Water movement in the firn of Storglaciären, Sweden

Abstract

The hydraulic properties of the firn on Storglaciären, Sweden, were investigated in firn cores by water-table measurements and pumping tests. The mean density of the firn was 800 850 kg m³, giving an effective porosity of 0.073. The lower part of the firn layer was saturated with water, producing a maximum saturated layer of 5 m in late July. Hydraulic conductivity of the firn aquifer was determined from pumping tests to be 4.9 × 10⁵ m s¹. Percolation velocity, calculated from the time lag of maximal water input at the glacier surface and the water-level peaks, was 0.25 m h¹. Percolation velocity increased over the ablation season, indicating a widening of the percolation pathways. A decrease in percolation velocity with percolation depth was found, reflecting decreasing permeability. The firn–water table responded to water input at the glacier surface with a delay of about 3 days. No diurnal variations were found in an area which was not influenced by fast drainage, indicating a diffusion of diurnal variations in meltwater production. One borehole intersected a water-filled cavity. Water level in this cavity showed diurnal variations, which probably were caused by diurnally produced meltwater waves moving fast through englacial conduits.

Introduction

Water movement through the firn layer on glaciers plays an important role, linking water input on a glacier surface with output at the terminus. Temporal water storage in firn and snow is probably the main reason for the delay of runoff from glacial drainage basins (Stenborg, 1970). Thus, the hydraulic properties of the firn layer are important for calculating the volume of stored water in glaciers during summer. In addition, knowledge of water flux through the firn layer is required for modelling glacier hydraulics and dynamics.

Meltwater from the firn surface percolates through the firn layer until it reaches impermeable glacier ice (Ambach and others 1975, 1978; Behrens and others 1977, 1981: Schommer, 1977, 1979; Lang and others. 1979; Ambach and Eisner. 1981; Oerter and others, 1981; Oerter and Moser, 1982;Fountain, 1989; Schneider, 1994). A water-saturated layer forms above the firn–ice transition similar to common groundwater aquifers (Röthlisbergcr and Lang, 1987).

This study examines water flux through the firn layer of Storglaciären, Sweden. Several holes, drilled in the accumulation area, were used to measure water-table fluctuations throughout the ablation season. Density of the firn layer was obtained from two firn cores, and pumping tests were carried out to determine the hydraulic conductivity of the firn aquifer.

Physical Settings

Storglaciären is a polythermal valley glacier in northern Sweden with an area of 3 km² (Fig. 1; Jansson, 1996). The mean thickness of the glacier is 95 m and the maximum thickness is 250 m (Eriksson and others, 1993). Storglaciären has a perennial cold surface layer in the ablation area that is 20–60 m thick (Hooke and others, 1983; Holmlund and Eriksson. 1989). This cold laver is practically impermeable to water, so surface water in this part of the glacier can only drain through moulins or crevasses.

(Stenborg 1965, 1969, 1973) performed the first detailed investigations of the glacial hydrology of Storglaciären. He showed that the accumulation area was drained mainly through Nordjåkk, whereas Sydjåkk drained the main part of the ablation area. He found a longitudinal division of the englacial drainage into two semi-lateral systems, corresponding to areas with north- and south-striking oblique crevasses. The southern and northern halves of the glacier tongue drained directly into Sydjåkk and Nordjåkk (Fig. 1) respectively, while the centre of the tongue had no direct drainage to the front. This anomaly could be explained by introducing a topographical obstacle on the bottom of the glacier. Salt injections revealed transit times of about 0.5–1.5 hours in the southern drainage system, whereas no salt tracer could be detected in the northern system. The division of the drainage system was later confirmed by an autoregressive model which simulated water discharge of Storglaciären during a fine weather period (Nilsson and Sundblad, 1975). Östling and Hooke (1986) studied the water storage in Storglaciären. According to their results, storage was built up during late May to early June. Input and losses were more-or-less constant from early summer to early August. From the end of August to the end of the ablation season, water was released from storage. Östling and Hooke stated that water was first stored in englacial reservoirs such as crevasses, snow and firn, and later in the season (mid-July) was released into subglacial cavities. They found that Nordjåkk transported almost no sediment. They therefore assumed that Nordjåkk obtained water from the glacier surface and from the accumulation area, while Sydjåkk was fed by subglacial water that was in contact with sediment at the glacier bed. These assumptions were confirmed later by means of dye-trace studies. Dye injected in the lower ablation area was detected only in Sydjåkk. A dye-tracer injected above the equilibrium line passed an overdeepening situated below the injection point through englacial rather than subglacial conduits (Hooke and others, 1988). During a period of 35 days, about 75% of the dye passed the sampling point in Nordjåkk, indicating the division of the glacial drainage system. Maximum transit velocity was ~0.02 m s¹, but the mean velocity was much less than this. Transit velocity increased almost linearly with discharge, which was explained by an increase in water pressure in the englacial conduits, combined with a decrease in effective sinuosity as discharge increased (Seaberg and others, 1988). More detailed dye-tracer experiments confirmed the division of the internal drainage system of Storglaciaren (Kohler, 1992). From dye-tracer tests, Hock and Hooke (1993) found the subglacial drainage network to be a multi-branched arborescent network of passages. Almost all investigations of the hydrology of Storglaciaren were carried out in the ablation area.

Fig. 1. Map if Storglaciären and the investigation area. Borehole C1 was used as the pumping well during the pumping tests. P1–P14 were boreholes drilled into the firn layer with an electrothermal drill and were used as piezometers to measure water-table fluctuations. The weather station was located at stake 16 and discharge was meaxssured at Nordjåkk.

Methods

The investigation site was a gently sloping (2.5°) area located in the central part of the accumulation area ofStorglaciaren (~1510 m a.s.l.) at the base of a slope descending from the northern part of the accumulation area (Fig. 1). Physical properties of firn were determined from two firn cores (C1 and C2 in Fig. 1) which were drilled with an electrothermal and a mechanical drill, respectively. Water movement in the firn layer was investigated by measuring water-table fluctuations in boreholes. The holes, 3–5 cm in diameter, were drilled with an electrothermal drill, reaching a depth below the firn ice transition (P1–P14 in Fig. 1). In these holes water level was measured by means of pressure transducers. Percolation velocity through the unsaturated part of the firn layer was estimated from rainfall-induced water-input peaks into the firn layer and corresponding water-table peaks. A pumping test was carried out to determine hydraulic properties of the firn aquifer (P1–P12, C1 in Fig. 1).

Firn Characteristics

The total volume of a firn sample, V _t, can be divided into a solid part, V _s, and a pore part, V _p (Freeze and Cherry, 1979). The porosity, n, of the firn sample is given by n = V _p/V _t. Under saturated conditions all pores are completely filled with water. Like the porosity of a soil sample (Freeze and Cherry, 1979), the porosity of a firn sample, free of liquid water, can be calculated as

. (1)

where ρ _t is the density of the total firn sample and ρ _t is the density of the solid part of the sample which consists of pure ice. Due to capillary and adsorptive forces, immovable water resides in unsaturated temperate firn in the same way as in soils. The difference between total pore volume and immovable water volume is the effective pore volume, V _e. Accordingly, an effective porosity, n _e, is defined as

. (2)

The density of firn was determined by dividing the weight of the firn sample by its volume. The liquid-water content of the firn was not taken into account. This means that the weight of the firn sample was the weight of the firn plus the weight of the immovable water. Accordingly, porosity calculated with Equation (1) is an estimate of effective porosity. Kawashima and others (1993) found water content in unsaturated firn to be 4–8% of total firn volume. Therefore, differences in density between water and ice can be neglected.

A 22.7 m, 13 cm diameter, core (C1 in Fig. 1) was drilled with an electrothermal drill between 3 and 21 July 1992. The hole had a diameter of 20 cm and was later used as a pumping well during pumping tests. At 21.2 m depth there was a sharp transition between firn and ice. This was used as the lower boundary of the firn aquifer. Unfortunately, some parts of this core were deformed by the drilling and could not be used to determine density. Therefore, a second core (C2 in Fig. 1), 17.7 m long, was drilled mechanically on 5–6 September 1992, with a PICO (Polar Ice Coring Office, Fairbanks, Alaska) coring auger, giving a core diameter of 7.5 cm. From this core the mean density of the firn layer (5–16 m below firn surface) was calculated to be 800 kg m⁻³, and 850 kg m⁻³ at the depth of the water-saturated layer (15 m). The effective porosity of the firn layer at the depth of the firn aquifer was calculated from density to be 0.073 using Equation (1) (ρ _t = 850 kg m⁻³; ρ _s = 917 kg m⁻³ (Kell, 1967)).

Firn–Water Level

In order to further investigate the firn aquifer, 12 holes (PI–P12 in Fig. 1) were drilled between 26 and 30 June 1992, in a 30 m² area. The holes were 21–30 m deep and served as piezometers to record the fluctuation of the firn-water table during pumping tests. In addition, two holes were drilled some 100 m south of the pumping-test site (P13 and P14 in Fig. 1). During the drilling of P14 the drill dropped from 18 m depth to 32 m below the surface. P14 intersected an englacial cavity or former crevasse below the firn layer, which was filled with water.

The water level in the boreholes was determined manually with an electronic plumb at intervals of 1–5 days in July and August 1992. To investigate shorter time-scale fluctuations and to obtain continuous records of water level, five Druck PDCR830 pressure transducers, connected to a Campbell Scientific CR10 data logger, were used. Water levels were recorded hourly and, during pumping tests, every minute. The pressure transducers and the electrical plumb were accurate to ±1cm. All water-level measurements were made relative to the glacier surface at the site of the borehole. These levels were later converted to altitude to facilitate comparison. The temporal variations in surface altitude due to ablation and accumulation were measured at ablation stake 29 (Fig. 1).

The firn-water level on 22 July was used to draw an equipotential map (Fig. 2). The hydraulic gradient in the firn aquifer was determined from this map to be 0.1 (5.7°). Manual and automatic water-level measurements in boreholes yielded an almost continuous record from late June to early September 1992 (Fig. 3). The fluctuation of the firn-water table was delayed compared with the fluctuation of water input at the surface and discharge at the terminus of the glacier (Fig. 3). Proglacial discharge showed fast response to water input, whereas the firn-water table lagged discharge peaks by ~3 days, due to percolation through the firn layer. The firn aquifer reached its maximum thickness of ~5 m around late July to early August. In mid-August, water input into the firn aquifer decreased due to lack of rainfall. In late August, high temperatures and a rainfall event caused an increase of the firn–water level. At the pumping-test site, the firn–water table reached a level similar to that during the maximum earlier in the summer, although water input was relatively small (P9 in Fig. 3).

Fig. 2. Equipotential map of the firn aquifer on Storglaciären, 24 July 1992. The altitude of the firn water table is given in m a.s.l.

Fig. 3. Firn–water level, discharge and meteorological conditions, Storglaciären, 1992. The meteorological station was located at stake 16; discharge was measured at Nordjåkk (Fig. 1). From 1 September, discharge was measured at Rännan, a gauging station 1.5 km downstream of the glacier terminus, and temperature (T_TRS) and precipitation (P_TRS) were measured at Tarfala Research Station (dashed line). P14 intersected a water-filled cavity. Dots connected with a dashed line show manual measurements.

Vallon and others (1976) found a rise of the firn-ice transition at the Vallée Blanche glacier, French Alps, of 3.5 m a⁻¹. They stated that the mean annual rise of the firn–ice transition was equal to the vertical velocity of the firn at the base of the firn aquifer. Vertical velocity, w _s, can be calculated as

(3)

where b _n is the net mass balance, u _s is the horizontal velocity and α is the surface slope (Hooke, 1998). Measurements of u _s near P9 gave a velocity of ~12 m a⁻¹. The mean net mass balance (1988–92) at the same site was ~2.l m (unpublished data from Tarfala Research Station). With a surface slope of 2.5°, w _s could be calculated to be ~1.5 m a⁻¹ as a mean value at P9. The rise of the firn–water table at the end of the ablation period was of the same magnitude and was therefore probably caused by a rise of the firn–ice transition and not by an increase of stored water.

Water level at P14 and P9 showed similar fluctuations until the end of July. From mid-August to the end of the investigation period, the water-level rise at P14 was smaller then that at P9 (Fig. 3). A possible explanation is that lower net mass balance at Pl4 caused a smaller rise of the firn–ice transition. Another reason could be that the area around P14 was drained more efficiently at the end than at the start of the ablation season. This is supported by the fact that P14 intersected a water-filled cavity, which might have been connected to an englacial drainage system. At the start of the ablation season, this drainage system was not fully developed, drainage was inefficient and a thick water-saturated layer was built up in the firn around this crevasse. During summer, the drainage system became more efficient, more percolating meltwater could be discharged and the water-saturated layer became thinner.

Diurnal fluctuations of the firn–water level were observed by Fountain (1989) on South Cascade Glacier, Washington State, U.S.A., and Ambach and others (1978) at Kesselwandferner, Ötztal Alps, but not by Schommer (1977) on Ewigschneefeld, Swiss Alps, or Oerter and Moser (1982) on Vernagtferner, Ötztal Alps. Fountain (1989) explained diurnal variations of the firn–water on South Cascade Glacier by diurnally generated meltwater, which percolated through the firn layer. These meltwater waves were not distorted, because of disintegration of ice layers in the snowpack that otherwise would have retarded the flow. An alternative explanation might be preferred percolation pathways in the firn layer with higher permeability, and thus higher percolation velocity (Wakahama, 1968; Fountain, 1989). On Storglaeiaren there were diurnal variations in P14 but not in P9 (Fig. 1). In contrast to the conditions on South Cascade Glacier and Kesselwandferner, the firn–water table at P14 was probably connected to an englacial drainage system. The area around P9 was not influenced by fast drainage, and no diurnal fluctuations were observed during the investigation period. Thus, the diurnal signal was distorted in the firn layer. The water level at P14 showed diurnal fluctuations at the end of August (Figs 3 and 4). Whether there were similar fluctuations in P14 at the start of the ablation period is unknown as no continuous measurements were carried out in P14 before 15 August. The fluctuations had a magnitude of a few cm and were steeper at falling water level than at rising water level (Fig. 4). These diurnal water-level fluctuations were probably caused by variations in englacial water pressure. The borehole intersected a water pocket, which was connected to the englacial drainage system. Meltwater was generated in diurnal cycles and drained fast through englacial conduits. Water-pressure variations in the englacial system in the accumulation area were probably caused by diurnal water input into crevasses up-glacier of P14 (Fig. 1).

Fig. 4. Water-level fluctuations at two different locations of the firn area on Storglaciären, 1992. Discharge was measured at Nordjåkk, and meteorological data at stake 16 (Fig. 1). From 1 September, discharge was measured at Rännan, a gauging station 1.5 km downstream if the glacier terminus, and temperature at Tarfala Research Station (dashed line).

Hooke (1991) and Jansson (1996) reported similar water-pressure fluctuations in boreholes in the ablation area of Storglaciaren. These occurred mainly in the lower part of the ablation area, where water-pressure variations are clearly governed by water input from diurnal surface runoff input into moulins.

Percolation Velocity

Two rainfall events were examined more closely to estimate vertical flow velocity through the firn layer (Fig. 5). High precipitation accompanied by relatively high air temperature caused distinct water pulses that percolated down to the firn aquifer. Both events had a precipitation peak before and after maximum temperature and caused one peak at the firn–water table (Fig. 5) due to the propagation of percolating water as a shock front (Colbeck, 1972). Percolation velocity was calculated as the ratio between the depth of the firn–water table below surface and the time difference between the precipitation and water-table peaks (Fig. 5; Table 1). The mean percolation velocity for each event was calculated as the arithmetic mean of velocities from the different precipitation peaks.

Fig. 5. Calculation of percolation velocity from precipitation events and peaks in firn–water level. The time differences of the first and second precipitation peaks of each event were used to calculate different percolation times Δt₁ and Δt₂, respectively. Precipitation, P, and temperature, T, were measured at stake 16. Together with percolation depth (depth of the firn water level below glacier surface), D, percolation velocity was calculated (cf. Table 1). For location of P6, P7 and P9 see Figure 1.

Table 1. Percolation velocity, v, calculated as the ratio of percolation depth, D, and the time difference between maximum precipitation and maximum firn–water level

There was a time lag of about 2–3 days between the maximum of the firn–water table and the maximum input at the glacier surface. The mean percolation velocity in the upper 16 m of the firn layer was 0.25 m h⁻¹ (Table 1). The percolation velocity of water through the firn layer of temperate glaciers is 0.12–0.35 m h⁻¹ (Table 2). The results from Storglaciaren relate well to this general pattern. The percolation velocity was inversely proportional to percolation depth (Fig. 6). Furthermore, all velocity values show an increase as the melt season progressed. This indicates less permeable firn early in the ablation season. As percolation velocity increases with increasing pore size, it can be concluded that the firn pores became wider at the end of the melt season. Melting due to heat transfer from warmer percolating water may have caused widening of firn pores. Additionally, disintegration of ice lenses in the upper part of the firn layer can cause an increase in percolation velocity. In fact, the percolation velocity decreases with increasing percolation depth, which indicates a decreasing permeability with depth.

Table 2. Percolation velocity m firn and snow from different investigations

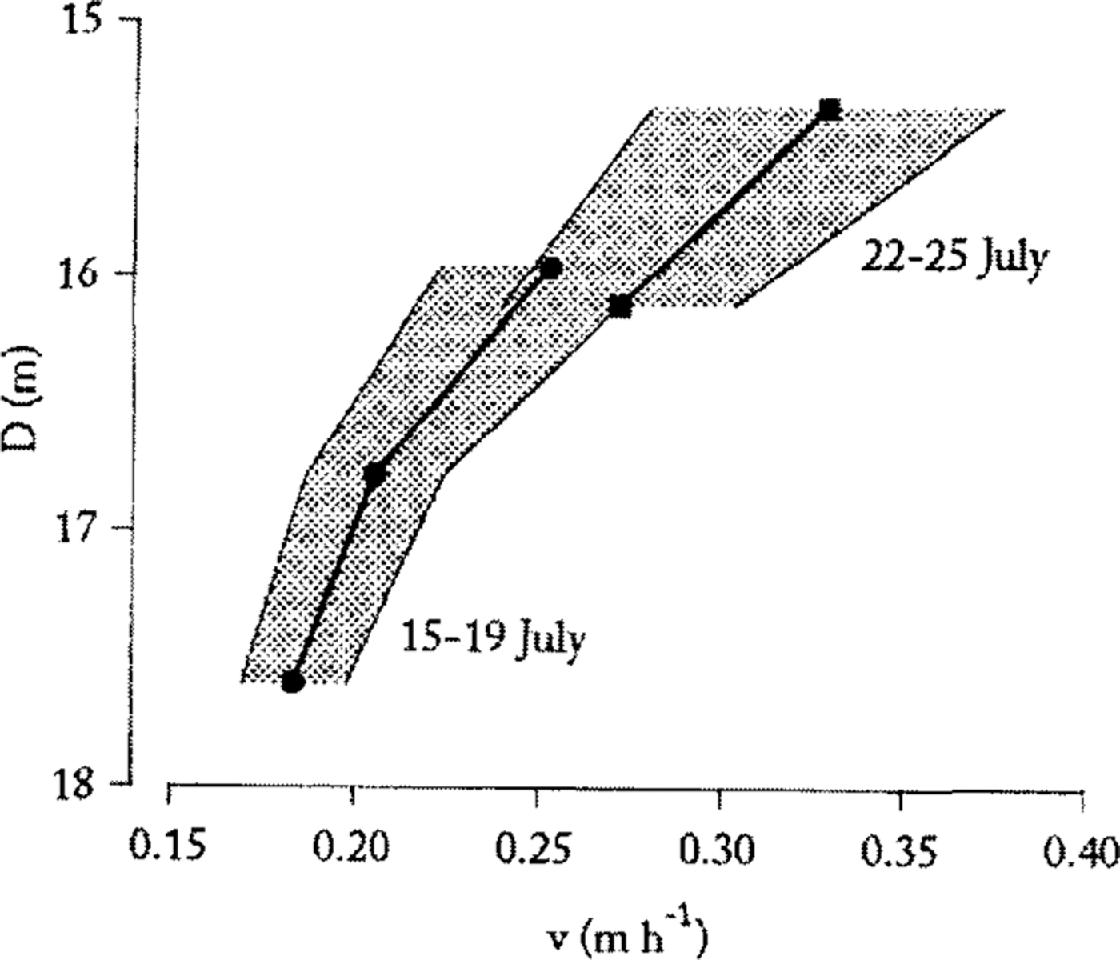
Fig. 6. Percolation velocity as a function of percolation depth. Notice the increase in percolation velocity as the ablation season progresses. The bold line is mean percolation velocity calculated as the arithmetic mean of velocities obtained from the different precipitation events (thin lines which define shaded area).

Water Movement in the Firn Aquifer

A pumping test is a common method to determine hydrogeological properties of a groundwater aquifer. When water is pumped out of an aquifer, the water level around the pumping well is lowered as a drawdown cone is formed. The spatial and temporal changes of the water table depend on the hydraulic properties of the storage medium, the physical properties of the fluid and the pumping rate. Today, pumping tests under transient-flow conditions are most common and there are several evaluation methods, all based on Theis’ (1935) theory, which are summarized by Kruseman and de Ridder (1991). All the applied methods for analyzing the pumping tests on Storglaciären are based on Theis’ well function and are described below. Theis used an analogy to heat-flow theory to develop an analytical solution of the drawdown during a pumping test in a confined aquifer under non-steady-state flow conditions.

The equation of the spatial and temporal change of the drawdown, s(r, t), is

. (4)

where r is the distance to the well, t is the time since start of pumping, Q is the pumping rate and T is transmissivity, defined as hydraulic conductivity, K, multiplied by the thickness of the aquifer. The function W(u) is called Theis’ well function and is defined as

(5)

where S is the storage coefficient. Theis’ well function is listed in Kruseman and de Ridder (1991). By plotting W(u) vs 1/u on a logarithmic scale, the so-called Theis-type curve is obtained. The Thesis-type curve is superimposed on the drawdown curve (s vs t), and a match point is obtained graphically, consisting of paired values of W(u) and s. T is then calculated as:

. (6)

According to Cooper and Jacob (1946), the sum of the infinite series of the well function (Equation (5)) becomes negligible for small u, so that

. (7)

Since Q, r, T and S are constants, the drawdown, s, vs log t should plot as a straight line. Thus, T can be calculated as

. (8)

where Δs is the drawdown for one log cycle of t, i.e. the slope of the straight line.

After shutting down the pump, water level in the well and the piezometers will begin to rise. This rise is referred to as residual drawdown, s′, and is defined as the difference between initial water table before pumping and the drawdown at the time, t′, which is the time since the shutdown of the pump. s′ during the recovery period can be calculated using Equation (5) as

. (9)

The transmissivity is obtained by

. (10)

where Δs′ is the recovery for one log cycle t/t′, i.e. the slope of the straight line, obtained by plotting s vs log t/t′.

Theis’ well function describes drawdown in an ideal aquifer. In reality, no natural aquifer is ideal. It is possible to draw conclusions about the hydraulic properties of the aquifer by comparing the shape of a drawdown with a type curve. Methods to correct measured values are summarized by Stober (1986). Those used in the analysis of the firn aquifer on Storglaciären will be described below.

Theis’ theory was developed for a confined porous aquifer. In such aquifers the cross-sectional area is constant during the pumping test since no dewatering occurs in the aquifer. Under unconfined conditions, as in the firn aquifer, the cross-sectional area changes. According to Dupuit’s assumptions (Thiem, 1906), drawdown, s, has to be reduced to s _r, as

. (11)

where H is aquifer thickness.

Theis assumed that the well had a small diameter, i.e. water storage in the well can be neglected. The pumping well on Storglaciären had a diameter of 20 cm. Thus water was stored in the well, and at the start of a pumping test this water was pumped instead of water from the aquifer. The duration of well storage can be determined from the drawdown curve or evaluated theoretically. According to Stober (1986), the duration of well storage, t _w, is calculated as:

,

where T _w is the radius of the well and T is transmissivity. With T = 2.4 × 10⁻⁴ m² s⁻¹ and T _w = 0.1 m, t _w was calculated to be ~21 min. This means that only pumping tests lasting longer than 21 min gave reliable results. Three pumping tests were performed, but due to the well storage only one pumping test, on 30 July, could be analyzed.

Pumping tests in the firn area of Storglaciären were carried out following the recommendations ofLangguth and Voigt (1980). All pumping tests were run under transient-flow conditions. The pumping well (C1) reached pure glacier ice, thus fully penetrating the firn aquifer. A Grundfos SP2-A9 submersible pump was used for the pumping test. It was placed at the bottom of the well, and pumping lasted for the time required to empty the well. The water pumped was released about 80 m down-glacier, which was sufficient not to influence the pumping tests. The drawdown of the water table was measured in the pumping well, C1, and in the piezometer holes P9A, P9, P4 and P5 (Fig. 1) by storing 1 min averages of 5 s samplings on a data logger. Whenever necessary, the drawdown and recovery values were corrected for regional variations of the water table during the pumping test. The pumping rate was determined every 5 min by measuring the time to fill a calibrated 20 L bucket. The pumping rate was within ±10% of the mean pumping rate during all the pumping tests (Fig. 7).

Fig. 7. Drawdown in the pumping well C1, s_T, and pumping rate, Q, during the pumping test on 30 July 1992. Variations in pumping rate caused unreliable drawdown data in the pumping well. s_T was reduced according to Dupuit’s assumptions (see text). t, time since start of pumping.

Transmissivity was determined from drawdown data recorded by the piezometers P4, P9, P9A and the pumping well C1. Some of the piezometers, 3 and 7 m from the well (P2, 3, 5, 8,10, 11 in Fig. 1), showed only a small drawdown. The borcholes, 15 m from the well (P1, 6, 7, 12), showed no response to the pumping test at all. The drawdown and the recovery in the well and the piezometers are shown in Figures 8–10. The pumping test gave a transmissivity of 2.4 × 10⁻⁴ m² s⁻¹. With an aquifer thickness of about 4.8 m, the hydraulic conductivity of the water-saturated firn layer was calculated to be 4.9 × 10⁻⁵ m s⁻¹ (Table 3). The hydraulic conductivity of the firn aquifer of temperate glaciers has a magnitude of 1–5 × 10⁻⁵ m s⁻¹ (Table 4).

Fig. 8. Log–log plot of drawdown, s_r, vs pumping time, t, during the pumping test on 30 July 1992. The Theis-type curve was used for the analysis of these curves. s_T was reduced according to Dupuit’s assumptions (see text).

Fig. 9. Semi-log plot of drawdown, s_r, vs pumping time, t, during the pumping test on 30 July 1992. The slope of the straight part of the curves gives transmissivity according to Equation (8) (Cooper and Jacob, 1946). s_r was reduced according to Dupuit’s assumptions (see text).

Fig. 10. Semi-log plot of residual drawdown, s^′_r, vs t/t^′ during the pumping test on 30 July 1992. t, duration of pumping; t^′, time since shutdown of pump. s^′_r was reduced according to Dupuit’s assumptions (see text). The slope of the straight part of the curves gives transmissivity according to Equation (10) (Theis, 1935).

Table 3. Results from the analysis of the pumping test on Storglaciären

Table 4. Hydraulic conductivity, K, of firn on temperate glaciers

Average Linear Velocity

Water flow through a water-saturated porous medium follows Darcy’s law:

. (12)

where Q is the flow rate, K is the hydraulic conductivity, A is the cross-sectional area normal to the flow direction, and dh/dl is the hydraulic gradient. The specific discharge or filter velocity, v, is defined as the hydraulic conductivity multiplied by the hydraulic gradient. Filter velocity is not the true velocity since the concept assumes that water flows through the entire cross-section. Average linear velocity, ν _a, is of more interest when studying transport processes as it considers the actual flow volume. In a porous medium, ν _a is given by

. (13)

where n is porosity. Under saturated conditions, the total pore volume is available for the movement of water, since no capillary forces exist and adhesion around the grains can be neglected if pores are not too small. The density of the firn core from Storglaciären revealed an effective porosity of 0.073. But total porosity is unknown for Storglaciären. Investigations from other glaciers (Oerter and Moser, 1982; Fountain, 1989) showed that total porosity is approximately twice the effective porosity. Thus, porosity was estimated to be 0.15. The hydraulic gradient was derived from the equipotential map of the firn aquifer (Fig. 2) to be 0.1. The pumping tests yielded K = 4.91 × l0⁻⁵ m s⁻¹. ν _a was calculated by Equation (13) to be 3.3 × 10⁻⁵ m s⁻¹ (= 0.12 m h⁻¹).

Conclusions

The firn–ice transition was found at about 21 m below firn surface. A water-saturated layer with a maximum thickness of 5 m existed during the melt season above the firn–ice transition. Water-table fluctuations were correlated to general weather conditions with a time lag of about 3 days. This time was required for water to move through the firn layer.

The percolation velocity of meltwater through the firn layer increased during summer. This can be explained by a widening of the pores by percolating meltwater and a disintegration of ice lenses in the upper part of the firn layer which delayed vertical movement at the start of the melt season. Percolation velocity decreased with percolation depth, indicating a decrease of permeability with depth.

Maximum water level in the firn aquifer occurred in late July. A second maximum in late August was probably caused by a rising firn–ice transition during the ablation season. The firn–water table showed no diurnal fluctuations, indicating that diurnally generated meltwater waves were distorted. One borehole intersected a water-filled cavity. The water level in this borehole showed diurnal fluctuations and long-term fluctuations at the same time. The diurnal fluctuations were caused by diurnally produced meltwater, which moved quickly through the englacial system. Long-term fluctuations were a result of water percolating slowly through the firn layer.

It would be useful to determine the thickness and extent of the firn aquifer across the whole accumulation area of Storglaciaren. With the results of such a study and the characteristic parameters from this investigation, accurate calculations of water storage in the accumulation area would be possible. Water drainage from the firn layer of a temperate glacier is a complex process, which depends on spatial and temporal variations of the englacial drainage system. More theoretical modelling is required to describe changes in the efficiency of the englacial drainage system. Repeated dye-tracing experiments through a whole ablation season coupled to water-table and meteorological measurements would provide a useful database to help expand the understanding of water flow out of the accumulation area of a temperate glacier.