1. Introduction
Over the past decade, agricultural commodity prices have been more volatile than in any period since the 1970s (Peters, Langley, and Westcott, 2009). Recent price variability has primarily been attributed to weather shocks, the growth of biofuels, associated links between agriculture and energy markets, and volatile economic conditions in emerging markets that buy and sell agricultural commodities (FAO et al., 2011; Hertel and Beckman, Reference Hertel, Beckman, Graff Zivin and Perloff2012; McPhail, Du, and Muhammad, Reference McPhail, Du and Muhammad2012).Footnote 1 Variability has also been blamed on growing speculative activity in futures and cash markets (Yang, Balyeat, and Leatham, Reference Yang, Balyeat and Leatham2005).
Whatever the source, price variability is often viewed as harmful, increasing the risk for producers who make planting decisions months prior to harvest and providing mixed signals to buyers of agricultural commodities. High variability also presents resource allocation challenges for firms and policy makers. Variability need not be detrimental to the market if prices are reacting to fundamentals such as increased uncertainty about production or stocks and use. However variability is detrimental if prices fluctuate without regard to fundamental factors. That is, when price variability reflects excessive speculative noise, it could impede the flow of fundamental information across markets. Thus, price variability may or may not be harmful to the overall agricultural economy.
This study addresses the issue of whether price variability improves or muddles the flow of information between the futures and cash markets for soybeans and soybean meal. Soybean markets were chosen for analysis because there are established cash and futures markets for both soybeans and soymeal. This allows us to compare cash and futures price relationships of a processed good with those of a related unprocessed product. However, other commodity markets, such as corn and wheat, face similar questions about the flow of information during periods of high price variability.
Specifically, this study analyzes the relationships between cash and futures prices for U.S. soybeans and soybean meal to determine whether an exogenous measure of price variability influences the speed with which prices adjust to equilibrium. Using daily cash and futures prices, error correction models (ECMs) are estimated. An exogenous variable representing price variability (from the recent past) is included in the model and used to measure the impact that price variability has on the speed with which futures and cash markets converge to their long-run equilibrium relationship. Relative adjustment rates derived from the estimated ECM are then used to estimate price discovery weights for cash and futures markets for the two soybean products. Thus, this study also evaluates the effect that price variability has on the relative contribution that cash and futures markets make to the price discovery process.
The results reveal that price variability influences both adjustment speeds and price discovery weights; weights that reveal both cash and futures markets contribute to the discovery of soybean and soybean meal prices. Also, adjustment speeds and price discovery weights have changed over time as has the overall level of price variability. Section 2 discusses the relationship between futures and cash markets and the role price variability may have on this relationship. Following that, there is a short discussion of relevant literature (Section 3). Our model is introduced in Section 4, along with an explanation of the method for calculating price discovery weights in Section 5. After a short discussion of the data (Section 6), the empirical results are presented and discussed in Sections 7–9. The final sections include a discussion of policy implications (Section 10) and conclusions (Section 11).
2. Cash and Futures Price Relationships
Economists have argued that an effective futures market should absorb information on the evolution of prices and then transmit that information to other markets (Mattos and Garcia, Reference Mattos and Garcia2004; Tomek and Gray, Reference Tomek and Gray1970). That is, prices are “discovered” in the futures market. However, if participants in futures markets (such as portfolio managers) also trade in nonagricultural markets while participants in cash markets (farmers and grain elevator operators) are closely tied to a particular agricultural commodity, then information contained in the cash markets may be a more accurate reflection of market fundamentals and may relate more closely to price discovery. This, in particular, may be true during periods when speculative activity is high, periods that are often thought to be related to periods of high price variability.
Etienne, Irwin, and Garcia (Reference Etienne, Irwin and Garcia2014) challenge the view that long periods of price variability relate to speculative activity. They show that price bubbles in the futures market for agricultural commodities often last less than 3 weeks, have become increasingly short lived, and are less important than market fundamentals in explaining agricultural price variability. This is critical because if participants in one market believe that a second market's price movements are speculative, they may not respond as forcefully to price signals from that market. In this case, price variability could slow or impede the flow of information between markets and reduce the second market's role in the price discovery process. However, if price variability reflects changing market fundamentals, the flow of fundamental information between markets could be amplified by constantly changing prices. For example, if the second market's prices strongly react to the arrival of meaningful information, clear and robust price signals would be sent to other markets. In this case, the second market's role in the price discovery process would be enhanced.
The force of both arguments highlights the need for continued empirical investigation into the relationship between futures and cash markets over periods where the long-run level of price variability is changing. Particularly useful would be evidence that can provide insights on whether (1) price variability improves or impedes the transmission of information between marketsFootnote 2 and (2) whether the role played by cash and futures prices in the price discovery process is influenced by the level of price variability.
3. Some Related Studies
In the past, economists used various causality-related tests and/or cointegration methods to measure price discovery. Using a framework developed by Garbade and Silber (Reference Garbade and Silber1983), Schroeder and Goodwin (Reference Schroeder and Goodwin1991) found that, in the short run, livestock prices tend to be discovered in futures markets and transferred to cash markets. Applying Granger causality tests to differenced prices, Oellermann, Brorsen, and Farris (Reference Oellermann, Brorsen and Farris1989) found that futures prices of feeder cattle explained cash prices but not the reverse. Koontz, Garcia, and Hudson (Reference Koontz, Garcia and Hudson1990) tested the relationship between spatially separated cash and futures markets for livestock and found that prices in both cash and futures markets interact in both directions and that the nature of the interaction has changed over time. Applying causality tests to ECM models, Yang, Balyeat, and Leatham (Reference Yang, Balyeat and Leatham2005) found that the futures market dominates the price discovery process for most agricultural markets and this finding held regardless of the commodity's storability.
In other literature, Mattos and Garcia (Reference Mattos and Garcia2004) estimated ECMs for Brazilian commodities, which included soybeans, and applied causality tests to the lagged price difference variables, which were included in their ECM model. Their causality tests provided mixed results. However, these authors also chose to test the significance of adjustment rate coefficients in the futures price equation and the cash price equation, a test that can be said to have anticipated methods later used by other authors investigating price discovery. These authors found that for most commodities (including soybeans) cash prices adjusted to the futures price.
Although causality testing can be informative, these tests focus on the impact of lagged prices on current prices and can be viewed as backward looking. Furthermore, when used for price discovery purposes, these tests implicitly give one market a weight of 1 and the other market a weight of 0. In contrast, price discovery is about market absorption of new information. Plato and Hoffman (Reference Plato and Hoffman2011) used the Gonzalo-Granger method to calculate price discovery weights for each market. These authors estimated ECM models for Brazil soybean futures and U.S. (Chicago) soybean futures and emphasized the role that adjustment rates play in determining price discovery weights. Adjustment rates represent the response to lagged error terms of a long-run price relationship equation. These long-run errors (sometimes called innovations) better reflect new or emerging information than the lagged prices that are used in causality testing. In any case, when using closing futures prices for both markets, these authors found that Chicago dominates price discovery for soybean futures. However, using the opening prices for Chicago and closing futures prices for Brazil, they found that Brazil dominates the price discovery process.
None of the previously discussed studies evaluated how price variability may influence the way markets exchange information. However, Adrangi, Chatrath, and Raffiee (Reference Adrangi, Chatrath and Raffiee2006) used an ECM to evaluate the relationship between the futures prices of soybeans, soy oil, and soymeal and used generalized autoregressive conditional heteroskedasticity methods to account for volatility spillovers between markets. They found that the soybean market adjusts to soymeal markets. However, they also found that the price spread between soybeans and soybean oil diverges. Separately, these authors found that there were volatility spillovers between markets for soy-related commodities (volatility for either beans, meal, or oil influences volatility in the other markets). However, these authors did not investigate how this volatility may influence the interaction of prices in each market.
Whatever the case, it is notable that few studies have used ECM models to calculate price discovery weights for agricultural commodity markets.Footnote 3 To our knowledge, no study has explicitly investigated the influence that price variability has on the speed with which prices adjust to equilibrium or explored how variability influences the price discovery process. However, studies by Adrangi, Chatrath, and Raffiee (Reference Adrangi, Chatrath and Raffiee2006) and Vercammen and Doroudian (Reference Vercammen and Doroudian2014) have investigated closely related issues.
4. An Error Correction Model of Cash and Futures Prices
In this study, an ECM model is specified that allows an exogenous measure of price variability to influence the speed of price adjustment between futures and cash markets. Estimates of absolute adjustment rates are related to market efficiency. That is, short-run efficiency is defined by the speed with which a displaced futures price and/or a displaced cash price returns (or converges) to the long-run equilibrium relationship between cash and futures prices (McKenzie and Holt, Reference McKenzie and Holt2002). If information fully transmits across markets, prices should quickly converge.
Estimates of relative adjustment rates are then used to measure the relative contribution that futures and cash markets make to the price discovery process. Unlike past studies, which rely on causality tests and relationships of prices with their lag values, this study examines how the response to unexpected information (errors from a long-run model) influences price discovery. We directly evaluate the role that price variability plays in influencing this response and the subsequent effect it has on price discovery weights. A typical ECM embodies the long-run relationship among variables and the disequilibrium relationship. The long-run price relationship between cash and futures prices can be written as follows:
where Psi csh, t and Psi fut, t represent cash prices and futures prices, respectively, for the ith soybean product in time period t. The term c represents a constant and takes into account differences in the cash and futures prices. The term ut represents the long-run error, which is zero in equilibrium. In the superscript si, s = soy and i = beans or meal. If c = 0 and βfut = 1, then markets are long-run efficient (Tomek and Gray, Reference Tomek and Gray1970).
The two-price ECM contains this long-run relationship and can be written as follows:
 $$\begin{eqnarray}
\Delta P_{{\rm csh},t}^{si} &=& {\rm \gamma }_{{\rm csh}} \left( {P_{{\rm csh},t - 1}^{si} - {\rm \beta }_{{\rm fut}} P_{{\rm fut},t - 1}^{si} - c} \right) + \mathop \sum \nolimits_{i = 1}^k {\rm \eta }_{11,i} \Delta P_{{\rm csh},t - i}^{si}\nonumber\\
&& + \mathop \sum \nolimits_{i = 1}^k {\rm \eta }_{12,i} \Delta P_{{\rm fut},t - i}^{si} + {\rm \varepsilon }_{{\rm csh},t},\end{eqnarray}$$
$$\begin{eqnarray}
\Delta P_{{\rm csh},t}^{si} &=& {\rm \gamma }_{{\rm csh}} \left( {P_{{\rm csh},t - 1}^{si} - {\rm \beta }_{{\rm fut}} P_{{\rm fut},t - 1}^{si} - c} \right) + \mathop \sum \nolimits_{i = 1}^k {\rm \eta }_{11,i} \Delta P_{{\rm csh},t - i}^{si}\nonumber\\
&& + \mathop \sum \nolimits_{i = 1}^k {\rm \eta }_{12,i} \Delta P_{{\rm fut},t - i}^{si} + {\rm \varepsilon }_{{\rm csh},t},\end{eqnarray}$$ $$\begin{eqnarray}
\Delta P_{{\rm fut},t}^{si} &=& {\rm \gamma }_{{\rm fut}} \left( {P_{{\rm csh},t - 1}^{si} - {\rm \beta }_{{\rm fut}} P_{{\rm fut},t - 1}^{si} - c} \right) + \mathop \sum \nolimits_{i = 1}^k {\rm \eta }_{21,i} \Delta P_{{\rm csh},t - i}^{si} \nonumber\\
&&+ \mathop \sum \nolimits_{i = 1}^k {\rm \eta }_{22,i} \Delta P_{{\rm fut},t - i}^{si} + {\rm \varepsilon }_{{\rm fut},t},
\end{eqnarray}$$
$$\begin{eqnarray}
\Delta P_{{\rm fut},t}^{si} &=& {\rm \gamma }_{{\rm fut}} \left( {P_{{\rm csh},t - 1}^{si} - {\rm \beta }_{{\rm fut}} P_{{\rm fut},t - 1}^{si} - c} \right) + \mathop \sum \nolimits_{i = 1}^k {\rm \eta }_{21,i} \Delta P_{{\rm csh},t - i}^{si} \nonumber\\
&&+ \mathop \sum \nolimits_{i = 1}^k {\rm \eta }_{22,i} \Delta P_{{\rm fut},t - i}^{si} + {\rm \varepsilon }_{{\rm fut},t},
\end{eqnarray}$$where ΔPsi csh, t and ΔPsi fut, t represent the daily change in cash prices and futures prices, respectively, for the ith soybean product. The term on the right-hand side in parentheses contains a one period lag of the error term from the long-run relationship between cash and futures prices. The next two terms represent lag price differences (whose length is often determined by empirical tests, three lags in this study), and the fourth term represents an equation error. The parameters γcsh and γfut are adjustment rate parameters. They represent the speed with which a displaced futures (or cash) price returns to its long-run equilibrium relationship with the cash (futures) price.
Within the long-run component of equations (2a) and (2b), the term in parentheses, the cash market price has a positive sign. Therefore, if γcsh < 0, cash prices return to their equilibrium relationship with the futures price. The futures price is expected to have a negative sign in equations (2a) and (2b), with βfut > 0. Therefore, the futures price returns to equilibrium when γfut> 0. If γcsh = −1 and γfut = 1, then markets are short-run efficient (McKenzie and Holt, Reference McKenzie and Holt2002). That is, cash and futures prices return to their equilibrium relationship within one period (with our analysis this is a day). What is critical is that the relative magnitude of the two adjustment rate coefficients reveals which market bears “the burden of convergence” (Adrangi, Chatrath, and Raffiee, Reference Adrangi, Chatrath and Raffiee2006, p. 79).
It is often more intuitive to write equations (2a) and (2b) explicitly in terms of the long-run model error (from equation 1) or as follows:
Price differences are a function of their own lags, and lagged errors of the long-run equation.
Therefore, to evaluate the role that price variability plays in influencing market efficiency, the following system was estimated:
 $$\begin{eqnarray}
\Delta P_{{\rm{csh}},t}^{si} &=& {{\rm{\gamma }}_{{\rm{csh}}}}{u_{t - 1}} + {{\rm{\theta }}_{{\rm{csh}}}}v{p_{{\rm{csh}},t}}{u_{t - 1}} + \mathop \sum \nolimits_{i = 1}^k {{\rm{\eta }}_{11,i}}\Delta P_{{\rm{csh}},t - i}^{si}\nonumber\\
&& + \mathop \sum \nolimits_{i = 1}^k {{\rm{\eta }}_{12,i}}\Delta P_{{\rm{fut}},t - i}^{si} + {{\rm{\varepsilon }}_{{\rm{csh}},{\rm{t}}}},
\end{eqnarray}$$
$$\begin{eqnarray}
\Delta P_{{\rm{csh}},t}^{si} &=& {{\rm{\gamma }}_{{\rm{csh}}}}{u_{t - 1}} + {{\rm{\theta }}_{{\rm{csh}}}}v{p_{{\rm{csh}},t}}{u_{t - 1}} + \mathop \sum \nolimits_{i = 1}^k {{\rm{\eta }}_{11,i}}\Delta P_{{\rm{csh}},t - i}^{si}\nonumber\\
&& + \mathop \sum \nolimits_{i = 1}^k {{\rm{\eta }}_{12,i}}\Delta P_{{\rm{fut}},t - i}^{si} + {{\rm{\varepsilon }}_{{\rm{csh}},{\rm{t}}}},
\end{eqnarray}$$ $$\begin{eqnarray}
\Delta P_{{\rm{fut}},t}^{si} &=& {{\rm{\gamma }}_{{\rm{fut}}}}{u_{t - 1}} + {{\rm{\theta }}_{{\rm{fut}}}}v{p_{{\rm{fut}}}}{u_{t - 1}} + \mathop \sum \nolimits_{i = 1}^k {{\rm{\eta }}_{21,i}}\Delta P_{{\rm{csh}},t - i}^{si}\nonumber\\
&& + \mathop \sum \nolimits_{i = 1}^k {{\rm{\eta }}_{22,i}}\Delta P_{{\rm{fut}},t - i}^{si} + {{\rm{\varepsilon }}_{{\rm{fut}},t}},
\end{eqnarray}$$
$$\begin{eqnarray}
\Delta P_{{\rm{fut}},t}^{si} &=& {{\rm{\gamma }}_{{\rm{fut}}}}{u_{t - 1}} + {{\rm{\theta }}_{{\rm{fut}}}}v{p_{{\rm{fut}}}}{u_{t - 1}} + \mathop \sum \nolimits_{i = 1}^k {{\rm{\eta }}_{21,i}}\Delta P_{{\rm{csh}},t - i}^{si}\nonumber\\
&& + \mathop \sum \nolimits_{i = 1}^k {{\rm{\eta }}_{22,i}}\Delta P_{{\rm{fut}},t - i}^{si} + {{\rm{\varepsilon }}_{{\rm{fut}},t}},
\end{eqnarray}$$where vpi is a lagged 12-day moving variance of the ith price. This term could be viewed as a measure of the expected level of price variability. In any case, lagging the variance of prices ensures that vpi is exogenous (see footnote 11). In equations (4a) and (4b), the adjustment rate term includes an interactive variable that allows the level of price variability in each market to influence the estimated adjustment rate. If the θcsh coefficient is significant and negative, the adjustment rate is faster, meaning that a higher level of price variability allows cash prices to return more quickly to their long-run equilibrium relationship. That is, price variability improves short-run market efficiency. If θcsh is significant and positive, a higher level of price variability slows down the adjustment process and reduces market efficiency. The opposite is true for the sign on the θfut coefficient in the futures price equation.
Our decision to include an exogenous measure of price variability in the disequilibrium part of the model reflects the idea that when markets adjust toward equilibrium, an excessive level of past variability could either aid or confuse markets in finding the most efficient path toward equilibrium. Lagged price variability is not included in the long-run model for two reasons: in equilibrium price variability is theoretically zero, and in equilibrium lagged information should not induce prices to move. Using daily data, covering the period 1992 to October 2013, distinct cash/futures ECM systems were estimated for soybeans and soymeal. Engle and Granger's (Reference Engle and Granger1987) two-step method was used to estimate each ECM system. That is, for each commodity, a single ordinary least square equation was estimated to capture the long-run relationship between the cash price and futures price. Next, a set of two price difference equations was estimated to capture the disequilibrium relationship among prices. Right-hand-side exogenous variables included the lagged error terms from the long-run model, lags of the price difference variables, and a variable representing the interaction of vpi, a measure of past price variability, and the lagged error term.
5. Price Discovery Cash or Futures
Schwarz and Szakmary (Reference Schwarz and Szakmary1994) and Theissen (Reference Theissen2002) developed a technique for calculating price discovery weights from estimated adjustment coefficients from a two-variable ECM model. There is an intuitive appeal to using error adjustment rates to measure a market's role in the price discovery process. Unlike the lags of a Granger test, errors in the long-run model contain new or unpredicted information.
In any case, the Schwarz-Szakmary/Theissen method allows us to directly determine whether price variability has an influence on the relative importance of cash and futures markets in price discovery. We evaluate whether the price discovery weights on the futures and cash markets changed after agricultural prices became more volatile after 2005 (see coefficient of variation [CV] 2 in Table 1), a period when the growth of corn ethanol linked agricultural commodities more tightly to volatile energy markets (Westcott Reference Westcott2007).
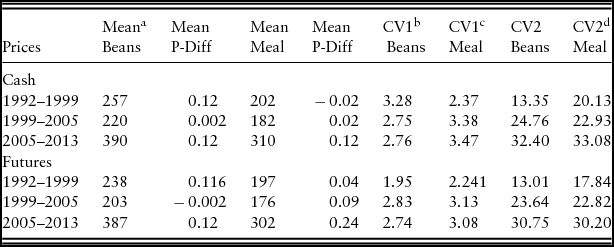
Table 1. Mean and Coefficient of Variation of Prices

a Average prices are dollars per metric ton, mean. P-Diff is the average first difference of daily price. For example, in the 1992–1999 period, the average daily change in the price is plus 12 cents for soybeans and minus 2 cents for soymeal.
b CV is the coefficient of variation represented by the standard deviation of price over its mean multiplied by 100.
c CV1 is the coefficient of variation derived from a 12-day moving average measure of the variance. This represents variability of a short period of time, and its lagged value is used in our model.
d CV2 is the coefficient of variation derived from the variance of the price over the entire listed subperiod. This represents long-run variability, reflecting overall changes in price movements over the period. Such a measure of variability would be endogenous if it were used in our model.
Estimated price discovery weights reflect the contribution each market makes to the price discovery process. In the Schwarz and Szakmary (Reference Schwarz and Szakmary1994) and Theissen (Reference Theissen2002) approach, the market whose price adjusts the least receives the higher price discovery weight, a point also made by Mattos and Garcia (Reference Mattos and Garcia2004). That is, prices are more likely to be formed in a market that does little adjusting to new information contained in the error of the long-run model. In contrast, price discovery weights are low for the market that adjusts relatively more. That is, prices are not likely to be formed in a market that is constantly forced to adjust to new information contained in the error of the long-run model. Underlying such analysis is the view that the market that does not adjust (or need not adjust) may be the source of the new information.
6. Data
The daily cash price of soybeans and soymeal was obtained from the U.S. Department of Agriculture's (USDA) Agricultural Marketing Service (AMS) (1992 through October 2013; USDA-AMS, 2013). Futures prices were obtained from Quandl (1992 through October 2013; Quandl, 2014). Futures prices were represented by the settlement price. Seven soybean contracts are traded within one calendar year. Following the approach applied in most studies that use futures prices, we roll over from the nearby contract (S1) to the next nearby contract (S2) on the last day of month prior to the delivery period.Footnote 4 Thus, the futures price series do not include the delivery months, and this study's estimated adjustment rates and price discovery weights do not refer to the delivery period. The cash price series for soybeans was obtained from USDA-AMS, Decatur–Central Illinois (1992 through October 2013; USDA-AMS, 2013), average price of the truck-rail low and high bid. The soybean meal (high protein) cash prices series was obtained from USDA-AMS, Decatur–Central Illinois, average price of the truck-rail low and high bid (USDA-AMS, 2013). These prices reflect a basis range for soybean meal as of 2:30 p.m. daily. The cash price (bid price) that is reported is computed by applying this basis range to the nearby futures price to reflect price offers over the previous hours of the day.Footnote 5, Footnote 6
Finally, each commodity had several dates for which one price was not available while the other price was available. For these observations, a synthetic price was created by averaging the previous day's price and next day's price. To ensure that this process did not influence the results, a dummy variable was created to represent those observations with a synthetic price and was tested for significance in subsequent models.
Table 1 reports the average prices over three periods: 1992–1999, 1999–2005, and 2005–2013. All prices fall from the first to the second period and rise significantly in the final period. Cash and futures prices are clearly related; in no period was the correlation coefficient between cash and futures prices below 0.987 for soybeans and 0.94 for soymeal. The table also reports two measures of the CV (the standard deviation over the mean). The first measure (CV1) is derived from a 12-day moving average estimate of the standard deviation of prices. Its lagged value was used in the subsequent model because traders tend to respond to price movements over a short period of time. For soybean cash price (futures), there is a slight fall (rise) in this measure of short-run price variability during the 1992–1999 period and little change over the latter two periods. For soymeal, the CV1 measure for both cash and futures prices rises after the first period. In contrast, CV2 is derived from the standard deviation of prices over each entire subperiod. It reflects the overall level of variability over the subperiods. Such a measure of variability would be endogenous if it were to be used in our model and serves mainly to provide an indicator of the environment in which traders operated during each period. This measure indicates that long-run price variability has risen over time and is particularly large for the 2005–2013 time period.
7. Results
Dickey-Fuller UR tests were applied to all four prices (cash and futures for soybeans and soymeal). It was not possible to reject the null hypothesis of nonstationarity for each price series over the entire period (1992–2013). Next, a series of UR equations was estimated for each price series while constantly altering the time period (changing starting and terminal dates) in order to determine if the coefficient on the lagged price term was stable. This method, which is similar to the Zivot and Andrews (Reference Zivot and Andrews1992) test for structural breaks, led to division of the data into three subperiods: 1992–1999, 1999–2005, and 2005–2013. The former two periods were characterized by relatively low long-run price variability, whereas the latter period experienced relative high price variability.Footnote 7 Interestingly, corn-based ethanol grew dramatically in 2005 and 2006 (Wescott, Reference Westcott2007), which further linked agricultural markets to volatile energy markets.
UR tests were applied to each time period, and it was not possible to reject the null hypothesis of nonstationary cash and futures prices, for both soybean and soymeal. All Dickey-Fuller Tau statistics were insignificant. We then carried out an Engle-Granger test, an appropriate method for testing cointegration between two variables. UR tests were applied to the errors from each long-run cash and futures price equation, and each Tau statistic was found to be statistically significant at the 0.01 confidence level. That is, the null hypothesis of nonstationary errors could be rejected. This combination of results revealed that cash and futures prices for both soybean and soybean meal were cointegrated for each of the three time periods in which the analysis took place.
8. Price Adjustment and Variability
Following the UR test, one set of ECM equations was estimated for each commodity price pair over the entire 1992–2013 period. Next, these data were broken into the three time periods (each characterized by different degrees of long-run price variability) and analyzed to determine whether the adjustment rate coefficients had changed over time and to determine if the impact of price variability on the adjustment rate differed across time periods. Thus, all models were estimated four times over, once for each of the subperiods and once over the entire 1992–2013 period.
Table 2 reports estimates of the long-run equilibrium models for soybeans and soymeal that were estimated over the entire period. The high R 2 values indicate that there is a close relationship between cash and futures prices for both commodities. Table 3 reports estimates of second-stage disequilibrium models representing the entire 1992–2013 period. For both commodities, each ECM model included three lags of each price difference term,Footnote 8 the lagged error term from the long-run model, and a variable that captures the interaction of lagged price variability (vpi) with the long-run lagged error term. This interaction term allowed us to determine how price variability influences the speed of price adjustment to equilibrium.
Table 2. Long-Run Cash/Futures Models of Soy Prices: 1992–2013

a The dependent variable is the cash price, con is the constant, and F price represents the futures price. The high R 2 values indicate that cash and futures prices are closely related over the long run.
b DVM is a dummy variable representing the delivery (rollover) month.
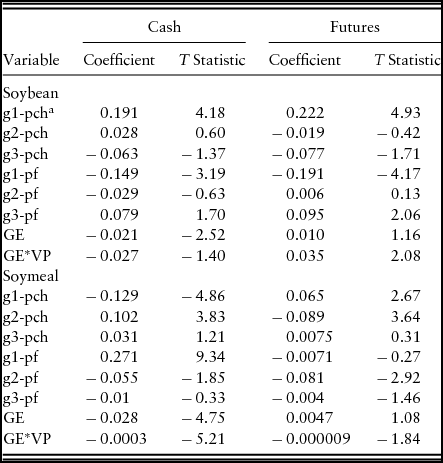
Table 3. Error Correction Model for Soybeans 1992–2013

a gi-pch (gi-pf) is the ith lag of the differenced cash (futures) price, GE is the lag error from the long-run model, and GE*VP is the lagged long-run error with a measure of lagged price variances. Dummy variable used to represent the few observations with filled in prices that were not significant and were dropped from the model.
A likelihood ratio test was performed to determine if each vpi variable contributed to the fit of each ECM system. A significant test statistic indicates that model performance improves when an exogenous price variability measure is included in the model. Table 4 reports χ2 statistics of the likelihood ratio tests. The test statistics reveal that the lagged (exogenous) price variability measure was significant (0.01 confidence level) for soybean and soymeal models that were estimated over the entire period (1992–2013), over the first period (1992–1999), and over the last period (2005–2013). This provides clear evidence that the level of price variability (measured by lagged 12-day estimate of the price variance) can influence both the adjustment rate and price discovery process for soybeans and soymeal.Footnote 9, Footnote 10 However, over the second period (1999–2005), the variability measure was not significant in the soybean model and was only significant at the 0.10 level in the soymeal model.
Table 4. Testing whether Price Variability Influences Adjustment RatesFootnote a

a Likelihood ratio tests were applied to test if the coefficient on the lagged vpi, lagged error interaction was zero in each error correction model. The numbers in the table refer to the subsequent test statistic. A significant test static reveals that inclusion of the variable significantly improves model performance.
b The asterisks (*, **, and ***) indicate significance at the 0.1, 0.05, and 0.01 confidence level, respectively.
Table 5 reports the estimated adjustment rates for soybeans and soymeal. In all long-run models, the cash price represented the dependent variable. Therefore, movement toward equilibrium requires a negative coefficient on the long-run error in the cash price equation and requires a positive coefficient on the long-run error in the futures price equation. The adjustment half-life, representing the time for prices to adjust halfway to equilibrium, is also reported.Footnote 11 The results reveal that for the models that include the vpi/error interaction term, soybean cash prices took 41 days to adjust halfway to equilibrium in the 1992–1999 period, 13 days in the 2000–2005 period, and 37 days in the final (2005–2013) period. In contrast, the futures prices adjusted in 37 days in the first period, adjusted the wrong way in the second period, and took 46 days to adjust halfway in the final high price variability period (2005–2013). The lack of futures price adjustment in the second period (1999–2005) reflects the dominance of the futures market in the price discovery process. That is, a price that fails to correct for deviations from the long-run equilibrium relationship but instead moves away from that relationship can be viewed as leading the market in its own direction.
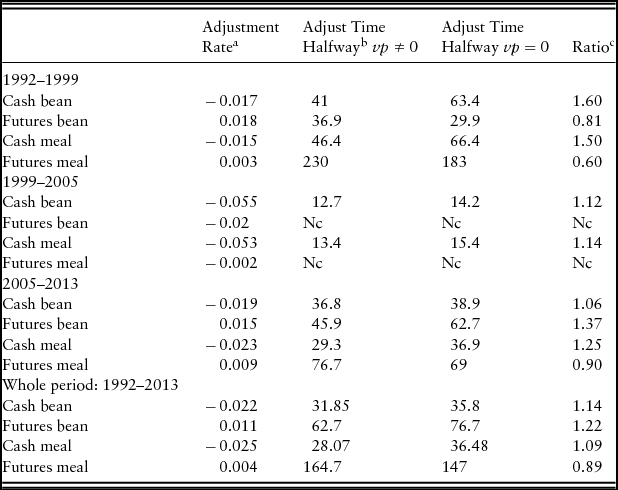
Table 5. Estimated Adjustment Rates

a Price adjustment rates are estimated from an error correction model. Adjustment rate coefficients should be negative for cash markets and positive for the futures price. Nc stands for “not converge” and is where the cash prices market does all the adjustment.
b The half-life or number of days it takes to adjust halfway to equilibrium (Kontolemis, Reference Kontolemis2002).
c Ratio represents a ratio of the estimated adjustment rate compared with what it would be if the measure of price variability were zero. A ratio <1 indicates the price variability slows the rate of adjustment to market equilibrium and thus impedes market efficiency.
For soymeal, there is an even larger change in the adjustment rates over time. Cash prices for soymeal take 46 days to adjust halfway in the first period, 13 days in the second period, and 29 days in the final period. Futures prices take 230 days to adjust in the first period and 77 days in the last period. As with soybean futures, soymeal prices adjust the wrong way in the 1999–2005 period. The slow adjustment of futures prices in the first period reflects the dominance of the futures market, which appears to be forcing cash prices to do most of the adjusting to the error term of the long-run model.
Table 5 also reports estimates half-life adjustment estimates, when the lagged level of price variability is set equal to zero. The ratio reported in the final column of this table represents two adjustment estimates from the same model: adjustment rates when the price variance is nonzero over the adjustment estimate when the price variance is zero. For example, for the cash market, this ratio is (γcsh + θcshvp csh)/γcsh. As constructed, a ratio greater than 1 means that when prices are more variable the estimated speed of adjustment increases; thus markets are more efficient. For the soybean cash price, the adjustment ratio is greater than 1 in every period, indicating that price variability increased the rate with which soybean cash prices returned to their long-run equilibrium value. However, price variability only increased the rate of adjustment for soybean futures prices in the 2005–2013 period.
There was a similar impact for soymeal price variability, increasing the speed of adjustment for cash prices in every period and slowing adjustment speeds of futures prices in two periods. Overall, it could be said that price variability increased the speed of adjustment of cash prices and slowed the speed of adjustment of futures prices. Because price discovery weights are inversely related to adjustments speeds, variability appears to have enhanced the role that futures prices play in price discovery.
9. Price Discovery Weights
Table 6 reports price discovery weights for each time period. For soybeans, an estimated weight of 0.52 on the cash price and 0.48 on the futures price indicate that both cash and futures markets contributed almost equally to price discovery in the first period. The wrong-way adjustment of futures prices in the second period is a sign of complete dominance of the futures market in price discovery. This finding suggests that the futures price does not correct for an error but instead responds to it positively and may be leading the market in a new direction, leaving the cash market to do all the adjusting. However, for the final period with high price variability, the futures market dominates slightly contributing 58% to the price discovery process. Finally, price discovery rates calculated for a model estimated over the entire period show the futures market dominating, contributing 66% to the price discovery process. What is notable is that the model representing the entire period obscures the changing role played by each market across time periods characterized by different levels of long-run price variability.
Table 6. Price Discovery Weights: Cash and FuturesFootnote a

a The reported price discovery weights and adjustment rates have been slightly rounded, so the two vectors may not appear to be exactly orthogonal (see Appendix). However, without rounding, the vector containing two adjustment rates is exactly orthogonal to the two price discovery rates (see Appendix).
b Nc represents periods when cash and futures prices did not converge in the nondelivery months. In each of these cases, the futures price moved away from equilibrium leaving cash prices to do all the adjusting. In such situations, prices are exclusively discovered in the futures market.
In contrast, the futures market dominates price discovery for soymeal in every period, contributing 83.5% in the first period, completely dominating price discovery in the second period, and contributing 72% to price discovery in the final period. Price discovery rates calculated for soymeal estimated over the entire period show the futures market contributing 86% to the price discovery process over the entire period.
What is also interesting is that for two of the three periods the cash market played a significant role in soybean price discovery, but for soybean meal, the cash markets played a small role in every period. The more dominant influence of the soymeal futures may reflect differences in the makeup of market participants. Individual producers and grain elevator operators are likely to participate in the soybean market. In contrast, producers are likely to play a smaller role in soymeal markets, a commodity that requires considerable processing to produce an output. Buyers and sellers of processed products are likely to represent larger established firms that have strong links to financial markets. Thus, it is no surprise that soymeal prices were primarily discovered in the futures market in every period.
10. Policy Implications
For policy makers, it is important to know whether futures markets or cash markets dominate the setting of price. Agricultural policy makers often focus on cash markets, whereas many economists argue that futures markets are more liquid, can absorb new information more quickly, and thus contribute more to price discovery than cash markets. Our results show that from 1992 to 1999 the soybean cash market played a slightly larger role in price discovery, but after 1999, the futures market came to dominate price discovery. The futures market dominated price discovery for soymeal in all periods. This serves as a reminder that both producers and policy makers should pay closer attention to futures markets when evaluating and forecasting economic outcomes in agriculture. In using a method that allows price discovery to be a weighted average of both prices, rather than claiming price discovery is an all-or-nothing phenomena, this study reminds both producers and policy markets that neither the cash market nor the futures market can be completely ignored. Our study illustrates that as the level of variability can change over time so can the relative importance of each market to the price discovery process.
It is also notable that in the final period (2005–2013) price discovery weights on the cash market were 42% for soybeans and 28% for soybean meal. Over this period, even when electronically based traders with links to financial markets were believed to have increased their agricultural trading, the cash market remained an important contributor to price discovery. If variable cash prices reflected changes in market fundamentals as claimed by McPhail, Du, and Muhammad (Reference McPhail, Du and Muhammad2012) and Hertel and Beckman (Reference Hertel, Beckman, Graff Zivin and Perloff2012), then paying attention to the cash market made sense for traders. So it should be for producers and policy makers.
Perhaps the most important message of this study is that policy makers should not always view price variability as harmful. Table 5 reveals that the speed by which prices return to equilibrium increased in 10 out 14 cases, when the impact variability is taken into account. In particular, price variability increases adjustment speeds in the cash markets. Tomek and Gray (Reference Tomek and Gray1970, p. 379) speculated that government-induced price stability “could be achieved at the cost of confusing and obliterating price signals for inventory or production responses.” Our results both reinforce and broaden this statement. Policies that reduce price variability can impede cash markets from quickly navigating toward equilibrium. That is, policies that reduce price volatility could make it difficult for market participants to detect the proper price signals and slow the process of price adjustment. Our findings indicate that this may confuse not only producers but also market traders themselves.
11. Conclusion
In the past decade, commodity markets have experienced a considerable amount of price variability, which is often viewed as a problem. This view ignores the possibility that variability can enhance market efficiency by providing clear price signals to market participants concerning changing market conditions. This study estimates the relationship between cash prices and futures prices for soybeans and soymeal. The first goal was to determine whether price variability influenced the speed with which cash and futures prices absorb new information and adjust to long-run equilibrium. If price variability increases the adjustment rate, then variability makes markets more efficient in the short run. If it slows the adjustment rate, variability makes markets less efficient. Our second goal was to determine how price variability influenced the relative importance of cash and futures markets in the price discovery process.
To achieve both goals, an ECM that included an exogenous measure of (lagged) price variability was specified and estimated. Allowing adjustment rates to be a function of an outside exogenous variable (rather than stand-alone coefficient) represents the main innovation of our ECM model. The impact lagged price variability had on the rate of adjustment to equilibrium was measured and tested. Statistical tests indicated that price variability has a significant impact on the adjustment rates. This implies that price variability influences convergence speeds, short-run market efficiency, and thus the relative importance that markets play in the price discovery process.
The analysis covered three time periods, each experiencing a different degree of long-run price variability. Modeling results indicated that for both soybeans and soybean meal variability increased the speed of adjustment of cash prices in every period. In contrast, price variability tended to slow the speed of adjustment of futures prices. The combined effect of these differences served to enhance the role of the futures market in the price discovery process.
The one exception was a large increase in the speed of adjustment of soybean futures during the 2005–2013 period, a period of high long-run price variability. In this period, both cash and futures prices returned to equilibrium more quickly. This result, combined with the higher adjustment speeds in the cash markets in every period, supports the view that in general price variability improves short-run market efficiency. At a minimum, the analysis in this study can serve as a challenge to those who claim price variability reduces market efficiency.
The results in this study also reveal that the role futures markets play in soybean price discovery was larger after 2000 than before it. The futures market played a much larger role in price discovery in the soymeal markets than soybean markets. Finally, in the latest period (2005–2013), in which variability was high, the cash market played a more significant role in price discovery than in the 1999–2005 period. This final result may reflect the perception that the futures market contained more speculative noise over the years from 2005 to 2013 than the cash market.
Further work along these lines, in other markets, is needed to draw conclusions about the price variability's effect on commodity markets in general. Future work also could explore how different aspects of price volatility influence market efficiency. For example, it would be interesting to compare how different measures of price volatility (other than the variances of prices) influence market efficiency. Or it may be interesting to compare the impact of price variability at different frequencies (daily, weekly, or monthly) on market interaction and the price discovery process. Finally, other factors (such as producer demographics) might be included in the model to help understand the changing role of the cash and futures markets in the price discovery process.
Appendix: Price Discovery Weights in a Two-Variable Model
Gonzalo and Granger (Reference Gonzalo and Granger1995) developed a method for measuring changes in the common factor underlying the long-run relationship among economic variables. A number of economists have applied this technique toward the issue of market price discovery (Figuerola-Ferretti and Gonzalo, Reference Figuerola-Ferretti and Gonzalo2010; Plato and Hoffman, Reference Plato and Hoffman2011). The goal is to determine which market is primarily responsible for generation of new price information.
Within the Gonzalo-Granger model, an error correction model (ECM) is estimated that contains only one long-run relationship. Differences in adjustments rates, to the same error term, determine the role different markets play in the price discovery process and in establishing a common long-run stochastic trend among prices.
Theissen (Reference Theissen2002) showed how the price discovery weights can be explicitly derived from estimated adjustment rate coefficients when a model consists of only two prices (also see Schwarz and Szakmary, Reference Schwarz and Szakmary1994). Price discovery weights for models with more than two prices are derived through a procedure similar to the Johansen eigenvalue test for cointegration (Gonzalo and Granger, Reference Gonzalo and Granger1995; Plato and Hoffman, Reference Plato and Hoffman2011). The Gonzalo-Granger eigenvector method for price discovery is similar to the Johansen (Reference Johansen1995) eigenvalue test for cointegration using residual matrices from two vector autoregression models. A different product matrix is calculated from these matrices, and the minimum eigenvector (rather maximum eigenvalue) is calculated to determine price discovery weights (Gonzalo and Granger, Reference Gonzalo and Granger1995; Plato and Hoffman, Reference Plato and Hoffman2011).
When prices are cointegrated, they follow to a common stochastic trend, a trend that is often said to be caused by some underlying common factor that influences the prices. The innovation of Gonzalo-Granger was to show that the missing common factor could be approximated as a weighted average of a model's endogenous variables. Call ε the linear combination of prices that produces the common stochastic price trend. This can be written as follows:
where the vector ![]() ${{\boldsymbol{\gamma}}_ \bot } = \left\{ {{{\rm{\gamma }}_{ \bot {\rm{csh}},}}{{\rm{\gamma }}_{ \bot {\rm{fut}}}}} \right\}$ is called the complement of the adjustment rate vector of the ECM (i.e.,
${{\boldsymbol{\gamma}}_ \bot } = \left\{ {{{\rm{\gamma }}_{ \bot {\rm{csh}},}}{{\rm{\gamma }}_{ \bot {\rm{fut}}}}} \right\}$ is called the complement of the adjustment rate vector of the ECM (i.e., ![]() ${\boldsymbol{\gamma }} = \{ {{\rm{\gamma }}_{{\rm{csh}},}}{{\rm{\gamma }}_{{\rm{fut}}}}\} $). To qualify as a complement vector, the following orthogonality condition must be met:
${\boldsymbol{\gamma }} = \{ {{\rm{\gamma }}_{{\rm{csh}},}}{{\rm{\gamma }}_{{\rm{fut}}}}\} $). To qualify as a complement vector, the following orthogonality condition must be met: ![]() ${{\boldsymbol{\gamma }}_ \bot }'{\boldsymbol{\gamma }} = 0$. That is, the multiplication of the complement vector and the estimated coefficients of the error correction vector must equal zero.
${{\boldsymbol{\gamma }}_ \bot }'{\boldsymbol{\gamma }} = 0$. That is, the multiplication of the complement vector and the estimated coefficients of the error correction vector must equal zero.
Harris, McInish, and Wood (Reference Harris, McInish and Wood2002) showed that a relative adjustment rate complement represents that market's contribution to a common stochastic price trend and can be thought of as a price discovery weight. In a cash/futures price model, the weights (Wgi) are
Expanding on the work of Schwarz and Szakmary (Reference Schwarz and Szakmary1994), Theissen (Reference Theissen2002) showed that in a two-variable model price discovery weights, Wg, can be directly derived from estimated error correction coefficients. Using this study's model, the Schwarz and Szakmary/Theissen weights are as follows:
where ![]() ${{\rm{\hat \gamma }}_{{\rm{\ csh\ }}}}{\rm{\ and\ }}{{\rm{\hat \gamma }}_{{\rm{\ fut\ }}}}$represent the adjustment rate coefficients estimates from this study's ECM.
${{\rm{\hat \gamma }}_{{\rm{\ csh\ }}}}{\rm{\ and\ }}{{\rm{\hat \gamma }}_{{\rm{\ fut\ }}}}$represent the adjustment rate coefficients estimates from this study's ECM.