No CrossRef data available.
Article contents
Jet-induced vortices of a row of distributed engines at vertical take-off condition
Published online by Cambridge University Press: 12 February 2024
Abstract
The aerodynamic performance of a wing model with a row of distributed engines are investigated at the vertical take-off condition. The engines are installed near the trailing edge of the wing. During vertical take-off, the jets exit from the engines and impinge perpendicularly to the ground, providing a thrust for the aircraft. Due to the ground effects, complex vortex structures are induced by the jets. The vortices are categorised into the spanwise vortices and the chordwise vortices. The underwing vortices can lead to low-pressure regions on the lower surface of the wing, resulting in an undesirable downward force. The underwing vortex structures are affected by the ratio of the engine distance to the engine diameter (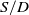 $S/D$). At a small
$S/D$). At a small 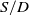 $S/D$ = 1.10, the flow field is dominated by the spanwise vortices; at a large
$S/D$ = 1.10, the flow field is dominated by the spanwise vortices; at a large 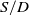 $S/D$ = 2.78, the flow field is dominated by the chordwise vortices. The range and strength of the spanwise vortices are affected by the vortices interaction. Competition mechanism exists between the range and strength effects, which results in the non-linear variation of the wing lift coefficient with engine spacing. The details of the flow physics underneath the wing and its mechanism on the lift of the wing during take-off are investigated.
$S/D$ = 2.78, the flow field is dominated by the chordwise vortices. The range and strength of the spanwise vortices are affected by the vortices interaction. Competition mechanism exists between the range and strength effects, which results in the non-linear variation of the wing lift coefficient with engine spacing. The details of the flow physics underneath the wing and its mechanism on the lift of the wing during take-off are investigated.
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Royal Aeronautical Society



