Sensitivity of mass balance and equilibrium-line altitude to climate change in the French Alps

Abstract

Assessment of the sensitivity of surface mass balance and equilibrium-line altitude (ELA) to climate change is crucial for simulating the future evolution of glaciers. Such an assessment has been carried out using an extensive dataset comprising numerous measurements of snow accumulation and snow and ice ablation made on four French glaciers over the past 16 years. Winter mass balance shows a complicated pattern with respect to altitude, with no clear linear relationship. Although the ratios of winter mass balance to valley precipitation differ considerably from site to site, they are relatively constant over time. Relationships between snow/ice ablation and temperature are stable, with no link with altitude. The mean snow and ice positive degree-day (PDD) factors are 0.003 and 0.0061 m w.e. °C⁻¹ d⁻¹. This analysis shows that, at a given site, ablation depends mainly on the amount of snow precipitation and on cumulative PDDs. The sensitivity of annual ablation to temperature change increases almost linearly from 0.25 m w.e. °C⁻¹ at 3500 m to 1.55 m w.e. °C⁻¹ at 1650 m. ELA sensitivity to temperature change was found to range from 50 to 85 m °C⁻¹.

1. Introduction

Glacier surface mass balance is widely recognized as being highly sensitive to climate variations in remote areas located at high altitudes (Kaser and others, 2006; Huss, 2012; IPCC, 2013). A change in climatic forcing is immediately reflected in a change in accumulation or ablation. Knowing the sensitivity of surface mass balance to climatic parameters is indispensable for assessing present climate change in high-altitude areas where meteorological data are sparse. It is also essential for estimating the changes glaciers will undergo for different future climate scenarios.

The sensitivity of glacier surface mass balance to climate change has been widely studied (e.g. Oerlemans and Fortuin, 1992; Wagnon and others, 1999; Braithwaite and Zhang, 2000; Oerlemans and Reichert, 2000; Vincent, 2002; Gerbaux and others, 2005; Huss and others, 2008; Sicart and others, 2008). It has been analysed either using the physical energy-balance approach or empirical relationships. Physical methods are the best way to study the relationships between mass balance and energy exchanges and many such studies have been performed, although the required measurements on the glacier surface are still rare and not available for long periods (Hock, 2005). Empirical relationships make it possible to link the surface mass balance to simple meteorological data to study mass-balance sensitivity to precipitation or temperature (e.g. Greuell, 1992; Braun and others, 1994; Hock, 1999; Braithwaite and Zhang, 2000; Vincent, 2002; Braithwaite, 2008; Huss and others, 2008; Six and others, 2009; Thibert and others, 2013). Although the physical processes are not taken into account, these simple relationships are very useful because air temperature and precipitation are the most reliable data that can be extracted from future climatic scenarios.

Previous studies have found a strong relationship between ablation and air temperature for glaciers in the European Alps (Chen and Funk, 1990; Vincent and others, 1997; Vincent, 2002; Thibert and others, 2013), which has not always been the case in other mountainous areas (Wagnon and others, 1999; Favier and others, 2004). To link ablation to temperature, snow and ice ablation must be separated (Braithwaite and Olesen, 1989; Braithwaite, 1995) because surface melt is highly sensitive to spatial and temporal albedo variations (Brock and others, 2000; Jonsell and others, 2003). However, many questions and uncertainties remain due to the lack of long time series of measurements. First, the physical cause of the strong relationship between ablation and temperature remains open to discussion (e.g. Oerlemans, 2000; Ohmura, 2001; Sicart and others, 2008). Second, many studies suggest that these relationships are improved when potential solar radiation is taken into account, although how this should be done remains controversial (Hock, 1999, 2005; Pelliciotti and others, 2005; Vincent and Six, 2013). Third, some studies suggest that ablation–temperature relationships could be affected by long-term changes in incoming shortwave radiation (Huss and others, 2009) or by changes in albedo due to dust deposition (Oerlemans and others, 2009) or black carbon (Painter and others, 2013). Fourth, accumulation is characterized by marked spatial variability, and the relationships between accumulation and precipitation are complex (Dadic and others, 2010; Sold and others, 2013).

For these reasons, major uncertainties remain concerning the relationships between ablation and temperature (Hock, 2005) and between accumulation and precipitation (Vin-cent, 2002; Machguth and others, 2006; Huss and others, 2009). The values cited in the literature for the sensitivity of the equilibrium-line altitude (ELA) of alpine glaciers to climate change therefore diverge greatly, ranging from 60 to 160 m °C⁻¹ (Kuhn, 1989; Oerlemans and Hoogendoorn, 1989; Wallinga and Van de Wal, 1998; Braithwaite and Zhang, 2000; Oerlemans, 2001; Vincent, 2002; Zemp and others, 2007; Thibert and others, 2013). However, most of these results were obtained from measurements made over short periods or from modelling. As mentioned by Ohmura and others (1992) and Rabatel and others (2005), the ELA is a very good indicator of the glacier mass balance. Understanding climate at the ELA is important for predicting glacier evolution.

In this paper, we reanalyse mass-balance sensitivity to temperature and precipitation using an extensive network of ablation and accumulation measurements made on four glaciers in the French Alps. This analysis goes beyond previously published evaluations of parts of this dataset (e.g. Vincent, 2002; Vincent and others, 2005, 2009; Vincent and Six, 2013). First, we have used all the measurements carried out over a 16 year period at 130 sites, including very contrasted years with high or low winter accumulation and with low or high ablation, representative of very different situations that could be observed in the future. Second, in the new dataset, numerous ablation measurements performed four to five times during summer are available. This allows us to separate ice and snow ablation and consequently to take into account the role of albedo in summer melt and its sensitivity to temperature change. Finally, the present network covers very different aspects and slopes, over a wide range of altitudes. In addition, many of the measurements were made around the ELA, enabling us to determine ELA sensitivity to temperature change from extensive field measurements.

2. Site Description, Meteorological Data and Method

2.1. Site description

For this study, we chose a dataset comprising measurements made on four French glaciers: Glacier de Saint-Sorlin (Grandes Rousses area), Glacier de Gébroulaz (Vanoise area), Glacier d’Argentière and Mer de Glace (both in the Mont Blanc range), between 1995 and 2011. Figure 1a shows a map of the French Alps, and Figure 1b–e are maps of the four glaciers. Table 1 lists the characteristics (length, surface, main aspect) of each glacier. The mass-balance site number is also given for each glacier (30–40 sites, distributed over both accumulation and ablation areas). Mer de Glace and Glacier d’Argentière are large glaciers with numerous tributary glaciers. The major contributors are also included in this study: Tour Noir (ablation zone) and Amethystes (accumulation area) for Glacier d’Argentière, and Talèfre and Leschaux (both are ablation areas) for Mer de Glace. Mer de Glace is also divided into three sections in this work: lower and middle ablation area and Géant (accumulation area) (Fig. 1e). Most of the data and measurement methods can be consulted on the website http://www-lgge.ujfgrenoble.fr/ServiceObs/.

Fig. 1. (a) Map of the western part of the Alps (from Vincent, 2002). Triangles show the locations of the glaciers: 1. Saint-Sorlin, 2. Gébroulaz, 3. Argentière, 4. Mer de Glace. Red dots show the locations of the meteorological stations (Besse en Oisans, Bourg Saint-Maurice and Chamonix). Lyon, not on this map, is located 80 km northwest of Grenoble. (b–e) Maps of Glacier de Gébroulaz (b), Glacier d’Argentière (c), Glacier de Saint-Sorlin (d) and Mer de Glace (e), with accumulation (blue) and ablation (red) sites. Tributary glaciers of Argentière and Mer de Glace are also shown.

Table 1. Main characteristics of the four measured glaciers and their major adjacent contributors. The number of measured sites in the ablation and accumulation areas is also given. The minimum elevation (snout position) was measured in 2012

During the period 1995–2011, the winter mass balance was measured at the end of April/beginning of May and the summer mass balance at the end of September/beginning of October. In addition, four or five regular visits were made during summer to monitor changes in ice and snow ablation in the accumulation and ablation areas. However, these regular summer visits were not possible on Glacier de Gébroulaz or on the top of Mer de Glace (Géant), mainly for reasons of accessibility. Measurements were therefore made only twice a year on Glacier du Géant (May for the winter mass balance and October at the end of the ablation season) and three times a year on Glacier de Gébroulaz (in May, at the end of August and in October).

In the accumulation area, cores were drilled to measure winter mass balances from snow layering (stratigraphy) and density. Stakes were inserted in the boreholes down to the previous summer surface. This technique makes it easy to measure the winter snow remaining at the end of summer by reading the stakes and prevents any possible misinterpretation of snow layering. In the ablation zone, winter mass balances were also measured by drilling cores. Annual mass balances were determined from wood stakes inserted in the ice. The summer mass balance was inferred from the difference between these two balance terms. Uncertainty on accumulation measurements was 0.21 m w.e. a⁻¹. Uncertainties on ablation measurements were 0.14 or 0.27 m w.e. a⁻¹ depending on whether the ablation concerned ice or firn (Thibert and others, 2008). The mean ELA was obtained from the mass balance measured on stakes around the ELA. The ELA of Mer de Glace could not be calculated accurately as it is usually located in a huge serac zone.

2.2. Meteorological data

The meteorological dataset used in this study was extracted from the Météo-France network at suitable nearby climate stations. For Glacier d’Argentière and Mer de Glace, daily precipitation and temperature data are available for the 1995–2011 period at Chamonix station (located very close to both glaciers, <10 km from the lowest stakes), at 1000 m a.s.l. For Glacier de Gébroulaz, we used data from Bourg Saint-Maurice (z = 865 m a.s.l.), located 37 km from the glacier. For Glacier de Saint-Sorlin, we used temperatures from Lyon–Bron station (125 km away, z = 200 m a.s.l.), and precipitation from Besse en Oisans (9 km away, z = 1525 m a.s.l.). Although Lyon–Bron station is far from Glacier de Saint-Sorlin, previous studies have shown that Lyon temperature data are strongly correlated with data from the nearest meteorological station available on shorter series (Vincent and others, 1997, 2004).

In August 2005 and June 2006, we set up two complete automatic weather stations (AWS) on the moraines of Saint-Sorlin and Argentière glaciers respectively (Fig. 1b and d). Half-hourly data (ventilated temperature, relative humidity, wind speed and direction, incident shortwave and longwave radiation) were recorded at 2720 and 2450 m respectively. Using these two AWS, the air temperature lapse rate can be calculated between valley stations and glaciers. For the following analysis related to degree-day factors, the determination of an air temperature lapse rate is crucial. We first tested the validity of using a constant air temperature lapse rate over a large altitudinal range, which can reach 2000 m on Mer de Glace between the lowest and highest stakes. Tests performed on meteorological data from Chamonix (1000 m), Argentière (2400 m) and Aiguille du midi (3800 m, weather station located in the vicinity of Mer de Glace accumulation zone) reveal very similar air temperature lapse rates (0.59°C (100 m)⁻¹ between Chamonix and Aiguille du midi, compared to 0.61°C (100 m)⁻¹ between Chamonix and Argentière, during the summer period).

Note that the air temperature lapse rate can change with the season and within the area under study. As generally observed, the summer air temperature lapse rate (calculated from 1 May to 30 September) is different from the mean annual lapse rate (Jabot and others, 2012). We compared annual and summer temperature lapse rates over the period 2006–12. The mean annual lapse rate between Saint-Sorlin and Lyon is 0.54°C (100 m)⁻¹, and the mean summer lapse rate is 0.59°C (100 m)⁻¹ (respectively 0.57°C (100 m)⁻¹ and 0.61°C (100 m)⁻¹ between Argentière and Chamonix). The differences in these summer lapse rates are therefore small given that Argentière and Saint-Sorlin glaciers are located 110 km apart. In the following analysis, we use a lapse rate value of 0.6°C (100 m)⁻¹ when the whole summer is taken into account. Due to the absence of other high weather stations close to Glacier de Gébroulaz, the same lapse rate is used for this glacier. Given the large monthly variations of the air temperature lapse rate, we can question the use of a single lapse rate value over the entire summer season. Meteorological data analysis reveals monthly variations from 0.68°C (100 m)⁻¹ in May to 0.54°C (100 m)⁻¹ in September between Chamonix and Argentière weather stations (and from 0.63°C (100 m)⁻¹ in May to 0.54°C (100 m)⁻¹ in September between Lyon and Saint-Sorlin weather stations). Neglecting such monthly variations could modify the sensitivity of ablation to temperature, particularly close to the equilibrium line, where snow ablation mostly occurs in May–July and ice ablation from August to September. The influence of air temperature lapse rate on ablation sensitivity is discussed in Section 4.

2.3. Method

The method used in this study to determine ablation sensitivity to climate parameters is a simple temperature-index method, widely used on glaciers as already mentioned. It assumes a linear relationship between melt and positive air temperature. Ablation at a given altitude j (A_j ) is the sum of snow ablation (A _s) and ice ablation (A _i) and is calculated by the degree-day model (Braithwaite and Olesen, 1989):

A_j = A _s + A _i = f _snowCPDD_snow + f _iceCPDD_ice

where CPDD_snow and CPDD_ice are the sums of positive air temperature (cumulative positive degree-day, or CPDD) at altitude j, for the snowmelt and ice melt periods respectively. f _snow and f _ice are the positive degree-day (PDD) factors for snow and ice (m w.e. °C⁻¹ d⁻¹). A review of PDD factors can be found in Braithwaite and Zhang (2000, table 4) or Hock (2003). As mentioned by Braithwaite and Zhang (2000), there is no evidence of unique values of f _snow and f _ice that can be used worldwide.

In the present study, we use separate sets of snow ablation A _s and ice ablation A _i to determine the snow and ice PDD factors respectively. Data with ablation of both snow and ice were removed from our dataset for this analysis.

3. Results

3.1. Temporal fluctuations in annual mass balance since 1995

Figure 2 shows the cumulative annual mass balance for the four glaciers since 1995. The annual mass balances are calculated with a linear model of variance over the entire surface area and adjusted with volume losses obtained from photogrammetric measurements (Vincent, 2002; Vincent and others, 2009). The cumulative annual mass balances are –26.5 m w.e., –23 m w.e., –19 m w.e. and –14 m w.e. on Saint-Sorlin, Mer de Glace, Argentière and Gébroulaz glaciers respectively. Figure 2 also shows acceleration in the negative mass balance over the past 10 years. The five most negative annual mass balances have occurred since 2003. When the whole period is separated into two periods, 1995–2002 and 2003–11, the mean annual mass balances are respectively –0.71 and –2.23 m w.e. on Glacier de Saint-Sorlin, –0.73 and –1.88 m w.e. on Mer de Glace, –0.55 and –1.54 m w.e. on Glacier d’Argentière and –0.31 and –1.18 m w.e. on Glacier de Gébroulaz, i.e. approximately three times higher over the second period. Such a comparison allows us to assess the stability of the ablation sensitivity to temperature change over time (Section 3.4).

Fig. 2. Cumulative annual mass balance as a function of time for Saint-Sorlin, Argentière, Gébroulaz and Mer de Glace and the linear trend from 1995 to 2011. Annual mass balances were calculated using a linear model of variance applied to stake measurements made over the entire surface of the glaciers.

Figure 3 shows deviations in the annual mass balance from the average value for 1995–2011, obtained using a method that has been applied widely in previous studies (Letréguilly and Reynaud, 1990; Vincent and others, 2004). For this purpose, each annual glacier mass balance was reduced by subtracting the 1995–2011 average mass balance of each glacier to obtain a mean-centred value. Figure 3 highlights the striking consistency and the common climatic signal of data from glaciers scattered throughout the French Alps (Saint-Sorlin and Argentière are located 110 km apart), despite the fact the size, aspect and slope of the glaciers are not the same. Table 2 summarizes mean winter and summer mass balances for each glacier. Only measurements made between 2750 and 2800 m a.s.l. are presented, to ensure that the comparison is relevant irrespective of the topographic characteristics of each glacier. These stake measurements are usually located in the ablation zone. No data were available on Mer de Glace for this altitude range. The table shows that summer mass balances are much more variable than winter mass balances. For Saint-Sorlin and Gébroulaz glaciers, there is a factor of 2 between winter and summer mass-balance variability. The factor is 1.5 for Glacier d’Argentière. For each glacier, Figure 4a and b show the winter and summer mass balances for the period concerned.

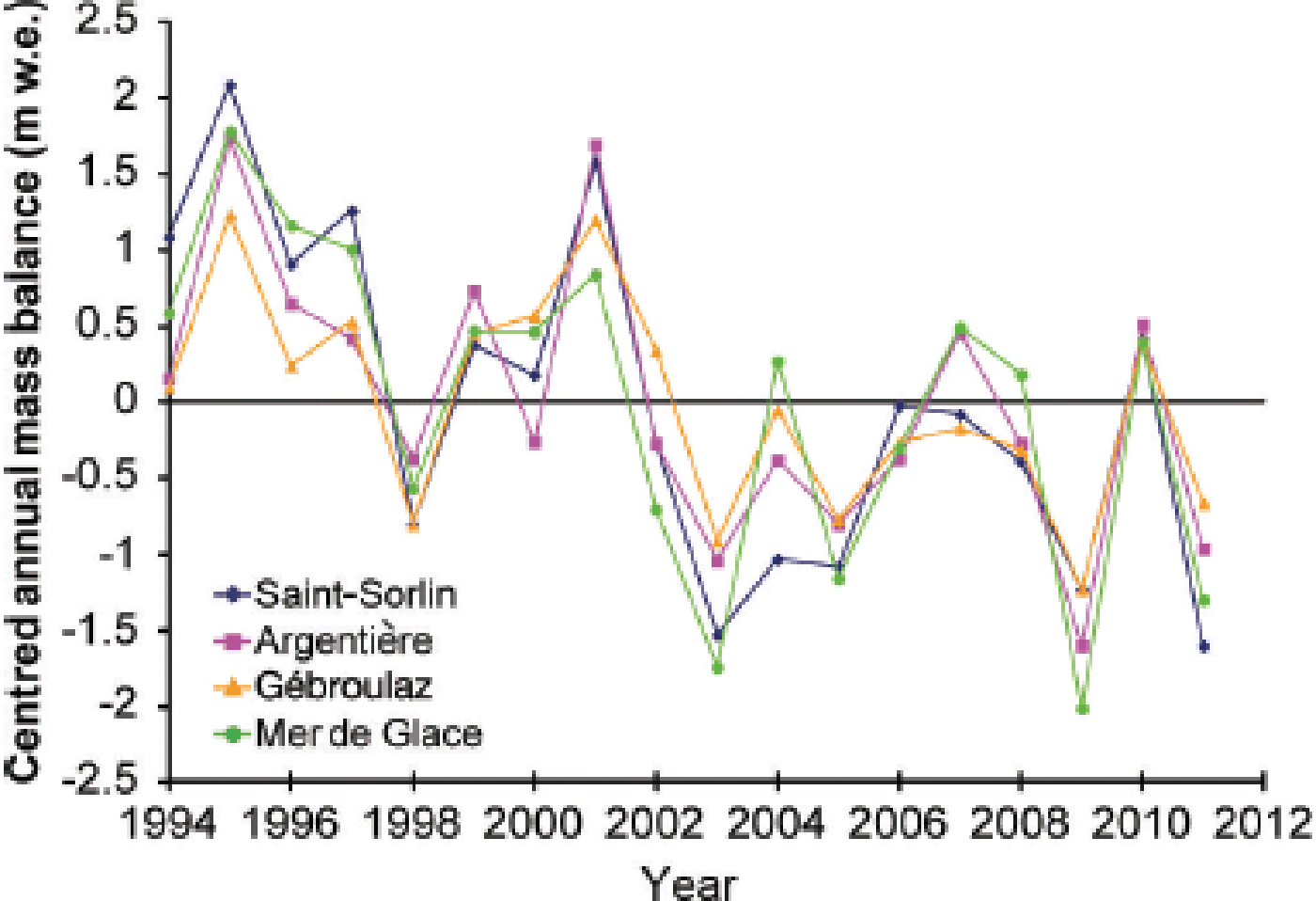
Fig. 3. Centred annual mass balance (annual mass balances minus average of each glacier for the period) for the four glaciers, from 1995 to 2011.

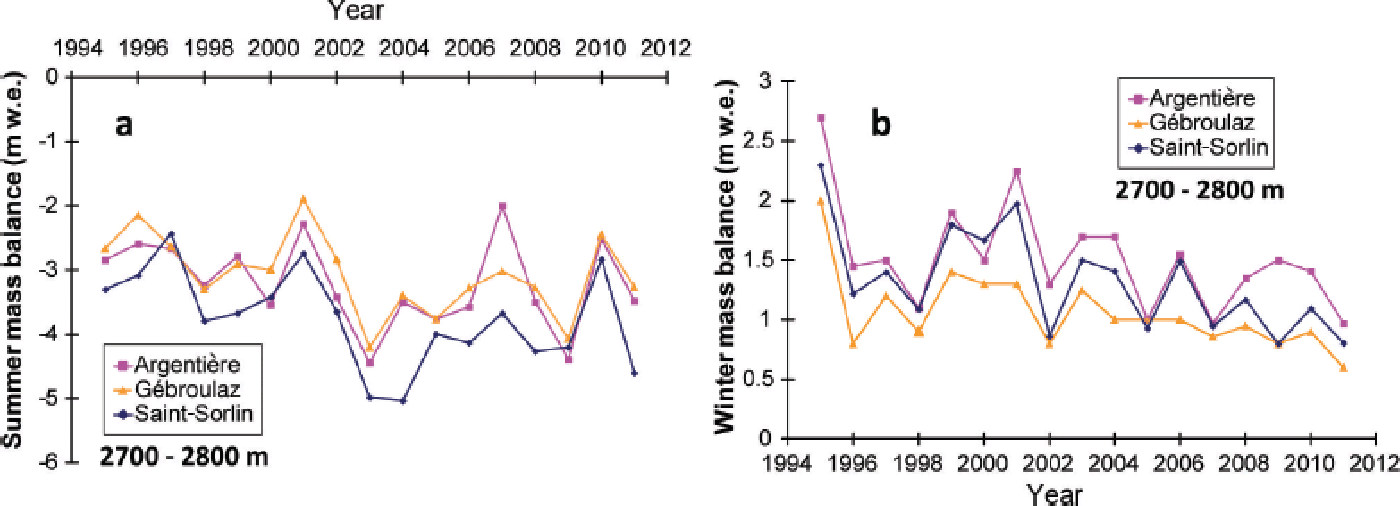
Fig. 4. Annual summer (a) and winter (b) mass balance around 2750 m a.s.l. on Argentière, Gébroulaz and Saint-Sorlin glaciers, for the period 1995–2011. No data are available for Mer de Glace in this altitude range.

Table 2. Means and standard deviations (m w.e.; calculated over the 1995–2011 period) of winter and summer mass balances (w.m.b. and s.m.b. respectively) on Argentière, Gébroulaz and Saint-Sorlin glaciers between 2750 and 2800 m a.s.l. No data are available for this altitude range on Mer de Glace

A slight decrease in winter mass balance was observed on the three glaciers over the entire period (also observed irrespective of the altitude of the site; not shown here). There was a decrease both in winter accumulation and in the standard deviation. On Glacier de Gébroulaz, winter accumulation decreased from 1.21 m w.e. before 2003 to 0.93 m w.e. after 2003, and the standard deviation decreased from 0.4 m w.e. to 0.17 m w.e. On Glacier d’Argentière, winter accumulation decreased from 1.76 m w.e. to 1.35 m w.e. and the standard deviation decreased from 0.53 m w.e. to 0.30 m w.e. Conversely, we observed an increase in summer ablation. Comparing the periods before and after 2003, summer ablation increased from 2.7 m w.e. to 3.4 m w.e. on Glacier de Gébroulaz, from 3.0 to 3.5 m w.e. on Glacier d’Argentière and from 3.25 to 4.19 m w.e. on Glacier de Saint-Sorlin.

The correlation between annual and summer mass balance was strong. For example, it reached R ² = 0.89 and R ² = 0.92 for all the stakes in the ablation zone of Glacier de Saint-Sorlin for the periods 1995–2002 and 2003–11 respectively. From this analysis, we conclude that the annual summer mass balance is largely responsible for changes in the annual mass balance. In addition, we conclude that the decrease in the annual mass balance after 2002 is mainly due to the increase in summer ablation.

3.2. Winter accumulation and precipitation

We compared the winter accumulation measured at each stake in the accumulation zone of the four glaciers with the cumulative valley precipitation calculated over the same period (Fig. 5). The Météo-France meteorological stations used were Besse en Oisans for Glacier de Saint-Sorlin, Bourg Saint-Maurice for Glacier de Gébroulaz, and Chamonix for the other glaciers. Precipitation at temperatures below 2°C (at the elevation of the observation) was taken into account. This temperature threshold was selected based on the best correlation found between winter mass balance and precipitation. Above this temperature, precipitation is rain and is assumed to run off the glacier and hence not contribute to the mass balance. No observations are reported below 2100 m a.s.l. because melting in winter is by no means negligible and can influence the winter mass balance significantly. Figure 5 shows the marked differences, which cannot be explained by orographic effects alone, in the ratio between winter mass balance and valley precipitation. For each glacier, the pattern is highly variable, very far from a linear function of altitude. For instance, the part of Glacier d’Argentière located between 2800 and 2980 m a.s.l. shows strong winter mass-balance ratios similar to those of the Amethystes tributary glacier located between 3250 and 3440 m. The strong winter mass balance found between 2800 and 2980 m is caused by the surrounding very steep non-glacial slopes which capture precipitation over a larger area.

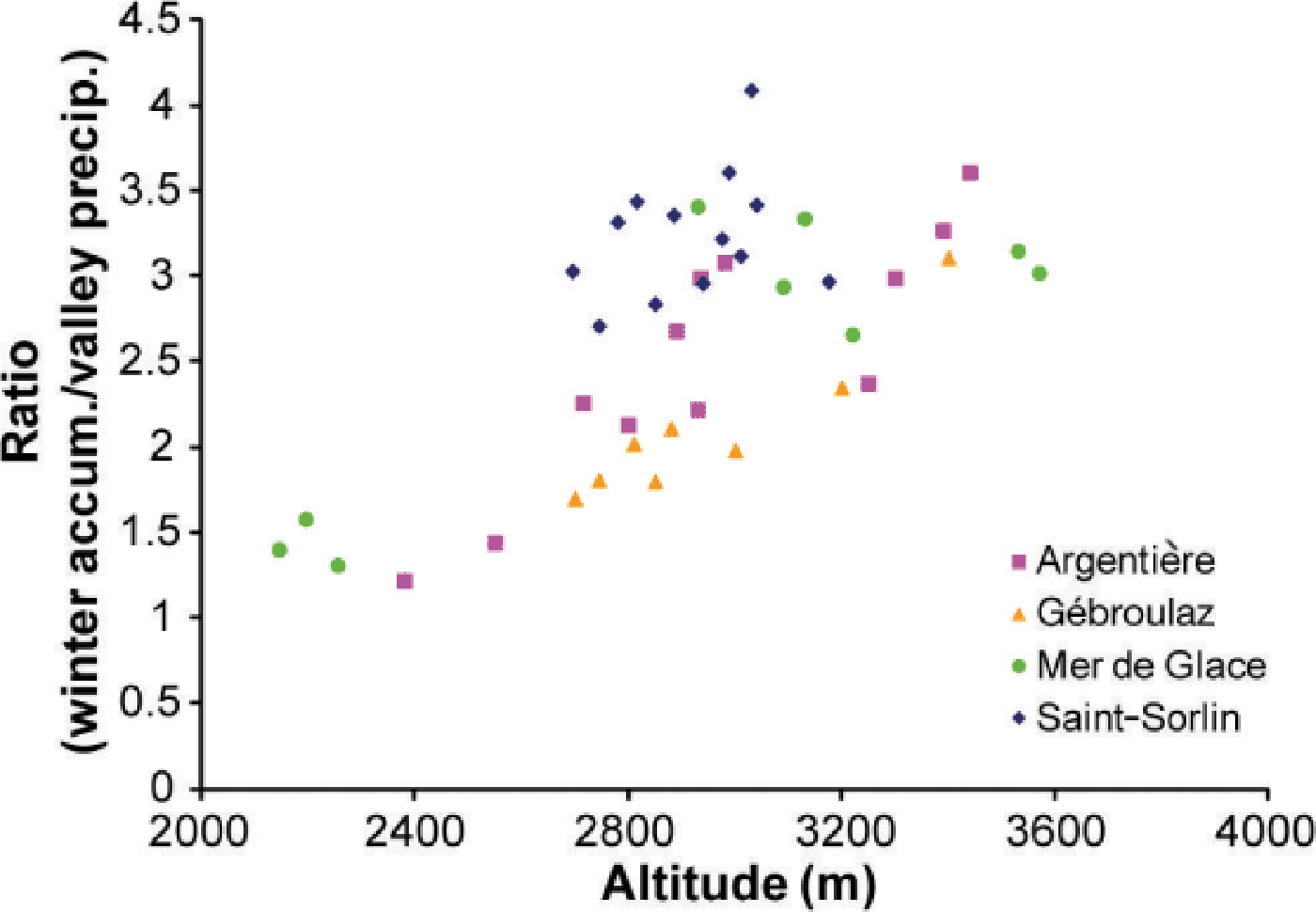
Fig. 5. Mean ratio (1995–2011) between the measured accumulation in winter and valley precipitation, as a function of altitude for Gébroulaz, Argentière, Mer de Glace and Saint-Sorlin. Precipitation data are from Bourg Saint-Maurice meteorological station for Gébroulaz, Chamonix for Argentière and Mer de Glace, and Besse en Oisans for Saint-Sorlin.

The ratio between winter accumulation and precipitation varied considerably from site to site, but when we compare the sites, the ratios are very similar to those obtained by Vincent (2002), showing that they remained relatively constant over time. However, the two study periods are probably not long enough to determine consistent changes in the ratios.

3.3. Summer ablation and temperature

In a first step, total measured summer ablation (May– October) for each altitude range and each year on Mer de Glace was compared with CPDD obtained from Chamonix data for the period 1995–2011. A fixed lapse rate of 0.60° C (100 m)⁻¹ was applied. Calculation of CPDD takes into account the beginning and end dates of the ablation measurements. In this first analysis, considering total summer ablation, snow and ice ablation data are not separated. We chose data for Mer de Glace because numerous detailed measurements had been made over a wide range of altitudes and very different aspects. Relationships were established for each of the altitude ranges located between 1625 and 3070 m a.s.l. in the ablation area, and for two sites in the accumulation area (Fig. 6). Our results revealed a strong linear relationship between ablation and CPDD, confirming previous results on this dataset (Vincent, 2002). Large dispersion was observed on the glacier tongue (‘lower ablation zone’, <1750 m a.s.l.) due to the debris cover which is highly variable in space and time. This led to very different ablation values for the same CPDD. On Glacier de Talèfre, with a south aspect, the ablation was high compared with that observed on Mer de Glace at similar altitudes. In the middle ablation zone of Mer de Glace (1900–2200 m a.s.l.), we found a stronger relationship between ablation and temperature (R ² = 0.80), probably due to the regular clean ice encountered on this part of the glacier. Moreover, at these low altitudes, snow disappears quickly, meaning that summer ablation is mainly driven by ice ablation, which explains the close relationship. Large dispersion was observed on the upper part of the glacier because there is both snow ablation and ice ablation, for which the degree-day factors are very different (see analysis below). Moreover, the ratio between snow and ice ablation differs considerably from year to year, according to the amount of snow accumulation. Consequently for the same CPDD during the ablation period, ablation can differ greatly depending on the winter accumulation value. In addition, in the very high-accumulation area (i.e. Glacier du Géant located above 3400 m), the relationship is poor due to possible snow precipitation in summer which can significantly affect the relationship between the summer mass balance and CPDD.

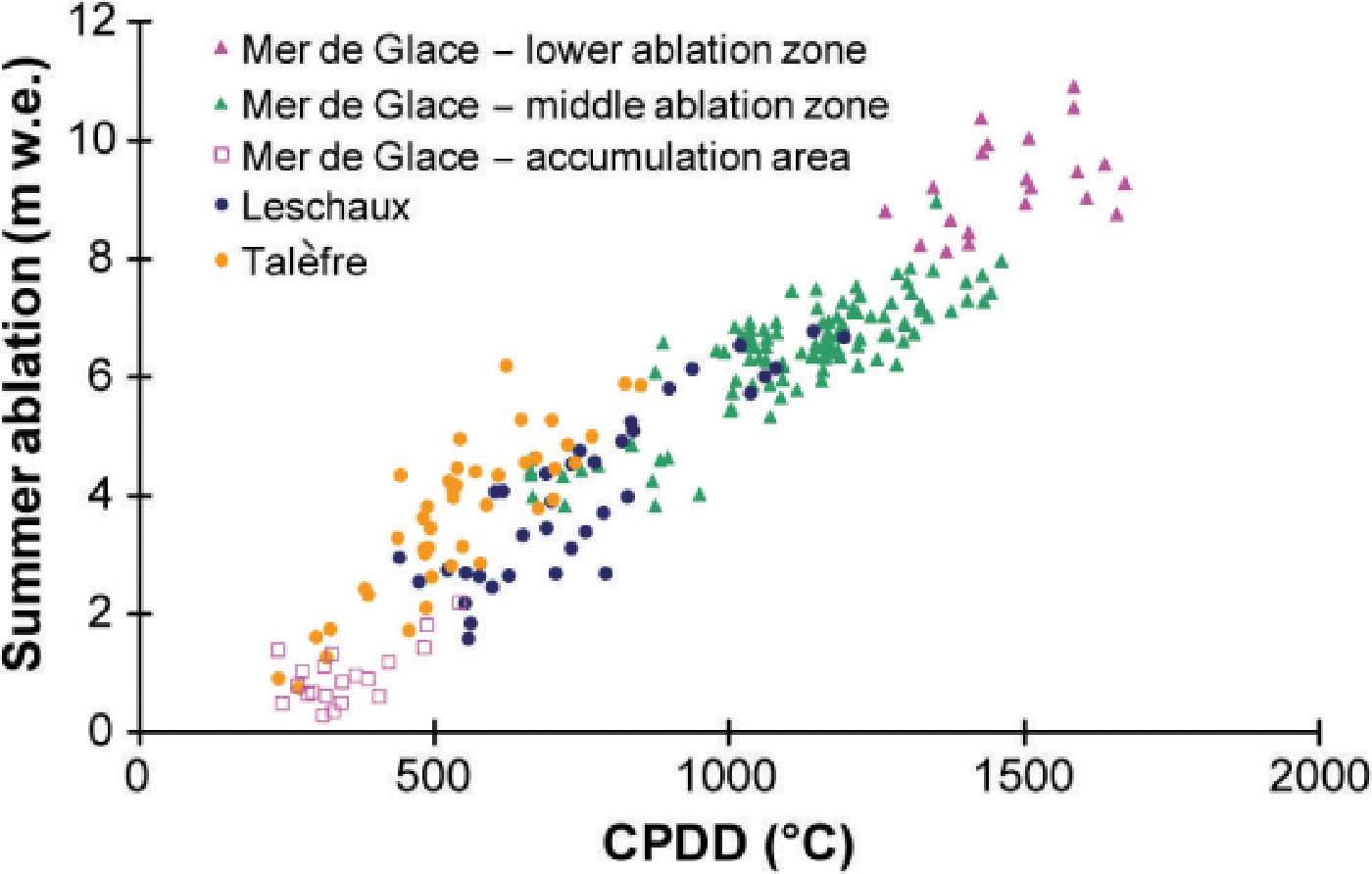
Fig. 6. Total summer ablation vs CPDD, calculated for various altitude ranges on Mer de Glace and tributary glaciers (Talèfre and Leschaux), for the period 1995–2011, using data from Chamonix meteorological station. For clarity, only part of the dataset is presented; data from some stakes are not included.

Figure 6 and previous studies (Hock, 2005) show that the relationship between summer mass balance and CPDD depends to a great extent on the surface albedo (snow, ice, debris). Thanks to the many measurements made during summer, our dataset allows us to separate the mass-balance sensitivity for ice from that for snow. This is not crucial at low altitudes, where snow disappears rapidly in spring, but is essential in other regions, especially near the ELA (2700– 3000 m in the French Alps), where large dispersion is observed because the winter snow layer disappears at different times during the summer from year to year, depending on winter accumulation.

In a second step, snow ablation was separated from ice ablation for our entire dataset. For clarity, we first focus our analysis on some selected sites. Figure 7a–d show, for example, the relationship between CPDD and snow and ice ablation for four selected sites, two on Saint-Sorlin (~2775 and ~2825 m) and two on Argentière glacier (~2500 and ~2700 m). Figure 6 reveals a dependence on exposure (e.g. the marked sensitivity of Glacier de Talèfre which is exposed to the south). In Figure 7, data were selected at certain sites to avoid the dependence of the PDD factor on exposure (Vincent and Six, 2013) or albedo (Van de Wal and others, 1992; Brock and others, 2000). Snow and ice data were selected manually from the dataset, depending on the amount of winter accumulation and the amount of snow still present on the measurement date. Data showing ablation of both snow and ice were removed from our dataset for this analysis.

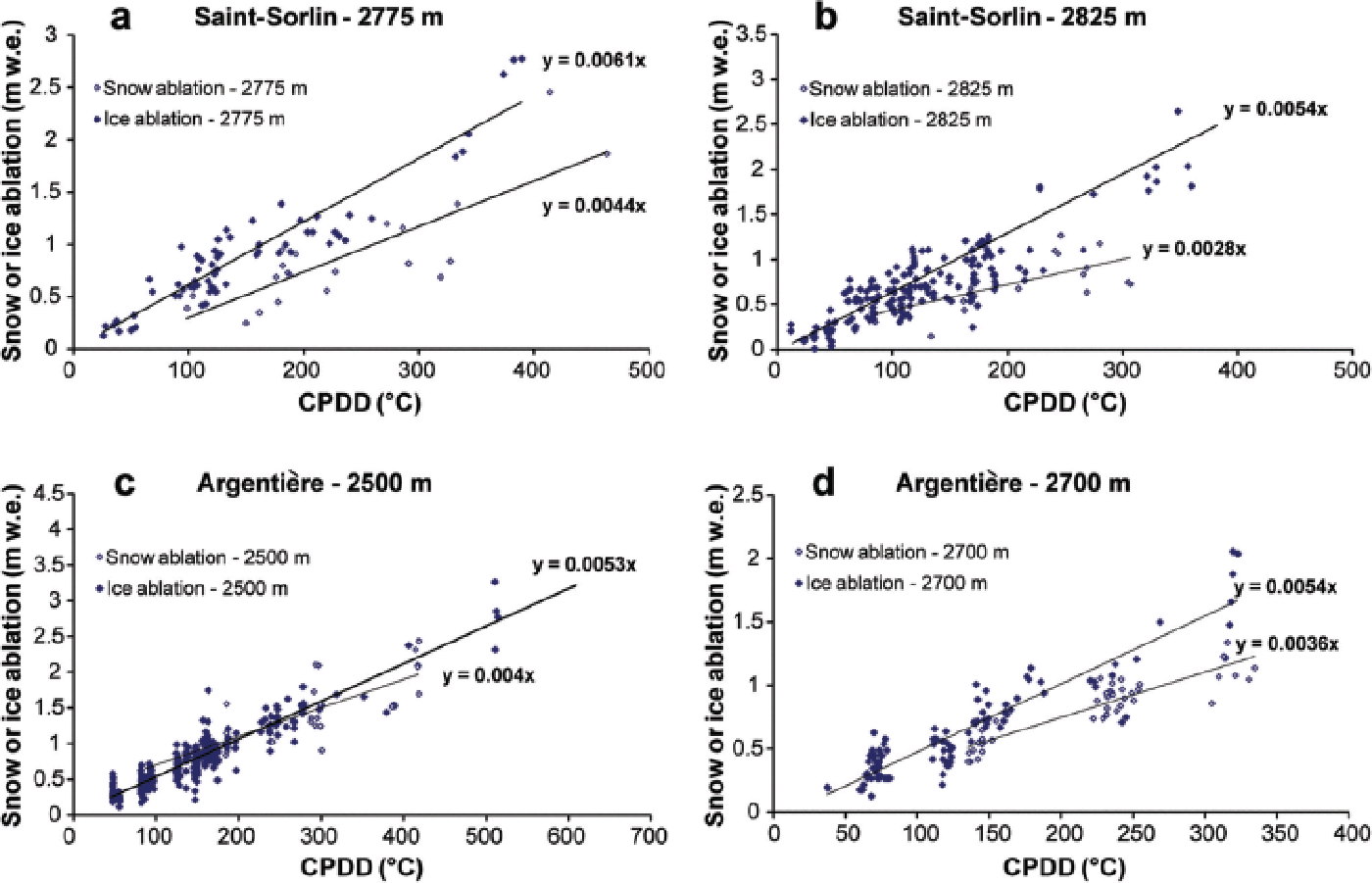
Fig. 7. Observed summer snow ablation and ice ablation on Saint-Sorlin ((a) ~2775 m and (b) ~2825 m) and Argentière ((c) ~2500 m and (d) ~2700 m) vs CPDD calculated from data measured at Lyon and Chamonix meteorological stations (stakes measured between 1995 and 2011).

CPDD values were calculated for the same period as ablation measurements. The PDD factors f _snow and f _ice were determined as the slope of the linear regression between CPDD and snow or ice ablation. For instance, the PDD factor was 0.0061 m w.e. °C⁻¹ d⁻¹ for ice ablation and

0.0044 m w.e. °C⁻¹ d⁻¹ for snow ablation for Glacier de Saint-Sorlin at 2775 m a.s.l., in agreement with results of the previous studies on this glacier (Vincent and Vallon, 1997; Vincent 2002). The percentage of explained ice ablation variance with temperature was generally higher than for snow (R ² = 0.9 and 0.7 respectively at 2775 m).

As in Figure 7a–d, the relationships between snow ablation or ice ablation and CPDD were obtained for the four glaciers and for all altitude ranges covered by each glacier. Thus, 49 PDD factors were deduced from these relationships. Figure 8 shows the PDD factors as a function of altitude, separating ice data (in the ablation area) and snow data (in the accumulation area and in the ablation area at the beginning of the ablation season). Figure 8 shows an important feature: on the one hand, the mean ice PDD factor was 0.0061 m °C⁻¹ d⁻¹ between 1600 and 2500 m a.s.l., with no dependence on altitude (standard deviation (SD) 0.0005 m °C⁻¹ d⁻¹); on the other hand, the mean PDD factor for snow above 3000 m was 0.003 m °C⁻¹ d⁻¹ (SD 0.0004 m °C⁻¹ d⁻¹) and, as for ice, did not depend on altitude.

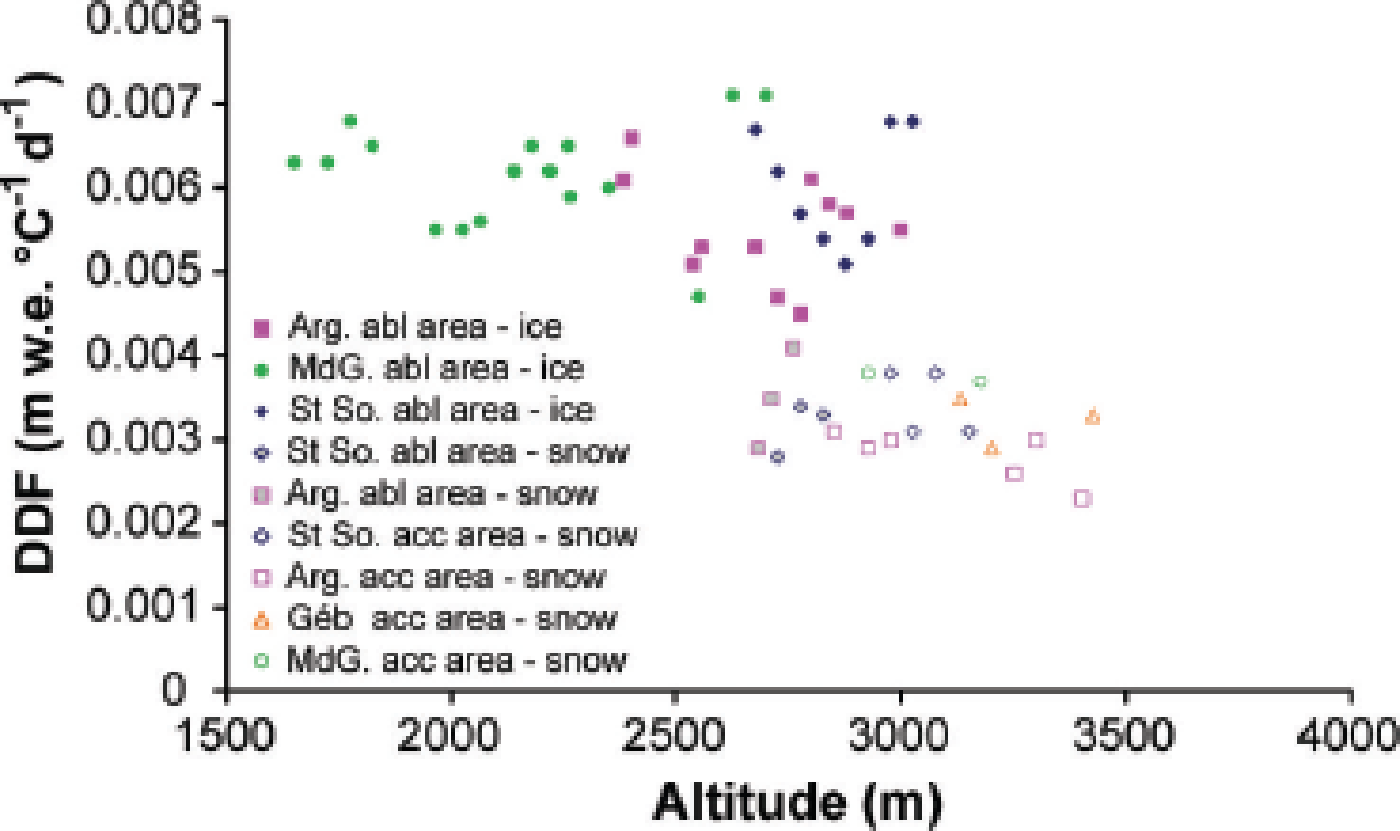
Fig. 8. All positive degree-day factors on the four glaciers as a function of altitude for the period 1995–2011. Snow and ice ablation measurements are treated separately for the calculation of each snow PDD factor in the accumulation (‘acc’) area (empty symbols) and ablation area (grey symbols) and each ice PDD factor in the ablation (‘abl’) area (full symbols).

Greater variability was observed between 2500 and 3000 m a.s.l. near the ELA, even though snow and ice ablation were treated separately. It is clear that the PDD factor depends mainly on the surface albedo (snow or ice) and, in this region, frequent snowfalls can occur during summer, which probably increases the uncertainty. There was a drop between values measured at ~0.006 and ~0.003 m °C⁻¹ d⁻¹, with no dependence on altitude. For instance, the PDD factor obtained for snow ablation in the ablation zone of Saint-Sorlin is very similar to that obtained for snow ablation in the accumulation zone of Saint-Sorlin and Gébroulaz glaciers. Note that the snow PDD factors ranged from 0.0025 to 0.004 m w.e. °C⁻¹ d⁻¹ whatever the region of the glacier (accumulation or ablation zone). As mentioned by Vincent and Six (2013), there is a strong dependence on aspect. In our dataset, we observed high values close to 0.007 m w.e. °C⁻¹ d⁻¹ on Glacier de Talèfre (south aspect) and the south part of Glacier de Saint-Sorlin between 3025 and 2975 m. Vincent and Six (2013) showed that the high spatial variability of ice ablation on Glacier de Saint-Sorlin depends mainly on potential solar radiation variations, while the temporal variations are highly correlated with temperature. This previous study was performed on a small area of the glacier. Extending this calculation over the entire glacier, we found that cumulative potential solar radiation calculated on the south slope of Saint-Sorlin is 25% higher than on the north slope at the same altitude (accumulated between 15 July and 1 October). For these two sites, we found ice PDD factors of 0.0051 and 0.007 m w.e. °C⁻¹ d⁻¹, indicating a value 40% higher on the slope with a south aspect. As discussed below, exposure can significantly influence ablation sensitivity to temperature change.

3.4. Sensitivity of annual ablation to temperature change

In order to estimate ablation sensitivity to temperature change over the whole summer, each degree-day factor shown in Figure 8 was used. We calculated the melting of snow and ice using these degree-day factors and the daily average temperature at Lyon, Bourg Saint-Maurice and Chamonix for the 1995–2011 period, calculated at the altitude of each site and enhanced by 1°C. These calculations were made using a mean accumulation scenario (mean value of the period), a low winter accumulation scenario and a high winter accumulation scenario measured during this period (lowest and highest accumulation observed in 2011 and 2001 respectively). It is important to consider these scenarios because the amount of snow present at the beginning of the melting period (and the time it will remain present at the surface) will affect the surface albedo. The albedo feedback will impact on the melt through the snow PDD factor which is lower than the ice PDD factor. Annual ablation sensitivity to temperature change is shown in Figure 9 for a mean accumulation scenario. This figure shows a marked decrease with increasing altitude, with annual ablation sensitivity to temperature change ranging from close to +1.55 m w.e. °C⁻¹ on the lower part of Mer de Glace (1650 m) to +0.25 m w.e. °C⁻¹ in the higher zone of Glacier d’Argentière (3440 m). This general pattern has already been observed in previous studies (Vallon and others, 1998; Braithwaite and Zhang, 2000; Vincent, 2002). Note that at a similar altitude (2600 m), the sensitivity of ablation to temperature change differed significantly depending on aspect (+1.23 m w.e. °C⁻¹ at Glacier de Talèfre for south exposure and +0.85 m w.e. °C⁻¹ for north exposure at Glacier de Leschaux, although these glaciers are located <1 km apart).

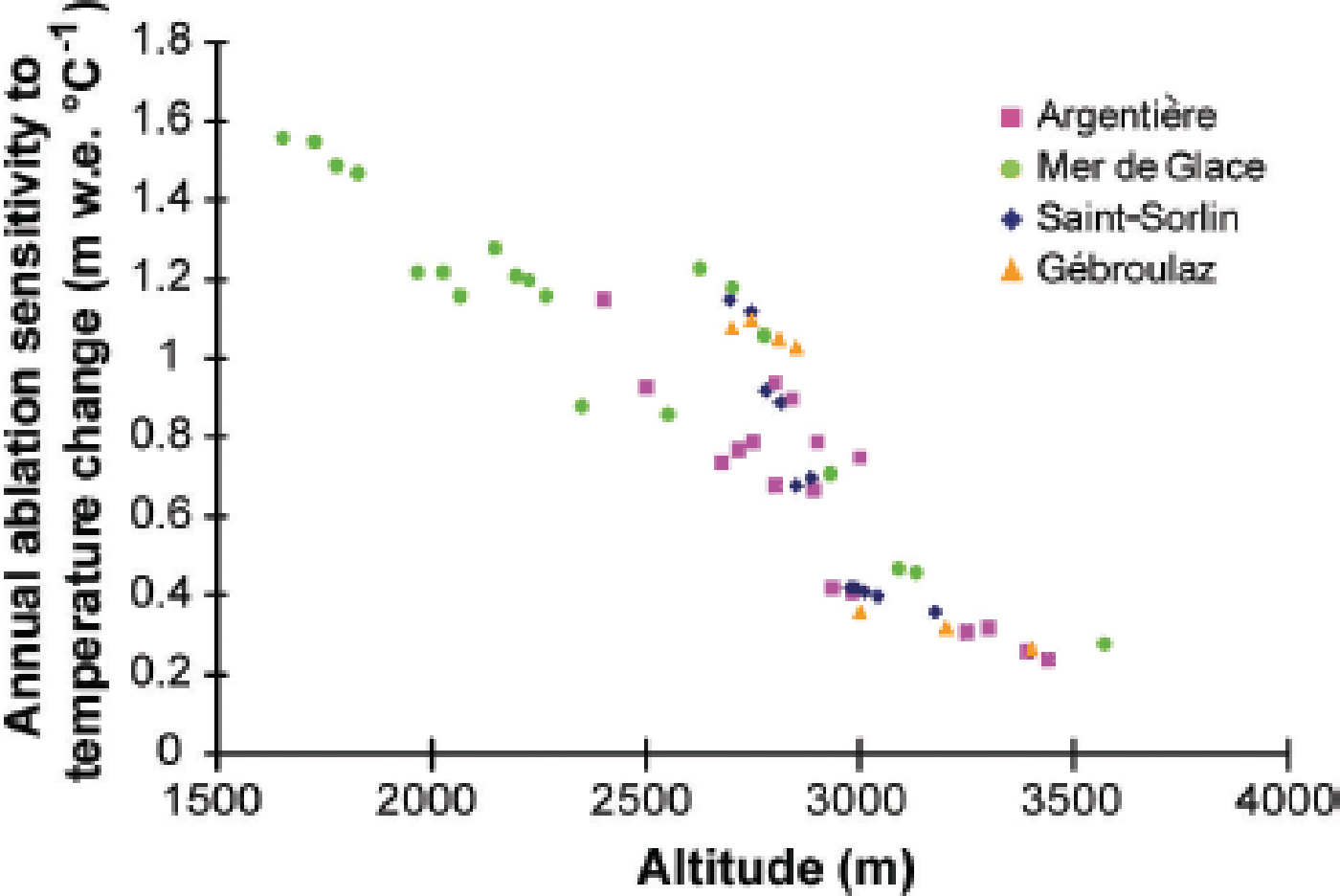
Fig. 9. Annual ablation sensitivity to temperature as a function of altitude for a mean accumulation scenario over the period. Depending on the altitude, PDD factors calculated for ice ablation or snow ablation (Fig. 8) were used.

Conversely, the sensitivity of ablation to temperature change was similar whatever the selected accumulation scenarios, except for the altitude range in the vicinity of the ELA where sensitivity can decrease by 20% for the high-accumulation scenario and increase by 10% for the low-accumulation scenario (the increase is lower because the low scenario is not so different from the mean in the measurement period). Our results are similar to those obtained by Vincent (2002) in the lower and upper part of glaciers. Conversely, we found marked discrepancies in the equilibrium-line area. The use of snow and ice PDD factors very likely improved the accuracy of the sensitivity values. Differences reached +0.15 to +0.25 m w.e. °C⁻¹ between Vincent’s (2002) study and this analysis.

3.5. Sensitivity of ELA to temperature change

From our surface mass-balance measurements made in the vicinity of the ELA, we calculated the annual mass-balance gradient db /dz for each glacier, in order to determine the annual values of ELA. Gradients around the ELA are 0.6, 0.65 and 1.07 m w.e. (100 m)⁻¹ for Gébroulaz, Saint-Sorlin and Argentière glaciers respectively. The average db /dz gradients calculated over the entire glaciers were also calculated. They are lower than those calculated with data from the ELA region for Argentière and Gébroulaz and higher for Saint-Sorlin (Table 3). For different altitudes within this ELA range, we were able to determine the number of positive degree-days required to melt the mean winter accumulation (highor low-accumulation scenario), using the snow PDD factor calculated in Section 3.3. The CPDD of the mean ELA was calculated using mean daily positive air temperature over the period and enhanced by 1°C (with a fixed lapse rate of 0.6°C (100 m)⁻¹). For each site around the ELA, we determined the increase in ablation due to a 1°C increase. Thus, the increase in ablation duration is taken into account. Finally, using the mass-balance gradient obtained from our dataset (around the ELA and over the entire glacier), we can determine the increase in ELA for a 1°C increase (Table 3). For a 1°C increase, we found an ELA increase of +75 m on Saint-Sorlin, +50 m on Argentière and +85 m on Gébroulaz. The choice of db /dz will influence the sensitivity of ELA to temperature change (see Table 3; Section 4).

Table 3. Mean ELA measured over 1995–2011, mass-balance gradients calculated around ELA and ELA increase for a 1°C rise for Saint-Sorlin, Argentière and Gébroulaz glaciers. The ELA increase is also presented for mass-balance gradients calculated with all the stakes over each glacier (two rightmost columns)

4. Discussion and Conclusions

We have analysed changes in the surface winter and summer mass balances since 1995 using an extensive dataset from four glaciers located in the French Alps. Based on these numerous measurements, we were able to separately study surface snow accumulation and snow/ice ablation over different periods. This allowed us to analyse the sensitivity of the surface mass balance to changes in snow precipitation and air temperature.

As mentioned in previous studies using parts of this dataset (e.g. Vincent, 2002; Vincent and others, 2005, 2009, 2014; Vincent and Six, 2013), glacier mass balances have been very negative since the beginning of the 1980s. In addition, in the present study, we observed a sharp increase in mass loss after 2002, and the five most negative annual mass balances for Argentière and Gébroulaz glaciers occurred after 2002.

Both winter and summer mass balances have been thoroughly studied. From our analysis, we confirm that summer mass balance is mainly responsible for changes in the annual mass balances; summer mass balance explains >90% of the variance.

Winter mass balance shows a complicated pattern, with no linear relationship with altitude, as shown in previous studies (Machguth and others, 2006; Sold and others, 2013). The spatial variation of accumulation on the glacier surface is influenced by snowdrifting and avalanches (Vincent, 2002; Vincent and others, 2007; Huss and others, 2008). Modelling accumulation distribution over a mountain glacier remains a challenging task (Sold and others, 2013).

We found that the ratios calculated between winter mass balance and valley precipitation differ considerably from site to site but that the values remain fairly constant over time. Although the two study periods are probably not long enough to determine consistent changes in the ratios, these ratios could be used for future simulations, as already done in other studies (e.g. Gerbaux and others, 2005), assuming that the ratios do not change over the coming decades.

Summer mass balances were compared to the cumulative PDDs calculated from valley meteorological stations. Over the past 16 years, the number of PDDs between 1 May and 1 October has increased by 30 days at 2800 m on Glacier de Saint-Sorlin (near the equilibrium line) based on data measured at Lyon, 19 days on Gébroulaz based on data measured at Bourg Saint-Maurice and 26 days on Glacier d’Argentière and Mer de Glace based on data measured at Chamonix. The CPDD increased by 92°C on Saint-Sorlin, 121°C on Gébroulaz and 184°C on Argentière and Mer de Glace (again at 2800 m).

We compared the periodically observed snow and ice ablation separately with the CPDD, in order to obtain snow and ice PDD factors. The snow PDD factor ranged between 0.0025 and 0.004 m w.e. °C⁻¹ d⁻¹, and the ice PDD factor between 0.0045 and 0.007 m w.e. °C⁻¹ d⁻¹. The mean ice PDD factor was 0.0061 m w.e. °C⁻¹ d⁻¹, and the mean snow PDD factor was 0.003 m w.e. °C⁻¹ d⁻¹.

These PDD factors were obtained for a fixed air temperature lapse rate over summer of 0.6°C (100 m)⁻¹. However, as mentioned in Section 2, the lapse rate varies over the ablation season. In order to study snow and ice PDD factor sensitivity to this lapse rate change, we analysed the influence of different air temperature lapse rates. First, we calculated the snow PDD factor using (1) a fixed lapse rate over summer (0.6°C (100 m)⁻¹), (2) the lapse rate commonly used in the literature (0.65°C (100 m)⁻¹) and (3) the lapse rate of May and June, during which maximum snowmelt occurs (0.68°C (100 m)⁻¹ on Argentière and 0.63°C (100 m)⁻¹ on Saint-Sorlin). We found that, at 2700 m a.s.l., in the ablation area of Argentière, the snow PDD factors are 0.0041, 0.0042 and 0.0045 m w.e. °C⁻¹ d⁻¹ respectively. Consequently the snow PDD factor may be underestimated by 10% using the fixed summer lapse rate. Secondly, the ice PDD factors were calculated using (1) the constant lapse rate over summer (0.60°C (100 m)⁻¹), (2) the lapse rate commonly used (0.65°C (100 m)⁻¹) and (3) the lapse rate of August/September during which maximum ice ablation occurs (0.58°C (100 m)⁻¹). On Argentière at 2700 m, the ice PDD factor varies from 0.0056 and 0.0060 m w.e. °C⁻¹ d⁻¹ to 0.0053 m w.e. °C⁻¹ d⁻¹. The ice PDD factor is overestimated by 5% using the fixed summer lapse rate on Argentière and up to 10% on Saint-Sorlin. At low altitudes (<2500 m) we also noticed that differences were limited because whatever the air temperature lapse rate used, temperature is positive most of the time during summer (differences are <5%). The differences are significant in the accumulation zone. In this area, the difference in snow PDD factor between a fixed summer lapse rate and a commonly used lapse rate (0.65°C (100 m)⁻¹) can reach 20%. We conclude that uncertainties of the ice and snow PDD factors are significant and should influence the sensitivity of ablation to temperature change if an incorrect air temperature lapse rate is used. Not using a correct air temperature lapse rate will introduce 20% uncertainty on the snow PDD factor in the accumulation area, 10–15% on the snow PDD factor in the ablation area near the ELA, 10% on the ice PDD factor close to the ELA and <5% on the ice PDD factor elsewhere.

Uncertainties of the air temperature lapse rate also imply a range of uncertainty in the determination of the ablation sensitivity to temperature change (Section 3.4). It is close to the ELA that the uncertainty of the snow/ice PDD factors will most affect this sensitivity. Again, it will depend on the amount of snow present at the end of spring. For this reason, different accumulation scenarios are proposed in this study (mean, low and high winter accumulation as mentioned in Section 3.4). For instance, considering Argentière at 2700 m, ablation sensitivity to temperature increases by 0.2 m w.e. °C⁻¹ (from 1 m w.e. °C⁻¹ to 1.20 m w.e. °C⁻¹) for a high-accumulation scenario and by +0.1 m w.e. °C⁻¹ for a low-accumulation scenario. Thus, these sensitivities can be over- or underestimated by 20% according to the air temperature lapse rate used.

The absence of a link between these snow and ice PDD factors and altitude is clear in the lower and higher parts of the glaciers. To our knowledge, our study is the first to separately analyse snow and ice ablation with temperature over such a wide range of altitudes, thanks to our large dataset. Previous studies based on the comparison between degree-day modeled mass balance and observations showed that the degree-day factors obtained from glaciers in Iceland, Norway and Greenland at different elevations were similar (Jóhannesson and others, 1995). Ambach (1988) found smaller degree-day factors at lower elevations of the Greenland ice sheet resulting from a larger contribution of sensible heat to melt energy. In an overview paper relative to the temperature index methods, Hock (2003) asserted that under otherwise similar conditions, degree-day factors are expected to increase with elevation. In our study, we found no relationship between the PDD factors and elevation. The ice PDD factors appear to depend on exposure since glaciers exposed to the south showed the largest ice PDD factors. However, they could also depend on local surface snow or ice albedo. This needs to be confirmed by a thorough analysis comparing the PDD factors with the solar radiation and surface albedo measurements in a future study. According to the results of the present study, the relationships are stable irrespective of whether the wide glacier mass balances are positive or negative. Given that this analysis covered 16 years with highly contrasted mass balances, we conclude that these snow and ice PDD factors can be used during the coming decades. This means that, for a given site, ablation depends mainly on the amount of snow precipitation and the CPDDs.

The age of the snow could be taken into account to improve this relationship. Indeed, on Glacier de Saint-Sorlin, we observed a small increase in the snow degree-day factor in the accumulation area. For fresh spring snow, the snow PDD factor was 0.0025 m w.e. °C⁻¹ d⁻¹, whereas it was 0.004 m w.e. °C⁻¹ d⁻¹ for old autumn snow. This is likely one effect of the absorbed shortwave radiation due to a change in albedo with the age of the snow (Six and others, 2009). Future studies should be carried out to confirm this effect.

Our results also allowed us to study ELA sensitivity to temperature increase. First, we compared our results to previous results obtained on the same glaciers. Vincent (2002) calculated such sensitivities for a shorter period (1995–2001) without distinguishing between snow and ice ablation sensitivity. He found a rise in the ELA of 60–70 m for a 1°C increase in temperature, slightly lower than the values we obtained on Saint-Sorlin and Gébroulaz glaciers, and higher than on Glacier d’Argentière. This was firstly because the CPDD factor used by Vincent (2002) did not distinguish ice and snow and also because he used a gradient-with-altitude of 0.7–0.8 m (100 m)⁻¹, higher on Gébroulaz and Saint-Sorlin than the mass-balance gradient obtained from our dataset (lower on Argentière). Using observed mass-balance gradients around the ELA, we found a lower sensitivity on Argentière and Gébroulaz and a higher sensitivity on Saint-Sorlin than using the mass-balance gradients calculated with all the stakes (Table 3). As mentioned by Thibert and others (2013), ELA sensitivity to temperature is highly dependent on the adopted altitudinal dependence of mass balance. In the present study, the altitudinal dependence of mass balance comes from direct surface mass-balance observations, but the weight given to the selected stakes (all the stakes on the glacier or stakes located around the ELA) influences the sensitivity. The major differences in ELA sensitivity to a temperature increase seem to be mainly driven by the mass-balance gradient with altitude. For example, on Glacier d’Argentière, using a common mass-balance gradient of 0.6 m (100 m)⁻¹, the sensitivity reaches 73 m °C⁻¹ instead of 50 m °C⁻¹, corresponding to a 40% increase. The uncertainty of the snow PDD factor near the accumulation line also contributes to uncertainty of the sensitivity of the ELA to temperature change. In fact, if the snow PDD factor is overestimated by 20%, then ELA sensitivity to temperature change is also overestimated by 20%. For instance, the ELA sensitivity rises from +75 m °C⁻¹ to +90 m °C⁻¹ on Saint-Sorlin, +85 m °C⁻¹ to +102 m °C⁻¹ on Gébroulaz and +50 m °C⁻¹ to +60 m °C⁻¹ on Argentière (for a 20% overestimation). This is a major issue in the determination of ELA increase in the future, and the consequences are very great for the future of glaciers.

Another way to calculate ELA sensitivity is to use satellite images, although comparing these with field measurements can lead to large differences given that (1) satellite images are not always available at the end of the ablation season and (2) the snowline detected on satellite images does not always correspond to the ELA. This method has been used for 43 glaciers in the French Alps including those in our study (Rabatel and others, 2013) for the period 1984–2011. Rabatel and others (2013) found a sensitivity of +115 m °C⁻¹ for all 43 glaciers, higher than our values. Using the mean ELA determined in their study for Argentière, Saint-Sorlin and Gébroulaz glaciers (see table II, supplementary material in their paper), restricted to the 1995–2011 period, we calculate ELA sensitivity to temperature change for each glacier using our mass-balance gradients near the ELA. The sensitivities are close to our sensitivities for all three glaciers (differences <5 m on Argentière and Saint-Sorlin and <10 m on Gébroulaz), even if the ELAs are lower by 60 m on Argentière, 90 m on Gébroulaz and 20 m on Saint-Sorlin.

More generally, we compared our results with those of previous studies, including those obtained from surface energy-balance models. Thibert and others (2013) found a sensitivity of +93 m °C⁻¹ on the south-exposed Glacier de Sarennes around its mean equilibrium line (3100 m). Gerbaux and others (2005) found +125 to +160 m °C⁻¹ on Glacier de Saint-Sorlin. Oerlemans and Hoogendoorn (1989) determined a value of +130 m °C⁻¹ for a fictitious glacier, and Wallinga and Van de Wal (1998) deduced ELA sensitivity to be 127 m °C⁻¹ on Rhonegletscher, Switzerland. Braithwaite and Zhang (2000) reported sensitivities between +90 and +115 m °C⁻¹ on Swiss glaciers. Zemp and others (2007) reported an average deviation of the regional climatic ELA of 100 m for a temperature change of 1°C. Kuhn (1989) found a value of +65 m °C⁻¹ on Hintereisferner, Austria. The discrepancies are large, with a factor of >2 between the lowest and the highest value. Note also that ELA sensitivity to meteorological data obtained from surface energy-balance models (Oerlemans and Hoogendoorn, 1989; Wallinga and Van de Wal, 1998; Gerbaux and others, 2005) provided the highest values. This could mean either that these models overestimate ELA sensitivity or that the empirical relationships lack all the necessary feedback. Quantifying ELA sensitivity to temperature from empirical regression of ablation to degree days integrates the effect of ablation not only of the measured temperature variations but also of all meteorological parameters that control ablation (summer and winter precipitation, downward longwave radiation, cloud cover, moisture and global radiation). However, given that the measurements used to assess this sensitivity have been carried out over a 16 year period, we can assume that these observations integrate very different meteorological conditions.

For the future, a combined approach using a surface energy-balance model and the many measurements made in this study for the purpose of validation will be required to calculate the sensitivity of the surface mass balance and ELA to meteorological data and to validate the empirical approach. Empirical relationships have the advantage of using simple and reliable available meteorological data in future climatic scenarios.