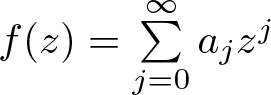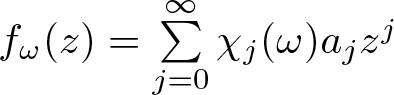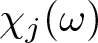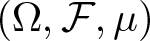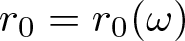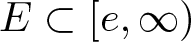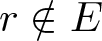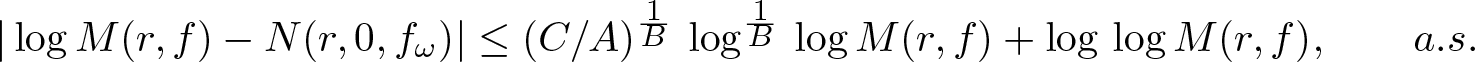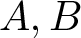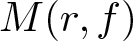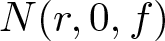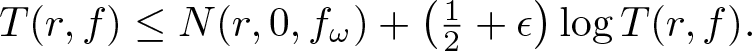1. Introduction
Let f be a transcendental entire function of the form
 \begin{align}
f(z)=\sum_{j=0}^{\infty} a_j z^j,
\end{align}
\begin{align}
f(z)=\sum_{j=0}^{\infty} a_j z^j,
\end{align} where ![]() $z, a_j \in \mathbb{C}$.
$z, a_j \in \mathbb{C}$.
Let ![]() $(\Omega, \mathcal{F}, \mu)$ be a probability space, where
$(\Omega, \mathcal{F}, \mu)$ be a probability space, where ![]() $\mathcal{F}$ is a σ-algebra of subset of Ω and µ is a probability measure on
$\mathcal{F}$ is a σ-algebra of subset of Ω and µ is a probability measure on ![]() $(\Omega,\, \mathcal{F})$. Along with the function (1.1), we consider the random functions on the probability space
$(\Omega,\, \mathcal{F})$. Along with the function (1.1), we consider the random functions on the probability space ![]() $(\Omega,\, \mathcal{F}, \, \mu)$ as follows:
$(\Omega,\, \mathcal{F}, \, \mu)$ as follows:
 \begin{equation}
f_\omega(z)=\sum_{j=0}^{\infty}\chi_j(\omega) a_j z^j,
\end{equation}
\begin{equation}
f_\omega(z)=\sum_{j=0}^{\infty}\chi_j(\omega) a_j z^j,
\end{equation} where ![]() $z, a_j \in \mathbb{C}$,
$z, a_j \in \mathbb{C}$, ![]() $\omega \in \Omega$,
$\omega \in \Omega$, ![]() $\chi_j(\omega)$ (
$\chi_j(\omega)$ (![]() $j=0, 1, 2, \ldots$) are independent and identically distributed complex-valued random variables. Further, we assume that the expectation and variance of χj are zero and one, respectively. It is clear that
$j=0, 1, 2, \ldots$) are independent and identically distributed complex-valued random variables. Further, we assume that the expectation and variance of χj are zero and one, respectively. It is clear that ![]() $f_\omega(z)$ is an entire function for almost all
$f_\omega(z)$ is an entire function for almost all ![]() $\omega \in \Omega$ (see [Reference Kahane6]).
$\omega \in \Omega$ (see [Reference Kahane6]).
In general, we consider three cases regarding ![]() $\chi_j(\omega)$. Gaussian entire functions: χj (
$\chi_j(\omega)$. Gaussian entire functions: χj (![]() $j=0, 1, \ldots$) are complex-valued Gaussian random variables with standard Gaussian distribution; Rademacher entire functions: χj (
$j=0, 1, \ldots$) are complex-valued Gaussian random variables with standard Gaussian distribution; Rademacher entire functions: χj (![]() $j=0, 1, \ldots$) are Rademacher random variables, which take the values ±1 with probability 1/2 each; Steinhaus entire functions:
$j=0, 1, \ldots$) are Rademacher random variables, which take the values ±1 with probability 1/2 each; Steinhaus entire functions:  $\chi_j={\rm e}^{2\pi i\theta_j}$ (
$\chi_j={\rm e}^{2\pi i\theta_j}$ (![]() $j=0, 1, \ldots$) are Steinhaus random variables, where θj (
$j=0, 1, \ldots$) are Steinhaus random variables, where θj (![]() $j=0, 1, \ldots$) are independent real-valued random variables with uniform distribution in the interval [0,1].
$j=0, 1, \ldots$) are independent real-valued random variables with uniform distribution in the interval [0,1].
The study of random polynomials was initiated by Bloch and Pólya in 1932. Since then, there are a lot of publications on random polynomials. Moreover, the research on random transcendental entire functions, especially, on Gaussian, Rademacher and Steinhaus entire functions, has drawn a lot of attention, too (e.g. [Reference Buhovsky, Glücksam and Sodin1, Reference Hough, Krishnapur, Peres and Virág4, Reference Kabluchko and Zaporozhets5, Reference Mahola and Filevych9, Reference Mahola and Filevych10, Reference Nazarov, Nishry and Sodin13, Reference Nazarov, Nishry and Sodin14, Reference Sodin16, Reference Sun and Chen17]). Recently, Nazarov et al. [Reference Nazarov, Nishry and Sodin13, Reference Nazarov, Nishry and Sodin14] made a breakthrough on the logarithmic integrability of Rademacher Fourier series and obtained several important results on the distribution of zeros of Rademacher entire functions. Their results extended earlier work of Littlewood and Offord [Reference Littlewood and Offord7, Reference Littlewood and Offord8]. Also, in 1982, Murai [Reference Murai12] proved the Nevanlinna defect identity for Rademacher entire functions. In 2000, Sun and Liu [Reference Sun and Liu18] obtained the Nevanlinna defect identity for ![]() $f(z)+X(\omega)g(z)$ (where
$f(z)+X(\omega)g(z)$ (where ![]() $f ,g$ are entire, g is a small function of f and
$f ,g$ are entire, g is a small function of f and ![]() $X(\omega)$ is a non-degenerated complex-valued random variable). Later, Mohola and Filevych [Reference Mahola and Filevych9, Reference Mahola and Filevych10] obtained Nevanlinna’s second main theorem for Steinhaus entire functions.
$X(\omega)$ is a non-degenerated complex-valued random variable). Later, Mohola and Filevych [Reference Mahola and Filevych9, Reference Mahola and Filevych10] obtained Nevanlinna’s second main theorem for Steinhaus entire functions.
In this paper, we first define a family ![]() $\mathcal{Y}$ of random entire functions, which includes Gaussian, Rademacher and Steinhaus entire functions. Thus, we can deal with these three classes of famous random entire functions all together. Then, we prove several inequalities concerning the maximum modulus
$\mathcal{Y}$ of random entire functions, which includes Gaussian, Rademacher and Steinhaus entire functions. Thus, we can deal with these three classes of famous random entire functions all together. Then, we prove several inequalities concerning the maximum modulus ![]() $M(r, f)$,
$M(r, f)$, ![]() $\sigma(r, f)$ and the integrated counting function
$\sigma(r, f)$ and the integrated counting function ![]() $N(r, a, f_\omega)$ for the random entire functions in the family
$N(r, a, f_\omega)$ for the random entire functions in the family ![]() $\mathcal{Y}$. These inequalities show that the zero-counting functions of almost all randomly perturbed functions fω are close to the maximum modulus of f, up to an error term. We also carefully treat the error terms in these inequalities. Our Lemma 4.3 verifies that the family
$\mathcal{Y}$. These inequalities show that the zero-counting functions of almost all randomly perturbed functions fω are close to the maximum modulus of f, up to an error term. We also carefully treat the error terms in these inequalities. Our Lemma 4.3 verifies that the family ![]() $\mathcal{Y}$ includes Gaussian, Rademacher and Steinhaus entire functions. The ingredients in our proofs involve the techniques used by Nazarov–Nishry–Sodin, Mohola–Filevych and Offord. As a by-product of our results, we also establish Nevanlinna’s second main theorems for random entire functions with a careful treatment of its error term. Thus, we obtain that the characteristic function of almost all functions in the family is bounded above by an integrated counting function, rather than by two integrated counting functions as in the classical Nevanlinna theory.
$\mathcal{Y}$ includes Gaussian, Rademacher and Steinhaus entire functions. The ingredients in our proofs involve the techniques used by Nazarov–Nishry–Sodin, Mohola–Filevych and Offord. As a by-product of our results, we also establish Nevanlinna’s second main theorems for random entire functions with a careful treatment of its error term. Thus, we obtain that the characteristic function of almost all functions in the family is bounded above by an integrated counting function, rather than by two integrated counting functions as in the classical Nevanlinna theory.
The paper is organized as follows. We devote ![]() $\S$ 2 to some preliminaries and previous results. In
$\S$ 2 to some preliminaries and previous results. In ![]() $\S$ 3, we state our main results and Nevanlinna’s second main theorems for random entire functions. In
$\S$ 3, we state our main results and Nevanlinna’s second main theorems for random entire functions. In ![]() $\S$ 4, we give some lemmas, which are needed in the proofs of our results, where Lemma 4.3 is one of the key lemmas in the section. In
$\S$ 4, we give some lemmas, which are needed in the proofs of our results, where Lemma 4.3 is one of the key lemmas in the section. In ![]() $\S$ 5, we first prove Theorem 3.1, with which, then, we prove a lemma that has its own interests and is needed in the proof of Theorem 3.2. All corollaries are proved in this section, too.
$\S$ 5, we first prove Theorem 3.1, with which, then, we prove a lemma that has its own interests and is needed in the proof of Theorem 3.2. All corollaries are proved in this section, too.
2. Preliminaries
Let X be a complex-valued random variable. We denote the expectation and the variance of X by ![]() $\mathbb{E}(X)$ and
$\mathbb{E}(X)$ and ![]() $\mathbb{V}(X)$, respectively. In particular, if X is either a standard complex-valued Gaussian random variable (its probability density function is
$\mathbb{V}(X)$, respectively. In particular, if X is either a standard complex-valued Gaussian random variable (its probability density function is  $ {\rm e}^{-|z|^2}/\pi$ with respect to Lebesgue measure m in the complex plane), or a Rademacher random variable or a Steinhaus random variable, then
$ {\rm e}^{-|z|^2}/\pi$ with respect to Lebesgue measure m in the complex plane), or a Rademacher random variable or a Steinhaus random variable, then ![]() $\mathbb{E}(X)=0$ and
$\mathbb{E}(X)=0$ and ![]() $\mathbb{V}(X)=\mathbb{E}(|X|^2)=1$. We also denote the probability of an event A by
$\mathbb{V}(X)=\mathbb{E}(|X|^2)=1$. We also denote the probability of an event A by ![]() $\mathbb{P}(A)$. For a set
$\mathbb{P}(A)$. For a set ![]() $E\subset[1,+\infty)$, we say E has a finite logarithmic measure if
$E\subset[1,+\infty)$, we say E has a finite logarithmic measure if  $\int_E1/t\,\textrm{d}t \lt +\infty$.
$\int_E1/t\,\textrm{d}t \lt +\infty$.
For the reader’s convenience, we recall some standard notation in function theory and state some important theorems in Nevanlinna theory for meromorphic functions g in the complex plane ![]() $\mathbb{C}$. These notation and theorems will be used to prove new theorems in Nevanlinna theory as corollaries of our main results for random entire functions. In the sequel, the values of constants, such as
$\mathbb{C}$. These notation and theorems will be used to prove new theorems in Nevanlinna theory as corollaries of our main results for random entire functions. In the sequel, the values of constants, such as ![]() $C, C_1, r_0\,\textrm{and}\, r_1$, may be different in each appearance of these constants.
$C, C_1, r_0\,\textrm{and}\, r_1$, may be different in each appearance of these constants.
We define the proximity function of g by
 \begin{equation*}
m(r, g)=\frac1{2\pi}\int_0^{2\pi}\log^+|g(re^{it})| \, \textrm{d}t,
\end{equation*}
\begin{equation*}
m(r, g)=\frac1{2\pi}\int_0^{2\pi}\log^+|g(re^{it})| \, \textrm{d}t,
\end{equation*} and for any ![]() $a\in \mathbb{C}$, we define
$a\in \mathbb{C}$, we define
 \begin{equation*}
m(r,a, g)=\frac1{2\pi}\int_0^{2\pi}\log^+\frac1{|g(re^{it})-a|}\, \textrm{d}t,
\end{equation*}
\begin{equation*}
m(r,a, g)=\frac1{2\pi}\int_0^{2\pi}\log^+\frac1{|g(re^{it})-a|}\, \textrm{d}t,
\end{equation*}and the (integrated) counting function of a-value of g by
 \begin{equation*}
N(r, a, g)=\int_0^{r}\frac{n(t, a, g)-n(0, a, g)}t \textrm{d}t +n(0, a, g)\log r,
\end{equation*}
\begin{equation*}
N(r, a, g)=\int_0^{r}\frac{n(t, a, g)-n(0, a, g)}t \textrm{d}t +n(0, a, g)\log r,
\end{equation*} where ![]() $n(t, a, g)$ is the number of zeros of g–a in the disk
$n(t, a, g)$ is the number of zeros of g–a in the disk ![]() $D(0, t)$. For
$D(0, t)$. For ![]() $a=\infty$,
$a=\infty$, ![]() $N(r,\infty,g)$, sometimes expressed as
$N(r,\infty,g)$, sometimes expressed as ![]() $N(r,g)$, is called the counting function of poles of g. We denote the Nevanlinna characteristic function of g by
$N(r,g)$, is called the counting function of poles of g. We denote the Nevanlinna characteristic function of g by
and the maximum modulus of g by
 \begin{equation*} M(r, g)=\max_{|z|=r}|g(z)|.\end{equation*}
\begin{equation*} M(r, g)=\max_{|z|=r}|g(z)|.\end{equation*}Theorem 2.1. (Jensen Formula, e.g. [Reference Cherry and Ye2, Reference Hayman3])
If g is a meromorphic function, then
 \begin{equation*}
\log |c_{g}(0)| + N(r, 0, g)=\frac1{2\pi}\int_0^{2\pi}\log |g(re^{it})|\, \textrm{d}t,
\end{equation*}
\begin{equation*}
\log |c_{g}(0)| + N(r, 0, g)=\frac1{2\pi}\int_0^{2\pi}\log |g(re^{it})|\, \textrm{d}t,
\end{equation*} where ![]() $c_{g}(0)$ is the first non-zero coefficient of Laurent series of g(z) in the neighbourhood of the point z = 0.
$c_{g}(0)$ is the first non-zero coefficient of Laurent series of g(z) in the neighbourhood of the point z = 0.
The Jensen formula also implies the so-called Nevanlinna’s first main theorem.
Theorem 2.2. (First Main Theorem, e.g. [Reference Cherry and Ye2, Reference Hayman3])
Let g be a meromorphic function in the complex plane and ![]() $a\in \mathbb{C}$. Then
$a\in \mathbb{C}$. Then
where ![]() $ |\epsilon(a, r)| \le \log^+|a| +\log 2.$
$ |\epsilon(a, r)| \le \log^+|a| +\log 2.$
There are many versions of the second main theorem in Nevanlinna theory. Here, when g is an entire function, we use the one with a better error term.
Theorem 2.3. (Second Main Theorem, e.g. [Reference Cherry and Ye2, Reference Hayman3])
Let g be an entire function in the complex plane and let dj (![]() $j=1, 2$) be two distinct complex numbers. Then
$j=1, 2$) be two distinct complex numbers. Then
for all large r outside a set E of finite Lebesgue measure, where the error term is
It is known (e.g. [Reference Cherry and Ye2, Reference Ye19]) that the coefficient 1 in the front of ![]() $\log T(r, g)$ in the inequality is the best possible, and, clearly, the term O(1) depends on
$\log T(r, g)$ in the inequality is the best possible, and, clearly, the term O(1) depends on ![]() $c_{g}(0)$ and dj.
$c_{g}(0)$ and dj.
We say that functions defined in Equation (1.2) have a certain property almost surely (a.s.) if there is a set ![]() $F\subset \Omega$ such that
$F\subset \Omega$ such that ![]() $\mu(F)=0$ and the functions with
$\mu(F)=0$ and the functions with ![]() $\omega \in \Omega \setminus F$ possessing the said property.
$\omega \in \Omega \setminus F$ possessing the said property.
For ![]() $\omega\in\Omega$, we define
$\omega\in\Omega$, we define
 \begin{equation*}
\sigma^2(r, f_\omega)=\sum_{j=0}^{\infty}|a_j\chi_j(\omega)|^2r^{2j}=\int_0^{2\pi}|f_{\omega}(r\,{\rm e}^{i\theta})|^2\,\frac{\textrm{d}\theta}{2\pi},
\end{equation*}
\begin{equation*}
\sigma^2(r, f_\omega)=\sum_{j=0}^{\infty}|a_j\chi_j(\omega)|^2r^{2j}=\int_0^{2\pi}|f_{\omega}(r\,{\rm e}^{i\theta})|^2\,\frac{\textrm{d}\theta}{2\pi},
\end{equation*} and  $ \sigma^2(r, f)=\sum\limits_{j=0}^{\infty}|a_j|^2r^{2j}$. Further, if
$ \sigma^2(r, f)=\sum\limits_{j=0}^{\infty}|a_j|^2r^{2j}$. Further, if ![]() $\mathbb{E}(\chi_j)=0$ and
$\mathbb{E}(\chi_j)=0$ and ![]() $\mathbb{V}(\chi_j)=1$, then
$\mathbb{V}(\chi_j)=1$, then
 \begin{equation*}
\sigma^2(r, f)=\mathbb{E}(|f_\omega(r\,{\rm e}^{i\theta})|^2)=\sum_{j=0}^{\infty}|a_j|^2r^{2j}.
\end{equation*}
\begin{equation*}
\sigma^2(r, f)=\mathbb{E}(|f_\omega(r\,{\rm e}^{i\theta})|^2)=\sum_{j=0}^{\infty}|a_j|^2r^{2j}.
\end{equation*}Set
 \begin{eqnarray}
\hat{f_\omega}(r\,{\rm e}^{i \theta})\stackrel{{def}}{=}\frac{f_\omega(r\,{\rm e}^{i\theta})}{\sigma(r, f)}=\sum_{j=0}^{\infty}\chi_j(\omega) \frac{a_jr^j}{\sigma(r,f)}{\rm e}^{ij\theta}\stackrel{{def}}{=}\sum_{j=0}^{\infty}\chi_j(\omega) \widehat{a_j}(r){\rm e}^{ij\theta},
\end{eqnarray}
\begin{eqnarray}
\hat{f_\omega}(r\,{\rm e}^{i \theta})\stackrel{{def}}{=}\frac{f_\omega(r\,{\rm e}^{i\theta})}{\sigma(r, f)}=\sum_{j=0}^{\infty}\chi_j(\omega) \frac{a_jr^j}{\sigma(r,f)}{\rm e}^{ij\theta}\stackrel{{def}}{=}\sum_{j=0}^{\infty}\chi_j(\omega) \widehat{a_j}(r){\rm e}^{ij\theta},
\end{eqnarray} where  $ \sum_{j=0}^{\infty}|\widehat{a_j}(r)|^2=1$ for all r. Let
$ \sum_{j=0}^{\infty}|\widehat{a_j}(r)|^2=1$ for all r. Let
 \begin{equation*}
X_r= \frac{1}{2\pi}\int_{0}^{2\pi}|\log|\hat{f_\omega}(r\,{\rm e}^{i\theta})|| \textrm{d}\theta, \quad \mbox{for} \ r \in \mathbb{R}^+.
\end{equation*}
\begin{equation*}
X_r= \frac{1}{2\pi}\int_{0}^{2\pi}|\log|\hat{f_\omega}(r\,{\rm e}^{i\theta})|| \textrm{d}\theta, \quad \mbox{for} \ r \in \mathbb{R}^+.
\end{equation*}Definition 2.1. Let f and fω be defined as in Equations (1.1) and (1.2), respectively. Then, the random entire function fω belongs to the family ![]() $\mathcal{Y}$ if and only if fω satisfies Condition Y, i.e., there are three positive constants A, B and C such that for all r > 0,
$\mathcal{Y}$ if and only if fω satisfies Condition Y, i.e., there are three positive constants A, B and C such that for all r > 0,
In § 4, we will prove that all Gaussian, Rademacher and Steinhaus entire functions are in family ![]() $\mathcal{Y}$. Indeed, if fω is Gaussian, Rademacher or Steinhaus, then fω satisfies Condition Y when we choose
$\mathcal{Y}$. Indeed, if fω is Gaussian, Rademacher or Steinhaus, then fω satisfies Condition Y when we choose ![]() $A\in (0, 2)$ and B = 1; A is close to zero and
$A\in (0, 2)$ and B = 1; A is close to zero and ![]() $B=1/6$;
$B=1/6$; ![]() $A\in (0,1/3)$ and B = 1, respectively.
$A\in (0,1/3)$ and B = 1, respectively.
Observe that if χj (![]() $j=0, 1, 2, \ldots$) are standard complex-valued Gaussian random variables, then
$j=0, 1, 2, \ldots$) are standard complex-valued Gaussian random variables, then ![]() $\mathbb{E}(X_r)$ is a positive constant. Therefore, for any Gaussian entire function fω,
$\mathbb{E}(X_r)$ is a positive constant. Therefore, for any Gaussian entire function fω,
 \begin{equation*}
\sup_{r \gt 0}\mathbb{E}(|N(r, 0, f_\omega)-\log\sigma(r, f)|)\le C,
\end{equation*}
\begin{equation*}
\sup_{r \gt 0}\mathbb{E}(|N(r, 0, f_\omega)-\log\sigma(r, f)|)\le C,
\end{equation*}where C is a constant.
In 2010 and 2012, Mahola and Filevych proved the following result, which can be regarded as a version of Nevanlinna’s second main theorem.
Theorem 2.4. ([Reference Mahola and Filevych9, Reference Mahola and Filevych10], Theorem 1)
Let f be an entire function as defined in Equation (1.1) and let ![]() $f_\omega(z)$ be a Steinhaus or a Gaussian entire function on
$f_\omega(z)$ be a Steinhaus or a Gaussian entire function on ![]() $(\Omega,\, \mathcal{F}, \, \mu)$ of the form (1.2). Then, there is a set E of finite logarithmic measure on
$(\Omega,\, \mathcal{F}, \, \mu)$ of the form (1.2). Then, there is a set E of finite logarithmic measure on ![]() $(0, \infty)$ such that for every
$(0, \infty)$ such that for every ![]() $a\in \mathbb{C}$, the inequality
$a\in \mathbb{C}$, the inequality
holds, where ![]() $C_1 \gt 0$ is an absolute constant.
$C_1 \gt 0$ is an absolute constant.
Remark 1. Mahola and Filevych [Reference Mahola and Filevych9] proved a similar inequality to that in Theorem 2.4 for the Steinhaus entire functions. In 2012, they proved Theorem 2.4 and other interesting results in [Reference Mahola and Filevych10] for the Steinhaus entire functions. Further, in 2012, Filevych stated that the inequality in Theorem 2.4 is also true for the Gaussian entire functions. Recently, Filevych told one of the authors that although the proof of the statement has not been published, it is essentially a repetition of the considerations from Mahola’s Ph.D. dissertation [Reference Mahola11].
Nazarov, Nishry and Sodin proved
Theorem 2.5. ([Reference Nazarov, Nishry and Sodin14], Theorem 1.1)
Let fω be a Rademacher entire function. There exists a set ![]() $E\subset [1, \infty)$ (depending on
$E\subset [1, \infty)$ (depending on ![]() $|a_k|$ only) of finite logarithmic length such that
$|a_k|$ only) of finite logarithmic length such that
(i) for almost every
 $\omega\in \Omega$, there exists
$\omega\in \Omega$, there exists  $r_0(\omega) \in [1, \infty)$ such that for every
$r_0(\omega) \in [1, \infty)$ such that for every  $r\in [r_0(\omega), \infty)\setminus E$ and every
$r\in [r_0(\omega), \infty)\setminus E$ and every  $\gamma \gt 1/2$,
$\gamma \gt 1/2$,
 \begin{equation*}
|n(r,0,{f_\omega }) - r{\mkern 1mu} {{\rm{d}} \over {{\rm{d}}r}}\log \sigma (r,f)| \le C(\gamma ){\left( {r{\mkern 1mu} {{\rm{d}} \over {{\rm{d}}r}}{\mkern 1mu} \log \sigma (r,f)} \right)^\gamma };
\end{equation*}
\begin{equation*}
|n(r,0,{f_\omega }) - r{\mkern 1mu} {{\rm{d}} \over {{\rm{d}}r}}\log \sigma (r,f)| \le C(\gamma ){\left( {r{\mkern 1mu} {{\rm{d}} \over {{\rm{d}}r}}{\mkern 1mu} \log \sigma (r,f)} \right)^\gamma };
\end{equation*}(ii) for every
 $r\in [1, \infty)\setminus E$ and every
$r\in [1, \infty)\setminus E$ and every  $\gamma \gt 1/2$,
$\gamma \gt 1/2$,
 \begin{equation*}
{\Bbb E}|n(r,0,{f_\omega }) - r{\mkern 1mu} \frac{{\text{d}}}{{{\text{d}}r}}\log \sigma (r,f)| \leqslant C(\gamma ){\left( {r{\mkern 1mu} \frac{{\text{d}}}{{{\text{d}}r}}{\mkern 1mu} \log \sigma (r,f)} \right)^\gamma }.
\end{equation*}
\begin{equation*}
{\Bbb E}|n(r,0,{f_\omega }) - r{\mkern 1mu} \frac{{\text{d}}}{{{\text{d}}r}}\log \sigma (r,f)| \leqslant C(\gamma ){\left( {r{\mkern 1mu} \frac{{\text{d}}}{{{\text{d}}r}}{\mkern 1mu} \log \sigma (r,f)} \right)^\gamma }.
\end{equation*}
3. Our results
In this section, we state several inequalities concerning the maximum modulus ![]() $M(r, f)$,
$M(r, f)$, ![]() $\sigma(r, f)$ and the integrated counting function
$\sigma(r, f)$ and the integrated counting function ![]() $N(r, 0, f_\omega)$ for the random entire functions in the family
$N(r, 0, f_\omega)$ for the random entire functions in the family ![]() $\mathcal{Y}$ with careful treatment of their error terms. A relationship between
$\mathcal{Y}$ with careful treatment of their error terms. A relationship between ![]() $\log \sigma(r, f_\omega)$ and
$\log \sigma(r, f_\omega)$ and ![]() $\log \sigma(r, f)$ is stated and proved in
$\log \sigma(r, f)$ is stated and proved in ![]() $\S$ 5.
$\S$ 5.
Theorem 3.1. If ![]() $f_\omega \in \mathcal{Y}$, then, for any constant C > 1, there exists a constant
$f_\omega \in \mathcal{Y}$, then, for any constant C > 1, there exists a constant ![]() $r_0=r_0(\omega)$ such that, for
$r_0=r_0(\omega)$ such that, for ![]() $r \gt r_0$,
$r \gt r_0$,
 \begin{equation*}
|\log \sigma(r, f)- N(r,0, f_\omega)|\le (C/A)^{1/{B}}\,\log^{1/{B}}\,\log \sigma(r,f), \qquad \mbox{a.s.}
\end{equation*}
\begin{equation*}
|\log \sigma(r, f)- N(r,0, f_\omega)|\le (C/A)^{1/{B}}\,\log^{1/{B}}\,\log \sigma(r,f), \qquad \mbox{a.s.}
\end{equation*}where the constants A and B are from Condition Y.
Remark 2. Theorem 3.1 tells us that the number of zeros of almost all fω can be controlled from above and below by ![]() $\log \sigma(r, f)$ and an error term, which are independent of ω.
$\log \sigma(r, f)$ and an error term, which are independent of ω.
Sometimes, it is easier for one to calculate ![]() $M(r, f)$ rather than
$M(r, f)$ rather than ![]() $\sigma(r,f)$. By Lemma 4.6, we obtain:
$\sigma(r,f)$. By Lemma 4.6, we obtain:
Corollary 3.1. If ![]() $f_\omega \in \mathcal{Y}$, then, for any constant C > 1, there are a constant
$f_\omega \in \mathcal{Y}$, then, for any constant C > 1, there are a constant ![]() $r_0=r_0(\omega)$ and a set
$r_0=r_0(\omega)$ and a set ![]() $E\subset [e, \infty)$ of finite logarithmic measure such that, for
$E\subset [e, \infty)$ of finite logarithmic measure such that, for ![]() $r \gt r_0$ and
$r \gt r_0$ and ![]() $r\notin E$,
$r\notin E$,
 \begin{equation*}
|\log M(r, f)- N(r,0, f_\omega)|\le (C/A)^{1/{B}}\,\log^{1/{B}}\,\log M(r,f) +\log\,\log M(r, f), \qquad \mbox{a.s.},
\end{equation*}
\begin{equation*}
|\log M(r, f)- N(r,0, f_\omega)|\le (C/A)^{1/{B}}\,\log^{1/{B}}\,\log M(r,f) +\log\,\log M(r, f), \qquad \mbox{a.s.},
\end{equation*}where the constants A and B are from Condition Y.
Example. Let ![]() $f(z)=e^z$ and its random perturbation function fω in the family
$f(z)=e^z$ and its random perturbation function fω in the family ![]() $\mathcal{Y}$. Then, the corollary tells us that, for almost all fω, its integrated zero-counting function in the disk
$\mathcal{Y}$. Then, the corollary tells us that, for almost all fω, its integrated zero-counting function in the disk ![]() $D(0, r)$ is close to r although ez does not take the value zero at all.
$D(0, r)$ is close to r although ez does not take the value zero at all.
Now, we state Nevanlinna’s second main theorem (involving the integrated zero-counting function only) for random entire functions as corollaries of above results.
Corollary 3.2. If ![]() $f_\omega \in \mathcal{Y}$, then, for any constant C > 1, there exists a constant
$f_\omega \in \mathcal{Y}$, then, for any constant C > 1, there exists a constant ![]() $r_0=r_0(\omega)$ such that, for
$r_0=r_0(\omega)$ such that, for ![]() $r \gt r_0$,
$r \gt r_0$,
 \begin{equation*}
T(r, f)\leq N(r,0, f_\omega)+(C/A)^{1/{B}}\,\log^{1/{B}} T(r,f), \qquad \mbox{a.s.}
\end{equation*}
\begin{equation*}
T(r, f)\leq N(r,0, f_\omega)+(C/A)^{1/{B}}\,\log^{1/{B}} T(r,f), \qquad \mbox{a.s.}
\end{equation*}and
 \begin{equation*}
T(r, f_\omega)\leq N(r,0, f_\omega)+(C/A)^{1/{B}}\,\log^{1/{B}} T(r,f_\omega), \qquad \mbox{a.s.}
\end{equation*}
\begin{equation*}
T(r, f_\omega)\leq N(r,0, f_\omega)+(C/A)^{1/{B}}\,\log^{1/{B}} T(r,f_\omega), \qquad \mbox{a.s.}
\end{equation*}where the constants A and B are from Condition Y.
When fω is a Gaussian, or Rademacher or Steinhaus entire function, we have the following corollary.
Corollary 3.3. Let f and fω be defined as in Equations (1.1) and (1.2), respectively. Then, for any ϵ > 0, there exists ![]() $r_0=r_0(\omega, \epsilon)$ such that, for
$r_0=r_0(\omega, \epsilon)$ such that, for ![]() $r \gt r_0$,
$r \gt r_0$,
(i) if fω is a Gaussian entire function, then
 \begin{equation*}
T(r, f) \leq N(r,0, f_\omega)+\frac{1+\epsilon}{2}\, \log T(r,f) \qquad \mbox{a.s.}
\end{equation*}
\begin{equation*}
T(r, f) \leq N(r,0, f_\omega)+\frac{1+\epsilon}{2}\, \log T(r,f) \qquad \mbox{a.s.}
\end{equation*}(ii) if fω is a Rademacher entire function, then
where the constant C 0 is from Lemma 4.1. \begin{equation*}
T(r, f) \leq N(r,0, f_\omega)+ \left(\left(\frac{eC_0}6\right)^6 +\epsilon \right) \log^6 T(r,f)\qquad \mbox{a.s.},
\end{equation*}
\begin{equation*}
T(r, f) \leq N(r,0, f_\omega)+ \left(\left(\frac{eC_0}6\right)^6 +\epsilon \right) \log^6 T(r,f)\qquad \mbox{a.s.},
\end{equation*}(iii) if fω is a Steinhaus entire function, then
 \begin{equation*}
T(r, f) \leq N(r,0, f_\omega)+(3+\epsilon)\, \log T(r,f) \qquad \mbox{a.s.}
\end{equation*}
\begin{equation*}
T(r, f) \leq N(r,0, f_\omega)+(3+\epsilon)\, \log T(r,f) \qquad \mbox{a.s.}
\end{equation*}
Now we consider the case when fω takes any value ![]() $a\in \mathbb{C}$.
$a\in \mathbb{C}$.
Theorem 3.2. Let ![]() $f_\omega \in \mathcal{Y}$ and define
$f_\omega \in \mathcal{Y}$ and define
 \begin{equation*}
f^*_\omega(z)=zf^{\prime}_\omega(z)=\sum_{j=1}^{\infty}ja_j\chi_jz^j.
\end{equation*}
\begin{equation*}
f^*_\omega(z)=zf^{\prime}_\omega(z)=\sum_{j=1}^{\infty}ja_j\chi_jz^j.
\end{equation*} If ![]() $f^*_\omega$ satisfies Condition Y (maybe with different constants A and B), then, for any constant C > 1, there exists a set E of finite logarithmic measure such that, for every
$f^*_\omega$ satisfies Condition Y (maybe with different constants A and B), then, for any constant C > 1, there exists a set E of finite logarithmic measure such that, for every ![]() $a\in \mathbb{C}$, there is
$a\in \mathbb{C}$, there is ![]() $r_1=r_1(\omega,a)$ such that, for
$r_1=r_1(\omega,a)$ such that, for ![]() $r \gt r_1$ and
$r \gt r_1$ and ![]() $r\not\in E$,
$r\not\in E$,
 \begin{equation*}
|\log \sigma(r, f)- N(r,a, f_\omega)|\le (C/A)^{1/{B}}\,\log^{1/{B}}\,\log \sigma(r,f) +(1+o(1))\,\log\,\log\sigma(r, f), \qquad \mbox{a.s.}
\end{equation*}
\begin{equation*}
|\log \sigma(r, f)- N(r,a, f_\omega)|\le (C/A)^{1/{B}}\,\log^{1/{B}}\,\log \sigma(r,f) +(1+o(1))\,\log\,\log\sigma(r, f), \qquad \mbox{a.s.}
\end{equation*}where the constants A and B are from Condition Y.
Remark 3. The first error term of the above inequality only appears in the lower bound for ![]() $N(r,a, f_\omega)$. In addition, if f is a Gaussian, or Rademarcher or Steinhaus entire function, then it follows from Lemma 4.3 that both fω and
$N(r,a, f_\omega)$. In addition, if f is a Gaussian, or Rademarcher or Steinhaus entire function, then it follows from Lemma 4.3 that both fω and ![]() $f^*_\omega$ satisfy Condition Y.
$f^*_\omega$ satisfy Condition Y.
The following corollary is a straightforward consequence of the above theorem and Lemma 4.6.
Corollary 3.4. Under the assumptions of Theorem 3.2, we have that, for any constant C > 1, there exists a set E of finite logarithmic measure such that, for every ![]() $a\in \mathbb{C}$, there is
$a\in \mathbb{C}$, there is ![]() $r_1=r_1(\omega,a)$ such that, for
$r_1=r_1(\omega,a)$ such that, for ![]() $r \gt r_1$ and
$r \gt r_1$ and ![]() $r\not\in E$,
$r\not\in E$,
 \begin{equation*}
|\log M(r, f)- N(r,a, f_\omega)|\le (C/A)^{1/{B}}\,\log^{1/{B}}\,\log M(r,f) +(2+o(1))\,\log\,\log M(r, f), \mbox{a.s.},
\end{equation*}
\begin{equation*}
|\log M(r, f)- N(r,a, f_\omega)|\le (C/A)^{1/{B}}\,\log^{1/{B}}\,\log M(r,f) +(2+o(1))\,\log\,\log M(r, f), \mbox{a.s.},
\end{equation*}where the constants A and B are from Condition Y.
When fω is Gaussian, Rademacher or Steinhuas, Theorem 3.2 and Lemma 4.3 give:
Corollary 3.5. Let f and fω be defined as in Equations (1.1) and (1.2), respectively. Then, for any ϵ > 0, there exists a set E of finite logarithmic measure such that, for every ![]() $a\in \mathbb{C}$, there exists
$a\in \mathbb{C}$, there exists ![]() $r_0=r_0(\omega, \epsilon, a)$ such that, for
$r_0=r_0(\omega, \epsilon, a)$ such that, for ![]() $r \gt r_0$ and
$r \gt r_0$ and ![]() $r\not\in E$, we have:
$r\not\in E$, we have:
(i) if fω is a Gaussian entire function, then
 \begin{equation*}
\log \sigma (r, f) \leq N(r,a, f_\omega)+(3/2+\epsilon) \log\, \log\sigma (r, f) \qquad \mbox{a.s.}
\end{equation*}
\begin{equation*}
\log \sigma (r, f) \leq N(r,a, f_\omega)+(3/2+\epsilon) \log\, \log\sigma (r, f) \qquad \mbox{a.s.}
\end{equation*}(ii) if fω is a Rademacher entire function, then
where the constant C 0 is from Lemma 4.1. \begin{equation*}
\log \sigma (r, f) \leq N(r,a, f_\omega)+ \left(\left(\frac{eC_0}6\right)^6 +\epsilon \right) \log^6 \,\log \sigma(r,f)\qquad \mbox{a.s.},
\end{equation*}
\begin{equation*}
\log \sigma (r, f) \leq N(r,a, f_\omega)+ \left(\left(\frac{eC_0}6\right)^6 +\epsilon \right) \log^6 \,\log \sigma(r,f)\qquad \mbox{a.s.},
\end{equation*}(iii) if fω is a Steinhaus entire function, then
 \begin{equation*}
\log\sigma(r, f) \leq N(r,a, f_\omega)+(4+\epsilon) \log\, \log\sigma(r,f) \qquad \mbox{a.s.}
\end{equation*}
\begin{equation*}
\log\sigma(r, f) \leq N(r,a, f_\omega)+(4+\epsilon) \log\, \log\sigma(r,f) \qquad \mbox{a.s.}
\end{equation*}
Remark 4. Corollary 3.5 shows that the constant in the error term is ![]() $3/2 +\epsilon$ and
$3/2 +\epsilon$ and ![]() $2+ \epsilon$ in Gaussian and Steinhaus cases, rather than a constant
$2+ \epsilon$ in Gaussian and Steinhaus cases, rather than a constant ![]() $C_1 \gt 0$ in Theorem 2.4. It is interesting to know whether these coefficients are the best possible coefficients in these error terms.
$C_1 \gt 0$ in Theorem 2.4. It is interesting to know whether these coefficients are the best possible coefficients in these error terms.
The following is Nevanlinna’s second main theorem for random entire functions. It verifies that the characteristic function for almost all random entire functions can be bounded above by one integrated counting function, rather than two integrated counting functions as in the classical case (e.g. Theorem 2.3). The proof of the following corollary is a straightforward consequence of Theorem 3.2 and Lemma 4.4 as we have seen the proof of Corollary 3.2.
Corollary 3.6. If fω and ![]() $f^*_\omega$ satisfy Condition Y, then, for any constant C > 1, there exists a set E of finite logarithmic measure such that, for every
$f^*_\omega$ satisfy Condition Y, then, for any constant C > 1, there exists a set E of finite logarithmic measure such that, for every ![]() $a\in \mathbb{C}$, there is
$a\in \mathbb{C}$, there is ![]() $r_1=r_1(\omega,a)$ such that, for
$r_1=r_1(\omega,a)$ such that, for ![]() $r \gt r_1$ and
$r \gt r_1$ and ![]() $r\not\in E$,
$r\not\in E$,
 \begin{equation*}
T(r, f)\leq N(r,a, f_\omega)+(C/A)^{1/{B}}\,\log^{1/{B}} T(r,f)+(1+o(1))\log T(r,f),\qquad \mbox{a.s.},
\end{equation*}
\begin{equation*}
T(r, f)\leq N(r,a, f_\omega)+(C/A)^{1/{B}}\,\log^{1/{B}} T(r,f)+(1+o(1))\log T(r,f),\qquad \mbox{a.s.},
\end{equation*}and
 \begin{equation*}
T(r, f_\omega)\leq N(r,a, f_\omega)+(C/A)^{1/{B}}\,\log^{1/{B}} T(r,f_\omega)+(1+o(1))\log T(r,f_\omega), \qquad \mbox{a.s.},
\end{equation*}
\begin{equation*}
T(r, f_\omega)\leq N(r,a, f_\omega)+(C/A)^{1/{B}}\,\log^{1/{B}} T(r,f_\omega)+(1+o(1))\log T(r,f_\omega), \qquad \mbox{a.s.},
\end{equation*}where the constants A and B are from Condition Y.
4. Some lemmas
In this section, in order to prove our main results, we give several lemmas.
Lemma 4.1. (Log-integrability, [Reference Nazarov, Nishry and Sodin13])
Let fω be a Rademarcher entire function. Then, for any ![]() $p\geq1$,
$p\geq1$,
 \begin{equation*}
\mathbb{E}\left(\int_{0}^{2\pi}|\log|\hat{f_\omega}||^p \,\frac{\textrm{d}\theta}{2\pi}\right)\leq (C_0p)^{6p},
\end{equation*}
\begin{equation*}
\mathbb{E}\left(\int_{0}^{2\pi}|\log|\hat{f_\omega}||^p \,\frac{\textrm{d}\theta}{2\pi}\right)\leq (C_0p)^{6p},
\end{equation*}where C 0 is an absolute constant.
Lemma 4.2. (Offord [Reference Offord15])
Let ![]() $f_\omega(z)$ be a Steinhaus entire function on
$f_\omega(z)$ be a Steinhaus entire function on ![]() $(\Omega,\, \mathcal{F}, \, \mu)$ of the form (1.2), and let
$(\Omega,\, \mathcal{F}, \, \mu)$ of the form (1.2), and let ![]() $\hat{f_\omega}$ be of the form (2.1). For all
$\hat{f_\omega}$ be of the form (2.1). For all ![]() $t\geq0$,
$t\geq0$, ![]() $\phi\in[0,2\pi)$, set
$\phi\in[0,2\pi)$, set
 \begin{equation*}A^*=\{\omega\in\Omega:|{\rm Re}(\hat{f_\omega})\cos\phi+{\rm Im}(\hat{f_\omega})\sin\phi| \lt t\}.\end{equation*}
\begin{equation*}A^*=\{\omega\in\Omega:|{\rm Re}(\hat{f_\omega})\cos\phi+{\rm Im}(\hat{f_\omega})\sin\phi| \lt t\}.\end{equation*}Then,
 \begin{equation*}
\mathbb{P}(A^*)\leq C\max\left\{t,t^{1/{3}}\right\},
\end{equation*}
\begin{equation*}
\mathbb{P}(A^*)\leq C\max\left\{t,t^{1/{3}}\right\},
\end{equation*}where C is an absolute constant.
Lemma 4.3. Let ![]() $f_\omega(z)\in \mathcal{Y}$ and let
$f_\omega(z)\in \mathcal{Y}$ and let  $\hat{f_\omega}(re^{i\theta})$ be defined by Equation (2.1). Then for any positive constant C and all x > 1, there is a positive constant C 1 such that
$\hat{f_\omega}(re^{i\theta})$ be defined by Equation (2.1). Then for any positive constant C and all x > 1, there is a positive constant C 1 such that
 \begin{equation}
\mathbb{P}\left(X_r\ge \left(\frac{C}{A}\,\log x\right)^{1/{B}}\right)\le \frac{C_1}{x^{C}}.
\end{equation}
\begin{equation}
\mathbb{P}\left(X_r\ge \left(\frac{C}{A}\,\log x\right)^{1/{B}}\right)\le \frac{C_1}{x^{C}}.
\end{equation}In particular, we have the following:
(i) If fω is a Gaussian entire function, then for any τ > 0, there is a constant
 $C_1=C_1(\tau)$ such that
$C_1=C_1(\tau)$ such that
 \begin{equation*}
\mathbb{P}\left(X_r\ge \frac{1+2\tau}{2}\,\log x\right)\le \frac{C_1}{x^{(({1+2\tau})/({1+\tau}))}}.
\end{equation*}
\begin{equation*}
\mathbb{P}\left(X_r\ge \frac{1+2\tau}{2}\,\log x\right)\le \frac{C_1}{x^{(({1+2\tau})/({1+\tau}))}}.
\end{equation*}(ii) If fω is a Rademacher entire function, then for any τ > 0,
 $\epsilon\in(0, (6/{(eC_0)})^6)$ (C 0 is from Lemma 4.1), there is a constant
$\epsilon\in(0, (6/{(eC_0)})^6)$ (C 0 is from Lemma 4.1), there is a constant  $C_1=C_1(\epsilon)$ such that
$C_1=C_1(\epsilon)$ such that
 \begin{equation*}
\mathbb{P}\left(X_r\ge \left(\frac{1+\tau}{\epsilon}\right)^6\log^6 x\right)\le \frac{C_1}{x^{1+\tau}}.
\end{equation*}
\begin{equation*}
\mathbb{P}\left(X_r\ge \left(\frac{1+\tau}{\epsilon}\right)^6\log^6 x\right)\le \frac{C_1}{x^{1+\tau}}.
\end{equation*}(iii) If fω is a Steinhaus entire function, then for any τ > 0, there is a constant
 $C_1=C_1(\tau)$ such that
$C_1=C_1(\tau)$ such that
 \begin{equation*}
\mathbb{P}\big(X_r\ge 3(1+\tau)^2\log x\big)\le \frac{C_1}{x^{1+\tau}}.
\end{equation*}
\begin{equation*}
\mathbb{P}\big(X_r\ge 3(1+\tau)^2\log x\big)\le \frac{C_1}{x^{1+\tau}}.
\end{equation*}
Proof. By Markov’s inequality, we obtain
 \begin{equation*}
\mathbb{P}\left(X_r\ge \left(\frac{C}{A}\,\log x\right)^{1/{B}}\right)\le \frac{\mbox{E}(\exp(AX_r^B))}{\exp(C\,\log x))}\stackrel{{def}}{=} \frac{C_1}{x^{C}}.
\end{equation*}
\begin{equation*}
\mathbb{P}\left(X_r\ge \left(\frac{C}{A}\,\log x\right)^{1/{B}}\right)\le \frac{\mbox{E}(\exp(AX_r^B))}{\exp(C\,\log x))}\stackrel{{def}}{=} \frac{C_1}{x^{C}}.
\end{equation*}Now. we give the proof of (i). Since χj are independent standard complex-valued Gaussian random variables, then
 \begin{equation*}
\mathbb{E}(\hat{f_\omega})=0
\quad \mbox{and} \quad
\mathbb{V}(\hat{f_\omega}) = \mathbb{E}(|\hat{f_\omega}|^2)=1.
\end{equation*}
\begin{equation*}
\mathbb{E}(\hat{f_\omega})=0
\quad \mbox{and} \quad
\mathbb{V}(\hat{f_\omega}) = \mathbb{E}(|\hat{f_\omega}|^2)=1.
\end{equation*} It follows that ![]() $\hat{f}_\omega$ is a standard complex-valued Gaussian random variable. For any x > 0,
$\hat{f}_\omega$ is a standard complex-valued Gaussian random variable. For any x > 0,
 \begin{equation*}\mathbb{P}(|\log|\hat{f_\omega}|| \lt x) = \mathbb{P}(-x \lt \log|\hat{f_\omega}| \lt x) ={\rm e}^{-{\rm e}^{-2x}}-{\rm e}^{-{\rm e}^{2x}}.\\
\end{equation*}
\begin{equation*}\mathbb{P}(|\log|\hat{f_\omega}|| \lt x) = \mathbb{P}(-x \lt \log|\hat{f_\omega}| \lt x) ={\rm e}^{-{\rm e}^{-2x}}-{\rm e}^{-{\rm e}^{2x}}.\\
\end{equation*} Consequently, the probability density function of  $ |\log|\hat{f_\omega}||$ is
$ |\log|\hat{f_\omega}||$ is  $2\,{\rm e}^{-{\rm e}^{-2x}}\,{\rm e}^{-2x}+2{\rm e}^{-{\rm e}^{2x}}{\rm e}^{2x}$ for x > 0 and is 0 for
$2\,{\rm e}^{-{\rm e}^{-2x}}\,{\rm e}^{-2x}+2{\rm e}^{-{\rm e}^{2x}}{\rm e}^{2x}$ for x > 0 and is 0 for ![]() $x\le 0$. It follows that the expected value
$x\le 0$. It follows that the expected value  $\mathbb{E}|\log |\hat{f_\omega}||$ is independent of θ. Thus, we have
$\mathbb{E}|\log |\hat{f_\omega}||$ is independent of θ. Thus, we have
 \begin{align}
\mathbb{E}({\rm e}^{\frac{2}{1+\tau}X_r})
&=\sum_{n=0}^{\infty}\frac{2^n}{n!(1+\tau)^n} \mathbb{E}X_r^n
\end{align}
\begin{align}
\mathbb{E}({\rm e}^{\frac{2}{1+\tau}X_r})
&=\sum_{n=0}^{\infty}\frac{2^n}{n!(1+\tau)^n} \mathbb{E}X_r^n
\end{align} \begin{align}
&=\sum_{n=0}^{\infty}\frac{2^n}{n!(1+\tau)^n} \mathbb{E}\left( \frac{1}{2\pi}\int_{0}^{2\pi}|\log |\hat{f_\omega}||{\rm d}\theta \right)^n
\end{align}
\begin{align}
&=\sum_{n=0}^{\infty}\frac{2^n}{n!(1+\tau)^n} \mathbb{E}\left( \frac{1}{2\pi}\int_{0}^{2\pi}|\log |\hat{f_\omega}||{\rm d}\theta \right)^n
\end{align} \begin{align}
&\leq\sum_{n=0}^{\infty}\frac{2^n}{n!(1+\tau)^n}\left( \frac{1}{2\pi}\int_{0}^{2\pi} \mathbb{E}|\log |\hat{f_\omega}||^n {\rm d}\theta \right)
\end{align}
\begin{align}
&\leq\sum_{n=0}^{\infty}\frac{2^n}{n!(1+\tau)^n}\left( \frac{1}{2\pi}\int_{0}^{2\pi} \mathbb{E}|\log |\hat{f_\omega}||^n {\rm d}\theta \right)
\end{align} \begin{align}
&= \mathbb{E}\left({\rm e}^{\frac{2}{1+\tau}|\log|\hat{f_\omega}||}\right)
\end{align}
\begin{align}
&= \mathbb{E}\left({\rm e}^{\frac{2}{1+\tau}|\log|\hat{f_\omega}||}\right)
\end{align} \begin{align}
&=\int_0^{\infty}{\rm e}^\frac{2x}{1+\tau}
\left(2{\rm e}^{-{\rm e}^{-2x}}\,{\rm e}^{-2x}+2{\rm e}^{-{\rm e}^{2x}}\,{\rm e}^{2x}\right)\, \textrm{d}x\stackrel{{def}}{=}C_1 \lt \infty,
\end{align}
\begin{align}
&=\int_0^{\infty}{\rm e}^\frac{2x}{1+\tau}
\left(2{\rm e}^{-{\rm e}^{-2x}}\,{\rm e}^{-2x}+2{\rm e}^{-{\rm e}^{2x}}\,{\rm e}^{2x}\right)\, \textrm{d}x\stackrel{{def}}{=}C_1 \lt \infty,
\end{align} where C 1 is a positive constant. It follows that Gaussian entire functions are in the family ![]() $\mathcal{Y}$ by taking
$\mathcal{Y}$ by taking ![]() $A=(2/({1+\tau}))$ and B = 1. Set
$A=(2/({1+\tau}))$ and B = 1. Set ![]() $C=({(1+2\tau)}/{(1+\tau)})$. Then, by Equation (4.1) and for
$C=({(1+2\tau)}/{(1+\tau)})$. Then, by Equation (4.1) and for ![]() $x\ge 1$, we get
$x\ge 1$, we get
 \begin{equation*}
\mathbb{P}\left(X_r\ge \frac{1+2\tau}{2}\,\log x\right)\le \frac{C_1}{x^{{((1+2\tau)}/{(1+\tau)})}}.
\end{equation*}
\begin{equation*}
\mathbb{P}\left(X_r\ge \frac{1+2\tau}{2}\,\log x\right)\le \frac{C_1}{x^{{((1+2\tau)}/{(1+\tau)})}}.
\end{equation*}This completes the proof of (i).
Next, we prove (ii). By Lemma 4.1, we have, for any positive integer ![]() $n\ge 6$,
$n\ge 6$,
 \begin{align*}
{\Bbb E}X_r^{n/6} = {\Bbb E}{\left( {\int_0^{2\pi } | \log |\widehat {{f_\omega }}||{\mkern 1mu} \frac{{{\text{d}}\theta }}{{2\pi }}} \right)^{n/6}} \leqslant {\Bbb E}\left( {\int_0^{2\pi } | \log |\widehat {{f_\omega }}|{|^{n/6}}{\mkern 1mu} \frac{{{\text{d}}\theta }}{{2\pi }}} \right) \leqslant {\left( {\frac{{{C_0}n}}{6}} \right)^n},
\end{align*}
\begin{align*}
{\Bbb E}X_r^{n/6} = {\Bbb E}{\left( {\int_0^{2\pi } | \log |\widehat {{f_\omega }}||{\mkern 1mu} \frac{{{\text{d}}\theta }}{{2\pi }}} \right)^{n/6}} \leqslant {\Bbb E}\left( {\int_0^{2\pi } | \log |\widehat {{f_\omega }}|{|^{n/6}}{\mkern 1mu} \frac{{{\text{d}}\theta }}{{2\pi }}} \right) \leqslant {\left( {\frac{{{C_0}n}}{6}} \right)^n},
\end{align*} where C 0 is the constant from Lemma 4.1. Thus, when ![]() $\epsilon \in
(0, ({6}/{eC_0})^6)$,
$\epsilon \in
(0, ({6}/{eC_0})^6)$,
 \begin{equation}
C_1\stackrel{{def}}{=}\mathbb{E} \left(\exp\left(\epsilon X_r^{1/{6}}\right) \right)=\sum_{n=0}^{\infty}\frac{\mathbb{E}|\epsilon X_r|^{{n}/{6}}}{n!}\leq \sum_{n=6}^{\infty}\left(\frac{C_0\epsilon^{1/6} n}{6}\right)^n\frac1{n!}+O(1) \lt +\infty.
\end{equation}
\begin{equation}
C_1\stackrel{{def}}{=}\mathbb{E} \left(\exp\left(\epsilon X_r^{1/{6}}\right) \right)=\sum_{n=0}^{\infty}\frac{\mathbb{E}|\epsilon X_r|^{{n}/{6}}}{n!}\leq \sum_{n=6}^{\infty}\left(\frac{C_0\epsilon^{1/6} n}{6}\right)^n\frac1{n!}+O(1) \lt +\infty.
\end{equation} Therefore, Rademacher entire functions satisfy the condition Y by choosing ![]() $A=\epsilon$ and
$A=\epsilon$ and ![]() $B=1/{6}$. Using the inequality (4.1) for
$B=1/{6}$. Using the inequality (4.1) for ![]() $C=1+\tau$, we get
$C=1+\tau$, we get
 \begin{align*}
\mathbb{P}\left(X_r\ge \left(\frac{1+\tau}{\epsilon}\right)^6\log^6 x\right)&=\mathbb{P} \left(\exp\left(\epsilon X_r^{1/{6}}\right)\geq x^{1+\tau} \right)\leq \frac{\mathbb{E} \left(\exp\left(\epsilon X_r^{1/{6}}\right) \right)}{x^{1+\tau}}=\frac{C_1}{x^{1+\tau}}.
\end{align*}
\begin{align*}
\mathbb{P}\left(X_r\ge \left(\frac{1+\tau}{\epsilon}\right)^6\log^6 x\right)&=\mathbb{P} \left(\exp\left(\epsilon X_r^{1/{6}}\right)\geq x^{1+\tau} \right)\leq \frac{\mathbb{E} \left(\exp\left(\epsilon X_r^{1/{6}}\right) \right)}{x^{1+\tau}}=\frac{C_1}{x^{1+\tau}}.
\end{align*}Now, we prove (iii).
For any non-negative integer j and any ![]() $\varphi\in[0,2\pi)$, set
$\varphi\in[0,2\pi)$, set
 \begin{equation*} b_j=\widehat{a_j}(r)\chi_j\,{\rm e}^{ij\theta}=\widehat{a_j}(r)\,{\rm e}^{ij\theta}\,{\rm e}^{i2\pi \theta_j} \quad \mbox{and} \quad
B_j=\mbox{Re}(b_j)\cos \varphi +\mbox{Im}(b_j)\sin \varphi.
\end{equation*}
\begin{equation*} b_j=\widehat{a_j}(r)\chi_j\,{\rm e}^{ij\theta}=\widehat{a_j}(r)\,{\rm e}^{ij\theta}\,{\rm e}^{i2\pi \theta_j} \quad \mbox{and} \quad
B_j=\mbox{Re}(b_j)\cos \varphi +\mbox{Im}(b_j)\sin \varphi.
\end{equation*} Thus,  $\hat{f_\omega}=\sum\limits_{j=0}^\infty b_j$, and Bj is a real random variable. Further, we deduce that
$\hat{f_\omega}=\sum\limits_{j=0}^\infty b_j$, and Bj is a real random variable. Further, we deduce that ![]() $
B_j=u\,\cos(2\pi\theta_j)+v\,\sin(2\pi \theta_j),
$ where
$
B_j=u\,\cos(2\pi\theta_j)+v\,\sin(2\pi \theta_j),
$ where
 \begin{align*}
u ={\rm Re}(\widehat{a_j}(r))\cos (j\theta) \cos \varphi & + {\rm Re}(\widehat{a_j}(r))\sin (j\theta) \sin \varphi \\
& -{\rm Im}(\widehat{a_j}(r))\sin (j\theta) \cos \varphi+{\rm Im}(\widehat{a_j}(r))\cos (j\theta) \sin \varphi,\\
v = {\rm Re}(\widehat{a_j}(r))\cos (j\theta) \sin \varphi & -{\rm Re}(\widehat{a_j}(r))\sin (j\theta) \cos \varphi \\
& -{\rm Im}(\widehat{a_j}(r))\cos (j\theta) \cos \varphi-{\rm Im}(\widehat{a_j}(r))\sin (j\theta) \sin \varphi,
\end{align*}
\begin{align*}
u ={\rm Re}(\widehat{a_j}(r))\cos (j\theta) \cos \varphi & + {\rm Re}(\widehat{a_j}(r))\sin (j\theta) \sin \varphi \\
& -{\rm Im}(\widehat{a_j}(r))\sin (j\theta) \cos \varphi+{\rm Im}(\widehat{a_j}(r))\cos (j\theta) \sin \varphi,\\
v = {\rm Re}(\widehat{a_j}(r))\cos (j\theta) \sin \varphi & -{\rm Re}(\widehat{a_j}(r))\sin (j\theta) \cos \varphi \\
& -{\rm Im}(\widehat{a_j}(r))\cos (j\theta) \cos \varphi-{\rm Im}(\widehat{a_j}(r))\sin (j\theta) \sin \varphi,
\end{align*} and ![]() $u^2+v^2=|b_j|^2$. The characteristic function of Bj is
$u^2+v^2=|b_j|^2$. The characteristic function of Bj is
 \begin{equation*}
\int_0^1\exp[it(u\, \cos(2\pi x)+v\,\sin(2\pi x))]\, \textrm{d}x,
\end{equation*}
\begin{equation*}
\int_0^1\exp[it(u\, \cos(2\pi x)+v\,\sin(2\pi x))]\, \textrm{d}x,
\end{equation*} which depends only on ![]() $|b_j|$. Similarly, we obtain that, for
$|b_j|$. Similarly, we obtain that, for ![]() $\varphi\in[0,2\pi)$,
$\varphi\in[0,2\pi)$,
 \begin{equation*}
\mbox{E}(|\log|\mbox{Re} (\hat{f_\omega})\cos \varphi+\mbox{Im}(\hat{f_\omega})\sin\varphi||^n)
\end{equation*}
\begin{equation*}
\mbox{E}(|\log|\mbox{Re} (\hat{f_\omega})\cos \varphi+\mbox{Im}(\hat{f_\omega})\sin\varphi||^n)
\end{equation*}is independent of φ for any non-negative integer n.
Since
 \begin{align*}
\mbox{Re} (\hat{f_\omega})\cos \varphi+\mbox{Im}(\hat{f_\omega})\sin\varphi =
\sqrt{\mbox{Re}^2(\hat{f_\omega})+\mbox{Im}^2 (\hat{f_\omega})}\sin(\varphi+\varphi_0) =|\hat{f_\omega}|\sin(\varphi+\varphi_0),
\end{align*}
\begin{align*}
\mbox{Re} (\hat{f_\omega})\cos \varphi+\mbox{Im}(\hat{f_\omega})\sin\varphi =
\sqrt{\mbox{Re}^2(\hat{f_\omega})+\mbox{Im}^2 (\hat{f_\omega})}\sin(\varphi+\varphi_0) =|\hat{f_\omega}|\sin(\varphi+\varphi_0),
\end{align*} (where  $\sin\varphi_0=\mbox{Re} (\hat{f_\omega})/|\hat{f_\omega}|$ and
$\sin\varphi_0=\mbox{Re} (\hat{f_\omega})/|\hat{f_\omega}|$ and  $\cos\varphi_0=\mbox{Im} (\hat{f_\omega})/|\hat{f_\omega}|$), it follows that
$\cos\varphi_0=\mbox{Im} (\hat{f_\omega})/|\hat{f_\omega}|$), it follows that
 \begin{align*}
\matrix {\log |\widehat {{f_\omega }}|{\text{ }}} \hfill & { = \int_0^{2\pi } {\log } |{\text{Re}}(\widehat {{f_\omega }})\cos \varphi + {\text{Im}}(\widehat {{f_\omega }})\sin \varphi |{\mkern 1mu} \frac{{{\text{d}}\varphi }}{{2\pi }} - \int_0^{2\pi } {\log } |\sin (\varphi + {\varphi _0})|{\mkern 1mu} \frac{{{\text{d}}\varphi }}{{2\pi }}} \hfill \\ {} \hfill & { = \int_0^{2\pi } {\log } |{\text{Re}}(\widehat {{f_\omega }})\cos \varphi + {\text{Im}}(\widehat {{f_\omega }})\sin \varphi |{\mkern 1mu} \frac{{{\text{d}}\varphi }}{{2\pi }} + \log 2.} \hfill \\
\end{align*}
\begin{align*}
\matrix {\log |\widehat {{f_\omega }}|{\text{ }}} \hfill & { = \int_0^{2\pi } {\log } |{\text{Re}}(\widehat {{f_\omega }})\cos \varphi + {\text{Im}}(\widehat {{f_\omega }})\sin \varphi |{\mkern 1mu} \frac{{{\text{d}}\varphi }}{{2\pi }} - \int_0^{2\pi } {\log } |\sin (\varphi + {\varphi _0})|{\mkern 1mu} \frac{{{\text{d}}\varphi }}{{2\pi }}} \hfill \\ {} \hfill & { = \int_0^{2\pi } {\log } |{\text{Re}}(\widehat {{f_\omega }})\cos \varphi + {\text{Im}}(\widehat {{f_\omega }})\sin \varphi |{\mkern 1mu} \frac{{{\text{d}}\varphi }}{{2\pi }} + \log 2.} \hfill \\
\end{align*}This together with Jensen inequality gives, for any A > 0,
 \begin{align*}\matrix {{\Bbb E}({e^{A{X_r}}})} \hfill & { = \sum\limits_{n = 0}^\infty {\frac{{{A^n}}}{{n!}}} {\Bbb E}X_r^n} \hfill \\ {} \hfill & { \leqslant {\Bbb E}({{\text{e}}^{A|\log |\widehat {{f_\omega }}||}})} \hfill \\ {} \hfill & { \leqslant {2^A}{\Bbb E}\left( {{{\text{e}}^{A|(1/2\pi )\int_0^{2\pi } {\log } |{\text{Re}}(\widehat {{f_\omega }})\cos \varphi + {\text{Im}}(\widehat {{f_\omega }})\sin \varphi |{\kern 1pt} {\text{d}}\varphi |}}} \right)} \hfill \\ {} \hfill & { \leqslant {2^A}\sum\limits_{n = 0}^\infty {\frac{{{A^n}}}{{n!}}} \frac{1}{{2\pi }}\int_0^{2\pi } {\Bbb E} (|\log |{\text{Re}}(\widehat {{f_\omega }})\cos \varphi + {\text{Im}}(\widehat {{f_\omega }})\sin \varphi |{|^n}{\mkern 1mu} {\text{d}}\varphi )} \hfill \\ {} \hfill & { \leqslant {C_0}{\Bbb E}\left( {{{\text{e}}^{A|\log |{\text{Re}}(\widehat {{f_\omega }})\cos \varphi + {\text{Im}}(\widehat {{f_\omega }})\sin \varphi ||}}} \right),} \hfill \\
\end{align*}
\begin{align*}\matrix {{\Bbb E}({e^{A{X_r}}})} \hfill & { = \sum\limits_{n = 0}^\infty {\frac{{{A^n}}}{{n!}}} {\Bbb E}X_r^n} \hfill \\ {} \hfill & { \leqslant {\Bbb E}({{\text{e}}^{A|\log |\widehat {{f_\omega }}||}})} \hfill \\ {} \hfill & { \leqslant {2^A}{\Bbb E}\left( {{{\text{e}}^{A|(1/2\pi )\int_0^{2\pi } {\log } |{\text{Re}}(\widehat {{f_\omega }})\cos \varphi + {\text{Im}}(\widehat {{f_\omega }})\sin \varphi |{\kern 1pt} {\text{d}}\varphi |}}} \right)} \hfill \\ {} \hfill & { \leqslant {2^A}\sum\limits_{n = 0}^\infty {\frac{{{A^n}}}{{n!}}} \frac{1}{{2\pi }}\int_0^{2\pi } {\Bbb E} (|\log |{\text{Re}}(\widehat {{f_\omega }})\cos \varphi + {\text{Im}}(\widehat {{f_\omega }})\sin \varphi |{|^n}{\mkern 1mu} {\text{d}}\varphi )} \hfill \\ {} \hfill & { \leqslant {C_0}{\Bbb E}\left( {{{\text{e}}^{A|\log |{\text{Re}}(\widehat {{f_\omega }})\cos \varphi + {\text{Im}}(\widehat {{f_\omega }})\sin \varphi ||}}} \right),} \hfill \\
\end{align*} where C 0 is a positive constant. For fixed ![]() $\theta\in(0,2\pi]$, let
$\theta\in(0,2\pi]$, let
 \begin{equation*}
V_\omega(\varphi,r)=|{\rm{Re}} (\hat{f_\omega})\cos \varphi+{\rm{Im}} (\hat{f_\omega})\sin\varphi|,
\end{equation*}
\begin{equation*}
V_\omega(\varphi,r)=|{\rm{Re}} (\hat{f_\omega})\cos \varphi+{\rm{Im}} (\hat{f_\omega})\sin\varphi|,
\end{equation*}and
Since  $
\mathbb{E}(|\hat{f_\omega}|^2)=1,
$ it follows that, for
$
\mathbb{E}(|\hat{f_\omega}|^2)=1,
$ it follows that, for ![]() $0 \lt A \lt 2$,
$0 \lt A \lt 2$,
 \begin{align*}
\int_{Y_1}{\rm e}^{A\,\log V_\omega(\varphi,r)}\, {\rm d}\mathbb{P}(\omega)&=\int_{Y_1}|\mbox{Re} (\hat{f_\omega})\cos \varphi+\mbox{Im} (\hat{f_\omega})\sin\varphi|^{A} \, {\rm d}\mathbb{P}(\omega)\\
&\leq \int_{Y_1}|\hat{f_\omega}|^{A} \, {\rm d}\mathbb{P}(\omega)
\leq \left( \int_{\Omega}|\hat{f_\omega}|^2 \, {\rm d}\mathbb{P}(\omega)\right)^{A/2}\\
&=\left(\mbox{E}(|\hat{f_\omega}|^2)\right)^{A/2}=1.
\end{align*}
\begin{align*}
\int_{Y_1}{\rm e}^{A\,\log V_\omega(\varphi,r)}\, {\rm d}\mathbb{P}(\omega)&=\int_{Y_1}|\mbox{Re} (\hat{f_\omega})\cos \varphi+\mbox{Im} (\hat{f_\omega})\sin\varphi|^{A} \, {\rm d}\mathbb{P}(\omega)\\
&\leq \int_{Y_1}|\hat{f_\omega}|^{A} \, {\rm d}\mathbb{P}(\omega)
\leq \left( \int_{\Omega}|\hat{f_\omega}|^2 \, {\rm d}\mathbb{P}(\omega)\right)^{A/2}\\
&=\left(\mbox{E}(|\hat{f_\omega}|^2)\right)^{A/2}=1.
\end{align*}On the set Y 2, by using Lemma 4.2, we have
 \begin{align*}
\matrix {\int_{{Y_2}} {{{\text{e}}^{A|\log {V_\omega }(\varphi ,r)|}}} } \hfill & {{\text{d}}{\Bbb P}(\omega ) = \int_0^\infty {\Bbb P} \left( {\left\{ {\omega \in {Y_2}:{{\text{e}}^{A|\log {V_\omega }(\varphi ,r)|}} \geqslant \lambda } \right\}} \right){\mkern 1mu} {\text{d}}\lambda } \hfill \\ {} \hfill & { = \int_0^\infty {\Bbb P} \left( {\left\{ {\omega \in {Y_2}:{{\text{e}}^{ - A{\kern 1pt} \log |{\text{Re}}(\widehat {{f_\omega }})\cos \varphi + {\text{Im}}(\widehat {{f_\omega }})\sin \varphi |}} \geqslant \lambda } \right\}} \right){\mkern 1mu} {\text{d}}\lambda } \hfill \\ {} \hfill & { = \int_0^\infty {\Bbb P} \left( {\left\{ {\omega \in {Y_2}:|{\text{Re}}(\widehat {{f_\omega }})\cos \varphi + {\text{Im}}(\widehat {{f_\omega }})\sin \varphi | \leqslant {{(1/\lambda )}^{1/A}}} \right\}} \right){\mkern 1mu} {\text{d}}\lambda } \hfill \\ {} \hfill & { \leqslant 1 + \int_1^\infty {\Bbb P} \left( {\left\{ {\omega \in \Omega :|{\text{Re}}(\widehat {{f_\omega }})\cos \varphi + {\text{Im}}(\widehat {{f_\omega }})\sin \varphi | \leqslant {{(1/\lambda )}^{1/A}}} \right\}} \right){\mkern 1mu} {\text{d}}\lambda } \hfill \\ {} \hfill & { \leqslant 1 + C\int_1^\infty {\frac{{d\lambda }}{{{\lambda ^{1/3A}}}}} .} \hfill \\
\end{align*}
\begin{align*}
\matrix {\int_{{Y_2}} {{{\text{e}}^{A|\log {V_\omega }(\varphi ,r)|}}} } \hfill & {{\text{d}}{\Bbb P}(\omega ) = \int_0^\infty {\Bbb P} \left( {\left\{ {\omega \in {Y_2}:{{\text{e}}^{A|\log {V_\omega }(\varphi ,r)|}} \geqslant \lambda } \right\}} \right){\mkern 1mu} {\text{d}}\lambda } \hfill \\ {} \hfill & { = \int_0^\infty {\Bbb P} \left( {\left\{ {\omega \in {Y_2}:{{\text{e}}^{ - A{\kern 1pt} \log |{\text{Re}}(\widehat {{f_\omega }})\cos \varphi + {\text{Im}}(\widehat {{f_\omega }})\sin \varphi |}} \geqslant \lambda } \right\}} \right){\mkern 1mu} {\text{d}}\lambda } \hfill \\ {} \hfill & { = \int_0^\infty {\Bbb P} \left( {\left\{ {\omega \in {Y_2}:|{\text{Re}}(\widehat {{f_\omega }})\cos \varphi + {\text{Im}}(\widehat {{f_\omega }})\sin \varphi | \leqslant {{(1/\lambda )}^{1/A}}} \right\}} \right){\mkern 1mu} {\text{d}}\lambda } \hfill \\ {} \hfill & { \leqslant 1 + \int_1^\infty {\Bbb P} \left( {\left\{ {\omega \in \Omega :|{\text{Re}}(\widehat {{f_\omega }})\cos \varphi + {\text{Im}}(\widehat {{f_\omega }})\sin \varphi | \leqslant {{(1/\lambda )}^{1/A}}} \right\}} \right){\mkern 1mu} {\text{d}}\lambda } \hfill \\ {} \hfill & { \leqslant 1 + C\int_1^\infty {\frac{{d\lambda }}{{{\lambda ^{1/3A}}}}} .} \hfill \\
\end{align*} Thus, when ![]() $0 \lt A \lt 1/3$, we have
$0 \lt A \lt 1/3$, we have
 \begin{equation*}
\int_{Y_2} {\rm e}^{A |\log V_\omega(\varphi,r)|}\, {\rm d}\mathbb{P}(\omega)\leq 1+C\int_{1}^{\infty}\frac{\textrm{d}\lambda}{\lambda^{1/3A}} \lt +\infty.
\end{equation*}
\begin{equation*}
\int_{Y_2} {\rm e}^{A |\log V_\omega(\varphi,r)|}\, {\rm d}\mathbb{P}(\omega)\leq 1+C\int_{1}^{\infty}\frac{\textrm{d}\lambda}{\lambda^{1/3A}} \lt +\infty.
\end{equation*} Therefore, setting ![]() $A=1/3(1+\tau)$ as before, we obtain
$A=1/3(1+\tau)$ as before, we obtain
 \begin{align}
{\text{E}}\left( {{{\text{e}}^{\frac{1}{{3(1 + \tau )}}{X_r}}}} \right) \leqslant {C_0}\int_{{Y_1}} {{{\text{e}}^{A{\kern 1pt} \log {V_\omega }(\varphi ,r)}}} {\mkern 1mu} {\text{d}}{\Bbb P}(\omega ) + {C_0}\int_{{Y_2}} {{{\text{e}}^{A|\log {V_\omega }(\varphi ,r)|}}} {\mkern 1mu} {\text{d}}{\Bbb P}(\omega ) = {C_1} \lt + \infty .
\end{align}
\begin{align}
{\text{E}}\left( {{{\text{e}}^{\frac{1}{{3(1 + \tau )}}{X_r}}}} \right) \leqslant {C_0}\int_{{Y_1}} {{{\text{e}}^{A{\kern 1pt} \log {V_\omega }(\varphi ,r)}}} {\mkern 1mu} {\text{d}}{\Bbb P}(\omega ) + {C_0}\int_{{Y_2}} {{{\text{e}}^{A|\log {V_\omega }(\varphi ,r)|}}} {\mkern 1mu} {\text{d}}{\Bbb P}(\omega ) = {C_1} \lt + \infty .
\end{align}It follows that
 \begin{equation*}
\mathbb{P}\left(X_r\ge 3(1+\tau)^2\log x\right)\le \frac{C_1}{x^{1+\tau}}.
\end{equation*}
\begin{equation*}
\mathbb{P}\left(X_r\ge 3(1+\tau)^2\log x\right)\le \frac{C_1}{x^{1+\tau}}.
\end{equation*}This completes the proof of the lemma.
Lemma 4.4. Let f and fω be entire functions of the forms (1.1) and (1.2), respectively. Then, there is a constant ![]() $r_1 \gt 0$ such that, for
$r_1 \gt 0$ such that, for ![]() $r \gt r_1$,
$r \gt r_1$,
 \begin{equation*}
T(r,f)\leq \log\sigma(r,f)+\frac12\,\log2 \quad \mbox{and} \quad
T(r,f_\omega)\leq \log\sigma(r,f_\omega)+\frac12\,\log2.
\end{equation*}
\begin{equation*}
T(r,f)\leq \log\sigma(r,f)+\frac12\,\log2 \quad \mbox{and} \quad
T(r,f_\omega)\leq \log\sigma(r,f_\omega)+\frac12\,\log2.
\end{equation*}Proof. By Parseval identity and Jensen inequality, we obtain
 \begin{align*}\matrix {T(r,{f_\omega })} \hfill & { = \frac{1}{{2\pi }}\int_0^{2\pi } {{{\log }^ + }} |{f_\omega }\left( {r{\mkern 1mu} {{\text{e}}^{i\theta }}} \right)|{\text{d}}\theta \leqslant \frac{1}{{4\pi }}\int_0^{2\pi } {\log } \left( {|{f_\omega }\left( {r{\mkern 1mu} {{\text{e}}^{i\theta }}} \right){|^2} + 1} \right){\text{d}}\theta } \hfill \\ {} \hfill & { \leqslant \log \sigma (r,{f_\omega }) + \frac{1}{2}{\mkern 1mu} \log 2.} \hfill \\
\end{align*}
\begin{align*}\matrix {T(r,{f_\omega })} \hfill & { = \frac{1}{{2\pi }}\int_0^{2\pi } {{{\log }^ + }} |{f_\omega }\left( {r{\mkern 1mu} {{\text{e}}^{i\theta }}} \right)|{\text{d}}\theta \leqslant \frac{1}{{4\pi }}\int_0^{2\pi } {\log } \left( {|{f_\omega }\left( {r{\mkern 1mu} {{\text{e}}^{i\theta }}} \right){|^2} + 1} \right){\text{d}}\theta } \hfill \\ {} \hfill & { \leqslant \log \sigma (r,{f_\omega }) + \frac{1}{2}{\mkern 1mu} \log 2.} \hfill \\
\end{align*}The other inequality in the lemma can be proved in the same manner.
Lemma 4.5. (Plane Growth Lemma, e.g. [Reference Cherry and Ye2], p. 100)
Let F(r) be a positive, non-decreasing continuous function satisfying ![]() $F(r)\geq e$ for
$F(r)\geq e$ for ![]() $e \lt r_0 \lt r \lt \infty$. Let
$e \lt r_0 \lt r \lt \infty$. Let ![]() $\psi(r) \ge 1$ be a real-valued, continuous, non-decreasing function on the interval
$\psi(r) \ge 1$ be a real-valued, continuous, non-decreasing function on the interval ![]() $[e, \infty)$ and
$[e, \infty)$ and  $ \int_e^{\infty}({\textrm{d}r}/{(r\psi(r)))} \lt \infty$. Let
$ \int_e^{\infty}({\textrm{d}r}/{(r\psi(r)))} \lt \infty$. Let ![]() $\phi(r)$ be a positive, non-decreasing function defined for
$\phi(r)$ be a positive, non-decreasing function defined for ![]() $r_0\leq r \lt \infty$. Set
$r_0\leq r \lt \infty$. Set ![]() $R=r+\phi(r)/\psi(F(r))$. If
$R=r+\phi(r)/\psi(F(r))$. If ![]() $\phi(r)\le r$ for all
$\phi(r)\le r$ for all ![]() $r\ge r_0$, then there exists a closed set
$r\ge r_0$, then there exists a closed set ![]() $E\subset [r_0,\infty)$ with
$E\subset [r_0,\infty)$ with  $ \int_E({\textrm{d}r}/{\phi(r))} \lt \infty$ such that for all
$ \int_E({\textrm{d}r}/{\phi(r))} \lt \infty$ such that for all ![]() $r \gt r_0$,
$r \gt r_0$, ![]() $r\not\in E$, we have
$r\not\in E$, we have
and
 \begin{equation*}
\log\frac{R}{r(R-r)}\le \log \frac{\psi(F(r))}{\phi(r)}+\log 2.
\end{equation*}
\begin{equation*}
\log\frac{R}{r(R-r)}\le \log \frac{\psi(F(r))}{\phi(r)}+\log 2.
\end{equation*}Lemma 4.6. Let f be an entire function defined as in Equation (1.1). There is a set E of finite logarithmic measure such that, for all large ![]() $r\notin E$,
$r\notin E$,
Proof. For any R > r, by Cauchy–Schwarz inequality, we get
 \begin{align*}
M(r, f)&\le \sum_{j=0}^{\infty}|a_j|r^{j}= \sum_{j=0}^{\infty}|a_j|R^{j}\frac{r^{j}}{R^{j}}\\
&\le\left( \sum_{j=0}^{\infty}|a_j|^2 R^{2j} \right)^{1/2} \left( \sum_{j=0}^{\infty}\frac{r^{2j}}{R^{2j}} \right)^{1/2} \\
&\le\left( \sum_{j=0}^{\infty}|a_j|^2 R^{2j} \right)^{1/2} \left( \sum_{j=0}^{\infty}\frac{r^j}{R^j} \right)^{1/2} \\
&= \sigma(R, f)\left(\frac{R}{R-r}\right)^{1/2}.
\end{align*}
\begin{align*}
M(r, f)&\le \sum_{j=0}^{\infty}|a_j|r^{j}= \sum_{j=0}^{\infty}|a_j|R^{j}\frac{r^{j}}{R^{j}}\\
&\le\left( \sum_{j=0}^{\infty}|a_j|^2 R^{2j} \right)^{1/2} \left( \sum_{j=0}^{\infty}\frac{r^{2j}}{R^{2j}} \right)^{1/2} \\
&\le\left( \sum_{j=0}^{\infty}|a_j|^2 R^{2j} \right)^{1/2} \left( \sum_{j=0}^{\infty}\frac{r^j}{R^j} \right)^{1/2} \\
&= \sigma(R, f)\left(\frac{R}{R-r}\right)^{1/2}.
\end{align*} Applying Lemma 4.5 to ![]() $F(r)=\sigma(r,f)$,
$F(r)=\sigma(r,f)$, ![]() $\phi(r)=r$,
$\phi(r)=r$, ![]() $\psi(x)=(\log x)^2$ and
$\psi(x)=(\log x)^2$ and  $ R=r+\frac{r}{\psi(F(r))}$ gives
$ R=r+\frac{r}{\psi(F(r))}$ gives
 \begin{equation*}\log \sigma(R, f)\le \log \sigma(r, f)+1 \quad \mbox{and} \quad
\log \frac{R}{R-r}\le 2\, \log\, \log \sigma(r, f)+\log 2
\end{equation*}
\begin{equation*}\log \sigma(R, f)\le \log \sigma(r, f)+1 \quad \mbox{and} \quad
\log \frac{R}{R-r}\le 2\, \log\, \log \sigma(r, f)+\log 2
\end{equation*} for all large ![]() $r \notin E$. The lemma is proved.
$r \notin E$. The lemma is proved.
Remark 5. It is straightforward to show that ![]() $\sigma(r, f)\le M(r, f)$ for all r > 0.
$\sigma(r, f)\le M(r, f)$ for all r > 0.
Now we recall a generalized logarithmic derivative estimates of Gol’dberg–Grinshtein type. To state this result, we introduce some notation. Given a non-constant meromorphic function g and ![]() $a\in\mathbb{C}$, we can always write
$a\in\mathbb{C}$, we can always write ![]() $g(z)=(z-a)^m h(z)$, where integer m is called the order of g at the point a and is denoted by
$g(z)=(z-a)^m h(z)$, where integer m is called the order of g at the point a and is denoted by ![]() ${ord}_a g$. And, the first non-zero coefficient of Laurent series of g(z) in the neighbourhood of the point z = a is denoted by
${ord}_a g$. And, the first non-zero coefficient of Laurent series of g(z) in the neighbourhood of the point z = a is denoted by ![]() $c_{g}(a)$.
$c_{g}(a)$.
Lemma 4.7. ([Reference Cherry and Ye2], p. 96)
Let g be a meromorphic function in the complex plane and let ![]() $0 \lt \alpha \lt 1$. There exists a constant r 0 such that, for all
$0 \lt \alpha \lt 1$. There exists a constant r 0 such that, for all ![]() $r_0 \lt r \lt R \lt \infty$,
$r_0 \lt r \lt R \lt \infty$,
 \begin{align*}
\int_0^{2\pi}\left|\frac{rg^{\prime}(r\,{\rm e}^{i\theta})}{g(r\,{\rm e}^{i\theta})}\right|^\alpha\frac{\textrm{d}\theta}{2\pi} \leq
C(\alpha)\left(\frac{R}{R-r}\right)^{\alpha}(2T(R, g)+\beta_1)^{\alpha},
\end{align*}
\begin{align*}
\int_0^{2\pi}\left|\frac{rg^{\prime}(r\,{\rm e}^{i\theta})}{g(r\,{\rm e}^{i\theta})}\right|^\alpha\frac{\textrm{d}\theta}{2\pi} \leq
C(\alpha)\left(\frac{R}{R-r}\right)^{\alpha}(2T(R, g)+\beta_1)^{\alpha},
\end{align*}where
 \begin{equation*}
\beta_1=\beta_1(g,r_0)=|{ord}_0 g| \log^+\frac1{r_0}+\left|\log|c_g(0)| \right|+\log2
\end{equation*}
\begin{equation*}
\beta_1=\beta_1(g,r_0)=|{ord}_0 g| \log^+\frac1{r_0}+\left|\log|c_g(0)| \right|+\log2
\end{equation*}and
 \begin{equation*}C(\alpha)=2^\alpha+(8+2^{\alpha+1})\sec\frac{\alpha\pi}{2}.\end{equation*}
\begin{equation*}C(\alpha)=2^\alpha+(8+2^{\alpha+1})\sec\frac{\alpha\pi}{2}.\end{equation*}5. Proofs of our main theorems
5.1. Proof of Theorem 3.1
Let fω be a random entire function on ![]() $(\Omega,\, \mathcal{F}, \, \mu)$ of the form (1.2). For
$(\Omega,\, \mathcal{F}, \, \mu)$ of the form (1.2). For ![]() $\omega\in\Omega$, by Jensen formula,
$\omega\in\Omega$, by Jensen formula,
 \begin{align*}
\matrix {N(r,0,{f_\omega })} \hfill & { = \int_0^{2\pi } {\log } |{f_\omega }(r{\mkern 1mu} {{\text{e}}^{i\theta }})|\frac{{{\text{d}}\theta }}{{2\pi }} - \log |{c_{{f_\omega }}}(0)|} \hfill \\ {} \hfill & { = \log \sigma (r,f) + \int_0^{2\pi } {\log } |\widehat {{f_\omega }}(r{\mkern 1mu} {{\text{e}}^{i\theta }})|\frac{{{\text{d}}\theta }}{{2\pi }} - \log |{c_{{f_\omega }}}(0)|.} \hfill \\
\end{align*}
\begin{align*}
\matrix {N(r,0,{f_\omega })} \hfill & { = \int_0^{2\pi } {\log } |{f_\omega }(r{\mkern 1mu} {{\text{e}}^{i\theta }})|\frac{{{\text{d}}\theta }}{{2\pi }} - \log |{c_{{f_\omega }}}(0)|} \hfill \\ {} \hfill & { = \log \sigma (r,f) + \int_0^{2\pi } {\log } |\widehat {{f_\omega }}(r{\mkern 1mu} {{\text{e}}^{i\theta }})|\frac{{{\text{d}}\theta }}{{2\pi }} - \log |{c_{{f_\omega }}}(0)|.} \hfill \\
\end{align*}It follows that, for any r > 0,
 \begin{equation*}
|N(r,0,f_\omega)-\log\sigma(r, f)+ \log|c_{f_\omega}(0)||
\le \int_0^{2\pi}|\log|\hat{f_\omega}(r\,{\rm e}^{i\theta})| |\frac{\textrm{d}\theta}{2\pi}=X_r. \\
\end{equation*}
\begin{equation*}
|N(r,0,f_\omega)-\log\sigma(r, f)+ \log|c_{f_\omega}(0)||
\le \int_0^{2\pi}|\log|\hat{f_\omega}(r\,{\rm e}^{i\theta})| |\frac{\textrm{d}\theta}{2\pi}=X_r. \\
\end{equation*} Since ![]() $\log \sigma(r,f)$ is increasing and unbounded, for any positive integer n, there is rn such that
$\log \sigma(r,f)$ is increasing and unbounded, for any positive integer n, there is rn such that ![]() $\log \sigma(r_n, f)=n$ and the sequence
$\log \sigma(r_n, f)=n$ and the sequence ![]() $\{r_n\}$ is increasing. Since
$\{r_n\}$ is increasing. Since ![]() $f_\omega \in \mathcal{Y}$, there are positive constants A and B such that
$f_\omega \in \mathcal{Y}$, there are positive constants A and B such that ![]() $\mbox{E}(\exp(AX_r^B))=C_1 \lt +\infty$. For any C > 1, set
$\mbox{E}(\exp(AX_r^B))=C_1 \lt +\infty$. For any C > 1, set
 \begin{equation*}
A_n=\left\{\omega\in\Omega: |N(r_n,0, f_\omega)-\log \sigma(r_n, f)+ \log|c_{f_\omega}(0)||\ge \left(\frac{C}{A}\,\log n\right)^{1/{B}}\right\}.
\end{equation*}
\begin{equation*}
A_n=\left\{\omega\in\Omega: |N(r_n,0, f_\omega)-\log \sigma(r_n, f)+ \log|c_{f_\omega}(0)||\ge \left(\frac{C}{A}\,\log n\right)^{1/{B}}\right\}.
\end{equation*}Therefore, by Equation (4.1) in Lemma 4.3,
 \begin{equation*}\mathbb{P}(A_n)\le \mathbb{P}\left(X_r\ge \left(\frac{C}{A}\log n\right)^{1/{B}}\right)\le \frac{C_1}{n^{C}}.\end{equation*}
\begin{equation*}\mathbb{P}(A_n)\le \mathbb{P}\left(X_r\ge \left(\frac{C}{A}\log n\right)^{1/{B}}\right)\le \frac{C_1}{n^{C}}.\end{equation*} Consequently, ![]() $ \sum\mathbb{P}(A_n) \lt \infty$ and by Borel–Cantelli lemma,
$ \sum\mathbb{P}(A_n) \lt \infty$ and by Borel–Cantelli lemma,
Thus, for ![]() $\omega \in \Omega\setminus A$, there exist j 0 such that for all
$\omega \in \Omega\setminus A$, there exist j 0 such that for all ![]() $n \gt j_0$, we have
$n \gt j_0$, we have
 \begin{equation*}
|N(r_n,0, f_\omega)-\log \sigma(r_n, f)+ \log|c_{f_\omega}(0)|| \lt \left(\frac{C}{A}\,\log n\right)^{1/{B}}.
\end{equation*}
\begin{equation*}
|N(r_n,0, f_\omega)-\log \sigma(r_n, f)+ \log|c_{f_\omega}(0)|| \lt \left(\frac{C}{A}\,\log n\right)^{1/{B}}.
\end{equation*} It follows that, for ![]() $r\in (r_n, r_{n+1}]$ with
$r\in (r_n, r_{n+1}]$ with ![]() $n \gt j_0$, for almost all
$n \gt j_0$, for almost all ![]() $\omega\in\Omega$, we have
$\omega\in\Omega$, we have
 \begin{align}
& \le N(r_n,0, f_\omega)+(C/A)^{1/B}(\log\, \log \sigma(r_n, f))^{1/B} +1+\log|c_{f_\omega}(0)|
\end{align}
\begin{align}
& \le N(r_n,0, f_\omega)+(C/A)^{1/B}(\log\, \log \sigma(r_n, f))^{1/B} +1+\log|c_{f_\omega}(0)|
\end{align} \begin{align}
&\le N(r,0,f_\omega)+(C/A)^{1/B}(\log\, \log \sigma(r, f))^{1/B}+1+\log|c_{f_\omega}(0)|,
\end{align}
\begin{align}
&\le N(r,0,f_\omega)+(C/A)^{1/B}(\log\, \log \sigma(r, f))^{1/B}+1+\log|c_{f_\omega}(0)|,
\end{align}and
 \begin{align}
N(r,0, f_\omega)& \le N(r_{n+1},0, f_\omega)\le \log \sigma(r_{n+1}, f)+ (C/A)^{1/B}(\log \,\log \sigma(r_{n+1}, f))^{1/B} \\
& \quad +\log|c_{f_\omega}(0)|
\end{align}
\begin{align}
N(r,0, f_\omega)& \le N(r_{n+1},0, f_\omega)\le \log \sigma(r_{n+1}, f)+ (C/A)^{1/B}(\log \,\log \sigma(r_{n+1}, f))^{1/B} \\
& \quad +\log|c_{f_\omega}(0)|
\end{align} \begin{align}
& \le \log \sigma(r_n, f)+1+(C/A)^{1/B}(\log\, \log \sigma(r_n, f))^{1/B}+O(1)+\log|c_{f_\omega}(0)|
\end{align}
\begin{align}
& \le \log \sigma(r_n, f)+1+(C/A)^{1/B}(\log\, \log \sigma(r_n, f))^{1/B}+O(1)+\log|c_{f_\omega}(0)|
\end{align} \begin{align}
&\le \log \sigma(r, f)+(C/A)^{1/B}(\log\, \log \sigma(r, f))^{1/B}+O(1)+\log|c_{f_\omega}(0)|.
\end{align}
\begin{align}
&\le \log \sigma(r, f)+(C/A)^{1/B}(\log\, \log \sigma(r, f))^{1/B}+O(1)+\log|c_{f_\omega}(0)|.
\end{align} Now we estimate the term ![]() $\log|c_{f_\omega}(0)|$. Since
$\log|c_{f_\omega}(0)|$. Since  $f_\omega(z)=\sum\limits_{j=0}^{\infty} a_j \chi_j(\omega) z^j$, we denote all the j satisfying
$f_\omega(z)=\sum\limits_{j=0}^{\infty} a_j \chi_j(\omega) z^j$, we denote all the j satisfying ![]() $a_j\neq0$ by the non-decreasing sequence
$a_j\neq0$ by the non-decreasing sequence ![]() $\{j_k\}_{k=0}^{\infty}$. It suffices to estimate
$\{j_k\}_{k=0}^{\infty}$. It suffices to estimate ![]() $|\chi_{j_k}(\omega)|$. Define
$|\chi_{j_k}(\omega)|$. Define
and
 \begin{equation*}
B^{\prime}_{km}=\{\omega\in B_k: m \lt |\chi_{j_k}(\omega)|\le m+1\}.
\end{equation*}
\begin{equation*}
B^{\prime}_{km}=\{\omega\in B_k: m \lt |\chi_{j_k}(\omega)|\le m+1\}.
\end{equation*}It is trivial to see that
Thus, for almost every ![]() $\omega\in\Omega$, there exist unique k and m such that
$\omega\in\Omega$, there exist unique k and m such that ![]() $\omega\in B^{\prime}_{km}$. Therefore,
$\omega\in B^{\prime}_{km}$. Therefore,
This together with Equations (5.1) and (5.2) gives, for r sufficiently large,
The proof of Theorem 3.1 is complete.
5.2. Proof of Theorem 3.2
To prove Theorem 3.2, we need the following lemma, whose proof is based on the result of our Theorem 3.1.
Lemma 5.1. Let ![]() $f_\omega(z) \in \mathcal{Y}$. Then there exists a constant
$f_\omega(z) \in \mathcal{Y}$. Then there exists a constant ![]() $r_0=r_0(\omega)$ such that, for
$r_0=r_0(\omega)$ such that, for ![]() $r \gt r_0$, we have
$r \gt r_0$, we have
and
where C > 1 is any constant, and constants A and B are from Condition Y.
Proof. Let φ be a non-negative increasing function. Since
 \begin{equation*}
\mathbb{E} (\sigma^2(r,f_\omega))=
\sum_{j=0}^{\infty}\mathbb{E}(|\chi_j(\omega)|^2)|a_n|^2 r^{2n}=\sigma^2(r,f),
\end{equation*}
\begin{equation*}
\mathbb{E} (\sigma^2(r,f_\omega))=
\sum_{j=0}^{\infty}\mathbb{E}(|\chi_j(\omega)|^2)|a_n|^2 r^{2n}=\sigma^2(r,f),
\end{equation*}by Markov’s inequality, we have
 \begin{equation*}
\mathbb{P}\left(\sigma^2(r,f_\omega) \gt \sigma^2(r,f)\varphi(\sigma(r,f))\right)\leq \frac{\mathbb{E} (\sigma^2(r,f_\omega))}{\sigma^2(r,f)\varphi(\sigma(r,f))}=\frac1{\varphi(\sigma(r,f))}.
\end{equation*}
\begin{equation*}
\mathbb{P}\left(\sigma^2(r,f_\omega) \gt \sigma^2(r,f)\varphi(\sigma(r,f))\right)\leq \frac{\mathbb{E} (\sigma^2(r,f_\omega))}{\sigma^2(r,f)\varphi(\sigma(r,f))}=\frac1{\varphi(\sigma(r,f))}.
\end{equation*} For any positive integer n, there is rn such that ![]() $\sigma(r_n, f)=e^n$ and the sequence
$\sigma(r_n, f)=e^n$ and the sequence ![]() $\{r_n\}$ is increasing. Set
$\{r_n\}$ is increasing. Set
Thus, by taking ![]() $\varphi(x)=(\log x)^2$, we have
$\varphi(x)=(\log x)^2$, we have
 \begin{equation*}
\mathbb{P}(B_n)\le \frac{1}{\varphi(\sigma(r_n,f))}= \frac{1}{n^2}.
\end{equation*}
\begin{equation*}
\mathbb{P}(B_n)\le \frac{1}{\varphi(\sigma(r_n,f))}= \frac{1}{n^2}.
\end{equation*} Consequently, ![]() $ \sum\mathbb{P}(B_n) \lt +\infty$. Thus, by Borel–Cantelli lemma, for almost all
$ \sum\mathbb{P}(B_n) \lt +\infty$. Thus, by Borel–Cantelli lemma, for almost all ![]() $\omega \in\Omega $, there is
$\omega \in\Omega $, there is ![]() $j_1=j_1(\omega)$, when
$j_1=j_1(\omega)$, when ![]() $n \gt j_1$,
$n \gt j_1$, ![]() $r\in (r_n, r_{n+1}]$, we have
$r\in (r_n, r_{n+1}]$, we have
 \begin{align*}
\sigma^2(r,f_\omega)&\leq \sigma^2(r_{n+1},f_\omega)\leq\sigma^2(r_{n+1},f)\varphi(\sigma(r_{n+1},f))\\
&= ({\rm e}^{n+1})^2(n+1)^2={\rm e}^2\sigma^2(r_n,f)(\log \sigma(r_n,f)+1)^2\\
&\leq {\rm e}^2\sigma^2(r,f)(\log \sigma(r,f)+1)^2.
\end{align*}
\begin{align*}
\sigma^2(r,f_\omega)&\leq \sigma^2(r_{n+1},f_\omega)\leq\sigma^2(r_{n+1},f)\varphi(\sigma(r_{n+1},f))\\
&= ({\rm e}^{n+1})^2(n+1)^2={\rm e}^2\sigma^2(r_n,f)(\log \sigma(r_n,f)+1)^2\\
&\leq {\rm e}^2\sigma^2(r,f)(\log \sigma(r,f)+1)^2.
\end{align*} For ![]() $r \gt r_0$ sufficiently large, we get
$r \gt r_0$ sufficiently large, we get
On the other hand, by Theorems 3.1 and 2.2 and Lemma 4.4, for any C > 1, there is a constant ![]() $r_0=r_0(\omega)$, for
$r_0=r_0(\omega)$, for ![]() $r \gt r_0(\omega)$,
$r \gt r_0(\omega)$,
 \begin{align*}
\log \sigma(r,f)&\leq N(r,0,f_\omega)+(C/A)^{1/B}(\log\, \log \sigma(r, f))^{1/B}\\
&\leq T(r,f_\omega)+(C/A)^{1/B}(\log\, \log \sigma(r, f))^{1/B}\\
&\leq \log \sigma(r,f_\omega)+(C^{\prime}/A)^{1/B}(\log\, \log \sigma(r, f))^{1/B}.
\end{align*}
\begin{align*}
\log \sigma(r,f)&\leq N(r,0,f_\omega)+(C/A)^{1/B}(\log\, \log \sigma(r, f))^{1/B}\\
&\leq T(r,f_\omega)+(C/A)^{1/B}(\log\, \log \sigma(r, f))^{1/B}\\
&\leq \log \sigma(r,f_\omega)+(C^{\prime}/A)^{1/B}(\log\, \log \sigma(r, f))^{1/B}.
\end{align*}This completes the proof of this lemma.
We are now ready to prove Theorem 3.2.
Proof of Theorem 3.2
By applying Theorem 3.1 to ![]() $f^*_\omega$, we obtain two positive constants A, B such that for any positive constant C > 1, there exists a constant
$f^*_\omega$, we obtain two positive constants A, B such that for any positive constant C > 1, there exists a constant ![]() $r_0=r_0(\omega) \gt 0$, so that for
$r_0=r_0(\omega) \gt 0$, so that for ![]() $r \gt r_0$,
$r \gt r_0$,
 \begin{equation*}
\log \sigma(r,f^*)\leq N(r, 0, f^*_\omega)+(C/A)^{1/B}(\log\,\log \sigma(r, f^*) )^{1/B}\qquad \mbox{a.s.}
\end{equation*}
\begin{equation*}
\log \sigma(r,f^*)\leq N(r, 0, f^*_\omega)+(C/A)^{1/B}(\log\,\log \sigma(r, f^*) )^{1/B}\qquad \mbox{a.s.}
\end{equation*} Since ![]() $\sigma(r,f^*)\geq\sigma(r,f)\geq e$ for all large r, say,
$\sigma(r,f^*)\geq\sigma(r,f)\geq e$ for all large r, say, ![]() $r \gt r_0$, and the function
$r \gt r_0$, and the function ![]() $y(x)=x-C_0\,\log x $ is increasing on
$y(x)=x-C_0\,\log x $ is increasing on ![]() $[x_0,+\infty)$, we have
$[x_0,+\infty)$, we have
 \begin{equation}
\log \sigma(r,f)\leq N(r, 0, f^*_\omega)+(C/A)^{1/B}(\log\,\log \sigma(r, f) )^{1/B}\qquad \mbox{a.s.}
\end{equation}
\begin{equation}
\log \sigma(r,f)\leq N(r, 0, f^*_\omega)+(C/A)^{1/B}(\log\,\log \sigma(r, f) )^{1/B}\qquad \mbox{a.s.}
\end{equation} By Jensen formula and Theorem 2.2, we have, for any r < R and ![]() $0 \lt \alpha \lt 1$,
$0 \lt \alpha \lt 1$,
 \begin{align*}
\matrix {{\mkern 1mu} N(r,0,f_\omega ^*) - N(r,a,{f_\omega })} \hfill & { = \frac{1}{{2\pi }}\int_0^{2\pi } {\log } \left| {\frac{{f_\omega ^*(r{\mkern 1mu} {{\text{e}}^{i\theta }})}}{{{f_\omega }(r{\mkern 1mu} {{\text{e}}^{i\theta }}) - a}}} \right|{\mkern 1mu} {\text{d}}\theta - \log \frac{{|{c_{f_\omega ^*}}(0)|}}{{|{c_{{f_\omega }}}(a)|}}} \hfill \\ {} \hfill & { = \frac{1}{\alpha }\int_0^{2\pi } {\log } {{\left| {\frac{{f_\omega ^*(r{\mkern 1mu} {{\text{e}}^{i\theta }})}}{{{f_\omega }(r{\mkern 1mu} {{\text{e}}^{i\theta }}) - a}}} \right|}^\alpha }{\mkern 1mu} \frac{{{\text{d}}\theta }}{{2\pi }} - \log \frac{{|{c_{f_\omega ^*}}(0)|}}{{|{c_{{f_\omega }}}(a)|}}} \hfill \\ {} \hfill & { \leqslant \frac{1}{\alpha }\log \left( {\int_0^{2\pi } {{{\left| {\frac{{f_\omega ^*(r{\mkern 1mu} {{\text{e}}^{i\theta }})}}{{{f_\omega }(r{\mkern 1mu} {{\text{e}}^{i\theta }}) - a}}} \right|}^\alpha }} {\mkern 1mu} \frac{{{\text{d}}\theta }}{{2\pi }}} \right) - \log \frac{{|{c_{f_\omega ^*}}(0)|}}{{|{c_{{f_\omega }}}(a)|}}.} \hfill \\
\end{align*}
\begin{align*}
\matrix {{\mkern 1mu} N(r,0,f_\omega ^*) - N(r,a,{f_\omega })} \hfill & { = \frac{1}{{2\pi }}\int_0^{2\pi } {\log } \left| {\frac{{f_\omega ^*(r{\mkern 1mu} {{\text{e}}^{i\theta }})}}{{{f_\omega }(r{\mkern 1mu} {{\text{e}}^{i\theta }}) - a}}} \right|{\mkern 1mu} {\text{d}}\theta - \log \frac{{|{c_{f_\omega ^*}}(0)|}}{{|{c_{{f_\omega }}}(a)|}}} \hfill \\ {} \hfill & { = \frac{1}{\alpha }\int_0^{2\pi } {\log } {{\left| {\frac{{f_\omega ^*(r{\mkern 1mu} {{\text{e}}^{i\theta }})}}{{{f_\omega }(r{\mkern 1mu} {{\text{e}}^{i\theta }}) - a}}} \right|}^\alpha }{\mkern 1mu} \frac{{{\text{d}}\theta }}{{2\pi }} - \log \frac{{|{c_{f_\omega ^*}}(0)|}}{{|{c_{{f_\omega }}}(a)|}}} \hfill \\ {} \hfill & { \leqslant \frac{1}{\alpha }\log \left( {\int_0^{2\pi } {{{\left| {\frac{{f_\omega ^*(r{\mkern 1mu} {{\text{e}}^{i\theta }})}}{{{f_\omega }(r{\mkern 1mu} {{\text{e}}^{i\theta }}) - a}}} \right|}^\alpha }} {\mkern 1mu} \frac{{{\text{d}}\theta }}{{2\pi }}} \right) - \log \frac{{|{c_{f_\omega ^*}}(0)|}}{{|{c_{{f_\omega }}}(a)|}}.} \hfill \\
\end{align*} Thus, by using Lemma 4.7 and the estimate of ![]() $\log|c_{f_\omega}(0)|$ as in the proof of Theorem 3.1, we obtain
$\log|c_{f_\omega}(0)|$ as in the proof of Theorem 3.1, we obtain
 \begin{align*}
N(r, 0, f^*_\omega)-N(r, a, f_\omega)&\le \frac1{\alpha}\,\log \left(C(\alpha)\left(\frac{R}{R-r}\right)^{\alpha}(2T(R, f_\omega-a)+\beta_1)^{\alpha} \right)+O(1) \\
&\le \frac1{\alpha}\,\log\left(C_1^\alpha C(\alpha) \left(\frac{R}{R-r}\right)^{\alpha}T^{\alpha}(R, f_\omega-a) \right) +O(1)\\
&\le \log T(R,f_\omega)+\log\frac{R}{R-r}+O(1),
\end{align*}
\begin{align*}
N(r, 0, f^*_\omega)-N(r, a, f_\omega)&\le \frac1{\alpha}\,\log \left(C(\alpha)\left(\frac{R}{R-r}\right)^{\alpha}(2T(R, f_\omega-a)+\beta_1)^{\alpha} \right)+O(1) \\
&\le \frac1{\alpha}\,\log\left(C_1^\alpha C(\alpha) \left(\frac{R}{R-r}\right)^{\alpha}T^{\alpha}(R, f_\omega-a) \right) +O(1)\\
&\le \log T(R,f_\omega)+\log\frac{R}{R-r}+O(1),
\end{align*} where β 1 is a random constant related to ![]() $\log|c_{f_\omega}(0)|$, and C 1 is an absolute constant.
$\log|c_{f_\omega}(0)|$, and C 1 is an absolute constant.
It follows from Lemma 4.4 and Lemma 5.1 that, for any r < R,
 \begin{align}
N(r, 0, f^*_\omega)&\le N(r, a, f_\omega)+\log\,\log \sigma(R,f_\omega)+\log\frac{R}{R-r}+O(1)\\
&\le N(r, a, f_\omega)+\log\,\log \sigma(R,f)+\log\,\log\,\log \sigma(R,f)+\log\frac{R}{R-r}+O(1).
\end{align}
\begin{align}
N(r, 0, f^*_\omega)&\le N(r, a, f_\omega)+\log\,\log \sigma(R,f_\omega)+\log\frac{R}{R-r}+O(1)\\
&\le N(r, a, f_\omega)+\log\,\log \sigma(R,f)+\log\,\log\,\log \sigma(R,f)+\log\frac{R}{R-r}+O(1).
\end{align} Applying Lemma 4.5 to the functions ![]() $F(r)=\log \sigma(r,f)$,
$F(r)=\log \sigma(r,f)$, ![]() $\phi(r)=r$,
$\phi(r)=r$,  $\psi(r)=\log^2r$ and
$\psi(r)=\log^2r$ and  $ R=r+\frac{r}{\psi(F(r))}$, we get a set
$ R=r+\frac{r}{\psi(F(r))}$, we get a set ![]() $E\subset[r_0,+\infty)$ of finite logarithmic measure, so that for all large r, say,
$E\subset[r_0,+\infty)$ of finite logarithmic measure, so that for all large r, say, ![]() $r \gt r_0$, and
$r \gt r_0$, and ![]() $r\not\in E$,
$r\not\in E$,
and
 \begin{equation*}\log \frac{R}{R-r} \le 2 \log\, \log\,\log\sigma(r, f)+\log 2.
\end{equation*}
\begin{equation*}\log \frac{R}{R-r} \le 2 \log\, \log\,\log\sigma(r, f)+\log 2.
\end{equation*}Thus, plugging the above two estimates to Equation (5.4) gives
for ![]() $r \gt r_0$ and
$r \gt r_0$ and ![]() $r \notin E$.
$r \notin E$.
It follows from Equations (5.3) and (5.5) that there is ![]() $r_1=r_1(a, r_0)$ such that
$r_1=r_1(a, r_0)$ such that
for ![]() $r \gt r_1$ and
$r \gt r_1$ and ![]() $r \notin E$.
$r \notin E$.
On the other hand, by Nevanlinna’s first main theorem, Lemma 4.4 and Lemma 5.1,
 \begin{align*}
N(r, a, f_\omega)& \le T(r, a, f_\omega)=T(r, f_\omega)+O(1)\\
& \le \log \sigma(r, f_\omega)+O(1)\\
&\le \log\sigma(r,f)+(1+o(1))\log\,\log\sigma(r,f).
\end{align*}
\begin{align*}
N(r, a, f_\omega)& \le T(r, a, f_\omega)=T(r, f_\omega)+O(1)\\
& \le \log \sigma(r, f_\omega)+O(1)\\
&\le \log\sigma(r,f)+(1+o(1))\log\,\log\sigma(r,f).
\end{align*}Combining this with Equation (5.6) completes the proof of the theorem.
5.3. Proof of Corollaries
Proof of Corollary 3.2
Since the function ![]() $x-(C/A\,\log x)^{1/B}$ is an increasing function for all large x and using Lemma 4.4, we have
$x-(C/A\,\log x)^{1/B}$ is an increasing function for all large x and using Lemma 4.4, we have
The rest is a straightforward consequence of Theorem 3.1.
Proof of Corollary 3.3
Let fω be a Gaussian entire function. By Equation (4.2) in the proof of Lemma 4.3, we have, for any τ > 0, r > 0,
 \begin{equation*}
\mathbb{E}\left({\rm e}^{\frac2{1+\tau}X_r}\right) \lt \infty.
\end{equation*}
\begin{equation*}
\mathbb{E}\left({\rm e}^{\frac2{1+\tau}X_r}\right) \lt \infty.
\end{equation*} Thus, ![]() $f_\omega \in \mathcal{Y}$ by choosing
$f_\omega \in \mathcal{Y}$ by choosing ![]() $A=2/(1+\tau)$ and B = 1. Applying Corollary 3.2 for
$A=2/(1+\tau)$ and B = 1. Applying Corollary 3.2 for ![]() $A=2/(1+\tau)$, B = 1 and
$A=2/(1+\tau)$, B = 1 and ![]() $C=1+\tau$, we can finish the proof of the corollary in this case.
$C=1+\tau$, we can finish the proof of the corollary in this case.
Similarly, if fω is a Steinhaus entire function or Rademacher entire function, we can choose ![]() $A=1/3(1+\tau)$, B = 1,
$A=1/3(1+\tau)$, B = 1, ![]() $C=1+\tau$ and
$C=1+\tau$ and ![]() $A=\epsilon\in(0, ({6}/({eC_0}))^6)$,
$A=\epsilon\in(0, ({6}/({eC_0}))^6)$, ![]() $B=1/6$,
$B=1/6$, ![]() $C=1+\tau$, respectively. This completes the proof of Corollary 3.3.
$C=1+\tau$, respectively. This completes the proof of Corollary 3.3.
Acknowledgements
The authors would like to thank Professors P. V. Filevych, I. Laine, A. Nishry and M. Sodin for their help during the preparation of the manuscript and the referee for her/his valuable suggestions and comments.
Funding Statement
Hui Li would like to thank the University of North Carolina Wilmington for its hospitality during her visit from 2019 to 2020 and was supported by China Scholarship Council (no. 201906470026) and National Natural Science Foundation of China (nos. 12071047 and 12301096). Jun Wang was supported by National Natural Science Foundation of China (no. 11771090). Xiao Yao was supported by National Natural Science Foundation of China (nos. 11901311 and 12371074) and National Key R&D Program of China (no. 2020YFA0713300).