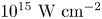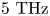1 Introduction
Very significant progress has recently been made at the Lawrence Livermore National Laboratory in the generation of high-energy-density conditions required for fusion energy gain. The August 2021 experiment, where a fusion yield of 1.3 MJ was obtained on the National Ignition Facility, confirmed that the Lawson criterion had been satisfied for the first time (Abu-Shawareb et al. Reference Abu-Shawareb2022; Zylstra et al. Reference Zylstra2022). Subsequently, in December 2022, more energy was released in fusion products than was delivered to target, with exquisite measurements of a 3.12 MJ yield (Abu-Shawareb et al. Reference Abu-Shawareb2024). These results mark a major milestone in the progress of inertial confinement fusion (ICF) research, which have reinvigorated worldwide efforts to explore routes to higher fusion gain for applications such as nuclear stockpile stewardship and inertial fusion energy.
One of the leading contenders for higher gains at current laser facility energy levels is the direct-drive ICF approach, principally due to the significantly larger energy coupling to the target that results in higher hydrodynamic efficiency of the implosions (Craxton et al. Reference Craxton2015; Campbell et al. Reference Campbell2021). A major problem for direct-drive ICF is the generation of highly energetic (hot) electrons which can prematurely raise the temperature of the fusion fuel and subsequently degrade the implosion performance. The source of these hot electrons are parametric instabilities that are driven as the laser beams propagate through the coronal plasma surrounding the target. When one of the decay products of a parametric instability is an electron plasma wave – as is the case for the two-plasmon decay (TPD) instability – hot electrons are generated (Vu et al. Reference Vu, DuBois, Myatt and Russell2012a,Reference Vu, DuBois, Russell and Myattb). The fraction of laser energy converted into hot electrons has to be limited to about $0.1\,\%$![]() for a successful implosion (Craxton et al. Reference Craxton2015).
for a successful implosion (Craxton et al. Reference Craxton2015).
Progress in the understanding of the impact of TPD on ICF experiments has been considerable in the recent years. The TPD instability is a three-wave instability in which an electromagnetic wave decays into a pair of electron plasma waves. Frequency matching between the waves is possible only in a spatially localised region near the quarter critical density (figure 1a). Hot electron generation typically occurs when the instability is in the so-called absolute regime in which wave amplitudes grow exponentially at a fixed point in space; saturation therefore only occurs through nonlinear processes, resulting in a plasma in a highly turbulent state, which accelerates the electrons stochastically (DuBois, Russell & Rose Reference DuBois, Russell and Rose1995; DuBois, Rose & Russell Reference DuBois, Rose and Russell1996; Vu et al. Reference Vu, DuBois, Myatt and Russell2012a,Reference Vu, DuBois, Russell and Myattb). When multiple laser beams are arranged in a cone (as is the case in real experimental facilities) they can cooperatively drive the instability by sharing a common plasma wave along the axis of symmetry (DuBois, Bezzerides & Rose Reference DuBois, Bezzerides and Rose1992) (see figure 1b). This results in substantial TPD growth even when the single beam thresholds are far from exceeded (Michel et al. Reference Michel, Maximov, Short, Delettrez, Edgell, Hu, Igumenshchev, Myatt, Solodov, Stoeckl, Yaakobi and Froula2013; Myatt et al. Reference Myatt, Zhang, Short, Maximov, Seka, Froula, Edgell, Michel, Igumenshchev, Hinkel, Michel and Moody2014). While the shared plasma wave along the cone axis is high-$k$![]() and grows convectively, it has been shown recently that multiple laser beams can drive a low-$k$
and grows convectively, it has been shown recently that multiple laser beams can drive a low-$k$![]() absolute mode cooperatively, with a lower threshold compared with the high-$k$
absolute mode cooperatively, with a lower threshold compared with the high-$k$![]() one (Zhang et al. Reference Zhang, Myatt, Short, Maximov, Vu, DuBois and Russell2014). Simulations and experiments of hot electrons driven by the multi-beam TPD instability show that the fraction of laser energy converted into hot electrons is near $0.1\,\%$
one (Zhang et al. Reference Zhang, Myatt, Short, Maximov, Vu, DuBois and Russell2014). Simulations and experiments of hot electrons driven by the multi-beam TPD instability show that the fraction of laser energy converted into hot electrons is near $0.1\,\%$![]() at overlapped intensities of about $10^{15}\,\text {W}\,\text {cm}^{-2}$
at overlapped intensities of about $10^{15}\,\text {W}\,\text {cm}^{-2}$![]() , rising to about $1\,\%$
, rising to about $1\,\%$![]() at $1.5 \times 10^{15}\,\text {W}\, \text {cm}^{-2}$
at $1.5 \times 10^{15}\,\text {W}\, \text {cm}^{-2}$![]() (Follett et al. Reference Follett, Myatt, Shaw, Michel, Solodov, Edgell, Yaakobi and Froula2017). In addition to generating hot electrons, TPD has been recently shown to be responsible for a large amount of anomalous absorption of laser energy (up to ${\simeq }30\,\%$
(Follett et al. Reference Follett, Myatt, Shaw, Michel, Solodov, Edgell, Yaakobi and Froula2017). In addition to generating hot electrons, TPD has been recently shown to be responsible for a large amount of anomalous absorption of laser energy (up to ${\simeq }30\,\%$![]() ) near the quarter critical density region (Seka et al. Reference Seka, Myatt, Short, Froula, Katz, Goncharov and Igumenshchev2014; Turnbull et al. Reference Turnbull, Maximov, Edgell, Seka, Follett, Palastro, Cao, Goncharov, Stoeckl and Froula2020). This is likely to be problematic as it increases the distance over which thermal energy needs to be conducted through in order to reach the ablation surface. Taming laser plasma instabilities at high intensities is therefore highly beneficial for direct-drive target designs (Paddock et al. Reference Paddock, Martin, Ruskov, Scott, Garbett, Haines, Zylstra, Aboushelbaya, Mayr, Spiers, Wang and Norreys2021, Reference Paddock, Martin, Ruskov, Scott, Garbett, Haines, Zylstra, Campbell, Collins, Craxton, Thomas, Goncharov, Aboushelbaya, Feng, von der Leyen, Ouatu, Spiers, Timmis, Wang and Norreys2022; Schmitt & Obenschain Reference Schmitt and Obenschain2023a,Reference Schmitt and Obenschainb; Trickey et al. Reference Trickey, Goncharov, Betti, Campbell, Collins and Follett2024).
) near the quarter critical density region (Seka et al. Reference Seka, Myatt, Short, Froula, Katz, Goncharov and Igumenshchev2014; Turnbull et al. Reference Turnbull, Maximov, Edgell, Seka, Follett, Palastro, Cao, Goncharov, Stoeckl and Froula2020). This is likely to be problematic as it increases the distance over which thermal energy needs to be conducted through in order to reach the ablation surface. Taming laser plasma instabilities at high intensities is therefore highly beneficial for direct-drive target designs (Paddock et al. Reference Paddock, Martin, Ruskov, Scott, Garbett, Haines, Zylstra, Aboushelbaya, Mayr, Spiers, Wang and Norreys2021, Reference Paddock, Martin, Ruskov, Scott, Garbett, Haines, Zylstra, Campbell, Collins, Craxton, Thomas, Goncharov, Aboushelbaya, Feng, von der Leyen, Ouatu, Spiers, Timmis, Wang and Norreys2022; Schmitt & Obenschain Reference Schmitt and Obenschain2023a,Reference Schmitt and Obenschainb; Trickey et al. Reference Trickey, Goncharov, Betti, Campbell, Collins and Follett2024).

Figure 1. (a) An illustration of an imploding ICF pellet, together with its surrounding coronal plasma. The plot shows an illustration of the density gradient in the corona and the region near the quarter critical density where the TPD instability is excited. (b) An illustration of a set of six laser beams arranged in a cone, as well as a wavevector diagram showing how, due to the cone geometry, a pair of electromagnetic waves ($\boldsymbol {k}_{0,1}$![]() and $\boldsymbol {k}_{0,2}$
and $\boldsymbol {k}_{0,2}$![]() ) can share a plasma wave along the cone axis ($\boldsymbol {K}_{\text {EPW},c}$
) can share a plasma wave along the cone axis ($\boldsymbol {K}_{\text {EPW},c}$![]() , in blue). The wavenumber matching condition due to the $j$
, in blue). The wavenumber matching condition due to the $j$![]() th beam in the cone is $\boldsymbol {k}_{0,j} = \boldsymbol {K}_{\text {EPW},c} + \boldsymbol {K}_{\text {EPW}j}$
th beam in the cone is $\boldsymbol {k}_{0,j} = \boldsymbol {K}_{\text {EPW},c} + \boldsymbol {K}_{\text {EPW}j}$![]() , where $\boldsymbol {K}_{\text {EPW}j}$
, where $\boldsymbol {K}_{\text {EPW}j}$![]() (in red) is the second plasma wave involved in TPD which is distinct for each beam.
(in red) is the second plasma wave involved in TPD which is distinct for each beam.
It has been known for some time that increasing the temporal bandwidth of the driving laser pulse significantly reduces the growth rates and increases the thresholds for the onset of parametric instabilities (Thomson & Karush Reference Thomson and Karush1974; Thomson Reference Thomson1975; Laval, Pellat & Pesme Reference Laval, Pellat and Pesme1976; Obenschain, Luhmann & Greiling Reference Obenschain, Luhmann and Greiling1976; Laval et al. Reference Laval, Pellat, Pesme, Ramani, Rosenbluth and Williams1977; Lu Reference Lu1988, Reference Lu1989; DuBois et al. Reference DuBois, Bezzerides and Rose1992; Pesme et al. Reference Pesme, Berger, Williams, Bourdier and Bortuzzo-Lesne1992). The Omega Laser Facility at the Laboratory for Laser Energetics is currently undergoing the FLUX upgrade (Dorrer, Hill & Zuegel Reference Dorrer, Hill and Zuegel2020; Dorrer et al. Reference Dorrer, Spilatro, Herman, Borger and Hill2021) in which fractional bandwidths of up to $\Delta \omega / \omega _0 = 1\unicode{x2013}2\,\%$![]() will be generated in order to experimentally test these ideas (Turnbull et al. Reference Turnbull, Boni, Colaitis, Dorrer, Edgell, Follett, Froula, Goncharov, Haberberger, Hill, Katz, Milder, Palastro, Shah, Shvydky, Solodov and Zuegel2023). Bandwidths of such order are expected to mitigate all laser plasma instabilities in Omega experiments (Follett et al. Reference Follett, Shaw, Myatt, Wen, Froula and Palastro2021; Bates et al. Reference Bates, Follett, Shaw, Obenschain, Myatt, Weaver, Wolford, Kehne, Myers and Kessler2023). Here $\Delta \omega$
will be generated in order to experimentally test these ideas (Turnbull et al. Reference Turnbull, Boni, Colaitis, Dorrer, Edgell, Follett, Froula, Goncharov, Haberberger, Hill, Katz, Milder, Palastro, Shah, Shvydky, Solodov and Zuegel2023). Bandwidths of such order are expected to mitigate all laser plasma instabilities in Omega experiments (Follett et al. Reference Follett, Shaw, Myatt, Wen, Froula and Palastro2021; Bates et al. Reference Bates, Follett, Shaw, Obenschain, Myatt, Weaver, Wolford, Kehne, Myers and Kessler2023). Here $\Delta \omega$![]() is the full width at half maximum of the laser power spectrum, and $\omega _0$
is the full width at half maximum of the laser power spectrum, and $\omega _0$![]() the frequency around which it is centred. The thresholds for the onset of parametric instabilities are typically set by inhomogeneity, and calculating them is of great importance. Follett et al. (Reference Follett, Shaw, Myatt, Dorrer, Froula and Palastro2019) recently compared the analytic model of Lu (Reference Lu1989) based on their effective Hamiltonian method against simulations utilising the Laser Plasma Simulation Environment (LPSE) code (Myatt et al. Reference Myatt, Follett, Shaw, Edgell, Froula, Igumenshchev and Goncharov2017), and found disagreements as large as a factor of ${\sim }20$
the frequency around which it is centred. The thresholds for the onset of parametric instabilities are typically set by inhomogeneity, and calculating them is of great importance. Follett et al. (Reference Follett, Shaw, Myatt, Dorrer, Froula and Palastro2019) recently compared the analytic model of Lu (Reference Lu1989) based on their effective Hamiltonian method against simulations utilising the Laser Plasma Simulation Environment (LPSE) code (Myatt et al. Reference Myatt, Follett, Shaw, Edgell, Froula, Igumenshchev and Goncharov2017), and found disagreements as large as a factor of ${\sim }20$![]() times in the case of the TPD threshold. Given the great promise of controlling laser plasma instabilities with laser bandwidth, it is crucial that theoretical models describe the results of experiments and simulations well, and in some of the most important cases (absolute TPD and Raman scattering) the reliability of current models is somewhat uncertain.
times in the case of the TPD threshold. Given the great promise of controlling laser plasma instabilities with laser bandwidth, it is crucial that theoretical models describe the results of experiments and simulations well, and in some of the most important cases (absolute TPD and Raman scattering) the reliability of current models is somewhat uncertain.
The broadband parametric instability problem suffers from complications similar to those involved in the study of turbulence. Laser bandwidth introduces fluctuations in the laser pulse electric field whose minute details are unknown or too difficult to describe. Hence a statistical approach to the problem must be pursued, only seeking to model some small set of averaged properties of the fluctuations – for example their spectra. But difficulties arise as one attempts to carry out statistical predictions about a system's evolution, and one is frequently faced with the statistical closure problem (Krommes Reference Krommes2002, Reference Krommes2015; Krommes & Parker Reference Krommes and Parker2019). Most statistical closures such as the commonly used random phase approximation (Nazarenko Reference Nazarenko2011; Connaughton, Nazarenko & Quinn Reference Connaughton, Nazarenko and Quinn2015) assume homogeneous statistics – meaning that the statistical properties of the fields of interest do not vary in space. This immediately causes trouble if one is interested in analysing convective growth or non-uniform plasmas – both of which are crucially important for understanding parametric instabilities (Michel Reference Michel2023). As discussed below it is also problematic even in a uniform plasma, when a zero-order perturbation is present.
Lately there has been some significant progress in moving beyond homogeneous statistical closures. For example, the quasi-linear interaction of inhomogeneous turbulence with plasma has been a long-standing problem where only recently a definitive theory was put forward (Dodin Reference Dodin2022). Similarly substantial developments in the theory of drift-wave turbulence interacting with zonal flows in tokamaks have been enabled by new insights about how to properly model the inhomogeneous statistics of the turbulent fields (Parker Reference Parker2014; Krommes Reference Krommes2015; Parker Reference Parker2016; Ruiz et al. Reference Ruiz, Parker, Shi and Dodin2016; Krommes & Parker Reference Krommes and Parker2019; Ruiz, Glinsky & Dodin Reference Ruiz, Glinsky and Dodin2019; Zhu Reference Zhu2020; Zhu, Zhou & Dodin Reference Zhu, Zhou and Dodin2020; Zhu & Dodin Reference Zhu and Dodin2021), improving upon initial work based on the traditional wave-kinetic approach (Smolyakov, Diamond & Shevchenko Reference Smolyakov, Diamond and Shevchenko2000; Trines et al. Reference Trines, Bingham, Silva, Mendonça, Shukla and Mori2005, Reference Trines, Bingham, Dunlop, Vaivads, Davies, Mendonça, Silva and Shukla2007, Reference Trines, Bingham, Silva, Mendonça, Shukla, Murphy, Dunlop, Davies, Bamford, Vaivads and Norreys2009). This drift-wave zonal-flow (DW-ZF) problem which is thought important in regulating turbulent transport in tokamaks, also bears resemblance to that of the broadband parametric instabilities in the sense that both seek to describe instabilities of some broad spectrum of waves – the drift-wave turbulence on the one hand, and the broad spectrum of electromagnetic waves on the other.
Here a statistical theory of the broadband TPD instability in a homogeneous plasma is presented for the first time, valid under laser fields with arbitrary power spectra. The same closure procedure as that used to study the DW-ZF problem is applied, namely the second-order cumulant expansion, also known as CE2, which allows for inhomogeneous statistics. Despite the fact that here one does not impose a density gradient, this is still crucial as inhomogeneity in statistics arises due the strong partially incoherent electromagnetic mode, i.e. the broadband laser pulse which is considered a zero-order perturbation (DuBois & Bezzerides Reference DuBois and Bezzerides1976; DuBois Reference DuBois2000). The CE2 closure captures the exact coupling of the stochastic fluctuations to the mean field, and ignores all cumulants of order ${\geq }3$![]() .Footnote 1 This implies that the stochastic fluctuations follow (jointly) normal distributions, and that they interact quasi-linearly with the mean field. The Weyl symbol calculus (McDonald Reference McDonald1988; Tracy et al. Reference Tracy, Brizard, Richardson and Kaufman2014; Dodin Reference Dodin2022) is employed in this article, which greatly facilitates the derivation of the equations governing the correlation functions. This new work is a generalisation of the approach of Santos, Silva & Bingham (Reference Santos, Silva and Bingham2007), which considered the broadband Raman scattering instability.Footnote 2 Their key insight was that extending the Wigner–Moyal formalism of quantum mechanics provides a natural statistical framework for describing laser pulse propagation inside the plasma, resulting in their generalised photon kinetics model (Santos & Silva Reference Santos and Silva2005; Silva & Bingham Reference Silva and Bingham2013). Generalised photon kinetics is, in essence, the Wigner–Moyal representation of the Klein–Gordon equation which describes laser pulse propagation in a plasma. They did not face a closure problem as they assumed the electrostatic fluctuations associated with electron plasma waves to be non-random. In the case of the TPD this is not possible, and one has to provide a statistical description of the plasma as well. It should be noted that were they to allow for stochasticity of the plasma, then they would effectively use the same closure as the one described here, and their model would have the same statistical content as the new one presented here.
.Footnote 1 This implies that the stochastic fluctuations follow (jointly) normal distributions, and that they interact quasi-linearly with the mean field. The Weyl symbol calculus (McDonald Reference McDonald1988; Tracy et al. Reference Tracy, Brizard, Richardson and Kaufman2014; Dodin Reference Dodin2022) is employed in this article, which greatly facilitates the derivation of the equations governing the correlation functions. This new work is a generalisation of the approach of Santos, Silva & Bingham (Reference Santos, Silva and Bingham2007), which considered the broadband Raman scattering instability.Footnote 2 Their key insight was that extending the Wigner–Moyal formalism of quantum mechanics provides a natural statistical framework for describing laser pulse propagation inside the plasma, resulting in their generalised photon kinetics model (Santos & Silva Reference Santos and Silva2005; Silva & Bingham Reference Silva and Bingham2013). Generalised photon kinetics is, in essence, the Wigner–Moyal representation of the Klein–Gordon equation which describes laser pulse propagation in a plasma. They did not face a closure problem as they assumed the electrostatic fluctuations associated with electron plasma waves to be non-random. In the case of the TPD this is not possible, and one has to provide a statistical description of the plasma as well. It should be noted that were they to allow for stochasticity of the plasma, then they would effectively use the same closure as the one described here, and their model would have the same statistical content as the new one presented here.
The paper is organised as follows. In § 2 the dispersion relation for the TPD instability is derived, one that is valid for laser fields with arbitrary power spectra in a uniform plasma. Emphasis is made on the details of the statistical closure. In § 3 the broadband dispersion relation is applied to some cases of interest – namely, it is shown that it reduces to the well-known dispersion relation for a single monochromatic beam, as well as multiple monochromatic non-interfering ones; following that, the effects of temporal incoherence on the instability as driven by a single broadband laser beam are considered; and lastly the extent to which a laser power spectrum consisting of multiple discrete spectral lines spread over a bandwidth $\Delta \omega$![]() approximates the instability-quenching properties of a continuous spectrum is explored. To conclude the article, a summary and a discussion of the new results are presented in § 4.
approximates the instability-quenching properties of a continuous spectrum is explored. To conclude the article, a summary and a discussion of the new results are presented in § 4.
2 Model
The TPD instability is a three-wave parametric instability in which an electromagnetic wave decays into a pair of plasma waves. Due to the Manley–Rowe relations, the frequencies and wavenumbers of the interacting waves must be matched (Michel Reference Michel2023). This localises the instability spatially near the quarter critical density – the point where the laser frequency is equal to twice the local plasma frequency (see figure 1a). Furthermore, since all of the waves are high in frequency, the ion motion can be neglected in the linear stage of the instability. The response of the electrons in the presence of the laser field can be analysed using non-relativistic fluid equations. Kinetic effects can be ignored provided $k \lambda _{De} \ll 1$![]() . Relativistic effects are negligible under conventional hot-spot ignition ICF where the laser intensity is of order $I_{{L}} \sim 10^{15} \, \text {W}\,\text {cm}^{-2}$
. Relativistic effects are negligible under conventional hot-spot ignition ICF where the laser intensity is of order $I_{{L}} \sim 10^{15} \, \text {W}\,\text {cm}^{-2}$![]() and the laser wavelength is $\lambda _{{L}} \sim 350 \ {\mu }\text {m}$
and the laser wavelength is $\lambda _{{L}} \sim 350 \ {\mu }\text {m}$![]() . This is because the quiver velocity of the electrons $\boldsymbol {v}_{\text {os}}(t,\boldsymbol {x}) = e \boldsymbol {A}_0/m_e$
. This is because the quiver velocity of the electrons $\boldsymbol {v}_{\text {os}}(t,\boldsymbol {x}) = e \boldsymbol {A}_0/m_e$![]() in the presence of an electromagentic wave described by the vector potential $\boldsymbol {A}_0(t,\boldsymbol {x})$
in the presence of an electromagentic wave described by the vector potential $\boldsymbol {A}_0(t,\boldsymbol {x})$![]() is $v_{\text {os}}/c \sim 0.01$
is $v_{\text {os}}/c \sim 0.01$![]() under such conditions. Finally, for the motion of the ions to be neglected, we need the amplitude of electrostatic waves to be low enough such that $\sqrt {W_e} \ll k \lambda _{De}$
under such conditions. Finally, for the motion of the ions to be neglected, we need the amplitude of electrostatic waves to be low enough such that $\sqrt {W_e} \ll k \lambda _{De}$![]() , where $W_e = \tfrac 12 \epsilon _0 |\boldsymbol {\nabla } \varphi |^2/n_e T_e$
, where $W_e = \tfrac 12 \epsilon _0 |\boldsymbol {\nabla } \varphi |^2/n_e T_e$![]() . This ensures that the nonlinear terms which couple the electron and ion motion are of higher order and negligible. So, the following ordering will be assumed from now on:
. This ensures that the nonlinear terms which couple the electron and ion motion are of higher order and negligible. So, the following ordering will be assumed from now on:

Assuming a purely electrostatic perturbation, linearising the continuity and momentum equations for the electron fluid gives (Liu & Rosenbluth Reference Liu and Rosenbluth1976; Simon et al. Reference Simon, Short, Williams and Dewandre1983)

Here $n(t,\boldsymbol {x})$![]() is the electron density perturbation normalised to the equilibrium density $n_{0}$
is the electron density perturbation normalised to the equilibrium density $n_{0}$![]() which will be assumed uniform for simplicity, $\psi (t,\boldsymbol {x})$
which will be assumed uniform for simplicity, $\psi (t,\boldsymbol {x})$![]() is the velocity potential of the electrons meaning $\boldsymbol {u} = \boldsymbol {\nabla } \psi$
is the velocity potential of the electrons meaning $\boldsymbol {u} = \boldsymbol {\nabla } \psi$![]() , where $\boldsymbol {u}$
, where $\boldsymbol {u}$![]() is the electron fluid velocity, $\omega _{\textrm {pe}}^{2} = e^2 n_0/\epsilon _0 m_e$
is the electron fluid velocity, $\omega _{\textrm {pe}}^{2} = e^2 n_0/\epsilon _0 m_e$![]() is the equilibrium plasma frequency and $v_{\textrm {th}e}^{2} = T_e/m_e$
is the equilibrium plasma frequency and $v_{\textrm {th}e}^{2} = T_e/m_e$![]() is the electron thermal velocity. Since the goal is to develop a description of the instability under broad-bandwidth (stochastic) laser fields, $n, \psi$
is the electron thermal velocity. Since the goal is to develop a description of the instability under broad-bandwidth (stochastic) laser fields, $n, \psi$![]() and $\boldsymbol {v}_{\textrm {os}}$
and $\boldsymbol {v}_{\textrm {os}}$![]() are assumed to be random variables.
are assumed to be random variables.
The wave equation governing the electron plasma waves is
where the right-hand side contains the TPD driving terms. One can express the driving terms through the Wigner functions describing the correlations between the pump field $\boldsymbol {v}_{\textrm {os}}$![]() and the plasma waves, as has been done in the case of inhomogeneous Navier–Stokes turbulence (Tsiolis, Zhou & Dodin Reference Tsiolis, Zhou and Dodin2020) (see Appendix B):
and the plasma waves, as has been done in the case of inhomogeneous Navier–Stokes turbulence (Tsiolis, Zhou & Dodin Reference Tsiolis, Zhou and Dodin2020) (see Appendix B):
Here ${\boldsymbol{\mathsf{W}}}_{\psi \boldsymbol {v}}(\boldsymbol {x},\boldsymbol {k}) = \mathscr {W} [ \left | \psi \right \rangle \left \langle \boldsymbol {v}_{\textrm {os}} \right | ]$![]() , with $\mathscr {W}$
, with $\mathscr {W}$![]() being the Wigner transform, and the bra-ket notation is used as in Dodin (Reference Dodin2022); ${\boldsymbol{\mathsf{W}}}_{\psi \boldsymbol {v}}^{\intercal }$
being the Wigner transform, and the bra-ket notation is used as in Dodin (Reference Dodin2022); ${\boldsymbol{\mathsf{W}}}_{\psi \boldsymbol {v}}^{\intercal }$![]() denotes the transpose of ${\boldsymbol{\mathsf{W}}}_{\psi \boldsymbol {v}}$
denotes the transpose of ${\boldsymbol{\mathsf{W}}}_{\psi \boldsymbol {v}}$![]() . The Wigner transform $\mathscr {W}[\hat {A}]$
. The Wigner transform $\mathscr {W}[\hat {A}]$![]() of some generic operator $\hat {A}$
of some generic operator $\hat {A}$![]() is called the Weyl symbol of $\hat {A}$
is called the Weyl symbol of $\hat {A}$![]() , and is defined as
, and is defined as
The Moyal star product $\star$![]() between two symbols is defined as $\textsf {A} \star \textsf {B} \doteq \mathscr {W}[\hat {A} \hat {B}]$
between two symbols is defined as $\textsf {A} \star \textsf {B} \doteq \mathscr {W}[\hat {A} \hat {B}]$![]() ; it is given by $\textsf {A}(\boldsymbol {x},\boldsymbol {k}) \star \textsf {B}(\boldsymbol {x},\boldsymbol {k}) = \textsf {A}(\boldsymbol {x},\boldsymbol {k})\, \textrm {e}^{\textsf {i} \hat {\mathcal {P}}/2} \textsf {B}(\boldsymbol {x},\boldsymbol {k})$
; it is given by $\textsf {A}(\boldsymbol {x},\boldsymbol {k}) \star \textsf {B}(\boldsymbol {x},\boldsymbol {k}) = \textsf {A}(\boldsymbol {x},\boldsymbol {k})\, \textrm {e}^{\textsf {i} \hat {\mathcal {P}}/2} \textsf {B}(\boldsymbol {x},\boldsymbol {k})$![]() , with $\hat {\mathcal {P}}$
, with $\hat {\mathcal {P}}$![]() being the Poisson bracket $\hat {\mathcal {P}} = \overset {{\scriptscriptstyle \leftarrow }}{\partial}_{\boldsymbol {x}} \boldsymbol {{\cdot }} \overset {{\scriptscriptstyle \rightarrow }}{\partial}_{\boldsymbol {k}} - \overset {{\scriptscriptstyle \leftarrow }}{\partial}_{\boldsymbol {k}} \boldsymbol {{\cdot }} \overset {{\scriptscriptstyle \rightarrow }}{\partial}_{\boldsymbol {x}}$
being the Poisson bracket $\hat {\mathcal {P}} = \overset {{\scriptscriptstyle \leftarrow }}{\partial}_{\boldsymbol {x}} \boldsymbol {{\cdot }} \overset {{\scriptscriptstyle \rightarrow }}{\partial}_{\boldsymbol {k}} - \overset {{\scriptscriptstyle \leftarrow }}{\partial}_{\boldsymbol {k}} \boldsymbol {{\cdot }} \overset {{\scriptscriptstyle \rightarrow }}{\partial}_{\boldsymbol {x}}$![]() , and the arrows indicating the directions in which the derivatives are acting. Element-wise application of the Moyal star product $\star$
, and the arrows indicating the directions in which the derivatives are acting. Element-wise application of the Moyal star product $\star$![]() and the usual matrix multiplication rules are assumed, meaning that for any two matrix symbols ${\boldsymbol{\mathsf{A}}}$
and the usual matrix multiplication rules are assumed, meaning that for any two matrix symbols ${\boldsymbol{\mathsf{A}}}$![]() and ${\boldsymbol{\mathsf{B}}}$
and ${\boldsymbol{\mathsf{B}}}$![]() one applies the Moyal product as follows: $( {\boldsymbol{\mathsf{A}}} \star {\boldsymbol{\mathsf{B}}} )_{ij} = \sum _k ({\boldsymbol{\mathsf{A}}})_{ik} \star ({\boldsymbol{\mathsf{B}}})_{kj}$
one applies the Moyal product as follows: $( {\boldsymbol{\mathsf{A}}} \star {\boldsymbol{\mathsf{B}}} )_{ij} = \sum _k ({\boldsymbol{\mathsf{A}}})_{ik} \star ({\boldsymbol{\mathsf{B}}})_{kj}$![]() . A brief introduction to the Weyl symbol calculus can be found in Appendix A. With these definitions, one can see that the quantity ${\boldsymbol{\mathsf{W}}}_{\psi \boldsymbol {v}}(\boldsymbol {x},\boldsymbol {k})$
. A brief introduction to the Weyl symbol calculus can be found in Appendix A. With these definitions, one can see that the quantity ${\boldsymbol{\mathsf{W}}}_{\psi \boldsymbol {v}}(\boldsymbol {x},\boldsymbol {k})$![]() is given by
is given by
After ensemble averaging, ${\boldsymbol{\mathsf{W}}}_{\psi \boldsymbol {v}}(\boldsymbol {x},\boldsymbol {k})$![]() will represent the correlations of the laser pulse field $\boldsymbol {v}_{\textrm {os}}$
will represent the correlations of the laser pulse field $\boldsymbol {v}_{\textrm {os}}$![]() with the the velocity potential $\psi$
with the the velocity potential $\psi$![]() . The second driving term is rewritten in a completely analogous manner leading to the quantity ${\boldsymbol{\mathsf{W}}}_{n \boldsymbol {v}}(\boldsymbol {x},\boldsymbol {k})$
. The second driving term is rewritten in a completely analogous manner leading to the quantity ${\boldsymbol{\mathsf{W}}}_{n \boldsymbol {v}}(\boldsymbol {x},\boldsymbol {k})$![]() which will represent the correlations between $\boldsymbol {v}_{\textrm {os}}$
which will represent the correlations between $\boldsymbol {v}_{\textrm {os}}$![]() and the density perturbation $n$
and the density perturbation $n$![]() .
.
Taking the Fourier transform of the wave equation, and ensemble averaging, leads to
where $D_e(\varOmega, \boldsymbol {K}) = \varOmega ^2 - \omega _{\textrm {pe}}^{2} - 3 v_{\textrm {th}e}^{2} K^2 = \varOmega ^2 - \omega _{e\boldsymbol {K}}^2$![]() is the dispersion function for the electron plasma waves, and the Fourier transformed quantities are denoted as follows: $\mathring {n}(\varOmega,\boldsymbol {K}) = \int \textrm {d} t \textrm {d} \boldsymbol {x} \, n(t,\boldsymbol {x}) \,\textrm {e}^{\textsf {i} \varOmega t - \textsf {i} \boldsymbol {K} \boldsymbol {{\cdot }} \boldsymbol {x}}$
is the dispersion function for the electron plasma waves, and the Fourier transformed quantities are denoted as follows: $\mathring {n}(\varOmega,\boldsymbol {K}) = \int \textrm {d} t \textrm {d} \boldsymbol {x} \, n(t,\boldsymbol {x}) \,\textrm {e}^{\textsf {i} \varOmega t - \textsf {i} \boldsymbol {K} \boldsymbol {{\cdot }} \boldsymbol {x}}$![]() . The overline represents ensemble averaging. Here one now faces the closure problem – to calculate the mean field $\bar {n}$
. The overline represents ensemble averaging. Here one now faces the closure problem – to calculate the mean field $\bar {n}$![]() , knowledge is needed of second-order quantities: $\bar {{\boldsymbol{\mathsf{W}}}}_{\psi \boldsymbol {v}}$
, knowledge is needed of second-order quantities: $\bar {{\boldsymbol{\mathsf{W}}}}_{\psi \boldsymbol {v}}$![]() and $\bar {{\boldsymbol{\mathsf{W}}}}_{n \boldsymbol {v}}$
and $\bar {{\boldsymbol{\mathsf{W}}}}_{n \boldsymbol {v}}$![]() . The powerful toolbox of the Weyl symbol calculus is now applied to derive and solve the equations governing these quantities.
. The powerful toolbox of the Weyl symbol calculus is now applied to derive and solve the equations governing these quantities.
The basic idea is as follows: if one writes down the governing equations of the system in Schrödinger form, then all of the second-order correlation functions describing the system will be governed by the Wigner–Moyal equation (see Appendix A). A similar procedure was carried out for the case of inhomogeneous fluid turbulence by Tsiolis et al. (Reference Tsiolis, Zhou and Dodin2020). The TPD equations (2.2) are first order in time and are readily put in Schrödinger form. The vector potential $\boldsymbol {A}_{0}$![]() describing the propagation of an electromagnetic mode in a plasma obeys a Klein–Gordon equation and therefore $( \partial _t^2 - c^2 \nabla ^2 + \omega _{\textrm {pe}}^{2} ) \boldsymbol {v}_{\textrm {os}} = 0$
describing the propagation of an electromagnetic mode in a plasma obeys a Klein–Gordon equation and therefore $( \partial _t^2 - c^2 \nabla ^2 + \omega _{\textrm {pe}}^{2} ) \boldsymbol {v}_{\textrm {os}} = 0$![]() , since $\boldsymbol {v}_{\textrm {os}}$
, since $\boldsymbol {v}_{\textrm {os}}$![]() differs from $\boldsymbol {A}_0$
differs from $\boldsymbol {A}_0$![]() only by a constant factor (Kruer Reference Kruer2019; Michel Reference Michel2023). There are no source or sink terms in this equation since the linear stage of the instability is considered and hence pump depletion is ignored. This second-order-in-time equation can be decomposed into two first-order ones by defining the auxiliary fields $\boldsymbol {\phi }, \boldsymbol {\chi } = \frac 12 ( \boldsymbol {v}_{\textrm {os}} \pm \textsf {i} \omega _{\textrm {pe}}^{-1} \partial _t \boldsymbol {v}_{\textrm {os}} )$
only by a constant factor (Kruer Reference Kruer2019; Michel Reference Michel2023). There are no source or sink terms in this equation since the linear stage of the instability is considered and hence pump depletion is ignored. This second-order-in-time equation can be decomposed into two first-order ones by defining the auxiliary fields $\boldsymbol {\phi }, \boldsymbol {\chi } = \frac 12 ( \boldsymbol {v}_{\textrm {os}} \pm \textsf {i} \omega _{\textrm {pe}}^{-1} \partial _t \boldsymbol {v}_{\textrm {os}} )$![]() (Santos & Silva Reference Santos and Silva2005).
(Santos & Silva Reference Santos and Silva2005).
The system of the decomposed Klein–Gordon equation, together with the two TPD equations are then written as a Schrödinger equation, $\textsf {i} \partial _t \boldsymbol {\varPsi } = \widehat{\boldsymbol{\mathsf{H}}} \boldsymbol {\varPsi }$![]() , with the following matrix Hamiltonian and state vector:
, with the following matrix Hamiltonian and state vector:

where $\boldsymbol {\eta } \doteq \boldsymbol {\nabla } n$![]() and $\boldsymbol {u} \doteq \boldsymbol {\nabla } \psi$
and $\boldsymbol {u} \doteq \boldsymbol {\nabla } \psi$![]() . The Wigner matrix ${\boldsymbol{\mathsf{W}}} = \mathscr {W} [ \left | \boldsymbol {\varPsi } \right \rangle \left \langle \boldsymbol {\varPsi } \right | ]$
. The Wigner matrix ${\boldsymbol{\mathsf{W}}} = \mathscr {W} [ \left | \boldsymbol {\varPsi } \right \rangle \left \langle \boldsymbol {\varPsi } \right | ]$![]() satisfies the Wigner–Moyal equation:
satisfies the Wigner–Moyal equation:
with ${\boldsymbol{\mathsf{H}}} \doteq \mathscr {W}[\widehat{\boldsymbol{\mathsf{H}}}]$![]() being the symbol of the matrix Hamiltonian. It is useful to write out the contents of the Wigner matrix and the symbol of the matrix Hamiltonian explicitly:
being the symbol of the matrix Hamiltonian. It is useful to write out the contents of the Wigner matrix and the symbol of the matrix Hamiltonian explicitly:


where the quantities which have a vector index in the second slot such as ${\boldsymbol{\mathsf{W}}}_{n \boldsymbol {\phi }}$![]() are row vectors; similarly ${\boldsymbol{\mathsf{W}}}_{\boldsymbol {\phi }n}$
are row vectors; similarly ${\boldsymbol{\mathsf{W}}}_{\boldsymbol {\phi }n}$![]() is a column vector; and quantities such as ${\boldsymbol{\mathsf{W}}}_{\boldsymbol {\phi } \boldsymbol {\phi }}$
is a column vector; and quantities such as ${\boldsymbol{\mathsf{W}}}_{\boldsymbol {\phi } \boldsymbol {\phi }}$![]() with two vector indices are matrices.
with two vector indices are matrices.
Note that the relevant Wigner functions in (2.7) are related to the components of this Wigner matrix above through ${\boldsymbol{\mathsf{W}}}_{n \boldsymbol {v}} = {\boldsymbol{\mathsf{W}}}_{n \boldsymbol {\phi }} + {\boldsymbol{\mathsf{W}}}_{n \boldsymbol {\chi }}$![]() and ${\boldsymbol{\mathsf{W}}}_{\psi \boldsymbol {v}} = {\boldsymbol{\mathsf{W}}}_{\psi \boldsymbol {\phi }} + {\boldsymbol{\mathsf{W}}}_{\psi \boldsymbol {\chi }}$
and ${\boldsymbol{\mathsf{W}}}_{\psi \boldsymbol {v}} = {\boldsymbol{\mathsf{W}}}_{\psi \boldsymbol {\phi }} + {\boldsymbol{\mathsf{W}}}_{\psi \boldsymbol {\chi }}$![]() , and so one needs only to compute the evolution equations of the upper right $2\times 2$
, and so one needs only to compute the evolution equations of the upper right $2\times 2$![]() corner of ${\boldsymbol{\mathsf{W}}}$
corner of ${\boldsymbol{\mathsf{W}}}$![]() . Doing so and taking sums and differences of the equations in the resulting system, one gets equations for ${\boldsymbol{\mathsf{W}}}_{n \boldsymbol {v}}$
. Doing so and taking sums and differences of the equations in the resulting system, one gets equations for ${\boldsymbol{\mathsf{W}}}_{n \boldsymbol {v}}$![]() and ${\boldsymbol{\mathsf{W}}}_{\psi \boldsymbol {v}}$
and ${\boldsymbol{\mathsf{W}}}_{\psi \boldsymbol {v}}$![]() , which upon ensemble averaging results in the following system:
, which upon ensemble averaging results in the following system:

Here $\omega _{\boldsymbol {k}}^2 = \omega _{\textrm {pe}}^{2} + k^2 c^2$![]() is the electromagnetic wave frequency. All of the ${\boldsymbol{\mathsf{B}}}$
is the electromagnetic wave frequency. All of the ${\boldsymbol{\mathsf{B}}}$![]() quantities are not of interest and simply facilitate the calculation; they are defined as follows: ${\boldsymbol{\mathsf{B}}}_{n \boldsymbol {v}} \doteq {\boldsymbol{\mathsf{W}}}_{n \boldsymbol {\phi }} - {\boldsymbol{\mathsf{W}}}_{n \boldsymbol {\chi }}, {\boldsymbol{\mathsf{B}}}_{\psi \boldsymbol {v}} \doteq {\boldsymbol{\mathsf{W}}}_{\psi \boldsymbol {\phi }} - {\boldsymbol{\mathsf{W}}}_{\psi \boldsymbol {\chi }}, {\boldsymbol{\mathsf{B}}}_{\boldsymbol {v} \boldsymbol {v}} \doteq {\boldsymbol{\mathsf{W}}}_{\boldsymbol {\phi } \boldsymbol {\phi }} + {\boldsymbol{\mathsf{W}}}_{\boldsymbol {\chi } \boldsymbol {\phi }} - {\boldsymbol{\mathsf{W}}}_{\boldsymbol {\phi } \boldsymbol {\chi }} - {\boldsymbol{\mathsf{W}}}_{\boldsymbol {\chi } \boldsymbol {\chi }}$
quantities are not of interest and simply facilitate the calculation; they are defined as follows: ${\boldsymbol{\mathsf{B}}}_{n \boldsymbol {v}} \doteq {\boldsymbol{\mathsf{W}}}_{n \boldsymbol {\phi }} - {\boldsymbol{\mathsf{W}}}_{n \boldsymbol {\chi }}, {\boldsymbol{\mathsf{B}}}_{\psi \boldsymbol {v}} \doteq {\boldsymbol{\mathsf{W}}}_{\psi \boldsymbol {\phi }} - {\boldsymbol{\mathsf{W}}}_{\psi \boldsymbol {\chi }}, {\boldsymbol{\mathsf{B}}}_{\boldsymbol {v} \boldsymbol {v}} \doteq {\boldsymbol{\mathsf{W}}}_{\boldsymbol {\phi } \boldsymbol {\phi }} + {\boldsymbol{\mathsf{W}}}_{\boldsymbol {\chi } \boldsymbol {\phi }} - {\boldsymbol{\mathsf{W}}}_{\boldsymbol {\phi } \boldsymbol {\chi }} - {\boldsymbol{\mathsf{W}}}_{\boldsymbol {\chi } \boldsymbol {\chi }}$![]() . Here, the fact that ${\boldsymbol{\mathsf{W}}}_{\boldsymbol {v} \boldsymbol {v}} = {\boldsymbol{\mathsf{W}}}_{\boldsymbol {\phi } \boldsymbol {\phi }} + {\boldsymbol{\mathsf{W}}}_{\boldsymbol {\chi } \boldsymbol {\phi }} + {\boldsymbol{\mathsf{W}}}_{\boldsymbol {\phi } \boldsymbol {\chi }} + {\boldsymbol{\mathsf{W}}}_{\boldsymbol {\chi } \boldsymbol {\chi }}$
. Here, the fact that ${\boldsymbol{\mathsf{W}}}_{\boldsymbol {v} \boldsymbol {v}} = {\boldsymbol{\mathsf{W}}}_{\boldsymbol {\phi } \boldsymbol {\phi }} + {\boldsymbol{\mathsf{W}}}_{\boldsymbol {\chi } \boldsymbol {\phi }} + {\boldsymbol{\mathsf{W}}}_{\boldsymbol {\phi } \boldsymbol {\chi }} + {\boldsymbol{\mathsf{W}}}_{\boldsymbol {\chi } \boldsymbol {\chi }}$![]() is used, which follows from the linearity of the Wigner transform.
is used, which follows from the linearity of the Wigner transform.
The crucial step, which is the essence of the CE2 closure, is the splitting of the average of the product, into the product of the averages, for the third-order quantities: $\overline {\boldsymbol {\eta }^{\top } \star {\boldsymbol{\mathsf{W}}}} = \bar {\boldsymbol {\eta }}^{\top } \star \bar {{\boldsymbol{\mathsf{W}}}}$![]() . This effectively assumes the third-order cumulant $\overline { \tilde {\boldsymbol {\eta }}^{\top } \star \widetilde {{\boldsymbol{\mathsf{W}}}}}$
. This effectively assumes the third-order cumulant $\overline { \tilde {\boldsymbol {\eta }}^{\top } \star \widetilde {{\boldsymbol{\mathsf{W}}}}}$![]() to be negligible (the tilde denotes the fluctuating part of the quantity) (Krommes & Parker Reference Krommes and Parker2019). It is exactly zero for fields obeying jointly normal (Gaussian multivariate) statistics. In contrast to turbulence, here this assumption is easier to justify. One does not expect the interactions between the fluctuations to be of interest, which is what is being neglected when one discards higher-order cumulants and assumes Gaussianity. They would not be of interest since such effects are what leads to fluctuation intermittency, or are responsible for the typical turbulent energy cascades, neither of which is assumed here to be of relevance in the linear stage of the instability. The fluctuations in the electric field of the laser pulse are prescribed in a sense (their power spectrum $\bar {{\boldsymbol{\mathsf{W}}}}_{\boldsymbol {v} \boldsymbol {v}}$
to be negligible (the tilde denotes the fluctuating part of the quantity) (Krommes & Parker Reference Krommes and Parker2019). It is exactly zero for fields obeying jointly normal (Gaussian multivariate) statistics. In contrast to turbulence, here this assumption is easier to justify. One does not expect the interactions between the fluctuations to be of interest, which is what is being neglected when one discards higher-order cumulants and assumes Gaussianity. They would not be of interest since such effects are what leads to fluctuation intermittency, or are responsible for the typical turbulent energy cascades, neither of which is assumed here to be of relevance in the linear stage of the instability. The fluctuations in the electric field of the laser pulse are prescribed in a sense (their power spectrum $\bar {{\boldsymbol{\mathsf{W}}}}_{\boldsymbol {v} \boldsymbol {v}}$![]() is given), and are expected to be normal for both temporally incoherent pulses (Goodman Reference Goodman2015), as well as transversely incoherent fields produced by a random phase plate for example (Rose & DuBois Reference Rose and DuBois1993; Garnier Reference Garnier1999), where in both cases this is a consequence of the central limit theorem. Hence the driving field $\boldsymbol {v}_{\textrm {os}}$
is given), and are expected to be normal for both temporally incoherent pulses (Goodman Reference Goodman2015), as well as transversely incoherent fields produced by a random phase plate for example (Rose & DuBois Reference Rose and DuBois1993; Garnier Reference Garnier1999), where in both cases this is a consequence of the central limit theorem. Hence the driving field $\boldsymbol {v}_{\textrm {os}}$![]() is safely assumed a Gaussian random process. It should be noted that the Wigner–Moyal formalism is also very useful in deriving more sophisticated closures such as the quasi-normal one as shown by Ruiz et al. (Reference Ruiz, Glinsky and Dodin2019).
is safely assumed a Gaussian random process. It should be noted that the Wigner–Moyal formalism is also very useful in deriving more sophisticated closures such as the quasi-normal one as shown by Ruiz et al. (Reference Ruiz, Glinsky and Dodin2019).
The Wigner function is bilinear and therefore ${\boldsymbol{\mathsf{B}}}_{\boldsymbol {v} \boldsymbol {v}} = {\boldsymbol{\mathsf{W}}}_{(\boldsymbol {\phi } + \boldsymbol {\chi )}(\boldsymbol {\phi } - \boldsymbol {\chi )}}$![]() . If the laser field $\boldsymbol {v}_{\textrm {os}}$
. If the laser field $\boldsymbol {v}_{\textrm {os}}$![]() is statistically stationary, it is shown in Appendix C that the ensemble-averaged Wigner function $\bar {{\boldsymbol{\mathsf{W}}}}_{\boldsymbol {v}\boldsymbol {v}}$
is statistically stationary, it is shown in Appendix C that the ensemble-averaged Wigner function $\bar {{\boldsymbol{\mathsf{W}}}}_{\boldsymbol {v}\boldsymbol {v}}$![]() and the associated quantity $\bar {{\boldsymbol{\mathsf{B}}}}_{\boldsymbol {v} \boldsymbol {v}}$
and the associated quantity $\bar {{\boldsymbol{\mathsf{B}}}}_{\boldsymbol {v} \boldsymbol {v}}$![]() are related as follows: $\bar {{\boldsymbol{\mathsf{B}}}}_{\boldsymbol {v} \boldsymbol {v}}(\boldsymbol {k}) = \omega _{\textrm {pe}}^{-1} \omega _{\boldsymbol {k}} \bar {{\boldsymbol{\mathsf{W}}}}_{\boldsymbol {v}\boldsymbol {v}}(\boldsymbol {k})$
are related as follows: $\bar {{\boldsymbol{\mathsf{B}}}}_{\boldsymbol {v} \boldsymbol {v}}(\boldsymbol {k}) = \omega _{\textrm {pe}}^{-1} \omega _{\boldsymbol {k}} \bar {{\boldsymbol{\mathsf{W}}}}_{\boldsymbol {v}\boldsymbol {v}}(\boldsymbol {k})$![]() . This is an important step in the derivation as it makes all symbol products in (2.12) have one of the quantities being a function of $\boldsymbol {x}$
. This is an important step in the derivation as it makes all symbol products in (2.12) have one of the quantities being a function of $\boldsymbol {x}$![]() or $\boldsymbol {k}$
or $\boldsymbol {k}$![]() only. Taking the Fourier transform of the system results in
only. Taking the Fourier transform of the system results in

where the quantities with superscripts $\pm$![]() are evaluated at $\boldsymbol {k}_{\pm } = \boldsymbol {k} \pm \tfrac 12 \boldsymbol {K}, \mathring {\bar {\boldsymbol {\eta }}}$
are evaluated at $\boldsymbol {k}_{\pm } = \boldsymbol {k} \pm \tfrac 12 \boldsymbol {K}, \mathring {\bar {\boldsymbol {\eta }}}$![]() and $\mathring {\bar {\boldsymbol {u}}}$
and $\mathring {\bar {\boldsymbol {u}}}$![]() are functions of $\boldsymbol {K}$
are functions of $\boldsymbol {K}$![]() only (the Fourier image of $\boldsymbol {x}$
only (the Fourier image of $\boldsymbol {x}$![]() ) and all other quantities are functions of both $\boldsymbol {k}$
) and all other quantities are functions of both $\boldsymbol {k}$![]() and $\boldsymbol {K}$
and $\boldsymbol {K}$![]() .
.
In order to keep the model self-consistent under the assumed ordering, the growth rate of the instability can be calculated only up to order $v_{\textrm {os}}/c$![]() and higher-order terms need to be discarded (Kruer Reference Kruer2019). The way this works in the present case is as follows. To close the system (2.13), $\mathring {\boldsymbol {u}}$
and higher-order terms need to be discarded (Kruer Reference Kruer2019). The way this works in the present case is as follows. To close the system (2.13), $\mathring {\boldsymbol {u}}$![]() can be expressed in terms of $\mathring {\boldsymbol {\eta }}$
can be expressed in terms of $\mathring {\boldsymbol {\eta }}$![]() and $\mathring {{\boldsymbol{\mathsf{W}}}}_{\psi \boldsymbol {v}}$
and $\mathring {{\boldsymbol{\mathsf{W}}}}_{\psi \boldsymbol {v}}$![]() through the second equation in the TPD system (2.2). Then the equations containing $\mathring {\boldsymbol {u}}$
through the second equation in the TPD system (2.2). Then the equations containing $\mathring {\boldsymbol {u}}$![]() will involve terms which are $\propto \mathring {{\boldsymbol{\mathsf{W}}}}_{\psi \boldsymbol {v}} \mathring {{\boldsymbol{\mathsf{W}}}}_{\boldsymbol {v} \boldsymbol {v}}$
will involve terms which are $\propto \mathring {{\boldsymbol{\mathsf{W}}}}_{\psi \boldsymbol {v}} \mathring {{\boldsymbol{\mathsf{W}}}}_{\boldsymbol {v} \boldsymbol {v}}$![]() . As in the standard derivation in Kruer (Reference Kruer2019), this introduces terms of order $(v_{\textrm {os}}/c)^2 \ll 1$
. As in the standard derivation in Kruer (Reference Kruer2019), this introduces terms of order $(v_{\textrm {os}}/c)^2 \ll 1$![]() in the growth rate which are ignored, and therefore in (2.13) one uses the approximation $\mathring {\boldsymbol {u}} = \textsf {i} (\varOmega /K^2) \mathring {\boldsymbol {\eta }}$
in the growth rate which are ignored, and therefore in (2.13) one uses the approximation $\mathring {\boldsymbol {u}} = \textsf {i} (\varOmega /K^2) \mathring {\boldsymbol {\eta }}$![]() .
.
Solving the system for the quantities of interest, $\mathring {\bar {{\boldsymbol{\mathsf{W}}}}}_{\psi \boldsymbol {v}}$![]() and $\mathring {\bar {{\boldsymbol{\mathsf{W}}}}}_{n \boldsymbol {v}}$
and $\mathring {\bar {{\boldsymbol{\mathsf{W}}}}}_{n \boldsymbol {v}}$![]() , in terms of the laser field $\bar {{\boldsymbol{\mathsf{W}}}}_{\boldsymbol {v} \boldsymbol {v}}$
, in terms of the laser field $\bar {{\boldsymbol{\mathsf{W}}}}_{\boldsymbol {v} \boldsymbol {v}}$![]() and substituting them into (2.7) results in the homogeneous broadband TPD dispersion relation:
and substituting them into (2.7) results in the homogeneous broadband TPD dispersion relation:
where $\varOmega _- = \omega _{\boldsymbol {k}} - \varOmega$![]() , the integral is to be taken along the Landau contour, $\boldsymbol {k}_- \doteq \boldsymbol {k} - \boldsymbol {K}$
, the integral is to be taken along the Landau contour, $\boldsymbol {k}_- \doteq \boldsymbol {k} - \boldsymbol {K}$![]() has been redefined and the colon denotes double matrix contraction.Footnote 3 This is the main result of the new model. For a statistically stationary random process, the two-point correlation function and the power spectrum form a Fourier pair (Wiener–Khinchin theorem) (Goodman Reference Goodman2015). So one can notice that the expression has a familiar form and a simple physical interpretation: the broadband dispersion relation is the monochromatic one integrated over the laser field power spectrum $\bar {{\boldsymbol{\mathsf{W}}}}_{\boldsymbol {v} \boldsymbol {v}} (\boldsymbol {k})$
has been redefined and the colon denotes double matrix contraction.Footnote 3 This is the main result of the new model. For a statistically stationary random process, the two-point correlation function and the power spectrum form a Fourier pair (Wiener–Khinchin theorem) (Goodman Reference Goodman2015). So one can notice that the expression has a familiar form and a simple physical interpretation: the broadband dispersion relation is the monochromatic one integrated over the laser field power spectrum $\bar {{\boldsymbol{\mathsf{W}}}}_{\boldsymbol {v} \boldsymbol {v}} (\boldsymbol {k})$![]() , given by
, given by
This dispersion relation allows one to study the homogeneous TPD under laser fields with arbitrary power spectra.
3 Applications
3.1 Monochromatic beams
The broadband TPD dispersion relation (2.14) reduces to the well-known result for a monochromatic plane wave. Consider a pump of the form $\boldsymbol {v}_{\textrm {os}}(t,\boldsymbol {x}) = \tfrac 12 v_{\textrm {os}} \boldsymbol {\sigma } \,\textrm {e}^{\textsf {i} \boldsymbol {k}_0 \boldsymbol {{\cdot }} \boldsymbol {x} - \textsf {i} \omega _0t} + \textrm {c.c.}$![]() , where $\omega _0 \equiv \omega _{\boldsymbol {k}_0}$
, where $\omega _0 \equiv \omega _{\boldsymbol {k}_0}$![]() is the laser frequency and $\boldsymbol {\sigma }$
is the laser frequency and $\boldsymbol {\sigma }$![]() is the laser polarisation. The polarisation $\boldsymbol {\sigma }$
is the laser polarisation. The polarisation $\boldsymbol {\sigma }$![]() is allowed to be complex to take into account circularly polarised laser beams as well. The Wigner function of this field isFootnote 4
is allowed to be complex to take into account circularly polarised laser beams as well. The Wigner function of this field isFootnote 4
Substituting this in (2.14), and as usual ignoring the anti-Stokes term for being off-resonant, reduces to the familiar expression (see Kruer Reference Kruer2019):

where one has used the approximation $\varOmega \simeq \varOmega _{-} \simeq \omega _{\textrm {pe}}$![]() in the numerator.
in the numerator.
In the case of multiple monochromatic non-interfering laser beams, the Wigner function is (ignoring the anti-Stokes terms)
The dispersion relation in this case becomes

This agrees with the result of Michel et al. (Reference Michel, Maximov, Short, Delettrez, Edgell, Hu, Igumenshchev, Myatt, Solodov, Stoeckl, Yaakobi and Froula2013).
3.2 Single temporally incoherent beam
Next, consider a single temporally incoherent laser beam. The Wigner function describing such a field is of the form (again ignoring the anti-Stokes term)
where $G(k_{\parallel })$![]() is the power spectrum centred around $k_0$
is the power spectrum centred around $k_0$![]() and normalised such that it integrates to unity. Also, $k_\parallel \doteq \boldsymbol {k} \boldsymbol {{\cdot }} \hat {\boldsymbol {\kappa }}, \boldsymbol {k}_\perp \doteq \boldsymbol {k} - k_\parallel \hat {\boldsymbol {\kappa }}$
and normalised such that it integrates to unity. Also, $k_\parallel \doteq \boldsymbol {k} \boldsymbol {{\cdot }} \hat {\boldsymbol {\kappa }}, \boldsymbol {k}_\perp \doteq \boldsymbol {k} - k_\parallel \hat {\boldsymbol {\kappa }}$![]() with $\hat {\boldsymbol {\kappa }} \doteq \boldsymbol {k}_0/k_0$
with $\hat {\boldsymbol {\kappa }} \doteq \boldsymbol {k}_0/k_0$![]() being the unit vector in the direction of propagation. For $\Delta \omega / \omega _0 \ll 1$
being the unit vector in the direction of propagation. For $\Delta \omega / \omega _0 \ll 1$![]() , the wavenumber spread $\Delta k$
, the wavenumber spread $\Delta k$![]() is related to the frequency bandwidth through $\Delta \omega = v_{g0} \Delta k$
is related to the frequency bandwidth through $\Delta \omega = v_{g0} \Delta k$![]() , where $v_{g0} = \partial \omega _{\boldsymbol {k}} / \partial k |_{k_{0}}$
, where $v_{g0} = \partial \omega _{\boldsymbol {k}} / \partial k |_{k_{0}}$![]() is the group velocity of electromagnetic waves at the peak of the power spectrum. Most commonly one considers broadband lasers with top-hat (flat), Lorentzian or Gaussian power spectra (Follett et al. Reference Follett, Shaw, Myatt, Dorrer, Froula and Palastro2019). Upon substitution of (3.5) in (2.14), the dispersion relation has the form
is the group velocity of electromagnetic waves at the peak of the power spectrum. Most commonly one considers broadband lasers with top-hat (flat), Lorentzian or Gaussian power spectra (Follett et al. Reference Follett, Shaw, Myatt, Dorrer, Froula and Palastro2019). Upon substitution of (3.5) in (2.14), the dispersion relation has the form
Here, in the same way as before $\boldsymbol {K}_{\perp } \doteq \boldsymbol {K} - \boldsymbol {K}\boldsymbol {{\cdot }} \hat {\boldsymbol {\kappa }}$![]() . The integral $\mathscr {I}$
. The integral $\mathscr {I}$![]() is given by
is given by

in which the integration variables have been changed from $\boldsymbol {k}$![]() to $\omega _{\boldsymbol {k}}$
to $\omega _{\boldsymbol {k}}$![]() in order to deal with the pole in the integrand more easily; note that the integral should be taken along the Landau contour $C_{{L}}$
in order to deal with the pole in the integrand more easily; note that the integral should be taken along the Landau contour $C_{{L}}$![]() . The function $\textsf {C}$
. The function $\textsf {C}$![]() has been defined as $\textsf {C} (k_{\parallel }) \doteq (K^2 \varOmega _- - k_-^2 \varOmega )^2/(K k_-)^2$
has been defined as $\textsf {C} (k_{\parallel }) \doteq (K^2 \varOmega _- - k_-^2 \varOmega )^2/(K k_-)^2$![]() . Note that $\textsf {C}$
. Note that $\textsf {C}$![]() is a function of $\varOmega$
is a function of $\varOmega$![]() and $\boldsymbol {K}$
and $\boldsymbol {K}$![]() as well, but those have been dropped for brevity. Of course here by $k_-$
as well, but those have been dropped for brevity. Of course here by $k_-$![]() one means $k_- = |\boldsymbol {K} - k_{\parallel } \hat {\boldsymbol {\kappa }}|$
one means $k_- = |\boldsymbol {K} - k_{\parallel } \hat {\boldsymbol {\kappa }}|$![]() . In order not to make the notation too cumbersome, functions such as $\textsf {C}$
. In order not to make the notation too cumbersome, functions such as $\textsf {C}$![]() , the spectrum $G$
, the spectrum $G$![]() , or $\omega _{e\boldsymbol {k}_-}$
, or $\omega _{e\boldsymbol {k}_-}$![]() which are defined as functions of $k_{\parallel }$
which are defined as functions of $k_{\parallel }$![]() , one evaluates in terms of the frequency implicitly as follows: $\textsf {C}(\omega _{k_\parallel }) \equiv \textsf {C}[\textsf {K}(\omega _{k_\parallel })]$
, one evaluates in terms of the frequency implicitly as follows: $\textsf {C}(\omega _{k_\parallel }) \equiv \textsf {C}[\textsf {K}(\omega _{k_\parallel })]$![]() , where $\textsf {K}(\omega _{\boldsymbol {k}}) \doteq c^{-1} \sqrt {\omega _{\boldsymbol {k}}^2 - \omega _{\textrm {pe}}^2} = k$
, where $\textsf {K}(\omega _{\boldsymbol {k}}) \doteq c^{-1} \sqrt {\omega _{\boldsymbol {k}}^2 - \omega _{\textrm {pe}}^2} = k$![]() allows one to go from the laser frequency to the laser wavenumber.
allows one to go from the laser frequency to the laser wavenumber.
In the monochromatic case, the TPD growth rate maximises to a value of $\gamma _0 = \tfrac 14 k_0 v_{\textrm {os}}$![]() . This tells one that $\gamma _0/\omega _{\textrm {pe}}\ll 1$
. This tells one that $\gamma _0/\omega _{\textrm {pe}}\ll 1$![]() since $\gamma _0/\omega _{\textrm {pe}} \sim k_0 v_{\textrm {os}}/\omega _{\textrm {pe}} \sim v_{\textrm {os}}/c \ll 1$
since $\gamma _0/\omega _{\textrm {pe}} \sim k_0 v_{\textrm {os}}/\omega _{\textrm {pe}} \sim v_{\textrm {os}}/c \ll 1$![]() . The right-hand side of (3.6) is of order $\gamma _0^2 \ll \omega _{\textrm {pe}}^2$
. The right-hand side of (3.6) is of order $\gamma _0^2 \ll \omega _{\textrm {pe}}^2$![]() . Therefore it is possible to assume that the real part of the frequency satisfies the linear dispersion relation: $\varOmega = \omega _{e\boldsymbol {K}} + \textsf {i} \gamma$
. Therefore it is possible to assume that the real part of the frequency satisfies the linear dispersion relation: $\varOmega = \omega _{e\boldsymbol {K}} + \textsf {i} \gamma$![]() . With this the growth rate becomes
. With this the growth rate becomes
and the integral $\mathscr {I}$![]() is
is

The integrand of $\mathscr {I}$![]() has one pole of interest which occurs at a wavenumber $k_{{p}}(\boldsymbol {K})$
has one pole of interest which occurs at a wavenumber $k_{{p}}(\boldsymbol {K})$![]() such that $\omega _{k_{{p}}} - \omega _{e\boldsymbol {K}} - \omega _{e\boldsymbol {k}_{-}} = 0$
such that $\omega _{k_{{p}}} - \omega _{e\boldsymbol {K}} - \omega _{e\boldsymbol {k}_{-}} = 0$![]() . This is the frequency-matching condition which for a given $k_{{p}}$
. This is the frequency-matching condition which for a given $k_{{p}}$![]() defines a circle in $\boldsymbol {K}$
defines a circle in $\boldsymbol {K}$![]() -space centred around $(K_{\parallel },K_{\perp }) = (k_0/2,0)$
-space centred around $(K_{\parallel },K_{\perp }) = (k_0/2,0)$![]() . In the limit of large bandwidth $\Delta \omega \gg \gamma$
. In the limit of large bandwidth $\Delta \omega \gg \gamma$![]() one evaluates $\mathscr {I}$
one evaluates $\mathscr {I}$![]() using Plemelj's formula:
using Plemelj's formula:
with $\mathscr {P} \displaystyle\int$![]() denoting the principal value integral and $\zeta, \varepsilon \in \mathbb{\text{R}}$
denoting the principal value integral and $\zeta, \varepsilon \in \mathbb{\text{R}}$![]() . Physically this is due to the fact that for small growth rates, the resonance is very sharp and the instability is driven only by the part of the power spectrum which can perfectly satisfy the matching conditions. Evaluating the imaginary part at the pole:
. Physically this is due to the fact that for small growth rates, the resonance is very sharp and the instability is driven only by the part of the power spectrum which can perfectly satisfy the matching conditions. Evaluating the imaginary part at the pole:
This gives the growth rate of the TPD instability in a uniform plasma in the case of a single temporally incoherent laser beam:
where one uses the fact that $({K_{\perp }^2v_{\textrm {os}}^2}/{8 \omega _{e\boldsymbol {K}} \omega _0}) \textsf {C}(k_{{p}},\boldsymbol {K}) \simeq ({K_{\perp }^2v_{\textrm {os}}^2}/{16})({(K^2 - |\boldsymbol {K} - k_{{p}} \hat {\boldsymbol {\kappa }}|^2)^2}/{K^2 |\boldsymbol {K} - k_{{p}} \hat {\boldsymbol {\kappa }}|^2}) = \gamma _{0\boldsymbol {K}}^2$![]() , and $\gamma _{0\boldsymbol {K}}$
, and $\gamma _{0\boldsymbol {K}}$![]() is the monochromatic growth rate. The reader is reminded here that the wavenumber at which the resonance occurs $k_{{p}}$
is the monochromatic growth rate. The reader is reminded here that the wavenumber at which the resonance occurs $k_{{p}}$![]() is a function of $\boldsymbol {K}$
is a function of $\boldsymbol {K}$![]() and is determined from the frequency-matching condition: $\omega _{k_{{p}}} - \omega _{e\boldsymbol {K}} - \omega _{e\boldsymbol {k}_{-}} = 0$
and is determined from the frequency-matching condition: $\omega _{k_{{p}}} - \omega _{e\boldsymbol {K}} - \omega _{e\boldsymbol {k}_{-}} = 0$![]() .
.
Consider next the maximum value that $\gamma _{\boldsymbol {K}}$![]() attains over all wavenumbers $\boldsymbol {K}$
attains over all wavenumbers $\boldsymbol {K}$![]() . Evaluating that for the top-hat and Lorentzian power spectra: for the top hat $G(k_0) = 1/\Delta k$
. Evaluating that for the top-hat and Lorentzian power spectra: for the top hat $G(k_0) = 1/\Delta k$![]() and so the growth rate is $\gamma _{\textrm {TH}} = \pi \gamma _0^2 / \Delta \omega$
and so the growth rate is $\gamma _{\textrm {TH}} = \pi \gamma _0^2 / \Delta \omega$![]() . For the Lorentzian $G(k) = (1/\pi ) ({\Delta k/2}/({(k-k_0)^2 + (\Delta k /2)^2}))$
. For the Lorentzian $G(k) = (1/\pi ) ({\Delta k/2}/({(k-k_0)^2 + (\Delta k /2)^2}))$![]() one has $G(k_0) = 2/\pi \Delta k$
one has $G(k_0) = 2/\pi \Delta k$![]() and so $\gamma _{{L}} = 2 \gamma _0^2/\Delta \omega$
and so $\gamma _{{L}} = 2 \gamma _0^2/\Delta \omega$![]() . Here $\gamma _0 = \tfrac 14 k_0 v_{\textrm {os}}$
. Here $\gamma _0 = \tfrac 14 k_0 v_{\textrm {os}}$![]() is the value at which $\gamma _{0\boldsymbol {K}}$
is the value at which $\gamma _{0\boldsymbol {K}}$![]() maximises. These results agree with the well-known scaling of the growth rate as $\gamma \sim \gamma _0^2/\Delta \omega$
maximises. These results agree with the well-known scaling of the growth rate as $\gamma \sim \gamma _0^2/\Delta \omega$![]() , but also include the dependence of the result on the laser spectral shape. It is interesting to note that while the coherence times for the two power spectra are (for the top hat and Lorentzian, respectively) $\tau _c = 2\pi /\Delta \omega, 2/\Delta \omega$
, but also include the dependence of the result on the laser spectral shape. It is interesting to note that while the coherence times for the two power spectra are (for the top hat and Lorentzian, respectively) $\tau _c = 2\pi /\Delta \omega, 2/\Delta \omega$![]() (see also § 3.3 for a definition of $\tau _{{c}}$
(see also § 3.3 for a definition of $\tau _{{c}}$![]() ) (Goodman Reference Goodman2015; Follett et al. Reference Follett, Shaw, Myatt, Dorrer, Froula and Palastro2019), the growth rates differ by less than a factor of $\pi$
) (Goodman Reference Goodman2015; Follett et al. Reference Follett, Shaw, Myatt, Dorrer, Froula and Palastro2019), the growth rates differ by less than a factor of $\pi$![]() . This shows that at least in the homogeneous case, it is not the coherence time per se which is the most relevant metric, but rather the fraction of laser energy which satisfies the resonance conditions. At first glance this is somewhat at odds with the results of Follett et al. (Reference Follett, Shaw, Myatt, Dorrer, Froula and Palastro2019), which found that the coherence time provides a universal scaling for the absolute Raman and TPD thresholds, meaning that the thresholds were the same for fields with the same coherence times but different spectral shapes. More formally, it appears that the peak growth rates of the instability scale with $G(k_0)$
. This shows that at least in the homogeneous case, it is not the coherence time per se which is the most relevant metric, but rather the fraction of laser energy which satisfies the resonance conditions. At first glance this is somewhat at odds with the results of Follett et al. (Reference Follett, Shaw, Myatt, Dorrer, Froula and Palastro2019), which found that the coherence time provides a universal scaling for the absolute Raman and TPD thresholds, meaning that the thresholds were the same for fields with the same coherence times but different spectral shapes. More formally, it appears that the peak growth rates of the instability scale with $G(k_0)$![]() , and the absolute thresholds with $\int |G(k)|^2 \,\textrm {d} k$
, and the absolute thresholds with $\int |G(k)|^2 \,\textrm {d} k$![]() . The reason for this difference in behaviour is unknown but the problem of an absolute instability near the quarter critical density in an inhomogeneous plasma is significantly more complicated and there is little reason to expect that it should be affected by bandwidth in the same way as the temporal growth rate in a homogeneous plasma, which has been calculated here.
. The reason for this difference in behaviour is unknown but the problem of an absolute instability near the quarter critical density in an inhomogeneous plasma is significantly more complicated and there is little reason to expect that it should be affected by bandwidth in the same way as the temporal growth rate in a homogeneous plasma, which has been calculated here.
Having explored how bandwidth affects the maximum value the growth rate attains, one now turns to how it modifies the spectrum of excited plasma waves. First in the monochromatic case, plasma waves are driven at wavenumbers near the intersection of the circles defined by the frequency-matching condition, and the hyperbolas defined by $K_{\perp }^2 = K_{\parallel }(K_{\parallel } - k_0)$![]() at which the monochromatic growth rate $\gamma _{0\boldsymbol {K}}$
at which the monochromatic growth rate $\gamma _{0\boldsymbol {K}}$![]() maximises. This is shown in the left-hand panel in figure 2. In the middle and right-hand panels the growth rate $\gamma _{\boldsymbol {K}}$
maximises. This is shown in the left-hand panel in figure 2. In the middle and right-hand panels the growth rate $\gamma _{\boldsymbol {K}}$![]() is presented, for a Lorentzian power spectrum of varying bandwidths. One sees that increasing the laser bandwidth significantly broadens the range of unstable wavenumbers excited by the TPD instability. In the right-hand panel virtually the entire TPD hyperbolas are observed since the ultra-large laser bandwidth allows all relevant wavenumbers to satisfy the frequency-matching conditions. What is most interesting is that even for relatively modest amounts of bandwidth such as $20 \ \textrm {THz}$
is presented, for a Lorentzian power spectrum of varying bandwidths. One sees that increasing the laser bandwidth significantly broadens the range of unstable wavenumbers excited by the TPD instability. In the right-hand panel virtually the entire TPD hyperbolas are observed since the ultra-large laser bandwidth allows all relevant wavenumbers to satisfy the frequency-matching conditions. What is most interesting is that even for relatively modest amounts of bandwidth such as $20 \ \textrm {THz}$![]() (middle panel) the broadening of the spectrum is substantial. Such effects may change the nature of the instability. For example, in an inhomogeneous plasma, at lower densities the TPD modes are fairly high in $\boldsymbol {K}$
(middle panel) the broadening of the spectrum is substantial. Such effects may change the nature of the instability. For example, in an inhomogeneous plasma, at lower densities the TPD modes are fairly high in $\boldsymbol {K}$![]() as illustrated by the left-hand panel in figure 2, and tend to be convective. Absolute modes occur near $|\boldsymbol {K}| \to 0$
as illustrated by the left-hand panel in figure 2, and tend to be convective. Absolute modes occur near $|\boldsymbol {K}| \to 0$![]() , which would typically be excited only in regions very close to the quarter critical density (Yan, Maximov & Ren Reference Yan, Maximov and Ren2010). One sees that laser bandwidth favours the absolute instability at lower densities too.
, which would typically be excited only in regions very close to the quarter critical density (Yan, Maximov & Ren Reference Yan, Maximov and Ren2010). One sees that laser bandwidth favours the absolute instability at lower densities too.

Figure 2. Effect of laser bandwidth on the range of unstable wavenumbers excited by the TPD instability as driven by a single broadband laser beam. The laser has a Lorentzian power spectrum, an intensity of $I_{{L}} = 10^{15} \, \textrm {W}\, \textrm {cm}^{-2}$![]() and wavelength $\lambda = 350 \ \textrm {nm}$
and wavelength $\lambda = 350 \ \textrm {nm}$![]() ; the plasma conditions are $T_e = 2 \ \textrm {keV}$
; the plasma conditions are $T_e = 2 \ \textrm {keV}$![]() and $n_e = 0.23 n_{c}$
and $n_e = 0.23 n_{c}$![]() ($n_{c}$
($n_{c}$![]() being the critical density). The growth rates are normalised to the maximal growth rate corresponding to each configuration. The left-hand panel represents the monochromatic case by solving (3.2) so it is normalised to $\gamma _{\textrm {max}} = \gamma _0 = \tfrac 14 k_0 v_{\textrm {os}}$
being the critical density). The growth rates are normalised to the maximal growth rate corresponding to each configuration. The left-hand panel represents the monochromatic case by solving (3.2) so it is normalised to $\gamma _{\textrm {max}} = \gamma _0 = \tfrac 14 k_0 v_{\textrm {os}}$![]() . The middle and right-hand panels show the analytical broadband solution $\gamma _{\boldsymbol {K}}$
. The middle and right-hand panels show the analytical broadband solution $\gamma _{\boldsymbol {K}}$![]() and are thus normalised to $\gamma _{\textrm {max}} = \gamma _{{L}} = 2 \gamma _0^2/\Delta \omega$
and are thus normalised to $\gamma _{\textrm {max}} = \gamma _{{L}} = 2 \gamma _0^2/\Delta \omega$![]() .
.
The analytical results presented so far have relied upon the assumption that the bandwidth is large compared with the growth rate $\Delta \omega \gg \gamma _0$![]() , which was used in the evaluation of the integral $\mathscr {I}$
, which was used in the evaluation of the integral $\mathscr {I}$![]() in (3.9). To explore the growth rates of the instability in the intermediate regime $\Delta \omega \sim \gamma _0$
in (3.9). To explore the growth rates of the instability in the intermediate regime $\Delta \omega \sim \gamma _0$![]() , the integral is evaluated numerically for finite $\gamma$
, the integral is evaluated numerically for finite $\gamma$![]() . Figure 3 shows the growth rate calculated along the lower branch of the TPD hyperbolas as a function of the magnitude of the wavenumber $K$
. Figure 3 shows the growth rate calculated along the lower branch of the TPD hyperbolas as a function of the magnitude of the wavenumber $K$![]() . One sees that even at the fairly low bandwidth of $5 \, \textrm {THz}$
. One sees that even at the fairly low bandwidth of $5 \, \textrm {THz}$![]() ($\Delta \omega / \gamma _0 = 2.8$
($\Delta \omega / \gamma _0 = 2.8$![]() ) and at intensity $I_{{L}} = 10^{15} \, \textrm {W}\, \textrm {cm}^{-2}$
) and at intensity $I_{{L}} = 10^{15} \, \textrm {W}\, \textrm {cm}^{-2}$![]() , the growth rate is half its monochromatic value. It is also approximately a third for $\Delta \omega /2\pi = 10 \textrm {THz}$
, the growth rate is half its monochromatic value. It is also approximately a third for $\Delta \omega /2\pi = 10 \textrm {THz}$![]() (corresponding to the intrinsic bandwidth of an argon fluoride laser). As shown below, laser wavelength does not affect the peak values of the growth rate and therefore the results just quoted are unchanged by it. Decreasing the wavelength though does reduce the broadening effect in the plasma wave spectrum shown in figure 2.
(corresponding to the intrinsic bandwidth of an argon fluoride laser). As shown below, laser wavelength does not affect the peak values of the growth rate and therefore the results just quoted are unchanged by it. Decreasing the wavelength though does reduce the broadening effect in the plasma wave spectrum shown in figure 2.

Figure 3. Numerically evaluated growth rates $\gamma$![]() in the intermediate-bandwidth regime calculated along the lower branch of the TPD hyperbolas defined by $K_{\perp }^2 = K_{\parallel }(K_{\parallel } - k_0)$
in the intermediate-bandwidth regime calculated along the lower branch of the TPD hyperbolas defined by $K_{\perp }^2 = K_{\parallel }(K_{\parallel } - k_0)$![]() . The inset shows the middle panel of figure 2 along with the aforementioned hyperbola as represented by the red dashed line. The plasma conditions and laser parameters are the same as those described in figure 2. The growth rate is normalised to the monochromatic one $\gamma _0$
. The inset shows the middle panel of figure 2 along with the aforementioned hyperbola as represented by the red dashed line. The plasma conditions and laser parameters are the same as those described in figure 2. The growth rate is normalised to the monochromatic one $\gamma _0$![]() , and the horizontal axis represents the magnitude of the wavenumber $K = \sqrt {K_\parallel ^2 + K_{\perp }^2}$
, and the horizontal axis represents the magnitude of the wavenumber $K = \sqrt {K_\parallel ^2 + K_{\perp }^2}$![]() . The circles represent the estimate of the maximum growth rate as given by (3.14).
. The circles represent the estimate of the maximum growth rate as given by (3.14).
In addition, it is possible to calculate the peak of the growth rates analytically in this regime. This is done by ignoring the thermal correction in the dispersion functions and assuming the wavenumber $\boldsymbol {K}$![]() is along the TPD hyperbola, leading to an expression for the maximum growth rate of the form
is along the TPD hyperbola, leading to an expression for the maximum growth rate of the form

For a Lorentzian spectrum centred at $\omega _0 = 2 \omega _{\textrm {pe}}$![]() the integral can be evaluated exactly, leading to
the integral can be evaluated exactly, leading to
This reproduces the two relevant limits: for $\Delta \omega \to 0, \gamma _{\textrm {max}} \to \gamma _0$![]() ; and for $\Delta \omega \to \infty, \gamma _{\textrm {max}} \to \gamma _{{L}} = 2\gamma _0^2/\Delta \omega$
; and for $\Delta \omega \to \infty, \gamma _{\textrm {max}} \to \gamma _{{L}} = 2\gamma _0^2/\Delta \omega$![]() . Since $\gamma _0$
. Since $\gamma _0$![]() does not depend on laser wavelength, then $\gamma _{\textrm {max}}$
does not depend on laser wavelength, then $\gamma _{\textrm {max}}$![]() does not either. The circles in figure 3 represent $\gamma _{\textrm {max}}$
does not either. The circles in figure 3 represent $\gamma _{\textrm {max}}$![]() as given by the result above, showing excellent agreement with the numerically calculated growth rate.
as given by the result above, showing excellent agreement with the numerically calculated growth rate.
3.3 Well-separated discrete spectral lines
Another implication concerns the extent to which a power spectrum consisting of $N$![]() well-separated sharp spectral lines spread over a bandwidth $\Delta \omega$
well-separated sharp spectral lines spread over a bandwidth $\Delta \omega$![]() , such as that shown in figure 4(a), approximates the instability reduction properties of a continuous power spectrum (Bodner Reference Bodner2023). For sufficiently low number of spectral lines, such that only a single line is contained within the instability resonance, $\Delta \omega /(N-1) > \gamma _0$
, such as that shown in figure 4(a), approximates the instability reduction properties of a continuous power spectrum (Bodner Reference Bodner2023). For sufficiently low number of spectral lines, such that only a single line is contained within the instability resonance, $\Delta \omega /(N-1) > \gamma _0$![]() , following the generalised dispersion relation presented here, the instability growth rate will be $\gamma = \gamma _0/\sqrt {N}$
, following the generalised dispersion relation presented here, the instability growth rate will be $\gamma = \gamma _0/\sqrt {N}$![]() . From the aforementioned inequality, this reduction will be somewhat lower than the expected $\pi \gamma _0^2/\Delta \omega$
. From the aforementioned inequality, this reduction will be somewhat lower than the expected $\pi \gamma _0^2/\Delta \omega$![]() in the continuous case, but still significant. For example for $N=10$
in the continuous case, but still significant. For example for $N=10$![]() , the reduction is similar to that of $10 \ \textrm {THz}$
, the reduction is similar to that of $10 \ \textrm {THz}$![]() continuous bandwidth (see figure 3). At first glance this reduction cannot be explained by the coherence properties of the power spectrum, since formally if each line is delta-shaped, the coherence time is infinite.
continuous bandwidth (see figure 3). At first glance this reduction cannot be explained by the coherence properties of the power spectrum, since formally if each line is delta-shaped, the coherence time is infinite.

Figure 4. (a) A power spectrum $G(\omega )$![]() consisting of $N=7$
consisting of $N=7$![]() well-separated spectral lines, centred around $\omega _0$
well-separated spectral lines, centred around $\omega _0$![]() and spread over a bandwidth of $\Delta \omega$
and spread over a bandwidth of $\Delta \omega$![]() . Their thickness is finite for the purposes of visualisation. (b) The normalised correlation function $|\varGamma (\tau )|^2$
. Their thickness is finite for the purposes of visualisation. (b) The normalised correlation function $|\varGamma (\tau )|^2$![]() as a function of the time separation $\tau$
as a function of the time separation $\tau$![]() of a set of $N$
of a set of $N$![]() delta-shaped spectral lines spread over a bandwidth $\Delta \omega$
delta-shaped spectral lines spread over a bandwidth $\Delta \omega$![]() .
.
To investigate this, one follows Goodman (Reference Goodman2015). Consider a power spectrum containing $N$![]() discrete delta-shaped spectral lines, uniformly spread over a bandwidth of $\Delta \omega$
discrete delta-shaped spectral lines, uniformly spread over a bandwidth of $\Delta \omega$![]() , and centred around $\omega _0$
, and centred around $\omega _0$![]() (figure 4a):
(figure 4a):

This is the power spectrum of the complex analytic signal $Y(t)$![]() where the actual signal is $y(t) = \textrm {Re} Y(t)$
where the actual signal is $y(t) = \textrm {Re} Y(t)$![]() . By the Wiener–Khinchin theorem, the correlation function $C(\tau ) = \overline {Y^*(t) Y(t + \tau )}$
. By the Wiener–Khinchin theorem, the correlation function $C(\tau ) = \overline {Y^*(t) Y(t + \tau )}$![]() is given by the (inverse) Fourier transform of $G(\omega )$
is given by the (inverse) Fourier transform of $G(\omega )$![]() :
:
Defining the normalised correlation function $\varGamma (\tau ) = C(\tau )/C(0)$![]() , the coherence time for a random process is given by
, the coherence time for a random process is given by
It can be shown that the correlation function for the discrete power spectrum $G(\omega )$![]() is
is
Formally, the integral of this will always diverge for any finite $N$![]() . In the limit of $N \to \infty$
. In the limit of $N \to \infty$![]() one recovers the normalised correlation function for a continuous top hat spectrum which has a finite coherence time:
one recovers the normalised correlation function for a continuous top hat spectrum which has a finite coherence time:
Figure 4(b) shows what $|\varGamma (\tau )|^2$![]() looks like for different numbers of spectral lines. One sees that for small $\tau$
looks like for different numbers of spectral lines. One sees that for small $\tau$![]() the correlation functions closely resemble the sinc profile expected in the continuous case. In contrast, the discrete case exhibits correlations for larger $\tau$
the correlation functions closely resemble the sinc profile expected in the continuous case. In contrast, the discrete case exhibits correlations for larger $\tau$![]() , and the time scale over which these correlations occur increases with the number of spectral lines $N$
, and the time scale over which these correlations occur increases with the number of spectral lines $N$![]() . The $k$
. The $k$![]() th peak occurs at time delay $T_k = 2(N-1) \pi k / \Delta \omega$
th peak occurs at time delay $T_k = 2(N-1) \pi k / \Delta \omega$![]() . If $T_1$
. If $T_1$![]() , the time at which the first peak occurs, is much larger than the typical time scale of interest (such as $\gamma _0^{-1}$
, the time at which the first peak occurs, is much larger than the typical time scale of interest (such as $\gamma _0^{-1}$![]() ) then the coherence properties of the continuous spectrum are well approximated by the discrete one. Using $T_1 \gg \gamma _0^{-1}$
) then the coherence properties of the continuous spectrum are well approximated by the discrete one. Using $T_1 \gg \gamma _0^{-1}$![]() translates to a condition on the number of spectral lines:
translates to a condition on the number of spectral lines:
For a laser intensity of $10^{15} \, \textrm {W} \, \textrm {cm}^{-2}$![]() at a wavelength of $350 \textrm {nm}$
at a wavelength of $350 \textrm {nm}$![]() and bandwidth of $\Delta \omega /\omega _0 = 1\,\%$
and bandwidth of $\Delta \omega /\omega _0 = 1\,\%$![]() , the right-hand side is ${\simeq } 1$
, the right-hand side is ${\simeq } 1$![]() . This suggests that even a low number of discrete spectral lines such as $N = 10$
. This suggests that even a low number of discrete spectral lines such as $N = 10$![]() might be a good approximation to the coherence properties of the continuous spectrum, as far as their effect on the instability is concerned.
might be a good approximation to the coherence properties of the continuous spectrum, as far as their effect on the instability is concerned.
4 Summary
In this paper, a novel statistical theory of the broadband TPD instability has been presented. It has been used to derive a dispersion relation in uniform plasma that is valid under laser electromagnetic fields with arbitrary power spectra. To achieve this, recent developments in inhomogeneous turbulence have been applied in order to derive the statistical closure required to treat the problem. The new dispersion relation is then applied to the study of the instability in a few cases of interest. For a single temporally incoherent laser beam, in the limit of large bandwidth $\Delta \omega \gg \gamma _0$![]() , the well-known reduction of the peak of the growth rate by a factor of approximately $\gamma _0/\Delta \omega$
, the well-known reduction of the peak of the growth rate by a factor of approximately $\gamma _0/\Delta \omega$![]() is confirmed, but it is also shown that the exact amount depends on the shape of the power spectrum. Namely, for a Lorentzian power spectrum the peak growth rate is $\gamma _{{L}} = 2 \gamma _0^2/\Delta \omega$
is confirmed, but it is also shown that the exact amount depends on the shape of the power spectrum. Namely, for a Lorentzian power spectrum the peak growth rate is $\gamma _{{L}} = 2 \gamma _0^2/\Delta \omega$![]() , and for a flat (top-hat) spectrum it is $\gamma _{\textrm {TH}} = \pi \gamma _0^2/\Delta \omega$
, and for a flat (top-hat) spectrum it is $\gamma _{\textrm {TH}} = \pi \gamma _0^2/\Delta \omega$![]() . This difference is less than what the difference in the coherence times of the two laser beams would imply. In addition, it has been shown that the laser bandwidth significantly broadens the range of wavenumbers excited by TPD. This implies that bandwidth favours the absolute instability in regions further away from the quarter critical density by allowing the $|\boldsymbol {K}| \to 0$
. This difference is less than what the difference in the coherence times of the two laser beams would imply. In addition, it has been shown that the laser bandwidth significantly broadens the range of wavenumbers excited by TPD. This implies that bandwidth favours the absolute instability in regions further away from the quarter critical density by allowing the $|\boldsymbol {K}| \to 0$![]() modes to be excited there too. The intermediate-bandwidth regime is explored numerically and it is shown that the growth rate is reduced to half its value for laser intensities of $10^{15} \, \textrm {W}\, \textrm {cm}^{-2}$
modes to be excited there too. The intermediate-bandwidth regime is explored numerically and it is shown that the growth rate is reduced to half its value for laser intensities of $10^{15} \, \textrm {W}\, \textrm {cm}^{-2}$![]() and relatively modest bandwidths of $5 \ \textrm {THz}$
and relatively modest bandwidths of $5 \ \textrm {THz}$![]() . A power spectrum consisting of $N$
. A power spectrum consisting of $N$![]() discrete lines spread over a bandwidth of $\Delta \omega$
discrete lines spread over a bandwidth of $\Delta \omega$![]() is also studied. It is shown that for a low number of spectral lines, the reduction in the peak growth rate is $1/\sqrt {N}$
is also studied. It is shown that for a low number of spectral lines, the reduction in the peak growth rate is $1/\sqrt {N}$![]() , which is somewhat smaller than in the continuous case but still significant.
, which is somewhat smaller than in the continuous case but still significant.
There some natural questions which arise as a consequence of this work. Firstly, can one model transversely incoherent laser fields such as those produced by a random phase plate (RPP), or a combination of transverse and temporal incoherence such as when a phase plate is combined with smoothing by spectral dispersion (SSD), as well as in the induced spatial coherence (ISI) scheme? Formally transverse incoherence can be straightforwardly incorporated by simply allowing the Wigner function (equivalently, the laser power spectrum) to have some finite angular spread in wavenumber. But since two laser fields which can have the same power spectrum can nonetheless still be very different, care should be taken when applying the generalised dispersion relation. The RPP field is such that it creates a speckle pattern at the focus which may cause the instability to be strongly localised within speckles with many times the average intensity (Follett et al. Reference Follett, Wen, Froula, Turnbull and Palastro2022). Such intermittent behaviour may break the Gaussianity assumption made in this work. Adding temporal incoherence by SSD or by using naturally broad-bandwidth lasers such as the excimer ones used in the ISI scheme causes the speckle pattern to move which may help smooth out this behaviour.
Secondly, the presence of a density gradient is primarily responsible for determining whether the dominant instability at the quarter critical density is the TPD or Raman scattering, with longer, ignition-relevant scale lengths favouring the Raman instability (Rosenberg et al. Reference Rosenberg, Solodov, Myatt, Seka, Michel, Hohenberger, Short, Epstein, Regan, Campbell, Chapman, Goyon, Ralph, Barrios, Moody and Bates2018). Therefore extending the present analysis to study the effects of laser bandwidth on the absolute instability in the presence of a density gradient is an important problem. The approach of Liu & Rosenbluth (Reference Liu and Rosenbluth1976) and Simon et al. (Reference Simon, Short, Williams and Dewandre1983) for a plane-wave laser field uses some rather specific mathematical manipulations to calculate the absolute threshold, for which it is not immediately clear how they might be carried out within the framework presented in this paper. So this remains an interesting open problem.
Acknowledgements
The authors acknowledge useful discussions with Dr R. Follett and Dr J. Palastro (Laboratory for Laser Energetics, University of Rochester), Dr S. Bodner (Naval Research Laboratory – Emeritus) and Dr A. Bott (Oxford), as well as the two anonymous referees for their valuable input.
Editor Alex Schekochihin thanks the referees for their advice in evaluating this article.
Funding
R.T.R. was supported by the Saven European Scholarship and UKRI-EPSRC. R.A. was supported by the Oxford-ShanghaiTech collaboration agreement. The research was conducted under UKRI grants EP/X035336/1 and ST/V001655/1.
Declaration of interest
The authors report no conflict of interest.
Appendix A. The Weyl symbol calculus
Here a very brief introduction to the Weyl symbol calculus is provided. Although quite concise, this should give the reader most of the necessary background to understand the results in this paper. For details and proofs, see McDonald (Reference McDonald1988), Tracy et al. (Reference Tracy, Brizard, Richardson and Kaufman2014) and Dodin (Reference Dodin2022) and references therein.
The symbol calculus is best presented in terms of abstract bra-kets and abstract operators acting on them. Therefore for any fields which might be of interest – the plasma density perturbation $n$![]() , the velocity potential $\psi$
, the velocity potential $\psi$![]() , the quiver velocity $\boldsymbol {v}_{\textrm {os}}$
, the quiver velocity $\boldsymbol {v}_{\textrm {os}}$![]() , etc. – one considers their abstract bra-ket representations. So for example, the position representation of the density perturbation is $n(\boldsymbol {x}) = \langle \boldsymbol {x} \! \mid \! n \rangle$
, etc. – one considers their abstract bra-ket representations. So for example, the position representation of the density perturbation is $n(\boldsymbol {x}) = \langle \boldsymbol {x} \! \mid \! n \rangle$![]() ; its Fourier transform, i.e. its wavenumber representation, is $\mathring {n}(\boldsymbol {k}) = \langle \boldsymbol {k} \! \mid \! n \rangle$
; its Fourier transform, i.e. its wavenumber representation, is $\mathring {n}(\boldsymbol {k}) = \langle \boldsymbol {k} \! \mid \! n \rangle$![]() .
.
One starts by defining the Wigner transform $\mathscr {W}$![]() of an abstract operator $\hat {A}$
of an abstract operator $\hat {A}$![]() as follows:
as follows:
where $\textsf {A}(\boldsymbol {x},\boldsymbol {k})$![]() is called the Weyl symbol of the operator $\hat {A}$
is called the Weyl symbol of the operator $\hat {A}$![]() . There is a close connection between the Wigner transform and correlation functions. The Wigner function of some field $\psi (\boldsymbol {x})$
. There is a close connection between the Wigner transform and correlation functions. The Wigner function of some field $\psi (\boldsymbol {x})$![]() is defined as
is defined as
where, from the definition, it is apparent that it can be thought of as the Fourier transform of the two-point correlation function of $\psi$![]() (modulo some averaging procedure). The Wigner function is the symbol of the density operator $\hat {\rho } \doteq \left | \psi \right \rangle \left \langle \psi \right |$
(modulo some averaging procedure). The Wigner function is the symbol of the density operator $\hat {\rho } \doteq \left | \psi \right \rangle \left \langle \psi \right |$![]() :
:
Analogously, one describes correlations between two different fields $\psi$![]() and $\phi$
and $\phi$![]() by considering the Wigner transform of $\left | \psi \right \rangle \left \langle \phi \right |$
by considering the Wigner transform of $\left | \psi \right \rangle \left \langle \phi \right |$![]() :
:
The Wigner transform possesses some nice properties:
for any integer $n$![]() , where ${\mathbb{1}}$
, where ${\mathbb{1}}$![]() is the identity operator, $\hat {\boldsymbol {x}}$
is the identity operator, $\hat {\boldsymbol {x}}$![]() is the abstract position operator with $\hat {x}_j$
is the abstract position operator with $\hat {x}_j$![]() being its $j$
being its $j$![]() th component; analogously for the wavenumber operator $\hat {\boldsymbol {k}}$
th component; analogously for the wavenumber operator $\hat {\boldsymbol {k}}$![]() , which is the abstract representation of $- \textsf {i} \partial _{\boldsymbol {x}}$
, which is the abstract representation of $- \textsf {i} \partial _{\boldsymbol {x}}$![]() .Footnote 5 As a consequence, any reasonably behaved function $F$
.Footnote 5 As a consequence, any reasonably behaved function $F$![]() of those operators satisfies
of those operators satisfies
This property makes it particularly easy to go from equations in the position representation as they are most commonly given to their abstract representation which is suitable for applying the Weyl symbol calculus. In the present work, this step does not even need be made explicit.
The symbol of a product of operators $\mathscr {W}[\hat {A} \hat {B}]$![]() is related to the individual symbols $\mathscr {W}[\hat {A}] = \textsf {A}(\boldsymbol {x},\boldsymbol {k})$
is related to the individual symbols $\mathscr {W}[\hat {A}] = \textsf {A}(\boldsymbol {x},\boldsymbol {k})$![]() and $\mathscr {W}[\hat {B}] = \textsf {B}(\boldsymbol {x},\boldsymbol {k})$
and $\mathscr {W}[\hat {B}] = \textsf {B}(\boldsymbol {x},\boldsymbol {k})$![]() through the Moyal star product $\star$
through the Moyal star product $\star$![]() as follows:
as follows:
where the star product between two symbols is defined as
with $\hat {\mathcal {P}}$![]() being the Poisson bracket, and the arrows over the derivatives denoting the direction in which they act; $\textsf {A} \hat {\mathcal {P}} \textsf {B}$
being the Poisson bracket, and the arrows over the derivatives denoting the direction in which they act; $\textsf {A} \hat {\mathcal {P}} \textsf {B}$![]() represents the Poisson bracket between $\textsf {A}$
represents the Poisson bracket between $\textsf {A}$![]() and $\textsf {B}$
and $\textsf {B}$![]() . The symbol product and the Wigner transform are related to each other like the convolution and the Fourier transform.
. The symbol product and the Wigner transform are related to each other like the convolution and the Fourier transform.
Frequently one needs to calculate symbol products where one of the symbols is only a function of space, or only a function of wavenumber. In such cases, the symbol product simplifies greatly when Fourier transformed. Denoting the Fourier transform of $\psi (\boldsymbol {x})$![]() as $\mathring {\psi }(\boldsymbol {k}) \doteq \mathscr {F}_{\boldsymbol {K}} [ \psi (\boldsymbol {x}) ] = \int \textrm {d} \boldsymbol {x}\, \psi (\boldsymbol {x}) \,\textrm {e}^{ - \textsf {i} \boldsymbol {K} \boldsymbol {{\cdot }} \boldsymbol {x}}$
as $\mathring {\psi }(\boldsymbol {k}) \doteq \mathscr {F}_{\boldsymbol {K}} [ \psi (\boldsymbol {x}) ] = \int \textrm {d} \boldsymbol {x}\, \psi (\boldsymbol {x}) \,\textrm {e}^{ - \textsf {i} \boldsymbol {K} \boldsymbol {{\cdot }} \boldsymbol {x}}$![]() , one has
, one has

for some generic functions $F, G$![]() and $W$
and $W$![]() . The proof of the first one is as follows:
. The proof of the first one is as follows:

The rest follow analogously.
For some field $\left | \psi \right \rangle$![]() governed by a Schrödinger-like equation $\textsf {i} \partial _t \left | \psi \right \rangle = \hat {H} \left | \psi \right \rangle$
governed by a Schrödinger-like equation $\textsf {i} \partial _t \left | \psi \right \rangle = \hat {H} \left | \psi \right \rangle$![]() the density operator satisfies the von-Neumann equation:
the density operator satisfies the von-Neumann equation:
Taking the Wigner transform of the above gives the so-called Wigner–Moyal equation which governs the Wigner function of the field:
with $\textsf {H} \doteq \mathscr {W}[\hat {H}]$![]() being the symbol of the Hamiltonian operator $\hat {H}$
being the symbol of the Hamiltonian operator $\hat {H}$![]() . This is what allows us to very efficiently go from the equations of motion (EOM) of some field $\psi$
. This is what allows us to very efficiently go from the equations of motion (EOM) of some field $\psi$![]() to the equation governing the correlation function of that field:
to the equation governing the correlation function of that field:
All of the above properties are also satisfied for vector fields $\boldsymbol {\varPsi } = (\psi _1, \psi _2, \ldots )$![]() and matrices of operators $\hat {\boldsymbol {A}}$
and matrices of operators $\hat {\boldsymbol {A}}$![]() as long as the usual matrix multiplication rules are respected. For example,
as long as the usual matrix multiplication rules are respected. For example,
where ${\boldsymbol{\mathsf{A}}}$![]() and ${\boldsymbol{\mathsf{B}}}$
and ${\boldsymbol{\mathsf{B}}}$![]() are arbitrary matrix symbols. In this work, matrix multiplication rules are implied between symbols.
are arbitrary matrix symbols. In this work, matrix multiplication rules are implied between symbols.
Appendix B. The driving terms
Here a calculation identical to the one in Tsiolis et al. (Reference Tsiolis, Zhou and Dodin2020) is reproduced which gives the form of the TPD driving terms. Consider the following:

Here $\hat {\boldsymbol{\mathsf{W}}}_{\psi \boldsymbol {v}} \doteq \left | \psi \right \rangle \left \langle \boldsymbol {v}_{\textrm {os}} \right |$![]() . So one sees that the expression $\boldsymbol {v}_{\textrm {os}} \boldsymbol {{\cdot }} \boldsymbol {\nabla } \psi$
. So one sees that the expression $\boldsymbol {v}_{\textrm {os}} \boldsymbol {{\cdot }} \boldsymbol {\nabla } \psi$![]() can be thought of as the matrix elements of the operator $\textsf {i} \hat {\boldsymbol {k}} \boldsymbol {{\cdot }} \hat {\boldsymbol{\mathsf{W}}}_{\psi \boldsymbol {v}}$
can be thought of as the matrix elements of the operator $\textsf {i} \hat {\boldsymbol {k}} \boldsymbol {{\cdot }} \hat {\boldsymbol{\mathsf{W}}}_{\psi \boldsymbol {v}}$![]() . For a general operator $\hat {A}$
. For a general operator $\hat {A}$![]() , it can be shown that these matrix elements can be related to the Weyl symbol $\textsf {A}(\boldsymbol {x},\boldsymbol {k})$
, it can be shown that these matrix elements can be related to the Weyl symbol $\textsf {A}(\boldsymbol {x},\boldsymbol {k})$![]() of the operator as follows (Dodin Reference Dodin2022):
of the operator as follows (Dodin Reference Dodin2022):
Hence using the Moyal star product, one writes
since
Note that the transpose is needed in order for the dot product to be taken into account in the symbol product since $\boldsymbol {k}$![]() is a column vector and ${\boldsymbol{\mathsf{W}}}_{\psi \boldsymbol {v}}$
is a column vector and ${\boldsymbol{\mathsf{W}}}_{\psi \boldsymbol {v}}$![]() is a row vector.
is a row vector.
Appendix C. Proof of the relationship between ${\boldsymbol{\mathsf{B}}}_{\boldsymbol {vv}} \doteq {\boldsymbol{\mathsf{W}}}_{(\boldsymbol {\phi } + \boldsymbol {\chi )}(\boldsymbol {\phi } - \boldsymbol {\chi )}}$ and ${\boldsymbol{\mathsf{W}}}_{\boldsymbol {v}\boldsymbol {v}} = {\boldsymbol{\mathsf{W}}}_{(\boldsymbol {\phi } + \boldsymbol {\chi )}(\boldsymbol {\phi } + \boldsymbol {\chi )}}$
and ${\boldsymbol{\mathsf{W}}}_{\boldsymbol {v}\boldsymbol {v}} = {\boldsymbol{\mathsf{W}}}_{(\boldsymbol {\phi } + \boldsymbol {\chi )}(\boldsymbol {\phi } + \boldsymbol {\chi )}}$
The solution of the Klein–Gordon equation for the vector potential in a uniform plasma is of the form
with $\omega _{\boldsymbol {k}} = \sqrt {\omega _{\textrm {pe}}^{2} + k^2 c^2}$![]() being the photon frequency. To calculate ${\boldsymbol{\mathsf{B}}}_{\boldsymbol {vv}}$
being the photon frequency. To calculate ${\boldsymbol{\mathsf{B}}}_{\boldsymbol {vv}}$![]() one needs $\partial _t \boldsymbol {v}_{\textrm {os}}$
one needs $\partial _t \boldsymbol {v}_{\textrm {os}}$![]() which is given by
which is given by
Let $\mathring {\boldsymbol {V}}$![]() denote the Fourier transform of $\partial _t \boldsymbol {v}_{\textrm {os}}$
denote the Fourier transform of $\partial _t \boldsymbol {v}_{\textrm {os}}$![]() :
:
It is straightforward to show that the Wigner function can be expressed in terms of the Fourier transforms of the fields as follows:
Therefore,

The equivalent expression for ${\boldsymbol{\mathsf{W}}}_{\boldsymbol {vv}}$![]() is
is
For spatially homogeneous fields, upon statistical averaging these wavenumber correlators will turn out to be deltas. To see that consider

For this to be independent of $\boldsymbol {x}$![]() one needs
one needs
Hence after statistical averaging and integrating out the delta, one gets the required relationship: