Introduction
Degradation of agriculturally productive land has become a pressing challenge to securing rural livelihoods across the world due to its detrimental effects on food production and agro-ecological stability (Gupta Reference Gupta2019). Approximately 20% of cropland worldwide is degraded (Malav et al. Reference Malav, Yadav, Tailor, Pattanayak, Singh and Kumar2022). In India, land degradation accounts for c. 29% of the total geographical area of the country (GoI 2016a), and the problem is more severe in arid and semi-arid regions (Kosoe et al. Reference Kosoe, Osumanu and Nabiebakye2020). Recognizing the urgent need for land management to ensure global food security, the United Nations General Assembly focused on attaining land degradation neutrality (LDN) as a Sustainable Development Goal by 2030. India has also joined the Bonn Challenge and aims to restore 26 Mha of degraded land by 2030 under the United Nations Convention to Combat Desertification (UNCCD) framework (Singh & Tewari Reference Singh and Tewari2021).
Soil and water erosion has emerged as one of the critical causes of impaired quality of land, impinging on the agricultural production and socio-economic status of farmers. Soil erosion is responsible for a third of total degraded land in USA, and in Europe, China and India the figures are 17%, 30% and 45%, respectively (Singh et al. Reference Singh, Chaudhary, Somasundaram, Sinha, Mohanty and Hati2020). Furthermore, c. 56% of the global degraded land area is affected by water erosion; in India, this affects 68% of the total land area (Bhattacharyya et al. Reference Bhattacharya, Ghosh, Mishra, Mandal, Rao and Sarkar2015).
Soil and water conservation measures (SWCMs) may be instrumental to restoring land quality and thus safeguarding the interests of rural households by increasing farm productivity and stabilizing yield, particularly in semi-arid regions, where land resource degradation is relentless (Palanisami et al. Reference Palanisami, Kumar, Wani and Giordano2009, Pathak Reference Pathak, Pal and Mohapatra2020). The commonly recommended SWCMs for these areas include contour bunding (constructing embankments or bunds along the contour lines of the land), graded bunding (constructing bunds with a specific slope), compartment bunding (dividing a piece of land into compartments using bunds), ridges and furrows, tied ridging (creating ridges and furrows in such a way that the soil is anchored or tied to reduce erosion), contour cultivation, set-furrow cultivation (creating furrows or rows in a planned manner to optimize water conservation and soil fertility), grass and tree stripping on bunds, agroforestry, orchard plantation and rejuvenation of ponds (Vittal et al. Reference Vittal, Sinha, Chary, Sankar, Srijaya and Ramakrishna2004, Mishra et al. Reference Mishra, Singh and Kumar2018). These limit the top-soil loss, improve water retention capacity of soil and increase groundwater availability (Stocking & Murnaghan Reference Stocking and Murnagham2001, Singha Reference Singha2017).
That adoption of SWCMs could help to restore land quality and improve farm productivity and income, as demonstrated in studies conducted in, for example, Ethiopia, Latin America, the Middle East, sub-Saharan Africa, northern Ghana and China (Barron et al. Reference Barron, Noel and Mikhail2009, Chen et al. Reference Chen, Zhu, Krotta, Calvo, Ganesh and Makot2013, Nkegbe & Shankar Reference Nkegbe and Shankar2014, Yaebiyo et al. Reference Yaebiyo, Tesfay and Assefa2015). Few studies have investigated the impacts of SWCMs on farm income in India (Datta Reference Datta2015, Singha Reference Singha2017, Kumar et al. Reference Kumar, Singh, Singh, Singh and Jha2020). Studies on the impacts of SWCMs on farm-specific technical efficiency (TE) – a measure of resource optimization at the farm level – in the Indian context to date are scarce. Mondal et al. (Reference Mondal, Singh and Jha2012), using a stochastic production frontier (SPF) model, made an explicit attempt at this by comparing farm-specific TEs in watersheds (treated areas with resource conservation practices) and control (untreated) areas in the Bundelkhand region of the Indian state of Madhya Pradesh. However, they made a simple comparison of TE estimates from two sets of samples (treated and control), which may have led to biased results because of the potential endogeneity issue associated with the farmers’ adoption decisions (Bravo-Ureta et al. Reference Bravo-Ureta, Greene and Solís2012, Morais et al. Reference Morais, Silva, Freitas and Braga2021). The adoption decision of farmers is usually influenced by observable factors (e.g., farm and producer characteristics, such as household size, income, schooling and experience) and unobservable factors (e.g., farmer’s managerial capacity). Failing to account for these characteristics tends to bias estimates of the impacts of SWCMs on the TE of farmers (Villano et al. Reference Villano, Bravo-Ureta, Solís and Fleming2015).
It is crucial to measure and evaluate the performance of farms in terms of their efficiency in using agricultural inputs if sustainable farming systems are to be implemented. Estimating TE can highlight the significance of practices such as modifying farm management (e.g., education and training programmes) and farm structure during the implementation stage of natural resource-based projects, with the aim of enhancing farm productivity levels.
A robust methodology to assess the impacts of SWCMs is lacking, and there is therefore a dearth of precise empirical estimates of the impacts of SWCMs on the TE of farms, especially those situated in arid and semi-arid regions. The primary objective of this paper is to address this gap in the Bundelkhand region, a typical semi-arid tropical region of central India grappling with profound natural resource degradation risks. We provide empirical evidence of the impacts on the rain-fed farms located there by comparing the impacts of SWCMs on the TE of adopter (treated) and non-adopter (control) farmers. We apply an econometric framework that addresses selectivity biases arising from observed and unobserved factors, and by allowing for selectivity bias we can also assess the factors influencing the adoption of SWCMs by farmers in the region.
Material and methods
Study area
This study was conducted in the Lalitpur district (latitudes 24°11’–25°14’ N and longitudes 78°10’–79°0’ E) of the Bundelkhand region of central India (Fig. S1). Of the total district area, c. 19% is degraded land, and c. 52% of the total degraded land is agricultural. Most of the population in the district is dependent on crop/livestock-based activities (GoI 2016b).
The prevalent undulating topography, hard rock geology, low soil fertility, scarce groundwater resources along with poor and erratic rainfall lead to frequent droughts and crop failure in the region (Garg et al. Reference Garg, Anantha, Nune, Venkataradha, Singh and Gumma2020, Singh et al. Reference Singh, Choudhary, Dwivedi, Arunachalam, Kumar and Dev2023). Farmers mainly cultivate crops such as groundnut, black gram, sesame and millet during the kharif (monsoon) and wheat, chickpea, barley, mustard and lentils during the rabi (October–February) season.
Three villages, namely Birdha, Purakhurd and Jhabar, in the Talbehat block of Lalitpur district were designated as treated villages, as all of the soil and water conservation activities were concentrated within their physical boundaries. Three adjacent villages, namely Gundera, Gebra and Viharipura, were chosen as control villages, which did not receive any soil- or water-based interventions but shared similarities with the treated villages in terms of agro-climatic conditions, infrastructure and socio-economic status.
Soil and water conservation measures in the study area
As a part of a project to double farmers’ income (KISAN MITrA) funded by the government of Uttar Pradesh State (India), various types of SWCMs were started in the study area in 2017 by the ICRISAT Development Center (IDC; Hyderabad) in a consortium with ICAR – Central Agroforestry Research Institute (CAFRI; Jhansi), ICAR – Indian Grassland and Fodder Research Institute (IGFRI; Jhansi) and a non-governmental organization (NGO) partner, Upman Mahila Sansthan.
Details of the SWCMs in the project villages are given in Table S1. As developing surface water and groundwater resources is crucial to enhancing farm productivity in rain-fed areas, a significant proportion of the total project expenditure was allocated for harvesting surface water through deepening and widening of the drainage network and the construction of water-harvesting structures such as farm ponds and havelis (traditional rainwater-harvesting tank systems to store runoff generated from the catchment during the monsoon and used for multiple purposes), which were present in almost every village in Bundelkhand (Meter et al. Reference Meter, Steiff, McLaughlin and Basu2016, Garg et al. Reference Garg, Anantha, Nune, Venkataradha, Singh and Gumma2020, Pathak et al. Reference Pathak, Pal and Mohapatra2020). All of these off-farm activities were being used for conserving soil and ensuring supplemental irrigation to nearby fields during dry periods.
Conceptual framework
The two primary methodologies employed in measuring farm TE are SPF analysis and data envelope analysis (DEA; Bravo-Ureta et al. Reference Bravo-Ureta, Greene and Solís2012, Wang et al. Reference Wang, Huo and Kabir2013, Choudhary et al. Reference Choudhary, Dev, Singh, Singh, Sharma and Chand2022). The DEA method is sensitive to outliers due to its reliance on the assumption of there being no sampling errors (Diagne et al. Reference Diagne, Demont, Seck and Diaw2013), and its applicability in agricultural studies, where output is particularly susceptible to random errors, is constrained (Koirala et al. Reference Koirala, Mishra and Mohanty2016). We therefore opted for the SPF approach to assess the TE of farmers, and the model was specified as in Equation 1:
where Y i is the output variable for the ith farmer, X i denotes the input variables and the adoption of SWCMs is encapsulated by the dummy variable d (1 = adopters, 0 = non-adopters). The error term ϵ i is delineated as the disparity between the stochastic error term (v i ) (v ∼ N(0, σv 2)) and a positive one-sided component (u i ) designed to account for the impact of inefficiency in the production process.
Several observed and unobserved factors exert influence on farmers’ adoption decisions, introducing self-selection bias in the case of SWCMs. Consequently, the dummy variable d i , signifying the technology adoption status of the farmers, is endogenously determined (Ma et al. Reference Ma, Renwick, Yuan and Ratna2018). Therefore, the sample selection equation for the adoption decision of farmers was formulated as in Equation 2:
where d i * serves as a latent variable denoting a farmer’s inclination towards adopting SWCMs; it signifies the adoption status, with d i taking a value of 1 for adopters and 0 for non-adopters. W i encompasses exogenous variables that impact the adoption decision of the farmer. The coefficient α represents unknown parameters, and e i represents the error term.
Selectivity bias correction
The propensity score matching (PSM) technique was employed to pair farmers from treated and control villages based on observed characteristics. The predicted probability of farmers adopting SWCMs, known as the propensity score, was generated by estimating Equation 2 through a binary-choice probit model. To ensure a balanced comparison between groups was achieved, a balancing test was conducted to confirm that farmers from treated and control villages were perfectly matched, indicating no systematic differences in observed characteristics such as age, education and landholdings. In order to address selectivity biases arising from unobserved factors such as attitude to risk, managerial ability and motivation of farmers within a SPF framework, we adopted Greene’s (Reference Greene2010) model, which is superior to Heckman’s self-selection specification for linear regression models (Bravo-Ureta et al. Reference Bravo-Ureta, Greene and Solís2012, Ma et al. Reference Ma, Renwick, Yuan and Ratna2018). The error structure in Greene’s (Reference Greene2010) model assumes correlation between the error term in the selection equation (ϵ i ) and the noise (v i ) in the stochastic frontier model. Mathematically, the error structures of Greene’s (Reference Greene2010) model can be expressed as in Equation 3:
where ρ represents the selectivity correction term, and a statistically significant coefficient for ρ would indicate the presence of selectivity bias arising from unobservable factors. U is a non-negative term accounting for technical inefficiency, V is a symmetric error term, σ is the standard deviation and N is the normal distribution function.
Sampling procedure and data collection
Given that the matching technique employed in this study necessitates a larger number of observations from control units, ideally in a ratio of c. 1:2 (Datta Reference Datta2015), data were collected from 150 farm households from the treated villages and 250 households from the control villages. Stratification of household heads was conducted based on land size categories within each village, and the probability proportional to size method was applied to select sample households from each village. Respondent household heads were then chosen using a random sampling technique.
The survey schedule comprehensively gathered information on various socio-economic parameters, including the age and education status of household members, the farming experience of the household head and the landholdings of the household. The crop farming data encompassed details on the area and production of each crop cultivated during the kharif and rabi seasons for the agricultural year 2021–2022. Additionally, the survey delved into the variable costs associated with diverse input categories such as human labour, machine labour, seeds, fertilizers and pesticides on a crop-by-crop basis.
Empirical techniques
We employed both PSM and the selectivity bias-corrected SPF model of Greene (Reference Greene2010) to control for biases arising from both observed and unobserved factors. Within PSM, we used kernel-based matching (KBM) with a bandwidth of 0.01 due to its reported effectiveness at minimizing biases (Ma et al. Reference Ma, Renwick, Yuan and Ratna2018). The application of KBM resulted in a total of 336 matched observations, comprising 150 farmers from the treated villages and 186 farmers from the control villages.
To evaluate the efficacy of the matching process, we conducted t-tests both before and after matching, as outlined by Leuven and Sianesi (Reference Leuven and Sianesi2003). These tests were employed to assess the null hypothesis that the means of observed characteristics for beneficiaries and non-beneficiaries are equal. Utilizing the propensity scores, we estimated the selectivity correction term (ρ) and incorporated it into the SPF framework, following the approach of Abdulai and Abdulai (Reference Abdulai and Abdulai2017). In the estimation of the production frontier, we compared both the Cobb–Douglas and translog functional forms using the likelihood ratio (LR) test. Based on the test results, we specified the Cobb–Douglas function as in Equation 4:
In the specified model, the dependent variable ln(Y i ) represents the log transformation of the total gross revenue (in INR) from the considered crop. The independent variable ln(X i ) is the log-transformed value of inputs, aggregated into four major categories, namely expenditures on labour, machinery, seeds and agrochemicals (fertilizers and pesticides). The parameter β i denotes the production elasticity of the ith input and was estimated. ϑ is the coefficient parameter of d (adoption status) and ϵ is the error term.
To compare the goodness of fit between two nested models, where one model is a constrained version of the other, we performed the LR test on both the unmatched and matched samples to examine potential technology disparities between the treated and control groups. Specifically, the restricted model assumes no disparities in technology adoption between the treated and control groups, whereas the unrestricted model permits differences in technology adoption (Equation 5).
where lnL P , lnL T and lnL C represent the log-likelihood function values estimated from the pooled sample, treated subsample and control subsample, respectively. If the null hypothesis indicating no differences in technology adoption between the treated and control groups was rejected based on the LR test, this implied that the parameters for the production frontiers differed between treated and control farmers. This rejection would suggest significant disparities in how technology is adopted and utilized by the treated and control groups; technology-related factors were influencing production outcomes differently for the two groups. The SPF for beneficiaries and non-beneficiaries was then estimated as in Equations 6 and 7:
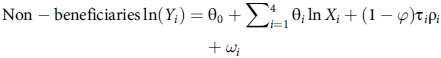 $$\eqalign{ & {\rm{Non}} - {\rm{beneficiaries}}\ln \left( {{Y_i}} \right) = {\theta _0} + \sum\nolimits_{i = 1}^4 {{\theta _i}} {\mkern 1mu} {\rm{ln}}{\mkern 1mu} {X_i} + \left( {1 - \varphi } \right){\tau _i}{\rho _i} \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + {\omega _i} \cr} $$
$$\eqalign{ & {\rm{Non}} - {\rm{beneficiaries}}\ln \left( {{Y_i}} \right) = {\theta _0} + \sum\nolimits_{i = 1}^4 {{\theta _i}} {\mkern 1mu} {\rm{ln}}{\mkern 1mu} {X_i} + \left( {1 - \varphi } \right){\tau _i}{\rho _i} \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + {\omega _i} \cr} $$
where ln(Y i ) and ln(X i ) are the logarithmic forms of gross revenue and input parameters, respectively, ρ i is a correction term, ϕ0 and θ0 are constant terms, δ i , θ i and τ i are parameters to be estimated and ϕ is a selectivity correction term that takes a value of 0 when unobserved selection bias issue is considered and 1 if this not considered in estimating the SPF. Both e and ω are error terms of their respective equations.
Results
Descriptive results and propensity score matching analysis
The variables used in both the sample selection equation and production frontier model, along with their descriptive statistics for the overall sample, are presented in Table 1.
Table 1. Summary statistics of the selected variables (USD = INR 83.02 as of 11 January 2024).

Prior to matching, there were discernible systematic differences in observed characteristics between households from treated and control villages (Table 2). Notably, household heads and female members from treated villages tended to exhibit higher education levels and to possess larger operational holdings than those from control villages. Nevertheless, following the implementation of the matching procedure, none of the mean differences in the selected variables between the treated and control groups were statistically significant, indicating that the matching process had effectively generated a balanced counterfactual (Table 2).
Table 2. Mean difference of the variables used in the sample selection equation.
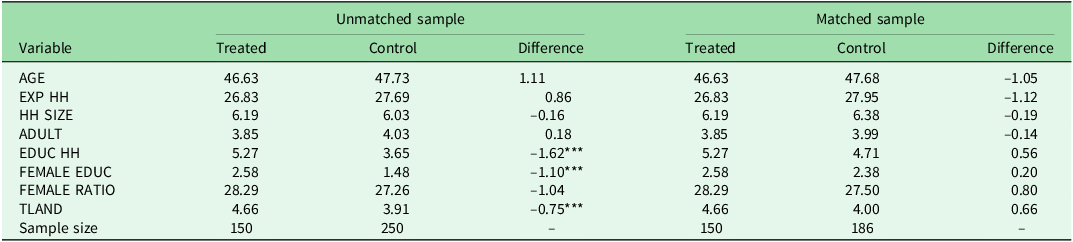
Note: For variable descriptions, see Table 1.
***p < 0.01.
This attests to the fulfilment of the balancing test requirement (Rosenbaum & Rubin Reference Rosenbaum and Rubin1983), as evident in the considerable drop of pseudo-R 2 from c. 31% to 9% before matching (Table S2). Furthermore, the non-significant p-values of the LR test and low mean standard bias (<20%) suggest that the propensity score specification achieved balance in the distribution of covariates between the treated and control groups (Table S2).
The propensity score distributions for both the treated group and the control group before and after matching (Fig. 1) suggest that the control group was now more similar to the treated group in terms of the confounding factors, suggesting that the assumption of common support – critical for PSM – is firmly upheld.
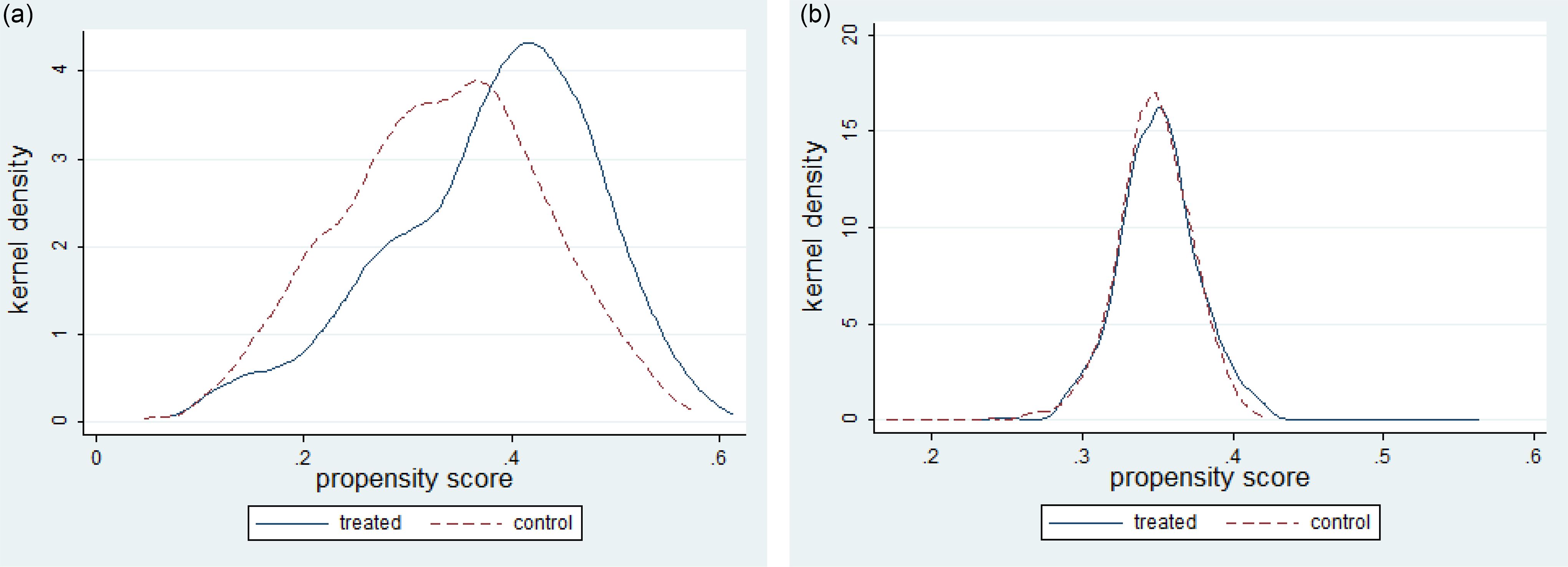
Figure 1. Propensity score distributions of treated and control farmers for (a) the unmatched sample and (b) the matched sample.
The test of means revealed that the total gross revenue for adopters was significantly higher than that of non-adopters (Table S3). It is evident that treated households on average were spending more on inputs than their control counterparts (Table S3).
Production frontier results
Table 3 presents the maximum likelihood estimates of the conventional and selectivity-corrected SPF models on the PSM subsample. Separate frontiers were estimated for the treated and control groups due to the rejection of the null hypothesis for technical homogeneity between beneficiaries and non-beneficiaries by the LR test (Equation 5; 79.36, p = 0.000).
Table 3. Parameter estimates of the stochastic production frontier (SPF) model for the matched sample. Figures in parentheses are standard errors:
![]() ${\rm{\gamma }} = {\rm{\sigma }}_u^2/\left( {{\rm{\sigma }}_u^2 + {\rm{\sigma }}_v^2} \right)$
.
${\rm{\gamma }} = {\rm{\sigma }}_u^2/\left( {{\rm{\sigma }}_u^2 + {\rm{\sigma }}_v^2} \right)$
.
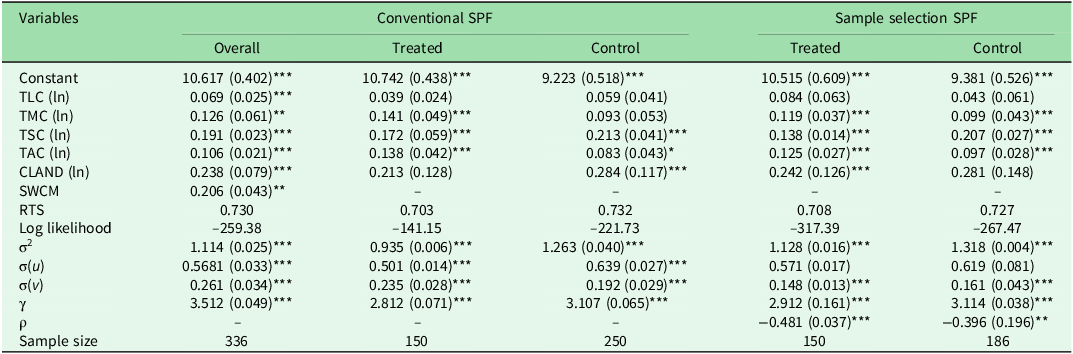
Note: For variable descriptions, see Table 1.
*p < 0.10, **p < 0.05, ***p < 0.01.
All of the estimated production elasticity coefficients were positive, as expected, although with varying magnitudes and levels of significance. The coefficient for the variable representing SWCMs for the overall sample under the conventional SPF model indicates that a SWCM on a farm had a direct and significant influence on total revenue from crop output. Amongst all of the estimated models, crop acreage and SWCM had the highest elasticity values.
The statistical significance of the error variance (σ2) in all cases indicates the goodness of fit of the model. The gamma coefficients (γ) were also significantly different from 0 at the 1% level, suggesting that farm technical inefficiency (TI) was indeed stochastic and that inefficiency caused variability in the observed output. This implies that there are unobserved factors affecting TI and that the estimated models accounted for this stochastic nature of TI.
The coefficients of the correction term (ρ) in the sample selection SPF models were statistically different from 0 for both the treated and control groups, confirming the presence of selection bias due to unobservable factors. Consequently, using conventional SPF models to estimate frontier efficiency would be inconsistent and would yield biased results for TE scores (Ma et al. Reference Ma, Renwick, Yuan and Ratna2018). Therefore, in our case, separate SPF models were justified for the treated and control groups within the sample selection framework.
The null hypothesis of simultaneous 0 values for all coefficients in both the matched and unmatched samples was rejected (Table 4), indicating that the estimated coefficients of these probit models could be compared. The lower number of statistically significant parameters in the matched sample was justified, as PSM reduced the variability between the treated and control groups, which can affect the significance of estimates. Off-farm income and training were important policy variables that positively influenced the economic efficiency of farmers (Table 4). A unit percentage increase in off-farm income and training increased the efficiency by 0.16% and 0.18%, respectively.
Table 4. Parameter estimates of the probit sample selection equation.
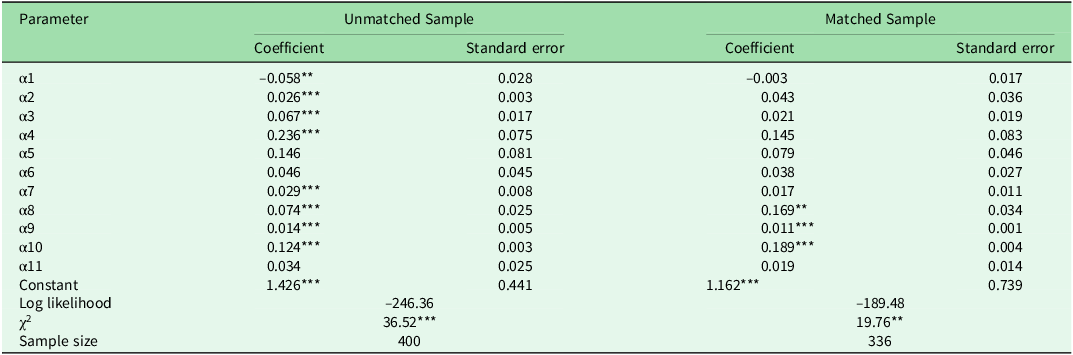
Note: For parameter descriptions, see Table 1.
**p < 0.05, ***p < 0.01.
Table 5 presents the mean TE scores for all of the estimated models in Table 3, along with TE estimates from the conventional SPF for the unmatched sample. The average TE for the treated group ranged from 68% to 72% and was higher than that of the control group in all cases (Table 5). The statistical differences in means indicate the existence of an efficiency gap between beneficiaries and non-beneficiaries of the soil and water conservation treatment. However, this gap is expected to narrow after implementing the matching technique, as PSM controls for selection bias arising from observable variables. Furthermore, the sample selection SPF for the matched sample further decreased the TE gap.
Table 5. Mean technical efficiency scores for the stochastic production frontier (SPF) models (standard errors are in parentheses).

***p < 0.01.
a A t-test is used to determine whether the technical efficiency means are significantly different between the treated and control groups.
Discussion
We found that SWCMs exhibited a direct and significant impact on total crop revenue, emphasizing the importance of these activities for enhancing agricultural outcomes. Area under crop and SWCMs emerged as key determinants of farm TE, having the highest elasticity values amongst all of the variables. Crop acreage exerted a direct influence on total revenue from agriculture by leveraging economies of scale. A larger cultivated area allowed farmers to spread fixed costs over a greater production volume, resulting in a lower per-unit cost of production and leading to increased efficiency (Duffy Reference Duffy2009). Economies of scale in agriculture are also realized through enhanced utilization of resources and streamlined operations on large farms (FAO 2017). Farmers adopting SWCMs are better positioned to optimize resource use, reduce production costs and ultimately increase total revenue by harnessing the intrinsic value of a healthier and more resilient agro-ecosystem (Choudhary et al. Reference Choudhary, Dev, Singh, Singh, Sharma and Chand2022). The return to scale, obtained by summing up all of the partial production elasticities, was consistently less than 1 for all of the SPF models. This suggests that upward adjustments in input usage by farmers will not result in a proportionate increase in output, which is consistent with prior studies on small and marginal farmers in less favourable areas (e.g., Chavas et al. Reference Chavas, Petrie and Roth2005, Solís et al. Reference Solís, Bravo-Ureta and Quiroga2007).
Off-farm income helps to alleviate the liquidity constraints faced by farmers and promotes efficient production. Contact with extension and training agencies facilitates knowledge and experience exchange, highlights suitable technologies and assists in efficient resource utilization, all of which play decisive roles in improving efficiency. These findings are consistent with the results of Choudhary et al. (Reference Choudhary, Dev, Singh, Singh, Sharma and Chand2022).
We show that the adoption of SWCMs significantly enhances the TE of farmers. The integration of SWCMs, coupled with access to valuable information through training and extension support, plays a crucial role in managing soil erosion, boosting groundwater levels to support irrigation and ultimately enhancing overall productivity. The empirical estimates of farm TE further demonstrate that without appropriate corrections for selection bias, farm TE tends to be underestimated, and the performance gap between treated farmers and their control counterparts would be overestimated. These findings are consistent with Mayen et al. (Reference Mayen, Balagtas and Alexander2010), Bravo-Ureta et al. (Reference Bravo-Ureta, Greene and Solís2012) and Ma et al. (Reference Ma, Renwick, Yuan and Ratna2018), who also reported bias correction on TE differentials between treated and control groups. Achieving precision in farm TE estimates is essential for identifying areas of improvement and implementing evidence-based policies that address specific challenges within the agricultural sector. By controlling biases, policymakers can ensure a more reliable foundation for decision-making, fostering sustainable agricultural practices, resource optimization and overall economic development in the farming industry. Moreover, the econometric analyses of the impacts of SWCMs on farm efficiency could inform effective adoption and successful implementation of such measures in semi-arid tropical areas elsewhere, where natural resource management is encouraged as an adaptation strategy for climate change.
Conclusion
By employing robust methodologies to address biases from observed and unobserved variables, we meticulously examine the farm TE in soil and water conservation activities in the Bundelkhand region of central India. Utilizing PSM and selectivity-corrected models for stochastic frontiers, the findings consistently indicate higher TE amongst beneficiary farmers, even after accounting for selectivity bias. The TE improvement for both treated and control farmers, coupled with a narrowed gap in post-bias correction, underscores the positive impacts of development projects on farm efficiency. Notably, a positive correlation is observed between TE and off-farm income, training and extension outreach. Prioritizing efforts to enhance off-farm income through government initiatives and strengthening extension services and training facilities emerge as crucial for optimizing farm production in this semi-arid region. Integrating participatory models such as farmer field schools and supporting local research institute demonstrations can play a pivotal role in advancing sustainable agriculture practices, and this should also be the case worldwide.
Supplementary material
To view supplementary material for this article, please visit https://doi.org/10.1017/S0376892924000146.
Acknowledgements
The support of the field staff of the KISAN MITrA project for data collection is duly acknowledged. Special thanks are given to the editor of the journal and reviewers for their critical comments that helped to improve the manuscript.
Financial support
None.
Competing interests
The authors declare none.
Ethical standards
None.










