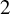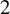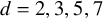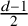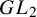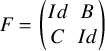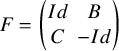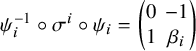Cyclic coverings of genus $2$ curves of Sophie Germain type

Abstract

We consider cyclic unramified coverings of degree d of irreducible complex smooth genus $2$ curves and their corresponding Prym varieties. They provide natural examples of polarized abelian varieties with automorphisms of order d. The rich geometry of the associated Prym map has been studied in several papers, and the cases $d=2, 3, 5, 7$ are quite well understood. Nevertheless, very little is known for higher values of d. In this paper, we investigate whether the covering can be reconstructed from its Prym variety, that is, whether the generic Prym Torelli theorem holds for these coverings. We prove this is so for the so-called Sophie Germain prime numbers, that is, for $d\ge 11$ prime such that $\frac {d-1}2$ is also prime. We use results of arithmetic nature on $GL_2$-type abelian varieties combined with theta-duality techniques.

1. Introduction

We consider cyclic unramified coverings of degree d of irreducible complex smooth genus- $2$ curves and their corresponding Prym varieties. They provide natural examples of polarized abelian varieties with automorphisms of order d. The rich geometry of the associated Prym map has been studied in several papers; see [1, 2, 7, 8, 11, 13], among others. Notice that the classical case, $d=2$ , is completely explained in [9, section 7] and [10]. Nevertheless, very little is known for higher values of d. In this article, we investigate whether the covering can be reconstructed from its Prym variety, that is, whether the generic Prym Torelli theorem holds for these coverings.

It is known that the Prym variety of an unramified cyclic covering (over any smooth curve) is isomorphic, as unpolarized varieties, to the product of two Jacobians (see [11]), and when the degree d is odd, the Jacobians are isomorphic. Moreover, when d is not prime, the existence of intermediate coverings gives a much more complicated scenario, which strongly depends on the decomposition of d in primes. For this reason, as in [13], we assume d to be an odd prime.

Putting this in a modular setting, we consider the moduli space ¹ $\mathcal R^d$ of isomorphism classes of cyclic unramified coverings $f:\widetilde C\rightarrow C$ , with $g(C)=2$ and $\deg (f)=d$ . Equivalently, $\mathcal R^d$ parametrizes isomorphism classes of pairs $(C,\langle \eta \rangle )$ , where $\eta $ is a d-torsion point in $JC$ generating a subgroup $\langle \eta \rangle \cong \mathbb Z/d\mathbb Z$ . We recall that the curve $\widetilde C$ is constructed by applying the $\mathrm {Spec}$ functor to the sheaf of $\mathcal O_{C}$ -algebras:

$$\begin{align*}\mathcal O_C \oplus \eta \oplus \eta^2 \oplus \ldots \eta^{d-1}. \end{align*}$$

Notice that $\widetilde C$ comes equipped with an automorphism $\sigma $ of order d such that $C=\widetilde C/\langle \sigma \rangle $ .

An important consequence of this construction is that it shows that any automorphism of C leaving $\langle \eta \rangle $ invariant lifts to an automorphism on $\widetilde C$ . This is the case of the hyperelliptic involution on C, which lifts to an involution j on $\widetilde C$ . Therefore, the dihedral group generated by $\sigma $ and j acts on $\widetilde C$ providing an interesting geometric structure in the several Jacobians and Pryms appearing naturally in the picture. We focus on the Prym variety $P(\widetilde C,C)$ defined as the component of the origin of the kernel of the norm map $J\widetilde C\rightarrow JC.$ It is a consequence of the Riemann–Hurwitz theorem that $g(\widetilde C)=d+1$ , and thus $\dim P(\widetilde C,C)=d-1$ . Moreover, the principal polarization on $J\widetilde C$ induces on $P(\widetilde C,C)$ a polarization $\tau $ of type $(1,\ldots ,1,d)$ . We can define the Prym map as the map of moduli stacks:

$$\begin{align*}{\mathcal P}_d:{\mathcal R}^{d} \longrightarrow {\mathcal A}_{d-1}^{(1,\ldots,1,d)}, \end{align*}$$

which maps $f:\widetilde C\rightarrow C$ to the isomorphism class of $(P(\widetilde C,C), \tau )$ .

It is known that the generic fiber of ${\mathcal P}_d$ is positive dimensional for $d=3,5$ ([2]), for $d=7$ the degree onto its image is $10$ ([8]) and the map is generically finite for $d\ge 7$ ([1]). In this paper, we prove:

Theorem 1.1. The Prym map $\mathcal P_d$ is generically injective for every prime $d\ge 11$ such that $k:=\frac {d-1}2$ is also prime.

Remark 1.2. It is conjectured that there are infinitely many pairs of prime numbers of the form $(k,2k+1)$ . These are called Sophie Germain prime numbers. Under this hypothesis on d and k, we will say that $f: \widetilde C \rightarrow C$ is of Sophie Germain type.

Our proof has ingredients of different nature. We use arithmetic arguments on abelian varieties of $GL_2$ -type to analyze the endomorphism algebra of some Jacobians, combined with the use of theta-duality techniques inspired by the Fourier–Mukai transform.

More precisely: The automorphism $\sigma $ on $\widetilde C$ induces an automorphism, denoted by the same letter, on $P:=P(\widetilde C,C)$ preserving the polarization $\tau $ and fixing point-wise the kernel of $\lambda _{\tau }:P\rightarrow P^{\vee }$ . We prove first that $\sigma $ is, generically, completely determined by $(P,\tau )$ . Then, we consider the curve $C_0:=\widetilde C/\langle j \rangle $ , where j is a lifting of the hyperelliptic involution on C. In the second step, using a result of arithmetic nature ([5, 15]), we prove that for a generic covering, the only automorphisms of $C_0$ are the identity and, possibly, the hyperelliptic involution.

Next, we consider the isomorphisms $JC_0\times JC_0 \rightarrow P$ studied in [13] and [11]. We prove, using step 2, that these isomorphisms are unique in general, which allows us to recover canonically from $(P,\tau )$ the curve $C_0$ and a set of automorphisms $\beta _i$ on $JC_0$ .

Finally, we show how to reconstruct the covering $f:\widetilde C\rightarrow C$ from these data. The key argument is that the whole diagram (2.1) is determined by the map $h_0:C_0\rightarrow \mathbb P^1$ . We recover explicitly the fibers of $h_0$ in the following way: We fix a point $x\in C_0$ to embed $C_0$ in $JC_0$ , and then we compute the theta dual (as introduced in [12] and used in [6]) of the curves $\beta _i(C_0)\subset JC_0$ . This gives a translation of the Brill–Noether locus $W_{k-3}(C_0)$ by an effective degree $2$ divisor defined by two points in the fiber $h_0^{-1}(h_0(x))$ . Varying i, we recover the whole fiber of $h_0$ at $h_0(x)$ , and this ends the proof.

In the last sections of the paper, we consider the cases $d=9$ and $d=13$ , which illustrate that without our assumptions the generic injectivity requires a case-by-case analysis which depends on the decomposition of d and k in prime numbers.

When $d=9$ , since d is not prime, we have additional curves in the diagram. In this case, a deeper analysis of the automorphisms that appear in step 3 combined with Galois theory arguments allows us to conclude the following (see Theorem 4.6):

Theorem 1.3. The Prym map $\mathcal P_{9}$ is generically injective.

We finish by studying the case $d=13$ , providing a necessary condition for the generic injectivity of the Prym map $\mathcal P_{13}$ .

2. Setup and notations

The content of this section is borrowed from [13] and [11]. We will state the results of these two papers without further quoting. Let $f: \widetilde C \rightarrow C$ be a cyclic d-covering of a curve C of genus $2$ associated to a nontrivial d-torsion point $\eta \in JC[d]$ . We denote by $\sigma $ both the automorphism of order d on $\widetilde C$ and the induced automorphism on $J\widetilde C$ . The Prym variety of the covering, $P:=P(\widetilde C,C)$ , is the component of the origin of the kernel of the norm map. One easily checks that $\sigma $ leaves P invariant, so we keep the notation $\sigma $ for the restriction to P. The polarization on $J\widetilde C$ induces on P a polarization $\tau $ of type $(1,\ldots ,1,d)$ which is invariant by $\sigma $ , that is, there is a line bundle $L\in Pic(P)$ representing $\tau \in NS(P)$ such that $\sigma ^*(L)\cong L$ . Moreover, we have:

Lemma 2.1. The set of fixed points of $\sigma $ on P is exactly the kernel $K(\tau )$ of the polarization map $\lambda _{\tau }:P\rightarrow P^{\vee }$ . Moreover, $K(\tau )= P\cap f^*(JC)$ .

From now on, we assume that d is an odd prime, and we set $d=2k+1$ .

The hyperelliptic involution $\iota $ on C lifts to an involution j on $\widetilde C$ . The dihedral group with $2d$ elements generated by j and $\sigma $ acts on $\widetilde C$ . Notice that all the automorphisms $j\circ \sigma ^i$ are involutions on $\widetilde C$ lifting $\iota $ . We define the following curves:

$$\begin{align*}C_0:=\widetilde C/\langle j \rangle, \quad C_1:=\widetilde C/\langle j\sigma \rangle, \quad \ldots \quad C_{d-1}:=\widetilde C/\langle j\sigma^{d-1} \rangle. \end{align*}$$

And we denote by $\pi _i:\widetilde C\rightarrow C_i$ , $i=0,\ldots , d-1$ the quotient maps. These curves fit in the following commutative diagram:

(2.1)

where the maps $\varepsilon , \pi _0,\ldots , \pi _{d-1}$ are of degree $2$ and the maps $f, h_0, h_1,\ldots ,h_{d-1}$ of degree d. Moreover, since d is odd, all the involution in the dihedral group are conjugate to each other, therefore all the curves $C_i$ are mutually isomorphic. Moreover, $g(C_0)=g(C_1)=\ldots = g(C_{d-1})=k$ . In fact, all the maps $\pi _i$ ramify in six points, one in each preimage by f of the Weierstrass points of C. In particular, $\pi _i^*:JC_i \rightarrow J\widetilde C$ is injective. From now on, we identify $JC_i$ with its image in $J\widetilde C$ .

Proposition 2.2. (Ortega, Ries). With the notations in the diagram (2.1) and denoting by P the Prym variety $P(\widetilde C,C)$ , the following statements hold for any $i=0,\ldots , d-1$ :

1. a) $JC_i\subset P$ .

2. b) The automorphism $\sigma ^i$ sends $JC_0$ to $JC_{d-2i}$ for $i\leq k$ , and to $JC_{2d-2i}$ for $i> k$ .

3. c) The automorphism $\beta _i:=\sigma ^i+\sigma ^{-i}$ leaves invariant $JC_0$ .

A crucial ingredient for the proof of our main theorem is the existence of k isomorphisms:

$$\begin{align*}\psi_i: JC_0 \times JC_0 \longrightarrow JC_0 \times JC_{d-2i} \longrightarrow P, \end{align*}$$

where the first map sends $(x,y)$ to $(x,\sigma ^i(y))$ (for $i=1,\ldots ,k$ ), and the second is the addition map.

Let us denote by $\lambda _N:JN\rightarrow JN^{\vee }$ the isomorphism attached to the natural principal polarization on a smooth irreducible curve N. We will keep this notation for the rest of the paper.

The pull-back of the polarization $\tau $ to $JC_0\times JC_0$ gives rise to the following commutative diagram:

(2.2)

where $M_i$ is the matrix

$$\begin{align*}\left( \begin{array}{cc} 2 & \beta_i \\ \beta_i & 2 \end{array} \right), \end{align*}$$

and the automorphisms $\beta _i$ , for $i=1,\ldots ,k$ of $JC_0$ are those appearing in the previous proposition.

It will also be useful to know the pull-back of the automorphisms $\sigma ^i$ to $JC_0\times JC_0$ through the isomorphisms $\psi _i$ . Indeed, we have the following:

Proposition 2.3. For any $i=1,\ldots ,k$ we have the equality:

$$\begin{align*}\sigma^i \circ \psi_i= \psi_i\circ \begin{pmatrix}0 & -1\\1&\beta_i\end{pmatrix}. \end{align*}$$

Remark 2.4. Notice that a priori $\psi _i^*(\langle \sigma \rangle )$ yields $d-1$ automorphisms of $JC_0\times JC_0$ . The crucial point is that only one among them is of type

$$ \begin{align*} \begin{pmatrix} 0 & *\\1 & * \end{pmatrix}. \end{align*} $$

3. Proof of the main theorem

Our aim is to prove the generic injectivity of the map

$$\begin{align*}\mathcal P_d:\mathcal R^d \longrightarrow \mathcal A_{d-1}^{(1,\ldots,1,d)}, \end{align*}$$

with $d=2k+1$ , assuming k and d primes.

3.1. First step: uniqueness of $\sigma $ .

We want to use the automorphism $\sigma $ in order to read from $(P,\tau )$ relevant information to reconstruct $(\widetilde C,C)$ . We shall show that the only automorphisms of P of order d preserving $\tau $ and in fact, fixing point-wise $K(\tau )$ (see Lemma 2.1) are the powers $\sigma ^i $ .

Proposition 3.1. Let P be a general element in $Im(\mathcal {P}_d)$ . Then the group of automorphisms

$$ \begin{align*}\{ \epsilon \in Aut((P,\tau)) \ \mid \ \epsilon (x)=x, \ \forall x\in K(\tau) \}\end{align*} $$

is $\langle \sigma \rangle \simeq \mathbb Z/d\mathbb Z$ .

Proof. Let P and $\epsilon \neq \mathrm {Id}$ be as in the statement. We will see that $\epsilon =\sigma ^i$ for some $i=1,\ldots ,d-1$ , where $\sigma $ is as in Section 2. Due to Lemma 2.1, there is an automorphism $\tilde \epsilon : J\widetilde C \rightarrow J\widetilde C$ such that the following diagram is commutative:

where $\mu :f^*JC \times P \rightarrow J\widetilde C$ stands for the addition map. According to the diagram, $\mu ^* \tilde \epsilon ^* \mathcal O_{J\widetilde C}(\widetilde \Theta )$ equals, as polarizations, $\mu ^*\mathcal O_{J\widetilde C}(\widetilde \Theta )$ . Since $\mu $ is an isogeny, the kernel of $\mu ^*$ is finite and therefore

$$\begin{align*}\tilde \epsilon ^{\,*} \mathcal O_{J\widetilde C}(\widetilde \Theta)\otimes \mathcal O_{J\widetilde C}(-\widetilde \Theta ) \end{align*}$$

is a torsion sheaf, in particular belongs to $Pic^0(J\widetilde C)$ . Hence, $\tilde \epsilon ^* \mathcal O_{J\widetilde C}(\widetilde \Theta )$ induces the canonical polarization on $J\widetilde C$ , and thus, by the Torelli theorem, there is an automorphism $\tilde \epsilon _0$ on $\widetilde C$ inducing $\tilde \epsilon $ . Notice that, by construction, $\tilde \epsilon $ is the identity on $f^*(JC)$ . We claim that $Norm_f (Id-\widetilde \epsilon )=0$ . Indeed, for all $x\in J\widetilde C$ we write $x=y+f^*(z)$ , where $y\in P$ and $z\in JC$ . Then:

$$\begin{align*}(Id-\widetilde \epsilon )(x)=y+f^*(z)- (\widetilde \epsilon (y)+f^*(z))= y-\widetilde \epsilon (y). \end{align*}$$

Since $\widetilde \epsilon $ leaves invariant P, we obtain that $Norm_f(Id-\widetilde \epsilon )=0$ . Let $p_1,p_2\in \widetilde C$ be two points with $f(p_1)=f(p_2)$ . Then the norm of $p_1-p_2-\widetilde \epsilon _0(p_1)+\widetilde \epsilon _0(p_2)$ is zero. This implies that $f(\widetilde \epsilon _0(p_1))=f(\widetilde \epsilon _0(p_2))$ , hence $\tilde \epsilon _0$ descends to an automorphism of C. Since C is generic, this automorphism must be either the identity or the hyperelliptic involution. The latter it is not possible, since the hyperelliptic involution induces $-Id$ in $f^*(JC)$ .

So $\tilde \epsilon _0$ preserves the fibers of f and descends to the identity automorphism of C. Therefore, $\tilde \epsilon _0$ belongs to the Galois group of $\widetilde C$ over C which is the cyclic group generated by $\sigma $ .

3.2. Second step: determination of the automorphisms on $C_0$

This subsection is devoted to the study of the possible automorphisms on $C_0$ that will appear in the third step. From now on, the covering $\widetilde C\rightarrow C$ is generic in $\mathcal R^d$ . Given an abelian variety A, we denote by $End(A)$ its endomorphism ring and by $End^0(A)$ the endomorphism algebra $End(A)\otimes _{\mathbb {Z}}\mathbb {Q}$ . Recall that a CM-field E is a number field with exactly one complex multiplication, equivalently E is a totally imaginary quadratic extension of a totally real number field. A CM-algebra is a finite product of CM-fields.

Definition 3.2. The abelian variety A is said to be of $GL_2$ -type if for some number field E such that $[E:\mathbb {Q}]=\dim A$ , there is an embedding of $\mathbb {Q}$ -algebras $E\hookrightarrow End^0(A)$ .

Definition 3.3. The abelian variety A is said to be of CM-type if for some CM-field E such that $[E:\mathbb {Q}]=2\dim A$ , there is an embedding of $\mathbb {Q}$ -algebras $E\hookrightarrow End^0(A)$ .

Proposition 3.4. The Jacobian variety $JC_0$ is of $GL_2$ -type.

Proof. This is a straightforward check of Definition 3.2 for the Jacobian variety $JC_0$ . The automorphism $\beta _1$ determines the subfield $E:=\mathbb {Q}(\xi +\xi ^{-1})\subseteq End^0(JC_0)$ , where $\xi $ is a primitive d-root of the unity. Since $[E:{\mathbb Q}] =(d-1)/2=k=\dim JC_0$ the claim follows.

Remark 3.5. Notice that the subfield E is totally real and that the Rosati involution acts here as the identity.

Hence, we can state the following:

Proposition 3.6. For a generic $(\widetilde C,C)\in \mathcal R^d$ , any nontrivial automorphism of $C_0$ has order 2.

Proof. Let $\phi $ be an automorphism of $C_0$ . Let us assume that it has order prime $p \geq 3$ . This yields the inclusion $\mathbb {Q}(\zeta _p)\hookrightarrow End^0(JC_0)$ , where $\zeta _p$ is a p-th primitive root of the unity. It is well known that for every $m|(p-1)=|Gal(\mathbb {Q}(\zeta _p)/\mathbb {Q})|$ there exists a subfield $K_m\subseteq \mathbb {Q}(\zeta _p)$ with degree m over $\mathbb {Q}.$ Thus, in particular, there exists a subfield $K_2:=\mathbb {Q}(\alpha )\subseteq \mathbb {Q}(\zeta _p)$ with degree $2$ over $\mathbb {Q}.$ So we have the inclusion $\mathbb {Q}(\alpha , \xi +\xi ^{-1})\subseteq End^0(JC_0)$ with

$$\begin{align*}[\mathbb{Q}(\alpha, \xi+\xi^{-1}): \mathbb{Q}]= [\mathbb{Q}(\alpha, \xi+\xi^{-1}):\mathbb{Q}(\xi+\xi^{-1})][\mathbb{Q}(\xi+\xi^{-1}): \mathbb{Q}] = 2k.\end{align*}$$

Therefore, $JC_0$ is a CM-type abelian variety, but this is impossible since there are only countably many such abelian varieties and $JC_0$ is a generic element in a positive dimensional family ([3][Section 9.6, Example 6.6]).

By analogous reasons, we can exclude the case $\text {ord}(\phi )=2^t$ with $t>1$ . Indeed, the imaginary unit i would determine a totally imaginary extension of our totally real field E. Finally, if $\text {ord}(\phi )$ is not prime nor of the form $2^t$ with $t>1$ , we can factorize $\phi $ through maps of smaller prime order and thus conclude the result. Therefore, it only remains the case $p=2$ .

In [15] (see also [5]), the author shows the following:

Proposition 3.7 ([15], Proposition 1.5).

Let A be an abelian variety of $GL_2$ -type.

1. 1 If A is not a CM abelian variety, then A is isogenous to $A_1^r$ , where $A_1$ is a simple abelian variety of $GL_2$ -type and $r\in {\mathbb {N}}$ .

2. 2 If A is a CM abelian variety, then A is isogenous either to $A_1^r$ , where $A_1$ is a simple CM abelian variety and $r\in {\mathbb {N}}$ , or to $A_1^{r_1}\times A_2^{r_2}$ , where $A_i$ is a simple CM abelian variety and $r_i\in {\mathbb {N}}$ for $i = 1, 2$ and $r_1 \dim A_1 = r_2 \dim A_2$ .

Applying this result to our situation, we have the following:

Proposition 3.8. Assume k be a prime number. Then, any automorphism $\phi $ of $C_0$ is either the identity or, potentially, the hyperelliptic involution. In particular, the induced automorphism on $JC_0$ is $\pm Id$ .

Proof. Due to Proposition 3.6, we can assume that the automorphism is an involution. Since there are only countably many CM abelian varieties, by Proposition 3.7, we have the following two possibilities: Either $JC_0$ is simple or it is isogenous to $A_1^r$ . Suppose that $JC_0$ is simple: Either $\phi =Id$ , or the quotient of the covering map $C_0\rightarrow C_0/\langle \phi \rangle $ is $\mathbb {P}^1$ . In the latter case, $C_0$ is hyperelliptic and thus, on $JC_0$ , the automorphism is $-Id$ . Suppose now that $JC_0$ is not simple, namely $JC_0\sim A_1^r$ . This yields $k=r\dim A_1$ . Since k is prime, the only possibility is $r=k$ and $\dim A_1=1$ . This leads to a contradiction, since $C_0$ varies in a three-dimensional family (see Remark 3.9), whereas the moduli space of elliptic curves is one-dimensional.

3.3. Third step: recovering $(C_0,\beta _1,\ldots , \beta _k)$

The dihedral construction of diagram (2.1) gives a morphism

$$ \begin{align*}\psi: \mathcal{R}^d \rightarrow \mathcal{M}_{k}\end{align*} $$

sending $[C,\eta ]$ to $[C_0]$ . Notice that this map is well defined since all the curves $C_0,\ldots ,C_{d-1}$ are isomorphic. According to Diagram (2.2), the curve $C_0$ together with the automorphisms $\beta _i$ of $JC_0$ determine $(P, \tau )$ as a polarized abelian variety. Let us consider the moduli space $\widetilde {\mathcal D}_k$ , of the isomorphism classes of objects $(C_0,j,\beta _1,\ldots ,\beta _k)$ , where $C_0$ is genus k curve with an embedding $j: JC_0 \hookrightarrow P$ and the $\beta _i's$ are automorphisms of P leaving $JC_0$ invariant. Let $\widetilde {\mathcal D}_k\rightarrow \mathcal D_k$ be the forgetful map $(C_0,j,\beta _1,\ldots ,\beta _k)\mapsto C_0$ . Since the pair $(P,\tau )$ can be constructed from these data (see diagram (2.2)), we have a factorization of the Prym map $\mathcal P_d$ as follows:

Remark 3.9. By means of this factorization, Albano and Pirola showed that the generic fibers of $\mathcal P_d$ have the same dimension as the dimension of the fibers of $\psi $ . Using this, they prove that the fibers of $\mathcal P_3$ and $ \mathcal P_5$ are positive dimensional (see [2, Remark 2.8]).

The aim of this step is to prove that $\mathcal P_{d,2} $ is generically injective. In the fourth step, we will show that $\mathcal P_{d,1}$ also has degree $1$ .

We consider isomorphisms $\varphi : JN\times JN\rightarrow P$ , where N is a smooth curve of genus k. We say that such an isomorphism $\varphi $ satisfies the property (*) if and only if the pull-back of $\tau $ is as in diagram (2.2), that is:

(*) $$ \begin{align} \varphi ^{\vee }\circ \lambda_{\tau } \circ \varphi = \begin{pmatrix} 2 \lambda_N & \lambda_N \circ \gamma \\ \lambda_N \circ \gamma & 2 \lambda _N \end{pmatrix},\end{align} $$

for some $\gamma \in Aut(JN)$ . In the same way, property (**) holds if $\varphi $ behaves as in Proposition 2.3, that is, for some automorphism $\gamma $ of $JN$ and some exponent i we have:

(**) $$ \begin{align} \sigma ^i \circ \varphi =\varphi \circ \begin{pmatrix} 0 & -1 \\ 1 & \gamma \end{pmatrix}. \end{align} $$

Then, we define the intrinsic set attached to $(P,\tau , \langle \sigma \rangle )$ :

(3.1) $$ \begin{align} \Lambda (P,\tau, \langle \sigma \rangle):= \{ (N,\varphi) \mid \varphi: JN\times JN \stackrel{\cong}{\longrightarrow } P \text{ satisfies } (*), (**) \text{ for the same } \gamma \in Aut(JN)\}. phi. \end{align} $$

Proposition 3.10. Let $(P,\tau , \langle \sigma \rangle )$ be generic in the image of $\mathcal {P}_d$ . Then for all $(N, \varphi ) \in \Lambda (P,\tau , \langle \sigma \rangle )$ , we have that:

1. a) $N\cong C_0$ ;

2. b) $\gamma =\beta _i$ for an i in $1,\cdots , k$ .

Proof. Let $(N, \varphi ) \in \Lambda (P,\tau , \langle \sigma \rangle )$ . We fix i, the exponent appearing in $(**)$ . The composition:

whose associated matrix is of type 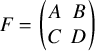$F=\begin {pmatrix} A & B\\ C & D \end {pmatrix}$ , provides an isomorphism such that the polarization in $JC_0 \times JC_0$ with matrix:

$$\begin{align*}\Lambda_0:=\begin{pmatrix} 2 \lambda_{C_0} & \lambda_{C_0} \circ \beta_i \\ \lambda_{C_0} \circ \beta_i & 2 \lambda_{C_0} \end{pmatrix}, \end{align*}$$

pulls-back to the polarization on $JN \times JN$ with matrix:

$$\begin{align*}\Lambda_N:=\begin{pmatrix} 2 \lambda_{N} & \lambda_{N} \circ \gamma\\ \lambda_{N} \circ \gamma & 2 \lambda_{N} \end{pmatrix}. \end{align*}$$

Considering the restriction to $JN\times \{0\}$ and projecting to the first factor $JC_0$ , we get a commutative diagram as follows:

(3.2)

Indeed, the dual of $\iota $ is $pr_1$ and the polarization induced by $\Lambda _N$ on $JN$ is exactly $\lambda _N$ . Therefore, the map $pr_1\circ F\circ \iota : JN\rightarrow JC_0$ satisfies that the pull-back of twice the canonical polarization on $JC_0$ is twice the canonical polarization on $JN$ . Hence, $(JN,\Theta _N)\cong (JC_0,\Theta _{C_0})$ . By the Torelli theorem, $N\cong C_0$ . This proves a).

In order to prove b), we fix an isomorphism $N\cong C_0$ and we look again at diagram (3.2) (by an abuse of notation we still use the letter F). The composition $pr_1\circ F\circ \iota : JC_0\rightarrow JC_0$ corresponds to the piece A in the matrix of F. Hence,

$$\begin{align*}2\lambda_0= 2A^\vee\lambda_0 A, \end{align*}$$

that is, A preserves the polarization on $JC_0$ . Thus, A comes from an automorphism of $C_0$ . By Proposition 3.8, we obtain $A=\pm Id$ . Replacing $\iota $ by $\iota _2$ (the restriction to the second factor of $JC_0\times JC_0$ ) and, analogously, $pr_1$ by $pr_2$ in diagram (3.2), we obtain $D=\pm Id$ . In order to study the terms B and C recall that, by assumptions (property (**)), for a certain unique i, we have

(3.3) $$ \begin{align} \sigma^i\circ \varphi=\varphi\circ \begin{pmatrix} 0 & -1\\ 1 & \gamma \end{pmatrix}, \end{align} $$

and, thanks to Proposition 2.3, the same occurs for $\psi _i$ with 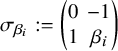$\sigma _{\beta _i}:=\begin {pmatrix} 0 & -1\\ 1 & \beta _i \end {pmatrix}$ . Therefore, we have the following diagram:

(3.4)

where $\sigma _{\gamma }$ is the matrix in (3.3). Now, we analyze the possibilities for F.

1. 1. Let $F=\begin {pmatrix} Id & B\\ C & Id \end {pmatrix}$ . The commutativity of the diagram above says that $B=-C=0$ and $\gamma =\beta _i$ .

2. 2. Let $F=\begin {pmatrix} Id & B\\ C & -Id \end {pmatrix}$ in this case $B=-C$ and $\gamma =\beta _i$ .

And the same occurs for the other configurations. This ends the proof.

3.4. Fourth step: theta duality.

The first three steps show that the curve $C_0$ and the set of automorphisms $\{\beta _1, \ldots ,\beta _k\}$ of $JC_0$ can be recovered from the initial data $(P, \tau , \langle \sigma \rangle )$ . We shall prove that these automorphisms determine the map $h_0:C_0 \rightarrow \mathbb P^1$ appearing in Diagram (2.1).

Let us recall the definition of the theta-dual of a subvariety X of a principally abelian variety $(A,\tau _A)$ , with $\dim (X) \leq \dim A -2$ . Fix an effective theta divisor $\Theta $ representing the polarization $\tau _{A}$ .

Definition 3.11. The theta-dual $T(X)$ of X is set-theoretically defined by

$$\begin{align*}T(X)=\{a\in A \mid X\subset \Theta +a\}. \end{align*}$$

That is, we consider the set of translates of X contained in the theta divisor or, equivalently, the set of $a\in A$ such that X is contained in $t_{-a}^*(\Theta )$ , where $t_{a}$ stands for the translation $x\mapsto x+a$ . Notice that changing the effective divisor representing the principal polarization $T(X)$ is modified by a translation.

Pareschi and Popa gave a natural scheme structure to $T(X)$ for any closed reduced subscheme X (see [12, Def. 4.2]) by defining $T(X)$ in terms of the Fourier–Mukai transform on A; more precisely, $T(X)$ becomes the support of an explicit sheaf on A. They also proved (see [12, Section 8]) that for a smooth curve N embedded in its Jacobian it holds, up to translation, $T(N)=-W_{g(N)-2}(N)$ , where $W_{g(N)-2}(N)$ stands for the Brill–Noether locus of effective divisors of degree $g(N)-2$ translated to $JN$ by subtracting some $\alpha \in Pic^{g(N)-2}(N)$ . Similar results for Prym curves in their Prym varieties are obtained in [6].

The key idea in this part is to compute the theta-dual of the curve $\beta _i(C_0)$ embedded in $JC_0$ and use this to recover the whole map $h_0$ .

Observe that in the Jacobian $JC_0$ (of genus k), we can give a canonical definition of the set $T(X)$ by representing it in the torsor $Pic^{k-1}(C_0)$ , where the theta divisor is canonically identified with $W_{k-1}(C_0)$ . We change slightly the notation to avoid confusion, so for any subscheme $X\subset JC_0$ we define the following:

Definition 3.12. The canonical theta-dual $T'(X)$ of $X\subset JC_0$ is set-theoretically defined by

$$\begin{align*}T'(X)=\{\psi \in Pic^{k-1}(C_0) \mid X+\psi \subset \Theta^{can}= W_{k-1}(C_0)\}. \end{align*}$$

Let us fix from now on a point $x \in C_0$ , and consider the injection $\iota _x: C_0\hookrightarrow JC_0, p\mapsto [p-x]$ . Our aim is to compute $T'(\beta _i(\iota _x(C_0)))\subset Pic^{k-1}(C_0)$ .

Observe that to use the definition of $\beta _i$ we need to see $JC_0=\pi _0^*(JC_0)$ as a subvariety of P. Given a point p in $C_{0}$ , $\iota _x(p)=[p-x]$ appears as $[p'+j(p')-x'-j(x')]\in P$ , where $x',p'\in \widetilde C$ are preimages of $x,p$ , respectively. We denote by

$$\begin{align*}p', p^{\prime}1:=\sigma (p'),\ldots ,p^{\prime}{d-1}=p^{\prime}{2k}:=\sigma ^{d-1}(p') \end{align*}$$

the whole fiber $f^{-1}(f(p'))$ and analogously for $x'$ . We denote by $p_i$ (resp. $x_i$ ) the image of $p^{\prime }i$ (resp. $x^{\prime }i$ ) in $C_0$ . With these notations, we have:

Proposition 3.13. Assume that $k \ge 4$ , then the following equality holds in $Pic^{k-1}(C_0)$ :

$$\begin{align*}T'(\beta_i(\iota_x(C_0)))=x_i+x_{d-i}+W_{k-3}(C_0). \end{align*}$$

Proof. Following the previous notation, the action of $\beta _i=\sigma ^i+\sigma ^{-i}$ on $[p'+j(p')-x'-j(x')]$ is as follows:

$$ \begin{align*} & [\sigma ^i(p')+\sigma^i(j(p'))+\sigma ^{-i}(p')+\sigma^{-i}(j(p')) -\sigma ^i(x')-\sigma^i(j(x'))-\sigma ^{-i}(x')-\sigma^{-i}(j(x'))]= \\ & [p^{\prime}i+j(p^{\prime}{d-i})+p^{\prime}{d-i}+ j(p^{\prime}{i}) - x^{\prime}i-j(x^{\prime}{d-i})-x^{\prime}{d-i}-j(x^{\prime}{i})]= \\ & (1+j)([p^{\prime}i+p^{\prime}{d-i}-x^{\prime}i-x^{\prime}{d-i}]). \end{align*} $$

Then, as element in $JC_0$ , we have obtained that:

$$\begin{align*}\beta_i ( [p-x])=[p_i+p_{d-i}-x_i-x_{d-i}]. \end{align*}$$

Observe that these points describe the fiber $h_0^{-1}(h_0(x))$ , more precisely, as divisors:

(3.5) $$ \begin{align} h_0^{-1}(h_0(x))=x+x_1+\ldots +x_{d-1}. \end{align} $$

By definition, $\xi \in T'(\beta _i(\iota _x(C_0))) $ means that:

$$\begin{align*}h^0(C_0,\xi + p_i+p_{d-i}-x_i-x_{d-i})>0,\qquad \text{for all } p\in C_0. \end{align*}$$

If $\xi $ is of the form $x_i+x_{d-i}+E$ for some effective divisor E, the condition is satisfied trivially, hence $x_i+x_{d-i}+W_{k-3}(C_0)\subset T'(\beta _i(\iota _x(C_0))).$ To prove the opposite inclusion, we consider $\xi \in T'(\beta _i(\iota _x(C_0)))$ . If $h^0(C_0, \xi -x_i-x_{d-i})>0$ , then we are done. So assume $h^0(C_0, \xi -x_i-x_{d-i})=0$ . Set $L:= K_{C_0}-(\xi -x_i-x_{i-d})$ . By Riemann–Roch theorem,

$$ \begin{align*}h^0(C_0, L)=2k-2-(k-3)-k+1=2.\end{align*} $$

Hence, L is a line bundle of degree $k+1$ with $h^0(C_0,L)=2$ and such that $h^0(C_0, L-p_{i}-p_{d-i})>0$ for all $p_i, p_{d-i}\in C_0$ , namely, L gives a $g^1_{k+1}$ whose associated map $\varphi _L$ satisfies $\varphi _L(p_i)=\varphi _L(p_{d-i})$ .

Now, let us take $p\in C_0$ such that no points in the fiber $h_0^{-1}(h_0(p))$ are in the base locus of L. Then this shows, as before, that $\varphi _L (p_i) = \varphi _L(p_{d-i})$ . Set now $q = p_{d-2i}$ . The same argument proves that $\varphi _L (p_{d-i}) = \varphi _L(q_i) = \varphi _L(q_{d-i}) = \varphi _L(p_{2d-3i})$ .

Proceeding in this way, one can prove that $\varphi _L(p_i) = \varphi _L(p_{d-i}) =\ldots = \varphi _L(p_{i+h(d-2i)})$ for all h. Since d is an odd prime which does not divide i, we can write every element $p_j$ in the form $p_j= p_{i+h(d-2i)}$ for a certain h. This shows that the whole $h_0^{-1}(h_0(p))$ is contained in the fiber of $\varphi _L$ , which is impossible since $h_0$ has degree $d=2k+1$ .

Remark 3.14. The proposition allows recovering intrinsically the class of the divisors $x_i+x_{d-i}$ since there are no translations leaving invariant $W_{k(g-1)-3}(C_0)$ . It may well happen that $x_i+x_{d-i}$ would belong to a $g^1_2$ linear series, since we have not excluded the possibility of $C_0$ being hyperelliptic. Assume that this is so for a generic point in $C_0$ , that is, for a generic p there is an index i such that $h^0(C,\mathcal{O}(p_i+p_{d-i}))=2$ . We can assume that $h^0(C,\mathcal{O}(x_1+x_{d-i}))=2$ for the fixed point x we used to embed the curve. Then $\beta_1(p-x)=p_1+p_{d-1}-x_i-x_{d-1}$ . Replacing p for a convenient point $p'$ in the same fiber we obtain $\beta_1(p'-x)=p_i+p_{d-i}-x_i-x_{d-1}=0$ since both divisors represent the hyperelliptic linear series. This contradicts that $\beta_1$ is an automorphism.

Proof of Theorem 1.1.

In order to show that the Prym map $\mathcal {P}^d$ has generically degree one, we factorize it as $\mathcal {P}^d_2\circ \mathcal {P}^d_1$ and we show that both maps $\mathcal {P}^d_i$ have generically degree one.

Let $(P(\widetilde C, C), \tau )$ be a generic element in $Im(\mathcal {P}^d)$ . The first three steps of the proof are devoted to the generic injectivity of $\mathcal {P}^d_2$ . First, we show that the triplet $(P(\widetilde C, C), \tau , \sigma )$ is uniquely determined by $(P(\widetilde C, C), \tau )$ . In the second step, we show that the only possible automorphisms of $JC_0$ are $\pm Id$ . This allows us to prove in the third step, that the fiber of $\mathcal {P}^d_2$ above $(P(\widetilde C, C), \tau )$ is given by the element $(C_0, \beta _1, \dots , \beta _k)$ .

The last step is devoted to the generic injectivity of $\mathcal {P}^d_1$ . Let $(C_0, \beta _1, \dots , \beta _k)$ be a generic element in $Im(\mathcal {P}^d_1)$ . According to Proposition 3.13; for a fixed $x\in C_0$ , we obtain intrinsically the subset $x_i+x_{d-i}+W_{k-3}(C_0)$ . A classical result of Weil (cf. [14, Hilfssatz 3]) states that $W_{k-3}(C_0)$ is not ‘translation invariant’, that is, if $\alpha \in JC_0$ satisfies that $\alpha + W_{k-3}(C_0)=W_{k-3}(C_0)$ , then $\alpha =0$ . This says that $x_i+x_{d-i}$ is uniquely determined in $C_0$ . Varying $i=1,\ldots ,k$ and using (3.5), we get that for all $x\in C_0$ the fiber of $h_0$ containing x is recovered. Now, by construction the map $h_0$ is ramified over six points in ${\mathbb P}^1$ , which are also the images of the Weierstrass points of C by $\varepsilon $ . Therefore, $\varepsilon : C\rightarrow \mathbb P^1$ is determined by $h_0$ . The fiber product of $\varepsilon : C\rightarrow \mathbb P^1$ and $h_0:C_0 \rightarrow \mathbb P^1$ gives the map $\widetilde C \rightarrow C$ . This finishes the proof.

4. Case $d=9$

This section is devoted to the analysis of the case $d=9$ , which is no longer a prime number. Due to the structure of the dihedral group $D_9$ , the corresponding diagram is more complicated since new intermediate quotients of the curve $\widetilde C$ and of the curves $C_i$ appear. Indeed, the situation can be summarized in the following diagram:

(4.1)

The curves $C_i$ correspond to the quotients $\widetilde C/ \langle j \sigma ^i\rangle $ , the curve $C':=\widetilde C/\langle \sigma ^3\rangle $ and, finally, the curves $E_i$ are obtained as $\widetilde C/\langle j\sigma ^i, \sigma ^3\rangle $ . Hence, $E_i$ and $ E_j$ are exactly the same curve if $i-j$ is a multiple of $3$ . The map $f'$ is étale of degree 3, while the maps $\widetilde C \rightarrow E_i$ (composing $\widetilde C \rightarrow C_i$ with $C_i\rightarrow E_i$ ) are Galois of degree 6 with Galois group $\langle j\sigma ^i, \sigma ^3\rangle \cong D_3$ . We have that $g(C')=4$ , $g(C_i)=4$ and $g(E_i)=1$ . By congruence modulo 3, it is sufficient to consider the first three quotient curves $C_0, C_1,C_2$ (respectively, $E_0, E_1, E_2$ ). Moreover, since the three dihedral groups $\langle j, \sigma ^3\rangle , \langle j\sigma , \sigma ^3\rangle $ , and $\langle j\sigma ^2, \sigma ^3\rangle $ are conjugated in $D_9$ , all the curves $E_i$ are isomorphic. Finally, notice that the non-Galois degree 9 maps $h_i: C_i\rightarrow {\mathbb P}^1$ factor as noncyclic triple covers $f_i:C_i\rightarrow E_i$ composed with some degree 3 maps $E_i\rightarrow {\mathbb P}^1$ ramified exactly over the Weiestrass points of C. The map $f_0: C_0\rightarrow E_0$ decomposes $JC_0$ up to isogeny as the product $ E_0\times P(C_0,E_0)$ , where $P(C_0,E_0)$ is the three-dimensional abelian variety defined as the Prym variety associated with $f_0$ .

A step-by-step analysis of Proposition 2.2 and Proposition 2.3 shows that they remain true in case $d=9$ too. Indeed, we have:

Proposition 4.1. For $i=1,\dots , 4$ the following properties hold.

1. 1. The automorphisms $\beta _i=\sigma ^i+\sigma ^{-i}$ restrict to automorphisms of $JC_0$ .

2. 2. The maps $\psi _i: JC_0\times JC_0\rightarrow P$ , sending $(x,y)$ to $x+\sigma ^i(y)$ are isomorphisms of polarized abelian varieties such that

   • • $\psi _i ^{\vee }\circ \lambda _{\tau } \circ \psi _i = \begin {pmatrix} 2 \lambda _{C_0} & \lambda _{C_0} \circ \beta _i \\ \lambda _{C_0} \circ \beta _i & 2 \lambda _{C_0} \end {pmatrix}$ ;

   • • $\psi _i ^{-1}\circ \sigma ^i \circ \psi _i = \begin {pmatrix} 0 &-1\\ 1 &\beta _i \end {pmatrix}$ .

Since both $\pi _0$ and $f_0$ are ramified maps, we have the inclusions $E_0\subset JC_0\subset J\widetilde C$ . More precisely, we have the following:

Proposition 4.2. The map $f_0: C_0\rightarrow E_0$ is given by the composition $C_0\hookrightarrow JC_0\xrightarrow {(1+\beta _3)} E_0$ . In particular, $E_0=Im(1+j)(1+\beta _3).$

Proof. Let us focus on the following part of diagram (4.1):

(4.2)

Let

$$\begin{align*}x, \sigma(x), \dots, \sigma^8(x)\quad \text{resp.} \quad jx, \sigma(jx), \dots, \sigma^8(jx) \end{align*}$$

be the whole fibers $f^{-1}(f(x))$ , resp. $f^{-1}(f(jx))$ . By construction, the map $f'$ identifies $[x]=[\sigma ^3(x)]= [\sigma ^6(x)]$ . By the commutativity of the diagram, we also have $E_0= C'/\langle j\rangle $ . Thus, in $E_0$ , we get the $6:1$ identification

(4.3) $$ \begin{align} [x]=[\sigma^3(x)]= [\sigma^6(x)]=[jx]=[j\sigma^3(x)]= [j\sigma^6(x)]. \end{align} $$

Obviously, the analogous holds true for the fiber of $\sigma (x) $ and of $\sigma ^2(x)$ .

By definition, in $C_0$ , we have $[x]=[jx]$ , $[\sigma ^3(x)]=[j\sigma ^3(x)]=[\sigma ^6(jx)]$ , and $[\sigma ^6(x)]=[j\sigma ^6(x)]=[\sigma ^3(jx)]$ . The commutativity of Equation (4.2), together with Equation (4.3), gives us the 3:1 map $f_0$ . As we already know, $JC_0=Im(1+j)$ . Thus, we get $JE_0\cong E_0=Im(1+j)(1+\sigma ^3+\sigma ^6)$ . Finally, it is easy to check that composing with the natural injection $\iota _x: C_0\hookrightarrow JC_0, \, p\mapsto [p-x]$ , we obtain the map $f_0$ .

As a consequence, we get the following:

Proposition 4.3. The automorphisms $\beta _1,\beta _2,\beta _4$ restrict to $-Id$ on $E_0$ , while $\beta _3$ acts as multiplication by 2.

Proof. It is a straightforward computation using that $E_0=Im (1+j)(1+\sigma ^3+\sigma ^6)$ , the fact that $\beta _i$ commutes with $(1+j)$ and that $1+\sigma +\dots +\sigma ^8=0$ on $J\widetilde C$ .

Let $\xi $ be a ninth primitive root of unity. In what follows, we want to describe more explicitly the automorphisms $\beta _i$ . First, we recall that the following equalities hold:

(4.4) $$ \begin{align} [\mathbb{Q}(\xi): \mathbb{Q}]= [\mathbb{Q}(\xi): \mathbb{Q}(\xi+\xi^{-1})][\mathbb{Q}(\xi+\xi^{-1}): \mathbb{Q}]=2\cdot 3=6. \end{align} $$

The action of $\sigma $ on $H^0(\widetilde C, \omega _{\widetilde C})$ decomposes as follows ([7, Section 3])

(4.5) $$ \begin{align} H^0(\widetilde C, \omega_{\widetilde C})= \bigoplus_{i=0}^8 H^0( C, \omega_{ C}\otimes \eta^i), \end{align} $$

where $H^0( C, \omega _{ C}\otimes \eta ^i)$ is the eigenspace corresponding to the eigenvalue $\xi ^i$ . This yields the following:

Proposition 4.4. The automorphisms $\beta _i$ act on $T_0JC_0$ as the diagonal matrices

$$ \begin{align*}diag(\xi^i+\xi^{-i}, \xi^{2i}+\xi^{-2i}, \xi^{3i}+\xi^{-3i}, \xi^{4i}+\xi^{-4i}).\end{align*} $$

Therefore, up to permutation of the eigenspaces, the automorphisms $\beta _1,\beta _2,\beta _4$ correspond to the matrix ${diag}(\xi +\xi ^{8}, \xi ^2+\xi ^{7}, \xi ^4+\xi ^5, -1)$ while $\beta _3$ is given by $diag(-1,-1,-1,2)$ . As an immediate consequence, we get the following:

Proposition 4.5. The Prym variety $P(C_0, E_0)$ is of $GL_2$ -type.

Proof. Using the description of the automorphisms $\beta _i: JC_0\rightarrow JC_0$ as a diagonal matrix, together with Proposition 4.3, we obtain that they restrict to automorphisms of $P(C_0, E_0)$ . Therefore, $F:=\mathbb {Q}(\xi +\xi ^{-1})$ is embedded in $End_0(P(C_0, E_0))$ . Since, by Equation (4.4), F is a totally real cubic field, we conclude that $P(C_0, E_0)$ is of $GL_2$ -type.

Now, we have all the ingredients to prove the following:

Theorem 4.6. The Prym map $\mathcal {P}_9: \mathcal {R}^9\rightarrow \mathcal {A}_8^{(1,\dots ,1,9)}$ is generically injective.

Proof. The proof traces the one given in case of $d, k$ prime numbers. The main difference here is that instead of recovering $h_0: C_0\rightarrow {\mathbb P}^1$ , we recover the map $f_0: C_0\rightarrow E_0$ .

Let $(P,\tau )$ be a general element in $Im(\mathcal {P}_9)$ . By Proposition 3.1, we obtain the triplet $(P, \tau , \langle \sigma \rangle )$ . Thus, as in Equation (3.1), we define the set $\Lambda (P,\tau , \langle \sigma \rangle )$ . Since, by Proposition 4.1 also in case of $d=9$ the maps $\psi _i$ are isomorphisms of polarized abelian varieties, we can use Proposition 3.10 to recover the curve $C_0$ . Using the same proposition (the second part of its proof where property $(\ast \ast $ ) is exploited) one can show that $\gamma $ is of the form $\phi ^{-1}\beta _i\phi $ for an $i \in \{ 1,2,3,4 \}$ and for $\phi $ an automorphism of $JC_0$ (compatible with the principal polarization, but this will not be used).

Now, using the obtained automorphisms $\gamma $ ’s, we consider the one-dimensional images $Im(\gamma +Id)$ . By Proposition 4.3, these images are the curves $E_0$ or $\phi (E_0)$ . We do not take into account higher-dimensional images, that is, the ones coming from $\beta _i$ or from $\phi ^{-1}\beta _i\phi $ for $i=1,2,4$ . By Proposition 4.2, we get the map $f_0$ in case of $\gamma =\beta _3$ , resp. the map $C_0\rightarrow \phi (E_0)$ in case of $\gamma =\phi ^{-1}\beta _3\phi $ . In this way, we conclude the result. Indeed, by definition, the Galois closure of $\widetilde C\rightarrow E_0$ does not depend on the automorphism of the base. This yields the element $\widetilde C\rightarrow C \in \mathcal {R}^9$ we are looking for.

5. Case $d=13$

This section is devoted to the analysis of the case $d=13$ , where d is a prime number, whereas $k=6$ no longer is. This prevents us to use the full Proposition 3.10, so one has to characterize the set $\Lambda (P,\tau , \langle \sigma \rangle )$ defined as in Equation (3.1). The diagram to keep in mind is the following:

(5.1)

We recall that $g(C_0)=6$ and that $\beta _i=\sigma ^i+\sigma ^{-i}$ are automorphisms of $JC_0$ not preserving the polarization. The second step of Section 3 yields the following:

Proposition 5.1. The Jacobian variety $JC_0$ is of $GL_2$ -type which is either simple or is isogenous to $X^r$ , where X is a simple abelian variety of $GL_2$ -type and $r\in \mathbb {N}$ . Moreover, any automorphism of the curve $C_0$ is an involution.

Proof. It follows from Propositions 3.4, 3.6 and 3.7(§1).

We have the following:

Corollary 5.2. For a general $\widetilde C\rightarrow C$ , the Jacobian variety $JC_0$ is either simple or isogenous to the square of a simple abelian threefold. In the first case, any involution induced on $JC_0$ from an automorphism of $C_0$ is $\pm Id$ .

Proof. Indeed, we have to exclude that $JC_0$ is one of the following cases:

1. 1. $E^6$ , where E is an elliptic curve,

2. 2. $S^3$ , where S is a $GL_2$ -type abelian surface.

This follows from a dimensional argument. The first case is excluded because the moduli of elliptic curves is one-dimensional. In the second case the moduli of abelian surfaces is three-dimensional, but the endomorphism algebra of the generic element is $\mathbb {Z}$ , and this is not compatible with our assumptions on the endomorphism algebra of S, so it can be also ruled out.

Thus, in order to conclude the generic injectivity of $\mathcal P_{13}$ , it only remains to exclude the case $JC_0\sim T^2$ (which prevents us to obtain a result as in Proposition 3.10). Such configuration is realized when an involution $\phi $ acts on $C_0$ with quotient a genus 3 curve $C^{\prime }0$ . That is, the 2:1 covering $C_0\rightarrow C^{\prime }0=C_0/\langle \phi \rangle $ is branched in two points and such that $T\sim JC^{\prime }0\sim P(C_0,C^{\prime }0)$ is a $GL_2$ -type threefold. One should then show that this does not occur for the general curve $C_0$ of the three-dimensional family appearing as a quotient of $\tilde C$ .