1. Introduction
The algebraic structures we now call involutive Stone algebras appear to have been first considered by Roberto Cignoli and Marta Sagastume along with their investigation of finite-valued Łukasiewicz logics, in connection with Łukasiewicz-Moisil algebras (Cignoli and Sagastume Reference Cignoli and Sagastume1981, Reference Cignoli and Sagastume1983). Formally, involutive Stone algebras are usually presented as expansions of De Morgan algebras (whose languages consist of a conjunction
![]() $\land$
, a disjunction
$\land$
, a disjunction
![]() $\lor$
, a negation
$\lor$
, a negation
![]() $\sim$
and the lattice bounds
$\sim$
and the lattice bounds
![]() $\bot, \top$
) in one of the following two alternative term-equivalent ways (we shall soon see that a third one has been recently proposed):
$\bot, \top$
) in one of the following two alternative term-equivalent ways (we shall soon see that a third one has been recently proposed):
-
1. by adding a unary “possibility” operator (usually denoted by
 $\nabla$
in the literature);
$\nabla$
in the literature); -
2. by adding an “intuitionistic” (namely, a pseudo-complement) negation (denoted by
 $\neg$
) satisfying the well-known Stone equation:
$\neg$
) satisfying the well-known Stone equation:
 $\neg x \lor \neg \neg x \approx \top$
.
$\neg x \lor \neg \neg x \approx \top$
.
Though obviously arising as “algebras of logic,” the class of involutive Stone algebras was not employed as an algebraic semantics for logical systems in the above-mentioned seminal works; rather, this has been pursued in a series of recent papers which focused in particular on the logic that preserves the lattice order of involutive Stone algebras (Cantú Reference Cantú2019; Cantú and Figallo Reference Cantú and Figallo2018, 2022; Marcelino and Rivieccio Reference Marcelino and Rivieccio2022).
In the paper Gomes et al. (Reference Gomes, Greati, Marcelino, Marcos and Rivieccio2022), which is the immediate predecessor of the present one, we built on the observation (made in Cantú and Figallo Reference Cantú and Figallo2018) that the logic of involutive Stone algebras may be viewed as a Logic of Formal Inconsistency in the sense of Marcos (Reference Marcos2005a), Carnielli et al. (Reference Carnielli, Coniglio, Marcos, Gabbay and Guenthner2007), and axiomatized it as such. This was possible due to the fact that involutive Stone algebras may be presented in a third term-equivalent way, namely:
-
3. by adding a unary “perfection” operator (denoted by
 $\circ$
) of the kind discussed in Marcos (Reference Marcos2005b).
$\circ$
) of the kind discussed in Marcos (Reference Marcos2005b).
Reformulated in this language (i.e.,
![]() $\{ \land, \lor, {\sim },{\circ }, \bot, \top \}$
), involutive Stone algebras have been renamed perfect paradefinite algebras (PP-algebras) in Gomes et al. (Reference Gomes, Greati, Marcelino, Marcos and Rivieccio2022). In the latter paper we axiomatized the
$\{ \land, \lor, {\sim },{\circ }, \bot, \top \}$
), involutive Stone algebras have been renamed perfect paradefinite algebras (PP-algebras) in Gomes et al. (Reference Gomes, Greati, Marcelino, Marcos and Rivieccio2022). In the latter paper we axiomatized the ![]() logic of order of PP-algebras, called
logic of order of PP-algebras, called
![]() $\mathcal{PP}_{\!\leq }$
, and also showed that
$\mathcal{PP}_{\!\leq }$
, and also showed that
![]() $\mathcal{PP}_{\!\leq }$
is semantically determined by a finite matrix based on the six-element algebra (there dubbed
$\mathcal{PP}_{\!\leq }$
is semantically determined by a finite matrix based on the six-element algebra (there dubbed
![]() $\mathbf{PP_6}$
) that generates the class of PP-algebras as a variety. Actually, we developed most of our results with respect to a Set-Set version of this logic, called
$\mathbf{PP_6}$
) that generates the class of PP-algebras as a variety. Actually, we developed most of our results with respect to a Set-Set version of this logic, called
![]() $\mathcal{PP}_{\!\leq }^{{\rhd }}{}$
. The Set-Set axiomatization we presented for it is analytic and thus suitable for automated reasoning. We then used all those results to aid in the study of
$\mathcal{PP}_{\!\leq }^{{\rhd }}{}$
. The Set-Set axiomatization we presented for it is analytic and thus suitable for automated reasoning. We then used all those results to aid in the study of
![]() $\mathcal{PP}_{\!\leq }$
.
$\mathcal{PP}_{\!\leq }$
.
In the present paper, further pursuing this approach, we shall focus on the question of how to add an implication connective to Set-Set and ![]() logics associated with PP-algebras. In an effort to proceed in a systematic fashion, we shall be guided by the following main principles:
logics associated with PP-algebras. In an effort to proceed in a systematic fashion, we shall be guided by the following main principles:
-
• the resulting system must be conservative over the logics being extended;
-
• the new connective must indeed qualify as an implication according to some general standard.
In order to narrow down our search and to eventually converge upon a short list of candidates, we shall presently consider a third guiding principle as well, namely:
-
• the new logic must also qualify as the logic of order of a suitable class of algebras.
In the present setting, as we shall see, the above principle turns out to be equivalent to requiring the logic to be self-extensional (see Definitions 3, 4 and general results on self-extensional logics in Jansana Reference Jansana2006, Section 3).
The approach outlined above for the study of implicational extensions is reminiscent of – indeed, directly inspired by – Avron’s proposal for extending Belnap’s logic (Avron Reference Avron2020), in which two main requirements are entertained: first, that the new connective should be an implication relative to a given set of designated elements (condition
![]() $(\textsf{A}1)$
in Subsection 2.4); second, that the resulting logic should be self-extensional
$(\textsf{A}1)$
in Subsection 2.4); second, that the resulting logic should be self-extensional
![]() $(\textsf{A}2)$
. We shall discuss these requirements at length in Section 4, where we show that in our case there is unfortunately no implication connective that meets both of them (Theorem 20). This is where we shall choose to retain the latter requirement (self-extensionality) instead of the former, which we find too restrictive, as we shall also discuss. As this choice still leaves plenty of room for a large collection of alternative implications, we shall follow two North Stars: Algebra and Tradition.
$(\textsf{A}2)$
. We shall discuss these requirements at length in Section 4, where we show that in our case there is unfortunately no implication connective that meets both of them (Theorem 20). This is where we shall choose to retain the latter requirement (self-extensionality) instead of the former, which we find too restrictive, as we shall also discuss. As this choice still leaves plenty of room for a large collection of alternative implications, we shall follow two North Stars: Algebra and Tradition.
Algebra suggests that, for a wide family of logics, a well-behaved implication connective may be obtained by considering, whenever available, the residuum of the algebraic operation that realizes the logical conjunction (see e.g., Galatos et al. Reference Galatos, Jipsen, Kowalski and Ono2007): this leads us to expand the logics of PP-algebras by a relative pseudo-complement implication, which we shall call a Heyting implication, for our definition mirrors the standard one for the implication on Heyting algebras.
Tradition, in the present setting, happens to point in the same direction as algebra. In fact, it turns out that a substantial part of the theory of involutive Stone algebras had already been developed, even prior to Cignoli and Sagastume’s works, in Monteiro (Reference Monteiro1980), itself a collection of earlier material. The main subject of Monteiro’s monograph is the class of symmetric Heyting algebras, providing an algebraic counterpart to Moisil’s symmetric modal logic. These algebras are presented precisely in the traditional language of involutive Stone algebras (with the
![]() $\nabla$
operator which Monteiro dubs “possibility”) enriched with a Heyting implication.
$\nabla$
operator which Monteiro dubs “possibility”) enriched with a Heyting implication.
The formal relation between the class of PP-algebras enriched with an implication that we shall define and Monteiro’s symmetric Heyting algebras is discussed in detail in Section 7. For the time being, let us conclude the present introductory remarks by mentioning an alternative proposal concerning our main question – how to add an implication to logics of PP-algebras, one of them being
![]() $\mathcal{PP}_{\!\leq }$
– which can be retrieved from a recent paper by Coniglio and Rodrigues (Reference Coniglio and Rodrigues2023). The purpose of the latter is to add a “classicality” operator
$\mathcal{PP}_{\!\leq }$
– which can be retrieved from a recent paper by Coniglio and Rodrigues (Reference Coniglio and Rodrigues2023). The purpose of the latter is to add a “classicality” operator
![]() $\circ$
to the well-known Belnap-Dunn four-valued logic, but the authors actually start from a logic which is itself a conservative expansion of the Belnap-Dunn logic with a classic-like implication (in the sense of Definition 13). The resulting logic – dubbed
$\circ$
to the well-known Belnap-Dunn four-valued logic, but the authors actually start from a logic which is itself a conservative expansion of the Belnap-Dunn logic with a classic-like implication (in the sense of Definition 13). The resulting logic – dubbed
![]() ${\textrm{LET}_{\textrm{K}}^{+}}$
– turns out to be determined by a six-valued matrix that (if we disregard the implication) coincides with the matrix
${\textrm{LET}_{\textrm{K}}^{+}}$
– turns out to be determined by a six-valued matrix that (if we disregard the implication) coincides with the matrix
![]() $\langle \mathbf{PP_6},{{\uparrow }{\mathbf{b}}} \rangle$
which determines the logic
$\langle \mathbf{PP_6},{{\uparrow }{\mathbf{b}}} \rangle$
which determines the logic
![]() $\mathcal{PP}_{\!\leq }$
(see Gomes et al. Reference Gomes, Greati, Marcelino, Marcos and Rivieccio2022). As noted in Coniglio and Rodrigues (Reference Coniglio and Rodrigues2023, Subsec. 5.1), it follows that the implication-free fragment of
$\mathcal{PP}_{\!\leq }$
(see Gomes et al. Reference Gomes, Greati, Marcelino, Marcos and Rivieccio2022). As noted in Coniglio and Rodrigues (Reference Coniglio and Rodrigues2023, Subsec. 5.1), it follows that the implication-free fragment of
![]() ${\textrm{LET}_{\textrm{K}}^{+}}$
coincides with
${\textrm{LET}_{\textrm{K}}^{+}}$
coincides with
![]() $\mathcal{PP}_{\!\leq }$
. The implication connective of
$\mathcal{PP}_{\!\leq }$
. The implication connective of
![]() ${\textrm{LET}_{\textrm{K}}^{+}}$
consists thus in a candidate for expanding
${\textrm{LET}_{\textrm{K}}^{+}}$
consists thus in a candidate for expanding
![]() $\mathcal{PP}_{\!\leq }$
with an implication. An inspection of its truth table (see Coniglio and Rodrigues Reference Coniglio and Rodrigues2023, Def. 3.9) reveals (see also Section 4) that this implication satisfies (with respect to the designated set
$\mathcal{PP}_{\!\leq }$
with an implication. An inspection of its truth table (see Coniglio and Rodrigues Reference Coniglio and Rodrigues2023, Def. 3.9) reveals (see also Section 4) that this implication satisfies (with respect to the designated set
![]() ${{\uparrow }{\mathbf{b}}}$
) the first among Avron’s requirements,
${{\uparrow }{\mathbf{b}}}$
) the first among Avron’s requirements,
![]() $(\textsf{A}1)$
, and therefore destroys self-extensionality (or, one may say, preserves the non-self-extensional character of paraconsistent Nelson logic). This leads to an interesting observation, namely, that
$(\textsf{A}1)$
, and therefore destroys self-extensionality (or, one may say, preserves the non-self-extensional character of paraconsistent Nelson logic). This leads to an interesting observation, namely, that
![]() ${\textrm{LET}_{\textrm{K}}^{+}}$
is determined by a refinement of the non-deterministic matrix introduced in Section 4, and may be obtained, thus, from the corresponding logic by adding suitable rules. In this sense, we may say our approach subsumes that of Coniglio and Rodrigues (Reference Coniglio and Rodrigues2023), at least insofar as the task of conservatively expanding
${\textrm{LET}_{\textrm{K}}^{+}}$
is determined by a refinement of the non-deterministic matrix introduced in Section 4, and may be obtained, thus, from the corresponding logic by adding suitable rules. In this sense, we may say our approach subsumes that of Coniglio and Rodrigues (Reference Coniglio and Rodrigues2023), at least insofar as the task of conservatively expanding
![]() $\mathcal{PP}_{\!\leq }$
is concerned.
$\mathcal{PP}_{\!\leq }$
is concerned.
Our paper is organized as follows. After the preliminary sections in which we fix the notation and basic definitions, we delve into the problem of expanding the logics of order of PP-algebras with an implication. To that effect, we first consider in Section 4 adding an implication satisfying at once
![]() $(\textsf{A}1)$
and
$(\textsf{A}1)$
and
![]() $(\textsf{A}2)$
. After proving the impossibility of this task, we focus first on
$(\textsf{A}2)$
. After proving the impossibility of this task, we focus first on
![]() $(\textsf{A}1)$
, which makes the implication qualify as classic-like. We explore possibilities of doing so using the semantical framework of non-deterministic logical matrices, providing analytic axiomatizations for the obtained Set-Set logics, from which we can readily obtain
$(\textsf{A}1)$
, which makes the implication qualify as classic-like. We explore possibilities of doing so using the semantical framework of non-deterministic logical matrices, providing analytic axiomatizations for the obtained Set-Set logics, from which we can readily obtain ![]() axiomatizations for the corresponding
axiomatizations for the corresponding ![]() companions.
companions.
Next, turning our focus to
![]() $(\textsf{A}2)$
, and having observed that the matrix
$(\textsf{A}2)$
, and having observed that the matrix
![]() $\langle \mathbf{PP_6},{{\uparrow }{\mathbf{b}}} \rangle$
, which determines
$\langle \mathbf{PP_6},{{\uparrow }{\mathbf{b}}} \rangle$
, which determines
![]() $\mathcal{PP}_{\!\leq }^{{\rhd }}$
and
$\mathcal{PP}_{\!\leq }^{{\rhd }}$
and
![]() $\mathcal{PP}_{\!\leq }$
, is based on an algebra (i.e.,
$\mathcal{PP}_{\!\leq }$
, is based on an algebra (i.e.,
![]() $\mathbf{PP_6}$
) that is a finite distributive lattice, in Section 5 we enrich its language with an operation
$\mathbf{PP_6}$
) that is a finite distributive lattice, in Section 5 we enrich its language with an operation
![]() $\Rightarrow _{\textsf{H}}$
that corresponds to the relative pseudo-complement implication determined by the lattice order. In fact, the six-element Heyting algebra thus obtained (denoted by
$\Rightarrow _{\textsf{H}}$
that corresponds to the relative pseudo-complement implication determined by the lattice order. In fact, the six-element Heyting algebra thus obtained (denoted by
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
) turns out to be a symmetric Heyting algebra in Monteiro’s sense. We then consider the family of all matrices
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
) turns out to be a symmetric Heyting algebra in Monteiro’s sense. We then consider the family of all matrices
![]() $\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, D \rangle$
such that
$\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, D \rangle$
such that
![]() $D$
is a non-empty lattice filter of the lattice reduct of
$D$
is a non-empty lattice filter of the lattice reduct of
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
. The (Set-Set and
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
. The (Set-Set and ![]() ) logics determined by this family are the order-preserving logics induced by the variety
) logics determined by this family are the order-preserving logics induced by the variety
![]() $\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
, guaranteed to be self-extensional.
$\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
, guaranteed to be self-extensional.
In Section 6, we proceed to axiomatize both the Set-Set and the ![]() logics thus defined. First focusing on the Set-Set logic, we present an axiomatization after a detailed analysis of the algebraic structure of the matrices and of their designated sets. The calculus we present is not only sound and complete, but also analytic. From such axiomatization, moreover, we show how to extract an axiomatization for the corresponding
logics thus defined. First focusing on the Set-Set logic, we present an axiomatization after a detailed analysis of the algebraic structure of the matrices and of their designated sets. The calculus we present is not only sound and complete, but also analytic. From such axiomatization, moreover, we show how to extract an axiomatization for the corresponding ![]() logic of order.
logic of order.
In Section 7, we look at the algebraic models that correspond to the ![]() logics
logics
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
and
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
and
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
(the
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
(the
![]() $\top$
-assertional logic associated with
$\top$
-assertional logic associated with
![]() $\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
) within the general theory of algebraization of logics. We begin by observing that both logics are closely related to Moisil’s “symmetric modal logic,” whose algebraic counterpart is the class of symmetric Heyting algebras (Definition 70). Indeed,
$\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
) within the general theory of algebraization of logics. We begin by observing that both logics are closely related to Moisil’s “symmetric modal logic,” whose algebraic counterpart is the class of symmetric Heyting algebras (Definition 70). Indeed,
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
is (term-equivalent to) a symmetric Heyting algebra, and the class of algebras providing an algebraic semantics for both
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
is (term-equivalent to) a symmetric Heyting algebra, and the class of algebras providing an algebraic semantics for both
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
and
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
and
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
is precisely the subvariety
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
is precisely the subvariety
![]() $\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
of symmetric Heyting algebras generated by
$\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
of symmetric Heyting algebras generated by
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
(Theorem 78); an equational presentation for
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
(Theorem 78); an equational presentation for
![]() $\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
is introduced in Definition 72, and shown to be sound and complete in Theorem 77. The algebraizability of Moisil’s logic (Proposition 71) entails that
$\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
is introduced in Definition 72, and shown to be sound and complete in Theorem 77. The algebraizability of Moisil’s logic (Proposition 71) entails that
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
is also algebraizable; its equivalent algebraic semantics is precisely
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
is also algebraizable; its equivalent algebraic semantics is precisely
![]() $\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
, and its reduced matrix models are the matrices of the form
$\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
, and its reduced matrix models are the matrices of the form
![]() $\langle \mathbf{A}, \{ \top \} \rangle$
with
$\langle \mathbf{A}, \{ \top \} \rangle$
with
![]() $\mathbf{A} \in \mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
(Theorem 78). On the other hand,
$\mathbf{A} \in \mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
(Theorem 78). On the other hand,
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
is not algebraizable (Proposition 36) but its algebraic counterpart is also
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
is not algebraizable (Proposition 36) but its algebraic counterpart is also
![]() $\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
; the shape of the reduced matrix models of
$\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
; the shape of the reduced matrix models of
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
is described in Proposition 81. We conclude the section by looking at the subvarieties of
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
is described in Proposition 81. We conclude the section by looking at the subvarieties of
![]() $\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
. There are only three of them (corresponding precisely to the self-extensional extensions of
$\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
. There are only three of them (corresponding precisely to the self-extensional extensions of
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
) which can be axiomatized by adding the axioms that translate the equations shown in Corollary 79.
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
) which can be axiomatized by adding the axioms that translate the equations shown in Corollary 79.
In Section 8, we draw some conclusions regarding interpolation for the implicative extensions of interest, as well as amalgamation for the class of algebraic models of
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
. Further directions of investigation are highlighted in Section 9.
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
. Further directions of investigation are highlighted in Section 9.
2. Preliminaries
In this section, we introduce the main concepts related to algebras, logics, and axiomatizations, with particular attention to perfect paradefinite algebras and their logics. We also fix what we shall understand as an implication and the selection criteria we will employ in investigating expansions of a logic by the addition of an implication.
2.1 Algebras, languages, and logics
A propositional signature is a family
![]() $\Sigma \,{:=}\, \{\Sigma _k\}_{k \in \omega }$
, where each
$\Sigma \,{:=}\, \{\Sigma _k\}_{k \in \omega }$
, where each
![]() $\Sigma _k$
is a collection of
$\Sigma _k$
is a collection of
![]() $k$
-ary connectives. A
$k$
-ary connectives. A
![]() $\Sigma$
-multialgebra is a structure
$\Sigma$
-multialgebra is a structure
![]() $\mathbf{A} \,{:=}\, \langle A, \cdot ^{\mathbf{A}} \rangle$
, where
$\mathbf{A} \,{:=}\, \langle A, \cdot ^{\mathbf{A}} \rangle$
, where
![]() $A$
is a non-empty set called the carrier of
$A$
is a non-empty set called the carrier of
![]() $\mathbf{A}$
and, for each
$\mathbf{A}$
and, for each
![]() $\unicode{x00A9} \in \Sigma _k$
, the multioperation
$\unicode{x00A9} \in \Sigma _k$
, the multioperation
![]() $\unicode{x00A9}^{\mathbf{A}} : A^k \to \wp (A)$
is the interpretation of
$\unicode{x00A9}^{\mathbf{A}} : A^k \to \wp (A)$
is the interpretation of
![]() $\unicode{x00A9}$
in
$\unicode{x00A9}$
in
![]() $\mathbf{A}$
. We say that
$\mathbf{A}$
. We say that
![]() $\mathbf{A}$
is a
$\mathbf{A}$
is a
![]() $\Sigma$
-algebra (or deterministic
$\Sigma$
-algebra (or deterministic
![]() $\Sigma$
-multialgebra) when
$\Sigma$
-multialgebra) when
![]() $\unicode{x00A9}^{\mathbf{A}}(a_1,\ldots, a_k)$
is a singleton for every
$\unicode{x00A9}^{\mathbf{A}}(a_1,\ldots, a_k)$
is a singleton for every
![]() $a_1,\ldots, a_k \in A$
,
$a_1,\ldots, a_k \in A$
,
![]() $\unicode{x00A9} \in \Sigma _k$
and
$\unicode{x00A9} \in \Sigma _k$
and
![]() $k \in \omega$
. If
$k \in \omega$
. If
![]() $\unicode{x00A9}^{\mathbf{A}}(a_1,\ldots, a_k) \neq \varnothing$
for every
$\unicode{x00A9}^{\mathbf{A}}(a_1,\ldots, a_k) \neq \varnothing$
for every
![]() $a_1,\ldots, a_k \in A$
,
$a_1,\ldots, a_k \in A$
,
![]() $\unicode{x00A9} \in \Sigma _k$
and
$\unicode{x00A9} \in \Sigma _k$
and
![]() $k \in \omega$
, we say that
$k \in \omega$
, we say that
![]() $\mathbf{A}$
is total. Note that the notion of
$\mathbf{A}$
is total. Note that the notion of
![]() $\Sigma$
-algebra matches the usual notion of algebra in Universal Algebra (cf. Sankappanavar Reference Sankappanavar1987). Given
$\Sigma$
-algebra matches the usual notion of algebra in Universal Algebra (cf. Sankappanavar Reference Sankappanavar1987). Given
![]() $\Sigma ^\prime \subseteq \Sigma$
(i.e.,
$\Sigma ^\prime \subseteq \Sigma$
(i.e.,
![]() $\Sigma ^\prime _k \subseteq \Sigma _k$
for all
$\Sigma ^\prime _k \subseteq \Sigma _k$
for all
![]() $k \in \omega$
), the
$k \in \omega$
), the
![]() $\Sigma '$
-reduct of a
$\Sigma '$
-reduct of a
![]() $\Sigma$
-multialgebra
$\Sigma$
-multialgebra
![]() $\mathbf{A}$
is the
$\mathbf{A}$
is the
![]() $\Sigma '$
-multialgebra over the same carrier of
$\Sigma '$
-multialgebra over the same carrier of
![]() $\mathbf{A}$
that agrees with
$\mathbf{A}$
that agrees with
![]() $\mathbf{A}$
on the interpretation of the connectives in
$\mathbf{A}$
on the interpretation of the connectives in
![]() $\Sigma '$
.
$\Sigma '$
.
A
![]() $\Sigma$
-homomorphism between
$\Sigma$
-homomorphism between
![]() $\Sigma$
-multialgebras
$\Sigma$
-multialgebras
![]() $\mathbf{A}$
and
$\mathbf{A}$
and
![]() $\mathbf{B}$
is a mapping
$\mathbf{B}$
is a mapping
![]() $h : A \to B$
such that
$h : A \to B$
such that
![]() $h(\unicode{x00A9}^{\mathbf{A}}(a_1,\ldots, a_k)) \in \unicode{x00A9}^{\mathbf{B}}(h(a_1),\ldots, h(a_k))$
for all
$h(\unicode{x00A9}^{\mathbf{A}}(a_1,\ldots, a_k)) \in \unicode{x00A9}^{\mathbf{B}}(h(a_1),\ldots, h(a_k))$
for all
![]() $a_1,\ldots, a_k \in A$
,
$a_1,\ldots, a_k \in A$
,
![]() $\unicode{x00A9} \in \Sigma _k$
and
$\unicode{x00A9} \in \Sigma _k$
and
![]() $k \in \omega$
. Note that for
$k \in \omega$
. Note that for
![]() $\Sigma$
-algebras this definition coincides with the usual notion of homomorphism. The collection of all
$\Sigma$
-algebras this definition coincides with the usual notion of homomorphism. The collection of all
![]() $\Sigma$
-homomorphisms between two
$\Sigma$
-homomorphisms between two
![]() $\Sigma$
-multialgebras
$\Sigma$
-multialgebras
![]() $\mathbf{A}$
and
$\mathbf{A}$
and
![]() $\mathbf{B}$
is denoted by
$\mathbf{B}$
is denoted by
![]() $\textsf{Hom}(\mathbf{A},\mathbf{B})$
.
$\textsf{Hom}(\mathbf{A},\mathbf{B})$
.
Given a denumerable set
![]() $P \supseteq \{p, q, r, s, x, y\}$
of propositional variables, the absolutely free
$P \supseteq \{p, q, r, s, x, y\}$
of propositional variables, the absolutely free
![]() $\Sigma$
-algebra freely generated by
$\Sigma$
-algebra freely generated by
![]() $P$
, or simply the language over
$P$
, or simply the language over
![]() $\Sigma$
(generated by
$\Sigma$
(generated by
![]() $P$
), is denoted by
$P$
), is denoted by
![]() $\mathbf{L}_{\Sigma }(P)$
, and its members are called
$\mathbf{L}_{\Sigma }(P)$
, and its members are called
![]() $\Sigma$
-formulas. The collection of all subformulas of a formula
$\Sigma$
-formulas. The collection of all subformulas of a formula
![]() $\varphi$
is denoted by
$\varphi$
is denoted by
![]() $\textsf{sub}(\varphi )$
and we let
$\textsf{sub}(\varphi )$
and we let
![]() $\textsf{sub}(\Phi ) \,{:=}\, \bigcup _{\varphi \in \Phi }\textsf{sub}(\varphi )$
, for all
$\textsf{sub}(\Phi ) \,{:=}\, \bigcup _{\varphi \in \Phi }\textsf{sub}(\varphi )$
, for all
![]() $\Phi \subseteq L_{\Sigma }(P)$
. Similarly, the collection of all propositional variables occurring in
$\Phi \subseteq L_{\Sigma }(P)$
. Similarly, the collection of all propositional variables occurring in
![]() $\varphi \in L_{\Sigma }(P)$
is denoted by
$\varphi \in L_{\Sigma }(P)$
is denoted by
![]() $\textsf{props}(\varphi )$
, and we let
$\textsf{props}(\varphi )$
, and we let
![]() $\textsf{props}(\Phi ) \,{:=}\, \bigcup _{\varphi \in \Phi }\textsf{props}(\varphi )$
, for all
$\textsf{props}(\Phi ) \,{:=}\, \bigcup _{\varphi \in \Phi }\textsf{props}(\varphi )$
, for all
![]() $\Phi \subseteq L_{\Sigma }(P)$
. The elements of
$\Phi \subseteq L_{\Sigma }(P)$
. The elements of
![]() $\textsf{Hom}(\mathbf{L}_{\Sigma }(P), \mathbf{A})$
will sometimes be referred to as valuations on
$\textsf{Hom}(\mathbf{L}_{\Sigma }(P), \mathbf{A})$
will sometimes be referred to as valuations on
![]() $\mathbf{A}$
. When
$\mathbf{A}$
. When
![]() $\mathbf{A}$
is
$\mathbf{A}$
is
![]() $\mathbf{L}_{\Sigma }(P)$
, valuations are endomorphisms on
$\mathbf{L}_{\Sigma }(P)$
, valuations are endomorphisms on
![]() $\mathbf{L}_{\Sigma }(P)$
and are usually dubbed substitutions. The set of all substitutions is denoted by
$\mathbf{L}_{\Sigma }(P)$
and are usually dubbed substitutions. The set of all substitutions is denoted by
![]() $\textsf{End}(\mathbf{L}_{\Sigma }(P))$
. Given
$\textsf{End}(\mathbf{L}_{\Sigma }(P))$
. Given
![]() $h,h' \in \textsf{Hom}(\mathbf{L}_{\Sigma }(P), \mathbf{A})$
, we shall say that
$h,h' \in \textsf{Hom}(\mathbf{L}_{\Sigma }(P), \mathbf{A})$
, we shall say that
![]() $h'$
agrees with
$h'$
agrees with
![]() $h$
on
$h$
on
![]() $\Phi \subseteq L_{\Sigma }(P)$
provided that
$\Phi \subseteq L_{\Sigma }(P)$
provided that
![]() $h'(\varphi )=h(\varphi )$
for all
$h'(\varphi )=h(\varphi )$
for all
![]() $\varphi \in \Phi$
. In case
$\varphi \in \Phi$
. In case
![]() $p_1,\ldots, p_k$
are the only propositional variables occurring in
$p_1,\ldots, p_k$
are the only propositional variables occurring in
![]() $\varphi \in L_{\Sigma }(P)$
, we say that
$\varphi \in L_{\Sigma }(P)$
, we say that
![]() $\varphi$
is
$\varphi$
is
![]() $k$
-ary and denote by
$k$
-ary and denote by
![]() $\varphi ^{\mathbf{A}}$
the
$\varphi ^{\mathbf{A}}$
the
![]() $k$
-ary multioperation on
$k$
-ary multioperation on
![]() $A$
such that
$A$
such that
![]() $\varphi ^{\mathbf{A}}(a_1,\ldots, a_k) \,{:=}\, \{ h(\varphi ) : h \in \textsf{Hom}(\mathbf{L}_{\Sigma }(P), \mathbf{A}) \text{ with } h(p_i) = a_i \text{ for each } 1 \leq i \leq k \}$
, for all
$\varphi ^{\mathbf{A}}(a_1,\ldots, a_k) \,{:=}\, \{ h(\varphi ) : h \in \textsf{Hom}(\mathbf{L}_{\Sigma }(P), \mathbf{A}) \text{ with } h(p_i) = a_i \text{ for each } 1 \leq i \leq k \}$
, for all
![]() $a_1,\ldots, a_k \in A$
. Also, if
$a_1,\ldots, a_k \in A$
. Also, if
![]() $\psi _1,\ldots, \psi _k \in L_{\Sigma }(P)$
, we let
$\psi _1,\ldots, \psi _k \in L_{\Sigma }(P)$
, we let
![]() $\varphi (\psi _1,\ldots, \psi _k)$
denote the formula resulting from substituting each
$\varphi (\psi _1,\ldots, \psi _k)$
denote the formula resulting from substituting each
![]() $p_i$
in
$p_i$
in
![]() $\varphi$
by
$\varphi$
by
![]() $\psi _i$
, for all
$\psi _i$
, for all
![]() $1 \leq i \leq k$
. For a set
$1 \leq i \leq k$
. For a set
![]() $\Theta$
of formulas
$\Theta$
of formulas
![]() $\varphi (p_1,\ldots, p_k)$
, we let
$\varphi (p_1,\ldots, p_k)$
, we let
![]() $\Theta (\psi _1,\ldots, \psi _k) \,{:=}\, \{ \varphi (\psi _1,\ldots, \psi _k) : \varphi \in \Theta \}$
.
$\Theta (\psi _1,\ldots, \psi _k) \,{:=}\, \{ \varphi (\psi _1,\ldots, \psi _k) : \varphi \in \Theta \}$
.
A
![]() $\Sigma$
-equation is a pair
$\Sigma$
-equation is a pair
![]() $(\varphi, \psi )$
of
$(\varphi, \psi )$
of
![]() $\Sigma$
-formulas that we denote by
$\Sigma$
-formulas that we denote by
![]() $\varphi \approx \psi$
, and a
$\varphi \approx \psi$
, and a
![]() $\Sigma$
-multialgebra
$\Sigma$
-multialgebra
![]() $\mathbf{A}$
is said to satisfy
$\mathbf{A}$
is said to satisfy
![]() $\varphi \approx \psi$
if
$\varphi \approx \psi$
if
![]() $h(\varphi )=h(\psi )$
for every
$h(\varphi )=h(\psi )$
for every
![]() $h \in \textsf{Hom}(\mathbf{L}_{\Sigma }(P), \mathbf{A})$
. For any given collection of
$h \in \textsf{Hom}(\mathbf{L}_{\Sigma }(P), \mathbf{A})$
. For any given collection of
![]() $\Sigma$
-equations, the class of all
$\Sigma$
-equations, the class of all
![]() $\Sigma$
-algebras that satisfy such equations is called a
$\Sigma$
-algebras that satisfy such equations is called a
![]() $\Sigma$
-variety. An equation is said to be valid in a given variety if it is satisfied by each algebra in the variety. The variety generated by a class
$\Sigma$
-variety. An equation is said to be valid in a given variety if it is satisfied by each algebra in the variety. The variety generated by a class
![]() $\textsf{K}$
of
$\textsf{K}$
of
![]() $\Sigma$
-algebras, denoted by
$\Sigma$
-algebras, denoted by
![]() $\mathbb{V}(\textsf{K})$
, is the closure of
$\mathbb{V}(\textsf{K})$
, is the closure of
![]() $\textsf{K}$
under homomorphic images, subalgebras and direct products. We denote the latter operations, respectively, by
$\textsf{K}$
under homomorphic images, subalgebras and direct products. We denote the latter operations, respectively, by
![]() $\mathbb{H}$
,
$\mathbb{H}$
,
![]() $\mathbb{S}$
and
$\mathbb{S}$
and
![]() $\mathbb{P}$
. We write
$\mathbb{P}$
. We write
![]() $\textsf{Cng}\mathbf{A}$
to refer to the collection of all congruence relations on
$\textsf{Cng}\mathbf{A}$
to refer to the collection of all congruence relations on
![]() $\mathbf{A}$
, which is known to form a complete lattice under inclusion.
$\mathbf{A}$
, which is known to form a complete lattice under inclusion.
In what follows, we assume the reader is familiar with basic notations and terminology of lattice theory (Davey and Priestley Reference Davey and Priestley2002). We denote by
![]() $\Sigma ^{\textsf{bL}}$
the signature containing but two binary connectives,
$\Sigma ^{\textsf{bL}}$
the signature containing but two binary connectives,
![]() $\land$
and
$\land$
and
![]() $\lor$
, and two nullary connectives
$\lor$
, and two nullary connectives
![]() $\top$
and
$\top$
and
![]() $\bot$
, and by
$\bot$
, and by
![]() $\Sigma ^{\textsf{DM}}$
the extension of the latter signature by the addition of a unary connective
$\Sigma ^{\textsf{DM}}$
the extension of the latter signature by the addition of a unary connective
![]() $\sim$
. Moreover, by adding the unary connective
$\sim$
. Moreover, by adding the unary connective
![]() $\nabla$
to
$\nabla$
to
![]() $\Sigma ^{\textsf{DM}}$
we obtain a signature we shall call
$\Sigma ^{\textsf{DM}}$
we obtain a signature we shall call
![]() $\Sigma ^{\textsf{IS}}$
, and by adding instead the unary connective
$\Sigma ^{\textsf{IS}}$
, and by adding instead the unary connective
![]() $\circ$
we obtain a signature we shall call
$\circ$
we obtain a signature we shall call
![]() $\Sigma ^{\textsf{PP}}$
. We provide below the definitions and some examples of De Morgan algebras and of involutive Stone algebras, in order to illustrate some of the notions introduced above.
$\Sigma ^{\textsf{PP}}$
. We provide below the definitions and some examples of De Morgan algebras and of involutive Stone algebras, in order to illustrate some of the notions introduced above.
Definition 1.
Given a
![]() $\Sigma ^{\textsf{DM}}$
-algebra whose
$\Sigma ^{\textsf{DM}}$
-algebra whose
![]() $\Sigma ^{\textsf{bL}}$
-reduct is a bounded distributive lattice, we say that it constitutes a De Morgan algebra if it satisfies the equations:
$\Sigma ^{\textsf{bL}}$
-reduct is a bounded distributive lattice, we say that it constitutes a De Morgan algebra if it satisfies the equations:
Example 1.
Let
![]() $\mathcal{V}_4 \,{:=}\, \{{\mathbf{t}},{\mathbf{b}},{\mathbf{n}},{\mathbf{f}}\}$
and let
$\mathcal{V}_4 \,{:=}\, \{{\mathbf{t}},{\mathbf{b}},{\mathbf{n}},{\mathbf{f}}\}$
and let
![]() $\mathbf{DM}_4 \,{:=}\, \langle \mathcal{V}_4, \cdot ^{\mathbf{DM}_4} \rangle$
be the
$\mathbf{DM}_4 \,{:=}\, \langle \mathcal{V}_4, \cdot ^{\mathbf{DM}_4} \rangle$
be the
![]() $\Sigma ^{\textsf{DM}}$
-algebra known as the Dunn-Belnap lattice, whose interpretations for the lattice connectives are those induced by the Hasse diagram in Fig. 1(a), and the interpretation for
$\Sigma ^{\textsf{DM}}$
-algebra known as the Dunn-Belnap lattice, whose interpretations for the lattice connectives are those induced by the Hasse diagram in Fig. 1(a), and the interpretation for
![]() $\sim$
is such that
$\sim$
is such that
![]() ${\sim }^{\mathbf{DM}_4}{\mathbf{f}} \,{:=}\,{\mathbf{t}}$
,
${\sim }^{\mathbf{DM}_4}{\mathbf{f}} \,{:=}\,{\mathbf{t}}$
,
![]() ${\sim }^{\mathbf{DM}_4}{\mathbf{t}} \,{:=}\,{\mathbf{f}}$
and
${\sim }^{\mathbf{DM}_4}{\mathbf{t}} \,{:=}\,{\mathbf{f}}$
and
![]() ${\sim }^{\mathbf{DM}_4} a \,{:=}\, a$
, for
${\sim }^{\mathbf{DM}_4} a \,{:=}\, a$
, for
![]() $a \in \{{\mathbf{n}},{\mathbf{b}}\}$
; as expected, for the nullary connectives, we have
$a \in \{{\mathbf{n}},{\mathbf{b}}\}$
; as expected, for the nullary connectives, we have
![]() $\top ^{\mathbf{DM}_4} \;\,{:=}\,\;{\mathbf{t}}$
and
$\top ^{\mathbf{DM}_4} \;\,{:=}\,\;{\mathbf{t}}$
and
![]() $\bot ^{\mathbf{DM}_4} \;\,{:=}\,\;{\mathbf{f}}$
. In Fig. 1(a), besides depicting the lattice structure of
$\bot ^{\mathbf{DM}_4} \;\,{:=}\,\;{\mathbf{f}}$
. In Fig. 1(a), besides depicting the lattice structure of
![]() $\mathbf{DM}_4$
, we also show its subalgebras
$\mathbf{DM}_4$
, we also show its subalgebras
![]() $\mathbf{DM}_3$
and
$\mathbf{DM}_3$
and
![]() $\mathbf{DM}_2$
, which coincide with the three-element Kleene algebra and the two-element Boolean algebra. These three algebras are the only subdirectly irreducible De Morgan algebras (Balbes and Dwinger Reference Balbes and Dwinger1975
, Sec. XI.2, Thm. 6).
$\mathbf{DM}_2$
, which coincide with the three-element Kleene algebra and the two-element Boolean algebra. These three algebras are the only subdirectly irreducible De Morgan algebras (Balbes and Dwinger Reference Balbes and Dwinger1975
, Sec. XI.2, Thm. 6).
Definition 2.
Given a
![]() $\Sigma ^{\textsf{IS}}$
-algebra whose
$\Sigma ^{\textsf{IS}}$
-algebra whose
![]() $\Sigma ^{\textsf{DM}}$
-reduct is a De Morgan algebra, we say that it constitutes an involutive Stone algebra (IS-algebra) if it satisfies the equations:
$\Sigma ^{\textsf{DM}}$
-reduct is a De Morgan algebra, we say that it constitutes an involutive Stone algebra (IS-algebra) if it satisfies the equations:
Example 2.
Let
![]() $\mathcal{V}_6 \,{:=}\, \mathcal{V}_4 \cup \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}}\}$
and let
$\mathcal{V}_6 \,{:=}\, \mathcal{V}_4 \cup \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}}\}$
and let
![]() $\mathbf{IS}_6 \,{:=}\, \langle \mathcal{V}_6, \cdot ^{\mathbf{IS}_6} \rangle$
be the
$\mathbf{IS}_6 \,{:=}\, \langle \mathcal{V}_6, \cdot ^{\mathbf{IS}_6} \rangle$
be the
![]() $\Sigma ^{\textsf{IS}}$
-algebra whose lattice structure is depicted in Fig. 1(b) and interprets
$\Sigma ^{\textsf{IS}}$
-algebra whose lattice structure is depicted in Fig. 1(b) and interprets
![]() $\sim$
and
$\sim$
and
![]() $\nabla$
as per the following:
$\nabla$
as per the following:
 \begin{equation*} {\sim }^{\mathbf {IS}_6} a \,{:=}\, \begin {cases} {\sim }^{\mathbf {DM}_4} a & a \in \mathcal {V}_4\\ {\hat {\mathbf {f}}} & a = {\hat {\mathbf {t}}}\\ {\hat {\mathbf {t}}} & a = {\hat {\mathbf {f}}}\\ \end {cases}\qquad \nabla ^{\mathbf {IS}_6} a \,{:=}\, \begin {cases} {\hat {\mathbf {t}}} & a \in \mathcal {V}_6\setminus \{{\hat {\mathbf {f}}}\}\\ {\hat {\mathbf {f}}} & a = {\hat {\mathbf {f}}}\\ \end {cases} \end{equation*}
\begin{equation*} {\sim }^{\mathbf {IS}_6} a \,{:=}\, \begin {cases} {\sim }^{\mathbf {DM}_4} a & a \in \mathcal {V}_4\\ {\hat {\mathbf {f}}} & a = {\hat {\mathbf {t}}}\\ {\hat {\mathbf {t}}} & a = {\hat {\mathbf {f}}}\\ \end {cases}\qquad \nabla ^{\mathbf {IS}_6} a \,{:=}\, \begin {cases} {\hat {\mathbf {t}}} & a \in \mathcal {V}_6\setminus \{{\hat {\mathbf {f}}}\}\\ {\hat {\mathbf {f}}} & a = {\hat {\mathbf {f}}}\\ \end {cases} \end{equation*}
The subalgebras of
![]() $\mathbf{IS}_6$
exhibited in Fig. 1(b) constitute the only subdirectly irreducible IS-algebras (Cignoli and Sagastume Reference Cignoli and Sagastume1983).
$\mathbf{IS}_6$
exhibited in Fig. 1(b) constitute the only subdirectly irreducible IS-algebras (Cignoli and Sagastume Reference Cignoli and Sagastume1983).
The notion of residuation in
![]() $\Sigma$
-algebras will be essential for us here, as it is tightly connected to the intuitionistic implication. Let
$\Sigma$
-algebras will be essential for us here, as it is tightly connected to the intuitionistic implication. Let
![]() $\textsf{K}$
be a class of
$\textsf{K}$
be a class of
![]() $\Sigma$
-algebras, with
$\Sigma$
-algebras, with
![]() $\Sigma \supseteq \Sigma ^{\textsf{bL}}$
, whose
$\Sigma \supseteq \Sigma ^{\textsf{bL}}$
, whose
![]() $\{ \land, \top \}$
-reducts are meet-semilattices with a greatest element assigned to
$\{ \land, \top \}$
-reducts are meet-semilattices with a greatest element assigned to
![]() $\top$
. Given
$\top$
. Given
![]() $\mathbf{A} \in \textsf{K}$
, we say that
$\mathbf{A} \in \textsf{K}$
, we say that
![]() $\unicode{x00A9}$
is the residuum of
$\unicode{x00A9}$
is the residuum of
![]() $\land$
in
$\land$
in
![]() $\mathbf{A}$
provided that
$\mathbf{A}$
provided that
![]() $a \,\land ^{\mathbf{A}}\, b \leq c$
if, and only if,
$a \,\land ^{\mathbf{A}}\, b \leq c$
if, and only if,
![]() $a \leq b \,\unicode{x00A9}^{\mathbf{A}}\, c$
for all
$a \leq b \,\unicode{x00A9}^{\mathbf{A}}\, c$
for all
![]() $a,b,c \in A$
. It is well-known that in classical logic and in intuitionistic logic the implication plays the role of residuum of conjunction. We will also consider the notion of pseudo-complement of
$a,b,c \in A$
. It is well-known that in classical logic and in intuitionistic logic the implication plays the role of residuum of conjunction. We will also consider the notion of pseudo-complement of
![]() $a \in A$
: this will be defined as the greatest element
$a \in A$
: this will be defined as the greatest element
![]() $\neg a \in A$
such that
$\neg a \in A$
such that
![]() $a \land ^{\mathbf{A}} \neg a = \bot ^{\mathbf{A}}$
. When every element of
$a \land ^{\mathbf{A}} \neg a = \bot ^{\mathbf{A}}$
. When every element of
![]() $\mathbf{A}$
has a pseudo-complement (unique by definition), we may think of
$\mathbf{A}$
has a pseudo-complement (unique by definition), we may think of
![]() $\neg ^{\mathbf{A}}$
as a unary operation, known as the pseudo-complement operation of
$\neg ^{\mathbf{A}}$
as a unary operation, known as the pseudo-complement operation of
![]() $\mathbf{A}$
.
$\mathbf{A}$
.

Figure 1. The subdirectly irreducible De Morgan (a) and the subdirectly irreducible IS-algebras (b).
We move now to the logical preliminaries. A ![]() logic (over
logic (over
![]() $\Sigma$
) is a consequence relation
$\Sigma$
) is a consequence relation
![]() $\vdash$
on
$\vdash$
on
![]() $L_{\Sigma }(P)$
and a Set-Set logic (over
$L_{\Sigma }(P)$
and a Set-Set logic (over
![]() $\Sigma$
) is a generalized consequence relation
$\Sigma$
) is a generalized consequence relation
![]() $\rhd$
on
$\rhd$
on
![]() $L_{\Sigma }(P)$
(Humberstone Reference Humberstone2011). The
$L_{\Sigma }(P)$
(Humberstone Reference Humberstone2011). The ![]() companion of a given Set-Set logic
companion of a given Set-Set logic
![]() $\rhd$
is the
$\rhd$
is the ![]() logic
logic
![]() $\vdash _{\rhd }$
such that
$\vdash _{\rhd }$
such that
![]() $\Phi \vdash _{\rhd } \psi$
if, and only if,
$\Phi \vdash _{\rhd } \psi$
if, and only if,
![]() $\Phi \rhd \{\psi \}$
. We will write
$\Phi \rhd \{\psi \}$
. We will write
![]() $\Phi \;{\lhd \rhd } \; \Psi$
when
$\Phi \;{\lhd \rhd } \; \Psi$
when
![]() $\Phi \; \rhd \; \Psi$
and
$\Phi \; \rhd \; \Psi$
and
![]() $\Psi \; \rhd \; \Phi$
; that being the case, we say these sets are logically equivalent. We will adopt the convention of omitting curly braces when writing sets of formulas in statements involving (generalized) consequence relations. The complement of a given Set-Set logic
$\Psi \; \rhd \; \Phi$
; that being the case, we say these sets are logically equivalent. We will adopt the convention of omitting curly braces when writing sets of formulas in statements involving (generalized) consequence relations. The complement of a given Set-Set logic
![]() $\rhd$
, that is,
$\rhd$
, that is,
![]() $(\wp L_{\Sigma }(P) \times \wp L_{\Sigma }(P)){\setminus }\rhd$
, will be denoted by
$(\wp L_{\Sigma }(P) \times \wp L_{\Sigma }(P)){\setminus }\rhd$
, will be denoted by
![]() $\blacktriangleright _{}$
.
$\blacktriangleright _{}$
.
Let
![]() $\rhd$
and
$\rhd$
and
![]() $\rhd '$
be Set-Set logics over signatures
$\rhd '$
be Set-Set logics over signatures
![]() $\Sigma$
and
$\Sigma$
and
![]() $\Sigma '$
, respectively, with
$\Sigma '$
, respectively, with
![]() $\Sigma \subseteq \Sigma '$
. We say that
$\Sigma \subseteq \Sigma '$
. We say that
![]() $\rhd '$
expands
$\rhd '$
expands
![]() $\rhd$
when
$\rhd$
when
![]() $\rhd ' \supseteq \rhd$
. When
$\rhd ' \supseteq \rhd$
. When
![]() $\Sigma = \Sigma '$
, we say more simply that
$\Sigma = \Sigma '$
, we say more simply that
![]() $\rhd '$
extends
$\rhd '$
extends
![]() $\rhd$
. It is worth recalling that the collection of all extensions of a given logic forms a complete lattice under inclusion. We say that
$\rhd$
. It is worth recalling that the collection of all extensions of a given logic forms a complete lattice under inclusion. We say that
![]() $\rhd '$
is a conservative expansion of
$\rhd '$
is a conservative expansion of
![]() $\rhd$
when
$\rhd$
when
![]() $\rhd '$
expands
$\rhd '$
expands
![]() $\rhd$
and, for all
$\rhd$
and, for all
![]() $\Phi, \Psi \subseteq L_{\Sigma }(P)$
, we have
$\Phi, \Psi \subseteq L_{\Sigma }(P)$
, we have
![]() $\Phi \rhd ' \Psi$
if, and only if,
$\Phi \rhd ' \Psi$
if, and only if,
![]() $\Phi \rhd \Psi$
. The finitary companion of a Set-Set logic
$\Phi \rhd \Psi$
. The finitary companion of a Set-Set logic
![]() $\rhd$
is the Set-Set logic
$\rhd$
is the Set-Set logic
![]() $\rhd _{\textsf{fin}}$
such that
$\rhd _{\textsf{fin}}$
such that
![]() $\Phi \rhd _{\textsf{fin}} \Psi$
if, and only if, there are finite
$\Phi \rhd _{\textsf{fin}} \Psi$
if, and only if, there are finite
![]() $\Phi ' \subseteq \Phi$
and
$\Phi ' \subseteq \Phi$
and
![]() $\Psi ' \subseteq \Psi$
such that
$\Psi ' \subseteq \Psi$
such that
![]() $\Phi ' \rhd \Psi '$
. The latter concepts may be straightforwardly adapted to
$\Phi ' \rhd \Psi '$
. The latter concepts may be straightforwardly adapted to ![]() logics.
logics.
We call special attention to the notion of self-extensionality, as it will play an important role in the implicative extensions we consider in this paper:
Definition 3.
A logic
![]() $\rhd$
over the signature
$\rhd$
over the signature
![]() $\Sigma$
is called self-extensional (or congruential) if logical equivalence is compatible with each connective in the signature, that is, for every
$\Sigma$
is called self-extensional (or congruential) if logical equivalence is compatible with each connective in the signature, that is, for every
![]() $\unicode{x00A9} \in \Sigma _k$
, it is the case that
$\unicode{x00A9} \in \Sigma _k$
, it is the case that
![]() $\unicode{x00A9}(\varphi _1,\ldots, \varphi _k) \,{\lhd \rhd } \, \unicode{x00A9}(\psi _1,\ldots, \psi _k)$
whenever
$\unicode{x00A9}(\varphi _1,\ldots, \varphi _k) \,{\lhd \rhd } \, \unicode{x00A9}(\psi _1,\ldots, \psi _k)$
whenever
![]() $\varphi _i \,{\lhd \rhd } \, \psi _i$
for every
$\varphi _i \,{\lhd \rhd } \, \psi _i$
for every
![]() $1\leq i \leq k$
. For
$1\leq i \leq k$
. For ![]() logics, just replace “
logics, just replace “
![]() $\rhd$
” by “
$\rhd$
” by “
![]() $\vdash$
”.
$\vdash$
”.
A partial non-deterministic
![]() $\Sigma$
-matrix (or, more simply,
$\Sigma$
-matrix (or, more simply,
![]() $\Sigma$
-PNmatrix)
$\Sigma$
-PNmatrix)
![]() $\mathfrak{M}$
is a structure
$\mathfrak{M}$
is a structure
![]() $\langle \mathbf{A}, D \rangle$
where
$\langle \mathbf{A}, D \rangle$
where
![]() $\mathbf{A}$
is a
$\mathbf{A}$
is a
![]() $\Sigma$
-multialgebra and the members of
$\Sigma$
-multialgebra and the members of
![]() $D \subseteq A$
are called designated values. We will write
$D \subseteq A$
are called designated values. We will write
![]() $\overline{D}$
to refer to
$\overline{D}$
to refer to
![]() $A{\setminus{}}D$
. When
$A{\setminus{}}D$
. When
![]() $\mathbf{A}$
is a
$\mathbf{A}$
is a
![]() $\Sigma$
-algebra,
$\Sigma$
-algebra,
![]() $\mathfrak{M}$
is called a
$\mathfrak{M}$
is called a
![]() $\Sigma$
-matrix, and coincides with the usual definition of logical matrix in the literature. A refinement of
$\Sigma$
-matrix, and coincides with the usual definition of logical matrix in the literature. A refinement of
![]() $\mathfrak{M}$
is a
$\mathfrak{M}$
is a
![]() $\Sigma$
-PNmatrix obtained from
$\Sigma$
-PNmatrix obtained from
![]() $\mathbf{A}$
by deleting values from some entries of the interpretations of the connectives in
$\mathbf{A}$
by deleting values from some entries of the interpretations of the connectives in
![]() $\mathbf{A}$
(the resulting interpretations are also said to be refinements of the ones in
$\mathbf{A}$
(the resulting interpretations are also said to be refinements of the ones in
![]() $\mathbf{A}$
). The mappings in
$\mathbf{A}$
). The mappings in
![]() $\textsf{Hom}(\mathbf{L}_{\Sigma }(P), \mathbf{A})$
are called
$\textsf{Hom}(\mathbf{L}_{\Sigma }(P), \mathbf{A})$
are called
![]() $\mathfrak{M}$
-valuations. Every
$\mathfrak{M}$
-valuations. Every
![]() $\Sigma$
-PNmatrix determines a
$\Sigma$
-PNmatrix determines a ![]() logic
logic
![]() $\rhd _{\mathfrak{M}}$
such that
$\rhd _{\mathfrak{M}}$
such that
![]() $\Phi\;{\rhd_{\mathfrak{M}}}\;\Psi$
iff
$\Phi\;{\rhd_{\mathfrak{M}}}\;\Psi$
iff
![]() $h(\Phi ) \cap \overline{D} \neq \varnothing$
or
$h(\Phi ) \cap \overline{D} \neq \varnothing$
or
![]() $h(\Psi ) \cap D \neq \varnothing$
for all
$h(\Psi ) \cap D \neq \varnothing$
for all
![]() $\mathfrak{M}$
-valuations
$\mathfrak{M}$
-valuations
![]() $h$
, as well as a
$h$
, as well as a ![]() logic
logic
![]() $\vdash _{\mathfrak{M}}$
with
$\vdash _{\mathfrak{M}}$
with
![]() $\Phi \vdash _{\mathfrak{M}} \psi$
iff
$\Phi \vdash _{\mathfrak{M}} \psi$
iff
![]() $h(\Phi ) \cap \overline{D} \neq \varnothing$
or
$h(\Phi ) \cap \overline{D} \neq \varnothing$
or
![]() $h(\psi ) \in D$
for all
$h(\psi ) \in D$
for all
![]() $\mathfrak{M}$
-valuations
$\mathfrak{M}$
-valuations
![]() $h$
(notice that
$h$
(notice that
![]() $\vdash _{\mathfrak{M}}$
is the
$\vdash _{\mathfrak{M}}$
is the ![]() companion of
companion of
![]() $\rhd _{\mathfrak{M}}$
). Given a
$\rhd _{\mathfrak{M}}$
). Given a ![]() logic
logic
![]() $\rhd$
(resp. a
$\rhd$
(resp. a ![]() logic
logic
![]() $\vdash$
), if
$\vdash$
), if
![]() $\rhd \;\subseteq \;\rhd _{\mathfrak{M}}$
(resp.
$\rhd \;\subseteq \;\rhd _{\mathfrak{M}}$
(resp.
![]() $\vdash \;\subseteq \; \vdash _{\mathfrak{M}}$
), we shall say that
$\vdash \;\subseteq \; \vdash _{\mathfrak{M}}$
), we shall say that
![]() $\mathfrak{M}$
is a matrix model of
$\mathfrak{M}$
is a matrix model of
![]() $\rhd$
(resp.
$\rhd$
(resp.
![]() $\vdash$
), and if the converse also holds we shall say that
$\vdash$
), and if the converse also holds we shall say that
![]() $\mathfrak{M}$
determines
$\mathfrak{M}$
determines
![]() $\rhd$
(resp.
$\rhd$
(resp.
![]() $\vdash$
). The
$\vdash$
). The ![]() (resp.
(resp. ![]() ) logic determined by a class
) logic determined by a class
![]() $\mathcal{M}$
of
$\mathcal{M}$
of
![]() $\Sigma$
-matrices is given by
$\Sigma$
-matrices is given by
![]() $\bigcap \{\rhd _{\mathfrak{M}} : \mathfrak{M} \in \mathcal{M}\}$
(resp.
$\bigcap \{\rhd _{\mathfrak{M}} : \mathfrak{M} \in \mathcal{M}\}$
(resp.
![]() $\bigcap \{\vdash _{\mathfrak{M}} : \mathfrak{M} \in \mathcal{M}\}$
).
$\bigcap \{\vdash _{\mathfrak{M}} : \mathfrak{M} \in \mathcal{M}\}$
).
Example 3.
The
![]() $\Sigma ^{\textsf{DM}}$
-matrix
$\Sigma ^{\textsf{DM}}$
-matrix
![]() $\langle \mathbf{DM}_4, \{{\mathbf{b}},{\mathbf{t}} \} \rangle$
determines the logic known as the 4-valued Dunn-Belnap logic (Belnap Reference Belnap1977
), or First-Degree Entailment, which we hereby denote by
$\langle \mathbf{DM}_4, \{{\mathbf{b}},{\mathbf{t}} \} \rangle$
determines the logic known as the 4-valued Dunn-Belnap logic (Belnap Reference Belnap1977
), or First-Degree Entailment, which we hereby denote by
![]() $\mathcal{B}$
. Extensions of
$\mathcal{B}$
. Extensions of
![]() $\mathcal{B}$
are known as super-Belnap logics (Rivieccio Reference Rivieccio2012
).
$\mathcal{B}$
are known as super-Belnap logics (Rivieccio Reference Rivieccio2012
).
Example 4.
Classical Logic, henceforth denoted by
![]() $\mathcal{CL}$
, is determined by the
$\mathcal{CL}$
, is determined by the
![]() $\Sigma ^{\textsf{DM}}$
-matrix
$\Sigma ^{\textsf{DM}}$
-matrix
![]() $\langle \mathbf{DM}_2, \{{\mathbf{t}}\} \rangle$
(see Fig. 1(a)).
$\langle \mathbf{DM}_2, \{{\mathbf{t}}\} \rangle$
(see Fig. 1(a)).
Given a
![]() $\Sigma$
-matrix
$\Sigma$
-matrix
![]() $\mathfrak{M} = \langle \mathbf{A}, D \rangle$
, a congruence
$\mathfrak{M} = \langle \mathbf{A}, D \rangle$
, a congruence
![]() $\theta \in \textsf{Cng} \mathbf{A}$
is said to be compatible with
$\theta \in \textsf{Cng} \mathbf{A}$
is said to be compatible with
![]() $\mathfrak{M}$
when
$\mathfrak{M}$
when
![]() $b \in D$
whenever both
$b \in D$
whenever both
![]() $a \in D$
and
$a \in D$
and
![]() $a \theta b$
, for all
$a \theta b$
, for all
![]() $a,b \in A$
. We denote by
$a,b \in A$
. We denote by
![]() $\Omega ^{\mathfrak{M}}$
the Leibniz congruence associated with
$\Omega ^{\mathfrak{M}}$
the Leibniz congruence associated with
![]() $\mathfrak{M}$
, namely the greatest congruence of
$\mathfrak{M}$
, namely the greatest congruence of
![]() $\mathbf{A}$
compatible with
$\mathbf{A}$
compatible with
![]() $\mathfrak{M}$
. The matrix
$\mathfrak{M}$
. The matrix
![]() ${\mathfrak{M}}^{\ast } = \langle \mathbf{A}/\Omega ^{\mathfrak{M}}, D/\Omega ^{\mathfrak{M}} \rangle$
is the reduced version of
${\mathfrak{M}}^{\ast } = \langle \mathbf{A}/\Omega ^{\mathfrak{M}}, D/\Omega ^{\mathfrak{M}} \rangle$
is the reduced version of
![]() $\mathfrak{M}$
. It is well-known that
$\mathfrak{M}$
. It is well-known that
![]() $\rhd _{\mathfrak{M}} = \rhd _{{\mathfrak{M}}^{\ast }}$
(and thus
$\rhd _{\mathfrak{M}} = \rhd _{{\mathfrak{M}}^{\ast }}$
(and thus
![]() $\vdash _{\mathfrak{M}} \;=\; \vdash _{{\mathfrak{M}}^{\ast }}$
) and, since every logic is determined by a class of matrix models, we have that every logic coincides with the logic determined by its reduced matrix models. As a shortcut, we call a matrix reduced when it coincides with its own reduced version (or, equivalently, when its Leibniz congruence is the identity relation on
$\vdash _{\mathfrak{M}} \;=\; \vdash _{{\mathfrak{M}}^{\ast }}$
) and, since every logic is determined by a class of matrix models, we have that every logic coincides with the logic determined by its reduced matrix models. As a shortcut, we call a matrix reduced when it coincides with its own reduced version (or, equivalently, when its Leibniz congruence is the identity relation on
![]() $A$
).
$A$
).
When a
![]() $\Sigma$
-algebra
$\Sigma$
-algebra
![]() $\mathbf{A}$
has a lattice structure with underlying order
$\mathbf{A}$
has a lattice structure with underlying order
![]() $\leq$
, for any
$\leq$
, for any
![]() $a\in A$
we write
$a\in A$
we write
![]() ${\uparrow }a$
to refer to the set
${\uparrow }a$
to refer to the set
![]() $\{b \in A : a \leq b\}$
. For instance, over
$\{b \in A : a \leq b\}$
. For instance, over
![]() $\mathbf{IS_6}{}$
we may consider the set
$\mathbf{IS_6}{}$
we may consider the set
![]() ${{\uparrow }{\mathbf{b}}} = \{{\mathbf{b}},{\mathbf{t}},{\hat{\mathbf{t}}}\}$
(see Fig. 1B). We may employ the same notation to write the designated set of a
${{\uparrow }{\mathbf{b}}} = \{{\mathbf{b}},{\mathbf{t}},{\hat{\mathbf{t}}}\}$
(see Fig. 1B). We may employ the same notation to write the designated set of a
![]() $\Sigma$
-matrix having a lattice as underlying algebra. A lattice filter of a meet-semilattice
$\Sigma$
-matrix having a lattice as underlying algebra. A lattice filter of a meet-semilattice
![]() $\mathbf{A}$
with a top element
$\mathbf{A}$
with a top element
![]() $\top ^{\mathbf{A}}$
is a subset
$\top ^{\mathbf{A}}$
is a subset
![]() $D \subseteq A$
with
$D \subseteq A$
with
![]() $\top ^{\mathbf{A}} \in D$
and closed under
$\top ^{\mathbf{A}} \in D$
and closed under
![]() $\land ^{\mathbf{A}}$
; moreover,
$\land ^{\mathbf{A}}$
; moreover,
![]() $D$
is a proper lattice filter of
$D$
is a proper lattice filter of
![]() $\mathbf{A}$
when
$\mathbf{A}$
when
![]() $D \neq A$
. A principal filter of
$D \neq A$
. A principal filter of
![]() $\mathbf{A}$
is a lattice filter of the form
$\mathbf{A}$
is a lattice filter of the form
![]() ${\uparrow } a$
, for some
${\uparrow } a$
, for some
![]() $a \in A$
. Note that, if
$a \in A$
. Note that, if
![]() $\mathbf{A}$
is finite, every lattice filter is principal. If
$\mathbf{A}$
is finite, every lattice filter is principal. If
![]() $\mathbf{A}$
also has a join-semilattice structure, a prime filter of
$\mathbf{A}$
also has a join-semilattice structure, a prime filter of
![]() $\mathbf{A}$
is a proper lattice filter
$\mathbf{A}$
is a proper lattice filter
![]() $D$
of
$D$
of
![]() $\mathbf{A}$
such that
$\mathbf{A}$
such that
![]() $a \lor b \in D$
iff
$a \lor b \in D$
iff
![]() $a \in D$
or
$a \in D$
or
![]() $b \in D$
, for all
$b \in D$
, for all
![]() $a,b \in A$
.
$a,b \in A$
.
2.2 Logics associated with classes of (ordered) algebras
Throughout this section, consider a propositional signature
![]() $\Sigma \supseteq \Sigma ^{\textsf{bL}}$
. In addition, for a set of
$\Sigma \supseteq \Sigma ^{\textsf{bL}}$
. In addition, for a set of
![]() $\Sigma$
-formulas
$\Sigma$
-formulas
![]() $\Phi \,{:=}\, \{ \varphi _1,\ldots, \varphi _n \}$
, let
$\Phi \,{:=}\, \{ \varphi _1,\ldots, \varphi _n \}$
, let
![]() $\bigwedge \Phi \,{:=}\, \varphi _1 \land \ldots \land \varphi _n$
and
$\bigwedge \Phi \,{:=}\, \varphi _1 \land \ldots \land \varphi _n$
and
![]() $\bigvee \Phi \,{:=}\, \varphi _1 \lor \ldots \lor \varphi _n$
, while, by convention, let
$\bigvee \Phi \,{:=}\, \varphi _1 \lor \ldots \lor \varphi _n$
, while, by convention, let
![]() $\bigwedge \varnothing \,{:=}\, \top$
and
$\bigwedge \varnothing \,{:=}\, \top$
and
![]() $\bigvee \varnothing \,{:=}\, \bot$
. Moreover, let the inequality
$\bigvee \varnothing \,{:=}\, \bot$
. Moreover, let the inequality
![]() $\varphi \leq \psi$
abbreviate the equation
$\varphi \leq \psi$
abbreviate the equation
![]() $\varphi \approx \varphi \land \psi$
.
$\varphi \approx \varphi \land \psi$
.
Definition 4.
Let
![]() $\textsf{K}$
be a class of
$\textsf{K}$
be a class of
![]() $\Sigma$
-algebras such that each
$\Sigma$
-algebras such that each
![]() $\mathbf{A} \in \textsf{K}$
has a bounded distributive lattice reduct with greatest element
$\mathbf{A} \in \textsf{K}$
has a bounded distributive lattice reduct with greatest element
![]() $\top ^{\mathbf{A}}$
and a least element
$\top ^{\mathbf{A}}$
and a least element
![]() $\bot ^{\mathbf{A}}$
. The order-preserving logic associated with
$\bot ^{\mathbf{A}}$
. The order-preserving logic associated with
![]() $\textsf{K}$
, denoted by
$\textsf{K}$
, denoted by
![]() $\rhd _{\textsf{K}}^{\leq }$
, is such that
$\rhd _{\textsf{K}}^{\leq }$
, is such that
![]() $\Phi \, \rhd _{\textsf{K}}^{\leq } \, \Psi$
if, and only if, there are finite
$\Phi \, \rhd _{\textsf{K}}^{\leq } \, \Psi$
if, and only if, there are finite
![]() $\Phi '\subseteq \Phi$
and
$\Phi '\subseteq \Phi$
and
![]() $\Psi '\subseteq \Psi$
such that
$\Psi '\subseteq \Psi$
such that
![]() $\bigwedge \Phi ' \leq \bigvee \Psi '$
is valid in
$\bigwedge \Phi ' \leq \bigvee \Psi '$
is valid in
![]() $\textsf{K}$
.
$\textsf{K}$
.
For any order-preserving logic
![]() $\rhd _{\textsf{K}}^{\leq }$
associated with an appropriate class
$\rhd _{\textsf{K}}^{\leq }$
associated with an appropriate class
![]() $\textsf{K}$
of algebras, the following characterization in terms of prime filters applies:
$\textsf{K}$
of algebras, the following characterization in terms of prime filters applies:
Proposition 5.
![]() $\rhd _{\textsf{K}}^{\leq }$
is the finitary companion of the logic determined by
$\rhd _{\textsf{K}}^{\leq }$
is the finitary companion of the logic determined by
![]() $ \mathcal{M^{{{\uparrow }\lor }}} \,{:=}\, \{ \langle \mathbf{A}, D \rangle : \mathbf{A} \in \textsf{K}\text{ and } D \text{ is a prime filter of $\mathbf{A}$}\}$
.
$ \mathcal{M^{{{\uparrow }\lor }}} \,{:=}\, \{ \langle \mathbf{A}, D \rangle : \mathbf{A} \in \textsf{K}\text{ and } D \text{ is a prime filter of $\mathbf{A}$}\}$
.
Proof.
To start with, assume that
![]() $\Phi \rhd _{\textsf{K}}^{\leq }\Psi$
. So, (i) there are finite
$\Phi \rhd _{\textsf{K}}^{\leq }\Psi$
. So, (i) there are finite
![]() $\Phi '\subseteq \Phi$
and
$\Phi '\subseteq \Phi$
and
![]() $\Psi '\subseteq \Psi$
such that
$\Psi '\subseteq \Psi$
such that
![]() $\Phi '\rhd _{\textsf{K}}^{\leq }\Psi '$
. Let
$\Phi '\rhd _{\textsf{K}}^{\leq }\Psi '$
. Let
![]() $\langle \mathbf{A}, D \rangle \in \mathcal{M^{{{\uparrow }\lor }}}$
and
$\langle \mathbf{A}, D \rangle \in \mathcal{M^{{{\uparrow }\lor }}}$
and
![]() $v \in \textsf{Hom}(\mathbf{L}_{\Sigma }(P), \mathbf{A})$
be a valuation. Assume that
$v \in \textsf{Hom}(\mathbf{L}_{\Sigma }(P), \mathbf{A})$
be a valuation. Assume that
![]() $v[\Phi '] \subseteq D$
. Thus
$v[\Phi '] \subseteq D$
. Thus
![]() $v(\bigwedge \Phi ') \in D$
, as
$v(\bigwedge \Phi ') \in D$
, as
![]() $D$
is a lattice filter. By (i), we know that
$D$
is a lattice filter. By (i), we know that
![]() $v(\bigwedge \Phi ') \leq v(\bigvee \Psi ')$
, so
$v(\bigwedge \Phi ') \leq v(\bigvee \Psi ')$
, so
![]() $v(\bigvee \Psi ') \in D$
. Since
$v(\bigvee \Psi ') \in D$
. Since
![]() $D$
is prime, we must have
$D$
is prime, we must have
![]() $v(\psi ) \in D$
for some
$v(\psi ) \in D$
for some
![]() $\psi \in \Psi '$
and we are done.
$\psi \in \Psi '$
and we are done.
Conversely, assume that (ii) follows from in the finitary companion of
![]() $\rhd_{\mathcal{M}^{{{\uparrow }\lor }}}$
. Thus
$\rhd_{\mathcal{M}^{{{\uparrow }\lor }}}$
. Thus
![]() $\Phi ' \rhd _{\mathcal{M^{{{\uparrow }\lor }}}} \Psi '$
for finite
$\Phi ' \rhd _{\mathcal{M^{{{\uparrow }\lor }}}} \Psi '$
for finite
![]() $\Phi '\subseteq \Phi$
and
$\Phi '\subseteq \Phi$
and
![]() $\Psi '\subseteq \Psi$
. Let
$\Psi '\subseteq \Psi$
. Let
![]() $\mathbf A \in \textsf{K}$
and
$\mathbf A \in \textsf{K}$
and
![]() $v \in \textsf{Hom}(\mathbf{L}_{\Sigma }(P), \mathbf{A})$
. Let
$v \in \textsf{Hom}(\mathbf{L}_{\Sigma }(P), \mathbf{A})$
. Let
![]() $a \,{:=}\, v(\bigwedge \Phi ')$
(note that
$a \,{:=}\, v(\bigwedge \Phi ')$
(note that
![]() $a = \top ^{\mathbf{A}}$
if
$a = \top ^{\mathbf{A}}$
if
![]() $\Phi ' = \varnothing$
). If
$\Phi ' = \varnothing$
). If
![]() $a = \bot ^{\mathbf{A}}$
, the result is straightforward. Otherwise,
$a = \bot ^{\mathbf{A}}$
, the result is straightforward. Otherwise,
![]() ${\uparrow }a$
is a proper filter. Suppose, by reductio, that
${\uparrow }a$
is a proper filter. Suppose, by reductio, that
![]() $a \not \leq v(\bigvee \Psi ')$
, that is,
$a \not \leq v(\bigvee \Psi ')$
, that is,
![]() $v(\bigvee \Psi ') \not \in{{\uparrow }a}$
. Since
$v(\bigvee \Psi ') \not \in{{\uparrow }a}$
. Since
![]() $\mathbf{A}$
is distributive, consider, by the Prime Filter Theorem, the extension of
$\mathbf{A}$
is distributive, consider, by the Prime Filter Theorem, the extension of
![]() ${\uparrow }a$
to a prime filter
${\uparrow }a$
to a prime filter
![]() $D \supseteq{{\uparrow }a}$
such that
$D \supseteq{{\uparrow }a}$
such that
![]() $v(\bigvee \Psi ') \not \in D$
. Since
$v(\bigvee \Psi ') \not \in D$
. Since
![]() $a \leq v(\varphi )$
for each
$a \leq v(\varphi )$
for each
![]() $\varphi \in \Phi '$
, we have
$\varphi \in \Phi '$
, we have
![]() $v(\varphi ) \in{{\uparrow }a} \subseteq D$
, for all
$v(\varphi ) \in{{\uparrow }a} \subseteq D$
, for all
![]() $\varphi \in \Phi '$
and, by (ii), we have
$\varphi \in \Phi '$
and, by (ii), we have
![]() $v(\psi ) \in D$
for some
$v(\psi ) \in D$
for some
![]() $\psi \in \Psi '$
. Since
$\psi \in \Psi '$
. Since
![]() $v(\psi ) \leq v(\bigvee \Psi ')$
, we must have
$v(\psi ) \leq v(\bigvee \Psi ')$
, we must have
![]() $v(\bigvee \Psi ') \in D$
. As this leads to a contradiction, we conclude that
$v(\bigvee \Psi ') \in D$
. As this leads to a contradiction, we conclude that
![]() $a \leq v(\bigvee \Psi ')$
, as desired.
$a \leq v(\bigvee \Psi ')$
, as desired.
For a variety generated by a single finite distributive lattice, we have this simpler characterization in terms of a finite family of finite matrices:
Proposition 6.
Let
![]() $\textsf{K} = \mathbb{V}(\{ \mathbf{B}\})$
, for
$\textsf{K} = \mathbb{V}(\{ \mathbf{B}\})$
, for
![]() $\mathbf{B}$
a finite distributive lattice. Then
$\mathbf{B}$
a finite distributive lattice. Then
![]() $\rhd _{\textsf{K}}^{\leq }$
is determined by
$\rhd _{\textsf{K}}^{\leq }$
is determined by
![]() $ \mathcal{M}^{{{\uparrow }\lor }}_{\textsf{fin}} \,{:=}\, \{ \langle \mathbf{B}, D \rangle : D \text{ is a prime filter of $\mathbf{B}$}\}$
.
$ \mathcal{M}^{{{\uparrow }\lor }}_{\textsf{fin}} \,{:=}\, \{ \langle \mathbf{B}, D \rangle : D \text{ is a prime filter of $\mathbf{B}$}\}$
.
Proof.
As
![]() $\mathcal{M}^{{{\uparrow }}\lor }_{\textsf{fin}} \subseteq \mathcal{M}^{{{\uparrow }}\lor }$
, we have
$\mathcal{M}^{{{\uparrow }}\lor }_{\textsf{fin}} \subseteq \mathcal{M}^{{{\uparrow }}\lor }$
, we have
![]() $\rhd _{\textsf{K}}^{\leq } \subseteq \rhd _{\mathcal{M}^{{{\uparrow }}\lor }_{\textsf{fin}}}$
. Conversely, suppose that
$\rhd _{\textsf{K}}^{\leq } \subseteq \rhd _{\mathcal{M}^{{{\uparrow }}\lor }_{\textsf{fin}}}$
. Conversely, suppose that
![]() $\Phi \; \,\blacktriangleright _{\textsf{K}}^{\leq } \; \Psi$
. Consider finite
$\Phi \; \,\blacktriangleright _{\textsf{K}}^{\leq } \; \Psi$
. Consider finite
![]() $\Phi ' \subseteq \Phi$
and
$\Phi ' \subseteq \Phi$
and
![]() $\Psi ' \subseteq \Psi$
. We want to show that
$\Psi ' \subseteq \Psi$
. We want to show that
![]() $\Phi ' \,\blacktriangleright _{\mathcal{M}^{{{\uparrow }}\lor }_{\textsf{fin}}} \Psi '$
. By the hypothesis, we know that
$\Phi ' \,\blacktriangleright _{\mathcal{M}^{{{\uparrow }}\lor }_{\textsf{fin}}} \Psi '$
. By the hypothesis, we know that
![]() $\bigwedge \Phi ' \leq \bigvee \Psi '$
fails in
$\bigwedge \Phi ' \leq \bigvee \Psi '$
fails in
![]() $\textsf{K}$
, thus it fails in
$\textsf{K}$
, thus it fails in
![]() $\mathbf{B}$
, say under a valuation
$\mathbf{B}$
, say under a valuation
![]() $v$
. Let
$v$
. Let
![]() $b \,{:=}\, v(\bigwedge \Phi ')$
. So,
$b \,{:=}\, v(\bigwedge \Phi ')$
. So,
![]() $b \not \leq v(\bigvee \Psi ')$
. Note that
$b \not \leq v(\bigvee \Psi ')$
. Note that
![]() ${\uparrow }b$
must be proper. As
${\uparrow }b$
must be proper. As
![]() $v(\bigvee \Psi ') \not \in{{\uparrow }b}$
, consider the extension of
$v(\bigvee \Psi ') \not \in{{\uparrow }b}$
, consider the extension of
![]() ${\uparrow }b$
to a prime filter
${\uparrow }b$
to a prime filter
![]() $D$
, by the Prime Filter Theorem, such that
$D$
, by the Prime Filter Theorem, such that
![]() $v(\bigvee \Psi ') \not \in D$
. Since
$v(\bigvee \Psi ') \not \in D$
. Since
![]() $\mathbf{B}$
is finite, we have that
$\mathbf{B}$
is finite, we have that
![]() $D$
is principal. Clearly, we must have
$D$
is principal. Clearly, we must have
![]() $v(\psi ) \not \in D$
for every
$v(\psi ) \not \in D$
for every
![]() $\psi \in \Psi '$
, as
$\psi \in \Psi '$
, as
![]() $v(\psi ) \leq v(\bigvee \Psi ')$
and
$v(\psi ) \leq v(\bigvee \Psi ')$
and
![]() $D$
is upwards closed, and
$D$
is upwards closed, and
![]() $v(\varphi ) \in D$
for every
$v(\varphi ) \in D$
for every
![]() $\varphi \in \Phi '$
. Therefore,
$\varphi \in \Phi '$
. Therefore,
![]() $\Phi ' \,\blacktriangleright _{\mathcal{M}^{{{\uparrow }}\lor }_{\textsf{fin}}} \Psi '$
, as desired.
$\Phi ' \,\blacktriangleright _{\mathcal{M}^{{{\uparrow }}\lor }_{\textsf{fin}}} \Psi '$
, as desired.
Definition 7.
Let
![]() $\textsf{K}$
be a class of
$\textsf{K}$
be a class of
![]() $\Sigma$
-algebras as in Definition 4
. The
$\Sigma$
-algebras as in Definition 4
. The ![]() order-preserving logic induced by
order-preserving logic induced by
![]() $\textsf{K}$
, which we denote by
$\textsf{K}$
, which we denote by
![]() $\vdash _{\textsf{K}}^{\leq }$
, is such that
$\vdash _{\textsf{K}}^{\leq }$
, is such that
![]() $\Phi \vdash _{\textsf{K}}^{\leq } \psi$
if, and only if, there are
$\Phi \vdash _{\textsf{K}}^{\leq } \psi$
if, and only if, there are
![]() $\varphi _1,\ldots, \varphi _n \subseteq \Phi$
(
$\varphi _1,\ldots, \varphi _n \subseteq \Phi$
(
![]() $n \geq 1$
) for which
$n \geq 1$
) for which
![]() $\bigwedge _i \varphi _i \leq \psi$
is valid in
$\bigwedge _i \varphi _i \leq \psi$
is valid in
![]() $\textsf{K}$
.
$\textsf{K}$
.
Notice that
![]() $\vdash _{\textsf{K}}^{\leq }$
is the
$\vdash _{\textsf{K}}^{\leq }$
is the ![]() companion of
companion of
![]() $\rhd _{\textsf{K}}^{\leq }$
.
$\rhd _{\textsf{K}}^{\leq }$
.
The above logics are particularly interesting for us in view of the following:
Proposition 8.
![]() $\rhd _{\textsf{K}}^{\leq }$
and
$\rhd _{\textsf{K}}^{\leq }$
and
![]() $\vdash _{\textsf{K}}^{\leq }$
are self-extensional.
$\vdash _{\textsf{K}}^{\leq }$
are self-extensional.
Proof.
Directly from Jansana (Reference Jansana2006, Sec. 3) and from the fact that
![]() $\vdash _{\textsf{K}}^{\leq }$
is the
$\vdash _{\textsf{K}}^{\leq }$
is the ![]() companion of
companion of
![]() $\rhd _{\textsf{K}}^{\leq }$
.
$\rhd _{\textsf{K}}^{\leq }$
.
We close by defining the
![]() $\top$
-assertional logics (also known as 1-assertional logics) associated with a class of bounded lattices.
$\top$
-assertional logics (also known as 1-assertional logics) associated with a class of bounded lattices.
Definition 9.
Let
![]() $\textsf{K}$
be a class of algebras with a bounded lattice reduct. The
$\textsf{K}$
be a class of algebras with a bounded lattice reduct. The
![]() $\top$
-assertional logics
$\top$
-assertional logics
![]() $\rhd ^\top _{\textsf{K}}$
and
$\rhd ^\top _{\textsf{K}}$
and
![]() $\vdash ^{\top }_{\textsf{K}}$
correspond respectively to the
$\vdash ^{\top }_{\textsf{K}}$
correspond respectively to the ![]() and
and ![]() logics determined by the class of matrices
logics determined by the class of matrices
![]() $\{\langle \mathbf{A}, \{\top ^{\mathbf{A}}\} \rangle : \mathbf{A} \in \textsf{K}\}$
.
$\{\langle \mathbf{A}, \{\top ^{\mathbf{A}}\} \rangle : \mathbf{A} \in \textsf{K}\}$
.
Notice that
![]() $\vdash ^{\top }_{\textsf{K}}$
is the
$\vdash ^{\top }_{\textsf{K}}$
is the ![]() companion of
companion of
![]() $\rhd ^\top _{\textsf{K}}$
.
$\rhd ^\top _{\textsf{K}}$
.
2.3 Hilbert-style axiomatizations
Based on Shoesmith and Smiley (Reference Shoesmith and Smiley1978) and Caleiro and Marcelino (Reference Caleiro, Marcelino, Iemhoff, Moortgat and Queiroz2019), we define a symmetrical (Hilbert-style) calculus
![]() $\textsf{R}$
(or
$\textsf{R}$
(or ![]() calculus, for short) as a collection of pairs
calculus, for short) as a collection of pairs
![]() $(\Phi, \Psi ) \in \wp{L_{\Sigma }(P)}\times \wp{L_{\Sigma }(P)}$
, denoted by
$(\Phi, \Psi ) \in \wp{L_{\Sigma }(P)}\times \wp{L_{\Sigma }(P)}$
, denoted by
![]() $\frac{\Phi }{\Psi }$
and called (symmetrical or
$\frac{\Phi }{\Psi }$
and called (symmetrical or ![]() ) inference rules, where
) inference rules, where
![]() $\Phi$
is the antecedent and
$\Phi$
is the antecedent and
![]() $\Psi$
is the succedent of the said rule. We will adopt the convention of omitting curly braces when writing sets of formulas and leaving a blank space instead of writing
$\Psi$
is the succedent of the said rule. We will adopt the convention of omitting curly braces when writing sets of formulas and leaving a blank space instead of writing
![]() $\varnothing$
when presenting inference rules and statements involving (generalized) consequence relations. We proceed to define what constitutes a proof in such calculi.
$\varnothing$
when presenting inference rules and statements involving (generalized) consequence relations. We proceed to define what constitutes a proof in such calculi.
A finite bounded rooted tree
![]() $t$
is a finite poset
$t$
is a finite poset
![]() $\langle \textsf{nds}(t), {\leq }^t \rangle$
with a single minimal element
$\langle \textsf{nds}(t), {\leq }^t \rangle$
with a single minimal element
![]() $\textsf{rt}(t)$
, the root of
$\textsf{rt}(t)$
, the root of
![]() $t$
, such that, for each node
$t$
, such that, for each node
![]() $n \in \textsf{nds}(t)$
, the set
$n \in \textsf{nds}(t)$
, the set
![]() $\{n' \in \textsf{nds}(t) : n' {\leq }^t n \}$
of ancestors of
$\{n' \in \textsf{nds}(t) : n' {\leq }^t n \}$
of ancestors of
![]() $n$
(or the branch up to
$n$
(or the branch up to
![]() $n$
) is linearly ordered under
$n$
) is linearly ordered under
![]() ${\leq }^t$
, and every branch of
${\leq }^t$
, and every branch of
![]() $t$
has a maximal element (a leaf of
$t$
has a maximal element (a leaf of
![]() $t$
). We may assign a label
$t$
). We may assign a label
![]() $l^{t}(n) \in \wp{L_{\Sigma }(P)} \cup \{\ast \}$
to each node
$l^{t}(n) \in \wp{L_{\Sigma }(P)} \cup \{\ast \}$
to each node
![]() $n$
of
$n$
of
![]() $t$
, in which case
$t$
, in which case
![]() $t$
is said to be labeled. Given
$t$
is said to be labeled. Given
![]() $\Psi \subseteq L_{\Sigma }(P)$
, a leaf
$\Psi \subseteq L_{\Sigma }(P)$
, a leaf
![]() $n$
is
$n$
is
![]() $\Psi$
-closed in
$\Psi$
-closed in
![]() $t$
when
$t$
when
![]() $l^{t}(n) \;=\; \ast$
or
$l^{t}(n) \;=\; \ast$
or
![]() $l^{t}(n) \cap \Psi \neq \varnothing$
. The tree
$l^{t}(n) \cap \Psi \neq \varnothing$
. The tree
![]() $t$
itself is
$t$
itself is
![]() $\Psi$
-closed when all of its leaves are
$\Psi$
-closed when all of its leaves are
![]() $\Psi$
-closed. The immediate successors of a node
$\Psi$
-closed. The immediate successors of a node
![]() $n$
with respect to
$n$
with respect to
![]() ${\leq }^t$
are called the children of
${\leq }^t$
are called the children of
![]() $n$
in
$n$
in
![]() $t$
.
$t$
.

Figure 2. Graphical representation of
![]() $\textsf{R}$
-derivations, where
$\textsf{R}$
-derivations, where
![]() $\textsf{R}$
is a
$\textsf{R}$
is a ![]() system. The dashed edges and blank circles represent other branches that may exist in the derivation. We usually omit the formulas inherited from the parent node, exhibiting only the ones introduced by the applied rule of inference. Recall that, in both cases, we must have
system. The dashed edges and blank circles represent other branches that may exist in the derivation. We usually omit the formulas inherited from the parent node, exhibiting only the ones introduced by the applied rule of inference. Recall that, in both cases, we must have
![]() $\Pi \subseteq \Phi$
.
$\Pi \subseteq \Phi$
.
Let
![]() $\textsf{R}$
be a symmetrical calculus. An
$\textsf{R}$
be a symmetrical calculus. An
![]() $\textsf{R}$
-derivation is a finite labeled bounded rooted tree such that for every non-leaf node
$\textsf{R}$
-derivation is a finite labeled bounded rooted tree such that for every non-leaf node
![]() $n$
of
$n$
of
![]() $t$
there exists a rule of inference
$t$
there exists a rule of inference
![]() $\textsf{r} = \frac{\Pi }{\Theta } \in \textsf{R}$
and a substitution
$\textsf{r} = \frac{\Pi }{\Theta } \in \textsf{R}$
and a substitution
![]() $\sigma$
such that
$\sigma$
such that
![]() $\sigma (\Pi ) \subseteq l^{t}(n)$
, and the set of children of
$\sigma (\Pi ) \subseteq l^{t}(n)$
, and the set of children of
![]() $n$
is either (i)
$n$
is either (i)
![]() $\{n^\varphi : \varphi \in \sigma (\Theta )\}$
, in case
$\{n^\varphi : \varphi \in \sigma (\Theta )\}$
, in case
![]() $\Theta \neq \varnothing$
, where
$\Theta \neq \varnothing$
, where
![]() $n^\varphi$
is a node labeled with
$n^\varphi$
is a node labeled with
![]() $l^{t}(n) \cup \{\varphi \}$
, or (ii) a singleton
$l^{t}(n) \cup \{\varphi \}$
, or (ii) a singleton
![]() $\{n^\ast \}$
with
$\{n^\ast \}$
with
![]() $l^{t}(n^\ast )\;=\;\ast$
, in case
$l^{t}(n^\ast )\;=\;\ast$
, in case
![]() $\Theta \;=\;\varnothing$
. Such node
$\Theta \;=\;\varnothing$
. Such node
![]() $n$
is said to be expanded by an application of
$n$
is said to be expanded by an application of
![]() $\textsf r$
. Fig. 2 illustrates the general shape of
$\textsf r$
. Fig. 2 illustrates the general shape of
![]() $\textsf{R}$
-derivations. We say that
$\textsf{R}$
-derivations. We say that
![]() $\Phi \; \rhd _{\textsf{R}}\; \Psi$
whenever there is a
$\Phi \; \rhd _{\textsf{R}}\; \Psi$
whenever there is a
![]() $\Psi$
-closed derivation
$\Psi$
-closed derivation
![]() $t$
such that
$t$
such that
![]() $\Phi \;\supseteq \;\textsf{rt}(t)$
; such a tree consists in a proof that
$\Phi \;\supseteq \;\textsf{rt}(t)$
; such a tree consists in a proof that
![]() $\Psi$
follows from
$\Psi$
follows from
![]() $\Phi$
in
$\Phi$
in
![]() $\textsf{R}$
. As a matter of simplification when drawing such trees, we usually avoid copying the formulas inherited from the parent nodes (see Example 5 below, where we display some proof trees). The relation
$\textsf{R}$
. As a matter of simplification when drawing such trees, we usually avoid copying the formulas inherited from the parent nodes (see Example 5 below, where we display some proof trees). The relation
![]() $\rhd _{\textsf{R}}$
so defined is a
$\rhd _{\textsf{R}}$
so defined is a ![]() logic and, when
logic and, when
![]() $\rhd _{\textsf{R}} = \rhd$
, we say that
$\rhd _{\textsf{R}} = \rhd$
, we say that
![]() $\textsf{R}$
axiomatizes
$\textsf{R}$
axiomatizes
![]() $\rhd$
. It is worth emphasizing that we restrict ourselves to finite derivations because we are interested in finitary
$\rhd$
. It is worth emphasizing that we restrict ourselves to finite derivations because we are interested in finitary ![]() logics, but in general they could be infinite and cover also non-finitary logics (cf. Marcelino and Caleiro Reference Marcelino and Caleiro2021, Figure 1, for an example). A rule
logics, but in general they could be infinite and cover also non-finitary logics (cf. Marcelino and Caleiro Reference Marcelino and Caleiro2021, Figure 1, for an example). A rule
![]() $\frac{\Phi }{\Psi }$
is sound in a PNmatrix
$\frac{\Phi }{\Psi }$
is sound in a PNmatrix
![]() $\mathfrak{M}$
when
$\mathfrak{M}$
when
![]() $\Phi \;\rhd _{\mathfrak{M}}\;\Psi$
. It should be pointed out that this proof formalism generalizes the conventional (
$\Phi \;\rhd _{\mathfrak{M}}\;\Psi$
. It should be pointed out that this proof formalism generalizes the conventional (![]() ) Hilbert-style calculi: the latter corresponds to symmetrical calculi whose rules have, each, a finite antecedent and a singleton as succedent.
) Hilbert-style calculi: the latter corresponds to symmetrical calculi whose rules have, each, a finite antecedent and a singleton as succedent.
Remark 10. Observe that any application of a rule of inference that creates a node labeled with the same set of formulas as the label of the node being expanded is superfluous (cf. Greati Reference Greati2022, Prop. 35); in this way, loops in these derivations may be readily averted.
The process of building an
![]() $\textsf{R}$
-derivation, in principle, does not necessarily terminate, since there may be infinitely many rule instances that are applicable. We now introduce a notion of analyticity that allows a limit to be set on the search space in such a way that this process is guaranteed to finish. Given
$\textsf{R}$
-derivation, in principle, does not necessarily terminate, since there may be infinitely many rule instances that are applicable. We now introduce a notion of analyticity that allows a limit to be set on the search space in such a way that this process is guaranteed to finish. Given
![]() $\Lambda \subseteq L_{\Sigma }(P)$
, we write
$\Lambda \subseteq L_{\Sigma }(P)$
, we write
![]() $\Phi \rhd _{\textsf{R}}^\Lambda \Psi$
whenever there is a proof of
$\Phi \rhd _{\textsf{R}}^\Lambda \Psi$
whenever there is a proof of
![]() $\Psi$
from
$\Psi$
from
![]() $\Phi$
using only formulas in
$\Phi$
using only formulas in
![]() $\Lambda$
. Given
$\Lambda$
. Given
![]() $\Theta, \Xi \subseteq L_{\Sigma }(P)$
, we define the set
$\Theta, \Xi \subseteq L_{\Sigma }(P)$
, we define the set
![]() $\Upsilon ^\Xi$
of
$\Upsilon ^\Xi$
of
![]() $\Xi$
-generalized subformulas of
$\Xi$
-generalized subformulas of
![]() $\Theta$
as the set
$\Theta$
as the set
![]() $\textsf{sub}(\Theta ) \cup \{ \sigma (\varphi ) : \varphi \in \Xi \mbox{ and } \sigma : P \to \textsf{sub}(\Theta )\}$
. We say that
$\textsf{sub}(\Theta ) \cup \{ \sigma (\varphi ) : \varphi \in \Xi \mbox{ and } \sigma : P \to \textsf{sub}(\Theta )\}$
. We say that
![]() $\textsf{R}$
is
$\textsf{R}$
is
![]() $\Xi$
-analytic when, for all
$\Xi$
-analytic when, for all
![]() $\Phi, \Psi \subseteq L_{\Sigma }(P)$
, we always have
$\Phi, \Psi \subseteq L_{\Sigma }(P)$
, we always have
![]() $\Phi \rhd _{\textsf{R}}^{\Upsilon ^\Xi } \Psi$
whenever we have
$\Phi \rhd _{\textsf{R}}^{\Upsilon ^\Xi } \Psi$
whenever we have
![]() $\Phi \;\rhd _{\textsf{R}}\;\Psi$
; intuitively, it means that proofs in
$\Phi \;\rhd _{\textsf{R}}\;\Psi$
; intuitively, it means that proofs in
![]() $\textsf{R}$
that
$\textsf{R}$
that
![]() $\Psi$
follows from
$\Psi$
follows from
![]() $\Phi$
, whenever they exist, do not need to use more material than subformulas of
$\Phi$
, whenever they exist, do not need to use more material than subformulas of
![]() $\Phi \cup \Psi$
or substitution instances of the formulas in
$\Phi \cup \Psi$
or substitution instances of the formulas in
![]() $\Xi$
built from the subformulas of
$\Xi$
built from the subformulas of
![]() $\Phi \cup \Psi$
. Searching for proofs in a finite
$\Phi \cup \Psi$
. Searching for proofs in a finite
![]() $\Xi$
-analytic calculus is then guaranteed to terminate because (i) due to analyticity, there are finitely many rule instances to be considered when expanding a node and (ii) in view of Remark Reference Caleiro and Marcelino10, loops may always be averted.
$\Xi$
-analytic calculus is then guaranteed to terminate because (i) due to analyticity, there are finitely many rule instances to be considered when expanding a node and (ii) in view of Remark Reference Caleiro and Marcelino10, loops may always be averted.
A general method is introduced in Caleiro and Marcelino (Reference Caleiro, Marcelino, Iemhoff, Moortgat and Queiroz2019), Marcelino and Caleiro (Reference Marcelino and Caleiro2021) for obtaining analytic calculi (in the sense of analyticity introduced in the previous paragraph) for logics given by a
![]() $\Sigma$
-PNmatrix
$\Sigma$
-PNmatrix
![]() $\langle \mathbf{A}, D\rangle$
whenever a certain expressiveness requirement (called “monadicity” in Shoesmith and Smiley Reference Shoesmith and Smiley1978) is met: for every
$\langle \mathbf{A}, D\rangle$
whenever a certain expressiveness requirement (called “monadicity” in Shoesmith and Smiley Reference Shoesmith and Smiley1978) is met: for every
![]() $a,b \in A$
, there is a single-variable formula
$a,b \in A$
, there is a single-variable formula
![]() $\textrm{S}$
such that
$\textrm{S}$
such that
![]() $\textrm{S}^{\mathbf{A}}(a) \in D$
and
$\textrm{S}^{\mathbf{A}}(a) \in D$
and
![]() $\textrm{S}^{\mathbf{A}}(b) \not \in D$
or vice-versa. We call such formula a separator (for
$\textrm{S}^{\mathbf{A}}(b) \not \in D$
or vice-versa. We call such formula a separator (for
![]() $a$
and
$a$
and
![]() $b$
).
$b$
).
The following example illustrates a symmetrical calculus for
![]() $\mathcal{B}$
generated by this method, as well as some proofs in this calculus.
$\mathcal{B}$
generated by this method, as well as some proofs in this calculus.
Example 5.
The matrix
![]() $\langle \mathbf{DM}_4,{\uparrow }{\mathbf{b}} \rangle$
fulfills the above-mentioned expressiveness requirement, with the following set of separators:
$\langle \mathbf{DM}_4,{\uparrow }{\mathbf{b}} \rangle$
fulfills the above-mentioned expressiveness requirement, with the following set of separators:
![]() $\mathcal{S} \,{:=}\, \{p,{\sim } p\}$
. We may therefore apply the method introduced in Marcelino and Caleiro (Reference Marcelino and Caleiro2021) to obtain for
$\mathcal{S} \,{:=}\, \{p,{\sim } p\}$
. We may therefore apply the method introduced in Marcelino and Caleiro (Reference Marcelino and Caleiro2021) to obtain for
![]() $\mathcal{B}$
the following
$\mathcal{B}$
the following
![]() $\mathcal{S}$
-analytic axiomatization we call
$\mathcal{S}$
-analytic axiomatization we call
![]() $\textsf{R}_{\mathcal{B}}$
:
$\textsf{R}_{\mathcal{B}}$
:
Fig. 3 illustrates proofs in
![]() $\textsf{R}_{\mathcal{B}}$
.
$\textsf{R}_{\mathcal{B}}$
.
Remark 11. Avron et al. (Reference Avron, Ben-Naim and Konikowska2007) employed essentially the same sufficient expressiveness condition – further discussed in Caleiro and Marcos (Reference Caleiro and Marcos2012)– as the one described above to provide cut-free sequent calculi for logics determined by finite non-deterministic matrices. In this work, we focus, instead, on Hilbert-style systems for their proximity with the logics being axiomatized (rules are simply consequence statements involving an antecedent and a succedent), which facilitates the algebraic study thereof. On what concerns the underlying decision procedures, we emphasize that analytic ![]() calculi admit straightforward (in general exponential-time) proof-search procedures.
calculi admit straightforward (in general exponential-time) proof-search procedures.
2.4 Implication connectives and criteria for implicative expansions
In the present study, we will follow some very specific research paths with the goal of adding an implication to given logics; we will refer to the resulting logics as implicative expansions. First of all, it is important to define precisely what we mean by an implication connective on ![]() and
and ![]() logics. Throughout this subsection, let
logics. Throughout this subsection, let
![]() $\Sigma$
be an arbitrary signature with a binary connective
$\Sigma$
be an arbitrary signature with a binary connective
![]() $\lor$
and denote by
$\lor$
and denote by
![]() $\Sigma _{\Rightarrow }$
the signature resulting from adding to
$\Sigma _{\Rightarrow }$
the signature resulting from adding to
![]() $\Sigma$
the binary connective
$\Sigma$
the binary connective
![]() $\Rightarrow$
. In what follows, let
$\Rightarrow$
. In what follows, let
![]() $\bigvee \{ \psi _1,\ldots, \psi _m \} \,{:=}\, \psi _1 \lor (\psi _2 \lor \ldots (\ldots \lor \psi _n)\ldots )$
.
$\bigvee \{ \psi _1,\ldots, \psi _m \} \,{:=}\, \psi _1 \lor (\psi _2 \lor \ldots (\ldots \lor \psi _n)\ldots )$
.

Figure 3. Proofs in
![]() $\textsf{R}_{\mathcal{B}}$
witnessing that
$\textsf{R}_{\mathcal{B}}$
witnessing that
![]() ${\sim }(p \land q) \;{\lhd \rhd }_{\mathcal{B}}\;{\sim } p \lor{\sim } q$
and
${\sim }(p \land q) \;{\lhd \rhd }_{\mathcal{B}}\;{\sim } p \lor{\sim } q$
and
![]() $p \lor \bot \;{\lhd \rhd }_{\mathcal{B}} \; p, r$
.
$p \lor \bot \;{\lhd \rhd }_{\mathcal{B}} \; p, r$
.
Definition 12.
The connective
![]() $\Rightarrow$
is an implication in a
$\Rightarrow$
is an implication in a ![]() logic
logic
![]() $\rhd{}$
over
$\rhd{}$
over
![]() $\Sigma _\Rightarrow$
provided, for all
$\Sigma _\Rightarrow$
provided, for all
![]() $\Phi, \{ \psi _1,\ldots, \psi _m \}, \{ \varphi, \psi \} \subseteq L_{\Sigma }(P)$
,
$\Phi, \{ \psi _1,\ldots, \psi _m \}, \{ \varphi, \psi \} \subseteq L_{\Sigma }(P)$
,
Note that the above definition reduces in ![]() to the deduction-detachment theorem (DDT) that holds, for example, in intuitionistic and classical logics, and this is indeed what we will take to be an implication in
to the deduction-detachment theorem (DDT) that holds, for example, in intuitionistic and classical logics, and this is indeed what we will take to be an implication in ![]() , in this paper. That is,
, in this paper. That is,
![]() $\vdash$
has the DDT with respect to
$\vdash$
has the DDT with respect to
![]() $\Rightarrow$
in case
$\Rightarrow$
in case
![]() $\Phi, \varphi \vdash \psi$
if, and only if,
$\Phi, \varphi \vdash \psi$
if, and only if,
![]() $\Phi \vdash \varphi \Rightarrow \psi$
for all
$\Phi \vdash \varphi \Rightarrow \psi$
for all
![]() $\Phi, \{ \varphi, \psi \} \subseteq L_{\Sigma }(P)$
. What we did above was a convenient generalization of the DDT for
$\Phi, \{ \varphi, \psi \} \subseteq L_{\Sigma }(P)$
. What we did above was a convenient generalization of the DDT for ![]() logics, using it to abstractly characterize what we expect of an implication connective (namely, an internalization of the consequence relation that allows formulas to be discharged from the antecedent).
logics, using it to abstractly characterize what we expect of an implication connective (namely, an internalization of the consequence relation that allows formulas to be discharged from the antecedent).
Based on the behavior of implication in classical logic, we also consider the following stronger notion of implication:
Definition 13.
The connective
![]() $\Rightarrow$
is a classic-like implication in a
$\Rightarrow$
is a classic-like implication in a ![]() logic
logic
![]() $\rhd{}$
over
$\rhd{}$
over
![]() $\Sigma _\Rightarrow$
provided, for all
$\Sigma _\Rightarrow$
provided, for all
![]() $\Phi, \Psi, \{ \varphi, \psi \} \subseteq L_{\Sigma }(P)$
,
$\Phi, \Psi, \{ \varphi, \psi \} \subseteq L_{\Sigma }(P)$
,
It should be clear enough that, for logics
![]() $\rhd$
with
$\rhd$
with
![]() $\lor$
satisfying
$\lor$
satisfying
![]() $p \rhd p \lor q$
;
$p \rhd p \lor q$
;
![]() $q \rhd p \lor q$
; and
$q \rhd p \lor q$
; and
![]() $p \lor q \rhd p,q$
, classic-like implications are implications in the sense of Definition 12. The converse, however, might not hold (see Remark Reference Monteiro32).
$p \lor q \rhd p,q$
, classic-like implications are implications in the sense of Definition 12. The converse, however, might not hold (see Remark Reference Monteiro32).
In this paper, we shall require two minimal criteria on implicative expansions:
 $(\textsf{I}1)$
The connective being added must qualify as an implication (Definition 12);
$(\textsf{I}1)$
The connective being added must qualify as an implication (Definition 12); $(\textsf{I}2)$
The expansion must be conservative.
$(\textsf{I}2)$
The expansion must be conservative.
We will prove below some facts regarding the connections among the notions of implication, residuation, and characterizability via a single PNmatrix.
Proposition 14.
Let
![]() $\Rightarrow ^{\mathbf{A}}$
be the residuum of
$\Rightarrow ^{\mathbf{A}}$
be the residuum of
![]() $\land ^{\mathbf{A}}$
in each
$\land ^{\mathbf{A}}$
in each
![]() $\mathbf{A} \in \textsf{K}$
, where
$\mathbf{A} \in \textsf{K}$
, where
![]() $\textsf{K}$
is a class of
$\textsf{K}$
is a class of
![]() $\Sigma _\Rightarrow$
-algebras, with
$\Sigma _\Rightarrow$
-algebras, with
![]() $\Sigma _\Rightarrow \supseteq \Sigma ^{\textsf{bL}}$
, whose
$\Sigma _\Rightarrow \supseteq \Sigma ^{\textsf{bL}}$
, whose
![]() $\{ \land, \top \}$
-reducts are
$\{ \land, \top \}$
-reducts are
![]() $\land$
-semilattices with a greatest element assigned to
$\land$
-semilattices with a greatest element assigned to
![]() $\top$
. Then
$\top$
. Then
![]() $\Rightarrow$
is an implication in
$\Rightarrow$
is an implication in
![]() $\rhd _{\textsf{K}}^{\leq }$
(recall Definition 4).
$\rhd _{\textsf{K}}^{\leq }$
(recall Definition 4).
Proof.
Let
![]() $\Phi, \Psi, \{ \varphi \} \subseteq L_{\Sigma }(P)$
with
$\Phi, \Psi, \{ \varphi \} \subseteq L_{\Sigma }(P)$
with
![]() $\Psi \neq \varnothing$
finite. From the left to the right, suppose that
$\Psi \neq \varnothing$
finite. From the left to the right, suppose that
![]() $\Phi, \varphi \rhd _{\textsf{K}}^{\leq } \Psi$
. Then
$\Phi, \varphi \rhd _{\textsf{K}}^{\leq } \Psi$
. Then
![]() $\Phi ' \rhd _{\textsf{K}}^{\leq } \Psi '$
, for finite
$\Phi ' \rhd _{\textsf{K}}^{\leq } \Psi '$
, for finite
![]() $\Phi ' \subseteq \Phi \cup \{ \varphi \}$
and
$\Phi ' \subseteq \Phi \cup \{ \varphi \}$
and
![]() $\Psi ' \subseteq \Psi$
, and thus (
$\Psi ' \subseteq \Psi$
, and thus (
![]() $\star$
)
$\star$
)
![]() $\Phi '',\varphi \rhd _{\textsf{K}}^{\leq } \Psi '$
, for
$\Phi '',\varphi \rhd _{\textsf{K}}^{\leq } \Psi '$
, for
![]() $\Phi ' \cup \{ \varphi \} = \Phi '' \cup \{ \varphi \}$
and
$\Phi ' \cup \{ \varphi \} = \Phi '' \cup \{ \varphi \}$
and
![]() $\varphi \not \in \Phi ''$
. Let
$\varphi \not \in \Phi ''$
. Let
![]() $\mathbf{A} \in \textsf{K}$
. By (
$\mathbf{A} \in \textsf{K}$
. By (
![]() $\star$
), we have that
$\star$
), we have that
![]() $\bigwedge \Phi '' \land \varphi \leq \bigvee \Psi '$
is valid in
$\bigwedge \Phi '' \land \varphi \leq \bigvee \Psi '$
is valid in
![]() $\mathbf{A}$
, thus
$\mathbf{A}$
, thus
![]() $\bigwedge \Phi '' \land \varphi \leq \bigvee \Psi$
is valid in
$\bigwedge \Phi '' \land \varphi \leq \bigvee \Psi$
is valid in
![]() $\mathbf{A}$
; hence, by residuation,
$\mathbf{A}$
; hence, by residuation,
![]() $\bigwedge \Phi '' \leq \varphi \Rightarrow \bigvee \Psi$
is valid in
$\bigwedge \Phi '' \leq \varphi \Rightarrow \bigvee \Psi$
is valid in
![]() $\mathbf{A}$
, thus
$\mathbf{A}$
, thus
![]() $\Phi \rhd _{\textsf{K}}^{\leq } \varphi \Rightarrow \bigvee \Psi$
. From the right to the left, suppose that
$\Phi \rhd _{\textsf{K}}^{\leq } \varphi \Rightarrow \bigvee \Psi$
. From the right to the left, suppose that
![]() $\Phi \rhd _{\textsf{K}}^{\leq } \varphi \Rightarrow \bigvee \Psi$
. Then, by definition, we have that
$\Phi \rhd _{\textsf{K}}^{\leq } \varphi \Rightarrow \bigvee \Psi$
. Then, by definition, we have that
![]() $\Phi ' \rhd _{\textsf{K}}^{\leq } \varphi \Rightarrow \bigvee \Psi$
, for some finite
$\Phi ' \rhd _{\textsf{K}}^{\leq } \varphi \Rightarrow \bigvee \Psi$
, for some finite
![]() $\Phi ' \subseteq \Phi$
. Let
$\Phi ' \subseteq \Phi$
. Let
![]() $\mathbf{A} \in \textsf{K}$
. We have that
$\mathbf{A} \in \textsf{K}$
. We have that
![]() $\bigwedge \Phi ' \leq \varphi \Rightarrow \bigvee \Psi$
is valid in
$\bigwedge \Phi ' \leq \varphi \Rightarrow \bigvee \Psi$
is valid in
![]() $\mathbf{A}$
. By residuation, we have
$\mathbf{A}$
. By residuation, we have
![]() $\bigwedge \Phi ' \land \varphi \leq \bigvee \Psi$
also valid in
$\bigwedge \Phi ' \land \varphi \leq \bigvee \Psi$
also valid in
![]() $\mathbf{A}$
, from which we easily obtain that
$\mathbf{A}$
, from which we easily obtain that
![]() $\Phi, \varphi \rhd _{\textsf{K}}^{\leq } \Psi$
.
$\Phi, \varphi \rhd _{\textsf{K}}^{\leq } \Psi$
.
Observe that the above result extends to
![]() $\vdash _{\textsf{K}}^{\leq }$
(recall Definition 7) since it is the
$\vdash _{\textsf{K}}^{\leq }$
(recall Definition 7) since it is the ![]() companion of
companion of
![]() $\rhd _{\textsf{K}}^{\leq }$
. This also looks like the right moment to introduce intuitionistic-like implications:
$\rhd _{\textsf{K}}^{\leq }$
. This also looks like the right moment to introduce intuitionistic-like implications:
Definition 15.
A Heyting implication in an algebra
![]() $\mathbf{A} \in \textsf{K}$
, with
$\mathbf{A} \in \textsf{K}$
, with
![]() $\textsf{K}$
as described in Proposition 14
, is an implication that corresponds to the residuum of
$\textsf{K}$
as described in Proposition 14
, is an implication that corresponds to the residuum of
![]() $\land ^{\mathbf{A}}$
.
$\land ^{\mathbf{A}}$
.
Inspired by Avron (Reference Avron2020), we also consider the following additional criteria to guide our investigations:
 $(\textsf{A}1)$
The expanded logic is determined by the single PNmatrix
$(\textsf{A}1)$
The expanded logic is determined by the single PNmatrix
 $\langle \mathbf A, D \rangle$
, and, for all
$\langle \mathbf A, D \rangle$
, and, for all
 $a,b \in A$
, we have
$a,b \in A$
, we have
 $a \Rightarrow ^{\mathbf A} b \subseteq D$
if, and only if, either
$a \Rightarrow ^{\mathbf A} b \subseteq D$
if, and only if, either
 $a \not \in D$
or
$a \not \in D$
or
 $b \in D$
.
$b \in D$
. $(\textsf{A}2)$
The expanded logic is self-extensional (Definition 3).
$(\textsf{A}2)$
The expanded logic is self-extensional (Definition 3).
Note that, for ![]() logics, the criterion
logics, the criterion
![]() $(\textsf{A}1)$
is strong to the point of forcing the referred implication to be classic-like:
$(\textsf{A}1)$
is strong to the point of forcing the referred implication to be classic-like:
Proposition 16.
Let
![]() $\mathfrak{M} \,{:=}\, \langle \mathbf A, D \rangle$
be a
$\mathfrak{M} \,{:=}\, \langle \mathbf A, D \rangle$
be a
![]() $\Sigma _{\Rightarrow }$
-PNmatrix. Then
$\Sigma _{\Rightarrow }$
-PNmatrix. Then
![]() $\Rightarrow$
is a classic-like implication in
$\Rightarrow$
is a classic-like implication in
![]() $\rhd _{\mathfrak{M}}$
if, and only if,
$\rhd _{\mathfrak{M}}$
if, and only if,
![]() $\mathfrak{M}$
satisfies
$\mathfrak{M}$
satisfies
![]() $(\textsf{A}1)$
.
$(\textsf{A}1)$
.
Proof.
We have that
![]() $\Phi, \varphi \, \,\blacktriangleright _{\mathfrak{M}} \, \psi, \Psi$
if, and only if,
$\Phi, \varphi \, \,\blacktriangleright _{\mathfrak{M}} \, \psi, \Psi$
if, and only if,
![]() $v[\Phi \cup \{\varphi \}\}] \subseteq D$
and
$v[\Phi \cup \{\varphi \}\}] \subseteq D$
and
![]() $v[\{\psi \}\cup \Psi \}] \subseteq \overline{D}$
for some valuation
$v[\{\psi \}\cup \Psi \}] \subseteq \overline{D}$
for some valuation
![]() $v$
if, and only if,
$v$
if, and only if,
![]() $v[\Phi ] \subseteq D$
and
$v[\Phi ] \subseteq D$
and
![]() $v(\psi ) \in \overline{D}$
and
$v(\psi ) \in \overline{D}$
and
![]() $v(\varphi \Rightarrow \psi ) \in \overline{D}$
for some valuation
$v(\varphi \Rightarrow \psi ) \in \overline{D}$
for some valuation
![]() $v$
if, and only if,
$v$
if, and only if,
![]() $\Phi \,\,\blacktriangleright _{\mathfrak{M}}\, \varphi \Rightarrow \psi, \Psi$
.
$\Phi \,\,\blacktriangleright _{\mathfrak{M}}\, \varphi \Rightarrow \psi, \Psi$
.
3. Perfect Paradefinite Algebras and Their Logics
In this section, we present the main definitions concerning perfect paradefinite algebras and the logics associated with them. Most of the materials come from Gomes et al. (Reference Gomes, Greati, Marcelino, Marcos and Rivieccio2022), where these objects were first introduced and investigated.
Definition 17.
Given a
![]() $\Sigma ^{\textsf{PP}}$
-algebra whose
$\Sigma ^{\textsf{PP}}$
-algebra whose
![]() $\Sigma ^{\textsf{DM}}$
-reduct is a De Morgan algebra, we say that it constitutes a perfect paradefinite algebra (PP-algebra) if it satisfies the equations:
$\Sigma ^{\textsf{DM}}$
-reduct is a De Morgan algebra, we say that it constitutes a perfect paradefinite algebra (PP-algebra) if it satisfies the equations:
Example 6.
An example of PP-algebra is
![]() $\mathbf{PP}_6 \,{:=}\, \langle \mathcal{V}_6, \cdot ^{\mathbf{PP}_6} \rangle$
, the
$\mathbf{PP}_6 \,{:=}\, \langle \mathcal{V}_6, \cdot ^{\mathbf{PP}_6} \rangle$
, the
![]() $\Sigma ^{\textsf{PP}}$
-algebra defined as
$\Sigma ^{\textsf{PP}}$
-algebra defined as
![]() $\mathbf{IS}_6$
in Example 2, differing only in that, instead of containing an interpretation for
$\mathbf{IS}_6$
in Example 2, differing only in that, instead of containing an interpretation for
![]() $\nabla$
, it contains the following interpretation for
$\nabla$
, it contains the following interpretation for
![]() $\circ$
:
$\circ$
:
 \begin{equation*} {\circ }^{\mathbf {PP}_6} a \,{:=}\, \begin {cases} {\hat {\mathbf {f}}} & a \in \mathcal {V}_6{\setminus }\{{\hat {\mathbf {f}}},{\hat {\mathbf {t}}}\}\\ {\hat {\mathbf {t}}} & a \in \{{\hat {\mathbf {f}}},{\hat {\mathbf {t}}}\}\\ \end {cases} \end{equation*}
\begin{equation*} {\circ }^{\mathbf {PP}_6} a \,{:=}\, \begin {cases} {\hat {\mathbf {f}}} & a \in \mathcal {V}_6{\setminus }\{{\hat {\mathbf {f}}},{\hat {\mathbf {t}}}\}\\ {\hat {\mathbf {t}}} & a \in \{{\hat {\mathbf {f}}},{\hat {\mathbf {t}}}\}\\ \end {cases} \end{equation*}
Other examples are the algebras
![]() $\mathbf{PP}_i$
, the subalgebras of
$\mathbf{PP}_i$
, the subalgebras of
![]() $\mathbf{PP}_6$
having, respectively, the same lattice structures of the algebras
$\mathbf{PP}_6$
having, respectively, the same lattice structures of the algebras
![]() $\mathbf{IS}_i$
, for
$\mathbf{IS}_i$
, for
![]() $2 \leq i \leq 5$
, exhibited in Fig. 1(b).
$2 \leq i \leq 5$
, exhibited in Fig. 1(b).
We denote by
![]() $\mathbb{PP}$
the variety of PP-algebras. This variety is term-equivalent to the variety of involutive Stone algebras (Gomes et al. Reference Gomes, Greati, Marcelino, Marcos and Rivieccio2022, Thm. 3.6) – in particular,
$\mathbb{PP}$
the variety of PP-algebras. This variety is term-equivalent to the variety of involutive Stone algebras (Gomes et al. Reference Gomes, Greati, Marcelino, Marcos and Rivieccio2022, Thm. 3.6) – in particular,
![]() $\nabla x \,{:=}\, x \lor{\sim }{\circ } x$
. Also, it holds that
$\nabla x \,{:=}\, x \lor{\sim }{\circ } x$
. Also, it holds that
![]() $\mathbb{PP} = \mathbb{V}(\{\mathbf{PP_6}\})$
(Gomes et al. Reference Gomes, Greati, Marcelino, Marcos and Rivieccio2022, Prop. 3.8). As it occurs with IS-algebras, we may define, in the language of PP-algebras, a pseudo-complement satisfying the Stone equation; to that effect, it suffices to set
$\mathbb{PP} = \mathbb{V}(\{\mathbf{PP_6}\})$
(Gomes et al. Reference Gomes, Greati, Marcelino, Marcos and Rivieccio2022, Prop. 3.8). As it occurs with IS-algebras, we may define, in the language of PP-algebras, a pseudo-complement satisfying the Stone equation; to that effect, it suffices to set
![]() $\neg x \;\,{:=}\,\;{\sim } x \land{\circ } x$
(alternatively, one might simply set
$\neg x \;\,{:=}\,\;{\sim } x \land{\circ } x$
(alternatively, one might simply set
![]() $\neg x \;\,{:=}\,\;{\sim }\nabla x$
, as usual).
$\neg x \;\,{:=}\,\;{\sim }\nabla x$
, as usual).
We shall denote by
![]() $\mathcal{PP}_{\!\leq }^{{\rhd }}$
and
$\mathcal{PP}_{\!\leq }^{{\rhd }}$
and
![]() $\mathcal{PP}_{\!\leq }$
, respectively, the
$\mathcal{PP}_{\!\leq }$
, respectively, the ![]() and
and ![]() order-preserving logics induced by
order-preserving logics induced by
![]() $\mathbb{PP}$
(cf. Subsection 2.2). In addition, we shall denote by
$\mathbb{PP}$
(cf. Subsection 2.2). In addition, we shall denote by
![]() $\mathcal{PP}_{\top }^{{\rhd }}{}$
and
$\mathcal{PP}_{\top }^{{\rhd }}{}$
and
![]() $\mathcal{PP}_\top{}$
, respectively, the
$\mathcal{PP}_\top{}$
, respectively, the ![]() and
and ![]()
![]() $\top$
-assertional logics induced by
$\top$
-assertional logics induced by
![]() $\mathbb{PP}$
. We know that
$\mathbb{PP}$
. We know that
![]() $\mathcal{PP}_{\!\leq }^{{\rhd }}{} \;=\;\rhd _{\langle \mathbf{PP_6},{{\uparrow }{\mathbf{b}}} \rangle }$
and thus
$\mathcal{PP}_{\!\leq }^{{\rhd }}{} \;=\;\rhd _{\langle \mathbf{PP_6},{{\uparrow }{\mathbf{b}}} \rangle }$
and thus
![]() $\mathcal{PP}_{\!\leq }{} \;=\;\vdash _{\langle \mathbf{PP_6},{{\uparrow }{\mathbf{b}}} \rangle }$
(Gomes et al. Reference Gomes, Greati, Marcelino, Marcos and Rivieccio2022, Theorem 3.11). We will sometimes refer to as
$\mathcal{PP}_{\!\leq }{} \;=\;\vdash _{\langle \mathbf{PP_6},{{\uparrow }{\mathbf{b}}} \rangle }$
(Gomes et al. Reference Gomes, Greati, Marcelino, Marcos and Rivieccio2022, Theorem 3.11). We will sometimes refer to as
Taking a proof-theoretical perspective, from Gomes et al. (Reference Gomes, Greati, Marcelino, Marcos and Rivieccio2022, Cor. 4.3) we know that
![]() $\mathcal{PP}_{\!\leq }^{{\rhd }}{}$
is axiomatized by a
$\mathcal{PP}_{\!\leq }^{{\rhd }}{}$
is axiomatized by a
![]() $\{p,{\sim } p,{\circ } p\}$
-analytic
$\{p,{\sim } p,{\circ } p\}$
-analytic ![]() calculus, which we now recall:
calculus, which we now recall:
Definition 18.
Let
![]() $\textsf{R}_{\mathcal{PP}_{\!\leq }^{{\rhd }}}$
be the
$\textsf{R}_{\mathcal{PP}_{\!\leq }^{{\rhd }}}$
be the ![]() calculus containing the rules in Example
5 together with the following rules:
calculus containing the rules in Example
5 together with the following rules:
In the mentioned paper, the above calculus was transformed into a ![]() axiomatization for
axiomatization for
![]() $\mathcal{PP}_{\!\leq }$
, using a technique that we shall detail and employ in Section 6.
$\mathcal{PP}_{\!\leq }$
, using a technique that we shall detail and employ in Section 6.
It is perhaps worth calling attention to the contribution played by rules
![]() $\textsf{r}_{24}$
and
$\textsf{r}_{24}$
and
![]() $\textsf{r}_{25}$
in making the perfection operator,
$\textsf{r}_{25}$
in making the perfection operator,
![]() $\circ$
, restore “classicality,” as described in the so-called Derivability Adjustment Theorems (for a semantical perspective, see Marcos Reference Marcos2005b, Sec. 2, and more specifically Gomes et al. Reference Gomes, Greati, Marcelino, Marcos and Rivieccio2022, Thm. 3.29).
$\circ$
, restore “classicality,” as described in the so-called Derivability Adjustment Theorems (for a semantical perspective, see Marcos Reference Marcos2005b, Sec. 2, and more specifically Gomes et al. Reference Gomes, Greati, Marcelino, Marcos and Rivieccio2022, Thm. 3.29).
Finally, we have that the
![]() $\top$
-assertional logics
$\top$
-assertional logics
![]() $\mathcal{PP}_{\top }^{{\rhd }}{}$
and
$\mathcal{PP}_{\top }^{{\rhd }}{}$
and
![]() $\mathcal{PP}_\top{}$
are determined by a single three-valued matrix. In fact, it can be shown that such logics are term-equivalent to the three-valued Łukasiewicz logic (in
$\mathcal{PP}_\top{}$
are determined by a single three-valued matrix. In fact, it can be shown that such logics are term-equivalent to the three-valued Łukasiewicz logic (in ![]() and
and ![]() , respectively) – in a language containing a “possibility” operator definable by setting
, respectively) – in a language containing a “possibility” operator definable by setting
![]() $\nabla x \,{:=}\, x \lor{\sim }{\circ } x$
, as above.
$\nabla x \,{:=}\, x \lor{\sim }{\circ } x$
, as above.
Proposition 19 (Gomes et al. Reference Gomes, Greati, Marcelino, Marcos and Rivieccio2022, Prop. 3.12).
![]() $\mathcal{PP}_{\top }^{{\rhd }}{} \;=\; \rhd ^{\top }_{\mathbb{V}(\mathbf{PP}_3)} \;=\; \rhd _{\langle \mathbf{PP}_3, \{{\hat{\mathbf{t}}}\} \rangle }$
, and thus
$\mathcal{PP}_{\top }^{{\rhd }}{} \;=\; \rhd ^{\top }_{\mathbb{V}(\mathbf{PP}_3)} \;=\; \rhd _{\langle \mathbf{PP}_3, \{{\hat{\mathbf{t}}}\} \rangle }$
, and thus
![]() $\mathcal{PP}_\top{} \;=\; \vdash ^{\top }_{\mathbb{V}(\mathbf{PP}_3)} \;=\; \vdash _{\langle \mathbf{PP}_3, \{{\hat{\mathbf{t}}}\} \rangle }$
(recall the definition of
$\mathcal{PP}_\top{} \;=\; \vdash ^{\top }_{\mathbb{V}(\mathbf{PP}_3)} \;=\; \vdash _{\langle \mathbf{PP}_3, \{{\hat{\mathbf{t}}}\} \rangle }$
(recall the definition of
![]() $\mathbf{PP}_3$
in Example
6
).
$\mathbf{PP}_3$
in Example
6
).
We have at this point all the relevant facts about the logics of PP-algebras we are interested in. Let us move to the main goal of the paper: adding an implication to them.
4. Conservatively Expanding
 $\mathcal{PP}_{\!\leq }^{{\rhd }}$
and
$\mathcal{PP}_{\!\leq }^{{\rhd }}$
and
 $\mathcal{PP}_{\!\leq }$
by Adding a Classic-Like Implication to Their Matrix
$\mathcal{PP}_{\!\leq }$
by Adding a Classic-Like Implication to Their Matrix
The first path we shall entertain amounts to modifying the logical matrix of
![]() $\mathcal{PP}_{\!\leq }^{{\rhd }}$
, namely
$\mathcal{PP}_{\!\leq }^{{\rhd }}$
, namely
![]() $\langle \mathbf{PP_6},{{\uparrow }{\mathbf{b}}} \rangle$
, by enriching its algebra with a new multioperation
$\langle \mathbf{PP_6},{{\uparrow }{\mathbf{b}}} \rangle$
, by enriching its algebra with a new multioperation
![]() $\Rightarrow _{\textsf{A}}$
, thus obtaining a multialgebra
$\Rightarrow _{\textsf{A}}$
, thus obtaining a multialgebra
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{A}}}}$
for which both criteria
$\mathbf{PP_6^{\Rightarrow _{\textsf{A}}}}$
for which both criteria
![]() $(\textsf{A}1)$
and
$(\textsf{A}1)$
and
![]() $(\textsf{A}2)$
mentioned in Section 2.4 hold, that is:
$(\textsf{A}2)$
mentioned in Section 2.4 hold, that is:
 $(\textsf{A}1)$
$(\textsf{A}1)$
 $a \Rightarrow _{\textsf{A}} b \subseteq{{\uparrow }{\mathbf{b}}}$
if, and only if, either
$a \Rightarrow _{\textsf{A}} b \subseteq{{\uparrow }{\mathbf{b}}}$
if, and only if, either
 $a \not \in{{\uparrow }{\mathbf{b}}}$
or
$a \not \in{{\uparrow }{\mathbf{b}}}$
or
 $b \in{{\uparrow }{\mathbf{b}}}$
.
$b \in{{\uparrow }{\mathbf{b}}}$
. $(\textsf{A}2)$
The resulting logic
$(\textsf{A}2)$
The resulting logic
 $\rhd _{\langle \mathbf{PP_6^{\Rightarrow _{\textsf{A}}}},{{\uparrow }{\mathbf{b}}} \rangle }$
is self-extensional.
$\rhd _{\langle \mathbf{PP_6^{\Rightarrow _{\textsf{A}}}},{{\uparrow }{\mathbf{b}}} \rangle }$
is self-extensional.
This path soon leads to a dead end, since:
Theorem 20.
There is no multialgebra
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{A}}}}$
simultaneously satisfying conditions
$\mathbf{PP_6^{\Rightarrow _{\textsf{A}}}}$
simultaneously satisfying conditions
![]() $(\textsf{A}1)$
and
$(\textsf{A}1)$
and
![]() $(\textsf{A}2)$
.
$(\textsf{A}2)$
.
Proof.
Let
![]() $\Rightarrow _{\textsf{A}}$
be an implication defined in
$\Rightarrow _{\textsf{A}}$
be an implication defined in
![]() $\mathbf{PP_6}$
that satisfies
$\mathbf{PP_6}$
that satisfies
![]() $(\textsf{A}1)$
and
$(\textsf{A}1)$
and
![]() $\mathfrak{M}^{\Rightarrow _{\textsf{A}}} \,{:=}\, \langle \mathbf{PP_6^{\Rightarrow _{\textsf{A}}}},{{\uparrow }{\mathbf{b}}} \rangle$
. Then, (
$\mathfrak{M}^{\Rightarrow _{\textsf{A}}} \,{:=}\, \langle \mathbf{PP_6^{\Rightarrow _{\textsf{A}}}},{{\uparrow }{\mathbf{b}}} \rangle$
. Then, (
![]() $\star$
) we have
$\star$
) we have
![]() $\rhd _{\mathfrak{M}^{\Rightarrow _{\textsf{A}}}} \, p \lor (p \Rightarrow \bot )$
, because, for every valuation
$\rhd _{\mathfrak{M}^{\Rightarrow _{\textsf{A}}}} \, p \lor (p \Rightarrow \bot )$
, because, for every valuation
![]() $v$
, either
$v$
, either
![]() $v (p ) \in{{\uparrow }{\mathbf{b}}}$
– in which case we have
$v (p ) \in{{\uparrow }{\mathbf{b}}}$
– in which case we have
![]() $v(p \lor (p \Rightarrow \bot )) \in v(p ) \lor v(p \Rightarrow \bot ) \subseteq{{\uparrow }{\mathbf{b}}}$
as well – or
$v(p \lor (p \Rightarrow \bot )) \in v(p ) \lor v(p \Rightarrow \bot ) \subseteq{{\uparrow }{\mathbf{b}}}$
as well – or
![]() $v (p ) \notin{{\uparrow }{\mathbf{b}}}$
, which gives us
$v (p ) \notin{{\uparrow }{\mathbf{b}}}$
, which gives us
![]() $ v(p \Rightarrow \bot ) \in v(p ) \Rightarrow v(\bot ) \subseteq{{\uparrow }{\mathbf{b}}}$
by
$ v(p \Rightarrow \bot ) \in v(p ) \Rightarrow v(\bot ) \subseteq{{\uparrow }{\mathbf{b}}}$
by
![]() $(\textsf{A}1)$
.
$(\textsf{A}1)$
.
Note that, for a valuation
![]() $v$
such that
$v$
such that
![]() $v(p) ={\mathbf{b}}$
, using
$v(p) ={\mathbf{b}}$
, using
![]() $(\textsf{A}1)$
we have
$(\textsf{A}1)$
we have
![]() $v(p \Rightarrow \bot ) \in{\mathbf{b}} \Rightarrow{\hat{\mathbf{f}}} \not \subseteq{{\uparrow }{\mathbf{b}}}$
, which means that
$v(p \Rightarrow \bot ) \in{\mathbf{b}} \Rightarrow{\hat{\mathbf{f}}} \not \subseteq{{\uparrow }{\mathbf{b}}}$
, which means that
![]() $v(p \Rightarrow \bot )$
may take a value in
$v(p \Rightarrow \bot )$
may take a value in
![]() $\{{\mathbf{n}},{\mathbf{f}},{\hat{\mathbf{f}}} \}$
. Hence, this being the case,
$\{{\mathbf{n}},{\mathbf{f}},{\hat{\mathbf{f}}} \}$
. Hence, this being the case,
![]() $v(p \lor (p \Rightarrow \bot )) \in{\mathbf{b}} \lor v(p \Rightarrow \bot ) \in \{{\mathbf{b}},{\mathbf{t}} \}$
, which entails
$v(p \lor (p \Rightarrow \bot )) \in{\mathbf{b}} \lor v(p \Rightarrow \bot ) \in \{{\mathbf{b}},{\mathbf{t}} \}$
, which entails
![]() $v ( \circ (p \lor (p \Rightarrow \bot )) ) ={\hat{\mathbf{f}}}$
. Thus
$v ( \circ (p \lor (p \Rightarrow \bot )) ) ={\hat{\mathbf{f}}}$
. Thus
![]() $\,\blacktriangleright _{\mathfrak{M}^{\Rightarrow _{\textsf{A}}}} \, {\circ} (p \lor (p \Rightarrow \bot ))$
.
$\,\blacktriangleright _{\mathfrak{M}^{\Rightarrow _{\textsf{A}}}} \, {\circ} (p \lor (p \Rightarrow \bot ))$
.
This prevents the logic from being self-extensional. Indeed, assuming
![]() $(\textsf{A}2)$
, from (
$(\textsf{A}2)$
, from (
![]() $\star$
) we would have that
$\star$
) we would have that
![]() $p \lor (p \Rightarrow \bot )$
and
$p \lor (p \Rightarrow \bot )$
and
![]() $\top$
are logically equivalent, thus we would be able to conclude that
$\top$
are logically equivalent, thus we would be able to conclude that
![]() $\circ (p \lor (p \Rightarrow \bot ))$
and
$\circ (p \lor (p \Rightarrow \bot ))$
and
![]() ${\circ}\top$
are logically equivalent too. Since
${\circ}\top$
are logically equivalent too. Since
![]() $\rhd _{\mathfrak{M}^{\Rightarrow _{\textsf{A}}}} \, {\circ} \top$
, we would conclude that
$\rhd _{\mathfrak{M}^{\Rightarrow _{\textsf{A}}}} \, {\circ} \top$
, we would conclude that
![]() $\rhd _{\mathfrak{M}^{\Rightarrow _{\textsf{A}}}} \, \circ (p \lor (p \Rightarrow \bot ))$
, against what we have shown.
$\rhd _{\mathfrak{M}^{\Rightarrow _{\textsf{A}}}} \, \circ (p \lor (p \Rightarrow \bot ))$
, against what we have shown.
In view of the preceding result, in this section we shall proceed by pursuing
![]() $(\textsf{A}1)$
, thus necessarily admitting non-self-extensional logics. In the subsequent sections, we will explore instead some avenues that arise when we opt for abandoning
$(\textsf{A}1)$
, thus necessarily admitting non-self-extensional logics. In the subsequent sections, we will explore instead some avenues that arise when we opt for abandoning
![]() $(\textsf{A}1)$
.
$(\textsf{A}1)$
.
The space of binary multioperations over
![]() $\mathcal{V}_6$
satisfying
$\mathcal{V}_6$
satisfying
![]() $(\textsf{A}1)$
is finite but very large, consisting of total refinementsFootnote 1 of the multioperation
$(\textsf{A}1)$
is finite but very large, consisting of total refinementsFootnote 1 of the multioperation
![]() $\Rightarrow _{\textsf{A1}}$
defined as:
$\Rightarrow _{\textsf{A1}}$
defined as:
 \begin{equation*} \Rightarrow _{\textsf {A1}}(a, b) \,{:=}\, \begin {cases} {{\uparrow }{\mathbf {b}}} & \text {if $a \not \in {{\uparrow }{\mathbf {b}}}$ or $b \in {{\uparrow }{\mathbf {b}}}$ }\\ \mathcal {V}_6{\setminus }{{\uparrow }{\mathbf {b}}} & \text {otherwise.} \end {cases} \end{equation*}
\begin{equation*} \Rightarrow _{\textsf {A1}}(a, b) \,{:=}\, \begin {cases} {{\uparrow }{\mathbf {b}}} & \text {if $a \not \in {{\uparrow }{\mathbf {b}}}$ or $b \in {{\uparrow }{\mathbf {b}}}$ }\\ \mathcal {V}_6{\setminus }{{\uparrow }{\mathbf {b}}} & \text {otherwise.} \end {cases} \end{equation*}
Denote by
![]() $\mathbf{PP_6}^{\!\!\Rightarrow _{\textsf{A1}}}$
the multialgebra obtained from
$\mathbf{PP_6}^{\!\!\Rightarrow _{\textsf{A1}}}$
the multialgebra obtained from
![]() $\mathbf{PP_6}$
by expanding its signature with
$\mathbf{PP_6}$
by expanding its signature with
![]() $\Rightarrow$
and interpreting this connective as
$\Rightarrow$
and interpreting this connective as
![]() $\Rightarrow _{\textsf{A1}}$
. Let
$\Rightarrow _{\textsf{A1}}$
. Let
![]() $\mathfrak{M}^{\Rightarrow _{\textsf{A1}}} \,{:=}\, \langle \mathbf{PP_6}^{\Rightarrow _{\textsf{A1}}},{{\uparrow }{\mathbf{b}}} \rangle$
. We will soon see that the logic induced by this matrix plays an important role regarding the conservative expansions of
$\mathfrak{M}^{\Rightarrow _{\textsf{A1}}} \,{:=}\, \langle \mathbf{PP_6}^{\Rightarrow _{\textsf{A1}}},{{\uparrow }{\mathbf{b}}} \rangle$
. We will soon see that the logic induced by this matrix plays an important role regarding the conservative expansions of
![]() $\mathcal{PP}_{\!\leq }^{{\rhd }}$
by a classic-like implication; but let us first present an analytic axiomatization for it.
$\mathcal{PP}_{\!\leq }^{{\rhd }}$
by a classic-like implication; but let us first present an analytic axiomatization for it.
Definition 21.
Let
![]() $\textsf{R}_{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}}$
be the calculus given by all inference rules in
$\textsf{R}_{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}}$
be the calculus given by all inference rules in
![]() $\textsf{R}_{\mathcal{PP}_{\!\leq }^{{\rhd }}}$
plus the following three inference rules:
$\textsf{R}_{\mathcal{PP}_{\!\leq }^{{\rhd }}}$
plus the following three inference rules:
Remark 22. The rule
![]() $\textsf{r}_2^{\mathcal{CL}}$
is responsible for the classicality of
$\textsf{r}_2^{\mathcal{CL}}$
is responsible for the classicality of
![]() $\Rightarrow$
in
$\Rightarrow$
in
![]() $\textsf{R}_{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}}$
. One may observe, in particular, that in the presence of this rule, the connective defined by setting
$\textsf{R}_{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}}$
. One may observe, in particular, that in the presence of this rule, the connective defined by setting
![]() $\neg p := p \Rightarrow \bot$
satisfies the “law of excluded middle” (
$\neg p := p \Rightarrow \bot$
satisfies the “law of excluded middle” (
![]() $p \lor \neg p$
is provable).
$p \lor \neg p$
is provable).
In a PNmatrix
![]() $\mathfrak{M} \,{:=}\, \langle \mathbf{A}, D \rangle$
, a set
$\mathfrak{M} \,{:=}\, \langle \mathbf{A}, D \rangle$
, a set
![]() $\mathcal{S}_a$
of unary formulas is said to isolate
$\mathcal{S}_a$
of unary formulas is said to isolate
![]() $a \in A$
if for every
$a \in A$
if for every
![]() $b \neq a \in A$
there is in
$b \neq a \in A$
there is in
![]() $\mathcal{S}_a$
a separator for
$\mathcal{S}_a$
a separator for
![]() $a$
and
$a$
and
![]() $b$
. A discriminator for
$b$
. A discriminator for
![]() $\mathfrak{M}$
is a family
$\mathfrak{M}$
is a family
![]() $\{ (\Omega _{a}, \mho _{a}) \}_{a \in A}$
such that
$\{ (\Omega _{a}, \mho _{a}) \}_{a \in A}$
such that
![]() $\Omega _{a} \cup \mho _{a}$
isolates
$\Omega _{a} \cup \mho _{a}$
isolates
![]() $a$
, where
$a$
, where
![]() $\textrm{S}^{\mathbf{A}}(a) \subseteq D$
whenever
$\textrm{S}^{\mathbf{A}}(a) \subseteq D$
whenever
![]() $\textrm{S} \in \Omega _{a}$
, and
$\textrm{S} \in \Omega _{a}$
, and
![]() $\textrm{S}^{\mathbf{A}}(a) \subseteq \overline D$
whenever
$\textrm{S}^{\mathbf{A}}(a) \subseteq \overline D$
whenever
![]() $\textrm{S} \in \mho _{a}$
. We say that a PNmatrix is monadic in case there is a discriminator for it. Discriminators play an essential role in the axiomatization of monadic PNmatrices, as we shall see in the following results.
$\textrm{S} \in \mho _{a}$
. We say that a PNmatrix is monadic in case there is a discriminator for it. Discriminators play an essential role in the axiomatization of monadic PNmatrices, as we shall see in the following results.
Theorem 23.
![]() $\textsf{R}_{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}}$
is
$\textsf{R}_{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}}$
is
![]() $\{ p,{\sim }p,{\circ }p \}$
-analytic and axiomatizes
$\{ p,{\sim }p,{\circ }p \}$
-analytic and axiomatizes
![]() $\rhd _{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}}$
.
$\rhd _{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}}$
.
Proof.
We consider the axiomatization method presented by Marcelino and Caleiro (Reference Marcelino and Caleiro2021, Theorems 3.5 and 3.12), which can be applied because
![]() $\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}$
is monadic, with the same discriminator as that of
$\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}$
is monadic, with the same discriminator as that of
![]() $\mathfrak{M}_6$
(see Table 1). The method can be seen essentially as a process of refining fully indeterministic six-valued interpretations of the connectives (i.e., interpretations where
$\mathfrak{M}_6$
(see Table 1). The method can be seen essentially as a process of refining fully indeterministic six-valued interpretations of the connectives (i.e., interpretations where
![]() $\mathcal{V}_6$
appears at every entry) by imposing soundness of some collections of inference rules, until obtaining the desired interpretations (in our case, the ones of
$\mathcal{V}_6$
appears at every entry) by imposing soundness of some collections of inference rules, until obtaining the desired interpretations (in our case, the ones of
![]() $\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}$
). For the connectives
$\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}$
). For the connectives
![]() $\land, \lor, {\sim }$
and
$\land, \lor, {\sim }$
and
![]() $\circ$
, the method produces the calculus
$\circ$
, the method produces the calculus
![]() $\textsf{R}_{\mathcal{PP}_{\!\leq }^{{\rhd }}}$
after some simplifications (Gomes et al. Reference Gomes, Greati, Marcelino, Marcos and Rivieccio2022). Thus, since the method is modular on the connectives, we only need to check what happens when we run it on the new connective
$\textsf{R}_{\mathcal{PP}_{\!\leq }^{{\rhd }}}$
after some simplifications (Gomes et al. Reference Gomes, Greati, Marcelino, Marcos and Rivieccio2022). Thus, since the method is modular on the connectives, we only need to check what happens when we run it on the new connective
![]() $\Rightarrow _{\textsf{A1}}$
and then add the resulting rules to
$\Rightarrow _{\textsf{A1}}$
and then add the resulting rules to
![]() $\textsf{R}_{\mathcal{PP}_{\!\leq }^{{\rhd }}}$
. The rules that are imposed will have the following shape:
$\textsf{R}_{\mathcal{PP}_{\!\leq }^{{\rhd }}}$
. The rules that are imposed will have the following shape:
for each
![]() $c \in \mathcal{V}_6{\setminus } (a \Rightarrow _{\textsf{A1}} b)$
and each
$c \in \mathcal{V}_6{\setminus } (a \Rightarrow _{\textsf{A1}} b)$
and each
![]() $a,b \in \mathcal{V}_6$
, where the sets
$a,b \in \mathcal{V}_6$
, where the sets
![]() $\Omega _{d}$
and
$\Omega _{d}$
and
![]() $\mho _{d}$
for each
$\mho _{d}$
for each
![]() $d \in \mathcal{V}_6$
are given in Table 1:
$d \in \mathcal{V}_6$
are given in Table 1:
Table 1. Discriminator for
![]() $\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}$
. They give, for example,
$\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}$
. They give, for example,
![]() $\Omega _{{\mathbf{b}}} = \{ p,{\sim } p \}$
and
$\Omega _{{\mathbf{b}}} = \{ p,{\sim } p \}$
and
![]() $\mho _{{\mathbf{n}}} = \{ p,{\circ } p,{\sim } p \}$
$\mho _{{\mathbf{n}}} = \{ p,{\circ } p,{\sim } p \}$

These rules at first do not seem to relate to the three rules for
![]() $\Rightarrow$
in
$\Rightarrow$
in
![]() $\textsf{R}_{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}}$
. However, we will see below that each of them is a “dilution” of one of the latter (i.e., they are obtained from the latter by adding formulas on the antecedents and succedents). Then, because these three rules for implication are sound, it follows trivially that we can use only them and discard its dilutions without harm for completeness and for analyticity.
$\textsf{R}_{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}}$
. However, we will see below that each of them is a “dilution” of one of the latter (i.e., they are obtained from the latter by adding formulas on the antecedents and succedents). Then, because these three rules for implication are sound, it follows trivially that we can use only them and discard its dilutions without harm for completeness and for analyticity.
First, consider the entries of
![]() $a \Rightarrow _{\textsf{A1}} b$
for
$a \Rightarrow _{\textsf{A1}} b$
for
![]() $b \in{{\uparrow }{\mathbf{b}}}$
. The values
$b \in{{\uparrow }{\mathbf{b}}}$
. The values
![]() $c \in \mathcal{V}_6{\setminus } (a \Rightarrow _{\textsf{A1}} b)$
are precisely
$c \in \mathcal{V}_6{\setminus } (a \Rightarrow _{\textsf{A1}} b)$
are precisely
![]() $\mathbf{n}$
,
$\mathbf{n}$
,
![]() $\mathbf{f}$
and
$\mathbf{f}$
and
![]() $\hat{\mathbf{f}}$
. Then
$\hat{\mathbf{f}}$
. Then
![]() $q \in \Omega _{b}(q)$
and
$q \in \Omega _{b}(q)$
and
![]() $p\Rightarrow q \in \mho _{c}(p\Rightarrow q)$
, thus the above rules are all dilutions of
$p\Rightarrow q \in \mho _{c}(p\Rightarrow q)$
, thus the above rules are all dilutions of
![]() $\textsf{r}_1^{\mathcal{CL}}$
.
$\textsf{r}_1^{\mathcal{CL}}$
.
Second, consider the entries of
![]() $a \Rightarrow _{\textsf{A1}} b$
for
$a \Rightarrow _{\textsf{A1}} b$
for
![]() $a \not \in{{\uparrow }{\mathbf{b}}}$
. The values
$a \not \in{{\uparrow }{\mathbf{b}}}$
. The values
![]() $c \in \mathcal{V}_6{\setminus } (a \Rightarrow _{\textsf{A1}} b)$
are precisely
$c \in \mathcal{V}_6{\setminus } (a \Rightarrow _{\textsf{A1}} b)$
are precisely
![]() $\mathbf{n}$
,
$\mathbf{n}$
,
![]() $\mathbf{f}$
and
$\mathbf{f}$
and
![]() $\hat{\mathbf{f}}$
. Then
$\hat{\mathbf{f}}$
. Then
![]() $p \in \mho _{a}(p)$
and
$p \in \mho _{a}(p)$
and
![]() $p\Rightarrow q \in \mho _{c}(p\Rightarrow q)$
, thus the above rules are all dilutions of
$p\Rightarrow q \in \mho _{c}(p\Rightarrow q)$
, thus the above rules are all dilutions of
![]() $\textsf{r}_2^{\mathcal{CL}}$
.
$\textsf{r}_2^{\mathcal{CL}}$
.
Finally, consider the entries of
![]() $a \Rightarrow _{\textsf{A1}} b$
for
$a \Rightarrow _{\textsf{A1}} b$
for
![]() $a \in{{\uparrow }{\mathbf{b}}}$
and
$a \in{{\uparrow }{\mathbf{b}}}$
and
![]() $b \not \in{{\uparrow }{\mathbf{b}}}$
. The values
$b \not \in{{\uparrow }{\mathbf{b}}}$
. The values
![]() $c \in \mathcal{V}_6{\setminus } (a \Rightarrow _{\textsf{A1}} b)$
are precisely
$c \in \mathcal{V}_6{\setminus } (a \Rightarrow _{\textsf{A1}} b)$
are precisely
![]() $\mathbf{b}$
,
$\mathbf{b}$
,
![]() $\mathbf{t}$
and
$\mathbf{t}$
and
![]() $\hat{\mathbf{t}}$
. Then
$\hat{\mathbf{t}}$
. Then
![]() $p \in \Omega _{a}(p)$
,
$p \in \Omega _{a}(p)$
,
![]() $p\Rightarrow q \in \Omega _{c}(p\Rightarrow q)$
and
$p\Rightarrow q \in \Omega _{c}(p\Rightarrow q)$
and
![]() $q \in \mho _{b}(q)$
, thus the above rules are all dilutions of
$q \in \mho _{b}(q)$
, thus the above rules are all dilutions of
![]() $\textsf{r}_3^{\mathcal{CL}}$
.
$\textsf{r}_3^{\mathcal{CL}}$
.
Remark 24. For a discriminator in the language of involutive Stone algebras, check Cantú and Figallo (Reference Cantú and Figallo2022, Prop. 4.3).
Remark 25. The above result could have been obtained by another strategy, observing that
![]() $\rhd _{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}}$
is induced by the strict product (Caleiro and Marcelino Reference Caleiro and Marcelino2023, Definition 10) of
$\rhd _{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}}$
is induced by the strict product (Caleiro and Marcelino Reference Caleiro and Marcelino2023, Definition 10) of
![]() $\mathfrak{M}_6$
and the matrix
$\mathfrak{M}_6$
and the matrix
![]() $\mathfrak{M}_2$
over the signature containing only
$\mathfrak{M}_2$
over the signature containing only
![]() $\Rightarrow$
, in which the algebra has carrier
$\Rightarrow$
, in which the algebra has carrier
![]() $\{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
and interprets
$\{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
and interprets
![]() $\Rightarrow$
as in classical logic (
$\Rightarrow$
as in classical logic (
![]() $a \Rightarrow ^{\mathfrak{M}_2} b ={\hat{\mathbf{f}}}$
if, and only if,
$a \Rightarrow ^{\mathfrak{M}_2} b ={\hat{\mathbf{f}}}$
if, and only if,
![]() $a ={\hat{\mathbf{t}}}$
and
$a ={\hat{\mathbf{t}}}$
and
![]() $b ={\hat{\mathbf{f}}}$
), and the designated set is
$b ={\hat{\mathbf{f}}}$
), and the designated set is
![]() $\{{\hat{\mathbf{t}}} \}$
. By Caleiro and Marcelino (Reference Caleiro and Marcelino2023, Theorem 12), this implies that
$\{{\hat{\mathbf{t}}} \}$
. By Caleiro and Marcelino (Reference Caleiro and Marcelino2023, Theorem 12), this implies that
![]() $\rhd _{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}}$
is the disjoint fibring of
$\rhd _{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}}$
is the disjoint fibring of
![]() $\mathcal{PP}_{\!\leq }^{{\rhd }}$
and
$\mathcal{PP}_{\!\leq }^{{\rhd }}$
and
![]() $\rhd _{\mathfrak{M}_2}$
(i.e., the smallest
$\rhd _{\mathfrak{M}_2}$
(i.e., the smallest ![]() logic in the signature
logic in the signature
![]() $\Sigma _\Rightarrow$
extending both logics). One can then show that, because both logics have analytic
$\Sigma _\Rightarrow$
extending both logics). One can then show that, because both logics have analytic ![]() axiomatizations, it is enough to merge both calculi in order to axiomatize their disjoint fibring. As it is well-known that
axiomatizations, it is enough to merge both calculi in order to axiomatize their disjoint fibring. As it is well-known that
![]() $\rhd _{\mathfrak{M}_2}$
is axiomatized by the
$\rhd _{\mathfrak{M}_2}$
is axiomatized by the
![]() $\{ p \}$
-analytic calculus given by the three rules for implication in Definition 21, the desired result follows.
$\{ p \}$
-analytic calculus given by the three rules for implication in Definition 21, the desired result follows.
From the above, we have that
![]() $\rhd _{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}}$
is special in the sense of being the smallest conservative expansion of
$\rhd _{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}}$
is special in the sense of being the smallest conservative expansion of
![]() $\mathcal{PP}_{\!\leq }^{{\rhd }}$
in which the added implication is classic-like (cf. Definition 13):
$\mathcal{PP}_{\!\leq }^{{\rhd }}$
in which the added implication is classic-like (cf. Definition 13):
Proposition 26.
Let
![]() $\rhd$
be a conservative expansion of
$\rhd$
be a conservative expansion of
![]() $\mathcal{PP}_{\!\leq }^{{\rhd }}$
over
$\mathcal{PP}_{\!\leq }^{{\rhd }}$
over
![]() $\Sigma ^{\textsf{PP}}_\Rightarrow$
in which
$\Sigma ^{\textsf{PP}}_\Rightarrow$
in which
![]() $\Rightarrow$
is a classic-like implication. Then
$\Rightarrow$
is a classic-like implication. Then
![]() $\rhd _{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}} \subseteq \rhd$
.
$\rhd _{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}} \subseteq \rhd$
.
Proof.
It is easy to see that any classic-like implication must satisfy the three rules for implication in the calculus for
![]() $\rhd _{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}}$
, and this is all we need for the present result.
$\rhd _{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}}$
, and this is all we need for the present result.
We observe that each proper refinement of
![]() $\Rightarrow _{\textsf{A1}}$
produces a proper extension of
$\Rightarrow _{\textsf{A1}}$
produces a proper extension of
![]() $\rhd _{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}}$
. In fact, following again the axiomatization method in Caleiro and Marcelino (Reference Caleiro, Marcelino, Iemhoff, Moortgat and Queiroz2019), for each such extension we can use the monadicity of
$\rhd _{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}}$
. In fact, following again the axiomatization method in Caleiro and Marcelino (Reference Caleiro, Marcelino, Iemhoff, Moortgat and Queiroz2019), for each such extension we can use the monadicity of
![]() $\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}$
to obtain
$\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}$
to obtain ![]() rules that hold in it but not in
rules that hold in it but not in
![]() $\textsf{R}_{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}}$
, and they will be precisely the rules that need to be added to the latter to obtain a
$\textsf{R}_{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}}$
, and they will be precisely the rules that need to be added to the latter to obtain a
![]() $\{ p,{\sim }p,{\circ }p \}$
-analytic calculus for these extensions.
$\{ p,{\sim }p,{\circ }p \}$
-analytic calculus for these extensions.
Proposition 27.
Let
![]() $\mathfrak{M}$
be obtained from
$\mathfrak{M}$
be obtained from
![]() $\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}$
by refining
$\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}$
by refining
![]() $\Rightarrow _{\textsf{A1}}$
. Then
$\Rightarrow _{\textsf{A1}}$
. Then
![]() $\textsf{R}_{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}}$
with the following rules provide a
$\textsf{R}_{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}}$
with the following rules provide a
![]() $\{ p,{\sim }p,{\circ }p \}$
-analytic calculus for
$\{ p,{\sim }p,{\circ }p \}$
-analytic calculus for
![]() $\mathfrak{M}$
:
$\mathfrak{M}$
:
for each
![]() $c \in (a \Rightarrow _{\textsf{A1}} b){\setminus } (a \Rightarrow ^{\mathfrak{M}} b)$
and each
$c \in (a \Rightarrow _{\textsf{A1}} b){\setminus } (a \Rightarrow ^{\mathfrak{M}} b)$
and each
![]() $a,b \in \mathcal{V}_6$
.
$a,b \in \mathcal{V}_6$
.
Proof. Directly from the method in Marcelino and Caleiro (Reference Marcelino and Caleiro2021, Theorems 3.5 and 3.12).
For an example of the latter axiomatization technique in action, if we remove the value
![]() $\mathbf{n}$
from the entry
$\mathbf{n}$
from the entry
![]() ${\mathbf{b}} \Rightarrow _{\textsf{A1}}{\hat{\mathbf{f}}}$
, we axiomatize the resulting logic by adding the following rule:
${\mathbf{b}} \Rightarrow _{\textsf{A1}}{\hat{\mathbf{f}}}$
, we axiomatize the resulting logic by adding the following rule:
which clearly does not hold in
![]() $\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}$
under a valuation
$\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}$
under a valuation
![]() $v$
with
$v$
with
![]() $v(p) ={\mathbf{b}}$
,
$v(p) ={\mathbf{b}}$
,
![]() $v(q) ={\hat{\mathbf{f}}}$
and
$v(q) ={\hat{\mathbf{f}}}$
and
![]() $v(p \Rightarrow q) ={\mathbf{n}}$
, but holds in the new logic precisely because this valuation was forbidden when we deleted
$v(p \Rightarrow q) ={\mathbf{n}}$
, but holds in the new logic precisely because this valuation was forbidden when we deleted
![]() $\mathbf{n}$
from that entry.
$\mathbf{n}$
from that entry.
As another application of this technique, we show how to axiomatize the logic
![]() ${\textrm{LET}_{\textrm{K}}^{+}}$
of Coniglio and Rodrigues (Reference Coniglio and Rodrigues2023) with a
${\textrm{LET}_{\textrm{K}}^{+}}$
of Coniglio and Rodrigues (Reference Coniglio and Rodrigues2023) with a
![]() $\{ p,{\sim }p,{\circ }p \}$
-analytic calculus, as it fits precisely in this setting, that is, it is determined by a refinement of
$\{ p,{\sim }p,{\circ }p \}$
-analytic calculus, as it fits precisely in this setting, that is, it is determined by a refinement of
![]() $\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}$
. In fact, its implication is given by the following truth table:
$\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}$
. In fact, its implication is given by the following truth table:

Then, to obtain the desired axiomatization, it is enough to add to
![]() $\textsf{R}_{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}}$
the following inference rules:
$\textsf{R}_{\mathfrak{M}^{\Rightarrow _{\textsf{A1}}}}$
the following inference rules:
The attentive reader will notice that they are not quite the same rules as the ones produced by the recipe in Proposition 27. In fact, they are simplifications thereof, following the streamlining procedures described in Marcelino and Caleiro (Reference Marcelino and Caleiro2021). Still, it is not hard to confirm that these rules produce the desired refinements of
![]() $\Rightarrow _{\textsf{A1}}$
in a similar way as we did in the previous example.
$\Rightarrow _{\textsf{A1}}$
in a similar way as we did in the previous example.
5. Logics of PP-Algebras Expanded with a Heyting Implication
In the light of Theorem 20, as we proceed to expand our logic with an implication we shall necessarily have to drop either
![]() $(\textsf{A}1)$
or
$(\textsf{A}1)$
or
![]() $(\textsf{A}2)$
. In this section we explore the first option, that is, we stick to
$(\textsf{A}2)$
. In this section we explore the first option, that is, we stick to
![]() $(\textsf{A}2)$
while dropping
$(\textsf{A}2)$
while dropping
![]() $(\textsf{A}1)$
. Having fixed a (deterministic) implication operator (say, on
$(\textsf{A}1)$
. Having fixed a (deterministic) implication operator (say, on
![]() $\mathbf{PP_6}$
), a straightforward way to ensure that the resulting logic will be self-extensional (cf. Proposition 8) is to consider, as in the implication-less case, the
$\mathbf{PP_6}$
), a straightforward way to ensure that the resulting logic will be self-extensional (cf. Proposition 8) is to consider, as in the implication-less case, the ![]() consequence relation that preserves the lattice order of
consequence relation that preserves the lattice order of
![]() $\mathbf{PP_6}$
(or, to be more precise, of the resulting class of algebras augmented with an implication). Indeed, as shown by Jansana (Reference Jansana2006, Sec. 3), when a conjunction is present, every self-extensional logic turns out to be the consequence associated with a suitably defined partial order. We shall thus follow this route, which still leaves us free to choose among the implication operators for
$\mathbf{PP_6}$
(or, to be more precise, of the resulting class of algebras augmented with an implication). Indeed, as shown by Jansana (Reference Jansana2006, Sec. 3), when a conjunction is present, every self-extensional logic turns out to be the consequence associated with a suitably defined partial order. We shall thus follow this route, which still leaves us free to choose among the implication operators for
![]() $\mathbf{PP_6}$
. Since on
$\mathbf{PP_6}$
. Since on
![]() $\mathbf{PP_6}$
we cannot define a classic-like implication suitable for our purposes – that is one satisfying both
$\mathbf{PP_6}$
we cannot define a classic-like implication suitable for our purposes – that is one satisfying both
![]() $(\textsf{A}1)$
and
$(\textsf{A}1)$
and
![]() $(\textsf{A}2)$
– we suggest introducing a Heyting implication. From an algebraic point of view, such an operator is readily available. Indeed, since
$(\textsf{A}2)$
– we suggest introducing a Heyting implication. From an algebraic point of view, such an operator is readily available. Indeed, since
![]() $\mathbf{PP_6}$
has a (finite) distributive lattice reduct, the meet operation has a residuum (we will denote it by
$\mathbf{PP_6}$
has a (finite) distributive lattice reduct, the meet operation has a residuum (we will denote it by
![]() $\Rightarrow _{\textsf{H}}$
), which is precisely the relative pseudo-complement operation.
$\Rightarrow _{\textsf{H}}$
), which is precisely the relative pseudo-complement operation.
Definition 28.
Let
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
be the algebra obtained by expanding
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
be the algebra obtained by expanding
![]() $\mathbf{PP_6}$
with the operation
$\mathbf{PP_6}$
with the operation
![]() $\Rightarrow _{\textsf{H}}$
defined as follows:
$\Rightarrow _{\textsf{H}}$
defined as follows:
In accordance with the above definition, the truth table of the implication in
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
looks as follows:
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
looks as follows:

![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
is obviously (i.e., has a reduct which is) a Heyting algebra. Furthermore, since it also carries a De Morgan negation, it may be called a De Morgan-Heyting algebra according to Sankappanavar (Reference Sankappanavar1987), or a symmetric Heyting algebra according to Monteiro (Reference Monteiro1980).Footnote 2 Indeed, since
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
is obviously (i.e., has a reduct which is) a Heyting algebra. Furthermore, since it also carries a De Morgan negation, it may be called a De Morgan-Heyting algebra according to Sankappanavar (Reference Sankappanavar1987), or a symmetric Heyting algebra according to Monteiro (Reference Monteiro1980).Footnote 2 Indeed, since
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
(as
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
(as
![]() $\mathbf{PP_6}$
) also has a Stone lattice reduct (i.e., a pseudo-complemented distributive lattice satisfying
$\mathbf{PP_6}$
) also has a Stone lattice reduct (i.e., a pseudo-complemented distributive lattice satisfying
![]() $\neg x \lor \neg \neg x \approx \top$
), we may be a bit more specific, observing that
$\neg x \lor \neg \neg x \approx \top$
), we may be a bit more specific, observing that
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
is also, in Monteiro’s terminology, a Stonean symmetric Heyting algebra (Monteiro Reference Monteiro1980, Ch. IV, Def. 1.1). These observations will be exploited in Section 7.
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
is also, in Monteiro’s terminology, a Stonean symmetric Heyting algebra (Monteiro Reference Monteiro1980, Ch. IV, Def. 1.1). These observations will be exploited in Section 7.
Remark 29. Before we proceed any further, one may wonder whether we are really adding something new to
![]() $\mathbf{PP_6}$
. In other words, was the implication
$\mathbf{PP_6}$
. In other words, was the implication
![]() $\Rightarrow _{\textsf{H}}$
already term-definable in this algebra? The answer is negative. To see why, observe that
$\Rightarrow _{\textsf{H}}$
already term-definable in this algebra? The answer is negative. To see why, observe that
![]() $\mathbf{PP_6}$
is a subdirectly irreducible algebra having a single non-trivial congruence
$\mathbf{PP_6}$
is a subdirectly irreducible algebra having a single non-trivial congruence
![]() $\theta$
, which is the one that identifies (only) the elements in the set
$\theta$
, which is the one that identifies (only) the elements in the set
![]() $\{{\mathbf{t}},{\mathbf{f}},{\mathbf{b}},{\mathbf{n}} \}$
. By adding the Heyting implication, we obtain a simple algebra, in which
$\{{\mathbf{t}},{\mathbf{f}},{\mathbf{b}},{\mathbf{n}} \}$
. By adding the Heyting implication, we obtain a simple algebra, in which
![]() $\theta$
is no longer a congruence (indeed,
$\theta$
is no longer a congruence (indeed,
![]() ${\mathbf{b}} \theta{\mathbf{n}}$
, but it is not the case that
${\mathbf{b}} \theta{\mathbf{n}}$
, but it is not the case that
![]() $({\mathbf{b}} \Rightarrow _{\textsf{H}}{\mathbf{b}}) \theta ({\mathbf{b}} \Rightarrow _{\textsf{H}}{\mathbf{n}})$
).
$({\mathbf{b}} \Rightarrow _{\textsf{H}}{\mathbf{b}}) \theta ({\mathbf{b}} \Rightarrow _{\textsf{H}}{\mathbf{n}})$
).
Before moving to the logics of order associated with the new algebra, we could first consider the ![]() logic determined by
logic determined by
![]() $\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\mathbf{b}}} \rangle$
, which is guaranteed to conservatively expand
$\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\mathbf{b}}} \rangle$
, which is guaranteed to conservatively expand
![]() $\mathcal{PP}_{\!\leq }^{{\rhd }}$
(with the implication
$\mathcal{PP}_{\!\leq }^{{\rhd }}$
(with the implication
![]() $\Rightarrow _{\textsf{H}}$
being the residuum of
$\Rightarrow _{\textsf{H}}$
being the residuum of
![]() $\land$
). Since
$\land$
). Since
![]() $\mathfrak{M}_6$
is monadic, we can axiomatize
$\mathfrak{M}_6$
is monadic, we can axiomatize
![]() $\Rightarrow _{\textsf{H}}$
straight away (similarly to what we did in the proof of Theorem 23) following the method of Marcelino and Caleiro (Reference Marcelino and Caleiro2021):
$\Rightarrow _{\textsf{H}}$
straight away (similarly to what we did in the proof of Theorem 23) following the method of Marcelino and Caleiro (Reference Marcelino and Caleiro2021):
Theorem 30.
The ![]()
![]() $\Sigma _\Rightarrow$
-logic induced by
$\Sigma _\Rightarrow$
-logic induced by
![]() $\mathfrak{M}_6$
expanded with
$\mathfrak{M}_6$
expanded with
![]() $\Rightarrow _{\textsf{H}}$
is axiomatized by the
$\Rightarrow _{\textsf{H}}$
is axiomatized by the
![]() $\{ p,{\sim }p,{\circ }p \}$
-analytic
$\{ p,{\sim }p,{\circ }p \}$
-analytic ![]() calculus given by
calculus given by
![]() $\textsf{R}_{\mathcal{PP}_{\!\leq }^{{\rhd }}}$
plus the following rules:
$\textsf{R}_{\mathcal{PP}_{\!\leq }^{{\rhd }}}$
plus the following rules:
Note however that
![]() $\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\mathbf{b}}} \rangle$
does not satisfy
$\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\mathbf{b}}} \rangle$
does not satisfy
![]() $(\textsf{A}1)$
: pick for instance
$(\textsf{A}1)$
: pick for instance
![]() $a \,{:=}\,{\mathbf{f}}$
and
$a \,{:=}\,{\mathbf{f}}$
and
![]() $b \,{:=}\,{\hat{\mathbf{f}}}$
. As for
$b \,{:=}\,{\hat{\mathbf{f}}}$
. As for
![]() $(\textsf{A}2)$
, we note that self-extensionality also fails. To see why, consider the formula
$(\textsf{A}2)$
, we note that self-extensionality also fails. To see why, consider the formula
![]() $\varphi :={\sim } (p \Rightarrow q) \land{\sim } (q \Rightarrow p )$
, and recall that
$\varphi :={\sim } (p \Rightarrow q) \land{\sim } (q \Rightarrow p )$
, and recall that
![]() $\nabla x \,{:=}\, x \lor{\sim }{\circ } x$
. While it is clear that both
$\nabla x \,{:=}\, x \lor{\sim }{\circ } x$
. While it is clear that both
![]() $\varphi$
and
$\varphi$
and
![]() $\nabla \bot$
are logically equivalent to
$\nabla \bot$
are logically equivalent to
![]() $\bot$
, the same does not hold for
$\bot$
, the same does not hold for
![]() $\nabla \varphi$
. To see this, consider a valuation such that
$\nabla \varphi$
. To see this, consider a valuation such that
![]() $v(p) ={\mathbf{b}}$
and
$v(p) ={\mathbf{b}}$
and
![]() $v(q) ={\mathbf{n}}$
. Then
$v(q) ={\mathbf{n}}$
. Then
![]() $v (\nabla ({\sim } (p \Rightarrow q) \land{\sim } (q \Rightarrow p ))) = \nabla ^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}({\sim }^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}} ({\mathbf{b}} \Rightarrow ^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}{\mathbf{n}}) \land ^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}{\sim }^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}} ({\mathbf{n}} \Rightarrow ^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}{\mathbf{b}} )) ={\hat{\mathbf{t}}}$
. It follows that
$v (\nabla ({\sim } (p \Rightarrow q) \land{\sim } (q \Rightarrow p ))) = \nabla ^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}({\sim }^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}} ({\mathbf{b}} \Rightarrow ^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}{\mathbf{n}}) \land ^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}{\sim }^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}} ({\mathbf{n}} \Rightarrow ^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}{\mathbf{b}} )) ={\hat{\mathbf{t}}}$
. It follows that
![]() $\varphi \;{\lhd \rhd } \;\bot$
holds good, while
$\varphi \;{\lhd \rhd } \;\bot$
holds good, while
![]() $\nabla \varphi \;{\lhd \rhd } \;\nabla \bot$
does not hold. In fact, as we are going to show in Proposition 35, there is only one self-extensional
$\nabla \varphi \;{\lhd \rhd } \;\nabla \bot$
does not hold. In fact, as we are going to show in Proposition 35, there is only one self-extensional ![]() logic determined by a class of matrices based on the algebra
logic determined by a class of matrices based on the algebra
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
and principal filters.
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
and principal filters.
Let us now resume our discussion about the logics of order. Having obtained a new algebra
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
, we can consider the variety it generates, denoted
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
, we can consider the variety it generates, denoted
![]() $\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
, and the order-preserving logics associated with it. We denote by
$\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
, and the order-preserving logics associated with it. We denote by
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
and
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
and
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
, respectively, the
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
, respectively, the ![]() and
and ![]() order-preserving logics associated with
order-preserving logics associated with
![]() $\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
(cf. Subsection 2.2 for the precise definitions). By the residuation property, we clearly have that
$\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
(cf. Subsection 2.2 for the precise definitions). By the residuation property, we clearly have that
![]() $\Rightarrow _{\textsf{H}}$
is an implication in these logics (cf. Definition 12 and Proposition 14).
$\Rightarrow _{\textsf{H}}$
is an implication in these logics (cf. Definition 12 and Proposition 14).
Proposition 31.
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
and
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
and
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
are conservative expansions of
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
are conservative expansions of
![]() $\mathcal{PP}_{\!\leq }^{{\rhd }}$
and
$\mathcal{PP}_{\!\leq }^{{\rhd }}$
and
![]() $\mathcal{PP}_{\!\leq }$
, respectively. Moreover, they are self-extensional.
$\mathcal{PP}_{\!\leq }$
, respectively. Moreover, they are self-extensional.
Proof.
That both logics are conservative expansions of
![]() $\mathcal{PP}_{\!\leq }$
follows directly from their matrix characterizations (Proposition 6), while self-extensionality follows from Proposition 8.
$\mathcal{PP}_{\!\leq }$
follows directly from their matrix characterizations (Proposition 6), while self-extensionality follows from Proposition 8.
Remark 32. Observe that
![]() $p \lor q \rhd _{{\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }}} p, q$
(by the above proposition), while
$p \lor q \rhd _{{\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }}} p, q$
(by the above proposition), while
![]() $\,\blacktriangleright _{{\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }}} (p \lor q) \Rightarrow p, q$
(take a valuation
$\,\blacktriangleright _{{\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }}} (p \lor q) \Rightarrow p, q$
(take a valuation
![]() $v$
such that
$v$
such that
![]() $v(p) :={\mathbf{b}}$
and
$v(p) :={\mathbf{b}}$
and
![]() $v(q) :={\mathbf{n}}$
), showing that
$v(q) :={\mathbf{n}}$
), showing that
![]() $\Rightarrow _{\textsf{H}}$
is not a classic-like implication in
$\Rightarrow _{\textsf{H}}$
is not a classic-like implication in
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
(recall Definition 13). This is one of the main reasons for which we chose Definition 12 as a more general notion of implication in
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
(recall Definition 13). This is one of the main reasons for which we chose Definition 12 as a more general notion of implication in ![]() instead of the one in Definition 13.
instead of the one in Definition 13.
We may actually improve Proposition 31 by removing some redundancies from the classes of matrices that characterize the logics thereby considered:
Proposition 33.
The logics
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
and
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
and
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
are determined by the class of matrices
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
are determined by the class of matrices
![]() $\{ \langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\mathbf{f}}} \rangle, \langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\mathbf{b}}} \rangle, \langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\hat{\mathbf{t}}}} \rangle \}$
. Moreover, all the latter matrices are reduced.
$\{ \langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\mathbf{f}}} \rangle, \langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\mathbf{b}}} \rangle, \langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\hat{\mathbf{t}}}} \rangle \}$
. Moreover, all the latter matrices are reduced.
Proof.
Note that any matrix
![]() $\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, D \rangle$
with
$\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, D \rangle$
with
![]() $D \neq \mathcal{V}_6$
is reduced, because
$D \neq \mathcal{V}_6$
is reduced, because
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
is a simple algebra. Regarding
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
is a simple algebra. Regarding
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
, we observe that two of the matrices appearing in Proposition 6 may be safely omitted. Obviously this holds for
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
, we observe that two of the matrices appearing in Proposition 6 may be safely omitted. Obviously this holds for
![]() $\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\hat{\mathbf{f}}}} \rangle$
, which defines a trivial logic. Note further that
$\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\hat{\mathbf{f}}}} \rangle$
, which defines a trivial logic. Note further that
![]() $\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\mathbf{b}}} \rangle$
and
$\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\mathbf{b}}} \rangle$
and
![]() $\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\mathbf{n}}} \rangle$
are isomorphic, and thus determine the same logic; so one of them may also be omitted. Finally, note that the matrix with set of designated values
$\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\mathbf{n}}} \rangle$
are isomorphic, and thus determine the same logic; so one of them may also be omitted. Finally, note that the matrix with set of designated values
![]() ${\uparrow }{\mathbf{t}}$
is not considered as we only need to take prime filters into account. Thus only the matrices listed in the statement remain. Regarding
${\uparrow }{\mathbf{t}}$
is not considered as we only need to take prime filters into account. Thus only the matrices listed in the statement remain. Regarding
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
, the result follows from the observation that
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
, the result follows from the observation that
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
is the
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
is the ![]() companion of the
companion of the ![]() order-preserving logics.
order-preserving logics.
There is another ![]() logic that has
logic that has
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
as
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
as ![]() companion, namely the one determined by the class of matrices based on the algebra
companion, namely the one determined by the class of matrices based on the algebra
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
having as designated sets the principal filters of
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
having as designated sets the principal filters of
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
. We shall denote this logic by
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
. We shall denote this logic by
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
. By a similar argument to the one above, we see that
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
. By a similar argument to the one above, we see that
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
is determined by the class of matrices
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
is determined by the class of matrices
![]() $\{ \langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\mathbf{f}}} \rangle, \langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\mathbf{b}}} \rangle, \langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\mathbf{t}}} \rangle, \langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\hat{\mathbf{t}}}} \rangle \}$
– that is, the matrices from Proposition 33 together with the matrix
$\{ \langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\mathbf{f}}} \rangle, \langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\mathbf{b}}} \rangle, \langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\mathbf{t}}} \rangle, \langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\hat{\mathbf{t}}}} \rangle \}$
– that is, the matrices from Proposition 33 together with the matrix
![]() $\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\mathbf{t}}} \rangle$
. In this logic, however,
$\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\mathbf{t}}} \rangle$
. In this logic, however,
![]() $\Rightarrow$
is not an implication in our sense, since
$\Rightarrow$
is not an implication in our sense, since
![]() $\rhd _{\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}} (p \lor q) \Rightarrow (p \lor q)$
, but
$\rhd _{\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}} (p \lor q) \Rightarrow (p \lor q)$
, but
![]() $p \lor q \, \,\blacktriangleright _{{\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}}}\, p,q$
. Still, we will include
$p \lor q \, \,\blacktriangleright _{{\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}}}\, p,q$
. Still, we will include
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
in our next considerations in view of its close relationship with
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
in our next considerations in view of its close relationship with
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
and because our techniques will also apply very naturally to it, as we shall see.
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
and because our techniques will also apply very naturally to it, as we shall see.
The above results do not clarify whether one could find a single matrix to characterize those logics (as it happens with
![]() $\mathcal{PP}_{\!\leq }$
): the next result rules out this possibility.
$\mathcal{PP}_{\!\leq }$
): the next result rules out this possibility.
Theorem 34.
The logic
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
is not determined by a single logical matrix. The same holds also for the logics
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
is not determined by a single logical matrix. The same holds also for the logics
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
and
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
and
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
.
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
.
Proof.
Since the two ![]() logics share the same
logics share the same ![]() companion
companion
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
, it is enough to prove that the latter is not determined by a single logical matrix. To that effect, we use the fact that any
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
, it is enough to prove that the latter is not determined by a single logical matrix. To that effect, we use the fact that any ![]() logic
logic
![]() $\vdash$
that is determined by a single logical matrix respects the so-called uniformity property (cf. Wójcicki Reference Wójcicki1969), according to which
$\vdash$
that is determined by a single logical matrix respects the so-called uniformity property (cf. Wójcicki Reference Wójcicki1969), according to which
![]() $\Phi, \Psi \vdash \varphi$
implies
$\Phi, \Psi \vdash \varphi$
implies
![]() $\Phi \vdash \varphi$
for all
$\Phi \vdash \varphi$
for all
![]() $\Phi \cup \Psi \cup \{ \varphi \} \subseteq L_{\Sigma }(P)$
such that (1)
$\Phi \cup \Psi \cup \{ \varphi \} \subseteq L_{\Sigma }(P)$
such that (1)
![]() $\textsf{props}(\Phi \cup \{ \varphi \}) \cap \textsf{props}(\Psi ) = \varnothing$
and (2)
$\textsf{props}(\Phi \cup \{ \varphi \}) \cap \textsf{props}(\Psi ) = \varnothing$
and (2)
![]() $\Psi \not \vdash \psi$
for some
$\Psi \not \vdash \psi$
for some
![]() $\psi \in L_{\Sigma }(P)$
.
$\psi \in L_{\Sigma }(P)$
.
Consider now
![]() $\Phi := \varnothing$
,
$\Phi := \varnothing$
,
![]() $\Psi := \{ p \land{\sim } p \land q \land{\sim } q \land{\sim }{\circ }(p \Rightarrow q) \}$
and
$\Psi := \{ p \land{\sim } p \land q \land{\sim } q \land{\sim }{\circ }(p \Rightarrow q) \}$
and
![]() $\varphi := r \lor{\sim } r$
. Condition (1) is obviously satisfied. To see that condition (2) is also satisfied, one may consider the matrix
$\varphi := r \lor{\sim } r$
. Condition (1) is obviously satisfied. To see that condition (2) is also satisfied, one may consider the matrix
![]() $\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\mathbf{f}}} \rangle$
, and to see that
$\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\mathbf{f}}} \rangle$
, and to see that
![]() $\not \vdash _{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }} r \lor{\sim } r$
it suffices to consider the matrix
$\not \vdash _{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }} r \lor{\sim } r$
it suffices to consider the matrix
![]() $\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\mathbf{b}}} \rangle$
. Yet, one may now use the semantics of the order-preserving logic associated with
$\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\mathbf{b}}} \rangle$
. Yet, one may now use the semantics of the order-preserving logic associated with
![]() $\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
to confirm that
$\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
to confirm that
![]() $p \land{\sim } p \land q \land{\sim } q \land{\sim }{\circ }(p \Rightarrow q) \vdash _{{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }}} r \lor{\sim } r$
.
$p \land{\sim } p \land q \land{\sim } q \land{\sim }{\circ }(p \Rightarrow q) \vdash _{{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }}} r \lor{\sim } r$
.
As earlier anticipated, we now proceed to show that
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
is actually the only self-extensional
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
is actually the only self-extensional ![]() logic determined by a class of matrices based on the algebra
logic determined by a class of matrices based on the algebra
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
and principal filters.
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
and principal filters.
Proposition 35.
For
![]() $ \mathcal{V} \subseteq \mathcal{V}_6$
, let
$ \mathcal{V} \subseteq \mathcal{V}_6$
, let
![]() $\vdash _{\mathcal{V}}$
be the
$\vdash _{\mathcal{V}}$
be the ![]() logic determined by
logic determined by
![]() $\left \{ \langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{\uparrow } a \rangle : a \in \mathcal{V} \right \}$
. If the logic
$\left \{ \langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{\uparrow } a \rangle : a \in \mathcal{V} \right \}$
. If the logic
![]() $\vdash _{\mathcal{V}}$
is self-extensional, then
$\vdash _{\mathcal{V}}$
is self-extensional, then
![]() $\vdash _{\mathcal{V}} \, = \,{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }}$
.
$\vdash _{\mathcal{V}} \, = \,{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }}$
.
Proof.
By Jansana (Reference Jansana2006, Thm. 3.7), the finitary self-extensional extensions of
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
are in a one-to-one correspondence with the subvarieties of
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
are in a one-to-one correspondence with the subvarieties of
![]() $\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
. The matrices in
$\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
. The matrices in
![]() $\{ \langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{\uparrow } a \rangle : a \in \mathcal{V} \}$
are reduced models of
$\{ \langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{\uparrow } a \rangle : a \in \mathcal{V} \}$
are reduced models of
![]() $\vdash _{\mathcal{V}}$
, implying that
$\vdash _{\mathcal{V}}$
, implying that
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
belongs to the subvariety
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
belongs to the subvariety
![]() $\textsf{K} \subseteq \mathbb{V} (\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
associated with
$\textsf{K} \subseteq \mathbb{V} (\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
associated with
![]() $\vdash _{\mathcal{V}}$
. Then
$\vdash _{\mathcal{V}}$
. Then
![]() $\mathbb{V} (\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}) \subseteq \textsf{K}$
, so
$\mathbb{V} (\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}) \subseteq \textsf{K}$
, so
![]() $\mathbb{V} (\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}) = \textsf{K}$
, and thus
$\mathbb{V} (\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}) = \textsf{K}$
, and thus
![]() ${\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }} \,=\, \vdash _{\mathcal{V}}$
.
${\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }} \,=\, \vdash _{\mathcal{V}}$
.
Adopting the terminology of Jansana (Reference Jansana2006), we may say that
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
is semilattice-based relative to
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
is semilattice-based relative to
![]() $\land$
and to
$\land$
and to
![]() $\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
. This observation allows us to obtain further information: for instance, we know by Jansana (Reference Jansana2006, Thm. 3.12) that the class of algebra reducts of reduced matrices for
$\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
. This observation allows us to obtain further information: for instance, we know by Jansana (Reference Jansana2006, Thm. 3.12) that the class of algebra reducts of reduced matrices for
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
is precisely
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
is precisely
![]() $\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
. Semilattice-based logics are often non-algebraizable but have an algebraizable companion, that is, an extension that shares the same algebraic models. We establish this for
$\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
. Semilattice-based logics are often non-algebraizable but have an algebraizable companion, that is, an extension that shares the same algebraic models. We establish this for
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
below.
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
below.
Proposition 36.
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
is equivalential but not algebraizable. The following is a set of equivalence formulas for it:
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
is equivalential but not algebraizable. The following is a set of equivalence formulas for it:
or, equivalently (setting
![]() $\Delta x : = x \land{\circ } x$
),
$\Delta x : = x \land{\circ } x$
),
Proof.
To prove that
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
is equivalential, it suffices to verify that the following conditions are met (see Font Reference Font2016, Thm. 6.60):
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
is equivalential, it suffices to verify that the following conditions are met (see Font Reference Font2016, Thm. 6.60):
-
1.
 $\vdash _{{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }}} \Xi (x,x)$
$\vdash _{{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }}} \Xi (x,x)$
-
2.
 $x, \Xi (x,y) \vdash _{{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }}} y$
$x, \Xi (x,y) \vdash _{{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }}} y$
-
3.
 $\Xi (x,y) \vdash _{{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }}} \Xi ( \circ x, \circ y)$
and
$\Xi (x,y) \vdash _{{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }}} \Xi ( \circ x, \circ y)$
and
 $\Xi (x,y) \vdash _{{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }}} \Xi ({\sim } x,{\sim } y)$
$\Xi (x,y) \vdash _{{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }}} \Xi ({\sim } x,{\sim } y)$
-
4.
 $\Xi (x_1,y_1), \Xi (x_2,y_2) \vdash _{{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }}} \Xi ( x_1 \unicode{x00A9} x_2, y_1 \unicode{x00A9} y_2)$
for every binary connective
$\Xi (x_1,y_1), \Xi (x_2,y_2) \vdash _{{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }}} \Xi ( x_1 \unicode{x00A9} x_2, y_1 \unicode{x00A9} y_2)$
for every binary connective
 $\unicode{x00A9}$
; in the signature.
$\unicode{x00A9}$
; in the signature.
The verification of the above conditions is straightforward from the matrix characterization of
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
. Now, if
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
. Now, if
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
were algebraizable, then each set of designated elements would be equationally definable on the corresponding reduced matrix (see Font Reference Font2016, Def. 6.90). But this is not the case, because the matrices
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
were algebraizable, then each set of designated elements would be equationally definable on the corresponding reduced matrix (see Font Reference Font2016, Def. 6.90). But this is not the case, because the matrices
![]() $\{ \langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }a} \rangle : a \in \mathcal{V}_6 \setminus \{{\hat{\mathbf{f}}} \}\}$
, all based on the same algebra, are all reduced, and have distinct sets of designated elements.
$\{ \langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }a} \rangle : a \in \mathcal{V}_6 \setminus \{{\hat{\mathbf{f}}} \}\}$
, all based on the same algebra, are all reduced, and have distinct sets of designated elements.
The algebraizable companion of
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
is the
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
is the
![]() $\top$
-assertional logic associated with the variety
$\top$
-assertional logic associated with the variety
![]() $\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
, which we denote by
$\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
, which we denote by
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
. The reduced models of this logic are all matrices of the form
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
. The reduced models of this logic are all matrices of the form
![]() $\langle \mathbf A, \{ \top ^{\mathbf A} \} \rangle$
, where
$\langle \mathbf A, \{ \top ^{\mathbf A} \} \rangle$
, where
![]() $\mathbf A$
is an algebra in
$\mathbf A$
is an algebra in
![]() $\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
. One easily verifies that
$\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
. One easily verifies that
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
satisfies the following rules – any of them being in fact sufficient to distinguish
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
satisfies the following rules – any of them being in fact sufficient to distinguish
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
from
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
from
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
(given that they are sound in the former but not in the latter):
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
(given that they are sound in the former but not in the latter):
where
![]() $p \Rightarrow _{\textsf{W}} q \,{:=}\,{\sim } p \lor{\sim }{\circ } p \lor q$
and
$p \Rightarrow _{\textsf{W}} q \,{:=}\,{\sim } p \lor{\sim }{\circ } p \lor q$
and
![]() $\Delta p \,{:=}\, p \land{\circ } p$
.
$\Delta p \,{:=}\, p \land{\circ } p$
.
5.1 Characterizability by single finite PNmatrices
We saw in Theorem 34 that the logics we introduced in this section are not characterized by any single logical matrix. In this subsection, we will demonstrate the power of partial non-deterministic matrices by showing that both
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
and
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
and
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
are characterized by single finite PNmatrices. In consequence,
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
are characterized by single finite PNmatrices. In consequence,
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
will be characterized by either of these matrices. The essential idea is that the collections of matrices that characterize these logics can be packaged into a single structure using partiality.
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
will be characterized by either of these matrices. The essential idea is that the collections of matrices that characterize these logics can be packaged into a single structure using partiality.
The construction we will present makes use of the notion of total components of a
![]() $\Sigma$
-PNmatrix, which we now proceed to introduce. Let
$\Sigma$
-PNmatrix, which we now proceed to introduce. Let
![]() $\mathfrak{M} \,{:=}\, \langle \mathbf{A}, D \rangle$
be a
$\mathfrak{M} \,{:=}\, \langle \mathbf{A}, D \rangle$
be a
![]() $\Sigma$
-PNmatrix. For
$\Sigma$
-PNmatrix. For
![]() $X \subseteq A$
, denote by
$X \subseteq A$
, denote by
![]() $\mathfrak{M}_X$
the
$\mathfrak{M}_X$
the
![]() $\Sigma$
-PNmatrix
$\Sigma$
-PNmatrix
![]() $\langle \mathbf{A}_X, D \cap X \rangle$
, where
$\langle \mathbf{A}_X, D \cap X \rangle$
, where
![]() $\mathbf{A}_X \,{:=}\, \langle A \cap X, \cdot ^{\mathbf{A}_X} \rangle$
is a
$\mathbf{A}_X \,{:=}\, \langle A \cap X, \cdot ^{\mathbf{A}_X} \rangle$
is a
![]() $\Sigma$
-multialgebra such that
$\Sigma$
-multialgebra such that
![]() $\unicode{x00A9}^{\mathbf{A}_X}(a_1,\ldots, a_k) \,{:=}\, \unicode{x00A9}^{\mathbf{A}}(a_1,\ldots, a_k) \cap X$
for all
$\unicode{x00A9}^{\mathbf{A}_X}(a_1,\ldots, a_k) \,{:=}\, \unicode{x00A9}^{\mathbf{A}}(a_1,\ldots, a_k) \cap X$
for all
![]() $a_1,\ldots, a_k \in X$
,
$a_1,\ldots, a_k \in X$
,
![]() $k \in \omega$
and
$k \in \omega$
and
![]() $\unicode{x00A9} \in \Sigma _k$
. This PNmatrix is called the restriction of
$\unicode{x00A9} \in \Sigma _k$
. This PNmatrix is called the restriction of
![]() $\mathfrak{M}$
to
$\mathfrak{M}$
to
![]() $X$
. We say that
$X$
. We say that
![]() $X \neq \varnothing$
is a total component of
$X \neq \varnothing$
is a total component of
![]() $\mathfrak{M}$
whenever
$\mathfrak{M}$
whenever
![]() $\mathfrak{M}_X$
is total. A total component
$\mathfrak{M}_X$
is total. A total component
![]() $X$
is maximal if adding any other value to
$X$
is maximal if adding any other value to
![]() $X$
leads to a component that is not total. Denote by
$X$
leads to a component that is not total. Denote by
![]() $\mathbb{T}(\mathfrak{M})$
the collection of maximal total components of
$\mathbb{T}(\mathfrak{M})$
the collection of maximal total components of
![]() $\mathfrak{M}$
. Then we have that
$\mathfrak{M}$
. Then we have that
![]() $\rhd _{\mathfrak{M}} ={\rhd _{\{ \mathfrak{M}_X : X \in \mathbb{T}(\mathfrak{M})\}}}$
(Caleiro and Marcelino Reference Caleiro and Marcelino2023). The latter observation is key to us: the matrices induced by the maximal total components of the PNmatrices we will construct are precisely the ones in the classes that determine the logics
$\rhd _{\mathfrak{M}} ={\rhd _{\{ \mathfrak{M}_X : X \in \mathbb{T}(\mathfrak{M})\}}}$
(Caleiro and Marcelino Reference Caleiro and Marcelino2023). The latter observation is key to us: the matrices induced by the maximal total components of the PNmatrices we will construct are precisely the ones in the classes that determine the logics
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
and
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
and
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
.
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
.
We display below diagrams of the four matrices (see discussion after Proposition 33) that determine the logic
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
(in each case, the sets of designated elements are highlighted with an ellipse).
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
(in each case, the sets of designated elements are highlighted with an ellipse).

Below we depict the structure of the PNmatrix
![]() $\mathfrak{M}_{\textsf{up}}$
we propose for this logic, whose principle of construction is the combination of the above matrices, such that each of them consists of a total component of the PNmatrix. Note: There is nothing special about the dashed edge, it is pictured as dashed only because it crosses other edges.
$\mathfrak{M}_{\textsf{up}}$
we propose for this logic, whose principle of construction is the combination of the above matrices, such that each of them consists of a total component of the PNmatrix. Note: There is nothing special about the dashed edge, it is pictured as dashed only because it crosses other edges.

We try to make the above idea clearer in the following pictures, which show how to identify each of the four matrices inside
![]() $\mathfrak{M}_{\textsf{up}}$
.
$\mathfrak{M}_{\textsf{up}}$
.

The PNmatrix for
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
, which we dub
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
, which we dub
![]() $\mathfrak{M}_{\leq }$
, is essentially the same, the only difference being the absence of the dashed line.
$\mathfrak{M}_{\leq }$
, is essentially the same, the only difference being the absence of the dashed line.
After this informal presentation of the general approach, we proceed to a precise definition of the PNmatrices
![]() $\mathfrak{M}_{\textsf{up}}$
and
$\mathfrak{M}_{\textsf{up}}$
and
![]() $\mathfrak{M}_{\leq }$
, and prove that they indeed determine, respectively, the logics
$\mathfrak{M}_{\leq }$
, and prove that they indeed determine, respectively, the logics
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
and
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
and
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
.
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
.
Definition 37.
Let
![]() $\mathcal{V}_{10} \,{:=}\, \{{\hat{\mathbf{f}}},{\mathbf{f}}^-,{\mathbf{n}}^-,{\mathbf{b}}^-,{\mathbf{t}}^-,{\mathbf{f}}^+,{\mathbf{n}}^+,{\mathbf{b}}^+,{\mathbf{t}}^+,{\hat{\mathbf{t}}}\}$
and
$\mathcal{V}_{10} \,{:=}\, \{{\hat{\mathbf{f}}},{\mathbf{f}}^-,{\mathbf{n}}^-,{\mathbf{b}}^-,{\mathbf{t}}^-,{\mathbf{f}}^+,{\mathbf{n}}^+,{\mathbf{b}}^+,{\mathbf{t}}^+,{\hat{\mathbf{t}}}\}$
and
![]() $D \,{:=}\, \{{\mathbf{f}}^+,{\mathbf{n}}^+,{\mathbf{b}}^+,{\mathbf{t}}^+,{\hat{\mathbf{t}}}\} \subseteq \mathcal{V}_{10}$
. Consider the predicates
$D \,{:=}\, \{{\mathbf{f}}^+,{\mathbf{n}}^+,{\mathbf{b}}^+,{\mathbf{t}}^+,{\hat{\mathbf{t}}}\} \subseteq \mathcal{V}_{10}$
. Consider the predicates
![]() $\textsf{inc}_{\textsf{up}}$
and
$\textsf{inc}_{\textsf{up}}$
and
![]() $\textsf{inc}_{\leq }$
over
$\textsf{inc}_{\leq }$
over
![]() $\wp (\mathcal{V}_{10})$
, where
$\wp (\mathcal{V}_{10})$
, where
![]() $\textsf{inc}_{\textsf{up}}(X)$
(resp.
$\textsf{inc}_{\textsf{up}}(X)$
(resp.
![]() $\textsf{inc}_{\leq }(X)$
) means that
$\textsf{inc}_{\leq }(X)$
) means that
![]() $X$
is not contained in the image of valuations over
$X$
is not contained in the image of valuations over
![]() $\mathfrak{M}_{\textsf{up}}$
(resp.
$\mathfrak{M}_{\textsf{up}}$
(resp.
![]() $\mathfrak{M}_{\leq }$
), and can be defined as follows:
$\mathfrak{M}_{\leq }$
), and can be defined as follows:
 \begin{align*} \textsf{inc}_{\textsf{up}}(X) & \text{ iff }\\ &X\supseteq Y\text{, for some }Y\in \{\{d^-,d^+\}:d\in \{{\mathbf{f}},{\mathbf{n}},{\mathbf{b}},{\mathbf{t}}\}\}\cup \\ &\qquad \{\{{\mathbf{b}}^-,{\mathbf{f}}^+\}, \{{\mathbf{n}}^-,{\mathbf{f}}^+\},\{{\mathbf{b}}^+,{\mathbf{t}}^-\}, \{{\mathbf{n}}^+,{\mathbf{t}}^-\}, \{{\mathbf{n}}^+,{\mathbf{b}}^+,{\mathbf{f}}^-\}\} \end{align*}
\begin{align*} \textsf{inc}_{\textsf{up}}(X) & \text{ iff }\\ &X\supseteq Y\text{, for some }Y\in \{\{d^-,d^+\}:d\in \{{\mathbf{f}},{\mathbf{n}},{\mathbf{b}},{\mathbf{t}}\}\}\cup \\ &\qquad \{\{{\mathbf{b}}^-,{\mathbf{f}}^+\}, \{{\mathbf{n}}^-,{\mathbf{f}}^+\},\{{\mathbf{b}}^+,{\mathbf{t}}^-\}, \{{\mathbf{n}}^+,{\mathbf{t}}^-\}, \{{\mathbf{n}}^+,{\mathbf{b}}^+,{\mathbf{f}}^-\}\} \end{align*}
 \begin{align*} {\textsf{inc}_{\leq }(X)}& \text{ iff }\\ &X\supseteq Y\text{, for some }Y\in \{\{d^-,d^+\}:d\in \{{\mathbf{f}},{\mathbf{n}},{\mathbf{b}},{\mathbf{t}}\}\}\cup \\ &\qquad \{ \{{\mathbf{b}}^-,{\mathbf{f}}^+\}, \{{\mathbf{n}}^-,{\mathbf{f}}^+\},\{{\mathbf{b}}^+,{\mathbf{t}}^-\}, \{{\mathbf{n}}^+,{\mathbf{t}}^-\}, \{{\mathbf{n}}^+,{\mathbf{b}}^+,{\mathbf{f}}^-\}, \{{\mathbf{n}}^-,{\mathbf{b}}^-,{\mathbf{t}}^+\}\} \end{align*}
\begin{align*} {\textsf{inc}_{\leq }(X)}& \text{ iff }\\ &X\supseteq Y\text{, for some }Y\in \{\{d^-,d^+\}:d\in \{{\mathbf{f}},{\mathbf{n}},{\mathbf{b}},{\mathbf{t}}\}\}\cup \\ &\qquad \{ \{{\mathbf{b}}^-,{\mathbf{f}}^+\}, \{{\mathbf{n}}^-,{\mathbf{f}}^+\},\{{\mathbf{b}}^+,{\mathbf{t}}^-\}, \{{\mathbf{n}}^+,{\mathbf{t}}^-\}, \{{\mathbf{n}}^+,{\mathbf{b}}^+,{\mathbf{f}}^-\}, \{{\mathbf{n}}^-,{\mathbf{b}}^-,{\mathbf{t}}^+\}\} \end{align*}
Consider also the function
![]() $g:\mathcal{V}_{10} \to \{{\hat{\mathbf{f}}},{\mathbf{f}},{\mathbf{n}},{\mathbf{b}},{\mathbf{t}},{\hat{\mathbf{t}}}\}$
given by
$g:\mathcal{V}_{10} \to \{{\hat{\mathbf{f}}},{\mathbf{f}},{\mathbf{n}},{\mathbf{b}},{\mathbf{t}},{\hat{\mathbf{t}}}\}$
given by
![]() $g({\hat{\mathbf{f}}}) \,{:=}\,{\hat{\mathbf{f}}}$
,
$g({\hat{\mathbf{f}}}) \,{:=}\,{\hat{\mathbf{f}}}$
,
![]() $g({\hat{\mathbf{t}}}) \,{:=}\,{\hat{\mathbf{t}}}$
,
$g({\hat{\mathbf{t}}}) \,{:=}\,{\hat{\mathbf{t}}}$
,
![]() $g(a^i) \,{:=}\, a$
for
$g(a^i) \,{:=}\, a$
for
![]() $a\in \{{\mathbf{f}},{\mathbf{n}},{\mathbf{b}},{\mathbf{t}}\}$
and
$a\in \{{\mathbf{f}},{\mathbf{n}},{\mathbf{b}},{\mathbf{t}}\}$
and
![]() $i \in \{ +,- \}$
. We define the PNmatrices
$i \in \{ +,- \}$
. We define the PNmatrices
![]() $\mathfrak{M}_{\textsf{up}} \,{:=}\,{\langle \mathbf{A}_{\textsf{up}},D\rangle }$
and
$\mathfrak{M}_{\textsf{up}} \,{:=}\,{\langle \mathbf{A}_{\textsf{up}},D\rangle }$
and
![]() $\mathfrak{M}_{\leq } \,{:=}\,{\langle \mathbf{A}_{\leq },D\rangle }$
, with
$\mathfrak{M}_{\leq } \,{:=}\,{\langle \mathbf{A}_{\leq },D\rangle }$
, with
![]() $\mathbf{A}_{\textsf{up}} \,{:=}\, \langle \mathcal{V}_{10},\cdot _{\textsf{up}} \rangle$
and
$\mathbf{A}_{\textsf{up}} \,{:=}\, \langle \mathcal{V}_{10},\cdot _{\textsf{up}} \rangle$
and
![]() $\mathbf{A}_{\leq } \,{:=}\, \langle \mathcal{V}_{10},\cdot _{\leq } \rangle$
such that
$\mathbf{A}_{\leq } \,{:=}\, \langle \mathcal{V}_{10},\cdot _{\leq } \rangle$
such that
-
• for
 $\unicode{x00A9} \in \{{\sim },{\circ }\}$
,
$\unicode{x00A9} \in \{{\sim },{\circ }\}$
, \begin{align*} \unicode{x00A9}_{\textsf{up}}(a)& \,{:=}\, \{b\in \mathcal{V}_{10}:\unicode{x00A9}_{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}(g(a))=g(b) \text{ and not }{\textsf{inc}_{\textsf{up}}(\{ a,b \})}\}\\ \unicode{x00A9}_\leq (a)&\,{:=}\,\{b\in \mathcal{V}_{10}: \unicode{x00A9}_{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}(g(a))=g(b) \text{ and not }{\textsf{inc}_{\leq }(\{a,b\})} \} \end{align*}
\begin{align*} \unicode{x00A9}_{\textsf{up}}(a)& \,{:=}\, \{b\in \mathcal{V}_{10}:\unicode{x00A9}_{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}(g(a))=g(b) \text{ and not }{\textsf{inc}_{\textsf{up}}(\{ a,b \})}\}\\ \unicode{x00A9}_\leq (a)&\,{:=}\,\{b\in \mathcal{V}_{10}: \unicode{x00A9}_{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}(g(a))=g(b) \text{ and not }{\textsf{inc}_{\leq }(\{a,b\})} \} \end{align*}
-
• for
 $\unicode{x00A9}\in \{\land, \lor, \Rightarrow \}$
,
$\unicode{x00A9}\in \{\land, \lor, \Rightarrow \}$
, \begin{align*} \unicode{x00A9}_{\textsf{up}}(a,b)& \,{:=}\, \{c\in \mathcal{V}_{10}: \unicode{x00A9}_{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}(g(a),g(b))=g(c) \text{ and not }{\textsf{inc}_{\textsf{up}}(\{a,b,c\})}\}\\ \unicode{x00A9}_{\leq }(a,b)&\,{:=}\,\{c\in \mathcal{V}_{10}: \unicode{x00A9}_{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}(g(a),g(b))=g(c)\text{ and not }{\textsf{inc}_{\leq }(\{a,b,c\})} \} \end{align*}
\begin{align*} \unicode{x00A9}_{\textsf{up}}(a,b)& \,{:=}\, \{c\in \mathcal{V}_{10}: \unicode{x00A9}_{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}(g(a),g(b))=g(c) \text{ and not }{\textsf{inc}_{\textsf{up}}(\{a,b,c\})}\}\\ \unicode{x00A9}_{\leq }(a,b)&\,{:=}\,\{c\in \mathcal{V}_{10}: \unicode{x00A9}_{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}(g(a),g(b))=g(c)\text{ and not }{\textsf{inc}_{\leq }(\{a,b,c\})} \} \end{align*}
Proposition 38.
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
is determined by
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
is determined by
![]() $\mathfrak{M}_{\textsf{up}}$
and
$\mathfrak{M}_{\textsf{up}}$
and
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
is determined by
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
is determined by
![]() $\mathfrak{M}_{\leq }$
.
$\mathfrak{M}_{\leq }$
.
Proof.
We have that if
![]() $\{a,b,c\} \subseteq X$
and
$\{a,b,c\} \subseteq X$
and
![]() $\textsf{inc}_{\textsf{up}}(\{a,b,c\})$
then
$\textsf{inc}_{\textsf{up}}(\{a,b,c\})$
then
![]() $X$
is not contained in a total component of
$X$
is not contained in a total component of
![]() $\mathfrak{M}_{\textsf{up}}$
. In fact,
$\mathfrak{M}_{\textsf{up}}$
. In fact,
-
• if
 $b_1,b_2\in X$
withthen
$b_1,b_2\in X$
withthen \begin{equation*}\{b_1,b_2\}\in \{\{a^-,a^+\}:a\in \{{\mathbf {f}},{\mathbf {n}},{\mathbf {b}},{\mathbf {t}}\}\}\cup \{\{{\mathbf {b}}^-,{\mathbf {f}}^+\}, \{{\mathbf {n}}^-,{\mathbf {f}}^+\},\{{\mathbf {b}}^+,{\mathbf {t}}^-\}, \{{\mathbf {n}}^+,{\mathbf {t}}^-\}\}\end{equation*}
\begin{equation*}\{b_1,b_2\}\in \{\{a^-,a^+\}:a\in \{{\mathbf {f}},{\mathbf {n}},{\mathbf {b}},{\mathbf {t}}\}\}\cup \{\{{\mathbf {b}}^-,{\mathbf {f}}^+\}, \{{\mathbf {n}}^-,{\mathbf {f}}^+\},\{{\mathbf {b}}^+,{\mathbf {t}}^-\}, \{{\mathbf {n}}^+,{\mathbf {t}}^-\}\}\end{equation*}
 $b_1\land _{\textsf{up}} b_2=\varnothing$
.
$b_1\land _{\textsf{up}} b_2=\varnothing$
.
-
• if
 $\{{\mathbf{n}}^+,{\mathbf{b}}^+,{\mathbf{f}}^-\}\subseteq X$
, then
$\{{\mathbf{n}}^+,{\mathbf{b}}^+,{\mathbf{f}}^-\}\subseteq X$
, then
 ${\mathbf{n}}^+\land _{\textsf{up}}{\mathbf{b}}^+=\{{\mathbf{f}}^+\}$
and
${\mathbf{n}}^+\land _{\textsf{up}}{\mathbf{b}}^+=\{{\mathbf{f}}^+\}$
and
 ${\mathbf{f}}^-\land _{\textsf{up}}{\mathbf{f}}^+=\varnothing$
.
${\mathbf{f}}^-\land _{\textsf{up}}{\mathbf{f}}^+=\varnothing$
.
The maximal total components of
![]() $\mathfrak{M}_{\textsf{up}}$
are
$\mathfrak{M}_{\textsf{up}}$
are
since for every
![]() $X\in \mathbb{T}({\mathfrak{M}_{\textsf{up}}})$
and every
$X\in \mathbb{T}({\mathfrak{M}_{\textsf{up}}})$
and every
![]() $a,b,c\in X$
we have that
$a,b,c\in X$
we have that
![]() $\textsf{inc}_{\textsf{up}}(\{a,b,c\})$
is not the case. Thus, the restriction of
$\textsf{inc}_{\textsf{up}}(\{a,b,c\})$
is not the case. Thus, the restriction of
![]() $\mathfrak{M}_{\textsf{up}}$
to
$\mathfrak{M}_{\textsf{up}}$
to
![]() $X$
is isomorphic to (that is, it is the same up to renaming of truth values) some matrix with set of designated values
$X$
is isomorphic to (that is, it is the same up to renaming of truth values) some matrix with set of designated values
![]() $D_X ={{\uparrow }a}$
for
$D_X ={{\uparrow }a}$
for
![]() $a\in \mathcal{V}_6$
. The isomorphism is given by the restriction of
$a\in \mathcal{V}_6$
. The isomorphism is given by the restriction of
![]() $g$
to
$g$
to
![]() $X$
.
$X$
.
Similarly, the maximal total components of
![]() $\mathfrak{M}_{\leq }$
are
$\mathfrak{M}_{\leq }$
are
This is so because
![]() $\textsf{inc}_{\leq }(\{a,b,c\})$
iff
$\textsf{inc}_{\leq }(\{a,b,c\})$
iff
![]() $\textsf{inc}_{\textsf{up}}(\{a,b,c\})$
or
$\textsf{inc}_{\textsf{up}}(\{a,b,c\})$
or
![]() $\{{\mathbf{n}}^-,{\mathbf{b}}^-,{\mathbf{t}}^+\}\subseteq X$
, and the fact that if
$\{{\mathbf{n}}^-,{\mathbf{b}}^-,{\mathbf{t}}^+\}\subseteq X$
, and the fact that if
![]() $\{{\mathbf{n}}^-,{\mathbf{b}}^-,{\mathbf{t}}^+\}\subseteq X$
then
$\{{\mathbf{n}}^-,{\mathbf{b}}^-,{\mathbf{t}}^+\}\subseteq X$
then
![]() $X$
is not in a total component of
$X$
is not in a total component of
![]() $\mathfrak{M}_{\leq }$
, since
$\mathfrak{M}_{\leq }$
, since
![]() ${\mathbf{n}}^-\lor _{\textsf{up}}{\mathbf{b}}^-=\{{\mathbf{t}}^-\}$
and
${\mathbf{n}}^-\lor _{\textsf{up}}{\mathbf{b}}^-=\{{\mathbf{t}}^-\}$
and
![]() ${\mathbf{t}}^-\land _{\textsf{up}}{\mathbf{t}}^+=\varnothing$
.
${\mathbf{t}}^-\land _{\textsf{up}}{\mathbf{t}}^+=\varnothing$
.
6. Hilbert-Style Axiomatizations
Our goal in this section is to present analytic ![]() Hilbert-style axiomatizations for the implicative expansions
Hilbert-style axiomatizations for the implicative expansions
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
and
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
and
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
, as well as a
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
, as well as a ![]() axiomatization for
axiomatization for
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
. Unfortunately, the PNmatrices from the previous section do not allow us to extract automatically an analytic
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
. Unfortunately, the PNmatrices from the previous section do not allow us to extract automatically an analytic ![]() calculus for the corresponding logics using the technology of Caleiro and Marcelino (Reference Caleiro, Marcelino, Iemhoff, Moortgat and Queiroz2019), employed in Gomes et al. (Reference Gomes, Greati, Marcelino, Marcos and Rivieccio2022) and in the previous sections of the present paper, in view of the following:
calculus for the corresponding logics using the technology of Caleiro and Marcelino (Reference Caleiro, Marcelino, Iemhoff, Moortgat and Queiroz2019), employed in Gomes et al. (Reference Gomes, Greati, Marcelino, Marcos and Rivieccio2022) and in the previous sections of the present paper, in view of the following:
Proposition 39.
Neither
![]() $\mathfrak{M}_\leq$
nor
$\mathfrak{M}_\leq$
nor
![]() $\mathfrak{M}_{\textsf{up}}$
is monadic.
$\mathfrak{M}_{\textsf{up}}$
is monadic.
Proof.
Note that no unary formula can separate
![]() ${\mathbf{n}}^+$
from
${\mathbf{n}}^+$
from
![]() ${\mathbf{b}}^+$
, nor
${\mathbf{b}}^+$
, nor
![]() ${\mathbf{n}}^-$
from
${\mathbf{n}}^-$
from
![]() ${\mathbf{b}}^-$
. Indeed, one can show inductively on the structure of a unary formula
${\mathbf{b}}^-$
. Indeed, one can show inductively on the structure of a unary formula
![]() $\varphi (p)$
that, given valuations
$\varphi (p)$
that, given valuations
![]() $v_a$
,
$v_a$
,
![]() $v_b$
such that
$v_b$
such that
![]() $v_a(p)=a^s$
and
$v_a(p)=a^s$
and
![]() $v_b(p)=b^s$
for
$v_b(p)=b^s$
for
![]() $s\in \{+,-\}$
, we have that
$s\in \{+,-\}$
, we have that
![]() $v_x(\varphi )\in \{{\hat{\mathbf{f}}},x^s,{\hat{\mathbf{t}}}\}$
, and either
$v_x(\varphi )\in \{{\hat{\mathbf{f}}},x^s,{\hat{\mathbf{t}}}\}$
, and either
![]() $v_a(\varphi )=v_b(\varphi )$
or
$v_a(\varphi )=v_b(\varphi )$
or
![]() $v_a(\varphi )=a^s$
and
$v_a(\varphi )=a^s$
and
![]() $v_b(\varphi )=b^s$
.
$v_b(\varphi )=b^s$
.
We need, therefore, to delve into specific details of the logical matrices introduced above, and extract what is important to characterize their algebraic and logical structures in terms of formulas and ![]() rules of inference. We will do that and obtain analytic axiomatizations for the
rules of inference. We will do that and obtain analytic axiomatizations for the ![]() logics and then, taking advantage of the fact that in
logics and then, taking advantage of the fact that in
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
we have a disjunction (a notion we will soon make precise), we will convert the calculus for
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
we have a disjunction (a notion we will soon make precise), we will convert the calculus for
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
into a
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
into a ![]() axiomatization for
axiomatization for
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
.
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
.
6.1 Analytic axiomatizations for
 $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
and
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
and
 $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
We begin by the analytic ![]() axiomatizations. What follows is a succession of definitions introducing groups of rules of inference that capture particular aspects of the collections of logical matrices determining
axiomatizations. What follows is a succession of definitions introducing groups of rules of inference that capture particular aspects of the collections of logical matrices determining
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
and
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
and
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
. We check the soundness of each of them and ultimately arrive at the desired completeness results. Throughout the proofs, we will make use of the following abbreviations:
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
. We check the soundness of each of them and ultimately arrive at the desired completeness results. Throughout the proofs, we will make use of the following abbreviations:
Definition 40.
Set
![]() ${\uparrow } p \,{:=}\,{\circ }({\sim } p\Rightarrow p)$
and
${\uparrow } p \,{:=}\,{\circ }({\sim } p\Rightarrow p)$
and
![]() ${\downarrow } p \,{:=}\,{\circ }(p\Rightarrow{\sim } p)$
.
${\downarrow } p \,{:=}\,{\circ }(p\Rightarrow{\sim } p)$
.
By way of an example, the truth tables of the above-derived connectives interpreted in
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
are given in Table 2. A key feature of these connectives is that they characterize the values
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
are given in Table 2. A key feature of these connectives is that they characterize the values
![]() $\mathbf{f}$
and
$\mathbf{f}$
and
![]() $\mathbf{t}$
in the following sense: for each valuation
$\mathbf{t}$
in the following sense: for each valuation
![]() $v$
over
$v$
over
![]() $\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, D\rangle$
,
$\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, D\rangle$
,
![]() $v({\uparrow } p) \not \in D$
iff
$v({\uparrow } p) \not \in D$
iff
![]() $v(p) ={\mathbf{f}}$
and
$v(p) ={\mathbf{f}}$
and
![]() $v({\downarrow } p) \not \in D$
iff
$v({\downarrow } p) \not \in D$
iff
![]() $v(p) ={\mathbf{t}}$
, for
$v(p) ={\mathbf{t}}$
, for
![]() $D$
containing
$D$
containing
![]() $\hat{\mathbf{t}}$
and not containing
$\hat{\mathbf{t}}$
and not containing
![]() $\hat{\mathbf{f}}$
.
$\hat{\mathbf{f}}$
.
Table 2. Truth tables of the connectives
![]() $\uparrow$
and
$\uparrow$
and
![]() $\downarrow$
interpreted in
$\downarrow$
interpreted in
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$

Note that the above definitions introduce new connectives by means of abbreviations, so we have
![]() ${\textsf{sub}}({\uparrow } p) = \{p,{\sim } p,{\sim } p\Rightarrow p,{\circ }({\sim } p\Rightarrow p)\}$
(the case of
${\textsf{sub}}({\uparrow } p) = \{p,{\sim } p,{\sim } p\Rightarrow p,{\circ }({\sim } p\Rightarrow p)\}$
(the case of
![]() ${\textsf{sub}}({\downarrow } p)$
is similar).
${\textsf{sub}}({\downarrow } p)$
is similar).
Definition 41.
Let
![]() $\textsf{R}_{\Diamond }$
be the
$\textsf{R}_{\Diamond }$
be the ![]() calculus given by the following inference rules:
calculus given by the following inference rules:
Proposition 42.
The rules of
![]() $\textsf{R}_\Diamond$
are sound for any matrix
$\textsf{R}_\Diamond$
are sound for any matrix
![]() $\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, D \rangle$
with
$\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, D \rangle$
with
![]() $D$
containing
$D$
containing
![]() $\hat{\mathbf{t}}$
and not containing
$\hat{\mathbf{t}}$
and not containing
![]() $\hat{\mathbf{f}}$
.
$\hat{\mathbf{f}}$
.
Proof. We proceed rule by rule.
 $\textsf{r}^\Diamond _{{\uparrow }\textsf{or}{\downarrow }}$
: If
$\textsf{r}^\Diamond _{{\uparrow }\textsf{or}{\downarrow }}$
: If
 $v({\uparrow } p)\notin D$
, then
$v({\uparrow } p)\notin D$
, then
 $v({\uparrow } p)={\hat{\mathbf{f}}}$
, so
$v({\uparrow } p)={\hat{\mathbf{f}}}$
, so
 $v(p)={\mathbf{f}}$
and thus
$v(p)={\mathbf{f}}$
and thus
 $v({\downarrow } p)={\hat{\mathbf{t}}}\in D$
.
$v({\downarrow } p)={\hat{\mathbf{t}}}\in D$
. $\textsf{r}^\Diamond _{\textsf{id}}$
: Clearly,
$\textsf{r}^\Diamond _{\textsf{id}}$
: Clearly,
 $v({\circ }(p\Rightarrow p))={\hat{\mathbf{t}}}\in D$
.
$v({\circ }(p\Rightarrow p))={\hat{\mathbf{t}}}\in D$
. $\textsf{r}^\Diamond _{\textsf{trans}}$
: If
$\textsf{r}^\Diamond _{\textsf{trans}}$
: If
 $v({\circ } q)\notin D$
, we have
$v({\circ } q)\notin D$
, we have
 $v(q)\neq{\hat{\mathbf{f}}}$
, hence
$v(q)\neq{\hat{\mathbf{f}}}$
, hence
 $v({\circ }(p\Rightarrow q))={\hat{\mathbf{t}}}$
and
$v({\circ }(p\Rightarrow q))={\hat{\mathbf{t}}}$
and
 $v({\circ }(q\Rightarrow r))={\hat{\mathbf{t}}}$
, thus
$v({\circ }(q\Rightarrow r))={\hat{\mathbf{t}}}$
, thus
 $v(p)\leq v(q)\leq v(r)$
, and therefore
$v(p)\leq v(q)\leq v(r)$
, and therefore
 $v({\circ }(p \Rightarrow r))={\hat{\mathbf{t}}}$
.
$v({\circ }(p \Rightarrow r))={\hat{\mathbf{t}}}$
. $\textsf{r}^\Diamond _{\leq{\mathbf{t}}}$
: If
$\textsf{r}^\Diamond _{\leq{\mathbf{t}}}$
: If
 $v({\downarrow } p)\notin D$
, then
$v({\downarrow } p)\notin D$
, then
 $v(p)={\mathbf{t}}$
. If
$v(p)={\mathbf{t}}$
. If
 $v({\circ } q)\notin D$
, then
$v({\circ } q)\notin D$
, then
 ${\mathbf{f}}\leq v(q)\leq{\mathbf{t}}$
and therefore
${\mathbf{f}}\leq v(q)\leq{\mathbf{t}}$
and therefore
 $v({\circ }(q\Rightarrow p))={\hat{\mathbf{t}}}$
.
$v({\circ }(q\Rightarrow p))={\hat{\mathbf{t}}}$
. $\textsf{r}^\Diamond _{\geq{\mathbf{f}}}$
: If
$\textsf{r}^\Diamond _{\geq{\mathbf{f}}}$
: If
 $v({\uparrow } p)\notin D$
then
$v({\uparrow } p)\notin D$
then
 $v(p)={\mathbf{f}}$
and therefore
$v(p)={\mathbf{f}}$
and therefore
 $v({\circ }(p \Rightarrow q))={\hat{\mathbf{t}}}$
.
$v({\circ }(p \Rightarrow q))={\hat{\mathbf{t}}}$
. $\textsf{r}^\Diamond _{\textsf{incclass}_1}$
: If
$\textsf{r}^\Diamond _{\textsf{incclass}_1}$
: If
 $v({\uparrow } p)\in D$
and
$v({\uparrow } p)\in D$
and
 $v({\circ } p)\notin D$
then
$v({\circ } p)\notin D$
then
 $v(p)\in \{{\mathbf{b}},{\mathbf{n}},{\mathbf{t}}\}$
and if
$v(p)\in \{{\mathbf{b}},{\mathbf{n}},{\mathbf{t}}\}$
and if
 $v({\circ }(p\Rightarrow q))\in D$
then
$v({\circ }(p\Rightarrow q))\in D$
then
 $v(q)\in \{{\hat{\mathbf{f}}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}},{\hat{\mathbf{t}}} \}$
and therefore
$v(q)\in \{{\hat{\mathbf{f}}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}},{\hat{\mathbf{t}}} \}$
and therefore
 $v({\uparrow } q)={\hat{\mathbf{t}}}\in D$
.
$v({\uparrow } q)={\hat{\mathbf{t}}}\in D$
. $\textsf{r}^\Diamond _{\textsf{incclass}_2}$
: If
$\textsf{r}^\Diamond _{\textsf{incclass}_2}$
: If
 $v({\downarrow } q)\in D$
and
$v({\downarrow } q)\in D$
and
 $v({\circ } q)\notin D$
then
$v({\circ } q)\notin D$
then
 $v(q)\in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}}\}$
and if
$v(q)\in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}}\}$
and if
 $v({\circ }(p \Rightarrow q))\in D$
then
$v({\circ }(p \Rightarrow q))\in D$
then
 $v(p)\in \{{\hat{\mathbf{f}}},{\mathbf{f}},{\mathbf{b}},{\mathbf{n}}\}$
and therefore
$v(p)\in \{{\hat{\mathbf{f}}},{\mathbf{f}},{\mathbf{b}},{\mathbf{n}}\}$
and therefore
 $v({\downarrow } p)={\hat{\mathbf{t}}}\in D$
.
$v({\downarrow } p)={\hat{\mathbf{t}}}\in D$
. $\textsf{r}^\Diamond _{\textsf{incclass}_3}$
: If
$\textsf{r}^\Diamond _{\textsf{incclass}_3}$
: If
 $v({\uparrow } p),v({\downarrow } q)\in D$
and
$v({\uparrow } p),v({\downarrow } q)\in D$
and
 $v({\circ } q)\notin D$
then
$v({\circ } q)\notin D$
then
 $v(p) \neq{\mathbf{f}}$
and
$v(p) \neq{\mathbf{f}}$
and
 $v(q)\in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}}\}$
. Further, if
$v(q)\in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}}\}$
. Further, if
 $v({\circ }(p \Rightarrow q))\in D$
then
$v({\circ }(p \Rightarrow q))\in D$
then
 $v(p) \leq v(q)$
and so
$v(p) \leq v(q)$
and so
 $v(q \Rightarrow p)\in D$
.
$v(q \Rightarrow p)\in D$
. $\textsf{r}^\Diamond _{\textsf{just}_2}$
: If
$\textsf{r}^\Diamond _{\textsf{just}_2}$
: If
 $v({\downarrow } p), v({\uparrow } r)\in D$
and
$v({\downarrow } p), v({\uparrow } r)\in D$
and
 $v({\circ } p)\notin D$
then
$v({\circ } p)\notin D$
then
 $v(p)\in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}}\}$
and
$v(p)\in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}}\}$
and
 $v(r) \neq{\mathbf{f}}$
. If
$v(r) \neq{\mathbf{f}}$
. If
 $v({\circ }(p \Rightarrow q)),v({\circ }(p \Rightarrow q)) \not \in D$
, then
$v({\circ }(p \Rightarrow q)),v({\circ }(p \Rightarrow q)) \not \in D$
, then
 $v(p \Rightarrow q), v(q \Rightarrow r) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}}\}$
. Then
$v(p \Rightarrow q), v(q \Rightarrow r) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}}\}$
. Then
 $v(p), v(q),v(r) \in \{{\mathbf{b}},{\mathbf{n}} \}$
. Hence, either
$v(p), v(q),v(r) \in \{{\mathbf{b}},{\mathbf{n}} \}$
. Hence, either
 $v(p)=v(q)$
, in which case
$v(p)=v(q)$
, in which case
 $v(p\Rightarrow q)={\hat{\mathbf{t}}}\in D$
, or
$v(p\Rightarrow q)={\hat{\mathbf{t}}}\in D$
, or
 $v(q)=v(r)$
, in which case
$v(q)=v(r)$
, in which case
 $v(q \Rightarrow r)={\hat{\mathbf{t}}}\in D$
(both cases contradicting the assumptions) or
$v(q \Rightarrow r)={\hat{\mathbf{t}}}\in D$
(both cases contradicting the assumptions) or
 $v(p)=v(r)$
, in which case
$v(p)=v(r)$
, in which case
 $v(p \Rightarrow r)={\hat{\mathbf{t}}}\in D$
, as desired.
$v(p \Rightarrow r)={\hat{\mathbf{t}}}\in D$
, as desired.
Definition 43.
Let
![]() $\textsf{R}_{\Rightarrow }$
be the
$\textsf{R}_{\Rightarrow }$
be the ![]() calculus given by the following inference rules:
calculus given by the following inference rules:
Proposition 44.
The rules of
![]() $\textsf{R}_\Rightarrow$
are sound for any matrix
$\textsf{R}_\Rightarrow$
are sound for any matrix
![]() $\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, D \rangle$
with
$\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, D \rangle$
with
![]() $D ={{\uparrow }a}$
for some
$D ={{\uparrow }a}$
for some
![]() $a \gt{\hat{\mathbf{f}}}$
.
$a \gt{\hat{\mathbf{f}}}$
.
Proof. We proceed rule by rule.
 $\textsf{r}^{\Rightarrow }_{1}$
: If
$\textsf{r}^{\Rightarrow }_{1}$
: If
 $v({\circ } q)\in D$
then
$v({\circ } q)\in D$
then
 $v(q)\in \{{\hat{\mathbf{t}}},{\hat{\mathbf{f}}}\}$
, hence
$v(q)\in \{{\hat{\mathbf{t}}},{\hat{\mathbf{f}}}\}$
, hence
 $v({\circ } (p\Rightarrow q))\in D$
.
$v({\circ } (p\Rightarrow q))\in D$
. $\textsf{r}^{\Rightarrow }_{2}$
: If
$\textsf{r}^{\Rightarrow }_{2}$
: If
 $v(q)\in D$
, then
$v(q)\in D$
, then
 $v(q)\geq a$
and by analyzing the table of
$v(q)\geq a$
and by analyzing the table of
 $\Rightarrow _{\textsf{H}}$
we conclude that
$\Rightarrow _{\textsf{H}}$
we conclude that
 $v(p\Rightarrow q)\geq v(q)\geq a$
and thus
$v(p\Rightarrow q)\geq v(q)\geq a$
and thus
 $v(p \Rightarrow q)\in D$
.
$v(p \Rightarrow q)\in D$
. $\textsf{r}^{\Rightarrow }_{3}$
: If
$\textsf{r}^{\Rightarrow }_{3}$
: If
 $v(p),v(p\Rightarrow q)\in D$
then
$v(p),v(p\Rightarrow q)\in D$
then
 $v(p)\geq a$
and
$v(p)\geq a$
and
 $v(p\Rightarrow q)\geq a$
, and by analyzing the table of
$v(p\Rightarrow q)\geq a$
, and by analyzing the table of
 $\Rightarrow _{\textsf{H}}$
we conclude that
$\Rightarrow _{\textsf{H}}$
we conclude that
 $v(q)\geq a$
and thus
$v(q)\geq a$
and thus
 $v(q)\in D$
.
$v(q)\in D$
. $\textsf{r}^{\Rightarrow }_{4}$
: If
$\textsf{r}^{\Rightarrow }_{4}$
: If
 $v({\circ } p),v(p) \in D$
and
$v({\circ } p),v(p) \in D$
and
 $v({\circ } q) \not \in D$
, then
$v({\circ } q) \not \in D$
, then
 $v(p) ={\hat{\mathbf{t}}}$
and
$v(p) ={\hat{\mathbf{t}}}$
and
 $v(q) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
and
$v(q) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
and
 $v(p \Rightarrow q) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, so
$v(p \Rightarrow q) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, so
 $v({\circ }(p \Rightarrow q)) ={\hat{\mathbf{f}}} \not \in D$
.
$v({\circ }(p \Rightarrow q)) ={\hat{\mathbf{f}}} \not \in D$
. $\textsf{r}^{\Rightarrow }_{5}$
: If
$\textsf{r}^{\Rightarrow }_{5}$
: If
 $v({\circ } p),v(p) \in D$
and
$v({\circ } p),v(p) \in D$
and
 $v({\downarrow } q) \not \in D$
, then
$v({\downarrow } q) \not \in D$
, then
 $v(p) ={\hat{\mathbf{t}}}$
and
$v(p) ={\hat{\mathbf{t}}}$
and
 $v(q) ={\mathbf{t}}$
, thus
$v(q) ={\mathbf{t}}$
, thus
 $v(p \Rightarrow q) ={\mathbf{t}}$
and we are done.
$v(p \Rightarrow q) ={\mathbf{t}}$
and we are done. $\textsf{r}^{\Rightarrow }_{6}$
: If
$\textsf{r}^{\Rightarrow }_{6}$
: If
 $v({\circ } p),v(p) \in D$
and
$v({\circ } p),v(p) \in D$
and
 $v({\uparrow } q) \not \in D$
, then
$v({\uparrow } q) \not \in D$
, then
 $v(p) ={\hat{\mathbf{t}}}$
and
$v(p) ={\hat{\mathbf{t}}}$
and
 $v(q) ={\mathbf{f}}$
, thus
$v(q) ={\mathbf{f}}$
, thus
 $v(p \Rightarrow q) ={\mathbf{f}}$
and we are done.
$v(p \Rightarrow q) ={\mathbf{f}}$
and we are done. $\textsf{r}^{\Rightarrow }_{7}$
: If
$\textsf{r}^{\Rightarrow }_{7}$
: If
 $v({\uparrow } q) \in D$
, then
$v({\uparrow } q) \in D$
, then
 $v(q) \neq{\mathbf{f}}$
. But then
$v(q) \neq{\mathbf{f}}$
. But then
 $v(p \Rightarrow q) \neq{\mathbf{f}}$
, and
$v(p \Rightarrow q) \neq{\mathbf{f}}$
, and
 $v({\uparrow }(p \Rightarrow q)) ={\hat{\mathbf{t}}}$
.
$v({\uparrow }(p \Rightarrow q)) ={\hat{\mathbf{t}}}$
. $\textsf{r}^{\Rightarrow }_{8}$
: Similar to the proof for
$\textsf{r}^{\Rightarrow }_{8}$
: Similar to the proof for
 $\textsf{r}^{\Rightarrow }_{7}$
.
$\textsf{r}^{\Rightarrow }_{7}$
. $\textsf{r}^{\Rightarrow }_{9}$
: If
$\textsf{r}^{\Rightarrow }_{9}$
: If
 $v({\circ }(p \Rightarrow (q \Rightarrow p))) \not \in D$
, then
$v({\circ }(p \Rightarrow (q \Rightarrow p))) \not \in D$
, then
 $v(p \Rightarrow (q \Rightarrow p)) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. Then
$v(p \Rightarrow (q \Rightarrow p)) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. Then
 $v(p) \in \{{\mathbf{b}},{\mathbf{n}},{\mathbf{t}},{\hat{\mathbf{t}}} \}$
and
$v(p) \in \{{\mathbf{b}},{\mathbf{n}},{\mathbf{t}},{\hat{\mathbf{t}}} \}$
and
 $v(q \Rightarrow p) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. So,
$v(q \Rightarrow p) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. So,
 $v(q) \in \{{\mathbf{b}},{\mathbf{n}},{\mathbf{t}},{\hat{\mathbf{t}}} \}$
and
$v(q) \in \{{\mathbf{b}},{\mathbf{n}},{\mathbf{t}},{\hat{\mathbf{t}}} \}$
and
 $v(p) \in \{{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. If
$v(p) \in \{{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. If
 $v(p) ={\mathbf{b}}$
and
$v(p) ={\mathbf{b}}$
and
 $v(q \Rightarrow p) ={\mathbf{b}}$
, then
$v(q \Rightarrow p) ={\mathbf{b}}$
, then
 $v(p \Rightarrow (q \Rightarrow p)) ={\hat{\mathbf{t}}}$
. If
$v(p \Rightarrow (q \Rightarrow p)) ={\hat{\mathbf{t}}}$
. If
 $v(p) ={\mathbf{n}}$
, the proof is similar. If
$v(p) ={\mathbf{n}}$
, the proof is similar. If
 $v(p) ={\mathbf{t}}$
, then
$v(p) ={\mathbf{t}}$
, then
 $v(q \Rightarrow p) ={\hat{\mathbf{t}}}$
or
$v(q \Rightarrow p) ={\hat{\mathbf{t}}}$
or
 $v(q) ={\hat{\mathbf{t}}}$
. In all cases, we reach a contradiction.
$v(q) ={\hat{\mathbf{t}}}$
. In all cases, we reach a contradiction. $\textsf{r}^{\Rightarrow }_{10}$
,
$\textsf{r}^{\Rightarrow }_{10}$
,
 $\textsf{r}^{\Rightarrow }_{11}$
: If
$\textsf{r}^{\Rightarrow }_{11}$
: If
 $v(p),v({\circ } p)\notin D$
, then
$v(p),v({\circ } p)\notin D$
, then
 $v(p)={\hat{\mathbf{f}}}$
, thus
$v(p)={\hat{\mathbf{f}}}$
, thus
 $v(p\Rightarrow q)=v({\circ }(p\Rightarrow q))={\hat{\mathbf{t}}} \in D$
.
$v(p\Rightarrow q)=v({\circ }(p\Rightarrow q))={\hat{\mathbf{t}}} \in D$
. $\textsf{r}^{\Rightarrow }_{12}$
: If
$\textsf{r}^{\Rightarrow }_{12}$
: If
 $v({\circ } q) \in D$
and
$v({\circ } q) \in D$
and
 $v(q) \not \in D$
, then
$v(q) \not \in D$
, then
 $v(q) ={\hat{\mathbf{f}}}$
. If
$v(q) ={\hat{\mathbf{f}}}$
. If
 $v({\circ } p) \not \in D$
, then
$v({\circ } p) \not \in D$
, then
 $v(p) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. But then
$v(p) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. But then
 $v(p \Rightarrow q) ={\mathbf{f}} \not \in D$
.
$v(p \Rightarrow q) ={\mathbf{f}} \not \in D$
. $\textsf{r}^{\Rightarrow }_{13}$
: If
$\textsf{r}^{\Rightarrow }_{13}$
: If
 $v({\circ }(p \Rightarrow q)) \in D$
, then
$v({\circ }(p \Rightarrow q)) \in D$
, then
 $v(p \Rightarrow q) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
. Further, if
$v(p \Rightarrow q) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
. Further, if
 $v({\circ } q) \not \in D$
, then
$v({\circ } q) \not \in D$
, then
 $v(q) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, thus
$v(q) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, thus
 $v(p \Rightarrow q) ={\hat{\mathbf{t}}}$
.
$v(p \Rightarrow q) ={\hat{\mathbf{t}}}$
. $\textsf{r}^{\Rightarrow }_{14}$
: If
$\textsf{r}^{\Rightarrow }_{14}$
: If
 $v({\circ } p) \not \in D$
, then
$v({\circ } p) \not \in D$
, then
 $v(p) \in \{{\mathbf{b}},{\mathbf{n}},{\mathbf{t}}\}$
. If
$v(p) \in \{{\mathbf{b}},{\mathbf{n}},{\mathbf{t}}\}$
. If
 $v({\uparrow } q) \not \in D$
, then
$v({\uparrow } q) \not \in D$
, then
 $v(q) ={\mathbf{f}}$
. Thus
$v(q) ={\mathbf{f}}$
. Thus
 $v(p \Rightarrow q) \in \{{\mathbf{b}},{\mathbf{n}},{\mathbf{f}} \}$
, so
$v(p \Rightarrow q) \in \{{\mathbf{b}},{\mathbf{n}},{\mathbf{f}} \}$
, so
 $v({\circ }(p \Rightarrow q)) ={\hat{\mathbf{f}}}$
.
$v({\circ }(p \Rightarrow q)) ={\hat{\mathbf{f}}}$
. $\textsf{r}^{\Rightarrow }_{15}$
: If
$\textsf{r}^{\Rightarrow }_{15}$
: If
 $v({\circ } p) \not \in D$
, then
$v({\circ } p) \not \in D$
, then
 $v(p) \in \{{\mathbf{b}},{\mathbf{n}},{\mathbf{t}}\}$
. If
$v(p) \in \{{\mathbf{b}},{\mathbf{n}},{\mathbf{t}}\}$
. If
 $v({\uparrow } q) \not \in D$
, then
$v({\uparrow } q) \not \in D$
, then
 $v(q) ={\mathbf{f}}$
. Thus
$v(q) ={\mathbf{f}}$
. Thus
 $v(p \Rightarrow q) \in \{{\mathbf{b}},{\mathbf{n}},{\mathbf{f}} \}$
, so
$v(p \Rightarrow q) \in \{{\mathbf{b}},{\mathbf{n}},{\mathbf{f}} \}$
, so
 $v({\circ }(p \Rightarrow q)) ={\hat{\mathbf{f}}}$
.
$v({\circ }(p \Rightarrow q)) ={\hat{\mathbf{f}}}$
. $\textsf{r}^{\Rightarrow }_{16}$
: If
$\textsf{r}^{\Rightarrow }_{16}$
: If
 $v({\circ } p) \not \in D$
and
$v({\circ } p) \not \in D$
and
 $v({\downarrow } p) \in D$
, then
$v({\downarrow } p) \in D$
, then
 $v(p) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}} \}$
and
$v(p) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}} \}$
and
 $v(p \Rightarrow q) \neq{\mathbf{f}}$
, and thus
$v(p \Rightarrow q) \neq{\mathbf{f}}$
, and thus
 $v({\uparrow }(p \Rightarrow q)) ={\hat{\mathbf{t}}}$
.
$v({\uparrow }(p \Rightarrow q)) ={\hat{\mathbf{t}}}$
. $\textsf{r}^{\Rightarrow }_{17}$
: If
$\textsf{r}^{\Rightarrow }_{17}$
: If
 $v({\circ } p) \not \in D$
, then
$v({\circ } p) \not \in D$
, then
 $ v(p) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. Thus
$ v(p) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. Thus
 $v(p \Rightarrow q) \neq{\mathbf{t}}$
, and so
$v(p \Rightarrow q) \neq{\mathbf{t}}$
, and so
 $v({\downarrow }(p \Rightarrow q)) ={\hat{\mathbf{t}}}$
.
$v({\downarrow }(p \Rightarrow q)) ={\hat{\mathbf{t}}}$
. $\textsf{r}^{\Rightarrow }_{18}$
: If
$\textsf{r}^{\Rightarrow }_{18}$
: If
 $v({\uparrow } p) \in D$
and
$v({\uparrow } p) \in D$
and
 $v({\circ } p) \not \in D$
, then
$v({\circ } p) \not \in D$
, then
 $v(p) \in \{{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. If
$v(p) \in \{{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. If
 $v({\uparrow } q) \not \in D$
, then
$v({\uparrow } q) \not \in D$
, then
 $v(q) ={\mathbf{f}}$
. If
$v(q) ={\mathbf{f}}$
. If
 $v(p) ={\mathbf{b}}$
, then
$v(p) ={\mathbf{b}}$
, then
 $v(p \Rightarrow q) ={\mathbf{n}}$
, and then
$v(p \Rightarrow q) ={\mathbf{n}}$
, and then
 $v(p \Rightarrow (p \Rightarrow q)) ={\mathbf{n}}$
. Similarly, we have
$v(p \Rightarrow (p \Rightarrow q)) ={\mathbf{n}}$
. Similarly, we have
 $v(p \Rightarrow (p \Rightarrow q)) ={\mathbf{b}}$
if
$v(p \Rightarrow (p \Rightarrow q)) ={\mathbf{b}}$
if
 $v(p) ={\mathbf{n}}$
. If
$v(p) ={\mathbf{n}}$
. If
 $v(p) ={\mathbf{t}}$
, then
$v(p) ={\mathbf{t}}$
, then
 $v(p \Rightarrow q) ={\mathbf{f}}$
, and
$v(p \Rightarrow q) ={\mathbf{f}}$
, and
 $v(p \Rightarrow (p \Rightarrow q)) ={\mathbf{f}}$
. In any case,
$v(p \Rightarrow (p \Rightarrow q)) ={\mathbf{f}}$
. In any case,
 $v({\circ }(p \Rightarrow (p \Rightarrow q))) ={\hat{\mathbf{f}}}$
.
$v({\circ }(p \Rightarrow (p \Rightarrow q))) ={\hat{\mathbf{f}}}$
. $\textsf{r}^{\Rightarrow }_{19}$
: If
$\textsf{r}^{\Rightarrow }_{19}$
: If
 $v({\circ }(p \Rightarrow q)) \not \in D$
, we have
$v({\circ }(p \Rightarrow q)) \not \in D$
, we have
 $v(p \Rightarrow q) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. If
$v(p \Rightarrow q) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. If
 $v({\uparrow } q) \in D$
, we have
$v({\uparrow } q) \in D$
, we have
 $v(q) \neq{\mathbf{f}}$
. The case
$v(q) \neq{\mathbf{f}}$
. The case
 $v(p \Rightarrow q) ={\mathbf{f}}$
is impossible. If
$v(p \Rightarrow q) ={\mathbf{f}}$
is impossible. If
 $v(p \Rightarrow q) ={\mathbf{b}}$
, we have
$v(p \Rightarrow q) ={\mathbf{b}}$
, we have
 $v(q) ={\mathbf{b}}$
, and clearly
$v(q) ={\mathbf{b}}$
, and clearly
 $v({\circ }((p \Rightarrow q) \Rightarrow q)) ={\hat{\mathbf{t}}}$
. The case
$v({\circ }((p \Rightarrow q) \Rightarrow q)) ={\hat{\mathbf{t}}}$
. The case
 $v(p \Rightarrow q) ={\mathbf{n}}$
is similar to the previous case. If
$v(p \Rightarrow q) ={\mathbf{n}}$
is similar to the previous case. If
 $v(p \Rightarrow q) ={\mathbf{t}}$
, then
$v(p \Rightarrow q) ={\mathbf{t}}$
, then
 $v(p) ={\hat{\mathbf{t}}}$
, thus
$v(p) ={\hat{\mathbf{t}}}$
, thus
 $v({\circ }((p \Rightarrow q) \Rightarrow q)) ={\hat{\mathbf{t}}}$
.
$v({\circ }((p \Rightarrow q) \Rightarrow q)) ={\hat{\mathbf{t}}}$
.
Definition 45.
Let
![]() $\textsf{R}_{{\sim }}$
be the
$\textsf{R}_{{\sim }}$
be the ![]() calculus given by the following inference rules:
calculus given by the following inference rules:
Proposition 46.
The rules of
![]() $\textsf{R}_{\sim }$
are sound for any matrix
$\textsf{R}_{\sim }$
are sound for any matrix
![]() $\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, D \rangle$
with
$\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, D \rangle$
with
![]() $D ={{\uparrow }a}$
for some
$D ={{\uparrow }a}$
for some
![]() $a\gt{\hat{\mathbf{f}}}$
.
$a\gt{\hat{\mathbf{f}}}$
.
Proof. We proceed rule by rule.
 $\textsf{r}^{\sim }_1$
: If
$\textsf{r}^{\sim }_1$
: If
 $v({\circ } p)\in D$
and
$v({\circ } p)\in D$
and
 $v(p)\notin D$
then
$v(p)\notin D$
then
 $v(p)={\hat{\mathbf{f}}}$
and
$v(p)={\hat{\mathbf{f}}}$
and
 $v({\sim } p)={\hat{\mathbf{t}}}\in D$
.
$v({\sim } p)={\hat{\mathbf{t}}}\in D$
. $\textsf{r}^{\sim }_2$
: If
$\textsf{r}^{\sim }_2$
: If
 $v(p),v({\circ } p)\in D$
then
$v(p),v({\circ } p)\in D$
then
 $v(p)={\hat{\mathbf{t}}}$
and
$v(p)={\hat{\mathbf{t}}}$
and
 $v({\sim } p)={\hat{\mathbf{f}}}\notin D$
.
$v({\sim } p)={\hat{\mathbf{f}}}\notin D$
. $\textsf{r}^{\sim }_3$
: If
$\textsf{r}^{\sim }_3$
: If
 $v({\circ } p)\in D$
then
$v({\circ } p)\in D$
then
 $v(p),v({\sim } p)\in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}}\}$
and so
$v(p),v({\sim } p)\in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}}\}$
and so
 $v({\circ }{\sim } p) ={\hat{\mathbf{t}}}\in D$
.
$v({\circ }{\sim } p) ={\hat{\mathbf{t}}}\in D$
. $\textsf{r}^{\sim }_4$
: If
$\textsf{r}^{\sim }_4$
: If
 $v({\circ }{\sim } p)\in D$
then
$v({\circ }{\sim } p)\in D$
then
 $v({\sim } p),v( p)\in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}}\}$
and so
$v({\sim } p),v( p)\in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}}\}$
and so
 $v({\circ } p) ={\hat{\mathbf{t}}}\in D$
.
$v({\circ } p) ={\hat{\mathbf{t}}}\in D$
. ${\textsf{r}^{\sim }_5}$
: If
${\textsf{r}^{\sim }_5}$
: If
 $v({\downarrow } p)\notin D$
then
$v({\downarrow } p)\notin D$
then
 $v(p)={\mathbf{t}}$
, so
$v(p)={\mathbf{t}}$
, so
 $v({\sim } p)={\mathbf{f}}$
and hence
$v({\sim } p)={\mathbf{f}}$
and hence
 $v({\uparrow }{\sim } p)={\hat{\mathbf{f}}}\notin D$
.
$v({\uparrow }{\sim } p)={\hat{\mathbf{f}}}\notin D$
. $\textsf{r}^{\sim }_6$
: If
$\textsf{r}^{\sim }_6$
: If
 $v({\uparrow } p)\notin D$
then
$v({\uparrow } p)\notin D$
then
 $v(p)={\mathbf{f}}$
, so
$v(p)={\mathbf{f}}$
, so
 $v({\sim } p)={\mathbf{t}}$
and hence
$v({\sim } p)={\mathbf{t}}$
and hence
 $v({\downarrow }{\sim } p)={\hat{\mathbf{f}}}\notin D$
.
$v({\downarrow }{\sim } p)={\hat{\mathbf{f}}}\notin D$
. $\textsf{r}^{\sim }_7$
: If
$\textsf{r}^{\sim }_7$
: If
 $v({\downarrow } p)\in D$
then
$v({\downarrow } p)\in D$
then
 $v(p)\neq{\mathbf{t}}$
, hence
$v(p)\neq{\mathbf{t}}$
, hence
 $v({\sim } p)\neq{\mathbf{f}}$
and so
$v({\sim } p)\neq{\mathbf{f}}$
and so
 $v({\uparrow }{\sim } p)={\hat{\mathbf{t}}}\in D$
.
$v({\uparrow }{\sim } p)={\hat{\mathbf{t}}}\in D$
. $\textsf{r}^{\sim }_8$
: If
$\textsf{r}^{\sim }_8$
: If
 $v({\uparrow } p)\in D$
then
$v({\uparrow } p)\in D$
then
 $v(p)\neq{\mathbf{f}}$
, hence
$v(p)\neq{\mathbf{f}}$
, hence
 $v({\sim } p)\neq{\mathbf{t}}$
and so
$v({\sim } p)\neq{\mathbf{t}}$
and so
 $v({\downarrow }{\sim } p)={\hat{\mathbf{t}}}\in D$
.
$v({\downarrow }{\sim } p)={\hat{\mathbf{t}}}\in D$
.
Definition 47.
Let
![]() $\textsf{R}_{{\circ }}$
be the
$\textsf{R}_{{\circ }}$
be the ![]() calculus given by the following inference rule:
calculus given by the following inference rule:
Proposition 48.
The rules of
![]() $\textsf{R}_{\circ }$
are sound for any matrix
$\textsf{R}_{\circ }$
are sound for any matrix
![]() $\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, D \rangle$
with
$\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, D \rangle$
with
![]() ${\hat{\mathbf{t}}} \in D$
.
${\hat{\mathbf{t}}} \in D$
.
Proof.
Easily,
![]() $v({\circ}{\circ} p)={\hat{\mathbf{t}}}\in D$
.
$v({\circ}{\circ} p)={\hat{\mathbf{t}}}\in D$
.
Definition 49.
Let
![]() $\textsf{R}_{\land }$
be the
$\textsf{R}_{\land }$
be the ![]() calculus given by the following inference rules:
calculus given by the following inference rules:
Proposition 50.
The rules of
![]() $\textsf{R}_\land$
are sound for any matrix
$\textsf{R}_\land$
are sound for any matrix
![]() $\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, D \rangle$
with
$\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, D \rangle$
with
![]() $D ={{\uparrow }a}$
for some
$D ={{\uparrow }a}$
for some
![]() $a\gt{\hat{\mathbf{f}}}$
.
$a\gt{\hat{\mathbf{f}}}$
.
Proof. We proceed rule by rule:
 $\textsf{r}^{\land }_{1}$
: If
$\textsf{r}^{\land }_{1}$
: If
 $v({\circ } p), v({\circ } q) \in D$
, then
$v({\circ } p), v({\circ } q) \in D$
, then
 $v(p),v(q) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
, thus
$v(p),v(q) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
, thus
 $v(p \land q) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
, and
$v(p \land q) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
, and
 $v({\circ }(p \land q)) ={\hat{\mathbf{t}}}$
.
$v({\circ }(p \land q)) ={\hat{\mathbf{t}}}$
. $\textsf{r}^{\land }_{2}$
: Soundness follows from the fact that principal filters are closed under meets.
$\textsf{r}^{\land }_{2}$
: Soundness follows from the fact that principal filters are closed under meets. $\textsf{r}^{\land }_{3}$
,
$\textsf{r}^{\land }_{3}$
,
 $\textsf{r}^{\land }_{7}$
: If
$\textsf{r}^{\land }_{7}$
: If
 $v(p\land q)\geq a$
, then from
$v(p\land q)\geq a$
, then from
 $v(p) \geq v(p\land q)$
and
$v(p) \geq v(p\land q)$
and
 $v(q)\geq v(p\land q)$
we have that
$v(q)\geq v(p\land q)$
we have that
 $v(p),v(q)\in D$
.
$v(p),v(q)\in D$
. $\textsf{r}^{\land }_{4}$
,
$\textsf{r}^{\land }_{4}$
,
 $\textsf{r}^{\land }_{8}$
: If
$\textsf{r}^{\land }_{8}$
: If
 $v({\circ } q) \not \in D$
, then
$v({\circ } q) \not \in D$
, then
 $v(q) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. If
$v(q) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. If
 $v({\circ }(p \land q)) \in D$
, then
$v({\circ }(p \land q)) \in D$
, then
 $v(p \land q) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
. Thus if
$v(p \land q) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
. Thus if
 $v(p \land q) ={\hat{\mathbf{t}}}$
, then
$v(p \land q) ={\hat{\mathbf{t}}}$
, then
 $v(p) = v(q) ={\hat{\mathbf{t}}}$
, absurd. Otherwise, we must have
$v(p) = v(q) ={\hat{\mathbf{t}}}$
, absurd. Otherwise, we must have
 $v(p) ={\hat{\mathbf{f}}}$
. The proof is analogous for the other rule.
$v(p) ={\hat{\mathbf{f}}}$
. The proof is analogous for the other rule. $\textsf{r}^{\land }_{5}$
,
$\textsf{r}^{\land }_{5}$
,
 $\textsf{r}^{\land }_{9}$
: If
$\textsf{r}^{\land }_{9}$
: If
 $v({\circ } p) \in D$
, then
$v({\circ } p) \in D$
, then
 $v(p) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
. Then either
$v(p) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
. Then either
 $v(q \Rightarrow (p \land q)) = v(q \Rightarrow q) ={\hat{\mathbf{t}}}$
or
$v(q \Rightarrow (p \land q)) = v(q \Rightarrow q) ={\hat{\mathbf{t}}}$
or
 $v(q \Rightarrow (p \land q)) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
. In both cases, we are done. The proof is analogous to the other rule.
$v(q \Rightarrow (p \land q)) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
. In both cases, we are done. The proof is analogous to the other rule. $\textsf{r}^{\land }_{6}$
,
$\textsf{r}^{\land }_{6}$
,
 $\textsf{r}^{\land }_{10}$
: We have that
$\textsf{r}^{\land }_{10}$
: We have that
 $v(p\land q)\leq v(p)$
and
$v(p\land q)\leq v(p)$
and
 $v(p\land q)\leq v(q)$
hence
$v(p\land q)\leq v(q)$
hence
 $v((p\land q)\Rightarrow q)=v({\circ }((p\land q)\Rightarrow q))=v((p\land q)\Rightarrow p)=v({\circ }((p\land q)\Rightarrow p))={\hat{\mathbf{t}}}\in D$
.
$v((p\land q)\Rightarrow q)=v({\circ }((p\land q)\Rightarrow q))=v((p\land q)\Rightarrow p)=v({\circ }((p\land q)\Rightarrow p))={\hat{\mathbf{t}}}\in D$
. $\textsf{r}^{\land }_{11}$
,
$\textsf{r}^{\land }_{11}$
,
 $\textsf{r}^{\land }_{12}$
: If
$\textsf{r}^{\land }_{12}$
: If
 $v({\circ } p)\in D$
and
$v({\circ } p)\in D$
and
 $v(p)\notin D$
, or
$v(p)\notin D$
, or
 $v({\circ } q)\in D$
and
$v({\circ } q)\in D$
and
 $v(q)\notin D$
, then either
$v(q)\notin D$
, then either
 $v(p)={\hat{\mathbf{f}}}$
or
$v(p)={\hat{\mathbf{f}}}$
or
 $v(q)={\hat{\mathbf{f}}}$
. In any case we have that
$v(q)={\hat{\mathbf{f}}}$
. In any case we have that
 $v(p\land q)={\hat{\mathbf{f}}}$
and
$v(p\land q)={\hat{\mathbf{f}}}$
and
 $v({\circ }(p\land q))={\hat{\mathbf{t}}}\in D$
.
$v({\circ }(p\land q))={\hat{\mathbf{t}}}\in D$
. $\textsf{r}^{\land }_{13}$
: If
$\textsf{r}^{\land }_{13}$
: If
 $v({\circ }(p \land q)) \in D$
, then
$v({\circ }(p \land q)) \in D$
, then
 $v(p \land q) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
. If
$v(p \land q) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
. If
 $v(p) = v(q) ={\hat{\mathbf{t}}}$
, clearly
$v(p) = v(q) ={\hat{\mathbf{t}}}$
, clearly
 $v({\circ } p) = v({\circ } q) ={\hat{\mathbf{t}}}$
. If
$v({\circ } p) = v({\circ } q) ={\hat{\mathbf{t}}}$
. If
 $v(p) ={\hat{\mathbf{f}}}$
, then
$v(p) ={\hat{\mathbf{f}}}$
, then
 $v({\circ } p) ={\hat{\mathbf{t}}}$
. Analogously if
$v({\circ } p) ={\hat{\mathbf{t}}}$
. Analogously if
 $v(q) ={\hat{\mathbf{f}}}$
.
$v(q) ={\hat{\mathbf{f}}}$
. $\textsf{r}^{\land }_{14}$
,
$\textsf{r}^{\land }_{14}$
,
 $\textsf{r}^{\land }_{15}$
: Suppose
$\textsf{r}^{\land }_{15}$
: Suppose
 ${\circ }(p\Rightarrow q)\in D$
. Then either
${\circ }(p\Rightarrow q)\in D$
. Then either
 $v(q)={\hat{\mathbf{f}}}$
, in which case
$v(q)={\hat{\mathbf{f}}}$
, in which case
 $v(p \Rightarrow (p \land q))\in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}}\}$
and thus
$v(p \Rightarrow (p \land q))\in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}}\}$
and thus
 $v({\circ }(p \Rightarrow (p\land q)))={\hat{\mathbf{t}}}\in D$
; or
$v({\circ }(p \Rightarrow (p\land q)))={\hat{\mathbf{t}}}\in D$
; or
 $v(p)\leq v(q)$
, and so
$v(p)\leq v(q)$
, and so
 $v(p\land q)=v(p)$
, hence
$v(p\land q)=v(p)$
, hence
 $v({\circ }(p\Rightarrow (p\land q)))={\hat{\mathbf{t}}}\in D$
. The proof for
$v({\circ }(p\Rightarrow (p\land q)))={\hat{\mathbf{t}}}\in D$
. The proof for
 $\textsf{r}^{\land }_{15}$
is similar.
$\textsf{r}^{\land }_{15}$
is similar. $\textsf{r}^{\land }_{16}$
: If
$\textsf{r}^{\land }_{16}$
: If
 $v({\circ } p) \not \in D$
and
$v({\circ } p) \not \in D$
and
 $v({\downarrow } p) \in D$
, then
$v({\downarrow } p) \in D$
, then
 $v(p) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}} \}$
. If
$v(p) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}} \}$
. If
 $v({\uparrow }(p \land q)) \in D$
, then
$v({\uparrow }(p \land q)) \in D$
, then
 $v(p \land q) \neq{\mathbf{f}}$
. We may safely focus on cases in which
$v(p \land q) \neq{\mathbf{f}}$
. We may safely focus on cases in which
 $v(p) \neq v(q)$
. If
$v(p) \neq v(q)$
. If
 $v(p) ={\mathbf{f}}$
, then
$v(p) ={\mathbf{f}}$
, then
 $v(p \Rightarrow q) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
. If
$v(p \Rightarrow q) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
. If
 $v(p) ={\mathbf{b}}$
, we have
$v(p) ={\mathbf{b}}$
, we have
 $v(q) \not \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}}\}$
from the above assumptions, and this gives
$v(q) \not \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}}\}$
from the above assumptions, and this gives
 $v(p \Rightarrow q) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
. Similarly if
$v(p \Rightarrow q) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
. Similarly if
 $v(p) ={\mathbf{n}}$
.
$v(p) ={\mathbf{n}}$
.
Definition 51.
Let
![]() $\textsf{R}_{\lor }$
be the
$\textsf{R}_{\lor }$
be the ![]() calculus given by the following inference rules:
calculus given by the following inference rules:
Proposition 52.
The rules of
![]() $\textsf{R}_\lor$
are sound for any matrix
$\textsf{R}_\lor$
are sound for any matrix
![]() $\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, D \rangle$
with
$\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, D \rangle$
with
![]() $D ={{\uparrow }a}$
for some
$D ={{\uparrow }a}$
for some
![]() $a\gt{\hat{\mathbf{f}}}$
.
$a\gt{\hat{\mathbf{f}}}$
.
Proof. We proceed rule by rule.
 $\textsf{r}_1^\lor$
: If
$\textsf{r}_1^\lor$
: If
 $v({\circ } p), v({\circ } q) \in D$
, then
$v({\circ } p), v({\circ } q) \in D$
, then
 $v(p), v(q) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
, thus
$v(p), v(q) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
, thus
 $v(p \lor q) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
, and we are done.
$v(p \lor q) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
, and we are done. $\textsf{r}_2^\lor$
: If
$\textsf{r}_2^\lor$
: If
 $v({\circ } p) \in D$
and
$v({\circ } p) \in D$
and
 $v(p) \not \in D$
,
$v(p) \not \in D$
,
 $v(p) ={\hat{\mathbf{f}}}$
. Then
$v(p) ={\hat{\mathbf{f}}}$
. Then
 $v(p \lor q) = v(q)$
and we are done.
$v(p \lor q) = v(q)$
and we are done. $\textsf{r}_3^\lor$
,
$\textsf{r}_3^\lor$
,
 $\textsf{r}_7^\lor$
: As
$\textsf{r}_7^\lor$
: As
 $v(q) \leq v(p \lor q)$
, if
$v(q) \leq v(p \lor q)$
, if
 $v(q) \in D$
, then
$v(q) \in D$
, then
 $v(p \lor q) \in D$
. Similarly for the other rule.
$v(p \lor q) \in D$
. Similarly for the other rule. $\textsf{r}_4^\lor$
,
$\textsf{r}_4^\lor$
,
 $\textsf{r}_8^\lor$
: If
$\textsf{r}_8^\lor$
: If
 $v({\circ }(p \lor q)) \in D$
, then
$v({\circ }(p \lor q)) \in D$
, then
 $v(p \lor q) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
. If
$v(p \lor q) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
. If
 $v({\circ } q) \not \in D$
,
$v({\circ } q) \not \in D$
,
 $v(q) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. Then
$v(q) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. Then
 $v(p) ={\hat{\mathbf{t}}}$
. Similarly for the other rule.
$v(p) ={\hat{\mathbf{t}}}$
. Similarly for the other rule. $\textsf{r}_5^\lor$
,
$\textsf{r}_5^\lor$
,
 $\textsf{r}_9^\lor$
: We have that
$\textsf{r}_9^\lor$
: We have that
 $v(p\lor q)\geq v(p)$
and
$v(p\lor q)\geq v(p)$
and
 $v(p\lor q)\geq v(q)$
, hence
$v(p\lor q)\geq v(q)$
, hence
 $v(q\Rightarrow (p\lor q))= v({\circ }(q\Rightarrow (p\lor q)))=v(p\Rightarrow (p\lor q))= v({\circ }(p\Rightarrow (p\lor q)))={\hat{\mathbf{t}}} \in D$
.
$v(q\Rightarrow (p\lor q))= v({\circ }(q\Rightarrow (p\lor q)))=v(p\Rightarrow (p\lor q))= v({\circ }(p\Rightarrow (p\lor q)))={\hat{\mathbf{t}}} \in D$
. $\textsf{r}_{6}^\lor$
,
$\textsf{r}_{6}^\lor$
,
 $\textsf{r}_{10}^\lor$
: If
$\textsf{r}_{10}^\lor$
: If
 $v({\circ } p)\in D$
and
$v({\circ } p)\in D$
and
 $v(p)\notin D$
then
$v(p)\notin D$
then
 $v(p)={\hat{\mathbf{f}}}$
and
$v(p)={\hat{\mathbf{f}}}$
and
 $v(p\lor q)=v(q)$
, so
$v(p\lor q)=v(q)$
, so
 $v((p\lor q)\Rightarrow q) ={\hat{\mathbf{t}}}$
. Similarly if
$v((p\lor q)\Rightarrow q) ={\hat{\mathbf{t}}}$
. Similarly if
 $v({\circ } q)\in D$
and
$v({\circ } q)\in D$
and
 $v(q)\notin D$
.
$v(q)\notin D$
. $\textsf{r}_{11}^\lor$
,
$\textsf{r}_{11}^\lor$
,
 $\textsf{r}_{12}^\lor$
: If
$\textsf{r}_{12}^\lor$
: If
 $v(p),v({\circ } p)\in D$
, or
$v(p),v({\circ } p)\in D$
, or
 $v(q),v({\circ } q)\in D$
, then either
$v(q),v({\circ } q)\in D$
, then either
 $v(p)={\hat{\mathbf{t}}}$
or
$v(p)={\hat{\mathbf{t}}}$
or
 $v(q)={\hat{\mathbf{t}}}$
. In any case we have that
$v(q)={\hat{\mathbf{t}}}$
. In any case we have that
 $v(p\lor q)=v({\circ }(p\lor q))={\hat{\mathbf{t}}}\in D$
.
$v(p\lor q)=v({\circ }(p\lor q))={\hat{\mathbf{t}}}\in D$
. $\textsf{r}_{13}^\lor$
: If
$\textsf{r}_{13}^\lor$
: If
 $v({\circ } p),v({\circ } q) \not \in D$
, we have
$v({\circ } p),v({\circ } q) \not \in D$
, we have
 $v(p),v(q) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, thus
$v(p),v(q) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, thus
 $v(p \lor q) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, and
$v(p \lor q) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, and
 $v({\circ }(p \lor q)) \not \in D$
.
$v({\circ }(p \lor q)) \not \in D$
. $\textsf{r}_{14}^\lor$
,
$\textsf{r}_{14}^\lor$
,
 $\textsf{r}_{15}^\lor$
: Suppose
$\textsf{r}_{15}^\lor$
: Suppose
 ${\circ }(p\Rightarrow q)\in D$
. Then either
${\circ }(p\Rightarrow q)\in D$
. Then either
 $v(q)={\hat{\mathbf{f}}}$
, in which case
$v(q)={\hat{\mathbf{f}}}$
, in which case
 $v((p\lor q)\Rightarrow q)\in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}}\}$
and thus
$v((p\lor q)\Rightarrow q)\in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}}\}$
and thus
 $v({\circ }((p\lor q)\Rightarrow q))={\hat{\mathbf{t}}}\in D$
; or
$v({\circ }((p\lor q)\Rightarrow q))={\hat{\mathbf{t}}}\in D$
; or
 $v(p)\leq v(q)$
, so
$v(p)\leq v(q)$
, so
 $v(p\lor q)=v(q)$
, hence
$v(p\lor q)=v(q)$
, hence
 $v({\circ }((p\lor q)\Rightarrow q))={\hat{\mathbf{t}}}\in D$
. The proof for
$v({\circ }((p\lor q)\Rightarrow q))={\hat{\mathbf{t}}}\in D$
. The proof for
 $\textsf{r}_{15}^\lor$
is similar.
$\textsf{r}_{15}^\lor$
is similar. $\textsf{r}_{16}^\lor$
: If
$\textsf{r}_{16}^\lor$
: If
 $v({\circ } p) \not \in D$
and
$v({\circ } p) \not \in D$
and
 $v({\uparrow } q) \in D$
,
$v({\uparrow } q) \in D$
,
 $v(p) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
and
$v(p) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
and
 $v(q) \neq{\mathbf{f}}$
. If
$v(q) \neq{\mathbf{f}}$
. If
 $v(p) = v(q)$
, we are done, so suppose
$v(p) = v(q)$
, we are done, so suppose
 $v(p) \neq v(q)$
. If
$v(p) \neq v(q)$
. If
 $v({\downarrow }(p \lor q)) \in D$
, then
$v({\downarrow }(p \lor q)) \in D$
, then
 $v(p \lor q) \neq{\mathbf{t}}$
. If
$v(p \lor q) \neq{\mathbf{t}}$
. If
 $v(p) ={\mathbf{f}}$
, then
$v(p) ={\mathbf{f}}$
, then
 $v(p \Rightarrow q) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
, and we are done. If
$v(p \Rightarrow q) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}} \}$
, and we are done. If
 $v(p) ={\mathbf{b}}$
, the only non-obvious case is
$v(p) ={\mathbf{b}}$
, the only non-obvious case is
 $v(q) ={\mathbf{n}}$
, but this is impossible as
$v(q) ={\mathbf{n}}$
, but this is impossible as
 $v(p \lor q) \neq{\mathbf{t}}$
. If
$v(p \lor q) \neq{\mathbf{t}}$
. If
 $v(p) ={\mathbf{n}}$
, the proof is similar to the previous case. If
$v(p) ={\mathbf{n}}$
, the proof is similar to the previous case. If
 $v(p) ={\mathbf{t}}$
, the only non-obvious cases are those in which
$v(p) ={\mathbf{t}}$
, the only non-obvious cases are those in which
 $v(q) \in \{{\mathbf{b}},{\mathbf{n}} \}$
; yet they are impossible, again, because
$v(q) \in \{{\mathbf{b}},{\mathbf{n}} \}$
; yet they are impossible, again, because
 $v(p \lor q) \neq{\mathbf{t}}$
.
$v(p \lor q) \neq{\mathbf{t}}$
.
Definition 53.
Let
![]() $\textsf{R}_{\bot \top }$
be the
$\textsf{R}_{\bot \top }$
be the ![]() calculus given by the following inference rules:
calculus given by the following inference rules:
Proposition 54.
The rules of
![]() $\textsf{R}_{\top \bot }$
are sound for any matrix
$\textsf{R}_{\top \bot }$
are sound for any matrix
![]() $\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, D \rangle$
with
$\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, D \rangle$
with
![]() $D ={{\uparrow }a}$
for some
$D ={{\uparrow }a}$
for some
![]() $a\gt{\hat{\mathbf{f}}}$
.
$a\gt{\hat{\mathbf{f}}}$
.
Proof. Obvious.
The final rules we introduce encode the differences between the logics
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
and
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
and
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
.
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
.
Definition 55. Consider the following inference rules:
Proposition 56.
In the matrix
![]() $\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, D \rangle$
: (i) the rules
$\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, D \rangle$
: (i) the rules
![]() $\textsf{r}_{D_\land }$
and
$\textsf{r}_{D_\land }$
and
![]() $\textsf{r}_{D_\leq }$
are sound when
$\textsf{r}_{D_\leq }$
are sound when
![]() $D={\uparrow } a$
for
$D={\uparrow } a$
for
![]() $a\gt{\hat{\mathbf{f}}}$
; (ii) the rule
$a\gt{\hat{\mathbf{f}}}$
; (ii) the rule
![]() $\textsf{r}_{D\neq{\uparrow }{\mathbf{t}}}$
is sound when
$\textsf{r}_{D\neq{\uparrow }{\mathbf{t}}}$
is sound when
![]() $D$
is a prime filter; (iii) the rule
$D$
is a prime filter; (iii) the rule
![]() $\textsf{r}_{D\neq{\uparrow }{\mathbf{t}}}$
is not sound when
$\textsf{r}_{D\neq{\uparrow }{\mathbf{t}}}$
is not sound when
![]() $D ={\uparrow }{\mathbf{t}}$
.
$D ={\uparrow }{\mathbf{t}}$
.
Proof. We first check items (i) and (ii):
 $\textsf{r}_{D_\land }$
: If
$\textsf{r}_{D_\land }$
: If
 $v({\circ }(p \Rightarrow q)) \not \in D$
, then
$v({\circ }(p \Rightarrow q)) \not \in D$
, then
 $v(p \Rightarrow q) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. From that and the assumption that
$v(p \Rightarrow q) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. From that and the assumption that
 $v({\circ } p) \not \in D$
and
$v({\circ } p) \not \in D$
and
 $v({\downarrow } p) \in D$
, we have
$v({\downarrow } p) \in D$
, we have
 $v(p) \in \{{\mathbf{b}},{\mathbf{n}} \}$
. Also, we obtain
$v(p) \in \{{\mathbf{b}},{\mathbf{n}} \}$
. Also, we obtain
 $v(q) \in \{{\mathbf{f}},{\mathbf{n}},{\mathbf{b}} \}$
. Suppose
$v(q) \in \{{\mathbf{f}},{\mathbf{n}},{\mathbf{b}} \}$
. Suppose
 $v(p),v(q) \in D$
. If
$v(p),v(q) \in D$
. If
 $v(q) ={\mathbf{f}}$
, then
$v(q) ={\mathbf{f}}$
, then
 $D ={\uparrow }{\mathbf{f}}$
, and supposing
$D ={\uparrow }{\mathbf{f}}$
, and supposing
 $v({\circ } r) \not \in D$
, we have
$v({\circ } r) \not \in D$
, we have
 $v(r) \in D$
. If
$v(r) \in D$
. If
 $v(q) ={\mathbf{b}}$
, we must have
$v(q) ={\mathbf{b}}$
, we must have
 $v(p) ={\mathbf{n}}$
. Then again
$v(p) ={\mathbf{n}}$
. Then again
 $D ={\uparrow }{\mathbf{f}}$
, for the same reason as before. The case of
$D ={\uparrow }{\mathbf{f}}$
, for the same reason as before. The case of
 $v(q) ={\mathbf{n}}$
is analogous.
$v(q) ={\mathbf{n}}$
is analogous. $\textsf{r}_{D_\leq }$
: If
$\textsf{r}_{D_\leq }$
: If
 $v({\circ }(p\Rightarrow q)) \in D, v(p)\geq a$
and
$v({\circ }(p\Rightarrow q)) \in D, v(p)\geq a$
and
 $v(\circ q) \lt a$
, then
$v(\circ q) \lt a$
, then
 $v({\circ }(p\Rightarrow q))={\hat{\mathbf{t}}}$
.
$v({\circ }(p\Rightarrow q))={\hat{\mathbf{t}}}$
. $\textsf{r}_{D\neq{\uparrow }{\mathbf{t}}}$
: If
$\textsf{r}_{D\neq{\uparrow }{\mathbf{t}}}$
: If
 $v({\downarrow } r) \not \in D$
, we have
$v({\downarrow } r) \not \in D$
, we have
 $v(r) ={\mathbf{t}}$
. If
$v(r) ={\mathbf{t}}$
. If
 $v({\uparrow } q) \in D$
, we have
$v({\uparrow } q) \in D$
, we have
 $v(q) \neq{\mathbf{f}}$
. If
$v(q) \neq{\mathbf{f}}$
. If
 $v({\circ }(p \Rightarrow q)) \not \in D$
, we have
$v({\circ }(p \Rightarrow q)) \not \in D$
, we have
 $v(p \Rightarrow q) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. This gives
$v(p \Rightarrow q) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. This gives
 $v(p) \in \{{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
and
$v(p) \in \{{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
and
 $v(q) \in \{{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. We only consider the cases
$v(q) \in \{{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. We only consider the cases
 $v(p) \neq v(q)$
. If
$v(p) \neq v(q)$
. If
 $v(p) ={\mathbf{b}}$
, then
$v(p) ={\mathbf{b}}$
, then
 $v(q) ={\mathbf{n}}$
, and supposing
$v(q) ={\mathbf{n}}$
, and supposing
 $v(p),v(q) \not \in D$
, given that
$v(p),v(q) \not \in D$
, given that
 $D$
is prime we must have
$D$
is prime we must have
 $D ={\uparrow }{\hat{\mathbf{t}}}$
, and
$D ={\uparrow }{\hat{\mathbf{t}}}$
, and
 $v(r) \not \in D$
. If
$v(r) \not \in D$
. If
 $v(p) ={\mathbf{n}}$
, the proof is similar to the previous case. If
$v(p) ={\mathbf{n}}$
, the proof is similar to the previous case. If
 $v(p) ={\mathbf{t}}$
, again we have
$v(p) ={\mathbf{t}}$
, again we have
 $D ={\uparrow }{\hat{\mathbf{t}}}$
, and we are done.
$D ={\uparrow }{\hat{\mathbf{t}}}$
, and we are done.
For item (iii), a valuation
![]() $v$
such that
$v$
such that
![]() $v(r) ={\mathbf{t}}$
,
$v(r) ={\mathbf{t}}$
,
![]() $v(p) ={\mathbf{n}}$
and
$v(p) ={\mathbf{n}}$
and
![]() $v(q) ={\mathbf{b}}$
shows that
$v(q) ={\mathbf{b}}$
shows that
![]() $\textsf{r}_{D\neq{\uparrow }{\mathbf{t}}}$
is not sound when
$\textsf{r}_{D\neq{\uparrow }{\mathbf{t}}}$
is not sound when
![]() $D ={\uparrow }{\mathbf{t}}$
.
$D ={\uparrow }{\mathbf{t}}$
.
We are ready to define our ![]() axiomatizations and prove the desired completeness results.
axiomatizations and prove the desired completeness results.
Definition 57. Using the previous definitions, we set the two following collection of rules:
-
1.
 $\textsf{R}_{\textsf{up}} \,{:=}\,\textsf{R}_\Diamond \cup \textsf{R}_D\cup \textsf{R}_\Rightarrow \cup \textsf{R}_{\circ }\cup \textsf{R}_{\sim } \cup \textsf{R}_\land \cup \textsf{R}_\lor \cup \textsf{R}_{\top \bot } \cup \{\textsf{r}_{D_\land },\textsf{r}_{D_\leq }\}$
;
$\textsf{R}_{\textsf{up}} \,{:=}\,\textsf{R}_\Diamond \cup \textsf{R}_D\cup \textsf{R}_\Rightarrow \cup \textsf{R}_{\circ }\cup \textsf{R}_{\sim } \cup \textsf{R}_\land \cup \textsf{R}_\lor \cup \textsf{R}_{\top \bot } \cup \{\textsf{r}_{D_\land },\textsf{r}_{D_\leq }\}$
; -
2.
 $\textsf{R}_{\leq }\,{:=}\,\textsf{R}_{\textsf{up}} \cup \{\textsf{r}_{D\neq{\uparrow }{\mathbf{t}}}\}$
.
$\textsf{R}_{\leq }\,{:=}\,\textsf{R}_{\textsf{up}} \cup \{\textsf{r}_{D\neq{\uparrow }{\mathbf{t}}}\}$
.
Theorem 58.
![]() $\textsf{R}_{\textsf{up}}$
axiomatizes
$\textsf{R}_{\textsf{up}}$
axiomatizes
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
and
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
and
![]() $\textsf{R}_{\leq }$
axiomatizes
$\textsf{R}_{\leq }$
axiomatizes
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
. Moreover, both
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
. Moreover, both
![]() $\textsf{R}_{\textsf{up}}$
and
$\textsf{R}_{\textsf{up}}$
and
![]() $\textsf{R}_{\leq }$
are
$\textsf{R}_{\leq }$
are
![]() $\Theta$
-analytic calculi, for
$\Theta$
-analytic calculi, for
![]() $\Theta \,{:=}\, \{p,{\circ } p,{\circ }(p\Rightarrow q),{\uparrow } p,{\downarrow } p\}$
.
$\Theta \,{:=}\, \{p,{\circ } p,{\circ }(p\Rightarrow q),{\uparrow } p,{\downarrow } p\}$
.
Proof.
From the previous propositions, it easily follows that
![]() $\rhd _{\textsf{R}_{\textsf{up}}}\subseteq{\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}}$
and
$\rhd _{\textsf{R}_{\textsf{up}}}\subseteq{\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}}$
and
![]() $\rhd _{\textsf{R}_{\leq }}\subseteq{\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }}$
, thus guaranteeing soundness of the proposed axiomatizations. To check completeness for
$\rhd _{\textsf{R}_{\leq }}\subseteq{\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }}$
, thus guaranteeing soundness of the proposed axiomatizations. To check completeness for
![]() $\textsf{R}\in \{\textsf{R}_{\textsf{up}},\textsf{R}_{\leq }\}$
we need to show that each consequence statement of the form
$\textsf{R}\in \{\textsf{R}_{\textsf{up}},\textsf{R}_{\leq }\}$
we need to show that each consequence statement of the form
![]() $\Phi \blacktriangleright_{\textsf{R}} \Psi$
is witnessed by some valuation and some principal filter over the algebra
$\Phi \blacktriangleright_{\textsf{R}} \Psi$
is witnessed by some valuation and some principal filter over the algebra
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
. Let
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
. Let
![]() $\Lambda \,{:=}\,{\textsf{sub}}(\Phi \cup \Psi )$
. Recall that from
$\Lambda \,{:=}\,{\textsf{sub}}(\Phi \cup \Psi )$
. Recall that from
![]() $\Phi \blacktriangleright_{\textsf{R}}\Psi$
, by cut for sets, there is a partition
$\Phi \blacktriangleright_{\textsf{R}}\Psi$
, by cut for sets, there is a partition
![]() $(\Omega, \overline{\Omega })$
of
$(\Omega, \overline{\Omega })$
of
![]() $\Theta (\Lambda )$
such that
$\Theta (\Lambda )$
such that
![]() $\Omega \blacktriangleright_{\textsf{R}} \,\overline{\Omega }$
. Lemmas 59–66, below, will give us material to show how a partial valuation
$\Omega \blacktriangleright_{\textsf{R}} \,\overline{\Omega }$
. Lemmas 59–66, below, will give us material to show how a partial valuation
![]() $f$
on
$f$
on
![]() $\Lambda$
may be extended to the whole language to such an effect that we will have
$\Lambda$
may be extended to the whole language to such an effect that we will have
![]() $f(\Lambda \cap \Omega )\subseteq D$
and
$f(\Lambda \cap \Omega )\subseteq D$
and
![]() $f(\Lambda \cap \overline{\Omega })\subseteq \mathcal{V}_6{\setminus }D$
for some suitable
$f(\Lambda \cap \overline{\Omega })\subseteq \mathcal{V}_6{\setminus }D$
for some suitable
![]() $D$
(either principal or prime, depending on the case). Further, analyticity will follow from the fact that we will be using only instances of the rules in
$D$
(either principal or prime, depending on the case). Further, analyticity will follow from the fact that we will be using only instances of the rules in
![]() $\textsf{R}$
with formulas in
$\textsf{R}$
with formulas in
![]() $\Lambda$
, thus only formulas in
$\Lambda$
, thus only formulas in
![]() $\Theta (\Lambda ) \,{:=}\, \{\psi ^\sigma :\psi \in \Theta \text{ and }\sigma :\{p,q\}\to \Lambda \}$
will appear along this proof.
$\Theta (\Lambda ) \,{:=}\, \{\psi ^\sigma :\psi \in \Theta \text{ and }\sigma :\{p,q\}\to \Lambda \}$
will appear along this proof.
The following abbreviations will be helpful in what follows. Let
 \begin{align*} \Lambda _{{\hat{\mathbf{f}}}}& \,{:=}\,\{\varphi \in \Lambda : \varphi \in \overline{\Omega }\text{ and }{\circ } \varphi \in \Omega \} \\ \Lambda _{{\hat{\mathbf{t}}}}&\,{:=}\,\{\varphi \in \Lambda : \varphi, {\circ } \varphi \in \Omega \} \\ \Lambda _{\Diamond }&\,{:=}\,\{\varphi \in \Lambda :{\circ } \varphi \in \overline{\Omega } \}\\ \Lambda _{\mathbf{t}}&\,{:=}\,\{\varphi \in \Lambda _{\Diamond }:{\downarrow } \varphi \in \overline{\Omega } \}\\ \Lambda _{\mathbf{f}}&\,{:=}\, \{\varphi \in \Lambda _{\Diamond }:{\uparrow } \varphi \in \overline{\Omega } \}\\ \Lambda _{\textsf{mid}}&\,{:=}\,\{\varphi \in \Lambda _{\Diamond }:{\uparrow }\varphi, {\downarrow } \varphi \in \Omega \} \end{align*}
\begin{align*} \Lambda _{{\hat{\mathbf{f}}}}& \,{:=}\,\{\varphi \in \Lambda : \varphi \in \overline{\Omega }\text{ and }{\circ } \varphi \in \Omega \} \\ \Lambda _{{\hat{\mathbf{t}}}}&\,{:=}\,\{\varphi \in \Lambda : \varphi, {\circ } \varphi \in \Omega \} \\ \Lambda _{\Diamond }&\,{:=}\,\{\varphi \in \Lambda :{\circ } \varphi \in \overline{\Omega } \}\\ \Lambda _{\mathbf{t}}&\,{:=}\,\{\varphi \in \Lambda _{\Diamond }:{\downarrow } \varphi \in \overline{\Omega } \}\\ \Lambda _{\mathbf{f}}&\,{:=}\, \{\varphi \in \Lambda _{\Diamond }:{\uparrow } \varphi \in \overline{\Omega } \}\\ \Lambda _{\textsf{mid}}&\,{:=}\,\{\varphi \in \Lambda _{\Diamond }:{\uparrow }\varphi, {\downarrow } \varphi \in \Omega \} \end{align*}
We will also consider the relation
![]() $\equiv _\Diamond \,\subseteq \Lambda _\Diamond \times \Lambda _\Diamond$
given by
$\equiv _\Diamond \,\subseteq \Lambda _\Diamond \times \Lambda _\Diamond$
given by
![]() $\varphi \equiv _\Diamond \psi$
if, and only if,
$\varphi \equiv _\Diamond \psi$
if, and only if,
![]() ${\circ }(\varphi \Rightarrow \psi ),{\circ }(\psi \Rightarrow \varphi )\in \Omega$
.
${\circ }(\varphi \Rightarrow \psi ),{\circ }(\psi \Rightarrow \varphi )\in \Omega$
.
Lemma 59.
From
![]() $\textsf{R}^\Diamond \subseteq \textsf{R}$
, we obtain that
$\textsf{R}^\Diamond \subseteq \textsf{R}$
, we obtain that
-
1.
 $\Lambda _\Diamond =\Lambda _{\mathbf{f}}\cup \Lambda _{\mathbf{t}}\cup \Lambda _{\textsf{mid}}$
;
$\Lambda _\Diamond =\Lambda _{\mathbf{f}}\cup \Lambda _{\mathbf{t}}\cup \Lambda _{\textsf{mid}}$
; -
2. the relation
 $\equiv _\Diamond$
is an equivalence relation that partitions
$\equiv _\Diamond$
is an equivalence relation that partitions
 $\Lambda _\Diamond$
into at most four equivalence classes. In particular, each set
$\Lambda _\Diamond$
into at most four equivalence classes. In particular, each set
 $\Lambda _{\mathbf{f}}$
and
$\Lambda _{\mathbf{f}}$
and
 $\Lambda _{\mathbf{t}}$
consists of formulas belonging to a single
$\Lambda _{\mathbf{t}}$
consists of formulas belonging to a single
 $\equiv _\Diamond$
-class, and if
$\equiv _\Diamond$
-class, and if
 $\Lambda _{\textsf{mid}}\neq \varnothing$
then this set is partitioned into exactly two
$\Lambda _{\textsf{mid}}\neq \varnothing$
then this set is partitioned into exactly two
 $\equiv _\Diamond$
-classes, which we name
$\equiv _\Diamond$
-classes, which we name
 $\Lambda _{{\mathbf{b}}}$
and
$\Lambda _{{\mathbf{b}}}$
and
 $\Lambda _{\mathbf{n}}$
, such that, for
$\Lambda _{\mathbf{n}}$
, such that, for
 $\varphi, \psi \in \Lambda _{\textsf{mid}}$
and
$\varphi, \psi \in \Lambda _{\textsf{mid}}$
and
 $a \in \{{\mathbf{b}},{\mathbf{n}} \}$
, we have
$a \in \{{\mathbf{b}},{\mathbf{n}} \}$
, we have
 $\varphi, \psi \in \Lambda _{a}$
if, and only if,
$\varphi, \psi \in \Lambda _{a}$
if, and only if,
 ${\circ }(\varphi \Rightarrow \psi ) \in \Omega$
;
${\circ }(\varphi \Rightarrow \psi ) \in \Omega$
; -
3. for
 $\varphi \in \Lambda _a$
and
$\varphi \in \Lambda _a$
and
 $\psi \in \Lambda _b$
with
$\psi \in \Lambda _b$
with
 $a,b\in \{{\mathbf{f}},{\mathbf{n}},{\mathbf{b}},{\mathbf{t}}\}$
, we have
$a,b\in \{{\mathbf{f}},{\mathbf{n}},{\mathbf{b}},{\mathbf{t}}\}$
, we have
 $a \leq b$
if, and only if,
$a \leq b$
if, and only if,
 ${\circ }(\varphi \Rightarrow \psi )\in \Omega$
.
${\circ }(\varphi \Rightarrow \psi )\in \Omega$
.
Proof.
Note that since
![]() $\Omega \cap \overline{\Omega }=\varnothing$
we have that
$\Omega \cap \overline{\Omega }=\varnothing$
we have that
![]() $\Lambda _a\cap \Lambda _b=\varnothing$
for
$\Lambda _a\cap \Lambda _b=\varnothing$
for
![]() $a\neq b$
and
$a\neq b$
and
![]() $a,b\in \{{\mathbf{f}},{\mathbf{t}},\textsf{mid},{\hat{\mathbf{t}}},{\hat{\mathbf{f}}}\}$
. By
$a,b\in \{{\mathbf{f}},{\mathbf{t}},\textsf{mid},{\hat{\mathbf{t}}},{\hat{\mathbf{f}}}\}$
. By
![]() $\textsf{r}^{\sim }_{{\uparrow }\textsf{or}{\downarrow }}$
we know that
$\textsf{r}^{\sim }_{{\uparrow }\textsf{or}{\downarrow }}$
we know that
![]() $\Lambda _\Diamond = \Lambda _{\mathbf{f}}\cup \Lambda _{\mathbf{t}}\cup \Lambda _{\textsf{mid}}$
, and this takes care of item (1).
$\Lambda _\Diamond = \Lambda _{\mathbf{f}}\cup \Lambda _{\mathbf{t}}\cup \Lambda _{\textsf{mid}}$
, and this takes care of item (1).
For all that follows, recall that
![]() ${\circ } \varphi \in \overline \Omega$
for any
${\circ } \varphi \in \overline \Omega$
for any
![]() $\varphi \in \Lambda _\Diamond$
, by definition of
$\varphi \in \Lambda _\Diamond$
, by definition of
![]() $\Lambda _\Diamond$
. That
$\Lambda _\Diamond$
. That
![]() $\equiv _\Diamond$
is an equivalence relation follows by the fact that the definition is symmetric and by the presence of the rules
$\equiv _\Diamond$
is an equivalence relation follows by the fact that the definition is symmetric and by the presence of the rules
![]() $\textsf{r}_{\textsf{id}}$
and
$\textsf{r}_{\textsf{id}}$
and
![]() $\textsf{r}_{\textsf{trans}}$
.
$\textsf{r}_{\textsf{trans}}$
.
We show now that formulas in
![]() $\Lambda _{\mathbf{t}}$
and
$\Lambda _{\mathbf{t}}$
and
![]() $\Lambda _{\mathbf{f}}$
correspond to the same
$\Lambda _{\mathbf{f}}$
correspond to the same
![]() $\equiv _\Diamond$
-class. If
$\equiv _\Diamond$
-class. If
![]() $\varphi, \psi \in \Lambda _{\mathbf{t}}$
, then
$\varphi, \psi \in \Lambda _{\mathbf{t}}$
, then
![]() ${\downarrow } \varphi, {\downarrow } \psi \in \overline{\Omega }$
and by
${\downarrow } \varphi, {\downarrow } \psi \in \overline{\Omega }$
and by
![]() $\textsf{r}^\Diamond _{\leq{\mathbf{t}}}$
we obtain that
$\textsf{r}^\Diamond _{\leq{\mathbf{t}}}$
we obtain that
![]() $\varphi \equiv _\Diamond \psi$
. Similarly, if
$\varphi \equiv _\Diamond \psi$
. Similarly, if
![]() $\varphi, \psi \in \Lambda _{\mathbf{f}}$
, then
$\varphi, \psi \in \Lambda _{\mathbf{f}}$
, then
![]() ${\uparrow } \varphi, {\uparrow } \psi \in \overline{\Omega }$
and by
${\uparrow } \varphi, {\uparrow } \psi \in \overline{\Omega }$
and by
![]() $\textsf{r}^\Diamond _{\geq{\mathbf{f}}}$
we obtain that
$\textsf{r}^\Diamond _{\geq{\mathbf{f}}}$
we obtain that
![]() $\varphi \equiv _\Diamond \psi$
.
$\varphi \equiv _\Diamond \psi$
.
We will show that there are subsets of
![]() $\Lambda _{\textsf{mid}}$
corresponding to a partition of this set. Our candidates are precisely the classes
$\Lambda _{\textsf{mid}}$
corresponding to a partition of this set. Our candidates are precisely the classes
![]() $[\varphi ]_{\equiv _{\Diamond }}$
. They are clearly disjoint and their union yields
$[\varphi ]_{\equiv _{\Diamond }}$
. They are clearly disjoint and their union yields
![]() $\Lambda _{\textsf{mid}}$
, so it is enough to show that they are all subsets of
$\Lambda _{\textsf{mid}}$
, so it is enough to show that they are all subsets of
![]() $\Lambda _{\textsf{mid}}$
. In fact, if
$\Lambda _{\textsf{mid}}$
. In fact, if
![]() $\psi \in [\varphi ]_{\equiv _{{\Diamond }}}$
, we have
$\psi \in [\varphi ]_{\equiv _{{\Diamond }}}$
, we have
![]() ${\circ }\psi \in \overline{\Omega }$
and
${\circ }\psi \in \overline{\Omega }$
and
![]() ${\circ }(\varphi \Rightarrow \psi ),{\circ }(\psi \Rightarrow \varphi ) \in \Omega$
. Then we obtain
${\circ }(\varphi \Rightarrow \psi ),{\circ }(\psi \Rightarrow \varphi ) \in \Omega$
. Then we obtain
![]() ${\circ }\psi \in \overline{\Omega }$
and
${\circ }\psi \in \overline{\Omega }$
and
![]() ${\uparrow }\psi, {\downarrow }\psi \in \Omega$
by the rules
${\uparrow }\psi, {\downarrow }\psi \in \Omega$
by the rules
![]() $\textsf{r}^\Diamond _{\textsf{incclass}_1}$
and
$\textsf{r}^\Diamond _{\textsf{incclass}_1}$
and
![]() $\textsf{r}^\Diamond _{\textsf{incclass}_2}$
. Moreover, for
$\textsf{r}^\Diamond _{\textsf{incclass}_2}$
. Moreover, for
![]() $\varphi, \psi \in \Lambda _{\textsf{mid}}$
, we have that
$\varphi, \psi \in \Lambda _{\textsf{mid}}$
, we have that
![]() ${\circ }(\varphi \Rightarrow \psi )\in \Omega$
if, and only if,
${\circ }(\varphi \Rightarrow \psi )\in \Omega$
if, and only if,
![]() $\varphi \equiv _\Diamond \psi$
. The harder direction is left-to-right, and it follows by
$\varphi \equiv _\Diamond \psi$
. The harder direction is left-to-right, and it follows by
![]() $\textsf{r}^\Diamond _{\textsf{incclass}_3}$
.
$\textsf{r}^\Diamond _{\textsf{incclass}_3}$
.
Still,
![]() $\Lambda _{\textsf{mid}}$
might be partitioned into more than two
$\Lambda _{\textsf{mid}}$
might be partitioned into more than two
![]() $\equiv _\Diamond$
-equivalence classes. We avoid this with the rule
$\equiv _\Diamond$
-equivalence classes. We avoid this with the rule
![]() $\textsf{r}^{\sim }_{\textsf{just}_2}$
, which, together with the fact proved in the previous paragraph, prevents the existence of more than two
$\textsf{r}^{\sim }_{\textsf{just}_2}$
, which, together with the fact proved in the previous paragraph, prevents the existence of more than two
![]() $\equiv _\Diamond$
-equivalence classes in
$\equiv _\Diamond$
-equivalence classes in
![]() $\Lambda _{\textsf{mid}}$
. This concludes the proof of item (2).
$\Lambda _{\textsf{mid}}$
. This concludes the proof of item (2).
Finally, for item (3), let
![]() $\varphi \in \Lambda _a$
and
$\varphi \in \Lambda _a$
and
![]() $\psi \in \Lambda _b$
with
$\psi \in \Lambda _b$
with
![]() $a,b\in \{{\mathbf{f}},{\mathbf{n}},{\mathbf{b}},{\mathbf{t}}\}$
. From left-to-right, suppose that
$a,b\in \{{\mathbf{f}},{\mathbf{n}},{\mathbf{b}},{\mathbf{t}}\}$
. From left-to-right, suppose that
![]() $a \leq b$
. We want to prove
$a \leq b$
. We want to prove
![]() ${\circ }(\varphi \Rightarrow \psi ) \in \Omega$
. Note that we cannot have
${\circ }(\varphi \Rightarrow \psi ) \in \Omega$
. Note that we cannot have
![]() $a ={\mathbf{b}}$
and
$a ={\mathbf{b}}$
and
![]() $b ={\mathbf{n}}$
, nor
$b ={\mathbf{n}}$
, nor
![]() $a ={\mathbf{n}}$
and
$a ={\mathbf{n}}$
and
![]() $b ={\mathbf{b}}$
. The only cases we need to consider, then, are:
$b ={\mathbf{b}}$
. The only cases we need to consider, then, are:
-
1. If
 $a = b$
, we already have that each
$a = b$
, we already have that each
 $\Lambda _c$
, with
$\Lambda _c$
, with
 $c \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
forms an
$c \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
forms an
 $\equiv _\Diamond$
-class, so
$\equiv _\Diamond$
-class, so
 ${\circ }(\varphi \Rightarrow \psi ) \in \Omega$
by the definition of
${\circ }(\varphi \Rightarrow \psi ) \in \Omega$
by the definition of
 $\equiv _\Diamond$
.
$\equiv _\Diamond$
. -
2. If
 $a ={\mathbf{f}}$
, we obtain
$a ={\mathbf{f}}$
, we obtain
 ${\circ }(\varphi \Rightarrow \psi ) \in \Omega$
by
${\circ }(\varphi \Rightarrow \psi ) \in \Omega$
by
 $\textsf{r}^\Diamond _{\geq{\mathbf{f}}}$
.
$\textsf{r}^\Diamond _{\geq{\mathbf{f}}}$
. -
3. If
 $b ={\mathbf{t}}$
, we obtain
$b ={\mathbf{t}}$
, we obtain
 ${\circ }(\varphi \Rightarrow \psi ) \in \Omega$
by
${\circ }(\varphi \Rightarrow \psi ) \in \Omega$
by
 $\textsf{r}^\Diamond _{\leq{\mathbf{t}}}$
.
$\textsf{r}^\Diamond _{\leq{\mathbf{t}}}$
.
From right to left, we reason contrapositively. Suppose that
![]() $a \not \leq b$
. We want to conclude that
$a \not \leq b$
. We want to conclude that
![]() ${\circ }(\varphi \Rightarrow \psi ) \in \overline{\Omega }$
. We only need to consider the following cases:
${\circ }(\varphi \Rightarrow \psi ) \in \overline{\Omega }$
. We only need to consider the following cases:
-
1. If
 $a ={\mathbf{t}}$
, we have
$a ={\mathbf{t}}$
, we have
 $b \lt{\mathbf{t}}$
. Thus
$b \lt{\mathbf{t}}$
. Thus
 ${\downarrow }\psi \in \Omega$
. By
${\downarrow }\psi \in \Omega$
. By
 $\textsf{r}^\Diamond _{\textsf{incclass}_2}$
, we have
$\textsf{r}^\Diamond _{\textsf{incclass}_2}$
, we have
 ${\circ }(\varphi \Rightarrow \psi ) \in \overline \Omega$
.
${\circ }(\varphi \Rightarrow \psi ) \in \overline \Omega$
. -
2. If
 $a ={\mathbf{b}}$
or
$a ={\mathbf{b}}$
or
 $a ={\mathbf{n}}$
, and
$a ={\mathbf{n}}$
, and
 $b ={\mathbf{f}}$
, we obtain
$b ={\mathbf{f}}$
, we obtain
 ${\circ }(\varphi \Rightarrow \psi ) \in \overline \Omega$
by
${\circ }(\varphi \Rightarrow \psi ) \in \overline \Omega$
by
 $\textsf{r}^\Diamond _{\textsf{incclass}_1}$
.
$\textsf{r}^\Diamond _{\textsf{incclass}_1}$
. -
3. If
 $\{ a, b \} = \{{\mathbf{b}},{\mathbf{n}} \}$
, we have that
$\{ a, b \} = \{{\mathbf{b}},{\mathbf{n}} \}$
, we have that
 ${\circ }(\varphi \Rightarrow \psi ),{\circ }(\psi \Rightarrow \varphi )\in \overline{\Omega }$
by the definition of the sets
${\circ }(\varphi \Rightarrow \psi ),{\circ }(\psi \Rightarrow \varphi )\in \overline{\Omega }$
by the definition of the sets
 $\Lambda _{\mathbf{b}}$
and
$\Lambda _{\mathbf{b}}$
and
 $\Lambda _{\mathbf{n}}$
.
$\Lambda _{\mathbf{n}}$
.
Our candidate for partial valuation is
![]() $f:\Lambda \to \mathcal{V}_6$
given by
$f:\Lambda \to \mathcal{V}_6$
given by
![]() $f(\varphi ) \,{:=}\, a$
if
$f(\varphi ) \,{:=}\, a$
if
![]() $\varphi \in \Lambda _a$
. One can check without difficulty that this function is well defined (as a matter of fact, the sets
$\varphi \in \Lambda _a$
. One can check without difficulty that this function is well defined (as a matter of fact, the sets
![]() $\Lambda _a$
defined above are pairwise disjoint). We will prove that
$\Lambda _a$
defined above are pairwise disjoint). We will prove that
![]() $f$
is indeed the desired valuation using a succession of lemmas. Let us begin with proving that
$f$
is indeed the desired valuation using a succession of lemmas. Let us begin with proving that
![]() $f$
is a partial homomorphism.
$f$
is a partial homomorphism.
Lemma 60.
Suppose
![]() $\textsf{R}_\Rightarrow, \textsf{R}_\Diamond \subseteq \textsf{R}$
. If
$\textsf{R}_\Rightarrow, \textsf{R}_\Diamond \subseteq \textsf{R}$
. If
![]() $\{\varphi, \psi, \varphi \Rightarrow \psi \} \subseteq \Lambda$
, then
$\{\varphi, \psi, \varphi \Rightarrow \psi \} \subseteq \Lambda$
, then
![]() $f(\varphi \Rightarrow \psi )=f(\varphi )\Rightarrow _{\textsf{H}} f(\psi )$
.
$f(\varphi \Rightarrow \psi )=f(\varphi )\Rightarrow _{\textsf{H}} f(\psi )$
.
Proof.
By cases on the values of
![]() $f(\varphi )$
and
$f(\varphi )$
and
![]() $f(\psi )$
:
$f(\psi )$
:
-
1. If
 $f(\psi ) ={\hat{\mathbf{t}}}$
, we have
$f(\psi ) ={\hat{\mathbf{t}}}$
, we have
 ${\circ }\psi, \psi \in \Omega$
. We want
${\circ }\psi, \psi \in \Omega$
. We want
 $f(\varphi \Rightarrow \psi ) ={\hat{\mathbf{t}}}$
, which follows from
$f(\varphi \Rightarrow \psi ) ={\hat{\mathbf{t}}}$
, which follows from
 $\textsf{r}_1^\Rightarrow$
and
$\textsf{r}_1^\Rightarrow$
and
 $\textsf{r}_2^\Rightarrow$
.
$\textsf{r}_2^\Rightarrow$
. -
2. If
 $f(\varphi ) ={\hat{\mathbf{t}}}$
, we have
$f(\varphi ) ={\hat{\mathbf{t}}}$
, we have
 ${\circ }\varphi, \varphi \in \Omega$
and proceed by cases on the value of
${\circ }\varphi, \varphi \in \Omega$
and proceed by cases on the value of
 $f(\psi )$
. Note that we want to show that
$f(\psi )$
. Note that we want to show that
 $f(\varphi \Rightarrow \psi ) = f(\psi )$
:
$f(\varphi \Rightarrow \psi ) = f(\psi )$
:-
a. The case
 $f(\psi ) ={\hat{\mathbf{t}}}$
was already covered.
$f(\psi ) ={\hat{\mathbf{t}}}$
was already covered. -
b. If
 $f(\psi ) ={\hat{\mathbf{f}}}$
, it follows from
$f(\psi ) ={\hat{\mathbf{f}}}$
, it follows from
 $\textsf{r}_1^\Rightarrow$
and
$\textsf{r}_1^\Rightarrow$
and
 $\textsf{r}_3^\Rightarrow$
.
$\textsf{r}_3^\Rightarrow$
. -
c. If
 $f(\psi ) ={\mathbf{t}}$
, it follows from
$f(\psi ) ={\mathbf{t}}$
, it follows from
 $\textsf{r}_4^\Rightarrow$
and
$\textsf{r}_4^\Rightarrow$
and
 $\textsf{r}_5^\Rightarrow$
.
$\textsf{r}_5^\Rightarrow$
. -
d. If
 $f(\psi ) ={\mathbf{f}}$
, it follows from
$f(\psi ) ={\mathbf{f}}$
, it follows from
 $\textsf{r}_4^\Rightarrow$
and
$\textsf{r}_4^\Rightarrow$
and
 $\textsf{r}_6^\Rightarrow$
.
$\textsf{r}_6^\Rightarrow$
. -
e. If
 $f(\psi ) \in \{{\mathbf{b}},{\mathbf{n}} \}$
, it follows by
$f(\psi ) \in \{{\mathbf{b}},{\mathbf{n}} \}$
, it follows by
 $\textsf{r}_4^\Rightarrow$
,
$\textsf{r}_4^\Rightarrow$
,
 $\textsf{r}_7^\Rightarrow$
and
$\textsf{r}_7^\Rightarrow$
and
 $\textsf{r}_8^\Rightarrow$
that
$\textsf{r}_8^\Rightarrow$
that
 $f(\varphi \Rightarrow \psi ) \in \{{\mathbf{b}},{\mathbf{n}} \}$
. Then, by
$f(\varphi \Rightarrow \psi ) \in \{{\mathbf{b}},{\mathbf{n}} \}$
. Then, by
 $\textsf{r}_9^\Rightarrow$
and Lemma 59 we have
$\textsf{r}_9^\Rightarrow$
and Lemma 59 we have
 $f(\varphi \Rightarrow \psi ) = f(\psi )$
.
$f(\varphi \Rightarrow \psi ) = f(\psi )$
.
-
-
3. If
 $f(\varphi ) ={\hat{\mathbf{f}}}$
, we have
$f(\varphi ) ={\hat{\mathbf{f}}}$
, we have
 ${\circ }\varphi \in \Omega$
and
${\circ }\varphi \in \Omega$
and
 $\varphi \in \overline \Omega$
. We obtain that
$\varphi \in \overline \Omega$
. We obtain that
 $f(\varphi \Rightarrow \psi ) ={\hat{\mathbf{t}}}$
by
$f(\varphi \Rightarrow \psi ) ={\hat{\mathbf{t}}}$
by
 $\textsf{r}_{10}^\Rightarrow$
and
$\textsf{r}_{10}^\Rightarrow$
and
 $\textsf{r}_{11}^\Rightarrow$
.
$\textsf{r}_{11}^\Rightarrow$
. -
4. If
 $f(\psi ) ={\hat{\mathbf{f}}}$
, the case
$f(\psi ) ={\hat{\mathbf{f}}}$
, the case
 $f(\varphi ) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}}\}$
was already treated, so we consider
$f(\varphi ) \in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}}\}$
was already treated, so we consider
 $f(\varphi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
and want to prove
$f(\varphi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
and want to prove
 $f(\varphi \Rightarrow \psi ) ={\hat{\mathbf{f}}}$
. From the available information, we have that
$f(\varphi \Rightarrow \psi ) ={\hat{\mathbf{f}}}$
. From the available information, we have that
 ${\circ }\psi \in \Omega$
,
${\circ }\psi \in \Omega$
,
 $\psi \in \overline{\Omega }$
,
$\psi \in \overline{\Omega }$
,
 ${\circ } \varphi \in \overline \Omega$
. Then for any of the possibilities for
${\circ } \varphi \in \overline \Omega$
. Then for any of the possibilities for
 $f(\varphi )$
, the result follows by
$f(\varphi )$
, the result follows by
 $\textsf{r}_1^\Rightarrow$
and
$\textsf{r}_1^\Rightarrow$
and
 $\textsf{r}_{12}^\Rightarrow$
.
$\textsf{r}_{12}^\Rightarrow$
. -
5. In case
 $f(\varphi ),f(\psi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, we make intensive use of Lemma 59.
$f(\varphi ),f(\psi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, we make intensive use of Lemma 59.-
a. If
 $f(\varphi ) \leq f(\psi )$
, we want to show
$f(\varphi ) \leq f(\psi )$
, we want to show
 $f(\varphi \Rightarrow \psi ) ={\hat{\mathbf{t}}}$
. By Lemma 59, we already have
$f(\varphi \Rightarrow \psi ) ={\hat{\mathbf{t}}}$
. By Lemma 59, we already have
 ${\circ }(\varphi \Rightarrow \psi ) \in \Omega$
. The result then follows by
${\circ }(\varphi \Rightarrow \psi ) \in \Omega$
. The result then follows by
 $\textsf{r}^\Rightarrow _{13}$
.
$\textsf{r}^\Rightarrow _{13}$
. -
b. If
 $f(\psi ) \leq f(\varphi )$
and
$f(\psi ) \leq f(\varphi )$
and
 $f(\varphi ) \not \leq f(\psi )$
, we have
$f(\varphi ) \not \leq f(\psi )$
, we have
 ${\circ }(\varphi \Rightarrow \psi ) \in \overline \Omega$
and
${\circ }(\varphi \Rightarrow \psi ) \in \overline \Omega$
and
 ${\circ }(\psi \Rightarrow \varphi ) \in \Omega$
by Lemma 59, and consider the following subcases:
${\circ }(\psi \Rightarrow \varphi ) \in \Omega$
by Lemma 59, and consider the following subcases:-
i. If
 $f(\varphi ) ={\mathbf{t}}$
, we want
$f(\varphi ) ={\mathbf{t}}$
, we want
 $f(\varphi \Rightarrow \psi ) = f(\psi )$
, which follows by
$f(\varphi \Rightarrow \psi ) = f(\psi )$
, which follows by
 $\textsf{r}_{9}^\Rightarrow$
and
$\textsf{r}_{9}^\Rightarrow$
and
 $\textsf{r}_{14}^\Rightarrow$
.
$\textsf{r}_{14}^\Rightarrow$
. -
ii. If
 $f(\varphi ) \in \{{\mathbf{n}},{\mathbf{b}} \}$
and
$f(\varphi ) \in \{{\mathbf{n}},{\mathbf{b}} \}$
and
 $f(\psi ) ={\mathbf{f}}$
, we want
$f(\psi ) ={\mathbf{f}}$
, we want
 $f(\varphi \Rightarrow \psi ) ={\mathbf{b}}$
. This follows from by
$f(\varphi \Rightarrow \psi ) ={\mathbf{b}}$
. This follows from by
 $\textsf{r}^\Rightarrow _{15}$
,
$\textsf{r}^\Rightarrow _{15}$
,
 $\textsf{r}^\Rightarrow _{16}$
,
$\textsf{r}^\Rightarrow _{16}$
,
 $\textsf{r}^\Rightarrow _{17}$
and
$\textsf{r}^\Rightarrow _{17}$
and
 $\textsf{r}^\Rightarrow _{18}$
. The first two force
$\textsf{r}^\Rightarrow _{18}$
. The first two force
 $f(\varphi \Rightarrow \psi ) \in \{{\mathbf{b}},{\mathbf{n}} \}$
, while the third forces
$f(\varphi \Rightarrow \psi ) \in \{{\mathbf{b}},{\mathbf{n}} \}$
, while the third forces
 $f(\varphi ) \neq f(\varphi \Rightarrow \psi )$
.
$f(\varphi ) \neq f(\varphi \Rightarrow \psi )$
.
-
-
c. Otherwise,
 $\{f(\varphi ), f(\psi )\} = \{{\mathbf{b}},{\mathbf{n}}\}$
, thus we want
$\{f(\varphi ), f(\psi )\} = \{{\mathbf{b}},{\mathbf{n}}\}$
, thus we want
 $f(\varphi \Rightarrow \psi ) = f(\psi )$
, which is achieved by
$f(\varphi \Rightarrow \psi ) = f(\psi )$
, which is achieved by
 $\textsf{r}^\Rightarrow _{9}$
and
$\textsf{r}^\Rightarrow _{9}$
and
 $\textsf{r}^\Rightarrow _{19}$
together with Lemma 59.
$\textsf{r}^\Rightarrow _{19}$
together with Lemma 59.
-
Lemma 61.
Suppose
![]() $\textsf{R}_{\sim }, \textsf{R}_\Diamond \subseteq \textsf{R}$
. If
$\textsf{R}_{\sim }, \textsf{R}_\Diamond \subseteq \textsf{R}$
. If
![]() $\{\varphi, {\sim }\varphi \} \subseteq \Lambda$
, then
$\{\varphi, {\sim }\varphi \} \subseteq \Lambda$
, then
![]() $f({\sim }\varphi )={\sim }^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}(f(\varphi ))$
.
$f({\sim }\varphi )={\sim }^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}(f(\varphi ))$
.
Proof.
We reason by cases on the value of
![]() $f(\varphi )$
:
$f(\varphi )$
:
-
1. If
 $f(\varphi )={\hat{\mathbf{t}}}$
, then
$f(\varphi )={\hat{\mathbf{t}}}$
, then
 $\varphi, {\circ } \varphi \in \Omega$
, so
$\varphi, {\circ } \varphi \in \Omega$
, so
 ${\sim } \varphi \in \overline{\Omega }$
and
${\sim } \varphi \in \overline{\Omega }$
and
 ${\circ }{\sim } \varphi \in \Omega$
by
${\circ }{\sim } \varphi \in \Omega$
by
 $\textsf{r}^{\sim }_2$
and
$\textsf{r}^{\sim }_2$
and
 $\textsf{r}^{\sim }_3$
.
$\textsf{r}^{\sim }_3$
. -
2. If
 $f(\varphi )={\hat{\mathbf{f}}}$
, then
$f(\varphi )={\hat{\mathbf{f}}}$
, then
 ${\circ } \varphi \in \Omega$
and
${\circ } \varphi \in \Omega$
and
 $\varphi \in \overline{\Omega }$
, so
$\varphi \in \overline{\Omega }$
, so
 ${\sim } \varphi \in \Omega$
and
${\sim } \varphi \in \Omega$
and
 ${\circ }{\sim } \varphi \in \Omega$
by
${\circ }{\sim } \varphi \in \Omega$
by
 $\textsf{r}_1^{\sim }$
and
$\textsf{r}_1^{\sim }$
and
 $\textsf{r}_3^{\sim }$
.
$\textsf{r}_3^{\sim }$
. -
3. If
 $f(\varphi )={\mathbf{t}}$
, then
$f(\varphi )={\mathbf{t}}$
, then
 ${\circ }\varphi \in \overline \Omega$
and
${\circ }\varphi \in \overline \Omega$
and
 ${\downarrow } \varphi \in \overline{\Omega }$
. Thus, by
${\downarrow } \varphi \in \overline{\Omega }$
. Thus, by
 $\textsf{r}^{\sim }_4$
and
$\textsf{r}^{\sim }_4$
and
 $\textsf{r}^{\sim }_5$
we have that
$\textsf{r}^{\sim }_5$
we have that
 ${\circ }{\sim }\varphi \in \overline \Omega$
and
${\circ }{\sim }\varphi \in \overline \Omega$
and
 ${\uparrow }{\sim } \varphi \in \overline{\Omega }$
.
${\uparrow }{\sim } \varphi \in \overline{\Omega }$
. -
4. If
 $f(\varphi )={\mathbf{f}}$
, then
$f(\varphi )={\mathbf{f}}$
, then
 ${\circ }{\sim }\varphi \in \overline \Omega$
and
${\circ }{\sim }\varphi \in \overline \Omega$
and
 ${\uparrow } \varphi \in \overline{\Omega }$
. Thus by
${\uparrow } \varphi \in \overline{\Omega }$
. Thus by
 $\textsf{r}^{\sim }_4$
and
$\textsf{r}^{\sim }_4$
and
 $\textsf{r}^{\sim }_6$
we have
$\textsf{r}^{\sim }_6$
we have
 ${\circ }{\sim }\varphi \in \overline \Omega$
and
${\circ }{\sim }\varphi \in \overline \Omega$
and
 ${\downarrow }{\sim } \varphi \in \overline{\Omega }$
.
${\downarrow }{\sim } \varphi \in \overline{\Omega }$
. -
5. If
 $f(\varphi ) \in \{{\mathbf{b}},{\mathbf{n}} \}$
, then
$f(\varphi ) \in \{{\mathbf{b}},{\mathbf{n}} \}$
, then
 ${\circ } \varphi \in \overline \Omega$
and
${\circ } \varphi \in \overline \Omega$
and
 ${\uparrow } \varphi, {\downarrow } \varphi \in \Omega$
. By
${\uparrow } \varphi, {\downarrow } \varphi \in \Omega$
. By
 $\textsf{r}^{\sim }_4$
,
$\textsf{r}^{\sim }_4$
,
 $\textsf{r}^{\sim }_7$
and
$\textsf{r}^{\sim }_7$
and
 $\textsf{r}^{\sim }_8$
, we have
$\textsf{r}^{\sim }_8$
, we have
 ${\circ }{\sim }\varphi \in \overline \Omega$
and
${\circ }{\sim }\varphi \in \overline \Omega$
and
 ${\uparrow }{\sim }\varphi, {\downarrow }{\sim }\varphi \in \Omega$
. This gives us that
${\uparrow }{\sim }\varphi, {\downarrow }{\sim }\varphi \in \Omega$
. This gives us that
 $f({\sim } \varphi ) \in \{{\mathbf{b}},{\mathbf{n}} \}$
. Also, since we have
$f({\sim } \varphi ) \in \{{\mathbf{b}},{\mathbf{n}} \}$
. Also, since we have
 ${\circ }(\varphi \Rightarrow{\sim }\varphi ) ={\downarrow } \varphi \in \Omega$
, we must have
${\circ }(\varphi \Rightarrow{\sim }\varphi ) ={\downarrow } \varphi \in \Omega$
, we must have
 $f({\sim } \varphi ) = f(\varphi )$
by Lemma 59.
$f({\sim } \varphi ) = f(\varphi )$
by Lemma 59.
Lemma 62.
Suppose
![]() $\textsf{R}_{\circ } \subseteq \textsf{R}$
. If
$\textsf{R}_{\circ } \subseteq \textsf{R}$
. If
![]() $\{\varphi, {\circ }\varphi \} \subseteq \Lambda$
, then
$\{\varphi, {\circ }\varphi \} \subseteq \Lambda$
, then
![]() $f({\circ }\varphi )={\circ }^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}(f(\varphi ))$
.
$f({\circ }\varphi )={\circ }^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}(f(\varphi ))$
.
Proof.
Note that by
![]() $\textsf{r}_{1}^{\circ }$
we always have
$\textsf{r}_{1}^{\circ }$
we always have
![]() ${\circ }{\circ }\varphi \in \Omega$
. Hence, if
${\circ }{\circ }\varphi \in \Omega$
. Hence, if
![]() $f(\varphi )\in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}}\}$
, then
$f(\varphi )\in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}}\}$
, then
![]() ${\circ }\varphi \in \Omega$
and thus
${\circ }\varphi \in \Omega$
and thus
![]() $f({\circ }\varphi )={\hat{\mathbf{t}}}={\circ }^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}(f(\varphi ))$
. If
$f({\circ }\varphi )={\hat{\mathbf{t}}}={\circ }^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}(f(\varphi ))$
. If
![]() $f(\varphi )\notin \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}}\}$
, then
$f(\varphi )\notin \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}}\}$
, then
![]() ${\circ }\varphi \in \overline{\Omega }$
, thus
${\circ }\varphi \in \overline{\Omega }$
, thus
![]() $f({\circ }\varphi )={\hat{\mathbf{f}}}={\circ }^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}(f(\varphi ))$
.
$f({\circ }\varphi )={\hat{\mathbf{f}}}={\circ }^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}(f(\varphi ))$
.
Lemma 63.
Suppose
![]() $\textsf{R}_\land, \textsf{R}_\Diamond \subseteq \textsf{R}$
. If
$\textsf{R}_\land, \textsf{R}_\Diamond \subseteq \textsf{R}$
. If
![]() $\{\varphi, \psi, \varphi \land \psi \} \subseteq \Lambda$
, then
$\{\varphi, \psi, \varphi \land \psi \} \subseteq \Lambda$
, then
![]() $f(\varphi \land \psi )=f(\varphi )\land ^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}\!\! f(\psi )$
.
$f(\varphi \land \psi )=f(\varphi )\land ^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}\!\! f(\psi )$
.
Proof.
We proceed by cases on the values of
![]() $f(\varphi )$
and
$f(\varphi )$
and
![]() $f(\psi )$
:
$f(\psi )$
:
-
1. If
 $f(\varphi ) ={\hat{\mathbf{t}}}$
, we have
$f(\varphi ) ={\hat{\mathbf{t}}}$
, we have
 ${\circ }\varphi, \varphi \in \Omega$
. We want
${\circ }\varphi, \varphi \in \Omega$
. We want
 $f(\varphi \land \psi ) = f(\psi )$
.
$f(\varphi \land \psi ) = f(\psi )$
.-
a. If
 $f(\psi ) ={\hat{\mathbf{t}}}$
, we have
$f(\psi ) ={\hat{\mathbf{t}}}$
, we have
 ${\circ }\psi, \psi \in \Omega$
. Then we have
${\circ }\psi, \psi \in \Omega$
. Then we have
 ${\circ }(\varphi \land \psi ),\varphi \land \psi \in \Omega$
by
${\circ }(\varphi \land \psi ),\varphi \land \psi \in \Omega$
by
 $\textsf{r}_1^\land$
and
$\textsf{r}_1^\land$
and
 $\textsf{r}_2^\land$
.
$\textsf{r}_2^\land$
. -
b. If
 $f(\psi ) ={\hat{\mathbf{f}}}$
, we have
$f(\psi ) ={\hat{\mathbf{f}}}$
, we have
 ${\circ }\psi \in \Omega$
and
${\circ }\psi \in \Omega$
and
 $\psi \in \overline{\Omega }$
. Then we have
$\psi \in \overline{\Omega }$
. Then we have
 ${\circ }(\varphi \land \psi ) \in \Omega$
and
${\circ }(\varphi \land \psi ) \in \Omega$
and
 $\varphi \land \psi \in \overline{\Omega }$
by
$\varphi \land \psi \in \overline{\Omega }$
by
 $\textsf{r}_1^\land$
and
$\textsf{r}_1^\land$
and
 $\textsf{r}_3^\land$
.
$\textsf{r}_3^\land$
. -
c. If
 $f(\psi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, we have
$f(\psi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, we have
 ${\circ }\psi \in \overline \Omega$
and that
${\circ }\psi \in \overline \Omega$
and that
 $f(\varphi \land \psi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
by
$f(\varphi \land \psi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
by
 $\textsf{r}_4^\land$
. Then we have that
$\textsf{r}_4^\land$
. Then we have that
 ${\circ }(\psi \Rightarrow (\varphi \land \psi )),{\circ }((\varphi \land \psi ) \Rightarrow \psi ) \in \Omega$
by
${\circ }(\psi \Rightarrow (\varphi \land \psi )),{\circ }((\varphi \land \psi ) \Rightarrow \psi ) \in \Omega$
by
 $\textsf{r}_5^\land$
and
$\textsf{r}_5^\land$
and
 $\textsf{r}_6^\land$
. This, together with Lemma 59, gives the desired result.
$\textsf{r}_6^\land$
. This, together with Lemma 59, gives the desired result.
-
-
2. If
 $f(\psi ) ={\hat{\mathbf{t}}}$
, the argument is very similar to the previous one. The case
$f(\psi ) ={\hat{\mathbf{t}}}$
, the argument is very similar to the previous one. The case
 $f(\varphi ) ={\hat{\mathbf{t}}}$
was already covered.
$f(\varphi ) ={\hat{\mathbf{t}}}$
was already covered.-
a. If
 $f(\varphi ) ={\hat{\mathbf{f}}}$
, we have
$f(\varphi ) ={\hat{\mathbf{f}}}$
, we have
 ${\circ }\varphi \in \Omega$
and
${\circ }\varphi \in \Omega$
and
 $\varphi \in \overline{\Omega }$
. Then we have
$\varphi \in \overline{\Omega }$
. Then we have
 ${\circ }(\varphi \land \psi ) \in \Omega$
and
${\circ }(\varphi \land \psi ) \in \Omega$
and
 $\varphi \land \psi \in \overline{\Omega }$
by
$\varphi \land \psi \in \overline{\Omega }$
by
 $\textsf{r}_1^\land$
and
$\textsf{r}_1^\land$
and
 $\textsf{r}_7^\land$
.
$\textsf{r}_7^\land$
. -
b. If
 $f(\varphi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, we have
$f(\varphi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, we have
 ${\circ }\varphi \in \overline \Omega$
and also that
${\circ }\varphi \in \overline \Omega$
and also that
 $f(\varphi \land \psi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, in view of
$f(\varphi \land \psi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, in view of
 $\textsf{r}_8^\land$
. Then we have that
$\textsf{r}_8^\land$
. Then we have that
 ${\circ }(\varphi \Rightarrow (\varphi \land \psi )),{\circ }((\varphi \land \psi ) \Rightarrow \varphi ) \in \Omega$
by
${\circ }(\varphi \Rightarrow (\varphi \land \psi )),{\circ }((\varphi \land \psi ) \Rightarrow \varphi ) \in \Omega$
by
 $\textsf{r}_9^\land$
and
$\textsf{r}_9^\land$
and
 $\textsf{r}_{10}^\land$
. Then, by Lemma 59, we obtain the desired result.
$\textsf{r}_{10}^\land$
. Then, by Lemma 59, we obtain the desired result.
-
-
3. If
 $f(\varphi ) ={\hat{\mathbf{f}}}$
, we have
$f(\varphi ) ={\hat{\mathbf{f}}}$
, we have
 ${\circ }\varphi \in \Omega$
and
${\circ }\varphi \in \Omega$
and
 $\varphi \in \overline{\Omega }$
. By
$\varphi \in \overline{\Omega }$
. By
 $\textsf{r}_{11}^\land$
and
$\textsf{r}_{11}^\land$
and
 $\textsf{r}_{7}^\land$
, we have
$\textsf{r}_{7}^\land$
, we have
 ${\circ }(\varphi \land \psi ) \in \Omega$
and
${\circ }(\varphi \land \psi ) \in \Omega$
and
 $\varphi \land \psi \in \overline{\Omega }$
, as desired.
$\varphi \land \psi \in \overline{\Omega }$
, as desired. -
4. If
 $f(\psi ) ={\hat{\mathbf{f}}}$
, the argument is similar to the one above and follows by
$f(\psi ) ={\hat{\mathbf{f}}}$
, the argument is similar to the one above and follows by
 $\textsf{r}_{12}^\land$
and
$\textsf{r}_{12}^\land$
and
 $\textsf{r}_{3}^\land$
.
$\textsf{r}_{3}^\land$
. -
5. If
 $f(\varphi ),f(\psi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, we have
$f(\varphi ),f(\psi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, we have
 ${\circ }\varphi, {\circ }\psi \in \overline{\Omega }$
. Thus we have
${\circ }\varphi, {\circ }\psi \in \overline{\Omega }$
. Thus we have
 ${\circ }(\varphi \land \psi ) \in \overline{\Omega }$
by
${\circ }(\varphi \land \psi ) \in \overline{\Omega }$
by
 $\textsf{r}_{13}^\land$
and thus
$\textsf{r}_{13}^\land$
and thus
 $f(\varphi \land \psi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, as desired. Consider then the following cases:
$f(\varphi \land \psi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, as desired. Consider then the following cases:-
a. If
 $f(\varphi ) \leq f(\psi )$
, we want to obtain
$f(\varphi ) \leq f(\psi )$
, we want to obtain
 $f(\varphi \land \psi ) = f(\varphi )$
. By Lemma 59, it is enough to conclude
$f(\varphi \land \psi ) = f(\varphi )$
. By Lemma 59, it is enough to conclude
 ${\circ }(\varphi \Rightarrow (\varphi \land \psi )),{\circ }((\varphi \land \psi ) \Rightarrow \varphi ) \in \Omega$
, which follows by
${\circ }(\varphi \Rightarrow (\varphi \land \psi )),{\circ }((\varphi \land \psi ) \Rightarrow \varphi ) \in \Omega$
, which follows by
 $\textsf{r}_{10}^\land$
and
$\textsf{r}_{10}^\land$
and
 $\textsf{r}_{14}^\land$
.
$\textsf{r}_{14}^\land$
. -
b. If
 $f(\psi ) \leq f(\varphi )$
, we want to obtain
$f(\psi ) \leq f(\varphi )$
, we want to obtain
 $f(\varphi \land \psi ) = f(\psi )$
. Analogously to the previous item, by Lemma 59, it is enough to conclude
$f(\varphi \land \psi ) = f(\psi )$
. Analogously to the previous item, by Lemma 59, it is enough to conclude
 ${\circ }(\psi \Rightarrow (\varphi \land \psi )),{\circ }((\varphi \land \psi ) \Rightarrow \psi ) \in \Omega$
, which follows by
${\circ }(\psi \Rightarrow (\varphi \land \psi )),{\circ }((\varphi \land \psi ) \Rightarrow \psi ) \in \Omega$
, which follows by
 $\textsf{r}_{15}^\land$
and
$\textsf{r}_{15}^\land$
and
 $\textsf{r}_{6}^\land$
.
$\textsf{r}_{6}^\land$
. -
c. Otherwise, we have
 $f(\varphi ),f(\psi ) \in \{{\mathbf{b}},{\mathbf{n}} \}$
and
$f(\varphi ),f(\psi ) \in \{{\mathbf{b}},{\mathbf{n}} \}$
and
 $f(\varphi ) \neq f(\psi )$
. Note that by Lemma 59 we obtain
$f(\varphi ) \neq f(\psi )$
. Note that by Lemma 59 we obtain
 ${\circ }(\varphi \Rightarrow \psi ) \in \overline \Omega$
. We want to obtain here
${\circ }(\varphi \Rightarrow \psi ) \in \overline \Omega$
. We want to obtain here
 $f(\varphi \land \psi ) ={\mathbf{f}}$
, that is, we want to have
$f(\varphi \land \psi ) ={\mathbf{f}}$
, that is, we want to have
 ${\uparrow }(\varphi \lor \psi ) \in \overline \Omega$
, which is achieved by
${\uparrow }(\varphi \lor \psi ) \in \overline \Omega$
, which is achieved by
 $\textsf{r}_{16}^\land$
.
$\textsf{r}_{16}^\land$
.
-
Lemma 64.
Suppose
![]() $\textsf{R}_\lor, \textsf{R}_\Diamond \subseteq \textsf{R}$
. If
$\textsf{R}_\lor, \textsf{R}_\Diamond \subseteq \textsf{R}$
. If
![]() $\{\varphi, \psi, \varphi \lor \psi \} \subseteq \Lambda$
, then
$\{\varphi, \psi, \varphi \lor \psi \} \subseteq \Lambda$
, then
![]() $f(\varphi \lor \psi )=f(\varphi )\lor ^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}\!\! f(\psi )$
.
$f(\varphi \lor \psi )=f(\varphi )\lor ^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}\!\! f(\psi )$
.
Proof.
We proceed by cases on the values of
![]() $f(\varphi )$
and
$f(\varphi )$
and
![]() $f(\psi )$
:
$f(\psi )$
:
-
1. If
 $f(\varphi )={\hat{\mathbf{f}}}$
, we know that
$f(\varphi )={\hat{\mathbf{f}}}$
, we know that
 $\varphi \in \overline \Omega$
and
$\varphi \in \overline \Omega$
and
 ${\circ } \varphi \in{\Omega }$
. We want to obtain that
${\circ } \varphi \in{\Omega }$
. We want to obtain that
 $f(\varphi \lor \psi )=f(\psi )$
, since
$f(\varphi \lor \psi )=f(\psi )$
, since
 $f(\psi ) ={\hat{\mathbf{f}}} \lor ^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}\!\! f(\psi )$
.
$f(\psi ) ={\hat{\mathbf{f}}} \lor ^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}\!\! f(\psi )$
.-
a. If
 $f(\psi )={\hat{\mathbf{f}}}$
, the result follows by
$f(\psi )={\hat{\mathbf{f}}}$
, the result follows by
 $\textsf{r}_{1}^\lor$
and
$\textsf{r}_{1}^\lor$
and
 $\textsf{r}_{2}^\lor$
.
$\textsf{r}_{2}^\lor$
. -
b. If
 $f(\psi )={\hat{\mathbf{t}}}$
, the result follows by
$f(\psi )={\hat{\mathbf{t}}}$
, the result follows by
 $\textsf{r}_{1}^\lor$
and
$\textsf{r}_{1}^\lor$
and
 $\textsf{r}_{3}^\lor$
.
$\textsf{r}_{3}^\lor$
. -
c. If
 $f(\psi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, we have
$f(\psi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, we have
 ${\circ }\psi \in \overline \Omega$
and we know that
${\circ }\psi \in \overline \Omega$
and we know that
 $f(\varphi \lor \psi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
by
$f(\varphi \lor \psi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
by
 $\textsf{r}_4^\lor$
. Then we have that
$\textsf{r}_4^\lor$
. Then we have that
 ${\circ }(\psi \Rightarrow (\varphi \lor \psi )),{\circ }((\varphi \lor \psi ) \Rightarrow \psi ) \in \Omega$
by
${\circ }(\psi \Rightarrow (\varphi \lor \psi )),{\circ }((\varphi \lor \psi ) \Rightarrow \psi ) \in \Omega$
by
 $\textsf{r}_5^\lor$
and
$\textsf{r}_5^\lor$
and
 $\textsf{r}_6^\lor$
, which, together with Lemma 59, gives the desired result.
$\textsf{r}_6^\lor$
, which, together with Lemma 59, gives the desired result.
-
-
2. If
 $f(\psi )={\hat{\mathbf{f}}}$
, we know that
$f(\psi )={\hat{\mathbf{f}}}$
, we know that
 $\psi \in \overline \Omega$
and
$\psi \in \overline \Omega$
and
 ${\circ } \psi \in{\Omega }$
. We want to obtain that
${\circ } \psi \in{\Omega }$
. We want to obtain that
 $f(\varphi \lor \psi )=f(\varphi )$
, since
$f(\varphi \lor \psi )=f(\varphi )$
, since
 $f(\varphi ) = f(\varphi ) \lor ^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}{\hat{\mathbf{f}}}$
.
$f(\varphi ) = f(\varphi ) \lor ^{\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}}{\hat{\mathbf{f}}}$
.-
a. The case
 $f(\varphi )={\hat{\mathbf{f}}}$
was already covered.
$f(\varphi )={\hat{\mathbf{f}}}$
was already covered. -
b. If
 $f(\varphi )={\hat{\mathbf{t}}}$
, the result follows by
$f(\varphi )={\hat{\mathbf{t}}}$
, the result follows by
 $\textsf{r}_1^\lor$
and
$\textsf{r}_1^\lor$
and
 $\textsf{r}_7^\lor$
.
$\textsf{r}_7^\lor$
. -
c. If
 $f(\varphi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, we have
$f(\varphi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, we have
 ${\circ }\varphi \in \overline \Omega$
and that
${\circ }\varphi \in \overline \Omega$
and that
 $f(\varphi \lor \psi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
in view of
$f(\varphi \lor \psi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
in view of
 $\textsf{r}_8^\lor$
. So we have that
$\textsf{r}_8^\lor$
. So we have that
 ${\circ }(\varphi \Rightarrow (\varphi \lor \psi )),{\circ }((\varphi \lor \psi ) \Rightarrow \varphi ) \in \Omega$
by
${\circ }(\varphi \Rightarrow (\varphi \lor \psi )),{\circ }((\varphi \lor \psi ) \Rightarrow \varphi ) \in \Omega$
by
 $\textsf{r}_9^\lor$
and
$\textsf{r}_9^\lor$
and
 $\textsf{r}_{10}^\lor$
. By Lemma 59, then, we obtain the desired result.
$\textsf{r}_{10}^\lor$
. By Lemma 59, then, we obtain the desired result.
-
-
3. If either
 $f(\varphi ) ={\hat{\mathbf{t}}}$
or
$f(\varphi ) ={\hat{\mathbf{t}}}$
or
 $f(\psi ) ={\hat{\mathbf{t}}}$
, we know that either
$f(\psi ) ={\hat{\mathbf{t}}}$
, we know that either
 ${\circ }\varphi, \varphi \in \Omega$
or
${\circ }\varphi, \varphi \in \Omega$
or
 ${\circ }\psi, \psi \in \Omega$
. In any case, we obtain
${\circ }\psi, \psi \in \Omega$
. In any case, we obtain
 ${\circ }(\varphi \lor \psi ), \varphi \lor \psi \in \Omega$
by
${\circ }(\varphi \lor \psi ), \varphi \lor \psi \in \Omega$
by
 $\textsf{r}_{11}^\lor$
,
$\textsf{r}_{11}^\lor$
,
 $\textsf{r}_{7}^\lor$
,
$\textsf{r}_{7}^\lor$
,
 $\textsf{r}_{12}^\lor$
and
$\textsf{r}_{12}^\lor$
and
 $\textsf{r}_{3}^\lor$
, and therefore
$\textsf{r}_{3}^\lor$
, and therefore
 $f(\varphi \lor \psi ) ={\hat{\mathbf{t}}}$
, as desired.
$f(\varphi \lor \psi ) ={\hat{\mathbf{t}}}$
, as desired. -
4. If
 $f(\varphi ),f(\psi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, we know that
$f(\varphi ),f(\psi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, we know that
 ${\circ } \varphi, {\circ } \psi \in \overline \Omega$
, and so
${\circ } \varphi, {\circ } \psi \in \overline \Omega$
, and so
 ${\circ }(\varphi \lor \psi ) \in \overline \Omega$
, by
${\circ }(\varphi \lor \psi ) \in \overline \Omega$
, by
 $\textsf{r}_{13}^\lor$
, thus
$\textsf{r}_{13}^\lor$
, thus
 $f(\varphi \lor \psi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. Consider now the following cases:
$f(\varphi \lor \psi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. Consider now the following cases:-
a. If
 $f(\varphi ) \leq f(\psi )$
, we want to obtain
$f(\varphi ) \leq f(\psi )$
, we want to obtain
 $f(\varphi \lor \psi ) = f(\psi )$
. By Lemma 59, we know that
$f(\varphi \lor \psi ) = f(\psi )$
. By Lemma 59, we know that
 ${\circ }(\varphi \Rightarrow \psi ) \in \Omega$
. But then
${\circ }(\varphi \Rightarrow \psi ) \in \Omega$
. But then
 ${\circ }(\psi \Rightarrow (\varphi \lor \psi ))$
,
${\circ }(\psi \Rightarrow (\varphi \lor \psi ))$
,
 ${\circ }((\varphi \lor \psi ) \Rightarrow \psi ) \in \Omega$
, by
${\circ }((\varphi \lor \psi ) \Rightarrow \psi ) \in \Omega$
, by
 $\textsf{r}_5^\lor$
and
$\textsf{r}_5^\lor$
and
 $\textsf{r}_{14}^\lor$
, which gives us the desired result by invoking Lemma 59 again.
$\textsf{r}_{14}^\lor$
, which gives us the desired result by invoking Lemma 59 again. -
b. If
 $f(\psi ) \leq f(\varphi )$
, we reason analogously to the previous item, but now using
$f(\psi ) \leq f(\varphi )$
, we reason analogously to the previous item, but now using
 $\textsf{r}_9^\lor$
and
$\textsf{r}_9^\lor$
and
 $\textsf{r}_{15}^\lor$
.
$\textsf{r}_{15}^\lor$
. -
c. Otherwise, we have
 $f(\varphi ),f(\psi ) \in \{{\mathbf{b}},{\mathbf{n}} \}$
and
$f(\varphi ),f(\psi ) \in \{{\mathbf{b}},{\mathbf{n}} \}$
and
 $f(\varphi ) \neq f(\psi )$
. Note that by Lemma 59 we obtain
$f(\varphi ) \neq f(\psi )$
. Note that by Lemma 59 we obtain
 ${\circ }(\varphi \Rightarrow \psi ) \in \overline \Omega$
. We want to obtain here
${\circ }(\varphi \Rightarrow \psi ) \in \overline \Omega$
. We want to obtain here
 $f(\varphi \lor \psi ) ={\mathbf{t}}$
, that is, we want to have
$f(\varphi \lor \psi ) ={\mathbf{t}}$
, that is, we want to have
 ${\downarrow }(\varphi \lor \psi ) \in \overline \Omega$
, and this is achieved by
${\downarrow }(\varphi \lor \psi ) \in \overline \Omega$
, and this is achieved by
 $\textsf{r}_{16}^\lor$
.
$\textsf{r}_{16}^\lor$
.
-
Lemma 65.
Suppose
![]() $\textsf{R}_{\top \bot } \subseteq \textsf{R}$
. If
$\textsf{R}_{\top \bot } \subseteq \textsf{R}$
. If
![]() $\top \in \Lambda$
, then
$\top \in \Lambda$
, then
![]() $f(\top )={\hat{\mathbf{t}}}$
; if
$f(\top )={\hat{\mathbf{t}}}$
; if
![]() $\bot \in \Lambda$
, then
$\bot \in \Lambda$
, then
![]() $f(\bot ) ={\hat{\mathbf{f}}}$
.
$f(\bot ) ={\hat{\mathbf{f}}}$
.
Proof.
Obvious from the rules of
![]() $\textsf{R}_{\top \bot }$
and the definition of
$\textsf{R}_{\top \bot }$
and the definition of
![]() $f$
.
$f$
.
Lemma 66.
If
![]() $\{ \textsf{r}_{D_\land },\textsf{r}_{D_\leq }\},\textsf{R}_\Diamond \subseteq \textsf{R}$
, we have
$\{ \textsf{r}_{D_\land },\textsf{r}_{D_\leq }\},\textsf{R}_\Diamond \subseteq \textsf{R}$
, we have
![]() $f[\Omega \cap \Lambda ]={\uparrow } a\cap f[\Lambda ]$
for some
$f[\Omega \cap \Lambda ]={\uparrow } a\cap f[\Lambda ]$
for some
![]() $a\gt{\hat{\mathbf{f}}}$
; and if we also have
$a\gt{\hat{\mathbf{f}}}$
; and if we also have
![]() $\textsf{r}_{D\neq{\uparrow }{\mathbf{t}}}\in \textsf{R}$
, then
$\textsf{r}_{D\neq{\uparrow }{\mathbf{t}}}\in \textsf{R}$
, then
![]() $f[\Omega \cap \Lambda ]={\uparrow } a\cap f[\Lambda ]$
for some
$f[\Omega \cap \Lambda ]={\uparrow } a\cap f[\Lambda ]$
for some
![]() ${\hat{\mathbf{f}}}\lt a\neq{\mathbf{t}}$
.
${\hat{\mathbf{f}}}\lt a\neq{\mathbf{t}}$
.
Proof.
First of all, we show that (I): for
![]() $\varphi _1, \ldots, \varphi _n \in \Omega \cap \Lambda$
, if
$\varphi _1, \ldots, \varphi _n \in \Omega \cap \Lambda$
, if
![]() $\bigwedge _i f(\varphi _i) \in f[\Lambda ]$
, then
$\bigwedge _i f(\varphi _i) \in f[\Lambda ]$
, then
![]() $\bigwedge _i f(\varphi _i) \in f[\Omega \cap \Lambda ]$
. By induction on
$\bigwedge _i f(\varphi _i) \in f[\Omega \cap \Lambda ]$
. By induction on
![]() $n$
, consider the base case
$n$
, consider the base case
![]() $n = 2$
. The cases
$n = 2$
. The cases
![]() $f(\varphi ) \leq f(\psi )$
and
$f(\varphi ) \leq f(\psi )$
and
![]() $f(\psi ) \leq f(\varphi )$
are obvious, as
$f(\psi ) \leq f(\varphi )$
are obvious, as
![]() $f(\varphi ) \land f(\psi )$
will coincide either with
$f(\varphi ) \land f(\psi )$
will coincide either with
![]() $f(\varphi )$
or with
$f(\varphi )$
or with
![]() $f(\psi )$
and they are in
$f(\psi )$
and they are in
![]() $f[\Omega \cap \Lambda ]$
by assumption. The tricky case thus is when
$f[\Omega \cap \Lambda ]$
by assumption. The tricky case thus is when
![]() $\{ f(\varphi ),f(\psi ) \} = \{{\mathbf{b}},{\mathbf{n}} \}$
. Suppose that for some
$\{ f(\varphi ),f(\psi ) \} = \{{\mathbf{b}},{\mathbf{n}} \}$
. Suppose that for some
![]() $\theta \in \Lambda$
we have
$\theta \in \Lambda$
we have
![]() $f(\theta ) = f(\varphi ) \land f(\psi ) ={\mathbf{f}}$
. Then, by
$f(\theta ) = f(\varphi ) \land f(\psi ) ={\mathbf{f}}$
. Then, by
![]() $\textsf{r}_{D_\land }$
, we must have
$\textsf{r}_{D_\land }$
, we must have
![]() $\theta \in \Omega$
, and so
$\theta \in \Omega$
, and so
![]() $f(\theta ) ={\mathbf{f}} \in f[\Omega \cap \Lambda ]$
. In the inductive step, suppose that
$f(\theta ) ={\mathbf{f}} \in f[\Omega \cap \Lambda ]$
. In the inductive step, suppose that
![]() $b \,{:=}\, (f(\varphi _1) \land \ldots \land f(\varphi _n)) \land f(\varphi _{n+1}) \in f[\Lambda ]$
, for
$b \,{:=}\, (f(\varphi _1) \land \ldots \land f(\varphi _n)) \land f(\varphi _{n+1}) \in f[\Lambda ]$
, for
![]() $\varphi _1,\ldots, \varphi _{n+1} \in \Omega \cap \Lambda$
. Then either (i)
$\varphi _1,\ldots, \varphi _{n+1} \in \Omega \cap \Lambda$
. Then either (i)
![]() $b = (f(\varphi _1) \land \ldots \land f(\varphi _n))$
, or (ii)
$b = (f(\varphi _1) \land \ldots \land f(\varphi _n))$
, or (ii)
![]() $b = f(\varphi _{n+1})$
, or (iii)
$b = f(\varphi _{n+1})$
, or (iii)
![]() $b ={\mathbf{f}}$
and
$b ={\mathbf{f}}$
and
![]() $\{f(\varphi _1) \land \ldots \land f(\varphi _n),f(\varphi _{n+1})\} = \{{\mathbf{b}},{\mathbf{n}} \}$
. In case (i), we use the induction hypothesis. Case (ii) is obvious. As for case (iii), we use
$\{f(\varphi _1) \land \ldots \land f(\varphi _n),f(\varphi _{n+1})\} = \{{\mathbf{b}},{\mathbf{n}} \}$
. In case (i), we use the induction hypothesis. Case (ii) is obvious. As for case (iii), we use
![]() $\textsf{r}_{D_\land }$
as we did in the base case.
$\textsf{r}_{D_\land }$
as we did in the base case.
Second, we show that (II): for
![]() $\varphi \in \Omega \cap \Lambda$
and
$\varphi \in \Omega \cap \Lambda$
and
![]() $\psi \in \Lambda$
, if
$\psi \in \Lambda$
, if
![]() $f(\varphi ) \leq f(\psi )$
, then
$f(\varphi ) \leq f(\psi )$
, then
![]() $\psi \in \Omega$
. By cases on the value of
$\psi \in \Omega$
. By cases on the value of
![]() $f(\varphi )$
(note that
$f(\varphi )$
(note that
![]() $f(\varphi ) \neq{\mathbf{f}}$
as
$f(\varphi ) \neq{\mathbf{f}}$
as
![]() $\varphi \in \Omega$
):
$\varphi \in \Omega$
):
-
1. If
 $f(\varphi ) ={\hat{\mathbf{t}}}$
, we must have
$f(\varphi ) ={\hat{\mathbf{t}}}$
, we must have
 $f(\psi ) ={\hat{\mathbf{t}}}$
, thus
$f(\psi ) ={\hat{\mathbf{t}}}$
, thus
 $\psi \in \Omega$
.
$\psi \in \Omega$
. -
2. If
 $f(\varphi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, we have either
$f(\varphi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
, we have either
 $f(\psi ) ={\hat{\mathbf{t}}}$
, and thus
$f(\psi ) ={\hat{\mathbf{t}}}$
, and thus
 $\psi \in \Omega$
, or
$\psi \in \Omega$
, or
 $f(\psi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. In that case, by Lemma 59, we have
$f(\psi ) \in \{{\mathbf{f}},{\mathbf{b}},{\mathbf{n}},{\mathbf{t}} \}$
. In that case, by Lemma 59, we have
 ${\circ }(\varphi \Rightarrow \psi ) \in \Omega$
. Then
${\circ }(\varphi \Rightarrow \psi ) \in \Omega$
. Then
 $\psi \in \Omega$
follows by
$\psi \in \Omega$
follows by
 $\textsf{r}_{D_\leq }$
.
$\textsf{r}_{D_\leq }$
.
Let
![]() $a \,{:=}\, \bigwedge f[\Omega \cap \Lambda ]$
. Clearly,
$a \,{:=}\, \bigwedge f[\Omega \cap \Lambda ]$
. Clearly,
![]() $a \neq{\hat{\mathbf{f}}}$
. Since
$a \neq{\hat{\mathbf{f}}}$
. Since
![]() $a \leq b$
for each
$a \leq b$
for each
![]() $b \in f[\Omega \cap \Lambda ]$
, we must have
$b \in f[\Omega \cap \Lambda ]$
, we must have
![]() $f[\Omega \cap \Lambda ] \subseteq{\uparrow } a \cap f[\Lambda ]$
. It remains to show that
$f[\Omega \cap \Lambda ] \subseteq{\uparrow } a \cap f[\Lambda ]$
. It remains to show that
![]() ${\uparrow } a \cap f[\Lambda ] \subseteq f[\Omega \cap \Lambda ]$
. Suppose that there is
${\uparrow } a \cap f[\Lambda ] \subseteq f[\Omega \cap \Lambda ]$
. Suppose that there is
![]() $\theta \in \overline \Omega \cap \Lambda$
such that (a):
$\theta \in \overline \Omega \cap \Lambda$
such that (a):
![]() $a \leq f(\theta )$
. By cases:
$a \leq f(\theta )$
. By cases:
-
1. If
 $f(\theta ) \leq f(\varphi )$
for all
$f(\theta ) \leq f(\varphi )$
for all
 $\varphi \in \Omega \cap \Lambda$
, then
$\varphi \in \Omega \cap \Lambda$
, then
 $f(\theta ) = a$
, and thus
$f(\theta ) = a$
, and thus
 $\theta \in \Omega$
by (I).
$\theta \in \Omega$
by (I). -
2. If
 $f(\theta ) \not \leq f(\psi )$
for some
$f(\theta ) \not \leq f(\psi )$
for some
 $\psi \in \Omega$
, we have the following subcases:
$\psi \in \Omega$
, we have the following subcases:-
a. If
 $f(\psi ) \lt f(\theta )$
, by (II) we must have
$f(\psi ) \lt f(\theta )$
, by (II) we must have
 $\theta \in \Omega \cap \Lambda$
.
$\theta \in \Omega \cap \Lambda$
. -
b. If
 $f(\psi ) \not \leq f(\theta )$
, we have
$f(\psi ) \not \leq f(\theta )$
, we have
 $f(\psi ) ={\mathbf{b}}$
and
$f(\psi ) ={\mathbf{b}}$
and
 $f(\theta ) ={\mathbf{n}}$
or vice-versa. By (a), we have
$f(\theta ) ={\mathbf{n}}$
or vice-versa. By (a), we have
 $a \in \{{\mathbf{f}},{\mathbf{n}} \}$
. The case
$a \in \{{\mathbf{f}},{\mathbf{n}} \}$
. The case
 $a ={\mathbf{n}}$
was treated in (1), so we only consider
$a ={\mathbf{n}}$
was treated in (1), so we only consider
 $a ={\mathbf{f}}$
. This means that either
$a ={\mathbf{f}}$
. This means that either
 ${\mathbf{b}},{\mathbf{n}} \in f[\Omega \cap \Lambda ]$
or
${\mathbf{b}},{\mathbf{n}} \in f[\Omega \cap \Lambda ]$
or
 ${\mathbf{f}} \in f[\Omega \cap \Lambda ]$
, and the result follows from (II).
${\mathbf{f}} \in f[\Omega \cap \Lambda ]$
, and the result follows from (II).
-
Now, in case the rule
![]() $\textsf{r}_{D\neq{\uparrow }{\mathbf{t}}}$
is present in the calculus, we are able to show that if
$\textsf{r}_{D\neq{\uparrow }{\mathbf{t}}}$
is present in the calculus, we are able to show that if
![]() $\varphi, \psi \in \Omega \cap \Lambda$
and
$\varphi, \psi \in \Omega \cap \Lambda$
and
![]() $f(\varphi ) \lor f(\psi ) \in f[\Omega \cap \Lambda ]$
, then either
$f(\varphi ) \lor f(\psi ) \in f[\Omega \cap \Lambda ]$
, then either
![]() $f(\varphi ) \in f[\Omega \cap \Lambda ]$
or
$f(\varphi ) \in f[\Omega \cap \Lambda ]$
or
![]() $f(\psi ) \in f[\Omega \cap \Lambda ]$
, which essentially excludes the possibility of
$f(\psi ) \in f[\Omega \cap \Lambda ]$
, which essentially excludes the possibility of
![]() $a ={\mathbf{t}}$
. Suppose that for
$a ={\mathbf{t}}$
. Suppose that for
![]() $\theta \in \Lambda$
,
$\theta \in \Lambda$
,
![]() $f(\theta ) = f(\varphi ) \lor f(\psi ) \in f[\Omega \cap \Lambda ]$
. Then either
$f(\theta ) = f(\varphi ) \lor f(\psi ) \in f[\Omega \cap \Lambda ]$
. Then either
![]() $f(\theta ) = f(\varphi )$
, or
$f(\theta ) = f(\varphi )$
, or
![]() $f(\theta ) = f(\psi )$
or
$f(\theta ) = f(\psi )$
or
![]() $f(\theta ) ={\mathbf{t}}$
and
$f(\theta ) ={\mathbf{t}}$
and
![]() $\{f(\varphi ),f(\psi )\} = \{{\mathbf{b}},{\mathbf{n}} \}$
. The first two cases are obvious. The third one follows because the rule
$\{f(\varphi ),f(\psi )\} = \{{\mathbf{b}},{\mathbf{n}} \}$
. The first two cases are obvious. The third one follows because the rule
![]() $\textsf{r}_{D\neq{\uparrow }{\mathbf{t}}}$
forces
$\textsf{r}_{D\neq{\uparrow }{\mathbf{t}}}$
forces
![]() $\varphi \in \Omega$
in this situation.
$\varphi \in \Omega$
in this situation.
We are now finally ready to go back to the completeness proof we were working on before going through the above series of auxiliary results. Note that the above lemmas show that
![]() $f$
is a partial homomorphism over
$f$
is a partial homomorphism over
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
(which can of course be extended to a full homomorphism) and, in view of the above lemmas, by considering a set of designated values of the form
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
(which can of course be extended to a full homomorphism) and, in view of the above lemmas, by considering a set of designated values of the form
![]() ${\uparrow } a$
for appropriate
${\uparrow } a$
for appropriate
![]() $a$
we obtain a countermodel for
$a$
we obtain a countermodel for
![]() $\Phi \rhd _{{\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}}} \Psi$
or for
$\Phi \rhd _{{\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}}} \Psi$
or for
![]() $\Phi \rhd _{{\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }}}\Psi$
as desired. This finishes the proof of Theorem 58.
$\Phi \rhd _{{\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }}}\Psi$
as desired. This finishes the proof of Theorem 58.
6.2
 axiomatization for
axiomatization for
 $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
The ![]() calculus developed in the preceding subsection for the logic
calculus developed in the preceding subsection for the logic
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
induces a
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\!\leq }$
induces a ![]() logic for its
logic for its ![]() companion
companion
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
. We begin by defining this calculus, then indicate why it is complete for
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
. We begin by defining this calculus, then indicate why it is complete for
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
. In what follows, given a set of formulas
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
. In what follows, given a set of formulas
![]() $\Phi$
, let
$\Phi$
, let
![]() $\Phi \lor \psi \,{:=}\, \{ \varphi \lor \psi : \varphi \in \Phi \}$
and
$\Phi \lor \psi \,{:=}\, \{ \varphi \lor \psi : \varphi \in \Phi \}$
and
![]() $\bigvee \{ \varphi _1,\ldots, \varphi _m \} \,{:=}\, \varphi _1 \lor (\varphi _2 \lor \ldots (\ldots \lor \varphi _n)\ldots )$
.
$\bigvee \{ \varphi _1,\ldots, \varphi _m \} \,{:=}\, \varphi _1 \lor (\varphi _2 \lor \ldots (\ldots \lor \varphi _n)\ldots )$
.
Definition 67.
Let
![]() $\textsf{R}$
be a
$\textsf{R}$
be a ![]() calculus. We define
calculus. We define
![]() $\textsf{R}^{\lor }$
as the
$\textsf{R}^{\lor }$
as the ![]() calculus
calculus
the rule
![]() $\textsf{r}^\lor$
is set as:
$\textsf{r}^\lor$
is set as:
 $\begin{array}{l@{\quad}l}\textsf{r} & in\;case\; \Phi\; is\;empty\;and\; \Psi\; is\; a\; singleton\\ \frac{\Phi \lor s}{s}, & in\;case\;\Psi\;is\;empty \\ \frac{\Phi \lor s}{(\bigvee \Psi ) \lor s}, & otherwise\\ \end{array}$
$\begin{array}{l@{\quad}l}\textsf{r} & in\;case\; \Phi\; is\;empty\;and\; \Psi\; is\; a\; singleton\\ \frac{\Phi \lor s}{s}, & in\;case\;\Psi\;is\;empty \\ \frac{\Phi \lor s}{(\bigvee \Psi ) \lor s}, & otherwise\\ \end{array}$
In all cases,
![]() $s$
is chosen to be a propositional variable not occurring in the rules that belong to
$s$
is chosen to be a propositional variable not occurring in the rules that belong to
![]() $\textsf{R}$
.
$\textsf{R}$
.
Using the above recipe is straightforward, and this gives the reason why we decided to not spell out the whole axiomatization here. Before introducing the completeness result, we define what it means for a ![]() logic to have a disjunction. A
logic to have a disjunction. A ![]() logic
logic
![]() $\vdash$
over
$\vdash$
over
![]() $\Sigma$
has a disjunction provided that
$\Sigma$
has a disjunction provided that
![]() $\Phi, \varphi \lor \psi \;\vdash \; \xi$
if, and only if,
$\Phi, \varphi \lor \psi \;\vdash \; \xi$
if, and only if,
![]() $\Phi, \varphi \;\vdash \; \xi$
and
$\Phi, \varphi \;\vdash \; \xi$
and
![]() $\Phi, \psi \;\vdash \;\xi$
(for
$\Phi, \psi \;\vdash \;\xi$
(for
![]() $\lor$
a binary connective in
$\lor$
a binary connective in
![]() $\Sigma$
). The completeness result is immediate from the fact that
$\Sigma$
). The completeness result is immediate from the fact that
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
has a disjunction, in view of the following result:
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
has a disjunction, in view of the following result:
Lemma 68 (Shoesmith and Smiley Reference Shoesmith and Smiley1978, Thm. 5.37). Let
![]() $\textsf{R}$
be a
$\textsf{R}$
be a ![]() calculus over a signature containing a binary connective
calculus over a signature containing a binary connective
![]() $\lor$
. If
$\lor$
. If
![]() $\vdash _{\textsf{R}}$
has a disjunction, then
$\vdash _{\textsf{R}}$
has a disjunction, then
![]() $\vdash _{\textsf{R}^\lor } \;=\; \vdash _{\textsf{R}}$
.
$\vdash _{\textsf{R}^\lor } \;=\; \vdash _{\textsf{R}}$
.
From this it immediately follows that:
Theorem 69.
![]() $\vdash _{\textsf{R}_{\leq }^\lor } ={\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }}$
.
$\vdash _{\textsf{R}_{\leq }^\lor } ={\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }}$
.
7. Algebraic Study of
 $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
and
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
and
 $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
In this section, we look at the class of algebras that corresponds to
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
and
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
and
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
according to the general theory of algebraization of logics (Font Reference Font2016). In order to facilitate the exposition, here we will write a
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
according to the general theory of algebraization of logics (Font Reference Font2016). In order to facilitate the exposition, here we will write a
![]() $\Sigma$
-algebra
$\Sigma$
-algebra
![]() $\mathbf{A} \,{:=}\, \langle A, \cdot ^{\mathbf{A}} \rangle$
as
$\mathbf{A} \,{:=}\, \langle A, \cdot ^{\mathbf{A}} \rangle$
as
![]() $\langle A; \unicode{x00A9}_1^{\mathbf{A}},\ldots, \unicode{x00A9}_n^{\mathbf{A}} \rangle$
, with
$\langle A; \unicode{x00A9}_1^{\mathbf{A}},\ldots, \unicode{x00A9}_n^{\mathbf{A}} \rangle$
, with
![]() $\unicode{x00A9}_i \in \Sigma$
for each
$\unicode{x00A9}_i \in \Sigma$
for each
![]() $1 \leq i \leq n$
. We will further omit the superscript
$1 \leq i \leq n$
. We will further omit the superscript
![]() $\mathbf{A}$
from the interpretations of the connectives whenever there is no risk of confusion.
$\mathbf{A}$
from the interpretations of the connectives whenever there is no risk of confusion.
We begin by recalling that, as observed earlier, the algebra
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
is a symmetric Heyting algebra in Monteiro’s sense.
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
is a symmetric Heyting algebra in Monteiro’s sense.
Definition 70 (Monteiro Reference Monteiro1980, Def. 1.2, p. 61). A symmetric Heyting algebra (SHA) is a
![]() $\Sigma ^{\textsf{DM}}_{\Rightarrow }$
-algebra
$\Sigma ^{\textsf{DM}}_{\Rightarrow }$
-algebra
![]() $\langle A; \land, \lor, \Rightarrow, {\sim }, \bot, \top \rangle$
such that:
$\langle A; \land, \lor, \Rightarrow, {\sim }, \bot, \top \rangle$
such that:
-
(1)
 $\langle A; \land, \lor, \Rightarrow, \bot, \top \rangle$
is a Heyting algebra.
$\langle A; \land, \lor, \Rightarrow, \bot, \top \rangle$
is a Heyting algebra.
-
(2)
 $\langle A; \land, \lor, {\sim }, \bot, \top \rangle$
is a De Morgan algebra.
$\langle A; \land, \lor, {\sim }, \bot, \top \rangle$
is a De Morgan algebra.
As mentioned earlier, SHAs are alternatively known as De Morgan-Heyting algebras in the terminology introduced by Sankappanavar (Reference Sankappanavar1987). The logical counterpart of SHAs is Moisil’s “symmetric modal logic,” which is the expansion of the Hilbert-Bernays positive logic (the conjunction-disjunction-implication fragment of intuitionistic logic) by the addition of a De Morgan negation. One might expect Moisil’s logic to be closely related to
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
. In fact, as we shall see, the logic
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
. In fact, as we shall see, the logic
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
considered earlier (the
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
considered earlier (the
![]() $\top$
-assertional companion of
$\top$
-assertional companion of
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
) may be viewed as an axiomatic extension of Moisil’s logic; whereas we may obtain
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
) may be viewed as an axiomatic extension of Moisil’s logic; whereas we may obtain
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
from Moisil’s logic provided we extend it by appropriate axioms but also drop the contraposition rule schema (
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
from Moisil’s logic provided we extend it by appropriate axioms but also drop the contraposition rule schema (
![]() $\textsf{r}^{\textsf M}_{12}$
below). The following is a Hilbert-style calculus for Moisil’s logic (see Monteiro Reference Monteiro1980, p. 60):
$\textsf{r}^{\textsf M}_{12}$
below). The following is a Hilbert-style calculus for Moisil’s logic (see Monteiro Reference Monteiro1980, p. 60):
The Lindenbaum-Tarski algebras of Moisil’s logic are precisely the symmetric Heyting algebras (see Monteiro Reference Monteiro1980, Thm. 2.3, p. 62). Using this result, it is easy to obtain the following:
Proposition 71.
Moisil’s logic is algebraizable (in the sense of Blok and Pigozzi Reference Blok and Pigozzi1989
) with the same translations as positive logic (namely, equivalence formulas
![]() $\{ x \Rightarrow y, y \Rightarrow x \}$
and defining equation
$\{ x \Rightarrow y, y \Rightarrow x \}$
and defining equation
![]() $x \approx \top$
). Its equivalent algebraic semantics is the variety of symmetric Heyting algebras.
$x \approx \top$
). Its equivalent algebraic semantics is the variety of symmetric Heyting algebras.
Having verified that
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
is an axiomatic extension of Moisil’s logic (see our axiomatization below), we will immediately obtain that
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
is an axiomatic extension of Moisil’s logic (see our axiomatization below), we will immediately obtain that
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
is algebraizable with the translations mentioned in the preceding proposition; the equivalent algebraic semantics of
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
is algebraizable with the translations mentioned in the preceding proposition; the equivalent algebraic semantics of
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
is then bound to be a sub(quasi)variety of SHAs. As we will see, one may obtain
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
is then bound to be a sub(quasi)variety of SHAs. As we will see, one may obtain
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
from the above axiomatizations of Moisil’s logic by adding the following axioms (we use
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
from the above axiomatizations of Moisil’s logic by adding the following axioms (we use
![]() $\neg p$
as an abbreviation of
$\neg p$
as an abbreviation of
![]() $p \Rightarrow{\sim } (p \Rightarrow p)$
and
$p \Rightarrow{\sim } (p \Rightarrow p)$
and
![]() ${\circ } p$
as an abbreviation of
${\circ } p$
as an abbreviation of
![]() $\neg p \lor \neg{\sim } p)$
:
$\neg p \lor \neg{\sim } p)$
:
This axiomatization should be compared with the equational presentation given in Definition 72, and the claimed completeness of the axiomatization will follow from Theorems 77 and 78. Definition 72(2) matches
![]() $\textsf{r}^{\top }_{3}$
. Definition 72(1) says that the algebra has a PP-algebra reduct: as observed in Marcelino and Rivieccio (Reference Marcelino and Rivieccio2022, p. 3150), for an algebra that has a pseudo-complement negation (as all symmetric Heyting algebras do), it is sufficient to impose the equation
$\textsf{r}^{\top }_{3}$
. Definition 72(1) says that the algebra has a PP-algebra reduct: as observed in Marcelino and Rivieccio (Reference Marcelino and Rivieccio2022, p. 3150), for an algebra that has a pseudo-complement negation (as all symmetric Heyting algebras do), it is sufficient to impose the equation
![]() ${\sim } \neg \neg x \approx \neg x$
to obtain an involutive Stone algebra (i.e., modulo the language, a PP-algebra); clearly the equation
${\sim } \neg \neg x \approx \neg x$
to obtain an involutive Stone algebra (i.e., modulo the language, a PP-algebra); clearly the equation
![]() ${\sim } \neg \neg x \approx \neg x$
corresponds, via algebraizability, to
${\sim } \neg \neg x \approx \neg x$
corresponds, via algebraizability, to
![]() $\textsf{r}^{\top }_{1}$
and
$\textsf{r}^{\top }_{1}$
and
![]() $\textsf{r}^{\top }_{2}$
.
$\textsf{r}^{\top }_{2}$
.
One can also show that
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
may be obtained from the preceding axiomatization by taking as axioms all the valid formulas while dropping the contraposition rule of Moisil’s logic (see e.g., Bou et al. (Reference Bou, Esteva, Maria Font, Gil, Godo, Torrens and Verdú2011, p.11)).
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
may be obtained from the preceding axiomatization by taking as axioms all the valid formulas while dropping the contraposition rule of Moisil’s logic (see e.g., Bou et al. (Reference Bou, Esteva, Maria Font, Gil, Godo, Torrens and Verdú2011, p.11)).
We proceed to obtain further information on the subclass of symmetric Heyting algebras that are models of
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
and
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
and
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
. Monteiro (Reference Monteiro1980) carried out an extensive study of symmetric Heyting (and related) algebras; independently, some of Monteiro’s results were rediscovered and a number of new ones obtained in Sankappanavar (Reference Sankappanavar1987). From these works, we shall recall only a few results needed for our purposes.
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
. Monteiro (Reference Monteiro1980) carried out an extensive study of symmetric Heyting (and related) algebras; independently, some of Monteiro’s results were rediscovered and a number of new ones obtained in Sankappanavar (Reference Sankappanavar1987). From these works, we shall recall only a few results needed for our purposes.
The following example is of special relevance to us because, as we shall see, the symmetric Heyting algebras we are mostly interested in have the shape described therein:
Example 7 (Sankappanavar Reference Sankappanavar1987, p. 568). Let
![]() $\mathbf{A}[D]$
be a finite De Morgan algebra and let
$\mathbf{A}[D]$
be a finite De Morgan algebra and let
![]() $\mathbf{A}[C]^+_n$
and
$\mathbf{A}[C]^+_n$
and
![]() $\mathbf{A}[C]^-_n$
be two
$\mathbf{A}[C]^-_n$
be two
![]() $n$
-element chains, which we view as lattices. Denoting
$n$
-element chains, which we view as lattices. Denoting
![]() $C^+_n \,{:=}\, \{ c_1, \ldots, c_n \}$
, with
$C^+_n \,{:=}\, \{ c_1, \ldots, c_n \}$
, with
![]() $c_1 \lt \ldots \lt c_n$
, let
$c_1 \lt \ldots \lt c_n$
, let
![]() $C^-_n \,{:=}\, \{{\sim } c_1, \ldots, {\sim } c_n \}$
, with
$C^-_n \,{:=}\, \{{\sim } c_1, \ldots, {\sim } c_n \}$
, with
![]() ${\sim } c_n \lt \ldots \lt{\sim } c_1$
. Consider the ordinal sum of these lattices,
${\sim } c_n \lt \ldots \lt{\sim } c_1$
. Consider the ordinal sum of these lattices,
![]() $\mathbf{A}[D]^{\mathbf{A}[C]} : = \mathbf{A}[C]^-_n \oplus \mathbf{A}[D] \oplus \mathbf{A}[C]^+_n$
, in which the order and the De Morgan negation are defined as follows: for all
$\mathbf{A}[D]^{\mathbf{A}[C]} : = \mathbf{A}[C]^-_n \oplus \mathbf{A}[D] \oplus \mathbf{A}[C]^+_n$
, in which the order and the De Morgan negation are defined as follows: for all
![]() $d \in D$
and
$d \in D$
and
![]() $c_i \in C^+_n$
, we let
$c_i \in C^+_n$
, we let
![]() ${\sim } c_i\lt d\lt c_i$
and
${\sim } c_i\lt d\lt c_i$
and
![]() ${\sim }^{\mathbf{A}[D]^{\mathbf{A}[C]}} d ={\sim }^{\mathbf{A}[D]} d$
. Then,
${\sim }^{\mathbf{A}[D]^{\mathbf{A}[C]}} d ={\sim }^{\mathbf{A}[D]} d$
. Then,
![]() $\mathbf{A}[D]^{\mathbf{A}[C]}$
is a finite De Morgan algebra, and can therefore be endowed with the Heyting implication determined by the order, turning it into a symmetric Heyting algebra.
$\mathbf{A}[D]^{\mathbf{A}[C]}$
is a finite De Morgan algebra, and can therefore be endowed with the Heyting implication determined by the order, turning it into a symmetric Heyting algebra.
We now proceed to the axiomatization of
![]() $\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
. First, we define an equational class we shall call
$\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
. First, we define an equational class we shall call
![]() $\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
, then we show that it coincides with
$\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
, then we show that it coincides with
![]() $\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
.
$\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
.
Definition 72.
Let
![]() $\mathbf{A} \,{:=}\, \langle A; \land, \lor, \Rightarrow, {\sim },{\circ }, \bot, \top \rangle$
be a symmetric Heyting algebra expanded with an operation
$\mathbf{A} \,{:=}\, \langle A; \land, \lor, \Rightarrow, {\sim },{\circ }, \bot, \top \rangle$
be a symmetric Heyting algebra expanded with an operation
![]() $\circ$
. We say that
$\circ$
. We say that
![]() $\mathbf{A}$
is in the class
$\mathbf{A}$
is in the class
![]() $\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
if the following conditions are satisfied:
$\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
if the following conditions are satisfied:
-
(1) The reduct
 $\langle A; \land, \lor, {\circ },{\sim }, \bot, \top \rangle$
is a PP-algebra.
$\langle A; \land, \lor, {\circ },{\sim }, \bot, \top \rangle$
is a PP-algebra.
-
(2)
 $\mathbf{A}$
satisfies the following equation:
$\mathbf{A}$
satisfies the following equation:
 \begin{equation*} {{\circ }(x_1 \Rightarrow x_2) \land {\circ }(x_2\Rightarrow x_3) } \leq {{\circ } x_1 \lor {\circ } x_4 \lor {\circ }(x_4\Rightarrow x_3)} \lor {\circ }(x_3\Rightarrow x_2) \lor {\circ }(x_2\Rightarrow x_1). \end{equation*}
\begin{equation*} {{\circ }(x_1 \Rightarrow x_2) \land {\circ }(x_2\Rightarrow x_3) } \leq {{\circ } x_1 \lor {\circ } x_4 \lor {\circ }(x_4\Rightarrow x_3)} \lor {\circ }(x_3\Rightarrow x_2) \lor {\circ }(x_2\Rightarrow x_1). \end{equation*}
Our next aim is to check the following results:
![]() $\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
is the variety (and the quasi-variety) generated by
$\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
is the variety (and the quasi-variety) generated by
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
(Theorem 77), and
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
(Theorem 77), and
![]() $\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
is the equivalent algebraic semantics of the algebraizable logic
$\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
is the equivalent algebraic semantics of the algebraizable logic
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
(Theorem 78).
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
(Theorem 78).
We shall prove the above by relying on a few lemmas that also have an independent interest, in that they shed some light on the structures of symmetric Heyting algebras in general and of algebras in
![]() $\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
in particular.
$\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
in particular.
Adopting Monteiro’s notation, we shall use the abbreviations
![]() $\neg x := x \Rightarrow{\sim } (x \Rightarrow x)$
and
$\neg x := x \Rightarrow{\sim } (x \Rightarrow x)$
and
![]() $\Delta x : = \neg{\sim } x$
(recall that, on every algebra having a PP-algebra reduct (Gomes et al. Reference Gomes, Greati, Marcelino, Marcos and Rivieccio2022), one may take
$\Delta x : = \neg{\sim } x$
(recall that, on every algebra having a PP-algebra reduct (Gomes et al. Reference Gomes, Greati, Marcelino, Marcos and Rivieccio2022), one may take
![]() ${\circ } x \,{:=}\, \neg x \lor \Delta x$
and
${\circ } x \,{:=}\, \neg x \lor \Delta x$
and
![]() $\Delta x \,{:=}\, x \land{\circ } x$
). In
$\Delta x \,{:=}\, x \land{\circ } x$
). In
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
, we have:
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
, we have:
 \begin{equation*} \neg ^{\mathbf {PP_6^{\Rightarrow _{\textsf {H}}}}}(a) = \begin {cases} {\hat {\mathbf {t}}} & \text {if } a = {\hat {\mathbf {f}}},\\ {\hat {\mathbf {f}}} & \text {otherwise.} \end {cases} \quad \text {and} \quad \Delta ^{\mathbf {PP_6^{\Rightarrow _{\textsf {H}}}}}(a) = \begin {cases} {\hat {\mathbf {t}}} & \text { if } a = {\hat {\mathbf {t}}},\\ {\hat {\mathbf {f}}} & \text { otherwise.} \end {cases} \end{equation*}
\begin{equation*} \neg ^{\mathbf {PP_6^{\Rightarrow _{\textsf {H}}}}}(a) = \begin {cases} {\hat {\mathbf {t}}} & \text {if } a = {\hat {\mathbf {f}}},\\ {\hat {\mathbf {f}}} & \text {otherwise.} \end {cases} \quad \text {and} \quad \Delta ^{\mathbf {PP_6^{\Rightarrow _{\textsf {H}}}}}(a) = \begin {cases} {\hat {\mathbf {t}}} & \text { if } a = {\hat {\mathbf {t}}},\\ {\hat {\mathbf {f}}} & \text { otherwise.} \end {cases} \end{equation*}
Given a SHA
![]() $\mathbf{A}$
and a subset
$\mathbf{A}$
and a subset
![]() $F \subseteq A$
, we shall say that
$F \subseteq A$
, we shall say that
![]() $F$
is a filter if it is a non-empty lattice filter of the bounded lattice reduct of
$F$
is a filter if it is a non-empty lattice filter of the bounded lattice reduct of
![]() $\mathbf{A}$
. A filter
$\mathbf{A}$
. A filter
![]() $F$
will be called regular if
$F$
will be called regular if
![]() $\Delta a \in F$
whenever
$\Delta a \in F$
whenever
![]() $a \in F$
, for all
$a \in F$
, for all
![]() $a \in A$
. For example, the algebra
$a \in A$
. For example, the algebra
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
has only one proper regular filter, namely the singleton
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
has only one proper regular filter, namely the singleton
![]() $\{{\hat{\mathbf{t}}} \}$
. On every SHA, the regular filters form a closure system (hence, a complete lattice) and may be characterized in a number of alternative ways (see e.g., Monteiro Reference Monteiro1980, Thm. 4.3, p. 75, and Thm. 4.11, p. 80). In particular, it can be shown that regular filters coincide with the lattice filters
$\{{\hat{\mathbf{t}}} \}$
. On every SHA, the regular filters form a closure system (hence, a complete lattice) and may be characterized in a number of alternative ways (see e.g., Monteiro Reference Monteiro1980, Thm. 4.3, p. 75, and Thm. 4.11, p. 80). In particular, it can be shown that regular filters coincide with the lattice filters
![]() $F$
that further satisfy the contraposition rule, that is:
$F$
that further satisfy the contraposition rule, that is:
![]() ${\sim } b \Rightarrow{\sim } a \in F$
whenever
${\sim } b \Rightarrow{\sim } a \in F$
whenever
![]() $a \Rightarrow b \in F$
. By the algebraizability of Moisil’s logic, this observation yields the following result, which Sankappanavar proved in a more general (and purely algebraic) context:
$a \Rightarrow b \in F$
. By the algebraizability of Moisil’s logic, this observation yields the following result, which Sankappanavar proved in a more general (and purely algebraic) context:
Lemma 73 (Sankappanavar Reference Sankappanavar1987, Thm. 3.3). The lattice of congruences of each SHA
![]() $\mathbf{A}$
is isomorphic to the lattice of regular filters on
$\mathbf{A}$
is isomorphic to the lattice of regular filters on
![]() $\mathbf{A}$
.
$\mathbf{A}$
.
We now focus on a subvariety of SHAs (to which
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
obviously belongs) where regular filter generation admits a particularly simple description. As we will see, the following equation will play a key role:
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
obviously belongs) where regular filter generation admits a particularly simple description. As we will see, the following equation will play a key role:
Lemma 74 (Monteiro, Reference Monteiro1980, Thm. 4.17, p. 82). Let
![]() $\mathbf{A}$
be a SHA that satisfies
$\mathbf{A}$
be a SHA that satisfies
![]() $({\Delta\text{-idemp}})$
and let
$({\Delta\text{-idemp}})$
and let
![]() $B \subseteq A$
. The regular filter
$B \subseteq A$
. The regular filter
![]() $F(B)$
generated by
$F(B)$
generated by
![]() $B$
is given by:
$B$
is given by:
Lemma 75 (Sankappanavar, Reference Sankappanavar1987, Cor. 4.8). Let
![]() $\mathbf{A}$
be a SHA that satisfies
$\mathbf{A}$
be a SHA that satisfies
![]() $({\Delta\text{-idemp}})$
. The following are equivalent:
$({\Delta\text{-idemp}})$
. The following are equivalent:
-
(1)
 $\mathbf{A}$
is directly indecomposable.
$\mathbf{A}$
is directly indecomposable.
-
(2)
 $\mathbf{A}$
is subdirectly irreducible.
$\mathbf{A}$
is subdirectly irreducible.
-
(3)
 $\mathbf{A}$
is simple.
$\mathbf{A}$
is simple.
The subvariety of SHAs defined by the equation
![]() $({\Delta\text{-idemp}})$
is dubbed
$({\Delta\text{-idemp}})$
is dubbed
![]() $\mathbb{SDH}_1$
by Sankappanavar (Reference Sankappanavar1987), who observes that it is a discriminatorFootnote 3 variety (see Burris and Sankappanavar Reference Burris and Sankappanavar2011, Def. IV.9.3). This entails that
$\mathbb{SDH}_1$
by Sankappanavar (Reference Sankappanavar1987), who observes that it is a discriminatorFootnote 3 variety (see Burris and Sankappanavar Reference Burris and Sankappanavar2011, Def. IV.9.3). This entails that
![]() $\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
is also a discriminator variety. The discriminator term for
$\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
is also a discriminator variety. The discriminator term for
![]() $\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
is the following:
$\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
is the following:
where
![]() $x \Leftrightarrow y \,{:=}\, (x \Rightarrow y) \land (y \Rightarrow x)$
. To see this, consider Theorem 77 and note that on
$x \Leftrightarrow y \,{:=}\, (x \Rightarrow y) \land (y \Rightarrow x)$
. To see this, consider Theorem 77 and note that on
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
we have, for all
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
we have, for all
![]() $c,d \in \mathcal{V}_6$
,
$c,d \in \mathcal{V}_6$
,
 \begin{equation*} \Delta ^{\mathbf {PP_6^{\Rightarrow _{\textsf {H}}}}} (c \Leftrightarrow d) = \begin {cases} {\hat {\mathbf {t}}} & \text { if } c = d,\\ {\hat {\mathbf {f}}} & \text { otherwise.} \end {cases} \end{equation*}
\begin{equation*} \Delta ^{\mathbf {PP_6^{\Rightarrow _{\textsf {H}}}}} (c \Leftrightarrow d) = \begin {cases} {\hat {\mathbf {t}}} & \text { if } c = d,\\ {\hat {\mathbf {f}}} & \text { otherwise.} \end {cases} \end{equation*}
Recall that every variety of algebras is generated by its subdirectly irreducible members, which in our case (since
![]() $\mathbb{PP}^{\Rightarrow _{\textsf{H}}} \subseteq \mathbb{SDH}_1$
) are simple, by Lemma 75. By Lemma 73, this means that every such algebra
$\mathbb{PP}^{\Rightarrow _{\textsf{H}}} \subseteq \mathbb{SDH}_1$
) are simple, by Lemma 75. By Lemma 73, this means that every such algebra
![]() $\mathbf{A}$
with a top element
$\mathbf{A}$
with a top element
![]() $\top$
has (as we have seen of
$\top$
has (as we have seen of
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
) a single non-trivial regular filter, namely the singleton
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
) a single non-trivial regular filter, namely the singleton
![]() $\{ \top \}$
. The following is now the main lemma we need:
$\{ \top \}$
. The following is now the main lemma we need:
Lemma 76.
Every simple algebra
![]() $\mathbf{A} \in \mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
is (isomorphic to) a subalgebra of
$\mathbf{A} \in \mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
is (isomorphic to) a subalgebra of
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
.
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
.
Proof.
In the proof we shall use the equations
![]() $\Delta x \leq x$
and
$\Delta x \leq x$
and
![]() $\Delta (x \lor y) = \Delta x \lor \Delta y$
, which may be easily verified in
$\Delta (x \lor y) = \Delta x \lor \Delta y$
, which may be easily verified in
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
. If
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
. If
![]() $\mathbf{A}$
is simple, then
$\mathbf{A}$
is simple, then
![]() $\mathbf{A}$
has only one non-trivial congruence, corresponding to the regular filter
$\mathbf{A}$
has only one non-trivial congruence, corresponding to the regular filter
![]() $\{ \top \}$
– which in this case must be prime, as we now argue. In fact, since
$\{ \top \}$
– which in this case must be prime, as we now argue. In fact, since
![]() $\mathbf{A}$
satisfies
$\mathbf{A}$
satisfies
![]() $\Delta \Delta x \approx \Delta x$
, we have
$\Delta \Delta x \approx \Delta x$
, we have
![]() $\Delta a = \bot$
whenever
$\Delta a = \bot$
whenever
![]() $a \neq \top$
; otherwise, indeed, the regular filter
$a \neq \top$
; otherwise, indeed, the regular filter
![]() $F(a) = \{ b \in A : \Delta a \leq b \}$
would be proper (Lemma 74). Now, assume
$F(a) = \{ b \in A : \Delta a \leq b \}$
would be proper (Lemma 74). Now, assume
![]() $a_1 \lor a_2 = \top$
for some
$a_1 \lor a_2 = \top$
for some
![]() $a_1, a_2 \in A$
. We have
$a_1, a_2 \in A$
. We have
![]() $\Delta (a_1 \lor a_2) = \Delta a_1 \lor \Delta a_2 = \top = \Delta \top$
. Thus, if
$\Delta (a_1 \lor a_2) = \Delta a_1 \lor \Delta a_2 = \top = \Delta \top$
. Thus, if
![]() $a_1 \neq \top$
, then
$a_1 \neq \top$
, then
![]() $\Delta a_1 = \bot$
and
$\Delta a_1 = \bot$
and
![]() $a_2 \geq \Delta a_2 = \bot \lor \Delta a_2 = \Delta a_1 \lor \Delta a_2 = \top$
, so
$a_2 \geq \Delta a_2 = \bot \lor \Delta a_2 = \Delta a_1 \lor \Delta a_2 = \top$
, so
![]() $a_2 = \top$
. Thus
$a_2 = \top$
. Thus
![]() $\{\top \}$
is a prime filter (entailing, since
$\{\top \}$
is a prime filter (entailing, since
![]() $\mathbf{A}$
has a De Morgan algebra reduct, that
$\mathbf{A}$
has a De Morgan algebra reduct, that
![]() $\{ \bot \}$
is a prime ideal); hence the last elements of
$\{ \bot \}$
is a prime ideal); hence the last elements of
![]() $\mathbf{A}$
form a chain
$\mathbf{A}$
form a chain
![]() $C^+$
, and the first elements of
$C^+$
, and the first elements of
![]() $\mathbf{A}$
form a chain
$\mathbf{A}$
form a chain
![]() $C^-$
. This means that
$C^-$
. This means that
![]() $\mathbf{A}$
has the shape described in Example 7, except that it need not be finite.
$\mathbf{A}$
has the shape described in Example 7, except that it need not be finite.
Let
![]() $D : = A - \{ \bot, \top \}$
. We claim that any chain of elements in
$D : = A - \{ \bot, \top \}$
. We claim that any chain of elements in
![]() $D$
must have length at most
$D$
must have length at most
![]() $3$
. To see this, notice that, for all
$3$
. To see this, notice that, for all
![]() $a \in A$
, we have
$a \in A$
, we have
![]() $a \in D$
if, and only if,
$a \in D$
if, and only if,
![]() ${\circ } a = \bot$
. In fact, for
${\circ } a = \bot$
. In fact, for
![]() $a \in D$
, we have
$a \in D$
, we have
![]() $\neg a = \bot = \Delta a$
, so
$\neg a = \bot = \Delta a$
, so
![]() ${\circ } a = \neg a \lor \Delta a = \bot$
. Notice also that, for
${\circ } a = \neg a \lor \Delta a = \bot$
. Notice also that, for
![]() $a_1, a_2 \in D$
, we have
$a_1, a_2 \in D$
, we have
![]() ${\circ } (a_1 \Rightarrow a_2) = \bot$
if (and only if)
${\circ } (a_1 \Rightarrow a_2) = \bot$
if (and only if)
![]() $a_1 \not \leq a_2$
.
$a_1 \not \leq a_2$
.
Now assume, by way of contradiction, that there are elements
![]() $a_1, a_2, a_3, a_4 \in D$
such that
$a_1, a_2, a_3, a_4 \in D$
such that
![]() $a_1 \lt a_2 \lt a_3 \lt a_4$
, forming a four-element chain. Then the inequality in the second item of Definition 72 would fail, for we would have:
$a_1 \lt a_2 \lt a_3 \lt a_4$
, forming a four-element chain. Then the inequality in the second item of Definition 72 would fail, for we would have:
 \begin{align*} {{\circ }(a_1 \Rightarrow a_2) \land {\circ }(a_2\Rightarrow a_3) } &= {\circ } \top \land {\circ } \top\\ &= \top\\ &\not \leq \bot\\ &= {\circ } a_1 \lor {\circ } a_4 \lor {\circ }(a_4 \Rightarrow a_3) \lor {\circ }( a_3\Rightarrow a_2) \lor {\circ }( a_2\Rightarrow a_1). \end{align*}
\begin{align*} {{\circ }(a_1 \Rightarrow a_2) \land {\circ }(a_2\Rightarrow a_3) } &= {\circ } \top \land {\circ } \top\\ &= \top\\ &\not \leq \bot\\ &= {\circ } a_1 \lor {\circ } a_4 \lor {\circ }(a_4 \Rightarrow a_3) \lor {\circ }( a_3\Rightarrow a_2) \lor {\circ }( a_2\Rightarrow a_1). \end{align*}
Thus, all chains in
![]() $D$
have at most three elements. Hence, as
$D$
have at most three elements. Hence, as
![]() $\mathbf{A}$
is a distributive lattice, it is easy to verify that
$\mathbf{A}$
is a distributive lattice, it is easy to verify that
![]() $\mathbf{A}$
must be finite, with a coatom (call it
$\mathbf{A}$
must be finite, with a coatom (call it
![]() $\mathbf{t}$
) and an atom
$\mathbf{t}$
) and an atom
![]() $\mathbf{f}$
. This easily entails that
$\mathbf{f}$
. This easily entails that
![]() $\mathbf{A}$
must be isomorphic to one of the subalgebras of
$\mathbf{A}$
must be isomorphic to one of the subalgebras of
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
.
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
.
Theorem 77 below, the first of the announced goals, is then essentially an immediate corollary of Lemma 76:
Theorem 77.
![]() $\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
is the variety (and the quasi-variety) generated by
$\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
is the variety (and the quasi-variety) generated by
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
.
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
.
Proof. From Lemma 76 and, for the quasi-variety result, see for example Clark and Davey (Reference Clark and Davey1998, Thm. 1.3.6.ii).
We are also ready to prove the second of the goals:
Theorem 78.
![]() $\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
is the equivalent algebraic semantics of the algebraizable logic
$\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
is the equivalent algebraic semantics of the algebraizable logic
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
.
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
.
Proof.
We know from the algebraizability of Moisil’s logic (with respect to all SHAs) that
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
is algebraizable, with the same translations, with respect to a sub(quasi)variety of SHAs which is axiomatized by the equations that translate the new axioms. Recalling that the equation
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
is algebraizable, with the same translations, with respect to a sub(quasi)variety of SHAs which is axiomatized by the equations that translate the new axioms. Recalling that the equation
![]() $\neg x \approx{\sim } \neg \neg x$
guarantees that a Heyting algebra has an involutive Stone algebra reduct (see Cignoli and Sagastume Reference Cignoli and Sagastume1983, Remark 2.2), it is easy to verify that the translations of the new axioms are indeed equivalent to the equations introduced in Definition 72.
$\neg x \approx{\sim } \neg \neg x$
guarantees that a Heyting algebra has an involutive Stone algebra reduct (see Cignoli and Sagastume Reference Cignoli and Sagastume1983, Remark 2.2), it is easy to verify that the translations of the new axioms are indeed equivalent to the equations introduced in Definition 72.
Another consequence of Lemma 76 that has a logical impact is the following. Recall that the universes of subalgebras of
![]() $\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
are the same as those of
$\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}$
are the same as those of
![]() $\mathbf{PP_6}$
, minus the five-element chain. Let us denote the corresponding algebras by
$\mathbf{PP_6}$
, minus the five-element chain. Let us denote the corresponding algebras by
![]() $ \mathbf{PP_4^{\Rightarrow _{\textsf{H}}}}, \mathbf{PP_3^{\Rightarrow _{\textsf{H}}}}$
and
$ \mathbf{PP_4^{\Rightarrow _{\textsf{H}}}}, \mathbf{PP_3^{\Rightarrow _{\textsf{H}}}}$
and
![]() $\mathbf{PP_2^{\Rightarrow _{\textsf{H}}}}$
.
$\mathbf{PP_2^{\Rightarrow _{\textsf{H}}}}$
.
Corollary 79.
The (proper, non-trivial) subvarieties of
![]() $\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
are precisely the following (the axiomatizations are obtained by adding the mentioned equations to the axiomatization of
$\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
are precisely the following (the axiomatizations are obtained by adding the mentioned equations to the axiomatization of
![]() $\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
):
$\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
):
-
(1)
 $\mathbb{V} (\mathbf{PP_4^{\Rightarrow _{\textsf{H}}}})$
, axiomatized by the equation
$\mathbb{V} (\mathbf{PP_4^{\Rightarrow _{\textsf{H}}}})$
, axiomatized by the equation
 $ x \land{\sim } x \leq y \lor{\sim } y$
.
$ x \land{\sim } x \leq y \lor{\sim } y$
. -
(2)
 $\mathbb{V} (\mathbf{PP_3^{\Rightarrow _{\textsf{H}}}})$
, axiomatized by
$\mathbb{V} (\mathbf{PP_3^{\Rightarrow _{\textsf{H}}}})$
, axiomatized by
 $ x \lor (x \Rightarrow (y \lor \neg y ) ) \approx \top$
.
$ x \lor (x \Rightarrow (y \lor \neg y ) ) \approx \top$
. -
(3)
 $\mathbb{V} (\mathbf{PP_2^{\Rightarrow _{\textsf{H}}}})$
, axiomatized by
$\mathbb{V} (\mathbf{PP_2^{\Rightarrow _{\textsf{H}}}})$
, axiomatized by
 $x \lor{\sim } x \approx \top$
.
$x \lor{\sim } x \approx \top$
.
Note that
![]() $\mathbb{V} (\mathbf{PP_4^{\Rightarrow _{\textsf{H}}}})$
and
$\mathbb{V} (\mathbf{PP_4^{\Rightarrow _{\textsf{H}}}})$
and
![]() $\mathbb{V} (\mathbf{PP_3^{\Rightarrow _{\textsf{H}}}})$
are incomparable, while
$\mathbb{V} (\mathbf{PP_3^{\Rightarrow _{\textsf{H}}}})$
are incomparable, while
![]() $\mathbb{V} (\mathbf{PP_2^{\Rightarrow _{\textsf{H}}}})$
, which is (up a choice of language) just the variety of Boolean algebras, is included in both of them.
$\mathbb{V} (\mathbf{PP_2^{\Rightarrow _{\textsf{H}}}})$
, which is (up a choice of language) just the variety of Boolean algebras, is included in both of them.
Proof.
All claims are established by easy computations. The main observation we need is that, by Jónsson’s Lemma (see Burris and Sankappanavar Reference Burris and Sankappanavar2011, Cor. IV.6.10), for
![]() $\mathbf{A} \in \{ \mathbf{PP_4^{\Rightarrow _{\textsf{H}}}}, \mathbf{PP_3^{\Rightarrow _{\textsf{H}}}}, \mathbf{PP_2^{\Rightarrow _{\textsf{H}}}}\}$
, the subdirectly irreducible (here meaning simple) algebras in each
$\mathbf{A} \in \{ \mathbf{PP_4^{\Rightarrow _{\textsf{H}}}}, \mathbf{PP_3^{\Rightarrow _{\textsf{H}}}}, \mathbf{PP_2^{\Rightarrow _{\textsf{H}}}}\}$
, the subdirectly irreducible (here meaning simple) algebras in each
![]() $\mathbb{V} (\mathbf{A})$
are in
$\mathbb{V} (\mathbf{A})$
are in
![]() $ \mathbb{H} \mathbb{S} (\mathbf{A})$
, and
$ \mathbb{H} \mathbb{S} (\mathbf{A})$
, and
![]() $\mathbb{H}\mathbb{S} (\mathbf{A}) = \mathbb{S} (\mathbf{A})$
.
$\mathbb{H}\mathbb{S} (\mathbf{A}) = \mathbb{S} (\mathbf{A})$
.
By Theorem 78, the logic
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
is complete with respect to the class of all matrices
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
is complete with respect to the class of all matrices
![]() $\langle \mathbf{A}, \{ \top ^{\mathbf{A}} \} \rangle$
such that
$\langle \mathbf{A}, \{ \top ^{\mathbf{A}} \} \rangle$
such that
![]() $\mathbf{A} \in \mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
. But, by Theorem 77, we know that the single matrix
$\mathbf{A} \in \mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
. But, by Theorem 77, we know that the single matrix
![]() $\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, \{{\hat{\mathbf{t}}} \} \rangle$
suffices. Thus:
$\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, \{{\hat{\mathbf{t}}} \} \rangle$
suffices. Thus:
Proposition 80.
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
is determined by
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
is determined by
![]() $\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, \{{\hat{\mathbf{t}}} \} \rangle$
.
$\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, \{{\hat{\mathbf{t}}} \} \rangle$
.
This observation may be used to verify the following equivalence, which holds for all
![]() $\Phi \cup \{\varphi \} \subseteq L_{\Sigma }(P)$
:
$\Phi \cup \{\varphi \} \subseteq L_{\Sigma }(P)$
:
where
![]() $ \Delta \Phi : = \{ \Delta \psi : \psi \in \Phi \}$
. From the latter, relying on the DDT (recall Section 2.4) for
$ \Delta \Phi : = \{ \Delta \psi : \psi \in \Phi \}$
. From the latter, relying on the DDT (recall Section 2.4) for
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
, we can obtain the DDT for
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
, we can obtain the DDT for
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
: for all
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
: for all
![]() $\Phi, \{\varphi, \psi \} \subseteq L_{\Sigma }(P)$
,
$\Phi, \{\varphi, \psi \} \subseteq L_{\Sigma }(P)$
,
The class of algebraic reducts of reduced matrices for
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
is also
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
is also
![]() $\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
. In fact, it can be shown that
$\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
. In fact, it can be shown that
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
is complete with respect to the class of all matrices
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
is complete with respect to the class of all matrices
![]() $\langle \mathbf{A}, D \rangle$
with
$\langle \mathbf{A}, D \rangle$
with
![]() $\mathbf{A} \in \mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
and
$\mathbf{A} \in \mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
and
![]() $D$
a non-empty lattice filter of
$D$
a non-empty lattice filter of
![]() $\mathbf{A}$
. The reduced models of
$\mathbf{A}$
. The reduced models of
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
may be characterized as follows:
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
may be characterized as follows:
Proposition 81.
Given
![]() $\mathbf{A} \in \mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
, we have that a matrix
$\mathbf{A} \in \mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
, we have that a matrix
![]() $\langle \mathbf{A}, D \rangle$
is a reduced model of
$\langle \mathbf{A}, D \rangle$
is a reduced model of
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
if, and only if,
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
if, and only if,
![]() $D$
is a lattice filter that contains exactly one regular filter (namely
$D$
is a lattice filter that contains exactly one regular filter (namely
![]() $\{ \top ^{\mathbf{A}} \}$
).
$\{ \top ^{\mathbf{A}} \}$
).
Proof.
We shall prove both implications by contraposition. Assume first that
![]() $\langle \mathbf{A}, D \rangle$
is not reduced. Then, by the characterization of the Leibniz congruence given in Proposition 36, there are elements
$\langle \mathbf{A}, D \rangle$
is not reduced. Then, by the characterization of the Leibniz congruence given in Proposition 36, there are elements
![]() $a,b \in A$
such that
$a,b \in A$
such that
![]() $a \neq b$
and
$a \neq b$
and
Assuming
![]() $a \not \leq b$
, we have
$a \not \leq b$
, we have
![]() $a \Rightarrow b \neq \top$
. Recall that the regular filter generated by the element
$a \Rightarrow b \neq \top$
. Recall that the regular filter generated by the element
![]() $a \Rightarrow b$
is
$a \Rightarrow b$
is
From the assumption
![]() $\Delta (a \Rightarrow b) \in D$
, we have
$\Delta (a \Rightarrow b) \in D$
, we have
![]() $F(\{ a \Rightarrow b \}) \subseteq D$
. So
$F(\{ a \Rightarrow b \}) \subseteq D$
. So
![]() $D$
contains a regular filter distinct from
$D$
contains a regular filter distinct from
![]() $\{\top \}$
.
$\{\top \}$
.
Conversely, assume
![]() $D$
contains a regular filter
$D$
contains a regular filter
![]() $F \neq \{ \top \}$
. Then there is
$F \neq \{ \top \}$
. Then there is
![]() $a \in F$
such that
$a \in F$
such that
![]() $a \lt \top$
. This means that
$a \lt \top$
. This means that
![]() $\Delta (a \Rightarrow \top ) = \Delta \top = \top \in F$
and (since
$\Delta (a \Rightarrow \top ) = \Delta \top = \top \in F$
and (since
![]() $F$
is regular)
$F$
is regular)
![]() $\Delta (\top \Rightarrow a) = \Delta a \in F$
. Then, by the characterization of Proposition 36, the pair
$\Delta (\top \Rightarrow a) = \Delta a \in F$
. Then, by the characterization of Proposition 36, the pair
![]() $(a,\top )$
is identified by the Leibniz congruence of
$(a,\top )$
is identified by the Leibniz congruence of
![]() $D$
, which would make
$D$
, which would make
![]() $\langle \mathbf{A}, D \rangle$
not reduced.
$\langle \mathbf{A}, D \rangle$
not reduced.
8. On Interpolation for
 $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
and
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
and
 $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
, and Amalgamation for
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
, and Amalgamation for
 $\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
$\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
We begin by defining three basic notions of interpolation according to the terminology of Czelakowski and Pigozzi (Reference Czelakowski and Pigozzi1998, Def. 3.1). In this section we will focus only in ![]() logics, since this is the framework in which the properties of interpolation are commonly formulated and investigated in the literature.
logics, since this is the framework in which the properties of interpolation are commonly formulated and investigated in the literature.
Definition 82.
A ![]()
![]() $\Sigma$
-logic
$\Sigma$
-logic
![]() $\vdash$
has the
$\vdash$
has the
-
(1) extension interpolation property (EIP) if having
 $\Phi, \Psi \vdash \varphi$
implies that there is
$\Phi, \Psi \vdash \varphi$
implies that there is
 $\Pi \subseteq L_{\Sigma }(\textsf{props}({\Psi \cup \{ \varphi \})})$
such that
$\Pi \subseteq L_{\Sigma }(\textsf{props}({\Psi \cup \{ \varphi \})})$
such that
 $\Phi \vdash \psi$
for all
$\Phi \vdash \psi$
for all
 $\psi \in \Pi$
and
$\psi \in \Pi$
and
 $\Pi, \Psi \vdash \varphi$
.
$\Pi, \Psi \vdash \varphi$
. -
(2) Craig interpolation property (CIP) if, whenever
 $\textsf{props}(\Phi ) \cap \textsf{props}(\varphi ) \neq \varnothing$
, having
$\textsf{props}(\Phi ) \cap \textsf{props}(\varphi ) \neq \varnothing$
, having
 $\Phi \vdash \varphi$
implies that there is
$\Phi \vdash \varphi$
implies that there is
 $\Pi \subseteq L_{\Sigma }(\textsf{props}({\Phi }) \cap \textsf{props}(\varphi ))$
such that
$\Pi \subseteq L_{\Sigma }(\textsf{props}({\Phi }) \cap \textsf{props}(\varphi ))$
such that
 $\Phi \vdash \psi$
for all
$\Phi \vdash \psi$
for all
 $\psi \in \Pi$
and
$\psi \in \Pi$
and
 $\Pi \vdash \varphi$
.
$\Pi \vdash \varphi$
. -
(3) Maehara interpolation property (MIP) if, whenever
 $\textsf{props}(\Phi )\cap \textsf{props}({\Psi \cup \{ \varphi \})} \neq \varnothing$
, having
$\textsf{props}(\Phi )\cap \textsf{props}({\Psi \cup \{ \varphi \})} \neq \varnothing$
, having
 $\Phi, \Psi \vdash \varphi$
implies that there is
$\Phi, \Psi \vdash \varphi$
implies that there is
 $\Pi \subseteq L_{\Sigma }(\textsf{props}(\Phi )\cap \textsf{props}({\Psi \cup \{ \varphi \})})$
such that
$\Pi \subseteq L_{\Sigma }(\textsf{props}(\Phi )\cap \textsf{props}({\Psi \cup \{ \varphi \})})$
such that
 $\Phi \vdash \psi$
for all
$\Phi \vdash \psi$
for all
 $\psi \in \Pi$
and
$\psi \in \Pi$
and
 $\Pi, \Psi \vdash \varphi$
.
$\Pi, \Psi \vdash \varphi$
.
Note that the (MIP) implies the (CIP) – just take
![]() $\Psi = \varnothing$
. It also implies the (EIP) when the logic has theses (i.e., formulas
$\Psi = \varnothing$
. It also implies the (EIP) when the logic has theses (i.e., formulas
![]() $\varphi$
such that
$\varphi$
such that
![]() $\varnothing \vdash \varphi$
) on a single variable and every formula without variables is logically equivalent to some constant in the signature. Note that for the logics
$\varnothing \vdash \varphi$
) on a single variable and every formula without variables is logically equivalent to some constant in the signature. Note that for the logics
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
and
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
and
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
both conditions hold good.
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
both conditions hold good.
Let us see now which of these interpolation properties the logic
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
satisfies.
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
satisfies.
Theorem 83.
The logic
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
has the (EIP) but does not have the (CIP) nor the (MIP).
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
has the (EIP) but does not have the (CIP) nor the (MIP).
Proof.
Since
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
is finitary, we may consider only finite candidates for
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
is finitary, we may consider only finite candidates for
![]() $\Psi$
and
$\Psi$
and
![]() $\Pi$
. To see that
$\Pi$
. To see that
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
has (EIP), assume that
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
has (EIP), assume that
![]() $\Phi, \Psi \vdash _{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }} \varphi$
. The property is satisfied if we choose
$\Phi, \Psi \vdash _{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }} \varphi$
. The property is satisfied if we choose
![]() $\Pi \,{:=}\, \{\bigwedge \Psi \Rightarrow \varphi \}$
, since
$\Pi \,{:=}\, \{\bigwedge \Psi \Rightarrow \varphi \}$
, since
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
has the DDT (see Section 2.4).
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
has the DDT (see Section 2.4).
Given that (MIP) implies (CIP), it is enough to show that the latter fails. First of all, note that
![]() $(p \land{\sim } p \land q \land{\sim } q \land{\sim }{\circ }(p \Rightarrow q)) \lor s \vdash _{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }} (r \lor{\sim } r) \lor s$
(recall the proof of Theorem 34). Based on the definition of (CIP), let
$(p \land{\sim } p \land q \land{\sim } q \land{\sim }{\circ }(p \Rightarrow q)) \lor s \vdash _{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }} (r \lor{\sim } r) \lor s$
(recall the proof of Theorem 34). Based on the definition of (CIP), let
![]() $\Phi \,{:=}\, \{ (p \land{\sim } p \land q \land{\sim } q \land{\sim }{\circ }(p \Rightarrow q)) \lor s \}$
and
$\Phi \,{:=}\, \{ (p \land{\sim } p \land q \land{\sim } q \land{\sim }{\circ }(p \Rightarrow q)) \lor s \}$
and
![]() $\varphi \,{:=}\, (r \lor{\sim } r) \lor s$
. Note that
$\varphi \,{:=}\, (r \lor{\sim } r) \lor s$
. Note that
![]() $\textsf{props}(\Phi )\cap \textsf{props}(\varphi ) = \{ s \}$
. Assume there is such
$\textsf{props}(\Phi )\cap \textsf{props}(\varphi ) = \{ s \}$
. Assume there is such
![]() $\Pi$
, then
$\Pi$
, then
![]() $\psi (s) \,{:=}\, \bigwedge \Pi$
is a formula on a single variable
$\psi (s) \,{:=}\, \bigwedge \Pi$
is a formula on a single variable
![]() $s$
. We will see now that we cannot have both (i)
$s$
. We will see now that we cannot have both (i)
![]() $\Phi \vdash _{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }} \psi (s)$
and (ii)
$\Phi \vdash _{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }} \psi (s)$
and (ii)
![]() $\psi (s) \vdash _{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }} \varphi$
. Let us fix
$\psi (s) \vdash _{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }} \varphi$
. Let us fix
![]() $v(p) \,{:=}\,{\mathbf{b}}$
,
$v(p) \,{:=}\,{\mathbf{b}}$
,
![]() $v(q)\,{:=}\,{\mathbf{n}}$
,
$v(q)\,{:=}\,{\mathbf{n}}$
,
![]() $v(r)\,{:=}\,{\mathbf{b}}$
and
$v(r)\,{:=}\,{\mathbf{b}}$
and
![]() $v(s)\,{:=}\,{\hat{\mathbf{f}}}$
thus making
$v(s)\,{:=}\,{\hat{\mathbf{f}}}$
thus making
![]() $v(\Phi )=\{{\mathbf{f}} \}$
and
$v(\Phi )=\{{\mathbf{f}} \}$
and
![]() $v(\varphi )={\mathbf{b}}$
. Note that
$v(\varphi )={\mathbf{b}}$
. Note that
![]() $v(\psi )\in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}}\}$
. However, (i) fails when
$v(\psi )\in \{{\hat{\mathbf{f}}},{\hat{\mathbf{t}}}\}$
. However, (i) fails when
![]() $v(\psi )={\hat{\mathbf{f}}}$
, and (ii) fails when
$v(\psi )={\hat{\mathbf{f}}}$
, and (ii) fails when
![]() $v(\psi )={\hat{\mathbf{t}}}$
.
$v(\psi )={\hat{\mathbf{t}}}$
.
Let us now take a look at the situation for
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
. Recall that, in the previous section, we presented the DDT for this logic, which demands a (derived) connective different from
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
. Recall that, in the previous section, we presented the DDT for this logic, which demands a (derived) connective different from
![]() $\Rightarrow$
to play the role of implication. In the same way as in the proof of the above theorem, this DDT guarantees that the (EIP) holds for this logic. We show however that (CIP) and (MIP) also hold. In what follows, recall from Proposition 80 that
$\Rightarrow$
to play the role of implication. In the same way as in the proof of the above theorem, this DDT guarantees that the (EIP) holds for this logic. We show however that (CIP) and (MIP) also hold. In what follows, recall from Proposition 80 that
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
is determined by the single matrix
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
is determined by the single matrix
![]() $\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, \{{\hat{\mathbf{t}}} \} \rangle$
.
$\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}, \{{\hat{\mathbf{t}}} \} \rangle$
.
Theorem 84.
The logic
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
has the (EIP), the (CIP), and the (MIP).
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
has the (EIP), the (CIP), and the (MIP).
Proof.
It is enough to show it has the (MIP). Since
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
is finitary, it suffices to consider finite sets. Given
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
is finitary, it suffices to consider finite sets. Given
![]() $\Phi, \Psi \vdash _{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top } \varphi$
, let
$\Phi, \Psi \vdash _{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top } \varphi$
, let
![]() $\textsf{props}(\Phi )\cap \textsf{props}(\Psi \cup \{\varphi \})=\{p_1,\ldots, p_k\}\neq \varnothing$
. Consider
$\textsf{props}(\Phi )\cap \textsf{props}(\Psi \cup \{\varphi \})=\{p_1,\ldots, p_k\}\neq \varnothing$
. Consider
![]() $\mathcal{U} \,{:=}\, \{v\in \textsf{Hom} (L_{\Sigma }(\{p_1,\ldots, p_k\}), \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}) : v(\Phi )={\hat{\mathbf{t}}}\}$
. For each
$\mathcal{U} \,{:=}\, \{v\in \textsf{Hom} (L_{\Sigma }(\{p_1,\ldots, p_k\}), \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}}) : v(\Phi )={\hat{\mathbf{t}}}\}$
. For each
![]() $v\in \mathcal{U}$
and
$v\in \mathcal{U}$
and
![]() $1\leq i\leq k$
, let
$1\leq i\leq k$
, let
 \begin{align*} \varphi ^v_i(p)& \,{:=}\, \begin{cases} p\land{\circ } p & \mbox{ if }v(p_i)={\hat{\mathbf{t}}}\\{\sim }{\downarrow } p & \mbox{ if }v(p_i)={\mathbf{t}}\\{\uparrow } p\land{\downarrow } p \land{\sim }{\circ } p & \mbox{ if }v(p_i)\in \{{\mathbf{b}},{\mathbf{n}}\}\\{\sim }{\uparrow } p & \mbox{ if }v(p_i)={\mathbf{f}}\\{\sim } p\land{\circ } p & \mbox{ if }v(p_i)={\hat{\mathbf{f}}} \end{cases}\\ I^v_{\mathbf{b}}& \,{:=}\, \{i:v(p_i)={\mathbf{b}}\}\\ J^v_{\mathbf{n}}& \,{:=}\, \{j:v(p_j)={\mathbf{n}}\} \end{align*}
\begin{align*} \varphi ^v_i(p)& \,{:=}\, \begin{cases} p\land{\circ } p & \mbox{ if }v(p_i)={\hat{\mathbf{t}}}\\{\sim }{\downarrow } p & \mbox{ if }v(p_i)={\mathbf{t}}\\{\uparrow } p\land{\downarrow } p \land{\sim }{\circ } p & \mbox{ if }v(p_i)\in \{{\mathbf{b}},{\mathbf{n}}\}\\{\sim }{\uparrow } p & \mbox{ if }v(p_i)={\mathbf{f}}\\{\sim } p\land{\circ } p & \mbox{ if }v(p_i)={\hat{\mathbf{f}}} \end{cases}\\ I^v_{\mathbf{b}}& \,{:=}\, \{i:v(p_i)={\mathbf{b}}\}\\ J^v_{\mathbf{n}}& \,{:=}\, \{j:v(p_j)={\mathbf{n}}\} \end{align*}
and
 \begin{align*} \psi _v&\,{:=}\,\bigwedge _{1\leq i\leq k}\varphi ^v_i(p_i)\land \bigwedge _{i\in I_{\mathbf{b}}^v,j\in J_{\mathbf{n}}^v}{\sim }{\circ }(p_i\Rightarrow p_j)\\ \xi &\,{:=}\,\bigvee _{v\in \mathcal{U}}\psi _v \end{align*}
\begin{align*} \psi _v&\,{:=}\,\bigwedge _{1\leq i\leq k}\varphi ^v_i(p_i)\land \bigwedge _{i\in I_{\mathbf{b}}^v,j\in J_{\mathbf{n}}^v}{\sim }{\circ }(p_i\Rightarrow p_j)\\ \xi &\,{:=}\,\bigvee _{v\in \mathcal{U}}\psi _v \end{align*}
If we set
![]() $\equiv \; \subseteq \mathcal{V}_6\times \mathcal{V}_6$
such that
$\equiv \; \subseteq \mathcal{V}_6\times \mathcal{V}_6$
such that
![]() $a \equiv b$
iff
$a \equiv b$
iff
![]() $a=b$
or
$a=b$
or
![]() $\{a,b\}=\{{\mathbf{b}},{\mathbf{n}}\}$
we obtain that, for all
$\{a,b\}=\{{\mathbf{b}},{\mathbf{n}}\}$
we obtain that, for all
![]() $v'\in \textsf{Hom} (\mathbf{L}_{\Sigma }(P), \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
,
$v'\in \textsf{Hom} (\mathbf{L}_{\Sigma }(P), \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
,
 \begin{equation*}v'(\varphi ^v_i(p))= \begin {cases} {\hat {\mathbf {t}}} & \text {if } v'(p)\equiv v(p_i) \\ {\hat {\mathbf {f}}} & \text {otherwise.}\\ \end {cases} \end{equation*}
\begin{equation*}v'(\varphi ^v_i(p))= \begin {cases} {\hat {\mathbf {t}}} & \text {if } v'(p)\equiv v(p_i) \\ {\hat {\mathbf {f}}} & \text {otherwise.}\\ \end {cases} \end{equation*}
Thus, if
![]() $v'(\psi _v)={\hat{\mathbf{t}}}$
then
$v'(\psi _v)={\hat{\mathbf{t}}}$
then
![]() $v(p_i)\equiv v'(p_i)$
for every
$v(p_i)\equiv v'(p_i)$
for every
![]() $1\leq i\leq k$
.
$1\leq i\leq k$
.
Let us show that
![]() $\xi \vdash _{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top } \varphi$
. For every
$\xi \vdash _{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top } \varphi$
. For every
![]() $v'\in \textsf{Hom} (\mathbf{L}_{\Sigma }(P), \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
such that
$v'\in \textsf{Hom} (\mathbf{L}_{\Sigma }(P), \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
such that
![]() $v'(\xi )={\hat{\mathbf{t}}}$
, there is
$v'(\xi )={\hat{\mathbf{t}}}$
, there is
![]() $v\in \mathcal{U}$
such that
$v\in \mathcal{U}$
such that
![]() $v(p_i)\equiv v'(p_i)$
for every
$v(p_i)\equiv v'(p_i)$
for every
![]() $1\leq i\leq k$
. Also,
$1\leq i\leq k$
. Also,
![]() $\{{\mathbf{b}},{\mathbf{n}}\}=\{v(p_i),v(p_j)\}$
if, and only if,
$\{{\mathbf{b}},{\mathbf{n}}\}=\{v(p_i),v(p_j)\}$
if, and only if,
![]() $\{{\mathbf{b}},{\mathbf{n}}\}=\{v'(p_i),v'(p_j)\}$
, and therefore
$\{{\mathbf{b}},{\mathbf{n}}\}=\{v'(p_i),v'(p_j)\}$
, and therefore
![]() $v(\psi )=v'(\psi )$
for every
$v(\psi )=v'(\psi )$
for every
![]() $\psi$
such that
$\psi$
such that
![]() $\textsf{props}(\psi )\subseteq \{p_1,\ldots, p_k\}$
. Thus, without loss of generality, we proceed considering that
$\textsf{props}(\psi )\subseteq \{p_1,\ldots, p_k\}$
. Thus, without loss of generality, we proceed considering that
![]() $v(p_i)=v'(p_i)$
for
$v(p_i)=v'(p_i)$
for
![]() $1\leq i\leq k$
.
$1\leq i\leq k$
.
Considering
![]() $v''\in \textsf{Hom} (\mathbf{L}_{\Sigma }(P), \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
such that
$v''\in \textsf{Hom} (\mathbf{L}_{\Sigma }(P), \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
such that
 \begin{equation*}v''(p)\,{:=}\, \begin {cases} v(p) & p\in P{\setminus }\textsf {props}(\Phi )\\ v'(p) &p\in \textsf {props}(\Phi ){\setminus }\{p_1,\ldots, p_k\} \end {cases}\end{equation*}
\begin{equation*}v''(p)\,{:=}\, \begin {cases} v(p) & p\in P{\setminus }\textsf {props}(\Phi )\\ v'(p) &p\in \textsf {props}(\Phi ){\setminus }\{p_1,\ldots, p_k\} \end {cases}\end{equation*}
we have that
![]() $v''(\Phi )=v''(\Psi )={\hat{\mathbf{t}}}$
, thus from
$v''(\Phi )=v''(\Psi )={\hat{\mathbf{t}}}$
, thus from
![]() $\Phi, \Psi \vdash _{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top } \varphi$
we conclude that
$\Phi, \Psi \vdash _{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top } \varphi$
we conclude that
![]() $v''(\varphi )=v'(\psi )={\hat{\mathbf{t}}}$
and therefore
$v''(\varphi )=v'(\psi )={\hat{\mathbf{t}}}$
and therefore
![]() $\xi \vdash _{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top } \varphi$
. Finally, to see that
$\xi \vdash _{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top } \varphi$
. Finally, to see that
![]() $\Phi \vdash _{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top } \xi$
, note that if
$\Phi \vdash _{\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top } \xi$
, note that if
![]() $v(\Phi )=\{{\hat{\mathbf{t}}}\}$
then, by definition,
$v(\Phi )=\{{\hat{\mathbf{t}}}\}$
then, by definition,
![]() $v\in \mathcal{U}$
and therefore
$v\in \mathcal{U}$
and therefore
![]() $v(\psi _v)=v(\xi )={\hat{\mathbf{t}}}$
.
$v(\psi _v)=v(\xi )={\hat{\mathbf{t}}}$
.
When a ![]() logic satisfies some of the above interpolation properties and we know it is algebraizable, the class of algebras corresponding to the equivalent algebraic semantics satisfies so-called “amalgamation properties,” which we formulate below based on Czelakowski and Pigozzi (Reference Czelakowski and Pigozzi1998).
logic satisfies some of the above interpolation properties and we know it is algebraizable, the class of algebras corresponding to the equivalent algebraic semantics satisfies so-called “amalgamation properties,” which we formulate below based on Czelakowski and Pigozzi (Reference Czelakowski and Pigozzi1998).
Let
![]() $\textsf{K}$
be a class of
$\textsf{K}$
be a class of
![]() $\Sigma$
-algebras and
$\Sigma$
-algebras and
![]() $\mathbf{A},\mathbf{B} \in \textsf{K}$
. If
$\mathbf{A},\mathbf{B} \in \textsf{K}$
. If
![]() $\mathbf{A}$
is a subalgebra of
$\mathbf{A}$
is a subalgebra of
![]() $\mathbf{B}$
and
$\mathbf{B}$
and
![]() $S \subseteq B$
,
$S \subseteq B$
,
![]() $\mathbf{B}$
is said to be a
$\mathbf{B}$
is said to be a
![]() $\textsf{K}$
-free extension of
$\textsf{K}$
-free extension of
![]() $\mathbf{A}$
over
$\mathbf{A}$
over
![]() $S$
if for every
$S$
if for every
![]() $\mathbf{C} \in \textsf{K}$
, every homomorphism
$\mathbf{C} \in \textsf{K}$
, every homomorphism
![]() $h : \mathbf{A} \to \mathbf{C}$
and every
$h : \mathbf{A} \to \mathbf{C}$
and every
![]() $f : S \to C$
, there is a unique homomorphism
$f : S \to C$
, there is a unique homomorphism
![]() $g : \mathbf{B} \to \mathbf{C}$
such that
$g : \mathbf{B} \to \mathbf{C}$
such that
![]() $g \upharpoonleft A = h$
and
$g \upharpoonleft A = h$
and
![]() $g \upharpoonleft S = f$
, where
$g \upharpoonleft S = f$
, where
![]() $\upharpoonleft$
denotes domain restriction. Write
$\upharpoonleft$
denotes domain restriction. Write
![]() $f : \mathbf{A} \rightarrowtail \mathbf{B}$
to denote that
$f : \mathbf{A} \rightarrowtail \mathbf{B}$
to denote that
![]() $f$
is an injective homomorphism, and
$f$
is an injective homomorphism, and
![]() $f : \mathbf{A} \hookrightarrow \mathbf{B}$
to denote that
$f : \mathbf{A} \hookrightarrow \mathbf{B}$
to denote that
![]() $f$
is a free injection over
$f$
is a free injection over
![]() $\textsf{K}$
, meaning that
$\textsf{K}$
, meaning that
![]() $f$
is an injection and
$f$
is an injection and
![]() $f(\mathbf{B})$
is a
$f(\mathbf{B})$
is a
![]() $\textsf{K}$
-free extension of
$\textsf{K}$
-free extension of
![]() $\mathbf{B}$
over some set
$\mathbf{B}$
over some set
![]() $S$
of elements.
$S$
of elements.
Definition 85 (Czelakowski and Pigozzi Reference Czelakowski and Pigozzi1998, Def. 5.2). A class of algebras
![]() $\textsf{K}$
has the
$\textsf{K}$
has the
-
(1) ordinary amalgamation property (OAP) when for all
 $\mathbf{A},\mathbf{B},\mathbf{C} \in \textsf{K}$
, and all homomorphisms
$\mathbf{A},\mathbf{B},\mathbf{C} \in \textsf{K}$
, and all homomorphisms
 $f : \mathbf{C} \rightarrowtail \mathbf{A}$
and
$f : \mathbf{C} \rightarrowtail \mathbf{A}$
and
 $g : \mathbf{C} \rightarrowtail \mathbf{B}$
, there exists
$g : \mathbf{C} \rightarrowtail \mathbf{B}$
, there exists
 $\mathbf{D} \in \textsf{K}$
and homomorphisms
$\mathbf{D} \in \textsf{K}$
and homomorphisms
 $h : \mathbf{A} \rightarrowtail \mathbf{D}$
and
$h : \mathbf{A} \rightarrowtail \mathbf{D}$
and
 $k : \mathbf{B} \rightarrowtail \mathbf{D}$
such that
$k : \mathbf{B} \rightarrowtail \mathbf{D}$
such that
 $hf = kg$
.
$hf = kg$
. -
(2) flat amalgamation property (FAP) when for all
 $\mathbf{A},\mathbf{B},\mathbf{C} \in \textsf{K}$
, and all homomorphisms
$\mathbf{A},\mathbf{B},\mathbf{C} \in \textsf{K}$
, and all homomorphisms
 $f : \mathbf{C} \rightarrowtail \mathbf{A}$
and
$f : \mathbf{C} \rightarrowtail \mathbf{A}$
and
 $g : \mathbf{C} \hookrightarrow \mathbf{B}$
, there exists
$g : \mathbf{C} \hookrightarrow \mathbf{B}$
, there exists
 $\mathbf{D} \in \textsf{K}$
and homomorphisms
$\mathbf{D} \in \textsf{K}$
and homomorphisms
 $h : \mathbf{A} \hookrightarrow \mathbf{D}$
and
$h : \mathbf{A} \hookrightarrow \mathbf{D}$
and
 $k : \mathbf{B} \rightarrowtail \mathbf{D}$
such that
$k : \mathbf{B} \rightarrowtail \mathbf{D}$
such that
 $hf = kg$
.
$hf = kg$
. -
(3) Maehara amalgamation property (MAP) when, for all
 $\mathbf{A},\mathbf{B},\mathbf{C} \in \textsf{K}$
, and all homomorphisms
$\mathbf{A},\mathbf{B},\mathbf{C} \in \textsf{K}$
, and all homomorphisms
 $f : \mathbf{C} \rightarrowtail \mathbf{A}$
and
$f : \mathbf{C} \rightarrowtail \mathbf{A}$
and
 $g : \mathbf{C} \to \mathbf{B}$
, there exists
$g : \mathbf{C} \to \mathbf{B}$
, there exists
 $\mathbf{D} \in \textsf{K}$
and homomorphisms
$\mathbf{D} \in \textsf{K}$
and homomorphisms
 $h : \mathbf{A} \to \mathbf{D}$
and
$h : \mathbf{A} \to \mathbf{D}$
and
 $k : \mathbf{B} \rightarrowtail \mathbf{D}$
such that
$k : \mathbf{B} \rightarrowtail \mathbf{D}$
such that
 $hf = kg$
.
$hf = kg$
.
The reader is referred to Czelakowski and Pigozzi (Reference Czelakowski and Pigozzi1998, Thm. 5.3) for the relationships between the above notions of amalgamation. In particular, we have that (MAP) implies both (FAP) and (OAP).
Theorem 86.
![]() $\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
has the (OAP), the (FAP), and the (MAP).
$\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
has the (OAP), the (FAP), and the (MAP).
Proof.
Clearly, it suffices to show that
![]() $\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
has the (MAP). By Theorem 78, we know that
$\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
has the (MAP). By Theorem 78, we know that
![]() $\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
is the equivalent algebraic semantics of
$\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
is the equivalent algebraic semantics of
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
. We just saw that this logic satisfies (MIP); hence, by Czelakowski and Pigozzi (Reference Czelakowski and Pigozzi1998, Cor. 5.27),
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
. We just saw that this logic satisfies (MIP); hence, by Czelakowski and Pigozzi (Reference Czelakowski and Pigozzi1998, Cor. 5.27),
![]() $\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
satisfies (MAP).
$\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
satisfies (MAP).
9. Conclusions and Future Work
The present paper has initiated the study of implicative expansions of logics of perfect paradefinite algebras by considering classic-like and Heyting implications, both in the ![]() and in the
and in the ![]() framework. We investigated semantical characterizations (via classes of algebras and logical matrices) as well as proof-theoretical ones (via
framework. We investigated semantical characterizations (via classes of algebras and logical matrices) as well as proof-theoretical ones (via ![]() and
and ![]() Hilbert-style calculi) of these expansions. For the expansions with a Heyting implication, the new connective introduced a further challenge, for the resulting logic (
Hilbert-style calculi) of these expansions. For the expansions with a Heyting implication, the new connective introduced a further challenge, for the resulting logic (
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
) cannot be characterized by a single logical matrix; however, we have proved that it can be characterized by a single finite PNmatrix. Over such expansions, we also studied properties of interpolation and amalgamation for the corresponding algebraic models. We indicate below a few directions that we believe could prove worthwhile pursuing in future research.
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
) cannot be characterized by a single logical matrix; however, we have proved that it can be characterized by a single finite PNmatrix. Over such expansions, we also studied properties of interpolation and amalgamation for the corresponding algebraic models. We indicate below a few directions that we believe could prove worthwhile pursuing in future research.
Alternative expansions of the logics of PP-algebras
In Section 4 we have briefly considered other logics that may be obtained by conservatively adding an implication to the logics of PP-algebras
![]() $\mathcal{PP}_{\!\leq }^{{\rhd }}$
and
$\mathcal{PP}_{\!\leq }^{{\rhd }}$
and
![]() $\mathcal{PP}_{\!\leq }$
. We did not explore these alternatives much further, preferring instead (from Section 5 onward) to focus our attention on logics having a more straightforward connection to existing frameworks (Moisil’s logic and symmetric Heyting algebras). Nevertheless, we feel that such alternative systems may deserve further study, and the connection we noted with the recent work by Coniglio and Rodrigues (Reference Coniglio and Rodrigues2023) provides further motivation for this project. Additionally, it would be interesting to systematically investigate the logics determined by refinements of the PNmatrix
$\mathcal{PP}_{\!\leq }$
. We did not explore these alternatives much further, preferring instead (from Section 5 onward) to focus our attention on logics having a more straightforward connection to existing frameworks (Moisil’s logic and symmetric Heyting algebras). Nevertheless, we feel that such alternative systems may deserve further study, and the connection we noted with the recent work by Coniglio and Rodrigues (Reference Coniglio and Rodrigues2023) provides further motivation for this project. Additionally, it would be interesting to systematically investigate the logics determined by refinements of the PNmatrix
![]() $\mathfrak{M}_{\textsf{up}}$
, providing axiomatizations, classifying them within the hierarchies of algebraic logic (e.g., which among them are algebraizable?) and studying the corresponding classes of algebras as done in Section 7 for
$\mathfrak{M}_{\textsf{up}}$
, providing axiomatizations, classifying them within the hierarchies of algebraic logic (e.g., which among them are algebraizable?) and studying the corresponding classes of algebras as done in Section 7 for
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
. Lastly, further enlarging the scope, one might recall from Proposition 16 how condition
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
. Lastly, further enlarging the scope, one might recall from Proposition 16 how condition
![]() $(\textsf{A}1)$
corresponds to classic-like implications (Definition 13), and ask whether such condition could be relaxed, perhaps requiring the new implication to be axiomatized by the usual inference rules for Heyting implications. In this way, we could circumvent the limitation of Theorem 20 exploring alternative self-extensional expansions of the logics of PP-algebras.
$(\textsf{A}1)$
corresponds to classic-like implications (Definition 13), and ask whether such condition could be relaxed, perhaps requiring the new implication to be axiomatized by the usual inference rules for Heyting implications. In this way, we could circumvent the limitation of Theorem 20 exploring alternative self-extensional expansions of the logics of PP-algebras.
Extensions of
 $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
Our preliminary investigations suggest that the landscape of extensions of the base logics considered in the present paper is quite interesting and complex. Concerning the finitary ![]() extensions of
extensions of
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
we may affirm the following:
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
we may affirm the following:
-
• By Jansana (Reference Jansana2006, Thm. 3.7), the finitary
 self-extensional extensions of
self-extensional extensions of
 $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
are in one-to-one correspondence with the subvarieties of
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
are in one-to-one correspondence with the subvarieties of
 $\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
. Thus, by Corollary 79, there are only three of them, all of them axiomatic (none of them being conservative expansions of
$\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
. Thus, by Corollary 79, there are only three of them, all of them axiomatic (none of them being conservative expansions of
 $\mathcal{PP}_{\!\leq }$
). These logics may be axiomatized, relatively to
$\mathcal{PP}_{\!\leq }$
). These logics may be axiomatized, relatively to
 $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
, by adding axioms corresponding to the equations in Corollary 79, to wit:
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
, by adding axioms corresponding to the equations in Corollary 79, to wit:-
(1) the logic of
 $\mathbb{V} (\mathbf{PP_4^{\Rightarrow _{\textsf{H}}}})$
is axiomatized by
$\mathbb{V} (\mathbf{PP_4^{\Rightarrow _{\textsf{H}}}})$
is axiomatized by
 $(p \land{\sim } p) \Rightarrow (q \lor{\sim } q)$
;
$(p \land{\sim } p) \Rightarrow (q \lor{\sim } q)$
; -
(2) the logic of
 $\mathbb{V} (\mathbf{PP_3^{\Rightarrow _{\textsf{H}}}})$
by
$\mathbb{V} (\mathbf{PP_3^{\Rightarrow _{\textsf{H}}}})$
by
 $ p \lor (p \Rightarrow (q \lor \neg q ) )$
; and
$ p \lor (p \Rightarrow (q \lor \neg q ) )$
; and -
(3) the logic of
 $\mathbb{V} (\mathbf{PP_2^{\Rightarrow _{\textsf{H}}}})$
, which is (up to the choice of language) just classical logic, by
$\mathbb{V} (\mathbf{PP_2^{\Rightarrow _{\textsf{H}}}})$
, which is (up to the choice of language) just classical logic, by
 $p \lor{\sim } p$
.
$p \lor{\sim } p$
.
-
-
• The number of axiomatic
 extensions of
extensions of
 $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
(all logics which are obviously finitary) is larger but also finite, for each axiomatic extension may be characterized by the submatrices of the original matrices that satisfy the axioms.Footnote 4
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
(all logics which are obviously finitary) is larger but also finite, for each axiomatic extension may be characterized by the submatrices of the original matrices that satisfy the axioms.Footnote 4 -
• As we have seen (cf. Proposition 80), the assertional logic
 $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
is itself a (non-axiomatic, non-self-extensional) extension of
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
is itself a (non-axiomatic, non-self-extensional) extension of
 $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
. Algebraizability of
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
. Algebraizability of
 $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
(Theorem 78) entails that its axiomatic
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
(Theorem 78) entails that its axiomatic  extensions are in one-to-one correspondence with the subvarieties of
extensions are in one-to-one correspondence with the subvarieties of
 $\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
, so again we can conclude that there are only three of them.
$\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
, so again we can conclude that there are only three of them. -
• In contrast to the preceding results, we conjecture that it may be possible to construct countably many distinct (non-axiomatic)
 finitary extensions of
finitary extensions of
 $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
. The theory of algebraizability would then tell us that the variety
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
. The theory of algebraizability would then tell us that the variety
 $\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
has at least countably many subquasivarieties.
$\mathbb{PP}^{\Rightarrow _{\textsf{H}}}$
has at least countably many subquasivarieties.
Now considering the ![]() extensions of
extensions of
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
, we can say the following:
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
, we can say the following:
-
• Similarly to the
 setting, all axiomatic
setting, all axiomatic  extensions of
extensions of
 $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
are characterized by the sets of (sub)matrices in
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
are characterized by the sets of (sub)matrices in
 $ \{ \langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{\uparrow } a \rangle : a \in \mathcal{V} \}$
that satisfy the corresponding axioms, hence their cardinality is also finite. Their
$ \{ \langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{\uparrow } a \rangle : a \in \mathcal{V} \}$
that satisfy the corresponding axioms, hence their cardinality is also finite. Their  companions are obtained by adding the same axioms to
companions are obtained by adding the same axioms to
 $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
.
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
. -
• In consequence, there are at least three self-extensional
 extensions of
extensions of
 $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
, namely, the ones determined by the matrices which satisfy the corresponding axioms. (There may be more, but each of them will have as
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
, namely, the ones determined by the matrices which satisfy the corresponding axioms. (There may be more, but each of them will have as  companion one of the three self-extensional
companion one of the three self-extensional  extensions of
extensions of
 $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
mentioned earlier.)
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
mentioned earlier.) -
• The methods used in the previous sections may be used to obtain analytic
 axiomatizations for all the logics determined by sets of (sub)matrices in
axiomatizations for all the logics determined by sets of (sub)matrices in
 $ \{ \langle \mathbf{PP}_6^{\Rightarrow _{\textsf{H}}},{\uparrow } a \rangle : a \in \mathcal{V} \}$
.
$ \{ \langle \mathbf{PP}_6^{\Rightarrow _{\textsf{H}}},{\uparrow } a \rangle : a \in \mathcal{V} \}$
.
The preceding considerations suggest that a complete description of the lattice of all extensions of our base logics is well beyond the scope of the present work, and will have to be pursued in future investigations. We summarize such a research program in terms of the following couple of problems:
Problem 1.
Describe the lattice of all (
![]() ) extensions of
) extensions of
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
and the lattice of all (
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
and the lattice of all (
![]() ) extensions of
) extensions of
![]() $\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
.
$\mathcal{PP}^{\rhd, \Rightarrow _{\textsf{H}}}_{\textsf{up}}$
.
Problem 2.
Look at the same problem again, but now restricting one’s attention, on the one hand, to the sublattice consisting of all the ![]() extensions of
extensions of
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
, and on the other hand, to the sublattice consisting of all the
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
, and on the other hand, to the sublattice consisting of all the ![]() extensions of the
extensions of the ![]() logic determined by the matrix
logic determined by the matrix
![]() $\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\hat{\mathbf{t}}}} \rangle$
. Due to the algebraizability of
$\langle \mathbf{PP_6^{\Rightarrow _{\textsf{H}}}},{{\uparrow }{\hat{\mathbf{t}}}} \rangle$
. Due to the algebraizability of
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
, for finitary
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_\top$
, for finitary ![]() logics the problem may be rephrased as: describe the lattice of all subquasivarieties of
logics the problem may be rephrased as: describe the lattice of all subquasivarieties of
![]() $\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
.
$\mathbb{V}(\mathbf{PP_6^{\Rightarrow _{\textsf{H}}}})$
.
Fragments of the language of
 $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
A close inspection of the methods employed in the previous sections to axiomatize
![]() $\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
and its
$\mathcal{PP}^{\Rightarrow _{\textsf{H}}}_{\!\leq }$
and its ![]() companions suggests that these may also be applied so as to obtain analytic axiomatizations for the logics corresponding to those fragments of the language over the connectives in
companions suggests that these may also be applied so as to obtain analytic axiomatizations for the logics corresponding to those fragments of the language over the connectives in
![]() $\{ \land, \lor, \Rightarrow, {\sim },{\circ }, \bot, \top \}$
that are sufficiently rich to express an appropriate set of separators. Some of these, we believe, have intrinsic logical and algebraic interest, and may deserve further study. Let us single out, for instance, the fragments corresponding to the connectives
$\{ \land, \lor, \Rightarrow, {\sim },{\circ }, \bot, \top \}$
that are sufficiently rich to express an appropriate set of separators. Some of these, we believe, have intrinsic logical and algebraic interest, and may deserve further study. Let us single out, for instance, the fragments corresponding to the connectives
![]() $\{ \Rightarrow, {\circ } \}$
,
$\{ \Rightarrow, {\circ } \}$
,
![]() $\{ \Rightarrow, \Delta \}$
(recall that
$\{ \Rightarrow, \Delta \}$
(recall that
![]() $\Delta x : ={\sim } x \Rightarrow{\sim } (x \Rightarrow x)$
) and
$\Delta x : ={\sim } x \Rightarrow{\sim } (x \Rightarrow x)$
) and
![]() $\{ \Rightarrow, {\sim } \}$
. The first of them may be of interest in the study of implicative fragments of Logics of Formal Inconsistency, while the second could be studied in the setting of implicative fragments of algebras with modal operators. The study of the third could lead to an interesting generalization of Monteiro’s results on symmetric Heyting algebras and their logic.
$\{ \Rightarrow, {\sim } \}$
. The first of them may be of interest in the study of implicative fragments of Logics of Formal Inconsistency, while the second could be studied in the setting of implicative fragments of algebras with modal operators. The study of the third could lead to an interesting generalization of Monteiro’s results on symmetric Heyting algebras and their logic.
Acknowledgments
Vitor Greati acknowledges support from the FWF project P33548. Sérgio Marcelino’s research was supported by FCT - Fundação para a Ciência e Tecnologia, I.P. by project reference UIDB/50008/2020, and DOI identifier https://doi.org/10.54499/UIDB/50008/2020. João Marcos acknowledges research support received from CNPq. Umberto Rivieccio acknowledges support from the 2023-PUNED-0052 grant “Investigadores tempranos UNED-SANTANDER” and from the I+D+i research project PID2022-142378NB-I00 “PHIDELO," funded by the Ministry of Science and Innovation of Spain.









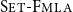 ) order-preserving logics are non-algebraizable self-extensional logics of formal inconsistency and undeterminedness determined by a six-valued matrix. We studied these logics extensively in Gomes et al. ((2022).
) order-preserving logics are non-algebraizable self-extensional logics of formal inconsistency and undeterminedness determined by a six-valued matrix. We studied these logics extensively in Gomes et al. ((2022).  order-preserving and
order-preserving and 




















