Introduction
The possible instability of the West Antarctic ice sheet has stimulated interest in its dynamics, especially in the role played by the ice streams which flow from the Siple Coast into the Ross Ice Shelf (e.g. Reference Hughes,Hughes, 1975). These ice streams are often highly crevassed and they move at speeds which are 2–3 orders of magnitude greater than the ice sheet in which they are embedded. In contrast to the fast-moving outlet glaciers and ice streams of Greenland (Reference Clarke, and Echelmeyer,Clarke and Echelmeyer, 1989; Reference Echelmeyer,Echelmeyer and others, 1991) and East Antarctica (Reference McIntyre,McIntyre, 1985; Reference Bentley,Bentley, 1987), these Siple Coast ice streams do not generally lie in over-deepened bedrock troughs. Their thickness is on the order of 1000 m, which is similar to that of the surrounding ice sheet (Reference Shabtaie, and Bentley,Shabtaie and others, 1987), and their surface slope is about 10−3. The resulting driving stresses are on the order of 0.1 × 105 Pa. Such low driving stresses and surface speeds which are on the order of 1000 m a−1 (e.g. Reference Bentley,Bentley, 1987; Reference Whillans, and Oerlemans,Whillans and others, 1987) imply that the resistance to flow is small compared to that normally found on ice sheets and non-surging valley glaciers.
Investigation of the controlling mechanisms for the flow of these ice streams has concentrated on basal processes. Seismic (Reference Blankenship,, Bentley,, Rooney, and Alley,Blankenship and others, 1987) and borehole studies (Engelhardt and others, 1990) in the vicinity of Upstream B Camp, about 300 km upstream of the grounding zone, have indicated that, locally, the bed of Ice Stream B consists of a weak, water-saturated till layer. The shear strength of this till layer is extremely low; measurements show it is on the order of 0.02 × 105 Pa (Reference Kamb,Kamb, 1991). These observations have led several authors to state or imply that the properties of this basal layer, and associated “sticky spots”, are key to an understanding of ice-stream flow, and that basal drag is the ultimate controlling factor in ice-stream dynamics (see, for instance, Reference Vornberger, and Whillans,Vornberger and Whillans, 1986; Reference Whillans,, Bolzan, and ShabtaieWhillans, 1987). However, some care must be taken in extrapolating these localized basal observations, which were made in a small and anomalously uncrevassed neighborhood of Upstream B Camp, to the remainder of Ice Stream B, which has a more highly crevassed surface. These crevasses may be indicative of other controlling mechanisms at play in ice-stream flow.
Studies on valley glaciers indicate that marginal drag at the valley walls is nearly equal in importance to basal drag as a controlling factor in glacier flow. However, on an ice stream such as Ice Stream B, the half-width is much greater than the depth (by about a factor of 15:1 at Upstream B Camp or 50:1 at Downstream B Camp (Fig. 1a), as opposed to about 3:1 for a valley glacier). Thus, the magnitude of marginal shear stresses on the West Antarctic ice streams must be nearly 10–50 times those at the bed in order to be important in the overall force balance of these ice streams.

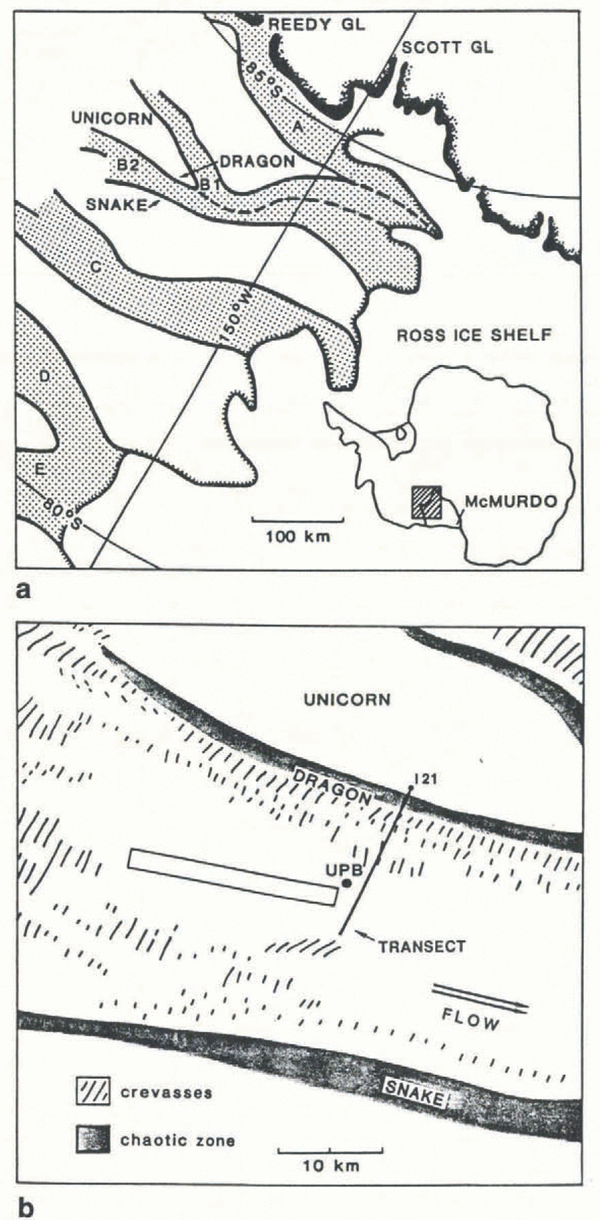
Fig. 1. (a) Location map, modified from Reference Blankenship,, Bentley,, Rooney, and Alley,Blankenship and others (1987) and Reference Shabtaie,, Whillans and BentleyShabtaie and Bentley (1987). The triangles mark the sites of Upstream B and Downstream B camps. The ice streams are stippled and end at their grounding lines at the Ross Ice Shelf, (b) Location of velocity profiles. The rectangle indicates the site of the Ohio State University strain net (Reference Whillans,, Jackson and TsengWhillans and others, 1987). The map is modified from Reference Vornberger, and Whillans,Vornberger and Whillans (1986).
In the limiting case of a glacier or ice stream which flows over a very weak, deformable bed, there must be a transfer of resistive forces from the bed to the margins and/or to longitudinal stress gradients. Such is the case for a floating ice shelf. Model results of Reference MacAyeal,MacAyeal (1989) show that marginal shear stresses and ice-shelf backpressure are important in determining the overall velocity field of the Siple Coast ice streams. In a second study, Reference MacAyeal,MacAyeal (1992) has used a velocity field determined from the motion of crevasses in the marginal zones of Ice Stream Ε to investigate the balance of forces along that ice stream. The velocity field obtained in this manner allows a direct investigation of marginal processes, as opposed to measurements made on crevasse-free regions. He again found that, while the existence of a deformable bed is important, the margins and ice-shelf back-pressure provide crucial controls on the flow.
Similar conclusions have been reached by Reference Jackson,Jackson (1991) on Ice Stream B. She used the motion of crevasses from repeat photography to determine the velocity field. Her results show that there exists important lateral shear across most of the ice stream in a region around Upstream B and, thus, concluded that marginal drag is an important control at that location. Whillans and others (1993) also argued for the importance of marginal drag on this ice stream using these data.
Reference Frolich, and Doake.Frolich and Doake (1988) found that lateral shear stresses are important only in narrow zones at the margins of Rutford Ice Stream. Basal shear stresses dominate over much of the central region of the ice stream, even near the grounding zone. These conclusions are based upon surveyed velocity profiles which do not, in most cases, extend across the marginal shear zones because extensive crevassing prohibited travel there.
Another factor that is important is the rheology of ice within marginal zones. Reference Hughes,Hughes (1975) has suggested that there may be a substantial softening of the ice there. Such softening may occur because of the preferred fabric developed during the accumulation of large shear strains in the deformational history of marginal ice (Reference Jacka, and Budd,Jacka and Budd, 1989). This enhanced flow within the margins may be important in determining the location and dynamics of ice streams.
In the present paper, we describe measurements made on Ice Stream B which are directed at the problem of the margins and their role in controlling ice-stream flow. Measurements of surface velocity were made along a transverse profile extending from near the center of the ice stream across the shear margin and into the slow-moving ice sheet. These observations are discussed in terms of flow models which indicate that the margins do play an important role in controlling ice-stream motion, with marginal drag being equal to or greater than basal drag at some locations. Inferences about the mean basal shear stress may be made from these models and a comparison with the strength of basal till from Upstream B as measured by Reference Kamb,Kamb (1991) is made. We also investigate the softening of ice within the marginal zones where the ice has a history of intense shearing and the viscous heating which is a consequence of the large strain rate and shear stress at the margins.
Morphology of the Ice Stream Along the Transverse Profile
In December 1989, a transverse-velocity profile in the vicinity of Upstream B Camp was surveyed across a line extending from near the ice-stream center line (about 3.3 km north of Upstream B Camp), through the south shear margin (the “Dragon”) and on to the relatively uncrevassed, slow-moving Unicorn (Fig. 1b). The ice stream is about 31 km wide at this location and the surveyed profile was 14.2 km in length. Near the north end of the profile (close to the ice-stream center line) there exists a zone of oblique crevassing of moderate density along a longitudinal topographic ridge (20 m in elevation relative to Upstream B). The cause of these crevasses is not clear. From the base of the ridge, the profile cut across relatively uncrevassed ice near where the strain grid of Reference Whillans,, Bolzan, and ShabtaieWhillans and others (1987) was situated (Fig. 1b). There are almost no large crevasses over a stretch of about 8 km, although there are small ones with a spacing of about 50–100 m which have little surface expression in the way of linear depressions or visible cracks. About 11 km from the center line, the 4–5 km wide marginal shear zone (the “Dragon”) is entered, as shown schematically in Figure 2a.

Fig. 2. Transverse profile. (a) Schematic diagram of the crevasse density and spacing across the section of Ice Stream B crossed by the velocity profile. Approximate crevasse orientations are shown, (b) Longitudinal component of the horizontal surface velocity, u, and its transverse derivative, ½∂u/∂y, along the line shown in Figure 1b. The dashed curve shows the velocity profile for a model in which the basal shear stress is zero, (c) Calculated transverse shear stress from Equation (2) and the simple linear model of Equation (3a).
During a ski traverse of this shear zone in 1989, three distinct sub-zones were identified. On the ice-stream side there is a 2 km wide region of large but somewhat organized crevasses whose density increases toward the margin. These crevasses roughly trend upstream at an angle of 40–70° to the margin, indicating an origin related to transverse shear. This sub-zone ends rather abruptly at the “chaotic” zone, which consists of highly disorganized crevasses and fractured ice blocks. Near-surface conditions suggest that there is great void space at depth. This chaotic sub-zone is also about 2 km in width. Within this region, about 14.3 km from the center line, there was a
Velocity Through the Margin
Approximately 20 markers were placed along the transverse profile, including several in the highly crevassed “Dragon”. The markers were surveyed three times at about 8 d intervals using a 1 s theodolite and an electronic distance meter. A retro-reflecting prism was mounted on each of the markers in the chaotic zone to avoid any re-occupation of these somewhat hazardous sites during the surveys.
Reduction of the survey data was accomplished by assuming that marker 121 (Reference Whillans,, Bolzan, and ShabtaieWhillans and others, 1987), which was situated at the end of our profile on the Unicorn, did not move. Such an assumption was necessary because of the lack of any absolute positioning at the time of the survey and by the geometry of the survey network. The geoceiver-survey results of I. Whillans (personal communication) during previous years indicate that marker 121 actually moves about 1 m a−1 obliquely into the ice stream. This slightly nonzero velocity will cause our calculated velocities to be somewhat lower than the true ones. Errors arising from this assumption will affect the calculated velocity of each marker in a similar manner and this systematic error is included in the estimated error bounds on the velocity measurements which are ±3–5 m a−1. Velocities calculated over the two different time intervals between surveys agree within these error bounds. In the following analysis, we take the x axis along the mean direction of flow, normal to the profile, the y axis approximately along the profile, directed to the south, and z upward.
The longitudinal component of surface velocity, u, resulting from these surveys is shown as a function of distance from the ice-stream center line in Figure 2b. Traversing outward from the center line, the speed shows a gradual decrease as one moves off the topographic ridge at the 2 km position. Across the uncrevassed part of the ice stream, the speed continues to show a slight decrease and, then, within the 4-5 km wide marginal shear zone the speed decreases rapidly to near-zero. Within the marginal zone, the small transverse component of velocity, v, (not shown here) is directed into the ice stream, as is typical of convergent flow. Between 13 and 14 km, just in from the longitudinal furrow, the curvature of the velocity profile changes sign and the magnitude of the transverse gradient of the longitudinal velocity, ∂u/∂y, reaches a maximum. Outward of this inflection point, the rate of decrease in speed is less than that found within most of the chaotic zone. The velocity profile is generally smooth but there are two significant jumps in ∂u/∂y, which may be caused by measurement error or by a change in ice-flow properties, as discussed below.
The observed velocity profile is similar to that observed on valley glaciers, in which the half-width to center-line depth ratio is relatively large, say 4–5. It is not reminiscent of true “plug flow” which has been observed on glaciers during surges (e.g. Reference Kamb,Kamb and others, 1985), because the speed is not constant in the center part of the profile and the marginal decrease is rapid but not extremely abrupt.
One-half of the transverse derivative of the longitudinal velocity, ½∂u/∂y, is also shown in Figure 2b. The derivative has been calculated discretely between each of the markers. Because the markers are not uniformly spaced, the error in ½∂u/∂y varies somewhat, ranging from 0.001 to 0.005 a−1. The velocity of several additional markers placed upstream of the transverse profile near and within the marginal zone shows that the longitudinal gradient of the transverse velocity, ∂u/∂x, is small and thus ∂u/∂y is approximately equal to the shear-strain rate,
The peak in the velocity gradient is centered in the chaotic zone, inside of the longitudinal furrow, not at the Unicorn–ice-stream boundary at 15 km. The width of this peak corresponds to the width of the crevassed marginal shear zone, with heavy crevassing ending at shear-strain rates below about 0.005 a−1. The chaotic crevassing occurs where the strain rate exceeds about 0.05 a−1. The peak shear-strain rate is about 0.08 a−1, a value similar to that found along the margins of some fast-moving valley glaciers.
Discussion
There are several interesting features of the observed velocity profile which are possibly unique to ice-stream flow. First, the center-line velocity is large in comparison with the surrounding ice sheet. Secondly, the velocity decreases rapidly within the narrow chaotic zone. The velocity does not vary much over the central part of the ice stream but the profile is not one of plug flow. And, lastly, there is the inflection point between 13 and 14 km, which is about 1.5 km into the ice stream from the contact between the ice stream and the relatively stagnant Unicorn.
In this section, we compare this profile with the velocity field obtained from analytical and numerical models of flow. The comparisons then allow us to address the following questions:
-
(1) What are the roles of the margins and of the bed in the force balance of the ice stream?
-
(2) How does the calculated basal shear stress compare with the measured strength of basal till samples (Reference Kamb,Kamb, 1991)?
-
(3) Does ice rheology vary across the ice stream?
-
(4) Is significant viscous heating likely within the margins?
We begin with a simplified estimate of the shear stress at the margin and of the importance of marginal drag on the overall force balance of the ice stream.
Based on our off-profile markers and the results of Reference Whillans, and Oerlemans,Whillans and others (1987) and Reference Jackson,Jackson (1991), we make the reasonable assumptions near the margins that

and that all gradients involving the vertical direction are small at the surface. For the purposes of this simple analysis, we assume that the strain rates are constant with depth. (In actuality, they may vary with depth because of changes in ice temperature, material properties and the basal boundary condition.)
Given these assumptions, a prediction of the shear stress τxy can be obtained from the power-law constitutive relation for ice

which is shown in Figure 2c. The maximum stress is about 2 × 105 Pa, and it occurs in the chaotic zone.
A first estimate of the importance of the margins in the force balance of the ice stream may be obtained by comparing the total down-slope gravitational force acting on the ice stream (= ρgHWsinα, where Η is the mean ice thickness (1100 m), sinα = 1.3 × 10−3 and W is the total width of the ice stream (∼31 km)) with the shear stress integrated over the margins. Taking a representative marginal shear stress as 1.7 × 105 Pa from Figure 2c, the total drag along the edges of the ice stream is about 3.7 × 108Ν per meter of length in the x direction, while the total gravitational driving force is 4.0 × 108 Ν per meter of length. This suggests that the margins provide a large proportion of the total resistive force on the ice stream at this location. Basal drag (and, to a lesser extent, longitudinal forces) must provide the remainder.
The velocity and estimated shear stress shown in Figure 2 may be compared with those obtained by a simple model in which we assume there is no basal drag and that the ice stream is restrained entirely by friction at the rigid margins. We also assume that the speed at the margins is zero and that material properties are constant throughout. Then, the shear stress would vary linearly with distance y out from the center (Reference Nye,Nye, 1965):
and by Equation (2) the velocity is given by

where ρ is the density of ice, g is the acceleration of gravity and α is the surface slope. We use a slope of 1.3 × 10−3 which is obtained by measurement along a 10–20 km length of the surface-elevation map of Reference Van der Veen, and Whillans,Shabtaie and others (1987) and on the higher-resolution map of Reference Retzlaff,, Lord, and Bentley,Retzlaff and others (1993). The peak stress occurring at the ice-stream-ice-sheet boundary is 1.8 × 105 Pa, as shown in Figure 2c. The center-line velocity predicted from this zero basal shear-stress model is about 420 m a−1, which is quite close to that observed. However, the shape of the predicted velocity profile does not resemble that observed, as shown in Figure 2b. The predicted profile is more rounded, without the abrupt decrease in velocity localized in the marginal zone. The inferred transverse shear stress is also not linear. These differences are related, in part, to the assumption of zero basal shear stress.
Introduction of basal shear stress
Reference Blankenship,, Bentley,, Rooney, and Alley,Blankenship and others (1987), Engelhardt and others (1990) and Reference Kamb,Kamb (1991) found that there is a layer of deformable till beneath the ice stream near Upstream B. This till has a finite shear strength of about 0.02 × 105 Pa and its thickness goes to zero in some areas, possibly placing bedrock in direct contact with the ice. This would imply that there is a distribution of non-zero basal shear stress, τb(y). This stress will provide additional restraint to the ice stream and it will influence the surface-velocity field.
In this section, we seek, in an approximate manner, a distribution of τb which leads to the observed velocity profile — both the center-line speed and the rapid decrease in speed which occurs in the margins. We note that
for any physically correct model, i.e. the bed cannot pull the ice downstream. The imposition of any non-zero τb satisfying Equation (4) will decrease the predicted center-line speed. The close match of center-line speeds with τb ≡ 0 implies that the ice must, in general, be softer than would be predicted by the assumed uniform −15°C temperature. We shall see that this is indeed the case.
We begin by again noting that Equation (1) holds near Upstream B and thus longitudinal stress gradients will be neglected. The stress-equilibrium equation in the down-glacier direction (x) is then given by

The ice stream is approximated by a slab of rectangular cross-section with uniform width W, thickness Η and surface slope α, as given above. The z axis is taken positive upward from the bed along the center line. Integrating Equation (5) over the ice thickness yields

where τd ≡ pgH sin α = 0.127 × 105 Pa is the driving stress,
As a first approximation, we assume ∂τxy/∂y is independent of depth. This assumption will be relaxed in the numerical model discussed later. Then

The flow law of ice may be used to express the shear stress τxy in terms of the measured strain rate at the surface, again assuming Equation (1) holds. The general form of the flow law is, following Reference Paterson,Paterson (1981),
where
Under the assumptions detailed above, the only nonzero stress component near the surface is τxy . Equation (8) can then be used to express τxy at the surface in a form similar to Equation (2). For the moment, we assume that ice temperature does not vary laterally. Then, Equation (7) can be written as

where ½∂u/∂y is given at the surface in Figure 2b.
If we assume that there is no variation in ice rheology across the ice stream, then the enhancement factor is constant and can be taken equal to 1. Any overall softening of the ice can be incorporated into the constant A. Such softening may be due to an error of our assumption about the mean temperature for the ice or some uniform softening related to the strain history of all the ice within the ice stream, which would lead to an error if Reference Paterson,Paterson’s (1981) values were assumed.
Taking the bulk ice temperature as −15°C and the value of A given by Reference Paterson,Paterson (1981) at this temperature, Equation (9) leads to negative basal shear stresses over much of the bed. This physically unrealistic result is to be expected, as explained above. Increasing A by a factor of 10 still produces negative τb in the chaotic zone, where the curvature of the velocity profile is large. Increasing A by a factor of 10 is equivalent to assuming all of the ice within the stream is close to the melting point.
If we increase A by a factor of 100, then τb inferred from Equation (9) is generally positive and, except near the margin, in the range 0−0.1 × 105 Pa. However, there are still areas in the chaotic zone where the calculated τb is slightly negative and A would have to be increased further in order to eliminate all negative values of τb .
The basal shear-stress distributions for each of the assumed values of A all lead to a value τb which is relatively constant at about 0.05 × 105 Pa over the first 10 km of the bed out from the center. Some variation about this value is found where the increased flow occurs off the longitudinal ridge near the ice-stream center line described earlier. This is reasonable, since the assumptions inherent to the model of uniform thickness and surface slope are not met there. This feature of τb , (y) may be taken to imply that basal conditions do not vary greatly over the first 10 km, at least as seen by the 1100 m thick filter of the ice stream. Variations over short distances across the bed could occur but the surface-velocity field would not reflect them.
The overall conclusion reached from these models is that, unless the ice rheology is substantially (two orders of magnitude or more) different than that published (e.g. Reference Paterson,Paterson, 1981), there is no physically reasonable distribution of Tb which can explain the observed velocity field when the ice rheology is taken to be uniform across the ice stream. The simple model described does have several assumptions which may not be strictly valid but, as will be seen below, relaxation of some of them in a numerical model does not change this conclusion.
Lateral variation of rheological properties
The ice in the marginal zones has been subjected to a history of rapid shear strain. The total strain which a parcel of marginal ice has undergone is dependent upon its time of transit through the marginal zone and on the stability of the margin. Taking the zone of intense shear to be about 2 km in width and ν ∼ 2–10 m a−1, the transit time is on the order of 200-1000 years. From Figure 2b, we see that the ice experiences an average rate of shear strain equal to about 0.04 a−1 and, thus, the total accumulated strain could be extremely large. Reference Hughes,Hughes (1975) suggested that ice undergoing such accumulated shear strain could be weaker than unstrained ice. According to Reference Jacka, and Budd,Jacka and Budd (1989), an enhancement factor Ε equal to 8 occurs when the accumulated shear strain reaches 0.15. Beyond that total strain, there appears to be no further increase in E. However, the extrapolation of this asymptotic value to the large strain accumulated during the few hundred year long passage through the shear margin may not be strictly valid and the resulting value of Ε could possibly be larger. In addition, ice temperatures may be elevated in the marginal zones, because of viscous heating (Reference Echelmeyer,, Wade, and Iken,Echelmeyer and others, 1992) which would further soften the ice. Such a lateral variation in ice-flow properties might lead to profiles of velocity and strain rate similar to those observed.
Equation (9) may be used to investigate this possibility. We are again subject to the assumptions leading to this equation. We again take the temperature to be constant at −15–C and use the value of A given by Reference Paterson,Paterson (1981) at this temperature. τb is now taken to be constant and Ε is a function of position across the ice stream, y. The variable Ε will encompass fabric development, strain heating and possibly other sources of enhanced flow.
Integration of Equation (9) over y from the center line outward gives

where we have used the condition that ∂u/∂y = 0 at the center line because the channel is symmetric. Assuming that ice near the center line has “standard” flow properties, or E(0) = 1, we obtain Tb from the limit

Extrapolating a smooth curve drawn through a plot of the quantity in the brackets of Equation (11) yields τb . (The plot is somewhat noisy due to the observed flow off the center-line ridge, as mentioned above.) This limiting value gives
Using this value of τb in Equation (10) yields the distribution of the enhancement factor Ε shown in Figure 3b. The discontinuous distribution of Ε is due to the discrete nature of the velocity data and measurement errors in u. Subject to the usual qualifications regarding anomalous flow induced by the center-line ridge (shown by the dotted line in Figure 3b), the results indicate that Ε is nearly constant over the first 10 km. There is then a softening of the ice at a position corresponding to the start of the crevassed Dragon. This softening reaches a peak (Ε ∼ 14) in the chaotic zone where shear-strain rates are the largest. Toward the Unicorn, the ice then again becomes stiffer.

Fig. 3. (a) Finite-element grid used in model calculations. The thickness of the basal layer is exaggerated for clarity, (b) Enhancement factors from Equation (10) (solid line) and those used in the finite-element model (dashed) along the Upstream B profile.
These values of the enhancement factor in the chaotic zone are somewhat greater than, but consistent with, those obtained by Reference Jacka, and Budd,Jacka and Budd (1989) in the laboratory for ice with a prolonged history of shear strain. The smaller values of Ε outside the chaotic zone (Ε ∼ 3-5) are also consistent with their results, given the picture of smaller strain rates and smaller total strain in these regions.
If a somewhat warmer bulk-ice temperature were assumed, the base value of A would increase. This would change the numerical values shown in Figure 3b but the pattern of variation would not change. A ten-fold increase in A (to that of near-temperate ice) would cause a transfer of some of the resistive drag to the bed and τb from Equation (11) would increase to about 0.09 × 105 Pa.
In summary, these simplified models indicate that there is no reasonable distribution of basal shear stress which can, by itself, explain the observed velocity profile. A picture which is consistent with the observations is as follows: nearly constant ice and bed properties out to 10 km, an approximate ten-fold softening of ice within the crevassed Dragon and somewhat stiffer ice and/or an increase in basal drag within the marginal part of the Unicorn. A basal shear stress of about 0.06 × 105 Pa over much of the bed results from this picture. This value is greater than the 0.02 × 105 Pa measured by Reference Kamb,Kamb (1991) in the laboratory. This larger value may be explained by postulating a distribution of weak, deformable till and bedrock protrusions or less-deformable till along the bed.
Of course, these models may not be unique. It is likely that there is some combination of laterally varying ice properties and basal drag which also lead to the observed velocity profile. What is important is that the resulting model matches the observed profile and not just the speed at a few points near the center line.
Finite-element analysis
In order to relax some of the assumptions and provide a more realistic estimate of the degree to which the margins help support the ice stream, we have conducted finite-element analysis of flow within a cross-section of a simplified ice-stream channel. The modeling scheme allows for flow in three dimensions within a two-dimensional cross-sectional grid. The three-dimensional stress-equilibrium equations are solved at each point in the grid. Stress and velocity gradients in x, which are directed out of the plane of the cross-section (in other words, longitudinal gradients along the ice stream) are taken to be zero. The power-law (n = 3) constitutive relation (Equation (8)) for incompressible flow is used with a spatially variable flow-law parameter, A(y, z). This allows us to account for temperature variation within the grid, as well as a spatially variable enhancement factor. Density is taken to be constant. (See Reference Echelmeyer,, Harrison,, Clarke, and Benson.Echelmeyer (1983) for details of the numerical algorithm.)
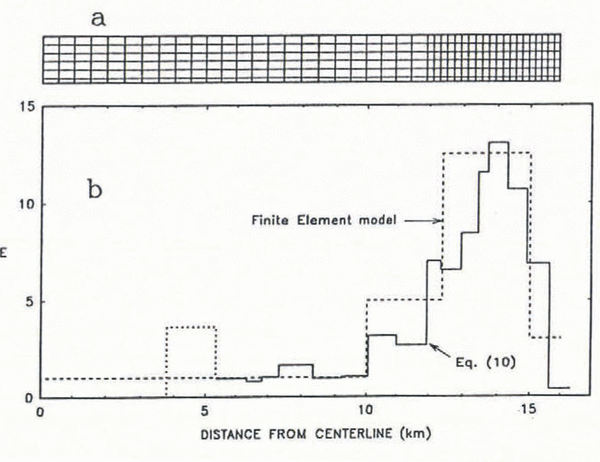
Because the exact cross-sectional shape of Ice Stream B along our profile is not known, we assume a simple rectangular cross-section 32 km wide with vertical sides positioned at the ice-stream–ice-sheet boundaries, a transversely horizontal surface and a total depth of 1100 m (Fig. 3a). This rectangular channel very closely approximates the depth profile measured by Reference Shabtaie, and Bentley,Shabtaie and Bentley (1988) at a nearby location on this ice stream, with variations from a rectangle being at most 10% near the center line and less elsewhere. Because the channel is assumed to be symmetric about the center line, we model only half of the cross-section. A grid of 264 quadrilateral isoparametric elements with linear shape functions was used (Fig. 3a). Clearly, some of the details of the observed velocity profile, such as the flow induced by the topographic ridge near the center, will not be modeled using such a simplified cross-section, but many of the essential features should be apparent.
A surface slope of 1.3 × 10−3 is used. Symmetry requires that the tangential shear stress and transverse velocity are zero down the center line. The outer margin of the channel is taken to be vertical and the velocity there is set equal to zero to approximate the no-slip interface with the stagnant ice of the Unicorn. There is no direct evidence that the ice-stream margin does not extend vertically down to the bed, although warmer ice near the bed may cause some tilting of this boundary at depth.
As described earlier, Reference Blankenship,, Bentley,, Rooney, and Alley,Blankenship and others (1987), Engelhardt and others (1990) and Reference Kamb,Kamb (1991) have found a thin (≤10m) layer of deformable till at the base of the ice stream near Upstream B. We incorporate this layer into our model by including a single layer of thin elements at the bed (Fig. 3a). Their thickness is included in the 1100 m total thickness stated above. A condition of no-slip is applied between the ice and the till, and at the bottom of the till. The rheology of the basal layer is assumed to follow the n = 3 power law for convenience. Model results do not depend strongly on this assumed constitutive relation. The variable flow-law parameter A(y, z) for this basal layer can be changed to simulate warm or cold ice, or a weak, deformable till. The layer thickness is taken to be 50 m in the final model in order to improve the accuracy of the stress calculations by keeping the aspect ratio of the thin elements relatively small. Tests were also done with a 10 m thick basal layer. Surface velocity and marginal stresses were not influenced by this change in layer thickness as long as the value of A in the bottom layer was adjusted suitably. Calculation of the basal shear stress required care when smoothing through the centroid of the elements in the 10 m thick layer but the final values did not appear to differ significantly from those found using the more accurate 50 m thick elements.
The flow-law parameter was adjusted in accordance with ice temperature. It is probable that marginal temperatures may be elevated because of viscous heating (Reference Echelmeyer,, Wade, and Iken,Echelmeyer and others, 1992) but we assume that the ice temperature measured in a borehole drilled at Upstream B Camp (Engelhardt and others, 1990) holds across the ice stream. We thus assume only a vertical variation in temperature, Τ = T(z). The measured temperature profile is approximated by a simple four-layer model, with layers at the following depths: 0–400 m at −24°C, 400–800 m at −20°C, 800–1050 m at −9°C and the basal layer at the melting point. The temperature-dependent flow-law parameter, A(z), is taken from Reference Paterson,Paterson (1981). A spatially variable enhancement factor, E(y, z) (Equation (8)), is introduced. This factor is again used to specify the softening of ice due to the combined effects of prolonged shear strain (Reference Jacka, and Budd,Jacka and Budd, 1989), elevated marginal ice temperatures and other factors. Knowledge of the specific source of the enhanced flow is not required. An enhancement factor is also introduced in the basal layer to allow lateral variations in its strength and in the basal shear stress.
Guided by the analytical results discussed above, several finite-element models of increasing complexity were run in order to illustrate the controlling mechanisms implied by the observed surface-velocity profile. Key features of the observed profile which must be fitted by any successful model include: the magnitude of the velocity at Upstream B Camp (420 m a−1), the decrease in speed over the reach from 8 to 12 km, the rapid decrease and associated peak in strain rate in the chaotic zone, reverse curvature of the profile as the Unicorn is approached, and nearly zero speed in the Unicorn.
Basic models confirm the analytical results. In one numerical model, the properties of the deformable basal layer were adjusted to make the basal shear stress equal to the shear strength of the till as measured by Reference Kamb,Kamb (1991) at Upstream B (0.02 × 105 Pa) and Ε set equal to 1 everywhere (no enhancement). In this case, the calculated center-line speed is only about half that observed and the resulting velocity profile differs significantly from that observed. It was instead more rounded, like that shown by the dashed profile in Figure 2b, but of reduced magnitude. In another model, Ε was chosen to approximate that calculated from Equation (10) and shown in Figure 3a. Properties of the basal layer were adjusted to fix τb at Reference Kamb,Kamb’s (1991) value of shear strength. The resulting surface speed was too large and the shape of the profile again differed from that observed.
An attempt was made to find a distribution of τb (or, equivalently, A in the basal layer) which would reproduce the observed velocity without requiring a lateral variation in Ε within the ice. The result was similar to that found analytically: no physically reasonable basal shear stress with acceptable but laterally uniform ice rheology could be found which yields the shape and magnitude of the observed velocity.
Thus, we are led to the following conclusions: some, but not all, of the ice within the cross-section must be softened, and there must be a weak deformable layer over much of the bed. The strength of this basal layer must, on average, be somewhat greater than that observed locally at Upstream B.
An exhaustive search for the distribution of material properties which yield the best fit to the observed velocity profile has not been attempted, nor can it be without adequate knowledge of englacial temperatures, accurate ice depths and the incorporation of longitudinal-stress gradients. However, we present a model (labeled “model A”), which displays all of the critical features of the observed velocity distribution and gives us substantial insight into the role of the bed and of the margins in controlling the flow of Ice Stream B.
Enhancement factors in the ice are given by the dashed line in Figure 3b. They approximate those determined using Equation (10) and their magnitude is reasonable given both the ideas of Reference Jacka, and Budd,Jacka and Budd (1989) and the expected elevation of ice temperature in the margins as detailed below. The flow-law parameter in the weak basal layer is adjusted to match the surface velocity at Upstream B; it is taken to be constant across the bed in this model.
The resulting velocity profile is shown by the dashed curve in Figure 4. There is close agreement with the observations (large dots). The calculated strain rate also compares well with that observed (Fig. 4). While this model is non-unique and simplified, the close agreement between model and observations, along with our search through “parameter” space in which E(y, z) and τb (y) were varied, lead to some general conclusions which are robust.

Fig. 4. Final flow models versus observed speed. Enhancement factors for model A (stiff er ice at margins; solid line) and model B (bed frozen at margins; dashed) are shown at the top of the figure. Observed and modeled transverse strain rates (righthand axis) are also shown.
First, flow properties of the ice and basal layer (or, equivalently, Ε and Tb) must be fairly constant over the first 10 km of the profile outward from the center line. Secondly, there must be a weak layer at the bed in order to match the center-line velocity — no amount of softening at the margins can lead to this speed. Thirdly, there must be soft ice in the marginal zones. If there is no softening, then the resulting velocity profile is much more rounded than that observed and there is no localized peak in shear-strain rate. No distribution of basal-till properties (or τb ) can produce such a profile by itself. We have taken the bed properties to be constant across the ice stream. This leads to an increase in Ε from 1 to 5 in a region encompassing the transition from the relatively uncrevassed ice stream to the Dragon (8–12+km), followed by an increase to Ε = 12.5 in the chaotic zone and then a drop to Ε = 3 in the region of the Dragon-Unicorn boundary. A more continuous variation in Ε might be expected physically, although the abrupt steps in the observed strain rate may indicate a discrete nature to the variation.
In our model, the basal shear stress is about 0.06 × 105 Pa away from the margins. This is similar to that obtained from Equation (11) and it is 3–4 times greater than the shear strength of the basal till layer sampled by Engelhardt and others (1990). Because the center-line speed is so closely linked to τb near the center, this again implies that the entire bed cannot be blanketed by a layer as weak as the samples indicate. There must be a distribution of weak and stiff regions at the bed. For example, if we assume that till in the layer has a strength of 0.02 × 105 Pa and that this till is interspersed with “sticky spots” (following Reference Van der Veen, and Whillans,Van der Veen and Whillans, 1989), where the basal shear stress is, say, 0.5 × 105 Pa, then the area fraction of “sticky spots” would be about 0.08, weak till thus covering 92% of the bed. Realistically, there must be some more continuous distribution of basal drag, ranging from that of weak till to bedrock protuberances. On average, an increase in basal drag as the margin is approached might also satisfy this requirement for a stiffer basal layer.
The non-uniquess of the model described above is illustrated by the following result. The inflection point within the marginal zone of the velocity profile can be modeled equally as well by imposing a frozen, non-rapidly deforming bed beneath the outer 1 km of the marginal zone (where Τ = −1°C, Ε = 1), while Ε = 10 in the ice above this basal layer (shown by the dotted line in Figure 4, model B). This is in lieu of prescribing a column of stiffer ice (E = 5) within this outer sub-zone of the margin as was shown in Figure 3b and in model A. Such a stiff basal layer is compatible with the scenario in which the margin of the ice stream signifies a change from a stiff bed beneath the slow-moving ice sheet to a deformable water-saturated basal layer beneath the faster-moving ice stream.
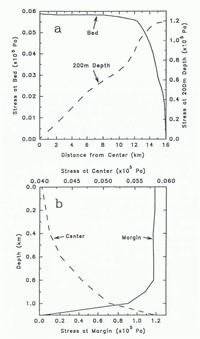
The effective shear stress (τ = (τ2 xy + τ2 xy )½) within the ice stream for model A is shown in Figure 5. Away from the bed τ ≈ τxy , while near the bed τxz becomes a significant component of τ. Numerical values of τxz indicate that the marginal shear stress approaches 1.2 × 105 Pa and the average basal shear stress is about 0.06 × 105 Pa. Integration of the basal shear stress across the total width of the ice stream gives 1.7 × 108N m−1, while vertical integration of the shear stress down the two margins (assumed symmetric) yields a total marginal drag force of 2.3 × 108 Ν per meter of length. Thus, the margins provide 58% and the bed supplies 42% of the total resistive drag required for equilibrium of the ice stream at Upstream B. Similar results apply for model B, except there is increased basal drag near the margins, as expected.

Fig. 5. (a) Smoothed horizontal profiles of τ, the effective shear stress (= (τxz 2 + τxy 2)½) across the ice stream at a depth of 200 m and along the bed. Lefthand axis corresponds to profile along bed (solid line), the righthand to the profile across at a depth of 200 m (dashed). (b) Smoothed vertical profiles of τ down the margin (lower axis, solid) and at position 0.5 km in from the center line (upper axis, dashed). These curves represent smoothed versions of the actual model results which are affected by discretization and interpolation noise.
Again, we note that this is only an illustrative example for one region of an active ice stream. Ice temperatures throughout the cross-section are not known, nor is the exact depth profile. Ambiguity in the surface slope also precludes a more exact treatment. If the surface slope quoted by Reference Alley,, Blankenship,, Bentley, and Rooney,Alley and others (1987; α= 2.7 × 10−3 versus our value of 1.3 × 10−3) is used, then the mean basal shear stress is about 0.17 × 105 kPa, that at the margins is 1.3 × 105kPa, and the resistive force of the margins drops to about one-third the total drag required to balance the increased driving force. Thus, while the ratio of basal to marginal drag may vary somewhat, the basic conclusion that the margins are important in the force balance at Upstream B remains.
If the marginal zones are not vertical but instead slope inward, mimicking typical “valley walls”, then the amount of softening in the marginal ice need not be as great. Similarly, since the actual ice-stream channel is not exactly rectangular in shape (Reference Shabtaie,, Whillans and BentleyShabtaie and Bentley, 1987), the enhancement factor in the basal layer need not be as large.
Flow at Downstream B Camp
Reference Bindschadler,, Stephenson,, MacAyeal, and ShabtaieBindschadler and others (1987) have measured a transverse-velocity profile at Downstream B approximately 240 km downstream of our profile. It also extends across the marginal shear zone. Downstream B is relatively close to the grounding zone and longitudinal stress gradients are important in the overall force balance (Reference Bindschadler,, Stephenson,, MacAyeal, and ShabtaieBindschadler and others, 1987). The ice stream is nearly 86 km wide at this location but only about 800 m thick. The southern boundary of Ice Stream B is the northern boundary of the slower-moving Ice Stream A and thus the geometry of marginal forces is not likely to be symmetric. The surface slope is much less at Downstream B, ranging from 0 to 0.4 × 10−3 depending on the length scale over which the gradient is determined (Reference Bindschadler,, Stephenson,, MacAyeal, and ShabtaieBindschadler and others, 1987). In the following, we use the large-scale average of 0.4 × 10−3 in our calculations, realizing that it represents an upper bound.
We have modeled the flow in a cross-section (again taken to be rectangular; 800 m deep and 43 km half-width). The important longitudinal stress gradients have been neglected — we are again interested in the relative importance of basal to marginal drag and we do not expect their ratio to depend too strongly on the longitudinal stress gradients just as the ratio does not depend strongly on surface slope. The temperature profile observed at Upstream B has been scaled to 800 m depth and the shear-zone width has been adjusted to fit that observed. No attempt was made to match accurately the observed velocity profile because of the relative sparseness of data and relatively large scatter in the published speeds within the critical marginal shear zone. The agreement between the observed (Reference Bindschadler,, Stephenson,, MacAyeal, and ShabtaieBindschadler and others, 1987) and modeled profiles at Downstream B, shown in Figure 6, is therefore not as close at that found at Upstream B but it still is quite good. The enhancement factors used for this model are shown along the top of Figure 6. They are similar to those found at Upstream B.

Fig. 6. Modeled and observed surface speed across a profile at Downstream B. Observed speed is taken from Reference Bindschadler,, Stephenson,, MacAyeal, and ShabtaieBindschadler and others (1987).
Marginal shear stresses are about 0.8 × 105 Pa, while the mean basal shear stress is about 0.014 × 105 Pa. Integration of the model shear stress over the width of the bed gives 1.1 × 108 Ν m−1, while integration down the two margins yields 1.2 × 108 Ν m−1. This indicates that at Downstream B the total marginal drag force is again nearly equal to the total basal drag. The strength of a deformable bed, if it exists at Downstream B, must be less than that observed at Upstream B, and less than that quoted by Reference Kamb,Kamb (1991). This makes sense, because the ice stream must be near flotation this close to the grounding zone. Pore-water pressure in any deformable layer must be high and “sticky spots” must be few and far between. The fit to the observed velocity profile could be improved if the basal drag increased outward to the margins, but then basal drag near the center line would be even less. If the smaller average value of local surface slope is pertinent to the flow here, then the importance of the margins will increase as will the importance of longitudinal stress gradients.
Viscous-Heat Dissipation in the Margins
The high shear-strain rates and shear stresses found in the margins will give rise to substantial viscous-heat dissipation in these narrow zones. This heating will be limited by the advection of cold ice moving into the ice stream from the sides. The amount of heating under steady-state conditions is readily estimated. Making the plausible assumptions that horizontal and longitudinal conduction and longitudinal advection are small, the governing two-dimensional advection–diffusion equation in the margins is given by

where Τ is the temperature, k is the thermal diffusivity,

where ΔT is the temperature change corresponding to the position change Δy. This result shows the inverse dependence of ΔT on the inflow velocity and the direct dependence on the width of the shear zone. The rate of increase of temperature is about 1.4 K per 100 years of residence time, or per 500 m at an average inflow rate of 5 m a−1, The total increase at a depth of 250 m or more is about 5.6 Κ for a 2 km wide margin. At lower inflow rates (ν ∼ 1–2 m a−1), which are probably more representative of the marginal part of the Upstream B profile, this increase could approach 15 K. Vertical advection and conduction will affect the temperature increase to depths of

Fig. 7. Temperature in the margin as a function of distance y from the outer edge for a constant transverse velocity v of 5 m a−1. The corresponding residence time t of the ice in the margin is also shown.
Ideally, Equation (14) should be integrated across the shear zone to take the variation in
This approximate analysis shows that substantial heating may occur within the margin under steady-state conditions. This heating will cause a softening of the ice found in the margins through the thermally activated flow-law parameter A. Increasing the temperature by 5–10 Κ could lead to an effective enhancement factor of 2–5, which would be imposed upon any enhancement arising due to preferred fabric development. The values of Ε shown in Figures 3b and 6 incorporate all possible sources of enhancement.
It is interesting to note that the margins of Jakobshavns Isbne, a fast-moving ice stream in Green-land, are a few degrees warmer than the center line (Reference Echelmeyer,, Harrison,, Clarke, and Benson.Echelmeyer and others, 1992). The in-flow velocity is large there but the viscous-heating term is also very large.
Conclusions
The magnitude and shape of transverse-velocity profiles have been used to investigate the roles of the shear margins and of the bed in the force balance of Ice Stream B. We find that the restraint supplied by marginal drag is equal to or somewhat greater than that of the integrated basal friction.
At the bed, there must be a weak, deformable layer and/or there must be greatly enhanced basal sliding. This result is constrained by the relatively large center-line speed and the small driving stress. While the basal shear stress at Upstream B must be low, it must, on average, be greater than the measured shear strength of basal till recovered by Engelhardt and others (1990). A distribution of saturated till and bedrock protrusions or other “sticky” spots across the bed could lead to the required basal shear stress.
Given unenhanced ice rheology, there is no physically reasonable distribution of basal shear stress which, by itself, can lead to the observed profiles of velocity. The curvature of the profiles requires a softening of ice in the marginal zones of both Upstream and Downstream B.
A good fit to the observed velocity is obtained by models with the following properties: a weak, deformable basal layer whose properties do not vary laterally, except possibly at the margin; constant, unenhanced ice rheology in the central part of the ice stream; soft ice within the marginal shear zones, with an enhancement factor equal to about 10 or 12 within the chaotic zone; and somewhat stiffer ice (E = 2–3) and/or increased basal drag in the slow-moving ice outside the ice stream.
These results depend critically on the detailed structure of the decrease in speed within the marginal zone. Of course, the distribution of Ε and basal shear stress is not unique. This is because there is a trade-off between basal friction and softening of the overlying ice. This trade-off is limited, however, because no amount of decrease in τb, can eliminate the requirement that there is soft ice at the margins.
These conclusions may possibly apply to other ice streams for which the driving stresses are small and the surface speeds are high. The enhanced flow properties of marginal ice were first suggested by Reference Hughes,Hughes (1975) to explain the general features of the Siple Coast ice streams. For an ice stream of fixed width, the lower the basal shear stress (i.e. the more deformable the bed or the greater the basal sliding), the greater the importance of the margins in the force balance. In the limiting case of a floating ice stream or ice shelf, the restraining force must come entirely from a combination of marginal drag and longitudinal stress gradients. For ice streams in which the driving stresses are larger, such as Jakobshavns Isbrae in Greenland, the basal shear stress need not be so small, because there is a high proportion of internal deformation within the ice (Reference Echelmeyer,Echelmeyer and others, 1991).
Strain heating in the margins may warm the ice significantly, as observed on Jakobshavns Isbrae, Greenland (Reference Echelmeyer,, Harrison,, Clarke, and Benson.Echelmeyer and others, 1992). The actual warming depends sensitively on the rate of convergence of cold ice into the ice stream from the ice sheet, because this determines the time that a parcel of ice is heated within the marginal zone. For values of the transverse velocity and viscous-heat dissipation at the margins typical of our final models, this heating amounts to about a 3–10 Κ increase in ice temperature. This temperature increase will lead to an additional softening of the marginal ice through the thermally activated flow-law parameter A. Therefore, strain heating in the margins may play an important role in ice-stream dynamics.
Acknowledgements
Financial support for this project was through the U.S. National Science Foundation grant DPP-8716604. We benefited from constructive comments made by R. Bindschadler, W. Budd, D. MacAyeal and C. Raymond. The manuscript was prepared by J. Ballew and P. Babcock, and the figures were drafted by J. DeMallie.
The accuracy of references in the text and in this list is the responsibility of the authors, to whom queries should be addressed.