No CrossRef data available.
Published online by Cambridge University Press: 05 June 2023
Least-squares analysis on the diffraction intensity values certified for NIST SRM676a and SRM1976c α-Al2O3 (corundum) have shown that the intensities of SRM1976c can be simulated by the March-Dollase preferred orientation model along the (001)-direction. Diffraction intensities of randomly oriented corundum crystallites have been calculated from electron density data obtained by conventional and density functional theory (DFT) calculations, on the assumption of independent and similar atomic displacements for Al and O atoms. The results of DFT calculations support that the strongest peak of randomly oriented α-Al2O3 crystalline powder should be 113-reflection, though the intensities simulated by DFT calculations are not closer to NIST SRM676a intensities than those expected for a fully ionized model 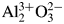 ${\rm Al}_2^{3 + } {\rm O}_3^{2-}$. Diffraction data of two types of relatively fine (nominally 2–3 μm and ca 0.3 μm) α-Al2O3 powder have been collected and processed by a deconvolutional treatment (DCT). Integrated peak intensities extracted from the DCT data by an individual peak profile fitting method also support that the 113-reflection is the strongest reflection of randomly oriented α-Al2O3 crystalline powder.
${\rm Al}_2^{3 + } {\rm O}_3^{2-}$. Diffraction data of two types of relatively fine (nominally 2–3 μm and ca 0.3 μm) α-Al2O3 powder have been collected and processed by a deconvolutional treatment (DCT). Integrated peak intensities extracted from the DCT data by an individual peak profile fitting method also support that the 113-reflection is the strongest reflection of randomly oriented α-Al2O3 crystalline powder.