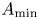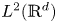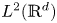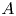General kernel estimates of Schrödinger-type operators with unbounded diffusion terms

Abstract

We first prove that the realization $A_{\mathrm {min}}$ of $A:={\operatorname {\mathrm {div}}}(Q\nabla )-V$ in $L^2({\mathbb {R}}^d)$ with unbounded coefficients generates a symmetric sub-Markovian and ultracontractive semigroup on $L^2({\mathbb {R}}^d)$ which coincides on $L^2({\mathbb {R}}^d)\cap C_b({\mathbb {R}}^d)$ with the minimal semigroup generated by a realization of $A$ on $C_b({\mathbb {R}}^d)$. Moreover, using time-dependent Lyapunov functions, we prove pointwise upper bounds for the heat kernel of $A$ and deduce some spectral properties of $A_{\min }$ in the case of polynomially and exponentially growing diffusion and potential coefficients.

1. Introduction

In this article, we are concerned with Schrödinger-type operators of the form

(1.1)\begin{equation} A\varphi ={\operatorname{\mathrm{div}}}(Q\nabla \varphi)-V\varphi , \quad \varphi \in C^2({\mathbb{R}}^d), \end{equation}

where the diffusion coefficients $Q$ and the potential $V$ are typically unbounded functions. Throughout, we make the following assumptions on $Q$ and $V$.

Hypothesis 1.1 We have $Q=(q_{ij})_{i,j=1, \ldots, d} \in C^{1+\zeta }({\mathbb {R}}^d; {\mathbb {R}}^{d\times d})$ and $0\leq V \in C^\zeta ({\mathbb {R}}^d)$ for some $\zeta \in (0,1)$. Moreover,

1. (a) the matrix $Q$ is symmetric and uniformly elliptic, i.e. there is $\eta >0$ such that

   \[ \sum_{i,j=1}^dq_{ij}(x)\xi_i\xi_j\ge \eta |\xi|^2 \quad \text{for all }x,\,\xi\in {\mathbb{R}}^d; \]

2. (b) there are $0\le Z\in C^{2}({\mathbb {R}}^d)$ and a constant $M\ge 0$ such that $\lim _{|x|\to \infty }Z(x)=\infty$, $AZ(x)\le M$ and $\eta \Delta Z(x)-V(x)Z(x)\leq M$ for all $x\in {\mathbb {R}}^d$.

In the last few years, second-order elliptic operators with polynomially growing coefficients and their associated semigroups have received a lot of attention, see for example [5–9, 13, 17, 18, 23–26] and the references therein.

Concerning the above operator $A$, it is well known (see [17, theorem 2.2.5] and [21]) that, assuming hypothesis 1.1, a suitable realization of $A$ generates a semigroup $T=(T(t))_{t\geq 0}$ on the space $C_b({\mathbb {R}}^d)$ that is given through an integral kernel; more precisely,

\[ T(t)f(x)=\int_{{\mathbb{R}}^d}p(t,x,y)f(y)\,{\rm d}y,\quad t>0,\,x\in {\mathbb{R}}^d,\,f\in C_b({\mathbb{R}}^d), \]

where the kernel $p$ is positive, $p(t,\cdot,\cdot )$ and $p(t,x,\cdot )$ are measurable for any $t>0,\,x\in {\mathbb {R}}^d$, and for a.e. fixed $y\in {\mathbb {R}}^d,\,p(\cdot,\cdot,y)\in C_{\mathrm {loc}}^{1+{\zeta }/{2},2+\zeta }((0,\infty )\times {\mathbb {R}}^d)$.

It is proved in § 2 that this semigroup can be extended to a symmetric sub-Markovian and ultracontractive $C_0$-semigroup on $L^2({\mathbb {R}}^d)$ and classical results show that this semigroup extrapolates to a positive $C_0$-semigroup of contractions in all $L^p({\mathbb {R}}^d)$, $p\in [1,\infty )$. Moreover, in the examples considered in § 4, these semigroups are compact and the spectra of their corresponding generators are independent of $p$.

Our second focus in this article lies in proving pointwise upper bounds for the kernel $p$. The case of (non-divergence type) Schrödinger operators

(1.2)\begin{equation} (1+|x|^m)\Delta - |x|^s \end{equation}

was discussed extensively in the literature and may serve as a model case. In this case, kernel estimates were obtained in [9] (see also [7] from which kernel estimates for the corresponding divergence form operators can be deduced) assuming that $m>2$ and $s>m-2$. The case $m\in [0,2)$ and $s>2$ was treated in [18]. Let us also mention that for $m=0$ and $s>0$ both upper and lower estimates were established in [22]. In the case of $V\equiv 0$, similar kernel estimates were obtained in [25].

As far as more general operators are concerned, in particular the case of bounded diffusion coefficients has received a lot of attention, see [1, 4, 16, 20]. These techniques were extended to include also unbounded diffusion coefficients in [14, 15].

In this article, we adopt the technique of time-dependent Lyapunov functions used in [1, 14, 15, 29] to our divergence form setting. This allows for a unified approach to obtain kernel bounds corresponding to [7, 22] in the divergence form setting. As a matter of fact, we can allow even more general conditions on $m$ and $s$, requiring merely that $m>0$ and $s>|m-2|$; moreover, we can drop the assumption $d\geq 3$ imposed in [7, 22].

As our approach does not depend on the specific structure of the coefficients, we can establish kernel estimates not only in the case where $Q(x) = (1+|x|^m)I$; an estimate of the quadratic form associated with $Q$ is enough, cf. equation (3.3). Moreover, we can even leave the setting of polynomially growing coefficients and consider coefficients of exponential growth; this includes the case $Q(x) = {\rm e}^{|x|^m}I$ and $V(x) = {\rm e}^{|x|^s}$ for $d\geq 1$ and $2\leq m < s$. Here, we would like to mention the paper [12] where pointwise estimates are obtained in the elliptic case for exponentially growing coefficients. We stress that these estimates can be improved by choosing a Lyapunov function as in § 4.2.

This article is organized as follows. In § 2, we adapt the techniques in [3] to prove that a realization of $A$ in $L^2({\mathbb {R}}^d)$ generates a symmetric sub-Markovian and ultracontractive semigroup $T_2(\cdot )$ on $L^2({\mathbb {R}}^d)$ which coincides with the semigroup $T(\cdot )$ on $L^2({\mathbb {R}}^d)\cap C_b({\mathbb {R}}^d)$. In § 3 we introduce time-dependent Lyapunov functions and establish sufficient conditions under which certain exponential functions are time-dependent Lyapunov functions in the case of polynomially and exponentially growing diffusion coefficients. In the subsequent § 4, we use these results to prove upper kernel estimates for our divergence form operator $A$. In the concluding § 4.3, we present some consequences of our result for the spectrum and the eigenfunctions of the operator $A_{\min }$ from § 2.

Notation

$B_r$ denotes the open ball of ${\mathbb {R}}^d$ of radius $r$ and centre $0$. For $0\leq a< b$, we write $Q(a,b)$ for $(a,b)\times {\mathbb {R}}^d$.

If $u: J\times {\mathbb {R}}^d\to {\mathbb {R}}$, where $J\subset [0,\infty )$ is an interval, we use the following notation:

\begin{align*} & \partial_t u =\frac{\partial u}{\partial t},\quad D_iu=\frac{\partial u}{\partial x_i},\quad D_{ij}u=D_iD_ju \\ & \nabla u=(D_1u, \ldots, D_du), \ {\operatorname{\mathrm{div}}}(F)=\sum_{i=1}^dD_iF_i \;\text{for }\;F:{\mathbb{R}}^d\to {\mathbb{R}}^d, \end{align*}

and

\[ |\nabla u|^2=\sum_{j=1}^d |D_j u|^2 , \quad |D^2u|^2=\sum_{i,j=1}^{d}|D_{ij} u|^2. \]

Let us define notations for function spaces. $C_b({\mathbb {R}}^d)$ is the space of bounded and continuous functions in ${\mathbb {R}}^d$. $\mathcal {D}({\mathbb {R}}^d)$ is the space of test functions. $C^\alpha ({\mathbb {R}}^d)$ denotes the space of all $\alpha$-Hölder continuous functions on ${\mathbb {R}}^d$. $C^{1,2}(Q(a,b))$ is the space of all functions $u$ such that $\partial _tu$, $D_iu$ and $D_{ij}u$ are continuous in $Q(a,b)$.

For $\Omega \subseteq {\mathbb {R}}^d,\,1\le k\le \infty,\,j\in \mathbb {N},\,W^{j}_{k}(\Omega )$ denotes the classical Sobolev space of all $L^k$-functions having weak derivatives in $L^k(\Omega )$ up to the order $j$. Its usual norm is denoted by $\|\cdot \|_{j,k}$ and by $\|\cdot \|_k$ when $j=0$. When $k=2$ we set $H^j(\Omega ):=W^{j}_{2}(\Omega )$ and $H_0^1(\Omega )$ denotes the closure of the set of test functions on $\Omega$ with respect to the norm of $H^1(\Omega )$.

For $0<\alpha \le 1$, we denote by $C^{1+\alpha /2 ,2+\alpha }(Q(a,b))$ the space of all functions $u$ such that $\partial _tu$, $D_iu$ and $D_{ij}u$ are $\alpha$-Hölder continuous in $Q(a,b)$ with respect to the parabolic distance $d((t,x),(s,y)):=|x-y|+|t-s|^{{1}/{2}}$. Local Hölder spaces are defined, as usual, requiring that the Hölder condition holds in every compact subset.

2. Generation of semigroups on $L^2({\mathbb {R}}^d)$

In this section, we show that a realization of $A$ in $L^2({\mathbb {R}}^d)$ generates a symmetric sub-Markovian and ultracontractive semigroup $T_2(\cdot )$ on $L^2({\mathbb {R}}^d)$ which coincides with the semigroup $T(\cdot )$ on $L^2({\mathbb {R}}^d)\cap C_b({\mathbb {R}}^d)$.

We recall that, given $\Omega \subset {\mathbb {R}}^d$, a $C_0$-semigroup $S(\cdot )$ on $L^2(\Omega )$ is called sub-Markovian if $S(\cdot )$ is a positive semigroup, i.e. $S(t)f\geq 0$ for all $t\geq 0$ and $f\geq 0$, and $L^\infty$-contractive, i.e.

\[ \|S(t)f\|_\infty \le \|f\|_\infty,\quad \forall t\ge 0,\,f\in L^2(\Omega)\cap L^\infty(\Omega). \]

It is called ultracontractive, if there is a constant $c>0$ such that

\[ \|S(t)\|_{{\mathcal{L}}(L^1, L^\infty)}\leq c t^{-({d}/{2})}, \]

for all $t>0$.

To establish ultracontractivity we use the following useful result, see [3, proposition 1.5], where we replace the $H^1$-norm with the $L^2$-norm of the gradient. The proof remains the same and is based on Nash's inequality:

\[ \|u\|^{1+{2}/{d}}_2 \leq c_d\| |\nabla u|\|_2\|u\|_1^{{2}/{d}} \]

for all $u\in L^1({\mathbb {R}}^d)\cap H^1({\mathbb {R}}^d)$.

Proposition 2.1 Let $S(\cdot )$ be a $C_0$-semigroup on $L^2({\mathbb {R}}^d)$ such that $S(\cdot )$ and $S^*(\cdot )$ are sub-Markovian. Assume that, for $\delta >0$, the generator $B$ of $S(\cdot )$ satisfies:

1. (a) $D(B)\subset H^1({\mathbb {R}}^d)$;

2. (b) $\langle -Bu,u\rangle \geq \delta \||\nabla u|\|_2^2 ,\ \forall u\in D(B)$;

3. (c) $\langle -B^*u,u\rangle \geq \delta \||\nabla u|\|_2^2 ,\ \forall u\in D(B^*)$.

Then, there is $c_\delta >0$ such that

\[ \left\Vert S(t)\right\Vert_{{\mathcal{L}}(L^1,L^\infty)}\leq c_\delta t^{-{ d}/2} ,\quad \forall t>0, \]

i.e. $S$ is ultracontractive.

We now take up our main line of study and consider the elliptic operator ${\mathcal {A}}$, defined by

\[ {\mathcal{A}} : H^1_{\rm{loc}}({\mathbb{R}}^d)\to\mathcal{D}({\mathbb{R}}^d)',\quad \mathcal{A}\varphi={\operatorname{\mathrm{div}}}(Q\nabla \varphi)-V\varphi. \]

Its maximal realization $A_{\max }$ in $L^2({\mathbb {R}}^d)$ is defined by

\begin{align*} D(A_{\max}) & = \{u\in L^2({\mathbb{R}}^d)\cap H^1_{\rm{loc}}({\mathbb{R}}^d), \,{\mathcal{A}} u\in L^2({\mathbb{R}}^d)\},\\ A_{\max} u & = {\mathcal{A}} u. \end{align*}

There is also a minimal realization $A_{\min }$ of ${\mathcal {A}}$. The minimal realization of ${\mathcal {A}}$ in $L^2({\mathbb {R}}^d)$ is the operator presented in the following theorem.

Theorem 2.2 There exists a unique operator $A_{\min }$ on $L^2({\mathbb {R}}^d)$ such that

1. (a) $A_{\min }\subset A_{\rm max};$

2. (b) $A_{\min }$ generates a positive, symmetric $C_0$-semigroup $T_2(\cdot )$ on $L^2({\mathbb {R}}^d);$

3. (c) if $B\subset A_{\rm max}$ generates a positive $C_0$-semigroup $S(\cdot )$, then $T_2(t)\leq S(t)$ for all $t\geq 0$.

The operator $A_{\min }$ and the semigroup $T_2(\cdot )$ have the following additional properties:

1. (d) $D(A_{\min })\subset H^1({\mathbb {R}}^d)$ and $-\langle A_{\min }u,u\rangle \geq \eta \| |\nabla u|\|_2^2$ for all $u\in D(A_{\min })$;

2. (e) $T_2(\cdot )$ is sub-Markovian and ultracontractive;

3. (f) the semigroup $T_2(\cdot )$ is consistent with $T(\cdot )$, i.e.

   \[ T_2(t)f=T(t)f,\quad t\ge 0,\,f\in L^2({\mathbb{R}}^d)\cap C_b({\mathbb{R}}^d). \]

Proof. We adapt the proof of theorem 1.1, proposition 1.2 and proposition 1.3 in [3] to our situation. For the reader's convenience we provide the details.

Step 1. We define approximate semigroups $T^{(\rho )}(\cdot )$ on $L^2(B_\rho )$. To that end, consider the bilinear form $\mathfrak {a}_\rho : H^1_0(B_\rho )\times H^1_0(B_\rho ) \to {\mathbb {C}}$, defined by

\[ \mathfrak{a}_\rho [u,v]= \int_{B_\rho} \sum_{i,j=1}^d q_{ij}D_i u D_j\bar v\,{\rm d}x + \int_{B_\rho} Vu\bar v\,{\rm d}x. \]

This form is obviously symmetric. Using that $Q$ and $V$ are bounded on $B_\rho$, an easy application of Hölder's inequality shows that $\mathfrak {a}_\rho$ is continuous. Moreover, the positivity of $V$, the uniform ellipticity of $Q$ and Poincaré's inequality yield coercivity of $\mathfrak {a}_\rho$. Now standard theory, see [27, proposition 1.51] implies that the associated operator $A_\rho$ generates a strongly continuous semigroup $T^{(\rho )}(\cdot )$ on $L^2(B_\rho )$. Making use of the Beurling–Deny criteria (see, e.g. corollary 4.3 and theorem 4.7 in [27]) we see that the semigroup $T^{(\rho )}(\cdot )$ is sub-Markovian.

Step 2. We prove that the semigroups $T^{(\rho )}(\cdot )$ are increasing to a semigroup $T_2(\cdot )$.

We now consider functions on $B_\rho$ to be defined on all of ${\mathbb {R}}^d$, by extending them with $0$ outside of $B_\rho$. Then, for any $0<\rho _1 <\rho _2$, the space $H^1_0(B_{\rho _1})$ is an ideal in $H^1_0(B_{\rho _2})$. Thus, by [30, corollary B.3] (see also [27, § 2.3]), we have $T^{(\rho _1)} (t) \leq T^{(\rho _2)}(t)$ for all $t\geq 0$. As every semigroup $T^{(\rho )}(\cdot )$ is sub-Markovian and thus contractive, we may define

\[ T_2(t)f := \sup_{n\in {\mathbb{N}}} T^{(n)}(t)f \]

for $0\leq f\in L^2({\mathbb {R}}^d)$ and then $T_2(t)f := T_2(t)f^+-T_2(t)f^-$ for general $f\in L^2({\mathbb {R}}^d)$. An easy computation shows that $T_2(\cdot )$ is a positive contraction semigroup. We prove that $T_2(\cdot )$ is strongly continuous. To that end, fix $0\leq f\in \mathcal {D}({\mathbb {R}}^d)$, and $\rho >0$ such that $\mathrm {supp} f\subset B_\rho$. Let $t_n\downarrow 0$. Then,

\begin{align*} & \limsup_{n\to\infty} \|T^{(\rho)}(t_n)f-T_2(t_n)f\|_2^2\\ & \quad= \limsup_{n\to\infty}\left[\|T^{(\rho)}(t_n)f\|_2^2 + \|T_2(t_n)f\|_2^2 - 2 \langle T^{(\rho)}(t_n)f, T_2(t_n)f\rangle_2\right]\\ & \quad\leq \limsup_{n\to\infty} \left[2\left\Vert f\right\Vert_2^2 -2 \langle T^{(\rho)}(t_n)f, T^{(\rho)}(t_n)f\rangle_2\right]= 2\|f\|_2^2 - 2\|f\|_2^2=0. \end{align*}

Here, in the third line we have used the contractivity of $T^{(\rho )}(\cdot )$ and $T_2(\cdot )$, that $0\leq T^{(\rho )}(t_n)f \leq T_2(t_n)f$ and the strong continuity of $T^{(\rho )}(\cdot )$. Thus, $T_2(t_n)f\to f$ as $n\to \infty$. Splitting $f\in \mathcal {D}({\mathbb {R}}^d)$ into positive and negative parts, we see that this is true for general $f$. In view of the contractivity of $T_2(\cdot )$, a standard $3\varepsilon$ argument yields strong continuity of $T_2(\cdot )$.

As the form $\mathfrak {a}_\rho$ is symmetric, the semigroup $T^{(\rho )}(\cdot )$ consists of symmetric operators and thus, so does the limit semigroup $T_2(\cdot )$. Likewise, sub-Markovianity of $T_2(\cdot )$ is inherited by that of $T^{(\rho )}(\cdot )$.

Step 3. We identify the generator $A_{\min }$ of $T_2(\cdot )$.

Let us first note that $R(\lambda, A_\rho )f \to R(\lambda, A_{\min })f$ as $\rho \to \infty$ for every $\lambda >0$; this follows from the construction of $T_2(\cdot )$ by taking Laplace transforms and using dominated convergence. Now fix a sequence $\rho _n\uparrow \infty$ and $f\in L^2({\mathbb {R}}^d)$. We put $u=R(1, A_{\min })f$ and $u_n = R(1, A_{\rho _n})f$. Then $u_n\to u$ and $A_{\rho _n}u_n = u_n - f \to u-f = A_{\min }u$ in $L^2({\mathbb {R}}^d)$ as $n\to \infty$. By coercivity of the form $\mathfrak {a}_{\rho _n}$, we have

(2.1)\begin{equation} \eta \limsup_{n\to\infty} \int |\nabla u_n|^2\,{\rm d}x \leq \limsup_{n\to\infty} \mathfrak{a}_{\rho_n}[u_n, u_n] = \limsup_{n\to\infty} - \langle A_{\rho_n} u_n, u_n\rangle ={-} \langle A_{\min}u, u\rangle. \end{equation}

It follows that $(u_n)_{n\in \mathbb {N}}$ is a bounded sequence in $H^1({\mathbb {R}}^d)$ and thus, by reflexivity of $H^1({\mathbb {R}}^d)$, $u_n\to u$ weakly in $H^1({\mathbb {R}}^d)$. Thus, $D(A_{\min })\subset H^1({\mathbb {R}}^d)$. Moreover, using the weak lower semicontinuity of norms, we see that (2.1) implies $-\langle A_{\min } u, u\rangle \geq \eta \||\nabla u|\|_2^2$.

Now fix $v\in \mathcal {D}({\mathbb {R}}^d)$. As $u_n$ converges to $u$ weakly in $H^1({\mathbb {R}}^d)$, we see that

\[ \langle {\mathcal{A}} u, v\rangle = \lim_{n\to\infty} \langle {\mathcal{A}} u_n, v\rangle = \lim_{n\to\infty} \langle A_{\rho_n}u_n, v\rangle = \langle A_{\min}u , v\rangle, \]

proving $A_{\min }\subset A_{\max }$. At this point, properties (a), (d) and (by definition of $A_{\min }$) (b) are proved.

Step 4. We establish the minimality property.

To this end, let $B\subset A_{\max }$ be such that $B$ generates a positive $C_0$-semigroup $S(\cdot )$ on $L^2({\mathbb {R}}^d)$. To prove $T_2(t)\leq S(t)$ for all $t\geq 0$ it suffices to prove $R(\lambda, A_{\min }) \leq R(\lambda, B)$ for all $\lambda >0$; this is an easy consequence of Euler's formula.

To see this, let us fix again a sequence $\rho _n \uparrow \infty$, $\lambda >0$ and $0\leq f\in L^2({\mathbb {R}}^d)$. We put $u= R(\lambda, A_{\min })f$, $v= R(\lambda, B)f$ and $u_n = R(\lambda, A_{\rho _n})f$. As $B \subset A_{\max }$, we have $v\in H^1_{\mathrm {loc}}({\mathbb {R}}^d)$ and

(2.2)\begin{equation} \lambda\int_{B_{\rho_n}}(u_n-v) w\,{\rm d}x+ \int_{B_{\rho_n}} \sum_{i,j=1}^d q_{ij}D_j(u_n-v)D_iw\,{\rm d}x + \int_{B_{\rho_n}} V(u_n-v) w\,{\rm d}x = 0 \end{equation}

for all $w\in H^1_0(B_{\rho _n})$. As the semigroup $S(\cdot )$ is positive, $v \geq 0$ and thus $(u_n -v)^+ \leq u_n$. As $H^1_0(B_{\rho _n})$ is an ideal in $H^1_{\mathrm {loc}}({\mathbb {R}}^d)$, $(u_n-v)^+\in H^1_0(B_{\rho _n})$. We may thus insert $w=(u_n-v)^+$ into (2.2). Taking the uniform ellipticity of $Q$ into account, this yields

\[ \lambda \int_{B_{\rho_n}} \left( (u_n -v)^+\right)^2\,{\rm d}x + \eta \int_{B_{\rho_n}} |\nabla (u_n - v)^+|^2\,{\rm d}x + \int_{B_{\rho_n}} V\left((u_n-v)^+\right)^2\,{\rm d}x \leq 0. \]

As $V\geq 0$, it follows that $(u_n - v)^+=0$ and thus $u_n \leq v$. Upon $n\to \infty$ we obtain $u\leq v$ and thus $R(\lambda, A_{\min })f \leq R(\lambda, B)f$ for $0\leq f\in L^2({\mathbb {R}}^d)$.

Step 5. We establish properties (e) and (f).

As we have already mentioned above, the semigroup $T_2(\cdot )$ is sub-Markovian and consists of symmetric operators. The latter implies that the generator $A_{\min }$ of $T_2(\cdot )$ is self-adjoint. In view of property (d), the ultracontractivity of the semigroup follows immediately from proposition 2.1.

As for consistency we note that the semigroup $T(\cdot )$ on $C_b({\mathbb {R}}^d)$ is obtained by a similar approximation procedure as for $T_2(\cdot )$, see [17, theorem 2.2.1]. Indeed, for all $\rho >0$ the operator $A$, endowed with the domain

\[ \{ u\in W^2_p(B_\rho) \text{ for all } 1\leq p<\infty \colon Au\in C_b(B_\rho), u|_{\partial B_\rho}=0\} \]

generates a semigroup $S^{(\rho )}(\cdot )$ on $C_b(B_\rho )$, that gives the unique solution of the following Cauchy–Dirichlet problem associated with ${\mathcal {A}}$ on $C_b(B_{\rho })$:

\[ \begin{cases} \partial_t u(t,x)= Au_\rho(t,x), & t>0,\, x\in B_\rho,\\ u(t,x)=0, & t>0,\, x\in \partial B_\rho,\\ u(0,x)=f(x), & x\in\overline{B}_\rho. \end{cases} \]

Given $f\in C_b({\mathbb {R}}^d)$, we may consider $S^{(\rho )}(t)f:= S^{(\rho )}(t)f|_{B_\rho }$ as a function on all of ${\mathbb {R}}^d$, extending with $0$ outside of $B_\rho$. It follows from the maximum principle that for $0\leq f \in C_b({\mathbb {R}}^d)$, the function $S^{(\rho )}(t)f$ is increasing in $\rho$. We may thus define

\[ T(t)f=\lim_{\rho\to\infty}S^{(\rho)}(t)f, \]

for all $0\leq f\in C_b({\mathbb {R}}^d)$ and then $T(t)f=T(t)f^+ -T(t)f^-$ for general $f\in C_b({\mathbb {R}}^d)$. As the semigroup $S^{(\rho )}(\cdot )$ is consistent with the semigroup $T^{(\rho )}(\cdot )$ on $L^2(B_{\rho })$ considered above, consistency of $T_2(\cdot )$ and $T(\cdot )$ follows.

Remark 2.3

1. (a) As the minimal realization $A_{\min }$ of the elliptic operator ${\mathcal {A}}$ generates a symmetric sub-Markovian $C_0$-semigroup $T_2(\cdot )$ on $L^2({\mathbb {R}}^d)$, it follows from [10, theorem 1.4.1], that $T_2(\cdot )$ extends to a positive $C_0$-semigroup of contractions $T_p(\cdot )$ on $L^p({\mathbb {R}}^d)$ for all $p\in [1,\infty )$. Moreover, these semigroups are consistent, i.e.

   \[ T_p(t)f=T_q(t)f,\quad \text{for all }f\in L^p({\mathbb{R}}^d)\cap L^q({\mathbb{R}}^d),\,t\ge 0. \]

2. (b) Since, by theorem 2.2, $T_2(\cdot )$ is ultracontractive, and $T_2(\cdot )$ coincides with $T(\cdot )$ on $L^2({\mathbb {R}}^d)\cap C_b({\mathbb {R}}^d)$, it follows that $T_2(\cdot )$ is given through an integral kernel which coincides with the kernel $p$ of the semigroup $T(\cdot )$.

3. Time-dependent Lyapunov functions for parabolic operators with polynomially and exponentially diffusion coefficients

As in [1, 15, 29], we use time-dependent Lyapunov functions to prove pointwise bounds of the kernel $p$. In this section, we give conditions under which certain exponentials are time-dependent Lyapunov functions for $L:=\partial _t+A$ also in the case of polynomially and exponentially growing diffusion coefficients.

We now introduce, as in [15, 29], time-dependent Lyapunov functions for $L$.

Definition 3.1 Let the function $Z$ be as in hypothesis 1.1(b). We say that a function $W:[0,T]\times {\mathbb {R}}^d\to [0,\infty )$ is a time-dependent Lyapunov function for $L$ if $W\in C^{1,2}((0,T)\times {\mathbb {R}}^d)\cap C([0,T]\times {\mathbb {R}}^d)$ such that $\lim _{|x|\to \infty }W(t,x)=\infty$ uniformly for $t$ in compact subsets of $(0,T],\,W\le Z$ and there is $0\le h\in L^1(0,T)$ such that

(3.1)\begin{equation} LW(t,x)\le h(t)W(t,x) \end{equation}

and

(3.2)\begin{equation} \partial_t W(t,x)+\eta\Delta W(t,x)-V(x)W(t,x)\leq h(t)W(t,x) \end{equation}

for all $(t,x)\in (0,T)\times {\mathbb {R}}^d$. To emphasize the dependence on $Z$ and $h$, we also say that $W$ is a time-dependent Lyapunov function for $L$ with respect to $Z$ and $h$.

The following result shows that time-dependent Lyapunov functions are integrable with respect to the measure $p(t,x,y)\,{\rm d}y$ for any $(t,x)\in (0,T)\times {\mathbb {R}}^d$.

Proposition 3.2 If $W$ is a time-dependent Lyapunov function for $L$ with respect to $h$, then for $\xi _W (t,x):=\int _{{\mathbb {R}}^d}p(t,x,y)W(t,y)\,{\rm d}y$, we have

\[ \xi_W (t,x)\le {\rm e}^{\int_0^th(s)\,{\rm d}s}W(0,x),\quad \forall (t,x)\in [0,T]\times {\mathbb{R}}^d. \]

Proof. The proof is similar to the one given in [29, proposition 2.3]. One has to approximate the coefficients $Q,\,F$ and $V$ by bounded functions, as in [16, lemma 2.3] and [19, theorem 6.2.10]. For more details, we refer to [28, propositions 1.5.2, 1.6.3]. We note that, as in [29], condition (3.2) is not needed for this proposition.

In what follows, we will often set $T=1$ for ease of notation. The following results give conditions under which certain exponentials are time-dependent Lyapunov functions. Here, $x\mapsto |x|_*^\beta$ denotes any $C^2$-function which coincides with $x\mapsto |x|^\beta$ for $|x|\ge 1$.

Proposition 3.3 Assume that there is a constant $c_q>0$ such that

(3.3)\begin{equation} \sum_{i,j=1}^dq_{ij}(x)\xi_i\xi_j\le c_q(1+|x|^m)|\xi|^2 \end{equation}

holds for all $\xi,\,x\in {\mathbb {R}}^d$ and some $m> 0$. Consider the function $W(t,x)={\rm e}^{\varepsilon t^\alpha |x|_*^\beta }$ for $(t,x)\in [0,1]\times {\mathbb {R}}^d$ with $\beta >(2-m)\vee 0,\,\varepsilon >0$ and $\alpha >{\beta }/{(\beta +m-2)}$. If

(3.4)\begin{equation} \limsup_{|x|\to \infty}|x|^{1-\beta -m}\left(G\cdot \frac{x}{|x|}-\frac{V}{\varepsilon \beta |x|^{\beta -1}}\right)<{-}\Lambda \end{equation}

is satisfied for $\Lambda >c_q\varepsilon \beta$ and

(3.5)\begin{equation} \lim_{\left\vert x\right\vert\to\infty} V(x) \left\vert x\right\vert^{2-2\beta-m}>c \end{equation}

holds true for some $c>0$, then $W$ is a time-dependent Lyapunov function for $L$ with respect to $Z(x)={\rm e}^{\varepsilon |x|_*^\beta }$ and $h(t)=C_1t^{\alpha -\gamma (2\beta +m-2)}$ for some $\gamma >{1}/{(\beta +m-2)}$ and some constant $C_1>0$. Here, $G_j:=\sum _{i=1}^dD_iq_{ij}$. Moreover,

\[ \xi_W (t,x)\le {\rm e}^{\int_0^1 h(s)\,{\rm d}s}=:C_2 \]

for all $(t,x)\in [0,1]\times {\mathbb {R}}^d$.

Proof. It is easy to see that $W\in C^{1,2}((0,1)\times {\mathbb {R}}^d)\cap C([0,1]\times {\mathbb {R}}^d)$, $\lim _{|x|\to \infty } W(t,x)=\infty$ uniformly for $t$ in compact subsets of $(0,1]$ and $W\le Z$. It remains to show that there is $0\le h\in L^1(0,1)$ such that (3.1) and (3.2) hold true.

In the following computations, we assume that $\left \vert x \right \vert \ge 1$ so that $\left \vert x \right \vert _*^s=\left \vert x \right \vert ^s$ for $s\ge 0$. Otherwise, if $\left \vert x \right \vert \le 1$, since $x\mapsto |x|_*^\beta$ is a $C^2$-function, one deduces easily that $W(t,x)^{-1}LW(t,x)\le Ct^{\alpha -1}+\widetilde {C}$ and $W(t,x)^{-1}[\partial _t W(t,x)+\eta \Delta W(t,x)-V(x)W(t,x)]\le Ct^{\alpha -1}+\widetilde {C}$ for any $(t,x)\in (0,1]\times B_1$ and some constants $C,\,\widetilde {C}>0$. Thus, by possibly choosing a larger constant $C_1$ we obtain that $LW(t,x)|\le h(t)$ and $\partial _t W(t,x)+\eta \Delta W(t,x)-V(x)W(t,x)\le h(t)$ for all $(t,x)\in (0,1]\times B_1$, with $\gamma >{1}/{(\beta +m-2)}$, where $h(t)=C_1t^{\alpha -\gamma (2\beta +m-2)}$.

Let $t\in (0,1)$ and $\left \vert x \right \vert \ge 1$. By straightforward computations we have

\begin{align*} D_jW(t,x)& =\varepsilon\beta t^\alpha \left\vert x\right\vert^{\beta-2} x_j W(t,x),\\ D_i(q_{ij}D_j W)(t,x)& = \varepsilon\beta t^\alpha \left\vert x\right\vert^{\beta-2} D_iq_{ij}(x)x_j W(t,x)\\ & \quad + \varepsilon\beta (\beta-2) t^\alpha \left\vert x\right\vert^{\beta-4} q_{ij}(x) x_i x_j W(t,x) \\ & \quad+ \varepsilon\beta t^\alpha \left\vert x\right\vert^{\beta-2} q_{ij}(x) \delta_{ij} W(t,x)\\ & \quad + \varepsilon^2\beta^2 t^{2\alpha} \left\vert x\right\vert^{2\beta-4} q_{ij}(x) x_i x_j W(t,x). \end{align*}

Then, we obtain

(3.6)\begin{align} LW(t,x)& = \partial_t W(t,x) +AW(t,x)\nonumber\\ & = \varepsilon\alpha t^{\alpha-1} \left\vert x\right\vert^{\beta} W(t,x) + \varepsilon\beta t^\alpha \left\vert x\right\vert^{\beta-2} W(t,x) \sum_{i,j=1}^d D_iq_{ij}(x)x_j \nonumber\\ & \quad+ \varepsilon\beta (\beta-2) t^\alpha \left\vert x\right\vert^{\beta-4} W(t,x) \sum_{i,j=1}^d q_{ij}(x) x_i x_j\nonumber\\ & \quad + \varepsilon\beta t^\alpha \left\vert x\right\vert^{\beta-2}W(t,x) \sum_{i,j=1}^d q_{ij}(x) \delta_{ij} \nonumber\\ & \quad+ \varepsilon^2\beta^2 t^{2\alpha} \left\vert x\right\vert^{2\beta-4}W(t,x) \sum_{i,j=1}^d q_{ij}(x) x_i x_j -V(x)W(t,x). \end{align}

We recall that $G_j:=\sum _{i=1}^dD_iq_{ij}$ and we use the polynomially growth of diffusion coefficients (3.3). We have

\begin{align*} LW(t,x)& \le \varepsilon\alpha t^{\alpha-1} \left\vert x\right\vert^{\beta} W(t,x) + \varepsilon\beta t^\alpha \left\vert x\right\vert^{\beta-2} W(t,x) G(x)\cdot x \\ & \quad+ c_q \varepsilon\beta (\beta-2)^+ t^\alpha \left\vert x\right\vert^{\beta-4} (1+\left\vert x\right\vert^m)\left\vert x\right\vert^2 W(t,x) \\ & \quad+ d c_q \varepsilon\beta t^\alpha \left\vert x\right\vert^{\beta-2} (1+\left\vert x\right\vert^m) W(t,x)\\ & \quad+ c_q \varepsilon^2\beta^2 t^{2\alpha} \left\vert x\right\vert^{2\beta-4} (1+\left\vert x\right\vert^m)\left\vert x\right\vert^2W(t,x) -V(x)W(t,x). \end{align*}

Since $(1+\left \vert x \right \vert ^m)\leq 2 \left \vert x \right \vert ^m$ and $t^\alpha \leq 1$, we arrange the terms as follows:

(3.7)\begin{align} LW(t,x)& \le \varepsilon\beta t^\alpha\left\vert x\right\vert^{2\beta+m-2} W(t,x)\left[ \frac{\alpha}{\beta t} \left\vert x\right\vert^{2-\beta-m}+2c_q ((\beta-2)^+{+}d) \left\vert x\right\vert^{-\beta} \right.\nonumber\\ & \quad\left. + c_q \varepsilon\beta t^\alpha +c_q \varepsilon\beta t^\alpha \left\vert x\right\vert^{{-}m} + \left\vert x\right\vert^{1-\beta-m} \left( G\cdot \frac{x}{\left\vert x\right\vert} - \frac{V}{\varepsilon\beta\left\vert x\right\vert^{\beta-1}}\right)\right]. \end{align}

Let $\gamma >{1}/{(\beta +m-2)}$. We distinguish two cases.

Case 1: $\displaystyle \left \vert x \right \vert >{1}/{t^\gamma }$.

Since $t^\alpha \le 1$ and using (3.7), we get

(3.8)\begin{align} LW(t,x)& \le \varepsilon\beta t^\alpha\left\vert x\right\vert^{2\beta+m-2} W(t,x) \left[ \frac{\alpha}{\beta} \left\vert x\right\vert^{{1}/{\gamma}+2-\beta-m}+2c_q ((\beta-2)^+{+}d) \left\vert x\right\vert^{-\beta} \right. \nonumber\\ & \quad\left. + c_q \varepsilon\beta +c_q \varepsilon\beta \left\vert x\right\vert^{{-}m} + \left\vert x\right\vert^{1-\beta-m} \left( G\cdot \frac{x}{\left\vert x\right\vert} - \frac{V}{\varepsilon\beta\left\vert x\right\vert^{\beta-1}}\right)\right]. \end{align}

We claim that, if we assume further that $\left \vert x \right \vert$ is large enough, then

\[ LW(t,x)\leq 0, \]

for all $t\in (0,1)$. To see this, let $\left \vert x \right \vert >K$ for some $K>1$. Combining (3.4) with (3.8) yields

(3.9)\begin{align} LW(t,x)& \le \varepsilon\beta t^\alpha\left\vert x\right\vert^{2\beta+m-2} W(t,x) \left[ \frac{\alpha}{\beta} \left\vert x\right\vert^{{1}/{\gamma}+2-\beta-m}+2c_q ((\beta-2)^+{+}d) \left\vert x\right\vert^{-\beta} \right. \nonumber\\ & \quad\left. + c_q \varepsilon\beta +c_q \varepsilon\beta \left\vert x\right\vert^{{-}m} -\Lambda \right]. \end{align}

Considering that $\gamma >{1}/{(\beta +m-2)}$, $\beta >0$ and $m> 0$, we infer that

\begin{align*} & \frac{\alpha}{\beta} \left\vert x\right\vert^{{1}/{\gamma}+2-\beta-m}+2c_q ((\beta-2)^+{+}d) \left\vert x\right\vert^{-\beta} + c_q \varepsilon\beta +c_q \varepsilon\beta \left\vert x\right\vert^{{-}m} -\Lambda\\ & \quad\le \left(\frac{\alpha}{\beta} +2c_q ((\beta-2)^+{+}d) + c_q \varepsilon\beta\right) K^{{-}l}+c_q \varepsilon\beta -\Lambda, \end{align*}

where $l:=\min ({-1}/{\gamma }-2+\beta +m, \beta, m)>0$. Since $\Lambda >c_q\varepsilon \beta$, choosing

\[ K\ge \left(\frac{{\alpha}/{\beta} +2c_q ((\beta-2)^+{+}d) + c_q \varepsilon\beta}{\Lambda-c_q \varepsilon\beta}\right)^{{1}/{l}}, \]

it follows that the quantity within square brackets on the right-hand side of (3.9) is negative. Thus $LW(t,x)\leq 0$ for $\left \vert x \right \vert >{1}/{t^\gamma }$, $\left \vert x \right \vert >K$ and for all $t\in (0,1)$.

For the remaining values of $x$, $\left \vert x \right \vert \leq K$, since $W\in C([0,1]\times {\mathbb {R}}^d)$, by (3.8), we have that $LW(t,x)\leq C$ for a certain constant $C>0$ and all $x\in \{y\in {\mathbb {R}}^d: 1\le |y|\le K\}$. Hence, $LW(t,x)\leq C$ for all $t\in (0,1]$ and ${1}/{t^\gamma }<\left \vert x \right \vert \le K$. Anyway, we conclude that

\[ LW(t,x)\leq CW(t,x), \]

for all $t\in (0,1]$ and $\left \vert x \right \vert >{1}/{t^\gamma }$.

Case 2: $\displaystyle \left \vert x \right \vert \leq {1}/{t^\gamma }$.

We assume that $\left \vert x \right \vert$ is large enough. Otherwise, by (3.7), we obtain $W(t,x)^{-1}LW(t,x)\le Ct^{\alpha -1}+\widetilde {C}$ and hence $LW(t,x)\leq h(t)$ for all $(t,x)\in (0,1]\times \{y\in {\mathbb {R}}^d: 1\le |y|\le K\}$ and any large constant $K$.

We combine (3.4) and (3.7) to deduce that

\begin{align*} LW(t,x)& \leq \left[\varepsilon\alpha t^{\alpha-1-\gamma\beta}+2c_q \varepsilon\beta((\beta-2)^+{+}d)t^{\alpha-\gamma(\beta+m-2)}+c_q \varepsilon^2 \beta^2 t^{2\alpha-\gamma(2\beta+m-2)}\right.\\ & \quad\left.+c_q \varepsilon^2 \beta^2 t^{2\alpha-\gamma(2\beta-2)}-\varepsilon\beta t^\alpha \left\vert x\right\vert^{2\beta+m-2}\Lambda\right]W(t,x). \end{align*}

We drop the term involving $\Lambda$ because it is negative. Moreover, since $\gamma >1/(\beta +m-2)$, we note that the leading term is $t^{\alpha -\gamma (2\beta +m-2)}$. Hence,

\[ LW(t,x)\leq h(t)W(t,x). \]

For the function $h(t)$ to be in the space $L^1((0,1))$, we set $\alpha >{\beta }/{(\beta +m-2)}$. In this way, choosing $\gamma <{(\alpha +1)}/{(2\beta +m-2)}$ so that $\alpha -\gamma (2\beta +m-2)>-1$, $h(t)$ is integrable in the interval $(0,1)$.

Summing up, considering a possibly larger constant $C_1$, we proved (3.1) for all $t\in (0,1)$ and $x\in {\mathbb {R}}^d$.

We now verify (3.2). An easy computation shows that

\[ \Delta W(t,x) = \varepsilon\beta (\beta+d-2) t^\alpha \left\vert x\right\vert^{\beta-2} W(t,x) +\varepsilon^2\beta^2 t^{2\alpha} \left\vert x\right\vert^{2\beta-2} W(t,x). \]

Thus, we get

(3.10)\begin{align} \partial_t W(t,x)+\eta\Delta W(t,x)-V(x)W(t,x) & = \varepsilon\alpha t^{\alpha-1} \left\vert x\right\vert^{\beta} W(t,x) \nonumber\\ & \quad+ \eta \varepsilon\beta (\beta+d-2) t^\alpha \left\vert x\right\vert^{\beta-2} W(t,x)\nonumber\\ & \quad+ \eta \varepsilon^2\beta^2 t^{2\alpha} \left\vert x\right\vert^{2\beta-2} W(t,x) \!-\!V(x)W(t,x). \end{align}

As in the first part of the proof, we let $\gamma >{1}/{(\beta +m-2)}$ and we distinguish two cases.

Case 1: $\left \vert x \right \vert >{1}/{t^\gamma }$.

Since $t^\alpha \leq 1$, by (3.10) we obtain

\begin{align*} & \partial_t W(t,x)+\eta\Delta W(t,x)-V(x)W(t,x)\\ & \quad\leq \varepsilon\beta t^\alpha\left\vert x\right\vert^{2\beta+m-2} W(t,x) \left[ \frac{\alpha}{\beta} \left\vert x\right\vert^{{1}/{\gamma}+2-\beta-m} +\eta(\beta+d-2) \left\vert x\right\vert^{-\beta-m}\right.\\ & \qquad\left.+ \eta \varepsilon\beta \left\vert x\right\vert^{{-}m} - \frac{1}{\varepsilon\beta}V(x)\left\vert x\right\vert^{2-2\beta-m}\right]. \end{align*}

If $\left \vert x \right \vert$ large enough, by (3.5) we have

\begin{align*} & \partial_t W(t,x)+\eta\Delta W(t,x)-V(x)W(t,x)\\ & \quad\leq \varepsilon\beta t^\alpha\left\vert x\right\vert^{2\beta+m-2} W(t,x) \left[ \frac{\alpha}{\beta} \left\vert x\right\vert^{{1}/{\gamma}+2-\beta-m}\right.\\ & \quad\left. +\eta(\beta+d-2) \left\vert x\right\vert^{-\beta-m} + \eta \varepsilon\beta \left\vert x\right\vert^{{-}m} - \frac{c}{\varepsilon \beta} \right]. \end{align*}

Arguing as in (3.9), we find that $\partial _t W(t,x)+\eta \Delta W(t,x)-V(x)W(t,x)$ is negative for $\left \vert x \right \vert$ large, whereas it is bounded for the remaining values of $x$. Therefore, we deduce that

\[ \partial_t W(t,x)+\eta\Delta W(t,x)-V(x)W(t,x)\leq C W(t,x), \]

for all $t\in (0,1)$ and $\left \vert x \right \vert >{1}/{t^\gamma }$.

Case 2: $\left \vert x \right \vert \leq {1}/{t^\gamma }$.

Since $V\geq 0$, (3.10) leads to

\begin{align*} \partial_t W(t,x)+\eta\Delta W(t,x)-V(x)W(t,x) & \leq \left[\varepsilon\alpha t^{\alpha-1-\gamma\beta} +\eta \varepsilon\beta((\beta -2)^+{+}d)t^{\alpha-\gamma(\beta-2)}\right.\\ & \quad\left.+\eta\varepsilon^2 \beta^2 t^{2\alpha-\gamma(2\beta-2)}\right]W(t,x). \end{align*}

We can control the right-hand side of the previous inequality with the function $h(t)W(t,x)$, obtaining that

\[ \partial_t W(t,x)+\eta\Delta W(t,x)-V(x)W(t,x)\leq h(t)W(t,x), \]

where the constant $C_1$ in the function $h$ has to be suitably adjusted. In both cases (3.2) holds true. We conclude that $W$ is a time-dependent Lyapunov function for $L$.

Moreover, by proposition 3.2, we have

\[ \xi_W (t,x)\le {\rm e}^{\int_0^t h(s)\,{\rm d}s} W(0,x) \le {\rm e}^{\int_0^1 h(s)\,{\rm d}s}=:C_2 \]

for all $(t,x)\in [0,1]\times {\mathbb {R}}^d$.

Remark 3.4 One can easily see that the same conclusion as in proposition 3.3 remains valid if we replace the operator $A$ with the more general operator $A_F:=A+F\cdot \nabla$ with $F\in C^\zeta ({\mathbb {R}}^d, {\mathbb {R}}^d)$ for some $\zeta \in (0,1)$, and condition (3.4) with

\[ \limsup_{|x|\to \infty}|x|^{1-\beta -m}\left((G+F)\cdot \frac{x}{|x|}-\frac{V}{\varepsilon \beta |x|^{\beta -1}}\right)<{-}\Lambda . \]

This generalizes proposition 2.3 in [1].

Proposition 3.5 Assume that there is a constant $c_e>0$ such that

(3.11)\begin{equation} \sum_{i,j=1}^dq_{ij}(x)\xi_i\xi_j\le c_e\,{\rm e}^{|x|^m}|\xi|^2 \end{equation}

holds for all $\xi,\,x\in {\mathbb {R}}^d$ and some $m\ge 2$. Consider the function

\[ W(t,x)=\exp\left(\varepsilon t^\alpha \int_0^{\left\vert x\right\vert_*}\,{\rm e}^{{\tau^\beta}/{2}}\,{\rm d}\tau\right) \]

for $(t,x)\in [0,1]\times {\mathbb {R}}^d$ with ${m}/{2}+1\le \beta \leq m,\,\varepsilon >0$ and $\alpha >{(2\beta +m-2)}/{2m}$. If

(3.12)\begin{equation} \limsup_{|x|\to \infty}|x|^{1-\beta-m}{\rm e}^{-({\left\vert x\right\vert^\beta}/{2})-\left\vert x\right\vert^m}\left(G\cdot \frac{x}{|x|}-\frac{V}{\varepsilon\,{\rm e}^{{\left\vert x\right\vert^\beta}/{2}}}\right)<{-}\Lambda \end{equation}

is satisfied for $\Lambda >0$ and

(3.13)\begin{equation} \lim_{\left\vert x\right\vert\to\infty} V(x) \left\vert x\right\vert^{1-\beta-m}\,{\rm e}^{-\left\vert x\right\vert^\beta-\left\vert x\right\vert^m}>c \end{equation}

holds true for some $c>0$, then $W$ is a time-dependent Lyapunov function for $L$ with respect to $Z(x)=\exp (\varepsilon \int _0^{\left \vert x \right \vert _*}\,{\rm e}^{{\tau ^\beta }/{2}}\,{\rm d}\tau )$ and $h(t)=C_3 t^{\alpha -\gamma \left (\beta +({3}/{2})m-1\right )}$ for some $\gamma >{1}/{m}$ and some constant $C_3>0$. Here, $G_j:=\sum _{i=1}^dD_iq_{ij}$. Moreover,

\[ \xi_W (t,x)\le {\rm e}^{\int_0^1 h(s)\,{\rm d}s}=:C_4 \]

for all $(t,x)\in [0,1]\times {\mathbb {R}}^d$.

Proof. As in the proof of proposition 3.3, one can assume from now on that $\left \vert x \right \vert \geq 1$ so that $\left \vert x \right \vert _*^s=\left \vert x \right \vert ^s$ for $s\ge 0$. The estimates can be extended to ${\mathbb {R}}^d$ by possibly choosing larger constants.

Let $t\in (0,1)$ and $\left \vert x \right \vert \ge 1$. By direct computations we have

\begin{align*} D_jW(t,x)& =\varepsilon t^\alpha \frac{x_j}{\left\vert x\right\vert}\,{\rm e}^{{\left\vert x\right\vert^\beta}/{2}} W(t,x),\\ D_i(q_{ij}D_j W)(t,x) & = \varepsilon t^\alpha \frac{1}{\left\vert x\right\vert}\,{\rm e}^{{\left\vert x\right\vert^\beta}/{2}} D_iq_{ij}(x)x_j W(t,x)\\ & \quad + \frac{1}{2}\varepsilon\beta t^\alpha \left\vert x\right\vert^{\beta-3}\,{\rm e}^{{\left\vert x\right\vert^\beta}/{2}} q_{ij}(x) x_i x_j W(t,x) \\ & \quad+ \varepsilon t^\alpha \frac{1}{\left\vert x\right\vert}\,{\rm e}^{{\left\vert x\right\vert^\beta}/{2}} q_{ij}(x) \delta_{ij} W(t,x)\\ & \quad - \varepsilon t^{\alpha} \frac{1}{\left\vert x\right\vert^3}\,{\rm e}^{{\left\vert x\right\vert^\beta}/{2}} q_{ij}(x) x_i x_j W(t,x)\\ & \quad+ \varepsilon^2 t^{2\alpha}\frac{1}{\left\vert x\right\vert^2}\,{\rm e}^{\left\vert x\right\vert^\beta} q_{ij}(x) x_i x_j W(t,x). \end{align*}

Hence, we deduce that

\begin{align*} LW(t,x)& = \partial_t W(t,x) +AW(t,x)\\ & = \varepsilon\alpha t^{\alpha-1} W(t,x) \int_0^{\left\vert x\right\vert} \,{\rm e}^{{\tau^\beta}/{2}}\,{\rm d}\tau + \varepsilon t^\alpha \frac{1}{\left\vert x\right\vert}\,{\rm e}^{{\left\vert x\right\vert^\beta}/{2}} W(t,x) \sum_{i,j=1}^d D_iq_{ij}(x)x_j \\ & \quad+ \frac{1}{2}\varepsilon\beta t^\alpha \left\vert x\right\vert^{\beta-3}\,{\rm e}^{{\left\vert x\right\vert^\beta}/{2}} W(t,x) \sum_{i,j=1}^d q_{ij}(x) x_i x_j\\ & \quad + \varepsilon t^\alpha \frac{1}{\left\vert x\right\vert}\,{\rm e}^{{\left\vert x\right\vert^\beta}/{2}} W(t,x) \sum_{i,j=1}^d q_{ij}(x) \delta_{ij} \\ & \quad- \varepsilon t^{\alpha} \frac{1}{\left\vert x\right\vert^3}\,{\rm e}^{{\left\vert x\right\vert^\beta}/{2}} W(t,x) \sum_{i,j=1}^d q_{ij}(x) x_i x_j\\ & \quad + \varepsilon^2 t^{2\alpha}\frac{1}{\left\vert x\right\vert^2}\,{\rm e}^{\left\vert x\right\vert^\beta} W(t,x) \sum_{i,j=1}^d q_{ij}(x) x_i x_j \\ & \quad-V(x)W(t,x). \end{align*}

First of all, we drop the negative term involving $\varepsilon$ on the right-hand side of the previous equality. Second, we use the exponentially growth of the diffusion coefficients (3.11) to obtain that

(3.14)\begin{align} LW(t,x)& \leq \varepsilon\alpha t^{\alpha-1} W(t,x) \int_0^{\left\vert x\right\vert}\,{\rm e}^{{\tau^\beta}/{2}}\,{\rm d}\tau + \varepsilon t^\alpha \frac{1}{\left\vert x\right\vert}\,{\rm e}^{{\left\vert x\right\vert^\beta}/{2}} W(t,x) G(x)\cdot x \nonumber\\ & \quad+ \frac{1}{2}c_e\varepsilon\beta t^\alpha \left\vert x\right\vert^{\beta-1}\,{\rm e}^{{\left\vert x\right\vert^\beta}/{2}+\left\vert x\right\vert^m} W(t,x) + d c_e\varepsilon t^\alpha \frac{1}{\left\vert x\right\vert}\,{\rm e}^{{\left\vert x\right\vert^\beta}/{2}+\left\vert x\right\vert^m} W(t,x) \nonumber\\ & \quad+ c_e\varepsilon^2 t^{2\alpha}\,{\rm e}^{\left\vert x\right\vert^\beta+\left\vert x\right\vert^m} W(t,x) -V(x)W(t,x). \end{align}

Since $t^\alpha \leq 1$, we can write the previous inequality as follows:

(3.15)\begin{align} LW(t,x)& \leq \varepsilon t^\alpha\left\vert x\right\vert^{\beta+m-1}\,{\rm e}^{\left\vert x\right\vert^\beta+\left\vert x\right\vert^m} W(t,x) \nonumber\\ & \quad\times \left[ \frac{\alpha}{t} \left\vert x\right\vert^{1-\beta-m}\,{\rm e}^{-\left\vert x\right\vert^\beta-\left\vert x\right\vert^m} \int_0^{\left\vert x\right\vert}\,{\rm e}^{{\tau^\beta}/{2}}\,{\rm d}\tau +\frac{1}{2}c_e \beta \left\vert x\right\vert^{{-}m}\,{\rm e}^{-{\left\vert x\right\vert^\beta}/{2}}\right.\nonumber\\ & \quad+ d c_e \left\vert x\right\vert^{-\beta-m}\,{\rm e}^{-{\left\vert x\right\vert^\beta}/{2}} +c_e\varepsilon t^\alpha \left\vert x\right\vert^{1-\beta-m}\nonumber\\ & \quad\left.+ \left\vert x\right\vert^{1-\beta-m}\,{\rm e}^{-{\left\vert x\right\vert^\beta}/{2}-\left\vert x\right\vert^m}\left( G\cdot \frac{x}{\left\vert x\right\vert} - \frac{V}{\varepsilon\,{\rm e}^{{\left\vert x\right\vert^\beta}/{2}}}\right)\right]. \end{align}

Let $\gamma >{1}/{m}$. We now distinguish two cases.

Case 1: ${\rm e}^{\left \vert x \right \vert ^m}\geq {1}/{t^{\gamma m}}$.

First, we observe that

\[ \int_0^{\left\vert x\right\vert}\,{\rm e}^{{\tau^\beta}/{2}}\,{\rm d}\tau\leq \left\vert x\right\vert\,{\rm e}^{{\left\vert x\right\vert^\beta}/{2}}. \]

Then, since $t^\alpha \leq 1$ and ${\rm e}^{-{\left \vert x \right \vert ^\beta }/{2}}\leq 1$, by (3.15) we get

\begin{align*} LW(t,x)& \leq \varepsilon t^\alpha\left\vert x\right\vert^{\beta+m-1}\,{\rm e}^{\left\vert x\right\vert^\beta+\left\vert x\right\vert^m} W(t,x) \left[\alpha \left\vert x\right\vert^{2-\beta-m}\,{\rm e}^{\left( {1}/{\gamma m}-1\right)\left\vert x\right\vert^m} \right.\\ & \quad +\frac{1}{2}c_e \beta \left\vert x\right\vert^{{-}m} + d c_e \left\vert x\right\vert^{-\beta-m} +c_e\varepsilon \left\vert x\right\vert^{1-\beta-m}\\ & \quad\left.+ \left\vert x\right\vert^{1-\beta-m}\,{\rm e}^{-{\left\vert x\right\vert^\beta}/{2}-\left\vert x\right\vert^m}\left( G\cdot \frac{x}{\left\vert x\right\vert} - \frac{V}{\varepsilon\,{\rm e}^{{\left\vert x\right\vert^\beta}/{2}}}\right)\right]. \end{align*}

Moreover, ${\rm e}^{( {1}/{\gamma m}-1)\left \vert x \right \vert ^m}\leq 1$ because $\gamma >{1}/{m}$. Thus, we derive that

\begin{align*} LW(t,x)& \leq \varepsilon t^\alpha\left\vert x\right\vert^{\beta+m-1}\,{\rm e}^{\left\vert x\right\vert^\beta+\left\vert x\right\vert^m} W(t,x) \left[ \alpha \left\vert x\right\vert^{2-\beta-m} +\frac{1}{2}c_e \beta \left\vert x\right\vert^{{-}m}\right.\\ & \quad+ d c_e \left\vert x\right\vert^{-\beta-m} +c_e\varepsilon \left\vert x\right\vert^{1-\beta-m}\\ & \quad\left.+ \left\vert x\right\vert^{1-\beta-m}\,{\rm e}^{-{\left\vert x\right\vert^\beta}/{2}-\left\vert x\right\vert^m}\left( G\cdot \frac{x}{\left\vert x\right\vert} - \frac{V}{\varepsilon\,{\rm e}^{{\left\vert x\right\vert^\beta}/{2}}}\right)\right]. \end{align*}

If $\left \vert x \right \vert$ is large enough, say $\left \vert x \right \vert >K$ for some $K>1$, we apply (3.12) to deduce that

\begin{align*} LW(t,x)& \leq \varepsilon t^\alpha\left\vert x\right\vert^{\beta+m-1}\,{\rm e}^{\left\vert x\right\vert^\beta+\left\vert x\right\vert^m} W(t,x) \left[ \alpha \left\vert x\right\vert^{2-\beta-m} +\frac{1}{2}c_e \beta \left\vert x\right\vert^{{-}m}\right.\\ & \quad\left. + d c_e \left\vert x\right\vert^{-\beta-m} +c_e\varepsilon \left\vert x\right\vert^{1-\beta-m}-\Lambda\vphantom{\left[ \alpha \left\vert x\right\vert^{2-\beta-m} +\frac{1}{2}c_e \beta \left\vert x\right\vert^{{-}m}\right.}\right]. \end{align*}

We now show that, for a suitable choice of $K$, the quantity within square brackets is negative. Since $\beta \ge {m}/{2}+1$ and $m\ge 2$, we have $\beta \ge 2$ and hence

\begin{align*} & \alpha \left\vert x\right\vert^{2-\beta-m} +\frac{1}{2}c_e \beta \left\vert x\right\vert^{{-}m}+ d c_e \left\vert x\right\vert^{-\beta-m} +c_e\varepsilon \left\vert x\right\vert^{1-\beta-m}-\Lambda\\ & \quad\leq \left(\alpha +\frac{1}{2}c_e \beta + d c_e +c_e\varepsilon \right) K^{{-}m}-\Lambda. \end{align*}

As a result, by taking

\[ K\geq \bigg(\frac{\alpha +({1}/{2})c_e \beta + d c_e +c_e\varepsilon }{\Lambda}\bigg)^{{1}/{m}}, \]

we finally get $LW(t,x)\leq 0$. For the remaining values of $x$, we argue as in the proof of proposition 3.3 to obtain that $LW$ is bounded by a constant. In both cases we have

\[ LW(t,x)\leq CW(t,x), \]

for all $t\in (0,1)$, ${\rm e}^{\left \vert x \right \vert ^m}\geq {1}/{t^{\gamma m}}$ and for some constant $C>0$.

Case 2: ${\rm e}^{\left \vert x \right \vert ^m}<{1}/{t^{\gamma m}}$.

Notice that $\left \vert x \right \vert < t^{-\gamma }$ and, since $\beta \leq m$, we have

\[ {\rm e}^{\left\vert x\right\vert^\beta}<\frac{1}{t^{\gamma m}} \,\text{for }\left\vert x\right\vert \ge 1. \]

Then, if $\left \vert x \right \vert$ is large enough, using $\beta >1$, and combining (3.12) and (3.15), we obtain that

\begin{align*} LW(t,x)& \leq \left[ \varepsilon \alpha t^{\alpha-1-\gamma \left({m}/{2}+1\right)}+\frac{1}{2}c_e \varepsilon \beta t^{\alpha-\gamma \left( \beta+({3}/{2})m-1\right)}+dc_e\varepsilon t^{\alpha-({3}/{2})\gamma m}\right.\\ & \quad\left. +c_e \varepsilon^2 t^{2\alpha-2\gamma m}-\Lambda \varepsilon t^\alpha \left\vert x\right\vert^{\beta+m-1} \,{\rm e}^{\left\vert x\right\vert^\beta+\left\vert x\right\vert^m}\vphantom{\left[ \varepsilon \alpha t^{\alpha-1-\gamma \left({m}/{2}+1\right)}+\frac{1}{2}c_e \varepsilon \beta t^{\alpha-\gamma \left( \beta+({3}/{2})m-1\right)}\right.}\right]W(t,x). \end{align*}

Dropping the last negative term, we find

\begin{align*} LW(t,x)& \leq \left[ \varepsilon \alpha t^{\alpha-1-\gamma \left({m}/{2}+1\right)}+\frac{1}{2}c_e \varepsilon \beta t^{\alpha-\gamma \left( \beta+({3}/{2})m-1\right)}\right.\\ & \quad \left. +dc_e\varepsilon t^{\alpha-({3}/{2})\gamma m}+c_e \varepsilon^2 t^{2\alpha-2\gamma m}\vphantom{\left[ \varepsilon \alpha t^{\alpha-1-\gamma \left({m}/{2}+1\right)}+\frac{1}{2}c_e \varepsilon \beta t^{\alpha-\gamma \left( \beta+({3}/{2})m-1\right)}\right.}\right]W(t,x). \end{align*}

Since $\gamma >{1}/{m}$ and $\beta \ge {m}/{2}+1$, the leading term is $t^{\alpha -\gamma \left (\beta +({3}/{2})m-1\right )}$. Therefore, we get

\[ LW(t,x)\leq C t^{\alpha-\gamma \left( \beta+({3}/{2})m-1\right)}W(t,x), \]

for all $t\in (0,1)$, ${\rm e}^{\left \vert x \right \vert ^m}<{1}/{t^{\gamma m}}$ and for some constant $C>0$.

To sum up, there exists a constant $C_3>0$ such that

\[ LW(t,x)\leq h(t) W(t,x), \]

for all $t\in (0,1)$ and $x\in {\mathbb {R}}^d$, where $h(t)=C_3 t^{\alpha -\gamma \left (\beta +({3}/{2})m-1\right )}$.

Moreover, we choose $\gamma <{(\alpha +1)}/{(\beta +({3}/{2})m-1)}$, which is possible since $\alpha >{(2\beta +m-2)}/{2m}$, so that $\alpha -\gamma \left (\beta +({3}/{2})m-1\right )>-1$ and $h\in L^1((0,1))$. We conclude that condition (3.1) is satisfied.

To show (3.2) we compute

\begin{align*} \Delta W(t,x) & = \frac{1}{2} \varepsilon\beta t^\alpha \left\vert x\right\vert^{\beta-1}\,{\rm e}^{{\left\vert x\right\vert^\beta}/{2}}W(t,x) +{\rm d}\varepsilon t^\alpha \frac{1}{\left\vert x\right\vert}\,{\rm e}^{{\left\vert x\right\vert^\beta}/{2}} W(t,x) \\ & \quad -\varepsilon t^\alpha \frac{1}{\left\vert x\right\vert}\,{\rm e}^{{\left\vert x\right\vert^\beta}/{2}} W(t,x)+\varepsilon^2 t^{2\alpha}\,{\rm e}^{\left\vert x\right\vert^\beta} W(t,x). \end{align*}

Hence,

(3.16)\begin{align} & \partial_t W(t,x)+\eta \Delta W(t,x)-V(x)W(t,x)\nonumber\\ & \quad = \varepsilon\alpha t^{\alpha-1}W(t,x) \int_0^{\left\vert x\right\vert}\,{\rm e}^{{\tau^\beta}/{2}}\,{\rm d}\tau + \frac{1}{2} \eta\varepsilon\beta t^\alpha \left\vert x\right\vert^{\beta-1}\,{\rm e}^{{\left\vert x\right\vert^\beta}/{2}}W(t,x) \nonumber\\ & \qquad+{\rm d}\eta\varepsilon t^\alpha \frac{1}{\left\vert x\right\vert}\,{\rm e}^{{\left\vert x\right\vert^\beta}/{2}} W(t,x) -\eta\varepsilon t^\alpha \frac{1}{\left\vert x\right\vert}\,{\rm e}^{{\left\vert x\right\vert^\beta}/{2}} W(t,x)\nonumber\\ & \qquad+\eta\varepsilon^2 t^{2\alpha}\,{\rm e}^{\left\vert x\right\vert^\beta} W(t,x)-V(x)W(t,x)\nonumber\\ & \quad\leq \varepsilon\alpha t^{\alpha-1}W(t,x) \int_0^{\left\vert x\right\vert}\,{\rm e}^{{\tau^\beta}/{2}}\,{\rm d}\tau + \frac{1}{2} \eta\varepsilon\beta t^\alpha \left\vert x\right\vert^{\beta-1}\,{\rm e}^{{\left\vert x\right\vert^\beta}/{2}}W(t,x) \nonumber\\ & \qquad+{\rm d}\eta\varepsilon t^\alpha \frac{1}{\left\vert x\right\vert}\,{\rm e}^{{\left\vert x\right\vert^\beta}/{2}} W(t,x) +\eta\varepsilon^2 t^{2\alpha}\,{\rm e}^{\left\vert x\right\vert^\beta} W(t,x)\nonumber\\ & \qquad-V(x)W(t,x). \end{align}

We use the same strategy as above. We let $\gamma >{1}/{m}$ and we consider two cases.

Case 1: ${\rm e}^{\left \vert x \right \vert ^m}\geq {1}/{t^{\gamma m}}$.

By (3.16) we obtain

\begin{align*} & \partial_t W(t,x)+\eta \Delta W(t,x)-V(x)W(t,x)\\ & \quad \leq \varepsilon t^\alpha \left\vert x\right\vert^{\beta+m-1}\,{\rm e}^{\left\vert x\right\vert^\beta+\left\vert x\right\vert^m}W(t,x)\left[\alpha \left\vert x\right\vert^{2-\beta-m}\,{\rm e}^{\left({1}/{\gamma m}-1\right) \left\vert x\right\vert^m}\right.\\ & \qquad +\frac{1}{2}\eta\beta\left\vert x\right\vert^{{-}m}+{\rm d}\eta \left\vert x\right\vert^{-\beta-m}+\eta\varepsilon \left\vert x\right\vert^{1-\beta-m}\\ & \qquad\left.-\frac{1}{\varepsilon} V(x) \left\vert x\right\vert^{1-\beta-m}\,{\rm e}^{-\left\vert x\right\vert^\beta-\left\vert x\right\vert^m}\right]. \end{align*}

Using (3.13) and the fact that $\gamma >{1}/{m}$, we get

\begin{align*} & \partial_t W(t,x)+\eta \Delta W(t,x)-V(x)W(t,x)\\ & \quad\leq \varepsilon t^\alpha \left\vert x\right\vert^{\beta+m-1}\,{\rm e}^{\left\vert x\right\vert^\beta+\left\vert x\right\vert^m}W(t,x)\left[\alpha \left\vert x\right\vert^{2-\beta-m}\right. \\ & \qquad \left.+\frac{1}{2}\eta\beta\left\vert x\right\vert^{{-}m}+{\rm d}\eta \left\vert x\right\vert^{-\beta-m}+\eta\varepsilon \left\vert x\right\vert^{1-\beta-m}-\frac{c}{\varepsilon}\right]. \end{align*}

If $\left \vert x \right \vert$ is large enough, the quantity within square brackets is negative. Otherwise, we can control it with a constant. In both cases, we deduce that

\[ \partial_t W(t,x)+\eta \Delta W(t,x)-V(x)W(t,x)\leq C, \]

for all $t\in (0,1)$, ${\rm e}^{\left \vert x \right \vert ^m}\geq {1}/{t^{\gamma m}}$ and for some constant $C>0$.

Case 2: ${\rm e}^{\left \vert x \right \vert ^m}<{1}/{t^{\gamma m}}$.

Since $\beta \leq m$ and $V\geq 0$, (3.16) yields

\begin{align*} \partial_t W(t,x)+\eta \Delta W(t,x)-V(x)W(t,x) & \leq \left[\varepsilon\alpha t^{\alpha-1-\gamma \left({m}/{2}+1\right)} +\frac{1}{2}\eta\varepsilon\beta t^{\alpha-\gamma \left( \beta+{m}/{2}-1\right)}\right.\\ & \quad\left.+{\rm d}\eta \varepsilon t^{\alpha-\gamma ({m}/{2})}+\eta\varepsilon^2 t^{2\alpha-\gamma m}\right]W(t,x)\\ & \leq C t^{\alpha-\gamma \left( \beta+({3}/{2})m-1\right)} W(t,x), \end{align*}

for some constant $C$. Therefore, by possibly choosing a larger $C_3$, we get (3.2). Then, $W$ is a time-dependent Lyapunov function for $L$. The last assertion follows from proposition 3.2.

4. Kernel estimates and spectral properties for general Schrödinger-type operators

In this section, we establish pointwise upper bounds for the kernel $p$ and study some spectral properties of $A_{\min }$ with either polynomial or exponential coefficients.

To obtain pointwise kernel estimates one needs the following assumptions.

Hypothesis 4.1 Fix $T>0,\,x\in {\mathbb {R}}^d$ and $0< a_0< a< b< b_0< T$. Let us consider two time-dependent Lyapunov functions $W_1,\,W_2$ with $W_1\le W_2$ and a weight function $1\le w\in C^{1,2}((0,T)\times {\mathbb {R}}^d)$ such that

1. (a) the functions $w^{-2}\partial _t w$ and $w^{-2}\nabla w$ are bounded on $Q(a_0,b_0)$;

2. (b) there exist $k>d+2$ and constants $c_1,\ldots,c_5$, possibly depending on the interval $(a_0,b_0)$, with

   \begin{align*} & w\le c_1w^{{(k-2)}/{k}}W_1^{{2}/{k}},\,|Q\nabla w|\le c_2w^{{(k-1)}/{k}}W_1^{{1}/{k}},\,|{\operatorname{\mathrm{div}}}(Q\nabla w)|\\ & \le c_3w^{{(k-2)}/{k}}W_1^{{2}/{k}}, |\partial_t w|\le c_4w^{{(k-2)}/{k}}W_1^{{2}/{k}},\,V^{{1}/{2}}\le c_5w^{-({1}/{k})}W_2^{{1}/{k}} \end{align*}
   on $[a_0,b_0]\times {\mathbb {R}}^d$.

The following result can be deduced as in [14, theorem 12.4] and [15, theorem 4.2].

Theorem 4.2 Assume hypotheses 1.1, 4.1, $k>d+2$ and $q_{ij},\,D_kq_{ij}$ are bounded on ${\mathbb {R}}^d$. Then there is a constant $C>0$ depending only on $d,\,k$ and $\eta$ such that

(4.1)\begin{align} w(t,y)p(t,x,y) & \le C\left[c_1^{{k}/{2}}\sup_{s\in (a_0,b_0)}\xi_{W_1}(s,x)+\left( c_2^k+\frac{c_1^{{k}/{2}}}{(b_0-b)^{{k}/{2}}}+c_3^{{k}/{2}} +c_4^{{k}/{2}}\right)\right.\nonumber\\ & \quad \left. \int_{a_0}^{b_0}\xi_{W_1}(s,x)\,{\rm d}s +c_5^k\int_{a_0}^{b_0}\xi_{W_2}(s,x)\,{\rm d}s\right], \end{align}

for all $(t,y)\in (a,b)\times {\mathbb {R}}^d$ and any fixed $x\in {\mathbb {R}}^d$.

Notice that the assumption of bounded diffusion coefficients was crucial to apply [15, theorem 3.7]. The fact that the constant $C$ does not depend on $\left \Vert Q \right \Vert _{\infty }$ will allow us to extend this result to the general case.

By an approximation argument one can extend the above result to the case of unbounded diffusion coefficients. The proof of the following result is similar to the one in [14, theorem 12.6]. The only difference is that here we are concerned with autonomous problems. This is the reason why we assume (4.3) for a fixed $t_0\in (0,T)$, similar as in [14, hypothesis 12.5].

Theorem 4.3 In addition to hypotheses 1.1, 4.1 and $k>d+2$, we assume that $|\nabla W_1|,|\nabla W_2|$ are bounded on $[0,T]\times B_R$ for all $R>0$ and that $\nabla Z(x)= f(x)W_1(t_0,x)$ for some nonnegative function $f$, some $t_0 \in (0, T)$ and all $x\in {\mathbb {R}}^d$. Moreover, we suppose that

1. (a) on $[a_0,b_0]\times {\mathbb {R}}^d$ we have

   (4.2)\begin{gather} |\Delta w|\le c_6w^{{(k-2)}/{k}}W_1^{{2}/{k}}; \end{gather}

2. (b) there is $t_0\in (0,T)$ such that

   (4.3)\begin{gather} |Q\nabla W_1(t_0, \cdot)|\le c_7W_1(t_0, \cdot)w^{-({1}/{k})}W_2^{{1}/{k}}; \end{gather}

3. (c) there are $c_0>0$ and $\sigma \in (0,1)$ such that

   (4.4)\begin{gather} W_2\leq c_0 Z^{1-\sigma} \end{gather}
   on $(0,T)\times {\mathbb {R}}^d$.

Then there is a constant $C>0$ depending only on $d,\,k$ and $\eta$ such that

(4.5)\begin{align} w(t,y)p(t,x,y) & \le C\left[c_1^{{k}/{2}}\sup_{s\in (a_0,b_0)}\xi_{W_1}(s,x)\right.\nonumber\\ & \quad\left. +\left( c_2^k+\frac{c_1^{{k}/{2}}}{(b_0-b)^{{k}/{2}}}+c_3^{{k}/{2}} +c_4^{{k}/{2}}+c_6^{{k}/{2}}\right)\int_{a_0}^{b_0}\xi_{W_1}(s,x)\,{\rm d}s\right.\nonumber\\ & \quad \left. +\left(c_5^k+c_2^{{k}/{2}}c_7^{{k}/{2}}\right)\int_{a_0}^{b_0}\xi_{W_2}(s,x)\,{\rm d}s\right], \end{align}

for all $(t,y)\in (a, b)\times {\mathbb {R}}^d$ and fixed $x\in {\mathbb {R}}^d$.

In the following subsections, we apply theorem 4.3 to obtain explicit kernel estimates in the case of polynomially or exponentially coefficients. Moreover, we prove in these cases the compactness of the semigroups and deduce estimates of the eigenfunctions.

4.1 Polynomially growing coefficients

Here, we apply the results of the previous sections to the case of operators with polynomial diffusion coefficients and potential terms.

Consider $Q(x)=(1+|x|^m_*)I$ and $V(x)=|x|^s$ with $s>|m-2|$ and $m>0$. To apply theorem 4.3 we set

\[ w(t,x)={\rm e}^{\varepsilon t^\alpha |x|_*^\beta} \text{ and } W_j(t,x)={\rm e}^{\varepsilon_j t^\alpha |x|_*^\beta}, \]

where $j=1,2$, $\beta ={(s-m+2)}/{2},\,0<\varepsilon <\varepsilon _1<\varepsilon _2<{1}/{\beta }$ and $\alpha >{\beta }/{(\beta +m-2)}$.

Theorem 4.4 Let $p$ be the integral kernel associated with the operator $A$ with $Q(x)=(1+|x|^m_*)I$ and $V(x)=|x|^s$, where $s>|m-2|$ and $m> 0$. Then

\[ p(t,x,y)\le C t^{1-(({\alpha(2m\vee s)})/({s-m+2})k}\,{\rm e}^{-({\varepsilon}/{2}) t^\alpha |x|_*^{({s-m+2})/{2}}}\,{\rm e}^{-({\varepsilon}/{2}) t^\alpha |y|_*^{{(s-m+2)}/{2}}} \]

for $k>d+2$ and any $t\in (0,1),\,x,y\in {\mathbb {R}}^d$.

Proof. Step 1. We apply proposition 3.3 to verify that the operator $A$ satisfies hypothesis 1.1 with

\[ Z(x)={\rm e}^{\varepsilon_2 |x|_*^\beta} \]

and that $W_1$ and $W_2$ are time-dependent Lyapunov functions for $L=\partial _t+A$. Clearly, (3.3) holds true with $c_q=1$. Since $s>|m-2|$, we have $\beta >(2-m)\vee 0$. It remains to check (3.4) and (3.5). Let $|x|\geq 1$ and set $G_j=\sum _{i=1}^d D_i q_{ij} = m |x|^{m-2}x_j.$ Then

\begin{align*} |x|^{1-\beta-m} \left(G\cdot \frac{x}{|x|}-\frac{V}{\varepsilon_j \beta |x|^{\beta -1}}\right) & = |x|^{1-\beta-m} \left(m |x|^{m-1}- \frac{|x|^s}{\varepsilon_j \beta |x|^{\beta -1}}\right)\\ & = m|x|^{-\beta} - \frac{1}{\varepsilon_j \beta}. \end{align*}

If $|x|$ is large enough, for example $|x|\ge K$ with

\[ K>\left( \frac{m}{{1}/{\varepsilon_j \beta}-1}\right)^{{1}/{\beta}}, \]

we get

\[ |x|^{1-\beta-m} \left(G\cdot \frac{x}{|x|}-\frac{V}{\varepsilon_j \beta |x|^{\beta -1}}\right) = m|x|^{-\beta} - \frac{1}{\varepsilon_j \beta}\leq m K^{-\beta}- \frac{1}{\varepsilon_j \beta} <{-}1, \]

where we have used that $\varepsilon _j <{1}/{\beta }$. Hence, (3.4) is satisfied if we choose $\Lambda :=1$. Moreover, we have

\[ \lim_{\left\vert x\right\vert\to\infty} V(x) \left\vert x\right\vert^{2-2\beta-m}=\lim_{\left\vert x\right\vert\to\infty} \left\vert x\right\vert^{2-2\beta-m+s}=1. \]

Consequently, (3.5) holds true for any $c<1$.

Step 2. We now show that $A$ satisfies hypothesis 4.1. Fix $T=1,\,x\in {\mathbb {R}}^d$, $0< a_0< a< b< b_0< T$ and $k>d+2$. Let $(t,y)\in [a_0,b_0]\times {\mathbb {R}}^d$. We assume that $|y|\geq 1$; otherwise, in a neighbourhood of the origin, all the quantities we are going to estimate are obviously bounded. First, since $\varepsilon <\varepsilon _1$, we have that

\[ w\le c_1w^{{(k-2)}/{k}}W_1^{{2}/{k}} \]

with $c_1=1$. Second, an easy computation shows that

(4.6)\begin{align} \frac{|Q(y)\nabla w(t,y)|}{w(t,y)^{{(k-1)}/{k}}W_1(t,y)^{{1}/{k}}} & = \varepsilon \beta t^\alpha |y|^{\beta-1}(1+|y|^m)\,{\rm e}^{-({1}/{k})(\varepsilon_1-\varepsilon)t^\alpha |y|^\beta}\nonumber\\ & \leq 2\varepsilon \beta t^\alpha |y|^{\beta+m-1}\,{\rm e}^{-({1}/{k})(\varepsilon_1-\varepsilon)t^\alpha |y|^\beta}. \end{align}

We make use of the following remark: since the function $t\mapsto t^p\,{\rm e}^{-t}$ on $(0,\infty )$ attains its maximum at the point $t=p$, then for $\tau, \gamma, z>0$ we have

(4.7)\begin{equation} z^\gamma\,{\rm e}^{-\tau z^\beta} =\tau^{-({\gamma}/{\beta})}(\tau z^\beta)^{{\gamma}/{\beta}}\,{\rm e}^{-\tau z^\beta}\leq \tau^{-({\gamma}/{\beta})} \left( \frac{\gamma}{\beta}\right)^{{\gamma}/{\beta}}\,{\rm e}^{-({\gamma}/{\beta})} =: C(\gamma,\beta) \tau^{-({\gamma}/{\beta})}. \end{equation}

Applying (4.7) to inequality (4.6) with $z=|y|$, $\tau =({1}/{k})(\varepsilon _1-\varepsilon )t^\alpha$, $\beta =\beta$ and $\gamma =\beta +m-1>0$ yields

\begin{align*} & \frac{|Q(y)\nabla w(t,y)|}{w(t,y)^{{(k-1)}/{k}}W_1(t,y)^{{1}/{k}}}\leq 2C(\beta+m-1, \beta)\varepsilon \beta t^\alpha \left[\frac{1}{k}(\varepsilon_1-\varepsilon)t^\alpha\right]^{-{(\beta+m-1)}/{\beta}}\\ & \quad\leq \overline{c} t^{-({(\alpha (m-1))}/{\beta})} \leq \overline{c} t^{-({\alpha m}/{\beta})} \leq \overline{c}a_0^{-\frac{\alpha m}{\beta}}. \end{align*}

Thus, we choose $c_2=\overline {c} a_0^{-({\alpha m}/{\beta })}$, where $\overline {c}$ is a universal constant. Similarly,

\begin{align*} & \frac{|{\operatorname{\mathrm{div}}}(Q(y)\nabla w(t,y))|}{w(t,y)^{{(k-2)}/{k}}W_1(t,y)^{{2}/{k}}}\!\leq\! \frac{m |y|^{m-1} |\nabla w(t,y)| \!+\! (1\!+\!|y|^m)|\Delta w|}{w(t,y)^{{(k-2)}/{k}}W_1(t,y)^{{2}/{k}}}\!\leq\! \varepsilon \beta t^\alpha \left[ m |y|^{\beta+m-2}\right.\\ & \quad\left. +2 ((\beta-2)^+{+}d) |y|^{\beta+m-2}+2\varepsilon\beta t^{\alpha} |y|^{2\beta +m-2} \right] {\rm e}^{-({2}/{k})(\varepsilon_1-\varepsilon)t^\alpha |y|^\beta}. \end{align*}

As a result, applying (4.7) to each term, we find that

\begin{align*} & \frac{|{\operatorname{\mathrm{div}}}(Q(y)\nabla w(t,y))|}{w(t,y)^{{(k-2)}/{k}}W_1(t,y)^{{2}/{k}}}\\ & \quad \leq C(\beta, m) \varepsilon \beta t^\alpha \left \lbrace [m+2((\beta-2)^+{+}d)] \left[\frac{2}{k}(\varepsilon_1-\varepsilon)t^\alpha\right]^{-({(\beta+m-2)}/{\beta})}\right. \\ & \qquad\left. +2\varepsilon\beta t^{\alpha}\left[\frac{2}{k}(\varepsilon_1-\varepsilon)t^\alpha\right]^{-({(2\beta+m-2)}/{\beta})}\right\rbrace \leq \overline{c} t^{-({(\alpha(m-2))}/{\beta})}\\ & \quad\leq \overline{c} t^{-({\alpha m}/{\beta})}\leq \overline{c}a_0^{-({\alpha m}/{\beta})}. \end{align*}

Therefore, we pick $c_3=\overline {c} a_0^{-({\alpha m}/{\beta })}$. In the same way, we have

\begin{align*} & \frac{|\partial_t w(t,y)|}{w(t,y)^{{(k-2)}/{k}}W_1(t,y)^{{2}/{k}}} = \varepsilon\alpha t^{\alpha-1} |y|^\beta\,{\rm e}^{-({2}/{k})(\varepsilon_1-\varepsilon)t^\alpha |y|^\beta} \\ & \quad\leq C(\beta) \varepsilon\alpha t^{\alpha-1}\left[\frac{2}{k}(\varepsilon_1-\varepsilon)t^\alpha\right]^{{-}1}\leq \overline{c} t^{{-}1}\leq \overline{c}a_0^{{-}1}. \end{align*}

Then, we take $c_4= \overline {c} a_0^{-1}$. Finally,

\begin{align*} & \frac{V(y)^{{1}/{2}}}{w(t,y)^{-({1}/{k})}W_2(t,y)^{{1}/{k}}} =|y|^{{s}/{2}}\,{\rm e}^{-({1}/{k})(\varepsilon_2-\varepsilon)t^\alpha |y|^\beta}\\& \quad\leq C(s,\beta)\left[\frac{1}{k}(\varepsilon_2-\varepsilon)t^\alpha\right]^{{-s}/{2\beta}} \leq \overline{c}t^{-({\alpha s}/{2\beta})}\leq \overline{c}a_0^{-({\alpha s}/{2\beta})}, \end{align*}

so we set $c_5=\overline {c} a_0^{-({\alpha s}/{2\beta })}.$

Step 3. We check the remaining hypotheses of theorem 4.3 assuming as above that $|y|\geq 1$. First, we have

\[ \frac{|\Delta w(t,y)|}{w(t,y)^{{(k-2)}/{k}}W_1(t,y)^{{2}/{k}}} = \varepsilon\beta t^\alpha \left[(\beta \!-\!2\!+\!d) |y|^{\beta-2} \!+\! \varepsilon\beta t^{\alpha} |y|^{2\beta-2}\right] {\rm e}^{-({2}/{k})(\varepsilon_1-\varepsilon)t^\alpha |y|^\beta}. \]

Recalling that $\left \vert y \right \vert \geq 1$ and applying (4.7), yields

\begin{align*} \frac{|\Delta w(t,y)|}{w(t,y)^{{(k-2)}/{k}}W_1(t,y)^{{2}/{k}}} & \leq \varepsilon\beta t^\alpha \left[((\beta-2)^+{+}d) |y|^{\beta} + \varepsilon\beta t^{\alpha} |y|^{2\beta}\right] {\rm e}^{-({2}/{k})(\varepsilon_1-\varepsilon)t^\alpha |y|^\beta}\\ & \leq C(\beta)\varepsilon\beta t^\alpha \left\lbrace ((\beta-2)^+{+}d)\left[\frac{2}{k}(\varepsilon_1-\varepsilon)t^\alpha\right]^{{-}1}\right.\\ & \quad\left. +\varepsilon\beta t^{\alpha}\left[\frac{2}{k}(\varepsilon_1-\varepsilon)t^\alpha\right]^{{-}2} \right\rbrace \leq \overline{c}. \end{align*}

Thus, (4.2) is verified by taking $c_6=\overline {c}$. To choose the constant $c_7$ in (4.3), we let $t_0\in (0,t)$. Then, we get

\begin{align*} \frac{|Q(y)\nabla W_1(t_0,y)|}{w(t,y)^{{-}1/k}W_1(t_0, y)W_2(t,y)^{1/k}} & =\frac{\varepsilon_1\beta t_0^\alpha |y|^{\beta-1}(1+|y|^m)W_1(t_0,y)}{w(t,y)^{{-}1/k}W_1(t_0, y)W_2(t,y)^{1/k}}\\ & \leq 2\varepsilon_1\beta t^\alpha |y|^{\beta+m-1}\,{\rm e}^{-({1}/{k})(\varepsilon_2-\varepsilon)t^\alpha |y|^\beta}\\ & \leq 2C(\beta,m)\varepsilon_1\beta t^\alpha\left[\frac{1}{k}(\varepsilon_2-\varepsilon)t^\alpha\right]^{-({(\beta+m-1)}/{\beta})}\\ & \leq \overline{c} t^{-({(\alpha(m-1))}/{\beta})} \leq \overline{c} t^{-({\alpha m}/{\beta})} \leq \overline{c}a_0^{-({\alpha m}/{\beta})}. \end{align*}

Consequently, we set $c_7=\overline {c} a_0^{-({\alpha m}/{\beta })}$. Finally, we observe that (4.4) is clearly satisfied.

To sum up, the constants $c_1, \dots, c_7$ are the following:

\begin{align*} & c_1=1, \quad c_2=c_3=c_7=\overline{c} a_0^{-({\alpha m}/{\beta})}, \quad c_4= \overline{c} a_0^{{-}1},\\ & c_5=\overline{c} a_0^{-({\alpha s}/{2\beta})}, \quad c_6=\overline{c}. \end{align*}

Step 4. We are now ready to apply theorem 4.3. Thus, there is a positive constant $C>0$ depending only on $d$ and $k$ such that

(4.8)\begin{align} w(t,y)p(t,x,y) & \le C\left[c_1^{{k}/{2}}\sup_{s\in (a_0,b_0)}\xi_{W_1}(s,x)\right.\nonumber\\ & \left. +\left( c_2^k+\frac{c_1^{{k}/{2}}}{(b_0-b)^{{k}/{2}}}+c_3^{{k}/{2}} +c_4^{{k}/{2}}+c_6^{{k}/{2}}\right)\int_{a_0}^{b_0}\xi_{W_1}(s,x)\,{\rm d}s\right.\nonumber\\ & \quad \left. +(c_5^k+c_2^{{k}/{2}}c_7^{{k}/{2}})\int_{a_0}^{b_0}\xi_{W_2}(s,x)\,{\rm d}s\right] \end{align}

for all $(t,y)\in (a,b)\times {\mathbb {R}}^d$ and fixed $x\in {\mathbb {R}}^d$. We set $a_0={t}/{4}$, $a={t}/{2}$, $b={(t+1)}/{2}$ and $b_0={(t+3)}/{4}$. Moreover, by proposition 3.3, there are two constants $H_1$ and $H_2$ not depending on $a_0$ and $b_0$ such that $\xi _{W_j}(s,x)\leq H_j$ for all $(s,x)\in [0,1]\times {\mathbb {R}}^d$, so

\[ \int_{a_0}^{b_0}\xi_{W_j}(s,x)\,{\rm d}s \leq H_j(b_0-a_0)= \frac{3}{4}t H_j. \]

If we now replace in (4.8) the values of the constants $c_1, \dots, c_7$ determined in step 3, we use the previous inequality and we consider $C$ as a positive constant that can vary from line to line, we obtain

(4.9)\begin{equation} w(t,y)p(t,x,y)\leq C \left[ t^{1-({\alpha m}/{\beta})k}+ t^{1-{k}/{2}}+t^{1-({\alpha s}/{2\beta})k}\right]. \end{equation}

We note that, since $\alpha >{\beta }/{(\beta +m-2)}$, $s>|m-2|$ and $\beta ={(s-m+2)}/{2}$, it follows that

\[ \frac{\alpha(m\vee {s}/{2})}{\beta}> \frac{m\vee {s}/{2}}{\beta+m-2}>\frac{s}{2(\beta+m-2)}= \frac{s}{s+m-2}>\frac{1}{2}. \]

Hence,

\[ t^{1-{k}/{2}}< t^{1-({\alpha\left(m\vee {s}/{2}\right)}{\beta})k}. \]

Consequently, by (4.9), we find that

\[ w(t,y)p(t,x,y)\leq C t^{1-({\alpha\left(m\vee {s}/{2}\right)k}/{\beta})}= C t^{1-({(\alpha(2m\vee s)k)}/{(s-m+2)}}. \]

Writing the expression of the weight function $w$ we get the following inequality:

(4.10)\begin{equation} p(t,x,y)\le C t^{1-({(\alpha(2m\vee s))}/{(s-m+2)})k}\,{\rm e}^{-\varepsilon t^\alpha |y|_*^{{(s-m+2)}/{2}}} \end{equation}

for $k>d+2$ and for any $t\in (0,1)$, $x,y\in {\mathbb {R}}^d$.

Step 5. Since $A^*=A$, applying (4.10) to $p^*(t,y,x)$, we derive that

\[ p(t,x,y)= p^*(t,y,x)\le C t^{1-({(\alpha(2m\vee s))}/{(s-m+2)})k}\,{\rm e}^{-\varepsilon t^\alpha |x|_*^{{(s-m+2)}/{2}}} \]

for all $t\in (0,1)$ and $x,y\in {\mathbb {R}}^d$. Combining this with (4.10) and considering that $p^*(t,x,y)=p(t,y,x)$ yields

\begin{align*} p(t,x,y)& =p(t,x,y)^{1/2}p(t,x,y)^{1/2}\\ & \quad \leq C t^{1-({(\alpha(2m\vee s))}/{(s-m+2)})k}\,{\rm e}^{-({\varepsilon}/{2}) t^\alpha |x|_*^{{(s-m+2)}/{2}}}\,{\rm e}^{-({\varepsilon}/{2}) t^\alpha |y|_*^{{(s-m+2)}/{2}}} \end{align*}

for $k>d+2$ and for any $t\in (0,1)$, $x,y\in {\mathbb {R}}^d$.

4.2 Exponentially growing coefficients

In this subsection, we apply theorem 4.3 to the case of operators with exponentially diffusion and potential terms.

Let $Q(x)={\rm e}^{\left \vert x \right \vert ^m}I$ and $V(x)={\rm e}^{\left \vert x \right \vert ^s}$ with $2\leq m< s$. Set

\[ w(t,x)=\exp\left( \varepsilon t^\alpha \int_0^{\left\vert x\right\vert_*}\,{\rm e}^{{\tau^\beta}/{2}}\,{\rm d}\tau\right)\text{ and } W_j(t,x)=\exp\left( \varepsilon_j t^\alpha \int_0^{\left\vert x\right\vert_*}\,{\rm e}^{{\tau^\beta}/{2}}\,{\rm d}\tau\right), \]

where $j=1,2$, ${m}/{2}+1\leq \beta \leq m$, $0<\varepsilon <\varepsilon _1<\varepsilon _2$ and $\alpha >{(2\beta +m-2)}/{2m}$.

Theorem 4.5 Let $p$ be the integral kernel associated with the operator $A$ with $Q(x)={\rm e}^{\left \vert x \right \vert ^m}I$ and $V(x)={\rm e}^{\left \vert x \right \vert ^s}$, where $2\leq m< s$. Then

\begin{align*} p(t,x,y)& \leq C t^{1-{k}/{2}} \exp({Ckt^{-\alpha}})\exp\left(- \frac{\varepsilon}{2} t^\alpha \int_0^{\left\vert x\right\vert_*}\,{\rm e}^{{\tau^\beta}/{2}}\,{\rm d}\tau\right)\\ & \quad\exp\left(- \frac{\varepsilon}{2} t^\alpha \int_0^{\left\vert y\right\vert_*}\,{\rm e}^{{\tau^\beta}/{2}}\,{\rm d}\tau\right), \end{align*}

for $k>d+2$ and any $t\in (0,1),\,x,y\in {\mathbb {R}}^d$.

Proof. Step 1. We check conditions (3.11)–(3.13) to apply proposition 3.5 and show that $W_1$ and $W_2$ are time-dependent Lyapunov functions for $L=\partial _t+A$. It is clear that (3.11) holds true with $c_e=1$. Moreover, since $s>m$, it follows that

\[ \lim_{\left\vert x\right\vert\to\infty} V(x) \left\vert x\right\vert^{1-\beta-m}\,{\rm e}^{-\left\vert x\right\vert^\beta-\left\vert x\right\vert^m}=\lim_{\left\vert x\right\vert\to\infty} \left\vert x\right\vert^{1-\beta-m}\,{\rm e}^{\left\vert x\right\vert^s-\left\vert x\right\vert^\beta-\left\vert x\right\vert^m}={+}\infty \]

and

\begin{align*} & \limsup_{\left\vert x\right\vert\to\infty}|x|^{1-\beta-m}\,{\rm e}^{-{\left\vert x\right\vert^\beta}/{2}-\left\vert x\right\vert^m}\left(G\cdot \frac{x}{|x|}-\frac{V}{\varepsilon\,{\rm e}^{{\left\vert x\right\vert^\beta}/{2}}}\right)\\ & \quad = \limsup_{\left\vert x\right\vert\to\infty} \left( m\left\vert x\right\vert^{-\beta}\,{\rm e}^{-{\left\vert x\right\vert^\beta}/{2}} -\frac{1}{\varepsilon}|x|^{1-\beta-m} \,{\rm e}^{\left\vert x\right\vert^s-\left\vert x\right\vert^\beta-\left\vert x\right\vert^m}\right)={-}\infty. \end{align*}

Consequently, there exist constants $c, \Lambda >0$ such that (3.12) and (3.13) hold true. By proposition 3.5 we conclude that $W_1$ and $W_2$ are time-dependent Lyapunov functions. In addition, we also note that hypothesis 1.1 is verified with

\[ Z(x)=\exp\left( \varepsilon_2 \int_0^{\left\vert x\right\vert_*}\,{\rm e}^{{\tau^\beta}/{2}}\,{\rm d}\tau\right). \]

Step 2. We prove that $A$ satisfies all the assumptions of theorem 4.3. Fix $T=1$, $x\in {\mathbb {R}}^d$, $0< a_0< a< b< b_0< T$ and $k>d+2$. Let $(t,y)\in [a_0,b_0]\times {\mathbb {R}}^d$. If $|y|\leq 1$, by continuity all the functions we are estimating are bounded by a constant. Thus, let $|y|\geq 1$. Since $\varepsilon <\varepsilon _1$, we have that $w\leq W_1$. Hence, the inequality

\[ w\le c_1w^{{(k-2)}/{k}}W_1^{{2}/{k}} \]

holds true with $c_1=1$. Observing that

(4.11)\begin{equation} \int_0^{\left\vert y\right\vert}\,{\rm e}^{{\tau^\beta}/{2}}\,{\rm d}\tau\geq \int_{\left\vert y\right\vert-1}^{\left\vert y\right\vert}\,{\rm e}^{{\tau^\beta}/{2}}\,{\rm d}\tau\geq\,{\rm e}^{{((\left\vert y\right\vert-1)^\beta)}/{2}} \end{equation}

we find

(4.12)\begin{align} \frac{|Q(y)\nabla w(t,y)|}{w(t,y)^{{(k-1)}/{k}}W_1(t,y)^{{1}/{k}}} & = \varepsilon t^\alpha \exp\left( \frac{\left\vert y\right\vert^\beta}{2}+\left\vert y\right\vert^m-\frac{(\varepsilon_1-\varepsilon)}{k}t^\alpha \int_0^{\left\vert y\right\vert}\,{\rm e}^{{\tau^\beta}/{2}}\,{\rm d}\tau\right)\nonumber\\ & \leq \varepsilon t^\alpha \exp\left( \frac{\left\vert y\right\vert^\beta}{2}+\left\vert y\right\vert^m-\frac{(\varepsilon_1-\varepsilon)}{k}t^\alpha\,{\rm e}^{{((\left\vert y\right\vert-1)^\beta)}/{2}}\right). \end{align}

We now consider the function

\[ f(r):=\frac{r^\beta}{2}+r^m-\tilde{\varepsilon} t^\alpha\,{\rm e}^{{((r-1)^\beta)}/{2}}, \]

where $r\geq 1$ and $\tilde {\varepsilon }:=(\varepsilon _1-\varepsilon )/{k}$. Considering that there exists a universal constant $\overline {c}>0$ (that can vary from line to line) depending on $\beta$ and $m$ such that

(4.13)\begin{equation} \frac{r^\beta}{2}+r^m\leq \overline{c}\,{\rm e}^{{((r-1)^\beta)}/{4}}, \quad \forall r\geq 1, \end{equation}

we get

\[ f(r)\leq \overline{c}\,{\rm e}^{{((r-1)^\beta)}/{4}}-\tilde{\varepsilon} t^\alpha\,{\rm e}^{{((r-1)^\beta)}/{2}}. \]

If we set $z={\rm e}^{{((r-1)^\beta )}/{2}}$ and we compute the maximum of the function $h(z)= \overline {c} \sqrt {z}-\tilde {\varepsilon } t^\alpha z$, we obtain that

\[ f(r)\leq \frac{\overline{c}^2}{4\tilde{\varepsilon}}t^{-\alpha}. \]

As a result, by (4.12) we derive

\[ \frac{|Q(y)\nabla w(t,y)|}{w(t,y)^{{(k-1)}/{k}}W_1(t,y)^{{1}/{k}}}\leq \varepsilon t^\alpha \exp\left(\frac{\overline{c}^2 }{4\tilde{\varepsilon}}t^{-\alpha}\right) \leq \varepsilon \exp\left(\frac{\overline{c}^2 }{4\tilde{\varepsilon}}a_0^{-\alpha}\right). \]

Then, we set $c_2:= \overline {c} \exp (\overline {c}a_0^{-\alpha })$. In a similar way, we have that

\begin{align*} \frac{|{\operatorname{\mathrm{div}}}(Q(y)\nabla w(t,y))|}{w(t,y)^{{(k-2)}/{k}}W_1(t,y)^{{2}/{k}}} & \leq \left[(d-1)\varepsilon t^\alpha \frac{1}{\left\vert y\right\vert}\,{\rm e}^{{\left\vert y\right\vert^\beta}/{2}+\left\vert y\right\vert^m} \right.\\ & \quad \left. +m\varepsilon t^\alpha \left\vert y\right\vert^{m-1} \,{\rm e}^{{\left\vert y\right\vert^\beta}/{2}+\left\vert y\right\vert^m} + \frac{\beta}{2}\varepsilon t^\alpha \left\vert y\right\vert^{\beta-1}\,{\rm e}^{{\left\vert y\right\vert^\beta}/{2}+\left\vert y\right\vert^m}\right.\\ & \quad \left.+\varepsilon^2 t^{2\alpha}\,{\rm e}^{\left\vert y\right\vert^\beta+\left\vert y\right\vert^m}\right] \exp\left(-\frac{2(\varepsilon_1\!-\!\varepsilon)}{k}t^\alpha \int_0^{\left\vert y\right\vert}\,{\rm e}^{{\tau^\beta}/{2}}\,{\rm d}\tau\right). \end{align*}

Using again (4.11), we deduce

\begin{align*} & \frac{|{\operatorname{\mathrm{div}}}(Q(y)\nabla w(t,y))|}{w(t,y)^{{(k-2)}/{k}}W_1(t,y)^{{2}/{k}}}\\ & \quad \leq (d-1)\varepsilon t^\alpha \exp\left( \frac{\left\vert y\right\vert^\beta}{2}+\left\vert y\right\vert^m -\frac{2(\varepsilon_1-\varepsilon)}{k}t^\alpha\,{\rm e}^{{((\left\vert y\right\vert-1)^\beta)}/{2}} \right)\\ & \qquad+m\varepsilon t^\alpha \exp\left( \log\left\vert y\right\vert^{m-1}+ \frac{\left\vert y\right\vert^\beta}{2}+\left\vert y\right\vert^m -\frac{2(\varepsilon_1-\varepsilon)}{k}t^\alpha\,{\rm e}^{{((\left\vert y\right\vert-1)^\beta)}/{2}}\right)\\ & \qquad+ \frac{\beta}{2}\varepsilon t^\alpha \exp\left( \log\left\vert y\right\vert^{\beta-1}+ \frac{\left\vert y\right\vert^\beta}{2}+\left\vert y\right\vert^m -\frac{2(\varepsilon_1-\varepsilon)}{k}t^\alpha\,{\rm e}^{{((\left\vert y\right\vert-1)^\beta)}/{2}}\right)\\ & \qquad +\varepsilon^2 t^{2\alpha} \exp\left( \left\vert y\right\vert^\beta+\left\vert y\right\vert^m-\frac{2(\varepsilon_1-\varepsilon)}{k}t^\alpha\,{\rm e}^{{((\left\vert y\right\vert-1)^\beta)}/{2}}\right). \end{align*}

The first term on the right-hand side of this inequality can be estimated exactly as above. As for the other three terms, we have to slightly modify the function $f$ considered above to match the argument of the exponential function. However, a short computation shows that also for these modified functions $f$ inequality (4.13) is valid so that we obtain the following estimate:

\begin{align*} & \frac{|{\operatorname{\mathrm{div}}}(Q(y)\nabla w(t,y))|}{w(t,y)^{{(k-2)}/{k}}W_1(t,y)^{{2}/{k}}}\\ & \quad \leq \left( (d-1) +m+\frac{\beta}{2}\right)\varepsilon t^\alpha \exp\left(\frac{\overline{c}^2}{8\tilde{\varepsilon}}t^{-\alpha}\right)+ \varepsilon^2 t^{2\alpha}\exp\left(\frac{\overline{c}^2}{8\tilde{\varepsilon}}t^{-\alpha}\right)\\ & \leq \overline{c} \varepsilon t^\alpha \exp\left(\frac{\overline{c}^2}{8\tilde{\varepsilon}}t^{-\alpha}\right)\leq \overline{c} \varepsilon \exp\left(\frac{\overline{c}^2}{8\tilde{\varepsilon}}a_0^{-\alpha}\right). \end{align*}

Thus, we choose $c_3=\overline {c} \exp (\overline {c}a_0^{-\alpha })$. Concerning $c_4$, we have

\begin{align*} \frac{|\partial_t w(t,y)|}{w(t,y)^{{(k-2)}/{k}}W_1(t,y)^{{2}/{k}}} & = \varepsilon \alpha t^{\alpha-1}\left(\int_0^{\left\vert y\right\vert}\,{\rm e}^{{\tau^\beta}/{2}}\,{\rm d}\tau\right)\\ & \quad \exp\left(-\frac{2(\varepsilon_1-\varepsilon)}{k}t^\alpha \int_0^{\left\vert y\right\vert}\,{\rm e}^{{\tau^\beta}/{2}}\,{\rm d}\tau\right)\\ & \leq \varepsilon \alpha \frac{k}{2(\varepsilon_1-\varepsilon)} t^{{-}1}\leq \varepsilon \alpha \frac{k}{2(\varepsilon_1-\varepsilon)} a_0^{{-}1}. \end{align*}

We take $c_4=\overline {c} a_0^{-1}$. Repeating the same procedure for the remaining estimates, we get $c_5= c_6=c_7=c_2.$

Step 3. As in the proof of theorem 4.4, we choose $a_0={t}/{4}$, $a={t}/{2}$, $b={(t+1)}/{2}$ and $b_0={(t+3)}/{4}$ and we notice that, by proposition 3.5, there are two constants $H_1$ and $H_2$ not depending on $a_0$ and $b_0$ such that

\[ \int_{a_0}^{b_0}\xi_{W_j}(s,x)\,{\rm d}s \leq H_j(b_0-a_0)= \frac{3}{4}t H_j. \]

Applying theorem 4.3, we infer that there exists a positive constant $C>0$ depending only on $d$ and $k$ such that

\begin{align*} w(t,y)p(t,x,y) & \le C\left[c_1^{{k}/{2}}\sup_{s\in (a_0,b_0)}\xi_{W_1}(s,x)\right.\\ & \quad\left. +\left( c_2^k+\frac{c_1^{{k}/{2}}}{(b_0-b)^{{k}/{2}}}+c_3^{{k}/{2}} +c_4^{{k}/{2}}+c_6^{{k}/{2}}\right)\int_{a_0}^{b_0}\xi_{W_1}(s,x)\,{\rm d}s\right.\nonumber\\ & \quad \left. +(c_5^k+c_2^{{k}/{2}}c_7^{{k}/{2}})\int_{a_0}^{b_0}\xi_{W_2}(s,x)\,{\rm d}s\right] \end{align*}

for all $(t,y)\in (a,b)\times {\mathbb {R}}^d$ and fixed $x\in {\mathbb {R}}^d$. We rewrite the previous inequality taking into account the values of the constants $c_1, \ldots, c_7$ found in step 2, keeping track only of powers of $t$ and absorbing all other constants into the constant $C$:

\begin{align*} w(t,y)p(t,x,y) & \leq C\left[ t^{1+k\alpha } \exp({\overline{c}kt^{-\alpha}}) +t^{1+{\alpha k}/{2}} \exp\left(\frac{\overline{c}k}{2}t^{-\alpha}\right)\right.\\ & \quad\left. +t^{1-{k}/{2}} +t \exp({\overline{c}kt^{-\alpha}})\vphantom{\left[ t^{1+k\alpha } \exp({\overline{c}kt^{-\alpha}}) +t^{1+{\alpha k}/{2}} \exp\left(\frac{\overline{c}k}{2}t^{-\alpha}\right)\right.}\right]\\ & \leq C t^{1-{k}/{2}} \exp({Ckt^{-\alpha}}). \end{align*}

Hence,

(4.14)\begin{equation} p(t,x,y)\leq C t^{1-{k}/{2}} \exp({Ckt^{-\alpha}})\exp\left(- \varepsilon t^\alpha \int_0^{\left\vert y\right\vert_*}\,{\rm e}^{{\tau^\beta}/{2}}\, d\tau\right) \end{equation}

for $k>d+2$ and for any $t\in (0,1)$, $x,y\in {\mathbb {R}}^d$, where $C$ depends only on $d, \eta, \beta$ and $m$.

Step 4. We conclude the proof by applying inequality (4.14) to $p^*(t,y,x)$. This is possible because $A^*=A$, so we obtain

\[ p^*(t,y,x)\leq C t^{1-{k}/{2}} \exp({Ckt^{-\alpha}})\exp\left(- \varepsilon t^\alpha \int_0^{\left\vert x\right\vert_*}\,{\rm e}^{{\tau^\beta}/{2}}\,{\rm d}\tau\right) \]

for all $t\in (0,1)$ and $x,y\in {\mathbb {R}}^d$. As a consequence, since $p^*(t,y,x)=p(t,x,y)$, we get the desired inequality as follows:

\begin{align*} p(t,x,y)& =p(t,x,y)^{{1}/{2}}p^*(t,y,x)^{{1}/{2}}\\ & \leq C t^{1-{k}/{2}} \exp({Ckt^{-\alpha}})\exp\left(- \frac{\varepsilon}{2} t^\alpha \int_0^{\left\vert x\right\vert_*}\,{\rm e}^{{\tau^\beta}/{2}}\,{\rm d}\tau\right)\\ & \quad\exp\left(- \frac{\varepsilon}{2} t^\alpha \int_0^{\left\vert y\right\vert_*}\,{\rm e}^{{\tau^\beta}/{2}}\,{\rm d}\tau\right), \end{align*}

for all $t\in (0,1)$ and $x,y\in {\mathbb {R}}^d$.

4.3 Spectral properties and eigenfunctions estimates

In this subsection, we study some spectral properties of $A_{\min }$ with either polynomial or exponential coefficients. In particular, we prove the following result.

Theorem 4.6 If $Q(x) = (1+|x|_*^m)I$ and $V(x)=|x|^s$ with $s>|m-2|$ and $m>0$ or $Q(x)={\rm e}^{\left \vert x \right \vert ^m}I$ and $V(x)={\rm e}^{\left \vert x \right \vert ^s}$, where $2\leq m< s$, then $T_p(t)$ is compact for all $t>0$ and $p\in (1,\infty )$. Moreover, the spectrum of the generator of $T_p(\cdot )$ is independent of $p$ for $p\in (1,\infty )$ and consists of a sequence of negative real eigenvalues which accumulates at $-\infty$.

Proof. By [10, theorem 1.6.3], it suffices to prove that $T_2(t)$ is compact for all $t>0$. For this purpose, let us assume that $Q(x)=(1+|x|^m_*)I$ and $V(x)=|x|^s$ with $s>m-2$ and $m>2$ or $Q(x)={\rm e}^{\left \vert x \right \vert ^m}I$ and $V(x)={\rm e}^{\left \vert x \right \vert ^s}$, where $2\leq m< s$. Applying [10, corollary 1.6.7], one deduces that the $L^2$-realization $A_0$ of ${\mathcal {A}}_0:={\operatorname {\mathrm {div}}}(Q\nabla )$ has compact resolvent and thus the semigroup $S(t)$ generated by $A_0$ in $L^2({\mathbb {R}}^d)$ is compact for all $t>0$, cf. [11, theorem 4.29]. Since $V\ge 0$ we have $0\le T_2(t)\le S(t)$ for all $t\ge 0$. Applying the Aliprantis–Burkinshaw theorem [2, theorem 5.15] we obtain the compactness of $T_2(t)$ for all $t>0$.

Let us now show the compactness of $T_2(t)$ in the case where $Q(x)=(1+|x|^m_*)I$ and $V(x)=|x|^s$ with $s>|m-2|$ and $0< m\le 2$. The operator $A_{\min }$ can be considered as the sum of the operator $\widetilde {A}_2u:=(1+|x|^m_*)\Delta u-|x|^su$ and the operator $Bu:=\nabla (1+|x|^m_*)\cdot \nabla u$. From [18, proposition 2.3] we know that $B$ is a small perturbation of $\widetilde {A}_2$. Hence, $R(\lambda,A_{\min })=R(\lambda, \widetilde {A}_2)(I-BR(\lambda,\widetilde {A}_2))^{-1}$ for all $\lambda \in \rho (\widetilde {A}_2)$. Moreover, by [18, proposition 2.10], we know that $\widetilde {A}_2$ has compact resolvent and hence $A_{\min }$ has compact resolvent too. Since $T_2(\cdot )$ is an analytic semigroup, we deduce that $T_2(t)$ is compact for all $t>0$.

Let us now estimate the eigenfunctions of $A_{\min }$. For this purpose, let us note first that, by the semigroup law and the symmetry of $p(t,\cdot,\cdot )$ for any $t>0$, we have

\[ p(t+s,x,y)=\int_{{\mathbb{R}}^d}p(t,x,z)p(s,y,z)\,{\rm d}z,\quad t,s>0,\,x,y\in {\mathbb{R}}^d. \]

Thus,

\[ p(t,x,x)=\int_{{\mathbb{R}}^d}p\left(\frac{t}{2},x,y\right)^2\,{\rm d}y,\quad t>0,\,x\in {\mathbb{R}}^d. \]

So, if we denote by $\psi$ an eigenfunction of $A_{\min }$ associated with the eigenvalue $\lambda$, then Hölder's inequality implies

\begin{align*} {\rm e}^{\lambda ({t}/{2})} |\psi(x)|& = |T_2(t/2)\psi(x)|\\ & \le \int_{{\mathbb{R}}^d} p\left(\frac{t}{2},x,y\right)|\psi(y)|\,{\rm d}y\\ & \le \left(\int_{{\mathbb{R}}^d}p\left(\frac{t}{2},x,y\right)^2\,{\rm d}y\right)^{{1}/{2}}\|\psi \|_2\\ & =p(t,x,x)^{{1}/{2}}\|\psi \|_2 \end{align*}

for any $t>0$ and any $x\in {\mathbb {R}}^d$. Therefore, if we normalize $\psi$, i.e. $\|\psi \|_2=1$, then

\[ |\psi(x)|\le {\rm e}^{-\lambda ({t}/{2})} p(t,x,x)^{{1}/{2}},\quad t>0,\,x\in {\mathbb{R}}^d. \]

So, by theorems 4.4 and 4.5 we have

Corollary 4.7 Let $\psi$ be any normalized eigenfunction of $A_{\min }$. Then,

1. (a) in the case of polynomially growing coefficients, i.e. $Q(x)=(1+|x|^m_*)I$ and $V(x)=|x|^s$, where $s>|m-2|$ and $m> 0$, we have

   \[ |\psi(x)| \le c_1\,{\rm e}^{{-}c_2 |x|_*^{{(s-m+2)}/{2}}},\quad x\in {\mathbb{R}}^d, \]
   for some constants $c_1,c_2>0$;

2. (b) in the case of exponentially growing coefficients, i.e. $Q(x)={\rm e}^{\left \vert x \right \vert ^m}I$ and $V(x)={\rm e}^{\left \vert x \right \vert ^s}$, where $2\leq m< s$, we have

   \[ |\psi(x)| \le c_1\exp\left({-}c_2 \int_0^{\left\Vert x\right\vert_*} {\rm e}^{{\tau^\beta}/{2}}\,{\rm d}\tau\right),\quad x\in {\mathbb{R}}^d, \]
   for some constants $c_1,c_2>0$.