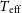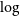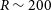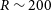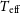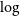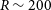1. Introduction
Very metal-poor (VMP, [Fe/H]<-2) stars are important relics of the galactic formation history since it offers rich information on the chemical and physical conditions of the first-generation stars in the universe. The Li abundance in VMP stars can provide estimates of the baryon-to-photon ratio, helping us to better refine the galaxy formation model (Beers and Christlieb Reference Beers and Christlieb2005; Frebel and Norris Reference Frebel and Norris2015; Frebel Reference Frebel2018).
Owing to large-scale sky survey projects, researchers have so far discovered a large number of VMP stars using photometry and spectroscopic methods. One of the earliest VMP search programmes was HK survey (Rhee, Beers, & Irwin Reference Rhee, Beers and Irwin2001), discovering approximately 2 000 cooler VMP stars by combining Artificial Neural networks and 2MASS JHK photometry, with a detection efficiency of between 60% and 70%. Christlieb et al. (Reference Christlieb, Schörck, Frebel, Beers, Wisotzki and Reimers2008) used CCD photometry to calibrate B-V colours in the Hamburg/ESO Survey (HES) spectra and found 10 times more VMP stars than the HK survey, with a rejection rate of 97% for stars with [Fe/H]>-2. The Pristine Inner Galaxy Survey (PIGS) photometry (Arentsen et al. Reference Arentsen2020) explored 1 300 VMP stars in the inner Galaxy with an efficiency exceeding 80%. For the spectroscopic survey, APOGEE (García Pérez et al. Reference García Pérez2013) also found a small number of VMP stars in the central part of the Milky Way. Besides, Matijevič et al. (2017) determined the metallicity of data from RAVE DR5 more reliably than the pipeline, with an accuracy of 0.2 dex, and found hundreds of VMP stars. Da Costa et al. (Reference Da Costa2019) discovered nearly 2 500 VMP stars from SkyMapper DR1.1 with the help of the follow-up low-resolution (
![]() $R\sim3\,000$
) spectroscopic research. Other surveys such as LAMOST (Li, Tan, & Zhao Reference Li, Tan and Zhao2018) and Southern African Large Telescope (SALT, Rasmussen et al. Reference Rasmussen, Zepeda, Beers, Placco, Depagne, Frebel, Dietz and Hartwig2020) also enlarge the sample pool of VMP stars.
$R\sim3\,000$
) spectroscopic research. Other surveys such as LAMOST (Li, Tan, & Zhao Reference Li, Tan and Zhao2018) and Southern African Large Telescope (SALT, Rasmussen et al. Reference Rasmussen, Zepeda, Beers, Placco, Depagne, Frebel, Dietz and Hartwig2020) also enlarge the sample pool of VMP stars.
Metal-poor stars tend to contain higher than average levels of carbon. If the carbon abundance ([C/Fe]) of the metal-poor ([Fe/H]<-1.0) stars is larger than +1.0, it is called the Carbon Enhanced Metal-poor (CEMP) stars (Beers and Christlieb Reference Beers and Christlieb2005). This threshold for classifying CEMP stars has been updated to [C/Fe]>+0.7 (Aoki et al. Reference Aoki, Beers, Christlieb, Norris, Ryan and Tsangarides2007). Measuring the carbon enhancement of metal-poor stars discovered from large-scale surveys is conducive to deriving CEMP stars, which are of vital importance for understanding the relationship between astrophysical s-process and carbon enhancement (Marsteller et al. Reference Marsteller, Beers, Rossi, Christlieb, Bessell and Rhee2005) and the nature of first-generation stars (Beers Reference Beers2011). Frebel et al. (Reference Frebel2006) proved that there is clear evidence that the proportion of carbon enrichment in metal-poor stars increases with decreasing metallicity. Lucatello et al. (Reference Lucatello, Beers, Christlieb, Barklem, Rossi, Marsteller, Sivarani and Lee2006) first analysed 94 VMP stars obtained by the Hamburg/ESO R-process Enhanced Star survey (HERES, Barklem et al. Reference Barklem2005) and found
![]() $21\pm2\%$
of VMP stars with [C/Fe] abundances above +1.0, which can be classified as CEMP stars. Lee et al. (Reference Lee2013) proposed a novel technique to obtain the fractions of CEMP stars in metal-poor stars from a large sample of SDSS/SEGUE low-resolution (
$21\pm2\%$
of VMP stars with [C/Fe] abundances above +1.0, which can be classified as CEMP stars. Lee et al. (Reference Lee2013) proposed a novel technique to obtain the fractions of CEMP stars in metal-poor stars from a large sample of SDSS/SEGUE low-resolution (
![]() $R\sim2\,000$
) spectra with precision over 0.35 dex. Placco et al. (Reference Placco, Frebel, Beers and Stancliffe2014) improved the frequency of CEMP stars in metal-poor stars and derived that 20% of VMP stars have [C/Fe] abundance greater than +0.7 utilizing the most extensive high-resolution samples from a variety of literature at that time.
$R\sim2\,000$
) spectra with precision over 0.35 dex. Placco et al. (Reference Placco, Frebel, Beers and Stancliffe2014) improved the frequency of CEMP stars in metal-poor stars and derived that 20% of VMP stars have [C/Fe] abundance greater than +0.7 utilizing the most extensive high-resolution samples from a variety of literature at that time.
In order to identify VMP and CEMP stars, the metallicity ([Fe/H]) and [C/Fe] abundance should first be determined. Many methods have been proposed to extract stellar atmospheric parameters (effective temperature
![]() $T_{\textrm{eff}}$
, surface gravity
$T_{\textrm{eff}}$
, surface gravity
![]() $\log$
g, and metallicity [Fe/H]) and chemical abundances from large amounts of spectral or photometric data. The spectral template fitting method is the most widely used method and has high reliability. Lee et al. (Reference Lee2008) proposed the SEGUE Stellar Parameter Pipeline (SSPP) using the line index method and
$\log$
g, and metallicity [Fe/H]) and chemical abundances from large amounts of spectral or photometric data. The spectral template fitting method is the most widely used method and has high reliability. Lee et al. (Reference Lee2008) proposed the SEGUE Stellar Parameter Pipeline (SSPP) using the line index method and
![]() $\chi^2$
minimum spectral fitting method and tested its performance on SDSS-iand SDSS-ii/SEGUE medium-resolution spectra. Koleva et al. (Reference Koleva and Prugniel2009) presented a full-spectrum fitting package ULySS by fitting the minimum observed spectra and model. Blanco-Cuaresma et al. (Reference Blanco-Cuaresma, Soubiran, Heiter and Jofrè2014) created iSpec using synthetic spectral fitting and equivalent width methods based on the SPECTRUM code and tested its effectiveness in the Gaia stellar spectral library. Wu et al. (Reference Wu, Du, Luo, Zhao, Yuan, Heavens, Starck and Krone-Martins2014) developed LAMOST stellar parameter pipeline (LASP) using the correlation function interpolation (CFI) and ULySS methods to automatically derive stellar parameters and radial velocity (
$\chi^2$
minimum spectral fitting method and tested its performance on SDSS-iand SDSS-ii/SEGUE medium-resolution spectra. Koleva et al. (Reference Koleva and Prugniel2009) presented a full-spectrum fitting package ULySS by fitting the minimum observed spectra and model. Blanco-Cuaresma et al. (Reference Blanco-Cuaresma, Soubiran, Heiter and Jofrè2014) created iSpec using synthetic spectral fitting and equivalent width methods based on the SPECTRUM code and tested its effectiveness in the Gaia stellar spectral library. Wu et al. (Reference Wu, Du, Luo, Zhao, Yuan, Heavens, Starck and Krone-Martins2014) developed LAMOST stellar parameter pipeline (LASP) using the correlation function interpolation (CFI) and ULySS methods to automatically derive stellar parameters and radial velocity (
![]() $V_r$
) for late A, FGK-type stars.
$V_r$
) for late A, FGK-type stars.
With the development of machine learning and the maturity of artificial intelligence technology, more and more deep learning methods are applied to stellar parameter measurement. Ness et al. (Reference Ness, Hogg, Rix, Ho and Zasowski2015) developed The Cannon, a data-driven model that does not rely on physical models, which allows us to derive stellar labels from low signal-to-noise (S/N) spectra. StarNet (Fabbro et al. Reference Fabbro and Venn2018) and SPCANet (Wang et al. Reference Wang2020) both employed Convolutional Neural Network (CNN), which is an approach capable of automatically learning data features without the need for manual feature design (Krizhevsky, Sutskever, & Hinton Reference Krizhevsky, Sutskever and Hinton2012; Szegedy et al. Reference Szegedy2015). This can save time and costs, making it more suitable for application to large astronomical datasets. Leung and Bovy (Reference Leung and Bovy2019) used the Artificial Neural Network (ANN), CNN, and Bayesian dropout variational inference to successfully obtain 18 element abundances of APOGEE high-resolution spectra. Ting et al. (Reference Ting, Conroy, Rix and Cargile2019) presented Payne by combining the neural network spectral interpolating method and physical models, which can determine a variety of stellar labels simultaneously.
These deep learning methods are a good solution to the problem of slow speed of traditional template matching methods, but most of them are still based on high-resolution spectra or spectra with
![]() $R\sim2\,000$
down to 1 000. The Chinese Space Station Telescope (CSST) (Zhan Reference Zhan2021) to be emitted in the future will acquire slitless spectra (Yuan, Deng, & Sun Reference Yuan, Deng and Sun2021), i.e. on the focal plane, all sources are able to disperse uniformly along the dispersion direction, which allows us to acquire the full spectrum of the entire field of view. However, the resulting mixing of the dispersion terms leads to contamination, which makes data processing more difficult and also further reduces the resolution (
$R\sim2\,000$
down to 1 000. The Chinese Space Station Telescope (CSST) (Zhan Reference Zhan2021) to be emitted in the future will acquire slitless spectra (Yuan, Deng, & Sun Reference Yuan, Deng and Sun2021), i.e. on the focal plane, all sources are able to disperse uniformly along the dispersion direction, which allows us to acquire the full spectrum of the entire field of view. However, the resulting mixing of the dispersion terms leads to contamination, which makes data processing more difficult and also further reduces the resolution (
![]() $R\sim200$
) and signal-to-noise ratio of the spectra. Moreover, the low metal abundance and weak spectral line features of VMP stars make most stellar parameter estimation methods inefficient for VMP stars. Both of these reasons increase the difficulty of using CSST spectral data to estimate stellar labels and identify VMP stars. So far, several studies have already shown the feasibility of estimating stellar parameters from very low-resolution spectra by using Gaia BP/RP spectra with a resolution of about 50 (Gavel et al. Reference Gavel, Andrae, Fouesneau, Korn and Sordo2022; Witten et al. Reference Witten2022). In this paper, we construct a two-dimensional CNN model composed of three convolutional layers and two fully connected layers. It can be an important supplement to the above methods and will be of great help for future studies of CSST. We use the spectral data obtained from LAMOST and reduce its resolution to
$R\sim200$
) and signal-to-noise ratio of the spectra. Moreover, the low metal abundance and weak spectral line features of VMP stars make most stellar parameter estimation methods inefficient for VMP stars. Both of these reasons increase the difficulty of using CSST spectral data to estimate stellar labels and identify VMP stars. So far, several studies have already shown the feasibility of estimating stellar parameters from very low-resolution spectra by using Gaia BP/RP spectra with a resolution of about 50 (Gavel et al. Reference Gavel, Andrae, Fouesneau, Korn and Sordo2022; Witten et al. Reference Witten2022). In this paper, we construct a two-dimensional CNN model composed of three convolutional layers and two fully connected layers. It can be an important supplement to the above methods and will be of great help for future studies of CSST. We use the spectral data obtained from LAMOST and reduce its resolution to
![]() $R\sim200$
to validate our model. MARCS synthetic spectra and other machine learning methods are also used to test whether our model has higher accuracy.
$R\sim200$
to validate our model. MARCS synthetic spectra and other machine learning methods are also used to test whether our model has higher accuracy.
The paper consists of five parts. The data selection and data pre-processing are introduced in Section 2. Then we describe the principles of CNN models and the structure of our model in Section 3. Section 4 presents the experiments and results. Section 5 discusses the comparison between CNN models and other machine learning algorithms. Brief conclusions can be seen in Section 6.
2. Data
The data used in the experiments in this paper are obtained from the LAMOST database and MARCS synthetic spectra. This section briefly introduces the data sources and selection process, as well as the pre-processing of the data.
2.1. LAMOST
2.1.1. Data introduction
In 2009, the Large Sky Area Multi-Object Fiber Spectroscopic Telescope (LAMOST) was successfully completed in China. As an exemplary representative among spectroscopic survey telescopes, LAMOST utilizes advanced thin mirror active optics and spliced mirror active optics technology, ingeniously combining a large field of view with a substantial aperture. This achievement has enabled LAMOST to provide an unparalleled understanding of the Milky Way and has significantly advanced the development of large-aperture astronomical telescopes in China (Li et al. Reference Li, Zeng, Wang, Du, Kong and Liao2022). Thanks to LAMOST’s enhanced observing capabilities and its ability to acquire large multi-fibre samples, the observation of medium or low-resolution spectra (
![]() $R\sim1\,000$
or 2 000) from LAMOST has made substantial contributions to the search for VMP stars (Wu et al. Reference Wu, Luo, Shi, Bai and Zhao2010; Li et al. Reference Li, Zhao, Christlieb, Wang, Wang, Zhang, Hou and Yuan2015, Reference Li, Tan and Zhao2018; Wang et al. Reference Wang, Huang, Yuan, Zhang, Xiang and Liu2022). To date, LAMOST has publicly released its eighth version of data, comprising an impressive collection of 10 633 515 low-resolution (
$R\sim1\,000$
or 2 000) from LAMOST has made substantial contributions to the search for VMP stars (Wu et al. Reference Wu, Luo, Shi, Bai and Zhao2010; Li et al. Reference Li, Zhao, Christlieb, Wang, Wang, Zhang, Hou and Yuan2015, Reference Li, Tan and Zhao2018; Wang et al. Reference Wang, Huang, Yuan, Zhang, Xiang and Liu2022). To date, LAMOST has publicly released its eighth version of data, comprising an impressive collection of 10 633 515 low-resolution (
![]() $R\sim 1\,800$
) spectra, covering 10 336 752 stars, 224 702 galaxies, and 72 061 quasars. The LAMOST stellar parameter pipeline (LASP) automatically derives the basic stellar atmospheric parameters for A, F, G, and K types of stars (Wu et al. Reference Wu, Du, Luo, Zhao, Yuan, Heavens, Starck and Krone-Martins2014), while the determination of M-type stars is carried out by LASP-M (Du et al. Reference Du2021).
$R\sim 1\,800$
) spectra, covering 10 336 752 stars, 224 702 galaxies, and 72 061 quasars. The LAMOST stellar parameter pipeline (LASP) automatically derives the basic stellar atmospheric parameters for A, F, G, and K types of stars (Wu et al. Reference Wu, Du, Luo, Zhao, Yuan, Heavens, Starck and Krone-Martins2014), while the determination of M-type stars is carried out by LASP-M (Du et al. Reference Du2021).
2.1.2. Data selection
In order to compare the ability of the model to estimate stellar parameters for VMP stellar spectra and non-VMP stellar spectra, and the accuracy of identifying VMP stars, we construct a dataset including VMP stars and non-VMP stars ([Fe/H]>-2.0) as positive and negative samples. To ensure the reliability of the stellar parameters, we combine two stellar parameter sources. For the VMP stellar sample, we choose the catalog containing 10 008 VMP stars obtained from LAMOST DR3 by Li et al. (Reference Li, Tan and Zhao2018) since it still provides researchers with the largest pool of bright and accurate VMP candidates to date. The stellar atmospheric parameters of these VMP stars are determined by line indices and by comparison with a grid of synthetic spectra, with metallicity ranging from −4.5 dex to −2.0 dex. For the negative sample dataset, we randomly select data with [Fe/H]>-2.0 from the LAMOST DR8 dataset that is recently made public to the world, where the stellar atmospheric parameters are determined by LASP (Wu et al. Reference Wu, Du, Luo, Zhao, Yuan, Heavens, Starck and Krone-Martins2014). To ensure that the accuracy of the stellar parameters of this dataset is comparable to that of the VMP stars dataset, we obtain 16 638 non-VMP stars with minor uncertainties and a signal-to-noise ratio larger than 10 at the g-band. In total, we construct a dataset including 26 646 stars. The resolution of all the spectral data is
![]() $R\sim 1\,800$
. The parameters of these stars range from 3 824.88 K<
$R\sim 1\,800$
. The parameters of these stars range from 3 824.88 K<
![]() $T_{\textrm{eff}}$
<8 866.15 K, 0.213 dex<
$T_{\textrm{eff}}$
<8 866.15 K, 0.213 dex<
![]() $\log$
g<4.897 dex, and −4.55 dex<[Fe/H]<0.699 dex. The errors of the parameters range from 0 K<
$\log$
g<4.897 dex, and −4.55 dex<[Fe/H]<0.699 dex. The errors of the parameters range from 0 K<
![]() $\sigma(T_{\textrm{eff}})$
<399 K, 0 dex<
$\sigma(T_{\textrm{eff}})$
<399 K, 0 dex<
![]() $\sigma(\log g)$
<0.94 dex, and 0 dex<
$\sigma(\log g)$
<0.94 dex, and 0 dex<
![]() $\sigma ([\textrm{Fe/H}])$
<0.4 dex. For subsequent model training and testing, we divide this dataset into a training set and a test set in the ratio of 7:3, including 18 652 and 7 994 stars, respectively. Fig. 1 depicts more clearly the distribution of the parameters in the training and test sets.
$\sigma ([\textrm{Fe/H}])$
<0.4 dex. For subsequent model training and testing, we divide this dataset into a training set and a test set in the ratio of 7:3, including 18 652 and 7 994 stars, respectively. Fig. 1 depicts more clearly the distribution of the parameters in the training and test sets.

Figure 1. The distribution of
![]() $T_{\textrm{eff}}$
(top panel),
$T_{\textrm{eff}}$
(top panel),
![]() $\log$
g (middle panel), and [Fe/H] (bottom panel) in the LAMOST training set and test set. The division of the training and test sets ensures the consistency of the data distribution.
$\log$
g (middle panel), and [Fe/H] (bottom panel) in the LAMOST training set and test set. The division of the training and test sets ensures the consistency of the data distribution.
To estimate the carbon abundance and identify CEMP stars in VMP stars, we need a dataset of VMP stars containing [C/Fe] labels. Since the VMP stars catalog mentioned above does not contain [C/Fe] values, Yuan et al. (Reference Yuan2020) cross-matched this catalog with Gaia DR2 and obtained a modified catalog including 9 690 stars with parameters derived by SEGUE Stellar Parameter Pipeline (SSPP, Lee et al. Reference Lee2008). We cross-match the VMP stars catalog (Li et al. Reference Li, Tan and Zhao2018) with the modified catalog (Yuan et al. Reference Yuan2020) and find 8 117 of 10 008 VMP stars with [C/Fe] labels. The range of the [C/Fe] labels is −2.018 dex<[C/Fe]<4.803 dex. For the aim of model training and testing, we divide the dataset into a training set and a test set in the ratio of 7:3, containing 5 681 and 2 436 stars, respectively.

Figure 2. The plots of spectra with resolution 1 800 (left) and 200 (right). Spectra with lower resolution have fewer characteristic points.
2.1.3. Data pre-processing
To obtain the data needed for the experiment, we preprocess the spectral data as follows:
-
(1) Resolution reduction:
Reduce the resolution of the spectra from
 $R\sim1\,800$
to
$R\sim1\,800$
to
 $R\sim200$
to simulate the low-resolution spectra acquired by CSST. The Coronagraph library provided in Python with the
$R\sim200$
to simulate the low-resolution spectra acquired by CSST. The Coronagraph library provided in Python with the
 $noise\_routines.construct\_lam()$
and
$noise\_routines.construct\_lam()$
and
 $downbin\_spec()$
functions can bring the data down to the resolution we need and output the degraded flux.
$downbin\_spec()$
functions can bring the data down to the resolution we need and output the degraded flux.Fig. 2 shows a comparison of the spectra with resolution
 $R\sim1\,800$
and
$R\sim1\,800$
and
 $R\sim200$
. Fewer features in the lower resolution spectra make the stellar parameter estimation more difficult.
$R\sim200$
. Fewer features in the lower resolution spectra make the stellar parameter estimation more difficult. -
(2) Interpolation:
Interpolate the flux data to the range of 4 000Å to 8 095Å, ensuring that the data is sampled at the same wavelengths. This results in a consistent flux range for all spectra and reduces the effect of noise at both ends of the spectrum.
-
(3) Normalization:
The flux values are then normalized by a linear function (Min-Max scaling), which can achieve equal scaling of the original data to convert the flux to the range of [0, 1], as follows.
(1) \begin{equation} Flux_{norm}=\frac{Flux-Flux_{\min}}{Flux_{\max}-Flux_{\min}},\end{equation}
\begin{equation} Flux_{norm}=\frac{Flux-Flux_{\min}}{Flux_{\max}-Flux_{\min}},\end{equation}
Finally, we obtain spectral data with 410 feature points. Section 4.1 shows the results of estimating stellar labels and identifying VMP stars in the LAMOST dataset using our CNN model.
2.2. MARCS dataset
To further test the validity of the CNN model for estimating stellar parameters, we use the MARCS synthetic spectra (Gustafsson et al. Reference Gustafsson, Edvardsson, Eriksson, Jørgensen, Nordlund and Plez2008). It is a grid of about
![]() $10^{4}$
model atmospheres with nearly 52 000 stellar spectra containing F, G, and K types of stars. This grid of one-dimensional LTE model atmospheres can be combined with atomic and molecular spectral line data and software to generate stellar spectra, which has been widely used in a variety of studies (Roederer et al. Reference Roederer, Preston, Thompson, Shectman, Sneden, Burley and Kelson2014; Lu et al. Reference Lu, Li, Lin and Qiu2018; Reggiani et al. Reference Reggiani2019; VandenBerg et al. Reference VandenBerg, Edvardsson, Casagrande and Ferguson2021; Salsi et al. Reference Salsi, Nardetto, Plez and Mourard2022).
$10^{4}$
model atmospheres with nearly 52 000 stellar spectra containing F, G, and K types of stars. This grid of one-dimensional LTE model atmospheres can be combined with atomic and molecular spectral line data and software to generate stellar spectra, which has been widely used in a variety of studies (Roederer et al. Reference Roederer, Preston, Thompson, Shectman, Sneden, Burley and Kelson2014; Lu et al. Reference Lu, Li, Lin and Qiu2018; Reggiani et al. Reference Reggiani2019; VandenBerg et al. Reference VandenBerg, Edvardsson, Casagrande and Ferguson2021; Salsi et al. Reference Salsi, Nardetto, Plez and Mourard2022).
We select 9 644 data from MARCS for the experiment. The range of the stellar parameters is 2 500 K<
![]() $T_{\textrm{eff}}$
<8 000 K, −0.5 dex<
$T_{\textrm{eff}}$
<8 000 K, −0.5 dex<
![]() $\log$
g<5.5 dex, −5 dex<[Fe/H]<−1 dex, and the step size of the parameters is 2 500 K for
$\log$
g<5.5 dex, −5 dex<[Fe/H]<−1 dex, and the step size of the parameters is 2 500 K for
![]() $T_{\textrm{eff}}$
, 0.5 dex for
$T_{\textrm{eff}}$
, 0.5 dex for
![]() $\log$
g, and 0.25 dex for [Fe/H]. We perform the same interpolation and normalization operations on the data and obtain spectral data with 746 feature points. The dataset is divided into a training set and a test in the ratio of 7:3, including 6 750 and 2 894 stars, respectively. Section 4.3 shows the results of estimating stellar parameters of the MARCS synthetic spectra using the CNN model.
$\log$
g, and 0.25 dex for [Fe/H]. We perform the same interpolation and normalization operations on the data and obtain spectral data with 746 feature points. The dataset is divided into a training set and a test in the ratio of 7:3, including 6 750 and 2 894 stars, respectively. Section 4.3 shows the results of estimating stellar parameters of the MARCS synthetic spectra using the CNN model.
3. Methodology
3.1. Introduction to the convolutional neural network (CNN)
In this paper, we construct a CNN model and test its performance in estimating stellar labels for low-resolution (
![]() $R\sim200$
) spectra and identifying VMP stars. This can enable us to better handle low-resolution spectra of CSST in the future and search for VMP stars.
$R\sim200$
) spectra and identifying VMP stars. This can enable us to better handle low-resolution spectra of CSST in the future and search for VMP stars.
The concept of deep learning originated from the study of artificial neural networks and was proposed by Hinton (Reference Hinton2008). CNN (Lecun et al. Reference Lecun, Bottou, Bengio and Haffner1998) is a typical supervised model of deep learning that has been widely applied to various fields in recent years. It is the first actual multilayer structure learning algorithm that uses spatial relative relationships to reduce the number of parameters to improve training performance. It adds a feature part to the original multilayer neural network; i.e. a convolutional layer and a pooling layer (dimensionality reduction layer) are added before the fully connected layer, and the network selects the features itself. CNN is a deep feedforward neural network that is widely used for supervised learning problems in image processing and natural language processing, such as computer vision (Krizhevsky et al. Reference Krizhevsky, Sutskever and Hinton2012), semantic segmentation (Ronneberger, Fischer, & Brox Reference Ronneberger, Fischer and Brox2015), object recognition (Redmon et al. Reference Redmon, Divvala, Girshick and Farhadi2016), etc.
While the CNN model can directly process one-dimensional sequences such as spectral data, most current CNN models demonstrate their power in processing two-dimensional image data. In the LAMOST dataset, the length of the 1D spectral data (
![]() $1\times410$
) we obtain is long, and collapsing it into 2D data (
$1\times410$
) we obtain is long, and collapsing it into 2D data (
![]() $21\times21$
) to simulate image data can perform cross-correlation operations and extract spectral features better and faster, thus speed up the network learning speed and parameter optimization efficiency. For MARCS spectral data (
$21\times21$
) to simulate image data can perform cross-correlation operations and extract spectral features better and faster, thus speed up the network learning speed and parameter optimization efficiency. For MARCS spectral data (
![]() $1\times746$
), we also collapse them into a two-dimensional matrix (
$1\times746$
), we also collapse them into a two-dimensional matrix (
![]() $28\times28$
) as the input to the CNN model. The following is a brief description of the structure and principles of the 2D CNN.
$28\times28$
) as the input to the CNN model. The following is a brief description of the structure and principles of the 2D CNN.
A complete CNN model must include convolutional layers, non-linear activation functions, pooling layers, and fully connected layers.
-
(1) Convolutional layer:
The convolutional layer is the core layer for establishing the CNN model, which can act as a filter and reduce the number of parameters. The discrete form of two-dimensional convolution is used.
Given a figure
 $\textbf{X}\in \textbf{R}^{M\times N}$
and a convolutional kernel
$\textbf{X}\in \textbf{R}^{M\times N}$
and a convolutional kernel
 $\textbf{W}\in\textbf{R}^{U\times V}$
. In general, U<M, V<N. The convolution between them can be denoted as (2)
$\textbf{W}\in\textbf{R}^{U\times V}$
. In general, U<M, V<N. The convolution between them can be denoted as (2) \begin{equation} \textbf{Y}=\textbf{W}*\textbf{X},\end{equation}
(3)
\begin{equation} \textbf{Y}=\textbf{W}*\textbf{X},\end{equation}
(3) \begin{equation} y_{ij}=\sum_{u=1}^{U}\sum_{v=1}^{V}w_{uv}x_{i-u+1,j-v+1}.\end{equation}
\begin{equation} y_{ij}=\sum_{u=1}^{U}\sum_{v=1}^{V}w_{uv}x_{i-u+1,j-v+1}.\end{equation}
An example of the convolution process is shown in Fig. 3. A two-dimensional input array (
 $3\times3$
) performs a mutual correlation operation with a two-dimensional convolutional kernel array (
$3\times3$
) performs a mutual correlation operation with a two-dimensional convolutional kernel array (
 $2\times2$
), resulting in a two-dimensional array (
$2\times2$
), resulting in a two-dimensional array (
 $2\times2$
). The convolution kernel slides over the input array from left to right and top to bottom.
$2\times2$
). The convolution kernel slides over the input array from left to right and top to bottom.The convolutional layer extracts features from local regions, and different convolutional kernels are equivalent to various feature extractors. Based on the standard definition of convolution, strides and zero padding of the convolutional kernel can be introduced to increase the diversity of convolution. Strides refer to the number of steps each convolutional kernel moves when performing a convolutional operation. Set stride=k, which means convolving k rows and k columns from left to right and from top to bottom. Zero padding represents adding zeros to the outer side of the image. Setting padding=d means supplementing d layers of zeros around the input vector. Zero padding allows us to obtain more detailed feature information and control the network structure.

Figure 3. Convolution process.
After the convolutional layer, an activation function is usually added as a non-linear factor, which can deal with problems that cannot be solved by linear models and enhance the ability of the network to interpret the model. A commonly used activation function is ReLU (Equation (4)). It has a small computational effort, and can effectively alleviate the gradient disappearance and gradient explosion problem because its derivative is maintained at 1.
(4) \begin{equation} f(x)=\max\!(0,x). \end{equation}
\begin{equation} f(x)=\max\!(0,x). \end{equation}
-
(2) Pooling layer:
The pooling layer (subsampling layer) is designed to reduce the number of features in the network, thereby reducing the number of parameters and avoiding overfitting. Local translation invariance is an essential property of pooling layers, which indicates that pooling is approximately invariant in its representation of the input when a small number of translations are performed on the input. Max-pooling is the most commonly used which means extracting the maximum value within the neighbourhood (see Fig. 4). It can reduce the offset of the estimated mean value caused by the parameter error of the convolutional layer, and retain more texture information.
-
(3) Fully connected layer:
The purpose of the fully connected layer is to connect the results of the last pooling layer to the output nodes and map the feature representation learned by the network to the label space of the samples. It acts as the ‘classifier’ of the network. It is important to note that when encoding the model, the last pooling layer needs to be flattened to a one-dimensional vector before connecting to the fully connected layer.
CNN extracts high-level semantic information from the input data gradually through a series of operations in these layers, formalizes the target task as an objective function, and generates the predicted values. This process is called Forward Propagation. The parameter optimization in the model is performed by Back Propagation. By calculating the loss between the predicted values and the true values, the CNN feeds the loss from the previous layer to the next layer, calculates the gradient of the loss on the parameters of each layer, and updates the corresponding parameters. Once all the parameters have completed one round of updates, the feedforward operation is performed again. This process is repeated iteratively until the model converges.

Figure 4. Max-pooling process.
3.2. The method of preventing overfitting
When the number of parameters in a model is large compared to the available training samples, overfitting can occur. This is manifested by high prediction accuracy on the training set and a significant decrease in accuracy on the test set.
The advent of dropout (Hinton et al. Reference Hinton, Srivastava, Krizhevsky, Sutskever and Salakhutdinov2012) has greatly alleviated this problem. During training, each neuron is retained with probability p and stops working with probability
![]() $1-p$
, and a different set of neurons is retained for each forward propagation. This approach reduces the reliance of the model on certain local features and has better generalization performance.
$1-p$
, and a different set of neurons is retained for each forward propagation. This approach reduces the reliance of the model on certain local features and has better generalization performance.

Figure 5. The structure of the proposed CNN model. The 1D spectral data is transformed into a 2D image-like matrix and is then input into the neural network consisting of three convolutional layers, three max-pooling layers, and two fully connected layers to extract the stellar parameters.
Another way is to add Batch Normalization (BN, Ioffe and Szegedy Reference Ioffe and Szegedy2015) layers after the convolutional and fully connected layers. During the training process of neural networks, parameter changes can lead to unstable distribution of activation values, which hinders the ability of subsequent layers to learn useful features. In addition to normalizing the input data of each layer and promoting a stable distribution of activation values, the BN layer can accelerate the convergence thus preventing model overfitting.
3.3. The structure of the proposed CNN model
After parameter tuning of the model, the final CNN model we construct is shown in Fig. 5. The convolutional layers filter the processed 2D spectra using a filter of size
![]() $9\times9$
, and the input is filled with zero space on the boundary so that the size of the output layer of the convolution is equal to the size of the input layer. The
$9\times9$
, and the input is filled with zero space on the boundary so that the size of the output layer of the convolution is equal to the size of the input layer. The
![]() $9\times9$
convolution kernel can acquire a larger field of perception and therefore can capture more characteristics. The kernels of each convolutional layer are 64, 128, and 256, respectively. Each convolutional layer is followed by a max-pooling layer of size
$9\times9$
convolution kernel can acquire a larger field of perception and therefore can capture more characteristics. The kernels of each convolutional layer are 64, 128, and 256, respectively. Each convolutional layer is followed by a max-pooling layer of size
![]() $2\times2$
with a step size set to two. Afterwards, two fully connected layers with 128 and 64 channels are added to combine the features previously extracted by the model. To prevent overfitting, a dropout layer can be set after each fully connected layer with a value of 0.2 to avoid the over-regularization of the model. BN and ReLU activation function layers are added between each layer to reduce overfitting and enhance the expressiveness of the model. The final output layer is the predicted values derived from the model.
$2\times2$
with a step size set to two. Afterwards, two fully connected layers with 128 and 64 channels are added to combine the features previously extracted by the model. To prevent overfitting, a dropout layer can be set after each fully connected layer with a value of 0.2 to avoid the over-regularization of the model. BN and ReLU activation function layers are added between each layer to reduce overfitting and enhance the expressiveness of the model. The final output layer is the predicted values derived from the model.
3.4. Experimental procedure
To test whether our model can better estimate stellar parameters and identify VMP stars, we conduct experiments using Python 3.8 on NVIDIA GeForce RTX GPU. As mentioned in Section 2, both the LAMOST dataset and the MARCS dataset are divided into training and testing sets in the ratio of 7:3 to train the model and test its effectiveness. The training and testing process is performed on
![]() $T_{\textrm{eff}}$
,
$T_{\textrm{eff}}$
,
![]() $\log$
g, [Fe/H], and [C/Fe] respectively.
$\log$
g, [Fe/H], and [C/Fe] respectively.
We set a total of 1 000 epochs for model training, and L1loss (MAE, Equation (5)) is used as the loss function. The training process is performed in batches, with the size of each batch set to 128. The Adam algorithm (Kingma and Ba Reference Kingma and Ba2014), with an initial learning rate set to 0.001, is chosen to be the optimizer, which is an extension of the stochastic gradient descent method. Adam optimizer can speed up convergence by adapting the learning rate, making it well-suited for deep learning problems. An early stopping mechanism is set when the loss function no longer decreases beyond 250 epochs, which can effectively prevent the model from overfitting.
3.4.1. Evaluation metrics
We use three main evaluation metrics to test the effectiveness of the model in estimating stellar parameters, Mean Absolute Error (MAE, Equation (5)), Standard Deviation (STD, Equation (6)), and R squared (
![]() $R^2$
, Equation (7)).
$R^2$
, Equation (7)).
Suppose that N is the number of samples contained in the test set, y denotes the true values, and
![]() $\hat y$
denotes the predicted values derived by the proposed model. Let
$\hat y$
denotes the predicted values derived by the proposed model. Let
![]() $e_{i}$
be
$e_{i}$
be
![]() $y_{i}-\hat y_{i}$
, and
$y_{i}-\hat y_{i}$
, and
![]() $\bar e_{i}$
be the average value of
$\bar e_{i}$
be the average value of
![]() $e_{i}$
.
$e_{i}$
.
-
(1) Mean absolute error (MAE): MAE is a loss function used in regression models, which can express the fitting ability of the model more intuitively.
(5) \begin{equation} MAE(y,\hat y)=\frac{1}{N}\sum_{i=0}^{N-1}|y_{i}-\hat y_{i}|. \end{equation}
\begin{equation} MAE(y,\hat y)=\frac{1}{N}\sum_{i=0}^{N-1}|y_{i}-\hat y_{i}|. \end{equation}
-
(2) Standard deviation (STD): Standard deviation reflects the degree of dispersion of a dataset.
(6) \begin{equation} STD(y,\hat y)=\sqrt {\frac{1}{N}\sum_{i=1}^{N}(e_{i}-\bar e_{i})^2}. \end{equation}
\begin{equation} STD(y,\hat y)=\sqrt {\frac{1}{N}\sum_{i=1}^{N}(e_{i}-\bar e_{i})^2}. \end{equation}
-
(3) R squared (
 $R^2$
): The numerator is the error between the predicted value and the true value, and the denominator is understood as the dispersion of the true value. The division of the two can eliminate the effect of the dispersion of the true value. The closer
$R^2$
): The numerator is the error between the predicted value and the true value, and the denominator is understood as the dispersion of the true value. The division of the two can eliminate the effect of the dispersion of the true value. The closer
 $R^2$
is to 1, the better the model fits the data. (7)
$R^2$
is to 1, the better the model fits the data. (7) \begin{equation} R^2(y,\hat y)=1-\frac{\sum\!(y-\hat y)^2}{\sum\!(y-\bar y)^2}. \end{equation}
\begin{equation} R^2(y,\hat y)=1-\frac{\sum\!(y-\hat y)^2}{\sum\!(y-\bar y)^2}. \end{equation}
Three other metrics can be used to test the effectiveness of the model in classifying stars, precision (Equation (8)), recall (Equation (9)), and accuracy rate (Equation (10)).
-
(1) True Positive (TP): VMP stars predicted as VMP stars.
-
(2) True Negative (TN): Common stars predicted as common stars.
-
(3) False Positive (FP): Common stars predicted as VMP stars.
-
(4) False Negative (FN): VMP stars predicted as common stars.
4. Results
In this section, we show the parameter estimation and classification results in the dataset described in Section 2 using the proposed CNN model.
Table 1. The prediction results of the three fundamental atmospheric parameters on the test set including 7 994 stars using the proposed CNN model.

4.1. Estimating stellar parameters and identifying VMP stars using the LAMOST dataset
We start our experiments with a total of 26 646 stars, including both VMP and non-VMP stars. The prediction results obtained on the test set are displayed in Table 1. For
![]() $T_{\textrm{eff}}$
, MAE=99.40 K, STD=183.33 K,
$T_{\textrm{eff}}$
, MAE=99.40 K, STD=183.33 K,
![]() $R^2$
=0.93; for
$R^2$
=0.93; for
![]() $\log$
g, MAE=0.22 dex, STD=0.35 dex,
$\log$
g, MAE=0.22 dex, STD=0.35 dex,
![]() $R^2$
=0.84; and for [Fe/H], MAE=0.14 dex, STD=0.26 dex,
$R^2$
=0.84; and for [Fe/H], MAE=0.14 dex, STD=0.26 dex,
![]() $R^2$
=0.94. We can see that the model is able to fit the three stellar parameters well and fits
$R^2$
=0.94. We can see that the model is able to fit the three stellar parameters well and fits
![]() $T_{\textrm{eff}}$
and [Fe/H] better than
$T_{\textrm{eff}}$
and [Fe/H] better than
![]() $\log$
g. Simultaneously, we plot the scatter density plots of the predicted and true values on the test set (see the left column of Fig. 6). The green dashed line indicates the first-degree polynomial fit curve of the predicted and true values, and the red line is the image of
$\log$
g. Simultaneously, we plot the scatter density plots of the predicted and true values on the test set (see the left column of Fig. 6). The green dashed line indicates the first-degree polynomial fit curve of the predicted and true values, and the red line is the image of
![]() $predicted\,value=true\,value$
. The closer the green dashed line is to the red solid line, the better the prediction results. From the figure, we can state that the fitting results of
$predicted\,value=true\,value$
. The closer the green dashed line is to the red solid line, the better the prediction results. From the figure, we can state that the fitting results of
![]() $T_{\textrm{eff}}$
and [Fe/H] are very close to the line of
$T_{\textrm{eff}}$
and [Fe/H] are very close to the line of
![]() $predicted\,value=true\,value$
, while the results of
$predicted\,value=true\,value$
, while the results of
![]() $\log$
g are relatively poor, which shows that the proposed CNN model has a better prediction for
$\log$
g are relatively poor, which shows that the proposed CNN model has a better prediction for
![]() $T_{\textrm{eff}}$
and [Fe/H], while
$T_{\textrm{eff}}$
and [Fe/H], while
![]() $\log$
g is relatively more difficult to estimate. In addition, the right column of Fig. 6 illustrates the variation of the residuals (true value-predicted value) with respect to the true values. The red line can show us more explicitly the turbulence of the residuals around zero.
$\log$
g is relatively more difficult to estimate. In addition, the right column of Fig. 6 illustrates the variation of the residuals (true value-predicted value) with respect to the true values. The red line can show us more explicitly the turbulence of the residuals around zero.

Figure 6. The left panel shows the true and predicted values of
![]() $T_{\textrm{eff}}$
(top side),
$T_{\textrm{eff}}$
(top side),
![]() $\log$
g (centre), and [Fe/H] (bottom side) obtained on the LAMOST test set. The red solid line is the plot of the function
$\log$
g (centre), and [Fe/H] (bottom side) obtained on the LAMOST test set. The red solid line is the plot of the function
![]() $y=x$
. The green dashed line represents the first-degree polynomial fit curve of the predicted values to the true values. The right panel are their residuals against the true values.
$y=x$
. The green dashed line represents the first-degree polynomial fit curve of the predicted values to the true values. The right panel are their residuals against the true values.
Furthermore, experiments can be conducted on 10 008 VMP stars and 16 638 non-VMP stars separately to test whether the CNN model has a significant difference in measuring the parameters of VMP stars and those of non-VMP stars. The prediction results on the two test sets involving 3 003 VMP stars and 4 992 non-VMP stars are listed in Table 2. Briefly, the MAE values for the predicted and true values are 118.26 K for
![]() $T_{\textrm{eff}}$
, 0.31 dex for
$T_{\textrm{eff}}$
, 0.31 dex for
![]() $\log$
g, and 0.17 dex for [Fe/H] for the VMP stars, and 75.84 K for
$\log$
g, and 0.17 dex for [Fe/H] for the VMP stars, and 75.84 K for
![]() $T_{\textrm{eff}}$
, 0.11 dex for
$T_{\textrm{eff}}$
, 0.11 dex for
![]() $\log$
g, and 0.08 dex for [Fe/H] for the non-VMP stars. We can clearly demonstrate that the proposed CNN model is much better at deriving the parameters of non-VMP stars than VMP stars, which specifies the necessity to develop a model that can effectively measure the parameters of VMP stars.
$\log$
g, and 0.08 dex for [Fe/H] for the non-VMP stars. We can clearly demonstrate that the proposed CNN model is much better at deriving the parameters of non-VMP stars than VMP stars, which specifies the necessity to develop a model that can effectively measure the parameters of VMP stars.
With the results obtained above, we can conclude that the proposed CNN model has good accuracy in estimating stellar atmospheric parameters, which suggests that we can use the method for VMP star identification. By analysing the metallicity of the total dataset containing VMP and non-VMP stars, setting the label of VMP stars with [Fe/H]<-2.0 to 1 and the label of non-VMP stars with [Fe/H]>-2.0 to 0, we find 2 999 VMP stars and 4 995 non-VMP stars in the test set. The confusion matrix of the true and predicted values is shown in Fig. 7. Then we can calculate the precision, recall, and accuracy of the proposed CNN model for predicting VMP stars (see Table 3). Among the 2 966 stars predicted to be VMP stars, 2 811 stars are true VMP stars, with a precision rate of 94.77% (2 811/2 966); among the test set including 2 999 VMP stars, 2 811 stars are correctly predicted to be VMP stars, with a recall rate of 93.73% (2 811/2 999). Overall, our CNN model is also able to classify VMP stars and non-VMP stars well, with an accuracy of 95.70%.
4.2. Estimating [C/Fe] and identifying CEMP stars using the VMP stars dataset
We perform experiments using the dataset obtained by cross-matching in Section 2.1, which includes 8 117 VMP stars with [C/Fe] values. The best prediction results obtained on the test set are MAE=0.26 dex, STD=0.38 dex, and
![]() $R^2$
=0.64. We also plot the scatter density plots of the predicted and true values of [C/Fe] and the residuals (Fig. 8). It can be seen from the figures that the proposed CNN model is also able to predict [C/Fe] well. By analysing the prediction results, we find that 240 stars are correctly predicted as CEMP stars, with a precision rate of 75.7% (240/317). The total accuracy rate is around 87.56%, indicating our model has good performance in classifying CEMP stars.
$R^2$
=0.64. We also plot the scatter density plots of the predicted and true values of [C/Fe] and the residuals (Fig. 8). It can be seen from the figures that the proposed CNN model is also able to predict [C/Fe] well. By analysing the prediction results, we find that 240 stars are correctly predicted as CEMP stars, with a precision rate of 75.7% (240/317). The total accuracy rate is around 87.56%, indicating our model has good performance in classifying CEMP stars.
4.3. Estimating stellar parameters using the MARCS synthetic spectra including 9 644 stars
This section shows the outcomes of predicting the stellar parameters of the 9 644 MARCS spectra using the CNN model. The results on the test set of 2 894 stars are shown in Table 4. For
![]() $T_{\textrm{eff}}$
, MAE=53.03 K, STD=80.78 K,
$T_{\textrm{eff}}$
, MAE=53.03 K, STD=80.78 K,
![]() $R^2$
=0.998; for
$R^2$
=0.998; for
![]() $\log$
g, MAE=0.056 dex, STD=0.097 dex,
$\log$
g, MAE=0.056 dex, STD=0.097 dex,
![]() $R^2$
=0.995; and for [Fe/H], MAE=0.047 dex, STD=0.093 dex,
$R^2$
=0.995; and for [Fe/H], MAE=0.047 dex, STD=0.093 dex,
![]() $R^2$
=0.995. Compared to the errors obtained using the LAMOST dataset, the results for the synthetic spectra are much smaller, and in particular the
$R^2$
=0.995. Compared to the errors obtained using the LAMOST dataset, the results for the synthetic spectra are much smaller, and in particular the
![]() $R^2$
values very close to 1 indicate a good fit of our model. The scatter density plots between the true and predicted values can be seen in Fig. 9, revealing there is only a little deviation between them.
$R^2$
values very close to 1 indicate a good fit of our model. The scatter density plots between the true and predicted values can be seen in Fig. 9, revealing there is only a little deviation between them.
Table 2. The prediction results of the three fundamental atmospheric parameters on VMP star test set and non-VMP stars test set.

Table 3. The results of classifying the VMP stars on test set including 7 994 stars.

Figure 7. The confusion matrix of classifying the VMP stars on test set including 7 994 stars.

Figure 8. The left panel shows the true and predicted values of [C/Fe] obtained on the test set including 2 436 stars. The red solid line is the plot of the function
![]() $y=x$
. The green dashed line represents the first-degree polynomial fit curve of the predicted values to the true values. The right panel is the residual against the true values.
$y=x$
. The green dashed line represents the first-degree polynomial fit curve of the predicted values to the true values. The right panel is the residual against the true values.
Table 4. The prediction results of the three fundamental atmospheric parameters on MARCS test set including 2 894 stars.


Figure 9. The true and predicted values of
![]() $T_{\textrm{eff}}$
(top panel),
$T_{\textrm{eff}}$
(top panel),
![]() $\log$
g (middle panel), and [Fe/H] (bottom panel) on MARCS test set including 2 894 stars.
$\log$
g (middle panel), and [Fe/H] (bottom panel) on MARCS test set including 2 894 stars.
5. Discussion
To further verify the effectiveness of the proposed CNN model, we introduce Random Forest (RF) and Support Vector Machine (SVM) algorithms to make comparisons. The dataset used in the comparison experiment is the same as that used in Section 4.1, which includes a total of 26 646 spectral data and fundamental stellar parameters of the VMP stars and non-VMP stars. The training and test sets are also selected in line with the previous experiments to test whether the CNN model outperforms other algorithms.
-
1. RF:
The RF algorithm (Breiman Reference Breiman2001) is a specific implementation of the bagging method, where multiple decision trees are trained and all results are combined. For regression problems, the prediction of the Random Forest is the average of all decision tree results. The advantage that this method can operate efficiently on large data sets and is not prone to overfitting has made it widely used in astronomical data analysis (Wang et al. Reference Wang, Zhen-Ping, Li-Li, Hui-Fen, Jing-Chang and Yu-De2019; Mahmudunnobe et al. Reference Mahmudunnobe2021).
The RandomForestRegressor function in the
 $Scikit-learn$
package in Python is imported to carry out experiments. To construct the optimal RF model, we tune the parameters for the number of decision trees (
$Scikit-learn$
package in Python is imported to carry out experiments. To construct the optimal RF model, we tune the parameters for the number of decision trees (
 $n\_estimators$
) and the maximum number of features (
$n\_estimators$
) and the maximum number of features (
 $max\_features$
). The GridSearchCV function in Python provides us with a convenient method to automatically derive the optimal parameters and the score. The specific parameter-tuning process is detailed in the Appendix. The MAE values on the test set are, 122.57 K for
$max\_features$
). The GridSearchCV function in Python provides us with a convenient method to automatically derive the optimal parameters and the score. The specific parameter-tuning process is detailed in the Appendix. The MAE values on the test set are, 122.57 K for
 $T_{\textrm{eff}}$
, 0.30 dex for
$T_{\textrm{eff}}$
, 0.30 dex for
 $\log$
g, and 0.26 dex for [Fe/H]. The precision, recall, and accuracy of classifying the VMP stars are 93.12%, 74.02%, and 88.20%, respectively.
$\log$
g, and 0.26 dex for [Fe/H]. The precision, recall, and accuracy of classifying the VMP stars are 93.12%, 74.02%, and 88.20%, respectively. -
2. SVM:
SVM (Cortes and Vapnik Reference Cortes and Vapnik1995) is a binary classification model, which is essentially an optimization algorithm for solving convex quadratic programming problems. In addition to classification problems, SVM can also be applied to regression problems (SVR), which centres on finding a regression plane such that all data in a set are closest to this plane. For non-linear regression problems, SVM can introduce a kernel function that turns the problem into an approximate linear regression problem.
To construct the optimal regression model, we use the SVR function of the
 $Scikit-learn$
library in Python, utilizing the third-degree polynomial kernel function for training and tuning two relatively important parameters C and gamma. C is the penalty factor of the target function and gamma is the coefficient of the kernel function. The tuning process is detailed in the Appendix. By using the optimal SVM model, the MAE values obtained on the test set are, 122.07 K for
$Scikit-learn$
library in Python, utilizing the third-degree polynomial kernel function for training and tuning two relatively important parameters C and gamma. C is the penalty factor of the target function and gamma is the coefficient of the kernel function. The tuning process is detailed in the Appendix. By using the optimal SVM model, the MAE values obtained on the test set are, 122.07 K for
 $T_{\textrm{eff}}$
, 0.26 dex for
$T_{\textrm{eff}}$
, 0.26 dex for
 $\log$
g, and 0.23 dex for [Fe/H]. The precision, recall, and accuracy of classifying the VMP stars are 95.37%, 77.66%, and 90.21%, respectively.
$\log$
g, and 0.23 dex for [Fe/H]. The precision, recall, and accuracy of classifying the VMP stars are 95.37%, 77.66%, and 90.21%, respectively.
The specific results of the comparison experiments are shown in Table 5. The MAE, STD, and
![]() $R^2$
values for estimating stellar parameters using the three machine learning methods are included. We can see that CNN estimates stellar parameters with higher accuracy than the other two methods from all three metrics.
$R^2$
values for estimating stellar parameters using the three machine learning methods are included. We can see that CNN estimates stellar parameters with higher accuracy than the other two methods from all three metrics.
Table 5. The prediction results of the three fundamental atmospheric parameters on the test set including 7,994 stars using RF, SVM, and CNN methods.

We also draw a bar chart of the results of identifying VMP stars with these three methods. From Fig. 10, we can clearly demonstrate that although the precision of the three methods is comparable, the recall rates of RF and SVM are much lower than that of the CNN, which indicates that the probability of VMP stars being predicted as common stars can be greatly reduced using the proposed CNN model. In terms of accuracy, the CNN model is also able to better classify VMP stars and common stars.

Figure 10. The bar chart of the precision rate, recall rate, and accuracy of identifying VMP stars using RF (green), SVM (blue), and CNN (orange).
Additionally, Wang et al. (Reference Wang, Huang, Yuan, Zhang, Xiang and Liu2022) carried out a fairly similar exercise to ours using neural networks. Similarly, they utilized the VMP stars catalog from Li et al. (Reference Li, Tan and Zhao2018) as a comparative reference. Employing their own method, they determined the [Fe/H] values within the sample. Their investigation yielded Standard Deviation (
![]() $\sigma$
) values of 0.299 dex and 0.219 dex for two kinds of [Fe/H] values ([Fe/H]-NN-PASTEL and [Fe/H]-NN-VMP, refer to Figure 21 in their study). In contrast to our VMP star results with an STD value of 0.24 dex (as shown in Table 2), the error of their improved [Fe/H] values ([Fe/H]-NN-VMP) is slightly better than ours, but the spectral resolution used by us is extremely low at only 200, which is much lower than the LAMOST low-resolution spectra (R
$\sigma$
) values of 0.299 dex and 0.219 dex for two kinds of [Fe/H] values ([Fe/H]-NN-PASTEL and [Fe/H]-NN-VMP, refer to Figure 21 in their study). In contrast to our VMP star results with an STD value of 0.24 dex (as shown in Table 2), the error of their improved [Fe/H] values ([Fe/H]-NN-VMP) is slightly better than ours, but the spectral resolution used by us is extremely low at only 200, which is much lower than the LAMOST low-resolution spectra (R
![]() $\sim$
1 800) employed by them. Consequently, it can be inferred that our model capably estimates stellar parameters even for spectra possessing a resolution as low as 200.
$\sim$
1 800) employed by them. Consequently, it can be inferred that our model capably estimates stellar parameters even for spectra possessing a resolution as low as 200.
6. Conclusion
This paper investigates the effectiveness of the CNN model in estimating stellar parameters for low-resolution spectra (
![]() $R\sim200$
) and the ability to identify VMP stars. We constructed a two-dimensional CNN model consisting of three convolutional and two fully connected layers and selected a catalog including 10 008 VMP stars and 16 638 non-VMP stars for our experiments. The resolution of these stellar spectra was scaled down from
$R\sim200$
) and the ability to identify VMP stars. We constructed a two-dimensional CNN model consisting of three convolutional and two fully connected layers and selected a catalog including 10 008 VMP stars and 16 638 non-VMP stars for our experiments. The resolution of these stellar spectra was scaled down from
![]() $R\sim1\,800$
to
$R\sim1\,800$
to
![]() $R\sim200$
to match the CSST’s spectral data, and then the spectral data with 410 features could be derived through interpolation and normalization. By collapsing these one-dimensional spectra into two-dimensional matrices and feeding them into the CNN model, we successfully estimated corresponding stellar parameters. The results show that for
$R\sim200$
to match the CSST’s spectral data, and then the spectral data with 410 features could be derived through interpolation and normalization. By collapsing these one-dimensional spectra into two-dimensional matrices and feeding them into the CNN model, we successfully estimated corresponding stellar parameters. The results show that for
![]() $T_{\textrm{eff}}$
, MAE=99.40 K, STD=183.33 K,
$T_{\textrm{eff}}$
, MAE=99.40 K, STD=183.33 K,
![]() $R^2$
=0.93; for
$R^2$
=0.93; for
![]() $\log$
g, MAE=0.22 dex, STD=0.35 dex,
$\log$
g, MAE=0.22 dex, STD=0.35 dex,
![]() $R^2$
=0.84; for [Fe/H], MAE=0.14 dex, STD=0.26 dex,
$R^2$
=0.84; for [Fe/H], MAE=0.14 dex, STD=0.26 dex,
![]() $R^2$
=0.94; and for [C/Fe], MAE=0.26 dex, STD=0.37 dex,
$R^2$
=0.94; and for [C/Fe], MAE=0.26 dex, STD=0.37 dex,
![]() $R^2$
=0.64. While the CNN model exhibited slightly diminished performance in deriving parameters of the VMP stars compared to non-VMP stars, it was still able to distinguish VMP stars with a precision rate of 94.77%, a recall rate of 93.73% and an accuracy of 95.70%. Impressively, the model also effectively identified CEMP stars in VMP stars, achieving an accuracy of 87.56%. Moreover, we illustrated the superiority of the CNN model over the RF and SVM algorithms in that it can predict stellar parameters with higher accuracy and identify VMP stars better, with a recall rate nearly 20% higher than the other two approaches. The efficiency of the CNN model was also tested on the MARCS synthetic spectra, and the MAE values obtained on the test set were 53.03 K for
$R^2$
=0.64. While the CNN model exhibited slightly diminished performance in deriving parameters of the VMP stars compared to non-VMP stars, it was still able to distinguish VMP stars with a precision rate of 94.77%, a recall rate of 93.73% and an accuracy of 95.70%. Impressively, the model also effectively identified CEMP stars in VMP stars, achieving an accuracy of 87.56%. Moreover, we illustrated the superiority of the CNN model over the RF and SVM algorithms in that it can predict stellar parameters with higher accuracy and identify VMP stars better, with a recall rate nearly 20% higher than the other two approaches. The efficiency of the CNN model was also tested on the MARCS synthetic spectra, and the MAE values obtained on the test set were 53.03 K for
![]() $T_{\textrm{eff}}$
, 0.056 dex for
$T_{\textrm{eff}}$
, 0.056 dex for
![]() $\log$
g, and 0.047 dex for [Fe/H].
$\log$
g, and 0.047 dex for [Fe/H].
To sum up, the CNN model proposed in this paper can productively measure the stellar parameters of spectra with a resolution of 200 and excels in identifying VMP stars. This work lays a robust foundation for future investigations of a large number of low-resolution spectra obtained by the CSST and searching for VMP stars from them. This will not only greatly expand the VMP star candidates, but also lead to a better understanding of the evolution of the Milky Way.
Acknowledgement
This work is supported by the National Natural Science Foundation of China under grant numbers 11873037, 11603012, and 11603014 and partially supported by the Young Scholars Program of Shandong University, Weihai (2016WHWLJH09), and the science research grants from the China manned Space Project with No CMS-CSST-2021-B05 and CMS-CSST-2021-A08.
Appendix A. Parameter-tuning process of RF and SVM
-
1. RFr
The RF model can be regarded as a decision tree model embedded into the bagging framework, so we first perform parameter selection on the outer bagging framework (
 $n\_estimators$
) and then on the inner decision tree model (
$n\_estimators$
) and then on the inner decision tree model (
 $max\_features$
). When optimizing a certain parameter, the other parameters need to be set as constants. The parameter-tuning process is performed on
$max\_features$
). When optimizing a certain parameter, the other parameters need to be set as constants. The parameter-tuning process is performed on
 $T_{\textrm{eff}}$
,
$T_{\textrm{eff}}$
,
 $\log$
g, and [Fe/H], respectively. For
$\log$
g, and [Fe/H], respectively. For
 $T_{\textrm{eff}}$
, when default values are used for all parameters, the best score is 0.914. After that, we perform a ten-fold cross-validation. The range of
$T_{\textrm{eff}}$
, when default values are used for all parameters, the best score is 0.914. After that, we perform a ten-fold cross-validation. The range of
 $n\_esimators$
is chosen to be 1–150 and the step size is 10. The best
$n\_esimators$
is chosen to be 1–150 and the step size is 10. The best
 $n\_esimators$
obtained is 110 and the score is 0.916. On the basis of
$n\_esimators$
obtained is 110 and the score is 0.916. On the basis of
 $n\_esimators$
of 110, the
$n\_esimators$
of 110, the
 $max\_features$
range is chosen to be 1–100 and the step size is 1. The best
$max\_features$
range is chosen to be 1–100 and the step size is 1. The best
 $max\_features$
obtained is 95, with a score of 0.918. It can be seen that there is a small increase in the score, indicating the parameter-tuning process is effective. Following the same steps, we obtain the optimal parameters for
$max\_features$
obtained is 95, with a score of 0.918. It can be seen that there is a small increase in the score, indicating the parameter-tuning process is effective. Following the same steps, we obtain the optimal parameters for
 $\log$
g is
$\log$
g is
 $n\_esimators$
=120,
$n\_esimators$
=120,
 $max\_features$
=94 with a score of 0.743, and for [Fe/H] is
$max\_features$
=94 with a score of 0.743, and for [Fe/H] is
 $n\_esimators$
=110,
$n\_esimators$
=110,
 $max\_features$
=52 with the score of 0.851.
$max\_features$
=52 with the score of 0.851. -
2. SVM
The tuning process for the SVM model is performed separately for
 $T_{\textrm{eff}}$
,
$T_{\textrm{eff}}$
,
 $\log$
g, and [Fe/H]. We use a grid search for 5-fold cross-validation, first tuning C, and then fixing the optimal C value to adjust gamma. C is set to 0.1, 1, 10, and gamma is set to 0.001, 0.01, 0.1, and ‘scale’ (gamma = 1/(n_features * X.var()), where n_features is the number of the input features, X.var() is the variance of the input features). The experimental results show that for
$\log$
g, and [Fe/H]. We use a grid search for 5-fold cross-validation, first tuning C, and then fixing the optimal C value to adjust gamma. C is set to 0.1, 1, 10, and gamma is set to 0.001, 0.01, 0.1, and ‘scale’ (gamma = 1/(n_features * X.var()), where n_features is the number of the input features, X.var() is the variance of the input features). The experimental results show that for
 $T_{\textrm{eff}}$
,
$T_{\textrm{eff}}$
,
 $\log$
g, and [Fe/H], the optimal C values are all 10, with scores of 0.87, 0.79, and 0.87, respectively. On this basis, optimal gamma values are obtained as 0.1, ‘scale’, and ‘scale’, with scores of 0.91, 0.81, and 0.88, respectively. Using the obtained optimal SVM model, we can conduct subsequent experiments.
$\log$
g, and [Fe/H], the optimal C values are all 10, with scores of 0.87, 0.79, and 0.87, respectively. On this basis, optimal gamma values are obtained as 0.1, ‘scale’, and ‘scale’, with scores of 0.91, 0.81, and 0.88, respectively. Using the obtained optimal SVM model, we can conduct subsequent experiments.