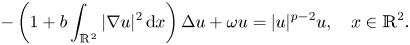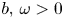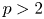Necessary and sufficient conditions for ground state solutions to planar Kirchhoff-type equations

Abstract

In this paper, we are concerned with the ground states of the following planar Kirchhoff-type problem:

\[ -\left(1+b\displaystyle\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)\Delta u+\omega u=|u|^{p-2}u, \quad x\in\mathbb{R}^2. \]

where $b,\, \omega >0$ are constants, $p>2$. Based on variational methods, regularity theory and Schwarz symmetrization, the equivalence of ground state solutions for the above problem with the minimizers for some minimization problems is obtained. In particular, a new scale technique, together with Lagrange multipliers, is delicately employed to overcome some intrinsic difficulties.

1. Introduction and main results

The stability of bound states of nonlinear Schrödinger equations in the attractive case has been studied since 1983. In particular, the ground state was described by minimizing the corresponding energy functionals in several manifolds with constrained conditions. In this paper, we study the bound states for the following Kirchhoff type equation

(1.1)\begin{equation} \begin{cases} -\left(1+b\displaystyle\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)\Delta u+\omega u=|u|^{p-2}u, \ x\in\mathbb{R}^2, \\ u\in H^1(\mathbb{R}^2), \end{cases} \end{equation}

where $b,\, \omega >0$ are constants, $p\in (2,\,+\infty )$. It is known that every solution to Eq. (1.1) is a critical point of the energy functional $S: H^1(\mathbb {R}^2)\rightarrow \mathbb {R}$, given by

\[ S(u)=\frac{1}{2}\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x+\frac{b}{4}\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2+\frac{\omega}{2}\int_{\mathbb{R}^2}|u|^2\,{\rm d}x-\frac{1}{p}\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x. \]

Equation (1.1) is related to the stationary form of the classical Kirchhoff equation

(1.2)\begin{equation} \begin{cases} u_{tt}-\left(1+b\displaystyle\int_{\Omega}|\nabla u|^2\,{\rm d}x\right)\Delta u=h(x,u), & \mathrm{in}\ \Omega, \\ u=0, & \mathrm{on}\ \partial\Omega, \end{cases} \end{equation}

where $\Omega \subset \mathbb {R}^N$ ($N\geq 1$) and $h\in C(\Omega \times \mathbb {R},\,\mathbb {R})$. Problem (1.2) was proposed by Kirchhoff [17] as an extensional the classical D'Alember's wave equation for free vibrations of elastic strings which corresponds to the case $b=0$ in (1.2). As we know, Kirchhoff's model takes into account modifications in length of the string produced by transversal vibrations. After the pioneering work of Lions [22], where an abstract framework was introduced, the stationary elliptic version of problem (1.2) has been widely studied in the literature, for example, we refer to the papers [1, 5, 7, 13–15, 21, 23–25, 28].

The existence and qualitative properties of positive solutions for the following Kirchhoff-type equation

(1.3)\begin{equation} \begin{cases} -\left(a+b\displaystyle\int_{\mathbb{R}^N}|\nabla u|^2\,{\rm d}x\right)\Delta u+u=f(x,u), \ x\in\mathbb{R}^N, \\ u\in H^1(\mathbb{R}^N) \end{cases} \end{equation}

have been extensively in the past several decades where $f\in C(\mathbb {R}^N\times \mathbb {R},\,\mathbb {R})$, $a,\,b>0$ are constants. It is well known that Eq. (1.3) is the Euler–Lagrange equation of the energy functional $I: H^1(\mathbb {R}^N)\rightarrow \mathbb {R}$ defined as

\[ I(u)=\frac{1}{2}\int_{\mathbb{R}^N}(a|\nabla u|^2+u^2)\,{\rm d}x+\frac{b}{4}\left(\int_{\mathbb{R}^N}|\nabla u|^2\,{\rm d}x\right)^2-\int_{\mathbb{R}^N}F(x,u)\,{\rm d}x, \]

where $F(x,\,u)=\int _0^uf(x,\,s)\,{\rm d}s$. Define

(1.4)\begin{equation} m=\inf\left\{I(v): v\in H^1(\mathbb{R}^N)\ \mathrm{is\;a\;nontrivial\;solution\;to\;equation\;(1.3)}\right\}. \end{equation}

A nontrivial solution $u$ to problem (1.3) is called a ground state if $I(u)=m$.

For $N=2$ or 3, by using the fountain theorem, Jin and Wu [16] proved that problem (1.3) has infinitely many radial solutions when $f$ satisfies some suitable assumptions. Later, on $\mathbb {R}^3$, He and Zou [11] studied (1.3) under the conditions that $f(x,\,u):=f(u)$ satisfies $\lim _{|u|\rightarrow 0}f(u)/|u|^3=0$, $\lim _{|u|\rightarrow \infty }f(u)/|u|^q=0$ for some $3< q<5$, $f(t)/t^3$ is strictly increasing for $t>0$ and

\[ 0<\theta\int_0^uf(s)\,{\rm d}s\leq f(u)u, \ \mathrm{for} \ \theta>4. \]

The authors obtained existence and concentration behavior of positive solutions and ground state solutions to (1.3) via using the mountain pass theorem and the Nehari manifold, respectively. When $f(x,\,u):=\lambda f(u)+|u|^4u$, where $f(u)$ satisfies some appropriate assumptions, Wang et al. [27], He et al. [12], Li and Ye [20] used the same arguments as in [11] to prove the existence of ground state solutions and concentration behavior of positive solutions. There are also some studies on ground state solutions and concentration behavior of positive solutions results, we refer to [8, 9, 14].

Recently, Li et al. [19] considered the existence of positive ground state solutions of (1.3) when $f(x,\,u):=u^p$ with $1< p<5$ on $\mathbb {R}^3$. Furthermore, they exploited the smoothness, symmetry and asymptotic behavior of positive solutions. Qi and Zou [26] studied the exact number and expressions of the positive solutions for problem (1.1) with the prescribed $L^2$-norm and the unknown frequency. Wei et al. [29] established the existence of ground state solution for problem (1.1) with critical exponential and periodic nonlinearity, see also [6] for some existence results for a Kirchhoff-type problem in $\mathbb {R}^2$ with critical exponential.

Inspired by the above work, we are interested in necessary and sufficient conditions for ground state solutions for Kirchhoff-type problems in the whole space $\mathbb {R}^2$, which have not been investigated in the literature until now. However, the main difficulty faced is that we have to consider the nonlocal term $b\int _{\mathbb {R}^2}|\nabla u|^2\,{\rm d}x$ in the whole space. For this, we introduce a new scale technique to deal with this problem.

Before stating our main results, we introduce the following functionals and sets, respectively.

(1.5)\begin{align} T(u)& =\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x+b\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2,\nonumber\\ V(u)& =\frac{1}{p}\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x-\frac{\omega}{2}\int_{\mathbb{R}^2}|u|^2\,{\rm d}x,\nonumber\\ Q(u)& =\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x+b\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2-\frac{p-2}{p}\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x,\nonumber\\ A& =\left\{u\!\in\! H^1(\mathbb{R}^2): u\neq0 \quad\mathrm{and}\quad \left(1\!+\!b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)\Delta u-\omega u+|u|^{p-2}u\!=\!0\right\},\nonumber\\ G& =\left\{u\in A: S(u)\leq S(v) \ \mathrm{for~all}\ v\in A\right\},\nonumber\\ N& =\{u\in H^1(\mathbb{R}^2): V(u)=0 \ \mathrm{and} \ u\neq0\}, \end{align}

(1.6)\begin{align} M& =\{u\in H^1(\mathbb{R}^2): Q(u)=0\ \mathrm{and} \ u\neq0\}. \end{align}

Now our main results are listed as follows.

Theorem 1.1 Assume $b,\,\omega >0$ and $p>2$. Then

1. (i) $A$ and $G$ are nonempty.

2. (ii) $u\in G$ if and only if $u$ solves the minimization problem

   (1.7)\begin{equation} \begin{cases} u\in N \ \text{and} \ \int_{\mathbb{R}^2}|u|^2\,{\rm d}x=\frac{2(4bd_N+1)-2\sqrt{4bd_N+1}}{\omega b(p-2)},\\ S(u)=d_N:=\min\{S(w): w\in N\}. \end{cases} \end{equation}

3. (iii) There exists a real-valued, positive, spherically symmetric, and decreasing function $\varphi \in G$ such that

   \[ G=\bigcup\{\varphi({\cdot}{-}y): y\in\mathbb{R}^2\}. \]

Theorem 1.2 Assume $b,\,\omega >0$ and $p>6$. If $u\in H^1(\mathbb {R}^2)$, then $u\in G$ if and only if $u$ solves the minimization problem

(1.8)\begin{equation} \begin{cases} u\in M,\\ S(u)=\min\{S(w): w\in M\}. \end{cases} \end{equation}

Remark 1.3 Note that our results are new even in the available literature concerning the case of $\mathbb {R}^N$ ($N\geq 3$). As a matter of fact, our scale technique seems difficult to be employed in $\mathbb {R}^N$ ($N\geq 3$). Of course, it would be interesting to extend our results to $\mathbb {R}^N$ ($N\geq 3$). In addition, our results could not be deduced if the nonlinearity $|u|^{p-2}u$ is replaced by the one with subcritical or critical exponential growth.

The paper is organized as follows. In § 2, we establish a regularity result and give the proof of theorem 1.1. In § 3, we deal with the proof of theorem 1.2.

2. Proof of theorem 1.1

If $u$ is a solution of problem (1.1), then

\[ \left(1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x=\int_{\mathbb{R}^2}\left(|u|^{p}-\omega|u|^2\right)\,{\rm d}x. \]

Now, $u$ is also the critical point of $S(u)$ in $H^1(\mathbb {R}^2)$. So we have the Pohozaev's identity $\frac {d}{d\lambda }|_{\lambda =1}S(u(\lambda ^{-1}x))=0$. This implies $V(u)=0$, that is,

\[ \int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x=\frac{\omega p}{2}\int_{\mathbb{R}^2}|u|^2\,{\rm d}x, \]

and hence

(2.1)\begin{equation} T(u)=\frac{\omega(p-2)}{2}\int_{\mathbb{R}^2}|u|^2\,{\rm d}x. \end{equation}

Consequently

\[ \int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x=\frac{\sqrt{1+2b(p-2)\omega\int_{\mathbb{R}^2}|u|^2\,{\rm d}x}-1}{2b}, \]

which leads to

(2.2)\begin{equation} \left. \begin{array}{rcl} S(u) & = & \displaystyle\dfrac{1}{2}\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x+\dfrac{b}{4}\left(\int_{\mathbb{R}^2}|\nabla u|^2dx\right)^2-V(u)\\ & = & \displaystyle\dfrac{1}{2}\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x+\dfrac{b}{4}\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2\\ & = & \displaystyle\dfrac{(p-2)\omega\int_{\mathbb{R}^2}|u|^2\,{\rm d}x}{8}+\dfrac{\sqrt{1+2b(p-2)\omega\int_{\mathbb{R}^2}|u|^2\,{\rm d}x}-1}{8b}. \end{array} \right. \end{equation}

Lemma 2.1 Assume $2< p<\infty$, $\omega >0$. If $u$ is a solution of (1.1). Then the following properties hold:

1. (i) $u\in W^{3,q}(\mathbb {R}^2)$ for every $2\leq q<+\infty$. In particular, $u\in C^2(\mathbb {R}^2)$ and $|D^\beta u(x)|\rightarrow 0$ as $|x|\rightarrow \infty$ for all $|\beta |\leq 2$.

2. (ii) There exists $\varepsilon >0$ such that $e^{\varepsilon |x|}(|u(x)|+|\nabla u(x)|)\in L^\infty (\mathbb {R}^2)$.

Proof. $(i)$ We borrow the idea from [4]. Let $u$ be a solution of problem (1.1). Thus,

\[ -\Delta u+\frac{\omega}{\left(1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)}u=\frac{1}{\left(1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)}|u|^{p-2}u. \]

Let $A=1+b\int _{\mathbb {R}^2}|\nabla u|^2\,{\rm d}x$ ($A<\infty$), $B=\frac {1+b\int _{\mathbb {R}^2}|\nabla u|^2\,{\rm d}x}{\omega ^2}$. Changing $u(x)$ to

\[ u(x)=\left(A/\omega\right)^{\frac{1}{p-2}}v(\sqrt{\omega/A}x), \]

we may assume that $v$ satisfies

(2.3)\begin{equation} {-}\Delta v+v=\frac{1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x}{\omega^2}|v|^{p-2}v=B|v|^{p-2}v. \end{equation}

Note that (2.3) can be written in the form

(2.4)\begin{equation} \mathcal{F}^{{-}1}((1+4\pi^2|\xi|^2)\mathcal{F}v)=B|v|^{p-2}v, \end{equation}

where $\mathcal {F}$ is the Fourier transform. For $K>0$, set

\[ \begin{array}{@{}ll} \displaystyle v_K & =\left\{\begin{array}{@{}ll} \displaystyle \pm K,\ \pm v>K,\\ \displaystyle v,\ |v|\leq K. \end{array}\right. \end{array} \]

Observing that, for $\beta \geq 1$,

\[ \int_{\mathbb{R}^2}|\nabla(|v_K|^{\beta-1}v)|^2\,{\rm d}x=\int_{\mathbb{R}^2}|v_K|^{2\beta-2}|\nabla v|^2\,{\rm d}x+(\beta^2-1)\int_{\mathbb{R}^2}|v_K|^{2\beta-2}|\nabla v_K|^2\,{\rm d}x, \]

we get

(2.5)\begin{align} & \displaystyle\frac{1}{\beta+1}\int_{\mathbb{R}^2}[|\nabla(|v_K|^{\beta-1}v)|^2+(|v_K|^{\beta-1}v)^2]\,{\rm d}x\nonumber\\ & =\displaystyle\frac{1}{\beta+1}\int_{\mathbb{R}^2}|v_K|^{2\beta-2}|\nabla v|^2\,{\rm d}x+(\beta-1)\int_{\mathbb{R}^2}|v_K|^{2\beta-2}|\nabla v_K|^2\,{\rm d}x\nonumber\\ & \quad +\frac{1}{\beta+1}\int_{\mathbb{R}^2}(|v_K|^{\beta-1}v)^2\,{\rm d}x\nonumber\\ & \leq \displaystyle\int_{\mathbb{R}^2}|v_K|^{2\beta-2}|\nabla v|^2\,{\rm d}x+\int_{\mathbb{R}^2}(|v_K|^{\beta-1}v)^2\,{\rm d}x\nonumber\\ & \quad +2(\beta-1)\int_{\mathbb{R}^2}|v_K|^{2\beta-2}|\nabla v_K|^2\,{\rm d}x. \end{align}

Taking the test function $\varphi =|v_K|^{2\beta -2}v$ in (2.3), we have

(2.6)\begin{align} & \int_{\mathbb{R}^2}|v_K|^{2\beta-2}|\nabla v|^2\,{\rm d}x+2(\beta-1)\int_{\mathbb{R}^2}|v_K|^{2\beta-2}|\nabla v_K|^2\,{\rm d}x+\int_{\mathbb{R}^2}(|v_K|^{\beta-1}v)^2\,{\rm d}x\nonumber\\ & \quad = B\int_{\mathbb{R}^2}|v_K|^{2\beta-2}|v|^2|v|^{p-2}\,{\rm d}x. \end{align}

It follows from (2.5) and (2.6) that

(2.7)\begin{equation} \frac{1}{\beta+1}\int_{\mathbb{R}^2}[|\nabla(|v_K|^{\beta-1}v)|^2+(|v_K|^{\beta-1}v)^2]\,{\rm d}x\leq B\int_{\mathbb{R}^2}|v_K|^{2\beta-2}v^2|v|^{p-2}\,{\rm d}x. \end{equation}

On one hand, by the Sobolev inequality, we have

\[ \int_{\mathbb{R}^2}[|\nabla(v_K|^{\beta-1}v)|^2+(|v_K|^{\beta-1}v)^2]\,{\rm d}x\geq S_{2p}\left[\int_{\mathbb{R}^2}(|v_K|^{\beta-1}v)^{2p}\,{\rm d}x\right]^{\frac{1}{p}}, \]

where

\[ S_{2p}=\inf_{u\in H^1(\mathbb{R}^2)\backslash\{0\}}\frac{\int_{\mathbb{R}^2}(|\nabla u|^2+u^2)\,{\rm d}x}{(\int_{\mathbb{R}^2}|u|^{2p}\,{\rm d}x)^{\frac{1}{p}}}. \]

On the other hand, by the Hölder inequality, we deduce that

\begin{align*} \int_{\mathbb{R}^2}|v_K|^{2\beta-2}v^2|v|^{p-2}\,{\rm d}x& =\displaystyle\left[\int_{\mathbb{R}^2}(|v_K|^{2\beta-2}v^2)^{\frac{2p}{p+2}}\,{\rm d}x\right]^{\frac{p+2}{2p}} \left[\int_{\mathbb{R}^2}|v|^{2p}\,{\rm d}x\right]^{\frac{p-2}{2p}}\\ & \leq S_{2p}^{-\frac{p-2}{2}}\|v\|^{p-2}\left[\int_{\mathbb{R}^2}(|v_K|^{2\beta-2}v^2)^{\frac{2p}{p+2}}\,{\rm d}x\right]^{\frac{p+2}{2p}}. \end{align*}

The symbol $\|\cdot \|$ is used only for the norm in $H^1(\mathbb {R}^2)$. Applying (2.7) and letting $K\rightarrow \infty$, we obtain

\[ \frac{S_{2p}}{\beta+1}|v|_{L^{2\beta p}}^{2\beta}\leq S_{2p}^{-\frac{p-2}{2}}\|v\|^{p-2}|v|_{L^{\frac{4\beta p}{p+2}}}^{2\beta}, \]

where $|\cdot |_{L^q}$ denotes the standard norm in $L^q(\mathbb {R}^2)$. It follows from the above inequality that

(2.8)\begin{equation} |v|_{L^{2\beta p}}\leq C(\beta+1)^{\frac{1}{2\beta}}\|v\|^\frac{p-2}{2\beta}|v|_{L^{\frac{4\beta p}{p+2}}}. \end{equation}

Set

\[ 2p\beta_{n-1}=\frac{4p}{p+2}\beta_n, \]

so that

\[ \beta_n=\left(\frac{p+2}{2}\right)^{n-1}, \quad n\in\mathbb{N}. \]

Consequently, $\beta _n\rightarrow \infty$ as $n\rightarrow \infty$. Therefore,

\[ \lim_{n\rightarrow\infty}(\beta_n+1)^{\frac{1}{2\beta_n}} =\displaystyle\lim_{n\rightarrow\infty}e^{\frac{\log(1+\beta_n)}{2\beta_n}} =1. \]

Doing iteration by (2.8), we obtain $v\in L^\infty (\mathbb {R}^2)$. Thus $|v|^{p-2}v\in L^2(\mathbb {R}^2)\cap L^\infty (\mathbb {R}^2)$, so that $v\in W^{2,q}(\mathbb {R}^2)$ and $|v|^{p-2}v\in W^{1,q}(\mathbb {R}^2)$ for all $2\leq q<\infty$. Therefore, it follows from (2.4) that $(-\Delta +I)\partial _jv\in L^q(\mathbb {R}^2)$, i.e., $\mathcal {F}^{-1}((1+4\pi ^2|\xi |^2)\mathcal {F}\partial _jv)\in L^q(\mathbb {R}^2)$. Thus $\partial _jv\in H^{2,q}(\mathbb {R}^2)=W^{2,q}(\mathbb {R}^2)$, and so $v\in W^{3,q}(\mathbb {R}^2)$. By the Sobolev's embedding theorem, $v\in C^{2,\delta }(\mathbb {R}^2)$ for $0<\delta <1$. Therefore, $|D^\beta v(x)|\rightarrow 0$ as $|x|\rightarrow \infty$ for all $|\beta |\leq 2$, so that $|D^\beta u(x)|\rightarrow 0$ as $|x|\rightarrow \infty$.

$(ii)$ Let $\varepsilon >0$ and $\theta _\varepsilon (x)=e^{\frac {|x|}{1+\varepsilon |x|}}$. $\theta _\varepsilon$ is bounded, Lipschitz continuous, and $|\nabla \theta _\varepsilon |\leq \theta _\varepsilon$ a.e. Taking the test function $\theta _\varepsilon v\in H^1(\mathbb {R}^2)$ in (2.3), we get

(2.9)\begin{equation} \int_{\mathbb{R}^2}\nabla v\nabla(\theta_\varepsilon v)\,{\rm d}x+\int_{\mathbb{R}^2}\theta_\varepsilon|v|^2\,{\rm d}x=\frac{1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x}{\omega^2}\int_{\mathbb{R}^2}\theta_\varepsilon|v|^p\,{\rm d}x. \end{equation}

Noting that

\begin{align*} \int_{\mathbb{R}^2}\nabla v\nabla(\theta_\varepsilon v)\,{\rm d}x& =\displaystyle\int_{\mathbb{R}^2}\theta_\varepsilon|\nabla v|^2\,{\rm d}x+\int_{\mathbb{R}^2}v\nabla\theta_\varepsilon\nabla v\,{\rm d}x\\ & \geq\displaystyle\int_{\mathbb{R}^2}\theta_\varepsilon|\nabla v|^2\,{\rm d}x-\int_{\mathbb{R}^2}|v||\nabla\theta_\varepsilon||\nabla v|\,{\rm d}x\\ & \geq\displaystyle\int_{\mathbb{R}^2}\theta_\varepsilon|\nabla v|^2\,{\rm d}x-\int_{\mathbb{R}^2}\theta_\varepsilon|v||\nabla v|\,{\rm d}x\\ & \geq\displaystyle\frac{1}{2}\int_{\mathbb{R}^2}\theta_\varepsilon|\nabla v|^2\,{\rm d}x-\frac{1}{2}\int_{\mathbb{R}^2}\theta_\varepsilon|v|^2\,{\rm d}x, \end{align*}

we obtain

(2.10)\begin{align} \frac{1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x}{\omega^2}\int_{\mathbb{R}^2}\theta_\varepsilon|v|^p\,{\rm d}x& =\displaystyle\int_{\mathbb{R}^2}\nabla v\nabla(\theta_\varepsilon v)\,{\rm d}x+\int_{\mathbb{R}^2}\theta_\varepsilon|v|^2\,{\rm d}x\nonumber\\ & \geq\displaystyle\frac{1}{2}\int_{\mathbb{R}^2}\theta_\varepsilon|v|^2\,{\rm d}x. \end{align}

Since $u\in H^1(\mathbb {R}^2)$, there exists $R>0$ such that $|v(x)|^{p-2}\leq \frac {1+b\int _{\mathbb {R}^2}|\nabla u|^2\,{\rm d}x}{4\omega ^2}$ for $|x|\geq R$. Thus

\begin{align*} & \displaystyle\frac{1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x}{\omega^2}\int_{\mathbb{R}^2}\theta_\varepsilon|v|^p\,{\rm d}x\\ & \quad =\displaystyle\frac{1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x}{\omega^2}\int_{\{|x|\leq R\}}\theta_\varepsilon|v|^p\,{\rm d}x+\frac{1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x}{\omega^2}\int_{\{|x|\geq R\}}\theta_\varepsilon|v|^p\,{\rm d}x\\ & \quad \leq \displaystyle\frac{1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x}{\omega^2}\int_{\{|x|\leq R\}}e^{|x|}|v|^p\,{\rm d}x+\frac{1}{4}\int_{\{|x|\geq R\}}\theta_\varepsilon|v|^{2}\,{\rm d}x\\ & \quad \leq \displaystyle\frac{1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x}{\omega^2}e^{R}\int_{\{|x|\leq R\}}|v|^p\,{\rm d}x+\frac{1}{4}\int_{\mathbb{R}^2}\theta_\varepsilon|v|^{2}\,{\rm d}x. \end{align*}

It follows from (2.10) that

\[ \int_{\mathbb{R}^2}\theta_\varepsilon|v|^2\,{\rm d}x\leq4\frac{1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x}{\omega^2}e^{R}\int_{\{|x|\leq R\}}|v|^p\,{\rm d}x. \]

Letting $\varepsilon \downarrow 0$, we deduce that

(2.11)\begin{equation} \int_{\mathbb{R}^2}e^{|x|}|v|^2\,{\rm d}x<{+}\infty. \end{equation}

Since $v$ is globally Lipschitz continuous by $(i)$, $|v(x)|^{4}e^{|x|}$ is bounded. Similarly, applying $\partial _j$ to equation (2.3) and multiplying the resulting equation by $\theta _\varepsilon \partial _j u$ for $j=1,\,2$, we have

\[ \int_{\mathbb{R}^2}\nabla(\partial_j v)\nabla(\theta_\varepsilon (\partial_j v))\,{\rm d}x+\int_{\mathbb{R}^2}\theta_\varepsilon|\partial_j v|^2\,{\rm d}x=\frac{1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x}{\omega^2}\int_{\mathbb{R}^2}\theta_\varepsilon|\partial_j v|^p\,{\rm d}x. \]

Applying the fact

\begin{align*} \int_{\mathbb{R}^2}\nabla (\partial_j v)\nabla(\theta_\varepsilon (\partial_j v))\,{\rm d}x& = \displaystyle\int_{\mathbb{R}^2}\theta_\varepsilon|\nabla \partial_j v|^2\,{\rm d}x+\int_{\mathbb{R}^2}(\partial_j v)\nabla\theta_\varepsilon\nabla (\partial_j v)\,{\rm d}x\\ & \geq \displaystyle\int_{\mathbb{R}^2}\theta_\varepsilon|\nabla (\partial_j v)|^2\,{\rm d}x-\int_{\mathbb{R}^2}|\partial_j v||\nabla\theta_\varepsilon||\nabla (\partial_j v)|\,{\rm d}x\\ & \geq \displaystyle\int_{\mathbb{R}^2}\theta_\varepsilon|\nabla (\partial_j v)|^2\,{\rm d}x-\int_{\mathbb{R}^2}\theta_\varepsilon|\partial_j v||\nabla (\partial_j v)|\,{\rm d}x\\ & \geq \displaystyle\frac{1}{2}\int_{\mathbb{R}^2}\theta_\varepsilon|\nabla (\partial_j v)|^2\,{\rm d}x-\frac{1}{2}\int_{\mathbb{R}^2}\theta_\varepsilon|\partial_j v|^2\,{\rm d}x, \end{align*}

we have

\begin{align*} \displaystyle\frac{1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x}{\omega^2}\int_{\mathbb{R}^2}\theta_\varepsilon|\partial_j v|^p\,{\rm d}x& =\displaystyle\int_{\mathbb{R}^2}\nabla (\partial_j v)\nabla(\theta_\varepsilon (\partial_j v))\,{\rm d}x+\int_{\mathbb{R}^2}\theta_\varepsilon|\partial_j v|^2\,{\rm d}x\\ & \geq \displaystyle\frac{1}{2}\int_{\mathbb{R}^2}\theta_\varepsilon|\nabla (\partial_j v)|^2\,{\rm d}x+\frac{1}{2}\int_{\mathbb{R}^2}\theta_\varepsilon|\partial_j v|^2\,{\rm d}x. \end{align*}

Consequently

(2.12)\begin{equation} \frac{1}{2}\int_{\mathbb{R}^2}\theta_\varepsilon|\partial_j v|^2\,{\rm d}x\leq\frac{1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x}{\omega^2}\int_{\mathbb{R}^2}\theta_\varepsilon|\partial_jv|^p\,{\rm d}x. \end{equation}

By $(i)$, there exists $R>0$ such that $|\partial _jv(x)|^{p-2}\leq \frac {1+b\int _{\mathbb {R}^2}|\nabla u|^2\,{\rm d}x}{4\omega ^2}$ for $|x|\geq R$. Thus

\begin{align*} & \displaystyle\frac{1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x}{\omega^2}\int_{\mathbb{R}^2}\theta_\varepsilon|\partial_jv|^p\,{\rm d}x\\ & \quad =\displaystyle\frac{1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x}{\omega^2}\int_{\{|x|\leq R\}}\theta_\varepsilon|\partial_jv|^p\,{\rm d}x\\ & \quad +\frac{1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x}{\omega^2}\int_{\{|x|\geq R\}}\theta_\varepsilon|\partial_jv|^p\,{\rm d}x\\ & \quad \leq \displaystyle\frac{1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x}{\omega^2}\int_{\{|x|\leq R\}}e^{|x|}|\partial_jv|^p\,{\rm d}x+\frac{1}{4}\int_{\{|x|\geq R\}}\theta_\varepsilon|\partial_jv|^{2}\,{\rm d}x\\ & \quad \leq \displaystyle\frac{1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x}{\omega^2}e^{R}\int_{\{|x|\leq R\}}|\partial_jv|^p\,{\rm d}x+\frac{1}{4}\int_{\mathbb{R}^2}\theta_\varepsilon|\partial_jv|^{2}\,{\rm d}x. \end{align*}

It follows from (2.12) that

\[ \int_{\mathbb{R}^2}\theta_\varepsilon|\partial_jv|^2\,{\rm d}x\leq4\frac{1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x}{\omega^2}e^{R}\int_{\{|x|\leq R\}}|\partial_jv|^p\,{\rm d}x. \]

Letting $\varepsilon \downarrow 0$, we deduce that

\[ \int_{\mathbb{R}^2}e^{|x|}|\nabla v|^2\,{\rm d}x<{+}\infty. \]

Since $\nabla v$ is globally Lipschitz continuous, similarly, we deduce that $|\nabla v(x)|^{4}e^{|x|}$ is bounded. The proof is now finished.

Lemma 2.2 Assume that $2< p<\infty$ and $b,\,\omega >0$. It follows that the minimization problem

(2.13)\begin{equation} d_N:=\min\{S(w): w\in N\}, \end{equation}

has a positive solution, where $N$ is defined in (1.5). Moreover, every solution of (2.13) is the solution of equation (1.1).

Proof. A similar argument to the proof of Theorem 8.1.5 in [4], we observe that $d_N>0$. Indeed, consider $u\in N$, it implies that $V(u)=0$, namely

\[ \int_{\mathbb{R}^2}|u|^2\,{\rm d}x=\frac{2}{\omega p}\int_{\mathbb{R}^2}|u|^p\,{\rm d}x. \]

It follows from the Gagliardo–Nirenberg inequality that there exists $C$ independent of $u$ such that

\[ \int_{\mathbb{R}^2}|u|^p\,{\rm d}x\leq C\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^{\frac{p-2}{2}}\int_{\mathbb{R}^2}|u|^2\,{\rm d}x. \]

From the above information, there exists $c>0$ such that $\int _{\mathbb {R}^2}|\nabla u|^2\,{\rm d}x\geq c$, and so

\begin{align*} S(u)& =\displaystyle\frac{1}{2}\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x+\frac{b}{4}\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2-V(u)\\ & =\displaystyle\frac{1}{2}\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x+\frac{b}{4}\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2\\ & > 0 \end{align*}

for all $u\in N$, which implies that $d_N>0$.

We recall the definition of the Schwarz symmetrization [3]. If $u\in L^2(\mathbb {R}^2)$ is a nonnegative function, we denote by $u^*$ the unique spherically symmetric, nonnegative, non-increasing function such that

\[ |\{x\in\mathbb{R}^2: u^*(x)>\lambda\}|=|\{x\in\mathbb{R}^2: |u(x)|>\lambda\}| \ \mathrm{for~all} \ \lambda>0. \]

In particular,

(2.14)\begin{equation} \begin{cases} \displaystyle\int_{\mathbb{R}^2}|u^*|^q\,{\rm d}x=\int_{\mathbb{R}^2}|u|^q\,{\rm d}x,\ \mathrm{for}\ 1\leq q<{+}\infty,\\ \displaystyle\int_{\mathbb{R}^2}|\nabla u^*|^2\,{\rm d}x\leq\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x. \end{cases} \end{equation}

The proof of lemma 2.2 is divided into three steps.

Step 1. we claim that the minimization problem (2.13) has a solution.

Similar to the proof of [2], it is clear that $N\neq \emptyset$. Let $\{v_n\}\subset N$ be a minimizing sequence of $S$, that is, $V(v_n)=0$, and $S(v_n)\rightarrow d_N$. Let $w_n=|v_n|^*$. It follows from (2.14) that $V(w_n)=V(v_n)$, and hence $\{w_n\}$ is also a minimizing sequence of $S$. Define now $u_n$ by $u_n(x)=w_n(\lambda ^{1/2}_nx)$, where

\[ \lambda_n=\frac{\int_{\mathbb{R}^2}|w_n|^2\,{\rm d}x}{\gamma}, \]

where

\[ \gamma=\frac{2(4bd_N+1)-2\sqrt{4bd_N+1}}{\omega b(p-2)}. \]

We deduce that

\begin{align*} \displaystyle\int_{\mathbb{R}^2}|u_n|^2\,{\rm d}x& = \displaystyle\int_{\mathbb{R}^2}|w_n|^2\frac{1}{\lambda_n}\,{\rm d}x\\ & = \displaystyle\gamma,\\ V(u_n)& =\displaystyle\frac{1}{p}\int_{\mathbb{R}^2}|w_n|^{p}\frac{1}{\lambda_n}\,{\rm d}x-\frac{\omega}{2}\int_{\mathbb{R}^2}|w_n|^2\frac{1}{\lambda_n}\,{\rm d}x\\ & =\displaystyle\frac{1}{\lambda_n}\left(\frac{1}{p}\int_{\mathbb{R}^2}|w_n|^{p}\,{\rm d}x-\frac{\omega}{2}\int_{\mathbb{R}^2}|w_n|^2\,{\rm d}x\right)\\ & =\displaystyle\frac{1}{\lambda_n}\left(\frac{1}{p}\int_{\mathbb{R}^2}(|v_n|^*)^{p}\,{\rm d}x-\frac{\omega}{2}\int_{\mathbb{R}^2}(|v_n|^*)^2\,{\rm d}x\right)\\ & =\displaystyle\frac{1}{\lambda_n}\left(\frac{1}{p}\int_{\mathbb{R}^2}|v_n|^{p}\,{\rm d}x-\frac{\omega}{2}\int_{\mathbb{R}^2}|v_n|^2\,{\rm d}x\right)\\ & = 0, \end{align*}

and

\begin{align*} \displaystyle T(u_n)& =\displaystyle\int_{\mathbb{R}^2}|\nabla u_n|^2\,{\rm d}x+b\left(\int_{\mathbb{R}^2}|\nabla u_n|^2\,{\rm d}x\right)^2\\ & =\displaystyle\int_{\mathbb{R}^2}|\nabla w_n|^2\lambda_n\cdot\frac{1}{\lambda_n}\,{\rm d}x+b\left(\int_{\mathbb{R}^2}|\nabla w_n|^2\lambda_n\cdot\frac{1}{\lambda_n}\,{\rm d}x\right)^2\\ & =\displaystyle\int_{\mathbb{R}^2}|\nabla w_n|^2\,{\rm d}x+b\left(\int_{\mathbb{R}^2}|\nabla w_n|^2\,{\rm d}x\right)^2. \end{align*}

These results imply

(2.15)\begin{equation} S(u_n)=S(w_n)\rightarrow d_N, \ \mathrm{as}\ n\rightarrow\infty. \end{equation}

We obtain that $\{u_n\}$ is also a minimizing sequence of $S$. It follows from (2.15) that $\{u_n\}$ is bounded in $H^1(\mathbb {R}^2)$. Therefore, there exist a subsequence of $u_n$ (denoted by itself) and $u\in H^1(\mathbb {R}^2)$ such that $u_n\rightharpoonup u$ weakly in $H^1(\mathbb {R}^2)$ and $u_n\rightarrow u$ strongly in $L^{p}(\mathbb {R}^2)$. By the Fatou's lemma,

\begin{align*} 0& = \lim_{n\rightarrow\infty}V(u_n)=\displaystyle\lim_{n\rightarrow\infty}\left(\frac{1}{p}\int_{\mathbb{R}^2}|u_n|^{p}\,{\rm d}x-\frac{\omega}{2}\int_{\mathbb{R}^2}|u_n|^2\,{\rm d}x\right)\\ & \leq \frac{1}{p}\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x-\frac{\omega}{2}\int_{\mathbb{R}^2}|u|^2\,{\rm d}x\\ & = V(u). \end{align*}

By the weak lower semicontinuity of the $L^2$ norm,

\[ T(u)\leq\liminf_{n\rightarrow\infty}T(u_n). \]

Therefore,

\[ V(u)\geq0, \quad \mathrm{and} \quad S(u)\leq d_N. \]

We claim that $V(u)=0$. Indeed, if $V(u)>0$, then $u\neq 0$. So there exists $\lambda \in (0,\,1)$ such that $v=\lambda u$ satisfies $V(v)=0$. Thus $v\in N$. Furthermore,

\begin{align*} \frac{1}{2}\int_{\mathbb{R}^2}|\nabla v|^2\,{\rm d}x+\frac{b}{4}\left(\int_{\mathbb{R}^2}|\nabla v|^2\,{\rm d}x\right)^2& = \displaystyle\frac{\lambda^2}{2}\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x+\frac{b}{4}\lambda^4\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2\\ & < \displaystyle\frac{1}{2}\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x+\frac{b}{4}\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2. \end{align*}

Noting that $d_N=\lim _{n\to \infty }S(u_n)$ and $V(u_n)=0$, then we have

\begin{align*} d_N& = \displaystyle\lim_{n\to\infty}S(u_n)\\ & = \displaystyle\lim_{n\to\infty}\left\{\frac{1}{2}\int_{\mathbb{R}^2}|\nabla u_n|^2\,{\rm d}x+\frac{b}{4}\left(\int_{\mathbb{R}^2}|\nabla u_n|^2\,{\rm d}x\right)^2-V(u_n)\right\}\\ & = \displaystyle\lim_{n\to\infty}\left\{\frac{1}{2}\int_{\mathbb{R}^2}|\nabla u_n|^2\,{\rm d}x+\frac{b}{4}\left(\int_{\mathbb{R}^2}|\nabla u_n|^2\,{\rm d}x\right)^2\right\}\\ & \geq \displaystyle\frac{1}{2}\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x+\frac{b}{4}\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2. \end{align*}

From the above information, we get

\begin{align*} S(v)& =\frac{1}{2}\int_{\mathbb{R}^2}|\nabla v|^2\,{\rm d}x+\frac{b}{4}\left(\int_{\mathbb{R}^2}|\nabla v|^2\,{\rm d}x\right)^2\\& <\frac{1}{2}\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x+\frac{b}{4}\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2\leq d_N. \end{align*}

This implies that $S(v)< d_N$. This contradicts (2.13) since $S(v)\geq d_N$. Therefore, $V(u)=0$. This implies that

\[ \lim_{n\rightarrow\infty}V(u_n)=V(u). \]

Consequently,

\[ \int_{\mathbb{R}^2}|u|^2\,{\rm d}x=\lim_{n\rightarrow\infty}\int_{\mathbb{R}^2}|u_n|^2\,{\rm d}x=\gamma, \]

and so $u$ satisfies (2.13).

Step 2. We claim that every solutions of (2.13) belongs to $A$.

Indeed, consider a solution $u$ of (2.13). There exists a Lagrange multiplier $\lambda$ such that

(2.16)\begin{equation} -\left(1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)\Delta u=\lambda(|u|^{p-2}u-\omega u). \end{equation}

For any $\varphi \in H^1(\mathbb {R}^2)$, it follows from (2.16) that

\[ \left(1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)\int_{\mathbb{R}^2}\nabla u\nabla\varphi \,{\rm d}x=\lambda\int_{\mathbb{R}^2}(|u|^{p-2}u-\omega u)\varphi \,{\rm d}x. \]

Taking the test function $\varphi =u$, we obtain

(2.17)\begin{equation} T(u)=\left(1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x=\lambda\int_{\mathbb{R}^2}(|u|^{p}-\omega |u|^2)\,{\rm d}x. \end{equation}

Noting that

\begin{align*} S(u)& =\displaystyle\frac{1}{2}\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x+\frac{b}{4}\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2\\ & = d_N, \end{align*}

we deduce that

\[ \int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x=\frac{-1+\sqrt{1+4bd_N}}{b}, \]

so that

\[ T(u)=\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x+b\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2=\frac{1+4bd_N-\sqrt{1+4bd_N}}{b}. \]

It follows from $V(u)=0$ and $\int _{\mathbb {R}^2}|u|^2\,{\rm d}x=\gamma$ that

\[ \int_{\mathbb{R}^2}|u|^{p}=\frac{p\gamma\omega}{2}. \]

Together with (2.17), there holds

\[ \frac{1+4bd_N-\sqrt{1+4bd_N}}{b}=\lambda\frac{(p-2)\gamma\omega}{2}=\lambda\frac{(p-2)\omega}{2}\cdot\frac{2(4bd_N+1)-2\sqrt{4bd_N+1}}{\omega b(p-2)}, \]

and so $\lambda =1$. Therefore, $u$ satisfies problem (1.1). So $A\neq \emptyset$.

Step 3. We claim that $u$ satisfies problem (2.13) if and only if $u\in G$.

Consider any solution $u$ of (2.13) and any $v\in A$. That is,

\[ -\left(1+b\int_{\mathbb{R}^2}|\nabla v|^2\,{\rm d}x\right)\Delta v=|v|^{p-2}v-\omega v. \]

By Pohozaev's identity, we get $V(v)=0$. This means $v\in N$, and

\begin{align*} \int_{\mathbb{R}^2}|v|^{p}\,{\rm d}x& =\frac{p\omega}{2}\int_{\mathbb{R}^2}|v|^2\,{\rm d}x,\\ T(v)& =\int_{\mathbb{R}^2}|v|^{p}\,{\rm d}x-\omega\int_{\mathbb{R}^2}|v|^2\,{\rm d}x=\frac{(p-2)\omega}{2}\int_{\mathbb{R}^2}|v|^2\,{\rm d}x. \end{align*}

From (2.2), there holds

(2.18)\begin{equation} S(v)=\frac{(p-2)\omega\int_{\mathbb{R}^2}|v|^2\,{\rm d}x}{8}+\frac{\sqrt{1+2b(p-2)\omega\int_{\mathbb{R}^2}|v|^2\,{\rm d}x}-1}{8b}. \end{equation}

Since $v\in N$, by the definition of $d_N$, we have

\[ S(v)\geq S(u)=d_N, \]

which implies that $u\in G\neq \emptyset$.

Assume further that $v\in G$. Since $u\in G$ also, we have $S(u)=S(v)$. Noting that $S(u)=d_N$ and $\int _{\mathbb {R}^2}|u|^2\,{\rm d}x=\gamma =\frac {2(4bd_N+1)-2\sqrt {4bd_N+1}}{\omega b(p-2)}$, we obtain

\[ d_N=\frac{(p-2)\gamma\omega}{8}+\frac{\sqrt{1+2b(p-2)\gamma\omega}-1}{8b}. \]

Applying (2.18), we have

\begin{align*} & \frac{(p-2)\gamma\omega}{8}+\frac{\sqrt{1+2b(p-2)\gamma\omega}-1}{8b}\\ & \quad =\frac{(p-2)\omega\int_{\mathbb{R}^2}|v|^2\,{\rm d}x}{8}+\frac{\sqrt{1+2b(p-2)\omega\int_{\mathbb{R}^2}|v|^2\,{\rm d}x}-1}{8b}, \end{align*}

which implies that $\gamma =\int _{\mathbb {R}^2}|v|^2\,{\rm d}x,$ which means that $v$ satisfies (2.13). Hence, the proof is complete.

Proof. Proof of theorem 1.1

Consider $u\in G$, it follows that

\[ -\left(1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)\Delta u+\omega u=|u|^{p-2}u, \]

and so

(2.19)\begin{equation} -\Delta u+\frac{\omega}{\overline{b}} u=\frac{a(x)}{\overline{b}}u, \end{equation}

where

\[ a(x)=|u(x)|^{p-2}, \quad \overline{b}=\left(1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right). \]

According to lemma 2.1, $u\in C^2(\mathbb {R}^2)$ and $a(x)\rightarrow 0$ as $|x|\rightarrow \infty$. Applying Theorem 2 in [10], we obtain that there exists a positive, spherically symmetric solution $\varphi$ of Eq. (2.19) and $y\in \mathbb {R}^2$ such that $u(\cdot )=\varphi (\cdot -y)$. Note that $\varphi$, being radially symmetric, satisfies the ordinary differential equation

\[ \left(1+b\int_0^\infty4\pi r^2u_r^2dr\right)\left(u_{rr}+\frac{1}{r}u_r\right)+\omega u(r)-u^{p-1}(r)=0. \]

Since $\int _0^\infty 4\pi r^2u_r^2dr$ is independent of choice of $u$, we deduce that $1+b\int _0^\infty 4\pi r^2u_r^2dr$ is a positive constant. As a result, we obtain that $\varphi$ is unique by applying the uniqueness results in [18] and [19]. The proof is now complete.

3. Proof of theorem 1.2

For the proof of theorem 1.2, we will use the following lemma.

Lemma 3.1 Given $u\in H^1(\mathbb {R}^2),\, u\neq 0$, and $\lambda >0$, set $\mathcal {P}(\lambda,\,u)(x)=\lambda u(\lambda x)$. Then following properties hold:

1. (i) There exists a unique $\lambda ^*(u)>0$ such that $\mathcal {P}(\lambda ^*(u),\,u)\in M$.

2. (ii) The function $\lambda \mapsto S(\mathcal {P}(\lambda,\,u))$ is convex on $(\lambda ^*(u),\,+\infty )$.

3. (iii) $\lambda ^*(u)<1$ if and only if $Q(u)<0$.

4. (iv) $\lambda ^*(u)=1$ if and only if $u\in M$.

5. (v) $S(\mathcal {P}(\lambda,\,u))< S(\mathcal {P}(\lambda ^*(u),\,u))$ for each $\lambda >0$, $\lambda \neq \lambda ^*(u)$.

6. (vi) $\frac {d}{d\lambda }S(\mathcal {P}(\lambda,\,u))=\frac {1}{\lambda }Q(\mathcal {P}(\lambda,\,u))$ for each $\lambda >0$.

7. (vii) $|\mathcal {P}(\lambda,\,u)|^*=\mathcal {P}(\lambda,\,|u|^*)$ for each $\lambda >0$, where $*$ is the Schwarz symmetrization.

8. (viii) If $u_m\rightharpoonup u$ in $H^1(\mathbb {R}^2)$ weakly and in $L^{p}(\mathbb {R}^2)$ strongly, then $\mathcal {P}(\lambda,\,u_m)\rightarrow \mathcal {P}(\lambda,\,u)$ in $H^1(\mathbb {R}^2)$ weakly and in $L^{p}(\mathbb {R}^2)$ strongly for each $\lambda >0$.

Proof. Let $u\in H^1(\mathbb {R}^2)$, $u\neq 0$, and let $u_\lambda =\mathcal {P}(\lambda,\,u)$. We have

\begin{align*} f(\lambda)& :=S(u_\lambda) =\frac{\lambda^2}{2}\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x+\frac{b\lambda^4}{4}\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2\\ & \quad +\frac{\omega}{2}\int_{\mathbb{R}^2}|u|^2\,{\rm d}x-\frac{\lambda^{p-2}}{p}\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x. \end{align*}

Then

\[ f'(\lambda)=\lambda\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x+b\lambda^3\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2-\frac{(p-2)\lambda^{p-3}}{p}\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x, \]

so that

\[ \frac{d}{d\lambda}S(\mathcal{P}(\lambda,u))=\frac{1}{\lambda}Q(\mathcal{P}(\lambda,u)), \]

Consequently, property (vi) holds. It follows from $f'(\lambda )=0$ that

(3.1)\begin{equation} \int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x+b\lambda^2\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2-\frac{(p-2)\lambda^{p-4}}{p}\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x=0. \end{equation}

Thus

\begin{align*} f''(\lambda)& =\displaystyle\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x+3b\lambda^2\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2\\ & \quad\displaystyle-\frac{(p-2)(p-3)\lambda^{p-4}}{p}\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x\\ & ={-}(p-4)\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x-b(p-6)\lambda^2\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2\\ & <\displaystyle0, \end{align*}

which implies that (3.1) has a unique positive solution $\lambda ^*(u)$ (by Rello's theorem). In particular, $f$ achieves its maximum at $\lambda ^*(u)$. Therefore, properties (i), (ii) and (v) follow.

(iii) Let $\lambda ^*(u)$ be the solution of (3.1), namely

(3.2)\begin{equation} \int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x+b(\lambda^*(u))^2\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2-\frac{(p-2)(\lambda^*(u))^{p-4}}{p}\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x=0. \end{equation}

If $Q(u)<0$. Then

\[ \int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x+b\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2-\frac{p-2}{p}\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x<0, \]

which implies that

\[ b\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2<\frac{p-2}{p}\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x. \]

If $\lambda ^*(u)\geq 1$. By (3.2), we deduce that

\begin{align*} 0& > \int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x+b\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2-\frac{p-2}{p}\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x\\ & \quad -\displaystyle\left[\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x+b(\lambda^*(u))^2\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2-\frac{(p-2)(\lambda^*(u))^{p-4}}{p}\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x\right]\\ & =\displaystyle\frac{p-2}{p}[(\lambda^*(u))^{p-4}-1]\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x+b(1-(\lambda^*(u))^2)\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2\\ & \geq \displaystyle\frac{p-2}{p}[(\lambda^*(u))^{p-4}-1]\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x+(1-(\lambda^*(u))^2)\frac{p-2}{p}\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x\\ & = \displaystyle\frac{p-2}{p}[(\lambda^*(u))^{p-4}-(\lambda^*(u))^2]\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x\\ & = \displaystyle\frac{p-2}{p}(\lambda^*(u))^2[(\lambda^*(u))^{p-6}-1]\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x, \end{align*}

which is impossible. This implies that if $Q(u)<0$ then $\lambda ^*(u)<1$. Now we claim that $Q(u)<0$ when $\lambda ^*(u)<1$. Indeed, $\lambda ^*(u)<1$ leads to

\[ b\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2\leq\frac{(p-2)(\lambda^*(u))^{p-6}}{p}\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x<\frac{p-2}{p}\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x. \]

Therefore,

\begin{align*} Q(u)& =\displaystyle\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x+b\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2-\frac{p-2}{p}\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x\\ & =\displaystyle\frac{(p-2)(\lambda^*(u))^{p-4}}{p}\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x-b(\lambda^*(u))^2\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2\\ & \quad +b\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2-\frac{p-2}{p}\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x\\ & =\displaystyle\frac{p-2}{p}[(\lambda^*(u))^{p-4}-1]\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x+b(1-(\lambda^*(u))^2)\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2\\ & <\displaystyle\frac{p-2}{p}[(\lambda^*(u))^{p-4}-1]\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x+(1-(\lambda^*(u))^2)\frac{p-2}{p}\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x\\ & =\displaystyle\frac{p-2}{p}[(\lambda^*(u))^{p-4}-(\lambda^*(u))^2]\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x\\ & =\displaystyle\frac{p-2}{p}(\lambda^*(u))^2[(\lambda^*(u))^{p-6}-1]\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x\\ & < 0. \end{align*}

Thus, property (iii) follows.

(iv) If $\lambda ^*(u)=1$, it follows from (3.2) that $u\in M$. On the other hand, assume $u\in M$, then

\[ \begin{cases} \displaystyle\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x+b\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2-\frac{p-2}{p}\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x=0,\\ \displaystyle\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x+b(\lambda^*(u))^2\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2-\frac{(p-2)(\lambda^*(u))^{p-4}}{p}\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x=0, \end{cases} \]

so that

(3.3)\begin{equation} \frac{p-2}{p}[1-(\lambda^*(u))^{p-4}]\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x+b((\lambda^*(u))^2-1)\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2=0. \end{equation}

If $\lambda ^*(u)>1$, using (3.3), we have

\begin{align*} 0& =\displaystyle\frac{p-2}{p}[1-(\lambda^*(u))^{p-4}]\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x+b((\lambda^*(u))^2-1)\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2\\ & <\displaystyle b[1-(\lambda^*(u))^{p-4}]\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2+b((\lambda^*(u))^2-1)\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2\\ & =\displaystyle b(\lambda^*(u))^2(1-(\lambda^*(u))^{p-6})\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2\\ & < 0. \end{align*}

Consequently, $\lambda ^*(u)\leq 1$. Similarly, we can reach a contradiction for the case of $\lambda ^*(u)<1$. As a result, $\lambda ^*(u)=1$.

Finally, property (vii) follows easily from the definition of Schwarz's symmetrization. For (viii), given $\lambda >0$, the operator $u\mapsto \mathcal {P}(\lambda,\,u)$ is linear and strongly continuous $H^1(\mathbb {R}^2)\rightarrow H^1(\mathbb {R}^2)$. Therefore, it is also weakly continuous. The $L^{p}(\mathbb {R}^2)$ continuity is immediate. Thus (viii) follows. This ends the proof.

Lemma 3.2 The set $M$ is nonempty. If we set

(3.4)\begin{equation} m=\inf\{S(u): u\in M\}, \end{equation}

then $Q(u)\leq S(u)-m$ for every $u\in H^1(\mathbb {R}^2)$ such that $Q(u)<0$.

Proof. The set $M$ is nonempty from lemma 3.1 (i). Let $u\in H^1(\mathbb {R}^2)$ such that $Q(u)<0$. By lemma 3.1 (ii) (iii), $f''(x)\leq 0$ on $(\lambda ^*(u),\, 1)$. Therefore,

\[ f(x)=f(1)+f'(1)(x-1)+\frac{f''(\xi)}{2}(x-1)^2\leq f(1)+f'(1)(x-1), \]

which means

\[ f(1)\geq f(\lambda^*(u))+f'(1)(1-\lambda^*(u)). \]

Applying lemma 3.1 (vi), we obtain

\begin{align*} S(u)& \geq f(\lambda^*(u))+(1-\lambda^*(u))Q(u)\\ & \geq f(\lambda^*(u))+Q(u). \end{align*}

Noting that $\lambda ^*(u)\in M$, we have $f(\lambda ^*(u))=S(\lambda ^*(u))\geq m$, and so

\[ S(u)\geq m+Q(u), \]

which completes the proof.

Proof. Proof of theorem 1.2

We proceed in three steps.

Step 1. We claim that the minimization problem (3.4) has a solution.

Since $M\neq \emptyset$, $S$ has a minimizing sequence $\{v_n\}$. In particular, $Q(v_n)=0$ and $S(v_n)\rightarrow m$. Let $w_n=|v_n|^*$, and $u_n=\mathcal {P}(\lambda ^*(w_n),\,w_n)$. It follows from lemma 3.1 (i) that $u_n\in M$. Furthermore, it follows from lemma 3.1 (vii) that $u_n=|\mathcal {P}(\lambda ^*(w_n),\,v_n)|^*$. Therefore,

\begin{align*} S(u_n)& \leq S(\mathcal{P}(\lambda^*(w_n),v_n))\leq S(\mathcal{P}(\lambda^*(v_n),v_n)) \ (\mathrm{by~Lemma~} 3.1\ (\mathrm{v}))\\ & \leq S(v_n) \ (\mathrm{since} \ \lambda^*(v_n)=1). \end{align*}

In particular, $\{u_n\}$ is a nonnegative, spherically symmetric, nonincreasing minimizing sequence of $S$. Furthermore, note that as $n\rightarrow \infty$

\begin{align*} m\displaystyle\leftarrow S(u_n)-\frac{1}{p-2}Q(u_n)& =\displaystyle\left(\frac{1}{2}-\frac{1}{p-2}\right)\int_{\mathbb{R}^2}|\nabla u_n|^2\,{\rm d}x \\ & \quad +b\left(\frac{1}{4}-\frac{1}{p-2}\right)\left(\int_{\mathbb{R}^2}|\nabla u_n|^2\,{\rm d}x\right)^2+\frac{\omega}{2}\int_{\mathbb{R}^2}|u_n|^2\,{\rm d}x\\ & \geq \displaystyle\left(\frac{1}{2}-\frac{1}{p-2}\right)\int_{\mathbb{R}^2}|\nabla u_n|^2\,{\rm d}x+\frac{\omega}{2}\int_{\mathbb{R}^2}|u_n|^2\,{\rm d}x, \end{align*}

which implies that $\{u_n\}$ is bounded in $H^1(\mathbb {R}^2)$. Since $Q(u_n)=0$, then

(3.5)\begin{equation} \frac{p}{p-2}\int_{\mathbb{R}^2}|\nabla u_n|^2\,{\rm d}x\leq\int_{\mathbb{R}^2}|u_n|^{p}\,{\rm d}x. \end{equation}

Therefore, by the Gagliardo–Nirenberg inequality and the boundedness of $\{u_n\}$ in $L^2(\mathbb {R}^2)$, there exists a constant $C>0$ such that

\[ \int_{\mathbb{R}^2}|\nabla u_n|^2\,{\rm d}x\leq C\left(\int_{\mathbb{R}^2}|\nabla u_n|^2\,{\rm d}x\right)^{\frac{p-2}{2}}. \]

We obtain that $|\nabla u_n|_{L^2}$ is bounded from below, and so it follows from (3.5) that

(3.6)\begin{equation} \int_{\mathbb{R}^2}|u_n|^{p}\,{\rm d}x\geq c, \ \mathrm{for~some}\ c>0. \end{equation}

Therefore, there exist $v\in H^1(\mathbb {R}^2)$ and a subsequence, which we still denoted by $\{u_n\}$, such that $u_n\rightharpoonup v$ in $H^1(\mathbb {R}^2)$ weakly and in $L^{p}(\mathbb {R}^2)$ strongly ($v\neq 0$, by (3.6)). Therefore, we may define $\zeta =\mathcal {P}(\lambda ^*(v),\,v)=\lambda ^*(v)v(\lambda ^*(v)x)$. By lemma 3.1 (i), it follows directly that $\zeta \in M$, and hence

\[ S(\zeta)\geq m. \]

On the other hand, according to lemma 3.1 (viii), we know that $\mathcal {P}(\lambda ^*(v),\,u_n)\rightharpoonup \zeta$ in $H^1(\mathbb {R}^2)$ weakly and in $L^{p}(\mathbb {R}^2)$ strongly. Therefore,

\begin{align*} S(\zeta)& \leq \displaystyle\liminf_{n\rightarrow\infty} S(\mathcal{P}(\lambda^*(v),u_n)) \\ & \leq \displaystyle\liminf_{n\rightarrow\infty} S(\mathcal{P}(\lambda^*(u_n),u_n))\\ & = \displaystyle\liminf_{n\rightarrow\infty} S(u_n)=m \ (\mathrm{since}\ \lambda^*(u_n)=1). \end{align*}

Consequently, we obtain $S(\zeta )=m$. Thus, $\zeta$ is the solution of (3.4).

Step 2. We claim that every solution of (3.4) satisfies equation (1.1).

Consider any solution $u$ of (3.4). We have

\[ S(u)=m. \]

Then $\langle S'(u),\,u\rangle _{H^{-1},\,H^1}=0$, where $S'$ is the gradient of the $C^1$ functional $S$, i.e.,

\[ S'(u)={-}\left(1+b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)\Delta u+\omega u-|u|^{p-2}u. \]

Notice that

\[ Q'(u)={-}\left(2+4b\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)\Delta u-(p-2)|u|^{p-2}u. \]

It follows from $u\in M$ that

\begin{align*} \langle Q'(u),u\rangle_{H^{{-}1},H^1}& = \displaystyle2\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x+4b\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2\\ & \quad -(p-2)\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x -pQ(u)\\ & =\displaystyle-(p-2)\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x-(p-4)b\left(\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)^2\\ & < 0. \end{align*}

Finally, since $u$ solves (3.4), there exists a Lagrange multiplier $\lambda$ such that

\[ S'(u)=\lambda Q'(u). \]

Thus,

\[ 0=\langle S'(u),u\rangle_{H^{{-}1},H^1}=\lambda \langle Q'(u),u\rangle_{H^{{-}1},H^1}. \]

Noting that $\langle Q'(u),\,u\rangle _{H^{-1},\,H^1}<0$, we obtain $\lambda =0$. Consequently, $S'(u)=0$, which means that $u$ solves problem (1.1).

Step 3. Conclusion.

Consider

(3.7)\begin{equation} l=\min\{S(u): u\in A\}. \end{equation}

Let $u\in G$ be such that $S(u)=l$. Now we claim that $u\in M$. Indeed, since $u$ is a solution of equation (1.1), we have $V(u)=0$ and

\[ T(u)=\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x-\omega\int_{\mathbb{R}^2}|u|^2\,{\rm d}x. \]

Thus

\begin{align*} Q(u)& = \displaystyle T(u)-\frac{p-2}{p}\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x\\ & = \displaystyle\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x-\omega\int_{\mathbb{R}^2}|u|^2\,{\rm d}x-\frac{p-2}{p}\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x\\ & =\displaystyle\frac{2}{p}\int_{\mathbb{R}^2}|u|^{p}\,{\rm d}x-\omega\int_{\mathbb{R}^2}|u|^2\,{\rm d}x\\ & =\displaystyle\frac{1}{2}V(u)\\ & = 0. \end{align*}

Therefore, $u\in M$, which implies that $S(u)\geq m$. In particular

(3.8)\begin{equation} l=S(u)\geq m. \end{equation}

Consider now a solution $v$ of (3.4). Since $S(v)=m$ and $v\in A$ (by Step 2), it follows from (3.7) that $m\geq l$. Combining with (3.8), we obtain $m=l$. The equivalence of the two problems follows easily. The proof is complete.