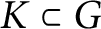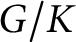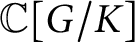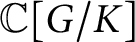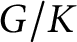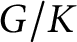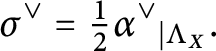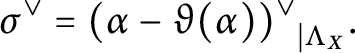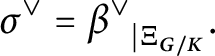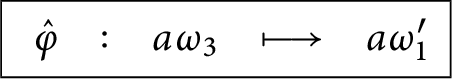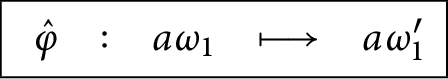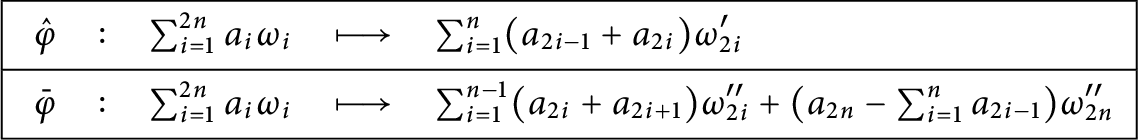1 Introduction
Let G be a connected semisimple complex algebraic group, and let
![]() $K \subset G$
be a reductive subgroup. Recall that the affine variety
$K \subset G$
be a reductive subgroup. Recall that the affine variety
![]() $G/K$
is called spherical if it contains an open orbit under a Borel subgroup of G. If this is the case, we will also say that K is a spherical subgroup, and that
$G/K$
is called spherical if it contains an open orbit under a Borel subgroup of G. If this is the case, we will also say that K is a spherical subgroup, and that
![]() $(G,K)$
is a reductive spherical pair. A fundamental example is that of the symmetric varieties, namely when K is the set of fixed points of an algebraic involution of G.
$(G,K)$
is a reductive spherical pair. A fundamental example is that of the symmetric varieties, namely when K is the set of fixed points of an algebraic involution of G.
By a result of Vinberg and Kimelfeld [Reference Vinberg and Kimelfeld34], reductive spherical subgroups are characterized by the property that the coordinate ring
![]() $\mathbb C[G/K]$
is a multiplicity-free G-module (that is, every isotypic component is irreducible).
$\mathbb C[G/K]$
is a multiplicity-free G-module (that is, every isotypic component is irreducible).
Fix a maximal torus
![]() $T \subset G$
and a Borel subgroup of G containing T, and let
$T \subset G$
and a Borel subgroup of G containing T, and let
![]() $\mathcal X(T)^+$
be the monoid of dominant weights of G. For
$\mathcal X(T)^+$
be the monoid of dominant weights of G. For
![]() $\lambda \in \mathcal X(T)^+$
, we denote by
$\lambda \in \mathcal X(T)^+$
, we denote by
![]() $V(\lambda )$
the irreducible G-module of highest weight
$V(\lambda )$
the irreducible G-module of highest weight
![]() $\lambda $
.
$\lambda $
.
Suppose now that X is an affine spherical homogeneous G-variety. Being multiplicity-free, the G-module structure of the coordinate ring of X is completely captured by the associated weight monoid, that is, the submonoid
![]() $\Lambda ^+_X \subset \mathcal X(T)^+$
formed by the highest weights of
$\Lambda ^+_X \subset \mathcal X(T)^+$
formed by the highest weights of
![]() $\mathbb C[X]$
. Such monoid is well understood, and can be combinatorially described (see, e.g., [Reference Brion and Pauer8]). On the other hand, the description of the G-algebra structure of
$\mathbb C[X]$
. Such monoid is well understood, and can be combinatorially described (see, e.g., [Reference Brion and Pauer8]). On the other hand, the description of the G-algebra structure of
![]() $\mathbb C[X]$
is still a widely open problem.
$\mathbb C[X]$
is still a widely open problem.
To be more precise, for
![]() $\lambda \in \Lambda _X^+$
, denote by
$\lambda \in \Lambda _X^+$
, denote by
![]() $E_X(\lambda ) \simeq V(\lambda )$
the irreducible component in
$E_X(\lambda ) \simeq V(\lambda )$
the irreducible component in
![]() $\mathbb C[X]$
of highest weight
$\mathbb C[X]$
of highest weight
![]() $\lambda $
. Then, we have the decomposition
$\lambda $
. Then, we have the decomposition
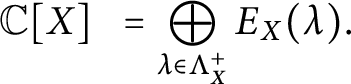 $$ \begin{align*}\mathbb C[X] \; \; = \bigoplus_{\lambda \in \Lambda_X^+} E_X(\lambda). \end{align*} $$
$$ \begin{align*}\mathbb C[X] \; \; = \bigoplus_{\lambda \in \Lambda_X^+} E_X(\lambda). \end{align*} $$
Given
![]() $\lambda , \mu \in \Lambda _X^+$
, let
$\lambda , \mu \in \Lambda _X^+$
, let
![]() $E_X(\lambda ) \cdot E_X(\mu )$
denote the submodule of
$E_X(\lambda ) \cdot E_X(\mu )$
denote the submodule of
![]() $\mathbb C[X]$
generated by the products
$\mathbb C[X]$
generated by the products
![]() $fg$
with
$fg$
with
![]() $f \in E_X(\lambda )$
and
$f \in E_X(\lambda )$
and
![]() $g \in E_X(\mu )$
. We will deal with the following problem: for which
$g \in E_X(\mu )$
. We will deal with the following problem: for which
![]() $\nu \in \Lambda ^+_X$
, does
$\nu \in \Lambda ^+_X$
, does
![]() $E_X(\nu )$
appear inside
$E_X(\nu )$
appear inside
![]() $E_X(\lambda ) \cdot E_X(\mu )$
?
$E_X(\lambda ) \cdot E_X(\mu )$
?
Clearly, there are some bounds on the range of weights which can occur inside
![]() $E_X(\lambda ) \cdot E_X(\mu )$
. For instance, if
$E_X(\lambda ) \cdot E_X(\mu )$
. For instance, if
![]() $\nu $
is such a weight, then
$\nu $
is such a weight, then
![]() $V(\nu )$
must appear as a submodule inside the tensor product
$V(\nu )$
must appear as a submodule inside the tensor product
![]() $V(\lambda ) \otimes V(\mu )$
.
$V(\lambda ) \otimes V(\mu )$
.
A more subtle bound comes from the spherical roots of X. Let indeed
![]() $\mathcal M_X^{\mathrm n} \subset \mathcal X(T)$
be the submonoid generated by the set of differences
$\mathcal M_X^{\mathrm n} \subset \mathcal X(T)$
be the submonoid generated by the set of differences
By a fundamental theorem of Knop [Reference Knop18], together with a recent result of Avdeev and Cupit-Foutou [Reference Avdeev and Cupit-Foutou2], the monoid
![]() $\mathcal M_X^{\mathrm n}$
is free. Let
$\mathcal M_X^{\mathrm n}$
is free. Let
![]() $\Delta _X^{\mathrm n}$
be the set of free generators of
$\Delta _X^{\mathrm n}$
be the set of free generators of
![]() $\mathcal M_X^{\mathrm n}$
, called the spherical roots of X (or, more precisely, the
$\mathcal M_X^{\mathrm n}$
, called the spherical roots of X (or, more precisely, the
![]() $\mathrm n$
-spherical roots, in the terminology of Section 4). Then,
$\mathrm n$
-spherical roots, in the terminology of Section 4). Then,
![]() $\Delta _X^{\mathrm n}$
is the base of a root system
$\Delta _X^{\mathrm n}$
is the base of a root system
![]() $\Phi ^{\mathrm n}_X$
, whose rank is called the rank of X. This root system, together with its Weyl group, encodes important information on the geometry of X and of its equivariant embeddings. When X is a symmetric variety, the root system
$\Phi ^{\mathrm n}_X$
, whose rank is called the rank of X. This root system, together with its Weyl group, encodes important information on the geometry of X and of its equivariant embeddings. When X is a symmetric variety, the root system
![]() $\Phi ^{\mathrm n}_X$
is essentially the restricted root system attached to X.
$\Phi ^{\mathrm n}_X$
is essentially the restricted root system attached to X.
Similarly to the weight monoid
![]() $\Lambda ^+_X$
, the set of spherical roots
$\Lambda ^+_X$
, the set of spherical roots
![]() $\Delta _X^{\mathrm n}$
is also well understood (see, e.g., [Reference Brion and Pauer8]). In the general context of spherical varieties, both the weight monoid and the spherical roots are a fundamental part of the combinatorial invariants attached by Luna to a spherical variety in his seminal paper [Reference Luna26].
$\Delta _X^{\mathrm n}$
is also well understood (see, e.g., [Reference Brion and Pauer8]). In the general context of spherical varieties, both the weight monoid and the spherical roots are a fundamental part of the combinatorial invariants attached by Luna to a spherical variety in his seminal paper [Reference Luna26].
Going back to the problem of decomposing the product of irreducible G-modules inside
![]() $\mathbb C[X]$
, by the very definition of the spherical roots, we see the implication
$\mathbb C[X]$
, by the very definition of the spherical roots, we see the implication
 $$ \begin{align*}E_X(\nu) \subset E_X(\lambda) \cdot E_X(\mu) \Longrightarrow \left\{ \begin{array}{c} V(\nu) \subset V(\lambda) \otimes V(\mu), \phantom{\Big|} \\ \lambda + \mu - \nu \in \mathbb N \Delta_X^{\mathrm n}. \end{array} \right. \end{align*} $$
$$ \begin{align*}E_X(\nu) \subset E_X(\lambda) \cdot E_X(\mu) \Longrightarrow \left\{ \begin{array}{c} V(\nu) \subset V(\lambda) \otimes V(\mu), \phantom{\Big|} \\ \lambda + \mu - \nu \in \mathbb N \Delta_X^{\mathrm n}. \end{array} \right. \end{align*} $$
In several cases, the condition on the right-hand side seems, indeed, close to give a characterization of the irreducible constituents of
![]() $E_X(\lambda ) \cdot E_X(\mu )$
. However, there are counterexamples (see, e.g., Example 6.4); thus, we are led to consider other possible descriptions.
$E_X(\lambda ) \cdot E_X(\mu )$
. However, there are counterexamples (see, e.g., Example 6.4); thus, we are led to consider other possible descriptions.
In particular, in the present paper, we will focus on the case of the affine spherical homogeneous spaces
![]() $X = G/K$
for a simple group G, whose spherical roots form a root system of type
$X = G/K$
for a simple group G, whose spherical roots form a root system of type
![]() $\mathsf A$
. The classification of the reductive spherical subgroups for a simple group was first obtained by Krämer [Reference Krämer23], and more recently in arbitrary characteristic by Knop and Röhrle [Reference Knop and Röhrle19]. For a complete list of the cases we will deal with, see the table at the end of Section 3 (for the symmetric cases) and the table at the beginning of Section 6 (for the non-symmetric cases).
$\mathsf A$
. The classification of the reductive spherical subgroups for a simple group was first obtained by Krämer [Reference Krämer23], and more recently in arbitrary characteristic by Knop and Röhrle [Reference Knop and Röhrle19]. For a complete list of the cases we will deal with, see the table at the end of Section 3 (for the symmetric cases) and the table at the beginning of Section 6 (for the non-symmetric cases).
When X is a symmetric variety with restricted root system of type
![]() $\mathsf A$
, a general conjectural rule for decomposing the product of two irreducible components of
$\mathsf A$
, a general conjectural rule for decomposing the product of two irreducible components of
![]() $\mathbb C[X]$
follows from a long-standing conjecture of Stanley [Reference Stanley33] on the multiplication of Jack symmetric functions (see Conjecture 3.2). Such conjectural description holds true when the rank of X is 1, as a consequence of a Pieri rule for the multiplication of Jack symmetric functions proved by Stanley himself [Reference Stanley33].
$\mathbb C[X]$
follows from a long-standing conjecture of Stanley [Reference Stanley33] on the multiplication of Jack symmetric functions (see Conjecture 3.2). Such conjectural description holds true when the rank of X is 1, as a consequence of a Pieri rule for the multiplication of Jack symmetric functions proved by Stanley himself [Reference Stanley33].
The connection between Stanley’s context and ours stems from the well-known fact that specializing the Jack symmetric functions to a suitable parameter defined by X (which is essentially the multiplicity of the restricted roots) and setting the extra variables to
![]() $0$
yields indeed a basis for the space
$0$
yields indeed a basis for the space
![]() $\mathbb C[X]^K$
of the spherical functions on X. This point of view was already exploited by Graham and Hunziker [Reference Graham and Hunziker16], who dealt with a problem similar to the one considered in this paper in the case of the symmetric varieties with restricted root system of type
$\mathbb C[X]^K$
of the spherical functions on X. This point of view was already exploited by Graham and Hunziker [Reference Graham and Hunziker16], who dealt with a problem similar to the one considered in this paper in the case of the symmetric varieties with restricted root system of type
![]() $\mathsf A$
.
$\mathsf A$
.
Our main contribution with the present paper is to show how a general conjectural rule for decomposing the product of two irreducible constituents in
![]() $\mathbb C[X]$
also follows from Stanley’s mentioned conjecture for all the nonsymmetric affine spherical homogeneous varieties whose spherical roots generate a root system of type
$\mathbb C[X]$
also follows from Stanley’s mentioned conjecture for all the nonsymmetric affine spherical homogeneous varieties whose spherical roots generate a root system of type
![]() $\mathsf A$
. When this root system is a direct sum of subsystems of rank 1, which happens in most cases, we will see (with the exception of one case) that such description holds true thanks to Stanley’s Pieri rule for Jack symmetric functions.
$\mathsf A$
. When this root system is a direct sum of subsystems of rank 1, which happens in most cases, we will see (with the exception of one case) that such description holds true thanks to Stanley’s Pieri rule for Jack symmetric functions.
To state the mentioned decomposition rule, we will introduce a different normalization for the spherical roots of X and will define a slight variation of
![]() $\Phi ^{\mathrm n}_X$
, where we replace some of the spherical roots of X with their half. More precisely, we will associate to X a based root datum
$\Phi ^{\mathrm n}_X$
, where we replace some of the spherical roots of X with their half. More precisely, we will associate to X a based root datum
![]() $\mathcal R_X$
(see Proposition 4.3 for its definition), having the same Weyl group of
$\mathcal R_X$
(see Proposition 4.3 for its definition), having the same Weyl group of
![]() $\Phi _X^{\mathrm n}$
and with the property that the weight monoid
$\Phi _X^{\mathrm n}$
and with the property that the weight monoid
![]() $\Lambda ^+_X$
can be naturally regarded as a submonoid of the dominant weights of
$\Lambda ^+_X$
can be naturally regarded as a submonoid of the dominant weights of
![]() $\mathcal R_X$
.
$\mathcal R_X$
.
Let
![]() $G_X$
be the complex reductive group associated to
$G_X$
be the complex reductive group associated to
![]() $\mathcal R_X$
, and for
$\mathcal R_X$
, and for
![]() $\lambda \in \Lambda ^+_X$
, denote by
$\lambda \in \Lambda ^+_X$
, denote by
![]() $V_X(\lambda )$
the irreducible
$V_X(\lambda )$
the irreducible
![]() $G_X$
-module associated to
$G_X$
-module associated to
![]() $\lambda $
(regarded as a dominant weight for
$\lambda $
(regarded as a dominant weight for
![]() $G_X$
). Then, we have the following conjecture (see Conjecture 5.1).
$G_X$
). Then, we have the following conjecture (see Conjecture 5.1).
Conjecture 1.1 Let X be an affine spherical homogeneous variety for a simple group G such that
![]() $\Phi _X^{\mathrm n}$
is of type
$\Phi _X^{\mathrm n}$
is of type
![]() $\mathsf A$
. Let
$\mathsf A$
. Let
![]() $\lambda , \mu , \nu \in \Lambda _X^+$
, then
$\lambda , \mu , \nu \in \Lambda _X^+$
, then
 $$ \begin{align*}E_X(\nu) \subset E_X(\lambda) \cdot E_X(\mu) \Longleftrightarrow \left\{ \begin{array}{c} V_X(\nu) \subset V_X(\lambda) \otimes V_X(\mu), \phantom{\Big|} \\ \lambda + \mu - \nu \in \mathbb N \Delta_X^{\mathrm n}. \end{array} \right. \end{align*} $$
$$ \begin{align*}E_X(\nu) \subset E_X(\lambda) \cdot E_X(\mu) \Longleftrightarrow \left\{ \begin{array}{c} V_X(\nu) \subset V_X(\lambda) \otimes V_X(\mu), \phantom{\Big|} \\ \lambda + \mu - \nu \in \mathbb N \Delta_X^{\mathrm n}. \end{array} \right. \end{align*} $$
Our main theorem is the following (see Propositions 5.8 and 5.12 and Corollary 5.10).
Theorem 1.2 Let X be an affine spherical homogeneous variety for a simple group G. Suppose that
![]() $\Phi _X^{\mathrm n}$
is of type
$\Phi _X^{\mathrm n}$
is of type
![]() $\mathsf A$
, and that
$\mathsf A$
, and that
![]() $X \neq \mathsf F_4/\operatorname {\mathrm {Spin}}(9)$
.
$X \neq \mathsf F_4/\operatorname {\mathrm {Spin}}(9)$
.
In the case of
![]() $\mathsf F_4/\operatorname {\mathrm {Spin}}(9)$
, which remains excluded from the previous theorem, Conjecture 1.1 is based on computational experiments.
$\mathsf F_4/\operatorname {\mathrm {Spin}}(9)$
, which remains excluded from the previous theorem, Conjecture 1.1 is based on computational experiments.
The strategy that we will adopt to prove the previous theorem is somehow homogeneous the various cases that we will consider. Indeed, we will show that in all cases (with the exception of
![]() $\mathsf F_4/\operatorname {\mathrm {Spin}}(9)$
, and three other cases that can be easily reduced to some other case), we can find a reductive overgroup
$\mathsf F_4/\operatorname {\mathrm {Spin}}(9)$
, and three other cases that can be easily reduced to some other case), we can find a reductive overgroup
![]() $\widehat G \supset G$
with a symmetric
$\widehat G \supset G$
with a symmetric
![]() $\widehat G$
-variety Y and a reductive subgroup
$\widehat G$
-variety Y and a reductive subgroup
![]() $H \subset G$
with a symmetric H-variety Z, respectively, endowed with a G-equivariant isomorphism and with an H-equivariant embedding
$H \subset G$
with a symmetric H-variety Z, respectively, endowed with a G-equivariant isomorphism and with an H-equivariant embedding
Both the symmetric varieties Y and Z will have a restricted root system of type
![]() $\mathsf A$
, and we will see that the previous maps induce an isogeny from the based root datum
$\mathsf A$
, and we will see that the previous maps induce an isogeny from the based root datum
![]() $\mathcal R_X$
to the direct sum
$\mathcal R_X$
to the direct sum
![]() $\mathcal R_Y \oplus \mathcal R_Z$
(see Proposition 5.6).
$\mathcal R_Y \oplus \mathcal R_Z$
(see Proposition 5.6).
This will allow us to show that the validity of Conjecture 1.1 in the various cases follows from the analogous statement for the symmetric varieties with restricted root system of type
![]() $\mathsf A$
, which in turn follows from Stanley’s conjecture, and from Stanley’s Pieri rule when
$\mathsf A$
, which in turn follows from Stanley’s conjecture, and from Stanley’s Pieri rule when
![]() $\Phi _X^{\mathrm n}$
is a direct sum of rank 1 root subsystems.
$\Phi _X^{\mathrm n}$
is a direct sum of rank 1 root subsystems.
The fact that the G-action on X can be extended to a
![]() $\widehat G$
-action making X into a symmetric
$\widehat G$
-action making X into a symmetric
![]() $\widehat G$
-variety will be basically a consequence of a suitable factorization of
$\widehat G$
-variety will be basically a consequence of a suitable factorization of
![]() $\widehat G$
as a product of two reductive subgroups (one of them being G, and the other one a symmetric subgroup of
$\widehat G$
as a product of two reductive subgroups (one of them being G, and the other one a symmetric subgroup of
![]() $\widehat G$
with the desired property). Such factorizations were first classified by Onishchik [Reference Onishchik29], and in arbitrary characteristic by Liebeck, Saxl, and Seitz [Reference Liebeck, Saxl and Seitz24].
$\widehat G$
with the desired property). Such factorizations were first classified by Onishchik [Reference Onishchik29], and in arbitrary characteristic by Liebeck, Saxl, and Seitz [Reference Liebeck, Saxl and Seitz24].
In the last section, we will also show that the same technique described above can also be applied in the case of the spherical variety
![]() $\operatorname {\mathrm {SO}}(2n+1)/\operatorname {\mathrm {GL}}(n)$
(whose spherical root system is not of type
$\operatorname {\mathrm {SO}}(2n+1)/\operatorname {\mathrm {GL}}(n)$
(whose spherical root system is not of type
![]() $\mathsf A$
), to decompose its root datum into the direct sum of those associated with two symmetric varieties of Hermitian type (see Theorem 6.1). This leads us to consider the decomposition problem also for another class of reductive spherical pairs
$\mathsf A$
), to decompose its root datum into the direct sum of those associated with two symmetric varieties of Hermitian type (see Theorem 6.1). This leads us to consider the decomposition problem also for another class of reductive spherical pairs
![]() $(G,K)$
, namely when K is a spherical Levi subgroup of G, in which case
$(G,K)$
, namely when K is a spherical Levi subgroup of G, in which case
 $\Phi _{G/K}^{\mathrm n}$
is of type
$\Phi _{G/K}^{\mathrm n}$
is of type
![]() $\mathsf B$
or
$\mathsf B$
or
![]() $\mathsf C$
. Here, the problem seems quite unexplored, even in the symmetric case. We show that the case of the spherical Levi subgroups reduces to that of the symmetric Levi subgroups (that is, to the case of the symmetric varieties of Hermitian type), and we formulate a conjectural rule for the decomposition of the product of two irreducible components in
$\mathsf C$
. Here, the problem seems quite unexplored, even in the symmetric case. We show that the case of the spherical Levi subgroups reduces to that of the symmetric Levi subgroups (that is, to the case of the symmetric varieties of Hermitian type), and we formulate a conjectural rule for the decomposition of the product of two irreducible components in
![]() $\mathbb C[G/K]$
in this case as well (see Conjecture 6.2).
$\mathbb C[G/K]$
in this case as well (see Conjecture 6.2).
2 Notation and preliminaries
If H is a connected algebraic group, we will denote by
![]() $\mathcal X(H)$
its character lattice. If H acts on a vector space V, we will denote by
$\mathcal X(H)$
its character lattice. If H acts on a vector space V, we will denote by
![]() $V^H$
the invariant subspace and by
$V^H$
the invariant subspace and by
![]() $V^{(H)}$
the semi-invariant subset, that is, the union of the semi-invariant subspaces
$V^{(H)}$
the semi-invariant subset, that is, the union of the semi-invariant subspaces
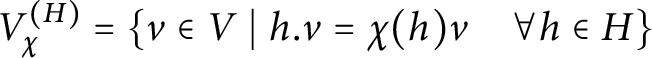 $$ \begin{align*}V^{(H)}_\chi = \{v \in V \; | \; h.v = \chi(h)v \quad \forall h \in H\} \end{align*} $$
$$ \begin{align*}V^{(H)}_\chi = \{v \in V \; | \; h.v = \chi(h)v \quad \forall h \in H\} \end{align*} $$
with
![]() $\chi \in \mathcal X(H)$
. If
$\chi \in \mathcal X(H)$
. If
![]() $\Xi $
is a lattice, we will denote by
$\Xi $
is a lattice, we will denote by
![]() $\Xi ^\vee $
its dual lattice, namely
$\Xi ^\vee $
its dual lattice, namely
![]() $\Xi ^\vee = \operatorname {\mathrm {Hom}}_{\mathbb Z}(\Xi , \mathbb Z)$
.
$\Xi ^\vee = \operatorname {\mathrm {Hom}}_{\mathbb Z}(\Xi , \mathbb Z)$
.
Let G be a semisimple complex algebraic group. If
![]() $K \subset G$
, we will denote by
$K \subset G$
, we will denote by
![]() $\mathrm N_G(K)$
the normalizer of K in G, and by
$\mathrm N_G(K)$
the normalizer of K in G, and by
![]() $Z_G(K)$
the centralizer of K in G. Fix a maximal torus
$Z_G(K)$
the centralizer of K in G. Fix a maximal torus
![]() $T \subset G$
and a Borel subgroup B containing T. We denote by
$T \subset G$
and a Borel subgroup B containing T. We denote by
![]() $\Phi $
the root system of G associated to T, and by
$\Phi $
the root system of G associated to T, and by
![]() $\Delta $
the base defined by B and by
$\Delta $
the base defined by B and by
![]() $\Phi = \Phi ^+ \sqcup \Phi ^-$
the corresponding decomposition into positive and negative roots. When
$\Phi = \Phi ^+ \sqcup \Phi ^-$
the corresponding decomposition into positive and negative roots. When
![]() $\Phi $
is an irreducible root system of rank n, we will order the set of simple roots
$\Phi $
is an irreducible root system of rank n, we will order the set of simple roots
![]() $\Delta = \{\alpha _1, \ldots , \alpha _n\}$
following Bourbaki’s notation.
$\Delta = \{\alpha _1, \ldots , \alpha _n\}$
following Bourbaki’s notation.
The monoid of dominant weights of G will be denoted by
![]() $\mathcal X(T)^+$
. Given
$\mathcal X(T)^+$
. Given
![]() $\lambda \in \mathcal X(T)^+$
, the irreducible representation of G of highest weight
$\lambda \in \mathcal X(T)^+$
, the irreducible representation of G of highest weight
![]() $\lambda $
will be denoted by
$\lambda $
will be denoted by
![]() $V_G(\lambda )$
, or simply by
$V_G(\lambda )$
, or simply by
![]() $V(\lambda )$
when no ambiguity is possible.
$V(\lambda )$
when no ambiguity is possible.
Let
![]() $G/K$
be an affine spherical variety. Equivalently, K is a reductive group, and the coordinate ring
$G/K$
be an affine spherical variety. Equivalently, K is a reductive group, and the coordinate ring
![]() $\mathbb C[G/K]$
is multiplicity-free as a G-module. By the multiplicity-free property, the description of the G-module structure of
$\mathbb C[G/K]$
is multiplicity-free as a G-module. By the multiplicity-free property, the description of the G-module structure of
![]() $\mathbb C[G/K]$
is equivalent to the description of the monoid of the spherical weights
$\mathbb C[G/K]$
is equivalent to the description of the monoid of the spherical weights
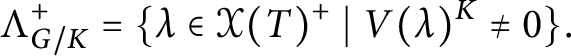 $$ \begin{align*}\Lambda^+_{G/K} = \{\lambda \in \mathcal X(T)^+ \; | \; V(\lambda)^K \neq 0\}. \end{align*} $$
$$ \begin{align*}\Lambda^+_{G/K} = \{\lambda \in \mathcal X(T)^+ \; | \; V(\lambda)^K \neq 0\}. \end{align*} $$
Because K is reductive, notice that
![]() $V(\lambda )$
admits a nonzero K-invariant vector if and only if the same holds for its dual
$V(\lambda )$
admits a nonzero K-invariant vector if and only if the same holds for its dual
![]() $V(\lambda )^*$
. Therefore, with this notation, we have the decomposition
$V(\lambda )^*$
. Therefore, with this notation, we have the decomposition
 $$ \begin{align*}\mathbb C[G/K] = \mathbb C[G]^K \simeq \bigoplus_{\lambda \in \mathcal X(T)^+} V(\lambda)^* \otimes V(\lambda)^K \simeq \bigoplus_{\lambda \in \Lambda_{G/K}^+} V(\lambda). \end{align*} $$
$$ \begin{align*}\mathbb C[G/K] = \mathbb C[G]^K \simeq \bigoplus_{\lambda \in \mathcal X(T)^+} V(\lambda)^* \otimes V(\lambda)^K \simeq \bigoplus_{\lambda \in \Lambda_{G/K}^+} V(\lambda). \end{align*} $$
For every
 $\lambda \in \Lambda _{G/K}^+$
, we denote by
$\lambda \in \Lambda _{G/K}^+$
, we denote by
![]() $E_{G/K}(\lambda )\simeq V(\lambda )$
the corresponding isotypic (irreducible) component in
$E_{G/K}(\lambda )\simeq V(\lambda )$
the corresponding isotypic (irreducible) component in
![]() $\mathbb C[G/K]$
.
$\mathbb C[G/K]$
.
The previous description can be generalized from the realm of K-invariant functions to that of K-semi-invariant functions, with respect to the right action of G on itself. Indeed, for every character
![]() $\chi \in \mathcal X(K)$
, the eigenspace
$\chi \in \mathcal X(K)$
, the eigenspace
 $\mathbb C[G]^{(K)}_\chi $
is also a multiplicity-free G-module. Inside
$\mathbb C[G]^{(K)}_\chi $
is also a multiplicity-free G-module. Inside
 $\mathbb C[G]^{(K)}_\chi $
, every
$\mathbb C[G]^{(K)}_\chi $
, every
![]() $\lambda \in \Lambda ^+$
with
$\lambda \in \Lambda ^+$
with
 $\big (V(\lambda )^*\big )^{(K)}_\chi \neq 0$
yields an isotypic component
$\big (V(\lambda )^*\big )^{(K)}_\chi \neq 0$
yields an isotypic component
![]() $E_{G/K}(\lambda ,\chi ) \simeq V(\lambda )$
. In this setting, the relevant weight monoid is that of the quasi-spherical weights
$E_{G/K}(\lambda ,\chi ) \simeq V(\lambda )$
. In this setting, the relevant weight monoid is that of the quasi-spherical weights
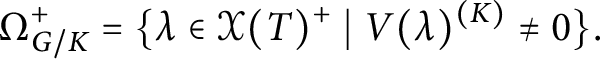 $$ \begin{align*}\Omega^+_{G/K} = \{\lambda \in \mathcal X(T)^+ \; | \; V(\lambda)^{(K)} \neq 0\}. \end{align*} $$
$$ \begin{align*}\Omega^+_{G/K} = \{\lambda \in \mathcal X(T)^+ \; | \; V(\lambda)^{(K)} \neq 0\}. \end{align*} $$
The algebra structure of the invariant ring
![]() $\mathbb C[G]^K$
is encoded by the associated spherical functions. For every
$\mathbb C[G]^K$
is encoded by the associated spherical functions. For every
 $\lambda \in \Lambda ^+_{G/K}$
, fix a nonzero element
$\lambda \in \Lambda ^+_{G/K}$
, fix a nonzero element
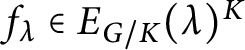 $f_\lambda \in E_{G/K}(\lambda )^K$
. The K-invariant space in
$f_\lambda \in E_{G/K}(\lambda )^K$
. The K-invariant space in
![]() $V(\lambda )$
is one-dimensional; thus, the spherical functions
$V(\lambda )$
is one-dimensional; thus, the spherical functions
 $\{f_\lambda \}_{\lambda \in \Lambda _{G/K}^+}$
form a basis for the space of K-invariant functions
$\{f_\lambda \}_{\lambda \in \Lambda _{G/K}^+}$
form a basis for the space of K-invariant functions
 $$ \begin{align*}\mathbb C[G]^{K\times K} = \bigoplus E_{G/K}(\lambda)^K.\end{align*} $$
$$ \begin{align*}\mathbb C[G]^{K\times K} = \bigoplus E_{G/K}(\lambda)^K.\end{align*} $$
More explicitly, if
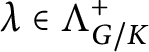 $\lambda \in \Lambda _{G/K}^+$
, the spherical function
$\lambda \in \Lambda _{G/K}^+$
, the spherical function
![]() $f_\lambda $
can be constructed (up to a scalar factor) as a matrix coefficient by taking nonzero K-invariants vectors
$f_\lambda $
can be constructed (up to a scalar factor) as a matrix coefficient by taking nonzero K-invariants vectors
![]() $v_\lambda \in V(\lambda )$
and
$v_\lambda \in V(\lambda )$
and
![]() $\psi _\lambda \in V(\lambda )^*$
and setting
$\psi _\lambda \in V(\lambda )^*$
and setting
The decomposition of the product of irreducible G-submodules inside
![]() $\mathbb C[G/K]$
is encoded in the structure constants for the multiplication of the corresponding spherical functions (see [Reference Ruitenburg31, Theorem 3.2]).
$\mathbb C[G/K]$
is encoded in the structure constants for the multiplication of the corresponding spherical functions (see [Reference Ruitenburg31, Theorem 3.2]).
Proposition 2.1 If
 $\lambda , \mu , \nu \in \Lambda _{G/K}^+$
and if
$\lambda , \mu , \nu \in \Lambda _{G/K}^+$
and if
 $f_\lambda f_\mu = \sum a_{\lambda ,\mu }^\nu f_\nu $
, then
$f_\lambda f_\mu = \sum a_{\lambda ,\mu }^\nu f_\nu $
, then
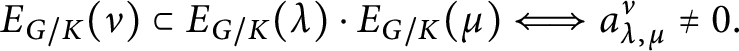 $$ \begin{align*}E_{G/K}(\nu) \subset E_{G/K}(\lambda) \cdot E_{G/K}(\mu) \Longleftrightarrow a_{\lambda,\mu}^\nu \neq 0. \end{align*} $$
$$ \begin{align*}E_{G/K}(\nu) \subset E_{G/K}(\lambda) \cdot E_{G/K}(\mu) \Longleftrightarrow a_{\lambda,\mu}^\nu \neq 0. \end{align*} $$
More generally, a similar characterization can be given in terms of the support of the tensor product of the K-semi-invariant vectors of the quasi-spherical representations (see [Reference Chirivì, Littelmann and Maffei9, Lemma 19], [Reference Bravi, Gandini and Maffei4, Lemma 1.2]).
Proposition 2.2 Let
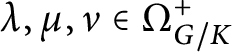 $\lambda , \mu , \nu \in \Omega _{G/K}^+$
, and let
$\lambda , \mu , \nu \in \Omega _{G/K}^+$
, and let
![]() $\chi , \chi ' \in \mathcal X(K)$
be such that the semi-invariant subspaces
$\chi , \chi ' \in \mathcal X(K)$
be such that the semi-invariant subspaces
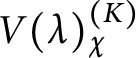 $V(\lambda )^{(K)}_\chi $
and
$V(\lambda )^{(K)}_\chi $
and
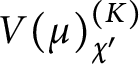 $V(\mu )^{(K)}_{\chi '}$
are nonzero. Let
$V(\mu )^{(K)}_{\chi '}$
are nonzero. Let
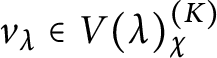 $v_\lambda \in V(\lambda )^{(K)}_\chi $
and
$v_\lambda \in V(\lambda )^{(K)}_\chi $
and
 $v_\mu \in V(\mu )^{(K)}_{\chi '}$
be nonzero, and let
$v_\mu \in V(\mu )^{(K)}_{\chi '}$
be nonzero, and let
![]() $\pi _\nu : V(\lambda ) \otimes V(\mu ) \rightarrow V[\nu ]$
denote the projection onto the isotypic component
$\pi _\nu : V(\lambda ) \otimes V(\mu ) \rightarrow V[\nu ]$
denote the projection onto the isotypic component
![]() $V[\nu ] \subset V(\lambda ) \otimes V(\mu )$
of highest weight
$V[\nu ] \subset V(\lambda ) \otimes V(\mu )$
of highest weight
![]() $\nu $
. Then,
$\nu $
. Then,
3 Multiplication of spherical functions of symmetric pairs of type A
Let G be semisimple and simply connected, and let
![]() $\vartheta : G \rightarrow G$
be an algebraic involution. We denote by
$\vartheta : G \rightarrow G$
be an algebraic involution. We denote by
![]() $K = G^\vartheta $
the set of fixed points. Then, K is a connected reductive subgroup of G, which has finite index in
$K = G^\vartheta $
the set of fixed points. Then, K is a connected reductive subgroup of G, which has finite index in
![]() $\mathrm N_G(K)$
.
$\mathrm N_G(K)$
.
Let
![]() $A \subset G$
be a maximal split torus, that is,
$A \subset G$
be a maximal split torus, that is,
![]() $\vartheta (a) = a^{-1}$
, for all
$\vartheta (a) = a^{-1}$
, for all
![]() $a \in A$
, and A is maximal with this property. Fix a maximal torus T containing A, then
$a \in A$
, and A is maximal with this property. Fix a maximal torus T containing A, then
![]() $\vartheta (T) = T$
. Let us denote by the same letter
$\vartheta (T) = T$
. Let us denote by the same letter
![]() $\vartheta $
the induced involution on
$\vartheta $
the induced involution on
![]() $\mathfrak t^*$
, then
$\mathfrak t^*$
, then
![]() $\vartheta (\Phi ) = \Phi $
and the Killing form is preserved by
$\vartheta (\Phi ) = \Phi $
and the Killing form is preserved by
![]() $\vartheta $
. We also choose the set of positive roots and the Borel subgroup
$\vartheta $
. We also choose the set of positive roots and the Borel subgroup
![]() $B \supset T$
in such a way that
$B \supset T$
in such a way that
![]() $\vartheta (\alpha ) \in \Phi ^-$
whenever
$\vartheta (\alpha ) \in \Phi ^-$
whenever
![]() $\alpha \in \Phi ^+$
and
$\alpha \in \Phi ^+$
and
![]() $\alpha \neq \vartheta (\alpha )$
(see [Reference De Concini, Procesi and Gherardelli11, Lemma 1.2]).
$\alpha \neq \vartheta (\alpha )$
(see [Reference De Concini, Procesi and Gherardelli11, Lemma 1.2]).
Denote
![]() $X = G/K$
, and let
$X = G/K$
, and let
![]() $A_X \simeq A/A\cap K$
be the image of A in X. Notice that
$A_X \simeq A/A\cap K$
be the image of A in X. Notice that
thus,
![]() $\mathcal X(A_X) = 2\mathcal X(A)$
is identified with the lattice
$\mathcal X(A_X) = 2\mathcal X(A)$
is identified with the lattice
Define
the set of restricted roots of X. Then,
![]() $\widetilde \Phi _X$
is a possibly nonreduced) root system in
$\widetilde \Phi _X$
is a possibly nonreduced) root system in
![]() $\Lambda _X \otimes \mathbb R \simeq \mathcal X(A) \otimes \mathbb R$
, with base
$\Lambda _X \otimes \mathbb R \simeq \mathcal X(A) \otimes \mathbb R$
, with base
and with Weyl group
The weight lattice and the root lattice of
![]() $\widetilde \Phi _X$
are, respectively, identified with
$\widetilde \Phi _X$
are, respectively, identified with
![]() $\Lambda _X \simeq \mathcal X(A_X)$
and with
$\Lambda _X \simeq \mathcal X(A_X)$
and with
![]() $\mathcal X(A/\mathrm N_A(K)) \subset \mathcal X(A_X)$
(see [Reference Vust36, Lemmas 2.3 and 3.1]). Finally, the monoid of the spherical weights
$\mathcal X(A/\mathrm N_A(K)) \subset \mathcal X(A_X)$
(see [Reference Vust36, Lemmas 2.3 and 3.1]). Finally, the monoid of the spherical weights
![]() $\Lambda _X^+$
is obtained by intersecting the monoid of the dominant weights with the sublattice of
$\Lambda _X^+$
is obtained by intersecting the monoid of the dominant weights with the sublattice of
![]() $\mathcal X(T)$
defined by
$\mathcal X(T)$
defined by
![]() $\mathcal X(A_X)$
(see [Reference Vust35, Théorème 3]):
$\mathcal X(A_X)$
(see [Reference Vust35, Théorème 3]):
By a result of Richardson [Reference Richardson30, Corollary 11.5], the restriction of functions yields an algebra isomorphism
Up to normalization, the restriction of the spherical function
![]() $f_\lambda $
to
$f_\lambda $
to
![]() $A_X$
is a specialization of the Jacobi polynomial
$A_X$
is a specialization of the Jacobi polynomial
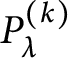 $P_\lambda ^{(k)}$
associated with the root system
$P_\lambda ^{(k)}$
associated with the root system
![]() $\widetilde \Phi _X$
(see [Reference Heckman, Opdam and Koornwinder17, Section 8.4]). More precisely, let
$\widetilde \Phi _X$
(see [Reference Heckman, Opdam and Koornwinder17, Section 8.4]). More precisely, let
![]() $m = (m_{\widetilde \alpha })$
be the multiplicity function of the restricted roots, that is, for
$m = (m_{\widetilde \alpha })$
be the multiplicity function of the restricted roots, that is, for
![]() $\widetilde \alpha \in \widetilde \Phi _X$
,
$\widetilde \alpha \in \widetilde \Phi _X$
,
Then, up to a scalar factor, the restriction
 ${f_\lambda }_{|A_X}$
coincides with the specialized Jacobi polynomial
${f_\lambda }_{|A_X}$
coincides with the specialized Jacobi polynomial
 $P_\lambda ^{(m/2)}$
.
$P_\lambda ^{(m/2)}$
.
Therefore, the decomposition of the products of the irreducible G-modules inside
![]() $\mathbb C[X]$
is encoded in the structure constants for the multiplication of the corresponding specialized Jacobi polynomials:
$\mathbb C[X]$
is encoded in the structure constants for the multiplication of the corresponding specialized Jacobi polynomials:
If
![]() $\lambda , \mu , \nu \in \Lambda _X^+$
and if
$\lambda , \mu , \nu \in \Lambda _X^+$
and if
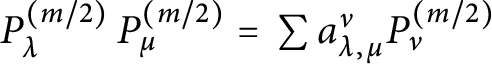 $P_\lambda ^{(m/2)} \, P_\mu ^{(m/2)} = \, \sum a_{\lambda ,\mu }^\nu P_\nu ^{(m/2)}$
, then
$P_\lambda ^{(m/2)} \, P_\mu ^{(m/2)} = \, \sum a_{\lambda ,\mu }^\nu P_\nu ^{(m/2)}$
, then
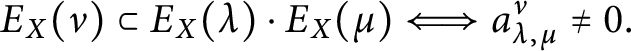 $$ \begin{align*}E_X(\nu) \subset E_X(\lambda) \cdot E_X(\mu) \Longleftrightarrow a_{\lambda,\mu}^\nu \neq 0. \end{align*} $$
$$ \begin{align*}E_X(\nu) \subset E_X(\lambda) \cdot E_X(\mu) \Longleftrightarrow a_{\lambda,\mu}^\nu \neq 0. \end{align*} $$
Let
![]() $\alpha \in \Phi $
be such that
$\alpha \in \Phi $
be such that
![]() $\alpha \neq \vartheta (\alpha )$
: then, either
$\alpha \neq \vartheta (\alpha )$
: then, either
![]() $\vartheta (\alpha ) = -\alpha $
, or
$\vartheta (\alpha ) = -\alpha $
, or
![]() $\alpha $
and
$\alpha $
and
![]() $\vartheta (\alpha )$
are orthogonal, or
$\vartheta (\alpha )$
are orthogonal, or
![]() $\langle \vartheta (\alpha ), \alpha ^\vee \rangle = 1$
(in which case,
$\langle \vartheta (\alpha ), \alpha ^\vee \rangle = 1$
(in which case,
![]() $\alpha - \vartheta (\alpha ) \in \Phi ^+$
; see [Reference Vust36, Lemma 2.3]). Thus, if
$\alpha - \vartheta (\alpha ) \in \Phi ^+$
; see [Reference Vust36, Lemma 2.3]). Thus, if
![]() $\sigma \in \widetilde \Delta _X$
, say
$\sigma \in \widetilde \Delta _X$
, say
![]() $\sigma = \alpha - \vartheta (\alpha )$
, we define the coroot
$\sigma = \alpha - \vartheta (\alpha )$
, we define the coroot
![]() $\sigma ^\vee \in \Lambda _X^\vee $
as follows:
$\sigma ^\vee \in \Lambda _X^\vee $
as follows:
-
(i) If
 $\vartheta (\alpha ) = -\alpha $
, then
$\vartheta (\alpha ) = -\alpha $
, then  $$ \begin{align*}\sigma^\vee = \tfrac{1}{2}{\alpha^\vee}_{|\Lambda_X}. \end{align*} $$
$$ \begin{align*}\sigma^\vee = \tfrac{1}{2}{\alpha^\vee}_{|\Lambda_X}. \end{align*} $$
-
(ii) If
 $\alpha $
and
$\alpha $
and
 $\vartheta (\alpha )$
are orthogonal, then
$\vartheta (\alpha )$
are orthogonal, then  $$ \begin{align*}\sigma^\vee = {\alpha^\vee}_{|\Lambda_X}. \end{align*} $$
$$ \begin{align*}\sigma^\vee = {\alpha^\vee}_{|\Lambda_X}. \end{align*} $$
-
(iii) If
 $\alpha - \vartheta (\alpha ) \in \Phi ^+$
, then
$\alpha - \vartheta (\alpha ) \in \Phi ^+$
, then  $$ \begin{align*}\sigma^\vee = {(\alpha- \vartheta(\alpha))^\vee}_{|\Lambda_X}. \end{align*} $$
$$ \begin{align*}\sigma^\vee = {(\alpha- \vartheta(\alpha))^\vee}_{|\Lambda_X}. \end{align*} $$
Notice that the previous definition only depends on
![]() $\sigma $
, and not on
$\sigma $
, and not on
![]() $\alpha $
. If indeed
$\alpha $
. If indeed
![]() $\lambda \in \Lambda _X$
, then in all cases, we have
$\lambda \in \Lambda _X$
, then in all cases, we have
 $$ \begin{align*}\langle \lambda, \sigma^\vee\rangle = \frac{2(\lambda, \alpha-\vartheta(\alpha))}{||\alpha-\vartheta(\alpha)||^2}. \end{align*} $$
$$ \begin{align*}\langle \lambda, \sigma^\vee\rangle = \frac{2(\lambda, \alpha-\vartheta(\alpha))}{||\alpha-\vartheta(\alpha)||^2}. \end{align*} $$
For later use, we now introduce a slight modification of the restricted root system. Denote
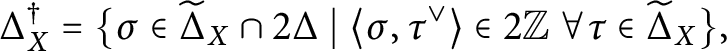 $$ \begin{align*}\Delta_X^\dagger=\{\sigma\in\widetilde \Delta_X \cap 2\Delta \;|\; \langle\sigma,\tau^\vee\rangle\in2\mathbb Z\ \forall \tau\in\widetilde\Delta_X\}, \end{align*} $$
$$ \begin{align*}\Delta_X^\dagger=\{\sigma\in\widetilde \Delta_X \cap 2\Delta \;|\; \langle\sigma,\tau^\vee\rangle\in2\mathbb Z\ \forall \tau\in\widetilde\Delta_X\}, \end{align*} $$
and define
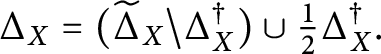 $$ \begin{align*}\Delta_X = (\widetilde \Delta_X \smallsetminus \Delta_X^\dagger) \cup \tfrac{1}{2}\Delta_X^\dagger. \end{align*} $$
$$ \begin{align*}\Delta_X = (\widetilde \Delta_X \smallsetminus \Delta_X^\dagger) \cup \tfrac{1}{2}\Delta_X^\dagger. \end{align*} $$
Then,
![]() $\Delta _X$
is the base of a (reduced) root system
$\Delta _X$
is the base of a (reduced) root system
![]() $\Phi _X$
(see, e.g., [Reference Knop and Sahi20, Proposition 3.1]): indeed, the scalar product between any two distinct elements in
$\Phi _X$
(see, e.g., [Reference Knop and Sahi20, Proposition 3.1]): indeed, the scalar product between any two distinct elements in
![]() $\Delta _X$
remains nonpositive, and the pairing among roots remains integer. Notice that
$\Delta _X$
remains nonpositive, and the pairing among roots remains integer. Notice that
![]() $\Phi _X$
has also Weyl group
$\Phi _X$
has also Weyl group
![]() $W_X$
. If moreover
$W_X$
. If moreover
![]() $\Delta _X$
is irreducible of rank
$\Delta _X$
is irreducible of rank
![]() $>1$
and distinct from
$>1$
and distinct from
![]() $\widetilde \Delta _X$
, then
$\widetilde \Delta _X$
, then
![]() $\Delta _X$
and
$\Delta _X$
and
![]() $\widetilde \Delta _X$
have necessarily dual types.
$\widetilde \Delta _X$
have necessarily dual types.
Accordingly, we extend the weight lattice with the normalized restricted roots, and we define
![]() $\Xi _X$
to be the lattice generated by
$\Xi _X$
to be the lattice generated by
![]() $\Lambda _X$
and
$\Lambda _X$
and
![]() $\Delta _X$
(namely by
$\Delta _X$
(namely by
![]() $\Lambda _X$
and
$\Lambda _X$
and
 $\tfrac 12\Delta _X^\dagger $
).
$\tfrac 12\Delta _X^\dagger $
).
For
![]() $\sigma \in \Delta _X$
, we define the coroot
$\sigma \in \Delta _X$
, we define the coroot
![]() $\sigma ^\vee \in \Xi _X^\vee $
similarly as we did before: if
$\sigma ^\vee \in \Xi _X^\vee $
similarly as we did before: if
![]() $\sigma \in \Phi ^+$
, then
$\sigma \in \Phi ^+$
, then
![]() $\sigma ^\vee \in \Xi _X^\vee $
is the restriction of the associated coroot in
$\sigma ^\vee \in \Xi _X^\vee $
is the restriction of the associated coroot in
![]() $\Lambda ^\vee $
; if instead
$\Lambda ^\vee $
; if instead
![]() $\sigma =2\alpha $
with
$\sigma =2\alpha $
with
![]() $\alpha \in \Delta $
, then we define
$\alpha \in \Delta $
, then we define
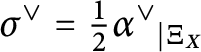 $\sigma ^\vee =\tfrac 12{\alpha ^\vee }_{|\Xi _X}$
; and finally, if
$\sigma ^\vee =\tfrac 12{\alpha ^\vee }_{|\Xi _X}$
; and finally, if
![]() $\sigma = \alpha - \vartheta (\alpha )$
with
$\sigma = \alpha - \vartheta (\alpha )$
with
![]() $\langle \vartheta (\alpha ), \alpha ^\vee \rangle = 0$
, then we define
$\langle \vartheta (\alpha ), \alpha ^\vee \rangle = 0$
, then we define
![]() $\sigma ^\vee = {\alpha ^\vee }_{|\Xi _X}$
.
$\sigma ^\vee = {\alpha ^\vee }_{|\Xi _X}$
.
Set
regarded as a subset of the dual lattice
![]() $\Xi _X^\vee $
. Then, the triple
$\Xi _X^\vee $
. Then, the triple
![]() $\mathcal R_X = (\Xi _X, \Delta _X, \Delta _X^\vee )$
is a based root datum, in the following (usual) sense.
$\mathcal R_X = (\Xi _X, \Delta _X, \Delta _X^\vee )$
is a based root datum, in the following (usual) sense.
A based root datum is a triple
![]() $(\Xi ,S,\alpha \mapsto \alpha ^\vee )$
such that:
$(\Xi ,S,\alpha \mapsto \alpha ^\vee )$
such that:
-
(i)
 $\Xi $
is a free abelian group of finite rank, S is a finite subset of
$\Xi $
is a free abelian group of finite rank, S is a finite subset of
 $\Xi $
, and
$\Xi $
, and
 $\alpha \mapsto \alpha ^\vee $
is a map from S into
$\alpha \mapsto \alpha ^\vee $
is a map from S into
 $\Xi ^\vee $
.
$\Xi ^\vee $
. -
(ii) For all
 $\alpha \in S$
, the pairing
$\alpha \in S$
, the pairing
 $\langle \alpha ,\alpha ^\vee \rangle $
is equal to 2.
$\langle \alpha ,\alpha ^\vee \rangle $
is equal to 2. -
(iii) The group W of automorphisms of
 $\Xi $
generated by the reflections with
$\Xi $
generated by the reflections with $$ \begin{align*} s_\alpha\colon \Xi\longrightarrow\Xi, \qquad \qquad \xi \longmapsto \xi-\langle x,\alpha^\vee\rangle\alpha,\end{align*} $$
$$ \begin{align*} s_\alpha\colon \Xi\longrightarrow\Xi, \qquad \qquad \xi \longmapsto \xi-\langle x,\alpha^\vee\rangle\alpha,\end{align*} $$
 $\alpha \in S$
is finite.
$\alpha \in S$
is finite.
-
(iv) The W-orbit of S is a reduced root system R in the real subspace of
 $\Xi _{\mathbb R}$
generated by S, and S is a base of R.
$\Xi _{\mathbb R}$
generated by S, and S is a base of R.
Notice that in our case the root datum
![]() $\mathcal R_X$
is semisimple, namely the base S spans
$\mathcal R_X$
is semisimple, namely the base S spans
![]() $\Xi _{\mathbb R}$
as a vector space.
$\Xi _{\mathbb R}$
as a vector space.
Let
be the monoid of the dominant weights of
![]() $\mathcal R_X$
. Then, we have a (possibly strict) inclusion
$\mathcal R_X$
. Then, we have a (possibly strict) inclusion
![]() $\Lambda _X^+ \subset \Xi _X^+$
, and
$\Lambda _X^+ \subset \Xi _X^+$
, and
![]() $\Xi _X^+ = \Xi _X \cap \Lambda ^+$
.
$\Xi _X^+ = \Xi _X \cap \Lambda ^+$
.
On the weight lattice
![]() $\Xi _X$
, we will consider the partial order
$\Xi _X$
, we will consider the partial order
![]() $\leqslant _X$
defined by
$\leqslant _X$
defined by
![]() $\widetilde \Delta _X$
as follows:
$\widetilde \Delta _X$
as follows:
When
![]() $\widetilde \Delta _X = \Delta _X$
, this is the usual dominance order on
$\widetilde \Delta _X = \Delta _X$
, this is the usual dominance order on
![]() $\Xi _X$
; otherwise, it is a refinement of the dominance order where the simple roots in
$\Xi _X$
; otherwise, it is a refinement of the dominance order where the simple roots in
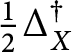 $\tfrac 12\Delta _X^\dagger $
are only taken with even coefficients.
$\tfrac 12\Delta _X^\dagger $
are only taken with even coefficients.
3.1 A conjectural rule when
 $\Phi _X$
is of type
$\Phi _X$
is of type
 $\mathsf A$
$\mathsf A$
When
![]() $\widetilde \Phi _X$
(or equivalently
$\widetilde \Phi _X$
(or equivalently
![]() $\Phi _X$
) is of type
$\Phi _X$
) is of type
![]() $\mathsf A$
, then up to a normalization, the Jacobi polynomials
$\mathsf A$
, then up to a normalization, the Jacobi polynomials
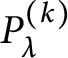 $P_\lambda ^{(k)}$
coincide with the Jack symmetric polynomials
$P_\lambda ^{(k)}$
coincide with the Jack symmetric polynomials
 $J_\lambda ^{(1/k)}$
(see, e.g., [Reference Beerends and Opdam3, Proposition 3.3]). Thus, in this case, the restriction of the spherical function
$J_\lambda ^{(1/k)}$
(see, e.g., [Reference Beerends and Opdam3, Proposition 3.3]). Thus, in this case, the restriction of the spherical function
![]() $f_\lambda $
to
$f_\lambda $
to
![]() $A_X$
is a scalar multiple of the specialized Jack polynomial
$A_X$
is a scalar multiple of the specialized Jack polynomial
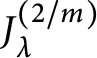 $J_\lambda ^{(2/m)}$
.
$J_\lambda ^{(2/m)}$
.
As is well known, when dealing with symmetric polynomials, it is often convenient to consider symmetric functions in infinitely many variables. Here, we do the same, and instead of working with the Jack polynomials, we pass to the Jack symmetric functions
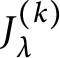 $J_\lambda ^{(k)}$
, which form a basis, when
$J_\lambda ^{(k)}$
, which form a basis, when
![]() $\lambda $
vary among all possible partitions, of the ring of symmetric functions in infinitely many variables with coefficients in
$\lambda $
vary among all possible partitions, of the ring of symmetric functions in infinitely many variables with coefficients in
![]() $\mathbb Q(k)$
. As a general reference on the Jack symmetric functions, see [Reference Stanley33] and [Reference Macdonald28, Section VI.10].
$\mathbb Q(k)$
. As a general reference on the Jack symmetric functions, see [Reference Stanley33] and [Reference Macdonald28, Section VI.10].
We now recall a conjecture of Stanley concerning the multiplication of the Jack symmetric functions.
Conjecture 3.1 [Reference Stanley33, Conjecture 8.3]
Write
 $J_\lambda ^{(k)} J_\mu ^{(k)} = \sum _\nu \frac {g_{\lambda ,\mu }^\nu (k)}{j_\nu (k)} J_\nu ^{(k)}$
. Then, the function
$J_\lambda ^{(k)} J_\mu ^{(k)} = \sum _\nu \frac {g_{\lambda ,\mu }^\nu (k)}{j_\nu (k)} J_\nu ^{(k)}$
. Then, the function
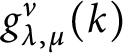 $g_{\lambda ,\mu }^\nu (k)$
is a polynomial in k, with nonnegative integer coefficients.
$g_{\lambda ,\mu }^\nu (k)$
is a polynomial in k, with nonnegative integer coefficients.
To explain the denominator
![]() $j_\nu (k)$
, recall that the Jack symmetric functions are pairwise orthogonal with respect to the scalar product
$j_\nu (k)$
, recall that the Jack symmetric functions are pairwise orthogonal with respect to the scalar product
![]() $\langle \ ,\ \rangle _k$
defined on the basis of the power-sum symmetric functions
$\langle \ ,\ \rangle _k$
defined on the basis of the power-sum symmetric functions
![]() $p_\lambda $
(
$p_\lambda $
(
![]() $\lambda $
being a partition) as follows:
$\lambda $
being a partition) as follows:
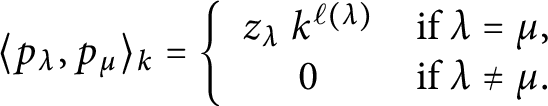 $$ \begin{align*}\langle p_\lambda, p_\mu \rangle_k = \left\{ \begin{array}{cc} z_\lambda \ k^{\ell(\lambda)} & \text{if}\ \lambda =\mu, \\ 0 & \text{if}\ \lambda \neq \mu. \end{array} \right. \end{align*} $$
$$ \begin{align*}\langle p_\lambda, p_\mu \rangle_k = \left\{ \begin{array}{cc} z_\lambda \ k^{\ell(\lambda)} & \text{if}\ \lambda =\mu, \\ 0 & \text{if}\ \lambda \neq \mu. \end{array} \right. \end{align*} $$
Here,
![]() $\ell (\lambda )$
denotes the length of
$\ell (\lambda )$
denotes the length of
![]() $\lambda $
, and if
$\lambda $
, and if
![]() $m_i$
is the number of parts in
$m_i$
is the number of parts in
![]() $\lambda $
equal to i, then
$\lambda $
equal to i, then
Therefore, expanding the product of two Jack symmetric functions in terms of Jack symmetric functions, one has
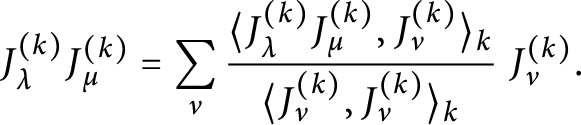 $$ \begin{align*}J_\lambda^{(k)} J_\mu^{(k)} = \sum_\nu \frac{\langle J_\lambda^{(k)} J_\mu^{(k)}, J_\nu^{(k)}\rangle_k}{\langle J_\nu^{(k)},J_\nu^{(k)}\rangle_k}\ J_\nu^{(k)} .\end{align*} $$
$$ \begin{align*}J_\lambda^{(k)} J_\mu^{(k)} = \sum_\nu \frac{\langle J_\lambda^{(k)} J_\mu^{(k)}, J_\nu^{(k)}\rangle_k}{\langle J_\nu^{(k)},J_\nu^{(k)}\rangle_k}\ J_\nu^{(k)} .\end{align*} $$
Then,
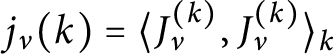 $j_\nu (k) = \langle J_\nu ^{(k)},J_\nu ^{(k)}\rangle _k$
, and
$j_\nu (k) = \langle J_\nu ^{(k)},J_\nu ^{(k)}\rangle _k$
, and
 $g_{\lambda ,\mu }^\nu (k)=\langle J_\lambda ^{(k)} J_\mu ^{(k)}, J_\nu ^{(k)}\rangle _k$
. There is a well-known combinatorial formula which expresses
$g_{\lambda ,\mu }^\nu (k)=\langle J_\lambda ^{(k)} J_\mu ^{(k)}, J_\nu ^{(k)}\rangle _k$
. There is a well-known combinatorial formula which expresses
![]() $j_\nu (k)$
as a polynomial in k with nonnegative integer coefficients in terms of hooks of
$j_\nu (k)$
as a polynomial in k with nonnegative integer coefficients in terms of hooks of
![]() $\nu $
(see [Reference Stanley33, Theorem 5.8]).
$\nu $
(see [Reference Stanley33, Theorem 5.8]).
It is known that the functions
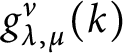 $g_{\lambda ,\mu }^\nu (k)$
are polynomials in k with integer coefficients: this follows from a result of Knop and Sahi [Reference Knop and Sahi20], showing that the coefficients of the expansion of the Jack symmetric functions in terms of the monomial symmetric functions are polynomial in k with nonnegative integer coefficients.
$g_{\lambda ,\mu }^\nu (k)$
are polynomials in k with integer coefficients: this follows from a result of Knop and Sahi [Reference Knop and Sahi20], showing that the coefficients of the expansion of the Jack symmetric functions in terms of the monomial symmetric functions are polynomial in k with nonnegative integer coefficients.
Conjecture 3.1 is known to be true when one of the two partitions
![]() $\lambda $
and
$\lambda $
and
![]() $\mu $
consists of a single row: this follows from a generalization of the Pieri rule for Jack symmetric functions proved by Stanley himself [Reference Stanley33, Theorem 6.1].
$\mu $
consists of a single row: this follows from a generalization of the Pieri rule for Jack symmetric functions proved by Stanley himself [Reference Stanley33, Theorem 6.1].
Let us come back to a symmetric space
![]() $X=G/K$
with restricted root system of type
$X=G/K$
with restricted root system of type
![]() $\mathsf A$
. If we normalize properly the spherical functions
$\mathsf A$
. If we normalize properly the spherical functions
![]() $f_\lambda $
and write
$f_\lambda $
and write
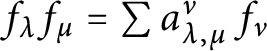 $f_\lambda f_\mu = \sum a_{\lambda ,\mu }^\nu \, f_\nu $
, then
$f_\lambda f_\mu = \sum a_{\lambda ,\mu }^\nu \, f_\nu $
, then
 $a_{\lambda ,\mu }^\nu = g_{\lambda ,\mu }^\nu (2/m)$
. On the other hand, by the very definition of the scalar product
$a_{\lambda ,\mu }^\nu = g_{\lambda ,\mu }^\nu (2/m)$
. On the other hand, by the very definition of the scalar product
![]() $\langle \ ,\ \rangle _k$
, specializing the Jack symmetric function
$\langle \ ,\ \rangle _k$
, specializing the Jack symmetric function
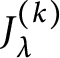 $J_\lambda ^{(k)}$
at
$J_\lambda ^{(k)}$
at
![]() $k = 1$
yields a nonzero scalar multiple of the Schur function
$k = 1$
yields a nonzero scalar multiple of the Schur function
![]() $s_\lambda $
. Thus,
$s_\lambda $
. Thus,
 $g_{\lambda ,\mu }^\nu (1)$
is nonzero if and only if the Littlewood–Richardson coefficient
$g_{\lambda ,\mu }^\nu (1)$
is nonzero if and only if the Littlewood–Richardson coefficient
 $c_{\lambda ,\mu }^\nu $
associated to
$c_{\lambda ,\mu }^\nu $
associated to
![]() $\lambda ,\mu ,\nu $
in the restricted root system associated to
$\lambda ,\mu ,\nu $
in the restricted root system associated to
![]() $G/K$
is nonzero.
$G/K$
is nonzero.
For a symmetric space X with restricted root system of type
![]() $\mathsf A$
, we get then
$\mathsf A$
, we get then
 $$ \begin{align} E_X(\nu) \subset E_X(\lambda) \cdot E_X(\mu) \Longleftrightarrow g_{\lambda, \mu}^\nu(2/m) \neq 0 , \end{align} $$
$$ \begin{align} E_X(\nu) \subset E_X(\lambda) \cdot E_X(\mu) \Longleftrightarrow g_{\lambda, \mu}^\nu(2/m) \neq 0 , \end{align} $$
and Stanley’s conjecture immediately implies
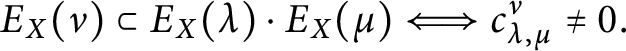 $$ \begin{align} E_X(\nu) \subset E_X(\lambda) \cdot E_X(\mu) \Longleftrightarrow c_{\lambda,\mu}^\nu \neq 0. \end{align} $$
$$ \begin{align} E_X(\nu) \subset E_X(\lambda) \cdot E_X(\mu) \Longleftrightarrow c_{\lambda,\mu}^\nu \neq 0. \end{align} $$
When the rank of the restricted root system is 1, only one-row partitions occur as dominant weights; therefore, equation (3.2) holds true thanks to Stanley’s generalization of the Pieri rule mentioned above.
To be more explicit, let
![]() $G_X$
be the connected semisimple group defined by the based root datum
$G_X$
be the connected semisimple group defined by the based root datum
![]() $\mathcal R_X = (\Xi _X, \Delta _X, \Delta _X^\vee )$
, and correspondingly, let
$\mathcal R_X = (\Xi _X, \Delta _X, \Delta _X^\vee )$
, and correspondingly, let
![]() $T_X \subset G_X$
and
$T_X \subset G_X$
and
![]() $B_X \subset G_X$
be a maximal torus and a Borel subgroup containing
$B_X \subset G_X$
be a maximal torus and a Borel subgroup containing
![]() $T_X$
inducing
$T_X$
inducing
![]() $\mathcal R_X$
. For
$\mathcal R_X$
. For
![]() $\pi \in \Xi _X^+$
(and in particular for
$\pi \in \Xi _X^+$
(and in particular for
![]() $\pi \in \Lambda _X^+$
), let
$\pi \in \Lambda _X^+$
), let
![]() $V_X(\pi )$
be the irreducible
$V_X(\pi )$
be the irreducible
![]() $G_X$
-module with highest weight
$G_X$
-module with highest weight
![]() $\pi $
. Then, Stanley’s Conjecture 3.1 yields the following (weaker) conjecture.
$\pi $
. Then, Stanley’s Conjecture 3.1 yields the following (weaker) conjecture.
Conjecture 3.2 Let X be a symmetric variety with restricted root system of type
![]() $\mathsf A$
, and let
$\mathsf A$
, and let
![]() $\lambda , \mu , \nu \in \Lambda _X^+$
. Then,
$\lambda , \mu , \nu \in \Lambda _X^+$
. Then,
 $$ \begin{align*}E_X(\nu) \subset E_X(\lambda) \cdot E_X(\mu) \Longleftrightarrow \left\{ \begin{array}{c} V_X(\nu) \subset V_X(\lambda) \otimes V_X(\mu), \phantom{\Big|} \\ \nu \leqslant_X \lambda + \mu. \end{array} \right. \end{align*} $$
$$ \begin{align*}E_X(\nu) \subset E_X(\lambda) \cdot E_X(\mu) \Longleftrightarrow \left\{ \begin{array}{c} V_X(\nu) \subset V_X(\lambda) \otimes V_X(\mu), \phantom{\Big|} \\ \nu \leqslant_X \lambda + \mu. \end{array} \right. \end{align*} $$
When the restricted root system of X is of type
![]() $\mathsf A_1$
, the previous conjecture holds true by Stanley’s Pieri rule for Jack symmetric functions.
$\mathsf A_1$
, the previous conjecture holds true by Stanley’s Pieri rule for Jack symmetric functions.
Notice that Conjecture 3.2 is easily shown when
![]() $G = H \times H$
and
$G = H \times H$
and
![]() $K = \operatorname {\mathrm {diag}}(H)$
for some reductive algebraic group H (even in types other than
$K = \operatorname {\mathrm {diag}}(H)$
for some reductive algebraic group H (even in types other than
![]() $\mathsf A$
), in which case
$\mathsf A$
), in which case
![]() $X \simeq H$
regarded as
$X \simeq H$
regarded as
![]() $H \times H$
-variety (see, e.g., [Reference De Concini and Popov10, Lemma 3.4]).
$H \times H$
-variety (see, e.g., [Reference De Concini and Popov10, Lemma 3.4]).
Remark 3.3 Notice that in all cases of Table 1 but case Sym.A1 with
![]() $n=2$
, it always holds the equality
$n=2$
, it always holds the equality
![]() $\Delta _X = \widetilde \Delta _X$
. In particular, in all these cases, Conjecture 3.2 follows immediately from (3.2), and the condition
$\Delta _X = \widetilde \Delta _X$
. In particular, in all these cases, Conjecture 3.2 follows immediately from (3.2), and the condition
![]() $\nu \leqslant _X \lambda +\mu $
is redundant. On the other hand, to deduce Conjecture 3.2 from (3.2) in the case
$\nu \leqslant _X \lambda +\mu $
is redundant. On the other hand, to deduce Conjecture 3.2 from (3.2) in the case
![]() $X = \operatorname {\mathrm {SL}}(2)/T$
, we need to use the saturation property of the tensor product of
$X = \operatorname {\mathrm {SL}}(2)/T$
, we need to use the saturation property of the tensor product of
![]() $\operatorname {\mathrm {SL}}(2)$
.
$\operatorname {\mathrm {SL}}(2)$
.
Remark 3.4 Rather than
![]() $\mathcal R_X$
, in Conjecture 3.2, it would have been more natural to use the based root datum
$\mathcal R_X$
, in Conjecture 3.2, it would have been more natural to use the based root datum
 $\widetilde {\mathcal R}_X = (\Lambda _X, \widetilde \Delta _X, \widetilde \Delta _X^\vee )$
, and define the semisimple group
$\widetilde {\mathcal R}_X = (\Lambda _X, \widetilde \Delta _X, \widetilde \Delta _X^\vee )$
, and define the semisimple group
![]() $G_X$
accordingly. Indeed, this formulation follows immediately from (3.2), and is also simpler, because the inequality
$G_X$
accordingly. Indeed, this formulation follows immediately from (3.2), and is also simpler, because the inequality
![]() $\nu \leqslant _X \lambda +\mu $
becomes redundant. However, computational experiments suggest that the formulation that we adopted is closer to possible generalizations (see Section 6, where we consider the case of the symmetric subgroups of Hermitian type).
$\nu \leqslant _X \lambda +\mu $
becomes redundant. However, computational experiments suggest that the formulation that we adopted is closer to possible generalizations (see Section 6, where we consider the case of the symmetric subgroups of Hermitian type).
In a slightly different form, Conjecture 3.2 was also considered by Graham and Hunziker [Reference Graham and Hunziker16].
For completeness, we list in Table 1 all the symmetric varieties with a restricted root system of type
![]() $\mathsf A$
. In all cases, we also give the simple restricted roots and a minimal set of generators for the weight monoid
$\mathsf A$
. In all cases, we also give the simple restricted roots and a minimal set of generators for the weight monoid
![]() $\Lambda ^+_X$
.
$\Lambda ^+_X$
.
Table 1: Symmetric pairs with restricted root system of type
![]() $\mathsf A_r$
$\mathsf A_r$
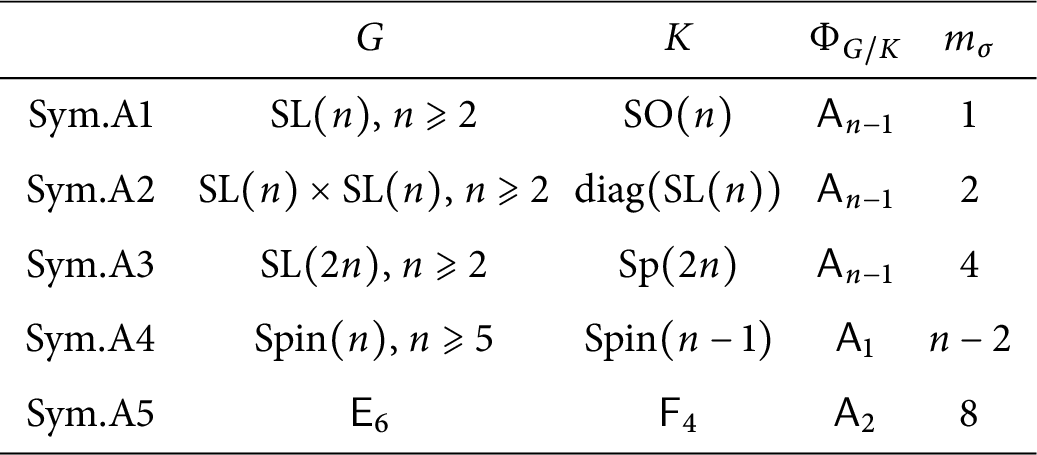
-
(i)
 $\mathbf {SL(2)/SO(2)}$
:
$\mathbf {SL(2)/SO(2)}$
:
 $\Delta _X = \{\alpha _1\}$
,
$\Delta _X = \{\alpha _1\}$
,
 $\Lambda ^+_X$
is generated by
$\Lambda ^+_X$
is generated by
 $2 \omega _1$
;
$2 \omega _1$
; -
(ii)
 $\mathbf {SL(n)/SO(n)}$
,
$\mathbf {SL(n)/SO(n)}$
,
 $n\geqslant 3$
:
$n\geqslant 3$
:
 $\Delta _X = \{2\alpha _i\ : \ 1\leqslant i\leqslant n-1\}$
,
$\Delta _X = \{2\alpha _i\ : \ 1\leqslant i\leqslant n-1\}$
,
 $\Lambda ^+_X$
is generated by the weights
$\Lambda ^+_X$
is generated by the weights
 $2 \omega _i$
with
$2 \omega _i$
with
 $ 1\leqslant i\leqslant n-1$
;
$ 1\leqslant i\leqslant n-1$
; -
(iii)
 $\big (\mathbf {SL(n)} \times \mathbf {SL(n)}\big )/\mathbf {diag(SL(n))}$
,
$\big (\mathbf {SL(n)} \times \mathbf {SL(n)}\big )/\mathbf {diag(SL(n))}$
,
 $n \geqslant 2$
:
$n \geqslant 2$
:
 $\Delta _X = \{\alpha _i + \alpha _i'\ :\ 1\leqslant i\leqslant n-1\}$
,
$\Delta _X = \{\alpha _i + \alpha _i'\ :\ 1\leqslant i\leqslant n-1\}$
,
 $\Lambda ^+_X$
is generated by the weights
$\Lambda ^+_X$
is generated by the weights
 $\omega _i + \omega _i'$
with
$\omega _i + \omega _i'$
with
 $ 1\leqslant i\leqslant n-1$
;
$ 1\leqslant i\leqslant n-1$
; -
(iv)
 $\mathbf {SL(2n)/Sp(2n)}$
,
$\mathbf {SL(2n)/Sp(2n)}$
,
 $n \geqslant 2$
:
$n \geqslant 2$
:
 $\Delta _X = \{\alpha _{2i-1} + 2\alpha _{2i}+\alpha _{2i+1}\ :\ 1\leqslant i\leqslant n-1\}$
,
$\Delta _X = \{\alpha _{2i-1} + 2\alpha _{2i}+\alpha _{2i+1}\ :\ 1\leqslant i\leqslant n-1\}$
,
 $\Lambda ^+_X$
is generated by the weights
$\Lambda ^+_X$
is generated by the weights
 $\omega _{2i}$
with
$\omega _{2i}$
with
 $ 1\leqslant i\leqslant n-1$
;
$ 1\leqslant i\leqslant n-1$
; -
(v)
 $\mathbf {Spin(2n+1)/Spin(2n)}$
,
$\mathbf {Spin(2n+1)/Spin(2n)}$
,
 $n \geqslant 2$
:
$n \geqslant 2$
:
 $\Delta _X = \{2(\sum _{i=1}^n\alpha _i)\}$
,
$\Delta _X = \{2(\sum _{i=1}^n\alpha _i)\}$
,
 $\Lambda ^+_X$
is generated by
$\Lambda ^+_X$
is generated by
 $\omega _1$
;
$\omega _1$
; -
(vi)
 $\mathbf {Spin(2n)/Spin(2n-1)}$
,
$\mathbf {Spin(2n)/Spin(2n-1)}$
,
 $n \geqslant 3$
:
$n \geqslant 3$
:
 $\Delta _X = \{2(\sum _{i=1}^{n-2}\alpha _i) + \alpha _{n-1} + \alpha _n\}$
,
$\Delta _X = \{2(\sum _{i=1}^{n-2}\alpha _i) + \alpha _{n-1} + \alpha _n\}$
,
 $\Lambda ^+_X$
is generated by
$\Lambda ^+_X$
is generated by
 $\omega _1$
;
$\omega _1$
; -
(vii)
 $\mathbf {E}_{\mathbf {6}}/\mathbf {F}_{\mathbf {4}}$
:
$\mathbf {E}_{\mathbf {6}}/\mathbf {F}_{\mathbf {4}}$
:
 $\Delta _X = \{2\alpha _1 + \alpha _2 + 2\alpha _3 + 2\alpha _4 + \alpha _5, \; \alpha _2 + \alpha _3 + 2\alpha _4 + 2\alpha _5 + 2\alpha _6\}$
,
$\Delta _X = \{2\alpha _1 + \alpha _2 + 2\alpha _3 + 2\alpha _4 + \alpha _5, \; \alpha _2 + \alpha _3 + 2\alpha _4 + 2\alpha _5 + 2\alpha _6\}$
,
 $\Lambda ^+_X$
is generated by
$\Lambda ^+_X$
is generated by
 $\omega _1$
and
$\omega _1$
and
 $\omega _6$
.
$\omega _6$
.
4 Root systems associated to a spherical homogeneous space
We now recall how to attach a based root system (or more precisely, three based root systems) to a spherical homogeneous space
![]() $G/K$
, which for the purposes of the present paper we can assume affine. General references for these constructions are [Reference Brion7, Reference Knop18].
$G/K$
, which for the purposes of the present paper we can assume affine. General references for these constructions are [Reference Brion7, Reference Knop18].
Let
![]() $\Lambda _{G/K}$
be the weight lattice of
$\Lambda _{G/K}$
be the weight lattice of
![]() $G/K$
, defined as
$G/K$
, defined as
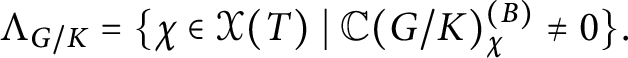 $$ \begin{align*}\Lambda_{G/K} = \{\chi \in \mathcal X(T) \; | \; \mathbb C(G/K)^{(B)}_\chi \neq 0\}. \end{align*} $$
$$ \begin{align*}\Lambda_{G/K} = \{\chi \in \mathcal X(T) \; | \; \mathbb C(G/K)^{(B)}_\chi \neq 0\}. \end{align*} $$
Because K is reductive, notice that
![]() $\Lambda _{G/K}$
is generated as a lattice by
$\Lambda _{G/K}$
is generated as a lattice by
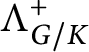 $\Lambda ^+_{G/K}$
. In all the cases that we will consider, we will actually have
$\Lambda ^+_{G/K}$
. In all the cases that we will consider, we will actually have
 $\Lambda ^+_{G/K} = \Lambda _{G/K} \cap \Lambda ^+$
.
$\Lambda ^+_{G/K} = \Lambda _{G/K} \cap \Lambda ^+$
.
Looking at the multiplication of spherical modules, we can associate three root systems to
![]() $G/K$
. For a fixed
$G/K$
. For a fixed
![]() $G/K$
, the three root systems will have the same Weyl group
$G/K$
, the three root systems will have the same Weyl group
![]() $W_{G/K}$
: what changes is only the root normalization.
$W_{G/K}$
: what changes is only the root normalization.
![]() $\bullet $
The
$\bullet $
The
![]() $\mathrm n$
-spherical roots of
$\mathrm n$
-spherical roots of
![]() $G/K$
. The first root system, that we denote by
$G/K$
. The first root system, that we denote by
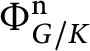 $\Phi ^{\mathrm n}_{G/K}$
, is defined by considering the multiplication of spherical modules inside the invariant space
$\Phi ^{\mathrm n}_{G/K}$
, is defined by considering the multiplication of spherical modules inside the invariant space
![]() $\mathbb C[G]^K$
. If
$\mathbb C[G]^K$
. If
 $\lambda , \mu , \nu \in \Lambda ^+_{G/K}$
is a triple of spherical weights such that
$\lambda , \mu , \nu \in \Lambda ^+_{G/K}$
is a triple of spherical weights such that
![]() $E(\nu ) \subset E(\lambda ) \cdot E(\mu )$
, then
$E(\nu ) \subset E(\lambda ) \cdot E(\mu )$
, then
![]() $\lambda +\mu -\nu \in \Lambda _{G/K} \cap \mathbb N\Delta $
. Denote by
$\lambda +\mu -\nu \in \Lambda _{G/K} \cap \mathbb N\Delta $
. Denote by
 $\mathcal M^{\mathrm n}_{G/K}$
the monoid generated by all possible differences
$\mathcal M^{\mathrm n}_{G/K}$
the monoid generated by all possible differences
![]() $\lambda +\mu -\nu \in \Lambda _{G/K}$
with
$\lambda +\mu -\nu \in \Lambda _{G/K}$
with
 $\lambda , \mu , \nu \in \Lambda ^+_{G/K}$
as above. This is a free monoid (see [Reference Knop18, Theorem 1.3], [Reference Avdeev and Cupit-Foutou2, Theorem 4.11]). Its (unique) set of free generators, denoted by
$\lambda , \mu , \nu \in \Lambda ^+_{G/K}$
as above. This is a free monoid (see [Reference Knop18, Theorem 1.3], [Reference Avdeev and Cupit-Foutou2, Theorem 4.11]). Its (unique) set of free generators, denoted by
 $\Delta ^{\mathrm n}_{G/K}$
, is the set of the
$\Delta ^{\mathrm n}_{G/K}$
, is the set of the
![]() $\mathrm n$
-spherical roots of
$\mathrm n$
-spherical roots of
![]() $G/K$
. It is the base of a reduced root system,
$G/K$
. It is the base of a reduced root system,
 $\Phi ^{\mathrm n}_{G/K}$
(see [Reference Knop18, Theorem 1.3]).
$\Phi ^{\mathrm n}_{G/K}$
(see [Reference Knop18, Theorem 1.3]).
![]() $\bullet $
The
$\bullet $
The
![]() $\mathrm {sc}$
-spherical roots of
$\mathrm {sc}$
-spherical roots of
![]() $G/K$
. The second root system, that we denote by
$G/K$
. The second root system, that we denote by
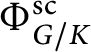 $\Phi ^{\mathrm {sc}}_{G/K}$
, is defined by considering the multiplication of quasi-spherical modules inside the semi-invariant space
$\Phi ^{\mathrm {sc}}_{G/K}$
, is defined by considering the multiplication of quasi-spherical modules inside the semi-invariant space
![]() $\mathbb C[G]^{(K)}$
. If
$\mathbb C[G]^{(K)}$
. If
 $\lambda , \mu , \nu \in \Omega ^+_{G/K}$
is a triple of quasi-spherical weights such that
$\lambda , \mu , \nu \in \Omega ^+_{G/K}$
is a triple of quasi-spherical weights such that
![]() $E_{\chi +\chi '}(\nu ) \subset E_\chi (\lambda ) \cdot E_{\chi '}(\mu )$
, then
$E_{\chi +\chi '}(\nu ) \subset E_\chi (\lambda ) \cdot E_{\chi '}(\mu )$
, then
![]() $\lambda +\mu -\nu \in \Lambda _{G/K} \cap \mathbb N \Delta $
. Let
$\lambda +\mu -\nu \in \Lambda _{G/K} \cap \mathbb N \Delta $
. Let
 $\mathcal M^{\mathrm {sc}}_{G/K}$
be the monoid generated by all possible differences
$\mathcal M^{\mathrm {sc}}_{G/K}$
be the monoid generated by all possible differences
![]() $\lambda +\mu -\nu $
with
$\lambda +\mu -\nu $
with
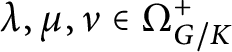 $\lambda , \mu , \nu \in \Omega ^+_{G/K}$
as above. Again, this is a free monoid (see [Reference Knop18, Corollary 7.6], [Reference Bravi, Gandini and Maffei4, Proposition 5]). Its (unique) set of free generators, denoted by
$\lambda , \mu , \nu \in \Omega ^+_{G/K}$
as above. Again, this is a free monoid (see [Reference Knop18, Corollary 7.6], [Reference Bravi, Gandini and Maffei4, Proposition 5]). Its (unique) set of free generators, denoted by
 $\Delta ^{\mathrm {sc}}_{G/K}$
, is the set of the
$\Delta ^{\mathrm {sc}}_{G/K}$
, is the set of the
![]() $\mathrm {sc}$
-spherical roots of
$\mathrm {sc}$
-spherical roots of
![]() $G/K$
. It is the base of a reduced root system,
$G/K$
. It is the base of a reduced root system,
 $\Phi ^{\mathrm {sc}}_{G/K}$
.
$\Phi ^{\mathrm {sc}}_{G/K}$
.
![]() $\bullet $
The minimal spherical roots of
$\bullet $
The minimal spherical roots of
![]() $G/K$
. By definition, we have inclusions
$G/K$
. By definition, we have inclusions
 $\mathcal M^{\mathrm n}_{G/K} \subset \mathcal M^{\mathrm {sc}}_{G/K} \subset \Lambda _{G/K}$
. The two root monoids
$\mathcal M^{\mathrm n}_{G/K} \subset \mathcal M^{\mathrm {sc}}_{G/K} \subset \Lambda _{G/K}$
. The two root monoids
 $\mathcal M^{\mathrm n}_{G/K}$
and
$\mathcal M^{\mathrm n}_{G/K}$
and
 $\mathcal M^{\mathrm {sc}}_{G/K}$
actually generate the same cone in
$\mathcal M^{\mathrm {sc}}_{G/K}$
actually generate the same cone in
![]() $\Lambda _{G/K} \otimes _{\mathbb Z} \mathbb Q$
. However, neither the
$\Lambda _{G/K} \otimes _{\mathbb Z} \mathbb Q$
. However, neither the
![]() $\mathrm n$
-spherical roots nor the
$\mathrm n$
-spherical roots nor the
![]() $\mathrm {sc}$
-spherical roots need to be primitive elements inside
$\mathrm {sc}$
-spherical roots need to be primitive elements inside
![]() $\Lambda _{G/K}$
: the set of the minimal spherical roots of
$\Lambda _{G/K}$
: the set of the minimal spherical roots of
![]() $G/K$
, denoted by
$G/K$
, denoted by
 $\Delta ^{\min }_{G/K}$
, is the set of the primitive elements in
$\Delta ^{\min }_{G/K}$
, is the set of the primitive elements in
![]() $\Lambda _{G/K}$
associated to the extremal rays of the cone generated by
$\Lambda _{G/K}$
associated to the extremal rays of the cone generated by
 $\mathcal M^{\mathrm n}_{G/K}$
in
$\mathcal M^{\mathrm n}_{G/K}$
in
![]() $\Lambda _{G/K} \otimes _{\mathbb Z} \mathbb Q$
. The minimal spherical roots of
$\Lambda _{G/K} \otimes _{\mathbb Z} \mathbb Q$
. The minimal spherical roots of
![]() $G/K$
form the base of a reduced root system, that we denote by
$G/K$
form the base of a reduced root system, that we denote by
 $\Phi ^{\min }_{G/K}$
.
$\Phi ^{\min }_{G/K}$
.
It is clear from their construction that the three root systems
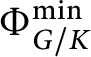 $\Phi ^{\min }_{G/K}$
,
$\Phi ^{\min }_{G/K}$
,
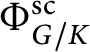 $\Phi ^{\mathrm {sc}}_{G/K}$
, and
$\Phi ^{\mathrm {sc}}_{G/K}$
, and
 $\Phi ^{\mathrm n}_{G/K}$
all have the same Weyl group
$\Phi ^{\mathrm n}_{G/K}$
all have the same Weyl group
![]() $W_{G/K}$
.
$W_{G/K}$
.
If
![]() $G/K$
is a symmetric variety, we have
$G/K$
is a symmetric variety, we have
 $\widetilde \Delta _{G/K} = \Delta ^{\mathrm n}_{G/K}$
(see [Reference Knop18, Theorem 6.7]).
$\widetilde \Delta _{G/K} = \Delta ^{\mathrm n}_{G/K}$
(see [Reference Knop18, Theorem 6.7]).
Both the
![]() $\mathrm n$
-spherical roots and the
$\mathrm n$
-spherical roots and the
![]() $\mathrm {sc}$
-spherical roots of
$\mathrm {sc}$
-spherical roots of
![]() $G/K$
arise as minimal spherical roots of a quotient of
$G/K$
arise as minimal spherical roots of a quotient of
![]() $G/K$
. Denote indeed by
$G/K$
. Denote indeed by
![]() $\bar K$
the spherical closure of K, defined as the kernel of the action of
$\bar K$
the spherical closure of K, defined as the kernel of the action of
![]() $\mathrm N_G(K)$
on
$\mathrm N_G(K)$
on
![]() $\mathcal X(K)$
. Then, both
$\mathcal X(K)$
. Then, both
![]() $\mathrm N_G(K)$
and
$\mathrm N_G(K)$
and
![]() $\bar K$
are spherical subgroups of G, which satisfy
$\bar K$
are spherical subgroups of G, which satisfy
 $$ \begin{align*}\Delta^{\mathrm n}_{G/K} = \Delta^{\min}_{G/\mathrm N_G(K)} \qquad \qquad \Delta^{\mathrm{sc}}_{G/K} = \Delta^{\min}_{G/\overline K}. \end{align*} $$
$$ \begin{align*}\Delta^{\mathrm n}_{G/K} = \Delta^{\min}_{G/\mathrm N_G(K)} \qquad \qquad \Delta^{\mathrm{sc}}_{G/K} = \Delta^{\min}_{G/\overline K}. \end{align*} $$
This explains our terminology. Moreover, we have equalities
 $$ \begin{align*}\Lambda_{G/\mathrm N_G(K)} = \mathbb Z \Delta^{\mathrm n}_{G/K} \qquad \qquad \Lambda_{G/\bar K} = \mathbb Z \Delta^{\mathrm{sc}}_{G/K}. \end{align*} $$
$$ \begin{align*}\Lambda_{G/\mathrm N_G(K)} = \mathbb Z \Delta^{\mathrm n}_{G/K} \qquad \qquad \Lambda_{G/\bar K} = \mathbb Z \Delta^{\mathrm{sc}}_{G/K}. \end{align*} $$
The inclusion
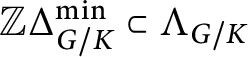 $\mathbb Z \Delta ^{\min }_{G/K} \subset \Lambda _{G/K}$
is strict in general: it is an equality precisely when
$\mathbb Z \Delta ^{\min }_{G/K} \subset \Lambda _{G/K}$
is strict in general: it is an equality precisely when
![]() $G/K$
admits a wonderful completion (which always happens for
$G/K$
admits a wonderful completion (which always happens for
![]() $G/\bar K$
and
$G/\bar K$
and
![]() $G/\mathrm N_G(K)$
). Notice that, in general, the minimal spherical roots of
$G/\mathrm N_G(K)$
). Notice that, in general, the minimal spherical roots of
![]() $G/K$
do not necessarily belong to the root lattice, differently from the
$G/K$
do not necessarily belong to the root lattice, differently from the
![]() $\mathrm n$
-spherical roots and from the
$\mathrm n$
-spherical roots and from the
![]() $\mathrm {sc}$
-spherical roots which by construction are always in the root lattice of G.
$\mathrm {sc}$
-spherical roots which by construction are always in the root lattice of G.
Remark 4.1 The weight lattices of
![]() $G/K$
,
$G/K$
,
![]() $G/\bar K$
, and
$G/\bar K$
, and
![]() $G/\mathrm N_G(K)$
allow easily to compare K,
$G/\mathrm N_G(K)$
allow easily to compare K,
![]() $\bar K$
, and
$\bar K$
, and
![]() $\mathrm N_G(K)$
: indeed, the quotient
$\mathrm N_G(K)$
: indeed, the quotient
![]() $\mathrm N_G(K)/ K$
is diagonalizable (see [Reference Brion and Pauer8, Corollaire 5.2]), and we have inclusions
$\mathrm N_G(K)/ K$
is diagonalizable (see [Reference Brion and Pauer8, Corollaire 5.2]), and we have inclusions
inducing isomorphisms (see, e.g., [Reference Gandini12, Lemma 2.4])
 $$ \begin{gather*} \mathcal X(\mathrm N_G(K)/K) \simeq \Lambda_{G/K}/\Lambda_{G/\mathrm N_G(K)},\\ \mathcal X\big(\mathrm N_G(K)/\bar K \big) \simeq \Lambda_{G/\bar K}/\Lambda_{G/\mathrm N_G(K)}, \qquad \qquad \mathcal X\big(\bar K/K \big) \simeq \Lambda_{G/K}/\Lambda_{G/\bar K}. \end{gather*} $$
$$ \begin{gather*} \mathcal X(\mathrm N_G(K)/K) \simeq \Lambda_{G/K}/\Lambda_{G/\mathrm N_G(K)},\\ \mathcal X\big(\mathrm N_G(K)/\bar K \big) \simeq \Lambda_{G/\bar K}/\Lambda_{G/\mathrm N_G(K)}, \qquad \qquad \mathcal X\big(\bar K/K \big) \simeq \Lambda_{G/K}/\Lambda_{G/\bar K}. \end{gather*} $$
As already anticipated in the case of a symmetric variety, we define a fourth normalization for the spherical roots, setting
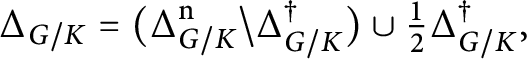 $$ \begin{align*}\Delta_{G/K} = (\Delta^{\mathrm n}_{G/K} \smallsetminus \Delta_{G/K}^\dagger) \cup \tfrac{1}{2}\Delta_{G/K}^\dagger, \end{align*} $$
$$ \begin{align*}\Delta_{G/K} = (\Delta^{\mathrm n}_{G/K} \smallsetminus \Delta_{G/K}^\dagger) \cup \tfrac{1}{2}\Delta_{G/K}^\dagger, \end{align*} $$
where
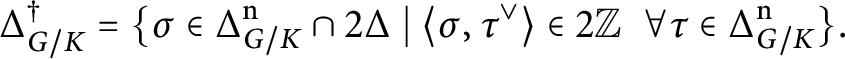 $$ \begin{align*}\Delta_{G/K}^\dagger=\{\sigma\in\Delta^{\mathrm n}_{G/K} \cap 2\Delta \;|\; \langle\sigma,\tau^\vee\rangle\in2\mathbb Z\ \; \forall \tau\in\Delta^{\mathrm n}_{G/K}\}. \end{align*} $$
$$ \begin{align*}\Delta_{G/K}^\dagger=\{\sigma\in\Delta^{\mathrm n}_{G/K} \cap 2\Delta \;|\; \langle\sigma,\tau^\vee\rangle\in2\mathbb Z\ \; \forall \tau\in\Delta^{\mathrm n}_{G/K}\}. \end{align*} $$
Because
 $\Delta ^{\mathrm n}_{G/K}$
is obtained from
$\Delta ^{\mathrm n}_{G/K}$
is obtained from
 $\Delta ^{\mathrm {sc}}_{G/K}$
by doubling some particular elements in
$\Delta ^{\mathrm {sc}}_{G/K}$
by doubling some particular elements in
 $\Delta ^{\mathrm {sc}}_{G/K} \cap \Delta $
(see [Reference Bravi and Luna5, Section 2.4]), it turns out that we also have
$\Delta ^{\mathrm {sc}}_{G/K} \cap \Delta $
(see [Reference Bravi and Luna5, Section 2.4]), it turns out that we also have
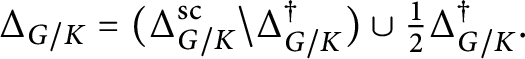 $$ \begin{align*}\Delta_{G/K} = (\Delta^{\mathrm{sc}}_{G/K} \smallsetminus \Delta_{G/K}^\dagger) \cup \tfrac{1}{2}\Delta_{G/K}^\dagger. \end{align*} $$
$$ \begin{align*}\Delta_{G/K} = (\Delta^{\mathrm{sc}}_{G/K} \smallsetminus \Delta_{G/K}^\dagger) \cup \tfrac{1}{2}\Delta_{G/K}^\dagger. \end{align*} $$
We denote by
![]() $\Phi _{G/K}$
the (reduced) root system generated by
$\Phi _{G/K}$
the (reduced) root system generated by
![]() $\Delta _{G/K}$
. Notice that
$\Delta _{G/K}$
. Notice that
![]() $\Phi _{G/K}$
has also Weyl group
$\Phi _{G/K}$
has also Weyl group
![]() $W_{G/K}$
. In all cases that we will be interested (see Table 3), we have indeed
$W_{G/K}$
. In all cases that we will be interested (see Table 3), we have indeed
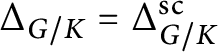 $\Delta _{G/K} = \Delta ^{\mathrm {sc}}_{G/K}$
: this is always true when K is connected.
$\Delta _{G/K} = \Delta ^{\mathrm {sc}}_{G/K}$
: this is always true when K is connected.
If
 $\sigma \in \Delta ^{\mathrm n}_{G/K}$
, then the following three possibilities occur (see [Reference Brion7, Théorème 2.6]): either
$\sigma \in \Delta ^{\mathrm n}_{G/K}$
, then the following three possibilities occur (see [Reference Brion7, Théorème 2.6]): either
![]() $\sigma \in \Phi ^+$
is a positive root, or
$\sigma \in \Phi ^+$
is a positive root, or
![]() $\sigma \in 2 \Delta $
is the double of a simple root, or
$\sigma \in 2 \Delta $
is the double of a simple root, or
![]() $\sigma = \alpha + \beta $
is the sum of two strongly orthogonal positive roots (that is, neither
$\sigma = \alpha + \beta $
is the sum of two strongly orthogonal positive roots (that is, neither
![]() $\alpha + \beta $
nor
$\alpha + \beta $
nor
![]() $\alpha -\beta $
is in
$\alpha -\beta $
is in
![]() $\Phi $
). Because
$\Phi $
). Because
![]() $\Delta _{G/K}$
and
$\Delta _{G/K}$
and
 $\Delta ^{\mathrm {sc}}_{G/K}$
are obtained from
$\Delta ^{\mathrm {sc}}_{G/K}$
are obtained from
 $\Delta ^{\mathrm n}_{G/K}$
by replacing some elements in
$\Delta ^{\mathrm n}_{G/K}$
by replacing some elements in
 $2\Delta \cap \Delta ^{\mathrm n}_{G/K}$
with the corresponding simple roots, the same description applies to
$2\Delta \cap \Delta ^{\mathrm n}_{G/K}$
with the corresponding simple roots, the same description applies to
 $\Delta ^{\mathrm {sc}}_{G/K}$
and
$\Delta ^{\mathrm {sc}}_{G/K}$
and
![]() $\Delta _{G/K}$
.
$\Delta _{G/K}$
.
There is actually a finite list of possible cases: the shape of an
![]() $\mathrm n$
-spherical root, written as sum of simple roots, is necessarily one of those reported in Table 2 (where we also specify the type of the root subsystem of
$\mathrm n$
-spherical root, written as sum of simple roots, is necessarily one of those reported in Table 2 (where we also specify the type of the root subsystem of
![]() $\Phi $
generated by the support of the spherical root).
$\Phi $
generated by the support of the spherical root).
Table 2:
![]() $\mathrm {sc}$
-spherical roots
$\mathrm {sc}$
-spherical roots

In general,
![]() $\Delta _{G/K}$
is not contained in
$\Delta _{G/K}$
is not contained in
![]() $\Lambda _{G/K}$
. Thus, we extend accordingly the weight lattice, and define
$\Lambda _{G/K}$
. Thus, we extend accordingly the weight lattice, and define
![]() $\Xi _{G/K}$
to be the lattice generated by
$\Xi _{G/K}$
to be the lattice generated by
![]() $\Lambda _{G/K}$
together with
$\Lambda _{G/K}$
together with
![]() $\Delta _{G/K}$
, namely by
$\Delta _{G/K}$
, namely by
![]() $\Lambda _{G/K}$
and
$\Lambda _{G/K}$
and
 $\tfrac {1}{2}\Delta _{G/K}^\dagger $
.
$\tfrac {1}{2}\Delta _{G/K}^\dagger $
.
The following lemma will allow us to define the spherical coroots in
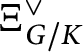 $\Xi _{G/K}^\vee $
, in analogy to what we did in the symmetric case.
$\Xi _{G/K}^\vee $
, in analogy to what we did in the symmetric case.
Lemma 4.2 Let
![]() $G/K$
be a spherical variety, and let
$G/K$
be a spherical variety, and let
 $\sigma \in \Delta ^{\mathrm {sc}}_{G/K} \smallsetminus \Phi ^+$
.
$\sigma \in \Delta ^{\mathrm {sc}}_{G/K} \smallsetminus \Phi ^+$
.
-
(i) If
 $\sigma = 2\alpha $
with
$\sigma = 2\alpha $
with
 $\alpha \in \Delta $
, then
$\alpha \in \Delta $
, then
 $\langle \lambda , \alpha ^\vee \rangle \in 2 \mathbb Z$
for all
$\langle \lambda , \alpha ^\vee \rangle \in 2 \mathbb Z$
for all
 $\lambda \in \Xi _{G/K}$
.
$\lambda \in \Xi _{G/K}$
. -
(ii) If
 $\sigma $
decomposes as a sum of two strongly orthogonal roots
$\sigma $
decomposes as a sum of two strongly orthogonal roots
 $\beta , \gamma \in \Phi ^+$
, then Moreover, any such decomposition of
$\beta , \gamma \in \Phi ^+$
, then Moreover, any such decomposition of $$ \begin{align*}{\beta^\vee}_{|\Xi_{G/K}} = {\gamma^\vee}_{|\Xi_{G/K}}. \end{align*} $$
$$ \begin{align*}{\beta^\vee}_{|\Xi_{G/K}} = {\gamma^\vee}_{|\Xi_{G/K}}. \end{align*} $$
 $\sigma $
yields the same result.
$\sigma $
yields the same result.
Proof (i) It is well known that
![]() $\langle \lambda , \alpha \rangle \in 2 \mathbb Z$
whenever
$\langle \lambda , \alpha \rangle \in 2 \mathbb Z$
whenever
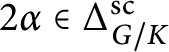 $2 \alpha \in \Delta ^{\mathrm {sc}}_{G/K}$
(see [Reference Luna26, Section 1.4]). It is indeed being part of Luna’s axioms which classify spherical varieties [Reference Bravi and Luna5, Section 1.2]. Thus, by the definition of
$2 \alpha \in \Delta ^{\mathrm {sc}}_{G/K}$
(see [Reference Luna26, Section 1.4]). It is indeed being part of Luna’s axioms which classify spherical varieties [Reference Bravi and Luna5, Section 1.2]. Thus, by the definition of
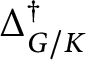 $\Delta ^\dagger _{G/K}$
, this property holds for all
$\Delta ^\dagger _{G/K}$
, this property holds for all
![]() $\lambda \in \Xi _{G/K}$
.
$\lambda \in \Xi _{G/K}$
.
(ii) We point out that, in [Reference Knop and Schalke21, Lemmas 6.2 and 6.4], a particular decomposition of
![]() $\sigma $
as a sum of two strongly orthogonal positive roots is considered, and the statement is proved for that decomposition.
$\sigma $
as a sum of two strongly orthogonal positive roots is considered, and the statement is proved for that decomposition.
Because
 $\Lambda ^+_{G/K} = \Lambda ^+_{G/\bar K}$
and
$\Lambda ^+_{G/K} = \Lambda ^+_{G/\bar K}$
and
 $\Delta ^{\mathrm {sc}}_{G/K} = \Delta ^{\mathrm {sc}}_{G/\bar K}$
, we may assume that
$\Delta ^{\mathrm {sc}}_{G/K} = \Delta ^{\mathrm {sc}}_{G/\bar K}$
, we may assume that
![]() $K =\bar K$
.
$K =\bar K$
.
Scrolling through the list of Table 2, we see that the
![]() $\mathrm {sc}$
-spherical roots that are neither positive roots nor the double of a simple root are those of the following table (we also report an extra datum, which is defined here below).
$\mathrm {sc}$
-spherical roots that are neither positive roots nor the double of a simple root are those of the following table (we also report an extra datum, which is defined here below).

The first case, with
![]() $\sigma $
of type
$\sigma $
of type
![]() $\mathsf A_1\times \mathsf A_1$
, is somewhat special, and the statement is well known (see [Reference Luna26, Proposition 3.2]). It is indeed part of Luna’s axioms to classify spherical varieties. Therefore, we will assume that
$\mathsf A_1\times \mathsf A_1$
, is somewhat special, and the statement is well known (see [Reference Luna26, Proposition 3.2]). It is indeed part of Luna’s axioms to classify spherical varieties. Therefore, we will assume that
![]() $\operatorname {\mathrm {supp}}(\sigma )$
is connected.
$\operatorname {\mathrm {supp}}(\sigma )$
is connected.
Denote
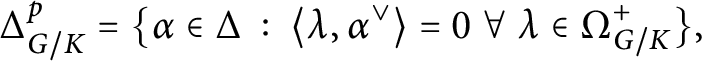 $$ \begin{align*}\Delta_{G/K}^p=\{\alpha\in \Delta\ :\ \langle\lambda,\alpha^\vee \rangle=0\ \forall\ \lambda\in\Omega^+_{G/K}\},\end{align*} $$
$$ \begin{align*}\Delta_{G/K}^p=\{\alpha\in \Delta\ :\ \langle\lambda,\alpha^\vee \rangle=0\ \forall\ \lambda\in\Omega^+_{G/K}\},\end{align*} $$
and let
![]() $\Delta ^{pp}(\sigma ) \subset \operatorname {\mathrm {supp}}(\sigma )$
be the set of simple roots orthogonal to
$\Delta ^{pp}(\sigma ) \subset \operatorname {\mathrm {supp}}(\sigma )$
be the set of simple roots orthogonal to
![]() $\sigma $
. Then, we have
$\sigma $
. Then, we have
 $\Delta ^{pp}(\sigma )\subset \Delta ^p_{G/K}$
whenever
$\Delta ^{pp}(\sigma )\subset \Delta ^p_{G/K}$
whenever
![]() $\sigma \not \in \Phi ^+$
(see [Reference Bravi and Luna5, Section 1.1]).
$\sigma \not \in \Phi ^+$
(see [Reference Bravi and Luna5, Section 1.1]).
Notice that in all cases of the previous table with
![]() $\operatorname {\mathrm {supp}}(\sigma )$
connected, there exists a unique simple root
$\operatorname {\mathrm {supp}}(\sigma )$
connected, there exists a unique simple root
![]() $\alpha \in \operatorname {\mathrm {supp}}(\sigma )$
not orthogonal to
$\alpha \in \operatorname {\mathrm {supp}}(\sigma )$
not orthogonal to
![]() $\sigma $
. Therefore, it is enough to check that, for any spherical root
$\sigma $
. Therefore, it is enough to check that, for any spherical root
 $\sigma \in \Delta ^{\mathrm {sc}}_{G/K} \smallsetminus (\Phi ^+ \cup 2\Delta )$
and for any decomposition
$\sigma \in \Delta ^{\mathrm {sc}}_{G/K} \smallsetminus (\Phi ^+ \cup 2\Delta )$
and for any decomposition
![]() $\sigma =\beta +\gamma $
as a sum of two strongly orthogonal positive roots, it holds
$\sigma =\beta +\gamma $
as a sum of two strongly orthogonal positive roots, it holds
which can easily be checked case by case.
For
![]() $\sigma \in \Delta _{G/K}$
, using Lemma 4.2, we define the coroot
$\sigma \in \Delta _{G/K}$
, using Lemma 4.2, we define the coroot
 $\sigma ^\vee \in \Xi _{G/K}^\vee $
as follows:
$\sigma ^\vee \in \Xi _{G/K}^\vee $
as follows:
-
(i) if
 $\sigma = 2\alpha $
with
$\sigma = 2\alpha $
with
 $\alpha \in \Delta $
, then
$\alpha \in \Delta $
, then  $$ \begin{align*}\sigma^\vee = \tfrac{1}{2}{\alpha^\vee}_{|\Xi_{G/K}}. \end{align*} $$
$$ \begin{align*}\sigma^\vee = \tfrac{1}{2}{\alpha^\vee}_{|\Xi_{G/K}}. \end{align*} $$
-
(ii) if
 $\sigma =\beta +\gamma $
with
$\sigma =\beta +\gamma $
with
 $\beta ,\gamma \in \Phi ^+$
strongly orthogonal, then
$\beta ,\gamma \in \Phi ^+$
strongly orthogonal, then  $$ \begin{align*}\sigma^\vee = {\beta^\vee}_{|\Xi_{G/K}}. \end{align*} $$
$$ \begin{align*}\sigma^\vee = {\beta^\vee}_{|\Xi_{G/K}}. \end{align*} $$
-
(iii) if
 $\sigma =\beta $
with
$\sigma =\beta $
with
 $\beta \in \Phi ^+$
, then
$\beta \in \Phi ^+$
, then  $$ \begin{align*}\sigma^\vee = {\beta^\vee}_{|\Xi_{G/K}}. \end{align*} $$
$$ \begin{align*}\sigma^\vee = {\beta^\vee}_{|\Xi_{G/K}}. \end{align*} $$
Set
 $\Delta _{G/K}^\vee = \{\sigma ^\vee \; | \; \sigma \in \Delta _{G/K}\}$
, then by construction we have the following.
$\Delta _{G/K}^\vee = \{\sigma ^\vee \; | \; \sigma \in \Delta _{G/K}\}$
, then by construction we have the following.
Proposition 4.3 The triple
 $\mathcal R_{G/K} = (\Xi _{G/K}, \Delta _{G/K}, \Delta _{G/K}^\vee )$
is a based root datum. Moreover, the intersection
$\mathcal R_{G/K} = (\Xi _{G/K}, \Delta _{G/K}, \Delta _{G/K}^\vee )$
is a based root datum. Moreover, the intersection
![]() $\Xi _{G/K} \cap \Lambda ^+$
is contained in the monoid of dominant weights of
$\Xi _{G/K} \cap \Lambda ^+$
is contained in the monoid of dominant weights of
![]() $\mathcal R_{G/K}$
$\mathcal R_{G/K}$
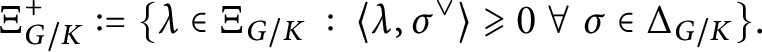 $$ \begin{align*}\Xi_{G/K}^+ :=\{\lambda\in\Xi_{G/K}\ :\ \langle\lambda,\sigma^\vee\rangle\geqslant0\ \forall\ \sigma\in \Delta_{G/K}\}. \end{align*} $$
$$ \begin{align*}\Xi_{G/K}^+ :=\{\lambda\in\Xi_{G/K}\ :\ \langle\lambda,\sigma^\vee\rangle\geqslant0\ \forall\ \sigma\in \Delta_{G/K}\}. \end{align*} $$
Differently from the symmetric case, notice that the based root datum
![]() $\mathcal R_{G/K}$
is not necessarily semisimple: by Remark 4.1, this happens if and only if K has finite index in its normalizer. When
$\mathcal R_{G/K}$
is not necessarily semisimple: by Remark 4.1, this happens if and only if K has finite index in its normalizer. When
![]() $\mathcal R_{G/K}$
is semisimple, every spherical weight is uniquely determined by its values against the spherical roots; otherwise, the extra information is obtained by restricting to the normalizer.
$\mathcal R_{G/K}$
is semisimple, every spherical weight is uniquely determined by its values against the spherical roots; otherwise, the extra information is obtained by restricting to the normalizer.
Lemma 4.4 Every
![]() $\lambda \in \Lambda _{G/K}$
is uniquely determined by its values against the spherical roots, together with its restriction to
$\lambda \in \Lambda _{G/K}$
is uniquely determined by its values against the spherical roots, together with its restriction to
![]() $B \cap \mathrm N_G(K)^\circ $
.
$B \cap \mathrm N_G(K)^\circ $
.
Proof Denote
![]() $K'= \mathrm N_G(K)^\circ $
, then the restriction of characters to
$K'= \mathrm N_G(K)^\circ $
, then the restriction of characters to
![]() $B \cap K'$
induces an exact sequence
$B \cap K'$
induces an exact sequence
 $$ \begin{align*}0 \longrightarrow \Lambda_{G/K'} \longrightarrow \Lambda_{G/K} \longrightarrow \mathcal X(B \cap K')^{B \cap K} \longrightarrow 0 \end{align*} $$
$$ \begin{align*}0 \longrightarrow \Lambda_{G/K'} \longrightarrow \Lambda_{G/K} \longrightarrow \mathcal X(B \cap K')^{B \cap K} \longrightarrow 0 \end{align*} $$
(see, e.g., [Reference Gandini12, Lemma 2.4]). On the other hand,
![]() $\Lambda _{G/\bar K}\subset \Lambda _{G/K'}$
is a sublattice of finite index, and
$\Lambda _{G/\bar K}\subset \Lambda _{G/K'}$
is a sublattice of finite index, and
 $\Lambda _{G/\bar K} = \mathbb Z \Delta ^{\mathrm {sc}}_{G/K}$
; thus, every element in
$\Lambda _{G/\bar K} = \mathbb Z \Delta ^{\mathrm {sc}}_{G/K}$
; thus, every element in
![]() $\Lambda _{G/ K'}$
is uniquely determined by its values against the spherical roots.
$\Lambda _{G/ K'}$
is uniquely determined by its values against the spherical roots.
5 Affine spherical varieties with root system of type A
We now consider generalizations of Conjecture 3.2 to other affine spherical homogeneous varieties for a simple algebraic group.
Let
![]() $(G,K)$
be a reductive spherical pair, and set
$(G,K)$
be a reductive spherical pair, and set
![]() $X = G/K$
. Let
$X = G/K$
. Let
![]() $G_X$
be the connected reductive group defined by the root datum
$G_X$
be the connected reductive group defined by the root datum
![]() $\mathcal R_X = (\Xi _X, \Delta _X, \Delta _X^\vee )$
, and correspondingly, let
$\mathcal R_X = (\Xi _X, \Delta _X, \Delta _X^\vee )$
, and correspondingly, let
![]() $T_X \subset G_X$
and
$T_X \subset G_X$
and
![]() $B_X \subset G_X$
be a maximal torus and a Borel subgroup containing
$B_X \subset G_X$
be a maximal torus and a Borel subgroup containing
![]() $T_X$
inducing
$T_X$
inducing
![]() $\mathcal R_X$
. For a spherical weight
$\mathcal R_X$
. For a spherical weight
![]() $\pi \in \Xi _X^+$
(in particular, for
$\pi \in \Xi _X^+$
(in particular, for
![]() $\pi \in \Lambda _X^+$
), let
$\pi \in \Lambda _X^+$
), let
![]() $V_X(\pi )$
be the irreducible
$V_X(\pi )$
be the irreducible
![]() $G_X$
-module with highest weight
$G_X$
-module with highest weight
![]() $\pi $
. In analogy with the symmetric case, we denote by
$\pi $
. In analogy with the symmetric case, we denote by
![]() $\leqslant _X$
the partial order on
$\leqslant _X$
the partial order on
![]() $\Xi _X$
defined by
$\Xi _X$
defined by
![]() $\Delta ^{\mathrm n}_X$
, namely
$\Delta ^{\mathrm n}_X$
, namely
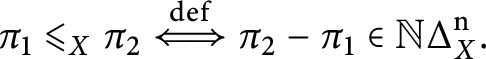 $$ \begin{align*}\pi_1 \leqslant_X \pi_2 \stackrel{\mathrm{def}}{\Longleftrightarrow} \pi_2 - \pi_1 \in \mathbb N \Delta^{\mathrm n}_X. \end{align*} $$
$$ \begin{align*}\pi_1 \leqslant_X \pi_2 \stackrel{\mathrm{def}}{\Longleftrightarrow} \pi_2 - \pi_1 \in \mathbb N \Delta^{\mathrm n}_X. \end{align*} $$
Conjecture 5.1 Let
![]() $(G,K)$
be a reductive spherical pair with G simple and with
$(G,K)$
be a reductive spherical pair with G simple and with
![]() $\Phi _{G/K}$
of type
$\Phi _{G/K}$
of type
![]() $\mathsf A$
, and set
$\mathsf A$
, and set
![]() $X = G/K$
. Let
$X = G/K$
. Let
![]() $\lambda , \mu , \nu \in \Lambda _X^+$
, then
$\lambda , \mu , \nu \in \Lambda _X^+$
, then
 $$ \begin{align*}E_X(\nu) \subset E_X(\lambda) \cdot E_X(\mu) \Longleftrightarrow \left\{ \begin{array}{c} V_X(\nu) \subset V_X(\lambda) \otimes V_X(\mu), \phantom{\Big|} \\ \nu \leqslant_X \lambda + \mu. \end{array} \right. \end{align*} $$
$$ \begin{align*}E_X(\nu) \subset E_X(\lambda) \cdot E_X(\mu) \Longleftrightarrow \left\{ \begin{array}{c} V_X(\nu) \subset V_X(\lambda) \otimes V_X(\mu), \phantom{\Big|} \\ \nu \leqslant_X \lambda + \mu. \end{array} \right. \end{align*} $$
With one exception (case Sph.A15 of Table 3), we will show that the previous conjecture holds true whenever
![]() $\Phi _X$
is a direct sum of rank 1 root systems—which happens in most of the cases—as a consequence of Stanley’s Pieri rule for Jack symmetric functions [Reference Stanley33, Theorem 6.1]. More generally, we will show that in all cases but case Sph.A15, the previous conjecture follows from Conjecture 3.2 (and in particular from Stanley’s Conjecture 3.1). Finally, in the remaining case Sph.A15, the conjecture is supported by computational experiments.
$\Phi _X$
is a direct sum of rank 1 root systems—which happens in most of the cases—as a consequence of Stanley’s Pieri rule for Jack symmetric functions [Reference Stanley33, Theorem 6.1]. More generally, we will show that in all cases but case Sph.A15, the previous conjecture follows from Conjecture 3.2 (and in particular from Stanley’s Conjecture 3.1). Finally, in the remaining case Sph.A15, the conjecture is supported by computational experiments.
For the remainder of the section, G will be a simple and simply connected algebraic group, and
![]() $K \subset G$
a connected reductive spherical subgroup such that the spherical root system
$K \subset G$
a connected reductive spherical subgroup such that the spherical root system
![]() $\Phi _{G/K}$
is of type
$\Phi _{G/K}$
is of type
![]() $\mathsf A$
. A list of such spherical pairs is given in Table 3 (where we omit the cases of Table 1). For a full list of the reductive spherical pairs
$\mathsf A$
. A list of such spherical pairs is given in Table 3 (where we omit the cases of Table 1). For a full list of the reductive spherical pairs
![]() $(G,K)$
with G simple and K connected, we refer to [Reference Knop and Röhrle19, Reference Krämer23].
$(G,K)$
with G simple and K connected, we refer to [Reference Knop and Röhrle19, Reference Krämer23].
Table 3: Reductive spherical pairs
![]() $(G,K)$
with root system of type
$(G,K)$
with root system of type
![]() $\mathsf A$
.
$\mathsf A$
.

Remark 5.2 As already pointed out in Remark 3.4 for the symmetric case, also in this case, it is possible to formulate Conjecture 5.1 using the based root datum
![]() $\mathcal R^{\mathrm n}_X = (\Lambda _X, \Delta ^{\mathrm n}_X, {\Delta ^{\mathrm n}_X}^{\!\!\vee })$
rather than
$\mathcal R^{\mathrm n}_X = (\Lambda _X, \Delta ^{\mathrm n}_X, {\Delta ^{\mathrm n}_X}^{\!\!\vee })$
rather than
![]() $\mathcal R_X$
, and defining the reductive group
$\mathcal R_X$
, and defining the reductive group
![]() $G_X$
accordingly. Using
$G_X$
accordingly. Using
![]() $\mathcal R^{\mathrm n}_X$
, the formulation becomes also simpler, because the inequality
$\mathcal R^{\mathrm n}_X$
, the formulation becomes also simpler, because the inequality
![]() $\nu \leqslant _X \lambda +\mu $
becomes redundant. However, the formulation that we adopted seems to be preferable, as it fits inside the more general framework that we will consider in Section 6. Notice also that in all cases but Sph.A10, it holds
$\nu \leqslant _X \lambda +\mu $
becomes redundant. However, the formulation that we adopted seems to be preferable, as it fits inside the more general framework that we will consider in Section 6. Notice also that in all cases but Sph.A10, it holds
![]() $\Delta _X = \Delta _X^{\mathrm n}$
, so that, in these cases, we have indeed
$\Delta _X = \Delta _X^{\mathrm n}$
, so that, in these cases, we have indeed
![]() $\mathcal R_X = \mathcal R_X^{\mathrm n}$
.
$\mathcal R_X = \mathcal R_X^{\mathrm n}$
.
Remark 5.3 Notice that the cases Sph.A7, Sph.A11, and Sph.A15 are actually symmetric, with nonreduced restricted root system of type
![]() $\mathsf {BC}_1$
.
$\mathsf {BC}_1$
.
Notice also that the unique cases where
![]() $\Phi _{G/K}$
is not a direct sum of subsystems of type
$\Phi _{G/K}$
is not a direct sum of subsystems of type
![]() $\mathsf A_1$
are cases Sph.A8 and Sph.A9. In the first case,
$\mathsf A_1$
are cases Sph.A8 and Sph.A9. In the first case,
![]() $G/K$
is the principal model variety of
$G/K$
is the principal model variety of
![]() $\operatorname {\mathrm {SL}}(n)$
: a homogeneous variety
$\operatorname {\mathrm {SL}}(n)$
: a homogeneous variety
![]() $G/H$
is said to be a model variety for G if it is spherical and
$G/H$
is said to be a model variety for G if it is spherical and
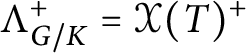 $\Lambda _{G/K}^+ = \mathcal X(T)^+$
(see [Reference Gelfand and Zelevinsky13, Reference Gelfand and Zelevinsky14]). In the latter case,
$\Lambda _{G/K}^+ = \mathcal X(T)^+$
(see [Reference Gelfand and Zelevinsky13, Reference Gelfand and Zelevinsky14]). In the latter case,
![]() $G/K$
is the homogeneous space which corresponds to the model variety of
$G/K$
is the homogeneous space which corresponds to the model variety of
![]() $\operatorname {\mathrm {SL}}(n)$
in Luna’s classification [Reference Luna27].
$\operatorname {\mathrm {SL}}(n)$
in Luna’s classification [Reference Luna27].
All other cases, where
![]() $\Phi _{G/K}$
is a direct sum of subsystems of type
$\Phi _{G/K}$
is a direct sum of subsystems of type
![]() $\mathsf A_1$
, are related to some transitive action of a compact Lie group on a projective space, on a sphere, or on a product of spheres. Let indeed
$\mathsf A_1$
, are related to some transitive action of a compact Lie group on a projective space, on a sphere, or on a product of spheres. Let indeed
![]() $G_{\mathbb R} \subset G$
and
$G_{\mathbb R} \subset G$
and
![]() $K_{\mathbb R} \subset K$
be the associated compact real forms, then we have the following descriptions for
$K_{\mathbb R} \subset K$
be the associated compact real forms, then we have the following descriptions for
![]() $G_{\mathbb R}/K_{\mathbb R}$
:
$G_{\mathbb R}/K_{\mathbb R}$
:
-
(i) It is isomorphic to
 $\mathbb P^n(\mathbb C)$
in case Sph.A7, to
$\mathbb P^n(\mathbb C)$
in case Sph.A7, to
 $\mathbb P^{2n}(\mathbb C)$
in case Sph.A10, to
$\mathbb P^{2n}(\mathbb C)$
in case Sph.A10, to
 $\mathbb P^n(\mathbb H)$
in case Sph.A11, and to
$\mathbb P^n(\mathbb H)$
in case Sph.A11, and to
 $\mathbb P^2(\mathbb O)$
in case Sph.A15 (where
$\mathbb P^2(\mathbb O)$
in case Sph.A15 (where
 $\mathbb H$
and
$\mathbb H$
and
 $\mathbb O$
denote, respectively, the algebras of the quaternions and of the octonions).
$\mathbb O$
denote, respectively, the algebras of the quaternions and of the octonions). -
(ii) It is isomorphic to
 $\mathbb S^{2n-1}$
in case Sph.A6, to
$\mathbb S^{2n-1}$
in case Sph.A6, to
 $\mathbb S^7$
in case Sph.A12, to
$\mathbb S^7$
in case Sph.A12, to
 $\mathbb S^{15}$
in case Sph.A13, to
$\mathbb S^{15}$
in case Sph.A13, to
 $\mathbb S^6$
in case Sph.A16, and to
$\mathbb S^6$
in case Sph.A16, and to
 $\mathbb S^7 \times \mathbb S^7$
in case Sph.A14.
$\mathbb S^7 \times \mathbb S^7$
in case Sph.A14.
By a theorem of Cartan, if
![]() $G_{\mathbb R}/H_{\mathbb R}$
is an irreducible compact Riemannian symmetric space of rank 1, then
$G_{\mathbb R}/H_{\mathbb R}$
is an irreducible compact Riemannian symmetric space of rank 1, then
![]() $H_{\mathbb R}$
acts transitively on the unit sphere in the isotropy representation of
$H_{\mathbb R}$
acts transitively on the unit sphere in the isotropy representation of
![]() $H_{\mathbb R}$
. This gives indeed rise to the transitive actions on spheres which correspond to cases Sph.A6 and Sph.A13 (which, respectively, come from the families of symmetric spaces corresponding to cases Sph.A7 and Sph.A15). More generally, transitive actions of compact Lie groups on spheres were classified by Montgomery–Samelson and Borel: those which are not related to a symmetric space of rank 1 correspond to cases Sph.A12 and Sph.A13 (see, e.g., [Reference Schlichtkrull, Trapa and Vogan32]).
$H_{\mathbb R}$
. This gives indeed rise to the transitive actions on spheres which correspond to cases Sph.A6 and Sph.A13 (which, respectively, come from the families of symmetric spaces corresponding to cases Sph.A7 and Sph.A15). More generally, transitive actions of compact Lie groups on spheres were classified by Montgomery–Samelson and Borel: those which are not related to a symmetric space of rank 1 correspond to cases Sph.A12 and Sph.A13 (see, e.g., [Reference Schlichtkrull, Trapa and Vogan32]).
There is indeed another transitive action on a sphere which is associated to a rank 1 symmetric space, which is not included in Table 3: it is the transitive action of
![]() $\operatorname {\mathrm {Sp}}(2,\mathbb R) \times \operatorname {\mathrm {Sp}}(2n,\mathbb R)$
on
$\operatorname {\mathrm {Sp}}(2,\mathbb R) \times \operatorname {\mathrm {Sp}}(2n,\mathbb R)$
on
![]() $\mathbb S^{4n-1}$
(which comes from the family of symmetric spaces corresponding to case Sph.A11). This action corresponds to the reductive spherical pair
$\mathbb S^{4n-1}$
(which comes from the family of symmetric spaces corresponding to case Sph.A11). This action corresponds to the reductive spherical pair
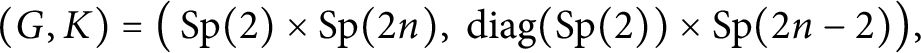 $$ \begin{align*}(G,K) = \big(\operatorname{\mathrm{Sp}}(2) \times \operatorname{\mathrm{Sp}}(2n), \ \operatorname{\mathrm{diag}}(\operatorname{\mathrm{Sp}}(2)) \times \operatorname{\mathrm{Sp}}(2n-2) \big), \end{align*} $$
$$ \begin{align*}(G,K) = \big(\operatorname{\mathrm{Sp}}(2) \times \operatorname{\mathrm{Sp}}(2n), \ \operatorname{\mathrm{diag}}(\operatorname{\mathrm{Sp}}(2)) \times \operatorname{\mathrm{Sp}}(2n-2) \big), \end{align*} $$
in which case
![]() $\Phi _{G/K}$
is of type
$\Phi _{G/K}$
is of type
![]() $\mathsf A_1 \times \mathsf A_1$
. Even though G is not simple, this case also fits in the general framework which allows us to deal with the cases of Table 3. We will analyze this case separately in Remark 5.11.
$\mathsf A_1 \times \mathsf A_1$
. Even though G is not simple, this case also fits in the general framework which allows us to deal with the cases of Table 3. We will analyze this case separately in Remark 5.11.
To deal with the cases of Table 3, a first useful remark is that cases Sph.A7, Sph.A9, and Sph.A11, respectively, follow (almost immediately) from the companion cases Sph.A6, Sph.A8, and Sph.A10. This will be explained in Section 5.3.
All the remaining cases of Table 3—with the exception of case Sph.A15—will follow from some cases of Table 1, thanks to a related factorization of a simple algebraic group as a product of two reductive subgroups. Such factorizations have been classified by Onishchik [Reference Onishchik29] in the context of compact Lie groups (see also [Reference Gorbatsevich, Onishchik and Onishchik15, Sections 4.5 and 4.6]) and by Liebeck, Saxl, and Seitz algebraically in arbitrary characteristic [Reference Liebeck, Saxl and Seitz24]. More precisely, in all the considered cases, the multiplication will reduce to that of some symmetric varieties, which correspond to a decomposition of
![]() $\Phi _{G/K}$
into two orthogonal components.
$\Phi _{G/K}$
into two orthogonal components.
In particular, we will find a reductive overgroup
![]() $\widehat G \supset G$
and a symmetric subgroup
$\widehat G \supset G$
and a symmetric subgroup
![]() $\widehat K \subset \widehat G$
such that
$\widehat K \subset \widehat G$
such that
![]() $\widehat G = G \cdot \widehat K$
and
$\widehat G = G \cdot \widehat K$
and
![]() $K = G \cap \widehat K$
, yielding a G-equivariant isomorphism
$K = G \cap \widehat K$
, yielding a G-equivariant isomorphism
and inducing a natural projection of weight monoids
 $$ \begin{align*}\hat \varphi: \Lambda^+_{G/K} \longrightarrow \Lambda^+_{\widehat G/\widehat K}. \end{align*} $$
$$ \begin{align*}\hat \varphi: \Lambda^+_{G/K} \longrightarrow \Lambda^+_{\widehat G/\widehat K}. \end{align*} $$
As a consequence of a theorem of Luna [Reference Luna25], notice that in the previous setting
![]() $G/K$
and
$G/K$
and
![]() $\widehat G/\widehat K$
are isomorphic as G-varieties if and only if
$\widehat G/\widehat K$
are isomorphic as G-varieties if and only if
![]() $G/K$
embeds G-equivariantly into
$G/K$
embeds G-equivariantly into
![]() $\widehat G/\widehat K$
as a dense open subset.
$\widehat G/\widehat K$
as a dense open subset.
We will also need to bring into the picture a second symmetric pair
![]() $(H,K)$
(possibly trivial), where H is a suitable connected reductive subgroup of G containing K and the connected center of
$(H,K)$
(possibly trivial), where H is a suitable connected reductive subgroup of G containing K and the connected center of
![]() $\mathrm N_G(K)$
, yielding an H-equivariant embedding
$\mathrm N_G(K)$
, yielding an H-equivariant embedding
and inducing a second projection of weight monoids
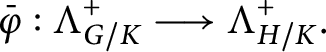 $$ \begin{align*}\bar \varphi:\Lambda^+_{G/K} \longrightarrow \Lambda^+_{H/K}. \end{align*} $$
$$ \begin{align*}\bar \varphi:\Lambda^+_{G/K} \longrightarrow \Lambda^+_{H/K}. \end{align*} $$
The two maps
![]() $\hat \varphi $
and
$\hat \varphi $
and
![]() $\bar \varphi $
will allow us to identify the spherical functions of
$\bar \varphi $
will allow us to identify the spherical functions of
![]() $G/K$
, and describe their products, in terms of those of
$G/K$
, and describe their products, in terms of those of
![]() $\widehat G/\widehat K$
and
$\widehat G/\widehat K$
and
![]() $H/K$
. Before treating the various cases in detail, let us explain here the general argument.
$H/K$
. Before treating the various cases in detail, let us explain here the general argument.
Suppose that we have:
-
(i) a connected reductive overgroup
 $\widehat G \supset G$
and a spherical subgroup
$\widehat G \supset G$
and a spherical subgroup
 $\widehat K \subset \widehat G$
such that
$\widehat K \subset \widehat G$
such that
 $G/K \simeq \widehat G/\widehat K$
, and
$G/K \simeq \widehat G/\widehat K$
, and -
(ii) a connected reductive subgroup
 $H\subset G$
containing K (and the connected center of
$H\subset G$
containing K (and the connected center of
 $\mathrm N_G(K)$
).
$\mathrm N_G(K)$
).
We also assume (it will always be true in our cases) that there is a compatible choice of Borel subgroups, that is, there exists a maximal torus and Borel subgroup
![]() $\widehat T \subset \widehat B$
of
$\widehat T \subset \widehat B$
of
![]() $\widehat G$
with
$\widehat G$
with
![]() $\widehat B \widehat K$
open in
$\widehat B \widehat K$
open in
![]() $\widehat G$
such that:
$\widehat G$
such that:
-
(i)
 $T = \widehat T \cap G$
is a maximal torus of G, and
$T = \widehat T \cap G$
is a maximal torus of G, and
 $B = \widehat B \cap G$
is a Borel subgroup of G with
$B = \widehat B \cap G$
is a Borel subgroup of G with
 $B K$
is open in G.
$B K$
is open in G. -
(ii)
 $T_H = T \cap H$
is a maximal torus of H, and
$T_H = T \cap H$
is a maximal torus of H, and
 $B_H = B \cap H$
is a Borel subgroup of H with
$B_H = B \cap H$
is a Borel subgroup of H with
 $B_H K$
is open in H.
$B_H K$
is open in H.
On the one hand, the restriction of the
![]() $\widehat G$
-action to G induces an isomorphism of G-modules
$\widehat G$
-action to G induces an isomorphism of G-modules
 $$ \begin{align*}\bigoplus_{\mu \in \Lambda^+_{\widehat G/\widehat K}} E_{\widehat G/\widehat K}(\mu) \; = \; \mathbb C[\widehat G/\widehat K] \stackrel{\sim}{\longrightarrow} \mathbb C[G/K] \quad = \bigoplus_{\lambda \in \Lambda^+_{G/K}} E_{G/K}(\lambda). \end{align*} $$
$$ \begin{align*}\bigoplus_{\mu \in \Lambda^+_{\widehat G/\widehat K}} E_{\widehat G/\widehat K}(\mu) \; = \; \mathbb C[\widehat G/\widehat K] \stackrel{\sim}{\longrightarrow} \mathbb C[G/K] \quad = \bigoplus_{\lambda \in \Lambda^+_{G/K}} E_{G/K}(\lambda). \end{align*} $$
Thus, for all
 $\lambda \in \Lambda ^+_{G/K}$
, there exists a unique
$\lambda \in \Lambda ^+_{G/K}$
, there exists a unique
 $\hat \lambda \in \Lambda ^+_{\widehat G/\widehat K}$
such that
$\hat \lambda \in \Lambda ^+_{\widehat G/\widehat K}$
such that
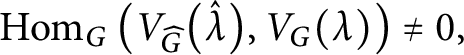 $$ \begin{align*}\operatorname{\mathrm{Hom}}_G\big(V_{\widehat G}\big(\hat \lambda\big),V_G(\lambda)\big) \neq 0, \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Hom}}_G\big(V_{\widehat G}\big(\hat \lambda\big),V_G(\lambda)\big) \neq 0, \end{align*} $$
and we define
 $\hat \varphi (\lambda ) = \hat \lambda $
.
$\hat \varphi (\lambda ) = \hat \lambda $
.
On the other hand, by definition, for all
 $\lambda \in \Lambda _{G/K}^+$
, the invariant space
$\lambda \in \Lambda _{G/K}^+$
, the invariant space
![]() $V_G(\lambda )^K$
is one-dimensional. Looking at the decomposition of
$V_G(\lambda )^K$
is one-dimensional. Looking at the decomposition of
![]() $V_G(\lambda )$
into simple H-modules, it follows that there exists a unique
$V_G(\lambda )$
into simple H-modules, it follows that there exists a unique
 $\bar \lambda \in \Lambda _{H/K}^+$
such that
$\bar \lambda \in \Lambda _{H/K}^+$
such that
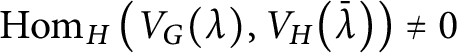 $$ \begin{align*}\operatorname{\mathrm{Hom}}_{H}\big(V_G(\lambda), V_{H}\big(\bar \lambda\big)\big) \neq 0 \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Hom}}_{H}\big(V_G(\lambda), V_{H}\big(\bar \lambda\big)\big) \neq 0 \end{align*} $$
(and the dimension of the latter is necessarily 1). Thus, we define
![]() $\bar \varphi (\lambda ) = \bar \lambda $
.
$\bar \varphi (\lambda ) = \bar \lambda $
.
Consider now the restriction of functions from
![]() $G/K$
to
$G/K$
to
![]() $H/K$
$H/K$
 $$ \begin{align*}\bigoplus_{\lambda \in \Lambda^+_{G/K}} E_{G/K}(\lambda) \; = \; \mathbb C[G/K] \stackrel{\rho}{\longrightarrow} \mathbb C[H/K] \quad = \bigoplus_{\mu \in \Lambda^+_{H/K}} E_{H/K}(\mu). \end{align*} $$
$$ \begin{align*}\bigoplus_{\lambda \in \Lambda^+_{G/K}} E_{G/K}(\lambda) \; = \; \mathbb C[G/K] \stackrel{\rho}{\longrightarrow} \mathbb C[H/K] \quad = \bigoplus_{\mu \in \Lambda^+_{H/K}} E_{H/K}(\mu). \end{align*} $$
In the following lemma, we show that
![]() $\rho (E_{G/K}(\lambda ))$
is nonzero; hence, it coincides with
$\rho (E_{G/K}(\lambda ))$
is nonzero; hence, it coincides with
 $E_{H/K}(\bar \lambda )$
.
$E_{H/K}(\bar \lambda )$
.
Lemma 5.4 Let
![]() $V \subset \mathbb C[G/K]$
be an irreducible G-submodule. Then,
$V \subset \mathbb C[G/K]$
be an irreducible G-submodule. Then,
![]() $\rho (V) \subset \mathbb C[H/K]$
is an irreducible H-submodule.
$\rho (V) \subset \mathbb C[H/K]$
is an irreducible H-submodule.
Proof By the discussion above, we only need to show that
![]() $\rho (V) \neq 0$
.
$\rho (V) \neq 0$
.
Suppose that
![]() $V \simeq V_G(\lambda )$
. Fix K-invariant vectors
$V \simeq V_G(\lambda )$
. Fix K-invariant vectors
![]() $v_\lambda \in V_G(\lambda )$
and
$v_\lambda \in V_G(\lambda )$
and
![]() $\psi _\lambda \in V_G(\lambda )^*$
, and define
$\psi _\lambda \in V_G(\lambda )^*$
, and define
Then,
![]() $f_{G,\lambda } \in V^K$
is a nonzero K-invariant function.
$f_{G,\lambda } \in V^K$
is a nonzero K-invariant function.
Similarly, if
 $v_{\bar \lambda } \in V_{H}(\bar \lambda )$
and
$v_{\bar \lambda } \in V_{H}(\bar \lambda )$
and
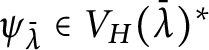 $\psi _{\bar \lambda } \in V_{H}(\bar \lambda )^*$
are K-invariant vectors, setting
$\psi _{\bar \lambda } \in V_{H}(\bar \lambda )^*$
are K-invariant vectors, setting
we get a nonzero K-invariant function on
![]() $H/K$
.
$H/K$
.
On the other hand, there is a unique H-equivariant embedding of
![]() $V_{H}(\bar \lambda )$
inside
$V_{H}(\bar \lambda )$
inside
![]() $V_G(\lambda )$
, and a unique H-equivariant embedding of
$V_G(\lambda )$
, and a unique H-equivariant embedding of
![]() $V_{H}(\bar \lambda )^*$
inside
$V_{H}(\bar \lambda )^*$
inside
![]() $V_G(\lambda )^*$
. With respect to such embeddings, we have equalities
$V_G(\lambda )^*$
. With respect to such embeddings, we have equalities
Because these invariant subspaces are one-dimensional, it follows that the K-invariant vectors
![]() $v_\lambda $
and
$v_\lambda $
and
![]() $v_{\bar \lambda }$
are proportional, and similarly for the K-invariant linear functions
$v_{\bar \lambda }$
are proportional, and similarly for the K-invariant linear functions
![]() $\psi _\lambda $
and
$\psi _\lambda $
and
![]() $\psi _{\bar \lambda }$
. Thus, the restriction
$\psi _{\bar \lambda }$
. Thus, the restriction
![]() $\rho (f_{G,\lambda })$
is a nonzero scalar multiple of
$\rho (f_{G,\lambda })$
is a nonzero scalar multiple of
![]() $f_{H,\bar \lambda }$
.
$f_{H,\bar \lambda }$
.
We now show that the two maps
![]() $\hat \varphi $
and
$\hat \varphi $
and
![]() $\bar \varphi $
, defined above, are actually morphisms of monoids.
$\bar \varphi $
, defined above, are actually morphisms of monoids.
Proposition 5.5 With notations and hypotheses as above, both the maps
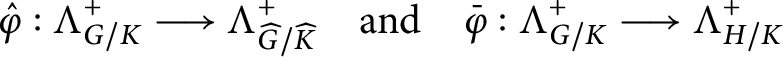 $$ \begin{align*}\hat \varphi : \Lambda^+_{G/K} \longrightarrow \Lambda^+_{\widehat G/\widehat K} \quad\mbox{and}\quad \bar \varphi : \Lambda^+_{G/K} \longrightarrow \Lambda^+_{H/K}\end{align*} $$
$$ \begin{align*}\hat \varphi : \Lambda^+_{G/K} \longrightarrow \Lambda^+_{\widehat G/\widehat K} \quad\mbox{and}\quad \bar \varphi : \Lambda^+_{G/K} \longrightarrow \Lambda^+_{H/K}\end{align*} $$
are additive maps.
Proof (i) Let
![]() $\Gamma (\widehat G,G)$
be the branching monoid associated to the pair
$\Gamma (\widehat G,G)$
be the branching monoid associated to the pair
![]() $(\widehat G,G)$
, namely
$(\widehat G,G)$
, namely
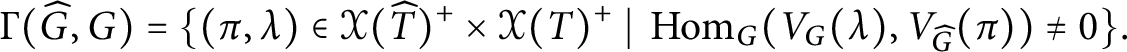 $$ \begin{align*}\Gamma(\widehat G,G) = \{(\pi,\lambda) \in \mathcal X(\widehat T)^+ \times \mathcal X(T)^+ \; | \; \operatorname{\mathrm{Hom}}_{G}(V_G(\lambda), V_{\widehat G}(\pi)) \neq 0 \}. \end{align*} $$
$$ \begin{align*}\Gamma(\widehat G,G) = \{(\pi,\lambda) \in \mathcal X(\widehat T)^+ \times \mathcal X(T)^+ \; | \; \operatorname{\mathrm{Hom}}_{G}(V_G(\lambda), V_{\widehat G}(\pi)) \neq 0 \}. \end{align*} $$
This is indeed a finitely generated monoid (see [Reference Akhiezer and Panyushev1]).
Consider the projections
 $$ \begin{align*}p : \Gamma(\widehat G,G) \rightarrow \mathcal X(\widehat T)^+, \qquad \qquad q : \Gamma(\widehat G,G) \rightarrow \mathcal X(T)^+. \end{align*} $$
$$ \begin{align*}p : \Gamma(\widehat G,G) \rightarrow \mathcal X(\widehat T)^+, \qquad \qquad q : \Gamma(\widehat G,G) \rightarrow \mathcal X(T)^+. \end{align*} $$
Because K is spherical in G, notice that
 $p^{-1}(\Lambda _{\widehat G/\widehat K}^+)$
is a submonoid of
$p^{-1}(\Lambda _{\widehat G/\widehat K}^+)$
is a submonoid of
![]() $\Gamma (\widehat G,G)$
, and that q induces an isomorphism
$\Gamma (\widehat G,G)$
, and that q induces an isomorphism
 $p^{-1}(\Lambda _{\widehat G/\widehat K}^+) \rightarrow \Lambda _{G/K}^+$
.
$p^{-1}(\Lambda _{\widehat G/\widehat K}^+) \rightarrow \Lambda _{G/K}^+$
.
If indeed
![]() $(\pi ,\lambda ) \in \Gamma (\widehat G,G)$
and
$(\pi ,\lambda ) \in \Gamma (\widehat G,G)$
and
 $\pi \in \Lambda _{\widehat G/\widehat K}^+$
, then by the isomorphism
$\pi \in \Lambda _{\widehat G/\widehat K}^+$
, then by the isomorphism
![]() $\mathbb C[G/K] \simeq \mathbb C[\widehat G/\widehat K]$
, it follows
$\mathbb C[G/K] \simeq \mathbb C[\widehat G/\widehat K]$
, it follows
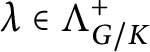 $\lambda \in \Lambda _{G/K}^+$
. Conversely, if
$\lambda \in \Lambda _{G/K}^+$
. Conversely, if
 $\lambda \in \Lambda _{G/K}^+$
, because
$\lambda \in \Lambda _{G/K}^+$
, because
![]() $\mathbb C[G/K] \simeq \mathbb C[\widehat G/\widehat K]$
, the multiplicity-free property implies that there is a unique
$\mathbb C[G/K] \simeq \mathbb C[\widehat G/\widehat K]$
, the multiplicity-free property implies that there is a unique
 $\pi \in \Lambda _{\widehat G/\widehat K}^+$
with
$\pi \in \Lambda _{\widehat G/\widehat K}^+$
with
![]() $(\pi ,\lambda ) \in \Gamma (\widehat G,G)$
, and by definition
$(\pi ,\lambda ) \in \Gamma (\widehat G,G)$
, and by definition
![]() $\pi = \hat \varphi (\lambda )$
.
$\pi = \hat \varphi (\lambda )$
.
It is now clear that, under the isomorphism
 $\Lambda _{G/K}^+ \simeq p^{-1}(\Lambda _{\widehat G/\widehat K}^+)$
, the map
$\Lambda _{G/K}^+ \simeq p^{-1}(\Lambda _{\widehat G/\widehat K}^+)$
, the map
![]() $\hat \varphi $
coincides with the restriction of the projection p. In particular, we see that
$\hat \varphi $
coincides with the restriction of the projection p. In particular, we see that
![]() $\hat \varphi $
is an additive map.
$\hat \varphi $
is an additive map.
(ii) The proof that
![]() $\bar \varphi $
is additive is similar to the previous one, by considering the branching monoid associated to the pair
$\bar \varphi $
is additive is similar to the previous one, by considering the branching monoid associated to the pair
![]() $(G,H)$
$(G,H)$
together with the projections
Then, p induces an isomorphism of monoids
 $q^{-1}(\Lambda _{H/K}^+) \rightarrow \Lambda _{G/K}^+$
, and
$q^{-1}(\Lambda _{H/K}^+) \rightarrow \Lambda _{G/K}^+$
, and
![]() $\bar \varphi $
corresponds to the restriction of q.
$\bar \varphi $
corresponds to the restriction of q.
Therefore, we can extend
![]() $\hat \varphi $
and
$\hat \varphi $
and
![]() $\bar \varphi $
to morphisms of the associated weight lattices. When the lattice
$\bar \varphi $
to morphisms of the associated weight lattices. When the lattice
![]() $\Xi _{G/K}$
is bigger than
$\Xi _{G/K}$
is bigger than
![]() $\Lambda _{G/K}$
, we will see in the cases under consideration that the extensions of
$\Lambda _{G/K}$
, we will see in the cases under consideration that the extensions of
![]() $\hat \varphi $
and
$\hat \varphi $
and
![]() $\bar \varphi $
to
$\bar \varphi $
to
![]() $\Xi _{G/K}$
, respectively, take values in
$\Xi _{G/K}$
, respectively, take values in
![]() $\Xi _{\widehat G/\widehat K}$
and
$\Xi _{\widehat G/\widehat K}$
and
![]() $\Xi _{H/K}$
. The description of the maps
$\Xi _{H/K}$
. The description of the maps
![]() $\hat \varphi $
and
$\hat \varphi $
and
![]() $\bar \varphi $
will immediately imply the following.
$\bar \varphi $
will immediately imply the following.
Proposition 5.6 Let
![]() $(G,K)$
be a reductive spherical pair with
$(G,K)$
be a reductive spherical pair with
![]() $\Phi _{G/K}$
of type
$\Phi _{G/K}$
of type
![]() $\mathsf A$
, and suppose that we are in one of the following cases of Table 3:
$\mathsf A$
, and suppose that we are in one of the following cases of Table 3:
Then, there exist a connected reductive subgroup
![]() $H \subset G$
containing K (possibly equal to K), a connected reductive overgroup
$H \subset G$
containing K (possibly equal to K), a connected reductive overgroup
![]() $\widehat G \supset G$
, and a symmetric subgroup
$\widehat G \supset G$
, and a symmetric subgroup
![]() $\widehat K \subset \widehat G$
with
$\widehat K \subset \widehat G$
with
![]() $\widehat K \cap G = K$
such that the map
$\widehat K \cap G = K$
such that the map
 $$ \begin{align*}(\hat \varphi,\bar \varphi) \; \colon \; \Xi_{G/K} \longrightarrow \Xi_{\widehat G/\widehat K} \oplus \Xi_{H/K}\end{align*} $$
$$ \begin{align*}(\hat \varphi,\bar \varphi) \; \colon \; \Xi_{G/K} \longrightarrow \Xi_{\widehat G/\widehat K} \oplus \Xi_{H/K}\end{align*} $$
is an isogeny of based root data
 $$ \begin{align*} \mathcal R_{G/K} \longrightarrow \mathcal R_{\widehat G/\widehat K} \oplus \mathcal R_{H/K}. \end{align*} $$
$$ \begin{align*} \mathcal R_{G/K} \longrightarrow \mathcal R_{\widehat G/\widehat K} \oplus \mathcal R_{H/K}. \end{align*} $$
To be clear about notation and terminology,
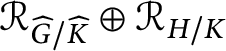 $\mathcal R_{\widehat G/\widehat K} \oplus \mathcal R_{H/K}$
is the based root datum defined by
$\mathcal R_{\widehat G/\widehat K} \oplus \mathcal R_{H/K}$
is the based root datum defined by
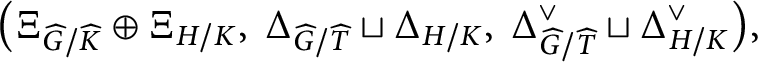 $$ \begin{align*}\big(\Xi_{\widehat G/\widehat K} \oplus \Xi_{H/K},\ \Delta_{\widehat G/\widehat T}\sqcup \Delta_{H/K},\ \Delta_{\widehat G/\widehat T}^\vee\sqcup \Delta_{H/K}^\vee\big),\end{align*} $$
$$ \begin{align*}\big(\Xi_{\widehat G/\widehat K} \oplus \Xi_{H/K},\ \Delta_{\widehat G/\widehat T}\sqcup \Delta_{H/K},\ \Delta_{\widehat G/\widehat T}^\vee\sqcup \Delta_{H/K}^\vee\big),\end{align*} $$
and
![]() $\varphi =(\hat \varphi ,\bar \varphi )$
is an isogeny of based root data in the following (usual) sense:
$\varphi =(\hat \varphi ,\bar \varphi )$
is an isogeny of based root data in the following (usual) sense:
-
(i)
 $\varphi : \Xi _{G/K} \rightarrow \Xi _{\widehat G/\widehat K} \oplus \Xi _{H/K}$
is injective with finite cokernel.
$\varphi : \Xi _{G/K} \rightarrow \Xi _{\widehat G/\widehat K} \oplus \Xi _{H/K}$
is injective with finite cokernel. -
(ii)
 $\varphi $
restricts to a bijection between
$\varphi $
restricts to a bijection between
 $\Delta _{G/K}$
and
$\Delta _{G/K}$
and
 $\Delta _{\widehat G/\widehat T}\sqcup \Delta _{H/K}$
.
$\Delta _{\widehat G/\widehat T}\sqcup \Delta _{H/K}$
. -
(iii) The dual map satisfies
 $\varphi ^\vee (\varphi (\sigma )^\vee )=\sigma ^\vee $
, for all
$\varphi ^\vee (\varphi (\sigma )^\vee )=\sigma ^\vee $
, for all
 $\sigma \in \Delta _{G/K}$
.
$\sigma \in \Delta _{G/K}$
.
In particular, we stress the following property.
Corollary 5.7 Every weight in
![]() $\Lambda _{G/K}$
is uniquely determined by its images in
$\Lambda _{G/K}$
is uniquely determined by its images in
![]() $\Lambda _{\widehat G/\widehat K}$
and in
$\Lambda _{\widehat G/\widehat K}$
and in
![]() $\Lambda _{H/K}$
.
$\Lambda _{H/K}$
.
In the next two subsections, we will deal with the various cases of Proposition 5.6.
For every spherical pair
![]() $(G,K)$
, we provide the groups
$(G,K)$
, we provide the groups
![]() $\widehat G$
,
$\widehat G$
,
![]() $\widehat K$
, and H with the required properties. The inclusions among the given groups are well known, and all the mentioned properties can be read off from the classification of the factorizations of simple algebraic groups [Reference Liebeck, Saxl and Seitz24, Reference Onishchik29] (see also [Reference Gorbatsevich, Onishchik and Onishchik15, Sections 4.5 and 4.6]).
$\widehat K$
, and H with the required properties. The inclusions among the given groups are well known, and all the mentioned properties can be read off from the classification of the factorizations of simple algebraic groups [Reference Liebeck, Saxl and Seitz24, Reference Onishchik29] (see also [Reference Gorbatsevich, Onishchik and Onishchik15, Sections 4.5 and 4.6]).
For each affine spherical variety
![]() $G/K$
,
$G/K$
,
![]() $\widehat G/\widehat K$
, and
$\widehat G/\widehat K$
, and
![]() $H/K$
, we describe the sets of spherical roots
$H/K$
, we describe the sets of spherical roots
![]() $\Delta _{G/K}$
,
$\Delta _{G/K}$
,
![]() $\Delta _{\widehat G/\widehat K}$
, and
$\Delta _{\widehat G/\widehat K}$
, and
![]() $\Delta _{H/K}$
(which we call normalized spherical roots), and minimal set of generators of the monoids
$\Delta _{H/K}$
(which we call normalized spherical roots), and minimal set of generators of the monoids
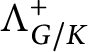 $\Lambda ^+_{G/K}$
,
$\Lambda ^+_{G/K}$
,
 $\Lambda ^+_{\widehat G/\widehat K}$
, and
$\Lambda ^+_{\widehat G/\widehat K}$
, and
 $\Lambda ^+_{H/K}$
(which we call fundamental spherical weights). These data are also well known, and can be read off, for example, from [Reference Bravi and Pezzini6].
$\Lambda ^+_{H/K}$
(which we call fundamental spherical weights). These data are also well known, and can be read off, for example, from [Reference Bravi and Pezzini6].
Finally, in each case, we describe the maps
![]() $\hat \varphi $
and
$\hat \varphi $
and
![]() $\bar \varphi $
. Being additive, it is enough to describe the images of the fundamental spherical weights of
$\bar \varphi $
. Being additive, it is enough to describe the images of the fundamental spherical weights of
![]() $G/K$
.
$G/K$
.
5.1 Indecomposable cases
We consider here the cases Sph.A12 and Sph.A16 where we take the subgroup
![]() $H \subset G$
as K itself (thus,
$H \subset G$
as K itself (thus,
![]() $\Xi _{H/K} = 0$
and
$\Xi _{H/K} = 0$
and
![]() $\Delta _{H/K} = \varnothing $
). The overgroup
$\Delta _{H/K} = \varnothing $
). The overgroup
![]() $\widehat G \supset G$
and the symmetric subgroup
$\widehat G \supset G$
and the symmetric subgroup
![]() $\widehat K \subset \widehat G$
with the prescribed properties are given below.
$\widehat K \subset \widehat G$
with the prescribed properties are given below.
From its explicit description, it will be clear that the map
 $$ \begin{align*}\hat \varphi : \Lambda_{G/K} \longrightarrow \Lambda_{\widehat G/\widehat K} \end{align*} $$
$$ \begin{align*}\hat \varphi : \Lambda_{G/K} \longrightarrow \Lambda_{\widehat G/\widehat K} \end{align*} $$
induces an isomorphism of root data
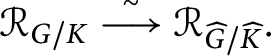 $$ \begin{align*} \mathcal R_{G/K} \stackrel{\sim}{\longrightarrow} \mathcal R_{\widehat G/\widehat K}. \end{align*} $$
$$ \begin{align*} \mathcal R_{G/K} \stackrel{\sim}{\longrightarrow} \mathcal R_{\widehat G/\widehat K}. \end{align*} $$
-
(Sph.A12)
 $G/K = \operatorname {\mathrm {Spin}}(7) / \mathsf G_2$
$G/K = \operatorname {\mathrm {Spin}}(7) / \mathsf G_2$
 $$ \begin{align*}\widehat G / \widehat K = \operatorname{\mathrm{SO}}(8) / \operatorname{\mathrm{SO}}(7).\end{align*} $$
$$ \begin{align*}\widehat G / \widehat K = \operatorname{\mathrm{SO}}(8) / \operatorname{\mathrm{SO}}(7).\end{align*} $$
 $$ \begin{align*}\begin{array}{|c|c|c|} \hline \phantom{\Big|} & \mbox{Norm. spherical roots} & \mbox{Fund. sph. weights}\\ \hline \hline \phantom{\Big|}G/K\phantom{\Big|} & \alpha_1 + 2 \alpha_2 + 3 \alpha_3 & \omega_3 \\ \hline \phantom{\bigg|}\widehat G / \widehat K\phantom{\bigg|} & 2(\alpha'_1 + \alpha'_2) + \alpha'_3 + \alpha'_4 & \omega'_1 \\ \hline \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{|c|c|c|} \hline \phantom{\Big|} & \mbox{Norm. spherical roots} & \mbox{Fund. sph. weights}\\ \hline \hline \phantom{\Big|}G/K\phantom{\Big|} & \alpha_1 + 2 \alpha_2 + 3 \alpha_3 & \omega_3 \\ \hline \phantom{\bigg|}\widehat G / \widehat K\phantom{\bigg|} & 2(\alpha'_1 + \alpha'_2) + \alpha'_3 + \alpha'_4 & \omega'_1 \\ \hline \end{array} \end{align*} $$
 $$ \begin{align*}\begin{array}{|ccccc|} \hline \phantom{\Big|} \hat \varphi & : & a\omega_3 & \longmapsto & a\omega_1' \\ \hline \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{|ccccc|} \hline \phantom{\Big|} \hat \varphi & : & a\omega_3 & \longmapsto & a\omega_1' \\ \hline \end{array}\end{align*} $$
-
(Sph.A16)
 $G / K = \mathsf G_2 / \operatorname {\mathrm {SL}}(3)$
$G / K = \mathsf G_2 / \operatorname {\mathrm {SL}}(3)$
 $$ \begin{align*}\widehat G / \widehat K = \operatorname{\mathrm{SO}}(7) / \operatorname{\mathrm{SO}}(6).\end{align*} $$
$$ \begin{align*}\widehat G / \widehat K = \operatorname{\mathrm{SO}}(7) / \operatorname{\mathrm{SO}}(6).\end{align*} $$
 $$ \begin{align*}\begin{array}{|c|c|c|} \hline \phantom{\Big|} & \mbox{Norm. spherical roots} & \mbox{sph. weights}\\ \hline \hline \phantom{\Big|} G/K \phantom{\Big|} & 4\alpha_1 + 2 \alpha_2 & \omega_1 \\ \hline \phantom{\bigg|}\widehat G / \widehat K\phantom{\bigg|} & 2(\alpha'_1 + \alpha'_2 + \alpha'_3) & \omega'_1 \\ \hline \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{|c|c|c|} \hline \phantom{\Big|} & \mbox{Norm. spherical roots} & \mbox{sph. weights}\\ \hline \hline \phantom{\Big|} G/K \phantom{\Big|} & 4\alpha_1 + 2 \alpha_2 & \omega_1 \\ \hline \phantom{\bigg|}\widehat G / \widehat K\phantom{\bigg|} & 2(\alpha'_1 + \alpha'_2 + \alpha'_3) & \omega'_1 \\ \hline \end{array} \end{align*} $$
 $$ \begin{align*}\begin{array}{|ccccc|} \hline \phantom{\Big|} \hat \varphi & : & a\omega_1 & \longmapsto & a\omega_1' \\ \hline \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{|ccccc|} \hline \phantom{\Big|} \hat \varphi & : & a\omega_1 & \longmapsto & a\omega_1' \\ \hline \end{array} \end{align*} $$
Proposition 5.8 Conjecture 5.1 holds true if
![]() $(G,K)$
is one of the spherical pairs Sph.A12 and Sph.A16 of Table 3.
$(G,K)$
is one of the spherical pairs Sph.A12 and Sph.A16 of Table 3.
Proof By restricting the action from
![]() $\widehat G$
to G, every spherical module for the pair
$\widehat G$
to G, every spherical module for the pair
![]() $(\widehat G, \widehat K)$
remains irreducible and yields a spherical module for the pair
$(\widehat G, \widehat K)$
remains irreducible and yields a spherical module for the pair
![]() $(G, K)$
. This gives a canonical bijection between the two: the restriction of every irreducible
$(G, K)$
. This gives a canonical bijection between the two: the restriction of every irreducible
![]() $\widehat G$
-module containing a nontrivial
$\widehat G$
-module containing a nontrivial
![]() $\widehat K$
-invariant subspace is irreducible as a G-module as well, and it is obviously K-spherical.
$\widehat K$
-invariant subspace is irreducible as a G-module as well, and it is obviously K-spherical.
In particular, the decomposition of the product of two spherical functions of
![]() $G/K$
immediately reduces to the decomposition of the product of the corresponding spherical functions of
$G/K$
immediately reduces to the decomposition of the product of the corresponding spherical functions of
![]() $\widehat G/\widehat K$
.
$\widehat G/\widehat K$
.
By Stanley’s Pieri rule for Jack symmetric functions, we know that Conjecture 3.2 holds true for the symmetric pair
![]() $(\widehat G,\widehat K)$
. On the other hand,
$(\widehat G,\widehat K)$
. On the other hand,
![]() $\hat \varphi $
induces an isomorphism of root data
$\hat \varphi $
induces an isomorphism of root data
 $\mathcal R_{G/K} \simeq \mathcal R_{\widehat G/\widehat K}$
. Thus, Conjecture 5.1 holds true for
$\mathcal R_{G/K} \simeq \mathcal R_{\widehat G/\widehat K}$
. Thus, Conjecture 5.1 holds true for
![]() $(G,K)$
as well.
$(G,K)$
as well.
5.2 Decomposable cases
We now consider the cases Sph.A6, Sph.A8, Sph.A10, Sph.A13, and Sph.A14 of Table 3: we define the subgroup
![]() $H \subset G$
, the overgroup
$H \subset G$
, the overgroup
![]() $\widehat G \supset G$
, and the symmetric subgroup
$\widehat G \supset G$
, and the symmetric subgroup
![]() $\widehat K \subset \widehat G$
with the required properties. Notice that H will always contain the connected center of
$\widehat K \subset \widehat G$
with the required properties. Notice that H will always contain the connected center of
![]() $\mathrm N_G(K)$
. As already mentioned, for the given inclusions among groups and their related properties, one can see [Reference Liebeck, Saxl and Seitz24, Reference Onishchik29] and also [Reference Gorbatsevich, Onishchik and Onishchik15, Sections 4.5 and 4.6].
$\mathrm N_G(K)$
. As already mentioned, for the given inclusions among groups and their related properties, one can see [Reference Liebeck, Saxl and Seitz24, Reference Onishchik29] and also [Reference Gorbatsevich, Onishchik and Onishchik15, Sections 4.5 and 4.6].
We also provide an explicit description of the maps
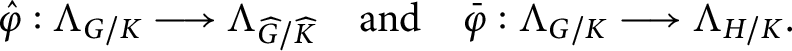 $$ \begin{align*}\hat \varphi: \Lambda_{G/K} \longrightarrow \Lambda_{\widehat G/\widehat K} \quad\mbox{and}\quad \bar \varphi: \Lambda_{G/K} \longrightarrow \Lambda_{H/K}. \end{align*} $$
$$ \begin{align*}\hat \varphi: \Lambda_{G/K} \longrightarrow \Lambda_{\widehat G/\widehat K} \quad\mbox{and}\quad \bar \varphi: \Lambda_{G/K} \longrightarrow \Lambda_{H/K}. \end{align*} $$
Proposition 5.6 will be an immediate consequence of these descriptions.
-
(Sph.A6)
 $G / K = \operatorname {\mathrm {SL}}(n) / \operatorname {\mathrm {SL}}(n-1)$
$G / K = \operatorname {\mathrm {SL}}(n) / \operatorname {\mathrm {SL}}(n-1)$
 $$ \begin{align*}\widehat G / \widehat K = \operatorname{\mathrm{SO}}(2n) / \operatorname{\mathrm{SO}}(2n-1),\end{align*} $$
$$ \begin{align*}\widehat G / \widehat K = \operatorname{\mathrm{SO}}(2n) / \operatorname{\mathrm{SO}}(2n-1),\end{align*} $$
 $$ \begin{align*}H / K = \operatorname{\mathrm{GL}}(n-1) / \operatorname{\mathrm{SL}}(n-1).\end{align*} $$
$$ \begin{align*}H / K = \operatorname{\mathrm{GL}}(n-1) / \operatorname{\mathrm{SL}}(n-1).\end{align*} $$
 $$ \begin{align*}\begin{array}{|c|c|c|} \hline \phantom{\Big|} & \text{Normalized spherical roots} & \text{Fund. sph. weights}\\ \hline \hline \phantom{\Big|} G/K \phantom{\Big|} & \alpha_1 + \cdots + \alpha_{n-1} & \omega_1, \ \omega_{n-1} \\ \hline \phantom{\bigg|}\widehat G / \widehat K\phantom{\bigg|} & 2(\alpha'_1 + \cdots + \alpha'_{n-2}) + \alpha'_{n-1} + \alpha'_n & \omega'_1 \\ \hline \phantom{\Big|}H/K \phantom{\Big|} & \text{ none } & \pm\omega''_{n-1}\\ \hline \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{|c|c|c|} \hline \phantom{\Big|} & \text{Normalized spherical roots} & \text{Fund. sph. weights}\\ \hline \hline \phantom{\Big|} G/K \phantom{\Big|} & \alpha_1 + \cdots + \alpha_{n-1} & \omega_1, \ \omega_{n-1} \\ \hline \phantom{\bigg|}\widehat G / \widehat K\phantom{\bigg|} & 2(\alpha'_1 + \cdots + \alpha'_{n-2}) + \alpha'_{n-1} + \alpha'_n & \omega'_1 \\ \hline \phantom{\Big|}H/K \phantom{\Big|} & \text{ none } & \pm\omega''_{n-1}\\ \hline \end{array} \end{align*} $$
 $$ \begin{align*}\begin{array}{|ccccl|} \hline \phantom{\Big|} \hat \varphi & : & a \omega_1 + b\omega_{n-1} & \longmapsto & (a+b)\omega'_1 \\ \hline \phantom{\Big|} \bar \varphi & : & a \omega_1 + b\omega_{n-1} & \longmapsto & (b-a) \omega''_{n-1} \\ \hline \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{|ccccl|} \hline \phantom{\Big|} \hat \varphi & : & a \omega_1 + b\omega_{n-1} & \longmapsto & (a+b)\omega'_1 \\ \hline \phantom{\Big|} \bar \varphi & : & a \omega_1 + b\omega_{n-1} & \longmapsto & (b-a) \omega''_{n-1} \\ \hline \end{array} \end{align*} $$
-
(Sph.A8)
 $G / K = \operatorname {\mathrm {SL}}(2n+1) / \operatorname {\mathrm {Sp}}(2n)$
$G / K = \operatorname {\mathrm {SL}}(2n+1) / \operatorname {\mathrm {Sp}}(2n)$
 $$ \begin{align*}\widehat G / \widehat K = \operatorname{\mathrm{SL}}(2n+2) / \operatorname{\mathrm{Sp}}(2n+2),\end{align*} $$
$$ \begin{align*}\widehat G / \widehat K = \operatorname{\mathrm{SL}}(2n+2) / \operatorname{\mathrm{Sp}}(2n+2),\end{align*} $$
 $$ \begin{align*}H / K = \operatorname{\mathrm{GL}}(2n) / \operatorname{\mathrm{Sp}}(2n).\end{align*} $$
$$ \begin{align*}H / K = \operatorname{\mathrm{GL}}(2n) / \operatorname{\mathrm{Sp}}(2n).\end{align*} $$
 $$ \begin{align*}\begin{array}{|c|c|c|} \hline \phantom{\Big|} & \text{Normalized spherical roots} & \text{Fund. spherical weights}\\ \hline \hline \phantom{\Big|} G/K \phantom{\Big|} & \alpha_i + \alpha_{i+1}\ (i=1,\ldots,2n-1) & \omega_i\ (i=1,\ldots,2n) \\ \hline \phantom{\bigg|}\widehat G / \widehat K\phantom{\bigg|} & \alpha'_{2i-1} + 2\alpha'_{2i} + \alpha'_{2i+1}\ (i=1,\ldots,n) & \omega'_{2i}\ (i=1,\ldots, n) \\ \hline \phantom{\Big|}H/K \phantom{\Big|} & \alpha''_{2i-1} + 2\alpha''_{2i} + \alpha''_{2i+1}\ (i=1,\ldots, n-1) & \omega''_{2i}\ (i=1,\ldots,n-1),\ \pm\omega''_{2n} \\ \hline \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{|c|c|c|} \hline \phantom{\Big|} & \text{Normalized spherical roots} & \text{Fund. spherical weights}\\ \hline \hline \phantom{\Big|} G/K \phantom{\Big|} & \alpha_i + \alpha_{i+1}\ (i=1,\ldots,2n-1) & \omega_i\ (i=1,\ldots,2n) \\ \hline \phantom{\bigg|}\widehat G / \widehat K\phantom{\bigg|} & \alpha'_{2i-1} + 2\alpha'_{2i} + \alpha'_{2i+1}\ (i=1,\ldots,n) & \omega'_{2i}\ (i=1,\ldots, n) \\ \hline \phantom{\Big|}H/K \phantom{\Big|} & \alpha''_{2i-1} + 2\alpha''_{2i} + \alpha''_{2i+1}\ (i=1,\ldots, n-1) & \omega''_{2i}\ (i=1,\ldots,n-1),\ \pm\omega''_{2n} \\ \hline \end{array} \end{align*} $$
 $$ \begin{align*}\begin{array}{|ccccl|} \hline \phantom{\Big|}\hat \varphi & : & \sum_{i=1}^{2n} a_i \omega_i & \longmapsto & \sum_{i=1}^n (a_{2i-1} + a_{2i}) \omega'_{2i} \\ \hline \phantom{\Big|}\bar \varphi & : & \sum_{i=1}^{2n} a_i \omega_i & \longmapsto & \sum_{i=1}^{n-1} (a_{2i}+a_{2i+1}) \omega''_{2i} + (a_{2n} - \sum_{i=1}^n a_{2i-1}) \omega''_{2n} \\ \hline \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{|ccccl|} \hline \phantom{\Big|}\hat \varphi & : & \sum_{i=1}^{2n} a_i \omega_i & \longmapsto & \sum_{i=1}^n (a_{2i-1} + a_{2i}) \omega'_{2i} \\ \hline \phantom{\Big|}\bar \varphi & : & \sum_{i=1}^{2n} a_i \omega_i & \longmapsto & \sum_{i=1}^{n-1} (a_{2i}+a_{2i+1}) \omega''_{2i} + (a_{2n} - \sum_{i=1}^n a_{2i-1}) \omega''_{2n} \\ \hline \end{array} \end{align*} $$
-
(Sph.A10)
 $G / K = \operatorname {\mathrm {Sp}}(2n) / [\operatorname {\mathrm {GL}}(1) \times \operatorname {\mathrm {Sp}}(2n-2)]$
$G / K = \operatorname {\mathrm {Sp}}(2n) / [\operatorname {\mathrm {GL}}(1) \times \operatorname {\mathrm {Sp}}(2n-2)]$
 $$ \begin{align*}\widehat G / \widehat K = \operatorname{\mathrm{SL}}(2n) / \operatorname{\mathrm{GL}}(2n-1),\end{align*} $$
$$ \begin{align*}\widehat G / \widehat K = \operatorname{\mathrm{SL}}(2n) / \operatorname{\mathrm{GL}}(2n-1),\end{align*} $$
 $$ \begin{align*}H / K = \operatorname{\mathrm{Sp}}(2) / \operatorname{\mathrm{GL}}(1).\end{align*} $$
$$ \begin{align*}H / K = \operatorname{\mathrm{Sp}}(2) / \operatorname{\mathrm{GL}}(1).\end{align*} $$
 $$ \begin{align*}\begin{array}{|c|c|c|} \hline \phantom{\Big|} & \text{Normalized spherical roots} & \text{Fund. sph. weights}\\ \hline \hline \phantom{\Big|}G/K\phantom{\Big|} & \alpha_1, \ \alpha_1 + 2(\alpha_2 + \cdots + \alpha_{n-1}) + \alpha_n & 2\omega_1, \ \omega_2 \\ \hline \phantom{\bigg|}\widehat G / \widehat K\phantom{\bigg|} & \alpha'_1 + \cdots + \alpha'_{2n-1} & \omega'_1 + \omega'_{2n-1} \\ \hline \phantom{\Big|}H/K \phantom{\Big|} & \alpha''_1 & 2\omega''_1\\ \hline \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{|c|c|c|} \hline \phantom{\Big|} & \text{Normalized spherical roots} & \text{Fund. sph. weights}\\ \hline \hline \phantom{\Big|}G/K\phantom{\Big|} & \alpha_1, \ \alpha_1 + 2(\alpha_2 + \cdots + \alpha_{n-1}) + \alpha_n & 2\omega_1, \ \omega_2 \\ \hline \phantom{\bigg|}\widehat G / \widehat K\phantom{\bigg|} & \alpha'_1 + \cdots + \alpha'_{2n-1} & \omega'_1 + \omega'_{2n-1} \\ \hline \phantom{\Big|}H/K \phantom{\Big|} & \alpha''_1 & 2\omega''_1\\ \hline \end{array} \end{align*} $$
 $$ \begin{align*}\begin{array}{|ccccl|} \hline \phantom{\Big|} \hat \varphi & : & 2a \omega_1+ b \omega_2 & \longmapsto & (a+b) (\omega'_1 + \omega'_{2n-1}) \\ \hline \phantom{\Big|} \bar \varphi & : & 2a \omega_1 + b \omega_2 &\longmapsto & 2a \omega''_1 \\ \hline \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{|ccccl|} \hline \phantom{\Big|} \hat \varphi & : & 2a \omega_1+ b \omega_2 & \longmapsto & (a+b) (\omega'_1 + \omega'_{2n-1}) \\ \hline \phantom{\Big|} \bar \varphi & : & 2a \omega_1 + b \omega_2 &\longmapsto & 2a \omega''_1 \\ \hline \end{array} \end{align*} $$
-
(Sph.A13)
 $G / K = \operatorname {\mathrm {Spin}}(9) / \operatorname {\mathrm {Spin}}(7)$
$G / K = \operatorname {\mathrm {Spin}}(9) / \operatorname {\mathrm {Spin}}(7)$
 $$ \begin{align*}\widehat G / \widehat K = \operatorname{\mathrm{SO}}(16) / \operatorname{\mathrm{SO}}(15),\end{align*} $$
$$ \begin{align*}\widehat G / \widehat K = \operatorname{\mathrm{SO}}(16) / \operatorname{\mathrm{SO}}(15),\end{align*} $$
 $$ \begin{align*}H/K = \operatorname{\mathrm{Spin}}(8) / \operatorname{\mathrm{Spin}}(7).\end{align*} $$
$$ \begin{align*}H/K = \operatorname{\mathrm{Spin}}(8) / \operatorname{\mathrm{Spin}}(7).\end{align*} $$
 $$ \begin{align*}\begin{array}{|c|c|c|} \hline \phantom{\Big|} & \text{Normalized spherical roots} & \text{Fund. sph. weights}\\ \hline \hline \phantom{\Big|}G/K \phantom{\Big|} & \alpha_1+\alpha_2+\alpha_3+\alpha_4, \ \alpha_2 + 2\alpha_3 + 3\alpha_4 & \omega_1, \ \omega_4 \\ \hline \phantom{\bigg|}\widehat G / \widehat K\phantom{\bigg|} & 2(\alpha'_1 + \cdots + \alpha'_6) + \alpha'_7+\alpha'_8 & \omega'_1 \\ \hline \phantom{\Big|} H/K \phantom{\Big|} & \alpha''_1+2\alpha''_2+\alpha''_3+2\alpha''_4 & \omega''_4\\ \hline \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{|c|c|c|} \hline \phantom{\Big|} & \text{Normalized spherical roots} & \text{Fund. sph. weights}\\ \hline \hline \phantom{\Big|}G/K \phantom{\Big|} & \alpha_1+\alpha_2+\alpha_3+\alpha_4, \ \alpha_2 + 2\alpha_3 + 3\alpha_4 & \omega_1, \ \omega_4 \\ \hline \phantom{\bigg|}\widehat G / \widehat K\phantom{\bigg|} & 2(\alpha'_1 + \cdots + \alpha'_6) + \alpha'_7+\alpha'_8 & \omega'_1 \\ \hline \phantom{\Big|} H/K \phantom{\Big|} & \alpha''_1+2\alpha''_2+\alpha''_3+2\alpha''_4 & \omega''_4\\ \hline \end{array} \end{align*} $$
 $$ \begin{align*}\begin{array}{|ccccl|} \hline \phantom{\Big|} \hat \varphi & : & a \omega_1 + b \omega_4 & \longrightarrow & (2a+b) \omega'_1 \\ \hline \phantom{\Big|} \bar \varphi & : & a \omega_1 + b \omega_4 & \longmapsto & b \omega''_4 \\ \hline \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{|ccccl|} \hline \phantom{\Big|} \hat \varphi & : & a \omega_1 + b \omega_4 & \longrightarrow & (2a+b) \omega'_1 \\ \hline \phantom{\Big|} \bar \varphi & : & a \omega_1 + b \omega_4 & \longmapsto & b \omega''_4 \\ \hline \end{array} \end{align*} $$
-
(Sph.A14)
 $G / K = \operatorname {\mathrm {Spin}}(8) / \mathsf G_2$
(where the two copies of
$G / K = \operatorname {\mathrm {Spin}}(8) / \mathsf G_2$
(where the two copies of $$ \begin{align*}\widehat G / \widehat K = \operatorname{\mathrm{Spin}}(8)/\operatorname{\mathrm{Spin}}(7) \times \operatorname{\mathrm{Spin}}(8)/\operatorname{\mathrm{Spin}}(7)\end{align*} $$
$$ \begin{align*}\widehat G / \widehat K = \operatorname{\mathrm{Spin}}(8)/\operatorname{\mathrm{Spin}}(7) \times \operatorname{\mathrm{Spin}}(8)/\operatorname{\mathrm{Spin}}(7)\end{align*} $$
 $\operatorname {\mathrm {Spin}}(7)$
are not conjugated in
$\operatorname {\mathrm {Spin}}(7)$
are not conjugated in
 $\operatorname {\mathrm {Spin}}(8)$
),
$\operatorname {\mathrm {Spin}}(8)$
),  $$ \begin{align*}H/K = \operatorname{\mathrm{Spin}}(7)/ \mathsf G_2.\end{align*} $$
$$ \begin{align*}H/K = \operatorname{\mathrm{Spin}}(7)/ \mathsf G_2.\end{align*} $$
 $$ \begin{align*}\begin{array}{|c|c|c|} \hline \phantom{\Big|} & \text{Normalized spherical roots} & \text{Fund. sph. weights}\\ \hline \hline \phantom{\Big|}G/K \phantom{\Big|} & \alpha_1+\alpha_2+\alpha_3, \ \alpha_1+\alpha_2+\alpha_4, \ \alpha_2 + \alpha_3 + \alpha_4 & \omega_1, \ \omega_3, \ \omega_4 \\ \hline \phantom{\bigg|}\widehat G / \widehat K\phantom{\bigg|} & 2\alpha'_1 + 2\alpha'_2 + \alpha'_3 + \alpha'_4, \ \alpha''_1 + 2\alpha''_2+ 2\alpha''_3 + \alpha''_4 & \omega'_1, \ \omega''_3 \\ \hline \phantom{\Big|} H/K \phantom{\Big|} & \alpha'''_1+2\alpha'''_2+3\alpha'''_3 & \omega'''_3\\ \hline \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{|c|c|c|} \hline \phantom{\Big|} & \text{Normalized spherical roots} & \text{Fund. sph. weights}\\ \hline \hline \phantom{\Big|}G/K \phantom{\Big|} & \alpha_1+\alpha_2+\alpha_3, \ \alpha_1+\alpha_2+\alpha_4, \ \alpha_2 + \alpha_3 + \alpha_4 & \omega_1, \ \omega_3, \ \omega_4 \\ \hline \phantom{\bigg|}\widehat G / \widehat K\phantom{\bigg|} & 2\alpha'_1 + 2\alpha'_2 + \alpha'_3 + \alpha'_4, \ \alpha''_1 + 2\alpha''_2+ 2\alpha''_3 + \alpha''_4 & \omega'_1, \ \omega''_3 \\ \hline \phantom{\Big|} H/K \phantom{\Big|} & \alpha'''_1+2\alpha'''_2+3\alpha'''_3 & \omega'''_3\\ \hline \end{array} \end{align*} $$
 $$ \begin{align*}\begin{array}{|ccccl|} \hline \phantom{\Big|} \hat \varphi & : & a \omega_1 + b \omega_3 + c \omega_4 & \longmapsto & (a+c)\omega'_1 + (b+c)\omega''_3 \\ \hline \phantom{\Big|} \bar \varphi & : & a \omega_1 + b \omega_3 + c \omega_4 & \longmapsto & (a+b)\omega'''_3 \\ \hline \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{|ccccl|} \hline \phantom{\Big|} \hat \varphi & : & a \omega_1 + b \omega_3 + c \omega_4 & \longmapsto & (a+c)\omega'_1 + (b+c)\omega''_3 \\ \hline \phantom{\Big|} \bar \varphi & : & a \omega_1 + b \omega_3 + c \omega_4 & \longmapsto & (a+b)\omega'''_3 \\ \hline \end{array} \end{align*} $$
Given
 $\lambda \in \Lambda _{G/K}^+$
, recall our notations
$\lambda \in \Lambda _{G/K}^+$
, recall our notations
 $\hat \lambda =\hat \varphi (\lambda )$
and
$\hat \lambda =\hat \varphi (\lambda )$
and
![]() $\bar \lambda =\bar \varphi (\lambda )$
. If
$\bar \lambda =\bar \varphi (\lambda )$
. If
 $\mu \in \Lambda ^+_{G/K}$
, we write
$\mu \in \Lambda ^+_{G/K}$
, we write
![]() $\mu \sim \lambda $
if
$\mu \sim \lambda $
if
 $\hat \mu =\hat \lambda $
. Identifying
$\hat \mu =\hat \lambda $
. Identifying
![]() $\mathbb C[\widehat G/ \widehat K] \simeq \mathbb C[G/K]$
, by definition, we have then
$\mathbb C[\widehat G/ \widehat K] \simeq \mathbb C[G/K]$
, by definition, we have then
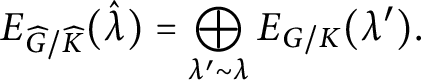 $$ \begin{align*}E_{\widehat G/\widehat K}(\hat \lambda) = \bigoplus_{\lambda' \sim \lambda} E_{G/K}(\lambda'). \end{align*} $$
$$ \begin{align*}E_{\widehat G/\widehat K}(\hat \lambda) = \bigoplus_{\lambda' \sim \lambda} E_{G/K}(\lambda'). \end{align*} $$
Theorem 5.9 Let
![]() $(G,K)$
be one of the following spherical pairs of Table 3:
$(G,K)$
be one of the following spherical pairs of Table 3:
Then, for all
 $\lambda ,\mu ,\nu \in \Lambda ^+_{G/K}$
, we have
$\lambda ,\mu ,\nu \in \Lambda ^+_{G/K}$
, we have
 $$ \begin{align*}\begin{array}{ccc} E_{G/K}(\nu) \subset E_{G/K}(\lambda) \cdot E_{G/K}(\mu) & \Longleftrightarrow & \left\{ \begin{array}{c} E_{\widehat G/\widehat K}\big(\hat\nu\big) \subset E_{\widehat G/\widehat K}\big(\hat\lambda\big) \cdot E_{\widehat G/\widehat K}\big(\hat\mu\big), \phantom{\Big|} \\ E_{H/K}(\bar \nu) \subset E_{H/K}(\bar \lambda) \cdot E_{H/K}(\bar\mu). \end{array}\right. \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ccc} E_{G/K}(\nu) \subset E_{G/K}(\lambda) \cdot E_{G/K}(\mu) & \Longleftrightarrow & \left\{ \begin{array}{c} E_{\widehat G/\widehat K}\big(\hat\nu\big) \subset E_{\widehat G/\widehat K}\big(\hat\lambda\big) \cdot E_{\widehat G/\widehat K}\big(\hat\mu\big), \phantom{\Big|} \\ E_{H/K}(\bar \nu) \subset E_{H/K}(\bar \lambda) \cdot E_{H/K}(\bar\mu). \end{array}\right. \end{array} \end{align*} $$
Proof Suppose that
![]() $E_{G/K}(\nu ) \subset E_{G/K}(\lambda ) \cdot E_{G/K}(\mu )$
. Looking at the associated
$E_{G/K}(\nu ) \subset E_{G/K}(\lambda ) \cdot E_{G/K}(\mu )$
. Looking at the associated
![]() $\widehat G$
-modules generated in the coordinate ring
$\widehat G$
-modules generated in the coordinate ring
![]() $\mathbb C[\widehat G/\widehat K]\ \simeq \mathbb C[G/K]$
, it follows that
$\mathbb C[\widehat G/\widehat K]\ \simeq \mathbb C[G/K]$
, it follows that
 $E_{\widehat G/\widehat K}\big (\hat \nu \big ) \subset E_{\widehat G/\widehat K}\big (\hat \lambda \big ) \cdot E_{\widehat G/\widehat K}\big (\hat \mu \big )$
as well. Similarly, looking at the images in
$E_{\widehat G/\widehat K}\big (\hat \nu \big ) \subset E_{\widehat G/\widehat K}\big (\hat \lambda \big ) \cdot E_{\widehat G/\widehat K}\big (\hat \mu \big )$
as well. Similarly, looking at the images in
![]() $\mathbb C[H/K]$
, we see that
$\mathbb C[H/K]$
, we see that
 $E_{H/K}(\bar \nu ) \subset E_{H/K}(\bar \lambda ) \cdot E_{H/K}(\bar \mu )$
.
$E_{H/K}(\bar \nu ) \subset E_{H/K}(\bar \lambda ) \cdot E_{H/K}(\bar \mu )$
.
Suppose conversely that both the inclusions
 $E_{\widehat G/\widehat K}(\hat \nu ) \subset E_{\widehat G/\widehat K}(\hat \lambda ) \cdot E_{\widehat G/\widehat K}(\hat \mu )$
and
$E_{\widehat G/\widehat K}(\hat \nu ) \subset E_{\widehat G/\widehat K}(\hat \lambda ) \cdot E_{\widehat G/\widehat K}(\hat \mu )$
and
 $E_{H/K}(\bar \nu ) \subset E_{H/K}(\bar \lambda ) \cdot E_{H/K}(\bar \mu )$
hold. By the first inclusion, the restriction of functions from
$E_{H/K}(\bar \nu ) \subset E_{H/K}(\bar \lambda ) \cdot E_{H/K}(\bar \mu )$
hold. By the first inclusion, the restriction of functions from
![]() $G/K$
to
$G/K$
to
![]() $H/K$
induces a commutative diagram as follows:
$H/K$
induces a commutative diagram as follows:
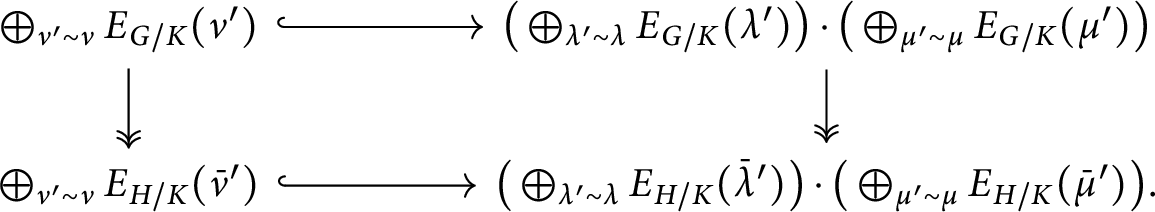
By the second inclusion, there are
![]() $\lambda ' \sim \lambda $
,
$\lambda ' \sim \lambda $
,
![]() $\mu '\sim \mu $
, and
$\mu '\sim \mu $
, and
![]() $\nu ' \sim \nu $
such that
$\nu ' \sim \nu $
such that
![]() $\bar \lambda ' = \bar \lambda $
,
$\bar \lambda ' = \bar \lambda $
,
![]() $\bar \mu ' = \bar \mu $
,
$\bar \mu ' = \bar \mu $
,
![]() $\bar \nu ' = \bar \nu $
, and
$\bar \nu ' = \bar \nu $
, and
![]() $E_{G/K}(\nu ') \subset E_{G/K}(\lambda ') \cdot E_{G/K}(\mu ')$
. On the other hand, by Corollary 5.7, the restriction of
$E_{G/K}(\nu ') \subset E_{G/K}(\lambda ') \cdot E_{G/K}(\mu ')$
. On the other hand, by Corollary 5.7, the restriction of
![]() $\bar \varphi $
to the fibers of
$\bar \varphi $
to the fibers of
![]() $\hat \varphi $
is injective. Thus,
$\hat \varphi $
is injective. Thus,
![]() $\lambda ' = \lambda $
,
$\lambda ' = \lambda $
,
![]() $\mu ' = \mu $
, and
$\mu ' = \mu $
, and
![]() $\nu ' = \nu $
, and we get
$\nu ' = \nu $
, and we get
![]() $E_{G/K}(\nu ) \subset E_{G/K}(\lambda ) \cdot E_{G/K}(\mu )$
.
$E_{G/K}(\nu ) \subset E_{G/K}(\lambda ) \cdot E_{G/K}(\mu )$
.
Corollary 5.10 Let
![]() $(G,K)$
be one of the following spherical pairs of Table 3:
$(G,K)$
be one of the following spherical pairs of Table 3:
If Conjecture 3.2 holds true, then Conjecture 5.1 holds true for
![]() $(G,K)$
. In particular, Conjecture 5.1 holds true in the cases
$(G,K)$
. In particular, Conjecture 5.1 holds true in the cases
Proof Set
![]() $X = G/K$
,
$X = G/K$
,
![]() $Y = \widehat G/\widehat K$
, and
$Y = \widehat G/\widehat K$
, and
![]() $Z = H/K$
. Then, by Proposition 5.6, we have an isogeny of reductive groups
$Z = H/K$
. Then, by Proposition 5.6, we have an isogeny of reductive groups
Notice that a
![]() $G_X$
-module is irreducible if and only if it is irreducible as a
$G_X$
-module is irreducible if and only if it is irreducible as a
![]() $(G_Y \times G_Z)$
-module under the previous map.
$(G_Y \times G_Z)$
-module under the previous map.
If
![]() $\lambda \in \Lambda _X^+$
, regarding
$\lambda \in \Lambda _X^+$
, regarding
![]() $V_X(\lambda )$
as a
$V_X(\lambda )$
as a
![]() $(G_Y \times G_Z)$
-module, by the definition of
$(G_Y \times G_Z)$
-module, by the definition of
![]() $\hat \lambda $
and
$\hat \lambda $
and
![]() $\bar \lambda $
, we see that
$\bar \lambda $
, we see that
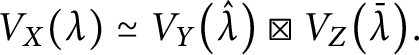 $$ \begin{align*}V_X(\lambda) \simeq V_Y \big(\hat \lambda\big) \boxtimes V_Z\big(\bar \lambda\big). \end{align*} $$
$$ \begin{align*}V_X(\lambda) \simeq V_Y \big(\hat \lambda\big) \boxtimes V_Z\big(\bar \lambda\big). \end{align*} $$
In particular, given
![]() $\lambda , \mu , \nu \in \Lambda ^+_X$
, we have
$\lambda , \mu , \nu \in \Lambda ^+_X$
, we have
 $$ \begin{align*}\begin{array}{ccc} V_X(\nu) \subset V_X(\lambda) \otimes V_X(\mu) \Longleftrightarrow \left\{\!\! \begin{array}{c} V_Y\big(\hat\nu\big) \subset V_Y \big(\hat\lambda\big) \otimes V_Y\big(\hat\mu\big), \phantom{\Big|} \\ V_Z(\bar \nu) \subset V_Z(\bar \lambda) \otimes V_Z(\bar\mu). \end{array}\right. \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ccc} V_X(\nu) \subset V_X(\lambda) \otimes V_X(\mu) \Longleftrightarrow \left\{\!\! \begin{array}{c} V_Y\big(\hat\nu\big) \subset V_Y \big(\hat\lambda\big) \otimes V_Y\big(\hat\mu\big), \phantom{\Big|} \\ V_Z(\bar \nu) \subset V_Z(\bar \lambda) \otimes V_Z(\bar\mu). \end{array}\right. \end{array} \end{align*} $$
Thus, by Theorem 5.9, we see that Conjecture 5.1 holds for X if and only if it holds both for Y and Z.
If both Y and Z are direct products of symmetric varieties with restricted root system of type
![]() $\mathsf A_1$
, then by Stanley’s Pieri rule for Jack symmetric functions, we see that Conjecture 3.2 holds true both for Y and Z. Thus, in this case, the claim follows for X as well.
$\mathsf A_1$
, then by Stanley’s Pieri rule for Jack symmetric functions, we see that Conjecture 3.2 holds true both for Y and Z. Thus, in this case, the claim follows for X as well.
Remark 5.11 There is another case which can be put in the framework outlined at the beginning of this subsection, even though G is not simple. In this case,
and
![]() $\Phi _{G/K}$
is of type
$\Phi _{G/K}$
is of type
![]() $\mathsf A_1 \times \sf A_1$
, and Conjecture 5.1 holds true thanks to the same arguments of Theorem 5.9 and Corollary 5.10. The corresponding symmetric varieties are
$\mathsf A_1 \times \sf A_1$
, and Conjecture 5.1 holds true thanks to the same arguments of Theorem 5.9 and Corollary 5.10. The corresponding symmetric varieties are
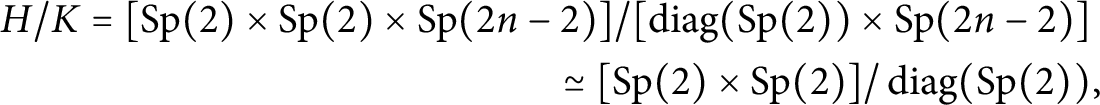 $$ \begin{align*} H/K = [\operatorname{\mathrm{Sp}}(2) \times \operatorname{\mathrm{Sp}}(2) \times \operatorname{\mathrm{Sp}}(2n-2)]/[\operatorname{\mathrm{diag}}(\operatorname{\mathrm{Sp}}(2)) \times \operatorname{\mathrm{Sp}}(2n-2)] & \\ \simeq [\operatorname{\mathrm{Sp}}(2) \times \operatorname{\mathrm{Sp}}(2) ]/\operatorname{\mathrm{diag}}(\operatorname{\mathrm{Sp}}(2))&, \end{align*} $$
$$ \begin{align*} H/K = [\operatorname{\mathrm{Sp}}(2) \times \operatorname{\mathrm{Sp}}(2) \times \operatorname{\mathrm{Sp}}(2n-2)]/[\operatorname{\mathrm{diag}}(\operatorname{\mathrm{Sp}}(2)) \times \operatorname{\mathrm{Sp}}(2n-2)] & \\ \simeq [\operatorname{\mathrm{Sp}}(2) \times \operatorname{\mathrm{Sp}}(2) ]/\operatorname{\mathrm{diag}}(\operatorname{\mathrm{Sp}}(2))&, \end{align*} $$
which have both restricted root system of type
![]() $\mathsf A_1$
. The associated spherical roots and spherical weights are described in the tables here below, together with the maps
$\mathsf A_1$
. The associated spherical roots and spherical weights are described in the tables here below, together with the maps
![]() $\hat \varphi $
and
$\hat \varphi $
and
![]() $\bar \varphi $
.
$\bar \varphi $
.
 $$ \begin{align*}\begin{array}{|c|c|c|} \hline \phantom{\Big|} & \text{Normalized spherical roots} & \text{Fund. spherical weights}\\ \hline \hline \phantom{\Big|} G/K & \alpha_0 + \alpha_1, \, \alpha_1 + 2(\alpha_2 + \cdots + \alpha_{n-1}) + \alpha_n & \omega_0+\omega_1, \ \omega_2 \\ \hline \phantom{\bigg|} \widehat G/\widehat K \phantom{\bigg|} & 2(\alpha'_1 + \cdots + \alpha'_{2n-2}) + \alpha'_{2n-1} + \alpha'_{2n} & \omega_1' \\ \hline \phantom{\Big|} H/K & \alpha_0'' + \alpha_1'' & \omega_0'' + \omega_1'' \\ \hline \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{|c|c|c|} \hline \phantom{\Big|} & \text{Normalized spherical roots} & \text{Fund. spherical weights}\\ \hline \hline \phantom{\Big|} G/K & \alpha_0 + \alpha_1, \, \alpha_1 + 2(\alpha_2 + \cdots + \alpha_{n-1}) + \alpha_n & \omega_0+\omega_1, \ \omega_2 \\ \hline \phantom{\bigg|} \widehat G/\widehat K \phantom{\bigg|} & 2(\alpha'_1 + \cdots + \alpha'_{2n-2}) + \alpha'_{2n-1} + \alpha'_{2n} & \omega_1' \\ \hline \phantom{\Big|} H/K & \alpha_0'' + \alpha_1'' & \omega_0'' + \omega_1'' \\ \hline \end{array} \end{align*} $$
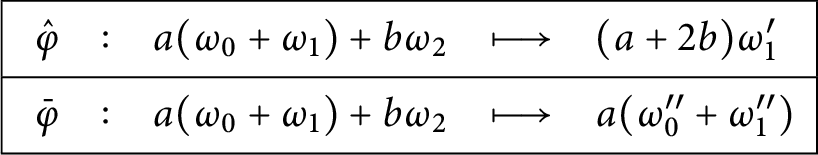 $$ \begin{align*}\begin{array}{|ccccl|} \hline \phantom{\Big|} \hat \varphi & : & a (\omega_0+\omega_1) + b\omega_2 & \longmapsto & (a+2b)\omega'_1 \\ \hline \phantom{\Big|} \bar \varphi & : & a (\omega_0+\omega_1) + b\omega_2 & \longmapsto & a (\omega_0''+\omega_1'') \\ \hline \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{|ccccl|} \hline \phantom{\Big|} \hat \varphi & : & a (\omega_0+\omega_1) + b\omega_2 & \longmapsto & (a+2b)\omega'_1 \\ \hline \phantom{\Big|} \bar \varphi & : & a (\omega_0+\omega_1) + b\omega_2 & \longmapsto & a (\omega_0''+\omega_1'') \\ \hline \end{array} \end{align*} $$
5.3 Other cases with restricted root system of type
 $\mathsf A$
$\mathsf A$
We now explain how the cases Sph.A7, Sph.A9, and Sph.A11 of Table 3 follow (almost immediately) from their companion cases Sph.A6, Sph.A8, and Sph.A10.
-
(Sph.A7)
 $G = \operatorname {\mathrm {SL}}(n), \ K = \operatorname {\mathrm {GL}}(n-1)$
. This case is immediately reduced to Sph.A6. Denote indeed
$G = \operatorname {\mathrm {SL}}(n), \ K = \operatorname {\mathrm {GL}}(n-1)$
. This case is immediately reduced to Sph.A6. Denote indeed
 $K' = \operatorname {\mathrm {SL}}(n-1)$
: then
$K' = \operatorname {\mathrm {SL}}(n-1)$
: then
 $K = \mathrm N_G(K')$
, and the spherical roots of
$K = \mathrm N_G(K')$
, and the spherical roots of
 $G/K$
are the same as those of
$G/K$
are the same as those of
 $G/K'$
. On the other hand,
$G/K'$
. On the other hand,
 $\Omega _{G/K} = \Lambda _{G/K'}$
, and
$\Omega _{G/K} = \Lambda _{G/K'}$
, and
 $V(\lambda )^{(K)} = V(\lambda )^{K'}$
for all
$V(\lambda )^{(K)} = V(\lambda )^{K'}$
for all
 $\lambda \in \Omega _{G/K}^+$
; therefore,
$\lambda \in \Omega _{G/K}^+$
; therefore,
 $\mathbb C[G]^{(K)} = \mathbb C[G]^{K'}$
.
$\mathbb C[G]^{(K)} = \mathbb C[G]^{K'}$
. -
(Sph.A9)
 $G = \operatorname {\mathrm {SL}}(2n+1), \ K = \operatorname {\mathrm {GL}}(1) \times \operatorname {\mathrm {Sp}}(2n)$
. This case is immediately reduced to Sph.A8. Consider indeed
$G = \operatorname {\mathrm {SL}}(2n+1), \ K = \operatorname {\mathrm {GL}}(1) \times \operatorname {\mathrm {Sp}}(2n)$
. This case is immediately reduced to Sph.A8. Consider indeed
 $K' = \operatorname {\mathrm {Sp}}(2n)$
: then
$K' = \operatorname {\mathrm {Sp}}(2n)$
: then
 $K = \mathrm N_G(K')$
, and the spherical roots of
$K = \mathrm N_G(K')$
, and the spherical roots of
 $G/K$
are the same as those of
$G/K$
are the same as those of
 $G/K'$
. Moreover, as in the previous case, we have
$G/K'$
. Moreover, as in the previous case, we have
 $\mathbb C[G]^{(K)} = \mathbb C[G]^{K'}$
.
$\mathbb C[G]^{(K)} = \mathbb C[G]^{K'}$
. -
(Sph.A11)
 $G = \operatorname {\mathrm {Sp}}(2n), \ K = \operatorname {\mathrm {Sp}}(2) \times \operatorname {\mathrm {Sp}}(2n-2)$
. This case is immediately reduced to Sph.A10. Set indeed
$G = \operatorname {\mathrm {Sp}}(2n), \ K = \operatorname {\mathrm {Sp}}(2) \times \operatorname {\mathrm {Sp}}(2n-2)$
. This case is immediately reduced to Sph.A10. Set indeed
 $K' = \operatorname {\mathrm {GL}}(1) \times \operatorname {\mathrm {Sp}}(2n-2)$
: then
$K' = \operatorname {\mathrm {GL}}(1) \times \operatorname {\mathrm {Sp}}(2n-2)$
: then
 $K' \subset K$
; thus, we have an inclusion
$K' \subset K$
; thus, we have an inclusion
 $\mathbb C[G]^K \subset \mathbb C[G]^{K'}$
. On the other hand, the unique spherical root of
$\mathbb C[G]^K \subset \mathbb C[G]^{K'}$
. On the other hand, the unique spherical root of
 $G/K$
is a spherical root of
$G/K$
is a spherical root of
 $G/K'$
as well, and if
$G/K'$
as well, and if
 $\lambda , \mu \in \Lambda _{G/K}$
, then
$\lambda , \mu \in \Lambda _{G/K}$
, then
 $\mu \leqslant _{G/K} \lambda $
if and only if
$\mu \leqslant _{G/K} \lambda $
if and only if
 $\mu \leqslant _{G/K'} \lambda $
.
$\mu \leqslant _{G/K'} \lambda $
.

As a consequence of the previous analysis, we get the following.
6 A conjectural rule in the case of spherical Levi subgroups
There is another case where we can apply the techniques of Section 5, and find two morphisms which decompose the root system of an affine spherical variety into those of two symmetric varieties. However, in this case, the root system generated by the spherical roots is of type
![]() $\mathsf B$
, and as far as we know, there is no rule (not even conjectural) to multiply spherical functions on a symmetric variety in this case.
$\mathsf B$
, and as far as we know, there is no rule (not even conjectural) to multiply spherical functions on a symmetric variety in this case.
6.1 The spherical pair
 $(\operatorname {\mathrm {SO}}(2p+1),\operatorname {\mathrm {GL}}(p))$
$(\operatorname {\mathrm {SO}}(2p+1),\operatorname {\mathrm {GL}}(p))$
Set
![]() $G = \operatorname {\mathrm {SO}}(2p+1)$
and
$G = \operatorname {\mathrm {SO}}(2p+1)$
and
![]() $K = \operatorname {\mathrm {GL}}(p)$
with
$K = \operatorname {\mathrm {GL}}(p)$
with
![]() $p\geqslant 3$
. Then, the homogeneous space
$p\geqslant 3$
. Then, the homogeneous space
![]() $G/K$
is spherical, and it is a model space for G (see [Reference Gelfand and Zelevinsky13, Reference Gelfand and Zelevinsky14, Reference Luna27]).
$G/K$
is spherical, and it is a model space for G (see [Reference Gelfand and Zelevinsky13, Reference Gelfand and Zelevinsky14, Reference Luna27]).
The spherical root system
![]() $\Phi _{G/K}$
is of type
$\Phi _{G/K}$
is of type
![]() $\mathsf B_{\lfloor p/2\rfloor } \times \mathsf B_{\lceil p/2\rceil }$
if
$\mathsf B_{\lfloor p/2\rfloor } \times \mathsf B_{\lceil p/2\rceil }$
if
![]() $p\geqslant 4$
, and of type
$p\geqslant 4$
, and of type
![]() $\mathsf A_1\times \mathsf B_2$
if
$\mathsf A_1\times \mathsf B_2$
if
![]() $p=3$
. In this case as well, it is possible to define reductive groups
$p=3$
. In this case as well, it is possible to define reductive groups
![]() $H \subset G \subset \widehat G$
and two symmetric varieties
$H \subset G \subset \widehat G$
and two symmetric varieties
![]() $H/K$
and
$H/K$
and
![]() $\widehat G/\widehat K$
endowed with equivariant morphisms
$\widehat G/\widehat K$
endowed with equivariant morphisms
which produce an isogeny of root data such as in Proposition 5.6. This will allow to extend Theorem 5.9 to this case as well, and to reduce the multiplication of the spherical functions on
![]() $G/K$
to the case of two symmetric varieties.
$G/K$
to the case of two symmetric varieties.
More precisely, define
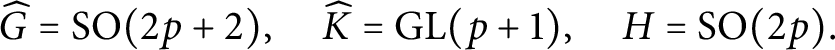 $$ \begin{align*}\widehat G = \operatorname{\mathrm{SO}}(2p+2), \quad \widehat K = \operatorname{\mathrm{GL}}(p+1), \quad H = \operatorname{\mathrm{SO}}(2p).\end{align*} $$
$$ \begin{align*}\widehat G = \operatorname{\mathrm{SO}}(2p+2), \quad \widehat K = \operatorname{\mathrm{GL}}(p+1), \quad H = \operatorname{\mathrm{SO}}(2p).\end{align*} $$
The root systems
![]() $\Phi _{\widehat G/\widehat K}$
and
$\Phi _{\widehat G/\widehat K}$
and
![]() $\Phi _{H/K}$
are of type
$\Phi _{H/K}$
are of type
![]() $\mathsf B$
, whereas the restricted root systems
$\mathsf B$
, whereas the restricted root systems
 $\widetilde \Phi _{\widehat G/\widehat K}$
and
$\widetilde \Phi _{\widehat G/\widehat K}$
and
 $\widetilde \Phi _{H/K}$
are either of type
$\widetilde \Phi _{H/K}$
are either of type
![]() $\mathsf B\mathsf C$
or of type
$\mathsf B\mathsf C$
or of type
![]() $\mathsf C$
, depending on the parity of p.
$\mathsf C$
, depending on the parity of p.
As in Section 5, the equivariant morphisms
![]() $H/K \hookrightarrow G/K \stackrel {\sim }{\to } \widehat G/\widehat K$
induce linear maps of the respective weight monoids
$H/K \hookrightarrow G/K \stackrel {\sim }{\to } \widehat G/\widehat K$
induce linear maps of the respective weight monoids
 $$ \begin{align*}\hat \varphi : \Lambda^+_{G/K} \longrightarrow \Lambda^+_{\widehat G/\widehat K} , \qquad \qquad \bar \varphi : \Lambda^+_{G/K} \longrightarrow \Lambda^+_{H/K}. \end{align*} $$
$$ \begin{align*}\hat \varphi : \Lambda^+_{G/K} \longrightarrow \Lambda^+_{\widehat G/\widehat K} , \qquad \qquad \bar \varphi : \Lambda^+_{G/K} \longrightarrow \Lambda^+_{H/K}. \end{align*} $$
For
 $\lambda \in \Lambda _{G/K}^+$
, we set
$\lambda \in \Lambda _{G/K}^+$
, we set
 $\hat \lambda = \hat \varphi (\lambda )$
and
$\hat \lambda = \hat \varphi (\lambda )$
and
![]() $\bar \lambda = \bar \varphi (\lambda )$
.
$\bar \lambda = \bar \varphi (\lambda )$
.
The spherical roots and the weight lattices, as well as the maps
![]() $\hat \varphi $
and
$\hat \varphi $
and
![]() $\bar \varphi $
, are described in the tables below. We separate the two cases p even and p odd.
$\bar \varphi $
, are described in the tables below. We separate the two cases p even and p odd.
(
![]() $p=2n$
even)
$p=2n$
even)
 $$ \begin{align*}\begin{array}{|c|c|c|} \hline \phantom{\Big|} & \text{Normalized spherical roots} & \text{Fund. sph. weights}\\ \hline \hline \phantom{\Big|}G/K \phantom{\Big|} & \begin{array}{l} \alpha_i+\alpha_{i+1} \ (i=1, \ldots, 2n-1),\ \alpha_{2n} \end{array} & \begin{array}{l}\omega_i\ (i=1, \ldots ,2n-1),\\ 2\omega_{2n} \end{array}\\ \hline \phantom{\Big|}\widehat G / \widehat K\phantom{\Big|} & \begin{array}{l} \alpha'_{2i-1} + 2\alpha'_{2i}+\alpha'_{2i+1}\ (i=1, \ldots, n-1) , \\ \alpha'_{2n-1} + \alpha'_{2n} + \alpha'_{2n+1} \end{array} & \begin{array}{l}\omega'_{2i}\ (i=1, \ldots ,n-1), \\ \omega'_{2n} + \omega'_{2n+1} \end{array}\\ \hline \phantom{\Big|}H/K\phantom{\Big|} & \begin{array}{l} \alpha''_{2i-1} + 2\alpha''_{2i}+\alpha''_{2i+1} \ (i=1, \ldots, n-1), \\ \alpha''_{2n} \end{array} & \begin{array}{l}\omega''_{2i}\ (i=1, \ldots ,n-1), \\ 2\omega''_{2n} \end{array}\\ \hline \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{|c|c|c|} \hline \phantom{\Big|} & \text{Normalized spherical roots} & \text{Fund. sph. weights}\\ \hline \hline \phantom{\Big|}G/K \phantom{\Big|} & \begin{array}{l} \alpha_i+\alpha_{i+1} \ (i=1, \ldots, 2n-1),\ \alpha_{2n} \end{array} & \begin{array}{l}\omega_i\ (i=1, \ldots ,2n-1),\\ 2\omega_{2n} \end{array}\\ \hline \phantom{\Big|}\widehat G / \widehat K\phantom{\Big|} & \begin{array}{l} \alpha'_{2i-1} + 2\alpha'_{2i}+\alpha'_{2i+1}\ (i=1, \ldots, n-1) , \\ \alpha'_{2n-1} + \alpha'_{2n} + \alpha'_{2n+1} \end{array} & \begin{array}{l}\omega'_{2i}\ (i=1, \ldots ,n-1), \\ \omega'_{2n} + \omega'_{2n+1} \end{array}\\ \hline \phantom{\Big|}H/K\phantom{\Big|} & \begin{array}{l} \alpha''_{2i-1} + 2\alpha''_{2i}+\alpha''_{2i+1} \ (i=1, \ldots, n-1), \\ \alpha''_{2n} \end{array} & \begin{array}{l}\omega''_{2i}\ (i=1, \ldots ,n-1), \\ 2\omega''_{2n} \end{array}\\ \hline \end{array} \end{align*} $$
 $$ \begin{align*}\begin{array}{|ccccl|} \hline \phantom{\Big|}\hat \varphi & : & \sum_{i=1}^{2n} a_i \omega_i & \longmapsto & \big(\sum_{i=1}^{n-1} (a_{2i-1} + a_{2i}) \omega'_{2i}\big) + (a_{2n-1}+\frac{a_{2n}}{2}) (\omega'_{2n} + \omega'_{2n+1})\\ \hline \phantom{\Big|}\bar \varphi & : & \sum_{i=1}^{2n} a_i \omega_i & \longmapsto & \big(\sum_{i=1}^{n-1} (a_{2i}+a_{2i+1}) \omega''_{2i}\big) + a_{2n} \omega''_{2n}\\ \hline \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{|ccccl|} \hline \phantom{\Big|}\hat \varphi & : & \sum_{i=1}^{2n} a_i \omega_i & \longmapsto & \big(\sum_{i=1}^{n-1} (a_{2i-1} + a_{2i}) \omega'_{2i}\big) + (a_{2n-1}+\frac{a_{2n}}{2}) (\omega'_{2n} + \omega'_{2n+1})\\ \hline \phantom{\Big|}\bar \varphi & : & \sum_{i=1}^{2n} a_i \omega_i & \longmapsto & \big(\sum_{i=1}^{n-1} (a_{2i}+a_{2i+1}) \omega''_{2i}\big) + a_{2n} \omega''_{2n}\\ \hline \end{array} \end{align*} $$
(
![]() $p=2n+1$
odd)
$p=2n+1$
odd)
 $$ \begin{align*}\begin{array}{|c|c|c|} \hline \phantom{\Big|} & \text{Normalized spherical roots} & \text{Fund. sph. weights}\\ \hline \hline \phantom{\Big|}G/K \phantom{\Big|} & \alpha_i+\alpha_{i+1} \ (i=1, \ldots, 2n),\ \alpha_{2n+1} & \begin{array}{l}\omega_i \ (i=1,\ldots ,2n), \\ 2\omega_{2n+1}\end{array} \\ \hline \phantom{\Big|}\widehat G / \widehat K\phantom{\Big|} & \begin{array}{l} \alpha'_{2i-1} + 2\alpha'_{2i}+\alpha'_{2i+1} \ (i=1, \ldots, n), \\ \alpha'_{2n+2} \end{array} & \begin{array}{l}\omega'_{2i} (i=1, \ldots, n), \\ 2\omega'_{2n+2}\end{array} \\ \hline \phantom{\Big|}H/K\phantom{\Big|} & \begin{array}{l} \alpha''_{2i-1} + 2\alpha''_{2i}+\alpha''_{2i+1} \ (i=1, \ldots, n-1), \\ \alpha''_{2n-1} + \alpha''_{2n} + \alpha''_{2n+1} \end{array} & \begin{array}{l}\omega''_{2i} (i=1, \ldots , n-1), \\ \omega''_{2n} + \omega''_{2n+1}\end{array} \\ \hline \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{|c|c|c|} \hline \phantom{\Big|} & \text{Normalized spherical roots} & \text{Fund. sph. weights}\\ \hline \hline \phantom{\Big|}G/K \phantom{\Big|} & \alpha_i+\alpha_{i+1} \ (i=1, \ldots, 2n),\ \alpha_{2n+1} & \begin{array}{l}\omega_i \ (i=1,\ldots ,2n), \\ 2\omega_{2n+1}\end{array} \\ \hline \phantom{\Big|}\widehat G / \widehat K\phantom{\Big|} & \begin{array}{l} \alpha'_{2i-1} + 2\alpha'_{2i}+\alpha'_{2i+1} \ (i=1, \ldots, n), \\ \alpha'_{2n+2} \end{array} & \begin{array}{l}\omega'_{2i} (i=1, \ldots, n), \\ 2\omega'_{2n+2}\end{array} \\ \hline \phantom{\Big|}H/K\phantom{\Big|} & \begin{array}{l} \alpha''_{2i-1} + 2\alpha''_{2i}+\alpha''_{2i+1} \ (i=1, \ldots, n-1), \\ \alpha''_{2n-1} + \alpha''_{2n} + \alpha''_{2n+1} \end{array} & \begin{array}{l}\omega''_{2i} (i=1, \ldots , n-1), \\ \omega''_{2n} + \omega''_{2n+1}\end{array} \\ \hline \end{array} \end{align*} $$
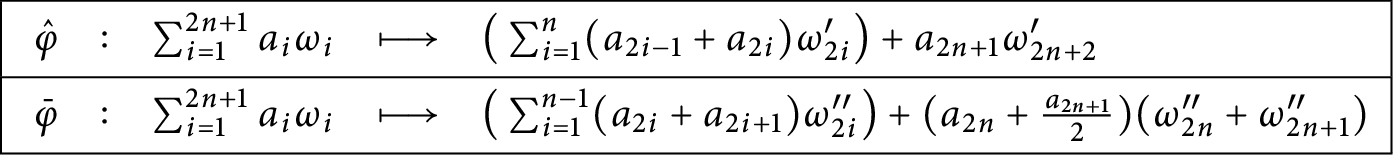 $$ \begin{align*}\begin{array}{|ccccl|} \hline \phantom{\Big|}\hat \varphi & : & \sum_{i=1}^{2n+1} a_i \omega_i & \longmapsto & \big(\sum_{i=1}^n (a_{2i-1} + a_{2i}) \omega'_{2i}\big) + a_{2n+1} \omega'_{2n+2}\\ \hline \phantom{\Big|}\bar \varphi & : & \sum_{i=1}^{2n+1} a_i \omega_i & \longmapsto & \big(\sum_{i=1}^{n-1} (a_{2i}+a_{2i+1}) \omega''_{2i}\big) + (a_{2n}+\frac{a_{2n+1}}{2}) (\omega''_{2n} + \omega''_{2n+1})\\ \hline \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{|ccccl|} \hline \phantom{\Big|}\hat \varphi & : & \sum_{i=1}^{2n+1} a_i \omega_i & \longmapsto & \big(\sum_{i=1}^n (a_{2i-1} + a_{2i}) \omega'_{2i}\big) + a_{2n+1} \omega'_{2n+2}\\ \hline \phantom{\Big|}\bar \varphi & : & \sum_{i=1}^{2n+1} a_i \omega_i & \longmapsto & \big(\sum_{i=1}^{n-1} (a_{2i}+a_{2i+1}) \omega''_{2i}\big) + (a_{2n}+\frac{a_{2n+1}}{2}) (\omega''_{2n} + \omega''_{2n+1})\\ \hline \end{array} \end{align*} $$
Therefore, in this case as well, we obtain the similar results as those in Proposition 5.6 and Theorem 5.9.
Theorem 6.1 Let
![]() $(G,K)$
be the spherical pair
$(G,K)$
be the spherical pair
![]() $(\operatorname {\mathrm {SO}}(2p+1),\operatorname {\mathrm {GL}}(p))$
, then with the above definitions:
$(\operatorname {\mathrm {SO}}(2p+1),\operatorname {\mathrm {GL}}(p))$
, then with the above definitions:
-
(i) The map
is an isogeny of based root data $$ \begin{align*}(\hat \varphi, \bar \varphi) : \Xi_{G/K} \longrightarrow \Xi_{\widehat G/\widehat K} \oplus \Xi_{H/K} \end{align*} $$
$$ \begin{align*}(\hat \varphi, \bar \varphi) : \Xi_{G/K} \longrightarrow \Xi_{\widehat G/\widehat K} \oplus \Xi_{H/K} \end{align*} $$
 $$ \begin{align*} \mathcal R_{G/K} \longrightarrow \mathcal R_{\widehat G/\widehat K} \oplus \mathcal R_{H/K}. \end{align*} $$
$$ \begin{align*} \mathcal R_{G/K} \longrightarrow \mathcal R_{\widehat G/\widehat K} \oplus \mathcal R_{H/K}. \end{align*} $$
-
(ii) For all
 $\lambda ,\mu ,\nu \in \Lambda ^+_{G/K}$
, we have
$\lambda ,\mu ,\nu \in \Lambda ^+_{G/K}$
, we have  $$ \begin{align*}\begin{array}{ccc} E_{G/K}(\nu) \subset E_{G/K}(\lambda) \cdot E_{G/K}(\mu) & \Longleftrightarrow & \left\{ \begin{array}{c} E_{\widehat G/\widehat K}(\hat \nu) \subset E_{\widehat G/\widehat K}(\hat \lambda) \cdot E_{\widehat G/\widehat K}(\hat \mu), \phantom{\Big|} \\ E_{H/K}(\bar \nu) \subset E_{H/K}(\bar \lambda) \cdot E_{H/K}(\bar \mu). \end{array}\right. \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ccc} E_{G/K}(\nu) \subset E_{G/K}(\lambda) \cdot E_{G/K}(\mu) & \Longleftrightarrow & \left\{ \begin{array}{c} E_{\widehat G/\widehat K}(\hat \nu) \subset E_{\widehat G/\widehat K}(\hat \lambda) \cdot E_{\widehat G/\widehat K}(\hat \mu), \phantom{\Big|} \\ E_{H/K}(\bar \nu) \subset E_{H/K}(\bar \lambda) \cdot E_{H/K}(\bar \mu). \end{array}\right. \end{array} \end{align*} $$
The symmetric variety
![]() $\operatorname {\mathrm {SO}}(2n)/\operatorname {\mathrm {GL}}(n)$
, however, is not covered by Conjecture 3.2. This prompts us to wonder how the conjecture should be rephrased in this case, and more generally in the case of the symmetric varieties of Hermitian type (that is, the symmetric varieties
$\operatorname {\mathrm {SO}}(2n)/\operatorname {\mathrm {GL}}(n)$
, however, is not covered by Conjecture 3.2. This prompts us to wonder how the conjecture should be rephrased in this case, and more generally in the case of the symmetric varieties of Hermitian type (that is, the symmetric varieties
![]() $G/K$
with K a Levi subgroup).
$G/K$
with K a Levi subgroup).
Notice that if
![]() $(G,K)$
is a spherical pair with K a Levi subgroup of G, then either
$(G,K)$
is a spherical pair with K a Levi subgroup of G, then either
![]() $G/K$
is a symmetric space of Hermitian type, or it is the pair
$G/K$
is a symmetric space of Hermitian type, or it is the pair
![]() $(\operatorname {\mathrm {SO}}(2p+1),\operatorname {\mathrm {GL}}(p))$
considered above, or it is the pair
$(\operatorname {\mathrm {SO}}(2p+1),\operatorname {\mathrm {GL}}(p))$
considered above, or it is the pair
![]() $(\operatorname {\mathrm {Sp}}(2p),\operatorname {\mathrm {GL}}(1) \times \operatorname {\mathrm {Sp}}(2p-2))$
which appeared as case Sph.A10 in Section 5.2. In particular, the analysis in this section reduces the case of the spherical Levi subgroups to the case of the Hermitian symmetric subgroups.
$(\operatorname {\mathrm {Sp}}(2p),\operatorname {\mathrm {GL}}(1) \times \operatorname {\mathrm {Sp}}(2p-2))$
which appeared as case Sph.A10 in Section 5.2. In particular, the analysis in this section reduces the case of the spherical Levi subgroups to the case of the Hermitian symmetric subgroups.
6.2 The Hermitian symmetric case
Let
![]() $X = G/K$
be a symmetric variety of Hermitian type, with G simple and simply connected. This means that the center of K has positive dimension, or equivalently that K is a Levi subgroup of G. In this case, the restricted root system
$X = G/K$
be a symmetric variety of Hermitian type, with G simple and simply connected. This means that the center of K has positive dimension, or equivalently that K is a Levi subgroup of G. In this case, the restricted root system
![]() $\widetilde \Phi _X$
is either of type
$\widetilde \Phi _X$
is either of type
![]() $\mathsf C$
or
$\mathsf C$
or
![]() $\mathsf {BC}$
, whereas the root system
$\mathsf {BC}$
, whereas the root system
![]() $\Phi _X$
is always of type
$\Phi _X$
is always of type
![]() $\mathsf B$
.
$\mathsf B$
.
For completeness, we list in Table 4 all the symmetric varieties of Hermitian type. In all cases, we also give the simple restricted roots and a minimal set of generators for the weight monoid
![]() $\Lambda ^+_X$
.
$\Lambda ^+_X$
.
-
(i)
 $\mathbf {SL(p+q)/S(GL(p)}L \times \mathbf {GL(q))}$
,
$\mathbf {SL(p+q)/S(GL(p)}L \times \mathbf {GL(q))}$
,
 $q> p \geqslant 1$
:
$q> p \geqslant 1$
:
 $\Delta _X = \{\alpha _i + \alpha _{p+q-i}\ :\ 1\leqslant i < p \}\cup \{\alpha _p + \cdots + \alpha _q \}$
,
$\Delta _X = \{\alpha _i + \alpha _{p+q-i}\ :\ 1\leqslant i < p \}\cup \{\alpha _p + \cdots + \alpha _q \}$
,
 $\Lambda ^+_X$
is generated by the weights
$\Lambda ^+_X$
is generated by the weights
 $\omega _i + \omega _{p+q-i}$
with
$\omega _i + \omega _{p+q-i}$
with
 $1\leqslant i\leqslant p$
.
$1\leqslant i\leqslant p$
. -
(ii)
 $\mathbf {SL(2p)/S(GL(p)} \times \mathbf {GL(p))}$
,
$\mathbf {SL(2p)/S(GL(p)} \times \mathbf {GL(p))}$
,
 $p \geqslant 1$
:
$p \geqslant 1$
:
 $\Delta _X = \{\alpha _i + \alpha _{2p-i}\ :\ 1\leqslant i < p\}\cup \{\alpha _p\}$
,
$\Delta _X = \{\alpha _i + \alpha _{2p-i}\ :\ 1\leqslant i < p\}\cup \{\alpha _p\}$
,
 $\Lambda ^+_X$
is generated by the weights
$\Lambda ^+_X$
is generated by the weights
 $\omega _i + \omega _{2p-i}$
with
$\omega _i + \omega _{2p-i}$
with
 $1\leqslant i < p$
, together with
$1\leqslant i < p$
, together with
 $2 \omega _p$
.
$2 \omega _p$
. -
(iii)
 $\mathbf {Spin(2p+1)/Spin(2)} \times \mathbf {Spin(2p-1)}$
,
$\mathbf {Spin(2p+1)/Spin(2)} \times \mathbf {Spin(2p-1)}$
,
 $p \geqslant 2$
:
$p \geqslant 2$
:
 $\Delta _X = \{\alpha _1, \; 2 (\alpha _2 + \cdots + \alpha _p)\}$
,
$\Delta _X = \{\alpha _1, \; 2 (\alpha _2 + \cdots + \alpha _p)\}$
,
 $\Lambda ^+_X$
is generated by
$\Lambda ^+_X$
is generated by
 $2\omega _1$
and
$2\omega _1$
and
 $\omega _2$
.
$\omega _2$
. -
(iv)
 $\mathbf {Spin(2p)/Spin(2)} \times \mathbf {Spin(2p-2)}$
,
$\mathbf {Spin(2p)/Spin(2)} \times \mathbf {Spin(2p-2)}$
,
 $p \geqslant 3$
:
$p \geqslant 3$
:
 $\Delta _X = \{\alpha _1, \; 2 (\alpha _2 + \cdots + \alpha _{p-2}) + \alpha _{p-1}+\alpha _p \}$
,
$\Delta _X = \{\alpha _1, \; 2 (\alpha _2 + \cdots + \alpha _{p-2}) + \alpha _{p-1}+\alpha _p \}$
,
 $\Lambda ^+_X$
is generated by
$\Lambda ^+_X$
is generated by
 $2\omega _1$
and
$2\omega _1$
and
 $\omega _2$
.
$\omega _2$
. -
(v)
 $\mathbf {Sp(2p)/GL(p)}$
,
$\mathbf {Sp(2p)/GL(p)}$
,
 $p \geqslant 2$
:
$p \geqslant 2$
:
 $\Delta _X =\{2\alpha _i\ :\ 1\leqslant i\leqslant p-1\}\cup \{\alpha _p\}$
,
$\Delta _X =\{2\alpha _i\ :\ 1\leqslant i\leqslant p-1\}\cup \{\alpha _p\}$
,
 $\Lambda ^+_X$
is generated by the weights
$\Lambda ^+_X$
is generated by the weights
 $2\omega _i$
with
$2\omega _i$
with
 $1 \leqslant i \leqslant p$
.
$1 \leqslant i \leqslant p$
. -
(vi)
 $\mathbf {Spin(4p+2)/GL(2p+1)}$
,
$\mathbf {Spin(4p+2)/GL(2p+1)}$
,
 $p \geqslant 1$
:
$p \geqslant 1$
:
 $\Delta _X =\{\alpha _{2i-1}+2\alpha _{2i}+\alpha _{2i+1}\, :\, 1\leqslant i < p\}\cup \{\alpha _{2p-1} + \alpha _{2p} + \alpha _{2p+1} \}$
,
$\Delta _X =\{\alpha _{2i-1}+2\alpha _{2i}+\alpha _{2i+1}\, :\, 1\leqslant i < p\}\cup \{\alpha _{2p-1} + \alpha _{2p} + \alpha _{2p+1} \}$
,
 $\Lambda ^+_X$
is generated by the weights
$\Lambda ^+_X$
is generated by the weights
 $\omega _{2i}$
with
$\omega _{2i}$
with
 $1 \leqslant i < p$
together with
$1 \leqslant i < p$
together with
 $\omega _{2p} + \omega _{2p+1}$
.
$\omega _{2p} + \omega _{2p+1}$
. -
(vii)
 $\mathbf {Spin(4p)/GL(2p)}$
,
$\mathbf {Spin(4p)/GL(2p)}$
,
 $p \geqslant 2$
:
$p \geqslant 2$
:
 $\Delta _X =\{\alpha _{2i-1}+2\alpha _{2i}+\alpha _{2i+1}\ :\ 1\leqslant i\leqslant p-1\}\cup \{ \alpha _{2p} \}$
,
$\Delta _X =\{\alpha _{2i-1}+2\alpha _{2i}+\alpha _{2i+1}\ :\ 1\leqslant i\leqslant p-1\}\cup \{ \alpha _{2p} \}$
,
 $\Lambda ^+_X$
is generated by the weights
$\Lambda ^+_X$
is generated by the weights
 $\omega _{2i}$
with
$\omega _{2i}$
with
 $1 \leqslant i < p$
, together with
$1 \leqslant i < p$
, together with
 $2 \omega _{2p}$
.
$2 \omega _{2p}$
. -
(viii)
 $\mathbf {E}_{\mathbf {6}}/{\mathbf {D}}_{\mathbf {5}} \times \mathbb C^*$
:
$\mathbf {E}_{\mathbf {6}}/{\mathbf {D}}_{\mathbf {5}} \times \mathbb C^*$
:
 $\Delta _X = \{\alpha _1 + \alpha _3 +\alpha _4+\alpha _5 + \alpha _6, \; 2\alpha _2 + \alpha _3 + 2\alpha _4 + \alpha _5 \}$
,
$\Delta _X = \{\alpha _1 + \alpha _3 +\alpha _4+\alpha _5 + \alpha _6, \; 2\alpha _2 + \alpha _3 + 2\alpha _4 + \alpha _5 \}$
,
 $\Lambda ^+_X$
is generated by
$\Lambda ^+_X$
is generated by
 $\omega _1+\omega _6$
and
$\omega _1+\omega _6$
and
 $\omega _2$
.
$\omega _2$
. -
(ix)
 $\mathbf {E}_{\mathbf {7}}/\mathbf {E}_{\mathbf {6}}\times \mathbb C^*$
:
$\mathbf {E}_{\mathbf {7}}/\mathbf {E}_{\mathbf {6}}\times \mathbb C^*$
:
 $\Delta _X = \{2\alpha _1 + \alpha _2 + 2\alpha _3 +2\alpha _4 + \alpha _5, \; \alpha _2 + \alpha _3 + 2(\alpha _4 + \alpha _5 + \alpha _6), \; \alpha _7\}$
,
$\Delta _X = \{2\alpha _1 + \alpha _2 + 2\alpha _3 +2\alpha _4 + \alpha _5, \; \alpha _2 + \alpha _3 + 2(\alpha _4 + \alpha _5 + \alpha _6), \; \alpha _7\}$
,
 $\Lambda ^+_X$
is generated by
$\Lambda ^+_X$
is generated by
 $\omega _1$
,
$\omega _1$
,
 $\omega _6$
, and
$\omega _6$
, and
 $2\omega _7$
.
$2\omega _7$
.
Table 4: Symmetric varieties of Hermitian type.

If
![]() $\widetilde \Phi _X$
is nonreduced, then K is self-normalizing, and the derived subgroup
$\widetilde \Phi _X$
is nonreduced, then K is self-normalizing, and the derived subgroup
![]() $K'$
is also spherical in G. If instead
$K'$
is also spherical in G. If instead
![]() $\widetilde \Phi _X$
is reduced, then K is not self-normalizing, and its derived subgroup is not spherical in G. Therefore, there are some Hermitian symmetric subgroups which have a nonsymmetric semisimple spherical counterpart, similarly to the cases Sph.A7 and Sph.A9 of Table 3.
$\widetilde \Phi _X$
is reduced, then K is not self-normalizing, and its derived subgroup is not spherical in G. Therefore, there are some Hermitian symmetric subgroups which have a nonsymmetric semisimple spherical counterpart, similarly to the cases Sph.A7 and Sph.A9 of Table 3.
We list such spherical pairs in Table 5. In all cases, we also give the simple restricted roots and a minimal set of generators for the weight monoid
![]() $\Lambda ^+_X$
.
$\Lambda ^+_X$
.
-
(i’)
 $\mathbf {SL(p+q)/SL(p)} \times \mathbf {SL(q))}$
,
$\mathbf {SL(p+q)/SL(p)} \times \mathbf {SL(q))}$
,
 $q> p \geqslant 1$
:
$q> p \geqslant 1$
:
 $\Delta _X = \{\alpha _i + \alpha _{p+q-i}\ :\ 1\leqslant i < p \}\cup \{\alpha _p + \cdots + \alpha _q \}$
,
$\Delta _X = \{\alpha _i + \alpha _{p+q-i}\ :\ 1\leqslant i < p \}\cup \{\alpha _p + \cdots + \alpha _q \}$
,
 $\Lambda ^+_X$
is generated by the weights
$\Lambda ^+_X$
is generated by the weights
 $\omega _i + \omega _{p+q-i}$
with
$\omega _i + \omega _{p+q-i}$
with
 $1\leqslant i < p$
together with
$1\leqslant i < p$
together with
 $\omega _p$
and
$\omega _p$
and
 $\omega _q$
.
$\omega _q$
. -
(vi’)
 $\mathbf {Spin(4p+2)/SL(2p+1)}$
,
$\mathbf {Spin(4p+2)/SL(2p+1)}$
,
 $p \geqslant 1$
:
$p \geqslant 1$
:
 $\Delta _X =\{\alpha _{2i-1}+2\alpha _{2i}+\alpha _{2i+1}\ :\ 1\leqslant i < p\}\cup \{\alpha _{2p-1} + \alpha _{2p} + \alpha _{2p+1} \}$
,
$\Delta _X =\{\alpha _{2i-1}+2\alpha _{2i}+\alpha _{2i+1}\ :\ 1\leqslant i < p\}\cup \{\alpha _{2p-1} + \alpha _{2p} + \alpha _{2p+1} \}$
,
 $\Lambda ^+_X$
is generated by the weights
$\Lambda ^+_X$
is generated by the weights
 $\omega _{2i}$
with
$\omega _{2i}$
with
 $1 \leqslant i < p$
together with
$1 \leqslant i < p$
together with
 $\omega _{2p}$
and
$\omega _{2p}$
and
 $\omega _{2p+1}$
.
$\omega _{2p+1}$
. -
(viii’)
 $\mathbf {E}_{\mathbf {6}}/\mathbf {D}_{\mathbf {5}}$
:
$\mathbf {E}_{\mathbf {6}}/\mathbf {D}_{\mathbf {5}}$
:
 $\Delta _X = \{\alpha _1 + \alpha _3 +\alpha _4+\alpha _5 + \alpha _6, \; 2\alpha _2 + \alpha _3 + 2\alpha _4 + \alpha _5 \}$
,
$\Delta _X = \{\alpha _1 + \alpha _3 +\alpha _4+\alpha _5 + \alpha _6, \; 2\alpha _2 + \alpha _3 + 2\alpha _4 + \alpha _5 \}$
,
 $\Lambda ^+_X$
is generated by
$\Lambda ^+_X$
is generated by
 $\omega _1$
,
$\omega _1$
,
 $\omega _2$
, and
$\omega _2$
, and
 $\omega _6$
.
$\omega _6$
.
Table 5: Nonsymmetric reductive spherical pairs
![]() $(G,K)$
with
$(G,K)$
with
![]() $G/\mathrm N_G(K)$
symmetric of Hermitian type.
$G/\mathrm N_G(K)$
symmetric of Hermitian type.

If
![]() $(G,K')$
is a spherical pair appearing in Table 5 and
$(G,K')$
is a spherical pair appearing in Table 5 and
![]() $K = \mathrm N_G(K')$
is the corresponding symmetric subgroup of Hermitian type, then we have
$K = \mathrm N_G(K')$
is the corresponding symmetric subgroup of Hermitian type, then we have
 $\Omega _{G/K}^+ =\Lambda _{G/K'}^+$
and
$\Omega _{G/K}^+ =\Lambda _{G/K'}^+$
and
 $\mathbb C[G]^{(K)} = \mathbb C[G]^{K'}$
, as in the cases Sph.A7 and Sph.A9. Thus, the problem of decomposing the product of two spherical functions on
$\mathbb C[G]^{(K)} = \mathbb C[G]^{K'}$
, as in the cases Sph.A7 and Sph.A9. Thus, the problem of decomposing the product of two spherical functions on
![]() $G/K$
reduces to the analogous problem on
$G/K$
reduces to the analogous problem on
![]() $G/K'$
.
$G/K'$
.
In the same spirit of Conjectures 3.2 and 5.1, we formulate the following for the multiplication of spherical functions in terms of the tensor product of the restricted root system, which by computational experiments seems to hold for all the Hermitian symmetric pairs but in case He.1a.
Conjecture 6.2 Let
![]() $(G,K)$
be a reductive spherical pair with G simple and K a Levi subgroup of G different from case He.1a. For all
$(G,K)$
be a reductive spherical pair with G simple and K a Levi subgroup of G different from case He.1a. For all
![]() $\lambda , \mu , \nu \in \Lambda _X^+$
, it holds
$\lambda , \mu , \nu \in \Lambda _X^+$
, it holds
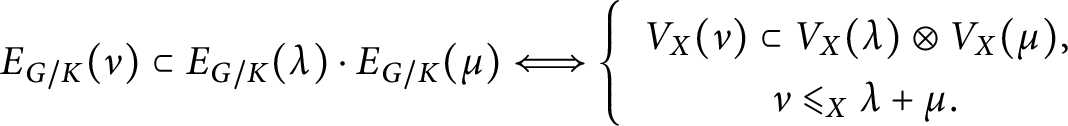 $$ \begin{align*}E_{G/K}(\nu) \subset E_{G/K}(\lambda) \cdot E_{G/K}(\mu) \Longleftrightarrow \left\{ \begin{array}{c} V_X(\nu) \subset V_X(\lambda) \otimes V_X(\mu), \phantom{\Big|} \\ \nu \leqslant_X \lambda + \mu. \end{array} \right. \end{align*} $$
$$ \begin{align*}E_{G/K}(\nu) \subset E_{G/K}(\lambda) \cdot E_{G/K}(\mu) \Longleftrightarrow \left\{ \begin{array}{c} V_X(\nu) \subset V_X(\lambda) \otimes V_X(\mu), \phantom{\Big|} \\ \nu \leqslant_X \lambda + \mu. \end{array} \right. \end{align*} $$
By Theorem 6.1 and Corollary 5.10, the previous conjecture immediately reduces to the case where
![]() $G/K$
is a symmetric variety of Hermitian type.
$G/K$
is a symmetric variety of Hermitian type.
Remark 6.3 In [Reference Bravi, Gandini and Maffei4, Section 9], the following question was considered. Suppose that G is simply laced, and let
![]() $X = G/K$
be a spherical variety with
$X = G/K$
be a spherical variety with
![]() $\Delta ^{\mathrm {sc}}_X \cap \Delta = \varnothing $
. Let
$\Delta ^{\mathrm {sc}}_X \cap \Delta = \varnothing $
. Let
![]() $\lambda , \mu , \nu \in \Lambda _X^+$
, is it true that
$\lambda , \mu , \nu \in \Lambda _X^+$
, is it true that
![]() $E_X(\nu ) \subset E_X(\lambda ) \cdot E_X(\mu )$
if and only if
$E_X(\nu ) \subset E_X(\lambda ) \cdot E_X(\mu )$
if and only if
![]() $V(\nu ) \subset V(\lambda ) \otimes V(\mu )$
and
$V(\nu ) \subset V(\lambda ) \otimes V(\mu )$
and
![]() $\nu \leqslant _{\Delta ^{\mathrm {sc}}_X} \lambda + \mu $
?
$\nu \leqslant _{\Delta ^{\mathrm {sc}}_X} \lambda + \mu $
?
This indeed seems to be true in several cases, and in particular in case He.1a. Assuming the validity of Conjecture 3.2, it is easy to see that when X is symmetric and both
![]() $\Phi $
and
$\Phi $
and
![]() $\Phi _X$
are of type
$\Phi _X$
are of type
![]() $\mathsf A$
, a positive answer to the previous question follows from the saturation theorem [Reference Knutson and Tao22]. See also [Reference Graham and Hunziker16], where a similar question is considered for the symmetric varieties with restricted root system of type
$\mathsf A$
, a positive answer to the previous question follows from the saturation theorem [Reference Knutson and Tao22]. See also [Reference Graham and Hunziker16], where a similar question is considered for the symmetric varieties with restricted root system of type
![]() $\mathsf A$
. However, the following example shows that the previous question does not always have a positive answer, at least when
$\mathsf A$
. However, the following example shows that the previous question does not always have a positive answer, at least when
![]() $\widetilde \Phi _X$
is nonreduced. Conjecture 6.2 is a partial attempt to fix the question.
$\widetilde \Phi _X$
is nonreduced. Conjecture 6.2 is a partial attempt to fix the question.
Example 6.4 Consider the symmetric variety
![]() $X = \operatorname {\mathrm {Spin}}(10)/\operatorname {\mathrm {GL}}(5)$
. The restricted root system
$X = \operatorname {\mathrm {Spin}}(10)/\operatorname {\mathrm {GL}}(5)$
. The restricted root system
![]() $\widetilde \Phi _X$
is of type
$\widetilde \Phi _X$
is of type
![]() $\mathsf {BC}_2$
, with base
$\mathsf {BC}_2$
, with base
Let us consider the highest root
![]() $\theta = \alpha _1 + 2\alpha _2 + 2\alpha _3 + \alpha _4 + \alpha _5$
: then
$\theta = \alpha _1 + 2\alpha _2 + 2\alpha _3 + \alpha _4 + \alpha _5$
: then
![]() $\theta \in \Lambda _X^+$
and
$\theta \in \Lambda _X^+$
and
![]() $\theta \leqslant _X 2 \theta $
. Moreover,
$\theta \leqslant _X 2 \theta $
. Moreover,
![]() $V(\theta ) \subset V(\theta )^{\otimes 2}$
; however, taking the product inside
$V(\theta ) \subset V(\theta )^{\otimes 2}$
; however, taking the product inside
![]() $\mathbb C[X]$
, we have
$\mathbb C[X]$
, we have
![]() $E_X(\theta ) \not \subset E_X(\theta )^2$
: indeed, the unique nonzero equivariant projection
$E_X(\theta ) \not \subset E_X(\theta )^2$
: indeed, the unique nonzero equivariant projection
is given by the bracket on the Lie algebra
![]() $\mathfrak g \simeq V(\theta )$
. It follows that
$\mathfrak g \simeq V(\theta )$
. It follows that
![]() $\pi (v \otimes v) = 0$
, for all
$\pi (v \otimes v) = 0$
, for all
![]() $v \in V(\theta )$
, and we conclude by Proposition 2.2.
$v \in V(\theta )$
, and we conclude by Proposition 2.2.
The same happens more generally for
![]() $\operatorname {\mathrm {Spin}}(2p)/\operatorname {\mathrm {GL}}(p)$
whenever p is odd, and for
$\operatorname {\mathrm {Spin}}(2p)/\operatorname {\mathrm {GL}}(p)$
whenever p is odd, and for
![]() $\mathsf E_6/\mathsf D_5 \times \mathbb C^*$
: indeed, in all these cases, the highest root is a spherical weight, and
$\mathsf E_6/\mathsf D_5 \times \mathbb C^*$
: indeed, in all these cases, the highest root is a spherical weight, and
![]() $V(\theta )$
occurs in
$V(\theta )$
occurs in
![]() $ V(\theta )^{\otimes 2}$
with multiplicity 1.
$ V(\theta )^{\otimes 2}$
with multiplicity 1.
Both these examples are instances of exceptional symmetric varieties of Hermitian type, that is, symmetric varieties of Hermitian type with nonreduced restricted root system. There is another instance of such a symmetric variety, namely
![]() $X = \operatorname {\mathrm {SL}}(p+q)/\mathrm S(\operatorname {\mathrm {GL}}(p) \times \operatorname {\mathrm {GL}}(q))$
when
$X = \operatorname {\mathrm {SL}}(p+q)/\mathrm S(\operatorname {\mathrm {GL}}(p) \times \operatorname {\mathrm {GL}}(q))$
when
![]() $p \neq q$
: however, in this case,
$p \neq q$
: however, in this case,
![]() $V(\theta )$
occurs in
$V(\theta )$
occurs in
![]() $ V(\theta )^{\otimes 2}$
with multiplicity 2, and the inclusion
$ V(\theta )^{\otimes 2}$
with multiplicity 2, and the inclusion
![]() $E_X(\theta ) \subset E_X(\theta )^2$
holds true inside
$E_X(\theta ) \subset E_X(\theta )^2$
holds true inside
![]() $\mathbb C[X]$
.
$\mathbb C[X]$
.
Acknowledgment
We would like to thank the anonymous referees for useful comments.