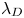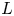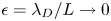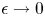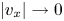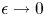1. Introduction
For a quasineutral plasma to exist next to a wall or a solid target, the most mobile charged species, typically electrons due to their smaller mass, must be reflected by the wall to achieve no net charge loss (and thus preserve quasineutrality). The wall is thus negatively charged and the region where electron reflection occurs is called the ‘sheath’ (Langmuir Reference Langmuir1923, Reference Langmuir1929; Tonks & Langmuir Reference Tonks and Langmuir1929). The sheath is positively charged and shields the quasineutral plasma from the negative charge on the wall. Its characteristic length scale is the Debye length, defined as $\lambda _{D} = \sqrt {\epsilon _0 T_{e} / n_{e} e^2}$![]() , where $n_{e}$
, where $n_{e}$![]() is the electron density, $e$
is the electron density, $e$![]() is the proton charge, $T_{e}$
is the proton charge, $T_{e}$![]() is the electron temperature (in units of energy) and $\epsilon _0$
is the electron temperature (in units of energy) and $\epsilon _0$![]() is the permittivity of free space. The characteristic length scale $L$
is the permittivity of free space. The characteristic length scale $L$![]() of unmagnetised plasmas, or magnetised plasmas where the magnetic field is perpendicular to the target, is defined to be the smallest one between: the collisional mean free path of ions, the ionisation mean free path of neutrals and the target curvature (Riemann Reference Riemann1991). It is usually much larger than the Debye length, such that the sheath is thin compared with the plasma
of unmagnetised plasmas, or magnetised plasmas where the magnetic field is perpendicular to the target, is defined to be the smallest one between: the collisional mean free path of ions, the ionisation mean free path of neutrals and the target curvature (Riemann Reference Riemann1991). It is usually much larger than the Debye length, such that the sheath is thin compared with the plasma
In magnetised plasmas with an oblique magnetic field impinging on the target, $L$![]() can also be the ion sound Larmor radius $\rho _{S} = \sqrt {m_{i}(ZT_{e} + T_{i})}/(ZeB)$
can also be the ion sound Larmor radius $\rho _{S} = \sqrt {m_{i}(ZT_{e} + T_{i})}/(ZeB)$![]() , where $T_{i}$
, where $T_{i}$![]() is the ion temperature, $B$
is the ion temperature, $B$![]() is the magnetic field strength, $m_{i}$
is the magnetic field strength, $m_{i}$![]() is the ion mass and $Z$
is the ion mass and $Z$![]() is the ionic charge state (Chodura Reference Chodura1982).Footnote 1 Once they reach the target, ions and electrons are absorbed, eventually recombine and are subsequently re-emitted as neutrals that penetrate back through the sheath all the way into the plasma before re-ionising.
is the ionic charge state (Chodura Reference Chodura1982).Footnote 1 Once they reach the target, ions and electrons are absorbed, eventually recombine and are subsequently re-emitted as neutrals that penetrate back through the sheath all the way into the plasma before re-ionising.
The physical principle treated in this paper states that the ions must reach the sheath at a minimum velocity, as first formalised by Bohm (Reference Bohm1949) assuming mono-energetic (cold) ions
Here, $u_{x} = \boldsymbol {u} \boldsymbol {\cdot } \boldsymbol {e}_x$![]() , where $\boldsymbol {u}$
, where $\boldsymbol {u}$![]() is the fluid velocity, $\hat {\boldsymbol {e}}_x$
is the fluid velocity, $\hat {\boldsymbol {e}}_x$![]() is a unit vector normal to the target plane and pointing away from it, $v_{B} = \sqrt {ZT_{e}/m_{i}}$
is a unit vector normal to the target plane and pointing away from it, $v_{B} = \sqrt {ZT_{e}/m_{i}}$![]() is the Bohm speed (or cold-ion sound speed) and $m_{i}$
is the Bohm speed (or cold-ion sound speed) and $m_{i}$![]() is the ion mass. The negative sign in the velocity component is related to the choice of placing the target at $x=0$
is the ion mass. The negative sign in the velocity component is related to the choice of placing the target at $x=0$![]() and the plasma at $x > 0$
and the plasma at $x > 0$![]() . The inequality (1.2) came to be known as the ‘Bohm criterion’. It holds at the ‘sheath entrance’ (or ‘sheath edge’), a position at this stage loosely defined as the distance from the wall below which collisions, ionisation, target curvature and curvature of ion Larmor orbits are negligible, and above which the space charge is negligible. It ensures an increasingly positive space charge in the sheath as the wall is approached, consistent with an increasing electric field directed towards the wall to reflect electrons.
. The inequality (1.2) came to be known as the ‘Bohm criterion’. It holds at the ‘sheath entrance’ (or ‘sheath edge’), a position at this stage loosely defined as the distance from the wall below which collisions, ionisation, target curvature and curvature of ion Larmor orbits are negligible, and above which the space charge is negligible. It ensures an increasingly positive space charge in the sheath as the wall is approached, consistent with an increasing electric field directed towards the wall to reflect electrons.
Since mono-energetic ions are a significant idealisation, a kinetic formulation of the Bohm criterion, valid for arbitrary ion velocity distributions, is desirable. This was first given by Harrison & Thompson (Reference Harrison and Thompson1959)
Here, $f$![]() is the ion distribution function of the velocity component normal to the target, $v_x = \boldsymbol {v}\boldsymbol {\cdot } \hat {\boldsymbol {e}}_x$
is the ion distribution function of the velocity component normal to the target, $v_x = \boldsymbol {v}\boldsymbol {\cdot } \hat {\boldsymbol {e}}_x$![]() with velocity $\boldsymbol {v}$
with velocity $\boldsymbol {v}$![]() , at the sheath entrance. By plasma quasineutrality at the sheath entrance, the electron density $n_{e}$
, at the sheath entrance. By plasma quasineutrality at the sheath entrance, the electron density $n_{e}$![]() satisfies
satisfies
The distribution $f$![]() is, in practice, the full three-dimensional distribution function which has been integrated over the velocity components tangential to the target. Note that the fluid criterion (1.2) is always fulfilled by the flow velocity $u_x$
is, in practice, the full three-dimensional distribution function which has been integrated over the velocity components tangential to the target. Note that the fluid criterion (1.2) is always fulfilled by the flow velocity $u_x$![]() defined by
defined by
provided that $f$![]() satisfies the kinetic criterion (1.3), as can be shown by two applications of Schwarz's inequality (Harrison & Thompson Reference Harrison and Thompson1959; Riemann Reference Riemann1991). In deriving (1.3), it has been assumed that no ions travel away from the target at the sheath entrance, such that $f(v_x) = 0$
satisfies the kinetic criterion (1.3), as can be shown by two applications of Schwarz's inequality (Harrison & Thompson Reference Harrison and Thompson1959; Riemann Reference Riemann1991). In deriving (1.3), it has been assumed that no ions travel away from the target at the sheath entrance, such that $f(v_x) = 0$![]() for $v_x > 0$
for $v_x > 0$![]() .
.
Although Harrison & Thompson's kinetic criterion (1.3) stood the test of time, Hall (Reference Hall1962) promptly criticised their derivation for implicitly assuming the conditions $f(0^-) \equiv \lim _{v_x \rightarrow 0^{-}} f(v_x) = 0$![]() and $f'(0^-) = 0$
and $f'(0^-) = 0$![]() without justification. The derivative of any function $G(\zeta )$
without justification. The derivative of any function $G(\zeta )$![]() of a single variable $\zeta$
of a single variable $\zeta$![]() is denoted $G'(\zeta ) \equiv \, {\rm d} G(\zeta )/ {\rm d} \zeta$
is denoted $G'(\zeta ) \equiv \, {\rm d} G(\zeta )/ {\rm d} \zeta$![]() . Performing a calculation that will be shown here to be flawed, Hall refutes $f'(0^-) = 0$
. Performing a calculation that will be shown here to be flawed, Hall refutes $f'(0^-) = 0$![]() and concludes that (1.3) ascribes ‘undue importance’ to the slow ions with $v_x \approx 0$
and concludes that (1.3) ascribes ‘undue importance’ to the slow ions with $v_x \approx 0$![]() .
.
In parallel, Caruso & Cavaliere (Reference Caruso and Cavaliere1962) recognised the asymptotic framework of the plasma-sheath transition as a singular perturbation theory (see § 7.2 of Bender & Orszag Reference Bender and Orszag1999), following work by Bertotti (Reference Bertotti1961). In the limit $\epsilon \rightarrow 0$![]() the equations on the plasma and sheath scales are distinct, and thus the two regions can be treated separately. The sheath entrance is defined in this limit by $x/L \rightarrow 0$
the equations on the plasma and sheath scales are distinct, and thus the two regions can be treated separately. The sheath entrance is defined in this limit by $x/L \rightarrow 0$![]() and $x/\lambda _{D} \rightarrow \infty$
and $x/\lambda _{D} \rightarrow \infty$![]() (Bertotti & Cavaliere Reference Bertotti and Cavaliere1965). In practice, any point $x_{\epsilon } = \epsilon ^q L$
(Bertotti & Cavaliere Reference Bertotti and Cavaliere1965). In practice, any point $x_{\epsilon } = \epsilon ^q L$![]() on an intermediate length scale with $q \in (0,1)$
on an intermediate length scale with $q \in (0,1)$![]() satisfies $\lim _{\epsilon \rightarrow 0} x_{\epsilon } / \lambda _{D} \rightarrow \infty$
satisfies $\lim _{\epsilon \rightarrow 0} x_{\epsilon } / \lambda _{D} \rightarrow \infty$![]() and $\lim _{\epsilon \rightarrow 0} x_{\epsilon }/L \rightarrow 0$
and $\lim _{\epsilon \rightarrow 0} x_{\epsilon }/L \rightarrow 0$![]() and is thus a valid reference choice for the sheath entrance.Footnote 2 The actual distribution function at this point is denoted $f_{\epsilon }(v_x)$
and is thus a valid reference choice for the sheath entrance.Footnote 2 The actual distribution function at this point is denoted $f_{\epsilon }(v_x)$![]() , and the asymptotic sheath entrance distribution function is defined by
, and the asymptotic sheath entrance distribution function is defined by
The Bohm criterion at the sheath entrance arises as a necessary condition for an electron-repelling sheath solution to exist in the limit $\epsilon \rightarrow 0$![]() .
.
In § 3.2 of his seminal review, Riemann (Reference Riemann1991) derived the kinetic Bohm criterion (1.3) in the limit $\epsilon \rightarrow 0$![]() , including ion reflection and re-emission from the wall. For comparison with this work, his derivation is considered for a perfectly absorbing wall. There, it is proven in an intermediate step that $f(0^-) = 0$
, including ion reflection and re-emission from the wall. For comparison with this work, his derivation is considered for a perfectly absorbing wall. There, it is proven in an intermediate step that $f(0^-) = 0$![]() , while the condition $f'(0^-) = 0$
, while the condition $f'(0^-) = 0$![]() emerges from the assumption that $f$
emerges from the assumption that $f$![]() can be represented by a Taylor expansion in kinetic energy $v_x^2 / 2$
can be represented by a Taylor expansion in kinetic energy $v_x^2 / 2$![]() near $v_x = 0$
near $v_x = 0$![]() . This assumption was criticised (Fernsler, Slinker & Joyce Reference Fernsler, Slinker and Joyce2005; Baalrud & Hegna Reference Baalrud and Hegna2011, Reference Baalrud and Hegna2012; Baalrud et al. Reference Baalrud, Scheiner, Yee, Hopkins and Barnat2015) for restricting the class of possible ion distribution functions at the sheath entrance. Another objection to (1.3) emphasises the divergence of its left-hand side when applied to the actual distribution function
. This assumption was criticised (Fernsler, Slinker & Joyce Reference Fernsler, Slinker and Joyce2005; Baalrud & Hegna Reference Baalrud and Hegna2011, Reference Baalrud and Hegna2012; Baalrud et al. Reference Baalrud, Scheiner, Yee, Hopkins and Barnat2015) for restricting the class of possible ion distribution functions at the sheath entrance. Another objection to (1.3) emphasises the divergence of its left-hand side when applied to the actual distribution function
caused by $f_{\epsilon }(0) \neq 0$![]() and $f_{\epsilon }'(0) \neq 0$
and $f_{\epsilon }'(0) \neq 0$![]() for finite $\epsilon$
for finite $\epsilon$![]() . Echoing (Hall Reference Hall1962) around 50 years later, Baalrud & Hegna (Reference Baalrud and Hegna2011, Reference Baalrud and Hegna2012) claim that the kinetic criterion places ‘undue importance’ on slow ions. While this assertion appears reasonable in light of (1.7), it is motivated by the misguided expectation that (1.3) should still apply as it is to $f_{\epsilon }$
. Echoing (Hall Reference Hall1962) around 50 years later, Baalrud & Hegna (Reference Baalrud and Hegna2011, Reference Baalrud and Hegna2012) claim that the kinetic criterion places ‘undue importance’ on slow ions. While this assertion appears reasonable in light of (1.7), it is motivated by the misguided expectation that (1.3) should still apply as it is to $f_{\epsilon }$![]() for small but finite $\epsilon$
for small but finite $\epsilon$![]() (Riemann Reference Riemann2012).
(Riemann Reference Riemann2012).
In the remainder of this article, the derivation of the kinetic Bohm criterion (1.3) is generalised to remove the assumption, and prove the physical legitimacy of, $f'(0^-) = 0$![]() . Condition (1.3) is shown to emerge from
. Condition (1.3) is shown to emerge from
by integrating (1.10) by parts and imposing (1.8) and (1.9). In (1.10), the electron density at $x_{\epsilon }$![]() was defined as $n_{e, \epsilon }$
was defined as $n_{e, \epsilon }$![]() . To conclude, (1.8)–(1.10) are combined to obtain the appropriate reformulation of (1.3) in terms of $f_{\epsilon }$
. To conclude, (1.8)–(1.10) are combined to obtain the appropriate reformulation of (1.3) in terms of $f_{\epsilon }$![]() . It is explained that the divergence (1.7) follows from an incautious interchange of the limits $\epsilon \rightarrow 0$
. It is explained that the divergence (1.7) follows from an incautious interchange of the limits $\epsilon \rightarrow 0$![]() and $v_x \rightarrow 0^-$
and $v_x \rightarrow 0^-$![]() .
.
2. Derivation of the kinetic Bohm criterion
In this section, the kinetic Bohm criterion is derived by imposing the requirement of an electron-repelling potential solution in the sheath near the sheath entrance. In § 2.1, the collisionless ion kinetic equation in the sheath is solved and Poisson's equation is thus derived (assuming adiabatic electrons). Then, in § 2.2 the ion density is expanded near the sheath entrance using a matched asymptotic expansion (Bender & Orszag Reference Bender and Orszag1999). Here, the only assumption on the form of the ion distribution function at the sheath entrance for $|v_x| \ll 1$![]() , $v_x < 0$
, $v_x < 0$![]() is that it has an asymptotic expansion in (possibly fractional) powers of $v_x$
is that it has an asymptotic expansion in (possibly fractional) powers of $v_x$![]() . In § 2.3, the charge density is evaluated for all possible values of the smallest exponent of $v_x$
. In § 2.3, the charge density is evaluated for all possible values of the smallest exponent of $v_x$![]() , associated with the largest term, in this expansion. Imposing an electron-repelling potential near the sheath entrance is shown in § 2.4 to lead to conditions (1.8) and (1.9) and to the inequality form of (1.10) and (1.3). Finally, in § 2.5 we verify that the equality form of the kinetic Bohm criterion (1.3) is consistent with an electron-repelling sheath solution.
, associated with the largest term, in this expansion. Imposing an electron-repelling potential near the sheath entrance is shown in § 2.4 to lead to conditions (1.8) and (1.9) and to the inequality form of (1.10) and (1.3). Finally, in § 2.5 we verify that the equality form of the kinetic Bohm criterion (1.3) is consistent with an electron-repelling sheath solution.
2.1. Poisson's equation in the sheath
The following dimensionless variables are introduced: the sheath-scale position $\xi = x / \lambda _{D}$![]() , the (negative of the) electrostatic potential relative to the sheath entrance $\chi = \lim _{\epsilon \rightarrow 0} e(\phi (x_{\epsilon }) - \phi (x))/T_{e}$
, the (negative of the) electrostatic potential relative to the sheath entrance $\chi = \lim _{\epsilon \rightarrow 0} e(\phi (x_{\epsilon }) - \phi (x))/T_{e}$![]() , the ion velocity component directed towards the wall $w = -v_x / v_{B}$
, the ion velocity component directed towards the wall $w = -v_x / v_{B}$![]() and the ion distribution function $g(w) = Zf (v_x) v_{B} /n_{e}$
and the ion distribution function $g(w) = Zf (v_x) v_{B} /n_{e}$![]() satisfying $\int _{0}^{\infty } g ( w ) \, {\rm d} w = 1$
satisfying $\int _{0}^{\infty } g ( w ) \, {\rm d} w = 1$![]() from (1.4).
from (1.4).
For $\epsilon \rightarrow 0$![]() , in the sheath $x \leqslant x_{\epsilon }$
, in the sheath $x \leqslant x_{\epsilon }$![]() , corresponding to $\xi \in [0, \infty ]$
, corresponding to $\xi \in [0, \infty ]$![]() , the ion distribution function $g_{\xi }(\xi, w)$
, the ion distribution function $g_{\xi }(\xi, w)$![]() satisfies the kinetic equation
satisfies the kinetic equation
Equation (2.1) results from the normalised full kinetic equation which has been integrated in the other two velocity components, after all the terms small in $\epsilon$![]() have vanished in the limit $\epsilon \rightarrow 0$
have vanished in the limit $\epsilon \rightarrow 0$![]() . The $\epsilon$
. The $\epsilon$![]() -dependent terms are related to the target curvature, collisions and ionisation in the plasma, the magnetic force on the ions and explicit time dependence on the plasma scale $v_{B} / L = \epsilon v_{B} / \lambda _{D}$
-dependent terms are related to the target curvature, collisions and ionisation in the plasma, the magnetic force on the ions and explicit time dependence on the plasma scale $v_{B} / L = \epsilon v_{B} / \lambda _{D}$![]() . By imposing the boundary condition at the sheath entrance $g_{\xi }(\infty, w) = g ( w )$
. By imposing the boundary condition at the sheath entrance $g_{\xi }(\infty, w) = g ( w )$![]() , assuming a perfectly absorbing wall, $g_{\xi }(0, w<0) = 0$
, assuming a perfectly absorbing wall, $g_{\xi }(0, w<0) = 0$![]() , and assuming no ion reflection within the sheath, $g_{\xi }(\xi, w<0) = 0$
, and assuming no ion reflection within the sheath, $g_{\xi }(\xi, w<0) = 0$![]() , one obtains $g_{\xi }(\xi, w) = g ( \sqrt {w^2 - 2\chi } )$
, one obtains $g_{\xi }(\xi, w) = g ( \sqrt {w^2 - 2\chi } )$![]() from (2.1). In order for no ions to be reflected, $\chi (\xi ) \geqslant 0$
from (2.1). In order for no ions to be reflected, $\chi (\xi ) \geqslant 0$![]() is required. For the electrons, a Boltzmann distribution is assumed, which is justified when the sheath reflects most electrons back into the bulk such that ${\rm e}^{-\chi (0)} \ll 1$
is required. For the electrons, a Boltzmann distribution is assumed, which is justified when the sheath reflects most electrons back into the bulk such that ${\rm e}^{-\chi (0)} \ll 1$![]() . Hence, Poisson's equation in the sheath is
. Hence, Poisson's equation in the sheath is
2.2. Matched asymptotic expansion of the ion density near the sheath entrance
In order to solve (2.2) for $\chi (\xi )$![]() locally near the sheath entrance (where $\chi = 0$
locally near the sheath entrance (where $\chi = 0$![]() ), the electron density may be expanded as a Taylor series in $\chi \ll 1$
), the electron density may be expanded as a Taylor series in $\chi \ll 1$![]() , $e^{-\chi } = 1 - \chi + \frac {1}{2}\chi ^2 + O(\chi ^3)$
, $e^{-\chi } = 1 - \chi + \frac {1}{2}\chi ^2 + O(\chi ^3)$![]() . The ion density integral for $\chi \ll 1$
. The ion density integral for $\chi \ll 1$![]() is calculated via a matched asymptotic expansion (see § 7.4 in Bender & Orszag Reference Bender and Orszag1999) hinging on the observation that the function $g ( \sqrt {w^2 - 2\chi } )$
is calculated via a matched asymptotic expansion (see § 7.4 in Bender & Orszag Reference Bender and Orszag1999) hinging on the observation that the function $g ( \sqrt {w^2 - 2\chi } )$![]() can be represented using two different approximations with a common range of validity. For $\bar w = \sqrt {w^2 - 2\chi } \ll 1$
can be represented using two different approximations with a common range of validity. For $\bar w = \sqrt {w^2 - 2\chi } \ll 1$![]() (slow ions), the function $g(\bar w)$
(slow ions), the function $g(\bar w)$![]() is expanded as an asymptotic series in (possibly fractional) powers of $\bar w$
is expanded as an asymptotic series in (possibly fractional) powers of $\bar w$![]() ,
,

where $p \equiv p_1 > -1$![]() (the density should remain finite) is defined to be the smallest power in the expansion of $g(\bar w)$
(the density should remain finite) is defined to be the smallest power in the expansion of $g(\bar w)$![]() near $\bar w = 0$
near $\bar w = 0$![]() , $g_p \equiv g_{p_1} > 0$
, $g_p \equiv g_{p_1} > 0$![]() is the corresponding positive constant coefficient ($g(w) > 0$
is the corresponding positive constant coefficient ($g(w) > 0$![]() ), $p_{\nu } > p_{\nu -1}$
), $p_{\nu } > p_{\nu -1}$![]() is the $\nu$
is the $\nu$![]() th power in the expansion for $\nu > 1$
th power in the expansion for $\nu > 1$![]() and $N_{3+}$
and $N_{3+}$![]() is the index corresponding to the smallest exponent in the expansion satisfying $p_{N_{3+}} > 3$
is the index corresponding to the smallest exponent in the expansion satisfying $p_{N_{3+}} > 3$![]() . By convention, it is considered that $g_{p'} = 0$
. By convention, it is considered that $g_{p'} = 0$![]() for $p'$
for $p'$![]() such that $p_{\nu } \neq p'$
such that $p_{\nu } \neq p'$![]() for all possible values of the index $\nu$
for all possible values of the index $\nu$![]() . The expansion in (2.3) is truncated such that terms $\ll \bar w^3$
. The expansion in (2.3) is truncated such that terms $\ll \bar w^3$![]() are not retained, as these terms will be negligible throughout the subsequent analysis. Note that the form of the distribution function $g(w)$
are not retained, as these terms will be negligible throughout the subsequent analysis. Note that the form of the distribution function $g(w)$![]() near $w=0$
near $w=0$![]() assumed here is much more general than in previous derivations of the kinetic Bohm criterion. For $\bar w \sim w \gg \sqrt {2\chi }$
assumed here is much more general than in previous derivations of the kinetic Bohm criterion. For $\bar w \sim w \gg \sqrt {2\chi }$![]() , $g ( \sqrt {w^2 - 2\chi } )$
, $g ( \sqrt {w^2 - 2\chi } )$![]() can be Taylor expanded near $g(w)$
can be Taylor expanded near $g(w)$![]()

The two approximations (2.3) and (2.4) have a common range of validity $\sqrt {2\chi } \ll w \ll 1$![]() . Therefore, (2.2) can be re-expressed by choosing a cutoff velocity parameter $w_{c}$
. Therefore, (2.2) can be re-expressed by choosing a cutoff velocity parameter $w_{c}$![]() , generally satisfying $\sqrt {2\chi } \ll w_{c} \ll 1$
, generally satisfying $\sqrt {2\chi } \ll w_{c} \ll 1$![]() , and using the approximation (2.3) for $w \leqslant w_{c}$
, and using the approximation (2.3) for $w \leqslant w_{c}$![]() and (2.4) for $w \geqslant w_{c}$
and (2.4) for $w \geqslant w_{c}$![]() . This results in
. This results in

with the zeroth-order, first-order, second-order and slow ion charge densities, respectively, defined by

The quasineutrality condition at the sheath entrance (where $\chi = 0$![]() and $\chi ''=0$
and $\chi ''=0$![]() ) was used in (2.6). The errors $O(\chi ^{3} w_{c}^{p-5}, \chi ^3)$
) was used in (2.6). The errors $O(\chi ^{3} w_{c}^{p-5}, \chi ^3)$![]() in (2.5) result from integrating the errors in (2.4) in the interval $w\in [w_{c}, \infty ]$
in (2.5) result from integrating the errors in (2.4) in the interval $w\in [w_{c}, \infty ]$![]() and from another $O(\chi ^3)$
and from another $O(\chi ^3)$![]() term in the expansion of the electron density. The error $O( \chi w_{c}^{p_{N_{3+}}-1})$
term in the expansion of the electron density. The error $O( \chi w_{c}^{p_{N_{3+}}-1})$![]() comes from the term $\bar Q_{(p_{N_{3+}}+1)/2}$
comes from the term $\bar Q_{(p_{N_{3+}}+1)/2}$![]() which has been neglected in (2.5). The terms $Q_2$
which has been neglected in (2.5). The terms $Q_2$![]() and $\bar Q_{(p_{\nu }+1)/2}$
and $\bar Q_{(p_{\nu }+1)/2}$![]() for $1< p_\nu \leqslant 3$
for $1< p_\nu \leqslant 3$![]() ($N_{1+} \leqslant \nu < N_{3+}-1$
($N_{1+} \leqslant \nu < N_{3+}-1$![]() ) are retained in (2.5), despite being $\ll \chi$
) are retained in (2.5), despite being $\ll \chi$![]() , in anticipation of a higher-order analysis that will be necessary for $p>1$
, in anticipation of a higher-order analysis that will be necessary for $p>1$![]() (see § 2.5). Hall (Reference Hall1962) uses a Taylor expansion instead of the more general expansion in (2.3), thus considering $p=0$
(see § 2.5). Hall (Reference Hall1962) uses a Taylor expansion instead of the more general expansion in (2.3), thus considering $p=0$![]() (and $p_\nu =\nu -1$
(and $p_\nu =\nu -1$![]() ) or $p=1$
) or $p=1$![]() (and $p_\nu =\nu$
(and $p_\nu =\nu$![]() ) while keeping terms up to order $\sim \chi$
) while keeping terms up to order $\sim \chi$![]() , but incorrectly takes $w_{c} \sim \sqrt {2\chi }$
, but incorrectly takes $w_{c} \sim \sqrt {2\chi }$![]() .Footnote 3 Even the more general expansion (2.5) is invalid for $w_{c} \sim \sqrt {2\chi }$
.Footnote 3 Even the more general expansion (2.5) is invalid for $w_{c} \sim \sqrt {2\chi }$![]() and $p\leqslant 1$
and $p\leqslant 1$![]() , since some of the neglected terms are of order $O(\chi ^{3}w_{c}^{p-5})$
, since some of the neglected terms are of order $O(\chi ^{3}w_{c}^{p-5})$![]() , which would be $O(\chi ^{(p+1)/2})$
, which would be $O(\chi ^{(p+1)/2})$![]() just like the dominant terms in (2.5). For (2.5) to have an error $\ll \chi$
just like the dominant terms in (2.5). For (2.5) to have an error $\ll \chi$![]() when $p\leqslant 1$
when $p\leqslant 1$![]() , it is required that $w_{c}$
, it is required that $w_{c}$![]() lie within the asymptotic region of overlap $\chi ^{1/2} \lesssim \chi ^{2/(5-p)} \ll w_{c} \ll 1$
lie within the asymptotic region of overlap $\chi ^{1/2} \lesssim \chi ^{2/(5-p)} \ll w_{c} \ll 1$![]() . In §§ 2.4 and 2.5, it will be seen that the asymptotic region of overlap changes with the value of $p$
. In §§ 2.4 and 2.5, it will be seen that the asymptotic region of overlap changes with the value of $p$![]() and with the order in $\chi$
and with the order in $\chi$![]() of the expansion. However, provided that such a region exists and $w_{c}$
of the expansion. However, provided that such a region exists and $w_{c}$![]() lies within it, the expansion up to the desired order is independent of the value of $w_{c}$
lies within it, the expansion up to the desired order is independent of the value of $w_{c}$![]() .
.
2.3. Evaluation of the charge density
The assumption of an electron-repelling sheath, $\chi (\xi ) \geqslant \chi (\infty ) = 0$![]() , requires that the charge density $\chi ''$
, requires that the charge density $\chi ''$![]() in (2.5) become positive in the sheath. The sign of $\chi ''$
in (2.5) become positive in the sheath. The sign of $\chi ''$![]() is established in the following cases sequentially: $-1< p < 1$
is established in the following cases sequentially: $-1< p < 1$![]() , $p=1$
, $p=1$![]() , $1< p<3$
, $1< p<3$![]() , $p=3$
, $p=3$![]() and $p>3$
and $p>3$![]() , thus covering all $p>-1$
, thus covering all $p>-1$![]() in (2.3). It will be convenient to first evaluate the density contributions (2.7)–(2.9). Equations (2.7) and (2.8) for $Q_1$
in (2.3). It will be convenient to first evaluate the density contributions (2.7)–(2.9). Equations (2.7) and (2.8) for $Q_1$![]() and $Q_2$
and $Q_2$![]() become
become


In (2.10), $N_{1-}$![]() is the index corresponding to the largest exponent in the expansion satisfying $p_{N_{1-}} < 1$
is the index corresponding to the largest exponent in the expansion satisfying $p_{N_{1-}} < 1$![]() , while $N_{1+}$
, while $N_{1+}$![]() is the index corresponding to the smallest exponent in the expansion satisfying $p_{N_{1+}} > 1$
is the index corresponding to the smallest exponent in the expansion satisfying $p_{N_{1+}} > 1$![]() . In (2.11), $N_{3-}$
. In (2.11), $N_{3-}$![]() is the index corresponding to the largest exponent in the expansion satisfying $p_{N_{3-}} < 3$
is the index corresponding to the largest exponent in the expansion satisfying $p_{N_{3-}} < 3$![]() . The derivation of (2.10) and (2.11) uses the following steps: (i) substitute $g(w) = g(w) - \sum _{\nu =1}^{N_{1-}} g_{p_\nu } w^{p_\nu } + \sum _{\nu =1}^{N_{1-}} g_{p_\nu } w^{p_\nu }$
. The derivation of (2.10) and (2.11) uses the following steps: (i) substitute $g(w) = g(w) - \sum _{\nu =1}^{N_{1-}} g_{p_\nu } w^{p_\nu } + \sum _{\nu =1}^{N_{1-}} g_{p_\nu } w^{p_\nu }$![]() in (2.7) and $g(w) = g(w) - \sum _{\nu =1}^{N_{3-}} g_{p_\nu } w^{p_\nu } + \sum _{\nu =1}^{N_{3-}} g_{p_\nu } w^{p_\nu }$
in (2.7) and $g(w) = g(w) - \sum _{\nu =1}^{N_{3-}} g_{p_\nu } w^{p_\nu } + \sum _{\nu =1}^{N_{3-}} g_{p_\nu } w^{p_\nu }$![]() in (2.8); (ii) integrate explicitly the integrals involving $\sum g_{p_\nu } w^{p_\nu }$
in (2.8); (ii) integrate explicitly the integrals involving $\sum g_{p_\nu } w^{p_\nu }$![]() to obtain the terms proportional to $1/ w_{c}^a$
to obtain the terms proportional to $1/ w_{c}^a$![]() with $a>0$
with $a>0$![]() ; (iii) integrate by parts (more than once for (2.8)) the integrals involving $g(w) - \sum g_{p_\nu } w^p$
; (iii) integrate by parts (more than once for (2.8)) the integrals involving $g(w) - \sum g_{p_\nu } w^p$![]() and use (2.3) to extract the boundary terms containing $\ln w_{c}$
and use (2.3) to extract the boundary terms containing $\ln w_{c}$![]() (present if $p_\nu = 1$
(present if $p_\nu = 1$![]() in (2.10) or $p_\nu = 3$
in (2.10) or $p_\nu = 3$![]() in (2.11) for some $\nu$
in (2.11) for some $\nu$![]() ); (iv) split the remaining integrals using $\int _{w_{c}}^{\infty }dw (\ldots ) = \int _{0}^{\infty }dw (\ldots ) - \int _0^{w_{c}} \, {\rm d} w (\ldots )$
); (iv) split the remaining integrals using $\int _{w_{c}}^{\infty }dw (\ldots ) = \int _{0}^{\infty }dw (\ldots ) - \int _0^{w_{c}} \, {\rm d} w (\ldots )$![]() and substitute (2.3) to evaluate the integrals $\int _0^{w_{c}} \, {\rm d} w (\ldots )$
and substitute (2.3) to evaluate the integrals $\int _0^{w_{c}} \, {\rm d} w (\ldots )$![]() . Equation (2.9) for $\bar Q_{(p_{\nu }+1)/2}$
. Equation (2.9) for $\bar Q_{(p_{\nu }+1)/2}$![]() becomes
becomes



where $A_{(p+1)/2}$![]() in (2.12) is defined by
in (2.12) is defined by

Gauss’ test can be used to show that the series in (2.13)–(2.15) are convergent for the given values of $p_{\nu }$![]() .
.
2.4. Electron-repelling potential in Poisson's equation: kinetic Bohm criterion
If $-1 < p< 1$![]() , (2.10) for $Q_1$
, (2.10) for $Q_1$![]() , (2.11) for $Q_2$
, (2.11) for $Q_2$![]() , (2.12) for $\bar Q_{(p+1)/2}$
, (2.12) for $\bar Q_{(p+1)/2}$![]() and (2.12), (2.13) or (2.14) for $\bar Q_{(p_\nu +1)/2}$
and (2.12), (2.13) or (2.14) for $\bar Q_{(p_\nu +1)/2}$![]() with $\nu \geqslant 2$
with $\nu \geqslant 2$![]() are inserted into (2.5) to obtain
are inserted into (2.5) to obtain
This equation is accurate for $\chi ^{1/2} \ll w_{c} \lesssim 1$![]() , where the restriction $w_{c} \ll 1$
, where the restriction $w_{c} \ll 1$![]() is not necessary because the integral in (2.2) is dominated by the region near $w=\sqrt {2\chi }$
is not necessary because the integral in (2.2) is dominated by the region near $w=\sqrt {2\chi }$![]() regardless of whether $g$
regardless of whether $g$![]() is approximated by (2.3) or (2.4) for $w \sim 1$
is approximated by (2.3) or (2.4) for $w \sim 1$![]() . Figure 1 is a plot of the numerical evaluation of $A_{(p+1)/2}$
. Figure 1 is a plot of the numerical evaluation of $A_{(p+1)/2}$![]() as a function of $p \in (-1,1) \cup (1, 3)$
as a function of $p \in (-1,1) \cup (1, 3)$![]() , illustrating that $A_{(p+1)/2} < 0$
, illustrating that $A_{(p+1)/2} < 0$![]() for $p \in (-1,1)$
for $p \in (-1,1)$![]() . This assumed interval for $p$
. This assumed interval for $p$![]() has therefore led to a negative charge density, $\chi '' \leqslant 0$
has therefore led to a negative charge density, $\chi '' \leqslant 0$![]() , in contradiction with an electron-repelling sheath. Hence, the form (2.3) requires $p \geqslant 1$
, in contradiction with an electron-repelling sheath. Hence, the form (2.3) requires $p \geqslant 1$![]() : the distribution function satisfies $g(0^+) = 0$
: the distribution function satisfies $g(0^+) = 0$![]() , corresponding to (1.8), and has a non-divergent (zero or finite) first derivative $g'(0^+)$
, corresponding to (1.8), and has a non-divergent (zero or finite) first derivative $g'(0^+)$![]() .
.

Figure 1. The quantity $A_{(p+1)/2}/(2^{(p+1)/2} g_p)$![]() is plotted as a function of $p$
is plotted as a function of $p$![]() in the intervals $p \in (-1, 1)$
in the intervals $p \in (-1, 1)$![]() and $p \in (1, 3)$
and $p \in (1, 3)$![]() . The asymptotes at $p=-1$
. The asymptotes at $p=-1$![]() , $1$
, $1$![]() and $3$
and $3$![]() are shown as dashed lines. The value of the curve at $p=0$
are shown as dashed lines. The value of the curve at $p=0$![]() and $2$
and $2$![]() is marked.
is marked.
If $p=1$![]() , (2.10) for $Q_1$
, (2.10) for $Q_1$![]() , (2.11) for $Q_2$
, (2.11) for $Q_2$![]() , (2.13) for $\bar Q_{1}$
, (2.13) for $\bar Q_{1}$![]() and (2.12) or (2.14) for $\bar Q_{(p_\nu +1)/2}$
and (2.12) or (2.14) for $\bar Q_{(p_\nu +1)/2}$![]() , $\nu \geqslant 2$
, $\nu \geqslant 2$![]() , are inserted into (2.5) to obtain
, are inserted into (2.5) to obtain
where $A_1$![]() and $B_1$
and $B_1$![]() are defined by
are defined by

Equation (2.17) is accurate for $\chi ^{1/2} \ll w_{c} \ll 1$![]() . This equation, which follows from the assumption $p=1$
. This equation, which follows from the assumption $p=1$![]() , is in contradiction with an electron-repelling sheath, since $B_1 < 0$
, is in contradiction with an electron-repelling sheath, since $B_1 < 0$![]() from (2.19) and $\ln (1/\chi ) \gg 1$
from (2.19) and $\ln (1/\chi ) \gg 1$![]() for $\chi \ll 1$
for $\chi \ll 1$![]() imply that $\chi '' \leqslant 0$
imply that $\chi '' \leqslant 0$![]() . Hence, $p>1$
. Hence, $p>1$![]() is required in (2.3), corresponding to $g'(0^+) = 0$
is required in (2.3), corresponding to $g'(0^+) = 0$![]() . This conclusively proves that condition (1.9) must be satisfied at the sheath entrance.
. This conclusively proves that condition (1.9) must be satisfied at the sheath entrance.
Considering $p>1$![]() and inserting (2.10) for $Q_1$
and inserting (2.10) for $Q_1$![]() , (2.11) for $Q_2$
, (2.11) for $Q_2$![]() , and (2.12) or (2.14) for $\bar Q_{(p_\nu +1)/2}$
, and (2.12) or (2.14) for $\bar Q_{(p_\nu +1)/2}$![]() in (2.5) gives
in (2.5) gives
Only when $p > 1$![]() does the asymptotic expansion of Poisson's equation in (2.5) up to and including terms of order $\sim \chi$
does the asymptotic expansion of Poisson's equation in (2.5) up to and including terms of order $\sim \chi$![]() become accurate for $\sqrt {2\chi } \leqslant w_{c} \ll 1$
become accurate for $\sqrt {2\chi } \leqslant w_{c} \ll 1$![]() , as seen from (2.20) upon enforcing the constraint $w_{c} \geqslant \sqrt {2\chi }$
, as seen from (2.20) upon enforcing the constraint $w_{c} \geqslant \sqrt {2\chi }$![]() arising from (2.2). This is because the part of the integral in (2.2) close to $w=\sqrt {2\chi }$
arising from (2.2). This is because the part of the integral in (2.2) close to $w=\sqrt {2\chi }$![]() is negligible compared with terms of order $\sim \chi$
is negligible compared with terms of order $\sim \chi$![]() irrespective of whether the approximation (2.3) or (2.4) is used there. Hence, the expansion in Hall (Reference Hall1962), which takes $w_{c} \sim \sqrt {2\chi }$
irrespective of whether the approximation (2.3) or (2.4) is used there. Hence, the expansion in Hall (Reference Hall1962), which takes $w_{c} \sim \sqrt {2\chi }$![]() , is correct only when the distribution function and its first derivative vanish at $w=0$
, is correct only when the distribution function and its first derivative vanish at $w=0$![]() , just like the expansion in Harrison & Thompson (Reference Harrison and Thompson1959) which was criticised by Hall. For (2.20) to be compatible with an electron-repelling sheath, the condition $\int _{0}^{\infty } \ln (1/w) g'' ( w ) \, {\rm d} w < 1$
, just like the expansion in Harrison & Thompson (Reference Harrison and Thompson1959) which was criticised by Hall. For (2.20) to be compatible with an electron-repelling sheath, the condition $\int _{0}^{\infty } \ln (1/w) g'' ( w ) \, {\rm d} w < 1$![]() is required, which is the dimensionless form of (1.10) without the equality. In order to prove (1.10), and consequently (1.3), it must still be verified that if the equality holds,
is required, which is the dimensionless form of (1.10) without the equality. In order to prove (1.10), and consequently (1.3), it must still be verified that if the equality holds,
the higher-order terms in (2.20) are consistent with an electron-repelling sheath solution with $\chi (\xi ) \geqslant 0$![]() .
.
2.5. Higher-order analysis for marginally satisfied kinetic Bohm criterion
If $1< p<3$![]() , inserting (2.10) for $Q_1$
, inserting (2.10) for $Q_1$![]() , (2.11) for $Q_2$
, (2.11) for $Q_2$![]() , (2.12) for $\bar Q_{(p+1)/2}$
, (2.12) for $\bar Q_{(p+1)/2}$![]() , (2.12) or (2.14) for $\bar Q_{(p_\nu +1)/2}$
, (2.12) or (2.14) for $\bar Q_{(p_\nu +1)/2}$![]() with $\nu \geqslant 2$
with $\nu \geqslant 2$![]() and (2.21) in (2.5) leads to
and (2.21) in (2.5) leads to
This equation is accurate for $\chi ^{1/2} \ll w_{c} \ll \chi ^{(p-1)/[2(p_{N_{3+}}-1)]}$![]() . From figure 1 it is seen that $A_{(p+1)/2} > 0$
. From figure 1 it is seen that $A_{(p+1)/2} > 0$![]() for $1< p<3$
for $1< p<3$![]() , which makes (2.22) consistent with a positive space charge, $\chi '' \geqslant 0$
, which makes (2.22) consistent with a positive space charge, $\chi '' \geqslant 0$![]() . If $p = 3$
. If $p = 3$![]() , inserting (2.10) for $Q_1$
, inserting (2.10) for $Q_1$![]() , (2.11) for $Q_2$
, (2.11) for $Q_2$![]() , (2.14) for $\bar Q_{2}$
, (2.14) for $\bar Q_{2}$![]() , (2.12) for $\bar Q_{(p_\nu +1)/2}$
, (2.12) for $\bar Q_{(p_\nu +1)/2}$![]() with $\nu \geqslant 2$
with $\nu \geqslant 2$![]() and (2.21) into (2.5) gives (note that $p=p_1 = 3$
and (2.21) into (2.5) gives (note that $p=p_1 = 3$![]() implies $N_{3+} = 2$
implies $N_{3+} = 2$![]() )
)
with

Equation (2.23) is accurate for $\chi ^{1/2} \ll w_{c} \ll \chi ^{1/(p_2-1)}$![]() , with $p_2 > 3$
, with $p_2 > 3$![]() , and is again consistent with a positive space charge, since $B_2 > 0$
, and is again consistent with a positive space charge, since $B_2 > 0$![]() from (2.25). If $p>3$
from (2.25). If $p>3$![]() , inserting (2.10) for $Q_1$
, inserting (2.10) for $Q_1$![]() , (2.11) for $Q_2$
, (2.11) for $Q_2$![]() , (2.12) for $\bar Q_{(p_\nu +1)/2}$
, (2.12) for $\bar Q_{(p_\nu +1)/2}$![]() and (2.21) into (2.5) gives
and (2.21) into (2.5) gives
Equation (2.26) requires $\sqrt {2\chi } \leqslant w_{c} \ll \chi ^{1/(p-1)}$![]() to be accurate. In (2.27), Schwartz's inequality and the equalities (2.6) and (2.21) constrain $\int _{0}^{\infty } \, {\rm d} w g ( w ) / w^4 \geqslant 1$
to be accurate. In (2.27), Schwartz's inequality and the equalities (2.6) and (2.21) constrain $\int _{0}^{\infty } \, {\rm d} w g ( w ) / w^4 \geqslant 1$![]() (Riemann Reference Riemann1991), such that $A_2 > 0$
(Riemann Reference Riemann1991), such that $A_2 > 0$![]() . Equation (2.26) is compatible with an electron-repelling sheath, and exhausts all possible remaining values of $p$
. Equation (2.26) is compatible with an electron-repelling sheath, and exhausts all possible remaining values of $p$![]() . This completes the proof that an electron-repelling sheath solution (with adiabatic electrons) exists if (1.8)–(1.10), which can be combined into (1.3), are satisfied.
. This completes the proof that an electron-repelling sheath solution (with adiabatic electrons) exists if (1.8)–(1.10), which can be combined into (1.3), are satisfied.
3. Discussion and conclusion
The physical interpretation of the kinetic Bohm criterion (1.3) in the limit $\epsilon \rightarrow 0$![]() is as follows. When entering the sheath, slower ions undergo a much larger relative velocity increment than faster ions for a given potential drop, and by continuity they have a larger contribution to the ion density drop. Hence, for mono-energetic ions there is a threshold velocity (1.2) above which the ion density drop is less than the electron density drop, consistent with the positive space charge expected in the sheath. Similarly, with an arbitrary velocity distribution instead of a mono-energetic one, conditions (1.8) and (1.9) limit the number of slow ions with $v_x \approx 0$
is as follows. When entering the sheath, slower ions undergo a much larger relative velocity increment than faster ions for a given potential drop, and by continuity they have a larger contribution to the ion density drop. Hence, for mono-energetic ions there is a threshold velocity (1.2) above which the ion density drop is less than the electron density drop, consistent with the positive space charge expected in the sheath. Similarly, with an arbitrary velocity distribution instead of a mono-energetic one, conditions (1.8) and (1.9) limit the number of slow ions with $v_x \approx 0$![]() to ensure that the ion density drop scales linearly with the potential drop, like the electron density drop, and not more strongly. Condition (1.3) then results from requiring that the ion density drop be smaller than the electron one. At this point, it should be unsurprising that slow ions with $|v_x| \ll v_{B}$
to ensure that the ion density drop scales linearly with the potential drop, like the electron density drop, and not more strongly. Condition (1.3) then results from requiring that the ion density drop be smaller than the electron one. At this point, it should be unsurprising that slow ions with $|v_x| \ll v_{B}$![]() have a larger weight in this condition, forcing the bulk ions to compensate by moving faster towards the wall and causing the over-satisfaction of (1.2).
have a larger weight in this condition, forcing the bulk ions to compensate by moving faster towards the wall and causing the over-satisfaction of (1.2).
If it is desirable to formulate (1.3) in terms of the actual distribution function $f_{\epsilon }$![]() , this can be done carefully as follows. Presuming that $f_\epsilon$
, this can be done carefully as follows. Presuming that $f_\epsilon$![]() is, just like its limit $f$
is, just like its limit $f$![]() in (1.6), differentiable at $v_x = 0$
in (1.6), differentiable at $v_x = 0$![]() , the two conditions (1.8) and (1.9) imply that $f_{\epsilon }(0) \sim \epsilon ^{r_1(q)} n_{e} / Z v_{B}$
, the two conditions (1.8) and (1.9) imply that $f_{\epsilon }(0) \sim \epsilon ^{r_1(q)} n_{e} / Z v_{B}$![]() and $f_{\epsilon }'(0) \sim \epsilon ^{r_2(q)} n_{e} / Z v_{B}^2$
and $f_{\epsilon }'(0) \sim \epsilon ^{r_2(q)} n_{e} / Z v_{B}^2$![]() , where $r_1(q) > 0$
, where $r_1(q) > 0$![]() and $r_2(q) > 0$
and $r_2(q) > 0$![]() depend on $q$
depend on $q$![]() in $x_{\epsilon } = \epsilon ^q L$
in $x_{\epsilon } = \epsilon ^q L$![]() . The small additional number of slow ions with $v_x \approx 0$
. The small additional number of slow ions with $v_x \approx 0$![]() at $x_{\epsilon }$
at $x_{\epsilon }$![]() is due to the replenishment of ions with $v_x \geqslant 0$
is due to the replenishment of ions with $v_x \geqslant 0$![]() occurring in the small region $x \in [0, x_{\epsilon }]$
occurring in the small region $x \in [0, x_{\epsilon }]$![]() , caused for example by rare (vanishing for $\epsilon \rightarrow 0$
, caused for example by rare (vanishing for $\epsilon \rightarrow 0$![]() ) collision or ionisation events in this region. Integrating the third condition (1.10) by parts twice gives
) collision or ionisation events in this region. Integrating the third condition (1.10) by parts twice gives
If the limits on the left-hand side of (3.1) are interchanged, all terms diverge; without the interchange, the second and third terms vanish by (1.8) and (1.9), recovering (1.3). The left-hand side of (1.7) results from interchanging the limits in (3.1) without retrieving the additional terms that no longer vanish (and diverge) after the interchange. The limits in (3.1) can be combined without interchange by taking $v_x = - v_{\epsilon }$![]() with $v_{\epsilon } = \epsilon ^r v_{B}$
with $v_{\epsilon } = \epsilon ^r v_{B}$![]() and $r \in (0,r_1(q))$
and $r \in (0,r_1(q))$![]() , such that $\lim _{\epsilon \rightarrow 0} f_\epsilon (-v_\epsilon ) / v_\epsilon = 0$
, such that $\lim _{\epsilon \rightarrow 0} f_\epsilon (-v_\epsilon ) / v_\epsilon = 0$![]() and $\lim _{\epsilon \rightarrow 0} f'_\epsilon (-v_\epsilon ) \ln (1/v_\epsilon ) = 0$
and $\lim _{\epsilon \rightarrow 0} f'_\epsilon (-v_\epsilon ) \ln (1/v_\epsilon ) = 0$![]() . This allows subsuming conditions (1.8), (1.9) and (3.1) into the single conditionFootnote 4
. This allows subsuming conditions (1.8), (1.9) and (3.1) into the single conditionFootnote 4
A small number (vanishing for $\epsilon \rightarrow 0$![]() ) of slow ions with $|v_x| < v_{\epsilon }$
) of slow ions with $|v_x| < v_{\epsilon }$![]() are ignored in (3.2) because their contribution to the density drop would be sharply overestimated due to the neglect of their replenishment in the region $x \leqslant x_{\epsilon }$
are ignored in (3.2) because their contribution to the density drop would be sharply overestimated due to the neglect of their replenishment in the region $x \leqslant x_{\epsilon }$![]() . Yet, the form of (3.2) confirms the importance of slow ions with $|v_x| \ll v_{B}$
. Yet, the form of (3.2) confirms the importance of slow ions with $|v_x| \ll v_{B}$![]() in the kinetic Bohm criterion.
in the kinetic Bohm criterion.
Acknowledgements
Editor Peter Catto thanks the referees for their advice in evaluating this article.
Declaration of interest
The authors report no conflict of interest.
Funding
This work has been carried out within the framework of the EUROfusion Consortium, via the Euratom Research and Training Programme (Grant Agreement No 101052200 – EUROfusion) and funded by the Swiss State Secretariat for Education, Research and Innovation (SERI). Views and opinions expressed are, however, those of the author(s) only and do not necessarily reflect those of the European Union, the European Commission or SERI. Neither the European Union nor the European Commission nor SERI can be held responsible for them.