Climate on the equilibrium line altitudes of glaciers: theoretical background behind Ahlmann's P/T diagram

Abstract

The climatic condition that prevails at a glacier equilibrium line altitude (ELA) is often parameterized in terms of summer air temperature (T) and annual precipitation (P). This simple parameterization was initially proposed by Hans W:son Ahlmann. The physical background of the relationship between P and T on the equilibrium line, however, has been left unexplained since Ahlmann first questioned the mathematical form of the relationship. This relationship can be explained when the thermal and hydrological processes of the ELA formation are investigated. The present authors studied the energy exchange processes that prevail on the ELA during the melt season. The inclusion of solar radiation brings Ahlmann's hypothesis closer to energy balance, and improves his P/T diagram. By comparing the observed fluxes from the polar through the mid-latitude to the equatorial glaciers, it was found that these glaciers in different climatic regions share important similarities at the ELA. Further, it was found that the classic P/T curve originally proposed by Ahlmann in the early 20th century is a concise expression of the conservation principle of energy and mass at the ELA of glaciers, and takes the form of a polynomial of the fourth order.

1. INTRODUCTION

The line or a zone on a glacier where the surface annual mass balance converges to zero is defined as the equilibrium line, and its altitude above the mean sea level is the equilibrium line altitude (ELA) (Cogley and others, 2011). Traditionally, glaciologists tended to consider the ELA in terms of the mean ELA averaged over a certain period, which was long enough to be climatic.

The ELA by definition divides the glacier surface into an accumulation and ablation area. This implies that the ELA represents the lowest boundary of the climatic glacierization, the existence of the ablation area being the consequence of the ice rheology. For the existence of glaciers, it is necessary that the ELA lies below topographic and glacier surfaces. Consequently, the upper limits of the lateral and medial moraines lie very close to the equilibrium line, a feature which is used in quaternary geology to estimate the ELA of the past (Hantke, 1978; Ballantyne, 1989). If the ELA is lifted above the highest bedrock or ice surface topography as a result of climate change, the glacier is doomed to disappear.

The ELA is also a useful concept as it is closely related to the annual mass balance. Where information of annual mass balance is lacking, the ELA provides an alternative way of estimating the annual mass balance (Liestøl, 1967; Paterson, 1969; Koerner, 1970; Schytt, 1981; Kulkarni, 1992; Seversky, 1997; Nesje and Dahl, 2000). This aspect also offers a method to estimate the change in mass balance as a result of climate change (Bradley, 1975; Kuhn, 1980, 1989; Ambach, 1989, 1993). Further, the altitudinal distributions of the annual mass balance, and especially of the summer balance, show the largest variations at or near the ELA (Ohmura and others, 1992). These features can be exploited to identify the ideal location for monitoring the atmosphere on the glacier in order to predict the meltwater discharge for agricultural irrigation and hydroelectric power generation. Therefore, the parameterization of the ELA is of primary importance not only for the theory of the glacier/climate relationship but also for applications such as water economy.

The glacier/climate relationship on the ELA was first expressed as a relationship between precipitation (P) and temperature (T) by Ahlmann (1924), in the form of what was later called the Ahlmann's P/T diagram. The diagram indicated a non-linear relationship between precipitation and temperature, which Ahlmann himself questioned. He considered two possible forms of the relationship, a second-order polynomial and exponential functions. Later workers also noticed the non-linearity of the relationship, and came up with an exponential curve (Ballantyne, 1989) and various polynomials (Kotlyakov and Krenke, 1982; Ohmura and others, 1992; Krenke and Khodakov, 1997). Andrews (1975) fitted the curve with three different straight line segments. More recently, Nesje and Dahl (2000) again used exponential curves. Authors used their intuition for selecting a function and fitting regression lines based on statistical means. The physical processes on ELAs, hence the physically based mathematical form of the function, have been left unidentified up to the present.

The objective of the present paper is (1) to examine the P/T relationship for the glaciers under diverse physical conditions, (2) to investigate the climatic conditions that determine the mean ELA with more abundant data of higher quality and (3) to present the main physical processes on ELAs in order to identify a mathematical form of the P/T diagram based on the theory of mass and energy conservation.

2. THE DEVELOPMENT OF ELA PARAMETERIZATION

2.1. Choice of parameters

The meteorological elements used in the present work are air temperature, precipitation and global solar radiation, three quantities that represent three major terms in the energy-balance equation for the glacier surface, as will be detailed later. Prior to the knowledge of the energy balance, the importance of temperature and precipitation was already known in the second half of the 19th century (Forbes, 1853; Hann, 1883). Forel and others (1909) and Maurer (1914) thought solar radiation to be a secondary but non-negligible heat source. It was however Ahlmann (1924) who characterized the ELA numerically by using temperature and precipitation, but abandoned solar radiation as unconvincing. The present paper demonstrates that all three elements are necessary.

For the air temperature, the free atmospheric temperature is preferred to the local temperature on the glacier. Lang (1968) reported a higher correlation between the melt and the air temperature measured outside the glacier. Using an extra-glacier temperature was also chosen later by Vincent (2002), Mernild and others (2013) and Pelto and others (2013). The present authors credit this tendency to the difficulty of defining the optimal temperature on the glacier owing to the strong temperature gradient near the glacier surface with respect to height and the horizontal expanse. Considering the temperature distribution over the glacier as the problem of turbulent heat diffusion, under the lower boundary condition of the melting temperature of the ice surface, which is constant, and the upper and lateral boundary conditions of external air, the temperature measured outside the direct glacier influence can be considered as the boundary conditions. Since the surface temperature is constant, the external air temperature becomes a sole factor to determine the solution. The air temperature between the glacier surface and the upper and lateral boundaries of the considered air volume becomes a solution with a strong vertical and horizontal gradient, which is impractical to characterize the glacier climate. In fact, if one approaches the glacier surface close to the roughness length, the air temperature is expected to become the melting point, and loses information on the energy fluxes. The external boundary condition is a more stable information-carrying parameter. The adoption of the free atmospheric temperature has another advantage compared with the near-glacier surface temperature. The free atmospheric temperature is much more easily and widely available, and also saves the cumbersome and uncertain task of downscaling (Ohmura and others, 1992), as is also shown by Rasmussen and Wenger (2009). The mean temperature of the three summer months of June, July and August (December, January and February for the Southern Hemisphere) is used as most of the annual ablation for the majority of glaciers at the ELA occurs during these three months.

For precipitation, the annual total precipitation represents annual accumulation better than the winter precipitation alone as precipitation in summer is often solid at high altitudes (Ahlmann, 1922; Müller-Lemans and others, 1993, 1997; Seversky, 1997; Braithwaite, 2008; Barrueto, 2009). Further, summer precipitation suppresses the melt through the higher albedo, larger cloud amount and lower air temperature (Ohmura and others, 1992). There are also regions where the main accumulation happens in summer, as in the interior of the Asian continent and the tropical Andes (Ohmura and others, 1990; Kang and others, 1996). These facts support the choice of annual precipitation rather than the winter accumulation or precipitation alone.

The present work chose annual precipitation as in the original works by Ahlmann (1922, 1924). However, the authors consider the possibility of a partial loss of the summer precipitation from the accumulation when it falls as liquid precipitation. To investigate the influence of the liquid precipitation on annual accumulation, the liquid precipitation at high-altitude observatories was evaluated, where the type and amount of the precipitation were observed by observers. The measured liquid precipitation at high-altitude stations is presented in Table 1, along with other information that helps to interpret the effect of the liquid precipitation on mass balance. When the observatory is located more than 200 m below the mean ELA, a temperature correction with a lapse rate of 0.65 K/100 m (Fliri, 1975; Schüepp and others, 1978; Auer and others, 2001) and liquid portion correction of 8%/K (Ohmura and others, 1999) was applied. The present survey shows that on an average, 9% of the annual total precipitation fell in liquid form at ELA during the summer. Although a part of the liquid precipitation might remain in the snow and firn layers as superimposed ice, this amount should be born in mind as a potential loss that would be unaccounted for as a contribution to the accumulation.

Table 1. Liquid precipitation observed at manned observatories near glacier equilibrium line altitudes. When the differences of the station altitude and ELA were more than 200 m, the temperature was corrected in accordance with the summer mean lapse rate of the region. The observed temperature before the correction is presented in the brackets

Sources: (1) Auer and others (2002); (2) Kang and others (1996); (3) Ohmura and others (1990); (4) Ohmura (1991); (5) Ohmura (1992); (6) Taylor-Alt (1975); (7) Chinese Meteorological Administration; (8) Austrian Meteorological and Geophysics Service; (9) German Weather Service; (10) Swiss Meteorology and Climatology Office.

Another possibility for estimating the annual precipitation at the ELA is a unique method proposed by Braithwaite and others (2006) and Braithwaite (2008). Braithwaite's method consists of estimating the annual melt based on the positive degree-days at ELA, which by definition must be the same as the annual accumulation. The uncertainty of this method is the variability of the degree-day coefficient. Once this problem is clarified, the present authors consider Braithwaite's method as a powerful method for estimating annual precipitation for high altitudes.

When Ahlmann (1924) presented the precipitation (ordinate) and temperature (abscissa) diagram (1924, P/T diagram in Fig. 5, P. 264), the relationship showed a certain scatter around the best-fit curve. Later works, for example, Loewe (1971) and Ohmura and others (1992), had an even larger scatter, mainly because more glaciers from much larger regions with diverse climatic conditions were considered. The authors realized that the adoption of a third variable besides P and T would reconcile the scatter in a systematic manner. This third variable was found to be solar global radiation (Forel and others, 1909; Maurer, 1914; Loewe, 1971; Ohmura and others, 2007).

2.2. Source for glaciological data

A single most comprehensive source of the surface mass balance and ELA is the ten volumes of Fluctuations of Glaciers, started by Kasser (1967), succeeded by Müller (1977), Haeberli and others (1985) and continued by Zemp and others (2011, 2012) (WGMS, 2012; World Glacier Monitoring Service). This series contains data covering the 51 years from 1959 to 2010. However, the series of publications was regularly updated with data older than 1959 that became newly available. The oldest mass balance and ELA published in this series is that of the Taku Glaciers starting in 1945. The information related to this series is available at http://wgms.ch/glacierapp/. Supplementary data are obtained from the series of 12 issues of Glacier Mass-Balance Bulletin started by Haeberli and Herren (1991) and continued to WGMS (2013) covering the period of 24 years from 1988 to 2011. The data for more recent years after Vol. 12 are available in WGMS (2015) under the new series title of Global Glacier Change Bulletin, and also directly from the WGMS. The current data at WGMS are available at http://wgms.ch/ggcb/. However, the data available from the website are by no means accurate and complete, and require corrections and amendments for which the glaciology community can contribute. There are a few other sources at the national level, for example, the results of the mass-balance survey published in Glasiologiske Undersökelser i Norge (Glaciological investigations in Norway) for glaciers in Norway, starting with Østrem and Liestøl (1964) and continued to Kjøllmoen (2011). The longest series of observation contained in this series is from Storbreen starting in 1949. Many research groups publish the results of the observations carried out during their projects, which often contain detailed information on mass balance and ELA (e.g. Cogley and others, 1995, for the White Glacier and Baby Glacier; Escher-Vetter and others, 2012, for Vernagtferner). For some glaciers, the pre-publication data of the mass balance and ELA were made available, for example, for Hofsjökull by T. Thorsteinsson of Icelandic Meteorological Service and for Langjökull by F. Pálsson of the University of Iceland. The oldest and the longest mass-balance/ELA observation (starting in 1914/15) has been carried out on Claridenfirn in the Glarner Alps by four generations of meteorologists at the Swiss Federal Office of Meteorology and Climatology where the data are available.

The mass-balance data are often re-evaluated after the publications. The authors encountered up to four different mass-balance evaluations for the same glacier. This sort of situation is not uncommon working with the mass-balance data. Usually, there is a legitimate reason for the re-evaluation, which makes usually the later re-evaluations better in quality. One of the important re-evaluations of the annual data is made by adjusting the annual data against geodetic survey. Some examples are the White Glacier on Axel Heiberg Island (Cogley and others, 1995; Thomson and others, 2017), Storglaciären in Sweden (Holmlund and others, 2005) and ten Norwegian glaciers (Andreassen and others, 2016, http://glacier.nve.no/viewer/CI/en/). Whenever necessary, the authors consulted the scientists involved in the original observations, evaluations and the subsequent re-evaluations for clarifying the reasons for the differences. The mean ELA and winter balance (B _w), which are averaged over the available period of the data, are presented in Table 2.

Table 2. Equilibrium line altitude (ELA), temperature, precipitation, global solar radiation and their sources

Data sources for mass balance and precipitation.

(1) Hattersley-Smith and Serson (1970); (2) Koerner (1979); (3) Sagar (1964); (4) Arnold (1968); (5) Kasser (1967); (6) Weiss (1984); (7) Alean (1977); (8) Kraus (1983); (9) Koerner (1966); (10) Müller (1977); (11) Mokievsky-Zubok and others (1985); (12) Schytt (1955); (13) Benson (1962); (14) H. Thomsen (personal communication); (15) Olesen (1986); (16) Weidick and Thomsen (1986); (17) R. Braithwaite (personal communication); (18) H. Björnsson (personal communication); (19) J. Dowdeswell (personal communication); (20) Meier and others (1971); (21) Tangborn and others (1977); (22) Marcus (1964); (23) Haeberli (1985); (24) Mokievsky-Zubok and others (1985); (25) Moser and others (1986); (26) Hoinkes (1970); (27) Kuhn (1981); (28) Funk (1985); (29) Funk and Alean (unpublished note); (30) Fujii and others (1976); (31) Ageta and Satow (1978); (32) Yasunari and Inoue (1978); (33) Timmis (1986); (34) Xie (1984); (35) Haeberli and Müller (1988); (36) IAHS/UNEP/UNESCO (1993); (37) IAHS/UNESCO (1998); (38) IUGG(CCS)/UNEP/UNESCO (2005); (39) Haeberli and others, Ed. (2008); (40) WGMS (2012); (41) Haeberli and Herren (1991); (42) Haeberli and others (1993); (43) Haeberli and others (1994); (44) Haeberli and others (1996); (45) Haeberli and others (1999); (46) Haeberli and others (2001); (47) Haeberli and others (2003); (48) Haeberli and others (2005); (49) Haeberli and others (2007); (50) Haeberli and others (2009); (51) WGMS (2011); (52) WGMS (2013); (53) WGMS (2015); (54) Kjøllmoen (2011); (55) Dyurgerov (2002); (56) Bessemoulin (1989); (57) Lundqvist (1953); (58) Hansen and others (2008); (60) T. Thorsteinsson (personal communication); (61) F. Pálsson (personal communication); (62) Higuchi and others (1982); (63) Böhm and Hiebl (2011/12); (64) H. Müller (personal communication); (65) Huss and others (2008); (66) A. Bauder (personal communication); (67) Cogley and others (1995); (68) Liu and others (2003); (69) Jin and Wang (2002); (70) Buffoni and Chlistovsky (1992); (71)) Service de la Météorologie, Québec (1978); (72) Atmospheric Environment Service of Canada (1984–1988); (73) Buffoni and others (1999); (74) Alpine Precipitation Grid Dataset (Isotta and others, 2014); (75) Agencia Estatal de Meteorologia, Madrid; (76) Icelandic Meteorological Office; (77) Norwegian Meteorological Institute; (78) Wang and others (2009); (79) Wang and others (2010); (80) Pelto and others (2013); (81) Müller-Lemans and others (1997); (82) Auer and others (2002); (83) Gerlitz and others (2016).

Data sources for solar global radiation.

(1) Atmospheric Environment Service (1982); (2) Sagar (1964); (3) Marshunova and Chernigovskiy (1971); (4) Andrews (1964); (5) Havens (1964); (6) Ohmura (1982); (7) Ohmura (1981); (8) Ohmura (1977); (9) Holmgren (1971); (10) Ambach (1963); (11) Ambach (1977); (12) Budyko (1963); (13) Braithwaite and Olesen (1984); (14) Young and Stanley (1976a); (15) Young and Stanley (1976b); (16) Mokievsky-Zubok and Stanley (1976b); (17) Mokievsky-Zubok and Stanley (1976a); (18) Palz and others (1979); (19) Ambach (1955); (20) Moser and others (1986); (21) Escher-Vetter (1985); (22) Kuhn (1981); (23) Wagner (1979); (24) Funk (1985); (25) Wang and others (2009); (26) Bai and others (1985); (27) Higuchi (1977); (28) Mani (1980); (29) Shanklin (1981); (30) Japanese Antarctic Research Expedition (1985); (31) Schwerdtfeger (1984); (32) Global Atmospheric Watch (GAW); (33) ECAHAM4-T106; (34) Escher-Vetter (1985); (35) Service de la Météorologie, Québec (1978); (36) Wild and others (2017); (37) Auer and others (2002).

Abbreviations for the organizations carrying out the mass balance observations.

AARI, Arctic and Antarctic Research Institute, Sankt Petersburg; ANARE, Australian National Antarctic Research Expeditions; ARC, Antarctic Research Centre, Wellington; ASGSSR, Academy of Sciences of Georgian SSR; ASKASSR, Institute of Geography, Academy of Sciences Kazakh SSR; ASKISSR, Tienshan Physical Geographical Station, Academy of Sciences of Kyrgyzstan SSR; CAIAG, Central Asian Institute of Applied Geosciences, Bishkek, Kyrgyzstan; CGI, Comitato Glaciologico Italiano, Torino; CNRS, Laboratory of Glaciology and Environmental Geophysics, Domaine Universitaire; CRREL, Cold Regions Research and Engineering Laboratory, Hanover, NH; DGGS, Department of Geography and Geology, University of Salzburg; DRB, Defence Research Board, Ottawa; DVNTS, Institute of Volcanology and Seismology, Far Eastern Branch, Russian Academy of Sciences; EPN, Escuela Politécnica Nacional, Quito; GGU, Geological Survey of Denmark and Greenland; Ingenieria 75 S.A., Madrid; IAA-DNA, Instituto Antártico Argentino, Dirección Nacional del Antártico, Buenos Aires; IDEAM, Institute for Hydrology, Meteorology and Environmental Studies, Bogota; IGAN, Institute of Geography, Academy of Sciences, Moscow; IHH, Instituto de Hidráulica e Hidrologia, Universidad Mayor de San Andrés, La Paz; IIMR, Institute of Interdisciplinary Mountain Research, Austrian Academy of Sciences, Innsbruck; IMGUI, Institute of Meteorology and Geophysics, University of Innsbruck; IMO, Icelandic Meteorological Service; IMONT, Italian Mountain Institute, Roma; INRENA, Unidad de Glaciología y Recursos Hídricos, Huaraz; ITPR, Institute of Tibetan Plateau Research, Chinese Academy of Sciences; JIRP, Jeneau Icefield Research Program, Nichols College; KGBAW, Commission of Glaciology, Bavarian Academy of Sciences, Munich; LIGG, Lanzhou Institute of Glaciology and Geocryology; MMA, Dirección General del Agua, Ministerio de Medio Ambiente, Madrid; MSC, Meteorological Service of Canada; NCD, Nichols College, Dudley, MA; NIWAR, National Institute of Water and Atmospheric Research, Christchurch; NPCR, National Power Company Reykjavik; NPI, Norwegian Polar Institute; NPSNC, North Cascades National Park; PAS, Polish Academy of Sciences; PCSP, Polar Continental Shelf Project, Ottawa; SANIIM, Central Asian Hydrometeorological Research Institute, Tashkent; SES, School of Environmental Science, Jawaharlal Nehru University, New Delhi; SMI, Società Meteorologica Italiana, Bussoleno; SPRI, Scott Polar Research Institute, Cambridge; TGU, Laboratory of Glacioclimatology, Tomsk State University; UAF, University of Alaska Fairbanks; UI/HA, Ufficio Idrografico/Hydrologisches Amt, Bolzano(Bozen); UFC, Universite de Franche Comté/CNRS Besançon; UGMS-NC, Hydrometeorological and Environmental Monitoring, Administration – North Caucasus; UNC, Universidad Nacional de Córdoba, Córdoba, Argentina; UPM, Departamento de Matemática Aplicada, Universidad Politécnica de Madrid; UW, Department of Atmospheric and Oceanic Sciences, University of Wisconsin; VAW, Institute of Hydraulics, Hydrology & Glaciology, ETH Zurich; WGMS, World Glacier Monitoring Service, Zurich; WRI, Water Resources Institute, University of Nagoya; ZAMG, Central Bureau of Meteorology and Geodynamics, Vienna.

2.3. Source for meteorological data

The free atmospheric temperature at the ELA was extracted from ERA-Interim Reanalysis (Dee and others, 2011). The temperature in the Antarctic coastal zones in the ERA-Interim is, however, greatly underestimated due to the inaccuracy of the model topography. For this zone, the climatological maps of the Free University of Berlin were used (Scherhag, 1969). There are at present no re-analyses that can reproduce precipitation accurately. The observed annual total precipitation near ELAs is available in limited cases from the national meteorological networks (e.g. glaciers in the Hohe Tauern in Austria, and in the eastern Swiss Alps). The observations made at high altitudes are also available in HISTALP (Historical Instrumental climatological Surface Time series of the greater Alpine region, Auer and others, 2007) and APGD (Alpine Precipitation Grid Dataset, Isotta and others, 2014), but direct observations near the ELA are rare, simply because there are few observatories and projects at such locations lasting long enough to provide climatic data. In the present paper, the measurements made by automatic stations are excluded, as the accuracy of the automatic stations at high altitudes is highly uncertain (Auer, 1992; Müller-Lemans and others, 1993; 1997; Barrueto, 2009). The best alternative for the annual precipitation at ELA, which is adopted in the present work, is to sum the winter accumulation (B _w) at the equilibrium line and the precipitation measured during summer at an altitude close to ELA (Ohmura and others, 1992; Braithwaite, 2008). Although the observations of annual precipitation at high altitudes are rare, there are a few observations made in summer, as many glaciological summer campaigns measure precipitation at high altitudes (e.g. Ohmura and Müller, 1978; Weber, 1997; WGMS, 2015). Only when the summer precipitation was not available, but winter accumulation was thought to be reliable, the ERA-Interim monthly precipitation from May to September (October to March in the Southern Hemisphere) was used in place of the locally measured summer precipitation. The present study, however, showed that the ERA-Interim underestimated precipitation by 17–40% for the glacierized regions, as indicated in columns 6 and 9 in Table 2. ERA-Interim evaluation presented by de Leeuw and others (2015) found a mean underestimation of 22% based on a comprehensive study for Great Britain. Therefore, when the ERA-Interim summer precipitation was used, it was increased by 22%.

As stated earlier in Section 2.1, the present work introduces solar global radiation as the third variable. This decision is based on the ten energy-balance measurements summarized in Section 3.2, which shows that solar radiation is the second largest heat source for the melt on all glaciers. The largest collection of solar global radiation is available in the Global Energy Balance Archive (GEBA, a part of Baseline Surface Radiation Network/World Climate Research Program and Global Climate Observing System) at E.T.H. Zurich. Presently, GEBA harbors monthly global solar radiation for ~1700 sites (Wild and others, 2017). The observation sites are dense enough for the present purpose for the Alps, Scandinavia and polar regions. For the radiation with more than 1000 m altitude difference, a correction was applied with the assumption of the vertical radiation gradient of +1 W m⁻²/100 m (Marty, 2000). The radiation from the areas with sparse observational networks, such as the high mountain regions of Asia, Latin America and Africa, global solar radiation was obtained from the GCM simulation with ECHAM4 T106. The shortwave irradiance simulated by ECHAM4 T106 was found to come closest to the observed values among all GCMs that participated in the Atmospheric Model Inter-comparison Program, AMIP II (Wild and others, 1998). Radiation data sources are presented for each glacier in Table 2.

3. NEW P/T DIAGRAM AND ENERGY BALANCE ON ELA DURING THE MELT SEASON

3.1. New P/T diagram based on selected glaciers

Out of more than 130 glaciers that have medium- to long-term observations of winter and summer balances and ELA, 104 glaciers with proximity to manned meteorological observations were selected (Table 2). The glaciers were also selected to represent major glacierized regions of the world. The geographical distribution of the 104 glaciers and their mean ELAs are illustrated in Figure 1. The new P/T diagram was constructed based on the data from 104 glaciers presented in Table 2, and illustrated in Figure 2. The correlation coefficient is 0.73, while the coefficient of determination is 0.63. Table 2 also contains all glaciological and meteorological data sources discussed in Section 2. The least-square linear and quadratic regression lines of all 104 glaciers are also presented in Figure 2. The numerical nature of the regression lines will be discussed later in Section 4. It was found that relatively large scatter of the diagram can be systematically grouped into narrow ranges according to solar global radiation as the third variable. The four curves in Figure 3 in Section 3.2 represent the best-fit linear regressions for the four groups, each spanning a range of 25 W m⁻². In the present study, the largest summer global radiation found was 305 W m⁻² in the Pamir, while the smallest was 165 W m⁻² in Svalbard. These relationships will be interpreted in light of the energy balance of the melt period in the next section.

Fig. 1. Geographic distribution of the locations and the altitudes of equilibrium lines of the glaciers used in the present work.

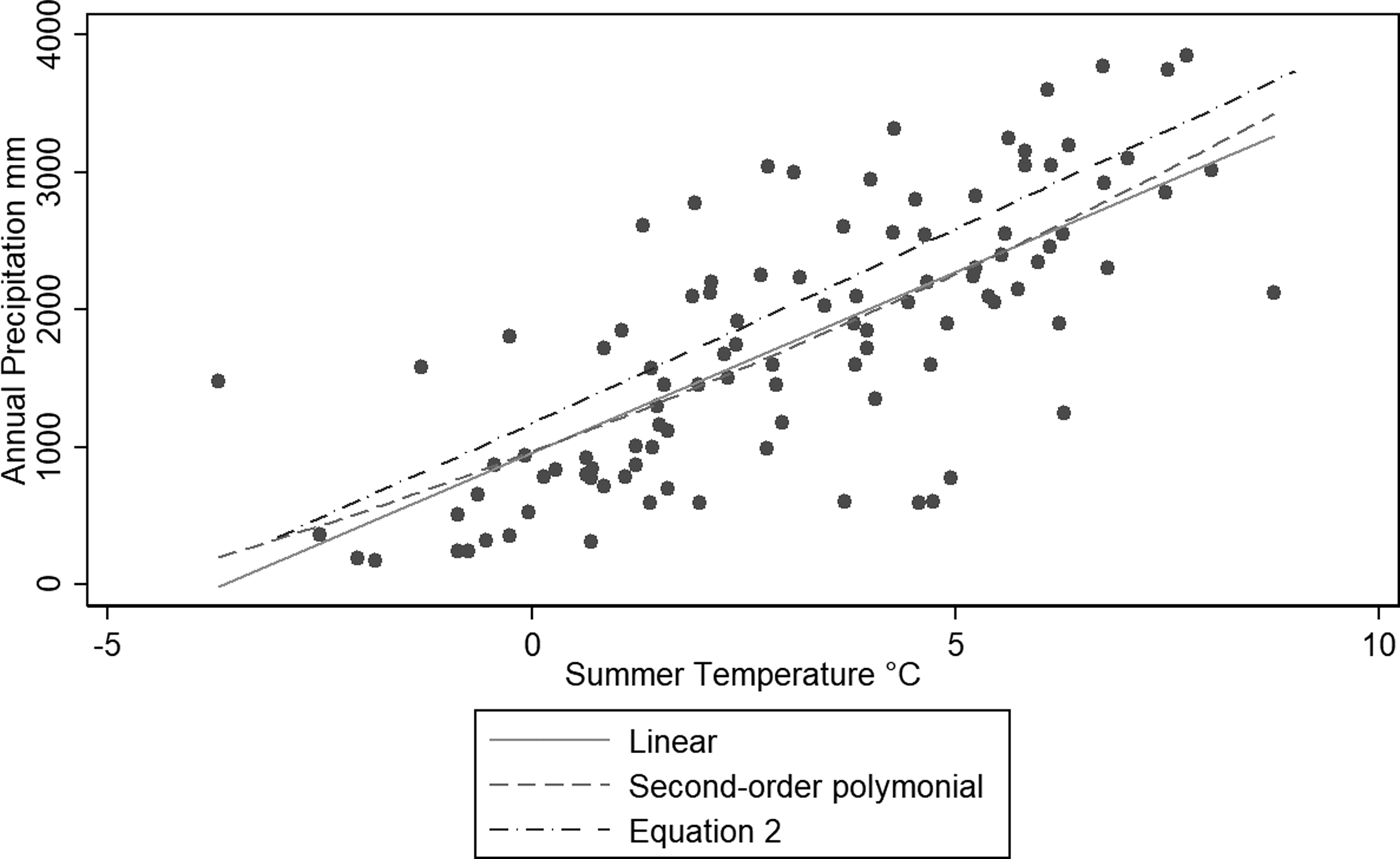
Fig. 2. Annual precipitation and summer (June, July, August or December January, February) mean air temperature at the equilibrium line altitude (ELA): R ² is 0.63. Two thin lines are linear and quadratic regression lines, while the dash and dot line is Eqn 2 discussed in Section 3.3.

Fig. 3. P/T diagram for four groups of glaciers classified by summer mean global solar radiation: triangles, more than 250 W m⁻²; squares, between 250 and 225 W m⁻²; open circles, between 225 and 200 W m⁻², black circles, <200 W m⁻². The four lines indicate the least-square linear regression lines with standard error of estimate (S.E.). The measure of the fit of regression lines is presented in Table 4.

3.2. Energy balance at ELA during the melt period

There are nine glaciers for which the full melt season energy-balance measurements were carried out in the equilibrium line areas. Table 3 summarizes the mean fluxes of the energy balance of individual glaciers. These glaciers represent a wide range of climatic conditions. They represent polar, mid-latitude and tropical glaciers. In terms of the ELAs, they range almost from the sea level to 5000 m a.s.l. The first four sites in Table 3 represent glaciers near the sea, while the following five sites the glaciers in continental interiors. The tenth experiment took place on a tropical high-altitude glacier. Despite the wide range of climatic conditions, these glaciers reveal strikingly similar energy-balance features during the melt period. Common to all glaciers is the dominance of longwave incoming radiation from the atmosphere. For all glaciers, this component is on average 70% of the total energy income, with extremes of maximum 86% (Meighen Ice Cap) to minimum 57% (Blue Glacier). For all glaciers, the absorbed solar radiation takes the second place as an energy source, on an average 25% of the total energy income, with extremes of maximum 35% (Vernagtferner) to minimum 15% (Meighen Ice Cap). The fact that the absorbed solar radiation is the second most important energy source at ELA was earlier recognized (Ohmura, 2001) and also used for improving the melt model (Pellicciotti and others, 2005). Sensible heat flux, or turbulent enthalpy flux, is 6% of the total energy on an average, with extreme cases of 19% (Rhonegletscher) and −1% (Meighen Ice Cap). The most important feature of the energy balance of ELA is the fact that longwave and shortwave incoming radiative fluxes are by far the dominant sources and turbulent components are one order of magnitude smaller. Since the major portion of the longwave radiation originates from the lowest 1 km of the atmosphere (Ohmura, 2001), the air temperature becomes particularly important information for calculating the melt. The majority of the energy gained by the surface is expended for radiative emission by the surface, which is almost constant near at the blackbody emission of the ice melting point, 315.7 W m⁻² during the melt period. The actually observed mean emission is 309 W m⁻² with a maximum of 316 W m⁻² (Ward Hunt Ice Shelf and Blue Glacier) and a minimum of 301 Wm⁻² (Vernagtferner). The mean emission is slightly smaller than the expected value from the blackbody emission at the melting point, as the glacier surface often re-freezes at night, allowing the surface to cool below the freezing point (Ambach, 1955). Although the surface emission is numerically the largest component of the energy balance, it is close to a constant. Therefore, among the fluxes of the heat sink, the latent heat of melt is the largest variable (mean of 91% of the available heat source), with two exceptions that show relatively large evapo-sublimation (Urumqi No.1 Glacier, 18% and Zongo Glacier, 60%). These are nevertheless amazingly similar features, when one considers the diverse climatic conditions under which these glaciers are located. This situation allows the following discussion in terms of the mean fluxes that are presented in the bottom line of Table 3. The mean energy balance on the ELA takes the following form:

(1)$$S(1 - {\rm a} ) + L \downarrow +\; \sigma T_o^4 + H + L_{\rm v} E + C = M,$$

where S is the solar global radiation, a is the albedo at ELA, L ↓ is the longwave incoming radiation, σ is the Stefan–Boltzmann constant (5.67 × 10⁻⁸ W m⁻² K⁻⁴), T _o is the glacier surface temperature at ELA, H is the sensible heat flux from the atmosphere, L _v is the latent heat of vaporization, E is the evaporation/sublimation rate, C is the subsurface energy flux mainly constituted by heat conduction and ice-internal absorption of solar radiation and M is the heat used for melt. The sign is taken positive when the flux is directed to the surface. Table 3 shows that longwave incoming radiation from the atmosphere is by far the most important energy source for the melt accounting for almost 70%. When this term is parameterized with standard screen-level air temperature, the effective emissivity of the overlying atmosphere becomes 0.84, allowing the approximation by L ↓ = εσT ⁴, ε = 0.84. Together with the sensible heat flux, longwave incoming radiation makes up 75% of the energy source. Since these two terms are strong functions of temperature, the temperature becomes the most important parameter representing the melt (Ohmura, 2001), hence the abscissa in the P/T diagram. The remaining 25% is supplied by absorbed solar global radiation. Solar radiation varies greatly depending on regions, and this is the reason for the improvement of the P/T diagram by adopting solar global radiation as the third variable. The energy sink is dominated by two terms, longwave outgoing radiation and the latent heat for melt. However, as pointed out earlier, the largest sink, longwave outgoing radiation is almost constant at the blackbody temperature close to the melting point. Because this numerically largest energy sink is a quasi-constant, the melt becomes predictable only with temperature and solar radiation. By definition, the total melt in summer must be equal to the annual accumulation, which in turn has been shown above to be close to the annual precipitation, P which was taken as the ordinate by Ahlmann (1924).

Table 3. Energy-balance fluxes at the equilibrium line altitudes of glaciers during the melt season. Unit in W m⁻²

Source: (1) Lister (1962); (2) Taylor-Alt (1975); (3) Ohmura and others (1994); (4) LaChapelle (1959); (5) Hoinkes and Untersteiner (1952), Hoinkes (1955); (6) Escher-Vetter (1980; 1985); (7) Wagner (1978, 1979, 1980), Tanzer (1986); (8) Funk (1985); (9) Calanca and Heuberger (1990); (10) Wagnon and others (1999).

3.3. ELA energy balance and the P/T diagram

A slight rearrangement of Eqn (1) has the following mass conservation relationship given energy-balance conditions at the ELA:

(2)$$P = d\displaystyle{M \over {L_{\rm f}}} = \displaystyle{d \over {L_{{\rm f}}}}\{ \varepsilon \sigma T^4 + S(1 - a) + \rho c_{\rm p} D_{\rm H} \bar u(T - T_0 ) - {\rm const}{\rm.} \}, \; $$

where P is the annual precipitation, hence summer total melt, d is the duration of the melt period, in the present case the three summer months, that is, 92 d (90 d for the Southern Hemisphere); L _f is the latent heat of fusion, 3.34 × 10⁵ J kg⁻¹, ρ is the density of the atmosphere, close to 1 kg m⁻³; c _p is the specific heat of air under constant pressure, 1004.67 J kg⁻¹ K⁻¹; D _H is the drag coefficient for heat, close to 0.0025 for wind speed at 10 m above the surface (Priestley, 1959), $\bar u$ is the wind-speed, T is the air temperature, T ₀ is the surface temperature, while ‘const.’ is the sum of the surface radiative emission, evapo-/sublimation and sub-surface heat flux, and ~315 W m⁻².

The numerical accuracy of Eqn (2) is tested against the observations of P and T for 104 glaciers presented in Table 2. The necessary values are presented in the previous paragraph and also in Table 2. The estimation of the sensible heat flux poses a slight problem, as this flux was not measured on most glaciers presented in Table 2. When wind was measured by glaciologists, often it was carried out not at the meteorological standard height of 10 m above the surface. The drag coefficient in micro-meteorology is traditionally referred to 10 m. Rather than estimating the drag coefficient and wind speed separately, the authors took a direct way to estimate $\rho c_{\rm p} D_{\rm H} \; \bar u$ by regressing sensible heat flux H against (T−T ₀), as is presented in Figure 4. The gradient of the regression line is $\rho c_{\rm p} D_{\rm H} \; \bar u$ with numerical value of 7.9 W m⁻² K⁻¹. R ² is 0.84. This value gives the approximate value of D _H as 0.003, which is close to 0.0025 given by Priestley (1959) and Brutsaert (2005).

Fig. 4. Relationship between sensible heat flux and the temperature difference between the surface and the atmosphere at the equilibrium line of glaciers during the melt season, obtained based on ten experiments on nine glaciers summarized in Table 3. The gradient of the regression line is $\rho c_{\rm p} D_{\rm H} \; \bar u$ with the numerical value of 7.9 Wm⁻² K⁻¹. R ² is 0.84. When detailed information such as the surface roughness length and the wind speed at the WMO standard height, that is 10 m above the surface, are not available, this relationship allows an order of magnitude estimation of the sensible heat flux on the glacier.

Equation (2) is plotted in Figure 2, together with the empirically obtained P/T relationships. There is an overestimation of P by 270 mm, equivalent to 11 W m⁻² between Eqn (2) and the best-fit empirical curves of 104 glaciers, which is small in comparison with the possible errors associated with the energy flux measurements. The difference may also stem from the possibility that the nine glaciers used for the derivation of Eqn (2) tended to have smaller evaporation than the mean condition of the majority of glaciers. In the present work, evaporation is not numerically treated, as it is small. It is included in the ‘constant’. However, if evaporation is larger, it must be treated as an independent term, and tends to pull the theoretical line downward, as postulated by Loewe (1971). This sampling problem can be reconciled, if further energy-balance observations are carried out on the glaciers representing mean climatic conditions.

4. DISCUSSION AND CONCLUSION

In summary, Eqn 2, the water-equivalent transformation of the energy-balance equation, is the P/T diagram originally proposed by Ahlmann (1924). When annual precipitation P is made a dependent variable, it becomes a fourth-order polynomial in T, summer air temperature. The Ahlmann's P/T curve expressing the climatic conditions at the ELA is a concise expression of the conservation principle. The mathematical shape of the P/T curve, which was earlier speculated to take various functional forms, is a polynomial of the fourth order that is derived from both the Stefan–Boltzmann equation and the difference approximation of turbulent sensible heat flux.

However, the narrow temperature range of the melt season at the ELA occupying only 10°C between −2 and +8°C offers a practical justification for approximating the P/T relationship with a lower order such as a quadratic or even a linear function, which offers a possibility for wide practical applications. These approximations are P = 5.87 T ² + 230 T + 966 and P = 264.1 T + 957, respectively, based on the least-square method for all 104 glaciers considered in the present study. The standard error of estimate (S.E.) of both regressions is almost identical at 648 and 650 mm, respectively. By taking solar global radiation into account, the best-fit approximation takes the following shape: P = (2.2 S–130) T + 3.12 S + 122 with S.E. of 510 mm, where T (°C) is the mean air temperature and S (W m⁻²) is the mean solar global radiation during the melt period. P (mm) is the annual precipitation at the ELA. The introduction of solar radiation brought about a considerable improvement over the previous temperature-only formulation. A better fit is, however, found for the four groups of glaciers that are classified by solar global radiation as presented in Table 4. Figure 3 offers regression lines and the standard error estimates for each group. Among them, the best fit with the smallest standard error of estimate was found for the group with solar global radiation ranging between 225 and 250 W m⁻². The reason for the best performance by glaciers of this class is not clear. The P/T combinations falling above these lines represent the climate of the accumulation area, while those below the lines indicate the climate of the ablation area or the area outside the glaciers.

Table 4. The best-fit linear regressions for the precipitation and temperature relationship at the equilibrium line altitudes (ELA) of glaciers, classified with respect to solar global radiation (S, W m⁻²). The coefficients are for the form of P (mm) = aT (°C) + b, S.E. is the standard error of estimate, and n is the number of the sampled glaciers

The introduction of solar global radiation improves the standard error of estimate of the regression lines from ~650 down to 500 mm, which corresponds to ~1.2°C in temperature scale. Given the wide range of variety of the climate where these glaciers are located, the present results are a considerable improvement over the earlier understanding on the climate at the glacier ELA. The present findings will contribute to the systematic understanding of the equilibrium line formation and of the total meltwater available from glaciers, and to reconstructing the temperature and precipitation on glaciers of the past.