Studies of herbicide fitness penalties commonly assume that either there is a penalty that is big enough to be detected with a statistical significance test of their data, or there is no penalty whatsoever (e.g., Du et al. Reference Du, Bai, Li, Qu, Yuan, Guo and Wang2017; Goggin et al. Reference Goggin, Beckie, Sayer and Powles2019; Keshtkar et al. Reference Keshtkar, Mathiassen and Kudsk2017; Patterson et al. Reference Patterson, Pettinga, Ravet, Neve and Gaines2018; Vila-Aiub et al. Reference Vila-Aiub, Neve and Powles2009, Reference Vila-Aiub, Goh, Gaines, Han, Busi, Yu and Powles2014). Such a conclusion, however, is based on false logic and reflects a much wider misinterpretation of nonsignificant results in weed science.
A significant difference between two means tells us that there is a high probability of a real effect. A nonsignificant difference does not tell us that there is zero effect, only that any effect (if there is one) is smaller than we can detect in that significance test. It is illogical to assume that absence of evidence is the same as evidence of absence. It is quite plausible that if we do so, we will make a type II error (in statistical parlance) or draw a “false-negative” conclusion. Just because two means are similar in magnitude does not rule out the possibility of such an error.
Let us, for the sake of argument, assume that biological systems are likely to show a broad variety of responses that can be depicted by a frequency distribution (Figure 1). In the case of herbicide-resistance fitness penalties, let us assume that there could (in theory) be large, small, or zero values, although most are small or zero, depending on the mode of action and the biochemistry involved. (It would be a highly unusual biological system in which values can only be zero or very large.)
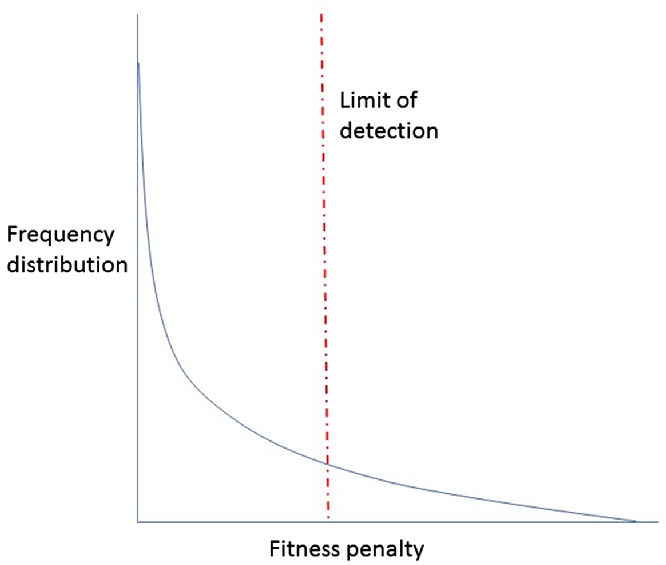
Figure 1. Hypothetical distribution of values of biological variable, in this case penalty resulting from herbicide resistance.
Now let us say that we sample cases from this distribution (a particular weed, particular herbicide resistance in a particular place) one by one, do a valid experiment on each (see Cousens and Fournier-Level Reference Cousens and Fournier-Level2018), measure plants with and without resistance alleles, and then compare the means using a significance test. If there is a very large fitness differential, we will probably reach the conclusion that it is “statistically significant” and report what that difference was (e.g., a 30% difference in fitness with vs. without resistance). What about smaller differences?
Because there will inevitably be experimental error and biological variation (“noise”), there will always be a size limit below which any real difference will likely not be concluded “statistically significant.” If we are using Fisher’s LSD for the statistical comparison, for example, this is a reasonable surrogate for the magnitude of real difference that is likely to be concluded to be “nonsignificant.” A standard error of 10% of the mean is typical in resistance “fitness” experiments (Cousens and Fournier-Level Reference Cousens and Fournier-Level2018), which would (depending on the experimental design) lead to an LSD of perhaps 25% of the mean. So, it is quite plausible that even a real 20% fitness penalty will be concluded “nonsignificant.” Indeed, most of the cases to the left of the vertical line in Figure 1 would be found to be nonsignificant. And yet, they are not zero (we specified at the outset of this hypothetical example that they are not)! Are we, then, prepared to argue that all the values to the left of the line cannot exist and that they must be zero! That is effectively what is being done in discussions of herbicide-resistance fitness penalties. Or in any other study in which nonsignificant is considered synonymous with “no difference.”
Analogies to the fitness penalty issue would be residue testing in food and performance-enhancement substances in sport: there is a lower limit to our ability to test for the presence of chemicals. If we fail to detect a chemical, it does not mean that there is zero chemical present or that such a small level of chemical would have zero impact. It is clearly inappropriate statistical inference to conclude that a nonsignificant result indicates that any fitness penalty is zero! It might be zero; but it might well not be. A fitness penalty of 2% may not be “meaningful” for management purposes, and it will seldom be statistically significant in an experiment, but that does not make the biological effect zero. So we must be extremely cautious in what we conclude and how we phrase the titles of our articles. Statisticians (and some weed scientists) have long warned against the dangers of treating statistical and biological significance as being one and the same thing (Cousens and Marshall Reference Cousens and Marshall1987). We need to decide what level of real effect is of interest to us; and we need to know whether our experiment is likely to be able to detect that size of effect (i.e., find it statistically significant) if it is there. Readers are advised to examine the sizes of the standard errors in their past work to better appreciate what sizes of real difference they would be unable to detect; and what they could do to their designs in order to make it possible to detect the sizes of effects that would be of interest to them. This simple procedure seems to be rarely used in weed science.
In light of this discussion, we need to be skeptical of papers seeking to establish summaries of cases where there is or is not a penalty (Vila-Aiub et al. Reference Vila-Aiub, Neve and Powles2009). Our aim should be to estimate the size of any penalty within each experiment, with confidence intervals for that estimate, and formal statistical meta-analyses should be considered when summarizing multiple studies (Cousens and Fournier-Level, Reference Cousens and Fournier-Level2018).
To conclude, it is worthwhile to remind readers, reviewers, and editors that the issue of the correct interpretation of “nonsignificant” is relevant to any experiment and not just those involving herbicide resistance. A nonsignificant result indicates that any difference is smaller than can be detected at that level of confidence: it does not prove the absence of any effect.



