Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-04-28T00:47:07.623Z Has data issue: false hasContentIssue false
  • English
  • Français

Temporal evolution of the turbulence interface of a turbulent plane jet

Published online by Cambridge University Press:  13 December 2024

Yuanliang Xie ,
Xinxian Zhang Open the ORCID record for Xinxian Zhang [Opens in a new window] ,
Xue-Lu Xiong Open the ORCID record for Xue-Lu Xiong [Opens in a new window]  and
Yi Zhou Open the ORCID record for Yi Zhou [Opens in a new window]
Yuanliang Xie
Affiliation:
School of Energy and Power Engineering, Nanjing University of Science and Technology, Nanjing 210094, PR China
Xinxian Zhang
Affiliation:
Institute of Applied Physics and Computational Mathematics, Beijing 100094, PR China
Xue-Lu Xiong
Affiliation:
School of Energy and Power Engineering, Nanjing University of Science and Technology, Nanjing 210094, PR China
Yi Zhou*
Affiliation:
School of Energy and Power Engineering, Nanjing University of Science and Technology, Nanjing 210094, PR China
*
†Email address for correspondence: yizhou@njust.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

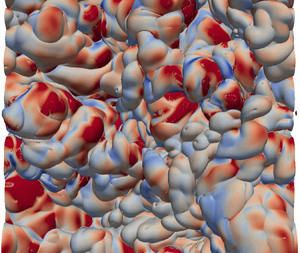
Direct numerical simulations are performed to explore the evolution behaviour of the turbulent/non-turbulent interface (TNTI) in a temporally evolving turbulent plane jet, using the evolution equation for the TNTI surface area. A novel algorithm is used to calculate the surface area of the TNTI and entrainment flux. It is shown that the surface area remains relatively constant, which leads to the mean entrainment velocity being inversely proportional to the square root of time. On average, the effects of the stretching and curvature/viscous terms on the TNTI area roughly counterbalance each other, while the curvature/inviscid term associated with vortex stretching is virtually zero. More specifically, the stretching term contributes to the production of the surface area, while the curvature/viscous term is associated with a destruction in the surface area. The local effect of the curvature/viscous term exhibits high spatial intermittency with small-scale extreme/intense events, whereas the effect of the large-scale stretching term is more continuous. To shed light on the contribution of curvature/viscous term to the evolution of the surface area, we decompose it into three components. The effect of the curvature/normal diffusion term (the curvature/viscous dissipation term) in the bulging regions (the valley regions) mainly contributes to the production of the area. The continuous decrease of the average mean curvature is associated with the production of the bulging regions and the destruction of the valley regions. Finally, although the entrainment velocity is mainly dominated by the normal diffusion effect, all three components related to the viscous effect are indispensable to the production and destruction of the TNTI area. This numerical study contributes to a better understanding of the evolution of the TNTI area.

JFM classification

Turbulent Flows: Turbulence theory Wakes/Jets: Jets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1001 , 25 December 2024 , A39
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Almagro, A., García-Villalba, M. & Flores, O. 2017 A numerical study of a variable-density low-speed turbulent mixing layer. J. Fluid Mech. 830, 569–601.CrossRefGoogle Scholar
Benzi, R. & Toschi, F. 2023 Lectures on turbulence. Phys. Rep. 1021, 1–106.CrossRefGoogle Scholar
Blakeley, B.C., Olson, B.J. & Riley, J.J. 2022 Self-similarity of scalar isosurface area density in a temporal mixing layer. J. Fluid Mech. 951, A44.CrossRefGoogle Scholar
Cafiero, G. & Vassilicos, J.C. 2019 Non-equilibrium turbulence scalings and self-similarity in turbulent planar jets. Proc. R. Soc. A 475 (2225), 20190038.CrossRefGoogle ScholarPubMed
Cafiero, G. & Vassilicos, J.C. 2020 Nonequilibrium scaling of the turbulent-nonturbulent interface speed in planar jets. Phys. Rev. Lett. 125 (17), 174501.CrossRefGoogle ScholarPubMed
Candel, S.M. & Poinsot, T.J. 1990 Flame stretch and the balance equation for the flame area. Combust. Sci. Tech. 70 (1-3), 1–15.CrossRefGoogle Scholar
Catrakis, H.J., Aguirre, R.C. & Ruiz-Plancarte, J. 2002 Area–volume properties of fluid interfaces in turbulence: scale-local self-similarity and cumulative scale dependence. J. Fluid Mech. 462, 245–254.CrossRefGoogle Scholar
Cleary, M.J. & Klimenko, A.Y. 2009 A generalised multiple mapping conditioning approach for turbulent combustion. Flow Turbul. Combust. 82, 477–491.CrossRefGoogle Scholar
Corrsin, S. & Kistler, A.L. 1955 Free-stream boundaries of turbulent flows. NACA Tech. Rep. 1224, 1033–1064.Google Scholar
Dairay, T., Obligado, M. & Vassilicos, J.C. 2015 Non-equilibrium scaling laws in axisymmetric turbulent wakes. J. Fluid Mech. 781, 166–195.CrossRefGoogle Scholar
Davidson, P.A. 2004 Turbulence, An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Dopazo, C., Martin, J., Cifuentes, L. & Hierro, J. 2018 Strain, rotation and curvature of non-material propagating iso-scalar surfaces in homogeneous turbulence. Flow Turbul. Combust. 101 (1–6), 1–32.CrossRefGoogle Scholar
Echekki, T. & Chen, J.H. 1999 Analysis of the contribution of curvature to premixed flame propagation. Combust. Flame 118 (1-2), 308–311.CrossRefGoogle Scholar
Er, S., Laval, J.-P. & Vassilicos, J.C. 2023 Length scales and the turbulent/non-turbulent interface of a temporally developing turbulent jet. J. Fluid Mech. 970, A33.CrossRefGoogle Scholar
Ewing, D., Frohnapfel, B., George, W.K., Pedersen, J.M. & Westerweel, J. 2007 Two-point similarity in the round jet. J. Fluid Mech. 577, 309–330.CrossRefGoogle Scholar
Gampert, M., Kleinheinz, K., Peters, N. & Pitsch, H. 2014 Experimental and numerical study of the scalar turbulent/non-turbulent interface layer in a jet flow. Flow Turbul. Combust. 92, 429–449.CrossRefGoogle Scholar
George, W.K. 1989 The self-preservation of turbulent flows and its relation to initial conditions and coherent structures. Adv. Turbul. 3973, 39–72.Google Scholar
Gutmark, E. & Wygnanski, I. 1976 The planar turbulent jet. J. Fluid Mech. 73 (3), 465–495.CrossRefGoogle Scholar
Hayashi, M., Watanabe, T. & Nagata, K. 2021 Characteristics of small-scale shear layers in a temporally evolving turbulent planar jet. J. Fluid Mech. 920, A38.CrossRefGoogle Scholar
Hickey, J.P., Hussain, F. & Wu, X. 2013 Role of coherent structures in multiple self-similar states of turbulent planar wakes. J. Fluid Mech. 731, 312–363.CrossRefGoogle Scholar
Holzner, M. & Lüthi, B. 2011 Laminar superlayer at the turbulence boundary. Phys. Rev. Lett. 106 (13), 134503.CrossRefGoogle ScholarPubMed
Huang, J., Burridge, H.C. & van Reeuwijk, M. 2023 Local entrainment across a TNTI and a TTI in a turbulent forced fountain. J. Fluid Mech. 977, A13.CrossRefGoogle Scholar
Jahanbakhshi, R. & Madnia, C.K. 2016 Entrainment in a compressible turbulent shear layer. J. Fluid Mech. 797, 564–603.CrossRefGoogle Scholar
Kempf, A., Klein, M. & Janicka, J. 2005 Efficient generation of initial- and inflow-conditions for transient turbulent flows in arbitrary geometries. Flow Turbul. Combust. 74 (1), 67–84.CrossRefGoogle Scholar
Krug, D., Holzner, M., Marusic, I. & van Reeuwijk, M. 2017 Fractal scaling of the turbulence interface in gravity currents. J. Fluid Mech. 820, R3.CrossRefGoogle Scholar
Laizet, S. & Lamballais, E. 2009 High-order compact schemes for incompressible flows: a simple and efficient method with the quasi-spectral accuracy. J. Comput. Phys. 228 (16), 5989–6015.CrossRefGoogle Scholar
Laizet, S., Lamballais, E. & Vassilicos, J.C. 2010 A numerical strategy to combine high-order schemes, complex geometry and parallel computing for high resolution DNS of fractal generated turbulence. Comput. Fluids 39 (3), 471–484.CrossRefGoogle Scholar
Laizet, S. & Li, N. 2011 Incompact3d, a powerful tool to tackle turbulence problems with up to $O(10^5)$ computational cores. Intl J. Numer. Meth. Fluids 67 (11), 1735–1757.CrossRefGoogle Scholar
Laizet, S., Nedić, J. & Vassilicos, J.C. 2015 Influence of the spatial resolution on fine-scale features in DNS of turbulence generated by a single square grid. Intl J. Comput. Fluid Dyn. 29 (3-5), 286–302.CrossRefGoogle Scholar
Lamballais, E., Fortuné, V. & Laizet, S. 2011 Straightforward high-order numerical dissipation via the viscous term for direct and large eddy simulation. J. Comput. Phys. 230 (9), 3270–3275.CrossRefGoogle Scholar
Lele, S.K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103 (1), 16–42.CrossRefGoogle Scholar
Mistry, D., Philip, J. & Dawson, J.R. 2019 Kinematics of local entrainment and detrainment in a turbulent jet. J. Fluid Mech. 871, 896–924.CrossRefGoogle Scholar
Nagata, R., Watanabe, T. & Nagata, K. 2018 Turbulent/non-turbulent interfaces in temporally evolving compressible planar jets. Phys. Fluids 30 (10), 105109.CrossRefGoogle Scholar
Neamtu-Halic, M.M., Krug, D., Mollicone, J.P., van Reeuwijk, M., Haller, G. & Holzner, M. 2020 Connecting the time evolution of the turbulence interface to coherent structures. J. Fluid Mech. 898, A3.CrossRefGoogle Scholar
Nedić, J., Vassilicos, J.C. & Ganapathisubramani, B. 2013 Axisymmetric turbulent wakes with new nonequilibrium similarity scalings. Phys. Rev. Lett. 111 (14), 144503.CrossRefGoogle ScholarPubMed
Phillips, O.M. 1972 The entrainment interface. J. Fluid Mech. 51 (1), 97–118.CrossRefGoogle Scholar
Pope, S.B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
van Reeuwijk, M., Vassilicos, J.C. & Craske, J. 2021 Unified description of turbulent entrainment. J. Fluid Mech. 908, A12.CrossRefGoogle Scholar
Sadeghi, H., Oberlack, M. & Gauding, M. 2018 On new scaling laws in a temporally evolving turbulent plane jet using lie symmetry analysis and direct numerical simulation. J. Fluid Mech. 854, 233–260.CrossRefGoogle Scholar
Sebastien, M.C. & Thierry, J.P. 1990 Flame stretch and the balance equation for the flame area. Combust. Sci. Tech. 70 (1–3), 1–15.Google Scholar
da Silva, C.B., Hunt, J.C.R., Eames, I. & Westerweel, J. 2014 Interfacial layers between regions of different turbulence intensity. Annu. Rev. Fluid Mech. 46, 567–590.CrossRefGoogle Scholar
da Silva, C.B., Lopes, D.C. & Raman, V. 2015 The effect of subgrid-scale models on the entrainment of a passive scalar in a turbulent planar jet. J. Turbul. 16 (4), 342–366.CrossRefGoogle Scholar
da Silva, C.B. & Métais, O. 2002 On the influence of coherent structures upon interscale interactions in turbulent plane jets. J. Fluid Mech. 473, 103–145.CrossRefGoogle Scholar
da Silva, C.B. & Pereira, J.C. 2008 Invariants of the velocity-gradient, rate-of-strain, and rate-of-rotation tensors across the turbulent/nonturbulent interface in jets. Phys. Fluids 20 (5), 055101.CrossRefGoogle Scholar
da Silva, C.B. & dos Reis, R.J.N. 2011 The role of coherent vortices near the turbulent/non-turbulent interface in a planar jet. Phil. Trans. R. Soc. Lond. A Math. Phys. Sci. 369 (1937), 738–753.Google Scholar
de Silva, C.M., Philip, J., Chauhan, K., Meneveau, C. & Marusic, I. 2013 Multiscale geometry and scaling of the turbulent-nonturbulent interface in high Reynolds number boundary layers. Phys. Rev. Lett. 111 (4), 044501.CrossRefGoogle ScholarPubMed
Silva, T.S., Zecchetto, M. & da Silva, C.B. 2018 The scaling of the turbulent/non-turbulent interface at high Reynolds numbers. J. Fluid Mech. 843, 156–179.CrossRefGoogle Scholar
Sreenivasan, K.R. & Antonia, R.A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29 (1), 435–472.CrossRefGoogle Scholar
Sreenivasan, K.R., Ramshankar, R. & Meneveau, C.H. 1989 Mixing, entrainment and fractal dimensions of surfaces in turbulent flows. Phil. Trans. R. Soc. Lond. A Math. Phys. Sci. 421 (1860), 79–108.Google Scholar
Stanley, S.A., Sarkar, S. & Mellado, J.P. 2002 A study of the flow-field evolution and mixing in a planar turbulent jet using direct numerical simulation. J. Fluid Mech. 450, 377–407.CrossRefGoogle Scholar
Taveira, R.R. & da Silva, C.B. 2013 Kinetic energy budgets near the turbulent/nonturbulent interface in jets. Phys. Fluids 25 (1), 015114.CrossRefGoogle Scholar
Taveira, R.R. & da Silva, C.B. 2014 Characteristics of the viscous superlayer in shear free turbulence and in planar turbulent jets. Phys. Fluids 26 (2), 021702.Google Scholar
Thomas, F. & Prakash, K. 1991 An experimental investigation of the natural transition of an untuned planar jet. Phys. Fluids 3 (1), 90–105.CrossRefGoogle Scholar
Townsend, A.A. 1956 The Structure of Turbulent Shear Flow, 1st edn. Cambridge University Press.Google Scholar
Townsend, A.A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Trouvé, A. & Poinsot, T. 1994 The evolution equation for the flame surface density in turbulent premixed combustion. J. Fluid Mech. 278, 1–31.CrossRefGoogle Scholar
Van Reeuwijk, M. & Holzner, M. 2014 The turbulence boundary of a temporal jet. J. Fluid Mech. 739, 254–275.CrossRefGoogle Scholar
Vassilicos, J.C. 2015 Dissipation in turbulent flows. Annu. Rev. Fluid Mech. 47, 95–114.CrossRefGoogle Scholar
Vassilicos, J.C. 2023 Beyond scale-by-scale equilibrium. Atmosphere 14 (4), 736.CrossRefGoogle Scholar
Watanabe, T., Sakai, Y., Nagata, K., Ito, Y. & Hayase, T. 2014 a Reactive scalar field near the turbulent/non-turbulent interface in a planar jet with a second-order chemical reaction. Phys. Fluids 26 (10), 105111.Google Scholar
Watanabe, T., Sakai, Y., Nagata, K., Ito, Y. & Hayase, T. 2014 b Vortex stretching and compression near the turbulent/non-turbulent interface in a planar jet. J. Fluid Mech. 758, 754–785.CrossRefGoogle Scholar
Watanabe, T., da Silva, C.B., Nagata, K. & Sakai, Y. 2017 Geometrical aspects of turbulent/non-turbulent interfaces with and without mean shear. Phys. Fluids 29 (8), 085105.CrossRefGoogle Scholar
Westerweel, J., Fukushima, C., Pedersen, J.M. & Hunt, J.C.R. 2009 Momentum and scalar transport at the turbulent/non-turbulent interface of a jet. J. Fluid Mech. 631, 199–230.CrossRefGoogle Scholar
Wolf, M., Holzner, M., Lüthi, B., Krug, D., Kinzelbach, W. & Tsinober, A. 2013 Effects of mean shear on the local turbulent entrainment process. J. Fluid Mech. 731, 95–116.CrossRefGoogle Scholar
Wolf, M., Lüthi, B., Holzner, M., Krug, D., Kinzelbach, W. & Tsinober, A. 2012 Investigations on the local entrainment velocity in a turbulent jet. Phys. Fluids 24 (10), 105110.CrossRefGoogle Scholar
Xie, Y.L., Yin, W.J., Zhang, X.X. & Zhou, Y. 2023 Visualization of the rotational and irrotational motions in a temporally evolving turbulent plane jet. J. Vis. 26, 1025–1036.CrossRefGoogle Scholar
Xu, C.Y., Long, Y.G. & Wang, J.J. 2023 Entrainment mechanism of turbulent synthetic jet flow. J. Fluid Mech. 958, A31.CrossRefGoogle Scholar
Yin, W.J., Xie, Y.L., Zhang, X.X. & Zhou, Y. 2023 On the structure of the turbulent/non-turbulent interface in a fully developed spatially evolving axisymmetric wake. Theor. Appl. Mech. Lett. 13 (2), 100404.CrossRefGoogle Scholar
Yurtoglu, M., Carton, M. & Storti, D. 2018 Treat all integrals as volume integrals: a unified, parallel, grid-based method for evaluation of volume, surface, and path integrals on implicitly defined domains. J. Inf. Sci. Engng 18 (2), 021013.Google ScholarPubMed
Zecchetto, M. & da Silva, C.B. 2021 Universality of small-scale motions within the turbulent/non-turbulent interface layer. J. Fluid Mech. 916, A9.CrossRefGoogle Scholar
Zhang, X.X., Watanabe, T. & Nagata, K. 2018 Turbulent/nonturbulent interfaces in high-resolution direct numerical simulation of temporally evolving compressible turbulent boundary layers. Phys. Rev. Fluids 3 (9), 094605.CrossRefGoogle Scholar
Zhang, X.X., Watanabe, T. & Nagata, K. 2023 Reynolds number dependence of the turbulent/non-turbulent interface in temporally developing turbulent boundary layers. J. Fluid Mech. 964, A8.CrossRefGoogle Scholar
Zhou, Y. & Vassilicos, J.C. 2017 Related self-similar statistics of the turbulent/non-turbulent interface and the turbulence dissipation. J. Fluid Mech. 821, 440–457.CrossRefGoogle Scholar