1. Basic Processes and Methodology
1.1. Historical background
The study of glacial erosion and drift is almost two centuries old. Around 1900, the processes of glacial erosion by temperate glaciers and the importance of glacial relative to hydraulic erosion were fiercely debated, appealing to field observations, not to theoretical models. At that time, all the processes that are known today had already been put forward. They are:
-
1. Subglacial chemical weathering, mainly of limestone.
-
2. Erosion by turbulent subglacial streams, which carry sand (Reference ChaixChaix, 1902).
-
3. Abrasion by rock debris that is present at the glacier sole, and provides glacial polish, striae and grooves. (The boundary between striae and grooves is conventional. A cross-sectional area of 10 mm2 may be adopted.)
-
4. Quarrying, also termed plucking, i.e. successive loosening, dislodging and dragging of boulders from the bedrock (Reference BaltzerBaltzer, 1898; Reference SalomonSalomon, 1900). The possibility of melting or refreezing at the glacier sole according to the location had already been an accepted idea at that time. Consequently, dislodging by regelation ice was conceivable. Nevertheless, continuous loosening of boulders under a temperate glacier was difficult to explain, as it is today. Therefore, Reference JohnsonJohnson (1899) emphasized frost-shattering in bergschrunds and marginal crevasses.
In the Alps, the amount of rock debris in the bottom ice is generally insignificant. For instance, bottom debris-laden ice is not found in the tongues of the three largest French glaciers: Mer de Glace, Glacier d’Argentière and Glacier Blanc. Therefore, Reference GeikieGeikie (1884), Reference DrygalskiDrygalski (1892) and Reference VallotVallot (1898) maintained that glacial erosion occurs only when a glacier has formed (or advances) on frost-shattered and loose ground, and that it becomes negligible several centuries later, once all the loose material has been removed as a bottom moraine. After the first French expeditions to Greenland, Reference BoyBoyé (1950) presented strong field arguments against steady subglacial erosion, although his idea that loose material had been pushed by the advancing ice was simplistic. More recent references and arguments are to be found in Reference LindströmLindström (1988).
While this point of view has always prevailed in Europe, American Quaternary geologists, impressed by the enormous overdeepenings and sheets of drift that are found in North America, think that glacial erosion, including quarrying that provides new abrasive material, always remains strong and can be considered as steady.
1.2. Scope of this study
I shall consider only monolithologic erosion, i.e. clasts eroding a bedrock with a similar pétrographie composition and strength, because it raises the main conceptual difficulties. This case is the most general in local mountain glaciers. Among the many glaciers that I have visited in the Alps and in the Andes, a single one lies on a bed with contrasted lithology: Glacier de Saint-Sorlin. (Its subglacial topography reflects this contrast. At the northwestern part, in soft dolomite, there is a longitudinal valley, whereas elsewhere, in metamorphic rock, the bed is flat.) Bedrock where chemical dissolution is essential, such as limestones or sandstones with a calcareous cement, will also be excluded.
Moreover, erosion by cold ice sheets will not be considered. In this case, there may be areas where, going downstream, freezing at the lower limit of the ice sheet replaces melting, a situation that favours soft sediments or lumps of permafrost to be caught up by the moving ice. Therefore, the key problem of discovering sources of abrading and grooving material becomes quite different and seems far easier to solve (cf. Reference SugdenSugden, 1978).
In this first part of this paper, assessments of erosion rates were reviewed, and the possibility of subglacial loosening of stones was examined. Since it will appear that no known process can operate in a steady way, Occam’s razor will be used. The methodology will be to estimate erosion rates without plucking. Only if these rates were insignificant, the hypothesis of continuous loosening by some unknown process would be necessary, but this will not be the case.
In the second part, sources of abrading and grooving material, and how they may reach the bed, will be examined. For a boulder to groove the bed, contact is not sufficient. In particular, it must have sharp corners and not be totally worn. The concentration of grooving boulders near the bed and their size distribution will be modelled. The concept of a “wearing distance” λ, over which a clast is totally worn, will yield a limiting value of the erosion rate.
Lastly, in the third part of this paper, the grooving process will be modelled, to estimate very roughly the influence of the sliding velocity, and how erosion rate varies with distance from the bergschrund. Although the mathematics will be more difficult, I do not claim to reach an accurate predictive formula. My aim is only to assess whether the “European” point of view appears to be acceptable. This is also to set out a methodology and to indicate to future investigators the observations, measurements and experiments that ought to be made.
1.3. Speculated formulae for erosion rates
To tackle large erosional forms as overdeepenings, some unwarranted formulae for erosion rates have been suggested, that assume implicitly this rate to be a constant during the life-time of a glacier.
Reference MartonneDe Martonne (1920) assumed an erosion rate proportional to σbUA, where σb is the basal normal stress (σb = Pgh cos α, with h denoting the glacier thickness and tanα the surface slope), U is the sliding velocity and A is an “adhesion factor”, i.e. the relative area of true contact between ice and bed. (Ice-bedrock separation was already known in Europe, although sliding was poorly understood.) De Martonne assumed A to be proportional to h/tan α. Therefore, the erosion rate would be proportional to Uρgh sin α. But he was unaware that ρgh sin α = τb is the bottom shear stress.
Reference AndrewsAndrews (1972) suggested directly an erosion rate proportional to τbU, a point of view that might be valid if most of the bottom drag were due to the solid friction of the clasts, as suggested later by Reference HalletHallet (1981).
Reference MazoMazo (1989) assumed an erosion rate proportional to τb and independent of U. (In his further calculations about glacier flow, he assumed explicitly that this sliding velocity is negligible.) With ice viscosity (that may be expressed in Pas) and rock strength (that may be expressed in Pa) as only dimensional quantities at hand, it is impossible to obtain a coefficient of proportionality with a dimension m s−1 Pa−1. This casts a doubt about the soundness of his model.
No progress can be made in this way – by speculating some relationship at the start. Even if some large-scale features could be explained by such relationships, many others might also explain them, maybe better. First, a physical model must be set up. It must take into account field observations but it must be sufficiently simple to allow reduction to a well-posed problem in mechanics.
This has been done by Reference BoultonBoulton (1979), and more convincingly by Reference HalletHallet (1979) and Reference ShoemakerShoemaker (1988). Nevertheless, at the beginning of his papers Reference Boulton and CoatesBoulton (1974, Reference Boulton1979) suggested the same erosion rate σb UA as De Martonne, subtracting from σb , “any water pressure pw that might exist between the glacier and the bed”. It seems that he has mixed two different space scales, since σb and pw have been defined (or, at least, are calculated) at the scale of the glacier.
Anyway, Hallett’s or Shoemaker’s treatments are only one-half of the story. Another theory must deal with the processes that provide abrading clasts at the ice-bed interface.
1.4. Assessment of erosion rates
Measured abrasion rates have been reviewed by Reference ReheisReheis (1975), by Reference VivianVivian (1975, p. 394) and by Reference DrewryDrewry (1986, p. 84, 87). Of course, I neglect measurements of erosion on a marble platen by a glacier that carries grains of quartz which are harder than calcite.
As quoted by Vivian, some field measurements have been made during temporary glacier advances. At Obergrindelwaldgletscher, in limestone, the erosion at 14 points during the 4 years 1921–24 of glacier coverage ranged between 0 and 39 mm, with 4.5 mm as the mean value. At Allalingletscher, during the 6 years 1919–25, 30 mm of somewhat weathered gneiss were eroded. Unfortunately, neither the amount of loose material dragged by the advancing glacier tongue, nor the sliding velocity, were measured. Obviously, these abrasion rates (1–5 mm a−1) cannot be extrapolated to the whole glacier or to a steady-state situation.
Many estimates of glacial erosion have been inferred from sediment transport in glacial streams. For instance, according to Kjeldsen (quoted by Reference DrewryDrewry (1986)), five glacier basins in Norway lead to mean erosion rates in the range 0.073–0.610 mm a−1, with 0.276 mm a−1 as the mean value. The best assessments come from hydroelectric agencies tapping subglacial streams. According to Reference Bezinge, Clark, Gurnell and WarburtonBezinge and others (1989), the load transport of tapped subglacial streams in the central Alps during 10 years corresponds to an erosion rate of 0.97–1.13 mm a−1.
The flaw in this method is that most of the load may come from the surrounding uncovered slopes and lateral moraines, and not from the bed. Subaerial erosion rates in rock cliffs above glaciers are in the order of 3 mm a−1: about 2.4 mm a−1 at the head of Glaciar Hatunraju, in Cordillera Blanca, Peru (Reference LliboutryLliboutry, 1986); 2.9–3.5 mm a−1 at the head of Laurichard rock glacier, just south of Col du Lautaret, French Alps (Reference Francou and ReynaudFrancou and Reynaud, unpublished). Of course, the extent of rock cliffs differs considerably from the head of one glacier to that of another. This topographic factor explains readily why larger values of load transport are found in the Alps than in Norway.
To circumvent this difficulty, Reference LanserLanser (1958) compared the sediment transports of Venter Ache at Vent (Oetztal) and Lech at Steeg (Tirol). Both watersheds are said to be similar, but the former is glaciated over 45.7% of its surface, whereas the latter has no glaciers. The erosion rate thus obtained is 0.6 mm a−1 in the former and 0.014 mm a−1 in the latter. This comparison is misleading. There is no reason for the amount of weathered debris in a watershed to remain in balance, especially when there are no glaciers. Then, weathered rocks form debris cones and screes at the foot of the cliffs, which increase with time and may deliver no load to the river. (Springs at the foot of the debris cones are quite clear.)
In conclusion, erosion rates of temperate glaciers on hard beds can be several millimetres per year during a glacier advance, but are one order of magnitude less when averaged over a long period.
Another way of assessing erosion rates, when the bedrock is not soluble, is to measure the corresponding drift. Reference Larsen and MangerudLarsen and Mangerud (1981) have estimated the drift produced in 700 years, during the Younger Dryas, by a glacier that existed in southern Norway, at 60 km from the Scandinavian ice sheet. They have found a mean erosion rate of 0.5–0.6 mm a−1. Nothing compels us to assume a constant erosion rate during seven centuries. Reference ReheisReheis (1975) suggested that at Arapaho Glacier (Front Range, Colorado) it is today 0.14–0.235 mm a−1, but has been 1.26–2.04 mm a−1 during a period of glacier advance, three centuries ago.
The maximum amount of glacial erosion is found in overdeepened piedmont lakes, fjords or continental shelves ahead of fjords. In the Alps, the largest over-deepenings are found in the lakes of Geneva (255 m), of Garda (281 m) and infilled with sediments below the town of Grenoble (~400 m). They reach 1210 m in Sögnefjord (Norway), 1460 m in Scoresby Sound (East Greenland), 1288 m in Messier Channel (Chilean Patagonia) and 2200 m in Lambert Fjord (East Antarctica) (Reference Grosval’d and GlazovskiyGrosval’d and Glazovskiy, 1982). These areas were repeatedly covered and uncovered by outlets of large ice sheets. In the Alps there should have been 13 glaciations during the last million years (Ma) (Reference KuklaKukla, 1977). Calving glaciers appeared in Greenland 2.7 Ma ago (it is the age of the first glacial drift on Rockall Plateau), in Patagonia 4.8 Ma ago and in East Antarctica 30 Ma ago. These figures may explain why overdeepenings in fjords are larger than in Alpine lakes.
In all these cases, frost-shattering of the area during interglacials can be ruled out, because the area was below water. Nevertheless, an advancing glacier should have transported ablation moraine that deposited when it receded. Moreover, most ice sheets were cold, a circumstance that favours the formation of a debris-laden bottom layer. Therefore, these large overdeepenings can be explained, but they are not pertinent to this study.
1.5. Rock fracture
Loosening of boulders involves joints that always exist in rocks. Joints are sometimes due to thermal contraction during cooling, after a magma chamber solidified. More frequently, they are attributed to tectonic stresses, either global (linked with plate tectonics) or local (linked with folding). Anyway, joints form at depth before denudation. New joints ought not to form at the surface, where the very existence of joints prevents horizontal tensile stresses and limits compressive stresses to a few MPa (Reference Jamison and CookJamison and Cook 1980). When concentration of tectonic stresses near the foot of a rock wall, by a factor that may reach 4 (Reference Gerber and ScheideggerGerber and Scheidegger, 1969) is accounted for, the differential stress
In fact, in mountains, the main deviatoric stresses at shallow depths are due to topography. A computation by Reference McTigue and MeiMcTigue and Mei (1981) is not pertinent here, because they assumed very small slopes (~0.1). Orders of magnitude may be obtained by using the following very crude model. Consider the plane-strain problem and a crenellated cross-sectional profile: parallel ranges of height Η and width a, separated by flat valleys of width b. Without solving exactly the elastic problem, we can assert that at the base of a range there is a vertical compressive stress in the order of Ρ = ρgH (where ρ is the rock density and g is gravity) and a transverse, horizontal normal stress close to zero. Since σg = 27 000 Pa m−1, when H = 1 000 m and Ρ = 27 MPa.
With Ε denoting Young’s modulus and v Poisson’s ratio, the transverse elastic strain at the base of the ranges is P(v+v2)/E. In the valleys there is a transverse compressive stress σy , which provides an elastic strain −σy(1 − v2)/Ε. Since the total transverse displacement must be zero, we have:

Without confining pressure, v vanishes because of rock porosity (Reference Jaeger and CookJaeger and Cook, 1979, p. 193). The conclusion is that topographic stresses are sufficient to cause sub-critical fracture, i.e. new joints, in steep slopes, on a very long time-scale, and probably never in glacier beds.
Therefore, once all loose rock has been plucked off by freezing of water infilling the joints, the formation of new joints in the bedrock at the time-scale of several centuries can hardly result from tectonic or topographic stresses. There must be another process. Reference Walder and HalletWalder and Hallet (1985) by theory, and Reference Hallet, Walder and StubbsHallet and others (1991) by experimentation have proved that sustained sub-zero temperatures lead to segregation ice growth in micro-cracks, propagation of these micro-cracks and final fracture. The micro-crack development is at a maximum between −3° and −6°C. Repeated cycles of freezing and thawing are not necessary for frost-shattering, contrary to what has been thought previously.
1.6. Subglacial rock fracture and overdeepenings
Beneath a temperate glacier, freezing within micro-cracks is totally excluded, although in bumps some heat flux goes steadily from the lee sides to the stoss sides. The reason is that water in micro-cracks is not free water. It freezes at about −1.5°C below the normal melting point and releases very little latent heat (Reference MellorMellor, 1970). Therefore, subglacial rock fracture by freezing is only possible when the bottom of the glacier is well below 0°C.
Many cirques that are actually covered by small temperate glaciers are strongly overdeepened in their lower parts, below the ablation zone. For instance, in the French Alps, Glacier du Cul du Nant (Massif de Bellecôte) has an overdeepening of 20 m, whereas the glacier thickness is 85 m when it is about 45 m elsewhere (Reference LliboutryLliboutry, 1976). Glacier Blanc (Massif des Ecrins) has an overdeepening of about 40 m, where the ice thickness is 230 m instead of about 250 m (Reference GluckGluck, 1969). Rock fracture, allowing further quarrying and an enhanced erosion rate, could not occur when the actually over-deepened area had not been glaciated, because a small lake would then occur there. But it might have happened subglacially with a more arid and much colder climate, when the cirque glacier was cold down to its bottom. Next, when the glacier became temperate and slid, plucking of loosened rock was possible. However, another explanation, with neither a cold episode nor quarrying, will be offered at the end of this paper.
An interesting case is Mer de Glace, whose bed all along the classical ski run “la Vallée Blanche” has been determined by Laboratoire de Glaciologie du CNRS between 1960 and 1974, with seismic exploration and boring. The upper part, within a cirque, has a gentle slope of 10%, without overdeepening. It is covered by a glacier of uniform thickness (145 m of ice and 33 m of firn) (Reference Lliboutry and VivetLliboutry and Vivet, 1961). The surface stands at 3550–3450 m. After a steep section (crevasses up to 45 m deep are found at its beginning), the slope decreases to 13% at La Bédière. Borings gave thicknesses ranging from 43 to 184 m over short distances, but the largest ones are very questionable since the velocity gradient and the crevasse pattern are very regular. After a major glacier fall (Séracs du Géant), where the velocity reaches 1000 m a−1, the valley has a parabolic cross-section over 3.5 km. The glacier, now a valley glacier, has its surface at 2350–2000 m, a width of about 800 m and a maximum thickness of 400 m. Five successive overdeepenings are found in this 3.5 km long section. Lastly, from 2000 m to the terminus at 1500 m, over 3.5 km, the cross-section of the valley has a V shape (Reference LliboutryLliboutry, 1978b).
Lithological factors cannot explain this contrasted bed topography; all the area is entirely granitic. The highest part has been evenly eroded and in the lowest one the V shape due to pre-Pleistocene fluvial erosion has not been destroyed. I suggest that the five overdeepenings that are found at about 2000 m correspond to at least five episodes of subglacial or periglacial rock fracture under colder and, above all, drier climates, when Mer de Glace was shorter and thinner than today. (Today, the area is very wet. During the period 1954–71 the mean precipitation at 3500 m, practically always snow, has been equivalent to 3.4 m a−1 and the summer melting to 0.2–0.4 m a−1.)
Before Walder and Hallet’s discovery of rock fracture by mere freezing, since repeated freezing and thawing at the same point cannot occur beneath temperate glaciers, other fracture processes had been suggested.
Several authors have put forward repeated high-punching contact forces by clasts squeezed against the bed, which consequently should be either scratching or grooving it (see Reference DrewryDrewry (1986) for references). The corresponding contact force will be estimated below. It may be very large. Nevertheless, it vanishes on the lee sides of bumps, because stream lines of flow in the ice diverge there, and it is precisely on the lee sides of bumps that quarrying is suspected. Moreover, known fatigue failure in rock has been obtained using boring tools, with cogs that impinge on the rock at the same point thousands of times. There is a vanishing probability of a similar repetition at a point on the glacier bed.
I have suggested another fatigue process (Reference LliboutryLliboutry, 1962), which has been taken up again by others. When there is a cavity at the lee of a bump that communicates with a subglacial stream, there are repeated variations in the water pressure in the cavity. This effect has been theoretically investigated by Reference IversonIverson (1991), assuming an instantaneous decrease in the water pressure by 0.6 MPa. Such variations have been subsequently measured (Reference Hantz and LliboutryHantz and Lliboutry, 1983) without making first an artificial large link between the cavity and the stream as other investigators did. Pressure variations may reach 5 bar (0.5 MPa) but they are not at all instantaneous; they span several days. This rate seems too low to cause significant effects and fatigue failure in this way remains to be proved.
My conclusion is that subglacial rock fracture has been possible where today there exists a temperate glacier, but under a different climate, when the glacier bottom was well below the melting point. Periglacial rock fracture by freezing has also been possible. Anyway, quarrying by a temperate glacier should cease when all loosened rock has been removed. The new point, which Walder and Hallet’s discovery has cleared up, is that the loosening process can reach important depths because it is caused by mere frost penetration, not by daily cycles of freeze-and-thaw. Therefore, small overdeepenings might be carved out after a single fracturing episode. We may speculate that, when actual plucking is observed, it is due to some rock fracture that occurred during the Younger Dryas, down to a depth of 30 m.
It has been argued in favour of rock fracture, after the onset of sliding and bed abrasion, that many roches moutonnées have rough lee faces. A simpler interpretation is that these lee faces are the original ones and were never abraded, because a cavity had been present there since the onset of sliding and abrasion (Reference LindströmLindström, 1988).
It remains to ascertain whether mere abrasion, scratching and grooving could provide a minimum glacial erosion rate in the order of 0.1–0.3 mm a−1.
2. Availability of Abrading and Grooving Material
The presence of clasts at the sole of an advancing glacier tongue is easy to understand, although many cases are possible. The glacier terminus may have encountered on its way bare rock, rock with moraine above it, ice-cored moraine, wet or frozen sediments, a snow cover or not, etc. Therefore, no general model, predicting how much material will be covered and carried by an advancing glacier, could be suggested. Let us now examine how many clasts can reach the sole of a steady-state glacier. Since subglacial plucking is assumed to have ended, such clasts must come from subaerial weathering. Secondly, sand may have been freed at the bed by chemical weathering.
2.1. Chemical weathering
In granite and granodiorite, hydration of feldspars causes the rock to decay into sand and silt. There is no reason for ruling out chemical weathering, which requires only water to operate. If weathering remains unnoticed, it is because the altered minerals are immediately abraded away by the hard angular quartz grains that have been freed. Contrary to frost-shattering, or to the speculated shattering by absorbed water (Reference WhiteWhite, 1976), chemical weathering attacks even polished rocks without microcracks at the surface.
Although this weathering has been described in many textbooks of geology, its rate has seldom been estimated. Old cathedrals not damaged by actual air pollution provide constraints on such rates. One century ago, Reference VélainVélain (1892) noted that the north side of the cathedral of Limoges, built of granite and then 400 years old, had lost nearly 1 cm by chemical weathering. This rate of about 0.02 mm a−1 should be pertinent to subglacial weathering of granite, since it concerns a wall never exposed to the sun, facing the dominant winds and hence plentifully watered. This rate is at least one order of magnitude lower than erosion rates reported above, and thus may be neglected for estimating them. Nevertheless, chemical processes might be the main source of polishing sand grains.
2.2. Marginal crevasses
In summer, at the sides of a glacier, scree may fall between ice and rock, or into marginal crevasses, which are the only ones that reach the bed.
In general, the accumulation zone of a glacier is concave, and stream lines veer towards the centre of the glacier, whereas the tongue is often convex and. stream lines veer away from the centre. Therefore, in the accumulation area, the debris that may fall into marginal crevasses should migrate progressively towards the centre. Nevertheless, the only source of debris for the central part of a glacier must be sought at the bergschrund.
Also, frost-shattering of the bedrock in marginal crevasses is possible, as observed by Reference AllixAllix (1922) at Glacier Blanc (Massif des Ecrins, French Alps). In August 1920, at 2470 m, the temperature at the bottom of marginal crevasses oscillated daily between 6.8°C and −2.7°C. Allix estimated the local frost-shattering of gneiss on these days was 1 cm d−1. Even if crevasses cover only 1/100 of the glacier side and frost-shattering occurs only a few weeks per year, Allix’s estimate yields a conspicuous mean erosion rate, in the order of 2 mm a−1, which would operate only at a shallow depth. Such a high value needs to be confirmed.
2.3. Bergschrunds
Many authors since Johnson have discussed the importance of frost-shattering within bergschrunds. Reference von KlebelsbergVon Klebelsberg (1948) made strong arguments against its importance. Anyway, there is no doubt that frost-shattering is more important at the rock walls above the bergschrund, where watering and frost are more intense, and these walls are far larger than the rocky wall of a bergschrund.
In normal years, above the bergschrund, an ice apron of cold ice stuck to the rock creates an overhang and, even when the bergschrund is open, most falling stones bounce over it. Nevertheless, there are from time to time very hot and dry summers, with gaping bergschrunds and melted ice aprons, such that clasts and boulders become free and can rush down the couloirs. (I remember such a summer in the Mont-Blanc massif in 1947, when I was an alpinist, not yet a glaciologist.) Moreover, when clasts do not enter the bergschrund, they may reach the glacier sole anyway, thanks to ice melting at this sole.
It is shown in Appendix I that a stone embedded in temperate glacier ice sinks through it, because of its buoyant weight, only by about 1 mm a−1, whatever its size. This very small effect may be ignored and we may consider that embedded stones follow the stream lines of the ice. There are stream lines that terminate at the bed, because there are sources of heat that melt ice. They are the geothermal flux φg , and the Newtonian energy dissipated in sliding τbU (U denoting the sliding velocity and τb the basal drag). The melting heat per unit volume of ice is M = 306.4 MPa. The melting rate at the glacier sole is:

The melting rate due to the geothermal flux, φg/Μ, is in the order of 0.01 ma−1. The term τbU/M yields the same value for U = 30 m a−1 and τb = 0.1 MPa. Let c be the volume fraction of debris in the bottom ice. There is at the glacier sole a volume accumulation rate of debris equal to mc. In a steady state, the only state that is considered, assuming that the debris at the bed does not form lodged till, the volumetric discharge of debris per unit width is:

The term Q0 is due to the clasts entering directly the bergschrund. It will be shown that clasts of any size move approximately at the sliding velocity U. Their volume per unit area of bed is then Q/U.
To obtain orders of magnitude for Q0 and c, assume that subaerial weathering destroys the relief at rate W, and that a slope of mean length D nourishes the upper end of the glacier with clasts, such that a part α falls into the bergschrund, and a part (1−α) within a distance x0 from it, with an even distribution. Near the bergschrund (x = 0), the surface mass balance of the glacier, in equivalent ice volume per unit area and unit time, is b 0. Then:

Realistic values for an Alpine glacier might be

With the above values, and m = 0.02 m a−1, xf = 4 km. After this distance, Q maintains a maximum and constant value. Nevertheless, the glacier may not be sufficiently long for this stage to be reached and some debris-laden bottom layer may still exist at the terminus.
2.4. Internal melting and external refreezing at the glacier sole
When a clast comes very close to the bed, we must consider other processes, which involve the micro-relief of the bedrock and the singular properties of temperate ice. They have been studied in detail in another paper (Reference LliboutryLliboutry, 1993), with the following results:
When the state of stress is not hydrostatic, most of the water present in temperate ice should be found as intergranular water lenses more or less perpendicular to the maximum compressive stress. They govern the temperature, which is then locally controlled by the stress. After a change in stress, it should take about 1 h for a new local thermodynamic equilibrium, hence a new temperature, to be reached. This concept of locally stress-controlled temperatures is valid only at space scales larger than the ice grain-size.
Given the stresses, and the corresponding temperatures, heat fluxes ensue according to Fourier’s law. They provide internal melting in a bottom layer, which is thinner on the lee sides of bumps but is never absent. Therefore, the water content first rises to its maximum value, which, from field evidence, is about 2%. Next, it exudes at the interface via the net of capillary veins. These veins can remain liquid even in domains of internal freezing, because of capillary effects.
On the stoss sides of bumps there is melting, with heat coming from the lee sides through the bedrock. On the lee sides, there is freezing, with heat beginning both through the ice and through the bedrock. (There are some changes in the precise areas of melting and freezing when the finite amplitude of the micro-relief is accounted for but they are of secondary importance.) Consequently, melting and refreezing at the very interface do not balance. Even when geothermal heat is taken into account, there is an important freezing trend made possible due to the water exuding from the ice.
Water moves from areas of melting to those of freezing through the ice and not as a continuous water film at the interface. This fact does not impede the possibility of cavitation. (The precise effects of cavitation on glacial erosion will not be attempted here.)
Internal melting and external freezing make the ice near the interface ascend to some distance hi from the bed. The order of magnitude of hi should be 3 cm. That geothermal heat and Newtonian energy dissipated by sliding melt over time, a large amount of ice does not contradict this result. Geothermal heat has been accounted for in the theory. Energy dissipation provides extra internal melting. Therefore, glacier stream lines do not reach the bed; they end as a single stream line, at a distance hi from it. Below, other stream lines begin from the bed and reach the singular stream line at a distance hi . (This is possible because ice permeability allows the continuity condition, that expresses mass conservation, to be violated.)
It follows from this last result that very small particles, say sand grains, of subaerial origin, embedded in the glacier, cannot reach the bottom interface. At most, they reach the singular stream line. Abrasion of the bed by sand grains and rock chips can occur only if they appear at the bed. Nevertheless, a question arises. Why should these small particles not be caught immediately by regelation ice and therefore could not leave the ice-bed interface?
These particles are smaller than ice crystals, and the theory summarized above (Reference LliboutryLliboutry, 1993) does not work at this minute space scale. When there is refreezing at the interface, water exudes via capillary veins and migrates between ice and rock over distances smaller than the ice crystals, before refreezing. When there is a particle between ice and rock, it should produce a very local overpressure that impedes refreezing. Even if the particle is caught on its sides by regelation ice, the strong contact forces linked with the abrasional process should often free it. It is only when small particles at the base are very abundant that they should rise and form the debris-rich layer of regelation ice that is often observed. (For instance, see Reference LewisLewis (1960) for such observations.) Of course, all these speculations have to be checked by field observations, together with the internal melting and bottom freezing that theory predicts.
Therefore, the primary process of steady erosion appears to be grooving by large stones, decimetric or metric in size. This point of view allows us to ignore the complex processes occurring within the bottom regelation layer some centimetres thick, because the stone size is at least one order of magnitude larger.
2.5. Behaviour of a large clast at the glacier sole
The motion of a stone of decimetric size that approaches the bed, but does not touch it, would be extremely difficult to predict accurately. An interesting attempt, with rigorous mathematics, has been made by Reference MorrisMorris (1979), in the case of a cylindrical stone near a piece-wise rough plane bed. She assumed the ice was dry and impermeable, and the pressure-melting point was reached at all the ice boundaries. This problem, in general, has no solution. The assumption of Newtonian viscosity cannot be the reason. Therefore, she suggested that in reality either the ice must be below the melting point at some places or that the ice is wet, but that there exists some additional “internal temperature”. This fuzzy “internal temperature” is precisely my locally stress-controlled temperature, but why it should be added to instead of replacing her calculated value is not at all clear. Another reason why the problem that she posed was too constrained to yield a solution is that she did not take into account ice permeability. If water fluxes are allowed, ever-growing water pockets might form.
Given these difficulties, I shall limit myself to qualitative considerations. Consider the stress field within the ice on the lee side of a bump. The pressure (i.e. the normal stress, sign apart) perpendicular to the bed increases with distance from the bed, tending towards the mean lithostatic pressure. When a rigid stone is introduced, this pressure must become equal on the upper and lower sides of the stone. This change demands a downward velocity of the stone with respect to ice. On the stoss side of a bump, it is the reverse. Thus, the centre of the stone oscillates about a stream line (as it exists without a stone). Without the melting trend m due to geothermal heat and energy dissipation, this effect may allow the stone to avoid the bumps of the bed. It may be insufficient, however, because the streamline about which the centre of the stone oscillates becomes progressively straight when the distance from the bed increases. With increasing stone size, the vertical oscillations due to pressure differences tend towards a maximum and the vertical oscillations due to the shape of the stream line tend towards zero. Thus, for a given distance between the lower side of a stone and a flat bed, the larger the stone is the more chance it has of hitting the stoss side of a bump downstream.
When a stone is close to the bed, if it is equant, it rotates more or less as the surrounding ice, at an angular velocity:

where τb is the bottom drag (τb ~0.1 MPa) and Β is a rheological factor, whose recommended value is B = 440 MPa−3 a−1 (Reference LliboutryLliboutry, 1987, p. 124 and 451). Flat clasts tend to become parallel to the bed and then their rotational velocity vanishes.
When a clast touches the bed, it may polish it by breaking off minute asperities that interlock with minute asperities of the clast, or it may scratch it making a glacial stria, or it may groove it. These three erosional forms have been well described by Reference Tricart and CailleuxTricart and Cailleux (1957). Striae have cross-sections in the order of 1 mm2, whereas grooves have cross-sections larger than 1 cm2. Obviously, grooves can be made by those large clasts that we are now considering but the reverse is not true; a large stone may rub the bed without grooving it.
This point will be considered in sections 2.7 (blunting of grooving corners) and 3.4 (probability ∏ for a stone with sharp corners to start a groove). This probability lowers progressively with wear but, to simplify the calculations, a piece-wise constant probability will be adopted in the model. Grooving rates will be calculated as though the stone was not worn at all during some time and next suddenly worn out.
When a clast slides on the bed, polishing or scratching it, small debris (rock chips) and gouge may infill more or less the interstices between the clast and the bed, as once observed by Reference Boulton and CoatesBoulton (1974). A clast of basalt 30 cm long was rubbing against a basaltic bed at three contact points, with one of them having become “a heavily striated and smoothed facet”. Between the three contact points, the gap between clast and bedrock was infilled with crushed debris. The clast velocity was 8.2 m a−1, and the ice velocity was 9.9 m a−1. (This differential velocity produced a 30 cm long cavity at the lee of the clast. However, since the clast was observed at the wall of a tunnel, this last feature may not be representative of subglacial conditions.) Probably, in such cases, the wear by small debris is considerably enhanced. The cushion of debris pressed by a clast should act as a rigid rasp, that rasps more as the normal pressure increases.
When plucking does not occur, grooving should be the essential process of glacial erosion, and I shall try to model it in section 3 of this paper. This modelling will yield the volume of bedrock that is carved per unit time by a single grooving clast, say
2.6. Size distribution
The size distribution of rock debris at a temperate glacier sole up to metric sizes is almost unknown. From the few data about morainic material found in textbooks on sedimentology it seems that, V(L) denoting the cumulative volume of debris with sizes inferior to L and L0 the minimum size allowed to sediment during analysis (L0 ~ 1µm), a logarithmic size distribution holds up to L ~8mm:
There is no reason for subglacial debris to fit the same distribution, especially for large sizes. At the glacier sole we may distinguish:
-
(a) Large clasts due to fracture along joints and frost-shattering.
-
(b) Minute rock debris, either chips produced by scratching and grooving or sand made free by chemical weathering.
-
(c) Very fine sand (finer than the grain-size of the rock) and rock flour due to abrasion.
Materials (b) and (c) might have a logarithmic distribution but we need to know the distribution of material (a), the only one able to groove the bed. Its distribution in glaciers has never been studied.
Reference BullBull (1964) has measured size distributions in debris flows and Reference O’Keefe and AhrensO’Keefe and Ahrens (1985) in fragmented material resulting from explosions. V(L) appears to be proportional to Lγ , with γ = 0.41 in the former case and γ = 0.55 ± 0.03 in the latter. Since, for large sizes, their distribution is mainly due to the distribution of the distances between joints in the rock, this power-law distribution will be adopted in our quite different context, with γ = 0.48 ± 0.07.
Of course, this distribution cannot be valid up to infinite size. There must be a maximum size Lm , corresponding to the distance between major joints. A minimum size Lm , either centimetric or decimetric, will be introduced to remove all small clasts unable to groove in any circumstance. Consequently, given clasts with sizes ranging from Lm to LM , whose total volume is V, the number of clasts with sizes in the interval [L, L + dL) is Vdf, with df such that:

2.7. Blunting of grooving corners
Monolithologic grooving, i.e. grooving by a stone with the same lithology as the bedrock, may seem paradoxical. Why should the grooving corner not have the same probability of breaking off as the bed? The reason must be sought in the geometry. The contact force increases very much the mean normal stress within the corner of the tool and the bottom of the groove, but less so on the rims of the groove. Since the shear stress needed for brittle fracture increases with the mean normal stress, it is a section of the rim, before the corner, that breaks off first. Thus, in general, before the grooving corner, the bedrock breaks off repeatedly, releasing each time a chip of 1–1000 cm3, whereas the corner only blunts progressively, with detachment of gouge smaller than the grain-size, as in frictional sliding (Reference Logan and TeufelLogan and Teufel, 1986). A progressive blunting of the grooving corner explains why some grooves become broader and more shallow downstream (Reference Tricart and CailleuxTricart and Cailleux, 1957).
It may happen that successive rotations of a boulder allow all its corners to blunt one after another, until it is completely worn out and unable to erode any more. This concept has been introduced by Reference RöthlisbergerRöthlisberger (1968). He reported that in medial moraines only some boulders are so worn out, testifying that they have been in contact with the bed for a long time.
In the same paper, Röthlisberger gave the following argument in favour of subglacial plucking: “If the content of abrasive is a very important factor in the total rate of erosion, one would expect that a long compound glacier should carve as many parallel (furrows) as there are medial moraines. One does not find this in Nature.” The argument loses its strength, however, either if boulders are worn out very fast or if glacial erosion is very low. In the latter case, since at depth lateral moraines spread progressively, no deep furrow will appear.
The case of worn clasts that are broken into smaller fragments with fresh angularities is assumed to be very marginal.
When a clast grooves the bed, its blunting removes a volume that should be more or less proportional to the volume of rock that it has grooved. When it is worn out, it has lost part of its volume. We may assume that both coefficients of proportionality are independent of the initial volume L3 of the clast (or, if they are mild functions of L, that their ratio is independent of L). Therefore, to take into account blunting in the model, the following assumption will be made:
“When a clast is worn out, it has grooved a volume kL3 of rock, the coefficient k being independent of L.”
A two-dimensional problem is assumed. (Thus, all clasts are assumed to come from the head wall.) A stone that appears at the bed at an abscissa x becomes worn out at abscissa x if:

It will be shown that v increases with size L much slower than L3 . Therefore, for given sliding velocities U(x′), the “wearing distance” λ is an increasing function of L. At distance × from the bergschrund, all clasts larger than some value L1 are not yet worn out. This limiting value is obtained by putting λ = × in Equation (9):

Clasts smaller than L1 can groove only if they have appeared at the bed at a shorter distance upstream than λ. According to Equation (3), their volume per unit area is mcλ/U. Therefore, the mean erosion rate by grooving at abscissa x, for clasts of any size, is:

This formula demands Lm < L < LM, to which corresponds, from Equation (10), xm < x < xM Also, we must have × < xf , with xf as given by Equation (5), because downstream of this limit no new clasts reach the bed. If xM < xf (we shall see that it is not the case), in the range xM < x < xf all the grooving clasts would have reached the bed at some distance downstream from the bergschrund. The volume of clasts that reach the bed per unit time and unit area is mc and the volume of grooved rock is k times this value. It would follow the very simple formula:
Although this formula is not obeyed, because xf < xM , it allows us to understand why blunting makes the grooving rate much less dependent on the sliding velocity and the rock strength than might be expected.
3. Estimation of Erosion Rates without Quarrying
3.1. Observed grooves
Grooves are furrows 2–5 times wider than deep, several metres long, with cross-sectional areas in the range 1–100 cm2 and even sometimes larger. They are observed mainly on side walls of glaciers (not necessarily large and fast ones), probably because large boulders are much more frequent there, but this case is put aside in our two-dimensional model.
Reference Boulton and CoatesBoulton (1974) mentioned boulders 3 m in size “having produced grooves up to 40 cm wide and 10 cm deep, having a very irregular floor and showing transverse fracturing”. This transverse fracturing is akin to chattermarks observed on quartzites without grooving. In the case of grooving, this fracturing shows that there is some overbreak, i.e. the cross-section of the groove is larger than the cross-section of the “tool”. The irregular floor contradicts the classical description of glacial grooves by geologists. Reference Boulton and CoatesBoulton (1974) suggested that grooves are subsequently polished, by streaming of the subglacial debris into the grooves.
The theory below yields important erosion rates only if grooving is much more ubiquitous than reported in the upper part of glaciers, for x < xf . (In the lower part, all small clasts are worn out and only large boulders can groove, making large grooves.) This point deserves unbiased statistics and not only reports on the most striking forms.
3.2. Equations for the motion of a rolling stone in ice
To model scratching or grooving, we must establish two sets of equations: a set that links the contact force with the motion of the stone relative to ice and another set that links the contact force with the strength of the bedrock and the geometry of the groove. Both problems will be examined in due course.
We consider only stones that are not too flat and are in contact with the bed at a single corner, because in this case their velocities relative to ice and their angular velocities are easy to estimate. The former may be calculated by taking a spherical stone as a model, and the latter, with less accuracy, with a cubic stone as a model. When a spherical stone embedded in temperate ice is subjected to a resultant force F, its velocity relative to the surrounding ice is Δu, as calculated in Appendix I. The angular velocity of a cubic stone subjected to a resultant moment Γ is calculated in Appendix II. Defining, in both cases, a size L of the stone such that its volume is L3 , the results are:


The terms in Α1 , A2 correspond to the melting-refreezing process and the terms in B1 , B2 to a viscous deformation of ice. These formulae are obtained assuming that at a large distance from the stone the ice is motionless. We assume that they still give correct orders of magnitude for any stone in contact with the bed over an area much smaller than L2 , although the bed modifies the flow of ice around the stone. This is permissible because we assume L > 3hi , i.e. the stone is of decimetric or metric size. Nevertheless, there is a general shear strain rate within the ice, that provides an additional angular velocity Ω0 , as given by Equation (6). Therefore, the angular velocity of the stone is Ω + Ω0 .
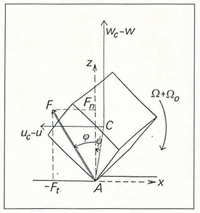
The resultant force on the stone is the sum of the contact force and of the buoyant weight of the stone. In Appendix I, it is shown that, when L < 5 m, the buoyant weight acting alone provides only a downward velocity of 1 mm a−1. This is much less than the mere vertical velocity due to bottom melting (which, in turn, is generally much less than the vertical velocities due to the micro-relief of the bed) and thus the buoyant weight will be neglected. Contrary to Reference HalletHallet (1979), rolling will be considered. It causes the velocity of the grooving corner A to differ from the velocity of the centre of the stone C (Fig. 1), especially during the sticking phases leading to repeated fractures of the rim of the groove.

Fig. 1. A grooving stone is modelled as a cube. Notations as used in the text. In this case Ψ and dΨ/dt are positive.
The contact force applies at point A. With the x axis along the local bed, pointing in the direction of glacier motion, and the z axis pointing upwards and, assuming a plane problem, the resultant force has two components: −Ft = −FsinΦ (tangential) and Fn = FcosΦ (normal). Let (uc, wc) be the components of the velocity of the centre of the stone. Let (u, w) be the velocity at the same point C in the ice, in the absence of stone. We assume that:
-
(a) Relation (13) gives the “relative velocity” Δu, defined by its components (uc − u) and (wc − w).
-
(b) This relative velocity has the same direction as the resultant force (which has been confused with the contact force):
(15)
-
(c) The angular velocity about C is (Ω + Ω0), obeying Equations (14) and (6), with Γ denoting the moment of the eccentric contact force about C. Taking again as a model a cube of size L, with its corner A in contact with the bed, the length CA = L√3/2. Assuming that the x − z plane is a plane of symmetry for the cube, its orientation is defined by a single angle, the angle Ψ of the contact radius CA with the z axis, as shown on Figure 1. Its sign is chosen in order that, t denoting time:
(16)
The velocity of A is (uA , 0). From geometry:
(17) (18)
(18)
Comparing Equations (15) and (17)
where, from Equations (14) and (18):(19) (20)
(20)
It follows that:
(21)
Given the ice velocity without rock debris (u, w) and the tilt of the contact radius Ψ, we have two equations for the three unknowns uA , F and Φ. To solve the problem, a third relation, either empirical or theoretical, is required.
3.3. Closure equations drawn from rock mechanics
Because of the lack of experiments on monolithologic grooving, we might call on engineering knowledge about drilling tools. A good review of rock drilling has been given by Reference MellorMellor (1977). Many values of the ratio Ft/Fn = tan Φ as a function of the rake angle (the tilt of the working face of the tool from the vertical) may be drawn from the figures reproduced in the paper, to which the following numbers refer.
In very weak rocks such as chalk tan Φ is very dependent on the rake angle (fig. 54) but in hard rocks it is much less sensitive. It is always larger than 1. In limestone (figs 11 and figs 19), tan Φ = 1.10–1.18; in andesite (figs 22 and figs 31), tanΦ = 1.56–1.89; in sandstone (figs 14, 21 and 31), tan Φ = 1.59–1.92; in quartzite (fig. 27), tan Ω = 1.79–2.27. These data, however, are for sharp very hard steel tools, and when they are considered to be worn out tan Φ decreases well below 1, as shown in Figure 76 of the quoted paper. (Anyone who has drilled a hole with a worn bit is well aware of this fact.) In the hardest rock, quartzite, tools are rapidly worn and tan tanΦ = 0.68 (figs 38 and 56) or even tan Φ = 0.20 (figs 57 and 58). Only these last results are pertinent to monolithologic grooving. Clearly, some important factor has been overlooked, and the required equation cannot be obtained from this approach. At most we may assert that tanΦ < 1 but this value is a mean during drilling. We shall see that, on very short time-scales, tan Φ should oscillate strongly.
Reference Kenny and JohnsonKenny and Johnson (1976) have investigated the wear of drilling tools. The worn volume of the tools was found to be independent of the rake angle and very quickly to become proportional to the distance travelled. If we assume that the worn volume of a clast is proportional to the grooved volume of bedrock, the latter also should very quickly become proportional to the travelled distance uAt In other words, the cross-sectional area of the groove, say s, very rapidly becomes a constant.
From the so-called “triaxial” tests, a uniaxial compressive strength is defined. It will be denoted C0, as in Reference Jaeger and CookJaeger and Cook (1979). Although at the head of a groove the state of stress is not uniaxial, it will be assumed that fracture occurs when the tangential force Ft equals SC0 . This assumption might be argued.
Note that rock strength is a macroscopic concept, which ignores individual grains. It cannot be used for modelling abrasion and scratching. In this case, the rock should not be considered as homogeneous. In monolithologic abrasion, harder grains can indent softer ones, with subsequent interlocking of hard grains. In Reference DrewryDrewry (1986), both size scales are unduly confused.
At the sole of a temperate glacier, the confining pressure due to the overburden of ice is some MPa. It is transmitted to the water that infills the micro-cracks and pores of the bedrock. Therefore, this confining pressure should not modify the strength of the bedrock, the difference between the two extreme principal stresses, σ1 − σ3 that allows brittle fracture (Reference PatersonPaterson, 1978, p. 77, 80). According to the data reviewed by Reference Jaeger and CookJaeger and Cook (1979) or Reference GoodmanGoodman (1980), the strength so defined is C0 = 200 ± 40 MPa for granite or gneiss, 250 ± 100 MPa for basalt and 400 ± 70 MPa for quartzite. (However, in quartzite grooves are not observed.) The value C0 = 200 MPa will be adopted in our calculations.
During grooving, fractures occur repeatedly, and the contact force oscillates on a very short time-scale. The elasticity of the whole system intervenes, and on this time-scale there is stick-slip motion. The two phases, stick and slip, must be considered separately.
During the stick phase, Equations (21) should be modified to take elasticity into account. When elasticity is ignored, putting uA = 0, Equations (21) yield a particular solution, say F = FM and Φ = ΦM Intuitively, when elasticity is introduced, the contact force increases with time and tends towards FM , and its tangential component Ft = F sin Φ increases faster, tending towards FMsinΦM . It will be assumed that, when brittle fracture occurs, F and Φ are approximately equal to the asymptotic values F and ΦM . Therefore, the cross-sectional area of the groove, s, is given by the following set of equations:

During the slip phase, Ft is the standard friction force for a corner sliding on a rough groove. It is given by Coulomb’s law: tan Φ has a fixed value f. For a plane rubbing on another plane, f ≈ 0.7, but for a corner sliding in a rough groove f ≈ 1. Since the contact force during the slip phase is constant, Equations (21), which ignore elasticity, hold. They yield F = Fm (so denoted because it is the minimum value of F during the entire process) and uA :

Nevertheless, what we need is the mean value of uA during the whole stick-slip process. Thus, the relative duration of the stick and slip phases must be estimated.
The elastic displacement at the end of the sticking phase, when a contact force sC0 acts on a stone of size L, is mainly due to the elasticity of ice, whose Young’s modulus is Ε = 9210 MPa. As a very rough estimation, this displacement is of the same order as for a rod of ice with a cross-section L2 and length 3L:

It will be shown that realistic values of s are s = 1.5 cm2 for L = 20 cm, and s = 25 cm2 for L = 1 m. In the former case, δ ~ 0.05 mm, when the length of the chip (of the same order as the displacement of the grooving corner before it sticks again) is in the order of 1 cm. In the latter case, δ ~ 0.16 mm, when the slipping length is in the order of 5 cm. Thus, the slip phase should be longer than the stick one by two orders of magnitude: several hours of slipping for several minutes of sticking. Consequently, uA as given by Equations (23) may be confused with its mean value.
3.4. Rolling velocity and grooving probability
The simplification above, ignoring the stick phase, is not valid when dΦ/dt is calculated by using Equation (20). Although the stick phase is very short, the instantaneous value of dΦ/dt is then very large. For this reason, the evolution of Φ with time will not be calculated. We limit ourselves to the following qualitative considerations.
Intuitively, with the cubic model of Figure 1, grooving by a corner demands that the facet acting as a tool make an angle with the vertical (henceforth called the rake angle, with a sign opposite to that in engineering use) smaller than some value. Otherwise, the stone would slip up out of the groove instead of breaking its rim. The calculation of this maximum value of the rake angle would need a thorough treatment of the fracture process, which has not been done. For clarity, assume that it is 60°. Since the angle of this facet with AC is arctan (l/√2) = 35.3°, the bounds of Φ are:
If the cube moved in the opposite direction to that of the one displayed in Figure 1, the bounds would be:

Given that the model is highly idealized, we may assume the mean values as bounds in any case:

Since 0 < Φ < 90°, it follows −45° < Φ + Ψ < 105°, and:

Therefore, according to Equation (20), dΨ/dt is always positive. A grooving stone must always roll.
When a stone hits the bed for the first time, if it is equisized, no particular value of Ψ is favoured. With the assumed value of the maximum rake angle, there are two chances out of three that Ψ is between the bounds that make grooving possible. As Ψ increases with time, sooner or later the upper bound is reached. Then the “tool” slips out from the groove and grooving is interrupted. According to some values of dΨ/dt calculated below for particular cases, the mean value of dΨ/dt should be about 1 rad a−1, and thus the duration of uninterrupted grooving should be in the order of 1 year.
However, when an equi-sized stone slides on the bed without grooving, it abrades and maybe scratches it. The corresponding contact forces favour rolling, as well as Ω0 . The calculations presented above are not valid in the case of several contact points but, intuitively, rolling goes on. Therefore, another corner may start a groove. The groove may begin as a stria that depends progressively or, more probably, it should start abruptly at some step, joint or hole in the bedrock.
All the processes considered in this section may be accounted for by introducing a “grooving probability” ∏. It is defined as the probability that a stone, with sharp corners and able to groove, which is in contact with the bed, indeed grooves. Since for a given size L this probability depends on the precise shape of the stone, a mean value is considered. We assume that, for a given lithology Π is independent of L. Although ∏ is an essential parameter of the theory, its value can only be guessed.
3.5. Estimations obtained with a particular value Ψ = 0
When the contact radius is normal to the bed (Ψ = 0), the equations of motion become simpler. Moreover, one may ignore the local perturbations of u due to the micro-relief and put u = U, the sliding velocity at the scale of the glacier. Also, since Ω0 ~ 0.22 a−1, L√3Ω0/2 is negligible compared with U and will be neglected. Then, Equations (22) and (23) read:
Slip phase:

End of the stick phase:

Recall that terms in A1 or A2 correspond to the melting-refreezing process, and terms in B1 or B2 correspond to the viscous deformation of ice.
Two examples will be given, assuming U = 10 ma−1 and −w = m, as given by Equation (2) when Φg/Μ 1 cm a−1 and τg = 0.1 MPa. It yields −w = 0.0133 m a−1. The values f = 1 and C0 = 200 MPa have been adopted; the Ai and Bi are given in Equations (13) and (14).
First example: L = 0.2 m
Fm = 2.35 kN and FM = 29.44 kN; Φm = 45° and ΦM = 87.0°. During the stick phase, Ft increases from 1.66 to 29.4 kN, whereas FN decreases insignificantly from 1.66 to 1.54 kN. (The neglected buoyant weight is 0.13 kN.)
U−uA = 0.167 ma−1, entirely due to melting-refreezing.
dΨ/dt = 1.12 rad a−1 during the slip phase (0.22 due to the general shear of bottom ice, 0.89 by melting-refreezing and 0.01 by ice viscosity).
dΨ/dt = 56.4 rad a−1 at the end of the stick phase, the contribution of the three processes being respectively 0.22, 15.7 and 40.5 rad a−1.
On the lefthand side of the first Equation (28), which gives the maximum tangential force, hence the crosssectional area, the contribution of melting-refreezing is 2.72 m a−1 and the contribution of ice deformation is 7.04 m a−1.
The cross-sectional area of the groove is s = 1.47 cm2.
Second example: L = 1 m
FM = 241 kN and FM = 489 kN; Φm= 45° and ΦΜ = 77.1°. During the stick phase, Ft increases from 170 to 477 kN, whereas Fn decreases from 170 to 109 kN. (The neglected buoyant weight is 16 kN.)
U − uA = 0.576 m a−1 (0.137 by melting-refreezing + 0.439 by ice deformation).
dΨ/dt = 0.22 + 0.146 + 0.505 = 0.871 rad a−1 during the slip phase.
dΨ/dt = 0.22 + 0.41 + 11.07 = 11.7 rad a−1 at the end of the stick phase.
On the lefthand side of Equation (28), the melting-refreezing term is 0.353 m a−1 and the viscous term is 9.584 m a−1. Lastly, s = 23.8 cm2.
An objection to the present theory might be that it yields a mean value of Ft which is somewhat larger than the mean value of Fn , when engineering practice indicates that this happens only with sharp steel tools. My answer is that once grooving has started because of a very local favourable geometry of the bed, its continuation is quite a different problem from that of rock drilling, which must be continuous. In rock drilling, ∏ = 1, and this certainty can be obtained only by continuous prodding of the rock.
Given the simplifications made by the model and the rough approximations made to solve the mechanical problem, for an admittedly rather heuristic treatment of glacial erosion, Equations (27) and (28) will be retained even when Ψ is not zero and evolves with time. Moreover, since in the first Equation (28), from which s is drawn, the viscous term is larger, or much larger, than the melting-refreezing term, the latter will be dropped. Also, it appears that

with the metre, the year and the MPa as units.
The two examples given show that U − uA ≪ U. Thus, the grooved volume per unit time is suA ≈ sU. Taking into account that a stone, in contact with the bed and not worn out, does not necessarily groove and not all the time because it rolls, the volume of bedrock per unit time grooved by a stone that is not worn out is, as a mean:

3.6. Rough estimation of erosion rates by grooving
With
and, comparing Equations (10) and (30):

where G denotes the following mild function of U:

For x < xm there are no worn-out clasts at the glacier sole. Therefore, Equation (11) has to be modified. The grooving rate is:

with J denoting the integral:

Adopting Lm = 0.1 m, LM and 7 = 0.48 ± 0.07, this integral is J = 3.48 ± 0.22 m −4/3 a−1/3. It is found, with the metre and the year as units:
Since Q0 ~ 0.1 m2 a−1 and U1/3 ~ 2 m1/3 a−1/3, a grooving probability ∏ in the order of 0.1 is favoured but this value may be questioned.
For x > xm , the smallest clasts, up to size L1 , may be worn out. Then, as long as x < xM and x < xf , Equation (11) holds. It yields:

where L1 is the function U and x defined by Equation (32). This grooving rate is still an increasing function of x but it is no longer linear in x. It is displayed in Figure 2 for the following values of the parameters: m = 0.02 m a−1, c = 0.01, k = 3, LM = 2 m, LM = 0.1 m, γ = 0.48, Q0 = 0.1 m2 a−1, ∏ = 0.1, C0 = 200 MPa and U = 8 m a−1. Then xm = 620 m and xM = 33700 m. Recall that an estimate of xf is 4000 m (cf. Equation (5)). Equations (32) and (37) read:

For × = xΜ = 33 700 m the second term of Equation (37) vanishes and ėgr = mck = 0.6 mm a−1. Nevertheless, Equation (38) is not valid for such a value of x, which is larger than xf , because no new stones appear at the bed by bottom melting.
For × > xf , the reasoning is as follows.
Since, up to × = xf , per unit width, over a distance dx, within a size interval (L, L + dL), mc dx df/U stones reach the bed and can groove over a distance λ, the number of grooving stones per unit area is:


From Equation (32), the condition λ < x is equivalent to L < L1 and the condition λ > x − xf is equivalent to L < L2 , with:

Therefore, only stones larger than L2 groove. (If L2 is smaller than Lm , a circumstance that occurs for x − xf < xm , then we must take L2 = Lm .) The grooving rate by stones of every size is:

Comparing with Equations (30) and (31), it follows:

With the same values of the parameters as above:


Fig. 2. a. Bounds of the integrals contributing to the erosion rate by grooving, as functions of x. The highest bound LM = 2 m is not represented, b. Erosion rates by grooving as a function of the distance × from the bergschrund (assuming that the glacier is sufficiently long). Note the change of scale for the abscissae at × = 10 km. No more new stones appear at the bed after x = xf. The model makes this limit very sharp. The assumed values of the parameters are given in the text..
This rate is displayed on Figure 2. Downstream of xf , where the number of grooving clasts is a maximum, no new clasts appear at the glacier sole and consequently the erosion rate diminishes. Between x = 4 km and x = 6 km it is halved. This fact produces, on the time-scale of 100 000 years, an over-deepening of the bed around x = xf (however, if the rock walls at the head that provide grooving clasts have not disappeared meanwhile by subaerial weathering). Note that the model is two-dimensional. If the convergence of streamlines from the bergschrunds around a cirque towards its centre was accounted for, this effect would be enhanced.
3.7. Total steady erosion rates (ignoring quarrying)
Glacial erosion also includes wear by the rock chips and gouge that grooving provides, and by sand grains freed by chemical weathering. The rate of chemical weathering is ėcr ~ 0.02 mm a−1 and one may assume that the rate at which sand grains are freed is one-half this value. Let β be the ratio of the volume that a clast loses by blunting to the volume of bedrock that it grooves, a ratio that should be in the order of 0.1. Since we are dealing with monolithologic erosion, the wear of the bedrock by small particles should be at most equal to the volume of these particles. Therefore, the total erosion rate by particles, stones and boulders of any size should be at most (when quarrying is excluded):

Ironically, these corrections to the erosion rate are insignificant but it is this wear that gives beds recently uncovered by glaciers their most peculiar appearance.
The erosion rates that have been suggested, as displayed in Figure 2, depend above all on the parameter k, which indicates how many times a stone has grooved its own volume before being worn out. This unknown parameter may be related to two other coefficients that are easier to guess. Let δ be the relative volume that has been lost by blunting when a clast is worn out. Considering that, when a cube becomes a perfect sphere, it has lost 47.6% of its volume, one may guess δ ~0.3. We have:
For this reason, k = 3 has been assumed in the calculations. The corresponding erosional rates are some tenths of a millimetre per year and some hundreds of metres during the whole of the Pleistocene. This agrees with the fact that, in general, glacial erosion cannot keep pace with the orogenic uplift of young mountain ranges, known to be in the order of 1 mm a−1.
4. Conclusion
The behaviour of rock debris at the glacier sole, in spite of its complexity, may be tackled with simple physical models and approximate mathematics. However, in the absence of detailed pertinent field observations and adhoc experiments, the models remain conjectural and the required parameters can only be assessed crudely. For this reason, numerical computations to determine exactly the evolution of Ψ with time, or for calculating ėgr when U depends on x, are premature.
Let us summarize the provisional, rather qualitative results that have been obtained.
Quarrying requires a previous cold episode during which rock was fractured by frost, maybe subglacially. Ignoring this process, glacial erosion of hard bedrock is important (several mm a−1 at least) when a glacier advances and drags loose material at its sole. Otherwise, in a steady-state situation, the primary erosion process is grooving by stones that have fallen into the bergschrund or in its vicinity, and into marginal crevasses. The theory of locally stress-controlled temperatures leads to the prediction that very near the bottom of a temperate glacier there is important internal melting, whereas at the very ice-bed interface there is a freezing trend. Therefore, in the lowest centimetres of the glacier, ice ascends and the minute particles that wear and polish the bedrock must be derived from the bed itself. In addition to sand grains freed by subglacial chemical weathering, they are mainly rock chips created by grooving and the gouge due to the wear itself. Thus, abrasion appears to be a secondary process, governed by prior grooving.
Stones that have fallen near the bergschrund reach the glacier sole within a distance xf of some kilometres, thanks to bottom melting due to geothermal heat and to the Newtonian energy that glacier sliding dissipates. Therefore, erosion should be much greater beneath temperate mountain glaciers that are surrounded by rock walls than beneath temperate ice caps from which only rarenunataks emerge. For x > xf , bottom ice is free of clasts and those already present at the bed lose progressively their ability to groove, because of blunting. (However, the largest boulders can still groove at some tens of kilometres downstream. Therefore, grooving is a maximum at x = xf . An over-deepening may form there very slowly, without the necessity of an episode of frost and subsequent quarrying.
The rock strength C0 and the sliding velocity U have less influence on the erosion rate than commonly thought. The harder the rock, the less easily stones can groove the bed but the longer they groove before being worn out. The faster the velocity, the more intense is grooving but also the more intense is blunting.
Unfortunately, the probability for a stone at the bed to groove when it is not worn out (∏) and the blunting parameter (β) are totally unknown. If k = δ/β ~ 10, grooving rates in the order of 1 mm a−1 would be found. My guess is k = 3 but it must be confirmed.
The theory has some limitations, besides dealing only with temperate glaciers. It does not consider the case of very high debris content in bottom ice, as in many glaciers fed mainly by avalanches (e.g. Khumbu Glacier). In this case, the clasts that appear at the glacier sole are so abundant that they should interact with each other. At the limit, the theory does not deal with bedrock erosion by rock glaciers, a topic that has never been investigated.
The effect of subglacial ice-bed separation (cavitation) has not been considered, nor has the possibility of almost horizontal faults at the bed, as found at some glacier tongues. The latter might allow the formation of stratified debris-laden bottom ice, which is sometimes found in temperate glaciers. (It is quite common in cold glaciers.) Today, any attempt to model erosion in all these complex cases would be highly speculative.
Clearly, more subglacial observations on temperate glaciers are needed. Not only in large natural cavities as those found beneath glacier d’Argentière, on a verrou where sliding velocities are very high, but in tunnels dug along the glacier sole where sliding velocities are small. When abrading clasts or grooving boulders are found, their shape and size, differential velocity, angular velocity, the dragged debris below, etc. should be measured and published. If stratified ice is found, it must be described in detail and information should be given about the glacier dynamics upstream from the site. (Seasonal variations of the surface velocity, that indicate the existence of ice-bed separation, are particularly relevant.)
The pushing, dragging as ground moraine, or capture of rock debris into bottom stratified ice by an advancing glacier should be examined, together with the abrasion, grooving and quarrying at the temporarily covered bedrock. This might be done in as little as two successive years, taking advantage of the temporary advance of any steady-state glacier during winter.
To estimate erosion rates, we need statistics about clasts that fall into a bergschrund and nearby. We need to know the size distribution of clasts and boulders in moraines up to the largest sizes.
Nevertheless, the most important data that are lacking could be obtained by experiments in rock mechanics which are remote from actual glaciers. It suffices that bare rock, polished during the Ice Age, be easily accessible. A stone having the same lithology might be plucked at a fixed velocity U over this past bed, with a superimposed load (i.e. with Fn fixed). No ice is needed but the bedrock must be fully watered. The onset of grooving could be observed. The cross-section of the groove for different values of the variables and the blunting coefficient could be measured. After many tests, the grooving probability ∏ might be estimated. These key factors would be easy and cheap to investigate. It is too late for the author to do it himself but he hopes that some younger scientists will hear and appreciate his suggestions.
After such field measurements and experimental investigations only, accurate calculations will become fruitful.
Dedication
I dedicate this article to the memory of André de Cayeux de Sénarpont, alias André Cailleux (1907–87). With continuing enthusiasm and youthfulness of mind, he fostered in France and Québec quantitative field studies on sedimentology and geomorphology. His enormous and diverse scientific production (he wrote as a single author about 500 papers and notes) is listed in a special issue of Cahiers Géologiques, No. 112 (1988).
In particular, he measured “indices of blunting” to distinguish pebbles of diverse origins. The present study has shown that, in the case of boulders of glacial origin, these indices may differ widely; only the blunting of very small pebbles and sand grains makes sense.
Acknowledgements
B. Hallet convinced me that plucking beneath temperate glaciers can be an important process, because frost-shattering needs a previous single cold event, and not repeated freeze and thaw. P. Molnar improved my style. With N. Iverson and an anonymous referee, he made well-chosen remarks about the first draft of this paper.
The accuracy of references in the text and in this list is the responsibility of the author, to whom queries should be addressed.
Appendix I Velocity of a Sphere Embedded in Temperate Ice
Ice is assumed to be motionless at an infinite distance. It provides against the sphere normal forces, which can be accounted for by replacing the weight of the sphere with the buoyant weight and shear forces. The latter are assumed to be negligible, because ice can easily overcome the minute asperities on the surface by a melting-refreezing process.
Other forces may act on the sphere but it is assumed that the way they are applied does not modify the flow around the sphere. For instance, the sphere may be pulled with a wire or pushed with a perfectly smooth thin rod. (Of course, this is not the case for a contact force; the calculation below then becomes only approximate.) The resultant of all the forces, buoyant weight included, is denoted by F.
Deforming temperate ice is assumed to have an isotropic, non-linear viscous behavior, with Glen’s coefficient n = 3 (transient creep is ignored). It means that τij and

The viscosity B is dependent on water content. The value that I recommend for the bulk of a temperate glacier is B = 440 MP a−3 a−1 (Reference LliboutryLliboutry, 1987, p. 451).
The velocity permitted by the viscous deformation of ice, say uv , may be bounded by the variational method (Reference LliboutryLliboutry, 1978a, p. 359–67). The result is:

By comparison with the volume of the sphere V = 4/3R3 , Equations (I.2) reads:

When temperate ice slides over a sinusoidal profile, the sliding velocity um due to melting-refreezing processes is about the same with locally stress-controlled temperatures as with the standard theory, which assumes ice to be dry and impermeable (Reference LliboutryLliboutry, 1993). It will be assumed that it is also the case with the present problem. The calculation of um using the standard theory is much simpler.
Define a pressure δ by F = 2ΠR2δ. The first harmonic of the normal pressure on the surface of the sphere has to be, from the equilibrium condition:

where pi denotes the hydrostatic pressure at a large distance and θ is the angle of the considered radius with the direction of motion. (With this approximate value of pn , the problem in mechanics and the problem in thermies are decoupled, as it is rigorously the case with a Newtonian viscous fluid.)
Since ice is assumed to be dry, the temperature is a harmonic function outside the sphere, as it is inside. It will be denoted Text and Τint , respectively. At the interface, Text = Tint = −CmPn and at infinity Text = −Cmpi . With the approximate value of pn as given by Equations (I.4), the solution is:

Let Kb and Ki denote the thermal conductivities of the spheric material and of ice, respectively, and let M denote the latent heat of fusion per unit volume. The melting rate at the interface (the freezing rate when negative) is, in thickness of ice melted per unit time:

As in Reference LliboutryLliboutry (1993), the following thermal parameter is introduced:
The normal velocity at the surface, given by Equations (I.6), corresponds to a velocity um , of the rigid sphere. Thus, melting and refreezing yield an additional velocity:

In the following, Kb = Ki will be assumed. The total velocity is u = uv + um .
Sinking of a Sphere Subject only to its Buoyant Weight
In particular, assume that F is only the buoyant weight, and that the sphere has a density ρ = 2700 kg m−3. Then, where, g = 10 m s−2 is the gravity,
It follows:

Unless boulders larger than 100 m3 are considered, uv ≪ um .
Appendix II Rotation of a Cube Embedded in Temperate Ice Subject to a Torque
The angular velocity of a cube subject to a torque with moment Γ can be roughly estimated, assuming that this driving moment is parallel to four ridges of the cube (with length L) and that the relation between Γ/L and the angular velocity Ω is the same as for a very long square prism rotating about its long axis. In this case, only two dimensions need to be considered. With the notations in Figure 3, the radius r is a periodic function of angle a. Its mean value and its first harmonic only will be kept, say:

Fig. 3. Approximation of a square by r =
This approximation will allow us to estimate the drag force along the periphery by using the formula for glacier sliding without cavitation on a sinusoidal profile.
First,

By using the formula:

it is found that:

Glacier sliding, without cavitation, on a sinusoidal profile z = a cos wx with finite amplitude a, when ice obeys the rheological law in Equation (I.1), has been calculated in (Reference LliboutryLliboutry 1987, p. 149, 157 and 356–59). The relationship between sliding velocity U and the mean bottom drag τb reads (assuming Kb = Ki ):

The standard theory of melting-refreezing has been used. The result is about the same, assuming locally stress-controlled temperatures (Reference LliboutryLliboutry, 1993). In the present case:

Comparing Equations (II.5) and (II. 6), it is found: