A random field describes the evolution of random observations over a multidimensional domain. Random fields are naturally used as probabilistic models for spatial and spatio-temporal data. Random fields find applications in numerous areas that include, but are not limited to, geosciences, image processing and health sciences. Analysis of spatial and spatio-temporal data extensively exploits different types of functionals of random fields [Reference Christakos2]. This research concentrates on two types of functionals that are nonlinear integral and maximum functionals, and studies their asymptotic properties under various scenarios.
Probabilistic analysis of integral functionals of random fields is required by both theoretical and practical needs. These functionals are also often applied in statistics of random fields as estimators of parameters. Thus, asymptotic distributions and rates of convergence of integral functionals of random fields are required for such important statistical procedures as hypothesis testing, prognostication and anomaly detection. As in the case of integral functionals, the probabilistic analysis of maximum functionals of random fields is required by theory as well as direct practical applications in econometrics, reliability theory and queuing theory.
In contrast to the classical Donsker–Prokhorov-type results, the presence of long-range dependence in random fields can lead to asymptotically non-Gaussian behaviour of integral functionals such that their finite-dimensional distributions deviate from the finite-dimensional distributions of the Wiener process.
One of the topics studied in this thesis is the asymptotic behaviour of the functionals
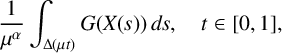$$ \begin{align*}\frac{1}{\mu^{\alpha}} \int_{\Delta(\mu t)}G(X(s))\,ds,\quad t\in[0,1],\end{align*} $$
as
$\mu \to \infty ,$
where
$G(\cdot )$
is a properly defined nonlinear function,
$X(\cdot )$
is a Gaussian random field and the number
$\alpha < d$
(d is a dimensionality of the space where
$X(\cdot )$
is defined) depends on the function
$G(\cdot )$
and the dependence structure of
$X(\cdot ).$
In statistical applications, the set
$\Delta $
plays the role of an observation window. Noncentral limit theorems show that the long-range dependence of the random field
$X(\cdot )$
significantly affects the asymptotic behaviour of the above functionals making the tails of their distributions heavier compared to Gaussian tails. In this case, the limiting processes are given in terms of multiple Wiener–Itô integrals and are called the generalised Hermite-type processes.
The first problem considered in the thesis is the derivation of new properties of generalised Hermite-type processes. The properties of generalised Hermite-type processes are not well studied. As the generalised Hermite-type processes are given in terms of stochastic integrals, one can show that their marginal distributions are stable. Also, it is known that in some cases, these distributions are absolutely continuous. However, not much is known about the properties of these processes in a general case. A rate of convergence in noncentral limit theorems has recently been estimated in [Reference Anh, Leonenko, Olenko and Vaskovych1]. However, new properties of the generalised Hermite-type processes can potentially be used to find the optimal rate of convergence. The properties of the generalised Hermite-type processes have not been well studied for observation windows with different topological and geometrical characteristics. This study shows there is a significant difference in the structures of increments of the generalised Hermite-type processes in one-dimensional and multidimensional cases. To prove the results, three different methodologies based on the stochastic integral representation of the generalised Hermite-type processes, Crofton’s mean value formula and integrals of potential kernels are used. The results obtained show interesting links between stochastics and differential geometry and can be used in other applications.
Next, Strong Laws of Large Numbers (SLLN) for maximum and integral functionals of random fields are studied. In contrast to central and noncentral limit theorems, SLLN are used to obtain point estimators of parameters of random fields. This research derives the SLLN for integral functionals of the form
$$ \begin{align*}\frac{1}{\mu^{d}} \int_{\Delta(\mu)}X(s)\,ds \quad \mbox{as} \ \mu\to\infty,\end{align*} $$
where d is a dimensionality of the space on which the random field
$X(\cdot )$
is defined. The results obtained allow random fields with unboundedly increasing covariances which generalises the results in the literature. To be more precise, the SLLN obtained are stated in terms of weaker conditions on variances and spatial dependencies allowing both short- and long-range dependent random fields. The main device used to obtain the results is a multidimensional analogue of the method of subsequences that works for both cases of processes defined on one-dimensional and multidimensional domains.
This thesis also obtains SLLN for the maximum functionals of random double arrays. The thesis considers the running maxima functionals
$$ \begin{align*} Y_{m,j} = \max_{1\leq k \leq m, 1\leq n\leq j}X_{k,n}-a_{m,j}, \quad m,j\geq 1,\end{align*} $$
of double arrays
$\{X_{k,n}, \ k,n\geq 1 \}$
consisting of
$\varphi $
-sub-Gaussian random variables, where
$\{ a_{m,j}, m,j\}$
are proper normalisations. The class of
$\varphi $
-sub-Gaussian random variables is introduced to generalise Gaussian variables. The main advantage of the SLLN obtained for running maxima is that it allows centred double arrays with more general exponential types of the tail distributions and random variables with unboundedly increasing
$\varphi $
-sub-Gaussian norms. As in the case of integral functionals, the derived SLLN for maximum functionals are stated in terms of simpler assumptions than in the known results for the one-dimensional case.
Finally, this research investigates multifractal random fields and associated multifractal random measures. Self-similar processes are invariant in distribution with respect to a proper rescaling in space and time. However, multifractal random processes have more complex scaling properties and deal with data that cannot be described by models with only one scaling rule. Under the so-called multifractal formalism, the Rényi function is linked to the multifractal spectrum by the Legendre transform and is an important tool in the analysis of multifractal processes. The main focus in this part of the thesis is to construct a multifractal measure
$\mu (\cdot )$
defined on a multidimensional domain as a limit of measures
$\mu _m(\cdot ), \ m\to \infty ,$
generated by cumulative fields
$A_m(\cdot )$
obtained as multifractal products of random fields. The cumulative fields are defined as
$$ \begin{align*}A_m(\boldsymbol{t}) := \int_{P_{n}[{\boldsymbol{0}},\boldsymbol{t}]} \prod_{i=0}^{m-1}\Lambda^{(i)}(b^i\boldsymbol{s})\,d \boldsymbol{s}, \quad m\in\mathbb{N},\ \boldsymbol{t}\in[0,1]^n,\end{align*} $$
where
$P_{n}[0,\boldsymbol {t}]$
is a hyperparallelepiped with the opposite vertices
${\boldsymbol {0}}$
and
$\boldsymbol {t}$
with
$\boldsymbol {t}=(t_1,t_2,\ldots ,t_n), t_j\in [0,1],\, j=1,2, \ldots , n, \Lambda ^{(i)}(\cdot ), \ i=0,1,\ldots ,$
is a family of independ ent stochastic copies of some nonnegative random field
$\Lambda (\cdot ),$
which is called a mother field, and
$b>1$
is a scaling parameter. The above product is also used to define nonnegative measures
$\mu _n(\cdot )$
on Borel subsets
$B\subseteq [0,1]^n$
as
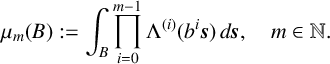$$ \begin{align*} \mu_m(B) := \int_{B} \prod_{i=0}^{m-1}\Lambda^{(i)}(b^i\boldsymbol{s})\,d\boldsymbol{s}, \quad m\in\mathbb{N}. \end{align*} $$
The thesis investigates the asymptotic properties of multifractal products of random fields. The limit theorems obtained provide conditions for the convergence of cumulative fields in the spaces
$L_q.$
New results on the rate of convergence are presented. The construction is also used to build random multifractal measures given on multidimensional domains. This study gives simple unified conditions for the limit theorems and the calculation of the Rényi function. A new important scenario of geometric
$\varphi $
-sub-Gaussian random fields is presented. In this case, the assumptions have a simple form and are expressed in terms of covariance functions only.
The theoretical results obtained in the thesis are confirmed by numerical studies. The detailed methodology for practical simulations of integral and maximum functionals of random fields and its implementation in the statistical programming language R is provided.
The results of the thesis have been published in the papers [Reference Donhauzer and Olenko3–Reference Hayek, Donhauzer, Giuliano, Olenko and Volodin6].
