A two-stage approach for passive sound source localization based on the SRP-PHAT algorithm

Abstract

This paper presents a different approach to tackle the Sound Source Localization (SSL) problem apply on a compact microphone array that can be mounted on top of a small moving robot in an indoor environment. Sound source localization approaches can be categorized into the three main categories; Time Difference of Arrival (TDOA), high-resolution subspace-based methods, and steered beamformer-based methods. Each method has its limitations according to the search or application requirements. Steered beamformer-based method will be used in this paper because it has proven to be robust to ambient noise and reverberation to a certain extent. The most successful and used algorithm of this method is the SRP-PHAT algorithm. The main limitation of SRP-PHAT algorithm is the computational burden resulting from the search process, this limitation comes from searching among all possible candidate locations in the searching space for the location that maximizes a certain function. The aim of this paper is to develop a computationally viable approach to find the coordinate location of a sound source with acceptable accuracy. The proposed approach comprises two stages: the first stage contracts the search space by estimating the Direction of Arrival (DoA) vector from the time difference of arrival with an addition of reasonable error coefficient around the vector to make sure that the sound source locates inside the estimated region, the second stage is to apply the SRP-PHAT algorithm to search only in this contracted region for the source location. The AV16.3 corpus was used to evaluate the proposed approach, extensive experiments have been carried out to verify the reliability of the approach. The results showed that the proposed approach was successful in obtaining good results compared to the conventional SRP-PHAT algorithm.

I. INTRODUCTION

Sound Source Localization (SSL) is an important part of a robot's auditory system. It is used by autonomous robots to locate a target based on acoustic signals gathered by microphones, this can help when other robot's systems, such as the vision system, are impaired, this can be due to bad lighting conditions or other reasons. The SSL system on the robot must locate the acoustic target with accuracy even if the acoustic signals are noisy, in addition, it must be able to work in a diverse environment. The robot auditory system is expected to be small enough to fit on the robot and to be economical, such constraints make it difficult to achieve the SSL requirements regarding its accuracy and robustness. The motivation of this work is to develop a robust, accurate, computationally non-intensive SSL system that can be used on a mobile robot to find the coordinates of a speech source in an indoor environment using a small microphone array.

SSL approaches can be categorized into three main categories [1]: approaches based on Time Difference of Arrival (TDOA), approaches based on high-resolution spectral calculations, and approaches based on maximizing a beamformer.

TDOA approaches are usually two-step approaches that involve the estimation of TDOAs between the signals of pairs of microphones as the first step, then mapping these TDOAs to an acoustic source location using geometrical relations. TDOA-based locators are widely used in localization applications because of their simplicity in implementation and their low computational burden, but such locators rely mainly on the accuracy of the TDOA estimation; a small error in TDOA estimates can lead to significant error in the location estimation.

Several efforts have been done and reported in the literature in order to overcome the limitations of the TDOA-based locators such as [2–10] which focused on increasing the robustness of the locator to ambient noise and reverberation. However, it is very difficult to obtain, using computationally viable algorithms, accurate acoustic location especially when small size microphone arrays are used.

The second category is the MUSIC-based locators. The MUSIC algorithm is a high-resolution spectral analysis algorithm that has been extensively used, and its derivatives [11–14], in speaker localization tasks. Originally it was intended for narrowband signals, but several modifications have extended their use to wideband signals such as those of audio signals. This class of algorithms, although having high resolution, suffer from the very high computational load. Even though there exists some efforts to reduce this computational burden, still all MUSIC-based algorithms need eigenvalue or singular value decompositions which are computationally extensive operations [15]. This computational limitations limit the use of such algorithms in commercial compact microphone arrays.

The beamforming-based methods search among possible candidate locations for the location that maximizes a certain function. The most successful and used algorithm in this category is the SRP-PHAT algorithm which finds the location that maximizes the SRP-PHAT function [16]. This algorithm has proven to be robust to ambient noise and reverberation to a certain extent. The main limitation of algorithms in this category is the computational burden resulting from the search process. The works of [17–23] are some of the efforts in the literature to improve the computational burden of the SRP-PHAT algorithm; however, they involve iterative optimization or statistical algorithms which can be complicated to implement. There are other limitations to the SRP-PHAT algorithm other than its computational burden that can affect the localization estimate and its resolution. High levels of noise and reverberation can lead to an unsatisfactory location estimates; moreover, discrete calculations involved in calculating the SRP-PHAT function can lead to a wrong location estimate; a wrong location can have slightly higher or similar SRP-PHAT value compared to that of the true location. The source of such errors is due to discrete calculations resulting from: low sampling frequency, using the FFT algorithm in GCC-PHAT estimation and interpolation, [24–27] addressed these limitations.

In this paper, a two-stage mixed near-field/far-field approach is adopted. First, the far-field model is adopted to estimate the Direction of Arrival (DoA) of the acoustic source in the closed form, then an uncertainty bound is applied to this DoA to form, along with a predefined search radius, a search region. The SRP-PHAT algorithm is applied on this contracted search region to extract the coordinates of the acoustic location. This approach has several merits: the search region is contracted to a smaller one with a very high degree of confidence that the acoustic source lies in it, this speeds up the SRP-PHAT search. Moreover, it would be highly unlikely that in the contracted search region would exist several maxima; therefore, the peak power found in that region would be that of the true source location. The main contribution of this work is finding a simple and effective way to contract the search region of the SRP-PHAT algorithm. This would make the already robust SRP-PHAT algorithm faster, hence, can be easily implemented. Moreover, since the search region is contracted, this could provide higher resolution in the estimated location. Finally, the region contraction process is carried out in one step in the closed form as opposed to similar approaches mentioned in the literature survey.

This paper is organized as follows: after this introduction, Section 2 details the proposed approach and explains the two stages of the algorithm. The results are then showed and analyzed in Section 3. Finally, Section 4 concludes this paper.

II. PROPOSED LOCALIZATION APPROACH

A two-stage approach to the acoustic localization problem is suggested. The aim is to minimize the search area for the SRP-PHAT algorithm and increase the reliability and accuracy of the localization system especially when using low-cost compact microphone arrays. The search area is minimized by estimating the DoA of the acoustic location and then forming a boundary around this estimated DoA according to the confidence level of this estimation along with the range of the microphone array. This can significantly reduce the number of maxima in the function since a majority of the original area has been eliminated as a possibility that the acoustic source originated from it. Therefore, the maximum found by the SRP-PHAT algorithm in this minimized area is most likely to be the only dominant peak and hence represents the true location; moreover, this is done in just one step, as the DoA can be estimated in the closed form, unlike optimization algorithms that can spend several iterations to find the peak, that if they did not get stuck in a local maxima. Figure 1 shows the idea of the localization approach.

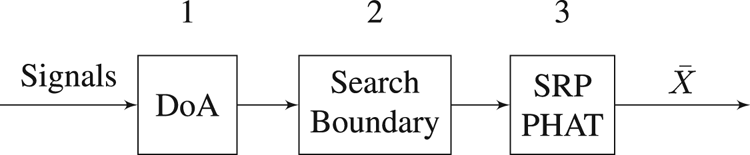
Fig. 1. Proposed localization scheme.

The DoA obtained from subsection A, in the closed form, is an estimate of the true DoA, this is due to several reasons, such as:

• • The TDOAs are inaccurate.

• • The equations from the previous section are derived based on the far-field assumption; therefore, the closer the sound source is to the microphone array the more the error will be in the DoA estimate.

• • Microphone array geometry can affect the DoA estimate.

• • Low sampling frequency and discrete calculations.

Lets assume that the DoA estimate is contaminated with a zero-mean Gaussian noise ɛ with a standard deviation σ. The standard deviation is dependent on the inaccuracies in the system mentioned above and hence can be estimated by analyzing the system's errors or through experiments on the localization system.

(1)\begin{align} \hat{\theta}&=\theta-\varepsilon_1 \tag{1}\end{align}

(2)\begin{align} \hat{\phi}&=\phi-\varepsilon_2 \tag{2}\end{align}

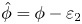
where $\hat {\phi }$ and $\hat {\theta }$ are the true azimuth and elevation angles, respectively. ϕ and θ are the estimated azimuth and elevation angles, respectively, obtained from subsection A. By sampling $N_1$ points from the normal distribution $\mathcal {N}_1(0,\sigma _1^2)$ and $N_2$ points from $\mathcal {N}_2(0,\sigma _2^2)$, where $\sigma _1$ and $\sigma _2$ are the standard deviations representing the errors in the azimuth and elevation, respectively, $N_1 \times N_2$ permutations of “possible” azimuth and elevation angles are formed. Applying these angles to equation 3 assuming $N_3$ points of $r \in [0,r_{\max }]$, where $r_{\max }$ is the acoustic range of the microphone array, a point cloud of $N_1 \times N_2 \times N_3 \quad xyz$ points is produced. Figure 2 shows an example of the search boundary produced from equation 3 in the 2D plane.

(3)\begin{equation} \begin{bmatrix} x \\ y \\ z \end{bmatrix} =r \times \begin{bmatrix} \sin(\theta)\cos(\phi) \\ \sin(\theta)\sin(\phi) \\ \cos(\theta) \end{bmatrix} \tag{3}\end{equation}

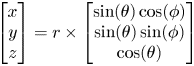
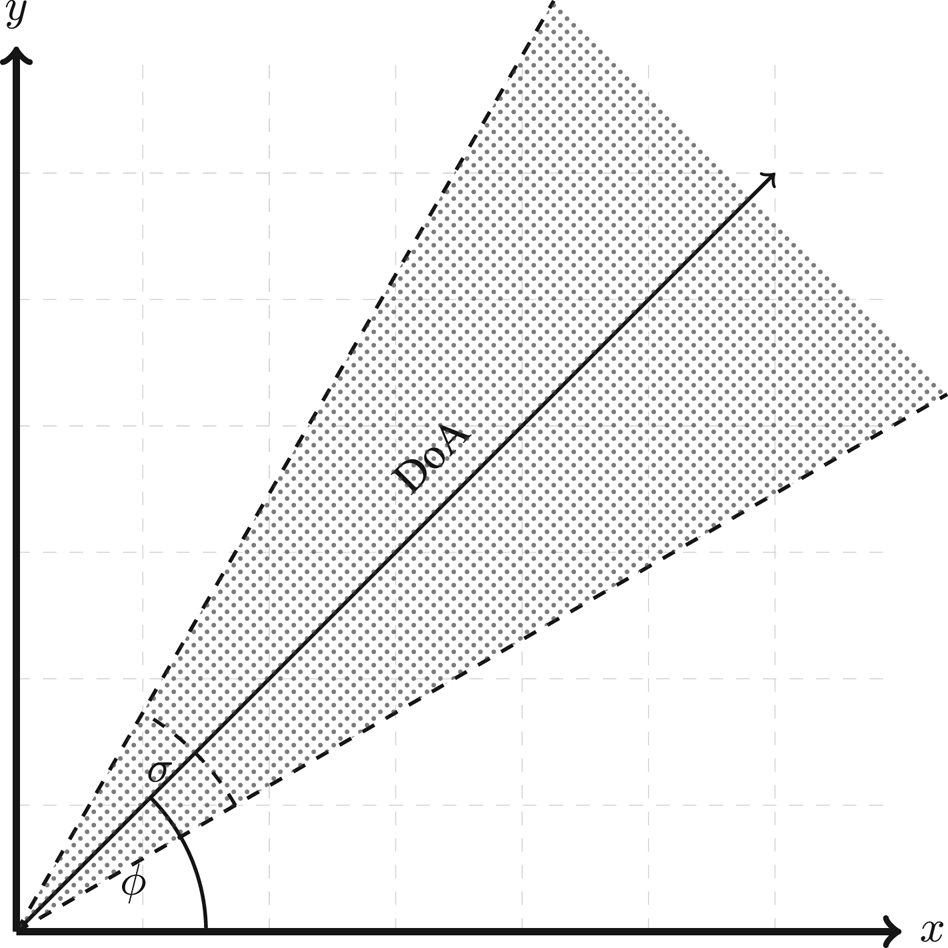
Fig. 2. Search boundary in the xy plane.

A) DoA in the closed form

Consider a microphone array consisting of M microphone elements each at location $m(m_x,m_y,m_z)$ arranged in the xyz plane in any arbitrary geometry as shown in Fig. 3, it is required to estimate the direction vector $\overrightarrow {u}$ pointing at the acoustic source X. The DoA can be estimated from the TDOA between pairs of microphones, where there exist $M(M-1)/2$ pairs of microphones.Let $\overrightarrow {u}$ be a unit direction vector pointing at the direction of the sound source:

(4)\begin{equation} \overrightarrow{u}=\begin{bmatrix} \cos(\theta)\cos(\phi) \\ \cos(\theta)\sin(\phi) \\ \sin(\theta) \end{bmatrix} =\begin{bmatrix} u_x \\ u_y \\ u_z \end{bmatrix} \tag{4}\end{equation}

where ϕ is the azimuth and θ is the elevation.

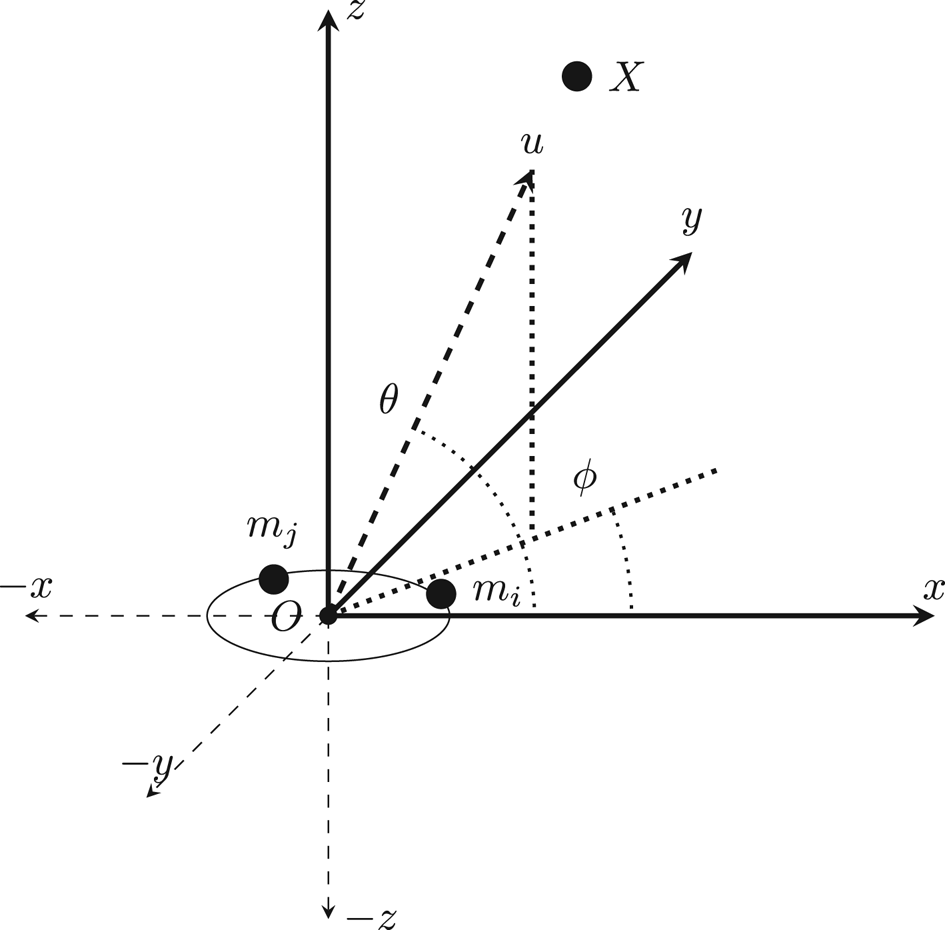
Fig. 3. Localization system's geometry.

The relationship between this direction vector and the TDOAs can be defined:

(5)\begin{align} \tau_{ij}(\phi,\theta) &=\frac{\overrightarrow{u}\cdot(\overrightarrow{m_i}-\overrightarrow{m_j})}{c} \tag{5}\end{align}

(6)\begin{align} &=\begin{bmatrix} \cos(\theta)\cos(\phi) \\ \cos(\theta)\sin(\phi) \\ \sin(\theta) \end{bmatrix} \cdot\left(\begin{bmatrix} x_i \\ y_i \\ z_i \end{bmatrix} - \begin{bmatrix} x_j \\ y_j \\z_j \end{bmatrix} \right) \cdot\frac{1}{c} \tag{6}\end{align}

let

\[ S=\left(\begin{bmatrix} x_i \\ y_i \\ z_i \end{bmatrix} - \begin{bmatrix} x_j \\ y_j \\ z_j \end{bmatrix} \right)^T \quad \text{and}\quad c \tau_{ij}=d.\]

Rearranging equation 6:

(7)\begin{equation} \boldsymbol d=\boldsymbol S \overrightarrow{u} \tag{7}\end{equation}

Equation 7 is an over-determined equation because there are $M(M-1)/2$ and only three variables; therefore, equation 7 can be solved in the closed-form using a simple least squares solution.

(8)\begin{equation} \overrightarrow{u}=-\boldsymbol S^+ \boldsymbol d =- \boldsymbol {(S^TS)}^{-1} \boldsymbol S^T \boldsymbol d \tag{8}\end{equation}

where $\boldsymbol S^+$ is the pseudoinverse of $\boldsymbol S$.

After calculating the direction vector $\overrightarrow {u}$ the azimuth and elevation angles can be easily calculated:

(9)\begin{align} \phi&=a\tan 2 \left(\frac{u_y}{u_x} \right) \tag{9}\end{align}

(10)\begin{align} \theta&=\sin^{-1} (u_z) \tag{10}\end{align}

Using the $a\tan 2$ function in equation 9 allows for an efficient way to find theta in the $[-\pi, \pi ]$ range provided that the microphone array has its elements distributed in the xy plane. In [28], they assumed that the elevation angle is equal to zero (for microphone array with all its elements in the xy plane) and estimated $\cos (\theta )=1$ and hence estimated the azimuth directly from the relations: $\phi =\cos ^{-1}(u_x)$ or $\phi =\sin ^{-1}(u_y)$. It was found that when assuming that the elevation is zero (which is not necessarily the case) the previous two relations will not yield the same azimuth angle, this is because the elevation angle greatly influence the azimuth estimate. Using equation 9 provides better estimate of azimuth since no assumptions are made that the elevation is zero, but rather the elevation term $\cos (\theta )$ will cancel each other.

The derivations of the previous equations can be found at [28,29].

B) The SRP-PHAT algorithm

The Steered Response Power (SRP) algorithm is a beamformer-based algorithm that searches for the location that maximizes the SRP function among a set of candidate locations. The Phase Transform (PHAT) weighting function has been extensively used in literature and has been shown to work well in real environments, it provides robustness against noise and reverberation. The SRP-PHAT algorithms combines the benefits of the SRP beamformer and the robustness of the PHAT weighting function, making it one of the most used algorithms for the acoustic localization task. The work of [30] showed that the SRP function is equivalent to summing all possible GCC combinations; therefore, the SRP-PHAT function can be written in terms of the Generalized Cross Correlation (GCC) as:

(11)\begin{align} P_{PHAT}(\bar{X}) & =\sum_{ij}^{M(M-1)/2}{GCC-PHAT(\tau_{ij}(\bar{X}))}\notag \\ & \qquad \qquad \qquad i=1:M,\ j=2:M, \ j > i \tag{11}\end{align}

where M is the number of microphones in the array. $\tau _{ij}(\bar {X})$ is the theoretical time delay between the signal received at microphone i and that at microphone j given the spatial location $\bar {X}$ and is calculated from the geometrical formula, given the spatial locations of the microphones $\bar {m}=[x,y,z]$ and the speed of sound c:

(12)\begin{equation} \tau_{ij}(\bar{X})=\frac{\left\Vert \bar{X}-\bar{m_i}\right\Vert -\left\Vert \bar{X}-\bar{m_j}\right\Vert}{c} \tag{12}\end{equation}

and $GCC-PHAT(\tau _{ij}(\bar {X}))$ is the value of the GCC-PHAT function at the theoretical time delay $\tau _{ij}(\bar {X})$. The GCC-PHAT function can be computed in the frequency domain as:

(13)\begin{equation} GCC-PHAT_{ij}(\omega)= \psi_{PHAT}(\omega)S_i(\omega)S^*_j(\omega) \tag{13}\end{equation}

In equation 13, $S_i(\omega )$ and $S_j(\omega )$ are the acoustic signals in the frequency domain computed by applying the Fast Fourier Transform (FFT) to the time domain signals $s_i(\tau )$ and $s_j(\tau )$ recorded from microphones i and j, respectively. $^*$ is the conjugate operator. $\psi _{PHAT}$ is the PHAT weighting function, it is defined as the magnitude of the Cross Power Spectrum between the two microphones signals and can be written as:

(14)\begin{equation} \psi_{PHAT}=\frac{1}{\vert S_i(\omega)S^*_j(\omega)\vert} \tag{14}\end{equation}

Substituting 14 into 13 and converting to the time domain:

(15)\begin{equation} GCC-PHAT_{ij}= \mathcal{F}^{-1}\left[\frac{S_i(\omega)S_j^*(\omega)}{\vert S_i(\omega)S_j^*(\omega)\vert}\right] \tag{15}\end{equation}

where $\mathcal {F}^{-1}$ is the Inverse Fourier Transform.

Finally, a grid of candidate locations $\bar {X}$ is formed and used to evaluate the SRP function in equation 11. The candidate location that produces the highest “Power” is said to be the location of the sound source.

(16)\begin{equation} \bar{X}=\mathbf{arg}\,\mathbf{max}(P_{PHAT}(\bar{X}))\tag{16}\end{equation}

Finding $\bar {X}$ that maximizes the SRP-PHAT function in the previous equation is a computationally intense problem. The function has several local maxima and a fine grid has to be formed and searched over to get reliable results. In order to alleviate the computational burden of the grid search, optimization-based techniques have been adopted and reported in the literature; however, there is no guarantee that these algorithms would find the global maximum of the function; moreover, due to factors such as excessive noise and reverberation or due to discrete calculations and interpolations involved in calculating the SRP-PHAT function, the global maximum of the function can deviate from the true location considerably.

III. RESULTS

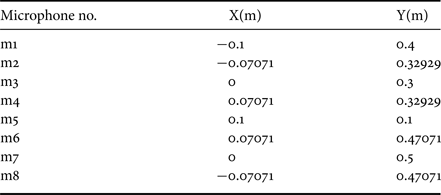
In order to evaluate the proposed approach, the “Audio Visual AV16.3” corpus was used [31]. The audio corpus of the AV16.3 is recorded in a meeting room context by means of two 0.1 m radius Uniform Circular Arrays (UCA) with eight-microphone elements each at a sampling frequency of 16 kHz. Table 1 shows the xyz locations of the first of the two arrays, the reference point is the middle point between the two arrays. The two UCAs are at plane Z = 0. The audio corpus consists of eight annotated sequences in a variety of situations, for this work sequence “seq01-1p-0000” is used. It was recorded for the purpose of SSL evaluation, the recording spans over 217 s for a single speaker at 16 different locations, static at each location and recording 10–11 segments at each location.

Table 1. Microphone locations of AV16.3 first array.

In the proposed approach the user is required to input only minimal settings namely: the number of points $N=N_1N_2N_3$ which will be used to fill the boundary area/volume (for 2D or 3D), the maximum range of the microphone array r and the standard deviations $\sigma _1$ and $\sigma _2$ that represent the error in the estimated azimuth and elevation, in addition to the frame window length and percentage overlap if required.

For the experiments presented here these settings are shown in Table 2. Since the microphones in the UCA of the AV16.3 corpus are distributed along the x and y axes only (z = 0), it is impossible to calculate the elevation part of the DoA vector; therefore, the boundary area is formed using the azimuth only hence forming a 2D area represented by a triangle as shown in Fig. 2, setting $\theta =0$ in equation 3, x and y are calculated from $x=rcos(\phi )$ and $y=rsin(\phi )$ and the z component is appended as uniform random values covering from the floor to the ceiling of the room $z\in U(z_{min},z_{\max })$. The z component was added this way and was not ignored because experiments showed that it had significant effect on the overall localization results. In Table 2, N is the total number of points that are distributed in the boundary volume; the distribution around the azimuth is a Gaussian with standard deviation $\sigma _1$ while the z values follow a uniform distribution from the floor to the ceiling of the room and has the same length N and was appended to the x and y values. The window used for the Fourier analysis is a Hanning window.

Table 2. Algorithm input parameters.

The measure used for the evaluation of the proposed approach is the Root Mean Square Error (RMSE) between the estimated location and the ground truth available in the AV16.3 corpus.

Since the proposed approach uses random numbers to fill in the search boundary, it is expected that this approach would result in different results at each run; therefore, each experiment at each location was run 1000 times and the RMSE of each run was recorded and the variance of these n = 1000 runs was calculated and reported to show that the proposed approach has a low variance, i.e. will give consistent results at each run. Moreover, the minimum and maximum as well as the mean of these 1000 runs were reported and compared to the results of the conventional SRP-PHAT algorithm.

As mentioned, the results from the proposed approach were compared to those of the conventional SRP-PHAT algorithm. The settings of the SRP-PHAT algorithm were the same as our proposed approached, i.e. the same window and overlap. A mesh-grid of 125 000 points in 3D was formed and fed to the SRP-PHAT algorithm for the search process, no optimizations were used in this search process. The conference room of the AV16.3 audio corpus was $8.2\,{\rm m} \times 3.6\,{\rm m} \times 2.4\,{\rm m}$, hence the mesh-grid was formed by taking 50 linearly spaced points along the x, y, and z axes creating a $50 \times 50 \times 50$ grid.

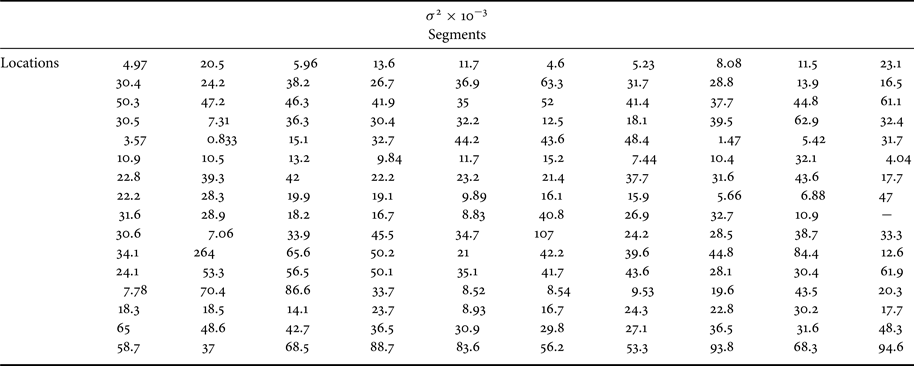
The variance resulted from the experiments on all 16 locations and 10 segments for each location is reported in Table 3. From the table it is clear that the proposed approach has low variance.

Table 3. Variance of the RMSE.

Figures 4–19 show the results for each of the 16 locations separately. Each figure compares the minimum, maximum, and mean RMSE of the proposed approach to that of the conventional SRP-PHAT algorithm. As it is clear from the graphs that the proposed approach yields lower RMSE results, in the majority of cases, than the conventional SRP-PHAT algorithm, even when comparing the maximum RMSE value. In locations 8,9,12,13,14, and 16 in Figs 11, 12, 15,16, 17, and 19, it was noticed that the RMSE of the SRP-PHAT algorithm was in some segments lower than the maximum RMSE of the proposed approach, this can be attributed to the low number of points of the proposed approach as compared to the high number of points used for the SRP-PHAT algorithm, this and the value of σ can affect the results; if σ is unrealistically small, i.e. has an overoptimistic, a search boundary can be formed where the true source location point lies on the boundaries or even outside the search area, and because of the Gaussian assumption, the points near the edge of the boundary are less represented than those around the mean DoA.

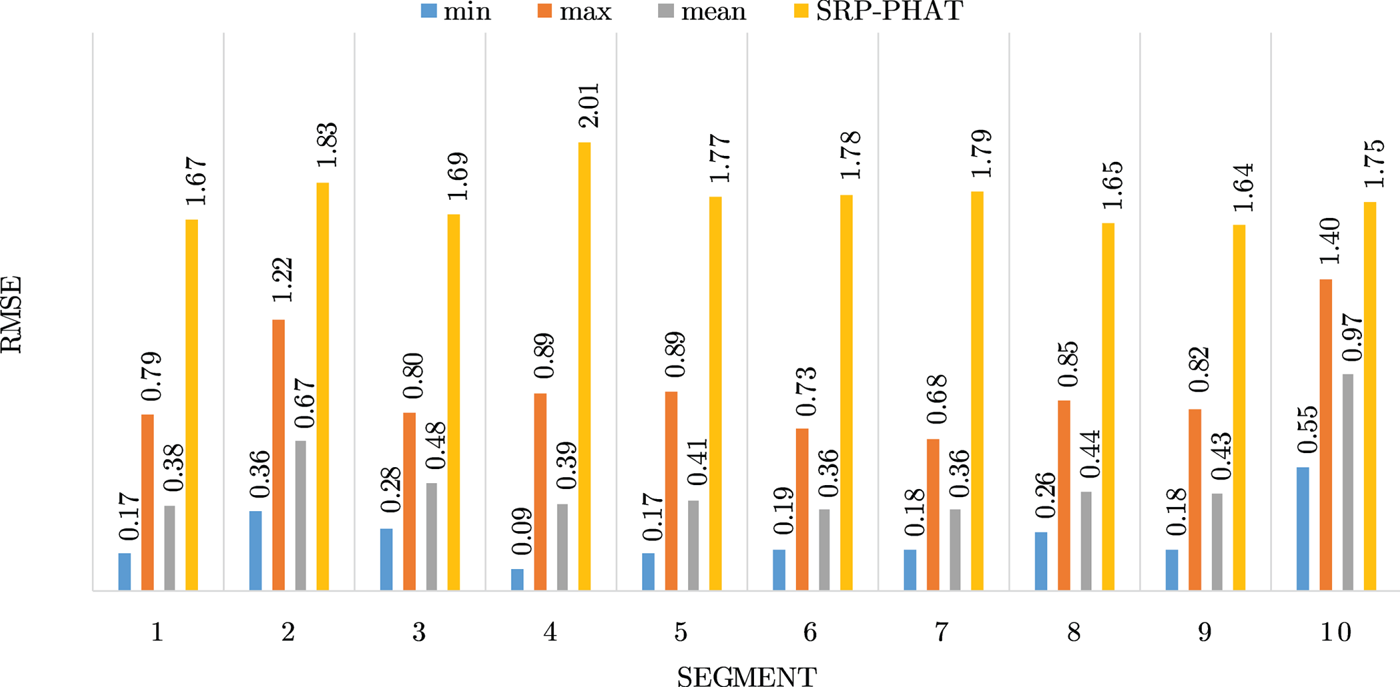
Fig. 4. Results for location 1.

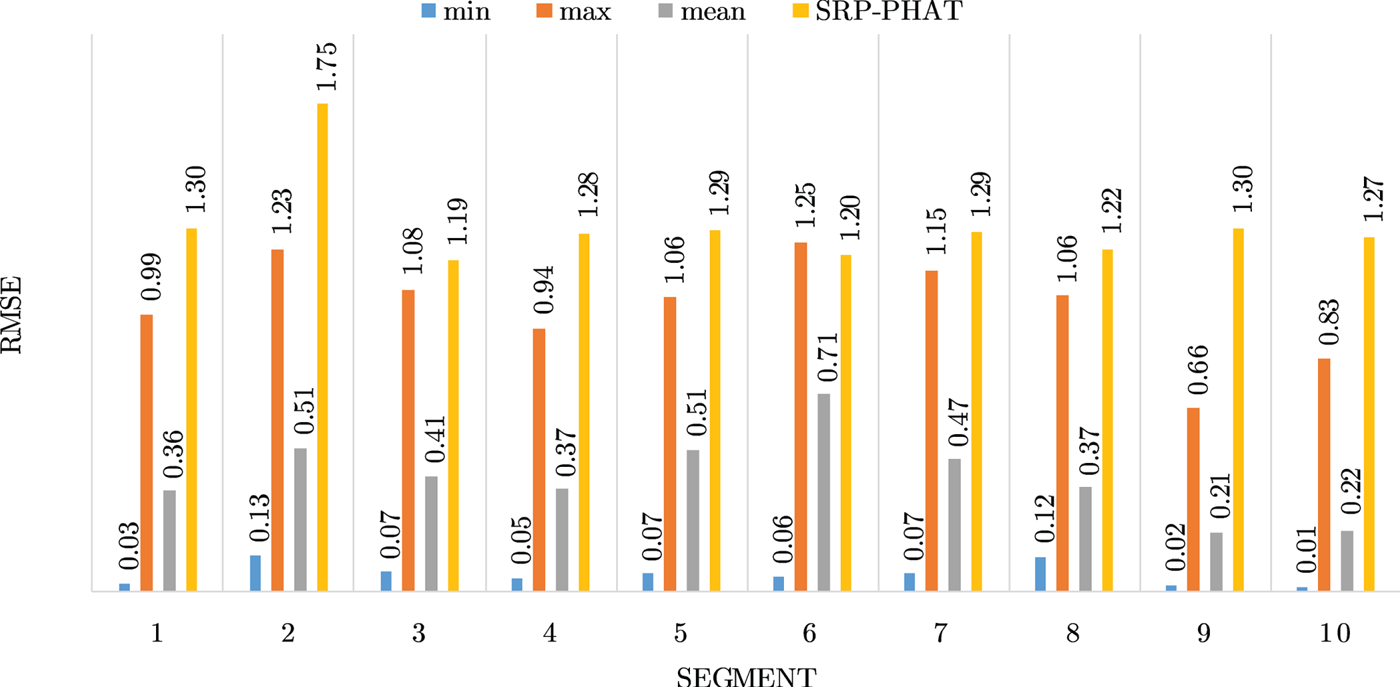
Fig. 5. Results for location 2.

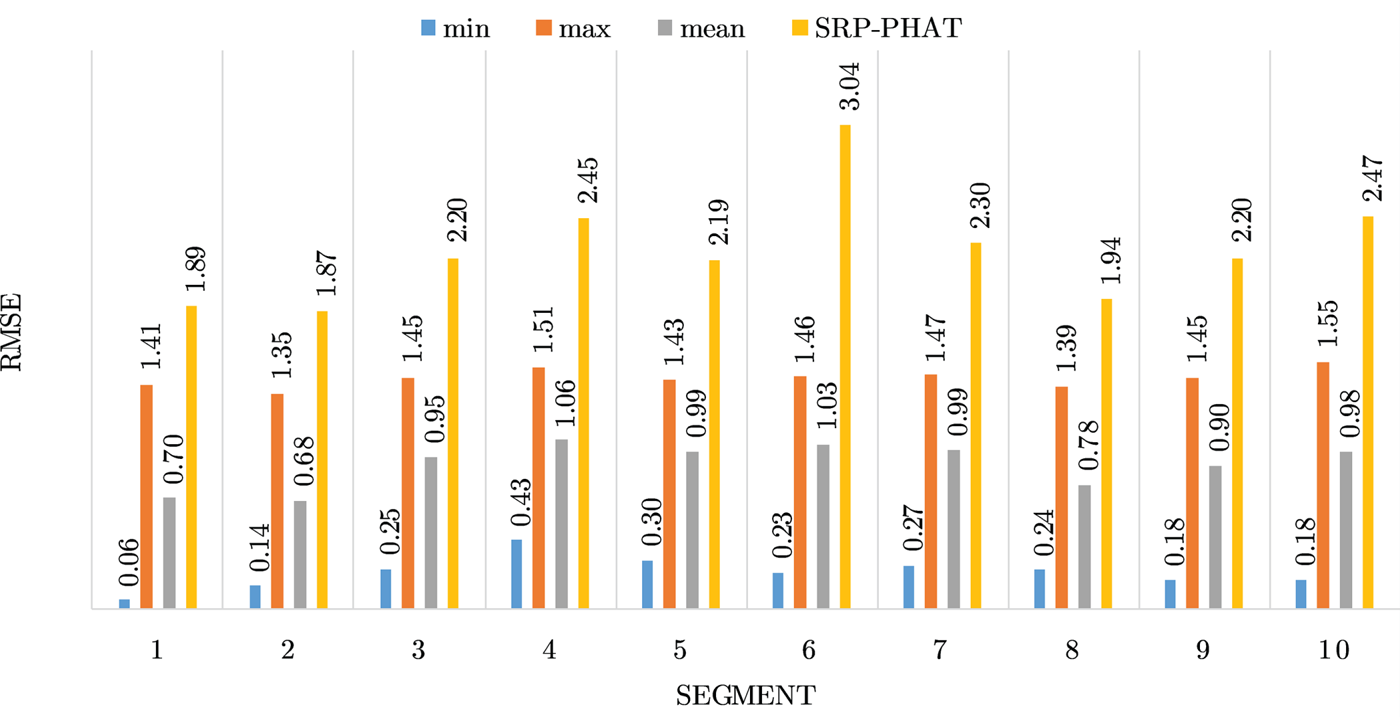
Fig. 6. Results for location 3.

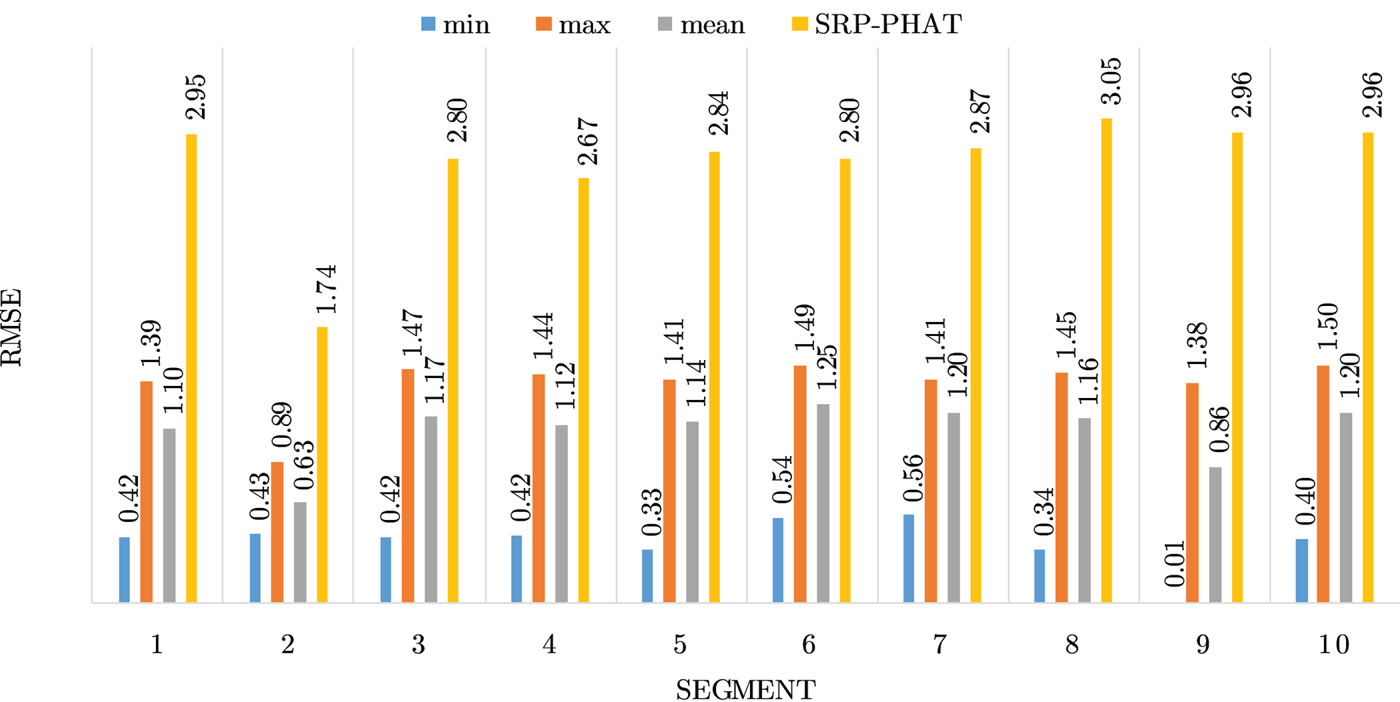
Fig. 7. Results for location 4.

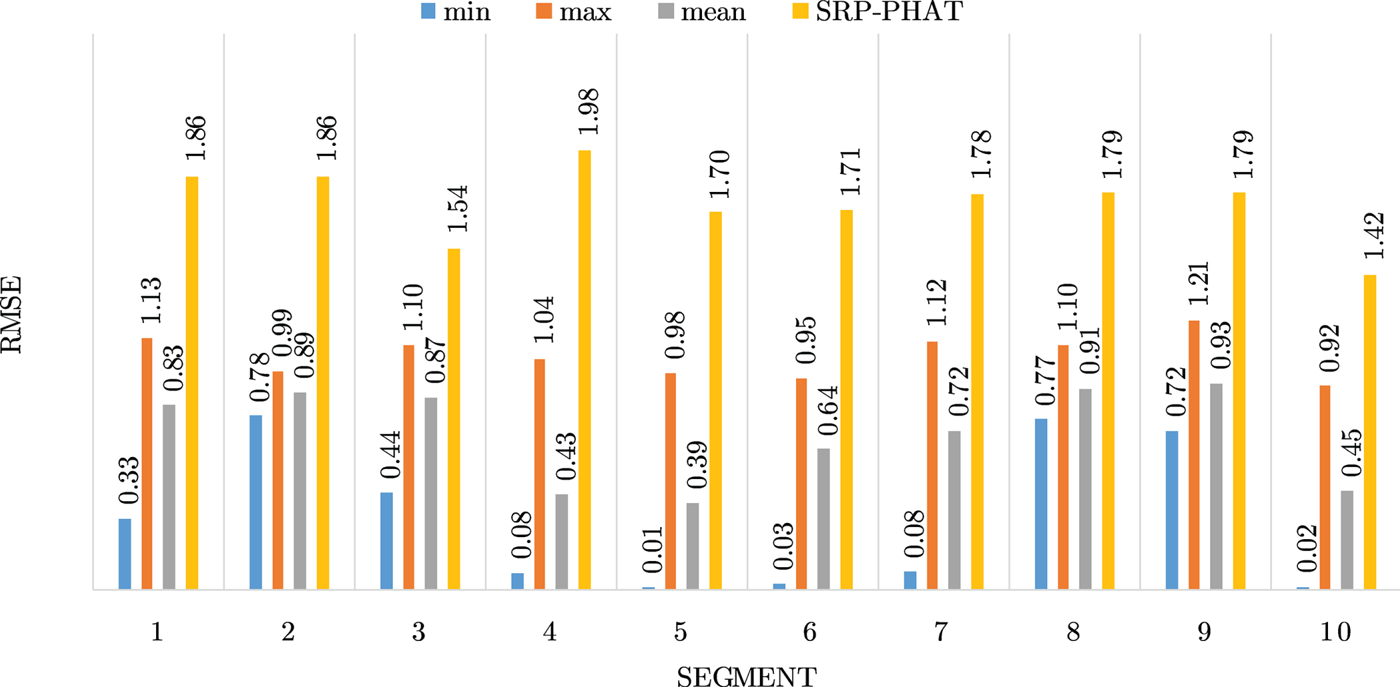
Fig. 8. Results for location 5.

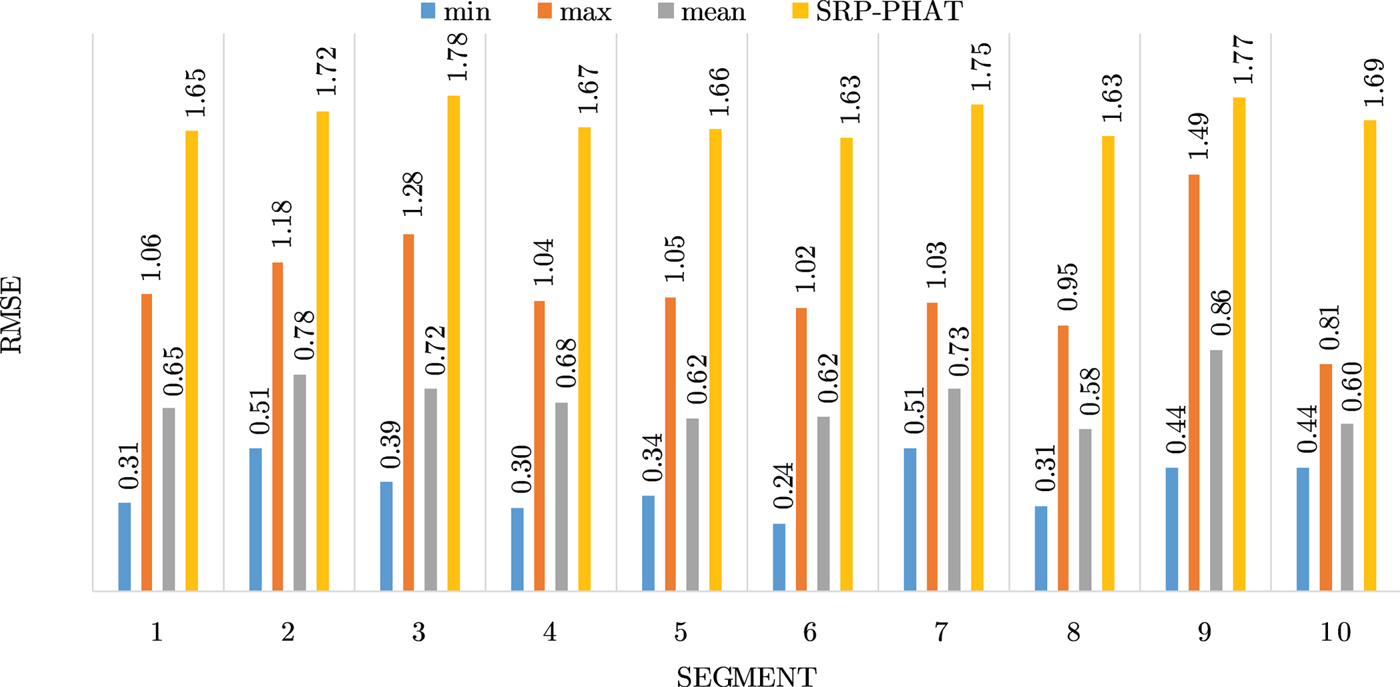
Fig. 9. Results for location 6.

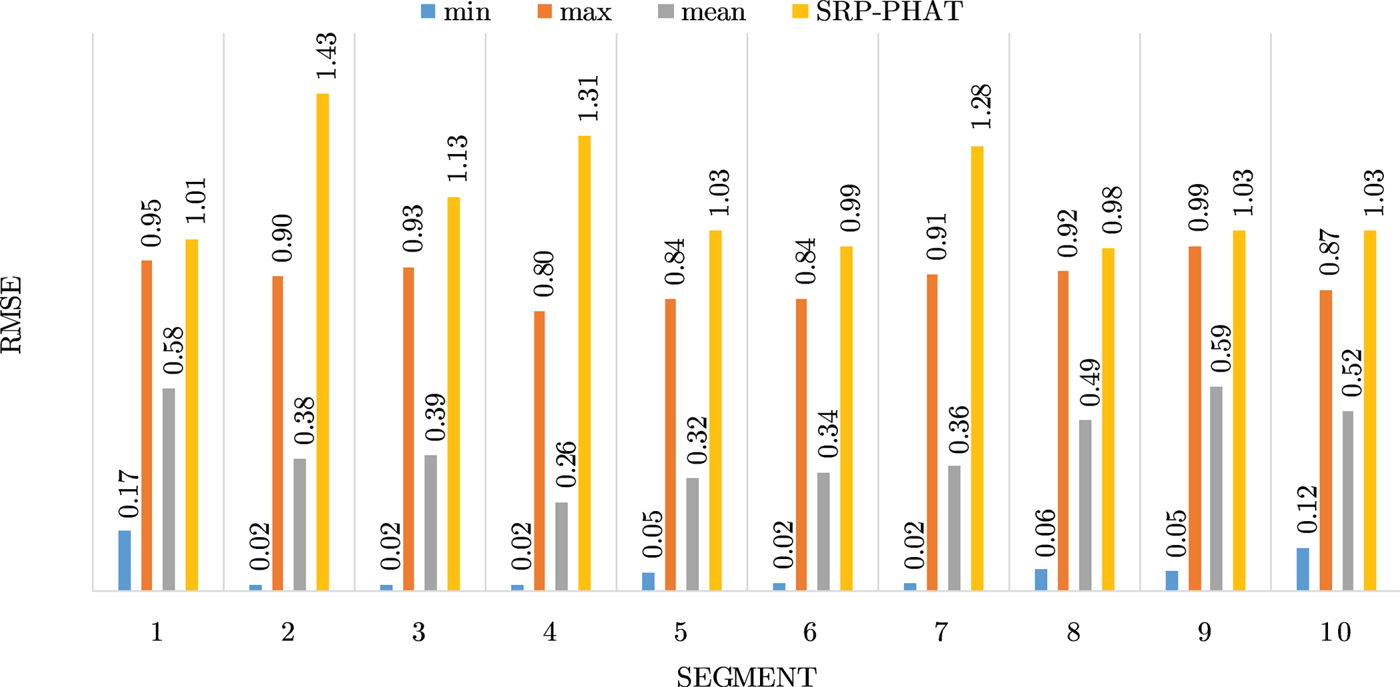
Fig. 10. Results for location 7.

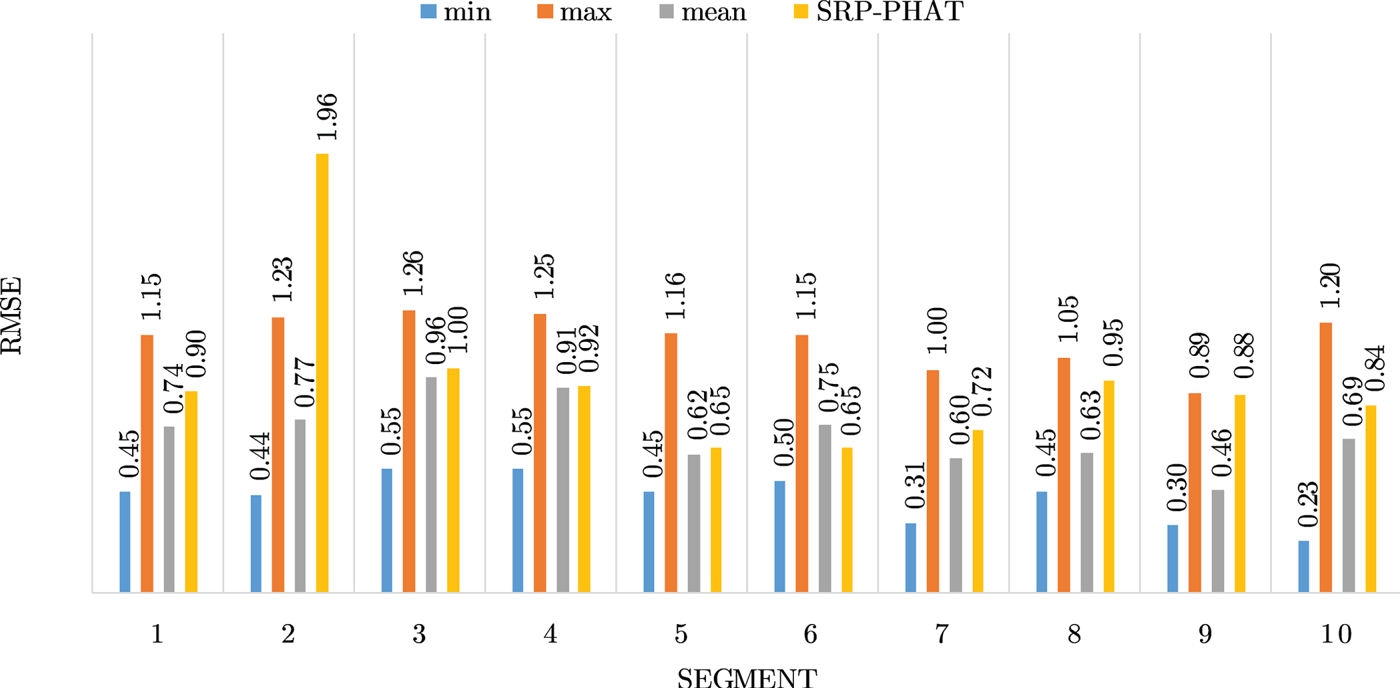
Fig. 11. Results for location 8.

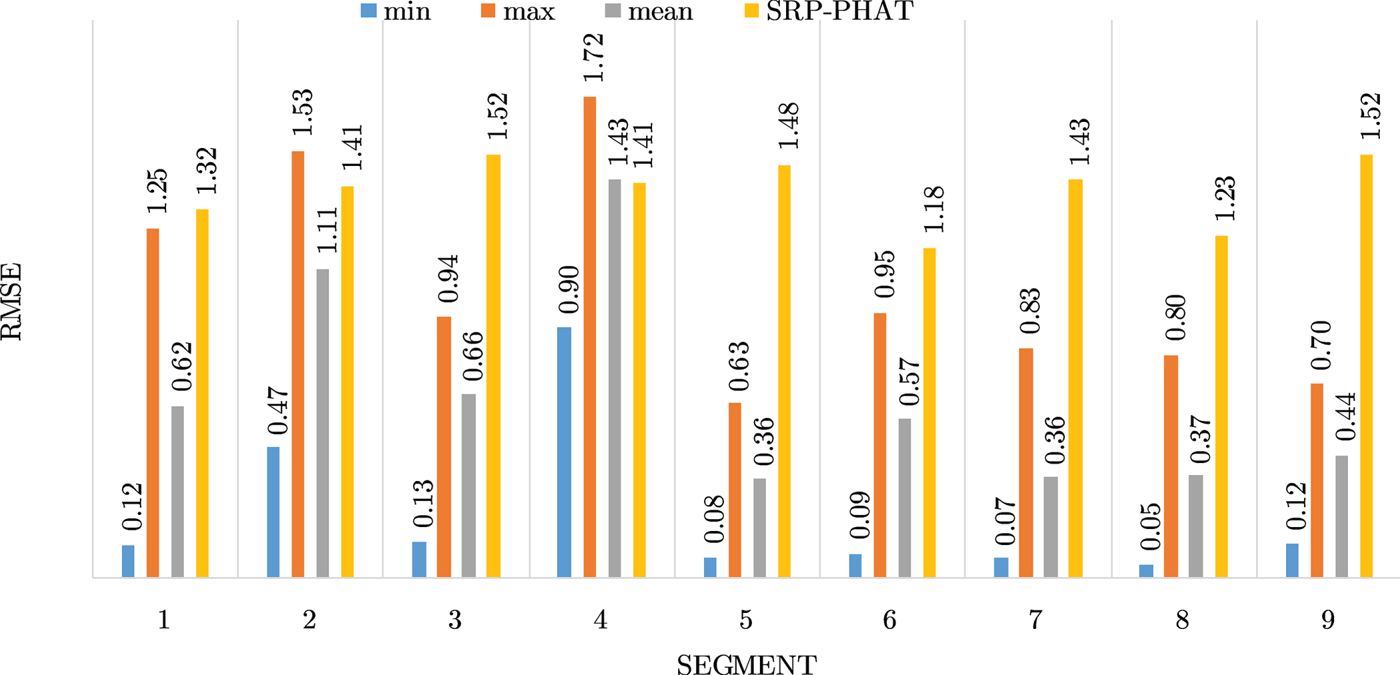
Fig. 12. Results for location 9.

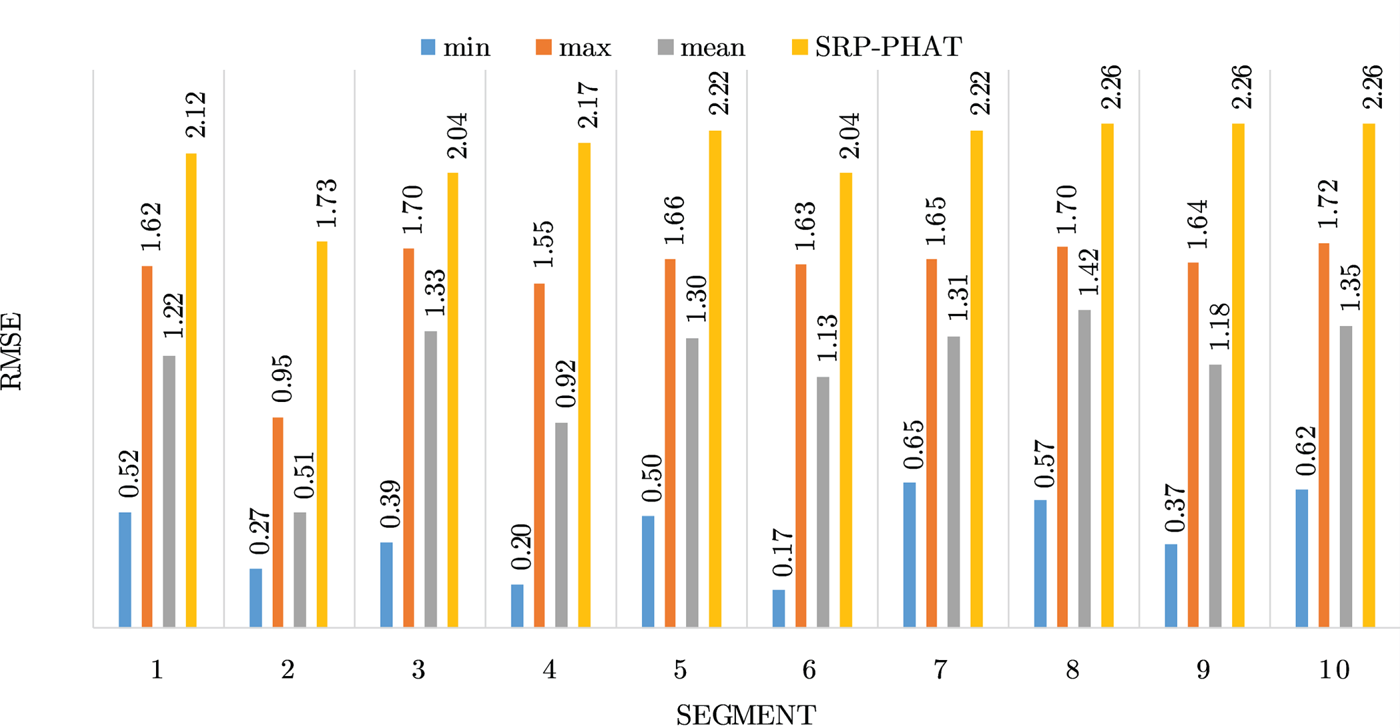
Fig. 13. Results for location 10.

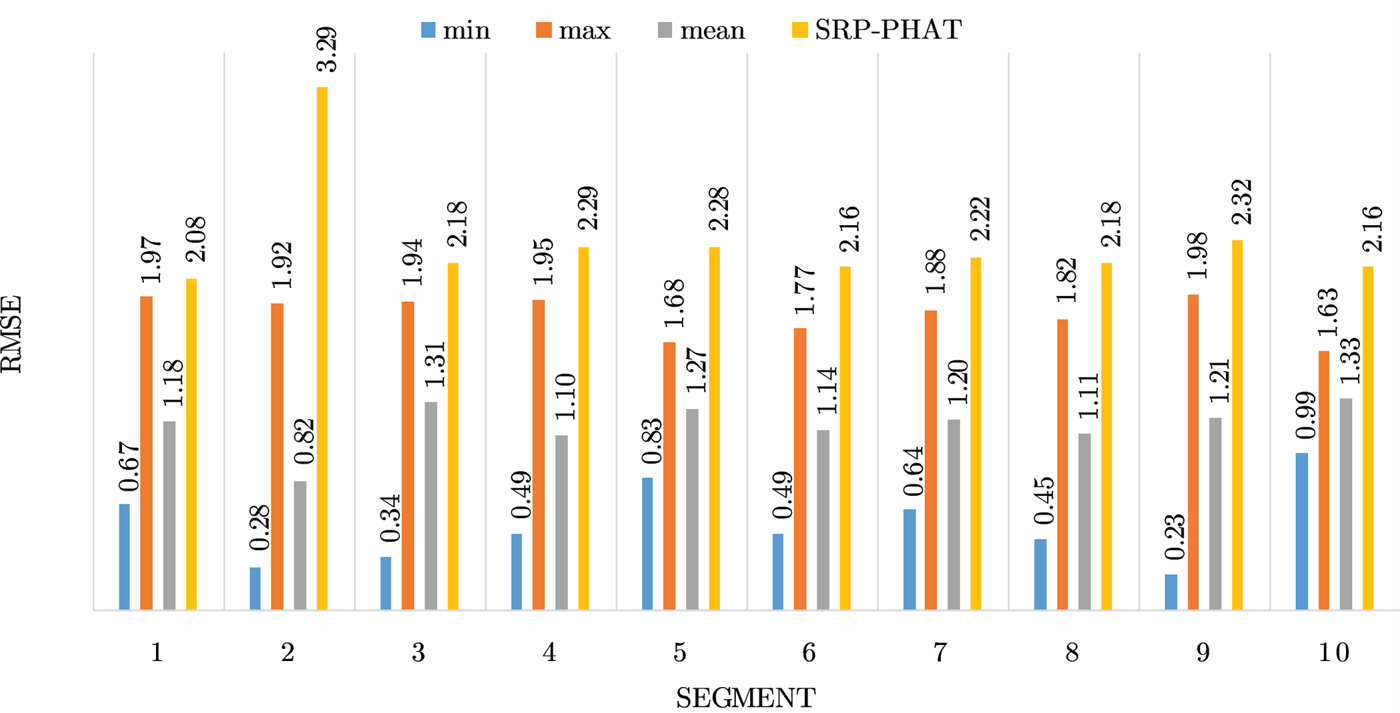
Fig. 14. Results for location 11.

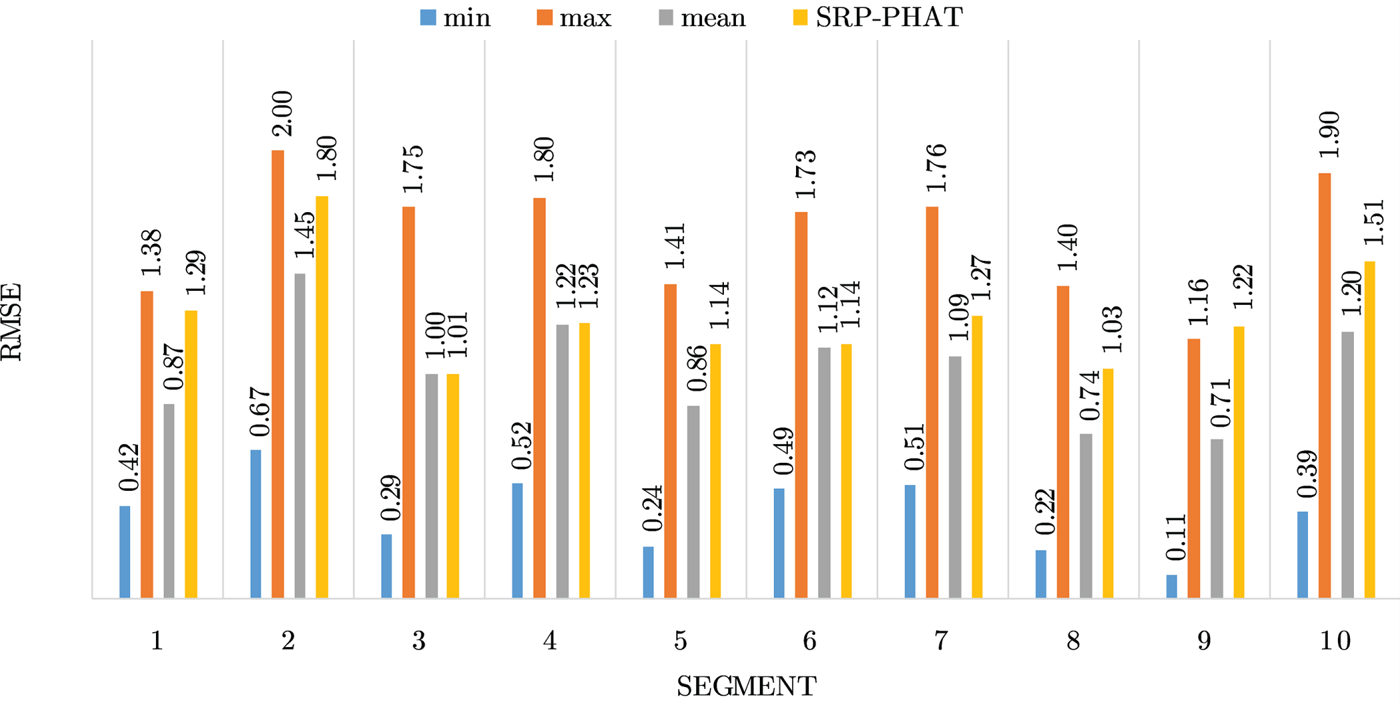
Fig. 15. Results for location 12.

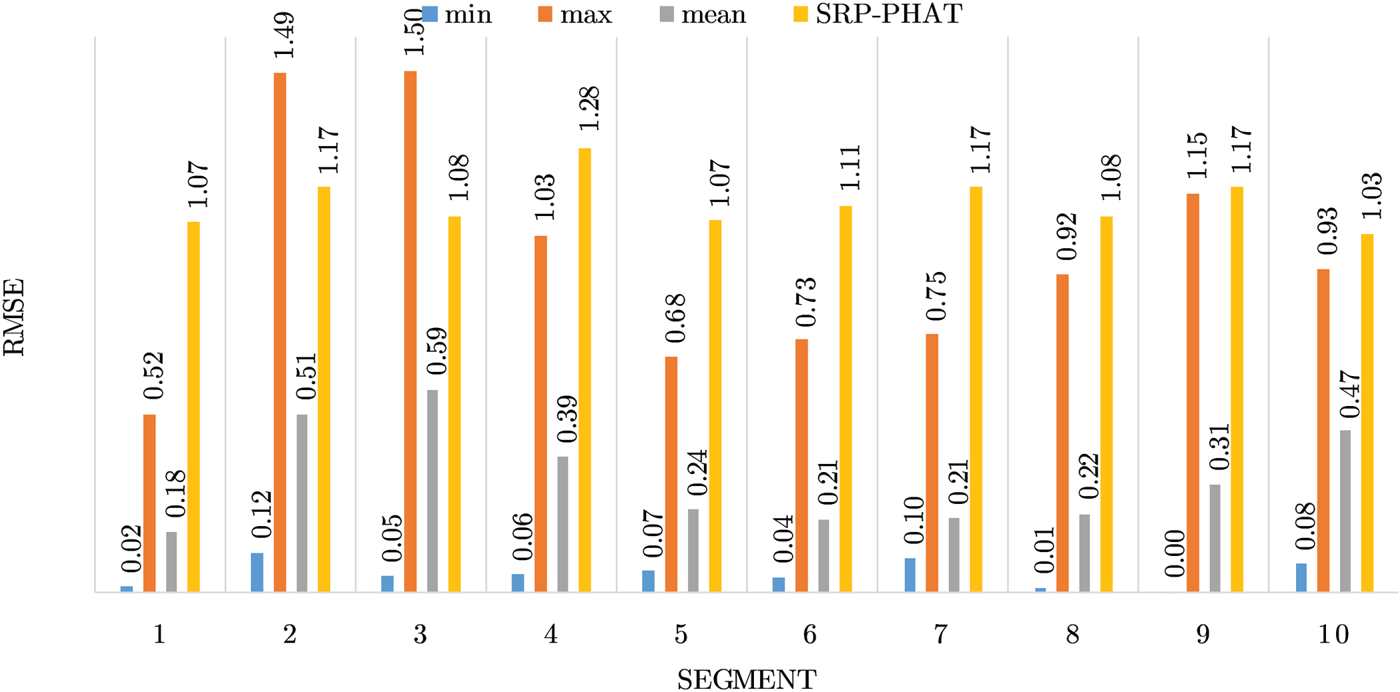
Fig. 16. Results for location 13.

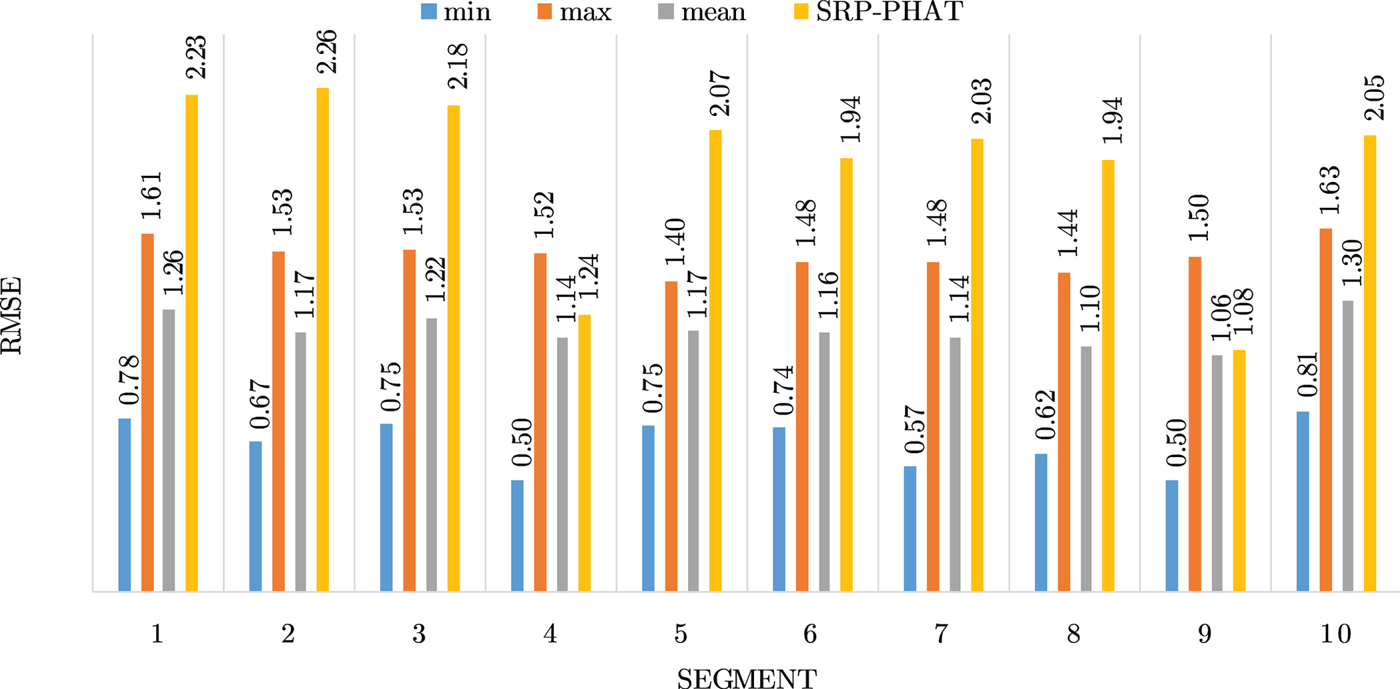
Fig. 17. Results for location 14.

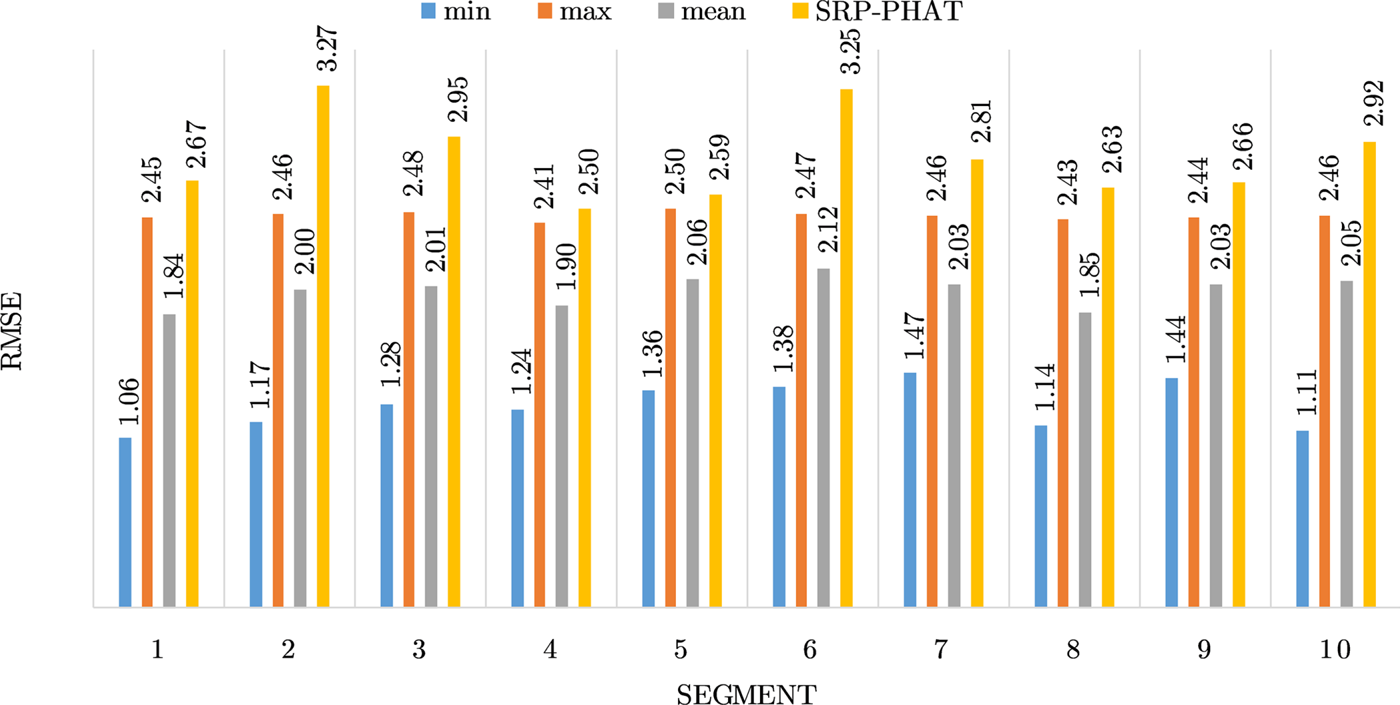
Fig. 18. Results for location 15.

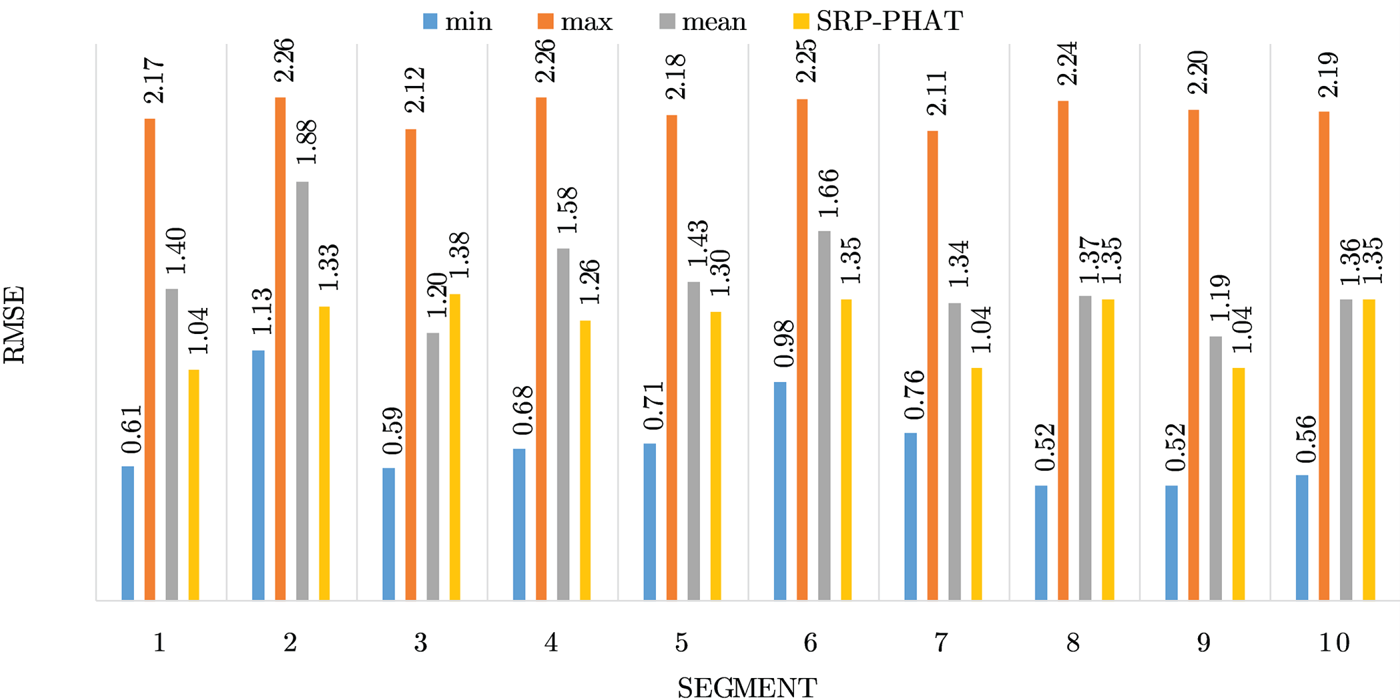
Fig. 19. Results for location 16.

IV. CONCLUSION

This paper presented a robust approach for the SSL problem. The proposed approach was developed with the aim to work with compact microphone arrays at low sampling frequencies and low computational burden, hence making it suitable to be used with small mobile robots. The proposed approach is based on a mixed far-field/near-field model, where as a first step, the DoA vector is estimated in the closed form using the far-field model, then, a search boundary is formed based on the DoA vector, the expected error in the DoA estimates and the microphone array range, finally, based on the near-field model, this boundary is searched using the conventional SRP-PHAT algorithm to find the source location. The AV16.3 corpus was used to evaluate the proposed approach, extensive experiments have been carried out to verify the reliability of the approach. The results showed that the proposed approach was successful in obtaining good results compared to the conventional SRP-PHAT algorithm eventhough only 1000 points were used for the search process as opposed to 125 000 used by the SRP-PHAT algorithm. Minimum user input is required to run the algorithm, namely, the number of points to fill the search boundary, the microphone array range and the expected error in the DoA estimation. Obviously, by increasing the number of points in the search boundary, the resolution will increase but so will the number of functional evaluations and hence the computational burden, but it was shown that even while using small number of points, good results can be obtained. The expected error in the DoA estimation $\sigma _1$ and $\sigma _2$ depends on factors related to the microphone array system as well as factors related to the environment. The number of microphone elements in the array, their types, and the array's geometry are some of the factors that affect the DoA estimation; moreover, factors such as the sampling frequency and discrete calculations and others contribute to this error and hence affect the values of $\sigma _1$ and $\sigma _2$. In addition, noise and reverberation and other environmental factors obviously affect $\sigma _1$ and $\sigma _2$ and cannot be easily predicted. All these factors make the calculation of $\sigma _1$ and $\sigma _2$ rather a difficult task. In this work, $\sigma _1$ was figured by observing some experiments and figuring out the DoA error of each experiment. Finally, it should be mentioned that in the experiments carried out in this paper, no efforts have been done to improve the SNR of the signals except for a simple second-order band pass filter (300 Hz–6 kHz) and this was applied to the proposed approach and to the SRP-PHAT algorithm. It is expected that using some further denoising techniques would further improve the results; moreover, it is possible to use some optimization techniques to search for the peak power in the search boundary instead of performing a point by point search.