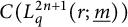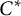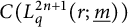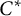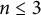1 Introduction
In the study of noncommutative geometry, many classical spaces have been given a quantum analogue. Due to Gelfand duality, there exists an equivalence between the categories of commutative
![]() $C^*$
-algebras and locally compact Hausdorff spaces. Hence, when studying quantum analogues of classical spaces, one often thinks of them as algebras of continuous functions on a nonexisting virtual space.
$C^*$
-algebras and locally compact Hausdorff spaces. Hence, when studying quantum analogues of classical spaces, one often thinks of them as algebras of continuous functions on a nonexisting virtual space.
A well-studied example is the quantum sphere by Vaksman and Soibelman [Reference Vaksman and Soibelman28], from which we define quantum lens spaces as fixed point algebras under the action of finite cyclic groups. In noncommutative geometry, quantum lens spaces are objects of increasing interest (see, e.g., [Reference Arici, Brain and Landi2, Reference Brzeziński and Fairfax7, Reference D’Andrea and Landi10]), where noncommutative line bundles with quantum lens spaces as total spaces are investigated.
In [Reference Hong and Szymański20], Hong and Szymański gave a description of quantum lens spaces as graph
![]() $C^*$
-algebras. This description was extended in [Reference Brzeziński and Szymański8] by Brzeziński and Szymański to also include weights that are not necessarily coprime with the order of the acting finite cyclic group. Unfortunately, the general description is incorrect, which was recently pointed out by Efren Ruiz.
$C^*$
-algebras. This description was extended in [Reference Brzeziński and Szymański8] by Brzeziński and Szymański to also include weights that are not necessarily coprime with the order of the acting finite cyclic group. Unfortunately, the general description is incorrect, which was recently pointed out by Efren Ruiz.
In the present paper, we first describe a new graph which is a modified version of the one given by Brzeziński and Szymański and prove that quantum lens spaces are indeed graph
![]() $C^*$
-algebras. Then we deal with classification of quantum lens spaces of dimension at most 7, with certain conditions on their weights. We remark that the work on classification has already been presented in an earlier preprint, unpublished, available on arXiv [Reference Gotfredsen and Mikkelsen18] by the present authors. After the submission of the preprint to arXiv, it was pointed out by Efren Ruiz that the graph
$C^*$
-algebras. Then we deal with classification of quantum lens spaces of dimension at most 7, with certain conditions on their weights. We remark that the work on classification has already been presented in an earlier preprint, unpublished, available on arXiv [Reference Gotfredsen and Mikkelsen18] by the present authors. After the submission of the preprint to arXiv, it was pointed out by Efren Ruiz that the graph
![]() $C^*$
-algebraic description of quantum lens spaces is incorrect in some cases. This affects to some extent the classification results presented in the first preprint. The present paper serves as an extension of the previous one, containing both the modified graph
$C^*$
-algebraic description of quantum lens spaces is incorrect in some cases. This affects to some extent the classification results presented in the first preprint. The present paper serves as an extension of the previous one, containing both the modified graph
![]() $C^*$
-algebraic description and the adjusted classification results.
$C^*$
-algebraic description and the adjusted classification results.
For the determination of isomorphism of quantum lens spaces, it is not sufficient only considering their K-groups and the order [Reference Eilers, Restorff, Ruiz and Sørensen13, Remark 7.10]. In [Reference Eilers, Restorff, Ruiz and Sørensen13], Eilers, Restorff, Ruiz, and Sørensen came with an important classification result of finite graph
![]() $C^*$
-algebras using the reduced filtered K-theory. As opposed to the classification of Cuntz–Krieger algebras given by Restorff in [Reference Restorff25], which the result in [Reference Eilers, Restorff, Ruiz and Sørensen13] is based on, quantum lens spaces fall within the scope of this classification. As an application of the classification result, Eilers, Restorff, Ruiz, and Sørensen investigated seven-dimensional quantum lens spaces for which all the weights are coprime with the order of the acting cyclic group
$C^*$
-algebras using the reduced filtered K-theory. As opposed to the classification of Cuntz–Krieger algebras given by Restorff in [Reference Restorff25], which the result in [Reference Eilers, Restorff, Ruiz and Sørensen13] is based on, quantum lens spaces fall within the scope of this classification. As an application of the classification result, Eilers, Restorff, Ruiz, and Sørensen investigated seven-dimensional quantum lens spaces for which all the weights are coprime with the order of the acting cyclic group
![]() ${\mathbb {Z}}_r$
. They managed to reduce the classification result to elementary matrix algebras using
${\mathbb {Z}}_r$
. They managed to reduce the classification result to elementary matrix algebras using
![]() $SL_{\mathcal {P}}$
-equivalence and to prove that the lowest dimension for which we get different quantum lens spaces is dimension
$SL_{\mathcal {P}}$
-equivalence and to prove that the lowest dimension for which we get different quantum lens spaces is dimension
![]() $7$
. Here, they showed that there exist two different quantum lens spaces when r is a multiple of 3, and precisely one when this is not the case.
$7$
. Here, they showed that there exist two different quantum lens spaces when r is a multiple of 3, and precisely one when this is not the case.
Further investigation of quantum lens spaces, as defined in [Reference Hong and Szymański20], was conducted in [Reference Jensen, Klausen and Rasmussen21] by Jensen, Klausen, and Rasmussen using
![]() $SL_{\mathcal {P}}$
-equivalence. For a fixed r, they showed how large the dimension of the quantum lens space
$SL_{\mathcal {P}}$
-equivalence. For a fixed r, they showed how large the dimension of the quantum lens space
![]() $C(L_q^{2n+1}(r;m_0,\ldots ,m_{n}))$
must be to obtain nonisomorphic quantum lens spaces. The work is based on computer experiments by Eilers, who came up with a suggestion for a number s such that for
$C(L_q^{2n+1}(r;m_0,\ldots ,m_{n}))$
must be to obtain nonisomorphic quantum lens spaces. The work is based on computer experiments by Eilers, who came up with a suggestion for a number s such that for
![]() $n<s$
, the quantum lens spaces are all isomorphic.
$n<s$
, the quantum lens spaces are all isomorphic.
In this paper, we will extend the result by Eilers, Restorff, Ruiz, and Sørensen to quantum lens spaces of dimension less than or equal to
![]() $7$
for which
$7$
for which
![]() $\gcd (m_i,r)\neq 1$
for one and only one i. The work builds on computer experiments, which were made in collaboration with Søren Eilers. We use a program written by Eilers in Maple 2019,Footnote
1
which has been optimized slightly by the present authors. Concretely, the program computes the adjacency matrices and isomorphism classes given the order r and the set
$\gcd (m_i,r)\neq 1$
for one and only one i. The work builds on computer experiments, which were made in collaboration with Søren Eilers. We use a program written by Eilers in Maple 2019,Footnote
1
which has been optimized slightly by the present authors. Concretely, the program computes the adjacency matrices and isomorphism classes given the order r and the set
![]() $\lbrace \gcd (m_i,r)\colon i=0,\dots , 3 \rbrace $
. We then came up with a suggestion for an invariant, depending on which weight that is not coprime with r, by considering various combinations of the values of r and the weights. In this way, experiments have played a crucial role in determining the statement of the presented theorems.
$\lbrace \gcd (m_i,r)\colon i=0,\dots , 3 \rbrace $
. We then came up with a suggestion for an invariant, depending on which weight that is not coprime with r, by considering various combinations of the values of r and the weights. In this way, experiments have played a crucial role in determining the statement of the presented theorems.
The structure of the paper is as follows: In Section 2, we present the classification result by Eilers, Restorff, Ruiz, and Sørensen in the case of type I graph
![]() $C^*$
-algebras. Section 3 contains a counterexample proving that the description of quantum lens spaces as graph
$C^*$
-algebras. Section 3 contains a counterexample proving that the description of quantum lens spaces as graph
![]() $C^*$
-algebras by Brzeziński and Szymański is incorrect. Moreover, it contains a new proof that quantum lens spaces are indeed graph
$C^*$
-algebras by Brzeziński and Szymański is incorrect. Moreover, it contains a new proof that quantum lens spaces are indeed graph
![]() $C^*$
-algebras. We emphasize that the content in this section has already been presented in the same format in [Reference Mikkelsen23, Chapter 2]. In Section 4, we describe the classification result by Eilers, Restorff, Ruiz, and Sørensen in the setting of quantum lens spaces and present the classification for quantum lens spaces for which all the weights are coprime to the order of the acting group.
$C^*$
-algebras. We emphasize that the content in this section has already been presented in the same format in [Reference Mikkelsen23, Chapter 2]. In Section 4, we describe the classification result by Eilers, Restorff, Ruiz, and Sørensen in the setting of quantum lens spaces and present the classification for quantum lens spaces for which all the weights are coprime to the order of the acting group.
The procedure to classify quantum lens spaces follows by first constructing the adjacency matrices, which are presented in Section 6. Afterward, we calculate an invariant using
![]() $SL_{\mathcal {P}}$
-equivalence, which involves some long calculations. Therefore, the proofs are postponed to Section 7, and the main theorems (Theorems 5.1 and 5.3) are stated in Section 5.
$SL_{\mathcal {P}}$
-equivalence, which involves some long calculations. Therefore, the proofs are postponed to Section 7, and the main theorems (Theorems 5.1 and 5.3) are stated in Section 5.
2 Preliminaries
We recall first some concepts of graph
![]() $C^*$
-algebras, which are needed in this paper. A directed graph
$C^*$
-algebras, which are needed in this paper. A directed graph
![]() $E=(E^0,E^1,r,s)$
consists of a countable set
$E=(E^0,E^1,r,s)$
consists of a countable set
![]() $E^0$
of vertices, a countable set
$E^0$
of vertices, a countable set
![]() $E^1$
of edges, and two maps
$E^1$
of edges, and two maps
![]() $r,s: E^1\to E^0$
called the range map and the source map, respectively. For an edge
$r,s: E^1\to E^0$
called the range map and the source map, respectively. For an edge
![]() $e\in E^1$
from v to w, we have
$e\in E^1$
from v to w, we have
![]() $s(e)=v$
and
$s(e)=v$
and
![]() $r(e)=w$
. For a directed graph E, we let
$r(e)=w$
. For a directed graph E, we let
![]() $A_E=[A(v,w)]_{v,w\in E^0}$
, where
$A_E=[A(v,w)]_{v,w\in E^0}$
, where
![]() $A(v,w)$
is the number of edges with source v and range w.
$A(v,w)$
is the number of edges with source v and range w.
![]() $A_E$
is called the adjacency matrix for E. Moreover, we let
$A_E$
is called the adjacency matrix for E. Moreover, we let
![]() $B_E:=A_E-I$
.
$B_E:=A_E-I$
.
A graph is called finite if it has finitely many edges and vertices. For a directed graph E, we recall that a vertex is regular if
![]() $s^{-1}(v)=\{e\in E^1| \ s(e)=v\}$
is finite and nonempty, and it is called singular if this is not the case. In the case where we have too many edges between two vertices to make a good drawing, we only draw one edge and indicate the number of edges as follows:
$s^{-1}(v)=\{e\in E^1| \ s(e)=v\}$
is finite and nonempty, and it is called singular if this is not the case. In the case where we have too many edges between two vertices to make a good drawing, we only draw one edge and indicate the number of edges as follows:
![]() $\bullet \overset {(m)}{\longrightarrow } \bullet $
if the number of edges is m.
$\bullet \overset {(m)}{\longrightarrow } \bullet $
if the number of edges is m.
A path
![]() $\alpha $
in a graph is a finite sequence
$\alpha $
in a graph is a finite sequence
![]() $\alpha =e_1e_2\cdots e_n$
of edges satisfying
$\alpha =e_1e_2\cdots e_n$
of edges satisfying
![]() $r(e_i)=s(e_{i+1})$
for
$r(e_i)=s(e_{i+1})$
for
![]() $i=1,\ldots ,n-1$
. A path
$i=1,\ldots ,n-1$
. A path
![]() $\alpha $
is called a cycle if
$\alpha $
is called a cycle if
![]() $s(\alpha )=r(\alpha )$
and a loop if
$s(\alpha )=r(\alpha )$
and a loop if
![]() $\alpha $
is a cycle of length 1. It is called a return path if
$\alpha $
is a cycle of length 1. It is called a return path if
![]() $\alpha $
is a cycle and
$\alpha $
is a cycle and
![]() $r(e_i)\neq r(\alpha )$
for
$r(e_i)\neq r(\alpha )$
for
![]() $i<n$
.
$i<n$
.
Let
![]() $v,w\in E^0$
, if there is a path from v to w in the graph, then we write
$v,w\in E^0$
, if there is a path from v to w in the graph, then we write
![]() $v\geq w$
. A subset
$v\geq w$
. A subset
![]() $H\in E^0$
is called hereditary if
$H\in E^0$
is called hereditary if
![]() $v\in H$
and
$v\in H$
and
![]() $w\in E^0$
is such that
$w\in E^0$
is such that
![]() $v\geq w$
, then
$v\geq w$
, then
![]() $w\in H$
.
$w\in H$
.
The graph
![]() $C^*$
-algebra of a directed graph is defined as follows (see, e.g., [Reference Bates, Pask, Raeburn and Szymański5, Reference Fowler, Laca and Raeburn16]).
$C^*$
-algebra of a directed graph is defined as follows (see, e.g., [Reference Bates, Pask, Raeburn and Szymański5, Reference Fowler, Laca and Raeburn16]).
Definition 2.1 Let
![]() $E=(E^0,E^1,r,s)$
be a directed graph. The graph
$E=(E^0,E^1,r,s)$
be a directed graph. The graph
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $C^*(E)$
is the universal
$C^*(E)$
is the universal
![]() $C^*$
-algebra generated by families of orthogonal projections
$C^*$
-algebra generated by families of orthogonal projections
![]() $\{p_v | \ v\in E^0\}$
and partial isometries
$\{p_v | \ v\in E^0\}$
and partial isometries
![]() $\{s_e | \ e\in E^1\}$
with mutually orthogonal ranges (i.e.,
$\{s_e | \ e\in E^1\}$
with mutually orthogonal ranges (i.e.,
![]() $s_e^*s_f=0, e\neq f$
) subject to the relations:
$s_e^*s_f=0, e\neq f$
) subject to the relations:
-
(CK1)
 $s_e^*s_e=p_{r(e)}$
.
$s_e^*s_e=p_{r(e)}$
. -
(CK2)
 $s_es_e^*\leq p_{s(e)}$
.
$s_es_e^*\leq p_{s(e)}$
. -
(CK3)
 $p_v=\underset {s(e)=v}{\sum }s_e s_e^*$
, if
$p_v=\underset {s(e)=v}{\sum }s_e s_e^*$
, if
 $\{e\in E^1| \ s(e)=v\}$
is finite and nonempty.
$\{e\in E^1| \ s(e)=v\}$
is finite and nonempty.
For at path
![]() $\alpha =e_1e_2\cdots e_n$
, we let
$\alpha =e_1e_2\cdots e_n$
, we let
![]() $s_{\alpha }=s_{e_1}s_{e_2}\cdots s_{e_n}$
.
$s_{\alpha }=s_{e_1}s_{e_2}\cdots s_{e_n}$
.
We can by universality define a circle action, called the gauge action,
![]() $\gamma : U(1)\to \text {Aut}(C^*(E))$
for which
$\gamma : U(1)\to \text {Aut}(C^*(E))$
for which
![]() $\gamma _z(p_v)=p_v \ \text {and} \ \gamma _z(s_e)=zs_e$
for all
$\gamma _z(p_v)=p_v \ \text {and} \ \gamma _z(s_e)=zs_e$
for all
![]() $v\in E^0, e\in E^1$
, and
$v\in E^0, e\in E^1$
, and
![]() $z\in U(1)$
.
$z\in U(1)$
.
If the graph has finitely many vertices, we say that a nonempty subset
![]() $S\subseteq E^0$
is strongly connected if for any pair of vertices
$S\subseteq E^0$
is strongly connected if for any pair of vertices
![]() $v,w\in S$
, there exists a path from v to w. It is called a strongly connected component if it is a maximal strongly connected subset. We let
$v,w\in S$
, there exists a path from v to w. It is called a strongly connected component if it is a maximal strongly connected subset. We let
![]() $\Gamma _E$
be the set of all strongly connected components and all singletons of singular vertices which are not the base of a cycle. Moreover, a strongly connected component is called a cyclic component if one of its vertices has exactly one return path.
$\Gamma _E$
be the set of all strongly connected components and all singletons of singular vertices which are not the base of a cycle. Moreover, a strongly connected component is called a cyclic component if one of its vertices has exactly one return path.
Let Prime
![]() $_{\gamma }(C^*(E))$
be the set of all proper ideals of
$_{\gamma }(C^*(E))$
be the set of all proper ideals of
![]() $C^*(E)$
which are prime and gauge-invariant. For at finite graph E, it follows by [Reference Eilers, Restorff, Ruiz and Sørensen13, Lemma 3.16] that there exists a homeomorphism
$C^*(E)$
which are prime and gauge-invariant. For at finite graph E, it follows by [Reference Eilers, Restorff, Ruiz and Sørensen13, Lemma 3.16] that there exists a homeomorphism
![]() $\nu _E: \Gamma _E\to $
Prime
$\nu _E: \Gamma _E\to $
Prime
![]() $_{\gamma }(C^*(E))$
such that
$_{\gamma }(C^*(E))$
such that
![]() $\gamma _1\geq \gamma _2$
if and only if
$\gamma _1\geq \gamma _2$
if and only if
![]() $\nu _E(\gamma _1)\supseteq \nu _E(\gamma _2)$
for
$\nu _E(\gamma _1)\supseteq \nu _E(\gamma _2)$
for
![]() $\gamma _1,\gamma _2\in \Gamma _E$
.
$\gamma _1,\gamma _2\in \Gamma _E$
.
The structure of Prime
![]() $_{\gamma }(C^*(E))$
, and hence of
$_{\gamma }(C^*(E))$
, and hence of
![]() $\Gamma _E$
, will become crucial in the application of
$\Gamma _E$
, will become crucial in the application of
![]() $SL_{\mathcal {P}}$
-equivalence.
$SL_{\mathcal {P}}$
-equivalence.
2.1 Classification of graph
 $C^*$
-algebras over finite graphs
$C^*$
-algebras over finite graphs
In this section, we briefly describe the classification result of finite graphs by Eilers, Restorff, Ruiz, and Sørensen in [Reference Eilers, Restorff, Ruiz and Sørensen13]. We restrict to the case of type I/postliminal
![]() $C^*$
-algebras. By [Reference Eilers, Restorff, Ruiz and Sørensen13, Lemma 4.20] and [Reference Deicke, Hong and Szymański11], a graph
$C^*$
-algebras. By [Reference Eilers, Restorff, Ruiz and Sørensen13, Lemma 4.20] and [Reference Deicke, Hong and Szymański11], a graph
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $C^*(E)$
is of type I if and only if no vertices support two distinct return paths.
$C^*(E)$
is of type I if and only if no vertices support two distinct return paths.
In [Reference Eilers, Restorff, Ruiz and Sørensen13, Theorem 6.1], finite graphs are classified up to stable isomorphism by their ordered reduced filtered K-theory, in which the main idea is to consider the K-theory of specific ideals, the corresponding quotients, and the maps between them. We will not describe this further. Instead, we consider type I graph
![]() $C^*$
-algebras for which the classification result is reduced to a question of
$C^*$
-algebras for which the classification result is reduced to a question of
![]() ${\text {SL}}_{\mathcal {P}}$
-equivalence as presented in [Reference Eilers, Restorff, Ruiz and Sørensen13, Reference Eilers, Restorff, Ruiz and Sørensen14].
${\text {SL}}_{\mathcal {P}}$
-equivalence as presented in [Reference Eilers, Restorff, Ruiz and Sørensen13, Reference Eilers, Restorff, Ruiz and Sørensen14].
![]() ${\text {SL}}_{\mathcal {P}}$
-equivalence boils down to elementary matrix algebras, which makes it a very useful tool in applications.
${\text {SL}}_{\mathcal {P}}$
-equivalence boils down to elementary matrix algebras, which makes it a very useful tool in applications.
We describe the definition of
![]() ${\text {SL}}_{\mathcal {P}}$
-equivalence; for this, we let
${\text {SL}}_{\mathcal {P}}$
-equivalence; for this, we let
![]() $\boldsymbol {n}=(n_i)_{i=1}^N, \boldsymbol {m}=(m_i)_{i=1}^N\in {\mathbb {N}}^N$
be multi-indices and
$\boldsymbol {n}=(n_i)_{i=1}^N, \boldsymbol {m}=(m_i)_{i=1}^N\in {\mathbb {N}}^N$
be multi-indices and
![]() $|\boldsymbol {n}|=n_1+\cdots +n_N$
. We denote by
$|\boldsymbol {n}|=n_1+\cdots +n_N$
. We denote by
![]() $\boldsymbol {1}$
the multi-index with
$\boldsymbol {1}$
the multi-index with
![]() $1$
on every entry.
$1$
on every entry.
Definition 2.2 Let
![]() $\mathcal {P}=\{1,2,3,\ldots ,N\}$
with
$\mathcal {P}=\{1,2,3,\ldots ,N\}$
with
![]() $N\in {\mathbb {N}}$
be a partially ordered set with order denoted
$N\in {\mathbb {N}}$
be a partially ordered set with order denoted
![]() $\preceq $
. Let
$\preceq $
. Let
![]() $\boldsymbol {m},\boldsymbol {n}\in {\mathbb {N}}^N$
be multi-indices such that
$\boldsymbol {m},\boldsymbol {n}\in {\mathbb {N}}^N$
be multi-indices such that
![]() $|\boldsymbol {m}|>0$
and
$|\boldsymbol {m}|>0$
and
![]() $|\boldsymbol {n}|>0$
. Then
$|\boldsymbol {n}|>0$
. Then
![]() $\mathfrak {M}_{\mathcal {P}}(\boldsymbol {m}\times \boldsymbol {n},\mathbb Z)$
is the set of block matrices
$\mathfrak {M}_{\mathcal {P}}(\boldsymbol {m}\times \boldsymbol {n},\mathbb Z)$
is the set of block matrices
 $$ \begin{align*}B=\begin{pmatrix} B\{1,1\} & \cdots & B\{1,N\} \\ \vdots & & \vdots \\ B\{N,1\} & \cdots & B\{N,N\} \end{pmatrix} \end{align*} $$
$$ \begin{align*}B=\begin{pmatrix} B\{1,1\} & \cdots & B\{1,N\} \\ \vdots & & \vdots \\ B\{N,1\} & \cdots & B\{N,N\} \end{pmatrix} \end{align*} $$
for which
where
![]() $B\{i,j\}\in M(m_i\times n_i,{\mathbb {Z}})$
. If
$B\{i,j\}\in M(m_i\times n_i,{\mathbb {Z}})$
. If
![]() $m_i=n_i=0$
, then
$m_i=n_i=0$
, then
![]() $B\{i,j\}$
is the empty matrix. Moreover, we denote
$B\{i,j\}$
is the empty matrix. Moreover, we denote
![]() $B\{i,i\}$
by
$B\{i,i\}$
by
![]() $B\{i\}$
. Note that condition (2.1) implies that the matrices in
$B\{i\}$
. Note that condition (2.1) implies that the matrices in
![]() $\mathfrak {M}_{\mathcal {P}}(\boldsymbol {m}\times \boldsymbol {n},\mathbb Z)$
are upper triangular block matrices.
$\mathfrak {M}_{\mathcal {P}}(\boldsymbol {m}\times \boldsymbol {n},\mathbb Z)$
are upper triangular block matrices.
Let
![]() $\mathfrak {M}_{\mathcal {P}}(\boldsymbol {n},\mathbb Z)$
denote
$\mathfrak {M}_{\mathcal {P}}(\boldsymbol {n},\mathbb Z)$
denote
![]() $\mathfrak {M}_{\mathcal {P}}(\boldsymbol {n}\times \boldsymbol {n},\mathbb Z)$
. We define
$\mathfrak {M}_{\mathcal {P}}(\boldsymbol {n}\times \boldsymbol {n},\mathbb Z)$
. We define
![]() ${\text {SL}}_{\mathcal {P}}(\boldsymbol {n},\mathbb Z)$
to be the matrices in
${\text {SL}}_{\mathcal {P}}(\boldsymbol {n},\mathbb Z)$
to be the matrices in
![]() $\mathfrak {M}_{\mathcal {P}}(\boldsymbol {n},\mathbb Z)$
such that all the nonempty diagonal blocks have determinant
$\mathfrak {M}_{\mathcal {P}}(\boldsymbol {n},\mathbb Z)$
such that all the nonempty diagonal blocks have determinant
![]() $ 1$
.
$ 1$
.
Definition 2.3 Let
![]() $A,B\in \mathfrak {M}_{\mathcal {P}}(\boldsymbol {m}\times \boldsymbol {n},\mathbb Z)$
, and we say that A and B are
$A,B\in \mathfrak {M}_{\mathcal {P}}(\boldsymbol {m}\times \boldsymbol {n},\mathbb Z)$
, and we say that A and B are
![]() ${\text {SL}}_{\mathcal {P}}$
-equivalent if there exist
${\text {SL}}_{\mathcal {P}}$
-equivalent if there exist
![]() $U\in {\text {SL}}_{\mathcal {P}}(\boldsymbol {m},\mathbb Z)$
and
$U\in {\text {SL}}_{\mathcal {P}}(\boldsymbol {m},\mathbb Z)$
and
![]() $V\in {\text {SL}}_{\mathcal {P}}(\boldsymbol {n},{\mathbb {Z}})$
such that
$V\in {\text {SL}}_{\mathcal {P}}(\boldsymbol {n},{\mathbb {Z}})$
such that
![]() $UAV=B$
.
$UAV=B$
.
The block structure of
![]() $B_E$
for a finite graph E is given by the conditions in [Reference Eilers, Restorff, Ruiz and Sørensen13, Definition 4.15]. Here, a partial ordered set
$B_E$
for a finite graph E is given by the conditions in [Reference Eilers, Restorff, Ruiz and Sørensen13, Definition 4.15]. Here, a partial ordered set
![]() $\mathcal {P}$
is defined such that there is an order-reversing isomorphism from
$\mathcal {P}$
is defined such that there is an order-reversing isomorphism from
![]() $\mathcal {P}$
to
$\mathcal {P}$
to
![]() $\Gamma _E$
and hence encodes the ideal structure.
$\Gamma _E$
and hence encodes the ideal structure.
Let E be a finite graph which has no vertices supporting two distinct return paths. From [Reference Eilers, Restorff, Ruiz and Sørensen13, Definition 4.15] and the following remark, it follows that
![]() $B_E$
can be assumed to have a
$B_E$
can be assumed to have a
![]() $1\times 1$
block structure, i.e.,
$1\times 1$
block structure, i.e.,
![]() $B_E\in \mathfrak {M}^{\circ }_{\mathcal {P}}(\boldsymbol {1},\mathbb Z)$
(see [Reference Eilers, Restorff, Ruiz and Sørensen13, Definition 4.15]).
$B_E\in \mathfrak {M}^{\circ }_{\mathcal {P}}(\boldsymbol {1},\mathbb Z)$
(see [Reference Eilers, Restorff, Ruiz and Sørensen13, Definition 4.15]).
![]() $SL_{\mathcal {P}}(\mathbf {1},\mathbb Z)$
is in this case given as the set of upper triangular matrices,
$SL_{\mathcal {P}}(\mathbf {1},\mathbb Z)$
is in this case given as the set of upper triangular matrices,
![]() $A=(a_{ij})$
, with
$A=(a_{ij})$
, with
![]() $1$
on the diagonal and which satisfies
$1$
on the diagonal and which satisfies
![]() $ a_{ij}\neq 0 \Rightarrow i\preceq j. $
$ a_{ij}\neq 0 \Rightarrow i\preceq j. $
![]() $SL_{\mathcal {P}}$
-equivalence simplifies in this case since the block structure consists of
$SL_{\mathcal {P}}$
-equivalence simplifies in this case since the block structure consists of
![]() $1\times 1$
matrices. Hence, working with
$1\times 1$
matrices. Hence, working with
![]() $SL_{\mathcal {P}}$
-equivalence becomes a linear problem. Note that
$SL_{\mathcal {P}}$
-equivalence becomes a linear problem. Note that
![]() $SL_{\mathcal {P}}(\mathbf {1},\mathbb Z)$
is a group under matrix multiplication.
$SL_{\mathcal {P}}(\mathbf {1},\mathbb Z)$
is a group under matrix multiplication.
Let
![]() ${E}_{\curlywedge }$
be the graph which is obtained from E by adding a loop to all sinks in E. For two finite graphs E and F, we say that
${E}_{\curlywedge }$
be the graph which is obtained from E by adding a loop to all sinks in E. For two finite graphs E and F, we say that
![]() $(B_E,B_F)$
is in standard form if the adjacency matrices for E and F have the same size and block structure; moreover, they must also have the same temperatures, i.e., the same types of gauge simple subquotients (see [Reference Eilers, Restorff, Ruiz and Sørensen13, Definition 4.22] for a precise definition). The partial ordered set
$(B_E,B_F)$
is in standard form if the adjacency matrices for E and F have the same size and block structure; moreover, they must also have the same temperatures, i.e., the same types of gauge simple subquotients (see [Reference Eilers, Restorff, Ruiz and Sørensen13, Definition 4.22] for a precise definition). The partial ordered set
![]() $\mathcal {P}$
is defined such that there is an order-reversing isomorphism from
$\mathcal {P}$
is defined such that there is an order-reversing isomorphism from
![]() $\mathcal {P}$
to
$\mathcal {P}$
to
![]() $\Gamma _E$
and
$\Gamma _E$
and
![]() $\Gamma _F$
.
$\Gamma _F$
.
Type I graph
![]() $C^*$
-algebras are classified by the following result.
$C^*$
-algebras are classified by the following result.
Theorem 2.1 ([Reference Eilers, Restorff, Ruiz and Sørensen13, Theorem 7.1] and [Reference Eilers, Restorff, Ruiz and Sørensen14, Proposition 14.8])
Let E and F be finite graphs which have no vertices supporting two distinct return paths. If
![]() $(B_E,B_F)$
is in standard form, then
$(B_E,B_F)$
is in standard form, then
![]() $C^*(E)$
and
$C^*(E)$
and
![]() $C^*(F)$
are isomorphic if and only if there exist matrices
$C^*(F)$
are isomorphic if and only if there exist matrices
![]() $U,V\in SL_{\mathcal {P}}(\mathbf {1},\mathbb Z)$
such that
$U,V\in SL_{\mathcal {P}}(\mathbf {1},\mathbb Z)$
such that
![]() $U{B_E}_{\curlywedge }V={B_F}_{\curlywedge }$
.
$U{B_E}_{\curlywedge }V={B_F}_{\curlywedge }$
.
3 Quantum Lens spaces as graph
 $C^*$
-algebras
$C^*$
-algebras
The quantum
![]() $(2n+1)$
-sphere by Vaksman and Soibelman, denoted
$(2n+1)$
-sphere by Vaksman and Soibelman, denoted
![]() $C(S_q^{2n+1})$
, is the universal
$C(S_q^{2n+1})$
, is the universal
![]() $C^*$
-algebra generated by
$C^*$
-algebra generated by
![]() $z_0,z_1,\ldots ,z_n$
with the following relations:
$z_0,z_1,\ldots ,z_n$
with the following relations:
 $$ \begin{align*} \begin{aligned} &z_jz_i=qz_iz_j, \;\;\; \text{for} \; i<j, \ \ z_iz_j^*=qz_j^*z_i, \;\;\; \text{for} \; i\neq j, \\ &z_i^*z_i=z_iz_i^*+(1-q^2)\sum_{j=i+1}^n z_jz_j^*, \; \text{for} \ i=0,\ldots ,n, \\ &\sum_{j=0}^n z_jz_j^*=1, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &z_jz_i=qz_iz_j, \;\;\; \text{for} \; i<j, \ \ z_iz_j^*=qz_j^*z_i, \;\;\; \text{for} \; i\neq j, \\ &z_i^*z_i=z_iz_i^*+(1-q^2)\sum_{j=i+1}^n z_jz_j^*, \; \text{for} \ i=0,\ldots ,n, \\ &\sum_{j=0}^n z_jz_j^*=1, \end{aligned} \end{align*} $$
where
![]() $q\in (0,1)$
(see [Reference Vaksman and Soibelman28]). It was shown in [Reference Hong and Szymański19] that
$q\in (0,1)$
(see [Reference Vaksman and Soibelman28]). It was shown in [Reference Hong and Szymański19] that
![]() $C(S_q^{2n+1})\cong C^*(L_{2n+1})$
where the graph
$C(S_q^{2n+1})\cong C^*(L_{2n+1})$
where the graph
![]() $L_{2n+1}$
has vertices
$L_{2n+1}$
has vertices
![]() $v_i, i=0,\ldots ,n$
, with edges
$v_i, i=0,\ldots ,n$
, with edges
![]() $e_{ij}, 0\leq i\leq j\leq n$
, and
$e_{ij}, 0\leq i\leq j\leq n$
, and
![]() $s(e_{ij})=v_i, r(e_{ij})=v_j$
.
$s(e_{ij})=v_i, r(e_{ij})=v_j$
.
Let
![]() $\underline {m}=(m_0,m_1,\ldots ,m_n)$
be a sequence of positive integers. The
$\underline {m}=(m_0,m_1,\ldots ,m_n)$
be a sequence of positive integers. The
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $C(S_q^{2n+1})$
admits, by universality, an action of
$C(S_q^{2n+1})$
admits, by universality, an action of
![]() $\mathbb Z_r$
for any
$\mathbb Z_r$
for any
![]() $r\in \mathbb {N}$
, given by
$r\in \mathbb {N}$
, given by
where
![]() $\theta $
is a generator of
$\theta $
is a generator of
![]() $\mathbb Z_r$
. The quantum lens space
$\mathbb Z_r$
. The quantum lens space
![]() $C(L_q^{2n+1}(r;\underline {m}))$
is defined as the fixed point algebra of
$C(L_q^{2n+1}(r;\underline {m}))$
is defined as the fixed point algebra of
![]() $C(S_q^{2n+1})$
under this action.
$C(S_q^{2n+1})$
under this action.
The action
![]() $\varrho _{\underline {m}}^r$
on
$\varrho _{\underline {m}}^r$
on
![]() $C(S_q^{2n+1})$
translates under the isomorphism with
$C(S_q^{2n+1})$
translates under the isomorphism with
![]() $C^*(L_{2n+1})$
, to the following action:
$C^*(L_{2n+1})$
, to the following action:
We also denote this action by
![]() $\varrho _{\underline {m}}^r$
. It then follows by [Reference Crisp9, Theorem 4.6] that
$\varrho _{\underline {m}}^r$
. It then follows by [Reference Crisp9, Theorem 4.6] that
 $$ \begin{align} C(L_q^{2n+1}(r;\underline{m}))\cong C(L_{2n+1})^{\varrho_{\underline{m}}^r}\cong \left(\sum_{i=0}^n p_{(v_i,0)}\right)C^*(L_{2n+1}\times_{ c}\mathbb{Z}_r)\left(\sum_{i=0}^n p_{(v_i,0)}\right). \end{align} $$
$$ \begin{align} C(L_q^{2n+1}(r;\underline{m}))\cong C(L_{2n+1})^{\varrho_{\underline{m}}^r}\cong \left(\sum_{i=0}^n p_{(v_i,0)}\right)C^*(L_{2n+1}\times_{ c}\mathbb{Z}_r)\left(\sum_{i=0}^n p_{(v_i,0)}\right). \end{align} $$
The graph
![]() $L_{2n+1}\times _{ c}\mathbb {Z}_r$
, called the skew product graph labeled by
$L_{2n+1}\times _{ c}\mathbb {Z}_r$
, called the skew product graph labeled by
![]() $c: e_{ij}\to m_i \ (\mathrm {mod}\ r)$
, has vertices
$c: e_{ij}\to m_i \ (\mathrm {mod}\ r)$
, has vertices
![]() $(v_i,k), i=0,\ldots ,n, k=0,\ldots ,r-1$
, and edges
$(v_i,k), i=0,\ldots ,n, k=0,\ldots ,r-1$
, and edges
![]() $(e_{ij}, k), i, j=0,\ldots ,n, i\leq j, k=0,\ldots ,r-1$
. The source and range maps are given as follows:
$(e_{ij}, k), i, j=0,\ldots ,n, i\leq j, k=0,\ldots ,r-1$
. The source and range maps are given as follows:
In [Reference Brzeziński and Szymański8, Theorem 2.2], it is stated that
![]() $C(L_q^{2n+1}(r;\underline {m}))$
is isomorphic to the graph
$C(L_q^{2n+1}(r;\underline {m}))$
is isomorphic to the graph
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $C^*(L_{2n+1}^{r;\underline {m}})$
. To define the graph
$C^*(L_{2n+1}^{r;\underline {m}})$
. To define the graph
![]() $L_{2n+1}^{r;\underline {m}}$
, we need the notion of an admissible path.
$L_{2n+1}^{r;\underline {m}}$
, we need the notion of an admissible path.
Definition 3.1 [Reference Brzeziński and Szymański8]
A path from
![]() $(v_i,s)$
to
$(v_i,s)$
to
![]() $(v_j,t)$
in
$(v_j,t)$
in
![]() $L_{2n+1}{\kern-1pt}\times _{c}\mathbb Z_r$
is called admissible if it does not pass through any
$L_{2n+1}{\kern-1pt}\times _{c}\mathbb Z_r$
is called admissible if it does not pass through any
![]() $(v_{\ell },k)$
for which
$(v_{\ell },k)$
for which
![]() $\ell {\kern-1pt}={\kern-1pt}i,\ldots ,j$
and
$\ell {\kern-1pt}={\kern-1pt}i,\ldots ,j$
and
![]() $k{\kern-1pt}={\kern-1pt}0,\ldots , \gcd (m_{\ell },r)-1$
.
$k{\kern-1pt}={\kern-1pt}0,\ldots , \gcd (m_{\ell },r)-1$
.
Remark 3.1 Comparing with the notion of 0-simple paths from [Reference Eilers, Restorff, Ruiz and Sørensen13, Definition 7.4], it is clear that the 0-simple paths are exactly the admissible paths when all weights are coprime to the order of the acting group.
Definition 3.2 [Reference Brzeziński and Szymański8]
The graph
![]() $L_{2n+1}^{r;\underline {m}}$
has vertices
$L_{2n+1}^{r;\underline {m}}$
has vertices
![]() $v_i^b,i=0,\ldots ,n, b=0,\ldots ,\gcd (m_i,r)-1$
and edges
$v_i^b,i=0,\ldots ,n, b=0,\ldots ,\gcd (m_i,r)-1$
and edges
![]() $e_{ij;a}^{st}$
,
$e_{ij;a}^{st}$
,
![]() $a=1,\ldots ,n_{ij}^{st}$
where
$a=1,\ldots ,n_{ij}^{st}$
where
The source and range maps are given by
The following example, which was pointed out by Efren Ruiz, shows that it is not in general true that
![]() $C(L_q^{2n+1}(r;\underline {m}))$
is isomorphic to the graph
$C(L_q^{2n+1}(r;\underline {m}))$
is isomorphic to the graph
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $C^*(L_{2n+1}^{r;\underline {m}})$
as stated in [Reference Brzeziński and Szymański8, Theorem 2.2].
$C^*(L_{2n+1}^{r;\underline {m}})$
as stated in [Reference Brzeziński and Szymański8, Theorem 2.2].
Example 3.2 Counterexample of [Reference Brzeziński and Szymański8, Theorem 2.2]
Let
![]() $n=1, r=4$
, and
$n=1, r=4$
, and
![]() $\underline {m}=(2,1)$
, then the skew product graph consists of two levels, both of which consist of four vertices, and the first level consists of two cycles as follows:
$\underline {m}=(2,1)$
, then the skew product graph consists of two levels, both of which consist of four vertices, and the first level consists of two cycles as follows:

We have
 $$ \begin{align*}\begin{aligned} C(L_q^3(4;(2,1)))&\cong (p_{(v_0,0)}+p_{(v_1,0)})C^*(L_3\times_c\mathbb Z_4)(p_{(v_0,0)}+p_{(v_1,0)}) \\ &= \overline{\operatorname{span}}\{s_{\mu}s_{\nu}^*| \ r(\mu)=r(\nu), s(\mu),s(\nu)\in \{(v_0,0),(v_1,0)\}\} \\ &=(p_{(v_0,0)}+p_{(v_1,0)})C^*(G)(p_{(v_0,0)}+p_{(v_1,0)}), \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} C(L_q^3(4;(2,1)))&\cong (p_{(v_0,0)}+p_{(v_1,0)})C^*(L_3\times_c\mathbb Z_4)(p_{(v_0,0)}+p_{(v_1,0)}) \\ &= \overline{\operatorname{span}}\{s_{\mu}s_{\nu}^*| \ r(\mu)=r(\nu), s(\mu),s(\nu)\in \{(v_0,0),(v_1,0)\}\} \\ &=(p_{(v_0,0)}+p_{(v_1,0)})C^*(G)(p_{(v_0,0)}+p_{(v_1,0)}), \end{aligned} \end{align*} $$
where G is the subgraph of
![]() $L_3\times _c\mathbb Z_4$
for which
$L_3\times _c\mathbb Z_4$
for which
The range and source maps are the ones from
![]() $L_3\times _c\mathbb Z_4$
restricted to G. The graph G is defined as above since we have no paths from
$L_3\times _c\mathbb Z_4$
restricted to G. The graph G is defined as above since we have no paths from
![]() $(v_0,0)$
or
$(v_0,0)$
or
![]() $(v_1,0)$
to
$(v_1,0)$
to
![]() $(v_0,1)$
and
$(v_0,1)$
and
![]() $(v_0,3)$
. Hence, we can remove the vertices
$(v_0,3)$
. Hence, we can remove the vertices
![]() $(v_0,i), i=1,3$
, and their outgoing edges. Note that
$(v_0,i), i=1,3$
, and their outgoing edges. Note that
![]() $G^0$
is the smallest hereditary subset of
$G^0$
is the smallest hereditary subset of
![]() $(L_3\times _c {\mathbb {Z}}_4)^0$
, which contains
$(L_3\times _c {\mathbb {Z}}_4)^0$
, which contains
![]() $(v_0,0)$
and
$(v_0,0)$
and
![]() $(v_1,0)$
.
$(v_1,0)$
.
Since G is a Cuntz–Krieger algebra, it follows by [Reference Arklint and Ruiz3, Corollary 4.10] that the corner is indeed a Cuntz–Krieger algebra, hence a graph
![]() $C^*$
-algebra.
$C^*$
-algebra.
The projection
![]() $p_{(v_0,0)}+p_{(v_1,0)}$
is full in
$p_{(v_0,0)}+p_{(v_1,0)}$
is full in
![]() $C^*(G)$
. Indeed, let I be the ideal generated by
$C^*(G)$
. Indeed, let I be the ideal generated by
![]() $p_{(v_0,0)}+p_{(v_1,0)}$
. By the Cuntz–Krieger relations, we have
$p_{(v_0,0)}+p_{(v_1,0)}$
. By the Cuntz–Krieger relations, we have
Hence,
Then
![]() $p_{(v_0,2)}\in I$
. Similarly, we can show that
$p_{(v_0,2)}\in I$
. Similarly, we can show that
![]() $p_{(v_1,1)}\in I$
using that
$p_{(v_1,1)}\in I$
using that
![]() $p_{(v_1,0)}\in I$
and so on. We obtain that
$p_{(v_1,0)}\in I$
and so on. We obtain that
![]() $p_w\in I$
for all
$p_w\in I$
for all
![]() $w\in G^0$
; hence,
$w\in G^0$
; hence,
![]() $I=C^*(G)$
and
$I=C^*(G)$
and
![]() $p_{(v_0,0)}+p_{(v_1,0)}$
is a full projection. By [Reference Brown6, Corollary 2.6],
$p_{(v_0,0)}+p_{(v_1,0)}$
is a full projection. By [Reference Brown6, Corollary 2.6],
![]() $(p_{(v_0,0)}+p_{(v_1,0)})C^*(G)(p_{(v_0,0)}+p_{(v_1,0)})$
is stably isomorphic to
$(p_{(v_0,0)}+p_{(v_1,0)})C^*(G)(p_{(v_0,0)}+p_{(v_1,0)})$
is stably isomorphic to
![]() $C^*(G)$
.
$C^*(G)$
.
We apply the collapse move defined in [Reference Sørensen26] a number of times until we obtain a finite graph with no sinks and sources such that every vertex is the base of at least one loop. The graphs below indicate how to obtain such a graph, and the vertex indicated with
![]() $\ast $
is the one we collapse in each step. The graph we obtain in the last step is denoted by E.
$\ast $
is the one we collapse in each step. The graph we obtain in the last step is denoted by E.

By [Reference Sørensen26, Lemma 5.1], we obtain
![]() $C^*(G)\otimes {\mathcal K} \cong C^*(E)\otimes {\mathcal K}$
and hence
$C^*(G)\otimes {\mathcal K} \cong C^*(E)\otimes {\mathcal K}$
and hence
It is a consequence of the claim [Reference Brzeziński and Szymański8, Theorem 2.2] made by Brzeziński and Szymański that
![]() $C(L_q^3(4;(2,1)))$
is isomorphic to the graph
$C(L_q^3(4;(2,1)))$
is isomorphic to the graph
![]() $C^*$
-algebra of the following graph:
$C^*$
-algebra of the following graph:

By considering the strongly connected components, we have
![]() $|\text {Prime}_{\gamma }C^*(E)|=2$
and
$|\text {Prime}_{\gamma }C^*(E)|=2$
and
![]() $|\text {Prime}_{\gamma }C^*(L_3^{4;(2,1)})|=3$
. Since
$|\text {Prime}_{\gamma }C^*(L_3^{4;(2,1)})|=3$
. Since
![]() ${\mathcal K}$
is central and simple, it follows that the ideal structure of the tensor product with
${\mathcal K}$
is central and simple, it follows that the ideal structure of the tensor product with
![]() ${\mathcal K}$
is completely determined by
${\mathcal K}$
is completely determined by
![]() $C^*(E)$
or
$C^*(E)$
or
![]() $C(L_q^3(4;(2,1)))$
(see, e.g., [Reference Drozd and Kirichenko12, Theorem 4.3.1]). Then
$C(L_q^3(4;(2,1)))$
(see, e.g., [Reference Drozd and Kirichenko12, Theorem 4.3.1]). Then
![]() $C(L_q^3(4;(2,1)))$
cannot be isomorphic to
$C(L_q^3(4;(2,1)))$
cannot be isomorphic to
![]() $C^*(L_{3}^{4;(2,1)})$
since it contradicts (3.2).
$C^*(L_{3}^{4;(2,1)})$
since it contradicts (3.2).
We will in Theorem 3.4 prove that the quantum lens spaces are indeed graph
![]() $C^*$
-algebras of a modified graph from which it follows that
$C^*$
-algebras of a modified graph from which it follows that
![]() $C(L_q^3(4;(2,1)))\cong C^*(E)$
.
$C(L_q^3(4;(2,1)))\cong C^*(E)$
.
Remark 3.3 The proof of [Reference Brzeziński and Szymański8, Theorem 2.2] follows by constructing an explicit isomorphism. The problem with the isomorphism is that
![]() $p_{v_i^b}$
is mapped to
$p_{v_i^b}$
is mapped to
![]() $p_{(v_i,b)}$
for
$p_{(v_i,b)}$
for
![]() $i=0,1,\ldots ,n, b=0,1,\ldots ,\gcd (m_i,r)-1$
. However,
$i=0,1,\ldots ,n, b=0,1,\ldots ,\gcd (m_i,r)-1$
. However,
![]() $p_{(v_i,b)}$
for
$p_{(v_i,b)}$
for
![]() $b\neq 0$
is not contained in the corner in (3.1) by orthogonality of the projections.
$b\neq 0$
is not contained in the corner in (3.1) by orthogonality of the projections.
3.1 A modified graph
We now define a graph for which the main idea behind the construction is similar to the one for
![]() ${L}_{2n+1}^{r;\underline {m}}$
. The main difference is that we restrict the set of vertices further.
${L}_{2n+1}^{r;\underline {m}}$
. The main difference is that we restrict the set of vertices further.
Definition 3.3 Let
![]() $n\geq 1$
be an integer, let
$n\geq 1$
be an integer, let
![]() $r\in {\mathbb {N}}$
, and let
$r\in {\mathbb {N}}$
, and let
![]() $\underline {m}=(m_0,\ldots ,m_n)$
be a sequence of positive integers. Let
$\underline {m}=(m_0,\ldots ,m_n)$
be a sequence of positive integers. Let
![]() $H_{r;\underline {m}}$
be the smallest hereditary subset of
$H_{r;\underline {m}}$
be the smallest hereditary subset of
![]() $(L_{2n+1}\times _c{\mathbb {Z}}_r)^0$
containing
$(L_{2n+1}\times _c{\mathbb {Z}}_r)^0$
containing
![]() $\{(v_i,0)| i=0,\ldots ,n\}$
. For each
$\{(v_i,0)| i=0,\ldots ,n\}$
. For each
![]() $i=0,\ldots ,n$
, let
$i=0,\ldots ,n$
, let
Note that
![]() $S_0=\{0\}$
. The graph
$S_0=\{0\}$
. The graph
![]() $\overline {L}_{2n+1}^{r;\underline {m}}$
is defined as follows:
$\overline {L}_{2n+1}^{r;\underline {m}}$
is defined as follows:
 $$ \begin{align*} \begin{aligned} (\overline{L}_{2n+1}^{r;\underline{m}})^0&:=\{v_i^k| \ i=0,\ldots ,n, k\in S_i\}, \\ (\overline{L}_{2n+1}^{r;\underline{m}})^1&:= \{e_{ij;a}^{st}| 0\leq i\leq j\leq n, s\in S_i, t\in S_j, a=1,\ldots ,n_{ij}^{st}\}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} (\overline{L}_{2n+1}^{r;\underline{m}})^0&:=\{v_i^k| \ i=0,\ldots ,n, k\in S_i\}, \\ (\overline{L}_{2n+1}^{r;\underline{m}})^1&:= \{e_{ij;a}^{st}| 0\leq i\leq j\leq n, s\in S_i, t\in S_j, a=1,\ldots ,n_{ij}^{st}\}, \end{aligned} \end{align*} $$
where
![]() $n_{ij}^{st}$
is the number of admissible paths from
$n_{ij}^{st}$
is the number of admissible paths from
![]() $(v_i,s)$
to
$(v_i,s)$
to
![]() $(v_j,t)$
. The range and source maps are given by
$(v_j,t)$
. The range and source maps are given by
The graph
![]() $\overline {L}_{2n+1}^{r;\underline {m}}$
then consists of
$\overline {L}_{2n+1}^{r;\underline {m}}$
then consists of
![]() $\sum _{i=0}^n |S_i|$
vertices, which we divide into
$\sum _{i=0}^n |S_i|$
vertices, which we divide into
![]() $n+1$
levels. The levels are denoted by level
$n+1$
levels. The levels are denoted by level
![]() $0$
to level n, where level i consists of the vertices
$0$
to level n, where level i consists of the vertices
![]() $v_i^k, k\in S_i$
. There only exist edges from a lower indexed level to a higher one, and each vertex is the base of precisely one loop. The graph is illustrated in Figure 1 without indicating any edges.
$v_i^k, k\in S_i$
. There only exist edges from a lower indexed level to a higher one, and each vertex is the base of precisely one loop. The graph is illustrated in Figure 1 without indicating any edges.

Figure 1: Illustration of
![]() $\left (\overline {L}_{2n+1}^{r; \underline {m}}\right ){}^0$
.
$\left (\overline {L}_{2n+1}^{r; \underline {m}}\right ){}^0$
.
The difference between the definition of
![]() $L_{2n+1}^{r;\underline {m}}$
and
$L_{2n+1}^{r;\underline {m}}$
and
![]() $\overline {L}_{2n+1}^{r;\underline {m}}$
is that we restrict the vertices to the ones in the smallest hereditary subset of
$\overline {L}_{2n+1}^{r;\underline {m}}$
is that we restrict the vertices to the ones in the smallest hereditary subset of
![]() $(L_{2n+1}\times _c{\mathbb {Z}}_r)^0$
. In this way, we avoid the problem in Example 3.2 since we remove the vertices that are not in the hereditary subset, i.e., the vertices
$(L_{2n+1}\times _c{\mathbb {Z}}_r)^0$
. In this way, we avoid the problem in Example 3.2 since we remove the vertices that are not in the hereditary subset, i.e., the vertices
![]() $(v_0,1)$
and
$(v_0,1)$
and
![]() $(v_0,3)$
.
$(v_0,3)$
.
The purpose of this section is to prove the following theorem.
Theorem 3.4 As
![]() $C^*$
-algebras, we have
$C^*$
-algebras, we have
Remark 3.5 If
![]() $\gcd (m_0,r)=1$
, then one can always find a path from
$\gcd (m_0,r)=1$
, then one can always find a path from
![]() $(v_0,0)$
to any given vertex in the skew-product graph, and hence
$(v_0,0)$
to any given vertex in the skew-product graph, and hence
![]() $\overline {L}_{2n+1}^{(r;\underline {m})}$
is the same as
$\overline {L}_{2n+1}^{(r;\underline {m})}$
is the same as
![]() $L_{2n+1}^{(r;\underline {m})}$
. It follows, in this particular case, that our description of quantum lens spaces as graph
$L_{2n+1}^{(r;\underline {m})}$
. It follows, in this particular case, that our description of quantum lens spaces as graph
![]() $C^*$
-algebras agrees with the one given in [Reference Brzeziński and Szymański8]. Consequently, all of the examples given in that paper as well as the work done in [Reference Eilers, Restorff, Ruiz and Sørensen13, Reference Hong and Szymański20] are still valid under the description given in Theorem 3.4
$C^*$
-algebras agrees with the one given in [Reference Brzeziński and Szymański8]. Consequently, all of the examples given in that paper as well as the work done in [Reference Eilers, Restorff, Ruiz and Sørensen13, Reference Hong and Szymański20] are still valid under the description given in Theorem 3.4
To show that
![]() $C(L_q^{2n+1}(r;\underline {m}))$
is isomorphic to
$C(L_q^{2n+1}(r;\underline {m}))$
is isomorphic to
![]() $C^*(\overline {L}_{2n+1}^{r;\underline {m}})$
, we need a couple of lemmas. With [Reference Brzeziński and Szymański8, Theorem 2.2] in mind, we will show the following.
$C^*(\overline {L}_{2n+1}^{r;\underline {m}})$
, we need a couple of lemmas. With [Reference Brzeziński and Szymański8, Theorem 2.2] in mind, we will show the following.
Lemma 3.6 There exists a
![]() $*$
-isomorphism
$*$
-isomorphism
 $$ \begin{align} \psi: C^*(\overline{L}_{2n+1}^{r;\underline{m}})\to \left(\sum_{\substack{(v_i,k) \\ i=0,\ldots ,n, \ k\in S_i}} p_{(v_i,k)}\right) C^*(L_{2n+1}\times_c\mathbb Z_r)\left(\sum_{\substack{(v_i,k) \\ i=0,\ldots ,n, \ k\in S_i}} p_{(v_i,k)}\right) \end{align} $$
$$ \begin{align} \psi: C^*(\overline{L}_{2n+1}^{r;\underline{m}})\to \left(\sum_{\substack{(v_i,k) \\ i=0,\ldots ,n, \ k\in S_i}} p_{(v_i,k)}\right) C^*(L_{2n+1}\times_c\mathbb Z_r)\left(\sum_{\substack{(v_i,k) \\ i=0,\ldots ,n, \ k\in S_i}} p_{(v_i,k)}\right) \end{align} $$
such that
For an admissible path
![]() $\alpha =(e_{ii_1},k+m_i)(e_{i_1,i_2},k_1)\cdots (e_{i_mi_{m+1}},k_m)(e_{i_{m+1}j},t)$
from
$\alpha =(e_{ii_1},k+m_i)(e_{i_1,i_2},k_1)\cdots (e_{i_mi_{m+1}},k_m)(e_{i_{m+1}j},t)$
from
![]() $(v_i,k)$
to
$(v_i,k)$
to
![]() $(v_j,t)$
with
$(v_j,t)$
with
![]() $i,j=0,\ldots ,n$
,
$i,j=0,\ldots ,n$
,
![]() $k\in S_i$
and
$k\in S_i$
and
![]() $t\in S_j$
, we let
$t\in S_j$
, we let
We denote from now on the corner in (
3.3
) by
![]() $C_{r,\underline {m}}$
.
$C_{r,\underline {m}}$
.
Proof Let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be two admissible paths between vertices in the set
$\beta $
be two admissible paths between vertices in the set
![]() $\{(v_i,k)| \ i=0,\ldots ,n, k\in S_i\}$
. Then
$\{(v_i,k)| \ i=0,\ldots ,n, k\in S_i\}$
. Then
![]() $s_{\alpha }^*s_{\beta }=0$
if
$s_{\alpha }^*s_{\beta }=0$
if
![]() $\alpha \neq \beta $
since the partial isometries in
$\alpha \neq \beta $
since the partial isometries in
![]() $C^*(\overline {L}_{2n+1}^{r;\underline {m}})$
have mutually orthogonal range projections. We then have to show that
$C^*(\overline {L}_{2n+1}^{r;\underline {m}})$
have mutually orthogonal range projections. We then have to show that
![]() $\psi (s_{\alpha }^*)\psi (s_{\beta })=0$
if
$\psi (s_{\alpha }^*)\psi (s_{\beta })=0$
if
![]() $\alpha \neq \beta $
. It follows that
$\alpha \neq \beta $
. It follows that
![]() $\psi (s_{\alpha }^*)\psi (s_{\beta })$
equals
$\psi (s_{\alpha }^*)\psi (s_{\beta })$
equals
![]() $s_{\beta '}$
if
$s_{\beta '}$
if
![]() $\beta =\alpha \beta '$
and
$\beta =\alpha \beta '$
and
![]() $s_{\alpha '}^*$
if
$s_{\alpha '}^*$
if
![]() $\alpha =\beta \alpha '$
; otherwise, it equals zero (see, e.g., [Reference Raeburn24, Corollary 1.14]). Since
$\alpha =\beta \alpha '$
; otherwise, it equals zero (see, e.g., [Reference Raeburn24, Corollary 1.14]). Since
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are admissible paths and
$\beta $
are admissible paths and
![]() $\alpha \beta '$
and
$\alpha \beta '$
and
![]() $\beta \alpha '$
are not, the two first cases cannot happen. Hence,
$\beta \alpha '$
are not, the two first cases cannot happen. Hence,
![]() $\psi (s_{\alpha }^*)\psi (s_{\beta })$
equals zero if
$\psi (s_{\alpha }^*)\psi (s_{\beta })$
equals zero if
![]() $\alpha \neq \beta $
.
$\alpha \neq \beta $
.
We will now show that the image of
![]() $p_{v_i^k}$
and
$p_{v_i^k}$
and
![]() $s_{\alpha }$
satisfies the defining relations in Definition 2.1 for
$s_{\alpha }$
satisfies the defining relations in Definition 2.1 for
![]() $\overline {L}_{2n+1}^{r;\underline {m}}$
. Then, by universality,
$\overline {L}_{2n+1}^{r;\underline {m}}$
. Then, by universality,
![]() $\psi $
is a
$\psi $
is a
![]() $*$
-homomorphism. Using the defining relations for graph
$*$
-homomorphism. Using the defining relations for graph
![]() $C^*$
-algebras, it follows by an easy calculation that
$C^*$
-algebras, it follows by an easy calculation that
![]() $\psi (s_{\alpha }^*)\psi (s_{\alpha })=p_{r(\alpha )}$
and
$\psi (s_{\alpha }^*)\psi (s_{\alpha })=p_{r(\alpha )}$
and
![]() $\psi (s_{\alpha })\psi (s_{\alpha }^*)\leq p_{s(\alpha )}$
, and hence conditions (CK1) and (CK2) are satisfied. For condition (CK3), we fix a
$\psi (s_{\alpha })\psi (s_{\alpha }^*)\leq p_{s(\alpha )}$
, and hence conditions (CK1) and (CK2) are satisfied. For condition (CK3), we fix a
![]() $v_i^k$
in
$v_i^k$
in
![]() $\left (\overline {L}_{2n+1}^{r;\underline {m}}\right )^0$
. Let A be the collection of all admissible paths from
$\left (\overline {L}_{2n+1}^{r;\underline {m}}\right )^0$
. Let A be the collection of all admissible paths from
![]() $(v_i,k)$
to a
$(v_i,k)$
to a
![]() $(v_j,t)$
with
$(v_j,t)$
with
![]() $j=0,\ldots ,n, t\in S_j$
. Since each outgoing edge of
$j=0,\ldots ,n, t\in S_j$
. Since each outgoing edge of
![]() $v_i^k$
to a
$v_i^k$
to a
![]() $v_j^t$
corresponds to an admissible path from
$v_j^t$
corresponds to an admissible path from
![]() $(v_i,k)$
to
$(v_i,k)$
to
![]() $(v_j,t)$
, we wish to show that
$(v_j,t)$
, we wish to show that
By condition (CK3) on
![]() $L_{2n+1}\times _c{\mathbb {Z}}_r$
and the identity
$L_{2n+1}\times _c{\mathbb {Z}}_r$
and the identity
![]() $s_e=s_ep_{r(e)}=p_{s(e)}s_e$
, we have
$s_e=s_ep_{r(e)}=p_{s(e)}s_e$
, we have
 $$ \begin{align} \begin{aligned} p_{(v_i,k)}&=\sum_{i_1=i}^n s_{(e_{ii_1},m_i+k)}s_{(e_{ii_1},m_i+k)}^* \\ &= \sum_{i_1=i}^n s_{(e_{ii_1},m_i+k)}p_{r((e_{ii_1}m_i+k))}s_{(e_{ii_1},m_i+k)}^* \\ &= \sum_{i_1=i}^n s_{(e_{ii_1},m_i+k)}p_{(v_{i_1},m_i+k)}s_{(e_{ii_1},m_i+k)}^*. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} p_{(v_i,k)}&=\sum_{i_1=i}^n s_{(e_{ii_1},m_i+k)}s_{(e_{ii_1},m_i+k)}^* \\ &= \sum_{i_1=i}^n s_{(e_{ii_1},m_i+k)}p_{r((e_{ii_1}m_i+k))}s_{(e_{ii_1},m_i+k)}^* \\ &= \sum_{i_1=i}^n s_{(e_{ii_1},m_i+k)}p_{(v_{i_1},m_i+k)}s_{(e_{ii_1},m_i+k)}^*. \end{aligned} \end{align} $$
For each
![]() $i_1\in \{i,\ldots ,n\}$
, if
$i_1\in \{i,\ldots ,n\}$
, if
![]() $e_{({ii_1},m_i+k)}$
is not in A, then we substitute
$e_{({ii_1},m_i+k)}$
is not in A, then we substitute
 $$ \begin{align*}p_{(v_{i_1},m_i+k)}=\sum_{i_2=i_1}^n s_{(e_{i_1i_2},m_i+m_{i_1}+k)}s_{(e_{i_1i_2},m_i+m_{i_1}+k)}^* \end{align*} $$
$$ \begin{align*}p_{(v_{i_1},m_i+k)}=\sum_{i_2=i_1}^n s_{(e_{i_1i_2},m_i+m_{i_1}+k)}s_{(e_{i_1i_2},m_i+m_{i_1}+k)}^* \end{align*} $$
in (3.5). Let
![]() $A_{1}$
be the set of all
$A_{1}$
be the set of all
![]() $(e_{{ii_1}},m_i+k), i_1=i,\ldots ,n$
, for which
$(e_{{ii_1}},m_i+k), i_1=i,\ldots ,n$
, for which
![]() $(e_{{ii_1}},m_i+k)$
is inside A. Moreover, let
$(e_{{ii_1}},m_i+k)$
is inside A. Moreover, let
![]() $I_1$
be the set of all
$I_1$
be the set of all
![]() $i_1$
for which
$i_1$
for which
![]() $(e_{{ii_1}},m_i+k)\in A_1$
. Note that
$(e_{{ii_1}},m_i+k)\in A_1$
. Note that
![]() $A_1$
is finite since the paths have to be admissible. Then
$A_1$
is finite since the paths have to be admissible. Then
 $$ \begin{align*} \begin{aligned} p_{(v_i,k)}&= \sum_{\substack{i_1=i \\ i_1\notin I_1}}^n \left( s_{(e_{ii_1},m_i+k)} \left(\sum_{i_2=i_1}^n s_{(e_{i_1i_2},m_i+m_{i_1}+k)}p_{(v_{i_2},m_i+m_{i_1}+k)}s_{(e_{i_1i_2},m_i+m_{i_1}+k)}^* \right) s_{(e_{ii_1},m_i+k)}^*\right) \\ &\quad + \ \ \sum_{\alpha\in A_1} s_{\alpha}s_{\alpha}^*. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} p_{(v_i,k)}&= \sum_{\substack{i_1=i \\ i_1\notin I_1}}^n \left( s_{(e_{ii_1},m_i+k)} \left(\sum_{i_2=i_1}^n s_{(e_{i_1i_2},m_i+m_{i_1}+k)}p_{(v_{i_2},m_i+m_{i_1}+k)}s_{(e_{i_1i_2},m_i+m_{i_1}+k)}^* \right) s_{(e_{ii_1},m_i+k)}^*\right) \\ &\quad + \ \ \sum_{\alpha\in A_1} s_{\alpha}s_{\alpha}^*. \end{aligned} \end{align*} $$
Similarly, let
![]() $A_2$
contain all paths
$A_2$
contain all paths
![]() $(e_{ii_1},m_i+k)(e_{i_1i_2},m_i+m_{i_1}+k)$
, which are contained in A. Let
$(e_{ii_1},m_i+k)(e_{i_1i_2},m_i+m_{i_1}+k)$
, which are contained in A. Let
![]() $I_2$
be the set of all
$I_2$
be the set of all
![]() $(i_1,i_2)$
for which
$(i_1,i_2)$
for which
![]() $(e_{ii_1},m_i+k)(e_{i_1i_2},m_i+m_{i_1}+k)\in A_2$
. Then
$(e_{ii_1},m_i+k)(e_{i_1i_2},m_i+m_{i_1}+k)\in A_2$
. Then
 $$ \begin{align*}\begin{aligned} p_{(v_i,k)}&= \sum_{\substack{i_1=i \\ i_1\notin I_1}}^n \sum_{\substack{i_2=i_1 \\ \ \ \ (i_1,i_2)\notin I_2}}^n s_{(e_{ii_1},m_i+k)} s_{(e_{i_1i_2},m_i+m_{i_1}+k)} \\ & \ \ \cdot \left( \sum_{i_3=i_2}^n s_{(e_{i_2i_3},m_i+m_{i_1}+m_{i_2}+k)}s_{(e_{i_2i_3},m_i+m_{i_1}+m_{i_2}+k)}^* \right) s_{(e_{i_1i_2},m_i+m_{i_1}+k)}^* s_{(e_{ii_1},m_i+k)}^* \\ & \ \ + \sum_{\alpha\in A_1\cup A_2} s_{\alpha}s_{\alpha}^*. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} p_{(v_i,k)}&= \sum_{\substack{i_1=i \\ i_1\notin I_1}}^n \sum_{\substack{i_2=i_1 \\ \ \ \ (i_1,i_2)\notin I_2}}^n s_{(e_{ii_1},m_i+k)} s_{(e_{i_1i_2},m_i+m_{i_1}+k)} \\ & \ \ \cdot \left( \sum_{i_3=i_2}^n s_{(e_{i_2i_3},m_i+m_{i_1}+m_{i_2}+k)}s_{(e_{i_2i_3},m_i+m_{i_1}+m_{i_2}+k)}^* \right) s_{(e_{i_1i_2},m_i+m_{i_1}+k)}^* s_{(e_{ii_1},m_i+k)}^* \\ & \ \ + \sum_{\alpha\in A_1\cup A_2} s_{\alpha}s_{\alpha}^*. \end{aligned} \end{align*} $$
Proceeding inductively, let
![]() $A_s$
contain the set of all paths
$A_s$
contain the set of all paths
 $$ \begin{align} \begin{aligned} &(e_{ii_1},m_i+k)(e_{i_1i_2},m_i+m_{i_1}+k)(e_{i_2i_3},m_i+m_{i_1}+m_{i_2}+k) \\ &\cdots\ (e_{i_{s-1}i_s},m_i+m_{i_1}+m_{i_2}+\cdots +m_{i_{s-1}}+k), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &(e_{ii_1},m_i+k)(e_{i_1i_2},m_i+m_{i_1}+k)(e_{i_2i_3},m_i+m_{i_1}+m_{i_2}+k) \\ &\cdots\ (e_{i_{s-1}i_s},m_i+m_{i_1}+m_{i_2}+\cdots +m_{i_{s-1}}+k), \end{aligned} \end{align} $$
which are contained in A. Let
![]() $I_s$
contain all
$I_s$
contain all
![]() $(i_1,i_2,\ldots ,i_s)$
for which the path in (3.6) is contained in
$(i_1,i_2,\ldots ,i_s)$
for which the path in (3.6) is contained in
![]() $A_s$
. Note that
$A_s$
. Note that
![]() $A_s$
consists of admissible paths of length s.
$A_s$
consists of admissible paths of length s.
Continuing as above, we will at some point obtain that all the paths are admissible; hence, the procedure terminates. This happens since we do not have any edges from a higher level to a lower one in the finite graph
![]() $L_{2n+1}\times _c{\mathbb {Z}}_r$
. Hence, there exists an
$L_{2n+1}\times _c{\mathbb {Z}}_r$
. Hence, there exists an
![]() $m\in \mathbb {N}$
such that
$m\in \mathbb {N}$
such that
![]() $(i_1,i_2,\ldots ,i_m)$
are all contained in
$(i_1,i_2,\ldots ,i_m)$
are all contained in
![]() $I_m$
. Then
$I_m$
. Then
Furthermore, since we in each step consider all the outgoing edges of a vertex, we construct indeed all admissible paths by this procedure. Hence,
![]() $A=A_1\cup A_2\cup \cdots \cup A_m$
, and we obtain (3.4).
$A=A_1\cup A_2\cup \cdots \cup A_m$
, and we obtain (3.4).
For surjectivity, we observe that
which follows by the fact that
 $$ \begin{align*}\left(\sum_{\substack{(v_i,k) \\ i=0,\ldots ,n, \ k\in S_i}} P_{(v_i,k)}\right)s_{\mu}s_{\nu}^*\left(\sum_{\substack{(v_i,k) \\ i=0,\ldots ,n, \ k\in S_i}} P_{(v_i,k)}\right) \end{align*} $$
$$ \begin{align*}\left(\sum_{\substack{(v_i,k) \\ i=0,\ldots ,n, \ k\in S_i}} P_{(v_i,k)}\right)s_{\mu}s_{\nu}^*\left(\sum_{\substack{(v_i,k) \\ i=0,\ldots ,n, \ k\in S_i}} P_{(v_i,k)}\right) \end{align*} $$
is nonzero if and only if
![]() $s(\mu ),s(\nu )\in \{(v_i,k), i=0,\ldots ,n, k\in S_i\}$
.
$s(\mu ),s(\nu )\in \{(v_i,k), i=0,\ldots ,n, k\in S_i\}$
.
Let
![]() $\mu $
and
$\mu $
and
![]() $\nu $
be paths such that
$\nu $
be paths such that
![]() $s_{\mu }s_{\nu }^*\in C_{r,\underline {m}}$
and for which the ranges of
$s_{\mu }s_{\nu }^*\in C_{r,\underline {m}}$
and for which the ranges of
![]() $\mu $
and
$\mu $
and
![]() $\nu $
are in
$\nu $
are in
![]() $\{(v_i,k), i=0,\ldots ,n, k\in S_i\}$
. Then we see immediately that
$\{(v_i,k), i=0,\ldots ,n, k\in S_i\}$
. Then we see immediately that
![]() $\mu =\mu _1\cdots \mu _s$
and
$\mu =\mu _1\cdots \mu _s$
and
![]() $\nu =\nu _1\cdots \nu _t$
for some admissible paths
$\nu =\nu _1\cdots \nu _t$
for some admissible paths
![]() $\mu _j,\nu _j$
, i.e.,
$\mu _j,\nu _j$
, i.e.,
![]() $\mu _i,\nu _i$
corresponds to edges in
$\mu _i,\nu _i$
corresponds to edges in
![]() $C^*(\overline {L}_{2n+1}^{r;\underline {m}})$
. Then
$C^*(\overline {L}_{2n+1}^{r;\underline {m}})$
. Then
Hence,
![]() $s_{\mu }s_{\nu }^*$
is in the image of
$s_{\mu }s_{\nu }^*$
is in the image of
![]() $\psi $
.
$\psi $
.
Let now
![]() $\mu $
and
$\mu $
and
![]() $\nu $
be paths with range not in
$\nu $
be paths with range not in
![]() $\{(v_i,k), i=0,\ldots ,n, k\in S_i\}$
such that
$\{(v_i,k), i=0,\ldots ,n, k\in S_i\}$
such that
![]() $s_{\mu }s_{\nu }^*\in C_{r,\underline {m}}$
. By using that
$s_{\mu }s_{\nu }^*\in C_{r,\underline {m}}$
. By using that
 $$ \begin{align*}s_{\mu}s_{\nu}^*=s_{\mu}\left(\sum_{\substack{e\in (L_{2n+1}\times_c{\mathbb{Z}}_r)^1 \\ s(e)=r(\mu)}} s_es_e^* \right)s_{\nu}^* \end{align*} $$
$$ \begin{align*}s_{\mu}s_{\nu}^*=s_{\mu}\left(\sum_{\substack{e\in (L_{2n+1}\times_c{\mathbb{Z}}_r)^1 \\ s(e)=r(\mu)}} s_es_e^* \right)s_{\nu}^* \end{align*} $$
a number of times, as in the proof of condition (CK3), we obtain that
 $$ \begin{align*}s_{\mu}s_{\nu}^*=\sum_{i=1}^m s_{\mu\alpha_i}s_{\nu\alpha_i}^*, \end{align*} $$
$$ \begin{align*}s_{\mu}s_{\nu}^*=\sum_{i=1}^m s_{\mu\alpha_i}s_{\nu\alpha_i}^*, \end{align*} $$
where
![]() $\alpha _i, i=1,\ldots ,m,$
are paths from
$\alpha _i, i=1,\ldots ,m,$
are paths from
![]() $r(\mu )$
to a vertex in
$r(\mu )$
to a vertex in
![]() $\{(v_i,k), i=0,\ldots ,n, k\in S_i\}$
. Then, for
$\{(v_i,k), i=0,\ldots ,n, k\in S_i\}$
. Then, for
![]() $i=1,\ldots ,m$
,
$i=1,\ldots ,m$
,
![]() $\mu \alpha _i$
and
$\mu \alpha _i$
and
![]() $\nu \alpha _i$
represent a path in
$\nu \alpha _i$
represent a path in
![]() $C^*(\overline {L}_{2n+1}^{r;\underline {m}})$
and
$C^*(\overline {L}_{2n+1}^{r;\underline {m}})$
and
![]() $s_{\mu }s_{\nu }^*$
is then in the image of
$s_{\mu }s_{\nu }^*$
is then in the image of
![]() $\psi $
.
$\psi $
.
Finally, to prove that
![]() $\psi $
is injective, we apply the generalized Cuntz–Krieger uniqueness theorem presented in [Reference Szymański27, Theorem 1.2]. We have that
$\psi $
is injective, we apply the generalized Cuntz–Krieger uniqueness theorem presented in [Reference Szymański27, Theorem 1.2]. We have that
![]() $\psi (p_{v_i^k})$
is nonzero for all
$\psi (p_{v_i^k})$
is nonzero for all
![]() $i=0,\ldots ,n,k\in S_i$
. By [Reference Szymański27, Theorem 1.2], we obtain that
$i=0,\ldots ,n,k\in S_i$
. By [Reference Szymański27, Theorem 1.2], we obtain that
![]() $\psi $
is injective if the spectrum of
$\psi $
is injective if the spectrum of
for each
![]() $k\in S_n$
contains the entire unit circle. By the last part of the proof of Theorem 2.4 in [Reference Kumjian, Pask and Raeburn22], it follows that this is indeed the case. Hence,
$k\in S_n$
contains the entire unit circle. By the last part of the proof of Theorem 2.4 in [Reference Kumjian, Pask and Raeburn22], it follows that this is indeed the case. Hence,
![]() $\psi $
is injective.
$\psi $
is injective.
Lemma 3.7 For each
![]() $v_i^k, i=0,\ldots ,n, k\in S_i$
, there is a path from
$v_i^k, i=0,\ldots ,n, k\in S_i$
, there is a path from
![]() $v_0^0$
to
$v_0^0$
to
![]() $v_i^k$
in
$v_i^k$
in
![]() $\overline {L}_{2n+1}^{r;\underline {m}}$
.
$\overline {L}_{2n+1}^{r;\underline {m}}$
.
Proof Let
![]() $v_i^k, i=0,\ldots ,n, k\in S_i$
, then
$v_i^k, i=0,\ldots ,n, k\in S_i$
, then
![]() $(v_i,k)\in H_{r;\underline {m}}$
by definition. Hence, there exists a path
$(v_i,k)\in H_{r;\underline {m}}$
by definition. Hence, there exists a path
![]() $\alpha $
from
$\alpha $
from
![]() $(v_j,0)$
for at least one
$(v_j,0)$
for at least one
![]() $j=0,\ldots ,n$
to
$j=0,\ldots ,n$
to
![]() $(v_i,k)$
. If the path is not admissible, we divide it into admissible subpaths. Furthermore, there is always an admissible path from
$(v_i,k)$
. If the path is not admissible, we divide it into admissible subpaths. Furthermore, there is always an admissible path from
![]() $(v_{\ell -1},0)$
to
$(v_{\ell -1},0)$
to
![]() $(v_{\ell },0)$
for any
$(v_{\ell },0)$
for any
![]() $\ell =0,\ldots ,n$
as follows:
$\ell =0,\ldots ,n$
as follows:
 $$ \begin{align*} (e_{(\ell-1)(\ell-1)},m_{l-1})(e_{(\ell-1)(\ell-1)},2m_{\ell-1})\cdots \left(e_{(\ell-1)(\ell-1)},\left(\frac{r}{\gcd(m_{\ell-1},r)}-1\right)m_{\ell-1}\right)(e_{(\ell-1)l},0). \end{align*} $$
$$ \begin{align*} (e_{(\ell-1)(\ell-1)},m_{l-1})(e_{(\ell-1)(\ell-1)},2m_{\ell-1})\cdots \left(e_{(\ell-1)(\ell-1)},\left(\frac{r}{\gcd(m_{\ell-1},r)}-1\right)m_{\ell-1}\right)(e_{(\ell-1)l},0). \end{align*} $$
Combining these paths, we obtain a path from
![]() $(v_0,0)$
to a
$(v_0,0)$
to a
![]() $(v_j,0)$
with
$(v_j,0)$
with
![]() $j=0,\ldots ,n$
, call the path
$j=0,\ldots ,n$
, call the path
![]() $\beta $
. Then we obtain a path
$\beta $
. Then we obtain a path
![]() $\beta \alpha $
from
$\beta \alpha $
from
![]() $(v_0,0)$
to
$(v_0,0)$
to
![]() $(v_i,k)$
which consists of admissible subpaths. Hence, there is indeed a path from
$(v_i,k)$
which consists of admissible subpaths. Hence, there is indeed a path from
![]() $v_0^0$
to
$v_0^0$
to
![]() $v_i^k$
.
$v_i^k$
.
Lemma 3.8 The projection
![]() $\sum _{i=0}^{n}p_{v_i^0}$
is full in
$\sum _{i=0}^{n}p_{v_i^0}$
is full in
![]() $C^*(\overline {L}_{2n+1}^{r;\underline {m}})$
.
$C^*(\overline {L}_{2n+1}^{r;\underline {m}})$
.
Proof Let I be the ideal generated by
![]() $\sum _{i=0}^{n}p_{v_i^0}$
. Note that we clearly have
$\sum _{i=0}^{n}p_{v_i^0}$
. Note that we clearly have
![]() $p_{v_i^0}\in I$
, for
$p_{v_i^0}\in I$
, for
![]() $i=0,\ldots ,n$
. We wish to show that for any
$i=0,\ldots ,n$
. We wish to show that for any
![]() $v_i^k, i=0,\ldots ,n, k\in S_i$
, we have
$v_i^k, i=0,\ldots ,n, k\in S_i$
, we have
![]() $p_{v_i^k}\in I$
, since then
$p_{v_i^k}\in I$
, since then
![]() $I=C^*(\overline {L}_{2n+1}^{r;\underline {m}})$
and
$I=C^*(\overline {L}_{2n+1}^{r;\underline {m}})$
and
![]() $\sum _{i=0}^{n}p_{v_i^0}$
is full.
$\sum _{i=0}^{n}p_{v_i^0}$
is full.
Let
![]() $\alpha =f_1f_2\cdots f_m$
with
$\alpha =f_1f_2\cdots f_m$
with
![]() $f_j\in (\overline {L}_{2n+1}^{r;\underline {m}})^1$
, for
$f_j\in (\overline {L}_{2n+1}^{r;\underline {m}})^1$
, for
![]() $j=1,\ldots ,m$
, be a path from
$j=1,\ldots ,m$
, be a path from
![]() $v_0^0$
to a
$v_0^0$
to a
![]() $v_i^k$
with
$v_i^k$
with
![]() $i\in \{0,\ldots ,n\}, k\in S_i$
which we know exists by Lemma 3.7. By the Cuntz–Krieger relations, we have
$i\in \{0,\ldots ,n\}, k\in S_i$
which we know exists by Lemma 3.7. By the Cuntz–Krieger relations, we have
Then
![]() $s_{f_1}s_{f_1}^*=s_{f_1}s_{f_1}^*p_{v_0^0}\in I$
and we obtain
$s_{f_1}s_{f_1}^*=s_{f_1}s_{f_1}^*p_{v_0^0}\in I$
and we obtain
![]() $s_{f_1}^*\in I$
, which implies that
$s_{f_1}^*\in I$
, which implies that
![]() $p_{r(f_1)}\in I$
. We can apply the same argument as above to show
$p_{r(f_1)}\in I$
. We can apply the same argument as above to show
![]() $p_{r(f_2)}\in I$
if we replace
$p_{r(f_2)}\in I$
if we replace
![]() $p_{v_0^0}$
with
$p_{v_0^0}$
with
![]() $p_{r(f_1)}$
and
$p_{r(f_1)}$
and
![]() $p_{r(f_1)}$
with
$p_{r(f_1)}$
with
![]() $p_{r(f_2)}$
. By continuing this argument, we obtain that
$p_{r(f_2)}$
. By continuing this argument, we obtain that
![]() $p_{v_i^k}=p_{r(f_m)}\in I$
.
$p_{v_i^k}=p_{r(f_m)}\in I$
.
Lemma 3.9 Let
![]() $E=(E^0,E^1,r,s)$
be a directed graph. For each
$E=(E^0,E^1,r,s)$
be a directed graph. For each
![]() $v\in E^0$
, choose an
$v\in E^0$
, choose an
![]() $a_v\geq 1$
. Define F (Figure 2
) to be the graph such that for each
$a_v\geq 1$
. Define F (Figure 2
) to be the graph such that for each
![]() $v\in E^0$
we add a head of
$v\in E^0$
we add a head of
![]() $a_v-1$
vertices to v.
$a_v-1$
vertices to v.

Figure 2: Illustration of the graph F.
Define another graph G (Figure 3 ) as follows:
The range and source maps extend from E to G for the edges in
![]() $E^1$
and
$E^1$
and

Figure 3: Illustration of the graph G.
Then, as
![]() $C^*$
-algebras,
$C^*$
-algebras,
![]() $C^*(F)\cong C^*(G)$
.
$C^*(F)\cong C^*(G)$
.
Proof Consider first the graph F, and we apply the
![]() $R^+$
-move, presented in [Reference Eilers and Ruiz15, Definition 3.9], on the regular vertices
$R^+$
-move, presented in [Reference Eilers and Ruiz15, Definition 3.9], on the regular vertices
![]() $v_i$
,
$v_i$
,
![]() $i=2,\ldots ,a_v$
, one by one for each
$i=2,\ldots ,a_v$
, one by one for each
![]() $v\in F$
. We then obtain a graph
$v\in F$
. We then obtain a graph
![]() $\overline {F}$
(Figure 4) defined as follows:
$\overline {F}$
(Figure 4) defined as follows:
where
![]() $s(\tilde {e}^v_i)=\tilde {v}_i$
and
$s(\tilde {e}^v_i)=\tilde {v}_i$
and
![]() $r(\tilde {e}^v_i)=v$
.
$r(\tilde {e}^v_i)=v$
.

Figure 4: Illustration of the graph
![]() $\overline {F}$
.
$\overline {F}$
.
By [Reference Eilers and Ruiz15, Theorem 3.10],
![]() $C^*(F)\cong C^*(\overline {F})$
.
$C^*(F)\cong C^*(\overline {F})$
.
For the graph G, we perform an out-split [Reference Bates and Pask4] (see also [Reference Eilers and Ruiz15, Definition 3.1]) of the vertex
![]() $\overline {w}$
by partition
$\overline {w}$
by partition
![]() $s^{-1}(\overline {w})$
into singleton sets. Then the out-split graph
$s^{-1}(\overline {w})$
into singleton sets. Then the out-split graph
![]() $G_O$
is precisely the graph
$G_O$
is precisely the graph
![]() $\overline {F}$
. By [Reference Bates and Pask4, Theorem 3.2],
$\overline {F}$
. By [Reference Bates and Pask4, Theorem 3.2],
![]() $C^*(G)\cong C^*(G_O)$
, and hence
$C^*(G)\cong C^*(G_O)$
, and hence
![]() $C^*(G)\cong C^*(F)$
.
$C^*(G)\cong C^*(F)$
.
We are now ready to prove Theorem 3.4.
Proof of Theorem 3.4
By Lemma 3.6 and (3.1), we obtain
 $$ \begin{align*} \begin{aligned} &C(L_q^{2n+1}(r;\underline{m})) \cong \left(\sum_{i=0}^n p_{(v_i,0)}\right)C^*(L_{2n+1}\times_{ c}\mathbb{Z}_r)\left(\sum_{i=0}^n p_{(v_i,0)}\right) \\ &= \left(\sum_{i=0}^n p_{(v_i,0)}\right)\left(\sum_{\substack{(v_i,k) \\ i=0,\ldots ,n, \ k\in S_i}} p_{(v_i,k)}\right)C^*(L_{2n+1}\times_{ c}\mathbb{Z}_r)\left(\sum_{\substack{(v_i,k) \\ i=0,\ldots ,n, \ k\in S_i}} P_{(v_i,k)}\right)\left(\sum_{i=0}^n p_{(v_i,0)}\right) \\ &\cong \left(\sum_{i=0}^{n}p_{v_i^0}\right)C^*(\overline{L}_{2n+1}^{r;\underline{m}})\left(\sum_{i=0}^{n}p_{v_i^0}\right). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &C(L_q^{2n+1}(r;\underline{m})) \cong \left(\sum_{i=0}^n p_{(v_i,0)}\right)C^*(L_{2n+1}\times_{ c}\mathbb{Z}_r)\left(\sum_{i=0}^n p_{(v_i,0)}\right) \\ &= \left(\sum_{i=0}^n p_{(v_i,0)}\right)\left(\sum_{\substack{(v_i,k) \\ i=0,\ldots ,n, \ k\in S_i}} p_{(v_i,k)}\right)C^*(L_{2n+1}\times_{ c}\mathbb{Z}_r)\left(\sum_{\substack{(v_i,k) \\ i=0,\ldots ,n, \ k\in S_i}} P_{(v_i,k)}\right)\left(\sum_{i=0}^n p_{(v_i,0)}\right) \\ &\cong \left(\sum_{i=0}^{n}p_{v_i^0}\right)C^*(\overline{L}_{2n+1}^{r;\underline{m}})\left(\sum_{i=0}^{n}p_{v_i^0}\right). \end{aligned} \end{align*} $$
Hence, it suffices to prove that
 $$ \begin{align} \left(\sum_{i=0}^{n}p_{v_i^0}\right)C^*(\overline{L}_{2n+1}^{r;\underline{m}})\left(\sum_{i=0}^{n}p_{v_i^0}\right) \cong C^*(\overline{L}_{2n+1}^{r;\underline{m}}). \end{align} $$
$$ \begin{align} \left(\sum_{i=0}^{n}p_{v_i^0}\right)C^*(\overline{L}_{2n+1}^{r;\underline{m}})\left(\sum_{i=0}^{n}p_{v_i^0}\right) \cong C^*(\overline{L}_{2n+1}^{r;\underline{m}}). \end{align} $$
We will follow the procedure in the proof of [Reference Arklint and Ruiz3, Theorem 4.8(1)] to construct a graph for which the corner in (3.7) is isomorphic to its graph
![]() $C^*$
-algebra. For proofs of the statement used in the construction, we refer to [Reference Arklint and Ruiz3, Theorem 4.8(1)].
$C^*$
-algebra. For proofs of the statement used in the construction, we refer to [Reference Arklint and Ruiz3, Theorem 4.8(1)].
For simplicity, we let
![]() $E:=\overline {L}_{2n+1}^{r;\underline {m}}$
and
$E:=\overline {L}_{2n+1}^{r;\underline {m}}$
and
![]() $P:=\sum _{i=0}^{n}p_{v_i^0}$
. Let
$P:=\sum _{i=0}^{n}p_{v_i^0}$
. Let
![]() $SE$
be the graph for which an infinite head has been added to each vertex.
$SE$
be the graph for which an infinite head has been added to each vertex.
![]() $SE$
is called the stabilization of E (Figure 5).
$SE$
is called the stabilization of E (Figure 5).

Figure 5: The stabilization when
![]() $E=\overline {L}_{3}^{4;(2,1)}$
.
$E=\overline {L}_{3}^{4;(2,1)}$
.
There exists an isomorphism
![]() $\phi : C^*\left (E\right )\otimes \mathcal {K}\to C^*(SE)$
such that
$\phi : C^*\left (E\right )\otimes \mathcal {K}\to C^*(SE)$
such that
for all
![]() $w\in E^0$
, where
$w\in E^0$
, where
![]() $\{e_{ij}\}$
is a set of matrix units in
$\{e_{ij}\}$
is a set of matrix units in
![]() $\mathcal {K}$
[Reference Abrams and Tomforde1, Proposition 9.8]. Then
$\mathcal {K}$
[Reference Abrams and Tomforde1, Proposition 9.8]. Then
Since P is full by Lemma 3.8, it follows by the proof of Proposition 4.7 in [Reference Arklint and Ruiz3] that there exists a finite hereditary subset T of
![]() $(SE)^0$
, which contains
$(SE)^0$
, which contains
![]() $E^0$
, such that
$E^0$
, such that
![]() $\phi (P\otimes e_{11})$
is Murray–von Neumann equivalent to
$\phi (P\otimes e_{11})$
is Murray–von Neumann equivalent to
We obtain T as follows: By an application of [Reference Arklint and Ruiz3, Lemma 4.3], there exist integers
![]() $a_v\geq 1$
such that
$a_v\geq 1$
such that
which follows since there is a path from
![]() $v_0^0$
to any
$v_0^0$
to any
![]() $v_i^k$
by Lemma 3.7. For a vertex
$v_i^k$
by Lemma 3.7. For a vertex
![]() $v\in E^0$
, we denote the first
$v\in E^0$
, we denote the first
![]() $a_{v}-1$
vertices in the infinite head added to v as follows:
$a_{v}-1$
vertices in the infinite head added to v as follows:

Let
![]() $v_1=v$
and denote by
$v_1=v$
and denote by
![]() $e_k$
the edge from
$e_k$
the edge from
![]() $v_k$
to
$v_k$
to
![]() $v_{k-1}$
for
$v_{k-1}$
for
![]() $k=2,\ldots ,a_v$
. By the Cuntz–Krieger relations, it follows that
$k=2,\ldots ,a_v$
. By the Cuntz–Krieger relations, it follows that
for
![]() $k=2,\ldots ,a_v$
. Hence,
$k=2,\ldots ,a_v$
. Hence,
![]() $[p_{v_k}]=[p_{v_{k-1}}]$
for
$[p_{v_k}]=[p_{v_{k-1}}]$
for
![]() $k=2,\ldots ,a_v$
from which it follows that
$k=2,\ldots ,a_v$
from which it follows that
![]() $[p_{v_{j}}]=[p_v]$
for
$[p_{v_{j}}]=[p_v]$
for
![]() $j=2,\ldots ,a_v$
and
$j=2,\ldots ,a_v$
and
 $$ \begin{align*}a_v[p_v]= [p_v]+\sum_{i=2}^{a_v} [p_{v_i}]. \end{align*} $$
$$ \begin{align*}a_v[p_v]= [p_v]+\sum_{i=2}^{a_v} [p_{v_i}]. \end{align*} $$
Let
then we obtain
 $$ \begin{align*} [\phi(P\otimes e_{11})]=[P]=\sum_{v\in E^0} a_v[p_v]= \sum_{v\in E^0}\left([p_v]+\sum_{i=2}^{a_v}[p_{v_i}]\right)=[P_T]. \end{align*} $$
$$ \begin{align*} [\phi(P\otimes e_{11})]=[P]=\sum_{v\in E^0} a_v[p_v]= \sum_{v\in E^0}\left([p_v]+\sum_{i=2}^{a_v}[p_{v_i}]\right)=[P_T]. \end{align*} $$
Then
By [Reference Arklint and Ruiz3, Theorem 3.15]
![]() $, P_TC^*(SE)P_T\cong C^*(F)$
, where
$, P_TC^*(SE)P_T\cong C^*(F)$
, where
![]() $F=(T,s_{SE}^{-1}(T),r_{SE},s_{SE})$
. The graph F consists then of the graph E where for each
$F=(T,s_{SE}^{-1}(T),r_{SE},s_{SE})$
. The graph F consists then of the graph E where for each
![]() $v\in E^0$
there is added a head consisting of
$v\in E^0$
there is added a head consisting of
![]() $a_v-1$
vertices (see Figure 2). We obtain by Lemma 3.9 that
$a_v-1$
vertices (see Figure 2). We obtain by Lemma 3.9 that
![]() $C^*(F)$
is isomorphic to
$C^*(F)$
is isomorphic to
![]() $C^*(G)$
. Hence, it remains to show that
$C^*(G)$
. Hence, it remains to show that
![]() $C^*(G)\cong C^*(E)= C^*(\overline {L}_{2n+1}^{r;\underline {m}})$
.
$C^*(G)\cong C^*(E)= C^*(\overline {L}_{2n+1}^{r;\underline {m}})$
.
For this, we apply [Reference Eilers, Restorff, Ruiz and Sørensen14, Theorem 14.6] on the graphs E and G. First, note that
![]() $E=\widetilde {E}=\widetilde {G}$
,
$E=\widetilde {E}=\widetilde {G}$
,
![]() $\underline {x}_E$
is the zero vector of size
$\underline {x}_E$
is the zero vector of size
![]() $|E^0|$
and
$|E^0|$
and
![]() $\underline {x}_G$
is a vector of size
$\underline {x}_G$
is a vector of size
![]() $|E_0|$
, which indicates the number of edges from
$|E_0|$
, which indicates the number of edges from
![]() $\overline {w}$
to each vertex in
$\overline {w}$
to each vertex in
![]() $E^0$
. Note that the first entry is
$E^0$
. Note that the first entry is
![]() $0$
since there are no edges from
$0$
since there are no edges from
![]() $\overline {w}$
to
$\overline {w}$
to
![]() $v_0^0$
.
$v_0^0$
.
The components of
![]() ${E}$
consist of singleton sets. They are all cyclic since every vertex is the base of precisely one loop. Recall that the graph
${E}$
consist of singleton sets. They are all cyclic since every vertex is the base of precisely one loop. Recall that the graph
![]() $E=\overline {L}_{2n+1}^{r;\underline {m}}$
consists of
$E=\overline {L}_{2n+1}^{r;\underline {m}}$
consists of
![]() $n+1$
levels for which we in level k have
$n+1$
levels for which we in level k have
![]() $|S_k|$
vertices. We denote the vertices in
$|S_k|$
vertices. We denote the vertices in
![]() $E^0$
as indicated in Figure 6.
$E^0$
as indicated in Figure 6.

Figure 6: Renaming of the vertices in
![]() $ \overline {L}_{2n+1}^{r; \underline {m}}$
.
$ \overline {L}_{2n+1}^{r; \underline {m}}$
.
A partial order on the set
![]() $\mathcal {P}=\{1,2,\ldots ,N\}$
with
$\mathcal {P}=\{1,2,\ldots ,N\}$
with
![]() $N:=\sum _{i=0}^{n} |S_i|$
is defined as follows: For
$N:=\sum _{i=0}^{n} |S_i|$
is defined as follows: For
![]() $i,j\in \mathcal {P}$
, we let
$i,j\in \mathcal {P}$
, we let
![]() $i\preceq j$
if there is a path from
$i\preceq j$
if there is a path from
![]() $v_i$
to
$v_i$
to
![]() $v_j$
. Let
$v_j$
. Let
![]() $\gamma _i:=\{v_i\}\in \Gamma _E$
, then the map
$\gamma _i:=\{v_i\}\in \Gamma _E$
, then the map
![]() $i\mapsto \gamma _i$
is clearly an order-reversing isomorphism from
$i\mapsto \gamma _i$
is clearly an order-reversing isomorphism from
![]() $\mathcal {P}$
to
$\mathcal {P}$
to
![]() $\Gamma _E$
. Furthermore, if
$\Gamma _E$
. Furthermore, if
![]() $i \preceq j$
, then
$i \preceq j$
, then
![]() $i\leq j$
, which is required. Then
$i\leq j$
, which is required. Then
![]() $B_{E}=B_{\widetilde {E}}=B_{\widetilde {G}}$
are contained in
$B_{E}=B_{\widetilde {E}}=B_{\widetilde {G}}$
are contained in
![]() $\mathfrak {M}^{\circ \circ \circ }_{\mathcal {P}}(\boldsymbol {1},{\mathbb {Z}})$
(see Definition in [Reference Eilers, Restorff, Ruiz and Sørensen13, p. 321]) and
$\mathfrak {M}^{\circ \circ \circ }_{\mathcal {P}}(\boldsymbol {1},{\mathbb {Z}})$
(see Definition in [Reference Eilers, Restorff, Ruiz and Sørensen13, p. 321]) and
 $$ \begin{align*}V_{c_2,\ldots ,c_{|E_0|}}=\begin{pmatrix} 1 & c_2 & \cdots & c_{|E^0|} \\ 0 & & & \\ \vdots & & I & \\ 0 & & & \end{pmatrix} \end{align*} $$
$$ \begin{align*}V_{c_2,\ldots ,c_{|E_0|}}=\begin{pmatrix} 1 & c_2 & \cdots & c_{|E^0|} \\ 0 & & & \\ \vdots & & I & \\ 0 & & & \end{pmatrix} \end{align*} $$
lies inside
![]() ${\text {SL}}_{\mathcal {P}}(\boldsymbol {1},{\mathbb {Z}})$
for any
${\text {SL}}_{\mathcal {P}}(\boldsymbol {1},{\mathbb {Z}})$
for any
![]() $c_j\in \mathbb {Z}$
since there is a path from
$c_j\in \mathbb {Z}$
since there is a path from
![]() $v_0^0$
to every other vertex by Lemma 3.7. Moreover, we have
$v_0^0$
to every other vertex by Lemma 3.7. Moreover, we have
![]() $B_{\widetilde {E}}V_{c_2,\ldots ,c_{|E_0|}}=B_{\widetilde {G}}$
and
$B_{\widetilde {E}}V_{c_2,\ldots ,c_{|E_0|}}=B_{\widetilde {G}}$
and
![]() $\underline {x}_G=\begin {pmatrix} 0 & k_2 & \cdots & k_{|E^0|} \end {pmatrix}^T $
with
$\underline {x}_G=\begin {pmatrix} 0 & k_2 & \cdots & k_{|E^0|} \end {pmatrix}^T $
with
![]() $k_i=a_{v_i}-1$
. Then
$k_i=a_{v_i}-1$
. Then
 $$ \begin{align*}V_{k_2,\ldots ,k_{|E_0|}}^T(\underline{1}+\underline{x}_E)=\begin{pmatrix} 1 \\ k_2+1 \\ \vdots \\ k_{|E_0|}+1 \end{pmatrix} =\underline{1}+\underline{x}_G. \end{align*} $$
$$ \begin{align*}V_{k_2,\ldots ,k_{|E_0|}}^T(\underline{1}+\underline{x}_E)=\begin{pmatrix} 1 \\ k_2+1 \\ \vdots \\ k_{|E_0|}+1 \end{pmatrix} =\underline{1}+\underline{x}_G. \end{align*} $$
Hence,
![]() $V_{k_2,\ldots ,k_{|E_0|}}^T(\underline {1}+\underline {x}_E)-(\underline {1}+\underline {x}_G)=\underline {0}$
, which is clearly in the image of
$V_{k_2,\ldots ,k_{|E_0|}}^T(\underline {1}+\underline {x}_E)-(\underline {1}+\underline {x}_G)=\underline {0}$
, which is clearly in the image of
![]() $B_{\widetilde {F}}^T$
. Then, by letting
$B_{\widetilde {F}}^T$
. Then, by letting
![]() $U=P=I$
in [Reference Eilers, Restorff, Ruiz and Sørensen14, Theorem 14.6], we obtain
$U=P=I$
in [Reference Eilers, Restorff, Ruiz and Sørensen14, Theorem 14.6], we obtain
![]() $C^*(G)\cong C^*(E)$
.
$C^*(G)\cong C^*(E)$
.
To summarize, we have shown
 $$ \begin{align*}\begin{aligned} C^*(L_{2n+1}^{r;\underline{m}})&\cong C^*(G)\cong C^*(F)\cong P_TC^*(SE)P_T \\ &\cong \phi(P\otimes e_{11})C^*(SE)\phi(P\otimes e_{11}) \\ &\cong PC^*(L_{2n+1}^{r;\underline{m}})P \cong C(L_q^{2n+1}(r;\underline{m})), \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} C^*(L_{2n+1}^{r;\underline{m}})&\cong C^*(G)\cong C^*(F)\cong P_TC^*(SE)P_T \\ &\cong \phi(P\otimes e_{11})C^*(SE)\phi(P\otimes e_{11}) \\ &\cong PC^*(L_{2n+1}^{r;\underline{m}})P \cong C(L_q^{2n+1}(r;\underline{m})), \end{aligned} \end{align*} $$
which proves the theorem.
4 A classification result of quantum lens spaces
We will in this section investigate quantum lens spaces
![]() $C(L_q^7(r,\underline {m}))$
for which
$C(L_q^7(r,\underline {m}))$
for which
![]() $\gcd (m_{\ell },r)=K$
for a single
$\gcd (m_{\ell },r)=K$
for a single
![]() $\ell \in \lbrace 0,1,2,3 \rbrace $
and the remaining weights are coprime to r. In the process of finding an invariant for seven-dimensional quantum lens spaces, we will also be able to calculate one for quantum lens spaces of dimension 5. We will in the following therefore have our focus on seven-dimensional quantum lens spaces.
$\ell \in \lbrace 0,1,2,3 \rbrace $
and the remaining weights are coprime to r. In the process of finding an invariant for seven-dimensional quantum lens spaces, we will also be able to calculate one for quantum lens spaces of dimension 5. We will in the following therefore have our focus on seven-dimensional quantum lens spaces.
Under the above assumptions on the weights, the skew product graph
![]() $L_{7}\times _{c}\mathbb Z_r$
consists of four levels, labeled by levels 0,1,2, and 3, with edges going from level i to j if
$L_{7}\times _{c}\mathbb Z_r$
consists of four levels, labeled by levels 0,1,2, and 3, with edges going from level i to j if
![]() $i<j$
. At the level on which
$i<j$
. At the level on which
![]() $\gcd (m_{\ell },r)=K$
, we have K cycles based on each of the vertices
$\gcd (m_{\ell },r)=K$
, we have K cycles based on each of the vertices
![]() $(v_{\ell },k), k=0,1,\ldots ,K-1$
. The graph
$(v_{\ell },k), k=0,1,\ldots ,K-1$
. The graph
![]() $\overline {L}_7^{r;\underline {m}}$
consists of four levels as before with four vertices when
$\overline {L}_7^{r;\underline {m}}$
consists of four levels as before with four vertices when
![]() $\gcd (m_0,r)=K$
and
$\gcd (m_0,r)=K$
and
![]() $K+3$
vertices when
$K+3$
vertices when
![]() $\gcd (m_i,r)=K, i\neq 0$
, which are all the base of a loop. There is one vertex in each level except for level i where
$\gcd (m_i,r)=K, i\neq 0$
, which are all the base of a loop. There is one vertex in each level except for level i where
![]() $\gcd (m_i,r)=K\neq 1, i\neq 0$
; here, we have K vertices. When
$\gcd (m_i,r)=K\neq 1, i\neq 0$
; here, we have K vertices. When
![]() $i=0$
, we have one vertex in each level. There is at least one edge going from a lower level to a higher one, but there are no edges between vertices at the same level. We will denote the vertices by
$i=0$
, we have one vertex in each level. There is at least one edge going from a lower level to a higher one, but there are no edges between vertices at the same level. We will denote the vertices by
![]() $v_i, i=1,\ldots ,K+3$
as indicated in Figure 6.
$v_i, i=1,\ldots ,K+3$
as indicated in Figure 6.
The partial order on
![]() $\Gamma _{\overline {L}_7^{r;\underline {m}}}$
is given as follows: Let
$\Gamma _{\overline {L}_7^{r;\underline {m}}}$
is given as follows: Let
![]() $\gamma _i:=\{v_i\}$
, then
$\gamma _i:=\{v_i\}$
, then
![]() $\gamma _j\leq \gamma _i$
if there is a path from
$\gamma _j\leq \gamma _i$
if there is a path from
![]() $v_i$
to
$v_i$
to
![]() $v_j$
. The set
$v_j$
. The set
![]() $\Gamma _{\overline {L}_7^{r;\underline {m}}}$
can be illustrated by its component graphs, which are depicted in Figure 7. In these graphs, an arrow from
$\Gamma _{\overline {L}_7^{r;\underline {m}}}$
can be illustrated by its component graphs, which are depicted in Figure 7. In these graphs, an arrow from
![]() $\gamma _i$
to
$\gamma _i$
to
![]() $\gamma _j$
indicates that
$\gamma _j$
indicates that
![]() $\gamma _i\geq \gamma _j$
.
$\gamma _i\geq \gamma _j$
.

Figure 7: Component graphs of seven-dimensional quantum lens spaces.
For
![]() $\gcd (m_0,r)=K$
, we let
$\gcd (m_0,r)=K$
, we let
![]() $\mathcal {P}=\{1,2,3,4\}$
and the partial ordering is linear. When
$\mathcal {P}=\{1,2,3,4\}$
and the partial ordering is linear. When
![]() $\gcd (m_i,r)=K, i\neq 0$
, we let
$\gcd (m_i,r)=K, i\neq 0$
, we let
![]() $\mathcal {P}=\{1,2,\ldots ,K+3\}$
and let
$\mathcal {P}=\{1,2,\ldots ,K+3\}$
and let
![]() $\ell $
be such that
$\ell $
be such that
![]() $\gcd (m_{\ell -1},r)=K$
. We define a partial order,
$\gcd (m_{\ell -1},r)=K$
. We define a partial order,
![]() $\preceq $
, on
$\preceq $
, on
![]() $\mathcal {P}$
by:
$\mathcal {P}$
by:
-
•
 $\ell -1\succeq \cdots \succeq 1$
,
$\ell -1\succeq \cdots \succeq 1$
, -
•
 $i\succeq \ell -1$
for
$i\succeq \ell -1$
for
 $i=\ell ,\ldots ,K+\ell -1$
,
$i=\ell ,\ldots ,K+\ell -1$
, -
•
 $K+\ell \succeq i$
for
$K+\ell \succeq i$
for
 $i=\ell ,\ldots ,K+\ell -1$
,
$i=\ell ,\ldots ,K+\ell -1$
, -
•
 $K+3 \succeq \cdots \succeq K+\ell $
.
$K+3 \succeq \cdots \succeq K+\ell $
.
The partial order satisfies that if
![]() $i\preceq j$
, then
$i\preceq j$
, then
![]() $i\leq j$
, which is the required assumption [Reference Eilers, Restorff, Ruiz and Sørensen13, Assumption 4.3]. It can easily be seen that there exists an order-reversing isomorphism
$i\leq j$
, which is the required assumption [Reference Eilers, Restorff, Ruiz and Sørensen13, Assumption 4.3]. It can easily be seen that there exists an order-reversing isomorphism
![]() $\gamma _{B_{\overline {L}_7^{r;\underline {m}}}}:\mathcal {P}\to \Gamma _{\overline {L}_7^{r;\underline {m}}}$
mapping i to
$\gamma _{B_{\overline {L}_7^{r;\underline {m}}}}:\mathcal {P}\to \Gamma _{\overline {L}_7^{r;\underline {m}}}$
mapping i to
![]() $\gamma _i$
.
$\gamma _i$
.
Let
![]() $\gcd (m_i,r)=K$
for one i. It follows immediately that
$\gcd (m_i,r)=K$
for one i. It follows immediately that
![]() $|\text {Prime}_{\gamma }(C^*(\overline {L}_7^{r;\underline {m}}))|=K+3$
when
$|\text {Prime}_{\gamma }(C^*(\overline {L}_7^{r;\underline {m}}))|=K+3$
when
![]() $i\neq 0$
and
$i\neq 0$
and
![]() $|\text {Prime}_{\gamma }(C^*(\overline {L}_7^{r;\underline {m}}))|=4$
if
$|\text {Prime}_{\gamma }(C^*(\overline {L}_7^{r;\underline {m}}))|=4$
if
![]() $i=0$
. By this result, we obtain nonisomorphic quantum lens spaces for different values of K when
$i=0$
. By this result, we obtain nonisomorphic quantum lens spaces for different values of K when
![]() $i\neq 0$
. Moreover, by Remark 6.9, it follows that K must also be the same in order to obtain isomorphic quantum lens spaces when
$i\neq 0$
. Moreover, by Remark 6.9, it follows that K must also be the same in order to obtain isomorphic quantum lens spaces when
![]() $i=0$
even though this is not immediately clear by considering the ideal structure.
$i=0$
even though this is not immediately clear by considering the ideal structure.
Fix a
![]() $K>1$
, and by considering the ideal structure, we obtain four different isomorphism classes of quantum lens spaces, one for each
$K>1$
, and by considering the ideal structure, we obtain four different isomorphism classes of quantum lens spaces, one for each
![]() $i=0,1,2,3$
for which
$i=0,1,2,3$
for which
![]() $\gcd (m_i,r)=K$
. We will in this section determine when two quantum lens spaces inside each of these four classes are isomorphic. Similarly, we have three different classes of quantum lens spaces of dimension
$\gcd (m_i,r)=K$
. We will in this section determine when two quantum lens spaces inside each of these four classes are isomorphic. Similarly, we have three different classes of quantum lens spaces of dimension
![]() $5$
to investigate.
$5$
to investigate.
To determine whether two quantum lens spaces in the same class are isomorphic, we will make use of [Reference Eilers, Restorff, Ruiz and Sørensen13, Theorem 7.1]. For the quantum lens spaces we are investigating, the block structure consists of
![]() $1\times 1$
-matrices and
$1\times 1$
-matrices and
![]() $(B_{\overline {L}_7^{r;\underline {m}}},B_{\overline {L}_7^{r;\underline {n}}})$
is in standard form for two quantum lens spaces in the same class when we order the vertices in the adjacency matrix as described above. Since
$(B_{\overline {L}_7^{r;\underline {m}}},B_{\overline {L}_7^{r;\underline {n}}})$
is in standard form for two quantum lens spaces in the same class when we order the vertices in the adjacency matrix as described above. Since
![]() $\overline {L}_{2n+1}^{r;\underline {m}}$
contains no sinks, Theorem 2.1 boils down to the following result.
$\overline {L}_{2n+1}^{r;\underline {m}}$
contains no sinks, Theorem 2.1 boils down to the following result.
Corollary 4.1 Let
![]() $\underline {m}=(m_0,m_1,m_2,m_3)$
and
$\underline {m}=(m_0,m_1,m_2,m_3)$
and
![]() $\underline {n}=(n_0,n_1,n_2,n_3)$
be in
$\underline {n}=(n_0,n_1,n_2,n_3)$
be in
![]() $\mathbb {N}^4$
. If
$\mathbb {N}^4$
. If
![]() $\gcd (m_i,r)=\gcd (n_i,r)$
, for each
$\gcd (m_i,r)=\gcd (n_i,r)$
, for each
![]() $i=0,1,2,3$
, then
$i=0,1,2,3$
, then
![]() $C^*(\overline {L}_7^{r;\underline {m}})$
and
$C^*(\overline {L}_7^{r;\underline {m}})$
and
![]() $C^*(\overline {L}_7^{r;\underline {n}})$
are isomorphic if and only if there exist matrices
$C^*(\overline {L}_7^{r;\underline {n}})$
are isomorphic if and only if there exist matrices
![]() $U,V\in SL_{\mathcal {P}}(\mathbf {1},{\mathbb {Z}})$
such that
$U,V\in SL_{\mathcal {P}}(\mathbf {1},{\mathbb {Z}})$
such that
![]() $UB_{\overline {L}_7^{r;\underline {m}}}V=B_{\overline {L}_7^{r;\underline {n}}}$
.
$UB_{\overline {L}_7^{r;\underline {m}}}V=B_{\overline {L}_7^{r;\underline {n}}}$
.
We remark that the natural generalization of Corollary 4.1 to quantum lens spaces of other dimensions is true if one defines the partial order in the obvious way. In particular, for dimension
![]() $5$
, we have a similar result by letting
$5$
, we have a similar result by letting
![]() $\mathcal {P}=\{1,2,\ldots ,K+2\}$
and defining the order in a similar way as the one for dimension
$\mathcal {P}=\{1,2,\ldots ,K+2\}$
and defining the order in a similar way as the one for dimension
![]() $7$
.
$7$
.
Eilers, Restorff, Ruiz, and Sørensen used Corollary 4.1, with
![]() $\mathcal {P}=\{1,2,3,4\}$
ordered linearly to completely classify the simplest case.
$\mathcal {P}=\{1,2,3,4\}$
ordered linearly to completely classify the simplest case.
Theorem 4.2 [Reference Eilers, Restorff, Ruiz and Sørensen13, Theorem 7.8]
Let
![]() $r\in {\mathbb {N}}$
,
$r\in {\mathbb {N}}$
,
![]() $r\geq 2$
, and let
$r\geq 2$
, and let
![]() $\underline {m}=(m_0,m_1,m_2,m_3)$
and
$\underline {m}=(m_0,m_1,m_2,m_3)$
and
![]() $\underline {n}=(n_0,n_1,n_2,n_3)$
be in
$\underline {n}=(n_0,n_1,n_2,n_3)$
be in
![]() ${\mathbb {N}}^4$
such that
${\mathbb {N}}^4$
such that
![]() $\gcd (m_i,r)=\gcd (n_i,r)=1$
for all i. Then
$\gcd (m_i,r)=\gcd (n_i,r)=1$
for all i. Then
![]() $C^*\left (\overline {L}_7^{(r,\underline {m})}\right )\cong C^*\left (\overline {L}_7^{(r,\underline {n})}\right )$
if and only if
$C^*\left (\overline {L}_7^{(r,\underline {m})}\right )\cong C^*\left (\overline {L}_7^{(r,\underline {n})}\right )$
if and only if
From the above, they concluded the following corollary.
Corollary 4.3 [Reference Eilers, Restorff, Ruiz and Sørensen13, Corollary 7.9]
If
![]() $3$
does not divide r, then
$3$
does not divide r, then
for all
![]() $\underline {m}\in {\mathbb {N}}^4$
with
$\underline {m}\in {\mathbb {N}}^4$
with
![]() $\gcd (m_i,r)=1$
.
$\gcd (m_i,r)=1$
.
If
![]() $3$
divides r and
$3$
divides r and
![]() $\underline {m}=(m_0,m_1,m_2,m_3)\in {\mathbb {N}}^4$
with
$\underline {m}=(m_0,m_1,m_2,m_3)\in {\mathbb {N}}^4$
with
![]() $\gcd (m_i,r)=1$
, then
$\gcd (m_i,r)=1$
, then
-
(i)
 $C^*\left (\overline {L}_7^{(r,\underline {m})}\right )\cong C^*\left ((\overline {L}_7^{(r,(1,1,1,1))}\right )$
if and only if
$C^*\left (\overline {L}_7^{(r,\underline {m})}\right )\cong C^*\left ((\overline {L}_7^{(r,(1,1,1,1))}\right )$
if and only if
 $m_1\equiv m_2 \ (\mathrm {mod}\ 3)$
,
$m_1\equiv m_2 \ (\mathrm {mod}\ 3)$
, -
(ii)
 $C^*\left (\overline {L}_7^{(r,\underline {m})}\right )\cong C^*\left (\overline {L}_7^{(r,(1,1,r-1,1))}\right )$
if and only if
$C^*\left (\overline {L}_7^{(r,\underline {m})}\right )\cong C^*\left (\overline {L}_7^{(r,(1,1,r-1,1))}\right )$
if and only if
 $m_1\not \equiv m_2 \ (\mathrm {mod}\ 3)$
.
$m_1\not \equiv m_2 \ (\mathrm {mod}\ 3)$
.
For dimension less than
![]() $7$
, Eilers, Restorff, Ruiz, and Sørensen observed that the adjacency matrices are independent of the weights; hence, all quantum lens spaces are isomorphic. We will see that this is not always the case when one of the weights is not coprime with r.
$7$
, Eilers, Restorff, Ruiz, and Sørensen observed that the adjacency matrices are independent of the weights; hence, all quantum lens spaces are isomorphic. We will see that this is not always the case when one of the weights is not coprime with r.
5 Classification of
 $C\left ( \overline {L}_{2n+1}(r; \underline {m})\right ), n\leq 3$
$C\left ( \overline {L}_{2n+1}(r; \underline {m})\right ), n\leq 3$
In this section, we fix the value of the order of the acting group, r, even though, as we will show later in Remark 6.9, r is in fact an invariant in most of the cases considered. Also, note that for the remainder of this paper, we will use the notation
![]() $\mathbb {Z}^{\times }_k$
to denote the subgroup of multiplicative units of the ring
$\mathbb {Z}^{\times }_k$
to denote the subgroup of multiplicative units of the ring
![]() $\mathbb {Z}_k$
, and we will use
$\mathbb {Z}_k$
, and we will use
![]() $\phi $
to denote Euler’s totient function, that is,
$\phi $
to denote Euler’s totient function, that is,
![]() .
.
Quantum lens spaces of dimension
![]() $3$
, with one and only one weight coprime with r, will be the same for any choice of weights. See Remark 6.4. For dimension
$3$
, with one and only one weight coprime with r, will be the same for any choice of weights. See Remark 6.4. For dimension
![]() $5$
. we obtain the following theorem.
$5$
. we obtain the following theorem.
Theorem 5.1 Let
![]() $r\in {\mathbb {N}}$
,
$r\in {\mathbb {N}}$
,
![]() $r\geq 2$
, and let
$r\geq 2$
, and let
![]() $\underline {m}=(m_0,m_1,m_2)$
and
$\underline {m}=(m_0,m_1,m_2)$
and
![]() $\underline {n}=(n_0,n_1,n_2)$
be in
$\underline {n}=(n_0,n_1,n_2)$
be in
![]() $\mathbb {N}^3$
such that
$\mathbb {N}^3$
such that
![]() $\gcd (m_{\ell },r)=\gcd (n_{\ell },r)=K$
for one
$\gcd (m_{\ell },r)=\gcd (n_{\ell },r)=K$
for one
![]() $0\leq \ell \leq 2 $
, and
$0\leq \ell \leq 2 $
, and
![]() $\gcd (m_i,r)=\gcd (n_i,r)=1$
whenever
$\gcd (m_i,r)=\gcd (n_i,r)=1$
whenever
![]() $i\neq \ell $
. Then:
$i\neq \ell $
. Then:
-
(i)
 $C^*\left (\overline {L}_5^{(r,\underline {m})}\right )\cong C^*\left (\overline {L}_5^{(r,\underline {n})}\right )$
if
$C^*\left (\overline {L}_5^{(r,\underline {m})}\right )\cong C^*\left (\overline {L}_5^{(r,\underline {n})}\right )$
if
 $\ell \in \lbrace 0,1\rbrace $
and
$\ell \in \lbrace 0,1\rbrace $
and -
(ii)
 $C^*\left (\overline {L}_5^{(r,\underline {m})}\right )\cong C^*\left (\overline {L}_5^{(r,\underline {n})}\right )$
if and only if
$C^*\left (\overline {L}_5^{(r,\underline {m})}\right )\cong C^*\left (\overline {L}_5^{(r,\underline {n})}\right )$
if and only if
 $m_1\equiv n_1 \ (\mathrm {mod}\ K)$
if
$m_1\equiv n_1 \ (\mathrm {mod}\ K)$
if
 $\ell =2$
.
$\ell =2$
.
The proof of Theorem 5.1 follows by a similar, but much easier, approach as the corresponding results in the seven-dimensional case, which is presented in Theorem 5.3. Therefore, we will not present the proof in the present paper.
Corollary 5.2 Let
![]() $\gcd (m_2,r)=K$
and
$\gcd (m_2,r)=K$
and
![]() $\gcd (m_i,r)=1$
for
$\gcd (m_i,r)=1$
for
![]() $i=0,1$
, then
$i=0,1$
, then
where
![]() $m_1\equiv k_1 \ (\mathrm {mod}\ K)$
with
$m_1\equiv k_1 \ (\mathrm {mod}\ K)$
with
![]() $k_1\in \mathbb {Z}^{\times }_r$
, and there are exactly
$k_1\in \mathbb {Z}^{\times }_r$
, and there are exactly
![]() $\phi (K)$
isomorphism classes of quantum lens spaces.
$\phi (K)$
isomorphism classes of quantum lens spaces.
We will now state our main theorem for quantum lens spaces of dimension
![]() $7$
, which is an extension of Theorem 4.2.
$7$
, which is an extension of Theorem 4.2.
Theorem 5.3 Let
![]() $r\in {\mathbb {N}}$
,
$r\in {\mathbb {N}}$
,
![]() $r\geq 2$
, and let
$r\geq 2$
, and let
![]() $\underline {m}=(m_0,m_1,m_2,m_3)$
and
$\underline {m}=(m_0,m_1,m_2,m_3)$
and
![]() $\underline {n}=(n_0,n_1,n_2,n_3)$
be in
$\underline {n}=(n_0,n_1,n_2,n_3)$
be in
![]() $\mathbb {N}^4$
such that
$\mathbb {N}^4$
such that
![]() $\gcd (m_{\ell },r)=\gcd (n_{\ell },r)=K$
for one
$\gcd (m_{\ell },r)=\gcd (n_{\ell },r)=K$
for one
![]() $0\leq \ell \leq 3 $
, and
$0\leq \ell \leq 3 $
, and
![]() $\gcd (m_i,r)=\gcd (n_i,r)=1$
whenever
$\gcd (m_i,r)=\gcd (n_i,r)=1$
whenever
![]() $i\neq \ell $
. Then
$i\neq \ell $
. Then
![]() $C^*\left (\overline {L}_7^{(r,\underline {m})}\right )$
is isomorphic to
$C^*\left (\overline {L}_7^{(r,\underline {m})}\right )$
is isomorphic to
![]() $C^*\left (\overline {L}_7^{(r,\underline {n})}\right )$
if and only if:
$C^*\left (\overline {L}_7^{(r,\underline {n})}\right )$
if and only if:
-
(0)
 $\left (m_2^{-1}m_1-n_2^{-1}n_1 \right ) \frac {r(r-1)(r-2)}{3} \equiv 0 \ \pmod {r}$
if
$\left (m_2^{-1}m_1-n_2^{-1}n_1 \right ) \frac {r(r-1)(r-2)}{3} \equiv 0 \ \pmod {r}$
if
 $\ell =0$
and
$\ell =0$
and
 $3\nmid K$
. If
$3\nmid K$
. If
 $3\mid K$
, then they are always isomorphic.
$3\mid K$
, then they are always isomorphic. -
(1)
 $\left (n_2^{-1}n_1-m_2^{-1}m_1 \right )\frac {r(r-1)(r-2)}{3}\equiv 0\ (\mathrm {mod}\ r)$
and
$\left (n_2^{-1}n_1-m_2^{-1}m_1 \right )\frac {r(r-1)(r-2)}{3}\equiv 0\ (\mathrm {mod}\ r)$
and
 $m_2\equiv n_2 \ \ \pmod {K}$
if
$m_2\equiv n_2 \ \ \pmod {K}$
if
 $\ell =1$
,
$\ell =1$
, -
(2)
 $\left (n_1^{-1}n_2-m_1^{-1}m_2 \right )\frac {r(r-1)(r-2)}{3}\equiv 0\ (\mathrm {mod}\ r)$
and
$\left (n_1^{-1}n_2-m_1^{-1}m_2 \right )\frac {r(r-1)(r-2)}{3}\equiv 0\ (\mathrm {mod}\ r)$
and
 $m_1\equiv n_1 \ \ \pmod {K}$
if
$m_1\equiv n_1 \ \ \pmod {K}$
if
 $\ell =2$
,
$\ell =2$
, -
(3)
 $\left (n_2^{-1}n_1-m_2^{-1}m_1 \right )\frac {r(r-1)(r-2)}{3}\equiv 0\ (\mathrm {mod}\ r)$
and
$\left (n_2^{-1}n_1-m_2^{-1}m_1 \right )\frac {r(r-1)(r-2)}{3}\equiv 0\ (\mathrm {mod}\ r)$
and
 $m_j\equiv n_j \ \ \pmod {K}, j=1,2$
if
$m_j\equiv n_j \ \ \pmod {K}, j=1,2$
if
 $\ell =3$
.
$\ell =3$
.
The proof is postponed to Section 7. From Theorem 5.3, we may derive the following results. They are in particular interesting for computational purposes, and it gives a precise determination of how many different spaces we obtain of each type. It also shows that the first case is somewhat degenerate.
Corollary 5.4 Let
![]() $r\in {\mathbb {N}}$
,
$r\in {\mathbb {N}}$
,
![]() $\underline {m}=(m_0,m_1,m_2,m_3)\in {\mathbb {N}}^4$
, and
$\underline {m}=(m_0,m_1,m_2,m_3)\in {\mathbb {N}}^4$
, and
![]() $\gcd (m_i,r)=K$
for precisely one i and
$\gcd (m_i,r)=K$
for precisely one i and
![]() $\gcd (m_j,r)=1$
when
$\gcd (m_j,r)=1$
when
![]() $j\neq i$
. Furthermore, let
$j\neq i$
. Furthermore, let
![]() $k_1,k_2\in {\mathbb {N}}$
be such that
$k_1,k_2\in {\mathbb {N}}$
be such that
![]() $0<k_1,k_2<K$
and
$0<k_1,k_2<K$
and
![]() $\gcd (k_1,K)=\gcd (k_2,K)=1$
.
$\gcd (k_1,K)=\gcd (k_2,K)=1$
.
If
![]() $3\mid K$
or
$3\mid K$
or
![]() $3\nmid r$
, then
$3\nmid r$
, then
![]() $C(L_q(r;\underline {m}))$
is isomorphic to a quantum lens space with precisely one of the following sets of weights:
$C(L_q(r;\underline {m}))$
is isomorphic to a quantum lens space with precisely one of the following sets of weights:
If
![]() $3\nmid K$
, then
$3\nmid K$
, then
![]() $C(L_q(r;\underline {m}))$
is isomorphic to a quantum lens space with one of the following set of weights:
$C(L_q(r;\underline {m}))$
is isomorphic to a quantum lens space with one of the following set of weights:
if
![]() $m_1\equiv m_2 \ \ \pmod {3}$
and
$m_1\equiv m_2 \ \ \pmod {3}$
and
if
![]() $m_1\not \equiv m_2 \ \ \pmod {3}$
.
$m_1\not \equiv m_2 \ \ \pmod {3}$
.
Proof First, note that in the case where
![]() $\gcd (m_0,r)=K$
and
$\gcd (m_0,r)=K$
and
![]() $3\nmid r$
, the invariant coincides with the analogous invariant in [Reference Eilers, Restorff, Ruiz and Sørensen13, Corollary 7.9], and we may make the same conclusion.
$3\nmid r$
, the invariant coincides with the analogous invariant in [Reference Eilers, Restorff, Ruiz and Sørensen13, Corollary 7.9], and we may make the same conclusion.
We now address the proof in the case where
![]() $\gcd (m_3,r)=K$
since the remaining follow by a similar approach. If
$\gcd (m_3,r)=K$
since the remaining follow by a similar approach. If
![]() $3$
does not divide r, we notice that we by Theorem 5.3 only need to consider the condition
$3$
does not divide r, we notice that we by Theorem 5.3 only need to consider the condition
![]() $m_i\equiv n_i \ (\mathrm {mod}\ K)$
. It is clear that if
$m_i\equiv n_i \ (\mathrm {mod}\ K)$
. It is clear that if
![]() $\gcd (m_i,r)= 1$
, then also
$\gcd (m_i,r)= 1$
, then also
![]() $\gcd (m_i,K)=1$
. Thus, it suffices to show that if
$\gcd (m_i,K)=1$
. Thus, it suffices to show that if
![]() $[k]_K\in \mathbb {Z}^{\times }_K$
, then
$[k]_K\in \mathbb {Z}^{\times }_K$
, then
![]() $[k]_K$
contains an element,
$[k]_K$
contains an element,
![]() $k'$
, such that
$k'$
, such that
![]() $\gcd (k',r)=1$
, since then each isomorphism class may be determined by a pair of units in
$\gcd (k',r)=1$
, since then each isomorphism class may be determined by a pair of units in
![]() $\mathbb {Z}_K$
. Indeed, let
$\mathbb {Z}_K$
. Indeed, let
![]() $[k]_K\in \mathbb {Z}_K^{\times }$
be arbitrary. We set p to be the product of
$[k]_K\in \mathbb {Z}_K^{\times }$
be arbitrary. We set p to be the product of
![]() $1$
and all prime factors of r which are factors of neither k nor K. Now, set
$1$
and all prime factors of r which are factors of neither k nor K. Now, set
![]() and assume that
and assume that
![]() $\gcd (k',r)\neq 1$
. Then there exists a common prime factor q of r and
$\gcd (k',r)\neq 1$
. Then there exists a common prime factor q of r and
![]() $k'$
. Since q divides
$k'$
. Since q divides
![]() $k'$
but only divides exactly one of
$k'$
but only divides exactly one of
![]() $Kp$
and k by construction, we have a contradiction, and
$Kp$
and k by construction, we have a contradiction, and
![]() $\gcd (k',r)=1$
as desired.
$\gcd (k',r)=1$
as desired.
If
![]() $3$
divides r, then we also need to consider the first part of the invariant. We observe the congruence
$3$
divides r, then we also need to consider the first part of the invariant. We observe the congruence
If
![]() $m_i\equiv \ell _i \ \ \pmod {K}$
for
$m_i\equiv \ell _i \ \ \pmod {K}$
for
![]() $i=1,2$
with
$i=1,2$
with
![]() $0<\ell _i<K$
and
$0<\ell _i<K$
and
![]() $\gcd (\ell _i,K)=1$
, then
$\gcd (\ell _i,K)=1$
, then
![]() $3$
must divide
$3$
must divide
![]() $\ell _2^{-1}\ell _1-m_2^{-1}m_1$
to get isomorphic quantum lens spaces. Also, notice that it follows by a computation that
$\ell _2^{-1}\ell _1-m_2^{-1}m_1$
to get isomorphic quantum lens spaces. Also, notice that it follows by a computation that
![]() $m_1\equiv m_2 \ (\mathrm {mod}\ 3)$
if and only if
$m_1\equiv m_2 \ (\mathrm {mod}\ 3)$
if and only if
![]() $\ell _1\equiv \ell _2 \ (\mathrm {mod}\ 3)$
. Hence,
$\ell _1\equiv \ell _2 \ (\mathrm {mod}\ 3)$
. Hence,
![]() $C(L_q(r;\underline {m}))$
is isomorphic to
$C(L_q(r;\underline {m}))$
is isomorphic to
![]() $C(L_q(r;(1,\ell _1,\ell _2,K)))$
where
$C(L_q(r;(1,\ell _1,\ell _2,K)))$
where
![]() $m_1\equiv m_2 \ (\mathrm {mod}\ 3)$
if and only if
$m_1\equiv m_2 \ (\mathrm {mod}\ 3)$
if and only if
![]() $\ell _1\equiv \ell _2 \ (\mathrm {mod}\ 3)$
.
$\ell _1\equiv \ell _2 \ (\mathrm {mod}\ 3)$
.
Let
![]() $\ell _1\not \equiv \ell _2 \ (\mathrm {mod}\ 3)$
, and we claim that there exist
$\ell _1\not \equiv \ell _2 \ (\mathrm {mod}\ 3)$
, and we claim that there exist
![]() $k_1,k_2$
with
$k_1,k_2$
with
![]() $0<k_i<K$
and
$0<k_i<K$
and
![]() $\gcd (k_i,K)=1$
for
$\gcd (k_i,K)=1$
for
![]() $i=1,2$
such that
$i=1,2$
such that
Let
![]() $k_1:=\ell _1$
. Assume first that
$k_1:=\ell _1$
. Assume first that
![]() $k_1\in [1]_3$
, then
$k_1\in [1]_3$
, then
![]() $\ell _2\in [2]_3$
. Let
$\ell _2\in [2]_3$
. Let
![]() $k_2=1$
, then
$k_2=1$
, then
and clearly
![]() $k_2\equiv k_1 \ (\mathrm {mod}\ 3)$
. If
$k_2\equiv k_1 \ (\mathrm {mod}\ 3)$
. If
![]() $k_1\in [2]_3$
, then
$k_1\in [2]_3$
, then
![]() $\ell _2\in [1]_3$
, and since
$\ell _2\in [1]_3$
, and since
![]() $3|r$
, we can by the first part of the proof (by letting
$3|r$
, we can by the first part of the proof (by letting
![]() $K=3$
) find
$K=3$
) find
![]() $k_2\in [2]_3$
such that
$k_2\in [2]_3$
such that
![]() $\gcd (k_2,r)=1$
and hence
$\gcd (k_2,r)=1$
and hence
![]() $\gcd (k_2,K)=1$
. Then
$\gcd (k_2,K)=1$
. Then
and we have proved the claim. Hence,
![]() $C(L_q(r;(1,\ell _1,\ell _2,K)))$
is isomorphic to
$C(L_q(r;(1,\ell _1,\ell _2,K)))$
is isomorphic to
![]() $C(L_q(r;(1,k_1,k_2(r-1),K)))$
for
$C(L_q(r;(1,k_1,k_2(r-1),K)))$
for
![]() $k_1,k_2$
such that
$k_1,k_2$
such that
![]() $0<k_i<K$
,
$0<k_i<K$
,
![]() $\gcd (k_i,K)=1$
and
$\gcd (k_i,K)=1$
and
![]() $k_1\equiv k_2 \ (\mathrm {mod}\ 3)$
.
$k_1\equiv k_2 \ (\mathrm {mod}\ 3)$
.
We will end the proof by showing that there is no overlap between the classes, i.e., we have to show that
when
![]() $0<k_i<K$
and
$0<k_i<K$
and
![]() $\gcd (k_i,K)=1$
for i=1,2. Assume that
$\gcd (k_i,K)=1$
for i=1,2. Assume that
![]() $k_2\equiv k_1 \ (\mathrm {mod}\ 3)$
, then
$k_2\equiv k_1 \ (\mathrm {mod}\ 3)$
, then
![]() $k_2(r-1)\equiv -k_1 \ (\mathrm {mod}\ 3)$
, but
$k_2(r-1)\equiv -k_1 \ (\mathrm {mod}\ 3)$
, but
![]() $k_1\not \equiv -k_1 \ (\mathrm {mod}\ 3)$
since
$k_1\not \equiv -k_1 \ (\mathrm {mod}\ 3)$
since
![]() $3\nmid k_1$
. The converse follows from a similar line of reasoning.
$3\nmid k_1$
. The converse follows from a similar line of reasoning.
From Corollary 5.4, it follows immediately that we can count the number of isomorphism classes as given in Table 1.
Table 1: The number of isomorphism classes.

6 Adjacency matrices
For each
![]() $i=0,\ldots ,n$
, let
$i=0,\ldots ,n$
, let
![]() $(L_{2n+1}\times _{c}{\mathbb {Z}}_r)\left < i\right>$
be the subgraph of
$(L_{2n+1}\times _{c}{\mathbb {Z}}_r)\left < i\right>$
be the subgraph of
![]() $L_{2n+1}\times _{c}{\mathbb {Z}}_r$
with vertex set
$L_{2n+1}\times _{c}{\mathbb {Z}}_r$
with vertex set
![]() $\{v_i\}\times {\mathbb {Z}}_r$
and edges
$\{v_i\}\times {\mathbb {Z}}_r$
and edges
![]() $\{e_{ii}\}\times {\mathbb {Z}}_r$
.
$\{e_{ii}\}\times {\mathbb {Z}}_r$
.
Definition 6.1 [Reference Eilers, Restorff, Ruiz and Sørensen13, Definition 7.4]
We call an admissible path
![]() $(e_{i_1,j_1},h_1)\cdots (e_{i_{\ell },j_{\ell }},h_{\ell })$
in
$(e_{i_1,j_1},h_1)\cdots (e_{i_{\ell },j_{\ell }},h_{\ell })$
in
![]() $L_{2n+1}\times _{c} {\mathbb {Z}}_r \ k$
-step if there exist integers
$L_{2n+1}\times _{c} {\mathbb {Z}}_r \ k$
-step if there exist integers
![]() $0<t_1<t_2<\cdots <t_{k+1}$
such that
$0<t_1<t_2<\cdots <t_{k+1}$
such that
![]() $t_1=i_1$
and
$t_1=i_1$
and
![]() $t_{k+1}=j_{\ell }$
, and for each
$t_{k+1}=j_{\ell }$
, and for each
![]() $2\leq \alpha \leq k$
, we have
$2\leq \alpha \leq k$
, we have
and
 $$ \begin{align*}\{r((e_{i_s,j_s},h_s))| 1\leq s\leq \ell\}\subseteq \bigcup_{i=1}^{k+1} ((L_{2n+1}\times_{c}{\mathbb{Z}}_r)\left< t_i \right>)^0. \end{align*} $$
$$ \begin{align*}\{r((e_{i_s,j_s},h_s))| 1\leq s\leq \ell\}\subseteq \bigcup_{i=1}^{k+1} ((L_{2n+1}\times_{c}{\mathbb{Z}}_r)\left< t_i \right>)^0. \end{align*} $$
Intuitively, an admissible path is k-step if it touches vertices from precisely
![]() $k-1$
different levels not including the level the path starts at and ends in. Below, we give formulae for the number of 1-step, 2-step, and 3-step admissible paths in each relevant case. For paths that only touch levels for which the corresponding weights are coprime to the order of the acting group, we refer to [Reference Eilers, Restorff, Ruiz and Sørensen13, Lemma 7.6], which describes this case to completion.
$k-1$
different levels not including the level the path starts at and ends in. Below, we give formulae for the number of 1-step, 2-step, and 3-step admissible paths in each relevant case. For paths that only touch levels for which the corresponding weights are coprime to the order of the acting group, we refer to [Reference Eilers, Restorff, Ruiz and Sørensen13, Lemma 7.6], which describes this case to completion.
Lemma 6.1 1-step admissible paths
Let
![]() $r\in {\mathbb {N}}$
,
$r\in {\mathbb {N}}$
,
![]() $r\geq 2$
, and let
$r\geq 2$
, and let
![]() $\underline {m}=(m_0,m_1,m_2,m_3)\in {\mathbb {N}}^4$
be such that for a single
$\underline {m}=(m_0,m_1,m_2,m_3)\in {\mathbb {N}}^4$
be such that for a single
![]() $\ell \in \lbrace 0,1,2,3\rbrace $
,
$\ell \in \lbrace 0,1,2,3\rbrace $
,
![]() $\gcd (m_{\ell },r)=K$
and
$\gcd (m_{\ell },r)=K$
and
![]() $\gcd (m_i,r)=1$
for
$\gcd (m_i,r)=1$
for
![]() $i\neq \ell $
. Let
$i\neq \ell $
. Let
![]() $t\in \lbrace 0,\dots , K-1 \rbrace $
, then:
$t\in \lbrace 0,\dots , K-1 \rbrace $
, then:
-
(1) For
 $i<\ell $
, there are
$i<\ell $
, there are
 $\frac {r}{K}$
1-step admissible paths from
$\frac {r}{K}$
1-step admissible paths from
 $(v_i,0)$
to
$(v_i,0)$
to
 $(v_{\ell },t)$
.
$(v_{\ell },t)$
. -
(2) For
 $i>\ell $
, there are
$i>\ell $
, there are
 $\frac {r}{K}$
1-step admissible paths from
$\frac {r}{K}$
1-step admissible paths from
 $(v_{\ell },t)$
to
$(v_{\ell },t)$
to
 $(v_i,0)$
.
$(v_i,0)$
.
Proof This follows since at the
![]() $\ell $
th level we have K loops each going through only one of the
$\ell $
th level we have K loops each going through only one of the
![]() $(v_{\ell },i)$
,
$(v_{\ell },i)$
,
![]() $i=0,1,\ldots ,K-1$
.
$i=0,1,\ldots ,K-1$
.
Notation 6.2 Consider a quantum lens space with set of weights
![]() $\underline {m}=(m_0,m_1,m_2,m_3)$
. We will in the following, if
$\underline {m}=(m_0,m_1,m_2,m_3)$
. We will in the following, if
![]() $\gcd (m_i,r)= 1$
, let
$\gcd (m_i,r)= 1$
, let
![]() $m_i^{-1}$
denote the fixed representative of the equivalence class
$m_i^{-1}$
denote the fixed representative of the equivalence class
![]() $[m_i]_r^{-1}$
in
$[m_i]_r^{-1}$
in
![]() ${\mathbb {Z}}_r^{\times }$
for which
${\mathbb {Z}}_r^{\times }$
for which
![]() $0< m_i^{-1} \leq r-1$
, and if
$0< m_i^{-1} \leq r-1$
, and if
![]() $K|r$
for some
$K|r$
for some
![]() $K\in {\mathbb {Z}}$
, we denote by
$K\in {\mathbb {Z}}$
, we denote by
![]() $a_i$
a fixed representative of
$a_i$
a fixed representative of
![]() $[m_i]^{-1}_K$
in
$[m_i]^{-1}_K$
in
![]() ${\mathbb {Z}}_K^{\times }$
for which
${\mathbb {Z}}_K^{\times }$
for which
![]() $0< a_i\leq K-1$
.
$0< a_i\leq K-1$
.
Lemma 6.3 2-step admissible paths
Let
![]() $r\in {\mathbb {N}}$
,
$r\in {\mathbb {N}}$
,
![]() $r\geq 2$
, and let
$r\geq 2$
, and let
![]() $\underline {m}=(m_0,m_1,m_2,m_3)\in {\mathbb {N}}^4$
be such that for a single
$\underline {m}=(m_0,m_1,m_2,m_3)\in {\mathbb {N}}^4$
be such that for a single
![]() $\ell \in \lbrace 0,1,2,3\rbrace $
,
$\ell \in \lbrace 0,1,2,3\rbrace $
,
![]() $\gcd (m_{\ell },r)=K$
and
$\gcd (m_{\ell },r)=K$
and
![]() $\gcd (m_i,r)=1$
for
$\gcd (m_i,r)=1$
for
![]() $i\neq \ell $
. Let
$i\neq \ell $
. Let
![]() $t\in \lbrace 0,\dots , K-1 \rbrace $
.
$t\in \lbrace 0,\dots , K-1 \rbrace $
.
-
(1) If
 $i<k<\ell -1$
, there are
$i<k<\ell -1$
, there are
 $\frac {r(r-K)}{2K}+\left (a_k\cdot t-1+q_t K\right )\frac {r}{K}$
2-step admissible paths from
$\frac {r(r-K)}{2K}+\left (a_k\cdot t-1+q_t K\right )\frac {r}{K}$
2-step admissible paths from
 $(v_i,0)$
to
$(v_i,0)$
to
 $(v_{\ell },t)$
passing through the kth level if
$(v_{\ell },t)$
passing through the kth level if
 $t\neq 0$
and
$t\neq 0$
and
 $\frac {r(r+K-2)}{2K}$
if
$\frac {r(r+K-2)}{2K}$
if
 $t=0$
.
$t=0$
. -
(2) If
 $i>k>\ell -1$
, there are
$i>k>\ell -1$
, there are
 $\frac {r(r-K)}{2K}-\left (a_k\cdot t-1+q_tK\right )\frac {r}{K}$
2-step admissible paths from
$\frac {r(r-K)}{2K}-\left (a_k\cdot t-1+q_tK\right )\frac {r}{K}$
2-step admissible paths from
 $(v_{\ell },t)$
to
$(v_{\ell },t)$
to
 $(v_i,0)$
passing through the kth level if
$(v_i,0)$
passing through the kth level if
 $t\neq 0$
and
$t\neq 0$
and
 $\frac {r(r-K)}{2K}$
if
$\frac {r(r-K)}{2K}$
if
 $t=0$
.
$t=0$
. -
(3) If
 $i<\ell <j$
, there are
$i<\ell <j$
, there are
 $\frac {r(r-K)}{2K}$
paths from
$\frac {r(r-K)}{2K}$
paths from
 $(v_i,0)$
to
$(v_i,0)$
to
 $(v_j,0)$
passing through the
$(v_j,0)$
passing through the
 $\ell $
th level,
$\ell $
th level,
where
![]() $a_k$
is defined in Notation 6.2 and
$a_k$
is defined in Notation 6.2 and
![]() $q_t\in \mathbb Z$
is such that
$q_t\in \mathbb Z$
is such that
![]() $a_kt-1+q_tK$
is an integer between
$a_kt-1+q_tK$
is an integer between
![]() $0$
and
$0$
and
![]() $K-1$
.
$K-1$
.
Proof
![]() $(1)$
First, note that there is only one path from
$(1)$
First, note that there is only one path from
![]() $(v_i,0)$
to
$(v_i,0)$
to
![]() $(v_k,sm_k)$
for
$(v_k,sm_k)$
for
![]() $s=1,2,\ldots ,r-1$
not coming back to
$s=1,2,\ldots ,r-1$
not coming back to
![]() $(v_i,0)$
and not going through any vertices at the kth level. We have an edge from
$(v_i,0)$
and not going through any vertices at the kth level. We have an edge from
![]() $(v_k,sm_k)$
into the cycle containing
$(v_k,sm_k)$
into the cycle containing
![]() $(v_{\ell },t)$
if and only if
$(v_{\ell },t)$
if and only if
![]() $ m_k(s+1)\equiv t \ (\mathrm {mod}\ K).$
Equivalently,
$ m_k(s+1)\equiv t \ (\mathrm {mod}\ K).$
Equivalently,
![]() $s\equiv a_kt-1 \ (\mathrm {mod}\ K)$
. Let
$s\equiv a_kt-1 \ (\mathrm {mod}\ K)$
. Let
![]() $q_t\in \mathbb Z$
be such that
$q_t\in \mathbb Z$
be such that
![]() $s_t:=a_kt-1+q_tK$
is an integer between
$s_t:=a_kt-1+q_tK$
is an integer between
![]() $0$
and
$0$
and
![]() $K-1$
. Hence,
$K-1$
. Hence,
![]() $(v_k,s_tm_k)$
is the first vertex in level k which has a path ending in the cycle containing
$(v_k,s_tm_k)$
is the first vertex in level k which has a path ending in the cycle containing
![]() $(v_{\ell },t)$
. The number of paths from
$(v_{\ell },t)$
. The number of paths from
![]() $(v_k,sm_k)$
for
$(v_k,sm_k)$
for
![]() $s=1,2,\ldots ,r-1$
to
$s=1,2,\ldots ,r-1$
to
![]() $(v_{\ell },t)$
is then
$(v_{\ell },t)$
is then
 $$ \begin{align*} \begin{aligned} &\frac{r-(s-h)}{K}, \ \text{if} \ s\equiv h=0,\ldots ,s_t \ (\mathrm{mod}\ K), \\ & \frac{r-(s-h)}{K}-1, \ \text{if} \ s\equiv h= s_t+1,\ldots ,K-1\ (\mathrm{mod}\ K). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\frac{r-(s-h)}{K}, \ \text{if} \ s\equiv h=0,\ldots ,s_t \ (\mathrm{mod}\ K), \\ & \frac{r-(s-h)}{K}-1, \ \text{if} \ s\equiv h= s_t+1,\ldots ,K-1\ (\mathrm{mod}\ K). \end{aligned} \end{align*} $$
The number of 2-step admissible paths then becomes
 $$ \begin{align*} \begin{aligned} &\sum_{h=0}^{s_t}\sum_{\substack{s=1, \\ s\equiv h \ (\mathrm{mod}\ K)}}^{r-1} \frac{r-(s-h)}{K} + \sum_{h=s_t+1}^{K-1} \sum_{\substack{s=1, \\ s\equiv h \ (\mathrm{mod}\ K) }}^{r-1} \left(\frac{r-(s-h)}{K}-1\right) \\ & =\sum_{h=0}^{K-1}\sum_{\substack{s=1, \\ s\equiv h \ (\mathrm{mod}\ K)}}^{r-1} \frac{r-(s-h)}{K}- \sum_{h=s_t+1}^{K-1} \sum_{\substack{s=1, \\ s\equiv h \ (\mathrm{mod}\ K) }}^{r-1}1 \\ &= \sum_{j=1}^{\frac{r-K}{K}} n\frac{r-jK}{K} + (K-1)\frac{r}{K} - (K-1-s_t)\frac{r}{K} \\ &= \frac{r(r-K)}{2K} + (a_kt-1+q_tK)\frac{r}{K}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\sum_{h=0}^{s_t}\sum_{\substack{s=1, \\ s\equiv h \ (\mathrm{mod}\ K)}}^{r-1} \frac{r-(s-h)}{K} + \sum_{h=s_t+1}^{K-1} \sum_{\substack{s=1, \\ s\equiv h \ (\mathrm{mod}\ K) }}^{r-1} \left(\frac{r-(s-h)}{K}-1\right) \\ & =\sum_{h=0}^{K-1}\sum_{\substack{s=1, \\ s\equiv h \ (\mathrm{mod}\ K)}}^{r-1} \frac{r-(s-h)}{K}- \sum_{h=s_t+1}^{K-1} \sum_{\substack{s=1, \\ s\equiv h \ (\mathrm{mod}\ K) }}^{r-1}1 \\ &= \sum_{j=1}^{\frac{r-K}{K}} n\frac{r-jK}{K} + (K-1)\frac{r}{K} - (K-1-s_t)\frac{r}{K} \\ &= \frac{r(r-K)}{2K} + (a_kt-1+q_tK)\frac{r}{K}. \end{aligned} \end{align*} $$
If
![]() $t=0$
, then
$t=0$
, then
![]() $q_0=1$
; hence, the number of 2-step admissible paths becomes
$q_0=1$
; hence, the number of 2-step admissible paths becomes
(2) Let
![]() $t>0$
. First, we have precisely one path from
$t>0$
. First, we have precisely one path from
![]() $(v_{\ell },t)$
to
$(v_{\ell },t)$
to
![]() $(v_k,m_kh)$
whose first vertex in the kth level is
$(v_k,m_kh)$
whose first vertex in the kth level is
![]() $(v_k,m_kh)$
if and only if
$(v_k,m_kh)$
if and only if
![]() $m_kh\equiv t \ (\mathrm {mod}\ K)$
for
$m_kh\equiv t \ (\mathrm {mod}\ K)$
for
![]() $h=1,2,\dots ,r-1$
. The number of paths from
$h=1,2,\dots ,r-1$
. The number of paths from
![]() $(v_k,m_kh)$
to
$(v_k,m_kh)$
to
![]() $(v_i,0)$
is
$(v_i,0)$
is
![]() $r-h$
. Hence, the total number of admissible 2-step paths is
$r-h$
. Hence, the total number of admissible 2-step paths is
 $$ \begin{align*} \begin{aligned} \sum_{\substack{h=1, \\ h\equiv a_kt \ (\mathrm{mod}\ K)}}^{r-1} (r-h) &= \sum_{j=0}^{\frac{r-K}{K}} (r-(a_kt+q_tK+jK)) = \frac{r(r+K)}{2K}-(a_kt+q_tK)\frac{r}{K} \\ &= \frac{r(r-K)}{2K}+\frac{r}{K}-(a_kt+q_tK)\frac{r}{K} =\frac{r(r-K)}{2K}-(a_kt-1+q_tK)\frac{r}{K}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \sum_{\substack{h=1, \\ h\equiv a_kt \ (\mathrm{mod}\ K)}}^{r-1} (r-h) &= \sum_{j=0}^{\frac{r-K}{K}} (r-(a_kt+q_tK+jK)) = \frac{r(r+K)}{2K}-(a_kt+q_tK)\frac{r}{K} \\ &= \frac{r(r-K)}{2K}+\frac{r}{K}-(a_kt+q_tK)\frac{r}{K} =\frac{r(r-K)}{2K}-(a_kt-1+q_tK)\frac{r}{K}, \end{aligned} \end{align*} $$
where
![]() $q_t\in \mathbb {Z}$
is such that
$q_t\in \mathbb {Z}$
is such that
![]() $0<a_kt+q_tK<K$
. If
$0<a_kt+q_tK<K$
. If
![]() $t=0$
, then the number of 2-step admissible paths becomes
$t=0$
, then the number of 2-step admissible paths becomes
 $$ \begin{align*} \sum_{j=1}^{\frac{r-K}{K}}(r-jK)=\frac{r(r-K)}{2K}. \end{align*} $$
$$ \begin{align*} \sum_{j=1}^{\frac{r-K}{K}}(r-jK)=\frac{r(r-K)}{2K}. \end{align*} $$
(3) Note that for each
![]() $t\in \lbrace 1,\dots ,K-1\rbrace $
and for each
$t\in \lbrace 1,\dots ,K-1\rbrace $
and for each
![]() $h\in \lbrace 1, \dots , \frac {r}{K}-1 \rbrace $
, there is precisely one edge from
$h\in \lbrace 1, \dots , \frac {r}{K}-1 \rbrace $
, there is precisely one edge from
![]() $(v_i,0)$
to
$(v_i,0)$
to
![]() $(v_{\ell },t+m_{\ell } h)$
, and the number of admissible paths from
$(v_{\ell },t+m_{\ell } h)$
, and the number of admissible paths from
![]() $(v_{\ell },t+m_{\ell } h)$
to
$(v_{\ell },t+m_{\ell } h)$
to
![]() $(v_j,0)$
is
$(v_j,0)$
is
![]() $\frac {r}{K}-h$
. Thus, the number of admissible 2-step paths is
$\frac {r}{K}-h$
. Thus, the number of admissible 2-step paths is
 $$ \begin{align*} \sum_{t=0}^{K-1}\sum_{h=1}^{\frac{r}{K}-1} \frac{r}{K}-h = \frac{r(r-K)}{2K}.\\[-34pt] \end{align*} $$
$$ \begin{align*} \sum_{t=0}^{K-1}\sum_{h=1}^{\frac{r}{K}-1} \frac{r}{K}-h = \frac{r(r-K)}{2K}.\\[-34pt] \end{align*} $$
Remark 6.4 For quantum lens spaces of dimension 3 (that is,
![]() $n=1$
), we see immediately by Lemma 6.3 that the adjacency matrices for a fixed r and K will all be the same. For quantum lens spaces of dimension
$n=1$
), we see immediately by Lemma 6.3 that the adjacency matrices for a fixed r and K will all be the same. For quantum lens spaces of dimension
![]() $5$
, the adjacency matrices are given by the following, which are obtained by adding the number of 1-step and 2-step admissible paths as found in Lemmas 6.1 and 6.3 and [Reference Eilers, Restorff, Ruiz and Sørensen13, Lemma 7.6]:
$5$
, the adjacency matrices are given by the following, which are obtained by adding the number of 1-step and 2-step admissible paths as found in Lemmas 6.1 and 6.3 and [Reference Eilers, Restorff, Ruiz and Sørensen13, Lemma 7.6]:

where
![]() $z_0=\frac {r(r+K)}{2K}$
,
$z_0=\frac {r(r+K)}{2K}$
,
![]() $z_t=\frac {r(r-K)}{2K}+\frac {r}{K}a_1t+q_tr$
for
$z_t=\frac {r(r-K)}{2K}+\frac {r}{K}a_1t+q_tr$
for
![]() $t=1,\dots ,K-1$
, and
$t=1,\dots ,K-1$
, and
![]() $a_1$
is defined in Notation 6.2 .
$a_1$
is defined in Notation 6.2 .
We will now calculate the adjacency matrices for seven-dimensional quantum lens spaces. Since the following pages are rather heavy on similarly looking matrices and formulae, we provide in Table 2 an overview of where the adjacency matrix of each of our four cases may be found in the following pages, both in terms of page numbering and lemma numbering.
Table 2: Reference table for adjacency matrices of seven-dimensional spaces.

Lemma 6.5 Let
![]() $r\in {\mathbb {N}}$
,
$r\in {\mathbb {N}}$
,
![]() $r\geq 2$
, and let
$r\geq 2$
, and let
![]() $\underline {m}=(m_0,m_1,m_2,m_3)$
be such that
$\underline {m}=(m_0,m_1,m_2,m_3)$
be such that
![]() $\gcd (m_3,r)=K$
and
$\gcd (m_3,r)=K$
and
![]() $\gcd (m_i,r)=1,i\neq 3$
. Then we may for each
$\gcd (m_i,r)=1,i\neq 3$
. Then we may for each
![]() $0\leq \ell < r-1$
and each
$0\leq \ell < r-1$
and each
![]() $0\leq t \leq K-1$
find
$0\leq t \leq K-1$
find
![]() $k_{\ell },s_t\in {\mathbb {Z}}$
such that
$k_{\ell },s_t\in {\mathbb {Z}}$
such that

where
and

For
![]() $t\geq 1$
, we have
$t\geq 1$
, we have
and
 $$ \begin{align*}\begin{aligned} x_t&\equiv-m_2^{-1}m_1\frac{r(r-2)(r-1)}{3K} + \sum_{\ell=1}^{r-2} \ell\frac{r(1-k_{\ell})}{K} \\ &+\mathop{\sum_{h=0}^{K-1}\sum_{\ell=1}^{r-2}}_{\ell\equiv m_2a_1h-1\ (\mathrm{mod}\ K)}\frac{\ell h}{K} - \mathop{\sum_{h=s_t+1}^{K-1}\sum_{\ell=1}^{r-2}}_{\ell\equiv m_2a_1h-1\ (\mathrm{mod}\ K)}\ell +\frac{r}{K}\left(a_2t+a_1t-1 \right) \ (\mathrm{mod}\ r), \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} x_t&\equiv-m_2^{-1}m_1\frac{r(r-2)(r-1)}{3K} + \sum_{\ell=1}^{r-2} \ell\frac{r(1-k_{\ell})}{K} \\ &+\mathop{\sum_{h=0}^{K-1}\sum_{\ell=1}^{r-2}}_{\ell\equiv m_2a_1h-1\ (\mathrm{mod}\ K)}\frac{\ell h}{K} - \mathop{\sum_{h=s_t+1}^{K-1}\sum_{\ell=1}^{r-2}}_{\ell\equiv m_2a_1h-1\ (\mathrm{mod}\ K)}\ell +\frac{r}{K}\left(a_2t+a_1t-1 \right) \ (\mathrm{mod}\ r), \end{aligned} \end{align*} $$
where
![]() $a_i$
is defined in Notation 6.2.
$a_i$
is defined in Notation 6.2.
Proof We will now calculate the number of 3-step admissible paths from
![]() $(v_0,0)$
to
$(v_0,0)$
to
![]() $(v_3,t)$
for
$(v_3,t)$
for
![]() $t=0,1,2,3$
. First, notice that there are exactly
$t=0,1,2,3$
. First, notice that there are exactly
![]() $\ell $
paths from
$\ell $
paths from
![]() $(v_0,0)$
to
$(v_0,0)$
to
![]() $(v_1,\ell m_1)$
not coming back to
$(v_1,\ell m_1)$
not coming back to
![]() $(v_0,0)$
, and exactly one edge from
$(v_0,0)$
, and exactly one edge from
![]() $(v_1,\ell m_1)$
to
$(v_1,\ell m_1)$
to
![]() $(v_2,(\ell +1)m_1)$
; hence, we wish to find the number of paths from
$(v_2,(\ell +1)m_1)$
; hence, we wish to find the number of paths from
![]() $(v_2,(\ell +1)m_1)$
to
$(v_2,(\ell +1)m_1)$
to
![]() $(v_3,t)$
, denoted
$(v_3,t)$
, denoted
![]() $P_{\ell }$
. Then the total number of 3-step admissible paths will be
$P_{\ell }$
. Then the total number of 3-step admissible paths will be
![]() $\sum _{\ell =1}^{r-2}\ell P_{\ell }$
.
$\sum _{\ell =1}^{r-2}\ell P_{\ell }$
.
We can express
![]() $(v_2,(\ell +1)m_1)$
as
$(v_2,(\ell +1)m_1)$
as
![]() $(v_2,sm_2)$
, where
$(v_2,sm_2)$
, where
![]() $0<s\leq r$
satisfies
$0<s\leq r$
satisfies
![]() $m_2s\equiv (\ell +1)m_1 \ (\mathrm {mod}\ r)$
. As in the proof of Lemma 6.3(1), we let
$m_2s\equiv (\ell +1)m_1 \ (\mathrm {mod}\ r)$
. As in the proof of Lemma 6.3(1), we let
![]() $s_t$
denote a representative of the class
$s_t$
denote a representative of the class
![]() $[a_2t-1]_K$
which lies between
$[a_2t-1]_K$
which lies between
![]() $0$
and
$0$
and
![]() $K-1$
, and let
$K-1$
, and let
![]() $k_{\ell }$
be an integer such that
$k_{\ell }$
be an integer such that
![]() $0 <m_2^{-1}m_1(\ell +1)+rk_{\ell }<r $
. By reasoning as in Lemma 6.3 (1), we have
$0 <m_2^{-1}m_1(\ell +1)+rk_{\ell }<r $
. By reasoning as in Lemma 6.3 (1), we have
if
![]() $s\equiv h=0,\ldots ,s_t \ (\mathrm {mod}\ K)$
, i.e.,
$s\equiv h=0,\ldots ,s_t \ (\mathrm {mod}\ K)$
, i.e.,
![]() $\ell \equiv m_2a_1h-1 \ (\mathrm {mod}\ K)$
and
$\ell \equiv m_2a_1h-1 \ (\mathrm {mod}\ K)$
and
if
![]() $s\equiv h=s_t+1,\ldots ,K-1 \ (\mathrm {mod}\ K)$
. The number of 3-step admissible paths becomes
$s\equiv h=s_t+1,\ldots ,K-1 \ (\mathrm {mod}\ K)$
. The number of 3-step admissible paths becomes

Adding up the 1-step, 2-step, and 3-step admissible paths, we arrive at the above adjacency matrix; here, we also make use of [Reference Eilers, Restorff, Ruiz and Sørensen13, Lemma 7.6(i) and (ii)].
Lemma 6.6 Let
![]() $r\in {\mathbb {N}}$
,
$r\in {\mathbb {N}}$
,
![]() $r\geq 2$
, and let
$r\geq 2$
, and let
![]() $\underline {m}=(m_0,m_1,m_2,m_3)$
be such that
$\underline {m}=(m_0,m_1,m_2,m_3)$
be such that
![]() $\gcd (m_0,r)=K$
and
$\gcd (m_0,r)=K$
and
![]() $\gcd (m_i,r)=1, i\neq 0$
. Then we may for each
$\gcd (m_i,r)=1, i\neq 0$
. Then we may for each
![]() $0\leq l < r-1$
find
$0\leq l < r-1$
find
![]() $k_{\ell },\in {\mathbb {Z}}$
such that
$k_{\ell },\in {\mathbb {Z}}$
such that

where
and

where
![]() $a_1$
is defined in Notation 6.2.
$a_1$
is defined in Notation 6.2.
Proof Notice that we only need to calculate the number of 3-step admissible paths from
![]() $(v_0,t)$
to
$(v_0,t)$
to
![]() $(v_3,0)$
, where
$(v_3,0)$
, where
![]() $t=0$
, but for the sake of completeness, we will count the remaining paths as well.
$t=0$
, but for the sake of completeness, we will count the remaining paths as well.
For each
![]() $0\leq t \leq K-1$
and
$0\leq t \leq K-1$
and
![]() $1 \leq \ell \leq r-1$
, there is a path from
$1 \leq \ell \leq r-1$
, there is a path from
![]() $(v_0,t)$
to
$(v_0,t)$
to
![]() $(v_1,m_1\ell )$
for which the latter is the first vertex in the first level, which is reached by the path, if and only if
$(v_1,m_1\ell )$
for which the latter is the first vertex in the first level, which is reached by the path, if and only if
![]() $m_1\ell \equiv t \ \ \pmod {K}$
. Consequently, the total number of paths from
$m_1\ell \equiv t \ \ \pmod {K}$
. Consequently, the total number of paths from
![]() $(v_0,t)$
to a general
$(v_0,t)$
to a general
![]() $(v_1,m_1\ell )$
not passing through
$(v_1,m_1\ell )$
not passing through
![]() $(v_1,0)$
is the same as the number of
$(v_1,0)$
is the same as the number of
![]() $1\leq \tilde {l}\leq \ell $
for which
$1\leq \tilde {l}\leq \ell $
for which
![]() $m_1\tilde {\ell } \equiv t \ \ \pmod {K}$
. Let
$m_1\tilde {\ell } \equiv t \ \ \pmod {K}$
. Let
![]() $q_{\ell }$
be the integer such that
$q_{\ell }$
be the integer such that
![]() $0 < a_1h + q_{\ell } K \leq K$
, then
$0 < a_1h + q_{\ell } K \leq K$
, then
is the least value,
![]() $\ell $
, for which there is an edge from the cycle starting at
$\ell $
, for which there is an edge from the cycle starting at
![]() $(v_0,t)$
to
$(v_0,t)$
to
![]() $(v_1,m_1\ell )$
. The number of paths from
$(v_1,m_1\ell )$
. The number of paths from
![]() $(v_0,t)$
to
$(v_0,t)$
to
![]() $(v_1,m_1\ell )$
not passing through
$(v_1,m_1\ell )$
not passing through
![]() $(v_1,0)$
is then given as follows:
$(v_1,0)$
is then given as follows:
if
![]() $\ell m_1\equiv h \ (\mathrm {mod}\ K)$
for
$\ell m_1\equiv h \ (\mathrm {mod}\ K)$
for
![]() $0\leq h<c_t$
and
$0\leq h<c_t$
and
if
![]() $\ell m_1\equiv h \ (\mathrm {mod}\ K)$
for
$\ell m_1\equiv h \ (\mathrm {mod}\ K)$
for
![]() $c_t\leq h<K$
. There is precisely one edge from
$c_t\leq h<K$
. There is precisely one edge from
![]() $(v_1,\ell m_1)$
to
$(v_1,\ell m_1)$
to
![]() $(v_2,m_1(\ell +1))$
. We can express
$(v_2,m_1(\ell +1))$
. We can express
![]() $(v_2,l(m_1+1))$
as
$(v_2,l(m_1+1))$
as
![]() $(v_2,sm_2)$
, i.e.,
$(v_2,sm_2)$
, i.e.,
![]() $m_1(\ell +1)\equiv sm_2 \ (\mathrm {mod}\ r)$
. Let
$m_1(\ell +1)\equiv sm_2 \ (\mathrm {mod}\ r)$
. Let
![]() $k_{\ell }$
be such that
$k_{\ell }$
be such that
![]() $0<m_2^{-1}m_1(\ell +1)+rk_{\ell }<K$
. Then the number of paths from
$0<m_2^{-1}m_1(\ell +1)+rk_{\ell }<K$
. Then the number of paths from
![]() $(v_1,\ell m_1)$
to
$(v_1,\ell m_1)$
to
![]() $(v_3,0)$
is
$(v_3,0)$
is
![]() $r-(m_2^{-1}m_1(\ell +1)+rk_{\ell }).$
The total number of 3-step admissible paths becomes
$r-(m_2^{-1}m_1(\ell +1)+rk_{\ell }).$
The total number of 3-step admissible paths becomes

For
![]() $t=0$
, we have
$t=0$
, we have
![]() $c_t=K$
; hence, the number of 3-step admissible paths is
$c_t=K$
; hence, the number of 3-step admissible paths is

Lemma 6.7 Let
![]() $r\in {\mathbb {N}}$
,
$r\in {\mathbb {N}}$
,
![]() $r\geq 2$
, and let
$r\geq 2$
, and let
![]() $\underline {m}=(m_0,m_1,m_2,m_3)$
be such that
$\underline {m}=(m_0,m_1,m_2,m_3)$
be such that
![]() $\gcd (m_2,r)=K$
and
$\gcd (m_2,r)=K$
and
![]() $\gcd (m_i,r)=1, i\neq 2$
. Then
$\gcd (m_i,r)=1, i\neq 2$
. Then

where
and
![]() $a_1$
is defined in Notation 6.2.
$a_1$
is defined in Notation 6.2.
Proof We will now calculate the number of 3-step admissible paths from
![]() $(v_0,0)$
to
$(v_0,0)$
to
![]() $(v_0,3)$
. First, we have
$(v_0,3)$
. First, we have
![]() $m_1^{-1}m_2\ell -1+tm_1^{-1}+rs_t$
paths from
$m_1^{-1}m_2\ell -1+tm_1^{-1}+rs_t$
paths from
![]() $(v_0,0)$
to each
$(v_0,0)$
to each
![]() $(v_1,\ell m_2-m_1+t)$
for
$(v_1,\ell m_2-m_1+t)$
for
![]() $t=0,\ldots ,K-1$
, where
$t=0,\ldots ,K-1$
, where
![]() $s_{\ell }$
is such that
$s_{\ell }$
is such that
![]() $0<m_1^{-1}m_2\ell -1+tm_1^{-1}+rs_{\ell }<r$
. The vertex
$0<m_1^{-1}m_2\ell -1+tm_1^{-1}+rs_{\ell }<r$
. The vertex
![]() $(v_1,\ell m_2-m_1+t)$
is connected to
$(v_1,\ell m_2-m_1+t)$
is connected to
![]() $(v_2,\ell m_2+t)$
by a single edge, and there are
$(v_2,\ell m_2+t)$
by a single edge, and there are
![]() $\frac {r}{K}-\ell $
paths from
$\frac {r}{K}-\ell $
paths from
![]() $(v_2,\ell m_2+t)$
to
$(v_2,\ell m_2+t)$
to
![]() $(v_3,0)$
. The total number of 3-step admissible paths becomes
$(v_3,0)$
. The total number of 3-step admissible paths becomes
 $$ \begin{align*} \begin{aligned} &\sum_{t=0}^{K-1}\sum_{\ell=1}^{\frac{r-K}{K}} \left(m_1^{-1}m_2\ell-1+tm_1^{-1}+rs_{\ell} \right) \left( \frac{r}{K}-\ell \right) \\ &\equiv K \sum_{\ell=1}^{\frac{r-K}{K}} -\ell\left(m_1^{-1}m_2\ell-1 \right)+\sum_{t=0}^{K-1}\sum_{\ell=1}^{\frac{r-K}{K}} tm_1^{-1}\left( \frac{r}{K}-\ell \right) \ (\mathrm{mod}\ r) \\ &\equiv -m_1^{-1}m_2 \frac{r(2r-K)(r-K)}{6K^2} + \frac{r(r-K)}{2K}+\sum_{t=0}^{K-1} tm_1^{-1}\frac{r(r-K)}{2K^2} \ (\mathrm{mod}\ r) \\ &\equiv -m_1^{-1}m_2 \frac{r(2r-K)(r-K)}{6K^2} + \frac{r(r-K)}{2K}+ m_1^{-1}\frac{r(r-K)(K-1)}{4K} \ (\mathrm{mod}\ r). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\sum_{t=0}^{K-1}\sum_{\ell=1}^{\frac{r-K}{K}} \left(m_1^{-1}m_2\ell-1+tm_1^{-1}+rs_{\ell} \right) \left( \frac{r}{K}-\ell \right) \\ &\equiv K \sum_{\ell=1}^{\frac{r-K}{K}} -\ell\left(m_1^{-1}m_2\ell-1 \right)+\sum_{t=0}^{K-1}\sum_{\ell=1}^{\frac{r-K}{K}} tm_1^{-1}\left( \frac{r}{K}-\ell \right) \ (\mathrm{mod}\ r) \\ &\equiv -m_1^{-1}m_2 \frac{r(2r-K)(r-K)}{6K^2} + \frac{r(r-K)}{2K}+\sum_{t=0}^{K-1} tm_1^{-1}\frac{r(r-K)}{2K^2} \ (\mathrm{mod}\ r) \\ &\equiv -m_1^{-1}m_2 \frac{r(2r-K)(r-K)}{6K^2} + \frac{r(r-K)}{2K}+ m_1^{-1}\frac{r(r-K)(K-1)}{4K} \ (\mathrm{mod}\ r). \end{aligned} \end{align*} $$
We state the final case without proof, as the proof is similar to that of Lemma 6.7.
Lemma 6.8 Let
![]() $r\in {\mathbb {N}}$
,
$r\in {\mathbb {N}}$
,
![]() $r\geq 2$
, and let
$r\geq 2$
, and let
![]() $\underline {m}=(m_0,m_1,m_2,m_3)$
be such that
$\underline {m}=(m_0,m_1,m_2,m_3)$
be such that
![]() $\gcd (m_1,r)=K$
and
$\gcd (m_1,r)=K$
and
![]() $\gcd (m_i,r)=1, i\neq 1$
. Then
$\gcd (m_i,r)=1, i\neq 1$
. Then

where
and
![]() $a_2$
is defined in Notation 6.2.
$a_2$
is defined in Notation 6.2.
Remark 6.9 It follows directly from the adjacency matrices and Lemma 6.1 that r is an invariant for
![]() $n>1$
whenever two quantum lens spaces share the same ideal structure and at most one of the weights is not coprime to the order of the acting group. To see this, note that it follows from a simple computation that
$n>1$
whenever two quantum lens spaces share the same ideal structure and at most one of the weights is not coprime to the order of the acting group. To see this, note that it follows from a simple computation that
![]() $SL_{\mathcal {P}}$
-equivalence preserves the elements directly above the main diagonal. Let now
$SL_{\mathcal {P}}$
-equivalence preserves the elements directly above the main diagonal. Let now
![]() $C(\overline {L}_q^{2n+1}(r;\underline {m}))$
and
$C(\overline {L}_q^{2n+1}(r;\underline {m}))$
and
![]() $C(\overline {L}_q^{2n+1}(r';\underline {n}))$
be two isomorphic quantum lens spaces for which only a single weight, say
$C(\overline {L}_q^{2n+1}(r';\underline {n}))$
be two isomorphic quantum lens spaces for which only a single weight, say
![]() $m_i$
and
$m_i$
and
![]() $n_i$
,
$n_i$
,
![]() $i\in \lbrace 0, \dots , n \rbrace $
is coprime to the order of the acting group. If
$i\in \lbrace 0, \dots , n \rbrace $
is coprime to the order of the acting group. If
![]() $i>0$
, the ideal structure guarantees that
$i>0$
, the ideal structure guarantees that
![]() $\gcd (m_i,r)=\gcd (n_i,r')$
, and by the structure of the adjacency matrices, we obtain directly that
$\gcd (m_i,r)=\gcd (n_i,r')$
, and by the structure of the adjacency matrices, we obtain directly that
![]() $r=r'$
. If
$r=r'$
. If
![]() $i=0$
, then we obtain from the adjacency matrix that
$i=0$
, then we obtain from the adjacency matrix that
![]() $\frac {r}{\gcd (m_0,r)}=\frac {r'}{\gcd (n_0,r')}$
and
$\frac {r}{\gcd (m_0,r)}=\frac {r'}{\gcd (n_0,r')}$
and
![]() $r=r'$
. From which it follows that
$r=r'$
. From which it follows that
![]() $\gcd (m_0,r)=\gcd (n_0,r')$
. Hence, r and the greatest common divisor are invariant whenever
$\gcd (m_0,r)=\gcd (n_0,r')$
. Hence, r and the greatest common divisor are invariant whenever
![]() $n>1$
. If
$n>1$
. If
![]() $n=1$
and
$n=1$
and
![]() $i=1$
, we obtain that r is an invariant by the same argument as for
$i=1$
, we obtain that r is an invariant by the same argument as for
![]() $n>1$
and
$n>1$
and
![]() $i\neq 0$
. If
$i\neq 0$
. If
![]() $n=1$
and
$n=1$
and
![]() $i=0$
, then something else happens. Let
$i=0$
, then something else happens. Let
![]() $\gcd (m_0,r)=K$
in this case
$\gcd (m_0,r)=K$
in this case
 $$ \begin{align*} A_{\overline{L}_3^{r;(m_0,m_1)}}=\begin{pmatrix} 1 & \frac{r}{K} \\ 0 & 1 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} A_{\overline{L}_3^{r;(m_0,m_1)}}=\begin{pmatrix} 1 & \frac{r}{K} \\ 0 & 1 \end{pmatrix}. \end{align*} $$
We can then obtain the same
![]() $C^*$
-algebra for different values of the order of the acting group and the greatest common divisor. For example, we have that
$C^*$
-algebra for different values of the order of the acting group and the greatest common divisor. For example, we have that
![]() $A_{\overline {L}_3^{4,(2,1)}}=A_{\overline {L}_3^{2,(1,1)}}$
and hence
$A_{\overline {L}_3^{4,(2,1)}}=A_{\overline {L}_3^{2,(1,1)}}$
and hence
![]() $C^*(\overline {L}_3^{(2,(1,1))})= C^*(\overline {L}_3^{(4,(2,1))})$
.
$C^*(\overline {L}_3^{(2,(1,1))})= C^*(\overline {L}_3^{(4,(2,1))})$
.
7 The invariant
We are now ready to prove Theorem 5.3.
Proof of Theorem 5.3
(0). Assume that the quantum lens spaces coming from the weights
![]() $\underline {m}=(m_0,m_1,m_2,m_3)$
and
$\underline {m}=(m_0,m_1,m_2,m_3)$
and
![]() $\underline {n}=(n_0,n_1,n_2,n_3)$
are isomorphic. We denote by
$\underline {n}=(n_0,n_1,n_2,n_3)$
are isomorphic. We denote by
![]() $x_0,y_0,a_1$
and
$x_0,y_0,a_1$
and
![]() $x_0',y_0',a_1'$
the elements coming from Lemma 6.6 corresponding to the system of weights
$x_0',y_0',a_1'$
the elements coming from Lemma 6.6 corresponding to the system of weights
![]() $\underline {m}$
and
$\underline {m}$
and
![]() $\underline {n}$
, respectively. See Notation 6.2 for the definition of
$\underline {n}$
, respectively. See Notation 6.2 for the definition of
![]() $a_1$
.
$a_1$
.
Consider the following expression:

Let
![]() $b_h$
be such that
$b_h$
be such that
![]() $1 \leq a_1h+b_hK \leq K$
. Then
$1 \leq a_1h+b_hK \leq K$
. Then

remarking that the corresponding terms for
![]() $\ell =0$
and
$\ell =0$
and
![]() $\ell =r-1$
vanish modulo r. We have
$\ell =r-1$
vanish modulo r. We have
 $$ \begin{align*} \begin{aligned} &\sum_{h=0}^{K-1}\left(a_1h+Kq_h\right)m_2^{-1}m_1 \sum_{k=0}^{\frac{r-K}{K}} \left(a_1h+b_hK+kK+1\right) \\ = & \sum_{h=0}^{K-1}\left(a_1h+Kq_h\right)m_2^{-1}m_1\left( \frac{r}{K}\left(a_1h+b_hK+1 \right) + \frac{r(r-K)}{2K} \right)\\ \equiv & \sum_{h=0}^{K-1}\left(a_1h+Kq_h\right)m_2^{-1}m_1\left( \frac{r}{K}\left(a_1h+1 \right) + \frac{r(r-K)}{2K} \right) \quad\pmod{r}\\ \equiv &\sum_{h=0}^{K-1}a_1hm_2^{-1}m_1\left( \frac{r}{K}\left(a_1h+1 \right) + \frac{r(r-K)}{2K} \right)+ \sum_{h=0}^{K-1}q_hm_2^{-1}m_1\left( \frac{r(r-K)}{2} \right) \pmod{r}\\ =&a_1m_2^{-1}m_1 \frac{r(K-1)}{2}\left(1+ \frac{(r-K)}{2}\right)+ a_1^2m_2^{-1}m_1\frac{r(K+1)(2K+1)}{6}+\sum_{h=0}^{K-1}q_hm_2^{-1}m_1\left( \frac{r(r-K)}{2} \right) \pmod{r}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\sum_{h=0}^{K-1}\left(a_1h+Kq_h\right)m_2^{-1}m_1 \sum_{k=0}^{\frac{r-K}{K}} \left(a_1h+b_hK+kK+1\right) \\ = & \sum_{h=0}^{K-1}\left(a_1h+Kq_h\right)m_2^{-1}m_1\left( \frac{r}{K}\left(a_1h+b_hK+1 \right) + \frac{r(r-K)}{2K} \right)\\ \equiv & \sum_{h=0}^{K-1}\left(a_1h+Kq_h\right)m_2^{-1}m_1\left( \frac{r}{K}\left(a_1h+1 \right) + \frac{r(r-K)}{2K} \right) \quad\pmod{r}\\ \equiv &\sum_{h=0}^{K-1}a_1hm_2^{-1}m_1\left( \frac{r}{K}\left(a_1h+1 \right) + \frac{r(r-K)}{2K} \right)+ \sum_{h=0}^{K-1}q_hm_2^{-1}m_1\left( \frac{r(r-K)}{2} \right) \pmod{r}\\ =&a_1m_2^{-1}m_1 \frac{r(K-1)}{2}\left(1+ \frac{(r-K)}{2}\right)+ a_1^2m_2^{-1}m_1\frac{r(K+1)(2K+1)}{6}+\sum_{h=0}^{K-1}q_hm_2^{-1}m_1\left( \frac{r(r-K)}{2} \right) \pmod{r}. \end{aligned} \end{align*} $$
Notice that if the parity of K and r is the same,
![]() $r-K$
is even and hence the leftmost and rightmost terms will vanish modulo r when we subtract the corresponding terms of
$r-K$
is even and hence the leftmost and rightmost terms will vanish modulo r when we subtract the corresponding terms of
![]() $Kx_0'$
. (For the first term, note that then either
$Kx_0'$
. (For the first term, note that then either
![]() $K-1$
or
$K-1$
or
![]() $\left (a_1m_2^{-1}m_1 - a_1'n_2^{-1}n_1 \right )$
is even). Additionally, it follows from a computation that
$\left (a_1m_2^{-1}m_1 - a_1'n_2^{-1}n_1 \right )$
is even). Additionally, it follows from a computation that
So, if the parity of r and K is the same, we have
We now consider the case where r is even and K is odd. We first let

so that we may rewrite the last term as
![]() $J_0K \frac {r}{2}$
and note that
$J_0K \frac {r}{2}$
and note that
![]() $J_0$
is an integer since K divides
$J_0$
is an integer since K divides
![]() $r-K$
. Consider next the first term. Since
$r-K$
. Consider next the first term. Since
![]() $K-1$
is even, we have
$K-1$
is even, we have
 $$ \begin{align*} \begin{aligned} \left(a_1m_2^{-1}m_1-a_1'n_2^{-1}n_1\right) \frac{r(K-1)}{2}\left(1+ \frac{(r-K)}{2}\right) \equiv \left(a_1m_2^{-1}m_1-a_1'n_2^{-1}n_1\right) \frac{r(K-1)}{2}\frac{(r-K)}{2} \quad\pmod{r},\end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \left(a_1m_2^{-1}m_1-a_1'n_2^{-1}n_1\right) \frac{r(K-1)}{2}\left(1+ \frac{(r-K)}{2}\right) \equiv \left(a_1m_2^{-1}m_1-a_1'n_2^{-1}n_1\right) \frac{r(K-1)}{2}\frac{(r-K)}{2} \quad\pmod{r},\end{aligned} \end{align*} $$
which we conclude has the form
![]() $KJ_1 \frac {r}{2}$
for an integer, using a similar argument as before
$KJ_1 \frac {r}{2}$
for an integer, using a similar argument as before
![]() $J_1$
. It follows that
$J_1$
. It follows that
![]() $K(x_0'-x_0)$
is equivalent to
$K(x_0'-x_0)$
is equivalent to
modulo r where
![]() $J=J_0-J_0'+J_1$
. Note that from the analysis above, we can conclude that
$J=J_0-J_0'+J_1$
. Note that from the analysis above, we can conclude that
![]() $KJ\frac {r}{2}\equiv 0\ \ \pmod {r}$
if the parity of r and K is the same.
$KJ\frac {r}{2}\equiv 0\ \ \pmod {r}$
if the parity of r and K is the same.
By an application of
![]() $SL_{\mathcal {P}}$
-equivalence (Corollary 4.1), we have that there exist integers
$SL_{\mathcal {P}}$
-equivalence (Corollary 4.1), we have that there exist integers
![]() $v_1,v_2,u$
such that
$v_1,v_2,u$
such that
Hence,
If r and K have the same parity, then the right-hand side is congruent to zero modulo r and
![]() $KJ\frac {r}{2}$
is congruent to zero modulo r.
$KJ\frac {r}{2}$
is congruent to zero modulo r.
Assume now that r and K have opposite parity (in particular, K is odd and r is even). We then obtain
where
![]() $M=v_2(r-K)+u(r+1)K-KJ$
. If
$M=v_2(r-K)+u(r+1)K-KJ$
. If
![]() $3\nmid r$
, then it is easy to see (remarking that the left-hand side is then an integer multiple of r) that M is even, recalling that in this case, either
$3\nmid r$
, then it is easy to see (remarking that the left-hand side is then an integer multiple of r) that M is even, recalling that in this case, either
![]() $3\mid (K+1)$
or
$3\mid (K+1)$
or
![]() $3\mid (2K+1)$
. If
$3\mid (2K+1)$
. If
![]() $3\mid r$
, then the expression may be rewritten as
$3\mid r$
, then the expression may be rewritten as
for some integer N, and consequently
from which it follows that M is even, and hence
Consider the term
It follows from an easy computation that if
![]() $3\nmid K$
, then this is congruent to zero modulo r, and consequently the invariant coincides with the analogous invariant for the other three cases, and we may make the same conclusion as in [Reference Eilers, Restorff, Ruiz and Sørensen13, Corollary 7.9]. If
$3\nmid K$
, then this is congruent to zero modulo r, and consequently the invariant coincides with the analogous invariant for the other three cases, and we may make the same conclusion as in [Reference Eilers, Restorff, Ruiz and Sørensen13, Corollary 7.9]. If
![]() $3$
divides both r and K, then
$3$
divides both r and K, then
![]() $a_1 \equiv m_1 \ \ \pmod {3}$
,
$a_1 \equiv m_1 \ \ \pmod {3}$
,
![]() $m_2^{-1}\equiv m_2 \ \ \pmod {3}$
, and so on, whereas neither of
$m_2^{-1}\equiv m_2 \ \ \pmod {3}$
, and so on, whereas neither of
![]() $(K+1), (2K+1), (r-1)$
, or
$(K+1), (2K+1), (r-1)$
, or
![]() $(r-2)$
is divisible by 3. So we in this case have
$(r-2)$
is divisible by 3. So we in this case have
if and only if
To see the “if” part of the statement, one should notice that the left-hand side of the second equation is always even and a multiple of
![]() $3$
under the given assumptions and hence a multiple of 6. Now, since
$3$
under the given assumptions and hence a multiple of 6. Now, since
![]() $(r-1)(r-2) \equiv 2 \ \ \pmod {3}$
and
$(r-1)(r-2) \equiv 2 \ \ \pmod {3}$
and
![]() $(K+1)(2K+1) \equiv 1 \ \ \pmod {3}$
and 2 is self-inverse modulo 3, the above is congruent to
$(K+1)(2K+1) \equiv 1 \ \ \pmod {3}$
and 2 is self-inverse modulo 3, the above is congruent to
which is
Furthermore, since
![]() $a_1' \equiv n_1 \ \ \pmod {3}$
and
$a_1' \equiv n_1 \ \ \pmod {3}$
and
![]() $a_1 \equiv m_1 \ \ \pmod {3}$
, this is true independent of the choice of weights, and hence this case is trivial.
$a_1 \equiv m_1 \ \ \pmod {3}$
, this is true independent of the choice of weights, and hence this case is trivial.
For the reverse implication, assume now that (7.2) holds. By appealing to (7.1), there is an integer s such that
We will make use of [Reference Eilers, Restorff, Ruiz and Sørensen13, Proposition 2.14]. Hence, we need to show that we can transform

into

by adding columns (rows) of either matrix to subsequent (prior) columns (rows) of the same matrix an integral number of times. This is done by the following operations: First, we add the second row to the first row J times to obtain
We can then transform this into
![]() $x_0'$
by adding the second column to the fourth
$x_0'$
by adding the second column to the fourth
![]() $s-JK\frac {r}{2}$
times (recall that J is even if r and K are both odd by the first part of the proof).
$s-JK\frac {r}{2}$
times (recall that J is even if r and K are both odd by the first part of the proof).
(3). Assume that the quantum lens spaces coming from the weights
![]() $\underline {m}=(m_0,m_1,m_2,m_3)$
and
$\underline {m}=(m_0,m_1,m_2,m_3)$
and
![]() $\underline {n}=(n_0,n_1,n_2,n_3)$
are isomorphic. We denote by
$\underline {n}=(n_0,n_1,n_2,n_3)$
are isomorphic. We denote by
![]() $x_0,\ldots ,x_{K-1}, y_0,\ldots ,y_{K-1},a_1,a_2$
, and
$x_0,\ldots ,x_{K-1}, y_0,\ldots ,y_{K-1},a_1,a_2$
, and
![]() $x_0',\ldots ,x_{K-1}'$
,
$x_0',\ldots ,x_{K-1}'$
,
![]() $y_0',\ldots ,y_{K-1}',a_1',a_2'$
the elements
$y_0',\ldots ,y_{K-1}',a_1',a_2'$
the elements
![]() $x_i$
and
$x_i$
and
![]() $y_i$
coming from Lemma 6.6 corresponding to
$y_i$
coming from Lemma 6.6 corresponding to
![]() $\underline {m}$
and
$\underline {m}$
and
![]() $\underline {n}$
, respectively. See Notation 6.2 for the definition of
$\underline {n}$
, respectively. See Notation 6.2 for the definition of
![]() $a_i$
. Then, by Corollary 4.1, we obtain the following equations:
$a_i$
. Then, by Corollary 4.1, we obtain the following equations:
for
![]() $j=0,1,\ldots ,K-1$
, where
$j=0,1,\ldots ,K-1$
, where
![]() $u_{\ell m}, v_{\ell m}\in \mathbb {Z}$
are the entries of the matrices U and V from the
$u_{\ell m}, v_{\ell m}\in \mathbb {Z}$
are the entries of the matrices U and V from the
![]() $SL_{\mathcal {P}}$
-equivalence.
$SL_{\mathcal {P}}$
-equivalence.
Note that since
![]() $y_0=y_0'$
, K divides
$y_0=y_0'$
, K divides
![]() $u_{23}$
. Then, by (7.3),
$u_{23}$
. Then, by (7.3),
and hence there exists a
![]() $k\in \mathbb Z$
such that
$k\in \mathbb Z$
such that
Then
![]() $\frac {a_2'-a_2}{K}\in \mathbb Z$
and
$\frac {a_2'-a_2}{K}\in \mathbb Z$
and
![]() $a_2'=a_2$
, which implies that
$a_2'=a_2$
, which implies that
![]() $m_2\equiv n_2 \ (\mathrm {mod}\ K)$
.
$m_2\equiv n_2 \ (\mathrm {mod}\ K)$
.
We now consider the sum of all the
![]() $x_i's$
. We have
$x_i's$
. We have

The last term is always congruent to
![]() $0$
modulo r; indeed, if K is odd, we are done, and if K is even, then
$0$
modulo r; indeed, if K is odd, we are done, and if K is even, then
![]() $a_1+a_2$
is even.
$a_1+a_2$
is even.
Since each
![]() $s_t$
corresponds uniquely to a number between
$s_t$
corresponds uniquely to a number between
![]() $0$
and
$0$
and
![]() $K-1$
, we may reiterate the penultimate sum accordingly:
$K-1$
, we may reiterate the penultimate sum accordingly:

Hence,
Using (7.3) and the fact that
![]() $(a_2-1)\frac {r(K-1)}{2}\equiv 0 \ (\mathrm {mod}\ r)$
, we have
$(a_2-1)\frac {r(K-1)}{2}\equiv 0 \ (\mathrm {mod}\ r)$
, we have
 $$ \begin{align*} \begin{aligned} &(x_0'+x_1'+\cdots+x_{K-1}')-(x_0+x_1+\cdots+x_{K-1})\equiv u_{12}(y_0+y_1+\cdots+y_{K-1})\\ &+Ku_{13}\frac{r}{K} + (v_{34}+v_{35}+\cdots+v_{3,K+3})\frac{r(r+1)}{2} \ (\mathrm{mod}\ r) \\ &\equiv u_{12}\left(\frac{r(r+K)}{2K}+ (K-1)\frac{r(r-K)}{2K}+a_2\frac{r}{K}\sum_{t=1}^{K-1} t\right)+(v_{34}+v_{35}+\cdots+v_{3,K+3})\frac{r(r+1)}{2} \ (\mathrm{mod}\ r) \\ &\equiv u_{12}\frac{r(r+1)}{2}+(v_{34}+v_{35}+\cdots+v_{3,K+3})\frac{r(r+1)}{2} \ (\mathrm{mod}\ r) \\ &\equiv (v_{34}+v_{35}+\cdots+v_{3,K+3})\frac{r(r+1)}{2}\ (\mathrm{mod}\ r) \equiv 0 \ (\mathrm{mod}\ r). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &(x_0'+x_1'+\cdots+x_{K-1}')-(x_0+x_1+\cdots+x_{K-1})\equiv u_{12}(y_0+y_1+\cdots+y_{K-1})\\ &+Ku_{13}\frac{r}{K} + (v_{34}+v_{35}+\cdots+v_{3,K+3})\frac{r(r+1)}{2} \ (\mathrm{mod}\ r) \\ &\equiv u_{12}\left(\frac{r(r+K)}{2K}+ (K-1)\frac{r(r-K)}{2K}+a_2\frac{r}{K}\sum_{t=1}^{K-1} t\right)+(v_{34}+v_{35}+\cdots+v_{3,K+3})\frac{r(r+1)}{2} \ (\mathrm{mod}\ r) \\ &\equiv u_{12}\frac{r(r+1)}{2}+(v_{34}+v_{35}+\cdots+v_{3,K+3})\frac{r(r+1)}{2} \ (\mathrm{mod}\ r) \\ &\equiv (v_{34}+v_{35}+\cdots+v_{3,K+3})\frac{r(r+1)}{2}\ (\mathrm{mod}\ r) \equiv 0 \ (\mathrm{mod}\ r). \end{aligned} \end{align*} $$
The last congruence follows by [Reference Eilers, Restorff, Ruiz and Sørensen13, Proof of Theorem 7.8]. Hence,
It remains to be shown that
![]() $m_1\equiv n_1 \ (\mathrm {mod}\ K)$
, i.e.,
$m_1\equiv n_1 \ (\mathrm {mod}\ K)$
, i.e.,
![]() $a_1=a_1'$
. For
$a_1=a_1'$
. For
![]() $h=s_t+1,\ldots ,K-1$
, let
$h=s_t+1,\ldots ,K-1$
, let
![]() $p_h\in \mathbb Z$
be such that
$p_h\in \mathbb Z$
be such that
![]() $0<m_2a_1h-1+Kp_h<K$
. First, we need to expand the following sum:
$0<m_2a_1h-1+Kp_h<K$
. First, we need to expand the following sum:
 $$ \begin{align*} \begin{aligned} &\mathop{\sum_{h=s_t+1}^{K-1}\sum_{\ell=1}^{r-2}}_{\ell\equiv m_2a_1h-1\ (\mathrm{mod}\ K)}\ell = \sum_{h=s_t+1}^{K-1}\sum_{k=0}^{\frac{r-K}{K}}\left( m_2a_1h-1+Kp_h+Kk\right) = \sum_{h=s_t+1}^{K-1}\left(\frac{r}{K}(m_2a_1h-1)+rp_h+\frac{r(r-K)}{2K} \right) \\ &\equiv \frac{r}{K}m_2a_1\left(\frac{K(K-1)}{2}+\frac{a_2t(1-a_2t)}{2}\right)+\frac{r}{K}(a_2t-K)+(K-a_2t)\frac{r(r-K)}{2K} \ (\mathrm{mod}\ r). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\mathop{\sum_{h=s_t+1}^{K-1}\sum_{\ell=1}^{r-2}}_{\ell\equiv m_2a_1h-1\ (\mathrm{mod}\ K)}\ell = \sum_{h=s_t+1}^{K-1}\sum_{k=0}^{\frac{r-K}{K}}\left( m_2a_1h-1+Kp_h+Kk\right) = \sum_{h=s_t+1}^{K-1}\left(\frac{r}{K}(m_2a_1h-1)+rp_h+\frac{r(r-K)}{2K} \right) \\ &\equiv \frac{r}{K}m_2a_1\left(\frac{K(K-1)}{2}+\frac{a_2t(1-a_2t)}{2}\right)+\frac{r}{K}(a_2t-K)+(K-a_2t)\frac{r(r-K)}{2K} \ (\mathrm{mod}\ r). \end{aligned} \end{align*} $$
We will now find an expression for
![]() $(x_0'-x_t')-(x_0-x_t)$
and then consider the expressions for
$(x_0'-x_t')-(x_0-x_t)$
and then consider the expressions for
![]() $t=1$
and
$t=1$
and
![]() $t=K-1$
. From the above, we have
$t=K-1$
. From the above, we have
 $$ \begin{align*} \begin{aligned} (x_0'-x_t')-(x_0-x_t)&\equiv \mathop{\sum_{h=s_t+1}^{K-1}\sum_{\ell=1}^{r-2}}_{\ell\equiv m_2a_1'h-1\ (\mathrm{mod}\ K)}\ell -\mathop{\sum_{h=s_t+1}^{K-1}\sum_{\ell=1}^{r-2}}_{\ell\equiv m_2a_1h-1\ (\mathrm{mod}\ K)}\ell + \frac{r}{K}(a_1-a_1')t \quad (\mathrm{mod}\ r) \\ &\equiv \frac{r}{K}\left(\frac{K(K-1)}{2}-\frac{a_2t(a_2t-1)}{2}\right)m_2(a_1'-a_1)+ \frac{r}{K}(a_1-a_1')t \quad\pmod{r}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} (x_0'-x_t')-(x_0-x_t)&\equiv \mathop{\sum_{h=s_t+1}^{K-1}\sum_{\ell=1}^{r-2}}_{\ell\equiv m_2a_1'h-1\ (\mathrm{mod}\ K)}\ell -\mathop{\sum_{h=s_t+1}^{K-1}\sum_{\ell=1}^{r-2}}_{\ell\equiv m_2a_1h-1\ (\mathrm{mod}\ K)}\ell + \frac{r}{K}(a_1-a_1')t \quad (\mathrm{mod}\ r) \\ &\equiv \frac{r}{K}\left(\frac{K(K-1)}{2}-\frac{a_2t(a_2t-1)}{2}\right)m_2(a_1'-a_1)+ \frac{r}{K}(a_1-a_1')t \quad\pmod{r}. \end{aligned} \end{align*} $$
On the other hand, by (7.3), we have
 $$ \begin{align*} \begin{aligned} (x_0'-x_t')-(x_0-x_t)&\equiv u_{12}(y_0-y_t)+(v_{34}-v_{3,t+4})\frac{r(r+1)}{2} \quad\pmod{r} \\ &\equiv -u_{12}a_2t\frac{r}{K} \quad\pmod{r}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} (x_0'-x_t')-(x_0-x_t)&\equiv u_{12}(y_0-y_t)+(v_{34}-v_{3,t+4})\frac{r(r+1)}{2} \quad\pmod{r} \\ &\equiv -u_{12}a_2t\frac{r}{K} \quad\pmod{r}, \end{aligned} \end{align*} $$
which follows since
![]() $v_{34}=-\frac {u_{23}}{K}$
. Indeed, we have
$v_{34}=-\frac {u_{23}}{K}$
. Indeed, we have
![]() $y_0'=y_0$
and
$y_0'=y_0$
and
hence,
![]() $rv_{3,t+4}+u_{23}\frac {r}{K}=(a_2'-a_2)t\frac {r}{K}=0$
and
$rv_{3,t+4}+u_{23}\frac {r}{K}=(a_2'-a_2)t\frac {r}{K}=0$
and
![]() $v_{3,t+4}=-\frac {u_{23}}{K}$
.
$v_{3,t+4}=-\frac {u_{23}}{K}$
.
Combining the two expressions for
![]() $(x_0'-x_t')-(x_0-x_t)$
, we get
$(x_0'-x_t')-(x_0-x_t)$
, we get
 $$ \begin{align*} \frac{r}{K}\left(\frac{K(K-1)}{2}-\frac{a_2t(a_2t-1)}{2}\right)m_2(a_1'-a_1)+ \frac{r}{K}(a_1-a_1')t+u_{12}a_2t\frac{r}{K}\equiv 0 \quad (\mathrm{mod}\ r). \end{align*} $$
$$ \begin{align*} \frac{r}{K}\left(\frac{K(K-1)}{2}-\frac{a_2t(a_2t-1)}{2}\right)m_2(a_1'-a_1)+ \frac{r}{K}(a_1-a_1')t+u_{12}a_2t\frac{r}{K}\equiv 0 \quad (\mathrm{mod}\ r). \end{align*} $$
Note that
 $$ \begin{align*} \frac{r}{K}\left(\frac{K(K-1)}{2}\right)m_2(a_1-a_1')=r\left(\frac{K-1}{2}\right)m_2(a_1-a_1')\equiv 0\quad \mod r, \end{align*} $$
$$ \begin{align*} \frac{r}{K}\left(\frac{K(K-1)}{2}\right)m_2(a_1-a_1')=r\left(\frac{K-1}{2}\right)m_2(a_1-a_1')\equiv 0\quad \mod r, \end{align*} $$
since if K is even, then
![]() $2$
divides
$2$
divides
![]() $a_1-a_1'$
, and if K is odd, then
$a_1-a_1'$
, and if K is odd, then
![]() $2$
divides
$2$
divides
![]() $K-1$
. Thus, we have
$K-1$
. Thus, we have
 $$ \begin{align} \left(\frac{r}{K}\frac{a_2t(a_2t-1)}{2}m_2+t\right)(a_1-a_1')+u_{12}a_2t\frac{r}{K}\equiv 0 \quad\pmod{r}. \end{align} $$
$$ \begin{align} \left(\frac{r}{K}\frac{a_2t(a_2t-1)}{2}m_2+t\right)(a_1-a_1')+u_{12}a_2t\frac{r}{K}\equiv 0 \quad\pmod{r}. \end{align} $$
By taking the sum of the expressions in (7.4) where we choose
![]() $t=1$
and
$t=1$
and
![]() $t=K-1$
, we arrive at
$t=K-1$
, we arrive at
Then
![]() $\frac {r}{K}a_2^2m_2(a_1-a_1')=rk$
for some
$\frac {r}{K}a_2^2m_2(a_1-a_1')=rk$
for some
![]() $k\in \mathbb {Z}$
; hence, K divides
$k\in \mathbb {Z}$
; hence, K divides
![]() $a_2^2m_2(a_1-a_1')$
. Since
$a_2^2m_2(a_1-a_1')$
. Since
![]() $a_2$
and
$a_2$
and
![]() $m_2$
are both relatively prime to K, we conclude that
$m_2$
are both relatively prime to K, we conclude that
![]() $a_1=a_1'$
.
$a_1=a_1'$
.
For the other direction, we will again make use of [Reference Eilers, Restorff, Ruiz and Sørensen13, Proposition 2.14] a number of times. Assume that
![]() $m_i\equiv n_i\ \ \pmod {K}$
,
$m_i\equiv n_i\ \ \pmod {K}$
,
![]() $i=1,2$
, and
$i=1,2$
, and
![]() $\left (m_2^{-1}m_1-n_2^{-1}n_1\right )\frac {r(r-1)(r-2)}{3} \ \ \pmod {r} \equiv 0 \ \ \pmod {r}$
, then the entries,
$\left (m_2^{-1}m_1-n_2^{-1}n_1\right )\frac {r(r-1)(r-2)}{3} \ \ \pmod {r} \equiv 0 \ \ \pmod {r}$
, then the entries,
![]() $y_t$
, in the second row of the adjacency matrices are identical, and it suffices to show for each t that
$y_t$
, in the second row of the adjacency matrices are identical, and it suffices to show for each t that
 $$ \begin{align*} \begin{aligned} x_t'-x_t\equiv\left(m_2^{-1}m_1-n_2^{-1}n_1\right)\frac{r(r-1)(r-2)}{3K} +\sum_{\ell=1}^{r-2}\ell\frac{r}{K}(k_{\ell}'-k_{\ell}) \quad\pmod{r} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} x_t'-x_t\equiv\left(m_2^{-1}m_1-n_2^{-1}n_1\right)\frac{r(r-1)(r-2)}{3K} +\sum_{\ell=1}^{r-2}\ell\frac{r}{K}(k_{\ell}'-k_{\ell}) \quad\pmod{r} \end{aligned} \end{align*} $$
is an integer multiple of
![]() $\tfrac {r}{K}$
. For the second term, this is obvious. Additionally, it is obvious that this is also true for the first term, whenever r is not a multiple of
$\tfrac {r}{K}$
. For the second term, this is obvious. Additionally, it is obvious that this is also true for the first term, whenever r is not a multiple of
![]() $3$
. If
$3$
. If
![]() $3\vert r$
, then one finds that
$3\vert r$
, then one finds that
![]() $3\vert m_2^{-1}m_1-n_2^{-1}n_1$
, and the claim follows.
$3\vert m_2^{-1}m_1-n_2^{-1}n_1$
, and the claim follows.
The adjacency matrices of each set of weights will then be identical after adding the third row to the first, and the first column to the tth column in each an appropriate number of times.
(2). Proceeding as in part (3), assume that the quantum lens spaces coming from the weights
![]() $\underline {m}=(m_0,m_1,m_2,m_3)$
and
$\underline {m}=(m_0,m_1,m_2,m_3)$
and
![]() $\underline {n}=(n_0,n_1,n_2,n_3)$
are isomorphic. We denote
$\underline {n}=(n_0,n_1,n_2,n_3)$
are isomorphic. We denote
![]() $x, a_1$
and
$x, a_1$
and
![]() $x',a_1'$
the elements coming from the adjacency matrix as written in Lemma 6.8 corresponding to
$x',a_1'$
the elements coming from the adjacency matrix as written in Lemma 6.8 corresponding to
![]() $\underline {m}$
and
$\underline {m}$
and
![]() $\underline {n}$
, respectively. See Notation 6.2 for the definition of
$\underline {n}$
, respectively. See Notation 6.2 for the definition of
![]() $a_1$
. In a similar manner, it follows from Corollary 4.1 and a computation that
$a_1$
. In a similar manner, it follows from Corollary 4.1 and a computation that
It follows that
![]() $m_1\equiv n_1 \ \ \pmod {K}$
. Moreover, we obtain from the adjacency matrices that
$m_1\equiv n_1 \ \ \pmod {K}$
. Moreover, we obtain from the adjacency matrices that
and using [Reference Eilers, Restorff, Ruiz and Sørensen13, Theorem 7.1], we obtain
![]() $k_0,k_1\in {\mathbb {Z}}$
such that
$k_0,k_1\in {\mathbb {Z}}$
such that
Consequently,
Multiplying both sides by
![]() $2K$
yields
$2K$
yields
Now, it is easy to check that the second term is always congruent to zero
![]() $\ (\mathrm {mod}\ r)$
, so we conclude that
$\ (\mathrm {mod}\ r)$
, so we conclude that
Conversely, assuming that
we may argue, as in the previous part, by showing that
![]() $x-x'$
is an integer multiple of
$x-x'$
is an integer multiple of
![]() $\frac {r}{K}$
. It follows by a computation that
$\frac {r}{K}$
. It follows by a computation that
 $$ \begin{align*}x-x'=\frac{r}{K}\left(\frac{2t+(m_1^{-1}-n_1^{-1})(r-K)(K-1)}{4} \right).\end{align*} $$
$$ \begin{align*}x-x'=\frac{r}{K}\left(\frac{2t+(m_1^{-1}-n_1^{-1})(r-K)(K-1)}{4} \right).\end{align*} $$
Since
![]() $(m_1^{-1}-n_1^{-1})(r-K)(K-1)$
is necessarily divisible by 4 (to see this, one can consider the different parities of K and r), it suffices to show that t is even, which one can conclude by considering (7.5).
$(m_1^{-1}-n_1^{-1})(r-K)(K-1)$
is necessarily divisible by 4 (to see this, one can consider the different parities of K and r), it suffices to show that t is even, which one can conclude by considering (7.5).
It remains to be shown that
![]() $\left ( n_2^{-1}n_1-m_2^{-1}m_1 \right )\frac {r(2r-K)(r-K)}{3K} \equiv 0 \ \ \pmod {r}$
if and only if
$\left ( n_2^{-1}n_1-m_2^{-1}m_1 \right )\frac {r(2r-K)(r-K)}{3K} \equiv 0 \ \ \pmod {r}$
if and only if
![]() $\left ( n_2^{-1}n_1-m_2^{-1}m_1 \right )\frac {r(r-1)(r-2)}{3} \equiv 0 \ \ \pmod {r}$
. It is routine to show that if
$\left ( n_2^{-1}n_1-m_2^{-1}m_1 \right )\frac {r(r-1)(r-2)}{3} \equiv 0 \ \ \pmod {r}$
. It is routine to show that if
![]() $3$
does not divide r, then
$3$
does not divide r, then
![]() $3$
divides either
$3$
divides either
![]() $2r-K$
or
$2r-K$
or
![]() $r-K$
, and the claim follows immediately. If
$r-K$
, and the claim follows immediately. If
![]() $\left (n_2^{-1}n_1-m_2^{-1}m_1 \right )\frac {r(r-1)(r-2)}{3} \equiv 0 \ \ \pmod {r}$
and
$\left (n_2^{-1}n_1-m_2^{-1}m_1 \right )\frac {r(r-1)(r-2)}{3} \equiv 0 \ \ \pmod {r}$
and
![]() $3\vert r$
, then
$3\vert r$
, then
![]() $3\vert \left ( n_2^{-1}n_1-m_2^{-1}m_1 \right )$
and one direction follows. The converse follows, remarking that
$3\vert \left ( n_2^{-1}n_1-m_2^{-1}m_1 \right )$
and one direction follows. The converse follows, remarking that
![]() $3\vert \left ( n_2^{-1}n_1-m_2^{-1}m_1 \right )$
is always true if
$3\vert \left ( n_2^{-1}n_1-m_2^{-1}m_1 \right )$
is always true if
![]() $\left ( n_2^{-1}n_1-m_2^{-1}m_1 \right )\frac {r(2r-K)(r-K)}{3K} \equiv 0 \ \ \pmod {r}$
.
$\left ( n_2^{-1}n_1-m_2^{-1}m_1 \right )\frac {r(2r-K)(r-K)}{3K} \equiv 0 \ \ \pmod {r}$
.
The proof of (1) is identical to that of (2), remarking that the adjacency matrix corresponding to the system of weights
![]() with
with
![]() $\gcd (m_1,r)=K$
and
$\gcd (m_1,r)=K$
and
![]() $\gcd (m_i,r)=1$
if
$\gcd (m_i,r)=1$
if
![]() $i\neq 2$
is the antitranspose of the adjacency matrix corresponding to the system
$i\neq 2$
is the antitranspose of the adjacency matrix corresponding to the system
![]() . By [Reference Golyshev and Steinstra17, Definition 1.7], the adjacency matrices are related by the identity
. By [Reference Golyshev and Steinstra17, Definition 1.7], the adjacency matrices are related by the identity
where J is the involutory matrix whose entries are
![]() $1$
on the second diagonal and
$1$
on the second diagonal and
![]() $0$
elsewhere.
$0$
elsewhere.
Remark 7.1 In this paper, we have only dealt with the case where a single weight is coprime to the order of the acting group, r. There is, however, no clear reason why a similar result should be unobtainable in a more general setting. In particular, if we consider a list of weights
![]() $(m_0,m_1,m_2,m_3)$
, then the methods for computing the adjacency matrices of the corresponding graph could very likely be identical or similar, albeit more tedious, to the ones used above if at least one of
$(m_0,m_1,m_2,m_3)$
, then the methods for computing the adjacency matrices of the corresponding graph could very likely be identical or similar, albeit more tedious, to the ones used above if at least one of
![]() $m_1$
or
$m_1$
or
![]() $m_2$
is coprime to r. If both weights are coprime, it is likely that an entirely different approach to counting is necessary since all methods employed so far have required one of them to be a unit of
$m_2$
is coprime to r. If both weights are coprime, it is likely that an entirely different approach to counting is necessary since all methods employed so far have required one of them to be a unit of
![]() ${\mathbb {Z}}_r$
.
${\mathbb {Z}}_r$
.
Acknowledgment
We would like to thank Søren Eilers for helpful discussions as well as providing a program which has been crucial to the investigation. We would also like to thank Efren Ruiz for pointing out the problem in the description of quantum lens spaces as graph
![]() $C^*$
-algebras and for his important guidance and help in constructing a new description. The authors also gratefully acknowledge helpful comments and suggestions from Wojciech Szymański and James Gabe. We would also like to thank the anonymous referee for comments and suggestions for improvements.
$C^*$
-algebras and for his important guidance and help in constructing a new description. The authors also gratefully acknowledge helpful comments and suggestions from Wojciech Szymański and James Gabe. We would also like to thank the anonymous referee for comments and suggestions for improvements.