Field Observations and Experimental and Theoretical Studies on the Superimposed Ice of McCall Glacier, Alaska

Abstract

The formation of superimposed ice in the accumulation area of sub-polar glaciers plays an important role in the heat and mass balance of the glaciers. In order to study the process of superimposed ice formation in detail, field observations were conducted on McCall Glacier, a sub-polar glacier in Arctic Alaska. It was found that the approximate thickness of superimposed ice formed in a whole summer was 20 cm in the upper region and 30—40 cm in the lower region of the accumulation area of the glacier. This difference in thickness may be attributed to the difference in the temperature of the underlying ice and the rate of supply of melt water. The ratio of the amount of superimposed ice formed in the accumulation area from May to July in 1972 to the total amount of melt was determined. Approximately 50% of the total melt water was discharged from the glacier as run-off water, and the remainder contributed to the formation of superimposed ice.

An experimental study on the artificial formation of superimposed ice was conducted in the cold laboratory to obtain the ratio of superimposed ice, that of run-off water, and that of free water suspended between snow grains, to the total amount of melt water produced in the snow. The ratios obtained in the laboratory experiment agree fairly well with those derived from the observational data on McCall Glacier.

Numerical calculations were conducted to examine the relationship between the growth rate of superimposed ice, the rale of snow melting, the rate of discharge of excess melt-water, and the temperature of the underlying ice. Calculations were made in reference to both the laboratory experiment and the field observations on McCall Glacier. It was found that the predominant factors controlling the growth rate or the total amount of superimposed ice in a sub-polar glacier are the rate of supply of melt water to the snow-ice interface and the initial temperature distribution in the underlying ice. By using the present calculation, it may be possible to estimate the growth rate, the total amount of superimposed ice, and the ratio of superimposed ice to the total amount of melting in the accumulation area of any sub-polar glacier, if observational data on the initial temperature distribution in ice and the rate of snow melting at the snow surface are available.

I. Introduction

In sub-polar glaciers, the total amount of melt water in the ablation season is not discharged from the glacier as run-off water, but a fairly large amount of it is stored as superimposed ice that forms by refreezing of melt water on to a continuous ice mass that underlies the winter accumulation. It has been known that superimposed ice thus formed in the accumulation area of a sub-polar glacier plays an important role in the mass balance of the glacier as has been reported by many workers (Schytt, 1949; Baird and others, 1952; Benson, 1962; Müller, 1962; Koerner, 1970; Holmgren, 1971). The amount of superimposed ice formed in a summer must depend on both the rate of snow melting, hence the rate of water supply to the firn—ice interface, and the temperature of ice on which superimposed ice forms. It is, therefore, important to know the amount of superimposed ice as a function of the rate of snow melting and the ice temperature.

In order to investigate the formation of the superimposed ice in connection with the mass balance of McCall Glacier, a sub-polar glacier in Arctic Alaska, glaciological observations were conducted by glaciologists from the Institute of Low Temperature Science, Hokkaido University and the Geophysical Institute, University of Alaska, under the Japan-U.S. Scientific Cooperative Program supported by the Japanese Society for Promotion of Science (No. 4R007, 1971-73) and the U.S. National Science Foundation (N.S.F. Grants GF29985 and GA28278X) in the summers of 1971 and 1972 (Wakahama and others, 1974). Laboratory experiments and numerical computations on the formation of superimposed ice were carried out to examine observational data obtained at the glacier (Wakahama and Hasemi, 1974).

II. Field Observations Of Superimposed Ice. On Mccall Glacifr

McCall Glacier is a small valley glacier located in the Romanzof Mountains of the north-eastern Brooks Range, Alaska. Figure 1 is a sketch map of the glacier showing contour lines and the usual position of the firn line (Wendler and others, 1972) The accumulation area of the glacier appears to consist of a wet-snow facies* and a superimposed-ice zone. The wet-snow facies seems to be much larger in area than the superimposed-ice zone, but the detailed argument of the zonal classification of the glacier will be described elsewhere by one of the present authors (C.S.B.).

Pit studies were made in the summers of 1971 and 1972 at eight sites in the wet-snow facies; LG, LC, LT in the “Lower Cirque”, MG in the “Middle Cirque” and UG, UG', UC, UT in the “Upper Cirque” as indicated in Figure 1. The stratificaLion of snow and ice was revealed by spraying blue ink onto the wall of the pit as shown in Figure 2(a) and (b). Ice-core drillings were made at the bottom of each pit to investigate further the stratigraphy of snow and ice down to a depth of 4 to 5 m. Vertical distributions of density, hardness, grain size and shape, free water content, and the temperature of snow and ice were measured from the pit walls, ice cores and bore holes. Figure 3 illustrates, as an example, the results of pit and ice-core studies made at LG and LC.

In the greater part of the accumulation area, the continuous ice mass was found at a depth of only 1-2 m directly beneath the firn as shown in Figures 2 and 4, and it was observed that the new superimposed ice was forming on to this continuous ice mass. The discontinuous structure found at the level labelled F-F in Figure 2 is the interface between and super-imposed ice. Figure 2(c) shows a close-up of the structure of firn and ice near the interface. In order to obtain the thickness of superimposed ice formed in a year, the stratigraphy was recorded at one and the same place at site LC in the summers of 1971 and 1972. The two stratigraphies were compared as shown in Figure 3(b), which indicates that the superimposed ice increased in thickness by 18 cm during this period.

Fig. 1. Schematic map of McCall Glacier, showing the contour lines anti the usual position of the firn line. Pit studies and ice-core drillings were made at the sites labelled LG. LC. LT, MG, UG', UG, UC and UT in three accumulation areas; the upper, middle and lower cirques

Fig. 2. The stratified structure of pit walls excavated at site LC on 24 August 1971 (a) and 6 July 1972 (b). and a close-up of the structure near the 1971 firn-ice interface, F-F. (a): Layers between S-S and FF consisted of very hard Jim, F-F is at the firn-ice interface. (b): Layers between C-C and D-D consist of firn, and the layer between D-D and F-F is the newly developed superimposed ice on the previous interface F-F.

It was found that the superimposed ice generally looked lighter in colour than the pre-existing ice as seen in Figure 2(b). In this figure, the new superimposed ice is located between F-F and D-D, and the old ice below D-D. Thus the new superimposed ice could easily be distinguished from the old ice by the difference in colour at any place in the accumulation area.

The data concerning the snow and the new superimposed ice observed at eight sites are listed in Table I. The approximate thickness of new superimposed ice formed in a whole summer was 20 cm at the higher altitude and 30-40 cm at the lower altitude of the accumulation area of the glacier. Table I also shows that approximately 50% of the total amount of ablation contributed to the formation of superimposed ice and the remainder was discharged from the accumulation area as run-off water.

The fact that the thickness of the new superimposed ice was less at the higher altitudes in each cirque may be attributed to the difference in the temperature of the underlying ice and the rate of supply of melt water. In fact, the temperature observed at 1om depth was — 2 to — 3⁰C at the higher altitude and — 10 to — 2⁰C at the lower altitude of the accumulation area (Trabant and others, 1975). This is mainly due to the presence of thicker snow and firn at the higher altitudes; this permeable material allows deeper penetration of percolating water, which releases latent heat as it freezes.

The rate of water supply to the snow-ice interface (including that due to rain in summer) may be larger in the lower region than in the higher region of the accumulation area, first because the air temperature is higher in the lower altitude and secondly because the amount of run-off water running along the snow-ice interface from the higher region increases with lowering altitude. These two factors, comparatively high temperature of underlying ice and the low rate of water supply, may reduce the formation of superimposed ice at the higher altitude of the accumulation area.

Fig. 3. Illustrations of stratigraphic sections of snow and ice. (a): Vertical distributions of density (G), hardness (R) grain size (D), free water content (W) and temperature (T) of snow and ice observed at site LG. (b): Comparison of the strati- graphics observed at one and the same place at site LC in 1971 (left) and 1972 (right). Labels F, D, S and C correspond to those indicated in Figure 2(a) and (b). seen in these two sections, new superimposed ice had formed a layer 18 cm in thickness at site LC between the beginning of the ablation season and 6 July 1972

Table I. Observations of superimposed ice growth at various sites in the accumulation area of mccall glacier, july 1972

* Average density of snow.

† Averaged free water content of snow (%).

In the higher region of the upper cirque, several thick ice layers of 60-80 cm in thickness separated by layers of snow and firn were found instead of continuous superimposed ice as shown in the stratigraphies of sites UC and UT in Figure 4. The thickness of each ice layer at UT has been measured by Benson and Trabant since 1969, and it was found that the thickness of each layer has been increasing by 5 to 10 cm per year. Since the physics involved when ice forms on a pre-existing ice layer or lens in snow or firn is the same as in the case of superimposed ice, the internal accumulation including ice layers, lenses, and ice glands, should be taken into account in the mass balance of the glacier as mentioned by Bazhev (1973). The detailed argument concerning internal accumulation will be presented elsewhere in connection with the facies classification of the glacier by one of the present authors (C.S.B.).

Fig. 4. Comparison of stratigraphies observed at eight sites in the accumulation area. In the lower and middle cirques, the snow and firn was less than 1.3 m in thickness and the continuous ice was found directly beneath the firn. In the higher regions of the upper cirque, however, a number of ice layers of 60-80 cm in thickness were found above the deeper continuous ice mass

It may be concluded, therefore, that the main part of the ice body which constitutes McCall Glacier is composed of superimposed ice formed by refreezing of melt water in the accumulation area. This argument may be generally applicable when considering the mass balance of many glaciers existing in sub-polar regions. In fact, Koerner (1970) showed that superimposed icc formed an important part of the positive balance of the Devon Island ice cap.

III. Laboratory Experiment On Superimposed Ice Formation

Fig. 5. (a); Experimental apparatus for making artificial superimposed ice. X: thermo-couples, L.C.: An automatic recording device for a rain gauge, (b): Changes of temperature profiles in ice and snow during the experiment

An experimental study on the formation of superimposed ice was conducted in a cold room, of the Institute of Low Temperature Science, Hokkaido University, to obtain the ratio of superimposed ice to the total amount of melt water. In order to simulate the process of formation of superimposed ice in the accumulation area of a glacier, a simple apparatus was made as illustrated schematically in Figure 5(a). A large block of snow (20 cm × 30 cm in cross-section, 80 cm in height, and average density 0.4 g/cm³) was placed on the slightly inclined surface of an ice block (20 cm × 30 cm in cross-section, 20 cm in height, and with a surface slope of 8⁰). The sides of the snow and ice blocks were thermally insulated with thick expanded polystyrene plates, while the bottom surface of the ice block was cooled by conduction through a copper plate exposed to the cold-room temperature of — 10⁰G. Melt water was produced by heating the snow surface. Some cosine powder (dye) was spread on the snow surface at the beginning of the experiment to allow us to examine the percolation of melt water in the snow. When the melt water reached the snow-ice interface, some of it began to refreeze, forming superimposed ice on the surface of the ice block. Thus the snow-ice interface gradually rose with time. When the air spaces in the snow near the interface were filled with melt water, additional melt water was discharged from the snow-ice interface as “run-off” water, and collected in the automatic recording rain gauge. Temperature profiles in the snow and ice were measured by thermocouples previously embedded at locations labelled in Figure 5(a). Figure 5(b) shows observed changes of temperature profiles in snow and ice as a function of time. The original location of the snow-ice interface was at the origin of the ordinate, but it rose with time. At a first glance, the temperature profiles of snow seen in Figure 5(b) seem unusual; the temperature of the overlying snow often showed a lower value than that of the snow-ice interface. This may be caused by the heterogeneous percolation of melt water in snow, which was revealed by the complex spreading of eosine dye within the snow. The change of the temperature profiles in the ice will be discussed in the following section.

After the heating of the snow surface had been stopped and the whole wet snow refrozen, the snow and ice were cut so that the amount of superimposed ice formed and the total weight of the snow could be measured. Since newly formed superimposed ice was slightly coloured by eosine dye, it was readily distinguishable from the original ice block.

The total amount of the melted snow Qs, of the superimposed ice Qi, of melt water drained from the snow-ice interface Qr, and of the free water Qt (suspended between snow grains) were measured, and ratios of Qi and Qr to Qs were calculated and are listed in Table II. These values obtained in the laboratory experiment agreed fairly well with those derived from the observational data at McCall Glacier.

Table 2. The total amount of melted snow qs, superimposed ice Qi free water Qt, And the ratios of Qi, Qf and Qr to Qs obtained in the laboratory experiment

IV. Numerical Simulations

The growth rate of superimposed ice may depend on the rate of water supply to the snow-ice interface, hence on the rate of melting of snow at the surface, and on the temperature of the underlying ice. Numerical calculations were conducted to examine the relationship between the growth rate of superimposed ice, the rate of snow melting, the rate of discharge of excess melt water from the snow-ice interface, and the temperature of underlying ice. The calculations were made in reference to both the laboratory experiment and the field observations on McCall Glacier.

(1) Model

The growth rate of superimposed ice at the interface may be obtained by solving the equation of one-dimensional heat conduction.

(1)

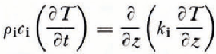
under the following boundary conditions:

(2)

(3)

(4)

where p_si, p_ws, and pi are the densities of the superimposed ice formed, the overlying wet snow, and the underlying ice, respectively, and w is the free water content of the wet snow, c _i, k _i and T are the specific heat capacity, thermal conductivity, and temperature of the superimposed ice, L the latent heat of freezing of water, H the thickness of the superimposed ice, t the time, and z the vertical coordinate (positive upwards). In order to simplify the thermal regime at the snow-ice interface, the following assumptions were made in our computation: (I) The temperature of wet snow is kept at 0⁰C and air spaces in the snow are assumed to be filled with water near the interface. (2) The initial temperature profile in ice is uniform and maintained at — T _B, that is T ₀ = — T _B Since the rate of growth of superimposed ice is governed by the rate of extraction of the latent heat released by solidification of melt water at the interface, it is necessary to know the change of temperature gradient in ice as a function of time and the successive locations of the proceeding interface. In order to do this, the computation was made using Savliev’s method and a forward differential form.

(2) Results

(a) Verification of the experimental results on the artificial formation of superimposed ice

A computation was made to verify experimental resul ts on the artificial formation of superimposed ice using the fo llowing data:

Fig. 6. Numerical simulations of the laboratory experiment, (a): Changes of computed temperature profiles in ice and growth of superinposed ice with time, (b): Changes of the thickness II and growth rate dH/dt of superimposed ice against time. (c) 'The growth rate of superimposed ice against the rate of water supply

• a. Verification of the experimental results on the artificial formation of superimposed ice

  A computation was made to verify experimental results on the artificial formation of superimposed ice using the following data:

  Figure 6{(a) illustrates computed results of temperature profiles in the ice and successive locations of the surface of growing superimposed ice as a function of time. Figure 6(b) shows computed values of the change of the thickness H and the growth rate, dH/dt, of superimposed ice with time. As seen in this figure, dH!!//dt has a high value at the initial stage of the development of superimposed ice but drops rapidly with time. After 24 h the thickness of superimposed ice attained 5.5 cm which agrees fairly well with the experimental results.

  Figure 6(c) represents the thickness of superimposed ice formed during 24 h against the rate of water supply. The growth rate of ice changes sensitively with the rate Qmof water supply when it is less than the critical value of 0.14 g/cm² h, while it becomes insensitive when Qm exceeds this critical value. This suggests that the rate Qm of water supply is the dominant factor for the growth of superimposed ice when Qm is less than 0.14 g/cm² h, whereas ice temperature becomes the controlling factor for larger Qm.

• b. Computation of the growth rate of superimposed ice in the lower cirque of McCall Glacier

  We shall calculate the growth rates of superimposed ice at the lower cirque of McCall Glacier to compare with those obtained in the summer of 1972. In order to compute these values, it is necessary to know the initial temperature distribution in the underlying ice formed in previous years and the rate of water supply to the snow-ice interface. Figure 7(a) shows a schematic diagram of the temperature distributions in ice at five observation sites located along the line drawn from site LT to LG in the lower cirque of McCall Glacier. Values of T _B, the temperature of ice at 10m depth, were estimated from the observational data obtained by Trabant and others (1975) at the end of ablation season of 1972. The value of T _B at the higher altitude is higher than that at low altitude, as mentioned before. Values of T ₀, the temperature at the snow-ice interface, were obtained immediately before the melting of snow started in 1972. Of these values, the only observed value was — 12⁰C at site LC, the other values have been calculated assuming an adiabatic lapse rate of 0.6 deg/100 m. It is also assumed that the initial temperature profile in ice at each site is given by a straight line which connects !T>₀ and T _B, and that the value of T _B does not change with time.

  The situation regarding water supply to the snow-ice interface at each site is schematically shown in Figure 7(a). At a given point on the interface, the dark arrow (Q _m) represents the flux of melt water from the snow surface and the shaded (Q _in ) and open arrow (Q _out) show fluxes of unfrozen water which flow in from up-stream and out to down-stream along the interface. The melt water is partly refrozen and the excess water is discharged down-stream from the area. Wendler and Ishikawa (1974) observed the rate and amount of ablation at various sites on the glacier as a function of altitude through the summer of 1972. The rates of snow melting at these five sites in the lower cirque were derived from the observational results obtained by Wendler and Ishikawa, assuming that the rates of snow melting at these sites were proportional to that observed at site MM shown in Figure 1. It was assumed that there was only Q _m from the surface and no inflow from up-stream at the interface of site LT. Some part of Q _m refreezes to form superimposed ice and the remainder flows out down-stream. At the interface located down-stream from LT, (Q _m+Q _in) — Q _out contributes to the formation of superimposed ice at the interface. Figure 7(b), shows, as an example, variations of Q _m, Q _out and Q _in at site LC for 36 d from 31 May to 6 July 1972. In this figure, the heavy solid curve indicates the total income of melt water (Q _m+Q _in) and Q _out represents the rate of melt-water discharge. Hence, the shaded area shows the net water frozen to form superimposed ice. The changes in the thickness H and the growth rate dH/dt of superimposed ice thus derived are illustrated in Figure 7(c). The total thickness of superimposed ice developed in 36 d was 18 cm, which agrees very well with the value observed at the site LG on 7 July 1972, i.e. 36 d after heavy snow melting started in the accumulation area.

  In Figure 8(a), the thickness of superimposed ice at five sites in the lower cirque is shown as a function of the lapse of time and altitude. As seen in this figure, the augmentation of superimposed ice at site LT located at a higher altitude is less than that at site LG located at lower altitude. This result agreed with the observational fact that the thickness of new superimposed ice formed in the summer of 1972 was larger at the lower altitude than that formed at the higher altitude in the accumulation area of McCall Glacier.

  Figure 8(b) shows the predicted change of the temperature profile in the underlying ice at the site LC. The initial temperature profile was linear, but it changed with time, which was caused by the release of latent heat at the interface. The temperature gradient near the interface on the 36th day agrees fairly well with that observed in the ice at the lower cirque on 7 July 1972, i.e. 36 d after heavy snow melting started in this area (cf. Fig. 3).

Fig. 7. Numerical simulations of the 1972field observations at the lower cirque of McCall Glacier. (a) : A schematic diagram of initial temperature distributions in ice and melt-water Jhw in snow and along the snow-ice interface at five sites in the lower cirque. Dark arrow: water supply from the surface ; shaded and open arrows: inflow and outflow along the interface, (b): Variations of Q_m. Q_in and Q_out with time at site LC. (c): Changes in thickness H and the growth rate dH/dt of superimposed ice at site LC

Fig. 8. (a): Calculated thickness of superimposed ice against time and altitude in the lower cirque, (h): Changes in the temperature distribution in the ice at site LC

(3) Discussion

As mentioned in the preceding section, our computation on the growth of superimposed ice was made under the assumption that the temperature of the overlying wet snow is o⁰C and that of the underlying ice is uniform and below the melting point. Therefore, at t = 0, there must be a discontinuous rise of temperature at the snow-ice interface. This assumption seems to be unreasonable, because the cold-wave penetration in the previous winter must be gradually removed by the percolation of melt water. However, the agreement between calculated result and observational data on the growth of superimposed ice shows that our assumption does not create any serious error in the computation.

Fig. 9. Predictions of the formation of superimposed ice under various thermal conditions in ice. The thickness of superimposed ice formed in 30 d as a function of the rate Q_m of water supply, and in terms of the temperature T₀ of the snow-ice interface, and the temperature, T_B. of ice at a depth of 10 m. (a); The set of solid curves show the thicknesses of superimposed ice for the case when the initial temperature distribution in ice is uniform, i.e. T_o = T_B The set oj dashed curves are those for the case when T_B is fixed at 90⁰C and T₀ variable. (b) : Thickness of superimposed ice for the case when the initial value of T₀ is 9⁰C and T _B variable.

The computed results described above are applicable only for the lower cirque of McCall Glacier, because the computation was simulated to the observational data obtained there. It is, therefore, desirable to predict the formation of superimposed ice under various thermal conditions on different sub-polar glaciers.

The thickness of superimposed ice formed in 30 d was computed as a function of the rate Q _m of water supply, and in terms of the temperature T ₀ of the snow—ice interface, and the temperature T _B of ice at to m depth. The computations were made for the following three cases of different initial temperature distribution in ice.

Case 1: Uniform initial temperature distribution in ice, i.e. T ₀ = T _B The thickness of superimposed ice for this case is given by a set of solid curves in Figure 9(a), for various rates Q _m of water supply.

Case 2: T _B is fixed at —9⁰C and T ₀ variable, assuming the initial temperature profile is linear. The thickness of ice is indicated by a set of dashed curves in Figure 9(a).

Case 3: The initial value of T ₀ is — 9⁰C and T _B variable, assuming the initial temperature profile is linear. The results are shown in Figure 9(b).

In both cases 1 and 2, the thickness of superimposed ice increases markedly with the lowering of the temperature at the interface T ₀ for larger values of water supply Q _m but the thickness of ice remains practically constant for any icc temperature lower than — 3⁰C when Q _m is less than 0.011 g/cm²h. It should be noted that the thicknesses of superimposed ice in these two cases are almost the same except for the case when T ₀ is higher than — 3⁰C. This suggests that the formation of superimposed ice is more sensitive to T ₀ than T _B. The growth rate of superimposed ice is rather insensitive to the temperature T _B as seen in Figure 9(b).

It should also be noted that the thickness of superimposed ice approaches the limiting value as the rate of melt-water supply increases in all the cases. The topmost heavy curves in Figure 9(a) and (b) indicate the upper-limit of the formation of superimposed ice; even if the rate Q _m is sufficiently large, further superimposed ice cannot be formed. This situation is reasonable, because the growth rate of ice rapidly decreases with time and excess water must be discharged as run-off. Values of the ratio of the total amount of superimposed ice to the total amount of melting are listed in Table III as a function of various values of initial temperature of the snow-ice interface (T ₀ = T _B) and the total amount of melting. As seen in this Table, when the underlying ice is cold enough and the amount of water supply is small, the melt water which comes to the interface is entirely refrozen to form superimposed ice.

The calculations and arguments described here may be applicable to the formation of superimposed ice in any glacier existing in sub-polar regions.

Table 3. Ratios or total amount or superimposed ice to the total. amount of melted snow for different temperature regimes in ice

V. Concluding Remarks

In the present paper, it was shown that the observed data on McCall Glacier and experimental results on the formation of superimposed ice can be explained by solving the differential equation for heat How under the various boundary conditions given by field observations and laboratory experiments. The predominant factors controlling the growth rate, or the total amount of superimposed ice in the accumulation area of a sub-polar glacier are the rate of supply of water to the snow-ice interface and the initial temperature distribution in the underlying ice. It may be possible to predict the growth rate and the total amount of superimposed ice, and the ratio of superimposed ice to the total amount of melting in the firn area, of any sub-polar glacier, if observational data on the initial temperature distribution in ice and the rate of water supply or the rate of snow melting at the snow surface are available.

Since level surfaces favour the growth of superimposed ice and steeply sloping ones do not, the slope of the underlying ice surface may be an important factor in the formation of superimposed ice. In our present work, however, it was fixed at 8⁰, the average surface slope of the underlying ice mass in the lower cirque of McCall Glacier, because both the laboratory experiments and the numerical calculations were made mainly for examining the observational data obtained there.

Acknowledgements

This work was part of the Japan-U.S. joint project on “Metamorphism of snow and the transformation of snow into glacier ice in Pacific and Arctic areas”, under the Japan-U.S. Scientific Cooperative Program supported by the Japan Society for Promotion of Science (Principal investigator: Daisuke Kuroiwa, Grant No. 4R007, 1971 -73) U.S, National Science Foundation (Principal investigator: Carl S. Benson, NSF Grants GF 29985 and GA-28278X). The authors wish to express their deepest appreciation to the Japan Society for Promotion of Science for the financial support. The authors are also indebted to Drs G. Wcndler, C. Fahl, and Messrs D. Trabant and N. Ishikawa of Geophysical institute, University of Alaska, Dr D. Kobayashi, the late Mr K. Tanuma, Messrs S. Kobayashi, Y. Endo and Mrs Y. Mizuno for their kind cooperation in the field observations on McCall Glacier.

Discussion

L. Lliboutry: To what extent do your results on artificial superimposed ice depend upon the slope of the ice surface below?

Wakahama; I don’t know the effect of the slope of the ice surface on the growth of artificial superimposed ice, but I agree it is necessary to examine the slope effect. Our experiment was made to simulate the superimposed ice formation at the lower cirque, so the angle of the slope was made the same as that of the snow- ice interface at site LG in the lower cirque of McCall Glacier.

R. Perla: HOW do you define and measure grain size for low density snow? I also address this question to Dr Zwally in connection with his paper on radiative scattering as a function of grain size.

Wakahama: We have consulted the International Classification of Snow in estimating the grain size for any density of snow. In field studies, we measure the grain size of snow by putting the snow grains on a 1 mm grid section paper which is placed in a transparent plastic case. In laboratory work, however, we usually measure the grain size by comparing the grains on a microscopic photograph of a thin section of snow with circles.

J. Zwally: The results I quoted were those of Dr A. J. Gow who took thin sections, estimated the mean diameter of each grain, and counted the number of each. Most of the grains consist of only one or two crystals.