This article concerns the uniform classification of infinite dimensional real topological vector spaces. We examine a recently isolated linearization procedure for uniform homeomorphisms of the form φ: X →Y, where X is a Banach space with non-trivial type and Y is any topological vector space. For such a uniform homeomorphism φ, we show that Y must be normable and have the same supremal type as X. That Y is normable generalizes theorems of Bessaga and Enflo. This aspect of the theory determines new examples of uniform non-equivalence. That supremal type is a uniform invariant for Banach spaces is essentially due to Ribe. Our linearization approach gives an interesting new proof of Ribe's result.

In this paper we prove a new version of the Cowling-Price theorem for Fourier transforms on Rn. Using this we formulate and prove an uncertainty principle for operators. This leads to an analogue of the Cowling-Price theorem for nilpotent Lie groups. We also prove an exact analogue of the Cowling-Price theorem for the Heisenberg group.

This paper concerns parabolic submonoids of a class of monoids known as singular Artin monoids. The latter class includes the singular braid monoid— a geometric extension of the braid group, which was created for the sole purpose of studying Vassiliev invariants in knot theory. However, those monoids may also be construed (and indeed, are defined) as a formal extension of Artin groups which, in turn, naturally generalise braid groups. It is the case, by van der Lek and Paris, that standard parabolic subgroups of Artin groups are canonically isomorphic to Artin groups. This naturally invites us to consider whether the same holds for parabolic submonoids of singular Artin monoids. We show that it is in fact true when the corresponding Coxeter matrix is of ‘type FC’ hence generalising Corran's result in the ‘finite type’ case.

The concept of loosely Markov dynamical systems is introduced. We show that for these systems the recurrence rates and pointwise dimensions coincide. The systems generated by hyperbolic exponential maps, arbitrary rational functions of the Riemann sphere, and measurable dynamical systems generated by infinite conformal iterated function systems are all checked to be loosely Markov.

In this article we study the Fourier space of a general hypergroup and its multipliers. The main result of this paper characterizes commutative hypergroups whose Fourier space forms a Banach algebra under pointwise product with an equivalent norm. Among those hypergroups whose Fourier space forms a Banach algebra, we identify a subclass for which the Gelfand spectrum of the Fourier algebra is equal to the underlying hypergroup. This subclass includes for instance, Jacobi hypergroups, Bessel-Kingman hypergroups.

We study the normed spaces of (equivalence classes of) Banach space-valued functions that are Dobrakov, S* or McShane integrable with respect to a Banach space-valued measure, where the norm is the natural one given by the total semivariation of the indefinite integral. We show that simple functions are dense in these spaces. As a consequence we characterize when the corresponding indefinite integrals have norm relatively compact range. On the other hand, we also determine when these spaces are ultrabornological. Our results apply to conclude, for instance, that the spaces of Birkhoff (respectively McShane) integrable functions defined on a complete (respectively quasi-Radon) probability space, endowed with the Pettis norm, are ultrabornological.

The stability properties of the family ℳ of all intersections of closed balls are investigated in spaces C(K), where K is an arbitrary Hausdorff compact space. We prove that ℳ is stable under Minkowski addition if and only if K is extremally disconnected. In contrast to this, we show that ℳ is always ball stable in these spaces. Finally, we present a Banach space (indeed a subspace of C[0, 1]) which fails to be ball stable, answering an open question. Our results rest on the study of semicontinuous functions in Hausdorff compact spaces.

In this paper we study the size of the value set of the Carmichael λ-functions.

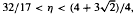Let P denote the set of prime numbers, and let P(n) denote the largest prime factor of an integer n > 1. We show that, for every real number , there exists a constant 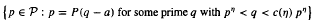c(η) > 1 such that for every integer a ≠ 0, the set has relative asymptotic density one in the set of all prime numbers. Moreover, in the range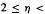 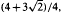, one can take c(η) = 1+ε for any fixed ε > 0. In particular, our results imply that for every real number 0.486 ≤ b.thetav; ≤ 0.531, the relation P(q − a) ≍ qθ holds for infinitely many primes q. We use this result to derive a lower bound on the number of distinct prime divisor of the value of the Carmichael function taken on a product of shifted primes. Finally, we study iterates of the map q ↦ P(q - a) for a > 0, and show that for infinitely many primes q, this map can be iterated at least (log logq)1+o(1) times before it terminates.