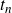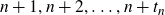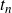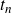1. Introduction
A question of Erdős, Graham and Selfridge ([Reference Erdős and Selfridge6] and [Reference Guy9, B30]) asks to find the least value of
![]() $t_n$
so that the integers
$t_n$
so that the integers
![]() $n+1, n+2, \dots, n+t_n $
contain a subset the product of whose members with n is a square. (If n is a square then we set
$n+1, n+2, \dots, n+t_n $
contain a subset the product of whose members with n is a square. (If n is a square then we set
![]() $t_n=0$
.) That is,
$t_n=0$
.) That is,
![]() $t_n \geq 0$
is the least integer such that there are integers
$t_n \geq 0$
is the least integer such that there are integers
![]() $1\leq j_1 < \cdots <j_s = t_n$
with
$1\leq j_1 < \cdots <j_s = t_n$
with
where “
![]() $m = \square$
” means that the integer m is a square. For instance, we easily compute that
$m = \square$
” means that the integer m is a square. For instance, we easily compute that
![]() $t_2 = 4, t_3 = 5$
and
$t_2 = 4, t_3 = 5$
and
![]() $t_5 = 5$
, since
$t_5 = 5$
, since
 \begin{align*}2\cdot 3\cdot 6 &= 6^2,\\ 3 \cdot 6 \cdot 8 &= 12^2,\\ 5 \cdot 8 \cdot 10 &= 20^2,\end{align*}
\begin{align*}2\cdot 3\cdot 6 &= 6^2,\\ 3 \cdot 6 \cdot 8 &= 12^2,\\ 5 \cdot 8 \cdot 10 &= 20^2,\end{align*}
and none of the last numbers in the products can be replaced by smaller integers.
One can interpret
![]() $t_n$
in terms of integer points on hyperelliptic curves. As an example, we have
$t_n$
in terms of integer points on hyperelliptic curves. As an example, we have
![]() $t_{14}=7$
from
$t_{14}=7$
from
![]() $14\cdot 15 \cdot 18\cdot 20\cdot 21=1260^2$
, and this gives rise to the integral point
$14\cdot 15 \cdot 18\cdot 20\cdot 21=1260^2$
, and this gives rise to the integral point
![]() $(x,y)=(14,1260)$
on the hyperelliptic curve
$(x,y)=(14,1260)$
on the hyperelliptic curve
![]() $y^2=x(x+1)(x+4)(x+6)(x+7)$
. Granville noted this connection [Reference Guy9, B30] and observed that effective versions of Faltings’ Theorem [Reference Faltings7] would lead to corresponding effective bounds on
$y^2=x(x+1)(x+4)(x+6)(x+7)$
. Granville noted this connection [Reference Guy9, B30] and observed that effective versions of Faltings’ Theorem [Reference Faltings7] would lead to corresponding effective bounds on
![]() $t_n$
. Granville mentioned that the ABC conjecture should lead, via work of Elkies [Reference Elkies4] and Langevin [Reference Langevin12], to stronger bounds on
$t_n$
. Granville mentioned that the ABC conjecture should lead, via work of Elkies [Reference Elkies4] and Langevin [Reference Langevin12], to stronger bounds on
![]() $t_n$
. He also stated that, presumably,
$t_n$
. He also stated that, presumably,
![]() $t_n > n^c $
for some fixed constant
$t_n > n^c $
for some fixed constant
![]() $ c > 0 $
, and perhaps one could prove this assuming the ABC conjecture.
$ c > 0 $
, and perhaps one could prove this assuming the ABC conjecture.
Our first result below shows that this supposition fails dramatically. A beautiful result of Granville and Selfridge [Reference Granville and Selfridge8, Corollary 1] shows that if the largest prime factor
![]() $P^+(n) $
of n satisfies
$P^+(n) $
of n satisfies
![]() $P^+(n) > \sqrt{2n}+1$
then
$P^+(n) > \sqrt{2n}+1$
then
![]() $t_n = P^+(n)$
. This inspired us to study closely the relationship between
$t_n = P^+(n)$
. This inspired us to study closely the relationship between
![]() $P^+(n)$
and
$P^+(n)$
and
![]() $t_n$
. While
$t_n$
. While
![]() $t_n$
and
$t_n$
and
![]() $P^+(n)$
may no longer be close if
$P^+(n)$
may no longer be close if
![]() $P^+(n) \leq \sqrt{2n}+1$
, we find the distribution of
$P^+(n) \leq \sqrt{2n}+1$
, we find the distribution of
![]() $t_n$
continues to follow that of
$t_n$
continues to follow that of
![]() $P^+(n)$
in larger ranges.
$P^+(n)$
in larger ranges.
Theorem 1·1.
For any fixed
![]() $c \in (0,1]$
,
$c \in (0,1]$
,
Remark 1. The right-hand side in the statement of Theorem 1·1 is equal to
![]() $\rho(1/c)$
, where
$\rho(1/c)$
, where
![]() $\rho(u)$
is the well-known Dickman–de Bruijn function which plays a prominent role in the theory of smooth numbers [Reference Hildebrand and Tenenbaum11]. Therefore, for every fixed
$\rho(u)$
is the well-known Dickman–de Bruijn function which plays a prominent role in the theory of smooth numbers [Reference Hildebrand and Tenenbaum11]. Therefore, for every fixed
![]() $c > 0$
a positive proportion of integers n satisfy
$c > 0$
a positive proportion of integers n satisfy
![]() $t_n \leq n^c$
.
$t_n \leq n^c$
.
Theorem 1·1 is a corollary of a slightly stronger theorem (Theorem 3·1) which we state and prove in Section 3 below.
Our next result shows there are integers n attaining even smaller values of
![]() $t_n$
, much smaller than
$t_n$
, much smaller than
![]() $n^c$
.
$n^c$
.
Theorem 1·2.
Let
![]() $\epsilon>0$
be fixed and sufficiently small, and let x be sufficiently large depending on
$\epsilon>0$
be fixed and sufficiently small, and let x be sufficiently large depending on
![]() $\epsilon$
. Then there are at least
$\epsilon$
. Then there are at least
![]() $x \exp\! \Big(\!-\!\big({3\sqrt{2}}/{2}+\epsilon \big)\sqrt{\log x \log \log x} \Big)$
integers
$x \exp\! \Big(\!-\!\big({3\sqrt{2}}/{2}+\epsilon \big)\sqrt{\log x \log \log x} \Big)$
integers
![]() $n\leq x$
such that
$n\leq x$
such that
![]() $t_n \leq \exp\! \left(\sqrt{(2+\epsilon)\log n \log \log n} \right)$
.
$t_n \leq \exp\! \left(\sqrt{(2+\epsilon)\log n \log \log n} \right)$
.
Suitable modification of the proof of Theorem 1·2 shows there exist hyperelliptic curves of large genus which have integral points of nontrivial height (see further comments and discussion at the end of Section 5).
Theorem 1·3.
Fix a constant
![]() $c \in (0,1)$
. There are arbitrarily large positive integers J such that the following is true: there exist N positive integers
$c \in (0,1)$
. There are arbitrarily large positive integers J such that the following is true: there exist N positive integers
![]() $1\leq j_1 < j_2 < \cdots < j_N < J$
with
$1\leq j_1 < j_2 < \cdots < j_N < J$
with
![]() $N \geq J^{1-c}$
and a positive integer
$N \geq J^{1-c}$
and a positive integer
![]() $x\geq \exp\! \left({c^2}{(\!\log J)^2}/({5\log \log J}) \right)$
such that
$x\geq \exp\! \left({c^2}{(\!\log J)^2}/({5\log \log J}) \right)$
such that
![]() $x(x+J)\prod_{i=1}^N(x+j_i)$
is a square.
$x(x+J)\prod_{i=1}^N(x+j_i)$
is a square.
In the complementary direction, we prove a lower bound on
![]() $t_n$
when n is not a square (recall
$t_n$
when n is not a square (recall
![]() $t_n=0$
when n is a square). The proof also uses a framework of hyperelliptic curves, and requires bounding the height of integral points on curves.
$t_n=0$
when n is a square). The proof also uses a framework of hyperelliptic curves, and requires bounding the height of integral points on curves.
Theorem 1·4. If n is a sufficiently large non-square integer, then
The implied constant is effectively computable.
The outline of the rest of the paper is as follows. In Section 2, we describe the notation and conventions of the paper. In Section 3, we state Theorem 3·1, of which Theorem 1·1 is essentially a special case; we assemble the ingredients for the proof and then prove Theorems 3·1 and 1·1. In Section 4, we prove Theorem 1·2. Section 5 contains the results and modifications of the proof of Theorem 1·2 necessary to prove Theorem 1·3; we close the section with some comments and discussion. We prove Theorem 1·4 in Section 6.
2. Notation and conventions
Given a positive integer n, the integer
![]() $t_n$
is the smallest nonnegative integer so that the integers
$t_n$
is the smallest nonnegative integer so that the integers
![]() $n+1, n+2, \dots, n+t_n $
contain a subset the product of whose members with n is a square. If n is a square then we define
$n+1, n+2, \dots, n+t_n $
contain a subset the product of whose members with n is a square. If n is a square then we define
![]() $t_n=0$
.
$t_n=0$
.
The expression
![]() $m = \square$
means that the integer m is a square. We write
$m = \square$
means that the integer m is a square. We write
![]() $P^+(n)$
for the largest prime factor of a positive integer n. We set
$P^+(n)$
for the largest prime factor of a positive integer n. We set
![]() $P^+(1)=1$
. We write
$P^+(1)=1$
. We write
![]() $\omega(n)$
for the number of distinct prime factors of n.
$\omega(n)$
for the number of distinct prime factors of n.
A number n is y–smooth if
![]() $P^+(n)\leq y$
. We write
$P^+(n)\leq y$
. We write
![]() $\Psi(x,y)$
for the number of y–smooth integers
$\Psi(x,y)$
for the number of y–smooth integers
![]() $n\leq x$
, and
$n\leq x$
, and
![]() $\rho(u)$
for the Dickman–de Bruijn function.
$\rho(u)$
for the Dickman–de Bruijn function.
We let
![]() $P^*(n)$
denote the largest prime which divides n to an odd power. Let
$P^*(n)$
denote the largest prime which divides n to an odd power. Let
![]() $S_\square(x,y) = \{n\leq x \;:\; P^*(n)\leq y\}$
, the set of integers
$S_\square(x,y) = \{n\leq x \;:\; P^*(n)\leq y\}$
, the set of integers
![]() $n\leq x$
which are a square times a y–smooth integer. As noted by Granville and Selfridge [Reference Granville and Selfridge8, p.4] we have
$n\leq x$
which are a square times a y–smooth integer. As noted by Granville and Selfridge [Reference Granville and Selfridge8, p.4] we have
![]() $P^*(n)\leq t_n$
. Therefore, if
$P^*(n)\leq t_n$
. Therefore, if
![]() $n\leq x$
and
$n\leq x$
and
![]() $t_n\leq y$
, then
$t_n\leq y$
, then
![]() $n \in S_\square(x,y)$
. So
$n \in S_\square(x,y)$
. So
One can easily show that
![]() $\Psi_\square(x,y) \sim \Psi(x,y)$
for
$\Psi_\square(x,y) \sim \Psi(x,y)$
for
![]() $y\geq (\!\log x)^3$
by results on
$y\geq (\!\log x)^3$
by results on
![]() $\Psi(x/d,y)/\Psi(x,y)$
like in [Reference de la Bretèche and Tenenbaum3].
$\Psi(x/d,y)/\Psi(x,y)$
like in [Reference de la Bretèche and Tenenbaum3].
Given two finite sets S and T, we write
![]() $S \Delta T$
for the symmetric difference of S and T. That is,
$S \Delta T$
for the symmetric difference of S and T. That is,
![]() $S\Delta T$
consists of those elements which are in one of S or T but not both:
$S\Delta T$
consists of those elements which are in one of S or T but not both:
![]() $S\Delta T = (S \cup T) \backslash (S \cap T)$
. By associativity one can consider the symmetric difference of any finite number of sets
$S\Delta T = (S \cup T) \backslash (S \cap T)$
. By associativity one can consider the symmetric difference of any finite number of sets
Given a finite set S we write
![]() $\# S$
or
$\# S$
or
![]() $|S|$
for the cardinality of S. The power set of S, i.e. the set that consists of all the subsets of S, is denoted by
$|S|$
for the cardinality of S. The power set of S, i.e. the set that consists of all the subsets of S, is denoted by
![]() $\mathcal{P}(S)$
.
$\mathcal{P}(S)$
.
The finite field with two elements is denoted as
![]() $\mathbb{F}_2$
.
$\mathbb{F}_2$
.
The real number x is always large. The notation o(1) denotes a quantity tending to zero as some other parameter, usually x, tends to infinity. We write
![]() $f \ll g, g \gg f$
, or
$f \ll g, g \gg f$
, or
![]() $f = O(g)$
if there exists a constant C such that
$f = O(g)$
if there exists a constant C such that
![]() $f \leq Cg$
. We write
$f \leq Cg$
. We write
![]() $f \sim g$
if
$f \sim g$
if
![]() $f = (1+o(1))g$
.
$f = (1+o(1))g$
.
In discussion, but not in proofs, we sometimes refer to the height of an integral point (x, y) on a curve. By this we mean the naive height
![]() $\max(|x|,|y|)$
. We similarly refer to the height of an integer polynomial, which is the maximum of the absolute value of its coefficients.
$\max(|x|,|y|)$
. We similarly refer to the height of an integer polynomial, which is the maximum of the absolute value of its coefficients.
3. The distribution of
 $t_n$
: Proof of Theorem 1·1
$t_n$
: Proof of Theorem 1·1
As mentioned in the introduction, Theorem 1·1 is a corollary of a somewhat stronger result, which we state here.
Theorem 3·1.
Let x be sufficiently large, and let c satisfy
![]() ${(\!\log \log \log x)^2}/{\log \log x} \leq c \leq 1$
. Then
${(\!\log \log \log x)^2}/{\log \log x} \leq c \leq 1$
. Then
 \begin{align*}\sum_{\substack{n\leq x \\ t_n \leq x^c}}1 = \sum_{\substack{n\leq x \\ P^+(n) \leq x^c}} 1 + O \Big(\frac{x}{c\log x} \Big)\end{align*}
\begin{align*}\sum_{\substack{n\leq x \\ t_n \leq x^c}}1 = \sum_{\substack{n\leq x \\ P^+(n) \leq x^c}} 1 + O \Big(\frac{x}{c\log x} \Big)\end{align*}
uniformly in c.
We prove Theorem 3·1 by proving upper bounds for
 \begin{align*}\sum_{\substack{n\leq x \\ t_n \leq x^c}}1 \ \ \ \ \ \ \ \text{ and } \ \ \ \ \ \ \ \sum_{\substack{n\leq x \\ P^+(n) \leq x^c}}1\end{align*}
\begin{align*}\sum_{\substack{n\leq x \\ t_n \leq x^c}}1 \ \ \ \ \ \ \ \text{ and } \ \ \ \ \ \ \ \sum_{\substack{n\leq x \\ P^+(n) \leq x^c}}1\end{align*}
in terms of each other. More precisely, the proof of Theorem 3·1 relies on the following two propositions.
Proposition 3·2 (
![]() $t_n$
less than
$t_n$
less than
![]() $P^+(n)$
on average). Let
$P^+(n)$
on average). Let
![]() $0 < c \leq 1$
. Then
$0 < c \leq 1$
. Then
 \begin{align*}\sum_{\substack{n\leq x \\ t_n \leq x^c}}1 \leq \sum_{\substack{n\leq x \\ P^+(n) \leq x^c}}1 + O(x\exp\!(\!-\!\sqrt{\log x}))\end{align*}
\begin{align*}\sum_{\substack{n\leq x \\ t_n \leq x^c}}1 \leq \sum_{\substack{n\leq x \\ P^+(n) \leq x^c}}1 + O(x\exp\!(\!-\!\sqrt{\log x}))\end{align*}
uniformly in c.
Proposition 3·3 (
![]() $P^+(n)$
less than
$P^+(n)$
less than
![]() $t_n$
on average). Let
$t_n$
on average). Let
![]() $0 < c \leq 1$
. Then
$0 < c \leq 1$
. Then
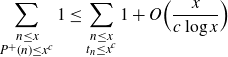 \begin{align*}\sum_{\substack{n\leq x \\ P^+(n) \leq x^c}}1 \leq \sum_{\substack{n\leq x \\ t_n \leq x^c}}1 + O \Big(\frac{x}{c\log x} \Big)\end{align*}
\begin{align*}\sum_{\substack{n\leq x \\ P^+(n) \leq x^c}}1 \leq \sum_{\substack{n\leq x \\ t_n \leq x^c}}1 + O \Big(\frac{x}{c\log x} \Big)\end{align*}
uniformly in c.
Proof of Theorem 3·1 assuming Propositions 3·2 and 3·3. From Proposition 3·2 we have
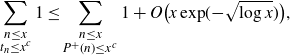 \begin{align*}\sum_{\substack{n\leq x \\ t_n \leq x^c}}1 \leq \sum_{\substack{n\leq x \\ P^+(n) \leq x^c}}1 + O\big(x\exp\!(\!-\!\sqrt{\log x})\big),\end{align*}
\begin{align*}\sum_{\substack{n\leq x \\ t_n \leq x^c}}1 \leq \sum_{\substack{n\leq x \\ P^+(n) \leq x^c}}1 + O\big(x\exp\!(\!-\!\sqrt{\log x})\big),\end{align*}
so from Proposition 3·3 we have
 \begin{align*}\sum_{\substack{n\leq x \\ t_n \leq x^c}}1 = \sum_{\substack{n\leq x \\ P^+(n) \leq x^c}}1 + O \Big(\frac{x}{c\log x} \Big).\end{align*}
\begin{align*}\sum_{\substack{n\leq x \\ t_n \leq x^c}}1 = \sum_{\substack{n\leq x \\ P^+(n) \leq x^c}}1 + O \Big(\frac{x}{c\log x} \Big).\end{align*}
That this asymptotic formula is non-trivial for the stated range of c follows from classical estimates for smooth numbers [Reference Hildebrand10, Reference Hildebrand and Tenenbaum11].
We first turn our attention to Proposition 3·2, since the proof is simpler and introduces some of the key ideas. The first result we need is a simple inequality relating
![]() $t_n$
and
$t_n$
and
![]() $P^+(n)$
.
$P^+(n)$
.
Lemma 3·4.
If
![]() $P^+(n)^2 \nmid n$
, then
$P^+(n)^2 \nmid n$
, then
![]() $t_n \geq P^+(n)$
.
$t_n \geq P^+(n)$
.
Proof. Let
![]() $p = P^+(n)$
. If
$p = P^+(n)$
. If
![]() $p^2 \nmid n$
, then n is not a square so by the definition of
$p^2 \nmid n$
, then n is not a square so by the definition of
![]() $t_n$
there are integers
$t_n$
there are integers
![]() $1\leq j_1 < \cdots < j_s =t_n$
with
$1\leq j_1 < \cdots < j_s =t_n$
with
![]() $n\prod_{i=1}^s (n+j_i) = \square$
. Since p divides the left-hand side to an even power but
$n\prod_{i=1}^s (n+j_i) = \square$
. Since p divides the left-hand side to an even power but
![]() $p^2 \nmid n$
there is some i such that
$p^2 \nmid n$
there is some i such that
![]() $p \mid n+j_i$
. Since
$p \mid n+j_i$
. Since
![]() $p\mid n$
and
$p\mid n$
and
![]() $p \mid n+j_i$
we have
$p \mid n+j_i$
we have
![]() $p \mid j_i$
, so
$p \mid j_i$
, so
![]() $t_n \geq j_i \geq p$
.
$t_n \geq j_i \geq p$
.
We also need a result quantifying that it is rare for an integer n to be divisible by the square of its largest prime factor (see also [Reference Erdős and Graham5, p. 345]).
Lemma 3·5 (Bound for exceptional set with
![]() $P^+(n)^2 \mid n$
). Let
$P^+(n)^2 \mid n$
). Let
![]() $\mathcal{E}$
denote the set of
$\mathcal{E}$
denote the set of
![]() $n\leq x$
such that
$n\leq x$
such that
![]() $P^+(n)^2 \mid n$
. Then
$P^+(n)^2 \mid n$
. Then
![]() $|\mathcal{E}| \ll x \exp\!(\!-\!\sqrt{\log x})$
.
$|\mathcal{E}| \ll x \exp\!(\!-\!\sqrt{\log x})$
.
Proof. Any
![]() $n \in \mathcal{E}$
may be written as
$n \in \mathcal{E}$
may be written as
![]() $n = p^2 m$
, where
$n = p^2 m$
, where
![]() $P^+(m) \leq p$
, and therefore
$P^+(m) \leq p$
, and therefore
 \begin{align*}|\mathcal{E}| &\leq \sum_{p\leq x^{1/2}} \sum_{\substack{m\leq x/p^2 \\ P^+(m) \leq p}} 1.\end{align*}
\begin{align*}|\mathcal{E}| &\leq \sum_{p\leq x^{1/2}} \sum_{\substack{m\leq x/p^2 \\ P^+(m) \leq p}} 1.\end{align*}
We introduce a parameter
![]() $10\leq P \leq x^{1/2}$
and split the sum over p at P. The contribution from
$10\leq P \leq x^{1/2}$
and split the sum over p at P. The contribution from
![]() $p > P$
is trivially
$p > P$
is trivially
![]() $\ll x/P$
. We bound the contribution from
$\ll x/P$
. We bound the contribution from
![]() $p\leq P$
using Rankin’s trick. Set
$p\leq P$
using Rankin’s trick. Set
![]() $\alpha = 1 - {1}/{\log P}$
, so that
$\alpha = 1 - {1}/{\log P}$
, so that
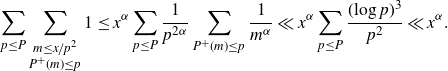 \begin{align*}\sum_{p\leq P}\sum_{\substack{m\leq x/p^2 \\ P^+(m) \leq p}} 1 &\leq x^{\alpha}\sum_{p\leq P} \frac{1}{p^{2\alpha}} \sum_{P^+(m) \leq p} \frac{1}{m^\alpha} \ll x^\alpha \sum_{p\leq P} \frac{(\!\log p)^3}{p^2} \ll x^\alpha.\end{align*}
\begin{align*}\sum_{p\leq P}\sum_{\substack{m\leq x/p^2 \\ P^+(m) \leq p}} 1 &\leq x^{\alpha}\sum_{p\leq P} \frac{1}{p^{2\alpha}} \sum_{P^+(m) \leq p} \frac{1}{m^\alpha} \ll x^\alpha \sum_{p\leq P} \frac{(\!\log p)^3}{p^2} \ll x^\alpha.\end{align*}
We have therefore proved
![]() $|\mathcal{E}| \ll x/P + x \exp\! ( - {\log x}/{\log P})$
, and the optimal choice is to take
$|\mathcal{E}| \ll x/P + x \exp\! ( - {\log x}/{\log P})$
, and the optimal choice is to take
![]() $P = \exp\! (\sqrt{\log x})$
.
$P = \exp\! (\sqrt{\log x})$
.
We now have the tools to prove Proposition 3·2.
Proof of Proposition 3·2. We split the integers
![]() $n\leq x$
according to whether or not
$n\leq x$
according to whether or not
![]() $P^+(n)^2 \mid n$
, so that
$P^+(n)^2 \mid n$
, so that
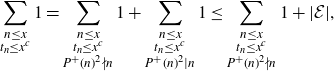 \begin{align*}\sum_{\substack{n\leq x \\ t_n \leq x^c}} 1 &= \sum_{\substack{n\leq x \\ t_n \leq x^c \\ P^+(n)^2 \nmid n}} 1 + \sum_{\substack{n\leq x \\ t_n \leq x^c \\ P^+(n)^2 \mid n}} 1 \leq \sum_{\substack{n\leq x \\ t_n \leq x^c \\ P^+(n)^2 \nmid n}} 1 + |\mathcal{E}|,\end{align*}
\begin{align*}\sum_{\substack{n\leq x \\ t_n \leq x^c}} 1 &= \sum_{\substack{n\leq x \\ t_n \leq x^c \\ P^+(n)^2 \nmid n}} 1 + \sum_{\substack{n\leq x \\ t_n \leq x^c \\ P^+(n)^2 \mid n}} 1 \leq \sum_{\substack{n\leq x \\ t_n \leq x^c \\ P^+(n)^2 \nmid n}} 1 + |\mathcal{E}|,\end{align*}
where
![]() $\mathcal{E}$
is the set in Lemma 3·5. If
$\mathcal{E}$
is the set in Lemma 3·5. If
![]() $P^+(n)^2 \nmid n$
then we have
$P^+(n)^2 \nmid n$
then we have
![]() $P^+(n) \leq t_n$
by Lemma 3·4, so
$P^+(n) \leq t_n$
by Lemma 3·4, so
 \begin{align*}\sum_{\substack{n\leq x \\ t_n \leq x^c \\ P^+(n)^2 \nmid n}} 1 = \sum_{\substack{n\leq x \\ t_n \leq x^c \\ P^+(n)\leq x^c \\ P^+(n)^2 \nmid n}} 1\leq \sum_{\substack{n\leq x \\ P^+(n) \leq x^c}} 1,\end{align*}
\begin{align*}\sum_{\substack{n\leq x \\ t_n \leq x^c \\ P^+(n)^2 \nmid n}} 1 = \sum_{\substack{n\leq x \\ t_n \leq x^c \\ P^+(n)\leq x^c \\ P^+(n)^2 \nmid n}} 1\leq \sum_{\substack{n\leq x \\ P^+(n) \leq x^c}} 1,\end{align*}
by positivity. Therefore
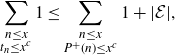 \begin{align*}\sum_{\substack{n\leq x \\ t_n \leq x^c}} 1 \leq \sum_{\substack{n\leq x \\ P^+(n) \leq x^c}} 1 + |\mathcal{E}|,\end{align*}
\begin{align*}\sum_{\substack{n\leq x \\ t_n \leq x^c}} 1 \leq \sum_{\substack{n\leq x \\ P^+(n) \leq x^c}} 1 + |\mathcal{E}|,\end{align*}
and we finish with an appeal to Lemma 3·5.
The proof of Proposition 3·3 is slightly more circuitous, and relies upon an analysis of the number of subsets S of an interval with
![]() $\prod_{n \in S} n = \square$
. For this we require two more lemmas, though the reader may wish to skip ahead and see how the lemmas are used in establishing Proposition 3·3 before examining their proofs.
$\prod_{n \in S} n = \square$
. For this we require two more lemmas, though the reader may wish to skip ahead and see how the lemmas are used in establishing Proposition 3·3 before examining their proofs.
Lemma 3·6 (Subset squares and
![]() $t_n$
in intervals). Let
$t_n$
in intervals). Let
![]() $I = (x,x+y]$
be an interval. The number of subsets S of
$I = (x,x+y]$
be an interval. The number of subsets S of
![]() $I \cap \mathbb{N}$
such that
$I \cap \mathbb{N}$
such that
![]() $\prod_{n \in S} n = \square$
is equal to
$\prod_{n \in S} n = \square$
is equal to
![]() $2^r$
, where
$2^r$
, where
Proof. The result is trivially true if
![]() $r=0$
, so assume
$r=0$
, so assume
![]() $r\geq 1$
. Let
$r\geq 1$
. Let
![]() $n_1 < \cdots < n_r$
be those integers with
$n_1 < \cdots < n_r$
be those integers with
![]() $x< n \leq n+t_n \leq x+y$
, and let
$x< n \leq n+t_n \leq x+y$
, and let
![]() $P_i$
be a non-empty product of integers in
$P_i$
be a non-empty product of integers in
![]() $[n_i,n_i+t_{n_i}]$
, including the endpoints, for which the product equals a square. Given
$[n_i,n_i+t_{n_i}]$
, including the endpoints, for which the product equals a square. Given
![]() $\ell_1 < \cdots < \ell_j \in (x,x+y]$
, define
$\ell_1 < \cdots < \ell_j \in (x,x+y]$
, define
![]() $v(\ell_1^{e_1}\cdots \ell_j^{e_j}) = \prod_{i : e_i \text{ odd}} \ell_i$
.
$v(\ell_1^{e_1}\cdots \ell_j^{e_j}) = \prod_{i : e_i \text{ odd}} \ell_i$
.
We claim that the
![]() $v(\prod_{i \in I} P_i), I \subset \{1,\ldots,r\}$
are distinct. If two are equal, select them minimally so that the
$v(\prod_{i \in I} P_i), I \subset \{1,\ldots,r\}$
are distinct. If two are equal, select them minimally so that the
![]() $P_i$
are distinct and therefore
$P_i$
are distinct and therefore
![]() $v(P_{i_1}\cdots P_{i_\ell}) = v(P_{j_1}\cdots P_{j_k})$
, say, with all the
$v(P_{i_1}\cdots P_{i_\ell}) = v(P_{j_1}\cdots P_{j_k})$
, say, with all the
![]() $i_*,j_*$
distinct. We may assume
$i_*,j_*$
distinct. We may assume
![]() $i_1 < j_1$
, and therefore
$i_1 < j_1$
, and therefore
![]() $n_1$
is part of the first product but not the second, a contradiction.
$n_1$
is part of the first product but not the second, a contradiction.
We claim that if
![]() $m_1 < \cdots < m_k \in (x,x+y]$
with
$m_1 < \cdots < m_k \in (x,x+y]$
with
![]() $m_1\cdots m_k = \square$
then
$m_1\cdots m_k = \square$
then
If not, select such a product with
![]() $m_1$
maximal. By definition
$m_1$
maximal. By definition
![]() $x<m_1\leq m_1+t_{m_1}\leq m_k \leq x+y$
, and so
$x<m_1\leq m_1+t_{m_1}\leq m_k \leq x+y$
, and so
![]() $m_1 = n_\ell$
for some
$m_1 = n_\ell$
for some
![]() $\ell$
. Then
$\ell$
. Then
![]() $\square = v(P_\ell m_1\cdots m_k) = v(n_\ell P_\ell m_2 \cdots m_k) = M_1\cdots M_k$
, where
$\square = v(P_\ell m_1\cdots m_k) = v(n_\ell P_\ell m_2 \cdots m_k) = M_1\cdots M_k$
, where
![]() $M_1 > m_1$
. By the maximality of
$M_1 > m_1$
. By the maximality of
![]() $m_1$
we have
$m_1$
we have
![]() $M_1 \cdots M_k = v(\prod_{i\in I}P_i)$
for some
$M_1 \cdots M_k = v(\prod_{i\in I}P_i)$
for some
![]() $I \subset \{1,\ldots,r\}$
, and so
$I \subset \{1,\ldots,r\}$
, and so
a contradiction.
We deduce there are
![]() $2^r$
products of distinct integers in
$2^r$
products of distinct integers in
![]() $(x,x+y]$
which give a square.
$(x,x+y]$
which give a square.
Lemma 3·7 (
![]() $t_n$
in intervals and smooth numbers). Let
$t_n$
in intervals and smooth numbers). Let
![]() $I = (x,x+y]$
be an interval. We have
$I = (x,x+y]$
be an interval. We have
Proof. Let
and let
![]() $\{n_1,\ldots,n_k\}$
be the largest subset of N such that if
$\{n_1,\ldots,n_k\}$
be the largest subset of N such that if
![]() $\prod_{i \in I} n_i$
is a square with
$\prod_{i \in I} n_i$
is a square with
![]() $I \subset \{1,\ldots,k\}$
then
$I \subset \{1,\ldots,k\}$
then
![]() $I = \varnothing$
(that is, they are the largest multiplicatively independent subset in
$I = \varnothing$
(that is, they are the largest multiplicatively independent subset in
![]() $\mathbb{Z}$
modulo squares), so
$\mathbb{Z}$
modulo squares), so
![]() $k\leq \pi(y)$
.
$k\leq \pi(y)$
.
Any subproduct of
![]() $n_{k+1}\cdots n_m$
is therefore dependent on
$n_{k+1}\cdots n_m$
is therefore dependent on
![]() $n_1,\ldots,n_k$
. That is, if
$n_1,\ldots,n_k$
. That is, if
![]() $J \subset \{k+1,\ldots,m\}$
then there exists
$J \subset \{k+1,\ldots,m\}$
then there exists
![]() $J = J(I) \subset \{1,\ldots,k\}$
such that
$J = J(I) \subset \{1,\ldots,k\}$
such that
These products are distinct since the sets J are distinct. The number of square products is therefore
![]() $\geq 2^{m-k}$
. Combining this with Lemma 3·6 yields
$\geq 2^{m-k}$
. Combining this with Lemma 3·6 yields
Proof of Proposition 3·3. If x is sufficiently large and
![]() $P^+(n) > x^{0.51}$
then [Reference Granville and Selfridge8, Corollary 1] implies
$P^+(n) > x^{0.51}$
then [Reference Granville and Selfridge8, Corollary 1] implies
![]() $P^+(n)=t_n$
, and therefore
$P^+(n)=t_n$
, and therefore
 \begin{align*}\sum_{\substack{n\leq x \\ P^+(n) \leq x^c}} 1 = \sum_{\substack{n\leq x \\ P^+(n) \leq x^{0.51}}} 1 + \sum_{\substack{n\leq x \\ x^{0.51}<t_n \leq x^c}} 1.\end{align*}
\begin{align*}\sum_{\substack{n\leq x \\ P^+(n) \leq x^c}} 1 = \sum_{\substack{n\leq x \\ P^+(n) \leq x^{0.51}}} 1 + \sum_{\substack{n\leq x \\ x^{0.51}<t_n \leq x^c}} 1.\end{align*}
The proposition in the case
![]() $c>0.51$
therefore follows from the proposition in the case
$c>0.51$
therefore follows from the proposition in the case
![]() $c\leq 0.51$
, so we may assume
$c\leq 0.51$
, so we may assume
![]() $c\leq 0.51$
.
$c\leq 0.51$
.
Let
![]() $I = (x,x+y]$
so Lemma 3·7 reads as
$I = (x,x+y]$
so Lemma 3·7 reads as
Now, since
![]() $P^*(n)\leq t_n$
we have
$P^*(n)\leq t_n$
we have
Combining the last two equations gives
![]() $\#\{n\in I \;:\; P^*(n)\leq y < t_n\} \leq \pi(y)$
, and so
$\#\{n\in I \;:\; P^*(n)\leq y < t_n\} \leq \pi(y)$
, and so
Summing this up over intervals of length y gives
Proof of Theorem 1·1. By [Reference Granville and Selfridge8, Corollary 1] we may assume
![]() $c\leq 0.51$
. We have
$c\leq 0.51$
. We have
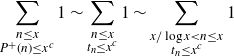 \begin{align*}\sum_{\substack{n\leq x \\ P^+(n) \leq x^c}} 1 \sim \sum_{\substack{n\leq x \\ t_n \leq x^c}} 1 \sim \sum_{\substack{x/\log x < n\leq x \\ t_n \leq x^c}} 1\end{align*}
\begin{align*}\sum_{\substack{n\leq x \\ P^+(n) \leq x^c}} 1 \sim \sum_{\substack{n\leq x \\ t_n \leq x^c}} 1 \sim \sum_{\substack{x/\log x < n\leq x \\ t_n \leq x^c}} 1\end{align*}
by Theorem 3·1 and trivial estimation. We split the sum acording to the size of
![]() $t_n$
so that
$t_n$
so that
 \begin{align*}\sum_{\substack{x/\log x < n\leq x \\ t_n \leq x^c}} 1 &\sim \sum_{\substack{n\leq x \\ t_n \leq n^c}} 1 + O \Big(\sum_{\substack{n\leq x \\ (x/\log x)^c < t_n \leq x^c}} 1 \Big).\end{align*}
\begin{align*}\sum_{\substack{x/\log x < n\leq x \\ t_n \leq x^c}} 1 &\sim \sum_{\substack{n\leq x \\ t_n \leq n^c}} 1 + O \Big(\sum_{\substack{n\leq x \\ (x/\log x)^c < t_n \leq x^c}} 1 \Big).\end{align*}
We must show
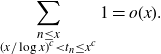 \begin{align*}\sum_{\substack{n\leq x \\ (x/\log x)^c < t_n \leq x^c}} 1 = o(x).\end{align*}
\begin{align*}\sum_{\substack{n\leq x \\ (x/\log x)^c < t_n \leq x^c}} 1 = o(x).\end{align*}
We split the sum over n according to whether or not
![]() $n \in \mathcal{E}$
, with
$n \in \mathcal{E}$
, with
![]() $\mathcal{E}$
as in Lemma 3·5. The size of
$\mathcal{E}$
as in Lemma 3·5. The size of
![]() $\mathcal{E}$
is o(x). If
$\mathcal{E}$
is o(x). If
![]() $n \not \in \mathcal{E}$
then
$n \not \in \mathcal{E}$
then
![]() $P^+(n) \leq t_n$
, and we may further split the sum with
$P^+(n) \leq t_n$
, and we may further split the sum with
![]() $n \not \in \mathcal{E}$
according to whether or not
$n \not \in \mathcal{E}$
according to whether or not
![]() $P^+(n) \leq (x/\log x)^c$
. Hence
$P^+(n) \leq (x/\log x)^c$
. Hence
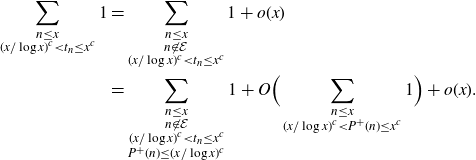 \begin{align*}\sum_{\substack{n\leq x \\ (x/\log x)^c < t_n \leq x^c}} 1 &= \sum_{\substack{n\leq x \\ n \not \in \mathcal{E} \\ (x/\log x)^c < t_n \leq x^c}} 1+o(x)\\&= \sum_{\substack{n\leq x \\ n \not \in \mathcal{E} \\ (x/\log x)^c < t_n \leq x^c \\ P^+(n) \leq (x/\log x)^c}} 1 + O \Big(\sum_{\substack{n\leq x \\ (x/\log x)^c < P^+(n) \leq x^c}} 1 \Big)+o(x).\end{align*}
\begin{align*}\sum_{\substack{n\leq x \\ (x/\log x)^c < t_n \leq x^c}} 1 &= \sum_{\substack{n\leq x \\ n \not \in \mathcal{E} \\ (x/\log x)^c < t_n \leq x^c}} 1+o(x)\\&= \sum_{\substack{n\leq x \\ n \not \in \mathcal{E} \\ (x/\log x)^c < t_n \leq x^c \\ P^+(n) \leq (x/\log x)^c}} 1 + O \Big(\sum_{\substack{n\leq x \\ (x/\log x)^c < P^+(n) \leq x^c}} 1 \Big)+o(x).\end{align*}
The O-term has size
![]() $\ll x({\log \log x}/{\log x})$
. For the other sum, we set
$\ll x({\log \log x}/{\log x})$
. For the other sum, we set
![]() $Y = (x/\log x)^c$
and note that
$Y = (x/\log x)^c$
and note that
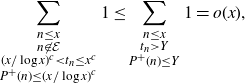 \begin{align*}\sum_{\substack{n\leq x \\ n \not \in \mathcal{E} \\ (x/\log x)^c < t_n \leq x^c \\ P^+(n) \leq (x/\log x)^c}} 1 &\leq \sum_{\substack{n\leq x \\ t_n > Y \\ P^+(n) \leq Y}} 1 = o(x),\end{align*}
\begin{align*}\sum_{\substack{n\leq x \\ n \not \in \mathcal{E} \\ (x/\log x)^c < t_n \leq x^c \\ P^+(n) \leq (x/\log x)^c}} 1 &\leq \sum_{\substack{n\leq x \\ t_n > Y \\ P^+(n) \leq Y}} 1 = o(x),\end{align*}
by the argument in the proof of Proposition 3·3.
Since we similarly have
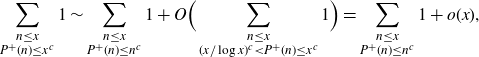 \begin{align*}\sum_{\substack{n\leq x \\ P^+(n) \leq x^c}} 1 \sim \sum_{\substack{n\leq x \\ P^+(n) \leq n^c}} 1 + O\Big(\sum_{\substack{n\leq x \\ (x/\log x)^c < P^+(n) \leq x^c}} 1 \Big) = \sum_{\substack{n\leq x \\ P^+(n) \leq n^c}} 1 + o(x),\end{align*}
\begin{align*}\sum_{\substack{n\leq x \\ P^+(n) \leq x^c}} 1 \sim \sum_{\substack{n\leq x \\ P^+(n) \leq n^c}} 1 + O\Big(\sum_{\substack{n\leq x \\ (x/\log x)^c < P^+(n) \leq x^c}} 1 \Big) = \sum_{\substack{n\leq x \\ P^+(n) \leq n^c}} 1 + o(x),\end{align*}
this completes the proof.
4. Small values of
 $t_n$
: Proof of Theorem 1·2
$t_n$
: Proof of Theorem 1·2
The proof of Theorem 1·2 uses estimates for smooth numbers and some elementary combinatorics. We introduce parameters
![]() $y < L \leq x^{o(1)}$
, and the first idea is to find many short intervals
$y < L \leq x^{o(1)}$
, and the first idea is to find many short intervals
![]() $I \subset [1,x]$
of length L which contain roughly the expected number of y–smooth numbers.
$I \subset [1,x]$
of length L which contain roughly the expected number of y–smooth numbers.
Lemma 4·1 (Many intervals with expected number of smooths). Let x be sufficiently large, and let
![]() $y < L \leq x^{o(1)}$
with
$y < L \leq x^{o(1)}$
with
![]() $y \geq \exp\! ((\!\log x)^{1/100})$
. Then there are
$y \geq \exp\! ((\!\log x)^{1/100})$
. Then there are
![]() $\gg \Psi(x,y)L^{-1}$
disjoint intervals
$\gg \Psi(x,y)L^{-1}$
disjoint intervals
![]() $I \subset [x/\log x,x]$
of length L such that
$I \subset [x/\log x,x]$
of length L such that
Proof. With y as in the statement of the lemma we have by [Reference Hildebrand10, Theorem 1] that the number of smooth numbers in
![]() $(x/\log x,x]$
is
$(x/\log x,x]$
is
![]() $\geq (1-o(1)) \Psi(x,y)$
.
$\geq (1-o(1)) \Psi(x,y)$
.
For k a positive integer write
![]() $I = I_k = (kL,(k+1)L]$
, and let
$I = I_k = (kL,(k+1)L]$
, and let
![]() $\mathcal{I}$
denote those I which are contained in
$\mathcal{I}$
denote those I which are contained in
![]() $(x/\log x,x]$
. By trivial estimation
$(x/\log x,x]$
. By trivial estimation
![]() $\# \mathcal{I} \asymp x/L$
. Let
$\# \mathcal{I} \asymp x/L$
. Let
![]() $\delta > 0$
be a sufficiently small positive constant, and write
$\delta > 0$
be a sufficiently small positive constant, and write
![]() $\mathcal{I} = \mathcal{G}\cup \mathcal{G}^c$
, where
$\mathcal{I} = \mathcal{G}\cup \mathcal{G}^c$
, where
![]() $I \in \mathcal{G}$
if
$I \in \mathcal{G}$
if
![]() $\# \{y-\text{smooth integers in } I\} > \delta L \Psi(x,y)/x$
. If
$\# \{y-\text{smooth integers in } I\} > \delta L \Psi(x,y)/x$
. If
![]() $\delta$
is sufficiently small the number of y-smooth integers in all of
$\delta$
is sufficiently small the number of y-smooth integers in all of
![]() $\mathcal{G}^c$
is
$\mathcal{G}^c$
is
![]() $O(\delta \Psi(x,y))$
. Since
$O(\delta \Psi(x,y))$
. Since
![]() $\# \{y-\text{smooth integers in } I\} \leq L$
we find that
$\# \{y-\text{smooth integers in } I\} \leq L$
we find that
![]() $\#\mathcal{G} \gg {\Psi(x,y)}/{L}$
.
$\#\mathcal{G} \gg {\Psi(x,y)}/{L}$
.
If a short interval contains sufficiently many y–smooth numbers, then we can construct an integer n with small
![]() $t_n$
.
$t_n$
.
Lemma 4·2 (Build small
![]() $t_n$
with many smooths). Let I be an interval of length L such that
$t_n$
with many smooths). Let I be an interval of length L such that
Then there exists an integer
![]() $n \in I$
with
$n \in I$
with
![]() $t_n \leq L$
.
$t_n \leq L$
.
Proof. Let
![]() $p_1 < \cdots < p_R$
be the primes
$p_1 < \cdots < p_R$
be the primes
![]() $\leq y$
, so that
$\leq y$
, so that
![]() $\pi(y) = R$
. A y–smooth integer n may be written as
$\pi(y) = R$
. A y–smooth integer n may be written as
![]() $n = \prod_{i=1}^R p_i^{e_i}$
, where
$n = \prod_{i=1}^R p_i^{e_i}$
, where
![]() $e_i$
is a nonnegative integer. By considering only the parity of
$e_i$
is a nonnegative integer. By considering only the parity of
![]() $e_i$
we obtain a map
$e_i$
we obtain a map
![]() $\theta\;:\; \{y-\text{smooth integers}\} \rightarrow \mathbb{F}_2^{R}$
given by
$\theta\;:\; \{y-\text{smooth integers}\} \rightarrow \mathbb{F}_2^{R}$
given by
Let
![]() $m_1,\ldots,m_M$
be the y–smooth integers in I. By assumption, we have
$m_1,\ldots,m_M$
be the y–smooth integers in I. By assumption, we have
![]() $M > R$
. Given
$M > R$
. Given
![]() $J \subset \{1,\ldots,M\}$
, let
$J \subset \{1,\ldots,M\}$
, let
![]() $n_J = \prod_{j \in J} m_j$
. The number
$n_J = \prod_{j \in J} m_j$
. The number
![]() $2^M$
of subsets of
$2^M$
of subsets of
![]() $\{1,\ldots,M\}$
is greater than
$\{1,\ldots,M\}$
is greater than
![]() $2^R = \#\mathbb{F}_2^R$
, so by the pigeonhole principle there exist distinct subsets J, J
′ of
$2^R = \#\mathbb{F}_2^R$
, so by the pigeonhole principle there exist distinct subsets J, J
′ of
![]() $\{1,\ldots,M\}$
such that
$\{1,\ldots,M\}$
such that
![]() $\theta(n_J) = \theta(n_{J'})$
. By the definition of
$\theta(n_J) = \theta(n_{J'})$
. By the definition of
![]() $\theta$
this implies
$\theta$
this implies
Since
![]() $J \neq J'$
we see that
$J \neq J'$
we see that
![]() $J \Delta J' \neq \varnothing$
and
$J \Delta J' \neq \varnothing$
and
![]() $\prod_{m \in J \Delta J'} m = \square$
. The least element n of
$\prod_{m \in J \Delta J'} m = \square$
. The least element n of
![]() $J \Delta J'$
is then the desired integer.
$J \Delta J'$
is then the desired integer.
Proof of Theorem 1·2. We define
![]() $y = \exp\!(\frac{\sqrt{2}}{2} \sqrt{\log x \log \log x})$
and
$y = \exp\!(\frac{\sqrt{2}}{2} \sqrt{\log x \log \log x})$
and
By [Reference Hildebrand10, Theorem 1] and Lemma 4·1 there are
![]() $\gg x L^{-1} \rho \big( {\log x}/{\log y}\big)$
intervals
$\gg x L^{-1} \rho \big( {\log x}/{\log y}\big)$
intervals
![]() $I \subset [x/\log x,x]$
of length L such that each interval I contains
$I \subset [x/\log x,x]$
of length L such that each interval I contains
![]() $\gg L \rho \Big( {\log x}/{\log y}\Big)$
numbers which are y–smooth. By [Reference Hildebrand and Tenenbaum11, Corollary 2·3], the number of y–smooth integers in each interval I of length L is therefore
$\gg L \rho \Big( {\log x}/{\log y}\Big)$
numbers which are y–smooth. By [Reference Hildebrand and Tenenbaum11, Corollary 2·3], the number of y–smooth integers in each interval I of length L is therefore
hence the number of y–smooth integers in each interval is
![]() $> \pi(y) \sim {y}/{\log y}$
. We conclude by applying Lemma 4·2.
$> \pi(y) \sim {y}/{\log y}$
. We conclude by applying Lemma 4·2.
We remark that our proof of Theorem 1·2 has some similarities to heuristic run-time analysis of factoring algorithms [Reference Pomerance13, p. 1477] (see also [Reference Croot, Granville, Pemantle and Tetali2] and [Reference Granville and Selfridge8, section 1]).
5. Large integral points on hyperelliptic curves: Proof of Theorem 1·3
As mentioned in the introduction, the proof of Theorem 1·3 draws on ingredients in the proof of Theorem 1·2. We also need an additional lemma, which provides for the existence of sets with large symmetric difference provided we have sufficiently many sets upon which to draw.
Lemma 5·1 (Many subsets implies a large symmetric difference). Let N be large and let
![]() $S_1,\ldots,S_K$
be distinct subsets of
$S_1,\ldots,S_K$
be distinct subsets of
![]() $\{1,\ldots,N\}$
. If
$\{1,\ldots,N\}$
. If
![]() $K \geq 2^Q$
with
$K \geq 2^Q$
with
![]() $Q \geq N^{1/100}$
, then there exist
$Q \geq N^{1/100}$
, then there exist
![]() $i\neq j$
such that
$i\neq j$
such that
Proof. Let A be an arbitrarily chosen (nonempty) subset
![]() $S_i$
. For any other subset S, we may uniquely write S as the disjoint union
$S_i$
. For any other subset S, we may uniquely write S as the disjoint union
![]() $S = S' \cup S_A$
, where
$S = S' \cup S_A$
, where
![]() $S' \cap A = \varnothing$
and
$S' \cap A = \varnothing$
and
![]() $S_A \subset A$
. Observe that
$S_A \subset A$
. Observe that
![]() $A \Delta S = (A \backslash S) \cup (S \backslash A) = (A \backslash S_A) \cup S'$
. Let
$A \Delta S = (A \backslash S) \cup (S \backslash A) = (A \backslash S_A) \cup S'$
. Let
![]() $\delta \geq {1}/{100}$
be a parameter. If
$\delta \geq {1}/{100}$
be a parameter. If
![]() $|A \Delta S |\leq \delta{Q}/{\log N}$
, then
$|A \Delta S |\leq \delta{Q}/{\log N}$
, then
![]() $|S'| \leq \delta{Q}/{\log N}$
and
$|S'| \leq \delta{Q}/{\log N}$
and
![]() $|A \backslash S_A| \leq \delta{Q}/{\log N}$
.
$|A \backslash S_A| \leq \delta{Q}/{\log N}$
.
The number of choices for the set S ′ is
and this is also a bound on the number of choices for the set
![]() $S_A$
. By the upper bound
$S_A$
. By the upper bound
![]() $\left(\substack{N\\[2pt] k}\right) \leq (eN/k)^k$
, valid for
$\left(\substack{N\\[2pt] k}\right) \leq (eN/k)^k$
, valid for
![]() $k\geq 1$
, we find
$k\geq 1$
, we find
It follows that the total number of choices of subset S such that
![]() $|A \Delta S| \leq \delta Q /\log N$
is
$|A \Delta S| \leq \delta Q /\log N$
is
![]() $\leq \exp\!(4\delta Q) < 1.95^Q$
, the last inequality following if we choose
$\leq \exp\!(4\delta Q) < 1.95^Q$
, the last inequality following if we choose
![]() $\delta = {1}/{6}$
, say. Since there are
$\delta = {1}/{6}$
, say. Since there are
![]() $K \geq 2^Q$
subsets, there must be some subset
$K \geq 2^Q$
subsets, there must be some subset
![]() $S_i$
such that
$S_i$
such that
![]() $|A \Delta S_i| > {Q}/(6\log N)$
.
$|A \Delta S_i| > {Q}/(6\log N)$
.
Proof of Theorem 1·3. Let x be a large integer. As in the proof of Theorem 1·2, we set our smoothness parameter
![]() $y = \exp\! \Big(({\sqrt{2}}/{2}) \sqrt{\log x \log \log x} \Big)$
. Given a constant
$y = \exp\! \Big(({\sqrt{2}}/{2}) \sqrt{\log x \log \log x} \Big)$
. Given a constant
![]() $C > \sqrt{2}$
, we also define a length parameter
$C > \sqrt{2}$
, we also define a length parameter
![]() $L = y^{C\sqrt{2}}$
.
$L = y^{C\sqrt{2}}$
.
We may apply Lemma 4·1 to deduce the existence of many disjoint intervals
![]() $I \subset [x/\log x, x]$
of length L such that the number of y–smooth integers in I is
$I \subset [x/\log x, x]$
of length L such that the number of y–smooth integers in I is
![]() $\gg L \Psi(x,y)/x$
. We fix one such interval I, and note that by the argument of Theorem 1·3 the number of y–smooth integers in I is
$\gg L \Psi(x,y)/x$
. We fix one such interval I, and note that by the argument of Theorem 1·3 the number of y–smooth integers in I is
![]() $\geq \exp\! \big((C - {\sqrt{2}}/{2} - o(1) )\sqrt{\log x \log \log x} \big)$
. If we let M denote the number of y–smooth integers in I, and
$\geq \exp\! \big((C - {\sqrt{2}}/{2} - o(1) )\sqrt{\log x \log \log x} \big)$
. If we let M denote the number of y–smooth integers in I, and
![]() $R = \pi(y)$
, then we see that
$R = \pi(y)$
, then we see that
Let
![]() $n_1,\ldots,n_M$
be the y–smooth integers in I. Given a subset
$n_1,\ldots,n_M$
be the y–smooth integers in I. Given a subset
![]() $S\subset\{1,\ldots,M\}$
we may construct the y–smooth integer
$S\subset\{1,\ldots,M\}$
we may construct the y–smooth integer
![]() $n_S = \prod_{s \in S} n_s$
, and then map
$n_S = \prod_{s \in S} n_s$
, and then map
![]() $n_S$
to
$n_S$
to
![]() $\mathbb{F}_2^R$
using the map
$\mathbb{F}_2^R$
using the map
![]() $\theta$
from (1). By the pigeonhole principle, there is some
$\theta$
from (1). By the pigeonhole principle, there is some
![]() $v \in \mathbb{F}_2^R$
and
$v \in \mathbb{F}_2^R$
and
![]() $\geq 2^{M-R}$
subsets S of
$\geq 2^{M-R}$
subsets S of
![]() $\{1,\ldots,M\}$
such that
$\{1,\ldots,M\}$
such that
![]() $\theta(n_S)=v$
for every such S. We apply Lemma 5·1 to obtain the existence of two subsets, call them S and T, of
$\theta(n_S)=v$
for every such S. We apply Lemma 5·1 to obtain the existence of two subsets, call them S and T, of
![]() $\{1,\ldots,M\}$
such that
$\{1,\ldots,M\}$
such that
By construction we have
![]() $\prod_{s \in S \Delta T} n_s = \square$
. We may arrange the integers
$\prod_{s \in S \Delta T} n_s = \square$
. We may arrange the integers
![]() $n_s$
in increasing order and write them as
$n_s$
in increasing order and write them as
![]() $n,n+j_1,\ldots,n+j_V$
for some integer
$n,n+j_1,\ldots,n+j_V$
for some integer
![]() $n\in [x/\log x,x]$
and some integers
$n\in [x/\log x,x]$
and some integers
![]() $1\leq j_1 < j_2 < \cdots < j_V \leq L$
. It follows that
$1\leq j_1 < j_2 < \cdots < j_V \leq L$
. It follows that
![]() $n(n+j_V)\prod_{i=1}^{V-1} (n+j_i)$
is a square.
$n(n+j_V)\prod_{i=1}^{V-1} (n+j_i)$
is a square.
We claim that setting
![]() $J = j_V$
gives rise to a J as in the statement of the theorem. First, note that
$J = j_V$
gives rise to a J as in the statement of the theorem. First, note that
![]() $V-1\geq L^{1 - \frac{\sqrt{2}}{2C} - o(1)}-2 \geq J^{1-c}$
, the last inequality holding if we set
$V-1\geq L^{1 - \frac{\sqrt{2}}{2C} - o(1)}-2 \geq J^{1-c}$
, the last inequality holding if we set
![]() $C = {\sqrt{2}}/{c}$
, say. Since
$C = {\sqrt{2}}/{c}$
, say. Since
![]() $x\leq n(\!\log n)^2$
we see that
$x\leq n(\!\log n)^2$
we see that
![]() $L \leq \exp\! \left((C+o(1))\sqrt{\log n \log \log n} \right)$
, which implies
$L \leq \exp\! \left((C+o(1))\sqrt{\log n \log \log n} \right)$
, which implies
![]() $\log n \geq \left(({1-o(1)})/({2C^2})\right)({(\!\log L)^2}/{\log \log L})$
. Recalling our choice for C and that
$\log n \geq \left(({1-o(1)})/({2C^2})\right)({(\!\log L)^2}/{\log \log L})$
. Recalling our choice for C and that
![]() $J\leq L$
we find
$J\leq L$
we find
Since every large x gives rise to such a J, and since
![]() $J \geq L^{1/3}$
, say, which tends to infinity with x, we may take J to be arbitrarily large, as claimed.
$J \geq L^{1/3}$
, say, which tends to infinity with x, we may take J to be arbitrarily large, as claimed.
We close this section with some comments on Theorem 1·3. In particular, it is worth comparing Theorem 1·3 with more trivial considerations.
First, we note that it is easy to obtain points (x, y) on a hyperelliptic curve of large genus if we allow
![]() $x=0$
(so that y is large). Indeed, consider the hyperelliptic curve
$x=0$
(so that y is large). Indeed, consider the hyperelliptic curve
![]() $y^2 = P(x)= x^g + D^2$
, where
$y^2 = P(x)= x^g + D^2$
, where
![]() $g\geq 5$
is large and D is a large positive integer. The point (0,D) clearly lies on the hyperelliptic curve and, since the height H of P is
$g\geq 5$
is large and D is a large positive integer. The point (0,D) clearly lies on the hyperelliptic curve and, since the height H of P is
![]() $D^2$
, we see the integral point (0,D) has height
$D^2$
, we see the integral point (0,D) has height
![]() $\gg H^{1/2}$
. We might expect that all integral points on a hyperelliptic curve
$\gg H^{1/2}$
. We might expect that all integral points on a hyperelliptic curve
![]() $y^2= P(x)$
have height
$y^2= P(x)$
have height
![]() $\ll H^{O(1)}$
, so this trivial construction is already fairly sharp.
$\ll H^{O(1)}$
, so this trivial construction is already fairly sharp.
Second, we consider hyperelliptic curves with integral points (x, y) where
![]() $x\neq 0$
. The hyperelliptic curve
$x\neq 0$
. The hyperelliptic curve
![]() $y^2 =P(x)= \prod_{i=1}^J (x+j), J \geq 5$
, is similar to the curves constructed in Theorem 1·3, and this curve has the integral point
$y^2 =P(x)= \prod_{i=1}^J (x+j), J \geq 5$
, is similar to the curves constructed in Theorem 1·3, and this curve has the integral point
![]() $(\!-\!J,0)$
. The polynomial P has height
$(\!-\!J,0)$
. The polynomial P has height
![]() $H=J!$
, so the point
$H=J!$
, so the point
![]() $(\!-\!J,0)$
on the curve has height
$(\!-\!J,0)$
on the curve has height
![]() $\gg \log H/\log \log H$
for large J. In contrast, Theorem 1·3 provides integral points (x, y) on curves
$\gg \log H/\log \log H$
for large J. In contrast, Theorem 1·3 provides integral points (x, y) on curves
![]() $y^2 = P(x)$
with
$y^2 = P(x)$
with
![]() $xy\neq 0$
and
$xy\neq 0$
and
where H is the height of P.
It would be very interesting to construct hyperelliptic curves of large genus having integral points (x, y) with
![]() $x\geq H^c$
, for
$x\geq H^c$
, for
![]() $c>0$
some fixed constant.
$c>0$
some fixed constant.
6. Lower bounds on
 $t_n$
: Proof of Theorem 1·4
$t_n$
: Proof of Theorem 1·4
If n is a large non-square integer, then by definition
![]() $n(n+t_n)\prod_{i=1}^s (n+j_i) = \square$
, where
$n(n+t_n)\prod_{i=1}^s (n+j_i) = \square$
, where
![]() $1\leq j_1 < \cdots < j_s < t_n$
are integers (obviously we must have
$1\leq j_1 < \cdots < j_s < t_n$
are integers (obviously we must have
![]() $s < t_n$
). If
$s < t_n$
). If
![]() $t_n$
is very small compared to n, then the curve
$t_n$
is very small compared to n, then the curve
contains an integral point with x extremely large (here and throughout the section we write
![]() $J = t_n$
in keeping with the notation of our other theorems). We rely on a uniform bound for the height of integral points on hyperelliptic curves due to Bérczes, Evertse and Győry [Reference Bérczes, Evertse and Győry1]. Their method utilises linear forms in logarithms.
$J = t_n$
in keeping with the notation of our other theorems). We rely on a uniform bound for the height of integral points on hyperelliptic curves due to Bérczes, Evertse and Győry [Reference Bérczes, Evertse and Győry1]. Their method utilises linear forms in logarithms.
We use different arguments depending on the size of s, with s as in (2). When
![]() $s=0$
trivial arguments suffice to bound the size of x. If
$s=0$
trivial arguments suffice to bound the size of x. If
![]() $s\geq 1$
but is smaller than a small power of J, then we consider the hyperelliptic equation (2) directly and apply the result of Bérczes, Evertse and Győry. When s is larger than a small power of J it is more efficient to extract a suitable system of generalised Pell equations from (2) and bound the size of solutions to these Pell equations. The coefficients of the Pell equations have size controlled by prime divisors
$s\geq 1$
but is smaller than a small power of J, then we consider the hyperelliptic equation (2) directly and apply the result of Bérczes, Evertse and Győry. When s is larger than a small power of J it is more efficient to extract a suitable system of generalised Pell equations from (2) and bound the size of solutions to these Pell equations. The coefficients of the Pell equations have size controlled by prime divisors
![]() $\leq J$
, and we can use some elementary arguments to find a system with coefficients that are smaller than what a trivial bound would give. The final bound results from balancing the arguments coming from small s and large s.
$\leq J$
, and we can use some elementary arguments to find a system with coefficients that are smaller than what a trivial bound would give. The final bound results from balancing the arguments coming from small s and large s.
Lemma 6·1 (Trivial case,
![]() $s=0$
). Let
$s=0$
). Let
![]() $J\geq 1$
be an integer. If x and y are positive integers with
$J\geq 1$
be an integer. If x and y are positive integers with
![]() $y^2 = x(x+J)$
, then
$y^2 = x(x+J)$
, then
![]() $x\leq J^2$
.
$x\leq J^2$
.
Proof. If x and
![]() $x+J$
have greatest common divisor
$x+J$
have greatest common divisor
![]() $d\geq 1$
, then
$d\geq 1$
, then
![]() $d \mid J$
. We change variables
$d \mid J$
. We change variables
![]() $x = dz$
and find
$x = dz$
and find
![]() $(y/d)^2 = z(z+J/d)$
, where
$(y/d)^2 = z(z+J/d)$
, where
![]() $(z,z+J/d)=1$
. Then
$(z,z+J/d)=1$
. Then
![]() $z=a^2$
and
$z=a^2$
and
![]() $z+J/d = b^2$
for some positive integers
$z+J/d = b^2$
for some positive integers
![]() $b>a$
. Then
$b>a$
. Then
so
![]() $a,b\leq J/d$
. Then
$a,b\leq J/d$
. Then
![]() $z=a^2\leq J^2/d^2$
and
$z=a^2\leq J^2/d^2$
and
![]() $x=dz \leq J^2/d\leq J^2$
.
$x=dz \leq J^2/d\leq J^2$
.
The next lemma is the theorem of Bérczes, Evertse and Győry [Reference Bérczes, Evertse and Győry1] in the special case we require.
Lemma 6·2 (Height of integral points). Let
![]() $P(x) = \sum_{i=0}^n a_i x^i \in \mathbb{Z}[x]$
with
$P(x) = \sum_{i=0}^n a_i x^i \in \mathbb{Z}[x]$
with
![]() $\deg(P)\geq 3$
and no repeated roots. Write
$\deg(P)\geq 3$
and no repeated roots. Write
![]() $\max_i |a_i| =H$
. If x and y are positive integers with
$\max_i |a_i| =H$
. If x and y are positive integers with
![]() $y^2 = P(x)$
then
$y^2 = P(x)$
then
Proof. This is [Reference Bérczes, Evertse and Győry1, Theorem 2·2] with
![]() $K = \mathbb{Q}$
and S equal to the infinite place of
$K = \mathbb{Q}$
and S equal to the infinite place of
![]() $\mathbb{Q}$
, where
$\mathbb{Q}$
, where
![]() $b=1$
in [Reference Bérczes, Evertse and Győry1, (2·5)].
$b=1$
in [Reference Bérczes, Evertse and Győry1, (2·5)].
The following lemma is useful when s is small.
Lemma 6·3 (Bound on height when is small). Let
![]() $J\geq 2$
be an integer, and let
$J\geq 2$
be an integer, and let
![]() $1\leq j_1 < \cdots < j_s < J$
be integers, where
$1\leq j_1 < \cdots < j_s < J$
be integers, where
![]() $s\geq 1$
. If x and y are positive integers with
$s\geq 1$
. If x and y are positive integers with
![]() $y^2 = x(x+J)\prod_{i=1}^s (x+j_i)$
then
$y^2 = x(x+J)\prod_{i=1}^s (x+j_i)$
then
![]() $\log x \leq \exp\! \big(O(s^5 \log J) \big)$
.
$\log x \leq \exp\! \big(O(s^5 \log J) \big)$
.
Proof. The integer polynomial
![]() $x(x+J)\prod_{i=1}^s (x+j_i)$
has degree
$x(x+J)\prod_{i=1}^s (x+j_i)$
has degree
![]() $s+2$
and clearly has no repeated roots. The coefficients of the polynomial all have size
$s+2$
and clearly has no repeated roots. The coefficients of the polynomial all have size
![]() $\leq J^{s+1}$
, so by Lemma 6·2 we see any solution to
$\leq J^{s+1}$
, so by Lemma 6·2 we see any solution to
![]() $y^2 = x(x+J)\prod_{i=1}^s (x+j_i)$
satisfies
$y^2 = x(x+J)\prod_{i=1}^s (x+j_i)$
satisfies
When s is large we argue more carefully. We use the following lemma to control the coefficients of an auxiliary hyperelliptic equation.
Lemma 6·4 (Finding numbers with fewer prime factors). Let J be a sufficiently large positive integer, and let
![]() $b_1,\ldots,b_t$
be positive integers all of whose prime factors are
$b_1,\ldots,b_t$
be positive integers all of whose prime factors are
![]() $\leq J$
. If
$\leq J$
. If
![]() $100\leq t \leq J^{1/2}/\log J$
and
$100\leq t \leq J^{1/2}/\log J$
and
![]() for all
for all
![]() $i\neq j$
, then there exist distinct
$i\neq j$
, then there exist distinct
![]() $b_i,b_j,b_k$
with
$b_i,b_j,b_k$
with
Proof. We observe that, by the prime number theorem, any distinct
![]() $b_i$
and
$b_i$
and
![]() $b_j$
have
$b_j$
have
![]() $\ll \log J/\log \log J\leq \log J$
prime factors in common, since
$\ll \log J/\log \log J\leq \log J$
prime factors in common, since
![]() $\text{gcd}(b_i,b_j)\leq J$
. Let
$\text{gcd}(b_i,b_j)\leq J$
. Let
![]() $s_i$
denote the set of prime factors of
$s_i$
denote the set of prime factors of
![]() $b_i$
. Note that
$b_i$
. Note that
![]() $|s_i \cap s_j| \leq \log J$
for any
$|s_i \cap s_j| \leq \log J$
for any
![]() $i\neq j$
, and that each
$i\neq j$
, and that each
![]() $s_i$
is contained in the set of all primes
$s_i$
is contained in the set of all primes
![]() $\leq J$
.
$\leq J$
.
Without loss of generality we may assume
![]() $|s_1| \geq |s_2| \geq \cdots \geq |s_t|$
. We claim that
$|s_1| \geq |s_2| \geq \cdots \geq |s_t|$
. We claim that
for each
![]() $1\leq r \leq t$
. This inequality trivially holds for
$1\leq r \leq t$
. This inequality trivially holds for
![]() $r=1$
, which provides the base case for an inductive argument. Let
$r=1$
, which provides the base case for an inductive argument. Let
![]() $A = s_1 \cup \cdots \cup s_r$
, so that by inclusion-exclusion and the induction hypothesis
$A = s_1 \cup \cdots \cup s_r$
, so that by inclusion-exclusion and the induction hypothesis
Since
![]() $|s_i \cap s_{r+1}| \leq \log J$
and
$|s_i \cap s_{r+1}| \leq \log J$
and
![]() $|s_r| \geq |s_{r+1}|$
, we obtain
$|s_r| \geq |s_{r+1}|$
, we obtain
![]() $|A \cap s_{r+1}| \geq (r+1)|s_{r+1}| - ({r(r+1)}/{2})\log J$
, as desired. This completes the proof of the claim.
$|A \cap s_{r+1}| \geq (r+1)|s_{r+1}| - ({r(r+1)}/{2})\log J$
, as desired. This completes the proof of the claim.
Applying (3) yields
![]() $|s_r| \leq ({1}/{r})|s_1 \cup \cdots \cup s_r| + ({r-1})\log J/{2}$
for any
$|s_r| \leq ({1}/{r})|s_1 \cup \cdots \cup s_r| + ({r-1})\log J/{2}$
for any
![]() $1\leq r \leq t$
. Since each set
$1\leq r \leq t$
. Since each set
![]() $s_i$
is contained in the set of all primes
$s_i$
is contained in the set of all primes
![]() $\leq J$
we have
$\leq J$
we have
![]() $|s_r| \ll {J}/{r\log J} + r\log J$
, and since
$|s_r| \ll {J}/{r\log J} + r\log J$
, and since
![]() $r\leq t\leq J^{1/2}/\log J$
we have
$r\leq t\leq J^{1/2}/\log J$
we have
![]() $|s_r| \ll {J}/{r\log J}$
. We finish the proof by taking
$|s_r| \ll {J}/{r\log J}$
. We finish the proof by taking
![]() $i=t-2,j=t-1$
, and
$i=t-2,j=t-1$
, and
![]() $k=t$
.
$k=t$
.
We are now ready to obtain a bound when s is large.
Lemma 6·5 (Bound on height when is large). Let J be a sufficiently large positive integer, and let
![]() $1\leq j_1 < \cdots < j_s < J$
be integers, where
$1\leq j_1 < \cdots < j_s < J$
be integers, where
![]() $J^{1/100}\leq s < J$
. If x and y are positive integers with
$J^{1/100}\leq s < J$
. If x and y are positive integers with
![]() $y^2 = x(x+J)\prod_{i=1}^s (x+j_i)$
then
$y^2 = x(x+J)\prod_{i=1}^s (x+j_i)$
then
where t is any integer satisfying
![]() $J^{1/100} \leq t \leq \min (s, J^{1/2}/\log J)$
.
$J^{1/100} \leq t \leq \min (s, J^{1/2}/\log J)$
.
Proof. We write
![]() $j_0 = 0$
and
$j_0 = 0$
and
![]() $j_{s+1} = J$
, so that the hyperelliptic equation is
$j_{s+1} = J$
, so that the hyperelliptic equation is
![]() $y^2 = \prod_{i=0}^{s+2} (x+j_i)$
. If
$y^2 = \prod_{i=0}^{s+2} (x+j_i)$
. If
![]() $d \mid( x+j_i)$
and
$d \mid( x+j_i)$
and
![]() $d\mid (x+j_{i'})$
then
$d\mid (x+j_{i'})$
then
![]() $d\mid |j_i - j_{i'}| \leq J$
, so the greatest common divisor of any two distinct
$d\mid |j_i - j_{i'}| \leq J$
, so the greatest common divisor of any two distinct
![]() $x+j_i$
is
$x+j_i$
is
![]() $\leq J$
. We may therefore uniquely write
$\leq J$
. We may therefore uniquely write
![]() $x+j_i = b_i z_i^2$
, where
$x+j_i = b_i z_i^2$
, where
![]() $b_i$
is squarefree and divisible only by primes
$b_i$
is squarefree and divisible only by primes
![]() $\leq J$
. Observe that
$\leq J$
. Observe that
![]() $\text{gcd}(b_i,b_{i'}) \leq J$
for
$\text{gcd}(b_i,b_{i'}) \leq J$
for
![]() $i\neq i'$
.
$i\neq i'$
.
Choose any t of the
![]() $b_i$
, with t as in statement of the lemma. By Lemma 6·4 there exist three distinct
$b_i$
, with t as in statement of the lemma. By Lemma 6·4 there exist three distinct
![]() $b_i,b_k$
, and
$b_i,b_k$
, and
![]() $b_\ell$
with
$b_\ell$
with
![]() $\omega(b_i),\omega(b_k),\omega(b_\ell) \ll {J}/{t\log J}$
. From the equations
$\omega(b_i),\omega(b_k),\omega(b_\ell) \ll {J}/{t\log J}$
. From the equations
we deduce
The quartic polynomial
![]() $b_kb_\ell(b_iz_i^2+j_k-j_i)(b_iz_i^2+j_\ell-j_i)$
has no repeated roots (since
$b_kb_\ell(b_iz_i^2+j_k-j_i)(b_iz_i^2+j_\ell-j_i)$
has no repeated roots (since
![]() $j_k \neq j_\ell$
) and has coefficients with absolute value
$j_k \neq j_\ell$
) and has coefficients with absolute value
We apply Lemma 6·2 to the hyperelliptic equation (4) to find
Since
![]() $x+j_i = b_i z_i^2$
this implies
$x+j_i = b_i z_i^2$
this implies
![]() $\log x \leq \exp\!\left( O \left( J/t\right) \right)$
.
$\log x \leq \exp\!\left( O \left( J/t\right) \right)$
.
Proof of Theorem 1·4. Let n be a large non-square integer. Write
![]() $J = t_n$
so that by definition we have
$J = t_n$
so that by definition we have
![]() $y^2 = n(n+J) \prod_{i=1}^s (n+j_i)$
for some integers
$y^2 = n(n+J) \prod_{i=1}^s (n+j_i)$
for some integers
![]() $1\leq j_i < \cdots < j_s< J$
and
$1\leq j_i < \cdots < j_s< J$
and
![]() $s\geq 0$
. If
$s\geq 0$
. If
![]() $s=0$
then Lemma 6·1 implies
$s=0$
then Lemma 6·1 implies
![]() $n\leq J^2$
. We may therefore assume
$n\leq J^2$
. We may therefore assume
![]() $s\geq 1$
.
$s\geq 1$
.
If J is bounded then by Lemma 6·2 we see n is effectively bounded in terms of J, so we may assume J is sufficiently large. We define
![]() $t = \lfloor (J/\log J)^{1/6}\rfloor$
. If
$t = \lfloor (J/\log J)^{1/6}\rfloor$
. If
![]() $1\leq s\leq t$
then Lemma 6·3 gives
$1\leq s\leq t$
then Lemma 6·3 gives
If
![]() $t\leq s < J$
then applying Lemma 6·5 gives
$t\leq s < J$
then applying Lemma 6·5 gives
Therefore, in any case
![]() $\log n \leq \exp\! \Big(O\big(J^{5/6}(\!\log J)^{1/6} \big) \Big)$
, which implies
$\log n \leq \exp\! \Big(O\big(J^{5/6}(\!\log J)^{1/6} \big) \Big)$
, which implies
![]() $\log \log n \ll J^{5/6} (\!\log J)^{1/6}$
. This last inequality implies in turn that
$\log \log n \ll J^{5/6} (\!\log J)^{1/6}$
. This last inequality implies in turn that
![]() $J \gg (\!\log \log n)^{6/5}(\!\log \log \log n)^{-1/5}$
.
$J \gg (\!\log \log n)^{6/5}(\!\log \log \log n)^{-1/5}$
.
One can likely obtain improvements to Theorem 1·4 by working with a version of Lemma 6·2 which exploits particular features of the hyperelliptic equation (2).
We expect that one can obtain a stronger result than Theorem 1·4.
Conjecture 1.
Let
![]() $c \in (0,1)$
be a fixed constant, and assume n is a non-square integer which is sufficiently large in terms of c. Then
$c \in (0,1)$
be a fixed constant, and assume n is a non-square integer which is sufficiently large in terms of c. Then
![]() $t_n \geq (\!\log n)^{1-c}$
.
$t_n \geq (\!\log n)^{1-c}$
.
Acknowledgements
We thank the anonymous referee for a careful reading of the manuscript and for helpful comments. We especially thank the referee for sharing with us the proof of Theorem 1·1 presented above, which is significantly shorter than our original proof. KP was supported by a post-doctoral research fellowship at All Souls College, University of Oxford, during the course of this work.