Introduction
Together with glaciers, permafrost is one of the clearest climate indicators in the cryosphere. The sensitivity of the upper permafrost layers to decadal climatic changes, and the potential effect of permafrost degradation on natural hazards in high-Alpine environments, makes knowledge of the spatial distribution of mountain permafrost fundamentally important (Reference HaeberliHaeberli, 1992). Models permitting estimations of permafrost distribution patterns are especially useful for planning hazard-mitigation measures such as flood and avalanche protection, or any other construction activity (Reference HoelzleKeller and Hoelzle, 1996; Reference KellerKeller and others, 1998). Various efforts have been undertaken in recent years to develop and improve spatial modelling of mountain permafrost distribution based on empirical and statistical data, including digital elevation models, meteorological data and topological classification of microclimatic situations (Reference KellerKeller, 1992; Reference Hoelzle and HaeberliHoelzle and Haeberli, 1995; Reference HoelzleHoelzle, 1996; Reference ImhofImhof, 1996; Reference Etzelmüller, Berthling and SollidEtzelmüller and others, 1998). These empirical models have the advantage of needing very few input variables. However, they lack deeper process understanding. In addition, they strongly depend on regional characteristics and must be adapted to specific conditions in different areas such as Scandinavia, the Alps and the Sierra Nevada. Therefore, they are of limited use for spatial and temporal extrapolations.
A better understanding of both the processes of Alpine permafrost formation or decay and the distribution of discontinuous mountain permafrost requires a detailed knowledge of the energy-exchange processes at the atmosphere/litho-sphere boundary. These processes determine the surface temperature regime (see Fig. 1) and are mainly controlled by climatic factors (solar radiation, clouds, etc.) and site-specific factors (aspect, slope, surface roughness, snow-cover thickness and duration, etc.) (Reference Williams and SmithWilliams and Smith, 1989).
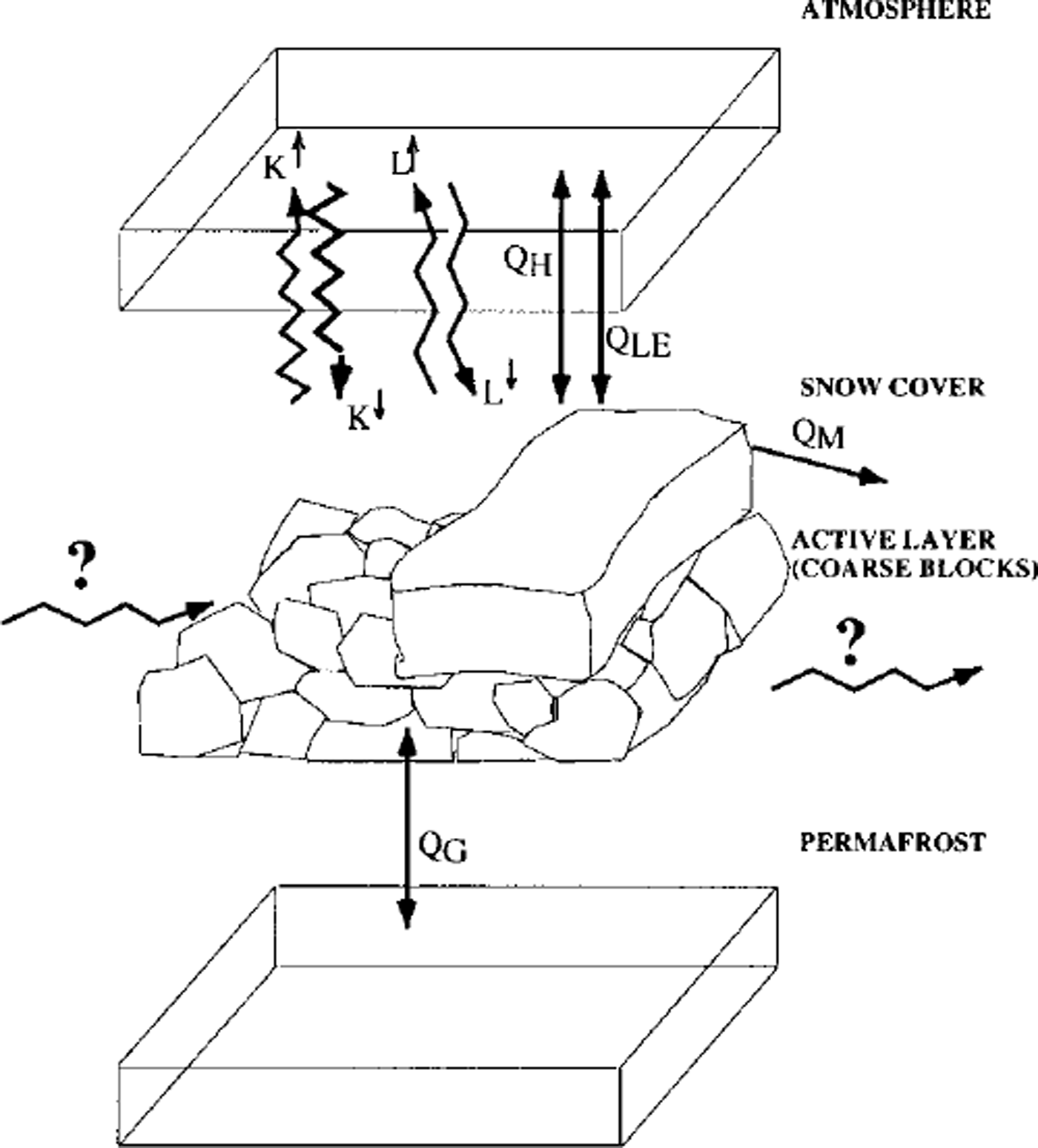
Fig. 1. Energy-exchange processes on a rock glacier. K↑, K↓ shortwave incoming and reflected radiation; L↓, L↑ longwave incoming and outgoing radiation; QH, QLE, sensible- and latent-heat flux; QM, snowmelt energy; QG, ground-heat flux.
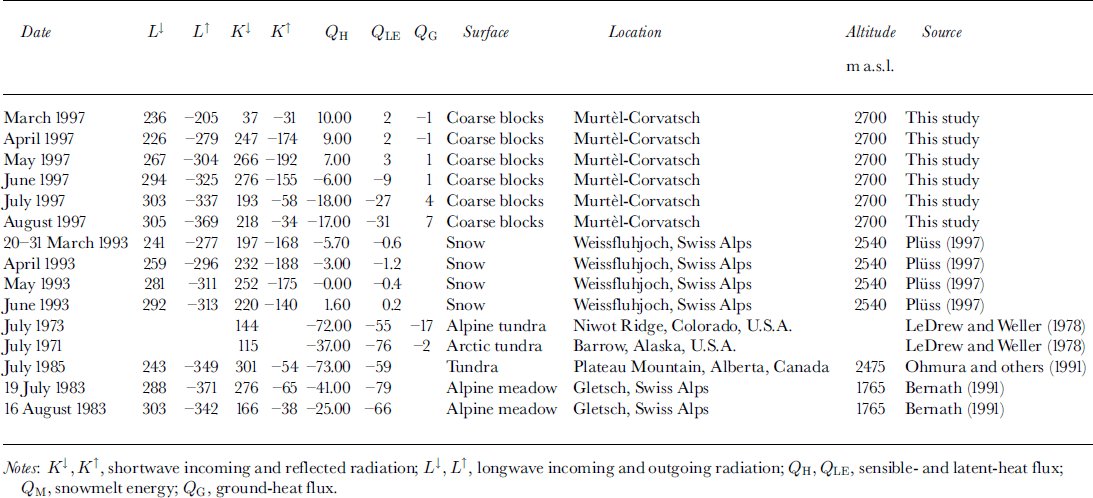
While measurements have been made in the Arctic (Reference Weller and HolmgrenWeller and Holmgren, 1974; Reference SmithSmith, 1975; Reference OhmuraOhmura, 1981; Reference Hinkel and OutcaltHinkel and Outcalt, 1994; Reference Outcalt and HinkelOutcalt and Hinkel, 1996), knowledge of mass- and heat-exchange processes in Alpine permafrost environments is still severely limited. Only a few studies of the thermal regime within the active layer of Alpine permafrost exist (Reference HumlumHumlum, 1997; Reference Harris and PedersenHarris and Pedersen, 1998), mainly because of complications involving highly variable small-scale topography, extreme surface roughness, high porosity of the active layer and pronounced slope inclination. In order to assess the possibilities related to the collection, analysis, interpretation and application for spatial modelling of continuously recorded data, measurements concerning near-surface energy-exchange processes were initiated in January 1997 on creeping permafrost at a high mountain site, the Murtèl-Corvatsch rock glacier, upper Engadin, Switzerland. The site was chosen because ground temperatures have been measured in a 60 m deep borehole on this rock glacier since 1987. The present paper presents and discusses the first results and analyses of the data for 2 year measurement period, 1997–99. It is hoped that evaluation of the most influential processes and parameters of the energy flux at the ground surface may later help to improve spatial modelling of permafrost occurrence and characteristics in rugged Alpine terrain.
Investigation Area
The Murtèi-Corvatsch rock glacier is located northwest of the Murtèl cable-car station (cable car Surlej, Piz Corvatsch) within the ski area Silvaplana/Piz Corvatsch (Fig. 2). Facing north-northwest, the rock glacier is 2620–2850 m a.s.l. and about 400 m long and 200 m wide. The ogive-like transverse ridges are a consequence of compressive flow in the lower, less steeply inclined part. The surface consists of a layer of coarse boulder blocks (e.g. 1–3 m) and has only sparse vegetation.

Fig. 2. Location of the energy-balance measurement station, Murtel.
A number of investigations have taken place on this rock glacier (e.g. Reference Vonder MuhllVonder Muhll, 1993; Reference HoelzleHoelzle, 1994; Reference KellerKeller, 1994; Reference WagnerWagner, 1996; Reference Kääb, Gudmundsson and HoelzleKääb and others, 1998). In 1987, a 60 m deep core drilling was performed in the centre and at the transition from extending to compressive flow (Reference Haeberli, Huder, Keusen, Pika, Rothlisberger and SennesetHaeberli and others, 1988). The borehole is equipped with thermistors for longterm temperature monitoring. With an average temperature of about –2°C at 10 m depth and palaeoclimatic effects from past colder decades, total permafrost thickness is estimated to exceed 100 m.
The structure of the rock glacier is as follows: Beneath a 3 m deep active layer consisting of blocky boulders, a layer with an extremely high ice content (90–100% by volume) extends downward to 28 m depth. Beneath this layer, the rock glacier consists of coarse blocks with ice-filled pores (around 40% by volume; Reference Haeberli and Vonder MuhllHaeberli and Vonder Muhll, 1996). Reference KellerKeller (1994) documented interactions between snow and permafrost through snow investigations (cf Reference Bernhard, Sutter, Haeberli and KellerBernhard and others, 1998). Reference HoelzleHoelzle (1994) modelled permafrost distribution in the Corvatsch-Furtschellas area utilizing BTS (bottom temperature of the snow cover) measurements and potential direct solar radiation calculations.
Methods: Automatic Micrometeorological Station
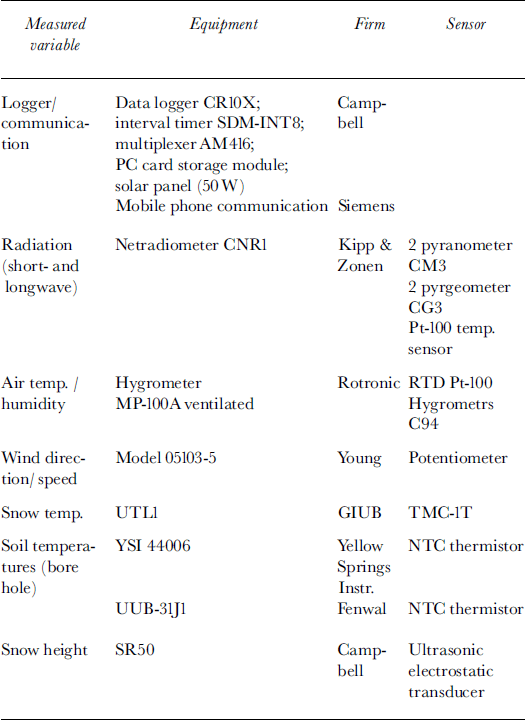
The energy-balance measurement station at Murtèl was established in January 1997 with the aim of collecting information about all energy fluxes at this site. The micrometeorological station consists of a 10 m high tower with various meteorological sensors (see Table 1) and is located 5 m from the borehole (Reference MittazMittaz, 1998). Air temperature, air humidity, wind speed and wind direction are measured at different heights (2, 6.50 and 9.10 m). Snow height and longwave and shortwave incoming and outgoing radiation are measured 1.50 m above the surface. Data are recorded every 15 s, averaged over a 30 min interval and transmitted by mobile phone to Zürich. Data collection started in January 1997 and is still in progress.
Table 1. Sensors and equipment of the micrometeorological station
Results
Radiation
All components of the radiation balance were measured directly. Shortwave incoming radiation reached daily values of up to 430 W m–2 but strongly varied with daily and annual cycles (Fig. 3). Superimposed on these regular fluctuations were fluctuations with irregular frequencies such as cloudiness and changes in surface characteristics (e.g. albedo). During the entire measurement period, outgoing longwave radiation exceeded incoming longwave radiation by about 40–80 W m–2, reaching values of up to 390 W m–2 (Fig. 3). The ground experienced only slow temperature change, unlike the air, which was mixed more quickly by turbulence. Therefore, the temporal variation of longwave outgoing radiation was much smaller than the variation of incoming radiation.

Fig. 3. Comparison of all energy-balance components for 1997 and l998. K↓ K↑ shortwave incoming and reflected radiation; L↓ L↑ longwave incoming and outgoing radiation; QH, QLE, sensible- and latent-heat flux; QM, snowmelt energy; QG, ground-heatflux.
Figure 4a compares air and surface temperature, the latter being calculated from longwave outgoing radiation by application of the Stefan-Boltzmann law. The emissivity of snow was set at εS = 0.99, and the emissivity of the ground material was set at εG = 0.815 (after Reference KondratyevKondratyev, 1972; Reference KellerKeller, 1994).
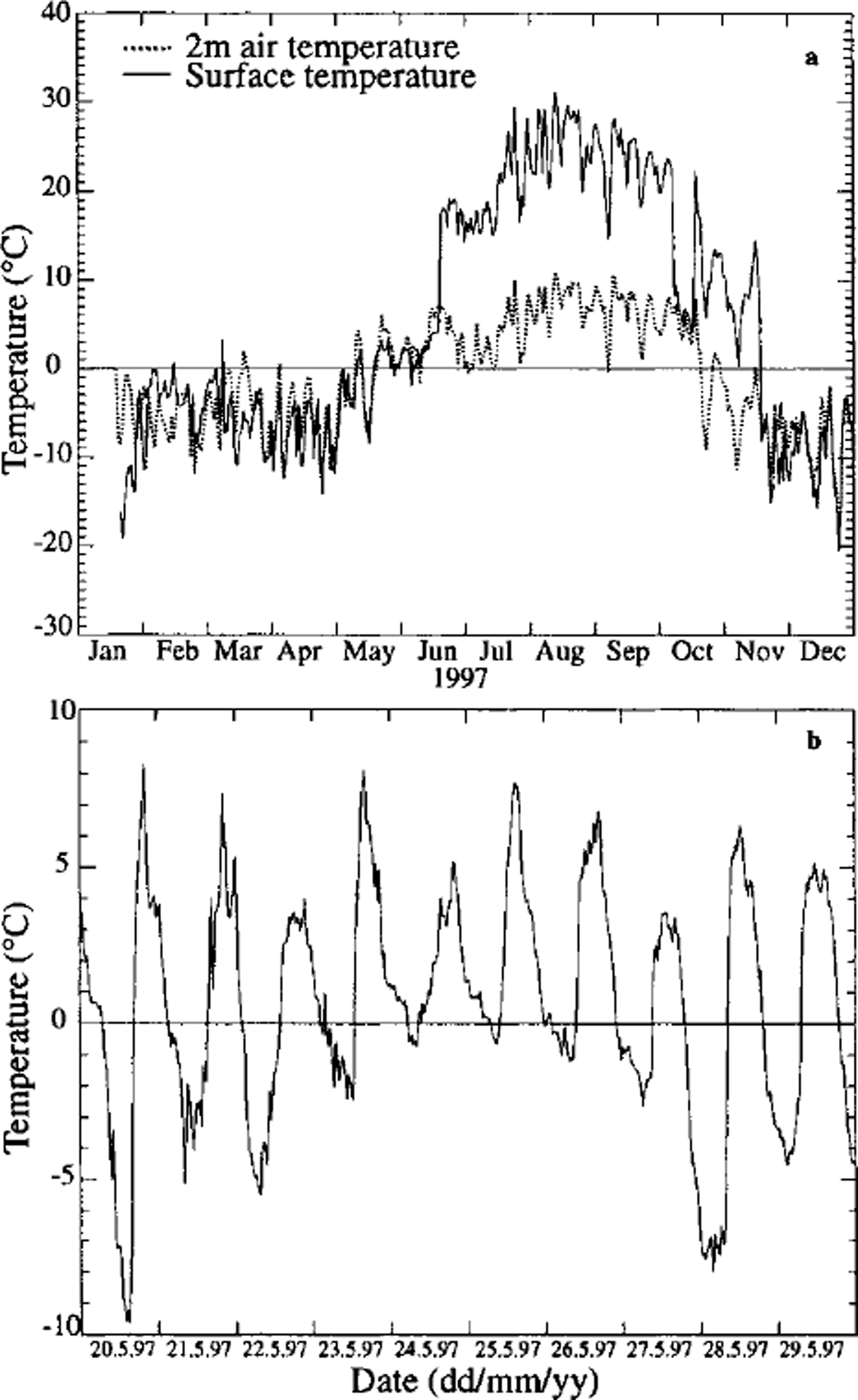
Fig. 3. (a) Suraface temperature and 2 m air temperature (daily values), 1997; (b) surface temperature during snowmelt period (daily values), 1997.
The surface temperature increased strongly as soon as the snow cover disappeared at the end of June, and reached very high daily values (up to 30°C). The highest measured surface temperature (30 min value) was 42.4°C. The large boulders (eg. 1–3 m) on the surface of the permafrost also experienced very high temperatures during snowmelt, in May-June. Although most of the area was still covered with snow, the tops of some large block-shaped rocks were snow-free, causing the measured surface temperatures to be positive during this period (the pyrgeometer was installed at a height of 1.50 m with a 150° field of view over an area of 5 m2). Figure 4b shows some daily surface temperature values during this period.
Turbulent fluxes
Measured wind-speed profiles were seldom logarithmic as expected (Reference OkeOke, 1987). In particular, when the surface was snow-covered, wind speed tended to decrease with increasing height. Cold air flowed downslope katabatically close to the surface, as on glaciers. Therefore turbulent fluxes were determined during winter using the bulk method, and not by the profile method:
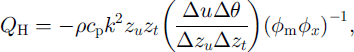
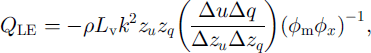
where QH and QLE are sensible- and latent-heat flux, respectively, p is air density, cp, is specific heat of air, k is von Kármán’s constant, Lv is latent evaporation energy, zu,t,q is roughness length for wind speed, temperature and humidity, respectively, Δ0, A≈ and Δq are differences of potential temperature, wind speed and humidity, respectively, between measurement level and surface, </>mx are Monin-Obukhov functions and Δzis measurement level (Reference OkeOke, 1987).
Measured wind speeds were always very low; the highest measured wind speed in 2 years was 12 m s–1. Therefore, the computed latent- and sensible-heat fluxes were small. The latent-heat flux had a monthly maximum in winter of ≤ 10 W m–2 and a minimum in summer of –50 W m–2. The maximum monthly sensible-heat flux in winter was 20 W m–2, and the minimum in summer was –35 W m–2 (Fig. 3).
The surface roughness length for wind speed was derived from the measured wind profiles and was different during winter (2 cm) and summer (14 cm) due to the presence or absence of snow.
Ground-heat flux
The ground-heat flux was calculated as pure heat conduction:
where QG is ground-heat flux, k is thermal conductivity of the ground and dT/dz is temperature gradient in the ground.
The temperature gradient was determined with the thermistors at depths of 0.6 and 3.6 m. A value of 2.49 for the thermal conductivity of the blocks was taken from Reference Vonder MuhllVonder Muhll (1988). The ground-heat flux stayed negative and small, ― 3 W nT2, during winter, but became positive in May when meltwater started penetrating into the still frozen active layer (Fig. 3). These measurements confirm results obtained by Reference Keller, Gubler and GuodongKeller and Gubler (1993) in the same region. During the snow-free period, ground-heat fluxes of up to +28 W nT2 were obtained. The insulating effect of the snow cover is obvious and has been described by several authors (e.g. Reference GoodrichGoodrich, 1982).
Heat flux through the snow cover
Like ground-heat flux, heat flux through the snow cover was calculated as pure heat conduction. To obtain a temperature gradient, the temperatures at the snow surface and at the bottom of the snow cover were measured using minature dataloggers (Reference Hoelzle, Wegmann and KrummenacherHoelzle and others, 1999). These were installed as recently as autumn 1997, so heat flux through the snow cover for winter and spring 1997 was calculated based on borehole temperatures (0.6 m thermistor) and temperatures at the snow surface (pyrgeometer). Thermal conductivity is a function of the snow density (after Reference MellorMellor, 1977; Reference KellerKeller, 1994). The density of the snow cover was assumed to be the same as in winter 1990/ 91 when it was measured by Reference KellerKeller (1994), since both winters had a relatively large snow accumulation of up to 2 m. The calculated heat fluxes varied between –1.5 and 2 WnT2, reflecting the insulating effect of the snow cover (Fig. 3).
Snowmelt energy
Latent melt energy was determined as a function of snow height and snow density. The measured minimum daily peaks reached –90 W m–2 , but affected the energy balance only during the melting period (Fig. 3).
Comparison of individual components
The results obtained during 1997 and 1998 are shown as monthly means in Figure 3. The radiation components are the dominant factors. Ground-heat flux, latent melt energy (during the snowmelt season) and turbulent fluxes during summer all vary within the same order of magnitude, but are much smaller than the radiation fluxes. Heat flux through the snow cover is too small to be included in this plot.
The sum of all measured components of the energy balance is also plotted in Figure 3. If all energy-balance components are determined correctly their sum should theoretically be zero. The calculated deviation from this theoretical case is negative during winter (minimum monthly value –78W m–2 (February 1997)) and positive during summer (maximum monthly value 130 W m–2 (July 1998)). The mean differences are given in Table 2.
Table 2. The calculated deviation (Wm–2) from the zero energy balance for different seasons
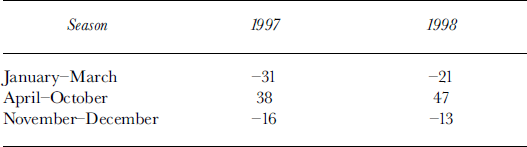
Discussion and Conclusions
Compared with other energy-balance data (Table 3), the data collected at Murtèl seem to be quite reasonable. Nevertheless, the deviation between a zero energy balance and the calculated sum of the energy-balance components averaged over lyear is 15W m–2 for 1997 and 24W m–2 for 1998; it amounts to more than half the radiation-balance values (28 W nT2 for 1997; 33 W nT2 for 1998).
Table 3. Compilation of energy-balance data at arctic and alpine sites in Wm–2
The most probable reason for the surplus/lack of energy in this study is the unmeasured energy flux from lateral advection within the active layer. A system of vertical funnels appearing within the snow cover on the rock glacier in early winter is a clear indicator of such a lateral energy flux within the layer of coarse boulder blocks (Reference Bernhard, Sutter, Haeberli and KellerBernhard and others, 1998).
The mean annual ground-surface temperature was determined as the average of the 0.6 m borehole temperature (1997), the minature datalogger temperature (1997/98) during winter and the surface temperature calculated from longwave radiation for summer. Mean annual ground-surface temperature reached maximum values of 5.9°C in 1997 and 5.0°C in 1998. Such high mean annual surface-temperature values at the top of perennially frozen ground clearly indicate that heat conduction is not the only energy-exchange process within the underlying active layer. Important advective fluxes of energy within the coarse boulder blocks surrounded by air must contribute to the difference between surface and ground temperature. In fact, a 0.6 m active-layer temperature calculated from mean ground-surface temperature and heat conduction differs from the measured 0.6 m borehole temperature by between –10°C during winter and +25°C in summer (1997) (see Fig. 5).
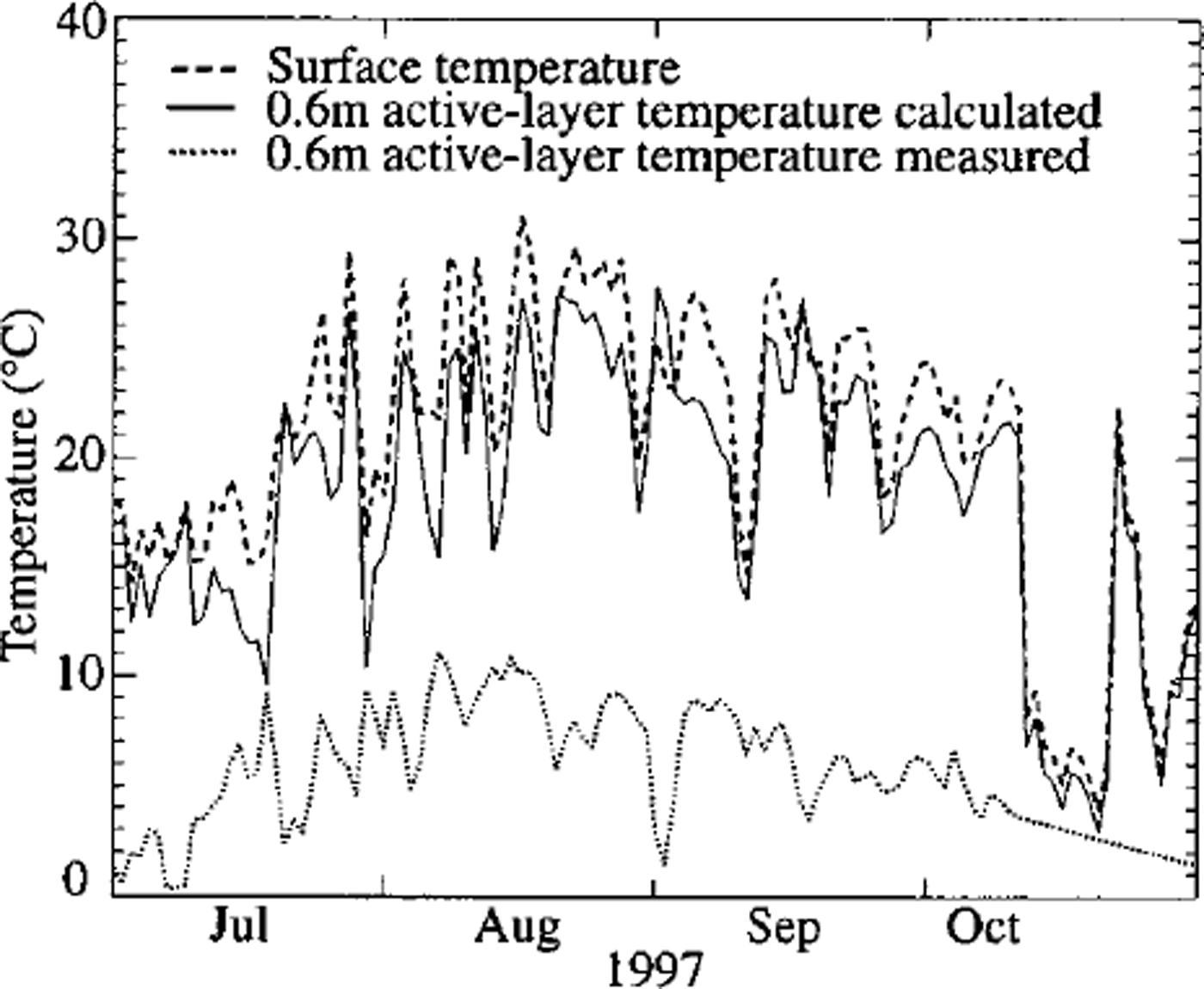
Fig. 5. Measured and calculated 0.6m active-layer temperature (daily values).
These differences may be due to unmeasured advective heat fluxes within the blocky surface layer. The difference can provide an estimate of the unmeasured advective heat flux: we calculated mean seasonal advective fluxes of +5W m–26 during winter and –26 W m–26 in summer. Although the processes causing such advection ― and the accuracy of the values ― are unknown, we propose that these numbers represent order-of-magnitude estimates of summer and winter advective heat fluxes and may account for the observed energy imbalance.
Perspectives
A realistic consideration of the advective energy flux in the active layer seems to be a fundamental precondition for linking near-surface temperatures to thermal conditions at depth (permafrost temperature and thickness). As a further step in the measurement program, a few small (1–2 m) boreholes will be drilled into some of the boulder blocks of the active layer. Data of the temperature profile within the blocks will then be obtained and should help characterize the advective energy flux within the active layer.
With a better knowledge of the energy-exchange processes at the atmosphere/lithosphere boundary, our understanding of Alpine permafrost formation, decay and distribution may be improved, as these processes determine the surface temperature regime. A complete understanding of the energy-exchange processes involved would open the way towards realistic parameterizations and spatial modelling of the essential energy fluxes by using meteorological data as input. However, the scientific and technical difficulties induced by the specific characteristics of Alpine permafrost surfaces cause a number of problems to be solved and make half-empirical approaches most promising in the near future. Potentially, the most important step at this time is to further develop documentation and quantification of the complex processes within the active layer.
Acknowledgements
We would like to thank the cable-car company Surlej-Corvatsch, and many colleagues for help in the field. We are indebted to the referees and E. Lutz for their careful suggestions that improved the clarity of the paper. This work was funded by the Federal Office for Education and Sciences (contract 97.0054–2) within the European Union programme ˚Permafrost and Climate in Europe" (PAGE; contract ENV4-GT97-0492).










