NOMENCLATURE
- L
Correlation or ice failure length (m)
- H
Ice thickness (m)
- v 0
Reference velocity (m s−1)
 $v,{\rm }\dot Y$
$v,{\rm }\dot Y$Ice velocity (m s−1)
- d
Segment width (m)
- D
Structural width (m)
- n
Number of segments
- K 0
Reference structural stiffness (kN m−1)
- K
Structural stiffness (kN m−1)
- ω n
Angular natural frequency of structure (rad s−1)
- f n
Natural frequency of the structure (Hz)
- f 0
Reference frequency (Hz)
- M
Mass of the structure (kg)
- C
Structural damping coefficient (kg s−1)
 $\ddot X$$
$\ddot X$$Structural acceleration (m s−2)
 $\dot X$$
$\dot X$$Structural velocity (m s−1)
- X
Structural displacement (m)
- F
Ice force (kN)
- T
Time (s)
- A
Magnification factor
- σ
Ice stress (kPa)
- q
Dimensionless fluctuation variable
- a, ε
Scalar parameters that control the q profile
- ω i
Angular frequency of ice force (rad s−1)
- f i
Ice failure frequency (Hz)
- B
Coefficient depending on ice properties
- Y
Ice displacement (m)
 $\ddot Y$$
$\ddot Y$$Ice acceleration (m s−2)
 $\dot \varepsilon $$
$\dot \varepsilon $$Strain rate (s−1)
- v r
Relative velocity between ice and structure (m s−1)
- λ
Dimensionless coefficient
- σ max
Maximum stress at ductile-brittle range (kPa)
- σ d, σb
Minimum stress at ductile and brittle range (kPa)
- α, β
Positive and negative indices to control the envelope profile
- v t
Transition ice velocity approximately in the middle of transition range (m s−1)
- ξ
Damping ratio
- ΔW t
Incremental work done by ice force
- ΔE m
Incremental change of mechanical energy in the structure
- ΔE d
Incremental heat dissipated by the structural damping
- ΔE p
Incremental change of potential energy in the structure
- ΔE k
Incremental change of kinetic energy in the structure
- f s
Frequency of structural displacement
- μ s
Static friction coefficient
- μ k
Kinetic friction coefficient
1. INTRODUCTION
Ice/structure interaction drew people's attention since the oil exploration and exploitation in Cook Inlet, Alaska, 1962. Large variations of ice properties (Peyton, Reference Peyton1966) and large amplitude ice-induced vibration (IIV) phenomenon (Blenkarn, Reference Blenkarn1970) were noticed and discussed from the data collected from this area. Although global warming had a negative effect on ice research activities during the past decade or two, there is an increasing interest on the possibility of using a new route in the Arctic Ocean from the Far East to Europe and oil and gas explorations in this area. Hence, it is essential to design ships and offshore structures which are resistant to possible ice impacts on the structure. However, because of the complex nature of ice and limited full-scale data, ice models and experiments show differences (Sodhi, Reference Sodhi1988) which makes the ice-related research still a challenging area.
Even after around half a century, the basic physical mechanism of the severest vibrations during ice/structure interaction, IIV, is still not fully understood. Blenkarn (Reference Blenkarn1970) and Määttänen (Reference Määttänen2015) argued that it was the reason of self-excited vibration because of the negative damping theory. On the other hand, Sodhi has forced vibration from resonance opinion as in Sodhi (Reference Sodhi1988) because negative damping explanation is not rigorous. Besides, Sodhi (Reference Sodhi1991a) found that energy always dissipates into ice, which rules out the chance of negative damping to occur.
In this study, before providing further explanations of ice mechanics, an extension of Ji and Oterkus (Reference Ji and Oterkus2016) model will be introduced first. This model is based on substituting an empirical parameter to include structural stiffness and ice velocity effects. Then, a series of reproduced numerical results based on the experiments done by Sodhi (Reference Sodhi, Jones, Tillotson, McKenna and Jordaan1991b) will be presented. Finally, the physical mechanism of ice/structure interaction process and ice force frequency lock-in during IIV will be discussed from both Määttänen and Sodhi's point of view by analysing negative damping phenomena, energy exchanges and stress variations based on the reproduced numerical results.
2. MODEL DESCRIPTION
2.1. Ice failure/correlation length parameter
Ice failure length is an idealised concept for numerical calculation based on the damage zone or crushing zone concept in experimental tests. Ice failure length is taken as a constant 1/3 of ice thickness in Ji and Oterkus (Reference Ji and Oterkus2016), which means ice fails at a certain length if ice thickness does not vary. However, it ranges from 1/2 to 1/5 of ice thickness according to the tests by Sodhi and Morris (Reference Sodhi and Morris1986) covering an area when it is used for ice force predominant frequency calculations. It is the reason that ice damage zone becomes smaller by increasing ice velocity (Kry, Reference Kry1981; Sodhi, Reference Sodhi1998). At low ice velocity, there is a large damage zone with radial cracks along with the contact area. When the velocity reaches a high level, the damage zone becomes much smaller with only microcracks near the interaction surface.
Sodhi (Reference Sodhi1998) proposed another concept, i.e. correlation length parameter L, to describe the size and the amount of damage zone of ice in relation to ice velocity. He proposed an equation to estimate this parameter in the form of L/H = (v 0/v)(d/H), where v 0 is a reference velocity, d = D/n is the segment width, n is the number of segments used as 1, 3, 5 or 7 to control the structural width D, and d/H the ratio is in the 1–3 range. It can be seen that the correlation length is decreasing with increasing ice velocity. In this paper, structural width is considered as one whole segment, i.e. n = 1. Thus, the equation is used in the form of L/H=(v0/v)(D/H). Assuming D/H = 2, then L/H = 2v 0/v which is done under the assumption that the ice failure length has a relationship to ice thickness and not to the structural width (Sodhi, Reference Sodhi1998).
In addition to ice velocity, structural stiffness has a linear relationship with ice failure length in ice force frequency calculation (Määttanen, Reference Määttanen1975; Sodhi and Nakazawa, Reference Sodhi and Nakazawa1990). Experimental test conducted by Sodhi (Reference Sodhi, Jones, Tillotson, McKenna and Jordaan1991b) also shows this relationship. These are Test 63, Test 66 and Test 67 under almost the same conditions except that the structural stiffness in each test was 3230, 1710 and 890 kN m−1, respectively. As listed in Table 1, the ice velocity, ice thickness and structural width are nearly the same. Time-history plotting of ice force in Sodhi (Reference Sodhi, Jones, Tillotson, McKenna and Jordaan1991b) showed that the average maximum value was ~15 kN in all tests. However, the frequency showed an approximately linearly decreasing trend when the structural stiffness decreases, with the value of 3.33, 2.17 and 1.25 Hz, respectively.
Table 1. Test configurations from Sodhi (Reference Sodhi, Jones, Tillotson, McKenna and Jordaan1991b)

Following the effect of ice velocity on ice failure from correlation length parameter and by adding up the linear structural stiffness effect, the general form of ice failure length can be written as
where K 0 is the reference structural stiffness and K is the structural stiffness. The constant value of 2 also satisfies the ratio of structural width to ice thickness in the range 1.67 and 2.08 as listed in Table 1. If the mass of the structure remains the same, the natural frequency of the structure will be proportional to the structural stiffness as ![]() $\omega _{\rm n} = \sqrt {K/M} $, where ω n is the angular natural frequency of the structure and M is the mass of the structure. Besides, the ISO 19906:2010 tends to use the structural natural frequency to define the highest ice velocity that lock-in condition can occur, v = γ vf n, where γ v = 0.06 m. Hence, (1) can be rewritten in the form of
$\omega _{\rm n} = \sqrt {K/M} $, where ω n is the angular natural frequency of the structure and M is the mass of the structure. Besides, the ISO 19906:2010 tends to use the structural natural frequency to define the highest ice velocity that lock-in condition can occur, v = γ vf n, where γ v = 0.06 m. Hence, (1) can be rewritten in the form of
by substituting the stiffness with the frequency, where f 0 is the reference frequency and f n is the natural frequency of the structure.
2.2. Main equations
In this study, governing equations and ice stress/strain rate relationship are adopted directly from Ji and Oterkus (Reference Ji and Oterkus2016). Unlike the experiment done by Sodhi (Reference Sodhi, Jones, Tillotson, McKenna and Jordaan1991b) in which an indenter is pushed through the ice sheet, in the current numerical model ice moves against a stationary structure. The ice/structure interaction model is taken as a mass-spring-damper system as illustrated in Figure 1. There are ‘internal effect’ and ‘external effect’ with regard to ice and structure. Internal effect corresponds to ice own failure characteristic and is represented by Van der Pol oscillator without forcing term. On the other hand, external effect corresponds to structural effects including structural displacement and structural velocity, i.e. relative displacement and the relative velocity between ice and structure. The Van der Pol oscillator and ice stain-stress function are coupled as ice force variations. Relative velocity is considered in ice strain rate/stress relationship and the right-hand side of Van der Pol oscillator. Relative displacement between ice and structure is also considered within the oscillator. Compressive stress results in ice deformation and when the deformation exceeds the natural ice failure length, ice failure occurs. Therefore, ice will fail under both internal and external effects. The model consists of equation of motion and Van der Pol equation, i.e.
 $$\left\{ \matrix{M\ddot X + C\dot X + KX = F(T) = ADH\sigma (q + a) \hfill \cr \ddot q + \varepsilon \omega _{\rm i} (q^2 - 1)\dot q + \omega _{\rm i} ^2 q = \displaystyle{{B\omega _{\rm i}} \over H}(\dot Y - \dot X) \hfill} \right.$$
$$\left\{ \matrix{M\ddot X + C\dot X + KX = F(T) = ADH\sigma (q + a) \hfill \cr \ddot q + \varepsilon \omega _{\rm i} (q^2 - 1)\dot q + \omega _{\rm i} ^2 q = \displaystyle{{B\omega _{\rm i}} \over H}(\dot Y - \dot X) \hfill} \right.$$in conjunction with the ice stress/strain rate relationship given in (4). In (3), X is the displacement of the structure, the ‘dot’ symbol represents the derivative with respect to time T, A is the magnification factor adjusted from experimental data, D is the structural width, q is the dimensionless fluctuation variable, A and ε are scalar parameters that control the lower bound of ice force value and saw-tooth ice force profile, respectively, ω i = 2πf i is the angular frequency of ice force, B is a coefficient depending on ice properties and Y is the displacement of ice.

Fig. 1. Schematic sketch of the dynamic ice-structure model.
2.3. Ice stress-strain rate equation
It is found and proved that ice uniaxial stress or indentation stress is a function of the strain rate as shown in Figure 2 (Blenkarn, Reference Blenkarn1970; Michel and Toussaint, Reference Michel and Toussaint1978; Palmer and others, Reference Palmer1983; Sodhi and Haehnel, Reference Sodhi and Haehnel2003). The strain rate is defined by v r/λD, where the dimensionless coefficient λ varies from 1 to 4 and D is the structural width (Yue and Guo, Reference Yue and Guo2011). It can be expressed by two separate dimensional power functions:
where σ max is the maximum stress at ductile-brittle range, σ d and σ b are the minimum stress at ductile and maximum stress at brittle range, respectively, α and β are positive and negative indices to control the envelope profile, respectively, and v t is the transition ice velocity approximately in the middle of transition range.
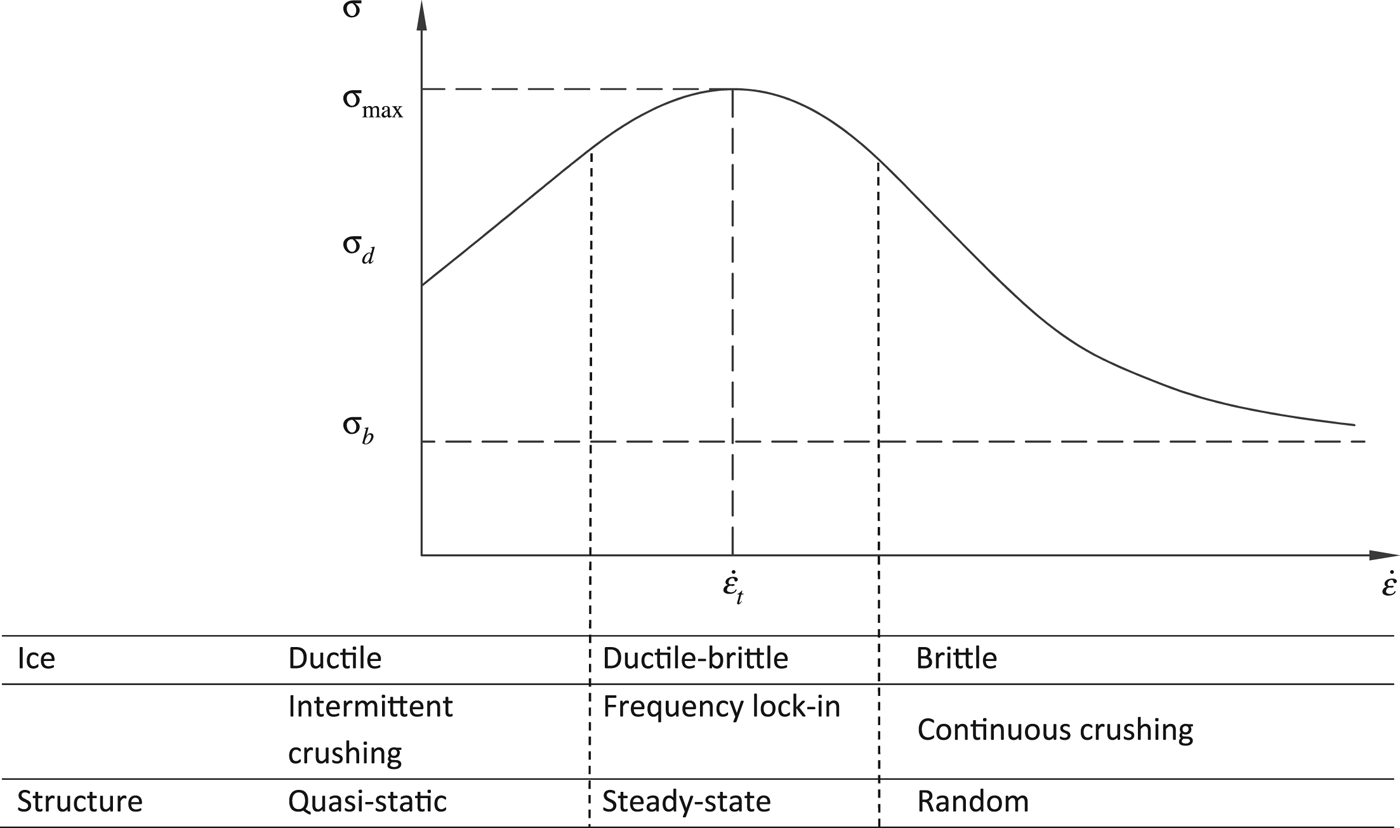
Fig. 2. Strain rate vs. uniaxial or indentation stress corresponding to ice failure and structural response mode.
2.4. Parameter values
Each parameter in the (3) and (4) is determined from the tests conducted by Sodhi (Reference Sodhi, Jones, Tillotson, McKenna and Jordaan1991b) and summarised in Table 1. In the equation of motion, A = 0.22 is the magnification factor adjusted by any one of the cases to determine the upper bound of the ice force except for the Test. 110 which is 0.15. a = 2 is set to assume that all force will drop to zero after each cycle of loading. D = 0.05 m and M = 600 kg are from the test configuration. ξ = 0.1 is not given but found in Figure 5 of Sodhi (Reference Sodhi1994). In the Van der Pol equation, ε = 4.6 is adjusted for better force envelope behaviour. B = 0.1 is calibrated by the results from Test. 63 and Test. 67. In the ice stress-strain rate equation, σ d = 8800 kPa because the maximum pressure is 8.8 MPa from Test. 64. In Test. 66, the effective failure pressure varies from 8 to 13 MPa under intermittent crushing. Therefore, σ max = 13000 kPa is used for maximum value and α = 0.35. In Test. 67, the pressure is 4.4 MPa. Therefore, σ b = 4400 kPa and β = −6 except for Test. 203 at high velocity, i.e. σ b = 1700 kPa from the data provided. Transition ice velocity is set to v t = 0.05 m s−1 because high velocity range described by Sodhi was above 0.1 m s−1 and the middle value is estimated. In the ice failure length equation, v 0 = 0.03 m s−1 is used as suggested by Sodhi (Reference Sodhi1998). K 0 = 710 kN m−1, i.e. f 0 = 5.47 Hz, is adjusted by the results from Test. 63 and Test. 67. Summary of all parameter values is listed below:
 $$\openup4pt\eqalign{D & = 0.05\,{\rm m},{\rm} \, M = 600\,{\rm kg,}\; \xi = 0.1, \cr&A = 0.22\,{\rm (}0.15{\rm \;for \; Test}{\rm. \,110)}, \, {\rm} a = 2; \,\varepsilon = 4.6, \, {\rm B} = 0.1, \cr& v_0 = 0.03 \, {\rm m\; s}^{ - 1} {\rm,} \; K_0 = 710 \, {\rm kN \, m}^{ - 1} {\rm,}\; f_0 = 5.47 \, {\rm Hz;} \cr& \sigma _{\rm d} = 8800 \, {\rm kPa,} \; \sigma _{\rm b} = 4300 \, {\rm kPa \, (1700 \, kPa \; for \; Test}{\rm. \, 203)}, \cr& \sigma _{\max} = 13000 \, {\rm kPa}, \; {\rm} \alpha = 0.35, \; \beta = - 6, \;{\rm} v_{\rm t} = 0.05 \, {\rm m\; s}^{ - 1} {\rm.}} $$
$$\openup4pt\eqalign{D & = 0.05\,{\rm m},{\rm} \, M = 600\,{\rm kg,}\; \xi = 0.1, \cr&A = 0.22\,{\rm (}0.15{\rm \;for \; Test}{\rm. \,110)}, \, {\rm} a = 2; \,\varepsilon = 4.6, \, {\rm B} = 0.1, \cr& v_0 = 0.03 \, {\rm m\; s}^{ - 1} {\rm,} \; K_0 = 710 \, {\rm kN \, m}^{ - 1} {\rm,}\; f_0 = 5.47 \, {\rm Hz;} \cr& \sigma _{\rm d} = 8800 \, {\rm kPa,} \; \sigma _{\rm b} = 4300 \, {\rm kPa \, (1700 \, kPa \; for \; Test}{\rm. \, 203)}, \cr& \sigma _{\max} = 13000 \, {\rm kPa}, \; {\rm} \alpha = 0.35, \; \beta = - 6, \;{\rm} v_{\rm t} = 0.05 \, {\rm m\; s}^{ - 1} {\rm.}} $$3. RESULTS
Based on the experimental results, reproduced results generated from the numerical model are shown in Figure 3, which are in a pretty good match with those from experiments. In these figures, records of variables are plotted with respect to time, such as ice force, displacement of the structure, acceleration of the structure and structural displacement with respect to the ice. Relative displacement is calculated by subtracting the structural displacement from ice displacement. Positive direction of the structural motion, i.e. the same direction as ice motion, is in the opposite direction with respect to Sodhi's results since the ice is assumed to move against the structure in the model whereas the indenter is set to move against the ice sheet in the Sodhi's experiments.

Fig. 3. Time history of ice force, structural displacement, acceleration and ice displacement with relative displacement at different structural stiffnesses and ice velocities. (a) Test. 63, K = 3230 kN m−1, v = 0.0411 m s−1. (b) Test. 66, K = 1710 kN m−1, v = 0.0411 m s−1. (c) Test. 67, K = 890 kN m−1, v = 0.0412 m s−1. (d) Test. 110, K = 2700 kN m−1, v = 0.1031 m s−1. (e) Test. 203, K = 1130 kN m−1, v = 0.1452 m s−1.
Figure 3a–c show results of Test. 63, Test. 66 and Test. 67, respectively, where all parameters are the same apart from the structural stiffness. The values of stiffness are 3230, 1710 and 890 kN m−1, respectively. Amplitude and frequency of ice force and displacement are almost the same as those in experiments, reaching at 15 kN, with ~14, 8 and 5 cycles of ice loading in 4 seconds, respectively. Although the ice failure forces are approximately the same, the ice failure frequency in each figure shows a clear dependence on the stiffness, because structural stiffness has a linear relationship with ice failure length as controlled by (1).
Acceleration in Figure 3a shows ~50% bigger than that in the test because there are some drops during loading phases. Moreover, there are some drops around the peak values, which are realistic since the stress varies with the relative velocity. When the force reaches the maximum, the relative velocity will become zero leading the force to drop to the corresponding stress value. In addition, this difference may be the reason of filtering process in experimental data that eliminates some sharp peak fluctuations and lowers the acceleration amplitude significantly.
If we take Figure 3c as an example in which force and displacement are plotted more clearly, there is almost no acceleration of the structure during loading phase in the detailed plot. At the instant of ice failure, the structure is in the maximum excursion place and the potential energy stored in the spring is then transformed into kinetic energy, moving the structure backwards against ice motion. The interaction force then drops to a much lower level suddenly at ~1/3 of the value at the instant of failure. It is the reason that crushed ice is in contact with and extruded by the backwards motion of the structure. After the extrusion, ice lost contact with the structure for a short time while the force is almost zero, which is called as separation phase according to Sodhi.
It can be noticed that there is some sudden unloading of ice force in Figs 3a and b because of the external effect appearance. It occurs when the structure is moving backwards with respect to ice motion at first. The compressive stress between ice and structure results in ice deformation and failure occurs when the deformation exceeds the natural ice failure length L can tolerate. So, the relative displacement is subtracted from the amount of L additionally leading to a negative value. Moreover, this external effect occurs after 3 cycles of loading in Figure 3a and 4 cycles in Figure 3b, respectively. Due to the space limit, simulations are all run in 16 seconds but plotted in 4 seconds only. The reason that there is no such external effect in Test No. 67 is because of structural stiffness, i.e. structural natural frequency, has an impact on the lock-in condition range as the ISO 19906:2010 revealed. As defined in (2), the higher the structural stiffness, the smaller the ice failure length. Therefore, lock-in condition will occur even under the same ice velocity if structural stiffness is high enough.
Figure 3d shows a steady-state vibration of the structure with a frequency close to its natural frequency. The ice force shows almost exactly the same periodic ‘spike’ like loading envelope profile as that in the test, in which the maximum amplitude of force is ~11 kN and a frequency of ~9 Hz. It can be noticed that range and amplitude of structural displacement and acceleration are different from those in the test. There are two reasons for this difference because of ice force. The first reason is that ice force is controlled to drop to zero during each cycle of loading. The second is only the maximum value is considered and predicted. A similar difference can also be found in Figure 3e, which shows the continuous crushing behaviour under high ice velocity. Ice force matches at ~2.5 kN with the test and no obvious vibration of the structure is found.
4. PHYSICAL MECHANISM
According to the definition from Den Hartog (Reference Den Hartog1947):
• In self-excited vibration, the alternating force that sustains the motion is created or controlled by the motion itself. When the motion stops, the alternating force disappears.
• In forced vibration, the sustaining alternating force exists independently apart from the motion and persists even when the vibratory motion is stopped.
Sodhi (Reference Sodhi1988) discussed IIV as forced vibration because ice force persists when the structure is prevented from moving. However, it is a fact that ice failed at a certain amount with a certain frequency (Neill, Reference Neill1976; Sodhi and Morris, Reference Sodhi and Morris1986; Kärnä and others, Reference Kärnä, Muhonen and Sippola1993; Sodhi, Reference Sodhi2001). So, the situation will be different if the analysis of ice failure process is restricted to just one single failure cycle when there is no feedback coming from the structure. There is a time interval after the first amount of ice fails and before another piece of ice approaches, which is a process for ice fragments to be removed. Both Sodhi (Reference Sodhi1988) and Määttänen (Reference Määttänen2015) pointed out this process and named ‘clearing process’ and ‘gap’, respectively, since ice force will vanish if the structure is stopped from moving. Therefore, it is not a forced vibration but self-excited vibration in this situation.
Depending on the number of ice elements in the system of interest, these two mechanisms can be converted. A similar statement can also be found in Ding (Reference Ding2012). If the studied system is extended to a macroscale, the external excitation caused forced vibration will be converted into the internal excitation that leads to self-excitation vibration, and vice versa. Taking ice as an example, if the ice and structure are coupled as one dynamic system, the IIV should belong to self-excited vibration category. On the contrary, if the structure is isolated from the ice and is considered as one dynamic system, the fluctuating force caused by ice failure would be an external excitation and IIV should be categorised as forced vibration. Therefore, there are internal and external effects from the structure point of view.
From the ice point of view, there are internal and external effects too. Internal from ice is the original ice failure characteristic. It is the behaviour under the assumption that ice fails against a theoretically rigid structure, which means there is no vibration or feedback coming from the external structure. But structure does vibrate in real cases. Hence, the structural vibration or oscillation effect is the external effect of the ice failure. Back in numerical modelling, the external effect is represented in the stress variations and the forcing term on the right-hand side of Van der Pol equation. If the stress is a constant and the forcing term is zero, then ice will fail under purely internal effect. Otherwise, relative velocity and relative displacement from structure will be effective in ice failure and lead to different ice force and structural movement behaviours, i.e., the general three responses shown in Figure 3c–e.
Further explanations can also be given from the ice point of view in analysing ice failure. If the ice velocity is slow, ice force will drop to almost zero after each failure which means that time interval for clearing process is relatively long. If the velocity increases, the time interval will consequently become shorter. At the intermediate velocity range, ice fails under the structural oscillation effect besides the original failure nature which means that when the structure moves backwards against the ice, compressive stress arises due to external structure feedback and lead to ice deformation and failure more predominantly.
4.1. Reasons of lock-in
Even though ice force frequency tends to increase with increasing ice velocity, it still locks in around the structural natural frequency because of the external structural oscillation feedback effect and related stress variations. The change of stress depends on the strain, i.e. relative velocity between ice and structure. When the structure and ice move in the same direction during IIV, the relative velocity is low and the value of stress is high. The increasing ice resistance decelerates the structure moving with respect to ice and results in ice failure frequency lagging behind the originally supposed frequency if the structure is considered as rigid without vibration. The lagging frequency is called hysteresis frequency. Once ice failure occurs, ice and structure start moving in opposite directions and the relative velocity becomes high. Hence, low ice stress value reduces the ice resistance and accelerates the structure backwards against ice (Määttänen, Reference Määttänen2015) exerting much lower ice force value upon the structure. More ice element failures result in higher ice force frequency than the originally supposed frequency. At the same time, during each interaction with the structure, the oncoming ice sheet will also decelerate the structural velocity and raise the stress value because of lower relative velocity. Once the structural deceleration and acceleration oscillation process is in a stable feedback condition when restoring force is equal to the ice force, the structure will be in a self-excited oscillation condition. Therefore, the structural natural frequency will be predominant of the oscillation and ice force predominant frequency locks in the structural natural frequency.
When ice velocities are above the IIV lock-in range, relative velocity will stay at higher range resulting in a very small time interval for the structure to give feedback to ice. Consequently, ice original failure characteristic becomes predominant and ice force frequency will increase with increasing ice velocity. At the same time, the response amplitude is decreasing with lower ice stress leading to the structure vibrating at the natural frequency with small amplitude or even diminish (Huang and others, Reference Huang, Shi and Song2007).
4.2. Damping
Damping cannot be negligible when the structure is oscillating, especially in IIV. Yue and Guo (Reference Yue and Guo2011) and Kärnä and others (Reference Kärnä2013) noticed that vibrating frequencies during IIV are slightly below the natural frequency. It is the reason when damping force is large compared with the spring or inertia forces that differ from the natural frequency appreciably (Den Hartog, Reference Den Hartog1947).
Mathematically, self-excited vibration occurs when there is an equilibrium between damping energy and external excitation energy during a full cycle of vibration (Ding, Reference Ding2012) so that the structure vibrates by itself without input from external excitation energy to the mechanical system. In other words, the excitation energy is totally dissipated by damping, i.e. zero net input energy in a cycle of vibration. Therefore, an alternative way of understanding for this mechanism is by adding the negative damping to free vibration (Den Hartog, Reference Den Hartog1947). It is therefore called ‘self-excited’ because there is no external excitation during a cycle of vibration.
Negative damping, in essence, is used as an external source of energy to increase the amplitude of vibration. As the characteristic of decreasing ice stress with increasing loading rate, Blenkarn (Reference Blenkarn1970) proposed ice force as a function of relative velocity and explained the increased vibration amplitude in IIV as negative damping theory:
For small motions, forcing term can be written as:
Hence, (5) becomes:
Sodhi (Reference Sodhi1988) expressed some disagreement even though he thought negative damping was realistic under some conditions. General reason was that the forcing term was not only controlled by relative velocity but also relative displacement, time, etc. Therefore, a more detailed relationship between ice force and relative velocity needs to be justified. Because of this reason, relative displacement effect is also considered in the current numerical model during ice force calculation. As Sodhi mentioned, a plot of ice force vs. relative velocity can be more persuasive. For instance, Figure 4 is the result of Test. 110 in which ice force can be taken as a function of relative velocity. It is clear that the slope, ∂F/∂v r, is sometimes positive and sometimes negative. The negative value can lead to net negative damping in (7) which will then lead the system to an unstable condition. The blue line is the first cycle of loading which has higher negative slope comparing with other stable conditions such as the red line in a cycle of ‘spike’ like ice loading under steady-state vibration and others in black dashed lines.
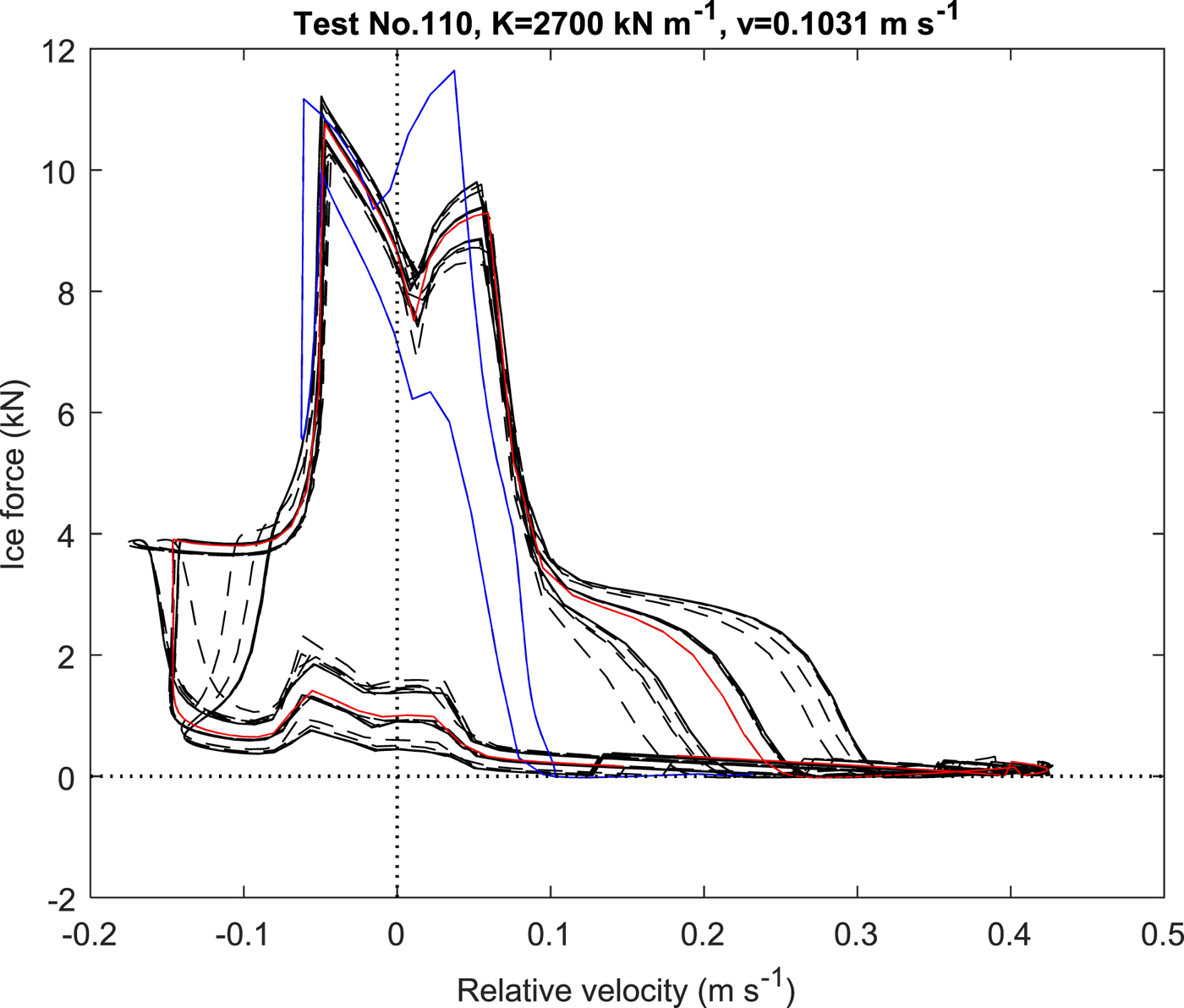
Fig. 4. Relative velocity vs. ice force in four seconds (black dashed): the first cycle of loading (blue) and ‘spike’ like loading (red).
4.3 Energy conservation
It is certain that energy is always conservative during ice/structure interaction process. The ultimate reason for increased structural vibration is due to more net energy input to structure. Force increases when ‘negative damping’ occurs and more energy transmits into the structure leading to increased vibration amplitude (Den Hartog, Reference Den Hartog1947). Note that the negative damping proposed by Blenkarn (Reference Blenkarn1970) is actually moving the external structural velocity related forcing term from the right-hand side of the equation of motion to the left-hand side.
Sodhi (Reference Sodhi1991a) presented further evidence that there is no real negative damping based on his experimental results given in Sodhi (Reference Sodhi, Jones, Tillotson, McKenna and Jordaan1991b). Instead, he found that the cumulative work done by the indenter is a non-decreasing function. According to the first law of thermodynamics, the frictional and damping force of the structure are always dissipating energy into heat. Therefore, a positive damping force does negative work. In the present model, the energy relationship satisfies the following equation during the interaction process:
where ΔW t is the incremental work done by ice, ΔE m is the incremental change of mechanical energy in the structure and ΔE dis the incremental heat dissipated by the structural damping since friction between ice and structure is not considered in the model. The incremental change of mechanical energy in the structure can be written as
where ΔE p and ΔE k are the incremental change of potential energy and kinetic energy in the structure, respectively. The computation of ΔW t between any two instants of time is through multiplying the average force by the corresponding incremental structural displacement, i.e. ![]() $\overline F \Delta X$. The change of kinetic energy and potential energy are obtained from
$\overline F \Delta X$. The change of kinetic energy and potential energy are obtained from ![]() $0.5M\Delta \dot X^2 $ and 0.5KΔX 2, respectively. The energy dissipated due to damping can be computed from (8). The cumulative form and integral form of (8) and (9) are
$0.5M\Delta \dot X^2 $ and 0.5KΔX 2, respectively. The energy dissipated due to damping can be computed from (8). The cumulative form and integral form of (8) and (9) are
Each parameter in (10) is shown in Figure 5 at four different tests such as total cumulative energy done by ice force (ΣΔW t) in red, potential energy (PE) in purple, kinetic energy (KE) in green, mechanical energy of the structure (PE + KE) in black and dissipated energy due to damping (ΣΔE d) in blue. It can be noticed that most of the energy arises from ice force dissipated by the damping of structure which is different from what Sodhi (Reference Sodhi1991a) found, i.e. energy supplied by carriage was dissipated mostly by the indenter. Because in the tests of Sodhi (Reference Sodhi, Jones, Tillotson, McKenna and Jordaan1991b), an indenter, i.e. structure, was attached to a carriage to move against the ice in a basin. To simplify the modelling and understanding, ice is moving towards the structure in the current numerical model. Therefore, subtracting the work done by carriage from indenter in the experiment is the same work done by the ice force in the present model.

Fig. 5. Time vs. total energy (red), potential energy (purple), kinetic energy (green), mechanical energy (black) and damping energy (blue) at different test configurations. (a) Test. 67, K = 890 kN m−1, v = 0.0412 m s−1. (b) Test. 63, K = 3230 kN m−1, v = 0.0411 m s−1. (c) Test. 110, K = 2700 kN m−1, v = 0.1031 m s−1. (d) Test. 203, K = 1130 kN m−1, v = 0.1452 m s−1.
According to the numerical results, there are three different energy exchange characteristics because of three different types of ice/structure interactions at different ice velocities which capture the general similar pattern with those in Sodhi (Reference Sodhi1991a). Figs 5a and b show the failure under intermittent crushing. During each cycle of loading, the structure moves with the increasing force, resulting in large displacement but relatively small velocity of the structure. Energy supplied by ice is mostly stored in the structural spring. After the failure of ice, the stored potential energy is then transferred to kinetic energy leading to the backwards movement of the structure and extrusion of ice. Damping mechanism consumes the energy all the time when the velocity of the structure increases and reaches a balance condition with the energy from ice force at the end of each cycle of ice failure. Figure 5c shows the energy exchange at steady-state vibration. From the enlarged detail of the dashed box, it can be seen that potential and kinetic energy are in a sinusoidal exchange relationship similar to what Sodhi (Reference Sodhi1991a) found. After the first few cycle of loading, the energy supplied by ice force in one cycle is equal to the energy dissipated by the damping. During the continuous crushing at high velocity, as shown in Figure 5d, most of the mechanical energy are in the form of potential energy remaining at around a constant and kinetic energy remains at almost zero. Because the structure is pushed by ice to a relatively static position, it vibrates at much lower amplitude.
4.4. Stress and force variations
Since 0.0412 and 0.1452 m s−1 in Sodhi (Reference Sodhi, Jones, Tillotson, McKenna and Jordaan1991b) was defined as intermediate and high velocity, respectively, estimated range of ice velocity at the test condition is between ~0.01 and 0.165 m s−1. Five sets of tests for the configurations in Table 1 were conducted except that ice velocities were used from 0.01 to 0.165 m s−1 at 0.005 m s−1 intervals. Histograms of time history plotting of stress values and ice force values in each set of tests show a similar pattern with each other as the ice velocity increases. Two sets of tests, Test. 67 and Test. 110, are chosen as shown in Figs 6a and b, respectively. During each 0.005 m s−1 ice velocity, time history plotting of stress and ice force points are counted and accumulated at 0.725 MPa and 0.5 kN intervals, i.e. 0.3625 MPa and 0.25 kN from both sides of each histogram, respectively. Ranges of stress and force are determined by the minimum and maximum values of them. Each histogram amplitude is then normalised into the relative amplitude by the maximum accumulated amplitude in each set of tests. Stress variations show a trend from low-velocity high stress to high-velocity low stress. Ice force variations show a concentration at around intermediate velocities range, i.e. IIV range, which means there is more integral of force over the same time interval, i.e. impulse energy, applied to increase the momentum of the structure. This situation occurs in the condition when stress values are relatively evenly distributed. These patterns may be worthwhile to be noticed from an energy conservation point of view.

Fig. 6. Histogram of stress and ice force variations at different ice velocities (a) Test. 67, K = 890 kN m−1. (b) Test. 110, K = 2700 kN m−1.
4.5. Type of vibration
It is debatable that whether IIV is forced vibration from resonance or self-excited vibration from negative damping as introduced earlier. One thing is certain that forced vibration does not need an initial condition. However, self-excited vibration needs to be trigged by forced vibration and it needs energy from an external source to sustain (Den Hartog, Reference Den Hartog1947).
No matter which type of vibration, both of them has the following relationship, f i = f s = f n, in which frequency of ice force, structural displacement and structural natural frequency are all equal. Commonly speaking, resonance is a special type of forced vibration which occurs when the external excitation frequency is equal to the structural natural frequency. For instance, making one fork to vibrate first will cause another identical fork to automatically vibrate. So, it is controlled by the external source. If the excitation frequency is different from the structural natural frequency, resonance will disappear. On the other hand, in self-excited vibration, vibrating frequency is equal to the natural frequency and the exciting force should be a function of the motion variables, such as displacement, velocity or acceleration (Rao, Reference Rao2004).
In IIV, vibration is self-excited predominantly because feedback from external structure makes more effect on ice failure and ice will affect the structure in return, like lock-in phenomenon. The reason for the increased vibration amplitude can be explained by the ‘negative damping’ theory in an alternative way by keeping in mind that the damping is not negative in reality. The increased vibration is attributed to more energy into the structure when there is higher ice force and the stress value is concentrated mainly in the higher range of stress values.
For vibrations below and above the IIV range, structure vibrates at forced vibration mechanism predominantly because the time interval between each cycle of vibration is so short that there is no time for the structure to give feedback to ice. So, the internal ice failure characteristic makes more effect with lower stress and ice force.
4.6. Friction-induced vibration
The frictional force is another important effect that builds up the ice force characteristic. With the formation of microcracks inside ice when it is interacting with structure, the static ice force is building up at the same time with the trend of sliding up and down motion along the vertical direction of interaction surface. Ice failure occurs when the crack propagates to a certain level that cannot hold the force perpendicular to the interaction surface. At the same time, the maximum static frictional force along the vertical direction of interaction surface is reached.
After the failure, ice force shows a typical transition instant from static friction to kinetic friction, which can be found at all ice velocity ranges in the tests from Sodhi (Reference Sodhi1991a), such as the creep deformation at very low ice velocity in Test. 64, the extrusion phase at intermittent crushing under intermediate velocity in Test. 204 and transition from intermittent crushing to continuous crushing at high velocity in Test. 206.
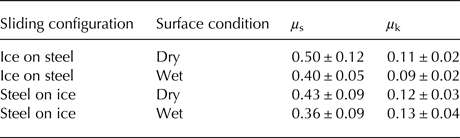
Sodhi (Reference Sodhi, Jones, Tillotson, McKenna and Jordaan1991b) found that effective pressure during continuous crushing is in an order of magnitude lower than the peak pressure during intermittent crushing from both full-scale and small-scale experiments. It can also be explained that kinetic friction occurs at higher velocities leading to much lower pressure. Sukhorukov (Reference Sukhorukov2013) found that the mean value of static and kinetic friction coefficients of ice on steel are 0.50 and 0.11 on a dry surface, and 0.40 and 0.09 on wet condition, respectively, as shown in Table 2, where μ s and μ k are the static and kinetic friction coefficients, respectively. Although values of steel on the ice have lower static friction coefficient, they are still much higher than the kinetic friction coefficients.
Table 2. Static and kinetic friction coefficients from ice-steel experiments (Sukhorukov, Reference Sukhorukov2013)
Ice stress variations in IIV is very similar to frictional coefficient variations in friction-induced vibration when considering relative velocity only as shown in the three-region Stribeck curve in Figure 7. A typical example is the self-excited vibration of a bowed violin string. The bow and string are moving in the same direction at first when the bow drags the string aside. The coefficient of friction is high because relative velocity is low and potential energy is storing in the string. When the maximum static force cannot hold the restoring force from string, the string will slip back releasing the energy to kinetic energy in the form of backward velocity. The decrease in coefficient of friction yields lower frictional force, which will then accelerate the velocity further to a certain level. However, the coefficient will raise again due to the coefficient curve as shown in Figure 7 and the system will be in a stable feedback condition when restoring force is equal to the frictional force. Less energy is lost than the input at first and the difference is enough to overcome the damping and sustain the vibration (Schmitz and Smith, Reference Schmitz and Smith2011), like the energy exchange in the steady-steady state shown in Figure 5c. The sound of vibrations is produced at its natural frequency since it determines the restoration of the string.
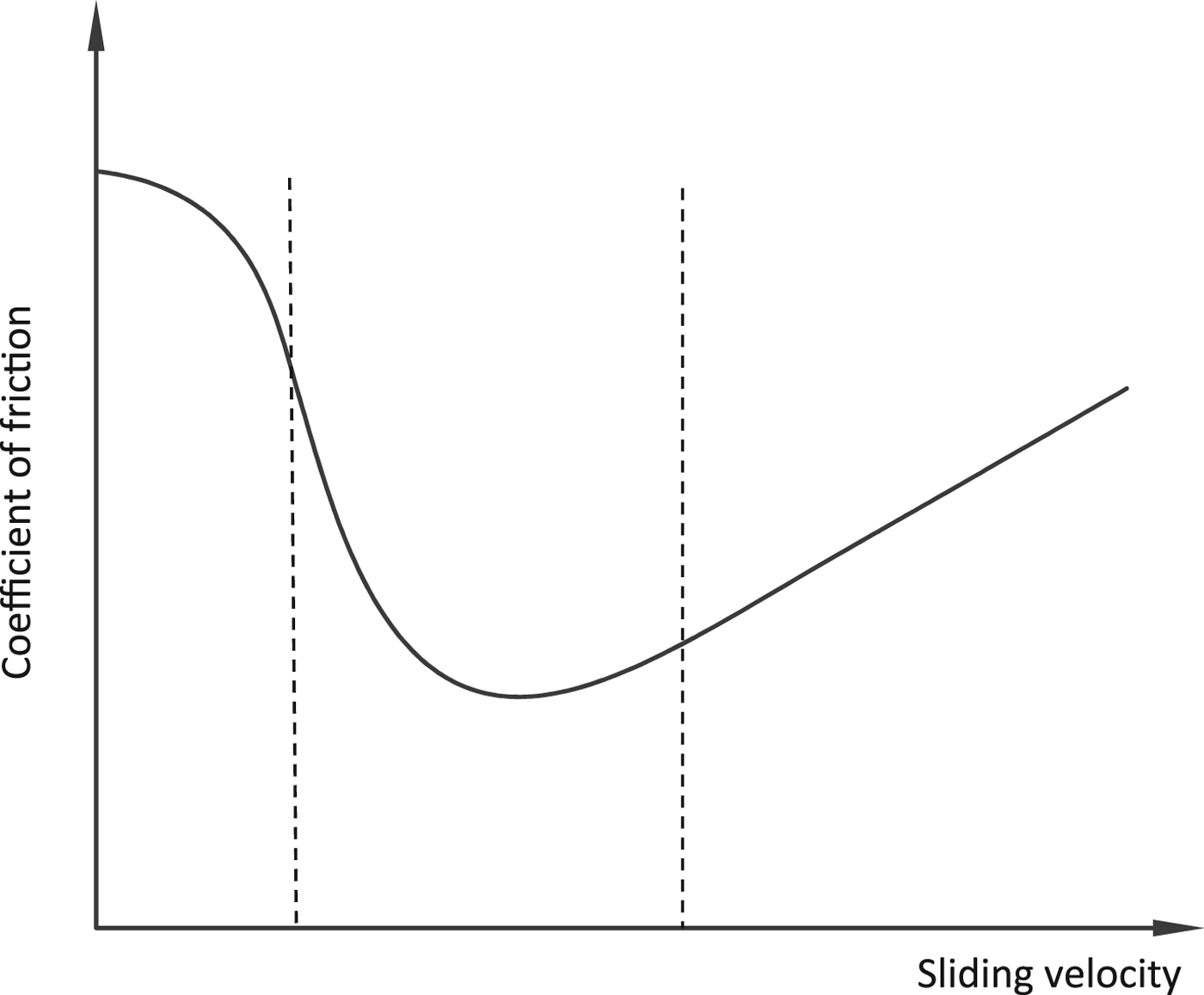
Fig. 7. Stribeck curve.
5. CONCLUSIONS
To obtain the effect of velocity and structural natural frequency (structural stiffness) on ice failure, an extended model based on the previous work of Ji and Oterkus (Reference Ji and Oterkus2016) was developed. A series of validation cases were conducted and compared with the results from Sodhi (Reference Sodhi, Jones, Tillotson, McKenna and Jordaan1991b) which show the typical three kinds of response; intermittent crushing, lock-in and continuous crushing and both numerical and experimental results are in a good agreement with each other.
Physical mechanism during ice/structure interaction process under different velocities was discussed based on the general branch of feedback mechanism and energy mechanism, respectively. Internal effect and external effect from ice and structure were both explained in the feedback branch. Energy exchanges of each type of energy were reproduced and coincided with analyses in Sodhi (Reference Sodhi1991a).
Reasons for the increased vibration amplitude during IIV and lock-in were presented and discussed starting from the disagreement between Sodhi and Määttänen and analyses were given from both perspectives. In addition, a study on the stress and force variations in the full range of velocities showed that there was more impulse energy during IIV range which can be an explanation for the increased vibration amplitude from the energy point of view.
IIV is in a resonant type of self-excited vibration because the structural effect is more predominant. Even though negative damping is not negative in reality, it can be used to explain the self-excited vibration in an alternative way. A general conclusion on the predominant type of vibration during the interaction process is forced, self-excited and forced in each of the three types of responses.
Similar variations between ice stress and coefficient of friction shows that there is a likelihood to use static and kinetic friction force to explain the pressure difference at high and low velocities as well as the unstable and stable conditions during IIV.
ACKNOWLEDGEMENTS
The first author would like to acknowledge the University Research Studentship provided by the University of Strathclyde.











