Over the last two decades, there has been an explosion in the use of principal components analysis (PCA) to identify dietary patterns in nutritional epidemiological studies( Reference Slattery, Boucher and Caan 1 – Reference Bertuccio, Rosato and Andreano 10 ). The main reason for the explosion of PCA is that recent results have raised questions about the role of diet in the aetiology of certain chronic diseases. A lack of empirical evidence from randomised controlled trials based on observational findings has been noted in chronic diseases such as asthma( Reference Shaheen, Newson and Rayman 11 ), cancer( Reference Greenberg, Baron and Tosteson 12 , Reference Schatzkin, Lanza and Corle 13 ) and CVD( Reference Hennekens, Buring and Manson 14 ), and it has been argued that single foods or nutrients may be less important than dietary patterns in causing disease. Since the use of a single variable to explore associations between diet and disease has led to unreliable results, an alternative is to look at a small number of dietary dimensions each made up of a combination of foods with the use of PCA.
PCA of data from FFQ allocates food items according to the degree with which their reported intakes are correlated. The principal components identified are referred to as ‘dietary patterns’ and can be investigated in relation to health and disease. This approach proved successful, for example, in two large US cohorts, in which the same two patterns of diet – a ‘prudent’ dietary pattern characterised by intake of vegetables, fruit, legumes, whole grains, fish and poultry and a ‘Western’ dietary pattern characterised by intake of red meat, processed meat, refined grains, sweets and desserts, French fries and high-fat dairy products – were identified and subsequently linked to differences in the occurrence of CHD( Reference Hu, Rimm and Stampfer 15 , Reference Fung, Willett and Stampfer 16 ), colon cancer( Reference Wu, Hu and Fuchs 17 , Reference Fung, Hu and Fuchs 18 ) and chronic obstructive pulmonary disease( Reference Varraso, Fung and Barr 19 , Reference Varraso, Fung and Hu 20 ).
PCA is often claimed to resolve the issue of confounding between different dietary exposures( Reference Randall, Marshall and Graham 21 , Reference Jacques and Tucker 22 ), though, even where there is a causal effect from diet, it is not clear whether the foods singled out in a PCA are those that are directly associated with the risk of disease, or are simply confounded with other foods. Some authors have also suggested that by aggregating the effects of different foods, PCA can demonstrate the effects that are too small to be detected by analysing each food separately( Reference Hu 2 , Reference Newby, Weismayer and Akesson 23 ). Slattery( Reference Slattery 24 ) claimed that eating patterns derived from PCA characterise the diet-associated disease risk better than any one food or nutrient. However, in order for this statement to be useful in disease prevention, we need PCA to identify all of the foods (and only those foods) that, in combination, increase or decrease the risk of disease.
As far as we are aware, justifications of this kind for using PCA have not been critically evaluated. We set out to investigate, using simulation, whether PCA really performs better in these respects than an analysis of individual food intakes.
Materials and methods
Simulation
Simulations were performed in Stata 10 (Stata Corporation). To simulate a dietary dataset with a realistic correlation structure, we sampled with replacement from a reference dataset of real FFQ data. We used two different sets of reference dietary data to allow replication of our findings. These datasets comprised 856 adults aged 16–50 years living in Greenwich who took part in the Food, Lifestyle and Asthma in Greenwich (F.L.A.G.) survey (dataset 1)( Reference Shaheen, Sterne and Thompson 25 ) and 201 adults aged 29–54 years living in Ipswich and Norwich who took part in the UK European Community Respiratory Health Survey (ECHRS) II diet survey (dataset 2)( Reference Hooper, Heinrich and Omenaas 26 ). Quantitative FFQ recorded frequencies of 217 different foods (from never to 6 d/week) in the FLAG survey and of seventy-four different foods (from never to 7 d/week) in the UK ECRHS II diet survey over the previous 12 months. Using both datasets, we created food intake variables by estimating weekly intake (g) of foods and food groups by multiplying frequency of consumption by the weight of standard portion sizes using British food composition tables( Reference Paul, Southgate and Buss 27 ). The UK ECHRS II study was conducted according to the guidelines laid down in the Declaration of Helsinki, and all procedures involving human participants were approved by the Ipswich Hospital and Norfolk and Norwich Hospital ethics committees in the UK( Reference Hooper, Heinrich and Omenaas 26 ). The F.L.A.G. survey was approved by the Greenwich Research Ethics Committee( Reference Shaheen, Sterne and Thompson 25 ). Written informed consent was obtained from all the participants in both studies.
In each simulation, we assumed that disease risk depended on a linear combination of m food intakes derived from the FFQ. Let us suppose that these foods are indexed i
1, i
2,…, i
m
, and absolute food intakes
![]() $$x _{ i _{1}},\, x _{ i _{2}},\,\ldots ,\, x _{ i _{ m }} $$
are standardised to have zero mean and unit standard deviation. We assumed a logistic model for the disease risk, p, that is:
$$x _{ i _{1}},\, x _{ i _{2}},\,\ldots ,\, x _{ i _{ m }} $$
are standardised to have zero mean and unit standard deviation. We assumed a logistic model for the disease risk, p, that is:
This model has been widely used in previous simulated epidemiological studies( Reference Fewell, Davey Smith and Sterne 28 , Reference Peduzzi, Concato and Kemper 29 ). We chose the constant a so that the baseline risk at the average intake of all foods was 0·15, i.e. a= ln(0·15/(1 − 0·15)). The constants b 1, b 2,…, b m were chosen so that the OR per standard deviation of food intake was 1·5 or 1/1·5 depending on whether the food was assumed to increase or decrease the risk of disease, i.e. b j = ± ln(1·5). This is comparable to significant OR for dietary patterns that were identified in the systematic review by Newby & Tucker( Reference Newby and Tucker 4 ).
The value of m was chosen to be about one in seven of the total number of foods on the FFQ, i.e. m= 30 (of 217) in dataset 1 and m= 10 (of 74) in dataset 2. The m foods were chosen in two different ways. First, they were randomly chosen in each simulation. Results of these simulations inform us about the average performance of different methods when we do not restrict a priori the combinations of foods that might be important for disease risk. We considered two models of this kind: in model 1, all m foods were assumed to be protective; in model 2, all m foods were assumed to increase the risk of disease. Second, they were predetermined in each simulation to be foods making up a ‘Western’ dietary pattern, which was assumed to be positively associated with the risk of disease (model 3). These foods are listed in Table 1, and were chosen as food intakes with the highest positive loadings on a ‘Western’ dietary pattern obtained using PCA from the original reference dataset (further details are available from the authors). Model 3 might be expected to favour PCA as a means of identifying dietary associations, since the model is based on a principal component in the population.
Table 1 List of foods comprising a ‘Western’ dietary pattern for each dataset*

* Dataset 1 is from the Food, Lifestyle and Asthma in Greenwich (F.L.A.G) survey( Reference Shaheen, Sterne and Thompson 25 ); Dataset 2 is from the UK European Community Respiratory Health Survey (ECRHS) II diet survey( Reference Hooper, Heinrich and Omenaas 26 ).
Having simulated the food intake data for a new individual in the sample, we then calculated the probability of the outcome, p, using equation 1. We determined whether or not the individual had the disease by generating a uniform random number between 0 and 1, and observing whether it was less than p.
The simulated dietary data were then subjected to a PCA (conducted on the correlation matrix of the reported food intakes) with varimax rotation, and the resulting dietary patterns were investigated for their associations with the risk of disease using logistic regression. We considered the results of extracting two, five and ten principal components, since this was the range of components identified in the majority of dietary pattern studies( Reference Kant 3 , Reference Newby and Tucker 4 ).
For comparison, we looked at the results of analysing each food on the FFQ separately in relation to the risk of disease, a process we refer to as an exhaustive single food analysis (ESFA). This is a univariate or independent screening approach as we know from, for example, SNP screening in statistical genetics( Reference Laird and SpringerLink 30 ). All regression analyses of dietary patterns and individual food intakes were adjusted for total energy intake. Adjustment for energy intake is strongly advised in the analysis of observational nutritional studies( Reference Willett 31 , Reference Jakes, Day and Luben 32 ). As pointed out by Willet( Reference Willett 31 ), adjustment for total energy intake should be considered because the level of intake might be a risk factor, might distort the effect of a food or a nutrient on the potential outcome, and variations in nutrient intake between individuals might reflect variations in individuals' energy intake levels.
ESFA was, in the first instance, unadjusted for the effects of other foods, but in order to deal with confounding, we also carried out ESFA adjusting for other foods using three different methods:
-
(a) Adjusting for the first five principal components of diet. Because net confounding by correlated foods and patterns could result in biased associations between diet and disease, adjustment for dietary patterns has been suggested in the literature( Reference Imamura, Lichtenstein and Dallal 33 ). We chose five components of diet because that was the number of dietary patterns of diet that were identified in the original populations (data not shown).
-
(b) Adjusting for all foods that were significant in the unadjusted ESFA. In this case, as a first step, we ran an ESFA procedure adjusting for total energy intake keeping the food variables (covariates) with those regression coefficient estimates that had a P value lower than a specific threshold. The threshold was determined by the procedure of Benjamini & Hochberg( Reference Benjamini and Hochberg 34 ), controlling the rate of our false discoveries at 20 %. Then, we re-ran an ESFA procedure adjusting for energy intake and for all these foods (covariates) that were significant in the first round of analysis (unadjusted ESFA). This method is conceptually similar to the iterative sure independence screening method proposed by Fan & Lv( Reference Fan and Lv 35 ). However, herein, we chose our covariates based on a multiple test procedure and not on a penalised likelihood method. Furthermore, we aimed to control the false discovery rate (FDR), whereas the iterative sure independence screening method focused on missed discoveries.
-
(c) Adjusting for a propensity score for predicting the amount of each index food intake consumed from other food intakes( Reference Imai and van Dyk 36 ). Once the propensity score was estimated, it was used as a confounder in our multivariate model( Reference Sturmer, Joshi and Glynn 37 ).
The process of simulation and testing was repeated a large number of times (10 000) in order to determine the long-run performance of PCA and ESFA in detecting the associations between diet and disease.
Using the ‘powerlog’ sample size calculation routine in Stata( 38 ), we determined that a sample size of 330 would achieve 80 % power at the 5 % significance level to detect an OR of 1·5 per standard deviation, using an unadjusted logistic regression with no allowance for multiple testing. We present results herein for sample sizes of 300, 1200 and 4800.
Evaluating the performance of exhaustive single food analysis and principal components analysis
First, we investigated the statistical power with which ESFA and PCA could detect whether there was any association between diet and disease. For the ESFA, we considered that an association had been found if any of the food intakes were significantly associated with the risk of disease after applying a Bonferroni correction for the number of foods tested (family-wise P< 0·05)( Reference Miller 39 ). For the PCA, we considered an association had been found if any of the dietary patterns were significantly associated with the risk of disease after applying a Bonferroni correction for the number of patterns identified.
We also wanted to see how well the two procedures identified the specific combination of food intakes that were causally associated with the risk of disease. We compared the power and the FDR of ESFA and PCA for detecting these associations. In this context, we extended the concept of ‘power’ to mean the proportion of foods included in the model that were correctly identified as significantly associated with the disease outcome (Fig. 1). The FDR is the proportion of discoveries, or significant findings, that are false (Fig. 1).
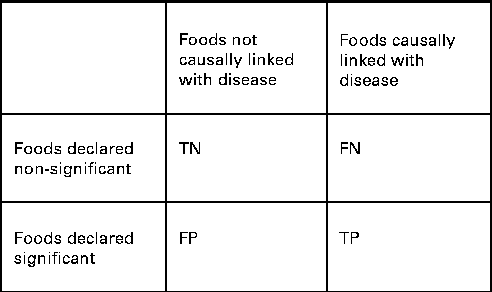
Fig. 1 How the results of dietary analyses can be broken down. TN, true negatives; FN, false negatives; FP, false positives; TP, true positives. Power = TP/(FN+TP). False discovery rate (FDR) = FP/(FP+TP) if FP+TP>0. FDR = 0 if FP+TP = 0.
For the ESFA, we considered that there was a ‘significant’ effect of a food if it was identified as such using the multiple testing procedure of Benjamini & Hochberg( Reference Benjamini and Hochberg 34 ), with a nominal FDR set to 20 %. For the PCA, we considered that there was a ‘significant’ effect of a food if it had a correlation >0·3 or < − 0·3 with a dietary pattern that was significantly associated with the risk of disease (P< 0·05) – this being the way in which individual foods tend to be highlighted in a PCA. It should be noted that the procedure of Benjamini & Hochberg( Reference Benjamini and Hochberg 34 ) is designed to control the FDR at no more than the nominal level, but here false discoveries (of foods) occur not just as random errors, but also because of confounding with other foods, so the nominal rate may be exceeded.
Results
Table 2 displays the estimates of the power of PCA and ESFA for detecting an association between diet and disease, for different sample sizes and numbers of principal component scenarios. In model 3, the estimates of power for a sample size of 300 were all close to 100 %, so the estimates for a sample size of 100 are also given. Neither method consistently outperformed the other in this respect.
Table 2 Power (%) of exhaustive single food analysis (ESFA) and principal components analysis (PCA) for detecting any association between diet and disease*

F.L.A.G., Food, Lifestyle and Asthma in Greenwich; ECRHS, European Community Respiratory Health Survey.
* All estimates of power have a standard error < 0·5 %.
† In models 1 and 2, one in seven foods (thirty in dataset 1 and ten in dataset 2) are selected at random in each replication from the foods on the FFQ. In model 1, all selected food intakes are negatively associated with the risk of disease; in model 2, all selected food intakes are positively associated with the risk of disease. In model 3, foods comprising a ‘Western’ dietary pattern (thirty in dataset 1 and ten in dataset 2; see Table 1) are used in each replication, with all these food intakes being positively associated with the risk of disease.
‡ Power of PCA exceeds that of ESFA.
Table 3 shows the estimates of the power and FDR of PCA and ESFA for identifying the combinations of food intakes that were causally associated with the risk of disease. In most parts of the table, ESFA ‘dominates’ PCA in the sense of having both a higher power and a lower FDR. In the remainder of the table, neither one dominates the other.
Table 3 Power and false discovery rate (FDR) (%) of exhaustive single food analysis (ESFA) and principal components analysis (PCA) for detecting the foods that are causally linked to the risk of disease*
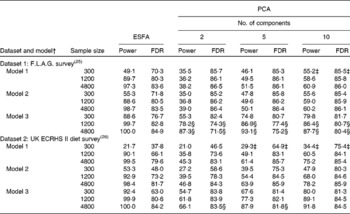
F.L.A.G., Food, Lifestyle and Asthma in Greenwich; ECRHS, European Community Respiratory Health Survey.
* All estimates of power and FDR have a standard error < 0·5 %.
† In models 1 and 2, one in seven foods (thirty in dataset 1 and ten in dataset 2) are selected at random in each replication from the foods on the FFQ. In model 1, all selected food intakes are negatively associated with the risk of disease; in model 2, all selected food intakes are positively associated with the risk of disease. In model 3, foods comprising a ‘Western’ dietary pattern (thirty in dataset 1 and ten in dataset 2; see Table 1) are used in each replication, with all these food intakes being positively associated with the risk of disease.
‡ Power of PCA exceeds that of ESFA, but FDR is also higher.
§ FDR of PCA is lower than that of ESFA, but power is also lower.
Adjusting for other foods that were significant in an unadjusted analysis successfully controlled the FDR at about the 20 % nominal level, though with some loss of power, particularly with low sample sizes (Table 4). Attempting to control the FDR of ESFA by adjusting for principal components of diet, or by adjusting for a propensity score, was not successful (Table 4).
Table 4 Power and false discovery rate (FDR) (%) of exhaustive single food analysis with different methods of adjustment for other foods*

F.L.A.G., Food, Lifestyle and Asthma in Greenwich; ECRHS, European Community Respiratory Health Survey.
* All estimates of power and FDR have a standard error < 0·5 %.
† In models 1–3, one in seven foods (thirty in dataset 1 and ten in dataset 2) are selected at random in each replication from the foods on the FFQ. In model 1, all selected food intakes are negatively associated with the risk of disease; in model 2, all selected food intakes are positively associated with the risk of disease. In model 3, foods comprising a ‘Western’ dietary pattern (thirty in dataset 1 and ten in dataset 2; see Table 1) are used in each replication, with all these food intakes being positively associated with the risk of disease.
Discussion
In some scenarios, ESFA had greater power than PCA to detect an association of diet with the risk of disease. Allowing for multiple testing using the procedure of Benjamini & Hochberg( Reference Benjamini and Hochberg 34 ), ESFA also typically had a higher power and a lower FDR for identifying the combinations of foods that were causally linked with the risk of disease than PCA in which foods were singled out if they correlated highly (>0·3 or < − 0·3) with a significant dietary pattern. Even when a simplified ‘Western’ dietary pattern was the real culprit, PCA could not outperform ESFA in reconstructing the foods that were linked with the risk of disease. These findings were replicated in two different FFQ datasets.
In principal components regression, there is no standard procedure for identifying foods as ‘significantly associated’ with the disease outcome. We used a definition that matches what researchers typically do when they single out a combination of foods to mention in their abstract( Reference Shaheen, Jameson and Syddall 40 ) or when they devise an intervention based on the results( Reference Bertuccio, Rosato and Andreano 10 ); that is, to list the foods that are highly correlated with a dietary pattern that is itself strongly associated with the disease outcome. We wanted to know whether this method was better at correctly identifying the combinations of foods that are associated with the risk of disease than an ESFA. ‘Significant’ foods are defined differently in each case (they are different methods), but the performance of each method is assessed using the same criterion: how often does it get it right? In fact, we use two criteria: FDR and power. The two methods can differ in both these respects, making comparison a little harder (think of two different diagnostic tests that might differ both in their sensitivity and specificity); nevertheless, if we observe one method to have both a lower FDR and a higher power, then we can conclude that it has superior performance.
It is common to try to control the FDR at a low level( Reference Benjamini and Hochberg 34 ). We have used a nominal FDR of 20 %; in genetic studies, where the use of FDR is well established, FDR between 5 and 20 % are recommended depending on the circumstances( Reference Benjamini and Yekutieli 41 ). It should be noted that 20 % is still well below the FDR of individual hypothesis testing using P< 0·05 as a cut-off( Reference Ioannidis 42 ). However, it is concerning that the observed FDR of both ESFA (nominally controlled at 20 %) and PCA increase in an uncontrolled fashion as the sample size and power increase (Table 3). It is worth noting that when one in seven foods are causally linked with the risk of disease, as here, an FDR of about 86 % would be achieved by selecting ‘significant’ foods entirely at random. The uncontrolled FDR occurs because all food intakes are correlated to some extent with the causal foods, leading to false positive findings (more so as power increases). We tried a variety of approaches to control for other foods in the ESFA, and found that the FDR could be successfully controlled at the nominal level by adjusting for foods that were significant in a univariate analysis. Achieving a given power requires about twice the sample size of an unadjusted ESFA (with its inflated FDR) and four times the sample size from our original calculation, i.e. for an unadjusted analysis with the criterion P< 0·05.
Our models included one in seven of the foods on the FFQ. We repeated our simulations with a smaller number of foods in the models, and obtained qualitatively similar findings (see online supplementary Tables S1–S3). We did not consider interactive effects of foods in our models; this requires further investigation. Studies have claimed that dietary constituents interact with each other in complex ways( Reference Messina, Lampe and Birt 43 , Reference Sacks, Obarzanek and Windhauser 44 ), and these interactions have an effect, for example, on the risk of CVD( Reference Halliwell 45 ) and breast cancer( Reference Edefonti, Randi and La Vecchia 46 ). PCA is often recommended as a way of dealing with interactions between foods( Reference Hu 2 , Reference Varraso, Fung and Hu 20 ). Furthermore, foods could be associated with the risk of disease in a non-linear way. However, it is questionable whether linear combinations of food intakes produced by the PCA adequately address the issues of modelling interactions or capture potential non-linear effects between diet and disease.
Although we considered a model based on a ‘Western’ dietary pattern, there is no reason why foods with truly causal effects should be foods that are highly correlated with each other in order to be associated with the risk of disease. Hence, in the present simulation study, foods associated with the risk of disease were not necessarily highly correlated. Note it is not obvious that ESFA will outperform PCA in this case, since ESFA must pay a much higher penalty for multiple testing of all the individual foods, while each principal component may include – even if only by chance – a number of foods that have causal effects in the same direction. Where disease risk is explained by other factors that are confounded with diet, however, this confounding is more likely to be at the level of a dietary pattern than with an individual food. A ‘prudent’ dietary pattern, for example, is associated with older age( Reference Agurs-Collins, Rosenberg and Makambi 47 ), female sex( Reference Robinson, Syddall and Jameson 48 ), non-smoking( Reference Fung, Rimm and Spiegelman 49 ), higher income( Reference Perrin, Dallongeville and Ducimetiere 50 ), higher educational level( Reference Raberg Kjollesdal, Holmboe-Ottesen and Wandel 51 ), exercise( Reference Lopez-Garcia, Schulze and Fung 52 ) and supplement use( Reference Heidemann, Schulze and Franco 53 ). These factors are likely to be associated with a number of food intakes contributing to a ‘prudent’ dietary pattern rather than with any one of these foods in particular. This is another reason for adjusting each food effect for others found to be significant, as we suggest this should help control for both measured and some unmeasured confounding. We did not include non-dietary confounders in our simulations because there are just too many different potential confounders and models for their effects to be considered. We suspect, however, that as long as there are foods with truly causal effects, the findings of the present study will generalise to situations where other confounders have been explicitly adjusted for.
PCA does not aim to obtain a clear picture of disease variation but to summarise the overall dietary intake variation in the population. As Jolliffe( Reference Jolliffe 54 ) points out, the mistake when PCA is employed for distinguishing between healthy and unhealthy individuals is to assume that the separation between these groups is along the axis of greatest variation in diet. More appropriate statistical approaches in this respect are linear discriminant analysis( Reference Jolliffe 54 ) and discriminant analysis of principal components( Reference Jombart, Devillard and Balloux 55 ).
Other multivariate approaches such as cluster analysis( Reference Reedy, Wirfalt and Flood 56 ), and data reduction techniques such as reduced-rank regression( Reference Hoffmann, Schulze and Schienkiewitz 57 ) provide an alternative way for identifying dietary patterns. The main advantage of cluster analysis over PCA is that cluster analysis creates mutually exclusive groups that can easily be used in the analysis. Reduced-rank regression constructs dietary patterns according to the covariance matrix of specific biomarkers (taken by blood samples, for example) that are associated with dietary intake variables and assumed to be linked with the investigated disease outcome. Thus, the dietary pattern that is identified to be associated with the risk of disease for a specific biological reason and the combinations of foods that characterise the pattern describe a specific biomarker in the causal pathway between diet and disease.
Another approach is factor analysis, an ambiguous term which in certain textbooks include both PCA and common factor analysis. Even when investigators say that they are employing factor analysis in nutritional studies, they may be employing PCA. This misconception depends on the statistical package that these studies have used, because certain statistical packages (e.g. SAS) treat PCA as a special category of factor analysis. Factor analysis, which is a different statistical technique from PCA( Reference Bartholomew, Steele and Moustaki 58 ), is not recommended for the analysis of nutritional data( Reference Hu 2 ), although factor analysis based on the principal factor method gives generally similar results to PCA( Reference Schulze and Hoffmann 59 ).
Since ESFA outperforms PCA in the present simulation study, dealing with high-dimensional multivariate dietary exposures could be treated as a problem of variable model selection, that is, finding the non-zero regression coefficients in an unknown regression model. Our adjusted ESFA is similar to the iterative sure independence screening method for ultra-high-dimensional data( Reference Fan and Lv 35 ). Other forms of penalised likelihood estimation methods have been developed in the last decade to cope with high-dimensional data and have been lately reviewed( Reference Fan and Lv 60 ). These methods could be potentially useful in nutritional epidemiological studies, and further research is needed.
There is a growing interest in designing dietary interventions around foods rather than nutrients( Reference Jacobs, Gross and Tapseli 61 ) and around particular foods rather than dietary patterns( Reference Jacobs, Gross and Tapseli 61 , Reference Mann and Aune 62 ). Specifically, Jacobs et al. ( Reference Jacobs, Gross and Tapseli 61 ) suggests that the evidence for beneficial effects of a ‘prudent’ diet comes from interventions that only modified the intake of one or two foods. Furthermore, McCann et al. ( Reference McCann, Weiner and Graham 63 ) suggests that fruits and vegetables alone provided the highest discrimination among endometrial cancer cases and controls compared with PCA and other methods of characterisation. Mann & Aune( Reference Mann and Aune 62 ), evaluating the evidence that fruits and vegetables can prevent diabetes, have called for more studies looking at the effects of specific fruits and vegetables.
In conclusion, an FFQ-wide study of associations between food intakes and disease risk outperforms an analysis of dietary patterns derived from PCA. Analysing each food adjusting for others allows truly causal effects to be identified with a low rate of false discoveries and surprisingly good power. Although PCA has proved extremely popular in nutritional epidemiology to date, we question its routine use in this context.
Supplementary material
To view supplementary material for this article, please visit http://dx.doi.org/10.1017/S0007114514000221
Acknowledgements
The present study is part of a programme of research funded by the Department of Health Policy Research Programme (DHTBX P16621).
All authors were responsible for the reported research and made substantial contributions to the conception and design of the simulation study, analysis and interpretation of the data, drafting of the manuscript or revising it critically for important intellectual content. I. B. prepared the manuscript, with R. H. and P. B. contributing to it. I. B. conducted the computer programming and simulation and data analysis. All authors read and approved the final version of the manuscript.
None of the authors has any personal, commercial, political, academic or financial conflicts of interest to declare.







