A signal adaptive diffusion filter for video coding: improved parameter selection

Abstract

In this paper we combine video compression and modern image processing methods. We construct novel iterative filter methods for prediction signals based on Partial Differential Equation (PDE)-based methods. The central idea of the signal adaptive filters is explained and demonstrated geometrically. The meaning of particular parameters is discussed in detail. Furthermore, thorough parameter tests are introduced which improve the overall bitrate savings. It is shown that these filters enhance the rate-distortion performance of the state-of-the-art hybrid video codecs. In particular, based on mathematical denoising techniques, two types of diffusion filters are constructed: a uniform diffusion filter using a fixed filter mask and a signal adaptive diffusion filter that incorporates the structures of the underlying prediction signal. The latter has the advantage of not attenuating existing edges while the uniform filter is less complex. The filters are embedded into a software based on HEVC with additional QTBT (Quadtree plus Binary Tree) and MTT (Multi-Type-Tree) block structure. Overall, the diffusion filter method achieves average bitrate savings of 2.27% for Random Access having an average encoder runtime increase of 19% and 17% decoder runtime increase. For UHD (Ultra High Definition) test sequences, bitrate savings of up to 7.36% for Random Access are accomplished.

I. INTRODUCTION

The increasing demand for high-resolution videos, together with limited transmission and memory capacity, is still driving the research on video compression. As a core technique in the state-of-the-art video codecs such as High Efficiency Video Coding (HEVC, [1]) a hybrid approach with block-based architecture is used. The term “hybrid” [2] refers to a combination of prediction from previous decoded frames (inter) or adjacent decoded blocks from the frame itself (intra prediction) together with transform coding of the resulting residual. Thus, the quality of the prediction signal has a large influence on the efficiency of video codecs. In this paper, a method first introduced in [3] based on the state-of-the-art mathematical denoising techniques is elaborated in more detail. The central idea of this method is to construct two types of prediction filters in order to improve prediction signals in a block-wise manner: a uniform diffusion filter using a fixed filter mask and a signal adaptive diffusion filter that incorporates the structures of the underlying prediction signal.

In particular, the employed techniques here come from the field of image smoothing for denoising and use Partial Differential Equation (PDE)-based methods. In the context of video coding, linear inpainting methods have been employed to replace intra prediction modes in general [4,5] or particular ones such as the planar prediction [6,7]. Due to their diffusion properties, these methods have the disadvantage that they cannot prolong edges well and are therefore not suitable to replace angular prediction modes. This is the reason why in this paper instead of replacing the prediction, the prediction provided by the video codec is chosen as initial condition.

Figure 1 shows a block diagram of a classic hybrid video encoder with enclosed decoder depicting the newly introduced additional prediction filter step that is applied on top of the selected prediction signal. So far, little work has been published on tools increasing the efficiency of the codec that operate at this particular location. Classically [8], linear filtering techniques have been applied to the reference samples before predicting to improve intra prediction. Furthermore after predicting, modern video codecs employ linear smoothing techniques for certain intra prediction modes, which are only applied on the block boundaries (boundary smoothing, see [8,9]).

Fig. 1. Block diagram of a hybrid video encoder with newly introduced prediction filter and enclosed decoder

In case of inter, most methods to improve prediction operate directly at the generation of the prediction block [10]: Weighted prediction approaches that superimpose different reference blocks can be applied to increase the accuracy of the current prediction, for example. Another classical method are the so-called interpolation filters, that use fixed sets of filter coefficients to interpolate in between the samples of the reference block(s) to generate fractional samples for an accurate inter prediction. In [11], adaptive interpolation filter coefficients have been proposed which are fitted and signaled frame by frame.

Well-known post-prediction methods have been suggested for the new video compression standard using affine linear models to compensate local illumination changes [12,13]. As the methods established in [3] and used here, this tool operates on the prediction signal.

The methods used here are signal adaptive in the sense that they have various configurations which are signaled block-wise. Thereby, they fit into the framework of classic video coding tools. Additionally, they are signal adaptive in the sense that the filter coefficients used depend on the underlying prediction signal.

The employed mathematical methods originate from image smoothing using PDE-based methods. One of the key challenges there is to filter out noise while keeping edges intact. Perona and Malik [14] suggested a non-linear diffusion method to avoid the blurring effects of linear smoothing.

Using a non-linear anisotropic diffusion model, interesting advances have been made on the topic of PDE-based image compression [15]. The authors of [15] compress images by firstly removing less significant samples from the image and then writing the remaining ones into a data stream. Secondly, to decode the picture, a generalized anisotropic Perona–Malik model is used to interpolate between the remaining sparse samples and thereby obtain a reconstruction of the original picture. Thus, in this case, the authors of [15] establish a kind of data compression by having to write less samples. In [16,17], these ideas are transferred to videos.

In contrast to that, in this paper, the anisotropic diffusion model is built into the framework of a hybrid video codec: The prediction filters make use of the a priori structural knowledge contained in the selected prediction signal. The anisotropic diffusion model is used to develop a highly signal adaptive prediction filter in order to improve the embodied prediction and thereby enhancing the coding efficiency.

This paper is organized as follows. In Section II an overview of the current state-of-the-art in video coding is given. In Section III, we will describe the PDE-based filtering approaches in a continuous setting and use them to construct a uniform and a signal adaptive prediction filter for video coding. Compared to [18] and [3], more details on the specific discrete implementation are given and the idea of the signal adaptive filtering is shown geometrically on a particular example. In Section IV, the employed experimental setup is described in detail. In contrast to [3], which was built into HEVC, here, the filter method is embedded into a software based on HEVC which uses a QTBT with MTT block structure (see subsection IV.A for more details). The impact of the filters is shown exemplarily on an intra prediction block. Additionally when compared to [18] and [3], in Section V, the meaning of the required parameters for the filter method is explained and illustrated. Furthermore, certain parameters are tested thoroughly using encoder-based tests, where the individual cost improvement is saved and later used to determine an improved parameter selection which leads to enhanced bitrate savings.

In this paper, as in [18] and [3], the diffusion filters are implemented such that they use the reconstructed samples on the boundary where they are applicable. In contrast to [18] and [3], here in Section VI, additionally, an alternative is shown which avoids accessing the reconstructed samples in the inter case: A Neumann boundary condition is implemented and tested empirically. In a discrete setting, this means that the samples are mirrored across the boundary. It is shown that the alternative boundary condition only affects the bitrate savings to a very small degree.

Eventually, in Section VII, we show results of up to $1.74 \%$ bitrate savings for All Intra at $43 \%$ encoding and $19 \%$ decoding complexity increase. In case of Random Access, $2.27 \%$ bitrate savings are achieved at $19 \%$ encoding and $17 \%$ decoding complexity increase. For individual UHD sequences, the method yields up to $7.36 \%$ bitrate savings for Random Access. Note that these results include the complexity reductions like the restriction on certain block sizes as described in [18].

II. STATE-OF-THE-ART VIDEO CODING

The standardization of video coding technology plays a major role in the broad adoption and growing popularity of video technology. The main purpose of a video coding standard is to define the interface between encoder and decoder to ensure interoperability among a wide range of devices. Video coding standards are designed to provide a maximal degree of freedom for the manufacturers to adapt the encoder to specific applications. More details can be found in [19].

All modern video codecs use the concept of hybrid coding. The term “hybrid” goes as far back as to the 1980s [2] and describes a combination of two fundamental concepts of video coding, predictive coding, and transform coding. The basic architecture of a hybrid video encoder together with an enclosed decoder is shown in Fig. 1, additionally depicting the new prediction filter step proposed here. The flow of the encoder is depicted using continuous lines.

For the sake of simplicity, here, we will describe the encoder only. Note that the standard does not imply a specific encoding approach. The following is to be read as an example of a particular encoder such as can be found in [20].

The video signal is divided into pictures and the pictures are split into blocks. Typically, the picture is divided into macroblocks of a fixed size consisting of a luma and two corresponding chroma components. In HEVC [1], the picture is divided into coding tree units (CTUs) of a size selected using a configuration parameter in the encoder. A CTU consists of a luma coding tree block (CTB) and two corresponding chroma CTBs. A CTB may contain only one coding unit (CU) or may be split into several CUs using a quadtree decomposition.

Assuming there are already reconstructed blocks in the picture storage, a prediction for the current block is formed using preceding blocks. If those blocks are spatially adjacent, the resulting prediction is called intra prediction. If they are taken from already reconstructed pictures, i.e. are temporally preceding, one speaks of inter prediction. The decision if intra or inter prediction is used is taken on CU level. To optimize the usage of already reconstructed pictures in the inter case, a motion estimation is performed. The residual between the prediction and the original block is calculated, transformed, and quantized using a certain quantization parameter (QP). The resulting coefficients are fed into the entropy coder. The entropy coder typically uses either variable-length coding (VLC) (e.g. Huffman codes [21]) or arithmetic coding (e.g. context-based adaptive binary arithmetic coding – CABAC [22]). To obtain the reconstructed samples, the quantized transform coefficients are rescaled and retransformed. Note that due to the quantization process, a loss of information takes place. Therefore, the reconstruction differs from the original. The reconstructed blocks are loop filtered and stored in the picture buffer where they are used to predict the following blocks.

III. MATHEMATICAL FRAMEWORK OF THE DIFFUSION FILTER

This section is primarily a review chapter and introduces the mathematical models to be used. Furthermore, it is described how these models are applied in the setting of video coding which is the main contribution of this paper. Here, the different types of uniform and signal adaptive diffusion models are described in a continuous setting. It is known that in a general, continuous setting, the problems that will be described in subsection B are not uniquely or not at all solvable. In a discrete setting, Weickert [23] has shown that they are uniquely solvable which makes the models suitable for our application.

A) Uniform diffusion model

In this subsection, a uniform diffusion model is described which originates from image smoothing. According to [24], such approaches were first introduced in 1959 in Japan [25]. This approach is a special case of the anisotropic case that will be presented in the sequel.

In order to use uniform diffusion in the context of video coding, let f be an image in $\mathbb {R}^2$ consisting of the given prediction block extended using the reconstructed pixels on the left and upper side. Then, we let the function $u \colon \mathbb {R}^2 \times \mathbb {R} \to \mathbb {R}$ be a solution of

(1)\begin{equation} \frac{\partial}{\partial t} u(x,t) = \mathrm{div} (\nabla u(x,t)), \end{equation}

with the initial condition

(2)\begin{equation} u(x,0) = f(x) \end{equation}

and boundary conditions

(3)\begin{align} u(x,t) &=f(x) \quad \forall x\in \Gamma_1, \nonumber\\ \frac{\partial}{\partial \nu} u(x,t) &=0 \quad \forall x\in \Gamma_2, \end{align}

for time $t\in [0,\infty )$, where ν denotes the outer normal and $\Gamma =\Gamma _1 \cup \Gamma _2$ the boundary of the prediction block. The upper and left boundary of the prediction block is denoted by $\Gamma _1$ and the lower and right boundary by $\Gamma _2$. Operator div denotes the divergence. The first boundary condition in Eq. (3) is chosen since in the application of video coding, the reconstructed samples on the upper and left sides are known. Here, the parameter t represents the duration of the filtering process and determines the strength of the filter.

The gradient is implemented using finite differences. Since $\mathrm {div} (\nabla u(x,t)) = \Delta u(x,t)$, Eq. (1) coincides with the heat equation. Solution u is a filtered version of the initial prediction f. The prediction in the codec is then replaced by its filtered descendant u restricted on the area of the prediction block.

Define the forward/backward differences operators as

\[ \mathcal{D}_{x_1}^+ u(x,t) = u(x+he_1,t) -u(x,t)\]

and

\[ \mathcal{D}_{x_1}^- u(x,t) = u(x,t)- u(x-he_1,t),\]

for unit vectors $e_i$, $i\in \{1,2\}$ and step size h>0. Operator $\mathcal {D}_{x_2}^\pm$ is defined analogously using unit vector $e_2 = (0,1)^T \in \mathbb {R}^2$. To discretize the time derivation, define

(4)\begin{equation} \mathcal{D}_t^+u(x,t) := \frac{1}{\tau}(u(x,t+\tau)-u(x,t)) \end{equation}

for parameter $\tau >0$. Now, Eq. (1) can be discretized as follows

(5)\begin{equation} \mathcal{D}_t^+u(x,t) = \mathcal{D}_{x_1}^- \mathcal{D}_{x_1}^+ u(x,t) + \mathcal{D}_{x_2}^- \mathcal{D}_{x_2}^+ u(x,t).\end{equation}

For sample x inside the block, Eq. (5) for $\tau =0.25$ results in

\begin{align*} u(x, t+\tau) &= \frac{1}{4} ( u(x+he_1,t) + u(x-he_1,t) \\ &\quad+u(x+he_2,t) +u(x-he_2,t) ). \end{align*}

In the discrete implementation, it is used that the latter can also be expressed as t-times correlating the initial prediction $u(x,0) = f(x)$ with the symmetric filter mask

\[ h = \frac{1}{4} \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \\ \end{pmatrix},\]

i.e.

\[ u(x,t) = \underbrace{h * \dots * h}_{\mbox{t-times}} *\, u(x,0).\]

Note that since h is a symmetric filter mask, correlation is equivalent to convolution.

An obvious disadvantage of this uniform smoothing is the fact that it does not only smooth noise, but also attenuates important features in the underlying image such as edges. This unwanted behavior can be prevented by using adaptive smoothing methods: Using this idea coming from image processing, we construct a filter which itself depends on local properties of the image – in our case the underlying prediction.

B) Anisotropic diffusion model

In order to identify features such as corners or to measure the local coherence of edges, the following model does not only consider the norm of the gradient but also takes its direction into account: Diffusion along edges should be preferred over diffusion perpendicular to them. To realize the combination of these aspects, a diffusion tensor which is based on the matrix $\nabla u \nabla u^T$ can be constructed as suggested by Cottet and Germain [26]. To avoid that noise contained in the image perturbs the edge selection process, the idea of Catté et al. [27] in the context of image restoration is transferred to the matrix $\nabla u \nabla u ^T$: matrix $\nabla u \nabla u ^T$ can be replaced by the Gaussian smoothed version

\[ J_\sigma (\nabla u) := K_\sigma * (\nabla u \nabla u ^T),\quad \sigma \geq 0.\]

with a Gaussian kernel $K_\sigma$ and standard deviation $\sigma \geq 0$. The correlation $*$ of $K_\sigma$ with $\nabla u \nabla u ^T$ is to be understood componentwise. Then, a matrix valued function $\tilde {q}(J_\sigma ) \colon \mathbb {R}^{2\times 2} \to \mathbb {R}^{2\times 2}$ can be defined which is referred to as diffusion tensor. In our application in video coding, the time update is neglected and $\nabla u \nabla u^T$ in the function $\tilde {q}(J_\sigma )$ is replaced by $\nabla f \nabla f^T$.

Using this, the anisotropic diffusion model reads

(6)\begin{equation} \frac{\partial}{\partial t} u = \mathrm{div} \Big(\tilde{q}(J_\sigma) \nabla u\Big)\end{equation}

with initial (2) and boundary conditions (3) as above. The model described in this subsection leads (under certain conditions) to a uniquely solvable problem (see [18]). Note that for $t \to \infty$, Eq. (6) converges to a steady state independently of the initial condition which is an inpainting solution [23]. But for $t << \infty$, the solution u can be understood as a smoothed version of prediction f. This makes it feasible for our application in video coding.

Since

(7)\begin{equation} J_\sigma := \frac{1}{4} \begin{pmatrix} g_{11} & g_{12}\\ g_{12} & g_{22} \end{pmatrix} \end{equation}

is a real symmetric matrix, it is diagonalizable by orthogonal matrices S. As shown below, the application of the matrix valued function $\tilde {q}$ on $J_{\sigma }$ is well defined by applying a suitable function q to its eigenvalues $\lambda _1$, $\lambda _2$, i.e.

(8)\begin{equation} \tilde{q}(J_\sigma) := S \begin{pmatrix} q(\lambda_1) & 0 \\ 0 & q(\lambda_2) \end{pmatrix} S^{T}. \end{equation}

Two different possibilities are considered here, which have been empirically tested.

1. i) A way of choosing $\tilde {q}$ is the following: Since $J_{\sigma }$ is diagonalizable, the term $I+J_{\sigma }^2$ is invertible and can be represented by an absolutely convergent power series

   \[ (I+J_{\sigma}^2)^{-1} =\sum_{k=0}^\infty \alpha_k J_{\sigma} ^{2k},\]
   with certain coefficients $\alpha _k$. Here, I denotes the identity matrix. Now, choose function $\tilde {q}$ as
   \[ \tilde{q}(J_{\sigma}) = (I+J_{\sigma}^2)^{-1}.\]
   Since $J_{\sigma }$ is diagonalizable, there exists an invertible matrix S such that $\Lambda = S^{-1} J_{\sigma } S$, where Λ is a diagonal matrix consisting of the eigenvalues $\lambda _1$, $\lambda _2$. It holds that
   \begin{align*} (I+J_{\sigma}^2)^{-1} &=\sum_{k=0}^\infty \alpha_k (S\Lambda S^{-1}) ^{2k} \\ &= S (I+\Lambda ^2)^{-1} S^{-1}. \end{align*}
   The term $(I+\Lambda ^2)^{-1}$ is defined by applying ${1}/({1+(\cdot )^2})$ to the entries of the diagonal matrix Λ.

2. ii) As a special case of case (i), function $\tilde {q}$ can be chosen as

   \[ \tilde{q}(J_{\sigma}) = \mathrm{exp}(J_{\sigma}).\]
   By definition, it holds that
   \[ \mathrm{exp}(J_{\sigma}) = \sum_{k=0}^\infty \frac{1}{k!}J_{\sigma}^k.\]
   This series always converges, thus $\mathrm {exp}(J_{\sigma })$ is well defined. Then, it holds
   \[ \mathrm{exp}(J_{\sigma}) = \sum_{k=0}^\infty \frac{1}{k!}(S\Lambda S^{-1})^k =S\ \mathrm{exp}(\Lambda )S^{-1},\]
   where S, Λ are defined as above. Thus, the term $\mathrm {exp}(\Lambda )$ is well defined as the application of the exponential function to the entries on the diagonal.

Therefore, the application of $\tilde {q}$ is well defined as the application of the following functions q on the eigenvalues of $J_{\sigma }$: Empirically, it has been decided that it is reasonable in case of intra to chose q as

(9)\begin{equation} q(s) = \mathrm{exp}\left(\frac{-s^2}{\mu}\right), \end{equation}

which corresponds to case (ii) and in case of inter as

(10)\begin{equation} q(s) = \frac{1}{1+ \frac{s^2}{\mu}}, \end{equation}

which corresponds to case (i). The two functions q are tabulated using integer look-up tables.

More details on the choice of parameter μ and the underlying empirical tests are given in Section V.

The finite discretization of Eq. (6) can be realized by the following ordered steps:

1. 1) Calculate discrete samples differences

   \[ EW(x) := (\mathcal{D}_{x_1}^+ + \mathcal{D}_{x_1}^-)u(x,t)\]
   and
   \[ NS(x) := (\mathcal{D}_{x_2}^+ + \mathcal{D}_{x_2}^-)u(x,t)\]
   for every sample $x \in \mathbb {R}^2$ and a fixed iteration step $t \in \mathbb {R}$.

2. 2) Calculate products $(EW \cdot EW)(x)$, $(EW \cdot NS)(x)$, $(NS \cdot NS)(x)$.

3. 3) Filter the three products with filter kernel $K_\sigma$ for obtaining the gradient arrays $g_{11}(x)$, $g_{12}(x)$, and $g_{22}(x)$ defined in Eq. (7).

4. 4) Determine the eigenvalues $\lambda _1 (x)$, $\lambda _2 (x)$ using look-up tables.

5. 5) Apply a function q set as Eqs. (9) or (10) to the eigenvalues using pre-defined look-up tables.

6. 6) Calculate S and $S^T$ to derive the integer entries of the diffusion tensor $\tilde {q}(J_\sigma )$ as in Eq. (8) using look-up tables.

7. 7) Derive the integer weighting arrays $w_N$, $w_S$, $w_W$, $w_E$, $w_{01}$, $w_{02}$, $w_{03}$, and $w_{04}$ using sample averages and set

   \begin{align*} u(x,t+\tau) &= u(x,t) + \tau \Big(\, w_E \big(u(x+he_1,t) -u(x,t)\big) \\ &\quad + w_W \big(u(x-he_1,t)-u(x,t)\big) \\ &\quad+ w_{01}\, u(x+he_1+he_2,t)\\ &\quad- w_{02}\, u(x+he_1-he_2,t)\\ &\quad- w_{03}\, u(x-he_1+he_2,t) \\ &\quad+ w_{04}\, u(x-he_1-he_2,t) \\ &\quad+ w_N \big(u(x+he_2,t) - u(x,t)\big) \\ &\quad+ w_S \big(u(x-he_2,t)-u(x,t)\big) \, \Big), \end{align*}
   for time discretization parameter τ.

C) The geometric meaning of the diffusion tensor

By definition, applying the linear transform $J_\sigma$ to its eigenvectors $ev_i$, a scaling of the eigenvector by the corresponding eigenvalue occurs, i.e. $J_\sigma ev_i = \lambda _i ev_i$ for i=1,2. The eigenvalue with the largest absolute value of its corresponding eigenvalue is called major eigenvector. In Fig. 2, the major eigenvectors of $J_\sigma$ scaled by their eigenvalues are depicted for an example image. As can be seen, the major eigenvectors point to the direction perpendicular to the main edge. Through the scaling with the corresponding eigenvalues, the vectors are larger and become more visible at the locations where the underlying image has strong edges. Therefore, by applying the functions q suggested above to the eigenvalues of $J_\sigma$, the diffusion solving Eq. (6) becomes small at these points.

Fig. 2. Left: original image, right: major eigenvectors of $J_\sigma$ scaled by their eigenvalues.

IV. IMPLEMENTATION AND EXPERIMENTAL SETUP

A) Experimental setup

In this paper, the presented tools are implemented into a software based on HEVC [28] that includes an additional QTBT block structure and MTT partitioning: That means that the quadtree structure of HEVC is replaced by a Quadtree plus Binary Tree (QTBT, [29]) block structure. An example for a QTBT partitioning is shown in Fig. 3. The CTUs are firstly divided in a quadtree manner and then further partitioned using a binary tree structure. QTBT allows more flexibility in the shape of the CU structure which can be rectangularly shaped now instead of only squared. In order to better capture objects in the center of blocks, instead of the binary partitioning the so-called Multi-Type-Tree (MTT) partitioning [30] is used here. In addition to quad-tree splitting and binary vertical and horizontal splitting, MTT introduces horizontal and vertical center-side triple-tree partitionings as depicted in Fig. 4.

Fig. 3. Illustration of a QTBT structure, taken from [31], ©2017 IEEE.

Fig. 4. Multi-Type-Tree structure, (a) quad-tree partitioning, (b) vertical binary-tree partitioning, (c) horizontal binary-tree partitioning, (d) vertical center-side triple-tree partitioning, (e) horizontal center-side triple-tree partitioning.

All other non-HEVC tools in [28] are turned off. The tests are configured using an All Intra (AI) configuration where only intra pictures are sent and a Random Access (RA) configuration. The corresponding configuration files can be found at [32]. To avoid long test runs, for some preliminary results, the number of frames has been limited to one frame for AI and 17 frames for RA. For the final results in Section VII however, full sequence runs were shown.

In this paper, the bitrate savings – also referred to as rate-distortion (RD) gains – are generally measured in terms of Bjøntegaard delta (BD) bitrate [33]. If not stated otherwise, per default quantization parameters $QP \in \{22,27,32,37\}$ are used. Additionally, simulations are run for the $QP \in \{27, 32, 37, 42\}$, which is a standard method [34,35]. The latter set of QP values represents a better approximation of achieving the bitrates specified in the CfP (Call for proposals of the international community for video coding standardization, [36]). Note that there is a logarithmic relationship between QP and stepsize, i.e. $stepsize = \Delta 2^{\lfloor {QP}/{6} \rfloor }$ for a parameter $\Delta >0$ ([37, p. 214]). Therefore, the adding of QP 42 doubles the stepsize. Since the rate distortion curve is well defined for four QPs and QPs much higher than 42 are visually not acceptable and QPs much lower than 22 not distinguishable, the range of practically feasible bitrates is quite well covered using the sets $QP \in \{22,27,32,37\}$ and $QP \in \{27, 32, 37, 42\}$. Accordingly, throughout the paper we test and report for the five QP values 22,27,32,37,42.

The results are shown with respect to the luma component Y and the chroma components U and V. Even though the introduced methods are only applied on the luma signal for complexity reasons, the results for the chroma components are shown as well here. This is not only for the sake of completeness but also to ensure that there is no major efficiency loss in the chroma components.

The test sequences for the All Intra (AI) and Random Access (RA) configurations are selected in a way that they represent the impact of the tool well. Therefore, the sequences for AI and RA differ slightly. To ensure a certain variety in the employed test set, at least one test sequence out of each sequence class 4K Panorama, 4K HDR (High Dynamic Range), 4K UHD (Ultra High Definition), and HD (High Definition) is included in the depicted test results.

B) Implementation

The encoder features a uniform version of the filter and a signal adaptive version as described above. The filters are applied on the luminance signal. The uniform filters apply a fixed filter mask (as elaborated in subsection III.A), while the signal adaptive filters as in subsection III.B use the underlying prediction signal to control the direction of the smoothing. While the latter preserves sharp edges in the prediction signal, the uniform version is less complex.

The flag for enabling the diffusion filter is tested and sent at CU level. If it is enabled, additionally the type of the diffusion model and the number of iteration steps as shown in Table 1 are signaled by sending the corresponding index. Since for each filter two options for its strength are given, in total, this corresponds to four different filter configurations. This is referred to as “diffusion filter method”. The particular numbers of iteration steps were tested empirically and lead to a good trade-off between complexity and bitrate savings.

Table 1. Overview of diffusion filter types.

In general, the matrix $J_\sigma (\nabla u)$ may be updated in every iteration step. To simplify the solution method and to make it complexity wise feasible for the state-of-the-art video coding, we neglect this update and set $J_\sigma = J_\sigma (\nabla f)$ constant for all iterations. Thereby, only the directions implied by the initial prediction signal f are taken into account when applying the anisotropic diffusion filter. This reduces the complexity while maintaining the signal adaptivity – which is a reasonable choice for its application in video coding introduced here.

C) Example

Figure 5 demonstrates the impact of diffusion filtering on an angular intra prediction block. On the left-hand side, the original intra prediction is depicted. In the middle, one can see the result of the uniform diffusion filter. On the right, the result of applying the signal adaptive diffusion filter is shown. It can be observed that the latter smooths the area in the bottom right corner of the prediction block in the same way as the uniform one. But while the uniform filter attenuates the edges of the underlying prediction, the signal adaptive filter preserves them.

Fig. 5. Left: original intra prediction. Middle: uniformly filtered prediction as in subsection III.A. Right: signal adaptive filtered prediction as in subsection III.B.

V. PARAMETER TESTS

To better understand the meaning of the edge parameter μ, it is reasonable to look at the one-dimensional case (similarly as has been done in [38]). Then, $\nabla u = {\partial }/{\partial x} u \in \mathbb {R}$ and Eq. (6) reduces to

\[ \frac{\partial}{\partial t} u = \Phi'\left(\frac{\partial}{\partial x} u\right),\]

where $\Phi (s)$ denotes the so-called flux function and $\Phi '$ its spatial derivative. The diffusivity functions q chosen as Eqs. (9) or (10) and its corresponding flux functions are depicted in Figs 6 and 7. Note that $\nabla u \nabla u^T$ translates to the notation $s^2$ used here. It can be seen that the diffusivity functions are positive and monotonically decreasing for ${\partial }/{\partial x} u >0$. For ${\partial }/{\partial x} u \to \infty$ they converge to zero. Thus, the larger ${\partial }/{\partial x} u$, the smaller the diffusion becomes.

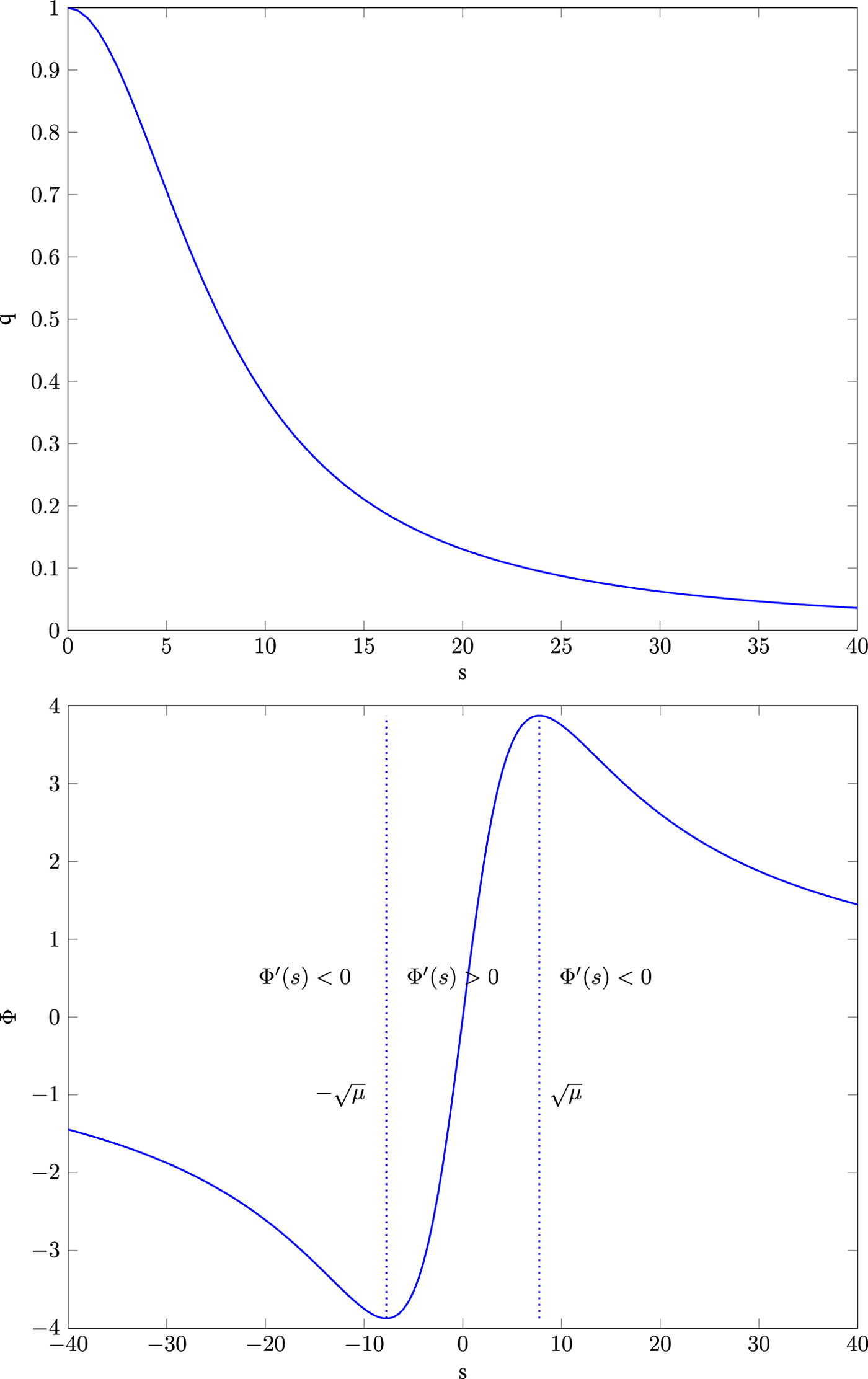
Fig. 6. Top: diffusivity function $q(s) =\frac {1}{1+ \frac {s^2}{\mu }}$, bottom: its flux function $\Phi (s)= \frac {s}{1+ \frac {s^2}{\mu }}$.

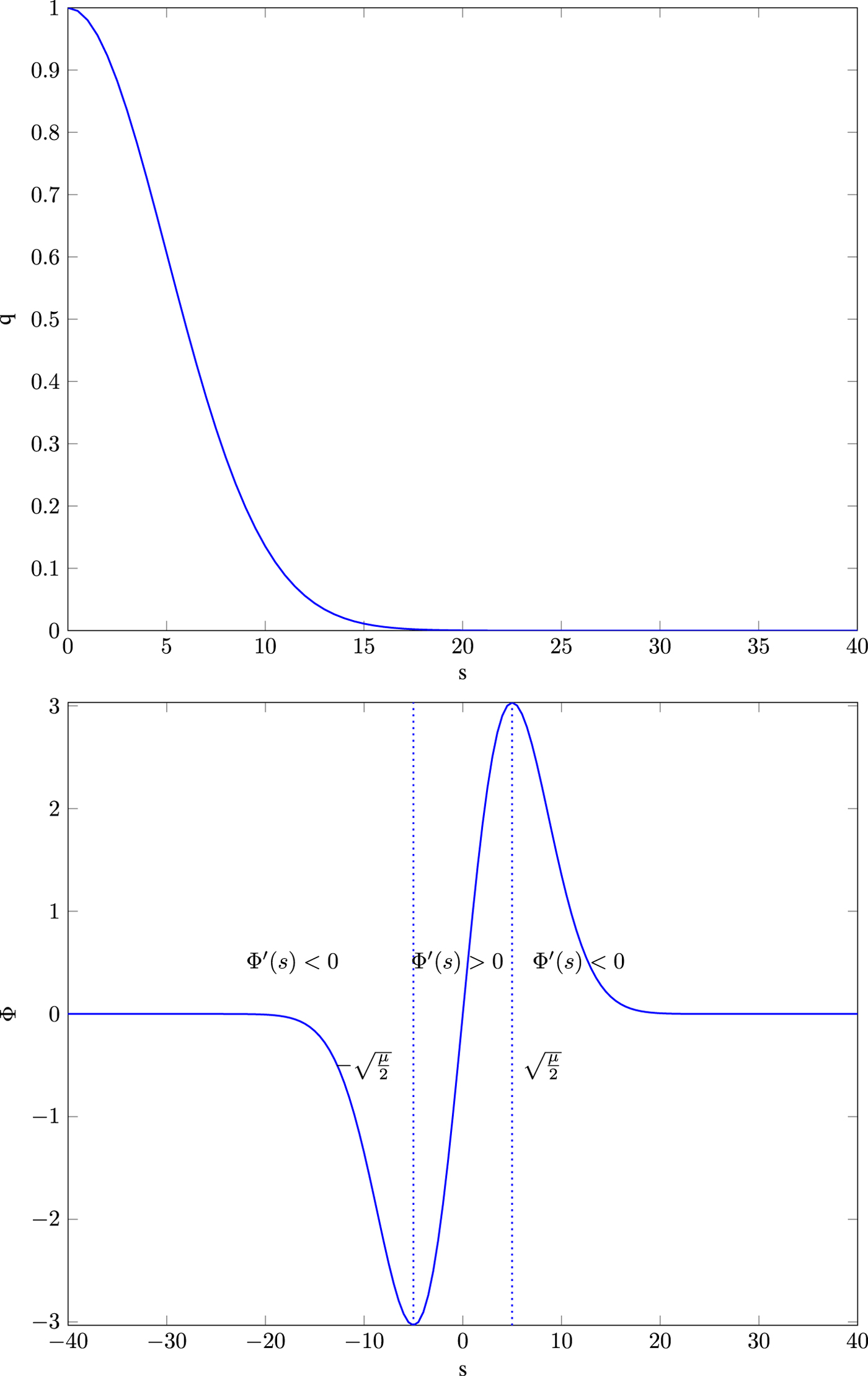
Fig. 7. Top: diffusivity function $q(s) = \mathrm {exp}(({-s^2})/{\mu })$, bottom: its flux function $\Phi (s)= s\,\mathrm {exp}(({-s^2})/{\mu })$.

In case of $q(s) = \frac {1}{1+ \frac {s^2}{\mu }}$, function $\Phi '(s)>0$ if

\[ - \sqrt{\mu} < \Phi(s) < \sqrt{\mu}\]

and $\Phi '(s)<0$ otherwise. Therefore, the corresponding effect of the model at this point is what can be called “forward diffusion” if

\[ -\sqrt{\mu} < \Phi \left(\frac{\partial}{\partial x} u (\bar{x})\right) < \sqrt{\mu}\]

for $\bar {x}\in \mathbb {R}$ and “backward diffusion” otherwise. This holds analogously in case of $q(s) =\mathrm {exp}(({-s^2})/{\mu })$ for threshold $\sqrt {{\mu }/{2}}$.

As there is no straightforward choice for μ, its setting was tested empirically. The parameter test features an encoder control that includes saving the original (meaning the cost of the non-filtered best choice) and the corresponding improved costs of the diffusion filter using a certain parameter μ. The difference of the costs is expressed in percentage and referred to as “cost improvement”. Hereby, only cases were considered where the diffusion filter was chosen, i.e. the RD gain was improved. The tested parameters were chosen as $\mu \in \{64, 100, 112, 151, 227, 310, 419, 550 \}.$ This interval was chosen as a result of several empirical tests. Choosing μ smaller than 64 or larger than 550 was tested and did not show any considerable improvements. In the encoder only test, no additional costs for the parameters were simulated since for the resulting tool the parameters will not be signaled but set fixed. The performed tests were evaluated on a large test set that included the sequences for which the results are shown in the following. As μ is only one single parameter, the risk of overfitting can be neglected here. The All Intra and Random Access configurations will be considered separately and it will be distinguished between intra and inter blocks. Further, it has been tested empirically that in case of inter, it makes sense to distinguish between different QPs, $QP \in [0, 51]$. This difference can be explained by the different nature of inter and intra predictions. For each class of block type, the number of occurrence of a certain parameter μ was multiplied by the corresponding percentage in cost improvement. The resulting number is referred to as “improvement weight” in the following. The idea is here that the larger the weight, the larger its presumable improvement impact is on the test set.

In Table 2, the three parameters with the best (i.e. largest) improvement weights for intra blocks are depicted. It has been tested empirically that $\mu =550$ results in the highest RD gain, which was highlighted in gray in Table 2.

Table 2. Best μ parameter for intra blocks.

In Table 3, a comparison of setting $\mu =64$ (left-hand side) and $\mu =550$ (right-hand side) is shown for All Intra configuration, using $QP \in \{22,27,32,37\}$, tested with one frame. It can be seen that the modification of parameter μ increases the RD gains of most sequences. Overall, the AI gain is increased from $-1.68 \%$ to $-1.77 \%$ for the luma component.

Table 3. All Intra comparison of $\mu =64$ (Y, U, V left-hand side) and $\mu =550$ ($Y_{impr}$, $U_{impr}$, $V_{impr}$ right-hand side), 1 frame, $QP \in \{22,27,32,37\}$, measured in BD rate.

In Table 6, the parameters μ for the best three improvement weights have been depicted separated by QP intervals for inter blocks. The best performing parameters (in terms of final bitrate savings) are highlighted in gray. In Tables 4 and 5, a comparison is shown for selected sequences setting $\mu =64$ fixed for inter and intra blocks on the left-hand side and varying μ by setting

(11)\begin{equation} \mu = \begin{cases} 550, & \hbox{for intra prediction}\\ 64, & \hbox{for inter prediction and QP} <33\\ 550, & \hbox{for inter prediction and QP} \geq 33 \end{cases} \end{equation}

on the right-hand side. Since inter predictions are naturally more diverse in terms of structures, it seems reasonable that they are also more sensitive toward change in quantization parameters.

Table 4. Random Access comparison of $\mu =64$ fixed for intra and inter blocks (Y, U, V left-hand side) and QP-dependent μ for inter blocks as in Eq. (11) ($Y_{impr}$, $U_{impr}$, $V_{impr}$ right-hand side), 17 frames, $QP \in \{22,27,32,37\}$, measured in BD rate.

Table 5. Random Access comparison of $\mu =64$ fixed for intra and inter blocks (Y, U, V left-hand side) and QP-dependent μ for inter blocks as in Eq. (11) ($Y_{impr}$, $U_{impr}$, $V_{impr}$ right-hand side), 17 frames, $QP \in \{27,32,37,42\}$, measured in BD rate.

Table 6. Best μ Parameter for inter blocks separated by QP intervals.

In Table 4, the results for $QP \in \{22,27,32,37\}$ are shown, and in Table 5, the results for $QP \in \{27,32,37,42\}$. The depicted results were configured with 17 frames using the RA configuration. It can be seen that the RD gains are improved overall, for luma by $0.07\%$ for $QP \in \{22,27,32,37\}$ and $0.3\%$ for $QP \in \{27,32,37,42\}$. While the results in Table 4 remain more or less stable and the average improvement stems from sequence Nebuta, in Table 5 most sequences are improved. This can be explained by the definition of μ in Eq. (11) where a different parameter is chosen for larger QPs while the initial results use $\mu =64$ set fixed.

VI. USING A NEUMANN BOUNDARY IN INTER CASE

From a hardware point of view, it can be beneficial to process intra and inter blocks in separate, parallel loops. In that case, the inter loop should not depend on reconstructed samples resulting from the intra loop. Hence, to avoid using the reconstructed boundary for the diffusion filter in the inter case, a Neumann boundary condition is used at the top and left boundary of the block (instead of fixed samples at the boundary). In a discrete setting, this means that the inner points of the prediction are mirrored at the boundary to replace the reconstructed samples. In Tables 7 and 8, the corresponding results are depicted, for 17 frames and for $QP \in \{22,27,32,37\}$ and for $QP \in \{27,32,37,42\}$.

Table 7. Neumann boundary condition for inter blocks, Random Access, 17 frames, $QP \in \{22,27,32,37\}$, measured in BD rate.

Table 8. Neumann boundary condition for inter blocks, Random Access, 17 frames, $QP \in \{27,32,37,42\}$, measured in BD rate.

It can be observed that in comparison to the right (improved) Luma results of Tables 4 and 5, the gains decrease slightly with the inter Neumann boundary condition but remain in a similar range. Thus, this version serves as a suitable alternative in case of hardware restrictions applying.

VII. RESULTS

In Tables 9 and 10, results are shown for full sequences for AI configuration. The corresponding full sequence results for RA are shown in Table 11 for $QP \in \{22,27,32,37\}$ and in Table 12 for $QP \in \{27,32,37,42\}$.

Table 9. All Intra, full sequences, $QP \in \{22,27,32,37\}$, measured in BD rate.

Table 10. All Intra, full sequences, $QP \in \{27,32,37,42\}$, measured in BD rate.

Table 11. Random Access, full sequences, $QP \in \{22,27,32,37\}$, measured in BD rate.

Table 12. Random Access, full sequences, $QP \in \{27,32,37,42\}$, measured in BD rate.

It can be seen in Tables 9, 10, 11, and 12 that the filter shows considerable rate-distortion gains with a reasonable complexity trade-off for AI and RA. The higher number of bitrate savings for RA can be explained by the signal adaptive nature of the tool: Since the noise in the predictor is uncorrelated to the noise of the current block, the filter is more likely to be applied. Furthermore, the tool is able to exhaust its full potential in inter predictions where the image structures are more diverse.

For AI, for test sequence Crosswalk, up to $-2.38\%$ RD gain are achieved. For RA, in test sequence Nebuta, a compression gain of $-7.36 \%$ can be observed.

This exceptional gain can be explained by taking a look at a close up of the sequence Nebuta in Fig. 8: It can be seen that there seems to be a kind of noise in the image and this might lead to distorted predictions. Knowing that the diffusion filter is based on mathematical denoising methods, it comes as no surprise that this tool works so well on this particular sequence.

Fig. 8. Excerpt taken from sequence Nebuta, QP32.

Overall, the gains for $QP \in \{27,32,37,42\}$ configuration are slightly less than for $QP \in \{22,27,32,37\}$. This can be explained by the nature of the tool. As sequences with high QPs are coarser, the filter cannot remove as much noise. Additionally, since four different settings of the diffusion filter are tested and signaled, the tool is quite expensive in case of low bitrates.

In Fig. 9, one can compare the rate-distortion (RD) plots for test sequence Nebuta for the five QPs 22, 27, 32, 37, and 42. Clearly, one can observe the higher RD gain in the lower QPs as the distance between the curves is larger. This corresponds to the fact that the tool generally works better for $QP \in \{22,27,32,37\}$ configuration.

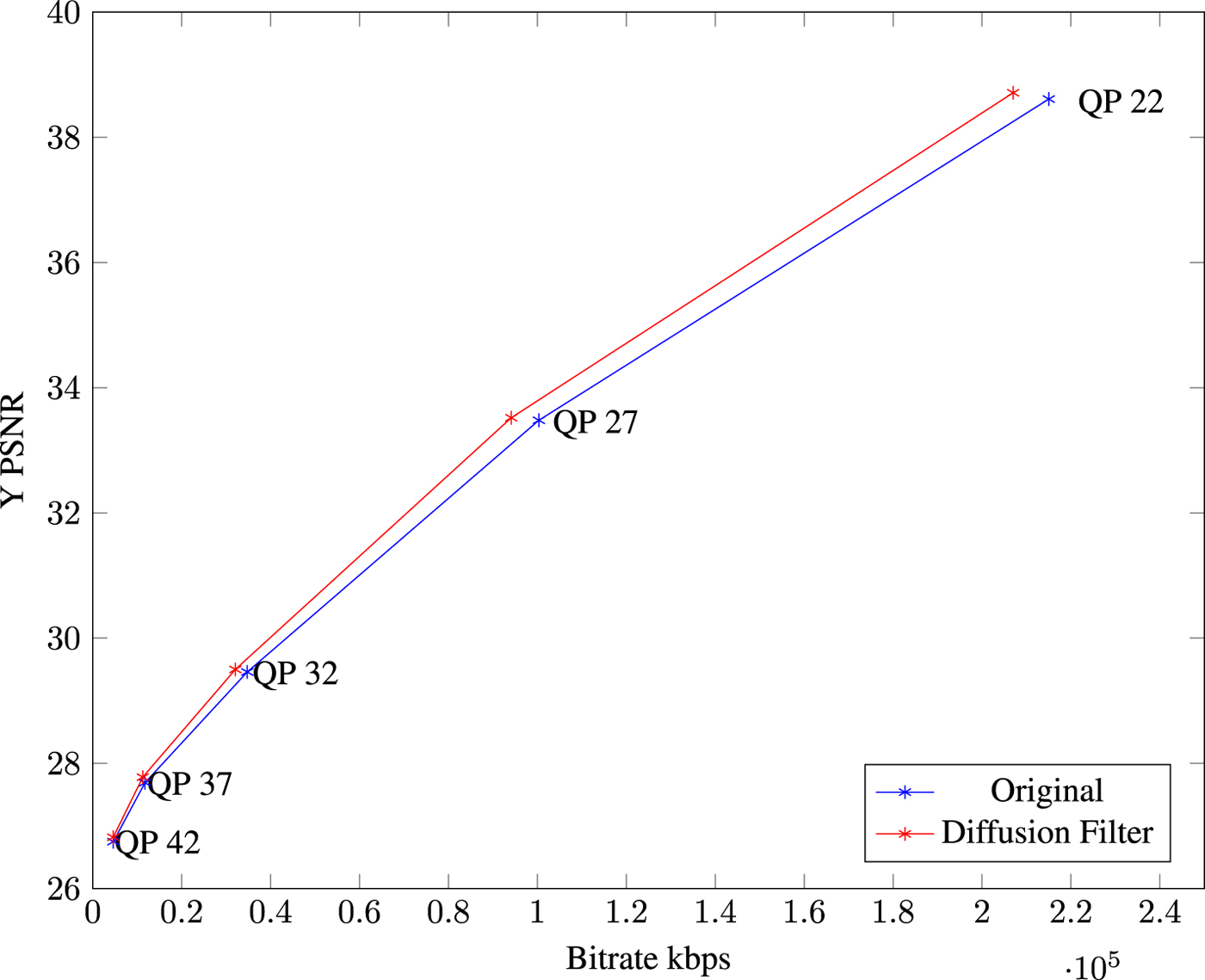
Fig. 9. RD plot for test sequence Nebuta, RA configuration.

VIII. CONCLUSION

It has been shown that mathematical methods coming from the field of image processing can be used to optimize prediction signals in video coding and significantly improve the rate-distortion performance. More specifically, prediction filters based on a continuous mathematical model have been developed for video coding. The resulting signal adaptive filters have been applied to intra as well as to inter predictions.

Based on a PDE-based class of diffusion models, two types of diffusion filters were constructed, one using a uniform diffusion with a fixed filter mask and one signal adaptive diffusion filter that incorporates the structures of the underlying prediction signal. For both filter types, two different sets of iteration steps (which corresponds to the filter strength) were used. The diffusion filter method introduced here consists of these resulting four filter configurations which are tested and signaled individually.

In case that hardware restrictions require to refrain in inter case from the usage of the reconstructed block boundary, an alternative was presented: Instead of using the reconstructed samples, a Neumann boundary condition is applied in inter case. Experimental results confirmed that the RD gains for Random Access (RA) only decrease slightly.

The filters were embedded into a software based on HEVC, a state-of-the-art video codec, and selected in a block-wise manner. Parameter tests incorporating the cost improvements were performed and it was shown that optimizing the employed parameters improved the RD gains.

Overall, the introduced diffusion filter method achieved an average bitrate saving of $1.74 \%$ for AI with $43 \%$ encoding and $19 \%$ decoding complexity increase and $2.27 \%$ for RA for $19 \%$ encoding and $17 \%$ decoding complexity increase. For individual UHD sequences, it was shown that the application of the diffusion filter method yields results of up to $2.38 \%$ for AI and $7.36 \%$ for Random Access (RA).