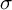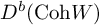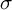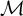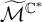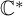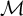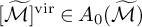1 Introduction
1.1 Brief historical background
Donaldson–Thomas (abbreviated as DT from now on) invariants constitute one of the main approaches for curve counting on Calabi–Yau threefolds. They naturally appear in many enumerative problems of interest in algebraic geometry and string theory and are conjecturally equivalent with other counting invariants, such as Gromov–Witten invariants, stable pair invariants [Reference Pandharipande and ThomasPT09] and Gopakumar–Vafa invariants [Reference Maulik and TodaMT18]. These relations have now been proven in many cases (for example, in [Reference Maulik, Nekrasov, Okounkov and PandharipandeMNOP06a, Reference Maulik, Nekrasov, Okounkov and PandharipandeMNOP06b, Reference TodaTod10]).
Let W be a smooth, projective Calabi–Yau threefold and
![]() $\gamma \in H^*(W, \mathbb {Q})$
. Classical DT theory was introduced in [Reference ThomasTho00] in order to obtain virtual counts of stable sheaves on W of Chern character
$\gamma \in H^*(W, \mathbb {Q})$
. Classical DT theory was introduced in [Reference ThomasTho00] in order to obtain virtual counts of stable sheaves on W of Chern character
![]() $\gamma $
. More precisely, Thomas considered the (coarse) moduli space
$\gamma $
. More precisely, Thomas considered the (coarse) moduli space
![]() $M := M^{ss}_L(\gamma )$
parameterizing Gieseker semistable sheaves on W of positive rank, fixed determinant L and Chern character
$M := M^{ss}_L(\gamma )$
parameterizing Gieseker semistable sheaves on W of positive rank, fixed determinant L and Chern character
![]() $\gamma $
. Assuming that every semistable sheaf is stable, M is proper and admits a perfect obstruction theory in the sense of Li-Tian [Reference Li and TianLT98] or Behrend–Fantechi [Reference Behrend and FantechiBF97] of virtual dimension zero. Thus, there exists a virtual fundamental cycle
$\gamma $
. Assuming that every semistable sheaf is stable, M is proper and admits a perfect obstruction theory in the sense of Li-Tian [Reference Li and TianLT98] or Behrend–Fantechi [Reference Behrend and FantechiBF97] of virtual dimension zero. Thus, there exists a virtual fundamental cycle
![]() $[M]^{\mathrm {vir}} \in A_0 \left ( M \right )$
and the classical DT invariant is defined as
$[M]^{\mathrm {vir}} \in A_0 \left ( M \right )$
and the classical DT invariant is defined as
One of its important properties is its invariance under deformation of the complex structure of W.
Another important feature of DT invariants is their motivic nature. Behrend [Reference BehrendBeh09] showed that the obstruction theory of M is symmetric in a certain sense and established an equality
where
![]() $\nu _{M} \colon M \to \mathbb {Z}$
is a canonical constructible function on M and the right-hand side a weighted Euler characteristic.
$\nu _{M} \colon M \to \mathbb {Z}$
is a canonical constructible function on M and the right-hand side a weighted Euler characteristic.
However, when stability and semistability of sheaves do not coincide, the above methods do not suffice and new techniques are required in order to define generalized DT invariants counting semistable sheaves. A main obstacle is that strictly semistable sheaves can have more automorphisms beyond
![]() $\mathbb {C}^{\ast }$
-scaling and, as a result, the stacks
$\mathbb {C}^{\ast }$
-scaling and, as a result, the stacks
![]() $\mathcal {M}^{ss}(\gamma )$
parameterizing semistable sheaves are generally Artin and no longer Deligne–Mumford (after rigidifying
$\mathcal {M}^{ss}(\gamma )$
parameterizing semistable sheaves are generally Artin and no longer Deligne–Mumford (after rigidifying
![]() $\mathbb {C}^*$
-scaling, cf. Subsection 6.3). This is necessary for the standard machinery of perfect obstruction theory and virtual cycles to apply.
$\mathbb {C}^*$
-scaling, cf. Subsection 6.3). This is necessary for the standard machinery of perfect obstruction theory and virtual cycles to apply.
In [Reference Joyce and SongJS12], Joyce and Song constructed generalized DT invariants of moduli stacks
![]() $\mathcal {M}^{ss}(\gamma )$
taking advantage of the above motivic behaviour and using motivic Hall algebras to obtain a generalization of the right-hand side of equation (†). Their DT invariant is easy to work with and amenable to computation. However, the proof of its deformation invariance is indirect and proceeds via wall-crossing to a stable pairs theory where semistability and stability coincide and thus a virtual cycle exists. Kontsevich and Soibelman [Reference Kontsevich and SoibelmanKS10] have also defined motivic generalized DT invariants using similar ideas. We also mention the related work of Behrend and Ronagh [Reference Behrend and RonaghBR19, Reference Behrend and RonaghBR16].
$\mathcal {M}^{ss}(\gamma )$
taking advantage of the above motivic behaviour and using motivic Hall algebras to obtain a generalization of the right-hand side of equation (†). Their DT invariant is easy to work with and amenable to computation. However, the proof of its deformation invariance is indirect and proceeds via wall-crossing to a stable pairs theory where semistability and stability coincide and thus a virtual cycle exists. Kontsevich and Soibelman [Reference Kontsevich and SoibelmanKS10] have also defined motivic generalized DT invariants using similar ideas. We also mention the related work of Behrend and Ronagh [Reference Behrend and RonaghBR19, Reference Behrend and RonaghBR16].
In [Reference Kiem, Li and SavvasKLS17], the authors develop a new direct approach towards defining generalized DT invariants of such a moduli stack
![]() $\mathcal {M}^{ss}(\gamma )$
. Their method adapts Kirwan’s partial desingularization procedure [Reference KirwanKir85] to define an invariant as the degree of a zero-dimensional virtual cycle in an associated Deligne–Mumford stack
$\mathcal {M}^{ss}(\gamma )$
. Their method adapts Kirwan’s partial desingularization procedure [Reference KirwanKir85] to define an invariant as the degree of a zero-dimensional virtual cycle in an associated Deligne–Mumford stack
![]() $\widetilde {\mathcal {M}}$
. The constructed invariant is called the generalized DT invariant via Kirwan blowups (or DTK invariant for short) and is a direct generalization of the left-hand side of equation (†). By the usual properties of virtual cycles, they establish the deformation invariance of DTK invariants.
$\widetilde {\mathcal {M}}$
. The constructed invariant is called the generalized DT invariant via Kirwan blowups (or DTK invariant for short) and is a direct generalization of the left-hand side of equation (†). By the usual properties of virtual cycles, they establish the deformation invariance of DTK invariants.
We make a final comment on the need for orientation data in the above approaches. Since motivic DT invariants are more refined, Kontsevich and Soibelman do need to assume the existence of such data to define their invariants. This assumption has been recently proved to hold in [Reference Joyce and UpmeierJU21]. Orientation data are not necessary for the definition of numerical generalized DT invariants given in [Reference Joyce and SongJS12] and [Reference Kiem, Li and SavvasKLS17]. This will be the case for the DTK invariant defined in this paper as well.
1.2 Statement of results
This paper serves as a sequel to [Reference Kiem, Li and SavvasKLS17]. We generalize the construction of DTK invariants to the case of moduli stacks
![]() $\mathcal {M} := \mathcal {M}^{\sigma -ss}(\gamma )$
parametrizing
$\mathcal {M} := \mathcal {M}^{\sigma -ss}(\gamma )$
parametrizing
![]() $\sigma $
-semistable objects of Chern character
$\sigma $
-semistable objects of Chern character
![]() $\gamma $
in the derived category
$\gamma $
in the derived category
![]() $D^b(\mathop{\mathrm { Coh}}\nolimits W)$
of coherent sheaves on W, where
$D^b(\mathop{\mathrm { Coh}}\nolimits W)$
of coherent sheaves on W, where
![]() $\sigma $
is one of the following stability conditions:
$\sigma $
is one of the following stability conditions:
-
1. A Bridgeland stability condition [Reference BridgelandBri07], as considered by Piyaratne–Toda [Reference Piyaratne and TodaPT19] and [Reference LiLi19].
-
2. A polynomial stability condition [Reference BayerBay09], as considered by Lo [Reference LoLo11, Reference LoLo13].
-
3. Gieseker and slope stability of sheaves. These are examples of weak stability conditions on
 $\mathop{\mathrm { Coh}}\nolimits W$
in the sense of Joyce–Song [Reference Joyce and SongJS12].
$\mathop{\mathrm { Coh}}\nolimits W$
in the sense of Joyce–Song [Reference Joyce and SongJS12].
More generally,
![]() $\sigma $
can be any nice stability condition (cf. Definition 6.1 and Definition 6.2).
$\sigma $
can be any nice stability condition (cf. Definition 6.1 and Definition 6.2).
Our main results are summarized in the following theorem, giving a definition of DTK invariants counting
![]() $\sigma $
-semistable complexes.
$\sigma $
-semistable complexes.
Theorem. Let W be a smooth, projective Calabi–Yau threefold,
![]() $\sigma $
a stability condition on
$\sigma $
a stability condition on
![]() $D^b(\mathop{\mathrm { Coh}}\nolimits W)$
as in Definition 6.2 and
$D^b(\mathop{\mathrm { Coh}}\nolimits W)$
as in Definition 6.2 and
![]() $\mathcal {M} := \mathcal {M}^{\sigma -ss}(\gamma )$
be the
$\mathcal {M} := \mathcal {M}^{\sigma -ss}(\gamma )$
be the
![]() $(\mathbb {C}^{\ast }$
-rigidified
$(\mathbb {C}^{\ast }$
-rigidified
![]() $)$
moduli stack parametrizing
$)$
moduli stack parametrizing
![]() $\sigma $
-semistable complexes of Chern character
$\sigma $
-semistable complexes of Chern character
![]() $\gamma $
. Then there exist:
$\gamma $
. Then there exist:
-
1. [Theorem-Construction 4.9, Theorem-Definition 6.6]
A canonical proper Deligne–Mumford stack
 $\widetilde {\mathcal {M}}^{\mathbb {C}^{\ast }} \to \mathcal {M}$
, called the
$\widetilde {\mathcal {M}}^{\mathbb {C}^{\ast }} \to \mathcal {M}$
, called the
 $\mathbb {C}^{\ast }$
-rigidified intrinsic stabilizer reduction of
$\mathbb {C}^{\ast }$
-rigidified intrinsic stabilizer reduction of
 $\mathcal {M}$
.
$\mathcal {M}$
.
 $\widetilde {\mathcal {M}}^{\mathbb {C}^{\ast }}$
is isomorphic to
$\widetilde {\mathcal {M}}^{\mathbb {C}^{\ast }}$
is isomorphic to
 $\mathcal {M}$
over the open
$\mathcal {M}$
over the open
 $\sigma $
-stable locus
$\sigma $
-stable locus
 ${\mathcal {M}}^{\sigma -s}(\gamma ) \subseteq \mathcal {M}$
.
${\mathcal {M}}^{\sigma -s}(\gamma ) \subseteq \mathcal {M}$
. -
2. [Theorem 5.11, Theorem-Definition 6.8]
A natural semiperfect obstruction theory of virtual dimension zero on
 $\widetilde {\mathcal {M}}^{\mathbb {C}^{\ast }}$
, which extends the symmetric obstruction theory of the Deligne–Mumford stack
$\widetilde {\mathcal {M}}^{\mathbb {C}^{\ast }}$
, which extends the symmetric obstruction theory of the Deligne–Mumford stack
 ${\mathcal {M}}^{\sigma -s}(\gamma )$
.
${\mathcal {M}}^{\sigma -s}(\gamma )$
.
We thus have a virtual fundamental cycle
and the generalized Donaldson–Thomas invariant via Kirwan blowups of
![]() $\mathcal {M}$
is defined as
$\mathcal {M}$
is defined as
By Theorem 6.12, this is invariant under deforming the complex structure of W.
1.3 Brief review of the case of sheaves and sketch of construction
We first give a brief account of the results of [Reference Kiem, Li and SavvasKLS17] and then explain the necessary adjustments in order to generalize their approach.
Let
![]() $\mathcal {M}$
be an Artin stack parametrizing Gieseker semistable sheaves of a fixed Chern character on a smooth, projective Calabi–Yau threefold. By construction (see [Reference Huybrechts and LehnHL10]),
$\mathcal {M}$
be an Artin stack parametrizing Gieseker semistable sheaves of a fixed Chern character on a smooth, projective Calabi–Yau threefold. By construction (see [Reference Huybrechts and LehnHL10]),
![]() $\mathcal {M}$
is obtained by geometric invariant theory (GIT) (see [Reference Mumford, Fogarty and KirwanMFK94]), meaning that it is a quotient stack of the form
$\mathcal {M}$
is obtained by geometric invariant theory (GIT) (see [Reference Mumford, Fogarty and KirwanMFK94]), meaning that it is a quotient stack of the form
where G is a reductive group acting on a projective space
![]() $\mathbb {P}^N$
via a homomorphism
$\mathbb {P}^N$
via a homomorphism
![]() $G\to GL(N+1,\mathbb {C})$
and X is an invariant closed subscheme of the GIT semistable locus
$G\to GL(N+1,\mathbb {C})$
and X is an invariant closed subscheme of the GIT semistable locus
![]() $X \subseteq (\mathbb {P}^N)^{ss}$
.
$X \subseteq (\mathbb {P}^N)^{ss}$
.
In order to define an invariant out of
![]() $\mathcal {M}$
, the first step in [Reference Kiem, Li and SavvasKLS17] is the construction of a proper Deligne—Mumford (DM) quotient stack
$\mathcal {M}$
, the first step in [Reference Kiem, Li and SavvasKLS17] is the construction of a proper Deligne—Mumford (DM) quotient stack
![]() $\widetilde {\mathcal {M}} := [\widetilde {X} / G]$
over
$\widetilde {\mathcal {M}} := [\widetilde {X} / G]$
over
![]() $\mathcal {M}$
, called the intrinsic stabilizer reduction of
$\mathcal {M}$
, called the intrinsic stabilizer reduction of
![]() $\mathcal {M}$
. This is produced by an iterative blowup procedure, which successively resolves the loci of closed G-orbits in X with stabilizer groups of maximum dimension. This procedure is an adaptation of Kirwan partial desingularization construction [Reference KirwanKir85] to singular GIT quotient stacks, using the notion of intrinsic blowup introduced in [Reference Kiem and LiKL13] and suitably generalized in [Reference Kiem, Li and SavvasKLS17].
$\mathcal {M}$
. This is produced by an iterative blowup procedure, which successively resolves the loci of closed G-orbits in X with stabilizer groups of maximum dimension. This procedure is an adaptation of Kirwan partial desingularization construction [Reference KirwanKir85] to singular GIT quotient stacks, using the notion of intrinsic blowup introduced in [Reference Kiem and LiKL13] and suitably generalized in [Reference Kiem, Li and SavvasKLS17].
The second step is to endow
![]() $\widetilde {\mathcal {M}}$
with a semiperfect obstruction theory [Reference Chang and LiCL11] of virtual dimension zero. This is a usual perfect obstruction theory in the sense of Behrend–Fantechi [Reference Behrend and FantechiBF97] defined on an étale cover of
$\widetilde {\mathcal {M}}$
with a semiperfect obstruction theory [Reference Chang and LiCL11] of virtual dimension zero. This is a usual perfect obstruction theory in the sense of Behrend–Fantechi [Reference Behrend and FantechiBF97] defined on an étale cover of
![]() $\widetilde {\mathcal {M}}$
together with compatibility data which play the role of suitable descent data. It is at this step where the existence of a virtual structure on
$\widetilde {\mathcal {M}}$
together with compatibility data which play the role of suitable descent data. It is at this step where the existence of a virtual structure on
![]() $\mathcal {M}$
plays a crucial role. More precisely, by [Reference Pantev, Toën, Vaquié and VezzosiPTVV13],
$\mathcal {M}$
plays a crucial role. More precisely, by [Reference Pantev, Toën, Vaquié and VezzosiPTVV13],
![]() $\mathcal {M}$
is the truncation of a
$\mathcal {M}$
is the truncation of a
![]() $(-1)$
-shifted symplectic derived Artin stack and it then follows that
$(-1)$
-shifted symplectic derived Artin stack and it then follows that
![]() $\mathcal {M}$
is a d-critical stack [Reference JoyceJoy15]. In particular, applying Luna’s étale slice theorem [Reference Drézet and WisniewskiDré04] and using the theory of d-critical loci developed in [Reference JoyceJoy15], we can obtain an explicit local description of
$\mathcal {M}$
is a d-critical stack [Reference JoyceJoy15]. In particular, applying Luna’s étale slice theorem [Reference Drézet and WisniewskiDré04] and using the theory of d-critical loci developed in [Reference JoyceJoy15], we can obtain an explicit local description of
![]() $\mathcal {M}$
: For every closed point
$\mathcal {M}$
: For every closed point
![]() $x \in \mathcal {M}$
with (reductive) stabilizer H, there exists a smooth affine scheme V with an H-action, an invariant function
$x \in \mathcal {M}$
with (reductive) stabilizer H, there exists a smooth affine scheme V with an H-action, an invariant function
![]() $f \colon V \to \mathbb {A}^1$
and an étale morphism
$f \colon V \to \mathbb {A}^1$
and an étale morphism
containing x in its image, where
![]() $U = \lbrace df = 0 \rbrace \subset V$
is the scheme-theoretic critical locus of f. Any two such local presentations can be compared as they give the same d-critical structure on
$U = \lbrace df = 0 \rbrace \subset V$
is the scheme-theoretic critical locus of f. Any two such local presentations can be compared as they give the same d-critical structure on
![]() $\mathcal {M}$
in the sense of [Reference JoyceJoy15].
$\mathcal {M}$
in the sense of [Reference JoyceJoy15].
To obtain the semiperfect obstruction theory of
![]() $\widetilde {\mathcal {M}}$
, consider the following H-equivariant four-term complex on U:
$\widetilde {\mathcal {M}}$
, consider the following H-equivariant four-term complex on U:
Around
![]() $u \in U$
with finite stabilizer group, this complex is quasi-isomorphic to a two-term complex which gives a symmetric perfect obstruction theory of
$u \in U$
with finite stabilizer group, this complex is quasi-isomorphic to a two-term complex which gives a symmetric perfect obstruction theory of
![]() $[U / H]$
and thus of
$[U / H]$
and thus of
![]() $\mathcal {M}$
near u.
$\mathcal {M}$
near u.
The intrinsic stabilizer reduction algorithm produces lifts of the étale morphisms (1.2) to give an étale cover
where
![]() $T = \lbrace \omega _S = 0 \rbrace \subseteq S$
for S a smooth affine H-scheme and
$T = \lbrace \omega _S = 0 \rbrace \subseteq S$
for S a smooth affine H-scheme and
![]() $\omega _S \in H^0(S, F_S)$
an invariant section of an H-equivariant vector bundle
$\omega _S \in H^0(S, F_S)$
an invariant section of an H-equivariant vector bundle
![]() $F_S$
on S. Moreover, there exists an effective invariant divisor
$F_S$
on S. Moreover, there exists an effective invariant divisor
![]() $D_S$
such that equation (1.3) lifts to a four-term complex
$D_S$
such that equation (1.3) lifts to a four-term complex
whose the first arrow is injective with locally free cokernel and the last arrow is surjective. Therefore, equation (1.5) is quasi-isomorphic to a two-term complex, whose dual can be shown to be a perfect obstruction theory on
![]() $[T/H]$
.
$[T/H]$
.
In [Reference Kiem, Li and SavvasKLS17], it is shown that these perfect obstruction theories satisfy the axioms of a semiperfect obstruction theory on
![]() $\widetilde {\mathcal {M}}$
of virtual dimension zero.
$\widetilde {\mathcal {M}}$
of virtual dimension zero.
Since, as usual, semiperfect obstruction theories produce virtual cycles,
![]() $\widetilde {\mathcal {M}}$
admits a virtual cycle
$\widetilde {\mathcal {M}}$
admits a virtual cycle
![]() $[\widetilde {\mathcal {M}}]^{\mathrm {vir}} \in A_0(\widetilde {\mathcal {M}})$
whose degree defines the DTK invariant counting Gieseker semistable sheaves parametrized by
$[\widetilde {\mathcal {M}}]^{\mathrm {vir}} \in A_0(\widetilde {\mathcal {M}})$
whose degree defines the DTK invariant counting Gieseker semistable sheaves parametrized by
![]() $\mathcal {M}$
. A relative version of the above construction, using derived symplectic geometry, implies its deformation invariance.
$\mathcal {M}$
. A relative version of the above construction, using derived symplectic geometry, implies its deformation invariance.
In the present paper, we work with moduli stacks
![]() $\mathcal {M}$
of semistable perfect complexes. These are truncations of
$\mathcal {M}$
of semistable perfect complexes. These are truncations of
![]() $(-1)$
-shifted symplectic derived Artin stacks as before; however, they are not global quotient stacks obtained by GIT of the form (1.1).
$(-1)$
-shifted symplectic derived Artin stacks as before; however, they are not global quotient stacks obtained by GIT of the form (1.1).
Our main contribution is to remove this assumption. To do this, we use several recent major technical results on the étale local structure of stacks [Reference Alper, Hall and RydhAHR19, Reference Alper, Hall and RydhAHR20], moduli spaces of objects in abelian categories [Reference Alper, Halpern-Leistner and HeinlothAHH18] and stability conditions in families [Reference Bayer, Lahoz, Macrì, Nuer, Perry and StellariBLM+21].
We generalize the requirement of a GIT presentation to the condition that
![]() $\mathcal {M}$
admit a good moduli space morphism [Reference AlperAlp13]. We show that such stacks (under additional reasonable assumptions) admit an intrinsic stabilizer reduction
$\mathcal {M}$
admit a good moduli space morphism [Reference AlperAlp13]. We show that such stacks (under additional reasonable assumptions) admit an intrinsic stabilizer reduction
![]() $\widetilde {\mathcal {M}}$
, which is a Deligne–Mumford stack and of independent interest in its own right (see Subsection 1.4 below).
$\widetilde {\mathcal {M}}$
, which is a Deligne–Mumford stack and of independent interest in its own right (see Subsection 1.4 below).
We then proceed to show that if in addition
![]() $\mathcal {M}$
is the truncation of a
$\mathcal {M}$
is the truncation of a
![]() $(-1)$
-shifted symplectic derived Artin stack, then the above statements about local models of
$(-1)$
-shifted symplectic derived Artin stack, then the above statements about local models of
![]() $\mathcal {M}$
and their comparison data carry over, using the main structural result of [Reference Alper, Hall and RydhAHR20] in place of Luna’s étale slice theorem. This allows us to define a semiperfect obstruction theory on
$\mathcal {M}$
and their comparison data carry over, using the main structural result of [Reference Alper, Hall and RydhAHR20] in place of Luna’s étale slice theorem. This allows us to define a semiperfect obstruction theory on
![]() $\widetilde {\mathcal {M}}$
and the associated DTK invariant.
$\widetilde {\mathcal {M}}$
and the associated DTK invariant.
Our approach thus works for a wide class of Artin stacks, which we call stacks of DT type (see Definition 3.4). Based on our discussion here, their two main characteristics can be summarized as the existence of a good moduli space and a derived enhancement that is
![]() $(-1)$
-shifted symplectic.
$(-1)$
-shifted symplectic.
Moduli stacks of semistable complexes fit into this context. This is the case by the recent results of [Reference Alper, Halpern-Leistner and HeinlothAHH18], which combine the theory of good moduli spaces with the notion of
![]() $\Theta $
-reductivity introduced in [Reference Halpern-LeistnerHal14] and apply to the stacks considered in the present paper.
$\Theta $
-reductivity introduced in [Reference Halpern-LeistnerHal14] and apply to the stacks considered in the present paper.
Finally, the deformation invariance of the DTK invariant follows from the compatibility of the intrinsic stabilizer reduction with base change and the recent results on stability conditions in [Reference Bayer, Lahoz, Macrì, Nuer, Perry and StellariBLM+21].
1.4 Relation to derived algebraic geometry
At the time of writing of this paper, intrinsic blowups and the intrinsic stabilizer reduction procedure were expected to be the classical shadow of a corresponding construction in derived algebraic geometry.
Subsequently, derived blowups were first defined in full generality in the work of Hekking [Reference HekkingHek21] and this expectation has recently been materialized by the results of [Reference Hekking, Rydh and SavvasHRS22], also using some of our results. Namely, the intrinsic blowup notion used in the present paper coincides with the classical truncation of an appropriate derived blowup of a derived scheme with a G-action along its derived fixed locus by the group G. Therefore, the intrinsic stabilizer reduction construction is indeed the classical truncation of a derived version of the Kirwan partial desingularization algorithm in GIT [Reference KirwanKir85] and its generalization to stacks with good moduli spaces by Edidin–Rydh [Reference Edidin and RydhER21], called derived stabilizer reduction. Moreover, the semiperfect obstruction theory constructed here is closely related to the derived cotangent complex of the stabilizer reduction of a
![]() $(-1)$
-shifted symplectic derived stack.
$(-1)$
-shifted symplectic derived stack.
1.5 Layout of the paper
In §2, we review background material on d-critical loci and
![]() $(-1)$
-shifted symplectic structures. In §3, we define the notion of stacks of DT type and establish their main properties that will be used throughout. §4 reviews the intrinsic stabilizer reduction procedure for GIT quotient stacks and generalizes it to stacks with good moduli spaces. In §5, we explain how to construct a semiperfect obstruction theory on stacks of DT type by following the arguments of [Reference Kiem, Li and SavvasKLS17]. Finally, in §6, we construct DTK invariants of semistable complexes by combining the above with the results of [Reference Alper, Halpern-Leistner and HeinlothAHH18] and
$(-1)$
-shifted symplectic structures. In §3, we define the notion of stacks of DT type and establish their main properties that will be used throughout. §4 reviews the intrinsic stabilizer reduction procedure for GIT quotient stacks and generalizes it to stacks with good moduli spaces. In §5, we explain how to construct a semiperfect obstruction theory on stacks of DT type by following the arguments of [Reference Kiem, Li and SavvasKLS17]. Finally, in §6, we construct DTK invariants of semistable complexes by combining the above with the results of [Reference Alper, Halpern-Leistner and HeinlothAHH18] and
![]() $\mathbb {G}_m$
-rigidification for Artin stacks and discuss their deformation invariance using recent work of [Reference Bayer, Lahoz, Macrì, Nuer, Perry and StellariBLM+21].
$\mathbb {G}_m$
-rigidification for Artin stacks and discuss their deformation invariance using recent work of [Reference Bayer, Lahoz, Macrì, Nuer, Perry and StellariBLM+21].
1.6 Notation and conventions
Here are the various notations and other conventions that we use throughout the paper:
-
– All schemes and stacks are defined over the field of complex numbers
 $\mathbb {C}$
or a smooth
$\mathbb {C}$
or a smooth
 $\mathbb {C}$
-scheme C, unless stated otherwise. For this reason, reductive group schemes will be linearly reductive automatically.
$\mathbb {C}$
-scheme C, unless stated otherwise. For this reason, reductive group schemes will be linearly reductive automatically. -
–
 $\mathcal {M}$
typically denotes an Artin stack, of finite type, with affine stabilizers and separated diagonal unless stated otherwise.
$\mathcal {M}$
typically denotes an Artin stack, of finite type, with affine stabilizers and separated diagonal unless stated otherwise. -
– W denotes a smooth, projective Calabi–Yau threefold over
 $\mathbb {C}$
and
$\mathbb {C}$
and
 $D^b(\mathop{\mathrm { Coh}}\nolimits W)$
its bounded derived category of coherent sheaves.
$D^b(\mathop{\mathrm { Coh}}\nolimits W)$
its bounded derived category of coherent sheaves. -
– C denotes a smooth quasi-projective scheme over
 $\mathbb {C}$
.
$\mathbb {C}$
. -
– G, H denote complex reductive groups. Usually, H will be a subgroup of G. T denotes the torus
 $\mathbb {C}^{\ast }$
.
$\mathbb {C}^{\ast }$
. -
– If
 $x \in \mathcal {M}$
,
$x \in \mathcal {M}$
,
 $G_x$
denotes the automorphism group/stabilizer of x. We will only consider stabilizers of closed points
$G_x$
denotes the automorphism group/stabilizer of x. We will only consider stabilizers of closed points
 $x \in \mathcal {M}$
. These will be reductive for most stacks of interest in this paper.
$x \in \mathcal {M}$
. These will be reductive for most stacks of interest in this paper. -
– If
 $U \hookrightarrow V$
is a closed embedding,
$U \hookrightarrow V$
is a closed embedding,
 $I_{U \subseteq V}$
or
$I_{U \subseteq V}$
or
 $I_U$
(when V is clear from context) denotes the ideal sheaf of U in V.
$I_U$
(when V is clear from context) denotes the ideal sheaf of U in V. -
– For a morphism
 $\rho \colon U \to V$
and a sheaf E on V, we systematically use
$\rho \colon U \to V$
and a sheaf E on V, we systematically use
 $E \vert _U$
to denote
$E \vert _U$
to denote
 $\rho ^* E$
, suppressing the pullback from the notation.
$\rho ^* E$
, suppressing the pullback from the notation. -
– If V is a G-scheme,
 $V^G$
is used to denote the fixed point locus of G in V.
$V^G$
is used to denote the fixed point locus of G in V. -
– If U is a scheme with a G-action, then
 $\widehat U$
is used to denote the Kirwan blowup of U with respect to G.
$\widehat U$
is used to denote the Kirwan blowup of U with respect to G.
 $\widetilde {U}$
denotes the intrinsic stabilizer reduction of U.
$\widetilde {U}$
denotes the intrinsic stabilizer reduction of U. -
– The abbreviations DT, DM, GIT, whenever used, stand for Donaldson–Thomas, Deligne–Mumford and geometric invariant theory, respectively.
2 D-Critical loci and
 $(-1)$
-shifted symplectic derived stacks
$(-1)$
-shifted symplectic derived stacks
This section collects background material and terminology that will be used throughout the rest of the paper.
We first briefly recall Joyce’s theory of d-critical loci, as developed in [Reference JoyceJoy15], and establish some notation and then proceed to quickly review shifted symplectic structures on derived stacks.
2.1 D-critical schemes
We begin by defining the notion of a d-critical chart.
Definition 2.1 (d-critical chart)
A d-critical chart for a scheme X is the data of
![]() $(U,V,f,i)$
such that:
$(U,V,f,i)$
such that:
![]() $U \subseteq X$
is Zariski open, V is a smooth scheme,
$U \subseteq X$
is Zariski open, V is a smooth scheme,
![]() $f \colon V \to \mathbb {A}^1$
is a regular function on V and
$f \colon V \to \mathbb {A}^1$
is a regular function on V and
![]() $U \xrightarrow {i} V$
is a closed embedding so that
$U \xrightarrow {i} V$
is a closed embedding so that
![]() $U = \lbrace d f=0 \rbrace = \mathop{\mathrm {Crit}}\nolimits (f) \subseteq V$
is the scheme-theoretic vanishing locus of the derivative of f.
$U = \lbrace d f=0 \rbrace = \mathop{\mathrm {Crit}}\nolimits (f) \subseteq V$
is the scheme-theoretic vanishing locus of the derivative of f.
If
![]() $x \in U$
, then we say that the d-critical chart
$x \in U$
, then we say that the d-critical chart
![]() $(U,V,f,i)$
is centered at x.
$(U,V,f,i)$
is centered at x.
Joyce defines a canonical sheaf
![]() $\mathcal {S}_X$
of
$\mathcal {S}_X$
of
![]() $\mathbb {C}$
-vector spaces with the property that for any Zariski open
$\mathbb {C}$
-vector spaces with the property that for any Zariski open
![]() $U \subseteq X$
and an embedding
$U \subseteq X$
and an embedding
![]() $U \hookrightarrow V$
into a smooth scheme V with ideal I,
$U \hookrightarrow V$
into a smooth scheme V with ideal I,
![]() $\mathcal {S}_X$
fits into an exact sequence
$\mathcal {S}_X$
fits into an exact sequence
For example, for a d-critical chart
![]() $(U,V,f,i)$
the element
$(U,V,f,i)$
the element
![]() $f+I^2 \in \Gamma (V, \mathcal {O}_V/I^2)$
gives a section of
$f+I^2 \in \Gamma (V, \mathcal {O}_V/I^2)$
gives a section of
![]() $\mathcal {S}_X|_U$
.
$\mathcal {S}_X|_U$
.
Definition 2.2 (d-critical scheme)
A d-critical structure on a scheme X is a section
![]() $s \in \Gamma (X, \mathcal {S}_X)$
such that X admits a cover by d-critical charts
$s \in \Gamma (X, \mathcal {S}_X)$
such that X admits a cover by d-critical charts
![]() $(U,V,f,i)$
and
$(U,V,f,i)$
and
![]() $s|_U$
is given by
$s|_U$
is given by
![]() $f+I^2$
as above on each such chart. We refer to the pair
$f+I^2$
as above on each such chart. We refer to the pair
![]() $(X,s)$
as a d-critical scheme.
$(X,s)$
as a d-critical scheme.
2.2 Equivariant d-critical loci
For our purposes, we need equivariant analogues of the results of Subsection 2.1. The theory works in parallel as before (cf. [Reference JoyceJoy15, Section 2.6]).
Definition 2.3 (Good action)
Let G be an algebraic group acting on a scheme X. We say that the action is good if X has a cover
![]() $\lbrace U_{\alpha } \rbrace _{\alpha \in A}$
, where every
$\lbrace U_{\alpha } \rbrace _{\alpha \in A}$
, where every
![]() $U_{\alpha } \subseteq X$
is a G-invariant Zariski open affine subscheme.
$U_{\alpha } \subseteq X$
is a G-invariant Zariski open affine subscheme.
Remark 2.1. If X is affine, then trivially every action of G on M is good.
Suppose now that a scheme X admits a good action by a reductive group G. Definitions 2.1, 2.2 extend naturally to this equivariant setting (cf. [Reference JoyceJoy15, Definition 2.40]) as follows: A G-invariant d-critical chart is given by the data
![]() $(U,V,f,i)$
of Definition 2.1, where
$(U,V,f,i)$
of Definition 2.1, where
![]() $U \subseteq X$
is a G-invariant Zariski open subscheme, V is a smooth scheme with a G-action,
$U \subseteq X$
is a G-invariant Zariski open subscheme, V is a smooth scheme with a G-action,
![]() $i \colon U \to V$
an equivariant closed embedding and
$i \colon U \to V$
an equivariant closed embedding and
![]() $f \colon V \to \mathbb {C}$
a G-invariant function. The sheaf
$f \colon V \to \mathbb {C}$
a G-invariant function. The sheaf
![]() $\mathcal {S}_X$
inherits a G-action by using a cover of X by G-invariant open subschemes
$\mathcal {S}_X$
inherits a G-action by using a cover of X by G-invariant open subschemes
![]() $U \subseteq X$
in equation (2.1). Then we say that the d-critical scheme
$U \subseteq X$
in equation (2.1). Then we say that the d-critical scheme
![]() $(X,s)$
is G-invariant if
$(X,s)$
is G-invariant if
![]() $s \in \Gamma (X, \mathcal {S}_X)^G$
is a G-invariant global section of the sheaf
$s \in \Gamma (X, \mathcal {S}_X)^G$
is a G-invariant global section of the sheaf
![]() $\mathcal {S}_X$
.
$\mathcal {S}_X$
.
Proposition 2.2 [Reference JoyceJoy15, Remark 2.47]
Let G be a complex reductive group with a good action on a scheme X. Suppose that
![]() $(X,s)$
is an invariant d-critical scheme. Then for any
$(X,s)$
is an invariant d-critical scheme. Then for any
![]() $x \in X$
fixed by G, there exists an invariant d-critical chart
$x \in X$
fixed by G, there exists an invariant d-critical chart
![]() $(U,V,f,i)$
centered at x, that is, an invariant open affine
$(U,V,f,i)$
centered at x, that is, an invariant open affine
![]() $U \ni x$
, a smooth scheme V with a G-action, an invariant regular function
$U \ni x$
, a smooth scheme V with a G-action, an invariant regular function
![]() $f \colon V \to \mathbb {A}^1$
and an equivariant embedding
$f \colon V \to \mathbb {A}^1$
and an equivariant embedding
![]() $i \colon U \to V$
so that
$i \colon U \to V$
so that
![]() $U = \mathop{\mathrm {Crit}}\nolimits (f) \subseteq V$
.
$U = \mathop{\mathrm {Crit}}\nolimits (f) \subseteq V$
.
Remark 2.3. If G is a torus
![]() $\left ( \mathbb {C}^{\ast } \right )^k$
, then Proposition 2.2 is true without the assumption that x is a fixed point of G.
$\left ( \mathbb {C}^{\ast } \right )^k$
, then Proposition 2.2 is true without the assumption that x is a fixed point of G.
Remark 2.4. One may replace Zariski open morphisms by étale morphisms without any difference to the essence of the theory. Another option is to work in the complex analytic topology.
2.3 D-critical Artin stacks
The theory of d-critical loci extends naturally to Artin stacks. For more details, we point the interested reader to Section 2.8 of [Reference JoyceJoy15]. We mention the following definition and basic properties which we will need in the form of remarks.
Definition 2.4 [Reference JoyceJoy15, Corollary 2.52, Definition 2.53]
Let
![]() $\mathcal {M}$
be an Artin stack. For every smooth morphism
$\mathcal {M}$
be an Artin stack. For every smooth morphism
![]() $\phi \colon U \to \mathcal {M}$
, where U is a scheme, the assignment
$\phi \colon U \to \mathcal {M}$
, where U is a scheme, the assignment
![]() $\mathcal {S}(U, \phi ) := \mathcal {S}_U$
defines a sheaf
$\mathcal {S}(U, \phi ) := \mathcal {S}_U$
defines a sheaf
![]() $\mathcal {S}_{\mathcal {M}}$
of
$\mathcal {S}_{\mathcal {M}}$
of
![]() $\mathbb {C}$
-vector spaces in the lisse-étale topology of
$\mathbb {C}$
-vector spaces in the lisse-étale topology of
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
A d-critical structure on
![]() $\mathcal {M}$
is a global section
$\mathcal {M}$
is a global section
![]() $s \in H^0(\mathcal {M}, \mathcal {S}_{\mathcal {M}})$
. We then say that
$s \in H^0(\mathcal {M}, \mathcal {S}_{\mathcal {M}})$
. We then say that
![]() $(\mathcal {M}, s)$
is a d-critical Artin stack.
$(\mathcal {M}, s)$
is a d-critical Artin stack.
Remark 2.5 [Reference JoyceJoy15, Example 2.55]
A d-critical structure can be equivalently described in terms of a groupoid presentation of
![]() $\mathcal {M}$
. It follows that d-critical structures on quotient stacks
$\mathcal {M}$
. It follows that d-critical structures on quotient stacks
![]() $\left [ X / G \right ]$
are in bijective correspondence with invariant d-critical structures on X.
$\left [ X / G \right ]$
are in bijective correspondence with invariant d-critical structures on X.
If
![]() $\mathcal {M}' \to \mathcal {M}$
is a smooth morphism of Artin stacks and
$\mathcal {M}' \to \mathcal {M}$
is a smooth morphism of Artin stacks and
![]() $\mathcal {M}$
is d-critical, then one may pull back the d-critical structure on
$\mathcal {M}$
is d-critical, then one may pull back the d-critical structure on
![]() $\mathcal {M}$
making
$\mathcal {M}$
making
![]() $\mathcal {M}'$
d-critical as well.
$\mathcal {M}'$
d-critical as well.
2.4 Shifted symplectic structures
Let
![]() ${\mathrm {cdga_{\mathbb {C}}^{\leq 0}}}$
be the category of nonpositively graded commutative differential graded
${\mathrm {cdga_{\mathbb {C}}^{\leq 0}}}$
be the category of nonpositively graded commutative differential graded
![]() $\mathbb {C}$
-algebras.
$\mathbb {C}$
-algebras.
There is a spectrum functor
![]() $\mathbf {Spec}\, \colon {\mathrm {cdga_{\mathbb {C}}^{\leq 0}}} \to \mathbf {dSt}_{\mathbb {C}}$
to the category of derived stacks (see [Reference Toën and VezzosiTV04, Definition 2.2.2.14] or [Reference ToënToë09, Definition 4.2]). An object of the form
$\mathbf {Spec}\, \colon {\mathrm {cdga_{\mathbb {C}}^{\leq 0}}} \to \mathbf {dSt}_{\mathbb {C}}$
to the category of derived stacks (see [Reference Toën and VezzosiTV04, Definition 2.2.2.14] or [Reference ToënToë09, Definition 4.2]). An object of the form
![]() $\mathbf {Spec}\, A$
is called an affine derived
$\mathbf {Spec}\, A$
is called an affine derived
![]() $\mathbb {C}$
-scheme. Such objects provide the Zariski local charts for general derived
$\mathbb {C}$
-scheme. Such objects provide the Zariski local charts for general derived
![]() $\mathbb {C}$
-schemes; see [Reference ToënToë09, Section 4.2]. An object
$\mathbb {C}$
-schemes; see [Reference ToënToë09, Section 4.2]. An object
![]() in
in
![]() $\mathbf {dSt}_{\mathbb {C}}$
is called a derived Artin stack if it is m-geometric (cf. [Reference ToënToë09, Definition 1.3.3.1]) for some m and its ‘classical truncation’
$\mathbf {dSt}_{\mathbb {C}}$
is called a derived Artin stack if it is m-geometric (cf. [Reference ToënToë09, Definition 1.3.3.1]) for some m and its ‘classical truncation’
![]() is an Artin stack (and not a higher stack). A derived Artin stack
is an Artin stack (and not a higher stack). A derived Artin stack
![]() admits an atlas, that is, a smooth surjective morphism
admits an atlas, that is, a smooth surjective morphism
![]() from a derived scheme. For a derived Artin stack
from a derived scheme. For a derived Artin stack
![]() , there exists a cotangent complex
, there exists a cotangent complex
![]() of finite cohomological amplitude in
of finite cohomological amplitude in
![]() $[-m,1]$
and a dual tangent complex
$[-m,1]$
and a dual tangent complex
![]() . Both are objects in a suitable stable
. Both are objects in a suitable stable
![]() $\infty $
-category
$\infty $
-category
![]() (see [Reference ToënToë09] or [Reference Toën and VezzosiTV04] for its definition).
(see [Reference ToënToë09] or [Reference Toën and VezzosiTV04] for its definition).
Shifted symplectic structures on derived Artin stacks were introduced by Pantev–Toën–Vaquié–Vezzosi in [Reference Pantev, Toën, Vaquié and VezzosiPTVV13]. The definition is given in the affine case first and then generalized by showing the local notion satisfies smooth descent. We recall the local definition: Let us set
![]() $\boldsymbol {M} = \mathbf {Spec}\, A$
so that
$\boldsymbol {M} = \mathbf {Spec}\, A$
so that
![]() $L_{\mathsf {qcoh}}(\boldsymbol {M}) \cong \mathbf {D}(\mathrm {dg}\textrm {-}\mathrm {Mod}_A)$
. For all
$L_{\mathsf {qcoh}}(\boldsymbol {M}) \cong \mathbf {D}(\mathrm {dg}\textrm {-}\mathrm {Mod}_A)$
. For all
![]() $p\geq 0$
, one can define the exterior power complex
$p\geq 0$
, one can define the exterior power complex
![]() $(\Lambda ^p \mathbb {L}_{\boldsymbol {M}},\mathrm {d}) \in L_{\mathsf {qcoh}}(\boldsymbol {M})$
, where the differential
$(\Lambda ^p \mathbb {L}_{\boldsymbol {M}},\mathrm {d}) \in L_{\mathsf {qcoh}}(\boldsymbol {M})$
, where the differential
![]() $\mathrm {d}$
is induced by the differential of the algebra A. For a fixed
$\mathrm {d}$
is induced by the differential of the algebra A. For a fixed
![]() $k \in \mathbb {Z}$
, define a k-shifted p-form on
$k \in \mathbb {Z}$
, define a k-shifted p-form on
![]() $\boldsymbol {M}$
to be an element
$\boldsymbol {M}$
to be an element
![]() $\omega ^0 \in (\Lambda ^p \mathbb {L}_{\boldsymbol {M}})^k$
such that
$\omega ^0 \in (\Lambda ^p \mathbb {L}_{\boldsymbol {M}})^k$
such that
![]() $\mathrm {d} \omega ^0 = 0$
. To define the notion of closedness, consider the de Rham differential
$\mathrm {d} \omega ^0 = 0$
. To define the notion of closedness, consider the de Rham differential
![]() $\mathrm {d}_{\mathrm {dR}}\colon \Lambda ^p \mathbb {L}_{\boldsymbol {M}} \to \Lambda ^{p+1} \mathbb {L}_{\boldsymbol {M}}$
. A k-shifted closed p-form is a sequence
$\mathrm {d}_{\mathrm {dR}}\colon \Lambda ^p \mathbb {L}_{\boldsymbol {M}} \to \Lambda ^{p+1} \mathbb {L}_{\boldsymbol {M}}$
. A k-shifted closed p-form is a sequence
![]() $(\omega ^0,\omega ^1,\ldots )$
, with
$(\omega ^0,\omega ^1,\ldots )$
, with
![]() $\omega ^i \in (\Lambda ^{p+i}\mathbb {L}_{\boldsymbol {M}})^{k-i}$
such that
$\omega ^i \in (\Lambda ^{p+i}\mathbb {L}_{\boldsymbol {M}})^{k-i}$
such that
![]() $\mathrm {d} \omega ^0 = 0$
and
$\mathrm {d} \omega ^0 = 0$
and
![]() $\mathrm {d}_{\mathrm {dR}} \omega ^i + \mathrm {d} \omega ^{i+1} = 0$
. When
$\mathrm {d}_{\mathrm {dR}} \omega ^i + \mathrm {d} \omega ^{i+1} = 0$
. When
![]() $p=2$
, any k-shifted
$p=2$
, any k-shifted
![]() $2$
-form
$2$
-form
![]() $\omega ^0 \in (\Lambda ^2 \mathbb {L}_{\boldsymbol {M}})^k$
induces a morphism
$\omega ^0 \in (\Lambda ^2 \mathbb {L}_{\boldsymbol {M}})^k$
induces a morphism
![]() $\omega ^0\colon \mathbb {T}_{\boldsymbol {M}} \to \mathbb {L}_{\boldsymbol {M}}[k]$
in
$\omega ^0\colon \mathbb {T}_{\boldsymbol {M}} \to \mathbb {L}_{\boldsymbol {M}}[k]$
in
![]() $L_{\mathsf {qcoh}}(\boldsymbol {M})$
, and we say that
$L_{\mathsf {qcoh}}(\boldsymbol {M})$
, and we say that
![]() $\omega ^0$
is nondegenerate if this morphism is an isomorphism in
$\omega ^0$
is nondegenerate if this morphism is an isomorphism in
![]() $L_{\mathsf {qcoh}}(\boldsymbol {M})$
.
$L_{\mathsf {qcoh}}(\boldsymbol {M})$
.
Definition 2.5 [Reference Pantev, Toën, Vaquié and VezzosiPTVV13, Definition 1.18]
A k-shifted closed
![]() $2$
-form
$2$
-form
![]() $\omega = (\omega ^0,\omega ^1,\ldots )$
is called a k-shifted symplectic structure if
$\omega = (\omega ^0,\omega ^1,\ldots )$
is called a k-shifted symplectic structure if
![]() $\omega ^0$
is nondegenerate. We say that
$\omega ^0$
is nondegenerate. We say that
![]() $(\boldsymbol {M},\omega )$
is a k-shifted symplectic (affine) derived scheme.
$(\boldsymbol {M},\omega )$
is a k-shifted symplectic (affine) derived scheme.
When
![]() $k=-1$
, it is shown in [Reference Ben-Bassat, Brav, Bussi and JoyceBBBBJ15] that if
$k=-1$
, it is shown in [Reference Ben-Bassat, Brav, Bussi and JoyceBBBBJ15] that if
![]() $\mathcal {M}$
is the classical truncation of a
$\mathcal {M}$
is the classical truncation of a
![]() $(-1)$
-shifted symplectic derived Artin stack, then
$(-1)$
-shifted symplectic derived Artin stack, then
![]() $\mathcal {M}$
admits an induced d-critical structure.
$\mathcal {M}$
admits an induced d-critical structure.
Theorem 2.6 [Reference Ben-Bassat, Brav, Bussi and JoyceBBBBJ15, Theorem 3.18]
Let
![]() be a
be a
![]() $(-1)$
-shifted symplectic derived Artin stack. Then the underlying classical Artin stack
$(-1)$
-shifted symplectic derived Artin stack. Then the underlying classical Artin stack
![]() extends in a canonical way to a d-critical Artin stack
extends in a canonical way to a d-critical Artin stack
![]() $(\mathcal {M},s)$
. This defines a ‘truncation functor’
$(\mathcal {M},s)$
. This defines a ‘truncation functor’
![]() $\tau $
from the
$\tau $
from the
![]() $\infty $
-category of
$\infty $
-category of
![]() $(-1)$
-shifted symplectic derived Artin stacks to the
$(-1)$
-shifted symplectic derived Artin stacks to the
![]() $2$
-category of d-critical Artin stacks.
$2$
-category of d-critical Artin stacks.
3 Stacks of DT type
In this section, we first give an account of results regarding the étale local structure of Artin stacks and the theory of good moduli spaces. We then proceed to define stacks of DT type, develop standard local models for them and describe how to compare these models.
3.1 Local structure of Artin stacks
The following theorem is an étale slice theorem for stacks, which generalizes Luna’s étale slice theorem [Reference Drézet and WisniewskiDré04]. It states that Artin stacks are étale locally quotient stacks.
Theorem 3.1 [Reference Alper, Hall and RydhAHR20, Theorem 1.2]
Let
![]() $\mathcal {M}$
be a quasi-separated Artin stack, locally of finite type over
$\mathcal {M}$
be a quasi-separated Artin stack, locally of finite type over
![]() $\mathbb {C}$
with affine stabilizers. Let
$\mathbb {C}$
with affine stabilizers. Let
![]() $x \in \mathcal {M}$
and
$x \in \mathcal {M}$
and
![]() $H \subseteq G_x$
a maximal reductive subgroup of the stabilizer of x. Then there exists an affine scheme U with an action of H, a point
$H \subseteq G_x$
a maximal reductive subgroup of the stabilizer of x. Then there exists an affine scheme U with an action of H, a point
![]() $u \in U$
fixed by H and a smooth morphism
$u \in U$
fixed by H and a smooth morphism
which maps
![]() $u \mapsto x$
and induces the inclusion
$u \mapsto x$
and induces the inclusion
![]() $H \hookrightarrow G_x$
of stabilizers at u. Moreover, if
$H \hookrightarrow G_x$
of stabilizers at u. Moreover, if
![]() $G_x$
is reductive, the morphism is étale. If
$G_x$
is reductive, the morphism is étale. If
![]() $\mathcal {M}$
has affine diagonal, then
$\mathcal {M}$
has affine diagonal, then
![]() $\Phi _x$
can be taken to be affine.
$\Phi _x$
can be taken to be affine.
3.2 Good moduli spaces
We now collect some useful results about the structure of a certain class of Artin stacks, namely those with affine diagonal admitting a good moduli space, following the theory developed by Alper ét al. All the material of the section can be found in [Reference AlperAlp13] and [Reference Alper, Hall and RydhAHR20].
We have the following definition of a good moduli space.
Definition 3.1 [Reference AlperAlp13, Definition 4.1]
A morphism
![]() $q \colon \mathcal {M} \to Y$
, where
$q \colon \mathcal {M} \to Y$
, where
![]() $\mathcal {M}$
is an Artin stack and Y an algebraic space, is a good moduli space for
$\mathcal {M}$
is an Artin stack and Y an algebraic space, is a good moduli space for
![]() $\mathcal {M}$
if the following hold:
$\mathcal {M}$
if the following hold:
-
1. q is quasi-compact and
 $q_* \colon \mathop{\mathrm {QCoh}}\nolimits (\mathcal {M}) \to \mathop{\mathrm { QCoh}}\nolimits (Y)$
is exact.
$q_* \colon \mathop{\mathrm {QCoh}}\nolimits (\mathcal {M}) \to \mathop{\mathrm { QCoh}}\nolimits (Y)$
is exact. -
2. The natural map
 $\mathcal {O}_Y \to q_* \mathcal {O}_{\mathcal {M}}$
is an isomorphism.
$\mathcal {O}_Y \to q_* \mathcal {O}_{\mathcal {M}}$
is an isomorphism.
The intuition behind the introduction of the notion of good moduli space is that stacks
![]() $\mathcal {M}$
that admit good moduli spaces behave like quotient stacks
$\mathcal {M}$
that admit good moduli spaces behave like quotient stacks
![]() $[X^{ss}/G]$
obtained from geometric invariant theory (GIT) with good moduli space morphism given by the map
$[X^{ss}/G]$
obtained from geometric invariant theory (GIT) with good moduli space morphism given by the map
![]() $[X^{ss}/G] \to X /\!\!/ G$
. In this sense, it is a generalization of GIT quotients for stacks.
$[X^{ss}/G] \to X /\!\!/ G$
. In this sense, it is a generalization of GIT quotients for stacks.
We state the following properties of stacks with good moduli space.
Proposition 3.2 [Reference AlperAlp13, Proposition 4.7, Lemma 4.14, Theorem 4.16, Proposition 9.1, Proposition 12.14]
Let
![]() $\mathcal {M}$
be locally noetherian over
$\mathcal {M}$
be locally noetherian over
![]() $\mathbb {C}$
and
$\mathbb {C}$
and
![]() $q \colon \mathcal {M} \to Y$
be a good moduli space. Then:
$q \colon \mathcal {M} \to Y$
be a good moduli space. Then:
-
1. q is surjective.
-
2. q is universally closed.
-
3. Two geometric points
 $x_1, x_2 \in \mathcal {M}(k)$
are identified in Y if and only if their closures
$x_1, x_2 \in \mathcal {M}(k)$
are identified in Y if and only if their closures
 $\overline {\lbrace x_1 \rbrace }$
and
$\overline {\lbrace x_1 \rbrace }$
and
 $\overline {\lbrace x_2 \rbrace }$
in
$\overline {\lbrace x_2 \rbrace }$
in
 $\mathcal {M} \times _{\mathop{\mathrm { Spec}}\nolimits \mathbb {C}} \mathop{\mathrm {Spec}}\nolimits k$
intersect.
$\mathcal {M} \times _{\mathop{\mathrm { Spec}}\nolimits \mathbb {C}} \mathop{\mathrm {Spec}}\nolimits k$
intersect. -
4. Every closed point of
 $\mathcal {M}$
has reductive stabilizer.
$\mathcal {M}$
has reductive stabilizer. -
5. Let
 $y \in |Y|$
be a closed point. Then there exists a unique closed point
$y \in |Y|$
be a closed point. Then there exists a unique closed point
 $x \in |q^{-1}(y)|$
.
$x \in |q^{-1}(y)|$
. -
6. If
 $\mathcal {Z}$
is a closed substack of
$\mathcal {Z}$
is a closed substack of
 $\mathcal {M}$
, then the morphism
$\mathcal {M}$
, then the morphism
 $\mathcal {Z} \to q(\mathcal {Z}) = \mathop{\mathrm {im}}\nolimits (\mathcal {Z})$
is a good moduli space morphism.
$\mathcal {Z} \to q(\mathcal {Z}) = \mathop{\mathrm {im}}\nolimits (\mathcal {Z})$
is a good moduli space morphism. -
7. Let

be a Cartesian diagram of Artin stacks such that
 $Y, Y'$
are algebraic spaces.
$Y, Y'$
are algebraic spaces.-
(a) If
 $\mathcal {M} \to Y$
is a good moduli space, then
$\mathcal {M} \to Y$
is a good moduli space, then
 $\mathcal {M}' \to Y'$
is a good moduli space.
$\mathcal {M}' \to Y'$
is a good moduli space. -
(b) If
 $Y' \to Y$
is fpqc and
$Y' \to Y$
is fpqc and
 $\mathcal {M}' \to Y'$
is a good moduli space, then
$\mathcal {M}' \to Y'$
is a good moduli space, then
 $\mathcal {M} \to Y$
is a good moduli space.
$\mathcal {M} \to Y$
is a good moduli space.
-
-
8. If
 $\mathcal {M}$
is of finite type, then Y is of finite type.
$\mathcal {M}$
is of finite type, then Y is of finite type.
The following notions will be useful for us.
Definition 3.2 [Reference AlperAlp13, Definition 6.1, Remark 6.2]
Let
![]() $\mathcal {M}$
be a locally noetherian Artin stack with a good moduli space
$\mathcal {M}$
be a locally noetherian Artin stack with a good moduli space
![]() $q \colon \mathcal {M} \to M$
. A Zariski open substack
$q \colon \mathcal {M} \to M$
. A Zariski open substack
![]() $\mathcal {U} \subseteq \mathcal {M}$
is called saturated if
$\mathcal {U} \subseteq \mathcal {M}$
is called saturated if
![]() $q^{-1}(q(\mathcal {U})) = \mathcal {U}$
.
$q^{-1}(q(\mathcal {U})) = \mathcal {U}$
.
If
![]() $\mathcal {U}$
is saturated, the morphism
$\mathcal {U}$
is saturated, the morphism
![]() $\mathcal {U} \to U := q(\mathcal {U})$
gives a good moduli space for
$\mathcal {U} \to U := q(\mathcal {U})$
gives a good moduli space for
![]() $\mathcal {U}$
fitting into a Cartesian diagram
$\mathcal {U}$
fitting into a Cartesian diagram

where
![]() $U \to M$
is an open embedding.
$U \to M$
is an open embedding.
Definition 3.3 [Reference Alper, Hall and RydhAHR19, Definition 3.13]
Let
![]() $\mathcal {M}',\ \mathcal {M}$
be Artin stacks with good moduli space morphisms
$\mathcal {M}',\ \mathcal {M}$
be Artin stacks with good moduli space morphisms
![]() $q' \colon \mathcal {M}' \to M'$
,
$q' \colon \mathcal {M}' \to M'$
,
![]() $q \colon \mathcal {M} \to M$
. A morphism
$q \colon \mathcal {M} \to M$
. A morphism
![]() $\mathcal {M}' \to \mathcal {M}$
is called strongly étale if the induced morphism
$\mathcal {M}' \to \mathcal {M}$
is called strongly étale if the induced morphism
![]() $M' \to M$
is étale and the diagram
$M' \to M$
is étale and the diagram

is Cartesian.
Remark 3.3. In the sequel, we will be using the fact that strongly étale morphisms are stabilizer-preserving.
We have the following theorem regarding the étale local structure of good moduli space morphisms for stacks with affine diagonal.
Theorem-Definition 3.4 ((Quotient chart) [Reference Alper, Hall and RydhAHR20, Theorem 4.12])
Let
![]() $\mathcal {M}$
be a locally noetherian Artin stack with a good moduli space
$\mathcal {M}$
be a locally noetherian Artin stack with a good moduli space
![]() $q \colon \mathcal {M} \to M$
such that q is of finite type with affine diagonal. If
$q \colon \mathcal {M} \to M$
such that q is of finite type with affine diagonal. If
![]() $x \in \mathcal {M}$
is a closed point with (reductive) stabilizer
$x \in \mathcal {M}$
is a closed point with (reductive) stabilizer
![]() $G_x$
, then there exists an affine scheme U with an action of
$G_x$
, then there exists an affine scheme U with an action of
![]() $G_x$
and a Cartesian diagram
$G_x$
and a Cartesian diagram

such that
![]() $\Phi _x$
has the same properties as in Theorem 3.1, is affine and
$\Phi _x$
has the same properties as in Theorem 3.1, is affine and
![]() $U_x /\!\!/ G_x$
is an étale neighbourhood of
$U_x /\!\!/ G_x$
is an étale neighbourhood of
![]() $q(x)$
.
$q(x)$
.
We refer to any choice of data
![]() $(U_x, \Phi _x)$
such that
$(U_x, \Phi _x)$
such that
![]() $\Phi _x \colon [U_x / G_x] \to \mathcal {M}$
is étale, affine and stabilizer-preserving as a quotient chart for
$\Phi _x \colon [U_x / G_x] \to \mathcal {M}$
is étale, affine and stabilizer-preserving as a quotient chart for
![]() $\mathcal {M}$
centered at x. We say that the quotient chart is strongly étale if the morphism
$\mathcal {M}$
centered at x. We say that the quotient chart is strongly étale if the morphism
![]() $\Phi _x$
is strongly étale.
$\Phi _x$
is strongly étale.
3.3 Stacks of DT type
We start with the following definition.
Definition 3.4 (Stack of DT type)
Let
![]() $\mathcal {M}$
be an Artin stack. We say that
$\mathcal {M}$
be an Artin stack. We say that
![]() $\mathcal {M}$
is of DT type if the following are true:
$\mathcal {M}$
is of DT type if the following are true:
-
1.
 $\mathcal {M}$
is quasi-separated and finite type over
$\mathcal {M}$
is quasi-separated and finite type over
 $\mathbb {C}$
.
$\mathbb {C}$
. -
2. There exists a good moduli space
 $q \colon \mathcal {M} \to M$
, where q is of finite type and has affine diagonal.
$q \colon \mathcal {M} \to M$
, where q is of finite type and has affine diagonal. -
3.
 $\mathcal {M}$
is the classical truncation of a
$\mathcal {M}$
is the classical truncation of a
 $(-1)$
-shifted symplectic derived Artin stack
$(-1)$
-shifted symplectic derived Artin stack
 .
.
Remark 3.5. By Theorem 2.6 a stack
![]() $\mathcal {M}$
of DT type admits a canonical d-critical structure
$\mathcal {M}$
of DT type admits a canonical d-critical structure
![]() $s \in H^0(\mathcal {M}, \mathcal {S}_{\mathcal {M}})$
.
$s \in H^0(\mathcal {M}, \mathcal {S}_{\mathcal {M}})$
.
Definition 3.5 (d-critical quotient chart)
Let
![]() $x \in \mathcal {M}$
and
$x \in \mathcal {M}$
and
![]() $\Phi \colon [U_x / G_x] \to \mathcal {M}$
be as in Theorem-Definition 3.4. We say that
$\Phi \colon [U_x / G_x] \to \mathcal {M}$
be as in Theorem-Definition 3.4. We say that
![]() $(U_x, V, f, \Phi _x)$
is a d-critical quotient chart centered at x if there exists a
$(U_x, V, f, \Phi _x)$
is a d-critical quotient chart centered at x if there exists a
![]() $G_x$
-invariant d-critical locus determined by data
$G_x$
-invariant d-critical locus determined by data
![]() $(U_x, V, f, i)$
.
$(U_x, V, f, i)$
.
A variant of the following proposition first appeared and was used in [Reference TodaTod16].
Proposition 3.6. Let
![]() $\mathcal {M}$
be a stack of DT type and
$\mathcal {M}$
be a stack of DT type and
![]() $x \in \mathcal {M}$
a closed point. Then there exists a d-critical quotient chart for
$x \in \mathcal {M}$
a closed point. Then there exists a d-critical quotient chart for
![]() $\mathcal {M}$
centered at x, which can be taken to be strongly étale.
$\mathcal {M}$
centered at x, which can be taken to be strongly étale.
Proof. By Theorem-Definition 3.4, we have a quotient chart
![]() $\Phi _x \colon [ U_x'' / G_x ] \to \mathcal {M}$
. By Proposition 2.2, Definition 2.4 and Remark 2.5, there exists a
$\Phi _x \colon [ U_x'' / G_x ] \to \mathcal {M}$
. By Proposition 2.2, Definition 2.4 and Remark 2.5, there exists a
![]() $G_x$
-invariant open affine
$G_x$
-invariant open affine
![]() $x \in U_x' \subseteq U_x''$
and an invariant d-critical chart
$x \in U_x' \subseteq U_x''$
and an invariant d-critical chart
![]() $(U_x', V', f, i)$
. We obtain a commutative diagram
$(U_x', V', f, i)$
. We obtain a commutative diagram

Applying the fundamental lemma [Reference AlperAlp10, Theorem 6.10] at x, there exists a Zariski open subscheme
![]() $R \subseteq U_x' /\!\!/ G_x$
such that the induced diagram
$R \subseteq U_x' /\!\!/ G_x$
such that the induced diagram

is Cartesian and
![]() $\Phi _x$
is strongly étale.
$\Phi _x$
is strongly étale.
Since
![]() $U^{\prime }_x /\!\!/ G_x$
is affine, we may take R to be affine as well. It is straightforward to check then that
$U^{\prime }_x /\!\!/ G_x$
is affine, we may take R to be affine as well. It is straightforward to check then that
![]() $(q')^{-1}(R) = [U_x / G_x]$
, where
$(q')^{-1}(R) = [U_x / G_x]$
, where
![]() $U_x$
is a
$U_x$
is a
![]() $G_x$
-invariant Zariski open affine subscheme of
$G_x$
-invariant Zariski open affine subscheme of
![]() $U^{\prime }_x$
, containing x, and also
$U^{\prime }_x$
, containing x, and also
![]() $R = U_x /\!\!/ G_x$
.
$R = U_x /\!\!/ G_x$
.
Setting
![]() $V = V' \setminus (U' \setminus U_x)$
, we have the d-critical chart
$V = V' \setminus (U' \setminus U_x)$
, we have the d-critical chart
![]() $(U_x,V,f|_V,i)$
. This concludes the proof.
$(U_x,V,f|_V,i)$
. This concludes the proof.
We now obtain the following key lemma, which gives a way to compare two choices of d-critical quotient charts.
Lemma 3.7. Let
![]() $\mathcal {M}$
be a stack of DT type. Let
$\mathcal {M}$
be a stack of DT type. Let
be two d-critical quotient charts with
![]() $V_{\alpha } , V_{\beta }$
affine and
$V_{\alpha } , V_{\beta }$
affine and
![]() $z \in [U_{\alpha } / G_{\alpha } ] \times _{\mathcal {M}} [U_{\beta }/G_{\beta }]$
a closed point with stabilizer
$z \in [U_{\alpha } / G_{\alpha } ] \times _{\mathcal {M}} [U_{\beta }/G_{\beta }]$
a closed point with stabilizer
![]() $G := G_z$
. Let
$G := G_z$
. Let
![]() $x_{\alpha } \in [U_{\alpha } /G_{\alpha } ]$
and
$x_{\alpha } \in [U_{\alpha } /G_{\alpha } ]$
and
![]() $x_{\beta } \in [U_{\beta }/G_{\beta }]$
be the two projections of z. Then the following hold:
$x_{\beta } \in [U_{\beta }/G_{\beta }]$
be the two projections of z. Then the following hold:
-
1. We have G-equivariant commutative diagrams for
 $\lambda = \alpha , \beta $
(3.2)
$\lambda = \alpha , \beta $
(3.2)
where the vertical arrows are unramified morphisms, the horizontal arrows are embeddings,
 $t \in T_{\alpha \beta }$
maps to
$t \in T_{\alpha \beta }$
maps to
 $x_{\lambda } \in U_{\lambda }$
and
$x_{\lambda } \in U_{\lambda }$
and
 $T_{\alpha \beta }, S_{\alpha \beta }$
are affine.
$T_{\alpha \beta }, S_{\alpha \beta }$
are affine. -
2. We have an induced diagram with étale arrows:
(3.3)
-
3. There exists a d-critical G-invariant quotient chart
 $(T_{\alpha \beta },S_{\alpha \beta },f_{\alpha \beta },\Phi _{\alpha \beta })$
for
$(T_{\alpha \beta },S_{\alpha \beta },f_{\alpha \beta },\Phi _{\alpha \beta })$
for
 $\mathcal {M}$
with
$\mathcal {M}$
with
 $t \in T_{\alpha \beta }$
fixed by G.
$t \in T_{\alpha \beta }$
fixed by G. -
4.
 $I := (\theta _{\lambda }^* df_{\lambda }) = (df_{\alpha \beta })$
as ideal sheaves in
$I := (\theta _{\lambda }^* df_{\lambda }) = (df_{\alpha \beta })$
as ideal sheaves in
 $\mathcal {O}_{S_{\alpha \beta }}$
and
$\mathcal {O}_{S_{\alpha \beta }}$
and
 $\theta _{\lambda }^* f_{\lambda } + I^2$
,
$\theta _{\lambda }^* f_{\lambda } + I^2$
,
 $f_{\alpha \beta } + I^2$
give the same invariant section
$f_{\alpha \beta } + I^2$
give the same invariant section
 $s|_{T_{\alpha \beta }} \in \Gamma (T_{\alpha \beta }, \mathcal {S}_{T_{\alpha \beta }})^G$
, where
$s|_{T_{\alpha \beta }} \in \Gamma (T_{\alpha \beta }, \mathcal {S}_{T_{\alpha \beta }})^G$
, where
 $\theta _{\lambda }$
are the morphisms defined above in diagram (3.2).
$\theta _{\lambda }$
are the morphisms defined above in diagram (3.2).
Proof. It follows by the second condition in Definition 3.4 that
![]() $\mathcal {M}$
must have affine diagonal. In particular, the Cartesian diagram
$\mathcal {M}$
must have affine diagonal. In particular, the Cartesian diagram

implies that
![]() $U_{\alpha \beta } := U_{\alpha } \times _{\mathcal {M}} U_{\beta }$
is affine.
$U_{\alpha \beta } := U_{\alpha } \times _{\mathcal {M}} U_{\beta }$
is affine.
Let us write
![]() $G_{\alpha \beta } = G_{\alpha } \times G_{\beta }$
. Since
$G_{\alpha \beta } = G_{\alpha } \times G_{\beta }$
. Since
![]() $U_{\alpha \beta }$
and
$U_{\alpha \beta }$
and
![]() $V_{\alpha } \times V_{\beta }$
are affine and the product embedding
$V_{\alpha } \times V_{\beta }$
are affine and the product embedding
![]() $U_{\alpha } \times U_{\beta } \hookrightarrow V_{\alpha } \times V_{\beta }$
is
$U_{\alpha } \times U_{\beta } \hookrightarrow V_{\alpha } \times V_{\beta }$
is
![]() $G_{\alpha \beta }$
-invariant, there exists a smooth affine scheme
$G_{\alpha \beta }$
-invariant, there exists a smooth affine scheme
![]() $V_{\alpha \beta }$
and a
$V_{\alpha \beta }$
and a
![]() $G_{\alpha \beta }$
-equivariant embedding fitting into a commutative diagram
$G_{\alpha \beta }$
-equivariant embedding fitting into a commutative diagram

Concretely, we may choose any
![]() $G_{\alpha \beta }$
-equivariant embedding
$G_{\alpha \beta }$
-equivariant embedding
![]() $U_{\alpha \beta } \hookrightarrow \mathbb {A}^N$
for big enough N and then take
$U_{\alpha \beta } \hookrightarrow \mathbb {A}^N$
for big enough N and then take
![]() $V_{\alpha \beta } = V_{\alpha } \times V_{\beta } \times \mathbb {A}^N$
with the obvious choices of morphisms that make the above diagram commute.
$V_{\alpha \beta } = V_{\alpha } \times V_{\beta } \times \mathbb {A}^N$
with the obvious choices of morphisms that make the above diagram commute.
Let
![]() $t \in U_{\alpha \beta }$
a representative of the point
$t \in U_{\alpha \beta }$
a representative of the point
![]() $z \in [U_{\alpha } / G_{\alpha } ] \times _{\mathcal {M}} [U_{\beta }/G_{\beta }] \simeq [U_{\alpha \beta } / G_{\alpha \beta }]$
(we are liberally abusing notation at this point). Using Luna’s étale slice theorem, take
$z \in [U_{\alpha } / G_{\alpha } ] \times _{\mathcal {M}} [U_{\beta }/G_{\beta }] \simeq [U_{\alpha \beta } / G_{\alpha \beta }]$
(we are liberally abusing notation at this point). Using Luna’s étale slice theorem, take
![]() $S_{\alpha \beta } \subseteq V_{\alpha \beta }$
to be an affine étale slice for t in
$S_{\alpha \beta } \subseteq V_{\alpha \beta }$
to be an affine étale slice for t in
![]() $V_{\alpha \beta }$
and
$V_{\alpha \beta }$
and
![]() $T_{\alpha \beta } := S_{\alpha \beta } \cap U_{\alpha \beta }$
the induced affine étale slice for
$T_{\alpha \beta } := S_{\alpha \beta } \cap U_{\alpha \beta }$
the induced affine étale slice for
![]() $t \in U_{\alpha \beta }$
.
$t \in U_{\alpha \beta }$
.
It is clear that conditions (1) and (2) are now satisfied and remain so even after G-invariant shrinking of
![]() $S_{\alpha \beta }$
around t.
$S_{\alpha \beta }$
around t.
For conditions (3) and (4), notice that by diagrams (3.2) and (3.3) and the properties of d-critical structures,
![]() $[T_{\alpha \beta } /G]$
is a d-critical stack and thus, up to possibly shrinking
$[T_{\alpha \beta } /G]$
is a d-critical stack and thus, up to possibly shrinking
![]() $S_{\alpha \beta } \ G$
-invariantly around t, there exists an induced d-critical G-invariant quotient chart
$S_{\alpha \beta } \ G$
-invariantly around t, there exists an induced d-critical G-invariant quotient chart
![]() $(T_{\alpha \beta }, S_{\alpha \beta }, f_{\alpha \beta }, \Phi _{\alpha \beta })$
for
$(T_{\alpha \beta }, S_{\alpha \beta }, f_{\alpha \beta }, \Phi _{\alpha \beta })$
for
![]() $\mathcal {M}$
centered at
$\mathcal {M}$
centered at
![]() $t \in T_{\alpha \beta }$
. Finally, since by construction
$t \in T_{\alpha \beta }$
. Finally, since by construction
![]() $S_{\alpha \beta }$
,
$S_{\alpha \beta }$
,
![]() $T_{\alpha \beta }$
are étale slices of
$T_{\alpha \beta }$
are étale slices of
![]() $V_{\lambda }, U_{\lambda }$
at t, we obtain that
$V_{\lambda }, U_{\lambda }$
at t, we obtain that
![]() $(df_{\alpha \beta })=(\theta _{\lambda }^* df_{\lambda })$
as ideals and
$(df_{\alpha \beta })=(\theta _{\lambda }^* df_{\lambda })$
as ideals and
![]() $\theta _{\lambda }^* f_{\lambda } + I^2, f_{\alpha \beta } + I^2$
both represent the pullback of the d-critical structure of
$\theta _{\lambda }^* f_{\lambda } + I^2, f_{\alpha \beta } + I^2$
both represent the pullback of the d-critical structure of
![]() $\mathcal {M}$
to
$\mathcal {M}$
to
![]() $[T_{\alpha \beta } / G]$
, which completes the proof.
$[T_{\alpha \beta } / G]$
, which completes the proof.
Remark 3.8. The above results only use the d-critical structure of
![]() $\mathcal {M}$
and not the existence of its
$\mathcal {M}$
and not the existence of its
![]() $(-1)$
-shifted symplectic derived enhancement. In fact, using the property that
$(-1)$
-shifted symplectic derived enhancement. In fact, using the property that
![]() $\mathcal {M}$
is the truncation of a
$\mathcal {M}$
is the truncation of a
![]() $(-1)$
-shifted symplectic derived Artin stack
$(-1)$
-shifted symplectic derived Artin stack
![]() , Proposition 3.6 may be strengthened. Since we won’t need this strengthening in this paper, we are content with just making this remark.
, Proposition 3.6 may be strengthened. Since we won’t need this strengthening in this paper, we are content with just making this remark.
Remark 3.9. We finally make a remark on the conditions in Definition 3.4. The first condition is there to ensure boundedness. The second condition implies the existence of quotient charts as in diagram (3.1), which will be necessary in order to construct the intrinsic stabilizer reduction
![]() $\widetilde {\mathcal {M}}$
and its good moduli space. The third condition is necessary to induce a d-critical structure on
$\widetilde {\mathcal {M}}$
and its good moduli space. The third condition is necessary to induce a d-critical structure on
![]() $\mathcal {M}$
which is the crucial component in obtaining a semiperfect obstruction theory for
$\mathcal {M}$
which is the crucial component in obtaining a semiperfect obstruction theory for
![]() $\widetilde {\mathcal {M}}$
.
$\widetilde {\mathcal {M}}$
.
4 Intrinsic stabilizer reduction
In this section, we review the notions of intrinsic and Kirwan blowups and then generalize the construction of the intrinsic stabilizer reduction of a quotient stack obtained by GIT given in [Reference Kiem, Li and SavvasKLS17] to the more general setting of stacks with good moduli space.
4.1 Kirwan blowups for affine schemes
We recall the notion of Kirwan blowup developed in [Reference Kiem, Li and SavvasKLS17].
Suppose that U is an affine scheme with an action of a reductive group G. For now, let us assume that G is connected, as this will be the case when we take blowups throughout the paper.
Suppose that we have an equivariant closed embedding
![]() $U \to V$
into a smooth affine G-scheme V, and let I be the ideal defining U. Since
$U \to V$
into a smooth affine G-scheme V, and let I be the ideal defining U. Since
![]() $U \subseteq V$
is G-invariant, G acts on I and we have a decomposition
$U \subseteq V$
is G-invariant, G acts on I and we have a decomposition
![]() $I = I^{\mathrm {fix}} \oplus I^{\mathrm {mv}}$
into the fixed part of I and its complement as G-representations.
$I = I^{\mathrm {fix}} \oplus I^{\mathrm {mv}}$
into the fixed part of I and its complement as G-representations.
Let
![]() $V^G$
be the fixed point locus of G inside V, defined by the ideal generated by
$V^G$
be the fixed point locus of G inside V, defined by the ideal generated by
![]() $\mathcal {O}_V^{\mathrm {mv}}$
, and
$\mathcal {O}_V^{\mathrm {mv}}$
, and
![]() $\pi \colon \mathrm {bl}_G(V) \to V$
the blowup of V along
$\pi \colon \mathrm {bl}_G(V) \to V$
the blowup of V along
![]() $V^G$
. Let
$V^G$
. Let
![]() $E\subseteq \mathrm {bl}_G(V)$
be its exceptional divisor and
$E\subseteq \mathrm {bl}_G(V)$
be its exceptional divisor and
![]() $\xi \in \Gamma ( \mathcal {O}_{\mathrm {bl}_G(V)}(E))$
the tautological defining equation of E.
$\xi \in \Gamma ( \mathcal {O}_{\mathrm {bl}_G(V)}(E))$
the tautological defining equation of E.
G-equivariance implies that (cf. [Reference Kiem, Li and SavvasKLS17, Section 2.2])
and consequently,
![]() $\xi ^{-1} \pi ^{-1} (I^{\mathrm {mv}}) \subseteq \mathcal {O}_{\mathrm {bl}_G(V)}$
, meaning that
$\xi ^{-1} \pi ^{-1} (I^{\mathrm {mv}}) \subseteq \mathcal {O}_{\mathrm {bl}_G(V)}$
, meaning that
![]() $\pi ^{-1}(I^{\mathrm {mv}})$
lies in the image of the inclusion
$\pi ^{-1}(I^{\mathrm {mv}})$
lies in the image of the inclusion
![]() $\mathcal {O}_{\mathrm {bl}_G(V)}(-E) \subseteq \mathcal {O}_{\mathrm {bl}_G(V)}$
, given by multiplication by
$\mathcal {O}_{\mathrm {bl}_G(V)}(-E) \subseteq \mathcal {O}_{\mathrm {bl}_G(V)}$
, given by multiplication by
![]() $\xi $
.
$\xi $
.
We define
![]() $I^{\mathrm {intr}}\subseteq \mathcal {O}_{\mathrm {bl}_G(V)}$
to be
$I^{\mathrm {intr}}\subseteq \mathcal {O}_{\mathrm {bl}_G(V)}$
to be
Definition 4.1 (Intrinsic blowup)
The G-intrinsic blowup of U is the subscheme
![]() $U^{\mathrm {intr}}\subseteq \mathrm {bl}_G(V)$
defined by the ideal
$U^{\mathrm {intr}}\subseteq \mathrm {bl}_G(V)$
defined by the ideal
![]() $I^{\mathrm {intr}}$
.
$I^{\mathrm {intr}}$
.
Lemma 4.1 [Reference Kiem, Li and SavvasKLS17, Lemma 2.6]
The G-intrinsic blowup of U is independent of the choice of G-equivariant embedding
![]() $U \subseteq V$
, and hence is canonical.
$U \subseteq V$
, and hence is canonical.
Proof. We give a brief outline of the proof and refer the reader to the proof of [Reference Kiem, Li and SavvasKLS17, Lemma 2.6] and [Reference Kiem and LiKL13, Subsection 3.1] for details.
If
![]() $U^G = \emptyset $
, then
$U^G = \emptyset $
, then
![]() $\widehat U = U$
, and there is nothing to show. So suppose this is not the case and
$\widehat U = U$
, and there is nothing to show. So suppose this is not the case and
![]() $u \in U^G$
.
$u \in U^G$
.
Let
![]() $U \rightarrow V_1,\ U \rightarrow V_2$
be two equivariant embeddings of U into smooth G-schemes. By composing with the equivariant inclusions
$U \rightarrow V_1,\ U \rightarrow V_2$
be two equivariant embeddings of U into smooth G-schemes. By composing with the equivariant inclusions
![]() $V_1 \times \lbrace u \rbrace \subseteq V_1 \times V_2$
and
$V_1 \times \lbrace u \rbrace \subseteq V_1 \times V_2$
and
![]() $\lbrace u \rbrace \times V_2 \subseteq V_1 \times V_2$
, we may reduce to the case of a sequence of equivariant embeddings
$\lbrace u \rbrace \times V_2 \subseteq V_1 \times V_2$
, we may reduce to the case of a sequence of equivariant embeddings
![]() $U \rightarrow V \xrightarrow {\Phi } W$
, where
$U \rightarrow V \xrightarrow {\Phi } W$
, where
![]() $V, W$
are smooth G-schemes.
$V, W$
are smooth G-schemes.
Applying the above construction using the two embeddings of U, we obtain G-intrinsic blowups
![]() $\widehat U^V$
, induced by the embedding
$\widehat U^V$
, induced by the embedding
![]() $U \rightarrow V$
, and
$U \rightarrow V$
, and
![]() $\widehat U^W$
, induced by the composite embedding
$\widehat U^W$
, induced by the composite embedding
![]() $U \rightarrow W$
.
$U \rightarrow W$
.
Then an identical argument as in the proof of [Reference Kiem and LiKL13, Lemma 3.1] shows that
![]() $\Phi $
gives rise to an isomorphism
$\Phi $
gives rise to an isomorphism
![]() $\widehat U^V \simeq \widehat U^W$
, which moreover is independent of the choice of
$\widehat U^V \simeq \widehat U^W$
, which moreover is independent of the choice of
![]() $\Phi $
interpolating between the two embeddings
$\Phi $
interpolating between the two embeddings
![]() $U \rightarrow V$
and
$U \rightarrow V$
and
![]() $U \rightarrow W$
. This proves that
$U \rightarrow W$
. This proves that
![]() $\widehat U$
is indeed canonical.
$\widehat U$
is indeed canonical.
Suppose U is an affine G-scheme with an equivariant embedding into a smooth affine G-scheme V as above. We can make sense of the notion of semistability of points in
![]() $U^{\mathrm {intr}}$
without ambiguity as follows.
$U^{\mathrm {intr}}$
without ambiguity as follows.
We first work on the ambient scheme V. As it is affine, we can think of all points of V as being semistable (in the usual sense of GIT). For the blowup
![]() $V^{\mathrm {intr}} := \mathrm {bl}_G (V)$
, G acts linearly on
$V^{\mathrm {intr}} := \mathrm {bl}_G (V)$
, G acts linearly on
![]() $E=\mathbb {P} N_{V^G/V}$
with respect to the natural G-linearization of
$E=\mathbb {P} N_{V^G/V}$
with respect to the natural G-linearization of
![]() $\mathcal {O}_E(1) := \mathcal {O}_E (-E)$
, and therefore we have a GIT notion of stability of points on the exceptional divisor E.
$\mathcal {O}_E(1) := \mathcal {O}_E (-E)$
, and therefore we have a GIT notion of stability of points on the exceptional divisor E.
Definition 4.2. We say that
![]() $v \in V$
is stable if its G-orbit is closed in V and its stabilizer finite. A point
$v \in V$
is stable if its G-orbit is closed in V and its stabilizer finite. A point
![]() $\widetilde {v} \in \mathrm {bl}_G (V)$
is unstable if either
$\widetilde {v} \in \mathrm {bl}_G (V)$
is unstable if either
![]() $\widetilde {v} \in E$
and
$\widetilde {v} \in E$
and
![]() $\widetilde {v}$
is unstable with respect to the linearization
$\widetilde {v}$
is unstable with respect to the linearization
![]() $\mathcal {O}_E(1)$
or
$\mathcal {O}_E(1)$
or
![]() $\widetilde {v} \notin E$
and its G-orbit closure meets the unstable locus of E. If
$\widetilde {v} \notin E$
and its G-orbit closure meets the unstable locus of E. If
![]() $\widetilde {v}$
is not unstable, we say that it is semistable.
$\widetilde {v}$
is not unstable, we say that it is semistable.
Thus, for any smooth affine G-scheme V, we can define its Kirwan blowup
![]() $\widehat V = \left ( \mathrm {bl}_G (V) \right )^{ss}$
. By [Reference KirwanKir85], it satisfies
$\widehat V = \left ( \mathrm {bl}_G (V) \right )^{ss}$
. By [Reference KirwanKir85], it satisfies
![]() $\widehat V^G = \emptyset $
.
$\widehat V^G = \emptyset $
.
Now, if we have an equivariant embedding
![]() $V \to W$
between smooth G-schemes, then
$V \to W$
between smooth G-schemes, then
![]() $(W^{\mathrm {intr}})^{ss} \cap V^{\mathrm {intr}} = (V^{\mathrm {intr}})^{ss}$
based on our description. Hence, we may define
$(W^{\mathrm {intr}})^{ss} \cap V^{\mathrm {intr}} = (V^{\mathrm {intr}})^{ss}$
based on our description. Hence, we may define
![]() $(U^{\mathrm {intr}})^{ss} := U^{\mathrm {intr}} \cap (V^{\mathrm {intr}})^{ss}$
for any equivariant embedding
$(U^{\mathrm {intr}})^{ss} := U^{\mathrm {intr}} \cap (V^{\mathrm {intr}})^{ss}$
for any equivariant embedding
![]() $U \to V$
into a smooth scheme V, which is independent of the choice of
$U \to V$
into a smooth scheme V, which is independent of the choice of
![]() $U \to V$
.
$U \to V$
.
Definition 4.3 (Kirwan blowup)
Let U be a possibly singular affine G-scheme with nonempty G-fixed locus. The Kirwan blowup of U associated with G is the scheme
![]() $\widehat U=(U^{\mathrm {intr}})^{ss}$
. It satisfies
$\widehat U=(U^{\mathrm {intr}})^{ss}$
. It satisfies
![]() $\widehat U^G = \emptyset $
.
$\widehat U^G = \emptyset $
.
The notion of semistability above is exactly motivated by the corresponding notion in GIT in Kirwan’s original blowup procedure in [Reference KirwanKir85]. This can be seen by the following theorem of Reichstein, which asserts that the locus of unstable points on
![]() $\mathrm {bl}_G(V)$
is exactly the locus of unstable points in the sense of GIT for the ample line bundle
$\mathrm {bl}_G(V)$
is exactly the locus of unstable points in the sense of GIT for the ample line bundle
![]() $\mathcal {O}_{\mathrm {bl}_G(V)}(-E)$
.
$\mathcal {O}_{\mathrm {bl}_G(V)}(-E)$
.
Theorem 4.2 [Reference ReichsteinRei89]
Let V as above, and let
![]() $q \colon V \to V /\!\!/ G$
denote the GIT quotient map. The unstable locus of
$q \colon V \to V /\!\!/ G$
denote the GIT quotient map. The unstable locus of
![]() $\mathrm {bl}_G(V)$
with respect to the line bundle
$\mathrm {bl}_G(V)$
with respect to the line bundle
![]() $\mathcal {O}_{\mathrm {bl}_G(V)}(-E)$
is the strict transform of the saturation
$\mathcal {O}_{\mathrm {bl}_G(V)}(-E)$
is the strict transform of the saturation
![]() $q^{-1}( q(V^G) )$
of
$q^{-1}( q(V^G) )$
of
![]() $V^G$
inside V.
$V^G$
inside V.
We obtain the following corollary.
Corollary 4.3. Let
![]() $\pi \colon \widehat {U} \to U$
be the Kirwan blowup of an affine G-scheme U with nonempty G-fixed locus. Then the quotient stack
$\pi \colon \widehat {U} \to U$
be the Kirwan blowup of an affine G-scheme U with nonempty G-fixed locus. Then the quotient stack
![]() $[\widehat {U}/G]$
admits a good moduli space, denoted by
$[\widehat {U}/G]$
admits a good moduli space, denoted by
![]() $q \colon [\widehat {U} / G] \to \widehat {U} /\!\!/ G$
.
$q \colon [\widehat {U} / G] \to \widehat {U} /\!\!/ G$
.
Proof. Let
![]() $U \to V$
be a G-equivariant embedding into a smooth affine G-scheme V. By Theorem 4.2,
$U \to V$
be a G-equivariant embedding into a smooth affine G-scheme V. By Theorem 4.2,
![]() $[\widehat V / G]$
admits a good moduli space
$[\widehat V / G]$
admits a good moduli space
![]() $\widehat V /\!\!/ G$
, and therefore the same is true for the closed substack
$\widehat V /\!\!/ G$
, and therefore the same is true for the closed substack
![]() $[\widehat U / G]$
by Proposition 3.2(6).
$[\widehat U / G]$
by Proposition 3.2(6).
Example 4.1. Suppose that
![]() $G = \mathbb {C}^{\ast }$
is the one-dimensional torus acting on the affine plane
$G = \mathbb {C}^{\ast }$
is the one-dimensional torus acting on the affine plane
![]() $V = \mathbb {C}^2_{x,y}$
with weights
$V = \mathbb {C}^2_{x,y}$
with weights
![]() $1$
and
$1$
and
![]() $-1$
on the coordinates x and y respectively and
$-1$
on the coordinates x and y respectively and
![]() $U \subseteq V$
is the closed G-invariant subscheme cut out by the ideal
$U \subseteq V$
is the closed G-invariant subscheme cut out by the ideal
![]() $I = (x^2 y, x y^2)$
.
$I = (x^2 y, x y^2)$
.
![]() $V^{\mathrm {intr}}$
is the blowup of V along the fixed locus
$V^{\mathrm {intr}}$
is the blowup of V along the fixed locus
![]() $V^G = \lbrace 0 \rbrace $
. The unstable points are the punctured x-axis and y-axis together with the points
$V^G = \lbrace 0 \rbrace $
. The unstable points are the punctured x-axis and y-axis together with the points
![]() $0, \infty $
of the exceptional divisor
$0, \infty $
of the exceptional divisor
![]() $\mathbb {P}^1$
. Thus, we have that
$\mathbb {P}^1$
. Thus, we have that
![]() $\widehat V = \mathop{\mathrm {Spec}}\nolimits [u ,v, v^{-1} ]$
, where G acts on
$\widehat V = \mathop{\mathrm {Spec}}\nolimits [u ,v, v^{-1} ]$
, where G acts on
![]() $u, v$
with weights
$u, v$
with weights
![]() $1, -2$
respectively and the blowdown map
$1, -2$
respectively and the blowdown map
![]() $\widehat V \to V$
is given on coordinates by
$\widehat V \to V$
is given on coordinates by
![]() $x \mapsto u, y \mapsto uv$
.
$x \mapsto u, y \mapsto uv$
.
![]() $\widehat U \subseteq \widehat V$
is the closed subscheme cut out by the ideal
$\widehat U \subseteq \widehat V$
is the closed subscheme cut out by the ideal
![]() $(u^2)$
so that
$(u^2)$
so that
We now explain how one can proceed if G is not connected.
Suppose that
![]() $U \to V$
is a G-equivariant embedding into a smooth G-scheme V. Let, as before, I be the ideal of U in V. Let
$U \to V$
is a G-equivariant embedding into a smooth G-scheme V. Let, as before, I be the ideal of U in V. Let
![]() $G_0$
be the connected component of the identity. This is a normal, connected subgroup of G of finite index. Let
$G_0$
be the connected component of the identity. This is a normal, connected subgroup of G of finite index. Let
![]() $I = I^{\mathrm {fix}} \oplus I^{\mathrm {mv}}$
be the decomposition of I into fixed and moving parts with respect to the action of
$I = I^{\mathrm {fix}} \oplus I^{\mathrm {mv}}$
be the decomposition of I into fixed and moving parts with respect to the action of
![]() $G_0$
. Using the normality of
$G_0$
. Using the normality of
![]() $G_0$
, we see that the fixed locus
$G_0$
, we see that the fixed locus
![]() $V^{G_0}$
is a closed, smooth G-invariant subscheme of V and also
$V^{G_0}$
is a closed, smooth G-invariant subscheme of V and also
![]() $I^{\mathrm {fix}},\ I^{\mathrm {mv}}$
are G-invariant.
$I^{\mathrm {fix}},\ I^{\mathrm {mv}}$
are G-invariant.
Let
![]() $\pi \colon \mathrm {bl}_{V^{G_0}} V \to V$
be the blowup of V along
$\pi \colon \mathrm {bl}_{V^{G_0}} V \to V$
be the blowup of V along
![]() $V^{G_0}$
with exceptional divisor E and local defining equation
$V^{G_0}$
with exceptional divisor E and local defining equation
![]() $\xi $
. Then, as before, take
$\xi $
. Then, as before, take
![]() $I^{\mathrm {intr}}$
to be the ideal generated by
$I^{\mathrm {intr}}$
to be the ideal generated by
![]() $\pi ^{-1}(I^{\mathrm {fix}})$
and
$\pi ^{-1}(I^{\mathrm {fix}})$
and
![]() $\xi ^{-1}\pi ^{-1}(I^{\mathrm {mv}})$
. Everything is G-equivariant and we define
$\xi ^{-1}\pi ^{-1}(I^{\mathrm {mv}})$
. Everything is G-equivariant and we define
![]() $U^{\mathrm {intr}}$
as the subscheme of
$U^{\mathrm {intr}}$
as the subscheme of
![]() $\mathrm {bl}_{V^{G_0}} V$
defined by the ideal
$\mathrm {bl}_{V^{G_0}} V$
defined by the ideal
![]() $I^{\mathrm {intr}}$
.
$I^{\mathrm {intr}}$
.
Finally, we need to delete unstable points. By the Hilbert–Mumford criterion (cf. [Reference Mumford, Fogarty and KirwanMFK94, Theorem 2.1]) it follows that semistability on E with respect to the action of G is the same as semistability with respect to the action of
![]() $G_0$
since every
$G_0$
since every
![]() $1$
-parameter subgroup of G factors through
$1$
-parameter subgroup of G factors through
![]() $G_0$
, and hence we may delete unstable points exactly as before and define the Kirwan blowup
$G_0$
, and hence we may delete unstable points exactly as before and define the Kirwan blowup
![]() $\widehat U$
.
$\widehat U$
.
One may check in a straightforwardly analogous way that this has the same properties (and intrinsic nature). It is obvious that if G is connected we recover Definition 4.3.
4.2 Kirwan blowups for GIT schemes
So far, we have defined Kirwan blowups for affine G-schemes (with nonempty fixed locus of the G-action). We now generalize the construction to any G-scheme with a G-action coming from GIT (see Definition 4.4 below) and the associated quotient stack, as performed in [Reference Kiem, Li and SavvasKLS17, Subsection 2.4].
We begin with an affine G-scheme whose G-fixed locus can now be possibly empty. Let
![]() $\mathcal {M} = [X / G]$
be a quotient Artin stack, where X is an affine G-scheme.
$\mathcal {M} = [X / G]$
be a quotient Artin stack, where X is an affine G-scheme.
Fix a G-equivariant closed embedding
![]() $X \to Y$
, where Y is a smooth affine G-scheme, and write
$X \to Y$
, where Y is a smooth affine G-scheme, and write
![]() $\mathcal {Y} = [ Y / G]$
. Let d be the maximum dimension of the stabilizers of closed points
$\mathcal {Y} = [ Y / G]$
. Let d be the maximum dimension of the stabilizers of closed points
![]() $x \in X$
. By possibly equivariantly shrinking Y, we may assume that the maximum dimension of stabilizers of closed points of Y is also equal to d.
$x \in X$
. By possibly equivariantly shrinking Y, we may assume that the maximum dimension of stabilizers of closed points of Y is also equal to d.
Kirwan’s partial desingularization, combined with Theorem 4.2, yields a smooth G-scheme
![]() $\widehat {Y}$
by blowing up the locus
$\widehat {Y}$
by blowing up the locus
![]() $Y_d \subseteq Y$
consisting of points satisfying
$Y_d \subseteq Y$
consisting of points satisfying
![]() $\dim G_y = d$
and deleting unstable points.
$\dim G_y = d$
and deleting unstable points.
![]() $\widehat {Y}$
satisfies the crucial property that its maximum stabilizer dimension is strictly less than d.
$\widehat {Y}$
satisfies the crucial property that its maximum stabilizer dimension is strictly less than d.
Now, for any point
![]() $x \in X$
with closed G-orbit and
$x \in X$
with closed G-orbit and
![]() $\dim G_x = d$
, let
$\dim G_x = d$
, let
![]() $S_x \subseteq Y$
be an étale slice for the G-orbit of x in Y. The Kirwan blowups
$S_x \subseteq Y$
be an étale slice for the G-orbit of x in Y. The Kirwan blowups
![]() $\widehat {S}_x$
(cf. Definition 4.3) of the slices
$\widehat {S}_x$
(cf. Definition 4.3) of the slices
![]() $S_x$
associated with
$S_x$
associated with
![]() $G_x$
provide natural strongly étale morphisms
$G_x$
provide natural strongly étale morphisms
![]() $\Psi _x \colon \widehat {S}_x \times _{G_x} G \to \widehat {Y}$
. The joint morphism
$\Psi _x \colon \widehat {S}_x \times _{G_x} G \to \widehat {Y}$
. The joint morphism
is an étale cover of an open neighbourhood
![]() $\widehat {Y}'$
of the restriction
$\widehat {Y}'$
of the restriction
![]() $E \times _{Y_d} X_d$
of the exceptional divisor E of
$E \times _{Y_d} X_d$
of the exceptional divisor E of
![]() $\widehat {Y}$
over the locus
$\widehat {Y}$
over the locus
![]() $X_d \subseteq Y_d$
.
$X_d \subseteq Y_d$
.
Let
![]() $T_x = X \cap S_x$
. Then
$T_x = X \cap S_x$
. Then
![]() $T_x$
is an étale slice for the G-orbit of x in X, and we have the Kirwan blowup
$T_x$
is an étale slice for the G-orbit of x in X, and we have the Kirwan blowup
![]() $\widehat {T}_x$
using the closed
$\widehat {T}_x$
using the closed
![]() $G_x$
-equivariant embedding
$G_x$
-equivariant embedding
![]() $T_x \subseteq S_x$
. In [Reference Kiem, Li and SavvasKLS17, Proposition 2.12], it is shown that the closed embedding
$T_x \subseteq S_x$
. In [Reference Kiem, Li and SavvasKLS17, Proposition 2.12], it is shown that the closed embedding
satisfies étale descent with respect to the morphism
![]() $\Psi $
and thus defines a closed subscheme
$\Psi $
and thus defines a closed subscheme
![]() $\widehat {X}' \subseteq \widehat {Y}'$
.
$\widehat {X}' \subseteq \widehat {Y}'$
.
![]() $\widehat {X}'$
glues naturally with the preimage of
$\widehat {X}'$
glues naturally with the preimage of
![]() $X - X_d$
in
$X - X_d$
in
![]() $\widehat {Y}$
under the blowup morphism
$\widehat {Y}$
under the blowup morphism
![]() $\widehat {Y} \to Y$
, defining a closed G-equivariant subscheme
$\widehat {Y} \to Y$
, defining a closed G-equivariant subscheme
![]() $\widehat {X}$
inside
$\widehat {X}$
inside
![]() $\widehat {Y}$
.
$\widehat {Y}$
.
Lemma 4.1 and the above discussion on stability imply that these are canonical and independent of any choices made regarding the embedding
![]() $X \to Y$
and étale slices
$X \to Y$
and étale slices
![]() $S_x$
.
$S_x$
.
If X is not affine, but is the GIT semistable locus of a G-scheme with a G-linearized ample line bundle, then it admits a cover by G-invariant Zariski open, saturated, affine subschemes
![]() $U_1, \ldots , U_n \subseteq X$
. Here, as in Definition 3.2, saturated means that the
$U_1, \ldots , U_n \subseteq X$
. Here, as in Definition 3.2, saturated means that the
![]() $U_i$
fit in Cartesian squares
$U_i$
fit in Cartesian squares

We may thus apply the Kirwan blowup to each
![]() $U_i$
. The Kirwan blowups
$U_i$
. The Kirwan blowups
![]() $\widehat {U}_i$
glue to the Kirwan blowup
$\widehat {U}_i$
glue to the Kirwan blowup
![]() $\widehat {X}$
of X, and we are led to the following definition.
$\widehat {X}$
of X, and we are led to the following definition.
Definition 4.4. Suppose that
![]() $[X/G]$
is a GIT quotient stack. Then we call
$[X/G]$
is a GIT quotient stack. Then we call
![]() $\widehat {X}$
and
$\widehat {X}$
and
![]() ${\widehat {\mathcal {M}} = [\widehat {X} / G]}$
the Kirwan blowups of X and
${\widehat {\mathcal {M}} = [\widehat {X} / G]}$
the Kirwan blowups of X and
![]() $\mathcal {M} = [X / G]$
, respectively.
$\mathcal {M} = [X / G]$
, respectively.
Remark 4.4. When X is not affine, we could also argue globally as in the affine case using an equivariant closed embedding
![]() $X \to Y$
into a smooth G-scheme Y, afforded by GIT. However, the more local argument using a cover by saturated, affine, G-invariant open subschemes is closer in spirit to the proof of Theorem-Construction 4.9.
$X \to Y$
into a smooth G-scheme Y, afforded by GIT. However, the more local argument using a cover by saturated, affine, G-invariant open subschemes is closer in spirit to the proof of Theorem-Construction 4.9.
4.3 Intrinsic stabilizer reduction for GIT quotient stacks
We quickly recall how the construction of the intrinsic stabilizer reduction works for GIT quotient stacks and some useful properties in that setting.
Let X be a G-scheme coming from GIT and
![]() $\mathcal {M} = [ X / G]$
the associated quotient stack.
$\mathcal {M} = [ X / G]$
the associated quotient stack.
Write
![]() $\mathcal {M}_0 = \mathcal {M}$
and
$\mathcal {M}_0 = \mathcal {M}$
and
![]() $X_0 = X$
. Taking Kirwan blowups, we obtain
$X_0 = X$
. Taking Kirwan blowups, we obtain
![]() $X_1 = \widehat {X}$
and
$X_1 = \widehat {X}$
and
![]() ${\mathcal {M}_1 = [\widehat {X} / G]}$
. The G-action on
${\mathcal {M}_1 = [\widehat {X} / G]}$
. The G-action on
![]() $\widehat {X}$
is still G-linearized, so
$\widehat {X}$
is still G-linearized, so
![]() $\mathcal {M}_1$
is a GIT quotient stack of lower maximum stabilizer dimension compared to
$\mathcal {M}_1$
is a GIT quotient stack of lower maximum stabilizer dimension compared to
![]() $\mathcal {M}_0$
. Thus, we may iterate the procedure to produce a canonical sequence of GIT quotient stacks
$\mathcal {M}_0$
. Thus, we may iterate the procedure to produce a canonical sequence of GIT quotient stacks
where
![]() $\mathcal {M}_{\ell }$
is a Deligne–Mumford stack since at each step the maximum stabilizer dimension strictly decreases.
$\mathcal {M}_{\ell }$
is a Deligne–Mumford stack since at each step the maximum stabilizer dimension strictly decreases.
Definition 4.5.
![]() $\widetilde {\mathcal {M}} := \mathcal {M}_{\ell }$
is called the intrinsic stabilizer reduction of
$\widetilde {\mathcal {M}} := \mathcal {M}_{\ell }$
is called the intrinsic stabilizer reduction of
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
4.4 Intrinsic stabilizer reduction for stacks with good moduli spaces
We now generalize the procedure of intrinsic stabilizer reduction to the case of stacks with good moduli spaces.
The following properties of Kirwan blowups will be useful, so we record them separately in a proposition before our main construction.
Proposition 4.5. Let
![]() $\varphi \colon G_1 \to G_2$
be a surjective homomorphism between reductive groups, and
$\varphi \colon G_1 \to G_2$
be a surjective homomorphism between reductive groups, and
![]() $X_i$
,
$X_i$
,
![]() $i=1,2$
, be affine
$i=1,2$
, be affine
![]() $G_i$
-schemes.
$G_i$
-schemes.
Suppose that
![]() $f \colon X_1 \to X_2$
is a smooth morphism which is equivariant with respect to
$f \colon X_1 \to X_2$
is a smooth morphism which is equivariant with respect to
![]() $\varphi $
and such that the induced morphism
$\varphi $
and such that the induced morphism
![]() $\underline {f} \colon [X_1 / G_1 ] \to [X_2 / G_2]$
on quotient stacks is strongly étale (cf. Definition 3.3).
$\underline {f} \colon [X_1 / G_1 ] \to [X_2 / G_2]$
on quotient stacks is strongly étale (cf. Definition 3.3).
Then there is a canonically induced smooth, affine morphism
![]() $\widehat {f} \colon \widehat {X}_1 \to \widehat {X}_2$
, equivariant with respect to
$\widehat {f} \colon \widehat {X}_1 \to \widehat {X}_2$
, equivariant with respect to
![]() $\varphi $
such that the associated quotient morphism
$\varphi $
such that the associated quotient morphism
![]() $\underline {\widehat {f}} \colon [\widehat {X}_1 / G_1] \to [\widehat {X}_2 / G_2]$
is strongly étale and fits in a Cartesian square
$\underline {\widehat {f}} \colon [\widehat {X}_1 / G_1] \to [\widehat {X}_2 / G_2]$
is strongly étale and fits in a Cartesian square

Proof. Let
![]() $x_1 \in X_1$
a point with closed
$x_1 \in X_1$
a point with closed
![]() $G_1$
-orbit and of maximum stabilizer dimension and
$G_1$
-orbit and of maximum stabilizer dimension and
![]() $x_2 = f(x_1) \in X_2$
. Since
$x_2 = f(x_1) \in X_2$
. Since
![]() $\underline {f}$
is strongly étale, the
$\underline {f}$
is strongly étale, the
![]() $G_2$
-orbit of
$G_2$
-orbit of
![]() $x_2$
is also closed, by Proposition 3.2(5), and
$x_2$
is also closed, by Proposition 3.2(5), and
![]() $x_2$
is of maximum stabilizer dimension.
$x_2$
is of maximum stabilizer dimension.
Up to
![]() $G_1$
-equivariant shrinking around
$G_1$
-equivariant shrinking around
![]() $x_1$
, we can find smooth, affine
$x_1$
, we can find smooth, affine
![]() $G_i$
-schemes
$G_i$
-schemes
![]() $Y_i$
,
$Y_i$
,
![]() $i=1,2$
and a smooth morphism
$i=1,2$
and a smooth morphism
![]() $g \colon Y_1 \to Y_2$
, equivariant with respect to
$g \colon Y_1 \to Y_2$
, equivariant with respect to
![]() $\varphi $
, fitting in a commutative diagram
$\varphi $
, fitting in a commutative diagram

where the horizontal arrows are equivariant closed embeddings. We may additionally assume that the induced morphism
![]() $\underline {g} \colon [Y_1 / G_1] \to [Y_2 / G_2]$
is strongly étale. This is because we can initially take g to map
$\underline {g} \colon [Y_1 / G_1] \to [Y_2 / G_2]$
is strongly étale. This is because we can initially take g to map
![]() $x_1$
to
$x_1$
to
![]() $x_2$
, be stabilizer-preserving at
$x_2$
, be stabilizer-preserving at
![]() $x_1$
and
$x_1$
and
![]() $\underline {g}$
to be étale at
$\underline {g}$
to be étale at
![]() $x_1$
, so using the fundamental lemma [Reference AlperAlp10, Theorem 6.10] at
$x_1$
, so using the fundamental lemma [Reference AlperAlp10, Theorem 6.10] at
![]() $x_1$
, after possible further shrinking around
$x_1$
, after possible further shrinking around
![]() $x_1$
, we may take
$x_1$
, we may take
![]() $\underline {g}$
to be strongly étale.
$\underline {g}$
to be strongly étale.
By the intrinsic nature of intrinsic blowups, using an identical argument as the one outlined in the proof of Lemma 4.1, one may consider diagram (4.2) as
![]() $x_1$
varies to obtain a canonical morphism
$x_1$
varies to obtain a canonical morphism
![]() $f^{\mathrm {intr}} \colon X_1^{\mathrm {intr}} \to X_2^{\mathrm {intr}}$
.
$f^{\mathrm {intr}} \colon X_1^{\mathrm {intr}} \to X_2^{\mathrm {intr}}$
.
By construction,
![]() $f^{\mathrm {intr}}$
is stabilizer-preserving and maps closed
$f^{\mathrm {intr}}$
is stabilizer-preserving and maps closed
![]() $G_1$
-orbits to closed
$G_1$
-orbits to closed
![]() $G_2$
-orbits, as this is the case for
$G_2$
-orbits, as this is the case for
![]() $g^{\mathrm {intr}}$
. It is moreover smooth and the associated quotient morphism
$g^{\mathrm {intr}}$
. It is moreover smooth and the associated quotient morphism
![]() $\underline {f}^{\mathrm {intr}} \colon [X_1^{\mathrm {intr}} / G_1] \to [X_2^{\mathrm {intr}} / G_2]$
is étale. This can be seen as follows: Let T be an affine, étale slice for the
$\underline {f}^{\mathrm {intr}} \colon [X_1^{\mathrm {intr}} / G_1] \to [X_2^{\mathrm {intr}} / G_2]$
is étale. This can be seen as follows: Let T be an affine, étale slice for the
![]() $G_1$
-orbit of
$G_1$
-orbit of
![]() $x_1$
in
$x_1$
in
![]() $X_1$
, whose stabilizer we denote by H. By the assumptions on the morphism f, we have a commutative diagram
$X_1$
, whose stabilizer we denote by H. By the assumptions on the morphism f, we have a commutative diagram

and the corresponding commutative diagram at the level of quotient stacks

has all étale arrows.
By definition, these give rise to identical diagrams with
![]() $T, X_1, X_2$
replaced by their intrinsic blowups. Varying
$T, X_1, X_2$
replaced by their intrinsic blowups. Varying
![]() $x_1$
, this immediately implies the smoothness and affineness of
$x_1$
, this immediately implies the smoothness and affineness of
![]() ${f^{\mathrm {intr}}}$
and étaleness of
${f^{\mathrm {intr}}}$
and étaleness of
![]() $\underline {f}^{\mathrm {intr}}$
. Moreover, a similar, straightforward local computation, using the definition of intrinsic blowup and the arguments of the proof of Lemma 4.1 and [Reference Kiem and LiKL13, Lemma 3.1], shows that the natural map
$\underline {f}^{\mathrm {intr}}$
. Moreover, a similar, straightforward local computation, using the definition of intrinsic blowup and the arguments of the proof of Lemma 4.1 and [Reference Kiem and LiKL13, Lemma 3.1], shows that the natural map
![]() $X_1^{\mathrm {intr}} \to X_1 \times _{X_2} X_2^{\mathrm {intr}}$
is an isomorphism.
$X_1^{\mathrm {intr}} \to X_1 \times _{X_2} X_2^{\mathrm {intr}}$
is an isomorphism.
Now, Corollary 4.3 lets us pass from intrinsic blowups to Kirwan blowups.
Finally, since
![]() $\underline {\widehat {f}}$
is étale, stabilizer-preserving and maps closed points to closed points, applying the fundamental lemma [Reference AlperAlp10, Theorem 6.10] at all closed points of
$\underline {\widehat {f}}$
is étale, stabilizer-preserving and maps closed points to closed points, applying the fundamental lemma [Reference AlperAlp10, Theorem 6.10] at all closed points of
![]() $[\widehat {X}_1/G_1]$
, we obtain that it is strongly étale. The existence of the isomorphism
$[\widehat {X}_1/G_1]$
, we obtain that it is strongly étale. The existence of the isomorphism
![]() $[\widehat {X}_1 / G_1] \to [X_1 / G_1] \times _{[X_2 / G_2]} [\widehat {X}_2 / G_2]$
is a direct consequence of the isomorphism
$[\widehat {X}_1 / G_1] \to [X_1 / G_1] \times _{[X_2 / G_2]} [\widehat {X}_2 / G_2]$
is a direct consequence of the isomorphism
![]() $X_1^{\mathrm {intr}} \to X_1 \times _{X_2} X_2^{\mathrm {intr}}$
and the definition of stability (Definition 4.2). This concludes the proof.
$X_1^{\mathrm {intr}} \to X_1 \times _{X_2} X_2^{\mathrm {intr}}$
and the definition of stability (Definition 4.2). This concludes the proof.
Before extending the notion of Kirwan blowup to stacks with good moduli space, it will be useful to generalize our definition of stability to this setting (cf. Definition 4.2).
Definition 4.6. Let
![]() $\mathcal {M}$
be an Artin stack of finite type and
$\mathcal {M}$
be an Artin stack of finite type and
![]() $q \colon \mathcal {M} \to M$
a good moduli space morphism of finite type with affine diagonal. The prestable locus
$q \colon \mathcal {M} \to M$
a good moduli space morphism of finite type with affine diagonal. The prestable locus
![]() $\mathcal {M}^{ps} \subseteq \mathcal {M}$
of
$\mathcal {M}^{ps} \subseteq \mathcal {M}$
of
![]() $\mathcal {M}$
is the (saturated) open substack whose closed points are the closed points
$\mathcal {M}$
is the (saturated) open substack whose closed points are the closed points
![]() $x \in \mathcal {M}$
satisfying
$x \in \mathcal {M}$
satisfying
![]() $ |q^{-1}(q(x))| = \lbrace x \rbrace $
. The stable locus
$ |q^{-1}(q(x))| = \lbrace x \rbrace $
. The stable locus
![]() $\mathcal {M}^s \subseteq \mathcal {M}$
is the saturated, open substack consisting of prestable points with finite stabilizer group.
$\mathcal {M}^s \subseteq \mathcal {M}$
is the saturated, open substack consisting of prestable points with finite stabilizer group.
This agrees with Definition 4.2 by the following proposition, which also explains why the stable locus is open and saturated since this is a property that can be checked strongly étale locally.
Proposition 4.6. With the same notation as above, for any strongly étale morphism
![]() $[U/G] \xrightarrow {\Phi } \mathcal {M}$
, we have that
$[U/G] \xrightarrow {\Phi } \mathcal {M}$
, we have that
![]() $\Phi ^{-1} (\mathcal {M}^s) = [U^s / G]$
, where
$\Phi ^{-1} (\mathcal {M}^s) = [U^s / G]$
, where
![]() $U^s$
is the open subscheme of
$U^s$
is the open subscheme of
![]() $u \in U$
with closed G-orbit and finite stabilizer.
$u \in U$
with closed G-orbit and finite stabilizer.
Proof. Any strongly étale morphism

induces an isomorphism of fibers
![]() $q_U^{-1}(q_U(u)) \simeq q^{-1}(q(x))$
whenever
$q_U^{-1}(q_U(u)) \simeq q^{-1}(q(x))$
whenever
![]() $\Phi (u) = x$
and we identify
$\Phi (u) = x$
and we identify
![]() $u \in U$
with its G-orbit as a point
$u \in U$
with its G-orbit as a point
![]() $u \in [U/G]$
. The conclusion is immediate by Proposition 3.2(5) and the fact that
$u \in [U/G]$
. The conclusion is immediate by Proposition 3.2(5) and the fact that
![]() $\Phi $
is stabilizer-preserving.
$\Phi $
is stabilizer-preserving.
We can now construct the Kirwan blowup of an Artin stack with good moduli space.
Theorem-Construction 4.7. Let
![]() $\mathcal {M}$
be an Artin stack of finite type over
$\mathcal {M}$
be an Artin stack of finite type over
![]() $\mathbb {C}$
with affine diagonal, which is not Deligne–Mumford. Moreover, suppose that
$\mathbb {C}$
with affine diagonal, which is not Deligne–Mumford. Moreover, suppose that
![]() $q \colon \mathcal {M} \to M$
is a good moduli space morphism with q of finite type and with affine diagonal.
$q \colon \mathcal {M} \to M$
is a good moduli space morphism with q of finite type and with affine diagonal.
Then there exists a canonical Artin stack
![]() $\widehat {\mathcal {M}}$
, called the Kirwan blowup of
$\widehat {\mathcal {M}}$
, called the Kirwan blowup of
![]() $\mathcal {M}$
, together with a morphism
$\mathcal {M}$
, together with a morphism
![]() $\pi \colon \widehat {\mathcal {M}} \to \mathcal {M}$
, such that:
$\pi \colon \widehat {\mathcal {M}} \to \mathcal {M}$
, such that:
-
1.
 $\widehat {\mathcal {M}}$
is of finite type over
$\widehat {\mathcal {M}}$
is of finite type over
 $\mathbb {C}$
, has affine diagonal and admits a good moduli space morphism
$\mathbb {C}$
, has affine diagonal and admits a good moduli space morphism
 $\widehat {q} \colon \widehat {\mathcal {M}} \to \widehat {M}$
with affine diagonal.
$\widehat {q} \colon \widehat {\mathcal {M}} \to \widehat {M}$
with affine diagonal. -
2. The maximum stabilizer dimension of closed points in
 $\widehat {\mathcal {M}}$
is strictly smaller than that of
$\widehat {\mathcal {M}}$
is strictly smaller than that of
 $\mathcal {M}$
.
$\mathcal {M}$
. -
3. For any strongly étale morphism
 $[U/G] \to \mathcal {M}$
, the base change
$[U/G] \to \mathcal {M}$
, the base change
 $\widehat {\mathcal {M}} \times _{\mathcal {M}} [U/G]$
is naturally isomorphic to the Kirwan blowup
$\widehat {\mathcal {M}} \times _{\mathcal {M}} [U/G]$
is naturally isomorphic to the Kirwan blowup
 $[\widehat U / G]$
.
$[\widehat U / G]$
. -
4.
 $\pi |_{\pi ^{-1}(\mathcal {M}^s)}$
is an isomorphism.
$\pi |_{\pi ^{-1}(\mathcal {M}^s)}$
is an isomorphism.
As is the case with Kirwan blowups of schemes,
![]() $\widehat {\mathcal {M}}$
is a semistable locus
$\widehat {\mathcal {M}}$
is a semistable locus
![]() $\widehat {\mathcal {M}} = (\mathcal {M}^{\mathrm {intr}})^{ss}$
, an open substack of a canonical Artin stack
$\widehat {\mathcal {M}} = (\mathcal {M}^{\mathrm {intr}})^{ss}$
, an open substack of a canonical Artin stack
![]() $\pi ^{\mathrm {intr}} \colon \mathcal {M}^{\mathrm {intr}} \to \mathcal {M}$
, called the intrinsic blowup of
$\pi ^{\mathrm {intr}} \colon \mathcal {M}^{\mathrm {intr}} \to \mathcal {M}$
, called the intrinsic blowup of
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Proof. Let
![]() $\mathcal {M}^{max}$
be the substack of
$\mathcal {M}^{max}$
be the substack of
![]() $\mathcal {M}$
whose points have stabilizers of the maximum possible dimension. This is a closed substack of
$\mathcal {M}$
whose points have stabilizers of the maximum possible dimension. This is a closed substack of
![]() $\mathcal {M}$
with good moduli space
$\mathcal {M}$
with good moduli space
![]() $M^{max}$
(cf. [Reference Edidin and RydhER21, Appendix B] for details on the algebraic structure of
$M^{max}$
(cf. [Reference Edidin and RydhER21, Appendix B] for details on the algebraic structure of
![]() $\mathcal {M}^{max}$
). For any closed point
$\mathcal {M}^{max}$
). For any closed point
![]() $x \in \mathcal {M}^{max}$
, applying Theorem-Definition 3.4, we have a Cartesian diagram
$x \in \mathcal {M}^{max}$
, applying Theorem-Definition 3.4, we have a Cartesian diagram

The morphisms
![]() $\Phi _x$
are affine, strongly étale and cover the locus
$\Phi _x$
are affine, strongly étale and cover the locus
![]() $\mathcal {M}^{max}$
. We may take the Kirwan blowup of each quotient stack
$\mathcal {M}^{max}$
. We may take the Kirwan blowup of each quotient stack
![]() $[U_x / G_x]$
to obtain good moduli space morphisms
$[U_x / G_x]$
to obtain good moduli space morphisms
![]() $[\widehat U_x / G_x] \to \widehat U_x /\!\!/ G_x$
.
$[\widehat U_x / G_x] \to \widehat U_x /\!\!/ G_x$
.
We need to check that these glue to give a stack
![]() $\widehat {\mathcal {M}}$
with a universally closed projection
$\widehat {\mathcal {M}}$
with a universally closed projection
![]() $\widehat {\mathcal {M}} \to \mathcal {M}$
and a good moduli space
$\widehat {\mathcal {M}} \to \mathcal {M}$
and a good moduli space
![]() $\widehat {\mathcal {M}} \to \widehat {M}$
satisfying the same conditions as
$\widehat {\mathcal {M}} \to \widehat {M}$
satisfying the same conditions as
![]() $\mathcal {M}$
and its good moduli space morphism. By the properties of the Kirwan blowup, the maximum stabilizer dimension of
$\mathcal {M}$
and its good moduli space morphism. By the properties of the Kirwan blowup, the maximum stabilizer dimension of
![]() $\widehat {\mathcal {M}}$
will be lower than that of
$\widehat {\mathcal {M}}$
will be lower than that of
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Suppose
![]() $x, y$
are two closed points of
$x, y$
are two closed points of
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $G_x, G_y$
are of maximum dimension. We obtain a Cartesian diagram of stacks
$G_x, G_y$
are of maximum dimension. We obtain a Cartesian diagram of stacks

where
![]() $U_{xy} := U_x \times _{\mathcal {M}} U_y$
is an affine scheme. This is due to the Cartesian diagram
$U_{xy} := U_x \times _{\mathcal {M}} U_y$
is an affine scheme. This is due to the Cartesian diagram

and the fact that
![]() $\mathcal {M}$
has affine diagonal.
$\mathcal {M}$
has affine diagonal.
Using Proposition 4.5, we obtain a diagram

with affine, strongly étale arrows and we have, moreover, canonical associated isomorphisms
![]() $[\widehat {U}_{xy} / (G_x \times G_y)] \to [\widehat U_x / G_x] \times _{\mathcal {M}} [U_y / G_y]$
and
$[\widehat {U}_{xy} / (G_x \times G_y)] \to [\widehat U_x / G_x] \times _{\mathcal {M}} [U_y / G_y]$
and
![]() $[\widehat {U}_{xy} / (G_x \times G_y)] \to [U_x / G_x] \times _{\mathcal {M}} [\widehat U_y / G_y]$
.
$[\widehat {U}_{xy} / (G_x \times G_y)] \to [U_x / G_x] \times _{\mathcal {M}} [\widehat U_y / G_y]$
.
Using the charts
![]() $[\widehat U_x / G_x]$
together with a cover of
$[\widehat U_x / G_x]$
together with a cover of
![]() $\mathcal {M} \setminus q^{-1}(M^{max})$
, we therefore obtain an atlas for a stack
$\mathcal {M} \setminus q^{-1}(M^{max})$
, we therefore obtain an atlas for a stack
![]() $\widehat {\mathcal {M}}$
with a map to
$\widehat {\mathcal {M}}$
with a map to
![]() $\mathcal {M}$
. By the canonical isomorphisms of the previous paragraph,
$\mathcal {M}$
. By the canonical isomorphisms of the previous paragraph,
![]() $\widehat {\mathcal {M}}$
is independent of the particular choices of charts for
$\widehat {\mathcal {M}}$
is independent of the particular choices of charts for
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Since the arrows in diagram (4.5) are strongly étale, we obtain a corresponding diagram of étale arrows at the level of good moduli spaces of the Kirwan blowups

where both rhombi are Cartesian.
By Proposition 3.2,
![]() $\mathcal {M} \setminus q^{-1} (M^{max}) \to M \setminus M^{max}$
is a good moduli space morphism. Hence, the morphisms
$\mathcal {M} \setminus q^{-1} (M^{max}) \to M \setminus M^{max}$
is a good moduli space morphism. Hence, the morphisms
![]() $[\widehat U_x / G_x] \to \widehat U_x /\!\!/ G_x$
for all
$[\widehat U_x / G_x] \to \widehat U_x /\!\!/ G_x$
for all
![]() $x \in \mathcal {M}^{max}$
together with an atlas of
$x \in \mathcal {M}^{max}$
together with an atlas of
![]() $\mathcal {M} \setminus q^{-1} (M^{max})$
glue to give a morphism
$\mathcal {M} \setminus q^{-1} (M^{max})$
glue to give a morphism
![]() $\widehat {\mathcal {M}} \to \widehat {M}$
. By Proposition 3.2 again, this is a good moduli space morphism.
$\widehat {\mathcal {M}} \to \widehat {M}$
. By Proposition 3.2 again, this is a good moduli space morphism.
![]() $\widehat {\mathcal {M}}$
has affine diagonal since we have a Cartesian diagram
$\widehat {\mathcal {M}}$
has affine diagonal since we have a Cartesian diagram

where the lower horizontal arrows give an étale cover of
![]() $\widehat {\mathcal {M}} \times \widehat {\mathcal {M}}$
and the left vertical arrow is affine.
$\widehat {\mathcal {M}} \times \widehat {\mathcal {M}}$
and the left vertical arrow is affine.
To see that
![]() $\widehat {\mathcal {M}} \to \widehat {M}$
also has affine diagonal, we consider the diagram
$\widehat {\mathcal {M}} \to \widehat {M}$
also has affine diagonal, we consider the diagram

where the right square is Cartesian. The diagonal of
![]() $\widehat {M}$
is separated [Sta23, Tag 04YQ]. Therefore, since the diagonal of
$\widehat {M}$
is separated [Sta23, Tag 04YQ]. Therefore, since the diagonal of
![]() $\widehat {\mathcal {M}}$
is affine, it follows by the usual cancellation property that
$\widehat {\mathcal {M}}$
is affine, it follows by the usual cancellation property that
![]() $\widehat {\mathcal {M}} \to \widehat {M}$
has affine diagonal.
$\widehat {\mathcal {M}} \to \widehat {M}$
has affine diagonal.
![]() $\widehat {\mathcal {M}}$
,
$\widehat {\mathcal {M}}$
,
![]() $\widehat {M}$
and the morphism
$\widehat {M}$
and the morphism
![]() $\widehat {\mathcal {M}} \to \widehat {M}$
thus have the same properties as
$\widehat {\mathcal {M}} \to \widehat {M}$
thus have the same properties as
![]() $\mathcal {M}$
, M and
$\mathcal {M}$
, M and
![]() $\mathcal {M} \to M$
, as desired. This establishes property (1) of the statement.
$\mathcal {M} \to M$
, as desired. This establishes property (1) of the statement.
Property (3) is true by construction and properties (2) and (4) can be checked strongly étale locally. But by the definition of Kirwan blowups of quotient stacks, they are both true in that case.
Finally, the last assertion about the intrinsic blowup
![]() $\mathcal {M}^{\mathrm {intr}}$
can be shown using the same arguments. Since we won’t be needing
$\mathcal {M}^{\mathrm {intr}}$
can be shown using the same arguments. Since we won’t be needing
![]() $\mathcal {M}^{\mathrm {intr}}$
, we leave the details to the reader.
$\mathcal {M}^{\mathrm {intr}}$
, we leave the details to the reader.
Remark 4.8. The fact that
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $q \colon \mathcal {M} \to M$
have affine diagonal is not crucial for the above proof to go through. In fact, by [Reference Alper, Hall and RydhAHR19, Theorem 13.1] and [Reference Alper, Hall and RydhAHR19, Corollary 13.11], it is enough to assume that
$q \colon \mathcal {M} \to M$
have affine diagonal is not crucial for the above proof to go through. In fact, by [Reference Alper, Hall and RydhAHR19, Theorem 13.1] and [Reference Alper, Hall and RydhAHR19, Corollary 13.11], it is enough to assume that
![]() $\mathcal {M}$
has affine stabilizers and separated diagonal. Since the stacks we are interested in will have affine diagonal, we make this assumption for convenience of presentation.
$\mathcal {M}$
has affine stabilizers and separated diagonal. Since the stacks we are interested in will have affine diagonal, we make this assumption for convenience of presentation.
As before, repeatedly applying the operation of Kirwan blowup we obtain the instrinsic stabilizer reduction. By construction of the Kirwan blowup, the stable locus is preserved at each step and hence stays invariant under the whole procedure.
Theorem 4.9. Let
![]() $\mathcal {M}$
be an Artin stack of finite type over
$\mathcal {M}$
be an Artin stack of finite type over
![]() $\mathbb {C}$
with affine diagonal, which is not Deligne–Mumford. Moreover, suppose that
$\mathbb {C}$
with affine diagonal, which is not Deligne–Mumford. Moreover, suppose that
![]() $q \colon \mathcal {M} \to M$
is a good moduli space morphism with q of finite type and with affine diagonal. Then there exists a canonical Deligne–Mumford stack
$q \colon \mathcal {M} \to M$
is a good moduli space morphism with q of finite type and with affine diagonal. Then there exists a canonical Deligne–Mumford stack
![]() $\widetilde {\mathcal {M}}$
, called the intrinsic stabilizer reduction of
$\widetilde {\mathcal {M}}$
, called the intrinsic stabilizer reduction of
![]() $\mathcal {M}$
, together with a morphism
$\mathcal {M}$
, together with a morphism
![]() $\pi \colon \widetilde {\mathcal {M}} \to \mathcal {M}$
which restricts to an isomorphism over the stable locus
$\pi \colon \widetilde {\mathcal {M}} \to \mathcal {M}$
which restricts to an isomorphism over the stable locus
![]() $\mathcal {M}^s \subseteq \mathcal {M}$
. Moreover,
$\mathcal {M}^s \subseteq \mathcal {M}$
. Moreover,
![]() $\widetilde {\mathcal {M}}$
admits a good moduli space
$\widetilde {\mathcal {M}}$
admits a good moduli space
![]() $\widetilde {M}$
and the good moduli space morphism
$\widetilde {M}$
and the good moduli space morphism
![]() $\widetilde {q} \colon \widetilde {\mathcal {M}} \to \widetilde {M}$
is proper.
$\widetilde {q} \colon \widetilde {\mathcal {M}} \to \widetilde {M}$
is proper.
Proof. We perform a sequence of Kirwan blowups by applying Theorem-Costruction 4.7 iteratively to get
At each step, the maximum stabilizer dimension strictly decreases, so we terminate as soon as
![]() $\mathcal {M}_{\ell }$
has finite stabilizers and is thus Deligne–Mumford. We define
$\mathcal {M}_{\ell }$
has finite stabilizers and is thus Deligne–Mumford. We define
![]() $\widetilde {\mathcal {M}} := \mathcal {M}_{\ell }$
.
$\widetilde {\mathcal {M}} := \mathcal {M}_{\ell }$
.
![]() $\widetilde {\mathcal {M}} \to \widetilde {M}$
admits a strongly étale cover by morphisms of the form
$\widetilde {\mathcal {M}} \to \widetilde {M}$
admits a strongly étale cover by morphisms of the form
![]() $[U/G] \to U /\!\!/ G$
, where G is finite, so its diagonal is finite (cf. [Reference Mumford, Fogarty and KirwanMFK94, Proposition 0.8]). Thus,
$[U/G] \to U /\!\!/ G$
, where G is finite, so its diagonal is finite (cf. [Reference Mumford, Fogarty and KirwanMFK94, Proposition 0.8]). Thus,
![]() $\widetilde {\mathcal {M}} \to \widetilde {M}$
is separated and by Proposition 3.2 also universally closed, hence proper.
$\widetilde {\mathcal {M}} \to \widetilde {M}$
is separated and by Proposition 3.2 also universally closed, hence proper.
Remark 4.10. If
![]() $\mathcal {M}^s$
is nonempty, then we are guaranteed that the intrinsic stabilizer reduction
$\mathcal {M}^s$
is nonempty, then we are guaranteed that the intrinsic stabilizer reduction
![]() $\widetilde {\mathcal {M}}$
is nonempty. While this is sufficient, it is not necessary, as can be seen for the quotient stack
$\widetilde {\mathcal {M}}$
is nonempty. While this is sufficient, it is not necessary, as can be seen for the quotient stack
![]() $\mathcal {M} = [U / G]$
in Example 4.1.
$\mathcal {M} = [U / G]$
in Example 4.1.
In general, if at some step of the procedure the stack
![]() $\mathcal {M}_i$
is a gerbe over a Deligne–Mumford stack (i.e.,
$\mathcal {M}_i$
is a gerbe over a Deligne–Mumford stack (i.e.,
![]() $\mathcal {M}_i$
has constant stabilizer dimension and every point is prestable), then
$\mathcal {M}_i$
has constant stabilizer dimension and every point is prestable), then
![]() $\widehat {\mathcal {M}}_i$
is empty. We could elect to terminate the procedure at this step instead and define
$\widehat {\mathcal {M}}_i$
is empty. We could elect to terminate the procedure at this step instead and define
![]() $\widetilde {\mathcal {M}} := \mathcal {M}_i$
. We choose not to do so as for our purpose of defining Donaldson–Thomas invariants, setting
$\widetilde {\mathcal {M}} := \mathcal {M}_i$
. We choose not to do so as for our purpose of defining Donaldson–Thomas invariants, setting
![]() $\widetilde {\mathcal {M}} = \emptyset $
in this case seems more geometrically motivated and better aligned with the BPS invariants considered in [Reference Joyce and SongJS12] and [Reference Davison and MeinhardtDM20].
$\widetilde {\mathcal {M}} = \emptyset $
in this case seems more geometrically motivated and better aligned with the BPS invariants considered in [Reference Joyce and SongJS12] and [Reference Davison and MeinhardtDM20].
Remark 4.11. Edidin–Rydh have also developed a blowup procedure for stacks with good moduli spaces in [Reference Edidin and RydhER21]. For smooth stacks, our stabilizer reduction is the same as theirs. For singular stacks, Kirwan blowups can be phrased in their language of saturated blowups; however, the resolution they obtain is a closed substack of the one here. Nevertheless, our construction is closely related to the Edidin–Rydh resolution of stabilizers performed at the level of derived stacks, using the recently developed notion of derived blowups in [Reference HekkingHek21] and the results of [Reference Hekking, Rydh and SavvasHRS22].
5 Obstruction theory
In this section, we first recall the basic principles of semiperfect obstruction theories and then explain how to construct such a gadget on the intrinsic stabilizer reduction of a stack of DT type. Our discussion goes through the notion of a local model and its obstruction theory, as used in [Reference Kiem, Li and SavvasKLS17].
5.1 Semiperfect obstruction theory
This subsection contains background material about semiperfect obstruction theories and their induced virtual cycles, as developed in [Reference Chang and LiCL11].
Let
![]() $U \to C$
be a morphism, where U is a scheme of finite type and C denotes a smooth quasi-projective scheme, which will typically be either a point or a smooth quasi-projective curve. We first recall the definition of perfect obstruction theory [Reference Behrend and FantechiBF97, Reference Li and TianLT98].
$U \to C$
be a morphism, where U is a scheme of finite type and C denotes a smooth quasi-projective scheme, which will typically be either a point or a smooth quasi-projective curve. We first recall the definition of perfect obstruction theory [Reference Behrend and FantechiBF97, Reference Li and TianLT98].
Definition 5.1 (Perfect obstruction theory [Reference Behrend and FantechiBF97])
A (truncated) perfect (relative) obstruction theory consists of a morphism
![]() $\phi \colon E \to L_{U/C}^{\geq -1}$
in
$\phi \colon E \to L_{U/C}^{\geq -1}$
in
![]() $D^b(\mathop{\mathrm {Coh}}\nolimits U)$
such that
$D^b(\mathop{\mathrm {Coh}}\nolimits U)$
such that
-
1. E is of perfect amplitude, contained in
 $[-1,0]$
.
$[-1,0]$
. -
2.
 $h^0(\phi )$
is an isomorphism and
$h^0(\phi )$
is an isomorphism and
 $h^{-1}(\phi )$
is surjective.
$h^{-1}(\phi )$
is surjective.
We refer to
![]() $\mathcal {O}b_{\phi } := \mathop {H^1}\nolimits (E^{\vee })$
as the obstruction sheaf of
$\mathcal {O}b_{\phi } := \mathop {H^1}\nolimits (E^{\vee })$
as the obstruction sheaf of
![]() $\phi $
.
$\phi $
.
Definition 5.2 (Infinitesimal lifting problem)
Let
![]() $\iota \colon \Delta \to \bar {\Delta }$
be an embedding with
$\iota \colon \Delta \to \bar {\Delta }$
be an embedding with
![]() $\bar {\Delta }$
local Artinian such that
$\bar {\Delta }$
local Artinian such that
![]() $I \cdot \mathfrak {m} = 0$
, where I is the ideal of
$I \cdot \mathfrak {m} = 0$
, where I is the ideal of
![]() $\Delta $
and
$\Delta $
and
![]() $\mathfrak {m}$
the closed point of
$\mathfrak {m}$
the closed point of
![]() $\bar {\Delta }$
. We call
$\bar {\Delta }$
. We call
![]() $(\Delta , \bar {\Delta }, \iota , \mathfrak {m})$
a small extension. Given a commutative square
$(\Delta , \bar {\Delta }, \iota , \mathfrak {m})$
a small extension. Given a commutative square

such that the image of g contains a point
![]() $p \in U$
, the problem of finding
$p \in U$
, the problem of finding
![]() $\bar {g} \colon \bar {\Delta } \to U$
making the diagram commutative is the ‘infinitesimal lifting problem of
$\bar {g} \colon \bar {\Delta } \to U$
making the diagram commutative is the ‘infinitesimal lifting problem of
![]() $U/C$
at p’.
$U/C$
at p’.
Definition 5.3 (Obstruction space)
For a point
![]() $p \in U$
, the intrinsic obstruction space to deforming p is
$p \in U$
, the intrinsic obstruction space to deforming p is
![]() $T_{p, U/ C}^1 := \mathop {H^1}\nolimits \left ( (L_{U/C}^{\geq -1})^{\vee } \vert _p \right )$
. The obstruction space with respect to a perfect obstruction theory
$T_{p, U/ C}^1 := \mathop {H^1}\nolimits \left ( (L_{U/C}^{\geq -1})^{\vee } \vert _p \right )$
. The obstruction space with respect to a perfect obstruction theory
![]() $\phi $
is
$\phi $
is
![]() $\mathop{\mathrm {Ob}}\nolimits (\phi ,p) := \mathop {H^1}\nolimits ( E^{\vee } \vert _p )$
.
$\mathop{\mathrm {Ob}}\nolimits (\phi ,p) := \mathop {H^1}\nolimits ( E^{\vee } \vert _p )$
.
Given an infinitesimal lifting problem of
![]() $U/C$
at a point p, there exists by the standard theory of the cotangent complex a canonical element
$U/C$
at a point p, there exists by the standard theory of the cotangent complex a canonical element
whose vanishing is necessary and sufficient for the lift
![]() $\bar {g}$
to exist.
$\bar {g}$
to exist.
Definition 5.4 (Obstruction assignment)
For an infinitesimal lifting problem of
![]() $U / C$
at p and a perfect obstruction theory
$U / C$
at p and a perfect obstruction theory
![]() $\phi $
the obstruction assignment at p is the element
$\phi $
the obstruction assignment at p is the element
Definition 5.5. Let
![]() $\phi \colon E \to L_{U / C}^{\geq -1}$
and
$\phi \colon E \to L_{U / C}^{\geq -1}$
and
![]() $\phi ' \colon E' \to L_{U / C}^{\geq -1}$
be two perfect obstruction theories and
$\phi ' \colon E' \to L_{U / C}^{\geq -1}$
be two perfect obstruction theories and
![]() $\psi \colon \mathcal {O}b_{\phi } \to \mathcal {O}b_{\phi '}$
be an isomorphism. We say that the obstruction theories give the same obstruction assignment via
$\psi \colon \mathcal {O}b_{\phi } \to \mathcal {O}b_{\phi '}$
be an isomorphism. We say that the obstruction theories give the same obstruction assignment via
![]() $\psi $
if for any infinitesimal lifting problem of
$\psi $
if for any infinitesimal lifting problem of
![]() $U/C$
at p
$U/C$
at p
We are now ready to give the definition of a semiperfect obstruction theory.
Definition 5.6 (semiperfect obstruction theory [Reference Chang and LiCL11, Definition 3.1])
Let
![]() $\mathcal {M}\to C$
be a morphism, where
$\mathcal {M}\to C$
be a morphism, where
![]() $\mathcal {M}$
is a DM stack, proper over C, of finite presentation and C is a smooth quasi-projective scheme. A semiperfect obstruction theory
$\mathcal {M}$
is a DM stack, proper over C, of finite presentation and C is a smooth quasi-projective scheme. A semiperfect obstruction theory
![]() $\phi $
consists of an étale covering
$\phi $
consists of an étale covering
![]() $\lbrace U_{\alpha } \rbrace _{\alpha \in A}$
of
$\lbrace U_{\alpha } \rbrace _{\alpha \in A}$
of
![]() $\mathcal {M}$
and perfect obstruction theories
$\mathcal {M}$
and perfect obstruction theories
![]() $\phi _{\alpha } \colon E_{\alpha } \to L_{U_{\alpha } / C}^{\geq -1}$
such that
$\phi _{\alpha } \colon E_{\alpha } \to L_{U_{\alpha } / C}^{\geq -1}$
such that
-
1. For each pair of indices
 $\alpha , \beta $
, there exists an isomorphism
$\alpha , \beta $
, there exists an isomorphism  $$ \begin{align*} \psi_{\alpha \beta} \colon \mathcal{O}b_{\phi_{\alpha}} \vert_{U_{\alpha\beta}} \longrightarrow \mathcal{O}b_{\phi_{\beta}} \vert_{U_{\alpha\beta}} \end{align*} $$
$$ \begin{align*} \psi_{\alpha \beta} \colon \mathcal{O}b_{\phi_{\alpha}} \vert_{U_{\alpha\beta}} \longrightarrow \mathcal{O}b_{\phi_{\beta}} \vert_{U_{\alpha\beta}} \end{align*} $$
so that the collection
 $\lbrace \mathcal {O}b_{\phi _{\alpha } }, \psi _{\alpha \beta } \rbrace $
gives descent data of a coherent sheaf on
$\lbrace \mathcal {O}b_{\phi _{\alpha } }, \psi _{\alpha \beta } \rbrace $
gives descent data of a coherent sheaf on
 $\mathcal {M}$
.
$\mathcal {M}$
. -
2. For each pair of indices
 $\alpha , \beta $
, the obstruction theories
$\alpha , \beta $
, the obstruction theories
 $E_{\alpha } \vert _{U_{\alpha \beta }}$
and
$E_{\alpha } \vert _{U_{\alpha \beta }}$
and
 $E_{\beta } \vert _{U_{\alpha \beta }}$
give the same obstruction assignment via
$E_{\beta } \vert _{U_{\alpha \beta }}$
give the same obstruction assignment via
 $\psi _{\alpha \beta }$
(as in Definition 5.5).
$\psi _{\alpha \beta }$
(as in Definition 5.5).
Remark 5.1. The obstruction sheaves
![]() $\lbrace \mathcal {O}b_{\phi _{\alpha } } \rbrace _{\alpha \in A}$
glue to define a sheaf
$\lbrace \mathcal {O}b_{\phi _{\alpha } } \rbrace _{\alpha \in A}$
glue to define a sheaf
![]() $\mathcal {O}b_{\phi }$
on
$\mathcal {O}b_{\phi }$
on
![]() $\mathcal {M}$
. This is the obstruction sheaf of the semiperfect obstruction theory
$\mathcal {M}$
. This is the obstruction sheaf of the semiperfect obstruction theory
![]() $\phi $
.
$\phi $
.
Suppose now that
![]() $\mathcal {M} \to C$
is as above and admits a semiperfect obstruction theory. Then, for each
$\mathcal {M} \to C$
is as above and admits a semiperfect obstruction theory. Then, for each
![]() $\alpha \in A$
, we have
$\alpha \in A$
, we have
where
![]() $\mathcal {C}_{U_{\alpha } /C}$
and
$\mathcal {C}_{U_{\alpha } /C}$
and
![]() $N_{U_{\alpha } /C}$
denote the intrinsic normal cone stack and intrinsic normal sheaf stack respectively, where by abuse of notation we identify a sheaf
$N_{U_{\alpha } /C}$
denote the intrinsic normal cone stack and intrinsic normal sheaf stack respectively, where by abuse of notation we identify a sheaf
![]() $\mathcal {F}$
on
$\mathcal {F}$
on
![]() $\mathcal {M}$
with its sheaf stack.
$\mathcal {M}$
with its sheaf stack.
We therefore obtain a cycle class
![]() $[\mathfrak {c}_{\phi _{\alpha } }] \in Z_* \mathcal {O}b_{\phi _{\alpha } }$
by taking the pushforward of the cycle
$[\mathfrak {c}_{\phi _{\alpha } }] \in Z_* \mathcal {O}b_{\phi _{\alpha } }$
by taking the pushforward of the cycle
![]() $[\mathcal {C}_{U_{\alpha } /C}] \in Z_* N_{U_{\alpha } /C}$
.
$[\mathcal {C}_{U_{\alpha } /C}] \in Z_* N_{U_{\alpha } /C}$
.
Theorem-Definition 5.2 [Reference Chang and LiCL11, Definition-Theorem 3.7]
Let
![]() $\mathcal {M}$
be a DM stack, proper over C, of finite presentation and C a point or a smooth quasi-projective curve such that
$\mathcal {M}$
be a DM stack, proper over C, of finite presentation and C a point or a smooth quasi-projective curve such that
![]() $\mathcal {M} \to C$
admits a semiperfect obstruction theory
$\mathcal {M} \to C$
admits a semiperfect obstruction theory
![]() $\phi $
. The classes
$\phi $
. The classes
![]() $[\mathfrak {c}_{\phi _{\alpha } }] \in Z_* \mathcal {O}b_{\phi _{\alpha } }$
glue to define an intrinsic normal cone cycle
$[\mathfrak {c}_{\phi _{\alpha } }] \in Z_* \mathcal {O}b_{\phi _{\alpha } }$
glue to define an intrinsic normal cone cycle
![]() $[\mathfrak {c}_{\phi }] \in Z_* \mathcal {O}b_{\phi }$
. Let s be the zero section of the sheaf stack
$[\mathfrak {c}_{\phi }] \in Z_* \mathcal {O}b_{\phi }$
. Let s be the zero section of the sheaf stack
![]() $\mathcal {O}b_{\phi }$
. The virtual cycle of
$\mathcal {O}b_{\phi }$
. The virtual cycle of
![]() $\mathcal {M}$
is defined to be
$\mathcal {M}$
is defined to be
where
![]() $s^{!} \colon Z_* \mathcal {O}b_{\phi } \to A_* \mathcal {M}$
is the Gysin map. This virtual cycle satisfies all the usual properties, such as deformation invariance.
$s^{!} \colon Z_* \mathcal {O}b_{\phi } \to A_* \mathcal {M}$
is the Gysin map. This virtual cycle satisfies all the usual properties, such as deformation invariance.
Remark 5.3. Observe that in Definition 5.6 it is not strictly necessary to take the
![]() $U_{\alpha } $
to be schemes. It is straightforward to generalize the definition and the construction of the associated virtual fundamental cycle to include étale covers by Deligne–Mumford stacks.
$U_{\alpha } $
to be schemes. It is straightforward to generalize the definition and the construction of the associated virtual fundamental cycle to include étale covers by Deligne–Mumford stacks.
5.2 Local models, standard forms and their blowups
Let V be a smooth affine G-scheme. The action of G on V induces a morphism
![]() ${\mathfrak {g} \otimes \mathcal {O}_V \rightarrow T_V}$
and its dual
${\mathfrak {g} \otimes \mathcal {O}_V \rightarrow T_V}$
and its dual
![]() $\sigma _V : \Omega _V \rightarrow \mathfrak {g}^{\vee } \otimes \mathcal {O}_V$
.
$\sigma _V : \Omega _V \rightarrow \mathfrak {g}^{\vee } \otimes \mathcal {O}_V$
.
Setup-Definition 5.4 [Reference Kiem, Li and SavvasKLS17, Setup-Definition 5.1]
Consider the quadruple
![]() $(V, F_V, \omega _V, D_V)$
, where
$(V, F_V, \omega _V, D_V)$
, where
![]() $F_V$
is a G-equivariant vector bundle on V,
$F_V$
is a G-equivariant vector bundle on V,
![]() $\omega _V$
a G-invariant section with scheme-theoretic zero locus
$\omega _V$
a G-invariant section with scheme-theoretic zero locus
![]() $U = \lbrace \omega _V = 0 \rbrace \subset V$
and
$U = \lbrace \omega _V = 0 \rbrace \subset V$
and
![]() $D_V \subset V$
an effective invariant divisor, satisfying:
$D_V \subset V$
an effective invariant divisor, satisfying:
-
1.
 $\sigma _V(-D_V) : \Omega _V ( -D_V ) \to \mathfrak {g}^{\vee } (-D_V)$
factors through a morphism
$\sigma _V(-D_V) : \Omega _V ( -D_V ) \to \mathfrak {g}^{\vee } (-D_V)$
factors through a morphism
 $\phi _V$
as shown (5.5)
$\phi _V$
as shown (5.5) $$ \begin{align} \Omega_V(-D_V) \longrightarrow F_V \xrightarrow{\phi_V} \mathfrak{g}^{\vee}(-D_V); \end{align} $$
$$ \begin{align} \Omega_V(-D_V) \longrightarrow F_V \xrightarrow{\phi_V} \mathfrak{g}^{\vee}(-D_V); \end{align} $$
-
2. The composition
 $\phi _V \circ \omega _V$
vanishes identically;
$\phi _V \circ \omega _V$
vanishes identically; -
3. Let R be the identity component of the stabilizer group of a closed point in V with closed orbit. Let
 $V^R$
denote the fixed point locus of R. Then
$V^R$
denote the fixed point locus of R. Then
 $\phi _V |_{V^R}$
composed with the projection
$\phi _V |_{V^R}$
composed with the projection
 $\mathfrak {g}^{\vee }(-D_V) \rightarrow \mathfrak {r}^{\vee }(-D_V)$
is zero, where
$\mathfrak {g}^{\vee }(-D_V) \rightarrow \mathfrak {r}^{\vee }(-D_V)$
is zero, where
 $\mathfrak {r}$
is the Lie algebra of R.
$\mathfrak {r}$
is the Lie algebra of R.
We say that the data
give a local model structure for U. Thinking of the quotient stack, we say that
![]() $[U/G]$
also has a local model structure and denote the data by
$[U/G]$
also has a local model structure and denote the data by
![]() $\Lambda _{[U/G]}$
.
$\Lambda _{[U/G]}$
.
Remark 5.5. Note that if
![]() $f \colon V \to \mathbb {A}^1$
is a G-invariant function on V, then
$f \colon V \to \mathbb {A}^1$
is a G-invariant function on V, then
![]() $(U, V, G, \Omega _V, df, 0, \sigma _V)$
give a local model for U, being equivalent to an invariant d-critical chart
$(U, V, G, \Omega _V, df, 0, \sigma _V)$
give a local model for U, being equivalent to an invariant d-critical chart
![]() $(U,V,f,i)$
for U. Therefore, an invariant d-critical locus is a particular case of a local model.
$(U,V,f,i)$
for U. Therefore, an invariant d-critical locus is a particular case of a local model.
Now, let
![]() $\Lambda _U= (U, V, G, F_V, \omega _V, D_V, \phi _V)$
define a local model structure on U. Since G is reductive, we have a splitting
$\Lambda _U= (U, V, G, F_V, \omega _V, D_V, \phi _V)$
define a local model structure on U. Since G is reductive, we have a splitting
Let now
![]() $\pi \colon \widehat V \to V$
be the Kirwan blowup of V. Define
$\pi \colon \widehat V \to V$
be the Kirwan blowup of V. Define
![]() $F_{\widehat V}$
as the kernel of the composite morphism
$F_{\widehat V}$
as the kernel of the composite morphism
![]() $\pi ^* F_V \to \pi ^* \left ( F_V |_{V^G} \right ) \to \pi ^* \left ( F_V |_{V^G}^{\mathrm {mv}} \right )$
so that we have an exact sequence
$\pi ^* F_V \to \pi ^* \left ( F_V |_{V^G} \right ) \to \pi ^* \left ( F_V |_{V^G}^{\mathrm {mv}} \right )$
so that we have an exact sequence
By equivariance,
![]() $\pi ^* \omega _V$
maps to zero under the second map and hence induces an invariant section
$\pi ^* \omega _V$
maps to zero under the second map and hence induces an invariant section
![]() $\omega _{\widehat V}$
of
$\omega _{\widehat V}$
of
![]() $F_{\widehat V}$
. A local computation shows the following.
$F_{\widehat V}$
. A local computation shows the following.
Proposition 5.6. The zero locus of
![]() $\omega _{\widehat V}$
is the Kirwan blowup
$\omega _{\widehat V}$
is the Kirwan blowup
![]() $\widehat U$
of U with respect to G.
$\widehat U$
of U with respect to G.
Proof. This is Proposition 2.11 in [Reference Kiem, Li and SavvasKLS17].
Local model structures are preserved under the operations of Kirwan blowups and taking étale slices.
Proposition 5.7. Let
![]() $(U, V, G, F_V, \omega _V, D_V, \phi _V)$
be the data of a local model. Then there exist induced data
$(U, V, G, F_V, \omega _V, D_V, \phi _V)$
be the data of a local model. Then there exist induced data
![]() $(\widehat U, \widehat V, G, F_{\widehat V}, \omega _{\widehat V}, D_{\widehat V}, \phi _{\widehat V})$
of a local model on the Kirwan blowup
$(\widehat U, \widehat V, G, F_{\widehat V}, \omega _{\widehat V}, D_{\widehat V}, \phi _{\widehat V})$
of a local model on the Kirwan blowup
![]() $\widehat U$
. The same is true for any étale slice T of a closed point of
$\widehat U$
. The same is true for any étale slice T of a closed point of
![]() $\widehat U$
with closed G-orbit.
$\widehat U$
with closed G-orbit.
Proof. This is [Reference Kiem, Li and SavvasKLS17, Lemma 5.3]. The fact that
![]() $F_{\widehat V}$
is locally free is discussed shortly after Definition 2.10 in [Reference Kiem, Li and SavvasKLS17]. Denoting the Kirwan blowup map
$F_{\widehat V}$
is locally free is discussed shortly after Definition 2.10 in [Reference Kiem, Li and SavvasKLS17]. Denoting the Kirwan blowup map
![]() $\widehat V \to V$
by
$\widehat V \to V$
by
![]() $\pi $
, the divisor
$\pi $
, the divisor
![]() $D_{\widehat V}$
is equal to
$D_{\widehat V}$
is equal to
![]() $\pi ^* D_V + 2E$
, where E is the exceptional divisor of
$\pi ^* D_V + 2E$
, where E is the exceptional divisor of
![]() $\widehat V$
. Finally,
$\widehat V$
. Finally,
![]() $\phi _{\widehat V}$
is induced by
$\phi _{\widehat V}$
is induced by
![]() $\phi _V$
through a diagram chase and the definition of
$\phi _V$
through a diagram chase and the definition of
![]() $F_{\widehat V}$
. The reasoning for étale slices is similar.
$F_{\widehat V}$
. The reasoning for étale slices is similar.
5.3 Obstruction theory of local model
Let
be the data of a local model structure. Consider the sequence
By [Reference Kiem, Li and SavvasKLS17, Lemma 5.5], this defines a G-equivariant perfect complex on U that descends to a perfect complex on
![]() $[U/G]$
, which we denote by
$[U/G]$
, which we denote by
![]() $\mathcal {K}_{[U/G]}$
.
$\mathcal {K}_{[U/G]}$
.
We have a morphism
given by the diagram

where I denotes the ideal sheaf of U in V. Observe that the diagram commutes since by Setup-Definition 5.4(2), the composition
![]() $\phi _V \circ \omega _V$
is identically zero.
$\phi _V \circ \omega _V$
is identically zero.
Let
![]() $U^s, V^s$
denote the stable loci of U and V respectively (cf. Definition 4.2). We thus have that
$U^s, V^s$
denote the stable loci of U and V respectively (cf. Definition 4.2). We thus have that
![]() $\sigma _V|_{V^s} \colon \Omega _V|_{V^s} \to \mathfrak {g}^{\vee }$
is surjective. By Setup-Definition 5.4, it follows that
$\sigma _V|_{V^s} \colon \Omega _V|_{V^s} \to \mathfrak {g}^{\vee }$
is surjective. By Setup-Definition 5.4, it follows that
![]() $\phi _V|_{U^s}$
is surjective and hence its dual is injective with locally free cokernel.
$\phi _V|_{U^s}$
is surjective and hence its dual is injective with locally free cokernel.
Therefore,
![]() $\mathcal {K}_{[U^s/G]} := \mathcal {K}_{[U/G]} |_{[U^s / G]}$
is a two-term perfect complex, whose dual
$\mathcal {K}_{[U^s/G]} := \mathcal {K}_{[U/G]} |_{[U^s / G]}$
is a two-term perfect complex, whose dual
![]() $E_{[U^s / G]}$
gives a perfect obstruction theory on the DM stack
$E_{[U^s / G]}$
gives a perfect obstruction theory on the DM stack
![]() $[U^s / G]$
via the diagrams (5.7) and (5.8).
$[U^s / G]$
via the diagrams (5.7) and (5.8).
Definition 5.7. Let
![]() $(U,V,G,F_V,\omega _V, D_V, \phi _V)$
be the data of a local model structure. Then
$(U,V,G,F_V,\omega _V, D_V, \phi _V)$
be the data of a local model structure. Then
![]() $E_{[U^s / G]}$
is the induced perfect obstruction theory on the stable locus
$E_{[U^s / G]}$
is the induced perfect obstruction theory on the stable locus
![]() $[U^s / G]$
.
$[U^s / G]$
.
5.4 Semiperfect obstruction theory of the intrinsic stabilizer reduction of a stack of DT type
Let
![]() $\mathcal {M}$
be an Artin stack of DT type. We now explain how to construct a semiperfect obstruction theory on its intrinsic stabilizer reduction
$\mathcal {M}$
be an Artin stack of DT type. We now explain how to construct a semiperfect obstruction theory on its intrinsic stabilizer reduction
![]() $\widetilde {\mathcal {M}}$
, one of the main results of this paper.
$\widetilde {\mathcal {M}}$
, one of the main results of this paper.
We begin by recording and abstracting some of the data associated to a stack of DT type.
Setup 5.8. For any closed point
![]() $x \in \mathcal {M}$
, by Proposition 3.6, there exists a strongly étale d-critical quotient chart for
$x \in \mathcal {M}$
, by Proposition 3.6, there exists a strongly étale d-critical quotient chart for
![]() $\mathcal {M}$
centered at x. In particular, we obtain a strongly étale cover
$\mathcal {M}$
centered at x. In particular, we obtain a strongly étale cover
where, by Remark 5.5, each quotient stack
![]() $[U_x / G_x]$
is equipped with data of a local model
$[U_x / G_x]$
is equipped with data of a local model
with
![]() $F_{V_x} = \Omega _{V_x}$
,
$F_{V_x} = \Omega _{V_x}$
,
![]() $\omega _{V_x} = df_x$
,
$\omega _{V_x} = df_x$
,
![]() $D_{V_x} = 0$
and
$D_{V_x} = 0$
and
![]() $\phi _{V_x} = \sigma _{V_x}$
.
$\phi _{V_x} = \sigma _{V_x}$
.
By Proposition 3.7, for any two closed points
![]() $x, y \in \mathcal {M}$
we have an étale cover
$x, y \in \mathcal {M}$
we have an étale cover
by d-critical quotient charts centered at closed points
![]() $z \in [U_x / G_x] \times _{\mathcal {M}} [U_y / G_y]$
so that we have local model structures on
$z \in [U_x / G_x] \times _{\mathcal {M}} [U_y / G_y]$
so that we have local model structures on
![]() $[T_z / G_z]$
given by the data
$[T_z / G_z]$
given by the data
with
![]() $F_{S_z} = \Omega _{S_z}$
,
$F_{S_z} = \Omega _{S_z}$
,
![]() $\omega _{S_z} = df_z$
,
$\omega _{S_z} = df_z$
,
![]() $D_{S_z} = 0$
and
$D_{S_z} = 0$
and
![]() $\phi _{S_z} = \sigma _{S_z}$
.
$\phi _{S_z} = \sigma _{S_z}$
.
For any morphism
![]() $[T_z / G_z] \to [U_x / G_x]$
in equation (5.11), Proposition 3.7 also produces the following data:
$[T_z / G_z] \to [U_x / G_x]$
in equation (5.11), Proposition 3.7 also produces the following data:
-
1. A commutative
 $G_z$
-equivariant diagram
$G_z$
-equivariant diagram 
where the horizontal arrows are closed embeddings and
 $\theta _{zx}$
is unramified, inducing the étale morphism
$\theta _{zx}$
is unramified, inducing the étale morphism
 $[T_z / G_z] \to [U_x / G_x]$
in equation (5.11).
$[T_z / G_z] \to [U_x / G_x]$
in equation (5.11). -
2. A surjective
 $G_z$
-equivariant morphism
$G_z$
-equivariant morphism
 $\eta _{zx} \colon F_{V_x} |_{S_z} \to F_{S_z}$
, compatible with the morphisms
$\eta _{zx} \colon F_{V_x} |_{S_z} \to F_{S_z}$
, compatible with the morphisms
 $\phi _{V_x}|_{S_z}$
and
$\phi _{V_x}|_{S_z}$
and
 $\phi _{S_z}$
such that
$\phi _{S_z}$
such that
 $\omega _z' := \eta _{zx} (\omega _{V_x}|_{S_z})$
and
$\omega _z' := \eta _{zx} (\omega _{V_x}|_{S_z})$
and
 $\omega _{S_z}$
are
$\omega _{S_z}$
are
 $\Omega $
-equivalent (cf. [Reference Kiem, Li and SavvasKLS17, Definition 5.9]).
$\Omega $
-equivalent (cf. [Reference Kiem, Li and SavvasKLS17, Definition 5.9]). -
3. An induced isomorphism
 $$ \begin{align*}\eta_{zx} \colon h^1(\mathcal{K}_{[U_x / G_x]})|_{[T_z / G_z]} \longrightarrow h^1(\mathcal{K}_{[T_z / G_z]}).\end{align*} $$
$$ \begin{align*}\eta_{zx} \colon h^1(\mathcal{K}_{[U_x / G_x]})|_{[T_z / G_z]} \longrightarrow h^1(\mathcal{K}_{[T_z / G_z]}).\end{align*} $$
-
4. Isomorphisms
 $$ \begin{align*}\psi_{xy} \colon h^1(\mathcal{K}_{[U_x / G_x]})|_{[U_x / G_x] \times_{\mathcal{M}} [U_y / G_y]} \longrightarrow h^1(\mathcal{K}_{[U_y / G_y]})|_{[U_x / G_x] \times_{\mathcal{M}} [U_y / G_y]}\end{align*} $$
$$ \begin{align*}\psi_{xy} \colon h^1(\mathcal{K}_{[U_x / G_x]})|_{[U_x / G_x] \times_{\mathcal{M}} [U_y / G_y]} \longrightarrow h^1(\mathcal{K}_{[U_y / G_y]})|_{[U_x / G_x] \times_{\mathcal{M}} [U_y / G_y]}\end{align*} $$
satisfying the cocycle condition and
 $\psi _{xy}|_{[T_z / G_z]} = \eta _{zy}^{-1} \circ \eta _{zx}$
.
$\psi _{xy}|_{[T_z / G_z]} = \eta _{zy}^{-1} \circ \eta _{zx}$
.
We abstract this situation by saying that the data of a strongly étale cover (5.9) equipped with a local model structure (5.10), an étale cover (5.11) with a local model structure (5.12) and compatibility data described by items (1)–(4) above constitute a virtual cycle (VC) package for an Artin stack
![]() $\mathcal {M}$
satisfying the conditions of Theorem-Construction 4.7. Note that if
$\mathcal {M}$
satisfying the conditions of Theorem-Construction 4.7. Note that if
![]() $\mathcal {M}$
is an Artin stack of DT type then, by our discussion, we may take the local model structures to correspond to invariant d-critical quotient charts; however, in general we only require local models that satisfy the compatibilities (1)–(4).
$\mathcal {M}$
is an Artin stack of DT type then, by our discussion, we may take the local model structures to correspond to invariant d-critical quotient charts; however, in general we only require local models that satisfy the compatibilities (1)–(4).
For a detailed account of
![]() $\Omega $
-equivalence, we refer the reader to [Reference Kiem, Li and SavvasKLS17, Section 5]. For the purposes of our discussion, it suffices to note that
$\Omega $
-equivalence, we refer the reader to [Reference Kiem, Li and SavvasKLS17, Section 5]. For the purposes of our discussion, it suffices to note that
![]() $\omega _z'$
being
$\omega _z'$
being
![]() $\Omega $
-equivalent to
$\Omega $
-equivalent to
![]() $\omega _{S_z}$
essentially means that we have another local model structure
$\omega _{S_z}$
essentially means that we have another local model structure
on
![]() $[T_z / G_z]$
such that the induced perfect obstruction theory
$[T_z / G_z]$
such that the induced perfect obstruction theory
![]() $E_{[T_z^s / G_z]}'$
naturally has the same obstruction sheaf and gives the same obstruction assignment with
$E_{[T_z^s / G_z]}'$
naturally has the same obstruction sheaf and gives the same obstruction assignment with
![]() $E_{[T_z^s / G_z]}$
.
$E_{[T_z^s / G_z]}$
.
The data of Setup 5.8 are preserved under Kirwan blowups and hence lift to the intrinsic stabilizer reduction of a stack of DT type.
Theorem 5.9. Let
![]() $\mathcal {M}$
be an Artin stack of DT type. Then its intrinsic stabilizer reduction
$\mathcal {M}$
be an Artin stack of DT type. Then its intrinsic stabilizer reduction
![]() $\widetilde {\mathcal {M}}$
admits a VC package.
$\widetilde {\mathcal {M}}$
admits a VC package.
Proof. By the discussion in Setup 5.8,
![]() $\mathcal {M}$
admits a VC package where moreover all local models corresponds to d-critical quotient charts.
$\mathcal {M}$
admits a VC package where moreover all local models corresponds to d-critical quotient charts.
By the construction of
![]() $\widetilde {\mathcal {M}}$
, it suffices to show that if a stack
$\widetilde {\mathcal {M}}$
, it suffices to show that if a stack
![]() $\mathcal {N}$
(satisfying the conditions of Theorem-Construction 4.7) admits a VC package, then its Kirwan blowup
$\mathcal {N}$
(satisfying the conditions of Theorem-Construction 4.7) admits a VC package, then its Kirwan blowup
![]() $\widehat {\mathcal {N}}$
admits a canonically induced VC package.
$\widehat {\mathcal {N}}$
admits a canonically induced VC package.
By the construction in the proof of Proposition 3.7, Proposition 4.5 and Theorem-Construction 4.7, we may obtain new étale covers 5.9 and 5.11 for
![]() $\widehat {\mathcal {N}}$
by replacing every stack by its Kirwan blowup.
$\widehat {\mathcal {N}}$
by replacing every stack by its Kirwan blowup.
By Proposition 5.7, there are canonically induced local model structures on these étale covers. It is moreover clear that condition (1) is satisfied.
Conditions (2)–(4) follow from [Reference Kiem, Li and SavvasKLS17, Lemma 6.1]. This concludes the proof.
Now, a VC package on a Deligne–Mumford stack naturally provides data of a semiperfect obstruction theory.
Theorem 5.10. Let
![]() $\mathcal {M}$
be a Deligne–Mumford stack equipped with a VC package. Then
$\mathcal {M}$
be a Deligne–Mumford stack equipped with a VC package. Then
![]() $\mathcal {M}$
admits an induced semiperfect obstruction theory and thus a virtual fundamental cycle
$\mathcal {M}$
admits an induced semiperfect obstruction theory and thus a virtual fundamental cycle
![]() $[\mathcal {M}]^{\mathrm {vir}} \in A_*(\mathcal {M})$
.
$[\mathcal {M}]^{\mathrm {vir}} \in A_*(\mathcal {M})$
.
Proof. Since
![]() $\mathcal {M}$
is Deligne–Mumford, all quotient stacks in equation (5.9) are also Deligne–Mumford and satisfy
$\mathcal {M}$
is Deligne–Mumford, all quotient stacks in equation (5.9) are also Deligne–Mumford and satisfy
![]() $[U_x / G_x] = [U_x^s / G_x]$
since all closed points are now stable.
$[U_x / G_x] = [U_x^s / G_x]$
since all closed points are now stable.
Thus, by Definition 5.7, the local model structures
![]() $\Lambda _{[U_x / G_x]}$
induce perfect obstruction theories
$\Lambda _{[U_x / G_x]}$
induce perfect obstruction theories
on each
![]() $[U_x / G_x]$
.
$[U_x / G_x]$
.
Conditions (3) and (4) of a VC package give descent data for the obstruction sheaves
![]() $h^1(E_x^{\vee })$
, while conditions (1) and (2) and the properties of
$h^1(E_x^{\vee })$
, while conditions (1) and (2) and the properties of
![]() $\Omega $
-equivalence imply that these descent data are compatible with obstruction assignments of infinitesimal lifting problems.
$\Omega $
-equivalence imply that these descent data are compatible with obstruction assignments of infinitesimal lifting problems.
Using Remark 5.3 and Theorem-Construction 5.2, we obtain a semiperfect obstruction theory on
![]() $\mathcal {M}$
and a virtual fundamental cycle
$\mathcal {M}$
and a virtual fundamental cycle
![]() $[\mathcal {M}]^{\mathrm {vir}} \in A_*(\mathcal {M})$
.
$[\mathcal {M}]^{\mathrm {vir}} \in A_*(\mathcal {M})$
.
Combining the above two theorems, we arrive at the main result of this section.
Theorem 5.11. Let
![]() $\mathcal {M}$
be an Artin stack of DT type. Then the intrinsic stabilizer reduction
$\mathcal {M}$
be an Artin stack of DT type. Then the intrinsic stabilizer reduction
![]() $\widetilde {\mathcal {M}}$
admits a semiperfect obstruction theory of virtual dimension zero and an induced, canonical virtual fundamental cycle
$\widetilde {\mathcal {M}}$
admits a semiperfect obstruction theory of virtual dimension zero and an induced, canonical virtual fundamental cycle
![]() $[\widetilde {\mathcal {M}}]^{\mathrm {vir}} \in A_0(\widetilde {\mathcal {M}})$
.
$[\widetilde {\mathcal {M}}]^{\mathrm {vir}} \in A_0(\widetilde {\mathcal {M}})$
.
Proof. The existence of the semiperfect obstruction theory follows immediately from Theorems 5.9 and 5.10.
The virtual dimension is zero since for a d-critical chart the rank of
![]() $F_V = \Omega _V$
is equal to
$F_V = \Omega _V$
is equal to
![]() $\dim V$
and the virtual dimension
$\dim V$
and the virtual dimension
![]() $\dim V - \mathop{\mathrm {rk}}\nolimits F_V$
is preserved under Kirwan blowups.
$\dim V - \mathop{\mathrm {rk}}\nolimits F_V$
is preserved under Kirwan blowups.
Finally, any two different étale covers (5.9) that are part of a VC package of
![]() $\mathcal {M}$
can be refined to a common étale cover. It is routine to check that the virtual fundamental cycle thus obtained is the same using this common refinement.
$\mathcal {M}$
can be refined to a common étale cover. It is routine to check that the virtual fundamental cycle thus obtained is the same using this common refinement.
Remark 5.12. The existence of the intrinsic stabilizer reduction of
![]() $\mathcal {M}$
and its obstruction theory only uses its
$\mathcal {M}$
and its obstruction theory only uses its
![]() $(-1)$
-shifted symplectic derived enhancement to deduce the existence of a d-critical structure on
$(-1)$
-shifted symplectic derived enhancement to deduce the existence of a d-critical structure on
![]() $\mathcal {M}$
. We could have thus used a weaker notion of stacks of DT type, replacing condition (3) in Definition 3.4 by the requirement that
$\mathcal {M}$
. We could have thus used a weaker notion of stacks of DT type, replacing condition (3) in Definition 3.4 by the requirement that
![]() $\mathcal {M}$
admits a d-critical structure. However, we will be interested in replicating our arguments in the relative case where
$\mathcal {M}$
admits a d-critical structure. However, we will be interested in replicating our arguments in the relative case where
![]() $\mathcal {M}$
is a stack over a base smooth scheme S. In that context, there is no well-developed theory of d-critical stacks to the author’s knowledge and the existence of a derived enhancement will allow us to still perform our constructions.
$\mathcal {M}$
is a stack over a base smooth scheme S. In that context, there is no well-developed theory of d-critical stacks to the author’s knowledge and the existence of a derived enhancement will allow us to still perform our constructions.
6 Donaldson–Thomas invariants of derived objects
In this section, W denotes a smooth, projective Calabi–Yau threefold over
![]() $\mathbb {C}$
. We first describe the stability conditions
$\mathbb {C}$
. We first describe the stability conditions
![]() $\sigma $
on
$\sigma $
on
![]() $D^b(\mathop{\mathrm {Coh}}\nolimits W)$
that we will be interested in. We then quote results in [Reference Alper, Halpern-Leistner and HeinlothAHH18] which imply that moduli stacks of
$D^b(\mathop{\mathrm {Coh}}\nolimits W)$
that we will be interested in. We then quote results in [Reference Alper, Halpern-Leistner and HeinlothAHH18] which imply that moduli stacks of
![]() $\sigma $
-semistable complexes are stacks of DT type and explain how to rigidify the
$\sigma $
-semistable complexes are stacks of DT type and explain how to rigidify the
![]() $\mathbb {C}^{\ast }$
-scaling automorphisms of objects. Finally, we define generalized DT invariants via Kirwan blowups and show their deformation invariance.
$\mathbb {C}^{\ast }$
-scaling automorphisms of objects. Finally, we define generalized DT invariants via Kirwan blowups and show their deformation invariance.
6.1 Stability conditions
By [Reference LieblichLie06], there is an Artin stack
![]() $\mathcal {P} := \mathop{\mathrm {Perf}}\nolimits (W)$
of (universally gluable) perfect complexes on W, which is locally of finite type and has separated diagonal. Following [Reference Alper, Halpern-Leistner and HeinlothAHH18], we will consider the following type of stability condition.
$\mathcal {P} := \mathop{\mathrm {Perf}}\nolimits (W)$
of (universally gluable) perfect complexes on W, which is locally of finite type and has separated diagonal. Following [Reference Alper, Halpern-Leistner and HeinlothAHH18], we will consider the following type of stability condition.
Definition 6.1 (Stability condition)
A stability condition
![]() $\sigma $
on
$\sigma $
on
![]() $D^b(\mathop{\mathrm {Coh}}\nolimits W)$
consists of the following data:
$D^b(\mathop{\mathrm {Coh}}\nolimits W)$
consists of the following data:
-
1. A heart
 $\mathcal {A} \subset D^b ( \mathop{\mathrm {Coh}}\nolimits W )$
of a t-structure on
$\mathcal {A} \subset D^b ( \mathop{\mathrm {Coh}}\nolimits W )$
of a t-structure on
 $D^b(\mathop{\mathrm {Coh}}\nolimits W)$
. Let
$D^b(\mathop{\mathrm {Coh}}\nolimits W)$
. Let
 $\mathcal {P}_{\mathcal {A}}$
denote the stack of perfect complexes in
$\mathcal {P}_{\mathcal {A}}$
denote the stack of perfect complexes in
 $\mathcal {A}$
.
$\mathcal {A}$
. -
2. A vector
 $\gamma \in H^* (W, \mathbb {Q})$
. Let
$\gamma \in H^* (W, \mathbb {Q})$
. Let
 $\mathcal {P}_{\mathcal {A}}^{\gamma }$
denote the stack of perfect complexes in
$\mathcal {P}_{\mathcal {A}}^{\gamma }$
denote the stack of perfect complexes in
 $\mathcal {A}$
with Chern character
$\mathcal {A}$
with Chern character
 $\gamma $
.
$\gamma $
. -
3. A locally constant function
 $$ \begin{align*} p_{\gamma} \colon \pi_0 (\mathcal{P}_{\mathcal{A}}) \longrightarrow V, \end{align*} $$
$$ \begin{align*} p_{\gamma} \colon \pi_0 (\mathcal{P}_{\mathcal{A}}) \longrightarrow V, \end{align*} $$
where V is a totally ordered abelian group,
 $p_{\gamma } (E) = 0$
for
$p_{\gamma } (E) = 0$
for
 $E \in \mathcal {P}_{\mathcal {A}}^{\gamma }$
and
$E \in \mathcal {P}_{\mathcal {A}}^{\gamma }$
and
 $p_{\gamma }$
is additive so that
$p_{\gamma }$
is additive so that
 $p_{\gamma }(E \oplus F) = p_{\gamma }(E) + p_{\gamma }(F)$
.
$p_{\gamma }(E \oplus F) = p_{\gamma }(E) + p_{\gamma }(F)$
.
We say that
![]() $E \in \mathcal {P}_{\mathcal {A}}^{\gamma }$
is semistable if for any subobject
$E \in \mathcal {P}_{\mathcal {A}}^{\gamma }$
is semistable if for any subobject
![]() $F \subseteq E$
we have
$F \subseteq E$
we have
![]() $p_{\gamma }(F) \leq 0$
and stable if
$p_{\gamma }(F) \leq 0$
and stable if
![]() $p_{\gamma } (F) < 0$
. If E is not semistable, we say it is unstable.
$p_{\gamma } (F) < 0$
. If E is not semistable, we say it is unstable.
In order for the stack of semistable objects to be of DT type, we will need to consider stability conditions satisfying certain properties.
Definition 6.2 (Nice stability condition)
Given a stability condition
![]() $\sigma $
on
$\sigma $
on
![]() $D^b(\mathop{\mathrm {Coh}}\nolimits W)$
, let
$D^b(\mathop{\mathrm {Coh}}\nolimits W)$
, let
![]() $\mathcal {M}$
be the stack of
$\mathcal {M}$
be the stack of
![]() $\sigma $
-semistable objects in
$\sigma $
-semistable objects in
![]() $\mathcal {P}_{\mathcal {A}}^{\gamma }$
. We say that
$\mathcal {P}_{\mathcal {A}}^{\gamma }$
. We say that
![]() $\sigma $
is nice if the following hold:
$\sigma $
is nice if the following hold:
-
1.
 $\mathcal {M}$
is an Artin stack of finite type.
$\mathcal {M}$
is an Artin stack of finite type. -
2.
 $\mathcal {M}$
is an open substack of
$\mathcal {M}$
is an open substack of
 $\mathop{\mathrm {Perf}}\nolimits (W)$
.
$\mathop{\mathrm {Perf}}\nolimits (W)$
. -
3.
 $\mathcal {M}$
satisfies the existence part of the valuative criterion of properness. We then say that
$\mathcal {M}$
satisfies the existence part of the valuative criterion of properness. We then say that
 $\mathcal {M}$
is quasi-proper or universally closed.
$\mathcal {M}$
is quasi-proper or universally closed.
Remark 6.1. The following are examples of nice stability conditions, by the results of the mentioned authors:
-
1. A Bridgeland stability condition in the sense of Piyaratne–Toda [Reference Piyaratne and TodaPT19] and Li [Reference LiLi19].
-
2. A polynomial stability condition in the sense of Lo [Reference LoLo11, Reference LoLo13].
-
3. Gieseker and slope stability. These are examples of a weak stability condition in the sense of Joyce–Song [Reference Joyce and SongJS12, Definition 3.5], where we take
 $\mathcal {A} = \mathop{\mathrm { Coh}}\nolimits W$
and
$\mathcal {A} = \mathop{\mathrm { Coh}}\nolimits W$
and
 $K(A) = N(W)$
.
$K(A) = N(W)$
.
6.2 Moduli stacks of semistable complexes are of DT type
The following theorem is an application of [Reference Alper, Halpern-Leistner and HeinlothAHH18, Theorem 7.25] to our context.
Theorem 6.2. Let
![]() $\sigma $
be a nice stability condition on
$\sigma $
be a nice stability condition on
![]() $D^b(\mathop{\mathrm {Coh}}\nolimits W)$
, and let
$D^b(\mathop{\mathrm {Coh}}\nolimits W)$
, and let
![]() $\mathcal {M}$
denote the stack of
$\mathcal {M}$
denote the stack of
![]() $\sigma $
-semistable complexes. Then
$\sigma $
-semistable complexes. Then
![]() $\mathcal {M}$
is an Artin stack of DT type with proper good moduli space M and affine diagonal.
$\mathcal {M}$
is an Artin stack of DT type with proper good moduli space M and affine diagonal.
Proof. By the niceness of
![]() $\sigma $
,
$\sigma $
,
![]() $\mathcal {M}$
is of finite type. By the results of [Reference Pantev, Toën, Vaquié and VezzosiPTVV13],
$\mathcal {M}$
is of finite type. By the results of [Reference Pantev, Toën, Vaquié and VezzosiPTVV13],
![]() $\mathop{\mathrm {Perf}}\nolimits (W)$
is the truncation of a
$\mathop{\mathrm {Perf}}\nolimits (W)$
is the truncation of a
![]() $(-1)$
-shifted symplectic derived Artin stack. Since
$(-1)$
-shifted symplectic derived Artin stack. Since
![]() $\mathcal {M}$
is an open substack of
$\mathcal {M}$
is an open substack of
![]() $\mathop{\mathrm {Perf}}\nolimits (W)$
, it is also such a truncation. By [Reference Alper, Halpern-Leistner and HeinlothAHH18, Theorem 7.25],
$\mathop{\mathrm {Perf}}\nolimits (W)$
, it is also such a truncation. By [Reference Alper, Halpern-Leistner and HeinlothAHH18, Theorem 7.25],
![]() $\mathcal {M}$
admits a good moduli space
$\mathcal {M}$
admits a good moduli space
![]() $\pi \colon \mathcal {M} \to M$
such that M is separated. By Proposition 3.2,
$\pi \colon \mathcal {M} \to M$
such that M is separated. By Proposition 3.2,
![]() $\pi $
is universally closed and since
$\pi $
is universally closed and since
![]() $\mathcal {M}$
is universally closed as well, it follows that M is universally closed. Thus, M must be proper.
$\mathcal {M}$
is universally closed as well, it follows that M is universally closed. Thus, M must be proper.
![]() $\mathcal {M}$
has affine diagonal by [Reference Alper, Halpern-Leistner and HeinlothAHH18, Lemma 7.19].
$\mathcal {M}$
has affine diagonal by [Reference Alper, Halpern-Leistner and HeinlothAHH18, Lemma 7.19].
6.3
 $\mathbb {C}^{\ast }$
-rigidified intrinsic stabilizer reduction
$\mathbb {C}^{\ast }$
-rigidified intrinsic stabilizer reduction
Let
![]() $\mathcal {M}$
be as in Theorem 6.2. We denote
$\mathcal {M}$
be as in Theorem 6.2. We denote
![]() $T = \mathbb {C}^{\ast }$
.
$T = \mathbb {C}^{\ast }$
.
To obtain a meaningful nonzero DT invariant, it will be necessary to rigidify the
![]() $\mathbb {C}^{\ast }$
-scaling automorphisms of objects in
$\mathbb {C}^{\ast }$
-scaling automorphisms of objects in
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
For each family of complexes
![]() $E_S \in \mathcal {M}(S)$
, there exists an embedding
$E_S \in \mathcal {M}(S)$
, there exists an embedding
which is compatible with pullbacks and moreover
![]() $\mathbb {G}_m (S)$
is central. In the terminology used in [Reference Abramovich, Graber and VistoliAGV08], we say that
$\mathbb {G}_m (S)$
is central. In the terminology used in [Reference Abramovich, Graber and VistoliAGV08], we say that
![]() $\mathcal {M}$
has a
$\mathcal {M}$
has a
![]() $\mathbb {G}_m$
-2-structure.
$\mathbb {G}_m$
-2-structure.
Using the results of [Reference Abramovich, Olsson and VistoliAOV08] or [Reference Abramovich, Graber and VistoliAGV08], we may take the
![]() $\mathbb {G}_m$
-rigification
$\mathbb {G}_m$
-rigification
![]() of
of
![]() $\mathcal {M}$
. From the properties of rigification, for any point
$\mathcal {M}$
. From the properties of rigification, for any point
![]() $x \in {\mathcal {M}}$
, one has
$x \in {\mathcal {M}}$
, one has
![]() . In particular, if
. In particular, if
![]() $x \in \mathcal {M}^s$
is stable, then
$x \in \mathcal {M}^s$
is stable, then
![]() .
.
Even though
![]() is not a stack of DT type, we show in the next two propositions that we can construct its intrinsic stabilizer reduction and equip it with a semiperfect obstruction theory of virtual dimension zero.
is not a stack of DT type, we show in the next two propositions that we can construct its intrinsic stabilizer reduction and equip it with a semiperfect obstruction theory of virtual dimension zero.
Proposition 6.3.
![]() satisfies the conditions of Theorem 4.9. It thus admits an intrinsic stabilizer reduction, which we denote by
satisfies the conditions of Theorem 4.9. It thus admits an intrinsic stabilizer reduction, which we denote by
![]() $\widetilde {\mathcal {M}}^{\mathbb {C}^*}$
.
$\widetilde {\mathcal {M}}^{\mathbb {C}^*}$
.
Proof. By [Reference RomagnyRom05, Theorem 5.1] or [Reference Abramovich, Olsson and VistoliAOV08, Theorem C.1.1],
![]() has the same good moduli space M. Since the morphism
has the same good moduli space M. Since the morphism
![]() is a
is a
![]() $\mathbb {G}_m$
-gerbe, it follows that
$\mathbb {G}_m$
-gerbe, it follows that
![]() and the good moduli space morphism
and the good moduli space morphism
![]() have affine diagonal.
have affine diagonal.
Proposition 6.4.
![]() is equipped with a VC package.
is equipped with a VC package.
Proof.
![]() $\mathcal {M}$
is a stack of DT type and hence admits a VC package by Setup 5.8. By the existence of the
$\mathcal {M}$
is a stack of DT type and hence admits a VC package by Setup 5.8. By the existence of the
![]() $\mathbb {G}_m$
-2-structure, T naturally embeds in each stabilizer group
$\mathbb {G}_m$
-2-structure, T naturally embeds in each stabilizer group
![]() $G_x$
. Replacing all such groups by their quotients
$G_x$
. Replacing all such groups by their quotients
![]() $G_x / T$
, we obtain a VC package for
$G_x / T$
, we obtain a VC package for
![]() .
.
Remark 6.5. In the case of semistable sheaves treated in [Reference Kiem, Li and SavvasKLS17], rigidification is much simpler since the moduli stack is a global GIT quotient stack
![]() $\mathcal {M} = [ X / G ]$
, where
$\mathcal {M} = [ X / G ]$
, where
![]() ${G = \mathop{\mathrm {GL}}\nolimits (N, \mathbb {C})}$
, and then one may work with
${G = \mathop{\mathrm {GL}}\nolimits (N, \mathbb {C})}$
, and then one may work with
![]() $[ X / \mathrm {PGL} (N, \mathbb {C}) ]$
as the
$[ X / \mathrm {PGL} (N, \mathbb {C}) ]$
as the
![]() $\mathbb {G}_m$
-rigidication.
$\mathbb {G}_m$
-rigidication.
We thus obtain the following.
Theorem-Definition 6.6.
![]() $\widetilde {\mathcal {M}}^{\mathbb {C}^*}$
is called the
$\widetilde {\mathcal {M}}^{\mathbb {C}^*}$
is called the
![]() $\mathbb {C}^{\ast }$
-rigidified intrinsic stabilizer reduction of
$\mathbb {C}^{\ast }$
-rigidified intrinsic stabilizer reduction of
![]() $\mathcal {M}$
. It is a proper DM stack with a semiperfect obstruction theory of virtual dimension zero.
$\mathcal {M}$
. It is a proper DM stack with a semiperfect obstruction theory of virtual dimension zero.
Proof. For properness, the good moduli space
![]() $q \colon \widetilde {\mathcal {M}}^{\mathbb {C}^{\ast }} \to \widetilde {M}^{\mathbb {C}^{\ast }}$
is proper. Since M is proper and
$q \colon \widetilde {\mathcal {M}}^{\mathbb {C}^{\ast }} \to \widetilde {M}^{\mathbb {C}^{\ast }}$
is proper. Since M is proper and
![]() $\widetilde {M}^{\mathbb {C}^{\ast }}$
is proper over M,
$\widetilde {M}^{\mathbb {C}^{\ast }}$
is proper over M,
![]() $\widetilde {\mathcal {M}}^{\mathbb {C}^{\ast }}$
is proper.
$\widetilde {\mathcal {M}}^{\mathbb {C}^{\ast }}$
is proper.
Everything else follows from Theorems 5.9, 5.10 as applied in the proof of Theorem 5.11.
Remark 6.7. By identical reasoning, all of the above hold in greater generality when
![]() $\mathcal {M}$
is an Artin stack of DT type with a
$\mathcal {M}$
is an Artin stack of DT type with a
![]() $\mathbb {G}_m$
-2-structure.
$\mathbb {G}_m$
-2-structure.
6.4 Generalized DT invariants via Kirwan blowups
Suppose as before that
![]() $\mathcal {M}$
is an Artin stack of DT type parametrizing
$\mathcal {M}$
is an Artin stack of DT type parametrizing
![]() $\sigma $
-semistable objects in a heart
$\sigma $
-semistable objects in a heart
![]() $\mathcal {A}$
of a t-structure on
$\mathcal {A}$
of a t-structure on
![]() $D^b(\mathop{\mathrm {Coh}}\nolimits W)$
with Chern character
$D^b(\mathop{\mathrm {Coh}}\nolimits W)$
with Chern character
![]() $\gamma $
, for a nice stability condition
$\gamma $
, for a nice stability condition
![]() $\sigma $
. Then, by Theorem-Definition 6.6, there is an induced
$\sigma $
. Then, by Theorem-Definition 6.6, there is an induced
![]() $\mathbb {C}^{\ast }$
-rigidified intrinsic stabilizer reduction
$\mathbb {C}^{\ast }$
-rigidified intrinsic stabilizer reduction
![]() $\widetilde {\mathcal {M}}^{\mathbb {C}^{\ast }}$
with a good moduli space
$\widetilde {\mathcal {M}}^{\mathbb {C}^{\ast }}$
with a good moduli space
![]() $\widetilde {M}^{\mathbb {C}^{\ast }}$
and an induced semiperfect obstruction theory and virtual cycle of dimension zero. We can now state the main theorem of this paper.
$\widetilde {M}^{\mathbb {C}^{\ast }}$
and an induced semiperfect obstruction theory and virtual cycle of dimension zero. We can now state the main theorem of this paper.
Theorem-Definition 6.8. Let W be a smooth, projective Calabi–Yau threefold,
![]() $\sigma $
a nice stability condition on a heart
$\sigma $
a nice stability condition on a heart
![]() $\mathcal {A} \subset D^b (\mathop{\mathrm {Coh}}\nolimits W)$
of a t-structure, as in Definition 6.1,
$\mathcal {A} \subset D^b (\mathop{\mathrm {Coh}}\nolimits W)$
of a t-structure, as in Definition 6.1,
![]() $\gamma \in H^*(W)$
, and let
$\gamma \in H^*(W)$
, and let
![]() $\mathcal {M}$
denote the stack parametrizing
$\mathcal {M}$
denote the stack parametrizing
![]() $\sigma $
-semistable complexes with Chern character
$\sigma $
-semistable complexes with Chern character
![]() $\gamma $
. Then we may define the associated generalized Donaldson–Thomas invariant via Kirwan blowups (DTK invariant) as
$\gamma $
. Then we may define the associated generalized Donaldson–Thomas invariant via Kirwan blowups (DTK invariant) as
Remark 6.9. In [Reference Kiem and SavvasKS21], the results of [Reference Kiem, Li and SavvasKLS17] and the present paper are refined to define a virtual structure sheaf
![]() $[\mathcal {O}_{\widetilde {\mathcal {M}}}^{\mathrm {vir}}] \in K_0(\widetilde {\mathcal {M}}^{\mathbb {C}^{\ast }})$
and a corresponding K-theoretic generalized DTK invariant.
$[\mathcal {O}_{\widetilde {\mathcal {M}}}^{\mathrm {vir}}] \in K_0(\widetilde {\mathcal {M}}^{\mathbb {C}^{\ast }})$
and a corresponding K-theoretic generalized DTK invariant.
6.5 Relative theory and deformation invariance
Let C be a smooth quasi-projective scheme over
![]() $\mathbb {C}$
and
$\mathbb {C}$
and
![]() $W \to C$
a smooth, projective family of Calabi–Yau threefolds. Without loss of generality, we assume that
$W \to C$
a smooth, projective family of Calabi–Yau threefolds. Without loss of generality, we assume that
![]() $H^*(W_t, \mathbb {Q})$
stays constant for
$H^*(W_t, \mathbb {Q})$
stays constant for
![]() $t \in C$
and identify it with
$t \in C$
and identify it with
![]() $H^*(W_0, \mathbb {Q})$
, where
$H^*(W_0, \mathbb {Q})$
, where
![]() $W_0$
is the fiber of the family over a point
$W_0$
is the fiber of the family over a point
![]() $0 \in C$
. Let
$0 \in C$
. Let
![]() $\gamma \in H^*(W_0, \mathbb {Q})$
. Moreover, let
$\gamma \in H^*(W_0, \mathbb {Q})$
. Moreover, let
![]() $\mathop{\mathrm {Perf}}\nolimits (W/S)$
denote the stack of (universally gluable) perfect complexes on the morphism
$\mathop{\mathrm {Perf}}\nolimits (W/S)$
denote the stack of (universally gluable) perfect complexes on the morphism
![]() $W \to C$
as in [Reference LieblichLie06].
$W \to C$
as in [Reference LieblichLie06].
We consider families
![]() $\sigma $
of stability conditions
$\sigma $
of stability conditions
![]() $\sigma _t$
, where, for each
$\sigma _t$
, where, for each
![]() $t \in C$
,
$t \in C$
,
![]() $\sigma _t$
is a stability condition on
$\sigma _t$
is a stability condition on
![]() $D^b(\mathop{\mathrm {Coh}}\nolimits W_t)$
as in Definition 6.2 with Chern character
$D^b(\mathop{\mathrm {Coh}}\nolimits W_t)$
as in Definition 6.2 with Chern character
![]() $\gamma \in H^*(W_t, \mathbb {Q}) = H^*(W_0, \mathbb {Q})$
. Let
$\gamma \in H^*(W_t, \mathbb {Q}) = H^*(W_0, \mathbb {Q})$
. Let
![]() $\mathcal {M} \to C$
be the stack parametrizing relatively semistable objects in
$\mathcal {M} \to C$
be the stack parametrizing relatively semistable objects in
![]() $D^b(\mathop{\mathrm {Coh}}\nolimits W)$
, that is, perfect complexes E such that the derived restriction
$D^b(\mathop{\mathrm {Coh}}\nolimits W)$
, that is, perfect complexes E such that the derived restriction
![]() $E_t := E|_{W_t}$
is
$E_t := E|_{W_t}$
is
![]() $\sigma _t$
-semistable for all
$\sigma _t$
-semistable for all
![]() $t \in C$
. We require that the conditions characterizing a nice stability condition hold relative to the base C as follows.
$t \in C$
. We require that the conditions characterizing a nice stability condition hold relative to the base C as follows.
Setup 6.10. We say that the family of stability conditions
![]() $\sigma _t$
is nice if the following hold.
$\sigma _t$
is nice if the following hold.
-
1.
 $\mathcal {M}$
is an Artin stack of finite type.
$\mathcal {M}$
is an Artin stack of finite type. -
2.
 $\mathcal {M}$
is an open substack of
$\mathcal {M}$
is an open substack of
 $\mathop{\mathrm {Perf}}\nolimits (W/C)$
.
$\mathop{\mathrm {Perf}}\nolimits (W/C)$
. -
3.
 $\mathcal {M} \to C$
admits a good moduli space
$\mathcal {M} \to C$
admits a good moduli space
 $M \to C$
, proper over C.
$M \to C$
, proper over C.
Remark 6.11. When we have a GIT description of
![]() $\mathcal {M} \to C$
, then the above conditions are satisfied. This is the case for Gieseker and slope stability of coherent sheaves.
$\mathcal {M} \to C$
, then the above conditions are satisfied. This is the case for Gieseker and slope stability of coherent sheaves.
When we are in the situation of the above setup, all of our results extend to the relative case.
Theorem 6.12. Let
![]() $W \to C$
be a smooth, projective family of Calabi–Yau threefolds over a smooth, quasi-projective scheme C,
$W \to C$
be a smooth, projective family of Calabi–Yau threefolds over a smooth, quasi-projective scheme C,
![]() $\lbrace \sigma _t \rbrace _{t \in C}$
a nice family of stability conditions on
$\lbrace \sigma _t \rbrace _{t \in C}$
a nice family of stability conditions on
![]() $D^b( \mathop{\mathrm {Coh}}\nolimits W)$
,
$D^b( \mathop{\mathrm {Coh}}\nolimits W)$
,
![]() $\gamma \in H^*(W_0, \mathbb {Q})$
and
$\gamma \in H^*(W_0, \mathbb {Q})$
and
![]() $\mathcal {M} \to C$
the stack of fiberwise
$\mathcal {M} \to C$
the stack of fiberwise
![]() $\sigma _t$
-semistable objects of Chern character
$\sigma _t$
-semistable objects of Chern character
![]() $\gamma $
in
$\gamma $
in
![]() $D^b(\mathop{\mathrm {Coh}}\nolimits W)$
.
$D^b(\mathop{\mathrm {Coh}}\nolimits W)$
.
Then there exists an induced
![]() $\mathbb {C}^{\ast }$
-rigidified intrinsic stabilizer reduction
$\mathbb {C}^{\ast }$
-rigidified intrinsic stabilizer reduction
![]() $\widetilde {\mathcal {M}} \to C$
, a DM stack proper over C, endowed with a semiperfect obstruction theory and a virtual fundamental cycle
$\widetilde {\mathcal {M}} \to C$
, a DM stack proper over C, endowed with a semiperfect obstruction theory and a virtual fundamental cycle
![]() $[\widetilde {\mathcal {M}}]^{\mathrm {vir}} \in A_0(\widetilde {\mathcal {M}})$
.
$[\widetilde {\mathcal {M}}]^{\mathrm {vir}} \in A_0(\widetilde {\mathcal {M}})$
.
Moreover, the fiber
![]() $\widetilde {\mathcal {M}}_t$
over
$\widetilde {\mathcal {M}}_t$
over
![]() $t \in C$
is the
$t \in C$
is the
![]() $\mathbb {C}^{\ast }$
-rigidified intrinsic stabilizer reduction of
$\mathbb {C}^{\ast }$
-rigidified intrinsic stabilizer reduction of
![]() $\mathcal {M}_t$
and the obstruction theory pulls back to the one constructed in the absolute case so that if
$\mathcal {M}_t$
and the obstruction theory pulls back to the one constructed in the absolute case so that if
![]() $i_t \colon \widetilde {\mathcal {M}}_t \to \widetilde {\mathcal {M}}$
is the inclusion, we have
$i_t \colon \widetilde {\mathcal {M}}_t \to \widetilde {\mathcal {M}}$
is the inclusion, we have
Proof. This is the generalization of [Reference Kiem, Li and SavvasKLS17, Theorem 7.17] adapted to our context. We briefly explain the steps and necessary changes.
![]() $\mathcal {M}$
admits a
$\mathcal {M}$
admits a
![]() $\mathbb {G}_m$
-2-structure. By conditions (1) and (3) of Setup 6.10,
$\mathbb {G}_m$
-2-structure. By conditions (1) and (3) of Setup 6.10,
![]() satisfies the conditions of Theorem 4.9, so using Proposition 6.3 we obtain the
satisfies the conditions of Theorem 4.9, so using Proposition 6.3 we obtain the
![]() $\mathbb {C}^{\ast }$
-rigidified intrinsic stabilizer reduction
$\mathbb {C}^{\ast }$
-rigidified intrinsic stabilizer reduction
![]() $\widetilde {\mathcal {M}}^{\mathbb {C}^{\ast }} \to \mathcal {M} \to C$
.
$\widetilde {\mathcal {M}}^{\mathbb {C}^{\ast }} \to \mathcal {M} \to C$
.
To see that the fiber over
![]() $t \in C$
is
$t \in C$
is
![]() $\widetilde {\mathcal {M}}_t^{\mathbb {C}^{\ast }}$
, observe that by definition
$\widetilde {\mathcal {M}}_t^{\mathbb {C}^{\ast }}$
, observe that by definition
![]() $\widetilde {\mathcal {M}}^{\mathbb {C}^{\ast }}$
is obtained by taking iterated Kirwan blowups of a cover by strongly étale quotient charts (where
$\widetilde {\mathcal {M}}^{\mathbb {C}^{\ast }}$
is obtained by taking iterated Kirwan blowups of a cover by strongly étale quotient charts (where
![]() $T = \mathbb {C}^{\ast }$
)
$T = \mathbb {C}^{\ast }$
)

Taking fibers over
![]() $t \in C$
, we obtain a cover of
$t \in C$
, we obtain a cover of
![]() by strongly étale quotient charts, so it suffices to show that
by strongly étale quotient charts, so it suffices to show that
![]() $(\widehat {\mathcal {N}}_x)_t = \widehat {(\mathcal {N}_x)}_t$
. But this is true by the same argument used in the proof of [Reference Kiem, Li and SavvasKLS17, Proposition 7.4].
$(\widehat {\mathcal {N}}_x)_t = \widehat {(\mathcal {N}_x)}_t$
. But this is true by the same argument used in the proof of [Reference Kiem, Li and SavvasKLS17, Proposition 7.4].
Constructing the obstruction theory of
![]() $\widetilde {\mathcal {M}}^{\mathbb {C}^{\ast }}$
is slightly more subtle. First, we observe that there is an obvious generalization of Setup-Definition 5.2 to define local model structures on G-schemes U over the base scheme C, cf. [Reference Kiem, Li and SavvasKLS17, Definition 7.11].
$\widetilde {\mathcal {M}}^{\mathbb {C}^{\ast }}$
is slightly more subtle. First, we observe that there is an obvious generalization of Setup-Definition 5.2 to define local model structures on G-schemes U over the base scheme C, cf. [Reference Kiem, Li and SavvasKLS17, Definition 7.11].
Using the fact that the morphism
![]() $\mathcal {M} \to C$
is the truncation of a
$\mathcal {M} \to C$
is the truncation of a
![]() $(-1)$
-shifted symplectic derived stack over C, we can show that
$(-1)$
-shifted symplectic derived stack over C, we can show that
![]() admits a VC package, as in Setup 5.8. The only difference is that, now in equation (5.10), we have
admits a VC package, as in Setup 5.8. The only difference is that, now in equation (5.10), we have
![]() $F_{V_x} = \Omega _{V_x/C}$
and
$F_{V_x} = \Omega _{V_x/C}$
and
![]() $\omega _{V_x}$
is a
$\omega _{V_x}$
is a
![]() $G_x$
-invariant
$G_x$
-invariant
![]() $1$
-form, and similarly in equation (5.12),
$1$
-form, and similarly in equation (5.12),
![]() $F_{S_z} = \Omega _{S_z / C}$
and
$F_{S_z} = \Omega _{S_z / C}$
and
![]() $\omega _{S_z}$
is a
$\omega _{S_z}$
is a
![]() $G_z$
-invariant
$G_z$
-invariant
![]() $1$
-form. The construction of the VC package follows verbatim the reasoning of Subsections 7.2 and 7.3 in [Reference Kiem, Li and SavvasKLS17]. We refer the reader there for details.
$1$
-form. The construction of the VC package follows verbatim the reasoning of Subsections 7.2 and 7.3 in [Reference Kiem, Li and SavvasKLS17]. We refer the reader there for details.
Finally, to see that the restriction of the semiperfect obstruction theory of
![]() $\widetilde {\mathcal {M}}^{\mathbb {C}^{\ast }}$
to
$\widetilde {\mathcal {M}}^{\mathbb {C}^{\ast }}$
to
![]() $\widetilde {\mathcal {M}}^{\mathbb {C}^{\ast }}_t$
agrees with the absolute semiperfect obstruction theory constructed using the d-critical structure of
$\widetilde {\mathcal {M}}^{\mathbb {C}^{\ast }}_t$
agrees with the absolute semiperfect obstruction theory constructed using the d-critical structure of
![]() , we use the fact that for any choice of relative local models in the VC package of
, we use the fact that for any choice of relative local models in the VC package of
![]() , the sections
, the sections
![]() $\omega _{V_x}$
can be taken so that
$\omega _{V_x}$
can be taken so that
![]() $\omega _{V_x}|_{(V_x)_t}$
is
$\omega _{V_x}|_{(V_x)_t}$
is
![]() $\Omega $
-equivalent to an exact
$\Omega $
-equivalent to an exact
![]() $1$
-form
$1$
-form
![]() $df_x$
induced by the d-critical structure of
$df_x$
induced by the d-critical structure of
![]() . As a consequence of properties of
. As a consequence of properties of
![]() $\Omega $
-equivalence (cf. [Reference Kiem, Li and SavvasKLS17, Lemma 5.14]), the construction of the semiperfect obstruction theory of
$\Omega $
-equivalence (cf. [Reference Kiem, Li and SavvasKLS17, Lemma 5.14]), the construction of the semiperfect obstruction theory of
![]() $\widetilde {\mathcal {M}}^{\mathbb {C}^{\ast }}_t$
can be performed equivalently using
$\widetilde {\mathcal {M}}^{\mathbb {C}^{\ast }}_t$
can be performed equivalently using
![]() $\omega _{V_x}|_{(V_x)_t}$
instead of
$\omega _{V_x}|_{(V_x)_t}$
instead of
![]() $df_x$
in the VC package of
$df_x$
in the VC package of
![]() . The necessary arguments are carried out in detail in [Reference Kiem, Li and SavvasKLS17, Subsection 7.4].
. The necessary arguments are carried out in detail in [Reference Kiem, Li and SavvasKLS17, Subsection 7.4].
In the case of Bridgeland stability conditions constructed in [Reference Piyaratne and TodaPT19] and [Reference LiLi19], the results of [Reference Bayer, Lahoz, Macrì, Nuer, Perry and StellariBLM+21] imply that we get nice families of Bridgeland stability conditions.
As an immediate corollary, we have the following theorem.
Theorem 6.13. The generalized DT invariant via Kirwan blowups for
![]() $\sigma $
-semistable objects on Calabi–Yau threefolds, where
$\sigma $
-semistable objects on Calabi–Yau threefolds, where
![]() $\sigma $
is a Bridgeland stability condition as in [Reference Piyaratne and TodaPT19] and [Reference LiLi19], is invariant under deformations of the complex structure of the Calabi–Yau threefold.
$\sigma $
is a Bridgeland stability condition as in [Reference Piyaratne and TodaPT19] and [Reference LiLi19], is invariant under deformations of the complex structure of the Calabi–Yau threefold.
Remark 6.14. In the case of Gieseker stability and slope stability of coherent sheaves, deformation invariance follows directly from the results of [Reference Kiem, Li and SavvasKLS17].
Acknowledgments
The author would like to thank his advisor Jun Li for introducing him to the subject, his constant encouragement and many enlightening discussions during the course of the completion of this work. He also benefited greatly by conversations with Jarod Alper, Jack Hall, Daniel Halpern-Leistner, Young-Hoon Kiem, Alex Perry, David Rydh and Ravi Vakil.
Competing Interests
The author(s) declare none.