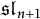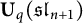1 Introduction
The classification of finite-dimensional irreducible representations of quantum affine algebras was given in [Reference Chari and Pressley9, Reference Chari and Pressley10] in terms of Drinfeld polynomials. However, generically the structure of these representations is far from being understood. Not even dimension formulas exist in contrast to the classical cases except for particular families of modules, e.g., (quantum) local Weyl modules, Kirillov–Reshetikhin (KR) modules (in short: KR modules) or minimal affinizations (see [Reference Chari and Pressley11, Reference Hernandez16, Reference Hernandez17, Reference Nakajima27] for instance). A well-established method to study these representations is to pass from quantum level to classical level by forming their classical limit (see, for instance, [Reference Chari and Pressley11, Section 4] for a sufficient condition for the existence of the classical limit). When the limit exists, it is a finite-dimensional module for the corresponding affine Lie algebra and hence a representation for the underlying standard maximal parabolic subalgebra – the current algebra. After a suitable twist, which is referred to as the graded limit in the literature, many interesting families of graded representations of current algebras appear in this way. Among them are the KR modules for current algebras (see [Reference Chari and Moura8, Reference Di Francesco and Kedem13, Reference Kedem21]) and their fusion products [Reference Naoi28] and also generalized Demazure modules appear in this context. Inspired by the results of [Reference Ardonne and Kedem1, Reference Ardonne, Kedem and Stone2, Reference Naoi28] the motivation of this paper is to fully understand the graded decompositions of the graded limits of the prime irreducible objects in the Hernandez–Leclerc (HL) category.
Let
![]() $\mathfrak {g}$
be the finite-dimensional complex simple Lie algebra
$\mathfrak {g}$
be the finite-dimensional complex simple Lie algebra
![]() $\mathfrak {sl}_{n+1}$
. In the seminal paper of HL [Reference Hernandez and Leclerc18], the authors presented an interesting subcategory
$\mathfrak {sl}_{n+1}$
. In the seminal paper of HL [Reference Hernandez and Leclerc18], the authors presented an interesting subcategory
![]() $\mathcal {C}_{q,\kappa }$
of the category of all finite-dimensional representations depending on a height function
$\mathcal {C}_{q,\kappa }$
of the category of all finite-dimensional representations depending on a height function
![]() $\kappa $
. Their main result states that
$\kappa $
. Their main result states that
![]() $\mathcal {C}_{q,\kappa }$
is closed under tensor products and categorifies a cluster algebra of the same type. The prime irreducible objects in that category, i.e., the ones which are not isomorphic to a tensor product of non-trivial representations, correspond precisely to the cluster variables and the frozen variables correspond to minimal affinizations. Moreover, an explicit description of the prime objects in terms of Drinfeld polynomials is given in [Reference Brito and Chari6, Reference Hernandez and Leclerc19] (see also Theorem 3) and their graded limits are isomorphic to stable prime Demazure modules in level two integrable highest weight representations [Reference Brito, Chari and Moura7]. In this paper, we give a description of the structure of these objects viewed as representations for the Hopf subalgebra
$\mathcal {C}_{q,\kappa }$
is closed under tensor products and categorifies a cluster algebra of the same type. The prime irreducible objects in that category, i.e., the ones which are not isomorphic to a tensor product of non-trivial representations, correspond precisely to the cluster variables and the frozen variables correspond to minimal affinizations. Moreover, an explicit description of the prime objects in terms of Drinfeld polynomials is given in [Reference Brito and Chari6, Reference Hernandez and Leclerc19] (see also Theorem 3) and their graded limits are isomorphic to stable prime Demazure modules in level two integrable highest weight representations [Reference Brito, Chari and Moura7]. In this paper, we give a description of the structure of these objects viewed as representations for the Hopf subalgebra
![]() $\mathbf {U}_q(\mathfrak {sl}_{n+1})$
.
$\mathbf {U}_q(\mathfrak {sl}_{n+1})$
.
For a finite-dimensional graded representation V for the current algebra with rth graded piece
![]() $V[r]$
, we denote by
$V[r]$
, we denote by
![]() $\tau _p^{*}V$
the graded vector space whose rth graded piece is
$\tau _p^{*}V$
the graded vector space whose rth graded piece is
![]() $V[r-p]$
. We encode the graded multiplicities as polynomials in an indeterminate q as follows:
$V[r-p]$
. We encode the graded multiplicities as polynomials in an indeterminate q as follows:
 $$ \begin{align*}\big[V: V(\mu)\big]_q= \sum_{p=0}^{\infty}\ [V: \tau_p^{*}V(\mu)] \cdot q^p.\end{align*} $$
$$ \begin{align*}\big[V: V(\mu)\big]_q= \sum_{p=0}^{\infty}\ [V: \tau_p^{*}V(\mu)] \cdot q^p.\end{align*} $$
Our aim is to determine these polynomials for a wide class of graded representations. In Section 4, we introduce the modules
![]() $M_{\boldsymbol \xi ,\lambda }$
depending on a pair
$M_{\boldsymbol \xi ,\lambda }$
depending on a pair
![]() $(\boldsymbol \xi ,\lambda )$
where
$(\boldsymbol \xi ,\lambda )$
where
![]() $\lambda $
is a dominant integral weight and
$\lambda $
is a dominant integral weight and
![]() $\boldsymbol \xi $
is a tuple of nonnegative integers indexed by the positive roots of
$\boldsymbol \xi $
is a tuple of nonnegative integers indexed by the positive roots of
![]() $\mathfrak {g}$
. Special choices of
$\mathfrak {g}$
. Special choices of
![]() $M_{\boldsymbol \xi ,\lambda }$
give many well-known families of representations such as truncated Weyl modules (see [Reference Barth and Kus3, Reference Fourier, Martins and Moura15, Reference Kus and Littelmann23] for instance) or the graded limits of certain representations for quantum affine algebras. We first describe the
$M_{\boldsymbol \xi ,\lambda }$
give many well-known families of representations such as truncated Weyl modules (see [Reference Barth and Kus3, Reference Fourier, Martins and Moura15, Reference Kus and Littelmann23] for instance) or the graded limits of certain representations for quantum affine algebras. We first describe the
![]() $\mathbf {U}^{-}$
structure of these representations in Proposition 4.2 by generators and relations. Subsequently, using the dual functional realization of loop algebras and the methods developed in [Reference Ardonne and Kedem1, Reference Ardonne, Kedem and Stone2], we give a functional description of the graded multiplicities of
$\mathbf {U}^{-}$
structure of these representations in Proposition 4.2 by generators and relations. Subsequently, using the dual functional realization of loop algebras and the methods developed in [Reference Ardonne and Kedem1, Reference Ardonne, Kedem and Stone2], we give a functional description of the graded multiplicities of
![]() $M_{\boldsymbol \xi ,\lambda }$
in Theorem 5. This space of functions can be always identified with a subalgebra (sometimes a representation) of the Cohomological Hall algebra (CoHA) of a quiver which was introduced by Kontsevich and Soibelman in [Reference Kontsevich and Soibelman22]. As of now, there are very few examples of modules or of subalgebras of the CoHA, so that this connection could be of independent interest; the details will appear elsewhere.
$M_{\boldsymbol \xi ,\lambda }$
in Theorem 5. This space of functions can be always identified with a subalgebra (sometimes a representation) of the Cohomological Hall algebra (CoHA) of a quiver which was introduced by Kontsevich and Soibelman in [Reference Kontsevich and Soibelman22]. As of now, there are very few examples of modules or of subalgebras of the CoHA, so that this connection could be of independent interest; the details will appear elsewhere.
Our goal is to figure out more explicit descriptions of these multiplicities, for example, combinatorial parametrizations; however, this question seems to be quite challenging for arbitrary pairs
![]() $(\boldsymbol \xi ,\lambda )$
. One possible explanation is the following. If
$(\boldsymbol \xi ,\lambda )$
. One possible explanation is the following. If
![]() $\boldsymbol {\xi }$
is a constant tuple, say each entry is equal to N, and
$\boldsymbol {\xi }$
is a constant tuple, say each entry is equal to N, and
![]() $\lambda =N\mu $
for a dominant integral weight
$\lambda =N\mu $
for a dominant integral weight
![]() $\mu $
, then the numerical multiplicity
$\mu $
, then the numerical multiplicity
![]() $[M_{\boldsymbol {\xi },\lambda }: V(\nu )]_{q=1}$
is exactly the Littlewood–Richardson coefficient describing how often
$[M_{\boldsymbol {\xi },\lambda }: V(\nu )]_{q=1}$
is exactly the Littlewood–Richardson coefficient describing how often
![]() $V(\nu )$
appears inside the tensor product
$V(\nu )$
appears inside the tensor product
![]() $V(\mu )^{\otimes N}$
(see [Reference Kus and Littelmann23] for instance).
$V(\mu )^{\otimes N}$
(see [Reference Kus and Littelmann23] for instance).
The main result of the paper gives a description of the graded multiplicities (see Theorem 4) of the graded limits
![]() $L(\boldsymbol {\pi })$
in terms of lattice points of convex polytopes when
$L(\boldsymbol {\pi })$
in terms of lattice points of convex polytopes when
![]() $\boldsymbol {\pi }$
is the Drinfeld polynomial whose corresponding representation
$\boldsymbol {\pi }$
is the Drinfeld polynomial whose corresponding representation
![]() $V_q(\boldsymbol {\pi })$
is a prime irreducible object in
$V_q(\boldsymbol {\pi })$
is a prime irreducible object in
![]() $\mathcal {C}_{q,\kappa }$
. In fact, the same methods can be applied for all representations whose generators and relations have a particular form, e.g., for certain generalized Demazure modules, minimal affinizations by parts or fusion products of level two and level one Demazure modules (see Theorem 6).
$\mathcal {C}_{q,\kappa }$
. In fact, the same methods can be applied for all representations whose generators and relations have a particular form, e.g., for certain generalized Demazure modules, minimal affinizations by parts or fusion products of level two and level one Demazure modules (see Theorem 6).
Organization of the paper: In Section 2, we introduce the main definitions and notations and discuss the prime irreducible objects in the HL category as well as their graded limits. In Section 3, we state the main results, and in Section 4, we present a class of truncated representations for current algebras and determine their
![]() $\mathbf {U}^-$
module structure. In Section 5, we recall the dual functional realization of loop algebras and discuss the graded characters of the aforementioned truncated representations. In Section 6, we prove the main theorem of the paper giving graded decompositions of the prime irreducible objects in the HL category in terms of lattice points of convex polytopes.
$\mathbf {U}^-$
module structure. In Section 5, we recall the dual functional realization of loop algebras and discuss the graded characters of the aforementioned truncated representations. In Section 6, we prove the main theorem of the paper giving graded decompositions of the prime irreducible objects in the HL category in terms of lattice points of convex polytopes.
2 Quantum loop algebras and prime representations in the HL category
2.1
Throughout this paper, we denote by
![]() $\mathbb {C}$
the field of complex numbers and by
$\mathbb {C}$
the field of complex numbers and by
![]() $\mathbb {Z}$
(resp.
$\mathbb {Z}$
(resp.
![]() $\mathbb {Z}_{+}$
,
$\mathbb {Z}_{+}$
,
![]() $\mathbb {N}$
) the subset of integers (resp. nonnegative, positive integers). Given an indeterminate t, we let
$\mathbb {N}$
) the subset of integers (resp. nonnegative, positive integers). Given an indeterminate t, we let
![]() $\mathbb C[t]$
(resp.
$\mathbb C[t]$
(resp.
![]() $\mathbb C[t,t^{-1}]$
,
$\mathbb C[t,t^{-1}]$
,
![]() $\mathbb C(t)$
) be the ring of polynomials (resp. Laurent polynomials, rational functions) in the variable t. For a Lie algebra
$\mathbb C(t)$
) be the ring of polynomials (resp. Laurent polynomials, rational functions) in the variable t. For a Lie algebra
![]() $\mathfrak {a}$
, let
$\mathfrak {a}$
, let
![]() $\mathbf {U}(\mathfrak {a})$
be the universal enveloping algebra of
$\mathbf {U}(\mathfrak {a})$
be the universal enveloping algebra of
![]() $\mathfrak {a}$
. Furthermore, let
$\mathfrak {a}$
. Furthermore, let
be the loop algebra (resp. current algebra) of
![]() $\mathfrak {a}$
with Lie bracket
$\mathfrak {a}$
with Lie bracket
A finite-dimensional
![]() $\mathbb {Z}$
-graded
$\mathbb {Z}$
-graded
![]() $\mathfrak {a}[t]$
-module is a
$\mathfrak {a}[t]$
-module is a
![]() $\mathbb {Z}$
-graded vector space admitting a compatible graded action of
$\mathbb {Z}$
-graded vector space admitting a compatible graded action of
![]() $\mathfrak {a}[t]$
:
$\mathfrak {a}[t]$
:
Given a
![]() $\mathbb {Z}$
-graded space V, let
$\mathbb {Z}$
-graded space V, let
![]() $\tau ^{*}_p V$
be the graded space whose rth graded piece is
$\tau ^{*}_p V$
be the graded space whose rth graded piece is
![]() $V[r-p]$
.
$V[r-p]$
.
2.2
Let
![]() $\mathfrak {g}$
be the Lie algebra
$\mathfrak {g}$
be the Lie algebra
![]() $\mathfrak {sl}_{n+1}$
with Cartan matrix
$\mathfrak {sl}_{n+1}$
with Cartan matrix
![]() $(c_{i,j})_{1\leq i,j\leq n}$
, and let
$(c_{i,j})_{1\leq i,j\leq n}$
, and let
![]() $\mathfrak {h}$
be a Cartan subalgebra of
$\mathfrak {h}$
be a Cartan subalgebra of
![]() $\mathfrak {g}$
. We denote by R the corresponding set of roots and
$\mathfrak {g}$
. We denote by R the corresponding set of roots and
![]() $\{\alpha _1,\dots ,\alpha _n\}$
and
$\{\alpha _1,\dots ,\alpha _n\}$
and
![]() $\{\varpi _1,\dots ,\varpi _n\}$
be a set of simple roots and fundamental weights, respectively. The set of positive roots is denoted by
$\{\varpi _1,\dots ,\varpi _n\}$
be a set of simple roots and fundamental weights, respectively. The set of positive roots is denoted by
![]() $R^+$
, the
$R^+$
, the
![]() $\mathbb {Z}$
(resp.
$\mathbb {Z}$
(resp.
![]() $\mathbb {Z}_+$
)-span of the simple roots by Q (resp.
$\mathbb {Z}_+$
)-span of the simple roots by Q (resp.
![]() $Q^+$
), and the
$Q^+$
), and the
![]() $\mathbb {Z}$
(resp.
$\mathbb {Z}$
(resp.
![]() $\mathbb {Z}_+$
)-span of the fundamental weights by P (resp.
$\mathbb {Z}_+$
)-span of the fundamental weights by P (resp.
![]() $P^+$
). We define as usual a partial order on P by
$P^+$
). We define as usual a partial order on P by
![]() $\lambda \succeq \mu $
if
$\lambda \succeq \mu $
if
![]() $\lambda -\mu \in Q^+$
. Note that for two positive roots
$\lambda -\mu \in Q^+$
. Note that for two positive roots
![]() $\alpha ,\beta \in R^+$
with
$\alpha ,\beta \in R^+$
with
![]() $\beta \succ \alpha $
, we either have
$\beta \succ \alpha $
, we either have
![]() $\beta -\alpha \in R^+$
or there exists
$\beta -\alpha \in R^+$
or there exists
![]() $\gamma _1,\gamma _2\in R^+$
such that
$\gamma _1,\gamma _2\in R^+$
such that
For
![]() $\gamma =\sum _{i=1}^nr_i\alpha _i\in Q^+$
, define its height by
$\gamma =\sum _{i=1}^nr_i\alpha _i\in Q^+$
, define its height by
![]() $|\gamma |=\sum _{i=1}^n r_i$
. Given a root
$|\gamma |=\sum _{i=1}^n r_i$
. Given a root
![]() $\alpha \in R^+$
, let
$\alpha \in R^+$
, let
![]() $x_{\alpha }^{\pm }$
be the corresponding root vector of weight
$x_{\alpha }^{\pm }$
be the corresponding root vector of weight
![]() $\pm \alpha $
and
$\pm \alpha $
and
![]() $h_{\alpha }$
the corresponding coroot. We have a triangular decomposition
$h_{\alpha }$
the corresponding coroot. We have a triangular decomposition
If
![]() $\alpha =\alpha _i+\cdots +\alpha _j$
and
$\alpha =\alpha _i+\cdots +\alpha _j$
and
![]() $1\leq i\leq j\leq n$
, we abbreviate in the rest of the paper
$1\leq i\leq j\leq n$
, we abbreviate in the rest of the paper
For
![]() $\lambda \in P^+$
, let
$\lambda \in P^+$
, let
![]() $V(\lambda )$
be the unique irreducible representation of
$V(\lambda )$
be the unique irreducible representation of
![]() $\mathfrak {g}$
of highest weight
$\mathfrak {g}$
of highest weight
![]() $\lambda $
and set
$\lambda $
and set
 $$ \begin{align*}\max(\lambda)=\max\{i: &\lambda(h_i)>0\},\ \ \min (\lambda)=\min\{i: \lambda(h_i)>0\},\ \ \mathrm{supp}_1(\lambda)=\{i: \lambda(h_i)>0\},\\&\mathrm{supp}_2(\lambda)=\{(i,j): i<j,\ [i,j]\cap \mathrm{supp}_1(\lambda)=\{i,j\}\}.\end{align*} $$
$$ \begin{align*}\max(\lambda)=\max\{i: &\lambda(h_i)>0\},\ \ \min (\lambda)=\min\{i: \lambda(h_i)>0\},\ \ \mathrm{supp}_1(\lambda)=\{i: \lambda(h_i)>0\},\\&\mathrm{supp}_2(\lambda)=\{(i,j): i<j,\ [i,j]\cap \mathrm{supp}_1(\lambda)=\{i,j\}\}.\end{align*} $$
Moreover, we set
2.3
Let
![]() $\widehat {\mathfrak {g}}$
be the untwisted affine Lie algebra associated with
$\widehat {\mathfrak {g}}$
be the untwisted affine Lie algebra associated with
![]() $\mathfrak {g}$
which is realized as
$\mathfrak {g}$
which is realized as
where K is required to be central and the Lie bracket is defined as
The commutator subalgebra
![]() $[\widehat {\mathfrak {g}},\widehat {\mathfrak {g}}]$
modulo the center is the loop algebra
$[\widehat {\mathfrak {g}},\widehat {\mathfrak {g}}]$
modulo the center is the loop algebra
![]() $\mathfrak {g}[t^{\pm 1}]$
, and note that the element d defines a grading on the loop algebra. The
$\mathfrak {g}[t^{\pm 1}]$
, and note that the element d defines a grading on the loop algebra. The
![]() $\mathbb {Z}_+$
-graded subalgebra is the current algebra
$\mathbb {Z}_+$
-graded subalgebra is the current algebra
![]() $\mathfrak {g}[t]$
associated with
$\mathfrak {g}[t]$
associated with
![]() $\mathfrak {g} $
. In the rest of the paper, we abbreviate
$\mathfrak {g} $
. In the rest of the paper, we abbreviate
 $$ \begin{align*}&\mathbf{U}=\mathbf{U}(\mathfrak{g}[t]),\ \ \mathbf{U}^{\pm}=\mathbf{U}(\mathfrak{n}^{\pm}[t]),\ \ \mathbf{U}^0=\mathbf{U}(\mathfrak{h}[t]),\\\mathbf{U}_{\ell}=\mathbf{U}(\mathfrak{g}[t^{\pm 1}]),\ \ &\mathbf{U}_{\ell}^{+}=\mathbf{U}(\mathfrak{n}^{+}[t^{\pm 1}]),\ \ \mathbf{U}_{\ell}^{-}=\mathbf{U}(\mathfrak{n}^{-}[t^{\pm 1}]),\ \ \mathbf{U}^0_{\ell}=\mathbf{U}(\mathfrak{h}[t^{\pm 1}]).\end{align*} $$
$$ \begin{align*}&\mathbf{U}=\mathbf{U}(\mathfrak{g}[t]),\ \ \mathbf{U}^{\pm}=\mathbf{U}(\mathfrak{n}^{\pm}[t]),\ \ \mathbf{U}^0=\mathbf{U}(\mathfrak{h}[t]),\\\mathbf{U}_{\ell}=\mathbf{U}(\mathfrak{g}[t^{\pm 1}]),\ \ &\mathbf{U}_{\ell}^{+}=\mathbf{U}(\mathfrak{n}^{+}[t^{\pm 1}]),\ \ \mathbf{U}_{\ell}^{-}=\mathbf{U}(\mathfrak{n}^{-}[t^{\pm 1}]),\ \ \mathbf{U}^0_{\ell}=\mathbf{U}(\mathfrak{h}[t^{\pm 1}]).\end{align*} $$
So as vector spaces,
2.4
Recall that
![]() $\mathbb {C}(q)$
denotes the field of rational functions in an indeterminate q. We discuss in the rest of this section quantum loop algebras, their representations (of type 1), and graded limits. Set
$\mathbb {C}(q)$
denotes the field of rational functions in an indeterminate q. We discuss in the rest of this section quantum loop algebras, their representations (of type 1), and graded limits. Set
 $$ \begin{align*}[m]=\frac{q^{m}-q^{-m}}{q-q^{-1}},\ \ [m]!=[m][m-1]\cdots [1],\ \ \begin{bmatrix}m \\r \end{bmatrix}=\frac{[m]!}{[r]![m-r]!},\ \ \ r,m\in \mathbb{Z}_+,\ m\geq r.\end{align*} $$
$$ \begin{align*}[m]=\frac{q^{m}-q^{-m}}{q-q^{-1}},\ \ [m]!=[m][m-1]\cdots [1],\ \ \begin{bmatrix}m \\r \end{bmatrix}=\frac{[m]!}{[r]![m-r]!},\ \ \ r,m\in \mathbb{Z}_+,\ m\geq r.\end{align*} $$
The quantum loop algebra
![]() $\mathbf {U}_q(\mathfrak {g}[t^{\pm 1}])$
is the
$\mathbf {U}_q(\mathfrak {g}[t^{\pm 1}])$
is the
![]() $\mathbb {C}(q)$
-algebra generated by elements
$\mathbb {C}(q)$
-algebra generated by elements
subject to the following relations:
 $$ \begin{align*}&\tilde{k}_i\tilde{k}_i^{-1} = \tilde{k}_i^{-1}\tilde{k}_i =1,\ \ [\tilde{k}_i,\tilde{k}_j]=[\tilde{k}_i,\tilde{h}_{j,r}] =[\tilde{h}_{i,r},\tilde{h}_{j,s}]=0,\ \ \tilde{k}_i\tilde{x}_{j,r}^{{}\pm{}}\tilde{k}_i^{-1} = q^{{}\pm c_{ij}}\tilde{x}_{j,r}^{{}\pm{}},\\&[\tilde{h}_{i,r} , \tilde{x}_{j,s}^{{}\pm{}}] = \pm\frac1r[rc_{ij}]\tilde{x}_{j,r+s}^{{}\pm{}},\\&\tilde{x}_{i,r+1}^{{}\pm{}}\tilde{x}_{j,s}^{{}\pm{}} -q^{{}\pm a_{ij}}\tilde{x}_{j,s}^{{}\pm{}}\tilde{x}_{i,r+1}^{{}\pm{}} =q^{{}\pm a_{ij}}\tilde{x}_{i,r}^{{}\pm{}}\tilde{x}_{j,s+1}^{{}\pm{}} -\tilde{x}_{j,s+1}^{{}\pm{}}\tilde{x}_{i,r}^{{}\pm{}},\\&[\tilde{x}_{i,r}^{{}\pm{}},\tilde{x}_{j,s}^{{}\pm{}}]=0,\ \text{if }c_{i,j}=0\\&\tilde{x}_{j,s}^{{}\pm{}} \tilde{x}_{i, r_{1}}^{{}\pm{}}\tilde{x}_{i,r_{2}}^{{}\pm{}}+\tilde{x}_{j,s}^{{}\pm{}} \tilde{x}_{i, r_{2}}^{{}\pm{}}\tilde{x}_{i,r_{1}}^{{}\pm{}}+x_{i, r_{1}}^{{}\pm{}}\tilde{x}_{i,r_{2}}^{{}\pm{}}\tilde{x}_{j,s}^{{}\pm{}}+x_{i, r_{2}}^{{}\pm{}}\tilde{x}_{i,r_{1}}^{{}\pm{}}\tilde{x}_{j,s}^{{}\pm{}}\\ &\quad=[2](\tilde{x}_{i, r_{1}}^{\pm} \tilde{x}_{j,s}^{{}\pm{}}\tilde{x}_{i, r_{2}}^{\pm}+\tilde{x}_{i, r_{2}}^{\pm} \tilde{x}_{j,s}^{{}\pm{}} \tilde{x}_{i, r_{1}}^{{}\pm{}}),\ i\neq j\\&[\tilde{x}_{i,r}^+ , \tilde{x}_{j,s}^-]=\delta_{ij} \frac{\phi_{i,r+s}^+ - \phi_{i,r+s}^-}{q - q^{-1}},\end{align*} $$
$$ \begin{align*}&\tilde{k}_i\tilde{k}_i^{-1} = \tilde{k}_i^{-1}\tilde{k}_i =1,\ \ [\tilde{k}_i,\tilde{k}_j]=[\tilde{k}_i,\tilde{h}_{j,r}] =[\tilde{h}_{i,r},\tilde{h}_{j,s}]=0,\ \ \tilde{k}_i\tilde{x}_{j,r}^{{}\pm{}}\tilde{k}_i^{-1} = q^{{}\pm c_{ij}}\tilde{x}_{j,r}^{{}\pm{}},\\&[\tilde{h}_{i,r} , \tilde{x}_{j,s}^{{}\pm{}}] = \pm\frac1r[rc_{ij}]\tilde{x}_{j,r+s}^{{}\pm{}},\\&\tilde{x}_{i,r+1}^{{}\pm{}}\tilde{x}_{j,s}^{{}\pm{}} -q^{{}\pm a_{ij}}\tilde{x}_{j,s}^{{}\pm{}}\tilde{x}_{i,r+1}^{{}\pm{}} =q^{{}\pm a_{ij}}\tilde{x}_{i,r}^{{}\pm{}}\tilde{x}_{j,s+1}^{{}\pm{}} -\tilde{x}_{j,s+1}^{{}\pm{}}\tilde{x}_{i,r}^{{}\pm{}},\\&[\tilde{x}_{i,r}^{{}\pm{}},\tilde{x}_{j,s}^{{}\pm{}}]=0,\ \text{if }c_{i,j}=0\\&\tilde{x}_{j,s}^{{}\pm{}} \tilde{x}_{i, r_{1}}^{{}\pm{}}\tilde{x}_{i,r_{2}}^{{}\pm{}}+\tilde{x}_{j,s}^{{}\pm{}} \tilde{x}_{i, r_{2}}^{{}\pm{}}\tilde{x}_{i,r_{1}}^{{}\pm{}}+x_{i, r_{1}}^{{}\pm{}}\tilde{x}_{i,r_{2}}^{{}\pm{}}\tilde{x}_{j,s}^{{}\pm{}}+x_{i, r_{2}}^{{}\pm{}}\tilde{x}_{i,r_{1}}^{{}\pm{}}\tilde{x}_{j,s}^{{}\pm{}}\\ &\quad=[2](\tilde{x}_{i, r_{1}}^{\pm} \tilde{x}_{j,s}^{{}\pm{}}\tilde{x}_{i, r_{2}}^{\pm}+\tilde{x}_{i, r_{2}}^{\pm} \tilde{x}_{j,s}^{{}\pm{}} \tilde{x}_{i, r_{1}}^{{}\pm{}}),\ i\neq j\\&[\tilde{x}_{i,r}^+ , \tilde{x}_{j,s}^-]=\delta_{ij} \frac{\phi_{i,r+s}^+ - \phi_{i,r+s}^-}{q - q^{-1}},\end{align*} $$
where
![]() $\phi _{i,r}^{\pm }$
is determined by equating coefficients of powers of u in
$\phi _{i,r}^{\pm }$
is determined by equating coefficients of powers of u in
 $$ \begin{align*}\Phi_i^{\pm}(u)=\sum_{r\in\mathbb{Z}}\phi_{i,\pm r}^{{}\pm{}}u^{{} r} = \tilde{k}_i^{{}\pm 1} \mathrm{exp}\left(\pm(q-q^{-1})\sum_{s=1}^{\infty}\tilde{h}_{i,\pm s} u^{{}s}\right).\end{align*} $$
$$ \begin{align*}\Phi_i^{\pm}(u)=\sum_{r\in\mathbb{Z}}\phi_{i,\pm r}^{{}\pm{}}u^{{} r} = \tilde{k}_i^{{}\pm 1} \mathrm{exp}\left(\pm(q-q^{-1})\sum_{s=1}^{\infty}\tilde{h}_{i,\pm s} u^{{}s}\right).\end{align*} $$
Denote by
![]() $\mathbf {U}_q(\mathfrak {g}) \left (\text {resp. } \mathbf {U}_q(\mathfrak {h}[t^{\pm 1}])\right )$
the subalgebra generated by
$\mathbf {U}_q(\mathfrak {g}) \left (\text {resp. } \mathbf {U}_q(\mathfrak {h}[t^{\pm 1}])\right )$
the subalgebra generated by
Then
![]() $\Lambda _{i,r}$
together with
$\Lambda _{i,r}$
together with
![]() $\tilde {k}_i^{\pm 1}$
,
$\tilde {k}_i^{\pm 1}$
,
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
![]() $r\in \mathbb {Z}$
, generate
$r\in \mathbb {Z}$
, generate
![]() $\mathbf {U}_q(\mathfrak {h}[t^{\pm 1}])$
as an algebra where the elements
$\mathbf {U}_q(\mathfrak {h}[t^{\pm 1}])$
as an algebra where the elements
![]() $\Lambda _{i,r}$
are obtained by equating powers of u in the formal power series
$\Lambda _{i,r}$
are obtained by equating powers of u in the formal power series
 $$ \begin{align*} \Lambda_i^\pm(u)=\sum_{r=0}^\infty \Lambda_{i,\pm r} u^{r}= \exp\left(-\sum_{s=1}^\infty\frac{\tilde{h}_{i,\pm s}}{[s]}u^s\right). \end{align*} $$
$$ \begin{align*} \Lambda_i^\pm(u)=\sum_{r=0}^\infty \Lambda_{i,\pm r} u^{r}= \exp\left(-\sum_{s=1}^\infty\frac{\tilde{h}_{i,\pm s}}{[s]}u^s\right). \end{align*} $$
2.5
We consider the dominant
![]() $\ell $
-weight lattice of
$\ell $
-weight lattice of
![]() $\mathbf {U}_q(\mathfrak {g}[t^{\pm 1}])$
defined as the monoid
$\mathbf {U}_q(\mathfrak {g}[t^{\pm 1}])$
defined as the monoid
![]() $\mathcal P^+$
of n-tuples of polynomials
$\mathcal P^+$
of n-tuples of polynomials
![]() $\boldsymbol {\pi } = (\boldsymbol {\pi }_1(u),\dots ,\boldsymbol {\pi }_n(u))$
with coefficients in
$\boldsymbol {\pi } = (\boldsymbol {\pi }_1(u),\dots ,\boldsymbol {\pi }_n(u))$
with coefficients in
![]() $\mathbb {C}(q)[u]$
(the polynomial algebra in an indeterminate u with coefficients in the field
$\mathbb {C}(q)[u]$
(the polynomial algebra in an indeterminate u with coefficients in the field
![]() $\mathbb {C}(q)$
) such that
$\mathbb {C}(q)$
) such that
![]() $\boldsymbol {\pi }_i(0)=1$
for all
$\boldsymbol {\pi }_i(0)=1$
for all
![]() $1\leq i\leq n$
. Given
$1\leq i\leq n$
. Given
![]() $a\in \mathbb {C}(q)^{\times }$
and
$a\in \mathbb {C}(q)^{\times }$
and
![]() $1\leq i\leq n$
, define the fundamental
$1\leq i\leq n$
, define the fundamental
![]() $\ell $
-weight
$\ell $
-weight
![]() $\boldsymbol {\varpi }_{i,a}\in \mathcal P^+$
by
$\boldsymbol {\varpi }_{i,a}\in \mathcal P^+$
by
The
![]() $\ell $
-weight lattice
$\ell $
-weight lattice
![]() $\mathcal P$
is the free abelian group generated by fundamental
$\mathcal P$
is the free abelian group generated by fundamental
![]() $\ell $
-weights. We consider the map
$\ell $
-weights. We consider the map
![]() $\boldsymbol {\Psi }:\mathcal {P}\rightarrow \mathbf {U}_q(\mathfrak {h}[t^{\pm 1}])^{*},\ \boldsymbol {\pi }\rightarrow \boldsymbol {\Psi }_{\boldsymbol {\pi }}$
(which turns out to be injective) by the following rule on the generators. For
$\boldsymbol {\Psi }:\mathcal {P}\rightarrow \mathbf {U}_q(\mathfrak {h}[t^{\pm 1}])^{*},\ \boldsymbol {\pi }\rightarrow \boldsymbol {\Psi }_{\boldsymbol {\pi }}$
(which turns out to be injective) by the following rule on the generators. For
![]() $\boldsymbol {\pi }=\boldsymbol {\pi }'\widetilde {\boldsymbol {\pi }}^{-1}$
with
$\boldsymbol {\pi }=\boldsymbol {\pi }'\widetilde {\boldsymbol {\pi }}^{-1}$
with
![]() $\boldsymbol {\pi }',\widetilde {\boldsymbol {\pi }}\in \mathcal {P}^+$
, let
$\boldsymbol {\pi }',\widetilde {\boldsymbol {\pi }}\in \mathcal {P}^+$
, let
![]() $\boldsymbol {\Psi }_{\boldsymbol {\pi }}$
be the algebra homomorphism determined by
$\boldsymbol {\Psi }_{\boldsymbol {\pi }}$
be the algebra homomorphism determined by
 $$ \begin{align*}\boldsymbol{\Psi}_{\boldsymbol{\pi}}(\tilde{k}_i^{\pm1})=q^{\pm \mathrm{wt}(\boldsymbol{\pi})(h_i)},\ \ \boldsymbol{\Psi}_{\boldsymbol{\pi}}(\Lambda^{\pm}_{i}(u))=\frac{\boldsymbol{\pi}^{\prime\pm}_i(u)}{\widetilde{\boldsymbol{\pi}}^{\pm}_i(u)},\end{align*} $$
$$ \begin{align*}\boldsymbol{\Psi}_{\boldsymbol{\pi}}(\tilde{k}_i^{\pm1})=q^{\pm \mathrm{wt}(\boldsymbol{\pi})(h_i)},\ \ \boldsymbol{\Psi}_{\boldsymbol{\pi}}(\Lambda^{\pm}_{i}(u))=\frac{\boldsymbol{\pi}^{\prime\pm}_i(u)}{\widetilde{\boldsymbol{\pi}}^{\pm}_i(u)},\end{align*} $$
where the weight map is the group homomorphism
![]() $\mathrm {wt}:\mathcal P \to P$
,
$\mathrm {wt}:\mathcal P \to P$
,
![]() $\mathrm {wt}(\boldsymbol \varpi _{i,a})=\varpi _i$
and
$\mathrm {wt}(\boldsymbol \varpi _{i,a})=\varpi _i$
and
![]() $\boldsymbol {\pi }^{+}_i(u)=\boldsymbol {\pi }^{}_i(u)$
whereas
$\boldsymbol {\pi }^{+}_i(u)=\boldsymbol {\pi }^{}_i(u)$
whereas
![]() $\boldsymbol {\pi }^{-}_i(u)$
is the polynomial obtained from
$\boldsymbol {\pi }^{-}_i(u)$
is the polynomial obtained from
![]() $\boldsymbol {\pi }_i(u)$
by replacing each
$\boldsymbol {\pi }_i(u)$
by replacing each
![]() $\boldsymbol {\varpi }_{i,a}$
by
$\boldsymbol {\varpi }_{i,a}$
by
![]() $\boldsymbol {\varpi }_{i,a^{-1}}$
.
$\boldsymbol {\varpi }_{i,a^{-1}}$
.
2.6
A nonzero vector v of a
![]() $\mathbf {U}_q(\mathfrak {g}[t^{\pm 1}])$
-module V is called
$\mathbf {U}_q(\mathfrak {g}[t^{\pm 1}])$
-module V is called
-
• an
 $\ell $
-weight vector of
$\ell $
-weight vector of
 $\ell $
-weight
$\ell $
-weight
 $\boldsymbol {\pi }\in \mathcal P$
if there exists
$\boldsymbol {\pi }\in \mathcal P$
if there exists
 $k\in \mathbb {N}$
such that
$k\in \mathbb {N}$
such that  $$ \begin{align*}(H-\boldsymbol{\Psi}_{\boldsymbol{\pi}}(H))^kv=0 \ \ \text{ for all }\ \ H\in \mathbf{U}_q(\mathfrak{h}[t^{\pm 1}]);\end{align*} $$
$$ \begin{align*}(H-\boldsymbol{\Psi}_{\boldsymbol{\pi}}(H))^kv=0 \ \ \text{ for all }\ \ H\in \mathbf{U}_q(\mathfrak{h}[t^{\pm 1}]);\end{align*} $$
-
• a highest
 $\ell $
-weight vector if we have
$\ell $
-weight vector if we have  $$ \begin{align*}Hv=\boldsymbol{\Psi}_{\boldsymbol{\pi}}(H)v \ \ \text{for all}\ \ H\in \mathbf{U}_q(\mathfrak{h}[t^{\pm 1}]) \ \ \text{and}\ \ \tilde{x}_{i,r}^+v=0 \quad\text{for all}\quad 1\leq i\leq n,\ r\in\mathbb Z.\end{align*} $$
$$ \begin{align*}Hv=\boldsymbol{\Psi}_{\boldsymbol{\pi}}(H)v \ \ \text{for all}\ \ H\in \mathbf{U}_q(\mathfrak{h}[t^{\pm 1}]) \ \ \text{and}\ \ \tilde{x}_{i,r}^+v=0 \quad\text{for all}\quad 1\leq i\leq n,\ r\in\mathbb Z.\end{align*} $$
Moreover, a module V is called
-
• an
 $\ell $
-weight module if every vector of V is a linear combination of
$\ell $
-weight module if every vector of V is a linear combination of
 $\ell $
-weight vectors;
$\ell $
-weight vectors; -
• a highest
 $\ell $
-weight module if it is generated by a highest
$\ell $
-weight module if it is generated by a highest
 $\ell $
-weight vector.
$\ell $
-weight vector.
Let
![]() $\mathcal C_q$
be the category of all finite-dimensional
$\mathcal C_q$
be the category of all finite-dimensional
![]() $\ell $
-weight modules of
$\ell $
-weight modules of
![]() $\mathbf {U}_q(\mathfrak {g}[t^{\pm 1}])$
. This category is abelian and stable under tensor product. Moreover, if V is an object of
$\mathbf {U}_q(\mathfrak {g}[t^{\pm 1}])$
. This category is abelian and stable under tensor product. Moreover, if V is an object of
![]() $\mathcal C_q$
, we have for
$\mathcal C_q$
, we have for
![]() $\mu \in P$
$\mu \in P$
where
![]() $V_{\boldsymbol {\pi }}\subseteq V$
denotes the subspace spanned by all
$V_{\boldsymbol {\pi }}\subseteq V$
denotes the subspace spanned by all
![]() $\ell $
-weight vectors of
$\ell $
-weight vectors of
![]() $\ell $
-weight
$\ell $
-weight
![]() $\boldsymbol {\pi }$
. In particular, V is a type 1 representation.
$\boldsymbol {\pi }$
. In particular, V is a type 1 representation.
The irreducible objects in
![]() $\mathcal C_q$
were classified and are obtained as follows. Let
$\mathcal C_q$
were classified and are obtained as follows. Let
![]() $\boldsymbol {\pi }\in \mathcal {P}^+$
and
$\boldsymbol {\pi }\in \mathcal {P}^+$
and
![]() $W_q(\boldsymbol {\pi })$
be the
$W_q(\boldsymbol {\pi })$
be the
![]() $\mathbf {U}_q(\mathfrak {g}[t^{\pm 1}])$
-module generated by an element
$\mathbf {U}_q(\mathfrak {g}[t^{\pm 1}])$
-module generated by an element
![]() $w_{\boldsymbol {\pi }}$
with defining relations
$w_{\boldsymbol {\pi }}$
with defining relations
Since
![]() $W_q(\boldsymbol {\pi })$
is a highest
$W_q(\boldsymbol {\pi })$
is a highest
![]() $\ell $
-weight module with
$\ell $
-weight module with
![]() $\dim (W_q(\boldsymbol {\pi })_{\boldsymbol {\pi }})=1$
, it has a unique irreducible quotient
$\dim (W_q(\boldsymbol {\pi })_{\boldsymbol {\pi }})=1$
, it has a unique irreducible quotient
![]() $V_q(\boldsymbol {\pi })$
. The next theorem can be derived from [Reference Chari and Pressley9, Reference Chari and Pressley10].
$V_q(\boldsymbol {\pi })$
. The next theorem can be derived from [Reference Chari and Pressley9, Reference Chari and Pressley10].
Theorem 1 Let V be an irreducible object in
![]() $\mathcal {C}_q$
. Then there exists a unique
$\mathcal {C}_q$
. Then there exists a unique
![]() $\boldsymbol {\pi }\in \mathcal {P}^+$
such that
$\boldsymbol {\pi }\in \mathcal {P}^+$
such that
![]() $V\cong V_q(\boldsymbol {\pi })$
.
$V\cong V_q(\boldsymbol {\pi })$
.
2.7
There are several ways to study the structure of these representations. One method would be to determine the classical decomposition with respect to the Hopf subalgebra
![]() $\mathbf {U}_q(\mathfrak {g})$
. If
$\mathbf {U}_q(\mathfrak {g})$
. If
![]() $V\in \mathcal {C}_q$
, then V can be viewed as a
$V\in \mathcal {C}_q$
, then V can be viewed as a
![]() $\mathbf {U}_q(\mathfrak {g})$
-module and hence (the category of finite-dimensional
$\mathbf {U}_q(\mathfrak {g})$
-module and hence (the category of finite-dimensional
![]() $\mathbf {U}_q(\mathfrak {g})$
-modules is semisimple)
$\mathbf {U}_q(\mathfrak {g})$
-modules is semisimple)
where
![]() $V_q(\mu )$
is the irreducible highest weight module of
$V_q(\mu )$
is the irreducible highest weight module of
![]() $\mathbf {U}_q(\mathfrak {g})$
of highest weight
$\mathbf {U}_q(\mathfrak {g})$
of highest weight
![]() $\mu $
.
$\mu $
.
We describe now the graded limit approach to the irreducible objects in
![]() $\mathcal {C}_q$
. Let
$\mathcal {C}_q$
. Let
![]() $\mathbf {A}=\mathbb {Z}[q,q^{-1}]$
and denote by
$\mathbf {A}=\mathbb {Z}[q,q^{-1}]$
and denote by
![]() $\mathbf {U}_{q,\mathbf {A}}(\mathfrak {g})$
and
$\mathbf {U}_{q,\mathbf {A}}(\mathfrak {g})$
and
![]() $\mathbf {U}_{q,\mathbf {A}}(\mathfrak {g}[t^{\pm 1}])$
the
$\mathbf {U}_{q,\mathbf {A}}(\mathfrak {g}[t^{\pm 1}])$
the
![]() $\mathbf {A}$
-form of
$\mathbf {A}$
-form of
![]() $\mathbf {U}_{q}(\mathfrak {g})$
and
$\mathbf {U}_{q}(\mathfrak {g})$
and
![]() $\mathbf {U}_{q}(\mathfrak {g}[t^{\pm 1}])$
, respectively (for a precise definition, see [Reference Lusztig26]). These are free modules over the ring
$\mathbf {U}_{q}(\mathfrak {g}[t^{\pm 1}])$
, respectively (for a precise definition, see [Reference Lusztig26]). These are free modules over the ring
![]() $\mathbf {A}$
such that
$\mathbf {A}$
such that
We could try to mimic the same kind of construction for an arbitrary irreducible object in
![]() $\mathcal {P}^+$
, but the existence is not guaranteed in general. Assume that
$\mathcal {P}^+$
, but the existence is not guaranteed in general. Assume that
![]() $V_q(\boldsymbol {\pi })$
admits an
$V_q(\boldsymbol {\pi })$
admits an
![]() $\mathbf {A}$
-form, i.e., there is a representation
$\mathbf {A}$
-form, i.e., there is a representation
![]() $V_{q,\mathbf {A}}(\boldsymbol {\pi })$
of
$V_{q,\mathbf {A}}(\boldsymbol {\pi })$
of
![]() $\mathbf {U}_{q,\mathbf {A}}(\mathfrak {g}[t^{\pm 1}])$
such that
$\mathbf {U}_{q,\mathbf {A}}(\mathfrak {g}[t^{\pm 1}])$
such that
If such an
![]() $\mathbf {A}$
-form exists, the classical limit is defined as
$\mathbf {A}$
-form exists, the classical limit is defined as
where
![]() $\mathbb {C}$
is viewed as an
$\mathbb {C}$
is viewed as an
![]() $\mathbf {A}$
-module by letting q act as
$\mathbf {A}$
-module by letting q act as
![]() $1$
. Since
$1$
. Since
![]() $\mathbf {U}_{q,\mathbf {A}}(\mathfrak {g}[t^{\pm 1}])\otimes _{\mathbf {A}} \mathbb {C}$
is a quotient of the universal enveloping algebra
$\mathbf {U}_{q,\mathbf {A}}(\mathfrak {g}[t^{\pm 1}])\otimes _{\mathbf {A}} \mathbb {C}$
is a quotient of the universal enveloping algebra
![]() $\mathbf {U}_{\ell }$
, we obtain that
$\mathbf {U}_{\ell }$
, we obtain that
![]() $\overline {V_{q}(\boldsymbol {\pi })}$
is a module for
$\overline {V_{q}(\boldsymbol {\pi })}$
is a module for
![]() $\mathbf {U}_{\ell }$
and hence for
$\mathbf {U}_{\ell }$
and hence for
![]() $\mathbf {U}$
by restriction. The graded limit
$\mathbf {U}$
by restriction. The graded limit
![]() $L(\boldsymbol {\pi })$
is obtained by pulling back the
$L(\boldsymbol {\pi })$
is obtained by pulling back the
![]() $\mathbf {U}$
-module
$\mathbf {U}$
-module
![]() $\overline {V_{q}(\boldsymbol {\pi })}$
via the automorphism
$\overline {V_{q}(\boldsymbol {\pi })}$
via the automorphism
So whenever
![]() $V_q(\boldsymbol {\pi })$
admits an
$V_q(\boldsymbol {\pi })$
admits an
![]() $\mathbf {A}$
-form, we can associate a representation
$\mathbf {A}$
-form, we can associate a representation
![]() $L(\boldsymbol {\pi })$
of
$L(\boldsymbol {\pi })$
of
![]() $\mathbf {U}$
with it.
$\mathbf {U}$
with it.
Remark It is not clear whether the graded limit is in fact a graded module for the current algebra. For the studied families of graded limits in the literature, this was a consequence of the fact that a presentation in terms of generators and relations was found for them; see, for example, Theorem 2(1) in the next subsection.
2.8
Let
![]() $\mathcal {P}^+_{\mathbb {Z}}$
be the submonoid of
$\mathcal {P}^+_{\mathbb {Z}}$
be the submonoid of
![]() $\mathcal {P}^+$
generated by the elements
$\mathcal {P}^+$
generated by the elements
![]() $\boldsymbol {\varpi }_{i,a}$
with
$\boldsymbol {\varpi }_{i,a}$
with
![]() $a\in q^{\mathbb {Z}}$
. Furthermore, we denote by
$a\in q^{\mathbb {Z}}$
. Furthermore, we denote by
![]() $\mathcal {P}_{\mathbb {Z}}^+(1)$
the subset of
$\mathcal {P}_{\mathbb {Z}}^+(1)$
the subset of
![]() $\mathcal {P}^+_{\mathbb {Z}}$
consisting of elements
$\mathcal {P}^+_{\mathbb {Z}}$
consisting of elements
such that
and
Then
![]() $V_q(\boldsymbol {\pi })$
admits an
$V_q(\boldsymbol {\pi })$
admits an
![]() $\mathbf {A}$
-form for all
$\mathbf {A}$
-form for all
![]() $\boldsymbol {\pi }\in \mathcal {P}^+_{\mathbb {Z}}(1)$
(see, for example, [Reference Chari and Pressley11]) and the corresponding graded limit
$\boldsymbol {\pi }\in \mathcal {P}^+_{\mathbb {Z}}(1)$
(see, for example, [Reference Chari and Pressley11]) and the corresponding graded limit
![]() $L(\boldsymbol {\pi })$
has been described in terms of generators and relations in [Reference Brito, Chari and Moura7]. Before we state their result, we introduce the following definition.
$L(\boldsymbol {\pi })$
has been described in terms of generators and relations in [Reference Brito, Chari and Moura7]. Before we state their result, we introduce the following definition.
Definition Let
![]() $\boldsymbol {\zeta }=(\lambda ,\lambda _0,\lambda _1,\lambda _2)$
be a quadrupel of dominant integral weights.
$\boldsymbol {\zeta }=(\lambda ,\lambda _0,\lambda _1,\lambda _2)$
be a quadrupel of dominant integral weights.
-
(1) We call
 $\boldsymbol {\zeta }$
admissible if
$\boldsymbol {\zeta }$
admissible if  $$ \begin{align*}\lambda_0,\lambda_1\in P^+(1),\ \lambda=2\lambda_0+\lambda_1+\lambda_2, \ \max(\lambda_0)<\min(\lambda_1),\ \max(\lambda_2)<\min(\lambda_1).\end{align*} $$
$$ \begin{align*}\lambda_0,\lambda_1\in P^+(1),\ \lambda=2\lambda_0+\lambda_1+\lambda_2, \ \max(\lambda_0)<\min(\lambda_1),\ \max(\lambda_2)<\min(\lambda_1).\end{align*} $$
-
(2) Given an admissible quadrupel
 $\boldsymbol {\zeta }$
, we denote by
$\boldsymbol {\zeta }$
, we denote by
 $N_{\boldsymbol {\zeta }}$
the graded
$N_{\boldsymbol {\zeta }}$
the graded
 $\mathbf {U}$
-module generated by an element v of grade zero with defining relations:
$\mathbf {U}$
-module generated by an element v of grade zero with defining relations:  $$ \begin{align*}&\mathfrak{n}^+[t]v=0,\ (h_i\otimes t^r)v=\delta_{r,0} \lambda(h_i), \ (x_i^{-}\otimes 1)^{\lambda(h_i)+1}v=0,\ r\in\mathbb{Z}_+,\ 1\leq i\leq n,\\&\left(x_i^{-}\otimes t^{(\lambda_0+\lambda_2)(h_i)}\right)^{}v=0,\ i\in \mathrm{supp}_1(\lambda_0),\ \ \left(x^{-}_{i,j}\otimes t\right)v=0,\ (i,j)\in \mathrm{supp}_2(\lambda_1).\end{align*} $$
$$ \begin{align*}&\mathfrak{n}^+[t]v=0,\ (h_i\otimes t^r)v=\delta_{r,0} \lambda(h_i), \ (x_i^{-}\otimes 1)^{\lambda(h_i)+1}v=0,\ r\in\mathbb{Z}_+,\ 1\leq i\leq n,\\&\left(x_i^{-}\otimes t^{(\lambda_0+\lambda_2)(h_i)}\right)^{}v=0,\ i\in \mathrm{supp}_1(\lambda_0),\ \ \left(x^{-}_{i,j}\otimes t\right)v=0,\ (i,j)\in \mathrm{supp}_2(\lambda_1).\end{align*} $$
Remark The above class of representations has been studied in [Reference Biswal, Chari, Shereen and Wand4, Section 2.2] in the context of Macdonald polynomials and fusion products of level two and level one Demazure modules. In their notation,
![]() $N_{\boldsymbol {\zeta }}$
was denoted by
$N_{\boldsymbol {\zeta }}$
was denoted by
![]() $M(\lambda _2,2\lambda _0+\lambda _1)$
and the defining relations look more complicated. However, the conditions
$M(\lambda _2,2\lambda _0+\lambda _1)$
and the defining relations look more complicated. However, the conditions
![]() $\max (\lambda _0)<\min (\lambda _1)$
and
$\max (\lambda _0)<\min (\lambda _1)$
and
![]() $\max (\lambda _2)<\min (\lambda _1)$
ensure that the defining relations of
$\max (\lambda _2)<\min (\lambda _1)$
ensure that the defining relations of
![]() $M(\lambda _2,2\lambda _0+\lambda _1)$
stated in [Reference Biswal, Chari, Shereen and Wand4, Section 2.2] can be simplified to the ones in the definition of
$M(\lambda _2,2\lambda _0+\lambda _1)$
stated in [Reference Biswal, Chari, Shereen and Wand4, Section 2.2] can be simplified to the ones in the definition of
![]() $N_{\boldsymbol {\zeta }}$
. To see this, we simply have to write
$N_{\boldsymbol {\zeta }}$
. To see this, we simply have to write
 $$ \begin{align*}\hspace{0,1cm} \left(x_{i,j}^{-}\otimes t^{(\lambda_0+\lambda_2)(h_{i,j})+\lceil\frac{m-r}{2}\rceil}\right)= \big[\cdots&\big[\big[\big[(x_{i,i_r-1}^{-}\otimes t^{(\lambda_0+\lambda_2)(h_{i,i_{r}-1})},(x_{i_r,i_{r+1}}^{-}\otimes t)\big]&\\&,(x_{i_{r+1}+1,i_{r+2}-1}^{-}\otimes 1)\big],(x_{i_{r+2},i_{r+3}}^{-}\otimes t)\big],\dots,(x_{i_{m-1}+1,j}^{-}\otimes 1)\big],\end{align*} $$
$$ \begin{align*}\hspace{0,1cm} \left(x_{i,j}^{-}\otimes t^{(\lambda_0+\lambda_2)(h_{i,j})+\lceil\frac{m-r}{2}\rceil}\right)= \big[\cdots&\big[\big[\big[(x_{i,i_r-1}^{-}\otimes t^{(\lambda_0+\lambda_2)(h_{i,i_{r}-1})},(x_{i_r,i_{r+1}}^{-}\otimes t)\big]&\\&,(x_{i_{r+1}+1,i_{r+2}-1}^{-}\otimes 1)\big],(x_{i_{r+2},i_{r+3}}^{-}\otimes t)\big],\dots,(x_{i_{m-1}+1,j}^{-}\otimes 1)\big],\end{align*} $$
where
![]() $\lambda _1=\varpi _{i_1}+\cdots +\varpi _{i_k}, 1\leq i_1<\cdots <i_k\leq n$
and m and r are determined by
$\lambda _1=\varpi _{i_1}+\cdots +\varpi _{i_k}, 1\leq i_1<\cdots <i_k\leq n$
and m and r are determined by
![]() $i_{r-1}<i\leq i_r$
and
$i_{r-1}<i\leq i_r$
and
![]() $i_{m-1}\leq j< i_m$
; we understand
$i_{m-1}\leq j< i_m$
; we understand
![]() $i_0=0$
and
$i_0=0$
and
![]() $i_{k+1}=n+1$
.
$i_{k+1}=n+1$
.
The first part of the next theorem has been proved in [Reference Brito, Chari and Moura7, Theorem 1], and the second part follows from [Reference Biswal, Chari, Shereen and Wand4, Proposition 2.5(i)] and Remark 2.8.
Theorem 2 Let
![]() $\boldsymbol {\zeta }=(\lambda ,\lambda _0,\lambda _1,\lambda _2)$
be an admissible quadrupel.
$\boldsymbol {\zeta }=(\lambda ,\lambda _0,\lambda _1,\lambda _2)$
be an admissible quadrupel.
-
(1) We have an isomorphism of graded
 $\mathbf {U}$
-modules
$\mathbf {U}$
-modules  $$ \begin{align*}L(\boldsymbol{\pi})\cong N_{(\mathrm{wt}(\boldsymbol{\pi}),0,\mathrm{wt}(\boldsymbol{\pi}),0)},\ \ \boldsymbol{\pi}\in \mathcal{P}^+_{\mathbb{Z}}(1).\end{align*} $$
$$ \begin{align*}L(\boldsymbol{\pi})\cong N_{(\mathrm{wt}(\boldsymbol{\pi}),0,\mathrm{wt}(\boldsymbol{\pi}),0)},\ \ \boldsymbol{\pi}\in \mathcal{P}^+_{\mathbb{Z}}(1).\end{align*} $$
-
(2) If
 $\lambda _2\in P^+(1)$
and
$\lambda _2\in P^+(1)$
and
 $\lambda _1=\varpi _{i_1}+\cdots +\varpi _{i_k}$
,
$\lambda _1=\varpi _{i_1}+\cdots +\varpi _{i_k}$
,
 $1\leq i_1<\cdots <i_k\leq n$
with
$1\leq i_1<\cdots <i_k\leq n$
with
 $k\geq 2$
, we have an exact sequence of
$k\geq 2$
, we have an exact sequence of
 $\mathbf {U}$
-modules (2.2)where
$\mathbf {U}$
-modules (2.2)where $$ \begin{align}0\rightarrow \tau_1^*N_{\boldsymbol{\zeta}_2} \rightarrow N_{\boldsymbol{\zeta}_1}\rightarrow N_{\boldsymbol{\zeta}}\rightarrow 0,\end{align} $$
$$ \begin{align}0\rightarrow \tau_1^*N_{\boldsymbol{\zeta}_2} \rightarrow N_{\boldsymbol{\zeta}_1}\rightarrow N_{\boldsymbol{\zeta}}\rightarrow 0,\end{align} $$
 $\boldsymbol {\zeta }_1$
and
$\boldsymbol {\zeta }_1$
and
 $\boldsymbol {\zeta }_2$
are the following admissible quadruples: (2.3)
$\boldsymbol {\zeta }_2$
are the following admissible quadruples: (2.3) $$ \begin{align}\boldsymbol{\zeta}_1=\left(\lambda,\lambda_0,\lambda_1-\varpi_{i_1},\lambda_2+\varpi_{i_1}\right),\end{align} $$
(2.4)
$$ \begin{align}\boldsymbol{\zeta}_1=\left(\lambda,\lambda_0,\lambda_1-\varpi_{i_1},\lambda_2+\varpi_{i_1}\right),\end{align} $$
(2.4) $$ \begin{align}\boldsymbol{\zeta}_2=\begin{cases} \left(\lambda-\alpha_{i_1,i_2},\lambda_0,\lambda_1-\alpha_{i_1,i_2}-\varpi_{i_1-1},\lambda_2+\varpi_{i_1-1}\right),& \text{ if }i_2+1<i_3\text{ or }k=2,\\ \\ \left(\lambda-\alpha_{i_1,i_2},\lambda_0+\varpi_{i_3},\varpi_{i_4}+\cdots+\varpi_{i_k},\lambda_2+\varpi_{i_1-1}\right),& \text{ otherwise.}\end{cases}\end{align} $$
$$ \begin{align}\boldsymbol{\zeta}_2=\begin{cases} \left(\lambda-\alpha_{i_1,i_2},\lambda_0,\lambda_1-\alpha_{i_1,i_2}-\varpi_{i_1-1},\lambda_2+\varpi_{i_1-1}\right),& \text{ if }i_2+1<i_3\text{ or }k=2,\\ \\ \left(\lambda-\alpha_{i_1,i_2},\lambda_0+\varpi_{i_3},\varpi_{i_4}+\cdots+\varpi_{i_k},\lambda_2+\varpi_{i_1-1}\right),& \text{ otherwise.}\end{cases}\end{align} $$
2.9
We describe now the importance of these representations and the relation to the HL category.
Definition We call
![]() $V_q(\boldsymbol {\pi })$
a prime irreducible representation of
$V_q(\boldsymbol {\pi })$
a prime irreducible representation of
![]() $\mathbf {U}_{q}(\mathfrak {g}[t^{\pm 1}])$
if
$\mathbf {U}_{q}(\mathfrak {g}[t^{\pm 1}])$
if
implies that
![]() $(s-1)$
factors are trivial representations.
$(s-1)$
factors are trivial representations.
It is clear that
![]() $V_q(\boldsymbol {\pi })$
is either prime or can be written as a tensor product of non-trivial prime representations; however, the uniqueness of such a decomposition is not known in general. The motivation of this paper is to determine the structure of the prime objects in the HL category by describing the graded characters of their graded limits. First, we recall the definition of the HL category.
$V_q(\boldsymbol {\pi })$
is either prime or can be written as a tensor product of non-trivial prime representations; however, the uniqueness of such a decomposition is not known in general. The motivation of this paper is to determine the structure of the prime objects in the HL category by describing the graded characters of their graded limits. First, we recall the definition of the HL category.
Let
![]() $\kappa : \{1,\dots ,n\}\rightarrow \mathbb {Z}$
be a (height) function satisfying
$\kappa : \{1,\dots ,n\}\rightarrow \mathbb {Z}$
be a (height) function satisfying
![]() $|\kappa (i+1)-\kappa (i)|= 1$
for
$|\kappa (i+1)-\kappa (i)|= 1$
for
![]() $1\leq i\leq n$
, and let
$1\leq i\leq n$
, and let
![]() $Q_{\kappa }$
be the corresponding quiver whose vertices are indexed by
$Q_{\kappa }$
be the corresponding quiver whose vertices are indexed by
![]() $\{1,\dots ,n\}$
and there is an edge
$\{1,\dots ,n\}$
and there is an edge
![]() $i\rightarrow i+1$
if
$i\rightarrow i+1$
if
![]() $\kappa (i)<\kappa (i+1)$
and
$\kappa (i)<\kappa (i+1)$
and
![]() $i\leftarrow i+1$
otherwise. The HL category
$i\leftarrow i+1$
otherwise. The HL category
![]() $\mathcal {C}_{q,\kappa }$
is the full subcategory of
$\mathcal {C}_{q,\kappa }$
is the full subcategory of
![]() $\mathcal {C}_q$
whose objects have all its Jordan–Hölder components of the form
$\mathcal {C}_q$
whose objects have all its Jordan–Hölder components of the form
where
![]() $\mathcal {P}_{\mathbb {Z}}^+(\kappa ,1)$
is the submonoid of
$\mathcal {P}_{\mathbb {Z}}^+(\kappa ,1)$
is the submonoid of
![]() $\mathcal {P}^+$
generated by
$\mathcal {P}^+$
generated by
![]() $\boldsymbol {\varpi }_{i,a},\ a\in \{q^{\kappa (i)},q^{\kappa (i)+2}\}, 1\leq i\leq n.$
The following results have been proved in [Reference Brito and Chari6, Reference Hernandez and Leclerc18, Reference Hernandez and Leclerc19].
$\boldsymbol {\varpi }_{i,a},\ a\in \{q^{\kappa (i)},q^{\kappa (i)+2}\}, 1\leq i\leq n.$
The following results have been proved in [Reference Brito and Chari6, Reference Hernandez and Leclerc18, Reference Hernandez and Leclerc19].
Theorem 3 The category
![]() $\mathcal {C}_{q,\kappa }$
is closed under tensor products. Let
$\mathcal {C}_{q,\kappa }$
is closed under tensor products. Let
![]() $V_q(\boldsymbol {\pi })$
be a prime irreducible object in
$V_q(\boldsymbol {\pi })$
be a prime irreducible object in
![]() $\mathcal {C}_{q,\kappa }$
. Then
$\mathcal {C}_{q,\kappa }$
. Then
![]() $\boldsymbol {\pi }\in \{\boldsymbol {\varpi }_{i,q^{\kappa (i)}}\boldsymbol {\varpi }_{i,q^{\kappa (i)+2}},\boldsymbol {\varpi }_{i,q^{\kappa (i)+2}},\boldsymbol {\varpi }_{i,q^{\kappa (i)}}\}$
for some
$\boldsymbol {\pi }\in \{\boldsymbol {\varpi }_{i,q^{\kappa (i)}}\boldsymbol {\varpi }_{i,q^{\kappa (i)+2}},\boldsymbol {\varpi }_{i,q^{\kappa (i)+2}},\boldsymbol {\varpi }_{i,q^{\kappa (i)}}\}$
for some
![]() $i\in \{1,\dots ,n\}$
or there exists an interval
$i\in \{1,\dots ,n\}$
or there exists an interval
![]() $J\subseteq [1,n]$
such that
$J\subseteq [1,n]$
such that
where
![]() $J_{\mathrm {sink}}$
(resp.
$J_{\mathrm {sink}}$
(resp.
![]() $J_{\mathrm {source}}$
) are the sinks (resp. sources) of
$J_{\mathrm {source}}$
) are the sinks (resp. sources) of
![]() $Q_{\kappa }$
contained in J. Conversely, all these representations are prime objects in
$Q_{\kappa }$
contained in J. Conversely, all these representations are prime objects in
![]() $\mathcal {C}_{q,\kappa }$
.
$\mathcal {C}_{q,\kappa }$
.
In fact, we have
The only nontrivial direction is derived as follows. Let
![]() $\boldsymbol {\pi }=\boldsymbol {\varpi }_{i_1,a_1}\cdots \boldsymbol {\varpi }_{i_k,a_k}\in \mathcal {P}_{\mathbb {Z}}^+(1)$
such that
$\boldsymbol {\pi }=\boldsymbol {\varpi }_{i_1,a_1}\cdots \boldsymbol {\varpi }_{i_k,a_k}\in \mathcal {P}_{\mathbb {Z}}^+(1)$
such that
![]() $a_2=a_1q^{(i_2-i_1+2)}$
, then we choose
$a_2=a_1q^{(i_2-i_1+2)}$
, then we choose
![]() $J=[i_1,i_k]$
and
$J=[i_1,i_k]$
and
![]() $\kappa $
to be the height function given by
$\kappa $
to be the height function given by
![]() $a_{1}=q^{\kappa (i_1)}$
and
$a_{1}=q^{\kappa (i_1)}$
and
![]() $i_1,i_3,\dots $
are the sinks and
$i_1,i_3,\dots $
are the sinks and
![]() $i_2,i_4,\dots $
are the sources. If
$i_2,i_4,\dots $
are the sources. If
![]() $a_2=a_1q^{-(i_2-i_1+2)}$
, we simply change the role of sinks and sources. Then we have
$a_2=a_1q^{-(i_2-i_1+2)}$
, we simply change the role of sinks and sources. Then we have
![]() $\boldsymbol {\pi }=\boldsymbol {\pi }_{\kappa ,J}$
.
$\boldsymbol {\pi }=\boldsymbol {\pi }_{\kappa ,J}$
.
Remark One of the main results of [Reference Hernandez and Leclerc18] shows that the category
![]() $\mathcal {C}_{q,\kappa }$
is a monoidal categorification of a cluster algebra
$\mathcal {C}_{q,\kappa }$
is a monoidal categorification of a cluster algebra
![]() $\mathcal {A}$
of type
$\mathcal {A}$
of type
![]() $A_n$
when
$A_n$
when
![]() $\kappa $
induces the sink–source orientation on
$\kappa $
induces the sink–source orientation on
![]() $Q_{\kappa }$
or
$Q_{\kappa }$
or
![]() $\kappa (i)=i$
for all
$\kappa (i)=i$
for all
![]() $1\leq i\leq n$
. This was later extended by representation theoretic methods to any height function in [Reference Brito and Chari6]. The isomorphism identifies the cluster variables in
$1\leq i\leq n$
. This was later extended by representation theoretic methods to any height function in [Reference Brito and Chari6]. The isomorphism identifies the cluster variables in
![]() $\mathcal {A}$
with the prime irreducible objects in
$\mathcal {A}$
with the prime irreducible objects in
![]() $\mathcal {C}_{q,\kappa }$
and cluster monomials are mapped to equivalence classes of irreducible objects in
$\mathcal {C}_{q,\kappa }$
and cluster monomials are mapped to equivalence classes of irreducible objects in
![]() $\mathcal {C}_{q,\kappa }$
.
$\mathcal {C}_{q,\kappa }$
.
3 The main results and recursion formulas
Our main result describes the graded character (see below for the definition) of certain objects including the graded limits of the prime irreducible objects in the HL category. It is formulated in Theorem 4 for
![]() $L(\boldsymbol {\pi })$
,
$L(\boldsymbol {\pi })$
,
![]() $\boldsymbol {\pi }\in \mathcal {P}_{\mathbb {Z}}^+(1)$
.
$\boldsymbol {\pi }\in \mathcal {P}_{\mathbb {Z}}^+(1)$
.
3.1
We shall view
![]() $V(\lambda )$
for
$V(\lambda )$
for
![]() $\lambda \in P^+$
as a
$\lambda \in P^+$
as a
![]() $\mathbb {Z}$
-graded space by declaring that each element has degree zero. Let M be a finite-dimensional and graded
$\mathbb {Z}$
-graded space by declaring that each element has degree zero. Let M be a finite-dimensional and graded
![]() $\mathbf {U}$
-module. Then there exists a decreasing filtration
$\mathbf {U}$
-module. Then there exists a decreasing filtration
of graded
![]() $\mathfrak {g}[t]$
-submodules such that
$\mathfrak {g}[t]$
-submodules such that
We denote by
![]() $[M: \tau _p^{*}V(\lambda )]$
the multiplicity of
$[M: \tau _p^{*}V(\lambda )]$
the multiplicity of
![]() $\tau _p^{*}V(\lambda )$
in the filtration (3.1) of M; note that this number is independent of the choice of the filtration. The graded character of M is defined as follows:
$\tau _p^{*}V(\lambda )$
in the filtration (3.1) of M; note that this number is independent of the choice of the filtration. The graded character of M is defined as follows:
 $$ \begin{align*}\mathrm{ch}_{\mathrm{gr}}(M):=\sum_{\mu\in P^+}[M: V(\mu)]_q \ \mathrm{ch}_{\mathfrak{h}} V(\mu),\ \ [M: V(\mu)]_q:= \sum_{p=0}^{\infty}\ [M: \tau_p^{*}V(\mu)] \cdot q^p,\end{align*} $$
$$ \begin{align*}\mathrm{ch}_{\mathrm{gr}}(M):=\sum_{\mu\in P^+}[M: V(\mu)]_q \ \mathrm{ch}_{\mathfrak{h}} V(\mu),\ \ [M: V(\mu)]_q:= \sum_{p=0}^{\infty}\ [M: \tau_p^{*}V(\mu)] \cdot q^p,\end{align*} $$
where
![]() $\mathrm {ch}_{\mathfrak {h}} V(\mu )$
denotes the usual
$\mathrm {ch}_{\mathfrak {h}} V(\mu )$
denotes the usual
![]() $\mathfrak {h}$
-character of
$\mathfrak {h}$
-character of
![]() $V(\mu )$
which can be computed, for example, with the Weyl character formula (see [Reference Humphreys20, Section 24.3]) or the various existing combinatorial models for
$V(\mu )$
which can be computed, for example, with the Weyl character formula (see [Reference Humphreys20, Section 24.3]) or the various existing combinatorial models for
![]() $V(\mu )$
(Young tableux, path model, Gelfand–Tsetlin pattern, etc.).
$V(\mu )$
(Young tableux, path model, Gelfand–Tsetlin pattern, etc.).
3.2
In order to state our results, we need some more notation. Given
![]() $\gamma =\sum _{i=1}^nr_i\alpha _i\in Q^+$
we write
$\gamma =\sum _{i=1}^nr_i\alpha _i\in Q^+$
we write
![]() $\boldsymbol {\mu }\vdash \gamma $
if
$\boldsymbol {\mu }\vdash \gamma $
if
![]() $\boldsymbol {\mu }$
is a multipartition
$\boldsymbol {\mu }$
is a multipartition
The tuple of empty partitions is denoted by
![]() $\boldsymbol {\emptyset }$
. We fix a dominant integral weight
$\boldsymbol {\emptyset }$
. We fix a dominant integral weight
![]() $\lambda \in P^+$
and a multipartition
$\lambda \in P^+$
and a multipartition
![]() $\boldsymbol {\mu }$
as in (3.2). We naturally identify a partition with a Young diagram and define
$\boldsymbol {\mu }$
as in (3.2). We naturally identify a partition with a Young diagram and define
-
•
 $\mu _i(s):= \text {number of boxes in the first }s\text { columns of }\mu _i$
,
$\mu _i(s):= \text {number of boxes in the first }s\text { columns of }\mu _i$
, -
•
 $m_{i,r}:= \text { number of rows of length }r\text { in }\mu _i$
,
$m_{i,r}:= \text { number of rows of length }r\text { in }\mu _i$
, -
•
 $d(\mu _i):= \text {number of rows of }\mu _i$
.
$d(\mu _i):= \text {number of rows of }\mu _i$
.
We set
and
 $$ \begin{align*}K^{\lambda}_{\boldsymbol{\mu}}=\sum_{i=1}^n\Big(\sum_{j=1}^{r_i}\big(2j\mu_i^{j}-\mu_{i+1}(\mu_i^{j})\big)-\lambda(h_i) \cdot d(\mu_i)\Big),\end{align*} $$
$$ \begin{align*}K^{\lambda}_{\boldsymbol{\mu}}=\sum_{i=1}^n\Big(\sum_{j=1}^{r_i}\big(2j\mu_i^{j}-\mu_{i+1}(\mu_i^{j})\big)-\lambda(h_i) \cdot d(\mu_i)\Big),\end{align*} $$
where we understand
![]() $\mu _0(\cdot )=\mu _{n+1}(\cdot )=0$
.
$\mu _0(\cdot )=\mu _{n+1}(\cdot )=0$
.
Example
-
(1) For the multipartition
 , we have
, we have  $$ \begin{align*}&P^{\boldsymbol{\mu},\lambda}_{1,1}=\lambda(h_1)-2\cdot 2+2,\ \ \ P^{\boldsymbol{\mu},\lambda}_{2,1}=\lambda(h_1)-2\cdot 2+3,\\&P^{\boldsymbol{\mu},\lambda}_{1,2}-2=\lambda(h_2)-2\cdot 3+2=P^{\boldsymbol{\mu},\lambda}_{2,2}=P^{\boldsymbol{\mu},\lambda}_{3,2},\end{align*} $$
$$ \begin{align*}&P^{\boldsymbol{\mu},\lambda}_{1,1}=\lambda(h_1)-2\cdot 2+2,\ \ \ P^{\boldsymbol{\mu},\lambda}_{2,1}=\lambda(h_1)-2\cdot 2+3,\\&P^{\boldsymbol{\mu},\lambda}_{1,2}-2=\lambda(h_2)-2\cdot 3+2=P^{\boldsymbol{\mu},\lambda}_{2,2}=P^{\boldsymbol{\mu},\lambda}_{3,2},\end{align*} $$
 $$ \begin{align*}\hspace{-12pt}K^{\lambda}_{\boldsymbol{\mu}}&=\big((2-\mu_2(1))+(4-\mu_2(1))-\lambda(h_1)\cdot 2\big)+\big(4+4-\lambda(h_2)\cdot 2\big)=10-2\cdot \lambda(h_{1,2}).\end{align*} $$
$$ \begin{align*}\hspace{-12pt}K^{\lambda}_{\boldsymbol{\mu}}&=\big((2-\mu_2(1))+(4-\mu_2(1))-\lambda(h_1)\cdot 2\big)+\big(4+4-\lambda(h_2)\cdot 2\big)=10-2\cdot \lambda(h_{1,2}).\end{align*} $$
-
(2) Let
 $n=7$
and
$n=7$
and
 $\lambda =\varpi _2+\varpi _3+\varpi _4+\varpi _5+\varpi _6$
. For the multipartitions a direct calculation gives
$\lambda =\varpi _2+\varpi _3+\varpi _4+\varpi _5+\varpi _6$
. For the multipartitions a direct calculation gives
 $K^{\lambda }_{\boldsymbol {\mu }_1}=7$
,
$K^{\lambda }_{\boldsymbol {\mu }_1}=7$
,
 $K^{\lambda }_{\boldsymbol {\mu }_2}=6$
and
$K^{\lambda }_{\boldsymbol {\mu }_2}=6$
and
 $K^{\lambda }_{\boldsymbol {\mu }_3}=4$
.
$K^{\lambda }_{\boldsymbol {\mu }_3}=4$
.
-
(3) Let
 $n=8$
and
$n=8$
and
 $\lambda =\varpi _2+\varpi _3+\varpi _4+\varpi _5+\varpi _7$
. For the multipartitions a direct calculation gives
$\lambda =\varpi _2+\varpi _3+\varpi _4+\varpi _5+\varpi _7$
. For the multipartitions a direct calculation gives
 $K^{\lambda }_{\boldsymbol {\mu }_1}=13$
and
$K^{\lambda }_{\boldsymbol {\mu }_1}=13$
and
 $K^{\lambda }_{\boldsymbol {\mu }_2}=10$
.
$K^{\lambda }_{\boldsymbol {\mu }_2}=10$
.
The following lemma gives certain relations which are needed later.
Lemma Let
![]() $\boldsymbol {\mu }$
be a multipartition and
$\boldsymbol {\mu }$
be a multipartition and
![]() $i\leq j$
such that
$i\leq j$
such that
![]() $m_{i,1},\dots ,m_{j,1}>0$
. We denote by
$m_{i,1},\dots ,m_{j,1}>0$
. We denote by
![]() $\boldsymbol {\tilde \mu }$
the multipartition obtained from
$\boldsymbol {\tilde \mu }$
the multipartition obtained from
![]() $\boldsymbol {\mu }$
by removing a box in the last row of each partition
$\boldsymbol {\mu }$
by removing a box in the last row of each partition
![]() $\mu _i,\dots ,\mu _j$
. For all
$\mu _i,\dots ,\mu _j$
. For all
![]() $\lambda \in P^+$
with
$\lambda \in P^+$
with
![]() $\lambda -\alpha _{i,j}\in P^+$
and
$\lambda -\alpha _{i,j}\in P^+$
and
![]() $\lambda (h_{i,j})=2$
, we have
$\lambda (h_{i,j})=2$
, we have
Proof Let
![]() $\boldsymbol {\tilde \mu }=(\tilde {\mu }_1,\dots ,\tilde {\mu }_n)$
. The lemma follows from the following equations:
$\boldsymbol {\tilde \mu }=(\tilde {\mu }_1,\dots ,\tilde {\mu }_n)$
. The lemma follows from the following equations:
 $$ \begin{align*}\lambda-\alpha_{i,j}=\lambda-\varpi_i-\varpi_j+\varpi_{i-1}+\varpi_{j+1},\ \ d(\mu_a)=\begin{cases}d(\tilde{\mu}_a)+1,& a\in\{i,\dots,j\}, \\ \\ d(\tilde\mu_a),& \text{otherwise}, \\\end{cases}\end{align*} $$
$$ \begin{align*}\lambda-\alpha_{i,j}=\lambda-\varpi_i-\varpi_j+\varpi_{i-1}+\varpi_{j+1},\ \ d(\mu_a)=\begin{cases}d(\tilde{\mu}_a)+1,& a\in\{i,\dots,j\}, \\ \\ d(\tilde\mu_a),& \text{otherwise}, \\\end{cases}\end{align*} $$
 $$ \begin{align*}\mu_a^b=\begin{cases}\tilde\mu^b_a,& a\notin\{i,\dots,j\}\text{ or }b\neq d(\mu_a), \\ \\ \tilde\mu^b_a+1,& \text{otherwise}, \end{cases}\ \ \ \ \ \ \mu_a(r)=\begin{cases}\tilde\mu_a(r),& a\notin\{i,\dots,j\}, \\ \\ \tilde\mu_a(r)+1,& \text{otherwise}, \end{cases}\end{align*} $$
$$ \begin{align*}\mu_a^b=\begin{cases}\tilde\mu^b_a,& a\notin\{i,\dots,j\}\text{ or }b\neq d(\mu_a), \\ \\ \tilde\mu^b_a+1,& \text{otherwise}, \end{cases}\ \ \ \ \ \ \mu_a(r)=\begin{cases}\tilde\mu_a(r),& a\notin\{i,\dots,j\}, \\ \\ \tilde\mu_a(r)+1,& \text{otherwise}, \end{cases}\end{align*} $$
 $$ \begin{align*}\sum_{b=1}^{r_a}\mu_{a+1}(\mu_a^b)=\begin{cases}\displaystyle\sum_{b=1}^{r_a}\tilde{\mu}_{a+1}(\tilde{\mu}_a^b),& a,a+1\notin\{i,\dots,j\} \\\displaystyle\sum_{b=1}^{r_a}\tilde{\mu}_{a+1}(\tilde{\mu}_a^b)+d(\tilde{\mu}_{a+1})+d(\tilde{\mu}_a)+1,& a,a+1\in\{i,\dots,j\}, \\ \displaystyle\sum_{b=1}^{r_a}\tilde{\mu}_{a+1}(\tilde{\mu}_a^b)+d(\tilde{\mu}_{a+1}),& a=j, \\ \displaystyle\sum_{b=1}^{r_a}\tilde{\mu}_{a+1}(\tilde{\mu}_a^b)+d(\tilde{\mu}_{a}),& a=i-1. \\\end{cases}\end{align*} $$
$$ \begin{align*}\sum_{b=1}^{r_a}\mu_{a+1}(\mu_a^b)=\begin{cases}\displaystyle\sum_{b=1}^{r_a}\tilde{\mu}_{a+1}(\tilde{\mu}_a^b),& a,a+1\notin\{i,\dots,j\} \\\displaystyle\sum_{b=1}^{r_a}\tilde{\mu}_{a+1}(\tilde{\mu}_a^b)+d(\tilde{\mu}_{a+1})+d(\tilde{\mu}_a)+1,& a,a+1\in\{i,\dots,j\}, \\ \displaystyle\sum_{b=1}^{r_a}\tilde{\mu}_{a+1}(\tilde{\mu}_a^b)+d(\tilde{\mu}_{a+1}),& a=j, \\ \displaystyle\sum_{b=1}^{r_a}\tilde{\mu}_{a+1}(\tilde{\mu}_a^b)+d(\tilde{\mu}_{a}),& a=i-1. \\\end{cases}\end{align*} $$
The next definition introduces the main combinatorial objects of this paper.
Definition Let
![]() $\gamma \in Q^+$
be a nonzero element,
$\gamma \in Q^+$
be a nonzero element,
![]() $\boldsymbol {\mu }\vdash \gamma $
be a multipartition,
$\boldsymbol {\mu }\vdash \gamma $
be a multipartition,
![]() $p\in \mathbb {Z}_+$
, and
$p\in \mathbb {Z}_+$
, and
![]() $\boldsymbol {\zeta }=(\lambda ,\lambda _0,\lambda _1,\lambda _2)$
be an admissible quadrupel. We define
$\boldsymbol {\zeta }=(\lambda ,\lambda _0,\lambda _1,\lambda _2)$
be an admissible quadrupel. We define
![]() $L^p_{\boldsymbol {\mu },\boldsymbol {\zeta }}$
to be the number of lattice points in the polytope
$L^p_{\boldsymbol {\mu },\boldsymbol {\zeta }}$
to be the number of lattice points in the polytope
![]() $\mathcal {S}^p_{\boldsymbol {\mu },\boldsymbol {\zeta }}$
consisting of all points
$\mathcal {S}^p_{\boldsymbol {\mu },\boldsymbol {\zeta }}$
consisting of all points
satisfying the following inequalities:
 $$ \begin{align}C_{d,r,i}\geq 0 \ \ \forall \ d,r,i,\ \ \ \ \sum_{d=1}^{m_{i,r}}C_{d,r,i}\leq P^{\boldsymbol{\mu},\lambda}_{r,i} \ \ \forall\ r,i, \ \ \ \ \sum_{d,r,i}d\cdot C_{d,r,i}=|\gamma|-p-K^{\lambda}_{\boldsymbol{\mu}},\end{align} $$
$$ \begin{align}C_{d,r,i}\geq 0 \ \ \forall \ d,r,i,\ \ \ \ \sum_{d=1}^{m_{i,r}}C_{d,r,i}\leq P^{\boldsymbol{\mu},\lambda}_{r,i} \ \ \forall\ r,i, \ \ \ \ \sum_{d,r,i}d\cdot C_{d,r,i}=|\gamma|-p-K^{\lambda}_{\boldsymbol{\mu}},\end{align} $$
 $$ \begin{align}\sum_{i=a}^{b}C_{m_{i,1},1,i}\geq 1,\ \ \forall (a,b)\in\mathrm{supp}_2(\lambda_1) ,\ \ \ \ C_{m_{i,1},1,i}\geq 1,\ \ \forall \ i\in \mathrm{supp}_1(\lambda_0).\end{align} $$
$$ \begin{align}\sum_{i=a}^{b}C_{m_{i,1},1,i}\geq 1,\ \ \forall (a,b)\in\mathrm{supp}_2(\lambda_1) ,\ \ \ \ C_{m_{i,1},1,i}\geq 1,\ \ \forall \ i\in \mathrm{supp}_1(\lambda_0).\end{align} $$
We extend our definition for
![]() $\gamma =0$
and set
$\gamma =0$
and set
![]() $L^p_{\boldsymbol {\emptyset },\boldsymbol {\zeta }}=\delta _{p,0}$
.
$L^p_{\boldsymbol {\emptyset },\boldsymbol {\zeta }}=\delta _{p,0}$
.
Remark We keep the notation of Definition 3.2. If
![]() $|\mathrm {supp}_1(\lambda _1)|\leq 1$
, then the first family of inequalities in (3.4) vanish and
$|\mathrm {supp}_1(\lambda _1)|\leq 1$
, then the first family of inequalities in (3.4) vanish and
![]() $\sum _{p\in \mathbb {Z}_+}L^p_{\boldsymbol {\mu },\boldsymbol {\zeta }}$
counts the number of lattice points of a polytope with inequalities
$\sum _{p\in \mathbb {Z}_+}L^p_{\boldsymbol {\mu },\boldsymbol {\zeta }}$
counts the number of lattice points of a polytope with inequalities
 $$ \begin{align*}C_{d,r,i}\geq 0 \ \ \forall \ d,r,i,\ \ \ \ \sum_{d=1}^{m_{i,r}}C_{d,r,i}\leq Q^{\boldsymbol{\mu},\lambda}_{r,i} \ \ \forall\ r,i,\end{align*} $$
$$ \begin{align*}C_{d,r,i}\geq 0 \ \ \forall \ d,r,i,\ \ \ \ \sum_{d=1}^{m_{i,r}}C_{d,r,i}\leq Q^{\boldsymbol{\mu},\lambda}_{r,i} \ \ \forall\ r,i,\end{align*} $$
where
![]() $Q^{\boldsymbol {\mu },\lambda }_{r,i}= P^{\boldsymbol {\mu },\lambda }_{r,i}-1$
if
$Q^{\boldsymbol {\mu },\lambda }_{r,i}= P^{\boldsymbol {\mu },\lambda }_{r,i}-1$
if
![]() $(r,i)\in \{1\}\times \mathrm {supp}_1(\lambda _0)$
and
$(r,i)\in \{1\}\times \mathrm {supp}_1(\lambda _0)$
and
![]() $Q^{\boldsymbol {\mu },\lambda }_{r,i}= P^{\boldsymbol {\mu },\lambda }_{r,i}$
otherwise. Hence,
$Q^{\boldsymbol {\mu },\lambda }_{r,i}= P^{\boldsymbol {\mu },\lambda }_{r,i}$
otherwise. Hence,
 $$ \begin{align}\sum_{\boldsymbol{\mu}\vdash \gamma}\sum_{p\in\mathbb{Z}_+}L^p_{\boldsymbol{\mu},\boldsymbol{\zeta}}=\sum_{\boldsymbol{\mu}\vdash \gamma}\prod_{i=1}^n\prod_{r=1}^{r_i}\begin{bmatrix}{Q^{\boldsymbol{\mu},\lambda}_{r,i} +m_{i,r}}\\{m_{i,r}}\end{bmatrix}=[N_{\boldsymbol{\zeta}}: V(\lambda-\gamma)]_{q=1},\end{align} $$
$$ \begin{align}\sum_{\boldsymbol{\mu}\vdash \gamma}\sum_{p\in\mathbb{Z}_+}L^p_{\boldsymbol{\mu},\boldsymbol{\zeta}}=\sum_{\boldsymbol{\mu}\vdash \gamma}\prod_{i=1}^n\prod_{r=1}^{r_i}\begin{bmatrix}{Q^{\boldsymbol{\mu},\lambda}_{r,i} +m_{i,r}}\\{m_{i,r}}\end{bmatrix}=[N_{\boldsymbol{\zeta}}: V(\lambda-\gamma)]_{q=1},\end{align} $$
where the last equation follows from the following two observations:
-
• If
 $|\mathrm {supp}_1(\lambda _1)|\leq 1$
, then
$|\mathrm {supp}_1(\lambda _1)|\leq 1$
, then
 $N_{\boldsymbol {\zeta }}$
is simply a tensor product of finite-dimensional irreducible
$N_{\boldsymbol {\zeta }}$
is simply a tensor product of finite-dimensional irreducible
 $\mathfrak {g}$
-modules (3.6)This can be derived from the generators and relations description [Reference Naoi28, Theorem B] of fusion products of KR modules and the fact that KR modules are classically irreducible in type A.
$\mathfrak {g}$
-modules (3.6)This can be derived from the generators and relations description [Reference Naoi28, Theorem B] of fusion products of KR modules and the fact that KR modules are classically irreducible in type A. $$ \begin{align}N_{\boldsymbol{\zeta}}\cong_{\mathfrak{g}} \bigotimes_{i=1}^n\left( V(\varpi_i)^{\otimes \lambda_2(h_i)}\otimes V(2\varpi_i)^{\otimes \lambda_0(h_i)}\right)\otimes V(\lambda_1).\end{align} $$
$$ \begin{align}N_{\boldsymbol{\zeta}}\cong_{\mathfrak{g}} \bigotimes_{i=1}^n\left( V(\varpi_i)^{\otimes \lambda_2(h_i)}\otimes V(2\varpi_i)^{\otimes \lambda_0(h_i)}\right)\otimes V(\lambda_1).\end{align} $$
-
• The numerical multiplicities in tensor products of finite-dimensional irreducible
 $\mathfrak {g}$
-modules corresponding to multiples of fundamental weights are given by sums of products of binomial coefficients (see, for example, [Reference Di Francesco and Kedem13]). In the case of (3.6), they are exactly given by the sums of products of binomials as in (3.5).
$\mathfrak {g}$
-modules corresponding to multiples of fundamental weights are given by sums of products of binomial coefficients (see, for example, [Reference Di Francesco and Kedem13]). In the case of (3.6), they are exactly given by the sums of products of binomials as in (3.5).
We will prove the following result in the rest of the paper.
Theorem 4 Let
![]() $p\in \mathbb {Z}_+$
,
$p\in \mathbb {Z}_+$
,
![]() $\nu \in P^+$
, and
$\nu \in P^+$
, and
![]() $\boldsymbol {\pi }=\boldsymbol {\varpi }_{i_1,a_1}\cdots \boldsymbol {\varpi }_{i_k,a_k}\in \mathcal {P}_{\mathbb {Z}}^+(1)$
. Then
$\boldsymbol {\pi }=\boldsymbol {\varpi }_{i_1,a_1}\cdots \boldsymbol {\varpi }_{i_k,a_k}\in \mathcal {P}_{\mathbb {Z}}^+(1)$
. Then
 $$ \begin{align*}\left[L(\boldsymbol{\pi}): \tau_p^{*}V(\nu)\right]=\begin{cases}\ 0,& \text{if }\nu\notin \mathrm{wt}(\boldsymbol{\pi})-Q^+,\\ \\ \ \displaystyle \sum_{\boldsymbol{\mu}\vdash \gamma} L^p_{\boldsymbol{\mu},\left(\mathrm{wt}(\boldsymbol{\pi}),0,\mathrm{wt}(\boldsymbol{\pi}),0\right)},& \text{if }\nu=\mathrm{wt}(\boldsymbol{\pi})-\gamma.\end{cases}\end{align*} $$
$$ \begin{align*}\left[L(\boldsymbol{\pi}): \tau_p^{*}V(\nu)\right]=\begin{cases}\ 0,& \text{if }\nu\notin \mathrm{wt}(\boldsymbol{\pi})-Q^+,\\ \\ \ \displaystyle \sum_{\boldsymbol{\mu}\vdash \gamma} L^p_{\boldsymbol{\mu},\left(\mathrm{wt}(\boldsymbol{\pi}),0,\mathrm{wt}(\boldsymbol{\pi}),0\right)},& \text{if }\nu=\mathrm{wt}(\boldsymbol{\pi})-\gamma.\end{cases}\end{align*} $$
The strategy of the proof is as follows; let
![]() $\boldsymbol {\zeta }=(\lambda ,\lambda _0,\lambda _1,\lambda _2)$
be an admissible quadrupel. We will use the dual functional realization of loop algebras to prove in Section 6.4 that
$\boldsymbol {\zeta }=(\lambda ,\lambda _0,\lambda _1,\lambda _2)$
be an admissible quadrupel. We will use the dual functional realization of loop algebras to prove in Section 6.4 that
Subsequently, we will show in Theorem 6 the reverse estimate under the restriction
![]() $\lambda _2\in P^+(1)$
. The key step for the reverse estimate is the following recursion satisfied by the numbers
$\lambda _2\in P^+(1)$
. The key step for the reverse estimate is the following recursion satisfied by the numbers
![]() $L_{\boldsymbol {\mu },\boldsymbol {\zeta }}^{p}$
; the main theorem is then obtained as a corollary by choosing the quadruple
$L_{\boldsymbol {\mu },\boldsymbol {\zeta }}^{p}$
; the main theorem is then obtained as a corollary by choosing the quadruple
![]() $(\mathrm {wt}(\boldsymbol {\pi }),0,\mathrm {wt}(\boldsymbol {\pi }),0)$
.
$(\mathrm {wt}(\boldsymbol {\pi }),0,\mathrm {wt}(\boldsymbol {\pi }),0)$
.
Proposition Let
![]() $\boldsymbol {\mu }$
be a multipartition,
$\boldsymbol {\mu }$
be a multipartition,
![]() $p\in \mathbb {Z}_+$
, and
$p\in \mathbb {Z}_+$
, and
![]() $\boldsymbol {\zeta }=(\lambda ,\lambda _0,\lambda _1,\lambda _2)$
be an admissible quadrupel. Suppose that
$\boldsymbol {\zeta }=(\lambda ,\lambda _0,\lambda _1,\lambda _2)$
be an admissible quadrupel. Suppose that
Then
 $$ \begin{align*}L^p_{\boldsymbol{\mu},\boldsymbol{\zeta}}=\begin{cases} L^p_{\boldsymbol{\mu},\boldsymbol{\zeta}_1},&\text{ if }\exists \ i\in\{i_1,\dots,i_2\}\text{ with }m_{i,1}=0,\\ \\ L^p_{\boldsymbol{\mu},\boldsymbol{\zeta}_1}-(1-\delta_{p,0})L^{p-1}_{\boldsymbol{\tilde \mu},\boldsymbol{\zeta}_2},&\text{ otherwise}, \end{cases}\end{align*} $$
$$ \begin{align*}L^p_{\boldsymbol{\mu},\boldsymbol{\zeta}}=\begin{cases} L^p_{\boldsymbol{\mu},\boldsymbol{\zeta}_1},&\text{ if }\exists \ i\in\{i_1,\dots,i_2\}\text{ with }m_{i,1}=0,\\ \\ L^p_{\boldsymbol{\mu},\boldsymbol{\zeta}_1}-(1-\delta_{p,0})L^{p-1}_{\boldsymbol{\tilde \mu},\boldsymbol{\zeta}_2},&\text{ otherwise}, \end{cases}\end{align*} $$
where
![]() $\boldsymbol {\tilde \mu }$
is the multipartition obtained from
$\boldsymbol {\tilde \mu }$
is the multipartition obtained from
![]() $\boldsymbol {\mu }$
by removing a box in the last row of each partition
$\boldsymbol {\mu }$
by removing a box in the last row of each partition
![]() $\mu _{i_1},\dots ,\mu _{i_2}$
and
$\mu _{i_1},\dots ,\mu _{i_2}$
and
![]() $\boldsymbol {\zeta }_1,\boldsymbol {\zeta }_2$
are defined as in (2.3) and (2.4).
$\boldsymbol {\zeta }_1,\boldsymbol {\zeta }_2$
are defined as in (2.3) and (2.4).
Proof If
![]() $m_{i,1}=0$
for some
$m_{i,1}=0$
for some
![]() $i\in \{i_1,\dots ,i_2\}$
, the defining inequalities of
$i\in \{i_1,\dots ,i_2\}$
, the defining inequalities of
![]() $\mathcal {S}^p_{\boldsymbol {\mu },\boldsymbol {\zeta }}$
and
$\mathcal {S}^p_{\boldsymbol {\mu },\boldsymbol {\zeta }}$
and
![]() $\mathcal {S}^p_{\boldsymbol {\mu },\boldsymbol {\zeta }_1}$
coincide and the statement is immediate. So suppose that
$\mathcal {S}^p_{\boldsymbol {\mu },\boldsymbol {\zeta }_1}$
coincide and the statement is immediate. So suppose that
![]() $m_{i,1}\geq 1$
for all
$m_{i,1}\geq 1$
for all
![]() $i\in \{i_1,\dots ,i_2\}$
and set
$i\in \{i_1,\dots ,i_2\}$
and set
![]() $\epsilon _i=1$
if
$\epsilon _i=1$
if
![]() $i\in \{i_1,\dots ,i_2\}$
and
$i\in \{i_1,\dots ,i_2\}$
and
![]() $\epsilon _i=0$
otherwise. In particular,
$\epsilon _i=0$
otherwise. In particular,
![]() $\boldsymbol {\mu }$
is not the tuple of empty partitions and we have
$\boldsymbol {\mu }$
is not the tuple of empty partitions and we have
![]() $L^0_{\boldsymbol {\mu },\boldsymbol {\zeta }}=0=L^0_{\boldsymbol {\mu },\boldsymbol {\zeta }_1}$
. Hence, we can assume
$L^0_{\boldsymbol {\mu },\boldsymbol {\zeta }}=0=L^0_{\boldsymbol {\mu },\boldsymbol {\zeta }_1}$
. Hence, we can assume
![]() $p\in \mathbb {N}$
in the rest of the proof. The definition of
$p\in \mathbb {N}$
in the rest of the proof. The definition of
![]() $\boldsymbol {\tilde \mu }$
implies
$\boldsymbol {\tilde \mu }$
implies
![]() $d(\tilde {\mu }_i)=d(\mu _i)-\epsilon _i$
and we consider the projection and inclusion maps
$d(\tilde {\mu }_i)=d(\mu _i)-\epsilon _i$
and we consider the projection and inclusion maps
 $$ \begin{align*}\rho:\mathbb{R}^{d(\mu_1)}&\times \cdots \times \mathbb{R}^{d(\mu_n)}\rightarrow \mathbb{R}^{d(\tilde\mu_1)}\times \cdots \times \mathbb{R}^{d(\tilde\mu_n)},\\\iota:\mathbb{R}^{d(\tilde\mu_1)}&\times \cdots \times \mathbb{R}^{d(\tilde\mu_n)}\rightarrow \mathbb{R}^{d(\mu_1)}\times \cdots \times \mathbb{R}^{d(\mu_n)}.\end{align*} $$
$$ \begin{align*}\rho:\mathbb{R}^{d(\mu_1)}&\times \cdots \times \mathbb{R}^{d(\mu_n)}\rightarrow \mathbb{R}^{d(\tilde\mu_1)}\times \cdots \times \mathbb{R}^{d(\tilde\mu_n)},\\\iota:\mathbb{R}^{d(\tilde\mu_1)}&\times \cdots \times \mathbb{R}^{d(\tilde\mu_n)}\rightarrow \mathbb{R}^{d(\mu_1)}\times \cdots \times \mathbb{R}^{d(\mu_n)}.\end{align*} $$
To be more precise, the projection
![]() $\rho $
applied to an element
$\rho $
applied to an element
![]() $\left (C_{d,r,i}\right )\in \mathbb {R}^{d(\mu _1)}\times \cdots \times \mathbb {R}^{d(\mu _n)}$
drops the entries
$\left (C_{d,r,i}\right )\in \mathbb {R}^{d(\mu _1)}\times \cdots \times \mathbb {R}^{d(\mu _n)}$
drops the entries
![]() $C_{m_{i_1,1},1,i_1},\dots ,C_{m_{i_2,1},1,i_2}$
corresponding to the last rows of the partitions
$C_{m_{i_1,1},1,i_1},\dots ,C_{m_{i_2,1},1,i_2}$
corresponding to the last rows of the partitions
![]() $\mu _{i_1},\dots ,\mu _{i_2}$
and the inclusion
$\mu _{i_1},\dots ,\mu _{i_2}$
and the inclusion
![]() $\iota $
fills the aforementioned places with zeros. By comparing once more the defining inequalities of the polytopes, we observe that
$\iota $
fills the aforementioned places with zeros. By comparing once more the defining inequalities of the polytopes, we observe that
![]() $\mathcal {S}^p_{\boldsymbol {\mu },\boldsymbol {\zeta }_1}$
is obtained from
$\mathcal {S}^p_{\boldsymbol {\mu },\boldsymbol {\zeta }_1}$
is obtained from
![]() $\mathcal {S}^p_{\boldsymbol {\mu },\boldsymbol {\zeta }}$
by dropping the inequality
$\mathcal {S}^p_{\boldsymbol {\mu },\boldsymbol {\zeta }}$
by dropping the inequality
![]() $C_{m_{i_1,1},1,i_1}+\cdots +C_{m_{i_2,1},1,i_2}\geq 1.$
Hence, we have a disjoint union
$C_{m_{i_1,1},1,i_1}+\cdots +C_{m_{i_2,1},1,i_2}\geq 1.$
Hence, we have a disjoint union
where
![]() $\mathcal {S}$
consists of all points
$\mathcal {S}$
consists of all points
![]() $\left (C_{d,r,i}\right )_{1\leq i\leq n,\hspace {0.2em} 1\leq r\leq r_i,\hspace {0.2em} 1\leq d\leq m_{i,r}}$
in
$\left (C_{d,r,i}\right )_{1\leq i\leq n,\hspace {0.2em} 1\leq r\leq r_i,\hspace {0.2em} 1\leq d\leq m_{i,r}}$
in
![]() $\mathcal {S}^p_{\boldsymbol {\mu },\boldsymbol {\zeta }_1}$
satisfying
$\mathcal {S}^p_{\boldsymbol {\mu },\boldsymbol {\zeta }_1}$
satisfying
We finish the proof by showing that
![]() $\rho (\mathcal {S})\subseteq \mathcal {S}^{p-1}_{\boldsymbol {\tilde \mu },\boldsymbol {\zeta }_2}$
and
$\rho (\mathcal {S})\subseteq \mathcal {S}^{p-1}_{\boldsymbol {\tilde \mu },\boldsymbol {\zeta }_2}$
and
![]() $\iota (\mathcal {S}^{p-1}_{\boldsymbol {\tilde \mu },\boldsymbol {\zeta }_2})\subseteq \mathcal {S}$
. Since both inclusions are proven similarly, we focus on the first one. From Lemma 3.2 (note that
$\iota (\mathcal {S}^{p-1}_{\boldsymbol {\tilde \mu },\boldsymbol {\zeta }_2})\subseteq \mathcal {S}$
. Since both inclusions are proven similarly, we focus on the first one. From Lemma 3.2 (note that
![]() $\lambda (h_{i_1,i_2})=2$
), we know that each point in
$\lambda (h_{i_1,i_2})=2$
), we know that each point in
![]() $\rho (\mathcal {S})$
satisfies the inequalities (3.3) of
$\rho (\mathcal {S})$
satisfies the inequalities (3.3) of
![]() $\mathcal {S}^{p-1}_{\boldsymbol {\tilde \mu },\boldsymbol {\zeta }_2}$
. The inequalities (3.4) of
$\mathcal {S}^{p-1}_{\boldsymbol {\tilde \mu },\boldsymbol {\zeta }_2}$
. The inequalities (3.4) of
![]() $\mathcal {S}^{p-1}_{\boldsymbol {\tilde \mu },\boldsymbol {\zeta }_2}$
read as follows:
$\mathcal {S}^{p-1}_{\boldsymbol {\tilde \mu },\boldsymbol {\zeta }_2}$
read as follows:
 $$ \begin{align*}\sum_{i=i_j+\delta_{j,2}}^{i_{j+1}}C_{m_{i,1},1,i}\geq 1,\ \ j\in J,\ \ \ \ C_{m_{i,1},1,i}\geq 1,\ \ \forall \ i\in \mathrm{supp}_1(\lambda_0),\end{align*} $$
$$ \begin{align*}\sum_{i=i_j+\delta_{j,2}}^{i_{j+1}}C_{m_{i,1},1,i}\geq 1,\ \ j\in J,\ \ \ \ C_{m_{i,1},1,i}\geq 1,\ \ \forall \ i\in \mathrm{supp}_1(\lambda_0),\end{align*} $$
where
![]() $J=\{2,\dots ,k-1\}$
if
$J=\{2,\dots ,k-1\}$
if
![]() $i_{2}+1<i_3$
or
$i_{2}+1<i_3$
or
![]() $k=2$
and
$k=2$
and
![]() $J=\{2,4,\dots ,k-1\}$
otherwise. Since
$J=\{2,4,\dots ,k-1\}$
otherwise. Since
![]() $\mathcal {S}\subseteq \mathcal {S}^p_{\boldsymbol {\mu },\boldsymbol {\zeta }_1}$
, they are obviously satisfied by all points in
$\mathcal {S}\subseteq \mathcal {S}^p_{\boldsymbol {\mu },\boldsymbol {\zeta }_1}$
, they are obviously satisfied by all points in
![]() $\rho (\mathcal {S})$
and thus
$\rho (\mathcal {S})$
and thus
![]() $\rho (\mathcal {S})\subseteq \mathcal {S}^{p-1}_{\boldsymbol {\tilde \mu },\boldsymbol {\zeta }_2}$
.
$\rho (\mathcal {S})\subseteq \mathcal {S}^{p-1}_{\boldsymbol {\tilde \mu },\boldsymbol {\zeta }_2}$
.
3.3
We end this section by discussing a few examples.
Example
-
(1) In some cases, the graded limit remains irreducible as a
 $\mathfrak {g}$
-module. For example, if we have
$\mathfrak {g}$
-module. For example, if we have
 $\boldsymbol {\pi }=\boldsymbol {\varpi }_{i_1,a}\boldsymbol {\varpi }_{i_2,aq^{\pm (i_2-i_1+2)}}$
for some
$\boldsymbol {\pi }=\boldsymbol {\varpi }_{i_1,a}\boldsymbol {\varpi }_{i_2,aq^{\pm (i_2-i_1+2)}}$
for some
 $a\in \mathbb {C}(q)$
and
$a\in \mathbb {C}(q)$
and
 $1\leq i_1< i_2\leq n$
, then (3.7)Although this is a well-known fact, we want to derive this example from our main theorem. In order to show
$1\leq i_1< i_2\leq n$
, then (3.7)Although this is a well-known fact, we want to derive this example from our main theorem. In order to show $$ \begin{align} L(\boldsymbol{\pi})\cong V(\varpi_{i_1}+\varpi_{i_2}). \end{align} $$
we fix a nontrivial multipartition
$$ \begin{align} L(\boldsymbol{\pi})\cong V(\varpi_{i_1}+\varpi_{i_2}). \end{align} $$
we fix a nontrivial multipartition $$ \begin{align*}L^p_{\boldsymbol{\mu},(\varpi_{i_1}+\varpi_{i_2},0,\varpi_{i_1}+\varpi_{i_2},0)}=0,\ \ \text{ for all }\ \ \boldsymbol{\mu}\neq \boldsymbol{\emptyset},\end{align*} $$
$$ \begin{align*}L^p_{\boldsymbol{\mu},(\varpi_{i_1}+\varpi_{i_2},0,\varpi_{i_1}+\varpi_{i_2},0)}=0,\ \ \text{ for all }\ \ \boldsymbol{\mu}\neq \boldsymbol{\emptyset},\end{align*} $$
 $\boldsymbol {\mu }$
with
$\boldsymbol {\mu }$
with
 $\mu _i\vdash r_i$
and suppose that
$\mu _i\vdash r_i$
and suppose that
 $u\in \{1,\dots ,n\}$
is maximal such that
$u\in \{1,\dots ,n\}$
is maximal such that
 $r_u\neq 0$
. We write
$r_u\neq 0$
. We write
 $\lambda =\varpi _{i_1}+\varpi _{i_2}$
and note that
$\lambda =\varpi _{i_1}+\varpi _{i_2}$
and note that
 $L^p_{\boldsymbol {\mu },(\lambda ,0,\lambda ,0)}\neq 0$
only if
$L^p_{\boldsymbol {\mu },(\lambda ,0,\lambda ,0)}\neq 0$
only if
 $P^{\boldsymbol {\mu },\lambda }_{r_i,i} \geq 0$
for all
$P^{\boldsymbol {\mu },\lambda }_{r_i,i} \geq 0$
for all
 $i\in \{1,\dots ,n\}$
. This gives (3.8)and hence by induction we get
$i\in \{1,\dots ,n\}$
. This gives (3.8)and hence by induction we get $$ \begin{align}2r_i\leq r_{i-1}+r_{i+1}+\lambda(h_i),\ \ 1\leq i\leq n,\end{align} $$
Now adding
$$ \begin{align}2r_i\leq r_{i-1}+r_{i+1}+\lambda(h_i),\ \ 1\leq i\leq n,\end{align} $$
Now adding $$ \begin{align*}(i+1)r_i\leq i r_{i+1}+\lambda(h_1)+2\lambda(h_2)+\cdots+i\lambda(h_i),\ \ 1\leq i\leq n.\end{align*} $$
$$ \begin{align*}(i+1)r_i\leq i r_{i+1}+\lambda(h_1)+2\lambda(h_2)+\cdots+i\lambda(h_i),\ \ 1\leq i\leq n.\end{align*} $$
 $(i+1)\lambda (h_{i+1})$
on both sides of the inequality and dividing by
$(i+1)\lambda (h_{i+1})$
on both sides of the inequality and dividing by
 $(i+1)$
gives Since the left-hand side is an integer, this yields
$(i+1)$
gives Since the left-hand side is an integer, this yields $$ \begin{align*}r_i+\lambda(h_{i+1})\leq r_{i+1}+\frac{1}{i+1}(\lambda(h_1)+2\lambda(h_2)+\cdots+(i+1)\lambda(h_{i+1}))\leq r_{i+1}+\frac{2i+1}{i+1}.\end{align*} $$
(3.9)Moreover, another condition for
$$ \begin{align*}r_i+\lambda(h_{i+1})\leq r_{i+1}+\frac{1}{i+1}(\lambda(h_1)+2\lambda(h_2)+\cdots+(i+1)\lambda(h_{i+1}))\leq r_{i+1}+\frac{2i+1}{i+1}.\end{align*} $$
(3.9)Moreover, another condition for $$ \begin{align}r_i+\lambda(h_{i+1})\leq r_{i+1}+1,\ \ 1\leq i\leq n.\end{align} $$
$$ \begin{align}r_i+\lambda(h_{i+1})\leq r_{i+1}+1,\ \ 1\leq i\leq n.\end{align} $$
 $L^p_{\boldsymbol {\mu },(\lambda ,0,\lambda ,0)}$
being nonzero is coming from
$L^p_{\boldsymbol {\mu },(\lambda ,0,\lambda ,0)}$
being nonzero is coming from
 $P^{\boldsymbol {\mu },\lambda }_{1,i}\geq 0$
: (3.10)Now we collect a few consequences from (3.8) (with index
$P^{\boldsymbol {\mu },\lambda }_{1,i}\geq 0$
: (3.10)Now we collect a few consequences from (3.8) (with index $$ \begin{align}\mu_{i-1}(1)\geq 2\mu_{i}(1)-\mu_{i+1}(1)-\lambda(h_i),\ \ 1\leq i\leq n.\end{align} $$
$$ \begin{align}\mu_{i-1}(1)\geq 2\mu_{i}(1)-\mu_{i+1}(1)-\lambda(h_i),\ \ 1\leq i\leq n.\end{align} $$
 $i+1$
) and (3.9). We have:
$i+1$
) and (3.9). We have:
-
(a)
 $\mu _u$
is a single box (use (3.9) for
$\mu _u$
is a single box (use (3.9) for
 $i=u$
).
$i=u$
). -
(b) If
 $r_{i+1}=r_{i+2}+1$
, then
$r_{i+1}=r_{i+2}+1$
, then
 $r_{i}=r_{i+1}-\lambda (h_{i+1})+1$
.
$r_{i}=r_{i+1}-\lambda (h_{i+1})+1$
. -
(c) If
 $r_{i+1}=r_{i+2}$
, then
$r_{i+1}=r_{i+2}$
, then
 $r_i=r_{i+1}-\lambda (h_{i+1})$
or
$r_i=r_{i+1}-\lambda (h_{i+1})$
or
 $r_i=r_{i+1}-\lambda (h_{i+1})+1$
.
$r_i=r_{i+1}-\lambda (h_{i+1})+1$
. -
(d) If
 $r_{i+1}=r_{i+2}-1$
, then
$r_{i+1}=r_{i+2}-1$
, then
 $r_i=r_{i+1}-\lambda (h_{i+1})-1$
or
$r_i=r_{i+1}-\lambda (h_{i+1})-1$
or
 $r_i=r_{i+1}-\lambda (h_{i+1})+1$
or
$r_i=r_{i+1}-\lambda (h_{i+1})+1$
or
 $r_i=r_{i+1}-\lambda (h_{i+1})$
.
$r_i=r_{i+1}-\lambda (h_{i+1})$
.
Case 1: In this case, we suppose that
 $u<i_1$
. Since
$u<i_1$
. Since
 $r_u=1=r_{u+1}+1$
(see part (a)), we obtain from part (b) that
$r_u=1=r_{u+1}+1$
(see part (a)), we obtain from part (b) that
 $r_{u-1}=2$
and from (3.10) that
$r_{u-1}=2$
and from (3.10) that
 $\mu _{u-1}$
is a column tableaux. Continuing in the same fashion, we get that
$\mu _{u-1}$
is a column tableaux. Continuing in the same fashion, we get that
 $r_i=u-i+1$
and
$r_i=u-i+1$
and
 $\mu _i$
is a column tableaux for all
$\mu _i$
is a column tableaux for all
 $i\in \{1,\dots ,u\}$
. But this contradicts
$i\in \{1,\dots ,u\}$
. But this contradicts
 $2r_1=2u\leq r_2=u-1$
, which we have from (3.10).
$2r_1=2u\leq r_2=u-1$
, which we have from (3.10).Case 2: In this case, we suppose that
 $u\geq i_2$
. Similarly as in the above case, we can show that In particular,
$u\geq i_2$
. Similarly as in the above case, we can show that In particular, $$ \begin{align*}r_i=u-i+1-\lambda(h_{i+1}),\ \text{and}\ \mu_i \text{ is a column tableaux for }i_2-1\leq i\leq u.\end{align*} $$
$$ \begin{align*}r_i=u-i+1-\lambda(h_{i+1}),\ \text{and}\ \mu_i \text{ is a column tableaux for }i_2-1\leq i\leq u.\end{align*} $$
 $r_{i_2-1}=r_{i_2}$
, which means that we have two choices for
$r_{i_2-1}=r_{i_2}$
, which means that we have two choices for
 $r_{i_2-2}$
by part (c). Either
$r_{i_2-2}$
by part (c). Either
 $r_{i_2-2}=r_{i_2-1}$
or
$r_{i_2-2}=r_{i_2-1}$
or
 $r_{i_2-2}=r_{i_2-1}+1$
. But part (b) forces in the latter case that we have to keep increasing until we reach index
$r_{i_2-2}=r_{i_2-1}+1$
. But part (b) forces in the latter case that we have to keep increasing until we reach index
 $i_1$
: Again by part (c), we have
$i_1$
: Again by part (c), we have $$ \begin{align*}r_{i_1-1}=r_{i_1}>\cdots >r_{i_2-2}>r_{i_2-1}.\end{align*} $$
$$ \begin{align*}r_{i_1-1}=r_{i_1}>\cdots >r_{i_2-2}>r_{i_2-1}.\end{align*} $$
 $r_{i_1-2}=r_{i_1-1}$
or
$r_{i_1-2}=r_{i_1-1}$
or
 $r_{i_1-2}=r_{i_1-1}+1$
and hence we have a weakly increasing sequence which contradicts once more
$r_{i_1-2}=r_{i_1-1}+1$
and hence we have a weakly increasing sequence which contradicts once more $$ \begin{align*}r_1\geq r_2\geq \cdots \geq r_{i_1-1},\end{align*} $$
$$ \begin{align*}r_1\geq r_2\geq \cdots \geq r_{i_1-1},\end{align*} $$
 $2r_1\leq r_2$
. In conclusion, we must have
$2r_1\leq r_2$
. In conclusion, we must have
 $r_{i_2-2}=r_{i_2-1}=r_{i_2}$
. Continuing with the same argument, we get and each partition
$r_{i_2-2}=r_{i_2-1}=r_{i_2}$
. Continuing with the same argument, we get and each partition $$ \begin{align*}r_{i_1-1}+1=r_{i_1}=\cdots=r_{i_2}=r_{i_2+1}+1\end{align*} $$
$$ \begin{align*}r_{i_1-1}+1=r_{i_1}=\cdots=r_{i_2}=r_{i_2+1}+1\end{align*} $$
 $\mu _{i_1},\dots ,\mu _{i_2}$
is a column tableaux by (3.10). This gives
$\mu _{i_1},\dots ,\mu _{i_2}$
is a column tableaux by (3.10). This gives
 $P^{\boldsymbol {\mu },\lambda }_{1,i}=0$
for
$P^{\boldsymbol {\mu },\lambda }_{1,i}=0$
for
 $i\in \{i_1,\dots ,i_2\}$
and hence
$i\in \{i_1,\dots ,i_2\}$
and hence
 $C_{r_{i_1},1,i_1}+\cdots +C_{r_{i_2},1,i_2}=0$
, which is a contradiction.
$C_{r_{i_1},1,i_1}+\cdots +C_{r_{i_2},1,i_2}=0$
, which is a contradiction.
Case 3: The last case
 $i_1\leq u<i_2$
works similarly, and we omit the details.
$i_1\leq u<i_2$
works similarly, and we omit the details.This proves that
 $L^p_{\boldsymbol {\mu },(\lambda ,0,\lambda ,0)}$
can only be nonzero if
$L^p_{\boldsymbol {\mu },(\lambda ,0,\lambda ,0)}$
can only be nonzero if
 $\boldsymbol {\mu }$
consists of empty partitions and we get (3.7) from Theorem 4.
$\boldsymbol {\mu }$
consists of empty partitions and we get (3.7) from Theorem 4. -
-
(2) Let
 $n=7$
and consider Therefore, the multipartitions
$n=7$
and consider Therefore, the multipartitions $$ \begin{align*} \gamma = \alpha_2+ 2\alpha_3 + 3\alpha_4 + 3\alpha_5 + 2\alpha_6 + \alpha_7, \quad i_1 = 2, i_2 = 3, i_3 = 4, i_4 = 5, i_5 = 6. \end{align*} $$
$$ \begin{align*} \gamma = \alpha_2+ 2\alpha_3 + 3\alpha_4 + 3\alpha_5 + 2\alpha_6 + \alpha_7, \quad i_1 = 2, i_2 = 3, i_3 = 4, i_4 = 5, i_5 = 6. \end{align*} $$
 $\boldsymbol {\mu }$
are of the form where
$\boldsymbol {\mu }$
are of the form where
 $\mu _3, \mu _6$
have two boxes and
$\mu _3, \mu _6$
have two boxes and
 $\mu _4,\mu _5$
have three boxes. Note that only multipartitions
$\mu _4,\mu _5$
have three boxes. Note that only multipartitions
 $\boldsymbol {\mu }$
, for which
$\boldsymbol {\mu }$
, for which
 $P^{\boldsymbol {\mu },\lambda }_{r,i} \ge 0$
for all
$P^{\boldsymbol {\mu },\lambda }_{r,i} \ge 0$
for all
 $1 \le i \le n$
and
$1 \le i \le n$
and
 $1 \le r \le r_i$
, need to be considered. A straightforward calculation yields that the relevant multipartitions are given by
$1 \le r \le r_i$
, need to be considered. A straightforward calculation yields that the relevant multipartitions are given by
 $\boldsymbol {\mu }_1,\boldsymbol {\mu }_2$
and
$\boldsymbol {\mu }_1,\boldsymbol {\mu }_2$
and
 $\boldsymbol {\mu }_3$
from Example 3.2(2). We deduce setting
$\boldsymbol {\mu }_3$
from Example 3.2(2). We deduce setting
 $\boldsymbol {\zeta }=(\mathrm {wt}(\boldsymbol {\pi }),0,\mathrm {wt}(\boldsymbol {\pi }),0)$
, and hence
$\boldsymbol {\zeta }=(\mathrm {wt}(\boldsymbol {\pi }),0,\mathrm {wt}(\boldsymbol {\pi }),0)$
, and hence $$ \begin{align*} L^p_{\boldsymbol{\mu}_1,\boldsymbol{\zeta}} &=| \lbrace C_{1,2,3} \in \mathbb{Z}_{+} \,\colon\, C_{1,2,3} \le 1, C_{1,2,3} + p =5 \rbrace|, \\ L^p_{\boldsymbol{\mu}_2,\boldsymbol{\zeta}} &=| \lbrace (C_{1,1,2}, C_{1,1,4}, C_{1,1,5}) \in \mathbb{Z}_{+}^3 \colon\, C_{1,1,2} = C_{1,1,4} = C_{1,1,5} = 1,\, p =3 \rbrace|, \\ L^p_{\boldsymbol{\mu}_3,\boldsymbol{\zeta}} &= 0,\end{align*} $$
$$ \begin{align*} L^p_{\boldsymbol{\mu}_1,\boldsymbol{\zeta}} &=| \lbrace C_{1,2,3} \in \mathbb{Z}_{+} \,\colon\, C_{1,2,3} \le 1, C_{1,2,3} + p =5 \rbrace|, \\ L^p_{\boldsymbol{\mu}_2,\boldsymbol{\zeta}} &=| \lbrace (C_{1,1,2}, C_{1,1,4}, C_{1,1,5}) \in \mathbb{Z}_{+}^3 \colon\, C_{1,1,2} = C_{1,1,4} = C_{1,1,5} = 1,\, p =3 \rbrace|, \\ L^p_{\boldsymbol{\mu}_3,\boldsymbol{\zeta}} &= 0,\end{align*} $$
 $$ \begin{align*}[L(\boldsymbol{\pi}):V(\mathrm{wt}(\boldsymbol{\pi})-\gamma)]_q= q^3 + q^4+q^5.\end{align*} $$
$$ \begin{align*}[L(\boldsymbol{\pi}):V(\mathrm{wt}(\boldsymbol{\pi})-\gamma)]_q= q^3 + q^4+q^5.\end{align*} $$
-
(3) Let
 $n=8$
and consider Again, we only have to consider multipartitions
$n=8$
and consider Again, we only have to consider multipartitions $$ \begin{align*}\gamma=\alpha_1+3(\alpha_2+\alpha_5)+4(\alpha_3+\alpha_4)+2\alpha_6+\alpha_7,\ \ i_1=2, i_2=3, i_3=4, i_4=5, i_5=7.\end{align*} $$
$$ \begin{align*}\gamma=\alpha_1+3(\alpha_2+\alpha_5)+4(\alpha_3+\alpha_4)+2\alpha_6+\alpha_7,\ \ i_1=2, i_2=3, i_3=4, i_4=5, i_5=7.\end{align*} $$
 $\boldsymbol {\mu }$
, for which
$\boldsymbol {\mu }$
, for which
 $P^{\boldsymbol {\mu },\lambda }_{r,i} \ge 0$
for all
$P^{\boldsymbol {\mu },\lambda }_{r,i} \ge 0$
for all
 $1 \le i \le n$
and
$1 \le i \le n$
and
 $1 \le r \le r_i$
. A long but straightforward calculation shows that the relevant multipartitions are given by
$1 \le r \le r_i$
. A long but straightforward calculation shows that the relevant multipartitions are given by 
 Moreover, the numbers described in Theorem 4 are only nonzero for the multipartitions
Moreover, the numbers described in Theorem 4 are only nonzero for the multipartitions
 $ \boldsymbol {\mu }_1$
and
$ \boldsymbol {\mu }_1$
and
 $\boldsymbol {\mu }_2$
from Example 3.2(3). We obtain for
$\boldsymbol {\mu }_2$
from Example 3.2(3). We obtain for
 $\boldsymbol {\zeta }=(\mathrm {wt}(\boldsymbol {\pi }),0,\mathrm {wt}(\boldsymbol {\pi }),0)$
, and hence
$\boldsymbol {\zeta }=(\mathrm {wt}(\boldsymbol {\pi }),0,\mathrm {wt}(\boldsymbol {\pi }),0)$
, and hence $$ \begin{align*} L^p_{\boldsymbol{\mu}_1,\boldsymbol{\zeta}} &=| \lbrace C_{1,2,5} \in \mathbb{Z}_{+} \,\colon\, C_{1,2,5}\le 1 , \, C_{1,2,5} + p = 5\rbrace|, \\ L^p_{\boldsymbol{\mu}_2,\boldsymbol{\zeta}} &=| \lbrace (C_{1,1,2}, C_{2,1,4}, C_{1,1,7}) \in \mathbb{Z}_{+}^3 \colon\, C_{1,1,2} = C_{2,1,4} = C_{1,1,7} = 1,\, p =4 \rbrace|, \end{align*} $$
$$ \begin{align*} L^p_{\boldsymbol{\mu}_1,\boldsymbol{\zeta}} &=| \lbrace C_{1,2,5} \in \mathbb{Z}_{+} \,\colon\, C_{1,2,5}\le 1 , \, C_{1,2,5} + p = 5\rbrace|, \\ L^p_{\boldsymbol{\mu}_2,\boldsymbol{\zeta}} &=| \lbrace (C_{1,1,2}, C_{2,1,4}, C_{1,1,7}) \in \mathbb{Z}_{+}^3 \colon\, C_{1,1,2} = C_{2,1,4} = C_{1,1,7} = 1,\, p =4 \rbrace|, \end{align*} $$
 $$ \begin{align*}\left[L(\boldsymbol{\pi}):V(\mathrm{wt}(\boldsymbol{\pi})-\gamma)\right]_q= 2q^4 + q^5.\end{align*} $$
$$ \begin{align*}\left[L(\boldsymbol{\pi}):V(\mathrm{wt}(\boldsymbol{\pi})-\gamma)\right]_q= 2q^4 + q^5.\end{align*} $$
4 The family of truncated modules for current algebras
4.1
We introduce the family of truncated
![]() $\mathfrak {g}[t]$
-modules indexed by pairs
$\mathfrak {g}[t]$
-modules indexed by pairs
![]() $(\boldsymbol {\xi },\lambda )$
where
$(\boldsymbol {\xi },\lambda )$
where
![]() $\boldsymbol {\xi }=(\xi _{\alpha })_{\alpha \in R^+}$
is a tuple of nonnegative integers indexed by the set of positive roots of
$\boldsymbol {\xi }=(\xi _{\alpha })_{\alpha \in R^+}$
is a tuple of nonnegative integers indexed by the set of positive roots of
![]() $\mathfrak {g}$
and
$\mathfrak {g}$
and
![]() $\lambda $
is a dominant integral weight (abbreviate as usual
$\lambda $
is a dominant integral weight (abbreviate as usual
![]() $\xi _{\alpha _{i,j}}=\xi _{i,j}$
etc.). We define
$\xi _{\alpha _{i,j}}=\xi _{i,j}$
etc.). We define
![]() $M_{\boldsymbol {\xi },\lambda }:=\mathbf {U}/\mathcal {I}_{\boldsymbol {\xi },\lambda }$
, where
$M_{\boldsymbol {\xi },\lambda }:=\mathbf {U}/\mathcal {I}_{\boldsymbol {\xi },\lambda }$
, where
![]() $\mathcal {I}_{\boldsymbol {\xi },\lambda }\subseteq \mathbf {U}$
is the left ideal generated by the elements
$\mathcal {I}_{\boldsymbol {\xi },\lambda }\subseteq \mathbf {U}$
is the left ideal generated by the elements
In other words,
![]() $M_{\boldsymbol {\xi },\lambda }$
is the cyclic quotient of the local Weyl module
$M_{\boldsymbol {\xi },\lambda }$
is the cyclic quotient of the local Weyl module
![]() $W_{\mathrm {loc}}(\lambda )$
by the submodule generated by
$W_{\mathrm {loc}}(\lambda )$
by the submodule generated by
where
![]() $w_{\lambda }$
is the highest weight generator of
$w_{\lambda }$
is the highest weight generator of
![]() $W_{\mathrm {loc}}(\lambda )$
. We call
$W_{\mathrm {loc}}(\lambda )$
. We call
![]() $\boldsymbol {\xi }$
normalized if
$\boldsymbol {\xi }$
normalized if
![]() $\xi _{\alpha }=\min \{\xi _{\beta }: \beta \succeq \alpha \}$
for all
$\xi _{\alpha }=\min \{\xi _{\beta }: \beta \succeq \alpha \}$
for all
![]() $\alpha \in R^+$
. Given an arbitrary
$\alpha \in R^+$
. Given an arbitrary
![]() $\boldsymbol {\xi }$
, we obviously have
$\boldsymbol {\xi }$
, we obviously have
![]() $M_{\boldsymbol {\xi },\lambda }\cong M_{\boldsymbol {\xi }',\lambda }$
, where
$M_{\boldsymbol {\xi },\lambda }\cong M_{\boldsymbol {\xi }',\lambda }$
, where
![]() $\boldsymbol {\xi }'$
is defined by
$\boldsymbol {\xi }'$
is defined by
![]() $\xi _{\alpha }':=\min \{\xi _{\beta }: \beta \succeq \alpha \}$
. Hence, we can replace
$\xi _{\alpha }':=\min \{\xi _{\beta }: \beta \succeq \alpha \}$
. Hence, we can replace
![]() $\boldsymbol {\xi }$
by the normalized tuple
$\boldsymbol {\xi }$
by the normalized tuple
![]() $\boldsymbol {\xi }'$
, and suppose in the rest of the paper without loss of generality that
$\boldsymbol {\xi }'$
, and suppose in the rest of the paper without loss of generality that
![]() $\boldsymbol {\xi }$
is normalized unless otherwise stated.
$\boldsymbol {\xi }$
is normalized unless otherwise stated.
Example
-
(1) If we choose
 $\xi _{\alpha }=1$
for all
$\xi _{\alpha }=1$
for all
 $\alpha \in R^+$
, we obtain the pullback of the irreducible representation
$\alpha \in R^+$
, we obtain the pullback of the irreducible representation
 $M_{\boldsymbol {\xi },\lambda }=\mathrm {ev}_0^{*}V(\lambda )$
where
$M_{\boldsymbol {\xi },\lambda }=\mathrm {ev}_0^{*}V(\lambda )$
where
 $\mathrm {ev}_0: \mathfrak {g}[t]\rightarrow \mathfrak {g}$
is the evaluation map at
$\mathrm {ev}_0: \mathfrak {g}[t]\rightarrow \mathfrak {g}$
is the evaluation map at
 $0$
.
$0$
. -
(2) Choosing
 $\xi _{\alpha }=\xi _{\beta }$
for all
$\xi _{\alpha }=\xi _{\beta }$
for all
 $\alpha ,\beta \in R^+$
, we obtain the truncated local Weyl modules whose structure has been partially determined in the series of articles [Reference Barth and Kus3, Reference Fourier, Martins and Moura15, Reference Kus and Littelmann23].
$\alpha ,\beta \in R^+$
, we obtain the truncated local Weyl modules whose structure has been partially determined in the series of articles [Reference Barth and Kus3, Reference Fourier, Martins and Moura15, Reference Kus and Littelmann23]. -
(3) For an admissible quadrupel
 $\boldsymbol {\zeta }=(\lambda ,\lambda _0,\lambda _1,\lambda _2)$
, we choose
$\boldsymbol {\zeta }=(\lambda ,\lambda _0,\lambda _1,\lambda _2)$
, we choose
 $\boldsymbol {\xi }$
as and obtain
$\boldsymbol {\xi }$
as and obtain $$ \begin{align*}\xi_{i,j}=(\lambda_0+\lambda_2)(h_{i,j})+\left\lceil \frac{\lambda_1(h_{i,j})}{2}\right\rceil,\ \ 1\leq i\leq j\leq n,\end{align*} $$
$$ \begin{align*}\xi_{i,j}=(\lambda_0+\lambda_2)(h_{i,j})+\left\lceil \frac{\lambda_1(h_{i,j})}{2}\right\rceil,\ \ 1\leq i\leq j\leq n,\end{align*} $$
 $N_{\boldsymbol {\zeta }}\cong M_{\boldsymbol {\xi },\lambda }$
from the discussion in Section 2.8. In particular,
$N_{\boldsymbol {\zeta }}\cong M_{\boldsymbol {\xi },\lambda }$
from the discussion in Section 2.8. In particular,
 $L(\boldsymbol {\pi })$
belongs to the family of truncated modules for all
$L(\boldsymbol {\pi })$
belongs to the family of truncated modules for all
 $\boldsymbol {\pi }\in \mathcal {P}^+_{\mathbb {Z}}(1)$
by Theorem 2(1).
$\boldsymbol {\pi }\in \mathcal {P}^+_{\mathbb {Z}}(1)$
by Theorem 2(1).
In fact, many more families of representations such as Demazure modules and generalized Demazure modules appear as
![]() $M_{\boldsymbol {\xi },\lambda }$
for a suitable choice of
$M_{\boldsymbol {\xi },\lambda }$
for a suitable choice of
![]() $\boldsymbol {\xi }$
and
$\boldsymbol {\xi }$
and
![]() $\lambda $
(see, for example, [Reference Chari and Venkatesh12, Reference Kus and Venkatesh24, Reference Kus and Venkatesh25]).
$\lambda $
(see, for example, [Reference Chari and Venkatesh12, Reference Kus and Venkatesh24, Reference Kus and Venkatesh25]).
4.2
The aim of this section is to describe the
![]() $\mathbf {U}^{-}$
structure of
$\mathbf {U}^{-}$
structure of
![]() $M_{\boldsymbol {\xi },\lambda }$
. We set
$M_{\boldsymbol {\xi },\lambda }$
. We set
![]() $x^{(r)}:=\frac {1}{r!} x^r$
for an element
$x^{(r)}:=\frac {1}{r!} x^r$
for an element
![]() $x\in \mathfrak {g}[t]$
,
$x\in \mathfrak {g}[t]$
,
![]() $r\in \mathbb {Z}_+$
and
$r\in \mathbb {Z}_+$
and
where the sum runs over all tuples
![]() $(b_0,\dots ,b_s)$
of nonnegative integers satisfying
$(b_0,\dots ,b_s)$
of nonnegative integers satisfying
![]() $b_0+\cdots +b_s=r$
and
$b_0+\cdots +b_s=r$
and
![]() $b_1+2b_2+\cdots + sb:s=s$
. The following result is a slight modification of [Reference Biswal and Kus5, Lemma 20].
$b_1+2b_2+\cdots + sb:s=s$
. The following result is a slight modification of [Reference Biswal and Kus5, Lemma 20].
Lemma Let V be a
![]() $\mathbf {U}$
-representation and
$\mathbf {U}$
-representation and
![]() $v\in V$
a weight vector such that
$v\in V$
a weight vector such that
Then we have for all
![]() $r,s\in \mathbb {Z}_+$
with
$r,s\in \mathbb {Z}_+$
with
![]() $r+s\geq 1+\lambda (h_i)$
,
$r+s\geq 1+\lambda (h_i)$
,
Proof From [Reference Biswal and Kus5, Proof of Lemma 20], we obtain up to a nonzero constant
 $$ \begin{align*}(h\otimes t^{\ell})\cdot \mathbf{x}_i^{-}(r,s)v=r\cdot \mathbf{x}_i^{-}(r,s+\ell)v-\sum_{j=0}^{\ell-1}(x_i^{-}\otimes t^j)\cdot \mathbf{x}_i^{-}(r-1,s+\ell-j)v.\end{align*} $$
$$ \begin{align*}(h\otimes t^{\ell})\cdot \mathbf{x}_i^{-}(r,s)v=r\cdot \mathbf{x}_i^{-}(r,s+\ell)v-\sum_{j=0}^{\ell-1}(x_i^{-}\otimes t^j)\cdot \mathbf{x}_i^{-}(r-1,s+\ell-j)v.\end{align*} $$
Hence, the above element lies in the
![]() $\mathbf {U}^-$
-span of elements of the form
$\mathbf {U}^-$
-span of elements of the form
![]() $\mathbf {x}_i^{-}(u,w)v$
with
$\mathbf {x}_i^{-}(u,w)v$
with
![]() $u+w\geq 1+\lambda (h_i)$
. The fact that an arbitrary product of elements in
$u+w\geq 1+\lambda (h_i)$
. The fact that an arbitrary product of elements in
![]() $(\mathfrak {h}\otimes t\mathbb {C}[t])$
applied to
$(\mathfrak {h}\otimes t\mathbb {C}[t])$
applied to
![]() $\mathbf {x}_i^{-}(r,s)v$
lies in the right-hand side of (4.1) follows from
$\mathbf {x}_i^{-}(r,s)v$
lies in the right-hand side of (4.1) follows from
![]() $[\mathfrak {h},\mathfrak {n}^{-}]\subseteq \mathfrak {n}^-$
and induction on the length. Now we consider the element
$[\mathfrak {h},\mathfrak {n}^{-}]\subseteq \mathfrak {n}^-$
and induction on the length. Now we consider the element
![]() $(x_i^+\otimes t^{a})\cdot \mathbf {x}_i^{-}(r,s)v$
. If
$(x_i^+\otimes t^{a})\cdot \mathbf {x}_i^{-}(r,s)v$
. If
![]() $a=1$
, then clearly (up to a constant)
$a=1$
, then clearly (up to a constant)
Otherwise, we choose
![]() $h\in \mathfrak {h}$
with
$h\in \mathfrak {h}$
with
![]() $\alpha _i(h)\neq 0$
and get
$\alpha _i(h)\neq 0$
and get
and the claim in this case (length one) follows by induction on a. Again, the general case follows by induction on the length and the Poincaré–Birkhoff–Witt (PBW) theorem.
By construction, we have an isomorphism of
![]() $\mathbf {U}^{-}$
-modules:
$\mathbf {U}^{-}$
-modules:
Proposition We have that
![]() $\mathcal {J}_{\boldsymbol {\xi },\lambda }$
is the left ideal in
$\mathcal {J}_{\boldsymbol {\xi },\lambda }$
is the left ideal in
![]() $\mathbf {U}^{-}$
generated by the elements
$\mathbf {U}^{-}$
generated by the elements
Proof We first show that each element in (4.2) and (4.3) is contained in
![]() $\mathcal {J}_{\boldsymbol {\xi },\lambda }$
. Let
$\mathcal {J}_{\boldsymbol {\xi },\lambda }$
. Let
![]() $\beta \in R^+$
such that
$\beta \in R^+$
such that
![]() $\beta \succeq \alpha $
and
$\beta \succeq \alpha $
and
![]() $\xi _{\beta }$
is minimal with this property. Either
$\xi _{\beta }$
is minimal with this property. Either
![]() $\alpha =\beta $
or
$\alpha =\beta $
or
![]() $\beta -\alpha \in R^+$
or we can find
$\beta -\alpha \in R^+$
or we can find
![]() $\gamma _1,\gamma _2\in R^+$
such that (2.1) holds. We assume that the latter holds, since all cases are treated similarly. We get
$\gamma _1,\gamma _2\in R^+$
such that (2.1) holds. We assume that the latter holds, since all cases are treated similarly. We get
Since
![]() $\mathfrak {n}^+[t]\subseteq \mathcal {I}_{\boldsymbol {\xi },\lambda }$
and
$\mathfrak {n}^+[t]\subseteq \mathcal {I}_{\boldsymbol {\xi },\lambda }$
and
![]() $(x_{\beta }^{-}\otimes t^{\xi _{\beta }})\in \mathcal {I}_{\boldsymbol {\xi },\lambda },$
we also have
$(x_{\beta }^{-}\otimes t^{\xi _{\beta }})\in \mathcal {I}_{\boldsymbol {\xi },\lambda },$
we also have
![]() $(x_{\alpha }^{-}\otimes t^{\xi _{\beta }+p})\in \mathcal {I}_{\boldsymbol {\xi },\lambda }\cap \mathbf {U}^-$
and all elements in (4.3) are contained in
$(x_{\alpha }^{-}\otimes t^{\xi _{\beta }+p})\in \mathcal {I}_{\boldsymbol {\xi },\lambda }\cap \mathbf {U}^-$
and all elements in (4.3) are contained in
![]() $\mathcal {J}_{\boldsymbol {\xi },\lambda }$
. The containment of (4.2) follows from the Garland identities (see, for example, [Reference Chari and Pressley11, Lemma 1.3] for the current formulation)
$\mathcal {J}_{\boldsymbol {\xi },\lambda }$
. The containment of (4.2) follows from the Garland identities (see, for example, [Reference Chari and Pressley11, Lemma 1.3] for the current formulation)
and the fact that
![]() $(x_i^-\otimes 1)^{(s+r)}\in \mathcal {I}_{\boldsymbol {\xi },\lambda }$
for all
$(x_i^-\otimes 1)^{(s+r)}\in \mathcal {I}_{\boldsymbol {\xi },\lambda }$
for all
![]() $r+s\geq 1+\lambda (h_i)$
. In order to finish the proof, we do the following procedure. We write each element in
$r+s\geq 1+\lambda (h_i)$
. In order to finish the proof, we do the following procedure. We write each element in
![]() $\mathcal {I}_{\boldsymbol {\xi },\lambda }$
in PBW order:
$\mathcal {I}_{\boldsymbol {\xi },\lambda }$
in PBW order:
After that, we take the projection of that element onto
![]() $\mathbf {U}^{-}\cdot \mathbf {U}(\mathfrak {h})$
and substitute
$\mathbf {U}^{-}\cdot \mathbf {U}(\mathfrak {h})$
and substitute
![]() $h=\lambda (h)$
for all
$h=\lambda (h)$
for all
![]() $h\in \mathfrak {h}$
. This gives an element in
$h\in \mathfrak {h}$
. This gives an element in
![]() $\mathcal {J}_{\boldsymbol {\xi },\lambda }$
and it is clear that each element in
$\mathcal {J}_{\boldsymbol {\xi },\lambda }$
and it is clear that each element in
![]() $\mathcal {J}_{\boldsymbol {\xi },\lambda }$
appears in this way. So the strategy of the proof is to show that by doing this procedure we only get elements in the left ideal in
$\mathcal {J}_{\boldsymbol {\xi },\lambda }$
appears in this way. So the strategy of the proof is to show that by doing this procedure we only get elements in the left ideal in
![]() $\mathbf {U}^{-}$
generated by the elements (4.2) and (4.3). Note that it is enough to project all elements in
$\mathbf {U}^{-}$
generated by the elements (4.2) and (4.3). Note that it is enough to project all elements in
 $$ \begin{align}\sum_{i=1}^n \mathbf{U}\cdot (x_i^-\otimes 1)^{\lambda(h_i)+1}+\sum_{\alpha\in R^+}\mathbf{U}\cdot (x^-_{\alpha}\otimes t^{\xi_{\alpha}}).\end{align} $$
$$ \begin{align}\sum_{i=1}^n \mathbf{U}\cdot (x_i^-\otimes 1)^{\lambda(h_i)+1}+\sum_{\alpha\in R^+}\mathbf{U}\cdot (x^-_{\alpha}\otimes t^{\xi_{\alpha}}).\end{align} $$
Using Lemma 4.2, we see that the projection of each element in (4.4) is contained in
 $$ \begin{align*}\sum_{i=1}^n\sum_{\substack{r,s:\\ r+s>\lambda(h_i)}} \mathbf{U}^{-}\cdot\mathbf{x}^-_i(r,s)+\sum_{\alpha\in R^+}\sum_{k\geq \min\{\xi_{\beta}: \beta\succeq \alpha\}}\mathbf{U}^{-}\cdot (x^-_{\alpha}\otimes t^{k})\mathbf{U}(\mathfrak{h}).\end{align*} $$
$$ \begin{align*}\sum_{i=1}^n\sum_{\substack{r,s:\\ r+s>\lambda(h_i)}} \mathbf{U}^{-}\cdot\mathbf{x}^-_i(r,s)+\sum_{\alpha\in R^+}\sum_{k\geq \min\{\xi_{\beta}: \beta\succeq \alpha\}}\mathbf{U}^{-}\cdot (x^-_{\alpha}\otimes t^{k})\mathbf{U}(\mathfrak{h}).\end{align*} $$
This finishes the proof of the proposition.
4.3
Our next goal is to understand the left ideal
![]() $\mathcal {L}_{\boldsymbol {\xi },\lambda }:=\mathbf {U}_{\ell }^-\mathcal {J}_{\boldsymbol {\xi },\lambda }$
generated by
$\mathcal {L}_{\boldsymbol {\xi },\lambda }:=\mathbf {U}_{\ell }^-\mathcal {J}_{\boldsymbol {\xi },\lambda }$
generated by
![]() $\mathcal {J}_{\boldsymbol {\xi },\lambda }$
in the loop algebra. The reason is that the same proof as in [Reference Naoi28, Lemma 4.2] shows that we have a linear isomorphism
$\mathcal {J}_{\boldsymbol {\xi },\lambda }$
in the loop algebra. The reason is that the same proof as in [Reference Naoi28, Lemma 4.2] shows that we have a linear isomorphism
preserving the
![]() $-Q^+$
-grading. This isomorphism is induced from the projection
$-Q^+$
-grading. This isomorphism is induced from the projection
![]() $\mathbf {U}_{\ell }^-\rightarrow \mathbf {U}^-$
with respect to the decomposition
$\mathbf {U}_{\ell }^-\rightarrow \mathbf {U}^-$
with respect to the decomposition
and its importance will be discussed later. The explicit generators of
![]() $\mathcal {L}_{\boldsymbol {\xi },\lambda }$
are given as follows. Let
$\mathcal {L}_{\boldsymbol {\xi },\lambda }$
are given as follows. Let
![]() $N=\text {max}\{\lambda (h_i),\xi _{i}: 1\leq i\leq n\}$
and define
$N=\text {max}\{\lambda (h_i),\xi _{i}: 1\leq i\leq n\}$
and define
 $$ \begin{align*}\widehat{X}_i^{-}(z)=\sum^N_{m=-\infty} (x_{i}^{-}\otimes t^m) z^{-m-1},\ 1\leq i\leq n.\end{align*} $$
$$ \begin{align*}\widehat{X}_i^{-}(z)=\sum^N_{m=-\infty} (x_{i}^{-}\otimes t^m) z^{-m-1},\ 1\leq i\leq n.\end{align*} $$
We denote by
![]() $\widehat {\mathbf {x}}_{i}^{-}(r,s)$
the coefficient in front of
$\widehat {\mathbf {x}}_{i}^{-}(r,s)$
the coefficient in front of
![]() $z^{-(r+s)}$
in the series
$z^{-(r+s)}$
in the series
![]() $\left (\widehat {X}_i^{-}(z)\right )^r$
.
$\left (\widehat {X}_i^{-}(z)\right )^r$
.
Lemma The
![]() $\mathbf {U}_{\ell }^-$
left ideal
$\mathbf {U}_{\ell }^-$
left ideal
![]() $\mathcal {L}_{\boldsymbol {\xi },\lambda }$
is generated by the elements
$\mathcal {L}_{\boldsymbol {\xi },\lambda }$
is generated by the elements
 $$ \begin{align}&\quad\notag \widehat{\mathbf{x}}_{i}^{-}(r,s),\ 1\leq i\leq n,\ r\in \mathbb{N},s\in\mathbb{Z}_+:\ r+s\geq 1+\lambda(h_i),\\&\quad (x^{-}_{\alpha}\otimes t^{k}),\ \alpha\in R^+,\ k\geq \min\{\xi_{\beta}: \beta\succeq \alpha\}.\end{align} $$
$$ \begin{align}&\quad\notag \widehat{\mathbf{x}}_{i}^{-}(r,s),\ 1\leq i\leq n,\ r\in \mathbb{N},s\in\mathbb{Z}_+:\ r+s\geq 1+\lambda(h_i),\\&\quad (x^{-}_{\alpha}\otimes t^{k}),\ \alpha\in R^+,\ k\geq \min\{\xi_{\beta}: \beta\succeq \alpha\}.\end{align} $$
Proof The proof is similar to the proof of [Reference Naoi28, Lemma 4.2] using Proposition 4.2.
Now we come back to the importance of the graded version of (4.5). Recall that
![]() $M_{\boldsymbol {\xi },\lambda }[p]$
denotes the pth graded piece of
$M_{\boldsymbol {\xi },\lambda }[p]$
denotes the pth graded piece of
![]() $M_{\boldsymbol {\xi },\lambda }$
for
$M_{\boldsymbol {\xi },\lambda }$
for
![]() $p\in \mathbb {Z}_+$
(similarly for
$p\in \mathbb {Z}_+$
(similarly for
![]() $\mathbf {U}^{-}$
). Setting
$\mathbf {U}^{-}$
). Setting
we obtain
 $$ \begin{align}[M_{\boldsymbol{\xi},\lambda}: \tau^{*}_p & V(\lambda-\gamma)]\notag=\text{dim} \left(M_{\boldsymbol{\xi},\lambda}[p]/\mathfrak{n}^-M_{\boldsymbol{\xi},\lambda}[p]\right)_{\lambda-\gamma}&\\&=\notag\text{dim}\left(\mathbf{U}^-[p]/\left(\mathfrak{n}^-\mathbf{U}^-[p]+\mathcal{J}_{\boldsymbol{\xi},\lambda}\cap \mathbf{U}^-[p]\right)\right)_{-\gamma}&\\&=\text{dim} \left(\mathbf{U}_{\ell}^-[p]/\left((\mathfrak{n}^-\otimes t^{-1} \mathbb{C}[t^{-1}])\mathbf{U}_{\ell}^-+\mathfrak{n}^-\mathbf{U}^-[p]+\mathcal{L}_{\boldsymbol{\xi},\lambda}\cap\mathbf{U}_{\ell}^-[p]\right)\right)_{-\gamma}.\end{align} $$
$$ \begin{align}[M_{\boldsymbol{\xi},\lambda}: \tau^{*}_p & V(\lambda-\gamma)]\notag=\text{dim} \left(M_{\boldsymbol{\xi},\lambda}[p]/\mathfrak{n}^-M_{\boldsymbol{\xi},\lambda}[p]\right)_{\lambda-\gamma}&\\&=\notag\text{dim}\left(\mathbf{U}^-[p]/\left(\mathfrak{n}^-\mathbf{U}^-[p]+\mathcal{J}_{\boldsymbol{\xi},\lambda}\cap \mathbf{U}^-[p]\right)\right)_{-\gamma}&\\&=\text{dim} \left(\mathbf{U}_{\ell}^-[p]/\left((\mathfrak{n}^-\otimes t^{-1} \mathbb{C}[t^{-1}])\mathbf{U}_{\ell}^-+\mathfrak{n}^-\mathbf{U}^-[p]+\mathcal{L}_{\boldsymbol{\xi},\lambda}\cap\mathbf{U}_{\ell}^-[p]\right)\right)_{-\gamma}.\end{align} $$
Hence, the graded character of
![]() $M_{\boldsymbol {\xi },\lambda }$
is determined by the numbers (4.7).
$M_{\boldsymbol {\xi },\lambda }$
is determined by the numbers (4.7).
5 Dual functional realization of loop algebras
In this subsection, we review the dual functional realization of
![]() $\mathbf {U}_{\ell }^-$
from [Reference Stoyanovskiĭ and Feĭgin29] (see also [Reference Ardonne and Kedem1, Reference Ardonne, Kedem and Stone2, Reference Feigin, Kedem, Loktev, Miwa and Mukhin14] for further developments).
$\mathbf {U}_{\ell }^-$
from [Reference Stoyanovskiĭ and Feĭgin29] (see also [Reference Ardonne and Kedem1, Reference Ardonne, Kedem and Stone2, Reference Feigin, Kedem, Loktev, Miwa and Mukhin14] for further developments).
5.1
In the rest of this section, we fix an element
![]() $\gamma = \sum ^n_{i=1}r_i \alpha _i$
of
$\gamma = \sum ^n_{i=1}r_i \alpha _i$
of
![]() $Q^+$
. Consider the generating current
$Q^+$
. Consider the generating current
The graded component
![]() $\left (\mathbf {U}_{\ell }^-\right )_{-\gamma }$
with respect to the
$\left (\mathbf {U}_{\ell }^-\right )_{-\gamma }$
with respect to the
![]() $\mathfrak {h}$
-grading is generated by the coefficients of products of generating currents of the form
$\mathfrak {h}$
-grading is generated by the coefficients of products of generating currents of the form
Note that we have two types of operator product expansion relations induced from the commutation relations and the Serre relations (see, for example, [Reference Ardonne and Kedem1, Section 4]). The commutation relation between currents implies the following: for
![]() $\alpha ,\beta \in R^+$
with
$\alpha ,\beta \in R^+$
with
![]() $\alpha +\beta \in R^+$
, we have that
$\alpha +\beta \in R^+$
, we have that
 $$ \begin{align}x^{-}_{\alpha}(z_1)x^{-}_{\beta}(z_2)=\frac{x^{-}_{\alpha+\beta}(z_2)}{(z_1-z_2)}+ \text{"terms with no pole at }z_1=z_2,\text{"}\end{align} $$
$$ \begin{align}x^{-}_{\alpha}(z_1)x^{-}_{\beta}(z_2)=\frac{x^{-}_{\alpha+\beta}(z_2)}{(z_1-z_2)}+ \text{"terms with no pole at }z_1=z_2,\text{"}\end{align} $$
where the expansion of the denominator is taken in the region
![]() $|z_1|>|z_2|$
. As a result of the Serre relations in
$|z_1|>|z_2|$
. As a result of the Serre relations in
![]() $\mathfrak {g}$
, we have
$\mathfrak {g}$
, we have
We will see at the end of this subsection that a typical element in the dual space of
![]() $\left (\mathbf {U}^-_{\ell }\right )_{-\gamma }$
can be viewed as a rational function in the variables
$\left (\mathbf {U}^-_{\ell }\right )_{-\gamma }$
can be viewed as a rational function in the variables
Due to the restrictions coming from the OPE relations (see (5.1) and (5.2)), we will get some restrictions on these rational functions. The first OPE relation (5.1) states that the functions will have at most a simple pole whenever
![]() $w_{i,r}=w_{i+1,s}$
. The second one (5.2) tells us that the evaluation of the functions at
$w_{i,r}=w_{i+1,s}$
. The second one (5.2) tells us that the evaluation of the functions at
![]() $w_{i,1}=w_{i,2}=w_{i\pm 1,1}$
must vanish. Moreover, since
$w_{i,1}=w_{i,2}=w_{i\pm 1,1}$
must vanish. Moreover, since
![]() $[x_{\alpha _{i}}^{-}(z),x_{\alpha _{i}}^{-}(w)]=0$
, the functions have a symmetry under the exchange of variables
$[x_{\alpha _{i}}^{-}(z),x_{\alpha _{i}}^{-}(w)]=0$
, the functions have a symmetry under the exchange of variables
![]() $w_{i,r}\leftrightarrow w_{i,s}$
. This motivates the next definition.
$w_{i,r}\leftrightarrow w_{i,s}$
. This motivates the next definition.
Definition Let
![]() $\mathbb {U}_{\gamma }$
be the subspace of rational functions in the variables
$\mathbb {U}_{\gamma }$
be the subspace of rational functions in the variables
![]() $\mathbf {w}_{\gamma }$
which are of the form
$\mathbf {w}_{\gamma }$
which are of the form
 $$ \begin{align*}g(\mathbf{w}_{\gamma})=\frac{f(\mathbf{w}_{\gamma})}{\Delta_{\gamma}},\ \ \ \ \Delta_{\gamma}:=\prod_{\substack{1\leq r\leq r_i,\ 1\leq s\leq r_{i+1},\\ 1\leq i\leq n-1}}(w_{i,r}-w_{i+1,s}),\end{align*} $$
$$ \begin{align*}g(\mathbf{w}_{\gamma})=\frac{f(\mathbf{w}_{\gamma})}{\Delta_{\gamma}},\ \ \ \ \Delta_{\gamma}:=\prod_{\substack{1\leq r\leq r_i,\ 1\leq s\leq r_{i+1},\\ 1\leq i\leq n-1}}(w_{i,r}-w_{i+1,s}),\end{align*} $$
where
![]() $f(\mathbf {w}_{\gamma })$
is a Laurent polynomial in the variables
$f(\mathbf {w}_{\gamma })$
is a Laurent polynomial in the variables
![]() $\mathbf{w}_{\gamma }$
, invariant under the action of the parabolic subgroup
$\mathbf{w}_{\gamma }$
, invariant under the action of the parabolic subgroup
![]() $S_{r_1}\times \cdots \times S_{r_n}$
(
$S_{r_1}\times \cdots \times S_{r_n}$
(
![]() $S_{r_i}$
permutes the variables
$S_{r_i}$
permutes the variables
![]() $w_{i,r},\ 1\leq r\leq r_i$
), and vanishing under the specialization
$w_{i,r},\ 1\leq r\leq r_i$
), and vanishing under the specialization
![]() $w_{i,1}=w_{i,2}=w_{i\pm 1,1}$
.
$w_{i,1}=w_{i,2}=w_{i\pm 1,1}$
.
The residue of
![]() $g(\mathbf{w}_{\gamma })\in \mathbb {U}_{\gamma }$
viewed as a function in
$g(\mathbf{w}_{\gamma })\in \mathbb {U}_{\gamma }$
viewed as a function in
![]() $w_{i,1}$
is defined as follows. We consider the Laurent series expansion of
$w_{i,1}$
is defined as follows. We consider the Laurent series expansion of
![]() $g(\mathbf{w}_{\gamma })$
in a punctured disk
$g(\mathbf{w}_{\gamma })$
in a punctured disk
![]() $\{0<|w_{i,1}|<\epsilon \}$
by expanding all
$\{0<|w_{i,1}|<\epsilon \}$
by expanding all
![]() $(w_{i,1}-w_{i+1,s})^{-1}$
(resp.
$(w_{i,1}-w_{i+1,s})^{-1}$
(resp.
![]() $(w_{i-1,r}-w_{i,1})^{-1}$
) in
$(w_{i-1,r}-w_{i,1})^{-1}$
) in
![]() $g(\mathbf{w}_{\gamma })$
by using
$g(\mathbf{w}_{\gamma })$
by using
where
![]() $\delta (z,w)=\sum _{r\geq 0}z^{-r-1}w^{r}$
. Then,
$\delta (z,w)=\sum _{r\geq 0}z^{-r-1}w^{r}$
. Then,
![]() $\text {Res}_{w_{i,1}}\left (g(\mathbf{x}_{\gamma })\right )$
is defined to be the coefficient of
$\text {Res}_{w_{i,1}}\left (g(\mathbf{x}_{\gamma })\right )$
is defined to be the coefficient of
![]() $\left (w_{i,1}\right )^{-1}$
in this series expansion. We set
$\left (w_{i,1}\right )^{-1}$
in this series expansion. We set
and view it as a function in
![]() $\mathbb {U}_{\gamma -\alpha _i}$
by re-indexing the set
$\mathbb {U}_{\gamma -\alpha _i}$
by re-indexing the set
![]() $\{w_{i,2},\dots ,w_{i,r_i}\}$
to
$\{w_{i,2},\dots ,w_{i,r_i}\}$
to
![]() $\{w_{i,1},\dots ,w_{i,r_i-1}\}$
which is possible by the symmetry of these functions. The following theorem can be found in [Reference Ardonne, Kedem and Stone2, Theorem 3.3].
$\{w_{i,1},\dots ,w_{i,r_i-1}\}$
which is possible by the symmetry of these functions. The following theorem can be found in [Reference Ardonne, Kedem and Stone2, Theorem 3.3].
Proposition The space of functions
![]() $\mathbb {U}_{\gamma }$
is dual to the graded component
$\mathbb {U}_{\gamma }$
is dual to the graded component
![]() $\left (\mathbf {U}^-_{\ell }\right )_{-\gamma }$
with pairing
$\left (\mathbf {U}^-_{\ell }\right )_{-\gamma }$
with pairing
given by the rule
for all
![]() $p_1,\dots ,p_k\in \mathbb {Z}$
and
$p_1,\dots ,p_k\in \mathbb {Z}$
and
![]() $i_1,\dots ,i_k\in \{1,\dots ,n\}$
with
$i_1,\dots ,i_k\in \{1,\dots ,n\}$
with
![]() $\gamma =\alpha _{i_1}+\cdots +\alpha _{i_k}$
.
$\gamma =\alpha _{i_1}+\cdots +\alpha _{i_k}$
.
5.2
Recall that the dual space of a quotient
![]() $V/W$
is isomorphic to the space of functions f in
$V/W$
is isomorphic to the space of functions f in
![]() $V^{*}$
satisfying
$V^{*}$
satisfying
![]() $f(W)=0$
. Hence, using Proposition 5.1, we get that the dual space of
$f(W)=0$
. Hence, using Proposition 5.1, we get that the dual space of
consists of all functions
![]() $g(\mathbf {w}_{\gamma })\in \mathbb {U}_{\gamma }$
satisfying
$g(\mathbf {w}_{\gamma })\in \mathbb {U}_{\gamma }$
satisfying
and
We claim that the above three conditions are equivalent to the conditions (5.4) and (5.5) and
To see this, we only have to show that a function satisfying (5.4)–(5.6) also satisfies (5.7). This claim is only nontrivial for elements in
![]() $\left (\mathbf {U}^-[q]\right )_{-\gamma +r\alpha _i}\widehat {\mathbf {x}}_i^{-}(r,s)$
considered as a subset of
$\left (\mathbf {U}^-[q]\right )_{-\gamma +r\alpha _i}\widehat {\mathbf {x}}_i^{-}(r,s)$
considered as a subset of
![]() $\mathcal {L}_{ \boldsymbol {\xi },\lambda }\cap \left (\mathbf {U}^-_{\ell }\right )_{-\gamma }$
. Obviously,
$\mathcal {L}_{ \boldsymbol {\xi },\lambda }\cap \left (\mathbf {U}^-_{\ell }\right )_{-\gamma }$
. Obviously,
So, if
![]() $q+s=p$
, then the latter element is contained in
$q+s=p$
, then the latter element is contained in
![]() $\mathcal {L}_{ \boldsymbol {\xi },\lambda }\cap \left (\mathbf {U}^-_{\ell }[p]\right )_{-\gamma }$
and the claim follows by our assumption. If
$\mathcal {L}_{ \boldsymbol {\xi },\lambda }\cap \left (\mathbf {U}^-_{\ell }[p]\right )_{-\gamma }$
and the claim follows by our assumption. If
![]() $q+s\neq p$
, then the claim follows from (5.4) and (5.5).
$q+s\neq p$
, then the claim follows from (5.4) and (5.5).
So summarizing, in order to determine (4.7), we are interested in all rational functions
![]() $g(\mathbf{w}_{\gamma })\in \mathbb {U}_{\gamma }$
satisfying (5.4), (5.5), and (5.7). The characterization of functions satisfying (5.4) is a slight modification of the result [Reference Naoi28, Lemma 4.6] and is stated in the next lemma.
$g(\mathbf{w}_{\gamma })\in \mathbb {U}_{\gamma }$
satisfying (5.4), (5.5), and (5.7). The characterization of functions satisfying (5.4) is a slight modification of the result [Reference Naoi28, Lemma 4.6] and is stated in the next lemma.
Lemma A function
![]() $g(\mathbf {w}_{\gamma })=\frac {f(\mathbf {w}_{\gamma })}{\Delta _{\gamma }}\in \mathbb {U}_{\gamma }$
satisfies (5.4) if and only if
$g(\mathbf {w}_{\gamma })=\frac {f(\mathbf {w}_{\gamma })}{\Delta _{\gamma }}\in \mathbb {U}_{\gamma }$
satisfies (5.4) if and only if
where we understand
![]() $r_0=r_{n+1}=0$
.
$r_0=r_{n+1}=0$
.
5.3
In this subsection, we investigate the meaning of (5.5) and (5.7). We set
![]() $e_{\gamma }=\sum _{i=1}^{n-1} r_ir_{i+1}$
.
$e_{\gamma }=\sum _{i=1}^{n-1} r_ir_{i+1}$
.
Lemma A function
![]() $g(\mathbf {w}_{\gamma })=\frac {f(\mathbf {w}_{\gamma })}{\Delta _{\gamma }}\in \mathbb {U}_{\gamma }$
satisfying (5.4) has in addition property (5.5) if and only if
$g(\mathbf {w}_{\gamma })=\frac {f(\mathbf {w}_{\gamma })}{\Delta _{\gamma }}\in \mathbb {U}_{\gamma }$
satisfying (5.4) has in addition property (5.5) if and only if
![]() $f(\mathbf {w}_{\gamma })$
is homogeneous of degree
$f(\mathbf {w}_{\gamma })$
is homogeneous of degree
![]() $-p-|\gamma |+e_{\gamma }$
.
$-p-|\gamma |+e_{\gamma }$
.
Proof The property (5.5) simply means that all terms in
![]() $g(\mathbf {w}_{\gamma })$
with strictly negative power with respect to each variable are homogeneous of degree
$g(\mathbf {w}_{\gamma })$
with strictly negative power with respect to each variable are homogeneous of degree
![]() $-p-|\gamma |$
. Since
$-p-|\gamma |$
. Since
![]() $g(\mathbf {w}_{\gamma })$
satisfies (5.4), hence
$g(\mathbf {w}_{\gamma })$
satisfies (5.4), hence
![]() $\text {deg}_{w_{i,r}}g(\mathbf {w}_{\gamma }) \leq -2$
, we have that
$\text {deg}_{w_{i,r}}g(\mathbf {w}_{\gamma }) \leq -2$
, we have that
![]() $g(\mathbf {w}_{\gamma })$
is homogeneous of degree
$g(\mathbf {w}_{\gamma })$
is homogeneous of degree
![]() $-p-|\gamma |$
and the rest follows by expanding each
$-p-|\gamma |$
and the rest follows by expanding each
![]() $(w_{j,r}-w_{j+1,s})$
using the function
$(w_{j,r}-w_{j+1,s})$
using the function
![]() $\delta $
.
$\delta $
.
It remains to observe the restrictions coming from (5.7). Recall that
![]() $(x^{-}_{i}\otimes t^{k})\in \mathcal {L}_{ \boldsymbol {\xi },\lambda }$
for all
$(x^{-}_{i}\otimes t^{k})\in \mathcal {L}_{ \boldsymbol {\xi },\lambda }$
for all
![]() $k\geq N$
. For
$k\geq N$
. For
![]() $r\leq r_i$
, we have
$r\leq r_i$
, we have
and hence the condition
means that the order of the pole of
![]() $g(\mathbf {w}_{\gamma })|_{w_{i,1}=\cdots =w_{i,r}=z}$
at
$g(\mathbf {w}_{\gamma })|_{w_{i,1}=\cdots =w_{i,r}=z}$
at
![]() $z=0$
can be at most
$z=0$
can be at most
![]() $\lambda (h_i)$
. In particular, a function
$\lambda (h_i)$
. In particular, a function
![]() $g(\mathbf{w}_{\gamma })$
satisfying (5.7) has this property by Lemma 4.3. The interpretation of (4.6) is explained in the proof of Theorem 5. First, we define the main object of this section.
$g(\mathbf{w}_{\gamma })$
satisfying (5.7) has this property by Lemma 4.3. The interpretation of (4.6) is explained in the proof of Theorem 5. First, we define the main object of this section.
Definition Let
![]() $\boldsymbol {\xi }=(\xi _{\alpha })_{\alpha \in R^+}$
be a normalized tuple,
$\boldsymbol {\xi }=(\xi _{\alpha })_{\alpha \in R^+}$
be a normalized tuple,
![]() $(\lambda ,p)\in P^+\times \mathbb {Z}_+$
, and
$(\lambda ,p)\in P^+\times \mathbb {Z}_+$
, and
![]() $\gamma =\sum _{i=1}^nr_i\alpha _i$
be an element of
$\gamma =\sum _{i=1}^nr_i\alpha _i$
be an element of
![]() $Q^+$
. We denote by
$Q^+$
. We denote by
![]() $\mathcal {V}_{ \boldsymbol {\xi },\lambda ,\gamma ,p}$
the vector space consisting of all rational functions
$\mathcal {V}_{ \boldsymbol {\xi },\lambda ,\gamma ,p}$
the vector space consisting of all rational functions
![]() $f(\mathbf {w}_{\gamma })\Delta _{\gamma }^{-1}\in \mathbb {U}_{\gamma }$
with
$f(\mathbf {w}_{\gamma })\Delta _{\gamma }^{-1}\in \mathbb {U}_{\gamma }$
with
![]() $f(\mathbf {w}_{\gamma })$
being a homogeneous Laurent polynomial of degree
$f(\mathbf {w}_{\gamma })$
being a homogeneous Laurent polynomial of degree
![]() $-p-|\gamma |+e_{\gamma }$
satisfying the following three properties:
$-p-|\gamma |+e_{\gamma }$
satisfying the following three properties:
-
(1) For all
 $1\leq i\leq n$
, we have
$1\leq i\leq n$
, we have
 $\text {deg}_{w_{i,1}}f(\mathbf {w}_{\gamma }) \leq r_{i-1}+r_{i+1}-2.$
$\text {deg}_{w_{i,1}}f(\mathbf {w}_{\gamma }) \leq r_{i-1}+r_{i+1}-2.$
-
(2) For all
 $1\leq i\leq n$
and
$1\leq i\leq n$
and
 $1\leq r\leq r_i$
, we have
$1\leq r\leq r_i$
, we have  $$ \begin{align*}z^{\lambda(h_i)}\cdot f(\mathbf{w}_{\gamma})\Big|_{w_{i,1}=w_{i,2}=\cdots=w_{i,r}=z}\in\mathbb{C}[w^{\pm 1}_{\ell,s}: (\ell,s)\neq (i,p), p=1,\dots,r ] [z].\end{align*} $$
$$ \begin{align*}z^{\lambda(h_i)}\cdot f(\mathbf{w}_{\gamma})\Big|_{w_{i,1}=w_{i,2}=\cdots=w_{i,r}=z}\in\mathbb{C}[w^{\pm 1}_{\ell,s}: (\ell,s)\neq (i,p), p=1,\dots,r ] [z].\end{align*} $$
-
(3) For all
 $1\leq i\leq j\leq n$
, we have that
$1\leq i\leq j\leq n$
, we have that  $$ \begin{align*}z^{\xi_{i,j}}\cdot f(\mathbf{w}_{\gamma})\Big|_{w_{i,1}=w_{i+1,1}=\cdots=w_{j,1}=z}\in \mathbb{C}[w^{\pm 1}_{\ell,s}: (\ell,s)\neq (k,1), k=i,\dots,j ] [z].\end{align*} $$
$$ \begin{align*}z^{\xi_{i,j}}\cdot f(\mathbf{w}_{\gamma})\Big|_{w_{i,1}=w_{i+1,1}=\cdots=w_{j,1}=z}\in \mathbb{C}[w^{\pm 1}_{\ell,s}: (\ell,s)\neq (k,1), k=i,\dots,j ] [z].\end{align*} $$
Now we state the main theorem of this section.
Theorem 5 Let
![]() $ \boldsymbol {\xi },\lambda ,\gamma ,p$
be as in Definition 5.3. We have an isomorphism of vector spaces
$ \boldsymbol {\xi },\lambda ,\gamma ,p$
be as in Definition 5.3. We have an isomorphism of vector spaces
and hence the graded character of
![]() $M_{ \boldsymbol {\xi },\lambda }$
is given by
$M_{ \boldsymbol {\xi },\lambda }$
is given by
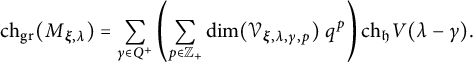 $$ \begin{align*}\mathrm{ch}_{\mathrm{gr}} (M_{ \boldsymbol{\xi},\lambda})=\sum_{\gamma\in Q^+} \left(\sum_{p\in\mathbb{Z}_+} \dim(\mathcal{V}_{ \boldsymbol{\xi},\lambda,\gamma,p}) \ q^p\right)\mathrm{ch}_{\mathfrak{h}} V(\lambda-\gamma).\end{align*} $$
$$ \begin{align*}\mathrm{ch}_{\mathrm{gr}} (M_{ \boldsymbol{\xi},\lambda})=\sum_{\gamma\in Q^+} \left(\sum_{p\in\mathbb{Z}_+} \dim(\mathcal{V}_{ \boldsymbol{\xi},\lambda,\gamma,p}) \ q^p\right)\mathrm{ch}_{\mathfrak{h}} V(\lambda-\gamma).\end{align*} $$
Proof It is clear that the space of all functions in
![]() $\mathbb {U}_{\gamma }$
satisfying the properties (5.4)–(5.7) describes the aforementioned dual space as a vector space. Using Lemmas 5.2 and 5.3 and the discussion preceding Definition 5.3, it has only to be checked that Definition 5.3(3) is equivalent to the fact that
$\mathbb {U}_{\gamma }$
satisfying the properties (5.4)–(5.7) describes the aforementioned dual space as a vector space. Using Lemmas 5.2 and 5.3 and the discussion preceding Definition 5.3, it has only to be checked that Definition 5.3(3) is equivalent to the fact that
 $$ \begin{align}\left\langle \left(\mathbf{U}_{\ell}^{-}\right)_{\gamma-\alpha}(x^{-}_{\alpha}\otimes t^k),\frac{f(\mathbf{x}_\gamma)}{\Delta_{\gamma}}\right\rangle =0,\ \ \alpha\in R^+,\ \ k\geq \xi_{\alpha}.\end{align} $$
$$ \begin{align}\left\langle \left(\mathbf{U}_{\ell}^{-}\right)_{\gamma-\alpha}(x^{-}_{\alpha}\otimes t^k),\frac{f(\mathbf{x}_\gamma)}{\Delta_{\gamma}}\right\rangle =0,\ \ \alpha\in R^+,\ \ k\geq \xi_{\alpha}.\end{align} $$
But if we write
for some
![]() $k_i,\dots ,k_{j}\in \mathbb Z$
with
$k_i,\dots ,k_{j}\in \mathbb Z$
with
![]() $k_1+\dots +k_{\ell }=k$
, this follows from
$k_1+\dots +k_{\ell }=k$
, this follows from
 $$ \begin{align} [R_{j,k_j},[R_{{j-1},k_{j-1}},&\dots,[R_{i+1,k_{i+1}},R_{i,k_i}]\dots]] \frac{f(\mathbf{x}_\gamma)}{\Delta_{\gamma}} &\\&\notag =\text{Res}_{w_{j,1}} \Big\{(w_{i,1}-w_{i+1,1})\cdots (w_{j-1,1}-w_{j,1}) \frac{f(\mathbf{x}_\gamma)}{\Delta_{\gamma}}\Big|_{w_{i,1}=\cdots=w_{j,1}=z}\cdot (w_{j,1})^k\Big\}, \end{align} $$
$$ \begin{align} [R_{j,k_j},[R_{{j-1},k_{j-1}},&\dots,[R_{i+1,k_{i+1}},R_{i,k_i}]\dots]] \frac{f(\mathbf{x}_\gamma)}{\Delta_{\gamma}} &\\&\notag =\text{Res}_{w_{j,1}} \Big\{(w_{i,1}-w_{i+1,1})\cdots (w_{j-1,1}-w_{j,1}) \frac{f(\mathbf{x}_\gamma)}{\Delta_{\gamma}}\Big|_{w_{i,1}=\cdots=w_{j,1}=z}\cdot (w_{j,1})^k\Big\}, \end{align} $$
which has been proved in [Reference Naoi28, Section 4.2]. So (5.8) is equivalent to the statement that the order of the pole of
 $$ \begin{align*}\left((w_{i,1}-w_{i+1,1})\cdots (w_{j-1,1}-w_{j,1})\frac{f(\mathbf{x}_\gamma)}{\Delta_{\gamma}}\right)|_{w_{i,1}=w_{i+1,1}=\cdots=w_{j,1}=z}\end{align*} $$
$$ \begin{align*}\left((w_{i,1}-w_{i+1,1})\cdots (w_{j-1,1}-w_{j,1})\frac{f(\mathbf{x}_\gamma)}{\Delta_{\gamma}}\right)|_{w_{i,1}=w_{i+1,1}=\cdots=w_{j,1}=z}\end{align*} $$
at
![]() $z=0$
is at most
$z=0$
is at most
![]() $\xi _{i,j}$
. The character equality follows from (4.7).
$\xi _{i,j}$
. The character equality follows from (4.7).
Remark A similar statement as above can be proven for any simple finite-dimensional Lie algebra with slightly more complicated property (5.9). The simplification of property (5.9) to a specialization property as in Definition 5.3(3) works at least in simply laced types. Nevertheless, we decided to restrict ourself to
![]() $\mathfrak {sl}_{n+1}$
(in particular the prime representations in
$\mathfrak {sl}_{n+1}$
(in particular the prime representations in
![]() $\mathcal {C}_{q,\kappa }$
) since the computation of
$\mathcal {C}_{q,\kappa }$
) since the computation of
![]() $\dim V_{\boldsymbol {\xi },\lambda ,\gamma ,p}$
seems to be quite difficult in general.
$\dim V_{\boldsymbol {\xi },\lambda ,\gamma ,p}$
seems to be quite difficult in general.
Example Let
![]() $n=2$
,
$n=2$
,
![]() $\xi _{\alpha _1}=\xi _{\alpha _2}=\xi _{\alpha _{1,2}}=2$
,
$\xi _{\alpha _1}=\xi _{\alpha _2}=\xi _{\alpha _{1,2}}=2$
,
![]() $\gamma =2\alpha _1+\alpha _2$
, and
$\gamma =2\alpha _1+\alpha _2$
, and
![]() $\lambda =7\varpi _1+5\varpi _2$
. We consider Laurent polynomials
$\lambda =7\varpi _1+5\varpi _2$
. We consider Laurent polynomials
![]() $f(\mathbf{w}_{\gamma })$
in the variables
$f(\mathbf{w}_{\gamma })$
in the variables
![]() $\{w_{1,1}, w_{1,2}, w_{2,1}\}$
which are symmetric under the exchange of variables
$\{w_{1,1}, w_{1,2}, w_{2,1}\}$
which are symmetric under the exchange of variables
![]() $w_{1,1} \leftrightarrow w_{1,2}$
and satisfying
$w_{1,1} \leftrightarrow w_{1,2}$
and satisfying
 $$ \begin{align*}w_{1,1}^{2} &f(\mathbf{w}_{\gamma})\in \mathbb{C}[w_{1,1}, w^{\pm 1}_{1,2},w^{\pm 1}_{2,1}],\ \ w_{2,1}^{2} f(\mathbf{w}_{\gamma})\in \mathbb{C}[x^{\pm 1}_{1,1}, w^{\pm 1}_{1,2},w_{2,1}],\ \ \text{deg}_{w_{2,1}}f(\mathbf{w}_{\gamma})\leq 0,\\&\text{deg}_{w_{1,1}}f(\mathbf{w}_{\gamma})\leq -1,\ \ z^{2} f(\mathbf{w}_{\gamma})\big|_{w_{1,1}=w_{2,1}=z}\in \mathbb{C}[w^{\pm 1}_{1,2}, z],\ \ f(\mathbf{w}_{\gamma})\big|_{w_{1,1}=w_{1,2}=w_{2,1}}=0.\end{align*} $$
$$ \begin{align*}w_{1,1}^{2} &f(\mathbf{w}_{\gamma})\in \mathbb{C}[w_{1,1}, w^{\pm 1}_{1,2},w^{\pm 1}_{2,1}],\ \ w_{2,1}^{2} f(\mathbf{w}_{\gamma})\in \mathbb{C}[x^{\pm 1}_{1,1}, w^{\pm 1}_{1,2},w_{2,1}],\ \ \text{deg}_{w_{2,1}}f(\mathbf{w}_{\gamma})\leq 0,\\&\text{deg}_{w_{1,1}}f(\mathbf{w}_{\gamma})\leq -1,\ \ z^{2} f(\mathbf{w}_{\gamma})\big|_{w_{1,1}=w_{2,1}=z}\in \mathbb{C}[w^{\pm 1}_{1,2}, z],\ \ f(\mathbf{w}_{\gamma})\big|_{w_{1,1}=w_{1,2}=w_{2,1}}=0.\end{align*} $$
This is a vector space of dimension 2 with basis
 $$ \begin{align*}f_1(\mathbf{w}_{\gamma})&=\left(w_{1,1}\right)^{-2}\left(w_{1,2}\right)^{-2}\left(w_{2,1}\right)^{-2}\left(\left(w_{2,1}\right)^2+w_{1,1}w_{1,2}-w_{1,2}w_{2,1}-w_{1,1}w_{2,1}\right),\\f_2(\mathbf{w}_{\gamma})&=\left(w_{1,1}\right)^{-2}\left(w_{1,2}\right)^{-2}\left(w_{2,1}\right)^{-2}\left(w_{1,2}\left(w_{2,1}\right)^2+w_{1,1}\left(w_{2,1}\right)^2-2w_{1,1}w_{1,2}w_{2,1}\right).\end{align*} $$
$$ \begin{align*}f_1(\mathbf{w}_{\gamma})&=\left(w_{1,1}\right)^{-2}\left(w_{1,2}\right)^{-2}\left(w_{2,1}\right)^{-2}\left(\left(w_{2,1}\right)^2+w_{1,1}w_{1,2}-w_{1,2}w_{2,1}-w_{1,1}w_{2,1}\right),\\f_2(\mathbf{w}_{\gamma})&=\left(w_{1,1}\right)^{-2}\left(w_{1,2}\right)^{-2}\left(w_{2,1}\right)^{-2}\left(w_{1,2}\left(w_{2,1}\right)^2+w_{1,1}\left(w_{2,1}\right)^2-2w_{1,1}w_{1,2}w_{2,1}\right).\end{align*} $$
So Theorem 5 implies
![]() $[M_{\boldsymbol {\xi },\lambda }: V(\lambda -\gamma )]_q=q^2+q^3$
.
$[M_{\boldsymbol {\xi },\lambda }: V(\lambda -\gamma )]_q=q^2+q^3$
.
6 Classical decompositions of the prime irreducible objects
In this section, we will focus on the modules
![]() $N_{\boldsymbol {\zeta }}$
from Definition 2.8 and prove our main result (see Theorem 4) concerning the graded decompositions of
$N_{\boldsymbol {\zeta }}$
from Definition 2.8 and prove our main result (see Theorem 4) concerning the graded decompositions of
![]() $L(\boldsymbol {\pi })$
for
$L(\boldsymbol {\pi })$
for
![]() $\boldsymbol {\pi }\in \mathcal {P}^+_{\mathbb {Z}}(1)$
. Recall from Example 4.1(3) that we can identify
$\boldsymbol {\pi }\in \mathcal {P}^+_{\mathbb {Z}}(1)$
. Recall from Example 4.1(3) that we can identify
![]() $N_{\boldsymbol {\zeta }}$
with a truncated representations and hence we have a formula for the graded character of
$N_{\boldsymbol {\zeta }}$
with a truncated representations and hence we have a formula for the graded character of
![]() $N_{\boldsymbol {\zeta }}$
(see Theorem 5) which we want to relate to lattice points in convex polytopes.
$N_{\boldsymbol {\zeta }}$
(see Theorem 5) which we want to relate to lattice points in convex polytopes.
We fix in the rest of this section an admissible quadruple
![]() $\boldsymbol {\zeta }=(\lambda ,\lambda _0,\lambda _1,\lambda _2)$
, the normalized tuple
$\boldsymbol {\zeta }=(\lambda ,\lambda _0,\lambda _1,\lambda _2)$
, the normalized tuple
![]() $\boldsymbol {\xi }$
from Example 4.1(3) and set
$\boldsymbol {\xi }$
from Example 4.1(3) and set
From the definition of
![]() $N_{\boldsymbol {\zeta }}$
, we need (4.6) in Lemma 4.3 for the module
$N_{\boldsymbol {\zeta }}$
, we need (4.6) in Lemma 4.3 for the module
![]() $N_{\boldsymbol {\zeta }}\cong M_{\boldsymbol {\xi },\lambda }$
only for the roots in the set
$N_{\boldsymbol {\zeta }}\cong M_{\boldsymbol {\xi },\lambda }$
only for the roots in the set
Hence, the third property in the definition of
![]() $\mathcal {V}_{\boldsymbol {\xi },\lambda ,\gamma ,p}$
(see Definition 5.3) can be relaxed for pairs in the set
$\mathcal {V}_{\boldsymbol {\xi },\lambda ,\gamma ,p}$
(see Definition 5.3) can be relaxed for pairs in the set
only and we use this fact without further comment.
6.1
We first record the following lemma.
Lemma Let
![]() $f(\mathbf {w}_{\gamma })$
be a polynomial in the variables
$f(\mathbf {w}_{\gamma })$
be a polynomial in the variables
![]() $\mathbf {w}_{\gamma }$
such that the specialization at
$\mathbf {w}_{\gamma }$
such that the specialization at
![]() $w_{i,1}=w_{i+1,1}=\cdots =w_{j,1}=z$
is divisible by z for all pairs
$w_{i,1}=w_{i+1,1}=\cdots =w_{j,1}=z$
is divisible by z for all pairs
![]() $(i,j)\in \{(i_{\ell },i_{\ell +1}):1\leq \ell \leq k-1\}$
. Then
$(i,j)\in \{(i_{\ell },i_{\ell +1}):1\leq \ell \leq k-1\}$
. Then
![]() $f(\mathbf {w}_{\gamma })$
is contained in the monomial ideal
$f(\mathbf {w}_{\gamma })$
is contained in the monomial ideal
Proof Suppose that we can write
where
![]() $A(\mathbf {w}_{\gamma })\in \mathcal {I}_{i_1,\dots ,i_k}$
and
$A(\mathbf {w}_{\gamma })\in \mathcal {I}_{i_1,\dots ,i_k}$
and
![]() $B(\mathbf {w}_{\gamma })$
is a nonzero polynomial with
$B(\mathbf {w}_{\gamma })$
is a nonzero polynomial with
![]() $B(\mathbf {w}_{\gamma })\notin \mathcal {I}_{i_1,\dots ,i_k}$
. Without loss of generality, we can assume that none of the monomials in
$B(\mathbf {w}_{\gamma })\notin \mathcal {I}_{i_1,\dots ,i_k}$
. Without loss of generality, we can assume that none of the monomials in
![]() $B(\mathbf {w}_{\gamma })$
is contained in
$B(\mathbf {w}_{\gamma })$
is contained in
![]() $\mathcal {I}_{i_1,\dots ,i_k}$
. We write
$\mathcal {I}_{i_1,\dots ,i_k}$
. We write
for some
![]() $a_1,\dots ,a_r\in \mathbb {C}^{\times }$
and monomials
$a_1,\dots ,a_r\in \mathbb {C}^{\times }$
and monomials
![]() $m_1(\mathbf {w}_{\gamma }),\dots ,m_r(\mathbf {w}_{\gamma })$
. Since
$m_1(\mathbf {w}_{\gamma }),\dots ,m_r(\mathbf {w}_{\gamma })$
. Since
![]() $m_1(\mathbf {w}_{\gamma })\notin \mathcal {I}_{i_1,\dots ,i_k}$
, there exists
$m_1(\mathbf {w}_{\gamma })\notin \mathcal {I}_{i_1,\dots ,i_k}$
, there exists
![]() $j\in \{1,\dots ,k-1\}$
with
$j\in \{1,\dots ,k-1\}$
with
![]() $m_1(\mathbf {w}_{\gamma })$
is independent of the variables
$m_1(\mathbf {w}_{\gamma })$
is independent of the variables
![]() $w_{i_j,1},w_{i_j+1,1},\dots ,w_{i_{j+1},1}$
. Now we collect all monomials which are independent of the aforementioned variables, say for simplicity
$w_{i_j,1},w_{i_j+1,1},\dots ,w_{i_{j+1},1}$
. Now we collect all monomials which are independent of the aforementioned variables, say for simplicity
![]() $m_1(\mathbf {w}_{\gamma }),\dots ,m_p(\mathbf {w}_{\gamma })$
for some
$m_1(\mathbf {w}_{\gamma }),\dots ,m_p(\mathbf {w}_{\gamma })$
for some
![]() $p\in \{1,\dots ,r\}$
, and the monomials
$p\in \{1,\dots ,r\}$
, and the monomials
![]() $m_{p+1}(\mathbf {w}_{\gamma }),\dots , m_r(\mathbf {w}_{\gamma })$
which depend on (at least) one of the aforementioned variables. This implies that
$m_{p+1}(\mathbf {w}_{\gamma }),\dots , m_r(\mathbf {w}_{\gamma })$
which depend on (at least) one of the aforementioned variables. This implies that
 $$ \begin{align*}a_1m_1(\mathbf{w}_{\gamma})+\cdots+a_p m_p(\mathbf{w}_{\gamma})=f(\mathbf{w}_{\gamma})-A(\mathbf{w}_{\gamma})-\sum^r_{k=p+1}a_{k}m_{k}(\mathbf{w}_{\gamma}) \end{align*} $$
$$ \begin{align*}a_1m_1(\mathbf{w}_{\gamma})+\cdots+a_p m_p(\mathbf{w}_{\gamma})=f(\mathbf{w}_{\gamma})-A(\mathbf{w}_{\gamma})-\sum^r_{k=p+1}a_{k}m_{k}(\mathbf{w}_{\gamma}) \end{align*} $$
is divisible by z after specializing
![]() $w_{i_j,1}=w_{i_j+1,1}=\dots =w_{i_{j+1},1}=z$
. This is a contradiction and we must have
$w_{i_j,1}=w_{i_j+1,1}=\dots =w_{i_{j+1},1}=z$
. This is a contradiction and we must have
![]() $B(\mathbf {w}_{\gamma })=0$
.
$B(\mathbf {w}_{\gamma })=0$
.
It is not difficult to translate the dimension of
![]() $\mathcal {V}_{\boldsymbol {\xi },\lambda ,\gamma ,p}$
into the language of linear algebra by multiplying the Laurent polynomials in Definition 5.3 by the factor
$\mathcal {V}_{\boldsymbol {\xi },\lambda ,\gamma ,p}$
into the language of linear algebra by multiplying the Laurent polynomials in Definition 5.3 by the factor
![]() $\prod _{i,r}w_{i,r}^{\lambda (h_i)}$
and using Lemma 6.1. We consider a typical polynomial
$\prod _{i,r}w_{i,r}^{\lambda (h_i)}$
and using Lemma 6.1. We consider a typical polynomial
 $$ \begin{align*}\sum_{\mathbf{c}}a_{\mathbf{c}} \prod_{i=1}^n w_{i,1}^{c_{i,1}}\cdots w_{i,r_i}^{c_{i,r_i}},\ \ a_{\mathbf{c}} \in \mathbb{C}.\end{align*} $$
$$ \begin{align*}\sum_{\mathbf{c}}a_{\mathbf{c}} \prod_{i=1}^n w_{i,1}^{c_{i,1}}\cdots w_{i,r_i}^{c_{i,r_i}},\ \ a_{\mathbf{c}} \in \mathbb{C}.\end{align*} $$
By the symmetry, we get
![]() $a_{\mathbf {c}}=a_{\sigma (\mathbf {c})}$
for each
$a_{\mathbf {c}}=a_{\sigma (\mathbf {c})}$
for each
![]() $\sigma \in S_{r_1}\times \cdots \times S_{r_n}$
. Hence, the coefficients are determined by complex numbers
$\sigma \in S_{r_1}\times \cdots \times S_{r_n}$
. Hence, the coefficients are determined by complex numbers
![]() $\left (a_{\boldsymbol {\mu }}\right )_{\boldsymbol {\mu }}$
where
$\left (a_{\boldsymbol {\mu }}\right )_{\boldsymbol {\mu }}$
where
![]() $\boldsymbol {\mu }=(\mu _1,\dots ,\mu _n)$
is a tuple of partitions and each
$\boldsymbol {\mu }=(\mu _1,\dots ,\mu _n)$
is a tuple of partitions and each
![]() $\mu _i$
is a partition with at most
$\mu _i$
is a partition with at most
![]() $r_i$
rows and whose entries are bounded by
$r_i$
rows and whose entries are bounded by
![]() $r_{i-1}+r_{i+1}-2+\lambda (h_i)$
by Definition 5.3(1). Continuing in this way gives a long list of constraints which is in general hard to calculate. In the next subsection, we use a different approach developed in [Reference Ardonne and Kedem1, Reference Ardonne, Kedem and Stone2].
$r_{i-1}+r_{i+1}-2+\lambda (h_i)$
by Definition 5.3(1). Continuing in this way gives a long list of constraints which is in general hard to calculate. In the next subsection, we use a different approach developed in [Reference Ardonne and Kedem1, Reference Ardonne, Kedem and Stone2].
6.2
We recall a filtration on the space of rational functions
![]() $\mathbb {U}_{\gamma }$
from [Reference Ardonne and Kedem1, Section 4.1]. Let
$\mathbb {U}_{\gamma }$
from [Reference Ardonne and Kedem1, Section 4.1]. Let
![]() $\boldsymbol \mu = (\mu _1,\dots ,\mu _n)$
be a multipartition such that
$\boldsymbol \mu = (\mu _1,\dots ,\mu _n)$
be a multipartition such that
![]() $\mu _i\vdash r_i$
for all
$\mu _i\vdash r_i$
for all
![]() $1\leq i\leq n$
. Recall that
$1\leq i\leq n$
. Recall that
![]() $m_{i,r}$
denotes the number of rows of length r in the partition
$m_{i,r}$
denotes the number of rows of length r in the partition
![]() $\mu _i$
. Our aim is to define a specialization map
$\mu _i$
. Our aim is to define a specialization map
where
![]() $\mathbb {H}_{\boldsymbol \mu }$
is the space of rational functions in the variables
$\mathbb {H}_{\boldsymbol \mu }$
is the space of rational functions in the variables
It means that we have a variable for each row in the multipartition. The specialization map
![]() $\varphi _{\boldsymbol \mu }$
does the following: for each
$\varphi _{\boldsymbol \mu }$
does the following: for each
![]() $i\in \{1,\dots ,n\}$
, we fill the boxes of
$i\in \{1,\dots ,n\}$
, we fill the boxes of
![]() $\mu _i$
with the variables
$\mu _i$
with the variables
![]() $x_{i,r}$
,
$x_{i,r}$
,
![]() $1\leq r\leq r_i$
, and specialize all variables in the uth row of length r in
$1\leq r\leq r_i$
, and specialize all variables in the uth row of length r in
![]() $\mu _i$
to
$\mu _i$
to
![]() $y_{i,r,u}$
. By the symmetry, this definition is independent of the filling.
$y_{i,r,u}$
. By the symmetry, this definition is independent of the filling.
Example Let
![]() $n=2$
and
$n=2$
and
![]() $\gamma =2\alpha _1+\alpha _1$
. Consider the multipartition
$\gamma =2\alpha _1+\alpha _1$
. Consider the multipartition
If we apply the specialization map to the functions in Example 5.3 (ignoring the fact that they are not contained in
![]() $\mathbb {U}_{\gamma }$
), we get
$\mathbb {U}_{\gamma }$
), we get
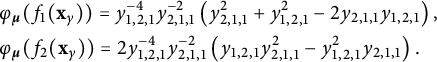 $$ \begin{align*}&\varphi_{\boldsymbol{\mu}}(f_1(\mathbf{x}_{\gamma}))=y_{1,2,1}^{-4}y_{2,1,1}^{-2}\left(y_{2,1,1}^2+y_{1,2,1}^2-2y_{2,1,1}y_{1,2,1}\right),\\&\varphi_{\boldsymbol{\mu}}(f_2(\mathbf{x}_{\gamma}))=2y_{1,2,1}^{-4}y_{2,1,1}^{-2}\left(y_{1,2,1}y_{2,1,1}^2-y_{1,2,1}^2y_{2,1,1}\right).\end{align*} $$
$$ \begin{align*}&\varphi_{\boldsymbol{\mu}}(f_1(\mathbf{x}_{\gamma}))=y_{1,2,1}^{-4}y_{2,1,1}^{-2}\left(y_{2,1,1}^2+y_{1,2,1}^2-2y_{2,1,1}y_{1,2,1}\right),\\&\varphi_{\boldsymbol{\mu}}(f_2(\mathbf{x}_{\gamma}))=2y_{1,2,1}^{-4}y_{2,1,1}^{-2}\left(y_{1,2,1}y_{2,1,1}^2-y_{1,2,1}^2y_{2,1,1}\right).\end{align*} $$
Now we recall the definition of a filtration on the space
![]() $\mathbb {U}_{\gamma }$
. First, we define a lexicographical ordering on the set of multipartitions. We say
$\mathbb {U}_{\gamma }$
. First, we define a lexicographical ordering on the set of multipartitions. We say
![]() $\boldsymbol \nu \succ \boldsymbol \mu $
if there exists some
$\boldsymbol \nu \succ \boldsymbol \mu $
if there exists some
![]() $j\in \{1,\dots ,n\}$
such that
$j\in \{1,\dots ,n\}$
such that
![]() $\nu _d=\mu _d$
for all
$\nu _d=\mu _d$
for all
![]() $d<j$
and
$d<j$
and
![]() $\nu _j>\mu _j$
, where the latter is the usual lexicographical order on partitions which is a total order. Let
$\nu _j>\mu _j$
, where the latter is the usual lexicographical order on partitions which is a total order. Let
Then we immediately get
and hence
![]() $(\Gamma _{\boldsymbol \mu })$
defines a filtration on
$(\Gamma _{\boldsymbol \mu })$
defines a filtration on
![]() $\mathbb {U}_{\gamma }$
:
$\mathbb {U}_{\gamma }$
:
where
![]() $\{\boldsymbol \mu _1\prec \cdots \prec \boldsymbol \mu _t\}$
is the set of multipartitions
$\{\boldsymbol \mu _1\prec \cdots \prec \boldsymbol \mu _t\}$
is the set of multipartitions
![]() $\boldsymbol \mu = (\mu _1,\dots ,\mu _n)$
with
$\boldsymbol \mu = (\mu _1,\dots ,\mu _n)$
with
![]() $\mu _i\vdash r_i$
for all
$\mu _i\vdash r_i$
for all
![]() $1\leq i\leq n$
. We say
$1\leq i\leq n$
. We say
Let
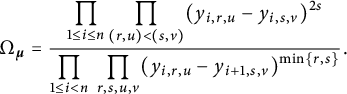 $$ \begin{align*}\Omega_{\boldsymbol\mu}=\frac{\displaystyle \prod_{1\leq i \leq n}\prod_{(r,u)<(s,v)} (y_{i,r,u}-y_{i,s,v})^{2s} } {\displaystyle \prod_{1\leq i<n}\ \prod_{r,s,u,v} (y_{i,r,u} - y_{i+1,s,v})^{\min\{r, s\}}}.\end{align*} $$
$$ \begin{align*}\Omega_{\boldsymbol\mu}=\frac{\displaystyle \prod_{1\leq i \leq n}\prod_{(r,u)<(s,v)} (y_{i,r,u}-y_{i,s,v})^{2s} } {\displaystyle \prod_{1\leq i<n}\ \prod_{r,s,u,v} (y_{i,r,u} - y_{i+1,s,v})^{\min\{r, s\}}}.\end{align*} $$
We recall the following important result from [Reference Ardonne, Kedem and Stone2, Theorem 3.6].
Lemma The induced map
![]() $\kern1pt\overline {\varphi }_{\boldsymbol \mu }: \Gamma _{\boldsymbol \mu }/\Gamma ^{\prime }_{\boldsymbol \mu }\rightarrow \mathbb {H}_{\boldsymbol \mu }$
of the specialization map
$\kern1pt\overline {\varphi }_{\boldsymbol \mu }: \Gamma _{\boldsymbol \mu }/\Gamma ^{\prime }_{\boldsymbol \mu }\rightarrow \mathbb {H}_{\boldsymbol \mu }$
of the specialization map
![]() $\varphi _{\boldsymbol \mu }$
is an isomorphism of graded vector spaces onto its image. Moreover, the image is the space of rational functions of the form
$\varphi _{\boldsymbol \mu }$
is an isomorphism of graded vector spaces onto its image. Moreover, the image is the space of rational functions of the form
where
![]() $h(\mathbf {y}_{\boldsymbol \mu })$
is an arbitrary Laurent polynomial in the variables
$h(\mathbf {y}_{\boldsymbol \mu })$
is an arbitrary Laurent polynomial in the variables
![]() $\mathbf {y}_{\boldsymbol \mu }$
, symmetric with respect to the exchange of variables
$\mathbf {y}_{\boldsymbol \mu }$
, symmetric with respect to the exchange of variables
![]() $y_{i,r,u}\leftrightarrow y_{i,r,v}$
.
$y_{i,r,u}\leftrightarrow y_{i,r,v}$
.
Now (6.1) induces a filtration
and hence
6.3
In what follows, we will describe the functions in
![]() $\varphi _{\boldsymbol \mu }(\mathcal {V}_{\boldsymbol \xi ,\lambda ,\gamma ,p}\cap \Gamma ^{}_{\boldsymbol \mu })$
. Recall the role of the space
$\varphi _{\boldsymbol \mu }(\mathcal {V}_{\boldsymbol \xi ,\lambda ,\gamma ,p}\cap \Gamma ^{}_{\boldsymbol \mu })$
. Recall the role of the space
![]() $\mathcal {V}_{\boldsymbol \xi ,\lambda ,\gamma ,p}$
from Theorem 5. By Definition 5.3, we have a list of restrictions to the function
$\mathcal {V}_{\boldsymbol \xi ,\lambda ,\gamma ,p}$
from Theorem 5. By Definition 5.3, we have a list of restrictions to the function
![]() $h(\mathbf {y}_{\boldsymbol \mu })$
. The second property implies that the Laurent polynomial
$h(\mathbf {y}_{\boldsymbol \mu })$
. The second property implies that the Laurent polynomial
![]() $h(\mathbf {y}_{\boldsymbol \mu })$
has a pole at
$h(\mathbf {y}_{\boldsymbol \mu })$
has a pole at
![]() $y_{i,r,u}$
of order at most
$y_{i,r,u}$
of order at most
![]() $\lambda (h_i)$
. Hence, we can write the Laurent polynomials in
$\lambda (h_i)$
. Hence, we can write the Laurent polynomials in
![]() $\varphi _{\boldsymbol \mu }(\mathcal {V}_{\boldsymbol \xi ,\lambda ,\gamma ,p}\cap \Gamma ^{}_{\boldsymbol \mu })$
as
$\varphi _{\boldsymbol \mu }(\mathcal {V}_{\boldsymbol \xi ,\lambda ,\gamma ,p}\cap \Gamma ^{}_{\boldsymbol \mu })$
as
 $$ \begin{align}\frac{\Omega_{\boldsymbol\mu}}{\displaystyle \prod_{1\leq i\leq n}\prod_{(r,u)}(y_{i,r,u})^{\lambda(h_i)}}\ h_1(\mathbf{y}_{\boldsymbol\mu}),\end{align} $$
$$ \begin{align}\frac{\Omega_{\boldsymbol\mu}}{\displaystyle \prod_{1\leq i\leq n}\prod_{(r,u)}(y_{i,r,u})^{\lambda(h_i)}}\ h_1(\mathbf{y}_{\boldsymbol\mu}),\end{align} $$
where
![]() $h_1(\mathbf {y}_{\boldsymbol \mu })$
is an arbitrary polynomial symmetric under the exchange of variables
$h_1(\mathbf {y}_{\boldsymbol \mu })$
is an arbitrary polynomial symmetric under the exchange of variables
![]() $y_{i,r,u}\leftrightarrow y_{i,r,v}$
. The first condition in Definition 5.3 implies that
$y_{i,r,u}\leftrightarrow y_{i,r,v}$
. The first condition in Definition 5.3 implies that
Since the degree of the first term in (6.2) with respect to the variable
![]() $y_{i,r,u}$
is given by
$y_{i,r,u}$
is given by
![]() $-P^{\boldsymbol {\mu },\lambda }_{r,i}-2r$
(recall the definition from Section 3), we obtain that
$-P^{\boldsymbol {\mu },\lambda }_{r,i}-2r$
(recall the definition from Section 3), we obtain that
Since the specialization map preserves the homogeneous degree, we have also that
![]() $\varphi _{\boldsymbol \mu }(g(\mathbf {x}_{\gamma }))$
is homogeneous of degree
$\varphi _{\boldsymbol \mu }(g(\mathbf {x}_{\gamma }))$
is homogeneous of degree
![]() $-p-|\gamma |$
and hence
$-p-|\gamma |$
and hence
 $$ \begin{align*}\mathrm{deg}(\Omega_{\boldsymbol\mu})=-p-|\gamma|-\mathrm{deg}(h_1(\mathbf{y}_{\boldsymbol\mu}))+\sum_{i=1}^n \lambda(h_i) \cdot d(\mu_i).\end{align*} $$
$$ \begin{align*}\mathrm{deg}(\Omega_{\boldsymbol\mu})=-p-|\gamma|-\mathrm{deg}(h_1(\mathbf{y}_{\boldsymbol\mu}))+\sum_{i=1}^n \lambda(h_i) \cdot d(\mu_i).\end{align*} $$
Let
![]() $j_{i,r,u}$
be the row index of
$j_{i,r,u}$
be the row index of
![]() $\mu _i$
corresponding to the pair
$\mu _i$
corresponding to the pair
![]() $(r,u)$
. Note that
$(r,u)$
. Note that
![]() $\mu _i^{j_{i,r,u}} = r$
. It follows that the degree of the numerator of
$\mu _i^{j_{i,r,u}} = r$
. It follows that the degree of the numerator of
![]() $\Omega _{\boldsymbol {\mu }}$
is given by
$\Omega _{\boldsymbol {\mu }}$
is given by
 $$ \begin{align*} \sum_{i=1}^n \sum_{(r,u) < (s,v)} 2s & = \sum_{i=1}^n \sum_{(s,v)} 2 ( j_{i,s,v}-1) \mu_i^{j_{i,s,v}} = \sum_{i=1}^n \sum_{j = 1}^{r_i} 2 (j-1) \mu_i^j\\ &= - 2|\gamma| + \sum_{i=1}^n \sum_{j = 1}^{r_i} 2 j \mu_i^j, \end{align*} $$
$$ \begin{align*} \sum_{i=1}^n \sum_{(r,u) < (s,v)} 2s & = \sum_{i=1}^n \sum_{(s,v)} 2 ( j_{i,s,v}-1) \mu_i^{j_{i,s,v}} = \sum_{i=1}^n \sum_{j = 1}^{r_i} 2 (j-1) \mu_i^j\\ &= - 2|\gamma| + \sum_{i=1}^n \sum_{j = 1}^{r_i} 2 j \mu_i^j, \end{align*} $$
where
![]() $(r,u) < (s,v)$
runs over all pairs of integer tuples satisfying
$(r,u) < (s,v)$
runs over all pairs of integer tuples satisfying
![]() $1 \le r,s \le r_i$
,
$1 \le r,s \le r_i$
,
![]() $1 \le u \le m_{i,r}$
, and
$1 \le u \le m_{i,r}$
, and
![]() $1 \le v \le m_{i,s}$
. Similarly, the degree of the denominator is given by
$1 \le v \le m_{i,s}$
. Similarly, the degree of the denominator is given by
 $$ \begin{align*} \sum_{i = 1}^{n-1} \sum_{r,u,s,v} \min\{ r,s \} &= \sum_{i = 1}^{n -1}\sum_{j = 1}^{r_i} \sum_{l = 1}^{r_{i+1}} \min\{ \mu_i^{j},\mu_{i+1}^{l} \} = \sum_{i = 1}^{n-1} \sum_{j = 1}^{r_i} \mu_{i+1}(\mu_i^j), \end{align*} $$
$$ \begin{align*} \sum_{i = 1}^{n-1} \sum_{r,u,s,v} \min\{ r,s \} &= \sum_{i = 1}^{n -1}\sum_{j = 1}^{r_i} \sum_{l = 1}^{r_{i+1}} \min\{ \mu_i^{j},\mu_{i+1}^{l} \} = \sum_{i = 1}^{n-1} \sum_{j = 1}^{r_i} \mu_{i+1}(\mu_i^j), \end{align*} $$
where the second sum runs over all
![]() $1 \le r \le r_i$
,
$1 \le r \le r_i$
,
![]() $1 \le u \le m_{i,r}$
,
$1 \le u \le m_{i,r}$
,
![]() $1 \le s \le r_{i+1}$
, and
$1 \le s \le r_{i+1}$
, and
![]() $1 \le u \le m_{i+1,s}$
. Therefore,
$1 \le u \le m_{i+1,s}$
. Therefore,
 $$ \begin{align*} \mathrm{deg}(\Omega_{\boldsymbol\mu})=-2 |\gamma|+K_{\boldsymbol{\mu}}^{\lambda}+\sum_{i=1}^n \lambda(h_i) \cdot d(\mu_i) \end{align*} $$
$$ \begin{align*} \mathrm{deg}(\Omega_{\boldsymbol\mu})=-2 |\gamma|+K_{\boldsymbol{\mu}}^{\lambda}+\sum_{i=1}^n \lambda(h_i) \cdot d(\mu_i) \end{align*} $$
and thus we get that
![]() $h_1(\mathbf {y}_{\boldsymbol \mu })$
is homogeneous of degree
$h_1(\mathbf {y}_{\boldsymbol \mu })$
is homogeneous of degree
![]() $-p+|\gamma |-K^{\lambda }_{\boldsymbol \mu }$
. Now we investigate the meaning of the last condition of Definition 5.3. Consider the polynomial
$-p+|\gamma |-K^{\lambda }_{\boldsymbol \mu }$
. Now we investigate the meaning of the last condition of Definition 5.3. Consider the polynomial
![]() $\tilde {f}(\mathbf {w}_{\gamma })=f(\mathbf {w}_{\gamma }) \prod _{i,r}w_{i,r}^{\lambda (h_i)}$
and note that the specializations
$\tilde {f}(\mathbf {w}_{\gamma })=f(\mathbf {w}_{\gamma }) \prod _{i,r}w_{i,r}^{\lambda (h_i)}$
and note that the specializations
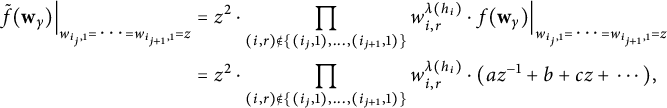 $$ \begin{align*} \tilde{f}(\mathbf{w}_{\gamma}) \Big|_{w_{i_{j},1}=\cdots=w_{i_{j+1},1}=z}&=z^2\cdot \prod_{(i,r)\notin \{(i_j,1),\dots,(i_{j+1},1)\}}w_{i,r}^{\lambda(h_i)}\cdot f(\mathbf{w}_{\gamma})\Big|_{w_{i_{j},1}=\cdots=w_{i_{j+1},1}=z}&\\&=z^2\cdot \prod_{(i,r)\notin \{(i_j,1),\dots,(i_{j+1},1)\}}w_{i,r}^{\lambda(h_i)}\cdot (a z^{-1}+b+cz+\cdots),\end{align*} $$
$$ \begin{align*} \tilde{f}(\mathbf{w}_{\gamma}) \Big|_{w_{i_{j},1}=\cdots=w_{i_{j+1},1}=z}&=z^2\cdot \prod_{(i,r)\notin \{(i_j,1),\dots,(i_{j+1},1)\}}w_{i,r}^{\lambda(h_i)}\cdot f(\mathbf{w}_{\gamma})\Big|_{w_{i_{j},1}=\cdots=w_{i_{j+1},1}=z}&\\&=z^2\cdot \prod_{(i,r)\notin \{(i_j,1),\dots,(i_{j+1},1)\}}w_{i,r}^{\lambda(h_i)}\cdot (a z^{-1}+b+cz+\cdots),\end{align*} $$
 $$ \begin{align*} \tilde{f}(\mathbf{w}_{\gamma}) \Big|_{w_{\ell,1}=z}&=z^{(2\lambda_0+\lambda_2)(h_{\ell})}\cdot \prod_{(i,r)\neq (\ell,1)}w_{i,r}^{\lambda(h_i)}\cdot f(\mathbf{w}_{\gamma})\Big|_{w_{\ell,1}=z}&\\&=z^{(2\lambda_0+\lambda_2)(h_{\ell})}\cdot \prod_{(i,r)\neq (\ell,1)}w_{i,r}^{\lambda(h_i)}\cdot (a z^{-(\lambda_0+\lambda_2)(h_{\ell})}+bz^{-(\lambda_0+\lambda_2)(h_{\ell})+1}+\cdots)\end{align*} $$
$$ \begin{align*} \tilde{f}(\mathbf{w}_{\gamma}) \Big|_{w_{\ell,1}=z}&=z^{(2\lambda_0+\lambda_2)(h_{\ell})}\cdot \prod_{(i,r)\neq (\ell,1)}w_{i,r}^{\lambda(h_i)}\cdot f(\mathbf{w}_{\gamma})\Big|_{w_{\ell,1}=z}&\\&=z^{(2\lambda_0+\lambda_2)(h_{\ell})}\cdot \prod_{(i,r)\neq (\ell,1)}w_{i,r}^{\lambda(h_i)}\cdot (a z^{-(\lambda_0+\lambda_2)(h_{\ell})}+bz^{-(\lambda_0+\lambda_2)(h_{\ell})+1}+\cdots)\end{align*} $$
are divisible by z for all
![]() $1\leq j<k$
and
$1\leq j<k$
and
![]() $\ell \in \mathrm {supp}_1(\lambda _0)$
; recall that
$\ell \in \mathrm {supp}_1(\lambda _0)$
; recall that
![]() $\lambda _0\in P^+(1)$
. Hence, we can apply Lemma 6.1 to
$\lambda _0\in P^+(1)$
. Hence, we can apply Lemma 6.1 to
![]() $\tilde {f}(\mathbf {w}_{\gamma })$
and obtain that
$\tilde {f}(\mathbf {w}_{\gamma })$
and obtain that
is contained in the intersection of ideals
 $$ \begin{align}\mathcal{Y}:=\bigcap_{\substack{s_{i_1},\dots,s_{i_k}\\ v_{i_1},\dots,v_{i_k}}}\mathcal{Y}_{\substack{s_{i_1},\dots,s_{i_k}\\ v_{i_1},\dots,v_{i_k}}}\cap \bigcap_{\substack{\ell\in\mathrm{supp}(\lambda_0),\\ 1\leq r\leq r_{\ell},\\ 1\leq u\leq m_{\ell,r}}}\left \langle y_{\ell,r,u} \right\rangle, \end{align} $$
$$ \begin{align}\mathcal{Y}:=\bigcap_{\substack{s_{i_1},\dots,s_{i_k}\\ v_{i_1},\dots,v_{i_k}}}\mathcal{Y}_{\substack{s_{i_1},\dots,s_{i_k}\\ v_{i_1},\dots,v_{i_k}}}\cap \bigcap_{\substack{\ell\in\mathrm{supp}(\lambda_0),\\ 1\leq r\leq r_{\ell},\\ 1\leq u\leq m_{\ell,r}}}\left \langle y_{\ell,r,u} \right\rangle, \end{align} $$
where
 $$ \begin{align*}\mathcal{Y}_{\substack{s_{i_1},\dots,s_{i_k}\\ v_{i_1},\dots,v_{i_k}}}:=\Big\langle y_{i_1,s_{i_1},v_{i_1}}^{c_{i_1}}y_{i_1+1,s_{i_1+1},v_{i_1+1}}^{c_{i_1+1}}\cdots y_{i_{k},s_{i_k},v_{i_k}}^{c_{i_{k}}}:\ \ \sum_{p=i_j}^{i_{j+1}} c_{p} = 1,\ \forall j\in[1,k)\Big\rangle.\end{align*} $$
$$ \begin{align*}\mathcal{Y}_{\substack{s_{i_1},\dots,s_{i_k}\\ v_{i_1},\dots,v_{i_k}}}:=\Big\langle y_{i_1,s_{i_1},v_{i_1}}^{c_{i_1}}y_{i_1+1,s_{i_1+1},v_{i_1+1}}^{c_{i_1+1}}\cdots y_{i_{k},s_{i_k},v_{i_k}}^{c_{i_{k}}}:\ \ \sum_{p=i_j}^{i_{j+1}} c_{p} = 1,\ \forall j\in[1,k)\Big\rangle.\end{align*} $$
Clearly, a polynomial
![]() $f(\mathbf {y}_{\boldsymbol {\mu }})$
is contained in
$f(\mathbf {y}_{\boldsymbol {\mu }})$
is contained in
![]() $\mathcal {Y}_{\substack {s_{i_1},\dots ,s_{i_k}\\ v_{i_1},\dots ,v_{i_k}}}$
if and only if
$\mathcal {Y}_{\substack {s_{i_1},\dots ,s_{i_k}\\ v_{i_1},\dots ,v_{i_k}}}$
if and only if
for all
![]() $j\in [1,k).$
However, this property is already satisfied by the prefactor of
$j\in [1,k).$
However, this property is already satisfied by the prefactor of
![]() $h_1(\mathbf {y}_{\boldsymbol {\mu }})$
in (6.3) unless there exists
$h_1(\mathbf {y}_{\boldsymbol {\mu }})$
in (6.3) unless there exists
![]() $j\in [1,k)$
with
$j\in [1,k)$
with
![]() $s_{i_j}=\cdots =s_{i_{j+1}}=1$
. Moreover, if there exists such a j with
$s_{i_j}=\cdots =s_{i_{j+1}}=1$
. Moreover, if there exists such a j with
![]() $s_{i_j}=\cdots =s_{i_{j+1}}=1$
, then the prefactor is a polynomial which has a nonzero constant term after evaluating the variables
$s_{i_j}=\cdots =s_{i_{j+1}}=1$
, then the prefactor is a polynomial which has a nonzero constant term after evaluating the variables
![]() $y_{i_j,s_{i_j},v_{i_j}}=\cdots =y_{i_{j+1},s_{i_{j+1}},v_{i_{j+1}}}=z$
(viewed as a polynomial in z). Hence, the discussion gives
$y_{i_j,s_{i_j},v_{i_j}}=\cdots =y_{i_{j+1},s_{i_{j+1}},v_{i_{j+1}}}=z$
(viewed as a polynomial in z). Hence, the discussion gives
-
• The expression (6.3) is contained in
 $\mathcal {Y}_{\substack {s_{i_1},\dots ,s_{i_k}\\ v_{i_1},\dots ,v_{i_k}}} \iff h_1(\mathbf {y}_{\boldsymbol {\mu }})$
satisfies (6.5) for all
$\mathcal {Y}_{\substack {s_{i_1},\dots ,s_{i_k}\\ v_{i_1},\dots ,v_{i_k}}} \iff h_1(\mathbf {y}_{\boldsymbol {\mu }})$
satisfies (6.5) for all
 $j\in [1,k)$
with
$j\in [1,k)$
with
 $s_{i_j}=\cdots =s_{i_{j+1}}=1$
.
$s_{i_j}=\cdots =s_{i_{j+1}}=1$
.
Similarly, the prefactor of
![]() $h_1(\mathbf {y}_{\boldsymbol {\mu }})$
in (6.3) is already contained in
$h_1(\mathbf {y}_{\boldsymbol {\mu }})$
in (6.3) is already contained in
 $\displaystyle \bigcap _{\substack {\ell \in \mathrm {supp}(\lambda _0),\\ 2\leq r\leq r_{\ell },\\ 1\leq u\leq m_{\ell ,r}}}\left \langle y_{\ell ,r,u} \right \rangle $
and thus
$\displaystyle \bigcap _{\substack {\ell \in \mathrm {supp}(\lambda _0),\\ 2\leq r\leq r_{\ell },\\ 1\leq u\leq m_{\ell ,r}}}\left \langle y_{\ell ,r,u} \right \rangle $
and thus
-
• The expression (6.3) is contained in
 $\displaystyle \bigcap _{\substack {\ell \in \mathrm {supp}(\lambda _0),\\ 1\leq r\leq r_{\ell },\\ 1\leq u\leq m_{\ell ,r}}}\left \langle y_{\ell ,r,u} \right \rangle \iff h_1(\mathbf {y}_{\boldsymbol {\mu }})\in \displaystyle \bigcap _{\substack {\ell \in \mathrm {supp}(\lambda _0),\\ 1\leq u\leq m_{\ell ,1}}}\left \langle y_{\ell ,1,u} \right \rangle $
.
$\displaystyle \bigcap _{\substack {\ell \in \mathrm {supp}(\lambda _0),\\ 1\leq r\leq r_{\ell },\\ 1\leq u\leq m_{\ell ,r}}}\left \langle y_{\ell ,r,u} \right \rangle \iff h_1(\mathbf {y}_{\boldsymbol {\mu }})\in \displaystyle \bigcap _{\substack {\ell \in \mathrm {supp}(\lambda _0),\\ 1\leq u\leq m_{\ell ,1}}}\left \langle y_{\ell ,1,u} \right \rangle $
.
This implies the following lemma.
Lemma The containment of (6.3) in the ideal (6.4) is equivalent to the fact that
![]() $h_1(\mathbf {y}_{\boldsymbol {\mu }})$
is contained in the intersection
$h_1(\mathbf {y}_{\boldsymbol {\mu }})$
is contained in the intersection
 $$ \begin{align*}\bigcap_{\substack{s_{i_1},\dots,s_{i_k}\\ v_{i_1},\dots,v_{i_k}}}\widetilde{\mathcal{Y}}_{\substack{s_{i_1},\dots,s_{i_k}\\ v_{i_1},\dots,v_{i_k}}}\cap \bigcap_{\substack{\ell\in\mathrm{supp}(\lambda_0),\\ 1\leq u\leq m_{\ell,1}}}\left \langle y_{\ell,1,u} \right\rangle,\end{align*} $$
$$ \begin{align*}\bigcap_{\substack{s_{i_1},\dots,s_{i_k}\\ v_{i_1},\dots,v_{i_k}}}\widetilde{\mathcal{Y}}_{\substack{s_{i_1},\dots,s_{i_k}\\ v_{i_1},\dots,v_{i_k}}}\cap \bigcap_{\substack{\ell\in\mathrm{supp}(\lambda_0),\\ 1\leq u\leq m_{\ell,1}}}\left \langle y_{\ell,1,u} \right\rangle,\end{align*} $$
where
![]() $\widetilde {\mathcal {Y}}_{\substack {s_{i_1},\dots ,s_{i_k}\\ v_{i_1},\dots ,v_{i_k}}}$
is the ideal generated by
$\widetilde {\mathcal {Y}}_{\substack {s_{i_1},\dots ,s_{i_k}\\ v_{i_1},\dots ,v_{i_k}}}$
is the ideal generated by
where for each
![]() $1\leq j\leq k-1$
we have
$1\leq j\leq k-1$
we have
 $$ \begin{align*}c_{i_j}+c_{i_j+1}+\cdots+c_{i_{j+1}}= \begin{cases}1,& \text{ if }s_{i_j}=\cdots=s_{i_{j+1}}=1,\\ 0,& \text{ otherwise. } \end{cases}\end{align*} $$
$$ \begin{align*}c_{i_j}+c_{i_j+1}+\cdots+c_{i_{j+1}}= \begin{cases}1,& \text{ if }s_{i_j}=\cdots=s_{i_{j+1}}=1,\\ 0,& \text{ otherwise. } \end{cases}\end{align*} $$
Example We consider
![]() $r_1=2$
and
$r_1=2$
and
![]() $r_2=1$
(
$r_2=1$
(
![]() $\lambda _1=\varpi _1+\varpi _2$
,
$\lambda _1=\varpi _1+\varpi _2$
,
![]() $\lambda _0=\lambda _2=0$
) with the two obvious tuples of partitions. In the case
$\lambda _0=\lambda _2=0$
) with the two obvious tuples of partitions. In the case
![]() $\boldsymbol {\mu }=(\mu _1,\mu _2)$
with
$\boldsymbol {\mu }=(\mu _1,\mu _2)$
with ![]() , we get that
, we get that
and in the other case ![]()
In the first case, we have no restriction on
![]() $h_1(\mathbf {y}_{\mu }), $
and in the second case, we actually need
$h_1(\mathbf {y}_{\mu }), $
and in the second case, we actually need
Proposition The dimension of
![]() $\varphi _{\boldsymbol {\mu }}(\mathcal {V}_{\boldsymbol {\xi },\lambda ,\gamma ,p}\cap \Gamma _{\boldsymbol {\mu }})$
is less or equal to the dimension of the space
$\varphi _{\boldsymbol {\mu }}(\mathcal {V}_{\boldsymbol {\xi },\lambda ,\gamma ,p}\cap \Gamma _{\boldsymbol {\mu }})$
is less or equal to the dimension of the space
![]() $\mathcal {W}$
consisting of all homogeneous polynomials
$\mathcal {W}$
consisting of all homogeneous polynomials
![]() $f(\mathbf {y}_{\boldsymbol \mu })$
of degree
$f(\mathbf {y}_{\boldsymbol \mu })$
of degree
![]() $-p+|\gamma |-K^{\lambda }_{\boldsymbol {\mu }}$
in the ideal
$-p+|\gamma |-K^{\lambda }_{\boldsymbol {\mu }}$
in the ideal
 $$ \begin{align}\bigcap_{\substack{s_{i_1},\dots,s_{i_k}\\ v_{i_1},\dots,v_{i_k}}}\widetilde{\mathcal{Y}}_{\substack{s_{i_1},\dots,s_{i_k}\\ v_{i_1},\dots,v_{i_k}}}\cap \bigcap_{\substack{\ell\in\mathrm{supp}(\lambda_0),\\ 1\leq u\leq m_{\ell,1}}}\left \langle y_{\ell,1,u} \right\rangle\end{align} $$
$$ \begin{align}\bigcap_{\substack{s_{i_1},\dots,s_{i_k}\\ v_{i_1},\dots,v_{i_k}}}\widetilde{\mathcal{Y}}_{\substack{s_{i_1},\dots,s_{i_k}\\ v_{i_1},\dots,v_{i_k}}}\cap \bigcap_{\substack{\ell\in\mathrm{supp}(\lambda_0),\\ 1\leq u\leq m_{\ell,1}}}\left \langle y_{\ell,1,u} \right\rangle\end{align} $$
symmetric with respect to the exchange of variables
![]() $y_{i,r,u}\leftrightarrow y_{i,r,v}$
and satisfying
$y_{i,r,u}\leftrightarrow y_{i,r,v}$
and satisfying
Proof The discussion in Section 6.3 shows that each element in
![]() $\varphi _{\boldsymbol {\mu }}(\mathcal {V}_{\boldsymbol {\xi },\lambda ,\gamma ,p}\cap \Gamma _{\boldsymbol {\mu }})$
is of the form (6.2) with
$\varphi _{\boldsymbol {\mu }}(\mathcal {V}_{\boldsymbol {\xi },\lambda ,\gamma ,p}\cap \Gamma _{\boldsymbol {\mu }})$
is of the form (6.2) with
![]() $h_1(\mathbf {y}_{\mu })\in \mathcal {W}$
and hence the upper bound for the dimension is obtained.
$h_1(\mathbf {y}_{\mu })\in \mathcal {W}$
and hence the upper bound for the dimension is obtained.
6.4
If we denote by
![]() $e_d^{(i,r)}(\mathbf {y}_{\boldsymbol \mu })$
,
$e_d^{(i,r)}(\mathbf {y}_{\boldsymbol \mu })$
,
![]() $1\leq d\leq m_{i,r}$
the dth elementary symmetric polynomial in the variables
$1\leq d\leq m_{i,r}$
the dth elementary symmetric polynomial in the variables
![]() $\{y_{i,r,1},\dots , y_{i,r,m_{i,r}}\}$
, we can rewrite the statement of Proposition 6.3 as follows. The dimension of
$\{y_{i,r,1},\dots , y_{i,r,m_{i,r}}\}$
, we can rewrite the statement of Proposition 6.3 as follows. The dimension of
![]() $\varphi _{\boldsymbol \mu }(\mathcal {V}_{\boldsymbol {\xi },\lambda ,\gamma ,p}\cap \Gamma _{\boldsymbol \mu })$
is less or equal to the dimension of the space spanned by all monomials
$\varphi _{\boldsymbol \mu }(\mathcal {V}_{\boldsymbol {\xi },\lambda ,\gamma ,p}\cap \Gamma _{\boldsymbol \mu })$
is less or equal to the dimension of the space spanned by all monomials
 $$ \begin{align*}\prod_{i=1}^n\prod_{r=1}^{r_i}\prod_{d=1}^{m_{i,r}} (e_d^{(i,r)}(\mathbf{y}_{\boldsymbol\mu}))^{C_{d,r,i}},\ \ C_{d,r,i}\in\mathbb{Z}_+\end{align*} $$
$$ \begin{align*}\prod_{i=1}^n\prod_{r=1}^{r_i}\prod_{d=1}^{m_{i,r}} (e_d^{(i,r)}(\mathbf{y}_{\boldsymbol\mu}))^{C_{d,r,i}},\ \ C_{d,r,i}\in\mathbb{Z}_+\end{align*} $$
with
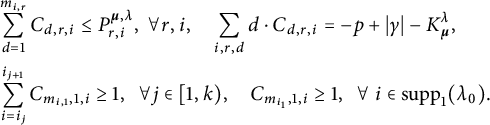 $$ \begin{align*}&\sum_{d=1}^{m_{i,r}}C_{d,r,i}\leq P^{{\boldsymbol\mu},\lambda}_{r,i},\ \forall r,i, \ \ \ \ \sum_{i,r,d}d\cdot C_{d,r,i}=-p+|\gamma|-K^{\lambda}_{\boldsymbol{\mu}},\\&\sum_{i=i_j}^{i_{j+1}}C_{m_{i,1},1,i}\geq 1, \ \ \forall j\in[1,k),\ \ \ \ C_{m_{i_1},1,i}\geq 1,\ \ \forall \ i\in\mathrm{supp}_1(\lambda_0).\end{align*} $$
$$ \begin{align*}&\sum_{d=1}^{m_{i,r}}C_{d,r,i}\leq P^{{\boldsymbol\mu},\lambda}_{r,i},\ \forall r,i, \ \ \ \ \sum_{i,r,d}d\cdot C_{d,r,i}=-p+|\gamma|-K^{\lambda}_{\boldsymbol{\mu}},\\&\sum_{i=i_j}^{i_{j+1}}C_{m_{i,1},1,i}\geq 1, \ \ \forall j\in[1,k),\ \ \ \ C_{m_{i_1},1,i}\geq 1,\ \ \forall \ i\in\mathrm{supp}_1(\lambda_0).\end{align*} $$
Therefore,
Now Theorem 4 follows from the next theorem and Theorem 2(1); the fact
![]() $[L(\boldsymbol {\pi }):\tau _p^*V(\nu )]=0$
for all
$[L(\boldsymbol {\pi }):\tau _p^*V(\nu )]=0$
for all
![]() $\nu \notin \mathrm {wt}(\boldsymbol {\pi })-Q^+$
is obvious by weight reasons.
$\nu \notin \mathrm {wt}(\boldsymbol {\pi })-Q^+$
is obvious by weight reasons.
Theorem 6 Let
![]() $\gamma \in Q^+$
,
$\gamma \in Q^+$
,
![]() $p\in \mathbb {Z}_+$
, and
$p\in \mathbb {Z}_+$
, and
![]() $\boldsymbol \zeta =(\lambda ,\lambda _0,\lambda _1,\lambda _2)$
be an admissible quadrupel such that
$\boldsymbol \zeta =(\lambda ,\lambda _0,\lambda _1,\lambda _2)$
be an admissible quadrupel such that
![]() $\lambda _2\in P^+(1)$
. Then
$\lambda _2\in P^+(1)$
. Then
Proof The proof is by induction on
![]() $|\mathrm {supp}_1(\lambda _1)|$
. In the case of
$|\mathrm {supp}_1(\lambda _1)|$
. In the case of
![]() $|\mathrm {supp}_1(\lambda _1)|\leq 1$
, the theorem follows from Remark 3.2 (see in particular (3.5)) since the assumption
$|\mathrm {supp}_1(\lambda _1)|\leq 1$
, the theorem follows from Remark 3.2 (see in particular (3.5)) since the assumption
![]() $[N_{\boldsymbol {\zeta }}:\tau _p^*V(\lambda -\gamma )]< \sum _{\boldsymbol \mu \vdash \gamma } L_{\boldsymbol \mu ,\boldsymbol {\zeta }}^p$
would lead together with (6.7) to a contradiction:
$[N_{\boldsymbol {\zeta }}:\tau _p^*V(\lambda -\gamma )]< \sum _{\boldsymbol \mu \vdash \gamma } L_{\boldsymbol \mu ,\boldsymbol {\zeta }}^p$
would lead together with (6.7) to a contradiction:
Now let
![]() $|\mathrm {supp}_1(\lambda _1)|\geq 2$
and write
$|\mathrm {supp}_1(\lambda _1)|\geq 2$
and write
![]() $\lambda _1=\varpi _{i_1}+\cdots +\varpi _{i_k},\ 1\leq i_1<\cdots <i_k\leq n$
. Since
$\lambda _1=\varpi _{i_1}+\cdots +\varpi _{i_k},\ 1\leq i_1<\cdots <i_k\leq n$
. Since
![]() $\lambda _2\in P^+(1)$
, we can use Theorem 2(2) and get
$\lambda _2\in P^+(1)$
, we can use Theorem 2(2) and get
Since
![]() $\boldsymbol {\zeta }_1$
is again admissible and
$\boldsymbol {\zeta }_1$
is again admissible and
![]() $\lambda _2+\varpi _{i_1}\in P^+(1)$
(see the definition in (2.3)), we can apply our induction hypothesis to get
$\lambda _2+\varpi _{i_1}\in P^+(1)$
(see the definition in (2.3)), we can apply our induction hypothesis to get
In general, we cannot apply the induction hypothesis to the second summand, but using (6.7) (which holds for all admissible quadruples), we can at least say
Hence,
where the last equality follows from Proposition 3.2. So the theorem is proved by using once more (6.7).
Acknowledgments
D.K. thanks the Hausdorff Research Institute for Mathematics and the organizers of the Trimester Program “New Trends in Representation Theory” for excellent working conditions. He also thanks Matheus Brito for many useful discussions and Rekha Biswal for many inspiring discussions and drawing our attention to the dual functional realization.
Editorial note of concern
The authors of this article, Professor Kus and Dr. Barth, have included an acknowledgement of the contributions of Dr. Rekha Biswal. Following acceptance of the manuscript for publication, the editors were contacted directly by Dr. Biswal, who alleges that she was a contributing author of the work whose name was removed from the submission without her permission. Dr. Biswal provided the editors with a copy of a report into this allegation by her then head-of-school, which has also been communicated to the other authors’ institution. Although this report is not conclusive, the journal’s Editors-in-Chief have decided it would be appropriate to include this note of concern communicating these facts along with the publication.
Henry Kim and Robert McCann, Editors-in-Chief, Canadian Journal of Mathematics.