Mechanical properties of two-dimensional materials and heterostructures

Abstract

Mechanical properties are of fundamental importance in materials science and engineering, and have been playing a great role in various materials applications in the human history. Measurements of mechanical properties of 2-dimensional (2D) materials, however, are particularly challenging. Although various types of 2D materials have been intensively explored in recent years, the investigation of their mechanical properties lags much behind that of other properties, leading to lots of open questions and challenges in this research field. In this review, we first introduce the nanoindentation technique with atomic force microscopy to measure the elastic properties of graphene and 2D transition metal dichalcogenides. Then we review the effect of defects on mechanical properties of 2D materials, including studies on naturally defective chemical-vapor-deposited and intentionally defective 2D materials. Lastly, we introduce a nano-electromechanical device, resonators, built on the basis of the excellent mechanical properties of 2D materials.

I. INTRODUCTION

Mechanical properties are probably the first aspect that people pay attention to in exploring a new material. Stone, bronze, and iron are the three milestone materials that appeared synchronically in ancient times. These materials were discovered, selected, and refined, mostly due to their outstanding mechanical properties, as well as cost-effective ways of production. Stone is rigid, but brittle and difficult to processing, while bronze and iron are stronger, tougher, and easier for shaping. Their utilizations have greatly changed the human history and they are used to name the ancient periods (i.e., Stone Age, Bronze Age, and Iron Age). As increasingly fast discoveries of new functional materials are made in modern times, mechanical properties are no longer the only properties that are concerned. However, they are still the key criteria in seeking super-strong or super-rigid materials for applications ranging from people's daily life to space exploration. ^1,2,3,4 In semiconductors, they are indispensable complements to electrical and optical properties of materials. ^5,6 Mechanical properties have also played vital roles in designs of flexible, stretchable, and epidermal electronics which may potentially dominate the future electronics industry. ^7,8,9

Nano-science and nano-technology have attracted intensive attention for the past 30 years. ^{10,11,12,13,14,15,16,17} In two-dimensional (2D) materials, electrons and phonons are limited in a planar dimension, and therefore many of their properties deviate from their 3D counterparts. ¹⁶ Two representative examples are graphene and most transition metal dichalcogenides (TMDs) such as molybdenum disulfide (MoS₂), which, in the monolayer limit features massless Dirac fermions ¹⁸ and an intrinsic direct band gap, respectively, ^19,20 leading to a variety of intriguing electrical and optical properties. ^{21,22,23,24,25,26,27,28} On the other hand, an important question arises: whether the mechanical properties of 2D materials become also different in the monolayer limit. In 3D, elastic modulus E and Poisson's ratio ν are used to determine elastic properties of materials. E is also called Young's modulus when the applied strain is uniaxial, following $E = {\sigma \mathord{\left/{\vphantom {\sigma \varepsilon }} \right\kern-\nulldelimiterspace} \varepsilon }$ , where σ is stress and ε is strain. Poisson's ratio ν is defined as the negative ratio of transverse to axial strain under uniaxial stress. Another important parameter is tensile strength, which describes the maximum tension that a material can withstand. Elastic modulus and tensile strength are scaled by the change of volumetric elastic energy, thus having a units of J/m³ or Pa. In 2D, however, these parameters have to be renormalized by the planar elastic energy, leading to a units of J/m² or N/m. Although 2D modulus and strength are more suitable to describe 2D materials, for the purpose of comparison between 2D and 3D materials, these 2D parameters can be converted to 3D ones by dividing the 2D values with the thickness of the 2D materials. With these concepts, the conventional elastic theory can be readily applied to 2D systems. However, there are many new aspects of mechanical properties in 2D systems that are different from 3D systems, as we will discuss later in this review. The first step to probe mechanical properties of 2D systems is more technical; that is, how to accurately measure the mechanical properties of 2D materials.

II. GRAPHENE—THE STRONGEST MATERIAL

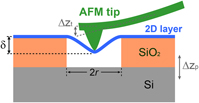
If the system is 1D, such as a carbon nanotube or an ultra-thin silicon nanowire, measurements of Young's modulus seem to be straightforward. Stretching a nanotube or nanowire is an effective way to directly determine its mechanical properties. ^1,29,30,31 However, the measurements of 2D systems appear to be more difficult, because uniformly stretching a 2D membrane is challenging. A breakthrough occurred in 2008, when Lee et al. in Columbia University utilized an atomic force microscope (AFM) nanoindentation to probe suspended, circular graphene membranes. ³ The AFM tip is pushing the center of the membrane (Fig. 1). When the tip radius is tiny (r _tip ≪ r _hole), the load applied by the AFM tip can be considered as a point load. In a simplified continuum mechanics model, the applied load is related to the deformation geometry of the membrane, ^3,32,33

(1) $$F = \left( {\sigma _0^{{\rm{2D}}}\pi } \right)\delta + \left( {{E^{{\rm{2D}}}}{{{q^3}} \over {{r^2}}}} \right){\delta ^3}\quad ,$$

where F is the applied point load force, δ is the indentation depth at the center of the membrane, r is the hole radius, q = 1/(1.05 − 0.15ν − 0.16ν²) is a dimensionless constant determined by the Poisson's ratio, ν, of the membrane, ${E^{{\rm{2D}}}}$ and $\sigma _0^{{\rm{2D}}}$ are the 2D modulus and the 2D pretension, respectively (Fig. 1). Equation (1) ignores contributions from the bending modulus because it is negligible in such an ultrathin monolayer membrane. Initially, the applied load scales linearly with the indentation depth when it is small (F ∼ δ), and the coefficient is dominated by the pretention; when the indentation depth is large, the load is dominated by the stiffness of the membrane with a cubic relationship (F ∼ δ³). Graphene and TMDs have a lattice with 6-fold- or 3-fold-symmetry, leading to nearly isotropic mechanical properties in the plane. Thus the above model can be applied to the measurements of mechanical properties of these 2D materials.

FIG. 1. Illustration of probing mechanical properties of 2D materials by AFM nanoindentation.

In Eq. (1), the Poisson's ratio is an important parameter because it determines q while ${E^{{\rm{2D}}}}$ scales reversely with the third power of q. The Poisson's ratio of graphene had been actually controversial for a few years. Bulk graphite was reported to have a Poisson's ratio of 0.16 in the basal plane. ³⁴ Ab initio calculation reveals an isotropic in-plane elastic response of graphene at small strains with a Poisson's ratio of 0.186, which, at large strains, becomes anisotropic and strongly dependent on the strain values. ³⁴ On the other hand, molecular dynamic simulations show a Poisson's ratio of 0.21 for bulk graphene, and the ratio significantly depends on the size and chirality in the case of graphene nanoribbons, with a larger value in the armchair direction than in the zigzag direction. ³⁵ Despite the wide distribution of Poisson's ratio ranging from 0.16 to 0.21, it merely introduces an error of ∼1% in the calculated constant q, or ∼3% for q ³, which is a negligible error for mechanical measurements.

Experimentally, monolayer graphene is mechanically exfoliated onto substrates drilled with holes with various diameters, such that the graphene membranes with desired diameters are suspended over the holes [Figs. 2(a) and 2(b)]. The indentation depth is determined by the displacement of the scanning piezo-tube of AFM (Δz _p) and the deflection of the AFM tip (Δz _t), and the applied load is obtained by multiplying the deflection of the AFM tip with its spring constant (Fig. 1). ${E^{{\rm{2D}}}}$ and $\sigma _0^{2{\rm{D}}}$ can be derived by a least-square fitting of the experimental force-displacement [F(δ)] curves with Eq. (1) [Fig. 2(c)]. By averaging over numerous times of measurements, Lee et al. obtained a mean value of E ^2D equal to 342 N/m, with a standard deviation of 30 N/m [Fig. 2(d)]. The uncertainty of their elastic modulus measurement is not large, only ∼14%. The derived values of ${\rm{\sigma }}_0^{2{\rm{D}}}$ ranges from 0.07 to 0.74 N/m, which are higher even than the fracture strength of many conventional materials. ³ The positive pretentions may result from adhesion of graphene membrane to the vertical wall of the hole, tautly stretching the graphene membrane [Fig. 2(b)]. Assuming an effective graphene thickness of 0.335 nm, the derived E ^2D corresponds to an ultrahigh 3D Young's modulus of 1.0 ± 0.1 TPa, very close to the theoretical value ^36,37 and the in-plane Young's modulus of bulk graphite. ³⁴

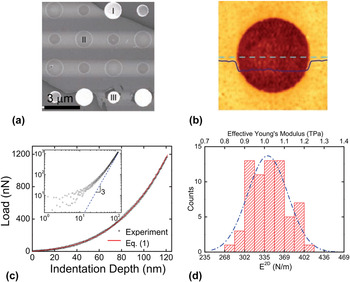
FIG. 2. Mechanical properties of exfoliated graphene: (a) scanning electron microscope image of a monolayer graphene exfoliated on a holey substrate, from Ref. 3; (b) detailed AFM image with a height profile across the dashed line, from Ref. 3; the diameter of the central hole is 1 μm; (c) typical experimental and fitted force–displacement curves, which reach the cubic behavior at high loads (inset), from Ref. 3; (d) statistical histogram and Gaussian distribution of measured E ^2D, from Ref. 3.

This nanoindentation process can also be used to probe the tensile strength of graphene by indenting it to its breaking point. Based on a continuum model, the maximum stress for a tightly clamped, linear elastic, and circular membrane under a spherical indenter is given by ³⁸

(2) $$\sigma _{\rm{m}}^{2{\rm{D}}} = {\left( {{{{\rm{F}}{{\rm{E}}^{2{\rm{D}}}}} \over {4\pi {r_{{\rm{tip}}}}}}} \right)^{1/2}}\quad ,$$

where F is the breaking force, and r _tip is the tip radius. Equation (2) shows that the breaking force scales with the tip radius. For graphene, the measured data yields a mean 2D tensile strength of 55 N/m, corresponding to a 3D tensile strength of 130 ± 10 GPa.

III. EFFECTS OF DEFECTS

Both the measured elastic modulus and tensile strength of graphene have the highest values among all natural materials. It arises from the extremely strong sp ² C–C bonding in graphene, as well as its free from notable microscopic defects when exfoliated from high-quality bulk graphite. However, defects exist ubiquitously in all materials. In graphene, carbon atoms could be lost or displaced, generating point defects including mono-vacancies, di-vacancies, and Stone–Wales defects (5–7 defects). Line defects such as grain boundaries are also observed in graphene by atomically resolved transmission electron microscopy (TEM). ³⁹ The existence of these defects raises a question of how the mechanical properties of graphene are affected by defects. Theoretical simulations show that point defects weaken the elastic modulus and tensile strength of graphene, ^40,41 but grain boundary defects can enhance or weaken the strength of graphene depending on the tilt angles, ^42,43 suggesting that not only defect density affects mechanical properties of graphene, but also the arrangements and interactions between defects are important. In addition, a movement of edge dislocation pairs along the zig-zag lattice direction was observed under a low-voltage, high resolution TEM by Warner et al. ⁴⁴ These edge dislocations result in a substantial bond compression or elongation of ±27%, and their movement may contribute to the plasticity of graphene, as dislocation movement is the key mechanism for materials plastic deformation. ⁴⁴

In large-area graphene synthesized by chemical vapor deposition (CVD), ^45,46 point defects and grain boundaries are very common [Figs. 3(a) and 3(c)]. ^39,48,49,50 CVD graphene thus provides a good platform to test the effect of defects and grain boundaries. Early experiments show that CVD graphene has much lower Young's modulus and tensile strength than exfoliated graphene. ^51,52 Ruiz-Vargas et al. reported an average modulus of 55 N/m and a breaking strength of ∼35 GPa, only 1/6 and 1/4 of the values of exfoliated, single-crystal graphene, respectively. ⁵¹ However, detailed studies reveal that the observed reduction in modulus and strength may originate from ripples or additional defects resulted from the transfer process. ^47,51 If polymethyl methacrylate (PMMA) is coated on graphene to assist the transfer, liquid acetone is usually needed to remove the PMMA at the last step, which introduces an additional surface tension on the suspended monolayer membrane, rippling the membrane and weakening its modulus and strength.

FIG. 3. Mechanical properties of CVD graphene: (a and b) a small-grain graphene: dark-field transition electron microscope (DF-TEM) image with false color (a) and histogram of its E ^2D (b), from Ref. 47; (c and d) DF-TEM images and E ^2D of a large-grain graphene, from Ref. 47; (e) bright-field TEM image of a small-grain graphene over a hole, from Ref. 47; (f) AFM indentation on different grain boundaries and on the center of the membrane as shown in (e), from Ref. 47.

Instead of PMMA, Lee et al. adopted polydimethylsiloxane (PDMS) as the transfer medium. They first transferred the graphene onto PDMS, and then stamped the graphene onto the target holey substrates. ⁴⁷ This dry transfer avoids surface tension and yields taut, suspended CVD graphene membrane, which is desired for measurements of intrinsic mechanical properties. With this effort, Lee et al. obtained an E ^2D of 328 ± 17 and 339 ± 17 N/m for small-grain and large-grain CVD graphene [Figs. 3(a)–3(d)], both very close to the value of exfoliated, single-crystal graphene (∼340 N/m). AFM indentations on grain boundaries show that facture occurs at a slightly lower load than the indentation at the center of a membrane [Figs. 3(e) and 3(f)]. The average breaking strength of graphene with small and well stitched grain, 33 N/m (98.5 GPa), is slightly smaller than that of exfoliated graphene (130 GPa). ^3,47 These experimental and simulating results are quite surprising because a common wisdom is that a reduction of both modulus and strength is expected by defects and grain boundaries. It indicates that defects or grain boundaries play very special roles beyond normal expectation in the mechanical properties of graphene, or even other 2D materials.

As CVD graphene is almost as strong as exfoliated ones, the role of defects in graphene seems to be contradictory to the common sense that defects often weaken the strength of materials. One possibility is that the defect density in CVD graphene, although considerable from an electronic point of view, is still too low to affect the mechanical strength. Therefore, quantification of the dependence of mechanical properties of graphene on defect density becomes necessary. For this purpose, defects need to be intentionally introduced into graphene. Zandiatashbar et al. generated defects in graphene by a gentle oxygen plasma etching. ⁵³ Defect types and densities are estimated from the ratio of the newly appearing D peak to the G peak in the Raman spectra [Figs. 4(a) and 4(b)]. ^55,56 When the etching time is short, sp ³-type defects form, while with increasing etching time, vacancy defects appear. The 2D modulus of graphene was found to be insensitive to defects in the sp ³-type defect regime, while in the vacancy-defect regime, it drops significantly [Fig. 4(a)]. In contrast, the breaking strength (scaling with square root of breaking load) of graphene decreases monotonically with increasing defect densities induced by the oxygen plasma, although it drops only by ∼14% over the entire sp ³-type defect region [Fig. 4(b)]. This discovery implies that in this regime graphene may be covalently bonded with itself or to the substrate, counteracting the weakening of mechanical properties. ⁵³

FIG. 4. Effects of defects on mechanical properties of graphene: (a and b) E ^2D and breaking strength of defective graphene induced by oxygen plasma etching, from Ref. 53; (c) E ^2D as a function of the density of defects introduced by Ar⁺ irradiation, showing a non-monotonic behavior, from Ref. 54; (d) schematic pictures of thermal fluctuation of a suspended graphene membrane, and (e) of a defective graphene, from Ref. 54.

Although oxygen plasma etching is an effective way to create defects, it is not a well-controlled method, because it is based on chemically reactive etching that has a fast etching rate, and tends to expand existing defects rather than generate new ones. Instead, López-Polín et al. controlled defects in monolayer graphene by a low-energy irradiation with argon ions (140 eV Ar⁺). ⁵⁴ This physical process creates defects uniformly and avoids the selective etching induced by oxygen plasma. With this more controlled technique, they reported an abnormal increase of E ^2D by almost a factor of 2 at a vacancy content of 0.2% [Fig. 4(c)]. Further increasing the defect density reduces E ^2D. The initial increase of E ^2D was attributed to dependence of E ^2D on the momentum of flexural modes predicted for 2D membranes. In graphene, the low bending rigidity introduces significant thermal fluctuations and strong anharmonic effects, which introduces a wavevector-dependent elastic modulus. Long-wavelength excitations are favorable in large and clean samples [Fig. 4(d)], but they are suppressed in defective samples [Fig. 4(e)], leading to an effective increase of the measured E ^2D. This abnormal increase of E ^2D cannot be thoroughly understood from the conventional continuum mechanics, and quantum and atomic-scale theories should be also considered in accurately describing the mechanics of 2D membranes. ⁵⁴

In multilayer graphene, an interesting topic is the effect of defects on the interaction between graphene layers. The interlayer interaction is crucial for many applications. For example, a weak interaction is desired for applications in high-performance electrochemical devices including batteries and supercapacitors that involve atomic intercalation into the space between layers. ⁵⁷ In defective graphene multilayers, however, whether the interlayer interaction of graphene is enhanced or weakened has been an open question. Liu et al. used high-energy irradiation with α particles to introduce defects in graphene with different number of layers, and explored their elastic modulus as a function of the irradiation dose by the AFM nanoindentation method. ⁵⁸ They found that in irradiated multilayer graphene, carbon atoms tend to form interlayer linking around the defects and partially restore the degraded modulus. As a result of such interlayer linking, the elastic modulus of multilayer graphene shows higher resistance to radiation damage as compared to monolayers. This finding reveals the importance of interlayer linking in graphene from the mechanical perspective, and the interlayer linking may also exist in other 2D materials and heterostructures. It also sheds light for possibly engineering mechanical properties of 2D materials with controlled defects.

IV. MECHANICAL PROPERTIES OF 2D TMDS

Although graphene has been proven to be the strongest material ever measured, its native zero band gap has limited its applications in semiconducting industry. ^59,60 As a result, TMDs, such as MoS₂, WS₂, and WSe₂, have attracted much attention in recent years due to the existence of a band gap, and their crossover from indirect band gap in bulk to direct band gap in the monolayer limit. ¹⁷ This opens up a wide range of applications for monolayer TMDs in electronics and optoelectronics. ^24,61,62 2D TMDs have also been used as key components in flexible electronics, ^63,64,65,66 in which their mechanical properties become relevant and important. The first reports on mechanical properties of TMD layers aim at less-defective, exfoliated flakes of MoS₂. Bertolazzi et al. utilized a similar AFM nanoindentation to measure the mechanical properties of exfoliated mono- and bi-layer MoS₂. ⁶⁷ The in-plane 2D modulus of monolayer MoS₂ was determined to be 180 ± 60 N/m (270 ± 100 GPa), and the average breaking strength 15 ± 3 N/m (23 GPa), which are several times lower than monolayer graphene but still much stronger than steel. The pretention lies between 0.02 and 0.1 N/m. In contrast, bilayer MoS₂ has a 2D modulus of 260 ± 70 N/m, corresponding to a lower 3D modulus of 200 ± 60 GPa, which is attributed to defects or interlayer sliding. ⁶⁷ On the other hand, Castellanos-Gomez et al. studied the elastic properties of suspended, thick MoS₂ sheets with 5–25 layers. ⁶⁸ In their work, the bending rigidity has to be considered and one more linear term, $\left[ {{{4\pi {{\rm{E}}^{2{\rm{D}}}}} \over {3(1 - {\upsilon ^2})}} \cdot {{{t^2}} \over {{r^2}}}} \right]\delta$ , needs to be added into Eq. (1), where t and r are the thickness and the radius of membrane, respectively. Despite this additional term, the modulus and the pretension can be similarly derived by fitting to the experimental force–displacement curves. They obtained a mean Young's modulus of 330 ± 70 GPa, and a pretention of 0.13 ± 0.10 N/m. ⁶⁸ Both values are higher than the results obtained by Bertolazzi et al., ⁶⁷ and both modulus values obtained by these two groups are higher than bulk MoS₂ (∼240 GPa). ⁶⁹

A similar question to that in graphene appears here in 2D TMDs, that is, whether CVD samples have similar mechanical properties as exfoliated samples. CVD is a widely applied method to grow large-area materials in cost-effective ways. But CVD samples are usually more defective compared to single crystals. So far, people have developed CVD methods to synthesize large-area, ^70,71,72,73 or even wafer-scale, ⁷⁴ 2D TMDs such as MoS₂. The as-grown samples consist of isolated triangles of monolayer crystals at positions on the substrate slightly far away from the precursors, and merged continuous film closer to the precursors [Figs. 5(a)–5(c)]. Liu et al. transferred CVD MoS₂ and WS₂ with a similar PDMS stamping process onto holey substrates [Figs. 5(d) and 5(f)], ⁷⁵ as Lee et al. did in CVD graphene, ⁴⁷ to avoid ripples that complicated the measurements of mechanical properties. They also employ the AFM nanoindentation to probe the modulus of monolayer CVD MoS₂ and WS₂, finding values of 171 ± 11 (264 GPa) and 177 ± 12 N/m (272 GPa), respectively [Figs. 5(f) and 5(g)]. The nearly identical values between MoS₂ and WS₂ originate from their similar lattice constants and bonding energies. First-principles calculations predict a 2D modulus of 123 N/m for MoS₂ and 137 N/m for WS₂, both lower than experimental values, which is consistent with the fact that the used DFT-GGA calculation usually underestimates the bulk modulus of semiconductor materials. ⁷⁶ Note that Liu et al. only measure the membranes with a single grain, so the effect of grain boundaries is not probed here. All of the elastic moduli and break strengths for 2D materials ever measured are listed in Table I. The modulus of CVD MoS₂ (∼170 N/m) is only ∼5% lower than that of exfoliated MoS₂ (∼180 N/m), ⁶⁷ similar to the case in CVD graphene versus exfoliated graphene. It may imply that point defects in CVD samples do not significantly affect the mechanical properties of CVD samples. However, there is no simple way to quantify the defects in 2D TMDs, because unlike graphene, 2D TMDs have no defect-related Raman peaks. This leaves an interesting topic for quantifying the relationship between mechanical properties and defects density in 2D TMDs.

FIG. 5. Measurements of CVD MoS₂ and WS₂ monolayers: (a–c) as-grown CVD MoS₂ samples (a), consisting of isolated-triangle part (b) and continuous film (c), from Ref. 75; (d) AFM image of an entire triangle transferred onto a holey substrate, from Ref. 75; (e) AFM image of a suspended membrane over a hole, from Ref. 75; (f and g) histograms of E ^2D for MoS₂ and WS₂, and the corresponding Guassian distribution, from Ref. 75.

TABLE I. Elastic properties of 2D materials ever measured.

Note: “1L” and “ML” indicate monolayer and multilayer, respectively.

V. 2D VAN DER WAALS HETEROSTRUCTURES

Stacking a 2D sheet onto another by van der Waals interactions and forming a heterostructure may be the most promising advantage of 2D materials in electronic applications (Fig. 6). ⁶⁰ This provides a simple, controllable way to build up heterostructures with desired band alignments. ⁷⁷ Their great potentials in optoelectronics and multi-junction solar cells have aroused lots of studies in recent years. ^78,79,80,81 Interlayer coupling has been found to play a great role in the performance of 2D heterostructure-based devices, and has been investigated intensively from the electrical or optical perspective. ^{82,83,84,85,86} However, mechanical probing of the heterostructures is still lacking.

FIG. 6. Schematic of van der Waals heterostructures, from Ref. 60.

There are some ways to investigate the interlayer coupling from a mechanical point of view. It seems to be not so difficult in 2D homostructures, such as multilayer graphene or bulk graphite. Tan et al. measured the interlayer shear Raman modes in low energies in multilayer graphene. ⁸⁷ The corresponding Raman peaks shift from bilayer graphene (∼31 cm⁻¹) to bulk graphite (∼43 cm⁻¹), suggesting that the peaks are related to interlayer interaction. With a deeper analysis, the shear modulus across the layer–layer interface is derived to be 4.3 GPa in graphite. ⁸⁸ This indirect method could be also applied to 2D heterostructures. Koren et al. used an AFM to apply lateral shear force on predesigned highly oriented pyrolytic graphite (HOPG) patterns. ⁸⁹ This induces a shear gliding along a random single basal plane in the HOPG patterns, from which the lateral shear force and the friction force can be obtained. The interface adhesion energy is measured to be 0.227 ± 0.005 J/m², which is agreement with theoretical models. It is a direct method to quantify the interlayer interaction in 2D homostructures, but it is not very suitable to probe heterostructures, because thick 2D materials are required in their method but it is difficult to form thick heterostructures by stacking monolayers, and the basal plane where the shear gliding occurs is difficult to be well controlled at the hetero-interface.

Mechanically probing the interlayer interaction in 2D heterostructures is still a challenge. With a purpose of attempting to address this, Liu et al. probed the elastic modulus of 2D bilayer heterostructures by the well-established nanoindentation process, along with their measurements of 2D TMD monolayers. ⁷⁵ They found that the measured E ^2D of bilayer heterostructures are always lower than the sum of E ^2D of each layer, implying an interlayer sliding that depends on the interlayer interaction [Fig. 7(a)]. In their experiments, the bilayer is suspended over a circular hole. The bottom layer in direct contact with the substrate is firmly clamped onto the substrate. In the extreme case of a very strong interlayer interaction, there is no interlayer sliding allowed, such that both layers contribute to the 2D modulus measured. In the opposite extreme, however, when the top layer is completely free to slide against the bottom layer, the measured modulus of the bilayer is solely given by the bottom layer that is clamped onto the substrate. With these considerations, they describe the measured modulus of a 2D bilayer with a phenomenological equation, $E_{\rm{t}}^{{\rm{2D}}} = E_{{\rm{bot}}}^{{\rm{2D}}} + \alpha \cdot E_{{\rm{top}}}^{2{\rm{D}}}$ , where $E_{\rm{t}}^{2{\rm{D}}}$ , $E_{{\rm{bot}}}^{2{\rm{D}}}$ , and $E_{{\rm{top}}}^{2{\rm{D}}}$ are the 2D modulus of the bilayer, the bottom layer, and the top layer, respectively. α is named “interaction coefficient,” which ranges from 0 to 1, qualitatively gauging the strength of the interlayer interaction. From their measurements, α is 0.80 in MoS₂/WS₂ heterostructure, comparable to 0.75 in MoS₂/MoS₂ bilayer, but it is only 0.69 in MoS₂/graphene heterostructure [Fig. 7(b)]. Although this method is not able to directly quantify the interlayer interaction, it provides a relatively simple way to explore the interlayer interaction in 2D heterostructures. Further investigation of α may be useful for extracting more intrinsic physical parameters, such as adhesion energy and friction coefficient, in bilayer heterostructures.

FIG. 7. Elastic properties of 2D heterostructures: (a) measured E ^2D and pretensions of various 2D monolayers and heterostructures, from Ref. 75; (b) defined interaction coefficients for different types of bilayers, from Ref. 75.

VI. RESONATORS BASED ON GRAPHENE AND MoS₂

2D materials are ultrathin and atomically flat, providing perfect candidates for planar nanoscale mechanical devices. Resonator is an electromechanical device that vibrates in response to an external applied force. ⁹⁰ As their resonant vibrations are sensitive to external environment, resonators can be used as sensors for mass, force, and charge, etc. The first prototype of graphene resonator was developed by Bunch et al. at Cornell University. ⁹¹ They mechanically exfoliated graphene nanosheets on predefined trenches that are etched into a SiO₂ surface. The resultant resonators are a doubly clamped, ultrathin, and microscale ribbon-like device [Fig. 8(a)]. These resonators are actuated by an electrical modulation that is realized by a time-varying radio frequency (rf) voltage on top of a constant voltage, or an optical modulation by using a modulated, focused diode laser at frequency f. The vibration of the resonators is monitored by the reflected light intensity from another laser beam with a photodiode. Multiple resonances are observed in graphene resonators, but the most prominent one at the lowest frequency is attributed to the fundamental vibrational mode, f ₀, which is related to the tension T and determined by ⁹¹

(3) $${f_0} = {\left\{ {{{\left[ {A{{\left( {{E \mathord{\left/ {\vphantom {E \rho }} \right. \kern-\nulldelimiterspace} \rho }} \right)}^{1/2}}{t \mathord{\left/ {\vphantom {t {{L^2}}}} \right. \kern-\nulldelimiterspace} {{L^2}}}} \right]}^2} + {{{A^2}0.57T} \mathord{\left/ {\vphantom {{{A^2}0.57T} {\rho {L^2}wt}}} \right. \kern-\nulldelimiterspace} {\rho {L^2}wt}}} \right\}^{1/2}}\quad ,$$

where A is the clamping coefficient (1.03 for doubly clamped ribbons and 0.162 for cantilevers), E is the Young's modulus, ρ is the mass density, t, w, and L are the thickness, width, and length of the ribbon. When the tension T is small, the second term in Eq. (3) can be ignored and f ₀ scales with t/L ². Their results show that f ₀ varies from 1 to 170 MHz, and the quality factor Q from 20 to 850 [Fig. 8(b)]. All of the data are plotted in Fig. 8(c), where the solid line corresponds to E = 1 TPa, and dashed lines to the estimated lowest modulus (0.5 TPa) and the highest (2 TPa). For the resonators with t > 7 nm, almost all data points lie between the two dashed lines, giving the resonators with the highest modulus to date. For the resonators with t < 7 nm, however, most of their resonant frequency are higher than predicted, which indicates that the tension is not negligible in this case. ⁹¹

FIG. 8. Graphene-based resonators: (a) schematic of a graphene resonator, from Ref. 91; (b) frequency response of a graphene resonator, with a Lorentzian fit, from Ref. 91; (c) scaling the frequency with t/L ², from Ref. 91; (d) large-area rGO film transferred on a pre-patterned substrate; rGO resonators are created by a similar transfer process, from Ref. 92; (e) frequency response of a rGO resonator, from Ref. 92; (f) experimental resonance frequencies at different film thicknesses and tensions, as well as theoretical values plotted for flat circular membranes with two different moduli, from Ref. 92.

Ultrahigh Young's modulus, extremely low mass, and large surface area make graphene resonators an ideal candidate for ultrasensitive sensors. Chen et al. developed an all-electrical, high-frequency mixing method for the actuation and detection of graphene resonances as mass sensors. ⁹³ In their method, an rf gate voltage δV _g ^f at a frequency of f is applied on top of a dc gate voltage V _g to drive the motion, and another rf voltage with a small offset frequency f + Δf is applied to the source. The mixed-down current I^Δf at the frequency difference Δf is measured to detect the motion because the conductance of monolayer graphene is gate responsive. Their devices also work in the megahertz range. They found that the interactions between adsorbates and the graphene sheet must be considered because adsorbates impart tension to the graphene. As a mass sensor, their best sample shows a sensitivity of ∼2 zg. The quality factor of the graphene resonator increases with lowering temperature, reaching 14,000 at 5 K, in contrast to a value of 125 at room temperature.

Although resonators based on exfoliated graphene are suitable for fundamental studies, large-area devices are much desired in realistic applications. Robinson et al. fabricated wafer-scale, few-monolayer reduced graphene oxide (rGO) films and then assembled them to mechanical resonators [Fig. 8(d)]. ^92,94 They utilized a well-established technique of laser interferometry to detect the resonance. The resonant frequencies of their devices lie in the megahertz range, and their modulus is moderately high (∼185 GPa), but their quality factors and figures of merit (f × Q) can reach up to 4000 and more than 10¹¹ Hz at room temperature [Fig. 8(e)], ⁹² which are much higher than the values of pure graphene resonators aforementioned. The experimental resonance frequencies are much higher than the theoretical values of relaxed films, suggesting considerable tensions that contribute to the high Q values [Fig. 8(f)]. This work not only opens up a way to produce large-area, high Young's modulus, low-density mechanical devices based on rGO films, but also reveals the importance of imposed tension for the Q factor of graphene resonators. The reason for the low Q factors in graphene resonators has been heavily debated. As the Q factor strongly depends on temperature, ⁹³ tension, ⁹² and damping, ⁹⁵ it implies that thermal fluctuation out of the plane in such atomically thin material might play a role. However, more experiments and simulations are needed for a full understanding, leaving an interesting topic in this research field.

Besides graphene, other 2D materials can also be adopted as the working component of mechanical resonators. MoS₂ is good candidate for this purpose because it is the mostly studied 2D TMDs with excellent mechanical properties. As discussed above, monolayer or thin-layer MoS₂ has a Young's modulus of 270–330 GPa, which reaches almost 1/3 of the value of graphene. ^67,68,75 Lee et al. reported multilayer MoS₂-based nanomechanical resonators with a minimum thickness of 6 nm (9 layers). ⁹⁶ Their devices exhibit a fundamental resonance frequency f ∼60 MHz and a figure of merit f × Q ∼2 × 10¹⁰ Hz, both are actually lower than graphene resonators. Castellanos-Gomez et al. studied the monolayer MoS₂ mechanical resonator. ⁹⁷ They report a similar range of values, f ranging from 10 to 30 MHz and quality factor being ∼55 at room temperature. The mechanics is found to be tension dominated for monolayer MoS₂ resonators, but bending rigidity dominated for multilayer MoS₂ devices, a similar conclusion drawn in graphene devices. As 2D TMDs has an intrinsic direct band gap that is tunable by strain, these findings on MoS₂ may illuminate novel devices that combine nanomechanical and optoelectronic properties of 2D TMDs.

VII. SUMMARY

We have summarized recent progresses on the studies of mechanical properties of 2D materials, 2D heterostructures, and their applications as a particular type of mechanical devices, resonators. We have also discussed the effect of defects on mechanical properties of graphene. Together with electrical, optical, and thermal properties, mechanical properties are among the most important and interesting properties of 2D materials. Graphene has been proven to be the strongest 2D material in nature. Other 2D materials, such as MoS₂, also have competent mechanical properties compared to conventional materials such as steel. Their large surface area, high Young's modulus, and extremely low mass have yielded high-performance resonators that are ideal for ultrasensitive mass, force, and charge sensors. The mechanical probing of 2D heterostructures provides valuable information for understanding the effect of interlayer interactions. The progresses are remarkable in both measurements and applications. However, there are still open questions and challenges remaining in this research field.

Although more and more types of 2D monolayers are explored, their mechanical properties are relatively less explored, lagging behind studies of their electrical, optical, or even thermal properties. So far, mechanical properties are only investigated for several 2D monolayers including graphene, MoS₂, and WS₂, and the atlas of mechanics has much empty phase space for a wide range of 2D materials. Filling-up of the atlas is technically feasible, and it is particularly important for the future design of flexible devices based on various 2D materials. Especially, investigation of the anisotropic mechanical properties of 2D materials with asymmetric in-plane lattices, such as black phosphorous, ⁹⁸ is much more challenging but will be very interesting. In 2D vertical heterostructures, interlayer interaction still needs to be quantified and understood. On the other hand, 2D planar heterostructures with a single atomic layer composed of two distinct materials attract much attention, but mechanical properties of these planar heterostructures are still unexplored. These topics will be particularly significant if the mechanical interactions in 2D heterostructures can be related to their electrical or optical properties.

Quantification of the relationship between defects and mechanical properties of 2D TMDs is also a question remained to be better answered. As 2D TMDs do not consist of a single type of atoms like graphene, the types of defects as well as their effects on mechanical properties of 2D TMDs would be more complicated. Unraveling these effects may yield lots of novel phenomena and enrich the understanding of defects in 2D TMDs. Particularly in 2D heterostructures, defects may enhance or weaken the interlayer interaction, and as a result, modulate the mechanical properties as well electrical, optical, and thermal properties of the system. These modulations provide new insights to the interlayer coupling, and will shed light on defect engineering of 2D heterostructures in general.