Hostname: page-component-6587cd75c8-gglxz Total loading time: 0.001 Render date: 2025-04-23T15:15:28.955Z Has data issue: false hasContentIssue false
  • English
  • Français

On the dimension of stationary measures for random piecewise affine interval homeomorphisms

Part of: Low-dimensional dynamical systems Random dynamical systems

Published online by Cambridge University Press:  04 August 2023

KRZYSZTOF BARAŃSKI  and
ADAM ŚPIEWAK Open the ORCID record for ADAM ŚPIEWAK [Opens in a new window]
KRZYSZTOF BARAŃSKI*
Affiliation:
Institute of Mathematics, University of Warsaw, ul. Banacha 2, 02-097 Warszawa, Poland
ADAM ŚPIEWAK
Affiliation:
Department of Mathematics, Bar-Ilan University, Ramat-Gan 5290002, Israel Institute of Mathematics, Polish Academy of Sciences, ul. Śniadeckich 8, 00-656 Warszawa, Poland (e-mail: [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study stationary measures for iterated function systems (considered as random dynamical systems) consisting of two piecewise affine interval homeomorphisms, called Alsedà–Misiurewicz (AM) systems. We prove that for an open set of parameters, the unique non-atomic stationary measure for an AM system has Hausdorff dimension strictly smaller than 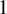$1$. In particular, we obtain singularity of these measures, answering partially a question of Alsedà and Misiurewicz [Random interval homeomorphisms. Publ. Mat. 58(suppl.) (2014), 15–36].

Keywords

random systemstationary measureinterval homeomorphism

MSC classification

Primary: 37E05: Maps of the interval (piecewise continuous, continuous, smooth)
Secondary: 37E10: Maps of the circle 37H10: Generation, random and stochastic difference and differential equations 37H15: Multiplicative ergodic theory, Lyapunov exponents
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 44 , Issue 6 , June 2024 , pp. 1473 - 1488
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alsedà, L. and Misiurewicz, M.. Random interval homeomorphisms. Publ. Mat. 58(suppl.) (2014), 15–36.10.5565/PUBLMAT_Extra14_01CrossRefGoogle Scholar
Barański, K. and Śpiewak, A.. Singular stationary measures for random piecewise affine interval homeomorphisms. J. Dynam. Differential Equations 33(1) (2021), 345–393.10.1007/s10884-019-09807-5CrossRefGoogle Scholar
Bradík, J. and Roth, S.. Typical behaviour of random interval homeomorphisms. Qual. Theory Dyn. Syst. 20(3) (2021), Paper no. 73, 20 pp.10.1007/s12346-021-00509-2CrossRefGoogle Scholar
Czernous, W.. Generic invariant measures for minimal iterated function systems of homeomorphisms of the circle. Ann. Polon. Math. 124(1) (2020), 33–46.10.4064/ap180518-12-4CrossRefGoogle Scholar
Czernous, W. and Szarek, T.. Generic invariant measures for iterated systems of interval homeomorphisms. Arch. Math. (Basel) 114(4) (2020), 445–455.10.1007/s00013-019-01405-7CrossRefGoogle Scholar
Czudek, K.. Alsedà–Misiurewicz systems with place-dependent probabilities. Nonlinearity 33(11) (2020), 6221–6243.10.1088/1361-6544/aba094CrossRefGoogle Scholar
Czudek, K. and Szarek, T.. Ergodicity and central limit theorem for random interval homeomorphisms. Israel J. Math. 239(1) (2020), 75–98.10.1007/s11856-020-2046-4CrossRefGoogle Scholar
Czudek, K., Szarek, T. and Wojewódka-Ścia̧żko, H.. The law of the iterated logarithm for random interval homeomorphisms. Israel J. Math. 246(1) (2021), 47–53.10.1007/s11856-021-2235-9CrossRefGoogle Scholar
Feller, W.. An Introduction to Probability Theory and Its Applications. Volume II, 2nd edn. John Wiley & Sons, Inc., New York–London–Sydney, 1971.Google Scholar
Gelfert, K. and Stenflo, Ö.. Random iterations of homeomorphisms on the circle. Mod. Stoch. Theory Appl. 4(3) (2017), 253–271.10.15559/17-VMSTA86CrossRefGoogle Scholar
Gharaei, M. and Homburg, A. J.. Skew products of interval maps over subshifts. J. Difference Equ. Appl. 22(7) (2016), 941–958.10.1080/10236198.2016.1164146CrossRefGoogle Scholar
Gharaei, M. and Homburg, A. J.. Random interval diffeomorphisms. Discrete Contin. Dyn. Syst. Ser. S 10(2) (2017), 241–272.Google Scholar
Ghys, É.. Groups acting on the circle. Enseign. Math. (2) 47(3–4) (2001), 329–407.Google Scholar
Hoeffding, W.. Probability inequalities for sums of bounded random variables. J. Amer. Statist. Assoc. 58 (1963), 13–30.10.1080/01621459.1963.10500830CrossRefGoogle Scholar
Jaroszewska, J. and Rams, M.. On the Hausdorff dimension of invariant measures of weakly contracting on average measurable IFS. J. Stat. Phys. 132(5) (2008), 907–919.10.1007/s10955-008-9566-3CrossRefGoogle Scholar
Łuczyńska, G.. Unique ergodicity for function systems on the circle. Statist. Probab. Lett. 173 (2021), Paper no. 109084, 7 pp.10.1016/j.spl.2021.109084CrossRefGoogle Scholar
Łuczyńska, G. and Szarek, T.. Limits theorems for random walks on Homeo $\left({S}^1\right)$ . J. Stat. Phys. 187(1) (2022), Paper no. 7, 13 pp.10.1007/s10955-022-02903-9CrossRefGoogle Scholar
Malicet, D.. Random walks on $\mathrm{Homeo}({S}^1)$ . Comm. Math. Phys. 356(3) (2017), 1083–1116.10.1007/s00220-017-2996-5CrossRefGoogle Scholar
Navas, A.. Groups of Circle Diffeomorphisms (Chicago Lectures in Mathematics). University of Chicago Press, Chicago, IL, 2011.10.7208/chicago/9780226569505.001.0001CrossRefGoogle Scholar
Navas, A.. Group actions on 1-manifolds: a list of very concrete open questions. Proceedings of the International Congress of Mathematicians—Rio de Janeiro 2018. Volume III. Invited Lectures. Eds. B. Sirakov, P. Ney de Souza and M. Viana. World Scientific Publishing, Hackensack, NJ, 2018, pp. 2035–2062.Google Scholar
Petersen, K.. Ergodic Theory (Cambridge Studies in Advanced Mathematics, 2). Cambridge University Press, Cambridge, 1983.10.1017/CBO9780511608728CrossRefGoogle Scholar
Prokaj, R. D. and Simon, K.. Piecewise linear iterated function systems on the line of overlapping construction. Nonlinearity 35(1) (2022), 245–277.10.1088/1361-6544/ac355eCrossRefGoogle Scholar
Szarek, T. and Zdunik, A.. Stability of iterated function systems on the circle. Bull. Lond. Math. Soc. 48(2) (2016), 365–378.10.1112/blms/bdw013CrossRefGoogle Scholar
Szarek, T. and Zdunik, A.. The central limit theorem for iterated function systems on the circle. Mosc. Math. J. 21(1) (2021), 175–190.10.17323/1609-4514-2021-21-1-175-190CrossRefGoogle Scholar
Toyokawa, H.. On the existence of a $\sigma$ -finite acim for a random iteration of intermittent Markov maps with uniformly contractive part. Stoch. Dyn. 21(3) (2021), Paper no. 2140003, 14 pp.10.1142/S0219493721400037CrossRefGoogle Scholar