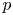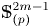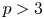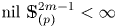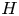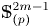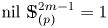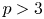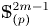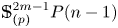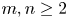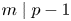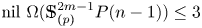Homotopy nilpotency of localized spheres and projective spaces

Abstract

For the $p$-localized sphere $\mathbb {S}^{2m-1}_{(p)}$ with $p >3$ a prime, we prove that the homotopy nilpotency satisfies $\mbox {nil}\ \mathbb {S}^{2m-1}_{(p)}<\infty$, with respect to any homotopy associative $H$-structure on $\mathbb {S}^{2m-1}_{(p)}$. We also prove that $\mbox {nil}\ \mathbb {S}^{2m-1}_{(p)}= 1$ for all but a finite number of primes $p >3$. Then, for the loop space of the associated $\mathbb {S}^{2m-1}_{(p)}$-projective space $\mathbb {S}^{2m-1}_{(p)}P(n-1)$, with $m,n\ge 2$ and $m\mid p-1$, we derive that $\mbox {nil}\ \Omega (\mathbb {S}^{2m-1}_{(p)}P (n-1))\le 3$.

Introduction

The homotopy nilpotency classes $\mbox {nil}\ X$ of associative $H$-spaces $X$ has been extensively studied, as well as their homotopy commutativity. In particular, Hopkins [10] made great progress by giving (co)homological criteria for homotopy associative finite $H$-spaces to be homotopy nilpotent. For example, he showed that if a homotopy associative finite $H$-space has no torsion in the integral homology, then it is homotopy nilpotent. Later, Rao [15, 16] showed that the converse of the above criterion is true in the case of groups $Spin(m)$ and $SO(m)$ and a connected compact Lie group is homotopy nilpotent if and only if it has no torsion in homology. Eventually, Yagita [21] proved that, when $G$ is a compact, simply-connected Lie group, its $p$-localization $G_{(p)}$ is homotopy nilpotent if and only if it has no torsion in the integral homology.

Although many results on the homotopy nilpotency have been obtained, the homotopy nilpotency classes have been determined in very few cases. It is well known that for the loop space $\Omega (\mathbb {S}^{m})$ of the $m$-sphere $\mathbb {S}^{m}$, we have $\mbox {nil}\ \Omega (\mathbb {S}^{m})=1$ if and only if $m=1,3,7$ and

\[ \mbox{nil}\ \Omega(\mathbb{S}^{m}) = \left\{\begin{array}{@{}ll} 2 & \mbox{for odd}\; m\; \mbox{and}\;m\not=1,3,7 \;\mbox{or}\, m=2;\\ 3 &\mbox{for even} \;m\ge 4. \end{array}\right. \]

Next, write $\mathbb {K}P^{m}$ for the projective $m$-space for $\mathbb {K}=\mathbb {R},\,\mathbb {C}$, the field of reals or complex numbers and $\mathbb {H}$, the skew $\mathbb {R}$-algebra of quaternions. Then, the homotopy nilpotency of $\Omega (\mathbb {K}P^{m})$ has been first studied by Ganea [7], Snaith [17] and then their $p$-localization $\Omega ((\mathbb {K}P^{m})_{(p)})$ by Meier [12]. The homotopy nilpotency of the loop spaces of Grassmann and Stiefel manifolds and their $p$-localization have been extensively studied in [8].

Now, let $\mathbb {S}^{2m-1}_{(p)}$ be the $p$-localization of the sphere $\mathbb {S}^{2m-1}$ at a prime $p$. The paper grew out of our desire to develop techniques in calculating the homotopy nilpotency classes of $\mathbb {S}^{2m-1}_{(p)}$ with respect to any homotopy associative $H$-structure for $p>3$. Its main result is the explicit determination of the homotopy nilpotence class of a wide range of homotopy associative multiplications on localized spheres $\mathbb {S}^{2m-1}_{(p)}$.

We begin with general results useful in the rest of the paper. In particular, we make use of [10, Theorem 2.1] to conclude the following corollary.

Corollary 1.4 Let $X$ be a finite simply-connected $CW$-complex with torsion-free homology $H_\ast (X,\mathbb {Z})$. If the $p$-localization $X_{(p)}$ for a prime $p$ admits a homotopy associative $H$-structure then $\mbox {nil}\ X_{(p)}<\infty$.

Next, we consider the homotopy nilpotency of $\mathbb {S}^{2m-1}_{(p)}$ with respect to any homotopy associative $H$-structures and the loop space $\Omega (\mathbb {S}^{2m-1}_{(p)}P(n-1))$ of the associated $\mathbb {S}^{2m-1}_{(p)}$-projective space $\mathbb {S}^{2m-1}_{(p)}P(n-1)$ for $p> 3$. First, we make use of Corollary 1.4, to prove the homotopy nilpotency of $\mathbb {S}^{2m-1}_{(p)}$.

Theorem 1.5 If $m\ge 2$ and $p>3$ is a prime then

\[ \mbox{nil}\ \mathbb{S}^{2m-1}_{(p)}<\infty \]

with respect to any homotopy associative $H$-structure on $\mathbb {S}^{2m-1}_{(p)}$.

Furthermore, we show that $\mathbb {S}^{2m-1}_{(p)}$ is homotopy associative and commutative for all but a finite number of primes $p$.

Then, we apply Zabrodsky's result [22, Lemma 2.6.6] to show the homotopy nilpotency of $\Omega (\mathbb {S}^{2m-1}_{(p)}P(n-1))$ under some conditions.

Theorem 3.12 Let $m\ge 2$ and $p> 3$ be a prime.

1. (1) If $n\ge 2$ and $m\mid p-1$ then

   \[ \mbox{nil}\ \Omega (\mathbb{S}^{2m-1}_{(p)}P(n-1))\le \mbox{nil}\ \mathbb{S}^{2m-1}_{(p)}+1\le 3; \]

2. (2) if $j=s= 1$ and $m \nmid p-1$, or if we have $s\ge 1$, $j\le p$, $j$ odd, and $m \mid p-1$, then

   \[ \mbox{nil}\ \Omega(\mathbb{S}^{2m-1}_{(p)}P(jp^{s}-1))=1. \]

1. Prerequisites

All spaces and maps in this note are assumed to be connected, based and of the homotopy type of $CW$-complexes. We also do not distinguish notationally between a continuous map and its homotopy class. We write $\Omega (X)$ (respectively $E(X)$) for the loop (respectively suspension) space on a space $X$, $\simeq$ for the homotopy relation and $[Y,X]$ for the set of homotopy classes of maps $Y\to X$.

Given a space $X$, we use the customary notation $X\vee X$ and $X\wedge X$ for the wedge and the smash product of $X$, respectively.

Recall that an $H$-space is a pair $(X,\mu )$, where $X$ is a space and $\mu : X \times X \to X$ is a map such that the diagram

commutes up to homotopy, where $\nabla : X\vee X\to X$ is the codiagonal map.

We call $\mu$ a multiplication or an $H$-structure on $X$. Two examples of $H$-spaces come in mind: topological groups and the spaces $\Omega (X)$ of loops on $X$. In the sequel, we identify an $H$-space $(X,\mu )$ with the space $X$.

An $H$-space $X$ is called a group-like space if $X$ satisfies all the axioms of groups up to homotopy. Recall that a homotopy associative an $H$-space always has a homotopy inverse. More precisely, according to [22, Corollary 1.3.2] (see also [3, Proposition 8.4.4]), we have the following result.

Proposition 1.1 If $X$ is a homotopy associative $H$-space then $X$ is a group-like space.

If $X$ is a homotopy associative $H$-space, then the functor $[ -, X]$ takes its values in the category of groups. One may then ask when this functor takes its values in various subcategories of groups.

For example, $X$ is homotopy commutative if and only if $[Y, X]$ is abelian for all $Y$.

For an integer $n\ge 1$, let $X^{\times n}$ and $X^{\wedge n}$ be the $n$-fold Cartesian and smash power of $X$, respectively. Write $q_{X,n} : X^{\times n}\to X^{\wedge n}$ for the quotient map. Given a group-like space $X$, we write $\gamma _{X,1}=\mbox {id}_X : X \to X$ and $\gamma _{X,2} : X \times X \to X$ for the commutator map of $X$. Since the restriction ${\gamma _{X,2}}_{\mid X\vee X}\simeq \ast$, we get a map $\bar {\gamma }_{X,2} : X \wedge X \to X$ with $\bar {\gamma }_{X,2}q_{X,2}\simeq \gamma _{X,2}$. Next, define inductively the maps

\[ \gamma_{X,n+1} : X^{{\times}(n+1)}\to X\quad \mbox{and}\quad \bar{\gamma}_{X,n+1} : X^{{\wedge}(n+1)}\to X \]

by $\gamma _{X,n+1}=\gamma _{X,2}\circ (\gamma _{X,1} \times \gamma _{X,n})$ and $\bar {\gamma }_{X,n+1}=\bar {\gamma }_{X,2}\circ (\gamma _{X,1} \wedge \bar {\gamma }_{X,n})$ for $n\ge 2$, respectively. Then, the diagram

commutes up to homotopy for $n\ge 2$.

One might ask if there is an upper bound for the nilpotency class of $[Y, X]$ that is independent of $Y$. The homotopy nilpotency class of $X$ defined by Berstein–Ganea [5] is the least $n$ such that $\gamma _{X,n+1}\simeq \ast$ and $\gamma _{X,n}\not \simeq \ast$. Equivalently, the homotopy nilpotency class of $X$ is the least $n$ such that $\bar {\gamma }_{X,n+1}\simeq \ast$ and $\bar {\gamma }_{X,n}\not \simeq \ast$. In this case, we write $\mbox {nil}\ X =n$ and call the homotopy associative $H$-space $X$ homotopy nilpotent. If no such integer exists, we put $\mbox {nil}\ X=\infty$.

Note that $\mbox {nil}\ X=1$ if and only if $X$ is homotopy commutative. Given a space $X$, the number $\mbox {nil}\ \Omega (X)$ (if any) is called the homotopy nilpotency class of $X$.

Now, let $MU$ be the complex Thom spectrum, $BP^{\ast }(-)$ the Brown–Peterson cohomology with coefficients $BP^{\ast } = \mathbb {Z}_{(p)}[v_1,\ldots ]$ and $K(n)$ the $n$th Morava $K$-theory at a prime $p$. Thus, $K(n)_\ast (pt) = \mathbb {Z}/p[v_n, v_n^{-1}]$ with $|v_n|=2p^{n}-2$. Hopkins [10] described a cohomological criteria for the homotopy nilpotence of finite connected associative $H$-spaces.

We recall Rao's formulation [15, Theorem 0.2] of Hopkins’ result [10, Theorem 2.1] needed in the sequel.

Theorem 1.2 Let $X$ be a finite homotopy associative $H$-space. Then the following conditions are equivalent:

1. (1) $X$ is homotopy nilpotent;

2. (2) $\widetilde {MU}^{\ast }(\bar {\gamma }_{X,n}) = 0$ for sufficiently large $n$;

3. (3) for every prime $p$, $\widetilde {BP}^{\ast } (\bar {\gamma }_{X,n})= 0$ for sufficiently large $n$;

4. (4) for every prime $p$ and positive integer m, $K(m)_\ast (\bar {\gamma }_{X,n})= 0$ for sufficiently large $n$.

Then, in [10, Corollary 2.2], it was deduced the following homological criterion for the homotopy nilpotency.

Corollary 1.3 If $X$ is a finite associative $H$-space and the integral homology $H_\ast (X,\mathbb {Z})$ is torsion free then $X$ is homotopy nilpotent.

Furthermore, we derive the following result the proof of which is essentially a small modification of Hopkins’ argument [10, Corollary 2.2].

Corollary 1.4 Let $X$ be a finite simply-connected $CW$-complex with torsion free homology $H_\ast (X,\mathbb {Z})$. If the $p$-localization $X_{(p)}$ for a prime $p$ admits a homotopy associative $H$-structure then $\mbox {nil}\ X_{(p)}<\infty$.

Proof. Note that $H\mathbb {Q}^{\ast }(\bar {\gamma }_n) = 0$ for the field of rationals $\mathbb {Q}$ sufficiently large $n$ since $X_{(p)}^{\wedge n}$ is at least $(n-1)$-connected. By assumption, the canonical map $MU^{\ast }(X_{(p)}^{\wedge n})\to MU^{\ast }(X_{(p)}^{\wedge n})\otimes \mathbb {Q}$ is injective, so by Theorem 1.2, it suffices to show that $MU^{\ast }(\bar {\gamma }_n)\otimes \mathbb {Q}=0$. But, for a finite $CW$-complex $X$, there is a natural isomorphism

\begin{align*} MU^{{\ast}}(X^{{\wedge} n}_{(p)})\otimes\mathbb{Q}&\approx MU^{{\ast}}(X^{{\wedge} n})\otimes\mathbb{Q}\approx MU^{{\ast}}(\mbox{pt})\otimes H\mathbb{Q}^{{\ast}}(X^{{\wedge} n})\\ &\approx MU^{{\ast}}(\mbox{pt})\otimes H\mathbb{Q}^{{\ast}}(X^{{\wedge} n}_{(p)}), \end{align*}

so the map $MU^{\ast }(\bar {\gamma }_n)\otimes \mathbb {Q}= 0$ as soon as $H\mathbb {Q}^{\ast }(\bar {\gamma }_n)=0$. This completes the proof.

Since the homology $H_\ast (\mathbb {S}^{2m-1},\mathbb {Z})$ are torsion free and $\mathbb {S}^{2m-1}$ is a finite $CW$-complex, Corollary 1.4 yields the result on the homotopy nilpotency of $\mathbb {S}^{2m-1}_{(p)}$.

Theorem 1.5 If $m\ge 2$ and $p>3$ is a prime then

\[ \mbox{nil}\ \mathbb{S}^{2m-1}_{(p)}<\infty \]

with respect to any homotopy associative $H$-structure on $\mathbb {S}^{2m-1}_{(p)}$.

In the sequel, we make use of the following. Let $f: X\to Y$ be an $H$-map of homotopy associative $H$-spaces. Recall from [22, Chapter II] that:

1. (1) it is said $\mbox {nil}\ f \le n$ if $f\bar {\gamma }_{X,n}\simeq \ast$;

2. (2) $f$ is called central if $\bar {\gamma }_{Y,2}(f \wedge \mbox {id}_Y)\simeq \ast$.

Notice that $\mbox {nil}\ f\le \min \{\mbox {nil}\ X,\mbox {nil}\ Y\}$.

Then, in view of [22, Lemma 2.6.6], we have the following techniques for the study of the homotopy nilpotency.

Proposition 1.6 Let $F\stackrel {i}{\to } E\stackrel {q}{\to } B$ be an $H$-fibration, i.e., $F\stackrel {i}{\to }E\stackrel {q}{\to }B$ is a fibration, $F,E$ and $B$ are $H$-spaces and the maps $i : F\to E$, and $q : E\to B$ are $H$-maps.

1. (1) If $\mbox {nil}\ q \le n$ and $i : F\to E$ is central then $\mbox {nil}\ E \le n+1$;

2. (2) if $\Omega (Y)\stackrel {i}{\to } E\stackrel {q}{\to } X$ is the induced $H$-fibration by an $H$-map $f : X\to Y$ then the map $i : \Omega (Y)\to E$ is central.

2. $A_m$-spaces

Recall that by Stasheff [18], an $A_m$-structure on a space $X$ consists on $m$-tuples

such that ${\frak q}_{n\ast } : \pi _k(\mathcal{E}_n(X),X)\to \pi _k(\mathcal {B}_n({X}))$ is an isomorphism for all $k\ge 1$, together with a contracting homotopy $h: C\mathcal {E}_{n-1}(X)\to \mathcal {E}_n(X)$ such that $h(C\mathcal {E}_{n-1}(X))\subseteq \mathcal {E}_n(X)$ for $n=2,\ldots ,m$. For the purposes of homotopy theory, in the light of [18, Proposition 2], we can think of $X\to \mathcal {E}_n(X)\stackrel {\frak {q}_n}{\to }\mathcal {B}_n(X)$, as a fibration.

An $A_m$-space for $m=0,1\ldots ,\infty$ is a space $X$ with a multiplication $\mu : X\times X\to X$ that is associative up to higher homotopies involving up to $n$ variables. Further, an $A_\infty$-space has all coherent higher associativity homotopies and is equivalent to a loop space $\Omega (Y)$ for a space $Y$ called the classifying space of $X$.

By [18, Theorem 5], classes of spaces with $A_m$-structures and $A_m$-spaces coincide.

Proposition 2.1 A space $X$ admits an $A_m$-structure if and only if $X$ is an $A_m$-space.

The $X$-projective $n$-space $XP(n)$ for $n\le m$, associated with an $A_m$-space X is the base space $\mathcal {B}_{n+1}(X)$ of the derived $A_m$-structure. The space $\mathcal {B}_1(X)$ is a point and $\mathcal {B}_2(X)$ can be recognized as the suspension $E(X)$. Notice that $\mathcal {B}_{m+1}(X)$ can be defined even when $\frak {p}_{m+1}$ cannot; it has the homotopy type of the mapping cone $C\mathcal {E}_m(X)\cup _{\frak {q}_m} \mathcal {B}_m(X)$. By means of [18, Theorem 11, Theorem 12], the spaces $\mathcal {E}_n(X)$ and $\mathcal {B}_{n+1}(X)$ have the homotopy types of the $n$th join $X^{\ast ^{n}}$ and $C\mathcal {E}_n(X)\cup _{\frak {p}_n} \mathcal {B}_n(X)$ for $n\le m$, respectively provided $X$ is path-connected. Because of a homotopy equivalence $X^{\ast ^{n}}\simeq E^{n-1}(X^{\wedge n})$ for the $(n-1)$th suspension $E^{n-1}$, we deduce that the fibration $X\to \mathcal {E}_n(X)\stackrel {\frak {q}_n}{\to }\mathcal {B}_n(X)$ is homotopy equivalent to

(2.2)\begin{equation} X\to E^{n-1}X^{{\wedge} n}\stackrel{q_n}{\longrightarrow} XP(n-1). \end{equation}

3. Localized spheres $\mathbb {S}^{2m-1}_{(p)}$ and $\mathbb {S}^{2m-1}_{(p)}$-projective spaces $\mathbb {S}^{2m-1}_{(p)}P(n-1)$

Let $\mathbb {S}^{2m-1}_{(p)}$ be the $p$-localization of the sphere $\mathbb {S}^{2m-1}$ at a prime $p$. It is known by [11, Theorem 1.4] that $\mathbb {S}^{2m-1}_{(2)}$ does not admit a homotopy associative multiplication if $m\not =1,2$. The sole obstruction to putting an $H$-structure on $\mathbb {S}^{2m-1}$ is the Whitehead square $[\iota _{2m-1},\iota _{2m-1}]$ of a generator $\iota _{2m-1}\in \pi _{2m-1}(\mathbb {S}^{2m-1})$. Since the order of $[\iota _{2m-1},\iota _{2m-1}]$ is $\le 2$, it follows that, if $p$ is an odd prime, $\mathbb {S}^{2m-1}_{(p)}$ admits an $H$-space structure. Which $p$-localized spheres $\mathbb {S}^{2m-1}_{(p)}$ with $p>2$ have an $H$-structures or loop structures is known by Adams [1]. More precisely, in view of [2] (see also [14, Proposition 11.2.2]), we have the following $H$-structure on $\mathbb {S}_{(p)}^{2m-1}$.

Proposition 3.1 If $p$ is an odd prime and $n\ge 1$ then there is an $H$-structure $\mu _A$ on $\mathbb {S}_{(p)}^{2m-1}$ $($unique up to homotopy if $p$ is an odd prime and $n\ge 2$ or if $n \ge 1$ and $p>3)$ such that the double suspension $E^{2} : \mathbb {S}_{(p)}^{2m-1}\to \Omega ^{2}\mathbb {S}_{(p)}^{2m+1}$ is an $H$-map.

Further:

1. (1) if $p>2$ then $(\mathbb {S}^{2m-1}_{(p)},\mu _A)$ is a homotopy commutative $H$-space;

2. (2) if $p>3$ then $(\mathbb {S}^{2m-1}_{(p)},\mu _A)$ is a homotopy associative $H$-space.

Loosely speaking, via the double suspension map $E^{2} : \mathbb {S}_{(p)}^{2m-1}\to \Omega ^{2}(\mathbb {S}_{(p)}^{2m+1})$, the multiplication on the double loop space $\Omega ^{2}\mathbb {S}_{(p)}^{2m+1}$ restricts to the multiplication $\mu _A$ on the bottom cell $\mathbb {S}_{(p)}^{2m-1}$. Next, by Mimura et al. [13, Proposition 6.8], Stasheff [18] and Sullivan [19], we have the result on $H$-structures on $\mathbb {S}_{(p)}^{2m-1}$.

Proposition 3.2 Let $m\ge 2$ and $p>3$ be a prime. Then:

1. (1) the $p$-localized sphere $\mathbb {S}_{(p)}^{2m-1}$ admits an $A_{p-1}$-structure;

2. (2) if $\mathbb {S}_{(p)}^{2m-1}$ admits an $A_{p}$-structure then $m\mid p-1$;

3. (3) $\mathbb {S}_{(p)}^{2m-1}$ admits an $A_\infty$-structure if and only if $m\mid p-1$ provided $p>3$.

This implies that $\mathbb {S}^{2m-1}_{(p)}$ does not admit an $A_{p}$-structure provided $m\nmid p-1$. We also point out that an $A_{p-1}$-structure on $\mathbb {S}^{2m-1}_{(p)}$ is induced from $\Omega ^{2}(\mathbb {S}_{(p)}^{2m+1})$ which is of course an $A_\infty$-space, via the double suspension map $E^{2} : \mathbb {S}_{(p)}^{2m-1}\to \Omega ^{2}(\mathbb {S}_{(p)}^{2m+1})$. Further, in view of Proposition 3.2, the sphere $\mathbb {S}_{(p)}^{2m-1}$ admits an $A_{p}$-structure if and only if it admits a classifying space.

Now, we show the nilpotency of $\mathbb {S}^{2m-1}_{(p)}$ provided $m\mid p-1$.

Proposition 3.3 If $m\mid p-1$ then $\mbox {nil}\ \mathbb {S}^{2m-1}_{(p)}\le 2$ with respect to the $A_\infty$-structure on $\mathbb {S}^{2m-1}_{(p)}$.

Proof. Sullivan [19], to construct a classifying space for $\mathbb {S}_{(p)}^{2m-1}$ with $m\mid p-1$, considered the space $K(\mathbb {Z}_p, 2)$, where $\hat {\mathbb {Z}}_p$ is the $p$-adic integers and the cyclic subgroup $\Gamma <\mathbb {Z}_{p-1}<\hat {\mathbb {Z}}_p^{\ast }$ (the $p$-adic units) of order $m$. Then $\Gamma$ acts freely on a model of $K(\hat {\mathbb {Z}}_p,2)$ and $X = K(\hat {\mathbb {Z}}_p,2)/\Gamma$ has cohomology $H^{\ast }(X,\mathbb {Z}/p\mathbb {Z}) = S(x,2m)$, the graded symmetric algebra generated by $x$ with degree $|x|=2m$ and $\pi _1(X) = \Gamma$. After completing $X$ at $p$ to $\hat {X}_p$, we have a space with $\pi _1(\hat {X}_p) = 0$ and $H^{\ast }(\hat {X}_p, \mathbb {Z}/p\mathbb {Z}) = S(x,2m)$. The map $\mathbb {S}^{2m-1}\to \Omega (\hat {X}_p)$ defines a homotopy equivalence $\mathbb {S}^{2m-1}_{(p)}\stackrel {\simeq }{\to } \Omega (\hat {X}_p)$ and $\hat {X}_p$ is a classifying space for $\mathbb {S}_{(p)}^{2m-1}$.

But, by [14, Chapter 2], the $p$-completion preserves a fibration of simply-connected spaces. Hence, the $p$-completion of the fibration $\Gamma \to K(\hat {\mathbb {Z}}_p,2)\to X$ leads to the fibration $\hat {\Gamma }_p\to K(\hat {\mathbb {Z}}_p,2)\to \hat {X}_p$. Consequently, we get the $H$-fibration

\[ \Omega( K(\hat{\mathbb{Z}}_p,2))= K(\hat{\mathbb{Z}}_p,1)\longrightarrow \Omega(X)\longrightarrow \Gamma. \]

Since the space $X = K(\hat {\mathbb {Z}}_p,2)/\Gamma$ is simply-connected, we have $\widehat {(\Omega (X))}_p=\Omega (\hat {X}_p)$. Then, by means of the $p$-completeness of $K(\hat {\mathbb {Z}}_p,1)$, the $p$-completion of the fibration above yields the $H$-fibration

\[ K(\hat{\mathbb{Z}}_p,1)\longrightarrow \Omega(\hat{X}_p)\longrightarrow \hat{\Gamma}_p \]

determined by the canonical $H$-map $\hat {\Gamma }_p\to K(\hat {\mathbb {Z}}_p,2)$.

Thus, by means of Proposition 1.6(2), we derive that the $H$-map $\Omega ( K(\hat {\mathbb {Z}}_p,2))= K(\hat {\mathbb {Z}}_p,1)\to \Omega (X)$ is central and so Proposition 1.6(1) yields

\[ \mbox{nil}\ \mathbb{S}^{2m-1}_{(p)}\le 2. \]

This completes the proof.

Then, Arkowitz, Ewing and Schiffman [4, Theorem 0.1] have proved the following result on $H$-structures on $\mathbb {S}^{2m-1}_{(p)}$.

Theorem 3.4 Let $p$ be an odd prime and $n$ a positive integer with $m\mid p-1$.

1. (1) If $m< p-1$ then $\mathbb {S}^{2m-1}_{(p)}$ has a unique $H$-structure which is both homotopy commutative and a loop multiplication.

2. (2) If $m=p-1$ then $\mathbb {S}^{2m-1}_{(p)}$ has precisely $p$ multiplications; one homotopy commutative and not a loop multiplication, and $(p-1)$ loop $H$-structures which are $H$-equivalent but not homotopy commutative.

Thus, the above and Theorem 3.4(2) yield the conclusion.

Corollary 3.5 If $m\mid p-1$ and $p>3$ then

\[ \mbox{nil}\ \mathbb{S}^{2m-1}_{(p)}= 2 \]

with respect to all $(p-1)$ loop $H$-structures on $\mathbb {S}^{2m-1}_{(p)}$.

We point out that Proposition 3.3 has been already shown by Meier [12] in the special case when $m = p-1$ using the result [20, Theorem 13.4].

Theorem 3.6 Let $p$ be an odd prime.

\[ \pi_{2m-1+k}(\mathbb{S}^{2m-1)}_{(p)}) \approx\begin{cases} \mathbb{Z}/p\mathbb{Z}\ \text{for}\ k = 2i(p-1)-1,\quad i = 1,\ldots, p-1,\ m\ge 2;\\ \mathbb{Z}/p\mathbb{Z}\ \text{for}\ k = 2i(p-1)-2,\quad i=m,\ldots,p-1;\\ 0\ \text{ortherwise}\ \text{for}\ 1\le k< 2p(p-1)-2. \end{cases} \]

Given a pointed connected topological space $X$ and a prime $p$, write $\pi _m(X;p)$ for the $p$-primary component of its $m$th homotopy group $\pi _m(X)$ for $m\ge 1$. Recall that by [6], the set of homotopy classes of possible $H$-structures on $\mathbb {S}^{2m-1}_{(p)}$ is in one-to-one correspondence with $[\mathbb {S}^{2m-1}_{(p)}\wedge \mathbb {S}^{2m-1}_{(p)},\mathbb {S}^{2m-1}_{(p)}]=\pi _{4m-2}(\mathbb {S}^{2m-1},p)$. Consequently, if $p>3$ then we may study the homotopy nilpotency of $\mathbb {S}^{2m-1}_{(p)}$.

Nevertheless, in some particular cases, an estimation for $\mbox {nil}\ \mathbb {S}^{2m-1}_{(p)}$ might be stated. First, notice that Theorem 3.6 implies that

(3.7)\begin{equation} \pi_{2m-1+k}(\mathbb{S}^{2m-1}_{(p)})=0 \end{equation}

provided $k<2p(p-1)-2$, $k\not =2i(p-1)-1$ for $i = 1,\ldots , p-1$ and $k\not =2i(p-1)-2$ for $i = m,\ldots , p-1$.

Certainly, the homotopy group $\pi _{4m-2}(\mathbb {S}^{2m-1})$ is finite and write $\sharp \pi _{4m-2}(\mathbb {S}^{2m-1})$ for its order. Then, for $p_m=\max \{p;\, p \,\mbox {is a prime with}\ p\mid \sharp \pi _{4m-2}(\mathbb {S}^{2m-1})\}$, we apply Theorem 3.6 to state the result on an $H$-structure on $\mathbb {S}^{2m-1}_{(p)}$.

Proposition 3.8 Let $p>3$ and $m\ge 3$.

If $m< p-1$ or $p>\max \{3,p_m\}$ then $\mathbb {S}^{2m-1}_{(p)}$ admits a unique homotopy associative and commutative $H$-structure and $\mbox {nil}\ \mathbb {S}^{2m-1}_{(p)}=1$.

Proof. If $m< p-1$ then $2m-1<2p-3$ and Equation (3.7) implies that

\[ [(\mathbb{S}^{2m-1}_{(p)})^{{\wedge} 2},\mathbb{S}^{2m-1}_{(p)}]=\pi_{2(2m-1)}(\mathbb{S}^{2m-1}_{(p)})=0. \]

If $p>\max \{3,p_m\}$ then $\pi _{2(2m-1)}(\mathbb {S}^{2m-1}_{(p)})=0$ as well. Then, Proposition 3.1 provides an existence of a unique homotopy associative and commutative $H$-structure on $\mathbb {S}^{2m-1}_{(p)}$ and the proof follows.

Now, we apply the results above to $\mathbb {S}^{2m-1}_{(p)}$-projective spaces $\mathbb {S}^{2m-1}_{(p)}P(n-1)$. Write $J_k(\mathbb {S}^{2n})$ for the $k$th stage of the James construction on the sphere $\mathbb {S}^{2m}$.

Since $\mathbb {S}^{2m-1}_{(p)}P(1)\simeq \mathbb {S}^{2m}_{(p)}$ and $\mathbb {S}^{2m-1}_{(p)}P(n-1)\simeq C\mathbb {S}^{2(n-1)m-1}_{(p)} \cup _{q_{n-1}}\mathbb {S}^{2m-1}_{(p)}P(n-2)$ for the fibration (2.2)

\[ q_{n-1} : \mathbb{S}^{2(n-1)m-1}_{(p)}\to \mathbb{S}^{2m-1}_{(p)}P(n-2) \]

with $X=\mathbb {S}^{2m-1}_{(p)}$, we can define inductively a map

\[ \mathbb{S}^{2m-1}_{(p)}P(n-1)\longrightarrow J_{n-1}(\mathbb{S}^{2m}_{(p)}). \]

for $p>3$ provided $n-1< p$ with $m\nmid p-1$ or any $n\ge 1$ with $m\mid p-1$.

Furthermore, one can state the result on some $\mathbb {S}^{2m-1}_{(p)}P(n-1)$.

Proposition 3.9 The canonical map

\[ \mathbb{S}^{2m-1}_{(p)}P(n-1)\longrightarrow J_{n-1}(\mathbb{S}^{2m}_{(p)}) \]

is an integral homology isomorphism for $p>3$ provided $n-1< p$ with $m\nmid p-1$ or any $n\ge 1$ with $m\mid p-1$.

Consequently, by means of the Whitehead Theorem, we get a homotopy equivalence $\mathbb {S}^{2m-1}_{(p)}P(n-1)\stackrel {\simeq }{\longrightarrow }J_{n-1}(\mathbb {S}^{2m}_{(p)})$ which yields an $H$-homotopy equivalence

\[ \Omega(\mathbb{S}^{2m-1}_{(p)}P(n-1))\stackrel{\simeq}{\longrightarrow}\Omega(J_{n-1}(\mathbb{S}^{2m}_{(p)})) \]

for $p>3$ provided $n-1< p$ with $m\nmid p-1$ or any $n\ge 1$ with $m\mid p-1$. But, Gray showed [9, Theorem 1 and the footnote on p. 182] that $\Omega (J_{jp^{s}-1}(\mathbb {S}^{2m}))$ with $p\ge 3$ is universal in the category of homotopy associative commutative $H$-spaces, with its generating subspace being the $(2mp-2)$-skeleton provided $p\ge 3$ with $s>0$ and an odd $j\le p$. Hence, Proposition 3.9 yields the conclusion on the $H$-structure on $\Omega (\mathbb {S}^{2m-1}_{(p)}P(jp^{s}-1))$.

Corollary 3.10 If $p>3$ and $m\ge 2$ then the associative $H$-space $\Omega (\mathbb {S}^{2m-1}_{(p)}P(jp^{s}-1))$ is homotopy commutative provided $j=s=1$ and $m\nmid p-1$ or $s\ge 1$, $j\le p$ is odd and $m\mid p-1$.

For further studies of the homotopy nilpotency of $\Omega (\mathbb {S}^{2m-1}_{(p)}P(n-1))$, we need to show an existence of some $H$-fibration.

Lemma 3.11 If $p> 3$ is a prime, $m\ge 2$ and $m\mid p-1$ then for a fixed $A_\infty$-structure on $\mathbb {S}^{2m-1}_{(p)}$ and $n\ge 2$ then there is an $H$-fibration

\[ \Omega (\mathbb{S}^{2mn-1}_{(p)})\longrightarrow \Omega (\mathbb{S}^{2m-1}_{(p)}P(n-1))\longrightarrow\mathbb{S}^{2m-1}_{(p)} \]

with the central map $\Omega (\mathbb {S}^{2mn-1}_{(p)})\longrightarrow \Omega (\mathbb {S}^{2m-1}_{(p)}P(n-1))$.

Proof. Recall that by Proposition 3.2(3) the space $\mathbb {S}^{2m-1}_{(p)}$ admits an $A_\infty$-structure provided $m\mid p-1$. Furthermore, for such the space $\mathbb {S}^{2m-1}_{(p)}$, Sullivan [19] constructed a classifying space denoted in the proof of Proposition 3.3 by $\hat {X}_p$.

Next, write $i_n : \mathbb {S}^{2mn-1}_{(p)}\hookrightarrow \mathbb {S}^{2m-1}_{(p)}P(n-1)$ and $j_n : \mathbb {S}^{2m-1}_{(p)}P(n-1)\hookrightarrow \hat {X}_p$ for the canonical inclusion maps and notice that $E^{n-1}(\mathbb {S}^{2m-1}_{(p)})^{\wedge n}=\mathbb {S}^{2mn-1}_{(p)}$. Since $\Omega (\hat {X}_p)\simeq \mathbb {S}^{2m-1}_{(p)}$, we get the Puppe fibration sequence

\[ \cdots\to \Omega(\mathbb{S}^{2mn-1}_{(p)})\stackrel{\Omega(i_n)}{\longrightarrow}\Omega(\mathbb{S}^{2m-1}_{(p)}P(n-1)) \stackrel{\Omega(j_n)}{\longrightarrow}\mathbb{S}^{2m-1}_{(p)}\stackrel{\partial_n}{\to} \mathbb{S}^{2mn-1}_{(p)}\stackrel{i_n}{\hookrightarrow}\mathbb{S}^{2m-1}_{(p)}P(n-1)\stackrel{j_n}{\hookrightarrow}\hat{X}_p. \]

But, the $H$-deviation [22, Definition 1.4.1.] of $\partial _n$ is a map $\mathbb {S}^{2m-1}_{(p)}\wedge \mathbb {S}^{2m-1}_{(p)}\to \mathbb {S}^{2mn-1}_{(p)}$ which is null homotopic for dimension and connectivity reasons if $n\ge 2$. Then, by Zabrodsky [22, Proposition 1.5.1.], $\partial _n$ is an $H$-map. Hence, Proposition 1.6(2) implies that $\Omega (i_n) : \Omega (\mathbb {S}^{2mn-1}_{(p)})\to \Omega (\mathbb {S}^{2m-1}_{(p)}P(n-1))$ is central in the $H$-fibration

\[ \Omega(\mathbb{S}^{2mn-1}_{(p)})\stackrel{\Omega(i_n)}{\longrightarrow}\Omega(\mathbb{S}^{2m-1}_{(p)}P(n-1)) \stackrel{\Omega(j_n)}{\longrightarrow}\mathbb{S}^{2m-1}_{(p)} \]

and this completes the proof.

Thus, Propositions 1.6(1), 3.3, Corollary 3.10 and Lemma 3.11 yield the result on the homotopy nilpotency of $\Omega (\mathbb {S}^{2m-1}_{(p)}P(n-1))$ under some conditions.

Theorem 3.12 Let $m\ge 2$ and $p> 3$ be a prime.

1. (1) If $n\ge 2$ and $m\mid p-1$ then

   \[ \mbox{nil}\ \Omega (\mathbb{S}^{2m-1}_{(p)}P(n-1))\le \mbox{nil}\ \mathbb{S}^{2m-1}_{(p)}+1\le 3; \]

2. (2) if $j=s= 1$ and $m \nmid p-1$, or if we have $s\ge 1$, $j\le p$, $j$ odd, and $m \mid p-1$, then

   \[ \mbox{nil}\ \Omega(\mathbb{S}^{2m-1}_{(p)}P(jp^{s}-1))=1. \]

To conclude, we point out that Theorem 3.12 applies to more cases than Meier's result [12, Theorem 5.4].

We close the paper with the following conjecture.

Conjecture 3.13 If $p> 3$ is a prime and $m,n\ge 2$ then

\[ \mbox{nil}\ \Omega (\mathbb{S}^{2m-1}_{(p)}P(n-1))<\infty. \]