Hostname: page-component-55f67697df-2mk96 Total loading time: 0 Render date: 2025-05-09T06:47:43.285Z Has data issue: false hasContentIssue false
  • English
  • Français

COLORING EQUILATERAL TRIANGLES

Part of: Graph theory Set theory

Published online by Cambridge University Press:  07 April 2025

JINDŘICH ZAPLETAL Open the ORCID record for JINDŘICH ZAPLETAL [Opens in a new window]
JINDŘICH ZAPLETAL*
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF FLORIDA GAINESVILLE, FL, 32611 USA
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

It is consistent relative to an inaccessible cardinal that ZF+DC holds, the hypergraph of equilateral triangles on a given Euclidean space has countable chromatic number, while the hypergraph of isosceles triangles on 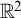$\mathbb {R}^2$ does not.

Keywords

geometric set theoryalgebraic hypergraphchromatic number

MSC classification

Primary: 03E35: Consistency and independence results 14P99: None of the above, but in this section 05C15: Coloring of graphs and hypergraphs
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 14
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bochnak, J., Coste, M., and Roy, M.-F., Real Algebraic Geometry , vol. 36, Springer Science & Business Media, New York, 2013.Google Scholar
Ceder, J., Finite subsets and countable decompositions of Euclidean spaces . Romanian Journal of Pure and Applied Mathematics , vol. 14 (1969), pp. 1247–1251.Google Scholar
Jech, T., Set Theory , Springer Verlag, New York, 2002.Google Scholar
Larson, P. and Zapletal, J., Geometric Set Theory , AMS Surveys and Monographs, American Mathematical Society, Providence, 2020.Google Scholar
Marker, D., Model Theory: An Introduction , Graduate Texts in Mathematics, 217, Springer Verlag, New York, 2002.Google Scholar
Schmerl, J. H., Triangle-free partitions of Euclidean space . Bulletin of the London Mathematical Society , vol. 26 (1994), pp. 483–486.Google Scholar
Schmerl, J. H., Countable partitions of Euclidean space . Mathematical Proceedings of the Cambridge Philosophical Society , vol. 120 (1996), pp. 7–12.Google Scholar
Schmerl, J. H., Avoidable algebraic subsets of Euclidean space . Transactions of the American Mathematical Society , vol. 352 (1999), pp. 2479–2489.Google Scholar
Zapletal, J., Coloring closed noetherian graphs . Journal of Mathematical Logic , vol. 24 (2024), no. 3, Paper No. 2350010, p. 21.Google Scholar
Zapletal, J., Coloring the distance graphs . European Journal of Mathematics , vol. 9 (2023), Paper No. 66, p. 16.Google Scholar
Zapletal, J., Triangles and Vitali sets, preprint, 2023. arXiv:2310.01759.Google Scholar