Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T15:16:54.443Z Has data issue: false hasContentIssue false
  • English
  • Français

The Fundamental Group of S1-manifolds

Published online by Cambridge University Press:  20 November 2018

Leonor Godinho  and
M. E. Sousa-Dias
Leonor Godinho*
Affiliation:
Departmento de Matem´atica, Instituto Superior T´ecnico, Lisbon, Portugal
*
[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We address the problem of computing the fundamental group of a symplectic 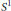${{S}^{1}}$-manifold for non-Hamiltonian actions on compact manifolds, and for Hamiltonian actions on non-compact manifolds with a proper moment map. We generalize known results for compact manifolds equipped with a Hamiltonian 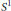${{S}^{1}}$-action. Several examples are presented to illustrate our main results.

Keywords

53D2037J1055Q05
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 62 , Issue 5 , 01 October 2010 , pp. 1082 - 1098
Copyright
Copyright © Canadian Mathematical Society 2010

Footnotes

Both authors were partially supported by FCT through program POCTI/FEDER; the first author was partially supported by FCT through grant POCTI/MAT/57888/2004 and by Fundação Calouste Gulbenkian

1

This generalized moment map is a special case of a Lie group-valued moment map (see [OR] and the references therein).

References

[A] Atiyah, M. F., Convexity and commuting Hamiltonians. Bull. London Math. Soc. 14(1982), no. 1, 1–15. doi:10.1112/blms/14.1.1Google Scholar
[Au] Audin, M., Torus actions on symplectic manifolds. Progress in Mathematics, 93, Birkhäuser Verlag, Basel, 2004.Google Scholar
[B] Bott, R., Nondegenerate critical manifolds. Ann. of Math. 60(1954), 248–261. doi:10.2307/1969631Google Scholar
[BHPV] Barth, W., Hulek, K., Peters, C., and Van de Ven, A., Compact complex surfaces. Results in Mathematics and Related Areas, 3rd Series, A Series of Modern Surveys in Mathematics, 4, Springer-Verlag, Berlin, 2004.Google Scholar
[BP] Brion, M. and Procesi, C., Action d’un tore dans une variété projective. In: Operator algebras, unitary representations, enveloping algebras, and invariant theory, Progress in Mathematics, 92, Birkhäuser, Boston, MA, 1990.Google Scholar
[CGKZ] Collins, D. J., Grigorchuk, R. I., Kurchanov, P. F., and Zieschang, H., Combinatorial group theory and applications to geometry. Reprint of the original English edition from the series Encyclopaedia of mathematical sciences, 58, Springer-Verlag, Berlin, 1998.Google Scholar
[F] Fulton, W., Introduction to toric varieties. Annals of Mathematics Studies, 131, Princeton University Press, Princeton, NJ, 1993.Google Scholar
[FG M] Fernández, M., Gray, A., and J.W. Morgan, Compact symplectic manifolds with free circle actions and Massey products. Michigan Math. J. 38(1991), no. 2, 271–283. doi:10.1307/mmj/1029004333Google Scholar
[G] Godinho, L., Blowing up symplectic orbifolds. Ann. Global Anal. Geom. 20(2001), no. 2, 117–162. doi:10.1023/A:1011628628835Google Scholar
[L] Lerman, E., Symplectic cuts. Math. Res. Lett. 2(1995), no. 3, 247–258.Google Scholar
[LT] Lerman, E. and Tolman, S., Hamiltonian torus actions on symplectic orbifolds and toric varieties. Trans. Amer. Math. Soc. 349(1997), no. 10, 4201–4230. doi:10.1090/S0002-9947-97-01821-7Google Scholar
[L MTW] Lerman, E., Meinrenken, E., Tolman, S., and C.Woodward, Nonabelian convexity by symplectic cuts. Topology 37(1998), no. 2, 245–259. doi:10.1016/S0040-9383(97)00030-XGoogle Scholar
[Li] Li, H., π1 of Hamiltonian S1 manifolds. Proc. Amer. Math. Soc. 131(2003), no. 11, 3579–3582. doi:10.1090/S0002-9939-03-06881-3Google Scholar
[K] Kotschick, D., Free circle actions with contractible orbits on symplectic manifolds. Math. Z. 252(2006), no. 1, 19–25. doi:10.1007/s00209-005-0841-6Google Scholar
[M] Matumoto, T., On diffeomorphisms of a K3 surface. In: Algebraic and topological theories (Kinosaki, 1984), Kinokuniya, Tokyo, 1986, pp. 616–621.Google Scholar
[MD1] Mc Duff, D., The moment map for circle actions on symplectic manifolds. J. Geom. Phys. 5(1998), no 2, 149–160. doi:10.1016/0393-0440(88)90001-0Google Scholar
[MD2] Mc Duff, D., Examples of simply-connected symplectic non-Kählerian manifolds. J. Differential Geom. 20(1984), no. 1, 267–277.Google Scholar
[Mi] Milnor, J., Morse theory. Annals of Mathematics Studies, 51, Princeton University Press, Princeton, NJ, 1963.Google Scholar
[O] Ono, K., Obstruction to circle group actions preserving symplectic structure. Hokkaido Math. J. 21(1992), no. 1, 99–102.Google Scholar
[OR] Ortega, J. P. and Ratiu, T. S., Momentum maps and Hamiltonian reduction. Progress in Mathematics, 222, Birkhäuser Boston, Boston, MA, 2004.Google Scholar
[R] Ranicki, A., High dimensional knot theory. In: Algebraic surgery in codimension 2, Springer Monographs in Mathematics, 26, Springer-Verlag, New York, 1998.Google Scholar