Migration–contagion processes

Abstract

Consider the following migration process based on a closed network of N queues with $K_N$ customers. Each station is a $\cdot$/M/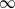$\infty$ queue with service (or migration) rate 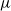$\mu$. Upon departure, a customer is routed independently and uniformly at random to another station. In addition to migration, these customers are subject to a susceptible–infected–susceptible (SIS) dynamics. That is, customers are in one of two states: I for infected, or S for susceptible. Customers can swap their state either from I to S or from S to I only in stations. More precisely, at any station, each susceptible customer becomes infected with the instantaneous rate 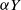$\alpha Y$ if there are Y infected customers in the station, whereas each infected customer recovers and becomes susceptible with rate 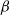$\beta$. We let N tend to infinity and assume that $\lim_{N\to \infty} K_N/N= \eta $, where 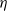$\eta$ is a positive constant representing the customer density. The main problem of interest concerns the set of parameters of such a system for which there exists a stationary regime where the epidemic survives in the limiting system. The latter limit will be referred to as the thermodynamic limit. We use coupling and stochastic monotonicity arguments to establish key properties of the associated Markov processes, which in turn allow us to give the structure of the phase transition diagram of this thermodynamic limit with respect to 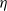$\eta$. The analysis of the Kolmogorov equations of this SIS model reduces to that of a wave-type PDE for which we have found no explicit solution. This plain SIS model is one among several companion stochastic processes that exhibit both random migration and contagion. Two of them are discussed in the present paper as they provide variants to the plain SIS model as well as some bounds and approximations. These two variants are the departure-on-change-of-state (DOCS) model and the averaged-infection-rate (AIR) model, which both admit closed-form solutions. The AIR system is a classical mean-field model where the infection mechanism based on the actual population of infected customers is replaced by a mechanism based on some empirical average of the number of infected customers in all stations. The latter admits a product-form solution. DOCS features accelerated migration in that each change of SIS state implies an immediate departure. This model leads to another wave-type PDE that admits a closed-form solution. In this text, the main focus is on the closed stochastic networks and their limits. The open systems consisting of a single station with Poisson input are instrumental in the analysis of the thermodynamic limits and are also of independent interest. This class of SIS dynamics has incarnations in virtually all queueing networks of the literature.

1. Introduction

The model described in the abstract aims to quantify the role of migration in the propagation of epidemics on the simplest possible migration model, namely a closed network of $\cdot/M/\infty$ queues, and for the simplest epidemic process, namely the susceptible–infected–susceptible (SIS) model. The thermodynamic limit discussed in the abstract is considered in order to further simplify the problem.

The epidemic interpretation of the SIS thermodynamic model is as follows: individuals move from place (station) to place, where places are indexed by, say, $\mathbb Z$ . The overall density of individuals is $\eta$ (i.e., the mean number of individuals per station is $\eta$ ). An individual stays at a place for an independent random time which is exponentially distributed with parameter $\mu$ . The last parameter can be seen as the migration rate. The departure rate of individuals from a given place is hence $\lambda=\mu \eta$ . When it leaves a place, an individual migrates to a place chosen independently and ‘at random’. At each station, individuals are subject to the SIS dynamics with parameters $(\alpha,\beta)$ . Infections and recoveries take place in stations and conditionally on the state of the stations.

In order to answer the question of the abstract, we first consider the problem of a single open station of the M/M/ $\infty$ type, referred to as the M/M/ $\infty$ SIS reactor. The input features two types of customers, infected and susceptible. The customer states change according to the mechanisms described in the abstract. The question is about the steady state of this queue. Of particular interest to us is the proportion $p_o$ of infected customers in the stationary output point process of this reactor in the steady state. This system has its steady state with a joint generating function characterized as a solution of a second-order wave-type partial differential equation (PDE) for which we have found no closed-form solution. We nevertheless derive several structural properties of this open system, which are of independent interest.

The connection of the SIS reactor with the problem of the abstract is the following: Fix all parameters $\lambda,\mu,\alpha,$ and $\beta$ of the thermodynamic limit as defined in the abstract. If the latter has a non-degenerate steady state (namely a steady state with survival), then there must exist a $0<p<1$ such that the open system with infected proportion p in input has a proportion of infected in output, $p_o$ , equal to p in the steady state. Conversely, if the SIS reactor has a stationary regime where $p_o(p)=p$ , for some $p=p^*>0$ , then the thermodynamic limit has a stationary regime where the epidemic persists for appropriate initial conditions. In addition, it will be shown that if the SIS reactor admits no p such that $p_o(p)=p$ , then for all initial conditions, when time tends to infinity, the proportion of infected customers tends to 0 in the thermodynamic limit. This is why we study the conditions on the parameters $\lambda,\mu,\alpha,$ and $\beta$ under which such a p exists, a situation that we will call survival, as well as conditions under which no such p exists, a situation that we call weak extinction.

More precisely, we prove that the SIS thermodynamic limit admits the following phase transition diagram: fix all parameters other than $\eta$ ; there exists a non-degenerate function $\eta_c(\alpha,\beta,\mu)$ such that, for $\eta\le\eta_c$ , there is strong extinction, whereas for $\eta>\eta_c$ , there is survival. We also derive bounds on the steady states of both the single open station model and the thermodynamic model. For instance, we give bounds on $\eta_c$ and $p^*$ for the latter. Some of these bounds are established under a hypothesis of negative correlation which is substantiated by simulation but not proved at this stage.

All the structural results on the SIS reactor are proved. All the results on the thermodynamic limit are proved under the assumption that the limits defining them exist—which we conjecture. This will be referred to as the thermodynamic propagation of chaos ansatz.

We also study the following variants of the SIS reactor:

• • The departure-on-change-of-state (DOCS) reactor, where the infection rate is the same as above, but where (a) an infection immediately leads to a departure, and (b) a recovery immediately leads to a departure. This problem is simpler in that the associated PDE can be solved.

• • The averaged-infection-rate (AIR) reactor, where (a) the infection rate of any susceptible is constant (rather than proportional to the actual number of infected), and (b) the recovery mechanism is as in the SIS case. This last model is a product-form Jackson network and admits a simple product-form solution.

In contrast to the plain SIS case, the stationary regimes of these two other open systems admit closed-form expressions. These two open-loop models in turn lead to thermodynamic limits. More precisely, the DOCS reactor leads to the DOCS thermodynamic limit, where customers leave the station as soon as they change their state and are immediately routed to another station chosen at random while keeping their new state. The AIR reactor leads to the AIR thermodynamic limit, which is a closed network (similar to the plain SIS thermodynamic limit) where, in any station, susceptible customers get infected with a rate that is proportional to the mean number of infected customers in all stations. The closed-form solutions alluded to above are used to quantify the phase diagram of the last two thermodynamic limits.

The AIR system is conjectured to provide bounds to the plain SIS system. These bounds are in the following sense. Consider two thermodynamic limits A and A ^′ with the same parameters $\alpha,\beta,\mu$ and with varying $\eta$ . System A will be said to have more infection in mean than system A ^′ if the mean number of infected customers is greater in A than in A ^′ in steady state. Assume that system A (resp. A ^′) admits a critical value $\eta_c$ (resp. $\eta^{\prime}_c$ ) such that if $\eta>\eta_c$ (resp. $\eta>\eta^{\prime}_c$ ), then there is survival, whereas otherwise there is extinction. System A ^′ will be said to be safer than system A if $\eta^{\prime}_c\ge \eta_c$ . If A has more infection in mean than A ^′, then A ^′ is safer than A. The converse is not true in general. It will be proved that, under a certain negative correlation conjecture which is backed by simulation, DOCS is safer than AIR. There is numerical evidence that plain SIS can be safer than DOCS, or vice versa, depending on the parameters.

The main probabilistic tools used in the paper are stochastic comparison, coupling, the rate conservation principle (RCP), various classes of Markov processes with both discrete and continuous state spaces, mean-field limits, and branching processes. The PDEs alluded to above are instrumental for finding solutions to the Kolmogorov equations of the generating functions of the discrete-state-space Markov chains in question.

The paper is structured as follows. A summary of the models (single-station models and thermodynamic limit models) is given in Section 2, so as to make navigation between them easier. The open SIS reactor is studied in Section 3. Its stationary generating function satisfies a wave-type PDE for which we have not found a closed-form solution so far. We then establish rate conservation equations which are useful throughout the paper. Section 4 discusses the DOCS open reactor and Section 5 the AIR open reactor. Both models can be solved in closed form. The wave-type PDE of the DOCS reactor has a closed-form solution, whereas the AIR reactor reduces to a product-form queueing network for which an explicit solution is already known. The closed-form expressions provide bounds on the SIS dynamics. Section 6 gathers results on the thermodynamic mean-field limit of the SIS dynamics. The analysis is based on structural properties of the open SIS reactor. The main result is a characterization of the structure of the phase diagram. The same is done in Sections 7 and 8 for the AIR and the DOCS thermodynamic limits, respectively. Section 9 gives a probabilistic interpretation for the phase transition thresholds in terms of branching conditions. Finally, Section 10 gathers additional numerical observations based on discrete event simulation.

The appendix contains the proofs of several central and auxiliary results. The extended arXiv version of the paper [2] contains further material and in particular inequalities that would follow from the conjectured property of anti-association (negative correlation) of certain random variables in this SIS dynamics.

We conclude this introduction with a brief overview of the relevant literature. In the absence of mobility, the problem has been extensively studied in the particle system literature [11], where the model is referred to as the contact process. This literature contains a large corpus of results on the phase diagrams of infinite graphs with finite degrees such as grids and regular trees. The problem has also been studied on finite deterministic graphs, where the main question is that of the separation between logarithmic and exponential growth of the time till extinction with respect to the size of the graph. There is also a series of studies of SIS epidemic models on populations partitioned into households and, in particular, on their correlation structure and time to extinction; see e.g. [5] and [4] and references therein.

The SIS dynamics has also been extensively studied on finite random graphs. For overviews on this class of questions, see e.g. [14] and [13]. Moment closure techniques [10, 9] provide an important tool in this context. The contact process has also been studied on infinite random graphs with unbounded degrees. The supercritical Bienaymé–Galton–Watson tree was studied in [15], where it was shown that some critical values can be degenerate. It has also been extensively studied on Euclidean point processes [7, 8, 12].

The analysis of the case with mobility is more recent. The situation where agents perform a random walk on a finite graph and agents meeting at a given point of the graph may infect each other was studied in [6]. The situation where agents form a Poisson point process and migrate in the Euclidean plane was studied in [3], which proposed a computational framework based on moment closure techniques for evaluating the role of mobility in the propagation of epidemics.

The queueing model studied here may be seen as a discrete version of the model in [3], or as a thermodynamic limit of that of [6].

Figure 1. On the left, the SIS reactor. On the right, the AIR reactor with parameter y.

2. The models

2.1. The open models

All models in this subsection feature an open queueing system with two types of customers. There are two independent Poisson external arrival point processes: that of susceptible customers, with intensity $\lambda q$ , and that of infected customers, with intensity $\lambda p$ , with $q=1-p$ .

2.1.1. The plain SIS reactor

The SIS reactor features a single M/M/ $\infty$ -type station (that will be referred to as a reactor). Service times of all customers in this queue are exponential with parameter $\mu$ . While waiting in the reactor, each susceptible customer becomes infected with the instantaneous rate $\alpha n$ when there are n infected customers, and each infected customer recovers and becomes susceptible with rate $\beta$ . It is because of this interaction that we call the queue a reactor (see the left panel of Figure 1).

Let X (resp. Y) denote the number of susceptible (resp. infected) customers in the steady state of the SIS reactor. By classical arguments, one gets that for all $0\le x\le 1$ , $0\le y\le 1$ , the joint generating function $\Phi(x,y)={\mathbb{E}}\big[x^Xy^Y\big]$ satisfies the PDE

(1) \begin{align}& \left( \lambda q(1-x) + \lambda p(1-y)\right) \Phi(x,y) \nonumber \\ & = \mu (1-x)\Phi_x(x,y) +\left(\mu (1-y)+ \beta(x-y)\right)\Phi_y(x,y) +\alpha y (y-x)\Phi_{xy}(x,y) .\end{align}

The term in $\Phi_{xy}(x,y)$ , which comes from the infection rate in XY, allows one to link this equation to the one-dimensional wave equation.

Remark 1. The one-dimensional wave equation reads $U_{tt} = c^2 U_{zz},$ with c velocity, t time, and z space. The last PDE leads (after a change of variables) to a relation between second derivatives of the form $\Psi_{xx}= \left(\frac y x\right)^2 \Psi_{yy}$ plus additional lower-order terms—that is, a velocity of $\frac y x$ when interpreting x as time and y as space. In this sense, the wave equation satisfied by the joint generating function involves a velocity that is not determined by the parameters of the dynamics but only by the variables of the joint generating function.

2.1.2. The AIR reactor

The AIR model features a network of two M/M/ $\infty$ stations. All infected arrivals are routed to the second station (that of the infected). The service rate in this station is $\nu=\mu+\beta$ . When a customer leaves this station, it leaves the network with probability $\frac{\mu}{\mu +\beta}$ and is routed to the first station otherwise. All susceptible customers are routed to the first station (that of the susceptible). At time t, the service rate in this station is $\mu + y(t) \alpha$ , where y(t) is a positive deterministic function that can be fixed at will. When a customer leaves this station, it leaves the network with probability $\frac{\mu}{\mu + y(t) \alpha}$ and is routed to the second station with probability $\frac{y(t) \alpha}{\mu + y(t) \alpha}$ . This is depicted in the right panel of Figure 1. The main difference from the SIS reactor is that the infection rate of a susceptible is a state-independent deterministic function here. In particular, when y(t) is constant, we will not need the PDE here but will rather use the theory of product-form queueing networks (see Section 5).

2.1.3. The averaging mean-field limit of the SIS reactor

The averaging mean-field limit of the plain SIS model is defined as the following limit of open networks. Consider a system with K stations. Each station is an M/M/ $\infty$ queue with service rate $\mu$ and arrival rate $\lambda$ . Each arrival is independently declared infected with probability p and susceptible otherwise. In each station, an infected customer turns susceptible with rate $\beta$ , and a susceptible customer turns infected with rate $\frac \alpha K \sum_{k=1}^K Y_k(t),$ where $Y_k(t)$ is the number of infected nodes in station k at time t. So in this model, which is depicted in the left panel of Figure 4, conditionally on the state, the infection rate of a susceptible in a station is proportional to the empirical mean of the number of infected customers in all stations (rather than to the number of infected customers in the same station in the SIS reactor). The averaging mean-field limit of SIS is obtained by letting $K\to \infty$ . The empirical mean in question then converges to a constant, which is also the mean number of infected customers in the typical station. When it exists, this limit features a typical station which is an AIR model with the constraint that $y(.)$ must be such that $y(t)={\mathbb{E}}_{y(.)}[Y(t)]$ for all t, where ${\mathbb{P}}_{y(.)}$ is the distribution at time t of the system with parameter $y(.)$ , and Y(t) is the number of infected customers at time t in the AIR station. The construction of such a system is discussed in Appendix D. A single AIR station where $y(.)={\mathbb{E}}_{y(.)}[Y(t)]$ will be referred to as an AIR averaging mean-field (AIR-AMF) reactor.

2.1.4. The DOCS reactor

The DOCS model features a single station as in the SIS case. The infection mechanism of the SIS model is replaced by a simultaneous infection and departure mechanism with the following characteristics: if the number of infected is Y(t), each susceptible gets infected with rate $\alpha Y(t)$ and, upon infection, it immediately leaves the system for good. There is also a ‘natural’ departure rate of susceptible customers, denoted by $\mu$ . The total departure rate of infected customers is hence $\nu=\mu+\beta$ , since when an infected customer recovers, it immediately leaves the system. Equivalently, the total departure rate is $\mu+\beta$ , and upon departure, the infected customer keeps its state with probability $\mu/(\mu+\beta)$ or swaps to susceptible with the complementary probability. See the left panel of Figure 2.

Figure 2. On the left, the DOCS reactor. On the right, the prelimit routing DOCS network with two stations.

In fact, if one just needs to determine ${\mathbb{E}} (X)$ in the DOCS reactor, the state of departing customers does not matter. Therefore, we may (and will) analyze a more general scheme where there are no recoveries but a general departure rate $\nu$ of infected customers, and where $\nu$ and $\mu$ are not linked as above.

The associated PDE for the stationary generating function of the general DOCS reactor is

(2) \begin{eqnarray}\left( \lambda q(1-x) +\lambda p (1-y)\right) \Phi(x,y) & \,=\, & \mu (1-x) \Phi_x(x,y) + \nu (1-y) \Phi_y(x,y)\nonumber\\ & & +\, \alpha y (1-x)\Phi_{xy}(x,y) .\end{eqnarray}

Remark 2. A wave-type equation shows up in the DOCS and the plain SIS systems, whereas it does not in the AIR model. This comes from the nonlinear infection rate of the form $\alpha XY$ whenever the state is (X, Y). This leads to the $\frac{\partial}{\partial x}$ and $\frac{\partial}{\partial y}$ terms in the corresponding PDEs, which in turn lead to the corresponding wave equations. In contrast, in the AIR system, this nonlinearity is replaced by the linear rate $\alpha X{\mathbb{E}}[Y]$ , with ${\mathbb{E}}[Y]$ seen as a parameter determined by a nonlinear relationship, which explains why the wave equation does not show up.

2.2. The routing mean-field limit of the DOCS reactor

The DOCS routing reactor, which will be essential below, is a variant of the DOCS reactor. It is based on a DOCS routing mean-field limit, which should not be confused with the DOCS thermodynamic limit (defined in Subsection 2.3 below). This routing mean-field limit is defined as follows. Consider first a network made of N DOCS reactors, as depicted in the right panel of Figure 2. For this network, the state variables in station $1\le n \le N$ will be denoted by $\widehat X_n(t)$ and $\widehat Y_n(t)$ . Each station is a $\cdot$ /M/ $\infty$ station with service rate $\mu$ and external arrival rate $\lambda$ . There is an external Poisson arrival process to each station, and each external arrival is independently declared infected with probability p and susceptible otherwise. In each station, an infected customer turns susceptible with rate $\beta$ . But rather than staying in the station (as in SIS), this newly susceptible customer instantaneously leaves, and rather than leaving for good as in the DOCS open reactor, it joins another station chosen at random and independently among the N stations. Similarly, in station n, a susceptible customer turns infected with rate $\alpha \widehat Y_n(t)$ at time t. But rather than staying in this station, the newly infected customer instantaneously joins another station chosen at random and independently among the N stations.

Figure 3. On the left, a closed network of three SIS reactors. On the right, the SIS TL.

Figure 4. On the left, a closed network of three AIR reactors. On the right, the AIR TL.

When N tends to infinity, we get the DOCS routing mean-field limit, which is a system with both external arrivals and internal customer routing. Again, the existence of this limit will not be discussed in the present paper. In the steady state of this limit, the overall arrival point process of infected customers in a typical station is Poisson with rate $\lambda p +\alpha {\mathbb{E}}[\widehat X\widehat Y]$ (sum of external and internal rates), and that of susceptible customers is independent and Poisson with rate $\lambda q +\beta {\mathbb{E}}[\widehat Y]$ (sum of external and internal rates again). Here $\widehat X$ and $\widehat Y$ represent the stationary state variables of a typical station in this limit. Here and in what follows, we use a hat on these variables to distinguish them from those of the DOCS reactor.

We will use the term routing DOCS reactor to refer to the typical station in question, namely a station which behaves as a DOCS reactor but where, in addition to an external infected (resp. susceptible) Poisson input point process of intensity $\lambda p(t)$ (resp. $\lambda q(t)$ ), there is an additional ‘re-routing’ infected (resp. susceptible) Poisson point process of intensity $\alpha {\mathbb{E}}\big[\widehat X(t)\widehat Y(t)\big]$ (resp. $\beta {\mathbb{E}}[X(t)]$ ).

For all $0\le x\le 1$ , $0\le y\le 1$ , in steady state, the joint generating function $\widehat\Phi(x,y)={\mathbb{E}}\big[x^{\widehat X}y^{\widehat Y}\big]$ satisfies the PDE

(3) \begin{eqnarray}& & \hspace{-.8cm} \left( \big(\lambda q+\beta {\mathbb{E}}[\widehat Y]\big)(1-x)+\big(\lambda p +\alpha {\mathbb{E}}[\widehat X\widehat Y]\big)(1-y)\right)\widehat \Phi(x,y) \nonumber\\& =\, & \mu (1-x)\widehat \Phi_x(x,y) +\left(\mu + \beta {\mathbb{E}}[\widehat Y] \right)(1-y) \widehat \Phi_y(x,y) +\alpha y (1-x)\widehat \Phi_{xy}(x,y) .\end{eqnarray}

This PDE is an instance of the DOCS PDE in (2) with the following specific parameters: $\lambda q$ is replaced by $\lambda q+\beta {\mathbb{E}}[\widehat Y]$ , $\lambda p$ by $\lambda p +\alpha {\mathbb{E}}[\widehat X\widehat Y]$ , and $\nu$ is taken equal to $\mu + \beta$ .

Here are a few observations on the routing DOCS models. Consider first the prelimit model with N stations. Consider the whole system as a single system. Any customer has an exponential lifetime in the queue with parameter $\mu$ . During its lifetime, an individual changes state but stays in the system. Since the total arrival rate to the system is $\lambda N$ , the total number of customers in the stationary regime is Poisson with parameter (and mean) $\lambda N/\mu$ . Because of the symmetry, the mean number of all customers in any station is hence $\lambda/\mu$ . Letting N tend to infinity and noting that uniform integrability holds, we conclude that the mean number of customers stays equal to $\lambda/\mu$ in the infinite system too. For all fixed N, in the stationary regime, the pairs of $(\widehat X,\widehat Y)$ vectors at different stations form an exchangeable family of dependent random vectors, with all coordinates summing up to a Poisson random variable.

2.3. The thermodynamic limits

2.3.1. Definition

The thermodynamic limits pertain to a family of closed networks as illustrated for SIS in the left panel of Figure 3 or for DOCS in the left panel of Figure 5.

They are all infinite-dimensional Markov systems. They can also be seen as certain nonlinear Markov processes (see Appendix D). Consequently, a wide range of asymptotic behaviors are possible for any given initial condition. For instance the dynamics could, e.g., converge to a stationary measure, or be periodic, or admit an attractor.

In this paper, for all cases considered, we assume that the thermodynamic limit exists and satisfies the following properties on any compact of time: (i) stations have independent dynamics; (ii) in each station, the arrival point process of susceptible (resp. infected) customers is (possibly non-homogeneous) Poisson, with these two processes being independent. This set of properties will be referred to as the thermodynamic propagation of chaos ansatz.

Figure 5. On the left, a closed network with two DOCS stations. At a fork, routing decisions are up or down with probability 1/2. On the right, the DOCS TL.

2.3.2. Examples

In all examples below, the prelimit is a closed system of N stations. Each station is again a $\cdot$ /M/ $\infty$ queue with departure rate $\mu$ . There is a total of $K_N$ customers, and we assume that $\lim_{N\to \infty} K_N/N= \lambda/\mu\,:\!=\,\eta$ . Here $\eta$ and $\lambda$ are positive constants representing the mean population per station and the arrival rate in a station, respectively. The routing is independent and uniform at random to all stations.

Plain SIS. We will call the SIS thermodynamic limit (SIS TL) the infinite-dimensional system obtained by letting N tend to infinity, assuming $K_N$ behaves as described above. This limit is illustrated in the right panel of Figure 3.

AIR. The AIR thermodynamic limit (AIR TL) is best described as the following variant of the closed system of the abstract, which is depicted in the left panel of Figure 4. There are N stations, with state variables $\widetilde X_n$ and $\widetilde Y_n$ . In any station, each susceptible customer swaps to infected with the instantaneous rate $\alpha \frac 1 N \sum_{k=1}^N \widetilde Y_k$ if there are $\widetilde Y_k$ infected customers in station k, whereas each infected customer recovers and becomes susceptible with rate $\beta$ . Letting $N\to \infty$ , one gets a variant of the SIS TL (again assumed to hold here), where stations are independent. In this limit, which is depicted in the right panel of Figure 4, each station behaves as an AIR AMF reactor (with $y(t)={\mathbb{E}}[\widetilde Y(t)]$ ) with the following constraint on the parameters: the external arrival rate of susceptible customers is equal to $\mu {\mathbb{E}}[\widetilde X(t)]$ , and that of infected customers is $\mu {\mathbb{E}}[\widetilde Y(t)]$ .

DOCS. The DOCS thermodynamic limit (DOCS TL) features a closed queueing network with N DOCS stations and a total of $K_N$ customers, as illustrated in the left panel of Figure 5. If station n has $X_n$ susceptible and $Y_n$ infected customers, each susceptible customer swaps to infected with the instantaneous rate $\alpha Y_n$ ; upon infection, it simultaneously leaves this station and is routed to one of the N stations chosen at random. Similarly, each infected customer becomes susceptible with rate $\beta$ ; upon recovery, it simultaneously leaves and is routed to a station chosen at random. In addition, as in the closed SIS network model, each customer (infected or susceptible) also leaves the station with a departure rate $\mu$ and is then also routed to a station chosen at random. We let N tend to infinity and assume that $K_N$ is such that the total input rate to a station tends to $\lambda$ (or equivalently that the density of customers is $\eta$ ). Then, in the limit when it exists, each station behaves as a routing DOCS reactor as defined in Subsection 2.2, with the additional consistency property that, in the latter, the external infected arrival rate $\lambda p^*(t)$ should match the external infected departure rate $\mu {\mathbb{E}}\big[\widehat Y(t)\big]$ , and similarly, $\lambda q^*(t)$ should be equal to $\mu {\mathbb{E}}\big[\widehat X(t)\big]$ . This fixed point, which characterizes the stationary distribution of the DOCS TL, is illustrated on the right in Figure 5.

2.3.3. Survival versus extinction

Below, for all thermodynamic limits, we assume that propagation of chaos holds. We will show that under this assumption, the dynamics of the infinite-dimensional Markov systems in question can be reduced to that of a finite-dimensional nonlinear Markov process.

Definition 1. In any thermodynamic limit, we will say that there is survival if the associated Markov system has a steady-state distribution with a fraction $0<p<1$ of susceptible customers. We will say that there is weak extinction if there exists no such p. We will say that there is strong extinction if, for all initial conditions, the associated Markov system converges to a regime without infected customers.

Remark 3. Weak extinction does not mean that the epidemic vanishes in the infinite-dimensional system as time tends to infinity. It only means that there is no initial condition for the associated infinite-dimensional Markov system to converge to a limiting regime with a positive fraction of infected customers.

Remark 4. As in many other models, survival in the thermodynamic limit should translate to the fact that the time to extinction in the prelimit at $N<\infty$ grows exponentially in N, where N is as defined in the abstract.

3. SIS reactor analysis

3.1. Preliminary observations

It is easy to check from the PDE (1) that $\Phi(z,z)= e^{-\frac \lambda \mu (1-z)}.$ A direct probabilistic argument also gives that $X+Y\sim Pois (\lambda/\mu)$ .

We were not able to solve this PDE. This is why we resort to other techniques based on the RCP [1]. A variety of conservation equations will be discussed. These are of independent interest and will also be used in what follows.

3.2. First-order relations

The simplest first-order relation states that the rate of arrivals, $\lambda$ , should match the rate of departures, namely $\mu {\mathbb{E}}[X+Y]$ . Note that there is no reason for the rate of arrivals of infected customers, $\lambda p$ , to match that of departures of infected customers, namely $\mu {\mathbb{E}}[Y]$ . This also holds for susceptible customers.

Lemma 1. The following relation holds:

(4) \begin{equation}\lambda p + \alpha {\mathbb{E}}[XY] = (\mu +\beta) {\mathbb{E}}[Y] .\end{equation}

Proof. We get this relation by differentiating the PDE (1) with respect to y and taking $x=y=1$ .

This has a simple RCP interpretation. We recognize in the left-hand side of (4) the increase rate of the mean number of infected customers in steady state (due to arrivals and infections), whereas the right-hand side is the mean decrease rate of the same quantity due to recoveries and departures from the reactor.

Also note that by differentiating the PDE (1) with respect to x and taking $x=y=1$ , we get

(5) \begin{equation}\lambda q +\beta {\mathbb{E}}[Y] = \mu {\mathbb{E}}[X] +\alpha {\mathbb{E}}[XY].\end{equation}

This equation is actually the same as that in the lemma (using the fact that ${\mathbb{E}}[X]+{\mathbb{E}}[Y]=\frac \lambda \mu$ ).

3.3. Second-order relations

Lemma 2. The following relations hold:

(6) \begin{equation}(\lambda p + \mu + \beta ) {\mathbb{E}} [Y] + \alpha {\mathbb{E}}\big[ XY^2\big] =(\mu +\beta) {\mathbb{E}}[Y^2],\end{equation}

and

(7) \begin{equation}(\lambda q + \mu) {\mathbb{E}} [X] +(\alpha+\beta) {\mathbb{E}}[XY] =\alpha {\mathbb{E}}\big[ X^2Y\big] +\mu {\mathbb{E}}[X^2].\end{equation}

Proof. The first relation is obtained by differentiating the PDE (1) with respect to y twice and taking $x=y=1$ , the second by differentiating the PDE with respect to x twice and taking $x=y=1$ .

3.4. Higher-order relations

Lemma 3. For all non-negative integers m and n, the RCP relation for $X^mY^n$ reads

(8) \begin{eqnarray}& & \hspace{-1cm}\lambda p {\mathbb{E}}[X^m\left((Y+1)^n-Y^n\right)] +\lambda q {\mathbb{E}}[\!\left((X+1)^m-X^m\right)Y^n]\nonumber \\& +\, &\beta {\mathbb{E}}[Y\left((X+1)^m(Y-1)^n-X^mY^n\right)] +\alpha {\mathbb{E}}[XY\left((X-1)^m(Y+1)^n-X^mY^n\right)]\nonumber \\& +\, &\mu {\mathbb{E}}[X\left((X-1)^m-X^m\right)Y^n ]+\mu {\mathbb{E}}[YX^m\left((Y-1)^n-Y^n\right)]=0.\end{eqnarray}

The proof is based on Equations (54), (55), and (56) in Appendix A.

4. DOCS reactor analysis

4.1. Preliminary observations

We start with a few observations on this system:

• • By either a simple probabilistic argument or a direct analytical derivation based on the PDE, we get that $\Phi(1,y)=e^{-\theta(1-y)}$ ; that is, Y is Poisson with mean $\theta=\frac{\lambda p}{\nu}$ (the Y process is that of an autonomous M/M/ $\infty$ queue with input rate $\lambda$ and service rate $\nu$ ).

• • Here, the random variable $X+Y$ has no reason to be Poisson.

• • The stationary output rate of infected customers, $\nu {\mathbb{E}}[Y]$ , should match the input rate of infected customers ( $\lambda p$ ). This is because the infected customers evolve as those of an M/M/ $\infty$ queue.

• • The stationary depletion rate of susceptible customers, $\mu {\mathbb{E}}[X]+ \alpha {\mathbb{E}}[XY]$ , should match the increase rate of susceptible customers ( $\lambda q$ ). This is because the susceptible customers evolve as in a stationary queue.

We summarize the last two observations in the following conservation equations:

(9) \begin{eqnarray}\lambda p = \nu{\mathbb{E}}[Y], \qquad \lambda q = \mu{\mathbb{E}}[X] +\alpha {\mathbb{E}}[XY].\end{eqnarray}

4.2. Analytical solution

By differentiating Equation (2) with respect to x and taking $x=1$ , we get

\begin{eqnarray*}-\lambda q \Phi(1,y)+\left(\lambda p (1-y) +\mu\right) \Phi_x(1,y)= \left(\nu (1-y) -\alpha y\right) \Phi_{xy}(1,y),\end{eqnarray*}

or equivalently, the function $\Psi(y)\,:\!=\, \Phi_x(1,y)$ satisfies the ordinary differential equation (ODE)

(10) \begin{eqnarray}\left(\nu (1-y) -\alpha y\right) \Psi^{\prime}(y)=\left(\lambda p (1-y) +\mu\right) \Psi(y) -\lambda q e^{-\theta(1-y)}.\end{eqnarray}

This can be rewritten as the first-order ODE

(11) \begin{eqnarray}\Psi^{\prime}(y)= h(y) \Psi(y) - g(y),\end{eqnarray}

with

(12) \begin{equation}h(y)\,:\!=\,\frac {\lambda p (1-y) +\mu} {\nu (1-y) -\alpha y}, \qquad g(y)\,:\!=\,\frac{ \lambda q e^{-\theta(1-y)}} {\nu (1-y) -\alpha y} .\end{equation}

Notice that the coefficients of this first-order ODE have a singularity at

$$y=y^*\,:\!=\, \frac{\nu}{\nu+\alpha}<1.$$

One can nevertheless work out the solution of this ODE for y in a neighborhood of 1 not including $y^*$ . The homogeneous equation has for a solution

$$ T(y)\,:\!=\, e^{\int_1^y h(z) dz}.$$

Hence, when looking for a solution of the form $\Psi(y)=T(y) a(y)$ , we get that

$$ a(y)= a(1) - \int_1^y g(u) e^{-\int_1^u h(z) dz} du.$$

Hence

(13) \begin{eqnarray}\Psi(y)= e^{\int_1^y h(z) dz}\left(\Psi(1) - \int_1^y g(u) e^{-\int_1^u h(z) dz} du\right).\end{eqnarray}

An expansion shows that for u in a right neighborhood of $y^*$ , $e^{-\int_1^u h(z) dz}\sim K (u-y^*)^{b}$ with K a constant and

$$b=\frac{ \lambda p \alpha +\mu(\alpha+\nu)}{(\alpha +\nu)^2}.$$

Hence the integral

$$\int_1^{y^*} g(u) e^{-\int_1^u h(z) dz} du$$

is well defined and finite despite the singularity of g at $y^*$ . This integral must match $\Psi(1)$ . Indeed, if this were not the case, the function $\Psi$ would have a singularity at $y^*$ , which is not possible. Hence

\begin{equation*}\Psi(1)=\int_1^{y^*} g(u) e^{-\int_1^u h(z) dz} du;\end{equation*}

that is,

(14) \begin{equation}{\mathbb{E}}[X]=\int_1^{\frac{\nu }{\nu+\alpha}}\frac{ \lambda q e^{-\frac{\lambda p}\nu (1-u)}} {\nu (1-u) -\alpha u}\exp\left({-}\int_1^u\frac {\lambda p (1-z) +\mu} {\nu (1-z) -\alpha z} dz\right) du.\end{equation}

Using the fact that

$$\int_1^u\frac {\lambda p (1-z) +\mu} {\nu (1-z) -\alpha z} dz=-\frac 1 {\nu +\alpha} \left(\lambda p (1-u) + \left(\mu +\lambda p\frac{\alpha}{\alpha +\nu}\right) \ln \left(\frac{u-y^*}{1-y^*}\right) \right),$$

with $y^*=\frac \nu{\nu +\alpha}$ , we get that

\begin{eqnarray*}{\mathbb{E}}[X] & \,=\, &\lambda q\int_1^{\frac{\nu }{\nu+\alpha}}e^{-\frac{\lambda p}\nu (1-u)}e^{\frac{\lambda p} {\nu+\alpha} (1-u)}\frac 1 {\nu (1-u) -\alpha u}\left( \frac{u-y^*}{1-y^*} \right)^{\frac \mu {\nu +\alpha} +\lambda p\frac{\alpha}{(\nu+\alpha)^2}}du .\end{eqnarray*}

That is,

(15) \begin{eqnarray}{\mathbb{E}}[X] & \,=\, & \frac {\lambda q} { (\nu+\alpha)\left(\frac{\alpha}{\nu+\alpha}\right)^{\frac \mu {\nu +\alpha} +\lambda p\frac{\alpha}{(\nu+\alpha)^2}} }\times \nonumber \\ & &\int_{\frac{\nu }{\nu+\alpha}}^1e^{-\frac{\lambda p \alpha}{\nu(\nu +\alpha)} (1-u)}\left( u-\frac \nu {\nu+\alpha} \right)^{\frac \mu {\nu +\alpha} +\lambda p\frac{\alpha}{(\nu+\alpha)^2}-1}du .\end{eqnarray}

Applying the change of variables $u= t \frac{\alpha}{\nu +\alpha} + \frac{\nu}{\nu +\alpha}$ , we get

(16) \begin{eqnarray}{\mathbb{E}}[X] & \,=\, & \frac {\lambda q}{\nu+\alpha}\int_{0}^1e^{-\frac{\lambda p \alpha^2}{\nu(\nu +\alpha)^2} (1-t)}t^{\frac \mu {\nu +\alpha} +\lambda p\frac{\alpha}{(\nu+\alpha)^2}-1}dt .\end{eqnarray}

4.3. Analysis of the routing DOCS reactor

Compared to the SIS reactor, the routing DOCS reactor (defined in Subsection 2.2) features much faster migration. This is because the natural departures (those happening with rate $\mu$ regardless of the state) are complemented by departures that are caused by a change of state. Because of the nature of the mean-field model, this goes with an increased arrival rate of both infected and susceptible customers, in that ‘external’ arrivals (those happening with rate $\lambda p(t)$ for infected and rate $\lambda q(t)$ for susceptible customers) are complemented by ‘internal’ arrivals (with respective rates $\alpha {\mathbb{E}}\big[\widehat X(t)\widehat Y(t)\big]$ for infected and $\beta {\mathbb{E}}\big[\widehat Y(t)\big]$ for susceptible customers). As we shall see (Lemma 4 below), this accelerated migration (in and out) preserves the mean queue size in steady state when it exists.

4.3.1. Stationary regime of the routing DOCS reactor

An important question is whether there exists a stationary regime for this reactor. A necessary condition is that there exists a probabilistic solution to the PDE (2) satisfying the above consistency equations. If this is the case, it follows from the observations preceding the remark of Subsection 2.2 and the results of Subsection 4.1 that $\widehat Y$ is Poisson with parameter

(17) \begin{equation}\widehat \theta= \frac {\lambda p +\alpha {\mathbb{E}}[\widehat X \widehat Y]} {\mu + \beta}.\end{equation}

The random variable $\widehat X+\widehat Y$ has no reason to be Poisson and the two terms of the sum have no reason to be independent. In fact we will see later on that they are neither Poisson nor independent.

4.3.2. First-order rate conservation

Assuming that the routing DOCS reactor has a stationary regime, one can apply the rate conservation equations to this system. The first-order RCP, which says that the input and output rates coincide, reads

(18) \begin{equation}\lambda q +\beta {\mathbb{E}}[\widehat Y] = \mu {\mathbb{E}}[\widehat X] +\alpha {\mathbb{E}}[\widehat X \widehat Y]\end{equation}

for susceptible customers and

(19) \begin{equation}\lambda p + \alpha {\mathbb{E}}[\widehat X \widehat Y] = (\beta + \mu) {\mathbb{E}}[\widehat Y]\end{equation}

for infected ones. Note that these match the first-order relations of the SIS reactor.

Lemma 4. In the stationary regime of the DOCS routing mean-field model, one also has

(20) \begin{equation}{\mathbb{E}}[\widehat Y] +{\mathbb{E}}[\widehat X] = \frac {\lambda} {\mu}.\end{equation}

Proof. The result is obtained by adding up the last two equations.

The fact that the mean total population is the same as in the SIS model is remarkable, as here, and in contrast to the SIS reactor, $\widehat X +\widehat Y$ is not Poisson.

4.3.3. Higher-order rate conservation

The setting is that of the last subsection. The RCP for $\widehat Y(\widehat Y-1)$ reads

(21) \begin{equation}\left(\lambda p + \mu +\beta\right) {\mathbb{E}}[\widehat Y]+ \alpha {\mathbb{E}}[\widehat X \widehat Y] {\mathbb{E}}[\widehat Y]= (\beta + \mu) {\mathbb{E}}[\widehat Y^2].\end{equation}

Note that it is similar to (6), except that ${\mathbb{E}}[XY^2]$ is replaced by ${\mathbb{E}}[\widehat X\widehat Y] {\mathbb{E}}[\widehat Y]$ . Similarly, the RCP for $\widehat X(\widehat X-1)$ reads

(22) \begin{equation}(\lambda q + \mu) {\mathbb{E}}[\widehat X] + \beta {\mathbb{E}}[\widehat Y] {\mathbb{E}}[\widehat X]+\alpha {\mathbb{E}}[\widehat X \widehat Y]= \alpha {\mathbb{E}}[\widehat X^2\widehat Y] + \mu {\mathbb{E}}[\widehat X^2],\end{equation}

which is similar to (7), except that $\beta {\mathbb{E}}[XY]$ is replaced by $\beta {\mathbb{E}}[\widehat X] {\mathbb{E}}[\widehat Y]$ . Finally, the RCP for $\widehat X \widehat Y$ reads

(23) \begin{equation}\left(\lambda q + \beta {\mathbb{E}}[\widehat Y]\right) {\mathbb{E}}[\widehat Y]+\left(\lambda p + \alpha {\mathbb{E}}[\widehat X \widehat Y]\right) {\mathbb{E}}[\widehat X]= (\beta + 2 \mu) {\mathbb{E}}[\widehat X \widehat Y]+ \alpha {\mathbb{E}}[\widehat X \widehat Y^2].\end{equation}

Note that the complexity of the last two equations remains similar to that of the corresponding equations in the initial system.

5. AIR reactor analysis

5.1. The reactor

Thanks to the linearity of the rates, the AIR queueing network defined in Section 2 has a product-form distribution in steady state which is the product of two Poisson distributions, with parameter $\frac {\lambda_1}{\mu}$ in station 1 and $\frac {\lambda_2}{\mu}$ in station 2. Direct computations based on the traffic equations

\begin{eqnarray*}\lambda_1 = \lambda q +\lambda_2 \frac \beta {\mu +\beta},\quad \quad \lambda_2 = \lambda p +\lambda_1 \frac {\alpha y} {\mu +\alpha y}\end{eqnarray*}

give that

$$\lambda_1 = \frac{(\mu+\alpha y)(\beta +\mu q)\lambda}{(\mu +\beta)(\mu+\alpha y)-\beta\alpha y}\ .$$

We also have $x=\frac {\lambda_1}{\mu+\alpha y}=\frac \lambda \mu -y$ , with x the mean queue size in station 1.

5.2. The averaging mean-field case

Consider the averaging mean-field limit when it exists. Denote by $\widetilde X$ the stationary number of susceptible customers in the typical station and by $\widetilde Y$ the stationary number of infected ones in this system. By arguments similar to those in Subsection 3.2, these state variables satisfy the relations

(24) \begin{equation}\lambda q+ \beta {\mathbb{E}}[\widetilde Y]= \mu {\mathbb{E}}[\widetilde X]+ \alpha {\mathbb{E}}[\widetilde X]{\mathbb{E}}[\widetilde Y],\end{equation}

where the independence comes from the fact that in the limit, the infection rate is constant and equal to $\alpha y=\alpha {\mathbb{E}}[\widetilde Y]$ . Using this and the fact that ${\mathbb{E}}[\widetilde X]=\frac \lambda \mu -y$ , one gets

(25) \begin{equation}\lambda q =\mu\left(\frac \lambda \mu - y\right)-\beta y + \alpha y\left(\frac \lambda \mu - y\right).\end{equation}

Thus, in the averaging mean-field version of the SIS reactor,

(26) \begin{equation} {\mathbb{E}}[\widetilde X] = \frac{\mu +\beta+\alpha \frac \lambda \mu-\sqrt{(\mu +\beta+\alpha \frac \lambda \mu )^2 -4\alpha\lambda \left(q+\frac \beta \mu \right)}}{2\alpha}\end{equation}

and

(27) \begin{equation} {\mathbb{E}}[\widetilde Y] = \frac \lambda \mu -\frac{\mu +\beta+\alpha \frac \lambda \mu-\sqrt{(\mu +\beta+\alpha \frac \lambda \mu )^2 -4\alpha\lambda \left(q+\frac \beta \mu \right)}}{2\alpha}.\end{equation}

6. SIS TL analysis

The natural parameters of the SIS TL are $(\eta,\mu,\alpha,\beta)$ with $\eta$ the density parameter (that is, the mean number of customers per station, whatever their state), $\mu$ the motion rate, $\alpha$ the infection rate, and $\beta$ the recovery rate. Note that the arrival rate in a station (whatever the state) is then $\lambda=\eta \mu$ . Another natural parameterization is hence $(\lambda,\mu,\alpha,\beta)$ .

6.1. Fixed-point equations for the SIS reactor

If this thermodynamic model admits a stationary regime, then there exists, in the open-loop SIS reactor with parameters $\eta,\mu,\alpha,\beta$ , a value of p, say $p^*$ , such that, for this value of p, the external arrival rate $\lambda p$ of infected customers matches the external departure rate of infected customers, namely $\lambda p^*=\mu {\mathbb{E}}[Y]$ (or equivalently $g(p^*)=p^*$ ). Similarly, we should also have $\lambda q^*= \mu {\mathbb{E}}[X]$ .

Note that since the total arrival rate of infected customers, $\lambda p^* +\alpha {\mathbb{E}}[XY]$ , necessarily matches the total departure rate of infected customers, $(\mu+\beta) {\mathbb{E}}[Y]$ , the fact that $\lambda p^*=\mu {\mathbb{E}}[Y]$ is equivalent to the fact that $\alpha {\mathbb{E}}[XY] = \beta {\mathbb{E}}[Y]$ .

6.1.1. Arrival versus departure rate of infected customers

Let $p_o$ denote the proportion of infected customers in the departure process of the SIS reactor in steady state, namely $ p_o= {\mathbb{E}}[Y] \frac \mu \lambda.$ Here is another representation of $p_0$ obtained by considering departures within the first busy cycle of an M/M/ $\infty$ queue (i.e., the cycle starting when the queue moves from empty to busy and ending at the next event of this type). By the strong law of large numbers, $p_o$ may be represented as $p_o = \frac{{\mathbb{E}} D_I(T)}{{\mathbb{E}} D(T)}$ , where T is the duration of a typical busy cycle, D(T) the number of customers served within the cycle, and $D_I(T)$ the number of customers departed from the system in the infected state within the cycle.

Let us fix strictly positive parameters $\mu,\alpha$ , and $\beta$ and consider $p_o$ as a function of p and $\eta$ only, say $p_o=g(p,\eta)$ . If $\eta$ is fixed too, then we write g(p) instead of $g(p,\eta)$ . Clearly, $g(0)=0$ and $g(1)<1$ .

The next lemmas are proved in Appendix B.

Lemma 5. The function g is an increasing, strictly concave, and differentiable function on $[0, 1]$ .

Lemma 6. Depending on the parameters $\eta$ , $\mu$ , $\alpha$ , and $\beta$ , either there is only one solution $p=0$ to the equation

(28) \begin{align}p=g(p)\end{align}

or there are exactly two solutions, $p=0$ and $p^*\equiv p^*(\eta,\mu,\alpha,\beta)\in (0, 1)$ . Let g^′(0) denote the right derivative of the function g(p) at 0, which exists by the previous lemma. Then $p^*$ exists if and only if $g^{\prime}(0)>1$ .

6.1.2. Main results on fixed point

In this subsection, we consider $p_o$ as a function of the two parameters p and $\eta$ , i.e. $p_o= g(p,\eta)$ . The proof of the following lemma is given in Appendix B.

Lemma 7. The function $\eta \to g^{\prime}(0,\eta)$ is strictly increasing.

Corollary 1. There exists a function $\eta_c^{(s)}(\alpha,\beta,\mu)=\eta_c(\alpha,\beta,\mu) \in [0,\infty)\cup \{\infty\}$ such that

• • $g^{\prime}(0,\eta)\le 1$ $\Leftrightarrow$ $p=0$ is the only solution to (28) $\Leftrightarrow$ $\eta \le \eta_c$ ;

• • $g^{\prime}(0,\eta)>1$ $\Leftrightarrow$ there are two solutions to Equation (28), $p=0$ and $p^*>0$ , $\Leftrightarrow$ $\eta >\eta_c$ .

Proof. These results follow directly from the previous lemmas.

6.2. Bounds

In this subsection, we provide sufficient conditions for the existence and the non-existence of solutions $p^*>0$ to the equation $p_o(p)=p$ . We also show that $\eta_c^{(s)}$ is finite and strictly positive.

Lemma 8. Fix the set of parameters $\alpha$ , $\beta$ , and $\mu$ . For $\eta$ (or equivalently $\lambda$ ) large enough, there exists $p_1 > 0$ such that if $0<p < p_1$ , then the fraction of infected customers of the output is larger than that of the input, namely $p_{o} > p$ .

Proof. An infected individual is guaranteed to leave infected if it departs before it recovers. The probability of this is $\mu/(\mu+\beta)$ . A susceptible individual (referred to as the target individual in what follows in this paragraph) is guaranteed to leave infected if (a) an infected individual (referred to as such in what follows in this paragraph) arrives before the target susceptible individual departs (the probability of this is $\lambda p/(\lambda p + \mu)$ ); then (b) the infected individual infects the target individual before the departure of either of them and before the recovery of the infected one (the probability of this is $\alpha/(\alpha+2\mu+\beta)$ ); and then either (c) the target individual departs before its own recovery (the probability of this is $\mu/(\mu+\beta)$ ), or (c^′) the target individual recovers before the departure of either one and before the recovery of the infected one (the probability of this is $\beta/(2\mu+2\beta)$ ) but gets infected by the infected one again, and so on. Thus,

(29) \begin{align}p_{o} \ge p \frac{\mu}{\mu+\beta} + (1-p) \frac{\lambda p}{\lambda p + \mu} \kappa,\end{align}

where

(30) \begin{align}\kappa = \frac{\alpha}{\alpha+2 \mu + \beta} \left(\frac{\mu}{\mu+\beta} + \frac{\beta}{2(\mu+\beta)}\kappa\right) = \frac{2 \alpha \mu}{2(\mu+\beta)(\alpha+2\mu + \beta) - \alpha \beta}.\end{align}

Note that $p_o>p$ follows if the right-hand side of (29) is strictly bigger than p, which is equivalent to $\frac{\mu}{\mu+\beta} + (1-p) \cdot \frac{\lambda \kappa}{\lambda p+\mu} >1$ , or to $(1-p)\frac{\lambda \kappa}{\lambda p+\mu} > \frac{\beta}{\mu+\beta}.$

Assume that, for some $C>1$ ,

(31) \begin{equation} \lambda \kappa > \frac{C\mu \beta}{\mu+\beta};\end{equation}

then $p_o > p$ for $ p < p_1 \equiv \frac{C-1}{\lambda/\mu +C}, $ so that there exists a $p^*>0$ solving $p_o(p)=p$ .

Corollary 2. It follows from Lemma 8 that for all $\alpha,\beta,\mu$ , the value of $\eta_c^{(s)}$ in Corollary 1 is finite, and more precisely

(32) \begin{equation}\eta_c^{(s)} \le \frac 1 \kappa \frac{\beta}{\mu+\beta},\end{equation}

with $\kappa$ defined in (30).

Here is another observation.

Lemma 9. Fix the set of parameters $\alpha$ , $\beta$ , and $\mu$ . For $\eta$ (or equivalently $\lambda$ ) small enough, $p_{o} < p$ for all p.

Proof. An individual is guaranteed to leave the system as susceptible in one of two scenarios. In the first scenario, it arrives as susceptible, finds no infected individuals in the system upon its arrival, and leaves before the arrival of an infected individual. The probability of this is $ (1-p) {\mathbb{P}}(Y=0) \frac{\mu}{\mu+\lambda p}$ , which can be bounded from below by

\begin{align*}& (1-p)(1-{\mathbb{E}}(Y)) \left(1-\frac{\lambda p}{\mu+\lambda p}\right) = (1-p)\left(1-p_{o} \frac{\lambda}{\mu}\right)\left(1-p\frac{\lambda}{\mu}\right)\\ & \ge \left(1-p\left(1+\frac{\lambda}{\mu}\right)\right)\left(1-p_{o} \frac{\lambda}{\mu}\right) \ge 1-p\left(1+\frac{\lambda}{\mu}\right) -p_{o} \frac{\lambda}{\mu}.\end{align*}

Finally, for a fixed $\mu$ and a small $\varepsilon>0$ , one can take $\lambda \le \varepsilon \mu$ so that the above is bounded from below by $ 1-p(1+\varepsilon) - \varepsilon p_{o}.$

In the second scenario, an individual arrives infected, finds no other individual in the system, recovers before any other individual arrives and then leaves before any infected individual arrives. The probability of this is

$$p e^{-\lambda/\mu} \frac{\beta}{\beta+\lambda+\mu}\frac{\mu}{\mu+\lambda p} \ge p \left(1-\frac{\lambda}{\mu}\right)\frac{\beta}{\beta+\lambda+\mu}\left(1-\frac{\lambda p}{\mu}\right) \ge p \left(1-\frac{\lambda}{\mu}\right)^2\frac{\beta}{\beta+\lambda+\mu}.$$

With the choice of small $\lambda$ already made, the above is bounded from below by

$$p(1-\varepsilon)^2 \frac{\beta}{\beta+\mu+\varepsilon\mu} \ge p(1-\varepsilon)^2 \frac{\beta}{\beta+\mu} \left(1-\varepsilon \frac{\mu}{\beta+\mu}\right) \ge p c (1-3 \varepsilon),$$

where $c = \beta/(\beta+\mu)$ . Combining the two scenarios, we conclude

$$1-p_{o} \ge 1-p(1+\varepsilon) - \varepsilon p_{o} + p c (1-3\varepsilon),$$

or equivalently

$$p_{o} \le p \frac{1-c+3 c\varepsilon}{1-\varepsilon} < p,$$

as long as $\varepsilon < c/(2+3c)$ .

From the proof of Lemma 9, one gets the following bound.

Corollary 3. For all $\alpha,\beta,\mu$ , the value of $\eta_c^{(s)}$ in Corollary 1 is strictly positive, and more precisely

(33) \begin{equation}\eta_c^{(s)} \ge \frac{\beta}{2\mu+5\beta}.\end{equation}

Remark 5. Note that the last lower bound does not depend on $\alpha$ . This may look surprising at first glance. The fact that this bound holds even for $\alpha =\infty$ can be explained as follows. For any fixed $\eta >0$ , in the M/M/ $\infty$ queue, there are busy cycles with only one customer. The smaller $\eta$ is, the closer to 1 is the probability $\mu/(\lambda+\mu)$ that a typical busy cycle will have only one customer to be served. Call such a cycle a 1-cycle. If a customer enters the queue as infected and if it is served in a 1-cycle, it has a chance close to $\beta/(\beta+\mu)$ of recovering before leaving the queue; and if it susceptible, it leaves the queue susceptible after service in a 1-cycle queue. So $p_0>p$ uniformly in all values of $\alpha$ , for all $\eta$ sufficiently small.

6.3. Survival versus extinction

The limiting system has only three parameters. Indeed, one can always take, say, $\beta=1$ by a time rescaling, so that only the other three parameters remain. Consider the parameterization $(\alpha,\mu,\eta)$ and the associated positive orthant.

6.3.1. Phase diagram in $\eta$

The following two results rely on the definitions of extinction and survival given in Definition 1. They show that the SIS TL admits a simple phase diagram with respect to $\eta$ , with critical value equal to $\eta_c^{(s)}$ as defined above.

Theorem 1. If the SIS thermodynamic propagation of chaos ansatz holds, then, in the SIS TL, there exists a constant $\eta_c$ such that there is survival if $\eta > \eta_c^{(s)}$ .

Proof. From Corollary 1, if $\eta > \eta_c^{(s)}$ , there exists $p^*>0$ such that $g(p^*)=p^*$ . If the ansatz holds, take as initial distribution in the nonlinear Markov representation of the SIS TL the law of the open SIS reactor with infected input rate $p=p^*$ . This distribution is a stationary distribution of this system.

Theorem 2. If the SIS thermodynamic propagation of chaos ansatz holds, then, in the SIS TL, there is strong extinction if $\eta \le \eta_c^{(s)}$ .

Proof. The proof is given in Appendix E.

Remark 6. Theorem 1 only shows that there exists an initial distribution ${\mathcal P}^*$ of the SIS TL that makes this limiting system stationary. A stronger result is proved in Corollary 6 in the appendix: for all initial distributions which are stochastically larger than ${\mathcal P}^*$ , the distribution of the SIS TL converges to ${\mathcal P}^*$ as time tends to infinity.

6.3.2. Phase diagrams in $\alpha$ and in $\beta$

Consider the SIS reactor. Fix all parameters except $\alpha$ (resp. $\beta$ ) and consider $0<\alpha_1<\alpha_2$ (resp. $0<\beta_2<\beta_1$ ). It is shown in Appendix C that there exists a coupling of the two associated models such that $X_1(t)+Y_1(t)=X_2(t)+Y_2(t)\,=\!:\,N(t)$ and $Y_1(t)\le Y_2(t)$ almost surely (a.s.), for all $t\ge 0$ , given that the two models start from the same initial condition $X_1(0)=X_2(0)$ and $Y_1(0)=Y_2(0)$ a.s.

Consider now a finite closed network of SIS reactors with N stations and $K_N$ customers. It is shown in Appendix C that the same monotonicity properties hold.

By arguments similar to those used with respect to $\eta$ , we have the following result.

Theorem 3. If the SIS thermodynamic propagation of chaos ansatz holds, then, in the SIS TL, there exists a constant $\alpha_c^{(s)}$ (resp. $\beta_c^{(s)}$ ) such that there is survival if $\alpha > \alpha_c^{(s)}$ (resp. $\beta < \beta_c^{(s)}$ ) and strong extinction otherwise.

6.3.3. Other phase diagrams

Phase diagrams with respect to $\mu$ will only be discussed numerically in Section 10. An example of a question of interest is whether there is a simple (monotonic as above) phase diagram with respect to $\mu$ when $\alpha$ , $\beta$ , and $\eta$ are fixed.

6.4. First- and second-order relations in the thermodynamic limit

In the thermodynamic limit, the first-order relation of Lemma 1 simplifies to

(34) \begin{equation}\alpha {\mathbb{E}}[XY] = \beta {\mathbb{E}}[Y].\end{equation}

Consider now the second-order relations of Lemma 2. Equation (6) can be rewritten as

(35) \begin{equation}(\eta\mu p + \mu + \beta ) p \eta + \alpha {\mathbb{E}}\big[ XY^2\big] =(\mu +\beta) {\mathbb{E}}[Y^2]\end{equation}

or equivalently

(36) \begin{align} (\mu + \beta ) ({\mathbb{E}}[Y^2] -{\mathbb{E}}[Y]^2 -{\mathbb{E}}[Y]) & = \alpha {\mathbb{E}}[XY] {\mathbb{E}}\left[Y \frac {\alpha XY}{{\mathbb{E}}[\alpha XY]}\right] -\beta{\mathbb{E}}[Y]\nonumber \\& = \beta {\mathbb{E}}[Y]({\mathbb{E}}_I^0[Y^-]-{\mathbb{E}}[Y]).\end{align}

Similarly, (7) can be rewritten as

(37) \begin{equation}(\eta\mu q + \mu) \eta q +(\alpha+\beta) {\mathbb{E}}[XY] =\alpha {\mathbb{E}}\big[ X^2Y\big] +\mu {\mathbb{E}}[X^2]\end{equation}

or equivalently

(38) \begin{eqnarray}&& \mu \left({\mathbb{E}}[X^2] -{\mathbb{E}}[X]^2-{\mathbb{E}}[X]\right) (\alpha+\beta) {\mathbb{E}}[XY] -\alpha{\mathbb{E}}[XY] {\mathbb{E}}\left[X \frac {\alpha XY}{{\mathbb{E}}[\alpha XY]}\right]\nonumber\\ & =\, & {\mathbb{E}}[XY] \alpha \left( 1 + \frac{\beta}{\alpha} - {\mathbb{E}}_I^0[X^-]\right) = {\mathbb{E}}[XY] \alpha \left(\frac{\beta}{\alpha} - {\mathbb{E}}_I^0[X^+]\right).\end{eqnarray}

Similarly, Equation (57) can be simplified to

(39) \begin{equation}\beta ({\mathbb{E}}_I^0[Y^-]-{\mathbb{E}}_R^0[Y^+]) = \mu {\mathbb{E}}_{D_I}^0[Y^+] -\eta\mu p,\end{equation}

whereas (58) can be simplified to

(40) \begin{equation}\beta( {\mathbb{E}}_{R}[X^-] - {\mathbb{E}}_{I}[ X^+])= \mu \frac q p {\mathbb{E}}_{D_s}[X^+]-\eta\mu q \frac q p.\end{equation}

7. AIR TL analysis

Let

(41) \begin{equation}\eta_c^{(a)} \,:\!=\, \frac \beta \alpha.\end{equation}

Theorem 4. Under the AIR TL propagation of chaos ansatz, if $\eta \le \eta_c^{(a)}$ , then there is weak extinction, whereas if $\eta> \eta_c^{(a)}$ , there is survival. In addition, if there is survival, in the stationary regime of the thermodynamic limit, ${\mathbb{E}}[\widetilde X] = \frac \beta \alpha$ , ${\mathbb{E}}[\widetilde Y]= \eta - \frac \beta \alpha$ , $1-\widetilde p^*= \widetilde q^* = \frac{\beta}{\eta \alpha}$ , and $ \widetilde X$ and $\widetilde Y$ are independent and Poisson. In addition, the departure rate from a station is $\lambda=\eta \mu$ .

If there is extinction, in the stationary regime, ${\mathbb{E}}[\widetilde X] = \frac \beta \alpha $ , ${\mathbb{E}}[\widetilde Y]= 0$ , $ 1-\widetilde p^*= \widetilde q^* = 1$ , and $ \widetilde X$ is Poisson. In addition, the departure rate from a station is $\lambda=\eta \mu$ .

Proof. Assuming existence of the thermodynamic limit and its convergence to a stationary distribution, the result is immediate from plugging in $y=p \eta$ in (25).

The AIR phase diagram is hence quite explicit. We have $\eta_c= \frac{\beta}{\alpha}$ , which does not depend on $\mu$ . In addition, the following continuity property holds: when $\eta\downarrow \eta_c$ , ${\mathbb{E}}[\widetilde Y] \downarrow 0$ . Similar statements can be formulated with respect to any parameter other than $\eta$ .

8. DOCS TL analysis

Since the behavior of a station in the DOCS TL is a specific instance of that of a station in the routing mean-field model, the following two results hold on the former: (i) The assumption that the ‘external’ arrival rate is $\lambda$ is equivalent to the assumption that the mean number of customers (of both types) in a station in steady state is $\frac{\lambda}{\mu}$ (see Equation (20)). By symmetry, this is equivalent to assuming that $\lim_{N\to \infty} K_N/N= \lambda/\mu\,:\!=\,\eta$ in the DOCS TL. (ii) The condition $\lambda p^*= \mu {\mathbb{E}}[\widehat Y]$ is equivalent to $\alpha {\mathbb{E}}[\widehat X \widehat Y]= \beta {\mathbb{E}}[\widehat Y]$ in view of (19). In words, in the DOCS TL, the stationary rate of ‘in-station’ infections matches the stationary rate of ‘in-station’ recoveries.

8.1. Analytical solution

In this section we use p in place of $p^*$ to lighten the notation.

8.1.1. Rate conservation equations

As shown above, in the thermodynamic limit, we have

(42) \begin{eqnarray}\lambda p & \,=\, & \mu {\mathbb{E}}[\widehat Y] \end{eqnarray}

(in words, the rate of ‘natural’ migration of infected customers matches that of ‘external’ arrivals of infected customers),

(43) \begin{eqnarray}\lambda q & \,=\, & \mu {\mathbb{E}}[\widehat X] \end{eqnarray}

(in words, the rate of ‘natural’ migration of susceptible customers matches that of ‘external’ arrivals of susceptible customers), and

(44) \begin{eqnarray}\alpha {\mathbb{E}}[\widehat X \widehat Y]& \,=\, & \beta {\mathbb{E}}[\widehat Y]\end{eqnarray}

(in words, the rate of ‘infections’ matches that of ‘recoveries’).

It follows that

$${\mathbb{E}}[\widehat Y] = \widehat \theta= \frac {\lambda p +\alpha {\mathbb{E}}[\widehat X \widehat Y]} {\mu + \beta}= \frac {\lambda p +\beta \widehat \theta} {\mu + \beta};$$

that is, $\widehat \theta=\frac{\lambda p}{\mu}$ , which is consistent with (42).

As for second-order relations, when using the fact that $\widehat Y$ is Poisson, one gets that (21) brings no information, whereas (22) leads to

(45) \begin{equation}\mu \left({\mathbb{E}}[\widehat X^2] -{\mathbb{E}}[\widehat X] -{\mathbb{E}}[\widehat X]^2 \right)= \alpha \left( {\mathbb{E}}[\widehat X\widehat Y] {\mathbb{E}}[\widehat X]+ {\mathbb{E}}[\widehat X\widehat Y] - {\mathbb{E}}[\widehat X^2\widehat Y] \right)\end{equation}

and (23) to

(46) \begin{equation}\lambda q {\mathbb{E}}[\widehat Y]+ \lambda p {\mathbb{E}}[\widehat X]+ \beta {\mathbb{E}}[\widehat Y] \frac \lambda \mu= (\beta + 2 \mu) \frac \beta \alpha {\mathbb{E}}[\widehat Y]+ \alpha {\mathbb{E}}[\widehat X \widehat Y^2].\end{equation}

8.1.2. Analytic treatment based on the DOCS ODE solution

The explicit solution of the open DOCS model is now used to analyze this thermodynamic limit. We recall that, in the DOCS TL, each station behaves as an open DOCS reactor with susceptible input rate

\begin{eqnarray*}\lambda q + \beta {\mathbb{E}}[\widehat Y] =\mu {\mathbb{E}}[\widehat X] + \frac{\beta}{\mu} \lambda p = \lambda q + \frac{\beta}{\mu} \lambda p,\end{eqnarray*}

infected input rate

\begin{eqnarray*}\lambda p + \alpha {\mathbb{E}}[\widehat X\widehat Y] & \,=\, & (\mu + \beta) {\mathbb{E}}[\widehat Y]= \frac{\mu+\beta}{\mu} \lambda p,\end{eqnarray*}

and susceptible departure rate $\nu=\mu +\beta$ . Hence, it follows from (16) that

(47) \begin{equation} {\mathbb{E}}[\widehat X] =\frac {\lambda q + \frac {\beta}{\mu} \lambda p} {\mu+\beta +\alpha }\int_{0}^1e^{-\frac{\lambda p \alpha^2}{\mu(\mu +\beta +\alpha)^2} (1-t)}t^{\frac \mu {\mu +\beta +\alpha} +\lambda p\frac{(\mu+\beta)\alpha}{\mu (\mu+\beta+\alpha)^2}-1} dt .\end{equation}

Since $\mu {\mathbb{E}}[\widehat X]= \lambda q$ , we have the following.

Proposition 1. In the DOCS TL, q satisfies the fixed-point relation

(48) \begin{equation}q = \frac{ q \mu + p \beta }{\mu+\beta +\alpha }\int_0^1e^{-\frac{\eta p \alpha^2}{(\mu +\beta +\alpha)^2} (1-t)}t^{\frac \mu {\mu +\beta +\alpha} +\eta p\frac{(\mu+\beta)\alpha}{(\mu+\beta+\alpha)^2}-1} dt ,\end{equation}

where the right-hand side is the analytic expression for $\frac{{\mathbb{E}}[\widehat X]}\eta$ in this context.

8.1.3. Monotonicity and convexity properties

Here we study the properties of the right-hand side of Equation (48) with respect to various parameters.

We consider the dependence on $\eta$ first. Rewriting the right-hand side of Equation (48) as

(49) \begin{align}\frac{q\mu + p\beta}{\mu+\alpha+\beta}\int_0^1 e^{ -\eta p \left( \frac{\alpha^2}{(\mu+\alpha+\beta)^2}(1-t)+ \frac{(\mu+\beta)\alpha}{(\mu+\beta+\alpha)^2} |\log t|\right)}t^{\frac \mu {\mu +\beta +\alpha} -1} dt,\end{align}

one gets that this right-hand side is a strictly decreasing function of $\eta$ when all other parameters are fixed.

The dependence on $\mu$ is more complicated. The integrand in the right-hand side of (48) is a monotone increasing function of $\mu$ since $\frac{(\mu+\beta)\alpha}{\mu(\mu+\beta+\alpha)^2}$ as a function of $\mu$ is decreasing. However, the coefficient $\frac{q\mu+p\beta}{\mu+\alpha+\beta}$ is equal to $q+ \frac{p\beta - q (\alpha+\beta)}{\mu+\alpha+\beta}$ , which is either an increasing or decreasing function of $\mu$ , depending on the sign of $p\beta - q (\alpha+\beta)$ .

Consider now the dependence in p. Clearly,

(50) \begin{align}p\to I(p)\,:\!=\,\int_0^1 e^{ -\eta \left( \frac{p\alpha^2}{(\mu+\alpha+\beta)^2}(1-t)+ \frac{p(\mu+\beta)\alpha}{(\mu+\beta+\alpha)^2} |\log t|\right)}t^{\frac \mu {\mu +\beta +\alpha} -1}dt\end{align}

is a positive and strictly decreasing function of p, when all other parameters $\eta,\mu,\alpha,\beta$ are fixed. The quantity

\begin{align*}I^{\prime\prime}(p)= \int_0^1 h_1^2(t) \exp ({-}p h_1(t)) h_2(t) dt\end{align*}

is positive, since

\begin{align*}h_1(t)\,:\!=\, \frac{\eta\alpha^2}{(\mu+\alpha+\beta)^2}(1-t) + \frac{\eta(\mu+\beta)\alpha}{(\mu+\beta+\alpha)^2} |\log t| \quad \text{and} \quad h_2(t)\,:\!=\,t^{\frac{\mu}{\mu+\beta+\alpha}-1}\end{align*}

are two strictly positive functions, and finite since $\lim_{t\to 0} t^r \log t = 0$ for any $r>0$ .

Furthermore, the numerator $q\mu + p\beta$ in the prefactor of the right-hand side of (49) may be represented as $\mu + p(\beta-\mu)$ , which is strictly positive. Hence, if $\beta\le \mu$ , the function in the right-hand side of (48) is strictly decreasing since its derivative with respect to p is

\begin{align*}D(p) \,:\!=\, \frac{1}{\mu+\alpha+\beta} \left((\beta-\mu)I(p) + (\mu+ p(\beta-\mu)) I{^{\prime}}(p)) \right) <0, \end{align*}

and strictly convex since its second derivative is

\begin{align*} \frac{1}{\mu+\alpha+\beta} \left(2(\beta-\mu)I^{\prime}(p) + (\mu+ p(\beta-\mu)) I{^{\prime\prime}}(p) \right) >0. \end{align*}

In particular,

(51) \begin{eqnarray} D(0) & \,=\, & \frac{\beta}{\mu}-1 -\eta\left( \frac{\alpha(\mu+\beta)}{\mu(\mu+\alpha +\beta)} + \frac{\alpha^2}{(\mu+\alpha+\beta)(2\mu+\alpha +\beta)} \right)\nonumber\\ & \equiv\, &\frac{\beta}{\mu}-1- \eta \cdot \frac{\alpha}{\mu}\left(1+\frac{\alpha}{2\mu+\beta}\right)^{-1}. \end{eqnarray}

8.2. Phase diagram

Let

(52) \begin{equation}\lambda_c^{(d)}\,:\!=\,\frac{\beta\mu}{\alpha}\left(1+\frac{\alpha}{2\mu+\beta}\right),\qquad \eta_c^{(d)} \,:\!=\, \frac{l_c^{(d)}}{\mu}= \frac{\beta}{\alpha}\left(1+\frac{\alpha}{2\mu+\beta}\right).\end{equation}

Here is an analogue of Corollary 1 for DOCS.

Lemma 10. In the DOCS TL, if $\beta\le \mu$ , then

• • $p=0$ is the only solution to (48) $\Leftrightarrow$ $\eta \le \eta_c^{(d)}$ ;

• • there are two solutions to Equation (48) ( $p=0$ and $p^*>0$ ) $\Leftrightarrow$ $\eta > \eta_c^{(d)}$ .

Proof. The left-hand side and the right-hand side of (48) coincide at $p=0$ , where both are equal to 1. At $p=1$ , the left-hand side of (48) is 0, whereas the right-hand side of (48) is positive. By (51), we have $D(0)<-1$ if and only if $\eta > \eta_c^{(d)}$ . When $\beta\le \mu$ , the right-hand side of (48) is a decreasing and convex function of p. Hence, if the first derivative of the right-hand side of (48) at 0 is less than $-1$ , then there is exactly one positive solution to (48), whereas if it is greater than or equal to $-1$ , there is no such solution.

In the general case, there is at least one positive solution if the first derivative of the right-hand side of (48) at 0 is less than $-1$ .

Theorem 5. Under the DOCS thermodynamic propagation of chaos ansatz, if $\eta\le\eta_c^{(d)}$ , then there is weak extinction, whereas if $\eta>\eta_c^{(d)}$ , then there is survival.

Note that the statement on weak extinction in the last theorem is only proved under the assumption $\beta\le \mu$ . There is numerical evidence that it also holds without this condition.

8.3. Interpretation of the results

Monotonicity. In DOCS, two contradictory phenomena are present:

1. 1. A larger motion rate implies smaller population density, which lowers local epidemic spread.

2. 2. A larger motion rate implies more global dissemination of the epidemic.

This possibly explains the following facts:

1. (a) The quantity $\eta_c^{(d)}$ is decreasing in $\mu$ (the motion rate); that is, if the population density per reactor is fixed, then increasing motion makes the system less safe. This is because only the phenomenon 2 is at play; the phenomenon 1 is blocked in this setting where $\eta$ is fixed.

2. (b) The quantity $\lambda_c^{(d)}$ is increasing in $\mu$ ; that is, if the overall arrival rate in a reactor is fixed, then increasing motion leads to a safer system. In this case the phenomena 1 and 2 compete and our formula shows that the phenomenon 1 (or locality) dominates.

9. On the thresholds of the thermodynamic limits

Here is first a general observation on the connections between the properties of the open reactors and the thresholds (with respect to $\eta$ ) of the thermodynamic limits. We have shown that survival in a thermodynamic limit is guaranteed as soon as the derivative at 0 of the $p\to p_0(p)$ function of the associated reactor is more than 1. Classical busy-cycle arguments show that the latter derivative can in turn be reinterpreted as the mean number of susceptible customers that a single infected customer arriving in the open reactor infects before leaving the reactor, given that the latter has only susceptible customers upon the arrival in question. This is precisely the $R_0$ parameter of epidemiologists. For SIS, the result is stronger: there is survival if the mean number of susceptible customers that a single infected customer infects is more than 1 and strong extinction otherwise. Of course, this mean number depends on the system considered. For AIR, the evaluation of this mean number is based on an averaging over the geometries of the random environments that a customer sees. For SIS or DOCS the evaluation takes the random and dynamic nature of the environment into account.

We now make some further observations on the thermodynamic limit thresholds in terms of the last mean value (or $R_0$ ) interpretation when the scales of the $(\lambda,\mu)$ or the $(\alpha,\beta)$ parameters, respectively, are changed.

Consider first a family of thermodynamic limits for DOCS indexed by n, and assume that $\lambda_n$ and $\mu_n$ both tend to infinity in such a way that the limit of the ratio $\lambda_n/\mu_n$ is a positive constant $\eta$ , whereas $\alpha$ and $\beta$ stay constant. Then $\eta_c^{(d,n)}$ tends to $\eta_c^{(a)}=\beta/\alpha$ . Here is a probabilistic interpretation of this fact. Take a unique infected customer in a large closed network of DOCS reactors, and assume that apart from this infected customer, the system contains only susceptible customers. As $\mu$ is very large, the infected customer travels very fast and visits many stations before recovering. The mean number of customers it infects before recovering is $N\,:\!=\, \eta \alpha/\beta$ . This formula uses that fact that the recovery time has mean $1/\beta$ , the infection rate is $\alpha$ , and some homogenization takes place over the population of susceptible customers seen before recovery, due to fast motion. In this limit ( $\lambda$ and $\mu$ high), the condition $\eta < \eta_c^{(d)}$ is then equivalent to the branching criticality condition $N < 1$ , which is that of AIR. The argument should extend to SIS: under the same assumptions, the threshold for SIS $\eta_c^{(s)}$ should tend to $\eta_c^{(a)}=\beta/\alpha$ as well.

Consider now a family of DOCS TLs, also indexed by n, and where $\beta_n$ and $\alpha_n$ both tend to infinity in such a way that the limit of the ratio $\beta_n/\alpha_n$ is a positive constant $\kappa$ , whereas $\lambda$ and $\mu$ stay constant. It is easy to see that $\eta_c^{(d)}$ tends to $1+\kappa$ . The condition $\eta> \eta_c^{(d)}$ then reads $M\,:\!=\, \eta \alpha/(\alpha+\beta) > 1$ ; that is, it is again like a branching condition stating that the mean number M of customers infected by a single infected customer is more than 1. Indeed, a single infected customer arriving at a station finds a mean of $\eta$ susceptible customers. For a tagged susceptible customer, start two exponential clocks, one of parameter $\alpha$ (for its own infection), and one of parameter $\beta$ (for the departure of the infected customer). The chance that the tagged customer gets infected is hence $\alpha/(\alpha+\beta)$ . This justifies the interpretation of M. Now each infected customer then immediately leaves for another queue far away, where its fate is the same and independent. This justifies the branching (independence) interpretation. Note that $\mu$ has disappeared because it is negligible with respect to $\alpha$ and $\beta$ . This interpretation is specific to DOCS.

10. Comparison and numerical results

10.1. Comparison of plain SIS TL and AIR TL

We conjecture that, in the stationary regime of the SIS TL, there is a negative correlation between X and Y. This negative correlation property is substantiated by simulation but unproved at this stage. It is proved in the arXiv version of this paper [2] that if this negative correlation property holds, then $\eta_c^{(s)}\ge \eta_c^{(a)}$ , that is, SIS is safer than AIR. A potential interpretation is as follows: replacing the infection rate $\alpha Y$ by $\alpha {\mathbb{E}}[Y]$ at the same time decreases the infection rate when Y is large and increases it when Y is small. In the thermodynamic limit, this last fact dominates and makes it more likely for the epidemic to survive in AIR than in plain SIS.

10.2. Comparison of plain SIS TL and DOCS TL

In this subsection, we use a mix of simulation and analysis to compare $\eta_c$ in the thermodynamic limits of SIS and DOCS. The main conclusion is that depending on the parameters, either SIS or DOCS may be safer. The evaluation of $\lambda_c^{(s)}$ is based on Theorems 1 and 2. The simulation of $\eta_c^{(s)}$ is based on its characterization in Corollary 1 in terms of the derivative at 0 of the function $p_0(p)$ . For DOCS, we use the evaluation of $\lambda_c^{(d)}$ in Lemma 10.

Figure 6 features a situation where both $\alpha$ and $\beta$ are moderate. We observe that $\eta_c^{(d)}< \eta_c^{(s)}$ , or equivalently, SIS is safer than DOCS.

Figure 6. Comparison of $\eta_c^{(s)}$ and $\eta_c^{(d)}$ for $\mu=1$ , $\beta=1$ , and $\alpha=1$ .

The left panel of Figure 7 features a situation where $\alpha$ is large and $\beta$ moderate. We observe that $\eta_c^{(s)}< \eta_c^{(d)}$ , or equivalently, DOCS is safer than SIS. One possible explanation is that although the mean population in each system is the same, in DOCS, in any station with infection present, infected customers leave immediately, which is safer than the SIS case where they stay and infect all other susceptible customers present in the station.

Figure 7. Left: comparison of $\eta_c^{(s)}$ and $\eta_c^{(d)}$ for $\mu=1$ , $\beta=1$ , and $\alpha=20$ ; Right: comparison of $\eta_c^{(s)}$ and $\eta_c^{(d)}$ for $\mu=1$ , $\beta=10$ , and $\alpha=1$ . On the left it is not clear which curve is higher at low values of $\lambda$ , but it is clear that the curve corresponding to DOCS is lower for high values of $\lambda$ and that, crucially, it reaches 1 later than the curve for SIS. On the right it is clear that the curve corresponding to DOCS reaches 1 earlier than that corresponding to SIS. The curves in both panels are produced by simulation, and for DOCS we also provide the exact curve that follows from our analytical results.

One can observe in Figure 6 that the curve corresponding to the derivative at $p=0$ for DOCS is higher (resp. lower) than that for SIS for low (resp. high) values of $\lambda$ and, crucially, reaches 1 at a lower value of $\lambda$ . Both curves are produced by simulation. We also present the exact curve for DOCS that follows from our analytic results; this can be observed to agree with simulations.

The right panel of Figure 7 features a situation where $\beta$ is large and $\alpha$ moderate. Here SIS is safer than DOCS again. The interpretation is that although the mean number of individuals per station is the same in either case, in DOCS any station with many infected customers is more quickly depleted because of their fast recovery.

10.3. Comparison of SIS-DOCS TL and AIR TL

It follows directly from the expressions for $\eta_c$ in both cases that $\eta_c^{(d)}>\eta_c^{(a)}$ . This can be rephrased by saying that DOCS is safer than AIR. A possible interpretation is again that extinction happens when Y fluctuates to small values throughout all reactors of a large system. Fixing Y to its means as in AIR, in the thermodynamic limit, makes these fluctuations less likely. This possibly explains why the AIR system is less safe than the DOCS system.

Figure 8. Graphs of the derivative at $p=0$ of g(p) in the SIS reactor as function of $\mu$ when $\eta$ , $\alpha$ , and $\beta$ are fixed. On the left, $\eta=\alpha=\beta=1$ ; on the right, $\eta=3$ , $\alpha=5$ , $\beta=1$ .

10.4. Phase diagram in $\mu$

For the SIS reactor and SIS TL, we have already characterized the phase diagrams: they turn out to be of the threshold type (survival in one interval, extinction in another). Another interesting question is what such a phase diagram looks like in $\mu$ . More specifically, one may be interested in fixing $\eta$ , $\alpha$ , and $\beta$ and asking for which values of $\mu$ the epidemic survives and for which it does not.

We have shown that, in order to answer such a question, one needs to examine the derivative at $p=0$ of the function g(p). Our findings were based on the monotonicity of this derivative with respect to the relevant parameters.

Numerical evidence shows that such monotonicity with respect to $\mu$ does not always hold. Indeed, Figure 8 contains graphs of the derivative as a function of $\mu$ , when the other parameters are fixed, in two scenarios. On the right, $\eta=3$ , $\alpha=5$ , $\beta=1$ , and one can observe the absence of monotonicity and convexity. On the left, however, when $\eta=\alpha=\beta=1$ , it appears that the derivative is monotone. This evidence suggests that the phase diagram in $\mu$ may be more complicated than in the case of other parameters. This is in line with what was observed in [3]. We plan to address the subject further in future research.

11. Conclusion and future research

We have rigorously proved the structure of the phase diagram of the SIS model under the assumption that the Poisson hypothesis holds. Future research on the basic model will consist in first proving the Poisson hypothesis (ansatz). Another key objective on the basic SIS model will be to establish the phase diagram for parameters other than population density. It would be nice to complement this with computational results like those established for the AIR and DOCS variants of the model. Several further variants of the basic model can also be considered, such as SIRS-type models where individuals go through a recovery phase (where they cannot be infected) before becoming susceptible again. We will also study further spatial SIS dynamics. Other basic queueing models, for instance finite-capacity queues, can also be considered. In fact, such epidemics can be devised on virtually all queueing network models in the literature.