Frost heave

Abstract

The deformation of the ground surface that is produced by frost heave has motivated almost a century of concerted laboratory, field and theoretical studies. Well before the development of equipment capable of resolving the microscopic films that support liquid transport towards growing ice lenses, early investigators predicted their occurrence and noted their importance. Idealized experiments continue to prompt theoretical advances that have been combined to develop predictive models for the macroscopic frost-heave characteristics that are seen in the field. This contribution highlights steps on the road to our current understanding of the physical interactions that control how ice forms in unconsolidated porous media.

Introduction

• Something there is that doesn’t love a wall,

• That sends the frozen-ground-swell under it,

• And spills the upper boulders in the sun …

‘Mending Wall’ (Frost, 1914)

The same year ‘Mending Wall’ was published, Stephen Taber began systematic investigations into Frost’s ‘something’: the forces exerted by growing crystals and the ‘needle-like ice columns that are commonly found on bare clayey soils after a cool night’ (Taber, 1916; see Fig. 1). A series of experiments led Taber to correctly deduce that the frozen-ground-swell that results from frost heave is unrelated to the reduction in water density upon freezing and is caused instead by liquid migration that supplies growing ice lenses (Taber, 1929, 1930). The precise mechanisms responsible for transport long remained elusive, though much was already known about the transport pathways. Earlier work had shown that surface energy (responsible for ‘capillary forces’) causes liquid to persist in thermodynamic equilibrium at subzero temperatures in fine-grained soils, and Taber (1916) further speculated that liquid transport ‘furnishing the material necessary for growth to a crystal surface that is under pressure, may consist of a layer so thin that the space must be classed as subcapillary rather than capillary in size’. The generation of such thin liquid (sometimes termed liquid-like, e.g. Gilpin, 1979) layers is now referred to as interfacial premelting (e.g. Dash, 1989; Dash and others, 1995, 2006), and the microscopic interactions that cause this behavior and lead to the liquid transport that produces frost heave have been rigorously incorporated within a continuum framework to enable predictions of the macroscopic features of heave (Rempel and others, 2004; Rempel, 2007, 2011). A review of the development of this contemporary understanding of frost heave follows.

Fig. 1. Needle ice growing from a dead branch, shown with a leaf for scale. Photograph by N. Page.

Freezing and Drying

The extension of roadways and rail lines in the north motivated substantial engineering efforts to understand the causes of frost damage and develop strategies to prevent it. Working for the Swedish Road Institute in Stockholm, Gunnar Beskow (1935) conducted extensive field and laboratory studies into the conditions under which varying degrees of frost damage would occur. Beskow recognized that the distribution of ice in soils, whether segregated into lenses that grow while excluding soil particles or distributed throughout the pore space without causing heave, depends on both environmental factors, such as the rate of freezing and the overburden pressure, and characteristics of the soil itself. Those soils most susceptible to heave are sufficiently fine-grained to enable significant quantities of liquid water to be held above the water table by capillary forces under warmer conditions, yet they are also sufficiently coarsegrained and permeable to enable a continued supply of unfrozen water to the segregated ice when freezing occurs. Though he noted the importance of ‘adsorbed’ water films (i.e. the subcapillary or interfacially premelted layers referred to above) as liquid conduits between soil grains and ice crystals during freezing, Beskow’s description of water migration towards the freezing front relied on ‘capillary suction’ associated with the curvature and surface energy of the ice-liquid interface in confined regions.

The misattribution of capillarity as the mechanism driving water transport in freezing soils is understandable. Along a curved ice-liquid interface, such as develops between sediment particles (see the schematic diagram in Fig. 2), the depression of the equilibrium temperature below the normal melting point is accompanied by a pressure difference between the ice and the adjacent liquid that is equal to the product of the curvature and the surface energy γil. Early models for liquid transport during freezing (e.g. Everett, 1961) identified the ice pressure with the overburden and suggested that liquid transport was a consequence of low liquid pressures in regions near the highly curved ice interface. An appealing precedent for this way of thinking comes from studies of liquid transport towards the gas-liquid interface of a drying front. At warmer temperatures, with the ice lens in Figure 2 replaced by the vapor phase, the gas pressure Pg along the drying front must be nearly uniform because its viscosity is very small in comparison with the liquid viscosity. The liquid pressure adjacent to highly curved portions of the interface is lower than P _g by the product of the gas-liquid surface energy p _g (equivalent to the surface tension; note that 1J m^-2 = 1 Nm^-1) and the curvature; liquid flow is produced whenever this causes the gradient in liquid pressure towards a connected reservoir to deviate from hydrostatic. A serious flaw in applying similar arguments to account for liquid transport during freezing is that the viscosity of ice is much greater than that of liquid water, making the assumption of uniform ice pressure somewhat tenuous.

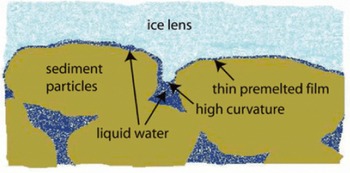
Fig. 2. Geometry of the ice-liquid interface near the base of an ice lens. Separate regions are highlighted in which liquid water forms a thin premelted film that separates the ice from the sediment particles where their surfaces are in close proximity and the area of high surface curvature where the ice-liquid interface is comparatively distant from the sediment particles.

A clear demonstration of the dynamic interactions that cause liquid to flow and supply frost heave was provided in an elegant experiment described by Wilenand Dash (1995). A disk of ice was grown on a microscope slide with its center cooled to a fixed subzero temperature and a liquid bath on its outer rim heated to melting to produce a temperature gradient along the upper interface with a flexible membrane. Over a period of several days the membrane height was monitored closely and found to gradually swell upwards in response to ice growth supplied by liquid flow along the thin premelted film that separated the membrane from the underlying ice. The curvature of the ice-liquid interface was negligible throughout the duration of the experiment, so capillarity cannot be implicated as the cause of liquid transport. Instead, quantitative agreement was found with model predictions (Wettlaufer and others, 1996; see also Wettlaufer and Worster, 2006) that described the liquid flow as a consequence of the same intermolecular forces responsible for producing the thin premelted film needed to supply ice growth. The thickness of the premelted film decreases with the size of the depression of the local temperature below melting and so gets thinner towards the center of the ice disk. As the separation between the membrane and ice decreases, the intermolecular forces that produce the premelted film cause the net force per unit area between the two solids (ice and membrane) to increase. With only air on the opposite side of the membrane, the uniform atmospheric pressure acts over its entire surface and the gradient in ice-membrane pressure implies that the liquid pressure must decrease with colder temperatures to satisfy force equilibrium. This is how the liquid pressure gradient is generated to cause flow towards colder temperatures. Some of the liquid freezes to maintain its equilibrium thickness as the film thins along the flow path; the additional ice accumulation produces the measured heave.

The Wilen and Dash (1995) experiment proved that frost heave can take place when surface-energy effects are negligible. This does not imply that surface energy is unimportant for frost heave in nature. Indeed, observations of changes in ice saturation with temperature produced by Beskow (1935, see figs 19, 20 and 23) and numerous others since (e.g. for a compilation see Andersland and Ladanyi, 2004) indicate clearly that the amount of unfrozen liquid contained within the pore space at subzero temperatures is strongly affected by the distribution of grain sizes; this is partly explained by the persistence of liquid in the vicinity of particle contacts where the interfacial curvature is high. Near the melting temperature, a theoretical model supported by experimental observations in mono-dispersed powders (Cahn and others, 1992; see also Dash and others, 2006) predicts that the fraction of liquid water in the immediate vicinity of highly curved regions dominates the total liquid fraction present. The fraction of liquid present along premelted films gains prominence as the temperature cools further. Similar results have been obtained in a more comprehensive treatment by HansenGoos and Wettlaufer (2010) which gives a particularly thorough description of the factors that control how the film thickness varies with temperature. Frost heave is made possible by liquid transport, and the role that surface energy plays in increasing the permeability of partially frozen soils is extremely important. Nevertheless, the generation of pressure gradients that drive liquid flow has little to do with capillarity and instead the intermolecular forces that produce premelted films are implicated.

Rejection and Trapping

A key characteristic of frost heave that goes beyond the simple fact of liquid flow is the tendency to form banded sequences of particle-free ice lenses separated by layers of ice-infiltrated soil. Under typical conditions, solidification takes place along the lower (or warmer) boundary of an ice lens for a finite period of time before a new lens forms beneath it and traps the layer of partially frozen sediments in between. In an effort to learn more about the controls on analogous behavior in a simpler system, Corte (1962) initiated a series of experiments to investigate the interaction of an ice-liquid interface with a single particle. The importance to the materials processing industry motivated much further study, leading to a general consensus on the major stages of behavior that are shown schematically in Figure 3. Initially the separation is large enough that the ice- liquid interface is unaffected by the presence of the particle (Fig. 3a). As the solidification front nears the particle (Fig. 3b), the interface shape adjusts so that a premelted film remains to separate the particle from the ice. The particle is pushed ahead of the ice-liquid interface at velocity U. A steady state can be established with the particle velocity equal to the freezing rate V so that the ice- particle separation remains constant and the particle is rejected from the growing ice. However, when the freezing rate is greater than some critical value that the particle velocity cannot exceed, the particle is eventually trapped within the ice (Fig. 3c).

Fig. 3. Schematic diagrams of the stages of interaction between a freezing front and a foreign solid particle in a temperature gradient ∇T.

A number of models have been developed to predict the particle behavior and understand how the critical freezing rate depends on the system parameters. The first substantially correct theories were developed independently in Canada by Gilpin (1980b) and in the Soviet Union by Chernov and his colleagues (Chernov and others, 1976; Chernov and Temkin, 1977). These authors recognized that a thin film of liquid separates the particle and the solid ice and that transport through this film is necessary in order for the particle to be pushed ahead of the advancing solidification front. By assuming an inverse relationship between the film thickness and the repulsive force per unit area that is exerted between the particle and ice surfaces, the net force on the particle produced by these intermolecular interactions can be calculated for a given interface geometry. As long as the temperature field is known (for simplicity a constant temperature gradient is often assumed), the interface geometry can be obtained by requiring that the film thickness depend in a specified way upon the temperature depression below the bulk melting temperature T_m. The velocity with which the particle is set in motion comes from balancing the net force of particle rejection with the effective suction force that results from the fluid pressure distribution needed to drive flow through the film and satisfy the mass-balance constraint on the solidifying front. When the freezing rate is not too large, the particle velocity can match it at a particular particle-ice separation. If the freezing rate increases slightly, the separation decreases so that the liquid film gets thinner and the net repulsive force on the particle increases. Below the critical freezing rate, the fluid flux can increase in response so that the suction force and repulsive force again balance with U = V. Beyond the critical freezing rate, the film has become so thin that the increased viscous resistance that must be overcome to supply liquid to the interface near the particle enables the suction force to balance the rejection force when the particle velocity is still lower than V. The discrepancy between U and V causes the intervening liquid film to shrink further and the particle velocity continues to drop until the particle is surrounded completely and only separated from the ice by a thin premelted film. The ingredients of this problem are essentially the same as those in the Wilen and Dash (1995) experiment, and the same description of the premelted layer can be used to specify both the temperature dependence of the film thickness and the net force per unit area exerted between the particle and the ice (e.g. Rempel and Worster, 1999). The analysis has been generalized to include such factors as the differing thermal properties of the system components, the buoyancy of the particle and even Marangoni effects for the case when the particle is replaced by a bubble (e.g. Park and others, 2006).

To better understand the dynamics at an ice-lens boundary similar to that shown in Figure 2, the single particle analysis has been extended to consider the interactions between an advancing solidification front and an array of particles (Worster and Wettlaufer, 1999). As expected, the model predicts that the particles are pushed ahead of the ice-lens surface as long as the freezing rate is lower than some critical value that is controlled by viscous resistance to the fluid flow needed to supply ice growth. The critical freezing rate decreases when an additional load is imposed on the particles to mimic the effects of overburden forces in nature. In the terminology coined by Miller (1978), the style of ice-lens growth that is characterized by steady particle rejection is known as ‘primary heave’. More significant ground deformation and frost damage take place in the ‘secondary heaving’ regime, when ice lenses grow with u< v so that the melting-temperature isotherm advances ever deeper beneath the growing ice lens until a new lens initiates and starts to grow while cutting off the water supply to the older lens above. Most of the physical ingredients that need to be included in a model to describe such a scenario are represented within the particle-trapping problem;only the question of how new lenses initiate remains to be addressed. The complicated geometry of the ice-liquid interface in natural porous media under conditions in which sequences of ice lenses form makes it impractical to calculate directly the net effect of interactions between the sediment particles and the ice in quite the same manner as the treatments for the simpler problems discussed thus far. A continuum treatment is required that remains faithful to the underlying physics on the microscopic length scales of the premelted films and nevertheless is able to make useful predictions of macroscopic variables like the rate of heave, the spacings between lenses and their thicknesses.

‘Rigid-Ice’ Models

Following a series of studies spanning many years of investigation, O’Neill and Miller (1985) put forward the first comprehensive and tractable model that can predict the characteristics of ice lenses and the rate of frost heave as a function of environmental conditions and sediment constitutive behavior. A key feature that their ‘rigid-ice’ model shares with many alternative descriptions of frost heave is the assumption that during secondary heave the ice penetrates a significant distance into the pore space beneath the growing ice lens to form a partially frozen zone referred to as a ‘frozen fringe’ (see Fig. 4). The pore ice in the fringe is attached to the growing lens above and moves relative to the surrounding soil particles by melting and refreezing as necessary. O’Neill and Miller developed their model as a series of differential equations that describe the conservation laws for mass and energy. The relative proportions of ice and liquid water in the fringe beneath the growing lens are controlled by the local temperature (with a slight dependence on the local water pressure as well) and allowed to vary according to an empirical description that accounts for the effects of surface energy and the presence of thin liquid films that coat sediment particles. Conservation of momentum in the liquid phase takes the form of Darcy’s law with a permeability that is sensitive to the ice content in the fringe. The predicted rate of heave is obtained by a force balance condition that is analogous to the controls on the particle velocity in the models discussed above. The overburden pressure is set equal to the sum of the liquid pressure adjacent to the ice- lens boundary and a term proportional to the local temperature depression below the normal melting point (with a small additional component proportional to the local liquid pressure) that approximates the net force supplied by interactions between the soil particles and the ice. The fringe gets thicker and the temperature on the lens boundary decreases over time whenever the heave rate is slower than the rate that isotherms progress relative to the ground surface.

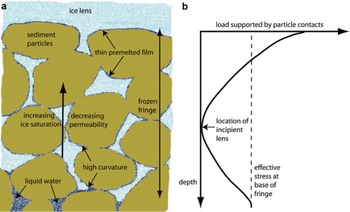
Fig. 4. (a) Schematic diagram showing the ice distribution in the frozen fringe beneath a growing ice lens. (b) The predicted load supported by particle contacts is shown. Above the base of the frozen fringe the load supported by particle contacts decreases at first, but eventually reaches a minimum because of the large gradients in liquid pressure that are needed to drive flow through the lower permeabilities that are caused by increasing ice saturation towards the base of the growing lens. As shown, the minimum load tends towards zero; this is where rigid-ice models predict that a new lens will form.

To generate banded sequences of ice lenses separated by ice-infiltrated sediments, in their model O’Neill and Miller (1985) proposed that a new lens initiates within the frozen fringe when the sediment contacts are unloaded at a particular depth beneath the actively growing lens. The local pore liquid pressure is obtained from the equation describing Darcy transport. The ice pressure is set to exceed this liquid pressure by an amount that is proportional to the local temperature; this is justified, for example, along portions of a curved ice-liquid interface that are outside the range of intermolecular interactions with the sediment particles. Using these pressure profiles, O’Neill and Miller calculated the load supported by each pore constituent according to the product of its local pressure with a weighting function. The initiation of a new lens is assumed to take place when the load borne by the pore constituents first reaches the overburden at a particular location within the fringe where the sediment particle contacts are no longer subject to a compressive stress (see Fig. 4).

As a continuum formulation, one of the most important advances made in the O’Neill and Miller (1985) model is the ability to predict frost-heave behavior without needing to resolve the detailed geometry of the ice-liquid interface explicitly. Instead the model keeps track of only two essential features of the ice content in the fringe: (1) spatial variations in the volume fraction of the pore space that is occupied by ice; and (2) spatial variations in the effective permeability caused by these changes in ice saturation. The temperature dependence of both of these parameters can be extracted from independent laboratory studies (e.g. Andersland and Ladanyi, 2004; Watanabe and Flury, 2008; Watanabe and Wake, 2009). While this greatly reduces the effort in comparison with previous modeling attempts (e.g. Gilpin, 1980a), in its original form the O’Neill and Miller model does still require considerable computational expense. Fowler (1989) (see also Fowler and Noon, 1993; Fowler and Krantz, 1994) addressed this problem using asymptotic analysis to reformulate the rigid-ice model and greatly improve its practical implementation.

Despite the success of the rigid-ice model in predicting the macroscopic features of frost heave, a difficulty remains in that the two force-balance conditions used to predict the heave rate and the initiation of new lenses lack a firm theoretical basis grounded in the underlying microscale physics. In particular, as the Wilen and Dash (1995) experiment and the particle-trapping problems show, the net force between the ice and sediment particles can be explained quantitatively as a result of the intermolecular forces that act between them and produce the intervening premelted films. An analysis of the force balance on a single regelating particle that is surrounded by a premelted film, as shown in Figure 3c, led to the development of a method to account rigorously for these forces in a continuum formulation of the frost-heave problem. On the warm side of the particle the premelted film is slightly thicker than on the cold side of the particle and so the strength of the repulsive pressure between the ice and the particle is slightly weaker; this sets the particle in motion. Independent of the particle shape and the details of the intermolecular forces responsible for the film’s presence, the net force that results from integrating the temperature-dependent ice-particle interaction pressure over the particle surface is proportional to the mass of ice that would otherwise fit within the volume occupied by the particle and the product of the temperature gradient with the ratio of the latent heat to the bulk melting temperature (Rempel and others, 2001). The net effect of intermolecular forces acting over an arbitrary surface that is separated from ice by premelted liquid can be accounted for as an effective thermodynamic buoyancy force that is proportional to the mass of ice that would otherwise fit within the enclosed volume; the precise shape of the ice- liquid surface is not important.

By applying the concept of thermodynamic buoyancy, for a known dependence of ice saturation on temperature it is possible to evaluate the net force per unit area supported by all of the ice-particle interactions over the connected ice surface from the lens boundary to the base of the fringe (e.g. Rempel and others, 2004). The net vertical force produced by the fluid pressure pushing against the ice surface similarly can be accounted for as an integral over the fringe depth that depends on the ice saturation and the saturation-dependent permeability. Balancing these two forces with the overburden in a modified rigid-ice model, the net rate of heave is predicted to depend not only on the local values of the liquid pressure and temperature at the boundary of the growing lens, but also on the distribution of these quantities throughout the depth of the fringe beneath. An integrated treatment is necessary because solid ice is able to transmit portions of the overburden load supported by particle-ice interactions throughout the fringe of connected pore ice. The lens initiation criterion similarly can be modified to avoid the use of arbitrary weighting functions and accurately account for the load transmitted by particle-ice interactions. This leads to a local description of the gradient in load supported by particle contacts within the fringe, and the initiation of new lenses can be predicted by solving for conditions when this load vanishes (e.g. Rempel, 2011, equation 4). With the intermolecular forces that ultimately produce macroscopic frost heave properly accounted for, a simple treatment of freezing in porous media can be used to delineate the parameter regimes in which: (1) a single ice lens or needle ice can grow without any further lens initiation; (2) multiple lenses can grow in succession to form the banded sequences characteristic of secondary heave; or (3) no lenses can initiate and freezing simply takes place within the pore space with no attendant heave (e.g. Rempel and others, 2004; Rempel, 2007).

Beyond ‘Rigid Ice’

Further developments in our understanding of frost heave have come as a result of challenges to the assumptions in the rigid-ice formulation. Mutou and others (1998) developed an apparatus to observe ice-lens behavior in glass beads that were sandwiched between two microscope slides and pulled through a fixed temperature gradient. Watanabe and Mizoguchi (2000) modified the apparatus to use Raman spectroscopy and monitor the pore constituents near the growing lens. Their measurements indicated that ice-lens growth took place without the presence of a detectable pore-ice-bearing fringe. Since sequences of ice lenses formed during these experiments, two explanations immediately present themselves: either the fringe was present, but the experimental resolution was insufficient to detect pore ice; or the fringe was absent and a different mechanism was responsible for nucleating new ice lenses.

Using a similar apparatus, Peppin and others (2006, 2007) and Peppin and Wettlaufer (2008) performed an extensive investigation of freezing morphologies in colloidal suspensions (e.g. bentonite and kaolinite). A wide variety of growth forms were observed that included conventional ice lenses, dendrites that extended in the direction of heat flow, and more complicated polygonal forms that resembled mud cracks. Quantitative agreement was found with a linear stability analysis of the conditions under which a planar ice lens would grow stably and reject the colloid particles to form a region of higher solids concentration adjacent to the ice surface, and conditions under which such a planar growth form was unstable. In this system, rearrangements of the solid particles to change the local porosity and alter the equilibrium melting temperature are a key factor in determining the solidification behavior. In the rigid-ice models discussed above, such particle rearrangements are typically neglected even though the load supported by particle contacts near the boundary of the growing lens often exceeds the effective stress at the base of the fringe (e.g. see Fig. 4). The possibility arises that ice might nucleate in a region of low particle concentration that is removed from the growing lens, and subsequent particle rearrangements near this freezing center might lead to the development of a new ice lens that is not connected to the one above. Indeed, such a scenario for ice- lens development might apply more generally in sediments that contain a sufficiently broad range of pore sizes, with lens nucleation occurring as the extension of one or more larger pores into an ice-filled crack (personal communication from J. Wettlaufer, 2010) in much the same way as occurs to promote frost damage to cohesive rocks and engineered structures (e.g. Walder and Hallet, 1985; Hallet and others, 1991; Murton and others, 2006). As O’Neill and Miller (1985) cautioned about the causes of secondary heave: ‘All of these processes interact in ways too devious to permit intuition or simplistic idealizations to tell us what to expect over periods of time ranging from as little as a few hours to as long as tens of years.’ More work is clearly needed to explain the variety of freezing morphologies that have been observed.

Conclusions

Nearly a century has passed since Taber’s first experiments on the crystallization of solids under stress. The forces that operate are now understood on a microscopic level and methods have been developed to account for these physical interactions in models that successfully predict many of the macroscopic features that they produce. Just as studies of frost heave at the beginning of the last century were largely driven by the expansion of commerce in the north, current concerns about permafrost degradation (e.g. Williams, 1995) motivate much renewed interest in how ground ice near anthropogenic structures will react to changing thermal and hydrological conditions. A firm theoretical basis has been developed to tackle these problems, though parameter uncertainties and the complexities of local surface and subsurface conditions make it challenging to predict exactly how the upper boulders will spill.