Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-15T15:17:46.110Z Has data issue: false hasContentIssue false
  • English
  • Français

The Jiang–Su Absorption for Inclusions of Unital C*-algebras

Published online by Cambridge University Press:  20 November 2018

Hiroyuki Osaka  and
Tamotsu Teruya
Hiroyuki Osaka
Affiliation:
Department of Mathematical Sciences, Ritsumeikan University, Kusatsu, Shiga, 525-8577 Japan e-mail: [email protected]
Tamotsu Teruya
Affiliation:
Faculty of Education, Gunma University, 4-2 Aramaki-machi, Maebashi City, Gunma, 371-8510, Japan e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

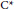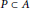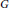We introduce the tracial Rokhlin property for a conditional expectation for an inclusion of unital ${{\text{C}}^{*}}$-algebras $P\,\subset \,A$ with index finite, and show that an action $\alpha$ from a finite group $G$ on a simple unital 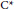${{\text{C}}^{*}}$- algebra $A$ has the tracial Rokhlin property in the sense of N. C. Phillips if and only if the canonical conditional expectation 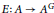$E:\,A\,\to \,{{A}^{G}}\,$ has the tracial Rokhlin property. 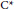Let $\mathcal{C}$ be a class of infinite dimensional stably finite separable unital ${{\text{C}}^{*}}$-algebras that is closed under the following conditions:

(1) If 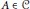$A\,\in \,\mathcal{C}$ and 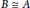$B\,\cong \,A$, then 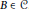$B\,\in \,\mathcal{C}$.

(2) If 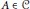$A\,\in \,\mathcal{C}$ and 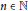$n\,\in \,\mathbb{N}$, then 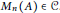${{M}_{n}}\left( A \right)\,\in \,\mathcal{C}$.

(3) If 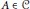$A\,\in \,\mathcal{C}$ and 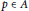$p\,\in \,A$ is a nonzero projection, then 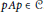$pAp\,\in \,\mathcal{C}$.

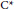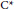Suppose that any ${{\text{C}}^{*}}$-algebra in $\mathcal{C}$ is weakly semiprojective. We prove that if $A$ is a local tracial ${{\text{C}}^{*}}$-algebra in the sense of Fan and Fang and a conditional expectation 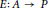$E:\,A\,\to \,P$ is of index-finite type with the tracial Rokhlin property, then $P$ is a unital local tracial $\mathcal{C}$-algebra.

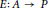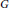The main result is that if $A$ is simple, separable, unital nuclear, Jiang–Su absorbing and $E:\,A\,\to \,P$ has the tracial Rokhlin property, then $P$ is Jiang–Su absorbing. As an application, when an action α from a finite group $G$ on a simple unital 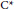${{\text{C}}^{*}}$-algebra $A$ has the tracial Rokhlin property, then for any subgroup 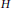$H$ of 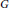$G$ the fixed point algebra 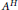${{A}^{H}}$ and the crossed product algebra 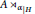$A{{\rtimes }_{{{\alpha }_{|H}}}}$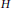$H$ is Jiang–Su absorbing. We also show that the strict comparison property for a Cuntz semigroup 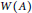$W\left( A \right)$ is hereditary to 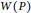$W\left( P \right)$ if $A$ is simple, separable, exact, unital, and 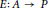$E:\,A\,\to \,P$ has the tracial Rokhlin property.

Keywords

46L5546L35Jiang–Su absorptioninclusion of C*-algebrastrict comparison
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 2 , 01 April 2018 , pp. 400 - 425
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Archey, D., Crossed product C*-algebras by finite group actions with the traded Rokhlin property. Rocky Mountain J. Math. 41(2011), no. 6,1755–1768.http://dx.doi.Org/10.1216/RMJ-2O11-41-6-1755 Google Scholar
[2] Blackadar, B., The stable rank of full corners in C*-algebras. Proc. Amer. Math. Soc. 132(2004), 2945–2950.http://dx.doi.Org/10.1090/S0002-9939-04-07148-5 Google Scholar
[3] Blackadar, B. and Handelman, D., Dimension functions and traces on C*-algebras. J. Funct. Anal. 45(1982), 297–340. http://dx.doi.org/10.1016/0022-1236(82)90009-X Google Scholar
[4] Brown, L. G. and Pedersen, G. K., C*-algebras of real rank zero. J. Funct. Anal. 99(1991), 131–149.http://dx.doi.Org/10.1016/0022-1236(91)90056-B Google Scholar
[5] Cuntz, J., The structure of multiplication and addition in simple C*-algebras.. Math. Scand. 40(1977), no. 2, 215–233.http://dx.doi.org/10.7146/math.scand.a-11691 Google Scholar
[6] Cuntz, J., Dimension functions on simple C*-algebras. Math. Ann. 233(1978), 145–153.http://dx.doi.org/10.1007/BF01421922 Google Scholar
[7] Elliott, G. A. and Niu, Z., On tracial approximation. J. Funct. Anal. 254(2008), 396–440.http://dx.doi.Org/10.1016/j.jfa.2007.08.005 Google Scholar
[8] Echterhoff, S., Luck, W., Phillips, N. C., and Walters, S., The structure of crossed products of irrational rotation algebras by finite subgroups ofSL2(ℤ). J. Reine Angew. Math. 639(2010), 173–221.http://dx.doi.Org/10.1515/CRELLE.2O10.015 Google Scholar
[9] Fan, Q. and Fang, X., Stable rank one and real rank zero for crossed products by finite group actions with the tracial Rokhlin property. Chin. Anal. Math. Ser. B 30(2009), 179–186.http://dx.doi.Org/10.1007/s11401-007-0563-7 Google Scholar
[10] Haagerup, U., Quasitraces on exact C*-algebras are traces. C. R. Math. Acad. Sci. Soc. Can. 36(2014), no. 2–3, 67–92.Google Scholar
[11] Hirshberg, I. and Orovitz, J., Tracially Z-absorbing C*-algebras. J. Funct. Anal. 265(2013), 765–785.http://dx.doi.Org/10.1016/j.jfa.2O13.05.005 Google Scholar
[12] Izumi, M., Inclusions of simple C*-algebras. J. Reine Angew. Math. 547(2002), 97–138.http://dx.doi.Org/10.1515/crll.2OO2.055 Google Scholar
[13] Izumi, M., Finite group actions on C*-algebras with the Rokhlin property. I. Duke Math. J. 122(2004), 233–280. http://dx.doi.Org/10.1215/S0012-7094-04-12221-3 Google Scholar
[14] Jeong, J. A. and Osaka, H., Extremally rich C*- crossed products and the cancellation property. J. Austral. Math. Soc. Ser. A 64(1998), 285–301.http://dx.doi.org/10.1017/S1446788700039161 Google Scholar
[15] Jeong, J. A. and Park, G. H., Saturated actions by finite dimensional Hopf*-algebras on C*-algebras. Intern. J. Math. 19(2008), 125–144.http://dx.doi.Org/10.1142/S0129167X08004583 Google Scholar
[16] Jiang, X. and Su, H., On a simple unital projectionless C*-algebras. Amer. J. Math. 121(1999), 359–413. http://dx.doi.Org/10.1353/ajm.1999.0012 Google Scholar
[17] Kirchberg, E., On the existence of traces on exact stably projectionless simple C*-algebras. In: Operator Algebras and their Applications (Waterloo, ON, 1884/1995), Fields Institute Communications , 13, American Mathematical Society, Providence, RI, 1997, pp. 171–172.Google Scholar
[18] Kishimoto, A., Outer automorphisms and reduced crossed products of simple C*-algebras. Commun. Math. Phys. 81(1981), 429–435.http://dx.doi.Org/10.1007/BF01209077 Google Scholar
[19] Kodaka, K., Osaka, H., and Teruya, T., The Rokhlin property for inclusions of C*-algebras with a finite Watatani Index. In: Operator structures and Dynamical Systems, Contemporary Mathematics , 503, American Mathematical Society, Providence, RI, 2009, pp. 177–195.http://dx.doi.Org/10.1090/conm/503/09900 Google Scholar
[20] Lin, H., Tracial AF C*-algebras. Trans. Amer. Math. Soc. 353(2001), 693–722.http://dx.doi.org/10.1090/S0002-9947-00-02680-5 Google Scholar
[21] Lin, H., The tracial topological rank of C*-algebras. Proc. London Math. Soc. (3) 83(2001), no. 1, 199–234.http://dx.doi.Org/10.1112/plms/83.1.199 Google Scholar
[22] Lin, H., An Introduction to the Classification of Amenable C*-algebras. World Scientific, River EdgeNJ, 2001. http://dx.doi.Org/10.1142/9789812799883 Google Scholar
[23] Lin, H., Simple nuclear C*-algebras of tracial topological rank one. J. Funct. Anal. 251(2007), 601–679.http://dx.doi.Org/10.1016/j.jfa.2007.06.016 Google Scholar
[24] Loring, T. A., Lifting Solutions to Perturbing Problems in C*-algebras. Fields Institute Monographs , 8, American Mathematical Society, Providence RI, 1997.Google Scholar
[25] Osaka, H., SP-Property for a pair of C*-algebras. J. Operator Theory 46(2001), 159–171.Google Scholar
[26] Osaka, H. and Phillips, N. C., Crossed products by finite group actions with the Rokhlin property. Math. Z. 270(2012), 19–42.http://dx.doi.Org/10.1007/s00209-010-0784-4 Google Scholar
[27] Osaka, H. and N. C. Phillips, in preparation.Google Scholar
[28] Osaka, H. and Teruya, T., Strongly self-absorbing property for inclusions of C*-algebras with a finite Watatani index. Trans. Amer. Math. Soc. 366(2014), no. 3,1685–1702.http://dx.doi.org/10.1090/S0002-9947-2013-05907-7 Google Scholar
[29] Osaka, H. and Teruya, T., Permanence of nuclear dimension for inclusions of unital C*-algebras with the Rokhlin property. Advances in Operator Theory 3(2018), 123–136.http://dx.doi.org/10.22034/aot.1703-1145 Google Scholar
[30] Phillips, N. C., The tracial Rokhlin property for actions of finite groups on C*-algebras. Amer. J. Math. 133(2011), no. 3, 581–636.http://dx.doi.org/10.1353/ajm.2011.0016 Google Scholar
[31] Rieffel, M. A., Dimension and stable rank in the K-theory of C*-algebras. Proc. London Math. Soc. 46(1983),301–333. http://dx.doi.Org/10.1112/plms/s3-46.2.301 Google Scholar
[32] Rordam, M., On the structure of simple C*-Algebras tensored with a UHF-algebra. J. Funct. Anal. 100(1991), 1–17.http://dx.doi.org/10.1016/0022-1236(91)90098-P Google Scholar
[33] Rordam, M., On the structure of simple C*-Algebras tensored with a UHF-algebra II. J. Funct. Anal. 107(1992), 255–269.http://dx.doi.org/10.1016/0022-1236(92)90106-S Google Scholar
[34] Rordam, M., The stable and the real rank of z-absorbing C*-algebras. Internat. J. Math. 15(2004), 1065–1084. http://dx.doi.org/10.1142/S0129167X04002661 Google Scholar
[35] Rordam, M. and Winter, W., The Jiang-Su algebra revisited. J. Reine Angew. Math. 642(2010), 129–155.http://dx.doi.org/10.1515/CRELLE.2010.039 Google Scholar
[36] Toms, A. S., Characterizing classifiable AH algebras. C. R. Math. Acad. Sci. Soc. R. Can. 33(2011), no. 4, 123–126.Google Scholar
[37] Toms, A. S. and Winter, W., Strongly self-absorbing C*-algebras. Trans. Amer. Math. Soc. 359(2007), 3999–4029.http://dx.doi.org/10.1090/S0002-9947-07-04173-6 Google Scholar
[38] Watatanxi, Y., Index for C*-subalgebras. Mem. Amer. Math. Soc. 424(1990).http://dx.doi.Org/10.1090/memo/0424 Google Scholar
[39] Winter, W. and Zacharias, J., The nuclear dimension of C*-algebras. Adv. Math. 224(2010), 461–498. http://dx.doi.Org/10.1016/j.aim.2009.12.005 Google Scholar
[40] Yang, X. and Fang, X., The tracial class property for crossed products by finite group actions. Abstr. Appl. Anal. , 2012, Art. ID 745369.Google Scholar