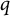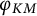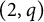The Kudla–Millson form via the Mathai–Quillen formalism

Abstract

A crucial ingredient in the theory of theta liftings of Kudla and Millson is the construction of a $q$-form $\varphi_{KM}$ on an orthogonal symmetric space, using Howe's differential operators. This form can be seen as a Thom form of a real oriented vector bundle. We show that the Kudla-Millson form can be recovered from a canonical construction of Mathai and Quillen. A similar result was obtaind by Garcia for signature $(2,q)$ in case the symmetric space is hermitian and we extend it to arbitrary signature.

1 Introduction

Let $(V,Q)$ be a quadratic space over $\mathbb {Q}$ of signature $(p,q)$ , and let G be its orthogonal group. Let $\mathbb {D}$ be the space of oriented negative q-planes in $V(\mathbb {R})$ and $\mathbb {D}^+$ one of its connected components. It is a Riemannian manifold of dimension $pq$ and an open subset of the Grassmannian. The Lie group $G(\mathbb {R})^+$ is the connected component of the identity and acts transitively on $\mathbb {D}^+$ . Hence, we can identify $\mathbb {D}^+$ with $G(\mathbb {R})^+ /K $ , where K is a compact subgroup of $G(\mathbb {R})^+$ and is isomorphic to $\operatorname {SO}(p)\times \operatorname {SO}(q)$ . Moreover, let L be a lattice in $ V(\mathbb {Q}),$ and let $\Gamma $ be a torsion-free subgroup of $G(\mathbb {R})^+$ preserving L.

For every vector v in $V(\mathbb {R})$ such that $Q(v,v)>0$ , there is a totally geodesic submanifold $\mathbb {D}^+_v$ of codimension q consisting of all the negative q-planes that are orthogonal to v. Let $\Gamma _v$ denote the stabilizer of v in $\Gamma $ . We can view $ \Gamma _v \backslash \mathbb {D}^+$ as a rank q vector bundle over $\Gamma _v \backslash \mathbb {D}_v^+$ , so that the natural embedding $\Gamma _v \backslash \mathbb {D}_v^+ $ in $ \Gamma _v \backslash \mathbb {D}^+$ is the zero section. In [6], Kudla and Millson constructed a closed $G(\mathbb {R})^+$ -invariant differential form

(1.1) $$ \begin{align} \varphi_{KM} \in \left [ \Omega^q(\mathbb{D}^+) \otimes \mathscr{S}(V(\mathbb{R})) \right ]^{G(\mathbb{R})^+}, \end{align} $$

where $G(\mathbb {R})^+$ acts on the Schwartz space $\mathscr {S}(V(\mathbb {R}))$ from the left by and on $\Omega ^q(\mathbb {D}^+) \otimes \mathscr {S}(V(\mathbb {R}))$ from the right by . In particular, $\varphi _{KM}(v)$ is a $\Gamma _v$ -invariant form on $\mathbb {D}^+$ . The main property of the Kudla–Millson form is its Thom form property: if $\omega $ in $\Omega _c^{pq-q}(\Gamma _v \backslash \mathbb {D}^+)$ is a compactly supported form, then

(1.2) $$ \begin{align} \int_{\Gamma_v \backslash \mathbb{D}^+} \varphi_{KM}(v) \wedge \omega = 2^{-\frac{q}{2}}e^{-\pi Q(v,v)}\int_{\Gamma_v \backslash \mathbb{D}^+_v} \omega. \end{align} $$

Another way to state it is to say that in cohomology, we have

(1.3) $$ \begin{align} [\varphi_{KM}(v)] = 2^{-\frac{q}{2}}e^{-\pi Q(v,v)} \operatorname{PD}(\Gamma_v \backslash \mathbb{D}^+_v) \in H^q \left (\Gamma_v \backslash \mathbb{D}^+ \right ), \end{align} $$

where $\operatorname {PD}(\Gamma _v \backslash \mathbb {D}^+_v)$ denotes the Poincaré dual class to $\Gamma _v \backslash \mathbb {D}^+_v$ .

1.1 Kudla–Millson theta lift

In order to motivate the interest in the Kudla–Millson form, let us briefly recall how it is used to construct a theta correspondence between certain cohomology classes and modular forms. For simplicity, ¹ assume that $p+q$ is even, and let $\omega $ be the Weil representation of the dual pair $\operatorname {SL}_2(\mathbb {R}) \times G(\mathbb {R})$ in $\mathscr {S}(V(\mathbb {R}))$ . We extend it to a representation in $\Omega ^q(\mathbb {D}^+) \otimes \mathscr {S}(V(\mathbb {R}))$ by acting in the second factor of the tensor product. Building on the work of [11], Kudla and Millson [7, 9] used their differential form to construct the theta series

(1.4)

where $\tau =x+iy$ is in $\mathbb {H}$ and $g_\tau $ is the matrix $\begin {pmatrix} \sqrt {y} & x\sqrt {y}^{-1} \\ 0 & \sqrt {y}^{-1} \end {pmatrix}$ in $\operatorname {SL}_2(\mathbb {R})$ that sends i to $\tau $ by Möbius transformation. This form is $\Gamma $ -invariant, closed and holomorphic in cohomology in the sense that $\frac {\partial }{\partial \overline {\tau }}\Theta _{KM}(\tau )$ is an exact form. Kudla and Millson showed that if we integrate this closed form on a compact q-cycle C in $\mathcal {Z}_q(\Gamma \backslash \mathbb {D}^+)$ , then

(1.5) $$ \begin{align} \int_C \Theta_{KM}(\tau)=c_0(C)+\sum_{n=1}^\infty \bigl < C,C_{2n} \bigr>e^{2i\pi n\tau} \end{align} $$

is a modular form of weight $\frac {p+q}{2}$ , where

(1.6)

and the special cycles $C_v$ are the images of the composition

(1.7) $$ \begin{align}\Gamma_v \backslash \mathbb{D}_v^+ \hookrightarrow \Gamma_v \backslash \mathbb{D}^+ \longrightarrow \Gamma \backslash \mathbb{D}^+.\end{align} $$

Thus, the Kudla–Millson theta series realizes a lift between the (co)-homology of $\Gamma \backslash \mathbb {D}^+$ and the space of weight $\frac {p+q}{2}$ modular forms.

1.2 The result

Let E be a $G(\mathbb {R})^+$ -equivariant vector bundle of rank q over $\mathbb {D}^+$ , and let $E_0$ be the image of the zero section. By the equivariance, we also have a vector bundle $\Gamma _v \backslash E$ over $\Gamma _v \backslash \mathbb {D}^+$ . The Thom class of the vector bundle is a characteristic class $\operatorname {Th}(\Gamma _v \backslash E)$ in $ H^{q}(\Gamma _v \backslash E,\Gamma _v \backslash (E-E_0))$ defined by the Thom isomorphism (see Section 3.6). A Thom form is a form representing the Thom class. It can be shown that the Thom class is also the Poincaré dual class to $\Gamma _v \backslash E_0$ . Let $s_v \colon \Gamma _v \backslash \mathbb {D}^+ \longrightarrow \Gamma _v \backslash E$ be a section whose zero locus is $\Gamma _v \backslash \mathbb {D}_v^+$ , then

(1.8) $$ \begin{align} s_v^\ast \operatorname{Th}(\Gamma_v \backslash E) \in H^q \left (\Gamma_v \backslash \mathbb{D}^+,\Gamma_v \backslash (\mathbb{D}^+-\mathbb{D}_v^+) \right ). \end{align} $$

Viewing it as a class in $H^q(\Gamma _v \backslash \mathbb {D}^+)$ it is the Poincaré dual class of $\Gamma _v \backslash \mathbb {D}_v^+$ . Since the Poincaré dual class is unique, property (1.3) implies that

(1.9) $$ \begin{align} [\varphi_{KM}(v)]= 2^{-\frac{q}{2}}e^{-\pi Q(v,v)} s_v^\ast \operatorname{Th}(\Gamma_v \backslash E) \in H^q \left (\Gamma_v \backslash \mathbb{D}^+\right ), \end{align} $$

on the level of cohomology.

For arbitrary real oriented metric vector bundles, Mathai and Quillen used the Chern–Weil theory to construct in [10] a canonical Thom form on E. We denote by $U_{MQ}$ the canonical Thom form in $\Omega ^{q}(E)$ of Mathai and Quillen. Since $U_{MQ}$ is $\Gamma $ -invariant, it is also a Thom form for the bundle $\Gamma _v \backslash E$ for every vector v. The main result is the following.

Theorem (Theorem 4.5)

For a natural choice of a bundle E and of a section $s_v$ , we have $\varphi _{KM}(v)= 2^{-\frac {q}{2}}e^{-\pi Q(v,v)} s_v^\ast U_{MQ}$ in $\Omega ^q(\Gamma _v \backslash \mathbb {D}^+).$

The bundle E is the tautological bundle of the Grassmannian $\mathbb {D}^+$ (see Section 3.6), and the section $s_v$ is defined in Section 4.1.

For signature $(2,q)$ , the spaces are Hermitian and the result was obtained by a similar method in [3] using the work of Bismut–Gillet–Soulé.

1.3 Generalizations

More generally, for a positive nondegenerate r-subspace $U \subset V$ spanned by vectors $v_1, \dots , v_r$ , Kudla and Millson also construct an $rq$ form $\varphi _{KM}(v_1,\dots ,v_r)$ . This form can also be recovered by the Mathai–Quillen formalism (see (3) of Section 5). Furthermore, in [7, 9], they not only construct forms for the symmetric space associated with $\operatorname {SO}(p,q)$ , but also for the Hermitian space associated with $U(p,q)$ . In this case, one should be able to recover their forms using the formalism of superconnections as in [10, Theorem 8.5]. We expect the computations to be closer to the computations done in [3].

2 The Kudla–Millson form

2.1 The symmetric space $\mathbb {D}$

Let $(V,Q)$ be a rational quadratic space, and let $(p,q)$ be the signature of $V(\mathbb {R})$ . Let $e_1, \dots , e_{p+q}$ be an orthogonal basis of $V(\mathbb {R})$ such that

(2.1) $$ \begin{align} Q(e_\alpha , e_\alpha) =1 \quad & \textrm{for} \quad \; 1 \leq \alpha \leq p, \nonumber \\ Q(e_\mu , e_\mu) =-1 \quad & \textrm{for} \quad \; p+1 \leq \mu \leq p+q. \end{align} $$

Note that we will always use letters $\alpha $ and $\beta $ for indices between $1$ and p, and letters $\mu $ and $\nu $ for indices between $p+1$ and $p+q$ . A plane z in $V(\mathbb {R})$ is a negative plane if $Q\big|{}_{z} $ is negative definite. Let

(2.2)

be the set of negative-oriented q-planes in $V(\mathbb {R})$ . For each negative plane, there are two possible orientations, yielding two connected components $\mathbb {D}^+ $ and $ \mathbb {D}^-$ of $\mathbb {D}$ . Let $z_0$ in $\mathbb {D}^+$ be the negative plane spanned by the vectors $e_{p+1}, \dots , e_{p+q}$ together with a fixed orientation. The group $G(\mathbb {R})^+$ acts transitively on $\mathbb {D}^+$ by sending $z_0$ to $gz_0$ . Let K be the stabilizer of $z_0$ , which is isomorphic to $\operatorname {SO}(p)\times \operatorname {SO}(q)$ . Thus, we have an identification

(2.3) $$ \begin{align} G(\mathbb{R})^+/K & \longrightarrow \mathbb{D}^+ \nonumber \\ gK & \longmapsto gz_0. \end{align} $$

For z in $\mathbb {D}^+$ , we denote by $g_z$ any element of $G(\mathbb {R})^+$ sending $z_0$ to z.

For a positive vector v in $V(\mathbb {R}),$ we define

(2.4)

It is a totally geodesic submanifold of $\mathbb {D}$ of codimension q. Let $\mathbb {D}_v^+$ be the intersection of $\mathbb {D}_v$ with $\mathbb {D}^+$ .

Let z in $\mathbb {D}^+$ be a negative plane. With respect to the orthogonal splitting of $V(\mathbb {R})$ as $z^\perp \oplus z$ , the quadratic form splits as

(2.5) $$ \begin{align} Q(v,v)={Q\big|{}_{z^\perp} }(v,v)+{Q\big|{}_{z} }(v,v). \end{align} $$

We define the Siegel majorant at z to be the positive-definite quadratic form

(2.6)

2.2 The Lie algebras $\mathfrak {g}$ and $\mathfrak {k}$

Let

(2.7)

(2.8)

be the Lie algebras of $G(\mathbb {R})^+$ and $K,$ where $\mathfrak {so}(z_0)$ is equal to $\mathfrak {so}(q)$ . The latter is the space of skew-symmetric q by q matrices. Similarly, we have $\mathfrak {so}(z_0^\perp )$ equals $\mathfrak {so}(p)$ . Hence, we have a decomposition of $\mathfrak {k}$ as $\mathfrak {so}(z_0^\perp ) \oplus \mathfrak {so}(z_0)$ that is orthogonal with respect to the Killing form. Let $\epsilon $ be the Lie algebra involution of $\mathfrak {g}$ mapping X to $-X$ . The $+1$ -eigenspace of $\epsilon $ is $\mathfrak {k}$ and the $-1$ -eigenspace is

(2.9)

We have a decomposition of $\mathfrak {g} $ as $\mathfrak {k} \oplus \mathfrak {p}$ and it is orthogonal with respect to the Killing form. We can identify $\mathfrak {p}$ with $\mathfrak {g}/\mathfrak {k}$ . Since $\epsilon $ is a Lie algebra automorphism, we have that

(2.10) $$ \begin{align} [\mathfrak{p},\mathfrak{p}] \subset \mathfrak{k}, \qquad \qquad [\mathfrak{k},\mathfrak{p} ] \subset \mathfrak{p}. \end{align} $$

We identify the tangent space of $\mathbb {D}^+$ at $eK$ with $\mathfrak {p}$ and the tangent bundle $T\mathbb {D}^+$ with $G(\mathbb {R})^+ \times _K \mathfrak {p}$ , where K acts on $\mathfrak {p}$ by the $\operatorname {Ad}$ -representation. We have an isomorphism

(2.11)

A basis of $\mathfrak {g}$ is given by the set of matrices

(2.12)

and we denote by $\omega _{ij}$ , its dual basis in the dual space $\mathfrak {g}^\ast $ . Let $E_{ij}$ be the elementary matrix sending $e_i$ to $e_j$ and the other $e_k$ ’s to $0$ . Then $\mathfrak {p}$ is spanned by the matrices

(2.13) $$ \begin{align}X_{\alpha \mu} = E_{\alpha \mu}+E_{\mu \alpha,}\end{align} $$

and $\mathfrak {k}$ is spanned by the matrices

(2.14) $$ \begin{align} X_{\alpha \beta} & = E_{\alpha \beta}-E_{\beta \alpha}, \nonumber \\ X_{\nu \mu} & = -E_{\nu \mu}+E_{\mu \nu}. \end{align} $$

2.3 Poincaré duals

Let M be an arbitrary m-dimensional real orientable manifold without boundary. The integration map yields a nondegenerate pairing [2, Theorem 5.11]

(2.15) $$ \begin{align} H^{q}(M) \otimes_{\mathbb{R}} H_c^{m-q}(M)& \longrightarrow \mathbb{R} \nonumber \\ [\omega]\otimes [\eta] & \longmapsto \int_M \omega \wedge \eta, \end{align} $$

where $H_c(M)$ denotes the cohomology of compactly supported forms on M. This yields an isomorphism between $H^{q}(M)$ and the dual $H_c^{m-q}(M)^\ast =\operatorname {Hom}(H_c^{m-q}(M),\mathbb {R})$ . If C is an immersed submanifold of codimension q in M, then C defines a linear functional on $H_c^{m-q}(M)$ by

(2.16) $$ \begin{align} \omega \longmapsto \int_C \omega. \end{align} $$

Since we have an isomorphism between $H_c^{m-q}(M)^\ast $ and $H^{q}(M)$ , there is a unique cohomology class $\operatorname {PD}(C)$ in $H^q(M)$ representing this functional, i.e.,

(2.17) $$ \begin{align} \int_M \omega \wedge \operatorname{PD}(C) = \int_C \omega \end{align} $$

for every class $[\omega ]$ in $H_c^{m-q}(M)$ . We call $\operatorname {PD}(C)$ the Poincaré dual class to C, and any differential form representing the cohomology class $\operatorname {PD}(C)$ a Poincaré dual form to C.

2.4 The Kudla–Millson form

The tangent plane at the identity $T_{eK} \mathbb {D}^+ $ can be identified with $\mathfrak {p}$ and the cotangent bundle $(T\mathbb {D}^+)^\ast $ with $G(\mathbb {R})^+ \times _K \mathfrak {p}^\ast $ , where K acts on $\mathfrak {p}^\ast $ by the dual of the $\operatorname {Ad}$ -representation. The basis $e_1, \dots , e_{p+q}$ identifies $V(\mathbb {R})$ with $\mathbb {R}^{p+q}$ . With respect to this basis, the Siegel majorant at $z_0$ is given by

(2.18)

Recall that $G(\mathbb {R})^+$ acts on $\mathscr {S}(\mathbb {R}^{p+q})$ from the left by $(g \cdot f)(v)= f(g^{-1}v)$ and on $\Omega ^q(\mathbb {D}^+) \otimes \mathscr {S}(\mathbb {R}^{p+q})$ from the right by . We have an isomorphism

(2.19) $$ \begin{align} \left [ \Omega^q(\mathbb{D}^+) \otimes \mathscr{S}(\mathbb{R}^{p+q}) \right ]^{G(\mathbb{R})^+} & \longrightarrow \left [ \sideset{}{^q}\bigwedge \mathfrak{p}^\ast \otimes \mathscr{S}(\mathbb{R}^{p+q}) \right ]^K \nonumber \\ \varphi & \longrightarrow \varphi_e \end{align} $$

by evaluating $\varphi $ at the basepoint $eK$ in $G(\mathbb {R})^+/K$ , corresponding to the point $z_0$ in $\mathbb {D}^+$ . We define the Howe operator

(2.20) $$ \begin{align}D \colon \sideset{}{^\bullet}\bigwedge \mathfrak{p}^\ast \otimes \mathscr{S}(\mathbb{R}^{p+q}) & \longrightarrow \sideset{}{^{\bullet+q}}\bigwedge \mathfrak{p}^\ast \otimes \mathscr{S}(\mathbb{R}^{p+q}) \end{align} $$

by

(2.21)

where $A_{\alpha \mu }$ denotes left multiplication by $\omega _{\alpha \mu }$ . The Kudla–Millson form is defined by applying D to the Gaussian:

(2.22)

Kudla and Millson showed that this form is K-invariant. Hence, by the isomorphism (2.19), we get a form

(2.23) $$ \begin{align} \varphi_{KM} \in \left [ \Omega^q(\mathbb{D}^+) \otimes \mathscr{S}(\mathbb{R}^{p+q}) \right ]^{G(\mathbb{R})^+}\!\!. \end{align} $$

In particular, since $g^\ast \varphi _{KM}(v)=\varphi _{KM}(g^{-1}v)$ for any $g \in G(\mathbb {R})^+$ , the form is $\Gamma _v$ -invariant and defines a form on $\Gamma _v \backslash \mathbb {D}^+$ . It is also closed and Kudla–Millson prove in [8, Proposition 5.2] that it satisfies the Thom form property: for every compactly supported form $\omega $ in $\Omega ^{pq-q}_c(\Gamma _v \backslash \mathbb {D}^+)$ , we have

(2.24) $$ \begin{align} \int_{\Gamma_v \backslash \mathbb{D}^+} \omega \wedge \varphi_{KM}(v) = 2^{-\frac{q}{2}}e^{-\pi Q(v,v)}\int_{\Gamma_v \backslash \mathbb{D}^+_v} \omega. \end{align} $$

3 The Mathai–Quillen formalism

We begin by recalling a few facts about principal bundles, connections, and associated vector bundles. For more details, we refer to [1, 5]. The Mathai–Quillen form is defined in Section 3.7 following [1] (see also [4]).

3.1 K-principal bundles and principal connections

Let K be $\operatorname {SO}(p)\times \operatorname {SO}(q)$ as before, and let P be a smooth principal K-bundle. Let

(3.1) $$ \begin{align} R \colon K \times P \longrightarrow P \nonumber \\ (k,p) \longmapsto R_k(p) \end{align} $$

be the smooth right action of K on P and

(3.2) $$ \begin{align} \pi \colon P \longrightarrow P/K \end{align} $$

the projection map. For a fixed $p $ in P, consider the map

(3.3) $$ \begin{align} R_p \colon K & \longrightarrow P \nonumber \nonumber \\ k & \longmapsto R_k(p). \end{align} $$

Let $V_pP$ be the image of the derivative at the identity

(3.4) $$ \begin{align} d_e R_p \colon \mathfrak{k} \longrightarrow T_pP, \end{align} $$

which is injective. It coincides with the kernel of the differential $d_p\pi $ . A vector in $V_pP$ is called a vertical vector. Using this map, we can view a vector X in $\mathfrak {k}$ as a vertical vector field on P. The space P can a priori be arbitrary, but in our case, we will consider either:

1. (1) P is $G(\mathbb {R})^+$ and $R_k$ the natural right action sending g to $gk$ . Then $P/K$ can be identified with $\mathbb {D}^+$ .

2. (2) P is $G(\mathbb {R})^+ \times z_0$ and the action $R_k$ maps $(g,w)$ to $(gk,k^{-1}w)$ . In this case, $P/K$ can be identified with $G(\mathbb {R})^+ \times _K z_0$ . It is the vector bundle associated with the principal bundle $G(\mathbb {R})^+$ as defined below.

A principal K-connection on P is a $1$ -form $\theta _P $ in $\Omega ^1(P, \mathfrak {k})$ such that:

• • $\iota _X \theta _P = X$ for any $X $ in $\mathfrak {k}$ ,

• • $R_k^\ast \theta _P=Ad(k^{-1}) \theta _P \quad $ for any k in K,

where $\iota _X$ is the interior product

(3.5)

and we view X as a vector field on P. Geometrically, these conditions imply that the kernel of $\theta _P$ defines a horizontal subspace of $TP$ that we denote by $HP$ . It is a complement to the vertical subspace, i.e., we get a splitting of $T_pP$ as $V_pP \oplus H_pP$ .

Let $\mathfrak {g}$ be the Lie algebra of $G(\mathbb {R})^+$ , and let $\mathcal {P}$ be the orthogonal projection from $\mathfrak {g}$ on $\mathfrak {k}$ . After identifying $\mathfrak {g}^\ast $ with the space $\Omega ^1(G(\mathbb {R})^+)^{G(\mathbb {R})^+}$ of $G(\mathbb {R})^+$ -invariant forms, we define a natural $1$ -form

(3.6) $$ \begin{align} \sum_{1 \leq i<j \leq p+q} \omega_{ij} \otimes X_{ij} \in \Omega^1(G(\mathbb{R})^+) \otimes \mathfrak{g} \end{align} $$

called the Maurer–Cartan form, where $X_{ij}$ is the basis of $\mathfrak {g}$ defined earlier and $\omega _{ij}$ its dual in $\mathfrak {g}^\ast $ . After projection onto $\mathfrak {k}$ , we get a form

(3.7)

where we identify $\Omega ^1(G(\mathbb {R})^+, \mathfrak {k})$ with $\Omega ^1(G(\mathbb {R})^+) \otimes \mathfrak {k}$ . A direct computation shows that it is a principal K-connection on P, when P is $G(\mathbb {R})^+$ .

If P is $G(\mathbb {R})^+ \times z_0$ , then the projection

(3.8) $$ \begin{align} \pi \colon G(\mathbb{R})^+ \times z_0 \longrightarrow G(\mathbb{R})^+ \end{align} $$

induces a pullback map

(3.9) $$ \begin{align} \pi^\ast \colon \Omega^1(G(\mathbb{R})^+) \longrightarrow \Omega^1(G(\mathbb{R})^+ \times z_0). \end{align} $$

The form

(3.10)

is a principal connection on $G(\mathbb {R})^+ \times z_0$ .

3.2 The associated vector bundles

Since $z_0$ is preserved by K, we have an orthogonal K-representation

(3.11)

where we will usually simply write $kw$ instead of ${k\big|{}_{z_0} }w$ . We can consider the associated vector bundle $P \times _K z_0$ which is the quotient of $P \times z_0$ by K, where K acts by sending $(p,w)$ to $ (R_k(p), \rho (k)^{-1}w)$ . Hence, an element $[p,w]$ of $P \times _K z_0$ is an equivalence class where the equivalence relation identifies $(p,w)$ with $(R_k(p), \rho (k)^{-1}w)$ . This is a vector bundle over $P/K$ with projection map sending $[p,w]$ to $\pi (p)$ . Let $\Omega ^i(P/K,P \times _Kz_0)$ be the space of i-forms valued in $P \times _Kz_0$ , when i is zero it is the space of smooth sections of the associated bundle.

In the two cases of interest to us, we define

(3.12)

Note that in both cases, P admits a left action of $G(\mathbb {R})^+$ and that the associated vector bundles are $G(\mathbb {R})^+$ -equivariant. Moreover, it is a Euclidean bundle, equipped with the inner product

(3.13)

on the fiber. Let $ \Omega ^i(P,z_0)$ be the space of $z_0$ -valued differential i-forms on P. A differential form $\alpha $ in $\Omega ^i(P,z_0)$ is said to be horizontal if $\iota _X\alpha $ vanishes for all vertical vector fields X. There is a left action of K on a differential form $\alpha $ in $\Omega ^i(P,z_0)$ defined by

(3.14)

and $\alpha $ is K-invariant if it satisfies $k\cdot \alpha = \alpha $ for any k in $K,$ i.e., we have $R_k^\ast \alpha = \rho (k^{-1}) \alpha $ . We write $\Omega ^i(P, z_0)^K$ for the space of K-invariant $z_0$ -valued forms on P. Finally, a form that is horizontal and K-invariant is called a basic form and the space of such forms is denoted by $\Omega ^i(P,z_0)_{\mathrm{bas}}$ .

Let $X_1, \dots , X_N$ be tangent vectors of $P/K$ at $\pi (p),$ and let $\widetilde {X}_i$ be tangent vectors of P at p that satisfy $d_p\pi (\widetilde {X}_i)=X_i$ . There is a map

(3.15) $$ \begin{align} \Omega^i(P,z_0)_{\mathrm{bas}} & \longrightarrow \Omega^i(P/K,P \times_K z_0) \nonumber \\ \alpha & \longmapsto \omega_\alpha \end{align} $$

defined by

(3.16) $$ \begin{align} {{\omega_\alpha}\big|{}_{\pi(p)} }(X_1 \wedge \cdots \wedge X_N)={{\alpha}\big|{}_{p} }(\widetilde{X}_1 \wedge \cdots \wedge \widetilde{X}_N). \end{align} $$

Proposition 3.1 The map is well-defined and yields an isomorphism between $\Omega ^i(P/K,P \times _K z_0)$ and $\Omega ^i(P,z_0)_{\mathrm{bas}}$ . In particular, if $z_0$ is one-dimensional, then $\Omega ^i(P/K)$ is isomorphic to $\Omega ^i(P)_{\mathrm{bas}}$ .

Proof In the case where i is zero, the horizontally condition is vacuous and the isomorphism simply identifies $\Omega ^0(P/K,P \times _K z_0)$ with $\Omega ^0(P,z_0)^K$ . We have a map

(3.17)

which is well defined since

(3.18) $$ \begin{align} f(R_k(p))=\rho(k)^{-1}f(p). \end{align} $$

Conversely, every smooth section s in $\Omega ^0(P/K,P \times _K z_0)$ is given by

(3.19) $$ \begin{align} s(\pi(p))=[p,f_s(p)] \end{align} $$

for some smooth function $f_s$ in $\Omega ^0(P,z_0)^K$ . The map sending s to $f_s$ is inverse to the previous one. The proof is similar for positive i.

3.3 Covariant derivatives

A covariant derivative on the vector bundle $P \times _K z_0$ is a differential operator

(3.20) $$ \begin{align} \nabla_P \colon \Omega^0(P/K,P \times_K z_0) & \longrightarrow \Omega^1(P/K,P \times_K z_0), \end{align} $$

such that for every smooth function f in $C^\infty (P/K),$ we have

(3.21) $$ \begin{align} \nabla_P(fs)=df\otimes s + f \nabla_P(s). \end{align} $$

The inner product on $P \times _Kz_0$ defines a pairing

(3.22) $$ \begin{align} \Omega^i(P/K,P \times_K z_0) \times \Omega^j(P/K,P \times_K z_0) & \longrightarrow \Omega^{i+j}(P/K) \nonumber \\ ( \omega_1 \otimes s_1 , \omega_2 \otimes s_2 ) & \longmapsto \langle \omega_1 \otimes s_1 , \omega_2 \otimes s_2 \rangle = \omega_1 \wedge \omega_2 \langle s_1,s_2 \rangle, \end{align} $$

and we say that the derivative is compatible with the metric if

(3.23) $$ \begin{align} d\langle s_1,s_2 \rangle = \langle \nabla_Ps_1,s_2 \rangle +\langle s_1,\nabla_Ps_2 \rangle \end{align} $$

for any two sections $s_1$ and $s_2$ in $\Omega ^0(P/K,P\times _Kz_0)$ . There is a covariant derivative that is induced by a principal connection $\theta _P$ in $\Omega ^1(P) \otimes \mathfrak {k}$ as follows. The derivative of the representation gives a map

(3.24) $$ \begin{align} d\rho \colon \mathfrak{k} \longrightarrow \mathfrak{so}(z_0) \subset \operatorname{End}(z_0), \end{align} $$

which we also denote by $\rho $ by abuse of notation. Note that for the representation (3.11), this is simply the map

(3.25) $$ \begin{align} \rho \colon \mathfrak{k} & \longrightarrow \mathfrak{so}(z_0) \nonumber \\ X & \longmapsto {{X}\big|{}_{z_0} }, \end{align} $$

since $\mathfrak {k}$ splits as $\mathfrak {so}(z_0^\perp ) \oplus \mathfrak {so}(z_0)$ . Composing the principal connection with $\rho $ defines an element

(3.26) $$ \begin{align} \rho(\theta_P) \in \Omega^1(P,\mathfrak{so}(z_0)). \end{align} $$

In particular, if s is a section of $P \times _K z_0$ , then we can identify it with a K-invariant smooth map $f_s$ in $\Omega ^0(P, z_0)^K$ . Since $\rho (\theta _P)$ is a $\mathfrak {so}(z_0)$ -valued form and $\mathfrak {so}(z_0)$ is a subspace of $\operatorname {End}(z_0),$ we can define

(3.27) $$ \begin{align} df_s+\rho(\theta_P) \cdot f_s \in \Omega^1(P, z_0). \end{align} $$

Lemma 3.2 The form $df_s+\rho (\theta _P) \cdot f_s$ is basic, hence gives a $P \times _K z_0$ -valued form on $P/K$ . Thus, $d+\rho (\theta _P)$ defines a covariant derivative on $P \times _K z_0$ . Moreover, it is compatible with the metric.

Proof See [1, p. 24]. For the compatibility with the metric, it follows from the fact that the connection $\rho (\theta _P)$ is valued in $\mathfrak {so}(z_0)$ that

(3.28) $$ \begin{align}\langle \rho(\theta_P) f_{s_1},f_{s_2} \rangle + \langle f_{s_1}, \rho(\theta_P)f_{s_2} \rangle =0. \end{align} $$

Hence, if we denote by $\nabla _P$ is the covariant derivative defined by $d+\rho (\theta _P),$ then

(3.29) $$ \begin{align}\langle \nabla_Ps_1,s_2 \rangle +\langle s_1,\nabla_Ps_2 \rangle = \langle df_{s_1},f_{s_2} \rangle + \langle f_{s_1}, df_{s_2} \rangle =d \langle f_{s_1},f_{s_2}\rangle=d\langle s_1,s_2 \rangle. \end{align} $$

Let us denote by $\nabla _P$ the covariant derivative $d+\rho (\theta _P)$ . It can be extended to a map

(3.30) $$ \begin{align} \nabla_P \colon \Omega^i(P/K,P \times_K z_0) & \longrightarrow \Omega^{i+1}(P/K,P \times_K z_0) \end{align} $$

by setting

(3.31)

where

(3.32) $$ \begin{align} \omega \otimes s \in \Omega^i(P/K) \otimes \Omega^0(P/K,P \times_K z_0) \simeq \Omega^i(P/K,P \times_K z_0). \end{align} $$

We define the curvature $R_P$ in $\Omega ^2(P,\mathfrak {k})$ by

(3.33)

for two vector fields X and Y on P. It is basic by [1, Proposition 1.13] and composing with $\rho $ gives an element

(3.34) $$ \begin{align} \rho(R_P)\in \Omega^2(P,\mathfrak{so}(z_0))_{\mathrm{bas}}, \end{align} $$

so that we can view it as an element in $\Omega ^2(P/K,P \times _K \mathfrak {so}(z_0)),$ where K acts on $\mathfrak {so}(z_0)$ by the $\operatorname {Ad}$ -representation. For a section s in $\Omega ^0(P/K,P \times _K z_0)$ , we have [1, Proposition 1.15]

(3.35) $$ \begin{align} \nabla_P^2s=\rho(R_p)s\in \Omega^2(P/K,P\times_K z_0). \end{align} $$

From now on, we denote by $\nabla $ and $\widetilde {\nabla }$ the covariant derivatives on E and $\widetilde {E}$ associated with $\theta $ and $\widetilde {\theta }$ defined in (3.7) and (3.10). Let R and $\widetilde {R}$ be their respective curvatures.

3.4 Pullback of bundles

The pullback of E by the projection map gives a canonical bundle

(3.36)

over E. We have the following diagram:

(3.37)

The projection induces a pullback of the sections

(3.38) $$ \begin{align} \pi^\ast \colon \Omega^i(\mathbb{D},E) \longrightarrow \Omega^i(E,\widetilde{E}). \end{align} $$

We can also pullback the covariant derivative $\nabla $ to a covariant derivative

(3.39) $$ \begin{align} \pi^\ast \nabla \colon \Omega^0(E,\pi^\ast E) \longrightarrow \Omega^1(E,\pi^\ast E) \end{align} $$

on $\pi ^\ast E$ . It is characterized by the property

(3.40) $$ \begin{align} (\pi^\ast \nabla)(\pi^\ast s)=\pi^\ast (\nabla s). \end{align} $$

Proposition 3.3 The bundles $\widetilde {E}$ and $\pi ^\ast E$ are isomorphic, and this isomorphism identifies $\widetilde {\nabla }$ and $\pi ^\ast \nabla $ .

Proof By definition, $([g_1,w_1],[g_2,w_2])$ are elements of $ \pi ^\ast E$ if and only if $g^{-1}_1g_2$ is in K. We have a $G(\mathbb {R})^+$ -equivariant morphism

(3.41) $$ \begin{align} \pi^\ast E & \longrightarrow \widetilde{E} \nonumber \\ ([g_1,w_1],[g_2,w_2]) & \longrightarrow [(g_1,g_1^{-1}g_2w_2),w_1]. \end{align} $$

This map is well defined and has as inverse

(3.42) $$ \begin{align} \widetilde{E} & \longrightarrow \pi^\ast E \nonumber \\ [(g,w_1),w_2] & \longrightarrow ([g,w_2],[g,w_1]). \end{align} $$

The second statement follows from the fact that $\widetilde {\theta }$ is $\pi ^\ast \theta $ .

3.5 A few operations on the vector bundles

We extend the K-representation $z_0$ to $\bigwedge ^j z_0$ by

(3.43) $$ \begin{align} k(w_1 \wedge \cdots \wedge w_j)=(kw_1) \wedge \cdots \wedge (k w_j). \end{align} $$

We consider the bundles $P \times _K \wedge ^j z_0$ and $ P \times _K \wedge z_0$ over $P/K$ , where $\bigwedge z_0$ is defined as $ \bigoplus _i \bigwedge ^iz_0$ . Denote the space of differential forms valued in $P \times _K \wedge ^j z_0$ by

(3.44)

The total space of differential forms

(3.45) $$ \begin{align} \Omega(P/K,P\times_K \wedge z_0) = \bigoplus_{i,j} \Omega_P^{i,j} \end{align} $$

is an (associative) bigraded $C^\infty (P/K)$ -algebra, where the product is defined by

(3.46)

This algebra structure allows us to define an exponential map by

(3.47)

where $\omega ^k$ is the k-fold wedge product $\omega \wedge \cdots \wedge \omega $ .

Remark 3.1 Suppose that $\omega $ and $\eta $ commute. Then the binomial formula

(3.48) $$ \begin{align} (\omega+\eta)^k=\sum_{l=0}^k \binom{k}{l}\omega^l\eta^{k-l} \end{align} $$

holds and one can show that $\exp (\omega +\eta )=\exp (\omega )+\exp (\eta )$ in the same way as for the real exponential map. In particular, the diagonal subalgebra $\bigoplus \Omega _P^{i,i}$ is a commutative, since for two forms $\omega $ and $\eta $ in $\Omega _P$ , we have

(3.49) $$ \begin{align} \omega \wedge \eta =(-1)^{\deg(\omega)+\deg(\eta)} \eta \wedge \omega \end{align} $$

and similarly for two sections s and t in $\Omega ^0(P/K,P \times _K z_0)$ .

The inner product $\langle - , - \rangle $ on $z_0$ can be extended to an inner product on $\bigwedge z_0$ by

(3.50)

If $e_1, \dots , e_q$ is an orthonormal basis of $z_0$ , then the set

(3.51) $$ \begin{align} \{ e_{i_1} \wedge \cdots \wedge e_{i_k} \; \vert \; 1 \leq k \leq q, \; i_1 < i_2< \cdots <i_k \}\end{align} $$

is an orthonormal basis of $\bigwedge z_0$ . We define the Berezin integral $\int ^B$ to be the orthogonal projection onto the top dimensional component, that is the map

(3.52) $$ \begin{align} \int^B \colon \bigwedge z_0& \longrightarrow \mathbb{R} \nonumber \\ w & \longmapsto \langle w \; , \;e_1\wedge \cdots \wedge e_q \rangle. \end{align} $$

The Berezin integral can then be extended to

(3.53) $$ \begin{align} \int^B \colon \Omega(P/K,P\times_K \wedge z_0) & \longrightarrow \Omega(P/K) \nonumber \\ \omega \otimes s & \longmapsto \omega \int^B s, \end{align} $$

where $\int ^B s$ in $C^\infty (P/K)$ is the composition of the section with the Berezinian in every fiber. Let $s_1, \dots , s_q$ be a local orthonormal frame of $P \times _K z_0$ . Then $s_1 \wedge \cdots \wedge s_q$ is in $\Omega ^0(P/K,\wedge ^q P \times _K z_0)$ and defines a global section. Hence, for $\alpha $ in $\Omega (P/K,P\times _K \wedge z_0),$ we have

(3.54) $$ \begin{align} \int^B\alpha=\langle \alpha, s_1 \wedge \cdots \wedge s_q \rangle. \end{align} $$

Finally, for every section s in $\Omega ^{0,1}$ , we can define the contraction

(3.55) $$ \begin{align} i(s) \colon \Omega_P^{i,j} & \longrightarrow \Omega_P^{i,j-1} \nonumber \\ \omega \otimes s_1 \wedge \cdots \wedge s_j & \longmapsto \sum_{k=1}^j (-1)^{i+k-1}\langle s,s_k \rangle \omega \otimes s_1\wedge \cdots \wedge \widehat{s_k} \wedge \cdots \wedge s_j, \end{align} $$

and extended by linearity, where the symbol $ \, \widehat {\cdot } \,$ means that we remove it from the product. Note that when j is zero, then $i(s)$ is defined to be zero. The contraction $i(s)$ defines a derivation on $\oplus \widetilde {\Omega }^{i,j}$ that satisfies

(3.56) $$ \begin{align} i(s)(\alpha \wedge \alpha')=(i(s) \alpha) \wedge \alpha'+(-1)^{i+j}\alpha \wedge (i(s)\alpha') \end{align} $$

for $\alpha $ in $\widetilde {\Omega }^{i,j}$ and $\alpha '$ in $\widetilde {\Omega }^{k,l}$ .

3.6 Thom forms

We denote by E the bundle $G(\mathbb {R})^+\times _K z_0$ . On the fibers of the bundle, we have the inner product given by . Let v be arbitrary vector in L and $\Gamma _v$ its stabilizer. Since the bundle is $G(\mathbb {R})^+$ -equivariant, we have a bundle

(3.57) $$ \begin{align} \Gamma_v \backslash E \longrightarrow \Gamma_v \backslash \mathbb{D}^+, \end{align} $$

and let $\operatorname {D}(\Gamma _v \backslash E)$ be the closed disk bundle. If we have a closed $(q+i)$ -form on $\Gamma _v \backslash E$ whose support is contained in $\operatorname {D}(\Gamma _v \backslash E)$ , then it has compact support in the fiber and represents a class in $H^{q+i}(\Gamma _v \backslash E,\Gamma _v \backslash E-\operatorname {D}(\Gamma _v \backslash E))$ . The cohomology group $H^{\bullet }(\Gamma _v \backslash E,\Gamma _v \backslash E-\operatorname {D}(\Gamma _v \backslash E))$ is equal to the cohomology group $H^{\bullet }(\Gamma _v \backslash E,\Gamma _v \backslash (E-E_0))$ that we used in the introduction, where $E_0$ is the zero section. Fiber integration induces an isomorphism on the level of cohomology

(3.58) $$ \begin{align} \operatorname{Th} \colon H^{q+i}(\Gamma_v \backslash E,\Gamma_v \backslash E-\operatorname{D}(\Gamma_v \backslash E)) & \longrightarrow H^i(\Gamma_v \backslash \mathbb{D}^+) \nonumber \\ [\omega] & \longmapsto \int_{\mathrm{fiber}} \omega \end{align} $$

known as the Thom isomorphism [2, Theorem 6.17]. When i is zero, then $H^i(\Gamma _v \backslash \mathbb {D}^+)$ is $\mathbb {R}$ and we call the preimage of $1$

(3.59)

the Thom class. Any differential form representating this class is called a Thom form, in particular, every closed q-form on $\Gamma _v \backslash E$ that has compact support in every fiber and whose integral along every fiber is $1$ is a Thom form. One can also view the Thom class as the Poincaré dual class of the zero section $E_0$ in E, in the same sense as for (2.24).

Let $\omega $ in $\Omega ^j(E)$ be a form on the bundle, and let $\omega _z$ be its restriction to a fiber $E_z=\pi ^{-1}(z)$ for some z in $\mathbb {D}^+$ . After identifying $z_0$ with $\mathbb {R}^q$ , we see $\omega _z$ as an element of $C^\infty (\mathbb {R}^q) \otimes \wedge ^j(\mathbb {R}^q)^\ast $ . We say that $\omega $ is rapidly decreasing in the fiber, if $\omega _z$ lies in $\mathscr {S}(\mathbb {R}^q) \otimes \wedge ^j(\mathbb {R}^q)^\ast $ for every z in $\mathbb {D}^+$ . We write $\Omega ^j_{\textrm {rd}}(E)$ for the space of such forms.

Let $\Omega ^\bullet _{\textrm {rd}}(\Gamma _v \backslash E)$ be the complex of rapidly decreasing forms in the fiber. It is isomorphic to the complex $\Omega ^\bullet _{\textrm {rd}}(E)^{\Gamma _v}$ of rapidly decreasing $\Gamma _v$ -invariant forms on E. Let $H_{\textrm {rd}}(\Gamma _v \backslash E)$ the cohomology of this complex. The map

(3.60) $$ \begin{align} h \colon \Gamma_v \backslash E & \longrightarrow \Gamma_v \backslash E \nonumber \\ w & \longrightarrow \frac{w}{\sqrt{1-\lVert {w} \rVert^2}} \end{align} $$

is a diffeomorphism from the open disk bundle $\operatorname {D}(\Gamma _v \backslash E)^\circ $ onto $\Gamma _v \backslash E$ . It induces an isomorphism by pullback

(3.61) $$ \begin{align} h^\ast \colon H_{\textrm{rd}}(\Gamma_v \backslash E) \longrightarrow H(\Gamma_v \backslash E,\Gamma_v \backslash E-\operatorname{D}(\Gamma_v \backslash E)), \end{align} $$

which commutes with the fiber integration. Hence, we have the following version of the Thom isomorphism:

(3.62) $$ \begin{align} H_{\textrm{rd}}^{q+i}(\Gamma_v \backslash E) & \longrightarrow H^i(\Gamma_v \backslash \mathbb{D}^+). \end{align} $$

The construction of Mathai and Quillen produces a Thom form

(3.63) $$ \begin{align} U_{MQ} \in \Omega_{\textrm{rd}}^q(E), \end{align} $$

which is $G(\mathbb {R})^+$ -invariant (hence, $\Gamma _v$ -invariant) and closed. We will recall their construction in the next section.

3.7 The Mathai–Quillen construction

As earlier, let $\widetilde {E}$ be the bundle $(G(\mathbb {R})^+ \times z_0) \times _K z_0$ . Let $ \wedge ^j \tilde {E} $ be the bundle $(G(\mathbb {R})^+ \times z_0) \times _K \wedge ^j z_0$ and

(3.64)

First, consider the tautological section $\mathbf{s}$ of $\widetilde {E}$ defined by

(3.65)

This gives a canonical element $\mathbf{s}$ of $\widetilde {\Omega }^{0,1}$ . Composing with the norm induced from the inner product, we get an element $\lVert \mathbf{s} \rVert ^2$ in $\widetilde {\Omega }^{0,0}$ .

The representation $\rho $ on $z_0$ induces a representation on $\wedge ^iz_0$ that we also denote by $\rho $ . The derivative at the identity gives a map

(3.66) $$ \begin{align} \rho \colon \mathfrak{k} \longrightarrow \mathfrak{so}(\wedge^i z_0). \end{align} $$

The connection form $\rho (\widetilde {\theta })$ in $\Omega ^1(G(\mathbb {R})^+ \times z_0,\wedge ^j z_0)$ defines a covariant derivative

(3.67) $$ \begin{align} \widetilde{\nabla} \colon \widetilde{\Omega}^{0,j} \longrightarrow \widetilde{\Omega}^{1,j} \end{align} $$

on $\wedge ^j \widetilde {E}$ . We can extend it to a map

(3.68) $$ \begin{align} \widetilde{\nabla} \colon \widetilde{\Omega}^{i,j} \longrightarrow \widetilde{\Omega}^{i+1,j} \end{align} $$

by setting

(3.69)

as in (3.30). The connection on $\widetilde {\Omega }^{i,j}$ is compatible with the metric. Finally, the covariant derivative $\widetilde {\nabla }$ defines a derivation on $\oplus \widetilde {\Omega }^{i,j}$ that satisfies

(3.70) $$ \begin{align} \widetilde{\nabla}(\alpha \wedge \alpha')=(\widetilde{\nabla} \alpha) \wedge \alpha'+(-1)^{i+j}\alpha \wedge (\widetilde{\nabla}\alpha') \end{align} $$

for any $\alpha $ in $\widetilde {\Omega }^{i,j}$ and $\alpha '$ in $\widetilde {\Omega }^{k,l}$ .

Taking the derivative of the tautological section gives an element

(3.71) $$ \begin{align} \widetilde{\nabla}\mathbf{s}=d\mathbf{s }+\rho(\widetilde{\theta}) \mathbf{s} \in \widetilde{\Omega}^{1,1}. \end{align} $$

Let $\mathfrak {so}(\widetilde {E})$ denote the bundle $(G(\mathbb {R})^+ \times z_0) \times _K \mathfrak {so}(z_0)$ and consider the curvature $\rho (\widetilde {R})$ in $\Omega ^2(\widetilde {E}, \mathfrak {so}(\widetilde {E}))$ . We have an isomorphism

(3.72) $$ \begin{align} {{T^{-1}}\big|{}_{z_0} } \colon \mathfrak{so}(z_0) & \longrightarrow \wedge^2 z_0 \nonumber \\ A & \longmapsto \sum_{i<j}\langle Ae_i,e_j\rangle e_i \wedge e_j. \end{align} $$

The inverse sends $v \wedge w$ to the endomorphism $ u \mapsto \langle v,u \rangle w-\langle w,u \rangle v$ , and is the isomorphism from (2.11) restricted to $z_0$ . Note that we have

(3.73) $$ \begin{align} T(v \wedge w) u =\iota(u) v \wedge w. \end{align} $$

Using this isomorphism, we can also identify $\mathfrak {so}(\widetilde {E})$ and $\wedge ^2 \widetilde {E}$ so that we can view the curvature as an element

(3.74) $$ \begin{align} \rho(\widetilde{R}) \in \widetilde{\Omega}^{2,2}. \end{align} $$

Lemma 3.4 The form lying in $\widetilde {\Omega }^{0,0} \oplus \widetilde {\Omega }^{1,1} \oplus \widetilde {\Omega }^{2,2}$ is annihilated by $\widetilde {\nabla }+ 2 \sqrt {\pi } i(\mathbf{s})$ . Moreover

(3.75) $$ \begin{align}d\int^B \alpha=\int^B \widetilde{\nabla} \alpha,\end{align} $$

for every form $\alpha $ in $\widetilde {\Omega }^{i,j}$ . Hence, $\int ^B exp(-\omega )$ is a closed form.

Proof We have

(3.76) $$ \begin{align} & \left (\widetilde{\nabla}+ 2 \sqrt{\pi} i(\mathbf{s}) \right ) \left ( 2 \pi \lVert \mathbf{s} \rVert^2+2 \sqrt{\pi}\widetilde{\nabla} \mathbf{s}-\rho(\widetilde{R}) \right ) \\ & = 2 \pi \widetilde{\nabla} \lVert \mathbf{s} \rVert^2 + 4\pi^{\frac{3}{2}}i(\mathbf{s}) \lVert \mathbf{s} \rVert^2 + 2 \sqrt{\pi} \widetilde{\nabla}^2 \mathbf{s}+4 \pi i(x) \widetilde{\nabla} \mathbf{s}-\widetilde{\nabla} \rho(\widetilde{R})-2 \sqrt{\pi} i(\mathbf{s}) \rho(\widetilde{R}). \nonumber \end{align} $$

It vanishes, because we have the following:

1. ∙ $i(\mathbf{s}) \lVert \mathbf{s} \rVert ^2=0$ since $\lVert \mathbf{s} \rVert $ is in $\widetilde {\Omega }^{0,0}$ ,

2. ∙ $\widetilde {\nabla } \rho (\widetilde {R})=0$ by Bianchi’s identity,

3. ∙ $\widetilde {\nabla }\lVert \mathbf{s} \rVert ^2= 2\langle \widetilde {\nabla }\mathbf{s},\mathbf{s} \rangle =-2 i(\mathbf{s}) \widetilde {\nabla }\mathbf{s} $ ,

4. ∙ $\widetilde {\nabla }^2\mathbf{s}=\rho (\widetilde {R})\mathbf{s} =i(\mathbf{s})\rho (\widetilde {R})$ .

For the last point, we used (3.73), where we view $\rho (\widetilde {R})$ as an element of $\Omega ^2(E,\mathfrak {so}(\widetilde {E}))$ , respectively of $\Omega ^2(E,\wedge ^2\widetilde {E})$ .

Let $s_1 \wedge \cdots \wedge s_q$ in $\Omega ^0(E,\wedge ^q \widetilde {E})$ be a global section, where $s_1, \dots , s_q$ is a local orthonormal frame for $\widetilde {E}$ . Then, for any $\alpha $ in $\widetilde {\Omega }^{i,j}$ , we have

(3.77) $$ \begin{align}\int^B\alpha=\langle \alpha, s_1 \wedge \cdots \wedge s_q \rangle. \end{align} $$

This vanishes if j is different from q, hence we can assume $\alpha $ is in $\widetilde {\Omega }^{i,q}$ . If we write $\alpha $ as $\beta s_1 \wedge \cdots \wedge s_q$ for some $\beta $ in $\Omega ^i(E)$ , then

(3.78) $$ \begin{align}\int^B \alpha = \beta.\end{align} $$

On the other hand, since the connection on $\widetilde {\Omega }^{i,q}$ is compatible with the metric, we have

(3.79) $$ \begin{align} 0 = d \langle s_1 \wedge \cdots \wedge s_q,s_1 \wedge \cdots \wedge s_q \rangle = 2 \langle \widetilde{\nabla}(s_1 \wedge \cdots \wedge s_q),s_1 \wedge \cdots \wedge s_q \rangle. \end{align} $$

Then we have

(3.80) $$ \begin{align} \int^B \widetilde{\nabla} \alpha & =\langle \widetilde{\nabla} \alpha, s_1 \wedge \cdots \wedge s_q \rangle \nonumber \\ & = \langle d\beta \otimes s_1 \wedge \cdots \wedge s_q + (-1)^i \beta \wedge \widetilde{\nabla}( s_1 \wedge \cdots \wedge s_q),s_1 \wedge \cdots \wedge s_q \rangle \nonumber \\ & = d \beta \nonumber \\ & = d \int^B \alpha. \end{align} $$

Since $\widetilde {\nabla } + 2 \sqrt {\pi }i(\mathbf{s})$ is a derivation that annihilates $\omega $ , we have

(3.81) $$ \begin{align} \left (\widetilde{\nabla} + 2 \sqrt{\pi}i(\mathbf{s}) \right ) \omega^k=0\end{align} $$

for positive k. Hence, it follows that

(3.82) $$ \begin{align} d \int^B \exp(-\omega) & = \int^B \widetilde{\nabla} \exp(-\omega) \nonumber \\ & = \int^B \left (\widetilde{\nabla}+2 \sqrt{\pi}i(\mathbf{s}) \right )\exp(-\omega) \nonumber \\ & =0.\\[-34pt]\nonumber \end{align} $$

In [10], Mathai and Quillen define the following form:

(3.83)

We call it the Mathai–Quillen form.

Proposition 3.5 The Mathai–Quillen form is a Thom form.

Proof From the previous lemma, it follows that the form is closed. It remains to show that its integral along the fibers is $1$ . The restriction of the form $U_{MQ}$ along the fiber $\pi ^{-1}(eK)$ is given by

(3.84) $$ \begin{align} U_{MQ} & = (- 1)^{\frac{q(q+1)}{2}} (2\pi)^{-\frac{q}{2}} e^{-2 \pi \lVert \mathbf{s} \rVert^2} \int^B \exp(-2 \sqrt{\pi} d \mathbf{s}) \nonumber \\ & = (- 1)^{\frac{q(q+1)}{2}} 2^{\frac{q}{2}} e^{-2 \pi \lVert \mathbf{s} \rVert^2} (-1)^q \int^B (dx_1 \otimes e_1) \wedge \cdots \wedge (dx_q \otimes e_q) \nonumber \\ & = 2^{\frac{q}{2}} e^{-2 \pi \lVert \mathbf{s} \rVert^2} dx_1 \wedge \cdots \wedge dx_q, \end{align} $$

and its integral over the fiber $\pi ^{-1}(eK)$ is equal to $1$ .

4 Computation of the Mathai–Quillen form

4.1 The section $s_v$

Let $\textrm {pr}$ denote the orthogonal projection of $V(\mathbb {R})$ on the plane $z_0$ . Consider the section

(4.1) $$ \begin{align} s_v \colon \mathbb{D}^+ & \longrightarrow E \nonumber \\ z \; & \longmapsto [g_z,\textrm{pr}(g_z^{-1}v)], \end{align} $$

where $g_z$ is any element of $G(\mathbb {R})^+$ sending $z_0$ to z. Let us denote by $L_g$ the left action of an element g in $G(\mathbb {R})^+$ on $\mathbb {D}^+$ . We also denote by $L_g$ the action on E given by $L_{g}[g_z,v]=[gg_z,v]$ . The bundle is $G(\mathbb {R})^+$ -equivariant with respect to these actions.

Proposition 4.1 The section $s_v$ is well-defined and $\Gamma _v$ -equivariant. Moreover, its zero locus is precisely $\mathbb {D}^+_v$ .

Proof The section is well-defined, since replacing $g_z$ by $g_zk$ gives

(4.2) $$ \begin{align}s_v(z)=[g_zk,\textrm{pr}(k^{-1}g_z^{-1}v)]=[g_zk,k^{-1}\textrm{pr}(g_z^{-1}v)]=[g,\textrm{pr}(g_z^{-1}v)]=s_v(z).\end{align} $$

Suppose that z is in the zero locus of $s_v$ , that is to say $\textrm {pr}(g_z^{-1}v)$ vanishes. Then $g_z^{-1}v$ is in $z_0^\perp $ . It is equivalent to the fact that $z=g_zz_0$ is a subspace of $v^\perp $ , which means that z is in $\mathbb {D}_v^+$ . Hence, the zero locus of $s_v$ is exactly $\mathbb {D}^+_v$ . For the equivariance, note that we have

(4.3) $$ \begin{align} s_v \circ L_{g}(z)=[gg_z,\operatorname{pr}(g_z^{-1}g^{-1}v)]=L_{g} \circ s_{g^{-1}v}(z). \end{align} $$

Hence, if $\gamma $ is an element of $\Gamma _v$ , we have

(4.4) $$ \begin{align} s_v \circ L_{\gamma}=L_\gamma \circ s_v. \end{align} $$

We define the pullback of the Mathai–Quillen form by $s_v$ . It defines a form

(4.5) $$ \begin{align} \varphi^0 \in C^\infty(\mathbb{R}^{p+q}) \otimes \Omega^q(\mathbb{D})^+. \end{align} $$

It is only rapidly decreasing on $\mathbb {R}^q$ , and in order to make it rapidly decreasing everywhere we set

(4.6)

It defines a form $ \varphi \in \mathscr {S}(\mathbb {R}^{p+q}) \otimes \Omega ^q(\mathbb {D})^+$ .

Proposition 4.2

1. (1) For fixed v in $V(\mathbb {R}),$ the form $\varphi ^0(v)$ in $\Omega ^q(\mathbb {D}^+)$ is given by

   (4.7) $$ \begin{align} \varphi^0(v) & = (- 1)^{\frac{q(q+1)}{2}} (2\pi)^{-\frac{q}{2}} \exp \left (2 \pi {Q\big|{}_{z_0} }(v,v) \right ) \int^B \exp \left (-2 \sqrt{\pi} \nabla s_v+\rho(R)\right ). \end{align} $$

2. (2) It satisfies $L_g^\ast \varphi ^0(v)=\varphi ^0(g^{-1}v)$ , hence

   (4.8) $$ \begin{align} \varphi^0 \in \left [\Omega^q(\mathbb{D}^+) \otimes C^\infty(\mathbb{R}^{p+q}) \right ]^{G(\mathbb{R})^+}.\end{align} $$

3. (3) It is a Poincaré dual of $\Gamma _v \backslash \mathbb {D}_v^+$ in $\Gamma _v \backslash \mathbb {D}^+$ .

Proof

1. (1) Recall that $\widetilde {\nabla }=\pi ^\ast \nabla $ and $\widetilde {R}=\pi ^\ast R$ . We pullback by $s_v$

   

   Since $\pi \circ s_v$ is the identity, we have

   (4.9) $$ \begin{align} s_v^\ast \widetilde{\nabla} = s_v^\ast \pi^\ast \nabla = \nabla. \end{align} $$

   Hence, the pullback connection $s_v^\ast \widetilde {\nabla }$ satisfies

   (4.10) $$ \begin{align} s_v^\ast (\widetilde{\nabla} \mathbf{s})= (s_v^\ast \widetilde{\nabla}) ( s_v^\ast \mathbf{s}) = \nabla s_v, \end{align} $$
   since $s_v^\ast \mathbf{s}=s_v$ . We also have $s_v^\ast \widetilde {R}=R$ and
   (4.11) $$ \begin{align}s_v^\ast \lVert \mathbf{s} \rVert^2= \lVert s_v \rVert^2= \langle s_v , s_v \rangle=-{Q\big|{}_{z_0} }(v,v). \end{align} $$

   The expression for $\varphi ^0$ then follows from the fact that $\exp $ and $s_v^\ast $ commute.

2. (2) The bundle E is $G(\mathbb {R})^+$ equivariant. By construction, the Mathai–Quillen form is $G(\mathbb {R})^+$ -invariant, so $L_g^\ast U_{MQ}=U_{MQ}$ . On the other hand, we also have

   (4.12) $$ \begin{align}s_v \circ L_g(z)=L_g \circ s_{g^{-1}v}(z),\end{align} $$

   and thus,

   (4.13) $$ \begin{align} L_g^\ast \varphi^0(v)=L_g^\ast s_v^\ast U_{MQ}=\varphi^0(g^{-1}v). \end{align} $$

3. (3) Since $s_v$ is $\Gamma _v$ -equivariant, we view it as a section

   (4.14) $$ \begin{align} s_v \colon \Gamma_v \backslash \mathbb{D}^+ \longrightarrow \Gamma_v \backslash E, \end{align} $$
   whose zero locus is precisely $\Gamma _v \backslash \mathbb {D}_v^+$ . Let $S_0$ (resp. $S_v$ ) be the image in $\Gamma _v \backslash E$ of the section $s_v$ (resp. the zero section). By [2, Proposition 6.24(b)], the Thom form $U_{MQ}$ is a Poincaré dual of the zero section $S_0$ of E. For a form $\omega $ in $\Omega _c^{m-q}(\Gamma _v \backslash \mathbb {D}^+),$ we have
   (4.15) $$ \begin{align} \int_{\Gamma_v \backslash \mathbb{D}^+} \varphi^0(v) \wedge \omega & = \int_{\Gamma_v \backslash \mathbb{D}^+} s_v^\ast \left ( U_{MQ} \wedge \pi ^\ast \omega \right ) \nonumber \\ & = \int_{S_v} U_{MQ} \wedge \pi ^\ast \omega \nonumber \\ & = \int_{S_v \cap S_0} \pi ^\ast \omega \nonumber \\ & = \int_{\Gamma_v \backslash \mathbb{D}_v^+} \omega. \end{align} $$

   The last step follows from the fact that $\pi ^{-1}(S_v \cap S_0)$ equals $\Gamma _v \backslash \mathbb {D}_v^+$ .

As in (2.19), we have an isomorphism

(4.16) $$ \begin{align} \left [ \Omega^q(\mathbb{D}^+) \otimes C^\infty(\mathbb{R}^{p+q}) \right ]^{G(\mathbb{R})^+} & \longrightarrow \left [ \sideset{}{^q}\bigwedge \mathfrak{p}^\ast \otimes C^\infty(\mathbb{R}^{p+q}) \right ]^K \end{align} $$

by evaluating at the basepoint $eK$ of $G(\mathbb {R})^+/K$ that corresponds to $z_0$ in $\mathbb {D}^+$ . We will now compute ${ {\varphi ^0}\big|{}_{eK} }$ .

4.2 The Mathai–Quillen form at the identity

From now on, we identify $\mathbb {R}^{p+q}$ with $V(\mathbb {R})$ by the orthonormal basis of (2.1), and let $z_0$ be the negative spanned by the vectors $e_{p+1}, \ldots , e_{p+q}$ . Hence, we identify $z_0$ with $\mathbb {R}^q$ and the quadratic form is

(4.17) $$ \begin{align} {Q\big|{}_{z_0} }(v,v)=-\sum_{\mu=p+1}^{p+q} x_\mu^2, \end{align} $$

where $x_{p+1}, \dots , x_{p+q}$ are the coordinates of the vector v.

Let $f_v$ in $\Omega ^0(G(\mathbb {R})^+,z_0)^K$ be the map associated with the section $s_v$ , as in Proposition 3.1. It is defined by

(4.18) $$ \begin{align} f_v(g)=\operatorname{pr}(g^{-1}v). \end{align} $$

Then $df_v+\rho (\theta ) f_v$ is the horizontal lift of $\nabla s_v$ , as discussed in Section 3.1. Let X be a vector in $\mathfrak {g}$ , and let $X_{\mathfrak {p}}$ and $X_{\mathfrak {k}}$ be its components with respect to the splitting of $\mathfrak {g}$ as $\mathfrak {p} \oplus \mathfrak {k}$ . We have

(4.19) $$ \begin{align} (df_v+\rho(\theta) f_v)_e(X)=d_ef_v(X_{\mathfrak{p}}). \end{align} $$

In particular, we can evaluate on the basis $X_{\alpha \mu }$ and get:

(4.20) $$ \begin{align} d_{e} f_v(X_{\alpha \mu}) & = \left. \frac{d}{dt} \right \rvert_{t=0} f_v(\exp tX_{\alpha \mu})\nonumber \\ & = -\operatorname{pr}(X_{\alpha \mu}v) \nonumber \\ & = -\operatorname{pr}(x_\mu e_\alpha+x_\alpha e_\mu) \nonumber\\ & = -x_{\alpha}e_\mu. \end{align} $$

So as an element of $\mathfrak {p}^\ast \otimes z_0$ , we can write

(4.21) $$ \begin{align}d_ef_v=-\sum_{\mu=p+1}^{p+q} \left ( \sum_{\alpha=1}^p x_\alpha \omega_{\alpha \mu} \right )\otimes e_\mu=-\sum_{\alpha=1}^p x_\alpha \eta_\alpha,\end{align} $$

with

(4.22)

Proposition 4.3 Let $\rho (R_e)$ in $\wedge ^2\mathfrak {p}^\ast \otimes \mathfrak {so}(z_0)$ be the curvature at the identity. Then after identifying $\mathfrak {so}(z_0)$ with $\wedge ^2 z_0$ , we have

(4.23) $$ \begin{align} \rho(R_e)= -\frac{1}{2} \sum_{\alpha=1}^p \eta_\alpha^2 \in \wedge^2\mathfrak{p}^\ast \otimes \wedge^2 z_0, \end{align} $$

where $\eta _\alpha ^2=\eta _\alpha \wedge \eta _\alpha $ .

Proof Using the relation $E_{ij}E_{kl}=\delta _{il}E_{kj}$ , one can show that

(4.24) $$ \begin{align} [X_{\alpha \mu},X_{\beta \nu}] =\delta_{\mu \nu} X_{\alpha \beta}+ \delta_{\alpha \beta} X_{\mu \nu} \end{align} $$

for two vectors $X_{\alpha \nu }$ and $ X_{\beta \mu }$ in $\mathfrak {p}$ . Hence, we have

(4.25) $$ \begin{align} R_e(X_{\alpha \nu} \wedge X_{\beta \mu}) & =[\theta(X_{\alpha \nu}), \theta(X_{\beta \mu})] -\theta([X_{\alpha \nu}, X_{\beta \mu}]) \nonumber \\ & =-\theta([X_{\alpha \nu}, X_{\beta \mu}]) \nonumber \\ & =-p\left (\delta_{\alpha \beta}X_{\nu \mu}+\delta_{\nu \mu}X_{\alpha \beta} \right ) \nonumber \\ & = -\delta_{\alpha \beta}X_{\nu \mu}. \end{align} $$

On the other hand, since $\eta _i(X_{jr})=\delta _{ij}e_r$ , we also have

(4.26) $$ \begin{align} \sum_{i=1}^p \eta_i^2(X_{\alpha \nu} \wedge X_{\beta \mu}) & = \sum_{i=1}^p \eta_i(X_{\alpha \nu}) \wedge \eta_i(X_{\beta \mu})-\eta_i(X_{\beta \mu}) \wedge \eta_i(X_{\alpha \nu}) \nonumber \\ & =2 \delta_{\alpha \beta}e_\nu \wedge e_\mu. \end{align} $$

The lemma follows since $\rho (X_{\nu \mu })=T(e_\nu \wedge e_\mu )$ in $\mathfrak {so}(z_0)$ , because

(4.27) $$ \begin{align}Q( \rho(X_{\nu \mu})e_\nu, e_\mu ) e_\nu \wedge e_\mu =-Q( e_\mu, e_\mu ) e_\nu \wedge e_\mu=e_\nu \wedge e_\mu.\\[-34pt]\nonumber \end{align} $$

Using the fact that the exponential satisfies $\exp (\omega +\eta )=\exp (\omega )\exp (\eta )$ on the subalgebra $\bigoplus \Omega ^{i,i}$ —see Remark 3.1—we can write

(4.28) $$ \begin{align} {{\varphi^0}\big|{}_{e} }(v) &= (- 1)^{\frac{q(q+1)}{2}} (2\pi)^{-\frac{q}{2}} \exp \left (2 \pi {Q\big|{}_{z_0} }(v,v) \right ) \int^B \prod_{\alpha=1}^p \exp \left ( 2 \sqrt{\pi} x_\alpha\eta_\alpha-\frac{1}{2}\eta_\alpha^2 \right ). \end{align} $$

We define the nth Hermite polynomial by

(4.29)

The first three Hermite polynomials are $H_0(x)=1$ , $H_1(x)=2x$ , and $H_2(x)=4x^2-2$ .

Lemma 4.4 Let $\eta $ be a form in $\bigoplus \Omega ^{i,i}$ . Then

(4.30) $$ \begin{align}\exp(2x \eta-\eta^2)=\sum_{n \geq 0} \frac{1}{n!}H_n(x)\eta^n, \end{align} $$

where $H_n$ is the nth Hermite polynomial.

Proof Since $\eta $ and $\eta ^2$ are in $\bigoplus \Omega ^{i,i}$ , they commute and we can use the binomial formula:

(4.31) $$ \begin{align} \exp(2x \eta-\eta^2) & =\sum_{k \geq 0} \frac{1}{k!} \left (2x\eta-\eta^2 \right)^k \nonumber \\ & = \sum_{k \geq 0} \frac{1}{k!} \sum_{l=0}^k {k \choose l}(2x \eta)^{k-l}\left (-\eta^2 \right)^{l} \nonumber \\ & = \sum_{k \geq 0} \frac{1}{k!} \sum_{l=0}^k {k \choose l}(2x)^{k-l} (- 1 )^{l} \eta^{l+k} \nonumber \\ & = \sum_{n \geq 0} P_n(x)\eta^n, \end{align} $$

where

(4.32)

The conditions on k and l imply that n is less than or equal to $2k$ . First, suppose that n is even. Then we have that k is between $\frac {n}{2}$ and n, so that the sum above can be written

(4.33) $$ \begin{align} \sum_{k=\frac{n}{2}}^{n}\frac{ (-1)^{n-k}}{(n-k)!(2k-n)!}(2x)^{2k-n}=&\sum_{m=0}^{\frac{n}{2}}\frac{(-1)^{\frac{n}{2}-m}}{(\frac{n}{2}-m)!(2m)!} (2x)^{2m}=\frac{1}{n!}H_n(x), \end{align} $$

where in the second step, we let m be $k-\frac {n}{2}$ . If n is odd, then k is between $\frac {n+1}{2}$ and n, so that the sum can be written

(4.34) $$ \begin{align} \sum_{k=\frac{n+1}{2}}^{n}\frac{ (-1)^{n-k}}{(n-k)!(2k-n)!}(2x)^{2k-n}=&\sum_{m=0}^{\frac{n-1}{2}}\frac{(-1)^{\frac{n-1}{2}-m}}{(\frac{n-1}{2}-m)!(2m+1)!} (2x)^{2m+1}=\frac{1}{n!}H_n(x). \end{align} $$

Applying the lemma to (4.28), we get

(4.35) $$ \begin{align} & \int^B \prod_{\alpha=1}^p \exp \left (2 \sqrt{\pi} x_\alpha\eta_\alpha-\frac{1}{2}\eta_\alpha^2 \right ) \nonumber \\ &= \int^B \prod_{\alpha=1}^p \exp \left (2 \sqrt{2\pi}x_\alpha \frac{\eta_\alpha}{\sqrt{2}}-\left (\frac{\eta_\alpha}{\sqrt{2}}\right)^2 \right ) \nonumber \\ & = \int^B \prod_{\alpha=1}^p \sum_{n \geq 0} \frac{2^{-n/2}}{n!}H_n\left (\sqrt{2\pi} x_\alpha \right )\eta_\alpha^n \nonumber \\ & = \sum_{n_1, \dots, n_p}\frac{2^{-\frac{n_1+\cdots +n_p}{2}}}{n_1! \ldots n_p!}H_{n_1}\left (\sqrt{2\pi} x_1 \right ) \ldots H_{n_p}\left (\sqrt{2\pi}x_p \right ) \int^B \eta_1^{n_1} \wedge \cdots \wedge \eta_p^{n_p}. \end{align} $$

If $n_1+ \cdots + n_p$ is different from q, then the Berezinian of $\eta _1^{n_1} \wedge \cdots \wedge \eta _p^{n_p}$ vanishes and we get

(4.36) $$ \begin{align} & \sum_{n_1, \dots, n_p}\frac{2^{-\frac{n_1+\cdots +n_p}{2}}}{n_1! \ldots n_p!}H_{n_1}\left (\sqrt{2\pi} x_1 \right ) \ldots H_{n_p}\left (\sqrt{2\pi}x_p \right )\int^B \eta_1^{n_1} \wedge \cdots \wedge \eta_p^{n_p} \nonumber \\ = & 2^{-\frac{q}{2}}\sum_{n_1+ \dots+ n_p=q}\frac{H_{n_1}\left (\sqrt{2\pi}x_1 \right ) \ldots H_{n_p}\left (\sqrt{2\pi} x_p \right )}{n_1! \ldots n_p!} \int^B \eta_1^{n_1} \wedge \cdots \wedge \eta_p^{n_p}. \end{align} $$

Note that

(4.37) $$ \begin{align} \eta_\alpha^{n_\alpha} & = \left ( \sum_{\mu=p+1}^{p+q} \omega_{\alpha \mu} \otimes e_\mu \right )^{n_\alpha} \nonumber \\ & = \sum_{\mu_1, \dots, \mu_{n_\alpha}} (\omega_{\alpha \mu_1} \otimes e_{\mu_1}) \wedge \cdots \wedge (\omega_{\alpha \mu_{n_\alpha}} \otimes e_{\mu_{n_\alpha}}) \nonumber \\ & = n_\alpha! \sum_{\mu_1< \dots< \mu_{n_\alpha}}(\omega_{\alpha \mu_1} \otimes e_{\mu_1}) \wedge \cdots \wedge (\omega_{\alpha \mu_{n_\alpha}} \otimes e_{\mu_{n_\alpha}}), \end{align} $$

where the sums are over all $\mu _i$ ’s between $p+1$ and $p+q$ . If $n_1+\cdots +n_p$ is equal to $q,$ we have

(4.38) $$ \begin{align} & \int^B \eta_1^{n_1} \wedge \cdots \wedge \eta_p^{n_p} \nonumber \\ & = \int^B \prod_{\alpha=1}^{p} \left ( \sum_{\mu=p+1}^{p+q} \omega_{\alpha \mu} \otimes e_\mu \right )^{n_\alpha} \nonumber \\ & = \int^B \prod_{\alpha=1}^{p} n_\alpha! \sum_{\mu_1< \dots< \mu_{n_\alpha}}(\omega_{\alpha \mu_1} \otimes e_{\mu_1}) \wedge \cdots \wedge (\omega_{\alpha \mu_{n_\alpha}} \otimes e_{\mu_{n_\alpha}}) \nonumber \\ & = n_1! \ldots n_p! \sum \int^B (\omega_{\alpha (p+1)} \otimes e_{1}) \wedge \cdots \wedge (\omega_{\alpha (p+q)} \otimes e_{q}) \nonumber \\ & = (- 1)^{\frac{q(q+1)}{2}} n_1! \ldots n_p! \sum \omega_{\alpha_1 (p+1)} \wedge \cdots \wedge \omega_{\alpha_q (p+q)}, \end{align} $$

where the sums in the last two lines go over all tuples $\underline {\alpha }=(\alpha _1, \dots , \alpha _q)$ with $\alpha $ between $1$ and p, and the value $\alpha $ appears exactly $n_{\alpha }$ -times in $\underline {\alpha }$ . Hence

(4.39) $$ \begin{align} {{\varphi^0}\big|{}_{e} }(v) = 2^{-q}\pi^{-\frac{q}{2}}\sum \omega_{\alpha_1 (p+1)}& \wedge \cdots \wedge \omega_{\alpha_q (p+q)} \otimes H_{n_1}\left (\sqrt{2\pi} x_1 \right ) \\ &\ldots H_{n_p}\left (\sqrt{2\pi} x_p \right )\exp \left (2\pi {Q\big|{}_{z_0} }(v,v) \right ). \nonumber \end{align} $$

After multiplying by $\exp \left (-\pi Q(v,v) \right )$ , we get

(4.40) $$ \begin{align} {{\varphi}\big|{}_{e} }(v) = 2^{-q}\pi^{-\frac{q}{2}} \sum \omega_{\alpha_1 (p+1)}& \wedge \cdots \wedge \omega_{\alpha_q (p+q)} \otimes H_{n_1}\left (\sqrt{2\pi} x_1 \right )\\ &\ldots H_{n_p}\left (\sqrt{2\pi} x_p \right )\exp \left (-\pi Q_{z_0}^+(v,v) \right ). \nonumber \end{align} $$

The form is now rapidly decreasing in v, since the Siegel majorant is positive definite. We have

(4.41) $$ \begin{align} {{\varphi}\big|{}_{e} } \in \left [ \sideset{}{^q} \bigwedge \mathfrak{p}^\ast \otimes \mathscr{S}(\mathbb{R}^{p+q})\right ]^K. \end{align} $$

Theorem 4.5 We have $2^{-\frac {q}{2}}\varphi (v)=\varphi _{KM}(v)$ .

Proof It is a straightforward computation to show that

(4.42) $$ \begin{align} (2 \pi)^{-n_\alpha/2}H_{n_\alpha}\left ( \sqrt{2 \pi}x_\alpha \right )\exp(-\pi x_\alpha^2) & = \left (x_\alpha - \frac{1}{2\pi}\frac{\partial}{\partial{x_\alpha}} \right )^{n_\alpha} \exp(-\pi x_\alpha^2). \end{align} $$

Hence, applying this, we find that the Kudla–Millson form, defined by the Howe operators in (2.22), is

(4.43) $$ \begin{align} {{\varphi_{KM}}\big|{}_{e} }(v) & = 2^{-q}(2\pi)^{-\frac{q}{2}} \sum \omega_{\alpha_1 (p+1)} \wedge \cdots \wedge \omega_{\alpha_q (p+q)} \otimes H_{n_1}\left (\sqrt{2\pi} x_1 \right ) \\ &\ldots H_{n_p}\left (\sqrt{2\pi} x_p \right )\exp \left (-\pi {Q\big|{}_{z_0} }(v,v) \right ) \nonumber \\ & = 2^{-\frac{q}{2}} e^{-\pi Q(v,v)}{{\varphi^0}\big|{}_{e} }(v).\nonumber\\[-34pt]\nonumber \end{align} $$

5 Examples and remarks

1. (1) Let us compute the Kudla–Millson as above in the simplest setting of signature $(1,1)$ . Let $V(\mathbb {R})$ be the quadratic space $\mathbb {R}^2$ with the quadratic form $Q(v,w)=x'y+xy'$ , where x and $x'$ (resp. y and $y'$ ) are the components of v (respectively of w). Let $e_1=\frac {1}{\sqrt {2}}(1,1)$ and $e_2=\frac {1}{\sqrt {2}}(1,-1)$ . The one-dimensional negative plane $z_0$ is $\mathbb {R} e_2$ . If r denotes the variable on $z_0$ , then the quadratic form is ${{Q}\big|{}_{z_0} }(r)=-r^2$ . The projection map is given by

   (5.1) $$ \begin{align} \operatorname{pr} \colon V(\mathbb{R}) & \longrightarrow z_0 \nonumber \\ v=(x,x') & \longmapsto \frac{x-x'}{\sqrt{2}}. \end{align} $$

   The orthogonal group of $V(\mathbb {R})$ is

   (5.2) $$ \begin{align} G(\mathbb{R})^+=\left \{ \begin{pmatrix} t & 0 \\ 0 & t^{-1} \end{pmatrix},t>0 \right \}, \end{align} $$
   and $\mathbb {D}^+$ can be identified with $\mathbb {R}_{>0}$ . The associated bundle E is $\mathbb {R}_{>0} \times \mathbb {R}$ and the connection $\nabla $ is simply d since the bundle is trivial. Hence, the Mathai–Quillen form is
   (5.3) $$ \begin{align} U_{MQ}=\sqrt{2}e^{-2\pi r^2}dr \in \Omega^1(E), \end{align} $$
   as in the proof of Proposition 3.5. The section $s_v \colon \mathbb {R}_{>0} \rightarrow E$ is given by
   (5.4) $$ \begin{align} s_v(t)=\left (t, \frac{t^{-1}x-tx'}{\sqrt{2}} \right ), \end{align} $$
   where x and $x'$ are the components of v. We obtain
   (5.5) $$ \begin{align} s_v^\ast U_{MQ}=e^{-\pi \left ( \frac{x}{t}-tx' \right )^2}\left ( \frac{x}{t}+tx' \right ) \frac{dt}{t}. \end{align} $$

   Hence, after multiplication by $2^{-\frac {1}{2}}e^{-\pi Q(v,v)}$ , we get

   (5.6) $$ \begin{align} \varphi_{KM}(x,x')= 2^{-\frac{1}{2}}e^{-\pi \left [ \left (\frac{x}{t} \right )^2+(tx')^2 \right ]}\left ( \frac{x}{t}+tx' \right ) \frac{dt}{t}. \end{align} $$

2. (2) The second example illustrates the functorial properties of the Mathai–Quillen form. Suppose that we have an orthogonal splitting of $V(\mathbb {R})$ as $\bigoplus _i^r V_i(\mathbb {R})$ . Let $(p_i,q_i)$ be the signature of $V_i(\mathbb {R})$ . We have

   (5.7) $$ \begin{align} \mathbb{D}_{1} \times \cdots \times \mathbb{D}_{r} \simeq \left \{ z \in \mathbb{D} \; \vert \; z = \bigoplus_{i=1}^r z \cap V_i(\mathbb{R}) \right \}. \end{align} $$

   Suppose, we fix $z_0= z_0^1 \oplus \cdots \oplus z_0^r$ in $\mathbb {D}^+_{1} \times \cdots \times \mathbb {D}^+_{r} \subset \mathbb {D}$ , where $z_0^i$ is a negative $q_i$ -plane in $V_i(\mathbb {R})$ . Let $G_i(\mathbb {R})$ be the subgroup preserving $V_i(\mathbb {R})$ , let $K_i$ be the stabilizer of $z_0^i$ , and $\mathbb {D}_i$ be the symmetric space associated with $V_i(\mathbb {R})$ .

   Over $\mathbb {D}^+_{1} \times \cdots \times \mathbb {D}^+_{r}$ the bundle E splits as an orthogonal sum $E_1 \oplus \cdots \oplus E_r$ , where $E_i$ is the bundle $G_i(\mathbb {R})^+ \times _{K_i} z_0^i$ . Moreover, the restriction of the Mathai–Quillen form to this subbundle is

   (5.8) $$ \begin{align} {{U_{MQ}}\big|{}_{E_1 \times \cdots \times E_r} }=U_{MQ}^1 \wedge \cdots \wedge U_{MQ}^r, \end{align} $$
   where $U_{MQ}^i$ is the Mathai–Quillen form on $E_i$ . The section $s_v$ also splits as a direct sum $\oplus s_{v_i}$ , where $v_i$ is the projection of v onto $v_i$ . In summary, the following diagram commutes
   (5.9)

   
   and we can conclude that
   (5.10) $$ \begin{align} {{\varphi_{KM}(v)}\big|{}_{\mathbb{D}_1^+ \times \cdots \times \mathbb{D}_r^+} }=\varphi_{KM}^1(v_1)\wedge \cdots \wedge \varphi_{KM}^r(v_r), \end{align} $$
   where $\varphi _{KM}^i$ is the Kudla–Millson form on $\mathbb {D}_i^+$ .

3. (2) Let $U \subset V$ be a nondegenerate r-subspace spanned by vectors $v_1, \dots , v_r$ . Let $(p',q')$ be the signature of U. Let $\mathbb {D}_U$ be the subspace

   (5.11)

   

   When U is positive, i.e., when $q'=0$ , then $\mathbb {D}_U$ is in fact

   (5.12)

   

   In particular, when U is spanned by a single positive vector v, then $\mathbb {D}_U=\mathbb {D}_v$ , where $\mathbb {D}_v$ is as in (2.4). Kudla and Millson construct an $rq$ -form $\varphi _{KM}(v_1,\dots ,v_r)$ that is a Poincaré dual to $\Gamma _U \backslash \mathbb {D}_U$ in $\Gamma _U \backslash \mathbb {D}$ , where $\Gamma _U$ is the stabilizer of U in $\Gamma $ . One of its properties [8][Lemma. 4.1] is that

   (5.13) $$ \begin{align} \varphi_{KM}(v_1,\dots,v_r)=\varphi_{KM}(v_1) \wedge \cdots \wedge \varphi_{KM}(v_r). \end{align} $$

   Let us explain how this form can also be recovered by the Mathai–Quillen formalism. Consider the bundle $E^r=E \oplus \cdots \oplus E$ of rank $rq$ over $\mathbb {D}$ . One can check that all the “ingredients” of the Mathai–Quillen form $U_{MQ}(E^r)$ are compatible with respect to the splitting as a direct sum, so that we have

   (5.14) $$ \begin{align} U_{MQ}(E^r)=U_{MQ}(E) \wedge \dots \wedge U_{MQ}(E). \end{align} $$

   On the other hand, the zero locus of the section of $E^r$ is precisely $\mathbb {D}_U$ . Hence, the pullback

   (5.15)

   
   is a Poincaré dual of $\mathbb {D}_U$ . Moreover, by (5.14), we have
   (5.16) $$ \begin{align} \varphi^0(v_1,\dots,v_r)=\varphi^0(v_1) \wedge \cdots \wedge \varphi^0(v_r). \end{align} $$

   Finally, after setting

   (5.17)

   
   we get
   (5.18) $$ \begin{align} 2^{-\frac{rq}{2}}\varphi(v_1,\dots, v_r) & = 2^{-\frac{rq}{2}} e^{-\pi \sum_{i=1}^r Q(v_i,v_i) }\varphi^0(v_1) \wedge \cdots \wedge \varphi^0(v_r) \nonumber\\ & = 2^{-\frac{rq}{2}} \varphi(v_1) \wedge \cdots \wedge \varphi(v_r) \nonumber\\ & = \varphi_{KM}(v_1) \wedge \cdots \wedge \varphi_{KM}(v_r) \nonumber \\ & = \varphi_{KM}(v_1,\dots,v_r). \end{align} $$

   The last two equalities use Theorem 4.5 and (5.13).