No CrossRef data available.
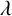 $\lambda $-QUIDDITIES OVER THE RINGS
$\lambda $-QUIDDITIES OVER THE RINGS 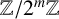 ${\mathbb {Z}}/2^{m}{\mathbb {Z}}$
${\mathbb {Z}}/2^{m}{\mathbb {Z}}$Published online by Cambridge University Press: 16 May 2024
The 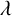 $\lambda $-quiddities of size n are n-tuples of elements of a fixed set, solutions of a matrix equation appearing in the study of Coxeter’s friezes. Their number and properties are closely linked to the structure and the cardinality of the chosen set. Our main objective is an explicit formula giving the number of
$\lambda $-quiddities of size n are n-tuples of elements of a fixed set, solutions of a matrix equation appearing in the study of Coxeter’s friezes. Their number and properties are closely linked to the structure and the cardinality of the chosen set. Our main objective is an explicit formula giving the number of 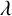 $\lambda $-quiddities of odd size, and a lower and upper bound for the number of
$\lambda $-quiddities of odd size, and a lower and upper bound for the number of 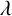 $\lambda $-quiddities of even size, over the rings
$\lambda $-quiddities of even size, over the rings 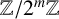 ${\mathbb {Z}}/2^{m}{\mathbb {Z}}$ (
${\mathbb {Z}}/2^{m}{\mathbb {Z}}$ (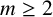 $m \geq 2$). We also give explicit formulae for the number of
$m \geq 2$). We also give explicit formulae for the number of 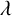 $\lambda $-quiddities of size n over
$\lambda $-quiddities of size n over 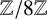 ${\mathbb {Z}}/8{\mathbb {Z}}$.
${\mathbb {Z}}/8{\mathbb {Z}}$.