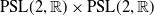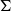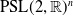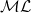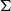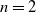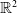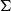1. Introduction
Let
![]() $\Sigma$
be a connected closed oriented surface of genus
$\Sigma$
be a connected closed oriented surface of genus
![]() $g\geq 2$
and let
$g\geq 2$
and let
![]() $\Gamma =\pi _1(\Sigma )$
be its fundamental group. For a real reductive Lie group
$\Gamma =\pi _1(\Sigma )$
be its fundamental group. For a real reductive Lie group
![]() $G$
, we denote by
$G$
, we denote by
![]() $\Xi (\Gamma,G)\;:\!=\;{\textrm{Hom}}_{red}(\Gamma,G)/G$
the character variety, namely the space of conjugacy classes of completely reducible representations
$\Xi (\Gamma,G)\;:\!=\;{\textrm{Hom}}_{red}(\Gamma,G)/G$
the character variety, namely the space of conjugacy classes of completely reducible representations
![]() $\rho \colon \Gamma \to G$
. The third named author used Weyl chamber valued length functions to construct the Weyl chamber length compactification of the character variety [Reference Parreau25], a compactification that generalizes Thurston’s compactification of the Teichmüller space
$\rho \colon \Gamma \to G$
. The third named author used Weyl chamber valued length functions to construct the Weyl chamber length compactification of the character variety [Reference Parreau25], a compactification that generalizes Thurston’s compactification of the Teichmüller space
![]() $\mathcal{T}=\mathcal{T}(\Sigma )$
, for which
$\mathcal{T}=\mathcal{T}(\Sigma )$
, for which
![]() $G=\textrm{PSL}(2,{\mathbb{R}})$
. The boundary
$G=\textrm{PSL}(2,{\mathbb{R}})$
. The boundary
![]() $\partial ^{\textrm{WL}}\Xi (\Gamma, G)$
of the character variety in the Weyl chamber length compactification is a compact subset of the set
$\partial ^{\textrm{WL}}\Xi (\Gamma, G)$
of the character variety in the Weyl chamber length compactification is a compact subset of the set
![]() ${\mathbb{P}}({{\overline{\mathfrak a}^+}}^\Gamma )$
of homothety classes of nonzero functions
${\mathbb{P}}({{\overline{\mathfrak a}^+}}^\Gamma )$
of homothety classes of nonzero functions
![]() $\overrightarrow{L}\colon \Gamma \to{{\overline{\mathfrak a}^+}}$
, where
$\overrightarrow{L}\colon \Gamma \to{{\overline{\mathfrak a}^+}}$
, where
![]() ${\overline{\mathfrak a}^+}$
is a fixed closed Weyl chamber of
${\overline{\mathfrak a}^+}$
is a fixed closed Weyl chamber of
![]() $G$
. Boundary points may be interpreted as projectivized
$G$
. Boundary points may be interpreted as projectivized
![]() ${\overline{\mathfrak a}^+}$
-length functions of actions on
${\overline{\mathfrak a}^+}$
-length functions of actions on
![]() $\mathbb{R}$
-buildings [Reference Parreau25].
$\mathbb{R}$
-buildings [Reference Parreau25].
In the case of
![]() $G=\textrm{PSL}(2,{\mathbb{R}})$
, we know much more: Thurston proved that the boundary of this compactification of Teichmüller space is the projectivization
$G=\textrm{PSL}(2,{\mathbb{R}})$
, we know much more: Thurston proved that the boundary of this compactification of Teichmüller space is the projectivization
![]() ${\mathbb{P}} ({\mathcal{ML}})$
of the space
${\mathbb{P}} ({\mathcal{ML}})$
of the space
![]() $\mathcal{ML}$
of measured geodesic laminations on
$\mathcal{ML}$
of measured geodesic laminations on
![]() $\Sigma$
, realized as the cone
$\Sigma$
, realized as the cone
![]() ${\mathcal{ML}}\subset{\mathbb{R}}_+^\Gamma$
of functions
${\mathcal{ML}}\subset{\mathbb{R}}_+^\Gamma$
of functions
![]() $\Gamma \to{\mathbb{R}}_+$
that are intersection functions of measured geodesic laminations (or equivalently, of measured foliations) on
$\Gamma \to{\mathbb{R}}_+$
that are intersection functions of measured geodesic laminations (or equivalently, of measured foliations) on
![]() $\Sigma$
[Reference Fathi, Laudenbach and Poénaru10, Reference Bonahon2]. This allowed him to prove that this boundary is a sphere of dimension
$\Sigma$
[Reference Fathi, Laudenbach and Poénaru10, Reference Bonahon2]. This allowed him to prove that this boundary is a sphere of dimension
![]() $6g-7$
and the compactification is a closed ball [Reference Fathi, Laudenbach and Poénaru10]. Boundary points may also be interpreted as projectivized length functions of actions on real trees [Reference Bestvina1, Reference Paulin27, Reference Morgan and Shalen17].
$6g-7$
and the compactification is a closed ball [Reference Fathi, Laudenbach and Poénaru10]. Boundary points may also be interpreted as projectivized length functions of actions on real trees [Reference Bestvina1, Reference Paulin27, Reference Morgan and Shalen17].
If
![]() $G$
is of Hermitian type, that is, if the associated symmetric space admits a
$G$
is of Hermitian type, that is, if the associated symmetric space admits a
![]() $G$
-invariant complex structure, the character variety contains a generalization of the Teichmüller space, the space of maximal representations, which we denote by
$G$
-invariant complex structure, the character variety contains a generalization of the Teichmüller space, the space of maximal representations, which we denote by
![]() $\Xi _{\text{Max}}(\Gamma,G)$
. We refer the reader to [Reference Burger, Iozzi, Labourie and Wienhard3, Reference Burger, Iozzi and Wienhard6] for the theory of maximal representations. Maximal representations share many features with the subset of the character variety consisting of Hitchin representations, which are defined for
$\Xi _{\text{Max}}(\Gamma,G)$
. We refer the reader to [Reference Burger, Iozzi, Labourie and Wienhard3, Reference Burger, Iozzi and Wienhard6] for the theory of maximal representations. Maximal representations share many features with the subset of the character variety consisting of Hitchin representations, which are defined for
![]() $G$
real split, and whose character variety we denote by
$G$
real split, and whose character variety we denote by
![]() $\Xi _{\text{Hit}}(\Gamma, G)$
. In [Reference Burger, Iozzi, Parreau and Pozzetti4, Reference Burger, Iozzi, Parreau and Pozzetti5] we used geodesic currents to study the Weyl chamber length compactification
$\Xi _{\text{Hit}}(\Gamma, G)$
. In [Reference Burger, Iozzi, Parreau and Pozzetti4, Reference Burger, Iozzi, Parreau and Pozzetti5] we used geodesic currents to study the Weyl chamber length compactification
![]() $\mathcal{X}^{\textrm{WL}}(\Gamma, G)$
of
$\mathcal{X}^{\textrm{WL}}(\Gamma, G)$
of
![]() $\mathcal{X}(\Gamma, G)$
, where
$\mathcal{X}(\Gamma, G)$
, where
![]() $\mathcal{X}(\Gamma, G)$
denotes either the Hitchin or the maximal character variety. We showed that, as soon as the group
$\mathcal{X}(\Gamma, G)$
denotes either the Hitchin or the maximal character variety. We showed that, as soon as the group
![]() $G$
has higher rank, the mapping class group admits a non-empty open domain of discontinuity for its action on the boundary
$G$
has higher rank, the mapping class group admits a non-empty open domain of discontinuity for its action on the boundary
![]() $\partial ^{\textrm{WL}}\mathcal{X}(\Gamma,G)$
, the so-called positive systole subset; moreover, for a dense subset of boundary points, the associated length function can be computed as intersection with a weighted multicurve. Natural questions arise: to determine the topology of
$\partial ^{\textrm{WL}}\mathcal{X}(\Gamma,G)$
, the so-called positive systole subset; moreover, for a dense subset of boundary points, the associated length function can be computed as intersection with a weighted multicurve. Natural questions arise: to determine the topology of
![]() $\mathcal{X}^{\textrm{WL}}(\Gamma,G)$
; to interpret boundary points in terms of geometric structures on the surface, in particular in the positive systole subset; and to relate such geometric structures with the associated actions on
$\mathcal{X}^{\textrm{WL}}(\Gamma,G)$
; to interpret boundary points in terms of geometric structures on the surface, in particular in the positive systole subset; and to relate such geometric structures with the associated actions on
![]() $\mathbb{R}$
-buildings, for example, by finding a nice invariant subset following the third named author’s work in the case of
$\mathbb{R}$
-buildings, for example, by finding a nice invariant subset following the third named author’s work in the case of
![]() $G=\textrm{PSL}(3,{\mathbb{R}})$
[Reference Parreau26].
$G=\textrm{PSL}(3,{\mathbb{R}})$
[Reference Parreau26].
In this text, we address all the questions introduced above in the case of
![]() $G=\textrm{PSL}(2,{\mathbb{R}})^n$
for
$G=\textrm{PSL}(2,{\mathbb{R}})^n$
for
![]() $n\geq 2$
. The product structure of
$n\geq 2$
. The product structure of
![]() $G$
lets us identify the space
$G$
lets us identify the space
![]() $\Xi _{\text{Max}}(\Gamma,G)$
with the product
$\Xi _{\text{Max}}(\Gamma,G)$
with the product
![]() $\mathcal{T}^n$
of
$\mathcal{T}^n$
of
![]() $n$
copies of the Teichmüller space
$n$
copies of the Teichmüller space
![]() $\mathcal{T}=\Xi _{\text{Max}}(\Gamma,\textrm{PSL}(2,{\mathbb{R}}))$
. A model Weyl chamber for
$\mathcal{T}=\Xi _{\text{Max}}(\Gamma,\textrm{PSL}(2,{\mathbb{R}}))$
. A model Weyl chamber for
![]() $G$
is
$G$
is
![]() ${{\overline{\mathfrak a}^+}}={\mathbb{R}}_+^n$
, hence boundary points are homothety classes of nonzero functions
${{\overline{\mathfrak a}^+}}={\mathbb{R}}_+^n$
, hence boundary points are homothety classes of nonzero functions
![]() $\overrightarrow{L}\colon \Gamma \to{\mathbb{R}}_+^n$
. Such functions can be identified with
$\overrightarrow{L}\colon \Gamma \to{\mathbb{R}}_+^n$
. Such functions can be identified with
![]() $n$
-tuples
$n$
-tuples
![]() $(L_i)_{i=1,\ldots,n}$
of functions
$(L_i)_{i=1,\ldots,n}$
of functions
![]() $L_i\colon \Gamma \to{\mathbb{R}}_+$
.
$L_i\colon \Gamma \to{\mathbb{R}}_+$
.
We identify the boundary of
![]() $\mathcal{T}^n$
in its vectorial length compactification with the projectivization of
$\mathcal{T}^n$
in its vectorial length compactification with the projectivization of
![]() $({\mathcal{ML}})^n$
; in particular, we show that, being a join of
$({\mathcal{ML}})^n$
; in particular, we show that, being a join of
![]() $n$
spheres, it is topologically a sphere of dimension
$n$
spheres, it is topologically a sphere of dimension
![]() $n(6g-6)-1$
. This also allows us to give a precise description of the open domain of discontinuity for the mapping class group alluded to before; for this we denote by
$n(6g-6)-1$
. This also allows us to give a precise description of the open domain of discontinuity for the mapping class group alluded to before; for this we denote by
![]() $({\mathcal{ML}})^n_{\gt 0}$
the set consisting of
$({\mathcal{ML}})^n_{\gt 0}$
the set consisting of
![]() $n$
-tuples of measured laminations with positive joint systole, namely
$n$
-tuples of measured laminations with positive joint systole, namely
![]() $n$
-tuples for which the function
$n$
-tuples for which the function
![]() $\sum _{i=1}^n L_i(\gamma )$
has a positive lower bound on
$\sum _{i=1}^n L_i(\gamma )$
has a positive lower bound on
![]() $\Gamma$
.
$\Gamma$
.
Theorem 1.1.
The boundary
![]() $\partial ^{\textrm{WL}}\Xi _{\text{Max}}(\Gamma,\textrm{PSL}(2,{\mathbb{R}})^n)$
is
$\partial ^{\textrm{WL}}\Xi _{\text{Max}}(\Gamma,\textrm{PSL}(2,{\mathbb{R}})^n)$
is
![]() ${\mathbb{P}}(({\mathcal{ML}})^n)$
, and
${\mathbb{P}}(({\mathcal{ML}})^n)$
, and
![]() $\textrm{MCG}(\Sigma )$
acts properly discontinuously on
$\textrm{MCG}(\Sigma )$
acts properly discontinuously on
![]() ${\mathbb{P}}(({\mathcal{ML}})^n_{\gt 0})$
.
${\mathbb{P}}(({\mathcal{ML}})^n_{\gt 0})$
.
We refer the reader to Section 4, and in particular to Corollary 4.4 for applications of this result to the study of compactifications induced by length functions on
![]() $\Gamma$
associated to various
$\Gamma$
associated to various
![]() $\textrm{PSL}(2,{\mathbb{R}})^n$
-invariant distance functions on the product
$\textrm{PSL}(2,{\mathbb{R}})^n$
-invariant distance functions on the product
![]() $(\mathcal H^2)^n$
of
$(\mathcal H^2)^n$
of
![]() $n$
hyperbolic planes.
$n$
hyperbolic planes.
Inspired by the work of Duchin–Leiniger–Rafi [Reference Duchin, Leininger and Rafi9] and of Morzadec [Reference Morzadec18], we give a geometric interpretation of boundary points in the case of
![]() $n=2$
. Duchin–Leiniger–Rafi introduced mixed structures to give a geometric compactification of the space of
$n=2$
. Duchin–Leiniger–Rafi introduced mixed structures to give a geometric compactification of the space of
![]() ${\textrm{Flat}}(\Sigma )$
of half translation structures on a compact surface
${\textrm{Flat}}(\Sigma )$
of half translation structures on a compact surface
![]() $\Sigma$
up to isometry. For the purposes of this paper, we define an
$\Sigma$
up to isometry. For the purposes of this paper, we define an
![]() ${\mathbb{R}}^2$
-mixed structure
Footnote 1 on
${\mathbb{R}}^2$
-mixed structure
Footnote 1 on
![]() $\Sigma$
as a triple
$\Sigma$
as a triple
![]() ${M}=(\Sigma^{\prime},{K},\overrightarrow{\lambda })$
where
${M}=(\Sigma^{\prime},{K},\overrightarrow{\lambda })$
where
![]() $\Sigma^{\prime}$
is an open geodesic subsurface of
$\Sigma^{\prime}$
is an open geodesic subsurface of
![]() $\Sigma$
,
$\Sigma$
,
![]() $K$
is a half-translation structure on
$K$
is a half-translation structure on
![]() $\Sigma^{\prime}$
, extendible at boundary components regarded as punctures, and
$\Sigma^{\prime}$
, extendible at boundary components regarded as punctures, and
![]() $\overrightarrow{\lambda }=(\Lambda, \nu _1,\nu _2)$
is a
$\overrightarrow{\lambda }=(\Lambda, \nu _1,\nu _2)$
is a
![]() $2$
-measured geodesic lamination, that is, a geodesic lamination
$2$
-measured geodesic lamination, that is, a geodesic lamination
![]() $\Lambda$
disjoint from
$\Lambda$
disjoint from
![]() $\Sigma^{\prime}$
and endowed with a pair of transverse measures
$\Sigma^{\prime}$
and endowed with a pair of transverse measures
![]() $(\nu _1,\nu _2)$
, with
$(\nu _1,\nu _2)$
, with
![]() $\textrm{supp}(\nu _1)\cup \textrm{supp}(\nu _2)=\Lambda$
. Note that the subsurface
$\textrm{supp}(\nu _1)\cup \textrm{supp}(\nu _2)=\Lambda$
. Note that the subsurface
![]() $\Sigma^{\prime}$
or the lamination
$\Sigma^{\prime}$
or the lamination
![]() $\Lambda$
may be empty, so the space
$\Lambda$
may be empty, so the space
![]() $\overrightarrow{\textrm{Mix}}(\Sigma )$
of mixed structures on
$\overrightarrow{\textrm{Mix}}(\Sigma )$
of mixed structures on
![]() $\Sigma$
contains both the space
$\Sigma$
contains both the space
![]() $\overrightarrow{\textrm{Flat}}(\Sigma )$
of half-translation structures (up to isotopy) and the space of
$\overrightarrow{\textrm{Flat}}(\Sigma )$
of half-translation structures (up to isotopy) and the space of
![]() $2$
-measured geodesic laminations. The half-translation structure is equipped with a natural pair
$2$
-measured geodesic laminations. The half-translation structure is equipped with a natural pair
![]() $(\mathcal{F}_1,\mathcal{F}_2)$
of transverse vertical/horizontal measured foliations. As a result, a mixed structure
$(\mathcal{F}_1,\mathcal{F}_2)$
of transverse vertical/horizontal measured foliations. As a result, a mixed structure
![]() $M$
defines a natural pair
$M$
defines a natural pair
![]() $(\lambda _{{M},1},\lambda _{{M},2})$
of associated “vertical/horizontal” measured geodesic laminations on
$(\lambda _{{M},1},\lambda _{{M},2})$
of associated “vertical/horizontal” measured geodesic laminations on
![]() $\Sigma$
. Taking intersection functions, we obtain a map
$\Sigma$
. Taking intersection functions, we obtain a map
extending the natural map
![]() $\overrightarrow{\textrm{Flat}}(\Sigma ) \to{\mathcal{ML}}\times{\mathcal{ML}}$
. We show in Proposition 5.8 that
$\overrightarrow{\textrm{Flat}}(\Sigma ) \to{\mathcal{ML}}\times{\mathcal{ML}}$
. We show in Proposition 5.8 that
![]() $I$
is a bijection, under which
$I$
is a bijection, under which
![]() $\overrightarrow{\textrm{Flat}}(\Sigma )$
corresponds to
$\overrightarrow{\textrm{Flat}}(\Sigma )$
corresponds to
![]() ${(\mathcal{ML})}^2_{\gt 0}$
. Together with Theorem 1.1 this implies the following:
${(\mathcal{ML})}^2_{\gt 0}$
. Together with Theorem 1.1 this implies the following:
Theorem 1.2.
Let
![]() $\overrightarrow{L}\colon \Gamma \to{\mathbb{R}}_+^2$
represent a point in the Weyl chamber length boundary of
$\overrightarrow{L}\colon \Gamma \to{\mathbb{R}}_+^2$
represent a point in the Weyl chamber length boundary of
![]() $\Xi _{\text{Max}}(\Gamma,\textrm{PSL}(2,{\mathbb{R}})^2)$
. Then
$\Xi _{\text{Max}}(\Gamma,\textrm{PSL}(2,{\mathbb{R}})^2)$
. Then
-
(1)
 $\overrightarrow{L}$
is the
$\overrightarrow{L}$
is the
 ${\mathbb{R}}^2$
-length function of a unique
${\mathbb{R}}^2$
-length function of a unique
 ${\mathbb{R}}^2$
-mixed structure
${\mathbb{R}}^2$
-mixed structure
 ${M}=(\Sigma^{\prime},{K},\overrightarrow{\lambda })$
on
${M}=(\Sigma^{\prime},{K},\overrightarrow{\lambda })$
on
 $\Sigma$
.
$\Sigma$
. -
(2) Every non-empty
 ${\mathbb{R}}^2$
-mixed structure on
${\mathbb{R}}^2$
-mixed structure on
 $\Sigma$
arises in this way.
$\Sigma$
arises in this way.
We now turn to the question of relating the geometric structures appearing in the boundary of
![]() $\Xi _{\text{Max}}(\Gamma,G)$
to the associated actions on
$\Xi _{\text{Max}}(\Gamma,G)$
to the associated actions on
![]() $\mathbb{R}$
-buildings and finding nice invariant subsets. In the case of
$\mathbb{R}$
-buildings and finding nice invariant subsets. In the case of
![]() $G=\textrm{PSL}(2,{\mathbb{R}})^n$
, the
$G=\textrm{PSL}(2,{\mathbb{R}})^n$
, the
![]() $\mathbb{R}$
-buildings appearing in the boundary of
$\mathbb{R}$
-buildings appearing in the boundary of
![]() $\Xi _{\text{Max}}(\Gamma,G)$
are products of
$\Xi _{\text{Max}}(\Gamma,G)$
are products of
![]() $n$
$n$
![]() $\mathbb{R}$
-trees, and hence boundary points are homothety classes of
$\mathbb{R}$
-trees, and hence boundary points are homothety classes of
![]() ${\overline{\mathfrak a}^+}$
-length functions of actions of
${\overline{\mathfrak a}^+}$
-length functions of actions of
![]() $\Gamma$
on a product of
$\Gamma$
on a product of
![]() $n$
$n$
![]() $\mathbb{R}$
-trees.
$\mathbb{R}$
-trees.
Notice that in his thesis [Reference Morzadec18] Morzadec used tree-graded spaces to obtain a geometric compactification of the space of flat structures and relate them with the mixed structures of [Reference Duchin, Leininger and Rafi9]. Also, in the case of
![]() $G=\textrm{PSL}(3,{\mathbb{R}})$
and
$G=\textrm{PSL}(3,{\mathbb{R}})$
and
![]() $\Gamma$
a punctured surface group, the third named author associates in [Reference Parreau26] to large families of boundary points of
$\Gamma$
a punctured surface group, the third named author associates in [Reference Parreau26] to large families of boundary points of
![]() $\Xi _{\text{Hit}}^{\textrm{WL}}(\Gamma,\textrm{PSL}(3,{\mathbb{R}}))$
explicit finite
$\Xi _{\text{Hit}}^{\textrm{WL}}(\Gamma,\textrm{PSL}(3,{\mathbb{R}}))$
explicit finite
![]() ${\overline{\mathfrak a}^+}$
-simplicial complexes whose universal cover, a tree-graded space with flat surface pieces, embeds equivariantly in the building preserving the natural
${\overline{\mathfrak a}^+}$
-simplicial complexes whose universal cover, a tree-graded space with flat surface pieces, embeds equivariantly in the building preserving the natural
![]() ${\overline{\mathfrak a}^+}$
-metric.
${\overline{\mathfrak a}^+}$
-metric.
Our last result takes these perspectives in the study of the compactification of the space of
![]() $\textrm{PSL}(2,{\mathbb{R}})\times \textrm{PSL}(2,{\mathbb{R}})$
-maximal representations. To be more precise, a tree-graded
$\textrm{PSL}(2,{\mathbb{R}})\times \textrm{PSL}(2,{\mathbb{R}})$
-maximal representations. To be more precise, a tree-graded
![]() ${\mathbb{R}}^2$
-space
${\mathbb{R}}^2$
-space
![]() $(X, d_1,d_2)$
is for us a space
$(X, d_1,d_2)$
is for us a space
![]() $X$
endowed with a pair
$X$
endowed with a pair
![]() $(d_1,d_2)$
of pseudometrics such that
$(d_1,d_2)$
of pseudometrics such that
![]() $d\;:\!=\;d_1+d_2$
is a metric, the
$d\;:\!=\;d_1+d_2$
is a metric, the
![]() $\ell ^1$
-metric, with respect to which
$\ell ^1$
-metric, with respect to which
![]() $X$
is tree-graded in the sense of [Reference Druţu and Sapir8]; we furthermore require that
$X$
is tree-graded in the sense of [Reference Druţu and Sapir8]; we furthermore require that
![]() $X$
admits an action of
$X$
admits an action of
![]() $\Gamma$
preserving each pseudometric. The
$\Gamma$
preserving each pseudometric. The
![]() ${\mathbb{R}}^2$
-length in
${\mathbb{R}}^2$
-length in
![]() $X$
of
$X$
of
![]() $\gamma \in \Gamma$
is then the pair
$\gamma \in \Gamma$
is then the pair
of translation lengths
of
![]() $\gamma$
for the pseudometric
$\gamma$
for the pseudometric
![]() $d_i$
.
$d_i$
.
We associate to each mixed structure
![]() $M$
an
$M$
an
![]() ${\mathbb{R}}^2$
-tree-graded space
${\mathbb{R}}^2$
-tree-graded space
![]() $(X_M, d_1,d_2)$
dual to
$(X_M, d_1,d_2)$
dual to
![]() $M$
, whose pieces are either flat surfaces or
$M$
, whose pieces are either flat surfaces or
![]() $\mathbb{R}$
-trees:
$\mathbb{R}$
-trees:
Theorem 1.3.
Let
![]() ${M}=(\Sigma^{\prime},{K},\overrightarrow{\lambda })$
be an
${M}=(\Sigma^{\prime},{K},\overrightarrow{\lambda })$
be an
![]() ${\mathbb{R}}^2$
-mixed structure on
${\mathbb{R}}^2$
-mixed structure on
![]() $\Sigma$
and
$\Sigma$
and
![]() $\overrightarrow{L}\colon \Gamma \to{\mathbb{R}}_+^2$
the associated
$\overrightarrow{L}\colon \Gamma \to{\mathbb{R}}_+^2$
the associated
![]() ${\mathbb{R}}^2$
-length function. Then there is a tree-graded
${\mathbb{R}}^2$
-length function. Then there is a tree-graded
![]() ${\mathbb{R}}^2$
-space
${\mathbb{R}}^2$
-space
![]() $X_M$
with length spectrum
$X_M$
with length spectrum
![]() $\overrightarrow{L}\colon \Gamma \to{\mathbb{R}}_+^2$
, and satisfying the following universal property: for any two actions of
$\overrightarrow{L}\colon \Gamma \to{\mathbb{R}}_+^2$
, and satisfying the following universal property: for any two actions of
![]() $\Gamma$
on
$\Gamma$
on
![]() $\mathbb{R}$
-trees
$\mathbb{R}$
-trees
![]() $T_1,T_2$
with length function
$T_1,T_2$
with length function
![]() $(L_{T_1},L_{T_2})=\overrightarrow{L}$
, there is an equivariant embedding
$(L_{T_1},L_{T_2})=\overrightarrow{L}$
, there is an equivariant embedding
preserving each pseudometric
![]() $d_i$
(and isometric for the
$d_i$
(and isometric for the
![]() $\ell ^1$
-metric).
$\ell ^1$
-metric).
In particular, for any point in the boundary
![]() $\partial ^{\textrm{WL}}\Xi _{\text{Max}}(\Gamma,\textrm{PSL}(2,{\mathbb{R}})^2)$
, with associated mixed structure
$\partial ^{\textrm{WL}}\Xi _{\text{Max}}(\Gamma,\textrm{PSL}(2,{\mathbb{R}})^2)$
, with associated mixed structure
![]() $M$
, the corresponding action on a
$M$
, the corresponding action on a
![]() $\mathbb{R}$
-building (here a product of two trees) preserves an
$\mathbb{R}$
-building (here a product of two trees) preserves an
![]() ${\overline{\mathfrak a}^+}$
-isometrically equivariantly embedded copy of
${\overline{\mathfrak a}^+}$
-isometrically equivariantly embedded copy of
![]() $X_{M}$
.
$X_{M}$
.
We construct the space
![]() $X_M$
by gluing the dual trees corresponding to the lamination components, endowed with the pair of pseudometrics induced by the pair of transverse measures, together with the completions of the flat components, endowed with the natural pair of horizontal and vertical pseudometrics (see Section 6 for more details). We show that the
$X_M$
by gluing the dual trees corresponding to the lamination components, endowed with the pair of pseudometrics induced by the pair of transverse measures, together with the completions of the flat components, endowed with the natural pair of horizontal and vertical pseudometrics (see Section 6 for more details). We show that the
![]() $\ell ^1$
-metric on
$\ell ^1$
-metric on
![]() $X_{M}$
corresponds to the path metric induced by the
$X_{M}$
corresponds to the path metric induced by the
![]() $\ell ^1$
-norm on the flat components (Lemma 5.3).
$\ell ^1$
-norm on the flat components (Lemma 5.3).
A more analytic and independent approach to compactifications of the space of maximal representations in rank 2 Hermitian Lie groups has been independently pursued by Ouyang [Reference Ouyang19], Ouyang–Tamburelli [Reference Ouyang and Tamburelli21, Reference Ouyang and Tamburelli22], and Martone–Ouyang–Tamburelli [Reference Martone, Ouyang and Tamburelli16]. In their work, they consider the length spectrum of the negatively curved metric induced on the unique invariant minimal surface associated to a maximal representation. They obtain in this way a compactification that they denote
![]() $\overline{\textrm{Ind}(S)}$
. In the case of
$\overline{\textrm{Ind}(S)}$
. In the case of
![]() $G=\textrm{PSL}(2,{\mathbb{R}})\times \textrm{PSL}(2,{\mathbb{R}})$
, Martone–Ouyang–Tamburelli [Reference Martone, Ouyang and Tamburelli16] also consider a refined compactification dominating
$G=\textrm{PSL}(2,{\mathbb{R}})\times \textrm{PSL}(2,{\mathbb{R}})$
, Martone–Ouyang–Tamburelli [Reference Martone, Ouyang and Tamburelli16] also consider a refined compactification dominating
![]() $\overline{\textrm{Ind}(S)}$
, which they prove is a ball of dimension
$\overline{\textrm{Ind}(S)}$
, which they prove is a ball of dimension
![]() $12g-12$
. Their notion of
$12g-12$
. Their notion of
![]() $(\overline{A_1^+\times A_1^+},2)$
-mixed structure introduced in this work is equivalent to our of
$(\overline{A_1^+\times A_1^+},2)$
-mixed structure introduced in this work is equivalent to our of
![]() ${\mathbb{R}}^2$
-mixed structure defined above. Moreover, they prove that also the boundary of
${\mathbb{R}}^2$
-mixed structure defined above. Moreover, they prove that also the boundary of
![]() $\Xi _{\text{Max}}(\Gamma,\textrm{PSL}(2,{\mathbb{R}})^2)$
in their refined compactification can be identified with such structures.
$\Xi _{\text{Max}}(\Gamma,\textrm{PSL}(2,{\mathbb{R}})^2)$
in their refined compactification can be identified with such structures.
Structure of the paper: The first two sections largely consist of preliminaries: we recall in Section 2 the construction of the Weyl chamber length compactification for
![]() $G=\textrm{PSL}(2,{\mathbb{R}})^n$
, and we discuss in Section 3 the relation between measured foliations, laminations, trees, and geodesic currents. The only new material in Section 3 is in Section 3.5 where we introduce the key notion of the
$G=\textrm{PSL}(2,{\mathbb{R}})^n$
, and we discuss in Section 3 the relation between measured foliations, laminations, trees, and geodesic currents. The only new material in Section 3 is in Section 3.5 where we introduce the key notion of the
![]() ${\mathbb{R}}^n$
-tree dual to an
${\mathbb{R}}^n$
-tree dual to an
![]() $n$
-measured geodesic lamination. With these at hand, we prove Theorem 1.1 in Section 4. We introduce and study mixed structures in Section 5, where we also prove Theorem 1.2. We construct in Section 6 the
$n$
-measured geodesic lamination. With these at hand, we prove Theorem 1.1 in Section 4. We introduce and study mixed structures in Section 5, where we also prove Theorem 1.2. We construct in Section 6 the
![]() ${\mathbb{R}}^2$
-tree-graded space
${\mathbb{R}}^2$
-tree-graded space
![]() $(X_{M}, d_1,d_2)$
dual to a mixed structure
$(X_{M}, d_1,d_2)$
dual to a mixed structure
![]() $M$
. We prove in Section 7 that this tree-graded space embeds isometrically in any product of trees (Proposition 7.1), which concludes the proof of Theorem 1.3.
$M$
. We prove in Section 7 that this tree-graded space embeds isometrically in any product of trees (Proposition 7.1), which concludes the proof of Theorem 1.3.
2. The Weyl chamber length compactification
2.1. Weyl chamber-valued and
 ${\mathbb{R}}^n$
-valued metrics
${\mathbb{R}}^n$
-valued metrics
Given a finite reflection group
![]() $({\mathfrak{a}},W)$
and a fixed model closed Weyl chamber
$({\mathfrak{a}},W)$
and a fixed model closed Weyl chamber
![]() ${\overline{\mathfrak a}^+}$
, we define a
${\overline{\mathfrak a}^+}$
, we define a
![]() ${\overline{\mathfrak a}^+}$
-valued pseudometric on a space
${\overline{\mathfrak a}^+}$
-valued pseudometric on a space
![]() $X$
as a function
$X$
as a function
![]() $\overrightarrow{d} \colon X \times X \to{{\overline{\mathfrak a}^+}}$
satisfying
$\overrightarrow{d} \colon X \times X \to{{\overline{\mathfrak a}^+}}$
satisfying
![]() $\overrightarrow{d}(x,x)=0$
and
$\overrightarrow{d}(x,x)=0$
and
-
Triangular inequality:
 $\overrightarrow{d}(x,z)\leq \overrightarrow{d}(x,y)+\overrightarrow{d}(y,z)$
;
$\overrightarrow{d}(x,z)\leq \overrightarrow{d}(x,y)+\overrightarrow{d}(y,z)$
; -
 $\text{opp}$
-symmetry:
$\text{opp}$
-symmetry:
 $\overrightarrow{d}(y,x)=\overrightarrow{d}(x,y)^{\text{opp}}$
,
$\overrightarrow{d}(y,x)=\overrightarrow{d}(x,y)^{\text{opp}}$
,
where
![]() $\text{opp}$
is the opposition involution on
$\text{opp}$
is the opposition involution on
![]() $\mathfrak{a}$
, and
$\mathfrak{a}$
, and
![]() $\mathfrak{a}$
is endowed with the partial order with positive cone the Euclidean dual
$\mathfrak{a}$
is endowed with the partial order with positive cone the Euclidean dual
![]() $({{\overline{\mathfrak a}^+}})^*$
of
$({{\overline{\mathfrak a}^+}})^*$
of
![]() ${\overline{\mathfrak a}^+}$
. We will call
${\overline{\mathfrak a}^+}$
. We will call
![]() $\overrightarrow{d}$
a
$\overrightarrow{d}$
a
![]() ${\overline{\mathfrak a}^+}$
-valued metric if in addition it is separated, namely
${\overline{\mathfrak a}^+}$
-valued metric if in addition it is separated, namely
![]() $\overrightarrow{d}(x,y)=0$
implies
$\overrightarrow{d}(x,y)=0$
implies
![]() $x=y$
.
$x=y$
.
In this article, we are interested only in the reflection group associated to the semisimple Lie group
![]() $G=\textrm{PSL}(2,{\mathbb{R}})^n$
, which is
$G=\textrm{PSL}(2,{\mathbb{R}})^n$
, which is
![]() ${\mathfrak{a}}={\mathbb{R}}^n$
with Weyl group
${\mathfrak{a}}={\mathbb{R}}^n$
with Weyl group
![]() $W=\{\pm{\textrm{id}}_{\mathbb{R}}\}^n$
. The model closed Weyl chamber is
$W=\{\pm{\textrm{id}}_{\mathbb{R}}\}^n$
. The model closed Weyl chamber is
![]() ${{\overline{\mathfrak a}^+}}={\mathbb{R}}_+^n$
. In this case, the involution opposition is trivial,
${{\overline{\mathfrak a}^+}}={\mathbb{R}}_+^n$
. In this case, the involution opposition is trivial,
![]() $({{\overline{\mathfrak a}^+}})^*={{\overline{\mathfrak a}^+}}={\mathbb{R}}_+^n$
so a
$({{\overline{\mathfrak a}^+}})^*={{\overline{\mathfrak a}^+}}={\mathbb{R}}_+^n$
so a
![]() ${\overline{\mathfrak a}^+}$
-valued (pseudo)metric amounts simply to a
${\overline{\mathfrak a}^+}$
-valued (pseudo)metric amounts simply to a
![]() $n$
-tuple
$n$
-tuple
of usual
![]() $\mathbb{R}$
-valued (pseudo)metric
$\mathbb{R}$
-valued (pseudo)metric
![]() $d_i$
. This gives rise to the equivalent notion of a
$d_i$
. This gives rise to the equivalent notion of a
![]() ${\mathbb{R}}^n$
-(pseudo)metric:
${\mathbb{R}}^n$
-(pseudo)metric:
Definition 2.1.
An
![]() ${\mathbb{R}}^n$
-pseudometric space is a set
${\mathbb{R}}^n$
-pseudometric space is a set
![]() $X$
together with an
$X$
together with an
![]() $n$
-tuple
$n$
-tuple
![]() $\overrightarrow{d}=(d_i)_{i=1,\ldots,n}$
of pseudometrics. We say that
$\overrightarrow{d}=(d_i)_{i=1,\ldots,n}$
of pseudometrics. We say that
![]() $(X,\overrightarrow{d})$
is an
$(X,\overrightarrow{d})$
is an
![]() ${\mathbb{R}}^n$
-metric space if
${\mathbb{R}}^n$
-metric space if
![]() $d\;:\!=\;\sum _{i=1}^n d_i$
is a metric.
$d\;:\!=\;\sum _{i=1}^n d_i$
is a metric.
Observe that even if
![]() $(X,\overrightarrow{d})$
is an
$(X,\overrightarrow{d})$
is an
![]() ${\mathbb{R}}^n$
-metric space, it is possible that none of the pseudo-metrics
${\mathbb{R}}^n$
-metric space, it is possible that none of the pseudo-metrics
![]() $d_i$
is separated.
$d_i$
is separated.
Example 2.2.
Examples of
![]() ${\mathbb{R}}^n$
-metric spaces are products
${\mathbb{R}}^n$
-metric spaces are products
of ordinary metric spaces, as well as subspaces thereof with the induced metric. Another example that will play an important role in our paper are the
![]() ${\mathbb{R}}^2$
-metric naturally induced on the universal cover of a half translation surface, see Section 5.1 for details. Another relevant example is given by simplicial trees with
${\mathbb{R}}^2$
-metric naturally induced on the universal cover of a half translation surface, see Section 5.1 for details. Another relevant example is given by simplicial trees with
![]() ${\mathbb{R}}^2$
-valued edge lengths. This is discussed, and generalized, in Section 3.5.
${\mathbb{R}}^2$
-valued edge lengths. This is discussed, and generalized, in Section 3.5.
In our case of interest,Footnote 2 it is easy to prove that, for any
![]() $W$
-invariant norm
$W$
-invariant norm
![]() $N\colon{\mathfrak{a}}={\mathbb{R}}^n\to{\mathbb{R}}_+$
,
$N\colon{\mathfrak{a}}={\mathbb{R}}^n\to{\mathbb{R}}_+$
,
![]() $N$
is not decreasing on each variable on
$N$
is not decreasing on each variable on
![]() ${{\overline{\mathfrak a}^+}}={\mathbb{R}}_+^n$
, that is, for the partial order introduced above. As a result, a
${{\overline{\mathfrak a}^+}}={\mathbb{R}}_+^n$
, that is, for the partial order introduced above. As a result, a
![]() ${\overline{\mathfrak a}^+}$
-valued (pseudo)metric
${\overline{\mathfrak a}^+}$
-valued (pseudo)metric
![]() $\overrightarrow{d}$
on
$\overrightarrow{d}$
on
![]() $X$
induces an
$X$
induces an
![]() $\mathbb{R}$
-valued (pseudo)metric by setting
$\mathbb{R}$
-valued (pseudo)metric by setting
Note that
![]() $\overrightarrow{d}(x,y)=0$
if and only if
$\overrightarrow{d}(x,y)=0$
if and only if
![]() $d_N(x,y)=0$
, in particular
$d_N(x,y)=0$
, in particular
![]() $\overrightarrow{d}$
is separated if and only if
$\overrightarrow{d}$
is separated if and only if
![]() $d_N$
is separated.
$d_N$
is separated.
Norms
![]() $N\colon{\mathbb{R}}^n\to{\mathbb{R}}$
of particular interest to us are the
$N\colon{\mathbb{R}}^n\to{\mathbb{R}}$
of particular interest to us are the
![]() $\ell ^2$
and
$\ell ^2$
and
![]() $\ell ^1$
norms, which we denote, respectively, by
$\ell ^1$
norms, which we denote, respectively, by
![]() $\|\cdot \|_2$
and
$\|\cdot \|_2$
and
![]() $\|\cdot \|_1$
. They give the associated Euclidean (pseudo)metric
$\|\cdot \|_1$
. They give the associated Euclidean (pseudo)metric
 \begin{align*}d_{\|\cdot \|_2}(x,y)\;:\!=\;\sqrt {\sum _{i=1}^n d_i(x,y)^2}\end{align*}
\begin{align*}d_{\|\cdot \|_2}(x,y)\;:\!=\;\sqrt {\sum _{i=1}^n d_i(x,y)^2}\end{align*}
and
![]() $\ell ^1$
-(pseudo)metric
$\ell ^1$
-(pseudo)metric
on
![]() $X$
. We will also denote
$X$
. We will also denote
![]() $d_{\|\cdot \|_2}$
by
$d_{\|\cdot \|_2}$
by
![]() $\lVert \overrightarrow{d} \rVert _2$
and
$\lVert \overrightarrow{d} \rVert _2$
and
![]() $d^1$
by
$d^1$
by
![]() $\| \overrightarrow{d} \|_1$
.
$\| \overrightarrow{d} \|_1$
.
Remark 2.3.
If
![]() $X=X_1\times \ldots \times X_n$
is a product, then
$X=X_1\times \ldots \times X_n$
is a product, then
![]() $d_{\|\cdot \|_2}$
is the usual product metric, in particular
$d_{\|\cdot \|_2}$
is the usual product metric, in particular
![]() $(X,d_{\|\cdot \|_2})$
is CAT(0) if and only if each of the
$(X,d_{\|\cdot \|_2})$
is CAT(0) if and only if each of the
![]() $X_i$
are. However, in general,
$X_i$
are. However, in general,
![]() $(X,d_{\|\cdot \|_2})$
is not a geodesic metric space. For example, if
$(X,d_{\|\cdot \|_2})$
is not a geodesic metric space. For example, if
![]() $X$
is a simplicial tree with
$X$
is a simplicial tree with
![]() ${\mathbb{R}}^2$
-valued edge lengths, the induced metric space
${\mathbb{R}}^2$
-valued edge lengths, the induced metric space
![]() $(X,d_{\|\cdot \|_2})$
is geodesic if and only if the two distance functions
$(X,d_{\|\cdot \|_2})$
is geodesic if and only if the two distance functions
![]() $d_i$
are proportional.
$d_i$
are proportional.
2.2. The Weyl chamber valued length function on
 $\textrm{PSL}(2,{\mathbb{R}})^n$
$\textrm{PSL}(2,{\mathbb{R}})^n$
The symmetric space associated to
![]() $\textrm{PSL}(2,{\mathbb{R}})^n$
is the product
$\textrm{PSL}(2,{\mathbb{R}})^n$
is the product
![]() $X=(\mathcal H^2)^n$
of
$X=(\mathcal H^2)^n$
of
![]() $n$
copies of the hyperbolic plane
$n$
copies of the hyperbolic plane
![]() $\mathcal H^2$
. On
$\mathcal H^2$
. On
![]() $X$
the natural Weyl-chamber valued distance
$X$
the natural Weyl-chamber valued distance
![]() $\overrightarrow{d} \colon X \times X \to{\mathbb{R}}_+^n$
is simply the product distance
$\overrightarrow{d} \colon X \times X \to{\mathbb{R}}_+^n$
is simply the product distance
The Weyl chamber length (or
![]() ${\mathbb{R}}^n$
-length) of
${\mathbb{R}}^n$
-length) of
![]() $g=(g_i)_{i=1,\ldots,n}\in \textrm{PSL}(2,{\mathbb{R}})^n$
can be defined as
$g=(g_i)_{i=1,\ldots,n}\in \textrm{PSL}(2,{\mathbb{R}})^n$
can be defined as
where the infimum is considered with respect to the partial order on
![]() ${\mathbb{R}}^n$
with positive cone
${\mathbb{R}}^n$
with positive cone
![]() ${\mathbb{R}}_+^n$
. As the metric space
${\mathbb{R}}_+^n$
. As the metric space
![]() $X$
is a product, it boils down to taking the list of the usual lengths in each factor:
$X$
is a product, it boils down to taking the list of the usual lengths in each factor:
Here
![]() ${L}(g)\;:\!=\;\inf _{x\in \mathcal H^2}d(x,gx)$
is the usual translation length of
${L}(g)\;:\!=\;\inf _{x\in \mathcal H^2}d(x,gx)$
is the usual translation length of
![]() $g$
on the hyperbolic plane
$g$
on the hyperbolic plane
![]() $\mathcal H^2$
. This ensures in particular that the infimum in (1.1) exists.
$\mathcal H^2$
. This ensures in particular that the infimum in (1.1) exists.
The length function of a representation
![]() $\rho \colon \Gamma \to \textrm{PSL}(2,{\mathbb{R}})$
is
$\rho \colon \Gamma \to \textrm{PSL}(2,{\mathbb{R}})$
is
Similarly, the Weyl chamber length function (or
![]() ${\mathbb{R}}^n$
-length function) of a representation
${\mathbb{R}}^n$
-length function) of a representation
![]() $\rho \colon \Gamma \to \textrm{PSL}(2,{\mathbb{R}})^n$
is
$\rho \colon \Gamma \to \textrm{PSL}(2,{\mathbb{R}})^n$
is
Of course when
![]() $\rho =(\rho _i)_{i=1,\ldots,n}$
, it holds
$\rho =(\rho _i)_{i=1,\ldots,n}$
, it holds
![]() $\overrightarrow{L}_\rho =(L_{\rho _i})_{i=1,\ldots,n}$
.
$\overrightarrow{L}_\rho =(L_{\rho _i})_{i=1,\ldots,n}$
.
2.3. The Weyl chamber length compactification
Here we define the Weyl chamber length compactification constructed in [Reference Parreau25], which has a simpler construction in our context. We endow the space
![]() $({\mathbb{R}}_+^n)^\Gamma$
of functions
$({\mathbb{R}}_+^n)^\Gamma$
of functions
![]() $\overrightarrow{L}\colon \Gamma \to{\mathbb{R}}_+^n$
with the topology of pointwise convergence, and the space
$\overrightarrow{L}\colon \Gamma \to{\mathbb{R}}_+^n$
with the topology of pointwise convergence, and the space
![]() ${\mathbb{P}}(({\mathbb{R}}_+^n)^\Gamma )$
of homothety classes of nonzero functions
${\mathbb{P}}(({\mathbb{R}}_+^n)^\Gamma )$
of homothety classes of nonzero functions
![]() $\overrightarrow{L}$
with the quotient topology. The map
$\overrightarrow{L}$
with the quotient topology. The map
 \begin{align*}\begin {array}{c@{\quad}c@{\quad}c@{\quad}c} \overrightarrow {\mathcal {L}}:&{\textrm {Hom}}(\Gamma,\textrm {PSL}(2,{\mathbb {R}})^n) &\to & ({\mathbb {R}}_+^n)^\Gamma \\[5pt] &\rho &\mapsto & \overrightarrow {L}\circ \rho \end {array}\end{align*}
\begin{align*}\begin {array}{c@{\quad}c@{\quad}c@{\quad}c} \overrightarrow {\mathcal {L}}:&{\textrm {Hom}}(\Gamma,\textrm {PSL}(2,{\mathbb {R}})^n) &\to & ({\mathbb {R}}_+^n)^\Gamma \\[5pt] &\rho &\mapsto & \overrightarrow {L}\circ \rho \end {array}\end{align*}
induces a continuous map
equivariant with respect to the mapping class group action. The injectivity of
![]() $\mathcal{T} \to{\mathbb{P}}{\mathbb{R}}_+^\Gamma$
implies that the map
$\mathcal{T} \to{\mathbb{P}}{\mathbb{R}}_+^\Gamma$
implies that the map
![]() ${\mathbb{P}}\overrightarrow{\mathcal{L}}$
is injective as well. The Weyl chamber length compactification
${\mathbb{P}}\overrightarrow{\mathcal{L}}$
is injective as well. The Weyl chamber length compactification
![]() $\overline{\mathcal{T}^n}^{\textrm{WL}}$
of
$\overline{\mathcal{T}^n}^{\textrm{WL}}$
of
![]() $\mathcal{T}^n$
is by definition the closure of its image (which is a compact set). We denote
$\mathcal{T}^n$
is by definition the closure of its image (which is a compact set). We denote
its boundary.
2.4. Other length compactifications
Recall from Section 2.1 that any
![]() $W$
-invariant norm
$W$
-invariant norm
![]() $N\colon{\mathbb{R}}^n\to{\mathbb{R}}$
induces a metric
$N\colon{\mathbb{R}}^n\to{\mathbb{R}}$
induces a metric
![]() $d_N\;:\!=\;N(\overrightarrow{d})$
on
$d_N\;:\!=\;N(\overrightarrow{d})$
on
![]() $X=(\mathcal H^2)^n$
, and thus a corresponding length function, the
$X=(\mathcal H^2)^n$
, and thus a corresponding length function, the
![]() $N$
-length function
$N$
-length function
![]() $L_{d_N}$
. We use this to construct the
$L_{d_N}$
. We use this to construct the
![]() $N$
-length compactification
$N$
-length compactification
![]() $\overline{\mathcal{T}^n}^{N}$
of
$\overline{\mathcal{T}^n}^{N}$
of
![]() $\mathcal{T}^n$
, associated to
$\mathcal{T}^n$
, associated to
![]() $L_{d_N}$
.
$L_{d_N}$
.
It is easy to verify that, since
![]() $N$
is not decreasing on each variable on
$N$
is not decreasing on each variable on
![]() ${{\overline{\mathfrak a}^+}}={\mathbb{R}}_+^n$
, and
${{\overline{\mathfrak a}^+}}={\mathbb{R}}_+^n$
, and
![]() $\mathcal{T}^n$
is a product, it holds
$\mathcal{T}^n$
is a product, it holds
![]() $L_{d_N}(g)=N(\overrightarrow{L}(g))$
. The Weyl chamber length compactification then dominates naturally
$L_{d_N}(g)=N(\overrightarrow{L}(g))$
. The Weyl chamber length compactification then dominates naturally
![]() $\overline{\mathcal{T}^n}^{N}$
: the restriction of the natural map
$\overline{\mathcal{T}^n}^{N}$
: the restriction of the natural map
induces a continuous
![]() $\textrm{Out}(\Gamma )$
-equivariant surjective map
$\textrm{Out}(\Gamma )$
-equivariant surjective map
restricting to identity on
![]() $\mathcal{T}^n$
.
$\mathcal{T}^n$
.
3. Trees dual to measured geodesic laminations
We refer the reader to [Reference Kapovich14, Chapter 11] for preliminaries on measured laminations, measured foliations, and the identification between equivalence classes of measured foliations and measured geodesic laminations on hyperbolic surfaces. The material in Sections 3.2, 3.3, and 3.4 is classical, while the viewpoint in Section 3.5 is new and important for our paper.
3.1. Measured foliations
Let
![]() $\mathcal{F}$
be a transverse measured foliation on a topological surface
$\mathcal{F}$
be a transverse measured foliation on a topological surface
![]() $\Sigma$
with fundamental group
$\Sigma$
with fundamental group
![]() $\Gamma$
. We denote by
$\Gamma$
. We denote by
![]() $i(\mathcal {F},c)$
the measure of a path
$i(\mathcal {F},c)$
the measure of a path
![]() $c\subset \Sigma$
with respect to
$c\subset \Sigma$
with respect to
![]() $\mathcal{F}$
. The intersection of
$\mathcal{F}$
. The intersection of
![]() $\mathcal{F}$
with
$\mathcal{F}$
with
![]() $\gamma \in \Gamma$
is defined as
$\gamma \in \Gamma$
is defined as
where the infimum is taken over all closed loops
![]() $c$
transverse to
$c$
transverse to
![]() $\Lambda$
and freely homotopic to
$\Lambda$
and freely homotopic to
![]() $\gamma$
. We denote by
$\gamma$
. We denote by
the corresponding intersection function.
This may be reformulated in terms of pseudometrics. We denote by
![]() $d_{\mathcal{F}}$
the pseudometric on the universal cover
$d_{\mathcal{F}}$
the pseudometric on the universal cover
![]() $\widetilde{\Sigma }$
of
$\widetilde{\Sigma }$
of
![]() $\Sigma$
associated with the lift
$\Sigma$
associated with the lift
![]() $\widetilde{\mathcal{F}}$
of
$\widetilde{\mathcal{F}}$
of
![]() $\mathcal{F}$
: it is defined by the formula
$\mathcal{F}$
: it is defined by the formula
where the infimum is taken on paths
![]() $c$
joining
$c$
joining
![]() $x$
to
$x$
to
![]() $y$
in
$y$
in
![]() $\widetilde{\Sigma }$
and transverse to
$\widetilde{\Sigma }$
and transverse to
![]() $\widetilde{\mathcal{F}}$
. The length function
$\widetilde{\mathcal{F}}$
. The length function
![]() $L_d\in ({\mathbb{R}}_+)^\Gamma$
of a pseudometric
$L_d\in ({\mathbb{R}}_+)^\Gamma$
of a pseudometric
![]() $d$
on a
$d$
on a
![]() $\Gamma$
-space
$\Gamma$
-space
![]() $X$
is defined as
$X$
is defined as
By definition, the length function of
![]() $d_{\mathcal{F}}$
on
$d_{\mathcal{F}}$
on
![]() $\widetilde{\Sigma }$
is the intersection function of
$\widetilde{\Sigma }$
is the intersection function of
![]() $\mathcal{F}$
:
$\mathcal{F}$
:
The dual tree of a measured foliation
![]() $\mathcal{F}$
is defined as the quotient metric space
$\mathcal{F}$
is defined as the quotient metric space
![]() $T(\mathcal{F})\;:\!=\;\widetilde{\Sigma }/d_{\mathcal{F}}$
of
$T(\mathcal{F})\;:\!=\;\widetilde{\Sigma }/d_{\mathcal{F}}$
of
![]() $\widetilde{\Sigma }$
by the pseudometric
$\widetilde{\Sigma }$
by the pseudometric
![]() $d_{\mathcal{F}}$
. The tree
$d_{\mathcal{F}}$
. The tree
![]() $T(\mathcal{F})$
inherits an action of
$T(\mathcal{F})$
inherits an action of
![]() $\Gamma$
by isometries, with associated length function
$\Gamma$
by isometries, with associated length function
3.2. Measured geodesic laminations
Let
![]() $\lambda =(\Lambda,\nu )$
be a measured lamination on
$\lambda =(\Lambda,\nu )$
be a measured lamination on
![]() $\Sigma$
. As for measured foliations, we denote by
$\Sigma$
. As for measured foliations, we denote by
![]() $i(\lambda, c)$
the
$i(\lambda, c)$
the
![]() $\lambda$
-measure of a path
$\lambda$
-measure of a path
![]() $c\colon [0,1] \to \Sigma$
transverse to
$c\colon [0,1] \to \Sigma$
transverse to
![]() $\Lambda$
. The intersection of
$\Lambda$
. The intersection of
![]() $\lambda$
with
$\lambda$
with
![]() $\gamma \in \Gamma$
is defined as
$\gamma \in \Gamma$
is defined as
where the infimum is taken over all closed loops
![]() $c$
transverse to
$c$
transverse to
![]() $\Lambda$
and freely homotopic to
$\Lambda$
and freely homotopic to
![]() $\gamma$
, and we denote by
$\gamma$
, and we denote by
the corresponding intersection function.
We denote by
![]() $d_\lambda$
the pseudometric on
$d_\lambda$
the pseudometric on
![]() $\widetilde{\Sigma }$
associated with
$\widetilde{\Sigma }$
associated with
![]() $\lambda$
: this is the pseudometric defined on
$\lambda$
: this is the pseudometric defined on
![]() $\widetilde{\Sigma }-\widetilde{\Lambda _0}$
, where
$\widetilde{\Sigma }-\widetilde{\Lambda _0}$
, where
![]() $\widetilde{\Lambda _0}$
is the set of atomicFootnote 3 leafs of the lift
$\widetilde{\Lambda _0}$
is the set of atomicFootnote 3 leafs of the lift
![]() $\tilde{\lambda }=(\widetilde{\Lambda },\nu )$
of
$\tilde{\lambda }=(\widetilde{\Lambda },\nu )$
of
![]() $\lambda$
, by the formula
$\lambda$
, by the formula
where the infimum is taken on paths
![]() $c$
joining
$c$
joining
![]() $x$
to
$x$
to
![]() $y$
in
$y$
in
![]() $\widetilde{\Sigma }$
and transverse to
$\widetilde{\Sigma }$
and transverse to
![]() $\widetilde{\Lambda }$
. By definition, the length function of
$\widetilde{\Lambda }$
. By definition, the length function of
![]() $d_\lambda$
on
$d_\lambda$
on
![]() $\widetilde{\Sigma }-\widetilde{\Lambda _0}$
is the intersection function of
$\widetilde{\Sigma }-\widetilde{\Lambda _0}$
is the intersection function of
![]() $\lambda$
:
$\lambda$
:
We refer to [Reference Kapovich14] for the classical correspondence between measured foliations and measured geodesic laminations on hyperbolic surfaces.
3.3. Geodesic currents
We refer to [Reference Bonahon2] or [Reference Martelli15, Section 8] for the background material in the case of closed geodesic surfaces, and for instance to [Reference Burger, Iozzi, Parreau and Pozzetti4] for the generalization to finite type surfaces.
A geodesic current on a finite type hyperbolic surface
![]() $\Sigma =\mathcal H^2/\Gamma$
is a flip-invariant
$\Sigma =\mathcal H^2/\Gamma$
is a flip-invariant
![]() $\Gamma$
-invariant positive Radon measure on the space of unoriented, unparametrized geodesics of
$\Gamma$
-invariant positive Radon measure on the space of unoriented, unparametrized geodesics of
![]() $\mathcal H^2$
, that may be identified with the space
$\mathcal H^2$
, that may be identified with the space
of distinct pairs of points in the boundary at infinity
![]() $\partial \mathcal H^2$
of
$\partial \mathcal H^2$
of
![]() $\mathcal H^2$
. A basic example is the current
$\mathcal H^2$
. A basic example is the current
![]() $\delta _c$
associated to a closed geodesic
$\delta _c$
associated to a closed geodesic
![]() $c$
in
$c$
in
![]() $\Sigma$
, which is defined as the sum of the Dirac masses on the lifts of
$\Sigma$
, which is defined as the sum of the Dirac masses on the lifts of
![]() $c$
to
$c$
to
![]() $\mathcal H^2$
. Recall that the Bonahon intersection
$\mathcal H^2$
. Recall that the Bonahon intersection
![]() $i(\mu,\nu )$
of two geodesic currents
$i(\mu,\nu )$
of two geodesic currents
![]() $\mu,\nu$
is defined as the
$\mu,\nu$
is defined as the
![]() $(\mu \times \nu )$
-measure of any Borel fundamental domain for the
$(\mu \times \nu )$
-measure of any Borel fundamental domain for the
![]() $\Gamma$
-action on the space
$\Gamma$
-action on the space
![]() $\mathcal{DG}(\mathcal H^2)\subset \mathcal{G}(\mathcal H^2)\times \mathcal{G}(\mathcal H^2)$
of pairs of transverse geodesics
$\mathcal{DG}(\mathcal H^2)\subset \mathcal{G}(\mathcal H^2)\times \mathcal{G}(\mathcal H^2)$
of pairs of transverse geodesics
![]() $(g,h)$
.
$(g,h)$
.
We refer for instance to [Reference Martelli15, Section 8.3.4] for the bijective correspondence
![]() $\lambda \mapsto \mu _ \lambda$
between measured geodesic laminations
$\lambda \mapsto \mu _ \lambda$
between measured geodesic laminations
![]() $\lambda =(\Lambda,\nu )$
of full support
$\lambda =(\Lambda,\nu )$
of full support
![]() $\Lambda$
and geodesic currents
$\Lambda$
and geodesic currents
![]() $\mu$
on
$\mu$
on
![]() $\Sigma$
with
$\Sigma$
with
![]() $i(\mu,\mu )=0$
, equivalently currents
$i(\mu,\mu )=0$
, equivalently currents
![]() $\mu$
such that no two geodesics in the support of
$\mu$
such that no two geodesics in the support of
![]() $\mu$
intersect transversally. The geodesic current
$\mu$
intersect transversally. The geodesic current
![]() $\mu _\lambda$
has support
$\mu _\lambda$
has support
![]() $\Lambda$
, and, for each geodesic arc
$\Lambda$
, and, for each geodesic arc
![]() $c$
transverse to
$c$
transverse to
![]() $\Lambda$
, the restriction of
$\Lambda$
, the restriction of
![]() $\mu _\lambda$
to the set of geodesics
$\mu _\lambda$
to the set of geodesics
![]() $g$
of
$g$
of
![]() $\Lambda$
intersecting
$\Lambda$
intersecting
![]() $c$
is the pullback of the
$c$
is the pullback of the
![]() $\lambda$
-measure on
$\lambda$
-measure on
![]() $c$
by the map
$c$
by the map
![]() $g \mapsto g\cap c$
. The notions of intersection then coincide as
$g \mapsto g\cap c$
. The notions of intersection then coincide as
for all closed geodesic
![]() $c$
in
$c$
in
![]() $\Sigma$
. Note that the union of two measured geodesic laminations with disjoint support corresponds to the sum of the associated currents. From now on, we will freely identify
$\Sigma$
. Note that the union of two measured geodesic laminations with disjoint support corresponds to the sum of the associated currents. From now on, we will freely identify
![]() $\lambda$
with
$\lambda$
with
![]() $\mu _\lambda$
whenever convenient.
$\mu _\lambda$
whenever convenient.
Given a geodesic current
![]() $\mu$
on
$\mu$
on
![]() $\Sigma$
and a geodesic subsurface
$\Sigma$
and a geodesic subsurface
![]() $\Sigma^{\prime}$
of
$\Sigma^{\prime}$
of
![]() $\Sigma$
, we denote by
$\Sigma$
, we denote by
![]() $\mu_{|{\Sigma^{\prime}}}$
the restriction of
$\mu_{|{\Sigma^{\prime}}}$
the restriction of
![]() $\mu$
to the subsurface
$\mu$
to the subsurface
![]() $\Sigma^{\prime}$
, namely the geodesic current
$\Sigma^{\prime}$
, namely the geodesic current
where
![]() $\chi _{\mathcal{G}(\Sigma^{\prime})}$
is the characteristic function of the set
$\chi _{\mathcal{G}(\Sigma^{\prime})}$
is the characteristic function of the set
![]() $\mathcal{G}(\Sigma^{\prime})$
of geodesics whose projection lies in
$\mathcal{G}(\Sigma^{\prime})$
of geodesics whose projection lies in
![]() $\Sigma^{\prime}$
. In general, a geodesic current of full support might restrict to the zero current on a proper subsurface (this is the case when
$\Sigma^{\prime}$
. In general, a geodesic current of full support might restrict to the zero current on a proper subsurface (this is the case when
![]() $\mu$
is the Liouville current of a hyperbolic structure), but if, for every boundary component
$\mu$
is the Liouville current of a hyperbolic structure), but if, for every boundary component
![]() $c$
of
$c$
of
![]() $\Sigma^{\prime}$
,
$\Sigma^{\prime}$
,
![]() $i(\mu,\delta _c)=0$
, then for every
$i(\mu,\delta _c)=0$
, then for every
![]() $\gamma \in \pi _1(\Sigma^{\prime})$
,
$\gamma \in \pi _1(\Sigma^{\prime})$
,
![]() $i(\mu,\delta _\gamma )=i(\mu_{|\Sigma^{\prime}},\delta _\gamma )$
[Reference Burger, Iozzi, Parreau and Pozzetti5, Proposition 4.13].
$i(\mu,\delta _\gamma )=i(\mu_{|\Sigma^{\prime}},\delta _\gamma )$
[Reference Burger, Iozzi, Parreau and Pozzetti5, Proposition 4.13].
3.4. Dual tree of a measured geodesic lamination
Let
![]() $\lambda =(\Lambda,\nu )$
be a measured geodesic lamination on an hyperbolic surface
$\lambda =(\Lambda,\nu )$
be a measured geodesic lamination on an hyperbolic surface
![]() $\Sigma$
. We now recall the construction of the associated dual
$\Sigma$
. We now recall the construction of the associated dual
![]() $\mathbb{R}$
-tree. We follow the construction of [Reference Kapovich14, Section 11.12].
$\mathbb{R}$
-tree. We follow the construction of [Reference Kapovich14, Section 11.12].
We first get rid of the atoms blowing-up along atomic leafs: for each isolated leaf
![]() $c$
of
$c$
of
![]() $\Lambda$
, cut
$\Lambda$
, cut
![]() $\Sigma$
along
$\Sigma$
along
![]() $c$
and insert an annulus
$c$
and insert an annulus
![]() $B(c)=c\times [0,1]$
, foliated by the parallel circles
$B(c)=c\times [0,1]$
, foliated by the parallel circles
![]() $c\times{t}$
. We endow
$c\times{t}$
. We endow
![]() $\Sigma ^b$
with the locally CAT(0) metric
$\Sigma ^b$
with the locally CAT(0) metric
![]() $m^b$
equal to the original metric
$m^b$
equal to the original metric
![]() $m$
of
$m$
of
![]() $\Sigma$
outside the annuli
$\Sigma$
outside the annuli
![]() $B(c)$
and to the flat metric on
$B(c)$
and to the flat metric on
![]() $B(c)$
. This gives a locally CAT(0) surface
$B(c)$
. This gives a locally CAT(0) surface
![]() $(\Sigma ^b,m^b)$
homeomorphic to
$(\Sigma ^b,m^b)$
homeomorphic to
![]() $\Sigma$
, with a geodesic lamination
$\Sigma$
, with a geodesic lamination
![]() $\Lambda ^b$
. We call
$\Lambda ^b$
. We call
![]() $(\Sigma ^b,\Lambda ^b)$
the blow-up of
$(\Sigma ^b,\Lambda ^b)$
the blow-up of
![]() $(\Sigma,\Lambda )$
. The blow-up of the transverse measure
$(\Sigma,\Lambda )$
. The blow-up of the transverse measure
![]() $\nu$
on
$\nu$
on
![]() $\Lambda$
is the non-atomic transverse measure
$\Lambda$
is the non-atomic transverse measure
![]() $\nu ^b$
on
$\nu ^b$
on
![]() $\Lambda ^b$
, obtained from
$\Lambda ^b$
, obtained from
![]() $\nu$
by giving to each foliated annulus
$\nu$
by giving to each foliated annulus
![]() $B(c)$
the transverse measure
$B(c)$
the transverse measure
![]() $\nu (c)dt$
on
$\nu (c)dt$
on
![]() $[0,1]$
. The pseudometric
$[0,1]$
. The pseudometric
![]() $d_{\lambda ^b}$
associated to the measured lamination
$d_{\lambda ^b}$
associated to the measured lamination
![]() $\lambda ^b\;:\!=\;(\Lambda ^b,\nu ^b)$
is then a continuous and everywhere-defined path pseudometric on
$\lambda ^b\;:\!=\;(\Lambda ^b,\nu ^b)$
is then a continuous and everywhere-defined path pseudometric on
![]() $\widetilde{\Sigma ^b}$
. The
$\widetilde{\Sigma ^b}$
. The
![]() $\mathbb{R}$
-tree dual to
$\mathbb{R}$
-tree dual to
![]() $\lambda$
is defined as the quotient metric space
$\lambda$
is defined as the quotient metric space
![]() $T(\lambda )\;:\!=\;\widetilde{\Sigma ^b}/d_\lambda ^b$
, whose metric will be denoted by
$T(\lambda )\;:\!=\;\widetilde{\Sigma ^b}/d_\lambda ^b$
, whose metric will be denoted by
![]() $d_\lambda$
.
$d_\lambda$
.
It is easy but crucial to see that the geodesics of
![]() $T(\lambda )$
are the projections of the
$T(\lambda )$
are the projections of the
![]() $m^b$
-geodesics of
$m^b$
-geodesics of
![]() $\widetilde{\Sigma ^b}$
. In the following lemma, and in the rest of the article, when we write geodesic we mean a path
$\widetilde{\Sigma ^b}$
. In the following lemma, and in the rest of the article, when we write geodesic we mean a path
![]() $t\mapsto c(t)$
that is additive for the distance
$t\mapsto c(t)$
that is additive for the distance
![]() $d$
, namely such that
$d$
, namely such that
![]() $d(c(t_1),c(t_3))=d(c(t_1),c(t_2))+d(c(t_2),c(t_3))$
for all
$d(c(t_1),c(t_3))=d(c(t_1),c(t_2))+d(c(t_2),c(t_3))$
for all
![]() $t_1\leq t_2\leq t_3$
. Observe that
$t_1\leq t_2\leq t_3$
. Observe that
![]() $c$
may then be constant on some subset of its domain of definition and needs not be parametrized at constant speed.
$c$
may then be constant on some subset of its domain of definition and needs not be parametrized at constant speed.
Proposition 3.1.
Let
![]() $c\colon I\to \widetilde{\Sigma ^b}$
be a
$c\colon I\to \widetilde{\Sigma ^b}$
be a
![]() $m^b$
-geodesic. Then
$m^b$
-geodesic. Then
![]() $c$
is a minimizing curve for
$c$
is a minimizing curve for
![]() $d_{\lambda ^b}$
, and the projection of
$d_{\lambda ^b}$
, and the projection of
![]() $c$
on the tree
$c$
on the tree
![]() $T(\lambda )$
is a geodesic.
$T(\lambda )$
is a geodesic.
Proof. Let
![]() $x,y$
be points of
$x,y$
be points of
![]() $\widetilde{\Sigma ^b}$
and
$\widetilde{\Sigma ^b}$
and
![]() $c\colon [0,1]\to \widetilde{\Sigma ^b}$
be the constant speed geodesic segment from
$c\colon [0,1]\to \widetilde{\Sigma ^b}$
be the constant speed geodesic segment from
![]() $x$
to
$x$
to
![]() $y$
. As the leafs of
$y$
. As the leafs of
![]() $\widetilde{\Lambda }^b$
are geodesics, and CAT(0) spaces are uniquely geodesic, the path
$\widetilde{\Lambda }^b$
are geodesics, and CAT(0) spaces are uniquely geodesic, the path
![]() $c$
cannot cross twice the same leaf of
$c$
cannot cross twice the same leaf of
![]() $\widetilde{\Lambda }^b$
, hence
$\widetilde{\Lambda }^b$
, hence
![]() $i(\lambda ^b,c)$
is minimal and
$i(\lambda ^b,c)$
is minimal and
![]() $d_{\lambda ^b}(x,y)=i(\lambda ^b,c)$
. Denote by
$d_{\lambda ^b}(x,y)=i(\lambda ^b,c)$
. Denote by
![]() $p\colon \widetilde{\Sigma ^b}\to T(\lambda )$
the canonical projection. The projection
$p\colon \widetilde{\Sigma ^b}\to T(\lambda )$
the canonical projection. The projection
![]() $\overline{c}=p\circ c$
of
$\overline{c}=p\circ c$
of
![]() $c$
in the dual tree
$c$
in the dual tree
![]() $T(\lambda )$
does not backtrack, hence is a geodesic.
$T(\lambda )$
does not backtrack, hence is a geodesic.
The tree
![]() $T(\lambda )$
inherits an action of
$T(\lambda )$
inherits an action of
![]() $\Gamma$
by isometries, with associated length function
$\Gamma$
by isometries, with associated length function
Note that when
![]() $\Sigma$
is closed the tree
$\Sigma$
is closed the tree
![]() $T(\lambda )$
is then minimal for the action of
$T(\lambda )$
is then minimal for the action of
![]() $\Gamma$
, namely there is no invariant proper subtree. Indeed an invariant proper subtree will lift as a proper closed invariant convex subset in
$\Gamma$
, namely there is no invariant proper subtree. Indeed an invariant proper subtree will lift as a proper closed invariant convex subset in
![]() $\widetilde{\Sigma ^b}$
, and taking the closure in the CAT(0) compactification we will then obtain a proper closed invariant subset of the boundary at infinity
$\widetilde{\Sigma ^b}$
, and taking the closure in the CAT(0) compactification we will then obtain a proper closed invariant subset of the boundary at infinity
![]() $\partial _\infty \widetilde{\Sigma ^b} \simeq \partial \mathcal H^2$
, which is impossible.
$\partial _\infty \widetilde{\Sigma ^b} \simeq \partial \mathcal H^2$
, which is impossible.
Note that the tree
![]() $T(\lambda )$
is essentially determined by its length function ; more generally, we will use the length rigidity of actions on minimal trees with length functions in
$T(\lambda )$
is essentially determined by its length function ; more generally, we will use the length rigidity of actions on minimal trees with length functions in
![]() $\mathcal{ML}$
: It is easily seen that for
$\mathcal{ML}$
: It is easily seen that for
![]() $\lambda \neq 0$
the action of
$\lambda \neq 0$
the action of
![]() $\Gamma$
on
$\Gamma$
on
![]() $T(\lambda )$
has no global fixed point in
$T(\lambda )$
has no global fixed point in
![]() $\partial _\infty T$
, where
$\partial _\infty T$
, where
![]() $\partial _\infty T$
denotes the boundary at infinity of
$\partial _\infty T$
denotes the boundary at infinity of
![]() $T$
. This in fact depends only on the length function, since having a fixed point at infinity is equivalent to the length function being of the form
$T$
. This in fact depends only on the length function, since having a fixed point at infinity is equivalent to the length function being of the form
![]() $\gamma \mapsto |h(\gamma )|$
, where
$\gamma \mapsto |h(\gamma )|$
, where
![]() $h:\Gamma \to{\mathbb{R}}$
is a morphism [Reference Culler and Morgan7, Corollary 2.3]. In particular, all minimal
$h:\Gamma \to{\mathbb{R}}$
is a morphism [Reference Culler and Morgan7, Corollary 2.3]. In particular, all minimal
![]() $\Gamma$
-trees with nonzero length function in
$\Gamma$
-trees with nonzero length function in
![]() $\mathcal{ML}$
have no fixed point at infinity, in particular are semisimple and not shifts in the sense of [Reference Culler and Morgan7]. It follows then from the length rigidity for minimal semisimple
$\mathcal{ML}$
have no fixed point at infinity, in particular are semisimple and not shifts in the sense of [Reference Culler and Morgan7]. It follows then from the length rigidity for minimal semisimple
![]() $\Gamma$
-trees [Reference Culler and Morgan7, Theorem 3.7] that if
$\Gamma$
-trees [Reference Culler and Morgan7, Theorem 3.7] that if
![]() $T$
and
$T$
and
![]() $T'$
are any two minimal
$T'$
are any two minimal
![]() $\Gamma$
-trees with the same length function in
$\Gamma$
-trees with the same length function in
![]() $\mathcal{ML}$
, then there is a unique equivariant isometry
$\mathcal{ML}$
, then there is a unique equivariant isometry
![]() $T\to T'$
.
$T\to T'$
.
3.5. The
 ${\mathbb{R}}^n$
-tree dual to a
${\mathbb{R}}^n$
-tree dual to a
 $n$
-measured geodesic lamination
$n$
-measured geodesic lamination
Let
![]() $n\in{\mathbb{N}}$
.
$n\in{\mathbb{N}}$
.
Definition 3.2.
A
![]() ${\mathbb{R}}^n$
-tree is a
${\mathbb{R}}^n$
-tree is a
![]() ${\mathbb{R}}^n$
-metric space
${\mathbb{R}}^n$
-metric space
![]() $(X, \overrightarrow{d}=(d_i)_{i=1,\ldots,n})$
which is a
$(X, \overrightarrow{d}=(d_i)_{i=1,\ldots,n})$
which is a
![]() $\mathbb{R}$
-tree for the associated
$\mathbb{R}$
-tree for the associated
![]() $\ell ^1$
-metric
$\ell ^1$
-metric
![]() $d^1(x,y)\;:\!=\;\sum _i d_i(x,y)$
.
$d^1(x,y)\;:\!=\;\sum _i d_i(x,y)$
.
Observe that, while we only assume that
![]() $d_i$
are pseudodistances, we require that their sum
$d_i$
are pseudodistances, we require that their sum
![]() $d^1$
is a distance, namely it separates points.
$d^1$
is a distance, namely it separates points.
Definition 3.3.
A
![]() $n$
-measured lamination
$n$
-measured lamination
![]() $\overrightarrow{\lambda }=(\Lambda,\overrightarrow{\nu })$
on a surface
$\overrightarrow{\lambda }=(\Lambda,\overrightarrow{\nu })$
on a surface
![]() $\Sigma$
is a lamination
$\Sigma$
is a lamination
![]() $\Lambda$
on
$\Lambda$
on
![]() $\Sigma$
, endowed with a
$\Sigma$
, endowed with a
![]() $n$
-tuple
$n$
-tuple
![]() $\overrightarrow{\nu }=(\nu _1,\ldots, \nu _n)$
of transverse measures of full joint support, namely
$\overrightarrow{\nu }=(\nu _1,\ldots, \nu _n)$
of transverse measures of full joint support, namely
![]() $\Lambda$
is the union of the supports
$\Lambda$
is the union of the supports
![]() $\Lambda _i$
of the measures
$\Lambda _i$
of the measures
![]() $\nu _i$
for
$\nu _i$
for
![]() $i=1,\ldots,n$
.
$i=1,\ldots,n$
.
It can equivalently be seen as a
![]() $n$
-tuple of parallel measured laminations
$n$
-tuple of parallel measured laminations
![]() $(\lambda _1,\ldots, \lambda _n)$
, that is, such that any two leafs of
$(\lambda _1,\ldots, \lambda _n)$
, that is, such that any two leafs of
![]() $\lambda _i$
and
$\lambda _i$
and
![]() $\lambda _j$
are either disjoint or equal.
$\lambda _j$
are either disjoint or equal.
When
![]() $\Sigma$
is endowed with a locally CAT(0) metric, a
$\Sigma$
is endowed with a locally CAT(0) metric, a
![]() $n$
-measured geodesic lamination
$n$
-measured geodesic lamination
![]() $\overrightarrow{\lambda }=(\Lambda,\overrightarrow{\nu })$
is called geodesic when
$\overrightarrow{\lambda }=(\Lambda,\overrightarrow{\nu })$
is called geodesic when
![]() $\Lambda$
is geodesic.
$\Lambda$
is geodesic.
When
![]() $\Sigma$
is a closed hyperbolic surface, seeing measured geodesic laminations as geodesic currents, a
$\Sigma$
is a closed hyperbolic surface, seeing measured geodesic laminations as geodesic currents, a
![]() $n$
-tuple
$n$
-tuple
![]() $(\lambda _1,\ldots, \lambda _n)$
of measured geodesic laminations is parallel if and only if
$(\lambda _1,\ldots, \lambda _n)$
of measured geodesic laminations is parallel if and only if
or equivalently that
Let
![]() $\overrightarrow{\lambda }=(\Lambda,\overrightarrow{\nu })$
be a
$\overrightarrow{\lambda }=(\Lambda,\overrightarrow{\nu })$
be a
![]() $n$
-measured lamination on a closed hyperbolic surface
$n$
-measured lamination on a closed hyperbolic surface
![]() $\Sigma$
. We now construct the associated dual
$\Sigma$
. We now construct the associated dual
![]() ${\mathbb{R}}^n$
-tree, adapting the construction of Section 3.4.
${\mathbb{R}}^n$
-tree, adapting the construction of Section 3.4.
We take the
![]() $\mathbb{R}$
-tree
$\mathbb{R}$
-tree
![]() $T(\lambda )\;:\!=\;\widetilde{\Sigma ^b}/d_\lambda ^b$
dual to the measured lamination
$T(\lambda )\;:\!=\;\widetilde{\Sigma ^b}/d_\lambda ^b$
dual to the measured lamination
![]() $\lambda =(\Lambda,\nu )$
where
$\lambda =(\Lambda,\nu )$
where
![]() $\nu =\sum _i\nu _i$
.
$\nu =\sum _i\nu _i$
.
Recall from Section 3.4 that
![]() $(\Sigma ^b,\Lambda ^b)$
is the blow-up of
$(\Sigma ^b,\Lambda ^b)$
is the blow-up of
![]() $(\Sigma,\Lambda )$
, which is a locally CAT(0) surface
$(\Sigma,\Lambda )$
, which is a locally CAT(0) surface
![]() $(\Sigma ^b,m^b)$
homeomorphic to
$(\Sigma ^b,m^b)$
homeomorphic to
![]() $\Sigma$
, with a geodesic lamination
$\Sigma$
, with a geodesic lamination
![]() $\Lambda ^b$
, and that
$\Lambda ^b$
, and that
![]() $\lambda ^b=(\Lambda ^b,\nu ^b)$
where
$\lambda ^b=(\Lambda ^b,\nu ^b)$
where
![]() $\nu ^b$
is the non-atomic transverse measure on
$\nu ^b$
is the non-atomic transverse measure on
![]() $\Lambda ^b$
obtained by blowing up
$\Lambda ^b$
obtained by blowing up
![]() $\nu$
, and that
$\nu$
, and that
![]() $d_{\lambda ^b}$
the associated continuous path pseudometric on
$d_{\lambda ^b}$
the associated continuous path pseudometric on
![]() $\widetilde{\Sigma ^b}$
.
$\widetilde{\Sigma ^b}$
.
Taking the blow-ups
![]() $\nu ^b_i$
of the transverse measure
$\nu ^b_i$
of the transverse measure
![]() $\nu _i$
, we obtained a
$\nu _i$
, we obtained a
![]() $n$
-tuple
$n$
-tuple
![]() $\overrightarrow{\nu }^b\;:\!=\;(\nu ^b_i)_i$
of non-atomic transverse measures on
$\overrightarrow{\nu }^b\;:\!=\;(\nu ^b_i)_i$
of non-atomic transverse measures on
![]() $\lambda ^b$
(not necessarily of full support), namely a
$\lambda ^b$
(not necessarily of full support), namely a
![]() $n$
-measured lamination
$n$
-measured lamination
![]() $\overrightarrow{\lambda }^b=(\Lambda ^b,\overrightarrow{\nu }^b)$
on
$\overrightarrow{\lambda }^b=(\Lambda ^b,\overrightarrow{\nu }^b)$
on
![]() $\Sigma ^b$
, which we will call the blow-up of
$\Sigma ^b$
, which we will call the blow-up of
![]() $\overrightarrow{\lambda }=(\Lambda,\overrightarrow{\nu })$
.
$\overrightarrow{\lambda }=(\Lambda,\overrightarrow{\nu })$
.
Each of the measured laminations
![]() $\lambda ^b_i=(\Lambda ^b,\nu ^b_i)$
then induces a continuous everywhere-defined path pseudometric
$\lambda ^b_i=(\Lambda ^b,\nu ^b_i)$
then induces a continuous everywhere-defined path pseudometric
![]() $d_{\lambda ^b_i}$
on
$d_{\lambda ^b_i}$
on
![]() $\widetilde{\Sigma ^b}$
.
$\widetilde{\Sigma ^b}$
.
Definition 3.4.
The
![]() ${\mathbb{R}}^n$
-tree
${\mathbb{R}}^n$
-tree
![]() $T(\overrightarrow{\lambda })$
dual to
$T(\overrightarrow{\lambda })$
dual to
![]() $\overrightarrow{\lambda }$
is defined as the
$\overrightarrow{\lambda }$
is defined as the
![]() $\mathbb{R}$
-tree
$\mathbb{R}$
-tree
![]() $T(\lambda )\;:\!=\;\Sigma ^b/d_\lambda ^b$
dual to the measured lamination
$T(\lambda )\;:\!=\;\Sigma ^b/d_\lambda ^b$
dual to the measured lamination
![]() $\lambda$
, endowed with the
$\lambda$
, endowed with the
![]() ${\mathbb{R}}^n$
-pseudometric given by the
${\mathbb{R}}^n$
-pseudometric given by the
![]() $n$
-tuple
$n$
-tuple
of quotient pseudometrics
![]() $d_{\lambda _i}$
induced by
$d_{\lambda _i}$
induced by
![]() $d_{\lambda ^b_i}$
.
$d_{\lambda ^b_i}$
.
It inherits an action of
![]() $\Gamma$
preserving
$\Gamma$
preserving
![]() $\overrightarrow{d}_\lambda$
, that is preserving each pseudometric
$\overrightarrow{d}_\lambda$
, that is preserving each pseudometric
![]() $d_{\lambda _i}$
.
$d_{\lambda _i}$
.
Proposition 3.5.
![]() $(T(\lambda ),\overrightarrow{d}_\lambda )$
is an
$(T(\lambda ),\overrightarrow{d}_\lambda )$
is an
![]() ${\mathbb{R}}^n$
-tree with associated
${\mathbb{R}}^n$
-tree with associated
![]() $\ell ^1$
-metric
$\ell ^1$
-metric
![]() $\lVert \overrightarrow{d}_\lambda \rVert _1=d_\lambda$
.
$\lVert \overrightarrow{d}_\lambda \rVert _1=d_\lambda$
.
Proof. The crucial fact is that, by Proposition 3.1, the infima involved in the definition of the pseudometrics
![]() $d_{\lambda _i}$
are in fact all realized simultaneously for a same path
$d_{\lambda _i}$
are in fact all realized simultaneously for a same path
![]() $c$
in
$c$
in
![]() $\widetilde{\Sigma ^b}$
, the
$\widetilde{\Sigma ^b}$
, the
![]() $m^b$
-geodesic. In particular,
$m^b$
-geodesic. In particular,
![]() $c$
is a minimizing curve for
$c$
is a minimizing curve for
![]() $d_{\lambda ^b}$
and its projection on
$d_{\lambda ^b}$
and its projection on
![]() $T(\lambda )$
is a minimizing path for
$T(\lambda )$
is a minimizing path for
![]() $\overrightarrow{d}_\lambda$
. This ensures that
$\overrightarrow{d}_\lambda$
. This ensures that
![]() $d_{\lambda }=\sum _i d_{\lambda _i}$
on
$d_{\lambda }=\sum _i d_{\lambda _i}$
on
![]() $T(\lambda )$
.
$T(\lambda )$
.
The separation of
![]() $\overrightarrow{d}_\lambda$
on
$\overrightarrow{d}_\lambda$
on
![]() $T(\lambda )$
follows: if
$T(\lambda )$
follows: if
![]() $\overrightarrow{d}_\lambda (x,y)=0$
then
$\overrightarrow{d}_\lambda (x,y)=0$
then
![]() $d_{\lambda }(x,y)=\sum _i d_{\lambda _i}(x,y)=0$
, hence
$d_{\lambda }(x,y)=\sum _i d_{\lambda _i}(x,y)=0$
, hence
![]() $x=y$
.
$x=y$
.
Remark 3.6.
Proposition 3.5 is special for the
![]() $\ell ^1$
-metric, and does not work for other distances, not even locally. For example, consider a minimal lamination
$\ell ^1$
-metric, and does not work for other distances, not even locally. For example, consider a minimal lamination
![]() $\lambda$
that supports two mutually singular measured laminations. Then the distance function
$\lambda$
that supports two mutually singular measured laminations. Then the distance function
![]() $\lVert \overrightarrow{d}_\lambda \rVert _2$
is not geodesic, not even locally.
$\lVert \overrightarrow{d}_\lambda \rVert _2$
is not geodesic, not even locally.
4. The boundary of
 $\Xi _{\text{Max}}(\Gamma,\textrm{PSL}(2,{\mathbb{R}})^n)$
is
$\Xi _{\text{Max}}(\Gamma,\textrm{PSL}(2,{\mathbb{R}})^n)$
is
 ${\mathbb{P}}(({\mathcal{ML}})^n)$
${\mathbb{P}}(({\mathcal{ML}})^n)$
In this section, we prove Theorem 1.1, that identifies
![]() $\partial ^{\textrm{WL}}{\mathcal{T}^n}$
with
$\partial ^{\textrm{WL}}{\mathcal{T}^n}$
with
![]() ${\mathbb{P}}(({\mathcal{ML}})^n)$
, and deduce some consequences for other length spectra compactifications.
${\mathbb{P}}(({\mathcal{ML}})^n)$
, and deduce some consequences for other length spectra compactifications.
4.1. Proof of Theorem 1.1
Theorem 1.1 is classical when
![]() $n=1$
and follows from the work of Thurston. Thurston furthermore proved [Reference Fathi, Laudenbach and Poénaru10, Expose 8] that
$n=1$
and follows from the work of Thurston. Thurston furthermore proved [Reference Fathi, Laudenbach and Poénaru10, Expose 8] that
![]() $\mathcal{ML}$
is homeomorphic to
$\mathcal{ML}$
is homeomorphic to
![]() ${\mathbb{R}}^{6g-6}$
, that it is projectivization
${\mathbb{R}}^{6g-6}$
, that it is projectivization
![]() ${\mathbb{P}}{\mathcal{ML}}$
is homeomorphic to
${\mathbb{P}}{\mathcal{ML}}$
is homeomorphic to
![]() $\mathbb S^{6g-7}$
, and that the resulting compactification is homeomorphic to a closed ball [Reference Martelli15, 8.3.13]. Using the latter fact, we can prove the following lemma, which ensures that given
$\mathbb S^{6g-7}$
, and that the resulting compactification is homeomorphic to a closed ball [Reference Martelli15, 8.3.13]. Using the latter fact, we can prove the following lemma, which ensures that given
![]() $L$
in
$L$
in
![]() $\mathcal{ML}$
, one can choose a sequence in
$\mathcal{ML}$
, one can choose a sequence in
![]() $\mathcal{T}$
converging to
$\mathcal{T}$
converging to
![]() $[L]$
with a fixed scale sequence. It will be crucial in the proof of Theorem 1.1.
$[L]$
with a fixed scale sequence. It will be crucial in the proof of Theorem 1.1.
Lemma 4.1.
Let
![]() $L\in{\mathcal{ML}}$
. Let
$L\in{\mathcal{ML}}$
. Let
![]() $(\lambda _k)$
be any increasing diverging sequence of positive real numbers. Then there exists a sequence of maximal representations
$(\lambda _k)$
be any increasing diverging sequence of positive real numbers. Then there exists a sequence of maximal representations
![]() $\rho _{k}\colon \Gamma \to \textrm{PSL}(2,{\mathbb{R}})$
such that
$\rho _{k}\colon \Gamma \to \textrm{PSL}(2,{\mathbb{R}})$
such that
![]() $\frac{1}{\lambda _k} L_{\rho _{k}}$
converges to
$\frac{1}{\lambda _k} L_{\rho _{k}}$
converges to
![]() $L$
in
$L$
in
![]() $({\mathbb{R}}_+)^\Gamma$
.
$({\mathbb{R}}_+)^\Gamma$
.
Proof. Given a finite generating set
![]() $S\subset \Gamma$
and an isometric action
$S\subset \Gamma$
and an isometric action
![]() $\rho$
of
$\rho$
of
![]() $\Gamma$
on a metric space
$\Gamma$
on a metric space
![]() $X$
, the minimal displacement of
$X$
, the minimal displacement of
![]() $\rho$
with respect to the generating set
$\rho$
with respect to the generating set
![]() $S$
is defined by
$S$
is defined by
 \begin{align*}\lambda _S(\rho )\;:\!=\;\inf _{x\in X}\sqrt {\sum _s d(x,\rho (s)x)^2}\;.\end{align*}
\begin{align*}\lambda _S(\rho )\;:\!=\;\inf _{x\in X}\sqrt {\sum _s d(x,\rho (s)x)^2}\;.\end{align*}
This defines a nonzero proper and continuous function
![]() $\lambda _S \colon \mathcal{T} \to{\mathbb{R}}_+$
(this is for example proven—in a much more general context—in [Reference Parreau24, Prop. 25]).
$\lambda _S \colon \mathcal{T} \to{\mathbb{R}}_+$
(this is for example proven—in a much more general context—in [Reference Parreau24, Prop. 25]).
We may suppose that
![]() $L$
is nonzero (otherwise we can take a constant sequence
$L$
is nonzero (otherwise we can take a constant sequence
![]() $\rho _k$
). Let
$\rho _k$
). Let
![]() $T$
be a
$T$
be a
![]() $\mathbb{R}$
-tree with minimal
$\mathbb{R}$
-tree with minimal
![]() $\Gamma$
-action, with length function
$\Gamma$
-action, with length function
![]() $L$
. Let
$L$
. Let
![]() $D$
be the minimal displacement of
$D$
be the minimal displacement of
![]() $\Gamma$
on
$\Gamma$
on
![]() $T$
with respect to the generating set
$T$
with respect to the generating set
![]() $S$
.
$S$
.
Fix a point
![]() $[\rho _0]$
in the Teichmüller space
$[\rho _0]$
in the Teichmüller space
![]() $\mathcal{T}$
. As the compactification
$\mathcal{T}$
. As the compactification
![]() $\overline{\mathcal{T}}$
of
$\overline{\mathcal{T}}$
of
![]() $\mathcal{T}$
is a closed ball, there exists a path
$\mathcal{T}$
is a closed ball, there exists a path
![]() $r(t)$
,
$r(t)$
,
![]() $t\in [0,1]$
from
$t\in [0,1]$
from
![]() $[\rho _0]$
to
$[\rho _0]$
to
![]() $[L]$
in
$[L]$
in
![]() $\overline{\mathcal{T}}$
such that
$\overline{\mathcal{T}}$
such that
![]() $r(t)$
belongs to
$r(t)$
belongs to
![]() $\mathcal{T}$
for
$\mathcal{T}$
for
![]() $t\in [0,1[$
. Let
$t\in [0,1[$
. Let
![]() $\rho _t$
be a representation with
$\rho _t$
be a representation with
![]() $[\rho _t]=r(t)$
. Then, as the map
$[\rho _t]=r(t)$
. Then, as the map
is continuous and diverges as
![]() $t$
goes to
$t$
goes to
![]() $1$
, there exists an increasing sequence
$1$
, there exists an increasing sequence
![]() $(t_k)_{k\geq K}$
in
$(t_k)_{k\geq K}$
in
![]() $[0,1[$
with limit
$[0,1[$
with limit
![]() $1$
such that
$1$
such that
![]() $\lambda _S(r(t_k))=D\lambda _k$
. Since
$\lambda _S(r(t_k))=D\lambda _k$
. Since
![]() $[\rho _k]=r(t_k)$
converges to
$[\rho _k]=r(t_k)$
converges to
![]() $[L]$
in
$[L]$
in
![]() $\overline{\mathcal{T}}$
, we have that
$\overline{\mathcal{T}}$
, we have that
![]() $\frac{1}{\lambda _S(\rho _k)} L_{\rho _k}$
converges to
$\frac{1}{\lambda _S(\rho _k)} L_{\rho _k}$
converges to
![]() $sL$
for some
$sL$
for some
![]() $s\in{\mathbb{R}}_+$
. Taking the asymptotic cone of this sequence (see for example [Reference Parreau25]), we also have that
$s\in{\mathbb{R}}_+$
. Taking the asymptotic cone of this sequence (see for example [Reference Parreau25]), we also have that
![]() $sL$
is the length function of an action of
$sL$
is the length function of an action of
![]() $\Gamma$
on a real tree
$\Gamma$
on a real tree
![]() $T_\omega$
with minimal displacement
$T_\omega$
with minimal displacement
![]() $1$
with respect to
$1$
with respect to
![]() $S$
.Footnote 4 Let
$S$
.Footnote 4 Let
![]() $T'\subset T_\omega$
be the minimal invariant subtree. As
$T'\subset T_\omega$
be the minimal invariant subtree. As
![]() $T'$
is a convex subset of
$T'$
is a convex subset of
![]() $T_\omega$
, the minimal displacement of
$T_\omega$
, the minimal displacement of
![]() $\Gamma$
in
$\Gamma$
in
![]() $T'$
is the same as in
$T'$
is the same as in
![]() $T_\omega$
. By length rigidity of actions on minimal trees with length function in
$T_\omega$
. By length rigidity of actions on minimal trees with length function in
![]() $\mathcal{ML}$
, the trees
$\mathcal{ML}$
, the trees
![]() $T$
and
$T$
and
![]() $\frac{1}{s}T'$
are equivariantly isometric, hence have same minimal displacement
$\frac{1}{s}T'$
are equivariantly isometric, hence have same minimal displacement
![]() $s=\frac{1}{D}$
. So we have that
$s=\frac{1}{D}$
. So we have that
![]() $\frac{1}{\lambda _k}L_{\rho _k} \to L$
as wanted.
$\frac{1}{\lambda _k}L_{\rho _k} \to L$
as wanted.
We now have the ingredients needed to prove Theorem 1.1, which we recall for the reader’s convenience:
Proposition 4.2.
The boundary of
![]() $\Xi _{\text{Max}}(\Gamma,\textrm{PSL}(2,{\mathbb{R}})^n)=\mathcal{T}^n$
in the Weyl chamber length compactification is
$\Xi _{\text{Max}}(\Gamma,\textrm{PSL}(2,{\mathbb{R}})^n)=\mathcal{T}^n$
in the Weyl chamber length compactification is
![]() ${\mathbb{P}}(({\mathcal{ML}})^n)$
.
${\mathbb{P}}(({\mathcal{ML}})^n)$
.
Proof. It is easy to see that
![]() $\partial ^{\textrm{WL}}(\mathcal{T}^n)\subset{\mathbb{P}}(({\mathcal{ML}})^n)$
. Let indeed
$\partial ^{\textrm{WL}}(\mathcal{T}^n)\subset{\mathbb{P}}(({\mathcal{ML}})^n)$
. Let indeed
![]() $\rho _k=(\rho _{k,i})_{i=1,\ldots,n}$
,
$\rho _k=(\rho _{k,i})_{i=1,\ldots,n}$
,
![]() $k\in{\mathbb{N}}$
, be a sequence in
$k\in{\mathbb{N}}$
, be a sequence in
![]() ${\textrm{Hom}}(\Gamma,\textrm{PSL}(2,{\mathbb{R}})^n)$
, which we identify with
${\textrm{Hom}}(\Gamma,\textrm{PSL}(2,{\mathbb{R}})^n)$
, which we identify with
![]() ${\textrm{Hom}}(\Gamma,\textrm{PSL}(2,{\mathbb{R}}))^n$
. We write a nonzero function
${\textrm{Hom}}(\Gamma,\textrm{PSL}(2,{\mathbb{R}}))^n$
. We write a nonzero function
![]() $\overrightarrow{L}\colon \Gamma \to{\mathbb{R}}^n$
as
$\overrightarrow{L}\colon \Gamma \to{\mathbb{R}}^n$
as
![]() $\overrightarrow{L}=(L_i)_{i=1,\ldots,n}$
with
$\overrightarrow{L}=(L_i)_{i=1,\ldots,n}$
with
![]() $L_i\colon \Gamma \to{\mathbb{R}}$
. The sequence of conjugacy classes
$L_i\colon \Gamma \to{\mathbb{R}}$
. The sequence of conjugacy classes
![]() $[\rho _k]$
converges to the homothety class
$[\rho _k]$
converges to the homothety class
![]() $[\overrightarrow{L}]$
in the Weyl chamber length compactification if and only if there exists a sequence of positive real numbers
$[\overrightarrow{L}]$
in the Weyl chamber length compactification if and only if there exists a sequence of positive real numbers
![]() $\lambda _k\to \infty$
(scale sequence) such that the renormalized Weyl chamber length function
$\lambda _k\to \infty$
(scale sequence) such that the renormalized Weyl chamber length function
![]() $\frac{1}{\lambda _k}\overrightarrow{L}_{\rho _k}$
converges to
$\frac{1}{\lambda _k}\overrightarrow{L}_{\rho _k}$
converges to
![]() $\overrightarrow{L}$
, that is, if
$\overrightarrow{L}$
, that is, if
![]() $\frac{1}{\lambda _k}L_{\rho _{k,i}}$
converges to
$\frac{1}{\lambda _k}L_{\rho _{k,i}}$
converges to
![]() $L_i$
for all
$L_i$
for all
![]() $i=1,\ldots,n$
[Reference Parreau25, Theorem 5.6]. Then either
$i=1,\ldots,n$
[Reference Parreau25, Theorem 5.6]. Then either
![]() $L_i=0$
or
$L_i=0$
or
![]() $[\rho _{k,i}]$
converges to
$[\rho _{k,i}]$
converges to
![]() $[L_i]$
in the length compactification
$[L_i]$
in the length compactification
![]() $\overline{\mathcal{T}}$
of
$\overline{\mathcal{T}}$
of
![]() $\mathcal{T}$
. As
$\mathcal{T}$
. As
![]() $\partial \mathcal{T}={\mathbb{P}}({\mathcal{ML}})$
, we have that each
$\partial \mathcal{T}={\mathbb{P}}({\mathcal{ML}})$
, we have that each
![]() $L_i$
belongs to
$L_i$
belongs to
![]() $\mathcal{ML}$
, hence
$\mathcal{ML}$
, hence
![]() $[\overrightarrow{L}]$
belongs to
$[\overrightarrow{L}]$
belongs to
![]() ${\mathbb{P}}(({\mathcal{ML}})^n)$
.
${\mathbb{P}}(({\mathcal{ML}})^n)$
.
The converse implication is a consequence of Lemma 4.1. Let
![]() $\overrightarrow{L}=(L_i)_{i=1,\ldots,n}\in ({\mathcal{ML}})^n$
. Using Lemma 4.1 with scale sequence
$\overrightarrow{L}=(L_i)_{i=1,\ldots,n}\in ({\mathcal{ML}})^n$
. Using Lemma 4.1 with scale sequence
![]() $\lambda _k=k$
, we can construct for each
$\lambda _k=k$
, we can construct for each
![]() $i=1,\ldots,n$
a sequence of maximal representations
$i=1,\ldots,n$
a sequence of maximal representations
![]() $\rho _{k,i}:\Gamma \to \textrm{PSL}(2,{\mathbb{R}})$
,
$\rho _{k,i}:\Gamma \to \textrm{PSL}(2,{\mathbb{R}})$
,
![]() $k\in{\mathbb{N}}$
, whose renormalized length function
$k\in{\mathbb{N}}$
, whose renormalized length function
![]() $\frac{1}{k}L_{\rho _{k,i}}$
converges to the length function
$\frac{1}{k}L_{\rho _{k,i}}$
converges to the length function
![]() $L_i$
in
$L_i$
in
![]() $({\mathbb{R}}_+)^\Gamma$
as
$({\mathbb{R}}_+)^\Gamma$
as
![]() $k\to \infty$
. We now consider for
$k\to \infty$
. We now consider for
![]() $k\in{\mathbb{N}}$
the product representation
$k\in{\mathbb{N}}$
the product representation
![]() $\rho _k\;:\! =\;(\rho _{k,i})_{i=1,\ldots,n}\colon \Gamma \to \textrm{PSL}(2,{\mathbb{R}})^n$
, which, being a product of maximal representations, is a maximal representation. Then
$\rho _k\;:\! =\;(\rho _{k,i})_{i=1,\ldots,n}\colon \Gamma \to \textrm{PSL}(2,{\mathbb{R}})^n$
, which, being a product of maximal representations, is a maximal representation. Then
![]() $\frac{1}{k}\overrightarrow{L}_{\rho _k}=(\frac{1}{k}L_{\rho _{k,i}})_{i=1,\ldots,n}$
converges to
$\frac{1}{k}\overrightarrow{L}_{\rho _k}=(\frac{1}{k}L_{\rho _{k,i}})_{i=1,\ldots,n}$
converges to
![]() $(L_i)_{i=1,\ldots,n}=\overrightarrow{L}$
as
$(L_i)_{i=1,\ldots,n}=\overrightarrow{L}$
as
![]() $k\to \infty$
. Hence,
$k\to \infty$
. Hence,
![]() $[\overrightarrow{L}]$
belongs to
$[\overrightarrow{L}]$
belongs to
![]() $\partial ^{\textrm{WL}}(\mathcal{T}^n)$
.
$\partial ^{\textrm{WL}}(\mathcal{T}^n)$
.
As a result, we deduce that
![]() ${\mathbb{P}}(({\mathcal{ML}})^n)\subset{\mathbb{P}}(({\mathbb{R}}_+^\Gamma )^n)$
is a sphere of dimension
${\mathbb{P}}(({\mathcal{ML}})^n)\subset{\mathbb{P}}(({\mathbb{R}}_+^\Gamma )^n)$
is a sphere of dimension
![]() $n(6g-6)-1$
, being the topological join of
$n(6g-6)-1$
, being the topological join of
![]() $n$
spheres:
$n$
spheres:
Corollary 4.3.
The boundary of
![]() $\Xi _{\text{Max}}(\Gamma,\textrm{PSL}(2,{\mathbb{R}})^n)=\mathcal{T}^n$
in the Weyl chamber length compactification is homeomorphic to
$\Xi _{\text{Max}}(\Gamma,\textrm{PSL}(2,{\mathbb{R}})^n)=\mathcal{T}^n$
in the Weyl chamber length compactification is homeomorphic to
![]() $\mathbb S^{n(6g-6)-1}$
.
$\mathbb S^{n(6g-6)-1}$
.
4.2. Applications to other length compactifications
As an application of Proposition 4.2, we can also understand various other compactifications of
![]() $\Xi _{\text{Max}}(\Gamma,\textrm{PSL}(2,{\mathbb{R}})^n)$
:
$\Xi _{\text{Max}}(\Gamma,\textrm{PSL}(2,{\mathbb{R}})^n)$
:
Corollary 4.4.
For any
![]() $W$
-invariant norm
$W$
-invariant norm
![]() $N\colon{\mathbb{R}}^n\to{\mathbb{R}}_+^n$
, the boundary of
$N\colon{\mathbb{R}}^n\to{\mathbb{R}}_+^n$
, the boundary of
![]() $\Xi _{\text{Max}}(\Gamma,\textrm{PSL}(2,{\mathbb{R}})^n)$
in the
$\Xi _{\text{Max}}(\Gamma,\textrm{PSL}(2,{\mathbb{R}})^n)$
in the
![]() $N$
-length compactification is the projectivization
$N$
-length compactification is the projectivization
![]() ${\mathbb{P}}(N(({\mathcal{ML}})^n))$
of the image
${\mathbb{P}}(N(({\mathcal{ML}})^n))$
of the image
![]() $N(({\mathcal{ML}})^n)$
of
$N(({\mathcal{ML}})^n)$
of
![]() $({\mathcal{ML}})^n$
by the map sending
$({\mathcal{ML}})^n$
by the map sending
![]() $\overrightarrow{L}\colon \Gamma \to{\mathbb{R}}^n$
to
$\overrightarrow{L}\colon \Gamma \to{\mathbb{R}}^n$
to
![]() $N\circ \overrightarrow{L}\colon \Gamma \to{\mathbb{R}}$
.
$N\circ \overrightarrow{L}\colon \Gamma \to{\mathbb{R}}$
.
In particular, the boundary of
![]() $\mathcal{T}^n$
in the
$\mathcal{T}^n$
in the
![]() $\ell ^1$
-length compactification is the projectivization
$\ell ^1$
-length compactification is the projectivization
![]() ${\mathbb{P}}(\sum _{i=1}^n{\mathcal{ML}})$
of the space of geodesic currents that can be decomposed as the sum of
${\mathbb{P}}(\sum _{i=1}^n{\mathcal{ML}})$
of the space of geodesic currents that can be decomposed as the sum of
![]() $n$
measured laminations.
$n$
measured laminations.
Remark 4.5.
While the map
![]() $({\mathcal{ML}})^2\to (\sum _{i=1}^2{\mathcal{ML}})$
has fibers of cardinality 2 on the set of geodesic currents with positive systole, the fiber over minimal measured laminations (and more generally over geodesic currents that admit a Bonahon-orthogonal decomposition
$({\mathcal{ML}})^2\to (\sum _{i=1}^2{\mathcal{ML}})$
has fibers of cardinality 2 on the set of geodesic currents with positive systole, the fiber over minimal measured laminations (and more generally over geodesic currents that admit a Bonahon-orthogonal decomposition
![]() $\mu =\mu _1+\mu _2$
with
$\mu =\mu _1+\mu _2$
with
![]() $\mu _1$
a minimal measured lamination) is higher dimensional. As a result it is, in general, not clear how to determine the topology of
$\mu _1$
a minimal measured lamination) is higher dimensional. As a result it is, in general, not clear how to determine the topology of
![]() ${\mathbb{P}}(\sum _{i=1}^2{\mathcal{ML}})$
. Indeed it follows from the arguments in [
Reference Duchin, Leininger and Rafi9, Theorem 2] that no finite set of simple closed curves is sufficient to separate points in
${\mathbb{P}}(\sum _{i=1}^2{\mathcal{ML}})$
. Indeed it follows from the arguments in [
Reference Duchin, Leininger and Rafi9, Theorem 2] that no finite set of simple closed curves is sufficient to separate points in
![]() ${\mathbb{P}}(\sum _{i=1}^2{\mathcal{ML}})$
. This is in strong contrast to
${\mathbb{P}}(\sum _{i=1}^2{\mathcal{ML}})$
. This is in strong contrast to
![]() ${\mathbb{P}}(({\mathcal{ML}})^2)$
: there is a collection of
${\mathbb{P}}(({\mathcal{ML}})^2)$
: there is a collection of
![]() $9g-9$
simple closed curves on
$9g-9$
simple closed curves on
![]() $\Sigma$
whose
$\Sigma$
whose
![]() ${\mathbb{R}}^2$
-length function already separate points in
${\mathbb{R}}^2$
-length function already separate points in
![]() ${\mathbb{P}}(({\mathcal{ML}})^2)$
.
${\mathbb{P}}(({\mathcal{ML}})^2)$
.
5.
 ${\mathbb{R}}^2$
-mixed structures
${\mathbb{R}}^2$
-mixed structures
The purpose of this section is to prove Theorem 1.2 from the introduction, which interprets points in
![]() ${\mathcal{ML}}\times{\mathcal{ML}}$
as length functions of mixed structures. For this we introduce the notion of flat structures in Section 5.1, mixed structures in Section 5.2, and their associated length functions in Section 5.3, and prove the result in Section 5.4.
${\mathcal{ML}}\times{\mathcal{ML}}$
as length functions of mixed structures. For this we introduce the notion of flat structures in Section 5.1, mixed structures in Section 5.2, and their associated length functions in Section 5.3, and prove the result in Section 5.4.
5.1. Flat structures
We will consider flat structures on a punctured finite type surfaces, namely the complement of a finite set of marked points considered as punctures in a compact topological surfaces. When dealing with mixed structures, the finite type surfaces will typically be obtained from geodesic subsurfaces of the original surface
![]() $\Sigma$
by collapsing each boundary components to a cusp point.
$\Sigma$
by collapsing each boundary components to a cusp point.
Definition 5.1.
A half-translation structure
![]() $K$
on a finite type surface
$K$
on a finite type surface
![]() $\Sigma$
is a
$\Sigma$
is a
![]() $({\mathbb{R}}^2\rtimes{\mathbb{Z}}/2{\mathbb{Z}},{\mathbb{R}}^2)$
-structure on
$({\mathbb{R}}^2\rtimes{\mathbb{Z}}/2{\mathbb{Z}},{\mathbb{R}}^2)$
-structure on
![]() $\Sigma$
, with conical singularities of angle
$\Sigma$
, with conical singularities of angle
![]() $k\pi$
,
$k\pi$
,
![]() $k\geq 2$
, extendible at punctures, with possibly angle
$k\geq 2$
, extendible at punctures, with possibly angle
![]() $\pi$
singularities at the punctures.
$\pi$
singularities at the punctures.
With a slight abuse of notation we denote by
![]() $\overrightarrow{\textrm{Flat}}(\Sigma )$
the moduli space of half-translation structures on
$\overrightarrow{\textrm{Flat}}(\Sigma )$
the moduli space of half-translation structures on
![]() $\Sigma$
, where two such structures are identified if they are isotopic. Note that the flat structures we consider here are directed (i.e.,, with a preferred vertical direction).
$\Sigma$
, where two such structures are identified if they are isotopic. Note that the flat structures we consider here are directed (i.e.,, with a preferred vertical direction).
Remark 5.2.
Duchin−Leiniger−Rafi [Reference Duchin, Leininger and Rafi9], as well as Ouyang−Tamburelli [Reference Ouyang and Tamburelli21] consider, instead, the space of flat structures on
![]() $\Sigma$
, where they identify isometric marked structures. As a result, we have fibrations
$\Sigma$
, where they identify isometric marked structures. As a result, we have fibrations
The fiber of
![]() $\overrightarrow{\textrm{Flat}}(\Sigma )\to{\textrm{Flat}}(\Sigma )$
is the circle
$\overrightarrow{\textrm{Flat}}(\Sigma )\to{\textrm{Flat}}(\Sigma )$
is the circle
![]() $\mathbb S^1$
, which acts on a half-translation surface by rotation. Since our structures are marked, and any half-translation structure induces a conformal structure on the surface, the space
$\mathbb S^1$
, which acts on a half-translation surface by rotation. Since our structures are marked, and any half-translation structure induces a conformal structure on the surface, the space
![]() $\overrightarrow{\textrm{Flat}}(\Sigma )$
fibers over the Teichmüller space. We will never need this fact, but it is well known that the fiber over
$\overrightarrow{\textrm{Flat}}(\Sigma )$
fibers over the Teichmüller space. We will never need this fact, but it is well known that the fiber over
![]() $X$
in this fibration identifies with the space of holomorphic quadratic differentials over the Riemann surface
$X$
in this fibration identifies with the space of holomorphic quadratic differentials over the Riemann surface
![]() $X$
.
$X$
.
Let
![]() $K$
be a flat structure on
$K$
be a flat structure on
![]() $\Sigma$
, and let
$\Sigma$
, and let
![]() $\mathcal{F}_1$
,
$\mathcal{F}_1$
,
![]() $\mathcal{F}_2$
be the vertical and horizontal measured foliations of
$\mathcal{F}_2$
be the vertical and horizontal measured foliations of
![]() $K$
. This is a pair of transverse measured foliations. For
$K$
. This is a pair of transverse measured foliations. For
![]() $i=1,2$
, we denote by
$i=1,2$
, we denote by
and by
![]() $d_{{K},i}\;:\!=\;d_{\mathcal{F}_i}$
the associated pseudometric on
$d_{{K},i}\;:\!=\;d_{\mathcal{F}_i}$
the associated pseudometric on
![]() $\widetilde{\Sigma }$
This defines the natural
$\widetilde{\Sigma }$
This defines the natural
![]() ${\mathbb{R}}^2$
-metric
${\mathbb{R}}^2$
-metric
on
![]() $\widetilde{\Sigma }$
. We denote
$\widetilde{\Sigma }$
. We denote
![]() $L_{{K},i}\;:\!=\;I_{\mathcal{F}_i}\colon \Gamma \to{\mathbb{R}}$
the corresponding length function. Let
$L_{{K},i}\;:\!=\;I_{\mathcal{F}_i}\colon \Gamma \to{\mathbb{R}}$
the corresponding length function. Let
![]() $T(\mathcal{F}_i)\;:\!=\;\widetilde{\Sigma }/d_{{K},i}$
be the dual tree of
$T(\mathcal{F}_i)\;:\!=\;\widetilde{\Sigma }/d_{{K},i}$
be the dual tree of
![]() $\mathcal{F}_i$
, and
$\mathcal{F}_i$
, and
![]() $p_i\colon \widetilde{\Sigma }\to T(\mathcal{F}_i)$
the corresponding projection.
$p_i\colon \widetilde{\Sigma }\to T(\mathcal{F}_i)$
the corresponding projection.
The universal cover
![]() $\widetilde{\Sigma }$
of
$\widetilde{\Sigma }$
of
![]() $\Sigma$
is a CAT(0) metric space for the flat metric associated to
$\Sigma$
is a CAT(0) metric space for the flat metric associated to
![]() $K$
, which we will denote by
$K$
, which we will denote by
![]() $d_{{\textrm{CAT}}(0)}$
. Note that
$d_{{\textrm{CAT}}(0)}$
. Note that
![]() $d_{{\textrm{CAT}}(0)}$
is not in general equal to the metric
$d_{{\textrm{CAT}}(0)}$
is not in general equal to the metric
![]() $\|\overrightarrow{d}_{K}\|_2$
induced from the
$\|\overrightarrow{d}_{K}\|_2$
induced from the
![]() ${\mathbb{R}}^2$
-metric
${\mathbb{R}}^2$
-metric
![]() $\overrightarrow{d}$
by taking the
$\overrightarrow{d}$
by taking the
![]() $\ell ^2$
-norm, nevertheless it is the associated length metric. We denote
$\ell ^2$
-norm, nevertheless it is the associated length metric. We denote
![]() $\widetilde{\Sigma }^c$
the completion of
$\widetilde{\Sigma }^c$
the completion of
![]() $\widetilde{\Sigma }$
with respect to
$\widetilde{\Sigma }$
with respect to
![]() $d_{{\textrm{CAT}}(0)}$
, which consists in adding one fixed point
$d_{{\textrm{CAT}}(0)}$
, which consists in adding one fixed point
![]() $x_{{\widetilde{c}}}$
for each parabolic subgroup
$x_{{\widetilde{c}}}$
for each parabolic subgroup
![]() $\Gamma _{{\widetilde{c}}}$
of
$\Gamma _{{\widetilde{c}}}$
of
![]() $\Gamma =\pi _1(\Sigma )$
(corresponding to lifts
$\Gamma =\pi _1(\Sigma )$
(corresponding to lifts
![]() $\widetilde{c}$
of punctures
$\widetilde{c}$
of punctures
![]() $c$
of
$c$
of
![]() $\Sigma$
), see for example [Reference Morzadec18, Lemma 7.2]. The flat structure extends on
$\Sigma$
), see for example [Reference Morzadec18, Lemma 7.2]. The flat structure extends on
![]() $\widetilde{\Sigma }^c$
. It is easy to see that
$\widetilde{\Sigma }^c$
. It is easy to see that
![]() $\mathcal{F}_i$
,
$\mathcal{F}_i$
,
![]() $d_{{K},i}$
, and
$d_{{K},i}$
, and
![]() $p_i$
extend naturally to the completion
$p_i$
extend naturally to the completion
![]() $\widetilde{\Sigma }^c$
of
$\widetilde{\Sigma }^c$
of
![]() $\widetilde{\Sigma }$
.
$\widetilde{\Sigma }$
.
We define the
![]() $\ell ^1$
-length metric on
$\ell ^1$
-length metric on
![]() $\widetilde{\Sigma }$
, as the Finsler metric
$\widetilde{\Sigma }$
, as the Finsler metric
![]() $d_{K}$
induced by the
$d_{K}$
induced by the
![]() $\ell ^1$
-norm
$\ell ^1$
-norm
![]() $||x||_1=|x_1|+|x_2|$
on
$||x||_1=|x_1|+|x_2|$
on
![]() ${\mathbb{R}}^2$
. This metric is clearly equivalent to the CAT(0) metric
${\mathbb{R}}^2$
. This metric is clearly equivalent to the CAT(0) metric
![]() $d_{CAT(0)}$
, in particular extends to
$d_{CAT(0)}$
, in particular extends to
![]() $\widetilde{\Sigma }^c$
. We denote by
$\widetilde{\Sigma }^c$
. We denote by
the corresponding length of
![]() $\gamma \in \Gamma$
. We now establish some basic properties of the
$\gamma \in \Gamma$
. We now establish some basic properties of the
![]() $\ell ^1$
-metric that we will need. Recall that in the following lemma, a geodesic is an additive path
$\ell ^1$
-metric that we will need. Recall that in the following lemma, a geodesic is an additive path
![]() $t\mapsto c(t)$
for the distance
$t\mapsto c(t)$
for the distance
![]() $d$
.
$d$
.
Lemma 5.3.
Let
![]() $K$
be a flat structure on a finite type surface
$K$
be a flat structure on a finite type surface
![]() $\Sigma$
. The following properties hold:
$\Sigma$
. The following properties hold:
-
(1) For any CAT(0) geodesic
 $c\colon I\to \widetilde{\Sigma }^c$
, the projections
$c\colon I\to \widetilde{\Sigma }^c$
, the projections
 $c_i=p_i\circ c$
of
$c_i=p_i\circ c$
of
 $c$
in the dual trees
$c$
in the dual trees
 $T(\mathcal{F}_i)$
are geodesics;
$T(\mathcal{F}_i)$
are geodesics;
-
(2) We have
 $d_{K}=d_{{K},1}+d_{{K},2}=\|\overrightarrow{d}_{K}\|_1$
on
$d_{K}=d_{{K},1}+d_{{K},2}=\|\overrightarrow{d}_{K}\|_1$
on
 $\widetilde{\Sigma }^c$
. In particular, the CAT(0) geodesics are geodesics for
$\widetilde{\Sigma }^c$
. In particular, the CAT(0) geodesics are geodesics for
 $d_{K}$
;
$d_{K}$
; -
(3) We have
 $L_{K}(\gamma )=L_{{K},1}(\gamma )+L_{{K},2}(\gamma )$
for all
$L_{K}(\gamma )=L_{{K},1}(\gamma )+L_{{K},2}(\gamma )$
for all
 $\gamma \in \Gamma$
.
$\gamma \in \Gamma$
.
Proof. We prove (1). Let
![]() $i\in \{1,2\}$
. As
$i\in \{1,2\}$
. As
![]() $T(\mathcal{F}_i)$
is a tree, we only need to prove that the path
$T(\mathcal{F}_i)$
is a tree, we only need to prove that the path
![]() $c_i$
does not backtrack. Let
$c_i$
does not backtrack. Let
![]() $t_1\leq t_2\leq t_3$
be real parameters in
$t_1\leq t_2\leq t_3$
be real parameters in
![]() $I$
such that
$I$
such that
![]() $c_i(t_1)=c_i(t_3)$
. Then the points
$c_i(t_1)=c_i(t_3)$
. Then the points
![]() $c(t_1)$
and
$c(t_1)$
and
![]() $c(t_3)$
are in a common leaf of the foliation
$c(t_3)$
are in a common leaf of the foliation
![]() $\mathcal{F}_i$
. As the leafs of the foliation are geodesic for the CAT(0) metric
$\mathcal{F}_i$
. As the leafs of the foliation are geodesic for the CAT(0) metric
![]() $d$
on
$d$
on
![]() $\widetilde{\Sigma }$
, we can deduce, by uniqueness of geodesics in CAT(0) metric spaces, that the point
$\widetilde{\Sigma }$
, we can deduce, by uniqueness of geodesics in CAT(0) metric spaces, that the point
![]() $c(t_2)$
is on the same leaf, hence that
$c(t_2)$
is on the same leaf, hence that
![]() $c_i(t_1)=c_i(t_2)=c_i(t_3)$
. This proves that
$c_i(t_1)=c_i(t_2)=c_i(t_3)$
. This proves that
![]() $c_i$
is a geodesic in the tree
$c_i$
is a geodesic in the tree
![]() $T(\mathcal{F}_i)$
. We now prove (2). The
$T(\mathcal{F}_i)$
. We now prove (2). The
![]() $\ell ^1$
-length of a path
$\ell ^1$
-length of a path
![]() $c$
is, by definition,
$c$
is, by definition,
![]() $\ell ^1(c)=\int _c|dx_1|+\int _c|dx_2| =\ell _1(c)+\ell _2(c)$
. We then clearly have that
$\ell ^1(c)=\int _c|dx_1|+\int _c|dx_2| =\ell _1(c)+\ell _2(c)$
. We then clearly have that
![]() $d(x,y)\geq d_1(x,y)+d_2(x,y)$
. On the other hand, if
$d(x,y)\geq d_1(x,y)+d_2(x,y)$
. On the other hand, if
![]() $c$
is the CAT(0) geodesic in
$c$
is the CAT(0) geodesic in
![]() $\widetilde{\Sigma }^c$
from
$\widetilde{\Sigma }^c$
from
![]() $x$
to
$x$
to
![]() $y$
, we know by (2) that both projections
$y$
, we know by (2) that both projections
![]() $c_i=p_i\circ c$
of
$c_i=p_i\circ c$
of
![]() $c$
are geodesic. So for
$c$
are geodesic. So for
![]() $i=1,2$
we have
$i=1,2$
we have
![]() $d_i(x,y)=d(p_i(x), p_i(y))=l(c_i)=\ell _i(c)$
and hence
$d_i(x,y)=d(p_i(x), p_i(y))=l(c_i)=\ell _i(c)$
and hence
![]() $\ell (c) = d_1(x,y)+d_2(x,y)$
.
$\ell (c) = d_1(x,y)+d_2(x,y)$
.
We finally prove (3). As
![]() $d=d_1+d_2$
we clearly have
$d=d_1+d_2$
we clearly have
![]() $L_{K}(\gamma )\geq L_{{K},1}(\gamma )+L_{{K},2}(\gamma )$
. If
$L_{K}(\gamma )\geq L_{{K},1}(\gamma )+L_{{K},2}(\gamma )$
. If
![]() $L_{K}(\gamma )=0$
, then we are done. Otherwise,
$L_{K}(\gamma )=0$
, then we are done. Otherwise,
![]() $\gamma$
has no fixed point in
$\gamma$
has no fixed point in
![]() $\widetilde{\Sigma }^c$
and, since
$\widetilde{\Sigma }^c$
and, since
![]() $\widetilde{\Sigma }^c/\Gamma$
is compact, there is a CAT(0) geodesic
$\widetilde{\Sigma }^c/\Gamma$
is compact, there is a CAT(0) geodesic
![]() $c$
in
$c$
in
![]() $\widetilde{\Sigma }^c$
translated by
$\widetilde{\Sigma }^c$
translated by
![]() $\gamma$
. By (2) both projections
$\gamma$
. By (2) both projections
![]() $c_i=p_i\circ c$
of
$c_i=p_i\circ c$
of
![]() $c$
are geodesics translated by
$c$
are geodesics translated by
![]() $\Gamma$
. So, for any
$\Gamma$
. So, for any
![]() $x$
on
$x$
on
![]() $c$
, and
$c$
, and
![]() $i=1,2$
$i=1,2$
Then
![]() $d(x,\gamma x)=L_{{K},1}(\gamma )+L_{{K},2}(\gamma )$
.
$d(x,\gamma x)=L_{{K},1}(\gamma )+L_{{K},2}(\gamma )$
.
5.2.
 ${\mathbb{R}}^2$
-mixed structures on a surface
${\mathbb{R}}^2$
-mixed structures on a surface
In this section, we introduce a natural notion of
![]() ${\mathbb{R}}^2$
-mixed structure on a surface. This generalizes flat structures and refines the notion of mixed structure introduced by Duchin−Leininger−Rafi and Morzadec [Reference Duchin, Leininger and Rafi9, Reference Morzadec18]. The definition follows the point of view of [Reference Duchin, Leininger and Rafi9], see Section 6 for the metric viewpoint analoguous to [Reference Morzadec18]. Note that an equivalent notion has been independently introduced in [Reference Martone, Ouyang and Tamburelli16, Definition 6.4].
${\mathbb{R}}^2$
-mixed structure on a surface. This generalizes flat structures and refines the notion of mixed structure introduced by Duchin−Leininger−Rafi and Morzadec [Reference Duchin, Leininger and Rafi9, Reference Morzadec18]. The definition follows the point of view of [Reference Duchin, Leininger and Rafi9], see Section 6 for the metric viewpoint analoguous to [Reference Morzadec18]. Note that an equivalent notion has been independently introduced in [Reference Martone, Ouyang and Tamburelli16, Definition 6.4].
Definition 5.4.
A
![]() ${\mathbb{R}}^2$
-mixed structure on a compact hyperbolic surface
${\mathbb{R}}^2$
-mixed structure on a compact hyperbolic surface
![]() $\Sigma$
with boundary is a triple
$\Sigma$
with boundary is a triple
![]() ${M}=(\Sigma^{\prime},{K},\overrightarrow{\lambda })$
where
${M}=(\Sigma^{\prime},{K},\overrightarrow{\lambda })$
where
-
•
 $\Sigma^{\prime}$
is a (possibly disconnected, possibly empty) open geodesic subsurface of
$\Sigma^{\prime}$
is a (possibly disconnected, possibly empty) open geodesic subsurface of
 $\Sigma$
, namely a union of complementary components of a collection of disjoint simple closed geodesics.
$\Sigma$
, namely a union of complementary components of a collection of disjoint simple closed geodesics.
-
•
 $K$
is a flat structure on
$K$
is a flat structure on
 $\Sigma^{\prime}$
extendible at punctures (when
$\Sigma^{\prime}$
extendible at punctures (when
 $\Sigma^{\prime}$
is compactified as a punctured surface),
$\Sigma^{\prime}$
is compactified as a punctured surface),
-
•
 $\overrightarrow{\lambda }=(\Lambda, \overrightarrow{\nu })$
is a
$\overrightarrow{\lambda }=(\Lambda, \overrightarrow{\nu })$
is a
 $2$
-measured geodesic lamination on
$2$
-measured geodesic lamination on
 $\Sigma -\Sigma^{\prime}$
, that is,
$\Sigma -\Sigma^{\prime}$
, that is,
 $\Lambda$
is a geodesic lamination on
$\Lambda$
is a geodesic lamination on
 $\Sigma$
, included in
$\Sigma$
, included in
 $\Sigma -\Sigma^{\prime}$
, and
$\Sigma -\Sigma^{\prime}$
, and
 $\overrightarrow{\nu }=(\nu _1,\nu _2)$
is a pair of transverse measures on
$\overrightarrow{\nu }=(\nu _1,\nu _2)$
is a pair of transverse measures on
 $\Lambda$
of full support, that is,
$\Lambda$
of full support, that is,
 $\Lambda =\textrm{supp}(\nu _1)\cup \textrm{supp}(\nu _2)$
.Footnote 5
$\Lambda =\textrm{supp}(\nu _1)\cup \textrm{supp}(\nu _2)$
.Footnote 5
This imposes topological restrictions on the subsurface
![]() $\Sigma^{\prime}$
: no connected component of
$\Sigma^{\prime}$
: no connected component of
![]() $\Sigma^{\prime}$
can be a pair of pants, since a pair of pants does not support any non-trivial flat structure.
$\Sigma^{\prime}$
can be a pair of pants, since a pair of pants does not support any non-trivial flat structure.
Example 5.5.
We illustrate an example of an
![]() ${\mathbb{R}}^2$
-mixed structure on a surface of genus
${\mathbb{R}}^2$
-mixed structure on a surface of genus
![]() $3$
in Figure 1. In this case, the support of the lamination
$3$
in Figure 1. In this case, the support of the lamination
![]() $\Lambda$
consists of the three colored curves
$\Lambda$
consists of the three colored curves
![]() $c_1$
,
$c_1$
,
![]() $c_2$
,
$c_2$
,
![]() $c_3$
, each with the given pair of weights
$c_3$
, each with the given pair of weights
![]() $(x_i,y_i)\in{\mathbb{R}}_+^2-\{(0,0)\}$
. Observe that in this example
$(x_i,y_i)\in{\mathbb{R}}_+^2-\{(0,0)\}$
. Observe that in this example
![]() $\textrm{supp}(\nu _1)=\{c_1,c_2\}$
and
$\textrm{supp}(\nu _1)=\{c_1,c_2\}$
and
![]() $\textrm{supp}(\nu _2)=\{c_2,c_3\}$
. The subsurface
$\textrm{supp}(\nu _2)=\{c_2,c_3\}$
. The subsurface
![]() $\Sigma^{\prime}$
is the disjoint union of a thrice punctured torus
$\Sigma^{\prime}$
is the disjoint union of a thrice punctured torus
![]() $\Sigma^{\prime}_1$
, bounded by the curve
$\Sigma^{\prime}_1$
, bounded by the curve
![]() $c_0$
and the curve
$c_0$
and the curve
![]() $c_1$
, and a twice punctured torus
$c_1$
, and a twice punctured torus
![]() $\Sigma^{\prime}_2$
, endowed with the flat structures
$\Sigma^{\prime}_2$
, endowed with the flat structures
![]() ${K}_1,{K}_2$
illustrated above in the picture. In the flat pictures, the parallel sides are identified, and the colored points correspond to punctures (corresponding to the curves, in
${K}_1,{K}_2$
illustrated above in the picture. In the flat pictures, the parallel sides are identified, and the colored points correspond to punctures (corresponding to the curves, in
![]() $\Sigma$
, of the same color). In particular, the two black punctures
$\Sigma$
, of the same color). In particular, the two black punctures
![]() $p_0,p_0'$
in
$p_0,p_0'$
in
![]() ${K}_1$
come from the same curve. Observe that, while
${K}_1$
come from the same curve. Observe that, while
![]() $c_0$
is a boundary component of
$c_0$
is a boundary component of
![]() $\Sigma^{\prime}$
, it does not belong to the lamination
$\Sigma^{\prime}$
, it does not belong to the lamination
![]() $\Lambda$
, since the curve is not contained in the support of neither transverse measure.
$\Lambda$
, since the curve is not contained in the support of neither transverse measure.
We denote by
![]() $\overrightarrow{\textrm{Mix}}(\Sigma )$
the moduli space of
$\overrightarrow{\textrm{Mix}}(\Sigma )$
the moduli space of
![]() ${\mathbb{R}}^2$
-mixed structures, where two
${\mathbb{R}}^2$
-mixed structures, where two
![]() ${\mathbb{R}}^2$
-mixed structures are identified if the subsurfaces and the laminations agree and the flat structures are equivalent, namely isotopic to each other.
${\mathbb{R}}^2$
-mixed structures are identified if the subsurfaces and the laminations agree and the flat structures are equivalent, namely isotopic to each other.
Remark 5.6.
Following up on Remark 5.2, observe that in the
![]() ${\mathbb{R}}^2$
-mixed structures we consider here, the flat part is always directed. Forgetting the vertical direction we obtain a map
${\mathbb{R}}^2$
-mixed structures we consider here, the flat part is always directed. Forgetting the vertical direction we obtain a map
![]() $\overrightarrow{\textrm{Mix}}(\Sigma )\to \textrm{Mix}(\Sigma )$
, where
$\overrightarrow{\textrm{Mix}}(\Sigma )\to \textrm{Mix}(\Sigma )$
, where
![]() $\textrm{Mix}(\Sigma )$
denotes the mixed structures studied in [Reference Duchin, Leininger and Rafi9]. In general, the map
$\textrm{Mix}(\Sigma )$
denotes the mixed structures studied in [Reference Duchin, Leininger and Rafi9]. In general, the map
![]() $\overrightarrow{\textrm{Mix}}(\Sigma )\to \textrm{Mix}(\Sigma )$
has fibers
$\overrightarrow{\textrm{Mix}}(\Sigma )\to \textrm{Mix}(\Sigma )$
has fibers
![]() $(\mathbb S^1)^k$
where
$(\mathbb S^1)^k$
where
![]() $k$
denotes the number of connected components of
$k$
denotes the number of connected components of
![]() $\Sigma^{\prime}$
. In [Reference Duchin, Leininger and Rafi9], the set
$\Sigma^{\prime}$
. In [Reference Duchin, Leininger and Rafi9], the set
![]() $\textrm{Mix}(\Sigma )$
is identified with the corresponding set of geodesic currents, a perspective that is generalized in [Reference Ouyang and Tamburelli21, Reference Ouyang and Tamburelli20], where the flat metrics associated to cubic (resp. quartic) differentials are considered.
$\textrm{Mix}(\Sigma )$
is identified with the corresponding set of geodesic currents, a perspective that is generalized in [Reference Ouyang and Tamburelli21, Reference Ouyang and Tamburelli20], where the flat metrics associated to cubic (resp. quartic) differentials are considered.

Figure 1. An
![]() ${\mathbb{R}}^2$
-mixed structure on a surface of genus 4.
${\mathbb{R}}^2$
-mixed structure on a surface of genus 4.
5.3. The
 ${\mathbb{R}}^2$
-length function of a mixed structure
${\mathbb{R}}^2$
-length function of a mixed structure
Let
![]() ${M}=(\Sigma^{\prime},{K},\overrightarrow{\lambda })$
be a
${M}=(\Sigma^{\prime},{K},\overrightarrow{\lambda })$
be a
![]() ${\mathbb{R}}^2$
-mixed structure on
${\mathbb{R}}^2$
-mixed structure on
![]() $\Sigma$
. Denote by
$\Sigma$
. Denote by
![]() $(\mathcal{F}_1,\mathcal{F}_2)$
the vertical and horizontal measured foliations on
$(\mathcal{F}_1,\mathcal{F}_2)$
the vertical and horizontal measured foliations on
![]() $\Sigma^{\prime}$
associated with the flat structure
$\Sigma^{\prime}$
associated with the flat structure
![]() $K$
. Let
$K$
. Let
![]() $\lambda _{{K},i}$
be the measured geodesic lamination on
$\lambda _{{K},i}$
be the measured geodesic lamination on
![]() $\Sigma^{\prime}$
corresponding to
$\Sigma^{\prime}$
corresponding to
![]() $\mathcal{F}_i$
, namely, with the same intersection function. It can be seen as a measured geodesic lamination on
$\mathcal{F}_i$
, namely, with the same intersection function. It can be seen as a measured geodesic lamination on
![]() $\Sigma$
. Let
$\Sigma$
. Let
![]() $\lambda _{{M},i}$
be the measured geodesic lamination on
$\lambda _{{M},i}$
be the measured geodesic lamination on
![]() $\Sigma$
obtained by taking the union of
$\Sigma$
obtained by taking the union of
![]() $\lambda _{{K},i}$
and of the measured geodesic lamination
$\lambda _{{K},i}$
and of the measured geodesic lamination
![]() $\lambda _i=(\Lambda _i, \nu _i)$
on
$\lambda _i=(\Lambda _i, \nu _i)$
on
![]() $\Sigma -\Sigma^{\prime}$
, where
$\Sigma -\Sigma^{\prime}$
, where
![]() $\Lambda _i\;:\!=\;\textrm{supp}(\nu _i)$
. Regarding measured geodesic laminations as geodesic currents on
$\Lambda _i\;:\!=\;\textrm{supp}(\nu _i)$
. Regarding measured geodesic laminations as geodesic currents on
![]() $\Sigma$
, we have
$\Sigma$
, we have
The
![]() ${\mathbb{R}}^2$
-length of
${\mathbb{R}}^2$
-length of
![]() $\gamma \in \Gamma$
with respect to the mixed structure
$\gamma \in \Gamma$
with respect to the mixed structure
![]() $M$
is then defined as the pair:
$M$
is then defined as the pair:
We denote
![]() $L_{M,i}(\gamma )\;:\!=\;i(\lambda _{M,i},\gamma )$
the factors. Note that if
$L_{M,i}(\gamma )\;:\!=\;i(\lambda _{M,i},\gamma )$
the factors. Note that if
![]() $\Sigma^{\prime}=\Sigma$
, then the length
$\Sigma^{\prime}=\Sigma$
, then the length
![]() $L_{M,i}$
agrees with
$L_{M,i}$
agrees with
![]() $L_{{K},i}$
.
$L_{{K},i}$
.
This gives a map
We will show in the next subsection that this is indeed a bijection.
5.4. Interpretation of
 ${\mathcal{ML}}\times{\mathcal{ML}}$
as
${\mathcal{ML}}\times{\mathcal{ML}}$
as
 $\overrightarrow {\textrm {Mix}}(\Sigma )$
$\overrightarrow {\textrm {Mix}}(\Sigma )$
The goal of the section is to provide an identification of
![]() ${\mathcal{ML}}\times{\mathcal{ML}}$
with
${\mathcal{ML}}\times{\mathcal{ML}}$
with
![]() $\overrightarrow{\textrm{Mix}}(\Sigma)$
, thus obtaining a geometric interpretation of the boundary
$\overrightarrow{\textrm{Mix}}(\Sigma)$
, thus obtaining a geometric interpretation of the boundary
![]() $\partial ^{\textrm{WL}}\Xi _{\text{Max}}(\Gamma,\textrm{PSL}(2,{\mathbb{R}})^n)$
for the case
$\partial ^{\textrm{WL}}\Xi _{\text{Max}}(\Gamma,\textrm{PSL}(2,{\mathbb{R}})^n)$
for the case
![]() $n=2$
. The main ingredient for this is the following application of the decomposition result of [Reference Burger, Iozzi, Parreau and Pozzetti4] to a sum of measured geodesic laminations (seen as geodesic currents), a result that works for general
$n=2$
. The main ingredient for this is the following application of the decomposition result of [Reference Burger, Iozzi, Parreau and Pozzetti4] to a sum of measured geodesic laminations (seen as geodesic currents), a result that works for general
![]() $n$
:
$n$
:
Proposition 5.7.
Let
![]() $\overrightarrow{L}=(L_i)_{i=1,\ldots,n}\in ({\mathcal{ML}})^n$
, and denote by
$\overrightarrow{L}=(L_i)_{i=1,\ldots,n}\in ({\mathcal{ML}})^n$
, and denote by
![]() $\mu _i$
the measured lamination with intersection function
$\mu _i$
the measured lamination with intersection function
![]() $L_i$
. Then there exists a canonical open geodesic subsurface
$L_i$
. Then there exists a canonical open geodesic subsurface
![]() $\Sigma^{\prime}$
, such that each
$\Sigma^{\prime}$
, such that each
![]() $\mu _i$
decomposes as a disjoint union
$\mu _i$
decomposes as a disjoint union
![]() $\mu _i=\mu ^i_{\Sigma^{\prime}}\cup \mu ^i_\Lambda$
of measured laminations, and
$\mu _i=\mu ^i_{\Sigma^{\prime}}\cup \mu ^i_\Lambda$
of measured laminations, and
-
(1)
 $\mu ^i_{\Sigma^{\prime}}$
is supported in
$\mu ^i_{\Sigma^{\prime}}$
is supported in
 $\Sigma^{\prime}$
,
$\Sigma^{\prime}$
,
 $\mu ^i_\Lambda$
in its complement;
$\mu ^i_\Lambda$
in its complement;
-
(2)
 $(\mu ^i_{\Sigma^{\prime}})_i$
have positive joint systole;
$(\mu ^i_{\Sigma^{\prime}})_i$
have positive joint systole;
-
(3)
 $(\mu ^i_\Lambda )_i$
are parallel, namely the union of their support is a geodesic lamination
$(\mu ^i_\Lambda )_i$
are parallel, namely the union of their support is a geodesic lamination
 $\Lambda$
(contained in
$\Lambda$
(contained in
 $\Sigma \setminus \Sigma^{\prime}$
).
$\Sigma \setminus \Sigma^{\prime}$
).
Proof. Let
![]() $\mu _i=(\Lambda _i,\nu _i)$
be the measured lamination on
$\mu _i=(\Lambda _i,\nu _i)$
be the measured lamination on
![]() $\Sigma$
corresponding to
$\Sigma$
corresponding to
![]() $L_i$
, that is, such that
$L_i$
, that is, such that
![]() $i(\mu _i,\cdot )=L_i$
on
$i(\mu _i,\cdot )=L_i$
on
![]() $\Gamma$
.
$\Gamma$
.
As in [Reference Burger, Iozzi, Parreau and Pozzetti4], we consider the collection
![]() $\mathcal E=\mathcal E_\mu$
of closed
$\mathcal E=\mathcal E_\mu$
of closed
![]() $\mu$
-short solitary geodesics. This is the collection, canonically associated to
$\mu$
-short solitary geodesics. This is the collection, canonically associated to
![]() $\mu$
, of simple closed geodesics in
$\mu$
, of simple closed geodesics in
![]() $\Sigma$
that have
$\Sigma$
that have
![]() $0$
-intersection with
$0$
-intersection with
![]() $\mu$
, and that do not intersect any geodesic that does not intersect the support of
$\mu$
, and that do not intersect any geodesic that does not intersect the support of
![]() $\mu$
. Applying the decomposition theorem [Reference Burger, Iozzi, Parreau and Pozzetti4, Corollary 1.9] to the geodesic current
$\mu$
. Applying the decomposition theorem [Reference Burger, Iozzi, Parreau and Pozzetti4, Corollary 1.9] to the geodesic current
![]() $\mu =\sum _{i=1}^n\mu _i$
, we get that the surface decomposes along the collection
$\mu =\sum _{i=1}^n\mu _i$
, we get that the surface decomposes along the collection
![]() $\mathcal E=\mathcal E_\mu$
in a finite number of open connected subsurfaces with geodesic boundary
$\mathcal E=\mathcal E_\mu$
in a finite number of open connected subsurfaces with geodesic boundary
![]() $\Sigma -\mathcal E=\bigcup _{v\in{\mathcal{V}}} \Sigma _v$
, and the current
$\Sigma -\mathcal E=\bigcup _{v\in{\mathcal{V}}} \Sigma _v$
, and the current
![]() $\mu$
decomposes as a sum
$\mu$
decomposes as a sum
where
![]() $\mu _v=\mu |_{\Sigma _v}$
is the restriction of
$\mu _v=\mu |_{\Sigma _v}$
is the restriction of
![]() $\mu$
to
$\mu$
to
![]() $\Sigma _v$
(recall Section 3.3).
$\Sigma _v$
(recall Section 3.3).
Furthermore, for every
![]() $v\in \mathcal E$
for which
$v\in \mathcal E$
for which
![]() $\mu _v\neq 0$
precisely one of the following holds:
$\mu _v\neq 0$
precisely one of the following holds:
-
(1) either
 $\textrm{Syst}_{\Sigma _v}(\mu _v)\gt 0$
,
$\textrm{Syst}_{\Sigma _v}(\mu _v)\gt 0$
, -
(2) or
 $\mu _v$
is a measured lamination.
$\mu _v$
is a measured lamination.
where
Let
![]() $i\in \{1,\ldots,n\}$
. We first see that no closed geodesic
$i\in \{1,\ldots,n\}$
. We first see that no closed geodesic
![]() $c\in \mathcal E$
intersects transversally the support of
$c\in \mathcal E$
intersects transversally the support of
![]() $\mu _i$
: indeed, since
$\mu _i$
: indeed, since
![]() $i(\mu,c)=i(\mu _1,c)+i(\mu _2,c)=0$
, we have
$i(\mu,c)=i(\mu _1,c)+i(\mu _2,c)=0$
, we have
![]() $i(\mu _i,c)=0$
. So the measured geodesic lamination
$i(\mu _i,c)=0$
. So the measured geodesic lamination
![]() $\mu _i$
decomposes as the union of measured geodesic laminations
$\mu _i$
decomposes as the union of measured geodesic laminations
![]() $\mu _{v,i}$
included in the open subsurface
$\mu _{v,i}$
included in the open subsurface
![]() $\Sigma _v$
, and possibly closed leafs
$\Sigma _v$
, and possibly closed leafs
![]() $c\in \mathcal E$
with transverse measure
$c\in \mathcal E$
with transverse measure
![]() $t_{c,i} \in{\mathbb{R}}_+$
. That is, seeing all those measured geodesic laminations as geodesic currents on
$t_{c,i} \in{\mathbb{R}}_+$
. That is, seeing all those measured geodesic laminations as geodesic currents on
![]() $\Sigma$
:
$\Sigma$
:
By uniqueness of the decomposition of
![]() $\mu$
along
$\mu$
along
![]() $\mathcal E$
, for each
$\mathcal E$
, for each
![]() $v\in{\mathcal{V}}$
we have
$v\in{\mathcal{V}}$
we have
and for each
![]() $c\in \mathcal E$
$c\in \mathcal E$
Let
![]() $v\in{\mathcal{V}}$
. If
$v\in{\mathcal{V}}$
. If
![]() $\mu _v$
is a measured lamination, then the measured laminations
$\mu _v$
is a measured lamination, then the measured laminations
![]() $\mu _{v,i}$
,
$\mu _{v,i}$
,
![]() $i=1,\ldots,n$
are parallel: indeed, as
$i=1,\ldots,n$
are parallel: indeed, as
![]() $i(\mu _v,\mu _v)=\sum _{1\leq i,j\leq n}i(\mu _{v,i},\mu _{v,j})=0$
, and
$i(\mu _v,\mu _v)=\sum _{1\leq i,j\leq n}i(\mu _{v,i},\mu _{v,j})=0$
, and
![]() $i(\mu _{v,i},\mu _{v,j})\geq 0$
, we get that
$i(\mu _{v,i},\mu _{v,j})\geq 0$
, we get that
![]() $i(\mu _{v,i},\mu _{v,j})=0$
for all
$i(\mu _{v,i},\mu _{v,j})=0$
for all
![]() $i,j\in \{1,\ldots,n\}$
.
$i,j\in \{1,\ldots,n\}$
.
We can now prove the main result of the section.
Proposition 5.8.
Any
![]() $\overrightarrow{L}=(L_1,L_2)$
in
$\overrightarrow{L}=(L_1,L_2)$
in
![]() ${\mathcal{ML}}\times{\mathcal{ML}}$
is the
${\mathcal{ML}}\times{\mathcal{ML}}$
is the
![]() ${\mathbb{R}}^2$
-length function of a unique
${\mathbb{R}}^2$
-length function of a unique
![]() ${\mathbb{R}}^2$
-mixed structure
${\mathbb{R}}^2$
-mixed structure
![]() $(\Sigma^{\prime},{K},\overrightarrow{\lambda })$
on
$(\Sigma^{\prime},{K},\overrightarrow{\lambda })$
on
![]() $\Sigma$
.
$\Sigma$
.
Note that a similar identification has been independently established in [Reference Martone, Ouyang and Tamburelli16], see for instance Theorem 6.8 therein.
Proof. As above we denote by
![]() $\mu _i$
the geodesic current corresponding to the lamination
$\mu _i$
the geodesic current corresponding to the lamination
![]() $(\Lambda _i,\nu _i)$
with length function
$(\Lambda _i,\nu _i)$
with length function
![]() $L_i$
. We use Proposition 5.7 to decompose
$L_i$
. We use Proposition 5.7 to decompose
![]() $\mu _i\;:\!=\;\mu ^i_{\Sigma^{\prime}}+\mu ^i_\Lambda$
.
$\mu _i\;:\!=\;\mu ^i_{\Sigma^{\prime}}+\mu ^i_\Lambda$
.
For any connected component
![]() $\Sigma _v$
of the positive systole subsurface
$\Sigma _v$
of the positive systole subsurface
![]() $\Sigma^{\prime}$
, we denote by
$\Sigma^{\prime}$
, we denote by
![]() $\Gamma _v=\pi _1(\Sigma _v)$
and
$\Gamma _v=\pi _1(\Sigma _v)$
and
![]() $L_{v,i}\colon \Gamma _v\to{\mathbb{R}}_+$
the intersection function of
$L_{v,i}\colon \Gamma _v\to{\mathbb{R}}_+$
the intersection function of
![]() $\mu _{v,i}$
on
$\mu _{v,i}$
on
![]() $\Sigma _v$
. Then
$\Sigma _v$
. Then
![]() $L_{v,i}$
is the intersection function
$L_{v,i}$
is the intersection function
![]() $I_{\mathcal{F}_i}$
of a measured foliation
$I_{\mathcal{F}_i}$
of a measured foliation
![]() $\mathcal{F}_i$
on the surface
$\mathcal{F}_i$
on the surface
![]() $\Sigma _v$
. Denote
$\Sigma _v$
. Denote
![]() $C=\textrm{Syst}_{\Sigma _v}(\mu _v)$
. We have that, for all non parabolic
$C=\textrm{Syst}_{\Sigma _v}(\mu _v)$
. We have that, for all non parabolic
![]() $\gamma$
in
$\gamma$
in
![]() $\Gamma _v$
,
$\Gamma _v$
,
It is known (see for example [Reference Gardiner and Wang12, Theorem 7]) that the two measured foliations
![]() $\mathcal{F}_1, \mathcal{F}_2$
are then transversely realisable, that is, up to replacing
$\mathcal{F}_1, \mathcal{F}_2$
are then transversely realisable, that is, up to replacing
![]() $\mathcal{F}_i$
by an equivalent measured foliation (an operation that does not change the length function), they arise as the vertical and horizontal measured foliation of a flat structure
$\mathcal{F}_i$
by an equivalent measured foliation (an operation that does not change the length function), they arise as the vertical and horizontal measured foliation of a flat structure
![]() ${K}_v$
on the surface
${K}_v$
on the surface
![]() $\Sigma _v$
. In particular, the measured geodesic laminations on
$\Sigma _v$
. In particular, the measured geodesic laminations on
![]() $\Sigma _v$
associated with
$\Sigma _v$
associated with
![]() ${K}_v$
are
${K}_v$
are
for
![]() $i=1,2$
. We denote by
$i=1,2$
. We denote by
![]() $K$
the flat structure on
$K$
the flat structure on
![]() $\Sigma^{\prime}$
equal to
$\Sigma^{\prime}$
equal to
![]() ${K}_v$
on each
${K}_v$
on each
![]() $\Sigma _v$
.
$\Sigma _v$
.
Let
![]() $\lambda _i$
be the measured geodesic lamination obtained by taking the union of
$\lambda _i$
be the measured geodesic lamination obtained by taking the union of
![]() $\mu _{v,i}$
, for the
$\mu _{v,i}$
, for the
![]() $v$
such that
$v$
such that
![]() $\mu _v$
is a lamination, and of the closed geodesics
$\mu _v$
is a lamination, and of the closed geodesics
![]() $c\in \mathcal E$
with weight
$c\in \mathcal E$
with weight
![]() $t_{c,i}$
. Then
$t_{c,i}$
. Then
![]() $\overrightarrow{\lambda }=(\lambda _1,\lambda _2)$
is a pair of parallel measured geodesic laminations on
$\overrightarrow{\lambda }=(\lambda _1,\lambda _2)$
is a pair of parallel measured geodesic laminations on
![]() $\Sigma$
, and
$\Sigma$
, and
![]() $M=(\Sigma^{\prime},{K},\overrightarrow{\lambda })$
is a mixed structure on
$M=(\Sigma^{\prime},{K},\overrightarrow{\lambda })$
is a mixed structure on
![]() $\Sigma$
, with associated pair of laminations
$\Sigma$
, with associated pair of laminations
In particular, taking intersection functions on
![]() $\Gamma$
we have
$\Gamma$
we have
![]() $L_i=L_{M,i}$
for each
$L_i=L_{M,i}$
for each
![]() $i$
.
$i$
.
The uniqueness of
![]() $M$
(up to isotopy of the flat part) is given by the uniqueness of the decomposition in Corollary 1.9 of [Reference Burger, Iozzi, Parreau and Pozzetti4] and by the injectivity of the natural map from quadratic differentials to pairs of equivalence classes of measured foliations [Reference Gardiner and Masur11, Theorem 3.1].
$M$
(up to isotopy of the flat part) is given by the uniqueness of the decomposition in Corollary 1.9 of [Reference Burger, Iozzi, Parreau and Pozzetti4] and by the injectivity of the natural map from quadratic differentials to pairs of equivalence classes of measured foliations [Reference Gardiner and Masur11, Theorem 3.1].
6. The
 ${\mathbb{R}}^2$
-tree-graded space dual to a mixed structure
${\mathbb{R}}^2$
-tree-graded space dual to a mixed structure
In this section, we construct the
![]() ${\mathbb{R}}^2$
-tree-graded space
${\mathbb{R}}^2$
-tree-graded space
![]() $X_M$
dual to a
$X_M$
dual to a
![]() ${\mathbb{R}}^2$
-mixed structure
${\mathbb{R}}^2$
-mixed structure
![]() $M=(\Sigma^{\prime},{K},\overrightarrow{\lambda })$
on a closed hyperbolic surface
$M=(\Sigma^{\prime},{K},\overrightarrow{\lambda })$
on a closed hyperbolic surface
![]() $\Sigma$
. In Section 6.1, we recall the definition of tree-graded space and discuss a general construction to glue pseudometrics which we use in Section 6.2 to construct the tree-graded space
$\Sigma$
. In Section 6.1, we recall the definition of tree-graded space and discuss a general construction to glue pseudometrics which we use in Section 6.2 to construct the tree-graded space
![]() $X_M$
dual to a mixed structure
$X_M$
dual to a mixed structure
![]() $M$
. In Section 6.3, we prove that space is indeed tree-graded and discuss its relevant geometric properties.
$M$
. In Section 6.3, we prove that space is indeed tree-graded and discuss its relevant geometric properties.
6.1. Generalities on
 ${\mathbb{R}}^n$
-tree-graded spaces
${\mathbb{R}}^n$
-tree-graded spaces
Recall from [Reference Druţu and Sapir8] the notion of tree-graded metric space:Footnote 6
Definition 6.1.
A geodesic metric space
![]() $(X,d)$
is tree-graded with respect to a collection
$(X,d)$
is tree-graded with respect to a collection
![]() $\mathcal{P}$
of geodesic subsets called pieces if
$\mathcal{P}$
of geodesic subsets called pieces if
-
(TG1) Any two different pieces have at most one common point.
-
(TG2) Any simple geodesic triangle in
 $X$
is contained in one piece.
$X$
is contained in one piece.
Here a geodesic triangle is simple if its sides meet only in the respective endpoints.
We now adapt this to define an tree-graded
![]() ${\mathbb{R}}^n$
-space, recall from Definition 2.1 the notion of an
${\mathbb{R}}^n$
-space, recall from Definition 2.1 the notion of an
![]() ${\mathbb{R}}^n$
-metric space:
${\mathbb{R}}^n$
-metric space:
Definition 6.2.
A
![]() ${\mathbb{R}}^n$
-metric space
${\mathbb{R}}^n$
-metric space
![]() $(X, \overrightarrow{d}=(d_i)_{i=1,\ldots,n})$
is tree-graded with respect to a collection
$(X, \overrightarrow{d}=(d_i)_{i=1,\ldots,n})$
is tree-graded with respect to a collection
![]() $\mathcal{P}$
of subsets if
$\mathcal{P}$
of subsets if
![]() $X$
is tree-graded (with respect to
$X$
is tree-graded (with respect to
![]() $\mathcal{P}$
) for the associated
$\mathcal{P}$
) for the associated
![]() $\ell ^1$
-metric
$\ell ^1$
-metric
![]() $d\;:\!=\;\sum _{i=1}^n d_i$
.
$d\;:\!=\;\sum _{i=1}^n d_i$
.
In the next subsection, we will construct the tree-graded space associated with a mixed structure on a surface
![]() $\Sigma$
as a quotient of a blowup
$\Sigma$
as a quotient of a blowup
![]() $\widetilde{\Sigma ^b}$
of
$\widetilde{\Sigma ^b}$
of
![]() $\Sigma$
by pseudometrics defined by gluing. We now recall the general construction of a global pseudometric on a CAT(0) surface
$\Sigma$
by pseudometrics defined by gluing. We now recall the general construction of a global pseudometric on a CAT(0) surface
![]() $\widetilde{\Sigma }$
obtained by gluing pseudometrics defined on geodesic pieces, the initial ingredient for the construction in the next section.
$\widetilde{\Sigma }$
obtained by gluing pseudometrics defined on geodesic pieces, the initial ingredient for the construction in the next section.
Let
![]() $\Sigma$
be a locally CAT(0) surface, and
$\Sigma$
be a locally CAT(0) surface, and
![]() $\mathcal E$
be a set of disjoint simple closed geodesics on
$\mathcal E$
be a set of disjoint simple closed geodesics on
![]() $\Sigma$
. We denote by
$\Sigma$
. We denote by
![]() $\widetilde{\mathcal E}$
the set of their lifts to the universal cover
$\widetilde{\mathcal E}$
the set of their lifts to the universal cover
![]() $\widetilde{\Sigma }$
. A piece of
$\widetilde{\Sigma }$
. A piece of
![]() $\widetilde{\Sigma }$
is defined as the closure
$\widetilde{\Sigma }$
is defined as the closure
![]() $\widetilde{P}$
of a complementary component
$\widetilde{P}$
of a complementary component
![]() $\widetilde{W}$
of
$\widetilde{W}$
of
![]() $\widetilde{\mathcal E}$
in
$\widetilde{\mathcal E}$
in
![]() $\widetilde{\Sigma }$
. Two different pieces are adjacent if they have non-empty intersection (which is then a geodesic in
$\widetilde{\Sigma }$
. Two different pieces are adjacent if they have non-empty intersection (which is then a geodesic in
![]() $\widetilde{\mathcal E}$
bounding each of the pieces). We denote by
$\widetilde{\mathcal E}$
bounding each of the pieces). We denote by
![]() $\mathcal P(\widetilde{\Sigma })$
the set of pieces of
$\mathcal P(\widetilde{\Sigma })$
the set of pieces of
![]() $\widetilde{\Sigma }$
.
$\widetilde{\Sigma }$
.
Definition 6.3.
A chain between two points
![]() $x,y$
in
$x,y$
in
![]() $\widetilde{\Sigma }$
is a sequence
$\widetilde{\Sigma }$
is a sequence
![]() $C=(x_0=x,x_1,\ldots,x_{k+1}=y)$
in
$C=(x_0=x,x_1,\ldots,x_{k+1}=y)$
in
![]() $\widetilde{\Sigma }$
such that any two consecutive points
$\widetilde{\Sigma }$
such that any two consecutive points
![]() $x_j$
and
$x_j$
and
![]() $x_{j+1}$
are in a same piece
$x_{j+1}$
are in a same piece
![]() ${\widetilde{P}}_j$
, with
${\widetilde{P}}_j$
, with
![]() ${\widetilde{P}}_j\neq{\widetilde{P}}_{j+1}$
.
${\widetilde{P}}_j\neq{\widetilde{P}}_{j+1}$
.
For
![]() $j=1,\ldots,k$
the pieces
$j=1,\ldots,k$
the pieces
![]() ${\widetilde{P}}_{j-1}$
and
${\widetilde{P}}_{j-1}$
and
![]() ${\widetilde{P}}_j$
are then adjacent and
${\widetilde{P}}_j$
are then adjacent and
![]() $x_j$
is on their common boundary geodesic
$x_j$
is on their common boundary geodesic
![]() ${\widetilde{c}}_j$
. Such a chain defines a path in the simplicial tree dual to
${\widetilde{c}}_j$
. Such a chain defines a path in the simplicial tree dual to
![]() $\widetilde{\mathcal E}$
. We call the chain straight if this path is geodesic, that is, if and only if
$\widetilde{\mathcal E}$
. We call the chain straight if this path is geodesic, that is, if and only if
![]() ${\widetilde{c}}_{j-1}\neq{\widetilde{c}}_{j}$
for
${\widetilde{c}}_{j-1}\neq{\widetilde{c}}_{j}$
for
![]() $j=1,\ldots,k$
. Then
$j=1,\ldots,k$
. Then
![]() ${\widetilde{c}}_1,\ldots{\widetilde{c}}_k$
is the ordered sequence of geodesics in
${\widetilde{c}}_1,\ldots{\widetilde{c}}_k$
is the ordered sequence of geodesics in
![]() $\widetilde{\mathcal E}$
separating
$\widetilde{\mathcal E}$
separating
![]() $x$
and
$x$
and
![]() $y$
(going from
$y$
(going from
![]() $x$
to
$x$
to
![]() $y$
).
$y$
).
Given a pseudometric
![]() $d^{\widetilde{P}}$
on each piece
$d^{\widetilde{P}}$
on each piece
![]() $\widetilde{P}$
of
$\widetilde{P}$
of
![]() $\widetilde{\Sigma }$
, we define the
$\widetilde{\Sigma }$
, we define the
![]() $d$
-length of a chain
$d$
-length of a chain
![]() $C$
as
$C$
as
 \begin{align*}\ell _d(C)=\sum _{j=0}^{k+1} d^{{\widetilde {P}}_j}(x_j,x_{j+1})\end{align*}
\begin{align*}\ell _d(C)=\sum _{j=0}^{k+1} d^{{\widetilde {P}}_j}(x_j,x_{j+1})\end{align*}
The induced pseudometric on
![]() $\widetilde{\Sigma }$
is then defined by
$\widetilde{\Sigma }$
is then defined by
where the infimum is taken over all chains
![]() $C$
joining
$C$
joining
![]() $x$
to
$x$
to
![]() $y$
. It is easy to see that we may restrict to straight chains
$y$
. It is easy to see that we may restrict to straight chains
![]() $C$
. If the restriction of
$C$
. If the restriction of
![]() $d^{{\widetilde{P}}}$
to the geodesics
$d^{{\widetilde{P}}}$
to the geodesics
![]() $\widetilde{c}$
of
$\widetilde{c}$
of
![]() $\widetilde{\mathcal E}$
is
$\widetilde{\mathcal E}$
is
![]() $0$
for each piece
$0$
for each piece
![]() $\widetilde{P}$
, then the pseudo-distance
$\widetilde{P}$
, then the pseudo-distance
![]() $d(x_j,x_{j+1})$
does not depend on the choice of
$d(x_j,x_{j+1})$
does not depend on the choice of
![]() $x_j$
on
$x_j$
on
![]() ${\widetilde{c}}_j$
, and thus all straight chains have the same length. In this case, we may alternatively define
${\widetilde{c}}_j$
, and thus all straight chains have the same length. In this case, we may alternatively define
![]() $d(x,y)$
as the
$d(x,y)$
as the
![]() $d$
-length of any straight chain, thus in particular
$d$
-length of any straight chain, thus in particular
![]() $d$
restricts to the original pseudometric
$d$
restricts to the original pseudometric
![]() $d^{\widetilde{P}}$
on each piece
$d^{\widetilde{P}}$
on each piece
![]() $\widetilde{P}$
.
$\widetilde{P}$
.
6.2. Construction of the
 ${\mathbb{R}}^2$
-space
${\mathbb{R}}^2$
-space
 $X_M$
$X_M$
Let
![]() $M=(\Sigma^{\prime},{K},\overrightarrow{\lambda })$
be a
$M=(\Sigma^{\prime},{K},\overrightarrow{\lambda })$
be a
![]() ${\mathbb{R}}^2$
-mixed structure on a closed hyperbolic surface
${\mathbb{R}}^2$
-mixed structure on a closed hyperbolic surface
![]() $\Sigma$
. Here, as always,
$\Sigma$
. Here, as always,
![]() $\overrightarrow{\lambda }=(\Lambda,\nu _1,\nu _2)$
.
$\overrightarrow{\lambda }=(\Lambda,\nu _1,\nu _2)$
.
We first resolve the atoms in the lamination part, by taking the blowup
![]() $(\Sigma ^b,\overrightarrow{\lambda }^b)$
of
$(\Sigma ^b,\overrightarrow{\lambda }^b)$
of
![]() $(\Sigma,\overrightarrow{\lambda })$
as in Section 3.5. Recall from Sections 3.4 and 3.5 that
$(\Sigma,\overrightarrow{\lambda })$
as in Section 3.5. Recall from Sections 3.4 and 3.5 that
![]() $\Sigma ^b$
denotes the CAT(0) surface obtained inserting in
$\Sigma ^b$
denotes the CAT(0) surface obtained inserting in
![]() $\Sigma$
a flat foliated annulus
$\Sigma$
a flat foliated annulus
![]() $B(c)=c\times [0,1]$
at each isolated leaf
$B(c)=c\times [0,1]$
at each isolated leaf
![]() $c$
of
$c$
of
![]() $\Lambda$
, and
$\Lambda$
, and
![]() $\Lambda ^b$
is the associated lamination whose non-atomic transverse measure
$\Lambda ^b$
is the associated lamination whose non-atomic transverse measure
![]() $\nu ^b_i$
is obtained by extending
$\nu ^b_i$
is obtained by extending
![]() $\nu _i$
with the transverse measure
$\nu _i$
with the transverse measure
![]() $\nu _i(c)dt$
on
$\nu _i(c)dt$
on
![]() $[0,1]$
for each foliated annulus
$[0,1]$
for each foliated annulus
![]() $B(c)$
.
$B(c)$
.
Our next goal is to define a
![]() ${\mathbb{R}}^2$
-pseudometric
${\mathbb{R}}^2$
-pseudometric
![]() $\overrightarrow{d}_M$
on
$\overrightarrow{d}_M$
on
![]() $\widetilde{\Sigma ^b}$
associated with
$\widetilde{\Sigma ^b}$
associated with
![]() $M$
, that is, a pair of pseudometrics
$M$
, that is, a pair of pseudometrics
![]() $(d_{M,i})_i$
on
$(d_{M,i})_i$
on
![]() $\widetilde{\Sigma ^b}$
. We first define the pieces which we will glue as outlined in Section 6.1. We denote by
$\widetilde{\Sigma ^b}$
. We first define the pieces which we will glue as outlined in Section 6.1. We denote by
![]() $\Sigma ^{'b}$
the open subsurface of
$\Sigma ^{'b}$
the open subsurface of
![]() $\Sigma ^b$
corresponding to
$\Sigma ^b$
corresponding to
![]() $\Sigma^{\prime}$
, and denote by
$\Sigma^{\prime}$
, and denote by
![]() $\mathcal E^b$
its set of boundary geodesics in
$\mathcal E^b$
its set of boundary geodesics in
![]() $\Sigma ^b$
. We denote by
$\Sigma ^b$
. We denote by
![]() $\widetilde{\mathcal E}^b$
the set of their lifts to
$\widetilde{\mathcal E}^b$
the set of their lifts to
![]() $\widetilde{\Sigma ^b}$
.
$\widetilde{\Sigma ^b}$
.
Definition 6.4.
A piece of
![]() $\widetilde{\Sigma ^b}$
is the closure
$\widetilde{\Sigma ^b}$
is the closure
![]() $\widetilde{P}$
of a complementary component
$\widetilde{P}$
of a complementary component
![]() $\widetilde{W}$
of
$\widetilde{W}$
of
![]() $\widetilde{\mathcal E}^b$
in
$\widetilde{\mathcal E}^b$
in
![]() $\widetilde{\Sigma ^b}$
. We will call such a piece
$\widetilde{\Sigma ^b}$
. We will call such a piece
-
• a flat piece if
 $\widetilde{W}$
projects in
$\widetilde{W}$
projects in
 $\Sigma ^{'b}$
, and
$\Sigma ^{'b}$
, and
-
• a lamination piece otherwise. Footnote 7
Example 6.5.
If
![]() $M$
is the mixed structure described in Example 5.5, the locally CAT(0) surface
$M$
is the mixed structure described in Example 5.5, the locally CAT(0) surface
![]() $(\Sigma ^b,m^b)$
is obtained by endowing
$(\Sigma ^b,m^b)$
is obtained by endowing
![]() $\Sigma$
with an hyperbolic metric and then gluing three flat cylinders
$\Sigma$
with an hyperbolic metric and then gluing three flat cylinders
![]() $C_i=[0,1]\times c_i$
to the hyperbolic surface
$C_i=[0,1]\times c_i$
to the hyperbolic surface
![]() $\Sigma \setminus \{c_1,c_2,c_3\}$
. The pieces in its universal cover
$\Sigma \setminus \{c_1,c_2,c_3\}$
. The pieces in its universal cover
![]() $\widetilde{\Sigma ^b}$
have four types: flat pieces isometric to the universal covers of the completion of
$\widetilde{\Sigma ^b}$
have four types: flat pieces isometric to the universal covers of the completion of
![]() $\Sigma^{\prime}_1$
and
$\Sigma^{\prime}_1$
and
![]() $\Sigma^{\prime}_2$
(up to now these pieces are endowed with a complete hyperbolic metric with geodesic boundary), lamination pieces of annular type, isometric to the universal cover of
$\Sigma^{\prime}_2$
(up to now these pieces are endowed with a complete hyperbolic metric with geodesic boundary), lamination pieces of annular type, isometric to the universal cover of
![]() $C_1$
, namely to the Euclidean strip
$C_1$
, namely to the Euclidean strip
![]() $[0,1]\times{\mathbb{R}}\subset{\mathbb{R}}^2$
, with measured geodesic lamination equal to the vertical foliation with transverse measures
$[0,1]\times{\mathbb{R}}\subset{\mathbb{R}}^2$
, with measured geodesic lamination equal to the vertical foliation with transverse measures
![]() $\nu _1=x_1dx$
,
$\nu _1=x_1dx$
,
![]() $\nu _2=y_1dx$
, and lamination pieces isometric the universal cover of
$\nu _2=y_1dx$
, and lamination pieces isometric the universal cover of
![]() $(\Sigma \setminus (\overline{\Sigma^{\prime}} \cup c_3))\cup C_2\cup C_3$
.
$(\Sigma \setminus (\overline{\Sigma^{\prime}} \cup c_3))\cup C_2\cup C_3$
.
We now define a new pseudometric on each piece. Let
![]() $i\in \{1,2\}$
. On each lamination piece
$i\in \{1,2\}$
. On each lamination piece
![]() $\widetilde{P}$
of
$\widetilde{P}$
of
![]() $\widetilde{\Sigma ^b}$
, we define
$\widetilde{\Sigma ^b}$
, we define
![]() $d^{\widetilde{P}}_{M,i}$
as the restriction to
$d^{\widetilde{P}}_{M,i}$
as the restriction to
![]() $\widetilde{P}$
of the pseudometric
$\widetilde{P}$
of the pseudometric
![]() $d_{\lambda ^b_i}$
associated to the non-atomic measured lamination
$d_{\lambda ^b_i}$
associated to the non-atomic measured lamination
![]() $\lambda ^b_i\;:\!=\;(\Lambda ^b,\nu ^b_i)$
. On each flat piece
$\lambda ^b_i\;:\!=\;(\Lambda ^b,\nu ^b_i)$
. On each flat piece
![]() $\widetilde{P}$
of
$\widetilde{P}$
of
![]() $\widetilde{\Sigma ^b}$
we, instead, define the pseudometric
$\widetilde{\Sigma ^b}$
we, instead, define the pseudometric
![]() $d^{\widetilde{P}}_{M,i}$
as intersection with the horizontal (resp. vertical) measured foliation of
$d^{\widetilde{P}}_{M,i}$
as intersection with the horizontal (resp. vertical) measured foliation of
![]() $K$
. More precisely we consider the canonical projection
$K$
. More precisely we consider the canonical projection
![]() ${\widetilde{P}}=\overline{{\widetilde{W}}}\to{\widetilde{W}^c}$
to the completion
${\widetilde{P}}=\overline{{\widetilde{W}}}\to{\widetilde{W}^c}$
to the completion
![]() $\widetilde{W}^c$
of
$\widetilde{W}^c$
of
![]() $\widetilde{W}$
with respect to the CAT(0) metric given by the flat structure
$\widetilde{W}$
with respect to the CAT(0) metric given by the flat structure
![]() $K$
, and we define the pseudometric
$K$
, and we define the pseudometric
![]() $d^{\widetilde{P}}_{M,i}$
as the pullback of the pseudo-distance
$d^{\widetilde{P}}_{M,i}$
as the pullback of the pseudo-distance
![]() $d_{{K},i}$
introduced in Section 5.1 through this projection. Note that the restriction of
$d_{{K},i}$
introduced in Section 5.1 through this projection. Note that the restriction of
![]() $d^{\widetilde{P}}_{M,i}$
to any boundary geodesic of a piece
$d^{\widetilde{P}}_{M,i}$
to any boundary geodesic of a piece
![]() $\widetilde{P}$
is always
$\widetilde{P}$
is always
![]() $0$
.
$0$
.
We define the pseudometric
![]() $d_{M,i}$
on
$d_{M,i}$
on
![]() $\widetilde{\Sigma ^b}$
as the gluing of the pseudometrics
$\widetilde{\Sigma ^b}$
as the gluing of the pseudometrics
![]() $d^{\widetilde{P}}_{M,i}$
on the pieces
$d^{\widetilde{P}}_{M,i}$
on the pieces
![]() ${\widetilde{P}}\in \mathcal P(\widetilde{\Sigma ^b})$
as in Section 6.1. We denote by
${\widetilde{P}}\in \mathcal P(\widetilde{\Sigma ^b})$
as in Section 6.1. We denote by
the corresponding
![]() ${\mathbb{R}}^2$
-pseudometric on
${\mathbb{R}}^2$
-pseudometric on
![]() $\widetilde{\Sigma ^b}$
, and by
$\widetilde{\Sigma ^b}$
, and by
the associated
![]() $\ell ^1$
-pseudometric on
$\ell ^1$
-pseudometric on
![]() $\widetilde{\Sigma ^b}$
. It follows from the construction that
$\widetilde{\Sigma ^b}$
. It follows from the construction that
![]() $d_M$
is the gluing of the
$d_M$
is the gluing of the
![]() $\ell ^1$
-pseudometrics
$\ell ^1$
-pseudometrics
![]() $d^{\widetilde{P}}_{M}=\sum _i d^{\widetilde{P}}_{M,i}$
on the pieces
$d^{\widetilde{P}}_{M}=\sum _i d^{\widetilde{P}}_{M,i}$
on the pieces
![]() ${\widetilde{P}}\in \mathcal P(\widetilde{\Sigma ^b})$
.
${\widetilde{P}}\in \mathcal P(\widetilde{\Sigma ^b})$
.
Definition 6.6.
The
![]() ${\mathbb{R}}^2$
-metric space
${\mathbb{R}}^2$
-metric space
![]() $X_M$
associated with
$X_M$
associated with
![]() $M$
is the quotient
$M$
is the quotient
of
![]() $\widetilde{\Sigma ^b}$
by the
$\widetilde{\Sigma ^b}$
by the
![]() $\ell ^1$
-pseudometric
$\ell ^1$
-pseudometric
![]() $d_M$
, endowed with the
$d_M$
, endowed with the
![]() ${\mathbb{R}}^2$
-metric induced by
${\mathbb{R}}^2$
-metric induced by
![]() $\overrightarrow{d}_M$
, that is, the pair of pseudometrics induced by
$\overrightarrow{d}_M$
, that is, the pair of pseudometrics induced by
![]() $d_{M,i}$
,
$d_{M,i}$
,
![]() $i=1,2$
.
$i=1,2$
.
The action of
![]() $\Gamma$
on
$\Gamma$
on
![]() $\widetilde{\Sigma ^b}$
induces an action of
$\widetilde{\Sigma ^b}$
induces an action of
![]() $\Gamma$
on
$\Gamma$
on
![]() $X_M$
preserving the
$X_M$
preserving the
![]() ${\mathbb{R}}^2$
-metric
${\mathbb{R}}^2$
-metric
![]() $\overrightarrow{d}_M$
.
$\overrightarrow{d}_M$
.
Example 6.7.
The pieces in the tree-graded
![]() ${\mathbb{R}}^2$
-space
${\mathbb{R}}^2$
-space
![]() $X_M$
associated to the mixed structure
$X_M$
associated to the mixed structure
![]() $M$
described in Example 5.5
have 4 isometry types:
$M$
described in Example 5.5
have 4 isometry types:
-
• flat pieces isometric to the completion of the universal cover of
 ${K}_1\setminus \{p_1, p_0,p_0'\}$
.
${K}_1\setminus \{p_1, p_0,p_0'\}$
. -
• flat pieces isometric to the completion of the universal cover of
 ${K}_2\setminus \{p_1,p_2\}$
,
${K}_2\setminus \{p_1,p_2\}$
, -
• closed segments of
 ${\mathbb{R}}^2$
-length
${\mathbb{R}}^2$
-length
 $(x_1,0)$
,
$(x_1,0)$
, -
•
 ${\mathbb{R}}^2$
-simplicial trees of infinite valence, obtain by attaching, to the dual tree to the curve
${\mathbb{R}}^2$
-simplicial trees of infinite valence, obtain by attaching, to the dual tree to the curve
 $c_3$
in the subsurface
$c_3$
in the subsurface
 $\Sigma \setminus \Sigma^{\prime}$
, a segment of
$\Sigma \setminus \Sigma^{\prime}$
, a segment of
 ${\mathbb{R}}^2$
-length
${\mathbb{R}}^2$
-length
 $(x_2,y_2)$
to the fixed points of the elements of
$(x_2,y_2)$
to the fixed points of the elements of
 $\Gamma$
corresponding to the curve
$\Gamma$
corresponding to the curve
 $c_2$
.
$c_2$
.
Observe that, in particular, the tree associated to the lamination pieces are, in this example, not minimal.
6.3. Basic properties of
 $X_M$
$X_M$
In this section, we prove that
![]() $X_M$
is indeed tree-graded, that its induced
$X_M$
is indeed tree-graded, that its induced
![]() ${\mathbb{R}}^2$
-length function corresponds to the pair
${\mathbb{R}}^2$
-length function corresponds to the pair
![]() $(\lambda _{M,1},\lambda _{M,2})$
of measured geodesic laminations associated with the mixed structure
$(\lambda _{M,1},\lambda _{M,2})$
of measured geodesic laminations associated with the mixed structure
![]() $M$
, and we discuss the isometry types of the pieces of
$M$
, and we discuss the isometry types of the pieces of
![]() $X_M$
.
$X_M$
.
Recall that we defined the laminations
![]() $\lambda _{M,i}$
as the sum of two measured geodesic laminations on
$\lambda _{M,i}$
as the sum of two measured geodesic laminations on
![]() $\Sigma$
$\Sigma$
where
![]() $(\lambda _{{K},i})_{i=1,2}$
are the measured geodesic laminations supported in
$(\lambda _{{K},i})_{i=1,2}$
are the measured geodesic laminations supported in
![]() $\Sigma^{\prime}$
induced by the horizontal (resp. vertical) foliation of the flat structure
$\Sigma^{\prime}$
induced by the horizontal (resp. vertical) foliation of the flat structure
![]() $K$
and
$K$
and
![]() $\lambda _i=(\Lambda,\nu _i)$
.
$\lambda _i=(\Lambda,\nu _i)$
.
We denote by
![]() $L_{X_{M,i}}$
,
$L_{X_{M,i}}$
,
![]() $i=1,2$
the length function of
$i=1,2$
the length function of
![]() $d_{M,i}$
on
$d_{M,i}$
on
![]() $X_M$
, namely
$X_M$
, namely
We denote by
![]() $\pi \colon \widetilde{\Sigma ^b}\to X_M$
the canonical projection. The pieces of
$\pi \colon \widetilde{\Sigma ^b}\to X_M$
the canonical projection. The pieces of
![]() $X_M$
are the images
$X_M$
are the images
![]() $X_{\widetilde{P}}\;:\!=\;\pi ({\widetilde{P}})$
in
$X_{\widetilde{P}}\;:\!=\;\pi ({\widetilde{P}})$
in
![]() $X_M$
of the pieces
$X_M$
of the pieces
![]() $\widetilde{P}$
of
$\widetilde{P}$
of
![]() $\widetilde{\Sigma ^b}$
. We denote by
$\widetilde{\Sigma ^b}$
. We denote by
![]() $\mathcal{P}(X_M)$
the set of pieces of
$\mathcal{P}(X_M)$
the set of pieces of
![]() $X_M$
. When a lamination piece
$X_M$
. When a lamination piece
![]() ${\widetilde{P}}\subset \widetilde{\Sigma ^b}$
does not meet the lamination
${\widetilde{P}}\subset \widetilde{\Sigma ^b}$
does not meet the lamination
![]() $\Lambda ^b$
, then the corresponding piece
$\Lambda ^b$
, then the corresponding piece
![]() $X_{\widetilde{P}}$
is reduced to a point. We will call the space
$X_{\widetilde{P}}$
is reduced to a point. We will call the space
![]() $(X_M,\overrightarrow{d}_M=(d_{M,1},d_{M,2}))$
the tree-graded
$(X_M,\overrightarrow{d}_M=(d_{M,1},d_{M,2}))$
the tree-graded
![]() ${\mathbb{R}}^2$
-space dual to
${\mathbb{R}}^2$
-space dual to
![]() $M$
.
$M$
.
Proposition 6.8.
-
(1) The
 ${\mathbb{R}}^2$
-metric space
${\mathbb{R}}^2$
-metric space
 $(X_M,\overrightarrow{d}_M)$
is tree-graded with respect to
$(X_M,\overrightarrow{d}_M)$
is tree-graded with respect to
 $\mathcal{P}(X_M)$
.
$\mathcal{P}(X_M)$
. -
(2) If
 $\widetilde{P}$
is a lamination piece,
$\widetilde{P}$
is a lamination piece,
 $(X_{\widetilde{P}}, \overrightarrow{d}_M)$
is isometric to the image of
$(X_{\widetilde{P}}, \overrightarrow{d}_M)$
is isometric to the image of
 $\widetilde{P}$
in the
$\widetilde{P}$
in the
 ${\mathbb{R}}^2$
-tree
${\mathbb{R}}^2$
-tree
 $T(\overrightarrow{\lambda })\;:\!=\;\Sigma ^b/d_\lambda ^b$
dual to the
$T(\overrightarrow{\lambda })\;:\!=\;\Sigma ^b/d_\lambda ^b$
dual to the
 $2$
-measured geodesic lamination
$2$
-measured geodesic lamination
 $\overrightarrow{\lambda }$
. In particular
$\overrightarrow{\lambda }$
. In particular
 $X_{\widetilde{P}}$
is then a
$X_{\widetilde{P}}$
is then a
 ${\mathbb{R}}^2$
-tree.
${\mathbb{R}}^2$
-tree.
-
(3) If
 $\widetilde{P}$
is a flat piece, then
$\widetilde{P}$
is a flat piece, then
 $X_{\widetilde{P}}$
is isometric to the complete flat surface
$X_{\widetilde{P}}$
is isometric to the complete flat surface
 $\widetilde{W}^c$
, the pseudometrics
$\widetilde{W}^c$
, the pseudometrics
 $d_{M,i}=d_{{K},i}$
are the vertical/horizontal pseudometrics, and
$d_{M,i}=d_{{K},i}$
are the vertical/horizontal pseudometrics, and
 $d_M$
is the
$d_M$
is the
 $\ell ^1$
-metric
$\ell ^1$
-metric
 $d_{K}$
(see Section 5.1
).
$d_{K}$
(see Section 5.1
).
-
(4) For all
 $\gamma \in \Gamma$
,
$\gamma \in \Gamma$
, \begin{align*} L_{X_{M,i}}(\gamma )=i(\lambda _{M,i},\gamma )=L_{M,i}(\gamma ) \end{align*}
\begin{align*} L_{X_{M,i}}(\gamma )=i(\lambda _{M,i},\gamma )=L_{M,i}(\gamma ) \end{align*}
Proof. The projection
![]() $\pi \colon \widetilde{\Sigma ^b}\to X_M$
sends each geodesic
$\pi \colon \widetilde{\Sigma ^b}\to X_M$
sends each geodesic
![]() ${\widetilde{c}}\in \widetilde{\mathcal E}^b$
to a point
${\widetilde{c}}\in \widetilde{\mathcal E}^b$
to a point
![]() $x_{\widetilde{c}}$
of
$x_{\widetilde{c}}$
of
![]() $X_M$
.
$X_M$
.
We first prove (2) and (3). By construction, the piece
![]() $X_{\widetilde{P}}$
is the biggest Hausdorff quotient of
$X_{\widetilde{P}}$
is the biggest Hausdorff quotient of
![]() $\widetilde{P}$
with respect to the
$\widetilde{P}$
with respect to the
![]() $\ell ^1$
-pseudometric
$\ell ^1$
-pseudometric
![]() $d_M$
, endowed with the quotient pseudometrics
$d_M$
, endowed with the quotient pseudometrics
![]() $d_{M,i}$
. As a result (3) holds.
$d_{M,i}$
. As a result (3) holds.
To check (2) observe that if
![]() $\widetilde{P}$
is a lamination piece, since
$\widetilde{P}$
is a lamination piece, since
![]() $d_{M,i}$
is the restriction of
$d_{M,i}$
is the restriction of
![]() $d_{\lambda ^b_i}$
, then
$d_{\lambda ^b_i}$
, then
![]() $d_M$
is the restriction of the pseudometric
$d_M$
is the restriction of the pseudometric
![]() $d_\lambda ^b$
induced by the measured lamination
$d_\lambda ^b$
induced by the measured lamination
![]() $\lambda ^b=(\Lambda ^b,\nu ^b_1+\nu ^b_2)$
on
$\lambda ^b=(\Lambda ^b,\nu ^b_1+\nu ^b_2)$
on
![]() $\Sigma ^b$
, and
$\Sigma ^b$
, and
![]() $(X_{\widetilde{P}}, d_{M,1}, d_{M,2})$
identifies with the image of
$(X_{\widetilde{P}}, d_{M,1}, d_{M,2})$
identifies with the image of
![]() $\widetilde{P}$
in the
$\widetilde{P}$
in the
![]() ${\mathbb{R}}^2$
-tree
${\mathbb{R}}^2$
-tree
![]() $T(\overrightarrow{\lambda })\;:\!=\;\Sigma ^b/d_\lambda ^b$
dual to the
$T(\overrightarrow{\lambda })\;:\!=\;\Sigma ^b/d_\lambda ^b$
dual to the
![]() $2$
-measured geodesic lamination
$2$
-measured geodesic lamination
![]() $\overrightarrow{\lambda }$
(see Section 3.5).
$\overrightarrow{\lambda }$
(see Section 3.5).
We now prove (1). Since all pieces
![]() $X_{\widetilde{P}}$
are geodesic for the
$X_{\widetilde{P}}$
are geodesic for the
![]() $\ell ^1$
-metric, it follows easily that
$\ell ^1$
-metric, it follows easily that
![]() $(X_M,d_M)$
is geodesic (a geodesic between
$(X_M,d_M)$
is geodesic (a geodesic between
![]() $x$
and
$x$
and
![]() $y$
is obtained by concatenating geodesics in the separating pieces).
$y$
is obtained by concatenating geodesics in the separating pieces).
We first prove (TG1), by showing that if two pieces
![]() $X_{\widetilde{P}}, X_{{\widetilde{P}}'}$
meet, then
$X_{\widetilde{P}}, X_{{\widetilde{P}}'}$
meet, then
![]() $X_{\widetilde{P}}\cap X_{{\widetilde{P}}'}=x_{\widetilde{c}}$
where
$X_{\widetilde{P}}\cap X_{{\widetilde{P}}'}=x_{\widetilde{c}}$
where
![]() $\widetilde{c}$
is the boundary component of
$\widetilde{c}$
is the boundary component of
![]() $\widetilde{P}$
separating
$\widetilde{P}$
separating
![]() $\widetilde{P}$
from
$\widetilde{P}$
from
![]() ${\widetilde{P}}'$
: we denote by
${\widetilde{P}}'$
: we denote by
![]() $\overline{x}$
the image in
$\overline{x}$
the image in
![]() $X_{\widetilde{P}}$
of a point
$X_{\widetilde{P}}$
of a point
![]() $x$
in
$x$
in
![]() $\widetilde{P}$
. Suppose that
$\widetilde{P}$
. Suppose that
![]() $\overline{x}=\overline{y}$
with
$\overline{x}=\overline{y}$
with
![]() $y\in{\widetilde{P'}}$
. Then
$y\in{\widetilde{P'}}$
. Then
 \begin{align} d_M(x,y)=0=\sum _{j=0}^{k+1} d^{{\widetilde{P}}_j}_M(x_j,x_{j+1}) \end{align}
\begin{align} d_M(x,y)=0=\sum _{j=0}^{k+1} d^{{\widetilde{P}}_j}_M(x_j,x_{j+1}) \end{align}
where
![]() $(x_0,\ldots,x_{k+1})$
is a straight chain from
$(x_0,\ldots,x_{k+1})$
is a straight chain from
![]() $x$
to
$x$
to
![]() $y$
. Recall that this means that
$y$
. Recall that this means that
![]() $x_0=x$
,
$x_0=x$
,
![]() $x_{k+1}=y$
and, for all
$x_{k+1}=y$
and, for all
![]() $j=1,\ldots,k$
, the point
$j=1,\ldots,k$
, the point
![]() $x_j$
belongs to the geodesic
$x_j$
belongs to the geodesic
![]() ${\widetilde{c}}_j$
, where
${\widetilde{c}}_j$
, where
![]() $({\widetilde{c}}_j)_{j=1,\ldots, k}$
is the ordered sequence of geodesics in
$({\widetilde{c}}_j)_{j=1,\ldots, k}$
is the ordered sequence of geodesics in
![]() $\widetilde{\mathcal E}^b$
separating
$\widetilde{\mathcal E}^b$
separating
![]() $x$
and
$x$
and
![]() $y$
, and we denote by
$y$
, and we denote by
![]() ${\widetilde{P}}_j$
the piece containing
${\widetilde{P}}_j$
the piece containing
![]() $x_j$
and
$x_j$
and
![]() $x_{j+1}$
. Then
$x_{j+1}$
. Then
![]() ${\widetilde{c}}_1={\widetilde{c}}$
and equation (6.1) implies that
${\widetilde{c}}_1={\widetilde{c}}$
and equation (6.1) implies that
![]() $d^{{\widetilde{P}}_0}_M(x,x_1)=0$
proving that
$d^{{\widetilde{P}}_0}_M(x,x_1)=0$
proving that
![]() $\overline{x}=x_{\widetilde{c}}=\overline{y}$
.
$\overline{x}=x_{\widetilde{c}}=\overline{y}$
.
We now verify (TG2). Consider a simple nontrivial geodesic triangle with vertices
![]() $\overline{x}, \overline{y},\overline{z}$
in
$\overline{x}, \overline{y},\overline{z}$
in
![]() $X_M$
, and lift its vertices to three points
$X_M$
, and lift its vertices to three points
![]() $x,y,z$
in
$x,y,z$
in
![]() $\widetilde{\Sigma ^b}$
. If
$\widetilde{\Sigma ^b}$
. If
![]() $x,y,z$
are not in a common piece of
$x,y,z$
are not in a common piece of
![]() $\widetilde{\Sigma ^b}$
, then there is a geodesic
$\widetilde{\Sigma ^b}$
, then there is a geodesic
![]() $\widetilde{c}$
in
$\widetilde{c}$
in
![]() $\widetilde{\mathcal E}^b$
separating one of the three points, say
$\widetilde{\mathcal E}^b$
separating one of the three points, say
![]() $x$
, from the others. Then the corresponding point
$x$
, from the others. Then the corresponding point
![]() $x_{\widetilde{c}}$
in
$x_{\widetilde{c}}$
in
![]() $X_M$
lies on each geodesic from
$X_M$
lies on each geodesic from
![]() $\overline{x}$
to
$\overline{x}$
to
![]() $\overline{y}$
and on each geodesic from
$\overline{y}$
and on each geodesic from
![]() $\overline{x}$
to
$\overline{x}$
to
![]() $\overline{z}$
in
$\overline{z}$
in
![]() $X_M$
. Hence, either the geodesic triangle is not simple or
$X_M$
. Hence, either the geodesic triangle is not simple or
![]() $x_{\widetilde{c}}=\overline{x}$
. In the second case, we can change representative and obtain a geodesic triangle in
$x_{\widetilde{c}}=\overline{x}$
. In the second case, we can change representative and obtain a geodesic triangle in
![]() $\widetilde{\Sigma ^b}$
with shorter lengths (for the CAT(0) distance). Since the elements in
$\widetilde{\Sigma ^b}$
with shorter lengths (for the CAT(0) distance). Since the elements in
![]() $\widetilde{\mathcal E}^b$
are uniformly separated, the process terminates and shows that we can find preimages in the same piece. We conclude proving (4). We have that
$\widetilde{\mathcal E}^b$
are uniformly separated, the process terminates and shows that we can find preimages in the same piece. We conclude proving (4). We have that
![]() $L_{d_{M,i}}(\gamma )=\inf _{x\in \widetilde{\Sigma ^b}}d_{M,i}(x,\gamma x)$
. Let
$L_{d_{M,i}}(\gamma )=\inf _{x\in \widetilde{\Sigma ^b}}d_{M,i}(x,\gamma x)$
. Let
![]() $x\in \widetilde{\Sigma ^b}$
. Let
$x\in \widetilde{\Sigma ^b}$
. Let
![]() $c$
be the geodesic segment from
$c$
be the geodesic segment from
![]() $x$
to
$x$
to
![]() $\gamma x$
in
$\gamma x$
in
![]() $\widetilde{\Sigma ^b}$
for the CAT(0) metric
$\widetilde{\Sigma ^b}$
for the CAT(0) metric
![]() $m^b$
. It crosses the decomposing geodesics
$m^b$
. It crosses the decomposing geodesics
![]() $\widetilde{\mathcal E}^b$
in a straight chain
$\widetilde{\mathcal E}^b$
in a straight chain
![]() $(x_0=x,x_1,\ldots,x_{k+1}=\gamma x)$
, hence
$(x_0=x,x_1,\ldots,x_{k+1}=\gamma x)$
, hence
 \begin{align*}d_{M,i}(x,\gamma x)=\sum _{j=0}^{k} d_{M,i}^{{\widetilde {P}}_j}(x_j,x_{j+1})\; .\end{align*}
\begin{align*}d_{M,i}(x,\gamma x)=\sum _{j=0}^{k} d_{M,i}^{{\widetilde {P}}_j}(x_j,x_{j+1})\; .\end{align*}
(see Section 6.1). Let
![]() $J_F$
be the set of
$J_F$
be the set of
![]() $j\in J=\{0,\ldots,k\}$
such that
$j\in J=\{0,\ldots,k\}$
such that
![]() ${\widetilde{P}}_j$
is a flat piece and
${\widetilde{P}}_j$
is a flat piece and
![]() $J_L$
be the set of
$J_L$
be the set of
![]() $j\in J$
such that
$j\in J$
such that
![]() ${\widetilde{P}}_j$
is a lamination piece. Recall that the measured geodesic lamination on
${\widetilde{P}}_j$
is a lamination piece. Recall that the measured geodesic lamination on
![]() $(\Sigma ^b,m^b)$
corresponding to
$(\Sigma ^b,m^b)$
corresponding to
![]() $\lambda _i$
is
$\lambda _i$
is
![]() $\lambda ^b_i=(\Lambda ^b,\nu ^b_i)$
. Denote by
$\lambda ^b_i=(\Lambda ^b,\nu ^b_i)$
. Denote by
![]() $\lambda ^b_{{K},i}$
the measured geodesic lamination on
$\lambda ^b_{{K},i}$
the measured geodesic lamination on
![]() $(\Sigma ^b,m^b)$
induced by
$(\Sigma ^b,m^b)$
induced by
![]() $\lambda _{{K},i}$
(which is included in the flat pieces).
$\lambda _{{K},i}$
(which is included in the flat pieces).
As the geodesic lamination
![]() $\lambda ^b_i$
is supported on lamination pieces, we have
$\lambda ^b_i$
is supported on lamination pieces, we have
 \begin{align*} \sum _{j\in J_L}d_{M,i}^{{\widetilde{P}}_j}(x_j,x_{j+1}) &= \sum _{j\in J_L}d_{\lambda ^b_i}(x_j,x_{j+1})\\[5pt] &=\sum _{j\in J}d_{\lambda ^b_i}(x_j,x_{j+1})\\[5pt] &=d_{\lambda ^b_i}(x,\gamma x)\\[5pt] &\geq i(\lambda ^b_i,\gamma ) \;. \end{align*}
\begin{align*} \sum _{j\in J_L}d_{M,i}^{{\widetilde{P}}_j}(x_j,x_{j+1}) &= \sum _{j\in J_L}d_{\lambda ^b_i}(x_j,x_{j+1})\\[5pt] &=\sum _{j\in J}d_{\lambda ^b_i}(x_j,x_{j+1})\\[5pt] &=d_{\lambda ^b_i}(x,\gamma x)\\[5pt] &\geq i(\lambda ^b_i,\gamma ) \;. \end{align*}
Similarly, since for any
![]() $x,y$
in (possibly different components of) the boundary
$x,y$
in (possibly different components of) the boundary
![]() $\partial{\widetilde{P}}$
of a flat piece
$\partial{\widetilde{P}}$
of a flat piece
![]() $\widetilde{P}$
it holds
$\widetilde{P}$
it holds
![]() $d_{M,i}^{{\widetilde{P}}}(x,y)=d_{\lambda _{{K},i}}(x,y)$
, and the geodesic lamination
$d_{M,i}^{{\widetilde{P}}}(x,y)=d_{\lambda _{{K},i}}(x,y)$
, and the geodesic lamination
![]() $\lambda ^b_{{K},i}$
is supported on flat pieces, we have
$\lambda ^b_{{K},i}$
is supported on flat pieces, we have
 \begin{align*} \sum _{j\in J_F}d_{M,i}^{{\widetilde{P}}_j}(x_j,x_{j+1}) &=\sum _{j\in J}d_{\lambda ^b_{{K},i}}(x_j,x_{j+1})\\ &=d_{\lambda ^b_{{K},i}}(x,\gamma x)\\ &\geq i(\lambda ^b_{{K},i},\gamma ). \end{align*}
\begin{align*} \sum _{j\in J_F}d_{M,i}^{{\widetilde{P}}_j}(x_j,x_{j+1}) &=\sum _{j\in J}d_{\lambda ^b_{{K},i}}(x_j,x_{j+1})\\ &=d_{\lambda ^b_{{K},i}}(x,\gamma x)\\ &\geq i(\lambda ^b_{{K},i},\gamma ). \end{align*}
Hence:
 \begin{align*} d_{M,i}(x,\gamma x) &\geq i(\lambda ^b_{{K},i},\gamma )+i(\lambda ^b_i,\gamma )\\ &=i(\lambda _{{K},i},\gamma )+i(\lambda _i,\gamma )\\ &= i(\lambda _{M,i},\gamma ). \end{align*}
\begin{align*} d_{M,i}(x,\gamma x) &\geq i(\lambda ^b_{{K},i},\gamma )+i(\lambda ^b_i,\gamma )\\ &=i(\lambda _{{K},i},\gamma )+i(\lambda _i,\gamma )\\ &= i(\lambda _{M,i},\gamma ). \end{align*}
If
![]() $x$
is on an axis of
$x$
is on an axis of
![]() $\gamma$
in the CAT(0) surface
$\gamma$
in the CAT(0) surface
![]() $(\widetilde{\Sigma ^b},m^b)$
, then there is equality.
$(\widetilde{\Sigma ^b},m^b)$
, then there is equality.
7. Embeddings in products of trees
If
![]() $X$
is a product
$X$
is a product
![]() $X=X_1\times \cdots \times X_n$
of metric spaces
$X=X_1\times \cdots \times X_n$
of metric spaces
![]() $(X_i,d_i)$
, the
$(X_i,d_i)$
, the
![]() $i\textrm{th}$
-factor pseudometric is the pseudometric
$i\textrm{th}$
-factor pseudometric is the pseudometric
![]() $d_i(x,y)=d_i(x_i,y_i)$
obtained by pulling back the metric on
$d_i(x,y)=d_i(x_i,y_i)$
obtained by pulling back the metric on
![]() $X_i$
via the canonical projection. The
$X_i$
via the canonical projection. The
![]() $\ell ^1$
-metric on
$\ell ^1$
-metric on
![]() $X$
is the metric given by
$X$
is the metric given by
![]() $d=\sum _i d_i$
.
$d=\sum _i d_i$
.
Proposition 7.1.
Consider a
![]() ${\mathbb{R}}^2$
-mixed structure
${\mathbb{R}}^2$
-mixed structure
![]() $M$
on
$M$
on
![]() $\Sigma$
with
$\Sigma$
with
![]() ${\mathbb{R}}^2$
-length function
${\mathbb{R}}^2$
-length function
![]() $\overrightarrow{L}$
, and a pair of isometric actions of
$\overrightarrow{L}$
, and a pair of isometric actions of
![]() $\Gamma$
on
$\Gamma$
on
![]() $\mathbb{R}$
-trees
$\mathbb{R}$
-trees
![]() $T_1,T_2$
with length functions
$T_1,T_2$
with length functions
![]() $(L_{T_1},L_{T_2})=\overrightarrow{L}$
. Let
$(L_{T_1},L_{T_2})=\overrightarrow{L}$
. Let
![]() $(X_M,(d_1,d_2))$
be the tree-graded
$(X_M,(d_1,d_2))$
be the tree-graded
![]() ${\mathbb{R}}^2$
-space associated with
${\mathbb{R}}^2$
-space associated with
![]() $M$
. There is an equivariant embedding
$M$
. There is an equivariant embedding
preserving each factor pseudometric
![]() $d_i$
. In particular,
$d_i$
. In particular,
![]() $f$
is isometric for the
$f$
is isometric for the
![]() $\ell ^1$
-metric
$\ell ^1$
-metric
![]() $d=d_1+d_2$
.
$d=d_1+d_2$
.
Example 7.2.
If
![]() $M$
is a flat surface, equivalently
$M$
is a flat surface, equivalently
![]() $\Sigma^{\prime}=\Sigma$
, the associated tree-graded
$\Sigma^{\prime}=\Sigma$
, the associated tree-graded
![]() ${\mathbb{R}}^2$
-space is the flat surface given by the universal cover
${\mathbb{R}}^2$
-space is the flat surface given by the universal cover
![]() $\widetilde{M}$
of
$\widetilde{M}$
of
![]() $M$
. The map
$M$
. The map
![]() $f$
gives an embedding of
$f$
gives an embedding of
![]() $\widetilde{M}$
in any product of trees with the correct length functions. Such embedding is isometric for the
$\widetilde{M}$
in any product of trees with the correct length functions. Such embedding is isometric for the
![]() $\ell ^1$
-metric, and bilipschitz for the CAT(0) metric (compare [
Reference Guirardel13, Example 4, Section 2.3]). Such embedding is never isometric for the CAT(0) metric.
$\ell ^1$
-metric, and bilipschitz for the CAT(0) metric (compare [
Reference Guirardel13, Example 4, Section 2.3]). Such embedding is never isometric for the CAT(0) metric.
If, instead,
![]() $M$
is a
$M$
is a
![]() $2$
-lamination, namely in the cases in which
$2$
-lamination, namely in the cases in which
![]() $\Sigma^{\prime}=\emptyset$
,
$\Sigma^{\prime}=\emptyset$
,
![]() $(X_M,d)$
is a tree. The map
$(X_M,d)$
is a tree. The map
![]() $f$
gives an equivariant embedding of this tree in any product of trees that induce the correct length function. This map is isometric if the product of trees is endowed with the
$f$
gives an equivariant embedding of this tree in any product of trees that induce the correct length function. This map is isometric if the product of trees is endowed with the
![]() $\ell ^1$
-metric. Observe, however, that there are laminations
$\ell ^1$
-metric. Observe, however, that there are laminations
![]() $\Lambda$
that support mutually singular transverse measures. For these the image of the
$\Lambda$
that support mutually singular transverse measures. For these the image of the
![]() ${\mathbb{R}}^2$
-tree will not be a geodesic subset of
${\mathbb{R}}^2$
-tree will not be a geodesic subset of
![]() $T_1\times T_2$
if
$T_1\times T_2$
if
![]() $T_1\times T_2$
is endowed with the CAT(0) metric. In general, when
$T_1\times T_2$
is endowed with the CAT(0) metric. In general, when
![]() $T_1\times T_2$
is endowed with the CAT(0) metric, it is possible to show that the embedding is isometric if and only if all the laminations are homothetic.
$T_1\times T_2$
is endowed with the CAT(0) metric, it is possible to show that the embedding is isometric if and only if all the laminations are homothetic.
Proof of Proposition 7.1. We first use rigidity of lengths in
![]() $\mathbb{R}$
-trees to reduce to the case where each
$\mathbb{R}$
-trees to reduce to the case where each
![]() $T_i$
is the tree
$T_i$
is the tree
![]() $T(\lambda _{M,i})$
dual to the measured geodesic lamination
$T(\lambda _{M,i})$
dual to the measured geodesic lamination
![]() $\lambda _{M,i}$
on
$\lambda _{M,i}$
on
![]() $\Sigma$
associated with
$\Sigma$
associated with
![]() $M$
: Let
$M$
: Let
![]() $T'_i$
denote the minimal subtree of
$T'_i$
denote the minimal subtree of
![]() $T_i$
invariant by
$T_i$
invariant by
![]() $\Gamma$
. The actions of
$\Gamma$
. The actions of
![]() $\Gamma$
on the trees
$\Gamma$
on the trees
![]() $T'_i$
and
$T'_i$
and
![]() $T(\lambda _{M,i})$
are minimal and have same length function, which belongs to
$T(\lambda _{M,i})$
are minimal and have same length function, which belongs to
![]() $\mathcal{ML}$
. Hence there is an equivariant isometry
$\mathcal{ML}$
. Hence there is an equivariant isometry
![]() $h_i\colon T(\lambda _{M,i})\overset{\sim }{\rightarrow } T'_i\subset T_i$
. Then the diagonal map
$h_i\colon T(\lambda _{M,i})\overset{\sim }{\rightarrow } T'_i\subset T_i$
. Then the diagonal map
![]() $h=(h_i)_i$
is an equivariant embedding
$h=(h_i)_i$
is an equivariant embedding
![]() $\prod _iT(\lambda _{M,i}) \to \prod _i T_i$
preserving each factor pseudometric
$\prod _iT(\lambda _{M,i}) \to \prod _i T_i$
preserving each factor pseudometric
![]() $d_i$
.
$d_i$
.
We now construct the canonical map
![]() $p_i\colon X_M\to T(\lambda _{M,i})$
. We denote
$p_i\colon X_M\to T(\lambda _{M,i})$
. We denote
![]() $T_{M,i}\;:\!=\; X_M/d_{M,i}$
the biggest Hausdorff quotient of
$T_{M,i}\;:\!=\; X_M/d_{M,i}$
the biggest Hausdorff quotient of
![]() $X_M$
with respect to the pseudometric
$X_M$
with respect to the pseudometric
![]() $d_{M,i}$
and by
$d_{M,i}$
and by
![]() $p_i\colon X_M \to T_{M,i}$
the corresponding projection. The tree
$p_i\colon X_M \to T_{M,i}$
the corresponding projection. The tree
![]() $T_{M,i}$
can be identified with
$T_{M,i}$
can be identified with
![]() $T(\lambda _{M,i})$
: since
$T(\lambda _{M,i})$
: since
![]() $T_{M,i}$
is tree-graded with
$T_{M,i}$
is tree-graded with
![]() $\mathbb{R}$
-trees pieces
$\mathbb{R}$
-trees pieces
![]() $p_i(X_{\widetilde{P}})={\widetilde{P}}/d_{M,i}$
, it is itself an
$p_i(X_{\widetilde{P}})={\widetilde{P}}/d_{M,i}$
, it is itself an
![]() $\mathbb{R}$
-tree. Since the action of
$\mathbb{R}$
-tree. Since the action of
![]() $\Gamma$
on
$\Gamma$
on
![]() $\widetilde{\Sigma ^b}$
is minimal, the action on
$\widetilde{\Sigma ^b}$
is minimal, the action on
![]() $T_{M,i}$
is minimal as well. The length function of this action is
$T_{M,i}$
is minimal as well. The length function of this action is
In particular, by rigidity of length functions for actions on minimal trees, there is an equivariant isometry
![]() $T_{M,i} \overset{\sim }{\rightarrow } T(\lambda _{M,i})$
. Then the diagonal map
$T_{M,i} \overset{\sim }{\rightarrow } T(\lambda _{M,i})$
. Then the diagonal map
![]() $p=(p_i)_i$
from
$p=(p_i)_i$
from
![]() $X_M$
to
$X_M$
to
![]() $\prod _i T(\lambda _{M,i})$
sends each pseudometric
$\prod _i T(\lambda _{M,i})$
sends each pseudometric
![]() $d_{M,i}$
on the factor pseudometric
$d_{M,i}$
on the factor pseudometric
![]() $d_i$
, hence it takes the metric
$d_i$
, hence it takes the metric
![]() $d_M=\sum _i d_{M,i}$
to the
$d_M=\sum _i d_{M,i}$
to the
![]() $\ell ^1$
-metric
$\ell ^1$
-metric
![]() $d=\sum _i d_i$
on
$d=\sum _i d_i$
on
![]() $\prod _i T(\lambda _{M,i})$
. The results follow taking the map
$\prod _i T(\lambda _{M,i})$
. The results follow taking the map
![]() $f=h\circ p$
.
$f=h\circ p$
.
Acknowledgements
Beatrice Pozzetti is supported by the Deutsche Forschungsgemeinschaft under Germany’s Excellence Strategy EXC-2181/1 – 390900948 (the Heidelberg STRUCTURES Cluster of Excellence), and acknowledges further support by DFG grant 338644254 (within the framework of SPP2026).