Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-26T01:04:16.629Z Has data issue: false hasContentIssue false
  • English
  • Français

Sharp gradient estimate, rigidity and almost rigidity of Green functions on non-parabolic RCD(0, N) spaces

Published online by Cambridge University Press:  17 January 2024

Shouhei Honda  and
Yuanlin Peng
Shouhei Honda
Affiliation:
Mathematical Institute, Tohoku University, Japan ([email protected])
Yuanlin Peng
Affiliation:
Mathematical Institute, Tohoku University; JSPS Research Fellow, Japan ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Inspired by a result in T. H. Colding. (16). Acta. Math. 209(2) (2012), 229-263 [16] of Colding, the present paper studies the Green function $G$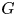 on a non-parabolic $\operatorname {RCD}(0,\,N)$ 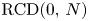space $(X,\, \mathsf {d},\, \mathfrak {m})$ 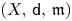for some finite $N>2$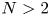. Defining $\mathsf {b}_x=G(x,\, \cdot )^{\frac {1}{2-N}}$ 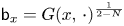for a point $x \in X$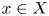, which plays a role of a smoothed distance function from $x$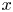, we prove that the gradient $|\nabla \mathsf {b}_x|$ 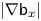has the canonical pointwise representative with the sharp upper bound in terms of the $N$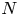-volume density $\nu _x=\lim _{r\to 0^+}\frac {\mathfrak {m} (B_r(x))}{r^N}$ 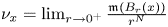of $\mathfrak {m}$ at $x$;

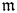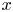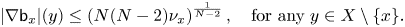
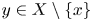\[ |\nabla \mathsf{b}_x|(y) \le \left(N(N-2)\nu_x\right)^{\frac{1}{N-2}}, \quad \text{for any }y \in X \setminus \{x\}. \]
Moreover the rigidity is obtained, namely, the upper bound is attained at a point $y \in X \setminus \{x\}$ if and only if the space is isomorphic to the $N$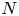-metric measure cone over an $\operatorname {RCD}(N-2,\, N-1)$ 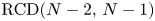space. In the case when $x$ 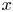is an $N$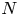-regular point, the rigidity states an isomorphism to the $N$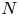-dimensional Euclidean space $\mathbb {R}^N$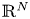, thus, this extends the result of Colding to $\operatorname {RCD}(0,\,N)$ spaces. It is emphasized that the almost rigidities are also proved, which are new even in the smooth framework.

Keywords

Ricci curvaturemetric measure spaceGreen functionsrigidityGromov–Hausdorff convergenceOptimal transportation theory
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 54
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ambrosio, L., Gigli, N. and Savaré, G.. Calculus and heat flow in metric measure spaces and applications to spaces with Ricci bounds from below. Invent. Math. 195 (2014), 289–391.CrossRefGoogle Scholar
Ambrosio, L., Gigli, N. and Savaré, G.. Metric measure spaces with Riemannian Ricci curvature bounded from below. Duke Math. J. 163 (2014), 1405–1490.CrossRefGoogle Scholar
Ambrosio, L. and Honda, S.. Local spectral convergence in $\text {RCD}^*(K,\, N)$ spaces. Nonlinear Anal. 177 (2018), 1–23.CrossRefGoogle Scholar
Ambrosio, L., Honda, S. and Tewodrose, D.. Short-time behavior of the heat kernel and Weyl's law on $\text {RCD}^*(K,\, N)$-spaces. Ann. Glob. Anal. Geom. 53 (2018), 97–119.CrossRefGoogle Scholar
Ambrosio, L. and Honda, S., New stability results for sequences of metric measure spaces with uniform Ricci bounds from below. Measure theory in non-smooth spaces, 1–51, Partial Differ. Equ. Meas. Theory, De Gruyter Open, Warsaw, 2017.CrossRefGoogle Scholar
Ambrosio, L., Mondino, A. and Savaré, G.. On the Bakry-Émery condition, the gradient estimates and the local-to-global property of $RCD^*(K,\,N)$ metric measure spaces. J. Geom. Anal. 26 (2016), 24–56.CrossRefGoogle Scholar
Ambrosio, L., Mondino, A. and Savaré, G., Nonlinear diffusion equations and curvature conditions in metric measure spaces, Mem. Amer. Math. Soc. (Vol. 262, 2019, 1270).CrossRefGoogle Scholar
Ambrosio, L., Calculus, heat flow and curvature-dimension bounds in metric measure spaces, Proceedings of the ICM 2018, Vol. 1, (World Scientific, Singapore, 2019, 301–340).CrossRefGoogle Scholar
Björn, A. and Björn, J.. Nonlinear Potential theory on metric measure spaces, EMS Tracts in Mathematics, vol. 17 (Zürich: European Mathematical Society, 2011).Google Scholar
Brena, C., Gigli, N., Honda, S. and Zhu, X.. Weakly non-collapsed $\text {RCD}$ spaces are strongly non-collapsed. J. Reine Angew. Math. 794 (2023), 215–252.Google Scholar
Bruè, E., Deng, Q. and Semola, D.. Improved regularity estimates for Lagrangian flows on $\text {RCD}\,(K,\, N)$ spaces. Nonlinear Anal. 214 (2022), 112609.CrossRefGoogle Scholar
Bruè, E. and Semola, D.. Constancy of dimension for $\text {RCD}^*(K,\,N)$ spaces via regularity of Lagrangian flows. Comm. Pure and Appl. Math. 73 (2019), 1141–1204.CrossRefGoogle Scholar
Cavalletti, F. and Milman, E.. The globalization theorem for the curvature dimension condition. Invent. Math. 226 (2021), 1–137.CrossRefGoogle Scholar
Cheeger, J. and Colding, T. H.. On the structure of spaces with Ricci curvature bounded below. I. J. Differ. Geom. 46 (1997), 406–480.CrossRefGoogle Scholar
Colding, T. H.. Ricci curvature and volume convergence. Ann. Math. 145 (1997), 477–501.CrossRefGoogle Scholar
Colding, T. H.. New monotonicity formulas for Ricci curvature and applications. I. Acta. Math. (2). 209 (2012), 229–263.CrossRefGoogle Scholar
Colding, T. H. and Minicozzi, W. P.. On uniqueness of tangent cones for Einstein manifolds. Invent. Math. 196 (2014), 515–588.CrossRefGoogle Scholar
Colding, T. H. and Naber, A.. Sharp Hölder continuity of tangent cones for spaces with a lower Ricci curvature bound and applications. Ann. Math. 176 (2012), 1173–1229.CrossRefGoogle Scholar
De Philippis, G. and Gigli, N.. From volume cone to metric cone in the nonsmooth setting. Geom. Funct. Anal. 26 (2016), 1526–1587.CrossRefGoogle Scholar
De Philippis, G. and Gigli, N.. Non-collapsed spaces with Ricci curvature bounded below. J. Ecole. Polytechn. 5 (2018), 613–650.Google Scholar
De Philippis, G. and Zimbrón, J. N.. The behavior of harmonic functions at singular points of RCD spaces. Manuscr. Math. 171 (2023), 155–168.CrossRefGoogle Scholar
Deng, Q., Hölder continuity of tangent cones in RCD(K,N) spaces and applications to non-branching, arXiv:2009.07956v2.Google Scholar
Ding, Y.. Heat kernels and Green's function on limit spaces. Comm. Anal. Geom. 10 (2002), 475–514.CrossRefGoogle Scholar
Eguchi, T. and Hanson, A. J.. Self-dual solutions to Euclidean gravity. Ann. Phys. 120 (1979), 82–105.CrossRefGoogle Scholar
Erbar, M., Kuwada, K. and Sturm, K.-T.. On the equivalence of the entropic curvature-dimension condition and Bochner's inequality on metric measure spaces. Invent. Math. 201 (2015), 993–1071.CrossRefGoogle Scholar
Fogagnolo, M., Mazzieri, L. and Pinamonti, A.. Geoetric aspects of $p$-capacitary potenttials. Ann. Inst. Henri. Poincare C Anal. Non Lineaire. 36 (2019), 1151–1179.CrossRefGoogle Scholar
Gigli, N., Kuwada, K. and Ohta, S.-I.. Heat flow on Alexandrov spaces. Commun. Pure Appl. Math. (3). 66 (2013), 307–331.CrossRefGoogle Scholar
Gigli, N., Mondino, A. and Savaré, G.. Convergence of pointed non-compact metric measure spaces and stability of Ricci curvature bounds and heat flows. Proc. Lond. Math. Soc. 111 (2015), 1071–1129.Google Scholar
Gigli, N. and Pasqualetto, E.. Lectures on Nonsmooth Differential Geometry. SISSA Springer Series 2 (New York, USA: Springer International Publishing, 2020).CrossRefGoogle Scholar
Gigli, N. and Rigoni, C.. A note about the strong maximum principle on RCD spaces. Canad. Math. Bull. 62 (2019), 259–266.CrossRefGoogle Scholar
Gigli, N. and Violo, I. Y.. Monotonicity formulas for harmonic functions in $\text {RCD}\,(0,\, N)$ spaces. J. Geom. Anal. 33 (2023), 100. https://doi.org/10.1007/s12220-022-01131-7CrossRefGoogle Scholar
Gigli, N., The splitting theorem in non-smooth context. ArXiv preprint 1302.5555.Google Scholar
Gigli, N., On the differential structure of metric measure spaces and applications. Mem. Amer. Math. Soc. (Vol. 236, 2015, 1113).CrossRefGoogle Scholar
Gigli, N., Nonsmooth differential geometry – An approach tailored for spaces with Ricci curvature bounded from below. Mem. Amer. Math. Soc. (Vol. 251, 2018, 1196).CrossRefGoogle Scholar
Gigli, N., De Giorgi and Gromov working together. ArXiv preprint: 2306.14604.Google Scholar
Grigor'yan, A.. Heat kernels on weighted manifolds and applications. Amer. Math. Soc. 398 (2006), 93–191.Google Scholar
Hajłasz, P. and Koskela, P., Sobolev met Poincaré. Mem. Amer. Math. Soc. (Vol. 145, 2000, 688).CrossRefGoogle Scholar
Heinonen, J., Koskela, P., Shanmugalingam, N. and Tyson, J., Sobolev spaces on metric measure spaces, New Mathematical Monographs, Vol. 27 (Cambridge University Press, Cambridge, 2015).CrossRefGoogle Scholar
Honda, S.. Ricci curvature and $L^p$-convergence. J. Reine Angew. Math. 705 (2015), 85–154.CrossRefGoogle Scholar
Honda, S.. New differential operators and $\text {RCD}$ spaces. Geom. Topol. 24 (2020), 2127–2148.CrossRefGoogle Scholar
Huang, Z.. Isometric immersions of $\text {RCD}\,(K,\, N)$ spaces via heat kernels. Calc. Var. PDEs. 62 (2023), 121. https://doi.org/10.1007/s00526-023-02460-3CrossRefGoogle Scholar
Jiang, R.. Cheeger-harmonic functions in metric measure spaces revisited. J. Funct. Anal. 266 (2014), 1373–1394.CrossRefGoogle Scholar
Jiang, R., Li, H. and Zhang, H.-C.. Heat kernel bounds on metric measure spaces and some applications. Potent. Anal. 44 (2016), 601–627.CrossRefGoogle Scholar
Ketterer, C.. Cones over metric measure spaces and the maximal diameter theorem. J. Math. Pures Appl. (9). 103 (2015), 1228–1275.CrossRefGoogle Scholar
Kuwada, K. and Li, X.-D.. Monotonicity and rigidity of the $\mathcal {W}$-entropy on $\text {RCD}\,(0,\, N)$ spaces. Manuscr. Math. 164 (2021), 119–149.CrossRefGoogle Scholar
Lott, J. and Villani, C.. Ricci curvature for metric-measure spaces via optimal transport. Ann. Math. 169 (2009), 903–991.CrossRefGoogle Scholar
Lytchak, A. and Stadler, S.. Ricci curvature in dimension $2$. J. Eur. Math. Soc. 25 (2023). https://doi.org/10.4171/JEMS/1196Google Scholar
Mondino, A. and Naber, A.. Structure theory of metric measure spaces with lower Ricci curvature bounds. J. Eur. Math. Soc. 21 (2019), 1809-–1854.CrossRefGoogle Scholar
Pan, J. and Wei, G.. Examples of Ricci limit spaces with non-integer Hausdorff dimension. Geom. Funct. Anal. 32 (2022), 676–685.CrossRefGoogle Scholar
Peng, Y., Zhang, H.-C. and Zhu, X.-P., Weyl's lemma on $\text {RCD}\,(K,\, N)$ metric measure spaces, arXiv:2212.09022.Google Scholar
Petrunin, A.. Alexandrov meets Lott–Villani–Sturm. Münst. J. Math. 4 (2011), 53–64.Google Scholar
Rajala, T.. Local Poincaré inequalities from stable curvature conditions on metric spaces. Calc. Var. Partial Differ. Equ. 44 (2012), 477–494.CrossRefGoogle Scholar
Sturm, K.-T.. On the geometry of metric measure spaces, I. Acta Math. 196 (2006), 65–131.CrossRefGoogle Scholar
Sturm, K.-T.. On the geometry of metric measure spaces, II. Acta Math. 196 (2006), 133–177.CrossRefGoogle Scholar
Taylor, M. E., Partial Differential Equations, II, Applied Mathematical Sciences, (Springer, 1996).CrossRefGoogle Scholar
Varopoulos, N.. The Poinsson kernel on positively curved manifolds. J. Funct. Anal. 44 (1981), 359–380.CrossRefGoogle Scholar
Zhang, H. and Zhu, X.. Ricci curvature on Alexandrov spaces and rigidity theorems. Commun. Anal. Geom. 18 (2010), 503–553.CrossRefGoogle Scholar