Article contents
On the emergence of secondary tones in airfoil noise
Published online by Cambridge University Press: 27 June 2023
Abstract
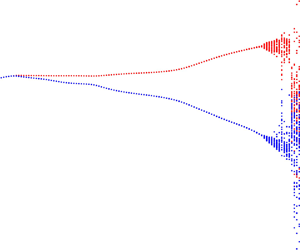
We present the results of direct numerical simulations of a NACA 0012 airfoil, with Mach number 0.3 and angle of attack of  $3^\circ$, examining the dynamics of the flow with increasing Reynolds numbers. Two-dimensional simulation results are obtained with chord-based Reynolds numbers in the range
$3^\circ$, examining the dynamics of the flow with increasing Reynolds numbers. Two-dimensional simulation results are obtained with chord-based Reynolds numbers in the range  $3.2 \times 10^3 \leq Re \leq 2.70 \times 10^4$, where each simulation uses the last time step of the previous one as a starting point, to capture the evolution of dynamics as a function of
$3.2 \times 10^3 \leq Re \leq 2.70 \times 10^4$, where each simulation uses the last time step of the previous one as a starting point, to capture the evolution of dynamics as a function of  $Re$. The development of the pressure fluctuations with time shows a transition from periodic to quasi-periodic attractor for
$Re$. The development of the pressure fluctuations with time shows a transition from periodic to quasi-periodic attractor for  $2.38 \times 10^4 \leq Re \leq 2.42 \times 10^4$, leading to the emergence of secondary tones in the wall and acoustic field pressure spectra, different from peaks related to the fundamental frequency
$2.38 \times 10^4 \leq Re \leq 2.42 \times 10^4$, leading to the emergence of secondary tones in the wall and acoustic field pressure spectra, different from peaks related to the fundamental frequency  $f_1$ and the respective harmonics; a second, incommensurate frequency
$f_1$ and the respective harmonics; a second, incommensurate frequency  $f_2$ appears, leading to several secondary tones with frequency
$f_2$ appears, leading to several secondary tones with frequency  $af_1 + bf_2$, with
$af_1 + bf_2$, with  $a$ and
$a$ and  $b$ integers. Further increase of the Reynolds number leads to the emergence of a tertiary frequency,
$b$ integers. Further increase of the Reynolds number leads to the emergence of a tertiary frequency,  $f_3$, indicating a route to chaos of the Ruelle–Takens–Newhouse type. Such a mechanism is related to the ladder-type characteristic structure of the tones, indicating that dynamic systems theory is an important tool for understanding airfoil tonal noise.
$f_3$, indicating a route to chaos of the Ruelle–Takens–Newhouse type. Such a mechanism is related to the ladder-type characteristic structure of the tones, indicating that dynamic systems theory is an important tool for understanding airfoil tonal noise.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 3
- Cited by



