Hostname: page-component-669899f699-ggqkh Total loading time: 0 Render date: 2025-04-25T08:55:59.266Z Has data issue: false hasContentIssue false
  • English
  • Français

Improved bounds for five-term arithmetic progressions

Part of: Extremal combinatorics

Published online by Cambridge University Press:  27 November 2024

JAMES LENG ,
ASHWIN SAH  and
MEHTAAB SAWHNEY
JAMES LENG
Affiliation:
Department of Mathematics, UCLA, Los Angeles, CA 90095, USA. e-mail: [email protected]
ASHWIN SAH
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. e-mails: [email protected], [email protected]
MEHTAAB SAWHNEY
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. e-mails: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $r_5(N)$ be the largest cardinality of a set in $\{1,\ldots,N\}$ which does not contain 5 elements in arithmetic progression. Then there exists a constant 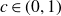$c\in (0,1)$ such that

\[r_5(N)\ll \frac{N}{\exp\!((\!\log\log N)^{c})}.\]
Our work is a consequence of recent improved bounds on the $U^4$-inverse theorem of J. Leng and the fact that 3-step nilsequences may be approximated by locally cubic functions on shifted Bohr sets. This, combined with the density increment strategy of Heath–Brown and Szemerédi, codified by Green and Tao, gives the desired result.

MSC classification

Primary: 05D10: Ramsey theory
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 177 , Issue 3 , November 2024 , pp. 371 - 413
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

†

Leng supported by an NSF Graduate research fellowship grant no. DGE-2034835.

‡

Sah and Sawhney were supported by NSF Graduate research fellowship program DGE-2141064.

References

Behrend, F. A.. On sets of integers which contain no three terms in arithmetical progression. Proc. Nat. Acad. Sci. U.S.A. 32 (1946), 331–332.Google Scholar
Bloom, T. F.. A quantitative improvement for Roth’s theorem on arithmetic progressions. J. Lond. Math. Soc. (2) 93 (2016), 643–663.Google Scholar
Bloom, T. F. and Sisask, O.. Breaking the logarithmic barrier in Roth’s theorem on arithmetic progressions. ArXiv:2007.03528.Google Scholar
Bloom, T. F. and Sisask, O.. An improvement to the Kelley-Meka bounds on three-term arithmetic progressions. ArXiv:2309.02353.Google Scholar
Bourgain, J.. On triples in arithmetic progression, Geom. Funct. Anal. 9 (1999), 968–984.CrossRefGoogle Scholar
Bourgain, Jean. Roth’s theorem on progressions revisited. J. Anal. Math. 104 (2008), 155–192.CrossRefGoogle Scholar
Gowers, W. T.. A new proof of Szemerédi’s theorem for arithmetic progressions of length four. Geom. Funct. Anal. 8 (1998), 529–551.CrossRefGoogle Scholar
Gowers, W. T.. Arithmetic progressions in sparse sets. Current developments in mathematics, 2000 (Int. Press, Somerville, MA, 2001), pp. 149–196.CrossRefGoogle Scholar
Gowers, W. T.. A new proof of Szemerédi’s theorem. Geom. Funct. Anal. 11 (2001), 465–588.CrossRefGoogle Scholar
Green, B. and Tao, T.. Quadratic uniformity of the Möbius function. Ann. Inst. Fourier (Grenoble) 58 (2008), 1863–1935.CrossRefGoogle Scholar
Green, B. and Tao, T.. The quantitative behaviour of polynomial orbits on nilmanifolds. Ann. of Math. (2) 175 (2012), 465–540.Google Scholar
Green, B., Tao, T., and Ziegler, T.. An inverse theorem for the Gowers $U^4$ -norm, Glasg. Math. J. 53 (2011), 1–50.CrossRefGoogle Scholar
Green, B. and Tao, T.. New bounds for Szemerédi’s theorem. II. A new bound for $r_4(N)$ . Analytic number theory (Cambridge University Press, Cambridge, 2009), pp. 180–204.Google Scholar
Green, B. and Tao, T.. New bounds for Szemerédi’s theorem, III: a polylogarithmic bound for $r_4(N)$ . Mathematika 63 (2017), 944–1040.CrossRefGoogle Scholar
Green, Ben, Tao, T. and Ziegler, T.. An inverse theorem for the Gowers $U^{s+1}[N]$ -norm. Ann. of Math. (2) 176 (2012), 1231–1372.Google Scholar
Heath-Brown, D. R.. Integer sets containing no arithmetic progressions. J. London Math. Soc. (2) 35 (1987), 385–394.Google Scholar
Host, B. and Kra, B.. Nilpotent structures in ergodic theory, Math. Surv. Monogr. 236 (American Mathematical Society, Providence, RI, 2018).Google Scholar
Kelley, Z. and Meka, R.. Strong bounds for 3-progressions, ArXiv:2302.05537.Google Scholar
Lazard, M.. Sur les groupes nilpotents et les anneaux de Lie. Ann. Sci. École Norm. Sup. (3) 71 (1954), 101–190.CrossRefGoogle Scholar
Leibman, A.. Polynomial sequences in groups. J. Algebra 201 (1998), 189–206.CrossRefGoogle Scholar
Leibman, A.. Polynomial mappings of groups. Israel J. Math. 129 (2002), 29–60.CrossRefGoogle Scholar
Leng, J.. Efficient equidistribution of nilsequences. ArXiv:2312.10772.Google Scholar
Leng, J.. Efficient equidistribution of periodic nilsequences and applications. ArXiv:2306.13820.Google Scholar
Manners, F.. Periodic nilsequences and inverse theorems on cyclic groups. ArXiv:1404.7742.Google Scholar
Peluse, S. and Prendiville, S.. A polylogarithmic bound in the nonlinear Roth theorem. Int. Math. Res. Not. IMRN (2022), 5658–5684.CrossRefGoogle Scholar
Peluse, S., Sah, A. and Sawhney, M.. Effective bounds for Roth’s theorem with shifted square common difference. ArXiv:2309.08359.Google Scholar
Pólya, Georg. Über ganzwertige ganze funktionen. Rendiconti del Circolo Matematico di Palermo (1884-1940) 40 (1915), 1–16.Google Scholar
Roth, K. F.. On certain sets of integers. II. J. London Math. Soc. 29 (1954), 20–26.CrossRefGoogle Scholar
Sanders, T.. On the Bogolyubov-Ruzsa lemma. Anal. PDE 5 (2012), 627–655.CrossRefGoogle Scholar
Sanders, Tom. On Roth’s theorem on progressions. Ann. of Math. (2) 174 (2011), 619–636.CrossRefGoogle Scholar
Sanders, Tom. On certain other sets of integers. J. Anal. Math. 116 (2012), 53–82.CrossRefGoogle Scholar
Schmidt, Wolfgang M.. Small fractional parts of polynomials, Regional Conference Series in Mathematics, no. 32 (American Mathematical Society, Providence, RI, 1977).Google Scholar
Szemerédi, E.. On sets of integers containing no four elements in arithmetic progression. Number Theory (Colloq., János Bolyai Math. Soc., Debrecen, 1968), Colloq. Math. Soc. János Bolyai, vol. 2 (North-Holland, Amsterdam-London, 1970), pp. 197–204.Google Scholar
Szemerédi, E.. On sets of integers containing no k elements in arithmetic progression. Acta Arith. 27 (1975), 199–245.Google Scholar
Szemerédi, E.. Integer sets containing no arithmetic progressions. Acta Math. Hungar. 56 (1990), 155–158.Google Scholar
Tao, T.. Higher order Fourier analysis, Grad. Stud. Math. 142 (American Mathematical Society, Providence, RI, 2012).Google Scholar
Tao, T. and Teräväinen, J.. Quantitative bounds for Gowers uniformity of the Möbius and von Mangoldt functions. ArXiv:2107.02158.Google Scholar