Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-04-27T12:32:58.422Z Has data issue: false hasContentIssue false
  • English
  • Français

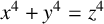POINTS ON $x^4+y^4=z^4$ OVER QUADRATIC EXTENSIONS OF 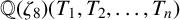${\mathbb {Q}}(\zeta _8)(T_1,T_2,\ldots ,T_n)$

Part of: Diophantine equations Arithmetic algebraic geometry

Published online by Cambridge University Press:  07 November 2024

NGUYEN XUAN THO Open the ORCID record for NGUYEN XUAN THO [Opens in a new window]
NGUYEN XUAN THO*
Affiliation:
School of Applied Mathematics and Informatics, Hanoi University of Science and Technology, Hanoi, Vietnam
*
e-mail: tho.nguyenxuan1@hust.edu.vn
Get access Rights & Permissions [Opens in a new window]

Abstract

Ishitsuka et al. [‘Explicit calculation of the mod 4 Galois representation associated with the Fermat quartic’, Int. J. Number Theory 16(4) (2020), 881–905] found all points on the Fermat quartic 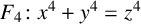${F_4\colon x^4+y^4=z^4}$ over quadratic extensions of 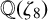${\mathbb {Q}}(\zeta _8)$, where 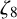$\zeta _8$ is the eighth primitive root of unity 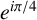$e^{i\pi /4}$. Using Mordell’s technique, we give an alternative proof for the result of Ishitsuka et al. and extend it to the rational function field 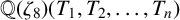${\mathbb {Q}}({\zeta _8})(T_1,T_2,\ldots ,T_n)$.

Keywords

Diophantine geometryDiophantine equationsFermat quarticsquadratic points

MSC classification

Primary: 11D25: Cubic and quartic equations
Secondary: 11G05: Elliptic curves over global fields
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 111 , Issue 1 , February 2025 , pp. 19 - 31
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The author is supported by the Vietnam National Foundation for Science and Technology Development (NAFOSTED) (grant number 101.04-2023.21).

Dedicated to Professor Andrew Bremner

References

Aigner, A., ‘Über die Möglichkeit von ${x}^4+{y}^4={z}^4$ in quadratische Körper’, J. Math. Verein. 43 (1934), 226–228.Google Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The MAGMA algebra system. I. The user language’, J. Symbolic Comput. 24(3–4) (1997), 235–265.CrossRefGoogle Scholar
Bremner, A. and Choudhry, A., ‘The Fermat cubic and quartic curves over cyclic fields’, Period. Math. Hungar. 80 (2019), 147–157.CrossRefGoogle Scholar
Cohen, H., Number Theory, Volume I: Tools and Diophantine Equations, Graduate Texts in Mathematics, 239 (Springer, New York, 2007).Google Scholar
Faddeev, D. K., ‘Group of divisor classes on the curve defined by the equation ${x}^4+{y}^4=1$ ’, Soviet Math. Dokl. 1 (1960), 1149–1151; Dokl. Akad. Nauk SSSR 134 (1960), 776–777 (in Russian).Google Scholar
Ishitsuka, Y., Ito, T. and Oshita, T., ‘Explicit calculation of the mod 4 Galois representation associated with the Fermat quartic’, Int. J. Number Theory 16(4) (2020), 881–905.CrossRefGoogle Scholar
Li, A., ‘The Diophantine equation ${x}^4+{2}^n{y}^4=1$ in quadratic number fields’, Bull. Aust. Math. Soc. 104 (2021), 21–28.CrossRefGoogle Scholar
Manley, E. D., ‘On quadratic solutions of ${x}^4+p{y}^4={z}^4$ ’, Rocky Mountain J. Math. 36(3) (2006), 1027–1031.Google Scholar
Mordell, L. J., ‘The Diophantine equation ${x}^4+{y}^4=1$ in algebraic number fields’, Acta Arith. 14 (1967/1968), 347–355.CrossRefGoogle Scholar
Mordell, L. J., Diophantine Equations, Pure and Applied Mathematics, 30 (Academic Press, London–New York, 1969).Google Scholar
Rohrlich, D. E., ‘Points at infinity on the Fermat curves’, Invent. Math. 39(2) (1977), 95–127.CrossRefGoogle Scholar