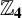 $\ \boldsymbol {\mathbb {Z}_{4}}$
$\ \boldsymbol {\mathbb {Z}_{4}}$Published online by Cambridge University Press: 03 June 2022
We present novel approaches for constructing linear codes over
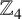 $\mathbb {Z}_{4}$
from the known ones. We obtain new linear codes, many of which are optimal. In particular, we find all optimal codes of type
$\mathbb {Z}_{4}$
from the known ones. We obtain new linear codes, many of which are optimal. In particular, we find all optimal codes of type
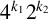 $4^{k_{1}}2^{k_{2}}$
for
$4^{k_{1}}2^{k_{2}}$
for
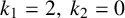 $k_{1}=2,~k_{2}=0$
and many optimal codes for
$k_{1}=2,~k_{2}=0$
and many optimal codes for
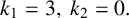 $k_{1}=3,~k_{2}=0.$
$k_{1}=3,~k_{2}=0.$
This research is supported by Institut Teknologi Bandung (ITB) and the Ministry of Education, Culture, Research and Technology (Kementerian Pendidikan, Kebudayaan, Riset dan Teknologi (Kemdikbud-ristek)), Republic of Indonesia.