No CrossRef data available.
Published online by Cambridge University Press: 13 September 2024
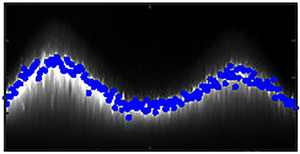
We study the behaviour of a particle bed immersed in water when a flow generated by an oscillating plate is induced above it. We first consider a rigid plate submerged and oscillated over a particle bed. During upward motion of the plate, a portion of the bed fails, allowing particle displacement, and the bed surface to deform into a heap. We have already determined the flow of the fluid above and within the bed. This work describes the particle motion within the failed region of the bed: when the particles are mobile, they follow the fluid. We depth average the balance of mass and obtain an evolution equation for the displacement of the bed surface. We solve this equation and compare the predictions with the measurements of surface displacement in earlier experiments on rigid square plates. We carry out new experiments to measure the surface displacements under elongated plates. Elongated rigid plates behave similarly to the rigid square ones. Flexible plates produce multiple heaps. We determine that the peaks of these heaps are correlated with the flexural modes of the plates and occur at points along the bed at which the fluid pressure has its extreme values. Different plate flexural modes, resulting in different numbers of heaps, are produced by driving the plate at different frequencies. The particle motion within the bed and heap evolution under a flexible plate can be roughly described by regarding it as two or more rigid plates. We test the predictions of the theory against experiments.