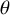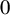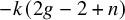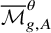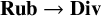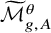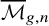1 Introduction
The strata of multiscale differentials are the loci
 $$ \begin{align*}\left\{(C,x_1,\cdots,x_n): (\omega^{\log})^{\otimes k}(\sum_{i=1}^n a_ix_i) \cong \mathcal{O}_C\right\} \end{align*} $$
$$ \begin{align*}\left\{(C,x_1,\cdots,x_n): (\omega^{\log})^{\otimes k}(\sum_{i=1}^n a_ix_i) \cong \mathcal{O}_C\right\} \end{align*} $$
in
![]() $\mathcal {M}_{g,n}$
for a vector
$\mathcal {M}_{g,n}$
for a vector
![]() $A = (a_1,\cdots ,a_n)$
of integers summing up to
$A = (a_1,\cdots ,a_n)$
of integers summing up to
![]() $-k(2g-2+n)$
. Extensions of these loci to the compactification
$-k(2g-2+n)$
. Extensions of these loci to the compactification
![]() $\overline {\mathcal {M}}_{g,n}$
have been the subject of a vast literature with different techniques and objectives. In its most algebraic incarnation, such an extension asks for a cycle
$\overline {\mathcal {M}}_{g,n}$
have been the subject of a vast literature with different techniques and objectives. In its most algebraic incarnation, such an extension asks for a cycle
of the expected dimension supported on the ‘double ramification locus’
of multiscale differentials for the partition A. The cycle
![]() $\mathsf {DR}^k_{g,A}$
is called the double ramification cycle, as when
$\mathsf {DR}^k_{g,A}$
is called the double ramification cycle, as when
![]() $k=0$
, it parametrizes functions ramified over two points of
$k=0$
, it parametrizes functions ramified over two points of
![]() $\mathbb {P}^1$
, namely zero and infinity. Even the definition of the cycle
$\mathbb {P}^1$
, namely zero and infinity. Even the definition of the cycle
![]() $\mathsf {DR}^k_{g,A}$
is subtle; the first rigorous definition was given in [Reference Graber and VakilGV05] for
$\mathsf {DR}^k_{g,A}$
is subtle; the first rigorous definition was given in [Reference Graber and VakilGV05] for
![]() $k=0$
via the relative Gromov-Witten theory of
$k=0$
via the relative Gromov-Witten theory of
![]() $\mathbb {P}^1$
, and in [Reference HolmesHol21, Reference Marcus and WiseMW20], in general, via Abel-Jacobi theory. Even subtler however is computing the class of
$\mathbb {P}^1$
, and in [Reference HolmesHol21, Reference Marcus and WiseMW20], in general, via Abel-Jacobi theory. Even subtler however is computing the class of
![]() $\mathsf {DR}^k_{g,A}$
in
$\mathsf {DR}^k_{g,A}$
in
![]() $\mathsf {CH}^g(\overline {\mathcal {M}}_{g,n})$
; what is meant by computing here is finding an expression of
$\mathsf {CH}^g(\overline {\mathcal {M}}_{g,n})$
; what is meant by computing here is finding an expression of
![]() $\mathsf {DR}^k_{g,A}$
in terms of generators of the tautological ring
$\mathsf {DR}^k_{g,A}$
in terms of generators of the tautological ring
![]() $\mathsf {R}^*(\overline {\mathcal {M}}_{g,n})$
. A remarkable such expression, known by now as Pixton’s formula, was discovered by Pixton and proven in [Reference Janda, Pandharipande, Pixton and ZvonkineJPPZ17].
$\mathsf {R}^*(\overline {\mathcal {M}}_{g,n})$
. A remarkable such expression, known by now as Pixton’s formula, was discovered by Pixton and proven in [Reference Janda, Pandharipande, Pixton and ZvonkineJPPZ17].
Perhaps surprisingly, the developments of [Reference Janda, Pandharipande, Pixton and ZvonkineJPPZ17] are not the final word on the subject. For instance, if one adopts the Gromov-Witten theory perspective, it is natural to ask for a calculation of the virtual fundamental class for (rubber) relative stable maps to
![]() $\mathbb {P}^2$
instead of
$\mathbb {P}^2$
instead of
![]() $\mathbb {P}^1$
, or in the multiscale language, for the corresponding classes and calculations of the ‘double double’ ramification loci
$\mathbb {P}^1$
, or in the multiscale language, for the corresponding classes and calculations of the ‘double double’ ramification loci
for two partitions
![]() $A,B$
of
$A,B$
of
![]() $k(2g-2+n)$
. For these problems, the methods of [Reference Janda, Pandharipande, Pixton and ZvonkineJPPZ17] have not been successfully adapted. To approach them, it has been understood ([Reference Holmes, Pixton and SchmittHPS19], [Reference RanganathanRan19], [Reference Holmes and SchwarzHS22], [Reference Molcho and RanganathanMR21], [Reference HerrHer19]) that one should study these problems in the context of logarithmic geometry. In this context, it is more natural to study instead the logarithmic double ramification cycle
$k(2g-2+n)$
. For these problems, the methods of [Reference Janda, Pandharipande, Pixton and ZvonkineJPPZ17] have not been successfully adapted. To approach them, it has been understood ([Reference Holmes, Pixton and SchmittHPS19], [Reference RanganathanRan19], [Reference Holmes and SchwarzHS22], [Reference Molcho and RanganathanMR21], [Reference HerrHer19]) that one should study these problems in the context of logarithmic geometry. In this context, it is more natural to study instead the logarithmic double ramification cycle
This is a certain refinement of
![]() $\mathsf {DR}^k_{g,A}$
, but it does not live on
$\mathsf {DR}^k_{g,A}$
, but it does not live on
![]() $\overline {\mathcal {M}}_{g,n}$
– or, better, it does not lie in
$\overline {\mathcal {M}}_{g,n}$
– or, better, it does not lie in
![]() $\mathsf {CH}(\overline {\mathcal {M}}_{g,n})$
, but rather in the logarithmic Chow ring
$\mathsf {CH}(\overline {\mathcal {M}}_{g,n})$
, but rather in the logarithmic Chow ring
![]() $\mathsf {logCH}(\overline {\mathcal {M}}_{g,n})$
([Reference BarrottBar18], [Reference Molcho, Pandharipande and SchmittMPS21]).
$\mathsf {logCH}(\overline {\mathcal {M}}_{g,n})$
([Reference BarrottBar18], [Reference Molcho, Pandharipande and SchmittMPS21]).
We will not define the
![]() $\mathsf {logDR}^k_{g,A}$
here (or the
$\mathsf {logDR}^k_{g,A}$
here (or the
![]() $\mathsf {DR}^k_{g,A}$
for that matter), but it is possible to explain the relevant aspects of the relationship between
$\mathsf {DR}^k_{g,A}$
for that matter), but it is possible to explain the relevant aspects of the relationship between
![]() $\mathsf {logDR}^k_{g,A}$
and
$\mathsf {logDR}^k_{g,A}$
and
![]() $\mathsf {DR}^k_{g,A}$
on general grounds. Let
$\mathsf {DR}^k_{g,A}$
on general grounds. Let
![]() $(X,D)$
be a smooth Deligne-Mumford stack with a normal crossings divisor D; the case of primary interest is of course
$(X,D)$
be a smooth Deligne-Mumford stack with a normal crossings divisor D; the case of primary interest is of course
![]() $X = \overline {\mathcal {M}}_{g,n}, D = \partial \overline {\mathcal {M}}_{g,n} = \overline {\mathcal {M}}_{g,n} - \mathcal {M}_{g,n}$
. The divisor D then stratifies X into the strata consisting of connected components of intersections
$X = \overline {\mathcal {M}}_{g,n}, D = \partial \overline {\mathcal {M}}_{g,n} = \overline {\mathcal {M}}_{g,n} - \mathcal {M}_{g,n}$
. The divisor D then stratifies X into the strata consisting of connected components of intersections
![]() $D_1 \cap \cdots \cap D_k$
of various irreducible components of D.Footnote
1
A simple blowup is the blowup of X along a smooth stratum closure. Such a blowup
$D_1 \cap \cdots \cap D_k$
of various irreducible components of D.Footnote
1
A simple blowup is the blowup of X along a smooth stratum closure. Such a blowup
![]() $p:X' \to X$
produces a new pair
$p:X' \to X$
produces a new pair
![]() $(X',D' = p^{-1}(D))$
. A blowup obtained by iterating this procedure a finite number of times is called an iterated blowup. A logarithmic modification of
$(X',D' = p^{-1}(D))$
. A blowup obtained by iterating this procedure a finite number of times is called an iterated blowup. A logarithmic modification of
![]() $(X,D)$
is any modificationFootnote
2
$(X,D)$
is any modificationFootnote
2
![]() $p:X' \to X$
which can be dominated by an iterated blowup of
$p:X' \to X$
which can be dominated by an iterated blowup of
![]() $(X,D)$
. Logarithmic modifications form an inverse system, with a map
$(X,D)$
. Logarithmic modifications form an inverse system, with a map
![]() $X" \to X'$
in the system if the modification
$X" \to X'$
in the system if the modification
![]() $X" \to X$
factors through
$X" \to X$
factors through
![]() $X' \to X$
. In this case, we say that
$X' \to X$
. In this case, we say that
![]() $X"$
is finer than
$X"$
is finer than
![]() $X'$
, or a refinement of it. The partial order determined by refinement yields a system of groups
$X'$
, or a refinement of it. The partial order determined by refinement yields a system of groups
![]() $\mathsf {CH}^{\text {op}}(X')$
indexed by Gysin pullback. Then
$\mathsf {CH}^{\text {op}}(X')$
indexed by Gysin pullback. Then
where
![]() $X' \to X$
ranges through logarithmic modifications of
$X' \to X$
ranges through logarithmic modifications of
![]() $(X,D)$
.Footnote
3
The ordinary Chow ring
$(X,D)$
.Footnote
3
The ordinary Chow ring
![]() $\mathsf {CH}(X)$
is contained in
$\mathsf {CH}(X)$
is contained in
![]() $\mathsf {logCH}(X)$
as a subring, and there is a retraction (which is not a ring homomorphism)
$\mathsf {logCH}(X)$
as a subring, and there is a retraction (which is not a ring homomorphism)
![]() $\mathsf {logCH}(X) \to \mathsf {CH}(X)$
by pushforward. Thus, to say that
$\mathsf {logCH}(X) \to \mathsf {CH}(X)$
by pushforward. Thus, to say that
![]() $\mathsf {logDR}^k_{g,A}$
is a nontrivial refinement of
$\mathsf {logDR}^k_{g,A}$
is a nontrivial refinement of
![]() $\mathsf {DR}^k_{g,A}$
in
$\mathsf {DR}^k_{g,A}$
in
![]() $\mathsf {logCH}(\overline {\mathcal {M}}_{g,n})$
is to say that
$\mathsf {logCH}(\overline {\mathcal {M}}_{g,n})$
is to say that
![]() $\mathsf {logDR}^k_{g,A} \notin \mathsf {CH}(\overline {\mathcal {M}}_{g,n}) \subset \mathsf {logCH}(\overline {\mathcal {M}}_{g,n})$
but its pushforward equals
$\mathsf {logDR}^k_{g,A} \notin \mathsf {CH}(\overline {\mathcal {M}}_{g,n}) \subset \mathsf {logCH}(\overline {\mathcal {M}}_{g,n})$
but its pushforward equals
![]() $\mathsf {DR}^k_{g,A}$
.
$\mathsf {DR}^k_{g,A}$
.
The ring
![]() $\mathsf {logCH}(X,D)$
is, apart from trivial cases, not finitely generated. However, any given element of it is determined by a finite amount of data: for each
$\mathsf {logCH}(X,D)$
is, apart from trivial cases, not finitely generated. However, any given element of it is determined by a finite amount of data: for each
![]() $x \in \mathsf {logCH}(X,D)$
, there exists some log modification
$x \in \mathsf {logCH}(X,D)$
, there exists some log modification
![]() $X' \to X$
and an element
$X' \to X$
and an element
![]() $x' \in \mathsf {CH}(X')$
so that
$x' \in \mathsf {CH}(X')$
so that
![]() $x = x'$
under the natural inclusion
$x = x'$
under the natural inclusion
![]() $\mathsf {CH}(X') \subset \mathsf {logCH}(X,D)$
. Such a pair
$\mathsf {CH}(X') \subset \mathsf {logCH}(X,D)$
. Such a pair
![]() $(X',x')$
is called a representative of x on
$(X',x')$
is called a representative of x on
![]() $X'$
. It is often the case, however, that several such representatives
$X'$
. It is often the case, however, that several such representatives
![]() $(X',x')$
exist, with none being preferable. For the sake of concreteness, one could have
$(X',x')$
exist, with none being preferable. For the sake of concreteness, one could have
![]() $(X_i',x_i'),i=1,2$
representing x, while by definition, there is a representative
$(X_i',x_i'),i=1,2$
representing x, while by definition, there is a representative
![]() $(X",x")$
dominating both, meaning
$(X",x")$
dominating both, meaning
![]() $p_i:X" \to X_i'$
is a modification and
$p_i:X" \to X_i'$
is a modification and
![]() $x"=p_i^*(x_i)$
; there may be no direct map
$x"=p_i^*(x_i)$
; there may be no direct map
![]() $X_1 \to X_2$
or vice versa.
$X_1 \to X_2$
or vice versa.
This is the case for
![]() $\mathsf {logDR}^k_{g,A}$
. Representatives of it can be found on any log modification
$\mathsf {logDR}^k_{g,A}$
. Representatives of it can be found on any log modification
![]() $p: \overline {\mathcal {M}}_{g,n}' \to \overline {\mathcal {M}}_{g,n}$
which is sufficiently fine in some sense that we do not make precise here, but which intuitively means that the closure of
$p: \overline {\mathcal {M}}_{g,n}' \to \overline {\mathcal {M}}_{g,n}$
which is sufficiently fine in some sense that we do not make precise here, but which intuitively means that the closure of
![]() $\mathsf {DRL}_{g,A}^k$
meets the boundary of
$\mathsf {DRL}_{g,A}^k$
meets the boundary of
![]() $\overline {\mathcal {M}}_{g,n}'$
sufficiently transversely. The log modifications
$\overline {\mathcal {M}}_{g,n}'$
sufficiently transversely. The log modifications
![]() $\overline {\mathcal {M}}_{g,n}'$
are, however, neither unique nor canonical, and there is no coarsest or finest log modification supporting a representative. So, in a sense, the ambiguity of choosing a representative is built into the
$\overline {\mathcal {M}}_{g,n}'$
are, however, neither unique nor canonical, and there is no coarsest or finest log modification supporting a representative. So, in a sense, the ambiguity of choosing a representative is built into the
![]() $\mathsf {logDR}^k_{g,A}$
problem.
$\mathsf {logDR}^k_{g,A}$
problem.
While the ambiguity of a representative of a class in
![]() $\mathsf {logCH}$
causes few conceptual difficulties, it can cause substantial ones on more practical matters. For instance, if one is interested in writing a formula for the class, several hurdles have to be overcome: from the offset, one must decide which generating set for the various
$\mathsf {logCH}$
causes few conceptual difficulties, it can cause substantial ones on more practical matters. For instance, if one is interested in writing a formula for the class, several hurdles have to be overcome: from the offset, one must decide which generating set for the various
![]() $\mathsf {CH}^{\text {op}}(X')$
to use. Fortunately, a good candidate for a generating set does exist, consisting of the Chow ring
$\mathsf {CH}^{\text {op}}(X')$
to use. Fortunately, a good candidate for a generating set does exist, consisting of the Chow ring
![]() $\mathsf {CH}(X)$
and the algebra of boundary strata of the various
$\mathsf {CH}(X)$
and the algebra of boundary strata of the various
![]() $X'$
, which is captured by combinatorial data: the algebra of piecewise polynomial functions on the tropicalization of X [Reference Molcho, Pandharipande and SchmittMPS21, Reference Molcho and RanganathanMR21, Reference BrionBri96, Reference PaynePay06, Reference Fulton and SturmfelsFS97]. Even so, while this choice of generating set determines the form of the answer, to write down an explicit formula, one generally needs to have precise control over the additional generators adjoined. In practice, this means choosing a representative
$X'$
, which is captured by combinatorial data: the algebra of piecewise polynomial functions on the tropicalization of X [Reference Molcho, Pandharipande and SchmittMPS21, Reference Molcho and RanganathanMR21, Reference BrionBri96, Reference PaynePay06, Reference Fulton and SturmfelsFS97]. Even so, while this choice of generating set determines the form of the answer, to write down an explicit formula, one generally needs to have precise control over the additional generators adjoined. In practice, this means choosing a representative
![]() $(X',x')$
with some sort of special presentation.
$(X',x')$
with some sort of special presentation.
Early approaches to the
![]() $\mathsf {logDR}^k_{g,A}$
focused on properties of the blowup
$\mathsf {logDR}^k_{g,A}$
focused on properties of the blowup
![]() $\overline {\mathcal {M}}_{g,n}' \to \overline {\mathcal {M}}_{g,n}$
supporting a representative. The idea here is that, since no best possible choice for
$\overline {\mathcal {M}}_{g,n}' \to \overline {\mathcal {M}}_{g,n}$
supporting a representative. The idea here is that, since no best possible choice for
![]() $\overline {\mathcal {M}}_{g,n}'$
exists, one might as well choose one that is fine enough that avoids as many pathologies as possible: choose an
$\overline {\mathcal {M}}_{g,n}'$
exists, one might as well choose one that is fine enough that avoids as many pathologies as possible: choose an
![]() $\overline {\mathcal {M}}_{g,n}'$
that is smooth, whose strata do not self-intersect, and so on. These approaches sufficed to prove soft properties of the
$\overline {\mathcal {M}}_{g,n}'$
that is smooth, whose strata do not self-intersect, and so on. These approaches sufficed to prove soft properties of the
![]() $\mathsf {logDR}^k_{g,A}$
, which depend on the form of the class; it was proven, for instance, that it is tautological [Reference Molcho and RanganathanMR21, Reference Holmes and SchwarzHS22]. But choosing least pathological models
$\mathsf {logDR}^k_{g,A}$
, which depend on the form of the class; it was proven, for instance, that it is tautological [Reference Molcho and RanganathanMR21, Reference Holmes and SchwarzHS22]. But choosing least pathological models
![]() $\overline {\mathcal {M}}_{g,n}'$
relies on abstract use of resolution of singularities, which makes the problem of finding an explicit formula essentially impossible.
$\overline {\mathcal {M}}_{g,n}'$
relies on abstract use of resolution of singularities, which makes the problem of finding an explicit formula essentially impossible.
In [Reference Holmes, Molcho, Pandharipande, Pixton and SchmittHMP+22], Pixton’s formula was extended to
![]() $\mathsf {logDR}^k_{g,A}$
. The strategy adopted there was in the opposite direction: the compactifications
$\mathsf {logDR}^k_{g,A}$
. The strategy adopted there was in the opposite direction: the compactifications
![]() $\overline {\mathcal {M}}_{g,n}'$
constructed were as closely tied with the geometry of the Abel-Jacobi section as possible. The reason for doing so was to connect the
$\overline {\mathcal {M}}_{g,n}'$
constructed were as closely tied with the geometry of the Abel-Jacobi section as possible. The reason for doing so was to connect the
![]() $\mathsf {logDR}^k_{g,A}$
with the DR cycle on the universal Picard stack, which had been calculated in [Reference Bae, Holmes, Pandharipande, Schmitt and SchwarzBHP+20] by a (rather elaborate) extension of the methods of [Reference Janda, Pandharipande, Pixton and ZvonkineJPPZ17]. The end result was, for each ‘universal stability condition’
$\mathsf {logDR}^k_{g,A}$
with the DR cycle on the universal Picard stack, which had been calculated in [Reference Bae, Holmes, Pandharipande, Schmitt and SchwarzBHP+20] by a (rather elaborate) extension of the methods of [Reference Janda, Pandharipande, Pixton and ZvonkineJPPZ17]. The end result was, for each ‘universal stability condition’
![]() $\theta $
[Reference Kass and PaganiKP19], which through works of [Reference Oda and SeshadriOS79, Reference CaporasoCap94, Reference Kass and PaganiKP19, Reference PandharipandePan96, Reference MeloMel19] produces a compactified Jacobian
$\theta $
[Reference Kass and PaganiKP19], which through works of [Reference Oda and SeshadriOS79, Reference CaporasoCap94, Reference Kass and PaganiKP19, Reference PandharipandePan96, Reference MeloMel19] produces a compactified Jacobian
![]() $\mathrm {Pic}^{\theta }$
, a log modification
$\mathrm {Pic}^{\theta }$
, a log modification
![]() $\overline {\mathcal {M}}_{g,A}^\theta \to \overline {\mathcal {M}}_{g,n}$
resolves the indeterminacies of the Abel-Jacobi section
$\overline {\mathcal {M}}_{g,A}^\theta \to \overline {\mathcal {M}}_{g,n}$
resolves the indeterminacies of the Abel-Jacobi section
The study of such resolutions was initiated in [Reference Abreu and PaciniAP21] via tropical methods, at least in the presence of some mild assumptions on the stability condition, but studying the problem logarithmically allows one to go further, by endowing
![]() $\overline {\mathcal {M}}_{g,A}^\theta $
with an explicit functor of points. In other words, the nonpathological compactifications
$\overline {\mathcal {M}}_{g,A}^\theta $
with an explicit functor of points. In other words, the nonpathological compactifications
![]() $\overline {\mathcal {M}}_{g,n}'$
were traded for modular ones. As the functor of points of
$\overline {\mathcal {M}}_{g,n}'$
were traded for modular ones. As the functor of points of
![]() $\overline {\mathcal {M}}_{g,A}^\theta $
can be understood completely explicitly when working logarithmically, this was sufficient to compute
$\overline {\mathcal {M}}_{g,A}^\theta $
can be understood completely explicitly when working logarithmically, this was sufficient to compute
![]() $\mathsf {logDR}^k_{g,A}$
on each
$\mathsf {logDR}^k_{g,A}$
on each
![]() $\overline {\mathcal {M}}_{g,A}^\theta $
.
$\overline {\mathcal {M}}_{g,A}^\theta $
.
However, the spaces
![]() $\overline {\mathcal {M}}_{g,A}^\theta $
are typically singular, and the calculation in [Reference Holmes, Molcho, Pandharipande, Pixton and SchmittHMP+22] expresses
$\overline {\mathcal {M}}_{g,A}^\theta $
are typically singular, and the calculation in [Reference Holmes, Molcho, Pandharipande, Pixton and SchmittHMP+22] expresses
![]() $\mathsf {logDR}^k_{g,A}$
as an operational class. Nevertheless, there are significant advantages to working with a nonsingular space. For instance, in [Reference Molcho and RanganathanMR21], the
$\mathsf {logDR}^k_{g,A}$
as an operational class. Nevertheless, there are significant advantages to working with a nonsingular space. For instance, in [Reference Molcho and RanganathanMR21], the
![]() $\mathsf {logDR}^k_{g,A}$
is approached via strict transforms and Segre classes and requires as inputs [Reference FultonFul98, Theorem 6.7] and [Reference AluffiAlu16], which do not work for singular toroidal spaces such as
$\mathsf {logDR}^k_{g,A}$
is approached via strict transforms and Segre classes and requires as inputs [Reference FultonFul98, Theorem 6.7] and [Reference AluffiAlu16], which do not work for singular toroidal spaces such as
![]() $\overline {\mathcal {M}}_{g,A}^\theta $
. Furthermore, ongoing work of Abreu-Pagani and myself aims to calculate the
$\overline {\mathcal {M}}_{g,A}^\theta $
. Furthermore, ongoing work of Abreu-Pagani and myself aims to calculate the
![]() $\mathsf {logDR}^k_{g,A}$
by Grothendieck-Riemann-Roch techniques, which require working with the class in the homological
$\mathsf {logDR}^k_{g,A}$
by Grothendieck-Riemann-Roch techniques, which require working with the class in the homological
![]() $\mathsf {CH}_*$
instead of the operational theory. For this approach, the singularities of
$\mathsf {CH}_*$
instead of the operational theory. For this approach, the singularities of
![]() $\overline {\mathcal {M}}_{g,A}^\theta $
cause difficulties.
$\overline {\mathcal {M}}_{g,A}^\theta $
cause difficulties.
The goal of this paper is to address these difficulties. For each universal stability condition
![]() $\theta $
, we construct a refinement
$\theta $
, we construct a refinement
and show the following:
Theorem 1.1. The stack
![]() $\widetilde {\mathcal {M}}_{g,A}^\theta $
is smooth. When
$\widetilde {\mathcal {M}}_{g,A}^\theta $
is smooth. When
![]() $\theta $
is nondegenerate, the induced map
$\theta $
is nondegenerate, the induced map
![]() $\widetilde {\mathcal {M}}_{g,A}^\theta \to \overline {\mathcal {M}}_{g,n}$
is a composition of a logarithmic modification with a root stack. Hence, it is proper, birational (an isomorphism over the compact type locus
$\widetilde {\mathcal {M}}_{g,A}^\theta \to \overline {\mathcal {M}}_{g,n}$
is a composition of a logarithmic modification with a root stack. Hence, it is proper, birational (an isomorphism over the compact type locus
![]() $\mathcal {M}_{g,n}^{\text {ct}})$
and of DM-type.
$\mathcal {M}_{g,n}^{\text {ct}})$
and of DM-type.
Furthermore, the refinement
![]() $\widetilde {\mathcal {M}}_{g,A}^\theta $
is modular:
$\widetilde {\mathcal {M}}_{g,A}^\theta $
is modular:
Theorem 1.2. Let S be a logarithmic scheme, and
![]() $S \to \overline {\mathcal {M}}_{g,n}$
be a logarithmic map, corresponding to a family of curves
$S \to \overline {\mathcal {M}}_{g,n}$
be a logarithmic map, corresponding to a family of curves
![]() $C \to S$
. Lifts of
$C \to S$
. Lifts of
![]() $S \to \widetilde {\mathcal {M}}_{g,A}^\theta $
correspond to pairs
$S \to \widetilde {\mathcal {M}}_{g,A}^\theta $
correspond to pairs
![]() $(C' \to C,\alpha )$
consisting of
$(C' \to C,\alpha )$
consisting of
-
• A destabilization
 $C' \to C$
,
$C' \to C$
, -
• An equidimensional piecewise linear function
 $\alpha $
on
$\alpha $
on
 $C'$
which twists
$C'$
which twists
 $(\omega ^{\log })^{\otimes k}(\sum a_ix_i)$
to a
$(\omega ^{\log })^{\otimes k}(\sum a_ix_i)$
to a
 $\theta $
-stable line bundle on
$\theta $
-stable line bundle on
 $C'$
.
$C'$
.
The notion of equidimensional piecewise linear function and twisting is explained in Section 4. Stability here is a minimality condition, also explained in 4, which ensures, among other things, finiteness of automorphisms groups. In particular, the strata of
![]() $\widetilde {\mathcal {M}}_{g,A}^\theta $
are entirely explicit and correspond to certain combinatorial/linear algebraic data, which we call
$\widetilde {\mathcal {M}}_{g,A}^\theta $
are entirely explicit and correspond to certain combinatorial/linear algebraic data, which we call
![]() $\theta $
-stable equidimensional flows. These are defined in 2.20.
$\theta $
-stable equidimensional flows. These are defined in 2.20.
In other words, the space
![]() $\widetilde {\mathcal {M}}_{g,A}^\theta $
is a ‘dream compactification’ of the double ramification problem: nonsingular and modular. In particular,
$\widetilde {\mathcal {M}}_{g,A}^\theta $
is a ‘dream compactification’ of the double ramification problem: nonsingular and modular. In particular,
![]() $\widetilde {\mathcal {M}}_{g,A}^\theta $
carries a universal family
$\widetilde {\mathcal {M}}_{g,A}^\theta $
carries a universal family
![]() $\widetilde {C}_{g,A}^\theta \to \widetilde {\mathcal {M}}_{g,A}^\theta $
and a universal line bundle
$\widetilde {C}_{g,A}^\theta \to \widetilde {\mathcal {M}}_{g,A}^\theta $
and a universal line bundle
![]() $\mathcal {L}$
on
$\mathcal {L}$
on
![]() $\widetilde {C}_{g,A}^\theta $
– that is, an Abel-Jacobi section
$\widetilde {C}_{g,A}^\theta $
– that is, an Abel-Jacobi section
The line bundle
![]() $\mathcal {L}$
is simply the pullback of the universal line bundle on
$\mathcal {L}$
is simply the pullback of the universal line bundle on
![]() $\mathrm {Pic}^\theta $
. The universal family
$\mathrm {Pic}^\theta $
. The universal family
![]() $\widetilde {C}_{g,A}^\theta $
is not the pullback but rather a blowup of the pullback of the universal family of
$\widetilde {C}_{g,A}^\theta $
is not the pullback but rather a blowup of the pullback of the universal family of
![]() $\mathrm {Pic}^\theta $
, which is also better behaved. Recall that a scheme is called quasi-smooth if every divisor is
$\mathrm {Pic}^\theta $
, which is also better behaved. Recall that a scheme is called quasi-smooth if every divisor is
![]() $\mathbb {Q}$
-Cartier. We have the following:
$\mathbb {Q}$
-Cartier. We have the following:
Theorem 1.3. The universal curve
![]() $\widetilde {C}_{g,A}^\theta $
is quasi-smooth.
$\widetilde {C}_{g,A}^\theta $
is quasi-smooth.
From the perspective of the semistable reduction theorems, this result is surprising. The semistable reduction theorem ensures that given a family of curves
![]() $C \to S$
, we can find blowups
$C \to S$
, we can find blowups
![]() $S' \to S$
and
$S' \to S$
and
![]() $C' \to C \times _S S'$
which are smooth; however, the blowup required on the base S depends on the family
$C' \to C \times _S S'$
which are smooth; however, the blowup required on the base S depends on the family
![]() $C \to S$
, which makes constructing the semistable family
$C \to S$
, which makes constructing the semistable family
![]() $C' \to S'$
explicitly very difficult in practice.
$C' \to S'$
explicitly very difficult in practice.
The connection with the double ramification cycle is as follows: when
![]() $\theta $
is nondegenerate and sufficiently close to the
$\theta $
is nondegenerate and sufficiently close to the
![]() $0$
stability condition,
$0$
stability condition,
![]() $\widetilde {\mathcal {M}}_{g,A}^\theta $
supports a representative of
$\widetilde {\mathcal {M}}_{g,A}^\theta $
supports a representative of
![]() $\mathsf {logDR}^k_{g,A}$
, and the methods of [Reference Holmes, Molcho, Pandharipande, Pixton and SchmittHMP+22] also apply.
$\mathsf {logDR}^k_{g,A}$
, and the methods of [Reference Holmes, Molcho, Pandharipande, Pixton and SchmittHMP+22] also apply.
Corollary 1.4. The universal
![]() $\mathsf {DR}$
formula for
$\mathsf {DR}$
formula for
![]() $\mathcal {L}$
computes the
$\mathcal {L}$
computes the
![]() $\mathsf {logDR}^k_{g,A}$
on
$\mathsf {logDR}^k_{g,A}$
on
![]() $\widetilde {\mathcal {M}}_{g,A}^\theta $
.
$\widetilde {\mathcal {M}}_{g,A}^\theta $
.
The smoothness of the spaces
![]() $\widetilde {\mathcal {M}}_{g,A}^\theta $
, however, also allows the use of alternative methods of calculation. This was, in fact, the main driver in writing the paper. Our motivations, ranked in order of confidence, can be listed as
$\widetilde {\mathcal {M}}_{g,A}^\theta $
, however, also allows the use of alternative methods of calculation. This was, in fact, the main driver in writing the paper. Our motivations, ranked in order of confidence, can be listed as
-
• Find a desingularization of
 $\overline {\mathcal {M}}_{g,A}^\theta $
in which one can calculate
$\overline {\mathcal {M}}_{g,A}^\theta $
in which one can calculate
 $\log \mathsf {DR}_{g,A}^k$
via traditional algebro-geometric techniques which avoid Gromov-Witten theory and localization.
$\log \mathsf {DR}_{g,A}^k$
via traditional algebro-geometric techniques which avoid Gromov-Witten theory and localization. -
• Highlight the following phenomenon:
 $\widetilde {\mathcal {M}}_{g,A}^\theta $
is constructed by combining two faraway ideas. Stability conditions from the universal Jacobian provide a compact space
$\widetilde {\mathcal {M}}_{g,A}^\theta $
is constructed by combining two faraway ideas. Stability conditions from the universal Jacobian provide a compact space
 $\overline {\mathcal {M}}_{g,A}^\theta $
. Techniques from stable maps then provide a desingularization relative to
$\overline {\mathcal {M}}_{g,A}^\theta $
. Techniques from stable maps then provide a desingularization relative to
 $\overline {\mathcal {M}}_{g,A}^\theta $
. We expect this phenomenon to be present in several moduli problems.
$\overline {\mathcal {M}}_{g,A}^\theta $
. We expect this phenomenon to be present in several moduli problems. -
• Optimize the computer calculations of
 $\log \mathsf {DR}_{g,A}^k$
.Footnote
4
Currently, the software deals with the singularities of
$\log \mathsf {DR}_{g,A}^k$
.Footnote
4
Currently, the software deals with the singularities of
 $\overline {\mathcal {M}}_{g,n}^\theta $
by desingularizing using a general desingularization algorithm for cones.
$\overline {\mathcal {M}}_{g,n}^\theta $
by desingularizing using a general desingularization algorithm for cones.
The construction of the spaces
![]() $\widetilde {\mathcal {M}}_{g,A}^\theta $
itself is, in fact, very simple. In the brilliant work of Marcus and Wise [Reference Marcus and WiseMW20], a modification
$\widetilde {\mathcal {M}}_{g,A}^\theta $
itself is, in fact, very simple. In the brilliant work of Marcus and Wise [Reference Marcus and WiseMW20], a modification
is constructed. The modification is not of finite type and is highly nonseparated; it is the universal modification which resolves the Abel-Jacobi section to the universal Picard stack
![]() $\mathbf {Pic}_{g,n}$
. Along with it, a further modification
$\mathbf {Pic}_{g,n}$
. Along with it, a further modification
is given, which is, up to orbifold corrections, a log modification as above. We briefly review these constructions in Section 6. The motivation of [Reference Marcus and WiseMW20] for these constructions is, in the case
![]() $k=0$
, to compare the double ramification locus
$k=0$
, to compare the double ramification locus
with the space of relative rubber maps to
![]() $\mathbb {P}^1$
, which is identified as
$\mathbb {P}^1$
, which is identified as
Our observation is simply that the spaces
![]() $\overline {\mathcal {M}}_{g,A}^\theta $
constructed in [Reference Holmes, Molcho, Pandharipande, Pixton and SchmittHMP+22] are open substacks of
$\overline {\mathcal {M}}_{g,A}^\theta $
constructed in [Reference Holmes, Molcho, Pandharipande, Pixton and SchmittHMP+22] are open substacks of
![]() $\mathbf {Div}_{g,A}$
, and that
$\mathbf {Div}_{g,A}$
, and that
![]() $\mathbf {Rub}_{g,A}$
is smooth. Combining the two properties gives the spaces
$\mathbf {Rub}_{g,A}$
is smooth. Combining the two properties gives the spaces
![]() $\widetilde {\mathcal {M}}_{g,A}^\theta $
as
$\widetilde {\mathcal {M}}_{g,A}^\theta $
as
Thus, the space
![]() $\widetilde {\mathcal {M}}_{g,A}^\theta $
is constructed by combining ideas from the theory of relative stable maps with universal stability conditions. Most of the work in the paper is devoted to understanding how this combination works – that is, what the functor of points of this fiber product is (a subtlety is that the fiber product is taken in the category of logarithmic schemes). The main technical tool that allows us to carry out this translation is the determination of a tropicalization of
$\widetilde {\mathcal {M}}_{g,A}^\theta $
is constructed by combining ideas from the theory of relative stable maps with universal stability conditions. Most of the work in the paper is devoted to understanding how this combination works – that is, what the functor of points of this fiber product is (a subtlety is that the fiber product is taken in the category of logarithmic schemes). The main technical tool that allows us to carry out this translation is the determination of a tropicalization of
![]() $\mathbf {Div}_{g,A}$
and the relevant auxiliary spaces. The tropicalization of
$\mathbf {Div}_{g,A}$
and the relevant auxiliary spaces. The tropicalization of
![]() $\mathbf {Div}_{g,A}$
is analogous to the tropicalization of the universal Jacobian, as discussed in [Reference Melo, Molcho, Ulirsch and VivianiMMUV22], and is perhaps of independent interest to tropical geometers. The analogy with the tropicalization of the universal Jacobian can, in fact, be made precise by recognizing
$\mathbf {Div}_{g,A}$
is analogous to the tropicalization of the universal Jacobian, as discussed in [Reference Melo, Molcho, Ulirsch and VivianiMMUV22], and is perhaps of independent interest to tropical geometers. The analogy with the tropicalization of the universal Jacobian can, in fact, be made precise by recognizing
![]() $\mathbf {Div}_{g,A}$
as the pullback of the universal Picard stack to
$\mathbf {Div}_{g,A}$
as the pullback of the universal Picard stack to
![]() $\overline {\mathcal {M}}_{g,n}$
via an Abel-Jacobi section, but we do not explore this direction here.
$\overline {\mathcal {M}}_{g,n}$
via an Abel-Jacobi section, but we do not explore this direction here.
The paper is roughly organized into three parts: combinatorial (Section 2), tropical Sections 3 and 4), and logarithmic (Sections 5 and 6). The parts are of increasing complexity, with the concepts in each part building upon the concepts in the preceding ones by endowing them with additional structure: metric structures turn combinatorial objects into tropical ones, and logarithmic structures turn tropical objects into algebraic ones.
Regardless, in its purest form, the map
![]() $\widetilde {\mathcal {M}}_{g,A}^\theta \to \overline {\mathcal {M}}_{g,n}$
is built by constructing a cone stack
$\widetilde {\mathcal {M}}_{g,A}^\theta \to \overline {\mathcal {M}}_{g,n}$
is built by constructing a cone stack
![]() $\Sigma _{\mathbf {Rub}_{g,A}^\theta }$
, which is identified with a subdivision of the tropicalization
$\Sigma _{\mathbf {Rub}_{g,A}^\theta }$
, which is identified with a subdivision of the tropicalization
![]() $\mathcal {M}_{g,n}^{\text {trop}}$
of
$\mathcal {M}_{g,n}^{\text {trop}}$
of
![]() $\overline {\mathcal {M}}_{g,n}$
(with an integral structure that is a finite index substructure of the induced one). This is constructed in Section 4. The cone stack
$\overline {\mathcal {M}}_{g,n}$
(with an integral structure that is a finite index substructure of the induced one). This is constructed in Section 4. The cone stack
![]() $\Sigma _{\mathbf {Rub}_{g,A}^\theta }$
is, in fact, a moduli space of tropical objects – tropical curves with piecewise linear functions on them that satisfy certain properties, which are discussed in Sections 3 and 4. The cones in
$\Sigma _{\mathbf {Rub}_{g,A}^\theta }$
is, in fact, a moduli space of tropical objects – tropical curves with piecewise linear functions on them that satisfy certain properties, which are discussed in Sections 3 and 4. The cones in
![]() $\Sigma _{\mathbf {Rub}_{g,A}^\theta }$
are indexed by the combinatorial data of Section 2. In fact, a cone in
$\Sigma _{\mathbf {Rub}_{g,A}^\theta }$
are indexed by the combinatorial data of Section 2. In fact, a cone in
![]() $\Sigma _{\mathbf {Rub}_{g,A}^\theta }$
can be thought of as parametrizing all possible ways to enrich a given combinatorial type with a metric structure. The space
$\Sigma _{\mathbf {Rub}_{g,A}^\theta }$
can be thought of as parametrizing all possible ways to enrich a given combinatorial type with a metric structure. The space
![]() $\widetilde {\mathcal {M}}_{g,A}^\theta $
is then built by algebraizing
$\widetilde {\mathcal {M}}_{g,A}^\theta $
is then built by algebraizing
![]() $\Sigma _{\mathbf {Rub}_{g,A}^\theta }$
via general techniques of logarithmic geometry, explained in Section 5. Section 6 is devoted to the analysis of the resulting algebraization and contains the final form of the results. Section 7 explains how to compute
$\Sigma _{\mathbf {Rub}_{g,A}^\theta }$
via general techniques of logarithmic geometry, explained in Section 5. Section 6 is devoted to the analysis of the resulting algebraization and contains the final form of the results. Section 7 explains how to compute
![]() $\Sigma _{\mathbf {Rub}_{g,A}^\theta }$
algorithmically, and Section 8 is devoted to an example. The reader is encouraged to skip ahead to the corresponding part of Sections 7 and 8 when coming upon an unfamiliar notion in the main sections, to see how it works in practice.
$\Sigma _{\mathbf {Rub}_{g,A}^\theta }$
algorithmically, and Section 8 is devoted to an example. The reader is encouraged to skip ahead to the corresponding part of Sections 7 and 8 when coming upon an unfamiliar notion in the main sections, to see how it works in practice.
2 Stable Flows
2.1 Graphs, divisors and flows
We begin with a short review of some essential notions from the theory of graphs. The notions are well-known, but we include them to avoid excessive referencing and to fix notation. We will follow the definitions of graphs and their morphisms from [Reference Melo, Molcho, Ulirsch and VivianiMMUV22], although we will substitute oriented edges in the place of half-edges in our presentation. Let
![]() $\Gamma $
be a graph. We write
$\Gamma $
be a graph. We write
![]() $V(\Gamma )$
for the set of vertices of
$V(\Gamma )$
for the set of vertices of
![]() $\Gamma $
,
$\Gamma $
,
![]() $\mathcal {E}(\Gamma )$
for the set of oriented edges,
$\mathcal {E}(\Gamma )$
for the set of oriented edges,
![]() $E(\Gamma )$
for the set of edges and
$E(\Gamma )$
for the set of edges and
![]() $L(\Gamma )$
for the set of legs. A genus function on
$L(\Gamma )$
for the set of legs. A genus function on
![]() $\Gamma $
is a function
$\Gamma $
is a function
The genus of
![]() $\Gamma $
is the natural number
$\Gamma $
is the natural number
When speaking about the genus of a graph, it is to be understood that a genus function has been specified. However, unless explicitly mentioned, our results do not require fixing the genus and apply equally well to graphs with or without a genus function. A marking on
![]() $\Gamma $
is a bijection between
$\Gamma $
is a bijection between
![]() $\{1,\cdots ,n\}$
and
$\{1,\cdots ,n\}$
and
![]() $L(\Gamma )$
. A graph with a marking is called an n-marked graph.
$L(\Gamma )$
. A graph with a marking is called an n-marked graph.
Definition 2.2. A divisor on
![]() $\Gamma $
is a formal
$\Gamma $
is a formal
![]() $\mathbb {Z}$
-linear combination of vertices of
$\mathbb {Z}$
-linear combination of vertices of
![]() $\Gamma $
. The group of divisors on
$\Gamma $
. The group of divisors on
![]() $\Gamma $
is denoted by
$\Gamma $
is denoted by
![]() $\mathsf {Div}(\Gamma )$
.
$\mathsf {Div}(\Gamma )$
.
Of course,
![]() $\mathsf {Div}(\Gamma )$
is nothing but the free abelian group
$\mathsf {Div}(\Gamma )$
is nothing but the free abelian group
![]() $\mathbb {Z}^{V(\Gamma )}$
on
$\mathbb {Z}^{V(\Gamma )}$
on
![]() $V(\Gamma )$
, but we insist on the notation for clarity.
$V(\Gamma )$
, but we insist on the notation for clarity.
Example 2.2.1. Let
![]() $\Gamma $
be an n-marked genus g graph. Let
$\Gamma $
be an n-marked genus g graph. Let
![]() $(a_1,\cdots ,a_n) \in \mathbb {Z}^n$
,
$(a_1,\cdots ,a_n) \in \mathbb {Z}^n$
,
![]() $k \in \mathbb {Z}$
. Let
$k \in \mathbb {Z}$
. Let
 $$\begin{align*}A = \sum_{v \in V(\Gamma)} k(2h_\Gamma(v)-2 + \text{val}(v))v + \sum_{i=1}^n a_iv_i, \end{align*}$$
$$\begin{align*}A = \sum_{v \in V(\Gamma)} k(2h_\Gamma(v)-2 + \text{val}(v))v + \sum_{i=1}^n a_iv_i, \end{align*}$$
where
![]() $\text {val}(v)$
is the valence of v – the number of oriented edges
$\text {val}(v)$
is the valence of v – the number of oriented edges
![]() $\vec {e}$
with
$\vec {e}$
with
![]() $\mathfrak {r}(\vec {e})=v$
plus the number of legs on v – and
$\mathfrak {r}(\vec {e})=v$
plus the number of legs on v – and
![]() $v_i$
is the vertex that contains the i-th leg. Then A is a divisor on
$v_i$
is the vertex that contains the i-th leg. Then A is a divisor on
![]() $\Gamma $
. When the
$\Gamma $
. When the
![]() $a_i$
are all
$a_i$
are all
![]() $0$
, A is called the log canonical divisor. When the
$0$
, A is called the log canonical divisor. When the
![]() $a_i$
are all
$a_i$
are all
![]() $-1$
, it is called the canonical divisor.
$-1$
, it is called the canonical divisor.
There is an evident two-to-one cover
![]() $\mathcal {E}(\Gamma ) \to E(\Gamma )$
from the set of oriented edges to the set of edges, and every choice of orientation
$\mathcal {E}(\Gamma ) \to E(\Gamma )$
from the set of oriented edges to the set of edges, and every choice of orientation
![]() $\vec {\Gamma }$
on
$\vec {\Gamma }$
on
![]() $\Gamma $
gives a section
$\Gamma $
gives a section
![]() $E(\Gamma ) \to \mathcal {E}(\Gamma )$
, whose image we denote by
$E(\Gamma ) \to \mathcal {E}(\Gamma )$
, whose image we denote by
![]() $E(\vec {\Gamma })$
.
$E(\vec {\Gamma })$
.
Definition 2.3. Given an oriented edge
![]() $\vec {e}$
, we write
$\vec {e}$
, we write
-
• e for the image of
 $\vec {e}$
in
$\vec {e}$
in
 $E(\Gamma )$
.
$E(\Gamma )$
. -
•
 for
for
 $\vec {e}$
with the opposite orientation.
$\vec {e}$
with the opposite orientation. -
•
 $\mathfrak {r}(\vec {e})$
for the initial point of
$\mathfrak {r}(\vec {e})$
for the initial point of
 $\vec {e}$
.
$\vec {e}$
. -
•
 for the terminal point of
for the terminal point of
 $\vec {e}$
.
$\vec {e}$
.
Definition 2.4. A flow on
![]() $\Gamma $
is a function
$\Gamma $
is a function
satisfying
![]() . We write
. We write
![]() $\mathsf {Flow}(\Gamma )$
for the group of flows on
$\mathsf {Flow}(\Gamma )$
for the group of flows on
![]() $\Gamma $
.
$\Gamma $
.
Of course, as above,
![]() $\mathsf {Flow}(\Gamma )$
can be identified with
$\mathsf {Flow}(\Gamma )$
can be identified with
![]() $\mathbb {Z}^{E(\vec {\Gamma })}$
after choosing an orientation on
$\mathbb {Z}^{E(\vec {\Gamma })}$
after choosing an orientation on
![]() $\Gamma $
.
$\Gamma $
.
Any flow on s on
![]() $\Gamma $
determines a divisor
$\Gamma $
determines a divisor
![]() $\mathsf {div}(s)$
on
$\mathsf {div}(s)$
on
![]() $\Gamma $
by setting
$\Gamma $
by setting
 $$ \begin{align*}\mathsf{ord}_v(s) = \sum_{\{\vec{e} : \mathfrak{t}(\vec{e}) = v\}} s(\vec{e}) \end{align*} $$
$$ \begin{align*}\mathsf{ord}_v(s) = \sum_{\{\vec{e} : \mathfrak{t}(\vec{e}) = v\}} s(\vec{e}) \end{align*} $$
and
Here, the notation
![]() $\{\vec {e}: \mathfrak {t}(\vec {e})=v\}$
means the set of oriented edges whose terminal point is v. This procedure gives a homomorphism
$\{\vec {e}: \mathfrak {t}(\vec {e})=v\}$
means the set of oriented edges whose terminal point is v. This procedure gives a homomorphism
Definition 2.5. Let
![]() $\Gamma $
be a graph. A basic subdivision of
$\Gamma $
be a graph. A basic subdivision of
![]() $\Gamma $
is a graph
$\Gamma $
is a graph
![]() $\Gamma '$
obtained from
$\Gamma '$
obtained from
![]() $\Gamma $
by replacing an oriented edge
$\Gamma $
by replacing an oriented edge
![]() $\vec {e}$
Footnote
5
with two oriented edges
$\vec {e}$
Footnote
5
with two oriented edges
![]() $\vec {e_1},\vec {e_2}$
and a new vertex u, and setting
$\vec {e_1},\vec {e_2}$
and a new vertex u, and setting
 $$ \begin{align*} \mathfrak{r}(\vec{e_1}) = \mathfrak{r}(\vec{e})\\ \mathfrak{t}(\vec{e_1}) = \mathfrak{r}(\vec{e_2}) = u \\ \mathfrak{t}(\vec{e_2}) = \mathfrak{t}(\vec{e}). \end{align*} $$
$$ \begin{align*} \mathfrak{r}(\vec{e_1}) = \mathfrak{r}(\vec{e})\\ \mathfrak{t}(\vec{e_1}) = \mathfrak{r}(\vec{e_2}) = u \\ \mathfrak{t}(\vec{e_2}) = \mathfrak{t}(\vec{e}). \end{align*} $$
There is an evident map
![]() $\Gamma ' \to \Gamma $
which sends
$\Gamma ' \to \Gamma $
which sends
![]() $e_1,e_2,u$
to e and all other vertices and edges to themselves.
$e_1,e_2,u$
to e and all other vertices and edges to themselves.
A subdivision of
![]() $\Gamma $
is a composition of basic subdivisions.
$\Gamma $
is a composition of basic subdivisions.
Let
![]() $\Gamma ' \to \Gamma $
be a subdivision. The additional vertices on
$\Gamma ' \to \Gamma $
be a subdivision. The additional vertices on
![]() $\Gamma '$
are called exceptional. A refinement of
$\Gamma '$
are called exceptional. A refinement of
![]() $\Gamma '$
is a further subdivision
$\Gamma '$
is a further subdivision
![]() $\Gamma " \to \Gamma '$
.
$\Gamma " \to \Gamma '$
.
Suppose
![]() $\Gamma ' \to \Gamma $
is a subdivision, and s is a flow on
$\Gamma ' \to \Gamma $
is a subdivision, and s is a flow on
![]() $\Gamma '$
. It is often desirable to find the minimal subdivision of
$\Gamma '$
. It is often desirable to find the minimal subdivision of
![]() $\Gamma $
on which s can be defined.
$\Gamma $
on which s can be defined.
Definition 2.6. We say that
![]() $\Gamma '$
is minimal with respect to s if
$\Gamma '$
is minimal with respect to s if
on all exceptional vertices v of
![]() $\Gamma '$
.
$\Gamma '$
.
Lemma 2.7. Suppose
![]() $\Gamma '$
is a subdivision of
$\Gamma '$
is a subdivision of
![]() $\Gamma $
, and s is a flow on
$\Gamma $
, and s is a flow on
![]() $\Gamma '$
. There is a unique minimal subdivision
$\Gamma '$
. There is a unique minimal subdivision
![]() $\Gamma _s \to \Gamma $
on which s can be defined.
$\Gamma _s \to \Gamma $
on which s can be defined.
Proof. Define
![]() $\Gamma _s$
as the subdivision of
$\Gamma _s$
as the subdivision of
![]() $\Gamma $
obtained by keeping only the exceptional vertices of
$\Gamma $
obtained by keeping only the exceptional vertices of
![]() $\Gamma '$
on which
$\Gamma '$
on which
Since the slope of s changes on the vertices v, any subdivision that supports s must refine
![]() $\Gamma _s$
, whereby the uniqueness of
$\Gamma _s$
, whereby the uniqueness of
![]() $\Gamma _s$
follows.
$\Gamma _s$
follows.
2.8 Equidimensionality
Let
![]() $\Gamma $
be a graph, and s a flow on
$\Gamma $
be a graph, and s a flow on
![]() $\Gamma $
. Then s defines a partial orientation on
$\Gamma $
. Then s defines a partial orientation on
![]() $\Gamma $
, by orienting the edges so that
$\Gamma $
, by orienting the edges so that
![]() $s(\vec {e})>0$
. The orientation is partial, as it is not defined on edges with
$s(\vec {e})>0$
. The orientation is partial, as it is not defined on edges with
![]() $s(e) = 0$
. We call such edges contracted. The flow s defines an honest orientation on the graph
$s(e) = 0$
. We call such edges contracted. The flow s defines an honest orientation on the graph
![]() $\overline {\Gamma }$
obtained from
$\overline {\Gamma }$
obtained from
![]() $\Gamma $
by contracting the contracted edges.
$\Gamma $
by contracting the contracted edges.
Definition 2.9. A flow s is called acyclic if the graph
![]() $\overline {\Gamma }$
has no oriented cycles for the orientation induced by s.
$\overline {\Gamma }$
has no oriented cycles for the orientation induced by s.
An acyclic flow s defines a partial order on the vertices of
![]() $\Gamma $
: the order is generated by the relation
$\Gamma $
: the order is generated by the relation
if
![]() $v,w$
are the endpoints of an oriented edge
$v,w$
are the endpoints of an oriented edge
![]() $\vec {e}$
from v to w in the orientation determined by s. Endpoints of contracted edges are not comparable to one another.
$\vec {e}$
from v to w in the orientation determined by s. Endpoints of contracted edges are not comparable to one another.
Definition 2.10. Let
![]() $\Gamma $
be a graph. An ordering on
$\Gamma $
be a graph. An ordering on
![]() $\Gamma $
is an acyclic flow s, together with the the choice of a total order among the vertices of the noncontracted edges of
$\Gamma $
is an acyclic flow s, together with the the choice of a total order among the vertices of the noncontracted edges of
![]() $\Gamma $
, extending the partial order determined by s. We say the ordering extends or is subordinate to s.
$\Gamma $
, extending the partial order determined by s. We say the ordering extends or is subordinate to s.
The flow s lifts to any subdivision
![]() $\Gamma ' \to \Gamma $
, by declaring
$\Gamma ' \to \Gamma $
, by declaring
![]() $s(\vec {e}_i)=s(\vec {e})$
whenever
$s(\vec {e}_i)=s(\vec {e})$
whenever
![]() $\vec {e} \in \mathcal {E}(\Gamma )$
is subdivided into
$\vec {e} \in \mathcal {E}(\Gamma )$
is subdivided into
![]() $\vec {e}_1,\cdots ,\vec {e_n}$
in
$\vec {e}_1,\cdots ,\vec {e_n}$
in
![]() $\Gamma '$
, and an ordering extending s on
$\Gamma '$
, and an ordering extending s on
![]() $\Gamma $
lifts to an ordering extending s on
$\Gamma $
lifts to an ordering extending s on
![]() $\Gamma '$
uniquely. We can rephrase the notion of ordering in the following convoluted way, which nevertheless will be meaningful in the next section:
$\Gamma '$
uniquely. We can rephrase the notion of ordering in the following convoluted way, which nevertheless will be meaningful in the next section:
Definition 2.11. A one-dimensional combinatorial target, or combinatorial line, is a graph X consisting of n-ordered vertices
![]() $v_1,\cdots ,v_n$
, with
$v_1,\cdots ,v_n$
, with
![]() $v_{i+1}$
joined to
$v_{i+1}$
joined to
![]() $v_i$
by a single edge
$v_i$
by a single edge
![]() $f_i$
, along with two legs – one on
$f_i$
, along with two legs – one on
![]() $v_1$
and one on
$v_1$
and one on
![]() $v_n$
.
$v_n$
.
One-dimensional combinatorial targets X come with a canonical orientation, in which
![]() $f_i$
is oriented from
$f_i$
is oriented from
![]() $v_i$
to
$v_i$
to
![]() $v_{i+1}$
. We denote the canonical orientation by
$v_{i+1}$
. We denote the canonical orientation by
![]() $E(\vec {X})$
.
$E(\vec {X})$
.
We can then consider maps
![]() $\Gamma \to X$
. Morphisms for us take cells into cells (i.e. vertices or edges into vertices or edges). A morphism
$\Gamma \to X$
. Morphisms for us take cells into cells (i.e. vertices or edges into vertices or edges). A morphism
![]() $\phi : \Gamma \to X$
also defines a partial order on
$\phi : \Gamma \to X$
also defines a partial order on
![]() $V(\Gamma )$
, by declaring
$V(\Gamma )$
, by declaring
![]() $v<w$
if
$v<w$
if
![]() $\phi (v) = v_i$
,
$\phi (v) = v_i$
,
![]() $\phi (w) = v_{j}$
, with
$\phi (w) = v_{j}$
, with
![]() $i < j$
. Vertices that map to the same vertex of X are incomparable with one another, and we do not define the order on vertices that map into edges of X. The following class of morphisms is then special:
$i < j$
. Vertices that map to the same vertex of X are incomparable with one another, and we do not define the order on vertices that map into edges of X. The following class of morphisms is then special:
Definition 2.12. A map
![]() $\Gamma \to X$
is equidimensional if it takes vertices to vertices.
$\Gamma \to X$
is equidimensional if it takes vertices to vertices.
Thus, an equidimensional morphism
![]() $\Gamma \to X$
defines a total order on the vertices of noncontracted edges (i.e., those edges which map to an edge instead of a vertex) of
$\Gamma \to X$
defines a total order on the vertices of noncontracted edges (i.e., those edges which map to an edge instead of a vertex) of
![]() $\Gamma $
.
$\Gamma $
.
Definition 2.13. Let
![]() $\Gamma $
be a graph, and s an acyclic flow on
$\Gamma $
be a graph, and s an acyclic flow on
![]() $\Gamma $
. An equidimensional lift of s is the data of a subdivision
$\Gamma $
. An equidimensional lift of s is the data of a subdivision
![]() $\Gamma ' \to \Gamma $
, a combinatorial line X and a morphism
$\Gamma ' \to \Gamma $
, a combinatorial line X and a morphism
![]() $\Gamma ' \to X$
compatible with the partial order on the vertices of
$\Gamma ' \to X$
compatible with the partial order on the vertices of
![]() $\Gamma '$
induced by (the lift of) s on
$\Gamma '$
induced by (the lift of) s on
![]() $\Gamma '$
. This data is stable if all vertices of X are images of vertices of
$\Gamma '$
. This data is stable if all vertices of X are images of vertices of
![]() $\Gamma $
.
$\Gamma $
.
We note that stability is not an absolute notion, but it depends on the original graph
![]() $\Gamma $
on which s is defined.
$\Gamma $
on which s is defined.
Suppose
![]() $\Gamma ' \to X$
is an equidimensional lift of s. Then
$\Gamma ' \to X$
is an equidimensional lift of s. Then
![]() $\Gamma ' \to X$
defines an ordering
$\Gamma ' \to X$
defines an ordering
![]() $\kappa $
extending s, as it orders the vertices of
$\kappa $
extending s, as it orders the vertices of
![]() $\Gamma '$
that lie on the noncontracted edges of
$\Gamma '$
that lie on the noncontracted edges of
![]() $\Gamma '$
(i.e., those on which
$\Gamma '$
(i.e., those on which
![]() $s \neq 0$
, which are precisely the subdivisions of the noncontracted edges of
$s \neq 0$
, which are precisely the subdivisions of the noncontracted edges of
![]() $\Gamma $
), and since
$\Gamma $
), and since
![]() $V(\Gamma ) \subset V(\Gamma ')$
, also the vertices of
$V(\Gamma ) \subset V(\Gamma ')$
, also the vertices of
![]() $\Gamma $
which lie on the noncontracted edges of
$\Gamma $
which lie on the noncontracted edges of
![]() $\Gamma $
. Conversely, given an ordering
$\Gamma $
. Conversely, given an ordering
![]() $\kappa $
extending s, we can define a combinatorial line
$\kappa $
extending s, we can define a combinatorial line
![]() $X_\kappa $
by taking one vertex
$X_\kappa $
by taking one vertex
![]() $v_i$
for each vertex of a noncontracted edge of
$v_i$
for each vertex of a noncontracted edge of
![]() $\Gamma $
according to the order determined by
$\Gamma $
according to the order determined by
![]() $\kappa $
. This defines an evident function
$\kappa $
. This defines an evident function
extending s. This is, however, not a morphism: edges of
![]() $\Gamma $
can map into unions of cells of
$\Gamma $
can map into unions of cells of
![]() $X_\kappa $
. There is a minimal subdivision
$X_\kappa $
. There is a minimal subdivision
![]() $\Gamma _\kappa $
which turns
$\Gamma _\kappa $
which turns
![]() $\Gamma \to X_\kappa $
into a morphism by adjoining the preimages of the vertices
$\Gamma \to X_\kappa $
into a morphism by adjoining the preimages of the vertices
![]() $\phi ^{-1}(v_i)$
to the noncontracted edges of
$\phi ^{-1}(v_i)$
to the noncontracted edges of
![]() $\Gamma _\kappa $
. The following lemma then follows:
$\Gamma _\kappa $
. The following lemma then follows:
Lemma 2.14. Orderings extending s are equivalent to stable equidimensional lifts of s, under the correspondence
2.15 Numerical stability conditions
Let
![]() $\Gamma $
be a graph.
$\Gamma $
be a graph.
Definition 2.16. A subdivision
![]() $\Gamma ' \to \Gamma $
is called a quasi-stable model of
$\Gamma ' \to \Gamma $
is called a quasi-stable model of
![]() $\Gamma $
if every edge in
$\Gamma $
if every edge in
![]() $\Gamma $
is subdivided at most once.
$\Gamma $
is subdivided at most once.
In other words, the subdivision
![]() $\Gamma ' \to \Gamma $
introduces at most one exceptional vertex on each edge of
$\Gamma ' \to \Gamma $
introduces at most one exceptional vertex on each edge of
![]() $\Gamma $
.
$\Gamma $
.
Definition 2.17. A divisor D on a quasi-stable model
![]() $\Gamma '$
of
$\Gamma '$
of
![]() $\Gamma $
is called admissible if its value on exceptional vertices is
$\Gamma $
is called admissible if its value on exceptional vertices is
![]() $1$
.
$1$
.
Finally, we recall that a stability condition
![]() $\theta $
on
$\theta $
on
![]() $\Gamma $
is simply a function
$\Gamma $
is simply a function
It is nondegenerate or generic if, for every
![]() $S \subset V(\Gamma )$
, we have
$S \subset V(\Gamma )$
, we have
where
![]() $\theta (S) = \sum _{v \in S} \theta (v)$
and
$\theta (S) = \sum _{v \in S} \theta (v)$
and
![]() $E(S,S^c)$
is the number of edges between S and its complement.
$E(S,S^c)$
is the number of edges between S and its complement.
A stability condition determines a list of semistable divisors on
![]() $\Gamma $
: those D for which
$\Gamma $
: those D for which
for all
![]() $S \subset V(\Gamma )$
. The divisor is stable if the inequalities are strict. Thus, a stability condition is nondegenerate if and only if all semistable divisors are stable.
$S \subset V(\Gamma )$
. The divisor is stable if the inequalities are strict. Thus, a stability condition is nondegenerate if and only if all semistable divisors are stable.
A stability condition on
![]() $\Gamma $
lifts canonically to a quasi-stable model
$\Gamma $
lifts canonically to a quasi-stable model
![]() $\Gamma ' \to \Gamma $
by declaring its value on exceptional vertices to be
$\Gamma ' \to \Gamma $
by declaring its value on exceptional vertices to be
![]() $0$
.
$0$
.
Definition 2.18. Let
![]() $\theta $
be a stability condition on
$\theta $
be a stability condition on
![]() $\Gamma $
, and
$\Gamma $
, and
![]() $\Gamma ' \to \Gamma $
a quasi-stable model. We call an admissible divisor D on
$\Gamma ' \to \Gamma $
a quasi-stable model. We call an admissible divisor D on
![]() $\Gamma '\ \theta $
-semistable if for every subgraph
$\Gamma '\ \theta $
-semistable if for every subgraph
![]() $S \subset \Gamma '$
, we have
$S \subset \Gamma '$
, we have
We note that if
![]() $\theta $
is generic, the inequalities above are strict for every divisor supported on
$\theta $
is generic, the inequalities above are strict for every divisor supported on
![]() $V(\Gamma ) \subset V(\Gamma ')$
. However, equality can hold for divisors that have support on exceptional vertices.Footnote
6
$V(\Gamma ) \subset V(\Gamma ')$
. However, equality can hold for divisors that have support on exceptional vertices.Footnote
6
We thus arrive at the key combinatorial notions of this paper. Let A denote a fixed divisor on
![]() $\Gamma $
, and
$\Gamma $
, and
![]() $\theta $
a stability condition.
$\theta $
a stability condition.
Definition 2.19. A
![]() $\theta $
-flow balancing A (or
$\theta $
-flow balancing A (or
![]() $\theta $
-flow for short) consists of a quasi-stable model
$\theta $
-flow for short) consists of a quasi-stable model
![]() $\Gamma ' \to \Gamma $
, a
$\Gamma ' \to \Gamma $
, a
![]() $\theta $
-semistable divisor D and an acyclic flow s with
$\theta $
-semistable divisor D and an acyclic flow s with
Definition 2.20. A
![]() $\theta $
-stable equidimensional flow (balancing A) consists of
$\theta $
-stable equidimensional flow (balancing A) consists of
-
• A quasi-stable model
 $\Gamma ' \to \Gamma $
.
$\Gamma ' \to \Gamma $
. -
• A
 $\theta $
-semistable divisor D on
$\theta $
-semistable divisor D on
 $\Gamma '$
.
$\Gamma '$
. -
• An acyclic flow s on
 $\Gamma '$
balancing D:
$\Gamma '$
balancing D:  $$ \begin{align*}\mathsf{div(s)} = A-D. \end{align*} $$
$$ \begin{align*}\mathsf{div(s)} = A-D. \end{align*} $$
-
• A stable equidimensional lift
 $\Gamma " \to X$
of s.
$\Gamma " \to X$
of s.
2.21 Specialization
The data discussed above specializes with respect to edge contractions. Namely, if
![]() $\overline {\Gamma }$
is obtained from
$\overline {\Gamma }$
is obtained from
![]() $\Gamma $
by contracting some edges, and
$\Gamma $
by contracting some edges, and
![]() $\phi : \Gamma \to \overline {\Gamma }$
denotes the contraction map,
$\phi : \Gamma \to \overline {\Gamma }$
denotes the contraction map,
-
(1) Divisors on
 $\Gamma $
specialize to divisors on
$\Gamma $
specialize to divisors on
 $\overline {\Gamma }$
by
$\overline {\Gamma }$
by
 $D \to \overline {D}$
$D \to \overline {D}$
 $$ \begin{align*}\overline{D}(v) = \sum_{w \in \phi^{-1}(v) \cap V(\Gamma)} D(w). \end{align*} $$
$$ \begin{align*}\overline{D}(v) = \sum_{w \in \phi^{-1}(v) \cap V(\Gamma)} D(w). \end{align*} $$
-
(2) Stability conditions specialize exactly analogously as
 $\overline {\theta }(v) = \sum \theta (w)$
.
$\overline {\theta }(v) = \sum \theta (w)$
. -
(3) Flows specialize by
 $s \to \overline {s}$
, with
$s \to \overline {s}$
, with  $$ \begin{align*}\overline{s}(\vec{e}) = s(\vec{e}) \end{align*} $$
$$ \begin{align*}\overline{s}(\vec{e}) = s(\vec{e}) \end{align*} $$
under the natural inclusion
 $\mathcal {E}(\overline {\Gamma }) \subset \mathcal {E}(\Gamma )$
.
$\mathcal {E}(\overline {\Gamma }) \subset \mathcal {E}(\Gamma )$
. -
(4) The genus function
 $h_{\overline {\Gamma }}$
of
$h_{\overline {\Gamma }}$
of
 $\overline {\Gamma }$
is defined by
$\overline {\Gamma }$
is defined by  $$\begin{align*}h_{\overline{\Gamma}}(v) = g_{\Gamma}(\phi^{-1}(v)) = \sum_{w \in V(\Gamma) \cap \phi^{-1}(v)} h_\Gamma(w) + \dim H_1(\phi^{-1}(v)). \end{align*}$$
$$\begin{align*}h_{\overline{\Gamma}}(v) = g_{\Gamma}(\phi^{-1}(v)) = \sum_{w \in V(\Gamma) \cap \phi^{-1}(v)} h_\Gamma(w) + \dim H_1(\phi^{-1}(v)). \end{align*}$$
All notions discussed, starting with subdivisions and culminating with
![]() $\theta $
-stable equidimensional flows, specialize under these definitions.
$\theta $
-stable equidimensional flows, specialize under these definitions.
Example 2.21.1. Let
![]() $\Gamma $
be an n-marked graph with a genus function
$\Gamma $
be an n-marked graph with a genus function
![]() $h_\Gamma $
. Let
$h_\Gamma $
. Let
![]() $(a_1,\cdots ,a_n) \in \mathbb {Z}^n$
,
$(a_1,\cdots ,a_n) \in \mathbb {Z}^n$
,
![]() $k \in \mathbb {Z}$
and
$k \in \mathbb {Z}$
and
 $$\begin{align*}A = \sum_{v \in V(\Gamma)} k(2h_\Gamma(v)-2 + \text{val}(v))v + \sum_{i=1}^n a_iv_i \end{align*}$$
$$\begin{align*}A = \sum_{v \in V(\Gamma)} k(2h_\Gamma(v)-2 + \text{val}(v))v + \sum_{i=1}^n a_iv_i \end{align*}$$
the divisor of example 2.2.1. Then A specializes to the analogous divisor
 $$\begin{align*}\sum_{v \in V(\overline{\Gamma})} k(2h_{\overline{\Gamma}}(v)-2 +\text{val}(v))v + \sum_{i=1}^na_i\overline{v}_i \end{align*}$$
$$\begin{align*}\sum_{v \in V(\overline{\Gamma})} k(2h_{\overline{\Gamma}}(v)-2 +\text{val}(v))v + \sum_{i=1}^na_i\overline{v}_i \end{align*}$$
under any contraction
![]() $\Gamma \to \overline {\Gamma }$
, where
$\Gamma \to \overline {\Gamma }$
, where
![]() $\overline {v}_i$
is the vertex of
$\overline {v}_i$
is the vertex of
![]() $\overline {\Gamma }$
that contains the i-th leg.
$\overline {\Gamma }$
that contains the i-th leg.
3 Abel-Jacobi Theory on Tropical Curves
The notions of the previous section are combinatorial. We extend them to tropical notions by introducing a metric on our graphs. We recall our convention: monoids M are sharp (they have no nontrivial units), finitely generated, integral and saturated. The category of monoids
![]() $\textbf {Mon}$
is dual to the category
$\textbf {Mon}$
is dual to the category
![]() $\textbf {RPC}$
of cones, which means rational polyhedral cones together with an integral structure, under the correspondence
$\textbf {RPC}$
of cones, which means rational polyhedral cones together with an integral structure, under the correspondence
 $$ \begin{align*} M \to M^{\vee}:= (\mathsf{Hom}(M,\mathbb{R}_{\ge 0}),\mathsf{Hom}(M,\mathbb{Z}))\\ \sigma^{\vee} = \{u \in \mathsf{Hom}(N,\mathbb{R}): u \ge 0 \text{ on }C\} \cap \mathsf{Hom}(N,\mathbb{Z}) \leftarrow \sigma = (C,N). \end{align*} $$
$$ \begin{align*} M \to M^{\vee}:= (\mathsf{Hom}(M,\mathbb{R}_{\ge 0}),\mathsf{Hom}(M,\mathbb{Z}))\\ \sigma^{\vee} = \{u \in \mathsf{Hom}(N,\mathbb{R}): u \ge 0 \text{ on }C\} \cap \mathsf{Hom}(N,\mathbb{Z}) \leftarrow \sigma = (C,N). \end{align*} $$
Let
![]() $\Gamma $
be a tropical curve metrized by a monoid M. In other words,
$\Gamma $
be a tropical curve metrized by a monoid M. In other words,
![]() $\Gamma $
is a graph together with a length function
$\Gamma $
is a graph together with a length function
from its set of edges to the nonzero elements of M. We denote the length of the edge e by
![]() $\ell _e$
.
$\ell _e$
.
Divisors and flows are combinatorial data and do not take into account the metric structure of
![]() $\Gamma $
. Piecewise linear functions on
$\Gamma $
. Piecewise linear functions on
![]() $\Gamma $
, however, are honest tropical notions:
$\Gamma $
, however, are honest tropical notions:
Definition 3.1. A piecewise linear function
![]() $\alpha $
is a function
$\alpha $
is a function
from the vertices of
![]() $\Gamma $
to the associated group of M, which satisfies the following condition: for every oriented edge
$\Gamma $
to the associated group of M, which satisfies the following condition: for every oriented edge
![]() $\vec {e}$
in
$\vec {e}$
in
![]() $\Gamma $
between
$\Gamma $
between
![]() $v,w \in \Gamma $
, there exists an integer
$v,w \in \Gamma $
, there exists an integer
![]() $s(\vec {e}) \in \mathbf Z$
such that
$s(\vec {e}) \in \mathbf Z$
such that
We write
![]() $\mathsf {PL}(\Gamma )$
for the group of piecewise linear functions on
$\mathsf {PL}(\Gamma )$
for the group of piecewise linear functions on
![]() $\Gamma $
.
$\Gamma $
.
Every piecewise linear function
![]() $\alpha $
on
$\alpha $
on
![]() $\Gamma $
determines a flow
$\Gamma $
determines a flow
![]() $s_\alpha $
by taking its underlying slopes:
$s_\alpha $
by taking its underlying slopes:
 $$ \begin{align*} \mathsf{PL}(\Gamma) \to \mathsf{Flow}(\Gamma)\\ \alpha \to s_{\alpha}, s_\alpha(\vec{e}) = \text{ slope of } \alpha \text{ on } \vec{e}. \end{align*} $$
$$ \begin{align*} \mathsf{PL}(\Gamma) \to \mathsf{Flow}(\Gamma)\\ \alpha \to s_{\alpha}, s_\alpha(\vec{e}) = \text{ slope of } \alpha \text{ on } \vec{e}. \end{align*} $$
In particular, we can talk about divisors of piecewise linear functions, orientations and so on, via the underlying flow. The flows that can arise from a piecewise linear function are constrained by the metric structure on
![]() $\Gamma $
.
$\Gamma $
.
Definition 3.2. We call a flow that arises as the underlying slopes of a piecewise linear function a twist on
![]() $\Gamma $
.
$\Gamma $
.
All flows that arise from piecewise linear functions are acyclic. The condition a flow must satisfy to be a twist, however, must involve the metric somehow. In short, we start with a flow s on
![]() $\Gamma $
and want to lift it to a function
$\Gamma $
and want to lift it to a function
![]() $\alpha $
. We can start at a vertex
$\alpha $
. We can start at a vertex
![]() $v \in \Gamma $
and assign a value of
$v \in \Gamma $
and assign a value of
![]() $\alpha (v) \in M^{\text {gp}}$
arbitrarily. But then, the rest of the values
$\alpha (v) \in M^{\text {gp}}$
arbitrarily. But then, the rest of the values
![]() $\alpha (w)$
are completely determined by the lengths of
$\alpha (w)$
are completely determined by the lengths of
![]() $\Gamma $
and the slopes of s (provided
$\Gamma $
and the slopes of s (provided
![]() $\Gamma $
is connected). For any oriented path
$\Gamma $
is connected). For any oriented path
![]() $P_{v \to w}$
from v to a vertex w, we must have
$P_{v \to w}$
from v to a vertex w, we must have
 $$\begin{align*}\alpha(w) = \alpha(v) + \sum_{\vec{e} \in P_{v \to w}} s(\vec{e})\ell_e, \end{align*}$$
$$\begin{align*}\alpha(w) = \alpha(v) + \sum_{\vec{e} \in P_{v \to w}} s(\vec{e})\ell_e, \end{align*}$$
and the function
![]() $\alpha $
is well-defined if and only if this expression is independent of path. This condition is most conveniently phrased in terms of the intersection pairing
$\alpha $
is well-defined if and only if this expression is independent of path. This condition is most conveniently phrased in terms of the intersection pairing
 $$ \begin{align*} \left \langle, \right \rangle : \mathsf{Flow}(\Gamma) \times \mathsf{Flow}(\Gamma) \to M^{\text{gp}} \\ \left \langle s, t \right \rangle = \frac{1}{2}\sum_{\vec{e} \in \mathcal{E}(\Gamma)} s(\vec{e})t(\vec{e})\ell_e. \end{align*} $$
$$ \begin{align*} \left \langle, \right \rangle : \mathsf{Flow}(\Gamma) \times \mathsf{Flow}(\Gamma) \to M^{\text{gp}} \\ \left \langle s, t \right \rangle = \frac{1}{2}\sum_{\vec{e} \in \mathcal{E}(\Gamma)} s(\vec{e})t(\vec{e})\ell_e. \end{align*} $$
In terms of the intersection pairing, the lifting problem amounts to the statement that for every
![]() $\gamma \in H_1(\Gamma )$
, we have
$\gamma \in H_1(\Gamma )$
, we have
Here,
![]() $H_1(\Gamma )$
is considered as embedded in
$H_1(\Gamma )$
is considered as embedded in
![]() $\mathsf {Flow}(\Gamma ) \cong \mathbb {Z}^{E(\vec {\Gamma })}$
after choosing an orientation, by writing a cycle
$\mathsf {Flow}(\Gamma ) \cong \mathbb {Z}^{E(\vec {\Gamma })}$
after choosing an orientation, by writing a cycle
![]() $\gamma $
as an oriented path
$\gamma $
as an oriented path
and associating to
![]() $\gamma $
the flow defined by
$\gamma $
the flow defined by
if
![]() $\vec {e}$
appears in the path with the same orientation as in
$\vec {e}$
appears in the path with the same orientation as in
![]() $\vec {\Gamma }$
, and
$\vec {\Gamma }$
, and
![]() $0$
if e is not in the path.
$0$
if e is not in the path.
Remark 3.3. This inclusion identifies
![]() $H_1(\Gamma )$
with the kernel of
$H_1(\Gamma )$
with the kernel of
This coincides with the usual identification of
![]() $H_1(\Gamma )$
with the kernel of
$H_1(\Gamma )$
with the kernel of
coming from the CW-complex structure on
![]() $\Gamma $
.
$\Gamma $
.
3.4 Subdivisions of tropical curves
Let
![]() $\Gamma $
be a tropical curve. A subdivision of
$\Gamma $
be a tropical curve. A subdivision of
![]() $\Gamma $
is a tropical curve
$\Gamma $
is a tropical curve
![]() $\Gamma '$
metrized by M, such that the underlying graph of
$\Gamma '$
metrized by M, such that the underlying graph of
![]() $\Gamma '$
is a subdivision of the underlying graph of
$\Gamma '$
is a subdivision of the underlying graph of
![]() $\Gamma $
and such that the lengths of the edges
$\Gamma $
and such that the lengths of the edges
![]() $e' \in E(\Gamma ')$
that subdivide an edge
$e' \in E(\Gamma ')$
that subdivide an edge
![]() $e \in E(\Gamma )$
add up to the length of e: if
$e \in E(\Gamma )$
add up to the length of e: if
![]() $\phi :E(\Gamma ') \to E(\Gamma )$
is the induced map of edges, we must have
$\phi :E(\Gamma ') \to E(\Gamma )$
is the induced map of edges, we must have
 $$ \begin{align*}\sum_{e' \in \phi^{-1}(e)} \ell_{e'} = \ell_e. \end{align*} $$
$$ \begin{align*}\sum_{e' \in \phi^{-1}(e)} \ell_{e'} = \ell_e. \end{align*} $$
Subdivisions
![]() $\Gamma '$
come with an evident map
$\Gamma '$
come with an evident map
![]() $\Gamma ' \to \Gamma $
. The collection of vertices in
$\Gamma ' \to \Gamma $
. The collection of vertices in
![]() $\Gamma '$
that are not in
$\Gamma '$
that are not in
![]() $\Gamma $
are called exceptional vertices. A refinenent of
$\Gamma $
are called exceptional vertices. A refinenent of
![]() $\Gamma ' \to \Gamma $
is a further subdivision
$\Gamma ' \to \Gamma $
is a further subdivision
![]() $\Gamma " \to \Gamma '$
.
$\Gamma " \to \Gamma '$
.
Suppose
![]() $\Gamma ' \to \Gamma $
is a subdivision, and
$\Gamma ' \to \Gamma $
is a subdivision, and
![]() $\alpha $
is a piecewise linear function on
$\alpha $
is a piecewise linear function on
![]() $\Gamma '$
. It is often desirable to find the minimal subdivision of
$\Gamma '$
. It is often desirable to find the minimal subdivision of
![]() $\Gamma $
on which
$\Gamma $
on which
![]() $\alpha $
can be defined.
$\alpha $
can be defined.
Definition 3.5. We say that
![]() $\Gamma '$
is minimal with respect to
$\Gamma '$
is minimal with respect to
![]() $\alpha $
if
$\alpha $
if
on all exceptional vertices v of
![]() $\Gamma '$
.
$\Gamma '$
.
Lemma 3.6. Suppose
![]() $\Gamma '$
is a subdivision of
$\Gamma '$
is a subdivision of
![]() $\Gamma $
, and
$\Gamma $
, and
![]() $\alpha $
is a piecewise linear function on
$\alpha $
is a piecewise linear function on
![]() $\Gamma '$
. There is a unique minimal subdivision
$\Gamma '$
. There is a unique minimal subdivision
![]() $\Gamma _\alpha \to \Gamma $
on which
$\Gamma _\alpha \to \Gamma $
on which
![]() $\alpha $
can be defined.
$\alpha $
can be defined.
Proof. Define
![]() $\Gamma _\alpha $
as the subdivision of
$\Gamma _\alpha $
as the subdivision of
![]() $\Gamma $
obtained by keeping only the exceptional vertices of
$\Gamma $
obtained by keeping only the exceptional vertices of
![]() $\Gamma '$
on which
$\Gamma '$
on which
Since the slope of
![]() $\alpha $
changes on the vertices v, any subdivision that supports
$\alpha $
changes on the vertices v, any subdivision that supports
![]() $\alpha $
must refine
$\alpha $
must refine
![]() $\Gamma _\alpha $
, whereby the uniqueness of
$\Gamma _\alpha $
, whereby the uniqueness of
![]() $\Gamma _\alpha $
follows.
$\Gamma _\alpha $
follows.
3.7 Equidimensional piecewise linear functions and twists
Any integral monoid
![]() $M \subset M^{\text {gp}}$
can be regarded as a partial order on
$M \subset M^{\text {gp}}$
can be regarded as a partial order on
![]() $M^{\text {gp}}$
: for
$M^{\text {gp}}$
: for
![]() $x,y \in M^{\text {gp}}$
, we declare
$x,y \in M^{\text {gp}}$
, we declare
![]() $x \le y$
if
$x \le y$
if
![]() $y - x \in M$
. Thus, a piecewise linear function
$y - x \in M$
. Thus, a piecewise linear function
![]() $\alpha $
on
$\alpha $
on
![]() $\Gamma $
comes with a partial ordering of its values
$\Gamma $
comes with a partial ordering of its values
![]() $\alpha (v) \in M^{\text {gp}}$
. This partial order is evidently compatible with the orientation on
$\alpha (v) \in M^{\text {gp}}$
. This partial order is evidently compatible with the orientation on
![]() $\Gamma $
induced by the underlying twist of
$\Gamma $
induced by the underlying twist of
![]() $\alpha $
.
$\alpha $
.
Definition 3.8. Let
![]() $\Gamma $
be a tropical curve. A piecewise linear function is totally ordered if its values
$\Gamma $
be a tropical curve. A piecewise linear function is totally ordered if its values
![]() $\alpha (v)$
,
$\alpha (v)$
,
![]() $v \in V(\Gamma )$
, are totally ordered.
$v \in V(\Gamma )$
, are totally ordered.
Remark 3.9. The condition that the values
![]() $\alpha (v)$
of the function
$\alpha (v)$
of the function
![]() $\alpha $
at the vertices v are totally ordered can be equivalently phrased in terms of the underlying flow s of
$\alpha $
at the vertices v are totally ordered can be equivalently phrased in terms of the underlying flow s of
![]() $\alpha $
. Since for any
$\alpha $
. Since for any
![]() $v,w$
we have that
$v,w$
we have that
 $$\begin{align*}\alpha(w) = \alpha(v) + \sum_{\vec{e} \in P_{v \to w}} s(\vec{e})\ell_e \end{align*}$$
$$\begin{align*}\alpha(w) = \alpha(v) + \sum_{\vec{e} \in P_{v \to w}} s(\vec{e})\ell_e \end{align*}$$
for any oriented path
![]() $P_{v \to w}$
, to say that
$P_{v \to w}$
, to say that
![]() $\alpha (w)$
comes after
$\alpha (w)$
comes after
![]() $\alpha (v)$
in a total order for
$\alpha (v)$
in a total order for
![]() $\alpha $
is to say that
$\alpha $
is to say that
 $$\begin{align*}\sum_{\vec{e} \in P_{v \to w}} s(\vec{e})\ell_e \in M \subset M^{\text{gp}} \end{align*}$$
$$\begin{align*}\sum_{\vec{e} \in P_{v \to w}} s(\vec{e})\ell_e \in M \subset M^{\text{gp}} \end{align*}$$
for any oriented path
![]() $P_{v \to w}$
, or, equivalently, that the evaluation
$P_{v \to w}$
, or, equivalently, that the evaluation
 $$\begin{align*}\sum_{\vec{e} \in P_{v \to w}} s(\vec{e})\ell_e(x) \ge 0 \end{align*}$$
$$\begin{align*}\sum_{\vec{e} \in P_{v \to w}} s(\vec{e})\ell_e(x) \ge 0 \end{align*}$$
for any
![]() $x \in \sigma = M^\vee $
.
$x \in \sigma = M^\vee $
.
Borrowing ideas from the theory of semistable reduction, we make the following definition.
Definition 3.10. A piecewise linear function
![]() $\alpha $
on
$\alpha $
on
![]() $\Gamma $
is equidimensional if
$\Gamma $
is equidimensional if
-
• The values
 $\alpha (v)$
are totally ordered.
$\alpha (v)$
are totally ordered. -
• For any edge e with endpoints
 $v,w$
that satisfy
$v,w$
that satisfy
 $\alpha (v)<\alpha (w)$
, and any vertex u with
$\alpha (v)<\alpha (w)$
, and any vertex u with
 $\alpha (v) \leq \alpha (u) \leq \alpha (w)$
, we necessarily have
$\alpha (v) \leq \alpha (u) \leq \alpha (w)$
, we necessarily have
 $\alpha (u) = \alpha (v)$
or
$\alpha (u) = \alpha (v)$
or
 $\alpha (u) = \alpha (w)$
.
$\alpha (u) = \alpha (w)$
.
While on its face the definition of equidimensionality seems dependent on the values of
![]() $\alpha $
, the definition is, in fact, invariant under translation of the values
$\alpha $
, the definition is, in fact, invariant under translation of the values
![]() $\alpha (v)$
by any common element
$\alpha (v)$
by any common element
![]() $x \in M^{\text {gp}}$
. Thus, the definition descends to twists, and it makes sense to talk about equidimensional twists.
$x \in M^{\text {gp}}$
. Thus, the definition descends to twists, and it makes sense to talk about equidimensional twists.
The definition of equidimensional piecewise linear function can perhaps be clarified by introducing its image, which is a one dimensional tropical target, also referred to as a tropical line.
Definition 3.11. A tropical line is the structure of a canonically orientedFootnote
7
one-dimensional polyhedral complex metrized by M on
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
We spell out the meaning of the definition: a tropical line is, thus, as a polyhedral complex, simply a combinatorial line X with a length assignment
![]() $\ell _{f_i} \in M-0$
for each of its edges. But to say that this polyhedral complex is a polyhedral complex structure on
$\ell _{f_i} \in M-0$
for each of its edges. But to say that this polyhedral complex is a polyhedral complex structure on
![]() $\mathbb {R}$
over M means that it furthermore comes with a chosen piecewise linear embedding
$\mathbb {R}$
over M means that it furthermore comes with a chosen piecewise linear embedding
This data is very similar to the definition of a piecewise linear function on a tropical curve: an element
for each vertex
![]() $v \in V(X)$
, such that
$v \in V(X)$
, such that
In particular, the ordering on the vertices has been chosen so that
![]() $\gamma _{i+1}>\gamma _i$
by assumption, which means that the piecewise linear structure is compatible with the canonical orientation
$\gamma _{i+1}>\gamma _i$
by assumption, which means that the piecewise linear structure is compatible with the canonical orientation
![]() $E(\vec {X})$
of definition 2.11 on X. We will also consider the trivial polyhedral decomposition as an allowable tropical line, where
$E(\vec {X})$
of definition 2.11 on X. We will also consider the trivial polyhedral decomposition as an allowable tropical line, where
![]() $\mathbb {R}$
is considered as a single cell. In that case, we will simply write
$\mathbb {R}$
is considered as a single cell. In that case, we will simply write
![]() $\mathbb {R}$
for the tropical line.
$\mathbb {R}$
for the tropical line.
Let
![]() $\Gamma $
be a tropical curve and X a tropical line metrized by M. By definition, a map of polyhedral complexes
$\Gamma $
be a tropical curve and X a tropical line metrized by M. By definition, a map of polyhedral complexes
![]() $\Gamma \to X$
is a piecewise linear map that respects the cell structure of the polyhedral decomposition: each cell (that is, vertex or edge) of
$\Gamma \to X$
is a piecewise linear map that respects the cell structure of the polyhedral decomposition: each cell (that is, vertex or edge) of
![]() $\Gamma $
maps into a cell of X (rather than a union of more than one cells). In particular, a piecewise linear function
$\Gamma $
maps into a cell of X (rather than a union of more than one cells). In particular, a piecewise linear function
![]() $\alpha $
on
$\alpha $
on
![]() $\Gamma $
can be tautologically thought of as a map
$\Gamma $
can be tautologically thought of as a map
to the trivial tropical line. The piecewise linear function
![]() $\alpha $
may or may not factor through X:
$\alpha $
may or may not factor through X:

Since
![]() $\iota _X$
is a monomorphism, the arrow
$\iota _X$
is a monomorphism, the arrow
![]() $\beta $
, if it exists, is unique.
$\beta $
, if it exists, is unique.
Definition 3.12. A map of polyhedral complexes
![]() $P \to Q$
is called equidimensional if it takes cells onto cells.
$P \to Q$
is called equidimensional if it takes cells onto cells.
As tropical curves and tropical lines are particularly simple examples of polyhedral complexes, the meaning of equidimensionality of a map
is very simple to describe: it says that each vertex
![]() $v \in \Gamma $
must map to a vertex in X.
$v \in \Gamma $
must map to a vertex in X.
Lemma 3.13. Let
![]() $\Gamma $
be a tropical curve metrized by M, and let
$\Gamma $
be a tropical curve metrized by M, and let
![]() $\alpha $
be a piecewise linear function on
$\alpha $
be a piecewise linear function on
![]() $\Gamma $
. Then
$\Gamma $
. Then
![]() $\alpha $
is equidimensional if, and only if, there exist a tropical line X and a factorization of
$\alpha $
is equidimensional if, and only if, there exist a tropical line X and a factorization of
![]() $\alpha $
through an equidimensional map
$\alpha $
through an equidimensional map
![]() $\beta : \Gamma \to X$
.
$\beta : \Gamma \to X$
.
Proof. Suppose e is an edge of
![]() $\Gamma $
with endpoints
$\Gamma $
with endpoints
![]() $v,w$
, and
$v,w$
, and
![]() $\alpha (w)> \alpha (v)$
. Suppose u is a vertex of
$\alpha (w)> \alpha (v)$
. Suppose u is a vertex of
![]() $\Gamma $
with
$\Gamma $
with
![]() $\alpha (v) \le \alpha (u) \le \alpha (w)$
. If
$\alpha (v) \le \alpha (u) \le \alpha (w)$
. If
![]() $\alpha $
factors through X, then
$\alpha $
factors through X, then
![]() $\beta (v)$
and
$\beta (v)$
and
![]() $\beta (w)$
must be consecutive vertices
$\beta (w)$
must be consecutive vertices
![]() $v_{i},v_{i+1}$
of X (otherwise, the edge e would map to a union of cells). But to say that
$v_{i},v_{i+1}$
of X (otherwise, the edge e would map to a union of cells). But to say that
![]() $\beta $
is equidimensional is to say that
$\beta $
is equidimensional is to say that
![]() $\beta (u)$
must be a vertex of X, and hence one of
$\beta (u)$
must be a vertex of X, and hence one of
![]() $v_{i},v_{i+1}$
. So either
$v_{i},v_{i+1}$
. So either
![]() $\alpha (u)=\alpha (v)$
or
$\alpha (u)=\alpha (v)$
or
![]() $\alpha (u)=\alpha (w)$
. Conversely, given an equidimensional function
$\alpha (u)=\alpha (w)$
. Conversely, given an equidimensional function
![]() $\alpha $
, we build X by taking one vertex
$\alpha $
, we build X by taking one vertex
![]() $v_i$
for each distinct value in {
$v_i$
for each distinct value in {
![]() $\alpha (v): v \in V(\Gamma )\}$
and define
$\alpha (v): v \in V(\Gamma )\}$
and define
to be the corresponding value.
Remark 3.14. Note that while the definition of equidimensionality requires that vertices of
![]() $\Gamma $
must map to vertices of X, edges can map either onto edges or vertices of X. Edges that map onto vertices of X are precisely those on which the slope of
$\Gamma $
must map to vertices of X, edges can map either onto edges or vertices of X. Edges that map onto vertices of X are precisely those on which the slope of
![]() $\alpha $
is
$\alpha $
is
![]() $0$
(i.e., the contracted edges). We point out that in order for a given
$0$
(i.e., the contracted edges). We point out that in order for a given
![]() $\alpha $
to factor through X (i.e., in order for
$\alpha $
to factor through X (i.e., in order for
![]() $\alpha = \iota _X \circ \beta $
to hold), strict constraints must hold between the lengths of the edges e of
$\alpha = \iota _X \circ \beta $
to hold), strict constraints must hold between the lengths of the edges e of
![]() $\Gamma $
and the edges f of X. Suppose
$\Gamma $
and the edges f of X. Suppose
![]() $\vec {f} \in E(\vec {X})$
is a canonically oriented edge of X (c.f. definition 2.11) between vertices
$\vec {f} \in E(\vec {X})$
is a canonically oriented edge of X (c.f. definition 2.11) between vertices
![]() $v_i$
and
$v_i$
and
![]() $v_{i+1}$
, and suppose an edge e of
$v_{i+1}$
, and suppose an edge e of
![]() $\Gamma $
maps to f. Then, orienting e so that
$\Gamma $
maps to f. Then, orienting e so that
![]() $s(\vec {e})> 0$
, we must have that
$s(\vec {e})> 0$
, we must have that
![]() $\beta $
maps the initial point
$\beta $
maps the initial point
![]() $\mathfrak {r}(\vec {e}) = v$
to
$\mathfrak {r}(\vec {e}) = v$
to
![]() $v_i$
and the terminal point
$v_i$
and the terminal point
![]() $\mathfrak {t}(\vec {e})=w$
to
$\mathfrak {t}(\vec {e})=w$
to
![]() $v_{i+1}$
, and furthermore,
$v_{i+1}$
, and furthermore,
Thus, in order for a given acyclic flow s to lift to an equidimensional twist with underlying combinatorial type
![]() $\Gamma \to X$
, the system of equations
$\Gamma \to X$
, the system of equations
needs to be satisfied. We note that this system of equations is stronger than the equations
![]() $\left \langle \gamma , s \right \rangle = 0$
required for the flow to lift to a twist: since X is contractible, the image of any loop
$\left \langle \gamma , s \right \rangle = 0$
required for the flow to lift to a twist: since X is contractible, the image of any loop
![]() $\gamma \in H_1(\Gamma )$
in X is an oriented path
$\gamma \in H_1(\Gamma )$
in X is an oriented path
![]() $P=\sum \vec {f}$
where each edge appears an equal number of times with opposite orientations. But then
$P=\sum \vec {f}$
where each edge appears an equal number of times with opposite orientations. But then
 $$\begin{align*}\left \langle s, \gamma \right \rangle = \sum_{\vec{e} \in \gamma} s(\vec{e})\ell_e = \sum_{\vec{f} \in P} o(\vec{f}) \ell_f = 0, \end{align*}$$
$$\begin{align*}\left \langle s, \gamma \right \rangle = \sum_{\vec{e} \in \gamma} s(\vec{e})\ell_e = \sum_{\vec{f} \in P} o(\vec{f}) \ell_f = 0, \end{align*}$$
where the
![]() $o(\vec {f})=1$
if
$o(\vec {f})=1$
if
![]() $\vec {f}$
is canonically oriented and
$\vec {f}$
is canonically oriented and
![]() $-1$
otherwise.
$-1$
otherwise.
Remark 3.15. The definition of equidimensionality may seem convoluted from the vantage of tropical curves metrized by monoids, but it is natural from the dual point of view of cone complexes and semistable reduction. We find the dual point of view more intuitive, but we stick with the tropical perspective as it is more ubiquitous in the literature. Namely, a tropical curve
![]() $\Gamma $
metrized by M is equivalent data to a map of cone complexes (with integral structure)
$\Gamma $
metrized by M is equivalent data to a map of cone complexes (with integral structure)
Plainly, one builds
![]() $\Sigma _C$
out of
$\Sigma _C$
out of
![]() $\Gamma $
as a fibration over
$\Gamma $
as a fibration over
![]() $\Sigma _S$
. The fiber over
$\Sigma _S$
. The fiber over
![]() $x \in \Sigma _S$
is obtained by attaching a vertex
$x \in \Sigma _S$
is obtained by attaching a vertex
![]() $v_x$
for each
$v_x$
for each
![]() $v \in V(\Gamma )$
and an edge of length
$v \in V(\Gamma )$
and an edge of length
![]() $\ell _e(x) \in \mathbb {R}_{\ge 0}$
for each
$\ell _e(x) \in \mathbb {R}_{\ge 0}$
for each
![]() $e \in E(\Gamma )$
. Then, a piecewise linear function
$e \in E(\Gamma )$
. Then, a piecewise linear function
![]() $\alpha $
on
$\alpha $
on
![]() $\Gamma $
corresponds to a piecewise linear map
$\Gamma $
corresponds to a piecewise linear map
![]() $\tilde {\alpha }$
$\tilde {\alpha }$

A tropical line X corresponds to a subdivision
![]() $\Sigma _X \to \Sigma _S \times \mathbb {R} \to \Sigma _S$
so that the composed map
$\Sigma _X \to \Sigma _S \times \mathbb {R} \to \Sigma _S$
so that the composed map
![]() $\Sigma _X \to \Sigma _S$
is equidimensional (maps cells onto cells) and furthermore sends integral structures onto integral structures, and an equidimensional piecewise linear function that factors through X corresponds to a factorization of
$\Sigma _X \to \Sigma _S$
is equidimensional (maps cells onto cells) and furthermore sends integral structures onto integral structures, and an equidimensional piecewise linear function that factors through X corresponds to a factorization of
![]() $\tilde {\alpha }$
through
$\tilde {\alpha }$
through
![]() $\Sigma _X$
that sends cells of
$\Sigma _X$
that sends cells of
![]() $\Sigma _C$
onto cells of
$\Sigma _C$
onto cells of
![]() $\Sigma _X$
. The name equidimensional comes from the fact that maps of fans which send cones onto cones are the ones that induce equidimensional maps of toric varieties.
$\Sigma _X$
. The name equidimensional comes from the fact that maps of fans which send cones onto cones are the ones that induce equidimensional maps of toric varieties.
Suppose
![]() $\alpha $
is a piecewise linear function or twist on
$\alpha $
is a piecewise linear function or twist on
![]() $\Gamma $
, and
$\Gamma $
, and
![]() $\Gamma ' \to \Gamma $
is a subdivision. Then
$\Gamma ' \to \Gamma $
is a subdivision. Then
![]() $\alpha $
lifts to a piecewise linear function on
$\alpha $
lifts to a piecewise linear function on
![]() $\Gamma '$
. Suppose
$\Gamma '$
. Suppose
![]() $\alpha $
is equidimensional on
$\alpha $
is equidimensional on
![]() $\Gamma '$
. We say that
$\Gamma '$
. We say that
![]() $\Gamma '$
is a minimal subdivision on which
$\Gamma '$
is a minimal subdivision on which
![]() $\alpha $
is equidimensional if the following stability condition holds:
$\alpha $
is equidimensional if the following stability condition holds:
![]() $(\star )$
For every exceptional vertex v of
$(\star )$
For every exceptional vertex v of
![]() $\Gamma '$
, there exists a nonexceptional vertex w of
$\Gamma '$
, there exists a nonexceptional vertex w of
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $\alpha (v) = \alpha (w)$
.
$\alpha (v) = \alpha (w)$
.
We remark that the minimal
![]() $\Gamma '$
on which
$\Gamma '$
on which
![]() $\alpha $
is equidimensional is, in general, finer than the minimal model
$\alpha $
is equidimensional is, in general, finer than the minimal model
![]() $\Gamma _\alpha $
on which
$\Gamma _\alpha $
on which
![]() $\alpha $
is defined. Furthermore, the model is unique if it exists. This is very similar to the combinatorial analogues in 2.14, but the tropical picture deviates here: a model where
$\alpha $
is defined. Furthermore, the model is unique if it exists. This is very similar to the combinatorial analogues in 2.14, but the tropical picture deviates here: a model where
![]() $\alpha $
becomes equidimensional may not exist, as the required combinatorial subdivisions may not lift with respect to the metric structure. Experts will recognize here that one can always find a minimal equidimensional model, but only after altering the base monoid M. However, one can say the following with relative ease:
$\alpha $
becomes equidimensional may not exist, as the required combinatorial subdivisions may not lift with respect to the metric structure. Experts will recognize here that one can always find a minimal equidimensional model, but only after altering the base monoid M. However, one can say the following with relative ease:
Lemma 3.16. Suppose that
![]() $\Gamma $
is a tropical curve with piecewise linear function
$\Gamma $
is a tropical curve with piecewise linear function
![]() $\alpha $
, and
$\alpha $
, and
![]() $\Gamma '$
is a subdivision on
$\Gamma '$
is a subdivision on
![]() $\Gamma $
on which
$\Gamma $
on which
![]() $\alpha $
is equidimensional. Then a minimal model
$\alpha $
is equidimensional. Then a minimal model
![]() $\mathsf {Eq}_{\Gamma }(\alpha )$
on which
$\mathsf {Eq}_{\Gamma }(\alpha )$
on which
![]() $\alpha $
is equidimensional exists.
$\alpha $
is equidimensional exists.
Proof. As in the construction of
![]() $\Gamma _\alpha $
, one obtains
$\Gamma _\alpha $
, one obtains
![]() $\mathsf {Eq}_\Gamma (\alpha )$
from
$\mathsf {Eq}_\Gamma (\alpha )$
from
![]() $\Gamma '$
by deleting all exceptional vertices in
$\Gamma '$
by deleting all exceptional vertices in
![]() $\Gamma '$
that violate
$\Gamma '$
that violate
![]() $(\star )$
.
$(\star )$
.
Definition 3.17. Suppose
![]() $\alpha $
is a piecewise linear function on
$\alpha $
is a piecewise linear function on
![]() $\Gamma $
, and that
$\Gamma $
, and that
![]() $\alpha $
lifts to an equidimensional function
$\alpha $
lifts to an equidimensional function
on some subdivision of
![]() $\Gamma $
. We call the lift stable if
$\Gamma $
. We call the lift stable if
![]() $\Gamma ' \to X$
is the minimal such lift (i.e., satisfies
$\Gamma ' \to X$
is the minimal such lift (i.e., satisfies
![]() $(\star )$
). We write
$(\star )$
). We write
for the minimal lift.
4 Tropical Moduli
This section closely follows [Reference Marcus and WiseMW20] in spirit, but in the tropical world.
4.1 Cone complexes and cone stacks
Since we want to build tropical moduli spaces parametrizing our objects – tropical curves with various types of piecewise linear functions on them – and our objects come with automorphisms, the notion of a cone complex is inadequate. Rather, we will use the formalism of cone stacks, developed in [Reference Cavalieri, Chan, Ulirsch and WiseCCUW20]. We recall only the very basics of the theory that we will use from loc. cit and refer the interested reader there for a comprehensive treatment.
A face morphism or face map of cones
![]() $\tau \to \sigma $
is an isomorphism of
$\tau \to \sigma $
is an isomorphism of
![]() $\tau $
with a face of
$\tau $
with a face of
![]() $\sigma $
. Note that in the definition we consider
$\sigma $
. Note that in the definition we consider
![]() $\sigma $
itself as a face, so arbitrary isomorphisms
$\sigma $
itself as a face, so arbitrary isomorphisms
![]() $\tau \to \sigma $
are considered face morphisms as well. A covering of a cone complex
$\tau \to \sigma $
are considered face morphisms as well. A covering of a cone complex
![]() $\Sigma $
by face morphisms is a collection of face maps
$\Sigma $
by face morphisms is a collection of face maps
![]() $\tau \to \Sigma $
that is jointly surjective. Such coverings generate a Grothendieck topology on the category of cone complexes. A cone stack is a stack on this site, with the (essentially straightforward) appropriate notion of algebraicity. Since face maps are, however, so simple, the notion of cone stack is, in fact, equivalent to the following much simpler definition [Reference Cavalieri, Chan, Ulirsch and WiseCCUW20][Proposition 2.19]:
$\tau \to \Sigma $
that is jointly surjective. Such coverings generate a Grothendieck topology on the category of cone complexes. A cone stack is a stack on this site, with the (essentially straightforward) appropriate notion of algebraicity. Since face maps are, however, so simple, the notion of cone stack is, in fact, equivalent to the following much simpler definition [Reference Cavalieri, Chan, Ulirsch and WiseCCUW20][Proposition 2.19]:
Definition 4.2. A cone stack is a category fibered in groupoids
where
![]() $\textbf {RPC}^f$
is the full subcategory of
$\textbf {RPC}^f$
is the full subcategory of
![]() $\textbf {RPC}$
with face maps as morphisms.
$\textbf {RPC}$
with face maps as morphisms.
Remark 4.3. Since the category of cones is equivalent to the category of monoids, we can consider
![]() $\Sigma $
equivalently as a category cofibered in groupoids over the category of monoids with morphisms being isomorphisms onto a quotient by a face. We will freely swap between conventions, as in our setup it is more convenient to work with the monoid M metrizing our tropical curves rather than its dual cone, but when writing
$\Sigma $
equivalently as a category cofibered in groupoids over the category of monoids with morphisms being isomorphisms onto a quotient by a face. We will freely swap between conventions, as in our setup it is more convenient to work with the monoid M metrizing our tropical curves rather than its dual cone, but when writing
![]() $\Sigma (M)$
, we formally mean the groupoid
$\Sigma (M)$
, we formally mean the groupoid
![]() $\Sigma (\sigma )$
, for
$\Sigma (\sigma )$
, for
![]() $\sigma = M^\vee $
.
$\sigma = M^\vee $
.
Most frequently, cone stacks natually arise as colimits. More precisely, suppose
![]() $\mathcal {D}$
is a category, and
$\mathcal {D}$
is a category, and
![]() $F: \mathcal {D} \to \textbf {RPC}^f$
is a functor. Concretely, this amounts to the data of cones
$F: \mathcal {D} \to \textbf {RPC}^f$
is a functor. Concretely, this amounts to the data of cones
![]() $\sigma _{\alpha }$
for
$\sigma _{\alpha }$
for
![]() $\alpha \in \text {Ob}(\mathcal {D})$
, and face morphisms
$\alpha \in \text {Ob}(\mathcal {D})$
, and face morphisms
![]() $u_{\alpha \to \beta }: \sigma _\alpha \to \sigma _\beta $
for any morphism
$u_{\alpha \to \beta }: \sigma _\alpha \to \sigma _\beta $
for any morphism
![]() $\alpha \to \beta $
in
$\alpha \to \beta $
in
![]() $\mathcal {D}$
. Then one constructs a cone stack
$\mathcal {D}$
. Then one constructs a cone stack
by taking the fiber over
![]() $\sigma $
to be the groupoid with objects
$\sigma $
to be the groupoid with objects
(the notation here means all
![]() $\textbf {RPC}$
morphisms, not just face morphisms) and with an isomorphism from
$\textbf {RPC}$
morphisms, not just face morphisms) and with an isomorphism from
![]() $\phi : \sigma \to \sigma _\alpha $
to
$\phi : \sigma \to \sigma _\alpha $
to
![]() $\psi :\sigma \to \sigma _\beta $
if there exists
$\psi :\sigma \to \sigma _\beta $
if there exists
![]() $\alpha \to \beta $
in
$\alpha \to \beta $
in
![]() $\mathcal {D}$
such that
$\mathcal {D}$
such that
![]() $u_{\alpha \to \beta } \circ \phi = \psi $
. We note that when all morphisms
$u_{\alpha \to \beta } \circ \phi = \psi $
. We note that when all morphisms
![]() $u_{\alpha \to \beta }$
appearing in
$u_{\alpha \to \beta }$
appearing in
![]() $F(\mathcal {D})$
are proper face morphisms (i.e., face morphisms to a proper face), the groupoid above is equivalent to a set. This way, one recovers the notion of generalized cone complexes of [Reference Abramovich, Caporaso and PayneACP15] or cone spaces of [Reference Cavalieri, Chan, Ulirsch and WiseCCUW20]. Moreover, when there exists at most one morphism between any two
$F(\mathcal {D})$
are proper face morphisms (i.e., face morphisms to a proper face), the groupoid above is equivalent to a set. This way, one recovers the notion of generalized cone complexes of [Reference Abramovich, Caporaso and PayneACP15] or cone spaces of [Reference Cavalieri, Chan, Ulirsch and WiseCCUW20]. Moreover, when there exists at most one morphism between any two
![]() $\sigma _\alpha \to \sigma _\beta $
, one gets an ordinary polyhedral complex. The following table, while simply an analogy, is perhaps helpful:
$\sigma _\alpha \to \sigma _\beta $
, one gets an ordinary polyhedral complex. The following table, while simply an analogy, is perhaps helpful:

Example 4.3.1. Fix a genus g and a number of markings n. There is a cone stack
![]() $\mathcal {M}_{g,n}^{\text {trop}} \to \mathbf {RPC}^f$
which over a cone
$\mathcal {M}_{g,n}^{\text {trop}} \to \mathbf {RPC}^f$
which over a cone
![]() $\sigma $
parametrizes genus g, n-marked curves
$\sigma $
parametrizes genus g, n-marked curves
![]() $\Gamma $
metrized by
$\Gamma $
metrized by
![]() $M = \sigma ^\vee $
, defined by
$M = \sigma ^\vee $
, defined by
For further details on the CFG structure, the interested reader is referred to [Reference Cavalieri, Chan, Ulirsch and WiseCCUW20].
4.4 Stacks of twists
We make the simplifying assumption that all graphs that appear have at least one leg.
Definition 4.5. We define cone stacks
by setting, for a cone
![]() $\sigma $
with dual monoid
$\sigma $
with dual monoid
![]() $M = \sigma ^\vee $
$M = \sigma ^\vee $
 $$ \begin{align*} \Sigma_{\textbf{Div}}(\sigma) = \{\Gamma, \alpha \in \mathsf{PL}(\Gamma)\} \\ \Sigma_{\textbf{Ord}}(\sigma) = \{\Gamma, \alpha \in \mathsf{PL}(\Gamma) \text{ which is totally ordered} \}\\ \Sigma_{\textbf{Rub}}(\sigma) = \{\Gamma, \alpha \in \mathsf{PL}(\Gamma), \mathsf{Eq}_\Gamma(\alpha) \to X \}, \end{align*} $$
$$ \begin{align*} \Sigma_{\textbf{Div}}(\sigma) = \{\Gamma, \alpha \in \mathsf{PL}(\Gamma)\} \\ \Sigma_{\textbf{Ord}}(\sigma) = \{\Gamma, \alpha \in \mathsf{PL}(\Gamma) \text{ which is totally ordered} \}\\ \Sigma_{\textbf{Rub}}(\sigma) = \{\Gamma, \alpha \in \mathsf{PL}(\Gamma), \mathsf{Eq}_\Gamma(\alpha) \to X \}, \end{align*} $$
where
-
•
 $\Gamma $
is metrized by M.
$\Gamma $
is metrized by M. -
•
 $\alpha $
vanishes on the vertex of
$\alpha $
vanishes on the vertex of
 $\Gamma $
containing the first leg.
$\Gamma $
containing the first leg.
Isomorphisms are isomorphism of graphs that respects the functions, orderings and equidimensional lifts.
Remark 4.6. The assumption that
![]() $\Gamma $
contains a leg is not serious, but we impose it to rigidify the problems above via the condition
$\Gamma $
contains a leg is not serious, but we impose it to rigidify the problems above via the condition
![]() $\alpha =0$
on the vertex. Otherwise, we have to talk about tropical line torsors, which we would rather avoid as all applications we have in mind involve curves that already have a marking.
$\alpha =0$
on the vertex. Otherwise, we have to talk about tropical line torsors, which we would rather avoid as all applications we have in mind involve curves that already have a marking.
Let
![]() $\textbf {CombDiv}$
be the category whose objects consist of a graph
$\textbf {CombDiv}$
be the category whose objects consist of a graph
![]() $\Gamma $
and an acyclic flow s. A map
$\Gamma $
and an acyclic flow s. A map
![]() $(\Gamma ,s) \to (\overline {\Gamma },\overline {s})$
in
$(\Gamma ,s) \to (\overline {\Gamma },\overline {s})$
in
![]() $\textbf {CombDiv}$
is given by a map
$\textbf {CombDiv}$
is given by a map
![]() $f: \Gamma \to \overline {\Gamma }$
, where
$f: \Gamma \to \overline {\Gamma }$
, where
![]() $\overline {\Gamma }$
is an edge contraction of
$\overline {\Gamma }$
is an edge contraction of
![]() $\Gamma $
, such that
$\Gamma $
, such that
![]() $\overline {s} \circ f = s$
(in particular, automorphisms respecting the flow are allowed). Similarly, we define
$\overline {s} \circ f = s$
(in particular, automorphisms respecting the flow are allowed). Similarly, we define
![]() $\textbf {CombOrd}$
to consist of pairs
$\textbf {CombOrd}$
to consist of pairs
![]() $(\Gamma ,s)$
and a total ordering
$(\Gamma ,s)$
and a total ordering
![]() $\kappa $
on
$\kappa $
on
![]() $\Gamma $
extending s, and
$\Gamma $
extending s, and
![]() $\textbf {CombRub}$
to consist of a pair
$\textbf {CombRub}$
to consist of a pair
![]() $(\Gamma ,s)$
and a stable equidimensional lift
$(\Gamma ,s)$
and a stable equidimensional lift
![]() $\Gamma ' \to X$
of s (2.13).
$\Gamma ' \to X$
of s (2.13).
For each
![]() $(\Gamma ,s) \in \textbf {CombDiv}$
, define a cone
$(\Gamma ,s) \in \textbf {CombDiv}$
, define a cone
consisting of the
![]() $\ell $
that satisfy the equations
$\ell $
that satisfy the equations
for all
![]() $\gamma \in H_1(\Gamma )$
. The pairing here is the intersection pairing of Section 3. By definition, the pairing requires a length on each edge of
$\gamma \in H_1(\Gamma )$
. The pairing here is the intersection pairing of Section 3. By definition, the pairing requires a length on each edge of
![]() $\Gamma $
. The subscript
$\Gamma $
. The subscript
![]() $\ell $
here means that on the point
$\ell $
here means that on the point
![]() $\ell = (\ell _{e})_{e \in E(\Gamma )}$
of
$\ell = (\ell _{e})_{e \in E(\Gamma )}$
of
![]() $\mathbb {R}_{\ge 0}^{E(\Gamma )}$
, we give the tautological length
$\mathbb {R}_{\ge 0}^{E(\Gamma )}$
, we give the tautological length
![]() $\ell _e$
to the edge e. Under a morphism
$\ell _e$
to the edge e. Under a morphism
![]() $(\Gamma ,s) \to (\overline {\Gamma },\overline {s})$
, we get a face morphism
$(\Gamma ,s) \to (\overline {\Gamma },\overline {s})$
, we get a face morphism
and so we may glue the cones into a cone stack
Similarly, as in the discussion in remark 3.14, for a triple
![]() $(\Gamma ,s,\Gamma ' \to X)$
in
$(\Gamma ,s,\Gamma ' \to X)$
in
![]() $\textbf {CombRub}$
, we take the cone
$\textbf {CombRub}$
, we take the cone
consisting of the
![]() $(\ell _{e},\ell _f)_{e \in E(\Gamma '),f \in E(X)}$
that satisfy
$(\ell _{e},\ell _f)_{e \in E(\Gamma '),f \in E(X)}$
that satisfy
whenever
![]() $\vec {e} \in \mathcal {E}(\Gamma ')$
maps to
$\vec {e} \in \mathcal {E}(\Gamma ')$
maps to
![]() $\vec {f}$
in
$\vec {f}$
in
![]() $E(\vec {X}) \subset \mathcal {E}(X)$
, and glue to a cone stack
$E(\vec {X}) \subset \mathcal {E}(X)$
, and glue to a cone stack
Finally, as in remark 3.9, for
![]() $(\Gamma ,s,\kappa ) \in \mathbf {CombOrd}$
, we take the cone
$(\Gamma ,s,\kappa ) \in \mathbf {CombOrd}$
, we take the cone
defined by the equations
for
![]() $\gamma \in H_1(\Gamma )$
, and the additional condition: for any two vertices
$\gamma \in H_1(\Gamma )$
, and the additional condition: for any two vertices
![]() $v,w$
such that w comes later than v in the ordering
$v,w$
such that w comes later than v in the ordering
![]() $\kappa $
, and an oriented path
$\kappa $
, and an oriented path
![]() $P_{v \to w}$
from v to w, we keep the lengths
$P_{v \to w}$
from v to w, we keep the lengths
![]() $\ell =(\ell _e)_{e \in E(\Gamma )} \subset \mathbb {R}_{\ge 0}^{E(\Gamma )}$
for which additionally,
$\ell =(\ell _e)_{e \in E(\Gamma )} \subset \mathbb {R}_{\ge 0}^{E(\Gamma )}$
for which additionally,
 $$\begin{align*}\sum_{\vec{e} \in P_{v \to w}} s(\vec{e})\ell_e \ge 0. \end{align*}$$
$$\begin{align*}\sum_{\vec{e} \in P_{v \to w}} s(\vec{e})\ell_e \ge 0. \end{align*}$$
Footnote
8
Equivalently, we can fix a minimal vertex
![]() $v_0$
for
$v_0$
for
![]() $\kappa $
, and an oriented path
$\kappa $
, and an oriented path
![]() $P_{v}$
from
$P_{v}$
from
![]() $v_0$
to v for each v, and keep the lengths
$v_0$
to v for each v, and keep the lengths
![]() $\ell $
such that
$\ell $
such that
 $$\begin{align*}\sum_{\vec{e} \in P_{v} } s(\vec{e})\ell_e \le \sum_{\vec{e} \in P_{w}} s(\vec{e})\ell_e \end{align*}$$
$$\begin{align*}\sum_{\vec{e} \in P_{v} } s(\vec{e})\ell_e \le \sum_{\vec{e} \in P_{w}} s(\vec{e})\ell_e \end{align*}$$
whenever
![]() $v \le w$
in the ordering
$v \le w$
in the ordering
![]() $\kappa $
(the advantage of doing so is that one has to consider fewer paths: one for each vertex v instead of one for each pair of vertices
$\kappa $
(the advantage of doing so is that one has to consider fewer paths: one for each vertex v instead of one for each pair of vertices
![]() $v,w$
). We glue these cones to a cone stack
$v,w$
). We glue these cones to a cone stack
Theorem 4.7. The cone stack
![]() $\Sigma _{\textbf {Div}}'$
represents the functor
$\Sigma _{\textbf {Div}}'$
represents the functor
![]() $\Sigma _{\textbf {Div}}$
, the cone stack
$\Sigma _{\textbf {Div}}$
, the cone stack
![]() $\Sigma _{\textbf {Ord}}'$
represents
$\Sigma _{\textbf {Ord}}'$
represents
![]() $\Sigma _{\textbf {Ord}}$
and the cone stack
$\Sigma _{\textbf {Ord}}$
and the cone stack
![]() $\Sigma _{\textbf {Rub}}'$
represents
$\Sigma _{\textbf {Rub}}'$
represents
![]() $\Sigma _{\textbf {Rub}}$
.
$\Sigma _{\textbf {Rub}}$
.
Proof. Let M be a monoid, with
![]() $M^\vee = \sigma $
. An element
$M^\vee = \sigma $
. An element
![]() $\Sigma _{\textbf {Div}}(M)$
is a tropical curve
$\Sigma _{\textbf {Div}}(M)$
is a tropical curve
![]() $\Gamma $
metrized by M, together with a piecewise linear function
$\Gamma $
metrized by M, together with a piecewise linear function
![]() $\alpha $
vanishing on the vertex containing the first leg. This data defines a map
$\alpha $
vanishing on the vertex containing the first leg. This data defines a map
 $$ \begin{align*} \sigma \to \mathbb{R}_{\ge 0}^{E(\Gamma)} \\ x \to (\ell_e(x)) \end{align*} $$
$$ \begin{align*} \sigma \to \mathbb{R}_{\ge 0}^{E(\Gamma)} \\ x \to (\ell_e(x)) \end{align*} $$
and an underlying flow
![]() $s_\alpha :=s$
. But the flow is a twist, and so
$s_\alpha :=s$
. But the flow is a twist, and so
is
![]() $0$
. So the
$0$
. So the
![]() $\ell _e(x)$
map into
$\ell _e(x)$
map into
![]() $\sigma _{(\Gamma ,s)}$
. Conversely, a map
$\sigma _{(\Gamma ,s)}$
. Conversely, a map
![]() $f: \sigma \to \sigma _{(\Gamma ,s)}$
defines a metric on
$f: \sigma \to \sigma _{(\Gamma ,s)}$
defines a metric on
![]() $\Gamma $
, by taking
$\Gamma $
, by taking
![]() $\ell _e \in M$
to be the composition
$\ell _e \in M$
to be the composition
of f with the e-th projection. The acyclic flow s is a twist on
![]() $\Gamma $
, since the lengths have been chosen so that the equations
$\Gamma $
, since the lengths have been chosen so that the equations
![]() $\left \langle s,\gamma \right \rangle = 0$
are satisfied. The twist only lifts to a piecewise linear function on
$\left \langle s,\gamma \right \rangle = 0$
are satisfied. The twist only lifts to a piecewise linear function on
![]() $\Gamma $
up to translation by an element of
$\Gamma $
up to translation by an element of
![]() $M^{\text {gp}}$
, but it lifts uniquely if we assume that its value is
$M^{\text {gp}}$
, but it lifts uniquely if we assume that its value is
![]() $0$
on the vertex containing the first leg. This shows
$0$
on the vertex containing the first leg. This shows
The proofs for
![]() $\textbf {Ord},\textbf {Rub}$
are similar, using the fact that the defining equations of the cones
$\textbf {Ord},\textbf {Rub}$
are similar, using the fact that the defining equations of the cones
![]() $\sigma _{(\Gamma ,s,\kappa )}$
and
$\sigma _{(\Gamma ,s,\kappa )}$
and
![]() $\sigma _{(\Gamma ,s,\Gamma ' \to \Gamma )}$
are, according to remarks 3.9 and 3.14, precisely the conditions necessary for s to lift to a totally ordered or equidimensional twist, respectively.
$\sigma _{(\Gamma ,s,\Gamma ' \to \Gamma )}$
are, according to remarks 3.9 and 3.14, precisely the conditions necessary for s to lift to a totally ordered or equidimensional twist, respectively.
There are evident maps
![]() $\Sigma _{\textbf {Rub}} \to \Sigma _{\textbf {Ord}} \to \Sigma _{\textbf {Div}}$
obtained by forgetting the additional structure at each step.
$\Sigma _{\textbf {Rub}} \to \Sigma _{\textbf {Ord}} \to \Sigma _{\textbf {Div}}$
obtained by forgetting the additional structure at each step.
Lemma 4.8. The map
![]() $\Sigma _{\textbf {Ord}} \to \Sigma _{\textbf {Div}}$
is a subdivision. The map
$\Sigma _{\textbf {Ord}} \to \Sigma _{\textbf {Div}}$
is a subdivision. The map
![]() $\Sigma _{\textbf {Rub}} \to \Sigma _{\textbf {Ord}}$
is a finite index inclusion.
$\Sigma _{\textbf {Rub}} \to \Sigma _{\textbf {Ord}}$
is a finite index inclusion.
Proof. We first look at
![]() $\Sigma _{\textbf {Ord}} \to \Sigma _{\textbf {Div}}$
. It is clear that the map is a monomorphism, so it suffices to show that the map is bijective on
$\Sigma _{\textbf {Ord}} \to \Sigma _{\textbf {Div}}$
. It is clear that the map is a monomorphism, so it suffices to show that the map is bijective on
![]() $\mathbb {N}$
points. Given a tropical curve
$\mathbb {N}$
points. Given a tropical curve
![]() $\Gamma $
with integer lengths, and an
$\Gamma $
with integer lengths, and an
![]() $\alpha : \Gamma \to \mathbb {R}$
, the values of
$\alpha : \Gamma \to \mathbb {R}$
, the values of
![]() $\alpha $
are elements of
$\alpha $
are elements of
![]() $\mathbb {Z}$
, and so automatically totally ordered.
$\mathbb {Z}$
, and so automatically totally ordered.
For the map
![]() $\Sigma _{\textbf {Rub}} \to \Sigma _{\textbf {Ord}}$
, it suffices to show that the map is bijective on
$\Sigma _{\textbf {Rub}} \to \Sigma _{\textbf {Ord}}$
, it suffices to show that the map is bijective on
![]() $\mathbb {Q}_{\ge 0}$
points. We start with an
$\mathbb {Q}_{\ge 0}$
points. We start with an
![]() $\alpha $
and an ordering
$\alpha $
and an ordering
![]() $\kappa $
of its values and build a tropical line X by taking one vertex
$\kappa $
of its values and build a tropical line X by taking one vertex
![]() $v_i$
for each distinct value
$v_i$
for each distinct value
![]() $\alpha (v)$
, with the ordering of
$\alpha (v)$
, with the ordering of
![]() $\kappa $
. We define an embedding
$\kappa $
. We define an embedding
![]() $\iota _X: X \to \mathbb {R}$
by
$\iota _X: X \to \mathbb {R}$
by
There is a map of topological spaces
![]() $\Gamma \to X$
, but it does not respect cell structures, as interior points of edges of
$\Gamma \to X$
, but it does not respect cell structures, as interior points of edges of
![]() $\Gamma $
map to vertices of X. We refine
$\Gamma $
map to vertices of X. We refine
![]() $\Gamma $
to
$\Gamma $
to
![]() $\Gamma '$
obtained by subdividing along the preimages of the vertices of X. This gives a stable equidimensional PL function on
$\Gamma '$
obtained by subdividing along the preimages of the vertices of X. This gives a stable equidimensional PL function on
![]() $\alpha $
.
$\alpha $
.
Remark 4.9. The argument in the proof essentially shows how the finite index inclusion in
![]() $\Sigma _{\textbf {Rub}} \to \Sigma _{\textbf {Ord}}$
arises. When subdividing
$\Sigma _{\textbf {Rub}} \to \Sigma _{\textbf {Ord}}$
arises. When subdividing
![]() $\Gamma $
to
$\Gamma $
to
![]() $\Gamma '$
, the new points may have rational coordinates; for instance, if an edge e from v to w has slope
$\Gamma '$
, the new points may have rational coordinates; for instance, if an edge e from v to w has slope
![]() $s(e)$
, and
$s(e)$
, and
![]() $\alpha (u)$
is an intermediate value between
$\alpha (u)$
is an intermediate value between
![]() $\alpha (v)$
and
$\alpha (v)$
and
![]() $\alpha (w)$
, the function
$\alpha (w)$
, the function
![]() $\alpha $
hits
$\alpha $
hits
![]() $\alpha (u)$
at the point
$\alpha (u)$
at the point
of e, and thus e needs to be subdivided there. This point is in
![]() $M_{\mathbb {Q}}^{\text {gp}}$
, but not necessarily in
$M_{\mathbb {Q}}^{\text {gp}}$
, but not necessarily in
![]() $M^{\text {gp}}$
.
$M^{\text {gp}}$
.
Lemma 4.10. The cone stack
![]() $\Sigma _{\textbf {Ord}}$
is simplicial and the cone stack
$\Sigma _{\textbf {Ord}}$
is simplicial and the cone stack
![]() $\Sigma _{\textbf {Rub}}$
is smooth.
$\Sigma _{\textbf {Rub}}$
is smooth.
Proof. It suffices to check that the cones
![]() $\sigma _{(\Gamma ,s,\Gamma ' \to X)}$
of
$\sigma _{(\Gamma ,s,\Gamma ' \to X)}$
of
![]() $\Sigma _{\textbf {Rub}}$
are isomorphic to
$\Sigma _{\textbf {Rub}}$
are isomorphic to
![]() $\mathbb {N}^k$
for some k. But the equations
$\mathbb {N}^k$
for some k. But the equations
for
![]() $\vec {e}$
mapping to
$\vec {e}$
mapping to
![]() $\vec {f} \in E(\vec {X})$
show that the coordinates of the noncontracted edges in
$\vec {f} \in E(\vec {X})$
show that the coordinates of the noncontracted edges in
![]() $E(\Gamma )$
are redundant, and the cone is, in fact, isomorphic to
$E(\Gamma )$
are redundant, and the cone is, in fact, isomorphic to
where
![]() $E^c(\Gamma )$
denotes the set of contracted edges of
$E^c(\Gamma )$
denotes the set of contracted edges of
![]() $\Gamma $
. The fact that
$\Gamma $
. The fact that
![]() $\Sigma _{\textbf {Ord}}$
is simplicial follows from the fact that its cones are isomorphic to those of
$\Sigma _{\textbf {Ord}}$
is simplicial follows from the fact that its cones are isomorphic to those of
![]() $\Sigma _{\textbf {Rub}}$
after tensoring with
$\Sigma _{\textbf {Rub}}$
after tensoring with
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
In fact, more can be said. From the isomorphism of the real points of a cone in
![]() $\Sigma _{\textbf {Ord}}$
with
$\Sigma _{\textbf {Ord}}$
with
![]() $\mathbb {R}_{\ge 0}^{E(X)} \times \mathbb {R}_{\ge 0}^{E^c(\Gamma )}$
, it follows that the rays (i.e., the one dimensional cones) in
$\mathbb {R}_{\ge 0}^{E(X)} \times \mathbb {R}_{\ge 0}^{E^c(\Gamma )}$
, it follows that the rays (i.e., the one dimensional cones) in
![]() $\Sigma _{\mathbf {Ord}}$
are precisely those that parametrize maps
$\Sigma _{\mathbf {Ord}}$
are precisely those that parametrize maps
![]() $\alpha $
consisting of
$\alpha $
consisting of
-
• Either a single contracted edge.
-
• Or, maps without contracted components to a target with exactly one edge.
In either case, the map
![]() $\alpha $
automatically lifts to an equidimensional one. Thus, the sublattice structure of
$\alpha $
automatically lifts to an equidimensional one. Thus, the sublattice structure of
![]() $\Sigma _{\textbf {Rub}}$
agrees with that of
$\Sigma _{\textbf {Rub}}$
agrees with that of
![]() $\Sigma _{\textbf {Ord}}$
on rays. Since
$\Sigma _{\textbf {Ord}}$
on rays. Since
![]() $\Sigma _{\textbf {Ord}}$
is simplicial, we obtain the following:
$\Sigma _{\textbf {Ord}}$
is simplicial, we obtain the following:
Corollary 4.11. Let
![]() $\sigma _{(\Gamma ,s,\kappa )}$
be a cone in
$\sigma _{(\Gamma ,s,\kappa )}$
be a cone in
![]() $\Sigma _{\textbf {Ord}}$
, and
$\Sigma _{\textbf {Ord}}$
, and
![]() $\sigma _{(\Gamma ,s,\Gamma ' \to X)}$
the corresponding cone in
$\sigma _{(\Gamma ,s,\Gamma ' \to X)}$
the corresponding cone in
![]() $\Sigma _{\textbf {Rub}}$
. The lattice of
$\Sigma _{\textbf {Rub}}$
. The lattice of
![]() $\sigma _{(\Gamma ,s,\Gamma ' \to X)}$
is the lattice freely generated by the primitive vectors along the rays of
$\sigma _{(\Gamma ,s,\Gamma ' \to X)}$
is the lattice freely generated by the primitive vectors along the rays of
![]() $\sigma _{(\Gamma ,s,\kappa )}$
.
$\sigma _{(\Gamma ,s,\kappa )}$
.
Proof. Since
![]() $\sigma _{(\Gamma ,s,\Gamma ' \to X)}$
is smooth (i.e., isomorphic to some
$\sigma _{(\Gamma ,s,\Gamma ' \to X)}$
is smooth (i.e., isomorphic to some
![]() $\mathbb {N}^k$
), its lattice must be the lattice generated by the primitive vectors along its rays. Since those primitive vectors are the same as the primitive vectors of
$\mathbb {N}^k$
), its lattice must be the lattice generated by the primitive vectors along its rays. Since those primitive vectors are the same as the primitive vectors of
![]() $\Sigma _{\textbf {Ord}}$
, the conclusion follows.
$\Sigma _{\textbf {Ord}}$
, the conclusion follows.
Thus,
![]() $\Sigma _{\textbf {Ord}}$
is in a certain sense a coarse moduli space of
$\Sigma _{\textbf {Ord}}$
is in a certain sense a coarse moduli space of
![]() $\Sigma _{\textbf {Rub}}$
: see, for example, [Reference Gillam and MolchoGM15, Subsection 3.2].
$\Sigma _{\textbf {Rub}}$
: see, for example, [Reference Gillam and MolchoGM15, Subsection 3.2].
4.12 Carving out small subcomplexes
The complexes
![]() $\Sigma _{\textbf {Div}}, \Sigma _{\textbf {Rub}}, \Sigma _{\textbf {Ord}}$
are very large: they are indexed by additional data over the category of all graphs, which is itself notoriously large. When algebraizing, as we will in the next section, the resulting schemes have infinitely many connected components and are highly nonseparated. Here, we want to impose several increasingly stringent conditions that carve out subcomplexes which algebraize to much more pleasant spaces.
$\Sigma _{\textbf {Div}}, \Sigma _{\textbf {Rub}}, \Sigma _{\textbf {Ord}}$
are very large: they are indexed by additional data over the category of all graphs, which is itself notoriously large. When algebraizing, as we will in the next section, the resulting schemes have infinitely many connected components and are highly nonseparated. Here, we want to impose several increasingly stringent conditions that carve out subcomplexes which algebraize to much more pleasant spaces.
First, we can, as usual, restrict our attention to genus g, n-marked graphs. We may then write
which decomposes
Similar descriptions are available for the order and rubber versions.
Given an n-marked graph
![]() $\Gamma $
, we can consider
$\Gamma $
, we can consider
![]() $n+1$
-marked graphs
$n+1$
-marked graphs
![]() $\Gamma _{c}$
, one for every cell c of
$\Gamma _{c}$
, one for every cell c of
![]() $\Gamma $
(vertex or edge), obtained by attaching a leg
$\Gamma $
(vertex or edge), obtained by attaching a leg
![]() $l_{n+1}$
on c when it is a vertex, and a bivalent vertex with a single leg
$l_{n+1}$
on c when it is a vertex, and a bivalent vertex with a single leg
![]() $l_{n+1}$
on c when it is an edge. A map
$l_{n+1}$
on c when it is an edge. A map
![]() $\Gamma _{c} \to \Gamma $
is obtained by deleting the latter vertex. There is a map
$\Gamma _{c} \to \Gamma $
is obtained by deleting the latter vertex. There is a map
which is an isomorphism when
![]() $c=v$
is a vertex, and which is the fiber product
$c=v$
is a vertex, and which is the fiber product

when e is an edge. Given a piecewise linear function
![]() $\alpha $
on
$\alpha $
on
![]() $\Gamma $
, with underlying flow
$\Gamma $
, with underlying flow
![]() $s=s_\alpha $
, it lifts canonically to a piecewise linear function on
$s=s_\alpha $
, it lifts canonically to a piecewise linear function on
![]() $\Gamma _c$
by not changing the slopes if e has been subdivided. The union of the cones
$\Gamma _c$
by not changing the slopes if e has been subdivided. The union of the cones
forms a subcomplex with a forgetful map to
![]() $\sigma _{(\Gamma ,s,n)}$
.
$\sigma _{(\Gamma ,s,n)}$
.
Lemma 4.13. The universal family of
![]() $\Sigma _{\mathbf {Div}_{n}}$
restricts to
$\Sigma _{\mathbf {Div}_{n}}$
restricts to
over
![]() $\sigma _{(\Gamma ,s,n)}$
.
$\sigma _{(\Gamma ,s,n)}$
.
Proof. Let
![]() $\mathcal {C} \to \Sigma _{\textbf {Div}_n}$
be the universal family, and
$\mathcal {C} \to \Sigma _{\textbf {Div}_n}$
be the universal family, and
![]() $\sigma $
a cone. A map
$\sigma $
a cone. A map
![]() $\sigma \to \mathcal {C}$
is a map
$\sigma \to \mathcal {C}$
is a map
![]() $\sigma \to \Sigma _{\textbf {Div}_n}$
, together with a section of
$\sigma \to \Sigma _{\textbf {Div}_n}$
, together with a section of
In other words, it consists of a tropical curve
![]() $\Gamma $
metrized by
$\Gamma $
metrized by
![]() $M = \sigma ^\vee $
, a piecewise linear function
$M = \sigma ^\vee $
, a piecewise linear function
![]() $\alpha $
and a section of
$\alpha $
and a section of
![]() $\Gamma $
. The section is a point of
$\Gamma $
. The section is a point of
![]() $\Gamma $
, which is either a vertex or lies on an edge. Sections that land in e are in bijection with subdivisions
$\Gamma $
, which is either a vertex or lies on an edge. Sections that land in e are in bijection with subdivisions
![]() $\Gamma '$
of
$\Gamma '$
of
![]() $\Gamma $
whose underlying graph is
$\Gamma $
whose underlying graph is
![]() $\Gamma _e$
, and are thus parametrized by the choice of lengths of the two pieces of e determined by the section. Since
$\Gamma _e$
, and are thus parametrized by the choice of lengths of the two pieces of e determined by the section. Since
![]() $\alpha $
lifts canonically to
$\alpha $
lifts canonically to
![]() $\Gamma '$
by not altering the slopes, the triples
$\Gamma '$
by not altering the slopes, the triples
![]() $(\Gamma ,\alpha ,\text {section through } e)$
are in bijection with maps
$(\Gamma ,\alpha ,\text {section through } e)$
are in bijection with maps
as claimed.
The analogous result does not hold for
![]() $\Sigma _{\textbf {Ord}}$
. The reason is that an ordering
$\Sigma _{\textbf {Ord}}$
. The reason is that an ordering
![]() $\kappa $
does not lift canonically to an ordering on the universal curve. All that can be said is that the universal curve of
$\kappa $
does not lift canonically to an ordering on the universal curve. All that can be said is that the universal curve of
![]() $\Sigma _{\textbf {Ord}}$
is the pullback of the universal curve of
$\Sigma _{\textbf {Ord}}$
is the pullback of the universal curve of
![]() $\Sigma _{\textbf {Div}}$
.
$\Sigma _{\textbf {Div}}$
.
The result is also false for
![]() $\Sigma _{\textbf {Rub}}$
, but a curious intermediate statement can be obtained. Points of
$\Sigma _{\textbf {Rub}}$
, but a curious intermediate statement can be obtained. Points of
![]() $\Sigma _{\textbf {Rub}}$
have more structure, contained in the map
$\Sigma _{\textbf {Rub}}$
have more structure, contained in the map
![]() $\Gamma ' \to X$
. Suppose
$\Gamma ' \to X$
. Suppose
![]() $\kappa $
is the induced ordering. The section of the universal curve in particular factors through some cell
$\kappa $
is the induced ordering. The section of the universal curve in particular factors through some cell
![]() $\Gamma ^{\prime }_c$
of
$\Gamma ^{\prime }_c$
of
![]() $\Gamma '$
now, and thus the ordering
$\Gamma '$
now, and thus the ordering
![]() $\kappa $
lifts canonically to
$\kappa $
lifts canonically to
![]() $\Gamma ^{\prime }_c$
: points in any cell of
$\Gamma ^{\prime }_c$
: points in any cell of
![]() $\Gamma '$
are in a unique order relative to
$\Gamma '$
are in a unique order relative to
![]() $\alpha $
. It follows that the universal curve of
$\alpha $
. It follows that the universal curve of
![]() $\Sigma _{\textbf {Rub}_n}$
factors through
$\Sigma _{\textbf {Rub}_n}$
factors through
![]() $\Sigma _{\textbf {Ord}_{n+1}} \to \Sigma _{\textbf {Div}_{n+1}}$
. However, it does not necessarily factor through
$\Sigma _{\textbf {Ord}_{n+1}} \to \Sigma _{\textbf {Div}_{n+1}}$
. However, it does not necessarily factor through
![]() $\Sigma _{\textbf {Rub}_{n+1}}$
. The reason is that while
$\Sigma _{\textbf {Rub}_{n+1}}$
. The reason is that while
![]() $\alpha $
and the total ordering lift canonically to
$\alpha $
and the total ordering lift canonically to
![]() $\Gamma ^{\prime }_c$
, the equidimensional lift
$\Gamma ^{\prime }_c$
, the equidimensional lift
does not. The induced map
is no longer equidimensional. Further subdivision of X and consequently of
![]() $\Gamma ^{\prime }_c$
is required, which may require extracting additional roots, as in 4.9. Nevertheless, the argument suffices to show the following:
$\Gamma ^{\prime }_c$
is required, which may require extracting additional roots, as in 4.9. Nevertheless, the argument suffices to show the following:
Lemma 4.14. The universal family of
![]() $\Sigma _{\textbf {Rub}}$
is simplicial.
$\Sigma _{\textbf {Rub}}$
is simplicial.
Remark 4.15. To get a smooth universal family, one can work instead with an alternative stack
![]() $\Sigma _{\textbf {AF}}$
Footnote
9
parametrizing (a strenghtening of) equidimensional maps on orbifold tropical curves. We do not introduce this here as
$\Sigma _{\textbf {AF}}$
Footnote
9
parametrizing (a strenghtening of) equidimensional maps on orbifold tropical curves. We do not introduce this here as
![]() $\Sigma _{\textbf {Rub}}$
is good enough for our purposes.
$\Sigma _{\textbf {Rub}}$
is good enough for our purposes.
We now continue our carving mission much more aggressively. As usual, we can fix the genus g of the graph, along with its n markings. This way, we obtain substacks
Next, we fix a universal stability condition
![]() $\theta $
[Reference Kass and PaganiKP19]. This means a stability condition for the universal family
$\theta $
[Reference Kass and PaganiKP19]. This means a stability condition for the universal family
![]() $\mathcal {C}_{g,n}^{\text {trop}} \to \mathcal {M}_{g,n}^{\text {trop}}$
of stable tropical curves: a numerical stability condition in the sense of Subsection 2.15 for each stable graph
$\mathcal {C}_{g,n}^{\text {trop}} \to \mathcal {M}_{g,n}^{\text {trop}}$
of stable tropical curves: a numerical stability condition in the sense of Subsection 2.15 for each stable graph
![]() $\Gamma $
of genus g with n legs, which are compatible with respect to all contractions of edges and automorphisms. We restrict to stable graphs here for simplicity but, in fact, a similar procedure even works for the cone stack of all genus g, n-marked tropical curves
$\Gamma $
of genus g with n legs, which are compatible with respect to all contractions of edges and automorphisms. We restrict to stable graphs here for simplicity but, in fact, a similar procedure even works for the cone stack of all genus g, n-marked tropical curves
![]() $\mathfrak {M}_{g,n}^{\text {trop}}$
.
$\mathfrak {M}_{g,n}^{\text {trop}}$
.
Let A be the divisor of example 2.2.1 associated to a vector
![]() $(a_1,\cdots ,a_n) \in \mathbb {Z}^n$
,
$(a_1,\cdots ,a_n) \in \mathbb {Z}^n$
,
![]() $k \in \mathbb {Z}$
, which is compatible with contractions according to example 2.21.1.
$k \in \mathbb {Z}$
, which is compatible with contractions according to example 2.21.1.

Figure 1 Above, a point of
![]() $\Sigma _{\textbf {Ord}}$
, representing a piecewise linear function
$\Sigma _{\textbf {Ord}}$
, representing a piecewise linear function
![]() $\alpha $
with
$\alpha $
with
![]() $\alpha (v)<\alpha (u)<\alpha (w)$
, and a lift to its universal family. The relation between
$\alpha (v)<\alpha (u)<\alpha (w)$
, and a lift to its universal family. The relation between
![]() $\alpha (u)$
and
$\alpha (u)$
and
![]() $\alpha (v_{n+1})$
on the universal family is undetermined. Below, an analogous point of
$\alpha (v_{n+1})$
on the universal family is undetermined. Below, an analogous point of
![]() $\Sigma _{\textbf {Rub}}$
. Here, the relation
$\Sigma _{\textbf {Rub}}$
. Here, the relation
![]() $\alpha (v_{n+1})<\alpha (u)=\alpha (u')$
is forced.
$\alpha (v_{n+1})<\alpha (u)=\alpha (u')$
is forced.
We write
![]() $\Sigma _{\mathbf {Div}_{g,A}^\theta } $
for the subcomplex of
$\Sigma _{\mathbf {Div}_{g,A}^\theta } $
for the subcomplex of
![]() $\Sigma _{\mathbf {Div}_{g,n}}$
consisting of the cones
$\Sigma _{\mathbf {Div}_{g,n}}$
consisting of the cones
![]() $\sigma _{(\Gamma ,s)}$
such that the graph
$\sigma _{(\Gamma ,s)}$
such that the graph
![]() $\Gamma $
is quasi-stable, and
$\Gamma $
is quasi-stable, and
![]() $D = A - \mathsf {div}(s)$
is
$D = A - \mathsf {div}(s)$
is
![]() $\theta $
-stable. In other words,
$\theta $
-stable. In other words,
![]() $(\Gamma ,s)$
is a
$(\Gamma ,s)$
is a
![]() $\theta $
-flow relative to the stabilization
$\theta $
-flow relative to the stabilization
![]() $\Gamma ^{\mathsf {st}}$
. We write
$\Gamma ^{\mathsf {st}}$
. We write
for the subcomplex consisting of
![]() $(\Gamma ,s,\kappa )$
with
$(\Gamma ,s,\kappa )$
with
![]() $\Gamma $
quasi-stable and
$\Gamma $
quasi-stable and
![]() $D = A - \mathsf {div}(s)\ \theta $
-stable, and
$D = A - \mathsf {div}(s)\ \theta $
-stable, and
for the subcomplex consisting of
![]() $(\Gamma ,s,\Gamma ' \to X)$
with
$(\Gamma ,s,\Gamma ' \to X)$
with
![]() $\Gamma $
quasi-stable,
$\Gamma $
quasi-stable,
![]() $D = A - \mathsf {div}(s)\ \theta $
-stable and
$D = A - \mathsf {div}(s)\ \theta $
-stable and
![]() $\Gamma ' \to X$
a stable equidimensional lift. In other words,
$\Gamma ' \to X$
a stable equidimensional lift. In other words,
![]() $(\Gamma ,s,\Gamma ' \to X)$
is a
$(\Gamma ,s,\Gamma ' \to X)$
is a
![]() $\theta $
-stable equidimensional flow relative to the stable graph
$\theta $
-stable equidimensional flow relative to the stable graph
![]() $\Gamma ^{\mathsf {st}}$
.
$\Gamma ^{\mathsf {st}}$
.
Lemma 4.16. The preimage of
![]() $\Sigma _{\mathbf {Div}_{g,A}^\theta }$
in
$\Sigma _{\mathbf {Div}_{g,A}^\theta }$
in
![]() $\Sigma _{\mathbf {Ord}_{g,n}}$
is
$\Sigma _{\mathbf {Ord}_{g,n}}$
is
![]() $\Sigma _{\mathbf {Ord}_{g,A}^\theta } $
, and the preimage of
$\Sigma _{\mathbf {Ord}_{g,A}^\theta } $
, and the preimage of
![]() $\Sigma _{\mathbf {Ord}_{g,A}^\theta }$
in
$\Sigma _{\mathbf {Ord}_{g,A}^\theta }$
in
![]() $\Sigma _{\mathbf {Rub}_{g,n}}$
is
$\Sigma _{\mathbf {Rub}_{g,n}}$
is
![]() $\Sigma _{\mathbf {Rub}_{g,A}^\theta } $
.
$\Sigma _{\mathbf {Rub}_{g,A}^\theta } $
.
Proof. The proof is immediate from the definition of the morphisms.
The space
![]() $\Sigma _{\mathbf {Div}^\theta _{g,A}}$
has a stabilization map to
$\Sigma _{\mathbf {Div}^\theta _{g,A}}$
has a stabilization map to
![]() $\mathcal {M}_{g,n}^{\text {trop}}$
. It is shown in theorem [Reference Holmes, Molcho, Pandharipande, Pixton and SchmittHMP+22, Theorem 23] that for nondegenerate
$\mathcal {M}_{g,n}^{\text {trop}}$
. It is shown in theorem [Reference Holmes, Molcho, Pandharipande, Pixton and SchmittHMP+22, Theorem 23] that for nondegenerate
![]() $\theta $
, this map factors isomorphically through a subdivision. We then get the following:
$\theta $
, this map factors isomorphically through a subdivision. We then get the following:
Corollary 4.17. Let
![]() $\theta $
be a nondegenerate stability condition. The map
$\theta $
be a nondegenerate stability condition. The map
factors isomorphically through the composition of a subdivision and a finite index sublattice inclusion.
5 Algebraizing and Globalizing
5.1 Tropicalization and tropical operations
In this paper, we use the language of logarithmic geometry as our main means to access algebro-geometric problems via combinatorial tools. We rapidly lay out our conventions. For a thorough treatment of logarithmic geometry, we refer the interested reader to [Reference KatoKat89] and [Reference OgusOgu18]. For a shallower treatment more adapted to our needs here, we refer to [Reference Holmes, Molcho, Pandharipande, Pixton and SchmittHMP+22, Reference Molcho and RanganathanMR21].
A log scheme (or log DM stack) is a pair
![]() $(S,M_S)$
consisting of a scheme (or DM stack) S with a log structure
$(S,M_S)$
consisting of a scheme (or DM stack) S with a log structure
![]() $M_S$
(i.e., a sheaf of monoids on the étale site of S with a homomorphism of monoids)
$M_S$
(i.e., a sheaf of monoids on the étale site of S with a homomorphism of monoids)
to the structure sheaf of S with its multiplicative monoid structure, such that
![]() $\epsilon ^{-1}(\mathcal {O}_S^*) \cong \mathcal {O}_S^*$
. As is common, we drop
$\epsilon ^{-1}(\mathcal {O}_S^*) \cong \mathcal {O}_S^*$
. As is common, we drop
![]() $M_S$
from the notation; however, when speaking about a log scheme S, it it to be understood that a log structure
$M_S$
from the notation; however, when speaking about a log scheme S, it it to be understood that a log structure
![]() $M_S$
is present.
$M_S$
is present.
The quotient
is a constructible sheaf on S, called the characteristic monoid. The characteristic monoid stratifies S; the strata are the connected components of the loci of S on which
![]() $\overline {M}_S$
is locally constant. As with our conventions on monoids, we will assume throughout that
$\overline {M}_S$
is locally constant. As with our conventions on monoids, we will assume throughout that
![]() $\overline {M}_S$
is a sheaf of finitely generated and saturated monoids.
$\overline {M}_S$
is a sheaf of finitely generated and saturated monoids.
The main example to keep in mind is a normal crossings pair – a smooth S with a normal crossings divisor D. This defines a log structure by setting, for an étale map
![]() $i: U \to S$
,
$i: U \to S$
,
The characteristic monoid
![]() $\overline {M}_S$
is, in that case, at a point x of the étale site of S, equal to
$\overline {M}_S$
is, in that case, at a point x of the étale site of S, equal to
where k is the number of distinct (in any sufficiently small étale neighborhood) branches of D that contain x.
The important point for us is that any cone stack, as in Section 4, can be given a functor of points in the category of log schemes: for a cone stack
![]() $\Sigma $
, one obtains a prestack
$\Sigma $
, one obtains a prestack
by defining
The associated stack is representable by an algebraic stack with logarithmic structure, referred to as an Artin fan. Instead of introducing Artin fans here, we will simply understand morphisms from a log scheme to
![]() $\Sigma $
to mean maps to the associated stack.
$\Sigma $
to mean maps to the associated stack.
Definition 5.2. Let S be a log DM stack. A tropicalization for S is a cone stack
![]() $\Sigma _S$
with a map
$\Sigma _S$
with a map
![]() $S \to \Sigma _S$
which is strict (i.e., induces an isomorphism on log structures) and has connected fibers.
$S \to \Sigma _S$
which is strict (i.e., induces an isomorphism on log structures) and has connected fibers.
In particular, under our definition, a tropicalization for S is not unique. For any log smooth DM stack S locally of finite type (for example, a normal crossings pair), one can construct a canonical tropicalization
![]() $\Sigma _S$
of S as follows. When S is sufficiently small – the technical term is atomic, meaning that S has a unique closed stratum and the restriction map
$\Sigma _S$
of S as follows. When S is sufficiently small – the technical term is atomic, meaning that S has a unique closed stratum and the restriction map
![]() $\overline {M}_S(S) \to \overline {M}_{S,x}$
is an isomorpism for any x in the closed stratum – it is easy to check that the rational polyhedral cone
$\overline {M}_S(S) \to \overline {M}_{S,x}$
is an isomorpism for any x in the closed stratum – it is easy to check that the rational polyhedral cone
![]() $\Sigma _S = \overline {M}_S(S)^{\vee }$
is a tropicalization. In general, we can find an étale cover U of S by atomic log schemes, and an étale cover V of
$\Sigma _S = \overline {M}_S(S)^{\vee }$
is a tropicalization. In general, we can find an étale cover U of S by atomic log schemes, and an étale cover V of
![]() $U \times _S U$
by atomic log schemes. Then, the coequalizer
$U \times _S U$
by atomic log schemes. Then, the coequalizer
considered as the cone stack associated to a colimit as in Section 4 is a tropicalization of S. It is straightforward to check that the composed map
![]() $U \to \Sigma _U \to \Sigma _S$
descends to a map
$U \to \Sigma _U \to \Sigma _S$
descends to a map
![]() $S \to \Sigma _S$
.
$S \to \Sigma _S$
.
Example 5.2.1. Let
![]() $\overline {\mathcal {M}}_{g,n}$
be the moduli space of genus g, n-marked stable curves. The divisor of singular curves is a normal crossings divisor and so endows
$\overline {\mathcal {M}}_{g,n}$
be the moduli space of genus g, n-marked stable curves. The divisor of singular curves is a normal crossings divisor and so endows
![]() $\overline {\mathcal {M}}_{g,n}$
with a logarithmic structure. A tropicalization for
$\overline {\mathcal {M}}_{g,n}$
with a logarithmic structure. A tropicalization for
![]() $\overline {\mathcal {M}}_{g,n}$
is
$\overline {\mathcal {M}}_{g,n}$
is
![]() $\mathcal {M}_{g,n}^{\text {trop}}$
.
$\mathcal {M}_{g,n}^{\text {trop}}$
.
Let S be a log DM stack with a tropicalization
![]() $S \to \Sigma _S$
. Then, any map
$S \to \Sigma _S$
. Then, any map
![]() $\Sigma \to \Sigma _S$
induces a map
$\Sigma \to \Sigma _S$
induces a map
The fiber product
![]() $S \times _{\Sigma _S} \Sigma $
is then an algebraic stack over S, and the map
$S \times _{\Sigma _S} \Sigma $
is then an algebraic stack over S, and the map
![]() $S \times _{\Sigma _S} \Sigma \to \Sigma $
is a tropicalization of
$S \times _{\Sigma _S} \Sigma \to \Sigma $
is a tropicalization of
![]() $S \times _{\Sigma _S} \Sigma $
. The importance of this observation for us is that, in this fashion, one can lift combinatorial operations one performs on
$S \times _{\Sigma _S} \Sigma $
. The importance of this observation for us is that, in this fashion, one can lift combinatorial operations one performs on
![]() $\Sigma _S$
to algebraic operations on S; often, they have clear geometric meaning. The ones we have encountered in Section 4 are:
$\Sigma _S$
to algebraic operations on S; often, they have clear geometric meaning. The ones we have encountered in Section 4 are:
-
• Subdivisions
 $\Sigma \to \Sigma _S$
. These lift to log modifications
$\Sigma \to \Sigma _S$
. These lift to log modifications
 $\widetilde {S} = S \times _{\Sigma _S} \Sigma \to S$
, which are proper, birational, surjective representable maps.
$\widetilde {S} = S \times _{\Sigma _S} \Sigma \to S$
, which are proper, birational, surjective representable maps. -
• Roots
 $\Sigma _S' \to \Sigma _S$
, which are maps that replace the integral structure of
$\Sigma _S' \to \Sigma _S$
, which are maps that replace the integral structure of
 $\Sigma _S$
with an integral structure coming from a finite index sublattice. These correspond to root stacks of S algebraically, which are proper, birational, nonrepresentable maps
$\Sigma _S$
with an integral structure coming from a finite index sublattice. These correspond to root stacks of S algebraically, which are proper, birational, nonrepresentable maps
 $S' \to S$
, which are bijective on geometric points – a generalization of roots along divisors of S. Details can be found in [Reference Borne and VistoliBV12] and [Reference Gillam and MolchoGM15].
$S' \to S$
, which are bijective on geometric points – a generalization of roots along divisors of S. Details can be found in [Reference Borne and VistoliBV12] and [Reference Gillam and MolchoGM15]. -
• Inclusion of a subcomplex
 $\Sigma \subset \Sigma _S$
. These lift to open inclusions
$\Sigma \subset \Sigma _S$
. These lift to open inclusions
 $V \subset S$
.
$V \subset S$
.
The three operations above are, furthermore, logarithmically étale and monomorphisms in the category of log schemes!
5.3 Logarithmic curves
Let
![]() $C \to S$
be a logarithmic curve (see [Reference Cavalieri, Chan, Ulirsch and WiseCCUW20, Section 7]). Applying the tropicalization construction of the previous subsection yields a map of cone stacks
$C \to S$
be a logarithmic curve (see [Reference Cavalieri, Chan, Ulirsch and WiseCCUW20, Section 7]). Applying the tropicalization construction of the previous subsection yields a map of cone stacks
Pulling back to S and unwinding the definitions, one arrives at the data of a family of tropical curvesFootnote
10
over the scheme S, referred to as the tropicalization of
![]() $C \to S$
in the literature:
$C \to S$
in the literature:
-
• For each point
 $x \in S$
, an underlying graph
$x \in S$
, an underlying graph
 $\Gamma _x$
: the dual graph of
$\Gamma _x$
: the dual graph of
 $C_x$
.
$C_x$
. -
• A tropical curve structure on
 $\Gamma _x$
metrized by
$\Gamma _x$
metrized by
 $\overline {M}_{S,x}$
: for each edge
$\overline {M}_{S,x}$
: for each edge
 $e \in E(\Gamma _x)$
, a length
$e \in E(\Gamma _x)$
, a length
 $\ell _e \in \overline {M}_{S,x}$
. The length
$\ell _e \in \overline {M}_{S,x}$
. The length
 $\ell _e$
is the ‘smoothing parameter’ of the corresponding node q in
$\ell _e$
is the ‘smoothing parameter’ of the corresponding node q in
 $C_x$
: there is a unique element
$C_x$
: there is a unique element
 $\ell _e$
in
$\ell _e$
in
 $\overline {M}_{S,x}$
such that under the map
$\overline {M}_{S,x}$
such that under the map $$ \begin{align*}\overline{M}_{C,q} \cong \overline{M}_{S,x} \oplus_{\mathbb{N}} {\mathbb{N}}^2\end{align*} $$
$$ \begin{align*}\overline{M}_{C,q} \cong \overline{M}_{S,x} \oplus_{\mathbb{N}} {\mathbb{N}}^2\end{align*} $$
 ${\mathbb {N}} \to \overline {M}_{S,x}$
sending
${\mathbb {N}} \to \overline {M}_{S,x}$
sending
 $1 \to \ell _e$
, and the diagonal
$1 \to \ell _e$
, and the diagonal
 ${\mathbb {N}} \to {\mathbb {N}}^2$
.
${\mathbb {N}} \to {\mathbb {N}}^2$
.
-
• Compatibility with étale specializations: for each étale specialization
 $\zeta : y \rightsquigarrow x$
, a map
$\zeta : y \rightsquigarrow x$
, a map
 $f_\zeta :\Gamma _x \to \Gamma _y$
compatible with the induced map
$f_\zeta :\Gamma _x \to \Gamma _y$
compatible with the induced map
 $\overline {M}_{S,x} \to \overline {M}_{S,y}$
.
$\overline {M}_{S,x} \to \overline {M}_{S,y}$
.
The geometric notions on tropical curves discussed in the previous section globalize to logarithmic curves. The globalization works the same way for all concepts, by working fiber by fiber and demanding compatibility with étale specializations: a notion A on a tropical curve globalizes to the analogous notion on a logarithmic curve as a system of
![]() $A_x$
on
$A_x$
on
![]() $\Gamma _x/\overline {M}_{S,x}$
for each
$\Gamma _x/\overline {M}_{S,x}$
for each
![]() $x \in S$
, compatible with étale specializations. For example, a piecewise linear function on
$x \in S$
, compatible with étale specializations. For example, a piecewise linear function on
![]() $C \to S$
is a collection of piecewise linear functions
$C \to S$
is a collection of piecewise linear functions
which are compatible with the maps
![]() $\Gamma _x \to \Gamma _y$
for each étale specialization
$\Gamma _x \to \Gamma _y$
for each étale specialization
![]() $y \rightsquigarrow x$
. It is ordered, equidimensional, stable, etc. if all
$y \rightsquigarrow x$
. It is ordered, equidimensional, stable, etc. if all
![]() $\alpha _x$
are. For divisors, we use the term tropical divisor to avoid confusion with the traditional algebro-geometric notion. Thus, a tropical divisor on
$\alpha _x$
are. For divisors, we use the term tropical divisor to avoid confusion with the traditional algebro-geometric notion. Thus, a tropical divisor on
![]() $C/S$
is a collection of divisors on each
$C/S$
is a collection of divisors on each
![]() $\Gamma _x$
compatible with the contractions that arise from étale specializations.
$\Gamma _x$
compatible with the contractions that arise from étale specializations.
Example 5.3.1. Let
![]() $C \to S$
be a logarithmic curve with n markings
$C \to S$
be a logarithmic curve with n markings
![]() $x_1,\cdots ,x_n$
, and let
$x_1,\cdots ,x_n$
, and let
![]() $(a_1,\cdots ,a_n)$
be a vector of integers (for instance, one adding up to
$(a_1,\cdots ,a_n)$
be a vector of integers (for instance, one adding up to
![]() $-k(2g-2+n)$
). The multidegree of
$-k(2g-2+n)$
). The multidegree of
![]() $\omega _{C/S}^{\log }(\sum a_ix_i)$
defines a tropical divisor on
$\omega _{C/S}^{\log }(\sum a_ix_i)$
defines a tropical divisor on
![]() $C/S$
: for each
$C/S$
: for each
![]() $x \in S$
, it is the divisor on
$x \in S$
, it is the divisor on
![]() $\Gamma _x/\overline {M}_{S,x}$
given by
$\Gamma _x/\overline {M}_{S,x}$
given by
for
![]() $v_i$
the vertex containing the marking
$v_i$
the vertex containing the marking
![]() $x_i$
, and where
$x_i$
, and where
![]() $\deg \omega _{C_x}^{\log }(v)$
is the degree of
$\deg \omega _{C_x}^{\log }(v)$
is the degree of
![]() $\omega _{C_x}^{\log }$
on the component of
$\omega _{C_x}^{\log }$
on the component of
![]() $C_x$
corresponding to v. The divisor A is then precisely the divisor of example 2.2.1 and so is compatible with étale specializations by example 2.21.1. We warn the reader that our terminology here clashes with that of the introduction: the tropical divisor A does require the vector of integers
$C_x$
corresponding to v. The divisor A is then precisely the divisor of example 2.2.1 and so is compatible with étale specializations by example 2.21.1. We warn the reader that our terminology here clashes with that of the introduction: the tropical divisor A does require the vector of integers
![]() $(a_1,\cdots ,a_n)$
as input but encodes more information.
$(a_1,\cdots ,a_n)$
as input but encodes more information.
Subdivisions deserve a special mention. A subdivision of the tropicalization of
![]() $C \to S$
is a subdivision of the fibers
$C \to S$
is a subdivision of the fibers
![]() $\Gamma _x/\overline {M}_{S,x}$
compatible with étale specializations. These subdivisions certainly give rise to logarithmic modifications
$\Gamma _x/\overline {M}_{S,x}$
compatible with étale specializations. These subdivisions certainly give rise to logarithmic modifications
![]() $C' \to C$
. However, the log modifications that arise this way are special, as the induced map
$C' \to C$
. However, the log modifications that arise this way are special, as the induced map
![]() $C' \to S$
remains a logarithmic curve.
$C' \to S$
remains a logarithmic curve.
Definition 5.4. We call a log modification
![]() $C' \to C$
that arises from a subdivision of the tropicalization a subdivision of
$C' \to C$
that arises from a subdivision of the tropicalization a subdivision of
![]() $C \to S$
.
$C \to S$
.
6 Algebraic Moduli
In this section, we will assume that all our curves come with at least one marking. This is analogous to the assumption in Section 4 that graphs have a leg and can be avoided. But nevertheless, we require it in order to simplify the presentation, as in our applications a marking is always present. We follow [Reference Marcus and WiseMW20] and define the following:
Definition 6.1. The stack
![]() $\textbf {Div}$
on
$\textbf {Div}$
on
![]() $\textbf {LogSch}$
parametrizing over S pairs
$\textbf {LogSch}$
parametrizing over S pairs
![]() $(C \to S,\alpha )$
, consisting of
$(C \to S,\alpha )$
, consisting of
-
• A logarithmic curve
 $C \to S$
.
$C \to S$
. -
• A piecewise linear function
 $\alpha $
on C, which is
$\alpha $
on C, which is
 $0$
on the component containing the first marking.
$0$
on the component containing the first marking.
Automorphisms are automorphisms of
![]() $\psi :C \to C$
fixing the underlying scheme of S, such that the induced automorphism
$\psi :C \to C$
fixing the underlying scheme of S, such that the induced automorphism
![]() $\overline {\psi }$
on the tropicalization of C respects
$\overline {\psi }$
on the tropicalization of C respects
![]() $\alpha $
:
$\alpha $
:
![]() $\overline {\psi } \circ \alpha = \alpha $
.
$\overline {\psi } \circ \alpha = \alpha $
.
Definition 6.2. The stack
![]() $\textbf {Ord}$
parametrizing pairs
$\textbf {Ord}$
parametrizing pairs
![]() $(C \to S, \alpha )$
of
$(C \to S, \alpha )$
of
-
• A log curve
 $C \to S$
.
$C \to S$
. -
• A piecewise linear function on C whose values are totally ordered and which is
 $0$
on the component containing the first marking.
$0$
on the component containing the first marking.
Definition 6.3. The stack
![]() $\textbf {Rub}$
parametrizing pairs
$\textbf {Rub}$
parametrizing pairs
![]() $(C \to S, \alpha , C' \to X)$
of
$(C \to S, \alpha , C' \to X)$
of
-
• A log curve
 $C \to S$
.
$C \to S$
. -
• A piecewise linear function
 $\alpha $
on C which is
$\alpha $
on C which is
 $0$
on the component containing the first marking.
$0$
on the component containing the first marking. -
• A subdivision
 $C' \to C$
with a stable lift of
$C' \to C$
with a stable lift of
 $\alpha $
to an equidimensional map
$\alpha $
to an equidimensional map  $$\begin{align*}C' \to X. \end{align*}$$
$$\begin{align*}C' \to X. \end{align*}$$
Automorphisms are defined as for
![]() $\mathbf {Div}$
.
$\mathbf {Div}$
.
Remark 6.4. The assumption that curves
![]() $C \to S$
carry a marking is put precisely in order to rigidify the stacks. We note, however, that in the case of
$C \to S$
carry a marking is put precisely in order to rigidify the stacks. We note, however, that in the case of
![]() $\textbf {Rub}$
, there is a canonical rigidification which does not depend on the presence of markings: the values of the function
$\textbf {Rub}$
, there is a canonical rigidification which does not depend on the presence of markings: the values of the function
![]() $\alpha $
are totally ordered, so we can always demand that
$\alpha $
are totally ordered, so we can always demand that
![]() $\alpha $
is
$\alpha $
is
![]() $0$
on the minimal value.
$0$
on the minimal value.
There are evident forgetful maps
![]() $\mathbf {Rub} \to \mathbf {Ord} \to \mathbf {Div}$
, and forgetful-stabilization morphisms
$\mathbf {Rub} \to \mathbf {Ord} \to \mathbf {Div}$
, and forgetful-stabilization morphisms
![]() $\mathbf {Div} \to \overline {\mathcal {M}}_{g,n}$
. We note here that we are potentially in an uncomfortable situation; in Section 4, we introduced cone stacks
$\mathbf {Div} \to \overline {\mathcal {M}}_{g,n}$
. We note here that we are potentially in an uncomfortable situation; in Section 4, we introduced cone stacks
![]() $\Sigma _{\mathbf {Div}},\Sigma _{\mathbf {Ord}},\Sigma _{\mathbf {Rub}}$
, whereas we should have reserved the notation for tropicalizations of
$\Sigma _{\mathbf {Div}},\Sigma _{\mathbf {Ord}},\Sigma _{\mathbf {Rub}}$
, whereas we should have reserved the notation for tropicalizations of
![]() $\mathbf {Div},\mathbf {Rub},\mathbf {Ord}$
. However, we have the following:
$\mathbf {Div},\mathbf {Rub},\mathbf {Ord}$
. However, we have the following:
Theorem 6.5. We have
Thus,
![]() $\textbf {Div} \to \Sigma _{\textbf {Div}}$
is a tropicalization for
$\textbf {Div} \to \Sigma _{\textbf {Div}}$
is a tropicalization for
![]() $\textbf {Div}$
. Analogous statements hold for
$\textbf {Div}$
. Analogous statements hold for
![]() $\mathbf {Ord},\mathbf {Rub}$
.
$\mathbf {Ord},\mathbf {Rub}$
.
Proof. We construct a map
![]() $\mathbf {Div} \to \Sigma _{\mathbf {Div}}$
. Let S be a log scheme; we must construct a map
$\mathbf {Div} \to \Sigma _{\mathbf {Div}}$
. Let S be a log scheme; we must construct a map
![]() $\mathbf {Div}(S) \to \Sigma _{\mathbf {Div}}(S)$
, which amounts to constructing a map locally around each
$\mathbf {Div}(S) \to \Sigma _{\mathbf {Div}}(S)$
, which amounts to constructing a map locally around each
![]() $x \in S$
, compatibly with any étale specialization
$x \in S$
, compatibly with any étale specialization
![]() $\zeta : y \rightsquigarrow x$
. So we may replace S with a sufficiently small neighborhood of x. Then, we can assume that x is in the closed stratum of S and that
$\zeta : y \rightsquigarrow x$
. So we may replace S with a sufficiently small neighborhood of x. Then, we can assume that x is in the closed stratum of S and that
![]() $\overline {M}_{S,x} = \overline {M}_{S}(S)$
. Furthermore,
$\overline {M}_{S,x} = \overline {M}_{S}(S)$
. Furthermore,
![]() $\overline {M}_{S,y}$
is a quotient of
$\overline {M}_{S,y}$
is a quotient of
![]() $\overline {M}_{S,x}$
by a face. Let
$\overline {M}_{S,x}$
by a face. Let
![]() $(C \to S,\alpha )$
be an element of
$(C \to S,\alpha )$
be an element of
![]() $\mathbf {Div}(S)$
.
$\mathbf {Div}(S)$
.
We write
![]() $\Gamma _x$
for the dual graph of
$\Gamma _x$
for the dual graph of
![]() $C_x$
, and
$C_x$
, and
![]() $\Gamma _y$
for the dual graph of
$\Gamma _y$
for the dual graph of
![]() $C_y$
. These have the structure of tropical curves metrized by
$C_y$
. These have the structure of tropical curves metrized by
![]() $\overline {M}_{S,x}$
and
$\overline {M}_{S,x}$
and
![]() $\overline {M}_{S,y}$
, respectively. Furthermore, they carry piecewise linear functions
$\overline {M}_{S,y}$
, respectively. Furthermore, they carry piecewise linear functions
![]() $\alpha _x,\alpha _y$
.
$\alpha _x,\alpha _y$
.
The map
![]() $\overline {M}_{S,x} \to \overline {M}_{S,y}$
canonically induces a tropical curve
$\overline {M}_{S,x} \to \overline {M}_{S,y}$
canonically induces a tropical curve
![]() $\overline {\Gamma }_x$
metrized by
$\overline {\Gamma }_x$
metrized by
![]() $\overline {M}_{S,y}$
, by contracting edges whose length is
$\overline {M}_{S,y}$
, by contracting edges whose length is
![]() $0$
in
$0$
in
![]() $\overline {M}_{S,y}$
, and a piecewise linear function
$\overline {M}_{S,y}$
, and a piecewise linear function
![]() $\overline {\alpha }_x$
. We thus get two maps
$\overline {\alpha }_x$
. We thus get two maps
![]() $\overline {M}_{S,y} \to \Sigma _{\mathbf {Div}}$
, corresponding to
$\overline {M}_{S,y} \to \Sigma _{\mathbf {Div}}$
, corresponding to
![]() $(\overline {\Gamma }_x,\overline {\alpha }_x)$
and
$(\overline {\Gamma }_x,\overline {\alpha }_x)$
and
![]() $(\Gamma _y,\alpha _y)$
.
$(\Gamma _y,\alpha _y)$
.
The specialization
![]() $\zeta $
induces a map
$\zeta $
induces a map
![]() $\overline {\Gamma }_x \to \Gamma _y$
, which, by definition of a piecewise linear function on C, takes
$\overline {\Gamma }_x \to \Gamma _y$
, which, by definition of a piecewise linear function on C, takes
![]() $\overline {\alpha }_x$
to
$\overline {\alpha }_x$
to
![]() $\alpha _y$
. This is precisely an isomorphism in
$\alpha _y$
. This is precisely an isomorphism in
![]() $\Sigma _{\mathbf {Div}}$
, and so the map is compatible with specializations. Thus, we get the desired map
$\Sigma _{\mathbf {Div}}$
, and so the map is compatible with specializations. Thus, we get the desired map
![]() $\mathbf {Div} \to \Sigma _{\mathbf {Div}}$
, and as a result, a map
$\mathbf {Div} \to \Sigma _{\mathbf {Div}}$
, and as a result, a map
However, an element of the fiber product is a log curve
![]() $C \to S$
, together with a piecewise linear function on its tropicalization; and so the map
$C \to S$
, together with a piecewise linear function on its tropicalization; and so the map
![]() $\mathbf {Div} \to \overline {\mathcal {M}}_{g,n} \times _{\mathcal {M}_{g,n}^{\text {trop}}} \Sigma _{\mathbf {Div}}$
is essentially surjective. Let S be the spectrum of an algebraically closed field,
$\mathbf {Div} \to \overline {\mathcal {M}}_{g,n} \times _{\mathcal {M}_{g,n}^{\text {trop}}} \Sigma _{\mathbf {Div}}$
is essentially surjective. Let S be the spectrum of an algebraically closed field,
![]() $C \to S$
a log curve, and
$C \to S$
a log curve, and
![]() $\Gamma $
its tropicalization, metrized by
$\Gamma $
its tropicalization, metrized by
![]() $M = \overline {M}_S(S)$
. The automorphism groups
$M = \overline {M}_S(S)$
. The automorphism groups
in the fiber product consist of pairs of an automorphism
![]() $\phi :\Gamma \to \Gamma $
with
$\phi :\Gamma \to \Gamma $
with
![]() $\phi \circ \alpha = \alpha $
, together with an automorphism
$\phi \circ \alpha = \alpha $
, together with an automorphism
![]() $\psi $
of C inducing
$\psi $
of C inducing
![]() $\phi $
(i.e., automorphisms
$\phi $
(i.e., automorphisms
![]() $\psi $
of C with
$\psi $
of C with
![]() $\overline {\psi } \circ \alpha = \alpha $
). These are exactly the automorphisms of
$\overline {\psi } \circ \alpha = \alpha $
). These are exactly the automorphisms of
![]() $\mathbf {Div}$
.
$\mathbf {Div}$
.
The statements for
![]() $\textbf {Ord},\textbf {Rub}$
are proved precisely the same way.
$\textbf {Ord},\textbf {Rub}$
are proved precisely the same way.
Thus,
![]() $\textbf {Div},\textbf {Ord},\textbf {Rub}$
are obtained from
$\textbf {Div},\textbf {Ord},\textbf {Rub}$
are obtained from
![]() $\overline {\mathcal {M}}_{g,n}$
by pulling back maps of cone stacks. Furthermore, the resulting maps
$\overline {\mathcal {M}}_{g,n}$
by pulling back maps of cone stacks. Furthermore, the resulting maps
![]() $\textbf {Rub} \to \textbf {Ord} \to \textbf {Div}$
are either subdivisions or roots. As corollaries, we obtain several theorems by combining the tropical results of Section 4 with the algebraization discussion of Section 5.
$\textbf {Rub} \to \textbf {Ord} \to \textbf {Div}$
are either subdivisions or roots. As corollaries, we obtain several theorems by combining the tropical results of Section 4 with the algebraization discussion of Section 5.
Theorem 6.6 ([Reference Marcus and WiseMW20, Corollary 5.3.5]).
The maps
![]() $\textbf {Rub} \to \mathbf {Ord} \to \mathbf {Div}$
are proper, log étale, birational log monomorphisms.
$\textbf {Rub} \to \mathbf {Ord} \to \mathbf {Div}$
are proper, log étale, birational log monomorphisms.
Theorem 6.7. The stack
![]() $\textbf {Rub}$
is nonsingular and its universal curve is quasi-smooth.
$\textbf {Rub}$
is nonsingular and its universal curve is quasi-smooth.
Theorem 6.8. The map
![]() $\textbf {Rub} \to \overline {\mathcal {M}}_{g,n}$
is of Deligne-Mumford type. The map
$\textbf {Rub} \to \overline {\mathcal {M}}_{g,n}$
is of Deligne-Mumford type. The map
![]() $\textbf {Rub} \to \textbf {Ord}$
is a relative coarse moduli space over
$\textbf {Rub} \to \textbf {Ord}$
is a relative coarse moduli space over
![]() $\overline {\mathcal {M}}_{g,n}$
.
$\overline {\mathcal {M}}_{g,n}$
.
Proof. This follows from corollary 4.11 and [Reference Gillam and MolchoGM15, Proposition 3.2.6] by observing that the cones in
![]() $\Sigma _{\textbf {Ord}},\Sigma _{\textbf {Rub}}$
provide local charts for
$\Sigma _{\textbf {Ord}},\Sigma _{\textbf {Rub}}$
provide local charts for
![]() $\textbf {Ord},\textbf {Rub}$
.
$\textbf {Ord},\textbf {Rub}$
.
Furthermore, if we fix a universal stability condition
![]() $\theta $
,
$\theta $
,
![]() $k \in \mathbb {Z}$
, and a vector of integers
$k \in \mathbb {Z}$
, and a vector of integers
![]() $(a_1,\cdots ,a_n)$
with
$(a_1,\cdots ,a_n)$
with
![]() $\sum a_i = -k(2g-2+n)$
, and let A be the divisor of example 5.3.1, we obtain:
$\sum a_i = -k(2g-2+n)$
, and let A be the divisor of example 5.3.1, we obtain:
Lemma 6.9. The stacks
![]() $\textbf {Div}_{g,A}^\theta $
,
$\textbf {Div}_{g,A}^\theta $
,
![]() $\textbf {Ord}_{g,A}^\theta $
,
$\textbf {Ord}_{g,A}^\theta $
,
![]() $\textbf {Rub}_{g,A}^\theta $
are open substacks of
$\textbf {Rub}_{g,A}^\theta $
are open substacks of
![]() $\mathbf {Div},\mathbf {Ord},\mathbf {Rub}$
.
$\mathbf {Div},\mathbf {Ord},\mathbf {Rub}$
.
However, we can restrict the natural map
![]() $\mathbf {Div}_{g,n} \to \overline {\mathcal {M}}_{g,n}$
to
$\mathbf {Div}_{g,n} \to \overline {\mathcal {M}}_{g,n}$
to
![]() $\mathbf {Div}_{g,A}^\theta $
, and also the composition
$\mathbf {Div}_{g,A}^\theta $
, and also the composition
![]() $\mathbf {Rub}_{g,A}^\theta \to \mathbf {Div}_{g,A}^\theta $
.
$\mathbf {Rub}_{g,A}^\theta \to \mathbf {Div}_{g,A}^\theta $
.
For the sake of completeness, we spell out the functor of points of
![]() $\textbf {Div}_{g,A}^\theta $
and
$\textbf {Div}_{g,A}^\theta $
and
![]() $\textbf {Rub}_{g,A}^\theta $
. It is simpler to do so in the category
$\textbf {Rub}_{g,A}^\theta $
. It is simpler to do so in the category
![]() $\textbf {LogSch}$
. For a log scheme S, the S points of
$\textbf {LogSch}$
. For a log scheme S, the S points of
![]() $\mathbf {Div}_{g,A}^\theta $
consist of
$\mathbf {Div}_{g,A}^\theta $
consist of
-
• A quasi-stable log curve
 $C \to S$
.
$C \to S$
. -
• A piecewise linear function
 $\alpha $
, vanishing along the first marking, such that is
$\alpha $
, vanishing along the first marking, such that is $$ \begin{align*}A-\mathsf{div}(\alpha) = D \end{align*} $$
$$ \begin{align*}A-\mathsf{div}(\alpha) = D \end{align*} $$
 $\theta $
-stable.
$\theta $
-stable.
The S-points of
![]() $\textbf {Rub}_{g,A}^\theta $
are, in addition to the above,
$\textbf {Rub}_{g,A}^\theta $
are, in addition to the above,
-
• A subdivision
 $C' \to C$
over S, a tropical target
$C' \to C$
over S, a tropical target
 $X \to S$
and an equidimensional map This data is required to be stable (i.e.,
$X \to S$
and an equidimensional map This data is required to be stable (i.e., $$ \begin{align*}C' \to X \end{align*} $$
$$ \begin{align*}C' \to X \end{align*} $$
 $C',X$
are minimal with this property).
$C',X$
are minimal with this property).
We can restrict the map
![]() $\mathbf {Div}_{g,n} \to \overline {\mathcal {M}}_{g,n}$
to its open substack
$\mathbf {Div}_{g,n} \to \overline {\mathcal {M}}_{g,n}$
to its open substack
![]() $\mathbf {Div}_{g,A}^\theta $
. The content of 4.17 and the discussion preceeding it is then that the restriction
$\mathbf {Div}_{g,A}^\theta $
. The content of 4.17 and the discussion preceeding it is then that the restriction
![]() $\mathbf {Div}_{g,A}^\theta \to \overline {\mathcal {M}}_{g,n}$
factors isomorphically through a log modification
$\mathbf {Div}_{g,A}^\theta \to \overline {\mathcal {M}}_{g,n}$
factors isomorphically through a log modification
![]() $\overline {\mathcal {M}}_{g,A}^\theta \to \overline {\mathcal {M}}_{g,n}$
; and the restriction of
$\overline {\mathcal {M}}_{g,A}^\theta \to \overline {\mathcal {M}}_{g,n}$
; and the restriction of
![]() $\mathbf {Rub}_{g,n} \to \overline {\mathcal {M}}_{g,n}$
to
$\mathbf {Rub}_{g,n} \to \overline {\mathcal {M}}_{g,n}$
to
![]() $\mathbf {Rub}_{g,A}^\theta $
factors through a log modification followed by a root
$\mathbf {Rub}_{g,A}^\theta $
factors through a log modification followed by a root
![]() $\widetilde {\mathcal {M}}_{g,A}^\theta \to \overline {\mathcal {M}}_{g,n}$
. We summarize as follows:
$\widetilde {\mathcal {M}}_{g,A}^\theta \to \overline {\mathcal {M}}_{g,n}$
. We summarize as follows:
Theorem 6.10. The stack
![]() $\widetilde {\mathcal {M}}_{g,A}^\theta $
is nonsingular. If
$\widetilde {\mathcal {M}}_{g,A}^\theta $
is nonsingular. If
![]() $\theta $
is nondegenerate, the map
$\theta $
is nondegenerate, the map
![]() $\widetilde {\mathcal {M}}_{g,A}^\theta \to \overline {\mathcal {M}}_{g,n}$
is proper, birational and of DM-type. The universal curve
$\widetilde {\mathcal {M}}_{g,A}^\theta \to \overline {\mathcal {M}}_{g,n}$
is proper, birational and of DM-type. The universal curve
![]() $\mathcal {C} \to \widetilde {\mathcal {M}}_{g,A}^\theta $
is quasi-smooth and carries a universal line bundle
$\mathcal {C} \to \widetilde {\mathcal {M}}_{g,A}^\theta $
is quasi-smooth and carries a universal line bundle
which is
![]() $\theta $
-stable.
$\theta $
-stable.
The line bundle
![]() $\mathcal {L}$
, in particular, gives an Abel-Jacobi section
$\mathcal {L}$
, in particular, gives an Abel-Jacobi section
and can be used to compute the DR cycle: when
![]() $\theta $
is small and nondegenerate, the ‘universal DR formula’ of [BHP+20] applies, as in [Reference Holmes, Molcho, Pandharipande, Pixton and SchmittHMP+22, Theorem A].
$\theta $
is small and nondegenerate, the ‘universal DR formula’ of [BHP+20] applies, as in [Reference Holmes, Molcho, Pandharipande, Pixton and SchmittHMP+22, Theorem A].
Remark 6.11. One can use the Abel-Jacobi section
to pull back the universal Jacobian
![]() $\text {Jac}$
of multidegree
$\text {Jac}$
of multidegree
![]() $0$
line bundles. The resulting space
$0$
line bundles. The resulting space
is the space
![]() $M^{\diamond }$
of [Reference HolmesHol21]. Its pullback to
$M^{\diamond }$
of [Reference HolmesHol21]. Its pullback to
![]() $\widetilde {\mathcal {M}}_{g,A}^\theta $
is a desingularization, denoted by
$\widetilde {\mathcal {M}}_{g,A}^\theta $
is a desingularization, denoted by
![]() $\mathsf {tDR}$
in [Reference Molcho and RanganathanMR21]. Pulling back further, replacing
$\mathsf {tDR}$
in [Reference Molcho and RanganathanMR21]. Pulling back further, replacing
![]() $\text {Jac}$
with its
$\text {Jac}$
with its
![]() $0$
section
$0$
section
![]() $0$
gives
$0$
gives
This is a compact locus which supports the cycle
![]() $\mathsf {DR}_{g,A}^k$
. When
$\mathsf {DR}_{g,A}^k$
. When
![]() $k=0$
, the further pullback
$k=0$
, the further pullback
can be identified with the rubber version of Bumsig Kim’s space of log stable maps to expansions of
![]() $\mathbb {P}^1$
. In fact, the tropical targets X are the cone stacks associated to expansions. But notice that in the definition of
$\mathbb {P}^1$
. In fact, the tropical targets X are the cone stacks associated to expansions. But notice that in the definition of
![]() $\textbf {Rub}$
, we demand that curves map to tropical targets and not expansions. It is precisely the point that there a lot more maps to tropical targets than algebraic ones, and it is in this space that we carve out the smooth spaces
$\textbf {Rub}$
, we demand that curves map to tropical targets and not expansions. It is precisely the point that there a lot more maps to tropical targets than algebraic ones, and it is in this space that we carve out the smooth spaces
![]() $\widetilde {\mathcal {M}}_{g,A}^\theta $
. The space of maps to algebraic targets is of much smaller dimension.
$\widetilde {\mathcal {M}}_{g,A}^\theta $
. The space of maps to algebraic targets is of much smaller dimension.
7 Algorithms
Let
![]() $\theta $
be a non-degenerate stability condition, and A a divisor on the universal family of
$\theta $
be a non-degenerate stability condition, and A a divisor on the universal family of
![]() $\mathcal {M}_{g,n}^{\text {trop}}$
. We explain how to construct the cone stack of
$\mathcal {M}_{g,n}^{\text {trop}}$
. We explain how to construct the cone stack of
![]() $\widetilde {\mathcal {M}}_{g,A}^\theta $
from that of
$\widetilde {\mathcal {M}}_{g,A}^\theta $
from that of
![]() $\overline {\mathcal {M}}_{g,n}$
algorithmically. The algorithm first constructs
$\overline {\mathcal {M}}_{g,n}$
algorithmically. The algorithm first constructs
![]() $\overline {\mathcal {M}}_{g,A}^\theta $
, precisely as in [Reference Holmes, Molcho, Pandharipande, Pixton and SchmittHMP+22]. It then finds the cones in
$\overline {\mathcal {M}}_{g,A}^\theta $
, precisely as in [Reference Holmes, Molcho, Pandharipande, Pixton and SchmittHMP+22]. It then finds the cones in
![]() $\widetilde {\mathcal {M}}_{g,A}^\theta $
by unpacking the discussion of 4. It suffices to work cone by cone in
$\widetilde {\mathcal {M}}_{g,A}^\theta $
by unpacking the discussion of 4. It suffices to work cone by cone in
![]() $\mathcal {M}_{g,n}^{\text {trop}}$
. We thus fix a stable graph
$\mathcal {M}_{g,n}^{\text {trop}}$
. We thus fix a stable graph
![]() $\Gamma $
of type
$\Gamma $
of type
![]() $g,n$
. We will write
$g,n$
. We will write
![]() $\Sigma _{\Gamma }$
for the cone corresponding to
$\Sigma _{\Gamma }$
for the cone corresponding to
![]() $\Gamma $
in
$\Gamma $
in
![]() $\overline {\mathcal {M}}_{g,n}$
,
$\overline {\mathcal {M}}_{g,n}$
,
![]() $\Sigma _{\Gamma }^\theta $
for the cone in
$\Sigma _{\Gamma }^\theta $
for the cone in
![]() $\overline {\mathcal {M}}_{g,A}^\theta $
, and
$\overline {\mathcal {M}}_{g,A}^\theta $
, and
![]() $\widetilde {\Sigma }_{\Gamma }^\theta $
for the cone in
$\widetilde {\Sigma }_{\Gamma }^\theta $
for the cone in
![]() $\widetilde {\mathcal {M}}_{g,A}^\theta $
.
$\widetilde {\mathcal {M}}_{g,A}^\theta $
.
Algorithm:
-
1. List all acyclic flows s on quasi-stable models of
 $\Gamma $
(without length assignments) with divisor
$\Gamma $
(without length assignments) with divisor
 $\mathsf {div}(s) = A -D$
. There is a finite number of possible such flows.
$\mathsf {div}(s) = A -D$
. There is a finite number of possible such flows. -
2. For each such flow, find the
 $x \in \Sigma _\Gamma $
such that
$x \in \Sigma _\Gamma $
such that
 $\left \langle s, \gamma \right \rangle _x = 0$
for any
$\left \langle s, \gamma \right \rangle _x = 0$
for any
 $\gamma \in H_1(\Gamma )$
. The collection of such x for a specific flow is a cone of
$\gamma \in H_1(\Gamma )$
. The collection of such x for a specific flow is a cone of
 $\Sigma _{\Gamma }^\theta $
. In other words,
$\Sigma _{\Gamma }^\theta $
. In other words,
 $\Sigma _{\Gamma }^\theta $
is the subdivision of
$\Sigma _{\Gamma }^\theta $
is the subdivision of
 $\Sigma _\Gamma $
into the cones where the various acyclic flows lift to actual twists.
$\Sigma _\Gamma $
into the cones where the various acyclic flows lift to actual twists. -
3. Over a cone of
 $\Sigma _\Gamma ^\theta $
corresponding to
$\Sigma _\Gamma ^\theta $
corresponding to
 $(\Gamma ',\alpha )$
, list all possible orderings
$(\Gamma ',\alpha )$
, list all possible orderings
 $\kappa $
extending
$\kappa $
extending
 $\alpha $
. Equivalently, lift the data
$\alpha $
. Equivalently, lift the data
 $\Gamma ',\alpha $
to stable equidimensional lifts
$\Gamma ',\alpha $
to stable equidimensional lifts
 $\Gamma " \to X$
of
$\Gamma " \to X$
of
 $\alpha $
. There is, again, only a finite number of such data.
$\alpha $
. There is, again, only a finite number of such data. -
4. Find the vectors
 $x \in \Sigma _\Gamma ^\theta $
that realize a given order
$x \in \Sigma _\Gamma ^\theta $
that realize a given order
 $\kappa $
. This means orienting the edges according to
$\kappa $
. This means orienting the edges according to
 $\kappa $
this total order,Footnote
11
choosing a minimal vertex v, and an oriented path
$\kappa $
this total order,Footnote
11
choosing a minimal vertex v, and an oriented path
 $P_{v \to w}$
for every
$P_{v \to w}$
for every
 $w \in V(\Gamma ')$
; for all given inequalities
$w \in V(\Gamma ')$
; for all given inequalities
 $\alpha (w) < \alpha (u)$
in the given order, find x such that
$\alpha (w) < \alpha (u)$
in the given order, find x such that  $$ \begin{align*}\sum_{\vec{e} \in P_{v \to w}} s(\vec{e})\ell_e \le \sum_{\vec{e} \in P_{v \to u}} s(\vec{e})\ell_e. \end{align*} $$
$$ \begin{align*}\sum_{\vec{e} \in P_{v \to w}} s(\vec{e})\ell_e \le \sum_{\vec{e} \in P_{v \to u}} s(\vec{e})\ell_e. \end{align*} $$
This determines the cones
 $\sigma \in \widetilde {\Sigma }_{\Gamma }^\theta $
.
$\sigma \in \widetilde {\Sigma }_{\Gamma }^\theta $
. -
5. For each cone
 $\sigma $
in
$\sigma $
in
 $\widetilde {\Sigma _{\Gamma }}^\theta $
, take a generating set for
$\widetilde {\Sigma _{\Gamma }}^\theta $
, take a generating set for
 $\sigma \cap N_{\Sigma _{\Gamma }^\theta }$
. For x in this generating set, find the minimal integral multiple
$\sigma \cap N_{\Sigma _{\Gamma }^\theta }$
. For x in this generating set, find the minimal integral multiple
 $kx$
of x for which the quantities
$kx$
of x for which the quantities  $$ \begin{align*}\frac{\alpha(u)-\alpha(v)}{s(f)},\frac{\alpha(w)-\alpha(v)}{s(f)} \end{align*} $$
$$ \begin{align*}\frac{\alpha(u)-\alpha(v)}{s(f)},\frac{\alpha(w)-\alpha(v)}{s(f)} \end{align*} $$
are integers when evaluated on
 $kx$
, where v ranges through all vertices of
$kx$
, where v ranges through all vertices of
 $\Gamma '$
, w is any vertex with
$\Gamma '$
, w is any vertex with
 $\alpha (w)$
the value consecutive to
$\alpha (w)$
the value consecutive to
 $\alpha (v)$
and f is any edge oriented away from v with other endpoint u. The sublattice generated by the
$\alpha (v)$
and f is any edge oriented away from v with other endpoint u. The sublattice generated by the
 $kx$
is the integral structure of
$kx$
is the integral structure of
 $\widetilde {\Sigma }_{\Gamma }^\theta $
.
$\widetilde {\Sigma }_{\Gamma }^\theta $
.Alternatively, the integral structure can be determined as the sublattice
 $$ \begin{align*}\oplus_{\rho \in \sigma(1)}{\mathbb{N}} x_{\rho} \subset {\mathbb{N}}^{E(\Gamma)} \end{align*} $$
$$ \begin{align*}\oplus_{\rho \in \sigma(1)}{\mathbb{N}} x_{\rho} \subset {\mathbb{N}}^{E(\Gamma)} \end{align*} $$
generated by the primitive vectors
 $x_\rho $
along the one dimensional faces
$x_\rho $
along the one dimensional faces
 $\rho $
of
$\rho $
of
 $\sigma $
.
$\sigma $
.
Remark 7.1. Steps
![]() $2$
and
$2$
and
![]() $4$
are the hardest steps to carry out, as they involve solving a collection of linear inequalities. However, as is explained in [Reference Holmes, Molcho, Pandharipande, Pixton and SchmittHMP+22], the difficulty of step
$4$
are the hardest steps to carry out, as they involve solving a collection of linear inequalities. However, as is explained in [Reference Holmes, Molcho, Pandharipande, Pixton and SchmittHMP+22], the difficulty of step
![]() $2$
is deceptive. In fact, it suffices to solve the equations
$2$
is deceptive. In fact, it suffices to solve the equations
![]() $\left \langle s, \gamma \right \rangle _x = 0$
only for acyclic flows s supported on
$\left \langle s, \gamma \right \rangle _x = 0$
only for acyclic flows s supported on
![]() $\Gamma $
rather than a quasi-stable model. The system of inequalities then simplifies significantly, as it reduces to a linear system of equalities. These flows determine the minimal cones of
$\Gamma $
rather than a quasi-stable model. The system of inequalities then simplifies significantly, as it reduces to a linear system of equalities. These flows determine the minimal cones of
![]() $\Sigma _\Gamma ^\theta $
, and all other cones are determined by how twists specialize (i.e., via the combinatorics of specializations rather than the tropical geometry). The same is true for step
$\Sigma _\Gamma ^\theta $
, and all other cones are determined by how twists specialize (i.e., via the combinatorics of specializations rather than the tropical geometry). The same is true for step
![]() $4$
: it suffices to solve the inequalities for total orders with the fewest possible strict inequalities. The other cones are determined by specializations. Thus, tropical geometry only enters to determine the shallowest strata. Afterwards, combinatorics takes over.
$4$
: it suffices to solve the inequalities for total orders with the fewest possible strict inequalities. The other cones are determined by specializations. Thus, tropical geometry only enters to determine the shallowest strata. Afterwards, combinatorics takes over.
8 Example
We present an example of the construction. We use the ramification vector
![]() $A = (-4,3,1)$
on
$A = (-4,3,1)$
on
![]() $\overline {\mathcal {M}}_{1,3}$
, and work out the subdivision of the cone
$\overline {\mathcal {M}}_{1,3}$
, and work out the subdivision of the cone
![]() $\mathbb {R}_{\ge 0}^3 = \left \langle \ell _1,\ell _2,\ell _3 \right \rangle $
corresponding to the triangular graph
$\mathbb {R}_{\ge 0}^3 = \left \langle \ell _1,\ell _2,\ell _3 \right \rangle $
corresponding to the triangular graph
![]() $\Gamma $
that consists of three vertices
$\Gamma $
that consists of three vertices
![]() $v_1,v_2,v_3$
with three edges
$v_1,v_2,v_3$
with three edges
![]() $e_1,e_2,e_3$
between them, depicted below:
$e_1,e_2,e_3$
between them, depicted below:

We choose a small perturbation of
![]() $\theta = 0$
which is negative on the component containing the first marking and positive on the others. The acyclic flows balancing
$\theta = 0$
which is negative on the component containing the first marking and positive on the others. The acyclic flows balancing
![]() $A-D$
, as D ranges through
$A-D$
, as D ranges through
![]() $\theta $
-stable divisors on
$\theta $
-stable divisors on
![]() $\Gamma $
are then given in the following list (with slopes depicted in red):
$\Gamma $
are then given in the following list (with slopes depicted in red):

The seven flows above contribute seven codimension
![]() $g=1$
cells in the subdivision
$g=1$
cells in the subdivision
![]() $S^\theta $
of
$S^\theta $
of
![]() $\mathbb {R}_{\ge 0}^3$
. For example, the first listed flow contributes the wall
$\mathbb {R}_{\ge 0}^3$
. For example, the first listed flow contributes the wall
In general, to complete the subdivision, it is necessary to consider all
![]() $\theta $
-semistable divisors D on quasi-stable models of
$\theta $
-semistable divisors D on quasi-stable models of
![]() $\Gamma $
as well. There are eight such flows, but in this case, we do not need to list them; since
$\Gamma $
as well. There are eight such flows, but in this case, we do not need to list them; since
![]() $g=1$
, the
$g=1$
, the
![]() $7$
codimension
$7$
codimension
![]() $1$
walls in fact determine the subdivision.Footnote
12
The desired subdivision looks as follows (we present the induced subdivision of the triangle obtained by cutting
$1$
walls in fact determine the subdivision.Footnote
12
The desired subdivision looks as follows (we present the induced subdivision of the triangle obtained by cutting
![]() $\mathbb {R}_{\ge 0}^3$
with the hyperplane
$\mathbb {R}_{\ge 0}^3$
with the hyperplane
![]() $\ell _1+\ell _2+\ell _3 = 1$
):
$\ell _1+\ell _2+\ell _3 = 1$
):

The shaded (slice of the) cone is special in
![]() $\Sigma _\Gamma ^\theta $
, as it is not simplicial. It is the region corresponding to the twist
$\Sigma _\Gamma ^\theta $
, as it is not simplicial. It is the region corresponding to the twist

The cone is subdivided further in
![]() $\widetilde {\Sigma }_\Gamma ^\theta $
, according to whether the piecewise linear function
$\widetilde {\Sigma }_\Gamma ^\theta $
, according to whether the piecewise linear function
![]() $\alpha $
is greater on the exceptional vertex u, or the vertex
$\alpha $
is greater on the exceptional vertex u, or the vertex
![]() $v_2$
. This corresponds to the three ways to make
$v_2$
. This corresponds to the three ways to make
![]() $\alpha $
equidimensional, namelyFootnote
13
$\alpha $
equidimensional, namelyFootnote
13

or

or, the degenerate case (note that no subdivision of
![]() $\Gamma '$
is required here)
$\Gamma '$
is required here)

More concretely, if the edge
![]() $e_2$
has been subdivided as
$e_2$
has been subdivided as
![]() $\ell _2' + \ell _2"$
, with
$\ell _2' + \ell _2"$
, with
![]() $\ell _2'$
the length of the edge connecting
$\ell _2'$
the length of the edge connecting
![]() $v_1$
to the exceptional vertex, the cone is subdivided along the hyperplane
$v_1$
to the exceptional vertex, the cone is subdivided along the hyperplane
This yields the simplicial subdivision

Next, we determine the integral structure of the two maximal cones. In fact, the one corresponding to the second equidimensional twist has the induced integral structure, so we describe it only for the first twist

The three rays of the corresponding cone are obtained by specializing the values
![]() $\alpha (v_1),\alpha (u),\alpha (v_2),\alpha (v_3)$
so that only two of them are distinct. There are thus three ways to do so, respecting the given total order
$\alpha (v_1),\alpha (u),\alpha (v_2),\alpha (v_3)$
so that only two of them are distinct. There are thus three ways to do so, respecting the given total order
![]() $\alpha (v_1) \le \alpha (u) \le \alpha (v_2) \le \alpha (v_3)$
:
$\alpha (v_1) \le \alpha (u) \le \alpha (v_2) \le \alpha (v_3)$
:
 $$ \begin{align*} \alpha(v_1) = \alpha(u) = \alpha(v_2) < \alpha(v_3)\\ \alpha(v_1) < \alpha(u) = \alpha(v_2) = \alpha(v_3)\\ \alpha(v_1) = \alpha(u) < \alpha(v_2) = \alpha(v_3) \end{align*} $$
$$ \begin{align*} \alpha(v_1) = \alpha(u) = \alpha(v_2) < \alpha(v_3)\\ \alpha(v_1) < \alpha(u) = \alpha(v_2) = \alpha(v_3)\\ \alpha(v_1) = \alpha(u) < \alpha(v_2) = \alpha(v_3) \end{align*} $$
The first of these is the specialization

Here, the subdivision demanded that
and
Since
![]() $\ell _1$
is contracted, this leads to the relation
$\ell _1$
is contracted, this leads to the relation
where the slope of
![]() $\alpha $
is
$\alpha $
is
![]() $2$
, and so to the equation
$2$
, and so to the equation
Thus, the specialization is the ray through the point
The other specializations are obtained similiarily, leading to the points
![]() $(1,2,0),(1,1,0)$
. The integral structure of the cone is then
$(1,2,0),(1,1,0)$
. The integral structure of the cone is then
Its index is computed as the determinant of the three vectors, and is found to be
![]() $2$
.
$2$
.
Acknowledgements
I’m grateful to David Holmes, Nicola Pagani, Rahul Pandharipande, Aaron Pixton, and Johannes Schmitt for several conversations related to double ramification cycles, the spaces
![]() $\overline {\mathcal {M}}_{g,A}^\theta $
and their desingularizations. I would also like to thank Paolo Aluffi for pointing out to me a broken reference in a previous version of the paper and explaining to me some points of his work. Special thanks are due to Dhruv Ranganathan and Alex Abreu. Dhruv listened to various versions of the results presented here, from the early to the late stages; our discussions benefited both content and exposition considerably. Alex Abreu’s questions on the construction of
$\overline {\mathcal {M}}_{g,A}^\theta $
and their desingularizations. I would also like to thank Paolo Aluffi for pointing out to me a broken reference in a previous version of the paper and explaining to me some points of his work. Special thanks are due to Dhruv Ranganathan and Alex Abreu. Dhruv listened to various versions of the results presented here, from the early to the late stages; our discussions benefited both content and exposition considerably. Alex Abreu’s questions on the construction of
![]() $\widetilde {\mathcal {M}}_{g,A}^\theta $
were numerous and remarkably poignant. They helped me understand several points about the structure of
$\widetilde {\mathcal {M}}_{g,A}^\theta $
were numerous and remarkably poignant. They helped me understand several points about the structure of
![]() $\widetilde {\mathcal {M}}_{g,A}^\theta $
that I had missed, especially regarding the universal family. I would like to extend my gratitude to both. Finally, I would like to thank the anonymous referee for several useful comments which helped fix errors and improve the exposition.
$\widetilde {\mathcal {M}}_{g,A}^\theta $
that I had missed, especially regarding the universal family. I would like to extend my gratitude to both. Finally, I would like to thank the anonymous referee for several useful comments which helped fix errors and improve the exposition.
Competing interest
The author has no competing interest to declare.
Financial support
I was supported by the grant ERC-2017-AdG-786580-MACI.